Течение газа через решетки турбомашин
ГЛАВА ВОСЬМАЯ
ПЕЧЕНИЕ ГАЗА ЧЕРЕЗ РЕШЕТКИ ТУРБОМАШИН
8-1. ГЕОМЕТРИЧЕСКИЕ И ГАЗОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ РЕШЕТОК.
ОСОБЕННОСТИ ПОТОКА В РЕШЕТКАХi
Преобразование энергии в ступени турбомашины .происходит в результате взаимодействия потока газа с неподвижными и вращающимися лопатками, которые образуют направляющую и рабочую решетки.
Решетки турбомашин в общем случае представляют собой систему лопаток одинаковой формы, равномерно размещенных на некоторой поверхности вращения. Частным случаем пространственной решетки является кольцевая решетка с радиально установленными лопатками, расположенными между соосными цилиндрическими поверхностями вращения.
Протекая через решетку, поток газа изменяет скорость и направление своего движения. При этом на решетку—Действует сила реакции. На вращающихся решетках турбины эта сила совершает работу; вращающиеся решетки компрессоров, наоборот, увеличивают энергию протекающего газа. В неподвижных решетках энергетического обмена с окружающей средой не происходит; здесь осуществляются необходимые преобразования анергии для получения требуемой скорости и поворот потока.
Классификация решеток может быть произведена по различным параметрам.
В зависимости от расчетных условий обтекания и соответствующих им геометрических параметров профиля и канала различают три основных типа решеток:
а) конфузорные — используются в турбинах в качестве как сопловых или направляющих ('неподвижных), так и реактивных рабочих (вращающихся);
448
6П2.2 Дейч Михаил Ефимович,
Д 27 Техническая газодинамика. Изд. 2-е, переработ. М.—Л. Госэнергоиздат, 1961
с черт. и илл. 6П2.2
design pashaok
Редактор Б. Я• Шумяцкий Техн. редактор А. М. Фридкин
ГЛАВА ВОСЬМАЯ ПЕЧЕНИЕ ГАЗА ЧЕРЕЗ РЕШЕТКИ ТУРБОМАШИН
8-1. ГЕОМЕТРИЧЕСКИЕ И ГАЗОДИНАМИЧЕСКИЕ ПАРАМЕТРЫ РЕШЕТОК.
ОСОБЕННОСТИ ПОТОКА В РЕШЕТКАХi
Преобразование энергии в ступени турбомашины ¦происходит в результате взаимодействия потока газа с неподвижными и вращающимися лопатками, которые образуют направляющую и рабочую решетки.
Решетки турбомашин в общем случае представляют собой систему лопаток одинаковой формы, равномерно размещенных на некоторой поверхности вращения. Частным случаем пространственной решетки является кольцевая решетка с радиально установленными лопатками, расположенными между соосными цилиндрическими поверхностями вращения.
Протекая через решетку, поток газа изменяет скорость и направление своего движения. При этом на решетку—Действует сила реакции. На вращающихся решетках турбины эта сила совершает работу; вращающиеся решетки компрессоров, наоборот, увеличивают энергию протекающего газа. В неподвижных решетках энергетического обмена с окружающей средой не происходит; здесь осуществляются необходимые преобразования анергии для получения требуемой скорости и поворот потока.
Классификация решеток может быть произведена по различным параметрам.
В зависимости от расчетных условий обтекания и соответствующих им геометрических параметров профиля и канала различают три основных типа решеток:
а) конфузорные — используются в турбинах в качестве как сопловых или направляющих ('неподвижных), так и реактивных рабочих (вращающихся);
б) активные — используются в турбинах в качестве рабочих (вращающихся);
в) диффузорные решетки — используются в компрессорах в качестве как направляющих (неподвижные), так и рабочих (вращающихся)
В зависимости от общего направления движения газа по отношению к оси вращения решетки подразделяются
а —кольцевая (цилиндрическая) решетка, б —прямолинейная решетка, в —плоская решетка.
на осевые и радиальные. В некоторых конструкциях машин поток газа движется под углом к оси вращения (диагональные решетки).
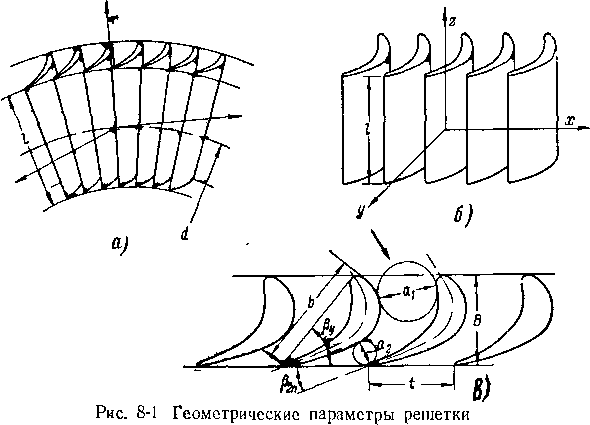
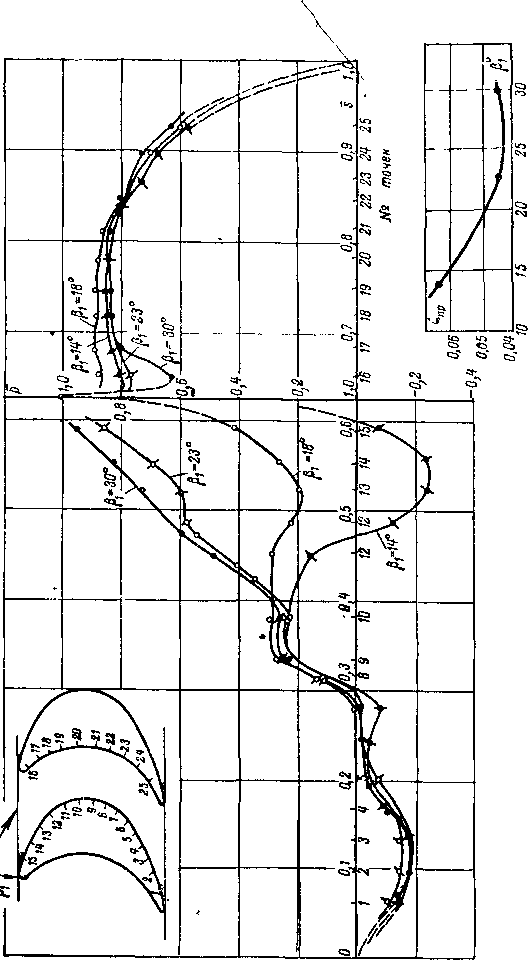
К числу важнейших геометрических параметров кольцевой (цилиндрической) решетки относятся: средний диаметр d, длина (высота) лопатки /, ширина решетки В, шаг профилей на среднем диаметре t, хорда Ь, угол установки ру и другие параметры профиля и канала (рис. 8-1), а также форма меридиональных обводов решетки.
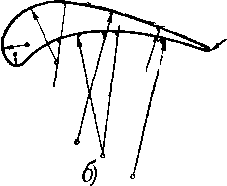
Существуют различные способы задания формьи профилей лопаток. Наибольшее распространение нашли координатный способ (рис. 8-2,а), а также способ построения профиля сопряженными дугами окружностей (рис. 8-2,6).
Если отношение среднего диаметра решетки d к высоте лопатки I велико, то для упрощения задачи можно считать решетку прямолинейной. При этом форма меж-лопаточного канала по высоте сохраняется постоянной. В простейшем случае, предполагая, что диаметр решетки, количество и длина лопаток неограниченно возрастают, получим плоскую бесконечную решетку (рис.
Переход от цилиндриче-
а)
Рис 8-2 Различные способы задания профиля лопатки.
а —координатный, б —дугами окружности
ской к плоской решетке осуществляется следующим опособом. Проведем два соосных цилиндрических сечения кольцевой решетки по среднему диаметру d и по диаметру d+Ad Полагая, что Ad мало, развернем на плоскость полученную кольцевую решетку весьма малой высоты. Увеличивая количество лопаток до бесконечности, получим плоскую бесконечную решетку, показанную на рис. 8-1,8.
Гипотеза плоских сечений, положенная в основу исследований и .расчетов современных турбомашин, была впервые плодотворно применена Н. Е. Жуковским в 1890 г. Ценность этой гипотезы подтверждена многочисленными экспериментами
Геометрические характеристики решеток задаются, как правило, в безразмерном виде. Например, относительный шаг профилей определяется по формуле
Относительная высота (или длина) лопатки
7 = —
1=4-
или
где а2 — ширина минимального (узкого) сечения канала (рис. 8-1).
Прямолинейную решетку располагают в системе координат х, у, г, причем направление х называют осью решетки (рис. 8-1,6). Все профили должны совпадать при поступательном перемещении вдоль оси решетки. Шаг t решетки равен расстоянию между любыми двумя соответственными точками.
При заданном профиле форма межлопаточного канала решетки зависит от относительного шага и угла установки профиля ру, который определяется как угол между осью решетки и хордой профиля (рис. 8-1,в).
Процесс течения газа через решетки лопаточной машины является весьма сложным. Теоретическое решение задачи нестационарного пространственного движения вязкой сжимаемой жидкости в решетке представляет большие трудности. Правильный подход к решению этой задачи заключается в исследовании упрощенных моделей действительного процесса, сохраняющих его наиболее существенные черты, с учетом и последующим анализом влияния второстепенных факторов.
В настоящее время наиболее разработана теория плоского стационарного периодического потока через решетку идеальной жидкости при докритических скоростях. Такое течение можно рассматривать как предельный случай действительного течения в решетке с малым влиянием вязкости (при больших числах Re).
Эта упрощенная схема позволяет установить основные характеристики потенциального потока в решетке. Однако .получаемые решения нуждаются в существенной корректировке. Наибольшие погрешности возникают за счет 'неучета вязкости Поэтому важной задачей является экспериментальная и теоретическая оценка влияния вязкости.
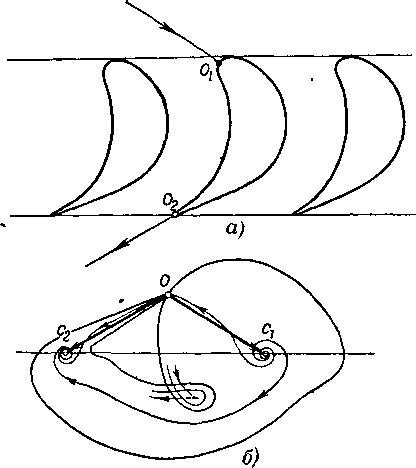
Рассмотрим некоторые особенности плоского потенциального течения идеальной несжимаемой жидкости на примере обтекания реактивной решетки (рис. 8-3). Вследствие периодичности потока достаточно изучить течение в одном межлопаточном канале или обтекание одного профиля. На рис. 8-3,а сплошными кривыми изображены линии тока ^ = const; пунктирными кривыми показаны изопотенциальные линии Ф=const, нормальные к линиям тока. Достаточно густая сеть, этих линий
Рис. 8-3. Течение идеальной несжимаемой жидкости через направляющую решетку. а—изопотенциальные линии и линии тока в решетке; б—годограф скорости; а —распределение относительных скоростей и коэффициентов давления по профилю.
хорошо характеризует течение. Скорость с в любой точке потока равна:
где S и п — криволинейные координаты соответственно вдоль линий тока и изопотенциальных линий.
Дифференциалы приближенно можно заменить конечными приращениями и получить:
С AS Ап '
При ДФ = A’JT = const в каждой точке Д5=Дп.Вэтом случае отдельные ячейки ортогональной сети линий Ф = = const и ЧГ = const в пределе (при AS->-0 и Дя-vO) становятся квадратами, поэтому сеть течения идеальной несжимаемой жидкости называют квадратной.
Другой важной характеристикой течения является план скоростей, или годограф скорости (рис. 8-3,6). Каждой линии тока и изопотенциальной линии соответствует в плоскости годографа геометрическое место концов векторов скорости на этой линии. Соответствующие геометрические места в плоскости годографа также образуют ортогональную сеть, которую можно считать сетью некоторого течения в плоскости годографа, ограниченного геометрическим местом концов векторов скорости на поверхности профиля и вызванного так называемым вихреисточником в конце вектора скорости С\ на бесконечности до решетки и вихрестоком в конце вектора скорости Сг за решеткой. Точки Оь С\ и с2 образуют треугольник скоростей решетки. На основании равенства расходов жидкости до и за решеткой
cj sin р! = сг^ sin
следует, что проекции скоростей с\ и с2 на нормаль к ф,ронту (оси) решетки равны или что прямая, проходящая через концы векторов С\ и с2 в плоскости годографа, параллельна фронту решетки. Рассматривая годограф скорости решетки, можно прийти к заключению, что в точках спинки профиля, касательные к которым параллельны направлениям скоростей на бесконечности до и за решеткой, скорости должны быть больше, чем соответственно сi и с2.
Большой интерес представляет распределение скорости или давления на поверхности профиля. На рис. 8-3,8 показано примерное распределение относительных ско-
? РГ2
= 1—с2 в функции длины дуги профиля S. Если известны величина С\ и направление Pi скорости на бесконечности до решетки, а также положение точки схода потока Oi (на вьиходной кромке), то течение через заданную решетку является определенным. В потоке идеальной несжимаемой жидкости при изменении величины скорости сi форма линий тока и изопотенциальных линий, а также величины относительных скоростей или давлений не изменяются.
На конечном расстоянии от решетки поле скоростей и давлений неравномерно. Линии «тока (при Pi=^90°) имеют волнообразную форму, периодически отклоняясь от своего направления в бесконечности. В соответствии с условиями неразрывности и при отсутствии вихрей средняя скорость вдоль любой линии ab (рис. 8-3,а) между двумя точками, отстоящими на целое число периодов t решетки, постоянна и равна скорости на бесконечности. Одна из линий тока разветвляется на входной кромке профиля, подходя к ,ней по нормали. В точке О\ (называемой иначе точкой входа) скорость становится равной нулю, а давление максимально. Начиная от точки разветвления, в которой ,S = 0 (рис. 8-3,в), скорость ¦на профиле резко возрастает. В зависимости от формы входной кромки, а также от направления скорости на входе (угла входа Pi) скорость вблизи точки разветвления может иметь один или два максимума. На спинке профиля скорость в среднем больше, а давление ниже, чем на вогнутой поверхности. Общий характер распределения скорости по профилю можно оценить, рассматривая ширину межлопаточного канала и кривизну контура профиля. В частности, сужение канала, характерное для турбинной решетки реактивного типа, приводит к ускорению потока; «а участке канала между профилями турбинной решетки активного типа с приблизительно постоянными шириной и кривизной средние значения скорости и давления мало изменяются (рис. 8-4); в компрессорной решетке межлопаточный канал расширяется и скорость соответственно уменьшается (рис. 8-5).
Распределение локальных скоростей в точках обвода
| Г--- | ||
| г\ |
с,=сг=1,0 | \ |
| 0 | ||
&Вог ф scn
Рис. 8-4. Течение идеальной несжимаемой жидкости через активную решетку а —профиль активной решетки; б—годограф скорости; в —распределение относительных скоростей по профилю.
профиля существенно зависит от формы вогнутой и выпуклой поверхностей и степени сужения канала, а также геометрических и режимных параметров решетки.
Увеличение кривизны на выпуклых участках профиля ¦приводит к увеличению скорости, и обратно. При скачкообразном изменении кривизны, например в точках сопряжения дуг окружностей, теоретические кривые рас-
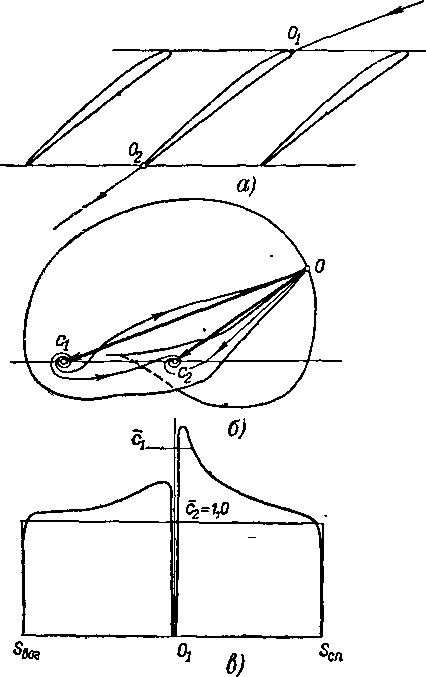
Рис. 8-5. Течение идеальной несжимаемой жидкости через компрессорную решетку.
о—профиль решетки; б—годограф скорости; в — распределение относительных скоростей по профилю
пределения давлений и скоростей претерпевают разрыв. На выступающих углах профиля скорость теоретически возрастает до бесконечности. Вследствие етого обводы профиля современных решеток выполняют с плавно изменяющейся кривизной.
У выходной кромки конечной толщины ', как и на вход-
1 Случай бесконечно тонкой кромки не рассматривается, как не имеющий практического значения.
ной, скорость имеет один или два максимума и она теоретически падает до нуля в точке схода, которая располагается на выходной кромке в области наибольшей кривизны. На большом .расстоянии за решеткой направление потока определяется углом р2.
Выше рассматривалось течение идеальной несжимаемой жидкости через решетку. В действительности с учетом влияния вязкости картина течения в решетке может существенно отличаться от рассмотренной.
При течении реальной вязкой жидкости на поверхности профиля образуется пограничный слой, в котором концентрируются потери энергии, обусловленные трением.
На участках канала с увеличением давления (диффу-зорных участках) может .происходить отрыв потока. Диффузорные участки в зависимости от формы профиля могут возникнуть внутри канала; появление диффузор-ных областей неизбежно на входных и выходных кромках профиля. На выходной кромке всегда происходит отрыв потока; в образующейся закромочной зоне движение вихревое. На границах закромочных зон происходит скачкообразное изменение скорости. В действительном потоке вязкой жидкости такое изменение скорости привело бы к появлению бесконечно больших сил трения; поэтому границы! от.рывных зон распадаются на отдельные вихри, уносимые потоком.
В результате отрыва давление за выходными кромками оказывается пониженным. На некотором небольшом расстоянии за кромками происходит выравнивание потока, сопровождающееся изменением статического давления, угла выхода потока и скорости.
При выравнивании потока за решеткой возникают потери кинетической энергии, составляющие вторую часть профильных потерь в решетках (кромочные потери).
В случае больших скоростей ('М>0,5) распределение скоростей в решетке претерпевает изменение («проявляется эффект сжимаемости). При атом обычно увеличиваются градиенты скоростей вдоль линий тока, изменяется форма линий тока, а также смещаются области максимальных и минимальных скоростей. При определенных значениях М<1 на некоторый частях поверхности профиля появляются сверхзвуковые скорости. Характер обтеканий решетки в этом случае резко изменяется; при сверхзвуковых скоростях возникают дополнительные потери в скачках.
Профильные потери характеризуют плоскую решетку. В -прямой и кольцевой решетках образуются дополнительные потери, обусловленные конечной длиной лопаток (концевые потери) и веерностью решетки.
Потери энергии в решетках, обусловленные при малых скоростях влиянием вязкости и периодической не-стационЗрностью, а также высокой турбулентностью потока, а при околозвуковых и сверхзвуковых скоростях — еще и необратимыми процессами изменения энергии в скачках, в значительной степени определяют к. п. д. лопаточной машины.
•При проектировании лопаточных решеток необходимо обеспечить заданное преобразование энергии потока с минимальными потерями. Отсюда вытекает необходимость детального изучения процесса обтекания решеток и установления влияния формы профиля и других геометрических параметров решетки на ее к. п. д. и угол выхода потока в широком диапазоне режимов, определяемых углом входа потока, числами М и Re и пр.
Выше частично была дана классификация решеток в зависимости от характера изменения параметров потока в межлопаточных каналах и направления движения газа относительно оси турбомашины.
Классификация применяемых решеток может быть существенно расширена. Так, в зависимости от скорости (числа М) все решетки следует разделить на три группы: дозвуковые, околозвуковые и сверхзвуковые. В пределах каждой группы .решетки различаются углом поворота потока (т. е. углами входа Pi и выхода рг).
Кроме того, применяемые решетки различают по относительной .высоте, характеризуемой отношением I —
= у: решетки малой высоты. 1,0 ч-1,5^ и решетки
большой высоты (Г>1,5-н2,0).
Вместе с тем разные решетки различаются веерностью 6=-р при малых 0(0<10) лопатки выполняются с переменным по высоте профилем (закрученные лопатки).
Учитывая, что характеристики решеток в олределен-
HoKi диапазоне изменений режимных и геометрический параметров меняются незначительно, число профилей, удовлетворяющих потребностям турбостроения, можно свести к необходимому минимуму.
8-2. РАСЧЕТ ПОТЕНЦИАЛЬНОГО ПОТОКА В РЕШЕТКАХ ПО ТЕОРИИ КАНАЛА
В теории .решеток и при их экспериментальном исследовании возникают две основные задачи. Одна из них, называемая прямой задачей, состоит в определении поля скоростей потенциального течения через решетку, состоящую из профилей заданной формы, и в последующей оценке потерь энергии при различных режимных (угол входа, числа М и Re) и геометрических (шаг, угол установки профиля, высота решетки и пр.) параметрах. Следовательно, прямая задача имеет большое значение при изучении переменного режима решеток и построении их аэродинамических характеристик.
Обратная задача заключается в построении решетки, отвечающей выбранному или заданному потоку в решетке99. В атой постановке практически важной является задача построения решетки с рациональным распределением скоростей (давлений) по поверхности профиля, обеспечивающим минимальные потери энергии.
В настоящее время разработаны методы расчета потенциального потока в решетках, использующие аппарат функций комплексного переменного. Однако эти методы оказываются громоздкими. Они подробно изложены в специальной литературе100.
Значительно более простые способы расчета, позволяющие с достаточной точностью решать прямую и обратную задачи, основаны на теории канала 101. К настоящему времени известно несколько методов расчета решеток по теории канала. Одним из первых был предложен метод Г. Флюгеля, развитый позднее Г. Ю. Степановым.
Задача обтекания решеток может бьить успешно сведена к расчету потока в канале только при умеренных значениях относительного шага. Кроме того, теория канала дает возможность расчета потока только в межло-паточном канале; в области входного участка спинки и в косом срезе необходимо использовать дополнительные приемьи, и точность расчета на этих участках снижается.
При расчете потока на входе и в косом срезе решетки необходимо с известным приближением определить гра
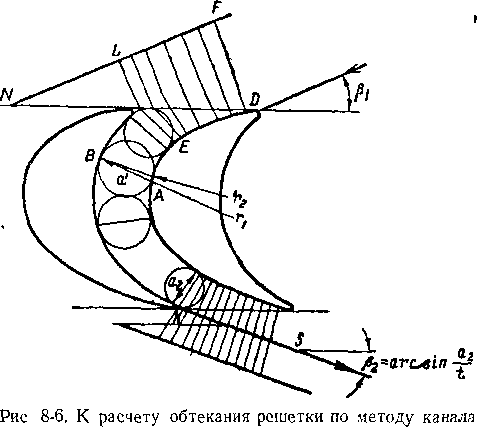
ничные линии тока. В простейшем случае граничные линии тока перед и за решеткой могут быть выбраны в виде отрезков прямых линий (рис. 8-6). Направление этих линий на входе в решетку задано (угол pi), а на выходе оно может быть определено одним из известных методов.
В действительности выделенные граничные линии тока до и после решетки искривляются вблизи входных и выходных кромок, причем это искривление тем значительнее, чем больше относительный шаг лопаток и циркуляция скорости. Некоторое влияние оказывает режим патока: угол входа, числа М и Re. По предложению JIM3 при расчете потока на входе рассматривается некоторый фиктивный входной участок EDFL (рис. 8-6), служащий непосредственным продолжением* межлопа-точ-ного канала. Одна граничная линия участка проходит под углом pi и является линией невозмущенного йотоКй, а вторая — спинкой профиля. Отрезок DN можно принять равным (1,5-г-2)^.
На выходе из канала граничные линии тока KS (рис. 8-6) строятся в предположении, что изопотенциалами являются лучи, ортогональные к опинке профиля. Линии тока KS в этом случае служат продолжением вогнутой поверхности соседнего профиля. На некотором расстоянии за решеткой (от точки S) линия тока переходит в прямую, проведенную под углом Р2102.
Распределение скоростей по сечению канала решетки в соответствии с § 3-5 выражается формулой (3-43).
При малых числах М (М<0,4) расчет распределения скоростей может быть произведен с помощью графиков, приведенных на рис. 3-14. Для сжимаемой жидкости необходимо учитывать изменение плотности. В атом случае можно воспользоваться методом, указанным в § 3-5.
Методика расчета скоростей сводится к следующему:
1. В ка,нал вписываются окружности (рис. 8-6). Через точки касания этих окружностей со стенками канала А и В проводятся эквипотенциальные линии (в виде дуг окружности). Определяются длины этих эквипотенциальных линий а и радиусов кривизны граничных линий в точках А и В (г\ и г2).
2. Для каждой эквипотенциальной линии вычисляются
безразмерные геометрические параметры: а=— ; гг — —;
Г\ Г1
а 2г2 — а
3. Определяются параметры газа на входе в решетку: безразмерная скорость Я,=-^-; приведенный расход q =
#
= q (Я) и отношение плотностей = / (Я,) по таблицам
Ро
газодинамических функций.
4. Средний приведенный расход удается определить по приведенному расходу на входе:
п _ ® Picit sin Pi „ t Й /й 1 \
qm-G---aSinP>- f8'1)
5. Отношение плотностей — определяется по вычис-
Ро
ленному среднему приведенному расходу qn с помощью таблиц газодинамических функций.
6. Объемный расход Q через рассматриваемое сечение а определяется по формуле
_Pi_
Ро
где Q1 = c1^1sinfi1 представляет собой объемный расход на входе в канал.
7. По формуле (3-44), которая в наших обозначениях имеет вид:
2К^г 1-/1+ 4 к,
a I 1 +4К,
2ft ,а
(или по графику на рис. 3-14) находим 8.
8. Скорость газа в точке А определяется соотношением
![]()
а по ней определяется величина Ха.
9. Скорость (безразмерная, а по ней — размерная) в точке В определяется по формуле
Л 1 + « —/С,аа
О точности определения скоростей в решетке по методу канала можно судить по рис. 8-7, на котором приведено сравнение расчетный и опытных данных для активной решетки. Как следует из рис. 8-7, заметное расхождение расчета и опыта наблюдается только вблизи входных и выходных кромок, что вполне закономерно.
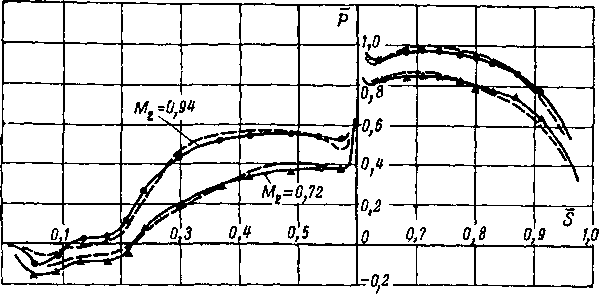
Рис 8-7 Сравнение расчета потенциального потока в решетке по методу канала с ^экспериментом (---опытные кривые;----
расчетные кривые)
8-3. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ПРОФИЛЬ В РЕШЕТКЕ. ТЕОРЕМА Н. Е. ЖУКОВСКОГО ДЛЯ РЕШЕТКИ
Для определения сил, действующих на профиль, выделим часть потока, как эта показано на рис. 8-8 и 8-9. Внешними границами выделенной области служат отрезки ab и dc, параллельные оси решетки и равные шагу t,
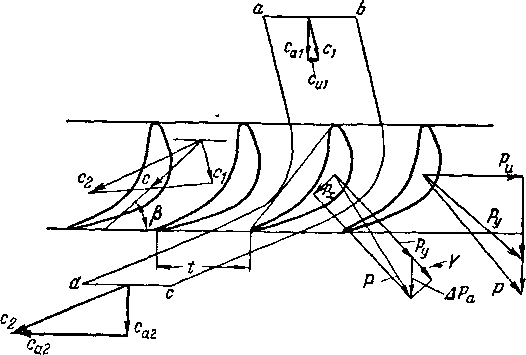
Рис. 8-8. Силы, действующие иа профиль в турбинной (конфузорной)
решетке.
и линии тока ad и Ьс. Линии ab и dc, строго говоря, должны находиться на бесконечно большом расстоянии от решетки, так как параметры 'потока вдоль этих линий предполагаются постоянными. Внутренней границей области служит контур профиля.
Проекции силы, с которой поток действует на профиль единичной длины, обозначим через Ри и Ра
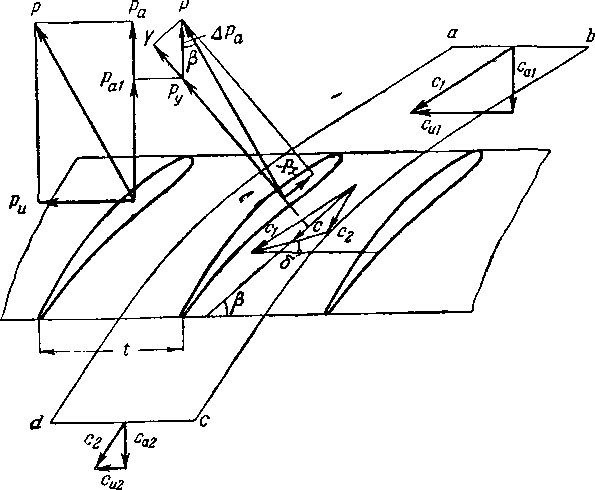
Рис. 8-9. Силы, действующие на профиль в компрессорной (диффузорной) решетке.
Величины этих сил можно определить по уравнению импульсов. Так как линии тока ad и Ьс эвидистантны, то результирующие сильи, действующие на выделенную этими линиями часть потока, равны по величине и противоположны по знаку. В проекции на направление, нормальное к оси решетки? изменение количества движения равно:
т = (Са\ — Са2> = * (Л — Pi) — Ра’
где Ра — составляющая силы Р в направлении, нормальном к оси решетки.
m = 9ica\t=z№J'
поэтому
ра = t [(Рас2а2 — р,^) + рг — а]- (8-4)
Проекция силы Р на ось решетки может быть выражена уравнением
Ри^гСа{{сиХ-си2). (8-5)
Уравнения (8-4) и (8-5) можно представить в другой форме, выразив силы Ри и Ра через циркуляцию скорости Г и параметры потока на входе и выходе из решетки. Согласно уравнению неразрывности
?iCa\ = РаСа2 = Р Са'
где р — средняя плотность газа.
Скорость с , входящую в это выражение, определим как среднюю арифметическую скоростей на входе и выходе:
г _ Са1 + саЧ
Са --з- •
Легко показать, что при этом „ _ 2Р1 Рз
(8-6)
Pi + р2 ‘
Циркуляция скорости вокруг профиля равна:
Г = Цси~си2), (8-7)
так как циркуляции по эквидистантным линиям ad и Ьс
одинаковы по величине и противоположны по знаку.
После простых преобразований из (8-4) и (8-5) получим:
Ра = t[Pi — Pi~ ?са (cal ~ Са2^’ (8‘8)
Ри = ?Тса. (8-9)
^ К, -'CJ =г^п (1 -с. к, - cj. (8-10)
2 2 I 2 2 2)2
С\— Са\+Си\ И С2— Са2+Си2’
си\ + си2
получим:
то, обозначив с,
Подставив это выражение в уравнение (8-8) и учитывая формулу (8-7), получим:
+ Р 1'си. (8-11)
— 1 V Ра Pi
Силу Ра удобно представить в виде суммы двух сил:
где
Pal = ?VCu
Pjl — ?± Рг Pi
(8-12)
Результирующую сил Ра и Ри обозначим через Р а общую результирующую силу — через Р (рис. 8-9). Силу Р определим по формуле
Подставив сюда значения Ри и Р , получим: -Рг =РгуГ с2 4-с2 .
и гг «1а
Но
где с — средняя векторная скорость. 30*
Следовательно, выражение для Ру при обтеканий 'решетки имеет такой же вид, как и в случае одиночного профиля (S 3-4):
Ру = ??с. (8-13)
Направление силы Ру перпендикулярно направлению средней векторной скорости с. Это следует из очевидного равенства
![]()
Итак, сила Жуковского, действующая на профиль в решетке, равна произведению средней плотности газа на циркуляцию скорости вокруг профиля и на среднюю векторную скорость. Направление силы р определяется поворотом вектора скорости с на 90° в сторону, противоположную направлению циркуляции.
Напомним, что плотность р соответствует среднему удельному объему, т. е.
![]()
Таким образом, мы установили, что в отличие от одиночного профиля результирующая сила, действующая на профиль в решетке, равна сумме силы Жуковского Ру и добавочной силы АРа, перпендикулярной оси решетки:
Важно отметить, что природа сил Ру и АРа различна. В то время как сила Ру зависит от циркуляции потока и обращается в нуль при Г=0, сила АРа от циркуляции непосредственно не зависит.
Сила, действующая на профиль, определена для общего случая движения газа. С помощью полученных общих соотношений нетрудно получить величину аэродинамической силы, действующей на профиль, для некоторых частных случаев. Так, например, переходя от решетки к одиночному профилю, увеличивая шаг решетки до бесконечности, «получим p2 = pi и р2 = р1; тогда АРа = Ри = 0 и, следовательйо, в случае изоэнтропическо-to обтекания изолированного профиля результирующая сила, Действующая на профиль, равна силе Жуковского:
где р и с — плотность и скорость набегающего потока.
Направление силы перпендикулярно направлению скорости набегающего потока.
Переходя к случаю обтекания решетки несжимаемой жидкостью, прежде всего следует обратить внимание на то, что в уравнении (8-12) второй член правой части пропорционален изменению потенциальной энергии потока (с учетом гидравлических потерь), т е
2 2
где p2t — теоретическое давление при отсутствии потерь. Следовательно,
ЬРа = -ЧР2{~Р*) = -*Арп.
Разность давлений Д/?п = — р% равна потере давления в решетке. Итак, в случае обтекания решетки пото
ком несжимаемой жидкости добавочная сила отрицательна и определяется потерей давления в решетке (не следует смешивать потерю давления Арп с разностью давлений
Рг~ Pi)-
При отсутствии потерь Арп = 0 и АРа = 0. В этом случае результирующая сила для несжимаемой жидкости равна силе Жуковского103:
S-4. КЛАССИФИКАЦИЯ ПОТЕРЬ И ОСНОВНЫЕ ХАРАКТЕРИСТИКИ РЕШЕТОК
При движении газа через решетки турбомашин возникают потери энергии: часть кинетической энергии потока вследствие вязкости необратимо преобразуется в тепло.
Рассмотренные в настоящей главе некоторые результаты теоретических и экспериментальных исследований потока газа в решетках позволяют классифицировать потери энергии по следующей схеме:
A. Профильные потери (в плоской решетке, т. е. при бесконечно большой высоте), включающие: 1) потери на трение в погра.ничном слое; 2) вихревые потери ори отрывах потока на профиле; 3) вихревые потери за выходной кромкой (кромочные потери).
Б. Концевые потери в прямой пространственной решетке (дополнительно к группе «А»).
B. Волновые потери (дополнительно к группам «А» и «Б» при околозвуковых и сверхзвуковых скоростях) в скачках уплотнения.
Г. Потери, вызванные нестационарностью и высокой турбулентностью потока.
Д. Веерные потери в кольцевой решетке, обусловленные отклонениями геометрических параметров решетки от оптимальных значений и радиальными перетеканиями газа.
Следует подчеркнуть, что профильные потери в решетке аналогичны профильному сопротивлению при обтекании одиночного крылового профиля (гл. 5). Различие состоит только в том, что при исследовании решеток устанавливаются относительные .потери энергии, а профильное сопротивление характеризуется силой сопротивления, отнесенной к скоростному напору набегающего потока. Физическая природа профильных потерь и профильного сопротивления тождественна. Вихревые потери при отрыве потока на профиле и за выходной кромкой эквивалентны сопротивлению давлений. Следовательно, профильные потери можно также рассматривать как сумму потерь трения и «потерь давления».
Потери, отнесенные к группам «Б», «Г» и «Д», являются специфическими для решеток. Волновые потери (группа «В») проявляются в решетках в специфической форме. Однако эта группа потерь, обусловленная необратимыми процессами в скачках, аналогична волновому сопротивлению при обтекании одиночного профиля.
При расчете ступени турбомашины необходимо знать направление потока на вьиходе из решетки (угол выхода потока) и энергетические или силовые характеристики решеток. Ниже рассмотрены отдельные составляющие потерь и указаны методьи расчета основных аэродинамических характеристик решеток.
Для оценки турбинной решетки в отличие от одиночного профиля вводятся главным образом энергетические характеристики. Компрессорные решетки характеризуются в основном силовыми коэффициентами.
Энергетической характеристикой решетки является коэффициент потерь, определяемый как отношение части кинетической энергии, необратимо перешедшей в тепло, к располагаемой кинетической энергии:
(8‘14)
где р01, р02 — давления полного торможения перед и за решеткой;
М2, — число М за решеткой в случае изоэнтропического течения.
Учитывая, что числитель выражения (8-14) представляет собой квадрат некоторого фиктивного числа Мф, подсчитываемого по параметрам торможения:
формулу для коэффициента потерь можно представить в виде:
_ <8-15)
Коэффициент полезного действия решетки определяется очевидным выражением
При экспериментальном исследовании решеток определяется поле давлений торможения перед и за решеткой Рои иРт и статических давлений ри и p2i. По этим данным с помощью формулы (8-14) подсчитываются точечные значения ?(.
Реальный поток на входе и на выходе из решетки является неравномерным: скорости, углы потока и статические давления меняются по шагу, поэтому значения местных коэффициентов потерь энергии, а также другие характеристики решетки приходится осреднять по шагу. Для определения осредненных характеристик следует сформулировать понятие идеального (теоретического) процесса в решетке при неравномерном потоке. Идеальным .процессом можно .считать такой изоэнтропический процесс, при котором в исследуемом сечении сохраняются неизменными по сравнению с реальным процессом поля статических давлений и направления скоростей *.
Коэффициент полезного действия .решетки в неравномерном потоке подсчитывается по формуле
t
J p2cacf sin (is
Jp2c2c|, sin p2?#
где c2— действительная скорость;
p2 — плотность газа в действительном потоке.
Введя в это выражение приведенный расход q, после элементарных преобразований получим:
t t
4 = °-*---^---. (8-17)
^2t^2t S^n ~p^x S‘n №t
~ const. Величина = -g—; \t, q2t— теоретическая ско-
^21
рость и приведенный расход в точке за решеткой.
Для расчетов по формуле (8-17) удобно пользоваться диаграммой, предложенной А. В. Губаревым (рис. 8-10).
Диаграмма строится для раздельного определения величин
А = и В = q2t .
Порядок построения и пользования диаграммой легко понять с помощью рис. 8-10. По значениям porJp^ и p2iJp0i в точке исследуемого потока определяются соответственно А? и Вг Затем производится раздельное суммирование величин i4(.sinp2/ и Вс sinp2(.. Окончательное выражение для к. п. д. решетки имеет вид:
П
X Л, Sin
i~ 1
Ч=—-’
г=1
где п — число выбранных участков в пределах шага решетки.
Кроме коэффициента потерь (к. п. д.) решетки, в расчетах ступени применяют коэффициент расхода, равный отношению действительного расхода к расходу в идеальном процессе. Так как расход газа [через один и тот же канал
t t Gi=i§rJРА sin fadt = g JP2c2 sin p2 dt, (8-18)
то, используя формулу (2-38), найдем коэффициент расхода в таком виде:
t,0 0,8 О,В 0,4 0,2
О о.г
о,и
<ts
as
Диаграммл А
___
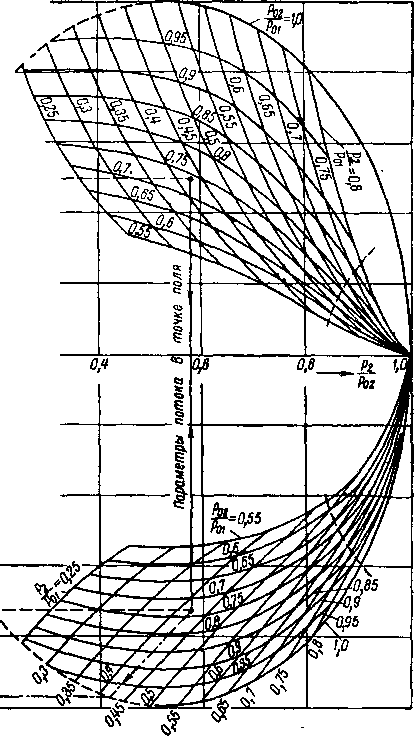
Рис. 8-10. Диаграмма для определения потерь в адиабатических потоках (k = 1,4).
П-0
I Ъ Pot
0,2
Диаграмма В
\
I
V
\
.?я\
02 Ро I
С помощью формулы (8-18) и (2-38) количество движения за решеткой может быть представлено в виде:
Ог
sin
t
~л7sin ^dt
9 = °-- , (8-20)
\q21 ^7sin M*
0
К
Л21
Легко показать, что диаграмма, построенная для определения т] (рис. 8-10), позволяет также найти ц и у в неравномерном потоке. Для определения достаточно на
диаграмме В найти значение Bt= q2U (на пересечении
экспериментальных значений рт!Р<>\ и PyJPa\) и Bt = q2t (на пересечении кривых p2Jpnl и p02i/pB1 = 1); тогда
П
V Bisin hi
![]()
i— i
sin hi
Для определения необходимо построить дополнительную диаграмму зависимости <р, = / (1^- ; —) .
V Р01 Ро 1/
Так как
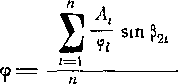
Yi B<Sin?2< (=1
Осредненное значение угла выхода потока определяется по уравнению количества движения. Средние значения проекций скорости за решеткой равны:
то
t
(С, COS р2)к д = в. jV„,<7A cos P. sin №'•
О
f
fa sin Р.)к д = ^ s* jVo^A sin2 р,Л.
О
Тогда средний угол
t
![]()
^ РюЯъЬъ sin2^3dt о
Р2кд = а^ё-Л-. (8-21)
8-5 ПОГРАНИЧНЫЙ СЛОИ И ПОТЕРИ НА ТРЕНИЕ В РЕШЕТКАХ
Определение структуры пограничного слоя, образующегося на профиле, установление точек перехода и отрыва слоя являются важной частью задачи о профильных потерях в решетках. Схема образования пограничного слоя на профиле в плоской решетке показана на рис 8-11,а.
Пользуясь графиком распределения скоростей по обводу профиля, проследим характер изменения слоя на вогнутой и выпуклой поверхностях лопаток.
На вогнутой поверхности за точкой торможения (критической точкой) толщина слоя вначале нарастает незначительно. В местах увеличивающейся кривизны, где скорость внешнего потока либо не меняется, ли&о падает, толщина пограничного слоя возрастает. В этих точках может возникнуть переход ламинарного слоя в турбулентный, а при некоторых режимах — даже местный отрыв слоя. На конфузорной участке вблизи узкого сечения, где давление интенсивно падает, а скорость
возрастает, толщина пограничного слоя уменьшается и достигает минимальных значений на сходе с профиля.
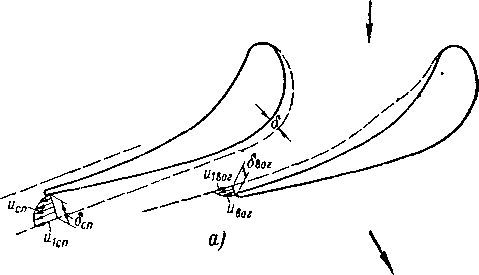
Рис 8-11. Схема образования пограничного слоя на профиле в решетке
а—без отрыва, б—отрыв на спинке лопатки
На спинке в направлении к узкому сечению толщина слоя также уменьшается Вдоль спинки в косом срезе заметно интенсивное нарастание толщины слоя, достигающей у выходной кромки максимальных значений Некоторая часть спинки в косом срезе обтекается, как правило, с положительным градиентом давления (диффузор-ный участок спинки), что иногда может привести к отрыву (рис 8-11,6).
При проектировании решетки практически существенным является определение положения области перехода ламинарного слоя в турбулентный и условий безотрывного обтекания профиля. Как показывают расчеты и опыты, точка перехода чаще всего совпадает с точкой минимума давлений на спинке или несколько смещается в диффузорную область. В тех случаях, когда поток сильно турбулизирован, точка перехода может существенно смещаться против течения (в конфузорную область) .
Рассмотрим некоторые результаты опытного исследования пограничного слоя в активной и реактивной турбинных решетках.
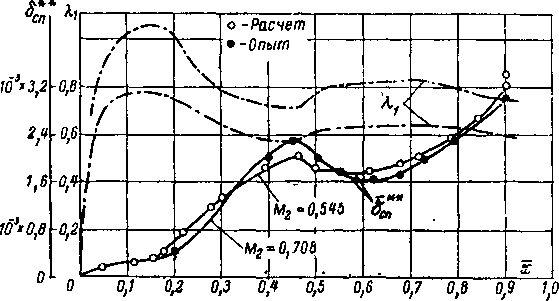
На рис. 8-12 приведены результаты измерений в пограничном слое на опинке профиля ТС-2А. Значительная конфузорность каналов этой решетки (рис. 8-12,а) создает благоприятные условия для сохранения ламинарного режима в слое. Однако при выходе в косой срез (5сп=0,5) ламинарный слой теряет устойчивость и переходит в турбулентный. Зона перехода вполне удовлетворительно определяется описанным в гл. 5 способом и занимает около 4% общего обвода профиля. Далее течение в пограничном слое носит явно выраженный турбулентный характер (рис. 8-12,6). За областью перехода в косом срезе на спинке отмечается интенсивное нарастание толщины потери импульса.
Пограничный слой на вогнутой поверхности до выходной кромки ламинарный. Отсюда можно заключить, что точки отрыва на вьиходной кромке расположены несимметрично относительно средней линии профиля.
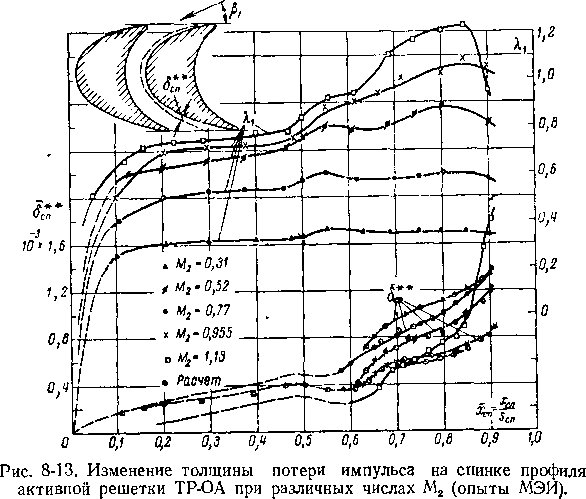
Результаты исследования пограничного слоя в активной решетке, составленной из профилей МЭИ ТР-ОА, показали, что и здесь при расчетном угле входа существуют три зоны течения в слое, которые располагаются таким же образом, как и в каналах реактивных решеток.
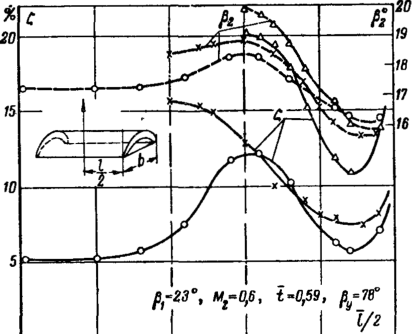
При оптимальном угле входа Pi = 23° (рис. 8-13) распределение скоростей вдоль спинки является конфузор-ным. Переходная зона при всех значениях М2 располагается за минимальным сечением канала при входе в косой срез и изменение режима по М и Re не приводит к заметному перераспределению протяженности ламинарных и турбулентных участков слоя.
|
У S | А | 1 CcfO,B6 :С„=0,В2 :en*0,68t | 2 0 |
1 | ||
| а й | 1 | |||||
| и- | Ja | |||||
| 3 | iу 8 А /• |
|||||
|
,^ | * |
0 > | ||||
|
0г—~ | к |
0.3 Ofl
0,5
0,7 0,в
0,9
Рис. 8-12. Распределение скоростей в пограничном слое на спинке профиля (а) и распределение толщин потери импульса вдоль спинки (б) для реактивной решетки ТС-2А.
1,0
0,6
О
0,7
0,6
0,5
0,4
0,3
0,2
0,1
103‘1,Ч
V ',0 0,8 0,6 М 0,2 О -
| • -Результаты расчетов | ||||||||
| LA-гРезильтаты опытов | ||||||||
| , | ||||||||
|
jH' | ||||||||
|
\ |
К* | |||||||
| А | т | |||||||
| i |
> | |||||||
| ,, j/ | У | |||||||
| / |
-¦-- | |||||||
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9
ч
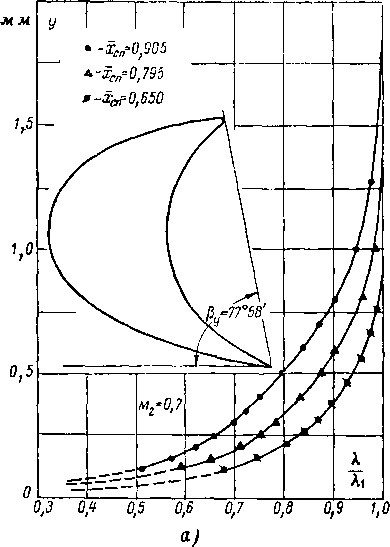
При малых углах входа ((^’==14°) весь пограничный слой на спинке оказывается турбулентным и толщина потери импульса у выходных кромок на спинке возрастает в 2— 2,5 раза по сравнению с р, = 23° (рис. 8-14). _
Существенные изменения в распределении толщины &** отмечаются и на вогнутой поверхности (рис. 8-15). Если
при ^ = 23° (Мг = 0,52)б”г оказалось порядка 0,7-10~а, то с переходом к (3, = 14° толщина 8**г уменьшилась до 0,27 • 10 ~3. Суммарная толщина потери импульса при уменьшении угла входа потока увеличивается на 60 — 70°/„. С увеличением возрастает 8** на вогнутой поверх
ности и уменьшается на спинке. Однако суммарная толщина потери импульса растет менее интенсивно, чем при уменьшении угла входа потока. Отсюда непосредственно следует, что при некотором оптимальном угле входа ?8** является минимальным. Зависимость толщины 8 у выходных кромок от ^ для реактивной решетки показана на
6)
Рис. 8-14. Профили скорости (а) и изменение толщины потери импульса вдоль спинки (б) для активной решетки при {!, = 14°.
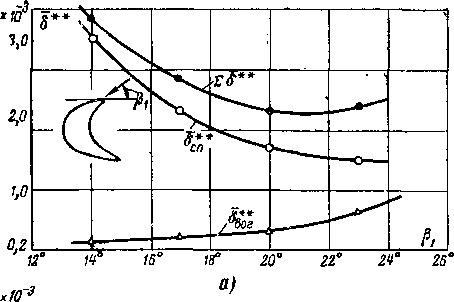
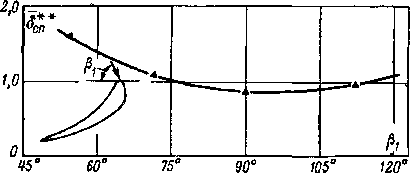
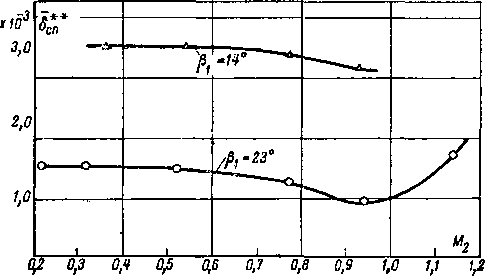
Рис. 8-15. Зависимость S** от угла входа потока р, для активной и реактивной решеток (опыты МЭИ).
В)
рис. 8-15, б. Чем меньше конфузорность потока в решетке, тем более интенсивным является изменение ES в зависимости от Pj.
Влияние двух других режимных параметров (Rea и М2) на структуру слоя в решетках можно проследить по графикам на рис. 8-13 и 8-15, в. С ростом Re2 и М2 толщина С заметно уменьшается.
Интенсивное уменьшение §** с ростом М2 объясняется в значительной степени изменением градиентов скорости в межлопаточном канале. Из приведенного на рис. 8-13 распределения скоростей отчетливо видно увеличение конфузорности на спинке с ростом Ма.
—
С переходом к сверхзвуковым скоростям величина б заметно возрастает в результате взаимодействия скачка уплотнения с пограничным слоем. В месте падения скачка на спинку в косом срезе может наблюдаться отрыв слоя.
Весьма существенное влияние на структуру пограничного слоя оказывает степень турбулентности потока, величина которой в ступенях турбомашин может достигать больших значений.
Влияние степени турбулентности на структуру пограничного слоя104 на спинке реактивного и активного профилей можно оценить по рис. 8-16, а и б. С увеличением турбулентности происходит перестройка профилей скорости в слое: увеличивается наполнение профилей скорости (гл. 5). Увеличение степени турбулентности приводит к сокращению участка ламинарного слоя и к возрастанию толщины турбулентного слоя.
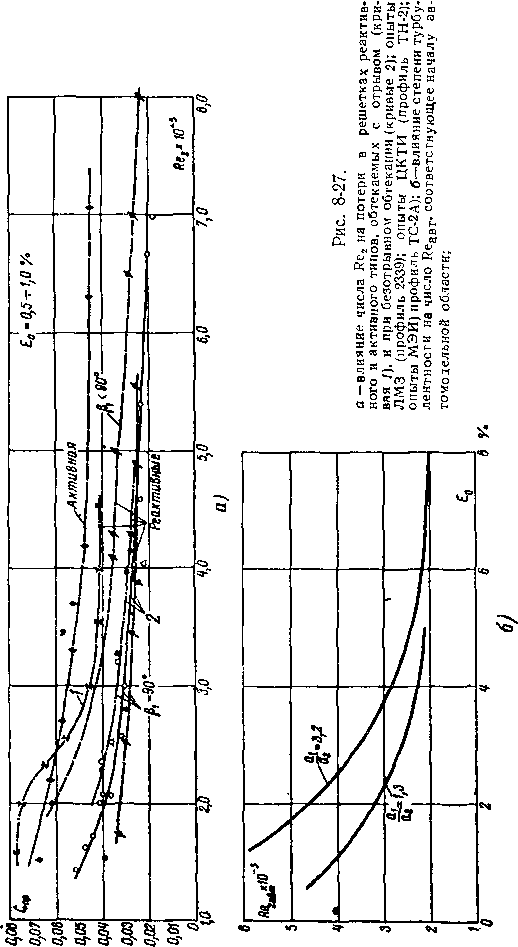
Характер изменения профильных потерь и потерь на трение в зависимости от степени турбулентности для двух типов решеток можно оценить по кривым на рис. 8-16, б. В реактивной решетке ТС-1А увеличение Е0 с 1 до 9°/0 приводит к возрастанию Стр с 2,6 до 4°/0. Для активной решетки ТР-ОА кривая Стр имеет минимум при Е0 = 3°/0. На участке 1°10<Е0 < 3°/0 происходит турбулизация слоя в точке отрыва на спинке и потери снижаются. При Е0^> > 3°/0 с ростом Е0 потери на трение возрастают более интенсивно, чем в конфузорной реактивной решетке.
Расчет пограничного слоя в решетках производится с помощью методики, изложенной в гл. 5. При этом предварительно должно быть рассчитано или определено опытным путем распределение скоростей по обводу профиля.
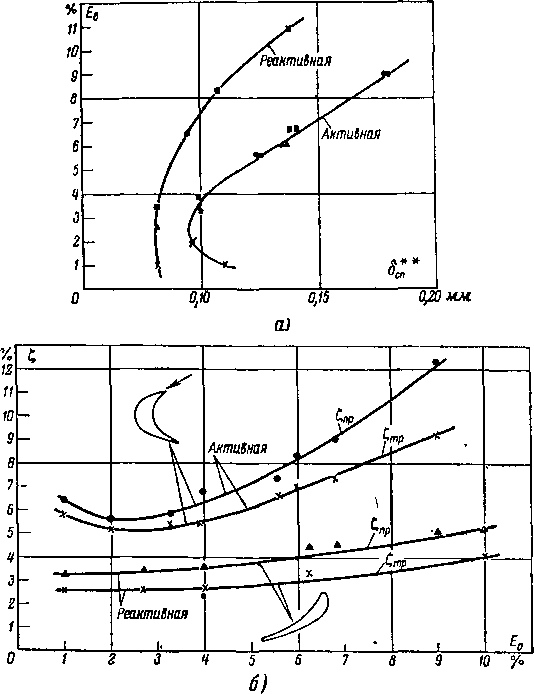
Рис. 8-16. Влияние степени турбулентности на распределение толщин 5** вдоль спинки (а) и на профильные потери и потери треиия в реактивной и активной решетках ТС-1А и ТР-ОА (б) (опыты МЭИ).
По нему производится расчет толщины потери импульса. Предварительно необходимо- правильно определить положение переходной области на спинке и вогнутой поверхности.
При отсутствии опытных данных 8 в зоне перехода можно определить по формулам, приведенным в § 5-10. При высоких степенях турбулентности переход совершается вблизи входной кромки; в этом случае отпадает необходимость учитывать ламинарный участок.
Потеря кинетической энергии в пограничном слое (потеря на трение) определяется по уравнению энергии, записанному для выходного сечения решетки:
• 00
{Г 00
j ри (и* — и2) dy
+
I О
- оо
^ рм (и2 — и2) dy
(8-21)
где и — скорость в данной точке слоя;
«j — скорость на внешней границе слоя; у — координата, нормальная к профилю в данной точке.
При отсутствии потерь кинетическая энергия за решеткой будет:
0ut F =' ' 2 g
(8-22)
где G— действительный расход через один канал, определяемый по формуле ~00 00
f (Рх«1 — р“)сп dy+ j* (pi“i — Ри)вог йУ
G—Gt g
, (8-23)
Lo О
где Gt, ut — теоретические расход и скорость на выходе из решетки.
Коэффициент потерь на трение равен:
Тр
Выразив Д?'тр и Et по формулам (8-21), (8-22) и (8-23) после некоторых преобразований можно получить:
(8-24)
тр t sin
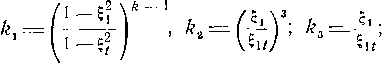
St = ——, ?4< = — --безразмерные скорости за решеткой
макс макс для действительного и теоретиче
ского процессов. Знак 2 указывает на суммирование по спинке и вогнутой поверхности.
Результаты проверки точности расчета слоя для нескольких решеток можно видеть на рис. 8-13 и 8-14. Сравнение показывает удовлетворительную сходимость опытных и расчетных значений 5 во всей области дозвуковых скорйстей (до М2 = 0,955).
После расчета толщины 8 определение потерь на трение не представляет труда, если известна величина Н* —
. Для расчета турбинных (конфузорных) решеток
можно принимать И = 1,8.
В диффузорных (компрессорных) решетках величина Н несколько повышается. Таким образом, потери на трение в первом приближении можно считать пропорциональными толщине потери импульса на выходной кромке профиля и по ее величине судить об относительной эффективности решеток.
8-6. КРОМОЧНЫЕ ПОТЕРИ В РЕШЕТКАХ
При сходе с выходных кромок профиля происходит отрыв пограничного слоя. В результате отрыва и взаимодействия слоев, стекающих с вогнутой и выпуклой поверхностей, с внешним потоком за выходной кромкой возникают вихри, которые образуют начальный участок кромочного следа (рис. 8-17).
В пределах начального участка и в том месте за ним, где образуется вихревая дорожка, взаимодействие между кромочным следом и ядром потока приводит к выравниванию поля потока за решеткой. В некотором сече-
Н‘Ий за решеткой вихревые следы соседних профилей смыкаются и поле скоростей, статических давлений и углов становится равномерным На участке до полного выравнивания среднее статическое давление потока увеличивается, а угол выхода уменьшается.
На поддержание вихревого движения за кромкой затрачивается часть кинетической энергии потока; допол-
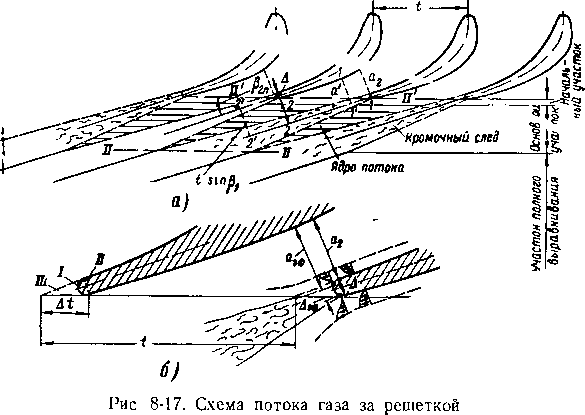
нительные потери кинетической энергии образуются на границе кромочного следа и ядра потока, где возникает интенсивный турбулентный обмен.
Образование вихревого движения в кромочном следе подтверждается экспериментально. На рис. 8-18 приведены кривые распределения полных и статических давлений, углов и температур торможения на некотором расстоянии за кромками реактивной решетки При малых расстояниях от кромки обнаруживается значительная неравномерность полей давлений, углов я, что особенно важно, температур торможения. В кромочном следе давление и температура торможения уменьшаются, что является характерным для вихревого движения. Изменение Та объясняется неравномерным распределе-йием скоростей и вихрейым эффектом за кромкой (§ 5-1 и 5-16). Быстрое выравнивание Т0 свидетельствует об интенсивном обмене между ядром шотока и кромочным следом.
При небольшой толщине кромки на структуру кромочного следа и кромочные потери решающее влияние оказывают толщина пограничного слоя и распределение
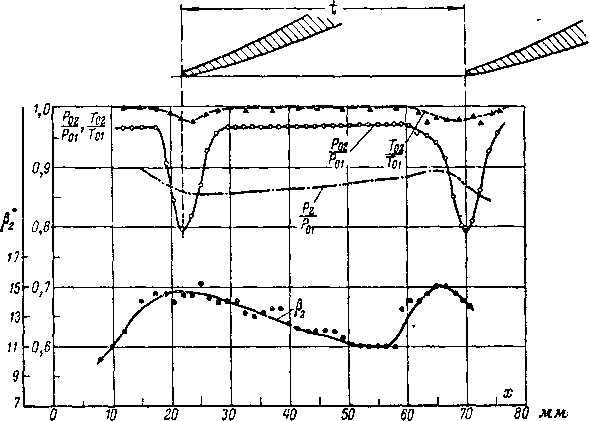
Рис. 8-18. Распределение параметров потока за выходными кромками реактивной решетки
скоростей вблизи точек отрыва потока, а также разность давлений в этих точках.
По мере увеличения толщины кромки заметное влияние приобретают потери, связанные с внезапным -расширением потока.
На рис. 8-19 показаны результаты дренирования выходной кромки. Как видно, давление вдоль кромки резко меряется. Со стороны вогнутой поверхности поток конфузорный, а со стороны спинки — диффузорньий. Следовательно, точки отрыва смещены к спинке лопатки.
При изменении толщины выходной кромки А (рис. 8-17) меняется распределение скоростей по обводу профиля и, следовательно, происходит некоторая перестройка пограничного слоя вблизи выходной кромки. Потери на трение при атом изменяются в соответствии с изменением толщины потери энергии на выходной кромке. Опыты В. С. Елизарова (рис. 8-20) отчетливо
|
1 ыр | ~f^2 m0j6 |
|
| Л */[ j | ||
| / /> | /\1Х^ТгЩ>т 0,(15 | |
| А |
'it' ч | i Номера, точен |
|
/~мг b |
f-(?S5 -0,55 |
3гГ |
| Рнр | м2- |
ар-ор | ||
| / а |
•мг-о,« | т0,6 f | ||
| о> / | /У ( |
о',в | :’з |
t',0 |
а) ?!
Рис. 8-19. Распределение давлений по выходной кромке реактивной решетки при различных режимах. '
. ?*** 1 <\*** подтвердили, что с увеличением Д сумма сп+°вог =
= #*?§** изменяется.
Значительное влияние на структуру потока за кромкой оказывает шаг лопаток. При малом шаге (рис. 8-19)
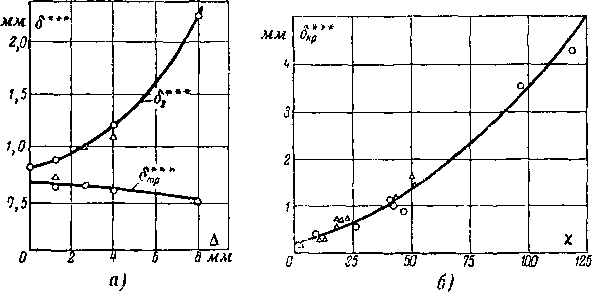
Рис. 8-20. Изменение толщин потери энергии на профиле и за решеткой (а) и S'** в зависимости от параметра у (б) по В. С. Елизарову.
за кромкой обнаруживается разрежение, несколько увеличивающееся с ростбм М2. По мере увеличения шага среднее давление за кромкой возрастает и при некотором шаге достигает значений, больших, чем давление за решеткой. Следовательно, с увеличением шага должны уменьшаться не только относительные, но и абсолютные значения кромочных потерь, что и подтверждается экспериментом.
Некоторое влияние на кромочные потери оказывает форма кромки, определяющая при известных условиях положение точек отрыва. Опыты показывают, что в случае скругленной кромки при дозвуковых скоростях начальный участок следа более узкий (точки отрыва смещены по потоку), чем у плоско срезанной кромки.
Теоретический расчет кромочных потерь весьма сложен, и эта задача до сих пор еще не решена. Имеющиеся полуэмпирические методы позволяют оценить кромочные потери и угол выхода из решетки на основании опытных данных, полученных для определенных классов профилей.
Параметры выровнявшегося потока за решеткой могут быть найдены путем совместного решения уравнений неразрывности, импульсов и энергии. Для жидкости, заключенной между контрольными поверхностями (рис. 8-17), расположенными параллельно друг другу на расстоянии, равном участку выравнивания, указанные уравнения могут быть записаны при следующих допущениях: а) плотность потока мало меняется в процессе смешения (между сечениями II—II и II'—IV); б) поля скоростей и давлений между кромками и в сечении
II—II являются однородными; в) спинка профиля в косом срезе выполнена прямолинейной.
В этом случае уравнение неразрывности можно представить в виде:
рс2 (t — ДО sin р2п = c2jt sin ра,
или
с,{\ — т) sin р2п = с2оо sink, (8-25)
At
где г=т;
At — толщина кромки в плоскости выходного сечения (рис. 8-17).
Уравнение импульсов в направлении оси решетки дает:
с\ cos р2п p(t — М) sin р2п = с^ cos j32pt sin 02. (8-26)
Уравнение импульсов в направлении, перпендикулярном оси решетки, можно написать в виде:
с2ооР sin2 К V - м) + А (t — ДО + РКМ =
кр
= C2ocPSin2P^ + /72J- (8‘27)
L'2ool'c’1“ Га* “Г/'гоо*
Из уравнений (8-25) и (8-26) легко получить:
P» = arctg[(l—t)tgpj. (8-28)
Уравнения (8-25) и (8-27) позволяют найти повышение давления за решеткой:
ДА = = [2 (1 - *) sin2 р2„ + ЯР] (8-29)
-jp 4
Для определения теоретической скорости на бесконечности за решеткой воспользуемся уравнением энергии,
которое при принятом допущении р2 = р2оо = р можно представить в виде:
'2 2
с2оо [ Pirn_ с1\Рг ,о ощ
2 I р 2 ' р ’ (о-30)
где с2оо — теоретическая скорость в сечении II — II.
С помощью уравнений (8-27), (8-28) и (8-30) получаем
коэффициент кромочных потерь
т sin2 89"—р„п
С =-=
кр-с.
(8-31)
КР 1-^200
Входящее в уравнения (8-29) и (8-31) безразмерное давление за кромками ркр должно быть определено по опытным данным.
Согласно (8-31) при увеличении толщины выходных кромок At целесообразно одновременно увеличивать относительный шаг t и уменьшать угол установки е тем* чтобы сохранить заданный угол выхода потока и обес* печить умеренные поггери.
Приведенные выше формулы, полученные Г. Ю. Степановым, удовлетворительно согласуются с опытными данными, однако практическое использование уравнения (8-31) затруднено, так как величина ркр может меняться в весьма широких пределах в зависимости от режимных и геометрических параметров решетки.
В. С. Елизаровым предложен приближенный метод определения кромочных потерь как разности потерь на определенном расстоянии за решеткой (профильных потерь) и потерь трения. Коэффициенты профильных потерь и потерь на трение могут быть выражены через соответствующие условные толщины потери энергии [формула (8-24)].
В соответствии с рассматриваемым методом толщина потери энергии в кромочном следе выражается формулой
о = о„ Но ,
кр 2 11 тр 105
где о2 — толщина потери энергии в сечении кромочного следа на выбранном расстоянии за решеткой.
Относительная толщина потери энергии в следе
кр _J2
(8-32)
(8-33)
тр тр
зависит в основном от комплекса
Д?8*" ДЕ5
.*** «*** гг* .** .**
<5 6 И д д
СП ВОГ сп вог
Соответствующая зависимость, полученная экспериментально для безотрывно обтекаемых профилей, приведена на рис. 8-20,6. Формула, аппроксимирующая эту зависимость, имеет вид:
Т*;= (0,21 х2 + 12,4 х + 220) • 10~3. (8-34)
Следовательно,
(8-35)
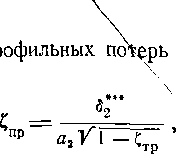
муле
где а2 — ширина узкого сечения канала;
Стр — коэффициент потерь на трение, определяемый по
формуле (8-24).
Таким образом, рассматриваемый способ расчета профильных потерь основан на установлении связи между кромочными потерями и потерями на трение причем эти потери определяются раздельно.
Очевидное преимущество метода состоит в том, что он позволяет учесть влияние различных геометрических и режимных параметров решетки на кромочные и профильные потери. При изменении этих параметров меняются условные толщины пограничного слоя, через которые выражаются коэффициенты ?пр и ?кр.
Однако фактически вид функции 8”*(х) может меняться в зависимости не только от типа решеток, но и от режима обтекания, что является недостатком метода.
Для решеток с толстыми кромками, толщина которых существенно больше толщины слоя (Д = Д/я2]>0,3), метод решения предложен А. Н. Шерстюком. Рассматривается течение в одном межлопа-точиом канале, границами которого за пределами выходных кромок служат прямые, проведенные под углом выхода потока р2 к фронту решетки (рис. 8-17).
Приближенно угол выхода потока определяется по эмпирической формуле
![]()
(8-36)
где т — опытный коэффициент.
При большой толщине выходных кромок можно считать, что переходы от сечения 1 — 1 к сечению 1' — Г и от сечения 2 — 2 к 2'— 2' (рис. 8-17) вызывают такие же потери энергии, как и при
где К = 0,2. Однако опыты показывают, что коэффициент К может меняться в весьма широких пределах в зависимости от геометрических и режимных параметров решетки (рис. 8-21).
Сопоставление различных приемов расчета кромочных потерь показывает, что лучшие результаты дает формула (8-34), учитывающая влияние чисел Re2 и М2 и основных геометрических параметров.
Внезапном расширении потока. Определив величину этих rtofe^b, можно получить приближенную формулу
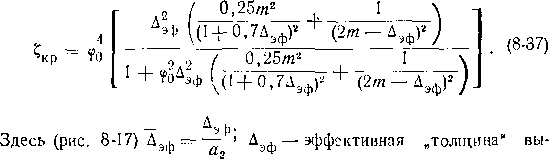
ходной кромки, определяемая как расстояние между точками отрывэ Д
ДЭф = 0,7 Д; аЭф = a2 + ~g- — эффективная „ширина" узкого сечения; — коэффициент скорости для бесконечно тонкой кромки.
Наиболее простая эмпирическая формула для определения кромочных потерь предложена Г. Флюгелем:
![]()
Влияние чисел Re2 и М2 (рис. 8-21,6 и в) объясняется главным образом перемещением точек перехода и отрыва по кромке, а также изменением потерь на трение (гл. 5). Особенно характерной является кривая ?кр(М2) для Д = = 0,42.. Первый максимум кривой объясняется смещением точек отрыва против потока (ламинарный отрыв). Турбу-лизация слоя в зоне отрыва приводит к перемещению точек отрыва по потоку („кризис сопротивления"). Второй максимум связан с образованием местных сверхзвуковых зон на кромке и перемещением отрыва против потока (Д_ф возрастает). Переход к сверхзвуковым скоростям сопровождается улучшением обтекания кромки. Таким образом, обтекание толстой кромки при различных Re2 и М2
0,1 0,2 0,3 0,4 0,5 0,6 0}7
а)
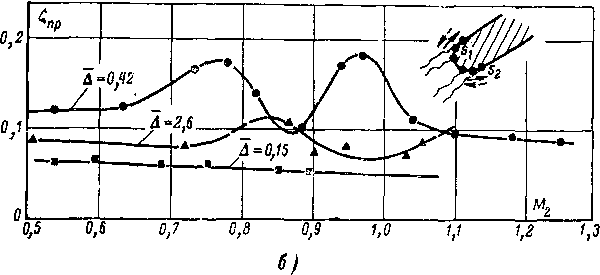
Рис. 8-21. Изменение кромочных потерь в зависимости от толщины кромки и относительного шага (а), чисел М2 (б).
качественно напоминает спектр обтекания плохо обтекаемого тела (§ 5-14).
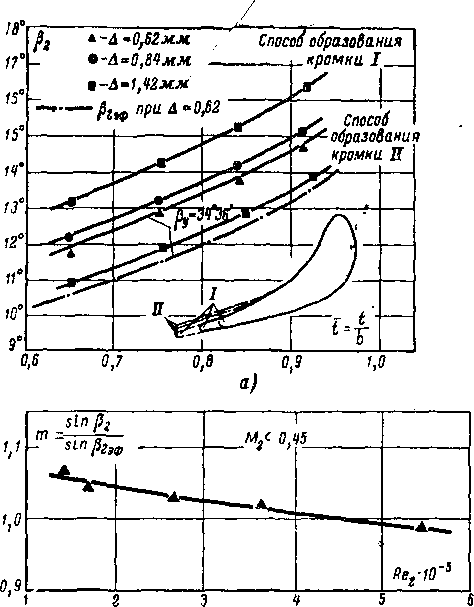
Влияние толщины кромки на угол выхода потока (рис. 8-22) оказывается различным в зависимости от способа образования кромки. При подрезке кромки по способу
I угол Р2 уменьшается с уменьшением Д. Подрезка вогнутой поверхности (по способу II) приводит к увеличению рг по мере* уменьшения Д. Следует подчеркнуть, что эффективный угол, определяемый по формуле (8-36), как пра-
В)
| т | йег> 6 * 10 |
5 | |||
| * | |||||
| < | > |
0,4 0,5 0,6 0,7 0,8 0,9
Рис 8-22. Зависимость угла выхода потока от относительного шага и толщины кромки (а), чисел Re (б) и чисел Мг (в).
вило, не совпадает с действительным углом [}2, причем Р2эф$Р2 (рис. 8-22,6). Поправочный коэффициент т. в формуле (8-36) позволяет перейти от Р2эф к рг. В соответствии
с физической природой явлений за кромками коэффициент т зависит от чисел Re2 и М2, а также от толщины кромки Д (рис. 8-22) и формы спинки выкосом срезе. Опыты показывают, что для профилей с прямолинейной спинкой в косом срезе угол |32 ^ Р2эф Длярыпуклой спинки |32
несколько меньше P2gJ)r
8-7. НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ ПЛОСКИХ РЕШЕТОК ПРИ ДОЗВУКОВЫХ СКОРОСТЯХ
Рассмотрим результаты опытного исследования профильных потерь и углов выхода потока в зависимости от геометрических и режимных параметров и формьи профиля для некоторых реактивных и активных решеток.
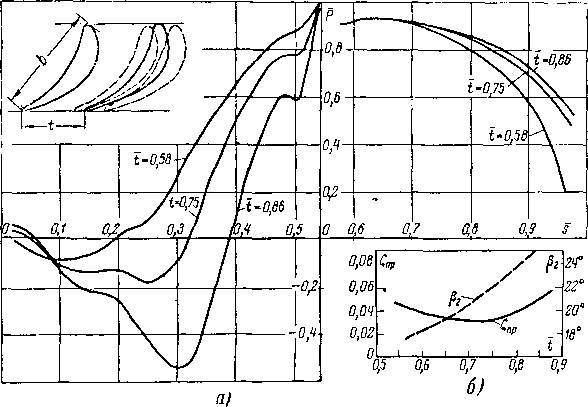
Рис. 8-23. Влияние шага на распределение давлений по профилю в решетке реактивного типа (я); профильные потери и угол выхода потока (б).
Влияние шага и угла установки профилей. Распределение давлений по профилю реактивной решетки (рис. 8-23) показывает, что при t =0,7 -f- 0,8 течение конфузорное по всему обводу профиля, за исключением коротких участков вблизи входной и выходной кромок. По мере уве-
личения шага точка минимума давлений на спинке смещается против потока, сокращаются области конфузор-ного течения в косом срезе; градиенты давлений в конфузорных и диффузорных областях возрастают. Следовательно, область перехода смещается против потока и
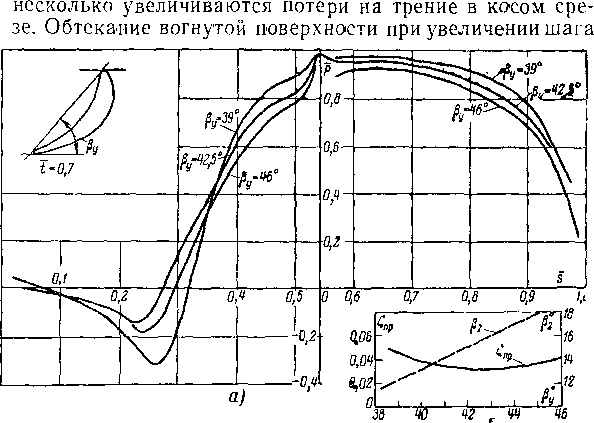
Рис. 8-24. Влияние угла установки профиля в решетке реактивного типа на распределение давлений (а), профильные потери и угол выхода потока (б).
становится благоприятным, так как конфузорность течения вблизи выходной кромки увеличивается. При малых шагах течение вдоль спинки в косом срезе более конфузорно, однако градиенты давлений уменьшаются.
Следовательно, с увеличением шага при безотрывном обтекании профиля потери на трение и кромочные потери меняются различно: ?Тр вначале уменьшается, так как снижается относительное значение толщины по-
тери импульса —-—, а при больших шагах возрастает
вследствие увеличения толщины «потери импульса; кромочные потери с ростом t уменьшаются непрерывно. В результате профильные потери вначале уменьшаются, а затем увеличиваются. Диапазон относительных шагов, сОотбетствующий минимуму профильных потбрь, называется оптимальным (рис. &23,б). Опыты отчетливо показывают, что диапазон оптимальных шагов зависит от формы профиля.
Изменение угла установки профиля ру вызывает изменение распределения давлений оо профилю (рис. 8-24). В соответствии с этим изменяются градиенты давления в диффузорных и конфузорных участках на профиле и структура пограничного слоя. В результате профильные потери при увеличении ру вначале уменьшаются, а затем возрастают (рис. 8-24,6), т. е. имеется определенный диапазон оптимальных углов установки. Необходимо отметить, что зтот диапазон зависит от шага решетки.
Угол выхода потока из решетки увеличивается при увеличении шага и угла установки. В интервале значений t0nT и ру.опт угол выхода при изменении шага меняется примерно пропорционально arcsin a2/t.
Слабое изменение ?Пр в широком диапазоне изменений шага и ру является важной особенностью реактивных решеток, составленных из хорошо обтекаемых профилей '. Абсолютное значение ?Пр не превосходит 2—3%.
Аналогично меняются профильные потери и угол выхода потока в зависимости orf и ру для решеток актив-ного типа, однако диапазон (опт и Ру. опт для активных решеток оказывается более узким, так как геометрическая и аэродинамическая конфузорность каналов таких решеток будет меньшей.
Отметим, что наличие .диффузорных участков на спинке в косом срезе с небольшими градиентами давле-ления не приводит к резкому возрастанию потерь, так как при малых степенях турбулентности переход в пограничном слое происходит быстрее и отрыв на выходных кромках смещается по потоку.
Влияние режимных параметров на профильные потери. В предыдущем параграфе было показано, что в зависимости от угла входа потока Pi меняется распределение толщин б** на вогнутой и выпуклой поверхностях, так как меняется распределение давлений по профилю ('рис. 8-25,а). Наиболее неблагоприятными являются режимы с 'малыми углами входа (Pi<45°), когда на вход-
НШ участке слинкй появляется заметный диффузорный участок. При этом ре^йо утолщается 'пограничный слой на обводе спинки, у/удшается распределение скоростей в слое и даже гари умеренных градиентах в диффузорной
области в косом срезе возникает отрыв; иногда отрыв может возникнуть и на входном участке спинки. При Рь больших расчетного,- диффузорная область обнаруживается на вогнутой поверхности. Однако в связи с ггем, что на сходе g этой поверхности течение конфузорное, отрыв,
Р
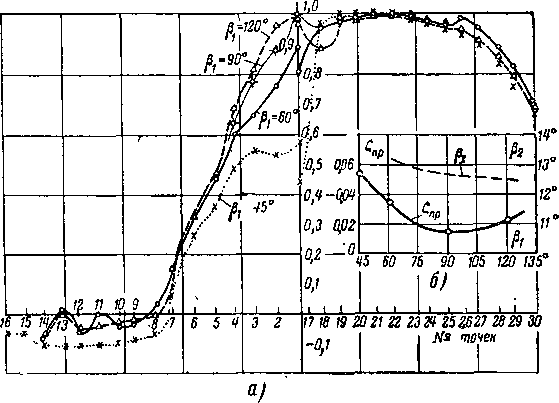
Рис. 8-25. Распределение давлений по профилю реактивной решетки (а), профильные потери и угол выхода потока (б) в зависимости от угла выхода р,; М2 —0,5; Re = 3,46-105
85
Рн
та . с «
go
?¦4
ш
»к
к
я
О)
ч
CQ
Ф
к
я
CO
Dh
л
я
л
ч
к
*©•
о
о-
с
gcv «(С
а®
s II
а
Ои
2
ts ^
tS •"
^QGU о b &ё
как правило, до выходной кромки не распространяется.
Аналогичная, но более резкая картина обнаруживается в решетках активного типа (рис. 8-26). Следовательно, ори малых углах входа отмечается значительно более резкое возрастание потерь, чем при больших (ом. также рис. 8-15). Сравнение реактивных и активных решеток при различных |3i отчетливо показывает, что решетки с меньшей геометрической конфузорностью ~
более чувствительны к изменению
При небольших дозвуковых скоростях, когда влиянием сжимаемости можно пренебречь, профильные потери зависят от числа Рейнольдса. Влияние Re2 особенно велико при отрывном обтекании епинки профиля, когда отрыв происходит до точки перехода ламинарного слоя в турбулентный. В этом случае при увеличении Re2 точка отрыва смещается по потоку. При этом потери в зависимости от числа Re2 меняются резко (рис. 8-27).
Влияние Re2 на профильные потери следует рассматривать при различных углах входа ^ и степенях турбулентности набегающего потока. Г'еометрическая конфузор-ность также влияет на характер зависимости Cnp(Re2).
При малых степенях турбулентности и расчетных углах входа отчетливо видно существенное влияние Rea на Спр при Re2<(6-r-8)- 105. С ростом Е0 (рис. 8-27,6) область практической автомодельности смещается в сторону меньших Re2 (§ 5-14). Уменьшение ReaBT отмечается также при малых р, <; ^ pacq и для решеток с небольшой конфузорностью каналов. Таким образом, значения чисел Re2, определяющих области автомодельного течения в решетках, могут изменяться в широких пределах в зависимости от формы профиля, геометрических параметров решетки, степени турбулентности и угла входа.
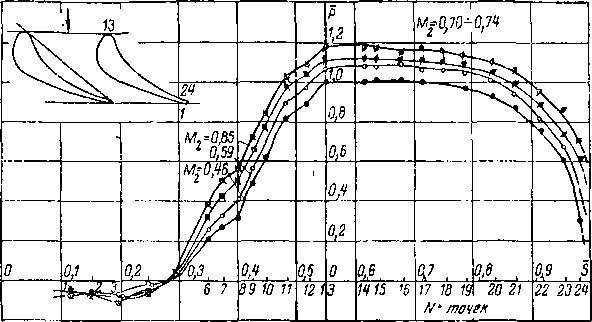
Влияние сжимаемости (числа М2) на характеристики решеток при докритических скоростях обнаруживается, начиная примерно с М2 > 0,5 (рис. 8-28). С увеличением М2 Спр уменьшается и достигает минимального значения М2 ^ 0,75 -г- 0,95 в зависимости от тица решетки и формы профиля.
Изменение Спр в зависимости от М2 в докритической области при безотрывном обтекании легко объяснить тем, что
градиенты давления в сжимаемой жидкости увеличиваются с ростом М2 (гл. 3).
При конфузорной обтекании профиля толщина потери импульса 8** уменьшается, а при диффузорном — соответственно возрастает (§ 8-5).
%
го
18
16
14
12
а)
0,6
6)
|
—- | Акта |
8ныз | _____ |
— | Р\ |
|
| 4 |
рпр | - | ||||
| ¦'-CZ |
,_а— | |||||
|
Реакп |
-и.-- швная |
м2 |
0,5
Рис. 8-28 Влияние числа М2 на распределение давлений, профильные потери и угол выхода потока для решеток реактивного и активного
типов.
По мере увеличения М2 точка минимума давлений в косом срезе несколько смещается по потоку и значение ~рыт1 снижается. В результате увеличивается протяженность конфузорного участка на спинке. По этим причинам по-
| / | ||||||
| тс- | га ¦тг/С | -ЗА | ||||
| • тс- |
0А | -V. | $ |
10 12 14 16 IS 2C 22
6)
%Ч A-0
| ' А-1 | |||||||||||
| V |
**пр | ч | А-2 | \ N | |||||||
| /\|! | 1 | А-3 < | |||||||||
| \TP-0A | |||||||||||
| ТР-1А | О |
С | ТР-ЗА | 'ТР' | 4А | .—Л* | |||||
| ?пр | | „ |
-- | \ |
||||||||
|
**пр |
"Т" 4*Лр | ||||||||||
14 18 22 26 30 34 38 42 46 50 54 5 8 60
Рис. 8-29. Профильные характеристики реактивных (а и б) и активных (в) решеток (А—О, А—1, А—2 а А—3—решетки старого типа).
тери снижаются. Аналогичные результаты получены и для активных решеток.
При больших дозвуковых скоростях (начиная с М2 = = М2* и при больших М2) в косом срезе канала и на кромках профиля появляются сверхзвуковые области, которые замыкаются скачками уплотнения. По этой причине появляются дополнительные волновые потери и Спр увеличивается.
Угол выхода потока в зависимости от М2 изменяется незначительно (рис. 8-28,6). С увеличением М2 угол 32 несколько уменьшается, а при М2>Мг» он возрастает, что объясняется увеличением потерь] в местной сверхзвуковой области.
Профильные характеристики решеток. Результаты измерений ?пр и р, в решетках различных типов показывают, что профильные характеристики являются сложными функциями большого числа параметров: С =?(3^, {Зу, Re2,
М2, Д, форма профиля) и могут быть установлены только опытным путем.
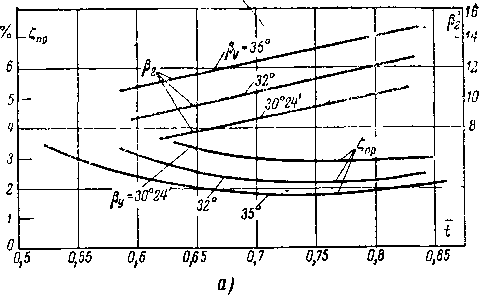
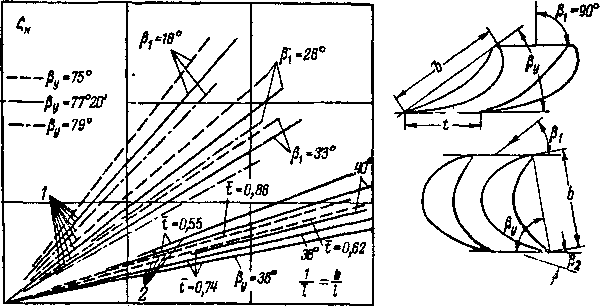
Примеры построения таких характеристик для решеток МЭИ реактивного и активного типов можно видеть на рис. 8-29. Как видно из рис. 8-29,6, профильные потери в реактивных решетках при fj, = 90° слабо зависят от угла в интервале р2 = 12 18°.
Профильные потери в активных решетках невелики (3,0 — 7°/0) и для каждой решетки в широком диапазоне меняются незначительно (рис. 8-29,в). Кривые Спр = / (Pj) для этой группы решеток имеют пологую огибающую. На рис. 8-29 приведены также кривые потерь в решетках старого типа, образованных дугами окружностей и отрезками прямых. Легко .видеть, что новые решетки, разработанные аэродинамическими методами, имеют значительно лучшие характеристики. Этот результат подтверждается также графиками распределения давлений для сравниваемых форм профилей при одинаковом угле входа потока.
8-8. ПРОСТРАНСТВЕННЫЙ ПОТОК ГАЗА В РЕШЕТКАХ.
КОНЦЕВЫЕ ПОТЕРИ И СПОСОБЫ ИХ УМЕНЬШЕНИЯ
В межлопаточных каналах решетки конечной высоты, как и в одиночном криволинейном канале *, возникают вторичные течения: под влиянием поперечного градиента давления происходит перетекание газа по плоским (или цилиндрическим) стенкам106 от вогнутой .поверхности к спинке (рис. 8-30).
На спинке, на некотором удалении от концов лопаток, пограничный слой, притекающий с плоских стенок, сливается с основным пограничным слоем, движущимся
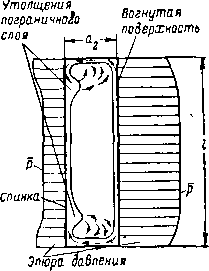
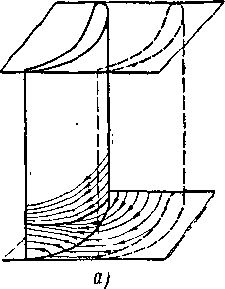
Рис. 8-30. Схема образования вторичных течений в межлопа-точном канале решетки.
а —линии тока на плоской стенке и на спинке; б— периферийные течения в пограничном слое у кондоз лопатки,
по траекториям, 'параллельным плоским стенкам; в результате здесь происходит интенсивное набухание пограничного слоя и появляются составляющие скорости, направленные в ядро потока. В ядре у концов лопатки возникает течение, направленное-от спинки к вогнутой поверхности, образующее вместе с периферийным течением вдоль торцовых стенок вихревые области. Таким образом, у спинки профиля на концах лопатки возникает парный вихрь, состоящий из двух вихревых областей. Вихри имеют противоположные направления .вращения.
На фотографии следов потока (рис. 8-31) отчетливо видно перетекание пограничного слоя «а плоских стенках и ,на спинке. Так как за областью возникновения вихрей продолжается притекание газа с торцовых стенок, то вихревое движение развивается к выходному сечению камаша; область дабухания пограничного слоя, а также ядро парного вихря смещаются к среднему сечению. При малых высотах вихревые области распространяются по всему сечению канала, образуя парный

?
Рис. 8-31. Следы периферийных перетеканий в межлопаточном канале.
вих,рь, характерный для криволинейных каналов квадратного сечения (§ 5-15).
Представленное на рис. 8-32 распределение потерь и углов выхода по высоте решетки показывает характерное для вихревых областей изменение этих величин. При удалении от торцовых стенок потери вначале у*мень-шаюГгся (|рис. 8-32,а), затем реако возрастают и .потом вновь уменьшаются к среднему сечению (шотери в среднем сечении цри достаточной высоте решетки равны профильным). Максимальные потери соответствуют области утолщенного пограничного слоя на спинке. Мини-¦мяльное значение ? у «плоских стенок можегг быть больше или меньше ?Пр в зависимости от интенсивности вторичных течений; для реактивной решетки минимум потерь, как правило, не обнаруживается (.рис. 8-32,6).
| 0 0,12 | 0,2 |
Ofi |
0,6 0 Ч |
,S | |
| С |
|||||
|
Ofi В | |||||
|
t‘0,72 | |||||
| 0,04 | - | ||||
| -и-,. t*0,61 | г |
||||
о
20мм
Рис. 8-32. Влияние вторичных перетеканий на распределение потерь и углов выхода потока по высоте активной (а) и реактивной (б) решеток при различных высотах.
ю
6)
В зоне вторичньих течений в соответствии с изменением ?, углы выхода вначале увеличиваются, а ватем к среднему сечению уменьшаются.
Концевые потери определяются как разность между суммарными и профильными потерями. Оценка влияния
на концевые потери высоты, шага, угла установки, формы профиля и канала, а также угла входа, чисел Re2 и М2 можегг быть произведена на основании опытных данных.
Опыты показывают, что, как и в случае одиночного криволинейного канала, любые изменения геометрических и режимных параметров, вызывающие увеличение поперечных градиентов давления в решетке, утолщение
0/18
0,04
О 12 3
Рис. 8-33 Изменение концевых потерь в зависимости от высоты, углов входа потока, углов установки и шага в активных (кривые 1) и реактивных (кривые 2) решетках.
пограничного слоя и появление диффузор,ных участков на выходе, приводят к 'росту концевых потерь.
С уменьшением высоты решетки до известных пределов сокращается плоский участок потока в средних сечениях канала; область повышенных потерь в зоне вихрей практически не меняется. Следовательно, коэффициенты! концевых потерь линейно изменяются в зависимо-1 ь „
сти от у =J. При некоторой минимальной высоте происходит смыкание вторичных течений; область увеличенных потерь занимает всю среднюю часть канала (рис. 8-32,а).
Характер зависимости концевых потерь от I существенно меняется дшя решеток различных типов. Наклон
линий lh=f(^jj уменьшается с уменьшением угла поворота потока в решетке Др=180—(Р1 + Р2) (рис. 8-33). Минимальные значения соответствуют реактивным решеткам, которые характеризуются большой конфузор-ностью каналов и малым углом поворота потока.
При увеличении шага реактивной решетки концевые потери вначале уменьшаются, так как возрастает конфу-зорность потока, достигают минимума, а затем увеличиваются в связи с ростом поперечного градиента давлений. Увеличение угла установки профиля при оптимальном шаге приводит к снижению концевых потерь, так как уменьшаются угол поворота потока и поперечный градиент давлений, а при мальих шагах с ростом ру концевые потери увеличиваются. Влияние шага особенно велико для активных решеток, причем минимальные концевые потери соответствуют такому шагу, при котором межлопаточный канал вначале расширяется (на входе), а затем сужается.
Интенсивное влияние угла входа потока Pi на (рис. 8-33) объясняется изменением поперечных градиентов давления в канале, появлением диффузорных участков на входе и в косом срезе и в некоторых случаях образованием отрывов. Концевые потери заметно возрастают при уменьшении Pi (увеличении Др). При постоянном значении Р] возрастает с уменьшением угла выхода Р2 (при малых р2<11-г-12°), так как при этом увеличивается кривизна канала (рис. 8-33).
Изменение концевых потерь в зависимости от числа Рейнольдса можно оценить по кривым на рис. 8-34. С увеличением Re2 концевые потери уменьшаются. Влияние числа Re2 на ?* велико при Re2<5- 105. Это объясняется тем, что с ростом Re2 пограничный слой утоняется.
Влияние сжимаемости при докринических скоростях сказывается в уменьшении концевых потерь с ростом числа М2 (рис. 8-34) в связи с тем, что поперечные градиенты давления в канале уменьшаются (§ 5-15) (см. также рис. 8-69).
Структура пространственного потока в кольцевых неподвижных решетках обладает некоторыми особенностями. Важнейшим следует считать наличие радиального градиента давления; давление у периферии выше, чем
0,09
| Ск | '1-----1----1-------- ¦¦ ¦- - Опыт/ при малой Hepafm. ——• — Опыты при большой неравл ста !ВЩ | vitfwc/n!/ wuep/t" - | ||||
| 1 2<&о,8 . |
»5 | - | ||||
| Я»г=9-ГС | 'S;Mt=qs |
м | ||||
| . | ±.Jl I I | |||||
1 2 3
Рис. 8-34. Влияние числел Re2 и М2 на концевые потери в решетке.
у корневого сечения 107. Вследствие этого развиваются радиальные перетекания вдоль лопаток, направленные от периферии к корневому сечению. Эти радиальные перетекания .накладываются на поперечные (рис. 8-35). Кроме того, в кольцевой решетке форма канала изменяется по высоте (из-за изменения шага и цилиндричности тор-
0,08
0,0б
0,02
цовых стенок) и поэтому интенсивность периферийных перетеканий у торцовых стенок различна. Как правило, потери энергии вблизи корневых сечений, где радиальные перетекания совпадают с поперечными, в кольцевой решетке, выше, чем на периферии. Отмеченное влияние веерности существенно зависит от параметра d/l, с уменьшением которого возрастает разность скоростей и давлений в корневом и периферийном сечениях.
Большой практический интерес представляет разработка способов уменьшения концевых потерь. Сниже-Ь'Ке .можно обеспечить, увеличивая относительную высоту лопатки, что при заданной абсолютной высоте достигается уменьшением хорды (ширины) профиля. Однако в связи с тем, что при изменении хорды меняются не только концевые, но и профильные потери, возни-
кает задача об установлении оптимальной хорды решетки.
Уменьшения концевых потерь можно также добиться соответствующим выбором геометрических параметров решетки и формы профиля (межлопаточного канала).
S, 91° 1Я° 17° 1Ь°
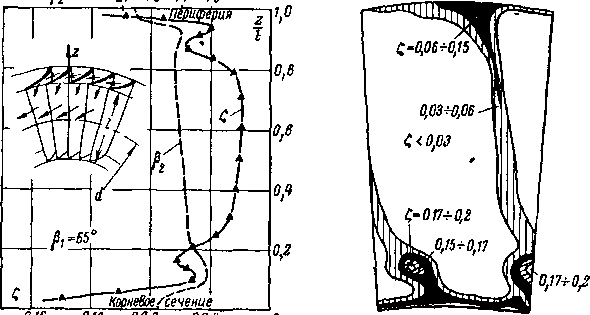
Рис. 8-35. Структура вторичных течений в кольцевой решетке
0,16 0,12 Oft В 0,0 4 О
а)
6)
Результаты исследования потока в криволинейных каналах показывают, что минимальная интенсивность вторичных течений в каналах активного типа обнаруживается в тех случаях, когда входная часть канала выполняется диффузорной. Аналогичные данные получены и для решеток активного типа
На рис. 8-36 приведены «результаты исследования двух решеток, имеющих одинаковые относительную» высоту, t и ру, ,а также форму спинки. Вогнутые поверхности сравниваемых профилей различаются радиусом кривизны: решетка ТР-1А имеет плавно суживающийся, а решетка ТР-1Ак — диффузорно-конфузорный канал. Распределение потерь по высоте для различных режимов показывает, что в решетке ТР-1Ак уровень потерь существенно ниже. Суммарные потери в сравниваемы* решетках в зависимости от угла входа Pi и - числа Мг
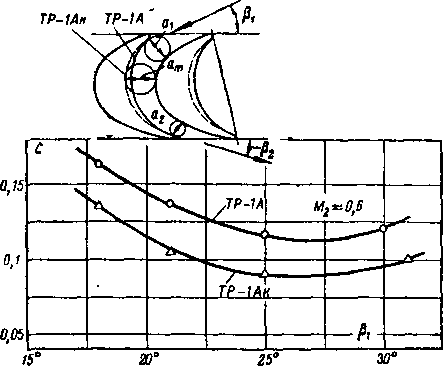
0,15
0,05
| Г> “ 0-1А |
-<у- | ||||
| >-1Ам |
|||||
ь,6 0,7 0,8 0,9 1,0
0,1
0,15
| с 1—. | |||||||
| Ч. |
Р-1А | & | -21° | ||||
| 7 | |||||||
| гг'' | -0,6 | ||||||
|
jp- | 1Аи^\ | ||||||
| Г 2 |
|||||||
S
В)
0,1
Рис. 8-36. Влияние формы канала на потери в активной решетке, а —изменение С в зависимости от р! для двух типов решеток; «—влияние числа М, на потери в решетках двух типов; в —распределение потерь С,по высоте решетки.
меняются аналогично г(рис. 8-36,а и б). Особенно существенны преимущества .решетки ТР-1Ак при небольших скоростях и малых углах входа.
Эффективность диффузорно-конфузорных решеток и
оптимальные геометрические соотношения и др.) зависят от угла поворота потока в решетке и
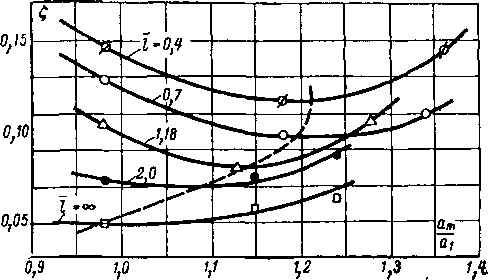
Рис. 8-37. Оптимальные значения ат в зависимости от относительной высоты I.
относительной высоты I (рис. 8-37). С увеличением угла поворота потока и уменьшением относительной высоты
ат
решетки оптимальное соотношение — 'вначале возра-
ai
стает, а затем уменьшается. Результаты опытов показывают, что решетки с диффузорно-конфузорньими каналами целесообразно применять при 1Пр<1,2-И,8 в зависимости от угла поворота потока; при больших Ар возрастает предельное значение /пр.
В реактивнььх (конфузорных) решетках существенного снижения концевых потерь можно добиться профилированием каналов по высоте (профилирование в мери-
к6 я е
|=Г то
диональной плоскости). Этот способ приобретает особенно большое значение для кольцевых решеток, в корневом сечении которых обычно обнаруживаются повышенные потери.
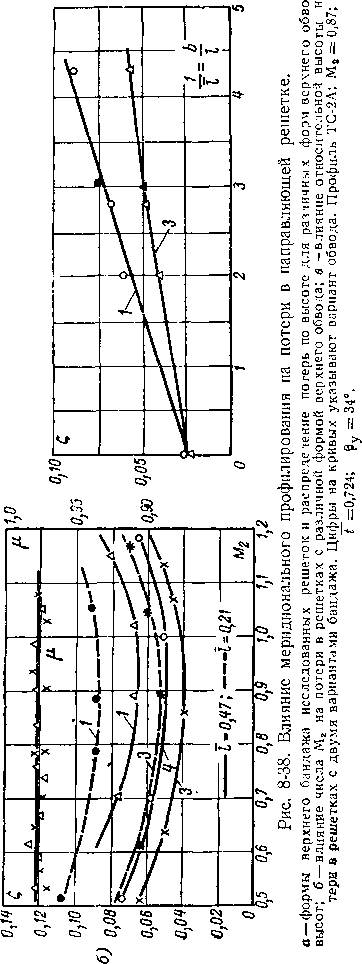
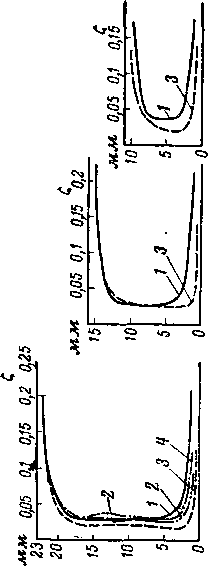
На рис. 8-38,а показаны схемы вариантов направляющей решетки с различными формами верхнего бандажа, а на рис. 8-38,6 и в — соответствующие результаты испытаний прямой решетки в статических условиях. Здесь же приведена кривая потерь в кольцевой решетке с цилиндрическими бандажами той же высоты!.
Опыты показывают значительное снижение потерь в 'решетке с профилированным 'верхним бандажом. Существенным является также перераспределение потерь по высоте решетки: у нижнего бандажа потери резко уменьшаются.
Профилирование верхнего бандажа позволяет также уменьшить разность реакций в корневом и периферийном сечениях, что повышает к. п. д. ступени турбины.
Кривые на рис. 8-39 позволяют объяснить преимущество решеток с профилированным бандажом: в таких решетках обеспечивается более конфузорное течение на спинке в косом срезе и точка минимума давления смещается к выходной кромке; кроме того, скорость потока перед основным поворотом потока в канале уменьшается, что приводит к снижению поперечного градиента на участке максимальной кривизны и, следовательно, интенсивности вторичных течений. Задаваясь рациональным распределением давления по 'каналу, (можно найти оптимальную форму бандажа.
Приведенные на рис. 8-38,в потери в зависимости от I показывают, что описываемый способ профилирования особенно эффективен при малых относительных высотах.
Следует отметить, что несимметричное поджатие верхнего обвода решетки расширяет диапазон оптимальных шагов и углов установки.
Оптимальная величина поджатая, определяемая l„ — h
отношением , меняется в зависимости от высоты
ч
решетки (рис. 8-39,6).
Необходимо подчеркнуть, что указанные способы уменьшения концевых потерь в активных (диффузорно-конфузорные каналы) и реактивных (несимметричное поджатие) решетках физически тождественны. В обоих случаях достигаются уменьшение скоростей на повороте потока в канале и увеличенная конфузорность на выходе из .решетки.
Условия на входе в решетку и, в частности, неравномерность поля скоростей по высоте и высокая турбу-равномерности и турбулентности 'растут толщина пограничного слоя на торцовых стенках и масса газа, участвующая в периферийном движении.
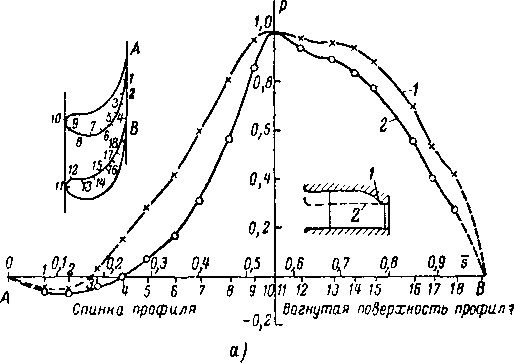
У°
v
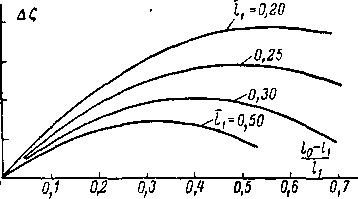
3
Рис. 8-39. 2
а —втнянне меридионального профилирования решеток на распределение давлений по ' профилю; б —уменьшение потерь в зависимости от lt и от степени поджатня Iq—IJIi. О
6)
лентаость потока оказывают большое влияние на концевые потери. Увеличение неравномерности по данным ВТИ вызывает рост концевых потерь (рис., 8-34). Повышение начальной турбулентности приводит к уменьшению угла наклона прямых = но суммарные
потери в реактивной решетке возрастают. Физически этот результат объясняется тем, что при увеличении не-
8-9. МЕТОДИКА РАСЧЕТА КОНЦЕВЫХ ПОТЕРЬ В РЕШЕТКАХ
Строгое решение задачи о концевых потерях в решетках должно основываться на уравнениях пространственного движения вязкой сжимаемой жидкости. В связи с очевидным,и трудностями такого решения можно использовать другой путь: на основании теории размерности построить, исходя из соображений о фщической природе вторичных течений, структурную формулу и ввести опытные коррективы [Л. 5].
В общем случае концевые потери энергии могут быть представлены как сумма:
Д Ек = Д Ех + 4?2 + Д Е„
где ДEi — часть концевых потерь, обусловленная взаимодейетвием пограничных слоев и периферийным движением;
ДЕг — потери на трение у торцовых стенок канала;
Д Ег—дополнительные вихревые потери, включающие потери от компенсирующих движений у концов.
Легко видеть, что вихревые потери \ЕХ и АЕа зависят от циркуляции скорости Г, а ДЕг не зависит от Г.
Анализ опытных данных показывает, что величина ДEk может быть выражена следующей функциональной зависимостью:
ДЕ^ = f (Г,р2, са2, Ь, Тг, {12) (8-38)
Запишем (8-38) в безразмерном виде:
ДЕй . ( Г \
W3a2bl ~ \ °*Ь ’ Si" h' R6a’ MV (8'39)
_ г
Разлагая выражение (8-39) в ряд по параметрам Г =-т-
Са2Ь
и sin р2, можио получить зависимость (8-39) в явном виде. Учитывая, что функция (8-39) четна относительно аргументов Г и sin р2 и при Г = 0 ие зависит от рг, получим:
AEk / Фх _ \
(Re^> Мг) ф0 Г2 sin2 P2J. (8-40)
Если предположить, что коэффициенты ф, и ф0 с изменением чисел М и Re изменяются пропорционально, т. е. ф,/ф0 = В, где В —
некоторая экспериментальная*константа, то нетрудно получить выражение для коэффициента ф0.
?А2Ь'4
Величину ДЕ2 можно выравить через толщину потери энергии 3*** по уравнению
ф..
д?2 = ?2c3n$'*'t sin р2= h°a2L 1..
tsin2p2j ’
тогда
Ь^Ч 7**7 Фо== 6^^7=170^ ¦ (841)
Для определения коэффициента концевых потерь найдем кинетическую энергию потока за решеткой:
Е = -7Г-.
Здесь G = g9iCa2F — действительный расход через канал решетки; F — эффективная площадь канала, которую легко определить, если воспользоваться толщиной вытеснения:
F = n-2ti'TOV-lfea-l»lm,
где 8*ор, 5*п, 5*ог — толщины вытеснения на торцовой стенке, на спинке я иа вогнутой поверхности профиля.
Следовательно,
Е — 2sin2 р2 [ 1 — 25тор — t (5сп + йвог ^ ] :
[/-23T*0p--J 4в],
(8-42)
где 5 -4-й =5
А СП 1 вог экв •
Величину Г sin fl2 представим в таком виде:
- ^{си\ ”Ь ^гг2^ —( Са\
-sin р2 = t [ — Ctg р, + ctg р2 J sin р2=
а2и \ са2
са\ ctgfA- Г
1+
t cos р2, (8-43)
где
'0) = ~Г*=Т' (8-44) ¦
са2 Pi
Для несжимаемой жидкости при турбулентном режиме течения в пограничном слое с достаточным основанием можно положить:
тор
Н*
0 2
= 6”; Н = —gi = 1,4;
О
« 0,036
Re!
С помощью формул, (8-40) — (8-43) и пренебрегая величиной
/
0,1 | =г—lj по сравнению с членом Re!p /, получим для несжимае мой жидкости:
0,13
R
Кк~
(8-45)
В общем случае для сжимаемой жидкости коэффициент концевых потерь определяется по формуле
Akx
(8-46)
Re0
3f{' + e['
Здесь k\ — поправочный множитель, учитывающий влияние сжимаемости. Его зависимость от безразмерной скорости Мг приведена на рис. 8-40.
Для определения числовых значений коэффициентов А и В на рис. 8-41 нанесены экспериментальные данные по концевым поте-
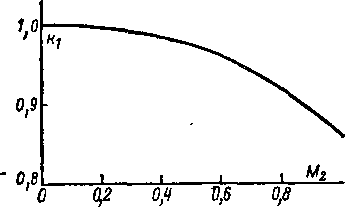
Рис. 8-40. Зависимость поправочного множителя кг от безразмерной скорости.
рям, полученные как для активных, так и для реактивных решеток при различных шагах, высотах, углах входа и выхода потока.
Здесь в качестве аргумента принят комплекс
а по оси ординат отложена функция -г-. В принятой системе
/г,
координат формула (8-46) изображается прямой, отсекающей на оси ординат отрезок, равный А, наклоненный к оси абсцисс под углом
S = arctg АВ.
Результаты указанной обработки i экспериментальных данных позволяют заключить,лто коэффициенты А и В существенно зависят от режима течения в пограничном слое и типа решетки. Для
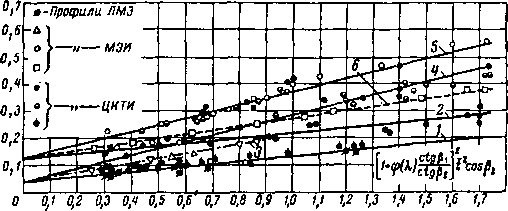
Рис. 8-41. Сопоставление расчетных и опытных значений конце-Bblx потерь для реактивных (прямые /, 2 и 3) и активных (прямые 4, 5 и 6) решеток.
реактивных решеток с плоскими торцовыми стенками экспериментальные точки довольно хорошо группируются в зависимости от режима течения в пограничном слое около .прямых / и 2. Для реактивных решеток с несимметричным поджатием наклон линии • меняется (прямая 3).
Прамые 4 и 5 характеризуют активные решетки с плавно суживающимися каналами, а прямая 6 — с диффузорно-«онфузорными каналами.
Значения коэффициентов, полученных на основании обработки опытных данных, приведены в табл. 8-1.
Интересно отметить, что для активных и реактивных решеток при наличии диффузарного участка на входе в решетку коэффициент Л = 0,13, что соответствует турбулентному режиму течения в пограничном слое. При переходе от одного режима течения к другому происходит параллельное смещение прямой, соответствующей данному типу решетки. Влияние формы межлотаточных каналов характеризуется коэффициентом, значения которого резко различны для разных типов решеток.
Формула (8-46) позволяет установить влияние некоторых геометрических и режимных параметров на концевые потери. Коэффициент t,h меняется обратно_ пропорционально относительной высоте I. С увеличением шага t коэффициент Zk вначале уменьшается, а затем возрастает. Уменьшение угла выхода р2 и увеличение угла поворота потока в решетке приводят к росту ?*¦ При возрастании
| Активные решетки без диффузор-ного участка на входе | Реактивные решетки без поджа-тия по высоте | ||||
|
Ламинарный пограничный слой |
Турбулентный пограничный слой | Ламинарный пограничный слой | Турбулентный noi раничиый слой | ||
| А | В | А В | А |
Я | А В |
| 0,45 | 5,5 | 0,13 1,90 | 0,45 | 2,0 |
0,13 0,7 |
| Активные решетки с диффузорно-конфузорными каналами | Реактивные решетки с несимметричным поджатием в косом срезе | ||||
| — |
— | 0,13 1.0 |
— | 0,13 0,3 | |
чисел Re2 и Мг концевые потери снижаются. Эти результаты хорошо согласуются с опытными данными108, приведенными в § 8-8
8-10. СТРУКТУРА ПОТОКА И ПОТЕРИ В РЕАКТИВНЫХ РЕШЕТКАХ ПРИ ОКОЛОЗВУКОВЫХ И СВЕРХЗВУКОВЫХ СКОРОСТЯХ
В реактивных решетках скорости на входе дозвуковые; переход к сверхзвуковым скоростям происходит в межлопаточном канале. В зависимости от положения минимального (переходного) сечения в канале реактивные решетки делятся на два типа: с суживающимися и 'расширяющимися межлопаточными каналами.
а) Решетки с суживающимися каналами. В таких решетках переход к сверхзвуковьвм.скоростям происходит в косом срезе.
Во многих случаях переход в околозвуковую область сопровождается значительным изменением характеристик .решеток. В этой связи необходимо знать критическое число М2и при котором в решетке появляются местные области сверхзвуковые скоростей.
На рис. 8-42,а даны кривые .максимальных скоростей на спинке профиля направляющей решетки в зависимости or М2 и относительного шага. За линией Мг=1 образуются замкнутые области сверхзвуковых скоростей. Местные сверхзвуковые скорости могут также возникать в области потока, примыкающей к выходной кромке
Критические числа М2* в зависимости от шага для реактивной решетки представлены на рис. 8-42,6. Отсюда
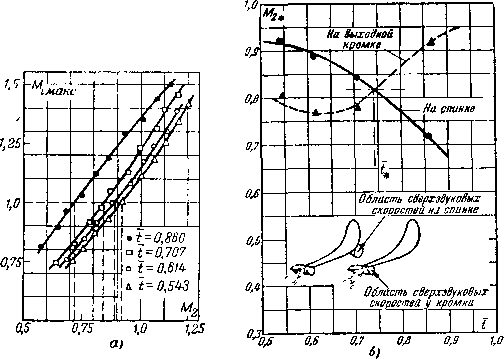
Рис. 8-42. Местные максимальные скорости на спинке профиля в зависимости от М2 (а), критические значения М2* в зависимости от шага для реактивной решетки (б).
следует, что для решеток существует такой шаг t„ при котором звуковые скорости достигаются одновременно у спинки и в области кромки. Этому шагу соответствует максимальное значение числа М2*.
Значения М2, для решетки, характер изменения М2,=
— а также положение и протяженность сверхзву
ковой области зависят от формы профиля (кривизны выходного участка спинки, толщины и формы выходной кромки). С увеличением М2> М2. сверхзвуковая область увеличивается и граница ее смещается внутрь канада.
При числе М2^ 1 линия перехода приближенно совпадает с узким сечением канала109 и сверхзвуковая область
0,95
0,90
0,85
0,30
0,75
0,70
| Рог Poi |
M2=0f61 |
Мг0,79 | ||
|
РЛ | А-о |
- ч>-о- | ||
| 1 ) \ \ \ \ |
ь' I ¦\1 1 Ц| 1 ¦Да • | ,'i 1^2 = ° |
М2= 1 ,98 | |
| № | i |
|||
| и» г ц i\ | г 5 | |||
| j | ||||
| ---- | 1 1 | |||
| 1/ хУ |
X t |
|||
Рис 8-43 Распределение давлений торможения по шагу в реактивной решетке при различных М2.
0 0,2 0,4 0,6 О,В 1,0
градиентов давления в конфузорной и диффузорной областях и смещение точек /?чин по потоку.
на спинке профиля соединяется с областью сверхзвуковые скоростей за выходной кромкой.
Наиболее характерной особенностью обтекания решеток потоком околозвуковых скоростей является возрастание
1,°
Показанные на рис. 8-43 графики распределения давлений торможения по шагу направляющей решетки позволяют заключить, что с увеличением М2 возрастает неравномерность потока: увеличивается глубина кромочных следов при переходе к околозвуковым скоростям, кромочный след расширяется.
Анализ кривых профильных потерь, представленных на рис. 8-44, показывает, что характер изменения Спр в зави-ff)
Рлс. 8-44. Влияние числа М2 иа профильные потери в реактивной решетке.
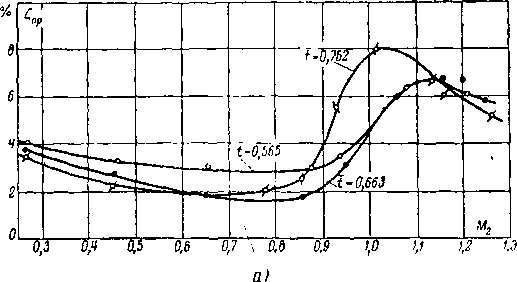
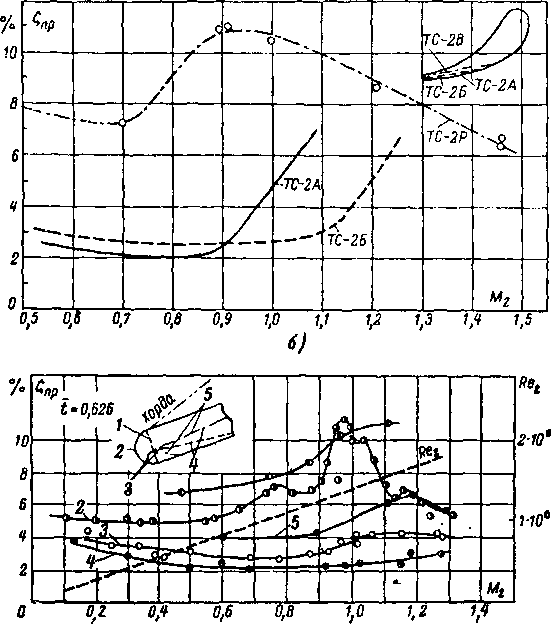
а “При изменении относительного шага t\ б—-при изменении формы спинки профиля в косом срезе; в —при изменении толщины и формы выходной кромки.
симости от М2 определяется формой профиля (главным образом), кривизной спинки в косом срезе, формой и толщиной кромки и геометрическими параметрами решетки. При этом следует различат^ две основные зоны изменения: до-критическую (М2<^М2„) и закритическую (М2 > М2,). В докритической области с увеличением М2 коэффициент потерь для большинства решеток несколько уменьшается. При отрывном обтекании спинки профиля увеличение М2 обычно приводит к возрастанию Спр.
При уменьшении шага интенсивность возрастания ?пр в околозвуковой зоне уменьшается, а значение М2„ после которого происходит рост потерь, увеличивается.
Важным следует считать обнаруженное в опытах Н. А. Скнаря влияние числа Рейнольдса, с возрастанием которого интенсивность увеличения Спр в околозвуковой зоне снижается. Эти данные относятся к малой степени турбулентности потока110. При искусственной турбулизации потока также наблюдается уменьшение степени возрастания потерь (Ма > Mg.).
Влияние формы спинки в косом срезе на потери в 'решетке показано на рис. 8-44,6. Потери в решетке ТС-2А интенсивно возрастают при М2>0,85, что обусловлено большой кривизной спинки. Для решетки ТС-2Б, профили которой имеют в косом срезе меньшую кривизну, рост потерь наблюдается только при М3> 1,05-г-1,1. Выполнение ©пинки профиля вогнутой в косом срезе позволяет область кризисного возрастания потерь сместить в зону еще больших чисел М2.
При изучении влияния сжимаемости на характеристики 'решеток следует учитывать толщину и форму выходной кромки. Показанные на рис. 8-44,в результаты опытов подтверждают влияние этих параметров на зависимость ?пр(М2).
При сверхкритических перепадах давлений в решетке в зоне узкого сечения межлопаточного канала111 устанавливается критическая скорость. За выходной кромкой давление ниже критического; поэтому при обтекании кромки (точки А, «рис. 8-45) давление падает — в косом срезе канала распространяется волна разрежения ABC. Необходимо подчеркнуть, что интенсивность волны ЛВС определяется закромочным давлением, а не давлением на бесконечности за решеткой. В первичной и отраженных от спинки профиля волнах разрежения поток перерасширяется: статическое давление на спинке профиля за волной ABC будет более низким, чем на бесконечности за решеткой.
Дальнейшее .развитие спектра зависит от структуры потока за выходной кромкой и степени перерасширения потока в волне ABC. Граничные струйки газа, сходящие с вогнутой и выпуклой поверхностей профиля, сближаются и на некотором расстоянии за кромкой 'резко поворачиваются. На границах начального участка юро-мочного следа возникает система скачков и волн уплотнения, сливающихся в косьпе скачки FC и FH.
Перерасширение потока в первичной и отраженные волнах разрежения частично «исправляется» первичным скачком FC. Скачок, взаимодействуя с пограничным слоем на спинке профиля в косом срезе, отражается и вновь попадает на кромочный след. В зависимости от среднего значения числа М в этом сечении 'кромочного следа отраженный скачок FC либо пересекает кромочный слещ (Мкр>1), либо отражается от его границы. Таким образом, поток, движущийся в косом срезе, последовательно проходит через первичную и отраженные волны разрежения, первичный и отраженный скачки112.
Поведение граничных линий тока при сходе с кромки (со стороны спинки профиля) существенно зависит от соотношения давлений в точке D и за выходной кромкой. Если давление в точке D более высокое, чем за кром-
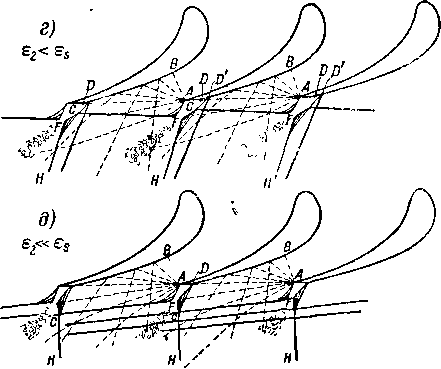
Рис. 8-45. Схемы истечения газа из направляющей решетки при сверхзвуковых скоростях.
кой, то в точке D образуется волна разрежения и обтекание кромки улучшается. Линия тока сходит с профиля не в точке D, а в точке Е. Волна разрежения DLKD замыкается системой слабых скачков уплотнения, сливающихся в криволинейный скачок FH. Система скачков FC и FH образует хвостовую ударную волну профиля.
Если давление вблизи точки D будет ниже давления за кромкой, то скачок образуется в точке D. В этом случае кромочный след оказывается более размытым В некоторых случаях скачок располагается выше по потоку относительно точки D.
Перерасширение потока в волнах разрежения, интенсивность кромочных скачков FC и FH, а также их положение определяются кривизной спинки профиля в косом срезе и толщиной и формой выходной кромки. Так, при уменьшении кривизны спинки перерасширение потока уменьшается и, следовательно, снижается интенсивность скачков Заданием спинке профиля в косом срезе обратной кривизны можно перерасширение потока свести к минимуму; кромочные скачки в этом случае будут ослаблены.
При пересечении системы' волн (разрежения и косых скачков отдельные линии тока многократно и различно деформируются, причем при е*<е? средний угол выхода потока увеличивается по сравнению с дозвуковым режимом: поток отклоняется в косом срезе.
С увеличением перепада давлений меняется спектр потока в косом срезе канала и за решеткой; изменяются интенсивность и характер расположения волн разрежения и скачков уплотнения. Увеличиваются протяженность и интенсивность первичной волны разрежения Углы первичного, отраженного и кромочного скачков уменьшаются, и точка падения косого скачка FC на спинку профиля (точка С) смещается по потоку. В соответствии с этим меняется и характер деформации отдельных линий тока. Однако интенсивность скачков возрастает только до определенного значения числа Мг, зависящего от геометрических параметров решетки.
Расширение потока в косом срезе решетки заканчивается три отношении давлений e2=es. Точное определение значения es затруднительно, однако можно считать предельным такой режим, при котором первичный ска-
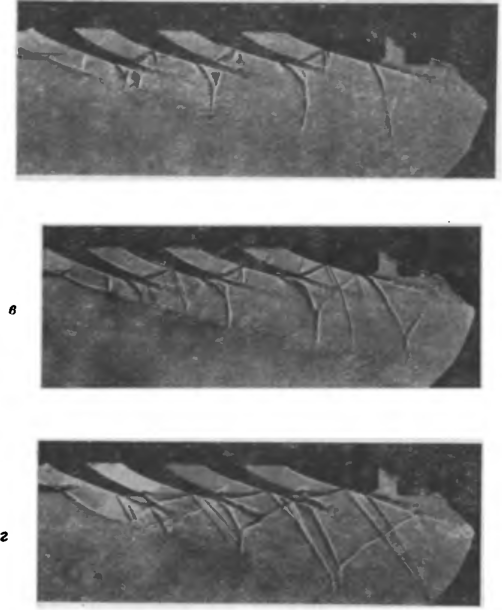
Рис. 8-46. Спектры течения воздуха через реактивную решетку с суживающимися каналами прн околозвуковых и сверхзвуковых скоростях Относительный шаг /=0,543; выходной угол профиля 15°52';
а — е, = 0,528, б — е, = 0.4ВД, в - еа = 0,379, г — е, = 0 2б I.
чок попадает в точку D (|рис. 8-45,в). В этом случае вместо трех скачков образуются только два: отраженный скачок СР сливается с кромочным FH.
Если E2<ES, то расширение потока частично происходит за пределами решетки (рис. 8-45,г). Система скачков на выходной кромке остается в основном прежней, но структура кромочного следа изменяется. Левая ветвь кромочного скачка FC попадает на дозвуковую часть кромочного следа и резко деформирует его. Давление за кромкой в этом случае определяется скачком, а следовательно, и противодавлением. При значительном уменьшении 62<es первичный скачок попадает в сверхзвуковую часть кромочного следа (рис. 8-45,<3). При этом обтекание выходной кромки профиля и кромочное давление определяются только геометрическими параметрами решетки и не зависят от противодавле-
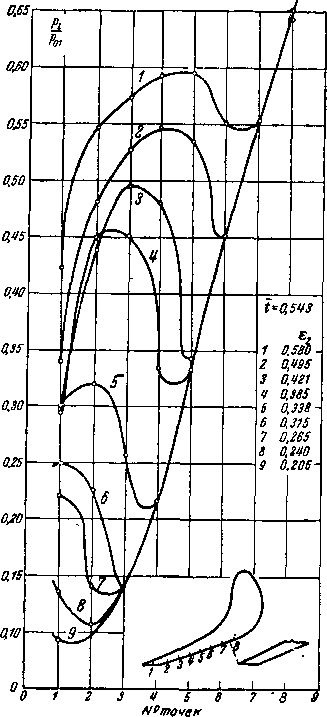
Рис 8-47. Распределение давлений вдоль ния- Это значение ег
спинки профиля в косом срезе реактив- соответствует второму
ной решетки с суживающимися канала- предельному режиму
ми при сверхкритическом истечении. ТбЧбНИЯ в рбШбТКб
Рассмотренные схемы истечения из реактивной решетки подтверждаются визуальными наблюдениями с помощью оптического
прибора (рис. 8-46).
На рис. 8-47 дано распределение Давлений на участке спинки профиля в косом срезе решетки при .различных отношениях 'е2=Рг/ро. За узким сечением (точки 2—6) -можно отметить значительное оерерасширение потока, которое заканчивается резким увеличением давления, что вызвано взаимодействием первичного и от.ра-
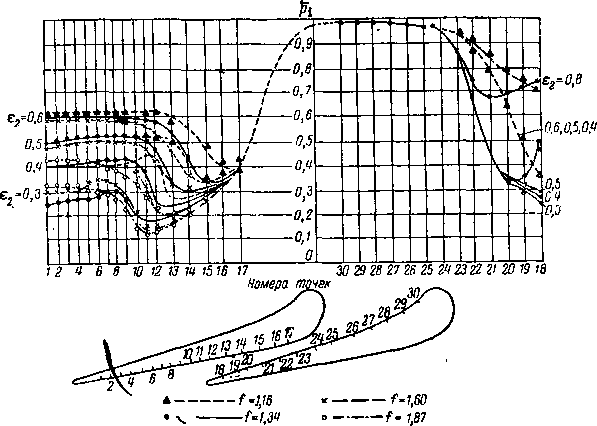
Рис. 8-48. Распределение давлений по профилю в решетках с расширяющимися межлопа1-очными каналами.
женного скачков с пограничным слоем. После скачков давление вдоль спинки падает. С уменьшением е2 зона максимального разрежения смещается по потоку к выходной кромке. На режиме предельного расширения (82^0,205) давление вдоль спинки профиля непрерывно падает.
б) Реактивные решетки с расширяющимися межлопаточньими каналами. Рассмотрим некоторые результаты опытного исследования таких решеток. На рис. 8-48 показано распределение давлений по профилю для четырех .решеток. Отсюда видно, что на определенных режимах в межлопаточном канале, как и в одиночном сопле Лаваля, возникают скачки уплотнения (диффузорный участок), причем их
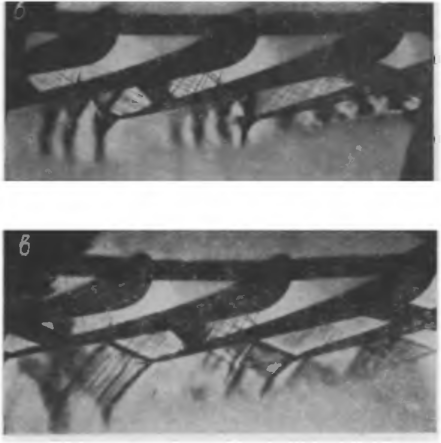
Рис. 8-49 Спектры потока в решетках с расширяющимися каналами а — е2 = 0,4; б — е2 = 0,3; в — е2 = 0,2.
положение и интенсивность зависят от 'режима е2 и гео-
F G.
метрического параметра f= -(рис. 8-53). По мере
г* мин
уменьшения е2 скачки перемещаются к выходному сечению канала. На расчетном режиме, определяемом по отношению /, образуются только кромочные скачки.
Характер изменения спектров течения в межлопаточ-ных каналах решетки можно проследить по фотографиям на рис. 8-49.
Кривые коэффициентов потерь (рис. 8-50) показы вают, что течение в решетках с расширяющимися каналами сопровождается резким увеличением потерь при
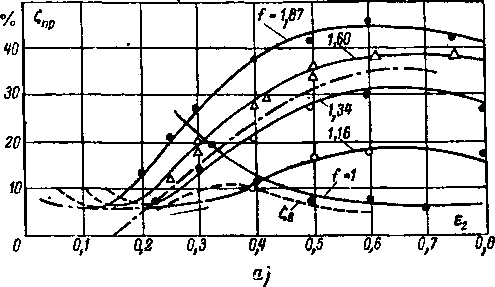
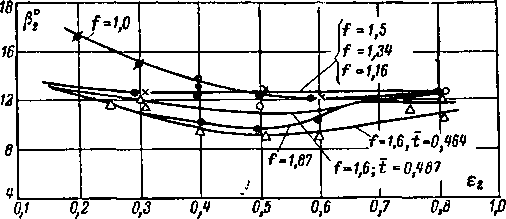
Рис. 8-50. Характеристики решеток с расширяющимися каналами.
6)
а - из 1ененне Спр в зависимости от t2 и /; б—зависимость угла выхода потока от е2 и f.
отклонениях режима от расчетного. Изменение коэффициента потерь оказывается тем значительнее, чем больше геометрический параметр f, т. е. чем выше расчетное значение М2р (см. гл. 6).
Наибольшее изменение потерь происходит при увеличении ег от расчетного до 0,5—0,6. При больших ег скачки располагаются вблизи минимального сечения; интенсивность скачков уменьшается, и ?пр снижается.
На режимах е2<е2Расч потери возрастают, так как
происходит расширение потока в косом срезе решетки. На режимах, близких к расчетным, потери для всех решеток невелики, причем профилирование расширяющейся части методом характеристик позволяет лишь незначительно снизить потери на таких .режимах.
На рис. 8-50,а приведена кривая коэффициента волновых потерь ?в Для .решетки с /=1,6, построенная по кривым распределения давлений (рис. 8-48) в предположении, что скачки прямые. Отсюда видно, что волновые потери невелики; основные потери на нерасчетном режиме обусловлены отрывом потока. На рис. 8-50,а нанесе-_ на также кривая ?Пр для решетки с суживающимися каналами. Точки пересечения кривой ?Пр для этой решетки с кривыми для решеток с расширяющимися каналами позволяет установить области рационального использования сравниваемых решеток.
Изменение среднего угла потока за 'решеткой в зависимости от е2 .показано .на рис. 8-50,6. Для .решеток с />1 средний угол потока слабо меняется во всем диапазоне изменений е2. Для .решетки с /=1,0 характерно увеличение р2 при сверхзвуковых скоростях, обусловленное отклонением потока в косом срезе.
8-11. РАСЧЕТ УГЛА ОТКЛОНЕНИЯ ПОТОКА В КОСОМ СРЕЗЕ И ПРОФИЛИРОВАНИЕ РЕАКТИВНЫХ РЕШЕТОК ПРИ ОКОЛОЗВУКОВЫХ И СВЕРХЗВУКОВЫХ СКОРОСТЯХ1
Существует несколько методов расчета угла отклонения потока в косом срезе решетки. Наиболее распространенными и простыми являются методы, основанные на уравнениях одномерного потока.
Предполагая, что поле потока в сечениях АА (рис. 8-51) и EF (выбранном на большом расстоянии за решеткой) равномерно, можно записать уравнение неразрывности следующим образом:
АА
р2с2sin = р2оос2ооsin р2оо, где sin р2 ==.
Разделим обе части этого выражения на рп а»; тогда получим:
<72 sin р2 = <72оо sin р2оо.
Учитывая, что при s2<^s, <72 = 1 и Р2оо = р2 -f- 8,
где 8 — угол отклонения потока в косом срезе, приходим к формуле Бэра:
S^arcsin/1—!—sinp2V—Р2. • (8-47)
\ ^2оо )
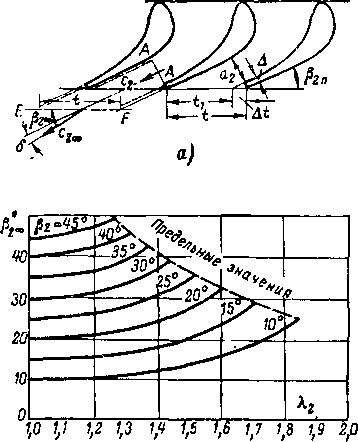
Рис. 8-51.
а г-к определению угла отклонения потока в косом срезе решетки; б— расчетная зависимость угла вы» хода потока из решетки от скорости Х2 и 02л*
6)
С учетом потерь между сечениями АА и EF формула Бэра принимает вид:
8 = arcsin (8-48)
\Ч2 оо "02 оо /
Отсюда следует, что с ростом потерь угол отклонения увеличивается. Существенным также является тот факт, что угол отклонения 6 зависит не только от скорости истечения и потерь, но и от расчетного угла выхода (рис. 8-51,6).
Формула Бэра справедлива только при гг зг ss, т. е. до тех пор, пока первичная волна разрежения находится в пределах косого среза. Угол отклонения, соответствующий предельному расширению в косом срезе, приближенно определяется по соотношению
![]()
где а — угол характеристики, совпадающей с выходным сечением.
Отсюда с помощью (8-47) получаем очевидное равенство
![]()
(8-49)
Выражая q2S через е5, находим отношение давлений для рассматриваемого режима:
= (sin %)k + l
Из уравнения (8-49) легко определяется предельный угол отклонения 8s.
С помощью уравнений неразрывности, импульсов и энергии, можно получить точное решение для угла отклонения потока в косом срезе решетки с кромками конечной толщины.
Полагая, что в сечениях АА и EF (рис. 8-51,а) поток равномерный, воспользуемся уравнениями сохранения, приведенными в §• 8-6. Решая эти уравнения совместно, можно получить расчетную формулу, предложенную А. С. Наталевичем:
tg8 =
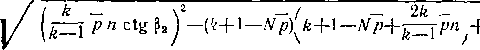
k2{k+\)
k—l
k + \—Np k _
pn ctg p2
(8-50)
k + \ —Np
При 8 <40° целесообразно пользоваться приближенным выражением
k(k + \) k —
(k + l-Np)
р = ——; Лг= (1 — /7 0—закромочное давление.
Рг 1 х\ /’гоо j к‘
Для случая бесконечно тонкой кромки формулы (8-50) и (8-51) были впервые даны Г. Ю. Степановым.
Решение системы трех уравнений дает возможность также определить волновые потери в косом срезе. Для случая бесконечно тонких кромок волновые потери определяются формулой Г. Ю. Степанова:
(1 -p)-i
(8-52)
С„=1
_ * 1
ь2со J
ft—1 cos i
k + u
Необходимо отметить, что коэффициент волновых потерь учитывает только потери, связанные с поворотом потока в косом срезе.
Потери, обусловленные взаимодействием скачков уплотнения с пограничным слоем, потери трения и потери на выравнивание потока обычно значительно превышают волновые потери, подсчитанные для идеальной жидкости. Поэтому угол отклонения как по формуле (8-47), так и по формулам Г. Ю. Степанова и А. С. На-талевича оказывается меньше действительного. Формула Бэрз с учетом потерь в косом срезе (8-48) дает близкое совпадение с экспериментом, но применение ее ограничено, так как необходимо предварительно определить потери.
В § 8-10 было показано, что угол выхода потока из решеток с расширяющимися каналами остается практически неизменным в широком диапазоне режимов Ма<М2р. Используя такой характер зависимости р2(М2), можно расчетным путем определить потери в решетке на переменный режимах.
Запишем уравнение неразрывности для критического сечения Р=ашш и сечения на бесконечности за решеткой в таком виде:
а1™ярД = Р.с,*8тр„
где рас2 — действительные параметры потока.
Разделим и умножим правую часть на p2ic2i и после преобразований получим:
(8-53)
(8-54)
(8-55)
P. Ро P 2t
Решив это уравнение относительно f, найдем:
F_
2
+ \\t k - 1
где
t sin I
1 k + V &k-\
\ ¦J
Знак минус в уравнении (8-54) не имеет физического смысла, так как <р>0.
В том случае, когда р2-= const, Ыпра = а2 и
(8-55а)
На рис. 8-52 представлены расчетные кривые зависи-
d ^
мости <р от еа и параметра /=—— при Р2 = const. Пред-
а мин
лагаемая методика дает возможность с достаточной точ-
Рис. 8-52. Расчетная зависимость $ от е2 для решетки с расширяющимися каналами (k — 1,4)
ностью определять дополнительные потери на нерасчетном режиме, если известна зависимость Р2 от г2.
Легко видеть, что для уменьшения потерь в широком диапазоне режимов е2 > г2р необходимо, чтобы угол выхода Р2 был переменным.
Идеальной в этом смысле является такая решетка, для которой изменение [32 соответствовало бы уравнению (8-54) при <р = 1. Отсюда после ряда преобразований можно получить следующий оптимальный закон изменения угла потока:

Следовательно, при Ni2t = 1 (q2t = 1) угол выхода потока должен быть минимальным, а при М2/ >1 — увеличиваться. Однако опыты показали, что для решеток с расширяющимися каналами такой характер изменения р2 невозможен.
Для решетки с суживающимися каналами ®MHH/^ = sinP2p. При этом условии получаем обычное уравнение Бэра для угла выхода потока (8-47).
Таким образом, для решеток с суживающимися каналами закон изменения р2 (М2) совпадает с теоретическим.
Однако, как известно, в таких решетках на нерасчетных режимах (г2 < е) потери интенсивно возрастают (рис. 8-44).
Это обусловлено появлением волновых потерь и взаимодействием скачков с пограничным слоем на спинке в косом срезе.
Как уже указывалось, интенсивность скачков в косом срезе при М2>1 зависит от кривизны спинки, причем минимальные волновые потери могут быть получены при выполнении спинки с обратной вогнутостью в косом срезе.
Исследования, проведенные в МЭИ, показали возможность созда,ния ,реактивных решеток с малыми потерями при М2>1 на расчетный и нерасчетных 'режимах В таких решетках рационально сочетаются положительные свойства решеток с расширяющимися и суживающимися каналами. При умеренных сверхзвуковые скоростях М2<1,3-М,4 межлопаточные каналы выполняются суживающимися, а спинка в косом срезе рассчитывается методом характеристик таким образом, чтобы вдоль спинки не происходило перерасширения потока. Метод характеристик может быть использован только для оценки стрелы прогиба спинки. Точка изменения кривизны спинки должна оыгь расположена внутри канала.
При больших сверхзвуковых .скоростях М2>1,3-ь1,4 целесообразно каналы' 'решеток выполнять с небольшим расширением (/=1,05-4-1,15), смещая узкое сечение
Рис. 8-53.
а — сверхзвуковая реактивная решетка МЭИ с вогнут ой спинкой в косом срезе и небольшим расширением межлопаточных каналов; б — влияние расширения канала на характеристики сверхзвуковых решеток с вогнутой спинкой в косом срезе (опыты МЭИ).
/—-*=1,17; f=0,46 (плоская спинка в косом срезе); 2— f = 1,17;
*=0,534; 3— /"1,10; /=0,581; 4 — f=I,0; /=0,680 (кривые 2, 3 и 4 — вогнутая спинка в косом срезе).
внутрь канала. При этом необходимая расчетная вогнутость опинки уменьшается и обводь^ профиля упрощаются. Целесообразность введения небольшого расширения канала до косого среза основывается «а кривых потерь, приведенных на рис. 8-50: при малых значениях параметра f интенсивность возрастания ?Пр на нерасчетных режимах резко снижается. С уменьшением числа М2 угол выхода .потока в таких решетках будет изменяться более интенсивно, чем в решетках с расширяющимися каналами.
На рис. 8-53 представлены некоторые результаты исследования решеток, спрофилированных указанным методом. Сравнение кривых показывает, что такие решетки имеют значительные преимущества не только на переменных, но и на расчетных режимах по сравнению с решетками, имеющими большое расширение канала (/>1,2). Опыты показывают также, что для околозвуковых скоростей (Ма<1,2) удовлетворительные результаты могут быть получены путем выполнения прямолинейной спинки в косом срезе; при этом точка разрыва кривизны на спинке располагается внутри канала.
8-12. СТРУКТУРА ПОТОКА В АКТИВНЫХ РЕШЕТКАХ ПРИ
ОКОЛОЗВУКОВЫХ И СВЕРХЗВУКОВЫХ СКОРОСТЯХ
Обтекание активных решеток потоком околозвуковых скоростей характеризуется наличием сверхзвуковых зон как на спинке в косом срезе, так и на входном участке спинки. Поэтому наряду с М2 —критическим числом М2, при котором возникают звуковые скорости в косом срезе, имеет смысл введение понятия второго критического числа М2 , определяющего такой режим обтекания, при котором звуковые скорости возникают на входной кромке. Так же как и М2 , величина М2 зависит от шага и угла установки. Кроме того, второе критическое число М2 решающим образом зависит от угла входа потока.
На рис. 8-54 представлены значения М2 и М2 в зависимости от t,$ и угла входа потока р,. Как видно, при малых р! и больших t М2 < М2, т. е. звуковые скорости в активной решетке возникают вначале на входных кромках лопаток. С увеличением шага М2 увеличивается. Характер изменения М2 и М2< в значительной степени определяется также фермой профиля: кривизной спинки в косом срезе и на входном участке и толщиной кромок.
На режимах М2 > М2 на входном участке спинки каждого профиля решетки образуется Я-образный скачок. При увеличении скорости этот скачок развивается в головной скачок для соседнего профиля (рис. 8-55). Непосредственно за каждым головным скачком поток дозвуковой, однако такая схема обтекания, очевидно, имеет место только в том случае, когда после каждого скачка поток ускоряется и перед следующим скачком скорость М>1. По мере увеличения скорости набегающего потока головные скачки приближаются к входным кромкам и искривляются. При этом поток за скачком вихревой и вдоль фронта решетки скорости меняются по величине и направлению.
При некотором значении , когда осевая со
ставляющая скорости сверхзвуковая, скачки, возникающие
Рис. 8-54. Влияние относительного шага t, угла установки Ру и угла входа потока ^ на критические значения М2 для активной решетки.
о,
о,
перед каждым профилем, сливаются в единый волнообразный скачок (рис. 8-55,6). Левые ветви головных скачков поворачиваются в направлении к вогнутой поверхности профиля. При дальнейшем увеличении Mj скачки входят в межлопаточный канал. Следовательно, на режимах
Мх соседние профили не оказывают влияния на по
ток перед входными кромками и поэтому обтекание входных участков таким сверхзвуковым потоком можно рассматривать изолированно.
Однако в большинстве встречающихся случаев скорости на входе в решетку недостаточно велики и осевая скорость потока значительно меньше звуковой. В этом случае влияние профилей распространяется в направлении против потока.
Рассмотрим обтекание сверхзвуковым потоком идеальной жидкости решетки с конечным числом профилей при условии, что осевая скорость меньше звуковой. Предположим, что толщина входной кромки равна нулю, конструктивный угол кромки весьма мал и спинка профиля до входного сечения канала образована прямой, угол наклона которой к фронту решетки равен рс.
Если вектор скорости на входе в решетку направлен под углом рс, со стороны спинки на входной кромке возникает слабый разрыв — характеристика. Вдоль прямолиней-

\ \ ^
Рис. 8-55. Схемы течения сверхзвуковог о потока в активной решетке.
ного участка спинки скорость сохраняется постоянной и, следовательно, перед кромками следующих профилей скорость потока равна скорости перед первым профилем (рис. 8-56,а). Таким образом, в этом случае поток перед решеткой с бесконечным числом профилей не отличается от потока на бесконечности.
В том случае, если вектор скорости на входе в решетку направлен под углом, меньшим рс, на входной кромке первого профиля (со стороны спинки) образуется волна разрежения, в которой поток ускоряется и поворачивается на угол 8 = рс —pj (рис. 8-56,6).
Вдоль прямолинейного, участка спинки профиля скорость сохраняется большей, чем скорость на бесконечности перед решеткой, и вектор ее направлен под углом P,=Pc>Pi. Поэтому на кромке следующего профиля возникает волна уплотнения и все ниже расположенные профили обтекаются потоком большей скорости, чем первый.
При Р, >рс на входной кромке первого профиля возникает скачок уплотнения, в котором происходят уменьшение скорости и поворот потока на угол 8 = pj-—j3,. Дальнейшие рассуждения аналогичны случаю, когда ^<[3^
Если при ф Рс рассмотреть решетку с бесконечным числом профилей, то необходимо допустить, что на бесконечности перед решеткой должны существовать или волна разрежения (при ), в которой поток поворачивается
на угол 5 = Рс — р,, или скачок уплотнения (при pi>pc). Это противоречит условию =^= р . Следовательно, при
/Wc
Рис. 8-56. Структура сверхзвукового потока на входе в активную решетку.
сверхзвуковой скорости перед решеткой поток на бесконечности может быть направлен только под углом р, = р .
В реальных условиях рабочая решетка обтекается совместно с направляющей. В этом случае все изменения структуры потока на входных кромках первого профиля локализуются в косом срезе направляющего канала, причем в такой системе можно обеспечить обтекание решетки
сверхзвуковым потоком при любом угле входа (до
наступления режимов „запирания”, § 8-13). При этом обтекание ниже расположенных профилей в значительной степени определяется системой скачков и волн разрежения, отраженных от стенки косого среза сопла. Структура потока перед решеткой усложняется, и нарушается однообразное обтекание всех профилей. Периодичность потока на входе в рабочую решетку при сверхзвуковых скоростях будет наблюдаться в интервале, кратном шагу направляющей решетки.
К. Осватичем было обнаружено, что даже в случае ножевой входной кромки при расчетных углах входа потока в решетке может- возникать сложная система скачков. Анализ этих результатов показывает, что головные скачки, возникающие перед решеткой, формально можно разделить на три основные группы: скачки, обусловленные толщиной и формой входной кромки, скачки, зависящие от формы межлопаточного канала (скачки „запирания" межлопаточного канала), и скачки (или волны разрежения), обусловленные нерасчетным углом входа потока в решетку (fij^^). В реальных условиях эти скачки разделить практически невозможно, так как они образуют единую сложную систему.
8-13. ПРИВЕДЕННЫЙ РАСХОД ГАЗА ЧЕРЕЗ РЕШЕТКУ.
ОСОБЫЙ РЕЖИМ АКТИВНОЙ РЕШЕТКИ В СВЕРХЗВУКОВОМ ПОТОКЕ
Запишем уравнение неразрывности для сечений входа и выхода из решетки (рис. 8-57) в следующей известной нам форме (см. § 8-11):
<7, sin р, = q2s0 sinpa; = (8-56)
Р 01
Это уравнение может быть использовано для графического ра.счета параметров потока в решетке.
Заметим, что осевая проекция qt равна:
Я Ха = Чг sin р, = <7гео sin р2 = q2aV (8-57)
Отсюда следует, что постоянному значению qa могут соответствовать различные значения Я и р. Следовательно, при qa = const конец вектора Я описывает в полярной си-
Рис 8-57 К выводу уравнения годографа
стеме координат (Я, (3) некоторую трансцендентную кривую. Эту кривую будем называть годографом вектора Я.
Задаваясь различными, но постоянными qa в пределах от qa = 0 до qa = 1 и от 0 до jt, в плоскости годографа можно построить группу кривых, позволяющих графически рассчитывать поток в рабочих решетках.
Форма годографа Я для некоторого q а показана на рис. 8-58. Окружность, соответствующая Я = 1, разделяет плоскость годографа на две области [дозвуковую (Я <[ 1) и сверхзвуковую (Я>1)].
При дозвуковых скоростях на входе использование графического метода не вызывает особых затруднений. Действительно, при е0 = 1 (идеальная жидкость) q2a = qUlи вектор Я2 при заданном ра находится на той же кривой [qa — const), что и вектор Я^ Следовательно, по известным Я j и Pj находим точку А, определяющую кривую q, = = const, a no ps в точках В а В' находим вектор Я2 (или Я2', если скорость на выходе сверхзвуковая)
Метод годографа можно распространить и на случай течения с потерями. С эшй целью построим кривую (пунктир на рис. 8-58) по уравнению
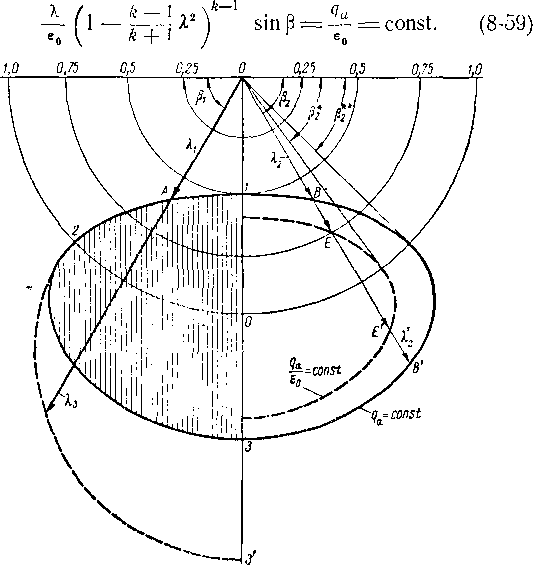
Рис 8-58 Графическое определение параметров потока в решетке.
На этой кривой находим точки Е н соответствующие скорости потока за решеткой с учетом потерь. Отсюда ввдно, что при Я2 1 скорость выхода потока из той же решетки при наличии потерь будет больше, чем в случае е0 = 1, а при Я2> 1 — меньше (при условии сохранения того же угла выхода потока).
Большой интерес представляет определение условий, при которых на входе или на выходе из решетки скорости достигают критических значений. Из (8-56) можно получить, что при = 1
pj = arcsin (<7ае0 sin fi2) = arcsin (q2a s0). (8-60)
При отсутствии потерь
РГ = arcsin q2a.
Легко видеть, что при
q2a = const ир;< р**. (8-60а)
Критическая скорость на выходе из решетки устанавливается в том случае, когда
р*= arcsin (8‘61)
При отсутствии потерь *
Р2*= arcsin q{a. (8-6 la)
Отсюда следует, что при
* Г\**
qla = const и р2>р2 .
Значения р* , р*, р", а также р” можно определить с помощью годографа (рис. 8-58).
При сверхзвуковых скоростях ,на >входе не все режимы, отвечающие годографу скорости, реально достижимы. Опыты показывают, что в некоторые случаях при ^i>l на входе в решетку возникают системы скачков, не связанные с обтеканием профилей; при пересечении этой системы скачков поток становится дозвуковым. Такие режимы обтекания активных решеток называют режимами «запирания».
Вместе с тем 'по условию непрерывности движения оказывается недостижимой некоторая другая группа режимов с дозвуковыми и сверхзвуковыми скоростями на входе. Установим «начале диапазон недостижимых значений А,1. Рассмотрим движение газа в системе подводящее сопло — решетка (рис. 8-59,а). Проходные сечения
в этой системе определяются очевидными соотношениями:
F' — al\ F1 = lLt sin^; /72 = /Sisin р2. (8-62)
Запишем уравнение неразрывности с учетом потерь:
Я F = <7 — Fj = <7 F (8-63)
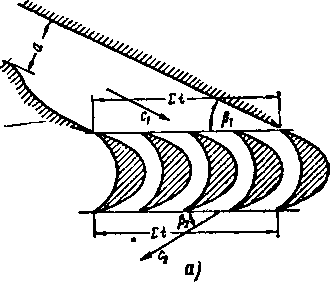
| — Y* 1 | SSSfSS^ 'ssssssff F„ F, | К h |
| 1— " | ?' ——\\ ... . |
6)
Рис 8-59 К анализу режимов .запирания" рабочей решетки.
Отсюда видно, что критическая скорость в сечении F, и, следовательно, сверхзвуковой поток на входе в решетку (в сечении Ft) могут возникнуть только при условиях Ft <Т2 и F </\j. При F поток перед решеткой будет дозву
ковым, а следовательно, не могут наблюдаться режимы „запирания®.
Подставив (8-62) в (8-63) и учтя, что sin (3j = <71а , а максимальный расход через систему соответствует получим:
Отсюда следует, что режимы, отвечающие условию
![]()
неосуществимы.
В плоскости годографа (рис. 8-58) область, соответствующая недостижимым на входе в решетку значениям Яь заштрихована. Таким образом, перед решеткой не могут быть осуществлены как .некоторые сверхзвуковые скорости (область 0—2—3), так и некоторые дозвуковые (0—1—2). Следует еще раз подчеркнуть, что область невозможных режимов на входе в решетку не совпадает с областью режимов «запирания». В последнем случае перед решеткой возникают скачки и, следовательно, режимы «запирания» могут образоваться только в том случае, когда в направляющем аппарате достигается сверхзвуковая скорость.
Для решения этой задачи удобно использовать упрощенную схему подводящее сопло —канал, в которой решетка заменена суживающимся каналом (рис. 8-59,6). В такой трубе переменного сечения при е > ет скорости всюду дозвуковые (sm — предельное отношение давления, при котором в критическом сечении Я# = 1). В случае e<CsOT в начальном участке после сечения /•* появляется сверхзвуковая зона, которая замыкается скачком уплотнения. Режимы s ет, где ет— отношение давлений, при котором скачок располагается в сечении F — F2, теоретически могут осуществляться тремя путями: со скач
ком в выходном сечении и в промежуточных сечениях сопла Fп и канала Fп. Однако первый и третий пути достижения e<Csmне могут быть реализованы, так как даже слабые возмущения выше по потоку приводят к срыву режима. Таким образом, на режимах sm>e>»sm при уменьшении противодавления сверхзвуковая область в начальном участке сверхзвукового сопла увеличивается — скачок уплотнения перемещается к выходному сечению Fг.
При s < еш сверхзвуковая зона остается постоянной и скачок располагается в сечении Fn, которое может быть определено из условия, при котором в сечении F2 устанавливается критическая скорость.
Дальнейшее снижение противодавления не изменяет режима течения в системе. При определенном соотношении Fa/F# и FJF^ сечение Fп совпадает с Fv В этом случае перед каналом и в канале возможно существование сверхзвуковых скоростей.
Следовательно, в системе сопло — канал сверхзвуковые скорости могут быть достигнуты только при Fg > F.... При определенном соотношении FJF1 и F1/F^i на режимах е<Сет на входе в канал возможно существование сверхзвуковых скоростей.
Возвращаясь к схеме сопло — решетка (рис. 8-59,а),
F, ?t sin В,
отметим, что отношение —-—— определяет расчет-
ное значение Я3 для расширяющегося сопла, a тг =
_ s}n Р2эjj sm]3j
Как было показано выше, сверхзвуковые скорости перед решеткой возможны только в том случае, когда удовлетворяется уравнение неразрывности с учетом потерь;
Здесь Pm/Pm — изменение давления торможения в прямом скачке, зависящее только от р02/р02'— изменение давления торможения в решетке.
Рис. 8-60. Диаграмма годографа X.
Формула (8-65) определяет в плоскости годографа кривую, ограничивающую область режимов, при которых сверхзвуковые скорости на входе в решетку недостижимы.
При Х1 — \ р! = Р2эф> т. е. кривые, описываемые формулой (8-65), совпадают с кривыми, построенными по формуле (8-59).
Для практического пользования целесообразно построить диаграмму годографов, соответствующих различным, но постоянным значениям qaX (рис. 8-60).
Диаграмма строится следующим образом. Задаваясь постоянной величиной qa и рядом значений q2, определяем по (8-59) соответствующие значения р. В области Я>1 строим также семейство кривых по формуле (8-65), причем в этом случае sin (39эф = <7а. Эти кривые используются для определения зоны возможных сверхзвуковых скоростей на входе в решетку.
Для удобства построения использования диаграммой внизу нанесены функции одномерного изоэнтропического потока:
Р Р Т Pol
q,\ —; —; -=- и т. п., а также q2 = J-^i-qi.
41 Ро Ро Го 4 Рог4
Рассмотрим на частном примерз использование этой диаграммы. Будем считать заданными значения qa — 0,5 и </, = 0,7.
0,5
Тогда sin Pj = q-j = 0,714 и j!, = 45°30' На горизонтальной оси
находим два значения: X, и XJ. Проведя из точки О радиусами X, и Х[ две окружности, получим на пересечении с лучом р, = 45°30' точки А к В, соответствующие годографу qa = 0,5. Определив указанным способом входной и выходной треугольники скоростей, мы можем иайти параметры потока Предваритечьно необходимо произвести проверку возможности достижения скорости X, на входе в решетку.
Для такой оценки необходимо знать р2э(,- Примем р2э{| = 36°50'. Тогда при сверхзвуковой скорости на выходе из решетки q2a = = sin р2эф = 0,6. Следовательно, перед решеткой сверхзвуковая скорость недостижима, так как точка В находится в области, ограниченной пунктирной кривой р2 эф = 36°50'.
Годограф Я можно использовать также для приближенного расчета углов отклонения потока в косом срезе как направляющей, так и рабочей рёшеток.
Для этого предварительно из уравнения неразрывности (8-56) при отсутствии потерь (е0=Л) получим:
Учитывая, что при рг = р1 и q2=q1 угол отклонения потока равен 8 = р, — Р2эф, приходим к заключению, что
Р, = Р,- -
При р1 = р3 — 5=0 и, следовательно, при любой сверхзвуковой скорости набегающего потока отклонения в косом срезе не происходит. В случае, когда (3, <р2/о <0, т. е. в косом срезе, происходит не расширение, а поджатие потока. К аналогичному выводу можно прийти и при анализе потока в плоскости годографа.
Такое поведение сверхзвукового потока в активных решетках связано с тем, что при сверхзвуковых скоростях возмущения не распространяются навстречу потоку и давление перед решеткой рх может быть выбрано произвольно. Это условие нарушается только на режимах „запирания", т. е. в том случае, если вектор Я лежит в области, ограниченной пунктирной кривой <?2а:=^Пр2эф-
Таким образом, до наступления режимов „запирания“ угол выхода потока из решетки можно определить по значению K — fiPz/Poi) на основном семействе кривых qa = = const, причем Р2 не зависит от геометрических параметров решетки и числа М. На режимах „запирания" вектор Я' находится внутри области, ограниченной пунктирной кривой qa = const; угол выхода определяется по Яа на кривой q а = sin р2эф > т- е- зависит от геометрических параметров решетки.
На рис. 8-61 представлены расчетные кривые зависимости угла выхода потока из решетки от р, и М2, при р2эф = 18°20' и М, =М2<> где М1р — расчетное значение числа М для подводящего сопла. На график нанесены гч
.гг
20
18
)6
|
4 | / | |||||||||||||
|
Рас | чет^ | |||||||||||||
| — | — | lit |
||||||||||||
|
jut: | — |
1,B_ | --- |
—»•* | ||||||||||
| - |
I | x^ | — |
— | — |
1 4 -JtL | ||||||||
| — | --- |
— | Mf - |
|||||||||||
| А* |
Kcnef. | mms |
im / | ?pa |
мг= | 1,62 | ||||||||
| /¦ |
i | |||||||||||||
| / |
i |
* |
fi | |||||||||||
Рис. 8-61. Зависимость угла выхода потока из акутной решетки от р, при М2< — !Л2р и р2э})= 18°20'.
1518 20 22 2426 28
также экспериментальные точки, полученные при М2,= = 1,62. Можно отметить удовлетворительное совпадение расчета с опытом.
8-14. ПРОФИЛИРОВАНИЕ И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТАЛЬНОГО ИССЛЕДОВАНИЯ
АКТИВНЫХ РЕШЕТОК ПРИ БОЛЬШИХ СКОРОСТЯХ
Проектирование и отработка профилей решеток для около- и сверхзвуковых скоростей осуществляются экспериментально.
Опыт показывает, что сверхзвуковые активные решетки имеют «альне .потери только в том случае, когда на входе в решетку поток затормаживается до малых сверхзвуковых скоростей. Рассмотрим два возможных метода профилирования сверхзвуковых активных решеток с торможением потока ,на входе.
Первый метод заключается в том, что торможение организуется на входном участке спинки проф-иля.
С этой целью входной участок спинки выполняется вогнутым для плавного торможения сверхзвукового потока (с возможным образованием отсоединенного криволинейного скачка) или с угловыми изломами для ступенчатого торможения 1 в системе косых скачков.
Второй метод основывается на торможении потока в криволинейном или косом скачках, организуемых во
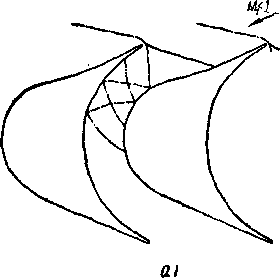
Рис. 8-62. Схемы активных сверхзвуковых решеток.
а —со ступенчатым торможением на входе; б —с плавным торможением вдоль спинках на входе; в~с торможением в косом или прямом скачках на вогнутой поверхности.
входном участке канала. При этом входной участок опинки выполняется прямолинейным или очень малой кривизны, а конструктивный угол входной кромки выбирается таким, чтобы торможение потока . происходило в скачке, возникающем со стороны вогнутой поверхности.
При небольших сверхзвуковых скоростях (Mj<1,25)
потери в прямом скачке невелики (1—1,5%). Потери при расширении потока в косом срезе также могут быть сведены к минимуму. Поэтому межлопаточный канал решетки, работающем при небольших сверхзвуковых скоростях, можно проектировать суживающимся так, чтобы перед нею возникал прямой .скачок «запирания». При больших сверхзвуковых скоростях целесообразно межлопаточный канал делать сужающе-расширяю-щимся.
Возможные формы профилей .и каналов активных ¦сверхзвуковых решеток -приведены на рис. 8-62.
Как показывает теоретический анализ, даже в меж-лопаточном ка.нале относительно большой кривизны можно избежать образования скачков уплотнения. Этот вывод подтверждается также данными эксперимента.
На рис. 8-63 представлены схема и фотографии спектров обтекания сверхзвуковым потоком активной решетки ТР-2А113, Перед толстой входной кромкой возникает скачок уплотнения а. На входной кромке и на спинке профиля поток ускоряется в волнах разрежения. Волны разрежения замыкаются скачком б, который вместе со скачком а образует головной А-образный скачок. В точке А наблюдается отрыв пограничного слоя. А-образный головной скачок 'вызывает излом границы вихревой зоны в точке В. Однако отрыв пограничного слоя сохраняется до выходного сечения межлопаточного канала, причем граница вихревой зоны и вогнутая поверхность профиля образуют фиктивный канал практически постоянной ширины. В месте падения кромочного скачка на спинку возникает локальный отрыв пограничного слоя вследствие кривизны спинки; за скачком (точка С) поток ускоряется. На подходе к выходной кромке образуется отсоединенный скачок уплотнения в. За^гсромкой возникает второй, кромочный, скачок е. Оба скачка сливаются в один А-образный скачок.
В решетках группы А при сверхзвуковых скоростях появляются дополнительные потери: в скачках уплотнения на входе, в вихревой зоне, образующейся вследствие отрыва пограничного слоя за скачком б, в кромочном и отраженном скачках d ив А-образном скачке. С увеличением скорости эти потери интенсивно увеличиваются.
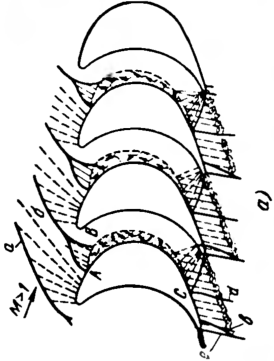
0 «>
tn 5 ьют о s fljOCO
f- x a<N«X)
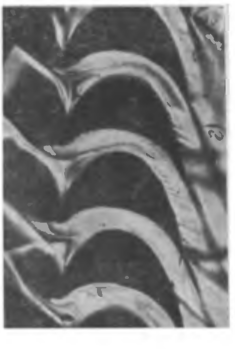
со I es 'i.
“? -S§TS
00 <e о S I I
• «о-Ё^А
S S с
иЙЧ <
1 ^ ^ I
I ЯО <u I Q O. tD >sj to
Решетки группы Б, разработанные в МЭИ для околозвуковых скоростей, характеризуются меньшими толщиной входной кромки и кривизной спинки на входном участке и в косом срезе. В этих решетках перед входной кромкой возникает криволинейный скачок а (рис. 8-64) меньшей интенсивности На криволинейной поверхности спинки (за точкой А) происходит интенсив-

Рис 8-64 Схема сверхзвукового потока в решетках группы Б.
ное ускорение потока. Замыкающий зону расширения скачок расположен внутри канала (канал № 1 на рис. 8-64). В том случае, когда перерасширение небольшое, торможение происходит только в головном скачке (в точке В, канал № 2 на рис. 8-64).
При большой конфузорности канала перед ним (не перед кромкой) возникает скачок уплотнения (режим «запирания», канал № 3 на рис. 8-64). Такое положение скачка обеспечивает устойчивое дозвуковое течение в межлопаточном канале. Если профилированием выходного участка спинки добиться малых потерь при расширении потока в косом срезе, то такая решетка может оказаться высокоэкономичной до чисел Mi — 1,25
На рис. 8-65 приведены кривые потерь в решетках .Групп А и Б. При Ма< 0,95 потери в решетке ТР-1А ниже, чем в решетках группы Б. Однако при М2>1 потери в решетке ТР-1А резко возрастают; в решетках грт-пы Б при MsЗа 0,95 -4-1,25 потери ниже.
Значение критического числа М^ для решетки группы Б во всех случаях выше, чем для решетки типа А.
В решетке ТР-2Б уменьшение потерь происходит до М2= 1,0. Однако при М2>1,1 наблюдается более интенсивный рост потерь, чем в решетке ТР-1Б. Это обуслов-
/
лено большей кривизной спинки профиля ТР-2Б в kocIom срезе.
На рис. 8-66 представлены! кривые распределения давлений по профилю решетки ТР-1В, спроектированной в МЭИ для сверхзвуковых скоростей по методу торможения потока в косом скачке, возникающем внутри канала со стороны вогнутой поверхности. Межлопаточный
|
?пр ТР-1В с под, спинной |
кзанной | 1 \/ |
ТР-1Б S' -/fr&w/srV |
0,59 |
|
^=======^^, |
А‘! 5 | 7° |
||
| 1 | ¦ч»--- > ТР-1А I | 1 |
- I | М, |
0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4
Рис 8-65. Зависимость профильных потерь в решетках групп А я Б
от 'числа М2
канал решетки сужающе-расширяющийся. Минимальное сечение расположено на входном участке (точки 8 и 7 и 13—14).
Торможение потока происходит перед входным сечением канала (точки 10—12). При Mi > 1,0 перед каналом возникает прямой скачок, который с увеличением числа Mi приближается к входному сечению.
При Mi >1,5 головные скачки входят в межлопаточный канал и торможение происходит в системе косых скачков; в канале поток ускоряется, причем в зоне минимального сечения на спинке профиля обнаруживается глубокое разрежение. При увеличении Mi минимальное давление уменьшается, а начало диффузорного участка, смещается по потоку.
На рис. 8-67 показаны .спектры обтекания решеток группы В. Характерно, что при достаточно больших числах Mi скорости в межлопаточных каналах сверхзвуковые, но скачки уплотнения отсутствуют, несмотря на большую кривизну каналов. На' входном участке профиля, перед кромкой, образуется система головных скачков.
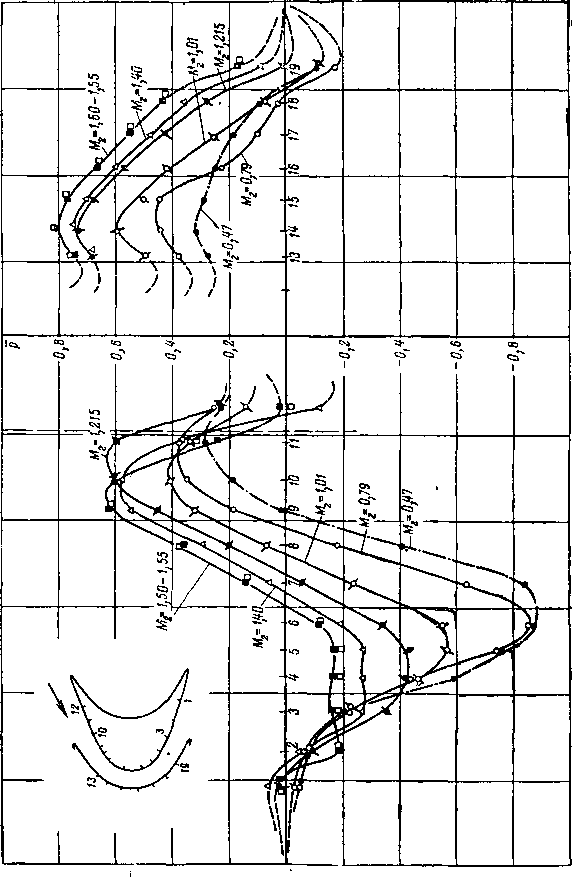
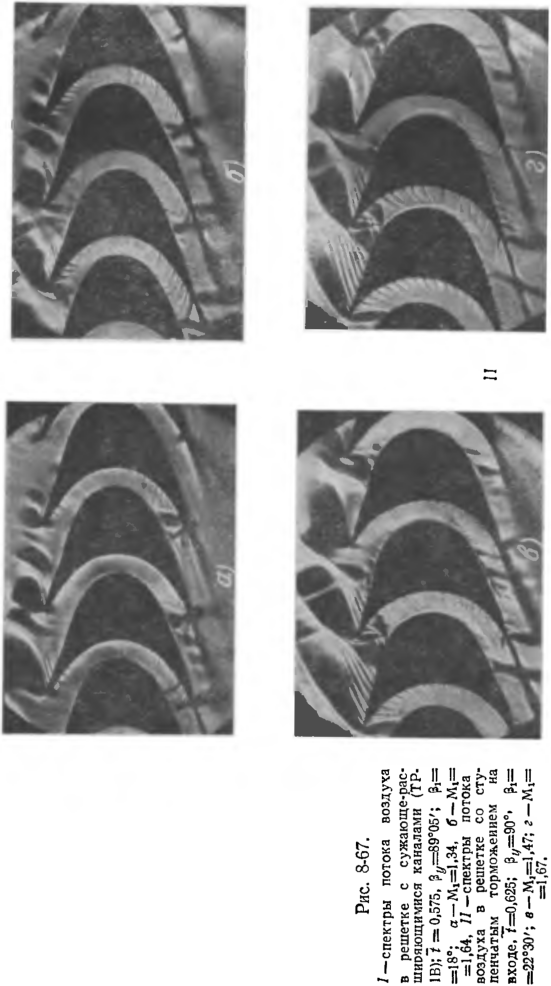
сверхзвуковых скоростях образуются два скачка, один из которые располагается в месте излома (рис. 8-67,6). На рис. 8-^)8 дано сравнение шотерь в активньих решетках, спроектированных по методу торможения потока вдоль опйнки профиля и по «етоду торможения в косрм скачке 'на вогнутой 'поверхности. Можно отметить, что первый метод позволяет добиться несколько лучших характеристик решетки при М2>1,3 (на 1—2,5%). Однако этот вывод сделан на основании ограниченного количества экспериментальных данных.
В том случае, когда решетка спроектирована по методу ступенчатого торможения потока вдоль опинки профиля (система косого — прямого скачков), при больших
%
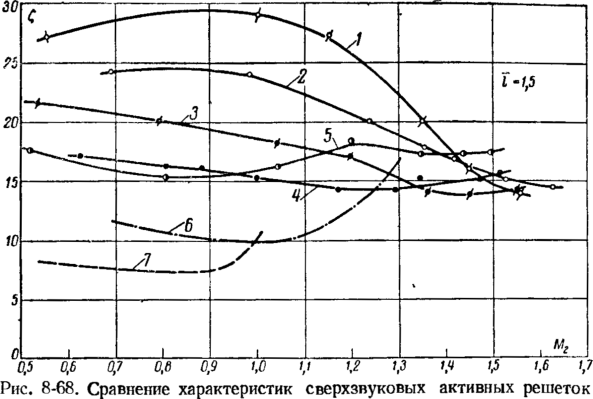
различных типов.
1, 2, 3, 4—решетки с сужающе расширяющимися каналами; 1,3—с торметкением в скачках на входе, 5—с постоянным сечением канала, б—ТР-1Б, 7*V?MA.
Рис. 8-69. Зависимость концевых потерь в решетках от числа М2.
/ —ТР 1Б при ?,=18°. 2 —ТР 1Б при р,=21°; .5 —ТР-1Б-1 при В,=18°; 4—ТР-2Б при р,=24°, 5— ТС-1А при р,=90°.
Опыты показывают, что при околозвуковых и сверхзвуковых скоростях концевые потери для всех решеток значительно уменьшаются (рис. 8-69). Уменьшается также неравномерность углов выхода потока по высоте решеток.
