Установившаяся и неустановившаяся фильтрация газа
ГЛАВА X
УСТАНОВИВШАЯСЯ И НЕУСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ ГАЗА
Течение газа через пористую среду можно рассматривать как установившееся, когда условия фильтрации со временем не изменяются, или неустановившееся, когда условия со временем изменяются. Падение давления в газовом месторождении при отборе газа является не-установившимся процессом.
Однако при определенных условиях формулы для установившегося течения можно применять и для расчета неустановившегося течения. Такие условия могут существовать при течении газа в зонах, прилегающих к забоям продуктивных скважин, или при работе скважины, которая, как говорят, «стабилизировалась».
Большой материал по установившемуся и неустано-вившемуся течению дан в двух книгах Маскета (Mus-kat) [I. 11, I. 12]. Работы Ван Эвердингена и Херста (Van Everdingen and Hurst) [X. 27], Ароновского, Дженкинса (Aronofsky, Jenkins) и других [X. 1—X. 5, X. 19,
X. X], Писмена, Ричфорда (Peaceman, Rahford) и других [VII. 6, X. 14] и Мак Робертса (Mac Roberts) [X. 21] вместе с книгами Маскета являются основными источниками материала данной главы. Дальнейшее развитие подобных работ дано в трудах Чатаса (Chatas) [X. 7], Меттхыоса, Бронса и Хазебрука (Matthews, Brons and Hazebroek) [X. 22], Корнелла и Катца (Cornelia and Katz) [11.42, X. 11], Джанисека и Катца (Janicek and Katz) [X. 18] и Уарреиа (Warren) [X. 28].
На рис. X. 1, б дано схематическое изображение скважины, дренирующей пласт ограниченной протяженности и пласт достаточно больших размеров, во всяком случае чтобы считать его бесконечным по протяженности (рис. X. 1, а). Изменение давления в скважине вызывает радиальное течение газа в пласте по направлению к скважине или от нее в зависимости от того, уменьшилось или увеличилось давление в скважине.
На рис. X. 2 приведены кривые, характеризующие изменение дебита скважины, работающей при постоянном давлении на забое, или изменение забойного давления при работе с постоянным дебитом газа для установившегося и неустановившегося течения.
В высокопроницаемых пластах характер течения обычно приближается к установившемуся. В малопроницаемых пластах характер течения ближе к неустано-вившемуся. Степень приближения характера течения к установившемуся или неустановившемуся режиму
1
V~ ' \
\
Время
\
\
Время
Рис. X, 2, Примеры установившегося и неустановившегося состояния.
а — случай, когда на скважине под-. держивается постоянное давление; 6 — случай, когда скважина работает с постоянным дебитом,
/ — установившееся состояние: 2 — неустановившееся состояние,
| *1 |
и | |
| _______ | ! 1 i i 1 i | ^-------- |
|
— 2 | 2 — с 3 | 3 у> |
ющая ограниченный (закры*
/ — скважина; 2 — пласт, простираю* щийся до бесконечности; 3 — ограниченный продуктивный пласт.
определяется, кроме проницаемости, и по другим параметрам пласта, которые будут рассматриваться ниже.
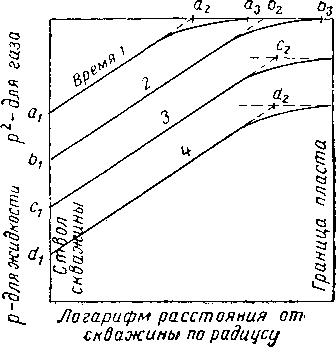
Общий характер распределения давления в пласте при неустановившемся течении к единичной скважине, эксплуатируемой с постоянным дебитом, показан на рис, X, 3. При установившемся течении изменение градиента давления в выбранных координатах (р для жидкостей или р2 для газов в зависимости от логарифма расстояния) изображается прямой линией, При неустановившемся течении прямолинейным является лишь участок кривой, соответствующий распределению давления вблизи скважины. На достаточно большом удалении от скважины наклон кривой постепенно изменяется и кривая стремится к горизонтальной линии, соответствующей максимальному давлению в пласте. Граница зоны, в которой градиент давления не равен нулю, со временем перемещается по пласту от скважины до тех пор, пока не достигнет границы пласта, Начиная с этого момента, пластовое давление снижается повсеместно, а распространение воронки депрессии прекращается, Рассмотрим вначале вывод формул для установившегося течения, а затем и для неустановившегося,
С3
Рис. X. 3, Изменение давления в пласте на разные моменты времени.
§ 1. УРАВНЕНИЯ УСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ
Уравнения установившегося течения выводятся из закона Дарси, выражающегося для случая течения вязких жидкостей уравнением (II. I). Уравнение для случая радиального течения интегрируется по переменной площади фильтрации. При высоких скоростях течения существенную роль начинает играть отклонение от закона Дарси. Поэтому для условий пласта необходимо пользоваться формулой, учитывающей как отклонение от закона Дарси, так и радиальный характер течения.
> = ±
1. РАДИАЛЬНОЕ ТЕЧЕНИЕ ГАЗА ПО ЗАКОНУ ДАРСИ
Радиальное течение, которое можно наблюдать при фильтрации газа к продуктивной скважине или от нагнетательной скважины, схематически изображено на рис. X. 4, Площадь сечения, через которую фильтруется газ, при радиальном течении — величина переменная,
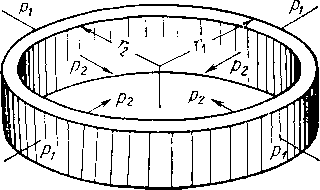
Рис. X. 4. Схема радиального течения,
и это должно учитываться при интегрировании уравнения (II. 1), Выразим площадь сечения A = 2nrh, где г — радиус в ж и h — мощность пласта в м. Для случая радиального течения газа уравнение (II. 1) принимает вид:
ifilnhkp (± dp)23
(X- 1)
Q
гТ pdr/r
где h — мощность пласта в м; k — проницаемость в мд; р — абсолютное давление в ат; г — коэффициент сжимаемости; Т — абсолютная температура фильтрующегося газа в °К; Iх — вязкость газа в ей; Q—дебит газа, приведенный к абсолютному давлению р = 1,033 ат и 15,5° С в м3/сутки.
Интегрируя уравнение радиального потока для постоянных значений k, Т, h, [х, z, получим
7,32Ай(р| — Pg)1
гГц 1п (г!/г2)
Эти единицы измерения в дальнейшем применяются в качестве «промысловых» единиц при расчетах фильтрации газа. Выражение 1 п(г,//"2) представляет собой натуральный логарифм отношения радиусов, измеренных от центра ствола скважины. Когда газ течет из пласта в скважину, индекс 1 относится к точке в пласте, а индекс 2 к точке на стенке ствола скважины. Если, наоборот, газ нагнетается в скважину и фильтруется в пласт, индекс 1 соответствует точке на стенке скважины, а индекс 2 — точке в пласте на некотором удалении от скважины.
Пример
При осуществлении сайклинг-процесса в газоконденсатный пласт нагнетается 141 500 м3/сутки газа удельного веса 0,6, Пласт имеет следующие параметры: /г = = 6 м; k = 60 мд; 7’ = 358°К. Радиус скважины гс=0,1 м.
Абсолютное давление нагнетания на забое скважины равно 161,69 ат. Рассчитать давление в точке пласта на удалении 15,25 м от центра скважины, принимая, что имеет место радиальное установившееся течение газа по закону Дарси,
Решение
Необходимо задаться давлением в пласте для определения значения вязкости и коэффициента сжимаемости газа. Принимаем р = 157,5 абс. ат.
Псевдокритическое абсолютное давление рс=48 ат; псевдопрнведенное давление рг = 3,35.
Псевдокритическая температура Тс = 198,5° К; псевдо-приведенная температура Тт= 1,803.
По графику на рис. IV. 16 2 = 0,893; [х =0,017 спз.
„ 141500 х 0,893 X 358 х 0,017 X 5,01
Р2 — 161,6924 7,39 x 6 x 60 '=
= 26144 — 1448 =24696. рз= 157,15 абс. ат при удалении от оси скважины на 15,25 м.
2. РАДИАЛЬНОЕ ТЕЧЕНИЕ ЖИДКОСТИ ПО ЗАКОНУ ДАРСИ
Формула для радиального течения жидкости выводится подобно формуле для газа и имеет вид:
0,05238 hi; (р, — р2)
(X. 3)
Q
ц In (г Jr.,)
где Q — дебит жидкости в м25/сутки; h — мощность пласта в м; k — проницаемость пласта в мд; р — абсолютное давление в ат; р.— вязкость жидкости в сп; г — радиус в м. Индекс 1 относится к пласту, индекс 2 — к стволу скважины.
1
Qo
Мощность пласта, м
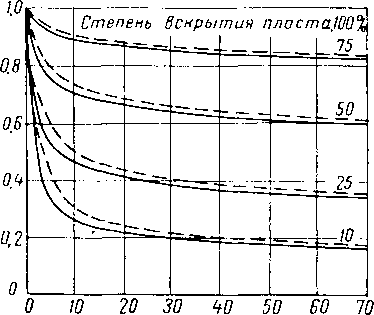
Рис. X. 5. Поправка дебита для скважин, не полностью вскрывших продуктивный пласт
Уравнения (X. 2) и (X. 3) справедливы для случая, когда скважина вскрывает всю мощность продуктивного пласта. Маскет [1.12] дает диаграмму (рис. X. 5),.по которой находится поправка для дебита, когда скважина вскрывает лишь часть мощности продуктивного пласта. На этой диаграмме Q/Qo представляет собой отношение производительности скважины, частично вскрывшей пласт, к производительности скважины, полностью вскрывшей этот же пласт. Сплошными линиями показаны кривые для случая, когда радиус скважины равен
+
0,076 м, а пунктирными — для радиуса скважины
0,152 м. Расстояние до границы пласта во всех случаях принято равным 200 м.
, г, 0,136цzTQ In (r1//'2)
Р\~Рг =-hk-+
3,038 X IО-17 PyQ4T
№
Единицы измерения величин, входящих в уравнения (X. 4) и (Х.5), те же, что и в уравнении (Х.2). Кроме того, здесь 7—удельный вес газа; |3—коэффициент 1 /см. Определяется он по лабораторным исследованиям или из графика (рис. 11.23).
Уравнение (X. 5) применяется для расчета градиента давления при радиальном течении газа в зоне, прилегающей к забою продуктивной или нагнетательной скважины, Еленбаас и Катц (Elenbaas and Katz) [X. 15] вывели формулу для течения при отклонении ог закона Дарси в несцементированной пористой среде, учитывающую коэффициенты трения для зерен песка.
Пример
По имеющимся данным о газовой скважине вычислить эффективную проницаемость эксплуатируемого песчаника.
Радиус скважины равен 0,15 м, расстояние до соседней закрытой скважины 137 м, мощность газоносного пласта 8,85 м, мощность пласта, вскрытая скважиной, 3,35 м.
При исследовании на приток дебит скважины равнялся 1 100 000 м?/сутки. Давление на забое скважины рг равнялось 49,58 ат. Давление в пласте вблизи скважины 50,82 ат. Температура газа в пласте 17,2° С. Удельный вес газа 0,6. Для решения уравнения (Х.5) обычным способом определяют коэффициент сжимаемости. Коэффициент сжимаемости оказался равным 0,892. Вязкость газа по графику на рис. IV. 107 равна 0,0117 спз. Тот факт, что скважина не полностью вскрывает пласт, означает, что ее дебит будет существенно меньше дебита скважины, совершенной по степени вскрытия. Согласно графику на рис. Х.5 дебит газа данной скважины составит лишь 62% дебита скважины, полностью вскрывшей пласт. 62% от 8,85 м составляет 5,5 м. Следовательно, эквивалентная мощность пласта Л = 5,5 м.
Решение
Решая уравнение (X. 5) относительно k и оставляя в качестве неизвестного, так как (3 в свою очередь зависит от k, получим
50,822 -49,58* = X 0.117 X 0.892
X
X 290,2 - 1 100 000(137/0,15)
124,49 =-г- + 12560 х 1(Г26р.
или
563697
Если пренебрежем 3 что течение принимается = 563697/124,49 = 4528 мд.
Из графика рис. 11.23 для k = 4528 мд ft = 1,87 X X ЮМ/сж. Подставляя это значение J3 в уравнение для определения k, получим
563 697
что эквивалентно тому, по закону Дарси, го
При установившемся течении количество жидкости (или газа) в пределах данного потока остается неизменным, При неустановившемся течении количество вещества, входящего в какой-то элемент объема пористой среды, может отличаться от количества вещества, выходящего из этого элемента. Следовательно, содержание жидкости в пористой среде со временем изменяется. Такие изменения количества жидкости в пористой среде возможны благодаря сжимаемости жидкости. Отсюда для выражения неустановившегося течения необходимо ввести дополнительные переменные, кроме тех, которые уже использовались для выражения установившегося течения: время, пористость пласта и сжимаемость жидкости. Пористость пласта является мерой способности пористой среды вмещать (содержать) жидкость. Сжимаемость определяет изменение содержания жидкости с изменением давления.
Решение задач неустановившегося течения обычно осуществляется по следующей методике.
1. Составляется уравнение материального баланса, учитывающее массу добытой (нагнетаемой) и остающейся в пласте жидкости, для рассматриваемой геометрии потока. Это уравнение называется уравнением неразрывности.
2. Уравнение неразрывности комбинируется с уравнением, описывающим движение жидкости, с уравнением, учитывающим изменение плотности в зависимости от температуры и давления. В результате получается уравнение течения в частных производных. В качестве уравнения движения жидкости обычно берется закон Дарси.
3. Математически формулируются граничные условия, которые устанавливают отсутствие фильтрации через непроницаемые границы системы, определяют скорость нагнетания или отбора жидкости (или газа), указывают характер распределения начального и текущего давления и т. д.
4. Решается уравнение в частных производных при заданных граничных условиях с целью получения формулы, пригодной для инженерных расчетов.
Для большинства инженерных расчетов нет никакой необходимости каждый раз придерживаться данной методики. Для определения дебита или падения давления можно применять полные решения задачи данного типа. При этом трудности будут не больше, чем при решении задач установившегося течения. Большинство инженерных задач можно решать с применением готовых решений, представленных в форме рабочих диаграмм или таблиц. Только в тех случаях, когда решается задача совершенно нового типа, необходимо следовать приведенной выше методике, используя геометрию системы и граничные условия, которые соответствуют новой задаче. Поэтому имеет смысл привести полный вывод уравнений, чтобы инженер был подготовлен для решения новой задачи. Кроме того, знание вывода уравнения дает более полное представление о преимуществах и недостатках рабочих диаграмм.
(ДуДг),
Уравнение неразрывности можно вывести, рассматривая входящий и выходящий поток из малого элемента объема. Такой поток лучше всего выражать как массу в единицу времени. Разность количества жидкости, вошедшей в элемент и вышедшей из него, составляет приращение массы в объеме элемента за некоторое время:
(Х.6)
вошло — вышло = приращение.
Уравнение неразрывности вначале будет выводиться для общего случая трехмерного потока, а затем для радиального потока, следуя методике Стритера (Stru-ter) [X. 26а].
Рассматривая случай трехмерного потока (рис. X. 6, а) возьмем элемент объема, имеющий стороны длиной Ах, Дг/ и Дг в системе координат х, у иг.
и, v и w — скорости соответственно в направлениях, х, у и г, рассматриваемые в центре элемента. Эти скорости определяются площадью поперечного сечения потока без учета пористости среды. Плотность жидкости в центре элемента равна р.
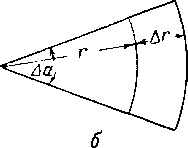
Рис. X. 6. Элемент объема, которым пользуются при выводе уравнения неразрывности. а — линейное течение; 6 — радиальное течение.
В направлении х скорость потока, входящего в элемент объема с левой стороны, равна [и — ди/дхАдс/2]. Скорость потока, выходящего из элемента с правой стороны, равна [и + ди/дхД*/2]. Подобным же образом плотность жидкости у левой грани элемента равна [р — др/дхАх/2] и плотность у правой грани [р+<3р/дх У, ХД*/2]. Площадь каждой грани равна hyh г.
Массовая скорость при течении через любую грань равна произведению скорости на плотность и на площадь. Соответственно массовая скорость потока в направлении х у левой грани равна
а массовая скорость потока в направлении х у правой грани равна
Результирующая скорость потока в элементарном объеме в направлении х находится перемножением приведенных выше выражений. Пренебрегая членами, со-
(Х.7)
(Х.8)
дх
(X. 13)
д (ра) ду
д (рw) дг
Д*Лг/Д г
(X. 14)
kp dt
1_ д2р2 2
(Х.9)
дх
Дг
2
-Дг\ ( 2
Р
ри г
-ф
(X. 10)
Накопление жидкости в пределах элементарного объема выражается также в единицах массовой скорости потока. Это накопление происходит благодаря изменению плотности жидкости во времени в элементарном объеме и выражается в виде
ФД*Дг/Дг ^ly-
где Ф—пористость среды (в долях единицы) a t — время.
Полагая, что разность входящего и выходящего потоков в элементарном объеме равна накоплению, и исключая ДяДг/Дг, получим уравнение неразрывности
2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ НЕУСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ
В качестве иллюстрации методики, по которой получаются дифференциальные уравнения, будет рассмотрен вывод уравнения для случая неустановившегося радиального течения газа. При замене ? на г в уравнении (II. 1) получим закон Дарси для случая радиалыюго потока;
k др
При выводе уравнения неразрывности не делалось никаких допущений.
Для случая радиального течения уравнение неразрывности выводится подобным же способом. Элементарный объем показан на рис. X. 6, б. Течение существует только в радиальном направлении со скоростью, обозначаемой и. Объем элемента ограничивается окружностями радиусом г и г+ Д г и углом Да . Высоту элемента можно считать равной h и пористость Ф.
Массовая скорость течения на входе в элемент равна
др
Накопление жидкости в элементе равно ФгЛДаДг щ.
Поступая так же, как и в предыдущем случае, получим уравнение неразрывности
д(ри) д(ри) д(рw) ^ /др
+ ду + дг
а на выходе из элемента д \ /Дг\
[(г + Дг) /гДа]
—ДяДг/Дг
д(?и)
дг
(/•ЛДа)
Подобным образом результирующие массовые скорости потока в элементарном объеме в направлениях у и г соответственно выражаются
на входе — на выходе =—АхАуДг
d (ри) = рdu + ud?, получаем следующее уравнение:
Г(3 (Ри)
держащими Д* в квадрате, вычитая скорость на выходе из скорости на входе и учитывая, что
д2Е1 _ , (?Р\2 /V
дг* -рдг* +[дг}‘ (Х-15)
При выводе уравнения (X. 14) и во время его применения следует помиить допущения, что k, г и Т являются постоянными, поэтому закон Дарси применим.
Уравнения в частных производных для других специфичных случаев неустановившегося течения могут быть выведены таким же путем, как для газа, так и для жидкости при лииейном или радиальном течении. В табл. X. 1 приведено несколько таких уравнений, причем вывод уравнений для жидкости основан на выражении плотности в виде
р = Роес - Ро), (х. 16)
где Ро — плотность при некотором стандартном давлении ро; С — постоянная, имеющая размерность 1 /ат\ р — давление, при котором определяется плотность.
Большинство расчетов неустановившегося течения жидкостей производится по уравнениям с одним дополнительным допущением, заключающимся в том, что таким выражением, как или пРенебре-
гается. Для малосжимаемых жидкостей это допущение, по-видимому, является вполне удовлетворительным.
3. БЕЗРАЗМЕРНЫЕ ПАРАМЕТРЫ В УРАВНЕНИЯХ НЕУСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ
При решении задач неустановившегося течения можно сделать большие упрощения, применяя безразмерные параметры. Показать в явной форме влияние на характер неустановившегося течения в пласте отдельных переменных (проницаемость, пористость, вязкость, скорость течения, давления, время и др.) невозможно. С другой стороны, указанные переменные могут группироваться вместе в виде нескольких безразмерных параметров, которыми легко пользоваться и которые дают простые соотношения между собой.
В табл. X. 2 приведены несколько наиболее распространенных безразмерных параметров. Самым важным из них является безразмерное ьремя tD. Расстояние, на
где М — молекулярный вес или удельный вес газа, умноженный на 29; R — газовая постоянная; Т — абсолютная температура; г — коэффициент сжимаемости. Газовая постоянная г имеет значение 0,082055 (табл. IV. 1) при плотности в кг/м3, давлении в абс. ат и температуре в °К.
Комбинируя уравнения (X. 12) и (X. 13) с целью исключения плотности газа, получим уравнение радиального неустановившегося течеиия газа
д2р2 , 1 др- р.Ф dp2
а7
Закон Дарси можно комбинировать с уравнением неразрывности для радиального потока (X. 10). Путем прямой подстановки получим
<РР,ЁЕ. д1 . Р^._ /V юл
Р дг'2 ' дг дг "r rdr ~~ k dt ' ' ’ ^
В уравнение (X. 12) входят четыре переменные р, г, t и р. Одна из переменных должна быть исключена. Путем введения уравнения, выражающего плотность газа, можно исключить плотность р:
Мр р - zRT
дг3 г
При выводе уравнения (X. 14) использовалось общее математическое соотношение
|
Фаза | Уравнение для выражения плотности фазы |
Геометрия системы, течение | У равнение неразрывн ости | Уравнения неустановившегося течения для ламинарного режима |
| Газ |
р = Mp/zRT |
Линейное | d(pu) др дх | д2р- пФ др- -тт = 'тг • (х- 17) дх1 kp dt ' |
|
Жидкость | Р = р0еС | Линей ное | д(р и) др дх dt |
d2P (dp\ 2 Ф?Сд_р dx2 +C(d*j ~ к dt (X' l8) |
|
Малосжимае-мая жидкость |
Р = р0еС<р ~Ро)* | Линейное | д(р и) др дх ~ - ф dt |
d2p U.C dp d=kit (X-19) |
|
Газ | р = Mp/zRl |
Радиаль ное |
д (рп) ри ^ др дг + г ~ф dt |
d2p2 1 dp2 Фи.dp Tfr^ + 7 Tr = k^df (X' 14) |
| Жидкость | p = pnec,'’-ft) |
Радиаль ное |
д(ри" ри др дг + г ~~фд( | d-^P ,C(d-?)2 ild-? x 20, dr2 + L [drj + r dr — К dt |
| Малосжи маемая жидкость | р = р0ес |
Радиаль ное | д(р и) ри др дг + г ~Фд< |
d*p 1 dp Ф C\i.dp dr* + r dr - k dt (Л- |
* —С (др/дх)г мало и им преиебрегается.
** _С (др/дг)2 мало и им преиебрегается.
Таблица X. 2
Продолжение табл. X. 2
| Название параметра |
Обозначе ние |
Безразмерный параметр в промысловых единицах | |
| течение жидкости | течение газа | ||
| Безразмерное изменение давления | pt |
В зависимости от постановки задачи | Изменяется в зависимости от постановки задачи |
| Безразмерная общая добыча | Qt |
То же | То же |
| Безразмерный дебит (одномерное течение) | m |
120p,Q hkPг> |
0,856(jl2T'Q hkP\ |
0,1365^7(3
hkp2n
19,1ц(?
hkpn
котором проявляется неустановившееся течение в пласте, зависит от безразмерного времени. Безразмерный дебит т представляет собой наклон градиента давления при неустановившемся течении, как это следует из уравнения (X. 3) или (Х.5), что показано на рис. X. 3. В табл. X. 2 приведено несколько безразмерных отноше-
Безразмерные параметры, применяемые при расчетах неустановившегося течения
| Название параметра |
Обозначе ние |
Безразмерный параметр в промысловых единицах | |
|
течение жидкости j течение газа | |||
| Безразмерное время (одномерное течение) |
1D | 0,0003486/ \1СФх2 | 0,000348ktp |жФх2 |
|
Безразмерное время (радиальное течение) | *0 |
0,00034 m \1СФг2 | 0,000348А/р р.Фг2 |
| Безразмерное расстояние по радиусу |
R | г г - ИЛИ -с к | г г - или — 'с 'к |
| Безразмерное отношение давлений |
Р/Рп Р — PjPn Р Рп/Рк Рп |
(,Р/Рп)2 (р2 — р2П)/р1 (Р2-Р2п) (Р2к--Рп) |
|
Безразмерный дебит (радиальное течение)
Ний давления. Они включают отношения текущего давления р к начальному давлению пласта рп, разности давления р—р„ к пластовому давлению рп а разность давлений р—р„ к максимально возможной разности давлений рк—рп, где рк — постоянное внешнее давление. Для случая течения газа применяются квадраты давления, как и в формулах установившегося течения.
При решении задач неустановившегося течения часто применяется член, выражающий безразмерное изменение давления Pt для случая постоянного дебита, или член, выражающий безразмерную добычу Qt для случая эксплуатации с постоянным рабочим давлением. Значения pt были найдены для нескольких типов задач и для любого значения безразмерного времени. Этот член позволяет вычислить падение давления при пуске скважины или возрастание давления при нагнетании. Подобным образом член Qt, выражающий безразмерную добычу, можно применять в расчетах количественного определения добычи для ряда типов промысловых задач.
Различные авторы при решении подобных задач применяли другие безразмерные параметры.
Применение таких видов безразмерных параметров имеет свои преимущества в некоторых типах расчетов. Тем не менее необходимость общих безразмерных параметров не вызывает сомнения. Поэтому безразмерные параметры, применяемые различными авторами, будут выражаться всякий раз, когда это возможно, с помощью общих безразмерных параметров, приведенных в табл. X. 2.
Следует стремиться представлять процесс при течении жидкости или газа, пользуясь безразмерными параметрами, а не отдельными переменными. Например, при течении газа расстояние, на которое распространяется возмущение в пласте, зависящее от безразмерного времени, помимо времени, определяется пластовым давлением и вязкостью газа.
4. ОБЩИЕ ПРЕДСТАВЛЕНИЯ О РАДИУСЕ ДРЕНИРОВАНИЯ
Радиус дренирования работающей скважины используется не только для более наглядной характеристики поведения пласта, но и при формулировке математического решения задач неустановившегося течения. Для различных целей имеется несколько определений этого радиуса. В общем термин «радиус дренирования» обозначает расстояние, в пределах которого жидкость движется по направлению к продуктивной скважине.
Теория утверждает, что любое изменение давления в скважине мгновенно создает возмущения, по крайней мере бесконечно малые на протяжении всего пласта. Следовательно, в строгом смысле слова радиус дренирования является радиусом всего продуктивного пласта, от которого может осуществляться фильтрация к скважине. Однако, учитывая, что могут быть лишь бесконечно малые изменения давления, такое определение не всегда полезно и им редко пользуются.
Более важным является определение установившегося радиуса дренирования или кажущегося радиуса дренирования.
При данных рабочем давлении, пластовом давлении, дебите, характеристике пласта и свойствах газа для вычисления радиуса, в пределах которого жидкость в пласте, по-видимому, течет по направлению к скважине, можно воспользоваться формулой установившегося радиального течения. Вся движущаяся по пласту жидкость высвобождается за счет изменения давления в пределах этого кажущегося радиуса дренирования. Кажущийся радиус дренирования вычисляется экстраполяцией прямолинейного участка кривой градиента давления вблизи забоя скважины до максимального пластового давления (рис. Х.З): точки а2, Ь2, с2 и d2 соответствуют значению установившегося или кажущегося радиуса дренирования для различных четырех моментов времени.
Другим определением является определение эффективного радиуса дренирования г-,ф. Точки аз, Ьз, сз и d3 на рис. X. 3 соответствуют значениям такого эффективного радиуса. Эффективный радиус дренирования больше установившегося радиуса дренирования. Однако очень незначительные изменения давления происходят и за пределами эффективного радиуса дренирования. После достижения границы продуктивной части пласта эффективный радиус дренирования становится тем же самым, что и радиус продуктивной части пласта. Более точное определение эффективного радиуса дренирования будет дано ниже.
Перемещение радиуса дренирования является очень важным моментом в поведении пласта. Установившийся и эффективный радиусы дренирования увеличиваются, в то время как скважина работает с постоянным дебитом и эффективный радиус еще не достиг границ пласта. Однако это увеличение радиуса дренирования, естественно, прекращается, когда достигается граница продуктивной части пласта. В течение перемещения радиуса дренирования работа скважины, как говорят, не стабилизирована, а когда перемещение его прекращается, то работа скважины стабилизируется, хотя в обоих случаях течение газа имеет неустановившийся характер. Эти термины будут рассмотрены в дальнейшем при определении характеристик поведения скважины.
5. МЕТОДЫ РЕШЕНИЯ УРАВНЕНИИ НЕУСТАНОВИВШЕГОСЯ ТЕЧЕНИЯ
Для решения различных уравнений неустановившегося течения, приведенных в табл. X. 1, имеется несколько методов.
Эти методы включают следующее.
1. Точные решения.
2. Аналитические решения с одним или более упрощающими допущениями.
3. Приближенные решения:
а) численные решения;
б) графические решения;
в) решения, полученные на электронных цифровых машинах.
4. Решения с использованием вычислительных устройств, основанных на принципе аналогии (пневматической, электрической, электронной).
Точные решения имеются лишь для случая течения малосжимаемых жидкостей. В них включены решения, взятые из задач по теплопроводности и обобщенные Черчиллем (Churchill) [X. 8], и решения, представленные Ван Эвердингеном и Херстом (Van Everdingen and Hurst) [X. 27]. Однако в известном смысле точных решений для таких задач по неустановившемуся течению нет, так как при выводе уравнений было необходимо допущение, что вязкость, коэффициенты сжимаемости, температура и проницаемость были постоянными. Это допущение позволяло пренебречь определенными параметрами. Однако если эти допущения принять, то можно непосредственно осуществить интегрирование и получить решение для уравнений (X. 19) и (X. 21).
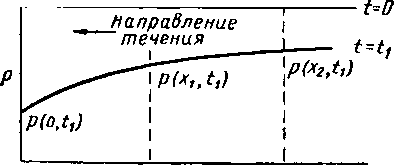
Математическое решение для линейного течения малосжимаемых жидкостей дано очень детально применительно к проблемам распространения тепла Черчиллем [X. 8]. На рис. X. 7 приводится схема, иллюстрирующая задачу линейного течения жидкости. Первый символ при р, которым обозначается давление, указывает положение точки, в которой замерено давление. Второй символ указывает время, в которое производилось измерение давления. Соответственно р(Х\, 11) указывает давление в точке Х\, замеренное в момент времени /[. Для простоты постоянное начальное давление обозначается
| Общее время | Время после закрытия скважины, ч | t |
D | Pt | 2 2 Рп - Рс, am2 абс. |
2 р с. am2 абс. | д t tf м | Рс, абс. am |
||
| после пуска |
после закрытия |
после пуска |
после закрытия |
разность | ||||||
| 0 | 0 |
0 | 0 |
0 | 19 774 |
140,62 | ||||
| 1 |
_ | 16 682 |
_ | 5,26 |
— | 5,26 |
1012,428 | 18761 |
— | 136,964 |
| 4 | _ |
66 728 | _ |
5,96 | _ |
5,96 | 1148,892 |
18 627 | — |
136,542 |
| 8 |
_ | 133 456 |
_ | 6,30 |
— | 6,30 |
1212,146 | 18 569 |
— | 136,261 |
| 12 | — |
200 184 | — |
6,55 | — |
6,55 | 1260,593 |
18513 | — |
136,120 |
| 16 |
266 912 | 6,74 |
6,76 | 1301,129 | 18 479 |
135,980 | ||||
| 20 |
_ | 333 640 | _ | 6,97 | — |
6,97 | 1341,172 |
18 434 | — |
135,769 |
| 24 |
0 | 400 368 |
0 | 7,16 |
0 | 7,16 |
1377,753 | 18 395 |
— | 135,628 |
|
26 | 2 |
433732 | 33 364 |
7,31 | 5,61 |
1,70 | 327,161 |
19 447 | 0,077 |
139,429 |
| 27 |
3 | 450 410 |
50 046 | 7,33 |
5,81 | 1,52 |
292,507. | 19 481 |
0,111 | 139,565 |
| 28 | 4 |
467 096 | 66 728 |
7,37 | 5,96 |
1,41 | 271,349 |
19 503 | 0,143 |
139,636 |
| 32 |
8 | 533 824 |
133 456 | 7,62 |
6,30 | 1,32 |
254,022 | 19 520 |
0,250 | 139,706 |
| 36 | 12 |
600 552 | 200 184 |
7,83 | 6,55 |
1,28 | 246,334 |
19 528 | 0,333 |
139,706 |
| 40 |
16 | 667 280 |
266 912 | 8,02 |
6,76 | 1,26 |
242,479 | 19 532 |
0,400 | 139,706 |
| 44 | 20 |
734 008 | 333 640 |
8,23 | 6,97 |
1,26 | 242,479 |
19 532 | 0,454 |
139,706 |
| 48 |
24 | 800 736 |
400 368 | 8,42 |
7,16 | 1,26 |
242,479 | 19 532 |
0,500 | 139,706 |
Р(О.О)
P(*t,°)
Р 1*2,0)
Pihc. X. 7. Схема линейного течения.
рп, а постоянное давление, действующее во внешней области, рс. Жидкость на схеме рис. X. 7 течет справа налево и вытекает из пористой среды к галерее, имеющей координату * = 0.
В зависимости от выбранных граничных условий можно получить несколько решений. Черчиллем рассмотрены три случая. В каждом случае начальное давление рп постоянно, когда время равно нулю и градиент давления равен нулю при х~ <х> для любого значения времени.
Случай I. Давление на галерее (х = 0) поддерживается постоянным. В этом случае давление на галерее (х = 0) мгновенно изменяется от рп до рс. Давление в любой точке пласта и в любой момент времени р(х, t) рассчитывается по уравнению Чарчилля
. 3,48 х 10~*Kt . |лСФ*2
Методика расчета распределения давления при не-установившемся течении заключается в следующем.
1. Вычисляется безразмерное время tD для данной точки и время для точек, где желательно знать давление.
При определении безразмерного времени для линейного течения в формуле, приведенной в табл. X. 2, вместо г подставляются расстояния от галереи (л: = 0) до выбранной точки в пласте.
2. Вычисляется величина 7г /д2.
3. Находится значение erfc (‘/г tp2) по соответствующей таблице.
4. Вычисляется р(х, t), когда известны рп и рс.
Пример
В лаборатории проводятся опыты на трубе, заполненной большими образцами керна, проницаемостью 15,6 мд и пористостью 12%. Система насыщена жидкостью вязкостью 0,20 спз и имеющей сжимаемость при данной температуре 0,00868 1 /ат. Начальное абсолютное давление в трубе равно 35,155 ат. Затем на одном конце абсолютное давление внезапно было снижено до 21 ат. Какое давление будет в точке, отстоящей от выходного конца на 6,095 м через 0,1 ч после сниження давления, принимая, что длина трубы достаточно велика?
Решение
3,48 X Ю-4 X 15,6 х 0,1
0,20 х 0,00868 х 0,12 х 6,195г = 0,0704,
1
2/‘/г
(X. 22)
= — erfc
2х 0,07041/2
erfc = 1
(X. 22а)
времени tD приведены а обозначение erfc расшифровывается как дополнительная фукция ошибки. Функции ошибок за-табулированы [X. 25]. Знак минус в уравнении (X. 22) соответствует случаю добычи жидкости. При нагнетании жидкости в пласт ставится знак плюс.
Р (*» 0 — Рп Г'с Рп безразмерного
интеграл вероятности.
Значения в табл. X. 2,
р (6,1; 0,1) = 35,155— 14,062 х 0,00752 = 35,049 абс. am.
Случай II. Поддерживается постоянный отбор (в точке х = 0). Течение линейное. Если жидкость отбирается на выходном конце (* = 0) с постоянным темпом отбора, то давление в любой точке пористой среды в произвольно
= 1,89. erfc (1,89) = 1 — 0,99248 = 0,00752.
быбранное время для неустановившегося течения определяется по уравнению
р (X, t) — рп
---= -mPt. (X. 23)
ГП
Безразмерный параметр т определяется по табл. X. 2 для линейного течения жидкости, а безразмерный параметр Pt, учитывающий изменение давления, рассчитывается по уравнению, полученному Черчиллем:
2 У Vi
erfc
(X. 24)
Pt ¦
Знак минус в правой стороне уравнения (X. 23) соответствует случаю добычи жидкости, а при нагнетании ставится знак плюс.
Так как равное нулю, нельзя подставлять непосредственно в уравнение (X. 23) или (X. 24), то для определения давления в этом случае необходимы специальные преобразования. Ниже уравнение (X. 23) дается для системы единиц (см, сек, ат, спз и др.):
Crt
dtr
2Q( UV \*/*
Р(0,/)-рп = Г(^) . (X- 25)
Обычно уравнение (X. 25) для решения промысловых задач не применяют, так как принятые допущения о линейности течения не удовлетворяют условиям вблизи отдельных скважин.
Случай III. Давление на галерее (* = 0) меняется произвольно. Если давление на эксплуатационной галерее *=0 меняется во времени произвольно
(X. 29)
Qt =
то решение (X. 8), по которому определяется давление в любой точке и времени, принимает вид:
Чг
X е_хЖ (X. 27)
где X —новая переменная интегрирования. При f(t) = =const уравнение (X. 27) переходит в уравнение (X. 22).
1 ^эф/гс на графиках (рис. X. гк/гР в тексте.
и X. 9) то же самое, что
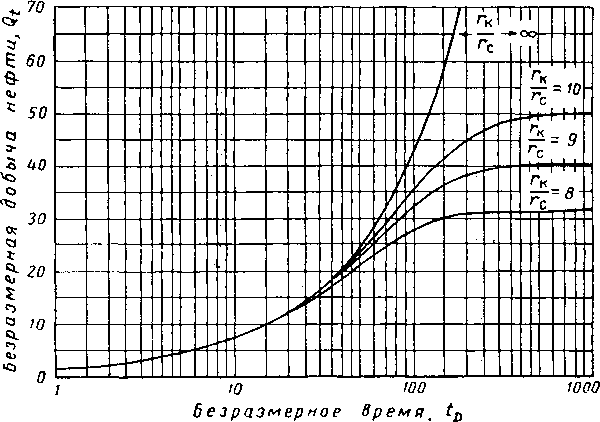
Рис. X. 8. Зависимость безразмерной добычи от безразмерного времени для ограниченного радиального пласта при постоянном давлении на скважине [X. 7]. гк— радиус пласта; гс — радиус скважины; к/гг —установившееся состояние не достигается: гк/гс = 10 — течение, установившееся при безразмерной добыче Q t — *=49,5: гк/гс = 9 — течение, установившее
ся при Q/ =40,0; гк/гс =8,0 — течение, уста новившееся при Q/ = 31,5.
Случаи IV. Постоянное забойное Давление. Радиальное течение в бесконечном пласте. Пользуясь приемами, аналогичными приемам при решении уравнений для линейного течения, Ван Эвердинген и Херст [X. 27] получили решение для случая радиального'течения малосжи-маемых жидкостей. Ниже будут даны уравнения в безразмерном виде и значения безразмерных параметров, затабулированных Ван Эвердингеном и Херстом и Чата-сом [X. 7]. Принимается, что в момент времени / = 0 давление равномерно распределено по пласту, а градиент давления на внешней границе конечного пласта, как и на бесконечном удалении в неограниченном пласте, равен нулю.
Для случая, когда на скважине поддерживается постоянное давление, при радиальной фильтрации в бесконечном пласте общее накопленное количество фильтрующейся в скважину жидкости за период времени от 0 до t обозначается QT: t (d
= 2*®Cr\h (pc — pj Qt, (X. 28)
где Qt—безразмерная общая добыча, определяемая из уравнения
др
dt р ' — Г . и
Рс—Рп
Если в уравнении (X. 28) гс и h выражены в м, то Qt получаем в м3 жидкости, количество которой измерено при пластовых условиях. Давление р и сжимаемость С должны быть в тех же самых единицах, т. е. в абс. ат. Величина Qt для любого значения безразмерного времени tD дается в табл. X. 4. На графике (рис. X. 8), взятом у Чатаса ((Chatas) [X. 7], даны значения Qt для рассматриваемой задачи (случай IV) '.
| Значения |
tD и Qt для |
радиального |
течения | Значения tD и Q | i для радиального |
течения | |
| в бесконечном пласте при рг = | const |
в бесконечном | пласте при рс = |
const | |||
| t D | Qt |
lD | Qt |
1 D | Qt |
lD | Qt |
| 0.00 |
0.000 | 41 |
21.298 | 96 |
41.735 | 355 |
121.966 |
| 0.01 |
0.112 | 42 |
21.701 | 97 |
42.084 | 360 |
123.403 |
| 0.05 |
0.278 | 43 |
22.101 | 98 |
42.433 | 365 |
124.838 |
| 0.10 |
0.404 | 44 |
22.500 | 99 |
42.781 | 370 |
126.270 |
| 0.15 |
0.520 | 45 |
22.897 | 100 |
43.129 | 375 |
127.699 |
| 0.20 |
0.606) | 46 |
23.291 | 105 |
44.858 | 380 |
129.126 |
| 0.25 |
0,689' | 47 |
23.684 | 110 |
46.574 | 385 |
130.550 |
| 0.30 |
0.758 | 48 |
24.076 | 115 |
48.277 | 390 |
131.972 |
| 0.40 |
0.89& | 49 |
24.466 | 120 |
49.968 | 395 |
133.391 |
| 0.50 |
1.020 | 50 |
24.855 | 125 |
51.648 | 400 |
134.808 |
| п йл | 1 1/ifi | № | 25.244 | 130 |
53.317 | 405 |
136.223 |
| и. ои П 7 П | 1. HU 1 |
'52 | 23.633 |
135 | 54.976 |
410 | 137.635 |
| и. /и П | 1 . | 53 | 26.020 |
140 | 56.625 |
415 | 139.045 |
| и. ои А ПА | 1 . OU«7 1 Л AQ | 54 |
26.406 | 145 |
58.265 | 420 |
140.453 |
| 0.У0 |
i .40^ | 55 |
26.791 | 150 |
59.895 | 425 |
141.859 |
| 1 |
1.569 | 56 |
27.J74 | 155 |
61.517 | 430 |
143.262 |
| 2 |
2.447 | 57 |
27.555 | 160 |
63.131 | 435 |
144.664 |
| 3 |
3.202 | 58 |
27.935 | 165 |
64.737 | 440 |
146.064 |
| 4 |
3.893 | 59 |
28.314 | 170 |
66.336 | 445 |
147.461 |
| 5 |
4.539 | 60 |
28.691 | 175 |
67.928 | 450 |
148.856 |
| 6 |
5.153 | 61 |
29.068 | 180 |
69.512 | 455 |
150.249 |
| 7 |
5.743 | 62 |
29.443 | 185 |
71.090 | 460 |
151'. 640 |
| 8 |
6.314 | 63 |
29.818 | 190 |
72.661 | 465 |
153.029 |
| 9 |
6.869 | 64 |
30.192 | 195 |
74.226 | 470 |
154.416 |
| 10 |
7.411 | 65 |
30.565 | 200 |
75.785 | 475 |
155.801 |
| 11 |
7.940 | 66 |
30.937 | 205 |
77.338 | 480, |
157.184 |
| 12 |
8.457 | 67 |
31.308 | 210 |
78.886 | 485 |
158.565 |
| 13 |
8.964 | 68 |
31.679 | 215 |
80.428 | 490 |
159(945 |
| 14 |
9.461 | 69 |
32.048 | 220 |
81.965 | 495 |
161.322 |
| 15 |
9.949 | 70 |
32.417 | 225 |
83.497 | 500 |
162.698 |
| 16 |
10.434 | 71 |
32.785 | 230 |
85.023 | 510 |
165:444 |
| 17 |
10.913 | 72 |
33.151 | 235 |
86.545 | 520 |
168.183 |
| 18 |
11.386 | 73 |
33.517 | 240 |
88.062 | 525 |
169.549 |
| 19 |
11.855 | 74 |
33.883 | 245 |
89.575 | 530 |
170.914 |
| 20 |
12.319 | 75 |
34.247 | 250 |
91.084 | 540 |
173.639 |
| 21 |
12.778 | 76 |
34.611 | 255 |
92.589 | 550 |
176.357 |
| 22 |
13.233 | 77 |
34.974 | 260 |
94.090 | 560 |
179.069 |
| 23 |
13.684 | 78 |
35.336 | 265 |
95.588 | 570 |
181.774 |
| 24 |
14.131 | 79 |
35.697 | 270 |
97.081 | 575 |
183.124 |
| 25 |
14.573 | 80 |
36.058 | 275 |
98.571 | 580 |
184.473 |
| 26 |
15,013 | 81 |
36.418 | 280 |
100,057 | 590 |
187.166 |
| 27 |
15.450 | 82 |
36.777 | 285 |
101.540 | 600 |
189.852 |
| 28 |
15.883 | 83 |
37.136 | 290 |
103.019 | 610 |
192.533 |
| 29 |
16.313 | 84 |
37.494 | 295 |
104.495 | 620 |
195.208 |
| 30 |
16.742 | 85 |
37,551 | 300 |
105.968 | 625 |
196.544 |
| 31 |
17*167 | 86 |
38.207 | 305 |
107,437 | 630 |
197.878 |
| 32 |
17 ,<590 | 87 |
38.(563 | 310 |
108.904 | 640 |
200.542 |
| 33 |
18.011 | 88 |
38.919 | 315 |
110.367 | 650 |
203.201 |
| 34 |
18.429 | 89 |
39.272 | 320 |
111.827 | 660 |
205.854 |
| 35 |
18.845 | 90 |
39.626 | 325 |
113.284 | 670 |
208.502 |
| 36 |
19,259 | 91 |
39.979 | 330 |
114.738 | 675 |
209.825 |
| 37 |
19.671 | 92 |
40.331 | 335 |
116.189 | .680 |
211.145 |
| 38 |
20.080 | 93 |
40.684 | 340 |
117.638 | 690 |
213.784 |
| 39 |
20.488 | 94 |
41.034 | 345 |
119.083 | 700 |
216.417 |
| 40 |
20^894 | 95 |
41.385 | 350 |
120.525 | 7 Ш |
319.046 |
| 720 |
221.670 | 1.175 |
337.142 |
| 725 |
222.980 | 1,180 |
338.376 |
| 730 |
224.289 | 1,190 |
340.843 |
| 740 | 226.904 | 1,200 | 343.308 |
|
750 | 229.514 |
1,210 | 345.770 |
| 760 | 232.120 |
1,220 | 348.230 |
| 770 | 234.721 |
1,225 | 349.460 |
| 775 | 236.020 |
1,230 | 350.688 |
| 780 | 237.318 |
1,240 | 353.144 |
| 790 | 239.912 | 1,250 | 355.597 |
| 800 |
242.501 | 1,260 |
358.048 |
| 810 |
245.086 | 1,270 |
360.496 |
| 820 |
247.668 | 1,275 |
361.720 |
| 825 | 248.957 | 1,280 | 362.942 |
|
830 | 250.245 |
1,290 | 365.386 |
| 840 | 252.819 |
1,300 | 367.828 |
| 850 | 255.388 |
1,310 | 370.267 |
| 860 | 257.953 |
1,320 | 372.704 |
| 870 | 260.515 |
1,325 | 373.932 |
| 875 | 261.795 | 1,330 | 375.139 |
| 880 |
263.073 | 1,340 |
377.572 |
| 890 |
265.629 | 1,350 |
380.003 |
| 900 |
268.181 | 1,360 |
382.432 |
| 910 | 270.729 | 1,370 | 384.859 |
|
920 | 273.274 |
1,375 | 386.070 |
| 925 | 274.545 |
1,380 | 387.283 |
| 930 | 275.815 |
1,390 | 389.705 |
| 940 | 278.353 |
1,400 | 392.125 |
| 950 | 280.888 |
1,410 | 394.543 |
| 960 | 283.420 | 1,420 | 396.959 |
| 970 |
285.948 | 1,425 |
398.167 |
| 975 |
287.211 | 1,430 |
399.373 |
| 980 |
288.473 | 1,440 |
401.786 |
| 990 | 290.995 | 1,450 | 404.197 |
|
1,000 | 293.514 |
1,460 | 406.606 |
| 1,010 | 296.030 |
1,470 | 409.013 |
| 1,020 | 298.543 | 1,475 | 410.214 |
| 1,025 |
299.799 | 1,480 |
411.418 |
| 1,030 |
301.053 | 1,490 |
413.820 |
| 1,040 | 303.560 | 1,500 | 416.220 |
|
1,050 | 306.065 |
1,525 | 422.214 |
| 1,060 | 308.567 |
1,550 | 428.196 |
| 1,070 | 311.066 | 1,575 | 434.168 |
| 1,075 |
312.314 | 1,600 |
440.128 |
| 1,080 |
313.562 | 1,625 |
446.077 |
| 1,090 | 316.055 | 1,650 | 452.016 |
|
1,100 | 318.545 |
1,675 | 457.945 |
| 1,110 | 321.032 |
1,700 | 463.863 |
| 1,120 | 323.517 | 1,725 | 469.771 |
| 1,125 |
324.760 | 1,750 |
475.669 |
| 1,130 |
326.000 | 1,775 |
481.558 |
| 1,140 | 328.480 | 1,800 | 487.437 |
|
1,150 | 330.958 |
1,825 | 493.307 |
| 1,160 | 333.433 |
1,850 | 499.167 |
| 1,170 | 335.906 | 1,875 | 505.019 |
| 24* |
|
1,900 | 510.861 |
4,050 | 990.108 |
| 1,925 | 516.695 |
4,100 | 1,000.858 |
| 1,950 | 522.520 | 4,150 | 1,011.595 |
| 1,975 |
528.337 | 4,200 |
1,022.318 |
| 2,000 | 534.145 | 4,250 | 1,033.028 |
|
2,025 | 539.945 |
4,300 | 1,043.724 |
| 2,050 | 545.737 |
4,350 | 1,054.409 |
| 2,075 | 551.522 | 4,400 | 1,005.082 |
| 2,100 |
557.299 | 4,450 |
1,075.743 |
| 2,125 | 563.068 | 4,500 | 1,086.390 |
|
2,150 | 568.830 |
4,550 | 1,097.024 |
| 2,175 | 574.585 |
4,600 | 1,107.646 |
| 2,200 | 580.332 | 4,650 | 1,118.257 |
| 2,225 |
586.072 | 4,700 |
1,128.854 |
| 2,250 | 591.806 | 4,750 | 1,139.439 |
|
2,275 | 597.532 |
4,800 | 1,150.012 |
| 2,300 | 603.252 |
4,850 | 1,160.574 |
| 2,325 | 608.965 | 4,900 | 1,171.125 |
| 2,350 |
614.672 | 4,950 |
1,181.666 |
| 2,375 | 620.372 | 5,000 | 1,192.198 |
|
2,400 | 626.066 |
5,100 | 1,213.222 |
| 2,425 | 631.755 |
5,200 | 1,234.203 |
| 2,450 | 637,437 | 5,300 | 1,255.141 |
| 2,475 |
643.113 | 5,400 |
1,276.037 |
| 2,500 | 648.781 | 5,500 | 1,296.893 |
|
2,550 | 660.093 |
5,600 | 1,317.709 |
| 2,600 | 671.379 |
5,700 | 1,338.486 |
| 2,650 | 682.640 | 5,800 | 1,359.225 |
| 2,700 |
693.877 | 5,900 |
1 ,-379.927 |
| 2,750 | 705.090 | 6,000 | 1,400.593 |
|
2,800 | 716.280 |
6,100 | 1,421.224 |
| 2,850 | 727.449 |
6,200 | 1,441.820 |
| 2,900 | 738.598 | 6,300 | 1,462.383 |
| 2,950 |
749.725 | 6,400 |
1,482.912 |
| 3,000 | 760.833 | 6,500 | 1,503.408 |
|
3,050 | 771.922 |
6,600 | 1,523.872 |
| 3,100 | 782.992 |
6,700 | 1,544.305 |
| 3,150 | 794.042 | 6,800 | 1,564.706 |
| 3,200 |
805.075 | 6,900 |
1,585.077 |
| 3,250 | 816.090 | 7,000 | 1,605.418 |
|
3,300 | 827.088 |
7,100 | 1,625.729 |
| 3,350 | 838.067 |
7,200 | 1,646.011 |
| 3,400 | 849.028 | 7,300 | 1,6(56 . 265 |
| 3,450 |
859.974 | 7,400 |
1,680.490 |
| 3,500 | 870.903 | 7,500 | 1,706.688 |
|
3,550 | 881.816 |
7,600 | 1,726.859 |
| 3,600 | 892.712 |
7,700 | 1,747.002 |
| 3,650 | 903.594 | 7,800 | 1,767.120 |
| 3,700 |
914.459 | 7,900 |
1,787.212 |
| 3,750 | 925.309 | 8,000 | 1,807.278 |
|
3,800 | 936.144 |
8,100 | 1,827.319 |
| 3,850 | 946.966 |
8,200 | 1,847.336 |
| 3,900 | 957.773 | 8,300 | 1,867.329 |
| 3,950 |
968.566 | 8,400 |
1,887.298 |
| 4,000 | 979.344 | 8-, 500 | 1,907.243 371 |
w з to
n> S
s s s a a
¦o ся Cj s C\ s
о
)S
fa
a
O CD О X
s =
ел О
4S?
to
-Я S
a s
to ?*
•s
Й
o>
*=»
| to |
н- | н- | Ср | 00 | <5 |
е> | Сл |
со | ю | ю |
и* | 1—1 | о |
00 | м | а | сл | СО |
to | — | ||||
| о | Сл |
Ь | о | о |
О | о | О |
о | с | сл |
о | Сл | о |
о | о | о |
о | о | о | о | Сл | о | Сл | to сл |
| X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X X | X |
о | |
| н- |
н- | н- | W* | н- | н- | |_ | N- | Н- | |_ | о | ||||||||||||||
| © | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о |
|
в | в | 0* | в | в | ||||||||||||||||||||
| to |
н- | н- | Н- | 00 | O'- |
Ср | & |
со | to | to |
н- | >— |
СО | н | а | 4- | со |
to | to | |||||
|
со | 00 | to |
't- | о | СО |
сл | со |
о | ?> | W | Ь |
Oi | to |
00 | О | со |
сл | J-* | ||||||
|
СО | to | сл |
СО | 05 |
а | ?» |
05 | to | 00 |
to | 05 | to |
00 | сл | СО | а | Oi |
о | со | |||||
| 00 | 00 | to |
?» | а |
сл | со |
4* | 05 |
to | 0г | СО |
*- | со | СО | Oi | 00 | 00 | © | ||||||
|
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
о |
| н- | н- | н- | н- |
и-* | м | н- | н- | ч со | ||||||||||||||||
| о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | ю |
| в» | в» |
«» | ||||||||||||||||||||||
| to | t—l | о |
00 | 0* |
Сл | * | со |
to | to | , . |
© | 00 | '№ | Сл |
со | to | W |
|||||||
| ь |
Сл | о | о |
о | о | о |
О | • о | ь |
сл | о | сл | о | о | о | о | о | о | о | о | сл | о | сл |
о |
| X | X | X | X | X | X | X | X | X | X | X | X | X | X | X | X |
XXX | X | X | X X | X | X | |||
| н- | и-» |
н- | н- | н- | н- | н- |
н- | н- | н- |
н- | н- | N- |
N- | |||||||||||
| о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
| *• | о |
о | о | о |
о | о | с |
о | о | о |
о | |||||||||||||
|
а | Сл | ?» | СО | to |
to | н- |
00 | |||||||||||||||||
|
а | Сл | Сл | А | СО |
со | to | ||||||||||||||||||
| со |
J-* | 'а |
00 | о | to |
сл | а |
to | ||||||||||||||||
| 4к |
о | to | Сл |
00 | м |
© | to | со |
Сл | s° |
о | 00 |
СО | о | о |
со | 00 | |||||||
| to | 00 | со | 00 | со |
СО | СЛ | to | СО | to |
сл | 00 | со | со | 00 |
СО | СЛ |
03 | 00 | ||||||
| X | X | X | X X | X X X X | X | X |
X X | X | X |
X | X X | X |
X | X | X X | X | X | |||||||
| N— | N— | w | N— |
N— | ||||||||||||||||||||
| о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
| - | © |
о | о | о |
о | о | о |
о | о | е |
о |
<в | <в | <е | ||||||||||
|
о | СО | 00 |
< | а |
сл | со | со | to |
to | ** | |||||||||||||||||||
| о | о | о | сл |
о | о | о |
о | сл | о |
сл | о | сл | to | о | СО | СО |
to | СО |
СО | СО |
СО | СО |
СО | ^о | 00 | 00 | 00 | 00 | |
| о | о |
о | о | о |
о | о | о |
о | о | о |
о | сл | о | сл | о |
СО | со |
05 | сл |
со | to |
о | to | *00 |
-1 | 05 | |||
|
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о | о | о | о | о | о | о | о | о | о | о | о |
о | о | ||
| о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о |
| сл |
со | to |
о | а |
Сл | Сл | со | со |
to | to | to |
to | to | to |
to | ьо | to |
to | to | to |
N- | — |
— | — | |||||
| сл | СО |
со | сл | о | со | С5 | 00 | о |
о | 05 | "н- | 05 | to |
"н- |
"н- | о |
о | о | о |
о | ъ | о |
со | о | |||||
|
00 | сл |
со | о |
а | сл | 00 | СО | О |
СО | со |
05 | 00 | о |
00 | 05 |
to | о | 00 |
05 | to |
о | 00 | 05 |
4*. | to | ||||
|
а | сл | о | 00 |
СО | о | о |
СО | СЛ |
сл | со |
4^ | 00 | со |
сл |
сл | СП |
сл | 05 |
05 | а | 05 | 05 | |||||||
| to | со | со | to |
о | о | to |
Сл | 00 |
со | СО |
00 | to | сл | 00 |
'О | to |
05 | -1 | о |
о | н- | ||||||||
|
00 | 00 | to |
сл | сл |
СО | СО |
•х | О |
to | о | С5 |
со | 05 |
05 | сл |
"I | 00 | 'sO | м |
ю | 'О |
05 | С5 | ||||||
| СО | 00 | СО | о |
а | 00 |
а | о | 00 |
о | 05 | сл | 00 | со | 05 | 00 | 00 |
05 | to | сл | 05 | |||||||||
|
со- 00 | о |
Сл | со |
to | to |
СО | 00 |
05 | сл |
со | to | to | СО |
00 | 05 |
сл | 4^ |
со | to | ||||||||||
|
о | о | о |
о | о | о |
о | сл | о |
Сл | о | о | о | о | о | о | о | о | сл | о |
сл | о | о |
о | о | о |
о | о | о |
сл |
| X X | X | X | X | X | X | X | X | X | X | X | к | X | X | X | X | X | X | X | X | X | X | X | X | X | X X | X X | |||
|
н- | н- |
н- | н- |
н- | Н- |
н- | и-> |
н- | _ |
Н- | Н- |
н- |
н- | н- | |||||||||||||||
| о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о |
| © |
® | * | во |
* |
* | * |
|||||||||||||||||||||||
| о | Сл |
со | to |
to | н- |
СО | 00 |
05 | о* |
сл | со |
to | to | н- | н- | о |
00 | 05 |
Сл | 4^ | со | .м | |||||||
| о |
о | to |
со | сл |
о* | со |
00 | itb |
00 | СО | о |
о | о |
05 | 05 |
о | о | 00 |
00 | 05 |
05 | сл | о | ||||||
| о | а |
to | а | to | 00 |
to | to | СО | 05 | to |
00 | со |
о | о | о |
о | сг |
сл | 00 |
05 | |||||||||
|
50 | а | о | 00 | о |
Сл | 00 | о | СО | Сл |
сл | 00 |
to | о |
00 | сл | 05 | 05 | 00 | СО |
о | |||||||||
| X X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X | X |
X | X X | X X | |||
|
н- | н- |
н- | н- |
н- | н- |
н- | н- |
Н- | н- |
н- | н- |
ь_,- | н- |
н- | н- | ||||||||||||||
|
о | о | о |
о | о во | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о | о |
| н- | н- |
н- | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
|
| to |
о | СО | 00 |
05 | Oi | со | to |
’н- | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | сГ | |||||
|
сл- | СО |
00 | 05 |
Сл | со | to | to | о | о | о | о | о | о | о | о | о | о | ||||||||||||||||||
| Сл | Сл |
СО | 00 |
05 | Сл |
со | to | Сл | |||||||||||||||||||||||||||
| о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | |
| СО |
00 | *00 | 05 | 05 |
Сл | сл | со | со | to | to | to | to | to | to | о | о | о | о | о | о | о | о | о | ||||||||||||
| 05 |
о | со | о | 05 | 05 | о | to | СО | 00 |
05 | сл |
со | о | 00 |
05 | <J} |
со | о | о |
СО | СО |
00 | 05 |
© | со | to | |||||||||
| 05 |
J-* | 00 |
to | to | 05 | to |
сл | СО |
00 | о |
о | 05 |
о | 00 |
to |
СО | ь |
СО | сл |
сл | |||||||||||||||
|
о | to | (0 |
05 | to |
Сл |
о | (0 | СЛ | о | о | 00 | СО |
со | to | 00 | сл | со | Сл |
to | о |
ш Сэ
W
=
X
S
а
¦Og ^
11 г s
л х а
п т ¦
5 о
6 г
to
)Я
S
to
ь
СГ
=
о
“1
о *S
05 сл ^ со to о о о о о
С5 Сл 4* СО tsi
о о о о о
СЛ о о 00 о о о о
| СО СЛ о | СО о о |
00 щ | 00 о о | сл о |
-ч| 8 | 05 Сл о | 05 8 | сл сл о | сл _8 |
Сл о | 8 | со сл о | со 8 |
to Сл о | to 8 | сл о | о о |
| о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о | о | о |
о |
CO 00
о о
ООО ооооо
S 8
1 Сл • Сл
Q9 сл до Сл до
|
со | со | со |
со | со | со | со | со |
со | со | со |
со | со | to | to | to | to | to | to | to | to | to | н- | н- |
н- | н- | н- | h- | |||||
| 05 | 05 |
05 | Сл | ?л |
со | to |
о | СО |
Vj | 05 | 05 |
СЛ | itb | со | to | CO |
00 | 05 | 05 |
Сл | со |
to | о | |||||||||
| сл | 09 |
?» | о | 05 |
>-* | 05 |
о | со | 05 |
05 | to |
to | сл |
00 | 00 | 05 | to | Сл |
о | Сл |
СО | со | 05 | ох. | ||||||||
| о | 00 | к | 05 |
?•> | Сл |
СО | со | to | со | CO |
о | Сл |
00 | to |
о | CO | о |
СЛ | Сл |
СО | а | to | Сл | 05- |
СО | |||||||
| Сл | to | 05 |
0> | со | о | 05 |
05 | to | CO | 00 | 00 | о | (0 |
to | о |
Сл |
со со
>?
о*
| L - 1.5 | R - 2.0 | R =* 2.5 | R - 3.0 | Я - | 3.5 | Я « |
4.0 | Я - | 4.5 |
Я *¦ 5.0 | Я = |
* 6.0 | Я => | 7.0 | Я | = 8.0 |
Я | - 9.0 | Я •= |
10.0 | |||||
| to |
tD |
tD | to |
Q> | tD |
Qt | tD |
ID | Qt |
to | to |
Qt | Id |
tD | Qt |
tD | to |
Qt | |||||||
| 5.0 X 10"* |
0.276 | 5.00 X Ю-* |
0.278 | 1.0 X 10-» | 0.408 | 3.0 X 10"» | 0.755 |
1 00 | 1.571 | 2.00 | 2.442 | 2.5 |
2.835 | 3.0 | 3. 195 |
6.0 | 5.148 | 9.00 | 6.861 | 9 |
6.861 | :o | 7.417 |
15 | 9.965 |
|
6.0 X 10‘* | 0.304 | 7.50 X Ю-* | 0.345 | 1.5 X Ю-» | 0.509 | 4.0 X 10"» |
0.895 | 1.20 | 1.761 | 2.20 | 2.598 |
3.0 | 3.196 | 3.5 |
3.542 | 6.5 | 5.440 | 9 50 | 7.127 |
10 | 7.398 | 15 |
9.945 | 20 | 12.32 |
| 7.0 X 10"* | 0.330 | 1.00 X 10'» | 0.404 |
2.0 X 10"» | 0.599 |
5.0 X 10"» | 1.023 |
1.40 | 1.940 | 2.40 |
2.748 | 3.5 | 3.537 | 4.0 | 3.875 |
7.0 | 5.724 | 10 |
7.389 | 11 | 7.920 | 20 | 12.26 |
22 | 13.22 |
| 8.0 X 10"» | 0.354 | 1.25 X 10"» | 0.458 | 2.5 X 10"» | 0.681 | 6.0 X 10"» | 1.143 | 1.60 | 2. Ill | 2.60 |
2.893 | 4.0 | 3.859 |
4.5 | 4.193 | 7.5 | 6.002 | 11 |
7.902 | 12 | 8.431 |
22 | 13. 13 | 24 | 14.09 |
| 9.0 X 10^* | 0.375 | . 1.50 X 10"» |
0.507 | 3.0 X Ю-» |
0.758 | 7.0 X Ю-» | 1.256 | 1.80 | 2.273 |
2.80 | 3.034 | 4.5 |
4.165 | 5.0 | 4.499 | 8.0 | 6.273 |
12 | 8.397 | 13 |
8.930 | 24 | 13.98 | 26 | 14.95 |
| 1.0 х ю-» | Ot 395 |
1.75 X 10"» | 0.553 | 3.5 X 10"» | 0.829 | 8.0 X 10"» | 1.363 | 2.00 | 2.427 | 3.00 | 3. 170 | 5.0 | 4.454 |
5.5 | 4.792 | 8 5 |
6.537 | 13 | 8.876 | 14 | 9.418 |
26 | 14.79 | 28 |
15.78 |
| 1.1 х ю-> |
0.414 | 2.00 X 10"» |
0.597 | 4.0 X 10"» |
0.897 | 9.0 X 10"» |
1.465 | 2.20 | 2.574 |
3.25 | 3.334 | 5.5 | 4.727 | 6.0 |
5.074 | 9.0 | 6.795 |
14 | 9.341 | 15 | 9.895 | 28 |
15.59 | 30 | 16.59 |
| 1.2 X 10"» | 0.431 | 2 25 X 10-* | 0.638 |
4.5 X 10"» | 0.962 |
1.00 | 1.563 | 2.40 |
2.715 | 3.50 | 3.493 | 6.0 | 4.986 |
6.5 | 5.345 | 9.5 |
7.047 | 15 | 9.791 | 16 | 10.361 |
30 | 16.35 | 32 |
17.38 |
| 1.3 х ю-» |
0.446 | 2.50 X 10"» |
0.678 | 5.0 X 10-* | 1.024 | 1.25 | 1.791 |
2.60 | 2.849 | 3.75 |
3.645 | 6.5 | 5.231 | 7.0 | 5.605 |
JO.O | •7.293 | 16 |
10.23 | 17 | 10.82 | 32 | 17. 10 |
34 | 18.16 |
| 1.4 X 10-» | 0.461 | 2.75 X 10"» | 0.715 | 5.5 X 10"» | 1.083 | 1.50 | 1.997 | 2.80 |
2.976 | 4 00 | 3.792 |
7.0 | 5.464 | 7.5 | 5.854 | 10.5 |
7.533 | 17 | 10.65 |
18 | 11.26 | 34 | 17.82 | 36 |
18.91 |
| 1.5 X Ю> |
0.474 | 3.00 X 10”» |
0.751 | 6.0 x Ю-» | 1.140 | 1.75 | 2. 184 |
3.00 | 3.098 | 4.25 |
3.932 | 7.5 | 5.684 | 8.0 | 6.094 |
11 | 7.767 | 18 |
11.06 | 19 | 11.70 | 36 | 18.52 |
38 | 19.65 |
| 1.6 X 10-» | 0.486 | 3.25 X lO"1 | 0.785 | 6.5 X 10-» | 1.195 | 2.00 |
2.353 | 3.25 | 3.242 | 4.50 | 4.068 |
8.0 | 5.892 | 8.5 |
6.325 | 12 | 8. 220 | 19 | 11.46 |
20 | 12.13 | 38 |
19.19 | 40 | 20.37 |
| 17 X 10-» | 0.497 | 3.50 X 10"» | 0.817 |
7.0 X Ю-» | 1.248 |
2.25 | 2.507 | 3-50 |
3.379 | 4.75 | 4.198 | 8.5 | 6.089 |
0.0 | 6.547 | 13 |
8.651 | 20 | 11.85 | 22 | 12.95 |
40 | 19.85 | 42 |
21.07 |
| 18 X Ю-> |
0.507 | 3.75 X JO”» |
0.848 | 7.5 X Ю-» | 1.299 | 2.50 | 2.646 |
3.75 | 3.507 | 5.00 |
4.323 | 9.0 | 6.276 | 95 | 6.760 |
14 | 9.063 | 22 |
12.58 | 24 | 13.74 | 42 | 20.48 |
44 | 21.76 |
| 1,9 X 10'» | 0.517 | 4.00 X lO"1 | 0.877 | 8.0 X 10"» | 1.348 | 2.75 | 2.772 | 4.00 |
3.628 | 5.50 | 4.560 |
9.5 | 6.453 | 10 | 6.965 | 15 |
9.456 | 24 | 13.27 |
26 | 14.50 | 44 | 21.09 | 46 |
22.42 |
| 2.0 X 10‘» |
0.525 | 4.25 X 10‘1 |
0.905 | 8.5 X Ю-» | 1.395 | 3.00 | 2.886 | 4 25 | 3.742 | 6.00 |
4.779 | 10 | 6.621 |
11 | 7.3-50 | 16 | 9.829 | 26 |
13.92 | 28 | 15.23 |
46 | 21.69 | 48 | 23.0> |
| 2.1 X 10-» | 0. 533 | 4.50 X 10"» |
0.932 | 9.0 X 10"» |
1.440 | 3.25 | 2.990 |
4.50 | 3.850 | 6.50 | 4.982 | 11 |
6.930 | 12 | 7.706 |
17 | 10.19 | 28 | 14.53 | 30 |
15.92 | 48 | 22.26 |
50 | 23.71 |
|
2.2 X 10-* | 0.541 | 4.75 X 10"1 | 0.958 | 9.5 X 10"! | 1.484 | 3.50 |
3.084 | 4.75 | 3-951 | 7.00 | 5.169 |
12 | 7.208 | 13 |
8,035 | 18 | 10.53 | 30 | 15. 11 |
34 | 17.22 | 50 |
22.82 | 52 | 24.33 |
| 2.3 X 10‘» | 0.548 | 5.00 X 10"» | 0.983 |
1.0 | 1.526 | 3.75 | 3.170 | 5.00 |
4.047 | 7.50 | 5.343 |
13 | 7.457 | 14 | 8.339 | 19 ‘ |
10.85 | 35 | 16.39 |
38 | 18.41 | 52 | 23.36 | 54 |
24.94 |
| 2.4 X 10”» |
0.554 | 5.50 X lO"1 |
1.028 | 1.1 | 1.605 |
4.00 | 3.247 | 5.50 | 4.222 | 8.00 |
5.504 | 14 | 7.680 |
15 | 8.620 | 20 | 11.16 | 40 |
17.49 | 40 | 18.97 |
54 | 23.89 | 56 | 25.53 |
| 2.5 X 10-» | 0.559 | 6,00 X 10“» |
1.070 | 1.2 | 1.679 | 4.25 | 3.317 |
6.00 | 4.378 | 8.50 |
5.653 | 15 | 7.880 | 16 | 8.879 |
22 | 11.74 | 45 |
18.43 | 45 | 20.26 | 56 | 24.39 |
58 | 26.11 |
| 2.6 X 10"» | 0.565 | 6.50 X 10"» | 1. 108 | ГЗ | 1.747 | 4.50 |
3.381 | 6.50 | 4.516 |
9.00 | 5.790 | 16 | 8.060 | 18 |
9.338 | 24 | 12.26 |
50 | 19.24 | 50 | 21.42 | 58 |
24.88 | 60 | 26.67 |
| 2.8 X 10"» | 0.574 | 7.00 X 10"» | 1.143 |
1.4 | 1.811 | 4.75 | 3.439 | 7.00 |
4.639 | 9.50 | 5.917 |
18 | 8.365 | 20 | 9.731 | 25 |
12.50 | 60 | 20.51 |
55 | 22.46 | 60 | 25.36 | 65 |
28.02 |
| 3.0 X 10"» |
0.582 | 7.50 X 10"» |
1.174 | 1.5 | 1.870 |
5.00 | 3.491 | 7.50 | 4.749 | 10 |
6.035 | 20 | 8.611 |
22 | 10.07 | 31 | 13.74 | 70 |
21.45 | 60 | 23.40 |
65 | 26.48 | 70 | 29.29 |
| 3.2 X 10-» | 0.588 | 8.00 X 10"» |
1.203 | 1.6 | 1.924 | 5.50 | 3.581 |
8.00 | 4.846 | 11 |
6.246 | 22 | 8.809 | 24 | 10.35 |
35 | 14.40 | 80 |
22.13 | 70 | 24.98 | 70 | 27.52 |
75 | 30.49 |
| Ъ.4 X Ю-» | 0.594 | 9.00 X 10-» | 1.253 | 1.7 |
1.975 | 6.00 | 3.656 |
8.50 | 4.932 | 12 | 6.425 | 24 |
8.968 | 26 | 10.59 |
39 | 14.93 | 90 | 22.63 | 80 |
26.26 | 75 | 28.48 |
80 | 31.61 |
|
3.6 X 10-» | 0.599 | 1.0 | 1.295 | 1.8 |
2.022 | 6.50 | 3.717 |
9.00 | 5.009 | 13 | 6.580 | 26 |
9.097 | 28 | 10.80 |
51 | 16.05 | 100 | 23.00 | 90 |
27.28 | 80 | 29.36 |
85 | 32.67 |
|
3.8 X Ю-» | G. 603 | 1.1 | 1.330 | 2.0 |
2.106 | 7.00 | 3.767 |
9.50 | 5.Q78 | 14 | 6.712 | 28 |
9.200 | 30 | 10.98 |
60 | 16.56 | 120 | 23.47 | 100 | 28. 11 | 85 | 30.18 |
90 | 33.66 |
| 4.0 X 10'» | 0.606 | 1.2 |
1.358 | 2.2 | 2.178 | 7.50 | 3.809 |
10.00 | 5. 138 | 15 |
6; 825 | 30 | 9.283 | 34 | 11.26 |
70 | 16.91 | 140 |
23.71 | 120 | 29.31 | 90 | 30.93 |
95 | 34.60 |
| 4.5 X Ю-» | 0.613 | 1.3 |
1.382 | 2.4 | 2. 241 | 8.00 | 3.843 |
11 | 5.241 | 16 |
6.922 | 34 | 9 404 | 38 | 11.46 |
80 | 17. 14 | 160 |
23.85 | 140 | 30.08 | 95 | 31.63 |
100 | 35.48 |
| 5.0 X Ю-» | 0.617 | 1.4 |
1. *402 | 2.0 | 2. 294 | 900 | 3.894 |
12 | 5.321 | 17 |
7.004 | 38 | 9.481 | 42 | 11.61 |
90. | 17.27 | 180 |
23.92 | 160 | 30.58 | 100 | 32.27 |
120 | 38.51 |
| Г 0 X 10-» | 0. 621 | 1.6 |
V432 | 2.8 | 2.340 | 10.00 | 3.928 |
13 | 5.385 | 18 |
7.076 | 42’ | 9.532 | 46 | 11.71 |
100 | 17.36 | 200 |
23.96 | 180 | 30.91 | 120 | 34.39 |
140 | 40.89 |
| 7.0 X Ю‘> | 0.623 | 1.7 |
1.444 | 3.0 | 2.380 | 11.00 | 3.951 |
14 | 5.435 | 20 |
7/189 | 46 | 9.565 | 50 | 11.79 |
110 | 17.41 | 500 |
24.00 | 200 | 31. 12 | 140 | 35.92 |
160 | 42.75 |
|
;fi.O X 10-» | 0.624 |
1.8 | 1.453 | 3.4 |
2.444 | 12.00 | 3.967 | 15 | 5.476 |
22 | 7.272 | 50 |
9.586 | 60 | 11.91 | 120 | 17.45 | 240 | 31.34 |
160 | 37.04 | 180 |
44 21 | ||
|
2.0 | 1.468 | 38 |
2.491 | 14.00 | 3.985 | 16 | 5.506 |
24 | 7.332 | 60 |
9.612 | 70 | 11.96 | 130 | 17.46 | 280 | 31.43 |
180 | 37.85 | 200 |
45.36 | ||||
|
2.6 | 1.487 | 4:2 |
2.525 | 16.00 | 3.993 | 17 | 5 531 |
26 | 7.377 | 70 |
9.621 | 80 | 11.98 | 140 | 17.48 | 320 | 31 47 |
200 | 38.44 | 240 |
46.95 | ||||
|
3.0 | 1 495 | 4.6 |
2.551 | 18.00 | 3.997 | 18 | 5.551 |
30 | 7.434 | 80 |
9.623 | 90 | 11.99 | 150 | 17.49 | 360 | 31 49 |
240 | 39. 17 | 280 |
47.04 | ||||
|
4.0 | 1.499 | 5.0 |
2.570 | 20.00 | 3.999 | 20 | 5.579 |
34 | 7.464 | 90 |
9.624 | 100 | 12.00 | 160 | 17.49 | 400 | 31.50 |
280 | 39 56 | 320 |
48.54 | ||||
|
G.O | 1.500 | 6.0 |
2.599 | 22.00 | 3.999 | 25 | 5.611 |
38 | 7.481 | 100 |
9.625 | 120 | 12.0 | 180 | 17 50 | 500 | 31.50 |
320 | 39 77 | 360 |
48 91 | ||||
| 7.0 | 2.613 |
24.00 | 4.000 | 30 |
5.621 | 42 | 7.490 | 200 | 17.50 | 360 | 39.88 |
400 | 49 14 | ||||||||||||
| , | 8.0 |
2.619 | 35 |
5.624 | 46 | 7.494 | 220 | 17 50 | 400 | 39.94 |
440 | 49 28 | |||||||||||||
| 9.0 |
2.622 | 40 |
5.625 | 50 | 7.497 |
440 |
39 97 | 480 | 49 36 |
||||||||||||||||
| !! | i |
10.0 | 2.624 | 480 |
39.9$. | ||||||||||||||||||||
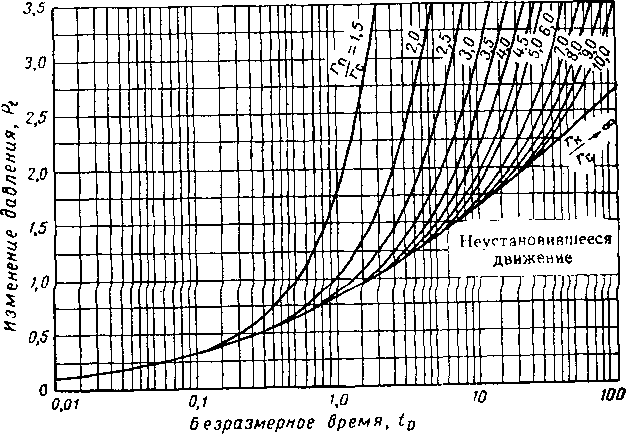
Рис. X. 9. То же, что на предыдущем рисунке, но скважина работает с постоянным дебитом [X. 7].
Пример
Начальное абсолютное давление в закрытой скважине 140,6 ат. Затем скважину открыли и она работала в течение нескольких часов с постоянным абсолютным давлением на забое, равным 105,45 ат. Значение безразмерного времени к концу этого периода равно 1500, гс =0,1525 м. /1 = 4,575 м. *„ = 0,20 и С=0,001714 1 /ат. Вычислить, сколько за это время добыто жидкости при радиальной фильтрации в бесконечном пласте.
=
Решение
Для ^с=1500 найдем но табл. X.4, что Qt = 416,220. По уравнению (X. 28) определяем QT:
QT = 2яФCr\h (рс — Pn)Qt = 2л х 4,575 х 0,2 х
X 0,001714 х 0,152527 х 35,15 X 416,22 = 3,351 м*.
Случай V. Постоянный дебит. Радиальное течение в бесконечном пласте. В случае постоянного дебита давление в любой точке пласта и в любой момент времени при радиальном течении жидкости рассчитывается но уравнению
(X. 30)
• mPt.
Р п
Знак минус перед правой частью уравнения ставится в случае эксплуатации скважины, а плюс при нагнетании. Значение m определяется из табл. X. 2. pt, выражающее безразмерное изменение давления, зависит только от безразмерного времени. Для tD = 1000 pt дано в табл. X. 5, а тдкже в виде графика иа рис. X. 9. При fD = 1000 pt рассчитывается по уравнению
?t = Vs (In tD + 0,80907). (X. 31)
При расчете давления для какого-то радиуса безразмерное время определяется именно для этого же радиуса.
Пример
Скважина, которая рассматривалась в предыдущем примере, после открытия работает с постоянным дебитом жидкости, равным 15,9 м28/сутки. Рассчитать давление в скважине спустя 24 ч после пуска, если К = 100 мд и (л = 1,8 сп.
Решение
3,480 X 10-4 X 100 х 24
to
Pt
tD
_j
6 0 X 10*
8 0 X 10’
1.0 X io-1.2 X 10-14 X 10
1 0 X 10-
1 8 X 10-
2.0 X 10-
2 2 X 10-2 4 X Ю-
2.6 X 10-2.8 X 10'
2.2 X 10
2.4 X 10-
2.6 X 10
2.8 X 10 3 0 X 10
3.2 X 10 3 4 X 10 36X10'
3 8 X 10
4 0 X 10
4 2 X 10-
4 4 X 10-
7.0 X IQ-в.0 X 10-
9.0 X 10' 1 0
2 0
3.0
5.0
1 .732
1.750 1.768 1 .784 1.801
1.817 1.832 1.847 1.862 1.890
0.251 0.288 0.322 0.355 ¦ 0.387
0. 420 0.452 0.484 0.51C 0 548
0.580 0,612 0 644 0 724 0.804
0.884
0.9621 1.044
1. 124
0.443
0,459
0.476
0.492
0,507
0 522 0.536 0 551 0 565 0 579
0.593 0 607 0.621 0.634 0.648
0.715
0.782
0.849
0.915
0.982
1.049
2,310
3.649
4 О X 10'
4 2 X 10“
9.5 X 10' 1.0 2.0
3.0
4.0
5.0
5.2 X 10-
5.4 x 10; 5.6 X 10-
6.0 X io-
6 5 X 10-
7 .0 X 10-
7.5 X 10 8.OX 10:
8.5 X 10
9.0 X 10
9.5 X 10 1.0 1.2 1.4 16
2.0
3.0
4.0
5.0
12.0
12.5
13.0
13.5
14.0
14.5 1§.0
15.5
16.0 17.0
0.565
0.576
0.587
0.598
0.608
0.018 0.628 0.638 0 04 0.057
.0.606
0.688
0.710
0.731
0.752
0.772
0.792
0.812
0.832
1215
1.596
1.977
2.358
ft 627 0.636 0.645 0.662 0.683
0.703 0 721 0.740 0 758 0 770
0 791 0 800
0.865
0.920
0.973
1.076
1 328 i.578 1.828
1 651
1.673
1.693
1.713
1.732
1.750
1.768
1.786
1.803
1.819
1 83Я 1.851
1 867 1.897
1.920
1.955 1; 983 2.037 2.090 2. 142
2 193 2.244 2.345 2 446
2 490
2.021
2.746
10
1.1
1.2
1.3
14
1.5
1.6
1.7
1.8 1.9
2 0
2 25 2.50 2.75
3 0
4.0
5.0
6.0
0 802
0.830
0.857
0.882
o.sOo
0.929
0 951 0.973
0.994 1.014
1.034
1 083 1.130
1. 176 1.221
1.401 1.579 \ 7 57
1.556 1.582 1.607 1.631
1 653
1.675 1.697 1.717 1.737 1.757
1.776
1.795
1.813
1.831
1.849
1.919 1.980 2.051 2. 110
2 ISO
2 340 2.499 2.658 2 817
10.0
10.5 11.0
11.5 12.0
12.5
13.0
13.5
14.0
14.5
15.0
15.5
16.0
17.0
18.0
19.0
20.0
22.6
24.0
26.0
28 0 30 0
34.0 38 0 40 0
45.0 50 0
1.5
1.6
1.7
1.8 1.9
2.0
2
2.4 2.6 2.8
3 0
3.5
4.0
4.5
5.0
5.5
6.0
6.5
7.0
8.0
9 0 Ю 0
0 927 0.948 0.968
0.988 1.007
1.025 1.059 1.09 2 1.123
1. 154
1. 184
1 .255 1.324 1.392 1.400
1.527 1.594 1.660 11727 1.861
1.994
2 127
1,023 1.040 1.056 1..072 1 087
1. 102 1110 1. lJO 1 144 1. 158
1.171 1.197
1.222 1.246 1.209
1. 167 1.180 1. 1-92 1.204 1.215
4.0
4.5
5.0
5.5
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5 10.0 11.0 12.0
13.0 14-0
15.0
16.0
17.0
18.0
19.0 20 0
25.0
30.0
1.275 1 .322 1.364 1-404 1.441
1.477 1.511 1.544 1.576 1.607
1.638 1.668 1.698 1.757
1 815
1.873 1.931 1.988 2.045 2. 103
2 160 2.217 2.274 2.500 2 846
6.0
6.5
7.0
7.5
8.0
8.5 9.0
9.5 10.0 11.0
12.0
13.0
14.0
15.0
16.0
17.0
18.0
19.0
20.0 22.0
24.0 ?6.0 28 0 30 0
1.436 1.470 1.501 1.531 1 559
1.586
1.613
1.638
1663
1.711
1.757 1 801 1 845 1.888 1.931
1.974
2.010 2.058 2. 100 2.184
2.267 2.3.>1 2.434 2.517
8.0
8.5
9.0
9.5 10.0
10.5
11.0
11.5 12.0
12.5
13.0
13.5
14.0
14.5
15.0
17.0
19.0
21.0 23 0
25.0
30.0 35 0
40.0 45 0
2.0
2. 1 2.2
2.3
2.4
2.5
2.6
2.7
2.8 2.9
3.0 3.2
3.4 3.6 3 8
4.0
4.5
5.0
5.5
0.0
7 0
8.0 9.0
10.0
11.0
12.0
13.0
14 0
15 0
3.0
3. 1 3.2 3 3
3.4
3.5
3.6
3.7
3
3.9
4.0 4:2
4 4
4.6
4.8
5.0 5. 5
6.0
6.5
7.0
7.5
8.0 9.0
10.0
110
1-2.0
13.0
14.0 15 0
1.227
238
249
259
270
1.91? 1 943 20. Oj 1.908 22.00 2.017 24. Of 2.063
18.С
19.С
1.281 1.301 1.321 1.340 1.360
1.378
1.424
1.469 K513 1.556
1.598 1.641 1.7Й5 1808 1 892
1 975 2.059
2 142 2 225
2. 108 2 151 2 194 2.236 2.278
2 319 2 360 2 401
2 004 2 806
3 008
26 28 30 32 0 34 0
36 0 38 0 40 0 50 0 60.0
70 0
1 292 1; 349 1.403 1.457 1 510
1 615 1.719 1.823 1.927
2 031
2. 135 2.‘239 2 343 2 447
0,5 + 2/п ЗЯ1 — 4/?4(1п?) — 2/?2-Pl = -ЦТ-Г ~ 4 (/?2 — I)2
где R = гк/гс.
При больших значениях безразмерного времени, которых нет в табл. X. 7 или на графике (рис. X. 9), определять pt можно по уравнению [X. 7]
А (X. 31 в)
Случай VIII. Постоянный дебит. Давление на внешней границе ограниченного пласта поддерживается постоянным. Радиальное течение. Градиент давления при эксплуатации конечного пласта, на границе которого постоянное давление, с постоянным дебитом рассчитывается по уравнению (X. 30), Р, находится по табл. X. 8.
Случай IX. Темп отбора периодически изменяется, причем каждый раз поддерживается свой постоянный дебит. Распределение давления довольно легко рассчитывается на любой момент времени и в том случае, если дебит газа меняется произвольное число раз. Прежде всего рассчитывается изменение давления за все время отбора газа при первом дебите. Затем рассчитывается изменение давления при следующем дебите за весь отрезок времени, прошедший после изменения дебита. Изменение давления при последующих изменениях дебита-рассчитывается по времени, прошедшему после каждого изменения дебита. Затем все изменения давления складываются вместе и в результате получают общее изменение давления по сравнению с начальным распределением давления.
1
= erfc
р1
Изменение давления после двух или более изменений дебита подсчитывается по уравнению
(X. 34)
P(r’() Р„ _ ,тг _ (тз _
где t\ — общее время с начала пуска скважины при первом дебите; f2 — общее время с начала работы скважины при втором дебите; tn — общее время с начала работы скважины при п = м дебите; т\ = первый безразмерный дебит; т2 — второй безразмерный дебит; тп—п-й безразмерный дебит; Рп — член, учитывающий изменение давления в безразмерном виде, определяемый при безразмерном времени tD для времени t\\ Рщ—член, учитывающий изменение давления в безразмерном виде при безразмерном времени tDn для времени tn.
Такой непосредственный расчет общего падения давления для нескольких последовательных периодов, в течение которых скважина работала с постоянными дебитами, прямым сложением, называется методом суперпозиции. Подобным методом можно решать задачи при работе скважины с переменным дебитом. Для этого общее время работы скважины делится на ряд периодов, в пределах которых дебит можно принять постоянным. Подобным же образом можно решать задачи, касающиеся работы скважины при переменном давлении.
(X. 36)
6. АНАЛИТИЧЕСКИЕ РЕШЕНИЯ ЗАДАЧ ТЕЧЕНИЯ ГАЗА С УПРОЩАЮЩИМИ ДОПУЩЕНИЯМИ
Для получения аналитических решений задач по фильтрации газа оказалось необходимым ввести несколько упрощающих допущений. Робертс (Roberts) [X.26] представил решение, в котором для замены р kp
в выражении уравнения линейного течения ис
пользована функция ах+b. Мак Робертс (Mac Roberts) получил аналитическое решение, которое применялось для расчета динамики процесса неустановившейся фазы радиального течения газа. Джанисек и Катц (Janicek and Katz) [X. 18] получили аналитическое решение, сделав допущение, что dp/dt не зависит от радиуса. Если вместо 1/С при определении безразмерного времени применить среднее давление р, тогда предыдущие решения, найденные для малосжимаемых жидкостей, применимы и для случая фильтрации газа [X. 12, X. 13]. Такое допущение не вводит больших ошибок, превышающих ошибки при определении свойств пласта, если, конечно, в пласте не происходит весьма существенных изменений давления. Если же изменения давления в пласте велики, то задачу для уменьшения ошибки надо разделить на несколько частей. Форма решений несколько изменяется, так как вместо давления в уравнениях для жидкости в уравнениях для газа появятся квадраты давления. Значения безразмерного времени и дебита должны рассчитываться по формулам для газа, приведенным в табл. X. 2.
Случай X. Давление на галерее (* = 0) поддерживается постоянным. Линейное течение газа. Этот случай соответствует случаю I для фильтрации жидкости. Для расчета применяется уравнение
Р2 (х, t) — р„
(X. 33)
Р2 -
НК
Случай XI. Дебит галереи поддерживается постоянным. Линейное течение газа. Этот случай подобен случаю II для течения жидкости:
р- (х, t) — pl
• — mPt.
Безразмерное изменение давления Pt определяется по уравнению (X. 24).
Случай XII. На скважине поддерживается постоянное давление. Радиальное течение газа в бесконечном пласте. Основным отличием случая XII от случая IV для жидкости заключается в том, что общая накопленная добыча газа обычно выражается в ж3, замеренная при стандартных условиях, а не в м3 газа в условиях пласта. Соответственно уравнение для выражения общей добычи газа принимает вид:
8,225яФ r\hp
^ = 1Гх-1,бзз'^-р°)^
(Х'35)
Значение Qt находится по табл. X. 4 или по графику на рис. X. 8.
Случай XIII. Постоянный дебит. Радиальное течение газа в бесконечном пласте. Уравнение X. 30, приведенное для решения в случае V применительно к случаю фильтрации газа, видоизменяется. Вместо давления вводятся квадраты давления:
Р- (г, t) - р2л
= — mPf
Рп
Значения Р( берутся из табл. X. 5, графика на рис. X. 9 или вычисляется по уравнению (X. 31).
Случай XIV. На скважине поддерживается постоянное давление. Радиальное течение газа в ограниченном пласте. Методика расчета та же, что и в случае VI, за исключением того, что применяется уравнение (X. 35).
Случай XV. Постоянный дебит. Радиальное течение газа в ограниченном пласте. Этот тип задач решается подобно тому, как решается задача для случая VII, для чего используют уравнение (X. 36) и определяют pt по табл. X. 7, графику на рис. X. 9 или уравнению (X. 31 в).
Случай XVI. Постоянный дебнт. Радиальное течение газа в ограниченном пласте. На внешней границе пласта поддерживается постоянное давление. Эта задача ре-
| R =¦ 1.5 | R а 2.0 | /2-2.5 | /2 — 3.0 | R = 3.5 |
ft = 4.0 | /2 -= 6Д) | |||||||
| Pt |
tD | Pt |
to | Pt |
to | Pt |
tu | Pt |
tu | Pt |
tD | Pt | |
|
6.0 X 10‘* | 0.230 | 2.0 X 10“» | 0 424 | 3.0 x Ю-» | 0.502 | 5.0 X 10‘> |
0.617 | 5.0 X 10-' |
0.020 | 1.0 | 0.802 |
4.0 | 1.275 |
|
в.5 X 10“* | 0 240 | 2.2 X Ю-> | 0 441 | 3.5 X 10-' | 0.535 | 5.5 X 10 » |
0 640 | 6 OX 10 » |
0 665 | 1.2 | 0.857 |
4.5 | 1 320 |
|
в.ОХ 10"* | 0 249 | 2 .4 X 10-» | 0 457 | 4 OX 10-' | 0.564 | 6.0 x io-i |
0.662 | 7 0 X Ю-* | 0 705 | 1.4 | 0.905 |
5.0 | 1 361 |
| 7.0 X 10-» | 0.266 | 2.6 X 10"» | 0 472 | 4.5 X 10"» |
0.591 | 7.0 X 10-» |
0.702 | 8 OX 10-' | 0 741 | 1.6 | 0.947 |
5.5 | 1 398 |
| 8.0 X 10-* | 0.282 | 2.8 X 10'1 | 0.485 | 5.0 X 10"» | 0.616 | 8.0 X ИП | 0.738 | 9 0 X 10-» |
0 774 | 18 | 0.986 |
6.0 | 1.432 |
|
9.0Х Ю"* | 0.292 | З.ОХ 10"» | 0.498 | 5.5 X 10"! | 0.638 | 9 .0 X lO-i | 0 770 | 1.0 | 0 804 | 2.0 | 1.020 |
6.5 | 1 462 |
|
1.0X10-1 | 0.307 | 3 .5 X 10-i | 0.527 | 6.0 X 10"» | 0.659 | 1.0 | 0 799 | 1.2 | 0.858 |
2.2 | 1.052 | 7.0 |
1.490 |
| 1.2 X Ю-» |
0.328 | 4.0 X Ю-i |
0.552 | 7.0 X lO-i | 0.696 | 1.2 | 0 850 |
1.4 | 0.904 | 2.4 |
1.080 | 7.5 | 1.516 |
| 1.4Х10-» | 0.344 | 4.5 X Ю-i | 0.573 |
8.0 X 10-» | 0.728 | 1.4 | 0.892 | 1.6 |
0.945 | 2.6 | 1.106 |
8.0 | 1.539 |
|
1.6 X 10-» | 0.356 | 5.0 X lO-i | 0.591 | 9.0 X 10-» | 0.755 | 1.6 |
0.927 | 1.8 | 0.981 |
2.8 | 1.130 | 8.5 | 1.561 |
| 1.8X10"» | 0.367 | 5.5 X 10"» |
0.606 | 1.0 | 0.778 | 1.8 | 0.-955 |
2.0 | 1.013 | 3.0 |
1.152 | 9.0 | 1 580 |
| 2.0Х 10-1 | 0.375 | 6.0 x io-i | 0.619 |
1.2 | 0.815 | 2.0 |
0.980 | 2.2 | 1.041 | 3.4 | 1.190 | 10 0 | 1 615 |
| 2.2 X 10"1 | 0.381 | 6.5 X Ю-i | 0 630 | 1.4 |
0.842 | 2.2 | 1.000 |
2.4 | 1.065 | 3.8 | 1.222 | 12.0 | 1 667 |
| 2.4 X Ю-» |
0.386 | 7.0 X 10-i | 0 639 | 1.6 | 0.861 |
2.4 | 1.016 | 2.6 |
1.087 | 4.5 | 1 266 | 14.0 | 1 704 |
| 2.6 X 10~» | 0.390 | 7.5 X НИ | 0.647 | 1.8 |
0.876 | 2.6 | 1.030 | 2.8 | 1.106 |
5.0 | 1.290 | 16.0 |
1 730 |
| 2.SXUT» |
0.393 | 8.0 X 10-» | 0 654 | 2.0 | 0.887 |
2.8 | k042 | 3.0 |
1.123 | 5.5 | 1 309 | 18.0 | 1.749 |
| З.ОХ 10"» | t>.396 |
8.5 X Ю-» | 0 660 |
2.2 | 0.895 | 3.0 |
1.051 | 3.5 | 1.158 | 6.0 | 1 325 |
20.0 | 1.762 |
| 3 5Х 10"» | 0.400 |
9.0X10"! | 0 665 | 2.4 | 0.900 | 3.5 |
1.069 | 4 0 | 1.183 |
7.0 | 1 347 | 22 0 | 1 771 |
| 4.0 X 10-» | 0.402 | ».«xio-> |
0 669 | 2.6 | 0.905 |
4.0 | 1.080 | 5.0 | 1.215 | 8.0 | 1 361 | 24.0 | 1.777 |
| 4.5Х10-* | 0.404 |
1.0 | 0.673 | 2.S | 0.908 | 4.5 |
1.087 | 6.0 | 1.232 |
9 0 | 1.370 | 26.0 | 1 781 |
| в.ох ю-» | 0.406 | 1.2 |
0.682 | 3.0 | 0.910 | 5.0 | 1.091 |
7.0 | 1.242 | 10 0 |
1.376 | 28.0 | 1.784 |
| в.0Х 10"» |
0.405 | 1.4 | 0.688 |
3.5 | 0.913 | 5.5 | 1.094 | 8.0 |
1.247 | 12.0 | 1.382 |
30.0 | 1.787 |
|
7.0X10-1 | 0.405 | 1.6 | 0 690 | 4.0 |
0.915 | 6.0 | 1.096 |
9.0 | 1.250 | 14 0 | 1.385 | 35.0 | 1 789 |
| 8.0 X 10"‘ |
0.405 | 1.8 | 0.692 |
4.5 | 0.916 | 6.5 | 1.097 | 10.0 |
1.251 | 16.0 | 1.386 |
40.0 | 1.791 |
| 2.0 | 0.692 |
5.0 | 0.916 | 7.0 | 1.097 | 12 0 |
1.252 | 18.0 | 1 38*» | 50.0 | 1.792 | ||
| 2.5 | 0.693 |
5.5 | 0.916 | 8.0 | 1.098 | 14.0 |
1.253 | ||||||
| 3.0 | 0.693 | 6.0 | 0.916 |
10.0 | 1.099 | 16.0 |
1.253 |
f | |||||
| /2*8.0 | ft = 10 | /2= 15 | /2-20 | ft = 25 | ft = 30 | ||||||
| tD | Pi |
tL> | P. |
Id | Pt |
tD | Pt |
tD | Pt | (d | Pt |
| 7.0 | 1.499 | 10 0 |
1.651 | 20.0 |
1.960 | 30.0 |
2.148 | 60.0 |
2.389 | 70.0 |
2.551 |
| 7.5 |
1.527 | 12.0 |
1.730 | 22.0 |
2.003 | 35.0 |
2.219 | 55.0 |
2.434 | 80.0 |
2.61S |
| &.0 |
1.554 | 14.0 |
1 798 | 24.0 |
2.043 | 40.0 |
2.282 | 60.0 |
2.476 | 90.0 |
2.672 |
| 8.5 |
1.580 | 16 0 |
1.856 | 26.0 |
2.080 | 45.0 |
2.338 | 65.0 |
2.514 | 100 |
2.723 |
| 9.0 |
1.604 | 18 0 |
1.907 | 28.0 |
2.114 | 50.0 |
2.388 | 70.0 |
2.550 | L20 | 2 812 |
| 9.5 |
1-627 | 20 0 |
1.952 | 30.0 |
2.146 | 60.0 |
2.475 | 75.0 |
2.583 | 140 |
2.886 |
| 10 0 |
1.648 | 25 0 |
2.043 | 35.0 |
2.218 | 70.0 |
2.547 | 80.0 |
2.614 | 160 | 2 950 |
| 12.0 |
1.724 | 30 0 | 2 111 | 40.0 |
2.279 | 80.0 |
2.609 | 85.0 | 2 643 | 165 | 2 965 |
| 14.0 |
1.786 | 35 0 |
2.160 | 45.0 |
2.332 | 90.0 |
2.658 | 90.0 |
2.671 | 170 |
2.979 |
| 16.0 |
1.837 | 40 0 |
2.197 | 50.0 |
2.379 | 100 |
2.707 | 95.0 |
2.697 | 175 |
2.992 |
| 18 0 |
1.879 | 45 0 |
2.224 | 60.0 |
2.455 | 105 |
2.728 | 100 |
2.721 | 180' |
3.006 |
| 20 0 |
1-914 | 50.0 |
2.245 | 70.0 |
2.513 | UO |
2.747 | 120 |
2.807 | 200 |
3.054 |
| 22.0 |
1-943 | 55 0 |
2.260 | 80.0 |
2.558 | 115 | 2. >64 | 140 |
2.878 | 250 |
3.150 |
| 24.0 |
1.967 | 60.0 |
2.271 | 90.0 |
2.592 | 120 |
2.781 | 160 |
2.936 | 300 |
3.219 |
| 26.0 |
1.986 | 65.0 |
2.279 | 100 |
2.619 | 125 |
2.796 | 180 |
2.984 | 350 |
3.269 |
| 28.0 |
2 002 | 70 0 |
2.285 | 120 |
2.655 | 130 |
2.810 | 200 |
3.024 | 400 |
3.3QS |
| 30.0 |
2.016 | 75 0 |
2.290 | 140 |
2.677 | 135 |
2.823 | 220 |
3.057 | 450 |
3.332 |
| 35.0 |
2 040 | 80 0 |
2.293 | 160 |
2.689 | 140 |
2.835 | 240 |
3.085 | 500 |
3.351 |
| 40.0 |
2.055 | 90.0 |
2.297 | 180 |
2.697 | 145 |
2.846 | 260 |
3.107 | 600 |
3.375 |
| 45.0 |
2.064 | 100 |
2.300 | 200 |
2.701 | 150 |
2.857 | 280 |
3.126 | 700 |
3.387 |
| 50.0 |
2.070 | UO |
2.301 | 220 |
2.704 | 160 |
2.876 | 300 |
3.142 | 800 |
3.394 |
| 60.0 |
2.076 | 120 |
2.302 | 240 |
2.706 | 180 |
2.906 | 350 |
3.171 | 900 |
3.397 |
| 70.0 |
2.078 | 130 |
2 302 | 260 |
2.707 | 200 |
2.929 | 400 |
3.189 | 1.000 |
3.399 |
| SO 0 |
2.079 | 140 |
2.302 | 280 |
2.707 | 240 |
2.958 | 450 | 3 200 | 1.200 | 3 401 |
| 160 |
2.303 | 300 |
2.708 | 280 |
2.975 | 500 |
3.207 | 1.400 |
3.401 | ||
| 300 |
2.980 | 600 |
3.214 | ||||||||
|
400 | 2.992 |
700 | 3.217 | ||||||||
| 500 |
2.995 | 800 |
3.218 | ||||||||
| 900 | 3 219 | ||||||||||
| ft =* 40 |
/2-50 | /2-60 |
/2 = 70 | ?-80 |
?«90 | /2-100 |
/2-200 | /2-300 |
/2-400 | /2-500 | /2-600 | /2-700 |
|||||||||||||
| tD | Pt |
tD | P< |
tD | Pt |
tD | Pt |
tD | Pt |
tD | Pt |
tD | Pt |
tD | Pt |
tD | Pt |
tD | Pt |
lD | Р, |
Pt | tD |
Р, | |
| 120 |
2 813 | 200 | 3.064 |
3.0 x 10* | 3 257 | 5.0 X 10» | 3.512 | 6.0 X Ю» | 3.603 | 8 .0 X 10* |
3.747 | 1 OX 10» | 3.859 | 15 X 10» | 4 061 |
6 .0 x 103 | 4 754 |
1.5 X НИ | 5.212 | 2.0 X НИ | 5.356 | 4.0 X 10* |
5 703 | 5 0 X НИ | 5 814 |
| 140 | 2.888 | 220 | 3.111 | 4.0 x Ю» | 3 401 | 6 .0 X 10» | 3.603 | 7.0-X 10» |
3.680 | 9 .0 X 10* | 3.806 | 1.2 X 10* | 3.949 |
2 0 X 10s | 4 205 | 8 .0 X 10* | 4 898 | 2 .0 X 10* | 5 356 | 2.5 X НИ |
5.468 | 4.5 X НИ | 5.762 | 6 0 X 10' | 5 905 |
| 160 | 2.953 |
240 | 3.154 | 5 .0 X Юз | 3 512 | 7.0 X 10* |
3.680 | 8.0 X Ю» | 3.747 | 1.0 X 10* | 3.858 |
1.4 X 10* | 4 026 | 2 5 X 10s | 4 317 | 10 .0 X 10» | 5 010 | 3.0 X 10* | 5 556 | 3.0 х ни |
5.559 | 5.0 X | 5 814 | 7 0 X 10' | 5 982 |
| 180 | 3.011 |
260 | 3.193 | 6.OX 10* | 3,602 | 8.0 X 10» |
3.746 | 9 .0 X 10» | 3.805 | 12 X Ю3 | 3.949 |
1.6 X 10* | 4.092 | 3.0 x ioj | 4 408 | 12.0 X 10» | 5 101 | 4 .0 X НИ | 5 689 | 3.5 X 10* |
5.636 | 6.0 X Ю' |
5.904 | 8 .0 X НИ | 6 048 |
| 200 | 3.063 |
280 | 3.229 | 7.0 X 10* | 3.676 | 9.0 X 10» |
3.803 | 10.0 X 10» |
3.857 | 1.3 X 10J |
3.988 | 18 X 10* | 4 150 | 3 5 X 10» | 4 485 |
14 0 X 10» | 5.177 | 5.0 X 10« | » 781 | 4.0 X НИ | 5.-702 | 7.0 X 10' |
5.979 | 9 0 X 10* | 6 105 |
| 220 | 3.109 |
300 | 3.263 | 8.OX 10s | 3 739 | 10 .0 X 10» | 3.854 | 12 .0 X 10» | 3.946 | 1.4 X 10* |
4.025 | 2 .0 X 10» | 4 200 | 4 OX 10» | 4 552 |
16 0 X ioj | 5 242 | 6 0 X 10* | 5.845 | 4.5 X 10* | 5 759 | 8.0 X 10' | 6.041 | 10 0 X Ю' |
6 156 |
| 240 |
3.152 | 350 | 3 339 |
9 OX lf»a | 3.792 |
12 .0 X 10* | 3.937 | 14,0 X 10* | 4.019 | 15 X 10* |
4 058 | 2 .5 X 10* | 4 303 | 5 0 X 103 | 4 663 | 18 0 X 10» | 5,299 | 7 0 X НИ | 5.889 |
5 .0 X НИ | 5.810 | 9 0 X Ю4 | 6.094 | 12 0 X 10* | 6 239 |
| 260 | 3.191 | 400 |
3.405 | 10.0 X IP | 3.832 | 14.0.X 10* | 4.003 |
15 .0 X 10» | 4.051 | 1.8 X 10J | 4 144 | 3 .0 X 10* | 4 379 | 6 0 X 103 | 4 754 | 20 0 X 10» | 5.348 | 8 0 X НИ | 5.920 | 6 0 X 10* |
5 894 | 10.0 X Ю4 |
6.139 | 14 .0 X НИ | б 305 |
| 230 | 3.226 |
450 | 3.461 | 12.OX 10s | 3.908 | 16.0 X 10» | 4.054 | 16.0 X 10» | 4.080 | 2.0 X 10J |
4.192 | 3 .5 X 10* |
4.434 | 7 0 X 10J |
4.829 | 24 .0 X 10» | 5.429 | 9 0 X Ю' | 5.942 |
7 .0 X НИ | 5 960 | 12.0 X НИ | 6.210 | 16 0 X 10» | 6.357 |
| 300 |
3.259 | 500 | 3.512 | 14 .0 X 10’ | 3.959 |
18.0 X 10» | 4.095 | 18.0 X 10* | 4.130 | 2 .5 X 10* |
4.285 | 4.0 X 10* |
4.478 | 8 .0 X 103 | 4 894 | 28 .0 X 10» | 5.491 | 10 0 x ни | 5.957 |
8.0 X 10* | 6 013 | 14.0 X 10* | 6.262 | 18.0 X 10* | 6.398 |
|
350 | 3.331 | 550 |
3.556 | 16.0 X 103 |
3.996 | 20.0 X 10* | 4.127 | 20.0 X 10» | 4.171 |
3 .0 X 10* | 4.349 | 4 .5 X 10* | 4.510 | 9 .0 X 10* |
4 94Q | 30 .0 X 10» | 5 517 | 11.0 X ни | 5.967 | 9.0 X НИ | 6.055 |
16.0 X ни | 6.299 | 20.0 X НИ | 6 430 |
| 400 | 3.391 | 600 |
3.595 | 18.0 X 10» | 4.023 | 25.0 X 10» | 4,181 |
25.0 X 10* | 4.248 | 3.5 X Ю3 | 4 394 | 5.0 X 10* | 4 534 | 10 OX 10* |
4.996 | 40.0 X 10» | 5 606 | 12.0 X НИ | 5 97Г | 10 .0 X ИИ | 6 088 |
18.0 X 10' | 6 326 | 25.0 X НИ | 6 484 |
| 450 | 3.440 | 650 |
3.630 | 20.0 X 10* | 4.043 | 30.0 X 10» | 4.211 |
30.0 X 10» | 4.297 | 4 .0 X 10J | 4 426 | 5 .5 X 10* | 4.552 | 12 0 X 10* |
5.072 | 50 0 X 10» | 5 652 | 12 .5 X НИ | 5 977 | 12 0 X НИ | 6.135 |
20 .0 X НИ | 6.345 | 30 .0 X НИ | 6 514 |
| 500 | 3.482 | 700 |
3.661 | 25.0 X 10* | 4.071 | 35.0 X 10* | 4.228 |
35.0 X 10» | 4.328 | 4 .5 X 103 | ¦I 448 | 6 .0 X 10* | 4.565 | 14 0 X IP |
5.129 | 60 0 X 10» | 5 676 | 13 .0 х ни | 5 980 | 14 0 X 10* | 6.164 |
25 0 X Ю' | 6.374 | 35.0 X НИ | 6 530 |
| 550 | 3.516 | 750 |
3.688 | 30 .0 X 10» | 4 084 | 40.0 X-10» | 4.237 |
40. OX 10» | 4.347 | 5.OX 10> | 4 464 | 6.5 X 10* | 4.579 | 16 0 X 10= |
5.171 | 70 .0 X 10» | 5.690 | 14 .0 X НИ | 5.983 |
16 0 X НИ | 6 183 | 30 0 X 10' | 6.387 | 40.0 X 10' |
6.540 |
| 600 |
3.545 | 800 | 3.713 |
35.0 X 10» | 4.090 | 45.0 X 10» | 4.242 | 45.0 X 10» | 4.360 | 6 .0 X 10* |
4.482 | 7 .0 X 10» | 4.583 | 18.0 X 10= | 5.203 |
80 .0 X 10» | 5 696 | 16 .0 х ни | 5.988 | 18 .0 X 10* | 6.195 | 35.0 Х-Ю' | 6.392 | 45.0 X НИ |
6.545 |
| €50 |
3.568 | 850 | 3 735 |
40.0 X 10» | 4.092 | 50.0 X 10» | 4.245 | 50.0 X 10» | 4.368 | 7 .0 X 10* |
4.491 | 7.5 X 10» | 4.588 | 20 .0 X 103 | 5.227 | 90.0 X 10» | 5.700 |
18.0 X НИ | 5.990 | 20 .0 X НИ | 6.202 | 40.0 X НИ | 6.395 | 50.0 X 10' |
6.543 |
| 700 |
3.588 | 900 | 3 754 |
45.0 X 10» | 4.093 | 55.0 X 10» | 4.247 | 60.OX 10» | 4.376 | 8.0 X 10* |
4 496 | 8 0 X 10* | 4.593 | 25 0 X 103 | 5.264 | 10 .0 X 10* | 5.702 |
20 .0 X НИ | 5 991 | 25 .0 X НИ | 6.2U | 50.0 X 10' |
6.397 | 60.0 X НИ |
6.550 |
| 800 |
3.619 | 950 | 3.771 |
50.0 X 10» | 4.094 | 60.0 X 10» | 4.247 | 70.0 X 10» | 4.380 | 9.0 X 10* |
4.498 | 9.0 X Ю1 |
4.598 | 30.0 X io> | 5.282 | 12.0 X 10* | 5 703 |
24.0 X НИ | 5.991 | 30 .0 X НИ | 6.213 | 60.0 X 1<И | 6.397 | 70.0 X НИ |
6.551 |
| 900 |
3.640 | 1.000 | 3-787 |
55.0 X 10» | 4.094 |
65.0 X 10» | 4.248 | 80.0 X 10» | 4.381 | 10 .0 X 10* | 4.499 | 10 .0 X Ю3 | 4.601 | 35 0 X 10» |
,5 290 | 14 .0 X НИ | 5 704 | 26.0 X 10' | 5.991 |
35 .0 X НИ | 6.214 | 80.0 X НИ | 6.551 |
||
| 1,000 | 3.655 |
1.200 | 3.833 | 70.0 X 10* | 4.2:48 | 90.0 X 10* | 4.382 | 11.0 X 103 | 4.499 | 12.5 X 10» | 4.604 | 40.0 X 10* | 5 294 | 15.0 X НИ |
5.704 | 40 .0 X НИ | 6 214 | ||||||||
| 1,200 | 3.572 | 1.400 | 3.862 | 75.0 X 10» | 4.248 |
10.0X10» | 4.382 | 12.0 X 103 | 4.500 | 15.0 X 10» | 4.605 | ||||||||||||||
| 1,400 | 3.681 | 1,600 |
3.881 | 80.0 X 10» |
4.248 | 11.OX 10» |
4.382 | 14 .0 X 10* | 4.500 | ||||||||||||||||
| 1,600 |
3.685 | 1,800 | 3.892 |
||||||||||||||||||||||
| 1.800 | 3.687 | 2,000 |
3.900 | ||||||||||||||||||||||
|
2,000 | 3.688 | 2,200 |
3.904 | ||||||||||||||||||||||
| 2,500 | 3.689 |
2,400 | 3.907 | ||||||||||||||||||||||
| 2,600 | 3.909 | ||||||||||||||||||||||||
| 2,800 |
3.910 | ||||||||||||||||||||||||
|
в — 800 | R = 900 | R = 1,000 | R = 1.200 | R = 1.400 | R = 1.600 | R - 1,800 | ft = 2.000 |
R - 2,200 | ft = 2,400 |
R = 2,600 | R = 2,800 | R = 3.000 | |||||||||||||
| Id | Р, |
Р, | tn |
Pi | tn |
Pi | in |
P, | to |
P, | to |
Pt | tn |
P, | to |
P, | to |
P, | to |
p, | to |
P, | Id |
Pt | |
| 7.ОХ 10* |
5 983 | 8 ОХ Ю* | 6 049 | I ОХ 10* | 6 161 |
2 OX 10s | 6 507 | 2 0 X 10* | 6 507 | 2 5 X 10* | 6.619 | 3 0 X 10* |
6 710 | 4.0 X 10* | 6.854 | 5 0 X 10* | 6.966 |
6 .0 X 10* | 7 057 | 7 .0 X 10* | 7.134 | 8 0 X 10* |
7.201 | 10 X 10е |
7 312 |
| 8 ОХ Ю4 | 6 049 | 9 ОХ Ю* |
6 108 | 1 2 х 10* | 6 252 | 3 0 X 10* | 6 704 |
2 5 X Iff | 6 619 | 3 0 X 10* | 6 710 | 4 0 X 10* |
6.854 | 5 0 X 10* | 6 966 | 5 5 X 10* | 7 013 |
7 0 X 10* | 7.134 | 8 .0 X 10* | 7.201 | 9 0 X 10* |
7.260 | 1 2 X 10й |
7 403 |
| 9.0 X 10* |
6.108 | 10 0 X 10* | 6 161 | 1.4 X 10s | 6 329 | 4 .0 X 10* | 6.833 |
3 0 X 10* | 6 709 | 3 5 X 10* | 6 787 | 5 0 X 10* | 6.965 | 6 0 X 10* |
7 056 | 6 0 X 10* | 7 057 | 8 .0 X 10* | 7.200 |
9 0 X 10* | 7,259 | 10 0 x 10* | 7.312 | 1.4 X 10е | 7,480 |
|
10 ох | 6.160 | 12 .0 X 10* | 6.251 | 1 6 X 10* |
6 395 | 5.OX 10* | 6.918 | 3 5 X 10* | 6 785 |
4 0 X 10* | 6 853 | 6 0 X 10* | 7.054 | 7 0 X 10* |
7 132 | 6 5 X 10* | 7.097 | 9 .0 X 10* | 7.259 |
10 0 X 10* | 7.312 | 12 .0 X 10* | 7.403 | 1 6 X 10» |
7 545 |
| 12.ОХ 10* |
6 249 | 14 0 X 10* | 6 327 | 1.8 X 10* | 6 452 |
6 0 X IO6 | 6 975 |
4 0 X 10* | 6 849 | 5 .0 X 10* | 6 962 | 7 0 X JO* |
7 120 | 8 0 X 10* | 7 196 | 7 0 X 10* | 7.133 |
10 0 X 10* | 7.3Ю | 12 .0 x 10* | 7.401 | 16 0 X 10* | 7.542 | 18 X 10» |
7 602 |
| 14 ОХ 10* |
6*322 | 16 о х ю* | 6 392 | 2 0 X 10* | 6.503 |
7 OX JO6 | 7 013 | 5 0 X 10* | 6.950 | 6 OX 10* |
7.046 | 8 0 X 10* |
7.188 | 9 0 X 10* | 7 251 | 7 5 X 10* | 7.167 |
12 .0 X 10* | 7.398 | 14 0 X 10* | 7.475 | 20.0 X 10* |
7.644 | 2 0 X 10е |
7 651 |
| 16 0 х io<;6.;kS2 | 18 ОХ 10* | 6 447 | 2 5 X 106 | 6.605 |
8 OX 10* | 7.038 | 6.OX 10* | 7.026 | 7 OX 10* |
7.114 | 9 0 X 10* |
7.238 | 10 0 X 10* | 7 298 | 8 0 X 10* | 7.199 |
16 0 X 10* | 7.526 | 16 0 X 10* | 7.536 | 24 0 X 10* |
7 719 | 2 .4 X 10е |
7.732 | |
| 18 ОХ 10* |
6 432 | 20 0 X 10* |
6.494 | 3 Ох 10* | 6 681 | 9 0 X 10* | 7.056 |
7 OX 10* | 7.082 | 8 .0 X 10* | 7.167 | 10 0 X 10* |
7.280 | 12 0 X IO | 7 374 | 8 .5 X 10* | 7 229 |
20 0 X 10* | 7611 | 18 0 X 10* | 7.588 | 28 .0 X 10* | 7.775 | 2 .S X 10» |
7.794 |
| 20 ОХ Ю* |
6 474 | 25 0 X 10* | в. 587 | 3 .5 х 10* | 6 738 |
10 0 X 10* | 7.0^7 | 8.OX 10* | 7.123 | 9 .0 X 10* |
7.310 | 15 0 X 10* | 7 407 | 14 0 X 10* | 7 431 |
9 0 X 10* | 7.256 | 24 .0 X 10* | 7.668 | 20 0 X 10* | 7.631 | 30 .0 X 10* |
7.797 | 3 .0 X 1C* | 7 820 |
| 25 ОХ Ю1 | 6 551 | 30 0 X 10* | 6.652 |
4 0 X 10* | 6 781 | 12 0 X 10* | 7 080 | 9 OX 10* |
7.154 | .10 0 X 10* |
7.244 | 20 0 X 10* | 7.459 | 16 0 X 10* | 7 474 |
10 0 X 10* | 7 307 | 28 0 X 10* | 7.706 | 24 0 X 10* |
7.699 | 35 0 X 10* |
7.840 | 3.5 X 10е |
7.871 |
| 30 ОХ ю* |
6 599 | 40 0 X 10* | 6 729 | 4 .5 X 10* | 6 813 |
14 OX 10* | 7 085 | 10 0 X 10* | 7.177 | 15 0 X 10* |
7.334 | 30 0 x 10* |
7.489 | 18 0 X 10* | 7 506 | 12 0 X 10* | 7.390 |
30 .0 X 10* | 7.720 | 28.0 X 10* | 7.746 | 40 0 X 10* |
7 870 | 4 ,0 X 10е |
7.908 |
| 35 ОХ №4 | 6 630 | 45.0 X 10* |
6 751 | 5 0 X 10* | 6 837 | 16 0 X 10* | 7.088 |
15 OX 10* | 7.229 | 20.0 X 10* | 7.364 | 40 0 x 10* |
7,495 | 20 0 X 10* | 7 530 | 16 0 X 10* | 7.507 |
35 0 X 10* | 7.745 | 30 0 X 10* | 7.765 | 50 0 X 10* | 7.905 | 4 .5 X 10е | 7 935 |
| 40.0 X Ю* | 6 650 | 50 ОХ Ю* |
6 766 | 5 .5 X Ю* | 6 854 | 18 OX 10* | 7 089 |
20 0 X 10* | 7.241 | 25 .0 X 10* | 7.373 | 50 0 X 10* |
7.495 | 25 0 X 10* | 7 566 | 20 0 X 10* | 7 579 |
40 0 X 10* | 7 760 | 35 0 X 10* | 7.799 | 60 0 X 10* | 7,922 | 5 0 X 10е | 7 955 |
| 45 ОХ Ю* | 6 663 | 55 ОХ 10* |
6 777 | 6 0 X 10* | 6 868 | 19 0 X 10* | 7.089 |
25 .0 X 10* | 7.243 | 30 .0 X 10* | 7.376 | 51.0 X 10* |
7. $95 | 30 0 X 10* |
7.584 | 25 0 X 10* | 7 631 | 50 0 X IO6 | 7 775 | 40 0 X 10* | 7.821 |
70 .0 X 10* | 7.930 | 6 0 X 10е | 7.979 |
|
50.ОХ Ю* | 6.671 | ¦60 о X 10* | 6.785 | 7 ОХ 10* |
6 885 | .20 OX 10* |
7.090 | 30 0 X 10* | 7.244 | 35 0 X 10* | 7.377 |
52 .0 X 10* | 7.495 | 35 0 X 10* | 7.593 | 30 0 X 10* |
7 661 | 60 0 X 10* |
7.780 | 50 0 X 10* | 7 845 | 80 0 X 10* | 7.934 |
7 .0 X 10е | 7.992 |
| 55 ОХ 10* | 6 676 | 70 Ох 10* | 6.794 | 8 0 X 10s | 6 895 | 21 0 X 104 | 7 090 | 31 0 X 10* | 7.244 | 40 .0 X 10* | 7 378 | 53 0 X 10* |
7.495 | 40 .0 X 10* | 7.597 | 35 0 X 10* | 7.677 |
70 0 X 10* | 7 782 | 60 0 X 10* | 7.856 | 90 0 X 10* |
7.936 | 8 0 X 10е |
7.999 |
| 60.0 X ю* |
6.679 | 80.0 X 10* |
6.798 | 9 ОХ 10* | 6.901 | 22 0 X 10* | 7 090 |
32 0 X 10* | 7.244 | 42 0 X 10* | 7 378 | 54 0 X 10* |
7.495 | 50 0 X 10* | 7 600 | 40 0 X 10* | 7.686 |
80 0 X 10* | 7 783 | 70 0 X 10* | 7.860 | 10 0 X 10* | 7.&37 | 9 0 X 10е | 8.002 |
| 70.ОХ 10* | 6.682 | 90.0 X 10* | 6.800 | 10 0 X 10* |
6.904 | 23 0 X 10* |
7,090 | 33 0 X 10* |
7.244 | 44 .0 X 10* | 7.378 | 56 0 X 10* | 7.495 |
60 0 X 10* | 7.601 | 50 0 X 10* | 7.693 | 90 .0 X 10* | 7.783 | 80 0 X 10* | 7.862 | 12 0 X 10* | 7.937 | 10 0 X 10е | 8 004 |
| 80 ОХ Ю* | 6.684 |
10 .0 X 10ь | 6.801 |
12 .0 X 10* | ft 907 |
24 OX IO6 | 7 090 |
64 0 X 10s | 7 fiOl |
60 .0 X 10* | 7.695 | 95 .0 X 10* | 7,78.3 | 90 0 X 10* | 7.863 | 13 OX 10* |
7 937 | 12 0 X 10е |
8.00*5 | ||||||
| 00.Ох ю* |
в 684 | 14.0 X 10“ | 6.907 | 70 0 X 10* | 7 696 | 10 0 x 10е |
7 863 | 15 0 X 10е | 8 006 | ||||||||||||||||
| 16 Г» х I06 | 6 909 | 80 0 X 10* | 7.696 | ||||||||||||||||||||||
шается так же, как и задача для случая VIII, при помощи уравнения (X. 36) и значения pt из табл. X. 8.
Случай XVII. Темп отбора периодически изменяется, но дебит каждый раз постоянный. Для случая фильтрации газа уравнение (X. 32) принимает вид:
dtr
1
= тхРи + (т2 — mt) Ри +
Ра (г, t)-p* Рп
+ (ma — m2) Pu + . . . + (m„ — m„ _ x)Ptn. (X. 37)
Обозначения те же, что и в уравнении (X. 32).
7. РЕШЕНИЕ ЗАДАЧ ПО ФИЛЬТРАЦИИ ГАЗА МЕТОДОМ СМЕНЫ СТАЦИОНАРНЫХ СОСТОЯНИИ
2m
Джанисек и Катц (Janicek and Katz) [X. 18] получили решения уравнений неустановившегося радиального течения газа, принимая, что dp/dt в любой данный момент не зависит от радиуса. Это допущение было названо Маскетом (Muskat) [1.11] «предположением смены стационарных состояний» и применялось для решения задач Метьюзом, Бронсом и Хазбруком (Matthews, Brons and Hazebrock) [X. 22]. Такое предположение наиболее приемлемо для ограниченных пластов, когда воронка депрессии скважины, работающей с постоянным дебитом, достигла границы пласта. Полученные Джани-секом и Катцем для этих условий решения затем были применены к бесконечным пластам по аналогии с более точными решениями. Ценность полученных Джанисеком и Катцем решений заключается в их математической простоте, которая во многих задачах позволяет легко понять существо явления, что невозможно при более строгом математическом описании.
рг_pz —-
п с — 2
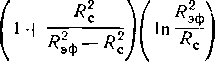
Уравнение для неустановившегося радиального течения газа (X. 14) можно переписать в виде
dp2 kp d2p2
(X. 38)
dt цФг2 д (Inг)2
Уравнение (X. 44) выражает темп падения давления в точке с любым значением радиуса для любого безразмерного дебита т и эффективного радиуса дренирования Ra ф.
Значение dP^/dtD. найденное из уравнения (X. 44), теперь можно подставлять в уравнение (X. 40). В результате получим выражение для градиента давления в любой момент времени
dP2
. . D. ,,----- Г R4 (In R) = т (1 - - ~L\ ,
ddntf) ( /?2 J
(X. 45) (X. 46)
где
Рп = Рп/Рп=1 и tfc = rc/rc= 1-
В этом уравнении для конечных пластов, когда градиент давления {воронка депрессии) достигает границы пласта, значение О равно единице. Для бесконечных пластов или для тех случаев, когда эффективный радиус дренирования еще не достиг внешней границы пласта, 6=постоянной Эйлера=0,5772.
Джанисек и Катц с помощью указанных методов получили ряд других уравнений для неустановившегося течения газа. Рассматривая фильтрацию газа в бесконечном пласте, они получили уравнение для оценки изменения давления в стволе скважины во времени
(X. 47)
дР2
dt п
(X. 39)
(X. 48)
Если использовать безразмерные значения Р = р/рП1 R = /-/г,, и tD = kpt/^Фг2, то уравнение (X. 38) можно
J_ д2Р2R2 a (Ini?)2 •
записать в виде
Pl-Pl=2 ln(4/De-4l). Эффективный радиус дренирования
D’
Принимая, что dP2/dtD не зависит от R, уравнение (X. 39) можно переписать в виде дР2 1 d2P2
dtD _ R2 d(Ini?)2 • (X> 40)
Граничные условия для случая постоянного дебита запишутся в следующем виде:
dP*
(Х.41)
т при R = 1.
d (Ini?)
Граничные условия на границе пласта записываются
в виде
Это уравнение подобно, но не идентично выражению, данному Мак Робертсом (Mac Roberts) [X. 21].
Чтобы найти отношение кажущегося или установившегося радиуса дренирования к эффективному радиусу дренирования, Джанисек и Катц предлагают применять отношение 0,749 для случая, когда эффективный радиус дренирования продолжает распространяться, и 0,606, когда эффективный радиус дренирования становится постоянным, достигнув границы пласта.
После того как эффективный радиус дренирования достиг границы пласта, что рассчитывается по уравнению (X. 48), и дальше не распространяется, падение давления во времени определяется по уравнению
d?2 dt
>2 р D .)
dP2 ' d (Ini?)
(X. 43)
d(lntf) г" ¦' "'эф’ (Х-42)
где Rэф представляет собой отношение упомина
емое раньше. Уравнение (X. 40) можно проинтегрировать в пределах R = 1 и R = ^эф:
^эф
= 0 при R = R
R4 (1п?) =
R - 1
сэф
где р П1— абсолютное давление в пласте в точке гк и в момент времени /к в ат; рПг— абсолютное давление в пласте в точке гк и в момент времени t в ат; t — общее время работы скважины в ч; гк — радиус внешней границы области, дренируемой скважиной, в м.\ z, Т, h, Ф и Q — в обычных промысловых единицах.
(X. 49)
Применяя к этим уравнениям принцип суперпозиции, получим уравнение для экстраполяции кривых восстановления давления при закрытии скважин
0,5143цгГ 0,000785kp (/а — tj
---lg---(х- 5°J
hk
где рс, — абсолютное давление на скважнне в момент ее закрытия (/1) в ат; рс2 —абсолютное давление на скважине в момент времени t% в ат\ Qi- — постоянный дебит скважины перед ее закрытием, т. е. в момент времени /1 (в ч), в м^/сутки, j-u z, Г, h, k, р, и гс — в обычных промысловых единицах.
8. УРАВНЕНИЯ В КОНЕЧНЫХ РАЗНОСТЯХ
Уравнения неустановившегося течения можно решать путем использования конечных приращений давления, расстояния и времени вместо дифференциалов dp, dx и dt. Уравнение в частных производных, написанное для таких конечных приращений, называется уравнением в конечных разностях. Уравнение в частных производных вначале преобразуется таким образом, что все чайные производные по расстоянию группируются иа одной стороне, а все частные производные но времени — на другой. Тогда по известному распределению давления от расстояния в начальный момент находится изменение давления в зависимости от расстояния для малых приращений расстояния и используется в уравнении для определения изменения давления при соответствующем приращении времени. Таким образом, кривую распределения давления в последующие моменты времени можно рассчитать путем последовательных операций, и решить уравнение неустановившегося течения газа. Частные производные давления по времени для какого-то фиксированного расстояния выражаются уравнением
(X. 54)
р\т — Дг, t) +
+ ( 1 + 2;) р2 = (^ + Д'-. О
др2 Др2 р2 (х, t + At)-~dt = ДГ = ДТ~
-Рг (x,t)
(X. 51)
Приведенные производные являются производными, в которых х в качестве переменной не фигурирует, так как в обоих случаях р2 оценивается для той же самой точки х. Значение р2 определяется для времени t и /+Д/. Таким образом, выражение в правой части уравнения (X. 51) является частной производной по времени в точке х.
Вторые производные выражаются таким же образом. В качестве примера приводятся частные производные по х при постоянном значении
д-рг Д (Др2) [р2 (х + Дх, /) — р2(х, /)] —
дх'1 (Дх)2 (Л*)2
— [р2 (х, /) — р2 (х — Дх, /) р2 (х + Дх, /) —
(Дх)2 ~ (Дх)2
- 2р2 (х, /) + р2 (к — Дх, /) (Дх)а
(X. 52)
Уравнение (X. 14) для неустановившегося радиального течения газа, выраженное через приведенные выше соотношения конечных разностей, принимает вид
Д tko
(*-2})р2(г-Ьг,0 +
,/)]. (X. 53)
р* (г. t + At)=
(Дг) 2цФ + (1 + ?)рг =(г + Лг
9. ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
Графический метод Шмидта, который широко используется для описания неустановившихся процессов теплопроводности, был применен [X. 11] для решения задач неустановившейся фильтрации газа. Этот метод довольно разносторонний и может использоваться для решения многих задач, включающих различные граничные условия. Можно применять его при решении различных промысловых задач. Для этого метода требуется минимальный математический аппарат и не нужны дорогие счетные машины.
В коэффициенте правой части уравнения (X. 14) предполагается постоянное среднее давление р. Значение приращения времени At выбирается таким образом, что составляет от У20 до 7м общего времени периода неустановившегося течения, который следует рассчитывать, и определяется Дг из уравнения
_ (Дг)уФп _ 2 kp
Используя значение Д г, полученное из уравнения (X. 54), уравнение (X. 53) можно написать в виде
Р2 (Г, / + Д/) = !/2
(X. 55)
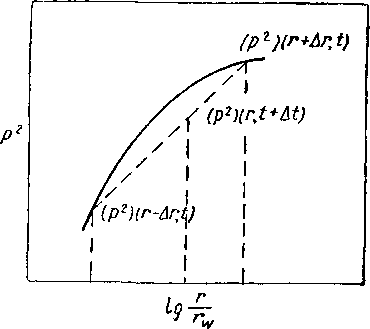
Рис. X. 10. Графическое решение задачи о неустановившемся радиальном течении [X. 11].
При помощи уравнения (X. 55) можно рассчитать неустановившееся радиальное течение, что иллюстрируется на графике (рис. X. 10). Этот график, если построить кривую р2 от lg(r/rc) для какого-то момента времени, выражает градиент давления. На графике проводятся три вертикальные линии, отстоящие друг от друга на расстоянии Д г. Пересечение линии, проведенной из точки р2(г—Дr,t) до р2(г+Дг,/), с вертикальной линией, соответствующей г, дает значение р2 при данном г через интервал времени At после первоначального градиента давления. Таким путем определяется полный градиент давления в последующие моменты времени и решается уравнение неустановившегося течения. Этот графический метод расчета, основан-
Рис. X. 11. Графическое определение градиентов пластового давления при смене темпа отбора жидкости (при постоянном дебите) [X. II].
/ — линии построения: //— конечный гради
ент давления; III —область влияния отклонения от закона Дарсн.
ный на применении уравнения (X. 55) можно свести к вычислению средневзвешенного давления в двух точках, отстоящих друг от друга на расстоянии 2Дг, по которым находится давление в более позднее время. Коэффициент взвешивания, как это видно из уравнения (X. 55), должен быть обратно пропорционален г.
Целесообразность применения логарифмической шкалы для г вытекает из графического расчета, ибо d(\nr) =dr/r и Д(1п г) =Дг/г.
Графические расчеты для периода неустановившегося течения при неизменной вязкости жидкости (газа) в бесконечном пласте, имеющем первоначально равномерно распределенное давление, выполняются, как следует ниже, для того, чтобы рассчитать градиент давления в пласте к концу переходного периода. Для этого необходимо зиать значения ft, Л, рп,1х, Ф. г. Т\ Q, р и гс.. Необходимо заранее считать среднее давление в возмущенной части пласта, чтобы определить ц, г и р. Затем берется лист полулогарифмической бумаги с соответствующим масштабом значений р2 на линейной шкале (ординате) и г на логарифмической шкале (абсциссе). Применяя уравнение (X. 54), можно выбирать значения Д* и Дг, после чего чертятся вертикальные линии, соответствующие г = Дг, 2 Дг, ЗДг и т. д., до 10Дг или 20 Д г в зависимости от желаемой точности. На рис. X. 11 показана такая диаграмма.
Затем из уравнения (X. 2) путем подстановки р\ = =рп, = 2 Дг и гг = гс определяется градиент давления при установившейся фильтрации. Значение pf, ко-
2
торое в этом случае является рс , вычисляется из уравнения (X. 2) и откладывается против г=гс. В результате получается линия, подобная линии I—I на рис. X. 11. Наклон этой линии соответствует градиенту давления при установившейся фильтрации. Все линии, соответствующие другим градиентам давления при установившейся фильтрации, для этого же значения дебита будут параллельны этой линии.
Как это видно из графика на рис. X. 10, давление в точках гс, Дг и ЗДг через интервал времени А/ со-^ ответствует точкам 2—2 на рис. X. 11. Через интервал времени 2Дt градиент давления дан точками 3—3 на рис. X. 11. Следует заметить, что наклон градиента давления вблизи ствола скважины всегда является наклоном, соответствующим установившемуся течению, и что влияние неустановившейся фильтрации проявляется в том, что изменяется наклон кривой, выражающей градиент давления, в точках на некотором удалении от скважины. Вычисления подобным же образом продолжаются до тех пор, пока не будет просчитано нужное время переходного периода.
Иногда необходимо в распределение градиента давления установившегося течения по закону Дарси ввести поправку на его отклонение вблизи ствола скважины, что делается при помощи уравнения (X. 56), которое выведено из уравнения (X. 5) для радиального течения:
— (г2 -г2 )- 3’038 X 10 хгГ TfQ,JP (Y ВД)
Это уравнение получено вычитанием уравнения, выражающего давление при условиях течения по закону Дарси, из подобного уравнения с учетом отклонения от закона Дарси. При этом значением 1/гь которое, видимо, мало по сравнению с 1 /г2, пренебрегаем. Введение поправки, учитывающей отклонение от закона Дарси, которая вычисляется по уравнению (X. 56), показано на рис. X. 11.
На рис. X. 12 показана методика расчета двух последовательных периодов. В конце первого переходного периода, в течение которого скважина работала с постоянным дебитом, наклон кривой градиента давления установившегося течения вблизи ствола скважины изменяется до наклона, соответствующего новому деби ¦ ту, и расчет продолжается по той же методике, по которой производился и до изменения дебита.
Рис. X. 12. Графическое определение градиентов пластового давления при смене темпа отбора жидкости (при постоянном дебите), причем g2>gi [X. 11]. Обозначения те же, что на рис. X. 11.
На рие. X. 13 иллюстрируется прием, который применяется для случая ограниченного пласта, имеющего непроницаемую внешнюю границу. В других отношениях расчет проводится, как и в предыдущих случаях.
Рис. X. 13. Графическое определение градиента пластового давления при постоянном темпе отбора в бесконечном пласте [X. II].
= 0,01,
1хФг2с
0,922
/ — построение; 2 — окончательное значение градиента.
\Ри
(из рис. X. 15) _
При последовательно изменяемых дебитах наклон кривой градиента установившегося течения вблизи ствола скважины изменяется так, что он соответствует измененному дебиту. Корнелл (Cornell) [X. 10] дал примерную задачу, включающую четыре последовательных увеличения дебита с поправкой на отклонение от закона Дарси. На рис. X. 14 приведена графическая часть этой задачи.
пример, если дебит равен
Градиенты давления в газовом пласте, эксплуатируемом при постоянном темпе отбора после того, как пласт был достаточно долгое время закрытым и пластовое давление выравнилось, были рассчитаны [X. 9, 11.42] и приведены в виде диаграммы на рис. X. 15 для различных значений безразмерного дебита т, отношения радиусов R, отношения давлений р и безразмерного времени tD. В значения, найденные из диаграммы на рис. X. 15, построенной для случая течения по закону Дарси при высоких дебитах, должна вноситься поправка на его отклонение вблизи ствола скважины. При помощи диаграммы иа рис. X. 15 можно решать самые различные задачи. Например, можно рассчитать перепад давления в скважине, зная свойства жидкостей, свойства пласта, пластовые условия и дебит газа. На диаграмме (рис. X. 15) приводится полный градиент давления по пласту. Также можно по известной кривой падения давления в скважине определить проницаемость пласта, зная другие параметры пласта и пластовые условия. Ниже приводится пример, из которого видно, как можно вычислить перепад давления, пользуясь графиком на рис. X. 15.
Пример
Газовая скважина,- которая на некоторое время была закрыта, должна вступить в эксплуатацию с дебитом
газа 141 500 м3/сутки. Характеристики пласта и газа приведены ниже. Надо рассчитать забойное давление, которое будет после 20 ч работы скважины, считая,'что течение газа ламинарное.
[>¦ — 0,022 с/п; г = 0,865; пористость Ф — 0,17; Т =362° К; k = 60 мд; мощность h = 3,66 м; давление в закрытой скважине рп =246,05 ат; радиус скважины гс = 0,1 м.
"абс г 1
Решение
m = 01365(1ОгГ =
hkp2n
0,1365 X 0,022 х 141500 х 0,865 х 362 3,66 X 60 х 246,05 х 246,05
3,480 х 10“
tD = ktp
3,480 X 60 X 20 X 239
^ 10000 х 0,022 х 0,1 х 0,1 х 0,1 “ 2668000.
При вычислении tD было принято абсолютное среднее давление, равное 239 ат. Из графика рис. X. 15
при — = 1,0, г
Рс = 246,05 х 0,922‘/г = 236,21 am.
И больше не требуется никаких испытаний.
Так как график на рис. X. 15 построен только для т = 0,01, для других значений дебита должна вводиться соответствующая поправка. Значения давлений можно корректировать посредством применения уравнения
(iff =1—1 \”п/ нсгтравл
Пример
Решить предыдущий 70 750 м3/сутки.
Решение
от = 0,005,
100 от. (X. 57)
tD = 2668000,
1,000 —(1,000—0,922) х (100 х 0,005 ) = 0,961, р = 246,05 х 0,961V* = 241,2 абс. am.
10 РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ НА ЦИФРОВЫХ СЧЕТНЫХ МАШИНАХ
В настоящее время известно множество решений, явившихся результатом расчетов на электронных цифровых машинах, использующих перфорированные карты. Очевидно, что на таких машинах целесообразно решать задачи (в отличие от решения задач аналитическими или графическими методами рассмотренных выше) в тех случаях, когда невозможно или нежелательно вводить упрощающие допущения, как, например, осреднение коэффициентов сжимаемости, вязкости, давления, или когда геометрия рассматриваемого пласта, чрезмерно сложна.
Из-за специфичного подхода к решению каждой задачи, осуществляемому с помощью счетной машины, невозможно представить общие решения, основанные на единственных кратких таблицах, как это делалось для любого из аналитических решений. Вместо этого для перекрытия диапазона принятых условий при каждом расчете на машине надо применять многочисленные таблицы и карты. Так как показать все эти таблицы и карты невозможно, приведем лишь несколько
Рис X 14. Расчетные значения градиентов давления при исследовании скважины методом различных отборов
Iprpf
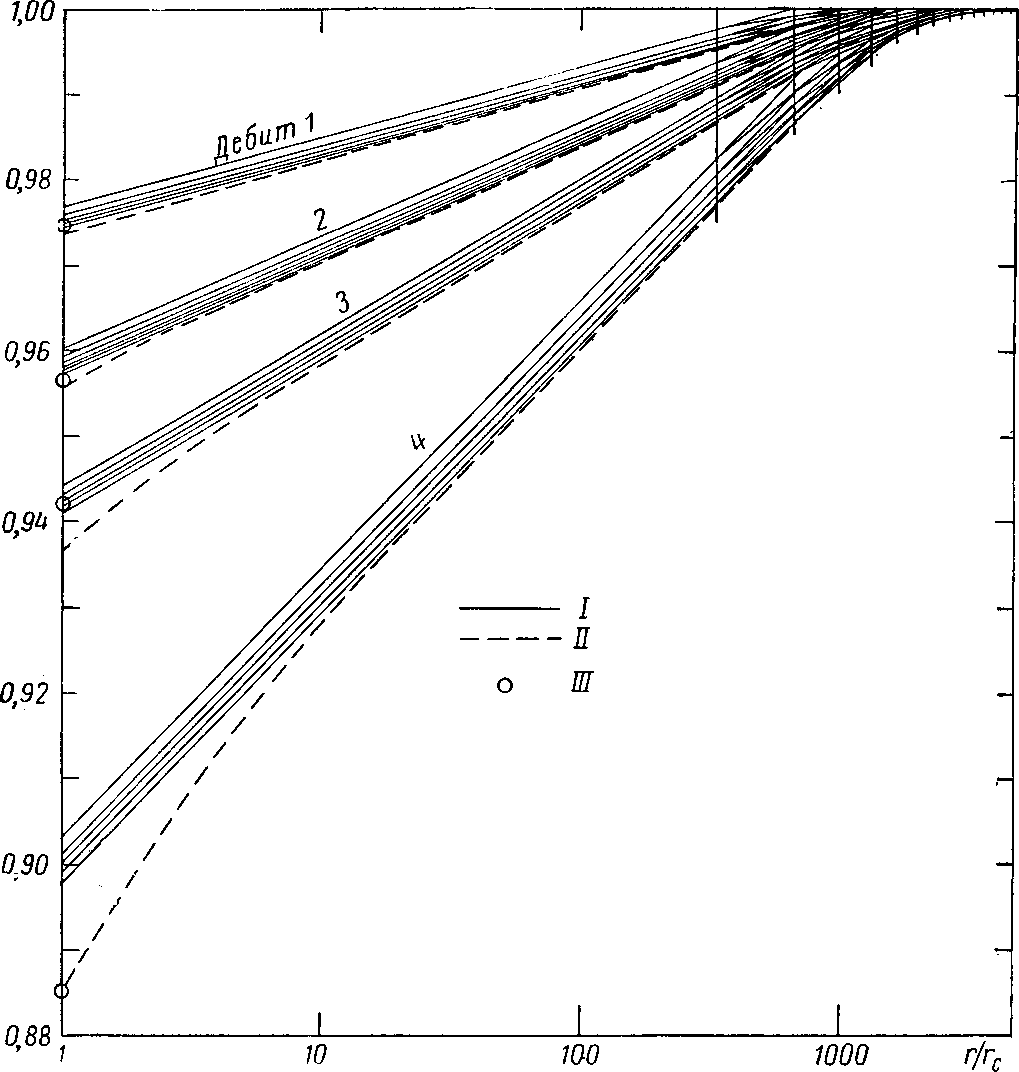
/ — линии построения; //—окончательное значение градиента давления, учитывающее поправку на отклонение от закона Дарси;
/// — значения давления, наблюдаемые на забое скважины.

Рис. X. 15. Обобщенная диаграмма для определения градиентов пластового давления, построенная для значения безразмерного параметра т = 0,010 [II. 42].
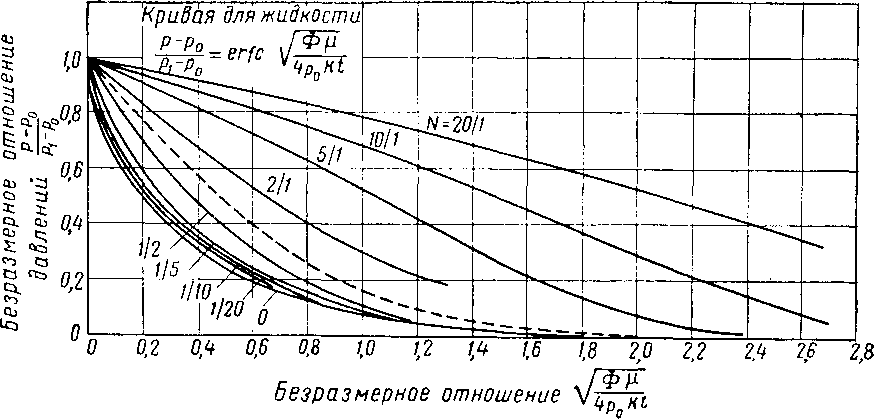
Рис. X. 16. Распределение давления в пласте бесконечной длины, в котором имеет место линейная
фильтрация газа [X. 1].
р— атмосферное давление; р —начальное давление в ат; pt — конечное давление в ат;
Ф — коэффициент пористости; р. — коэффициент вязкости в спз; к — коэффициент проницаемости в д\ X—расстояние в см\ t —время в сек\ N — отношение начального давления р9 к постоянному конечному давлению Pi.
решены Ароновским и Дженкинсом (Aronofsky arid Jenkins) [X. 1]. В качестве примера на рис. X. 16 приведены решения при постоянном конечном давлении для бесконечного пласта. Соответствующие обозначения приведены на графике. Параметр N представляет собой отношение начального давления ро к постоянному давлению рь
Радиальное течение газа. Решение уравнений, описывающих радиальную фильтрацию газа, полученные без допущений о среднем давлении газа, были выполнены численным методом Дженкинсом и Ароновским (Jenkins and Aronofsky) [X. 19] и Брюсом, Писменом, Ричфордом и Рисом (Bruce, Peaceman, Rachford and Rice) [X. 6]. Типичный результат из работы Дженкинса и Ароновского приведен на рис. X. 17. Этот график дает изменение забойного давления во времени при различных темпах нагнетания и отбора газа. Это семейство кривых получено вместо единственной кривой, фигурирующей в работе Ван Эвердингена и Херста (Van Everdingen and Hurst). Наличие нескольких кривых следует объяснить тем фактом, что давление в этом случае берется также в качестве переменной величины во всех частях дифференциального уравнения.
Безразмерное время tD
Рис. X. 17. Изменение давления на скважине во времени при эксплуатации бесконечного радиального пласта с различными темпами
отбора [X. 19].
Предельный случай, когда течение отсутствует, рассчитанный аналитически Карслоу и Джегером.
результатов для типичных случаев. С решением задач, учитывающих другие диапазоны переменных, не приведенных в данной книге, можно познакомиться по соответствующим оригинальным работам [X. 1, X. 2, X. 3, X. 4, X. 5, Х.6, X. 14, X. 19, X. 20, X. 28, X. 29, X. 24].
Линейиое течение газа. Несколько задач линейного течения газа (среднее давление не учитывалось) были
Графики, характеризующие результаты Брюса, Пис-мена, Ричфорда и Риса [X. 6], полученные для неуста-
а Ь с
Рис. X. 18. Расчет распределения давления при истощении радиального гэ'зонасыщемного пласта. to определяется по внешней границе пласта гк [Х.6].
новившегося радиального течения с постоянным дебитом в ограниченном пласте, приведены на рис. X. 18 (а, Ь, с). Эти кривые можно применять для расчета давления в любой точке пласта, соответствующей данному значению безразмерного параметра mtD, являющегося произведением безразмерного времени и безразмерного дебита.
11. РЕШЕНИЯ, ПОЛУЧЕННЫЕ С ПОМОЩЬЮ ВЫЧИСЛИТЕЛЬНЫХ УСТРОЙСТВ,
ОСНОВАННЫХ НА ПРИНЦИПЕ АНАЛОГИИ
Дифференциальные уравнения для неустановившейся фильтрации газа могут решаться на электрической, электронной или механической системах, которые подчиняются законам, подобным закону Дарси pVT, соотношениям и уравнению неразрывности. Например, электрическая сетка может набираться вместе с электрическими емкостями. Она моделирует в данном случае объем пласта, его пористость и сжимаемость. Электрическое сопротивление является аналогом проницаемости. Меняя сопротивление, можно варьировать вязкостью моделируемой жидкости (газа) и мощностью песчаника. Электрический ток в этом Случае будет аналогом фильтрующегося газа (жидкости). Напряжение будет соответствовать давлению. Отбор электрического тока из такой системы с постоянной скоростью будет моделировать неустановившееся течение газа по пласту при отборе его с постоянным дебитом.
Для моделирования неустановившегося течения газа в пласте можно применять пневматическую аналогию, основанную на использовании комбинации капиллярных трубок и резервуаров, заполненных газом. Для воспроизведения неустановившегося течения газа можно использовать и трубки, заполненные песком.
Для решений дифференциальных уравнений применением электронной аналогии комбинируются электронные схемы, на которых можно дифференцировать, интегрировать или производить другие необходимые функции.
В числе полученных с помощью вычислительных устройств, известных на сегодня решений, основанных на принципах аналогии, следует указать результаты, полученные с использованием пневматической аналогии, представленные Хоупертом (Houpeurt) [X. 17], и результаты, полученные на сетках электросопротивлений с емкостями Грином и Уилтсом (Green and Wilts [X. 16]. Миллер, Деес и Хатчинсон (Miller, Dyes and Hutchinson) [X, 23] также использовали сетки электросопротивлений с емкостями для решения задач восстановления давления в закрытых скважинах.
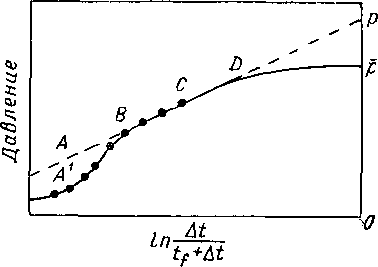
Рпс. 19. Кривая восстановления давления [X. 22].
стовым давлением». Выравнившееся пластовое давление представляет собой давление, которое должно существовать в пласте по прошествии такого отрезка времени, к концу которого миграция газа в истощенные зоны прекратилась и в пласте практически не существует градиентов давления.
Меттыоз, Броне и Хазброк (Matthews, Brons and Hazebroek) [X. 22] предлагают метод определения вырав-нившегося давления, основанный на использовании кривой восстановления давления во времени. После того как скважина эксплуатировалась в течение времени if, ее закрывают. Затем через интервалы времени A t фиксируется давление на забое скважины. По результатам измерений строится график, на котором забойное давление откладывается против lgA^f + A/ (рис. X. 19).
Прямолинейный участок полученной кривой, который прослеживается через сравнительно короткое время после закрытия скважины, экстраполируется до значения Kt/tf-\-M = \, т. е. до бесконечного времени. Давление, соответствующее точке пересечения экстраполированной кривой с ординатой lg A///f+A/ = 0, обозначенное на графике р *, больше, чем выравнившееся давление в закрытом пласте потому, что в процессе выравнивания происходит повсеместное падение давления по пласту.
Затем по графику находится выравнившееся пластовое давление (рис. X. 20). Этот график при соответствующих координатах можно использовать для случая течения по пласту как газа, так и жидкости.
Пример
Рассмотрим применение графика (рис. X. 20), построенного Маттыозом, Бронсом и Хазброком (Matthews, Rrons and Hazebroek) [X. 22], для расчета выравнип-шегося пластового давления в конечном пласте по прямолинейному участку кривой восстановления давления. В этом примере даются достаточные данные, чтобы рассчитать выравнившееся пластовое давление тремя методами.
1. Делается обыкновенный расчет материального баланса.
2. Делается расчет с использованием методики, по которой обычно рассчитываются показатели неустано-внвшегося течения. Расчет ведется для момента времени, к которому давление успевает выравниться.
3. Выравнившееся пластовое давление определяется по начальному участку кривой восстановления давления с применением графика па рис. X. 20.
Чтобы более ясно показать методику расчета, поправки, учитывающие отклонение реального процесса 07 теории, благодаря наличию явления скин-эффекта и других, опускаются.
1
СЬ»
C\j
|
- | |||||||||||||||||||||||||||
|
Шестиигольми | к |
у |
s' | У | |||||||||||||||||||||||
|
Квадратх | |||||||||||||||||||||||||||
| Рад но сторонний | \ | / | у | ||||||||||||||||||||||||
| Lb | си | V' | /1 |
Р | ом |
6 | |||||||||||||||||||||
| 77г | Г 1 1 1 1 ямпчгпл |
¦fh | 111 - | ||||||||||||||||||||||||
| - | - |
- |
У |
треугольник | |||||||||||||||||||||||
|
* | |||||||||||||||||||||||||||
002 0 04 0,1 0.2 0.3 0.4 0,6 0# 1
tj, _ 0.0000838 Kptf
3 4 6 8 10
Рис. X. 20. Функция давления одной скважины, расположенной в центре залежи, имеющей форму равносторонних геометрических фигур [X. 22].
пМ
0,01
TiR2
Рис, X. 21. Изменение безразмерного давления при эксплуатации ограниченного пласта с непроницаемой внешней границей R = rK/c=800 и с постоянным дебитом.
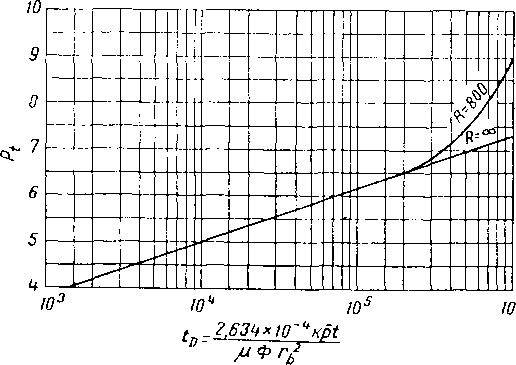
Условия
= 16640*.
1. Метод материального баланса. Принимаем, что Коэффициент сжимаемости не изменяется.
Уменьшение давления в пласте равно
QzRT _ 85000 X 0,89 X 0,082055 X 356 _ nQC,i
ппг2ккф 22,4 х 3,14 х 122* х 15,25 X 0,75 " '
(:г — объем 1 моль в л при (—15,5° С; R — газовая постоянная, равная 0,082055);
р = 140,6 — 0,923 = 139,677 абс. ат.
2. По кривым падения и восстановления давления в скважнне. Для расчета безразмерного времени принимаем абсолютное среднее пластовое давление, равное
133,5 ат:
_ 0,0003480/г*р _ 0,0003480 X 20 X 133,5*
р.фг2 0,016 х 0,15 х 0.15252
Определим безразмерный дебит:
m _ 0,1365|хгГ<Э _ 0,1365 х 0,016 х 0,89 х
X 356 х 85000 X 140,62
Рис, X. 22, Расчетные кривые падения и восстановления забойного давления в ограниченном пласте.
Начальное пластовое абсолютное давление 140,5 ат; выравнившееся пластовое абсолютное давление 139,6 ат.
е 140,5 Ч 140,0
8J 139,0
| 738,0
^ то
i 136,0 I 135,0
О 4 a 12 IB 20 24 28 32 36 40
Время, ч
Рис. X. 23. Расчетная кривая восстановления давления, используемая для определения р*.
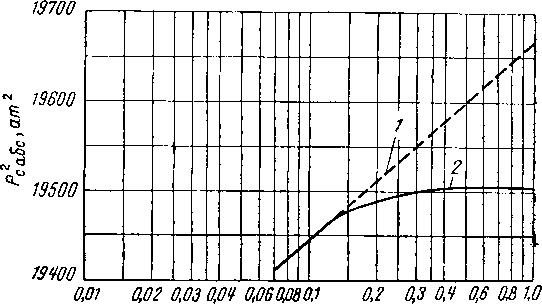
/ экстраполированное значение (р*)г\ 2 — действительное значение (р) 2•
Определяем значения Pt для R = 800 и постоянного дебита из конечного пласта для радиального течения при закрытой внешней границе. Для больших tD Чатас (C.hatas) [Х.7] дает уравнение (Х.31в). При R = 800 это уравнение принимает вид:
tr
+ 5,934.
3,2 хЮ5
Для несколько меньших значений tD м R — оо целесообразно применять уравнение (X. 31). На рис. X. 21 приведены зависимость pt от безразмерного времени при R = 800 и R = оо .
Результаты полного расчета гипотетических кривых падения и восстановления давления, произведенного по уравнению (X. 37), а также значений pt, приведенных на рис. X. 21, даны в табл. X. 3.
D
На рис. X. 22 приводятся расчетные кривые падения и восстановления давления. В этом случае выравнившееся абсолютное давление достигает значения
[(Р*
139,6 ат, которое было определено методом материального баланса, сравнительно за короткое время:
3. Метод Меттьюза, Бронса и Хазбрука. На графике рис. X. 23 приводится кривая восстановления давления. Начальные точки прямолинейного участка кривой экстраполируются до значения (р?Ьс)2 = 19550 ат2. Действительное значение давления также показано на графике. Однако эта часть кривой резко отличается от (рп)2 = 19770 ат2, потому что рассматривался конечный пласт.
Подсчитывается значение безразмерного времени для периода работы скважины:
tD = 16640 х 24 = 399360 400 000.
Значение абсциссы на рис. X. 20 равно
400000
= 0,199.
nR2 3,14 х 8002 Из рис. X. 20 для круговых пластов
= 1,85.
тр2п
Решая относительно р2, получим
р2 = 19510 абс. ат2 и р — 139,706 абс, ат•
После открытия газового месторождения следует планировать его разработку и находить рынок сбыта для газа. Чтобы правильно представить масштабы сбыта, необходимо подсчитать запасы газа. Для обеспечения потребителя требующимся количеством газа месторождение следует разбуривать достаточным количеством скважин. Разработка завершается при полном истощении месторождения.
