Глава ii однопролетные бескомпеисаторные надземные переходы
ГЛАВА II
ОДНОПРОЛЕТНЫЕ БЕСКОМПЕИСАТОРНЫЕ НАДЗЕМНЫЕ ПЕРЕХОДЫ
Надземные системы прокладки трубопроводов применяют при пересечении естественных и искусственных препятствий, при прокладке трубопроводов в сложных гидрогеологических условиях [30].
Для надземной прокладки можно использовать бескомпеисаторные системы прокладки, в которых напряжения от температурного воздействия воспринимаются трубопроводом, а перемещения ограничены опорами. Наи-¦ более часто применяют однопролетпые бескомпеисаторные переходы без специальных опор, работающие совместно с примыкающими подземными участками трубопровода. Рассмотрим поведение однопролетного надземного бескомпенсаторного перехода с примыкающими подземными участками под воздействием равцомерно распределенной поперечной нагрузки, изменения температуры н внутреннего давления продукта. Расчетная модель грунта принимается в виде упругого основания, т. е. считается, что сопротивление грунта пропорционально поперечным перемещениям трубы. Эта модель грунта достаточно хорошо описывает работу трубопровода па примыкающих подземных участках, учитывая малость поперечных перемещений.
Для расчета трубопровода на действие поперечной нагрузки н продольного усилия, обусловленного воздействием температуры и давления, приме ним способ, предложенный С. П. Тимошенко и заключающийся в том, что вначале выполняется расчет на поперечную нагрузку, при расчете же на продольное усилие действие поперечной нагрузки заменяется начальным прогибом, вызванным этой нагрузкой.
§ 1. Расчет на поперечную нагрузку
Определяем усилия и перемещения трубопровода от действия равномерно распределенной поперечной нагрузки. Уравнения равновесия для надземного и подземного участков трубопровода (рис. 52) имеют вид
EI-L —<?-0;
dx*
0.
EI-
41
dx*
(11.1)
Решения уравнений (11-1) записываются в виде: .. _ 9*4 ?4^ г &
~ + c2^ + c3t+c4.
(П.2)
24 EI
Oji cos — + А2 sin —^
е-? Ф Лд sin — + cos .
(П.3)
V Ф ф )
Здесь EI — изгибная жесткость трубы; oi, Vu — перемещения соответственно на надземном и подземном участках; <7 — интенсивность поперечной нагрузки; Ji=cvcDh коэффициент пропорциональности — произведение обобщенного коэффициента нормального сопротивления грунта и диаметра трубы; I — половина длины надземного участка трубопровода; |=хД относительная
Рнс. 52. Расчетная схема однопролетаого бескомпексдторного
перехода
координата; ф / 4EIIk/l —параметр, характеризующий относительное защемление концов надземного трубопровода.
Используя условия симметрии И сопряжения обоих участков (при принятой системе координат, см. рис. 52):
dv т.
Du —-5=0 при х—>- — оо;
dx
dvi A1 j j d ь-'j d ; 'j [
находим произвольные постоянные:
Cl . „ ql2 2 — Зф2
3 6?/ ' 1 + ф
С А ^(3ф2" 6ф 2) ¦
4 1 12 1 +ф
л/4 ф3(3фа 2)
Тор! ~Г~а ~ — Ац 0. (11.5)
12EI \ ф
Пз уравнения упругой лниип (112) определяем изгибающие моменты и перемещения.
Изгибающие моменты-для середины пролета (§=1)
24
для опорного сечення (| = 0)
oL2 —
М0^—-~-Мо. (11 .ту
Поперечные перемещения: для середины пролета
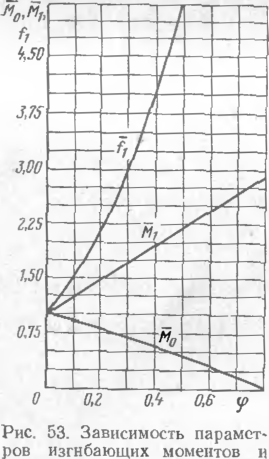
прогиба от относительного замещения концов перехода
f о -
(11.10)
(11.11)
/о —
(11.13)
Как следует из рис. 53, учет влияния примыкающих участков при расчете переходов па воздействие поперечной нагрузки] приводит к перераспределению изгибающих моментов между срединным и Опорным сечениями, и прп Ф=0,2 они ориентировочно равны. Угет этого фактора позволяет более полно использовать несущую способность трубопровода л увеличивать пролеты переходов.
§ 2. Расчет на воздействие температуры и внутреннего
давления
При расчете надземного перехода трубопровода иа воздействие температуры и внутреннего давлеиня продукта влияние поперечной нагрузки, как уже отмечалось, можно заменить первоначальным прогибом перехода обусловленным этой нагрузкой. С достаточной для практических расчетов точностью начальный прогиб можно представить в виде:
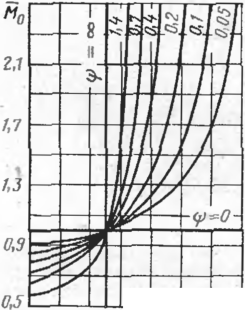
Ьезразмсрные параметры Mt, Л/0, ft, fa являются функцией величины <р, характеризующей относительное защемление кон цов подземного перехода, и определяются по формулам:
1 4- ф
ф2 (Зу* -f 6ф -f 2) 1 + ф
— 3<p2 + 3y-fl
1 + ф
4L-T
192EI
2 — Зф2
М0-
J = 6Ф4+12Ф3 10ф2 5Ф 1 . (И 12)
2 (1 + ф)
1>0 - fa sin2 nx!L при 0 ^ х ^
(11-14)
при —оо < х <0.
Vo (II)' 0
Стрелка начальною прогиба fo здесь определяется в соответствии с форму-] лой (11.8). В качество расчетной модели 1руита принимается упругое оено-( вание, сопротивление которого пропорционально поперечным и продольным перемещениям трубы и характеризуется соответствующими коэффициентами нормального Су о и касательного с* о сопротивлений. Продольное усилие по длине надземной части перехода принимается постоянным, на примыкающих участках учитывается сопротивление грунта продольным перемещениям.
Уравнения равновесия надземного и подземного участков трубопровода записываются в виде:
d\ dx2
d4\
dAv j dx4
(s,-^Ц + *О1, = 0, (11.15)
dx1 dx V dx J
ne So. Sx — полные продольные осевые сжимающие yen. ия, действующие
па элемент dx соответственно на надземном и подземном участках,
so "•= Р^св — А'0; 5 х — р/7с лs—(11,16)
/г=с„с?>я— коэффициент пропорциональности; р — внутреннее давление продукта; Fc* — площадь сечения трубы в свету; <V„, Nx—продольные осевые растягивающие усилия, действующие в стейках трубы соответственно на надземном н подземном участках, No определяется из условия неразрывности продольных перемещении обоих участков, Л'х определяется по формуле
Nx—-~ (а-ЫЕ — ЦОкц) F + (Л'о + aMEF — naKUf) ev*, (11.17)
Iздесь x изменяется от 0 до —оо), полное продольное усилие, согласно (II 16), можно представить в виде
SX=S0 [I _е** (JV0aAtEF-iia^F)], (11.18)
= [ лР„схв . (11.19)
EF
а — коэффициент линейного расширения материала, Дt — температурный перепад, положительный при нагревании; Е — модуль упругости материала; ц — коэффициент Пуассона; <т|!Ц — кольцевые напряжения от внутреннего давления; F — площадь поперечного сечения стенок трубы.
Граничные условия для уравнений (11,15) записываются также в виде
(11.4). Учитывая малость второго члена в выражении (11.18), нелинейное
уравнение (11.15) можио решить методом малою параметра Для нрактиче-екз х расчетов достаточно ограничиться первым членом разложения. Записываем решения уравнений (11.15). определенные с учетом граиичньгх условий
(11.4), в безразмерных параметрах:
- ms Г л, / to* - тл е I
где v — v/i- дополнительный прогиб, отнесенный к радиусу инерции сечеиня
трубы; — начальная стрепка прогиба, отнесенная к радиусу инерции
ее [синя трубы; тг — полное продольное сжимающее усилие, отнесенное
К критической силе для стержня с защемленными копнами:
т2 _ S0/Af3 -- S0L*t{4st*Ely, (11.22)
L — д шна надземного участка трубопровода; 0, . u, Р — безразмерные па
раметры. вычисляемые по формулам:
п полное продольное сжимающее усн—) лне, отнесенное к критической силе* для бесконечного стержня в упругой! среде: 1
(11.25)4
Из уравнений упругой линии тру бопровода следует, что область устой: чнвого равновесия существует прн в>0. График на рис. 54 показывает, что с уменьшением относительной же-t сткостн подземного участка трубопро4 вода (параметр п) область устойчивого равновесия значительно сужается.
Неизвестное продольное усилие N0, а следовательно, И S0 [см. формулу (11 16)] определяется из условия не-j разрывности продольных перемещений обоих участков
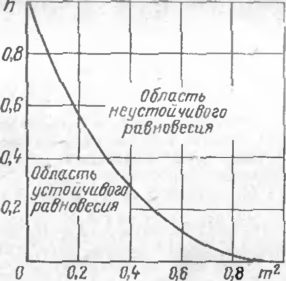
n = VA'kp = 5„/(2 Vf/ft).
Рис. 54. График областей равновесия надземного перехода
I
VuJ
(11 26>
где ut и и2 — продольные перемещения нулевого сечения надземной и подземной частой трубопровода.
Для определения продольного перемещения запишем связь деформации с перемещением, учитывая нелинейность и соотношение термоупругост'и для продольной деформации
dx 2 \ dx ) 2 \dxj 1
No
4- аДЛ
Е* =
EF
(U.28>
отсюда
du
¦Vo
EF
I aAt — ¦
i©’ тШ- <"»>
где E — модуль упругости материала трубы F — плошадь сечения стенок трубы; а — коэффициент линейного расширения материала трубы; At — ] температурный перепад, положительный при нагревании; yi — коэффициент! Пуассона материала трубы; dm, — кольцевые напряжения от внутреннего1] давления.
Тогда можно вычислить продольное перемещение нулевого (начального) сечения надземной части по формуле
г
(11 30)
Г du
dx.
Продольное перемещение подземной части трубопровода в месте стыка с надземной частью иг определяется в соответствии с решением, подученным в гл. 4
Из (1126) получаем уравнение для определения полного продольного усилия в сечении трубопровода.
При отсутствии участка предельного равновесия груита при продольны* перемещениях трубы уравнение для определения безразмерного параметра
продольного усилия т2 имеет вид
р7 1 + 1/у/
Критерием отсутствия участка предельного равновесия грунта является
условие
При наличии участка предельного равновесия груита уравнение для определения параметра т2 имеет вид
Безразмерный параметр гп2рт, характеризующий воздействие давления и тем-л1ературы (параметр нагрузки), оиредсляется по формуле
Безразмерный параметр к, характеризующий взаимодействие трубопровода с грунтом, определяется по формуле
_ tyyl
трТ
(11.35)
лаЕ1/Р
безразмерный параметр Ai, характеризующий сэмокомпенсацшо трубопровода, оиредсляется интегрированием упругой линии (11.14) и (11.20)
Мы видим, что величина А, зависит от искомого параметра продольного усилия ш2, т. с. уравиеиия_( 11.31) и (11.33) нелинейны относительно гп2. Подсчитанные223 значения Ai приведены на рис. 55 в функции ггР и ф при -стрелке начального прогиба ?о=1-
Для получения этих значений при других стрелках начального прогиба, а к следует из (П.36), величины, приведенные на рнс. 55, необходимо умножить на квадрат относительной начальной стрелки. Для удобства расчетов графики построены в функции
ф = n/rn2 ^ N3!NKP. (11.37)
Нелинейное относительно тг уравнение (11.31) можно решить графическим способом. На рис. 56 построен такой график для некоторых параметров, характеризующих защемление примыкающих подземных участков трубопроводов.
Сплошпыми линиями показаны зависимости продольного усилия от на-•рузки для случая полного зашемлояия концов надземного участка трубопровода (у/ — со, -ф — 0), что соответствует стержню с неподвижными опорами. Как следует из графиков, при одном и том же значении нагрузки гп2рт продольное усилие тг уменьшается с увеличением стрелки начального прогиба 5"- Пунктирным» линиями показаны эти же зависимости для промежуточных значении уI и ф, характеризующих соответственно сопротивление грунта продольным и поперечным перемещениям трубопровода иа подземном участке. Прямая пунктирная линия соответствует случаю равенства нулю сопротивления грунта продольным перемещениям (\'i—0), в этом случае продольное усилие не зависит от стрелки начального прогиба.
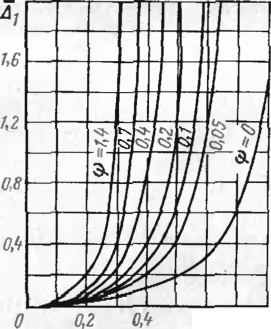
0,6 т*
Рис. 56. Зависимость продольного усилия от нагрузки при различных граничных условиях
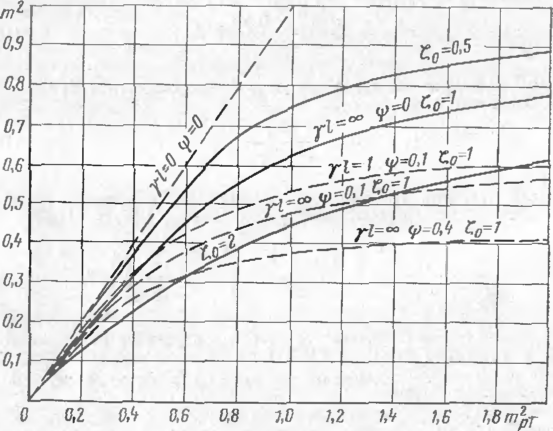
Рис. 55. Зависимость параметра самокомпеисашш от продольного усилия и относительной жесткости перехода
Определив по графику рис. 56 параметр продольного усилия т2, на основании (11.16) и (11.22) вычислим продольное растягивающее усилие
Лго=Р^св m2N%~ (11.38)
Зная параметр продольного усилия т2, определяют остальвые расчетные параметры надземного перехода
Исходя из уравнений упругой линии (дополнительных прогибов) надземного перехода (11.20), определяем значения изгибающих моментов и дополнительных поперечных перемещений трубы. Для начала надземного участка трубопровода (1=0):
М0 = Л1„; (П-39)
0 2 1— т1
v0 = А> —
т—¦ ¦ «о;
О1-40)
1 — т2
(11.41)
<7 <7,2 й4> «^/772
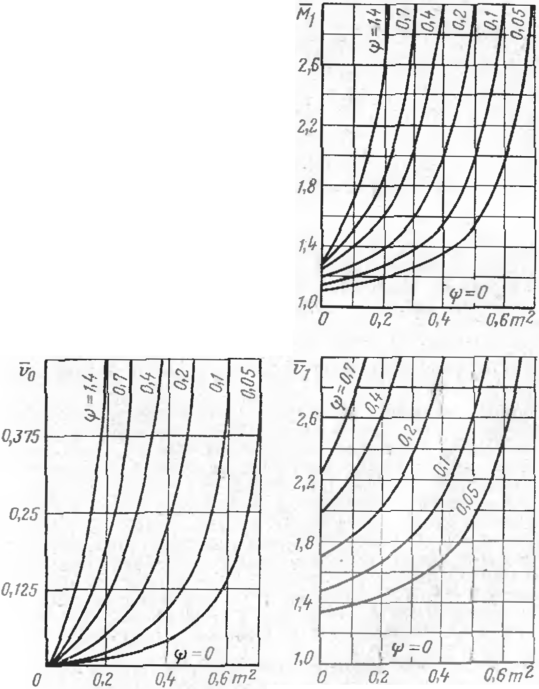
Рпс. 57. Зависимость безразмерных параметров от продольного усилия и относительной жесткости перехода
Вычисление по (11.41) проводится в том случае, если критерий (11.32) соблюдается, в противном случае продольное перемещение определяется по (11.42). Для середины надземного участка трубопровода (1 = 1):
Жг --Tl—Mv. (11.43)
Р 2 I — ma I
rrfi —
fi=h ---«I, (11.44)
I —tr?
Мй = тг{п\~ l)/0; (11.45)
»o=-—-; (11-46)
Mi = l +
2w2w* ; (11.47)
0 sin mn
mn
1 4-n. tg——
4 =---+ 1. (11.48)
На рис. 57 приведены значения безразмерных коэффициентов М0, ve. Mi, Vi в функции щ2 и ф. Используя полученные зависимости и графики, приведенные на рис. 55—57, определяют значения продольного осевого усилия и изгибающих моментов от воздействия температуры и внутреннего давления
§ 3. Анализ напряженно-деформируемого состояния перехода
Рассмотрим некоторые граничные условия и особенно обратим внимание на изменение продольных напряжений от внутреннего давления в зависимости от начальной кривизны трубопровода. Как следует из графика изменения параметра изгибающего момента на опоре и посередине пролета, при полном защемлении балки на опоре (ф=0) безразмерный параметр М=1 (см, рис. 57), т. е. соответствует известному решению продольно-поперечного изгиба балки с защемлением на опорах. При продольном усилии т2< 0,25, т. е. меньше усилия, соответствующего потере устойчивости стержня с шарнирным закреплением опор, с увеличением степени защемления (уменьшением параметра ф) изгибающий момент на опоре увеличивается. При от2>0,25 с уменьшением параметра ф изгибающий момент на опоре уменьшается. Изгибающий момент в середине пролета с уменьшением степени защемления увеличивается, особенно на границе области устойчивого равновесия.
Таким образом, учет влияния поперечных перемещений подземных участков трубопроводов, особенно для слабых грунтов, приводит к существенному изменению напряжении и перемещении примыкающего надземного перехода.
Уравнение для определения продольного усилия при надземном переходе со специальными опорами, обеспечивающими защемление пят трубо-
7
г
j
о
Рис. 58. График для определения продольного усилия от воз действия температуры и внутреннего давления для балки с неподвижными опорами
провода, т. е. при у=оо и ф=0, имеет вид
трГ = т2+Лр (11.49)
где
V.
16 [(1-т2)2 ]
На основании уравнений (11.49) и (11.50) построены графики тля определения усилия тг в зависимости от нагрузки т2РТ (рис. 58) Графики построены для различных стрелок начального прогиба трубопровода. Как пидио из этого графика, при воздействиях, превышающих критическую си.' у, т е прн т*рт>1 при наличии начального изгиба продольное усилие не может превысить критическую силу, т. е. m2< 1. С увеличением стрелки начального изгиба при одном и том же воздействии продольное усилие уменьшается. Посмотрим, как изменяется продольное осевое усилие в стейках трубы только прн воздействии внутреннего давления. Для прямолинейного перехода (?о=0) тг~тгРт- Тогда из (11.38) получаем, что продольные осевые напряжения сПр я — No/F в стенках трубы будут равны 0,3 (Тип. С увеличением стрелки начальною прогиба величина тг уменьшается и прн С->-оо т2-*-0, т е. из (1138) мы получаем, что для этого предельного случая Оцр х —0,5 Сть-ц. Таким образом, осевые продольные напряжения от внутреннего давления являются растягивающими и изменяются в пределе 0.3- -0,5 от кольцевых напряжений.
Рассмотрим открытый трубопровод с сальниковыми пли линзовыми компенсаторами Прн такой конструкции продольное осевос усилие в стенках трубы Лг0 равно нулю. Тогда из (11.38) получаем, что тг— pFcn/Ne. т е при действии внутреннего давления трубопровод изгибается что необходимо учитывать в расчетах. При ms= 1 эта конструкция теряет устойчивость. Возможность потерн устойчивости стержня трубчатою сечения от внутреннего давления при отсутствии продольной силы отмстил В. И. Феодосьсв [46].
Остановимся несколько подробнее на этом вопросе. В лаборатории прочности ВНИИСТа И П. Петровым и К И. Калошиным были проведены эксперименты по определению критической силы для стальных и алюминиевых труб с учетом влияния внутреннего давления. В отрезках труб с заглушками (доньями) созывалось внутреннее давление с помощью гидравлического масляною иасоса с ресивером Продольное усилие прикладывали с помощью
универсальной 50-тонной испытательной машины Опыты показали, что при данной схеме испытания внутреннее давление не оказывает влияния на критическую силу. Этот результат также объясняется на основании полученных ранее зависимостей. Продольное растягивающее усилие в стенках трубы
No — PFсв — Nam (11.51)
где pFсв — усилие от внутреннего давления, действующее на заглушку трубы; Л^вн — внешнее сжимающее продольное усилие.
Учитывая, что потере устойчивости соответствует равенство m2=S0/.Va= = 1, получаем
** э
т. е. внутреннее давление при наличии заглушек (доньев) не влияет иа критическое продольлое усилие.
Однако при сжатии труб с одновременным действием внутреннего давления увеличивается предел применимости формулы Эйлера. Формула Эй- j лера справедлива прн условии, что деформация сжатия стержня вплоть до момента потери устойчивости подчиняется закону Гука. Иными словами, критическое напряжение <тКр не должно превышать предела пропорциональности материала стержня сгПц
или для данной схемы эксперимента
п2Е pFzB ^ /lt rjI4
-------(Ц.о4)
A. F
где % — гибкость стержня
\[—приведенная длина стержня; i — радиус инерции сечсиия.
Предельная «упругая» \ ибкость трубы, т. е. наименьшая гибкость, при которой еше можио пользоваться формулой Эйлера;
^ = ЭТ/Л/---. (11.56)
W 7пц + ^св/?
Условие (11.53) получает вид
(11.57)
Таким образом, порученные решения хорошо объясняют поведение откры-1 того трубопровода под воздействием внутреннего давления.
Для динамического расчета перехода трубопровода необходимо зиать частоту собственных колебаний трубопровода. Известные зависимости строительной механики относятся к балкам с так называемыми конечными граничными условиями — шарнирными, жесткими или упругими опорами. В данном случае в качестве опор надземного перехода служат примыкающие подземные участки трубопровода. Для определения частоты собственных колебаний такой конструкции можно воспользоваться известной зависимостью, в которой соотношение частот колебаний балки с различными граничными условиями пропорционально квадратному корию из соотношения их статических прогибов. Тогда частоту собственных колебаний (основного тона) соо (в рал/с) надземного прямолинейного балочного одиопролстного перехода с примыкающими подземными участками (без специальных опор) можно определить по приближенной формуле
(11.58)
: = л Л/ —
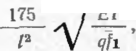
где I — половина длины надземного участка трубопровода, см; EI — жесткость сечения при изгибе, Н • см2; Ч — вес единицы длины трубопровода, Н/см; fI — коэффициент, учитывающий увеличение стрелки прогиба перехода без специальных опор по сравнению с переходом с защемленными опорами и определяемый по формуле (11.12) или по графику рис. 53.
Используя известное соотношение изменения частоты собственных колебаний балки при действии осевого сжимающего усилия, частоту собственных колебаний (основного тоиа) перехода с примыкающими подземными участками можно определять по формуле
Ю1=ю0д/-^^, (11.59)
V VI
где too — частота собственных колебаний; тг — параметр продольного осевого усилия; Vi — коэффициент, учитывающий увеличение стрелки прогиба, определяемый по (11.48) или по графику рис. 59.
Сравним полученное решение с результатами эксперимента. Экспери меит был проведен в лаборатории прочности ВНИИСТа224 на моделях одно-пролетного перехода, нагружение осуществлялось внутренним давлением сту-пенями но 2 МПа. Модели были изготовлены из отрезков стальных труб диаметром 38 мм и толщиной стенки 1,3 мм. Трубы иа опорах были неподвижно защемлены, и продольное усилие от заглушек воспринималось опорами. Расстояние между опорами 2/ 360 см. Испытывались модели с раз-тнчиыми стрелками начального прогиба. Полученные значения полного прогиба f=fo+fi в середине пролета при изменении внутреннего давления от О до 18 МПа показаны в виде точек па рис. 59. Там же построены соответствующие кривые, рассчитанные по зависимости (11.44). Величина т2 определялась с помощью графика рис. 58. Во время испытаний измерялись частоты колебаний моделей без воздействия внутреннего давленпя Wo и прн давлении соотношения частот toi/wo при изменении внутреннего давления, найденные экспериментально, показаны в виде отдельных точек на рис. 60, здесь же построены соответствующие кривые, рассчитанные по (11.59). Как видно из
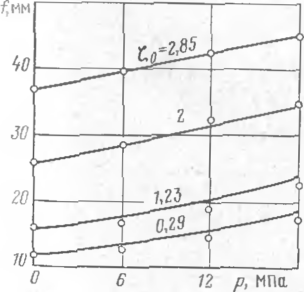
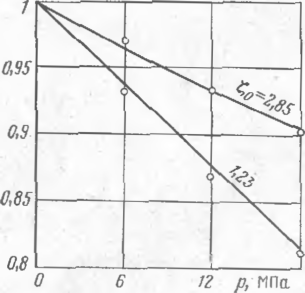
Р«с. 59. График экспернменталь- Рис. 60. График экспериментальных
ных и теоретических значений и теоретических значений частот соб-
прогиба от внутреннего давления стенных колебаний от внутреннего
давления
рис. 60, с повышением давления частота колебаний падает, хотя как было показано ранее, в стейках трубы возникают продольные растягивающие напряжения. Хорошее совпадение опытных данных с расчетными позволяет рекомендовать изменение частот колебаний трубопровода в качестве метода определения продольного усилия.
Таким образом, проведенный анализ показал, что примыкающие к надземному переходу подземные участки трубопровода оказывают существенное влияние иа напряженио-деформированное состояние трубопровода, а начальное искривление трубопровода изменяет продольное осевое усилие и что дчя практических расчетов прямолинейного перехода можно пренебречь само-компенсацией системы.
Проверить прочность надземного бескомпенсаториого перехода трубопровода без специальных опор пролетом в свегу 32 м. 'Примыкающие участки к переходу подземные. Модуль деформации груита Етр —2000 Н/см®, коэффициент Пуассона груита Цгр= 0,2. Трубопровод выполнен из труб размером 1420x16,5 мм, имеющих временное сопротивление 600 МПа и предел текучести 470 МПа. Трубопровод, относится к участку III категории. Интенсивность расчетной вертикальной нагрузки 9=100 Н/см. Рабочее давление р=7,5 МПа, положительный температурный перепад Д/=60°С.
Проверяем достаточность толщины стенки трубы. Кольцевые напряжения
МПа.
°кц = —~—" =-~—;- = d4b> в
Расчетное сопротивление
'm 600-0 9 R, = —— = ’ = 350,6 МПа.
Так как oKu<Ri, то по расчету иа внутреннее давление толщина стенки достаточна.
Расчет на поперечную нагрузку.
Обобщенный коэффициент нормального сопротивления грунта
0,012?гр 0,012-2000 (1 — Мтр) л/^н 0 0,22) д/Т42 ~ •
о -
Параметр, характеризующий относительное защемление концов иадземиого перехода:
| 1 // 4 EI |
1 | ,*/ 4-2,1-107-1,79-10® |
| «v* j О ? 1 | 1600 | I 2,1-142 |
= 0,53,
где
64 64
Безразмерные параметры изгибающих моментов пычнсляются по фор-муаам (11 10) и (11 11)
МХ 3 0-532 + 3-0,53+_1 2>24;
1 + 0,53
.. 100-32002 „ 0 с. 1П7 „
Мг --2,24 = 9,56-107 Н-см.
24
Изгибающий момент опорного сечсния вычисляется по формуле (11.7)
Л10 = — ^1м0 = — 10°'
32002 -0,38 - — 3,24-Ю7 Н м 12
12
Результаты расчетов показывают, что для надземного участка трубопровода с примыкающими подземными участками изгибающий момент в опорном сечении в 2,6 раза меньше по сравнению с переходом с жесткими опорами, а изгибающий момент посередине пролета в 2,24 раза больше по сравнению с переходом с жесткими опорами ив 35 раза меньше по сравнению с переходом с шарнирными опорами.
Безразмерные параметры прогибов вычисляются по формулам (11.12) и (11.13):
7 6-0,534 f 12 0,533+ ю • 0,532 + 5- 0,53 + 1 _ с
/1 — * " * »
1+0,53
7 0,532(3-0,532 + 6-0,53 + 2) , по
10 -
------- ----1 7 '-'О.
1 + 0 53
Прогиб посередине пролета по (11.8)
. 100-3200* _ _ ...
--5,7 = 4,14 см.
384-2,1 ¦ 107-1,79-10°
Перемещения «опоры» перехода вычисляются по формуле (11.9)
, 100-32001
f0^ ---1,08= 1,56 см.
192-2,1-ЮМ 79-10е
Результаты расчетов показывают, что для рассматриваемого перехода прогиб по середине пролета в 5,7 раз больше по сравнению с переходом с жесткими опорами и даже на 14 % больше по сравнению с переходом с шарнирными опорами.
Расчет на воздействие температуры и внутреннего давления.
Определяем параметр нагрузки по (11.34)
т2 (12-Ю—6~60-2,1-10» + 0,2-346,8) 728 1Ш. и ШрТ я!-2,М0« 1,79-10®
Принимаем т2—т2Р, г, т. е. пренебрегаем изменением продольного усилия, связанным с деформацией системы, тогда т2=0,11.
Определяем безразмерные параметры по формулам (11.37), (11.23), (11.24), (11 45), (11.47), (11.46) и (11.48):
n2 = J-<U)748_ = 12 7. n __ 3 52;
0,0748
0 = 0,11- (12,37+2-3,52 ctg Vo, И n — l) =3,4;
M0= —’11 (12,37 ~-J)_ 0,37;
3,4
— , , 2-0,11-3,52
Mt = 1 + -j--:— — 1,67;
3,4- sin д/0,11 я
v0 =-Pdi_-= 0,0364;
l+3,52tg^^l
r, =---h 1 = 1,47.
3,4
Изгибающий момент посередине пролета по (11.43)
16002 2 1 —0,11
Изгибающий момент для «пяты» перехода по (11.39)
эт2-2,1¦107-1,79-10е 4,14 0,11
Мп =-----—------0,37 = — 1,37 -107 Н - см.
1600* 2 1 —0,11
Прогиб посередине пролета перехода по (1144)
[. =4,14 - °—--1,47 -0,75 см.
Прогиб «пяты» перехода по (11 40)
е0= 4,14—Р’11--0,0364
0,02
см.
1—0,11
Суммарный изгибающий момент: для «пяти» перехода
Мв = — 3,24-Ю7— 1,37-107 = — 4,61 ¦ 107 Н ем;
д.1Я середины пролета
— 9,56-107 -(- 6,19-107 — 15,75-107 Н-см.
Продольное усилие от воздействия температуры и внутреннего давления по (11.38)
.. . 1М , n%EI 1,1 -7,5-я-138.72
N0 = PFcn — mгЛ/э —Р-:--—
4 Р 4
0,11я2-2,1-10б-1,78-10е
Частота собственных колебаний (основного тона) перехода по (11.58) 175
ю0 -
/2.М0М,79-10» V 100 5,7
16002
Частота собственных колебаний (основного тона) при воздействии температуры и внутреннего давления определяется по формуле (11.59)
= 17,5 л /J-^ 13,6 рад с.
0)1
V 1,47
Проверим прочность трубопровода в соответствии с нормами: продольные осевые напряжения
Лг0 —3,48 10*
°„пы = —~ =-1- - —47,8 МПа;
npN р ?28
¦ф3 = -| 1 — 0,75 -0,5- кц
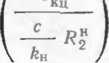
У
к
W 2I 2.1,79-10*
коэффициент, учитывающий двухосное напряженное состояние:
Г ' V
максимальные напряжения от изгиба
М MDH 15,75-105 142
= 62,4 МПа;
i-o.'TS /. 346.8^1 Y_0>5_346,8_M- = 0)3 .
/
1 - 470
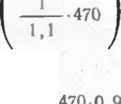
асчетное сопротивление
Щт х
R2 —--=274,7 МПа;
Мн 1,4 1,1
предельные допускаемые продольные осевые напряжения
Кр*] “ V?* 0,3-274,7 = 82,4 МПа;
предельные допускаемые максимальные продольные напряжения
= 0,635R„ (1 +г|>_) sin-^!-Mi-я = 0,635-274,7 (1 + 0,3) X
— 47,8 + 0,3-274,7 со МГ1
X sin -:—-— - я —68 МПа.
(1 + 0,3) 274,7
Тйк как [<7вь f<7nf. л-1 и [0м]>|«тм|, то условие прочности выполнено.
РАСЧЕТ НАДЗЕМНЫХ БЕСКОМПЕНСАТОРНЫХ БАЛОЧНЫХ СИСТЕМ ТРУБОПРОВОДОВ С ПРИМЕНЕНИЕМ ЭВМ
Даже для однопролстиого перехода аналитическое решение получается достаточно сложным. Для многопролетных систем решение существенно усложняется тем, что необходим учет начальных искривлений (начальных несовершенств), обусловленных сооружением перехода, геометрической нелинейности (продольно поперечный изгиб), особенностей поведения примыкающих к надземному переходу подземных участков трубопровода. Для расчета различных конструктивных решений многопролетных балочных систем трубопроводов был использован численный метод, реализованный на ЭВМ Составленная программа определяет напряженно деформированное состояние трубопровода и нагрузки на опоры.
§ I. Область применения программы НБП-2
Для расчета одно- и многопролетных надземных бсскомпенсаторных переходов трубопроводов можно использовать разработанную ВНИИСТом программу НБП-2 для ЭВМ ЕС любого типа [36]. С помошью этой программы можно рассчитывать надземные многонролетные переходы практически с любым числом пролетов (текст программы на машипных носителях хранится в организации-разработчике).
Промежуточные опоры могут быть как жесткие, так и упругие, причем опора может быть представлена как связь, препятствующая в топ или иной стспсни (в зависимости от заданной жесткости) угловым, поперечным и продольным перемещениям. В то же время крайние опоры могут и отсутствовать, их роль в этом случае выполняют примыкающие подземные участки.
При расчетах можно задаваться иячалышми искривлениями трубопро- , вода, обусловленными сваркой трубопровода из отдельных труб и условиями выполнения строительно монтажных работ.
Нагрузка по длине трубопровода принимается равномерно-распределенной, температурный перепад (положительный или отрицательный) и внутреннее давление одинаково по всей длине. Согласно этой программе расчет переходов производится только как плоских систем, поэтому при наличии нагрузок, воздействий и начального изгиба в двух плоскостях расчет производится для каждой плоскости в отдельности. Алгоритм программы учитывает геометрическую нелинейность (продольно-поперечный изгиб), поэтому проверку продольной устойчивости можно не производить. Если расчетная схема трубопровода в процессе монтажа отличается от расчетной схемы в процессе эксплуатации, то расчет трубопровода выполняется в два этапа. Вначале выполняется расчет на нагрузки, возникающие при монтаже. На вто- , ром этапе расчета трубопровод рассматривается с начальной погибью, величины которой определяются на первом этане расчета, под воздействием эксплуатационных нагрузок. Определенные на обоих этапах расчета напряже- ] ния алгебраически суммируются. Полные напряжения затем сравниваются ‘ с предельными.
§ 2. Матрица жесткости элемента
В качестве расчетной моде;Ти надземпого бескомпенсаторного перехода трубопровода принят стержень трубчатого сечеиия. Материал трубы принимается упругим, зависимость «напряжения деформации» принимается на основании обобщенного закона Гука. Считается, что в процессе нагружения системы остается плоской.
Для решения задачи используется метол конечных элементов в переме щеииях. В качестве конечного элемента принимается линейный Одномерный элемент. Рассчитываемая конструкция заменяется некоторым числом конечных дискретных элементов. Криволинейные участки перехода заменяются совокупностью прямых, соединенных иод углом друг к другу Узлы соединения конечных элементов должны обязательно назначаться в местах соединения трубопровода с любыми связями (опорами). Примыкающие к переходам подземпые участки трубопровода рассматриваются только прямолинейными. Поэтому для их описания используется так называемый полубес-конечный элемент.
Определим матрицу жесткости и грузовых членов для отдельного элемента — стержня, принимая местную систему координат, связанную с элементом. Номер элемента обозначим через i. Положительные направления усилий и перемещений изображены на рис. 61. При этом будем строить матрицу отдельно для начала и конца элемента. Тогда элементами матрицы жесткости будут являться реакции в соответствующей точке только от одного из единичных смещений при закреплении остальных точек, а элементами матрицы грузовых членов — реакции от нагрузки при закреплении граничных точек.
В соответствии с принятыми положительными направлениями усилий и перемещений можно записать матрицы жесткости и вектор реакций в виде
| 0ц | °13 | М0(Фо = | 1) |
М0 (v0 - 1) |
М„ ("о = 1) | |||
| /н = | Ojl | °82 |
аТЛ | -= | Qc (Фо = | 1) |
Со (t'o — 1) | Qo К = 1) |
|
а31 |
а32 |
°33 | «о (Фо = | 1) | So (t'o ~ 1) | Qo(“о = 1) |
|
й)2 | ^13 | ||
|
II | b2i |
^22 | ^23 |
|
Ьз1 | ^32 | ^33 |
| — Ml (Фо = Ij | — Mi(v0— — 1) | — Ml («„= 1) | |||
| = |
Qi (ф0= i) | Qi (^о = — 1) | Qi (u0T= •) | ||
| Si (Фо = 1) | St К= —1) |
& о || | |||
| ai р | Ь1Р | ||||
| II X to: | °2Р | ; ** = |
ь*р |
¦ | |
|
аз Р |
Ьзр | ||||
Здесь и в дальнейшем индекс элемента i опущен. Для элемента можио считать, что поперечные перемещения и углы поворота малы, поэтому реакции продольных связей от них равны нулю. Для определения реакций можио использовать независимые уравнения равновесия в поперечных и продольных перемещениях. При определении поперечных перемещений будем учитывать геометрическую нелинейность (продольно-поперечный изгиб), считая, что продольное усилие S, обусловленное воздействием температуры и внутреннего давления транспортируемого продукта, известно. Кроме того, учитывая особенности трубопровода, будем считать, что каждый элемент представляет собой балку трубчатого сечсния с заглушками (доньями) по концам.
Для вычисления верхних двух строк матрицы жесткости используем известное уравнение продольио-поперечного изгиба
EJdHi dx* + Sd^v dx2 = ?, (12.2)
где LI — пзгибная жесткость трубы; v — поперечное перемещение сечения
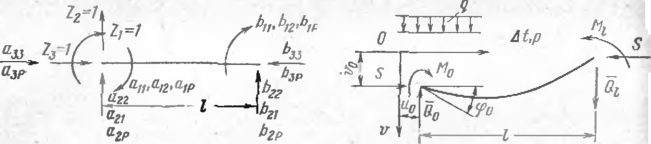
Рис. 61. Схема конечного элемента Рис. 62. Расчетная схема элемента
надземного участка трубопровода
надземного участка трубопровода
трубопровода на расстоянии х от начала координат; S продольное усилие, положительное при сжатии; Q— интенсивность поперечной нагрузки.
Решение этого уравнения запишем в форме начальных параметров Положительные направления начальных параметров приведены на рис. 62 Уравнения прогиба, угла поворота сечения, изгибающего момента и поперечной силы при S>0 имеют внд
I sin kx
I3
Ain
v (х) = vD 4 ф„
(kl — sin kx)-\-
Elm*
kl
EI
ql*
i2
(1 — cos kx) +
ф (x) = ф0 cos kx
EI kl QlB
Eim3
ei m2
(kx — sin kx);
1 4 cos kx Qo
(1 — cos foe) — Q0 ¦
M0 I . , — sin kx
k42 / fe2/2
ql2
klEI — I
Ф„-sin kx -(- M0 cos kx. 4- Q0 — sin kx -
I kl
Q (*) = Qo <7*.
• cos kx); (12.3)
где Do, фо, Mo, Qo — соответственно перемещение, угол поворота, изгибающий момент и поперечная сила; I — длина элемента; k2=S/EI— параметр
продольного усилия. _ _
Для удобства вычисления матрицы жесткости под поперечной силон Q понимается сила, направление которой перпендикулярно к недеформировап-ной оси элемента (см. рнс. 62).
При действии растягивающего усилия (S<0) соответствующие уравне ния можно получить (12.3), заменив fe2 на № и используя известные за висамостн для функций комплексных перемепных.
Используя приведенные решения и уравнение продольного сжатия, на-ходим искомые элементы матрицы жесткости и грузовых членов:
6 EI
M (x)
k42
AEI
и 1 —- ^12 — ^2
ап = —-— vi;
°12 -\2Е1
Qni> = boa -
2 EI
¦V-
Is
I — °23 = ^S1 = ^34 = ^13 "
_ . ql2 , ql
ал p — — o1 p —--i2~V3’ °2 P = 1 p ~ ~2 ’ (12.4)
Os р~ЪзР = аД tEF + PFCB— poKUF, (12.5)
где F — площадь сечения стенок трубы; At — температурный перепад, поло
жительный при нагревании; р — внутреннее давление; Fc в — площадь сечения трубы в свету; (Тип — кольцевые напряжения от внутреннего давления. Приведем формулы для определения v в функции безразмерного параметра
продольного усилия т* = \S\P/n2Ef: для S>0
Пт tg пт—пт
я т. п т
2 2~
пт пт — sin пт пт пт
8 tgiim tg
2
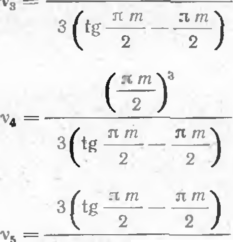
(лту, пт
для S<0
th пт пт
8И1Л/П пт пт
2 2
пт пт ¦— sh пт
4 sh пт ,, пт пт th----
я т
У
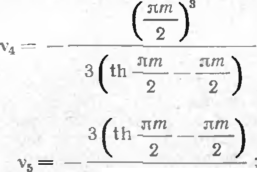
для S = 0 v, —v5= 1
Таким образом, получены матрицы жесткости и реакций для элемента открытое! (надземной) части трубопровода. Здесь индекс элемента i опущен, эти выражения используются для любого элемента с присвоением соответствующего индекса /.
Так как рассматривается надземный переход с примыкающими полу-бесконечиымп подземными участками, то необходимо записать также матрицу жесткости и вектор грузовых членов для начала полубесконечного уча' стка. В качестве расчетной модели грунта принимается упругое основание, т. е. считается, что по длине имеются распределенные поперечные и продольные связи, сопротивление которых пропорционально соответствующим перемещениям, т. е. т*=—Схои, qv =—cuov.
Уравнения иродольио-поперечиого изгиба и продольных перемещений для такой расчетной схемы (рис. 63) имеют вид:
di v cd-v
El —-----1 S--b kv - <7.
(12.6) (12 7)
dxi dx2
d*u dx2
+ n2u = 0,
где
к —' ci/o^hI
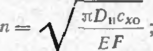
« — продольное перемещение трубопровода на расстоянии х от начала координат; cv о обобщенный коэффициент нормального сопротивления грунта;
DH наружный диаметр трубы, Сх о — обобщенный коэффициент касательного сопротивления груита.
На основании решений уравнений (12.6) и (12.7) через начальные параметры (см. гл. 4 и 6) находим искомые элементы матрицы жесткости и грузовых членов дЛи начала полубесконечного элемента:
Рис. 63. Схема полубесконечного подземного участка трубопровода, примыкающего к переходу
flla л]CyoDu EI',
al3 ~ c23 ” a3l ~ C82 aip “
2 л/Ci/c^r EI — S EI
aa g = EFn\
qEI
qEI
Й2р
(12.9)
^Cy0DuEl a3p = aAtEF •{ pFcn }^^кцГ •
^2 ^JcyoDuEI — S,
Этн элементы матрицы используются для описания только примыкающих к надземному переходу с обеих сторон подземных участков трубопровода.
§ 3. Уравнения равновесия узла
Как отмечалось раисс, вся рассчитываемая система заменяется конечными линейными элементами, соединенными в узлах. В нашем случае в каждом узле соединяются два элемента. Kpo*ie того, для общиости решения будем считать, что в каждом узле имеются три упруго-податливые опоры — угловая и две линейные, направленные поперек н вдоль элемента. Типовой узел рассчитываемой системы изображен па рис. 64. Особыми свойствами будут обладать только крайние узлы, где имеются полубескоиечные элементы.
Направление счета узлов и элементов гринимаем слева направо Обозначим номер узла через ?, длину элемента, предшествующего узлу, через U, последующего /(+1, угол между элементом и вертикальной осью, направленной винз, через у с соответствующим индексом, перемещение узлов обозначим через Z с соответствующим индексом, причем для узла t перемещения Z3 i_2, Zs i-1 и Zs i означают соответственно угловое, поперечное и продольное (осевое) перемещения в местной системе координат. Положительные на-
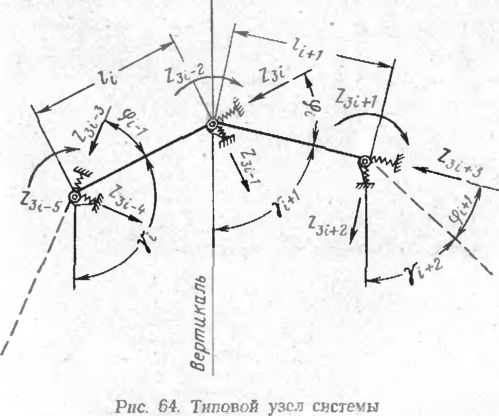
правления углов у и перемещений Z приведены на рис. 64. Угол между элементами определяется по формуле
<Г1 = Ti — Yi+i. (12.10)
причем угол tp, будет положительным, если вращение продолжения предыдущего элемента до совмещения с последующим будет происходить по ча-совой стрелке. Учитывая особенности крайних узлов, обозначим их номера соответственно индексам и и к.
Уравнения равновесия узла выражают условие равенства пулю суммы моментов и проекций всех сил па ортогональные оси от всех нагрузок и воздействий. Тогда для каждого узла в плоской системе получаем три уравнения, которые в матричной форме имеют вид
RHi-4Zi-i 'I' RHZi + *,(/+!)*(,+„ - V где векторы перемещений и грузовых реакций
(12.11)
(12.12)
|
1 5 | Zsi -i |
||
| 2/-i = | 4 |
5 | т os N |
| ^31—3 |
^ai |
| ^ (3i-2)p | |||
| 2y+i = | Z3i+2 |
» R p — |
R$i-l)p |
|
Z8i+3 | Л(3 i)P |
Матрица жесткости узла вычисляется на основании матрицы жесткости элементов, примыкающих к узлу, и матрицы жесткости связей с приведением ее к принятой (см. рис. 64) системе узловых перемещений:
'/(Ж) lli'K(i+i)’ (12.13)
где П, — матрица поворота; П,т—транспонированная матрица; С; — матрица жесткости связей;
П,- =
(12.14)
С/ —
| 0 | 0 | |
| — |
cos q>? | sin Ф, |
| — | sin q>c |
— cos <f>, |
| 1 <0 | 0 | 0 |
|
0 | C2 fx) |
0 |
| 0 | 0 | сз (0 |
Аналогичным образом вычисляется матрица грузовых членов
(12.15)
Уравнение (12.11) составляется для всех узлов системы путем присвоения индексу i всех значений номеров узлов. Отметим также, что при i=н или г=к матрицы жесткости соответствующих элементов берутся для подземной части. Кроме того, необходимо учесть, что если индекс при перемещениях Z меньше 3 н — 2 или больше 3 к, то соответствующие перемещения Z—0, так как крайние элементы приняты полу бесконечным и.
§ 4. Компоненты напряженно-деформированного состояния трубопровода
Из решения системы линейных уравнений (12.11), число которых равно л троенному произведению числа узлов, определяют неизвестные перемете пия 1 во пссх узлах. Далее, зная перемещения обоих концов элемента, можно определить грани-шые параметры. Под граничными параметрами здесь понимаются три компонента перемещений — поперечные, продольные перемещения и угол поворота — и три компонента усилий — поперечная, продольная силы и изгибающий момент. Для вычисления компонентов усилий используются элементы мзтрипы жесткости и матрицы грузовых членов.
Расчетные зависимости для вычисления граничные параметров имеют
вид:
и0 = Z3i_4 COS <г-f Zai-3 sin <PiI
Мв — G\q I 5^11 — (Z.ii—4 cos lJ i—i -|- 3 sin ^ a,I Z3f_2fcn+Zs
Qo = °2<7 "Ь ^3i—5a2l- (*3i 4 C0S *P« — 1 ^31—3S'n Vi—l) O.,o Z3l_tb2l -f- Zj, 1—^22;
1 М/= —biq — Zji-jflii—1^1? 1 (-^'з:—4C0S'W—IT
+ Zsi—s sin Ф/_1) ЬЛг — Zgi—sbuJ
— boq ' ^:u'- i &2Я ('/¦:<i 4 COS ф^_ 1 -j- -Zsi—g sin (ir 1) 2 ^:i? 5^21 •
(12.17)
Обычно для определения распределения перемещений и усилий по длине стержня считается удобным использовать метод начальных параметров. Од-иако как показал проведенный машинный эксперимент, использование этого метода приводит к численным ошибкам. Поэтому нам при численных методах решения пришлось отказаться от этого общепринятого метода и использовать уравнения в граничных параметрах:
ОЕ -= ы 1 - Ф, (DJ + ^Ф- (I) + Фо [®1 (1) - Ф- (I) ®1 (Ю - Ф8 (1) Фь (1 )1 +
+ Ф/Ф8(Ю + [Ф4 (?) - Ф4 (1) Ф7 (|) - Фй (5) Фэ (1)];
EJ
чг = {щ - vb) Фа ft) ь Фо [Ф= (D - Фю (?) Ф5 (1) - ®«(I) ®i (1)] + Ф;Фю О + + [фз © - Фз (1) °10 ® - ®9 (5)ф*
Щ = М0 f®5 (|) -ф, (1) Фи (I)] + М/Фц (I) + Qd (®1 (I) - Фд (1) Фп (?)] -
-<?[Ф2 © —ф« (!) Фи (1)1;
В этих уравнениях \=У./1 — безразмерная текущая координата, изменяющаяся от 0 до 1, а Ф — функция от ?. Значения введенных дополнительных Функций Ф(1) вычисляются по приведенным формулам, причем значения Функций изменяются в зависимости от знака продольного усилия:
Для S > О
(|) = —-— sin ят?;
я т
Ф* (I) = —~ (1 — cos пт\у, п2т2
Is
Фз (5) = (л/г;| — sin лт|);
n3m3
. /4 / nam2|2 _\
Ф* (1)----(---1 + cos ят 5 j ;
Ф5 (?,) — cos пт
_ пт
Фе (I)--—sin пт 1\
®i fi) = —— sh пт ?;
Tim
Фг(5) =--—— (1 — chnmE);
{3
ndm6
,ь t\ <4 Z' зт2т212 , , A
(S) --1---- 1 — ch лт 11
n*m* \ 2 J
Ф5Ш — ch ят|;
Ф6 (I) = — ~~ sh xml;
для S^O
®i (5) = Ie;
24
Вспомогательные функции вычисляются по формулам;
ф (|) = Ф1(1)ФЯ(6) Ф2(1)Фг(1) .
Ф,(1)Ф3(1)-Ф|(])
Ф6 (I) * ФЯ(1)Ф ;
Ф,Г?}~* Ф10)Ф2(?)-Ф»(1)Ф1(|) .
Ф,(1)Ф3П)-Ф| (1)
Ф (й) ан '1)Ф1(?)-Ф (ЦФ (I) .
(i>i (1) ф3(1)—ф! (I) фц:«) = ф«(|; Фв а)
при S 0 Фц(|)= I. (12.19)
Реакции связей, имеющихся в узлах, вычисляются как разность значений усилий, действующих л сечении трубопровода слева и справа от имеющейся связи:
Iji-2 - *«1+1 (б = 0) - Mi (1-1), l-ii-i — Qc+i (i*= 0) — Qt (I = 1);
Последняя формула в (12.20) учитывает, что продольное усилие постоянно по длине элемента.
Расчет по описанному алгоритму можно провести, если известно продольное усилие. Напомним, что под S понимается эквивалентное продольное усилие в сечении трубопровода (положительное при сжатии), обусловливающее его изгиб, а под N — усилие в стенках трубы (положительное при растяжении). Эти усилия связаны между собой cooti ошеннем
S=pFCB-N, (12.21)
1де /;/•’<• в — произведение давления и площади трубы в свету.
Если считать, что ось трубопровода не реформируема, то эквивалентное осевое усилие в сечеини трубы or внутреннего давления и температуры определяется по формуле
S3 — (аА/? 4- 0,2 сКц) F, (12.22)
где F ~ площадь сечения стейок трубы.
На первом этапе расчета усилие S принимается равным величине, вычисленной по (12.22). Далее, рассчитав систему и найдя перемещения, опре
деляют значения усилия с учетом деформативности системы. Расчетные формулы получены иа основе нелинейного уравнения, связывающего деформацию с перемещением.
Эквивалентное осевое усилие е учетом деформативности системы вычисляется по формуле:
Sa = —(Zg [_g cos cpf—j — ZSi ^ sintpf—i) G33 4 Z3{b^3 A,-;
Ai — fl<P(?)]3d!. (12.23)
2 o'
Такнл! образом, для определения осевою усилия использутется итерационный метод, в котором на каждом этапе расчета определяется усилие по перемещениям, определенным на предыдущем этапе расчета.
§ 5. Блок-схема программы расчета на ЭВМ
Приведем блок-схему расчета надземного беекомпенсаторного переходя трубопровода (рис. 65).
Блок 1. Исходной информацией для расчета являются значения нагрузоя и воздействий, физико механические характеристики металла труб и грунта иа примыкающих к надземному переходу подземных участках Tpy6onpoBoAaJ геометрические характеристики труб перехода. Здесь вычисляются эк к ива! лентное осевое усилие для первого этапа расчета н все вспомогательные naJ раметры.
Блок 2. Матрица жесткости вычисляется для вссх элементов открытой и подземной части трубопровода в соответствии с ранее приведенными формулами. В блоке 2 имеются три подблока для вычисления матрицы жесткости в зависимости от знака эквивалентного усилия.
Блок 3. Здесь вычисляется матрица реакций (грузовых членов) от поперечной нагрузки, воздействия температуры и внутреннего давления с учетом продольно-поперечного изгиба элемента. Последний фактор обусловил наличие таких же, как в блоке 2, трех подблоков.
Блок 4. На основании уравнения равновесия, составленного для произ-] вольного узла, формируется система линейных алгебраических уравнений. В нашем случае для плоской системы число уравнений равно числу узлов, умноженному на три. При этом для первого и последнего узла учитываются особенности двух примыкающих к нему элементов, а также граничные условия.
Ввод исходной информации
Продольное усилие 8>С | S<0 { s~ff~
т
Формирование системы уравнений равновесия
|
Решение системы линейных уравнений
| Эквивалентное продольное осевое усилие | ||
|
ь | Продольное усилие | |
| S >0 |
S^O | 5 = 0 | |
Напряженно-Вефорниро-ванное состояние трубопровода
Да
Критерий сходимости процесса итерации
Нет
Продольное усилие S>0 | S^O |~5=Р~
I
|
Расчет на прочность по | 10 | Вывод выходной инфор | ||
|
J | СНиП П +5-75 |
мации |
Рис. 65. Блок-схема расчета надземного беекомпенсаторного перехода
трубопровода
Блок 5. Здесь решается система лиисйиых уравнений, число которых
может быть равно в данной версии программы НБП-2 140 В результате
решения получаются обобщенные перемещения всех узлов. Далее, вычисляются граничные параметры элемента: три составляющих перемещения (про дольное, поперечное и угол поворота) и три составляющих усилия (продольное, поперечное и изгибающий момент).
Блок 6. На перпом этапе расчета продольное осевос усилие от всех на
грузок и воздействий принимается для всех элементов одинаковым и равным усилию для прямолинейного стержня с неподвижными опорами.
Вычислив перемещение системы, на основе уравнения (12.23) вычисляется новое значение эквивалентного усилия для каждого элемента. При этом интегрирование производится численным .методом.
Блок 7. Критерием сходимости процесса при определении фактического значения продольного осевого усилия является сравнение усилий двух последующих итераций. Нели установленный критерий не выполняется, то новое значение усилия засылается в блоки 2 и 3, где заново формируется матрица жесткости и матрица реакций элемента. При удовлетворении критерия сходимости переходят к блоку 8.
Блок 8. На основе граничных параметров для элемента, определенных в блоке 5, находятся продольные и поперечные перемещения, изгибающий момент, поперечная сила н продольное осевое усилие в стенках трубы, а также реакции опор. Продольные и поперечные перемещения, изгибающий момент определяются по уравнениям для любых сечений по длине трубопровода. Сечения, где необходимо определить эти параметры, указываются по входной информации. Реакции опор определяются по вычисленным значениям изгибающего момента, поперечной и продольной сил слева и справа от опорного сечения. Отметим, что продольное осевое усилие в стенках трубы определяется как алгебраическая сумма произведения внутреннего давления на площадь трубы в свету и эквивалентного продольного усилия.
Блок 9. Здесь по найденным усилиям определяются кольцевые и продольные напряжения по сечению трубы и выполняется расчет на прочность в соответствии с действующими нормами.
Блок 10. На печать выдаются значения изгибающих моментов, продольных н поперечных перемещений, продольных усилий и напряжений в крайних фибрах сечения. Кроме того, на печать выдаются значения предельных напряжений по установленным СНнПом 11-45—75 различным предельным состояниям.
Таким образом, изложенный алгоритм расчета учитывает влияние примыкающих к переходу подземных участков трубопроводов, геометрическую нелинейность, начальные несовершенства перехода, самокомпснсацню системы н жесткость опор.
§ 6. Подготовка исходных данных для расчета
Вначале вся рассчитываемая конструкция, состоящая из прямолинейных и криволинейных участков трубопровода, разбивается на отдельные прямолинейные элементы. Узловые точки (где соединяются два элемента)' обязательно назначаются в местах соединения подземной части с надземной расположения опор (связей) и соединения прямолинейных и криволинейных участков. Пролет трубопровода, имеющий начальный изгиб, рекомендуется, на основании численных экспериментов, разбить на 3—10 элементов, в зависимости от кривизны оси трубопровода. Кривые необходимо заменить рядом прямых, соединенных под углом друг к другу. Если опора (связь) находится ча кривой, то прн разбивке ее на элементы следует предусматривать, что к опоре должны примыкать с обеих сторон прямые, являющиеся продолжением друг друга. Далее, определяется угол между элементом и вертикалью (при расчете перехода трубопровода в вертикальной плоскости) или между элементом и перпендикуляром к оси, соединяющей крайние узлы (при рас-теге перехода в горизонтальной плоскости). Вычисляются действительные
жесткости опор (связей). Если связь в каком-либо направлении абсолют» жесткая, го в качестве ее характеристики вводится большое число, равяоЛ 0,1-1018. J
Физико-механические характеристики грунта задаются по данным hhkJ nepilo-reo.логических изысканий
Нагрузки, коэффициенты перегрузки и коэффициенты, характеризуют*^ предельные состояния, определяются в соответствии с требованиями норм Вхояная информация заносится в специально разработанную форму.
Первая строка формы содержит информацию общего плана: наименова! нне отдела, заказа, варианта и объекта.
Во вторую строку заносятся значения следующих характеристик: р -I внутреннее рабочее (нормативное) давление продукта; At температурным перепад, положительный при нагревании; Da — наружный диаметр трубьи б - толщина стенкн трубы; а — коэффициент линейного расширения маты риата труб; Е—модуль упругости материала труб; ft— коэффициент Пуао-! сона материала труб; q — интенсивность равномерно-распределенной поп« речной нагрузки; hv — расстояние от оси трубы до верха засыпки на примыкающих к переходу подземных участках трубопровода; Егр—модули деформации грунта р, р коэффициент Пуассона грунта; с* о — коэффициент касательного сопротивления lpyirra, г|—коэффициент снижения нормального сопротивления грунта.
В третью строку заносятся следующие характеристики: nQ — коэффицисм перегрузки для поперечной нагрузки; пь — коэффициент перегрузки для внутреннего давления продукта; Хк — параметр самокочпенсации, который может приниматься меньше единицы для системы со значительными перече~‘ щениями, вводится для ускорения процесса сходимости; m — коэффицием условия работы; k, коэффициент безопасности материала по временнозЯ сопротивлению, k-2 — коэффициент безопасности материала по текучести kK — коэффициент надежности; с — коэффициент, отражающий категории участка трубопровода; i?iH; R,” — предел прочности и текучести материала труб; | — шаг текущей координаты, для которой печатается выходная ик» формация для всех элементов.
Начиная с четвертой строки построчно ввовится информация для каждого элемента рассчитываемой системы Первым элементом явдяегся пояу~ бесконечный участок, поэтому информация о его геометрии не заносится У го 1 между элементом н вертикалью или соответствующим перпендикуляр ром вводится в градусах и долях от градуса. Далее, вводятся жесткости уп^ ругих связей: Ct—жесткость угловой связи; С2 — жесткость поперечной связи С'з - жесткость продольной связи. Положение опоры характеризуется концом элемента, так, например, если связь имеется в пятом узле, то ии* формацию о ней заносят в пятую строку. Последняя вертикальная графа этих строк характеризует шаг текущей координаты |спеК для соответствующего элемента. Если для всех элементов шаг текущей координаты одинаков, то информация в эту графу не заносится. После заполнения всех стро^ в первом столбце ставится знак *, являющийся признаком конпа исходных данных.
§ 7 Выходная информация и анализ результатов расчета
Выходная информация состоит из двух частей: исходные данные и результаты расчета. Исходные дздшые распечатываются с необходимыми комментариями и служат для контроля ввода их в программу. Результаты расчета включают в себя значения изгибающих моментов, фибровых напряжений от изгиба, осевых продольных усилий и продольных напряжений, поперечных и продольных перемещений и трех составляющих реакций упругих опор — вертикальной, горизонтальной и угловой.
Положительные значения расчетных величин означают для изгибающего момента и изгибных напряжений— растянуты нижние волокна:
для продольных усилий и напряжении — растяжение;
для поперечных перемещений — направление вииз перпендикулярно элементу;
для продольных перемещений — направление вдоль элемента слева направо;
для вертикальной реакции — направление вверх перпендикулярно элементу;
для горизонтальной реакции — направление вдоль элемента к Опоре слева направо;
для угловой реакции (изгибающего момента) — паправление по часовой стрелке относительно узла, где расположена опора.
Для магистральных трубопроводов проверка прочности надзе-мных переходов производится в соответствии с предельными состояниями, изложенными в СНиПе II-45—75 «Магистральные трубопроводы. Нормы проектц-оованняж
Предельные состояния для многопролетных бсскомпенсаторных балочных систем надземной прокладки при отсутствии или устранении резонансных колебаний трубопроводов в ветровом потоке имеют вид:
от расчетных нагрузок и воздействий
апр N I ^ %^2'
I % М
N°,635i?2 (1 + %) ^ - Г
(12.24)
от нормативных нагрузок
'°пРМ.зТС (12.25)
«н
гле
1, если о„р > 0;
О?
1- 0,75 / -\ — 0,5————, если <гПр<0:
^3 =
I
(12.26)
Ri— расчетное сопротивление металла; с — коэффициент, отражающий категорию участка трубопровода; R *—нормативное сопротивление металла;
— коэффициент надежности; с“ц — кольцевые напряжения от рабочего
(нормативного) давления.
В левые части формул (12.24, 12 25) входят значения расчетных параметров, определяемых программой НБП-2, Они содержатся в выходной нн формации, за исключением величины а“р, которая вычисляется по формуле
°гр ~ °прЛ' ± °прМ |* (12.27)
Отметим, что для проверки условия (12.25) необходимо рассчитать на
нормативные нагрузки и воздействия
Для использования формул (12.24) на рнс. 66 приведены вспомогательные афики, построенные в безразмерных параметрах-. По осп абсцисс отложено отношение продольных осевых напряжений сгПр n к расчетному сопротивлению Л, по оси ординат — отношение абсочютиой величины изгибных напряжений °пр м ( к расчетному сопротивлению R.2- Вычислив эти безразмерные параметры, находим точку на рис. 66 Если эта точка находится ниже кривой соответствующего значения ф3, вычисленного по формуле (12 26) то это оз-а^ает, что условия (12.24) выполнены. Затем проверяется условие (12 25).
Рис. 66. График для проверки предельного состояния бескомпен саторных переходов трубопроводов
Если условия (12.24) илн (12.25) не выполняются, то изменением конструн тивное решение переходов в основном за счет уменьшения пролетов, и рас чет повторяем заново. Используя вариантное проектирование, опредсляк! рациональное конструктивное решение, удовлетворяющее предельным cq стояниям.
В качестве иллюстрации применения программы ПБП-2 рассмотрим рас чет трехпролетного перехода с пролетами 3100, 3100 и 3300 см. На учаегке первых двух пролетов переход имеет начальное искривление. Геометрические параметры перехода приведены на рис. 67, о. Здесь же представлена раз бивка его па элементы. Открытая часть состоит из девяти элементов, первые два пролега состоят ил восьми элементов, последний пролет —из одного Примыкающие к переходу подземные участки имеют высоту засыпки грун том 80 см (над верхней образующей трубы). Физико-механические характс ристикн грунта: модуль деформации грунта ?гй=18 МПа, коэффициент Пу ассона груига р,гр = 0,3, обобщенный коэффициент касательного сопротивления грунта сх <,=2,5 H/cv3 J
Переход выполнен из труб размером 1420X19,5 мм, имеющих времен ное сопротивление 600 МПа и предел текучести 470 МПа. Переход распо ложен на участке II категории. Нагрузки и воздействия- распределенная по перечная нагрузка 99 Н/см, рабочее (нормативное) давление 7,5 МПа, теж пературный перепад +50 °С.
Все исходные данные, включая определяемые геометрические параметры трубы, распечатываются. Это Необходимо для контроля подготовки исход-них данных В результате расчета на печать выдаются значения изгибаю-щнх моментов, изгибных напряжений продольных усилий и напряжений, поперечных н продольных перемещений и три составляющие реакции промежуточных опор.
Ряс. 67. Схема трехпро-летного бескомпспсаторного перехода с определенными начальными искривлениями
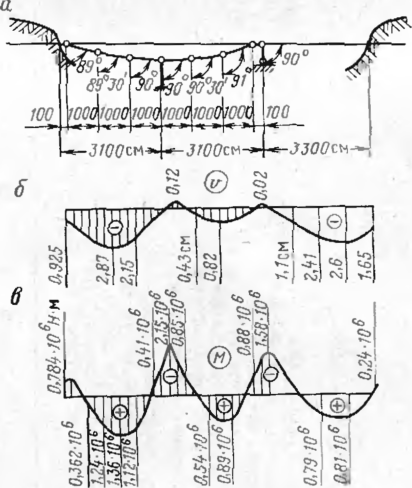
На рис. 67,6, в приведены построенные по полученным данным (см. рас печатку с ЭВМ) эпюры соответственно поперечных перемещений и изгибающих моментов. Наибольший изгибающий момент возникает на первой опоре, он равен 2,15-10е Н-м. Наибольшее усилие действует также на первую опору, оно равно 0,63-10® Н.
Для опорного сечения из результатов расчета (см. распечатку с ЭВМ) находим 0цР ,м=72,0 МПа, cr,Jr, я——37,7 МПа. Кроме того, в конце распечатки приведены значения ^2-278,6 МПа и фз=0,3153, которые служат для проверки предельных состояний.
Проверяем предельное состояние но формулам (12.24). Предельно-допл-скаемые продольные осевые напряжения
[anpiVJ 0,3153-278,6 — 87,7 МПа.
Предельно допускаемые продольные изгибные напряжения
[огрЛ11 =
о.езб-гте.е a + 0,3153) sin — 37,7 '
0,3?53-78'—п*=
97 МПа.
PMJ (14-0,3153)278,6
Так как |спр а- | <[о11Р л-] и |опр дг | <[оПр лг], то предельное состояние, установленное нормами, выполнено.
Выходная информация
Вариант:
ю
СЛ
о
Отдел:
Объект:
99
50
7,5
1.1
1.1
1,0
0,75
1.15
1.1
1,34
0.85
142
1.95
Момент инерции, см4 Момент сопротивления, см®
Площадь сечения, см3 Модуль упругости, МПа Коэффициент Пуассона металла Коэффициент линейного расширения Нормативное сопротивление Я", МПа Нормативное сопротивление Д"- МПа Модуль деформации грунта, МПа Высота засыпки над осью, см Коэффициент Пуассона грунта
0.2104Е 07 0.2963Е 05 860 0.210Е 06 0,3 0.12Е—04 600 470 18 151 0.3 2,5
| Элемент |
ft | <Р[ |
h | с, | С, | С» | 1 |
| J 2 3 4 5 6 7 8 9 10 |
90.00 90.00 89.00 89.30 90.00 90.00 90.30 91.00 90.00 90.00 | 0.0 1 00 —0.30 —0.70 0.0 -0.30 —0.70 1 00 0.0 0.0 | 9999.00 100.00 1000.00 1000.00 1000.00 1000.00 1000.00 1000.00 100.0 3300.0 |
0.0 0.0 0.0 0.0 0.0 0,0 0.0 0.0 0.0 о.о | 0.0 0.0 0.0 0.0 0.10Е 18 0.0 0.0 0.0 O.lOE is 0.0 | 0.0 0.0 0.0 * 0.0 0.0 0.0 0.0 о.о 0.0 0.0 | 1 OOOOOOOOOO В cS К! Ь? Ь ю fo 1 |
Поперечная нагрузка, Н/см Температурный перепад, °С Рабочее (норм.) давление, МПа Коэффициент перегрузки nqКоэффициент перегрузки прПараметр самокомленсащш Коэффициент условия работы Коэффициент безопасности по материалу, k2Коэффициент надежности Коэффициент безопасности по материалу,
Коэффициент, отраж. категорию Наружный диаметр трубы, см Толщина стеики т^убы, см
Р.чулыаты расчета
| Перемещении | ||||||||||
| Элемент | Момент, | 11-м | Ич1 ибаю цес | Продольное |
Occbog |
Реакции, 11 | ||||
|
координата |
иипряжепис, МПа | усилие, К | напряжение, МЛ а | |||||||
|
поперечное, см | продольное, сч | |||||||||
| 1 2 |
—.784Е | 06 | — 264 Е | 02 | —.325Е 07 |
—.378Е 02 | 0.92Е |
00 | 0.73E—02 | |
| 0.25 | —.786Е | 0G | — .265Е | 02 | 0.96Е | 00 |
||||
| 0.50 |
—.788Е | 0G | —.266Е | 02 | 0.10Е | 01 | ||||
|
0.75 | —.791Е | 06 |
- .267Е | 02 | 0.10Е | 01 | ||||
| 1.00 | —.795Е | 06 | - .268Е |
02 | 0.10Е |
01 | 0.76E—02 | |||
| 3 | —.795Е | 06 | —.268Е | 02 |
—.324Е 07 | —.378Е 02 |
0.10Е | 01 | 0.26E—01 | |
| 0.25 |
—.187Е | 06 | — .634 Е | 01 | 0.15E | 01 | ||||
|
0.50 | 0.361 Е | 06 |
0.122Е | 02 | 0 20 E | 01 | ||||
| 0 75 | 0.842Е | 06 | 0.284Е |
02 | 0.24E |
01 | ||||
| 1.00 | 0 124Е | 07 |
0.418Е | 02 |
0.27E | 01 | 0.28E—01 | |||
| 4 | 0 124Е | 07 | 0.418Е |
02 | — .325Е 07 | —.379Е 02 | 0 27E | 01 |
0.14E— 01 | |
| 0.25 |
0 134Е | 07 | 0 454 Е | 02 |
0.2SE | 01 | ||||
| 0.50 | 0.136Е |
07 | 0.459Е | 02 |
0.28E | 01 |
||||
| 0 75 |
0.128Е | 07 | 0.433Е | 02 | 0.28E | 01 | ||||
|
J 00 | 0 111Е | 07 | 0.3 76Е | 02 | 0.21 E | 01 |
0.15E 01 | |||
| 5 |
0.111Е | 07 | 0.376Е | 02 | —.323Е 07 |
—.376Е 02 | 0 21E | 01 | —.10E 01 | |
|
0.25 | 0.387Е | 06 |
0.130Е | 02 | 0Л5Е | 01 | ||||
| 0.50 | — .412Е | 06 | 0.139Е |
02 | 0 95 E |
00 | ||||
| 0.75 | - .126Е | 07 | - .426Е | 02 |
0 39E | 00 | ||||
| 1.00 | .215Е |
07 | —.726Е | 02 |
экстр | 0.G2E- |
-12 | -.83E-02 | 0.628E 06 | |
| б | —.215Е | 07 | —.726Е |
02 | —,326'Е 07 | —.377Е 02 | 0.62E | -12 |
—.83E—02 | |
| 0.25 | - .И8Е | 07 |
—.501Е | 02 | — .HE | 00 | ||||
| 0 >0 | — .849!' |
06 | ¦286Е | 02 | —.27E- |
-01 | ||||
| 0.7» | — ,23'iF. | 06 |
- .8G3E | 0( | 0.18E | DO | ||||
| 1.00 | 0.281 Е |
06 | 0.951Е | 01 | 0.43E | 00 | — .63E-02 | |||
Продолжение
ш
СО
сч
о
СЧ
О
I
Ш
ю
t—
7 ?
ш ш
СО СО
Ы
ш
| СЧ |
сч | ,—« |
|
о 1 | о 1 |
о 1 |
| 1 Ш |
1 Ш | ! ш |
| ю | о |
ю |
| оо | о | •*ч |
О О о о о
О о —*
о о о о
о о о о о
— — — — —
СО^ООСЧСОСОЛОО^.СЛФЕ—гГ^СЧСЧ —• CD CD ООО Г I Г I О ° О О О о
^ CD N Об N О О о О О О
О S
о о> Л
g*C
о Kg
OS*
Яг 292,2 МПа, Ri~ 278,6 МПа, ^ 0,315, *?*— признак .дельта
о!
СЛ Т-* сч СЧ СЧ СЧ О О о О О О О
1111
о о
S =
н ?
= 2
<y s
2 s
о *=t ч o. <Q°
ю
CN
о о о —•
ООО
^C^COCPtDC'OOCf'-NNNNNNlOcD^m
ОООООООООООООООООООО
»;ooo^t-Ncooc5hNhh.Ncocoh.r}-wc: оо ТГ ^ 1C со 00 щ сОщЛ1ПЮЮЮЮЮ(МО) —> -гг WlONOOOOOOCOCSlOO-H^^~4r4^.^NNOO(N
о о о о о о о | I I I j1 |' ' l' [ | О о I
-•CNINCMWWCI^IMWWC^WINC^C^-CMCNIO
ОООООООООООООООООООО
ИИЩШЩЩШШШИЩЩЩЩЩШИЩШЩ
•--^лсосло^с^со^-зз^счсотг^йоо^м uioo^cooaiNbowwrtcocoMrt'^oNiM ............CNlOlDLOLOWiniOC^CMCMCO
| <м | сч | сч |
сч |
| о | о | о | о |
|
Ш | из | ш | ш |
| о |
СП | о |
<У> |
| 00 |
N | со | N |
| со | СО |
СО | со |
| N |
N | N | N |
| о | О |
О | О |
|
Ш | Ш |
Ш | V.1 Н W |
| CD | ю |
'<?> | О ю |
| СМ | сч | S3 | и: сч |
| СО |
со | со | m со |
} О lO О to Q lO о Ю о tc о Ю о to о
i^NOoD^'OhO^NiChqOWiONO
Л СЛ /”1 -Q 1^1 Q гч -Л Л
(N Ю Ю й Й Ю
Г Г I Г I г
о о о —
НЕСУЩАЯ СПОСОБНОСТЬ НАДЗЕМНЫХ ПЕРЕХОДОВ ТРУБОПРОВОДОВ
В работе И. П. Петрова и В. В. Спиридонова [30] отмечалось, что предельное состояние, т. е. несущая способность надземного напорного трубопровода, определяется условием равенства максимальных продольных напряжений пределу текучести металла. Экспериментальные исследования, проведенные по ВНИИСТе, показали, что и после превышения продольных напряжений предела текучести несущая способность надземного трубопровода не исчерпывается, т. е. можно допустить в процессе эксплуатации трубопровода улруго-пластические деформации металла. Так как d процессе эксплуатации ¦ рубонровода нагрузки и воздействия могут из ми яться по величине, а ииогда н но знаку (например, нагревание и охлаждение трубопровода), то несущая способность трубопровода должна определяться не только его напряженным состоянием, но и условиями, исключающими накопление пластической деформации и пластическую усталость металла.
§ 1. Анализ упругой и упруго-пластической работы надземных переходов
Анализ упругой и упруго-пластической работы надземных переходов проводился иа основе экспериментальных исследований, отражающих условия работы напорного трубопровода. Экспериментальные исследования проводились на моделях (рис. 68) балочных переходов с защемленными концами пролетом 760 см из стальных труб размерам 76x2 мм, характеризуемых пределом текучести, рапным 347 МПа, временным сопротивлением 503 МПа и относительным удлинением при разрыве 21 %.
Модели балочных i ереходов испытывались на действие поперечной иа-\’зки и внутреннего давления. Защемление концов моделей трубопровода исключало перечачу усилия от давления к заглушке иа расчетный пролет трубопровода. Перемещения трубопровода в спорном сечении контролировались индикаторалш часового типа. Поперечная нагрузка прикладывалась с помощью одиночных грузов, равномерно распределенных по пролету. Закрепление трубопровода на опорах против продольных перемещений проводилось в некоторых экспериментах до приложения поперечной нагрузки, а п некоторых после, что нашло отражение при расчетах. Затем с помощью ручного гидравлического иасоса через ресивер в трубопроводе создавалось внутреннее давление: до 10 МПа этапами по 2,5 МПа и далее по 1 МПа. Значение давления фиксировалось образцовым маио(. етром
Прогибы трубопровода определялись в восьми точках по длине пролета прецизионным нивелиром. Деформации измерялись датчиками на бумажной и пленочной основе с базой 5 и 10 им с помощью автоматического измерителя деформации АИ-1. Для определения больших деформаций в сеть активных и компенсационных датчиков вводилось, по мере надобности, дополнительное сопротивление, которое тарировалось также иа АИ-1. Датчики наклеивались у обеих опор, в трех сечениях на расстоянии 35, 95 и 145 мм от поры н посередине пролета. В каждом сечении наклеивалось по восемь лаччнков в продольном направлении и перпендикулярно к ним (по окружности). Датчики, расположенные по нижней и верхней образующей, дублировались.
В двух экспериментах загружение производилось до разрушения трубо-Ровода. Разрыв трубы происходил по иижней образующей вие пролета между двумя опорами, закрепляющими один из концов трубопровода, при Давлениях р=27,2 МПа (<7=4,72 Н/см) и р=27,4 МПа (<7=3 Н/см).

Рис. 68. Модель надземного перехода
Для анализа экспериментальных данных получим теоретическое решение! для надземного прямолинейного бсекомпеисаторного перехода трубопровода] с защемленными концами, прн воздействии на него равномерно распределенной нагрузки температурного перепада и внутреннего давления Переход] рассматривается как балка трубчатого сечения, при атом принимаются обычи ные допущения теории балок: прогибы считаются малыми по сравнению^ с пролетом, не учитываются касательные и радиальные напряжения и дефор-1 мирование контура поперечного сечения трубы.
Учитывая, что модель трубопровода выполнена из пластичной стали! (От/Ов = 0,69; 65=21 %), а деформации при нагружении не превышали 0,7 %„1 условно принимаем зависимость напряжений от деформаций в виде диа-1 граммы Прандтля. ]
Так как первые шарниры пластичности образуются в опорных сечениях^ то для общности решения рассматривается балка с шарнирно-неподвижными опорами с фиктивным моментом Мв на обоих концах. Следуя концепции! пластического шарнира, будем считать, что величина Мо, вплоть до образоЛ вания полного пластического шарнира, определяется из условия, что угоЛ поворота на опоре равен нулю, т. е. фиктивный момент равен моменту в за-1 щемленной балке (Л10=^у„Р). При дальнейшем росте нагрузки момент] в опорном сечении Мп ие изменяется и равен пластическому (А1ь=МпП). ¦ Уравнение продольно-поперечного изгиба балки имеет вид j
d4 v
(13.1>
EI
dx4
с
S-= q.
dx*
Принимая ?/=const, S=const, дифференцируя (13.1) дважды по x:
dev
dx*
d4v
dx*
Учитывая, что по концам балки приложены изгибающие моменты Л/0, а продольные усилия, обусловленные деформациями от повышения темпера-TVpu и внутреннего давления, имеют реактивный характер, граничные условия записываются в виде
о г п. d2v Mo . d3v qL
при х. — О, L v — 0, —- ¦ ) -— it ———, (13.3)
dx2 El dx? 2 El
Решение уравнения (13.1) при первых двух граничных условиях для начальной и конечной точек"
и =_ Г (tg лт sin яте-*- cos я/п| — 1) (—^—
л2т2 [ Ч л2т2
МQ tg лт — лт Мупр л2т2 tg лт
¦ИЫ
?. (13 4)
Решение уравнения (13.2) при использовании всех трех граничных условий для начальной и конечной точек
X
| 24&, | cosnm(l —1) |
л*т* Г | Мо |
\ tg лт VI |
|
лЗта tg лт |
cos лт | 2 1 |
М-уцр | ^ лт J\ |
X 1(1 — 2) — 1}, (13.5)
где v—v/i — прогиб, отнесенный к радиусу инерции сечения; tq f<il' — отношение стрелки прогиба защемленной балки от равномерно-распределенной нагрузки к радиусу инерции (fq=qLl/384 Е!)\ 1=2x/L— безразмерная текущая координата; т2^5/АгКр — отношение осевого сжимающего усилия к критической силе защемленного стержня (N,-r=4 n2EI/Lz); Л10=Л1„/(от W'n.-i)—¦ отношение внешнего (фиктивного) момента, приложенного к концам рассматриваемой балки, к пластическому моменту прн изгибе (ст—предел текучести металла труб, Wпл — пластический момент сопротивления при из-ii(6c); Л1упр=Л1уПр/(0т U^'n л)—отношение момента на опоре балки с защемленными концами к пластическому моменту при изгибе.
Отметим, что отношение Л10/МупР характеризует вид опор по концам балки: iVfo/Afynp=l — неподвижные опоры; Afo/Alynp=0 — шарнирные опоры; 0<.Ио/Л1упр<1 —упругие опоры.
Ih (13.4) и (13.5) получаем соответствующие прогибы посередине про-
ii-та (1=1):
I Jlk. (_1__iV i____in (13
л2т‘2 | V cos лт )\л-тг Afynp л2т2 tg лт ) 2 J
1 =__/_L__! Г1 _ (I__)}}, (13.7)
лзтз tg лт I cos лт 2 [ Afynp V лт )
Графическое изображение зависимостей (13.6) и (13.7) для начальной с-р^_ки прогиба от поперечной нагрузки ?в=0,5 при различных отношениях ЛЬ/Мупр (соответственно сплошными и пунктирными линиями) приведено на рпс. .69. При Л1о/Мупр=1 решения (13.6) и (13.7) совпадают, т. с. для защемленного стержня известное решение и полученное нами решение из предположений об учете реактивного характера продольного усилия совпа--ают Отмстим, что при т2= 1 прогиб ? стремится к бесконечности, т е. критическое продольное усилие S^p=mzJVKp=4 iPEI/L* и соответствует критическому продольному усилию для защемленного стержня.
При Af0/AJy„p<l оба решения расходятся. Объясняется это разным критическим усилием. Как следует из решения (13.6), независимо от жест-
кости, упругих связей (0sg:Afo/Afynp<li при т2=0,25 т. е. критическое про?
дольное усилие равно SHP=m2NKII=n:lEIIli и соответствует критическому продольно) му усилию для шарнирного стержня. Каи следует из решения (13.7) ?-*-оо только прн т?= 1, те2=0,25 величина С имеет конечна значение независимо or отношений Alo/Alynp- '
| , ]?,^ГГ= | ||||
| / и | ||||
| 1 1 | А / / |
0,5 | ||
| 1 1 /1 | -Mol& |
|||
0,5 1,5 ?.,Ь 3,5 W С
%
0,8
0,6
Ofi о,г
Отсюда следует, что если учитывать реактивный характер продольного усилия, обусловленного воздействием, то критическое продольное усилие для стержня с упругими угловыми связями любой же^ сткости, в том числе и при шарнирном ¦! жестком закреплении концов, одинакова и равно критическому усилию стержня с защемленными концами, к которому приложены внешние сжимающие силы, т. с. SKp—4n2EI/L2.
о
Рис. 69. Зависимость дополнительного прогиба от продольного усилия при различных соотношениях момента иа опоре
Опорный момент для защемленной балки определим из условия, что до об] разования пластического шарнира угол поворота на опоре равен иулю,-т. е. dv\dx=0 при х—0, L. Из уравнения (13.5) находим
6V2 -г, у tgJtm — пт
Л/v,
(13.8)
упр -«кр ?,<? —г—-
я п*т2 tg пт
где
NKP -= 4п EIIa,FL . (13.9)
Таким образом, если исходить из концепции пластического шарнира, то опорный момент прн возрастании нагрузки и воздействий, вплоть до образования пластического шарнира (М0^МПл), определяется условием Мо4 = МупР; при дальнейшем возрастании нагрузки опорный момент остается постоянным и равным пластическому моменту, соответствующему образованию пластического шарнира в рассматриваемом сечении (Л10=Д1ПЛ).
В уравнениях (13.1) и (13.2) величина S является сжимающей силой в сеченин трубопровода, возникающей от воздействия температуры и внут-1 репного давления. В отличне от усилия в стенках трубы будем ее называть эквивалентным сжимающим усилием. Эквивалентное сжимающее усилие в се-* чеиии напорного трубопровода
S = pFCB — N, (13.10);
где pFc в — произведение внутреннего давления и площади трубы в свету; N — усилие в стенках трубы ог всех нагрузок и воздействий.
Продольное усилие определяется из условия продольного закрепления тр} бопропо ш на опорах я для рассматриваемого случая определяется из условия неподвижности опор L/2 Ш
LP-
0 0 0
(13.11)
где а — коэффициент линейного расширения материала: Дt ноложнтелД ный температурный перепад; ц — коэффициент Пуассона, окц кольцевые напряжения от внутреннего давления; v — прогиб балки от нагрузок и поз«| действий; ЕГ — жесткость трубы при растяжении.
Для упрощения решения по определению продольного усилия аппроксимируем уравнение упругой линии балки функцией v = t: sin2.-rx/L, в которой стрелка прогиба определяется по (13.7). Тогда из условия (13 11) поручаем следующее уравнение:
т2-|—— = т" т, (13.12)
16 р
где
т — S/N кр; m2pT=[aMEF 0,2 aKI/)/.VKp. (13.13)
Уравнение (13.12) нелинейно относительно т.2, так как стрелка прогиба 5, как следует из (13.17), также зависит от эквивалентного продольного усилия.
Продольное усилие, как следует из (13.10), принимая pFcn==:0,5 aKuF, определяют по формуле
N — 0,5oK4F — m2iVKp. (13.14)
Если не учитывать деформацию системы, т. е. пренебречь последним слагаемым в (13.12), то эквивалентное сжимающее усилие и продольное растя-гнвающее усилие в стенках трубы при повышении температуры и внутреннего давления определяются но формулам:
S - (0, 2скц + аШ) F\ (13.15)
N (0,3окц — аМЕ) F. (13.16)
Теперь необходимо иайти соотношение между силовыми факторами — изгибающим моментом и продольным осевым усилием, соответствующими образованию пластического шарнира.
Как указывалось ранее, в качестве расчетной схемы надземного перехода трубопровода принималась балка трубчатого сечения. Однако при этом необходимо учесть наличие кольцевых напряжений от внутреннего давления
Расчет такой балки прн двухосном напряженном состоянии можно свести
к расчету обычной балки (прн одноосном напряженном состоянии), материал которой имеет разные пределы текучести при сжатии и растяжении.
Пределы текучести в растянутой от р и сжатой ст с зонах сечения можно связать с пределом текучести при одноосном растяжении От зависимостью:
От.р — Ст'. Отс = Ф°т, (13 ¦17)
!де параметр ф, являющийся функцией внутреннего давления (рис. 70), определяется из принятого условия пластичности Сен Венана (сплошная кривая) или Мизеса — Губера — Генки (пунктирная кривая)
ф 1 —окц или ф = 1Л-0,75сгК11-0,5с7кц, (13.18)
зр Чцц=сТйп/от—безразмерное значенье кольцевых напряжений.
Здесь прн использовании условия Мизеса — Губера—Геики пренебрегаем превышением предела текучести в растянутой зоне сечения по сравнению
с От.
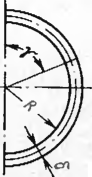
На рис. 71 изображена возможная эпюра распределения продольных напряжений, соответстт'ющая образованию пластического шарнира. 'Угол у, отсчитываемый от крайней фибры растянутой зоны, характеризует положение трального слоя сечения. Из условия равенства внешних и внутренних сил зап [съшаем, что
гДе г —средний радиус трубы; й — толщина стенки трубы.
<Р6г
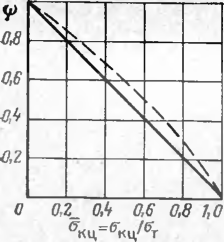
Рис. 70. Зависимость параметра ф от относительной всличи ш кольцевых напряжений
Рис. 71. Эпюра напряжений, cootJ ветствующая пластическому шар^ ниру
Интегрируя и переходя к безразмерным параметрам, получаем значение искомого угла у и изгибающего момента, соответствующего пластическому шарниру:
77 1 -Ьф
N+ ф У— . . я;
(13.21'
Мпл = - smy.
1 + ф 2
_ В формуле (13.21) использованы следующие безразмерные параметры:
N—N/ciF; Mlln=MnjI/aiWn„; =aW, для тонкостенных труб а=
=4/л ~ 1,27.
Запишем также условие достижения текучести в крайней фибре со ответ]' ственно растянутой и сжатой зон сечепня
1М1 ¦ " ,М| JL=ioT. (13.22)
, N + ~ = °'
W ' F
или в безразмерных параметрах
а | М | + N = 1,
а | М | —JV=^4p.
(13.23
Графическое изображение соотношений (13.21) и (13.23) приведено на рис. 72. Сплошные прямые линии соответствуют появлению текучести в ежа! той зоне, пунктирные прямые — в растя 1утой. Любая точка кривой соответ! ствует предельному состоянию сечения трубы (шарниру пластичности), т. с.. определяет для этого состояния соотношение между изгибающим моментом Af, продольным усилием N (положительным при растяжении) и i араметром внутреннего давления 4’- Для точек внутри кривой распределение напряжм ннй в сечении будет либо упругим, либо упруго пластическим в зависимое* от того, лежат ли они ниже или выше прямых, характеризующих появлений текучести в крайних волокнах сечения
Перейдем теперь к анализу экспериментальных данных.
На рис. 73 приведены значения прогибов посередине пролета модел^ подземного перехода трубопровода при различном внутреннем давлении нра дукта. Для каждого из экспериментов поперечная нагрузка q составила 3 3,67 4,2; 4,72 и 5,37 Н/см. Здесь же приведены для соответствующих попе речных нагрузок расчетные кривые, полученные по формулам (13 6) и (13.7)< Сплошные линии соответствуют «деформационному» расчету, т с. с учетом влияния перемещений иа продольное усиление по (13.12), пунктирные -Я «недеформациоппому», т. е. при постоянном продольном усилии, определяем мом по (13.15). «Деформационный» расчет был выполнен на ЭВМ по следующему алгоритму. Исходя из значений поперечной нагрузки и внутреннего^
Рис. 72. Зависимость изгибающего момента от продольного усилии нз условия образования пластического шарнира текучести в крайней фибре
давления, определялись tQ. ™2рт и ф. Далее, принимая в (13.6) или (13.7) Л/c/Afy.p^l, т.е. предполагая, что не произошло образования пластического шарнира, нз уравнения (13 12) с использованием (13 13) методом последопа-ельных приближений определялся параметр т2, затем N (13.14), и Мцл (13.21) н My up (13.8). Если условие Ипл$гА1удг выполнялось, то полученная величина т2 являлась искомой. Если Мил<Л1у1,-р, то все решения выпояия-
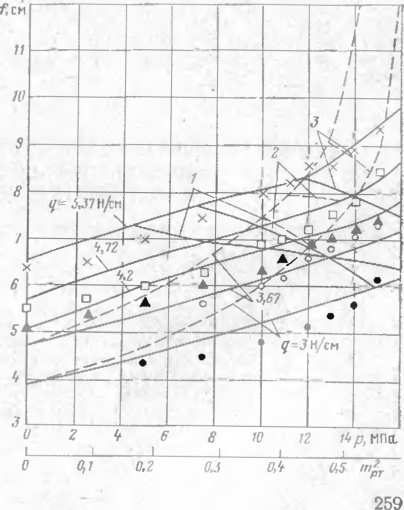
Рчс 73. Зависимость про-
i ябов посередине пролета от внутреннего давления при различной поперечной нагрузке:
1 ' фибровая текучесть в ежа-зоне: 2 — фибровая теку-' есть в растянутой зоне; 3 — разование полного пластического шарнира лись в соответствии_с действительным нх отношением. Кроме того, из условий (13.14) и Л1у0р/А!пл = 1 определялись давления, соответствующие началу текучести в растянутой и сжатой зоне и образованию полного пластического] шарнира в опорном сечснии.
Результаты эксперимента показывают, что начиная с момента появления ! пластических деформаций в крчйнем волокне сечения вплоть до образования полного пластического шарнира па onoDax продольные и кольцевые дефор-1 мании, а также поперечные перемещения (прогибы) продолжают быть одного порядка с упругими (не наблюдается значительного нарастания). После образования полного пластического шарнира на опорах также не проиехо-1 дит резкого увеличения прогибов Деформации поперечного сечения трубы после образования пластического шарнира незначительны, изменение поперечного размера составляет 0 4—0,7 %-
Таким образом, полу ченное решение для упругой и упруго-пластической работы металла труб достаточно хорошо согласуется с результатами экспериментов, что Показывает приемлемость принятых допущений и гипотез. Ре-1 зультаты проведенных исследований отражены в нормах проектирования ма-| гистральных трубопроводов (СНнП 11-45—75) и используются в практике 1 проектирования. р
В СНиПе Н-45-75 условие образования нолного пластического шарнира в сечении трубы записано с заменой предела текучести металла труб от на его расчетное сопротивление R2
апрМ ^ W.
<W«°,635Я2 (1 + %)
a(,;P^f22
"• I
где
— 0,75^-^H_j2 — 0,5-^5-. (13.24)
Если оПр к>0, то в формулах принимается f4=l.
Расчет по этим формулам выполняют только для балочных систем над-J земной прокладки, являющихся статически неопределимыми системами, при отсутствии динамических напряжений. Для других схем надземной прокладке
расчет выполняют из условия достижения текучести в крайнем волокне се-|
чения
°пр (13.25)|
§ 2 Влияние изменения нагрузок и воздействий на несущую способность трубопровода при пластических деформациях
При эксплуатации трубопровода может происходить изменение нагрузок и воздействий как по величине, так и по знаку, поэтому при определении] его несущей способности следует исходить также из условия исключения возможности накопления пластических деформаций и пластической усталости! в какой-либо зоне сечения. В связи с этим в нормах указано, что условны образования пластического шарнира как предельного состояния, принимается! только для статически неопределимых систем.
Определим предельное состояние для сечения статически определимой системы из условий, исключающих накопление пластической деформации и пластическую усталость металла. Расчет трубопровода при двухосном на-1 пряженном состоянии сводим к расчету балки прн одноосном напряженном , состоянии, материал которой имеет разные пределы текучести при сжатии и растяжении. Эти пределы текучести определяются в зависимости от внутреннего давления по формуле (13.17).
Приведенные на рис. 74 эпюры напряжений иллюстрируют возможность накопления продольных пластических деформаций в сечении напорного трубопровода. Если после образования полного пластического шарнира (рис. 74, а) происходит разгрузка трубопровода, то эпюра напряжений от разгрузки сраэгр изменяется по линейному закону по высоте сечения (рис. 74,6), причем для статически определимой системы соответствующие этой эпюре внутренний момент и продольное усилие равны по величине и про тнпоположки по знаку моменту и про дольной силе при первоначальном нагружении. В результате суммирования обеих эпюр (рис. 74, в) в части сечения между нейтральными осями суммарные напряжения превышают предел текучести, т. е. при повторных погружениях в этой зоне сечения происходит накопление пластических деформаций.
Согласно теоремы Блейха — Мелана при любом изменении усилий сечение приспосабливается, т. е не происходит неограниченного накопления пластических деформаций (прогрессивного разрушения), если для каждой точки сечения сумма остаточных и упругих повторных напряжений от любого возможного сочетания внешних нагрузок (при неограниченной упругости материала) не превышает предела текучести материала. Эго условие для точки, как показано Б. И. Любаровым [25], можно свести к интегральным условиям для всего сечения в целом.
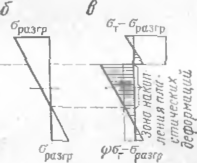
Рнс. 74. Эпюры напряжения б сечении трубопровода
Л Г ГОСТ -Г Л1оСТ "4" Муи.ат = Мп р’ N ПОСТ Ч" Л'ост -г- Агун.ог = Nnp, (13.26)
где Л1„ост и Nuост — постоянно действующие изгибающий момент и продольное усилие; Л10ст и Л'ОСт — момент и усилие, к которым сводится эпюра остаточных напряжений; МуП. ог и ЛуГ1 ог — момент и усилие, к которым сводится огибающая эпюра напряжений, полученная от любого возможного сочетания внешних нагрузок при неограниченной упругости материала, Мпр и Л'цр — момент и усилие, к которым сводится эпюра продольных напряжении, соответствующая образованию полного пластического шарнира в сечении.
Усилие (13.26) записано в безразмерных параметрах, выражающих отношение соответствующих моментов и усилий к пластическому моменту и пластическому усилию соответственно только при изгибе или растяжении, например ;Мос1=ЛГ0ст/(ат'Гпл), ArOCT=jVOCT/(oIF). Здесь —пластический
момент сопротивления, для тонкостенных труб U7n.-,=4 N^/я; W — упругий
момент сопротивления; F — площадь сечения стенок трубы.
Значения Afr.p и Апр определяются по формулам:
МПр = -lit. SI-n Y; W„p = V - 4>. (13.27)
2 rt
где у—угол, отсчитываемый от крайнего растянутого волокна сечения и ха рактернзующин положение нейтральной оси сечения при образовании пла стического шарнира.
Зависимость между Мпр и А?Пр, как следует из (13.27), имеет вид
ф Мпр--1 + ^ sin -— я =
0 (13.28)
и изображена иа рис. 75 и 76 сплошными кривыми.
Для определения Л1У„. от и Nyv_ ог строим огибающую эпюру упруги» напряжений (рис. 77). Величины напряжений ам и а к от переменных усилий ЛТ и N определяются при неограниченной, упругости материала.
На рис. 77 (о, б) построены огибающие эпюры соответственно Для двух счучасв А/>0 и N<10. При Л'^О в растянутой зоне ссчеиия напряжений от продольного усилия <Jn=N/F и момента gm=M/W суммируются, в сжатой зоне огибающая эпюра состоит только из напряжений от момента, при Л'<0,. наоборот, в растянутой зоне огибающая эпюра состоит только из напряжений от момента, а в сжатой зоне — из суммы напряжений от продо. ьной силы и момента. Положение же нейтральной оси пока неизвестно и определяется искомым углом Yor.
На основании построенных огибающих эпюр напряжений получаем значения Л' у п ог И Afyn. or. Например, для эпюры рнс. 77
yn.OI
где r, 6 — соответственно радиус и толщина стенкн трубы.
Интегрируя и переходя к безразмерным параметрам, получаем значения Л’у п. ог и Afyn. or в функции от Yor, которые подставляем в выражение (13.26)..
Согласно теореме о приспособляемости Вленха — Мелапа, следует подобрать самое невыгодное сочетание усилий, определяемое параметром у из условия достижения максимума фуикиии Ф(А?, А1), т. е. из усилии d0fdyor~0 которое с учетом (13.28) имеет вид
JL(cosJ!™ *
(13.31)
2 I ! + ¦ / <*Yor
Учитывая, что для статически определимых систем остаточные напряжения самоуравповешены: AfOCT=-0, Лгост=0, и подставляя в (13.31) значения производных, найденных из (13.27), получаем
Yor - 31 = У’ <13-32>
т. е. самой невыгодной эпюрой огибающих напряжений б\ дет такая эпюра, когда иа участке, где при однократном нагружении достигается предел текучести металла на растяжение 0т, принимаются положительные напря епия от любого возможного сочетания внешних нагрузок, а на участке, где достигается предел текучести на сжатие ф0т, отрицательные напряжения.
_Учитывая (1Х.Х2) и вводя безразмерные параметры а=Л'„огт/Д,г Р=МПоа/М, условия приспособляемости (13.26) для статически определимой балки запишутся в виде
-4 —
(а-\- y)N--(I — sin v) М (1 + Ч1) V — 'И
п
Afsinv+
f2p + -^--f Sln 2V- + i,(l+if)sinv (13.33)
V Я Я /
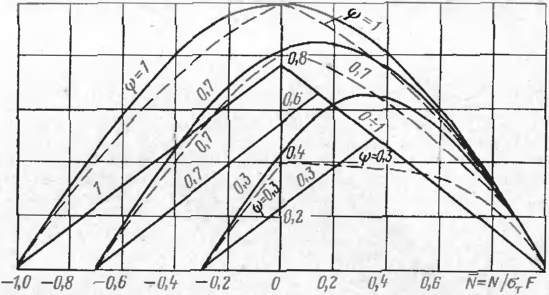
75. Зависимость изгибающего момента от продольного усилия из условия приспособляемости сечения
Рис.
Рпс. 76. Зависимость изгибающего момента от продольного усилия из условия пластической усталости сечення
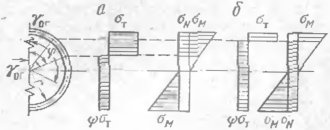
Piic. 77. Огибающие эпюры упругих напряжений при растягивающем (о) и сжимающем (б) продольных усилиях
при N< О
Решая системы уравнений (13.33) и (13.34), записанные в параметрической форме (параметр -у), находим значения усилий N и М, которые могут многократно повторяться в любой последовательности, не приводя к накоплению пластических деформаций в какой либо зоне сечения.
![]()
![]()
+ (2р + -^+-^+ ,)И = (1 4- ф) sin v (13.34>
На графике рис. 75 пунктирные кривые линии изображают графическое решение систем уравнений (13 33) и (13.34) для значений ф=1; 0,7 и 0,3-при аир, равных нулю, т. е. эти кривые определяют область тех значений N и Л1, многократное повторение которых не вызывает прогрессивного-разрушения. Для сравнения здесь же приведены прямые, определяющие область упругой работы сечения. На графике же рис. 76 для значения ф 0,3 приведено также решение для случая а=0,5; р—0,5 и a=P=co_j
Как видно из графиков и из анализа полученных решений, с умеиьше-1 иием значения ф влияние повторности нагружения па несущую способность сечения возрастает, предельный момент, полученный из условия приспособляемости сечения, для всех значений ф достигает максимума при N=0, тогда как предельный момент при однократном нагружении дости-] гает максимума при Л^=ф. Наибольшее снижение несущей способности се- , чения при многократных нагружениях наблюдается для N>0 при средних значениях N и достигает максимума при Лг=ф. Так, например, при ф=0,3, J 0,2<ЛГ<0,55 предельный момент, полученный из условия приспособляемости, оказывается меньше момента, полученного из условия упругости, т. е для этого случая при многократных нагружениях нельзя дотекать, никаких пластических деформаций.
Небольшое снижение несущей способности для значений ф<1 прп повторных нагружениях наблюдается даже при одном только изгибе (V —0). Прн N<0 для всех значений ф повторность нагружения весьма мало ска-j зывастся на несущей способности трубы При центральном растяжении —-I сжатии (Л1 0) повторность нагружения при всех значениях ф ие оказы- ' вает влияния иа несущую способность трубы.
Для трубопровода, кроме изменения нагрузок и воздействий в про- I цсссс эксплуатации по величине (многократное нагружение) возможно нз-1 менение некоторых нагрузок и воздействий по знаку (например, темпера- j турный перепад), т е. может иметь место повторно переменное иагр\жение. i В этом случае разрушение может произойти от переменной текучести J материала (пластическая усталость), если при упругой разгрузке в какой- 1 либо зоне сечения напряжения достигают предела текучести противополож-J ного знака. Для трубчатого сечения при наличии внутреннего давления условие, гарантирующее трубу от разрушения из-за пластической устало-1 сти, имеет вид сивного разрушения вследствие накопления пластических деформаций, при больших значениях N — условием пластической усталости. Когда усилия изменяясь, не меняют знака, условие (13 35) дает значения предельных усилий большее, чем значение предельных усилий при однократном нагружении н, следовательно, разрушение вследствие пластической усталости при многократном нагружении не может иметь место.
4
(13.35)
(1 — v) М ± (1 — Г)) N 1 -|- ф.
я
где т) и v — соответственно отношения минимальных значений сил и мо * ментов к их максимальным значениям.
Построенный на основании (13 35) для случая ф —0,3 график (см. J рис. 76) показывает, что наибольшее снижение несущей способности в ре- 1 зультате пластической \сталости имеет место при симметрично-м цикле из -менения усилий (г)=—1, v=—1). Как видно из графика, предельная несущая способность при малых значениях N определяется условием прогрес--]
Таким образом, при изменении в процессе эксплуатации нагрузок и воздействий в узких пределах несущая способность сечения определяется условием прогрессивного разрушения (13.33) и (13.34), а при изменении нагрузки в широких пределах, включая перемену знака, условием пластической усталости (13.35); в промежуточных случаях — минимальным значением N п Л1, определяемых из обоих условий.
Определить предельный изгибающий момент для надземного перехода, выполненного из труб размером 1420X20 мм, предел текучести которых 0т = 470 МПа. Трубопровод относится к III категории, рабочее (нормативное) давление р=7,5 МПа, температурный перепад Л/=50 °С.
Так как пример носит методический характер, не будем приводить расчет конкретного перехода, а рассмотрим две возможные конструктивные схемы надземного перехода: с полной компенсацией перемещений, без компенсации перемещений. Для первой схемы осевые продольные напряжения в стенках трубы
I 1 7 Ч 1ЧЯ
(тпр = 0,5сткц = 0.5-
-- ^ ¦ =
Н6’5 МПа’
для второй;
с pV *--а.МЕ -г Цок1, = —12 10-«-50 2, МО*’ + 0,3-293 = — 38,1 МПа.
Расчетное сопротивление mR"
о 9 470
-- = — — = 334,4 МПа.
По формуле (13.24)
0,5—— =0,213.
334,4
Предельные изгибные напряжения для первой схемы
а
-0,635 334,4 (1 + 0,213) sin
(146’~—°’213'334-4)п
= 263,1 МПа;
Л1 (1 + 0,213)334,4
Для второй:
о 0,635-334,4(1 -0,213) sin
(°’21--334,4)- =67,2
МПа.
Л1 (1 -1-0,213)334,4
Если рассчитывать из условия, чтобы напряжения в крайнем волокне не превышали предела текучести, то из условия (13 25) предельные изгиб ные напряжения для первой схемы
апрм 0,213 334,4 + 146,5 = 217,7 МПа;
для второй
СТ ы-0,213-334 4 - 38,1 = 33,1 МПа.
Пр-Л1
Можно считать, что пролет перехода прямо пропорционален корню квадратному из предельного изгибного напряжения. Тогда расчет из условия образования пластического шарнира по сравнению с расчетом из условия Достижения текучести в крайнем волокне сечения для первой схемы позволяет увеличить пролет на 10%. а для второй на 40%.
