Глава 1 основные воздействия и факторы, влияющие на прочность и устойчивость трубопроводов
ГЛАВА 1
ОСНОВНЫЕ ВОЗДЕЙСТВИЯ И ФАКТОРЫ, ВЛИЯЮЩИЕ НА ПРОЧНОСТЬ И УСТОЙЧИВОСТЬ ТРУБОПРОВОДОВ
§ 1. Основные предпосылки
Одним из основных силовых воздействий, влияющих на прочность магистральных трубопроводов, является внутреннее давление, на основе которого определяется толщина стеиок труб, т. с. такой важный параметр, как металлоемкость трубопроводов. Однако расчет тр} бопроводов иа воздействие одного только внутреннего давления недостаточен для обеспечения прочности и устойчивости трубопроводов.
Как известно, магистральные трубопроводы прокладываются на обширной территории нашей страны, характеризующейся большим разнообразием климатических, почвенных, гидрогеологических и других условий, и находятся под влиянием различных силовых воздействий, которые в той или иной степени влияют на их прочность и устойчивость. Как показала практика, эти воздействия в ряде случаев имеют большое значение в обшей проблеме обеспечения надежности трубопроводов, т. е. расчет трубопроводов на внутреннее давление есть условие, необходимое для обеспечения их эксплуатационной надежности, но недостаточное, поскольку трубопроводы в процессе эксплуатации подвергаются воздействию ряда факторов.
§ 2 Внутреннее давление
Внутреннее давление продукта - одно из основных силовых воздействий, определяющих напряженное состояпие трубопроводов. Толщина стенок труб магистральных трубопроводов обычно определяется, только исходя из внутреннего давления продукта. Однако при этом конструктивное решение трубопровода как строительной конструкции выбирается с учетом всех возможных воздействий Для принятой схемы прокладки трубопровода.
Под воздействием внутреннего давления в трубах возникают кольцевые растягивающие напряжения, которые рассчитывают по безмоментной теории тонкостенных цилиндрических оболочек, пренебрегая изменением радиальных напряжений по толщине трубы и начальным несовершенством формы поперечного сечения. Хотя вследствие овальности труб (отклонения формы поперечного сечения от круговой) наряду с кольцевыми растягивающими напряжениями и возникают ичгибные напряжения, но их в расчетах по предельным состояниям не учитывают. Это объясняется тем, что в пределах допусков, установленных на овальность (отношение фактического диаметра трубы к номинальному), разрушающее давление практически одинаково для труб с различной овальностью. Однако имеются случаи, когда предельным состоянием для трубопровода является ие его разрушение, а определенный уровень допускаемых напряжений. Это относится к трубопроводам, транспортирующим газ с содержанием сероводорода. Исследования показали, что склонность такого трубопровода к коррозионному разрушению тем выше, чем больше концентрация и парциальное давление сероводорода и напряженное состояние трубопровода. Для обеспечения надежной работы таких систем допускаемое максимальное напряжение определяется в зависимости от предела текучести металла труб. При определении же кольцевых напряжений от внутреннего давлепня необходимо учитывать начальную овальность сечения трубопровода.
Внутреннее давление в магистральных трубопроводах непостоянно, так как при движении транспортируемого продукта затрачивается значительная энергия на преодоление гидравлического сопротивления в трубах. Поэтому внутреннее давление по длине трубопроводов между компрессорными и насосными станциями постепенно уменьшается.
В случаях, если исключается возможность обратной перекачки продукта или если пе предполагается в будущем установка по трассе дополнительных компрессорных или насосных станций для увеличения пропускной способности трубопровода, при определении толщин стенок трубопровода можно учитывать фактическое давление иа конкретном участке трубопровода. Практически трубопровод между станциями разделяется на три участка, давление для каждого из которых принимается равным давлению в начале участка. При остановке перекачки, что происходит очень редко, в трубопроводе установится среднее давление. Это давление всегда будет меньше начального и даже в том случае, если оно превысит расчетное и возникнут дополнительные напряжения, которые носят кратковременный характер. Допускаемый уро пень напряженного состояния и этом случае может бы гъ повышен.
Внутреннее давление в трубопроводе вызывает не только кольцевые напряжения, но и продольные. Продольные напряжения зависят от очертания оси трубопровода и взаимодействия его с окружающей средой. Так, при прямолинейной оси трубопровода и отсутствии поперечных и продольных его перемещений продольные осевые напряжения равны примерно 30 % кольцевых, При иепрямолинейной оси трубопровода продольные осевые напряжения зависят от перемещений трубопровода, которые определяются взаимодействием его со средой (грунтом, опорами и др.). При этом продольные осевые напряжения могут достигать 50 % кольцевых.
§ 3. Воздействие температуры
Температура трубопровода изменяется во времени, так как при строительстве она определяется в основном температурой наружного воздуха, а в процессе эксплуатации — температурой транспортируемого продукта.
Для расчета трубопроводов па прочность и устойчивость используется понятие температурного перепада. Этот параметр определяет иапряженно-деформируемое состояние трубопроводной конструкции. Температурный перепад для рассчитываемой конструкции равен разности между температурой трубопровода в процессе эксплуатации (расчетный период) и температурой, при которой сооружена эта конструкция.
При расчете реальная конструкция заменяется расчетной схемой, которая отражает с точки зрения строительной механнкн распределение усилий, перемещений и напряжений в трубопроводной конструкции. Поэтому в нормах на проектирование магистральных трубопроводов записано, что под температурой сооружения понимается температура, при которой фиксируется расчетная схема трубопровода.
Для подземного трубопровода расчетная схема представляет собой стержень с поперечными и продольными связями, поэтому под температурой строительства следует понимать температуру уложенного на дно траншеи трубопровода в момент засыпки его грунтом.
Для надземного трубопровода расчетная схема представляет собой балку на опорах с определенными граничными условиями, отражающими влияние примыкающих к надземному трубопроводу конструктивных элементов. Поэтому для такой конструкции под температурой строительства следует понимать температуру, прн которой осуществляется строительство концевых участков: привариваются компенсаторы, соединяется подземная и надземная части трубопровода и др.
Продольные напряжения от температурного перепада определяются конструктивным решением трубопровода н взаимодействием трубопровода с ок ружающей его средой. Наибольшие температурные напряжения возникают при отсутствии поперечных и продольных перемещений. Допускаемый темпе ратурный перепад определяется расчетом для принятого конструктивного решения, исходя из установленного нормами предельного состояния трубопровода.
| Диэиетр i трубопровода, мм | Толщина стенки, им | Предел прочности» МПа | Предел теку чести, МПа | Допуска перепад радиусе 1500 | еыый темпе в СС) при Г упругого и 2000 | ратурный аз ли«ном згиба. ы 2500 |
| 1420 |
16,5 | 600 |
420 | 40 |
49 | 55 |
|
1420 | 16,5 |
600 | 470 |
66 | 75 |
81 |
| 1220 |
14,1 | 600 |
420 | 56 |
61 | 64 |
|
1220 | 14,1 |
600 | 450 |
71 | 76 |
80 |
Б табл. 1 приведены допускаемые температурные перепады, определенные в соответствии со СНиП II-45—75 в зависимости от радиуса упругого изгиба подземного трубопровода.
Данные таблицы показывают, что даже небольшое снижение температурного перепада позволяет укладывать трубопровод при значительно меньших ради>сах упругого изгиба.
Положительный температурный перепад при определенном своем значении вызывает в трубопроводе продольные осевые сжимающие напряжения, которые влияют на толщину стенки трубы. Поэтому температурный перепад обычно ограничивают значением, полученным из условия минимума толщины стенки. Температурный перепад в существенной мере определяет продольную устойчивость подземного трубопровода, которая обеспечивается выбором соответствующей кривизны трубопровода, глубины его заложения и балластировки.
Для уменьшения температурного перепада, который может быть особенно значительным для газопроводов больших диаметров, газ на выходе из компрессорной станции охлаждают.
§ 4. Воздействие деформаций грунта
Деформации грунта, влияющие иа напряженно-деформированное состояние трубопровода, могут быть связаны с перемещением грунта в результате горных разработок в районе прокладки трубопровода.
При разработке полезных ископаемых в недрах земли образуется сво бодное пространство, и верхние слои почвы перемещаются к центру образовавшейся пустоты. Район земной поверхности, подверженный влиянию горных разработок, образует так называемую «мульду сдвижения», представляющую собой участок, в котором происходит оседание земиой поверхности. В результате сползания грунта в «мульде сдвижения» в трубопроводе в связи с его защемлением возникают значительные растягивающие напряжения. Поэтому при расчете трубопроводов напряжения от воздействия этого фактора Должны быть определены и в проекте предусмотрены специальные конструктивные решения, обеспечивающие надежность работы трубопровода в этих }словиях.
Деформации грунта, влияющие на прочность трубопровода, ыотут быть связаны также с колебаниями грунта, возникающими при землетрясениях.
Как известно, в результате сейсмического толчка в грунте создаются и распространяются сейсмические волны. Поэтому подземный трубопровод, представляющий собой единую систему «грунт — труба», вовлекается в колебательный процесс. Сейсмическая волна, имеющая, как правило, большую скорость распространения в трубопроводе, чем в грунте, достигает по трубопроводу участков, еще не вовлеченных в колебательный процесс. На этих участках трубопровод можно рассматривать как генератор колебаний, а грунт — как демпфирующую подушку. Напряжения в трубопроводе на этих участках меньше, чем на участках, где колебания трубопроводу сообщались грунтом.
Таким образом, следует рассматривать две схемы работы трубопровода в условиях сейсмических колебаний: подземный трубопровод, вовлекаемый в колебательный процесс, при котором напряжения в трубах возникают в результате напряженного состояния грунта, и колеблющийся трубопровод, погруженный в грунтовую среду, препятствующую его колебаниям. Как показал анализ последствий ряда землетрясений, подземные стальные трубопроводы, проложенные вне зон разломов в сейсмически устойчивых грунтах, хорошо переносят землетрясения силой в 7—8 баллов. Поэтому нормы проектирования допускают сейсмические воздействия на подземный трубопровод до 8 баллов включительно. При большей балльности прочность трубопровода проверяют и на основании расчетов выбирают соответствующее конструктивное решение, обеспечивающее надежную работу трубопровода.
Воздействие грунта на трубопровод имеет место иа оползневых участках. Силовые воздействия оползающих грунтов на трубопроводы подразделяются на два вида. К первому виду относится такое воздействие грунта, при котором направление скольжения массы грунта совпадает с осью трубопровода, прокладываемого на продольных уклонах. А так как трубопровод защемлен в грунте, то в трубах возникают растягивающие напряжения на верхнем участке и сжимающие на нижпем их участке. Ко второму виду воздействий относятся такие, при которых направление движения оползневых масс перпендикулярно осн трубопровода или происходит под некоторым углом к ней. Этот вид силового воздействия грунта наиболее опасен, поскольку в этом случае наряду с продольными осевыми напряжениями возникают изгибные напряжения.
Если расчетная прочность трубопровода недостаточна, то необходимо выполнить ряд защитных мероприятий. К ним относится устройство подпорных стенок, основание которых должно быть заложено ниже плоскости
скольжения оползня, устройство шпунтовых стенок из свай, цементирование оползающего грунта и т. д.
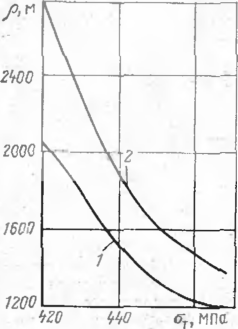
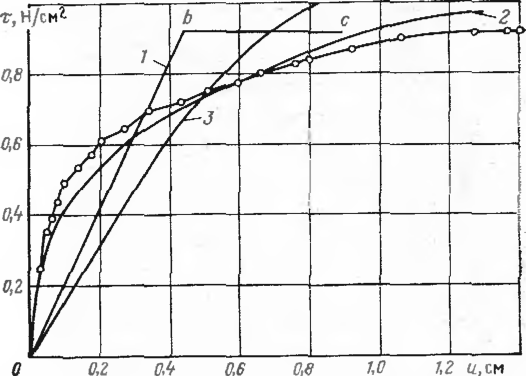
Рис. 1. Зависимость ради уса упругого изгиба трубопровода диаметром 1420 мм от предела текучести ме талла труб при временном сопротивлении 600 МПа (Д/=60 °С):
1 — 6—16,5 мм; 2 — 6=17,5 мм
§ 5. Предварительный изгиб трубопровода при сооружении
С целью уменьшения объемов земляных работ профиль траншей выполняют близким к профилю земной поверхности на данном участке. Профиль траншеи определяется условиями укладки трубопровода, т. е. возможностью изгиба трубопровода по принятому профилю -под действием собственной массы и напряженным состоянием трубопровода в процессе эксплуатации при воздействиях внутреннего давления и температурного перепада.
Обычно предварительный изгиб трубопровода характеризуется минимальным радиусом упругого изгиба оси трубопровода. Как показали исследования, предварительный упругий изгиб ие оказывает влияния на разрушающее давление. Однако с уменьшением радиуса оси трубопровода возрастают не только начальные напряжения, ио и напряжения, возникающие от эксплуатационных нагрузок. Изгиб трубопровода может привести к потере продольной устойчивости всего трубопровода или к потере местной устойчивости стенкн трубы в сжатой зоне сечения. Поэтому мниимальный радиус упругого изгиба оси трубопровода ограничивают из условия деформ ативиости.
Зависимость предельно допускаемого радиуса упругого изгиба от предела текучести металла труб представлена на рис. 1. График построен для газопровода диаметром 1420 мм при рабочем давлении 7,5 МПа и температурном перепаде 60 СС. Как видно нз графика, значение предела текучести оказывает существенное влияние па радиус изгиба, Так, с увеличением предела текучести от 420 до 470 МПа допускаемый радиус уменьшается с 2800 до 1350 м, т. е. в дга раза.
Проектирование вертикального профиля траншеи с использованием минимального радиуса упругого изгиба позволяет уменьшить объемы земляных работ. В то же время при проектировании трубопроводов иа обводненных и заболоченных участках следует учитывать, что с увеличением радиуса изгиба уменьшается балластировка трубопровода, необходимая ддя обеспечения его продольной устойчивости. Поэтому радиус упругого изгиба должен назначаться из условия деформативности металла трубы и условия продольной устойчивости на основе технико-экономического сравнения вариантов.
§ 1. Основные принципы расчета
Обеспечению высокой надежности трубопроводов как одной из важнейших задач развития технического лрогресса в области строительства объектов трубопроводного транспорта должно уделяться самое серьезное внимание. Расчет трубопроводов на прочность и устойчивость следует рассматривать как важнейшее звено в общей цепи формирования надежности трубопроводных систем.
В СНиП II-45—75 требования к материа-iy труб содержат максимальное отношение предела текучести к временному сопротивлению, минимальную удариую вязкость, минимальное относительное удлинение и направлены на предотвращение хрупкого разрушения трубопровода в процессе эксплуатации. Выполнение требований к сварочным материалам обеспечивает равнопроч-ность сварных стыков основному металлу труб.
Магистральные трубопроводы рассчитываются по методу предельных состояний. Сущность метода заключается в том, что рассматривается такое напряженное состояние трубопровода, при котором дальнейшая его эксплуатация невозможна.
Методика расчета магистральных трубопроводов по предельным состояниям создана впервые в нашей стране сотрудниками ВНИИСТ И. П. Петровым, А. Г. Камершгсйном, В. С. Туркиным и др>гими. Нормы проектирования магистральных трубопроводов (СНиП II-45—75), разработанные под руководством В. И. Прокофьева, основаны на этой методике.
Первое предельное состояние трубопровода — разрушение его под действием внутреннего давления Поэтому характеристикой несущей способности трубопровода является временное сопротивление.металла труб (предел прочности) .
Для обеспечения надежной работы трубопровода при определении расчетного сопротивления вводится ряд дифференцированных коэффициентов, отражающих вероятностный характер различных факторов, влияющих на несущую способность трубопровода. К ним относятся коэффициент безопасности по материалу, коэффициент условия работы трубопровода и коэффициент \ надежности.
1 Коэффициент- .безопасности по материалу отражает возможное уменьшение временного сопротивления металла труб по сравнению с его нормативным значением, возможное уменьшение толщины стенкн трубы по сравнению с ее номинальным значением и надежность конструкции трубы. Последний фактор зависит от технологии производства труб.
__ Коэффициент условия работы показывает возможное несоответствие при нятой расчетной схемы реальной трубопроводной конструкции, в том числе особенности взаимодействия трубопровода с окружающей средой. Кроме того, коэффициент условия работы показывает влияние последствий разрушения трубопроводов на здоровье людей, а также на приведенную стоимость выполнения ремонтно-восстановительных работ JJ Коэффициент надежности впервые введен в нормы проектирования магистральных трубопроводов в 1975 г., что вызвано увеличением диаметров сооружаемых трубопроводов и рабочего давления продукта. Коэффициент надежности учитывает следующие факторы, влияющие на надежность работы системы:
с увеличением диаметра возрастает поверхность, контактнруемая с грунтом, следовательно, трубопроводы больших диаметров при деформациях грунта находятся в более тяжелых условиях, чем трубопроводы малых диаметров;
с увеличением диаметра трубопровода резко возрастает его изгибная жесткость, поэтому при укладке может не быть обеспечено его опирание на дно траншеи но всей длине, в результате чего в нем могут возникнуть дополнительные изгибные напряжения;
с увеличением диаметра трубопровода возрастает его металлоемкость, общая длина сварных стыков и объем наплавленного металла, поэтому вероятность каких-либо технологических дефектов повышается;
с увеличением рабочего давления продукта и диаметра трубопровода возрастает пропускная способность системы, отказ которой может привести к большим народнохозяйственным потерям.
Коэффициент надежности назначается в соответствии со СНиП II-45—75 различный для газо- и нефтепроводов и зависит от диаметра трубопровода и давления продукта.
При определении напряженного состояния трубопровода для проверки первого предельною состояния учитывают только те напряжения, которые практически влияют на разрушающее давление.
На основаннн экспериментальных исследований установлено, что к ним относятся кольцевые напряжения от внутреннего давления и продольные осевые напряжения от всех нагрузок и воздействий.
В СНиП II-45—75 первое предельное состояние записано в виде равенства растягивающих кольцевых и растягивающих осевых продольных на пряжений расчетному сопротивлению, а при разнозначном напряженном со стоянии — равенства эквивалентных напряжений расчетному сопротивлению.
Для ограничения пластических деформаций СНиП II-45—75 предусматривает проверку трубопровода по второму предельному состоянию. Второе предельное состояние выражается через напряжения.
Напряжения определяются от всех нормативных нагрузок и воздействий (с учетом их сочетания) для наиболее напряженной точки сечения трубы Критерием выполнения второго предельного состояния является условие, при котором кольцевые и растягивающие продольные напряжения, а при разнозначном напряженном состоянии эквивалентные напряжения не должны превышать значений, определяемых пределом текучести металла труб. Отметим также, что при проверке по первому предельному состоянию согласпо нормам СНиП требуется выполнять расчет трубопроводов, исходя из упругопластической работы металла труб, а по второму — исходя нз упругой работы самих трубопроводов.
§ 2. Нагрузки и воздействия, принимаемые при расчете трубопроводов
При расчете трубопроводов следует учитывать нагрузки и воздействия, возникающие при их сооружении, испытании и эксплуатации. Основная нагрузка — рабочее (нормативное) давление транспортируемою продукта (устанавливается проектом). При расчете трубопроводов следует учитывать возможность увеличения этою давления, что оценивается коэффициентом перегрузки. Для нефтепроводов и нефтепродуктопроводов коэффициент перегрузки дифференцируется в зависимости от технологии перекачки. Для нефтепроводов и нефтепродуктопроводов диаметром 720—1420 мм на всех промежуточных насосных станциях, работающих без подключения емкостей, следит устанавливать устройства по защите линейной части трубопроводов от воздействия переходных процессов, возникающих при остановке иасосов, закрытии задвижек, изменении режима перекачки и т. д. Коэффициент перегрузки ие учитывает возможность повышения давления в результате гидравлического удара
При расчете трубопроводов следует учитывать температурный перепад в металле стенок труб, который определяется как разница _между максимально или минимально возможной температурой стенок при эксплуатации н наименьшей или наибольшей температурой, при которой фиксируется расчетная схема трубопровода.
Минимальную или максимальную температуру стенок труб при эксплуатации следует определять ^? подземных трубопроводов в зависимости от температуры транспортируемого продукта и грунта, а для надземных трубопроводов— от температуры наружного воздуха, с учетом солнечной радиации.
При укладке трубопроводов в болотистых н обводненных районах должна учитываться выталкивающая сила воды. При отсутствии течения воды выталкивающая сила иа единицу длины полностью погруженного трубопровода определяется по формуле
<?в = °.80?,Ув. (2-1)
где Dn — наружный диаметр трубы с учетом изоляциоипого покрытия и футеровки; ув — удельный вес воды с учетом растворимых в ней солей.
При расчете трубопроводов, прокладываемых на участках, сложенных грунтами, которые при обводнении переходят в жидкопластическое состояние, следует вместо объемного веса воды принимать объемный вес разжиженного грунта, определяемый по данным инженерных изысканий.
Нагрузки и воздействия,' связанные с осадками и пучением грунта, оползнями, деформациями земной поверхности в результате горных разработок и т. д., должны определяться на основании данных анализа грунтовых условий и их возможного изменения в процессе строительства и эксплуатации трубопровода.
При расчете надземных трубопроводов следует учитывать вес транспортируемых продуктов. Нормативный вес газа (в Н/м) в 1 м трубопровода qгаз можно определять по приближенной формуле
</га8 100 ipD*,. (2.2)
где р — нормативное давление, МПа; Dvп — внутренний диаметр трубы, м.
Нормативный вес нефти или нефтепродукта (в Н/м) в 1 м трубопровода Чпроя определяется по формуле
л?)вн
<?прод — Vh —-—> (2.3)
4
где уд — объемный вес нефти или нефтепродукта, Н/м8.
В случае, когда возможно обледенение трубопровода, нормативную нагрузку от обледенения (в Н/м) 1 м трубы д»еЯ следует определять по формуле
<7лсд 17 ЬВн, (2.4)
где b — толщина слоя льда, принимаемая в соответствии со СНиП, глава «Нагрузки и воздействия», мм; Du — наружный диаметр трубы, м.
Нормативная снеговая нагрузка на горизонтальную проекцию надземного трубопровода и примыкающего эксплуатационного мостика также определяется в соответствии с требованиями той же главы СНиП. При этом для одиночно прокладываемого трубопровода коэффициент перехода от веса
снегового покрова земли к снеговой нагрузке иа трубопровод принимается
равным 0,4.
Нормативную ветровую нагрузку, действующую перпендикулярно осевой вертикальной плоскости одиночно прокладываемого трубопровода, определяют по формуле
Цвет.и — (<?1кс + <7и.д) Du, (2.5)
где д„ с, <7п д — соответственно нормативные значения Статической и динамической составляющих ветровой нагрузки, Н/м!.
Статическую составляющую ветровой нагрузки определяют по формуле
<7н.с = <ДАс> (2.6)
где (/о — скоростной напор ветра, Н/мг; сх — аэродинамический коэффициент лобового сопротивления надземного трубопровода
Скоростной напор ветра qt, определяется ir зависимости от района расположения надземного трубопровода Районирование территории СССР по скоростным напорам приведено в СНнП, глава «Нагрузки и воздействия». Значения скоростного напора q0 для различных районов СССР следующие:
Районы СССР......... I II HI IV V VI VII
Скоростной Напор ветра, Н/м2 270 350 450 550 700 850 1000
Для трубопроводов, расположенных на высоте до 5 м над поверхностью земли разрешается спижать скоростной напор на 25 %, за исключением трубопроводов, сооружаемых в горной местности.
По известным скоростям ветра qo можно вычислить по формуле
(2-л
1 ,о
где а= (0,75+5/и) — поправочный коэффициент к скоростям ветра, полученным путем обработки наблюдений по флюгеру; v — скорость ветра ла высоте 10 м над поверхностью земли, наибольшая за пять лет, м/с.
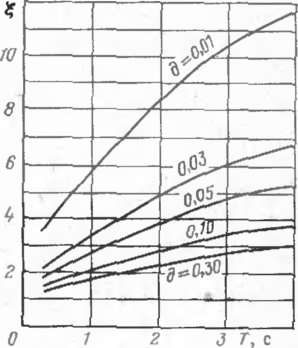
Коэффициент лобового сопротивления сх определяют в зависимости от числа Рейнольдса Не по графику рис. 2.
Число Рейнольдса вычисляется по формуле
Re = J!^, (2.8)
v
где v — учитываемая в расчете скорость ветра, м/с; v — кинематическая вязкость воздуха (при <=15 °С и атмосферном давлении 1000 Г Па принимают v=0,146-10-4 м /с).
При числе Рейнольдса Re>35-105 обычно принимают с*=0,7. Динамическую составляющую ветровой Нагрузки иа трубопровод можно приближенно определять как для сооружения постоянной жесткости и с равномерно распределенной массой.
Динамическая составляющая будет
q и.д — 0,35<7н.с5>
(2.9)
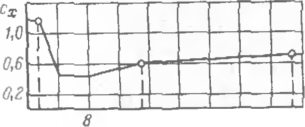
где 0,35 — коэффициент пульсации скоростного напора; | — коэффициент динамичности, зависящий от периода, соответствующего второй форме свободных горизонтальных колебапий, и логарифмического декремента колебаний надземного трубопровода.
1,5 h
12 15 20 RejW5
2b 28 32 3S
Рис. 2. График для определения коэффициента лобового сопротивления
Рис. 3. График Для определения
коэффициента динамичности
Значения коэффициента динамичности можно определять по графику рис. 3, где по оси абсцисс отложен период собственных горизонтальных колебаний. Если период колебании 7'<0,25 с, то динамическую составляющую ветрогон нагрузки не учитывают, т. е. принимают qB. д = 0
Логарифмический декремент колебаний трубопровода зависит от конструктивной схемы надземного перехода и определяется по записям виброграмм свободных затухающих колебаний
д = — In (Ai/Al+n), п
(2.10)
где п — число циклов на участке виброграммы; Л,- и Ai+„—амплитуды колебаний в начале и в конце рассматриваемого участка виброграммы.
Согласно [34] для предварительных расчетов логарифмический декремент рекомендуется принимать для горизонтальных колебаний — 0,05, для вертикальных колебаний (если нет устройства для гашения колебаний) — 0,03—0,05.
Для определения периода собственных колебаний надземных переходов трубопроводов Т находят частоту изгнбпых колебаний v (Т 1/v).
Собственную частоту нзгибных колебаний (в Гц) определяют по формуле
(2">
где I — расстояние между опорами, м; EI — изгибпая жесткость трубопровода, Н-м2; g — ускорение свободного падения, g=9,81 м/с2; q—расчетная вертикальная нагрузка на трубопровод, Н/м; m2=S/NKV — безразмерный параметр эквивалентного продольного усилия (здесь S эквивалентное продольное усилие, Н; NKр критическое продольное усилие, И); для переходов с компенсацией продольных перемещений ms=0, для бескомпенсаторных пере ходов определяется в соответствии с методикой, изложенной в гл. 9 и 12.
Значения параметра fec зависят от числа пролетов, условий закрепления концов трубопровода и формы собственных колебаний
Для балки с защемленными концами значения кс приведены в табл. 2. Здесь индекс 1 соответствует первой (одна полуволна в пролете), а индекс 2 — второй зопам сгущення частот, индексы (и) и (в) — пижней и верхней границам зон сгущения частот.
При определении fee по табл. 2 для многопролетных надземных переходов без крайних опор условно принимается число пролетов на два больше.
Например, для трехпролетиого надземного перехода с компенсатором на одном копде условно принимается число пролетов равным пяти, по табл. 2 находим значение kc. 1В=1,74.
Учесть действительные граничные условия для реальных схем надземных переходов трубопроводов представляется достаточно сложным. Для одно-
Таблица 2
Значение коэффициента kc
| ¦ Число пролетов | *С1Н |
*С1В | ^С2Н | *С2В |
| 1 | 3,56 |
9,82 | ||
|
2 | 2,46 | 3,56 |
7.96 | 9,82 |
|
3 | 2,01 | 3,56 |
7,16 | 9,82 |
|
4 | 1,83 | 3,56 |
6,82 | 9,82 |
|
Б * | 1,74 | 3,56 |
6,64 | 9,82 |
|
6 | 1,69 | 3,56 |
6,54 | 9,82 |
|
>6 | 1,57 | 3,56 |
6,28 | 9,82 |
Постоян
ные
Времен
ные
длитель
ные
Кратко
времен
ные
и воздействий
|
Нагрузки и воздействия |
Способ прокладки трубопровода | |
| подземный н в ии-сыпях |
надзем ный | |
|
Собственный вес трубопровода и обустройств | + |
+ |
| Воздействие предварительного напряжения трубопровода (упругий изгиб и др.) | + | ¦Ь |
| Давление (вес грунта) | + |
|
| Гидростатическое давление воды | + |
- |
| Внутреннее давление для газопроводов |
+ | + |
|
Внутреннее давление для нефтепроводов диаметром 700—1420 мм с промежуточными насосными станциями, работающими без подключения емкостей | + | + |
|
Внутреннее давление для нефтепроводов диаметром 700—1420 мм без промежуточных насосных станций или с промежуточными станциями, работающими постоянно только с подключенной емкостью, а также для нефтепроводов и нефтепродуктопроводов диаметром менее 720 мм |
+ | + |
|
Вес продукта или воды |
+ | + |
|
Температурное воздействие |
+ | + |
|
Воздействие неравномерных деформаций грунта, не сопровождающихся изменением его структуры (присадки, пучение и др.) |
+ | + |
| Снеговая нагрузка |
— | + |
|
Ветровая нагрузка |
— | + |
|
Гололедная нагрузка |
— | + |
|
Нагрузка и воздействие, возникающие при пропуске очистных устройств |
+ | |
|
Нагрузки и воздействие, возни-кающие при испытании трубопроводов |
+ | + |
Коэффи
циент
пере
грузки
1.15
1.1 (•)
1
1.2 (0,8) 1
1.1
1.1 1 (0.95) 1
1.5
1.4
1,2
1.3
1.2
|
Характер нагрузок и воздействий |
Нагрузки и воздействия | Способ прокладки трубопровода | Коэффи-j циент | |
| подземный н в насыпях |
надзем ный | пере грузки | ||
| Особые | Воздействие селевых потоков и оползней | + |
+ | 1 |
| Воздействие деформаций земной поверхности в районах горных разработок и карстовых районах |
+ | + |
1 | |
|
Воздействие деформаций грунта, сопровождающихся изменением его структуры (например, деформации просадочиых грунтов при замачивании) • | + |
+ | 1 |
|
Примечание Со знаком (-(-) даны нагрузки н воздействия, учитываемые при расчете в зависимости от способа прокладки, а со знаком ( ) неучитываемые нагрузки. Значения коэффициентов перегрузки, указанные в скобках, должны приниматься при расчете трубопроводов иа продольную устойчивость и устойчивость положения (например, при' расчете на всплытие), а также з других случаях, когда уменьшение нагрузки ухудшает условия работы трубопровода.
пролетного надземного перехода без компенсаторов с примыкающими подземными участками влияние упругого защемления опор можно учесть с помощью коэффициента X, на который умножается параметр kc для балки с защемленными концами. Коэффициент Л вычисляется по формуле
/
[(2.12)
Л
6у* + 12т*+ 1 Оу2 + 5у + 1
где
4EI
СуоВн
(2.13)
Здесь / — пролет перехода в свету; cv „—обобщенный коэффициент нормаль пого сопротивления грунта
Нагрузки и воздействия, учитываемые при расчете трубопроводов, под разделяются на постоянные, временные длительные, кратковременные н особые. В табл, 3 приведена классификация нагрузок и воздействий и даны коэффициенты перегрузки, характеризующие возможность увеличения или уменьшения соответствующих нормативных нагрузок и воздействий
Если по условиям испытаний или эксплуатации газопроводы могут пол ностью или частично заполняться водой, а нефтепроводы или иефтепродукто-проводы — воздухом или при эксплуатации возможно опорожнение последних, необходимо учитывать изменение нагрузки по длине трубопровода от массы продукта.
§ 3 Определение толщины стенок труб
Методика определения толщины стенки труб магистрального трубопровода основана иа принципе предельных состояний. За предельное состояние, при котором трубопровод перестает удовлетворять предъявляемым к нему требованиям, принимается состояпие разрушения. Поэтому расчетное сопротивление определяется, исходя из временного сопротивления материала труб (предела прочности).
Расчетное сопротивление материала труб определяют по формуле:
ЛГт
где R\u — нормативное значение временного сопротивления металла труб, \станавлнваемое стандартом и техническими условиями на трубы; т — коэффициент условий работы участка трубопровода; ki—коэффициент безопасности по материалу при расчете по временному сопротивлению; ки — коэффициент надежности.
Коэффициент безопасности по материалу устанавливается нормами на проектирование. Он характеризует изменение свойств металла труб в зависимости от технологии их изготовления, уменьшение толщины стенок труб по сравнению с ее номинальным значением, (допуски по толщине), конструкцию труб, способ их изготовления, степень контроля сварных соединений и основного металла, а также пластические свойства трубных сталей. Таким образом, определение толщины стенок труб тесно связано с их качеством. Так, термически упрочненные трубы, изготовленные из низколегированной стали, прокатанной по регулируемому режиму, и имеющие допуск по толщине стенки не более 5 % с обеспечением 100 % ного контроля листа и сварных соединений, рассчитываются с коэффициентом безопасности fei = 1,34. Спиральношовные трубы, изготовленные из горячекатаной низколегированной стали, сваренные в три слоя, и прямошовиые экспапдированныс трубы из нормализованной листовой стали, сваренные двухсторонним швом, рассчитываются с коэффициентом безопасности kl—1,47.
Коэффициент условий работы также устанавливается нормами на про ектированне. Он отражает особенности эксплуатации отдельных участков трубопроводов, последствия возможного разрушения, трудности ремонта и восстановления, требования безопасности и защиты окружающей среды и т. д. В зависимости от указанных факторов установлены три значения коэффициента условия работы: 0,9; 0,75 и 0,6. Так, для обычной линейной части трубопровода т=0,9. Для переходов магистральных трубопроводов через водные преграды, железные и автомобильные дороги, трудно проходимые болота, а также для участков, примыкающих к компрессорным и нефтеперекачивающим станциям, узлам пуска и приема очистных устройств, т=0,75. Для наиболее ответственных участков, к которым относятся трубопроводы, расположенные внутри зданий и в пределах территорий компрессорных, газораспределительных и нефтеперекачивающих станций, станций подземного хранения газа, а также для переходов мощных нефтепроводов диаметром 1020 мм и более через водные преграды т=0,6.
Коэффициент надежности учитывает народнохозяйственную значимость трубопровода, внутреннее давление и диаметр трубопровода.
Значения коэффициента безопасности, классификация участков трубопроводов по категориям и соответствующий коэффициент условий работы, а также значения коэффициента надежности приведены в СНиП II-45—75 Магистральные трубопроводы. Нормы проектирования».
Предельное состояние магистрального трубопровода характеризуется неравенством Cmax^ftmin, где ота1 — наибольшие возможные напряжения п трубопроводе от расчетных нагрузок и воздействий; Rmin — расчетное сопротивление металла труб.
Для подземных трубопроводов в качестве предельного состояния принято условие разрушения, характеризуемое расчетным сопротивлением Rit определяемым по формуле (2.14). При определении эквивалентных напряжений, влияющих па несущую способность подземных трубопроводов, принимаются •зо внимание только кольцевые и продольные осевые напряжения. Условие Для определения эквивалентных напряжений базируется на энергетической
°кц ^ °npjV °n:pjV0Ka ^ ^
При отсутствии продольных осевых напряжений или при однозначном на пряженном состоянии (продольное и кольцевое растяжение) предельное со стояиие записывается для компонентов эквивалентных напряженки:
°пр н ^ ^1’ (2.16
где окц, ОпРя — соответственно кольцевые и продольные осевые напряжения При отсутствии продольных осевых сжимающих напряжений или при наличии продольных осевых растягивающих напряжений (Ощ, n >0) тол щина стенок труб определяется по формуле
6 =-2--(2.17
2(/?! ч пр)
а при наличии продольных осевых сжимающих напряжений толщина стеиок труб определяется по формуле
6=-??Ё»-, (2.18;
2 + пр)
где п коэффициент перегрузки рабочего давления; р — рабочее (нормативное) давление в трубопроводе; Dn наружный диаметр трубы; ^—коэффициент, учитывающий двухосное напряженное состояние металла труб и определяемый по формуле
=
д/1 - 0.75 (-°7^-)2 ~ 0.5
' °ПМ
' • (2.19)
Так как в правой части выражения (2.15) предельное состояние принято Ru
то продольные осевые напряжения определяются, исходя из расчетных нагрузок и воздействий с учетом упругопластической работы металла труб, т. е. учитывается физическая нелинейность материала. Это также относится к кольцевым напряжениям, однако в этом случае расчетные формулы при упругой и упругопластической работе совпадают.
Продольные осевые напряжения оПр к должны определяться в зависимости от расчетных нагрузок и воздействий с учетом упругопластической работы металла труб, а также от конструктивной схемы трубопровода, продольных и поперечных перемещений трубы.
В СНиП 11-45—75 приведена формула определения продольных осевых напряжений для частного случая прокладки подземного защемленного прямолинейного и упругоизогнутого трубопровода от воздействия температурного перепада и внутреннего давления
°пр N - - + 0.25 -2^52- , (2.20)
где и — коэффициент линейного расширения металла труб; Af — температурный перепад (положительный при нагревании); Е — модуль упругости; Рил —коэффициент Пуассона при пластических деформациях металла; !)„,— внутренний диаметр трубопровода.
Из формулы (2.18) следует, что при наличии продольных осевых сжимающих напряжений, определяемых по (2.20), толщина стеики трубы зависит от положительного температурного перепада. Уменьшение температурного перепада может быть достигнуто охлаждением транспортируемого продукта
Толщина стенок труб магистральных трубопроводов определяется методом последовательных приближений. Вначале задаются ориентировочным
шачсиием толщины стсики. затем определяют по (2.20) стпр к, далее, по
2 )9) v]-, н по (2.18) толщину стен кн труб. Если эта толщина не совпадает заданным значением, то расчет повторяют в той же последовательности, принимая новое значение толщины стенки, близкое к определенному по
(bop.vWJ ам
Для частного случая прокладки подземного прямолинейного и упругоизогнутого участка трубопровода, когда продольные осевые напряжения определяются по выражению (2.20), можно получить решение в замкнутом
'ИД Решив совместно уравнения (2.18), (2.19) и (2.20), получим формулу чля непосредственного определения толщины стенки трубы при наличии продольных осевых сжимающих напряжений
Величина R\* вычисляется в зависимости от соотношений aAtE и при R]~Rt:
, Г (аМЕ\2
при 0,5Д,<аД??<Д, Я* = I/ —!-^-I—. (2.22)
“ 0,75
Проверка прочности трубопроводов осуществляется по формуле
где
**= л/1 ~0,75 (^У ~0,5 “л2" (224)
Здесь
— __ЯР&ВЙ ОсЛ
Прп ПрОДОЛЬНЫХ ОСОБЫХ рйСТЯГИВйЮЩИХ напряжениях ((7цр jv ^ 0) ф2=1.
Для ограничения максимальных (с учетом изгиба) напряжений и деформаций нормами проектирования установлено дополнительное условие (второе предельное состояние), при котором деформации труб ограничиваются соответствующим нормативным пределом текучести:
с#2 сЙ”
«пр^з-г1-; <226>
«н «н
где Спр" — максимальные продольные суммарные напряжения от нормативных нагрузок и воздействий;
\/ 1-0,75
( °кц- \
-0,5—^-; (2.27)
cR%l\ j cRfyk„
с — коэффициент, отражающий категорию участков трубопроводов, устанавливаемый СНиП II-45 — 75; R<2K— нормативное значение предела текучести металла труб, устанавливаемое стандартом и техническими условиями на трубы; сгкцн — кольцевые напряжения от (нормативного) рабочего давления
о« (2 28)
кц 26
Выполнение условия (2.26) обеспечивает местную устойчивость стенок труб и не допускает накопления пластических деформаций, а следонагельно, и долговечность конструкции. Отметим, что при проверке по второму предельному состоянию (2.26) расчет выполняют на нормативные нагрузки и воздействия, а продольные напряжения определяют для крайних волокон сечения трубы, исходя из упругой работы металла последней, с учетом по Перечных и продольных перемещений трубопровода (с учетом геометрнче слой нелинейности) в соответствии с правилами строительной мехаинкн.
В СПиП II-45—75 приведена формула определения максимальных (сум марных) продольных напряжений для частного случая прокладки подзем ного защемленного упругоизогнугого трубопровода от воздействия внутреннего давления и температурного перепада.
Максимальные продольные напряжения определяют по формуле
<р - Кц + °Л, + °Р = 0; 15 -^L _ aME ± , (2.29)
где р — минимальный радиус изгиба оси трубопровода.
Используя выражение (229), связывающее радиус изгиба трубопровода, толщину стенки и температурный перепад, из условия (2.26) определяют минимальный радиус оси изгиба:
р =-:-; (2-30)
р =-^. (2.31)
Из условия (2.23) можно определить предельно допускаемый температурный перепад, невызывающий увеличения толщины стенки трубы. Предельно допускаемый температурный перепад определяется по формулам: положительный
- ---; (2.32)
<хЕ
отрнцательный
0,25 — R,
м ^' (2-33)
аЕ
В табл. 4 приведены значения толщин стенок труб, применяемых для сооружения магистральных трубопроводов, рассчитанных по нормам СССР, США и ФРГ. Как видно из таблицы, только при высоком значении предела текучести, т.е. при отношении <ТтЛтврЭ*077, толщина стенок труб по нормам СССР больше по сравнению с зарубежными нормами.
| Технические условия | <Ц № ч <и | a ? о р. с о « <0 |
К S о V | Толщины стенок по нормам различных стран, мм | |||||
| К сЗ SE Iй «X |
Временное лен не, МП |
Предел те МПа | Р. га н е> | •3? |
S я Q~ | 1Л t'- йС | оХТ | США, КОД 1974 | | ФРГ, ДИН 2413 | |
| ТУ 56-72—73 (ФРГ) ТУ 56-46—74 (Италия) ТУ 48—75 (ФРГ) | 7,5 | 600 | 420 |
0,70 | 1,40 | 1420 |
16,5 | 17,4 | 19,8 |
| 7,5 |
600- | 470 | 0,77 |
1,34 | 1420 | 15,7 | 15,5 | 17,6 | |
| 7,5 | 600 | 450 | 0,75 | 1,34 |
1220 | 12,9 | 13,8 |
15,7 | |
| ТУ 14-3-446- 76 (СССР) ТУ 14-3-446- 76 (СССР) ЧМТУ 156-68 (СССР) ТУ 14-3-109—73 (СССР) ТУ 14-3-109—73 (СССР) | 7,5 | 600 |
420 | 0,70 |
1,40 | 1220 | 13,4 |
14,9 | 16,8 |
|
7,5 | 520 | 360 |
0,69 | 1,47 | 1220 | 16,4 | 17,4 |
19,6 | |
| 6,0 | 530 | 360 | 0,68 |
1,47 | 1020 | 10,6 |
11,6 | 13,1 | |
|
5,8 | 500 | 350 |
0,70 | 1,47 | 1020 | 11 | 11,6 | 13 | |
| 5,5 | 520 |
360 | 0,69 | 1,47 | 1020 | 10 |
10,5 | 11 | |
| ТУ 40-48—73 (Франция) | 6,0 |
600 | 420 | 0,7 |
1,40 | 1020 | 9 | 9,8 | 11,1 |
Метод предельных состояний, на котором основаны нормы проектирования СССР, практически всегда даст болсс экономичные решения, чем метод допускаемых напряжений, используемый в нормах США и ФРГ.
Пример /. Определить толщину стенок труб участка i азопровода III категории (/я= 0,9, л -1) диаметром Ды = 1420 мм при рабочем давлении р~ —7,5 МПа.
Для сооружения газопровода будут использованы горячеправленые, тер-мтески упрочненные трубы, изготовленные из нормалн'юваиноул учтенной ниш-легированной стали, прокатанной по регулируемому режиму. Согласно СНиП 11 45—75, коэффициент безопасности для этих труб k\ = 1,4, временное сопротивлекие <7Bp=#iB=600 МП а, предел текучести От=/?2п=470 МПа, модуль упругости ?=2,1-105 МПа.
Для определения минимальной (номинальной) толщины стенки определим расчетное сопротивление /?, по формуле (2.14)
*1 =
¦ 350 МПа.
Расчетную номинальную толщину стенки получим но формуле (2.17)
1,1-7,5-142
Проведем проверку кольцевых деформаций по формуле (2.26) и (2.28): „ 7,5(142 — 2.1,64)
317 МПа;
2-1,64
кц -- 1(1
Следовательно, условие (2 26) соблюдено
Определим максимально допускаемый положительный температурный перепад по формуле (2.32), для чего найдем значения акц, и апр .у соответственно но формулам (2.25), (2.24), (2.23).
1,1-7,5(142 — 2-1,64) „,п МГ1
-Тш— 349 МШ:
ф2 = Д А-0,75 — 0,5-^- 0,0096;
0[фN - 0,0096-350 - 3,5 МПа; 0,25 1,1-7,5(142 — 2-1 64)
I 64
Ы --—-- 70,6 СС.
12-10_в-2,Ы0ь
Определим максимально допускаемый отрицательный температурный перепад по формуле (2.33)
0,25^4^-^1^350
1 64
=-—-———--= —69,9 °С.
]2.10-«-2,1-105
Таким образом, если температура транспортируемого газа 60 ''С, то работы, при которых фиксируется длина газопровода, должны проводиться при температуре не ниже —10 °С.
Определим минимальный радиус упругого изгиба при полученных температурных перепадах, для чего найдем ф3 по формуле (2.27)
л/\—0,75(-—-V — 0,5-—--0,395,
V VI 470/1,1 ) 1-470/1,1
а по формулам (2.30) и (2.31):
при положительном температурном перепаде Л/=70,6 °С
__2,1 10М42_
= 1,733.10s см — 1733 м;
>|-^-470
—j^-0’—7’5^-4^
2—--12- 10—«-2,1 106-70, б||
= 4,3-10‘ см = 430 м:
прн отрицательном температурном перепаде Д?=—70 СС
_______2, ЫО5-142__
Pt 2 470 + + 12-10—e-2,1 - I06-7ojj
= 3,38-JO4 см = 338 m:
__2,M0»-142__
P2 2J— 470 -
^°»1о,1»5(И?~2'1:64)
-f 12-10—*- 2,1 ¦ 10». 70j| = 9,56-10* cm = 956
м.
Принимается большее значение искомого радиуса
Таким образом, радиус упругого изгиба трубопровода при Af=70,6 °С должен быть не менее 1733 м, а при Д^=—70 °С — ire менее 956 м.
Пример 2¦ Определить толщину стенки трубопровода при положительном температурном перепаде А/=85 °С. Техническая характеристика труб та же, что и в первом примере.
Так как данный температурный перепад превышает максимально допускаемый, полученный в предыдущем примере, то толщину стеики трубопровода следует определять по формуле (2.18). Продольные осевые напряжения запнеят от толщины стсики поэтому решение выполняется методом последовательных приближений. Принимаем вначале толщину стенки 6=2 см Продольные осевые напряжения определяем по формуле (2.20)
anpN = —
12-10—e-2,1-106-85 +
-0,25'1'Ь7’^(Н2"~2--2)
= -72 МПа.
По формуле (2.19) определяем коэффициент учитывающий двухосное разнозначное напряженное состояние.
д/1— 0,75 Г—ZH_V — о, %Л- =0,882.
V V 350 У 350
Толщину Стенки трубы определяем по формуле (2.18)
1,1.7,5-142
о-- 1,84 см.
2(0,882-350+ 1,1-7,5)
Принимаем новое значение толщины стенки 6=1,84 см и повторяем расчет:
о--12- 10е-2,1-
10ь-85 +
1,1-7,5(—2——,84)
= -59 МПа;
прлг 184
ф,--= а/ 1— 0,75 Г —— 0,5.-^_= 0,905,
1,1-7,5-142
о =- 1,80 см.
2(0,905-350+ 1,1-7,5)
Принимаем иовое значение толщины Стенки 6=1,78 см и выполняем расчет:
,= — 12-10-6-2,1-1Q6-85+
O’jj?0,1'?:5*142—2-1,78)
= _ 1,78 ^1“ а/ 1 —0,75^—Y —0,5——- =
0,914;
Таким образом, расчетная толщина стенки будет 6“1,78 см.
Как видно из расчетов, повышение температурного перепада по сравн нию с предельно допускаемым значением вызывает необходимость увелич пия толщины стенкн трубы.
Пример 3. Определить толщину стенок труб для исходных дапных npi мера 2. Используем решение (2.21).
Определим напряжение от температурного перепада.
0д, = аА<Е 12-10-0-85.2,1-10s = 214 МПа.
Величина R\ как следует из примера 2, равна 350 МПа Так как 214; >175, аА/?>0,5 Hi. Следовательно, согласно (2.22)
/ 350*-
214s
320 МПа.
,75
По формуле (2.21) толщина стенки будет
= 1,78 см.
2(320+ 1,1 7,5)
Пример 4. Определить ветровую нагрузку для двухпролетиого переход с одним компенсатором при длине пролета /=33 м Переход сооружаете; в III ветровом районе. Диаметр трубопровода 1420 мм, толщина стенга
20 мм
Скоростной напор ветра для III ветрового района
^0 = 450 Н/м2.
Скорость ветра, соответствующую данному скоростному капору, опредс ляем по формуле (2.7), принимая а 1:
v = V 1,6ft, = У1,6-450 = 26,8 м/с.
Число Рейнольдса определяем по формуле (2.8)
Re=,
2Г-’8'--'-2 -=
26-106.
По графику рис. 2 находим коэффициент лобового сопротивления, который равен сх=0,62.
Статическую составляющую ветровой нагрузки получим по формуле (2.6) <7„. с = 450 0,62 = 278 Н/м*.
Для определения динамической составляющей ветровой нагрузки по формуле (2.11) находим собственную частоту горизонтальных колебаний (для второй формы). Величину получаем по табл. 2, принимая условное число пролетов, равное четырем. Она составляет 6,82. Тогда
6,82 /2,1 •10и-2,1б6-10—*-9,81 t _
•v2r — -/\ / ---13,5 I ц
ЗЗ2 V 9,6-103
Период собственных горизонтальных колебаний
Tgr = —-— = —-— = 0,07 с-v2r 13,5
егы*---
Поскольку 7'2г<0,251 динамическое воздействие пульсаций скоростного на пора ветра не учитывается, т. е. 5=0, qn. л=0 Нормативную ветровую па-грузку определим по формуле (2 5)
РАСЧЕТНЫЕ МОДЕЛИ ГРУНТА, ВЗАИМОДЕЙСТВУЮЩЕГО С ТРУБОПРОВОДОМ
Расчетные модели грунта, взаимодействующего с трубопроводом обычно представляют в виде зависимости сопротивления грунта от продольных и поперечных перемещений трубы. Эти зависимости в основном устанавливаются на основании экспериментальных исследований.
§ 1. Физико-механические характеристики грунта
Подземные трубопроводы рассчитывают в зависимости от характеристик среды, в которой они будут находиться при эксплуатации. Эти характеристики определяются на основании инженерных изысканий трассы и прогнозирования изменения грунтовых условий, связанных со строительством и дальнейшей эксплуатацией трубопровода.
Под инженерными изысканиями следует понимать комплексный производственный процесс, обеспечивающий строительное проектирование исходными данными о природных и инженерно-геологических условиях трассы будущего трубопровода.
При изысканиях следует руководствоваться ие только нормативными документами, относящимися непосредственно к изысканиям, но и документами, регламентирующими нормы проектирования магистральных трубопроводов, конструкций, заглубленных в грунт, а также правилами производства и приемки земляных работ.
На основании инженерных изысканий в соответствии с номенклатурой грунтов устанавливаются типы, виды и разновидности грунтов по нх различным показателям, например по гранулометрическому составу, степени влажности, плотности, коэффициенту пористости, числу пластичности и т. п.
Основными параметрами физико-механических свойств грунтов, определяющих напряженно-деформированное состояние подземных трубопроводов, являются угол внутреннего трения q>rp, удельное сцепление сгр, модуль деформации нескальных грунтов Егр, объемный вес грунта \гр, удельный вес грунта \’у- гр, пористость е.
Методы определения основных показателей грунта изложены в соответ-ств>ющих стандартах, перечень которых приведен в СНиП 1Г9—78 Инженерные изыскания для строительства. Основные положения.
Физико-механические характеристики грунта при изысканиях определяют для каждого выделенного по трассе трубопровода инженерно - геологического элемента.
За нормативное значение всех характеристик грунта (за исключением удельного сцепления и угла внутреннего трения) принимают среднее арифметическое значение результатов частных определений
Нормативное значение характеристики грунта А" но результатам непосредственных определений, выполняемых в лабораторных или полевых условиях, вычисляется по формуле
![]()
где п — число определений характеристики; Л, — частное значение характеристик.
За нормативное значение удельного сцепления и угла внутреннего трения принимают параметры линейной зависимости сопротивления грунта
срезу т от давления, получаемые методом наименьших квадратов для всея совокупности опытных величин в инжснсрио-геологическом элементе:
(3 2)
где г — сопротивление образца грунта срезу; р — нормальное удельное давление, передаваемое на образец грунта.
Нормативные значения сгрн н tg фгрн вычисляются по формулам:
/ п п п п
![]()
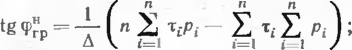
(3 4)
где
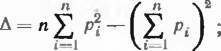
/I — число определений величин г.
В нормативное значение характеристики грунта может вводиться поправка на возможное изменение состава, состояния и свойств грунта в процессе строительства и эксплуатации трубопровода. Величина этой поправки устанавливается испытанием образцов грунта заданного (прогнозируемого) состава и (или) состояния, т. е. путем моделирования. Возможен учет этих факторов так называемыми коэффициентами перегрузки.
Все расчеты подземных трубопроводов на прочность и устойчивость выполняются с использованием расчетных характеристик грунтов А, которые определяются по формуле
(3 6)
А — AHJkrp,
где Ая нормативное значение данной характеристики; kTp коэффициент безопасности по грунту.
Коэффициент безопасности по грунту Агр устанавливается в зависимости от изменчивости нормативных характеристик, числа определений этих характеристик и от значения доверительной вероятности а, которую можно принимать равной 0,95 для трубопроводов категории В, 0,9 — для трубопроводов категории I и II и 0,85 для трубопроводов категории III и IV.
Категории трубопроводов устанавливаются согласно СНиП 11-45—75.
Коэффициент безопасности по грунту klp прн определении расчетных значений удельного сцепления сгр, угла внутреннего трения <ргР и объемного веса грунта \’гр вычисляется по формуле
![]()
где р — показатель точности оценки среднего значения характеристики грунта.
В формуле (3.7) знак перед величиной р принимается тот, который обеспечивает большую надежность рассчитываемого трубопровода, т. е. значение получае мого коэффициента безопасности идет в запас прочности или устойчивости. Показатель р вычисляется по формулам:
ДЛЯ Сгр и tg <ргр
Коэффициент ta для определения показателя точности оценки среднего значения характеристики грунта
|
Число степеней свободы (п — I) для Yrp’ (,‘ _ 2) для сгр н Фгр |
Коэффициент /а при односторонней доверительной вероятности а | Число степеней свободы (п — 1) для Vrp. («-2) для сгр н <frp |
Коэффициент ta при односторонней доверительной вероятности а | ||||
| 0,85 |
0,90 | 0.95 | 0,85 | 0,90 | 0,95 | ||
| 2 | 1,34 |
1,89 | 2,92 |
9 | 1 10 |
1,38 | 1,83 |
| 3 | 1,25 |
1,64 | 2,35 |
10 | 1 10 |
1,37 | 1 81 |
| 4 | 1,19 |
1,53 | 2 13 |
11 | 1,09 | 1 36 | 1 80 |
|
5 | 1,16 | 1 48 | 2 01 | 12 | 1,08 | 1,36 |
1 78 |
| 6 |
1 13 | 1 44 |
1,94 | 13 |
1,08 | 1 35 |
1,77 |
| 7 |
1,12 | 1 41 |
1,90 | 14 |
1,08 | 1,34 | 1 76 |
| 8 |
1,11 | 1,40 |
1,86 | 15 |
1,07 | 1,34 |
1,75 |
ДЛЯ \тр
P = (3 9)
V И
где ta — коэффициент, принимаемый по табл. 5 в зависимости от заданной доверительной вероятности а и числа степеней свободы. Под числом степеней свободы в данном случае понимается общее число определения угр и т; v — коэффициент вариации характеристик
v = —, (3.10)
где о - среднее квадратическое отклонение характеристики.
Величина ст вычисляется по формулам
Д.1Я Сгр И tg фгр
°-'гр = ^|/ ТХ/' И
г=а.лГг, (3.11)
где
Ох
д- определяется по формуле (3.5); для Yrp
Число частных определений п для вычисления нормативных и расчетных значений характеристик грунтов зависит в общем случае от степени
неоднородности грунтов основания, требуемой точности вычисления характер ристики и устанавливается программой исследований.
Число одноименных частных определений для каждого выделенного инженерно геологического элемента должно быть не менее шести. При этом для вычисления нормативных и расчетных значений сгр и ф,р должно быть] определепо не менее шести значений х для каждого значения нормального давления р.
Число частных определений для вычисления нормативного значения мо-| дуля деформации Егр, полученного по результатам испытаний грунта штампом в полевых условиях, должно быть не менее трех. Допускается ограни-' читься двумя значениями Егр, если эти значения отклоняются от среднего, не более чем на 25 %.
Число частных определений характеристик грунтов допускается уменьшить при наличии одноименных определений в материалах предыдущих изысканий, выполненных на той же трассе для того же инженерно-геологи-ческого элемента.
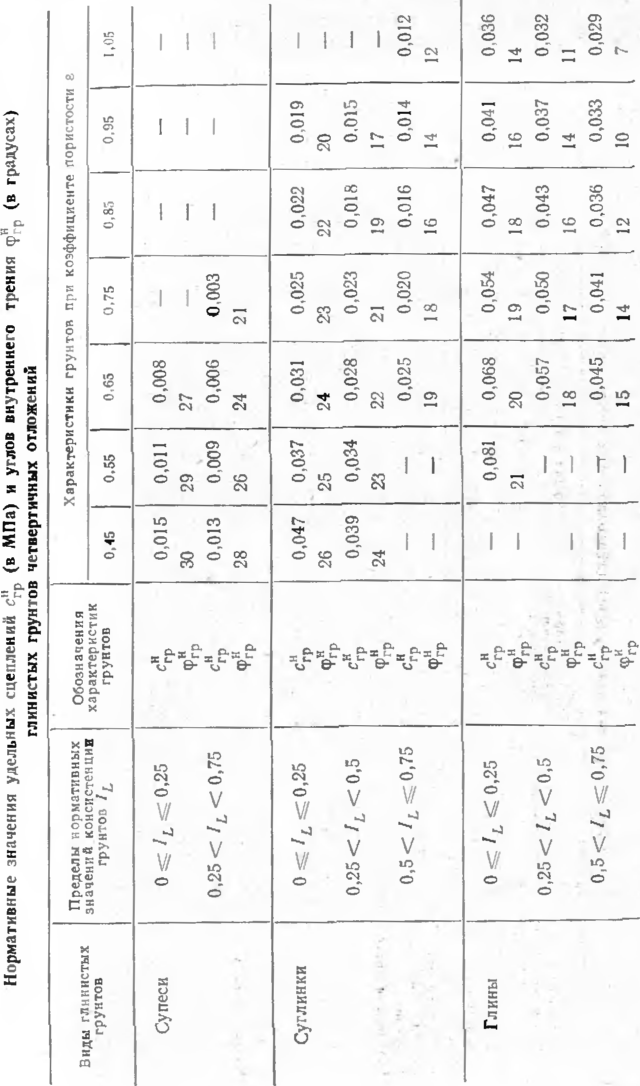
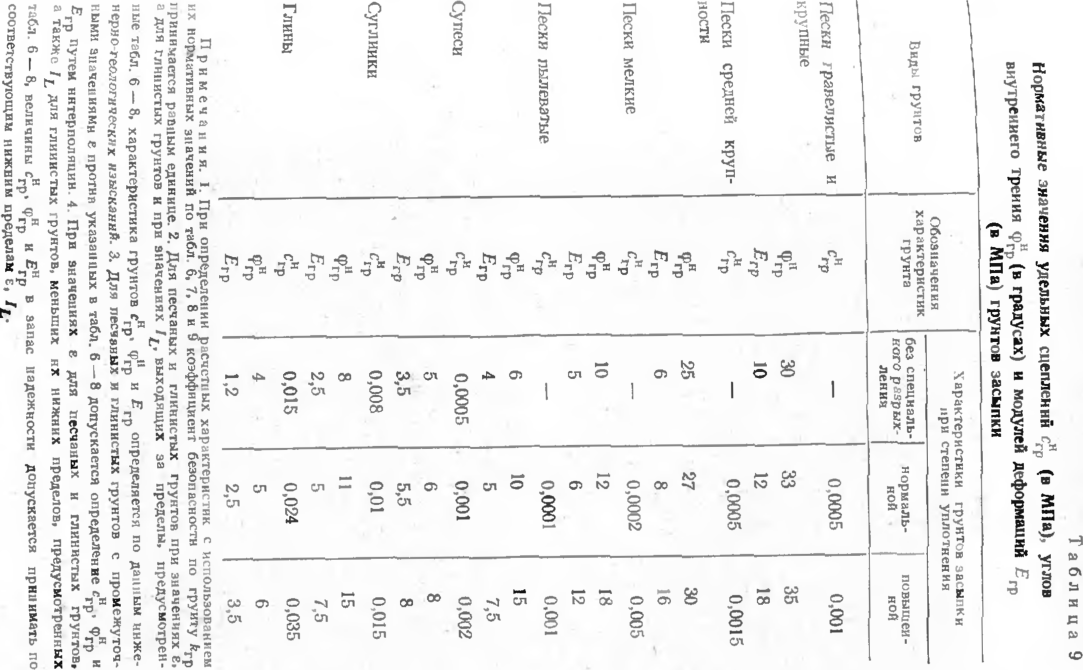
Для предварительных расчетов можно пользоваться данными табл. 6—9. Табл. 6™8 характеризуют грунты ненарушенной структуры, табл. 9 грунты засыпки.
Особое внимание при проектировании и расчете подземных трубопрово-J дов должно быть уделено учету как сезонных и многолетних колебаний уровня грунтовых вод (и верховодки), так и возможности формирования нового повышенного среднего уровня.
Таблица в Нормативные значения удельных сцеплений с^р (в МПа), углов внутреннего трення <р”р (в градусах) и модулей деформации ?Гр (в МПа) песчаных грунтов (независимо от происхождения, возраста и влажности)
|
Виды песчаных (VSLtt) грунтов |
'^Обозначения "характеристик | Характеристики грунтов основания Я при коэффициенте пористости в | |||
| грунтов | 0,45 | 0.SS |
0,65 | 0,75 | |
|
Пески гравелистые и | ?р |
0,002 | 0,001 | __ | _ j |
| крупные | Фгр | 43 |
40 | 38 | — |
| Егр | 50 |
40 | 30 | — 1 | |
| Пески средней круп |
0,003 | 0,002 |
0,001 | — | |
|
ности | |||||
| «р? | 40 |
38 | 35 | — |
|
| с *-гр |
50 | 40 | 30 |
— | |
| Пески мелкие |
Сгр | 0,006 |
0,004 | 0,002 | |
| фГр | 38 |
36 | 32 | 28 | |
| Егр | 48 | 38 | 28 | 18 | |
| Пески пылеватые |
0,008 | 0,006 |
0,004 | 0,002 | |
| 36 | 34 |
30 | 26 | ||
|
?Yp | 39 | 23 |
18 | И | |
*
|
Происхождение и возраст глинистых грунтов | Виды глинистых Грунтов |
Пределы нормативных значений консистенции грунтов | Модули деформации грунтов при коэффициенте пористости в | ||||||||||
| 0,35 | 0,45 |
0,55 | 0,65 |
0,75 | 0,85 |
0,95 | 1,05 |
1,2 | 1,4 | 1.6 | |||
| Четвертичные отло |
Супеси | 0</:.< 0,75 | 32 | 24 | Гб | Ш |
7 | ||||||
| жения: | |||||||||||||
| Аллювиальные | |||||||||||||
|
Делювиальные | Суглинки |
0 < //.< 0,25 |
•- | 34 |
27 | п |
17 | 14 |
11 | ||||
| Озерные | 0,25 < lL г^О 5 |
¦- | 32 |
25 | 19 |
14 | 11 |
8 | __ | ||||
|
Озерно-аллювиальные |
0,5 < У/. <0,75 | - | — | — |
17 | 12 |
8 | 6 | 5 | — | — |
— | |
| Глины |
0 < /? < 0,25 |
. | _ | 28 | 24 | 21 |
18 | 15 |
12 | ||||
| 0,25 < /^ ^: 0,5 |
- | — |
— | 21 | 18 | 15 | 12 |
9 | _ | _ |
|||
| 0,5 < IL <0,75 |
-- | - | — |
— | 15 | 12 | 9 | 7 |
— | — | — |
||
| Ф лювиог л яциальны е |
Супеси | OsS 1l <0,75 | — | 33 | 24 | 17 |
11 | 7 | |||||
|
Суглинки | 0 < It < 0,25 |
_ | 40 | 33 | 27 | 21 |
|||||||
| 0,25 < /l<0,5 | - | 35 |
28 | 22 |
17 | 14 | |||||||
| 0,5 < /i. <0,75 |
- | - | — |
17 | 13 |
10 | 7 |
— | — | — |
|||
| Моренные |
Супеси, | //,<0,5 |
75 | 55 |
45 | ||||||||
|
Суглинки | |||||||||||||
| Юрские отложения | Глины |
—0,25 < II <0 |
27 | 25 | 22 |
||||||||
| оксфордского яруса | 0 < /l <0,25 | ?.4 | 22 | 19 | 15 | ||||||||
| 0,25 </^.<0,5 |
1 | 16 | 12 |
10 | |||||||||
Возможные измеиепия уровня грунтовых вод следует прогнозировать в зависимости от геологических и гидрогеологических условий участка, времени и способ а выполнения строительно-монтажных работ, температуры трубопровода и окружающего его грунта в процессе эксплуатации.
§ 2. Сопротивление грунта продольным перемещениям трубы
Самой простейшей расчетной моделью грунта при продольных перемещениях трубы является линейная модель. Эта модель впервые была предложена проф Флориным и исходит из того, что сопротивление грунта прямс пропорционально его продольным перемещениям. С использованием это? модели был решен ряд практических задач. Однако, как показали проведен ные различными авторами исследования, эту модель можно использоват! только при рассмотрении «малых» перемещений, так как при «Зольших перемещениях имеет место существенная нелинейность между сопротивле нисм и перемещением. Жестко-пластическая модель грунта, с которой при нимается сопротивление грунта постоянным, может использоваться при ре шении задач, где рассматриваются большие перемещения.
Использование нелинейных моделей позволяет существенно повысит! точность результатов расчета.
Проведено большое число экспериментальных исследований по установ лению расчетной модели грунта н ее количественных параметров [8, 9, 29 Эксперименты проводились как на моделях трубопровода, так и в реаль ных условиях. Следует отметить, что количественные характеристики, полу ченные на моделях, не всегда отражают условия работы трубопровода. Объ ясняется это тем, что на механические и физические свойства грунта, ка физического тела, оказывают влияние нагрузки, обусловленные собственно массой грунта. Поэтому при моделировании взаимодействия сооружеии (трубопровода) с грунтом необходимо, как указывал проф. Г. И. Покров ский, воспроизводить то поле напряжений, которое обусловлено действие] силы тяжести.
На рис. 4 и 5 приведены результаты четырех из проведенных нами эк< периментов по определению зависимости сопротивления грунта от продол! ных перемещений трубы.
По оси абсцисс отложены продольные перемещения отрезка трубы, ка иедеформируемого тела, по оси ординат — средние значения сопротивлеин грунта сдвигу по периметру трубы.
Общая качественная характеристика зависимости сопротивления грунт от продольного сопротивления трубы соответствует приведенным диагра» мам. На диаграммах можно выделить три участка. Первый участок соо' ветствует стадии, когда между сопротивлением и перемещением имеете почти линейная зависимость. Это — первая фаза (по Н. М. Герссванову
Н. А. Цытовичу) напряженного состояния грунта фаза уплотнения, ког; грунт уплотняется н приобретает свойства упругого тела На втором учасп пропорциональность между сопротивлением и перемещением нарушается, ч-соответствует второй фазе, когда доля упругих деформаций уменьшается происходит нарастание остаточных деформаций. Этот факт иллюстрирует! полученными при экспериментах петлями гистерезиса (рнс. 4, а) Наконе третий участок — прямая, которая характеризует равномерное движение о резка трубы Эта третья фаза напряженного состояния грунта. Она хара теризует работу грунта в стадии предельного равновесия, т. е. когда меж, трубой и грунтом установилась пластическая связь, которая описывает свойством пластического тела Прандтля—Кулона.
Как показали эксперименты (см рис. Б), для связных грунтов (п сцеплении сгр>0) предельное сопротивление грунта сдвигу уменьшается сравнению с максимальным. Этот факт отмечеи П. П. Бородавкиным В. Д Тараном при проведении опытов на моделях. Касаясь природы это явления, Н Н. Маслов отмечает, что величина сцепления, определяемая j бораторными испытаниями грунтов, состоит из двух слагаемых: иеобра-
Рис 4. Диаграмма «сопротивление песчаного грунта — продольное перемещение»:
о — диаметр 720 мм. высота засыпки 100 см: / — при т—1,2 и; 2“ при г=»0.59 —
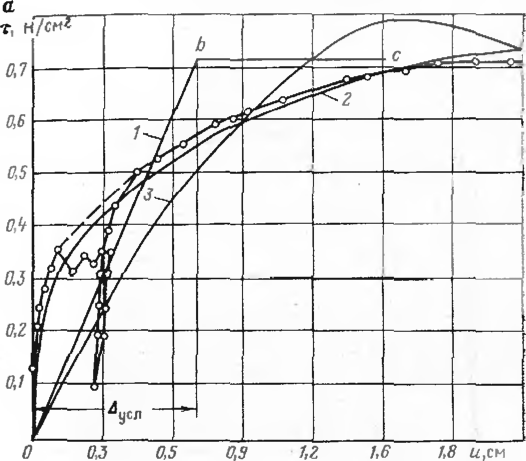
6
при т=*0,8 ^jti и; б — диаметр 529 мм. высота засыпки 120 см; / — при т=2,1 и, 2 — при Т—0,93 ii03*; 3 — при т—1.05 sin 1,54 и
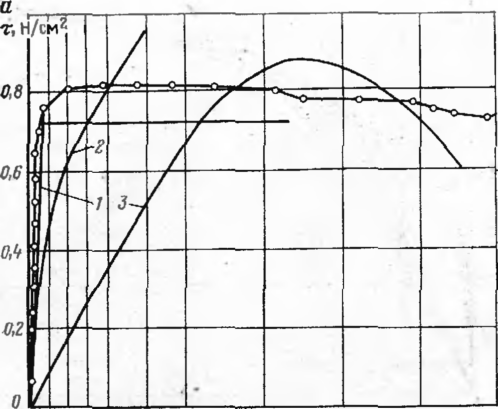
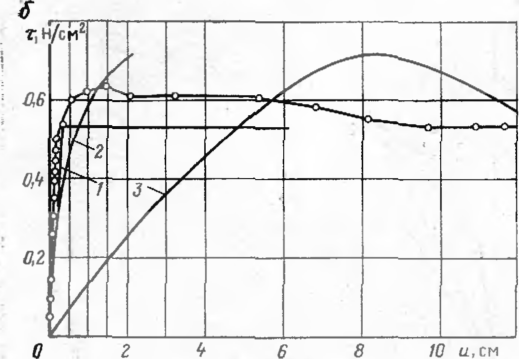
Рис 5. Диаграмма «сопротивление глинистого грунта — продольное перемещение»:
о —Диаметр 273 мм, высота засыпки ВО см; / — при т^>2.45 и\ 2— при t^O.63 при т—0,88 sin 0,21С и: 6 — диаметр 325 мм, высота засыпки 40 см; / при т=2 4 и; 2 — при т—0,58 3 — при т=--0.71 sin 0,184 и
п о сцепления и связности водно-коллопдиой природы обратимого харак-м ' f-ia предельное сопротивление грунта сдвигу оказывает влияние только
б рати мая часть сцепления. Специально поставленные опыты, проведеи-' t Ь Н. Жемочкпиым, также показали, что при медленном движении напущенные силы сцепления ие восстанавливаются.
*' Таким образом, качественный характер взаимодействия трубопровода и лнта при продольных перемещениях можио описать следующей схемой, д возникновения состояния предельного равновесия происходит деформация структуры, н касательные напряжения являются функцией перемеще-, fi При дальнейшем росте перемещений касательные напряжения остаются постоянными, притом их максимальная величина ограничивается напряже-,км сдвига 1рунта а минимальная — трением структуры.
Рассмотрим одну из возможных нелинейных зависимостей сопротнвле-н 1Я грунта от перемещения в области унруюпластичсских деформаций rpvm а в виде
тх = сигх, (3.14)
где г* — сопротивление грунта. Приходящееся на единицу площади; с—коэффициент, характеризующий максимальное значение сопротивления грунта; г — пока (атель не линейности; их продольное перемещение.
Инея результаты экспериментальных исследований, для определения искомых параметров сиг можио воспользоваться способом наименьших квадратов. Прп этом необходимо решить систему нелинейных уравнений. Вос-по ьзуемся способом определения параметров уравнения, предложенным Б П Демидовичем. Сущность ею заключается в следующем: искомая кривая описываемая уравнением (3.14), проходит через одну из характерных точек, в нашем случае через точку с координатами ит п Tmas- Тогда уравнение (3.14) можно представить в виде
(3.15)
т* = ттах («*/«т)г.
где тп,а*--максимальное сопротивление грунта сдвигу; ит — перемещение, соответствующее величине тгоах-
Иснользуя способ наименьших квадратов и приняв в качестве меры отклонения всличнпу
/1
Sm - - V (In С zlnHf lux,-)®,
(3.16)
находим из независимых выражений коэффициенты уравнении (3.14)
П
![]()
n
X 1 nullum
![]()
(3.171
Тля каждого нз опытов, имея п экспериментальных точкк, определяют гскомые параметры г и с.
Приведем данные, нолученные нами на основании проведенных 58 экспериментов с трубами диаметром от 114 до 729 мм Используя теорию математической статистики определим доверительный интервал параметров е заданной надежностью Р. Считая, что результаты всех измерений подчиняются нормальному распределению доверительный интервал величины г определяется но формуле
![]()
![]()
Здесь г —среднее значение коэффициента, г=Хг,/н, I t(P. п)—функция!
f=i
заданной вероятности (надежности оценки) и числа измерений (опытов) ггл значение I определяется но таблицам интеграла вероятности; s„ выбороч! ный стандарт
Обрабатывая результаты каждого из опытов н всех экспериментов, находим, что истинные значения искомых параметров с надежностью Р 0,9 составляют: для песчаных грунтов
О 278 <г<0,330,
0.0477 < с < 0,0605,
для глинистых грунтов
0,233 <г<0,298,
0,0552 < с < 0,0756
Как показали проведенные исследования и расчеты, в большинстве случаев зависимость сопротивления грунта от продольных перемещений а области упругонластических деформаций можно линеаризировать с помощью обобщенного коэффициента касательного сопротивления грунта сх о п представить искомую зависимость в виде
Т* - " сх оых» (3 19)
т. е. считать показатель нелинейности z в уравнении (3.14) равным единице. Отметим, однако, существенное различие меж чу параметрами с в уравнении
(3.14) и с* о в уравнении (3 19).
Обобщенный коэффициент касательного сопротивления грунта, отражающий его упругон.частичсскис деформации, определяем по имеющимся экспериментальным диаграммам т т(и) по способу, предложенному проф
Н. К. Снитко для определения обобщенного коэффициента сжатия. Для этого истинную диаграмму зависимости сопротивления грунта от продольных : перемещений заменяем идеализированной, построенной по аналогии с диаграммой Прандтля. Зная нредетьное сопротивление грунта сдвигу, определим обобщенный коэффициент из условия минимума ошибки. Для этого из начала координат проведем ломаную оЬг (ем рис. 4) так, чтобы площади, образованные экспериментальной кривой и ломаной линией были равны. Обобщенный коэффициент касательного сопротивления грунта сх 0 вычисляется как отношение tnp/Дуел, где ДуСл — перемещение, соответствующее предельному сопротивлению грунта сдвигу.
На основании проведенных нами и опубликованных в литературе результатов экспериментов, а также существующей нормативной классификации грунтов составлена таблица рекомендуемых значений обобщенного коэффициента касательного сопротивления грунта (табл. 10).
Отметим, что учет ynpyi оплаетнческой работы грунта с помощью обобщенного линейного коэффициента обычно даст удовлетворительные результаты для практических расчетов. Применение более точной аппроксимация для этого диапазона зависимости сопротивлений от перемещений обычно возникает при решении обратной задачи, когда по результатам фактических перемещений при сечения напряженною трубопровода определяется его напряженное состояние.
Важнейшим параметром, характеризующим диаграмму «сопротивление грунта — продольное перемещение», является предельное сопротивление грунта сдвигу тпр.
Предельное сопротивление грунта сдвигу зависит от радиальных со ставляющих давления грунта по поверхности трубы и от сцепления грунта. Так как радиальные составляющие различны по поверхности трубы, то для
Значение обобщенного коэффициента касательного сопротивления грунта сх0, МПа'см
|
Виды Грунтов | Пределы нормативных значений консистенции |
Характеристики грунтов прн коэффициенте пористости е | ||||
| грунтои t^ | < 0.5 [ | 0,5—0,6 | 0,61—0.7 |
0,71—0,8 | >0.8 | |
| Пески гравелистые, крупные и средней круп | ||||||
| ности | 0,033 | 0,030 |
0,027 | 0,025 | 0,025 | |
| Пески мелкие | 0,025 | 0,02] | 0,021 | 0,019 | 0 019 | |
| и пылеватые | ||||||
|
Супеси | 0,25 | 0,035 | 0,033 | 0,030 | 0 030 | 0 030 |
| 0,25 < //_ sj 0 75 | 0,035 |
0,032 | 0,030 | 0,025 |
0 025 | |
| Суглинки | 0 *= IL < 0,3 |
0 038 | 0,035 | 0,035 |
0,032 | 0,030 |
| 0,3 < /к 0,75 | 0,035 | 0,033 | 0,030 |
0,025 | 0,020 | |
|
Глины | 0 < IL s? 0,3 | 0,040 | 0,038 |
0,035 | 0,033 | 0,030 |
| 0,3 < ^0,75 |
0,045 | 0,040 | 0,035 | 0,030 | 0,030 |
|
раем гов целесообразно использовать интегральную сумму карательных напряжений по периметру грубы.
Каь. показали проведенные нами эксперименты, предельное сопротивление грунта сдвигу нелинейно зависит от высоты засыпки над трубой. Кроме то о. на предельное сопротивление грунта сдвигу оказывает влияние только необратимая часть сцепления, которую можно определять но методу повторны». сдвигов (при разной влажности) при нормальных напряжениях в грунтах, близких к действительным
На основания анализа опубликованных работ 18, 9, 49J и проведенных иа.\:и чксперичеитов Для определения предельного сопротивления грунта сзпнгу можно рекомендовать следующую формулу:
'гр =- <?тр ^ <РгР + 2Угрсля-°н ». р + С'6яСисгр, (3.20)
1де Рть- вес трубопровода с про-
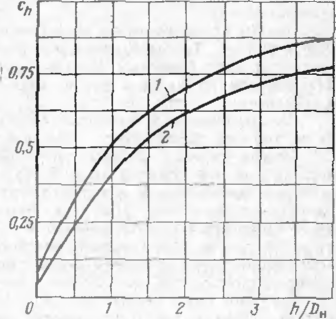
Рис. 6. Коэффициент, учитывающий образование свода обрушения:
/ — песчаный грунт; 2 — глинистый грунт
г.уктом; с(тр - угол внутреннего тре-«нк грунта; угр объемный вес грунта; ch безразмерный коэффи-t И' нт; ?>„ наружный диаметр трубы; сгр сцеилсние грунта.
Первое слагаемое этой формулы учитывает вес трубопровода с про-. укгом или отрицательную плавучесть. второе — давление грудта по периметру трубы и третье необратимую часть сцепления грунта по периметру трубы.
Коэффициент сь, отражающий образование свода обрзшения за-г-1 ят от отношения высоты засыпки «а: трубой к се диаметру h/Da и может быть получен по графику рпс. 6.
Для расчетов на ЭВМ кривые I ii 2 графика рис. б представлены ь виде многочленов. Коэффициент i'f определяется по формулам'
ch = 0,416 —--0.056 — -f- 0,095; (3.21)
для глинистых грунтов
сн = 0,367 ----0,046 0,06. (3.22)
0„ D2,
§ 3. Сопротивление грунта поперечным перемещениям трубьг
Сопротивление грунта поперечным перемещениям трубы зависит or 1 плоскости, в которой происходит перемещение. При перемещениях трубы, в вертикальной плоскости всчедствие различия свойств грунтов засыпки И: основания под трубой (их жесткости) сопротивление грунта различно. При перемещениях трубы в горизонтальной и юскостп сопротивление грунта зависит от ширины траншеи и свойств грунта нарушенной и ненарушенной структуры
В связи с этим расчетные модели грунта н се количественные параметры будут различны в зависимости от направления перемещений.
Сопротивление грунта поперечным (в вертикальной плоскости) перемещениям трубы вверх
В свят с необходимостью расчета трубопровода ла продольную устойчивость проведено достаточно много экспериментальных исследовании по со-противлению грунта поперечным перемещениям трубы вверх.
Результаты многих из этих исследований приведены в работах.
Э. М. Ясина [49], П. П. Бородавкина н других авторов. Учитывая, < го для расчета трубопроводов принималась, в основном, жесткопластическая мо~ дель, основное внимание уделялось определению предельной удерживающей способности грунта.
Особенностью проведенных иамн экспериментов было то, что труба нагружалась не статическим усилием, а прессовой нагрузкой, что позволило-получить зависимость сопротивления грунта от перемещения во всем их диапазоне.
Опыты проводились на заглубленных трубах длиной 4 м, диаметром 273,. 529 и 720 мм. Трубы поднимали лебедками с помощью тросов. Перемещения измеряли аротбомерамп Максимова, усилия—динамометрами растяжения. Нагружение на каждом этапе осуществляли с выдержкой во времени дестабилизации усилия.
Опыты проводили при различной высоте засыпки грунта над трубой (от
0 до 100 см). Кроме того, грунт использован! нескольких видов.
Общая картина зависимости сопротивления грунта от перемещения одинакова для всех опытов (рис. 7, 8). Вначале, пока перемещения невелики, • между сопротивлением q и поперечным перемещением у наблюдается почти-линейная зависимость. Достигнув максимума, сопротивление грунта снижа- I ется. Особенностью диаграммы (ля глинистых грунтов по сравнению с диаграммой для песчаных грунтов является то, что достижение сопротш i-нием максимума характеризуется наибольшим перемещением грубы, г. с. в этот период происходит более значительное уплотнение грунта над трубой.
Выразим зависимость между сопротивлением грунта qy н попер* ным перемещением у трубы на участке кривой, характеризующимся упругоила-стичсской работой грунта, с помощью обобщенного коэффициента нормального сопротивления грунта су 0:
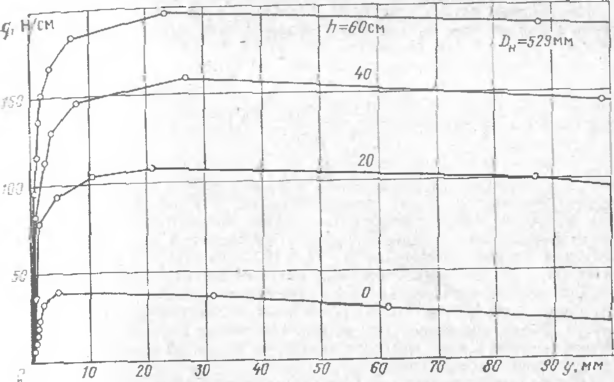
Рис 7. Диаграмма «сопротивление песчаного грунта — вертикальное перемещение (вверх)». (Днамегр трубы 529 мм)
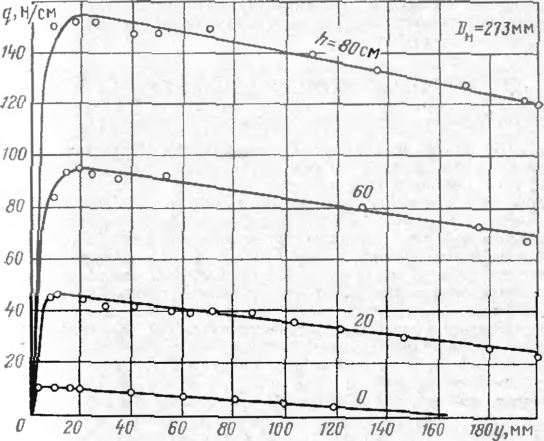
Р(;с 8 Диаграмма «сопротивление глинистого грунта — вертикальное перемещение (вверх)». (Днаметр трубы 273 мч)
На основании обработки результатов экспериментов с использование решения для штампа иа упругом основании зависимость обобщенного коэ^ фицнента нормального сопротивления грунта от свойств грунта и параме-ров заглубленного трубопровода может быть представлена в виде
/ 2Ло \
0,12?грТ}гр I р I
су о--
—-—— \1 — е /,
(3 24)
где су о — коэффициент нормального сопротивления грунта, ЛШа/см; ?гР —1 модуль деформации грунта ненарушенной Структуры, МПа; >],Р— коэффиИ циенг снижения моду тя деформации грунта засыпки по сравнению с грун-1 том ненарушенной структуры; цгр— коэффициент Пуассона грунта; /с,—J единичная длина трубопровода (/о=100 см); Он -наружный диаметр! трубы, см; Л0 - расстояние от верха засыпки до осн трубы, см.
Для определения предельной удерживающей способноети грунта за-1 сыпки над трубой, т. е его сопротивления, соответствующего потере устой* чивости грунта, существует ряд решении. Огметнм решение Ю. И. Соловьева! и метод расчета анкерных фундаментов, изложенный в нормах иа проекти-1 рование линий электропередач.
Обычно предельную удерживающую способность грунта определяют призмой выпора. Nчнтыная, что для реальных трубопроводов отношение глу-j бины его заложення к диаметру не превышает пяти можно считать, что во всех случаях угол откоса призмы определяется углом внутреннего трений грунта. Несколько сложнее со слагаемым, входящим в предельную удерживающую способность грунта и учитывающим сцепление грунта. Как показали исследования Г 11 Покровского и Д. А. Леонардса силы сцепления зависят от сил сжатия Снлы же сжатия, т е. нормальные напряжения п грунте, вызванные его собственным весом, для трубопроводов имеют незначительную величин*- и изменяются в пределах от 0 на поверхности до 0,02—0,04 i\Vna на глубине 2—2,5 м.
На основе обработки экспериментальных данных для определения предельного сопротивления грунта вертикальным вверх перемещениям трубы можио рекомендовать формулу
^P.rp-VrpDjho-0,39DH) Vrp^otg0,7<рГр (3.25)
COS U, / фгр
где уГ|1 — объемный вес грунта; Du — наружный диаметр трубы; h„ — расстояние от верха засыпки до оси трубы; qprp — угол внутреннего треиня грунта; е,.р сцепление грунта.
Нами определялось сопротивление грунта н при перемещениях, когда имела место потеря устойчивости грунта, т. е. сопротивление грунта уменьшалось но сравнению с максимальным его значением. Это означает, что, если бы мы рассматривали трубу как анкер, то при приложении постоянного усилия, равного максимальной удерживающей способности грунта, произошло бы выдергивание трубы. При небольших доиолпнтельиых перемещениях трубы к перемещению, соответствующему предельному сопротивлению грунта, последнее уменьшалось незначительно. При перемещениях, имеющих один и тог же порядок с высотой засыпьн, сопротивление значительно уменьшилось, гак как происходило разрушение грунта над трубой и «растекание» его по поверхности. Высота слоя грунта над трубой также уменьшалась. Физическая сущность этого явления очень сложна При больших перемещениях иа уменьшение высоты засыпки непосредственно над трубой в ре.'шД ных условиях будут оказывать влияние атмосферные факторы — увшж нение, ветер и т. п. Учитывая это, сопротивление 1рунта при перемещениях трубы выше предельных можио определять, исходя пз линейной зависимости, считая что при перемещениях, равных глубине заложення, сопротивление
грунта равно нулю:
?, = ?пр грО+Ср/*)-^ ПРИ *>У*Р гр.
че с. — коэффициент разгрузки;
Ср = «пр.гр/Я> k-cyoD„, (3.27)
- коэффициент пропорциональности; с/„г,. гр—перемещение, соответствующее предельному сопротивлению грунта, Н — расстояние от верха засыпки
о низа трубы.
д ,п анализа различных расчетных моделей грунта засылки нами было „ыполиено экспериментальное исследование поперечною изгиба в вертикальной плоскости подземного трубопровода.
Тр\бопровод диаметром 529 x 8 мм, длиной 90.1 м был уложен в траншею на глубину (33 см (до нижней образующей трубы). Грунт засыпки песок объемным весом \гр = 15.2 Н/м3 и углом внутреннего треиия <р,р=28° Посередине плети трубопровода имелся шурф с фундаментной плитой, где ow.7.4 установлены два гидравлических домкрата. При подъеме трубопровода фиксировалась поперечная сила (но показаниям манометров насосных станиий) и вертикальное перемещение трубопровода через каждые 5 .м но его длине (но результатам нивелирования выступающих стержней, приваренных к трубам). Результаты измерена я показаны на рис. 9. 10
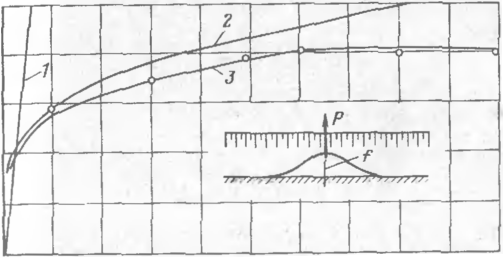
О 5 10 15 20 25 30 35 40 b5f,c м
Рис. 9. Зависимость стрелки прогиба от поперечной силы
250 v 230
I 150
« т
-I 50
Cs
? о
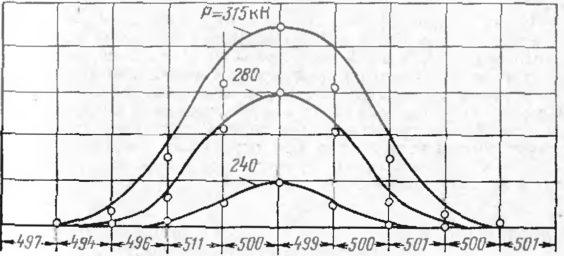
Расстояние между отметками , сн
Рис. 10. Упругая линия подземного трубопровода при изгибе его иоперсч-
иой силой
На рис. 9 приведены зависимости (экспериментальная и теоретическая} максимального поперечного перемещения трубопровода (стрелки прогиба) f от поперечной силы Р. Кривая 1 соответствует решению поперечного изгиба балки для упругой (винкдеровской) .модели среды g=ky; кривая 2 — для жесткопластической модели <?=<?пр. iP; кривая 3— для модели, учитывающей уменьшение сопротивление грунта <7 = <7пр. гр—cvy.
Зависимость максимального перемещения стрелки прогиба f от поперечного усилия Р для балки с нзгнбпой жесткостью П1, лежащей на упругом основании, как известно, имеет вид:
ван вариационный метод. Принимая упругую ось бал кн в виде функции «•=> ==f0sin3nJотвечающей граничным условиям (у=*у' =«/"=0 при х=0. L) абсолютно жесткого нижнего основания, находим зависимость поперечной] силы от прогиба и длины волны изгиба.
р 4QnpL 4йл4?// ^ 5CpLf
(3 29)
Нл 16L® * 16
где (?щ) — предельное сопротивление поперечным перемещениям вверх, равное нределыюму сопротивлению грунта и весу трубопровода; L — длина волны изгиба.
Длина волны изгиба определяется из условия dP/dL^Q
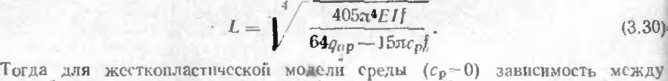
прогибом if поперечной силой нз (3.29) с учетом (3.30) будет иметь вид
Р = 3,76 V <?рЕ// •
(3.31}
Кривая /, 2 и 3 (рис. 9) построены соответственно по формулам (3.28),. (3.31) и (3.29) при параметрах груита засыпки, определенных на основании опытов на моделях: k~ 1,75 МПа; </ПГ1= 147 II/см; ср^0.011 МПа.
На рис. 10 приведены экспериментальные дашгые и упругие линии подземного участка трубопровода, рассчитанные для третьей модели среды в соответствии с зависимостями (3.29) и (3.30) и принятой формой волны изгиба.
Результаты проведенного эксперимента свидетельствуют о том. что если первая модель среды хорошо описывает поведение трубопровода прн максимальном прогибе до 3 см, вторая — от 1 до 5 см, то третья модель среды хорошо согласуется с результатами опыта при прогибе до 50 см. Таким образом, результаты этого опыта подтверждают необходимость учет» уменьшения сопротивления груита при поперечных перемещениях трубы вверх. Этот фактор существенен при расчетах продольной устойчивости вертикальных выпуклых кривых и при определении нагрузок на трубочклад чики при способе ремонта, предусматривающем подъем трубопровода ш засыпанной грунтом траншеи.
Сопротивление грунта поперечным (в вертикальной плоскости} перемещениям трубы вниз
Наиболее часто прп решении задач по изгибу балок иа упругом основании используется гипотеза Винклера Циммермана, согласно которой ме жду прогибом (осадкой) балки и реактивным давлением существует пря
пропорциональность Несмотря на имеющиеся недостатки, эта 1Ипо-теза пает удовлетворительные результаты при расчете различных строительных конструкций.
Экспериментальные исследования, проведенные на моделях трубопрово-
0 также показали, что можно принять линейную зависимость между со протяжением грунта и поперечным (вертикальным) перемещением трубы вшп Эта зависимость справедлива до тех пор, пока сопротивление грунта меньше его несущей способности. Далее, можно считать, что сопротивле-j | е грунта остается постоянным и не зависит от перемещения
Таким образом, принимая эффективную ширину балки равной диаметру гр) бы расчетную модель трубопровода при поперечных перемещениях трубы можно описать зависимостью:
Q c,j ,Р„У при !/=? КГР/С(,..:
(3 32)
q RVVDK при y>RTVciJC,
где с — сопротивление грунта поперечным перемещениям трубы; с„ „ — обобщенный коэффициент нормального сопротивления грунта; Dn — наружный диаметр трубы: «/ — поперечное перемещение Rrv—условная несущая способность грунта.
Обобщенный коэффициент нормального сопротивления грунта, как н ранее, -ожио свялать с модулем деформации грунта зависимостью
Су о
---’,2/ -Г1 ,
(3.33)
где ZTrj. — модуль деформации грунта, МПа; цП.—коэффициент Пуассона грунг = . 1й — единичная длина трубопровода (!о= 10(1 см), DH — наружный дкамегр трубы, см.
Сопротивление грунта поперечным (в горизонтальной плоскости) перемещениям трубы в траншее
При определении напряженно-деформированного состояния трубопровода, имеющего углы поворота в горизонтальной плоскости, необходима соответствующая расчетная модель грунта
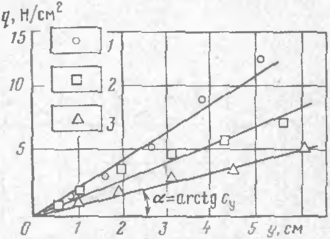
^ IbVnVL/IIUlUl В KJ4 1ЬЛ11Л 11- J «
I на проведенные С. К- Гпльзиным [13 , показали возможность исполь-3D имя пшенной зависимости между сопротивлением грунта и пе ре ме жегшем. Эксперименты проводи. и;ь на трубах песколькпх дна-" роз прн различном расстоянии от t оковой образующей трубы до стен»! траншеи.
На рис. 11 приведены некоторые in полученных экспериментальна кривых в координатах сопро-|*го-сане фунта g — перемещение у
II расстоянии от боковой образую-
ш tr трубы до стенки траншеи e= с 1* Зависимость сопротивления 411 см грунта от поперечных горизонталь
)ощий характер зависимости ных перемещений трубы
соирог1т.тения грунта от перемете- 1 при ?>„==219 мм: 2 — при ?>„ 325 мы;
пин одинаков для всех опытов 3 — при ?>„=529 мм в диапазоне перемещений от 1 до 6 см (при трубах диаметром до 529 мм). Для этого диапазона перемещений зависимость близка к линейной. При аппроксимации полученных кривых линейной функцией можио отметить, что коэффициент нормального сопротивления грунта, равный тангенсу угла наклона прямой, тем меньше, чем больше диаметр трубы, что соответствует физической сущности явления.
На основании проведенных экспериментов обобщенный коэффициент нормального сопротивления грунта рекомендуется вычислять по формуле
Коэффициент • Ii *>jI определяется в зависимости от отношения расстоя~ пия от боковой образующей трубы до стенкн траншеи о к расстоянию от оси трубы до верха засыпки h(l.
На рис, 12 приведен полученный на основе обработки экспериментальных данных в соответствии с формулой (3 34) график для определения коэффициента г|ГСр.
Как следует нз графика, при а=0 (прилегание трубы вплотную к стенке траншеи) коэффициент т]гор=0,93, т. с. зависимости (3.24) и (3.34) практически совпадают.
Принципиальным отличием моделей грунта при поперечных перемещениях трубы в I оризоптальной (в плане) и вертикальной (вверх) плоско етях, несмотря иа аналогию формул (3.24) и (3.34), является то, что прп поперечных перемещениях в плане линейная зависимость реализуется при значительных перемещениях трубы, составляющих примерно 0,1 диаметра трубы Однако при расчетах трубопровода, прокладываемого в слабых грунтах, в некоторых случаях поперечные перемещения могут быть и более указанного значения. Для таких случаев можно предложить два вида нелинейных моделей (рис. 13).
Первый вид модели (рис 13, а) соответствует условиям прокладки, когда предельная удерживающая способность грунта больше его условной несущей способности (с/пр.
Под предельной удерживающей способностью грунта qnp. гор понимается предельное сопротивление грунта перемещениям трубы в горизонтальной плоскости, определяемое также как пассивное боковое давление грунта при расчетах подпорной стеики:
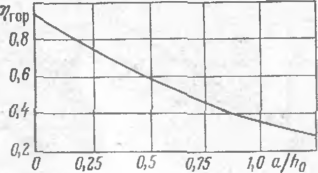
^пр.гор "|’гр^о^н^р- ( 35)
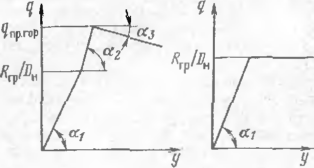
Рис. 12. График для определения Рпс. 13. Диаграммы сопротивления
коэффициента 1|ГОр грунта поперечным горизонтальным
перемещениям тру бы
*р tga (45
фг1,/2) 'гр
(tg 45 [ <Ггр2),
(3.36)
;vpA«i
где ifrp — >тол внутреннего трения грунта; сгр — сцепление грунта; у,р — объемный вес грунта.
Под несущей способностью грунта К,Р понимается критическое значение среднего давления, которое приведено в нормах иа проектирование оснований и фундаментов.
Второй вид модели (рис. 13,6) соответствует условиям прокладки, когда (?пр. roi><#ir>/?>H. В этом случае прн больших перемещениях ие про-исходит выхода линий скольжения на поверхность, и сопротивление грунта перемещению трубы не изменяется.
