Измерение и расчет фазовых соотношении в условиях равновесия для многокомпонентных смесей
ГЛАВА VI ИЗМЕРЕНИЕ И РАСЧЕТ ФАЗОВЫХ СООТНОШЕНИИ В УСЛОВИЯХ РАВНОВЕСИЯ ДЛЯ МНОГОКОМПОНЕНТНЫХ СМЕСЕЙ
Для измерения фазовых соотношений в условиях равновесия пара и жидкости в многокомпонентных смесях газа и нефти необходимо в первую очередь определить состав исследуемой смеси. Методы анализа фаз и оборудование, применяемое для достижения равновесия, описываются ниже.
Имея данные о составе каждой из фаз определенной смеси, можно построить графики коэффициентов распределения К =.у!х и на их основе устанавливать коэффициенты распределения для других смесей. В этой главе будут рассмотрены методы определений К при помощи различных корреляций и приведены графики, предназначенные для определения К некоторых систем.
Сочетание коэффициентов распределения и точек росы и начала кипения служит для создания методов определения фазовых границ углеводородных смесей. В последние годы в газовой промышленности применяют расчеты фазовых равновесий при помощи быстродействующих электронных вычислительных машин. Этот вопрос также рассматривается в настоящей главе.
Необходимым условием измерений равновесных соотношений пара и жидкости в многокомпонентных системах является применение надежного метода анализа газообразных и жидких компонентов. Для анализа смесей природного газа и летучих углеводородов применяют следующие методы.
1. Низкотемпературную ректификацию.
2. Аналитическую масс-спектрометрию.
3. Инфракрасную абсорбционную спектрометрию (ИКС).
4. Газовую хроматографию.
Эти методы определения состава углеводородного газа или жидкости будут кратко описаны в данной главе.
Общепринятые методы анализа газа путем абсорбции компонента в растворе описаны в учебниках по физической химии [V. 58] и в стандартах ASTM (например, метод D1136 [V. 6]). Плотность газа можно установить взвешиванием определенного объема [V 6, 1070-52].
Метод измерения плотности газа является вполне удовлетворительным анализом двухкомпонентных смесей, но при этом нельзя не учитывать отклонения от законов идеального состояния [IV’. 83]. Для анализа потоков стали применять элементы, измеряющие удельную теплопроводность, а также аппаратуру для измерения других характеристик [VI. 9].
НИЗКОТЕМПЕРАТУРНАЯ РЕКТИФИКАЦИЯ
До конца двадцатых годов не существовало систематических методов лабораторного определения состава природных газов. После сожжения пробы, при котором измерялись уменьшение объема вследствие сгорания компонентов газа и содержание двуокиси углерода в продуктах сгорания, компоненты природного газа выражались в метановом и этаповом эквиваленте. В. Дж. Подбельняк (W. J. Podbielniak) сконструировал и применил низкотемпературную фракционирующую колонку, в которой в качестве охлаждающего агента, создающего орошение, использовался жидкий воздух или азот (VI. 41).
На рис. VI. 1 показана одна из первых моделей аппарата для низкотемпературной ректификации. Для обеспечения орошения жидкого метана в. колонках последние помещались в посеребренные вакуумные рубашки.
Температуру кипения измеряли термопарой, установленной на верху колонны. Объем отогнанного газа определяли по повышению давления в вакуумирован-ном приемнике, измеряемому при помощи манометра. По очереди отгоняли метан, этан, пропан, изобутан, н-бутан и т. п. Когда точка кипения достигнет комнатной температуры (в обычных условиях изопентан кипит при 28° С), становится необходимым создать в колонке вакуум для предотвращения конденсации отходящих паров в соединительных линиях. Несколько изомеров гексана имеют относительно близкие температуры кипения и поэтому их объединяли в одну гекса-новую фракцию. Помимо гексанов, может испариться и остаток, состоящий из гептана и высших углеводородов, если предел выкипания этого остатка относительно низок. Чаще, однако, гептан и высшие углеводороды оставались на дне колонки в виде жидкости, плотность которой определяют путем взвешивания известного объема в пикнометре, а молекулярный вес — по понижению температуры замерзания бензола. Если имеется жидкий остаток, объем всех компонентов газа и объем жидкости выражается числом молей, откуда легко уже определить мольные доли каждого компонента. Из подаваемого в колонку газа обычно удаляют (при помощи твердой каустической соды) двуокись углерода и сероводород, так как эти соединения образуют твердые отложения во фракционной колонке. Содержание этих газов определяют на отдельном приборе путем абсорбции раствором едкого кали, для чего нужна вто-
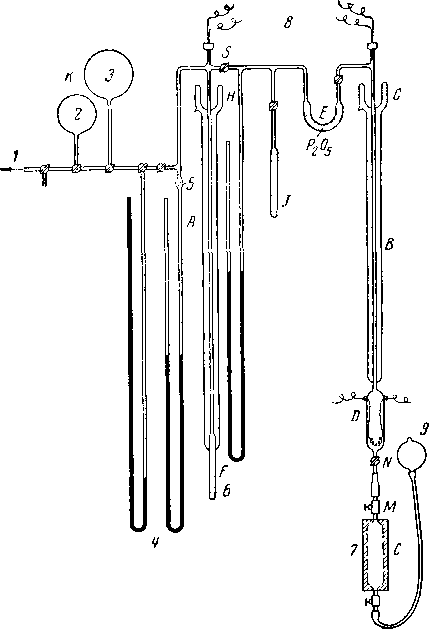
Рис. VI. 1. Одна из первых моделей для низкотемпературной фракциояировки, применявшаяся для анализа природных газов (Л) и смесей летучих жидкостей (В и Л).
/ — к вакууму; 2—1 л\ 3 — 2 л; 4 — манометры; 5 — запорный клапан; 6 — крошка пемзы; 7 — стальной контейнер с образцом»' 8 — к милливольтметру; 9— уравнительный сосуд.
рая проба газа. Содержание сероводорода можно установить и при помощи раствора йода [VI. 2].
С момента появления аппаратуры для низкотемпературной ректификации в нее были внесены значительные усовершенствования [VI. 44]: улучшена насадка,
введены автоматическая регистрация объема и температуры отогнанного газа, автоматическое регулирование охлаждения, увеличена скорость перегонки (рис. VI. 2 и VI. 3). Серьезным шагом вперед явилось измерение теплопроводности отходящих паров в качестве средства распознавания границ кипения фракций [VI. 43]. Американская Ассоциация газового бензина (NSAA) производит испытания, целью которых является определение точности анализа методом низкотемпературной ректификации, ибо этот метод часто является основой контрактов на поставку [VI. 35]. Объем образца газа, отбираемого для низкотемпературного анализа, обычно исчисляемого литрами, а продолжительность анализа часами.
Состав сложных жидких смесей, содержащих компоненты от метана до углеводородов с температурой кипения 121° С и выще, можно определить двухступенчатой низкотемпературной ректификацией. Г азы вплоть до пентанов анализируются подобно природному газу, а остаток образца ректифицируют во фракционирующей колонне с конденсацией отходящего продукта. Для жидкой части можно построить кривую разгонки, состав жидкой части можно также характеризовать последовательным рядом фракций, каждая из которых выкипает в узком температурном интервале. Фракции эти различаются по молекулярному весу и плотности. Используемые температурные пределы выкипания фракций иногда соответствуют температурам кипения нормальных предельных углеводородов, и тогда эти фракции именуют октановой, нонановой, декановой и т. п. В табл. VI. 1 показан состав пластовой жидкости, определенный комбинированным методом анализа [VI. 27].
Таблица VI. 1 Состав углеводородной смеси, содержащей газообразные и высококипящие компоненты [VI. 27] Состав пластовой нефти и газа, находящихся в равновесии при абсолютном давлении, равном 269 ат, и температуре 99° С
|
Компонент | Пластовая нефть | Пластовый |
газ | ||||
| мольные концентрации, % | плотность в жидком состоянии при 15° С, г/сма | моле-к уляр-ный вес | мольные концентрации, % | плотность в жидком состоянии при 15° С, г/см3 | моле куляр ный вес | ||
|
Метан | 52,00 | 91,35 | |||||
| Этан | 3,81 |
4,03 | |||||
|
Пропан | 2,37 | 1,53 | |||||
| Изобутан . | 0,76 |
0,39 | |||||
|
н-Бутан . . | 0,96 |
0,43 | |||||
| Изопентан . | 0,69 |
0,14 | |||||
|
н-Пентан | 0,51 |
0,19 | |||||
| Гексаны . . | 2,06 |
0,39 | |||||
|
Фракция 7* | 2.63 |
0,749 | 99 |
0,361 | 0,745 |
100 | |
| » |
8 | 2,34 |
0,758 | 110 |
0,285 | 0,753 |
114 |
| V |
9 | 2,35 |
0,779 | 121 |
0,222 | 0,773 |
128 |
| » |
10 | 2,240 |
0,786 | 132 |
0,158 | 0,779 |
142 |
| 11 | 2,412 | 0,798 |
145 | 0,121 |
0,793 | 156 | |
| ъ | 12 |
2,457 | 0,812 |
158 | 0,097 |
0,804 | 170 |
| 13 | 2,657 |
0,826 | 172 |
0,083 | 0,816 |
184 | |
| » |
14 | 3,262 |
0,846 | 186 |
0,069 | 0,836 |
198 |
| » |
15 | 3,631 |
0,854 | 203 |
0,050 | 0,840 |
212 |
| » |
16 | 2,294 |
0,852 | 222 |
0,034 | 0,839 |
226 |
| 17 | 1,714 | 0,838 |
238 | 0,023 |
0,835 | 240 | |
| » | 18 |
1,427 | 0,846 |
252 | 0,015 |
0,850 | 254 |
| » | 19 |
1,303 | 0,851 |
266 | 0,010 |
0,865 | 268 |
| » | 20 |
1,078 | 0,871 |
279 | 0,006 |
0,873 | 282 |
| » | 21 |
0,871 | 0,878 |
290 | 0,004 |
0,876 | 296 |
| » | 22 |
0,715 | 0,884 |
301 | 0,002 |
0,878 | 310 |
| ъ | 23 |
0,575 | 0,889 |
315 | |||
| ъ | 24 |
0,481 | 0,893 |
329 | |||
| » | 25 |
0,394 | 0,897 |
343 | |||
| » | 26 |
0,335 | 0,900 |
357 | |||
| 27 | 0,280 |
0,903 | 371 |
||||
|
28 | 0,250 |
0,906 | 385 | ||||
| » |
29 | 0,232 |
0,908 | 399 | |||
| » |
30 | 0,195 |
0,910 | 413 | |||
| » |
31 | 0,170 |
0,912 | 427 | |||
| » |
32 | 0,156 |
0,914 | 441 | |||
| » |
33 | 0,143 |
0,916 | 455 | |||
| 34 |
0,130 | 0,917 |
469 | ||||
| » | 35 |
0,118 | 0,918 |
483 | |||
| Всего. . | 100,000 | 100,000 |
1 | ||||
* Интервал выкипания фракции соответствует интервалу температур кипения нормальных предельных углеводородов с числом атомов, равным номеру фракции.
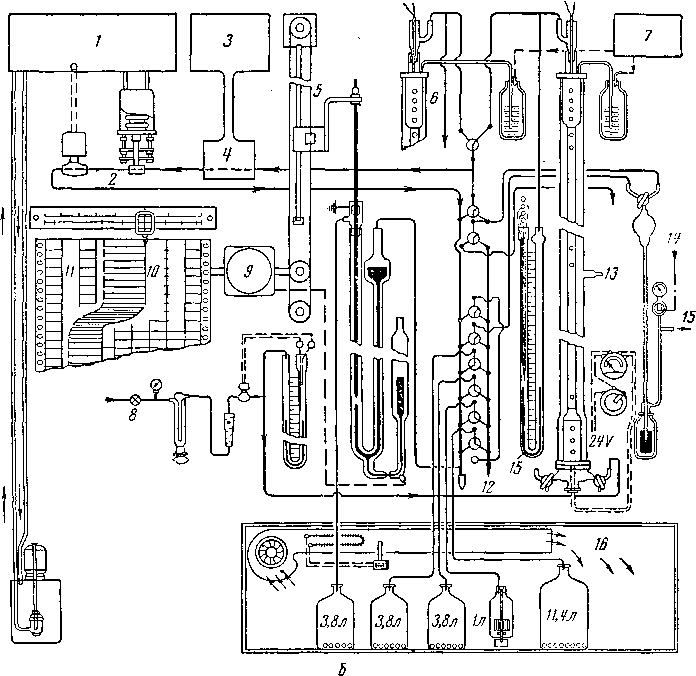

Рис. VI. 2. Современная аппаратура для низкотемпературной ректификации.
о — внешний вид* 6 — схема потока. I *— гидравлическо-электронный прибор для регулирования а контроля расхода дистиллята; 2 — парообразный дистиллят; «? — конгуры для измерения теплопроводности; 4 — датчик; 5 — регистрирующие манометр, кабельная связь и механизм, перемещающий картограмму; 6 — манометр колонны; 7—приборы, регулирующие давление в колонне и охлаждение флегмы; «5 — автоматическая подача образцов газа; 5 —двигатель; 10 теплопроводность; // — температура; 12 — вакуум; 13 — удаление паров; 14 — воздух; 15 — выпускное отверстие; 16 —. термостатическая воздушная баня.
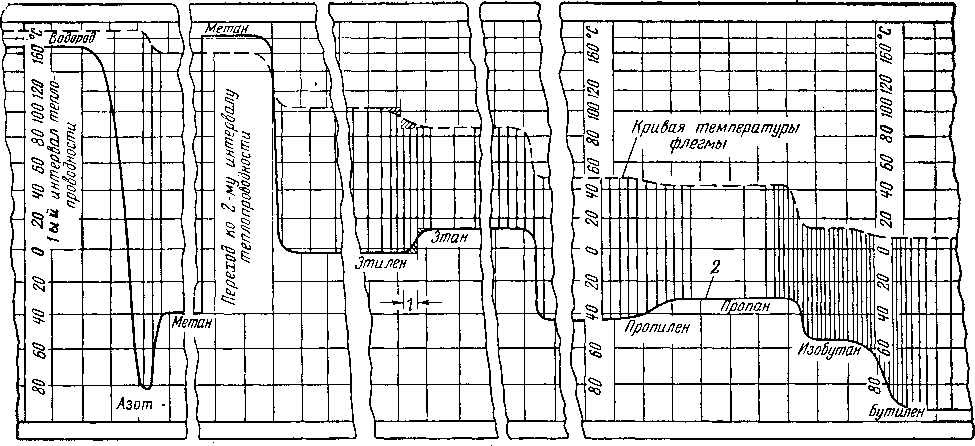
Рис. VI. 3. Запись на картограмме, полученная в результате низкотемпературной ректификации.
Образец —. иефтезаводский крекинг-газ. /-—разница в разрывах характерной кривой разгонки объясняется удержанием жидкости
во флегме: 2 — кривая теплопроводности дистиллята.
Масс-спектрометр ионизирует молекулы газа в условиях низкого давления и классифицирует образующиеся молекулярные и осколочные ионы в соответствии с их массами [VI. 12, VI. 1, VI. 6, VI. 63]. Схема действия масс-спектрометра показана на рис. VI. 4. Подлежащий анализу газ в количестве около 0,2 см3 при давлении
'.:2
11 у
16
1 ат помещают в баллон напуска. Масс-спектрометр может иметь также устройства, обеспечивающие испарение жидкостей с целью последующего анализа их в парообразном состоянии при низком давлении. Из баллона напуска погок газа через диафрагму (10—15 мк) поступает в ионизационную камеру, в которой происходит ионизация и диссоциация молекул и образование осколочных и молекулярных ионов. Ионизированные частицы под действием высокого напряжения приобре. тают ускорение и проходят через щель в магнитное поле. Эти частицы отклоняются магнитным полем в соответствии с их массой и фокусируются на выходную щель и коллектор. Ток в цепи коллектора усиливается и регистрируется. Изменяя ускоряющее напряжение ионов, можно получить спектр заряженных частиц с массой от 1 до 250 и более.
Фотография аналитического масс-спектрометра фирмы «Консолидейтед инжиниринг корпорейшн» показана на рис. VI. 5.
Регистрирующий прибор фиксирует высоту пики (рис. VI. 6) в зависимости от различных соотношений между массой и зарядом. Соотношение между высотой пики, выраженной в единицах шкалы, и давлением образца, выраженным в микронах, в первоначально поступившем объеме является постоянным. Эт0 соотношение называется чувствительностью Совокупность относительных высот пик по сравнению с высотой какого-либо пика, взятого в качестве эталона, является масс-спектром, являющимся функцией структуры молекулы. Различные молекулы одинакового молекулярного веса различаются распределением интенсивностей ионов в масс-спектре. Аналитический масс-спектрометр
Характерный образец: газ, жидкость Образец
i
Периодически отВираемыи образец расширяется до газообразного состояния при ~~ 0,05мм pm cm Просашбание газа
(Молекулы)+(е) ^\(аон)~+{ион)**{мткуло$* L ? (атом)+(е) ~ J
сн?+е-—сн}+сн?+сн$ + СН++С++Н+
+10006 -10006 и
Г-5
Г-7
13
IV-
17
Рис. VI. 4. Схема потока в масс-спектрометре, /—сосуд емкостью 3 л; 2— диафрагма; 3 — ионизирующая камера; 4 — поле электродвижущей силы;
5 — входная щель: 6 — ускоритель частиц; 7 — выходная щель; 8 — коллектор и усилитель; 9 — регистрирующий прибор; 10— ускоренные частицы; //— тяжелые ионы, 12 — легкие ноиы; J3 — коллектор;
14 — сигнал в усилитель; 15 — ионы в фокусе; 16 — сопротивление.
обеспечивает постоянство масс-спектров и чувствительности для каждого вида молекул независимо от времени и парциального давления компонентов в смеси. Американский нефтяной институт (API) составил справочные таблицы масс-спектров и чувствительностей для большого числа углеводородов [VI. 1]. Для выполнения аналитической работы масс-спектрометр калибруют по эта-

Рис. VI. 5. Приборный сгол масс-спектрометра фирмы «Консолидейтед» (Consolidated), модель 21-103В.
лонным образцам. Зная чувствительность и масс-спектр каждого компонента в смеси, определенные по эталонным образцам отдельных компонентов, можно вычислить состав смеси, решив ряд линейных уравнений, число которых равно числу компонентов в смеси.
Для решения этих уравнений часто применяют электронные вычислительные машины. Таким образом можно
определить состав сложных смесей, состоящих из двадцати и более компонентов. Более того, в благоприятных обстоятельствах прибор обнаруживает следы веществ, концентрация которых составляет несколько частей на 1 млн. В табл. VI. 2 приведены результаты анализов искусственной смеси, которые проводились периодически в течение 6 месяцев, и анализов образцов, взятых из газового пробоотборника и отправленных в лабораторию наряду с другими обычными образцами без указания, что они собой представляют.
Таблица VI. 2 Параллельные анализы газовых смесей масс-с пектрометром
А, Анализы искусственной смеси газа, проводившиеся периодически в течение 6 месяцев
Мольная доля
| состав ис | результаты |
анализов | |||
| Компонент | кусствен | ||||
| но состав | |||||
| ленной | № 1 |
№ 2 | № 3 | № 4 | |
| смесн |
|||||
|
0,83 | 0,82 |
0,73 | 0,80 |
0,79 | |
| 15,7 | 15,5 | 15,6 |
15,5 | 15,0 | |
| 70,0 | 70,0 | 69,8 | 70,0 |
70,1 | |
|
7,3 | 7,4 |
7,4 | 7,3 |
7,8 | |
| Пропан..... | 3,5 | 3,4 |
3,6 | 3,5 |
3,5 |
| Изобутан .... | 1,0 |
1,2 | 1,1 |
1,2 | 1,1 |
|
«-Бутан..... | 1,7 |
1,7 | 1,8 |
1,7 | 1,7 |

28
24
25
26 27
Масса /заряд
Продолжение табл. VI. 2 Б. Анализы образцов, последовательно взятых из газового пробоотборника
| Компонент |
Мольная доля | ||
|
результаты анализов | |||
|
№ I | № 2 | № 3 | |
| Гелий .... |
0,66 | 0,69 |
0,58 |
| Азот..... | 15,6 | 15,5 |
15,5 |
| Метан .... | 73,0 |
72,5 | 71,5 |
| Этан..... | 6,2 |
6,8 | 7,0 |
| Пропан .... | 3,7 | 3,6 | 4,4 |
| Изобутан . . . |
0,20 | 0,25 |
0,29 |
| «-Бутан . . . | 0,54 |
0,57 | 0,70 |
| Пентаны . . . | 0,07 | 0,07 | 0,02 |
Крупные углеводородные молекулы (содержащие шесть или более атомов углерода) вследствие более сложных спектров расщепления и возможного присутствия многих изомеров труднее поддаются анализу. Приходится калибровать спектры каждого соединения, но и при этом один и тот же спектр может быть характерным для целой группы изомеров.
В инфракрасном спектрометре получают спектр поглощения инфракрасных лучей образцом газа или жидкости [VI. 22]. Различные молекулы поглощают инфракрасные лучи различных частот, что позволяет определить содержание каждой из них в образце. Оптическая схема инфракрасного спектрометра приведена на рис. VI. 7.
При помощи инфракрасного спектрометра легко распознавать ненасыщенные и насыщенные молекулы, например молекулы с четырьмя атомами углерода (нормальный и изомерный бутаны, бутилены и бутадиен).
Инфракрасным спектрометром можно анализировать газы, жидкости, прозрачные твердые вещества или ве-
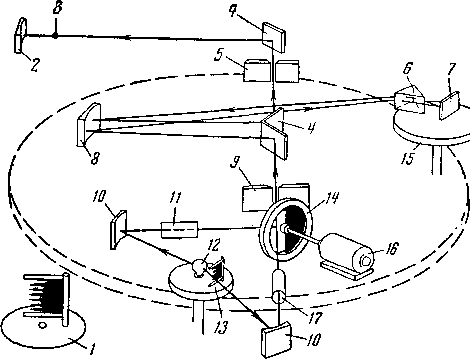
Рис. VI. 7. Схема оптической системы инфракрасного спектрометра [VI. 22].
/ — деталь гребневидной заслонки; 2 — приемное зеркало;
3 — болометр; 4 — зеркало, установленное под углом 45°;
5— выходная щель; 6 — призма с углом 60°; 7 — зеркало длины волн; 8 — прицельное зеркало; 9 — входная щель; 10 — вогнутое зеркало; // — сосуд с образцом; 12 — источник инфракрасных лучей; 13—гребневидная заслонка; 14 — вращающаяся отражательная заслонка; 15 — вращающийся столик; 16 — синхронный двигатель; 17 — сосуд с образцом, принятым за эталон.
щесТва в растворителях. При анализе жидкостей берут образцы объемом 1—2 см3 или меньше, а при анализе газа — образцы объемом 200 см3 или меньше.
Поглощение лучей различной длины волны регистрируют и сопоставляют со стандартными величинами поглощения, указанными на шкале спектрометра или взятыми из опубликованных работ [VI. 1].
Газовая хроматография — сравнительно новый метод анализа. Своим названием она обязана изменению окраски адсорбентов при поглощении определенных соединений. Во время анализа смеси разделяются на отдельные компоненты, при этом компоненты поглощаются на поверхности твердого адсорбента и каждый из них десорбируется в потоке газа--носителя [VI. 42,
VI. 18, VI. 43, VI. 8, VI. 17]. По теплопроводности выходящего потока газа можно судить о содержании каждого из компонентов.
При хроматографии пар адсорбируется или абсорбируется на поверхности пористого твердого вещества. Газ-носитель переносит индивидуальные соединения вперед по слою, где они распределяются по степени их адсорбируемости. К тому в^меии, когда соединения достигнут конца колонки, они оказываются уже раз-
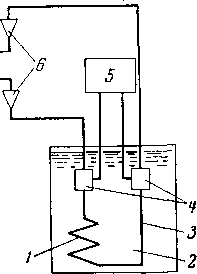
Рис. VI. 8. Схема газового хроматографа.
/—•змеевик с твердым адсорбентом или же с твердым материалом, покрытым нелетучим жидким абсорбентом; 2 —¦ термостатируемая
баня: 3— впуск образца:
4 —элемент для измерения теплопроводности; 5 — регистрирующий вольтметр; 6 —¦ расходомеры: 7 — поток ге
лия.
деленными и следуют один за другим в устройство, в котором измеряется их теплопроводность. Основное оборудование, необходимое для разделения и анализа, показано на рис. VI. 8. Проявляющей колонной может служить трубка диаметром 6,4 мм и длиной 1,2—1,8 м. Она заполняется гранулированным твердым веществом, например кирпичной крошкой, поверхность которой покрыта нелетучим абсорбентом, например триизобутиле-ном, диоктилфталатом или силиконом. На устройстве, измеряющем теплопроводность, показывается концентрация соединений в выходящем потоке газа-носителя. Переменными факторами при хроматографии являются диаметр насадки колонки, размеры колонки, температура, состав газа-носителя, скорость продвижения газа-носителя и объем образца. Для каждого данного вида анализа подбирают оптимальное сочетание параметров и тарируют аппарат по известным образцам.
Процедура анализа заключается в следующем.
1. Потоком газ а-носителя, например гелия, стабилизируется колонна при постоянной температуре.
2. Добавляют во входящий поток гелия порцию газа.
3. Регистрируют изменение теплопроводности во времени.
Хроматограмма показана на рис. VI. 9. Продолжительность анализа зависит от длины колонки и ее содержимого, скорости движения газа-носителя и объема
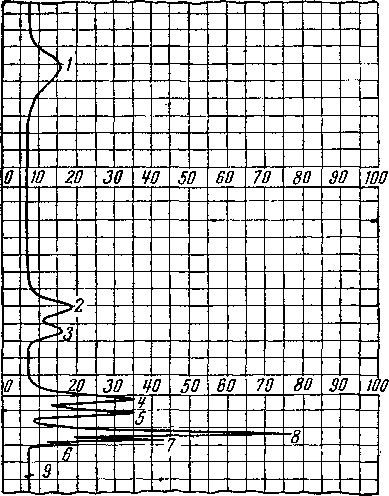
Рис. VI. 9. Хроматограмма деэтанизиро-ванного газового бензина.
Колонна высотой 1,8 м; поглотитель — трикрезил-фосфат на целине; температура 50° С; газ-носи-тель — гелий. / — «-гептан; 2—н-тексан; 3— изо-гексан; 4— «-пентач; 5 — изопентан; 6—пропаи;
7 — изобутаи; 8 — «-бутан; 9 — начало
образца. Соединения идентифицируют на основании времени, которое затрачивается на прохождение через слой.
Эта техника анализа непрерывно усовершенствуется, особенно в части методики выбора надлежащей адсорбционной колонны. Типовая аппаратура, применяемая в настоящее время, показана на рис. VI. 10.

Часто при изыскании источников получения гелия необходимо определить содержание его в природном газе. Хорошие результаты при этом дает использование масс-спектрометра. Горное бюро [VI. 3] разработало метод анализа на гелий, принятый в качестве стандартного. Этот метод состоит в адсорбции всех прочих газов на активированном угле при температурах жидкого азота и в измерении давления, создаваемого гелием.
ОПРЕДЕЛЕНИЕ СОДЕРЖАНИЯ СЕРОВОДОРОДА
Для определения содержания сероводорода в природном газе широко используется метод Тутвейлера (Tutweiler) [VI. 2]. Сероводород растворяют в воде и воздействуют на него стандартным раствором йода, используя в качестве индикатора крахмал. Обычно содержание H2S выражается в гранах серы на 100 куб. фут. газа (г/100 л3); 590 гран серы на 100 м3 (или 1360 г/100 м3 соответствуют 1% от объема (при 15,6° С и абсолютном давлении, ранном 1,03 ат).
§ 2. ИЗМЕРЕНИЕ РАВНОВЕСИЯ ПАР —ЖИДКОСТЬ
Для приведения в равновесие пара и жидкости используется аппаратура различных типов. Опыт может состоять в измерении упругости паров чистого вещества или же температур точек кипения и точек росы двойных смесей. Можно привести в равновесие сложные смеси, состоящие из природного газа и нефти, и взять для анализа образцы равновесных фаз. В промысловых условиях выходящий из скважины поток можно разделить на пар и жидкость, например, в сепараторах.
Аппаратура, примененная Сиднеем Юнгом (Sidney Jonng) [VI. 68] для определения упругости пара и плотности насыщенных фаз тридцати чистых веществ, показана на рис. VI. 11. Вещество «запирается» ртутью в стеклянных трубках, окруженных термостатирующими паровыми рубашками; достижение температуры начала кипения и точки росы устанавливается визуально. Кей (Kay) [III. 30] применял аналогичную аппаратуру при своих исследованиях двойных систем. Он вставлял небольшой стальной шарик в капиллярную стальную трубку и перемешивал жидкость при помощи соленоида, находящегося снаружи обогревательной рубашки.
Для приведения в равновесие многокомпонентных смесей при давлениях 350 ат и выше использовалась аппаратура различных типов. Толстостенные стальные сосуды, вмещающие 500—1000 см3, могут быть снабжены внутренней мешалкой [III. 26]. как показано на рис. VI. 12, и прикреплены к цапфе для качания [111. 68]. Для достижения в таких сосудах равновесия можно также пропускать пар через жидкость [VI. 11]. Оборудование этого типа позволяет получать равновесные образцы пара и жидкости для анализа.
Сейдж и Лес и (Sage and Lacey) и их сотрудники разработали аппаратуру для комбинированного определения объемных свойств и коэффициентов распределения пара и жидкости [VI. 55].
Общая схема этой аппаратуры показана на рис. VI. 13. Равновесный сосуд 1 погружают в масляную ванну с мешалкой, температуру которой регулируют с помощью обычных устройств, принятых для этой цели. Ртуть может быть введена в сосуд 1 из резервуара 2 через вентиль 3,
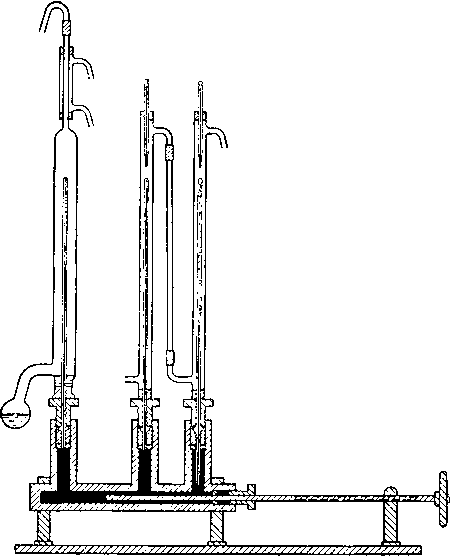
Рис. VI. 11. Аппарат Сиднея Юнга для определения свойств газа и жидкости.

На верхнем конце вертикального стержня 4, входящего в сосуд 1 снизу, находится указатель уровня ртути 5 с электрическим контактом. Электроконтакт и идущий от него по стержню электропровод изолированы от стержня и сосуда. Стержень 4 выведен из заполненной ртутью части сосуда через сальник, имеющийся в нижней стенке камеры 6. Этот сальник позволяет стержню двигаться вертикально лишь с очень ничтожной утечкой ртути из равновесного сосуда. Под сальником стержень присоединен к ходовому винту 7, который приводится в движение электродвигателем через червяк, находящийся в сцеплении с муфтой ходового винта. Счетчик числа оборотов 8, находящийся на валу червячной передачи, определяет после надлежащей калибровки положение точки контакта уровнемера 5 с точностью до 0,05 мм.
Во избежание изменений общего объема системы сосуда при подъеме или спуске стержня 4 к нижнему концу ходового винта присоединяют стержень такого же диаметра, что и стержень 4. Стержень 10 проходит через сальник в заполненную ртутью камеру 11, соединяющуюся с равновесным сосудом. Это компенсационное устройство не только устраняет какое бы то ни было влияние движения стержня на общий объем заполненной жидкостью системы, но служит также для предотвращения больших перемещений уровнемера 5, которые могли иметь место при изменении давления в сосуде. Благодаря компенсатору 10 при повышении давления наблюдаются лишь такие деформации, как упругое сжатие в винте 7 и упругое удлинение в окружающем его корпусе.
В стенку равновесного сосуда вделаны вентили 12 И 13. Через них сосуд присоединен к вакуум-насосу и К
Рис. VI. 12. Установка Катца и Гахмуса (Katz and Hachmuth) для изучения сщесей в равновесных условиях [111.26].
1— резервуар с ртутью; 2— насос для подачи ртутн;
3 — ртуть; 4 — сжатый азот; 5 — ртутный резервуар высокого давления; 6 манометр; 7 — к приборному щиту; 8 — термометр; 9 — манометр с надлежащим интервалом измерения; 10 — газовая фаза;
И—жидкая фаза; 12 — трубка для взятия образца газа; 13 — трубка для взятия образца жидкости;
14—мешалка; 15 — заземление; 16 — двигатель мешалки термостата; 17 — масляный или водяной термостат;
18 — двигатель мешалки сосуда; 19 — сосуд; 20 — нагреватель на 1000 вт\ 21 — к анализатору газа; 22 — к анализатору жидкости; 23 — вентиль понижения давления;
24 — вентиль для загрузки и очистки.
аппарату для ввода или извлечения образцов (через вентиль 13, а также вентиль 15 или 16). Вентиль 15 позволяет откачивать содержимое нижнего манифольда независимо от равновесного сосуда.
Установление равновесия в сосуде ускоряется при помощи спиральной мешалки 17, которая сконструирована так, что свободное поперечное сечение внутри сосуда остается неизменным в любой точке, за исключением точки, расположенной близ самого днища и самой крышки. Эта спиральная мешалка приводится в действие трубчатым валом, к которому внутри корпуса прикреплен якорь из мягкого железа. Корпус изготовлен из нержавеющей стали. Снаружи корпуса находится вращающийся электромагнит, вращающий спиральную мешалку со скоростью около 100 об/мин.
Детали уровнемера показаны на рис. VI. 14, а равновесного сосуда — на рис. VI. 15. Для определения давления применяют грузовой манометр. Предельное давление равно 700 кГ/см2, а интервал температур, который обеспечивает термостат, — от —1,1° С до +238,8" С с точностью +0,06° С.
Объемные и фазовые измерения производятся на взвешенном количестве материала. Газ поступает из
резервуара 19 через вентиль 20, а жидкость — из сосуда 21 через вентиль 16 (см. рис. VI. 13). Общий объем углеводородов в равновесном сосуде определяется посредством указателя ртути 5, а поверхность раздела углеводородного газа и жидкости — при помощи теплового индикатора. Объем системы, заполненный углеводородами, регулируют подачей и откачкой ртути через вентиль 3.
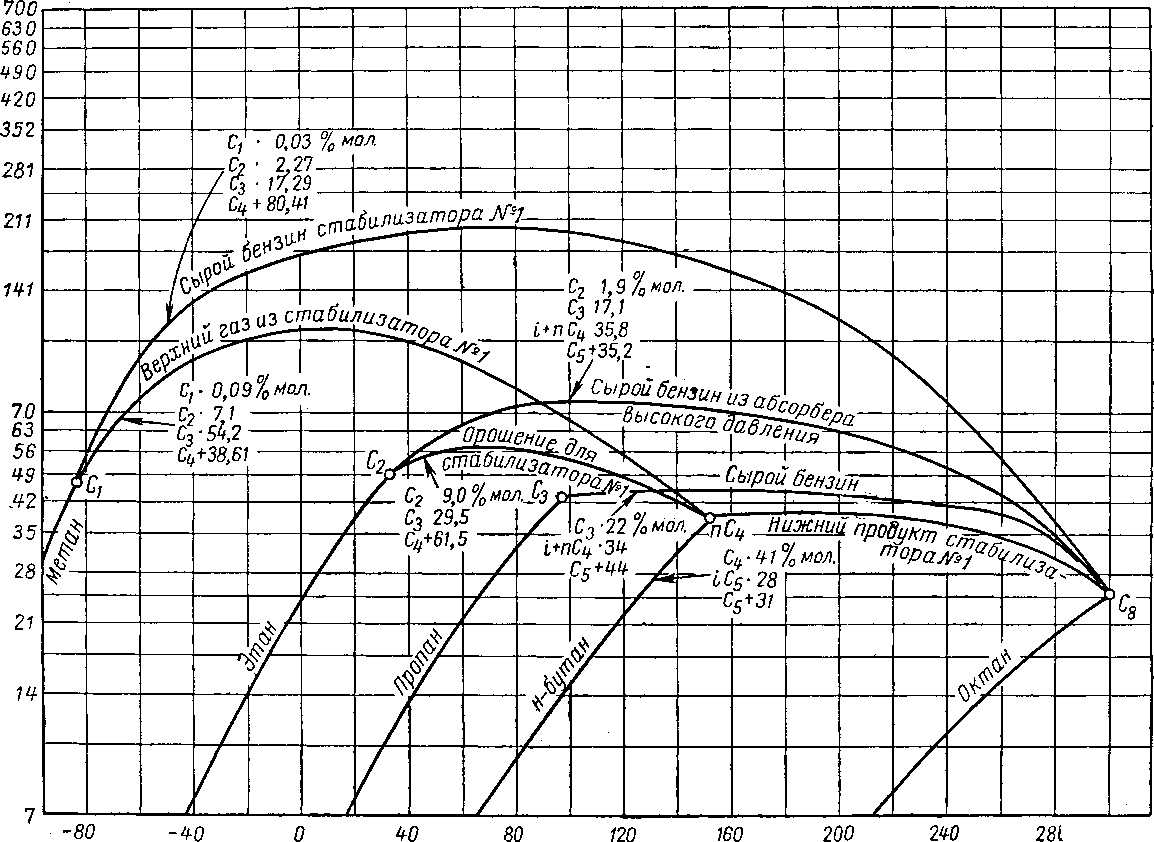
Результаты, полученные на описанном выше оборудовании для смесей, состав которых дан в табл. VI. 3, приведены на рис. VI. 16 и VI. 17.
Методы определения равновесий в системе газ — жидкость при низких температурах рассмотрены в работе Блумера и Перента (Bloomer and Parent) [III. 7].
В двухфазном потоке, движущемся по трубам к сепаратору, работающему при постоянных температуре и давлении, фазы обычно находятся в состоянии, близком к равновесному. Результаты анализа образцов двух фаз, взятых из промысловых сепараторов, приведены в табл. VI. 4.
| Компонент | Состав смеси (к рис. VI. 16) | Состав смеси (к рис. VI. 17) | ||
| весовой |
мольный | весовой |
мольный | |
| Метан .... | 0,0520 |
0,2632 | 0,3548 |
0,7155 |
| Этан..... | 0,0191 | 0,0517 | 0,0768 | 0,0826 |
| Пропан .... |
0,0424 | 0,0783 |
0,0771 | 0,0526 |
| Изобутан . . . |
0,0181 | 0,0254 |
0,0197 | 0,0110 |
| я-Бутан . . . | 0,0439 | 0,0615 | 0,0400 | 0,0222 |
|
Изопентан . . | 0,0252 | 0,0283 | 0,0182 | 0,0081 |
|
я-Пентан . . . | 0,0304 | 0,0343 | 0,0190 | 0,0085 |
|
Гексаны* . . . | 0,7678 | 0,4553 | 0,3894 | 0,0919 |
|
Двуокись углерода .... |
0,0011 | 0,0020 |
0,0104 | 0,0076 |
‘Средний молекулярный вес 137,1.
Состав образцов, взятых из промысловых сепараторов
Таблица VI. 4
| Газоконденсатные |
смеси с промыслов | |||||||
| Молярные долм | Эрат (Луизиана); абсолютное давление 154 ат, температура 38,3°С |
Оклахома; абсолютное давление 89,2 ат, температура 28,9° С |
Картидж (Техас); абсолютное давление 25,5 ат, температура 26,1° С |
Кеттлмен Хиллз (Ка-лифорння); абсолютное давление 35,7 ат температура 64,4° С |
||||
| газ |
жидкость | газ |
жидкость | газ |
жидкость | газ |
жидкость | |
|
Азот.............. | 0,0173 | |||||||
| Двуокись углерода....... | 0,0041 |
— | — |
— | 0,0060 |
_ | — |
— |
|
Метан............. | 0,9276 | 0,3406 | 0,8053 | 0,2732 | 0,9012 | 0,1110 | 0,8319 | 0,1000 |
|
Этан.............. | 0,0303 | 0,0415 | 0,1188 | 0,1544 | 0,0403 | 0,0302 | 0,0848 | 0,0613 |
|
Пропан ............ | 0,0136 | 0,0297 | 0,0519 | 0,1519 | 0,0152 | 0,0338 | 0,0437 | 0,0533 |
|
Изобутан............ | 0,0042 | 0,0152 | 0,0034 | 0,0095 | 0,0036 | 0,0193 | 0,0076 | 0,0224 |
|
я-Бутан ............ | 0,0038 | 0,0167 | 0,0132 | 0,0941 | 0,0073 | 0,0519 | 0,0168 | 0,0666 |
|
Изопентан........... |
0,0023 | 0,0142 |
0,0011 | 0,0189 |
0 0016 | 0,0385 |
0,0057 | 0,0384 |
| я-Пентан............ |
0,0016 | 0,0132 |
0,0044 | 0,0590 |
0,0034 | 0,0615 |
0,0032 | 0,0430 |
| Гексаны............ |
0,0026 | 0,0463 |
0,0037 | 0,0542 |
0,0016 | 0,1563 |
0,0063 | 0,6150 |
| Гептаны +........... |
0,0029 | 0,4826 |
.— | 0,1878 | 0,0025 | 0,4969 |
._ | |
|
Удельный вес: гептаны-f-.......... Молекулярный вес: гептаны-f-.......... |
— | 0,7994 159,5 | _ | 0,761 131 | 0,686 126,5 | 107,5 | ||
§ 3. КОЭФФИЦИЕНТЫ РАСПРЕДЕЛЕНИЯ (КОНСТАНТЫ РАВНОВЕСИЯ) СЛОЖНЫХ СМЕСЕЙ
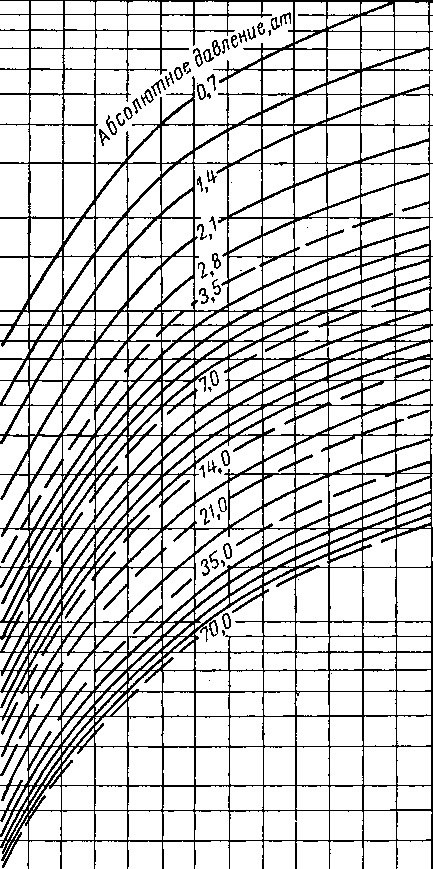
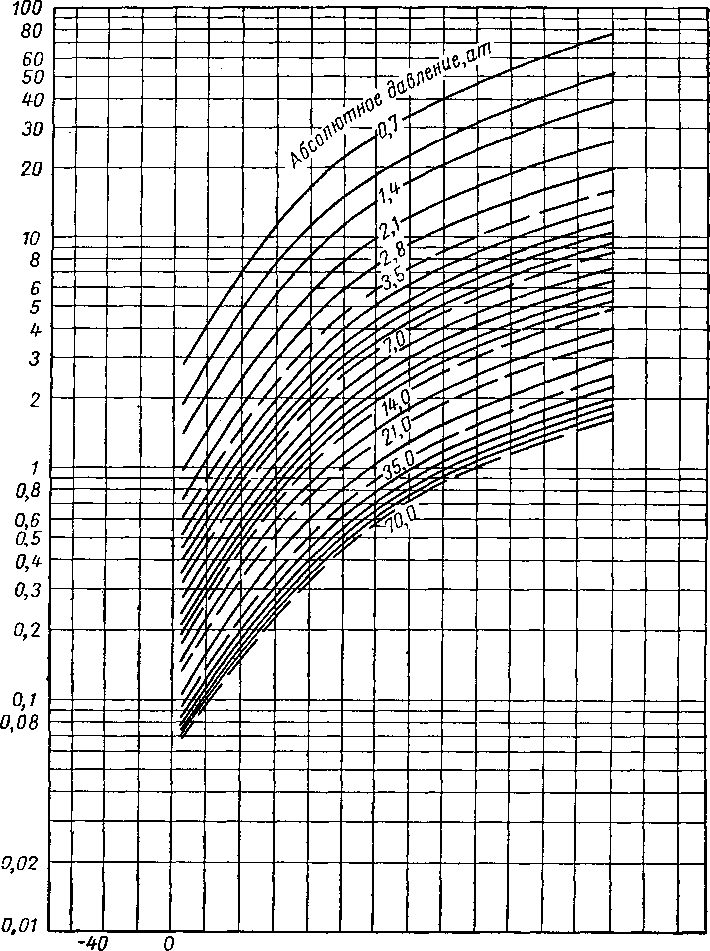
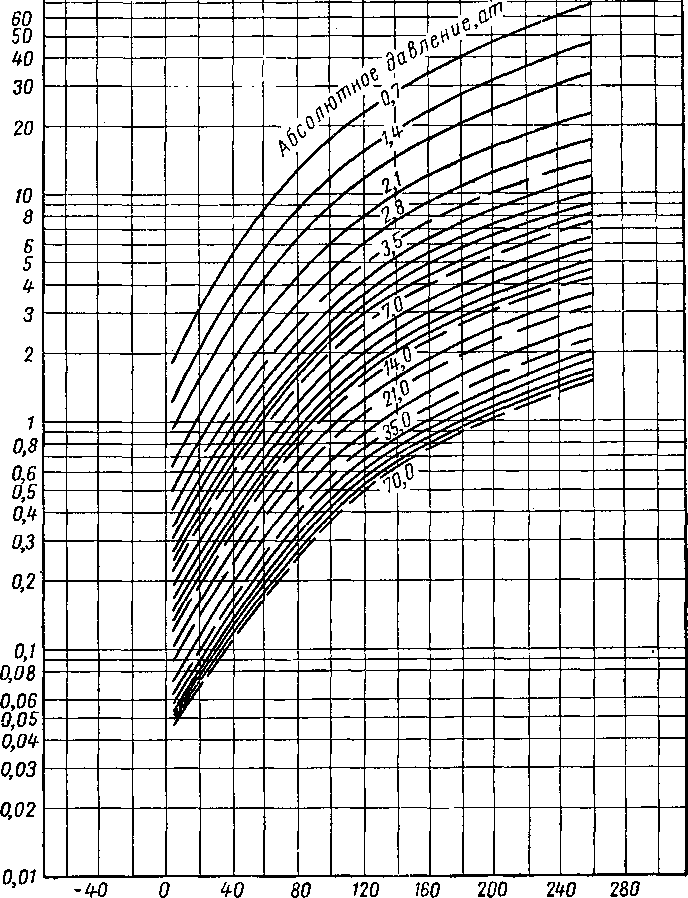
Первые диаграммы для определения констант равновесия были основаны на экстраполяции фугетивно-стей и их соотношений [III. 67, III. 41, VI. 30]. Такие диаграммы назывались «диаграммами идеальных констант равновесия», поскольку они строились для углеводородных смесей, подчиняющихся законам идеальных растворов. На рис. VI. 18—VI. 20 приведены идеальные константы равновесия, вычисленные Брауиом и Холкомбом (Brown and Holcomb) [VI. 14] для пропана, изобутана и я-бутана.
После юго как были получены экспериментальные данные по условиям равновесия газ—жидкость, для определения констант равновесия стали применять методы корреляции.
Условия, при которых были измерены в условиях равновесия составы сложных смесей, включающих компоненты природного газа, приведены в табл. VI. 5.
Один из методов определения констант равновесия заключается в построении графиков констант для подобных смесей в функции температуры и давления.
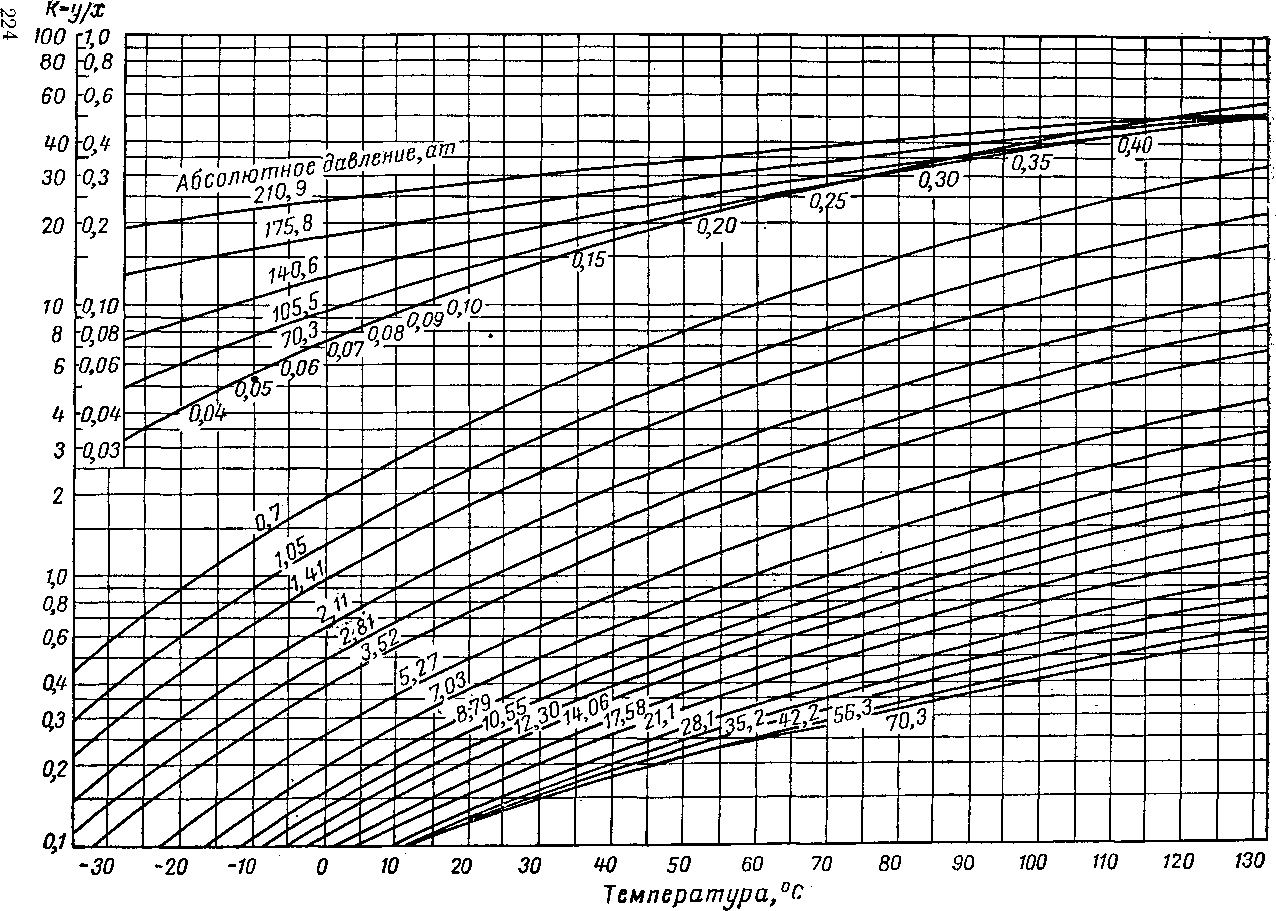
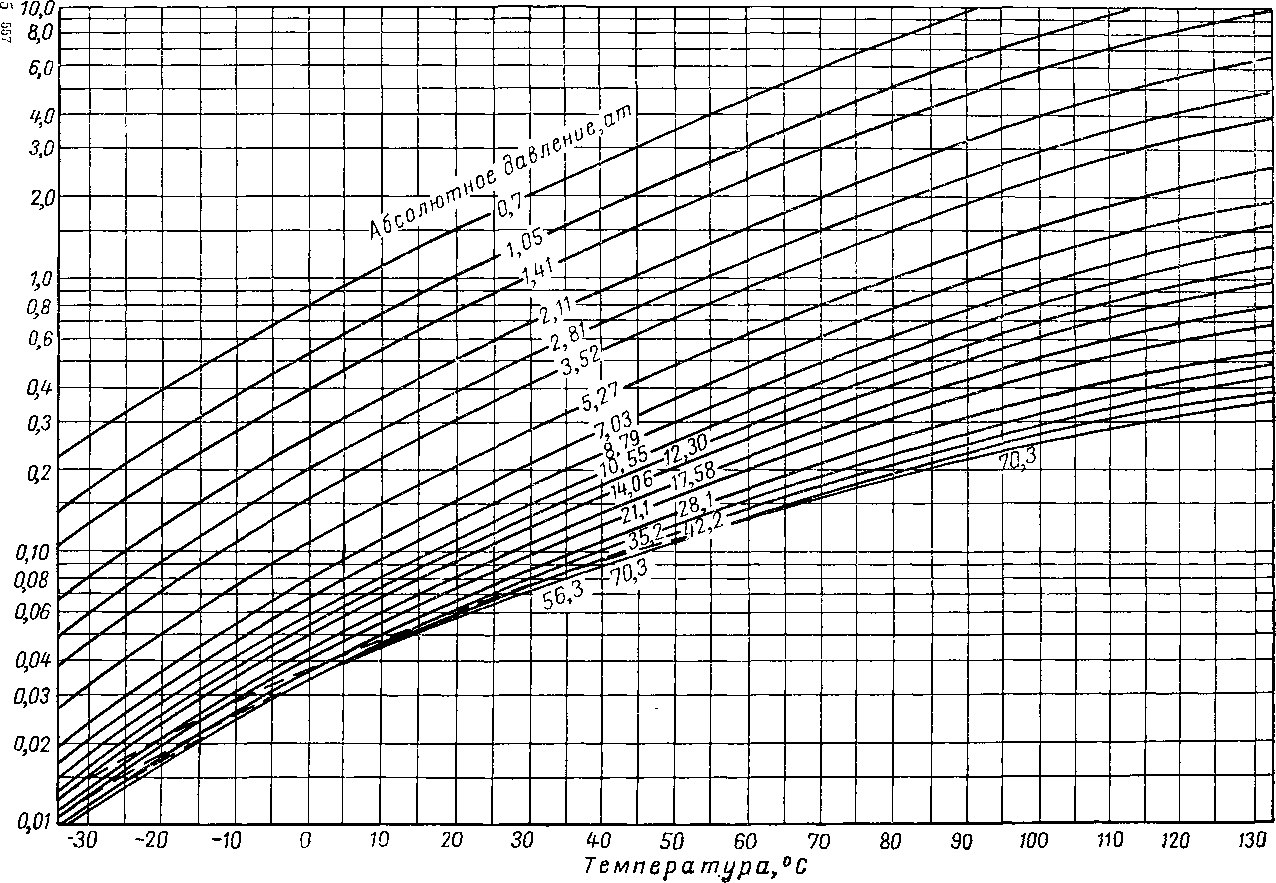
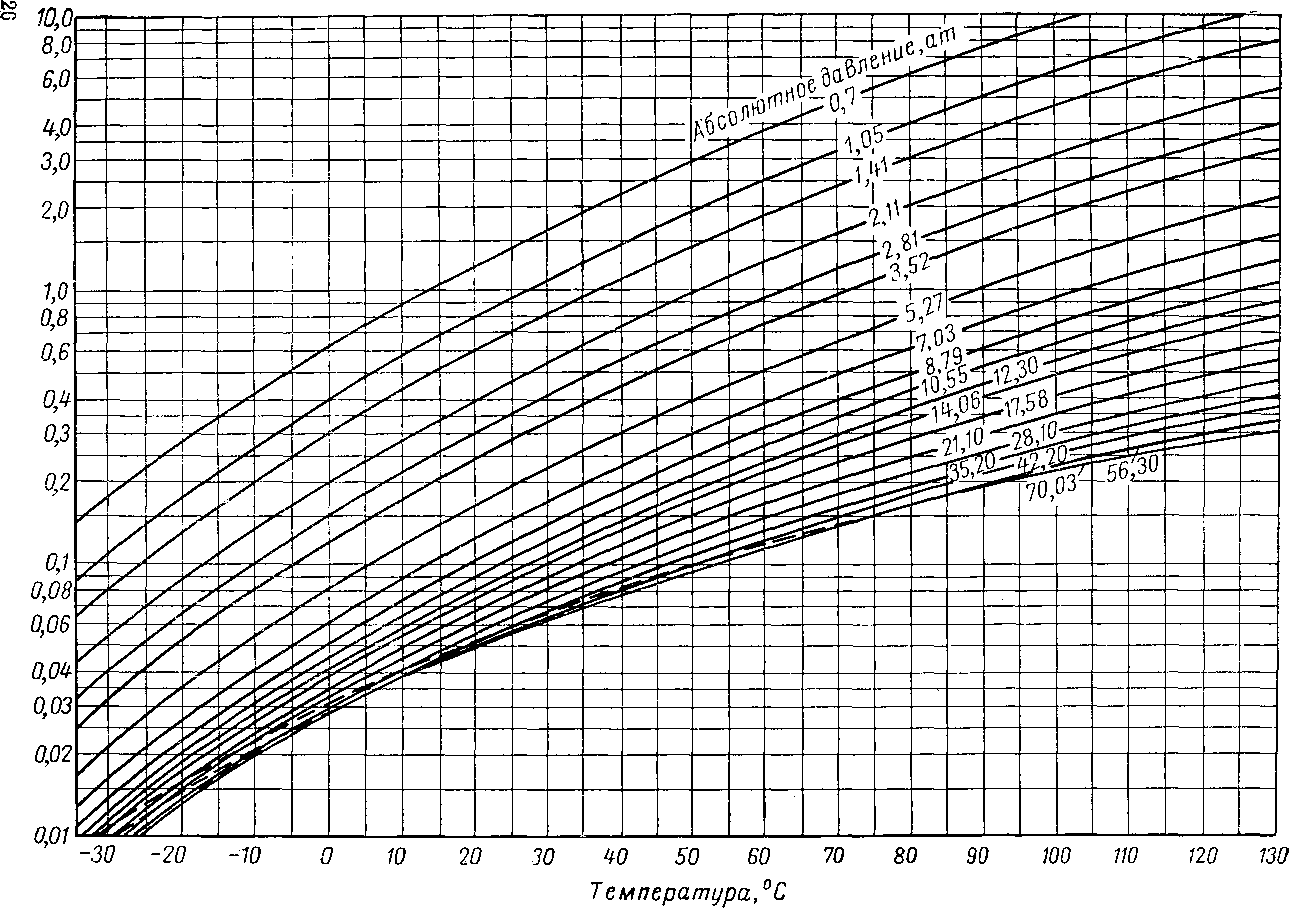
Для смесей оклахомской нефти и природного газа эта работа была проведена Катцем и Хахмусом (Katz and Hachmuth) [111.26]. Диаграммы рис. VI. 21—V. 29, а применимы для многих нефтей среднеконтинентальной платформы. Диаграммы для изобутана, я-бутана, изо-пентана и я-пентана были составлены в 1953 г. Хиндсом и Берроусом (Hinds and Burrows). Константа равновесия для гептана, умноженная на коэффициент 0,15, дает величину, достаточно точно выражающую константу равновесия для суммы гептанов и более тяжелых углеводородов оклахомской нефти. При использовании диаграмм для систем иефть — природный газ для вычисления констант равновесия метана, а также гептана и более тяжелых углеводородов может потребоваться
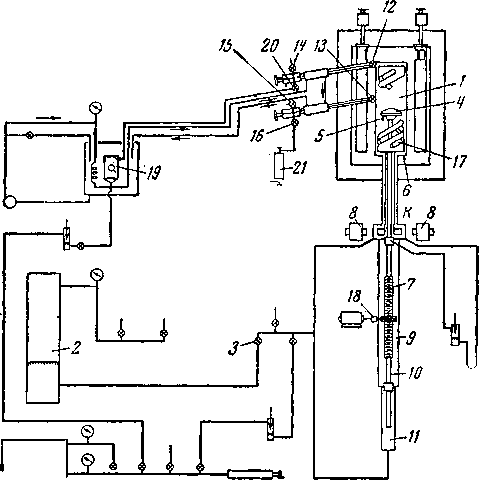
Рис. VI. 13. Аппарат конструкции Сейджа и Леси для определения объемных свойств и фазового поведения [VI. 55].
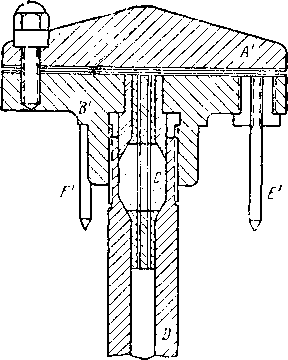
Рис. VI. 14. Деталь уровнемера [VI. 55].
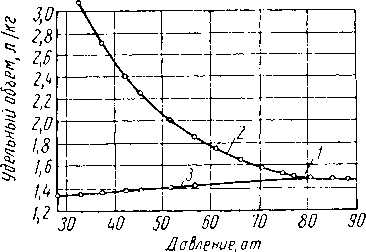
Рис, VI. 16. Объемное поведение смеси природного газа и яефти [VI. 55].
/ — точка начала кипения; 2 — две фазы при 37.8° С; 3 — жидкость при 37.8° С.
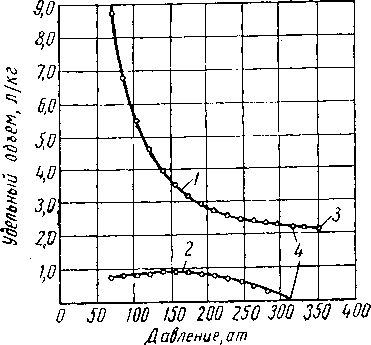
Рис. VI. 17. Объемное поведение углеводородной смеси, обнаруживающее ретроградную точку .росы [VI. 55].
/ — газовая и жидкая фазы; 2 — жидкая фаза; 3 — газовая фаза; 4 — ретроградная точка росы,
10
41 3
1
0,5
0,4
0,3
0,2
W 80 120 160 200 240 280
Температура, °C
Рис. VI. 18. Идеальные константы равновесия для пропана [IV. 14].
W 80 120 160 200 2kO 28<
0,06
0,05
0,04
0,03
Рис. VI. 19. Идеальные константы равновесия для изобутана [IV. 14].
Температура^С
Рис. VI. 20. Идеальные константы равновесия для «-бутана [IV. 14].
100 п во -
K-?
1000т 800
600
-30 -20 -10
по т
to
<Б

-30 -20 -10 0 10 20 30 kO 50 60 70 80 90 100 110 120 130 Температура, °С
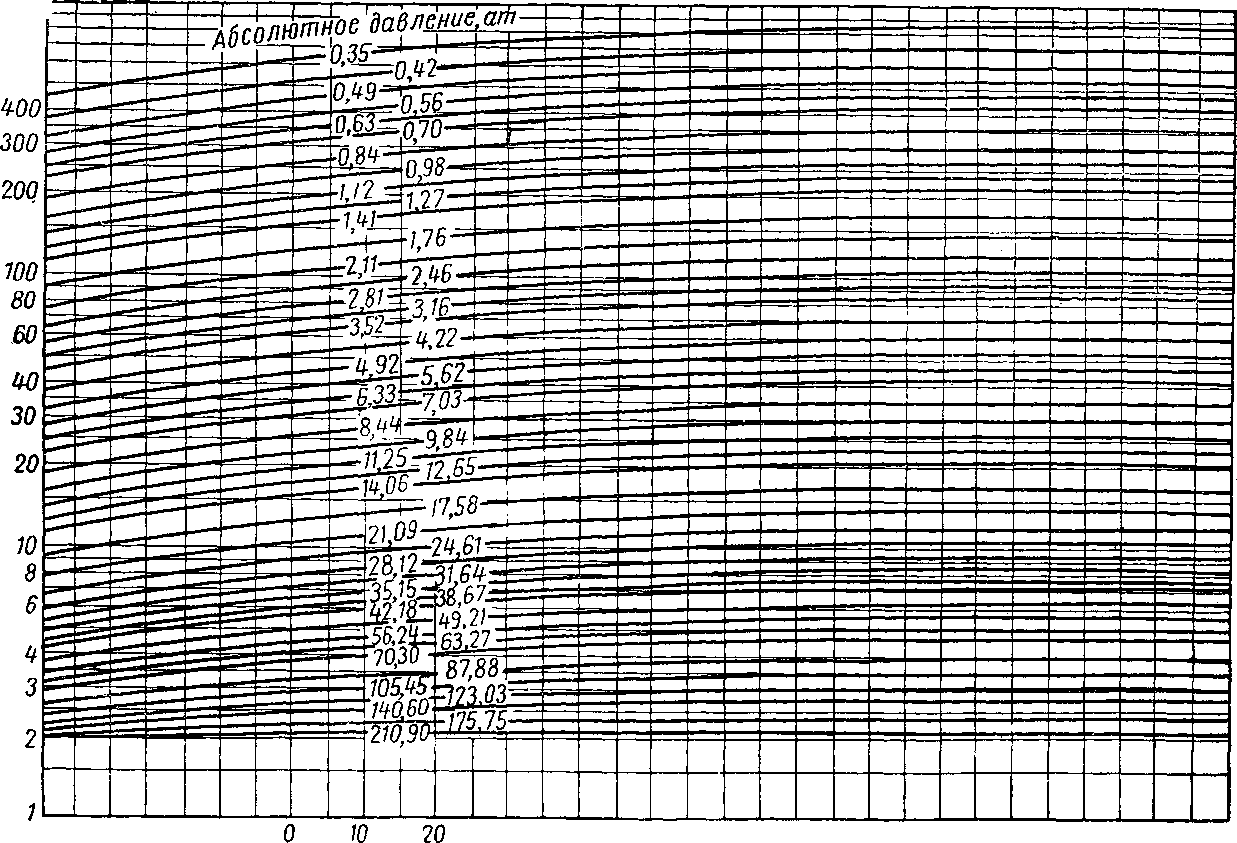
Рис. VI. 22 Коистаиты равновесия для этана в оклахомской нефти [111.26].
к~х
N0
N0
СЛ
н-лснтана
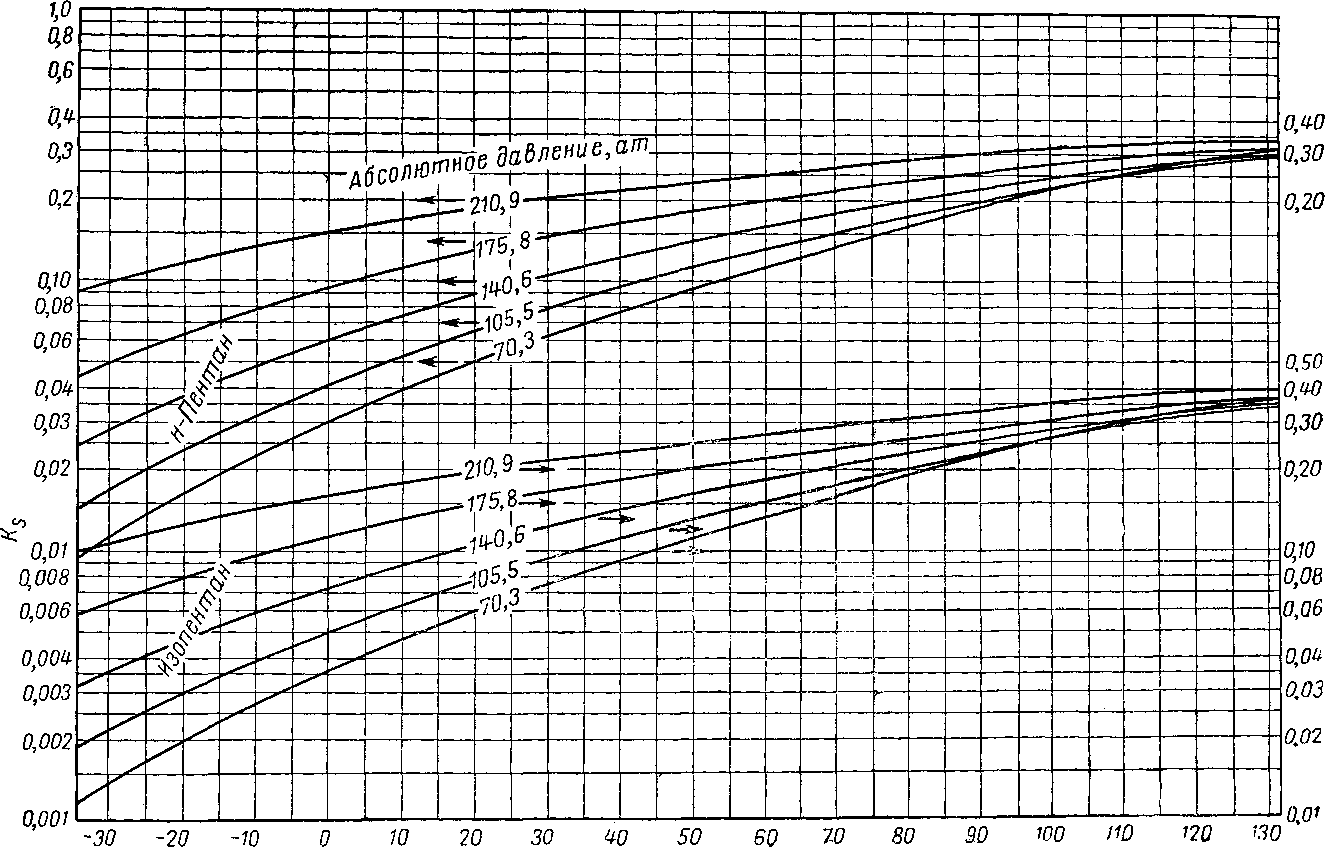
изопентана
-20 -10 0 10 20 30 Ц-0 50 60 70 80 90
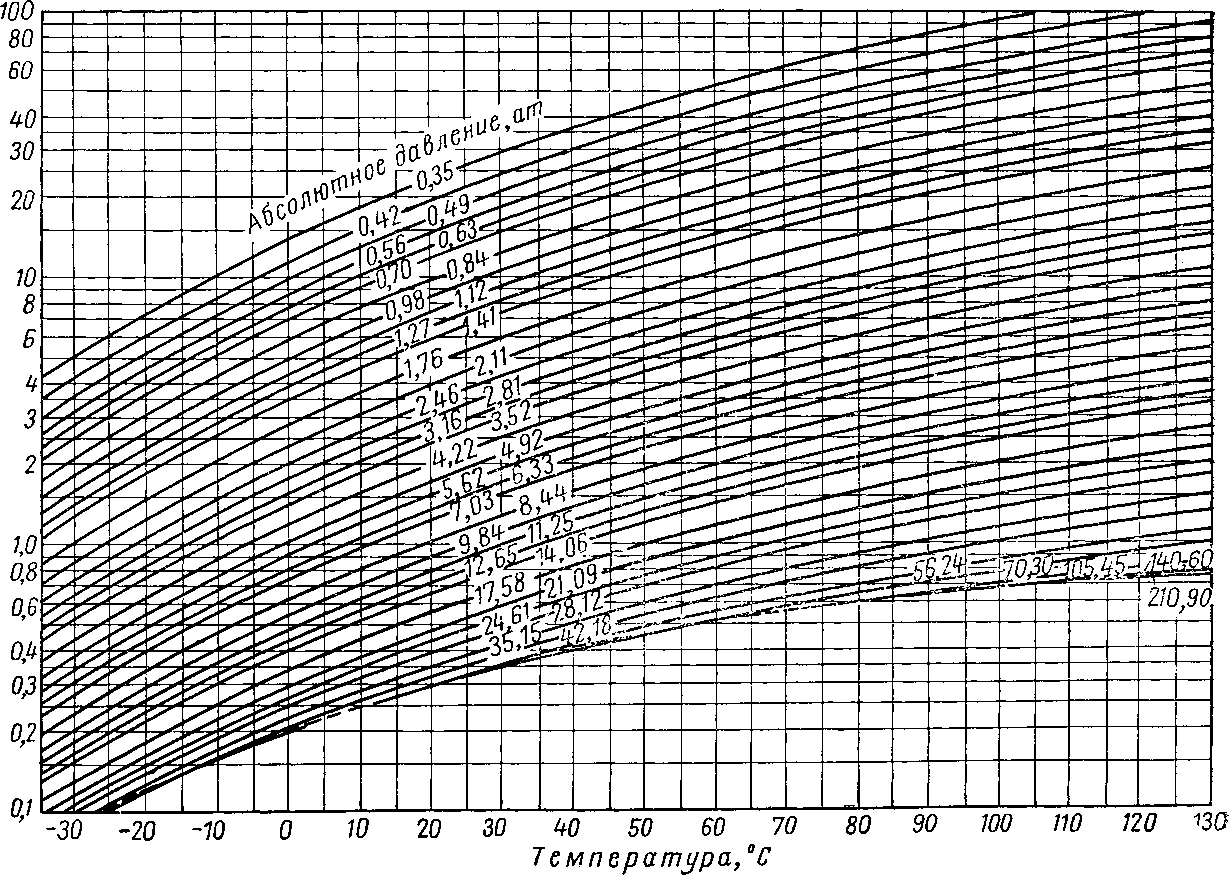
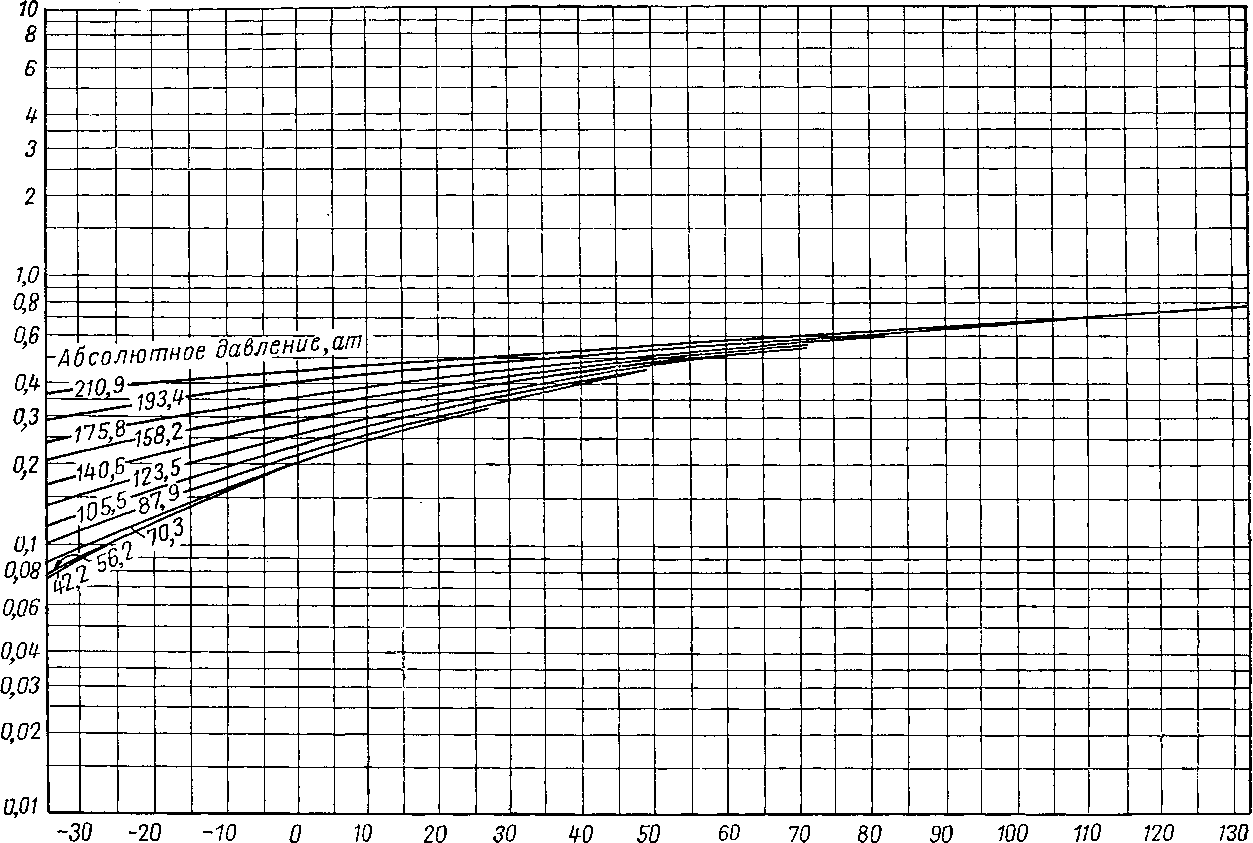
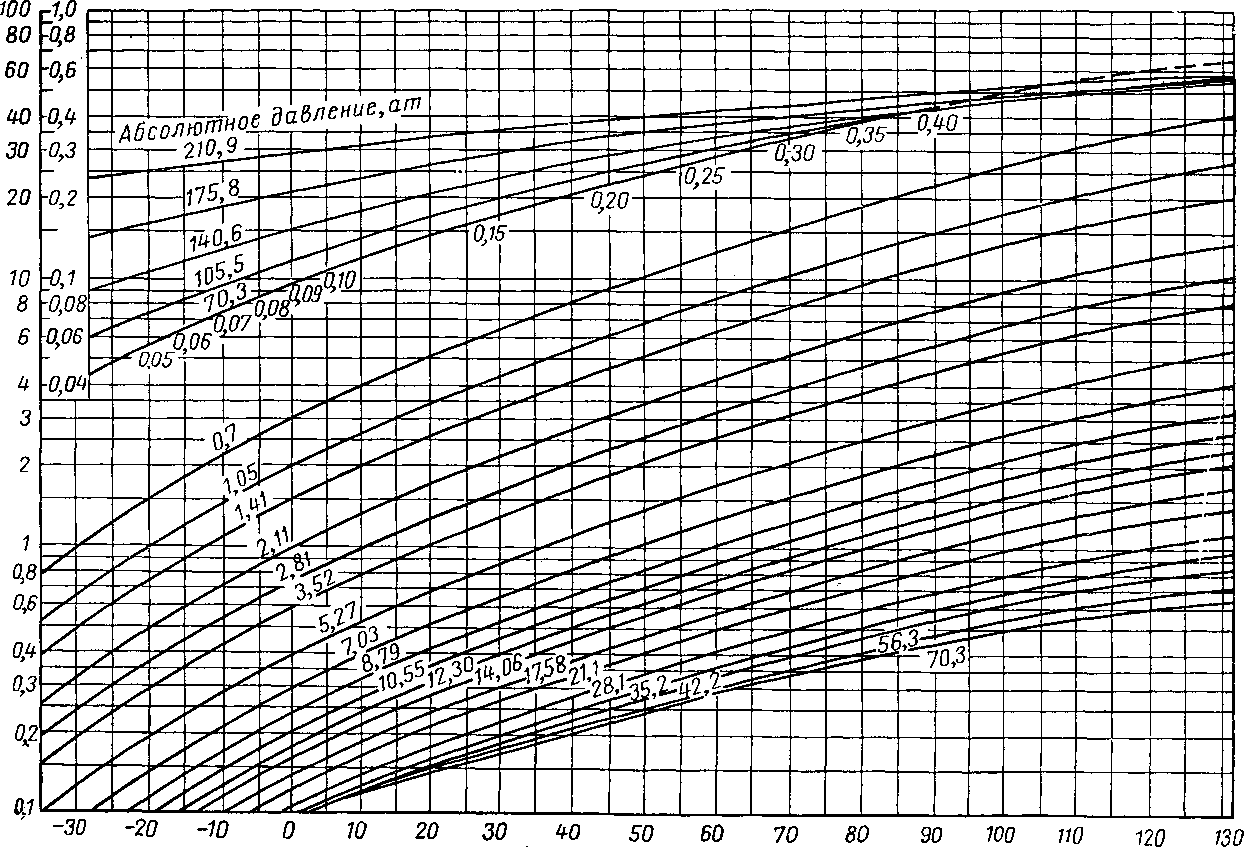
Рис. VI. 28. Константы равновесия для гексанов в оклахомской нефти [III. 26].
к=у/х
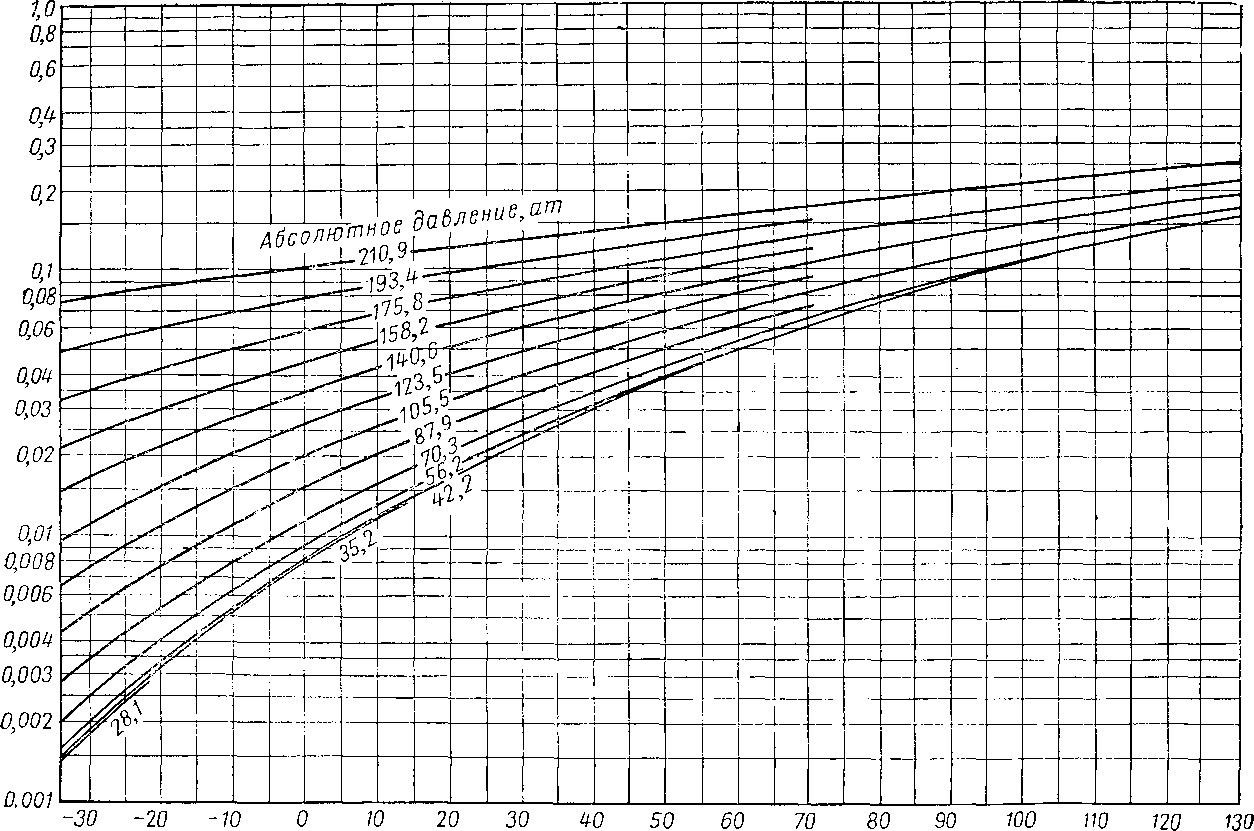
30 -20 -10 О W го 30 ч-о 50 60 70 80 90
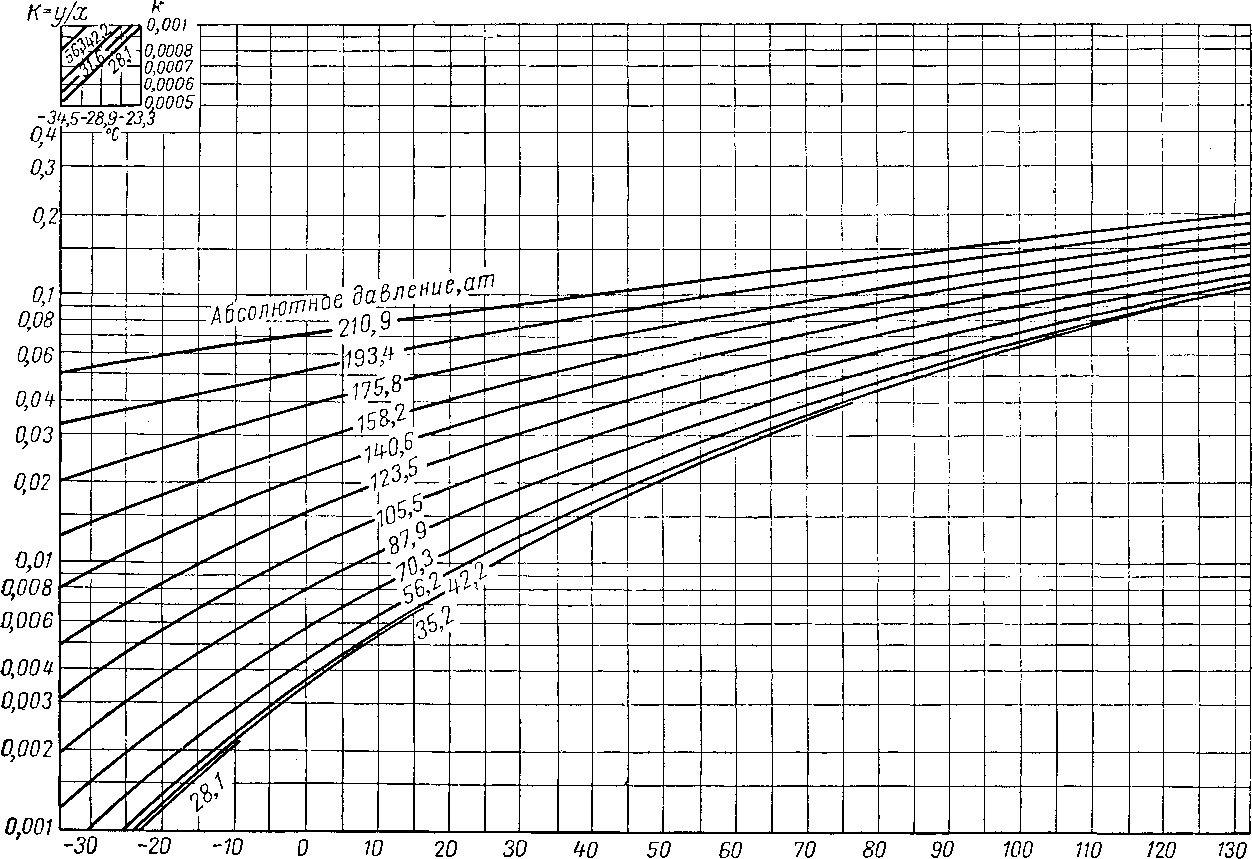
Таблица VI. 5
Экспериментальные данные по равновесиям фаз сложных углеводородных смесей
|
Наименование |
Температура, °С |
Абсолютное давление, ат |
Год исследования |
Литература | |||
|
Природный газ—нефть .... | 49,4; 48,9; |
0,98—232 | 1937 |
III. | 26 | ||
| 93,3 | |||||||
| Природный газ — абсорбционное |
масло | 0,6—82,2 | 7—350 | 1941 |
VI. | 64 | |
| Природный газ — дистиллят . | 4,4—93,3 |
14,280 | 1941 |
VI. | 49 | ||
|
Г аз дистиллят........ | 301,7—438,5 |
8,3—45,7 | 1942 |
VI. | 65 | ||
|
Газ абсорбционное масло . . |
17,8—34,4 |
8,7—225 | 1943 |
VI. | 31 | ||
|
Природный газ — нефть . . . |
1,7—121,1 |
70,3—576 | 1944 |
III. | 68 | ||
|
Природный газ—гексан . . . |
37,8 |
3,5—126 | 1945 |
VI. | 26 | ||
|
Природный газ — нефть . . . . |
48,9—93,3 |
70,3—654 | 1945 |
VI. | 50 | ||
|
Двуокись углерода — природный | газ — |
конденсат | 37,8—121,1 | 35—197 | 1946 | VI. | 45 |
| Природный газ........ |
54,4—115,6 |
7 | 1949 |
VI. | 61 | ||
|
Двуокись углерода — природный | газ — | нефть . . | 3,3—94,4 |
42—598 | 1951 |
VI. | 47 |
|
Газ — абсорбционные масла . . |
37,8—104,4 |
35—70 | 1952 |
VI. | 59 | ||
|
Двуокись углерода, сероводород, | природный газ, |
VI. |
|||||
| нефть и абсорбционные масла |
37,8—93,3 | 14—350 |
1952 | 29 | |||
| Газ — конденсат ....... | 93,9 | 35—210 | 1953 | VI. |
27 | ||
|
Сероводород—природный газ— |
нефть | 67,8 | 49—175 | 1954 | VI. | 62 |
|
| Природный газ — нефть . . . | 87,8 |
70—420 | 1956 |
VI. | 21 |
||
некоторая модификация этих диаграмм [VI. 53]. В работе Стендинга и Катца [III. 68] показано, что состав нефти имеет большое значение при высоких давлениях. Константы, полученные для нефти типа оклахомской, можно с достаточной достоверностью применить при расчетах, связанных с абсорбцией маслами. Данные Роланда, Смита и Кавелера, выполненные в виде графиков, могут быть использованы для расчета сепарации газоконденсатной смеси [VI. 49].
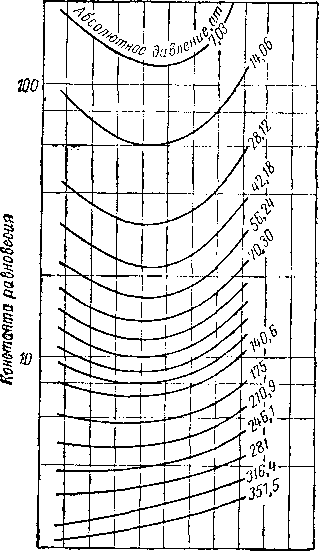
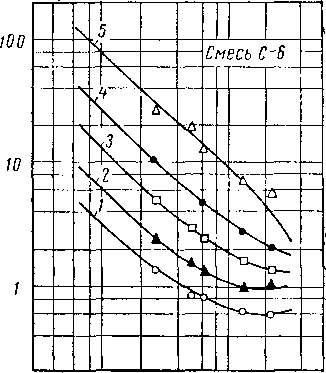
Как видно из табл. VI. 5, были исследованы и условия равновесия неуглеводородных компонентов — двуокиси углерода, азота и сероводорода. Диаграмма, составленная Поттменом (Poettmann) для двуокиси углерода в нефти, приведена на рис. VI. 30 [VI. 47]. Поттмен производил измерения при содержании двуокиси углерода в газовой фазе в 6—11 % мол. В сырой нефти из месторождения Биллингс растворялось больше двуокиси углерода, чем в конденсате из Эратского месторождения [VI. 45]. Якоби и Рзаса (Jacoby and Rzasa) [VI. 29] определили составы фаз системы нефть—природный газ (молекулярный вес С7 + равен 227, удельный вес 0,894), в которой содержалось азота, двуокиси углерода и сероводорода по 5% мол. Величины К для этих компонентов сопоставлены с величинами К для метана и этана на рис. VI. 31—VI. 33. Диаграммы для азота и сероводорода в этой системе приведены на рис. VI. 34 и VI. 35. Вагтборг (Vagtborg) [VI. 62] изучал естественную систему нефть — природный газ, содержавшую значительное количество сероводорода и небольшое — двуокиси углерода и азота. Он осуществлял дифференциальное испарение нефти, насыщенной при абсолютном давлении 175 ат и 67,8° С. Осредненные данные по дифференциальным составам фаз приведены в табл. VI. 7, а константы равновесия (все при 67,8° С)—в табл. VI. 8.
Таблица VI. 6
Опубликованные работы, в которых выведены корреляции констант равновесия жидкой и парообразной
фаз
| Наименование |
Год исследования | Литерату ра |
| Легкие парафины........ | 1932 |
VI. 57 |
| То же............. | 1932 |
III. 41 |
| » ..... | 1938 | VI. 54 |
| Метан в смесях......... |
1938 | VI. 53 |
| Сложные системы........ |
1948 | IV. 29 |
| Компоненты с высокой температурой кипения......... |
1949 | VI. 46 |
| Легкие углеводороды...... |
1950 | VI. 13 |
| Метан в смеси с легкими углеводородами ........... |
1952 | VI. 10 |
| Сложные системы........ |
1952 | VI. 51 |
| 1952 | VI. 37 | |
| 1952 |
VI. 67 | |
|
1953 | VI. 33 | |
| 1953 | VI. 25 | |
| Легкие углеводороды...... | 1953 | VI. 19 |
|
Сложные системы........ |
1955 | VI. 40 |
К=у/х

-10 О 10 20 30 40 50 60 70 80 90 100 110
Рис, VI. 30. Константы равновесия для двуокиси углерода в нефти Биллингса [VI. 47].
10
Рис. VI. 31. Константы равновесия для компонентов нефти при 37,8° С [VI. 29].
/ — сероводород; 2 — этан; 3— двуокись углерода; 4 — метан; 5 — азот*
СЭ
СХ
СЗ
5
сз
5
со
з:
о
си
:э
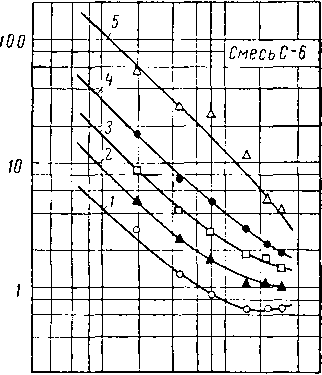
Рис. VI. 32. Константы равновесия для компонентов нефти при 65,50° С [VI. 29].
/ — сероводород; 2 — этан*, 3 — двуокись: углерода; 4 — метан; 5 =— азот.
сз
са.
сэ
е
а:
сз
е
Со
а;
о
5:
100
давление,ат
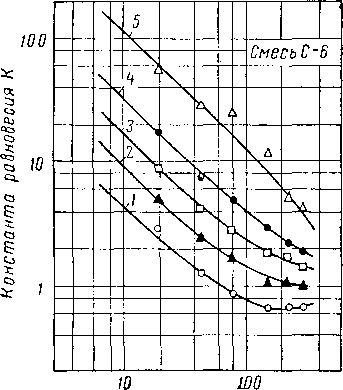
Рис. VI. 33. Константы равновесия для компонентов нефти при 93,3° С.
/ — сероводород; 2 — этан; 3 — двуокись углерода; 4 — метан; 5 азот.
го за т so 60 ю so зо wo по по по Температура/С-
Рис. VI. 34. Константы равновесия азота в нефти (смесь С-6) [VI. 29].
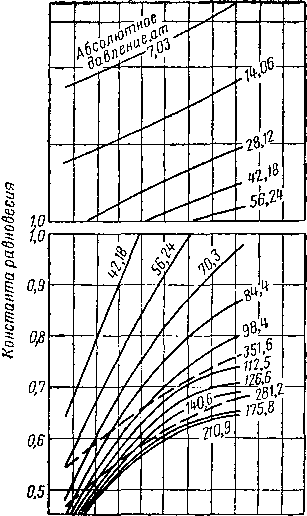
20 30 40 50 60 70 80 90 100 НО 120 130 Температура, °С
Рис. VI. 35. Константы равновесия сероводорода в нефти (смесь С-6) [VI. 29],
1,0 2,0 3,04,0 6,08,010 20 30 40 6080100 200300 600
moo
800
600
CO n
о * 3
m
300
2 oo
юо
80
60
w
30
20
I 2
В ,
las
0,6
0,4
0,3
0,2
0,1
0,08
0,06
0,04
0,03
0,02
Рис. VI. 36, Константы равновесия при 48,9° С.
/ — двойные системы Ci—Сх — пС4; С1!— nCt; Сг—пС4, С8 — лС,; 2 природный газ — нефть (Катц и Гахмус); «?-— природный газ— конденсат (Роуленд, Смит и Кейвлер);
4 — природный газ — нефть (Стендинг и Катц); 5 — метан; б—этан; 7 — пропан; 8 — бу-таны; 9 — пентаны; 10 — гексаны; — гептаны.
Таблица VI. 7
Состав фаз при выделении растворенного газа из Пластовой жидкости при 67,8° С [VI. 62]
Абсолютное давление, ат
|
Компонент | 1* | 51 |
78 | 109 | 144 | 1 175** |
|||||
| жидкость |
пар | жидкость |
пар | жидкость | | пар |
ЖИДКОСТЬ | | пар |
жидкость | пар | жидкость | |
|
Ci | 0,00 |
13,80 | 7,787 |
37,68 | 12,10 |
45,86 | 16,843 |
53,23 | 21,723 |
56,73 | 26,121 |
| С2 | 0,00 |
9,50 | 5,361 |
10,15 | 6,05 |
10,49 | 6,677 |
9,94 | 7,127 |
8,08 | 7,247 |
| С3 | 1,37 |
4.00 | 2,854 |
2,06 | 2,74 |
2.04 | 2,641 |
1,60 | 2,497 |
1,45 | 2,366 |
| с4 | 2,00 |
3,45 | 2,818 |
1,71 | 2,66 |
1,34 | 2,473 |
1,00 | 2,270 |
0,84 | 2,090 |
| с5 | 3,63 |
1,70 | 2,541 |
0,88 | 2,30 |
0,74 | 2,081 |
0,68 | 1,888 |
1,04 | 1,782 |
| с6+ | 92,23 | 0,87 | 40,677 |
0,44 | 34,86 |
0,48 | 30,023 |
0,64 | 25,971 |
0,83 | 22,812 |
| H2S | 0,77 |
64,55 | 36,761 |
43,28 | 37,70 |
34,60 | 37,267 |
29,06 | 36,135 |
25,72 | 34,227 |
| С02 | 0,00 |
1,45 | 0,818 |
2,27 | 1,03 |
2,36 | 1,216 |
2,36 | 1,374 |
2,33 | 1,494 |
| n2 | 0,00 |
0,68 | 0,383 |
1,63 | 0,56 |
2,09 | 0,779 |
2,49 | 1,015 |
2,98 | 1,261 |
* Состав жидкой фазы при атмосферном давлении определен экспериментально. Состав пара выражен «сглажен
ными» данными.
** Состав жидкости при температуре начала кипения дни.
(абсолютное давление 175). Определен путем экстраполя-
Таблица VI. 8 Константы равновесия для пластовой жидкости при 67,8° С [VI. 62]
| Компонент | Абсолютное давление, am |
|||
| 51 | 78 |
109 | | 144 | |
|
Cl | 4,826 |
3,790 | 3,101 |
2,612 |
| с2 | 1,893 | 1,734 |
1,489 | 1,133 |
| С3 | 0,722 | 0,745 | 0,606 |
0,581 |
|
С4 | 0,607 |
0,504 | 0,404 |
0,370 |
| с5 | 0,346 | 0,322 |
0,327 | 0,551 |
| с6+ | 0,011 | 0,014 | 0,021 | 0,032 |
|
HsS | 1,177 |
0,918 | 0,780 |
0,712 |
| со2 | 2,775 | 2,291 | 1,941 | 1,696 |
| N* | 4,256 | 3,732 | 3,196 |
2,936 |
КОРРЕЛЯЦИЯ КОНСТАНТ РАВНОВЕСИЯ
По правилу фаз для точного определения десятикомпонентной двухфазной системы в условиях постоянных температуры и давления требуется знание восьми фазовых концентраций. Корреляции констант равновесия для сложных систем, кроме температуры и давления, в значительной мере зависят от подобия углеводородных систем.
Хенсон и Браун (Hanson and Brown), [VI. 26] сопоставили различные системы при температуре 48,9° С (рис. VI.36). Они показали, что при одинаковом давлении схождения данный компонент даже при различном составе смеси будет иметь одинаковые константы равновесия. Первоначально применявшийся метод определения констант равновесия для систем с летучестью, промежуточной между исследованными системами, заключался в интерполяции диаграмм, подобных показанной на рис. VI. 36. Уайт и Браун (Whitte and Brown) [VI. 65] предложили простую методику отыскания кон-ртант равноиесия при известных кажущихся величинах давления схождения. Кривая идеальной константы равновесия по этому методу строится в координатах log К—log р. По таким диаграммам получаем величины минимума констант равновесия и давления, необходимого для минимума К, как функцию давления схождения и упругости паров данного компонента. Схема такого построения кривой константы равновесия показана на рис. VI. 37.
щи
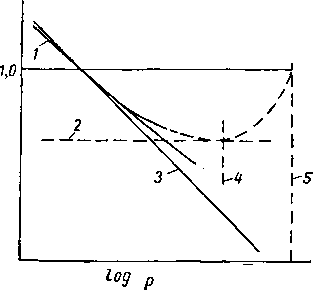
Рис. VI. 37. Определение величин К по давлению схождения.
/ — идеальная К; 2 — минимум К; 3 — по закону Рауля; 4 — давление минимума К',
5 — давление схождения.
Давления схождения или геометрические места критических точек двойных систем показаны на рис. III. 14. В общем можно констатировать, что в многокомпонентных системах повышение давления схождения вызывается либо добавлением к системе высоколетучих веществ, например азота и водорода, либо уменьшением содержания промежуточных компонентов. Высокое давление схождения приводит к замедленному повышению величин К для менее летучих компонентов и к ускоренному снижению величин К для более летучих компонентов при давлениях, при которых они не следуют больше законам идеальных растворов. Хеддн (Hadden) [VI. 24] составил корреляцию констант равновесия на основе давления схождения и метода приближения к давлению схождения [VI. 25]. Уинн (Winn) [VI. 67] разработал номограмму (рис. VI. 38) для нахождения констант равновесия при давлении схождения 350 ат.
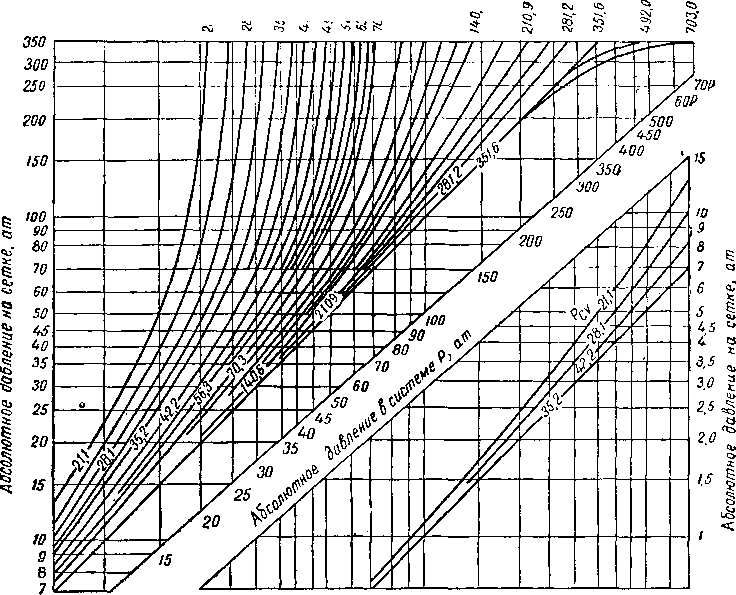
Прямая линия, соединяющая точку давление—температура на координатной сетке с точкой компонента, пересекает вертикальную ось констант в точке, соответствующей искомой константе равновесия. Для других давлений схождения в сочетании с рис. VI. 38 берут величины давления на координатной сетке, приведенный
"1 f л
emtpou**
®- I
6ем%ьпв
Абсолютное давление,а
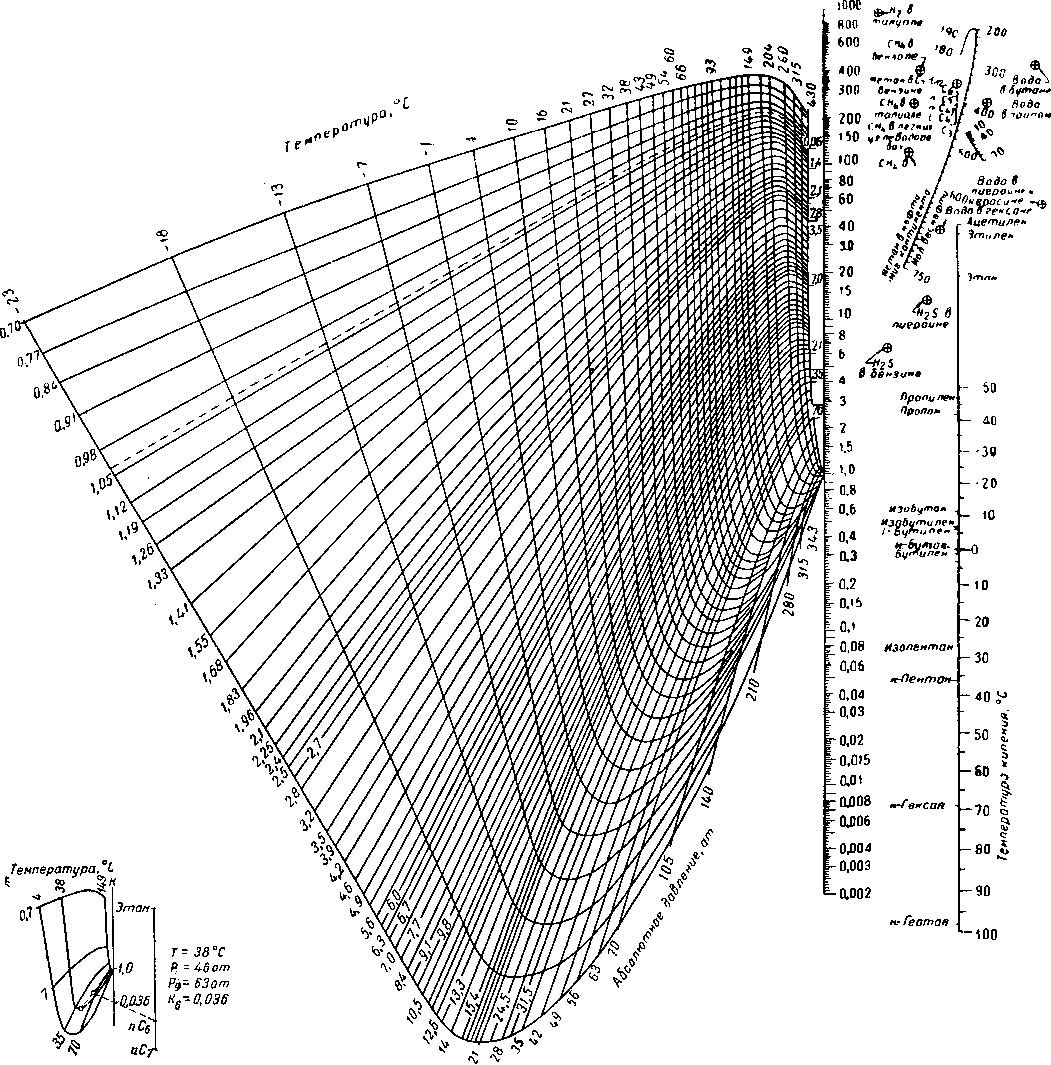
Абсолютное давление схождения Рси.ат
tr.
C\j С\| ГЪ frj t»J
( С\1 f>.' Q1* ж«ч* г-^*
10 0.2 Ц25 0.3 0,35 0*50,5 0,6 0,70,д 1,0 1,5 2,0 2,5 3.0 3,5 40 50 6 7
Абсолютное даВление 6 системе р, ат
PhCj VI. 39. График для определения сеточного давления при давлении схождения,
отличном от 350 кГ/см2 абс. [VI. 67].
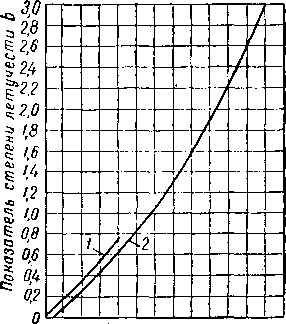
Рис. VI. 40. Показатель степени летучести в уравнении (VI. 1) [VI. 67].
1 •— чистые углеводороды; 2 — нефтяные фракции (погон уд. веса 0,78)* на рис. VI. 39. Методика определения К в этом случае заключается в следующем.
120 160 200 2Ь0 280 320 360 Температура нипеная при атмосферном давлении,
1. На рис. VI. 38 находим точку давления—температуры системы. Проводим прямую линию через эту точку и К = 1,0.
2. Находим точку пересечения этой линии с кривой давления, соответствующего давлению на сетке рис. VI. 39.
3. Проведя через эту точку пересечения и точку компонента прямую линию, определяем К.
Для компонентов с температурой кипения выше 98,9° С (гептан С7) константы определяем по следующему уравнению:
(V,'1)
где Кп—константа равновесия нефтяной фракции или смеси с высокой температурой кипения; Кг — константа равновесия этана при температуре, давлении и давлении схождения в системе; Кч — константа равновесия гептана при температуре, давлении и давлении схождения в системе; Ь — показатель степени летучести (рис. VI. 40).
Давления схождения Уинн (Winn) определяет по критическим кривым двойных систем, приведенным на рис. VI. 41. Для тройных и сложных систем Уинн предлагает следующее.
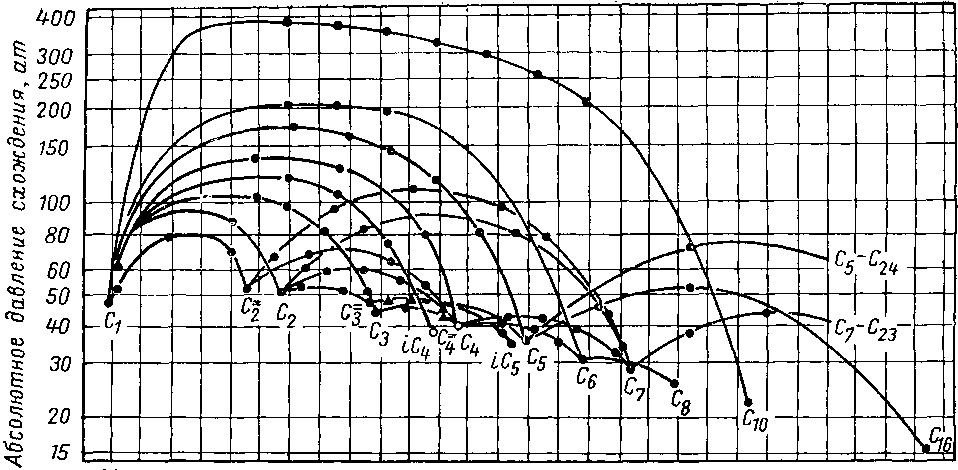
-40 0 40 80 120 160 200 240 280 320 360 400 4-4-0 480
Температура,°С
Рте. VI. 41. Давление схождения двойных углеводородных систем [VI. 67].
W00 в ООО 5000 4000
0 4-0 80 120 1Б0 200 74Q 280
Температура, °С
По рис. VI. 41 при температуре системы нужно найти давления на двух кривых, являющихся геометрическим местом критических точек двойных смесей’ самого легкого компонента с промежуточным и тяжелым ^компонентами. Если температура системы выше критической температуры промежуточного компонента, берем критическое давление этого компонента. Умножая эти две величины давления на соответствующие весовые доли промежуточного и тяжелого компонентов в жидкой фазе, складываем результаты и делим их на сумму весовых долей промежуточного и тяжелого компонентов в жидкой фазе.
Давление в системе для многокомпонентных систем определяют таким же образом, как и для тройных систем, т. е.
(MlW'i + (Рс, vhW2 + (Pc. vh У3 + • • •
где р Cf0 — абсолютное давление схождения системы в ат- {р c v) 1—давление на кривой критических точек Самого легкого компонента и компонента, обозначенного, данным подстрочным значком при температуре системы; W1 — весовая доля/компонента, обозначенного дан ным подстрочным значком, в жидкой фазе. Индексы 1,
2, 3 ... обозначают 1 — самый легкий компонент, 2 — следующий, более тяжелый компонент и т. п.
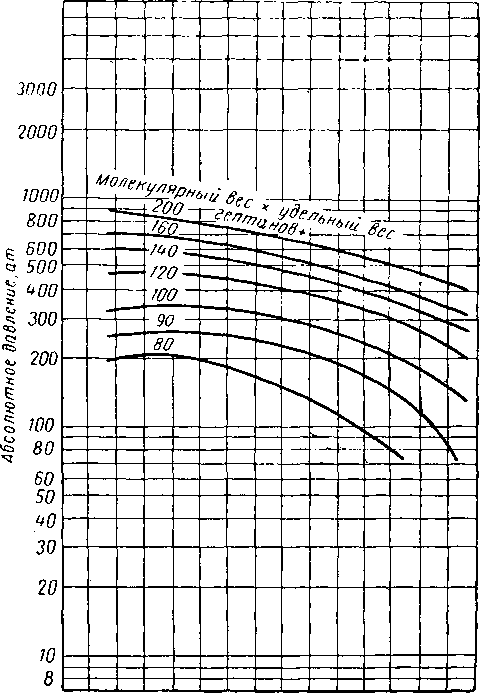
Рзаса, Гласс и Опфелль (Rzasa, Glass and Opfell) [VI. 51] разработали корреляцию величин К для сложных нефтяных систем, по которой давление схождения определяется из температуры и произведения молекулярного веса фракции гептана и более тяжелых углеводородов на ее удельный вес (рис. VI. 42).
Рис. VI. 42. Определение давления схождения по температуре и свойствам фракции гептанов и более тяжелых углеводородов [VI; 51 ].
Ч В 8 10 20 М 6080100 200 400600
Абсолютное давление,ат
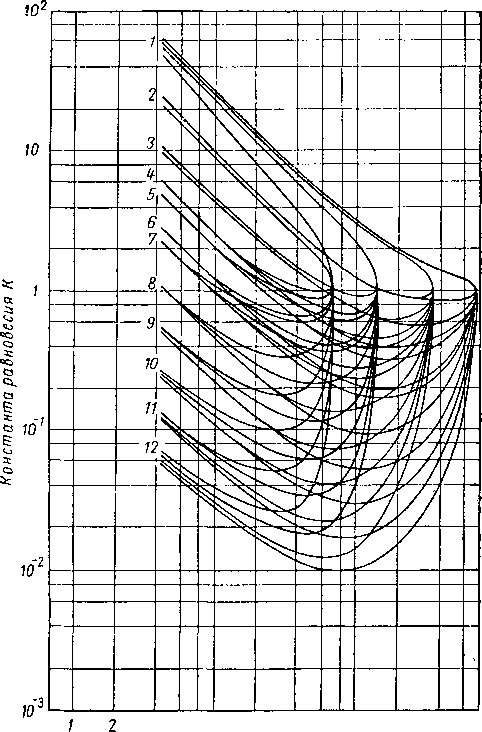
Рис. VI. 43. Константы равновесия для различных величин давления схождения при 126,7° С [VI. 51],
/ — метан; 2 — этан; 3— пропан; 4 — изобутан; 5 — «-бутан; б —I изопентан; 7— н-пентан; 8 — н-гексан; 9 — н-гептан; 10 — н-октан; // — н-нонан; 12 — «-декан.
Константы равновесия при различных давлениях схождения и температуре 126,7° С приведены на рис. VI. 43.
Для определения равновесий в системе природный газ—жидкость широкс применяют диаграммы фугетив-ности, составленные фирмой «Келлогг» [VI. 13]. Константу равновесия определяют по уравнению
(VI. 2)
где Цх — фугетивность компонента, деленная на его мольную долю в жидкой фазе; f/y — фугетивность компонента, деленная на его мольную долю в парообразной фазе.
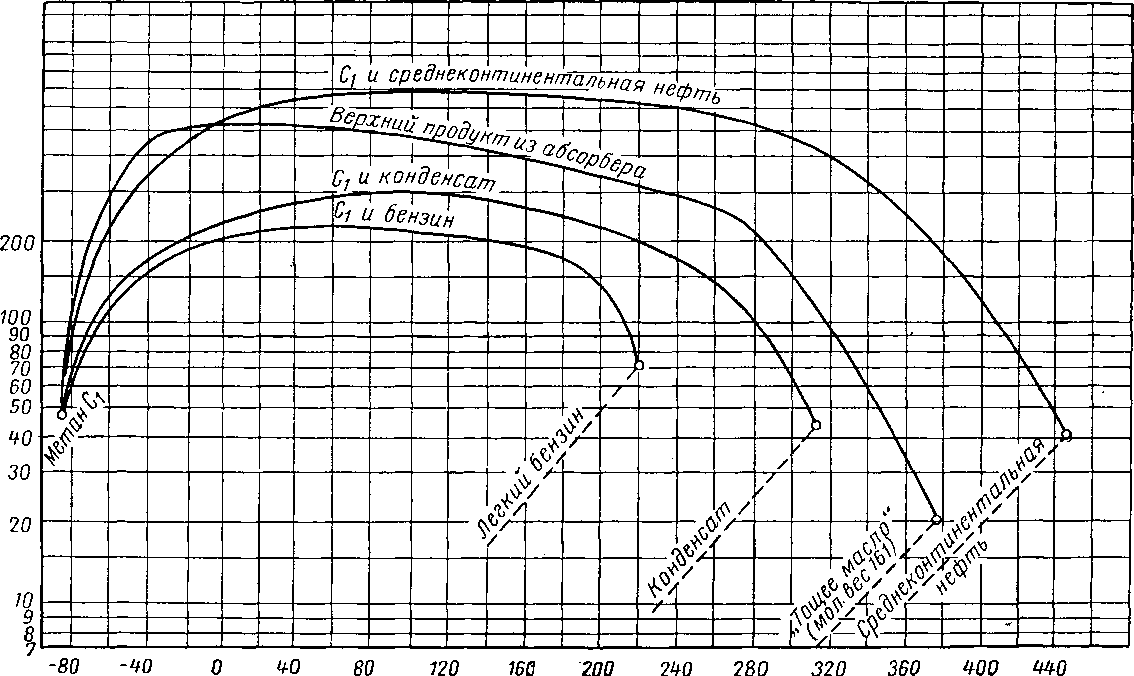
Соотношение между фугетивностью и мольной долей зависит от средней мольной температуры кипения фазы и выражается рядом диаграмм, каждая из которых дает это соотношение для данного компонента при данном давлении. Применение диаграмм (примером может являться диаграмма для метана, приведенная на рис. VI. 44) осуществляется по методу последовательных приближений. Для определения К исходят из четырех переменных: температуры, давления, мольных средних температур кипения жидкости и пара.
Другие методы корреляции и работы, в которых они приведены, перечислены в табл. VI. 6.
КОРРЕЛЯЦИЯ ОРГАНИКА—БРАУНА (ORGANICK—BROWN), ДИАГРАММЫ NGAA
(Американской ассоциации газового бензина)
Органик и Браун [VI. 37] разработали корреляцию констант равновесия, в которой кажущееся давление схождения вычисляется по средней мольной температуре кипения паровой фазы и средневзвешенному эквиваленту молекулярного веса жидкости. На диаграммах К выражены как функции температуры, давления и давления схождения.
Давление схождения определяют по двум диаграммам (рис. VI. 45 и VI. 46). Для данных температуры и давления равновесия находят среднемолекулярную температуру кипения пара и средневзвешенный молекулярный вес жидкости Мв. Задаются давлением схождения или корреляционным давлением рк и определяют соотношение р/рк. По рис. VI. 45 находят показатель степени в члене (ЮО/Мв)".
По рис. VI. 46 определяют ординату рк (ЮО/Мв)", сопоставляя ее с величиной, вычисленной по заданному значению рк и Мъ. Этот метод последовательных приближений в сочетании с повторными вычислениями фазовых равновесий очень трудоемок. Однако, пользуясь этим методом, можно получить точные величины К при любом давлении схождения.
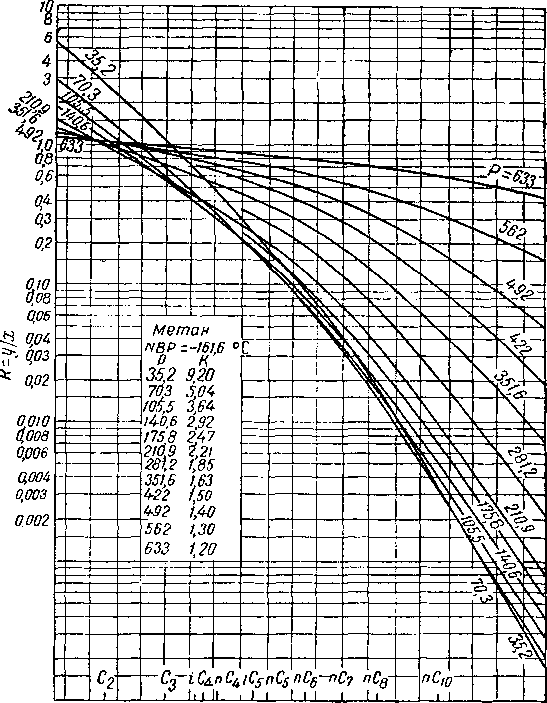
Можно построить график константы равновесия как функции нормальной температуры кипения компонента (NBP) при постоянной температуре и давлении. На рис. VI. 47—VI. 49 приведены такие графики, построенные для температуры 93° С и нескольких давлений, при трех давлениях схождения с использованием констант Органика и Брауна.
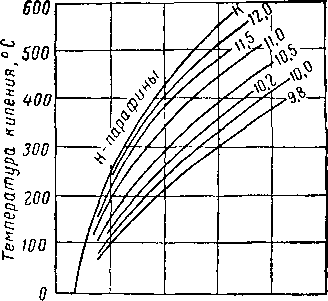
Если расчет ведется не для нормальных парафиновых углеводородов, а для других соединений, Органик и Браун рекомендуют применять эквивалентный молекулярный вес (рис. VI. 50). Данные о влиянии растворителя для ароматических и нафтеновых абсорбционных масел приведены в работе Киркбрайда и Бертетти (Kirkbride and Bertetti) [VI. 31].
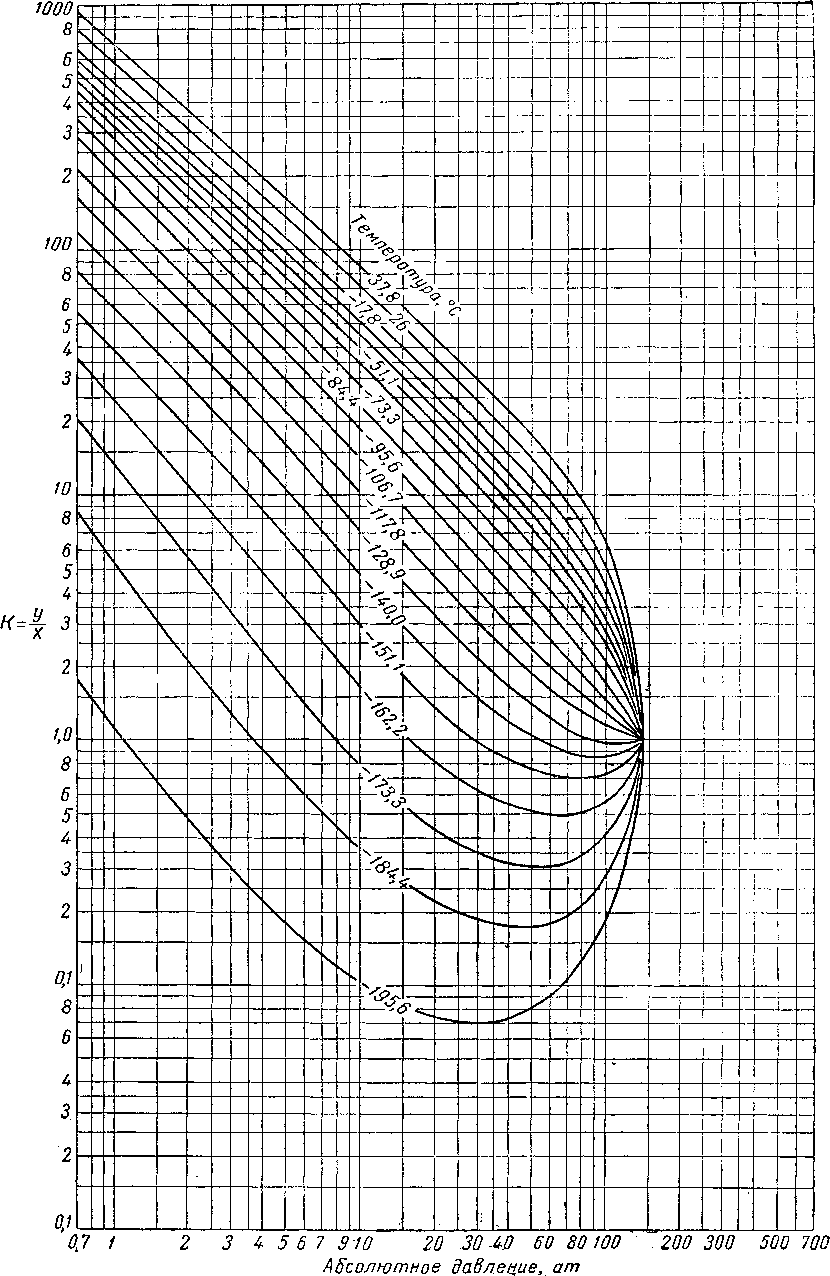
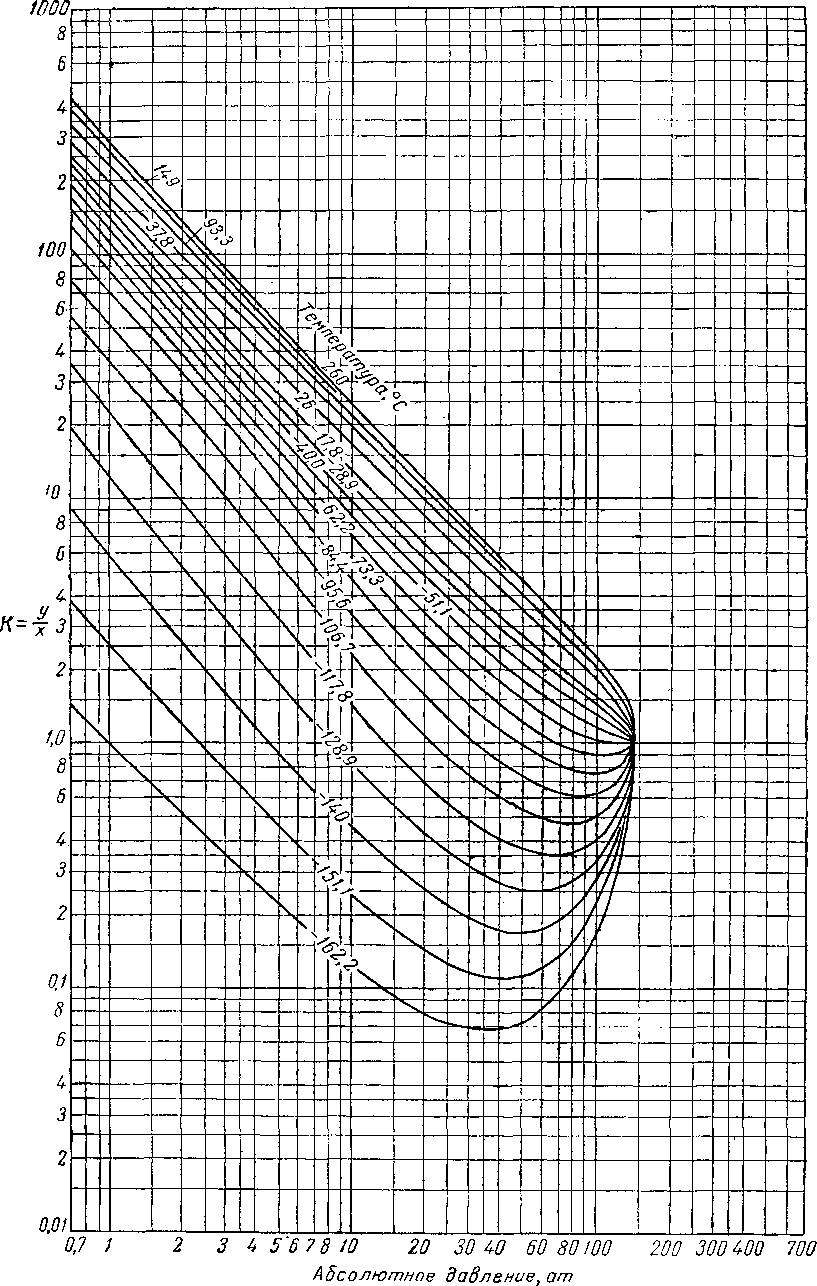
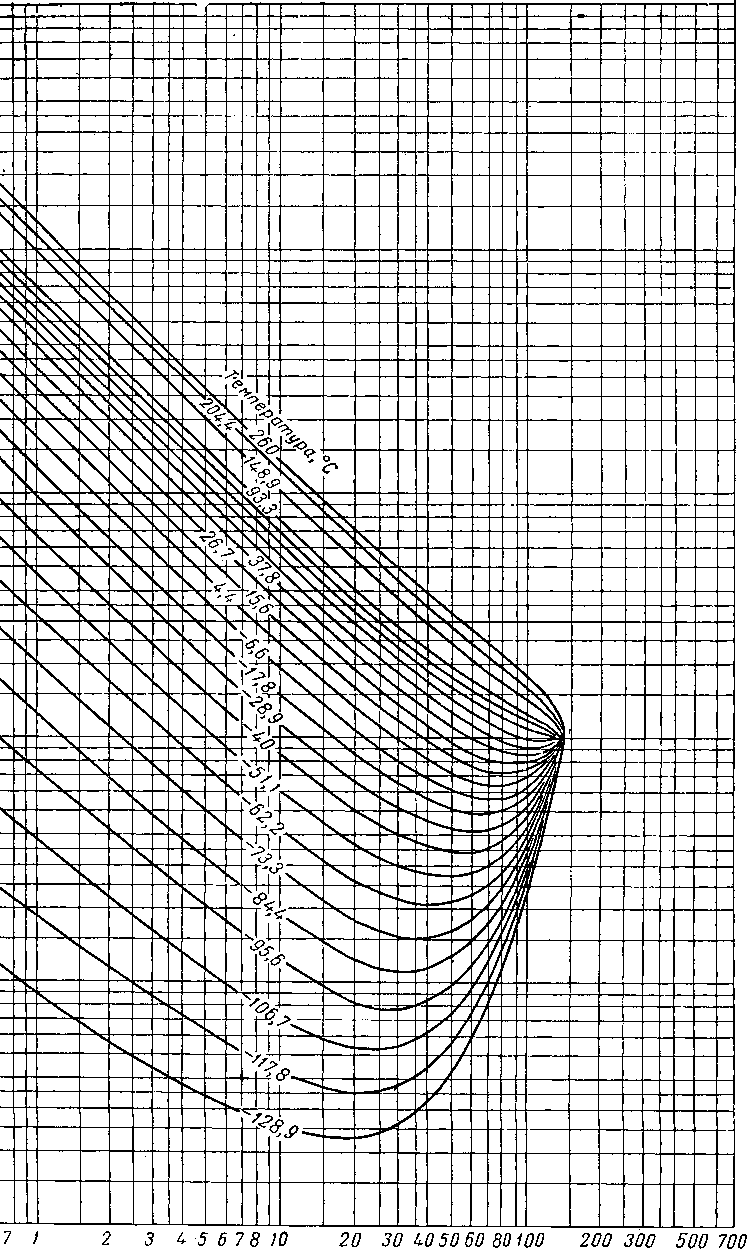
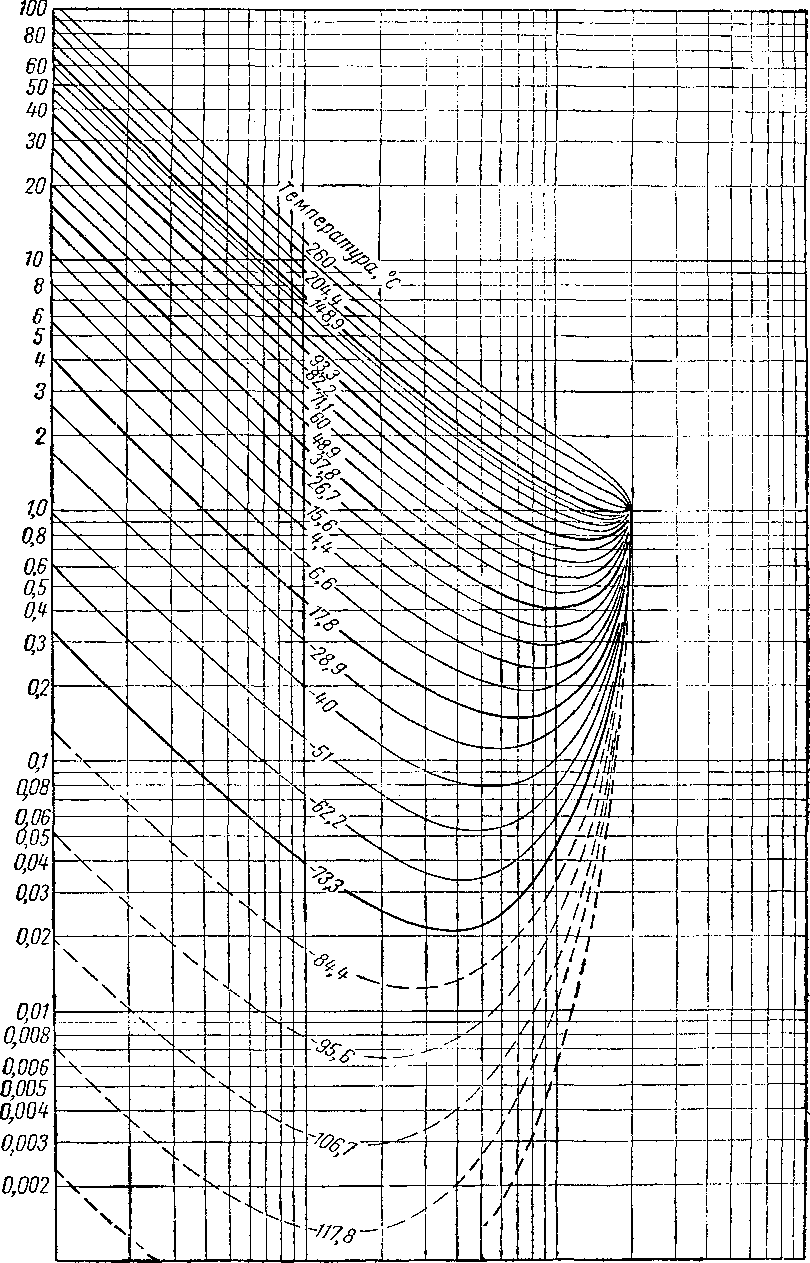
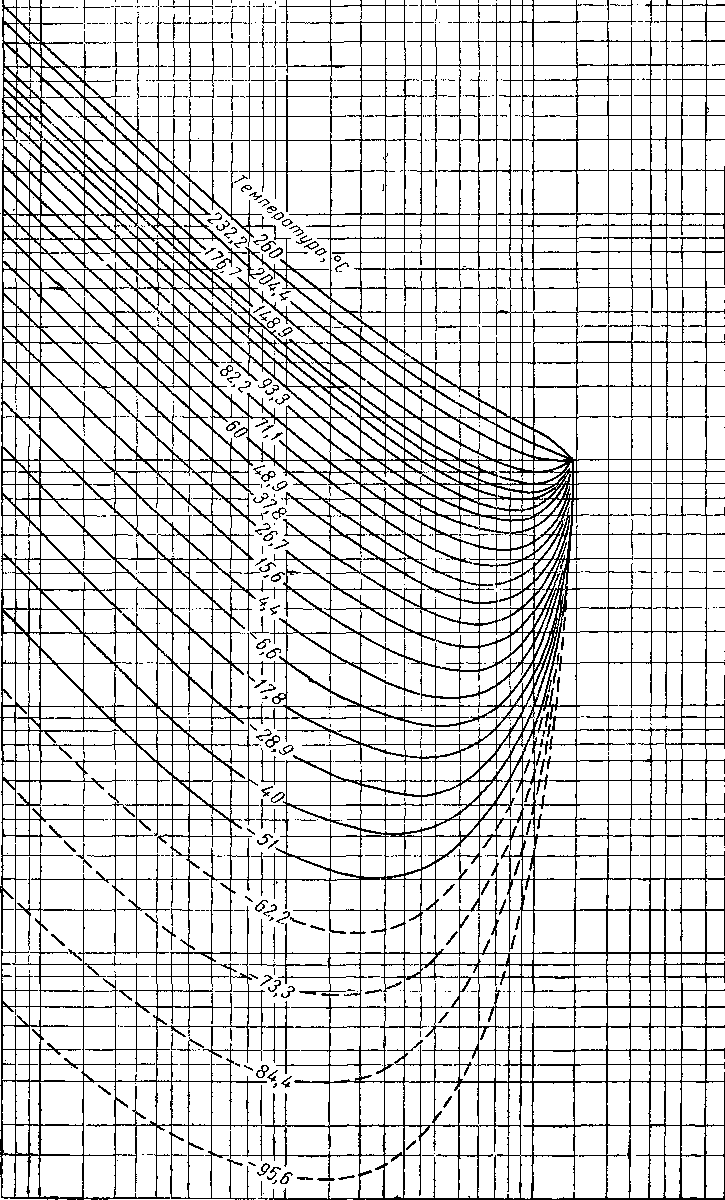
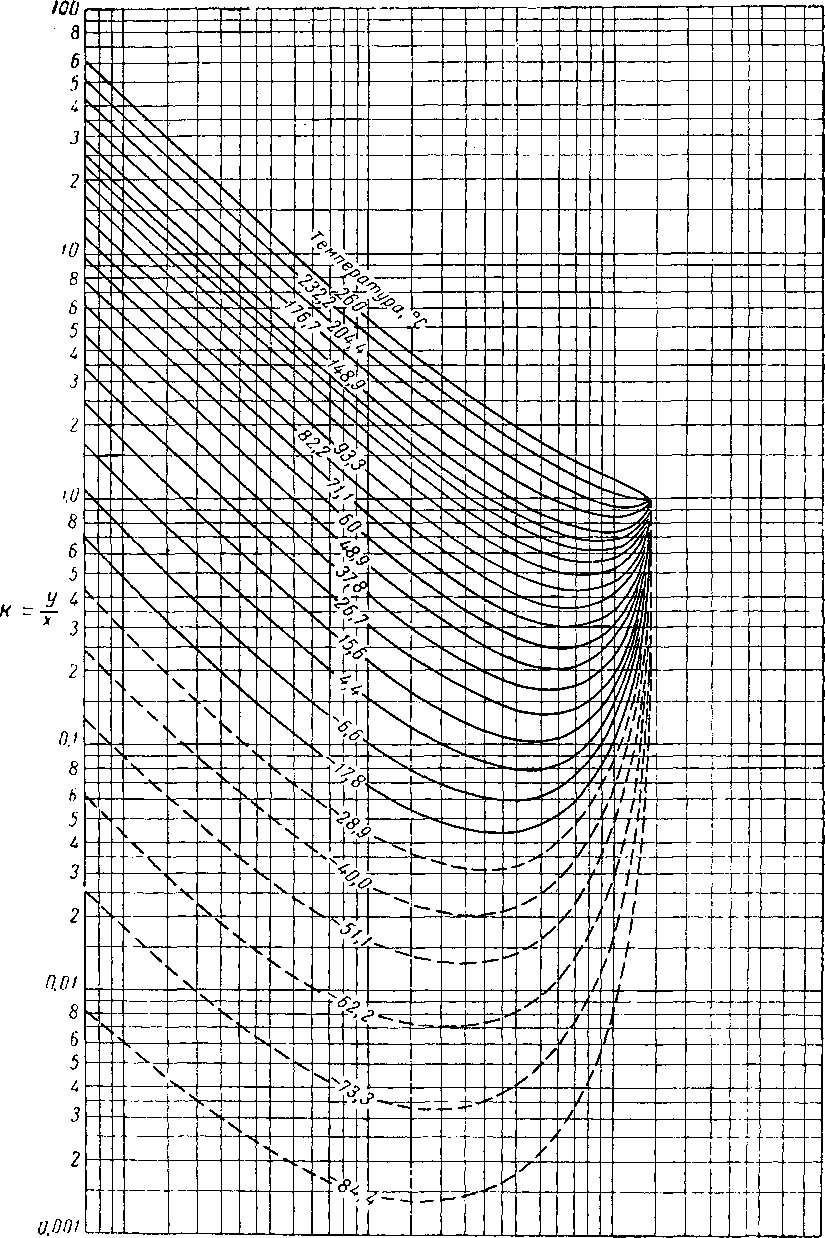
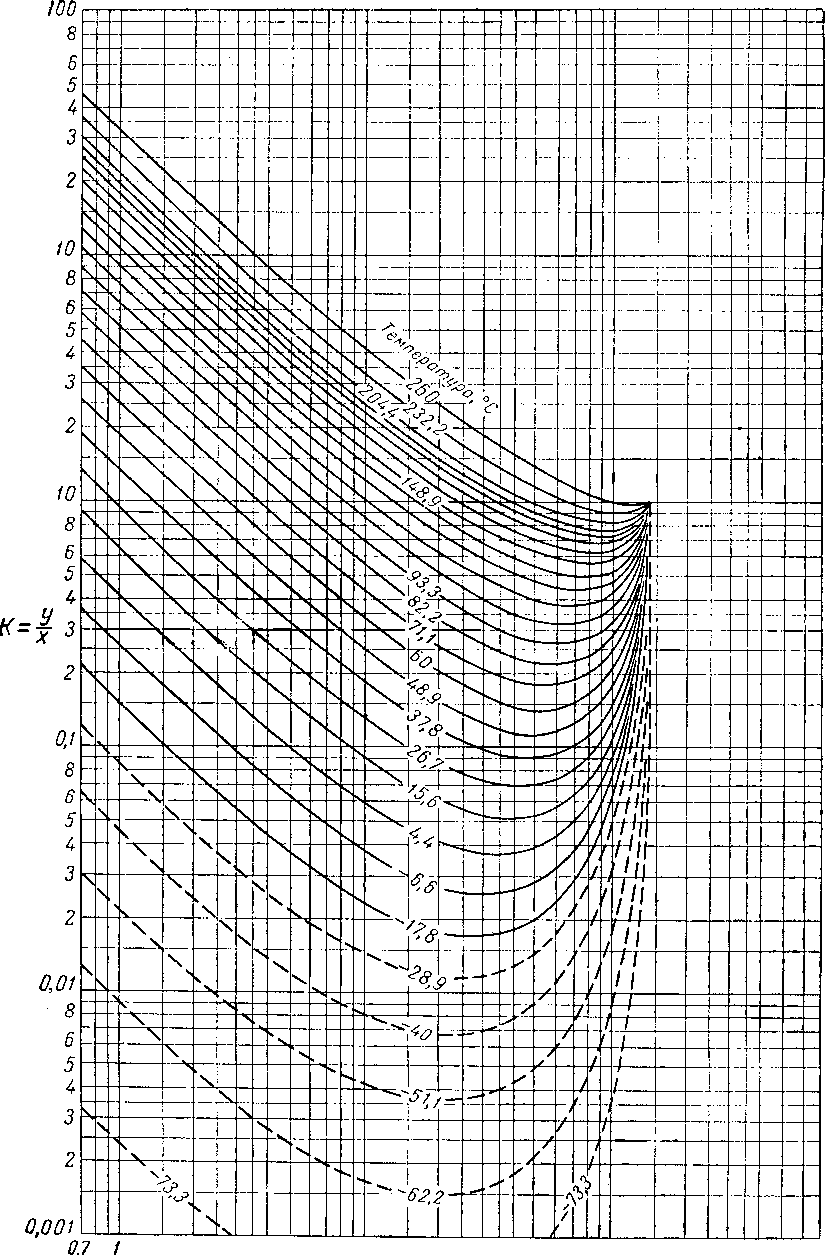
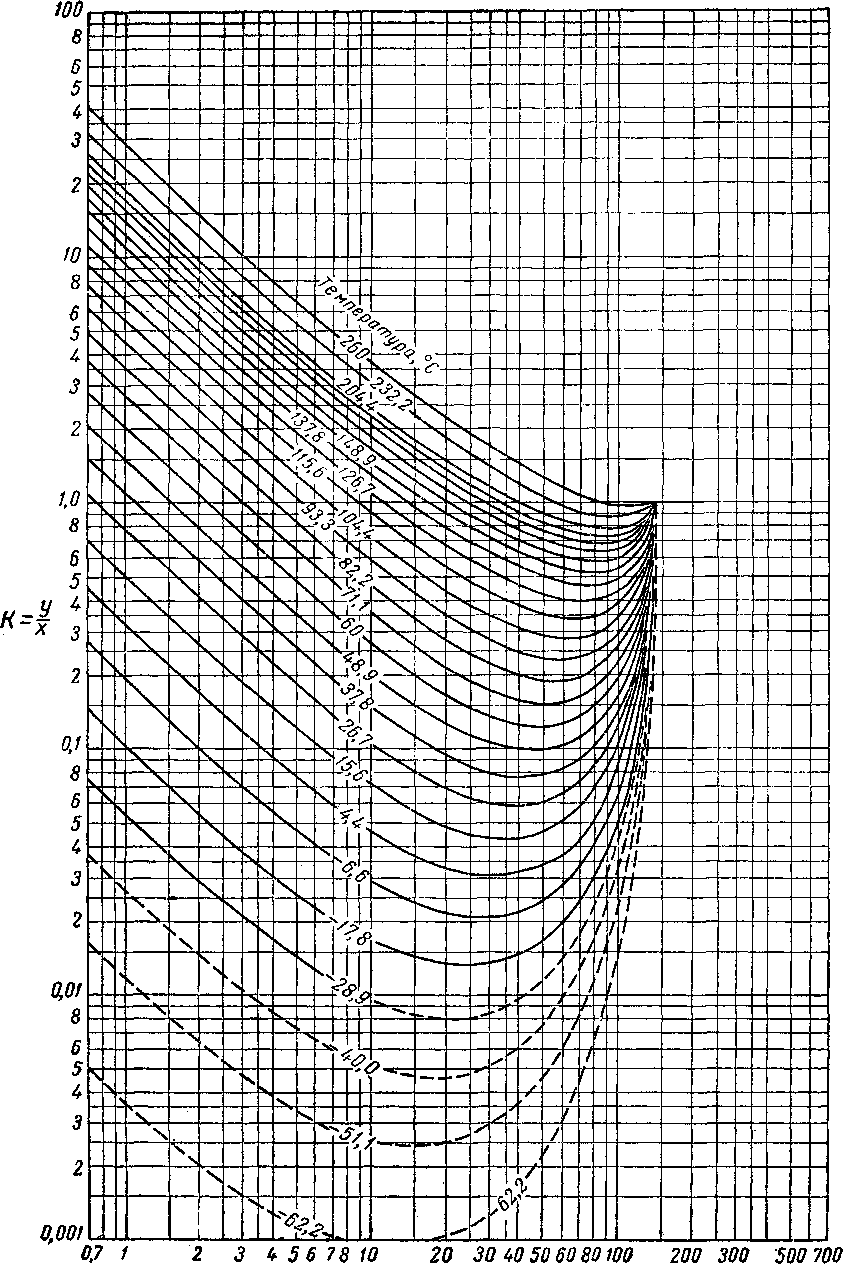
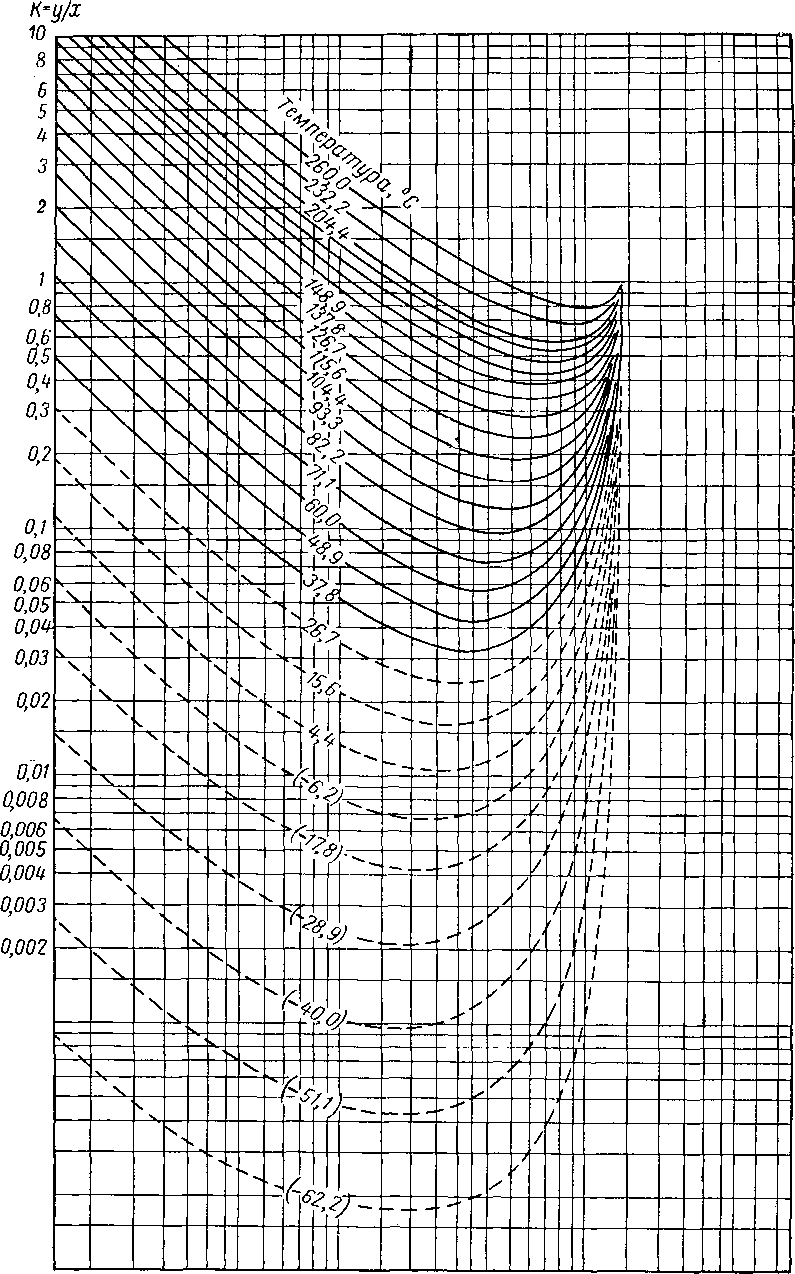
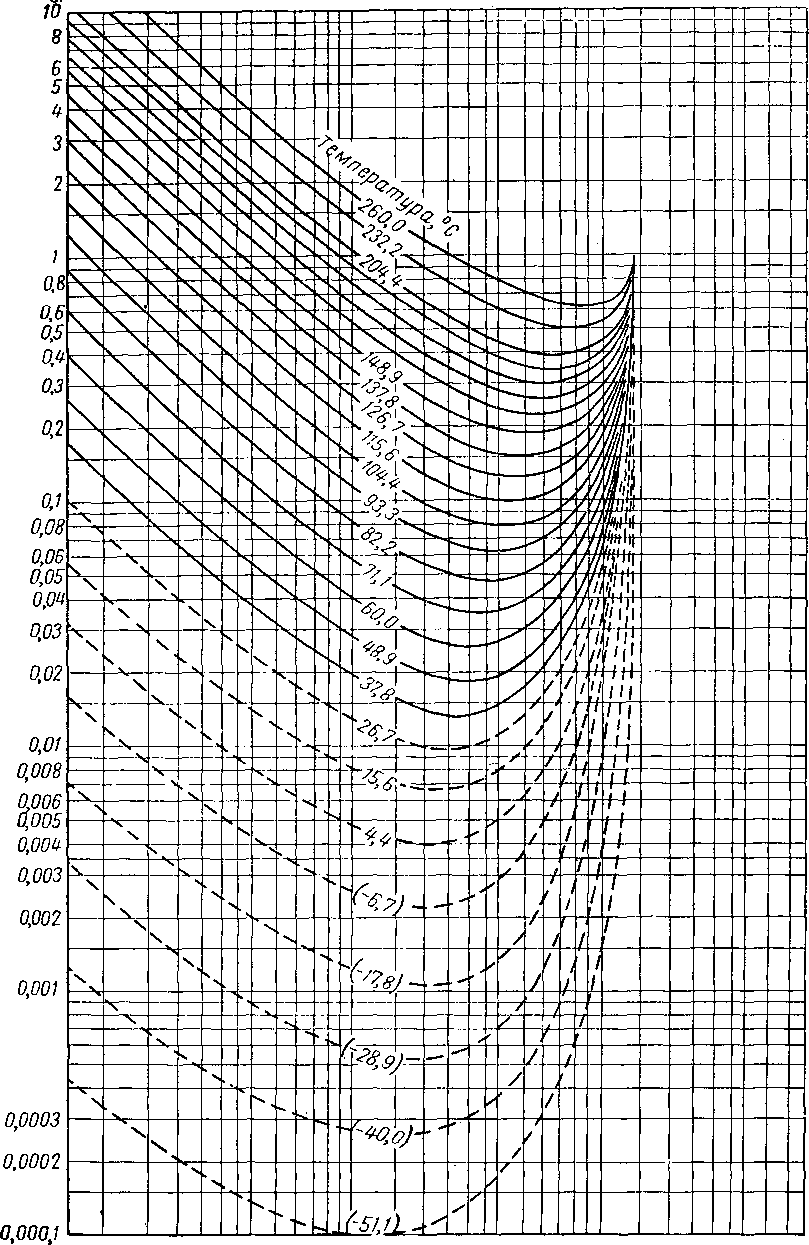
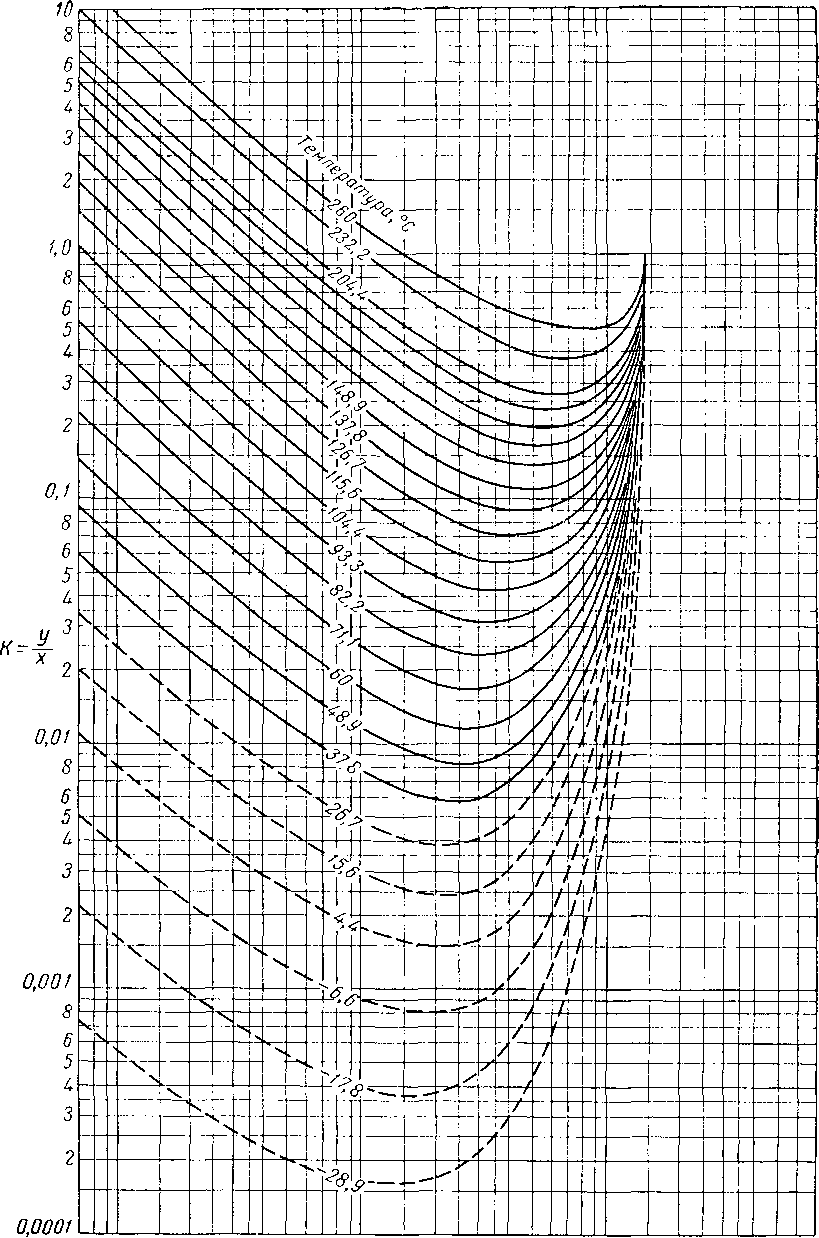
Вычислять давления схождения следует лишь в тех случаях, когда другие расчеты неприменимы. Американская ассоциация газового бензина (NQAA) выпустила сборник диаграмм констант равновесия и кривых давления схождения наиболее часто встречающихся смесей (рис. VI. 51—VI. 53). Диаграммы К при абсолютном давлении схождения, равном 140 ат, для некоторых компонентов природного газа приведены на рис. VI. 54—VI. 66. Имеются также диаграммы абсолютных давлений схождения, равных 42, 56, 70, 210, 280, 350, 700 и 1400 [V. 1].
Для двухкомпонентных смесей термины «давление схождения» и «критическое давление» являются синонимами. Точно так же для многокомпонентной смеси константы равновесия при критической температуре всей смеси будут иметь одно значение при критическом давлении. Проблема заключается в расчете сложных смесей, приближающихся к точке росы по мере повышения давления при постоянной температуре. Данные
Роланда (Roland) [VI. 50] показывают, что по мере приближения к точке росы константы могут и не сойтись и не иметь тенденцию к схождению (рис. VI. 67). Это явление можно отнести за счет присутствия в нефти асфальтенов. Точка росы в их присутствии становится нечеткой, ибо при этом остается пластическая твердая асфальтовая фаза. Отсюда следует, что для сложных систем природного газа и нефти вместо термина «давление схождения» правильнее применять «кажущееся давление схождения», или «корреляционное давление».
350
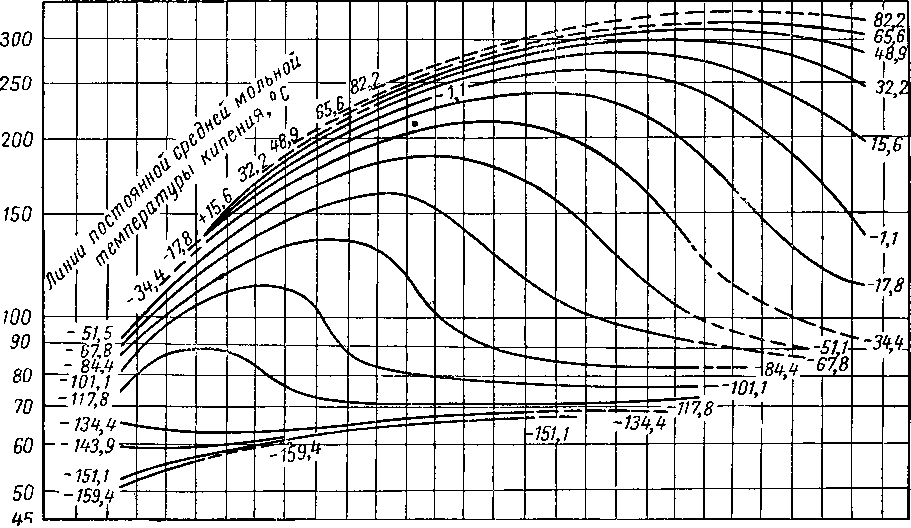
“-70-60 -40 -20 0 20 40 60 80 100 120 W 160 180 200
Температура, °С
Рис. VI. 44. График Келлога: фугетивность для метана при абсолютном давлении, равном 70 [VI, 13].
КОМПОНЕНТЫ С ВЫСОКОЙ ТЕМПЕРАТУРОЙ КИПЕНИЯ
В пластах высокого давления высококипящие компоненты при температуре пласта являются летучими. Гоффман, Крамп и Хокотт (Hoffman, Crump and Hocott) [VI. 27] приводят некоторые характеристики этих высоко-кипящих компонентов в пластовых условиях. Летучесть абсорбционного масла при некоторых условиях характеризуется в работе Веббера (Webber) [VI. 64].
Поттмен и Мейленд (Poettmann and Mayland) вывели корреляцию констант равновесия высококипящих компонентов [VI. 46] на основе диаграммы фугетивности, построенной Киркбрайдом.
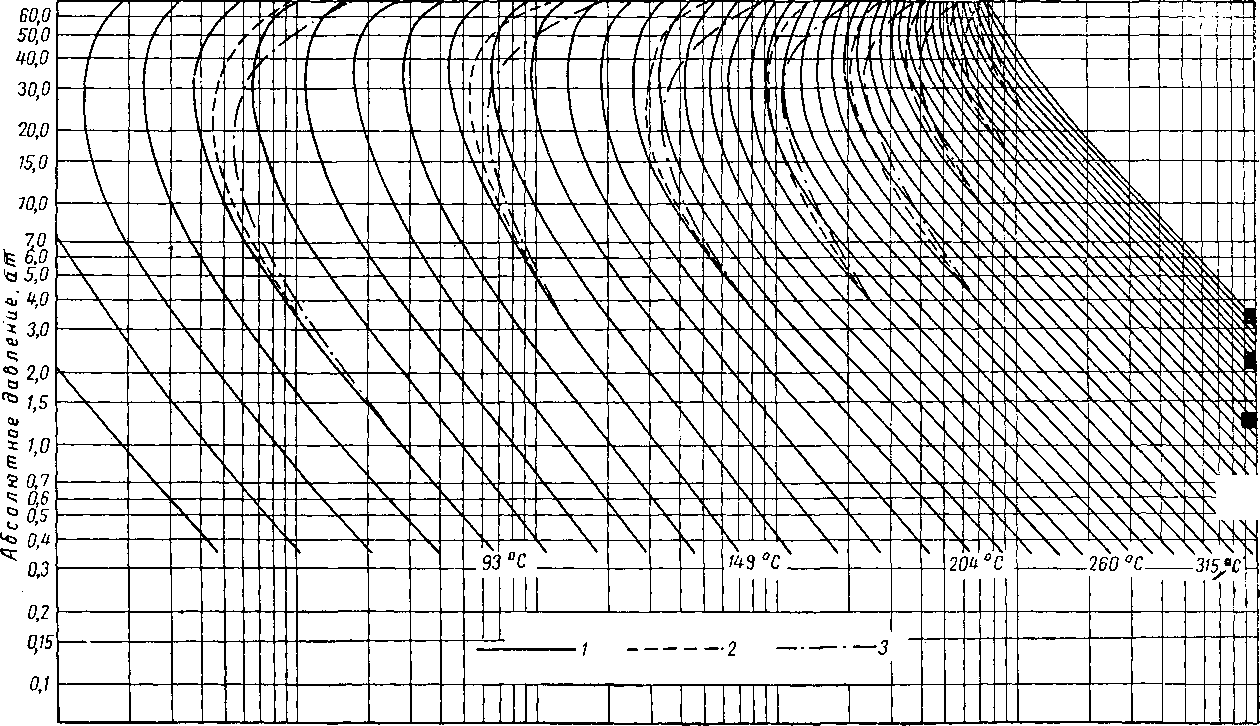
На рис. VI. 68 приведена диаграмма для компонентов с нормальной температурой кипения, равной 260°С. Компоненты рассматриваются раздельно, поскольку характер компонента влияет на давление схождения. На рис. VI. 69—VI. 71 представлены данные Гоффмана, Крампа и Хокотта [VI. 27], совмещенные с диаграммами Поттмена и Мейленда.
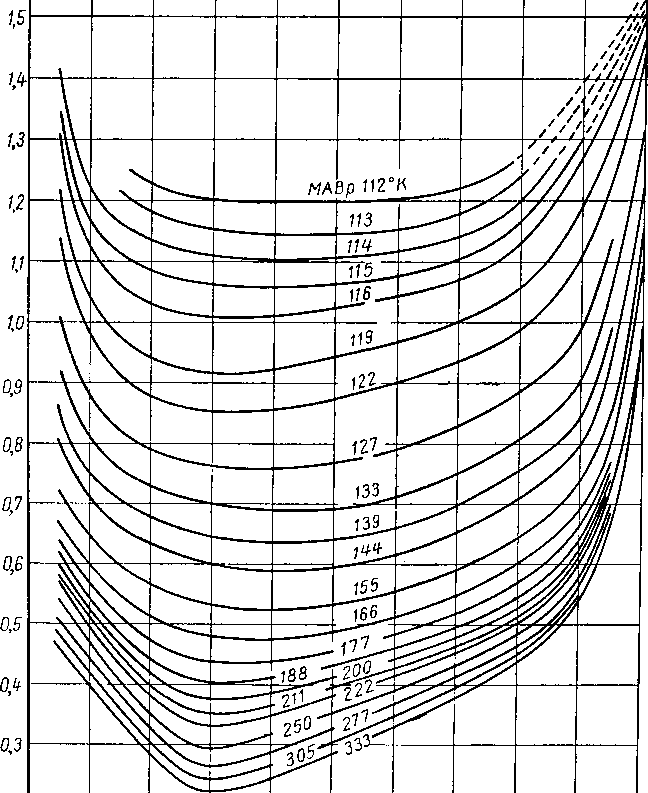
Показатель п
0,2
О 0,1 0,2 0,3 0,4- 0,5 0,6 OP 0,8 0,9 1,0р/рк
Рис. VI. 45. График 1 для определения давления схождения [VI. 37].
Равновесное давление к Корреляционное давление На кривых приведена среднемольная температура кипения паров (МАВР).
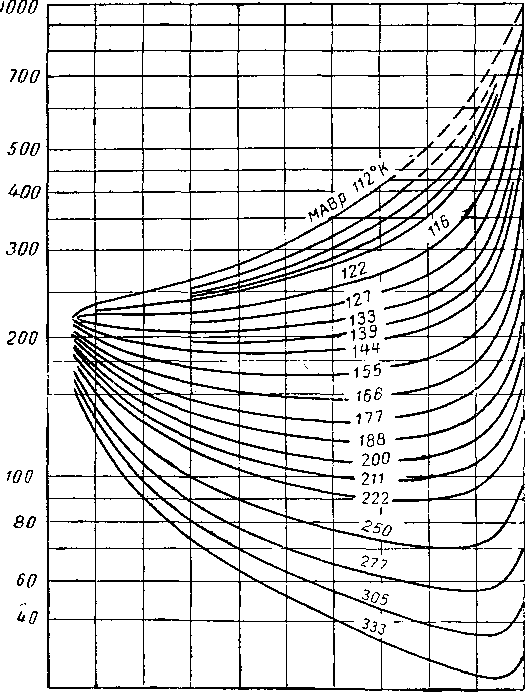
Рис. VI. 46. График 2 для определения давления схождения.
ю
СО
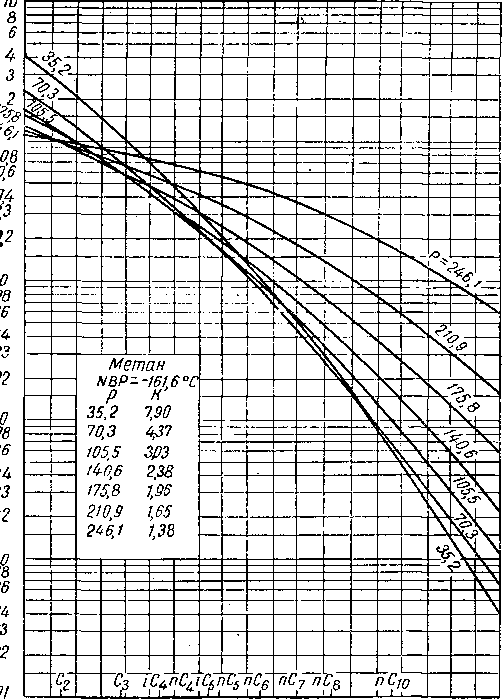
-100 -80 -4-0 0 b-0 80 120 tBO 200 24-0
нормальная температура кипения10 С
Рис. VI. 47. Константы равновесия как функция нормальной температуры кипения компонента при абсолютном давлении схождения, равном 280 кГ/сж2, и температуре 93° С.
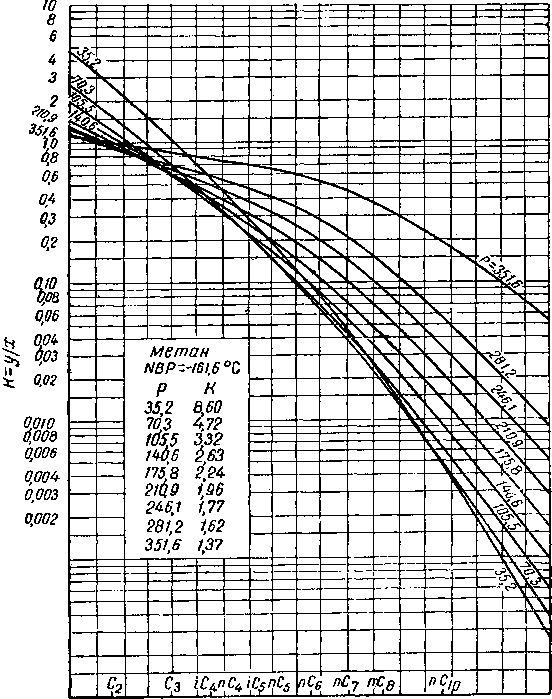
0,0001
-120 -80 -4-0 0 40 80 100 160 200 24-0
Пормольноя температура кипения, °С
опою
0008
0,0006
0,000b
0,0003
00002
Рис. VI. 48. Константы равновесия как функция нормальной температуры кипения компонента при абсолютном давлении схождения, равном 420 кГ/см2, и температуре 93°С.
ooow
0,0008
0,0006
0,0004-
0,0003
0,0002
0.0001
-120 -во -40 0 4О 80 120
iso гоо 2ьо °С
нормальная температура кипения,
Рис. VI. 49. Константы равновесия как функция нормальной температуры кипения компонента при абсолютном давлении схождения, равном 700 кГ/см2, и температуре 93° С.
200 400 600 800 1000
Эквивалентный молекилярнь/й Вес
Рис. VI. 50. Эквивалентные молекулярные веса углеводородов [VI. 37].
80 120 160 Температура,°С
Рис. IV. 51. Давления схождения для типовых смесей в стабилизационной колонне [VI, 40].
Абсолютное давление схождения,am
ЮОО 900 800 7 00 600
500
Ш
3 00
Абсолютное давление схождения,am
160 200 2W
Температура, °С
Рис. VI. 52. Давления схождения для типовых смесей в абсорбционных колоннах [VI. 40].
Абсолютное давление схождения, am
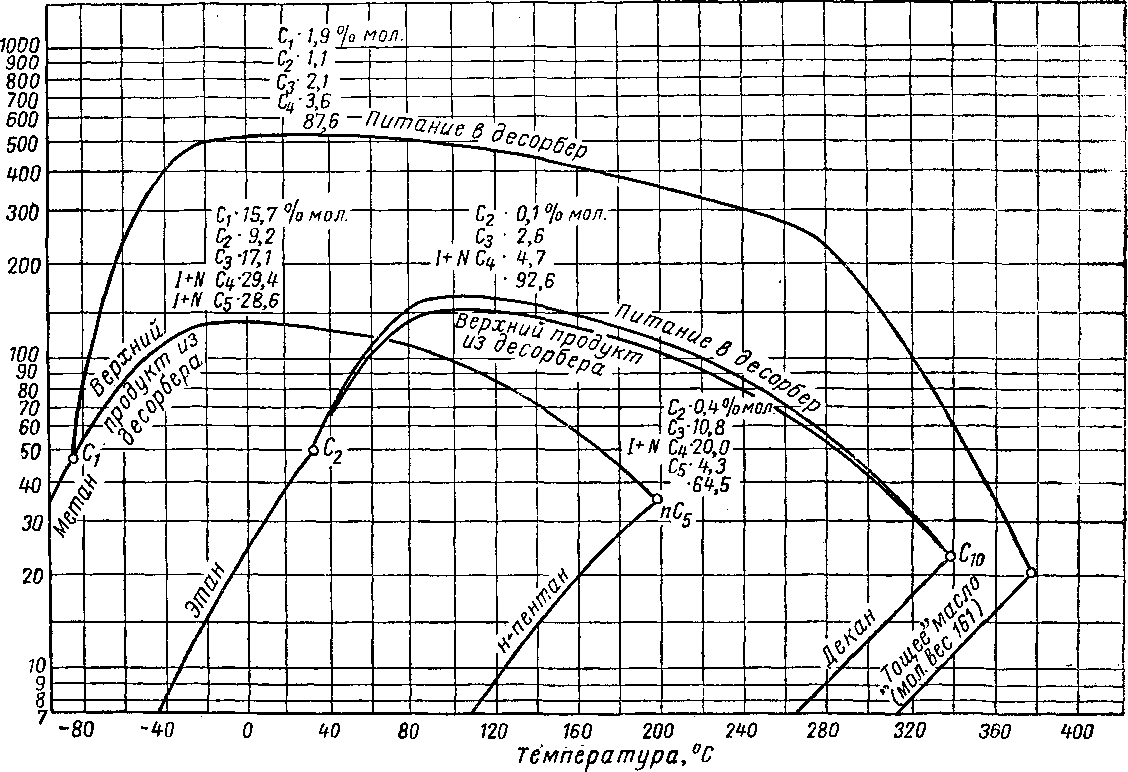
Рис. VI. 53. Давления схождения для типовых смесей в десорбционной колонне [VI. 40].
30 50 70 100 300 500 1000 3000 5000 10000
6 5 U
3 2
W
8
6
5
U
3
2
1,0
8
6
5
2
о;
8
б
5
U
3
0,1
8
6
5
4
3
2
0,001 __________________________________________U
0,7 / 2 3 4 5 6 8 /0 20 30 4-0 60 80 (00 200 300 500 700
0.7 I 2 3 С 5 6 7 8 10 20 30 UO 60 80 WO
Абсолютное давление, am
200 300 500 700
2 J 4 5 6 7 8 10 20 30 UO 60 80100 200 300 500 700
0,0001
0,001
0,0008
0,0006
0,0005
0,0004
0,0003
0,0002
1,0 2,0 3,0 4,05,0 7,0 10,0 20 30 4050 70 1П0 200 300 400 600
1.0 2.0 3,0 if,0 5,0 7,0 10,0 20 30 4050 70 /00
200 300 т 600
0,0008
0,0006
0,0005
0,0004
0,7 t 2 3 U 5 6 78910 20 30 UO 50 70 100 200 300 500
700

1 2 3 4 5 6 7 8 910 20 30 4050 60 80100 200 300 4 00
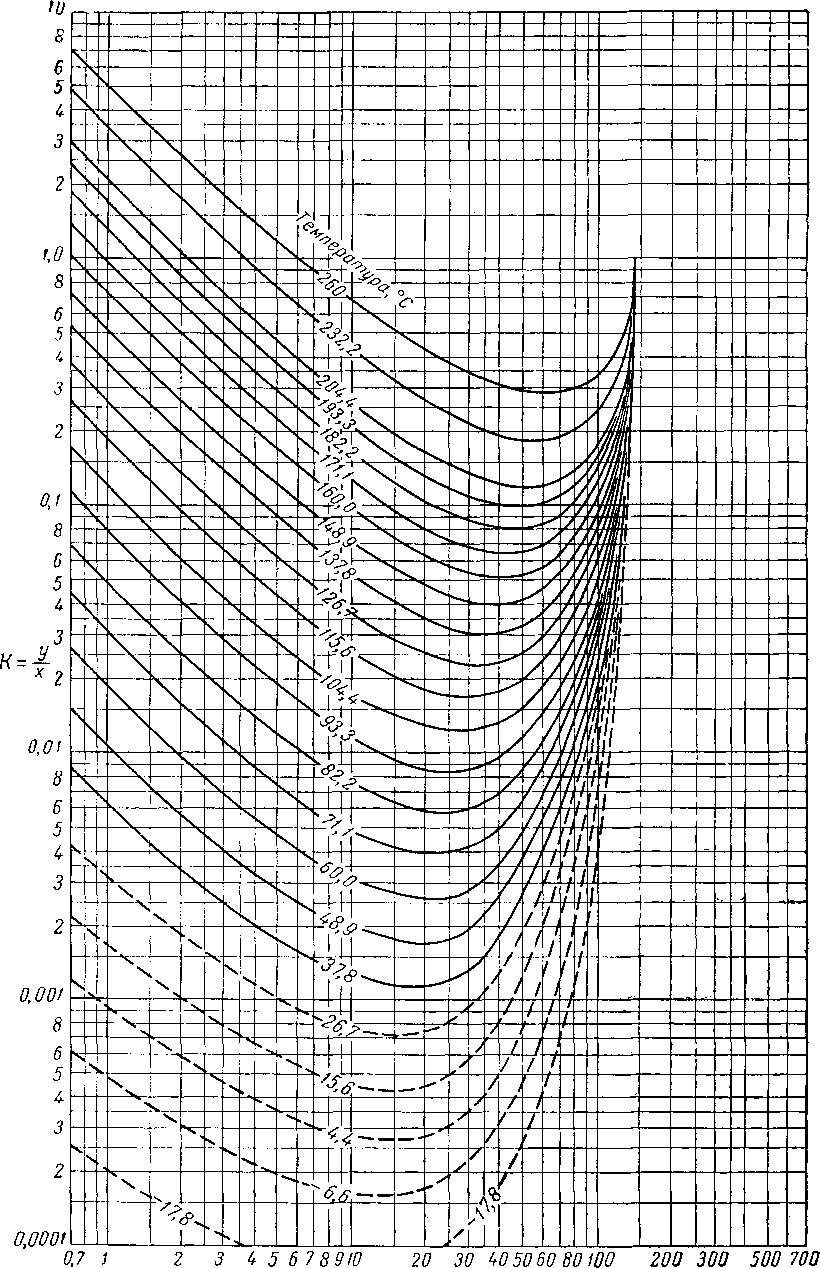
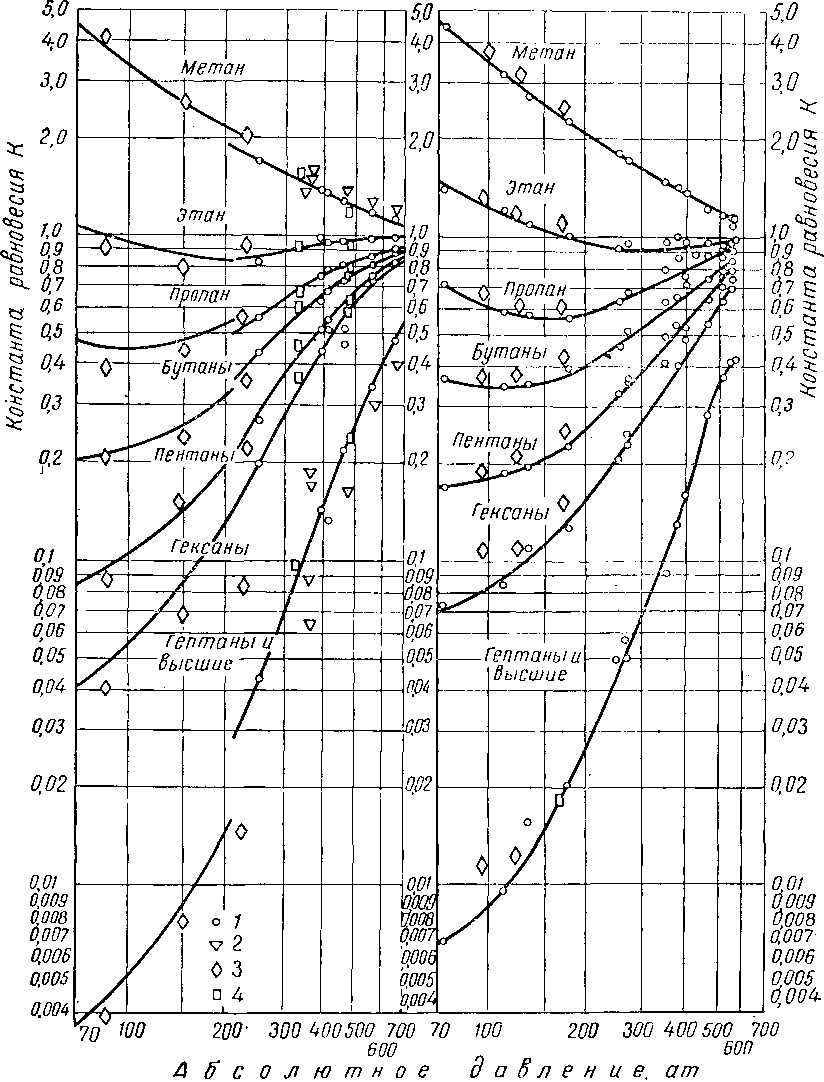
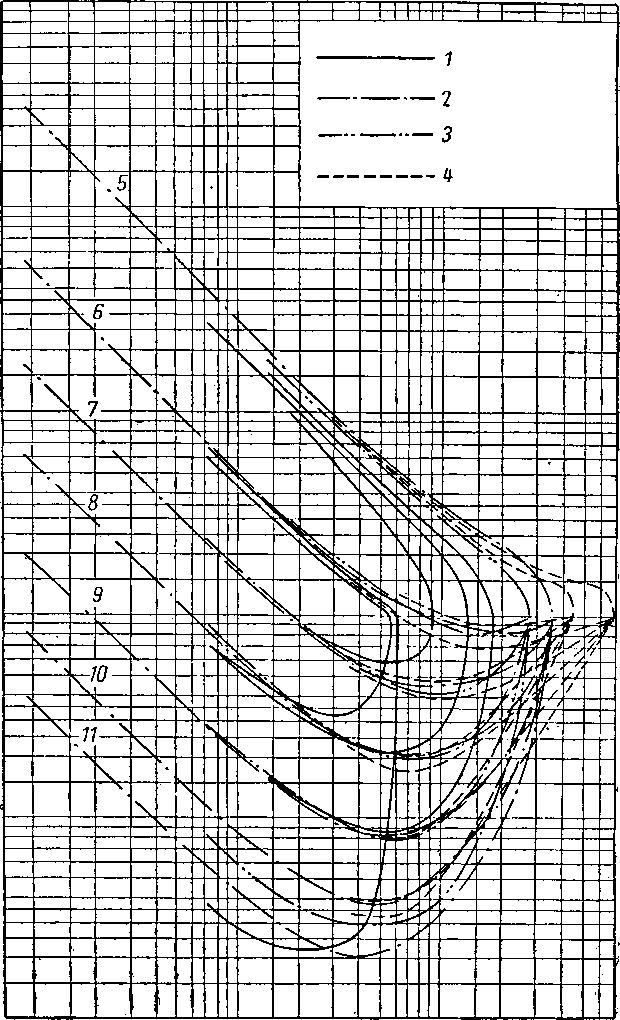
Рис. VI. 67. Константы равновесия для природного газа и нефти из месторождения
Биллингс.
/ — постоянный состав; 2—различные смеси; «У —данные Катца и Хахмуса; 4 — равновесия, полученные при абсолютной упругости паров, равной 656,2 кГ!смЪ
537 °С 482° О
Ц-26 °С
0,0001
0,6 1,0
3,0 6,0 10,0 Kt
0,03 0,06 0,1
0,0003 0,0006 0,001 0,003 0,006 0,01
Рис. VI. 68, График констант равновесия компонентов с нормальной температурой кипения 260° С. Характеристический фактор: / — 10,5; 2—11,5; 3 —12,5.
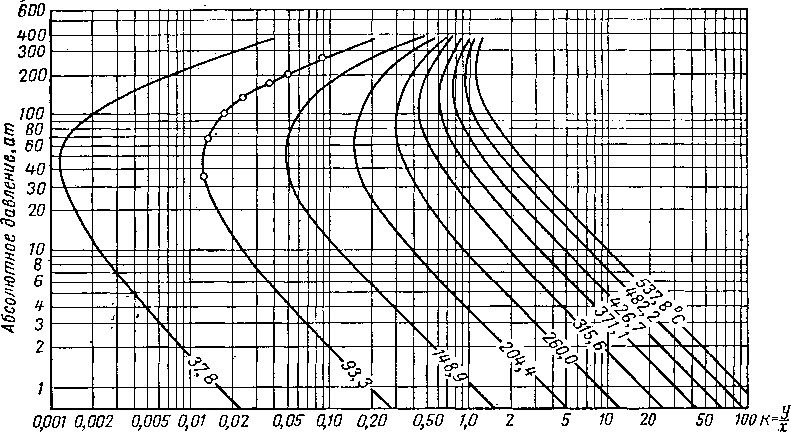
Рис. VI. 69. Константы равновесия компонента с нормальной температурой кипения
N9° С.
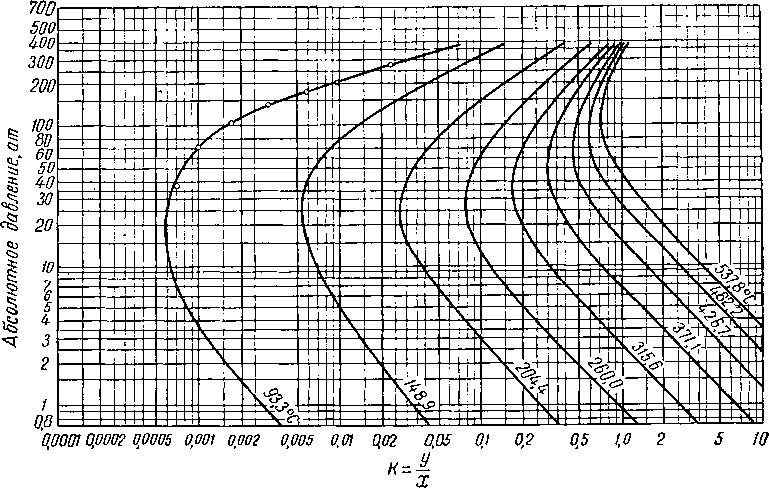
Рис. VI. 70. Константы равновесия компонента с нормальной температурой кипения
0,00010,0002 0,00050,001 0,002 0,005 0,01 0,02 0,05 0,1 0,2 0,5 1,0 2 5 10 К-.
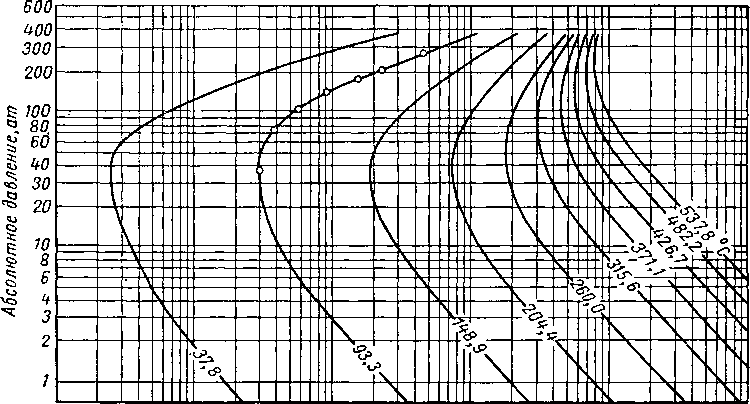
Рис. VI. 71. Константы равновесия компонента с нормальной температурой кипения
204° С.
§ 4. ВЫЧИСЛЕНИЕ РАВНОВЕСИЙ СИСТЕМ ПАР — ЖИДКОСТЬ
Для смесей, состав которых известен, температуру и давление точек начала кипения и точек росы, а также состав фаз смеси в данных условиях можно вычислить по константам равновесия. Количество и состав каждой фазы вычисляют по методу последовательных приближений [VI. 30, 111.27].
Точке начала кипения (или, как ее иначе называют, точка появления первого пузырька) соответствуют температура и давление, при которых сумма членов Кх равна единице:
где К — константа равновесия; х — мольная доля компонента в жидкой фазе; у — мольная доля в паровой фазе.
Таблица VI. 9 Вычисление давления точки начала кипения смеси при 49° С (измеренное абсолютное значение равно 85,75 ат)
|
Компонент | Мольная ДОЛЯ X | Давление 98 ат | Давление 84 ат | ||
| К |
Кх | К |
/С, | ||
| Метан....... | 0,2208 | 3,4 |
0,7507 | 3,9 |
0,8611 |
|
Этан........ | 0,0739 |
0,97 | 0,0716 |
1,02 | 0,0755 |
| Пропан....... | 0,0775 | 0,44 | 0,0341 |
0,44 | 0,0341 |
| Изобутан ..... |
0,0203 | 0,255 |
0,0052 | 0,245 |
0,0050 |
|
н-Бутан...... | 0,0420 |
0,212 | 0,0089 |
0,208 | 0,0087 |
| Изопентан..... |
0,0170 | 0,126 |
0,0021 | 0,115 |
0,0020 |
|
н-Пентан...... | 0,0270 | 0,108 | 0,0029 |
0,10 | 0,0027 |
| Гексан ....... |
0,0477 | 0,056 |
0,0027 | 0,048 |
0,0023 |
| Гептаны ..... | 0,4738 |
0,0051 | 0,0024 |
0,0042 | 0,0020 |
| 0,8806 |
0,9934 |
||||
Примечание. Путем экстраполирования получаем точку начала кипения, при температуре 49° С, равную 83,5 ат.
Вычисление точки начала кипения для газового бензина показано в табл. VI. 9. Мы видим, что величины Кх представляют собой мольные доли в момент появления первого пузырька пара, образовавшегося при равновесии до того, как его образование изменяет состав жидкости.
Точка росы — это температура, при которой образуется первая капля жидкости, и ей соответствуют температура и давление, при которых сумма членов у/К равна единице:
1у/К=1х=1. (VI. 4)
Пример расчета точки росы приведен в табл. VI. 10.
Таблица VI. 10
Вычисление температуры точки росы продукта, отходящего из фракционирующей колонны при абсолютном давлении, равном 9,1 ат
|
Компонент | Мольная доля | 54,4 | ° с | 65,6° С | |
| К | у/к |
к | У/К | ||
| 0,025 |
1,85 | 0,0135 |
2,2 | 0,0144 | |
| Изобутан ..... | 0,904 | 0,88 | 1,2730 | 1,1 | 0,8218 |
| н-Бутан...... |
0,071 | 0,65 |
0,109 | 0,83 |
0,0085 |
| 1,3955 | 0,8417 | ||||
Примечание. Путем интерполяции находим, что температура точки-росы при 9,1 ат равна 62,6° С.
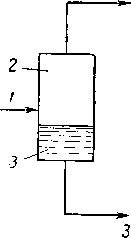
Равновесное или однократное испарение можно рассчитать для тех смесей, которые при определенных температуре и давлении разделяются на две фазы (рис. VI. 72). При этом весь пар находится в равновесии со всей жидкостью. Установление равновесия может иметь характер непрерывного или периодического про-
Подставляя значение х из (VI. 5) в (VI. 7), получим zF=-^L + yV. (VI. S)
При F = 1
Если числитель и знаменатель умножим на К и разделим их на V, то
Кг
zF
У —
L/K+V- V K + L/V
Кг
У—'
(*-1)1/+1 Для всех компонентов
F Кг V' K + L/V
Аналогично, подставляя значение (VI. 7), получим
F г г
х
1у= 1 = Х-
I ' К +L/V- (/С — 1) V + 1 •
Кг
V-X K + LjV -^K + LlV . (VI. 14)
Зная состав исходной смеси и константы равновесия для избранных температуры и давления, задаемся величиной V. Чтобы определить, правильно ли взята эта величина1 вычисляем
Mz/(K+L/V) или lz/(K+L/V).
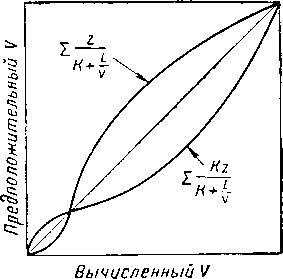
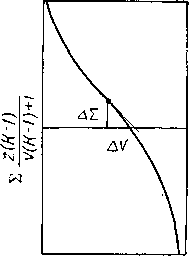
Диаграмма принятых и вычисленных величин V приведена на рис. VI. 73. Следует отметить, что кривые приближаются к начальной точке, даже если правильное решение находится где-то вдоль линии, проходящей под углом 45°. Пример расчета приведен в табл. VI. 11. Иной путь решения также по методу последователь-(VI. 7) ных приближений получаем при другом сочетании урав-
цесса. Ниже приводятся уравнения для расчета по методу последовательных приближений количества образующегося пара и жидкости и соответственно состава пара и жидкости.
Обозначим F — число молей исходной смеси; V — число молей пара; L — число молей жидкости, находящейся в равновесии; г — мольная доля компонента в исходной смеси; х— мольная доля компонента в жидкости; у — мольная доля компонента в паре; i — любой компонент.
По равновесию
— =Kl. CVI- 5)
Х1
По общему материальному балансу
F=L+V. (VI. 6)
По материальному балансу данного компонента
Рис. VI. 72. Равновесное испаре- Рис. VI. 73. Решение уравнения
ние при постоян- равновесного испарения,
ных температура и дазлении.
1 —исходная смесь [г]; 2 — пар; 3 — жидкость.
zF — xL + yV.
(VI. 9)
(VI. 10)
(VI. 11) у в уравнение
(VI. 12)
Х*= 1 = 2-у- д._|_ L/v . (VI. 13)
Пусть F— 1 моль, тогда по уравнениям (VI. 11) и
(VI. 13)
Таблица VI. 11
Пример решения задачи на равновесное испарение. Вычислить количества жидкости и пара и определить их состав при однократном испарении данной смеси при абсолютном давлении,
равном 112 am и 48,9° С
| Компонент |
Мольная доля в | К при абсолютном давлении 112 am и 48,9° С | Предполагаем V = 0,9009 | Предполагаем V = 0,885 | Мольная доля | |||
| смеси г | К+0,11 | гЦК+LV) | К + 0,13 |z/(K+L/V) | (жидкость) |
У (пар) | |||
|
Двуокись углерода . |
0,0046 | 1,65 |
1,76 | 0,0026 |
1,78 | 0,0026 |
0,0029 | 0,0048 |
| Метан....... | 0,8345 | 3,09 | 3,20 |
0,2603 | 3,22 |
0,2595 | 0,2943 |
0,9050 |
|
Этан........ | 0,0381 |
0,72 | 0,83 |
0,0459 | 0,85 |
0,0449 | 0,0510 |
0,0360 |
| Пропан ...... | 0,0163 |
0,39 | 0,50 |
0,0326 | 0,52 |
0,314 | 0,0356 |
0,0137 |
|
Изобутан...... | 0,0050 | 0,21 | 0,32 |
0,0156 | 0,34 |
0,0147 | 0,0167 |
0,0035 |
| к-Бутап ...... | 0,0074 |
0,175 | 0,285 |
0,0422 | 0,305 |
0,0242 | 0.0275 |
0,0048 |
| Пентаны ...... | 0,0287 |
0,093 | 0,203 |
0,1413 | 0,223 |
0,1288 | 0,1463 |
0,0134 |
|
Гексаны...... | 0,220 |
0,065 | 0,175 |
0,1258 | 0,195 |
0,1130 | 0,1283 |
0,0083 |
| Гептаны ...... | 0,0434 |
0,036 | 0,146 |
0,2970 | 0,166 |
0,2620 | 0,2974 |
0,0105 |
| Всего. . . | 1,000 |
0,9633 | 0,8811 |
1,0000 | 1,0000 |
|||
Примечание. Путем экстраполяции получим С, « 196; удельный вес С, + = 0,850.
V г= 0,887 мол, пара, Z, = 113 мол. жидкости. Молекулярный вес
Пример вычисления равновесного испарения методом повторных попыток (метод Ньютона)
| Предполагаем V | = 0,80 | Г1 редполагаем |
V = | 0,913 | |||||||||||||||
| Компонент | Моль ная доля | К при абсолютном давлении, равном 112 ат и 48,9* С | К— 1 | г(К- 1) | г (К - 1)“ | V (К- 1) | V (К- 1)+ 1 | 1 N | + 1 ? |
+ 1 | 1 | + 1 < | V, (К- 1) |
+ 1 | 1 N |
+ 1 | + 1 * |
1 N | + 1 |
| Двуокись углерода .... | 0,0046 | 1,65 |
0,65 | 0,00299 |
0,00194 | 0,52000 |
1,52000 | 0,00197 |
2,3104 | 0,00084 | 0,59345 | 1,59345 | 0,00188 |
2,53908 | 0,00076 |
||||
| Меган . . . |
0,8345 | 3,09 |
2,09 | 1,74411 |
3,64518 | 1,67200 |
2,67200 | 0,65273 |
7,13958 | 0,51055 | 1,90817 | 2,90817 | 0,59972 |
8,45745 | 0,43100 |
||||
| Этан .... |
0,0381 | 0,72 |
—0,28 | —0,01668 |
0,00467 | —0,22400 |
0,77600 | —0,02149 | 0,60218 |
0,00776 | —0,25564 |
0,74436 | —0,02241 | 0,55407 |
0,00843 | ||||
| Пропан . . | 0,0163 |
0,39 | —0,61 |
—0,00991 | 0,00605 |
—0,48800 | 0,51200 | —0,01935 | 0,26214 | 0,02308 |
—0,55693 | 0,44307 | —0,02237 | 0,19631 | 0,03082 | ||||
|
Изобутан . . | 0,0050 |
0,21 | —0,78 |
—0,00390 | 0,00304 |
—0,62400 | 0,37600 |
—0,01037 | 0,14138 | 0,02150 |
—0,71214 | 0,28786 | —0,01355 | 0,08286 | 0,03669 | ||||
|
к-Бутан . . | 0,0074 |
0,175 | —0,825 |
—0,00611 | 0,00504 |
—0,66000 | 0,34000 |
—0,01797 | 0,11560 | 0,04360 |
—0,75323 | 0,24677 | —0,02476 | 0,06089 | 0,00828 | ||||
|
Пентаны . . | 0,0287 |
0,093 | —0,907 |
—0,02603 | 0,02361 |
—0,72560 | 0,27440 |
—0,09486 | 0,07530 | 0,31354 |
—0,82809 | 0,17191 | —0,15142 | 0,02955 | 0,79898 | ||||
|
Гексаны . . | 0,0220 |
0,065 | —0,935 |
—0,02057 | 0,01923 |
—0,74800 | 0,25200 |
—0,08163 | 0,06350 | 0,30283 |
—0,85366 | 0,14634 | —0,14056 | 0,02142 | 0,89775 | ||||
|
Гептаны + . | 0,0434 |
0,036 | —0,964 |
—0,04184 | 0,04033 |
—0,77120 | 0,22880 |
—0,18287 | 0,05235 | 0,77039 |
—0,88013 | 0,11987 | —0,34904 | 0,01437 | 2,80654 | ||||
| 0,22616 | 1,99409— | —0,12251 |
5,01925 | ||||||||||||||||
V2 = 0,8 +
0,22616
1,99409 V2 = 0,8 + 0,1134 V2 = 0,913
l/„ = 0,913 .
0,12251
5,01925 Va = 0,913 — 0,0244 Va = 0,8886
Продолжение табл. VI. 12
| Компонент |
Предполагаем |
V = 0.8886 |
Предполагаем V ~ 0, | 8848 | ||||||
| V, (К - 1) | Vs (К - 1) + 1 |
г (К - 1) | IV (Л - 1)+ 13* | г (К - I)2 |
И* (/С—1) | IMK-D + 1 |
г (К- !) | Мольн X | ая доля У (пар) (жидкость) | |
| V (К — \ | [V (К- 1) + ip | V (К — 1) + 1 | ||||||||
| Двуокись углерода . . . |
0,57759 | 1,57759 |
0,00189 | 2,48879 |
0,00078 | 0,57511 |
1,57511 | 0,00189 |
0,00292 | 0,00482 |
| Метан......... |
1,85717 | 2,85717 |
0,61043 | 8,16342 |
0,44652 | 1,84921 |
2,84921 | 0,61213 |
0,29289 | 0,90503 |
| Этан ......... |
—0,24881 | 0,75119 |
—0,02220 | 0,56428 |
0,00828 | —0,24774 |
0,75226 | —0,00217 |
0,05065 | 0,03647 |
| Пропан........ |
—0,54205 | 0,45795 |
—0,02164 | 0,209718 |
0,02885 | —0,53972 |
0,46028 | —0,02153 |
0,03541 | 0,01381 |
| Изобутан....... |
—0,69311 | 0,30689 |
—0,01271 | 0,094181 |
0,03228 | —0,69014 |
0,31968 | —0,01219 |
0,01563 | 0,00328 |
| «-Бутан........ |
—0,73310 | 0,26690 |
—0,02289 | 0,07123 |
0,07076 | —0,72995 |
0,27005 | —0,02263 |
0,02740 | 0,00479 |
| Пентаны........ |
—0,80596 | 0,19404 |
—0,13415 | 0,03765 |
0,69709 | —0,80250 |
0,19750 | —0,13179 |
0,14532 | 0,01351 |
| Гексаны........ |
—0,83084 | 0,16916 |
—0,12160 | 0,02862 |
0,67190 | —0,82728 |
0,17272 | —0,11909 |
0,12737 | 0,00828 |
| Гептаны +....... |
—0,85661 | 0,14339 |
—0,29179 | 0,02056 |
1,96157 | —0,85294 |
0,14706 | —0,28451 |
0,29512 | 0,01062 |
| —0,01466 | 3,84803 | 0,00011 | ||||||||
V = 0,8886 —
0.01466
3,84803
V = 0,8886 — 0,00381
V = 0,88479
V = 0.8848
0
(VI. 16)
1,0
dV
нений (VI. 5), (VI. 6) и (VI. 7). Если вычтем уравнение (VI. 12) из (VI. 11), то получим
z(K— ])
. (VI.lt,
Если V определена верно, правый член уравнения [VI. 15] равен нулю.
Выбор величины V основан на определении угла наклона кривой при первоначально заданной величине V (рис. VI. 74). Угол наклона кривой при V получаем, дифференцируя по V выражение г(К- 1)
г (К— I)2
Величина z(K—l)/[V(K—1) + 1], полученная при первой попытке, и угол наклона кривой позволяют вычислить Л V, которую приплюсовывают к величине, заданной при первой попытке:
[V (K — 1) + l]2 '
•V(K- 1)+ 1
= X
Рис. VI. 74. Решение уравнения равновесного испарения (VI. 15) по методу Ньютона.
Профиль кривой может отклоняться от прямой линии между первой и второй точками (рис. VI. 74) и для получения точного ответа может понадобиться третья попытка. Величину V3 получаем из V2 точно так же, как V2 была получена из V|. Пример подобного решения приведен в табл. VI. 12,
. z(*-l)
' V(K- 1)+1
. z(/C-l)2 ¦
' IV/ (iC— 1) + l]2
(VI. 17)
Дифференциальное испарение отличается от равновесного однократного испарения тем, что пар в момент его образования выходит из контакта с жидкостью. Образование пара при этом дифференциальном процессе вызывается изменением температуры или давления. Каждое новое увеличение количества образовавшегося пара (dW) изменяет состав жидкости, вследствие чего изменяется и равновесное давление или температура, если только парообразование на этом не прекращается.
§ 5. ДИФФЕРЕНЦИАЛЬНОЕ ИСПАРЕНИЕ
Интегрируя это выражение, получаем !п (xf/x0)
(VI. 21)
К—I
K-l
(VI. 22)
(VI. 23)
(VI. 24) (VI. 25)
1
Расчеты дифференциального испарения ведутся на основе материального баланса, в котором количество компонента во вновь образовавшемся паре уравнивается с уменьшением количества этого компонента в жидкости в соответствии с уравнением
ydW = Wx — (W — dW) (x— dx), (VI. 18)
где W — число молей жидкости; * — мольная доля данного компонента в жидкости; у — мольная доля данного компонента в паре.
Раскрывая скобки, опуская dWdx и подставляя у = = Кх. получаем
xdW + Wdx = KxdW. (VI. 19)
После преобразования и интегрирования при допущении, что К — const, получим
I
CdW № ~К
(VI. 20)
Индекс 0 — первоначальное состояние и индекс f — окончательное состояние.
1-я попытка
|
Компонент | (Х‘)о | Принятое wf |
Принятое Рте. ата |
Кп | Кп~ 1 | 1 С * 1 | (*<)/ |
К (допускаем, что абсолютное давление равно 21,09) | i»t)f |
| С! | 0,1113 | 0,805 | 27,07 |
6,19 | 5,19 |
0,3245 | 0,0361 |
8,13 | 0,2935 |
| С3 | 0,8887 |
0,805 | 27,07 |
0,617 | —0,383 |
1,0865 | 0,9640 |
0,720 | 0,695 |
X = 0,9885
2-я попытка
Q 0,1113 0,8120 27,07 6,19 5,19 0,3395 0,0378 8,13 0,307
С3 0,888? 0,8120 27,07 0,617 —0,3831 1,0828 0,962 0,720 0,693
268 2 = 0,9998 ?=1,000
W о
h
In
Xo
W,\K-
-1 =1 X() 1^0/
В конце вычисления у нас будет
Х.*^ = 1,
lKfxi = 1.
Пример
Какое количество пара нужно дифференциально удалить при постоянной температуре (37,8° С) для того, чтобы получить жидкость с абсолютным давлением точки начала кипения, равным 21,1 ат, из жидкости, состоящей из 11,13% мол. метана и 88,87% мол. пропана. Точке начала кипения жидкости соответствует абсолютное давление, равное 33 ат при 37,8° С.
Решение
Применяем величины К из рис. III. 31.
Поэтому нужнс дифференциально испарить 18,8% жидкости.
Аналогичные уравнения можно вывести, заменив К отношением Kn/Ki- Таким образом, для приведенного
выше уравнения К не должно быть постоянным, но отношение величин К должно быть приблизительно постоянным. Если соотношение величин К значительно колеблется в том интервале давления или температур, в котором происходит испарение, вычисления нужно разбить на ряд этапов. Точность вычисления всегда можно проверить, произведя одни и те же расчеты сначала в один этап, а затем разделив их на два или больше этапов.
Пример
Определить конечное давление, необходимое для дифференциального испарения 25% мол. смеси, состоящей при температуре 37,8°С из 32% мол. метана и 68% мол. пропана. Точке начала кипения соответствует абсолютное давление, равное 70,3 ат.
Решение
Применяем величины К из рис. III. 31
Первая попытка Допускаем, что абсолютное давление рте— 63 ат.
|
fr" X | ||||
| X о с я о X |
кп |
Кп~ 1 | (We \ Кп-\ | (xi)> |
| С, |
2,295 | 1,295 |
0,6890 | 0,2205 |
| 0,511 | —0,489 | 1,1510 | 0,783 |
X = 1,0035
Вторая попытка Принимаем 'абсолютное давление равным рте =
= 62 ат.
| fr" X а> X | / 1 Кп— 1 |
(xiV | |||
|
о с 2 О * | (*<% |
Кп | кп- 1 | !^) | |
| 0,320 | 2,350 | 1,350 | 0,678 |
0,217 | |
| ^3 | 0,680 | 0,510 |
—0,490 | 1,1515 |
0,783 |
Определяем конечное давление путем вычисления точки начала кипения конечной жидкости.
Первая попытка Предположим, что абсолютное давление pf- = 56 ат.
| Компо нент |
К-п | («IV |
| Cl | 2,66 |
0,576 |
| С3 | 0,50 | 0,3915 |
S = 0,9675
Вторая попытка Предположим, что абсолютное давление р( =54 ат.
| Компонент | (у i)1 | |
| Cl | 2,805 | 0,6085 |
| Сэ | 0,500 | 0,3915 |
| 2 = 1,0000 | ||
|
Р те — среднее давление; |
||
Pf — конечное абсолютное давление, равное 54 ат.
§ 6. ПРИМЕНЕНИЕ ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН ДЛЯ РАСЧЕТОВ ИСПАРЕНИЯ
Расчеты испарения можно вести при помощи логарифмической линейки, однако этот метод очень трудоемок, а результаты получаются неточные. Настольные счетные машины повышают точность результатов, но все же расчеты остаются весьма трудоемкими. Поэтому для расчетов испарения, связанных с многочисленными повторениями большого числа сложных вычислений, все шире применяются цифровые электронные вычислительные машины [VI. 39, VI. 48, VI. 36, VI. 16].
Цифровая электронная вычислительная машина [VI. 7, VI. 28, VI. 66, VI. 15, VI. 5, VI. 4] производит арифметические действия с очень большой скоростью, превышающей 100 000 действий в секунду. В машину вводят исходные данные и команды с перфокарты или перфорированной ленты, которые она запоминает, затем она может выполнять команды по заданной программе. По существу машина может только складывать и сравнивать число с нулем. Все вычисления могут быть сведены к арифметическому действию сложения. Результаты вычислений, хранимые в ячейках памяти, печатаются в виде таблиц или же выдаются машиной в виде перфокарт или ленты.
Вопрос об использовании цифровой вычислительной машины для определенных расчетов решается двумя факторами: машинным временем с программированием и числом вычислителей, которые нужно привлечь для выполнения данных расчетов.
Стоимость аренды электронно-вычислительных машин очень высока. Поэтому затраты должны быть оправданы повышением точности и ускорением расчетов. Необходимо также учесть затраты на подготовку или программирование данной задачи для вычислительной машины. Если требуется решить задачу только для одного набора условий, требующего составления специальной программы, или же если задача имеет единственное решение, то использование вычислительных машин может оказаться неэкономичным. Однако, когда требуется решить задачу для большого числа условий, расходы по программированию обычно невелики, поскольку для каждого последующего решения (после первого) необходимо только включить в первоначальную программу новые исходные данные без до. полнительной подготовки.
Уже из этих кратких предварительных замечаний видно, что многие проблемы нецелесообразно решать при помощи электронно-вычислительной машины, при использовании которой все переменные должны быть связаны посредством математических уравнений или сведены в таблицы. Если подобные уравнения (или их приемлемые приближения) трудно получить, следует рассмотреть вопрос о применении моделирующих устройств. Но, несмотря на эти ограничения, вычислительные машины все более широко применяются при инженерных расчетах. Ниже рассматриваются принципы работы, относящиеся ко всем электронно-вычислительным машинам и лишь в отдельных случаях только к машинам модели «Дататрон» [VI. 4].
Вначале следует выполнить программирование — подготовку задачи для решения. При применении вычислительных машин для стандартных экономических и статистических вычислений одну и ту же программу вводят в машину периодически, что обеспечивает оптимальное использование вычислительной машины. Наоборот, при научных и инженерных расчетах составление такой программы, которая обеспечивала бы оптимальное использование вычислительных машин, потребовало бы слишком больших затрат времени квалифицированных работников и не оправдало бы себя. Хотя программы для большей части инженерных расчетов и не дают оптимального использования вычислительных машин, они обеспечивают оптимально возможное сочетание использования машинного времени и работы программистов. Фактически проектировщики могут составить программу для необходимых им расчетов, даже не будучи особенно компетентными 8 устройстве самой машины. После небольшой практики легко можно составить такую программу, которая позволила бы сэкономить время загрузки вычислительной машины.
Научиться программированию нетрудно, ибо всякий, кто решал ту или иную задачу, фактически уже программировал ее. Программирование сводится по существу к написанию инструкции по решению данной задачи для расчетчика, не знающего ни математики, ни инженерного дела, не. '-меющего пользоваться настольной вычислительной машиной. Поскольку наблюдается тенденция к использованию одноадресных электронно-вычислительных машин с хранимой в памяти программой, в данном разделе будут рассматриваться машины этого класса. Изменить программу для двухадресной машины нетрудно, по существу двухадресная машина может использоваться как одноадресная. Программист может рассматривать вычислительную машину просто как так называемый «черный ящик» и в основном не обращать внимания на детали механизма, выполняющего вычисления. Устройство электронно-вычислительных машин описывается здесь лишь в объеме, необходимом для выполнения программистом его работы.
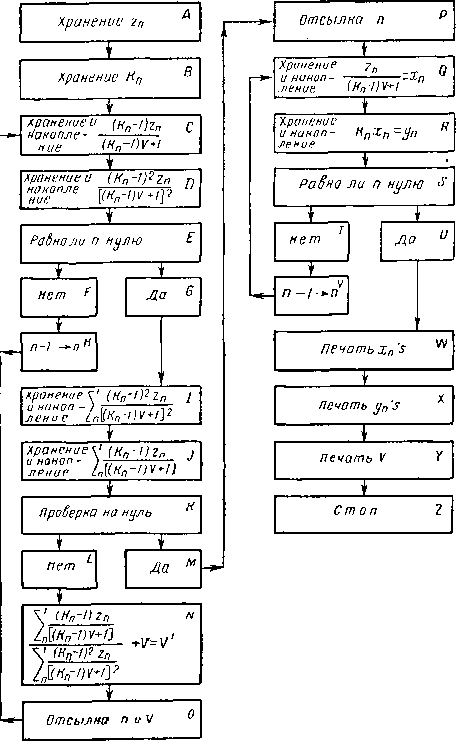
ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО ИЛИ ПАМЯТЬ
Вычислительная машина имеет ряд ячеек памяти, в которые можно помещать команды или исходные данные. Эти ячейки последовательно пронумерованы; одной из задач программиста является регистрация содержания каждой из ячеек. Когда в ячейку вводится какая-либо информация, автоматически стирается находившаяся в ней информация. Однако перевод исходных данных или команд иа ячейки памяти в вычислительное устройство не изменяет хранимой в ячейке информации. Номер каждой ячейки памяти называется «адресом» этой ячейки. Вычислительная машина выполняет команды, хранимые в ячейках памяти, в последовательности, определяемой их адресами, если только она не получает приказ изменить первоначальную последовательность команд.
РЕГИСТРЫ И КОД
Программист должен также знать, что арифметическое устройство вычислительной машины имеет ряд регистров, где числа, над которыми производятся действия, появляются на различных этапах вычислений. Эти регистры аналогичны имеющимся у настольной счетной машины. Действия, производимые над числами этими регистрами, почти сходны с соответствующими действиями настольных счетных машин, но с одним важным исключением: ответ всегда появляется в одном и том же регистре. Этот регистр имеет в 2 раза больше разрядов, чем любая ячейка памяти, плюс знаковый разряд. При сложении числа ответ (или сумма плюс знаковый разряд) появляется на левой половине регистра. Когда число в этом регистре умножается на другое число, взятое из памяти, произведение плюс знаковый разряд занимают весь регистр. С другой стороны, когда число в этом регистре делится на число, взятое из памяти, частное плюс знаковый разряд появляются в левой половине регистра, а остаток в правой. Этот регистр для удобства разделен на две части. Левую часть, или ответную, называют регистром А. Правую часть, где после деления появляется остаток, называют регистром R. Число, прежде чем над ним может производиться какое-либо действие, должно находиться в регистре А. После выполнения действия ответ автоматически появляется в некоторой форме в регистрах А и R и над ним можно производить последующие действия. Если сумма двух чисел имеет большое число цифр, не помещающихся в регистре А, регистр отбрасывает разряды, находящиеся справа. Это отбрасывание опять-таки аналогично действию настольного счетного устройства с тем исключением, что электронно-вычислительная машина в данном случае автоматически остановится и вспыхнет световой сигнал, означающий, что произошло «переполнение». Поэтому данные следует располагать в каждой ячейке памяти или в регистре А так, чтобы предотвратить возникновение «переполнения». Некоторые вычислительные машины имеют другие регистры, которые могут значительно облегчить задачу программиста, но рассмотрение их выходит за границы этого элементарного изложения, Регистр А и каждая ячейка памяти содержат несколько цифровых разрядов плюс знаковый разряд. Эти цифровые разряды в совокупности со знаковым разрядом называются кодом. Код для большинства вычислительных машин состоит из десяти цифровых разрядов и знакового разряда. Длина кода является фактором, определяющим число цифр, над которыми производятся действия.
Рис, VI. 75. Блок-схема вычислений на цифровой вычислительной машине.
Электронно-вычислительная машина рассматриваемого типа имеет ряд ячеек памяти, в которые можно поместить один код информации. Коды, вводимые в вычислительную машину, могут представлять собой либо команды, либо числа. Числа следует размещать в разрядах кода так, чтобы положение десятичной запятой было связано с положением десятичной запятой других используемых чисел. Кроме того, каждому из исходных данных должка соответствовать своя ячейка памяти или адрес.
(VI. 28) (VI. 29) (VI. 30)
F'
После того как все исходные данные получили свои адреса, составляют блок-схему, показывающую в деталях отдельные этапы вычисления (рис. VI. 75). Для примера запрограммируем вычисления контактного испарения с использованием метода, демонстрирующего возможности вычислительных машин.
Уравнение (VI. 15) для расчета испарения имеет форму, удобную для решения его на электронно-вычислительной машине:
^y-'Zx =
'Lyf^-)l)+l =F(V) = 0.
В качестве отправной точки используем график правого члена уравнения для различных величин V (рис. VI. 74). Поскольку сама вычислительная машина не может определить такую величину V, которая удовлетворяла бы уравнению (VI. 15), необходимо разработать метод для определения величины V на машине.
Рэчфорд и Райс (Rachford and Rice) [VI. 48] предложили использовать метод 20-ти итераций (попыток). Значения функции F(V) определяются для ряда значений V, выбранных таким образом, чтобы сузить область изменения переменной V, в которой находится решение уравнения [VI. 15]. Для определения корня функции F(V) возьмем сначала величину V, равную 0,5. Из рис. VI. 74 можно видеть, что если Ёг (К — 1)/[V(К — 1) + 1] — величина положительная, то значение V слишком мало, чтобы удовлетворить уравнению (VI. 15), следовательно, величина V должна быть больше 0,5. Если же значение функции отрицательное, то величина V слишком велика, чтобы удовлетворить уравнению (VI. 15), т. е. V должно быть меньше 0,5. Первая величина V сузила интервал изменения переменной V, в котором лежит решение уравнения (VI. 15), до половины предыдущего интервала изменения от 0 до 1. Теперь, если для нахождения значения функции F( V) взять другую величину V, находящуюся в середине интервала величин, в котором находится решение уравнения (VI. 15), то знак функции F(V) покажет, в какой из половин оставшегося интервала находится решение уравнения (VI. 15). Повторяя эту процедуру 20 раз, можно определить величину V, которая дает значение функции F(V), меньшее величины 10-8. Определив величину V, являющуюся решением уравнения (VI. 15), используют эту величину в уравнениях (VI. 10) и (VI. 12). Хотя этот метод был бы слишком трудоемким для настольного счетного устройства, электронно-вычислительная машина может при его использовании получить решение через 1 мин после ввода в нее исходных данных и программы.
Команда
Очистить, сложить
Сложить
Другим подходом к задаче определения V является так называемый метод Ньютона. В данной точке определяется тангенс угла наклона функции F(V) к V. Функция F( V), деленная на тангенс угла наклона, служит поправкой, которую нужно добавить к первому взятому значению V. Новое значение V будет гораздо ближе к величине, полученной при решении уравнения (VI. 15). Этот метод состоит в следующем:
Очистить, вычесть
F (У) = 0, (VI. 26)
F (V) = F (V;) + (У/+1 - Vjt F‘ (V,) + . . . , (VI. 27)
где /—номер итерации. Опуская члены второго порядка, получаем
Vj+\ — V j = — F’ (VJ "
F(V,)
Так, из уравнения (VI. 29) можно найти ряд последующих приближений из величины V, пока функция F(V) не станет меньше какого-то заданного числа. Для данной задачи по методу Ньютона получают ответ после нескольких итераций. Этот метод дает сходимость быстрее, чем метод 20 итераций. Однако в большинстве случаев удовлетворительными являются оба метода. Лишь при более сложной задаче, когда уравнение приходится решать много раз, лучше переходить с программы, составленной для метода 20 итераций, на программу, составленную по методу Ньютона. Блок-схема этапов вычислений по методу Ньютона показана на рис. VI. 75. Цель этой блок-схемы — дать программисту возможность увидеть процесс вычисления в целом и установить, какие промежуточные результаты следует сохранить для последующего использования (например, результаты в блоке С, которые потребуются в блоках / и N). Блок-схема позволяет также легко перегруппировать этапы вычислений, сводя к минимуму число операций, и тем самым получить оптимальную программу.
Этапы блок-схемы после ее составления переводятся в команды для вычислительной машины. Команда состоит из трех частей: 1) адреса ячейки памяти, в которой будет храниться команда; 2) кода операции; 3) адреса числа, над которым должно быть произведено действие. Некоторые из возможных команд перечислены в табл. VI. 13.
Таблица VI. 13 Перечень команд для вычислительной машины
Объяснение
Арифметические команды
Очистить регистр А и прибавить содержимое ячейки, адрес которой указан в команде
Прибавить содержимое ячейки, адрес которой указан в команде, к содержимому регистра А
Очистить регистр А и вычесть содержимое ячейки, адрес которой указан в команде, из содержимого регистра А
Команда
Запись
ПРОГРАММИРОВАНИЕ
Прежде чем программировать задачу однократного испарения, приведем в качестве упрощенного примера программу для решения следующего уравнения:
x = (D + B)C,
где ?>= 110,2345, В = 22,445566 и С = 33,557799. Программа показана в табл. VI. 14 в одной из применяемых форм.
Таблица VI. 14 Программа для х = (D +В)С
Оста нов.
Переполнение «включено», знаки различны
Переход при числе, отличном от нуля
X О * ’К Н Я о> к zS з* x cq
о а cl и * о
и К
Команды нлн даннь
команда
Считывание, начало вычисления
0001
Переход при нуле
| 0001 | 0110234500 | _ |
| 0002 |
0022445566 | _ |
| 0003 | 0033557799 |
_ |
| 0004 |
Очистить, сложить |
0001 |
| 0005 |
Сложить | 0002 |
| 0006 |
Умножить | 0003 |
Условный
переход
|
Команда | Объяснение |
| Вычесть |
Вычесть содержимое ячейки, адрес которой указан в команде, из содержимого регистра А |
|
Умножить | Умножить содержимое ячейки, адрес которой указан в команде, на содержимое регистра А и ввести 20-значное произведение в регистры А и R |
|
Умножить, округлить |
Умножить содержимое ячейки, адрес которой указан в команде, на содержимое регистра А. Округлить произведение до 10 знаков и очистить регистр R |
| Разделить |
Разделить 20-значиое содержимое регистров А и Я на содержимое ячейки, адрес которой указан в команде |
| Пе |
эедача информации |
| Запомнить | Передать содержимое регистра А в ячейку, адрес которой указан в команде |
| Запомнить, очистить | Передать содержимое регистра А в ячейку, адрес которой указан в команде, и очистить регистр А |
| Сдвинуть влево | Сдвинуть содержимое регистров А и R влево на число мест, указанное номером в адресе команды. Код операции не сдвигается |
|
Сдвинуть вправо Очистить R Округлить |
Сдвинуть содержимое регистров А и R вправо на число мест, указанное номером в адресной части команды. Код операции не сдвигается Очистить регистр R Округлить 20-значное содержимое регистров А и R до 10 знаков и очистить регистр R |
Безусловный
переход
Считывание
Считать, начать вычисления
Начать
числения
Принятие решения и разветвление
Остановить работу машины.
Если знак регистра А отличается от знака ячейки, адрес которой указан в команде, переполнение показывает «включено»
Проверить содержимое (не знак) регистра А:
а) если содержимое регистра А равно нулю, установить знак регистра А на нуль и продолжать счет в должной последовательности; б) если содержимое регистра А не равно нулю, передать управление ячейке, адрес которой указан в команде Проверить содержимое (не знак) регистра А:
а) если содержимое регистра А не равно нулю, продолжать счет в должной последовательности; б) если содержимое регистра А равно нулю, передать управление ячейке, адрес которой указан в команде Если переполнение показывает «включено», передать управление ячейке, адрес которой указан в команде, и вновь установить переполнение.
Если переполнение показывает «выключено», продолжать счет в должной последов атель ности Передать управление ячейке, адрес которой указан в команде Считываются несколько команд и исходных данных, число которых указано в скобках, и передаются в последовательно расположенные ячейки памяти, начиная с ячейки, адрес которой указан в команде Записать содержимое нескольких последовательно расположенных ячеек памяти, число которых указано в скобках, начиная с той ячейки, адрес которой указан в команде
Читать непрерывно исходные данные или команды и хранить их в последовательно расположенных ячейках памяти, начиная с ячейки, адрес которой указан в команде, пока не подойдет команда начать вычисления; передать управление ячейке, адрес которой указан в этой команде Начать вычисления, передав управление ячейке, адрес которой указан в команде
Ввести программу с перфокарт в память вычислительной машины, начиная с ячейки памяти 0001, пока не дойдет очередь кода, в состав которого будет входить команда начать вычисления; хранить D в ячейке 0001 Хранить D в ячейке 0001 Хранить В в ячейке 0002 Хранить С в ячейке 0003 Очистить регистр и прибавить D Прибавить В (в регистре А будет тогда D + В) Умножить на С
Объяснен не
Объяснение
| Я к X и к | Команды или данные | ||
| 1 Адрес ячей , где хранш информаци |
команда | : адрес I | Объяснение |
| 0007 | Сдвинуть влево | 0004 |
Переставить десятичную запятую Округлить число в регистре R |
| 0008 |
Округлить | — |
|
| 0009 |
Запомнить | 0013 |
Хранить (D + В) С в ячейке 0011 |
| 0010 | Запись (1) |
0013 | Записать (D + В) С |
| ООП |
Останов | — |
Прекратить вычисления |
| 0012 | Начать вычисления | 0004 |
Прекратить ввод данных и начать вычисления с ячейки 0004 |
На первом этапе программы электронно-вычислительная машина вводит сообщаемую информацию в последовательно расположенные ячейки памяти (начиная с ячейки 0001). Когда ввод дойдет до последнего кода, на ленте или перфокарте, ввод прекратится и управление будет передано ячейке 004. В данном случае вычисления начинают по команде очистить регистр А и прибавить содержимое ячейки 0001 или D к регистру А. После того как вычислительная машина завершила это действие, выполняется следующая команда и содержимое ячейки 0002, т. е. В, прибавляется к регистру А, который будет тогда содержать сумму D + В. После этого вычислительная машина производит еще одно действие, выполняя команду умножить эту сумму на содержимое ячейки 0003. Теперь в регистрах А и R будет находиться произведение (D + В)С.
ПЕРЕСТАНОВКА ДЕСЯТИЧНОЙ ЗАПЯТОЙ
При умножении и делении вычислительная машина всегда помещает десятичную запятую перед первым разрядом. Но в действительности в обоих умножаемых (или делимых) числах десятичная запятая обычно находится на другом месте, поэтому после выполнения умножения (или деления) запятую необходимо переставить в нужное место.
Для этого служат команды сдвига влево и вправо. Команда, находящаяся в ячейке 0007 (см. табл. VI. 14), перемещает произведение, находящееся в регистре, таким образом, что десятичная запятая оказывается на том же месте, что и в первоначально введенных в память данных. По следующей команде к последней цифре, находящейся в регистре А, прибавляется 1, если первая цифра в регистре R равна или больше 5. По следующим двум командам выдается (печатается) ответ (D + В)С. Команда, находящаяся в ячейке ООП, завершает процесс вычислений.
ПРОГРАММА ДЛЯ РАСЧЕТОВ ОДНОКРАТНОГО (КОНТАКТНОГО) ИСПАРЕНИЯ
В табл. VI. 15 показана программа для расчетов мгновенного испарения по методу Ньютона. Для упрощения берем систему, состоящую лишь из Десяти компонентов. Программа составлена так, что после ее ввода в вычислительную машину можно получить ряд решений, непосредственно считывая для каждого из них zn, Кп и первую предположительно взятую величину V. В ячейках памяти 0001—0010 находятся данные о составе исходной смеси z„, а в ячейках ООП—0020 — константы равновесия Кп для каждого компонента, расположенные в той же последовательности, что и данные
о составе каждого компонента в исходной смеси. Ячейки 0021—0090 оставлены для хранения промежуточных результатов. Величины, хранимые в ячейках 0091—0099, будут рассмотрены по мере их использования в программе. Данные о составе исходной смеси располагаются в ячейках памяти так, что десятичная запятая находится между первым и вторым разрядом слева. Десятичная запятая в константах равновесия ставится между третьим и четвертым разрядом слева, а в величинах V ставится перед первым разрядом слева.
Перед рассмотрением программы следует указать, что при ее составлении ставилась цель продемонстрировать возможности различных подходов к решению данной задачи, а не цель — получить совершенную и безукоризненную программу. Не экономились также ячейки памяти, поскольку предполагалось, что вычислительная машина имеет больше ячеек, чем необходимые для данной программы 250 адресов.
Команды, находящиеся в ячейках 0100—0113, ясно показывают этапы вычислений. Прежде всего очищаются регистры и прибавляется величина, находящаяся в ячейке ООП. Поскольку в этой ячейке находится величина Ль на регистре А появляется Ки как указано в колонке объяснений. Результаты каждого этапа вычислений вплоть до ячейки 0113 показаны в колонке объяснений. Команды с 0100 до 0113 можно дополнительно повторять еще 9 раз, по разу для каждого компонента. При этом необходимо лишь изменить адреса команд в ячейках 0100, 0102, 0103, 0107, ОНО, 0111 и 0113. При каждом повторении этапа к адресам команд указанных ячеек нужно прибавить 1. Так, для Кг команда в ячейке 0100 будет «очистить, прибавить 0012», и она будет храниться в ячейке 0114.
Таблица VI. 15 Программа для расчета однократного испарения по методу Ньютона
| Адрес ячейки памяти, где хранится информация | Код операции | Адрес числа, иад которым-нужно произвести действие |
Объяснение |
|
Считывание | 0001 |
Ввод данных в вычисли | |
| тельную машину | |||
| 0001 |
Ci | Хранение состава исходной | |
| смеси z в мольных фракциях | |||
|
0002 | с2 |
||
| 0003 |
С3 | ||
|
0004 | С1 | ||
| 0005 |
Сь | ||
| 0006 | св |
||
| 0007 |
С7 | ||
| 0008 | с» |
||
| 0009 |
с9 | ||
|
0010 | С10 |
||
| ООП |
Кг | Хранение констант равнове | |
| сия к | |||
| 0012 | Кг |
||
| 0013 |
К3 | ||
|
0014 | К« |
||
| 0015 |
Кб | ||
|
0016 | кв |
||
| 0017 |
К, | ||
|
0018 | Ks |
||
| 0019 |
К» | ||
|
0020 | К10 |
||
| . . . |
Ввести дан | 0093 |
Ввод в вычислительную ма |
| ные, начать |
шину первой предположи | ||
| работу |
тельно взятой величины V. | ||
| 0093 |
0000000001 | . . . |
Хранение постоянной 1 для |
|
переадресации команд | |||
| 0094 | 0000000009 |
. . . | Хранение постоянной 9 для |
| переадресации команд |
Код
операции
гг н
S3
< X
Н 2 S CL
X о
at
X 53
Объяснение
| 0141 | Запомнить |
0153 |
| 0142 |
Очистить, прибавить | 0113 |
|
0143 | Прибавить |
0095 |
| 0144 | Запомнить |
0155 |
| 0145 |
..... | |
| 0146 | Умножить |
0098 |
| 0147 |
Прибавить | 0099 |
| 0148 |
Запомнить | 0096 |
| 0149 | ||
| 0150 |
Безусловный переход |
0241 |
| 0151 | Запомнить |
0096 |
| 0152 |
||
| 0153 |
||
| 0154 |
Безусловный переход |
0244 |
| 0155 | Очистить, |
0095 |
| 0156 |
прибавить | |
|
0157 | Переход при нуле | 0161 |
|
0158 | Вычесть |
0093 |
| 0159 | Запомнить |
0095 |
| 0160 |
Безусловный переход | 0145 |
|
0161 | Очистить, прибавить | 0094 |
| 0(62 |
Запомнить | 0095 |
| 0163 |
Очистить, прибавить |
0041 |
| 0164 | Прибавить |
0042 |
| 0165 |
Прибавить | 0043 |
| 0166 |
Прибавить | 0044 |
| 0167 |
Прибавить | 0045 |
| 0168 |
Прибавить | 0046 |
| 0169 |
Прибавить | 0047 |
| 0170 |
Прибавить | 0048 |
| 0171 |
Прибавить | 0049 |
| 0172 |
Прибавить | 0050 |
| 0173 |
Запомнить | 0092 |
| 0174 |
Прибавить | 0051 |
| 0175 |
Очистить | |
|
0176 | Запомнить |
0091 |
| 0177 | Очистить, прибавить | 0174 |
| 0178 |
0095 | |
| 0179 |
Запомнить | 0181 |
Из 0138
(К - 1) V + 1 Из 0141, запомнить Переставить десятичную запятую и вычислить
(Л: — l)2z
Запомнить 0 в 0091 (fl-l)2z
Из 0132, К— 1
(/С - 1) V (K-\)V+\
Из 0135, К — 1 Переставить десятичную запятую и вычислить
К— 1
(К - 1) V + 1
(К — 1) z
(К-1)У + 1
Из 0114, запомнить
Если на регистре А стоит нуль, вычислить все компоненты
Переадресация команд
Возвратиться к вычислению следующего компонента
Восстановление команд
(*-l)z (К — 1) V + 1
(* - 1) z (/С - 1)У + 1
= F( V)
2 накопление
(*_1)У + 1
| Адрес ячейки памяти, где хранится информация | Код операции |
Адрес числа, над которым нужно произвести действие |
Объяснение |
| 0095 | 0000000009 |
Хранение постоянной 9 для | |
| Останов |
переадресации команд |
||
| 0096 | 0096 | Промежуточное запоминание | |
| 0097 |
5000000000 | • • • |
Хранение постоянной 0,5 |
| 0098 | 5000000000 | 0,5 | |
|
0099 | 001000000 | 1 | |
| 0100 |
Очистить, | 0011' | Очистить и прибавить К |
|
прибавить | |||
|
0101 | Вычесть |
0099 | К- 1 |
| 0102 |
Запомнить | 0021 |
|
| 0103 |
Очистить, прибавить |
0021 | К — 1 |
| 0104 |
Умножить | 0098 |
(ZC-l)V' |
| 0105 | Прибавить |
0099 | (К - 1) V + 1 |
| 0106 |
Запомнить | 0096 |
|
| 0107 |
Очистить, прибавить |
0021 | К— 1 К — 1 |
| 0108 |
Разделить | 0096 | (К- 1)У+ 1 |
| 0109 |
Запомнить | 0096 |
(К- \)г |
| 0110 |
Умножить | 0001 |
(K-\)V+\ |
|
0111 | Запомнить |
0041 | (К — I)2 2 |
| 0112 |
Умножить | 0096 |
(К-1)У+ 1 |
|
0113 | Запомнить |
0051 | |
|
0114 | Очистить, прибавить | 0100 |
|
| о: 15 |
Прибавить | 0095 |
|
| 0116 |
Запомнить | 0120 |
|
| 0117 |
Очистить, прибавить |
0102 | |
|
0118 | Прибавить |
0095 | |
|
0119 | Запомнить |
0122 | Из 0116 |
| 0120 |
Остановить | 0120 |
|
| 0121 |
Вычесть | 0099 | Из 0119 |
|
0122 | Остановить |
0122 | |
| 0123 | Очистить, прибавить | 0095 |
|
| 0124 |
Переход при | 0128 |
|
| 0125 |
нуле Вычесть |
0093 | Переадресация команд |
| 0126 |
Запомнить | 0095 | |
| 0127 |
Безусловный переход |
0114 | |
|
0128 | Очистить, прибавить | 0094 |
|
| 0129 |
Запомнить | 0095 |
|
| 0130 |
Очистить, прибавить |
0103 | |
|
0131 | Прибавить |
0095 | |
|
0132 | Запомнить |
0145 | |
|
0133 | Очистить, прибавить | 0107 |
|
| 0134 |
Прибавить | 0095 |
|
| 0135 |
Запомнить | 0149 |
|
| 0136 |
Очистить, прибавить |
0110 | |
|
0137 | Прибавить |
0095 | |
|
0138 | Запомнить |
0152 | |
|
0139 | Очистить, прибавить | 0111 |
|
| 0140 |
Прибавить | 0095 |
4>
-Г, Ft
о н Ф к
S 5
< с
| К * 0) к Ч X | 1 я s g S 4 3 о ? | ||
|
»=! "s'g* и н s а m к а 0 | Код операции | Ь: о-ЬЙ : о с« u 2 5 4 О) * Я S tf ж н е Zr О | Объяснение |
| Э Л D, I < С X S | ^ ж ж ш |
||
| 0180 |
Очистить, прибавить |
0091 | Из 0179 |
| 0181 |
Останов | 0181 |
(*- О2* „ (К - 1) У + 1 1 |
| 0182 | Запомнить |
0091 | |
| 0183 | Очистить, |
0095 | |
|
0184 | прибавить |
||
| Переход при | 0188 | ||
| 0185 | нуле |
||
| Вычесть | 0093 | ||
|
0186 | Запомнить |
0095 | |
|
0187 | Безусловный |
0177 | |
|
0188 | переход |
||
| Очистить, | 0092 | F(10 | |
| 0189 |
прибавить | ||
|
Сдвинуть | 0002 |
Сравнить F (У) с величиной | |
| вправо |
10-8 | ||
| 0190 | Переход при нуле | 0205 | |
|
0191 | Очистить, |
0092 | F<Y) F(V) |
|
прибавить | |||
|
0192 | Разделить |
0091 | |
| F' (У) | |||
|
0193 | Прибавить |
0098 | Новая р VJ + 1 - VJ + F' (У) |
| 0194 |
Запомнить | 0098 |
|
| 0195 |
Безусловный переход |
0128 | |
|
0196 | Очистить, |
0121 | К- 1 |
| прибавить |
(К - 1) V |
||
| 0197 |
Умножить | 0098 |
|
| 0198 |
Прибавить | 0099 |
(/С_1)У+ 1 |
|
0199 | Очистить, прибавить | 0001 |
Z |
| 0200 |
Сдвинуть вправо |
0004 | |
|
0201 | Разделить |
0096 | Z |
| 0202 | Запомнить | 0061 | (К— 1) V + 1 ~ у Кх=у |
| 0203 |
Умножить, округлить |
ООП | |
| 0204 | Запомнить |
0071 | |
| 0205 | Очистить, прибавить | 0195 |
|
| 0206 |
Прибавить | 0095 |
|
| 0207 |
Запомнить | 0220 |
|
| 0208 |
Очистить, | 0199 |
|
| прибавить | 0095 | ||
| 0209 | Прибавить | ||
| 0210 |
Запомнить | 0224 |
|
| 0211 |
Очистить, | 0202 |
|
| прибавить | 0095 | ||
| 0212 | Прибавить | ||
| 0213 |
Запомнить | 0227 |
|
| 0214 |
Очистить, прибавить |
0203 |
| J к L. -г * а К -и ™ К Н *Е о н s а |
Код операции | ' 0j и * 2 * ¦о а&Й U * 2 4 | Объяснение |
| &**¦§• |
Cf да О | ||
| 5 Я D, I < С X X | < X X Ш | ||
|
0215 | Прибавить |
0095 | |
|
0216 | Запомнить |
0228 | |
|
0217 | Очистить, прибавить | 0204 |
|
| 0218 |
Прибавить | 0095 |
|
| 0219 |
Запомнить | 0229 |
|
| 0220 |
Останов | 0220 |
Из 0207, К — 1 |
|
0221 | Умножить |
0098 | (Я-1) У |
| 0222 |
Прибавить | 0099 |
(К — 1)У + 1 |
| 0223 | Запомнить | 0096 | |
|
0224 | Останов |
0224 | Из 0210, z Z |
| 0225 |
Сдвинуть вправо |
0004 | |
| 0226 | Разделить |
0096 | {К — 1)У+ 1~* |
| 0227 |
Останов | 0227 |
Из 0213, запомнить х |
| 0228 | Останов |
0228 | Из 0216, Кх = у |
| 0229 |
Останов | 0229 |
Из 0219, запомнить у |
| 0230 |
Очистить, прибавить |
0095 | |
| 0231 | Переход при нуле |
0235 | Если на регистре А стоит нуль, вычислить все компоненты |
| 0232 | Вычесть | 0093 | Переадресация команд |
| 0233 |
Запомнить | 0095 |
Возвратиться к вычислению |
| 0234 |
Безусловный переход |
0205 | следующего компонента |
| 0235 | Запись (20) |
0001 | Выдать z и К |
| 0236 |
Запись (1) | 0098 | Выдать V |
|
0237 | Запись (20) |
0061 | Выдать х и у |
| 0238 |
Очистить, прибавить |
0094 | Переадресация команд |
| 0239 |
Запомнить | 0095 | Восстановление команд |
| 0240 |
Останов | 0240 |
|
| 0241 |
Сдвинуть вправо |
0001 | |
| 0242 | Разделить |
0096 | |
| 0243 | Безусловный переход | 0151 |
|
| 0244 |
Умножить | 0096 |
|
| 0245 |
Сдвинуть влево |
0001 | |
| 0246 | Округлить | ||
| 0247 |
Безусловный переход |
0114 | |
|
начать |
ПЕРЕАДРЕСАЦИЯ КОМАНД
Вычислительная машина должна производить все эти действия автоматически, поэтому по командам
команды, находящейся в ячейке 0114, данные команды в ячейке 0100 являются исходными, они прибавляются к числу на регистре А, после этого к полученной сумме добавляется содержимое ячейки 0095. Поскольку ячейка 0095 содержит число 0000000009, на регистре А находится число, которое, если превратить его в команду, будет означать «очистить, прибавить 0020», т. е. прибавить К для последнего компонента. Эта команда поступает затем в ячейку 0120, где она будет выполнена в нормальной последовательности. Таким образом, команда была выполнена путем изменения ее адреса (переадресации). Ячейка 0120, куда поступает измененная команда, обычно содержит фиктивную команду «останов по 0120», так что другие команды при вводе я вычислительную машину будут храниться в надлежащих ячейках. Команда «останов» служит для того, чтобы остановить вычислительную машину при достижении данного этапа, если введенная в нее программа не будет должным образом выполняться. Это имеет значение лишь во время отладки программы. Поэтому в программе приводится адрес ячейки, чтобы облегчить оператору установление места ошибки.
Следующие три команды 0117, 0118 и 0119 переадресуют команду 0102 и засылают ее в ячейку 0122. Код для следующих трех этапов будет:
0120— очистить, прибавить 0020;
0121 — вычесть 0099;
0122 — запомнить 0030.
Эта последовательность аналогична команде в первых трех командах с одним исключением: вместо вычисления К—1 для первого компонента она дает К—1 для последнего (т. е. десятого) компонента.
Далее вспомогательная команда переадресации прибавляется к команде регистра А, затем выполняется переход при нуле. Поскольку эта команда не равна нулю, выполняется следующий этап; из адреса команды переадресации вычитается 1, после чего он становится равным 8. Новая команда переадресации хранится в той же ячейке, что и прежняя, которая, естественно, уничтожается. Затем команда, находящаяся в ячейке 0127, изменяет последовательность, в которой работает вычислительная машина, передавая управление ячейке 0114. Таким образом повторяется описанный выше процесс переадресации и вычисления. Так как в ячейке 0095 теперь вместо девятого компонента находится восьмой, К—1 вычисляется для девятого компонента. Эту процедуру повторяют, пока не будут вычислены К — 1 для всех компонентов. К этому времени в ячейке 0095 будет храниться нуль, так что, когда команда переадресации будет сравниваться с нулем по команде 0124, последовательность будет изменена таким образом, что команды 0125—0127 будут опущены. Команды 0128 и 0129 восстанавливают первоначальную команду переадресации и направляют ее в ячейку 0095 для дальнейшего использования. Именно по этой причине команда переадресации запоминается дважды.
Описанный выше процесс переадресации и вычисления повторяется в ячейках 0130—0162 для команд, находящихся в ячейках 0103—0113. Следует отметить, что команды 0101, 0104, 0105, 0106, 0108, 0109 и 0112 не обязательны для программы, поскольку они не нуждаются в переадресации; они включены сюда лишь для того, чтобы упростить объяснение. Следует отметить также, что вычисление начинается с ячейки 0114. Команды 0163—0173 производят вычисление ?„(/(„ —
— l)zn/[(Kn — 1)У+1] без переадресации; ячейки 0174—0187 иллюстрируют вычисления аналогичной суммы 2(К— \)-zj[(K— 1)У + I]2 с переадресацией. Для суммирования и запоминания суммы без переадресации требуется 11 команд, с переадресацией—14. В данном случае время вычисления и число ячеек памяти минимальны при вычислении без переадресации. Однако, если цифровая вычислительная машина снабжена регистром переадресации, разница во времени будет незначительна, а число необходимых ячеек памяти снизится. При большом числе компонентов переадресация обеспечит и абсолютную экономию ячеек памяти.
РАЗВЕТВЛЕНИЕ ПРОГРАММЫ
По командам 0188—0190 производится сравнение „ <*»-!)*„
*{Kn-l)V+l с величиной 10~8. При этом определяется, решено ли уравнение (VI. 15). Команда 0189 сдвигает последние две цифры из регистра. Они заменяются нулями, занимающими первые два разряда. После этого сдвига, если в первых восьми разрядах F( V) находились нули, на регистре А будут находиться одни лишь нули. Изменив число сдвигаемых разрядов, данное число можно сравнить с любым числом 10 — п. Если /'(l7) не равно нулю, по методу Ньютона в соответствии с командами 0188—0193 вычисляют новое V, которое помещают затем в 0098, стирая старое V. Ячейка 0195 изменяет последовательность операций и возвращает к началу программы, чтобы пересчитать коэффициенты для нового l7. Это повторяется до тех пор, пока F(V) не станет меньше величины 10
Решив уравнение (VI. 15), вычисляют х„ и у„, используя переадресацию команд в соответствии с командами 0196—0234.
Затем ьсе необходимые данные, полученные в процессе решения, будут выданы в соответствии с командами, находящимися в ячейках 0235—0237. Команды 0238—0239 восстанавливают измененные команды так, что для решения следующей задачи необходимо лишь ввести новые значения z„, Кп и начать вычисления. Команда, находящаяся в ячейке 0240, останавливает вычислительную машину, когда вычисления закончены.
ПОПРАВКИ
Следующая группа команд является примером поправок к программе. При выполнении программы после деления, произведенного по команде ячейки 0150, произошло переполнение.
Проверка показала, что десятичная запятая для этого деления была неправильно установлена. Поправка была произведена путем изменения команды и последовательности операций, т. е. передачи управления в конец программы ячейкам 0241—0243. Здесь была правильно установлена десятичная запятая, выполнено деление и передано управление ячейке 0151. Если бы команда об установке десятичной запятой была вставлена непосредственно в программу, пришлось бы изменить адреса всех последующих и некоторых предыдущих команд.
Оказалось также необходимым переставить десятичную запятую после умножения по команде в ячейке 0154. Это, а также округление произведения было выполнено путем замены команды в ячейке 0154 с указанием новой последовательности операций, которые были перенесены в ячейки 0243—0246.
ПОДПРОГРАММЫ
Составление программ, пример которого был приведен выше, еще более упрощается с применением подпрограмм. Элементарные математические функции, такие, как синус, косинус, тангенс, котангенс, логарифм, показательная и т. п., для большей части вычислительных машин запрограммированы в виде подпрограмм. Эти подпрограммы хранятся в памяти вычислительной машины, так что программист может установить число на регистре А, передав управление адресу ячейки подпрограммы, которая вычислит функцию, а затем передаст управление главной программе. Такая подпрограмма вычисляет функцию путем разложения ее в ряд. Этот метод используется в связи с тем, что вычислительная машина, как и настольное вычислительное устройство, может выполнять лишь ограниченное число действий. Любой учебник по численному анализу может послужить хорошим пособием для выбора метода решения задачи на цифровой вычислительной машине.
Составление программы табулирования для некоторых сложных математических функций — очень трудоемкая операция. В таком
Таблица VI. 16 Функция х (пример пользования вспомогательными таблицами)
| ' | F W | X | F(x) |
| 0 | 84270 | 6 | 86614 |
| 1 | 84681 | 7 | 86947 |
| 2 | 85084 | 8 | 87333 |
| 3 | 85478 | 9 | 87680 |
| 4 | 85865 | 10 | 88021 |
| 5 | 86244 |
случае можно воспользоваться так называемыми «вспомогательными таблицами». Для примера неболь-_шая часть такой таблицы приведена в табл. VI. 16. При использовании мето-_да «вспомогательных таблиц» таблица должна храниться в каких-либо определенных ячейках памяти. В данном случае величины функции хранятся в ячейках, начиная с ячейки 1200. Величина х или аргумент определяется и хранится в ячейке 1199 как часть главной программы. Вычисление функции F(x) программируется следующим образом.
В этой программе первые три разряда аргумента х плюс 1200 образуют адрес ячейки, в которой хранится функция. Таким образом, сделав первые три цифры аргумента х частью адреса команды, можно определить табличные величины функции, между которыми находится искомая величина функции. Программа вводится в ячейку 1505 и х засылается в регистр А так, что первые три цифры х появляются в трех крайних справа разрядах. При сложении этой величины с командами, находящимися в ячейках 1502 и 1504, получается команда прибавить функцию F(х) к величине, находящейся в таблице непосредственно ниже х. При сложении этой же величины с величиной команды, находящейся в ячейке 1503, получается команда вычесть функцию F(x) из величины, находящейся в таблице непосредственно выше х. Чтобы вычислить линейной интерполяцией между этими двумя табличными величинами искомую величину функции, устанавливают х на регистре А и сдвигают его влево столько раз, чтобы первые три цифры вышли из регистра А. Оставшееся на регистре число будет коэффициентом интерполяции, на который умножается разность между двумя приведенными в таблице величинами, ближайшими к искомой.
Это произведение прибавляют к ближайшей величине функции, расположенной в таблице ниже х, получая хорошее приближение для значения функции в точке х.
Чтобы повысить точность вычислений, можно ввести в таблицу дополнительные величины. Можно также взять по таблице три ближайшие значения функции, по которым вычислительная машина составит уравнение
Таблица VI. 17 Программа для вычисления F(x) при помощи вспомогательных таблиц
| Адрес ячейки, в которой хранится информация | Команды | Адрес ячейки памяти, в которую нужно поместить результат |
Объяснение |
| 1199 1200 1201 1202 1203 1204 1205 1206 1207 1208 1209 1210 |
0010345000 0842700000 0846810000 0850840000 0854780000 0858650000 0862440000 0866140000 0869770000 0873330000 1876800000 0880210000 | л = 001,0345000 | |
| 1500 | • • • • | 00000001,03 | |
| 1501 |
4500000000 | ||
| 1502 | Очистить, прибавить | 1100 |
|
| 1503 |
Вычесть | 1101 |
|
| 1504 |
Прибавить | 1100 |
|
| 1505 |
Очистить, прибавить |
1199 | л = 001,0345000 |
| 1506 |
Сдвинуть вправо |
0005 | На регистре А находится 00000001,03 |
|
1507 | Запомнить |
1500 | |
|
1508 | Очистить, прибавить | 1199 |
|
| 1509 |
Сдвинуть влево |
0005 | На регистре А находится 4500000000 |
|
1510 | Запомнить |
1500 | |
|
1511 | Очистить, прибавить | 1502 |
На регистре А: очистить, прибавить 1100 |
| 1512 | Прибавить |
1510 | На регистре А находится, очистить, прибавить 1203 |
| 1513 |
Запомнить | 1520 |
Команда найти в таблице первую х |
| 1514 |
Очистить, прибавить | 1503 | На регистре А находится, вычесть 1101 |
| 1515 |
Прибавить | 1500 |
На регистре А находится, вычесть 1204 |
| 1516 | Запомнить |
1521 | Команда найти в таблице и вычесть вторую X |
| 1517 |
Очистить, прибавить |
1504 | На регистре А находится, прибавить 1100 |
| 1518 |
Вычесть | 1500 |
На регистре Л находится, прибавить 1203 |
| 1519 |
Запомнить | 1523 |
Команда найти в таблице и вычесть первую X |
| 1520 | Останов | 1520 | Команда из 1513 F(x) = 0854780000 |
| 1521 |
Останов | 1521 |
Команда из 1516/Г(лг) ~F(x)2 = = — 0003870000 |
|
1522 | Умножить |
1501 | Интерп ретация: —^(JC)][^(JC)! — — = = — 0001741500 |
| 1523 1523 | Останов Запомнить | 1523 |
Команда из 1519 F(x) = 0856521500 |
параболы. Затем это уравнение параболы используется для определения значения функции в точке х.
Рис. VI. 76. Электронная вычислительная машина «1ВМ 650» с вводом программы « данных на магнитный запоминающий барабан состоит из трех элементов. В одном шкафу помещаются вводное и выводное устройство, в двух других — запоминающее и вычислительное устройства. Запоминающее устройство имеет 20000 ячеек.
Широко используются стандартные программы для цифровых вычислительных машин, составленных на основе операторного программирования. Хотя основные принципы программирования одни и те же для всех классов цифровых вычислительных машин, специфические детали программирования могут быть поняты лишь с учетом того, на какой машине работает программист. Использование другой цифровой вычислительной машины заставляет менять и библиотеку стандартных программ, составленную для решения типовых задач.

Рис. VI. 77. Счетно-вычислительный центр фирмы «Берроус корпорейшн» с ЭВМ
«Дататрон».
Типичные из применяемых в настоящее время вычислительных машин показаны на рис. VI. 76 и VI. 77.
Природный газ должен транспортироваться от пласта до самого отдаленного потребителя с максимальной эффективностью.
