Глава 3 характеристики и режим работы лопастных насосов
ГЛАВА 3
ХАРАКТЕРИСТИКИ И РЕЖИМ РАБОТЫ ЛОПАСТНЫХ НАСОСОВ
§ 14. ТЕОРЕТИЧЕСКИЕ ХАРАКТЕРИСТИКИ НАСОСОВ
Основные параметры лопастных насосав (.подача, напор, мощность, коэффициент полезного действия и частота вращения) находятся в определенной зависимости, которая лучше всего уясняется из рассмотрения характеристических кривых.
Значения напора, мощности и КПД для различных значений подачи могут быть представлены в виде системы точек :в координатах Q—

Н, Q—N и Q—т|. Соединяя точки плаэньгми кривьими, получаем непрерывную характеристику зависимости рассматриваемых параметров от подачи насоса при постоянной частоте вращения. Основной характеристической кривой насоса является график, выражающий зависимость развиваемого напора от подачи H — f(Q) при постоянной частоте .вращения tt=<const.
Для построения теоретической характеристики Q—Н воспользуемся основным уравнением центробежного насоса. Если поток на входе в колесо не закручен, то
“2 а
Г1 т = - .
Идеальная подача насоса
Qt == ^ ^2 ^2 ^2г»
откуда
Qt
°2 г Я D2 Ь2 ’
где D2 — диаметр |рабочего колеса;
Ь2 — ширина рабочего колеса.
Из рис. 3.1 следует
02?i = u2———-Щ Р2
ИЛИ
Qt
°2Ц “2 JtD2b2tg&s '
Подставим полученное значение v2u в основное уравнение теоретического напора:
л D2 b2 tg Р2
или
g ngD2b2 tg P2
При n—const окружная скорость u2 будет постоянной. Очевидно,
что для рассматриваемого насоса !Д>, Ъ2 и tgf32 также являются постоян
ными величинами. Обозначая постоянные величины через коэффициенты А и В:
— = А; '-—--1-~=В,
g гс gD2b2 tg
получим:
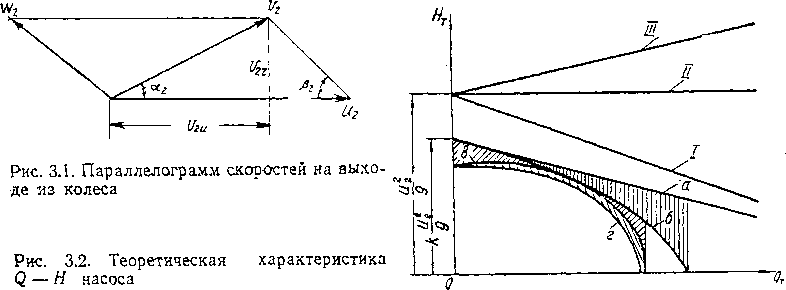
Таким образом, зависимость Ят от Qт выражается уравнением первой степени, которое в координатах Ят и QT графически изображается прямыми линиями; наклон этих прямых зависит от значения углового коэффициента, являющегося функцией угла рг-
На рис. 3.2 дана, графическая интерпретация уравнения (3.1) для различных значений углового коэффициента. Проанализируем положение прямых линий при р2<С90°, р2=90° и р2>90°.
Для построения графика зависимости Q—Я предположим, что QT = 0, тогда HT = u22]g-, при Ят = 0 QT — u2nD2b2tg$2.
При (32<С90° (лопатки отогнуты назад) tgj32>0, поэтому с ростом ,QT напор Ят, развиваемый насосом, уменьшается. Следовательно, линия зависимости теоретического напора (см. рис. 3.2, /) от подачи направлена наклонно вниз. Наклон прямой Iбудет тем больше, чем меньше tgp2, т. е. угол (32.
При р2=90 (лопатки направлены радиально) tgj32=oo, следовательно, второй член уравнения будет равен нулю: H^—i^lg, т. е. график зависимости Ят от QT выражается прямой II, параллельной оси абсцисс и отсекающей на оси ординат отрезок Н^-и? jg.

При р2>90° (лопатки загнуты вперед)- tgj32<0 — второй член уравнения (3.1) изменит знак минус на плюс. В этом случае с увеличением подачи возрастает напор, причем тем больше, чем больше f32. График зависимости Ят от QT выражается прямой III, поднимающейся
вверх. При <QT = 0 начальная ордината прямой /// также равна: HT = u2fg-
Как видно из графика (см. рис. 3.2, прямая III), рабочие колеса с лопатками, загнутыми вперед, создают значительно большее давление, чем колеса с лопатками, загнутыми назад, и в этом их основное преимущество. Однако преобразование динамического давления, создаваемого лопатками, в статическое путем уменьшения абсолютной скорости потока при выходе из рабочего колеса насоса, связано с большими потерями энергии. Ввиду этого рабочие колеса центробежных насосов, используемых для нагнетания жидкостей, как правило, изготовляют с лопатка.ми, загнутыми назад. Следовательно, практическое значение имеет' лишь одна из этих прямых (линия I) — теоретическая характеристика Qt—Ят, соответствующая работе насоса без учета потерь в нем.
Для получения действительной характеристики насоса необходимо внести поправки на гидравлические (в проточной части насоса) объемные и механические потери и на конечное число лопаток.
Теоретический напор при конечном числе лопаток Ят будет меньше теоретического напора при бесконечном числе лопаток Ят. Уменьшение теоретического напора учитывается поправочным коэффициентом на конечное число лопаток k. Поэтому линия теоретической характеристики QT—Ят (прямая а), учитывающая поправку на конечное число лопаток, понизится и отсечет на оси Я отрезок
#'=?#т
или
Прямая I и прямая а (см. рис. 3.2) пересекаются на оси Q, если принять, что коэффициент k не зависит от подачи или ниже оси Q, если он зависит от подачи. Потери сопротивления протеканию жидкости при турбулентном движении практически можно считать 'пропорциональными квадрату подачи, т.е. hn=SQ2. Таким образом, графически потери от трения в каналах изображаются параболой с вершиной в начале координат (см. рис. 3.2, кривая б). Откладывая значение этих потерь вниз от линии а, получим кривую б.
Потери на удар при входе жидкости на. лопатки или в направляющий аппарат вызываются резким изменением ' направления средней скорости.
Для расчетной подачи Qp углы наклона лопаток при входе и выходе из колеса или направляющего аппарата подбирают таким образом* чтобы, не было потерь от удара, т. е. чтобы Луд=0. При изменении подачи появляются потери на удар и растут пропорционально квадрату отклонения подачи:
- АуД= k' (Qx — Qp)2.
Графически этому уравнению соответствует параболическая кривая с вершиной в точке безударного входа Луд=0 при Qa:=Qp (см. рис. 3.2, кривая в).
¦В соответствии с уравнением Бернулли для увеличения статического (полезного) напора необходимо значительно уменьшить скорость потока у выходного патрубка. Из законов гидродинамики жидкости известно, что всякое изменение скорости потока сопровождается потерями, прямо пропорциональными квадрату потерянной скорости.
При построении кривой в не принималась в расчет утечка воды через зазоры. Если учитывать эти утечки, то полученные давления Я будут соответствовать меньшим фактическим подачам насоса и действительная характеристика Q—Я (кривая г) несколько сместится влево.
Так как утечка в современных конструкциях центробежных насосов не превышает 2—5%, то ее влияние дает незначительное смещение характеристики.
К механическим потерям относятся потери на трение дисков колеса о жидкость и потери на трение в подшипниках и сальниках. Эти потери почти не влияют на характеристику насоса, поэтому мы их здесь не рассматриваем.

Теоретическое построение
характеристик насосов по заданным размерам
встречается с большими трудностями.
Исследования, проведенные во
ВНИИГидромаше, показывают, что строить
теор-етическую характеристику лучше всего
комбинированным способом: по расчетному
направлению касательной в точке
оптимального значения КПД и по точке
холостого хода, полученной сопоставлением
относительной характеристики колеса такой
же конструкции и с таким же значением
коэффициента быстроходности ns.
Однако и в этом случае действительной
характеристики не получается ввиду
большого числа факто-56 ров,
которые не поддаются точному определению и
которыми приходится задаваться. Поэтому на
практике отдают предпочтение опытным
характеристикам.
§ 15. РАБОЧИЕ ХАРАКТЕРИСТИКИ НАСОСОВ И СПОСОБЫ ИХ ПОЛУЧЕНИЯ
Основная трудность в получении рабочих характеристик насосов расчетным путем заключается в выборе коэффициентов потерь, влияющих на подачу и напор насоса. Поэтому при расчете режима работы насоса пользуются опытными рабочими характеристиками, которые получают при испытаниях насосов. Насосы, изготовляемые насосостроч-тельными заводами Советского Союза, подвергаются испытаниям в соответствии с ГОСТ 6134—71*. Мелкие и средние насосы испытываются на заводском испытательно.м стенде. Крупные насосы допускается испытывать на месте эксплуатации при частоте вращения, отличающейся от номинальной не более чем на 5%.
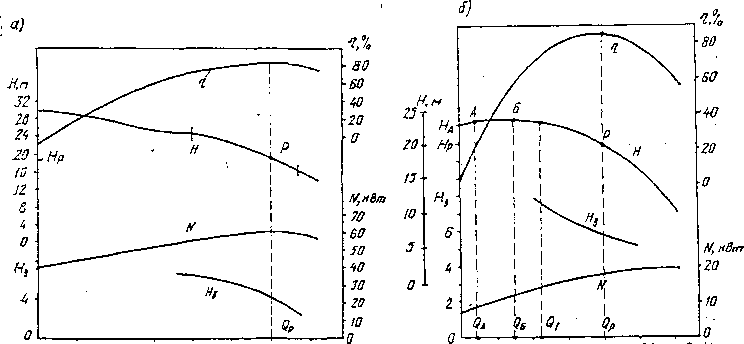
На основании опытных измерений вычисляют напор и коэффициент полезного действия насоса по формулам (2.2) и (2.10) для соответствующей подачи при постоянной частоте вращения. Полученные значения напора, мощности, коэффициента полезного действия и допустимой вакуумметрической высоты всасывания для ряда значений подачи можно представить в виде системы точек в координатах Н, N, г\, Нв и Q (рис. 3.3). Соединяя соответствующие точки плавными линиями, получаем кривые зависимости рассматриваемых параметров от подачи насоса при постоянной частоте вращения и определенном диаметре рабочего колеса.
Полученные кривые Q—Н, Q—N, Q—т] и Q—#в называются рабочими характеристиками центробежного насоса и вписываются в паспорт насоса. Из рис. 3.3, а (насос 12Д-49) видно, что максимальному значению КПД соответствует подача Qp и напор Яр (расчетные параметры). Точка Р характеристики Q—Н, отвечающая максимальному значению КПД, называется оптимальной режимной точкой.
Из теоретической зависимости Н от Q следует, что с уменьшением подачи напор возрастает и достигает максимального значения при подаче, равной нулю, т. е. при закрытой задвижке на напорном трубопроводе. Однако испытания насосов показывают, что некоторые насосы (например, 8^-18; рис. 3.3, б) развивают . максимальный напор после открывания-задвижки, т. е. напор возрастает при начальном уве-
20 i/О SO 80 100 Q//C
4-0 80 120 ISO ZOO 2*0 Q^/c
Ряс. 3.3. Рабочие характеристики центробежных насосов
личении подачи, а затем падает. Из рис. 3.3, б видно, что напору На соответствуют две подачи: Qa и Qi. Изменение подачи насоса наступает внезапно, сопровождается сильным шумом и гидравлическими ударами, сила которых зависит от диапазона изменения подачи и длины трубопровода.
Характеристические кривые Q—Н, имеющие максимальный напор при некоторой--промежуточной подаче, называются восходящими. Режим работы насоса в пределах подачи от нуля до Qi называется областью неустойчивой работы.
Характеристики, не имеющие возрастающей ветви, называются стабильными.
Форма рабочей характеристики Q—Я зависит от коэффициента быстроходности насоса ns (см. § 11):. чем больше коэффициент быстроходности, тем круче кривая Q—Я. Режим работы насосов, имеющих стабильную рабочую характеристику Q—Н, протекает устойчиво во всех точках кривой.
При стабильной пологой характеристике напор насоса, даже при значительном изменении расхода, изменяется незначительно. Насосы с пологими характеристиками целесообразно применять в системах, где при постоянном напоре требуется регулирование подачи в широких пределах, например, в безбашенной системе'водоснабжения.
Насосы со стабильной крутопадающей характеристикой обычно применяют в системах со значительными колебаниями напора при необходимости сохранения по возможности постоянной подачи, например на насосных станциях I подъема (на нерегулируемых реках).
Насосы с возрастающей рабочей характеристикой можно применять в системах, где подача не снижается до Qi (до подачи, соответствующей напору при закрытой задвижке).

Крутизну кривой Q—Я можно оценить по отношению
* = —^—“ 100%-Н х
где Я0 — напор насоса при работе с закрытой задвижкой;
Нх — напор насоса при максимальном КПД.
Пологая характеристика обычно имеет крутизну 8—12%, крутопадающая — 25—30 %.
Е. А. Прегер1 на основе анализа рабочих характеристик Q—Я составил уравнение, дающее аналитическую зависимость между параметрами Я и Q:
Н = Cto -j- Q -j- 0<i Q2..
Ограничиваясь лишь рабочей частью характеристик Q—Я, можно упростить указанное уравнение, а именно:
для водопроводных насосов
Н = а — bQ2;
для фекальных насосов
Н = а — bQ.
Приведенные уравнения справедливы в пределах, где рабочие характеристики Q—Я могут быть приняты за прямую или квадратичную кривую. Коэффициенты а и Ъ постоянны и установлены для выпускаемых типоразмеров насосов.
'Прегер Е. А. Аналитические зависимости между параметрами лопастных насосов. Научные труды ЛИСИ, вып. 20, 1955.
§ 16. ИЗМЕНЕНИЕ ХАРАКТЕРИСТИК НАСОСОВ ПРИ ИЗМЕНЕНИИ ЧАСТОТЫ ВРАЩЕНИЯ И ГЕОМЕТРИЧЕСКИХ РАЗМЕРОВ РАБОЧЕГО КОЛЕСА
В производственных условиях часто возникает необходимость пересчета рабочих характеристик, установленных при частоте вращения п для перехода на другую частоту вращения рабочего колеса пi при D2='const. Так как диаметр рабочего колеса по наружному обводу ос-
тается постоянным, то отношение D2fiD\2 будет равно единице. Тогда ¦из закона подобия центробежных насосов имеем (см. § 11)'-
(3.3)
Q___п_
, Qi ni
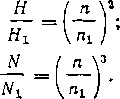
(3.4)
(3.5)
Полученные выражения называются законом пропорциональности.
Высота всасывания насоса при работе его с частотой вращения ni определяется по уравнению
![]()
где Я в —допускаемая вакуумметрическая высота всасывания при
частоте вращения пй Яв — то же, при частоте вращения, п.
Установленный закон пропорциональности позволяет по одной опытной характеристике Q—Я построить ряд характеристик насоса в широком диапазоне изменения частоты вращения.
Исключая из уравнений (3.3) и (3.4) частоту вращения, получим:
Hi = — Qf = const q\ ,
т. е.. уравнение параболы с вершиной в начале координат, проходящей через точку А с координатами QA и НА• Парабола OAi А2 А (рис. 3.4) представляет собой геометрическое место точек, определяющих режимы работы насоса, подобные режиму в точке А, и называется параболой подобных режимов.
Очевидно, что пересчет координат точки А для любой другой частоты вращения по формулам (3.3) и (З.б) приведет к точкам, располагающимся на параболах подобных режимов. Следовательно, пересчет всякой другой точки характеристики Q—Я при частоте вращения п на
частоту вращения пь п2,...; гсг- даст точки В2,..., С2,..., С* и
т.д., которые расположатся соответственно на параболах ОВь В; ОСъ ..., С. Соединяя точки А{, By Сi,... плавной кривой, получаем характеристику Qi—Я1 насоса для частоты вращения п{. Повторяя подобные операции для точек А2, Въ С2,..., Ai, В-ь Сь ..., получим соответственно характеристики Q—Я2,..., Q—Я* (см. рис. 3.4,а).
Параболы подобных режимов являются и линиями постоянного КПД. В действительности насос не сохраняет постоянства КПД, так как с увеличением п возрастают скорости потока и пропорционально их квадратам гидравлические потери. С другой стороны, механические потери сказываются сильнее при малых значениях п, т. е. когда мощность насоса мала. Оптимального значения КПД достигает при расчетном значении п0. При других п, меньших или больших nQt КПД будет уменьшаться по мере увеличения отклонения п от тг0.
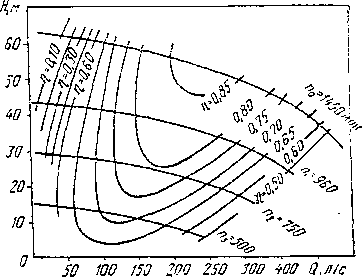
Отмечая на полученных характеристиках Q—Н, Q—Яь ... , Q—Hi точки с равными значениями КПД и соединяя их плавными кривыми, получают так называемую универсальную характеристику (см. рис. 3.4, б). Из рис. 3.4, б видно, что наибольшее значение КПД обеспечивают двигатели с частотой вращения 1450 мин-1.
а)
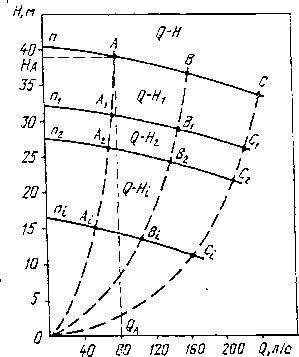

Рис. 3.4. Характеристики центробежных насосов
а — дри.изменении частоты вращения; б — универсальная
Универсальная характеристика позволяет наиболее полно исследовать работу насоса при переменных частоте вращения, КПД и мощности насоса для любой режимной точки.
Необходимо отметить, что режим работы насоса с пониженной частотой вращения допускается, но повышение частоты вращения в каждом случае следует согласовывать с заводом-изготовителем.
В практике проектирования и эксплуатации насосных станций часто для расширения поля работы насоса производят срезку рабочего колеса, т. е. уменьшают диаметр колеса D2, сохраняя b2—const.
Подачу Qcp и напор Яср насоса, имеющего срезанное рабочее колесо диаметром Оср, можно определить по уравнениям .закона подобия центробежных насосов (2.60), зная подачу Q и напор'Я насоса при номинальном (не срезанном) рабочем колесе диаметром
Из закона подобия при условии, что частота вращения rc=const и ширина колеса fr2—const, получим:
(3.6)
| Яср , | (А* |
| Н -1 |
1 г |
| Qcp |
Рср |
| ~Q~-Z |
\ D |
Экспериментальная проверка полученных равенств показывает, что для центробежных насосов, имеющих коэффициент быстроходности п3<с 150, лучшее соответствие расчетных величин QCp и Яср опытным данным получается при расчете срезки колеса по формулам:
{DcvV
Исследуем изменение режимных точек работы насоса при срезке рабочего колеса насоса. Из уравнений (3.6) следует, что
|
D2 | D2 __ ср |
| Н |
#ср |
| D2 |
D2 __ ср |
| Q | Qcp |
Отсюда
kxH =/^Q.
Принимая
kx
получим
H = kQ.
Следовательно, перемещение режимных точек в координатах Q—Я при уменьшении диаметра рабочего колеса происходит по прямым линиям I (рис. 3.5), проходящим через начало координат, т. е. точка А (находящаяся «а характеристике Q—Я, соответствующей DHom) перемещается в положение А\..
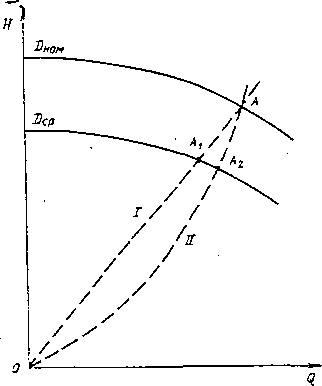
Рис. 3.5. Изменение положения режимнои тояки при срезке рабочего колеса
Проводя аналогичные исследования равенств (3.7), получим: Я=
=kQ2.
Таким образом, при расчете срезки рабочего колеса по уравнениям (3.7) режимные точки перемещаются по квадратичным параболам II с вершинами в начале координат (см. рис. 3.5), т. е. точка А перемещается в положение А2.
Изменение КПД насоса можно рассчитать по формуле Муди, которая применяется в гидротурбостроении для расчета оптимального значения полного КПД т]н (натуры) по значению т]м (модели):
_D
А
0,25
ср
Лер — 1 (1 'Ч)
Экспериментальное исследование- rfcp показывает, что при срезке колеса КПД изменяется незначительно в зависимости от коэффициента быстроходности. С достаточной степенью точности можно принять, что КПД насоса уменьшается на 1% на каждые 10% срезки колеса при коэффициенте быстроходности ns=60... 200 и на 1% на каждые 4°/о срезки при ns=200 ... 300.
В зависимости от коэффициента быстроходности рекомендуются следующие пределы срезки колес:
6Q<rtS<L20...................20—15%
120<л3<200 ................... 15—1.1%
200</г3< 300 ...............................11— 7%
В техническом паспорте насоса указываются характеристики Q—Я насоса для номинального рабочего колеса, например для насоса 10Д-9
D — 366 мм и рекомендуемой величины его срезки ^макс.ср == 325 ММ штрихлунктирная линия (рис. 3.6). Однако режимная точка Ь (предположим, с расчетными
параметрами Q = 150 л/с и Я=35 м) может не совпасть с указанными характеристиками. В этом случае необходимо произвести расчет срезки колеса в таких пределах, чтобы характеристика Q—Я срезанного колеса прошла через точку Ь.
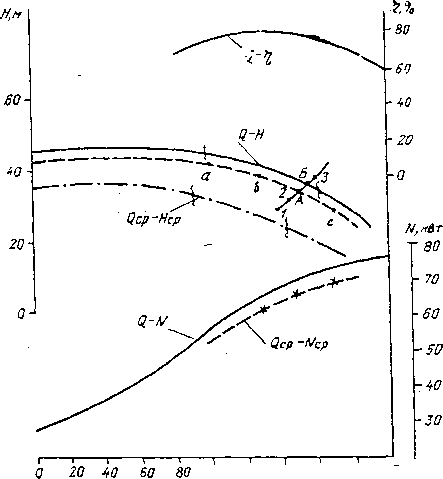
100 120
Рис. 3.6. Характеристика насоса ЮД-9 = 1450 мин-1) при срезке рабочего колеса
(Л:
Пример. Построим характеристику Qop — Яор, принимая во внимание, что коэффициент быстроходности насоса
ЮД-9 ns« 90.
Решение. Воспользуемся формулами (3.7) и построим параболу подобных режимов, проходящую через точку Ь:
D
366 Dc р
366 \2
QY = Н_ 150/ 35
а
Qcp
я
150
ср
Я_
35
D
Я = 35
н,
V150/ •
D,
а
ср
ср
ср
Для вычисления Я задаемся произвольно подачей Q (результаты вычислений при-зедены в табл. 3.1).
ТАБЛИЦА 3.1
| № точки (см. рис. 3.6) |
Q | <3/150 |
(Q/150)2 | н |
| 1 | 140 |
0,933 | 0,87 | 30,45 |
| 2 | 145 |
0,966 | 0,933 | 32,65 |
| 3 | 160 |
1,066- | 1,136 |
39,76 |
По данным табл. 3.1 строим параболу подобных режимов (см. рис. 3.6, кривая 1—5). Точка Б пересечения параболы с кривой Q—Я, соответствующей необточенному колесу 0 = 366 мм, и есть та точка, которая при срезке колеса переходит- в точку А. Из рис. 3.6 получим координаты точки Б: Q=.156,7 л/с. Отсюда имеем:
156,7 366 366-150
” 350,3 мм.
D
ср
СР 156,7
Срезка колеса составляет 4,3%. Следовательно, КПД насоса уменьшится приблизительно на 0,5%. Вычислив диаметр обточенного колеса, можем построить характеристику Qop—Яор:
Dc
150
Dr
Г) \2 ‘-'ср
~D~
¦'ср
D
и Яср = Я
Qcp — 0. 350,3
а
D,
ср
D
= 0,957;
= 0,9572 = 0,916.
366
Принимая произвольно Q и. определяя соответствующие ей Я по кривой Q—Я (при ?> = 366 мм), вычисляем координаты QCp, Яор (результаты вычислений сведены в табл. 3.2).
|
№ точки (см. рис. 3.6) | Q | ^ср | н ¦ : | ср |
|
а | 100 | 95,7 | 45 ¦ | 41,2 |
| ь | 13G |
124,4 | 41,8 | 38,3 |
| А | 156,7 |
150 | 38,21 | 35 |
| с | 170 |
162,7 | 33 | 30,2 |
По данным табл. 3.2 строим характеристику Q—Я (кривая аЬАс).
Оптимальный КПД соответствует расчетной подаче, поэтому насос следует подбирать так, чтобы рабочая подача соответствовала максимальному или близкому к максимальному значению КПД. Желательно, чтобы отклонения КПД насоса, выбранного для заданного-режима работы, составляли не более 5—10% максимального КПД.
Пространство (см. рис. 3.6), заключенное между характеристиками Q—Я для полного колеса и Qcр—Яср для максимально срезанного колеса и извилистыми линиями, соответствующими подачам при рекомендуемых отклонениях КПД, называется полем работы насоса.
В каталогах-справочниках приводятся сводные графики полей работы насосов различных типов. По этим графикам удобно подбирать насосы на заданный режим работы (см. приложения III—IX).
§ 17. НЕУСТАНОВИВШИЕСЯ И ПЕРЕХОДНЫЕ РЕЖИМЫ РАБОТЫ НАСОСОВ
Экспериментальные исследования показывают, что у центробежных насосов с коэффициентом быстроходности ns<ClOO наибольший напор достигается при некоторой промежуточной подаче и затем начинает падать. Такие насосы обеспечивают устойчивую работу системы при условии ЯСТ<Я0(ЯСТ — геометрическая высота подъ-H>M ем а воды; Я0 — напор насоса при Q = 0).
Q-Hrp
Q,J>/C
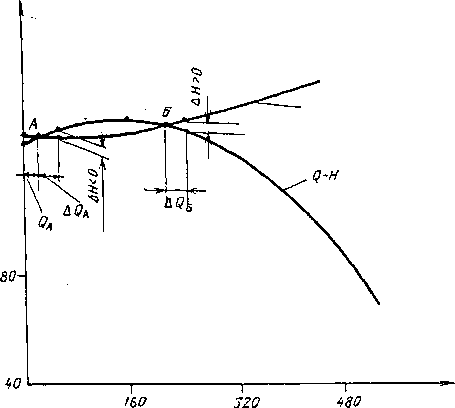
Рис. 3.7. Кривые неустановившейся работы яассхса
Рассмотрим режим работы насоса 14Д-6 (имею- н щего восходящую харак- ст теристику) с характерно- н° такой Q—Ятр. Пусть ха- 120 рактеристика Q—Ятр пересекает характеристику Q—Я насоса в двух точках: Л— на восходящей ветви и Б — на падающей ветви (рис. 3.7). В обеих режимных точках имеются все условия материального .и энергетического равновесия системы «насос— ^водоводы». При увеличении подачи на величину AQa вследствие кратковременного понижения требуемого напора в водоводах Ятр возникает отрицательная разность напоров ДЯ=Ятр—Я<0.
Избыток напора в системе Я по сравнению с требуемым Ятр вызывает увеличение кинетической энергии жидкости в системе, скорость движения и подача возрастают, что ведет к отклонению системы от равновесия в точке А и затем к выпадению системы из равновесия.
Предположим, что система «насос — водоводы» работает в режиме Б. В этом случае возникает положительная разность напоров
А Я = #тр — Я > 0.
Недостаток напора в системе' Я по сравнению с требуемым Ятр может быть компенсирован только за счет кинетической энергии жидкости в системе. Скорость движения жидкости при уменьшении Я падает, подача уменьшается, в результате чего достигается равновесие системы.
Следовательно, критерием устойчивой работы системы является знак разности напора ДЯ при увеличении подачи. Математическим критерием устойчивой работы в режимной точке является выполнение неравенства
аЯтр dtf
dQ > dQ *
Неустановившийся режим работы насоса недопустим по соображениям надежности работы всей системы. Поэтому при выборе насоса нужно стремиться к тому, чтобы заданный режим работы насоса лежал в поле рекомендуемой работы насоса.
В настоящее время в СССР уделяется большое внимание разработке конструкций насосов с n.s<ClOO с целью получения непрерывно падающих характеристик.
