Глава шестая истечение газа из суживающихся сопел и отверстий. сопла лаваля
ГЛАВА ШЕСТАЯ
ИСТЕЧЕНИЕ ГАЗА ИЗ СУЖИВАЮЩИХСЯ СОПЕЛ И ОТВЕРСТИЙ. СОПЛА ЛАВАЛЯ
6-1. СУЖИВАЮЩИЕСЯ СОПЛА
Суживающиеся сопла широко применяются для создания потоков дозвуковых и околозвуковых скоростей. Гидравлический расчет таких сопел весьма прост и сводится к определению размеров выходного сечения пс заданному расходу газа и заданной скорости истечения. При расчете считают, что течение газа в сопле адиабатическое, так как за 'короткое время протекания газовых частиц через сопло теплообмен с окружающей средой практически не устанавливается. Следовательно, для расчета сойла могут 'быть использованы уравнения адиабатического течения. Если пренебречь влиянием трения, то течение в сопле можно считать изоэнтроличе-ским. Как показывает опыт, потери на трение в коротких соплах невелики.
Обозначив, как и раньше, параметры полного торможения р0, Т0 и р„ (в рассматриваемом случае — это параметры газа в резервуаре), а параметры среды за соплом ра, Та и ра, можем определить скорость в выходном сечении F сопла по уравнению (2-10):
Ра
где еа=--отношение давления за соплом к давлению
Ро в резервуаре; k — 1 т = —т— .
К
По уравнению неразрывности можно найти весовой расход газа;
G = gFpc = Fyc = ~ .
Подставив сюда значение скорости из формулы (6-1), получим:
0 = /^^АТ..*У 1—*. (6-2)
Формула (6-2) дает расход газа в зависимости от давления и плотности газа в резервуаре и давления среды. Эта формула справедлива в предположении равномерного распределения скоростей в выходном сечении сопла F. Расход газа G в зависимости от еа меняется так же, как приведенный расход q.
6П2.2 Дейч Михаил Ефимович
Д 27 Техническая газодинамика. Изд. 2-е, переработ. М.—Л. Госэнергоиздат, 1961
с черт. и илл. 6П2.2
design pashaok
Редактор Б. Я• Шумяцкий Техн. редактор А. М. Фридкин
ГЛАВА ШЕСТАЯ
ИСТЕЧЕНИЕ ГАЗА ИЗ СУЖИВАЮЩИХСЯ СОПЕЛ И ОТВЕРСТИЙ. СОПЛА ЛАВАЛЯ
6-1. СУЖИВАЮЩИЕСЯ СОПЛА
Суживающиеся сопла широко применяются для создания потоков дозвуковых и околозвуковых скоростей. Гидравлический расчет таких сопел весьма прост и сво-
1 Напомним, что весь расчет выполнен без учета пограничного слоя: скорость берется на внешней границе слоя.
2 Выделение теплоты трения происходит только в тех областях
потока, где устанавливается неравномерное распределение скоростей, связанное с действием вязкости. /
3 Такая задача возникает при исследовании закрученного потока в ступени турбомашины (турбины илн компрессора).
дится к определению размеров выходного сечения пс заданному расходу газа и заданной скорости истечения. При расчете считают, что течение газа в сопле адиабатическое, так как за короткое время протекания газовых частиц через сопло теплообмен с окружающей средой практически не устанавливается. Следовательно, для расчета сойла могут 'быть использованы уравнения адиабатического течения. Если пренебречь влиянием трения, то течение в сопле можно считать изоэнтроличе-ским. Как показывает опыт, потери на трение в коротких соплах невелики.
Обозначив, как и раньше, параметры полного торможения ро, Т0 и р0 (в рассматриваемом случае — это параметры газа в резервуаре), а параметры среды за соплом ра, Та и ра, можем определить скорость в выходном сечении F сопла по уравнению (2-10):
где &а =--отношение давления за соплом к давлению
в резервуаре;
т = —7—. k
По уравнению неразрывности можно найти весовой расход газа;
G = gF?c = Ffc = ^.
Подставив сюда значение скорости из формулы (6-1), получим:
Формула (6-2) дает расход газа в зависимости от давления и плотности газа в резервуаре и давления среды. Эта формула справедлива в предположении равномерного распределения скоростей в выходном сечении сопла F. Расход газа G в зависимости от еа меняется так же, как приведенный расход q.
Действительно, так как G = gFq^a*, то после подстановки значений р* и а получаем:
1
= f (i -Iqrji-)6 ' ¦ («-3)
Из сопоставления уравнений (6-2) и (6-3) следует:
_i i_
l~‘ !-‘Г. (е'4>
Формулы (6-2) и (6-3) показывают, что максимальное значение расхода отвечает критической скорости Х=\ и соответственно критическому отношению давлений еа=е„.
Максимальный или критический расход получаем после подстановки еа = е# в уравнение (6-2) или 1 = 1 в уравнение (6-3):
ft+i
(6-5)
Формула (6-5) легко получается подстановкой I = 1 в уравнение (2-38).
Для
? = 1,4 G, = 2,145V/Vfo = 0.396f^= ; Для Л = 1,3 G, = 2,09VAJo~ 0,305/'-^?=.
(6-6)
г Г0
Уравнение расхода (6-2) показывает, что при заданном выходном сечении сопла с уменьшением sfl при &а > е, рас» ход газа увеличивается, а при еа <[ е, согласно уравнению (S-2) расход газа должен уменьшаться. Однако последнее не соответствует действительности. Следовательно, уравнение (6-2) неправильно описывает процесс истечения газа при еа<^е3, если в него подставлять отношение давления среды ра к давлению в резервуаре pQ.
Рассмотрим истечение из суживающегося сопла при фиксированных значениях давления и температуры в резервуаре и переменном давлении среды ра.
До тех пор, пока давление среды больше критического давления, подсчитанного по параметрам газа в резервуаре, любые изменения ра распространяются и внутрь сопла. В этом случае расход газа изменяется в соответствии с формулой (6-2). Когда уменьшающееся давление ра достигает критического значения р„ в выходном сечении суживающегося сопла устанавливается критическая скорость и дальнейшие изменения давления окружающей среды не могут проникнуть внутрь сопла. Следовательно, фактический перепад давлений, создающий расход газа через сопло при pa<i pt, вне зависимости от величины давления внешней среды будет критическим, а расход газа — максимальным и постоянным. Отсюда следует, что формула (6-2) при ра < р, только в этом случае дает правильные значения расхода, если в нее подставляется критическое давление, которое устанавливается в выходном сечении суживающегося сопла, вне зависимости от величины ра. В момент, когдя в выходном сечении достигаются критические параметры, происходит своеобразное явление „запирания" сопла136, в результате которого сопло и резервуар оказываются изолированными от внешней среды.
Таким образом, при &а < е, в формулу (6-2) необходимо подставлять е#. Расход газа при этом остается постоянным и определяется по формуле (6-6).
На характер зависимости G от га оказывает влияние распределение скоростей в выходном сечении сопла. Полученные выше формулы хорошо подтверждаются экспериментом только в том случае, когда профиль сопла выполнен плавным. Плавно суживающаяся форма сопла .приближает распределение скоростей в выходном сечении тс равномерному. С этой целью стенки сопла должны быть особым образом рассчитаны.
Профиль суживающегося сопла может быть рассчитан по формуле Витоши'нского:
г —-— . --
Величины, входящие в формулу (6-7), пояснены на рис.
6-1; I' = . Такой профиль пригоден для сопел, соеди
няющих две трубы различных диаметров, когда поток при
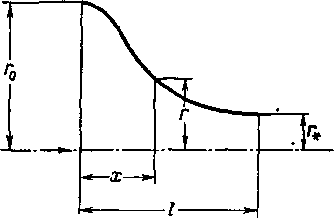
Рис. 6-1. К построению суживающегося сопла.
переходе в трубу меньшего диаметра должен быть ускорен, а скорости в каждой точке выходного сечения сопла должны быть одинаковыми. Сопла такого профиля применяются для аэродинамических труб дозвуковых скоростей.
Опыт показывает, что в широком диапазоне скоростей до Я = 0,90-н0,95 поле скоростей за соплом достаточно равномерно.
При подключении сопла непосредственно к резервуару его профиль может быть очерчен дугами окружности. Иногда профиль сопла очерчивается лемнискатами.
6-2. СУЖИВАЮЩЕЕСЯ СОПЛО ПРИ ПЕРЕМЕННОМ РЕЖИМЕ
При изменении параметров газа в резервуаре и за соплом меняются расход газа и спектр вытекающей струи. Пользуясь соотношениями (6-2) и (6-5), можно проайализи-
ровать изменение расхода при одновременном изменении давления в резервуаре ра и давления среды ра.
Обозначим:
Л)макс — максимальное давление в резервуаре;
G* макс — соответствующий этому давлению максимальный критический расход;
Роу G* — текущие значения давления в резервуаре и критического расхода.
На основании формулы (6-5) можно выразить отношение критических расходов:
Ро
(6-8)
1
G,
Ро I
Предполагая, что при изменении давления р0 температура газа в резервуаре Г0 сохраняется постоянной, получим:
С —п * ' '
макс Ро макс
При Т0 — const и неизменном давлении в резервуаре изменение расхода в зависимости от давления за соплом ра выражается уже известным над уравнением (6-2).
Легко заметить, что отношение расхода при данном противодавлении к критическому расходу равно:
^0 макс
Подставив О, в уравнение (6-10), получим:
Отсюда следует, что при изменении начального давления все точки кривой приведенного расхода сдвигаются пропорционально е0, т. е. пропорционально изменению давления перед соплом.
Следовательно, отношение расхода G к максимальному критическому расходу G#MaKc можно представить в зависи
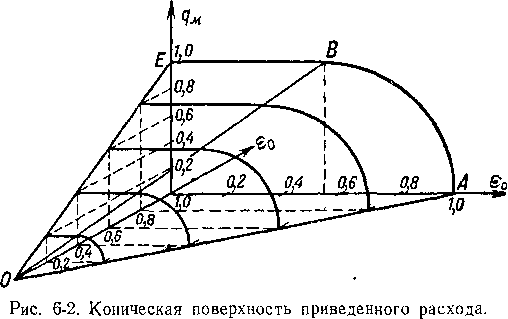
мости от еа и е0. Эта зависимость наглядно изображается в трехосной системе координат (рис. 6-2), где по трем осям отложены
Ро
Ро,
Ра Ро
В результате мы 'получаем некоторую коническую поверхность, каждая точка которой определяет расход газа через суживающееся сопло в зависимости от давлений перед соплом и за ним. Продолжением конической поверхности ОАВ (рис. 6-2) служит плоский треугольник ОЕВ, точки которого отвечают области критических расходов газа.
Уравнение (6-11) можно представить и в двухосной системе координат, построив кривые <7M=f(?a) для различных, но .постоянных значений ео. Тогда мы получаем сетку относительных расходов газа, которая представляет собой проекцию конической поверхности на плоскость (q, е). Сетка расходов (рис. 6-3) весьма удобна
для графического расчета сопла при изменениях режима *.
Многочисленные опыты показали, что уравнение поверхности расходов (6-11) можно упростить, заменяя точную формулу приведенного расхода q приближенным выражением. При докритических перепадах давлений
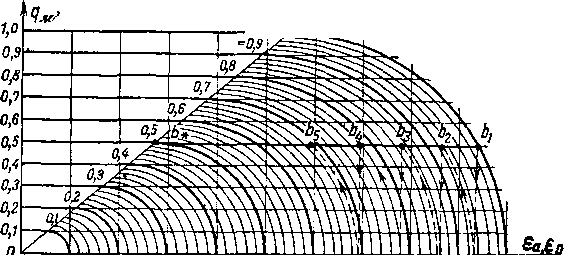
0,2 0,3 0,4 0,5 0,6 ?0,7 gOfl ?0,9# 1,0
Рис 6-3. Сетка приведенных расходов газа.
(еа> е ) зависимость q = q(za) может быть представлена дугой эллипса, уравнение которого имеет вид:
(6-12)
(1 —
Во всем диапазоне дозвуковых скоростей эта формула весьма точно аппроксимирует зависимость между q и efl. Заменив в уравнении (6-12)
получим:
1.
(6-13)
е2
О
(I-*.)137
Обозначим:
_ Р а Р„
Ра
: s
а О
Р0 макс Ро Р0 макс
откуда
9M=urr/(so“?,)K-30(2e.-l)]. (6-15)
При е0 — const уравнение (6-15) дает зависимость qM — = q (s'), так как для плавно суживающегося сопла е# зависит только от физических свойств газа и является при k =const величиной постоянной.
При изучении переменного режима сопла большой практический интерес представляет характер изменения спектра струи за соплом. Для докритических режимов истечения изменения параметров на входе в сопло и выходе из него слабо влияют на форму струи за соплом.
При сверхкритических перепадах давлений переход от критической скорости в выходном сечении к сверхзвуковой скорости происходит в свободной струе за соплом.
В этом случае кромка выходного сечения ААХ (рис. 6-4,а) является источником возмущения звукового потока. За выходным сечением струя встречает давление среды ра (р меньше критического) и, следовательно, в точках А и Ах (рис. 6-4,а) давление меняется от р, до ра. В результате от кромок сопла распространяются две волны разрежения: ЛЛД и А1АВ, крайними границами которых являются характеристики. Первая граница АА, представляет собой
характеристику, угол которой <*mI — ; вторая граница АВХ
.должна проходить в свободной струе под углом
am2 = arCS
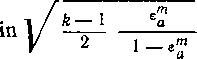
k—\ т — k ¦ (6-16)
Между двумя этими границами располагаются характе ристики, углы которых меняются в пределах
В действительности, однако, все характеристики, включая АВ\ и А{В, имеют переменный угол наклона и, следовательно, являются криволинейными, так как волны разрежения из тачек А и А\ в пределах струи пересекаются. Пересечение волн происходит в треугольнике AA\D. Кроме того, характеристики, попадая на
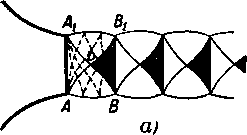
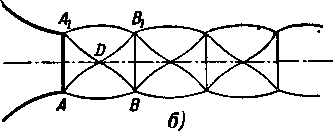
Рис. 6-4, Схемы спектров струи за сужи» вающимся соплом при нерасчетных ре жимах (еа]> е,).
свободную границу АВ и А\Ви отражаются от нее с обратным знаком и волны разрежения переходят в волны сжатия.
В результате пересечения в струе образуется клин разрежения ADAX, основание которого расположено в выходном сечении сопла. В пределах клина происходит значительное уменьшение давления, которое в этой зоне становится ниже давления среды ра.
Так как отраженные от свободной границы волны пересекаются в пределах второго клина DBBX, то здесь давление повышается до значения р в сечении BBV\ клин разрежения переходит в клин уплотнения. Следовательно, точки В и В\, давление в которых меняется от до ра, также являются источниками волн разрежения и спектр струи повторяется. Нетрудно заметить, что отрезки AAi и BBt равны. При пересечении клина
разрежения линии тока деформируются, отклоняясь of оси сопла: сечения струи увеличиваются, и струя
«разбухает». В пределах отраженных волн поток уплотняется и его сечения уменьшаются. Границы струи, симметричные относительно оси, приобретают волнистую форму.
На основании изложенного можно предвидеть характер изменения давления по оси струи. В пределах клина разрежения давление падает от до некоторого значения Pd<Ph, а в пределах клина уплотнение возрастает до р ; дальше процесс повторяется. Давление в струе меняется по некоторому периодическому закону, близкому к синусоидальному. Соответствующим будет и характер изменения скоростей вдоль оси струи. В сечениях АА, и ВВ1 скорости критические. Между этими сечениями скорости сверхкритические, причем в точке D скорость будет максимальной. Следовательно, вся область струи АВВХАУ является сверхзвуковой.
Спектры струи при рассматриваемых режимах сохраняются качественно одинаковыми для плоских и осесимметричных сопел, однако в последнем случае волны разрежения и уплотнения имеют коническую форму. В осесимметричной струе поэтому образуются конусы (а не клинья) разрежения и уплотнения. По мере повышения давления в резервуаре или снижения давления за соплом спектр течения постепенно перестраивается (рис. 6-4,6). Углы волн АВ\ и АУВ уменьшаются, высота клиньев ADA\ и DBBj увеличивается и углы при вершине клиньев (конусов) уменьшаются. Расстояния между сечениями AAt и ВВ\ увеличиваются.
Для осесимметричного сопла такая постепенная перестройка происходит до определенных пределов. При достижении некоторого отношения давлений ei картина течения за соплом меняется кризисным образом.
Благодаря интенсивному уменьшению давления газа в пределах конуса разрежения его образующие AD и A\D переходят в криволинейные скачки AD и A\Dy (рис. 6-5,а), а в ядре струи образуется прямой скачок DDy, замыкающий криволинейные скачки. Во внешнем потоке возникают криволинейные скачки DB и DiBh Таким образом, в струе за соплом возникает мостообразный скачок ADBByD\Ay. Скачки DB и DxBi выходят за свободную границу струи и отражаются от нее в виде волн разрежения. Волны разрежения также замыкаются криволинейными скачками.
Пр'И пересечении прямого скачка DDy скорости центральной части струи становятся дозвуковыми, а давление интенсивно возрастает (р'>ра). При переходе через скачки DB и DxBy скорости остаются сверхзвуковыми. Следовательно, линии DE и
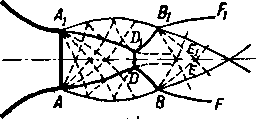
а)
D\Ey являются линиями тангенциального разрыва скоростей. В результате взаимодействия с внешним сверхзвуковым течением дозвуковое ядро потока ускоряется, а сечение его уменьшается до минимального ЕЕ 1, в котором звуковая скорость
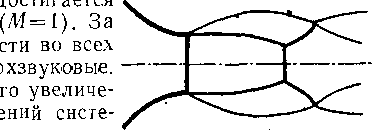
сечением ЕЕг скоро! точках струи свер По мере дальнейше ния перепада давл« ма скачков постепенно >пере-

страивается (рис. 6-5,6). Увеличивается протяженность прямого скачка, изменяется форма
криволинейного скачка, ограничивающего перерасширенное
сверхзвуковое ядро. Необходимо подчеркнуть, что внешние части струи ABFEDA и соответственно А\B\F\E\D\A\, так же как и ядро ADDiAu при любом значении еа<е^ остаются сверхзвуковыми. Дозвуковые скорости обнаруживаются только на небольшом участке внутри струи за скачком DD\. Следует иметь в виду, что все вышеприведенные рассуждения не учитывают влияния вязкости и, в частности, взаимодействия струи с окружающей средой.
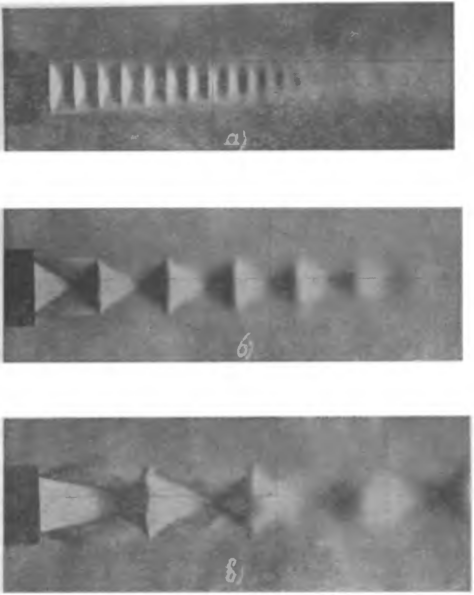
Спектры истечения из суживающегося осесимметричного сопла даны на рис. 6-6. Здесь отчетливо видны все стадии развития спектра струи при еа<е _ Заметим, что сверхзвуковые участки спектра для плоского сопла могут .быть рассчитаны методом характеристик.
Для оценки качества сопла служат коэффициент
-
Рис. 6-6. Истечение воздуха из суживающегося сопла при сверхкритйческих перепадах давлений. а—еа=0,51; б—еа=0,412; в—efl=0,267; г — гд=0,05.
расхода цс, 'коэффициент скорости фс и коэффициент потерь 1с.
Коэффициент расхода определяется по формуле
где G— действительный расход газа через сопло;
Gt — теоретический расход (при изоэнтропическом процессе).
Коэффициент скорости представляет собой отношение скоростей в действительном и теоретическом процессах:
?с=-^- (6‘18^
На рис. 6-7 и 6-8 приведены коэффициенты и ф для суживающихся профилированных и конических сопел в за-
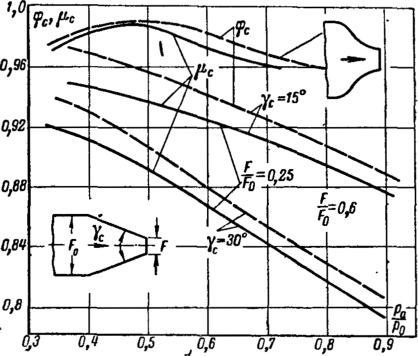
Рис. 6-7. Коэффициенты расхода у.с и коэффициенты скорости <рс для конических и профилированных сопе'л.
висимости от еа и Re. Кривые показывают, что при увеличении перепада давлений и уменьшении угла конусности коэффициент расхода возрастает. Аналогичный результат получен и для профилированного сопла. Однако максимум ц(
С
в последнем случае отвечает околокритическим скоростям. Абсолютные значения ^ получены более высокими для профилированного сопла. При еа3=0,7 кривые на рис. 6-7
'отражают не только влияние сжимаемости, но и числа Рейнольдса (рис. 6-8).
Коэффициент скорости конических сопел мало меняется в зависимости от угла конусности. В широком диапазоне eQ
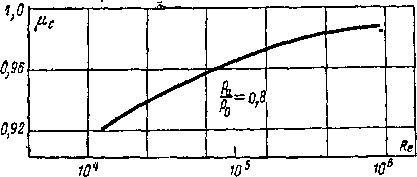
Рис. 6-8. Влияние числа Re на коэффициент расхода суживающегося сопла.
среднее значение <?с составляете 0,97. Для сопел, профилированных по формуле (6-7), значения 9с получаются более высокими (9^ = 0,985^-0,99).
Отмечаемое влияние отношения сечений, угла конусности и еа объясняется изменением структуры потока в струе за соплом.
С увеличением — уменьшаются потери на трение в соп-
О
ле, но вместе с тем поле потока на выходе становится более неравномерным. Аналогично влияет и увеличение угла конусности, с ростом которого поле потока на выходе приобретает все большую неравномерность.
В качестве примера применения сетки расходов рассмотрим течение газа в системе последовательно включенных сопел. Пусть в трубе установлены г суживающихся сопел с одинаковой площадью выходного сечения (рис. 6-9). Полагаем, что диаметр грубы значительно больше диаметра сопел; скоростью газа в трубе можно пренебречь.
При истечении через каждое сопло газ расширяется и скорость его возрастает. В промежуточной камере происходит процесс преобразования кинетической анергии в тепло. В рассматриваемой схеме аппарата осуществляется полное преобразование (полное гашение)
Кинетической энергии. Струя газа теряет скорость благодаря йзай-модействию с частицами в камере, а также удару о стенку следующего сопла.
Процесс гашения кинетической энергии в аппарате является изобарическим. При этом состояние газа на входе в сопла характеризуется условием !0i = const или r0=const (рис. 6-10).
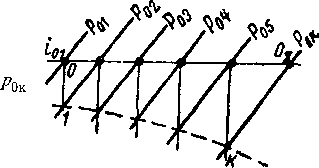
Рис. 6-9. Схема соплового Рис. 6-10. Изображение процесса аппарата с полным гашением в тепловой диаграмме для сопло-скорости в промежуточных вого аппарата,
камерах.
| 2 |
LUA | ч |
& | 2 |
Ро5 | '4 | |
| 1 | 1 |
1 | I | 1 | |||
| 1 |
/'/// | 1 |
>77М | ГГ7Т |
1 |
Характерной особенностью процесса в сопловом аппарате является увеличение энтропии в промежуточных камерах.
Расчет соплового аппарата осуществляется с помощью уравнений (6-3) и (6-12). Учитывая, что расход для всех сопел будет одинаковым, из указанных уравнений легко получаем:
Здесь qt — приведенный расход через первое сопло;
_ Pol _ po>i __ ^Ок
е°2~ Poi ’ е°га = Ра 1 ’ Е°к= Ро 1 ’ РоЬ Р°2’ Р°п ’
Рок — давления торможения соответственно перед и за первым соплом, за соплом (п — 1) и за аппаратом;
Ра (п + 1) Рйг
е =—---; е =-—отношение давлении на сопле
п Роп г Рак
п И Z.
Значение еп определяется по формуле (6-19):
>б-2о>
Отсюда заключаем, <trd так йай i0n <С ), Тб tn гя_| , Для каждого последующего сопла отношения давлений будут меньше, чем для предыдущего. В соответствии с этим безразмерные скорости вдоль соплового аппарата будут возрастать (Хп > Хп_{) и, следовательно, критическая скорость (X = I) появится в последнем сопле (вне зависимости от того, происходит ли полное или частичное гашение кинетической энергии в промежуточных камерах), если е0к е0 , где г0 —критическое отношение давлений для соплового аппарата.
К этому же выводу можно прийти из простых физических соображений. Действительно, с падением давления падает и плотность газа. Но так как выходные сечения сопел одинаковы, то для того чтобы расход газа оставался постоянным, необходимо, чтобы в каждом последующем сопле скорость возрастала. Очевидно, наибольшая скорость установится в последнем сопле
Из уравнения (6-J 9) для последнего сопла можно получить, что
РО* ( 2 V
при ег = —— = е, = ^ fe _j_ j j критическое отношение давлении
для соплового аппарата будет:
![]()
где — приведенный расход через первое сопло при критическом истечении из последнего.
Для каждого сопла при eQn — const можно нанести кривые q = q(e) (рис. 6-3). Линия критических расходов определена уравнением (6-21) (линия ОВ на рис. 6-3).
Следует подчеркнуть, что формула (6-21) полностью эквивалентна формуле (5-19), полученной для трубы постоянного сечения. Отсюда можно заключить, что вне зависимости от физических особенностей движения газа (без энергетического обмена с окружающей средой), но сопровождающегося ростом энтропии предельный режим этого движения, рассматриваемого в рамках одномерной схемы, описывается одинаковыми уравнениями.
С помощью диаграммы на рис. 6-3 можно решать следующие задачи:
1. Если заданы приведенный расход газа и число сопел в аппарате г, то можно определить е04, а также е0л и еп, т. е. установить распределение давлении в соплах.
2. Можно иайти число сопел, если известны расход qt и относительное давление за последним соплом е04 .
3. Для известного значения qt .можно определить критическое отношение давлений eQ и число сопел г.
Рассмотрим соответствующие примеры.
1. Допустим, что число сопел г = 4, а приведенный расход q, = 0,5.’На пересечении линии qi = 0,5 с кривой q = q(e) для первого сопла найдем точку bu которая определяет в,. Кривая b\ Ьг даст ту же зависимость для второго сопла. Следовательно, в точке b'2 получим e02 = e,e2. Повторив это построение до точки Ь'л , определим относительное давление eQk = е,е2е3е4.
2. Пусть заданы расход qt = 0,5 и отношение давлений e0ft=0,69. Тогда исходной точкой в сетке расходов будет точка Ьь на пересечении линии qt = 0,5 дуги эллипса eak = 0,69. Перемещаясь по этой линии до оси е и затем по вертикали до линии qt = 0,5, последова-
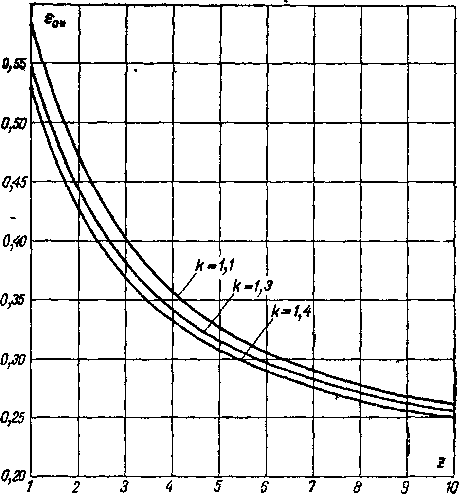
Рис. 6-11. Критическое отношение давлений для соплового аппарата в зависимости от числа сопел г для различных значений k.
тельно находим точки b[, 64, Ь'ъ, Ь3 и т. д. до точки Число вертикальных линий b\, 64, Ъ’ъ, Ъг и т. д. равно числу сопел аппарата г.
3. Найдем теперь число сопел при qt = 0,5, отвечающее критическому режиму соплового аппарата zQk = е0 . Определив на линии ОВ точку Ь, , соответствующую критической скорости в последнем сопле, находим линию q = q (е), проходяшую через эту точку, и далее последовательно определяем распределение давлений и число сопел г так же, как и в предыдущем случае.
Задаваясь различными значениями qt по (6-21), находим соответствующие значения и, решив задачу 3 описанным выше методом, олреде^яе^ число сопел при критическом режиме соплового аппарата.
Результаты таких расчетов прэдставлены на рис 6-11, где нанесены значения е0 в зависимости от г.
Большой практический интерес представляет также возможность определения расхода газа через сопловой аппарат при заданных eQk и г. Такая задача, однако, решается просто только в том случае, когда сотовой аппарат работает в критическом режиме (еой, < е0 J с полным гашением кинетической энергии в промежуточных камерах. В этом случае из графика на рис 6-11 находим критическое отношение давлений е0 для заданного числа сопел Величину приведенного расхода qy можно определить по формуле (6-21) или по рис. 6-3 (прямая АВ)
Отметим, что кривые на рис. 6-11 подчиняются уравнению
е°*_ /е2 -{-(! — )г' (6’22*
6-3. ИСТЕЧЕНИЕ ГАЗА ИЗ ОТВЕРСТИЯ С ОСТРОЙ КРОМКОЙ.
ВТОРОЕ КРИТИЧЕСКОЕ ОТНОШЕНИЕ ДАВЛЕНИЙ
Теоретические исследования и эксперимент обнаруживают некоторые новые свойства потока газа, вытекающего из отверстия с острой кромкой.
Теоретические решения этой задачи были даны в классических работах Н. Е. Жуковского и С. А. Чаплыгина как для небольших скоростей, так и для скоростей, соизмеримых со скоростью звука. Дальнейшее развитие метода С. А. Чаплыгина применительно к истечению из отверстия с острой кромкой было осуществлено Ф. И. Франклем для области звуковых и сверхзвуковых скоростей.
При истечении из суживающегося сопла плавный профиль стенок обеспечивает постепенное расширение потока и определяет форму линий тока. Возникающие на входе радиальные составляющие скоростей уменьшаются при течении по соплу и к выходному сечению обращаются в нуль. Поток в выходном сечении имеет равномерное поле скоростей. При сверхкритических перепадах давлений выходное сечение сопла совпадает с критическим.
Истечение из отверстия с острой кромкой происходит иначе (рис. 6-12). В сосуде на достаточно большом удалении от отверстия скорость газа равна нулю, а давление— Ро- За отверстием поддерживается давление ра<Ро-
Вблизи отверстия слева скорости газа интенсивно нарастают, струйки газа суживаются и искривляются.
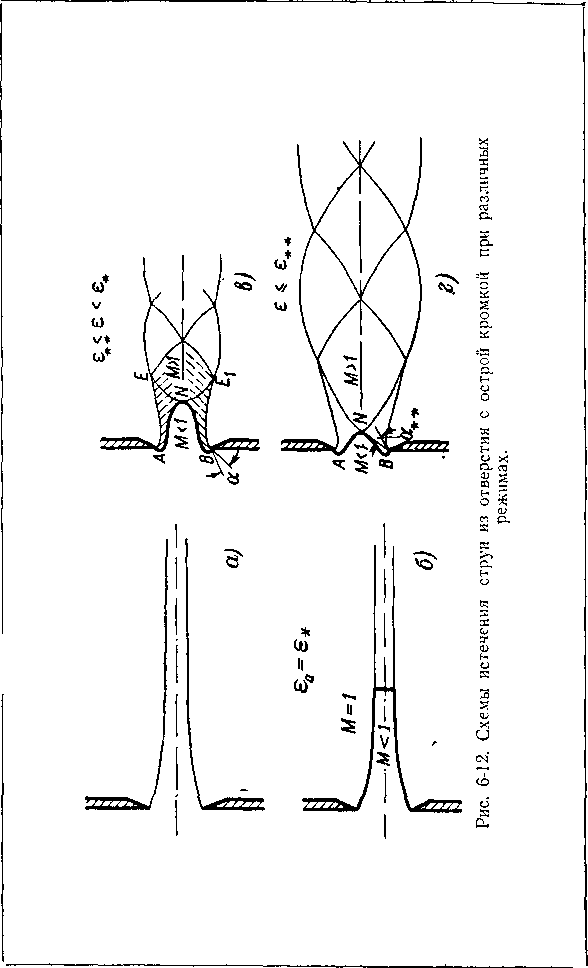
Поток газа срывается с острых кромок отверстия <й дальше движется, как свободная струя.
Спектр струи в отверстии показывает, что кривизна разных линий тока оказывается различной. Наиболее искривленными являются линии тока у границы струи, а наименее искривленными — линии тока вблизи оси. Поэтому скорости на внешних линиях тока будут больше, чем скорости в ядре струи. На выходе из отверстия устанавливается неравномерное распределение скоростей и давлений. Неравномерность потока усугубляется влиянием вязкости. Нетрудно видеть, что струя будет увлекать за собой газ окружающей среды и тормозиться. Средняя скорость струи будет уменьшаться, а поперечное сечение ее — увеличиваться. Размывание струи начинается непосредственно от кромок отверстия. Однако происходит оно достаточно медленно. На этом основании можно воспользоваться следующей идеализированной схемой истечения через отверстие. Предполагаем газ совершенным, а движение — безвихревым.
На острых кромках А и В будет происходить отрыв. Так как мы предполагаем, что трение отсутствует, то подмешивания окружающего газа к струе не будет. Следовательно, справа от отверстия образуются две области: свободная струя и неподвижный газ с давлением ра. Так как давление на границе струи является постоянным, то очевидно, что скорость на границе также постоянна.
Задача по определению формы такой струи и расхода газа через отверстие была решена в классической работе С. А. Чаплыгина „О газовых струях“. С. А. Чаплыгин рассмотрел случай плоской струи, когда отношение дав-.
лений еа = больше критического или близко к нему.
В этом случае струя имеет форму, изображенную на рис. 6-12,а. Струя непрерывно суживается, причем максимальное сужение имеет место на бесконечном удалении от отверстия. Если = , то на границе струи ско
рость течения равна критической. Внутри струи скорости меньше критической. С удалением от отверстия эпюры скоростей выравниваются и на некотором конечном расстоянии от отверстия скорости в струе становятся равными скорости на границе, причем выравнивание поля скоростей происходит вследствие поджатия струи и ускоре-
ййй ядра. Образующееся при этом сужение струи характер ризуется коэффициентом сужения, который определяется как отношение минимальной ширины струи к ширине отверстия (плоская задача).
Таким образом, при ?а = критическая скорость обнаруживается на границе струи и в поперечном сечении на конечном удалении от отверстия. Линия критических скоростей для такого режима показана на рис. 6-12,6. При дальнейшем понижении противодавления (е <6^) струя становится сверхзвуковой.
Переход через скорость звука совершается на линии звуковых скоростей AN В, которая идет от кромок отверстия и вдается в струю в виде „язычка" (рис. 6-12,в).
Следовательно, при sQ<Cs, спектр струи перестраивается. Линия звуковых скоростей (линия перехода), совпадавшая при sg = stic границей струи и минимальным сечением, по мере уменьшения eQ деформируется и приближается к выходному сечению отверстия. Справа от переходной линии течение сверхзвуковое. Деформация линии перехода объясняется перестройкой поля скоростей в выходном сечении АВ и в последующих сечениях, связанной с изменением кривизны граничных линий тока.
Внутри „язычка“ скорости дозвуковые. Характер деформации линии перехода свидетельствует о том, что сверхзвуковые скорости достигаются вначале во внешней части струи (на границе и вблизи нее), а затем в ядре, что полностью соответствует распределению скоростей в поперечном сечении струи. Граница струи расширяется. Деформация „язычка* при изменении га будет происходить до тех пор, пока линии слабых возмущений (характеристики), отходящие от границ АЕ и ВЕг, будут попадать на линию перехода AN В. Углы характеристик кт с уменьшением га уменьшаются (рис. 6-12,в).
Следовательно, деформация линии перехода-при уменьшении sfl не будет беспредельной. Существует такое значение внешнего давления /?##, при котором линия перехода занимает стабильное положение; дальнейшее снижение давления внешней среды уже не приводит к ее деформации. Этот режим соответствует такому углу первых характеристик, исходящих из точек А и В, при котором они касаются линии перехода, но не пересекая ее (рис. 6-12,г). Давление ры было названо Ф. И. Франклем вторым критическим давлением. Соответствующее отношение
Ро
будем называть вторым критическим отношением давлений.
Характерными особенностями стабилизировавшейся линии перехода являются участки, лежащие внутри сопла около точек А и В (рис. 6-12,г) которые показывают, что у краев отверстия со стороны резервуара скорости уже сверхзвуковые. Кроме того, при еа = ем линия перехода в струе занимает ближайшее к отверстию положение.
В соответствии с перестраивающейся (в зависимости от sj картиной течения изменяется расход газа через отверстие. Назовем коэффициентом расхода отверстия р.отв отношение действительного расхода через отверстие к расходу газа через суживающееся сопло, имеющее ту же площадь поперечного сечения на выходе при одном и том же перепаде давлений.
Значения коэффициента расхода при &а > st , подсчитанные С. А. Чаплыгиным для воздуха, приведены в первых пяти графах табл. 6-1. Для несжимаемой жидкости и =0,63.
Готв ’
Выше указывалось, что максимальный расход для сопла имеет место при критическом противодавлении и дальнейшее снижение противодавленйя не влияет на расход. При истечении из отверстия благодаря изменению формы линии перехода при &а<^расход газа будет увеличиваться до тех пор, пока га'>гм.
Таблица 6-1
| ° Ро | 0,676 |
0,641 | 0,606 | 0,559 |
0,529 | 0,037 |
|
^отв | 0,680 | 0,700 | 0,710 | 0,730 |
0,740 | 0,850 |
При га<г„ уменьшение противодавления не влияет на форму линии перехода и, следовательно, на расход
Таблица 6-2
LO
II
*1?
¦i tal-
о
o'
Ч
ч?
It
>fiijcs
00
О
<м
o'
I
fsj
II
Л|<3
со
сГ
II
•я
о
Я
W
*3
о
CQ
X
>>
СО
о
СО
и
>>
Я
к
*=с
о
CQ
СО
о
X
о
V
я
н
я *
О- * & W
»я О х о S
Q* О)
н
я
а>
я
s*
я
*&
>&
m
о
газа. Если внешнее давление равно второму критическому давлению, то коэффициент расхода имеет максимальное значение.
Значения коэффициента расхода р/тв и второго- критического отношения давлений ем для отверстий различной формы приведены в табл. 6-2.
На рис. 6-13 представлены кривые относительного расхода через суживающееся сопло и через отверстие с острой
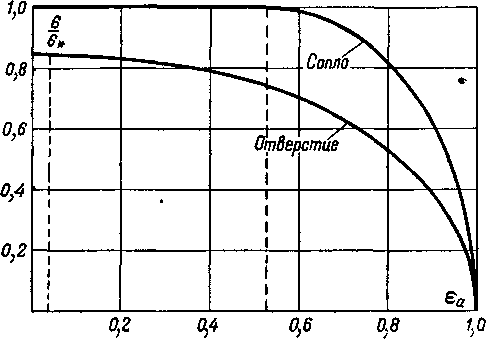
Рис. 6-13. Изменение расхода газа через сопло и отверстие с острой кромкой при одинаковой площади сечения (ft = 1,4).
кромкой при одинаковой площади поперечного сечения в зависимости от еа для воздуха. В обоих случаях расход отнесен к критическому расходу через сопло.
Установим теперь форму кривой зависимости ~^—=f(sa)
для отверстия с острой кромкой. Максимальный расход газа через отверстие может быть подсчитан по формуле
?~Н
°~=(rri (6-23)
где F — площадь отверстия;
|/тв — коэффициент расхода через отверстия при
Ро> То — параметры газа в резервуаре на значительном удалении от отверстия (параметры торможения).
Расход газа через отверстие при произвольном га можно найти по уравнению
i_
G = ^ОТВ F /тй 8* (1 - е" ). (6-24)
Обозначим приведенный расход через отверстие с острой кромкой
G
<7о =g~-w **
Тогда расход через отверстие
G = g0G^==(p^j(k ] VkgV-'0TBq„F VPSU- (6-24а)
Формула для приведенного расхода газа q0 на основании уравнений (6-23) и (6-24) принимает такой вид:
А + 1
Значения коэффициентов расхода [*отв и р/тв могут быть приняты по табл. 6-1 и 6-2.
Можно получить простое приближенное выражение
для q0, предположив, что зависимость q0 от еа при описыйается уравнением эллипса:
= (6‘26)
или
¦ (1 - г.,)2 <7о =1 - 2е» (! - еа) - е!. * (6-27)
Сопоставление точного и приближенного решений показывает, что уравнение эллипса с большой степенью точности описывает зависимость приведенного расхода q0
от вг для отверстия р рстрой кромкой, так же как и для
суживающегося сопла. Различие состоит только в том, что в случае сопла максимальный расход достигается при первом критическом отношении давлений s,, а в случае отверстия — при втором критическом отношении давлений ем.
Отсюда следует, что влияние формы отверстия на расход может быть учтено соответствующим выбором второго критического отношения давлений, так как следует ожидать, что эллиптическая зависимость будет точной для любого очертания стенок, если она точна для двух крайних случаев: сопла и отверстия с острыми кромками.
Опыты, поставленные с целью определения расхода воздуха и перегретого пара через отверстия различной формы, подтверждают эллиптическую зависимость q0 от sfl. Для перегретого водяного пара второе критическое отношение давлений по опытным данным составляет е^^О, 13 (табл. 6-2). Следовательно, с уменьшением k (показатели изоэнтропы) е#„ так же как и , увеличиваются. Отсюда можно заключить, что изменение физических констант газа влияет на е<# в том же направлении, что и на . Этот вывод отчетливо подтверждается данными, приведенными в табл. 6-2.
Таким образом, мы видим, что свойства струи, вытекающей из резервуара, существенно меняются в зависимости от характера распределения параметров в поперечном сечении струи. При неравномерном распределении параметров течения (истечение из отверстия или из щели) в потоке обнаруживаются новые свойства и уравнения, описывающие истечение равномерной струи, оказываются неприменимыми.
Заметим, что на спектр струи за отверстием и на коэффициент сужения струи оказывают некоторое влияние размеры камеры, из которой струя вытекает. Теоретическая зависимость коэффициента сужения плоской струи от размеров камеры и скорости в минимальном сечении М2 по Г. А. Домбровскому приведена на рис. 6-14. Кривые
показывают, что с ростом — (с увеличением относительно
ао
размера отверстия) и М2 коэффициент сужения возрастает. Влияние сказывается ощутимо только при — >0,3.
&q ад
Для расчета отверстия или щели при различных начальных и конечных давлениях можно использовать метод, описанный выше для сопла. Исходя из условия неизменной температуры в резервуаре, строят ' сетку относительных расходов газа через отверстие, каждая кривая кото-
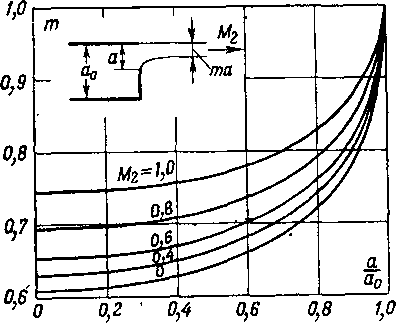
Рис. 6-14. [Зависимость коэффициента сужения плоской струи от размеров камеры и скорости в минимальном сечении по Г. А Домбровскому.
рой qa = /(еа) соответствует постоянному начальному отно-
Роп
сительному давлению в0п = —-— .
6-4. РАСЧЕТ СВЕРХЗВУКОВОГО СОПЛА
Сверхзвуковые сопла (сопла Лаваля) применяются для создания потакав газа оо сверхзвуковыми скоростями. Эти сопла используются в качестве одного из основных элементов реактивных двигателей, а также в паровых турбинах, эжекторах и других аппаратах.
Анализ одномерного течения показал, что поток со сверхзвуковой скоростью может быть получен в трубе с минимальным сечением, если в этом сечении будет достигнута критическая скорость138. В соответствии с этим
Сбпло Лаваля представляет собой трубу лерей1ейнб!Ч> сечения, состоящую из двух частей. Скорость газа, протекающего через нормально работающее сопло Лаваля, непрерывно увеличивается, причем в суживающейся части сопла скорость дозвуковая, а в расширяющейся — сверхзвуковая (рис. 6-16).
Элементарный расчет сверхзвуковых сопел производится по уравнению неразрывности, причем должны
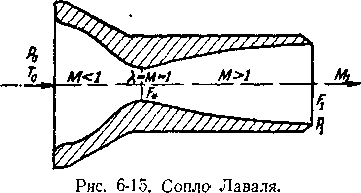
быть заданы параметры газа перед соплом, расход газа и скорость потока в выходном сечении.
Пренебрегая влиянием трения, можно считать, что критическая скорость устанавливается в минимальном сечении сопла. Размеры этого сечения определяются по уравнению (6-5):
ft ~Ь 1
_ /139 + 1ча(*-—ОG.VT, .
* Л 2 ) Y ek ро
Выходное сечение рассчитывается по формуле
Где F — промежуточное сечение;
X и s — соответствующие этому сёчению скорость и
![]()
относительное давление
Если задано распределение скоростей или давлений по оси сопла, то формула (6-29) определяет профиль сопла. Однако такой расчет промежуточных сечений, а тем самым и профиля (формы) сопла является приближенным и может не обеспечить заданного распределения давлений, так как скорость в сечении непостоянна ни по величине, ни по направлению и, следовательно, поток не является одномерным.
В случаях, когда важно получить лишь заданную среднюю скорость на выходе из сопла, а характер распределения скоростей по сечению не имеет большого значения, промежуточные сечения сопла не рассчитывают, а для простоты изготовления как суживающуюся, так и расширяющуюся части выполняют коническими. При этом в узком сечении и тем более на выходе поле скоростей получается неравномерным.
В некоторых случаях для уменьшения неравномерности поля скоростей суживающуюся часть сопла рассчитывают по формуле Витошинского (6-7), а угол раствора конической расширяющейся части выбирают малым (до 12°). Опыт показывает, однако, что эти меры не всегда достаточны для получения нужного поля скоростей.
Лучшие результаты можно получить, применяя профилированные сопла, расширяющаяся часть которых рассчитана методом характеристик. Рассматривая плоское сопло и пренебрегая влиянием трения, предположим, что все параметры течения остаются неизменными вдоль линий, нормальных к плоским стенкам. Допустим, что в узком сечении сопла АА' поток имеет равномерное поле скоростей М=1 (рис. 6-16).
Для ускорения потока, имеющего в сечении АА' критическую скорость, необходимо увеличивать сечение сопла. С этой целью повернем участки стенки ААХ и соответственно А'А\ на малый угол от оси сопла бо-Тогда з точках А и А' возникнут слабые волны разрежения. При пересечении этих волн поток ускоряется и приобретает скорость Xii2, которую можно определить
С Помощью диаграммы характеристик (рис. 6-16,6) иЛй с помощью таблиц.
Состояние потока в критическом сечении АА' в диаграмме характеристик изобразится точкой (Л,, Л,) на окружности Я= 1. Скорость потока в области 1 определяется в точке 1' на эпициклоиде Ах1', если провести луч из начала координат под углом 80 к направлению оси сопла х. Симметрично расположена точка 2', которая соответствует области 2 потока. Через точки Г и 2' проходит окружность, отвечающая скорости Я, 2.
Непрерывное расширение газа в стационарных волнах разрежения, возникающих в точках Л и Л', можно заменить, проводя из этих точек звуковые волны АЕ и А'Е *
под углом aml-j--y- к направлению оси сопла (ат1—-угол
звуковой волны, соответствующей скорости потока в области 1).
В диаграмме характеристик найдем точку Е', соответствие
вующую отклонению потока на угол , и определим
величины скорости ^Ае№а,е), отвечающей направлению звуковой волны АЕ'.
При переходе из областей 1 и 2 в область 3 линии тока пересекают волны ЕЕ1 и ЕЕг (поток ускоряется) и поворачиваются на угол о0 к оси сопла. Следовательно, в областях 3 скорости потока имеют направление, параллельное оси. В диаграмме характеристик легко определяется точка 3', отвечающая этой области течения.
В точках Аг и А[ (рис. 6-16,а) стенки сопла вновь поворачиваются на угол 8в. При переходе в области 4 и 5 поток ускоряется и приобретает скорость Я45=Я3. Аналогично можно найти величину и направление скорости в областях 6, 7, 8 и т. д., а также направления звуковых волн, которые являются границами этих областей.
В результате последовательного поворота стенок сопла образуются две стационарные волны разрежения конечной интенсивности, при переходе через которые поток расширяется и достигает заданного значения скорости.
Скорость Ai(Mi) будет достигнута в пределах зоны
пересечения волн разрежения на участке HL. За последней характеристикой LQ, угол наклона которой равен
amLQ = arcsin ла
поток должен иметь равномерное поле скоростей, в каждой точке которой скорость равна Мь Все линии тока
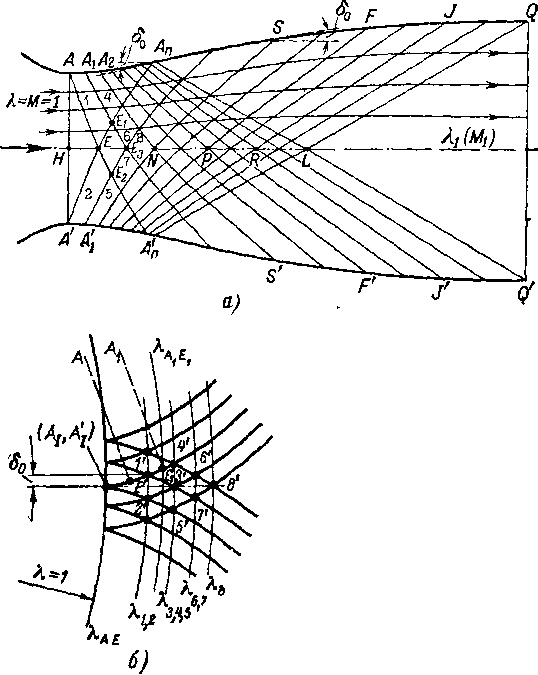
Рис. 6-16 Спектр волн разрежения в профилированном сопле Лаваля (а) и построение процесса в диаграмме характеристик (б).
правее LQ должны быть параллельными оси сопла. Отсюда следует, что каждую звуковую волну от противоположной стенки, выходящую за пределы AnL, необходимо погасить соответствующим поворотом стенки на угол, равный углу отклонения потока в такой волне.
Начиная от точки Ап> стенка сопла поворачивается так, чтобы падающие на нее волны NS, PF и т. д. не отражались.
Таким образом, на первом участке стенки сопла поворачиваются от оси сопла, а на втором участке, где волны от противоположной стенки гасятся, наклон стенки постепенно уменьшается и в точке Q бо=0. В пределе при уменьшении 6о ломаная стенка AAnQ переходит в плавно искривленную стенку.
Вблизи узкого сечения, где скорость течения незначительно превосходит критическую скорость, точность расчета методом характеристик первого участка сопла недостаточна, в особенности если расчетное значение Л1 невелико.
Подбор профиля стенки поэтому производят, начиная с некоторого начального сечения, где течение уже обладает сверхзвуковой скоростью. Распределение скоростей в начальном сечении должно быть известным.
В некоторых случаях начальный участок сопла выполняют коническим. Угол конусности выбирается в зависимости от заданного значения A,i и составляет половину максимального угла поворота потока при увеличении скорости от А,= 1 до А,1-
Широкое применение находят также аналитические методы расчета сверхзвуковых сопел, разработанные С. А. Христиановичем и др.
Методы расчета и .профилирования сверхзвуковых сопел не учитывают влияния вязкости. На стенке сопла образуется пограничный слой, толщина которого нарастает по длине сопла. Отметим, что в соответствии с выводами гл. 5 влияние трения приводит к смещению критического сечения, которое сдвигается в расширяющуюся часть сопла.
Пограничный слой на стенках вызывает некоторое перераспределение скоростей и давлений потока у стенок и смещение характеристических линий. Действительные скорости и давления в различных сечениях и на выходе из сопла будут отличаться от расчетных значений.
Для получения заданного распределения скорости и расчетного значения Ai необходимо увеличивать площадь поперечных сечений сопла, полученную при условии изоэнтропического течения. Точное решение такой задачй требует расчета пйграйичного слоя На стейках сопла (гл. 5).
Приближенное решение можно найти, если известно распределение коэффициентов сопротивления по оси сопла.
Удельную работу сил трения для трубы переменного сечения (сопла) можно представить в следующей форме:
с2 dx dLTр = ? 2g ' J) ’
— dx — D где dx = -рг—; D = ; Д, — диаметр горлового сечения сопла.
_ S
где S = —= — приведенная энтропия.
На основании (6-30) после несложных преобразований находим такое выражение для коэффициента сопротивления:
k \ \ k + 1 / dx
Учитывзя, что согласно формуле (5-12) d j 1 de0
dx ?о dx ’
где s =^-—отношение давлений торможения на входе в сопло Ро н в данном сечении, можем получить:
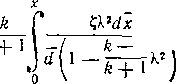
In е0 — и ¦ 1 \ • (6-31)
Если известен вид функции ? (х), то с помощью (6-31) нетрудно найти изменение s0 по длине сопла. Значения 'С, (х) можно принять по графику на рис. 5-12. В соответствии с уравнением неразрывности (2-41) связь между сечениями в действительном (F) н изоэнтропи-ческом (F0) потоках можно представить так:
f = fo~eo, (6-32)
t F с Ро ^tet Р с
где t = -б— ; = —; qt = — — ; q———; q и qt — приведенные
‘ * r* tV“# Р»
расходы для теоретического и действительного процессов.
Йсследойания, йробеденные йдд рукободстйом А. А. Гухманй, теоретически и экспериментально показали возможность линейной аппроксимации закона изменения энтропии по длине сопла. Следовательно, если принять
и. = —==-=— = const,
dx dx
то, положив в критическом сечении х = 0, с помощью (6-32) найдем (/«?< = >);
Ins0 = In (fq) = цх,
ИЛИ
Опыты показывают, что для сопел с полированной внутренней поверхностью можно принять jj. =5: 0,011 -г- 0,018.
Уравнение (6-33) используется для решения прямой и обратной задач. В первом случае заданными являются f (х) и jj.; по формуле {6-33) устанавдивается приведенный расход q (х); распределение параметров потока по длине канала (к, р, р, Г) устанавливается по таблицам газодинамических функций. При решении обратной задачи по известному распределению q (х) или X (х) устанавливаются те сечения, в которых достигаются заданные значения k(f(x)). Значения
0 (х) в обоих случаях можно найти по формуле (6-32) (при этом
Влияние трения на скорость и другие параметры в выходном сечении сопла оценивается с помощью коэффициента скорости, который выражается по формуле
где = rzTT'T- ( ~т — М “ коэффициент потерь энергии мн \ есГ J в сопле;
s0=——отношение давлений тормо-Рог жения на выходе и на входе в сопло;
Ми — теоретическое значение числа .М в выходном сечении.
Из формулы (6-34) следует, что величина е0 неоднозначно связана с коэффициентами и Сс. При одинаковых
значениях s0 коэффициенты у и Сс меняются в зависимости от величины располагаемой энергии, пропорциональной М21Г На рис. 6-17 приведены графики, устанавливающие связь между срс, е0 и М1Г
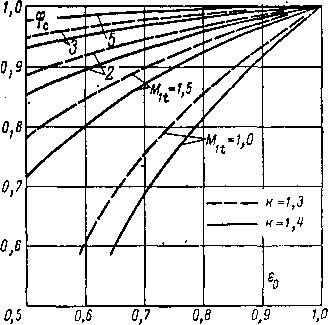
Рис. 6-17. Зависимость коэффициента скорости сопла <fc от е0 и Mlt.
6-5. ПЛОСКОЕ СОПЛО ЛАВАЛЯ ПРИ НЕРАСЧЕТНЫХ УСЛОВИЯХ
В условиях эксплуатации параметры, а также расход газа через сопло могут изменяться. Существенно при этом,
Ра
что меняется отношении давлении еа = — , где ра — по-
прежнему давление окружающей среды.
Рассмотрим работу сопла при переменных режимах в первом приближении, пренебрегая трением и теплопроводностью. На рис. 6-18 показано распределение давлений в сопле Лаваля при различных давлениях внешней среды ра. Кривая АОВ, построенная по уравнению (6-29), соответствует расчетному режиму течения в сопле, при котором
e=Sl = ^-.
“ Ро
Предположим, что при пострянном значении р0 давление внешней среды меняется в пределах и ПР0'
следим изменение структуры потока как внутри сопла, так и за ним. При этом можно выделить четыре характерные группы режимов; в пределах каждой группы режимов картина течения качественно сохраняется неизменной.
Первая группа режимов характеризуется пониженными
давлениями среды — < —. В этом случае в выходном се> Ро Ро
чении сопла устанавливается расчетное давление р1У так
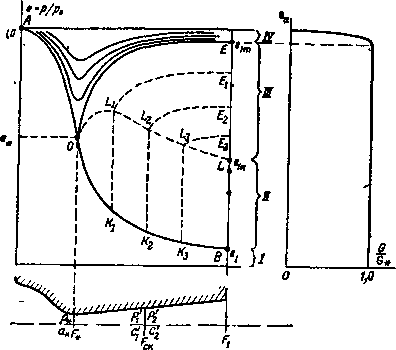
Рис. 6-18. Диаграмма распределения давлений в сопле Лаваля при различных режимах.
как параметры газа в резервуаре, а следовательно, и расход газа через сопло не меняются. Это очевидно также и потому, что в сверхзвуковой струе возмущение против течения не распространяется и, следовательно, падение давления среды не скажется в выходном сечении сопла. Во всех промежуточных сечениях сопла поэтому давления также остаются расчетными. Параметры течения изменяются только за соплом, в свободной сверхзвуковой струе.
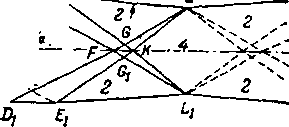
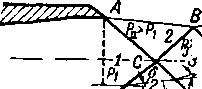
На рис. 6-19,а представлены схемы спектров струи на выходе из плоского сопла при'пониженном противодавлении. В угловых точках А и At давление меняется от значения Р\ Д° Ра. Линии тока в точках Л и Л, отклоняются на некоторый угол 8 в связи с возникновением в этих точках волн разрежения, вызывающих изоэнтропическое расширение газа от pt до ра. Вдоль характеристик АС, АгС и АВ, А1В1 в соответствии со свойствами прямолинейных харак-ip у у О v
1Z%?7777Z
Ш: *
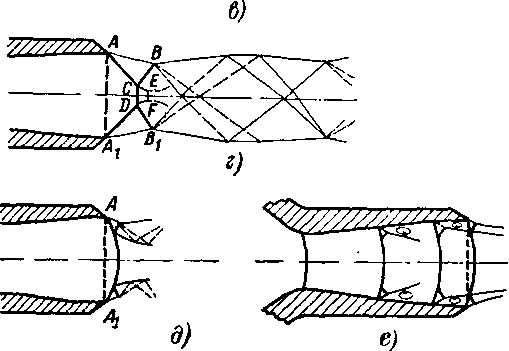
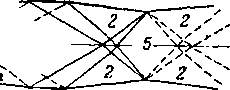
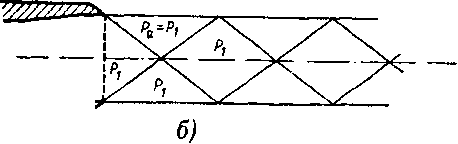
Рис. 6-19. Схемы спектров струи за плоским соплом при различных
режимах
теристик давление не меняется. Следовательно, в областях 2 устанавливаются постоянная скорость и давление ра, равное давлению окружающей среды. Волны разрежения и AlDEAl выходят на свободную границу струи, вдоль
которой давление остается неизменным и равным р В зоне СВС1В1 пересечения этих волн, как уже известно, происходит искривление характеристик. В результате угол звуковой волны BD становится меньше угла волны АХС и а <Г а ; соответственно а < а ; а <" а
BjD, "Me mC,H mBD тС,Н, mBiDl
От свободной границы волна разрежения отражается, как волна сжатия, при прохождении через которую линии тока деформируются, отклоняясь на угол 8 к оси струи. В точках L hLj волны сжатия выходйт на свободную границу.
За пересекающимися волнами разрежения (в области 3) устанавливается давление, меньшее давления окружающей среды (струя перерасширена). В области 4 после пересечения волн сжатия давление повышается до давления рг в выходном сечении сопла ААг. К сечению LLt струя суживается и ширина ее равна ширине выходного сечения АА,. В областях 1, 3 и 4 линии тока прямолинейны и параллельны оси сопла. В областях 2 линии тока также прямолинейны и параллельны, но расположены под углом 8 к оси сопла. Для рассматриваемой первой группы режимов при принятых допущениях потерь энергии в струе нет.
По мере повышения давления среды ра характеристики АВ, BD, АуВ^ BJ.315СХЕ и СХЕХ меняют свое положение в струе. Так как разность давлений в областях 1 и 2 при этом уменьшается, то углы указанных характеристик увеличиваются, интенсивность волн разрежения AD1E1A и A1DEA1 уменьшается. Углы отклонения линий тока в области 2 также уменьшаются. В пределе, при расчетном режиме (ра = р^, характеристики AEt и AtE сливаются с волнами /Ш, и A,D. Струя приобретает формулу, приведенную на рис. 6-19,6.
Вторая группа режимов характеризует истечение из сопла Лаваля при повышенном противодавлении среды или при пониженном начальном давлении (sa ]> Sj). Зная расчетную скорость в выходном сечении сопла /Ц, легко определить то значение давление среды, при котором в выходном сечении образуется прямой скачок уплотнения [рис. 6-18 и формула (4-20)];
Рассматриваемая бторая группа ре&имой характеризуется Следующим соотношением давлений среды: Pi<Pa<Pik. В этом случае в сечении AAt (рис. 6-19,е) также устанавливается расчетное давление рх. Если давление среды р сравнительно немного превышает давление р1Г то в точках ААХ образуются два косых скачка: АС и АгС, пересекающихся в точке С. Косые скачки выходят на свободную границу струи (после пересечения в точке С углы косых скачков увеличиваются). При прохождении через скачки АС и AtC линии тока отклоняются на угол S, который легко подсчитать. В областях 2 давление равно давлению окружающей среды, линии тока параллельны друг другу и свободной границе струи АВ и А1В1.
Из условия симметрии за скачками СВ и СВi скорость должна стать параллельной оси потока, т. е. линии тока должны повернуться в обратном направлении на угол б. В этой области устанавливается давление, повышенное по- сравнению с давлением среды. Следовательно, в точках В и Вх со стороны струи давление более высокое и из этих точек распространяются волны разрежения. При переходе через волны разрежения давление падает до давления окружающей среды и линии тока отклоняются от оси — струя расширяется. После пересечения волн разрежения давление равно pi. В точках выхода волн разрежения на свободную границу струя имеет ширину, равную ААг. Рассматриваемая группа режимов характеризуется потерями энергии в струе, обусловленными возрастанием энтропии в системе косых скачков уплотнения. Поле давлений по оси и в поперечных сечениях приобретает значительную неравномерность.
Описанная схема истечения возможна лишь при небольшом превышении давления ра над ри когда угол б невелик. При некотором давлении среды /?и
спектр струи на выходе из сопла меняется. Существование системы двух косых скачков уплотнения со сверхзвуковой скоростью за точкой их пересечения становится невозможным. При pa^Piu угол косых скачков, отходящих от кромок А и Ль достигает значения, лри котором в некоторой области за скачком скорости будут дозвуковыми и спектр истечения резко изменится (рис. 6-19,г и д).
Для плоского сопла угол отклонения линии тока 6mi (или угол скачка pmi), при котором изменится картина истечения, легко определяется с помощью диаграммы ударных поляр.
Ударная поляра АК1 (рис. 6-20) соответствует расчетной скорости А,] потока в выходном сечении сопла
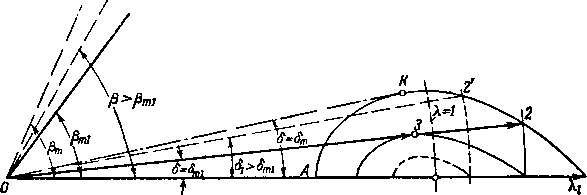
Рис. 6-20. Определение режима течения за скачками, образующимися при нерасчетных условиях в сопле Лаваля, с помощью диаграммы ударных поляр.
(отрезок 01) и, следовательно, во всей области 1 (рис. 6-19,в). При некотором давлении среды pa = p'\h скорость за скачком измеряется отрезком 02 (скорость в области 2 на рис. 6-19,в); предельная скорость за косыми скачками СВ и СВХ в области 3, где линии тока параллельны оси струи, определяется отрезком 03 (рис. 6-20).
Величина давления р'\и может быть определена по формуле (4-13):
(6-36)
k — '~2k
l ¦
В этом случае в струе за скачками СВ и СВг (рис. 6-19,в) скорости будут дозвуковыми.
Если ра>р'\ъ, то при пересечении скачков СВ и СВ\ поток уже не сможет повернуться на угол 6i>6mi (пунктирная линия на рис. 6-20), на который он повернулся при переходе через АС и А\С. Схема истечения при этом качественно изменится. На выходе из сопла образуется мостообразный скачок.
От угловых точек А и А\ (рис. 6-19,г) распространяются косые скачки АС и A\D, переходящие в прямой
sin2 Pj
k — 1
2k
ml
Pxk
k+\p'\k + i
'k+ fX'
(или — при неравномерном распределении скоростей — криволинейный) скачок, за которым скорости будуг дозвуковыми. За косыми скачками СВ и DB^ скорости остаются сверхзвуковыми, а давление оказывается более высоким, чем давление среды ра-
За прямым скачком CD давление значительно более высокое, чем за скачками СВ и DBX. Следовательно, в струе создается сложное распределение давлений по сечению: выравнивание давлений приводит к резкому уменьшению р в ядре струи, т. е. к ускорению ядра, что сопровождается уменьшением его сечения. Линии раздела СЕ и DF образуют суживающийся участок ядра, вдоль которого скорости растут и в сечении EF достигают звуковых значений. Кроме того, внутренний поток дозвуковых скоростей непосредственно за скачком CD ускоряется внешним сверхзвуковым потоком. Косые скачки СВ и DB\ отражаются от свободной границы в форме волн разрежения, которые также ускоряют ядро струи. В результате скорость внутреннего потока становится сверхзвуковой Интенсивность изменения давления в прямом скачке CD и за ним по данным А. А. Гухмана и А. Ф. Гандельсмана для двух режимов иллюстрируется кривыми на рис. 6-21. Опыты подтверждают, что на весьма коротком участке за скачком поток достигает расчетного давления р\ и соответственно сверхзвуковой скорости.
Итак, при давлении внешней среды pa>p'ih система пересекающихся косых скачков разрушается и переходит в мостообразный скачок Это явление анало1ично рассмотренным в гл 4 случаям неправильного отражения косого скачка от твердой стенки и пересечения скачков.
При дальнейшем повышении давления среды внутренняя дозвуковая область течения расширяется, а внешняя сверхзвуковая—суживается. Существует такое давление среды р"\к, при котором криволинейный скачок распространяется почти на все сечение; в этом случае за скачком АА\ скорости становятся дозвуковыми (рис. 6-19,5), за исключением узкой периферийной области. Этот криволинейный скачок располагается вблизи выходного сечения сопла.
Давление р"^ будет соответствовать такому режиму, при котором угол поворота б на скачках АС и A\D (рис. 6-19,г) становится равным максимальному углу 6,„ (штрихпунктирнйй Линия на рис. 6-2б). Определив t помощью ударной поляры угол соответствующий углу поворота бт, можно, пользуясь формулой (4-13) или (6-36) для косого скачка, подсчитать давление р”\\,\
2k ' k+ 1
' + 1'
k ~ ] j2 ‘ k + 1
мм pm cm.
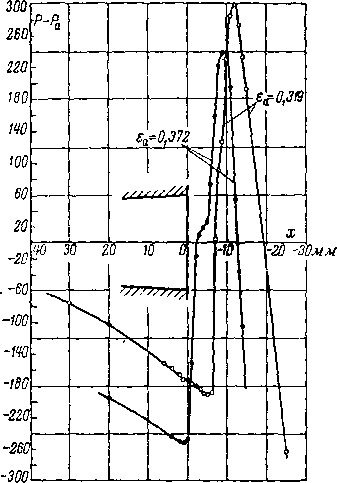
Рис. 6-21. Изменение давления вдоль оси сопла и в струе за соплом на режимах с мостообразным скачком в выходном сечении; М1==1,5. Опыты МО ЦКТИ.
РЛ
Pik~-
2k
(6-37)
При давлениях среды ра>р"ш скачок выпрямляется и при ра~pih [формула (6-35)] скачок должен стать прямым, располагаясь в выходном сечении сопла. Фактически вследствие неравномерного распределения скоростей в конических соплах и влияния пограничного слоя (вязкости) скачок входит .внутрь сопла несколько искривленным (рис. 6-19,е).
Если давление за соплом pa>p"\k, то в выходном сечении сопла давление будет меняться. Дальнейшее повышение давления среды {ра>рifc) вызывает перемещение системы скачков внутрь сопла, как показано на рис. 6-19,е.
Из формулы (6-36) для отношения давлений на границах скачка следует, что данной скорости %i сверхзвукового потока перед скачком соответствует вполне определенное •повышение давления в скачке. Если давление среды превысит величину рщ, то, очевидно, условия равновесия на прямом скачке нарушатся и он переместится в такое место в потоке, которое соответствует равновесному положению скачка при новых параметрах среды. Следует иметь в виду, что перемещение скачка внутрь сопла сопровождается новыми качественными изменениями потока (третья группа режимов). Давление за скачком в этом случае уже не равно давлению среды; оно оказывается меньше ра. Поэтому за скачком давление продолжает возрастать. Распределение давлений в потоке при промежуточных положениях прямого скачка показано на рис. 6-18 линиями KiLiEu K2L2E2 и т. д.
С ростом давления среды скачок продолжает перемещаться внутрь сопла к минимальному сечению. При этом изменяется соотношение между степенью восстановления давления на скачке и степенью изоэнтропиче-ского восстановления давлений за скачком. В соответствии с последовательным смещением скачка в область меньших скоростей отношение давлений на границах скачка уменьшается, а степень восстановления давления в расширяющейся части сопла за скачком увеличивается 140 (см. кривые LXE\, L2E2 и т. д. на рис. 6-18).
При некотором давлении среды р\т скачок входит в минимальное сечение сопла и здесь исчезает. В минимальном сечении сопла параметры потока при этом критические, но перехода в сверхзвуковую область не происходит. Линия ОЕ является границей между дозвуковыми и сверхзвуковыми режимами сопла При ра>р\т скорости в о всех точках сопла дозвуковые и мы полу-- чаем четвертую группу режимов сопла. Для этой группы характерны последовательное расширение потока в суживающейся части и сжатие в расширяющейся части сопла. Минимум давления достигается в узком сечении Известно, что таков характер распределения давлений в трубах Вентури, применяемых для измерения расхода газа.
До тех пор, пока ра<р\т, расход газа через сопло при различных противодавлениях сохраняется неизменным (в минимальном сечении сопла параметры газа критические, а начальные параметры остаются неизменными). Изменение расхода начинается только при противодавлениях, больших, чем ргт, т. е. в пределах четвертой группы режимов. На рис. 6-18 справа показано изменение расхода газа через сопло в зависимости от противодавления ра-
Величина давления р\т может быть определена, если известны геометрические характеристики сопла и параметры потока перед соплом. Пренебрегая потерями в расширяющейся части сопла, можно с помощью уравнения неразрывности получить:
It.
F, ’
Pj
где
ct\m'=—"
т•—приведенный
расход в выходном сече-р* а‘
нии сопла для рассматриваемого режима.
С другой стороны, дш можно выразить через отношение
давлений по формуле (6-4); тогда, имея в виду, что Ро
приходим к следующему уравнению для е{т:
JL t' JL
к Л * \ А— 1 * 1 /с оо
** Ч\ m
Нетрудно видеть, что уравнение (6-38) при f1 = 1 (су-
k
живающееся сопло) имеет корень elm = ’а ПРИ
f1 = оо (сопло, рассчитанное на максимальную скорость ^1макс)—два корня: е1от = 1 и е1ш = 0. Второе значение (slm=0) соответствует расчетному режиму сопла при Д = оо и поэтому не рассматривается.
Зависимость е1т от j- по формуле (6-38) представлена на рис. 6-22.
Для е1т можно получить более простую формулу, если воспользоваться эллиптической зависимостью между qlm
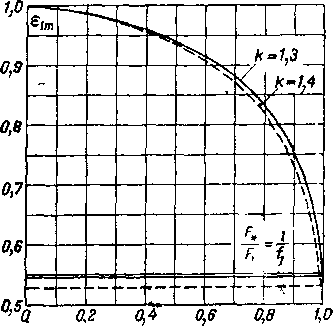
Рис. 6-22. Предельное отношение давлений на сопле в зависимости от f,.
Согласно уравнению (6-12) можно записать:
„ ' _ 1 f л (г1 т — .
отсюда _
elm==e. + (1 ~S.) j/"1--j2~ • (6-39)
В уравнение (6-39) можно ввести поправку, учитывающую потери в расширяющейся части сопла. В этом случае
•i« = e. + (1— е.) 1_тр (6'39а>
где
Ti = fiso = fi~-
Pa*
Из уравнения (6-39а) следует, что с возрастанием потерь в сопле величина предельного противодавления р1тп уменьшается.
При определении е1т с учетом потерь можно пользоваться графиком на рис. 6-22, откладывая по горизон-
1
тальнои оси величину -=-.
Вернемся к рассмотрению некоторых особенностей третьей группы режимов со скачками уплотнения внутри сопла. Необходимо учитывать, что в действительности в сопле создается не прямой скачок, а сложная система криволинейных скачков. Большое значение при этом имеет форма расширяющейся части сопла. При небольших углах раствора расширяющейся части в сопле возникают скачки, близкие ,по форме к прямым. Около стенок сопла происходит разветвление криволинейного скачка, принимающего форму мостоо-бразного скачка (рис. 6-19,е).
Третья группа режимов характеризуется значительными потерями энергии. Наряду с волновыми потерями в скачках возникают потери вследствие отры-ва потока от стенок сопла. Отрыв сопровождается образованием вихрей и характерным подсосом газа из окружающей среды.
В ряде случаев практический интерес представляет определение положения скачка внутри сопла и потерь в сопле при заданном отношении давлений. Так как структура скачков зависит от формы расширяющейся части сопла, то такая задача не может быть точно решена. Приближенное решение можно получить для простейшего случая, принимая скачок прямым и поток в сопле безотрывным.
Задача решается следующим образом. До скачка расширение газа следует по кривой АОВ (рис. 6-18), соответствующей расчетному режиму. Параметры газа на входе и в сечениях К связаны уравнениями изоэнтропического течения. Изменение состояния в сечении К определяется по формулам прямого скачка (линии .процесса К, L и'т. д.). Наконец, за скачком можно использовать данные, характеризующие потери в диффузоре (гл. 7).
Допустим, что прямой скачок возникает в некотором
где q — приведенный расход перед скачком.
Из формулы (6-40) можно выразить /ск через Х'ск или с помощью уравнения (6-4) через отношение давлений в =-?L. Приведенный расход в этом же сечении за скач-Ро
ком равен:
Р о ?0
Здесь р0’ — давление тормржения за скачком.
Из уравнения неразрывности для сечений FCK и F, получим:
(6-42)
1 ^ск Ро ^ск
где q" и qa — приведенные расходы за скачком и в выход-,ном сечении при заданном давлении рд;
Рйа
е0д = —77—изменение давления торможения в расширяюсь щейся части сопла за скачком141.
Тогда с помощью уравнения (6-40) получим:
^ск
/ !
Ро
где е0ск—~;--изменение давления торможения в скачке.
Ро
Подставляя в уравнение (6-43) значения q'CK и qa, находим:
I
¦'JV<
k+i
е„ " V 1 — е0 ск
6ск У 1 — еск
Здесь s' = — — относительное давленйе зй Соплом; “ Ро
ft— 1 m=—tг.
Если пренебречь потерями в сопле до скачка, то
в' =в = —
S“ S“ Ро '
Отношение давлений полного торможения на скачке
определяется по уравнению (4-35). Формула (6-44) при tt
Р(]
подстановке — из (4-35) становится весьма громоздкой;
Ро
значительно удобнее пользоваться уравнением (6-43), которое содержит табличные функции изоэнтропического потока и прямого скачка. Задаваясь величиной qCK в пределах от
<7ск —1 д0 ?ск = ?а’ находим /СК по формуле (6-43). Опрело'
делив по таблицам соответствующие значения —, найдем
Ро
//
величину q"K — q'CK . Оценка коэффициента е0д произвело
дится после расчета дск(\к) и -у*- . Затем определяется
^СК
величина qa = q"CKs0д. Зная е0д и е" — —, находим:
" Рйа
е = е --
а а р0
Таким образом, можно построить зависимости /ск от еа
для различных, но постоянных значений = . При
efl = sIm скачок располагается в горле сопла и /ск = 1. При efl = s1A скачок находится в выходном сечении сопла.
Анализ формулы (6-43) показывает, что в интервале изменений fcK от 1 до 2 зависимость /ск от еа может быть выражена приближенной формулой
+ (6-45)
где А — безразмерный коэффициент, зависящий от Д.
Подсчитав /ск по формуле (6-45), можно определить
t /
?ск и Кк (или еск) и изйти у-; тогда коэффициент потерь
энергии в скачке определяется по формуле (4-33) или по таблицам. Коэффициент потерь в расширяющейся части за скачком определяется по формуле
2 1
1
д k— 1 м"142
СК
Од
Коэффициент полных потерь в сопле в режимах третьей группы равен:
«¦ _«¦ ск y ск
с Чж ~од2 Г д^2 >
где Ма — безразмерная скорость, соответствующая отно-
„ Ра
шению давлении —.
Р о
С учетом отрыва потока потери и положение скачка будут отличаться от рассчитанных указанным способом. Отрыв потока за скачком приводит к резкому возрастанию потерь
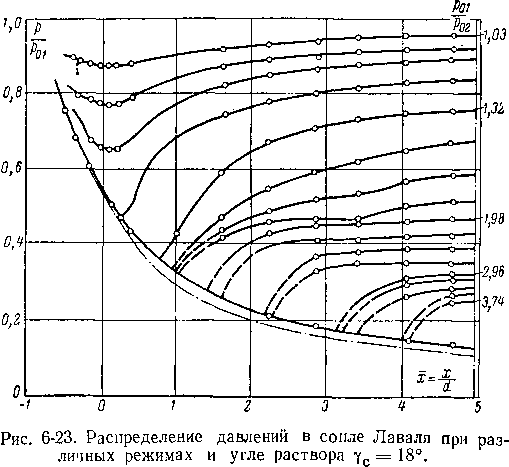
Результаты опытного исследования подтверждают .указанные особенности потока в сопле прн нерасчетных режимах.
Так, на рис. 6-23 приведено распределение давлений вдоль сопла при различных режимах. Штрихпунктирны-ми линиями показаны результаты расчета, выполненного указанным выше способом. С уменьшением угла раствора расчетные кривые сближаются с опытными. Однако совпадение расчета с опытом не является вполне удовлетворительным. Повышение давления в месте расположения скачка происходит хотя и весьма интенсивно, но не скачкообразно. Следовательно, только при весьма малых углах раствора скачки, соответствующие третьей группе режимов, близки к прямым. Заслуживает внимания также тот опытный факт, что .положение скачка в сопле зависит от того, каким путем меняется режим сопла: изменением начального давления ро или противодавления ра• Этот результат объясняется влиянием числа Рейнольдса при взаимодействии скачка уплотнения с пограничным слоем.
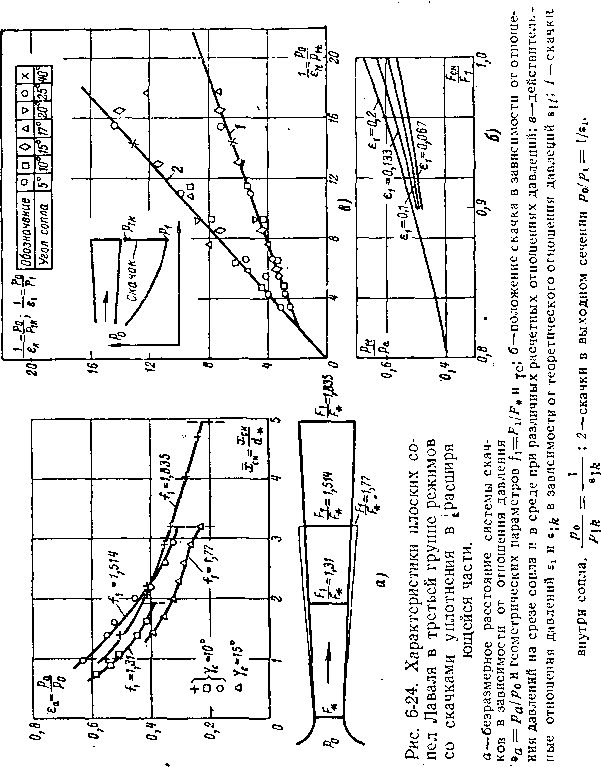
Графики «а рис. 6-24,а показывают \ что положение
• системы скачков сопла зависит от основного геометри-
ческого параметра f1=y: и угла раствора ус-. С увеличе-
нием ус система скачков при том же отношении давлений ъа смещается к минимальному сечению.
Относительное давление за скачком е А не зависит от 7С (кривая 1 на рис. 6-24,в) (точки при разных у ложатся на одну кривую).
Изменение положения скачка в зависимости от расчетного перепада давлений в сопле Sj (или, что то же, от /,) и отношения давлений в выходном сечении (/?,) и окружающей среде (ра) подтверждают графики на рис. 6-24,6.
Вместе с тем опыты подтвердили, что на режимах, соответствующих расположению скачков в выходном сечении
1 По данным Асвуда и Кросс?.
в)
г)

Рис. 6-25. Спектры потока в плоском сверхзвуковом сопле при нерасчетных условиях. Параметры расчетного режима: = 0,052,
.№,^=2,57; угол раствора сопла tc = 19°40'. а — еа =0,685: б — = 0,518; в — еа =0,362; г- еа =0,068.
сопЛа, давление fe этом сечении (и скорость перед скачкоМ не зависит от угла раствора ус (кривая 2 на рис. 6-24,в)
Отношение давлений е1 = -~ отличается от расчетного
только на величину, характеризующую потери на трение.
Последовательное развитие спектра в плоском сопле с углом раствора расширяющейся части ус = 19°40' показано на рис. 6-25. При давлении в среде рш'>Ра^>А (третья и вторая группы режимов) внутри сопла возникает
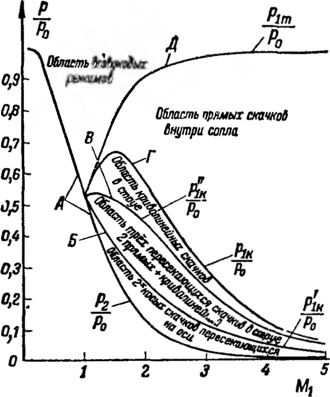
Рис. 6-26. Диаграмма нерасчетных режимов сопла Лаваля (по Б. Я- Шумяцкому).
система скачков. Замыкающим эту систему является скачок малой кривизны (рис. 6-25,а), за которым скорость дозвуковая. На некоторых режимах обнаруживаются колебательные движения струи за точкой отрыва (рис. 6-25,6).
С понижением давления среды ра скачки продвигаются от критического к выходному сечению; при некотором давлении внутри сопла образуется система пересекающихся косых скачков (рис. 6-25,в), которая с понижением давления среды перемещается к выходному сечению сопла и выходит в струю (рис. 6-25,г).
Режим работы плоского сверхзвукового сопла без учета влияния пограничного слоя можно определить с помощью
диаграммы, построенной Б. Я. Шумяцким (рис. 6-26). Г1о вертикальной оси здесь отложено относительное давление, а по горизонтальной—расчетное число М, для сопла. Если
Ра
известны отношение давлении sa = — и расчетное числа М,, то, пользуясь диаграммой, можно установить, на каком режиме будет работать данное сопло.
Кривая А соответствует расчетным значениям ~ . Точки,
лежащие ниже этой кривой, относятся к режимам первой группы, когда на срезе сопла образуются волны разрежения. Кривая Б соответствует предельному случаю двух пересекающихся скачков [формула (6-36)]. Между кривыми А и Б располагается область режимов с косыми скачками на срезе сопла. Кривая В отвечает случаю предельного отношения давлений за первым косым скачком [формула (6-37)]. Области между кривыми Б я В соответствуют режимы с мостообразным скачком на срезе. Кривая Г соответствует прямому скачку в выходном сечении сопла [формула (6-35)]. Режимы с криволинейным скачком располагаются в области между кривыми В я Г. Выше кривой Г находится область прямых скачков внутри сопла. Верхней границей этой области служит кривая Д, а нижней—кривая Г. Значе-
Ра „ и
ния —, соответствующие кривои Д, определяют режимы, Р о
при которых скачки в сопле исчезают (прямой скачок перемещается в минимальное сечение сопла, где М = 1).
Диаграмма на рис. 6-26 построена в предположении, что поток в сопле и струе плоский и симметричный и течение безотрывное.
Результаты опытов, приведенные на рис. 6-24,е, показывают, что отношение давлений, соответствующее положению скачка в выходном сечении сопла, с удовлетворительной точностью можно определить по формуле
SIА— 0,4 4- *
Потери энергии в плоских соплах Лаваля при различных режимах можно оценить по рис. 6-27. Здесь пунктиром нанесены коэффициенты волновых потерь в скачках уплотнения и коэффициенты потерь на расширяющемся участке сопла Кривые показывают, что на
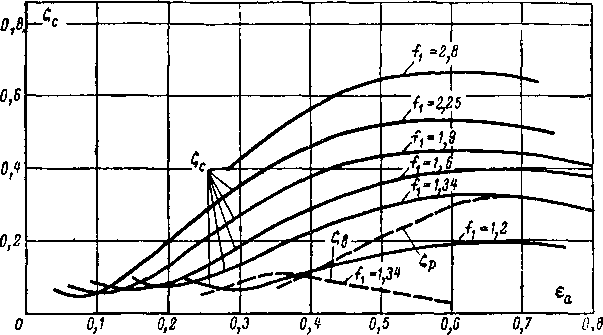
Рис. 6-27 Потери энергии в плоском сопле Лаваля при различных
режимах
—---опытные кривые,---волновые потери (расчет) н потерн в расши-
ряющейся части
режимах третьей группы, когда скачки располагаются вблизи минимального сечения, основное значение приобретают потери в диффузоре за скачком (потери трения и вследствие отрыва).
6-6 КОНИЧЕСКИЕ СОПЛА ЛАВАЛЯ
В НЕРАСЧЕТНЫХ УСЛОВИЯХ. РЕАКТИВНАЯ СИЛА
Истечение из осесимметричного сопла при расчетном и нерасчётном режимах обладает рядом особенностей 143
Рассмотрим вначале результаты опытного изучения спектра потока за соплом при истечении в среду с пониженным давлением (первая группа режимов).
На кромке выходного сечения АА\ (рис 6-28,а) образуется коническая волна разрежения, и давление падает от р 1 до ра. В ядре струи давление снижается до меньшего значения. В результате возникает пошеречный градиент давления, натравленный внутрь струи. Расширение потока в конической волне разрежения приводит к отклонению линии тока от оси и вызывает соответствующую деформацию внешней границы на участке AD. На участке DC граница струи под влиянием разности
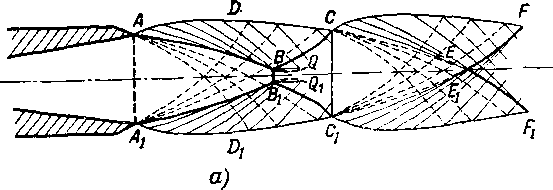
криволинейный скачок. В случае осесимметричной струи такой скачок имеет форму 'поверхности вращения с криволинейной образующей.
Скачок АВВХА\ (рис. 6-28,а) может зарождаться не у выходной кромки сопла, а в ядре струи, на некотором расстоянии от ее границы.
При значительном отклонении режима от расчетного (ра<рО скачок отходит непосредственно от кромки сопла. На оси струи возникает прямой скачок ВВХ, ,за которым скорость потока становится дозвуковой. Следовательно, при пониженном давлении за соплом в этом случае возникает мостообразный скачок.
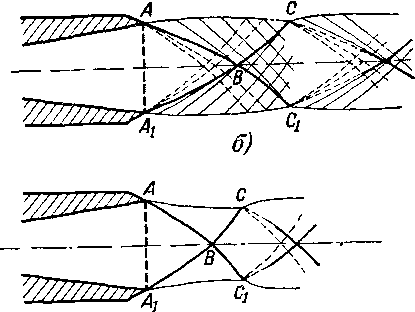
Криволинейный скачок СВВХСХ во внешней сверхзвуковой области является продолжением скачка АВВ{АХ. Струя суживается до того сечения, где скачок СВВ\С\ выходит на поверхность струи, и отражается в форме волны разрежения. Далее струя вновь разбухает. От ее границы обходят звуковые волны, пересекающиеся в ядре струи. В результате здесь образуется конический скачок EEiFFu замыкающий волну разрежения СЕЕ^Сх и выходящий на поверхность струи в точках F и Fь По мере повышения давления среды система скачков на выходе из сопла меняется мало и при расчетном режиме за выходным сечением сохраняются два осесимметричных криволинейных скачка (рис. 6-28,6). При дальнейшем возрастании давления среды (вторая группа режимов) форма границы струи меняется. За первым скачком линии тока отклоняются от оси струи (рис. 6-28,в).
Таким образом, для конического сопла первая группа режимов непрерывно переходит во вторую без существенных качественных изменений спектра течения внутри струи. В отличие от плоского сопла в коническом сопле при всех режимах в струе возникают скачки.
Если угол раствора сопла невелик, то в расчетном режиме отсутствуют внутренний прямой скачок и дозвуковое ядро. При повышенном противодавлении среды система скачков вновь перестраивается: два конических скачка соединяются прямым скачком, и внутренняя часть струи становится дозвуковой. Повышение противодавления приводит к расширению дозвуковой области и соответственно к сужению внешнего сверхзвукового течения (рис. 6-28,г). В этой группе режимов осесимметричная струя также имеет ряд особенностей. Криволинейные скачки АВ и А\ВХ разветвляются в точках В и В\, образуя уже известную мостообразную систему. В области 3 устанавливается повышенное давление и в сечении ССi скачок ВСВХСХ отражается в виде волны разрежения Однако в этом случае отраженные характеристики являются криволинейными
Характеристики, отходящие от свободных границ CF и C\F\, пересекаются. В результате, как и в случае, показанном на рис. 6-28,а, волна разрежения из точек С и Ci замыкается скачком CD (C1D1). На участке правее второго прямого скачка, расположенного на оси, поток ускоряется и становится сверхзвуковым. Далее процесс повторяется.
Дозвуковое ядро струи обнаруживается при всех режимах, отличных от расчетного Однако, как и во всех разобранных выше случаях, протяженность дозвукового ядра невелика. Внешняя сверхзвуковая часть струи ускоряет внутреннюю часть так, что уже на небольшом расстоянии за скачком ВВХ (рис. 6-28,а и г) поток на оси достигает сверхзвуковых скоростей На оси образуется как бы сопло Лаваля, границами которого служат линии раздела BQ и BiQx.
Для всех рассмотренных режимов характерной особенностью осесимметричной струи является различная кривизна ее границы, внутренних линий тока, скачков и волн разрежения. Действительно, как уже указывалось в гл. 4, при переходе через конический скачок линии тока непосредственно за скачком искривляются, причем их кривизна переменна вдоль скачка Если осесимметричный скачок имеет криволинейную образующую, то кривизна линий тока увеличивается. Линии тока искривляются и при переходе через коническую волну разрежения.
Форма расширяющейся части сопла оказывает значительное влияние на спектр струи за соплом. Опыт показывает, что в правильно профилированном осесимметричном сопле скачки уплотнения за выходным сечением возникают только при больших отклонениях режима ог расчетного (ра*€рО- На расчетном режиме и при незначительных отклонениях ог него (pa<pi) сопло работает без скачков уплотнения на выходе.
В конических соплах скачки в струе обнаруживаются при всех режимах С увеличением угла раствора расщи-
т ряющейся части интенсивность скачков и их крийизйа увеличиваются При больших углах раствора на выходе из сопла на 'расчетном режиме возникает мосгообраз-ный скачок (рис. 6-29)
Расширяющаяся часть непрофилированных сопел 'Лаваля выполняется, как правило, конической с неболь-


Рис 6-29 Спектры потока в струе за осесимметричным соплом Лаваля. Расчетные характеристики сопла } — 1,52, еи — 0,066, Mxt = 1,8.
а—ва = 0,546, б — ва “ 0,04, в — еа = 0,16.
шим углом раствора, равным 8+12° На расчетных режимах течение газа в сопле может быть безотрывным и при значительно больших углах раствора.
Величину предельного угла растзора плоского сопла, отвечающего безотрывному течению, на расчетном режиме можно легко определить по диаграмме характеристик (гл. 3) или с помощью таблиц (см. приложение), если задано расчетное значение Угол сопла должен быть не больше угла отклонения в волне разрежеййй при ускорении потока от А,= 1 до Xi.
Вместе с тем увеличение угла раствора оказывает значительное влияние на структуру потока в сопле при расчетном и нерасчетных режимах. По мере увеличения угла раствора растет величина отрицательного градиента давле-
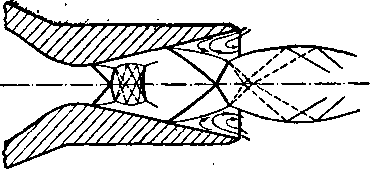
Рис. 6-30. Схема расположения сйачков в сопле Лаваля с большим углом раствора.
ления в расширяющейся части; возрастает неравномерность потока по оси струи и в выходном сечении.
Выше были приведены спектры потока в плоском сопле Лаваля с большим углом раствора. Опыт показывает, что и в конических соплах с большими углами раствора обнаруживаются аналогичные качественные изменения спектра. Схема перемещения системы скачков внутри конических сопел при различных режимах sa^>slk приведена на рис. 6-30.
Таким образом, характерные режимы сверхзвукового сопла с большим углом раствора нельзя определять по формулам, приведенным в предыдущем параграфе. Для такого сопла значения plk, plk и p^k ниже, чем для сопла с малым углом ус, и следовательно, переход в третью группу режимов происходит при меньших изменениях начального или конечного давления.
На рис. 6-31 приведены коэффициенты потерь Сс' для нескольких осесимметричных сопел.
Отсюда можно заключить, что минимальные потери соответствуют режиму истечения, близкому к расчетному. При возрастании еа потери в сопле резко увеличиваются и достигают максимальной величины вблизи критического значения еа ss 0,55 -е- б,65. При еще больших значениях еа потери уменьшаются. Такой характер кривых Сс объясняется изменением Волновых и вихревых потерь в сопле для второй и третьей групп режимов. Теоретически изме-
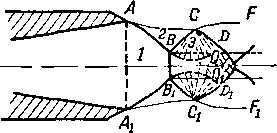
Рис. 6-28 Схемы спектров струи за коническим соплом при различных режимах,
давлений (давление среды более высокое) деформируется в противоположном направлении — струя сжимается (рис. 6-28,а). Все слабые волны, отходящие от границы, образуют с ней одинаковый угол (давления, скорости и температуры во всех точках границы одинаковы). При этом характеристики сходятся к оси струи. Как известно, сходящиеся характеристики образуют
г)
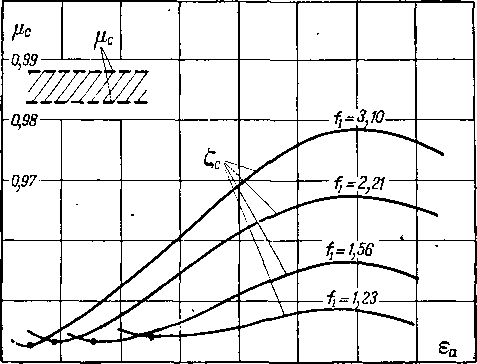
О 0,1 0,г 0,3 0,4 0,5 0,6 0,7
Рис. 6-31. Кривые коэффициентов потерь в зависимости от еа и
0,8
0,6
0,4
о,г
нение потерь должно происходить только при Однако, как показывает опыт, увеличение потерь с возрастанием sa происходит при меньших значениях е Повышение давления в системе скачков, возникающих в точках А и Аг при еа<^е)й, распространяется через дозвуковую часть пограничного слоя внутрь сопла и приводит к перераспределению параметров в выходном сечении. Максимальные волновые потери соответствуют режиму ea = e]ft. По мере перемещения скачков внутрь сопла (sa!>elft) волновые потери уменьшаются, а вихревые—увеличиваются. В соплах с небольшим углом раствора, когда скачок приближается к критическому сечению, отрыв потока имеет локальный характер. На небольшом расстоянии за скачком поток вновь подходит к стенкам сопла и вихревые потери уменьшаются. Поэтому коэффициент потерь начинает уменьшаться. На режимах еа еш волновые и вихревые потери в сопле
отсутствуют (режимы трубы Вентури); потери энергии возникают только из-за трения. Как видно из рис. 6-27 и 6-31, F,
с увеличением /i = -pr- потери на режимах третьей группы
увеличиваются и область максимальных значений Сс несколько смещается в сторону больших еа. Следует подчеркнуть, что суммарные потери в сопле значительно выше волновых
b с' с
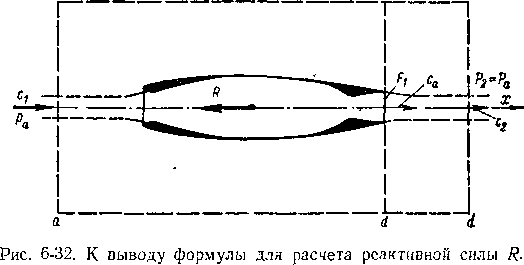
потерь при данном режиме sa5=slft. Заметим, что характер . кривых С = ?с (е ) остается одинаковым для плоских и осесимметричных сопел, однако абсолютные значения Сс несколько отличаются.
На рис. 6-31 указаны также значения коэффициентов расхода рс.
Сопла Лаваля весьма широко применяются в реактивных двигателях. В этой связи остановимся кратко на характеристиках сопел, необходимых для расчета реактивной силы.
Для определения реактивной силы, под действием которой осуществляется полет реактивного аппарата, воспользуемся уравнением импульсов. Для этого опишем около аппарата замкнутую цилиндрическую поверхность abed, все элементы которой удалены на достаточно большое расстояние (рис. 6-32). Возмущения, создаваемые аппаратом на выделенной замкнутой поверхности, будут бесконечно слабыми. Запишем уравнение количества движения в проекции на ось х (уравнение Эйлера):
\padF~ §P,dF + R = ~ j (c2-Cl)dGB+~ ^c2dGr.
0 0 0 0
(6-46)
Здесь pa — давление набегающего потока в сечении а — b; рг, сг — давление и скорость потока за аппаратом в сечении с — d; F — площадь сечений а — b и с — d; GJg— секундная масса воздуха, втекающая в контур; GJg — секундная масса горючего, подаваемого в двигатель; R — реактивная сила.
I Так как сечения а — b и с — d расположены на большом удалении от аппарата, то ра = р2. В этом случае силы давления в указанных сечениях уравновешиваются всюду, за исключением участка, равного площади выходного сечения сопла F,. Скорости отдельных струек, охватывающих аппарат, также мало различаются. Обозначив с а — скорость истечения из сопла; рх — давление в выход, ном сечении сопла Flt из (6-46) получим:
R = ~J jcorfG + j(A — PjdFv (6-48)
о
где G ¦— секундный расход рабочего тела.
В средних величинах формулу (6-48) можно записать так:
* = 7-Са + <Л-Д,)Л.
Заменив здесь
к
-J- Са =РгС1 Fl = kPiMl Fi=k (j~yif~~lp№„
окончательно получим:
Заметим, что добавочный член в уравнении (6-49) вводится только для первой и второй групп режимов работы сопла, т. е. при сверхзвуковых скоростях истечения.
При повышенных противодавлениях (pi>р2) реактивная сила уменьшается, так как разность р2—pi отрицательна. Наоборот, при расширении струи за соплом разность (р2—pi) положительна и R увеличивается.
Если скачки расположены внутри сопла, то истечение происходит с дозвуковыми скоростями (р2“pi) и второй член отпадает. Изменение реактивной силы в этом случае обусловливается уменьшением скорости истечения, которая должна быть определена с учетом потерь в системе скачков и в расширяющейся части сопла.
Реактивную силу удобно представить в безразмерном виде. С этой целью разделим (6-49) на величину p\Fx. После несложных преобразований получим:
R=$ +1) (1 - % )k~lfa - I. (6-50)
Для оценки эффективности сопла реактивного аппарата иногда вводится понятие коэффициента тяги
где R , Rt— реактивные силы в действительном и теоретическом (без потери в сопле) процессах.
Связь между Ra и Rt можно найти в таком виде:
где сэ—эквивалентная скорость:
Y (с0 — c1) + (p1-pa)F1
8
G и Gt — действительный и теоретический расходы через сопло;
си—теоретическая скорость истечения из сопла.
т. е. коэффициент тяги является произведением коэффициентов расхода и скорости.
0.7
| ь | А | 41. |
// | |
| .1,2 Ь V/ | г | |||
|
\ \ | т, lyw | • У |
||
| \ \ |
1 к |
|||
| А •3/5 \ \ | / |
1V | ||
|
Л | / / | ?а |
---Ус*12°
уcW Ус’36’
0,4
0,6
о,в
Рис. 6-33. Изменения коэффициента = [хсус в зависимости от режима (еа), отношения f{ и угла раствора сопла -у
Характеристики <pR по опытам В. Ф. Степанчука приведены на рис. 6-33 для сопел с различным параметром /, и для разных углов раствора.
1.0
В режимах первой группы J(ea<Csi) величина практически не меняется. В третьей группе режимов, когда система скачков входит в расширяющуюся часть сопла, величина падает в связи с появлением значительных волновых и вихревых потерь. Минимальное значение резко уменьшается с ростом Этот результат объясняется большей интенсивностью скачков и увеличением потерь в диффузоре за скачками в соплах с большим f,.
Для углов ус = 12° ч- 24° характеристики сопел Совпадают. Дальнейшее увеличение ус ведет к резкому снижению для третьей группы режимов.
При ус = 48° на кривой появляются два максимума, первый из которых соответствует расчетному режиму, а второй—-режиму работы сопла, как обычного суживающегося (рис. 6-33). Это означает, что при больших ус отрыв потока на режимах, соответствующих третьей группе, происходит вблизи критического сечения. Опыты подтвердили, что значение ед, при котором в расширяющейся части образуется отрыв, существенно зависит от угла раствора и растет с увеличением ус.
Таким образом, в соплах с углами раствора ус>-5-г-80 на режимах третьей группы возникает сложная система скачков. В соответствии с данными опыта чаще всего эта система может быть аппроксимирована двумя пересекающимися на оси косыми или коническими скачками. В этом случае для расчета третьей группы режимов работы сопла необходимо знать угол косого скачка в зависимости от При боЛЬШИХ уГЛЭХ рЭСТВОрЭ, КОГДЭ ПОТОК
за скачком отрывается, можно принять, что р”к ~ ра. По
известным значениям М1ск и нетрудно найти угол скач-
Рск
ков р. Если отрыва за скачком не образуется, то задача может быть решена только подбором.
6-7. СВЕРХЗВУКОВОЕ СОПЛО С КОСЫМ СРЕЗОМ
При расчетном режиме истечение из сверхзвукового сопла с косым срезом происходит с небольшими изменениями спектра потока. Эти изменения обусловлены влиянием пограничного слоя на стенке косого среза КА (рис. 6-34). '
При нерасчетном режиме, когда давление среды ра меньше расчетного (режим 1), дополнительное расширение сгруи происходит в косом срезе или за его пределами. Если угол первой характеристики меньше угла косого среза ф, то расширение потока происходит за пределами косого среза (рис. 6-34,а). В этом случае кромки сопла А и Ai создают стационарные волны разрежения, пересекающиеся не на оси струи, а в области, лежащей ближе к кромке А. По этой причине нарушается симметричность спектра истечения и струя отклоняется от оси сопла. Волны разрежения отражаются от границы
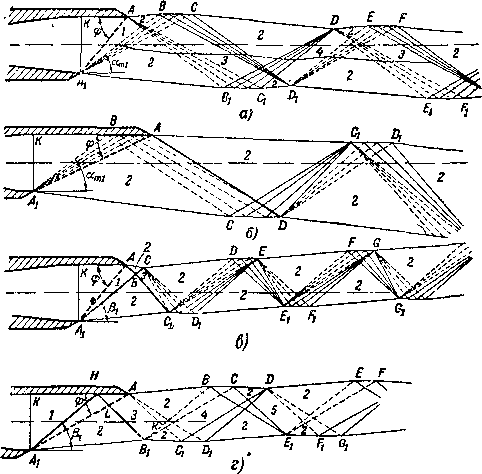
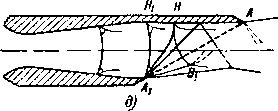
Рис. 6-34. Схемы спектров струи за соплом с косым срезом.
струи, как волны сжатия (BCDi и BiCxD), пересекающиеся вблизи противоположной границы. В зонах струи 2, примыкающих к границе, давление равно внешнему давлению ра, в зоне 3 (за пересечением волн разрежения) давление пониженное, а в зоне 4 — повышенное, равное давлению в косом срезе сопла pi.
При пересечении несимметрично расположенной системы волн углы отклонения линий тока меняются от
сечения к сечению. Соответственно меняется и средний угол отклонения струи.
Если первая волна разрежения из точки А частично или полностью лежит в пределах косого среза, то характер течения меняется (рис 6-34,6). Отраженная от стенки косого среза (частично или полностью) волна разрежения приводит к понижению давления, и у кромки А давление оказывается меньшим, чем ра¦ В результате в точке А образуется косой скачок уплотнения; система волн изменяется и углы отклонения будут уже другими, по сравнению с первым случаем В косом скачке AD линии тока отклоняются по часовой стрелке, поэтому средний угол отклонения струи несколько увеличивается. Такой характер истечения будет иметь место в том случае, когда угол косого среза
<p<arcsin —.
Для второй группы режимов (давление среды выше расчетного) на кромках А и Ах возникают косые скачки (рис 6-34,в), пересекающиеся за косым срезом, если угол Pi скачка из точки А\ меньше угла косого среза <р. Точка пересечения скачков В лежит у верхней границы струи. Поток отклоняется от оси струи, проходя несимметричную систему скачков и отраженных волн разрежения, причем поворот потока происходит в противоположном первому случаю направлении. Заметим, что для первой группы режимов (pa<pi), поворот струи происходит относительно точки А, а при ра>Р\ (вторая группа режимов) струя поворачивается относительно точки А\. Углы отклонения линий тока, а следовательно, и всей струи меняются вдоль потока, так же как и в первом случае, благодаря влиянию отраженны^ волн.
Если cp<Pi (рис. 6-34,г), то первый косой скачок лежит в пределах косого среза. В отраженном скачке НВу давление увеличивается до значения, большего, чем ра. В результате на участке НА и в области LAKBX давление повышенное. Из точек А и Вх распространяются волны разрежения ACiDx и В^ВС. В зонах 2 устанавливается давление ра. В зоне 4 давление равно р\, а в зоне 5 (за пересечением отраженных волн 'Сжатия) давление вновь повышается. Далее процесс повторяется. Легко заметить, что средний угол отклонения струи в этом случае может увеличиться. При дальнейшем повышении противодавления скачок АуН будет поворачиваться к сечению АуК. При некотором значении pa=p'ih нормальное отражение скачка АУН становится невозможным, так как скорость за первичным скачком близка к скорости звука. Скачок принимает форму ^-образного скачка

Рис. 6-35. Спектр потока за соплом Лаваля с косым срезом (волна разрежения в пределах косого среза).
AiHBi (рис. 6-34,д), и в косом срезе у стенки НА образуется отрыв струи.
Если pa~pik, то мостообразный скачок располагается в сечении сопла АуНу и спектр струи почти не отличается от рассмотренного выше для сопла с прямым срезом.
Расчет спектра и определение среднего угла отклонения на выходе из сопла с косым срезом могут быть произведены методом характеристик (режимы /) в комбинации с методом ударных поляр, если pa>pi (режимы //).
Приближенную оценку углов отклонения можно осуществить и более простыми способами, изложенными в гл. 8, с помощью уравнений неразрывности количества движения и энергии.
Опыты подтверждают рассмотренные выше спектры I истечения из сопла Лаваля с косым срезом. На рис. 6-35 отчетливо виден волновой спектр струи за косым срезом.
Заметим, что отклонение струи в косом срезе вызывает изменение реактивной силы, расчет которой должен быть произведен л о измененной формуле с учетом отклонения потока.
ДВИЖЕНИЕ ГАЗА В ДИФФУЗОРАХ.
СТУПЕНЬ ЭЖЕКТОРА
7-1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ И РАСЧЕТ ДИФФУЗОРОВ
В диффузорах происходит преобразование кинетической энергии потока в энергию давления. Уравнения одномерного течения (гл. 2) показывают, что такой процесс при дозвуковых скоростях можно осуществить в трубе с увеличивающимся вдоль потока сечением.
Течение газа в диффузоре характеризуется 'положительными градиентами давления, наличие которых создает условия для интенсивного нарастания пограничного слоя и в ряде случаев отрыва потока от стенок.
Влияние положительного градиента давления на структуру пограничного слоя было подробно рассмотрено в § 5-11. Графики на рис. 5-29 и 5-30 показывают, что с увеличением положительного градиента давления (параметр Г<0) резко возрастает толщина потери импульса 6** и уменьшается наполнение профиля скорости у стенки.
При значительных градиентах давления в диффузоре может возникнуть отрыв (гл. 5). В этом случае потери энергии резко возрастают и диффузор не обеспечивает заданного повышения давления.
Основная задача расчета сводится к установлению оптимальной формы диффузора, соответствующей безотрывному течению и минимуму потерь энергии при заданных режимных .параметрах (числах Re и М) и условиях на входе ’.
С этой целью выбирается такая эпюра распределения давлений по диффузору, который дает наименее интенсивный рост толщины потери импульса к выходному сечению и не приводит к отрыву слоя или смещает отрыв к выходному сечению. 11одо!бная задача может быть решена путем вариантных расчетов пограничного слоя методами, изложенными в гл. 5.
Выбрав рациональное распределение давлений, нетрудно рассчитать проходные сечения, установить фор-
1 Имеются в ввду длина, форма и шероховатость стенок входного участка диффузора, начальная степень турбулентности потока, распределение скоростей по сечению и пр.
му диффузора и определить Величину потерь в нём. В случае, когда форма диффузора является заданной, распределение давлений по оси рассчитывается по методу канала (§ 3-5).
В практике расчетов принято потери энергии в диффузорах рассматривать как сумму двух составляющих: потерь на трение в пограничном слое ?тр и потерь расширения ?р. По смыслу величина ?р характеризует потери, вызванные вихревым ^
![]()
потока, когда при переходе Рис- 7Л- Схема ДиФФуз°ра-
из узкой части трубы в более
широкую граница струи распадается и свертывается в вихри На поддержание вихревого движения затрачивается часть энергии потока. В результате внезапное
расширение сопровождается потерей давления, причем коэффициент потерь для несжимаемой жидкости при внезапном расширении (потери на удар) может быть определен по формуле
? _(ci — сг?__I }
УД
F.
где f = y — степень расширения диффузора [Fj— сечение
входа и F3— сечение выхода диффузора (рис. 7-1)].
Соответствующая потеря давления выражается формулой \
-чд=Ри - р.=4с=•х (• - й J • <7-2)
где p2t—давление за внезапным расширением при отсутствии потерь; я с2 — скорости в сечениях Fx и Ft.
В диффузоре (рис. 7-1) потери энергии и давления, обусловленные расширением сечений, будут меньше, так как сечения меняются постепенно.
Отношение
Д р„
* = i(?-3)
ууд
Где Арж — потеря давления в диффузоре, называют коэффициентом смягчения удара. Следовательно, коэффициент <]/ представляет собой отношение потерь давления в диффузоре к потерям давления при внезапном расширении.
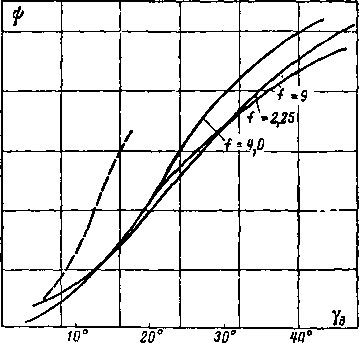
о
Рис. 7-2. Коэффициент смягчения удара в зависимости от угла раствора и параметра / для
диффузоров (-- — круглого сечения;
----квадратного сечения).
?
0,6
о,ч
0,2
Как видно из рис. 7-2, коэффициент <J> слабо зависит
Р
от отношения f—у и Ф°РМЫ сечения и в основном определяется углом раствора диффузора у .
Использование коэффициента ф для расчета диффузоров является формальным и может быть оправдано только тем, что обнаруживаемые потери в диффузорах оказываются большими, чем потери на трение, определяемые для без-градиентного течения.
Действительно, при вычислении потерь на трение, как правило, используют известную формулу (гл. 5):
dLT р = (7-4)
с коэффициентом 5, определяемым по одной из известных формул для безградиентного течения, например по формуле Блаузиуса:
Здесь C0 — скорость на оси диффузора; dx ¦— элемент длины; D — диаметр поперечного сечения рассматриваемого участка и
![]()
(7-6)
— число Рейнольдса.
Величина абсолютных потерь на трение, вычисленная таким способом, оказывается значительно меньше экспериментальных значений, даже при безотрывном течении, так как формула (7-5) не учитывает влияния градиента давления.
Потери в диффузорах любой формы при безотрывном течении могут быть вычислены с использованием теории пограничного слоя, например по методу А. Е. Зарянки-на, основанному на шрименении понятия толщины потери энергии.
Для конических диффузоров путем некоторых упрощений им получена формула для коэффициента потерь в следующем виде:
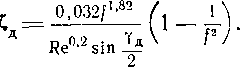
(7-7)
Используя этот коэффициент, можно вычислить потери давления в диффузоре:
д/>д = Дм-А = Сд-г-
(7-8)
Сравним результаты расчетов по формуле (7-7) с данными эксперимента.
Из кривых потерь на рис. 7-3 следует, что потери в изоградиентном диффузоре144 значительно больше, чем в коническом. Все диффузоры имели одну и ту же степень .расширения / = 2,25. Изменение потерь в зависимости от числа Mi<0,8 показывает, что е ростом скорости
потери несколько снижаются. Однако всюду величинй потерь в изоградиентном диффузоре примерно в 3 раза больше, чем в коническом, что указывает на отрывный характер течения в нем.
Оценка потерь по формуле (7-7) для конических диффузоров при Mi = 0,7 дает 5,5^/0 для уд=10° и 5°/0 для
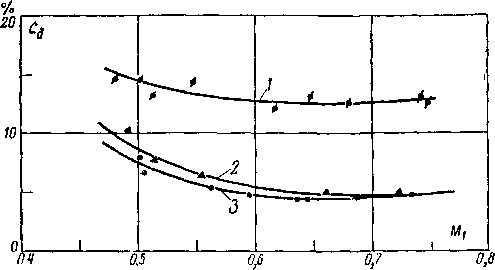
Рис 7-3. Изменение потерь в различных диффузорах в зависимости от числа М,
1 — изоградиентный дифф\зор, 2 —конический ди{>ф>зор (7Д = 6“);
3 —конический диффузор (7Д = И°)
уд = 6°. Эти значения 1д практически совпадают с данными эксперимента.
Для расчета распределения скоростей по оси диффузора проинтегрируем уравнение (5-10):
+ = (7-9)
\ У *
где элементарная работа трения dL^ может быть выражена через коэффициент потерь в диффузоре.
В результате интегрирования получим:
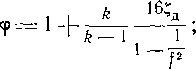
у As — 1
i / l k+l
![]()
![]()
(7-12)
Следуя методу, изложенному в работе [Л. 4], введем по аналогии с приведенным расходом в данном сечении q(l) функцию
![]()
При отсутствии потерь (Я) = (Я), поэтому функцию
qR (Я) можно назвать обобщенным приведенным расходом. Зная распределение скорости вдоль оси диффузора, по уравнению неразрывности с помощью этой формулы можно найти отношение давлений полного торможения в произвольном сечении диффузора [см. формулу (2-41)]:
и соответствующее отношение статических давлений:
Здесь а (2) = ^ q (2) (см. гл. 2).
Расчет распределения параметров потока вдоль оси диффузора с учетом вязкости показывает, что скорость потока в произвольном сечении больше, а статическое и полное давления меньше, чем соответствующие значения этих величин, полученные без учета влияния вязкости. Кривые р показывают, что восстановление статИ’ ческого давления в коническом диффузоре происходит наиболее интенсивно в начальном участке. Далее возрастание р резко замедляется, а, начиная с некоторого предельного значения /пред, дарление начинает снижаться,
Формула (7-15) отражает также влияние сжимаемости: с увеличением скорости на входе положительные градиенты давления возрастают особенно интенсивно на начальном участке.
Для оценки точности расчета по формуле (7-14) на рис. 7-4 приведены значения ео по данным К. С. Сцил-ларда для диффузора с / = 4,92 и уд = 4 и 8°. Совпадение расчетных и опытных данных следует признать удовлетворительным во всем диапазоне чисел
0,96
0,92
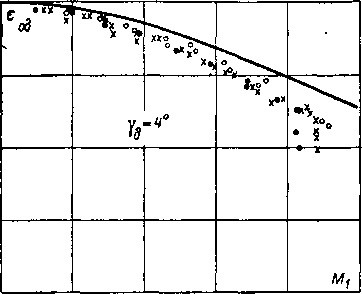
0.84
' 0 0,2 0,4 0,6 0,8 1,0
0,88
1,0
0,96
0,92
0,8В
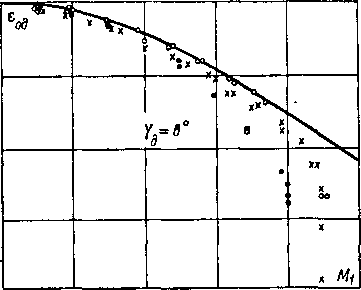
0,84
’О 0,2 0,4 0,6 0,8 1,0
Рис. 7-4. Сравнение расчетных и экспериментальных значений е0 для конических диффузоров с различными углами раствора (опыты к. С. Сцилларда).
Остановимся теперь на характеристиках диффузоров, получаемых лри экспериментальном исследовании.
Рассмотрим в тепловой диаграмме изменение состояния газа в дозвуковом диффузоре. Параметры полного торможения потока на входе в диффузор определяются
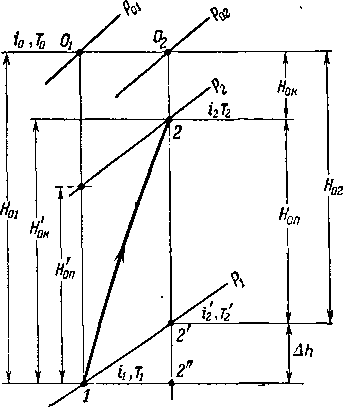
Рис. 7-5. Процесс изменения состояния газа в дозвуковом диффузоре в тепловой диаграмме.
точкой 01 (рис. 7-5), а параметры движущегося газа до диффузора—точкой 1.
Сжатие в диффузоре происходит с возрастанием энтропии. Этот процесс изобразится линией 1—2, причем точка 2 соответствует параметрам газа за диффузором. Точка 02 соответствует состоянию полностью заторможенного за диффузором потока. В тепловой диаграмме легко найти соответствующие энергетические характеристики: потерю кинетической энергии Ah, изменение потенциальной энергии Я0п и кинетическую энергию потока в выходном течении Я0к. Коэффициент потерь энергии в диффузоре, как и в случае скачка, определяется по формуле (4-ЗЗа):
где е0д=—¦—коэффициент восстановления давления тор-Pai можения в диффузоре.
Эффективность диффузора можно характеризовать также энергетическим к. п. д.
чд=т^ = 1-<д- (7-т
В некоторых случаях для оценки диффузора пользуются другим понятием к. п. д., определяя эту величину по формуле
- ^Оп
¦Г70к
где Нйп — изменение потенциальной энергии потока в диффузоре;
Hqk — разность кинетических энергий потока во входном и выходном сечениях диффузора.
После подстановки Н0п и Н0к можно получить к. п. д. диффузора в виде:
k - 1 .9 ft—I
k
1
k-\-\
\~2k-l *2_х2
(g) ]¦ <М6б>
Энергетический к. п. д. зависит только от потерь энергии в диффузоре, в то время «ак меняется лри изменении степени сжатия. Легко видеть, что ,Пд>'Пд/.
Выбор оптимального эпюра скоростей (или давлений) вдоль диффузора осуществляется на основании вариантных расчетов.
Величины б** и dpfdx, определяющие состояние потока в диффузоре, зависят от степени расширения (отношения f = F2/Fi) и угла раствора диффузора ул. Отсюда вытекает, что форма оптимального эпюра давлений зависит от этих геометрических .параметров.
В диффузорах с плавным изменением сечения (с малыми углами раствора) при безотрывном течении целесообразно выбирать эпюры с большими градиентами на входных участках (эпюры 2 или 5 на рис. 7-6,а) и с уменьшающимися значениями dp/dx в среднем и выходным участках; удовлетворительные результаты могут быть получены в диффузоре с прямолинейными стенками (эпюр 3 на рис. 7-6,а).
В диффузорах с большими углами растйора отрыв возникает в сечениях входного участка. Для того чтобы сместить отрыв к выходному сечению, необходимо
h
Ь2
Ь
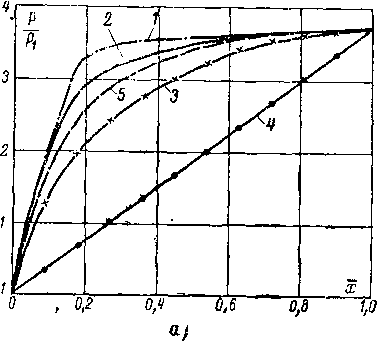
| F F, |
— j | |||
| i ( | У2^/ /У> | V |
г | |
|
ft | / s К | 3 |
У‘ | |
|
ft |
X |
1 'JT * х
' О 0,2 О,-* 0,5 ~~ 0,3 1,1}
б)
Рис. 7-6 Эпюры давлений и проходных сечений диффузоров различной формы.
уменьшить градиенты давления на входе, т. е. перейти к кривой dpjdx = const (эпюр 4 на риа. 7-6,а и др.). Изменение проходных сечений диффузоров, обеспечивающих эпюры указанных давлений, представлены на рис. 7-7,6.
Рассмотрим влияние основных геометрических и режимных параметров на эффективность плоских и конических диффузоров. Как указывалось, важнейшими геометрическими параметрами являются угол раствора уд и степень расширения f.
Из приведенных формул (§ 7-1) следует, что при заданном распределении скоростей значение параметра Г не зависит от уд и эта величина может быть выбрана произвольно. На основании формулы (7-11) можно заключить, что при 'больших углах уд потери в диффузоре уменьшаются.
Однако, как показывают опыты, при уд>8-н12° в конических диффузорах возникает отрыв; потери энергии при этом резко возрастают.
Можно полагать, что образование отрыва при больших углах раствора связано с неравномерным распределением скоростей на входе. В большинстве случаев переход от конфузорной части к коническому диффузору осуществляется с резким изменением кривизны стенок, причем скачок кривизны возрастает с увеличением уд. Такое местное нарушение граничных условий является причиной раннего отрыва пограничного слоя при увеличении угла Yfl- Влияние указанного нарушения особенно велико в тех случаях, когда пограничный слой на значительном расстоянии от входа ламинарный.
Отметим, что характер неравномерности поля скоростей на входе существенно влияет на потери в диффузоре. Особенно неблагоприятным является эпюр скоростей 1, вытянутый в средней части (рис. 7-7); менее существенно влияние неравномерности, если поток характеризуется повышенными скоростям и у стенок (эпюра 2). В этом случае потери могут оказаться меньшими по сравнению с равномерным полем скоростей (эпюра 3). Неравномерность, характеризуемая" эпюрой 2 на рис. 7-7, благоприятна потому, что в этом случае пограничный слой в диффузоре становится тоньше, а точка отрыва смещается по потоку.
При правильной организации потока на входе в диффузор угол раствора уд можно принимать увеличенным.
При определении оптимального угла раствора уд. опт, т. е. такого максимального угла, при котором еще не произошел отрьгв потока, можно для круглых диффузоров при >малых скоростях пользоваться формулой И. Е. Идельчика:
Y -0 43 Р Г + 1УШ5д-опт : ¦
где <рн — опытный коэффициент, учитывающий влияние неравномерности поля скоростей на входе в диффузор.
Следует подчеркнуть, что формулы для Тд.0Пт пРеД' ставляют эту величину в зависимости от числа Рейнольдса,
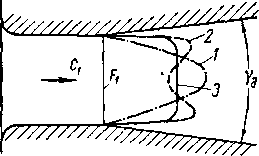
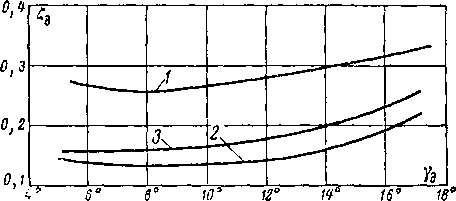
Рис. 7-7. Влияние характера неравномерности поля скоростей во входном сечении диффузора на потери; Re, = = 3-105; М, = 0,5.
функцией которого является коэффициент сопротивления 5. Расчеты показывают, что с ростом Rexудопт увеличивается.
По опытным данным К. С. Сцилларда с ростом числа Mj преимущество малых углов возрастает. Следовательно, с увеличением М, оптимальный угол раствора должен уменьшаться (рис. 7-4). Этот результат представляется очевидным, так как влияние сжимаемости проявляется в том, что увеличиваются продольные градиенты давления. Так, при увеличении числа М.г от 0 до 0,8 уд опт уменьшается на 0,7 — 0,9° (Re1 = 106). Эта зависимость Тд.олт от числа Mi оказывается менее интенсивной, чем от Rex.
Опыты показывают, что для круглых конических диффузоров оптимальные значения Тдопт можно принимать в пределах Тдопт = 615°. Наиболее употребительны средние значения 10—12°.
Важной геометрической характеристикой диффузора является отношение сечений /. При заданной скорости на входе повышение давления происходит только до определенных пределов, причем в коническом диффузоре и в диффузоре оптимальной формы наиболее бурный рост давления соответствует начальному участку.
Значение параметра f, отвечающее максимальной степени сжатия в диффузоре, называется предельным. Выполнение диффузора с большим отношением f нецелесообразно, так как при этом на выходном участке обнаруживается снижение давления.
Результаты расчета показывают, что /пред зависит от угла раствора диффузора уд> безразмерной скорости потока и числа Re! на входе. С увеличением уд и величина /пред. уменьшается. Физически этот результат объясняется тем, что с ростом уд и Я.1 увеличиваются градиенты давления. Возрастание числа Рейнольдса приводит к увеличению /пред, так как при этом уменьшаются потери на трение в диффузоре.
Следует отметить, что практически принимаемые значе-ния /п должны быть меньше расчетных. Действительно, наиболее интенсивное сжатие газа происходит во входном участке диффузора, так что в сечениях f = 2,5-н 3,5 повышение давления составляет около 9Q°/0 максимального, соответствующего /пред (для диффузоров с углами раствора т[д —8-*-15°). При окончательном выборе /пред следует производить детальный расчет пограничного слоя и оценивать вероятность образования отрыва по параметру
Результаты соответствующих расчетов для конических диффузоров показаны на рис. 7-8. Видно, что предельные
Значения /пред, определенные по условиям безотрывного течения (Г Г5) и максимального повышения давлений в ди($>узоре pjpl = 0,9 (а/М^кс > существенно ниже теоретических /пред, изображенных сплошными линиями.
Для диффузоров, построенных по рациональному распределению давлений, значения /пред могут быть выбраны
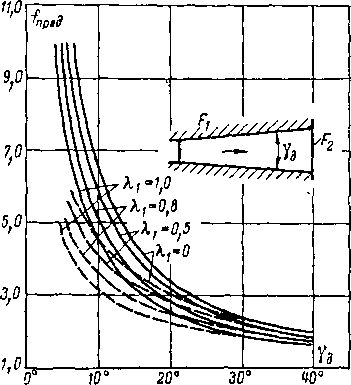
Рис. 7-8. Предельные степени расширения диффузора в зависимости от угла раствора и безразмерной скорости на входе.
большими, так ка'к в этом случае течение в диффузоре безотрывное.
Влияние формы диффузора на его основные характеристики частично рассматривалось в § 7-1. Как указывалось, решение этого вопроса не является универсальным; оптимальный эпюр давлений меняется в зависимости от двух основных геометрических параметров — отношения сечений f и длины диффузора. При малой длине и больших /, когда градиенты давления на входе весьма резко возрастают, возможно образование отрыва уже во входных сечениях. '
В этих случаях необходимо уменьшать dpjdx на входе, причем диффузоры с постоянным 1 градиентом давления оказываются более эффективными для больших углов рас-
Твора, т. е. при малой длине и больших f. Этот факт отчетливо подтверждается опытами И. Е. Идельчика с плоскими диффузорами (рис. 7-9).
Так как в изоградиентных диффузорах потери на трение больше (в связи с тем, что §** возрастает на выходе интенсивнее), то применение таких диффузоров следует считать целесообразным только при больших углах рас-
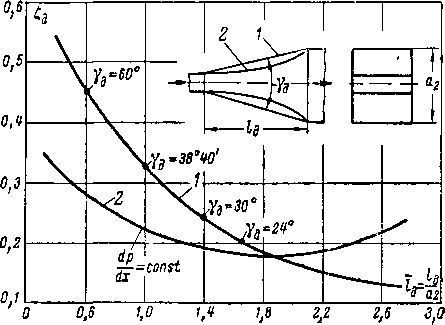
Рмс 7 9 Изменение коэффициента потерь в плоских диффузорах в зависимости от относительной длины /
твора удзз18°. В интервале хд=12-г-18° лучшие результаты дают диффузоры с прямолинейными стенками (Тд = const). При малых углах уд<12° следует переходить к диффузорам с криволинейными выпуклыми стенками (кривые 2 на рис. 7-6).
Возможно также применение комбинированных диффузоров, принципиальные схемы которых приведены на рис. 7-10. Особый интерес представляет ступенчатый диффузор. Повышение давления здесь происходит вначале в обычном плавно расширяющемся канале, а затем давление растет при внезапном расширении сечения. Такие диффузоры следует применять при малой длине и больших отношениях f. Для каждого значения f существует определенная оптимальная длина / , соответствующая минимальным потерям. При выбранных оптимальном угле раствора Уд0Пт
плавной части диффузора F'2.
Ступенчатые диффузоры имеют существенные преимущества в тех случаях, когда необходимо сократить длину диффузора. При малых уд применение ступенчатого диффузора нецелесообразно, так как суммарные потери при внезапном расширении возрастают.
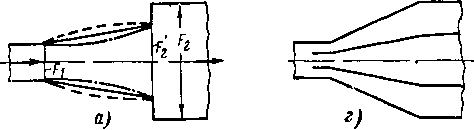
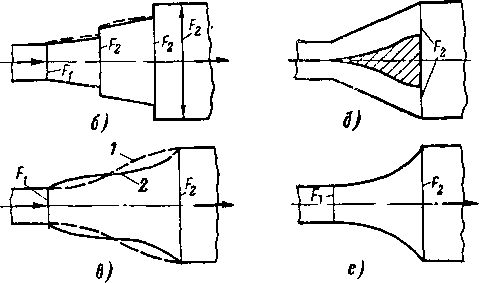
Рис. 7-10 Схемы комбинированных диффузоров.
а, б и д—ступенчатые диффузоры, в —диффузоры с малыми (/) и большими (2) градиентами давления иа входе, г —диффузор с разделительными стенками, е —изоградиентный диффузор.
Опыты показывают также, что на эффективность диффузора влияет форма его поперечных сечений. В круглых и плоских диффузорах потери энергии оказываются минимальными. В диффузорах квадратного или прямоугольного сечения с расширением в двух плоскостях потери выше. Это объясняется различным изменением давлений вдоль потока: градиенты давлений в круглых и плоских диффузорах при одинаковых Л и Р2 будут меньше, чем в квадратных. В некруглых диффузорах потери повышаются вследствие интерференции пограничных слоев в углах.
Опыты подтверждают значительное йлияние начальной турбулентности на характеристики диффузора в полном соответствии с тем, что 'было получено при исследовании пограничного слоя (гл. 5). Коэффициенты потерь интенсивно возрастают с увеличением начальной турбулентности.
Остановимся на оценке влияния основных режимных параметров, чисел Rei и Mi на характеристики диффу-
1,3
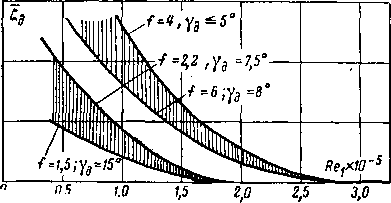
Рис 7-11. Влияние чисел Re, и М, на коэффициент потерь в конических диффузорах.
;д = Re, = 3.105.
V
V ' 1,0
зоров. Опыты показывают, что характер кривых ?n(Rei) зависит от геометрических характеристик диффузора: уд и [. Соответствующие кривые по данным различных исследований приведены на рис 7-11. Как видно, влияние Rei ощутимо ,при Rei<3- 105 в зависимости от уя, f2 и формы диффузора Отметим, что характеристики ?H(Rei) при больших углах раствора и [>4 протекают более полого. Здесь наблюдается аналогия с влиянием начальной турбулентности: при больших уд влияние Е0 ослабевает.
Возрастание числа Mi приводит к увеличению градиентов давления; в соответствии с этим потери на трение в диффузоре с ростом Mi начиная с Mi>0,7 увеличиваются. Сжимаемость приводит к росту вихревых потерь в диффузоре; при отрывном обтекании с увеличением Mi точка отрыва потока перемещается к входному сечению.
При околозвуковых скоростях на входе (при Mi<l) потери в диффузоре возрастают особенно интенсивно, так как градиенты давления во входном участке резко увеличиваются, что приводит к раннему отрыву даже при небольших углах раствора (рис. 7-4). Следует подчеркнуть, что кривые на рис. 7-3 отражают влияние не только сжимаемости, но и числа Рейнольдса. Уменьшение с ростом Mi при 0,1<М1<0,5 обусловлено изменением Reb так как в этом диапазоне чисел Mi влияние сжимаемости еще не сказывается.
Рассмотрим в заключение некоторые результаты опытов, проведенных с целью снижения потерь в диффузорах с большими углами раствора. По данным И. Е. Идельчика, наряду с применением изоградиентных диффузоров понижение потерь в диффузоре может быть достигнуто установкой сеток, разделительных стенок и организацией отсоса или сдува пограничного слоя, а также применением ступенчатых диффузоров.
Опыты В. Кмоничка показали, что установка проволочного пучка приводит к заметному уменьшению потерь в плоском диффузоре с большими углами раствора (рис. 7-12,а, бив). Аналогичные результаты были получены для круглых диффузоров при радиальном расположении проволок (рис. 7-12,г).
Обнаруживаемый эффект объясняется тем, что вводимое в диффузор сопротивление выравнивает поле скоростей на выходе из диффузора. Выравнивание скоростей приводит к смещению точки отрыва по потоку, так как -профиль скорости у стенок становится более полным (рис 7-7).
Оптимальное положение и форма проволочных решеток, вводимых в диффузор, существенно зависят от формы и угла раствора диффузора, а также от режима потока (чисел Mi и Rei).
Исследования В. Кмоничка проведены были с сопротивлениями, введенными внутрь диффузора. При этом оказалось, что для плоского диффузора с углом раствора уд= 15° оптимальным является вариант на рис. 7-12,а, для уд=30° лучшие результаты показали варианты б и s. Улучшение течения газа в диффузоре с большими углами раствора можно обеспечить* акже с помощью глубоких канавок, вытачиваемых на некотором расстоянии от входного сечения (рис. 7-12,5). Создаваемый канавками отсос слоя смещает отрыв по патоку, как это показано опытами В. К- Мигая,
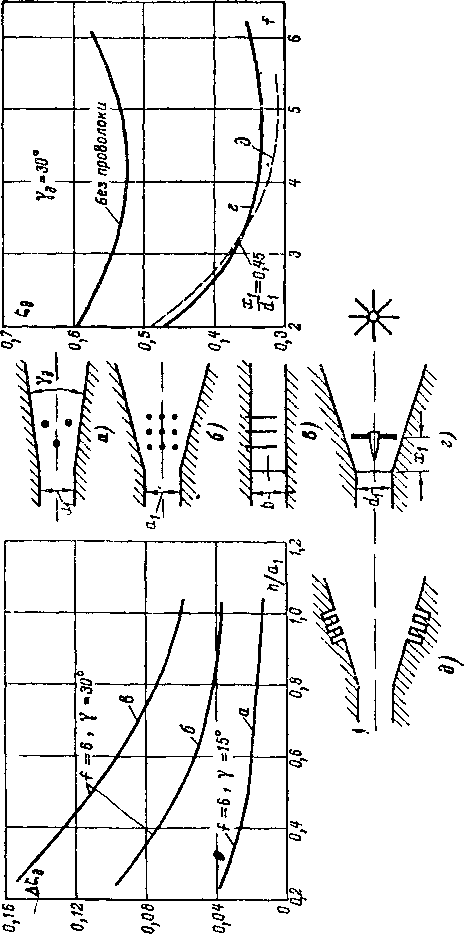
Рис. 7-12. Влияние местных сопротивлений на потери в плоских диффузорах при небольших скоростях.
Отвод газа из турбомашины осуществляется по оси вращения либо по конструктивным условиям под прямым углом к ней. Частичное преобразование кинетической энергии выхЛопа в потенциальную позволяет повысить к. п. д. турбомашины. Такое преобразование осу-
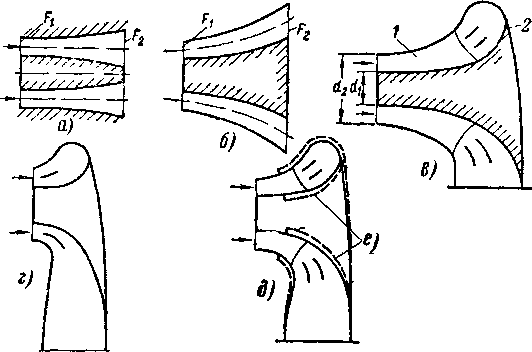
Рнс. 7-13 Рациональные схемы выхлопных патрубков турбомашин.
ществимо в диффузорных выхлопных патрубках, различные схемы которых приведены на рис. 7-13.
Первые две схемы (а и б) показывают наиболее простые криволинейные кольцевые диффузоры F2>FX с осевым или диагональным потоком газа.
Три других патрубка должны обеспечить поворот потока на угол 90° к оси вращения В схеме патрубка на рис. 7-13,в применен развитый кольцевой диффузор./ с диагональным или осевым направлением потока. В таком диффузоре в основном и происходит преобразование кинетической энергии в потенциальную; поворот потока на угол порядка 90° осуществляется уже при малых скоростях в улитке 2. Выходная часть патрубка (радиальный диффузор) имеет относительно малую длину.
Другая схема (рис. 7-13,г) обеспечивает восстановление давления после поворота в радиальном диффузоре. В таком патрубке поворот желательно осуществлять в конфузорном потоке или в 'Крайнем случае при постоянной скорости.
Как видно из сравнения схем виг, первая схема имеет значительно большие осевые размеры, а вторая — радиальные
Третья схема (рис. 7-13,д) является комбинированной. Здесь выполняются относительно короткие осевой (или диагональный) и радиальный диффузоры. Следовательно, восстановление давления в таком патрубке осуществляется частично до поворота и частично после него. Такая же задача решается в схеме е, выполненной со ступенчатым диагональным диффузором Эффективность каждой схемы существенно зависит о г организации поворота потока в улитке (при переходе из осевого в радиальный диффузор) Эта задача решается соответствующим выбором рациональной системы кольцевых поворотных направляющих лопаток и ребер, устанавливаемых на повороте.
Как указывалось в § 5-15, в криволинейных каналах возникают вторичные движения жидкости, связанные с неравномерным распределением давлений на повороте.
В кольцевых криволинейных каналах структура вторичных течений а зависимости от отношений диаметров d2/dl может существенно отличаться от обычной для простого поворота При больших значениях d2ldx опыт подтверждает существование двух вихрей в поперечном сечснии кольцевого канала. Если отношение диаметров близко к единице, то в поперечном сечении возникают четыре вихря, расположенных в сечении кольцевого канала (два внутренних и два наружных).
Имея в виду сказанное выше о влиянии формы сечения канала, можно заключить, что неизбежное переформирование сечения потока в патрубках турбомашин должно быть организовано с учетом дополнительных потерь, которые могут при этом возникнуть
Конструктивно неизбежными в патрубках являются-ребра жесткости. Выбор рациональной схемы расположения ребер и их формы, обеспечивающей минимальные потери, составляет важную задачу при конструировании патрубков.
Особенно сложными конструктивно являются выхлопные патрубки мощных паровых турбин Большие объемные расходы .пара в конденсатор при конструктивно ограниченных осевых и радиальных размерах приводят к сложной схеме патрубка с большим количеством ребер жесткости Пример рационального размещения ребер на 'повороте показан на рис. 7-13 и 7-17
При исследовании выхлопных патрубков экспериментально определяются основные характеристики,
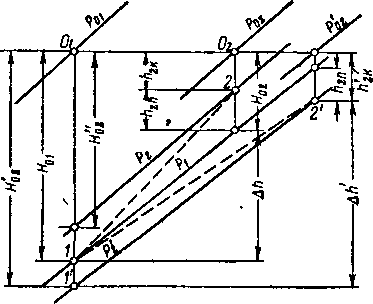
Рис 7 14 Процесс в выхлопном патрубке в тепловой диаграмме.
к числу которых относятся а) коэффициент, оценивающий энергетические потери патрубка; б) коэффициент восстановления давления, показывающий изменение статического давления; в) коэффициент неравномерности поля скоростей в выходном сечении.
Процесс в патрубке удобно рассмотреть в тепловой диаграмме (рис. 7-14). Обозначив через p0i и рог давления торможения на входе и на выходе из патрубка, Pi и р2 — статические давления в этих же сечениях, находим коэффициент потерь энергии по формуле (7-16).
Получив после коэффициентов потерь в выходном сечении патрубка, можно найти его среднее значение по уравнению энергии.
На рис. 7-14 рассмотрены два возможных случая: а) выхлопной патрубок турбомащины работает как диффузор (процесс 1—2); б) в выхлопном патрубке проис-
ХОДИТ СниЖенйе давления вследствие больших {потерь (процесс 1—2'). Здесь же можно указать величину кинетической энергии за .патрубком (h2k), изменение потенциальной энергии в патрубке (h2n) и потери (Ah или соответственно Ah').
В практике лабораторных исследований выхлопных патрубков находят применение и другие оценочные коэффициенты. Так, например, лаборатория турбин JIM3 использует для оценки патрубка величину
г
где Н0"2 —¦ изоэнтропический перепад, соответствующий расширению от давления торможения на входе рй1 до статического давления на выходе рг.
Связь между коэффициентом потерь энергии Сд и Сп
устанавливается следующими очевидными соотношениями (рис. 7-14):
Я0" « Яо1 - 1г2п = Я01 - (Я02 - h2k) = СДЯ01 + h2k, поэтому
Отсюда следует, что Сп включает кинетическую энергию на выходе из патрубка h2k = h2JH01. Нетрудно видеть, что если Сп>1 (Н^2^>Но1), то (выхлопной
патрубок не является диффузором); если Сп<[1» то /?2>Л-
Для несжимаемой жидкости коэффициент патрубка определяется по формуле
г _Рт Рг
а~ Pox — Pi '
С учетом сжимаемости Сп можно получить в таком виде:
Коэффициент tп позволяет вычислить потерю мощности й выхлопном патрубке:
![]()
(7-18)
i-де Ga — расход газа через выхлопной патрубок.
Вторая характеристика выхлопного патрубка — коэффициент восстановления — определяется по формуле
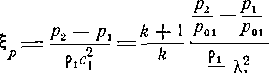
2
Ро 1
(7-19;
Из формулы (7-19) видно, что для определения величины 1р необходимо измерение статических давлений на входе а патрубок. Такой опыт оказывается трудоемким. Используя расходную характеристику Gn = f(p0i) и таблицу газодинамических функций, давление р\ можно получить расчетным .путем.
Тре1ья характеристика патрубка позволяет оценить неравномерность поля статических давлений и скоростей в выходном сечении.
Как указывалось, важным элементом выхлопного патрубка является криволинейный кольцевой диффузор. Опыты М. Хибша показали, что коэффициент потерь для такого диффузора зависит от следующих геометрических параметров (рис. 7-15,а):
р
отношения площадей сечений / = ; относительной вьг
г л
соты кольца на входе ajrml; относительной кривизны сред-
ней линии ; относительной длины средней линии —— К Гш1
и закона изменения площади f (х).
Примеры соответствующих зависимостей приведены на рис. 7-15,6. Кривые показывают, что оптимальное значение
-^г лежит в пределах 0,25—'0,4, причем с ростом f эта
величина увеличивается.
При расчете криволинейных диффузоров используют понятие эквивалентного конического диффузора, длина ко-toporo, а также площади Рг и Ps совпадают с Соответствующими геометрическими параметрами исходного диффузора. В соответствии с этим вводится понятие эквивалентного угла раствора.
Аналогичная характеристика может быть использована и для кольцевых криволинейных диффузоров.
Потери в кольцевом криволинейном диффузоре возрастают с увеличением f и с уменьшением ajrml.
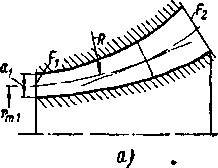
0,35
0,25
0,15
0,05
| ч | |||
|
/-4 | /ш 5 s | ||
|
*=2 | Vn1 т |
0.35
0,25
| Гт1 | ||||
|
Гт1 f | ||||
0,25
0,05
| J‘3,5 ^5^— | ||||
|
4" | 1L rml | |||
|
г | ||||
0,15
0,05
0,35
0,15
6)
г)
Рис 7-15. Схема (а) и коэффициенты потерь в криволинейном кольцевом диффузоре в зависимости от основных геометрических параметров (б, в и г).
Значительное влияние на потери оказывает форма диффузора в продольном разрезе. Вид функции f рс) определяет изменение давлений по диффузору, т. е. структуру пограничного слоя и 8** (х).
Выбор рациональной функции f (х) можно осуществить, например, путем оценки изменения 6” при различных эпюрах давления. При этом необходимо учитывать конструктивные особенности проектируемой машины.
Схемы часто применяемых кольцевых выхлопных патрубков приведены на рис. 7-16. Следует подчеркнуть, что потери в таких диффузорах, как правило, невелики, если указанные геометрические параметры близки к оптимальным. Вариант диффузора 4 (рис. 7-16) с максимальной кривизной образующих дает максимальные потери, а вариант диффузора 2 — минимальные.
Результаты исследования кольцевых диффузоров были положены в основу разработки выхлопного патрубка тур-
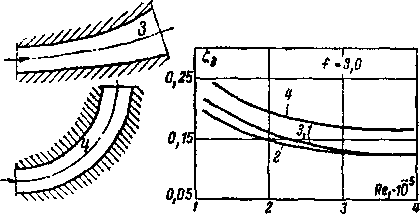
Рис 7-16 Схемы применяемых кольцевых выхлопных патрубков (а) и зависимость коэффициентов потерь от числа Ret(6).
т-
*77.
’77777777Т7'.
бины, схема которого приведена на рис. 7-17,а. Патрубок состоит из криволинейного кольцевого диффузора I и улитки 2 (выхлопной части), в которой происходит поворот потока на 90°. На входе в улитку при повороте поток раздваивается центральным ребром 3 и растекается по криволинейным каналам, образованным ребрами 4,4', 5,5 и т. д. Профилировка межреберных каналов осуществляется таким образом, чтобы потери от вторичных течений были минимальными. Это достигается выполнением канала вначале
[а а \
диффузорным, а затем конфузорным I — >> 1 и —¦ > 1 ).
\и 1 аг j
Представленные на рис. 7-17,6 результаты исследования такого патрубка показывают, что его эффективность существенно зависит от соотношения площадей кольцевого
р
диффузора и улитки f = ^ и f1 = FJF3. Наибольшие зна-
* 1
чения коэффициентов Сп получены для вариантов f — 2,5 и [1=1,46. С увеличением f до 3,32 и при соответствующем уменьшении f% до 1,1 Ся уменьшился до 0,75. Близкий к оптимальному вариант соответствовал отношениям сёчений f = 3,04 и f1=* 1,2.
Полученные при этом значения коэффициентов ?п и их изменение в зависимости от числа Rei отчетливо показывают, что при правильном выборе соотношения
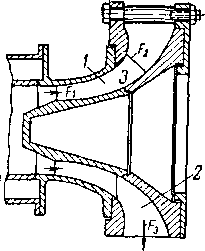
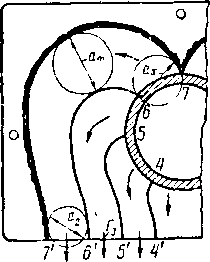
Ч)
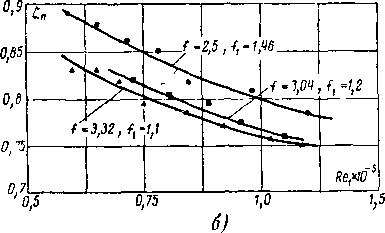
Рис. 7-17. Схема выхлопного патрубка турбины (а) и его характеристики (б).
проходных сечечий выхлопной патрубок менее резко реагирует на изменение этого режимного параметра.
Вариант комбинированного патрубка с коротким осевым и радиальным -диффузорами при условии правильного выбора соотношений проходных сечений дает результаты, близкие к тем, которые получены для первого варианта.
Влияние сжимаемости на характеристики выхлопного патрубка можно оценить по кривым на рис. 7-18. С ро-ctOim Mj отмечается возрастание потерь (?п увеличивается), особенно интенсивное при Mi>0,8. Характерно, что патрубки 'с развитым кольцевым диффузором менее Чувствительны к изменению Mj (кривые 1 и 2 на рис. 7-18). Патрубок без диффузора практически не реагирует на изменение Mi (кривая 4) и имеет ?п>1.
Таким образом, проведенные опыты показали, что введение осевого и радиального диффузоров в схему выхлопного патрубка позволяет существенно улучшить его характеристики и обеспечить частичное восстановление давления за турбомашиной.
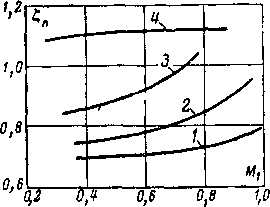
Рис. 7-18. Характеристики выхлопного патрубка с диффузором (1, 2 и 3) и без диффузора (4).
Правильным выбором формы и проходных сечений диффузоров и улитки, а также рациональным расположением ребер жесткости можно повысить эффективность патрубка.
Опыты показывают, что в некоторых случаях заметные преимущества имеет выхлопной патрубок с лопаточными решетками диффузорного типа, устанавливаемыми на повороте (рис. 7-13).
Практический интерес представляет вопрос о влиянии неравномерности (закрутки) потока на входе в патрубок. Соответствующие опыты показали, что отклонение от осевого входа в пределах ±15° не приводят к заметному изменению характеристик патрубка.
7-4. СВЕРХЗВУКОВЫЕ ДИФФУЗОРЫ
Из основного уравнения одномерного течения следует, что торможение сверхзвукового потока можно осуществить в трубе переменного сечения, входная часть которой выполнена суживающейся, а выходная — расширяющейся. В .первой части скорость уменьшается и достигает критического значения в минимальном сечении. Тогда в расширяющейся части продолжается процесс сжатия дозвукового потока.
Отсюда следует, что принципиально в качестве «идеального» диффузора можно использовать сверхзву-кбйоё СОпло С профилированными стёнкамй, предполагая течение в нем обращенным (рис. 7-19). Благодаря плавности профилированных стенок, в каждой точке которых поток совершает поворот на малый угол, во входной части диффузора должна возникнуть система слабых волн сжатия (характеристик). Проходя эту систему,

поток тормозится изоэнтропически. Система слабых волн сжатия при этом полностью совпадает с системой слабых волн разрежения (характеристик) в расширяющейся части сопла.
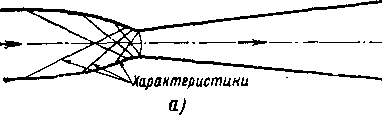
Скачон
А.
В горловине поток приобретает критическую скорость Я=1. В расширяющейся части диффузора скорости дозвуковые, уменьшающиеся в направлении потока.
В действительности, однако, такой диффузор осуществить не удается, так как течение в нем оказывается неустойчивым: малые возмущения потока на входе приводят к конечным возмущениям на выходе. Это объясняется тем, что при малом уменьшении числа М на входе в горловине не установится критическая скорость, в результате чего перед диффузором возникнет отошедшая волна. Фактически поле потока, поступающего в диффузор из сопла Лаваля, как правило, неравномерно и насыщенно скачками. Кроме того, вследствие возникновения потерь во входной части и образования пограничного слоя характер изменения проходных .сечений не будет соответствовать расчетному. В результате во входной части возникает система скачков.
Процесс движения газа в диффузоре в тепловой диаграмме строится известным способом (рис. 7-20). Точка 1 соответствует состоянию потока на входе в диффузор. Линия 1—2 условно изображает процесс сжатия газа в системе скачков в сверхзвуковой части диффузора. Соответствующее приращение энтропии As, характеризует в основном волновые потери во входной части диффузора. За скачками устанавливается давление P2s- ¦ ЕСЛИ P2s/P02<St, то после скачков поток еще сверхзвуковой и в суживающейся части диффузора продолжается сжатие газа.
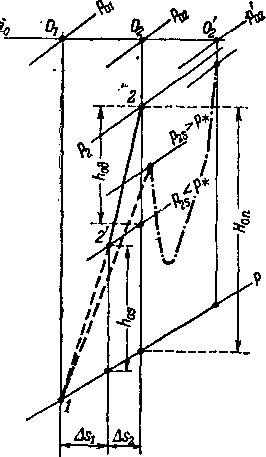
Если P2sIPo2>?*, ТО ПОТОК за скачками дозвуковой. Это означает, что в суживающейся части до минимального сечения поток будет ускоряться и давление его будет падать. Если в мини- рис. 7.20. Процесс изменения мальном сечении скорость состояния в сверхзвуковом диф-потока достигает критиче- фузоре в тепловой диаграмме, ского значения, то в расширяющейся части Х>1. В этом случае торможение потока будет происходить в системе скачков за узким сечением. Увеличение энтропии As2 обусловлено потерями в дозвуковой части диффузора.
Заметим, что полное .изменение потенциальной энергии в сверхзвуковом диффузоре #65 можно рассматривать как сумму изменения потенциальной энергии в системе скачков h0s и в дозвуковой части /г0д.
При небольших сверхзвуковых скоростях на входе (М!<1,5) можно применять обычные расширяющиеся дозвуковые диффузоры (рис. 7-19,6). В этом случае перед расширяющейся частью возникает прямой скачок уплотнения, в котором поток переходит к дозвуковым скоростям. В расширяющейся части продолжается сжатие дозвукового потока. Потери в таком диффузоре могут быть умеренными, так как при Mi <1,5 волновые потери в скачках невелики.
Гидравлический расчет сверхзвукового диффузора основан на уравнениях одномерного течения. С помощью уравнения энергии определяется энергетический к. п. д. диффузора по формулам (7-16) и (7-16а).
Сечения диффузора рассчитываются по уравнению неразрывности, которое (для суживающейся части) можно записать в виде:
/ I
где р и 2 — плотность и скорость в минимальном сечении диффузора.
После преобразования получим:
\/ (7-20)
F,д Мх V Рlpi <?, Pal V '
Если в узком сечении устанавливается критическая скорость Ml = 1, то
l!_. JLi/ р*р*__1 Ро“ (7-21)
JF,
F
\л~Мг У АР, ~П Poi [ }
ИЛИ
— 1 —т~т~\
(7-22)
k+ \ ?д1)
где Сд1 — коэффициент потерь в суживающейся части диффузора.
Формула (7-22) показывает, что с увеличением потерь в суживающейся части отношение сечений FJF увеличивается. Отсюда также следует, что при фиксированном значении FJF изменение параметров на входе приводит к изменению потерь в суживающейся части. Сравнивая
два режима течения при одинаковых начальных условиях с различными потерями, из выражения (7-22) можно получить формулу, показывающую, что минимальное сечение диффузора должно увеличиться пропорционально изменению давления торможения в сечении F :
или
= (7-23)
^.Д ^*Д Р°*
Здесь р —давление торможения в критическом сечении при данном режиме; p'Q — то же при другом режиме.
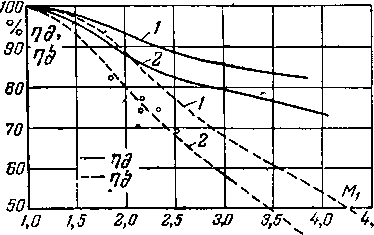
Рис. 7-21. Коэффициенты полезного действия сверхзвукового диффузора в зависимости от М /—с прямым скачком в горловине, 2 — с прямым скачком на входе.
Для расчета входной части диффузора необходимо знать величину коэффициента потерь С ,, а следовательно, структуру и положение скачков уплотнения на этом участке. В простейшем случае можно принять, что во входной части расположен только один прямой скачок. Величина Сд1 при этом зависит от положения прямого скачка. Если скачок возникнет в сечении Fx, потери энергии будут максимальными; если скачок расположится в узком сечении, потери значительно снизятся.
Для иллюстрации на рис. 7-21 приведены соответствующие к. п. д. диффузора 1]д и цд для двух предельных случаев (1 — с прямым скачком в горловине и 2 — с прямым скачком во входном сечении), а также опытные значения к. п. д. Сравнение показывает удовлетворительное совпадение расчетных и опытных величин.
Выходное сечение диффузора определяется по уравнению неразрывности. Коэффициент потерь в расширяющейся части диффузора ?д2 в первом приближении можно принять по данным испытаний дозвуковых диффузоров. Скоростью на выходе из диффузора задаются.
Полный коэффициент потерь в диффузоре можно найти по формуле (при X =1)
![]()
Давление торможения за диффузором определяется по уравнению
к
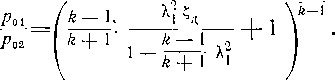
(7-24)
Волновые потери на входе можно уменьшить, вводя ступенчатое торможение потока во входном участке (гл 4).
Торможение в системе скачков осуществляется различными способами. Один из способов заключается в том, что стенки входного участка выполняют с изломами (рис. 7-22,а). Лучший результат можно получить с помощью профилированной иглы (рис. 7-22,6). В диффузорах реактивных двигателей применяется аналогичная система ступенчатого торможения (рис. 7-22,в).
Для уменьшения волновых потерь на входе используется также система отраженных скачков (рис. 7-22,г и (3).
Расчет сверхзвукового диффузора со ступенчатым торможением состоит из нескольких этапов. Вначале устанавливается система скачков на входе и определяются восстановление полного давления и коэффициент волновых ,потерь в системе скачков. Затем по заданному расходу рассчитывается критическое сечение;
дРог8одl]/Tov
Где е0д = —- — коэффициент вос^ановления полного дав* Poi ления в системе скачков.
Начальный участок расширяющейся части диффузора целесообразно выполнять коническим. Выходная часть диффузора рассчитывается по выбранному рациональному распределению давлений (§ 7-1).
Сначки
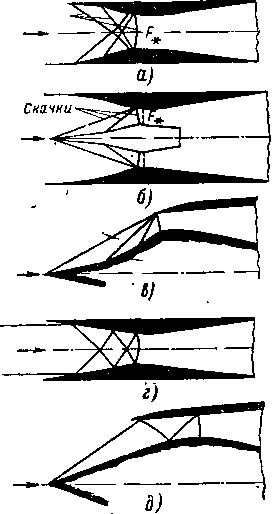
Рис 7-22 Схемы сверхзвуковых диффузоров со ступенчатым торможением потока в системе скачков уплотнения.
По результатам расчета пограничного слоя определяются потери энергии в дозвуковой части диффузора Сд2 и при выбранной площади выходного сечения F% скорость на выходе из диффузора
Рассмотрим некоторые особенности работы сверхзвукового диффузора при нерасчетных условиях. Режим в диффузоре может измениться в результате изменения параметров потока на входе (Х1, рх, р01 и, следовательно, расхода газа G) и давления на выходе р2.
Допустим вначале, что параметры потока на входе и расход через диффузор остаются неизменными, и проследим влияние меняющегося противодавления рг. Предположим, что в сечении скорость
равна критической,а давление среды значительно ниже расчетного (ра < /л). В этом случае расширяющаяся часть диффузора работает как сверхзвуковое сопло. На срезе выходной части в зависимости от ра возникают волны разрежения^ или косые скачки. По мере повышения ра система скачков перестраивается; при давле-*нии ра = р0к в выходном сечении располагается мостообразный скачок; при дальнейшем увеличении ра скачок перемещается внутрь расширяющейся части и движется к минимальному сечению. При некотором предельном противс-давлении ра — р2т скачок располагается в горловине диффузора (узкое сечение); при этом поток в расширяющейся части полностью дозвуковой. Такому режиму со скачком в горловине соответствует максимальная степень сжатия в диффузоре.
Соответствующие графики распределения давлений по диффузору при ра <Р2т показаны на рис. 7-23,а (кривые ОЛС, OADE и др.). Эта часть диаграммы давлений полностью соответствует диаграмме давлений в сопле для второй и третьей групп режимов.
Дальнейшее повышение противодавления приводит к изменению параметров потока (давления и плотности) в узком сечении и во входной части.
Рассмотрим теперь влияние изменения параметров потока на входе в диффузор. Допустим, что давление за диффузором поддерживается постоянным (ра<^р2т)- Скорость на
входе Хх увеличивается. При дозвуковых скоростях на входе (i[ <[1) в суживающейся части поток ускоряется и максимальная скорость достигается в узком сечении FПо мере увеличения Х{ растут расход газа и скорость в узком сечении X'.
При некотором значении X' < 1 скорость в сечении F, равна критической (ij = l). Дальнейшее увеличение расхода при неизменном статическом давлении перед диффузором становится невозможным. В соответствии с этим увеличение скорости Хх > Х{ повлечет за собой увеличение давления во входном сечении диффузора и во всех других сечениях суживающейся части; в результате при X'>1 перед диффузором возникнет скачок. С увеличением X' скачок приближается к диффузору и при некотором значении Хх располагается во входном сечении Ft. Если скачок на входе прямой, то в суживающейся части поток дозвуковой и ускоряющийся к минимальному сечению. Для того чтобы прямой скачок (или система скачков) проник в суживающуюся часть диффузора, необходимо дальнейшее увеличение скорости X' (X'^XJ.
Так как при движении скачка к горловине потери энергии уменьшаются, то в минимальном сечении может вновь воз-
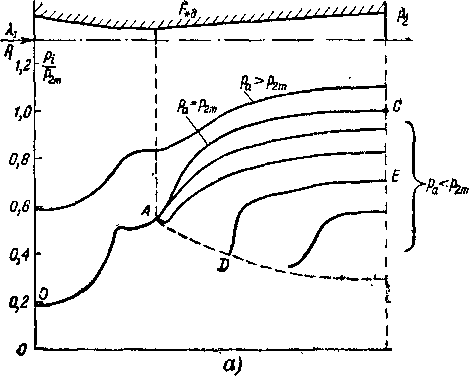
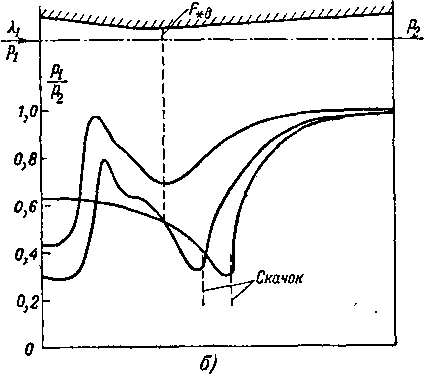
Рис. 7-23. Распределение давлений в сверхзвуковом диффузоре при различных режимах.
никнуть критическая скорость. В некоторых случаях при ра = р2т при переходе в расширяющуюся часть поток продолжает ускоряться и становится сверхзвуковым. Тогда и в расширяющейся части диффузора возникают скачки.
На Таких режимах потери в диффузоре резко возрастают
Рассмотренные режимы иллюстрируются графиками распределения давлений на рис. 7-23,6. При одновременном появлении скачков в суживающейся и расширяющейся частях диффузора кривые распределения давлений приобретают характерную петлеобразную форму.
Рассмотрение условий работы сверхзвукового диффузора при нерасчетных режимах показывает, что отношение сечений F, jFt должно изменяться при изменении параметров потока на входе или на выходе. В период пуска отношение FFi должно быть максимальным. В эксплуатации любое нарушение режима может быть частично компенсировано соответствующим изменением отношения F*JF1.
Проанализируем более подробно переменные режимы диффузора с меняющимся в процессе эксплуатации минимальным сечением. Если постепенно уменьшается минимальное сечение от F*a — F, до того значения, при котором скорость 1, то расход газа через диф
фузор будет-сохраняться неизменным (G = gf1p1c,). Однако если площадь горловины будет и далее уменьшаться, то расход через диффузор снизится. При этом вблизи узкого сечения возникнет скачок уплотнения, так как обуженная горловина представляет собой дополнительное сопротивление. Благодаря повышению энтропии в скачке давление в минимальном сечении падает, а скорость и температура сохраняются постоянными. Вследствие уменьшения плотности расход уменьшается в еще большей степени и скачок переместится против потока. При этом интенсивность скачка возрастет. Движение скачка в направлении против потока будет продолжаться до тех пар, пока он не выйдет за пределы входного сечения F{, скачок займет такое положение относительно Fv при котором часть газа будет выходить во внешний поток, минуя диффузор (рис. 7-24,а).
При дальнейшем уменьшении FtJl скачок будет перемещаться против потока, обеспечивая необходимое уменьшение расхода через диффузор; интенсивность скачка будет сохраняться практически неизменной.
Рассматривая теперь обратный процесс — увеличение F,A, можно заключить, что если F,A достигнет того значения, при котором впервые появился скачок, то скачок не исчезнет, так как уменьшенная плотность в горловине обусловливает частичное вытеснение массы газа во внешний поток. Следовательно, FtJk необходимо увеличить до таких пределов, чтобы компенсировать уменьшение плотности в горловине. Последующее увеличение F,A приведет к перемещению скачка внутрь диффузора и обеспечит постоянный максимальный расход через диффузор.
1 Рассматриваемый случай Показан штрихпунктирной линией на диаграмме i — s на рис. 7-20.
Изложенное показывает, что в диффузоре с переменным сечением горловины наблюдаются гистерезисные явления. Графики на рис. 7-24,6 дополнительно иллюстрируют эти явления. В диаграмме зависимости G/G0 от FtpjFi (G — расход через диффузор; G0 = gFtf^c^) можно указать точку А, соответствующую Ft = Ft (G=G0)- По мере умень-
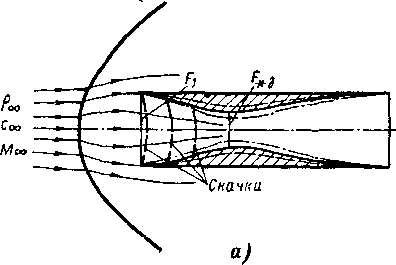
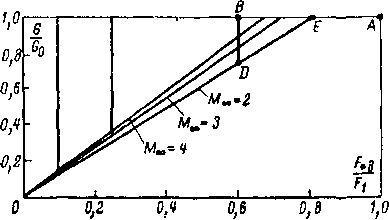
6}
Рис. 7-24. Схема диффузора с регулируемым минимальным сечением (а) и его расходная характеристика (б) при различных режимах.
шения F* расход сохраняется неизменным до точки В, которой соответствует М, = 1 в горловине; перед диффузором возникает скачок, и расход падает до значения в точке D. Дальнейшее уменьшение F д приводит к изменению расхода по линии DO.
При увеличении Р^а скачок перед диффузором сохраняется до того значения F^д, которое соответствует точке Е. К исходной точке А диффузор возвращается по линии ODEA. В результате образуется г.истерезионая петля EBDE и для того чтобы установить состояние потока в диффузоре при произвольном F д, необходимо знать, каким было направление изменения F .
Необходимо подчеркнуть, что режимы со скачками уплотнения перед диффузорам характеризуются резким возрастанием сопротивления Размер гистерезисной петли зависит от числа Mi, с возрастанием которого отрезок BD перемещается влево (рис. 7-24,6). Следует отметать, что область между кривыми 1 и 2 на рис. 7-24
характеризует неустойчивые режимы работы диффузора, при которых скачок может появиться и может исчезнуть.
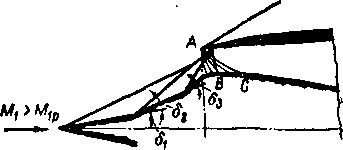
а.)
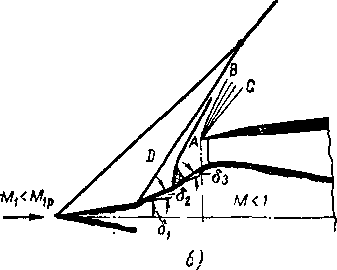
Рис. 7-25. Схемы спектров в диффузорах со ступенчатым торможением на входе при различных режимах.
Как указывалось, в практике применяются регулируемые сверхзвуковые диффузоры (рис. 7-23) со ступенчатым торможением на входе
В тех случаях, когда внутренний конус имеет возможщость осевых перемещений, можно не только улучшить условия пуска и эксплуатации сверхзвукового диффузора, но и обеспечить более высокий к. п. д. диффузора при расчетном и нерасчетном режимах.
Изменение скорости потока на входе» в такие диффузоры приводит к изменению углов наклона скачков' при Mi>Mij> углы скачков уменьшаются, а при Mi<MiP — увеличиваются.
В первом случае (рис. 7-25,си) взаимодействие скачков с противоположной стелкой будет происходить внутри горловины или в расширяющейся части. Возможно также иокривление скачков вблизи наружной поверхности диффузора. При обтекании кромки возникает волна разрежения АВС\ в результате поток на влоде в диффузор становится неравномерным.
Во втором случае, когда скачки не попадают на вход
ную кромку диффузора (рис. 7-25,6). По этой причине уменьшается расход газа через диффузор и возрастают волновые потери в скачках (гл 4). На входной кромке диффузора возникает волна разрежения ABC.
При уменьшении Mi скорость потока перед вторым поворотом (точка D) может стать меньше того значения, при котором еще
1,0
0,1)
0,6
0,4
о,г
| ?оЗ ч | ||||
| N | ||||
| V |
S. | |||
| \ |
||||
| и, |
1
Рис. 7-26. Коэффициенты восстановления давления торможения в сверхзвуковых диффузорах при переменных режимах. Цифры на пунктирных кривых указывают число скачков (по расчету). Опытные точки нанесены для четырехскачкового диффузора.
возможно существование прямолинейного скачка (угол 6з>6зт). В этом случае происходят искривление и отход скачка от угловой точки; потере на входе в диффузор заметно возрастают.
Характеристики регулируемого диффузора при переменных скоростях на 'входе представлены на рис. 7-26.
Положение замыкающего систему прямого скачка зависит от выходного сечения диффузора. Если выходное сечение становится больше расчетного, то прямой скачок в горловине не возникает — течение остается сверхзвуковым в расширяющейся части, где, кал указывалось выше, возникает система скачков, в которой поток переходит к дозвуковьим скоростям.
При уменьшении выходного сечения прямой скачок перемещается из горловины в направлении против потока. В обоих случаях возрастают волновые потери в диффузоре.
7 5. СТУПЕНЬ ЭЖЕКТОРА I
Газовые эжекторы находят широкое и разнообразное применение в технике. В таких а-ппаратах 'происходит
1 § 7-5 составлен при участии М. В. Цоливдвского; § 7-6 И 7-7 написавы совместно с А. В. Рсбожерым.
смешение газовых потоков (в простейшем и наиболее распространенном случае—двух). В результате смешения изменяются .параметры торможения и статические параметры смешиваемьих потоков. Основная особенность физического процесса в эжекторе заключается в том, что смешение потоков происходит при больших скоростях эжектирующего (активного) газа.
Принцип действия ступени эжектора можно уяснить из рассмотрения схемы, представленной на рис. 7-27.
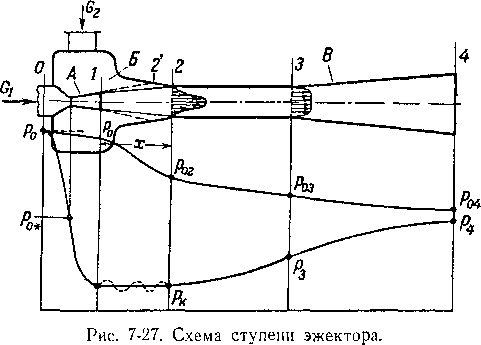
Основными элементами ступени являются сопло А, камера смешения Б и диффузор В 145. Эжектирующий газ под давлением подается к соплу А. Расширяясь в сопле, поток газа приобретает в сечении 1 сверхзвуковую скорость. В камере смешения Б струя активного газа взаимодействует с вжектируемой (.пассивной) средой и увлекает ее в диффузор, где и происходит сжатие образовавшейся смеси.
Опытное изучение механизма эжекции в камере смешения показывает, что наиболее существенное влияние на процесс смешения оказывают турбулентность потоков и волновая структура сверхзвуковой эжектирующей струи.
Изучение СпёКтроВ бсёсимметричной сверхзвуковой струи (рис. 6-28 и 6-29) позволяет установить, что по мере удаления от сопла на 'периферии струи образуется пограничный слой. В кольцевом пограничном слое скорости меняются от малых дозвуковых на периферии до сверхзвуковых на участке, примыкающем к ядру струи. Заметим, что в соответствии с волновым спектром струи статическое давление по оси ядра струи периодически меняется. По диаметру струи давления распределяются также неравномерно: в струе образуются поперечные градиентьи давления. В сечениях за скачками градиенты давления направлены к периферии струи, а в сечениях за волнами разрежения — к оси струи. В дозвуковом участке пограничного слоя статическое давление близко к давлению среды. На некотором расстоянии от сопла вся струя становится дозвуковой: в этой юбласти статическое давление распределяется по оси и по сечению практически равномерно.
Эти особенности поля осесимметричной сверхзвуковой затопленной струи позволяют заключить, что между внешней средой и струей происходит непрерывный обмен частицами. Поперечные перемещения частиц из пограничного слоя в ядро и из ядра в пограничный слой осуществляются с интенсивностью, переменной вдоль оси.
Вернемся к рассмотрению процесса в ступени эжектора (рис. 7-27). В сечении 2 смешанный поток с неравномерным профилем скоростей заполняет входную часть диффузора. На участке 2—3 в горловине диффузора происходит дальнейшее перемешивание потока'. На участке 1—2 процесс смешения можно приближенно считать изобарическим. На участке 2—3 смешение и выравнивание потока сопровождаются повышением среднего по сечению давления. В выходной части диффузора (участок 3—4) происходит дальнейшее повышение давления.
В литературе иногда рассматривается иная схема процесса смешения, когда расстояние между выходной кромкой сопла и входным сечением горловины диффузора х = 0. Такие эжекторы (компрессоры) называют эжекторами с цилиндрической камерой Смешения или с постоянной площадью смешения.
• Однако указанное деление не имеет особого смысла, так как рассмотренная схема (рис. 7-27) переходит в другую путем непрерывного уменьшения величины х до нуля.
Для определения параметров смешанного потока в выходном сечении горловиньи (сечение 3) воспользуемся уравнениями количества движения, сохранения энергии и неразрывности. В первом приближении будем считать, что поля давлений и скоростей в сечениях 1 я 3 равномерны; силовое воздействие стенки на поток отсутствует; сильи давления, действующие на поток от стенки горловины, не дают осевых составляющих; силами трения в первом приближении также можно пренебречь. Поэтому изменение количества движения между сечениями 1 я 3 равно разности импульсов сил давления в этих сечениях. Следовательно, уравнение количества движения для сечений 1—3 можно записать в виде:
![]()
(7-25)
где G — расход эжектирующего (активного) газа; си, рх — скорость и давление в выходном сечении сопла при изоэнтропическом истечении; ^
с2> — расход и скорость эжектируемого (пассивного)
газа;
с3, р3 — скорость и давление смешанного потока в выходном сечении горловины диффузора;
F, , —площади сечения горловины диффузора и вы
ходного сечения сопла.
В общем случае сумма количества движения и силы давления, т. е. импульс потока, выражается формулой Б. М. Киселева [(2-44) и (2-45)].
Подставив выражение (2-44) в уравнение (7-25), получим после несложных преобразований:
![]()
![]()
где х = G2jG1 — коэффициент эжекции; а»,, а,2 и а,3 — критические скорости активного, пассивного и смешанного потоков;
1и— безразмерная скорость на выходе из сопла при изоэнтропическом истечении.
' Расход активного газа можно выразить формулой Gi = ^PA„ где р,— плотность в критическом сечении сопла:
<7-27>
имея в виду, что а,,—
у/~^’^RT01, и вводя функцию ф
[формула (2-45)], представим уравнение (7-26) в
виде:
_ _!_
¦ил и 2k *i/т”\ [ fk + '\-xp*fF'B. л
= (1+х)/^;Ф(Л,), (7-28)
где Т03— температура торможения смешанного потока.
Отношения температур торможения Т02/Т01 и Т03/Т01можно выразить с помощью уравнения энергии:
^Voi ФЛа = (Gj -(~ G2) г03.
Отсюда, считая теплоемкости смешиваемых потоков одинаковыми, приходим к выражению
(7-29)
Заметим, что критические скорости ач и а»2, а», и а,3 потоков связаны очевидными соотношениями:
КУ+ф<’,1.+
fe + lV-iA IF<
= V(i+*)(!+«,)<!» (г,).
Fi
¦д
2 ) PAF
'с
гс
(7-30)
Уравнение (7-30) устанавливает связь между безразмерными газодинамическими параметрами pjp0, х, v1 и Х3 и геометрическими характеристиками эжектора Ft jFtc и FJF^.
Следует иметь в виду, что отношение также представ-
ляет собой функцию 1и. Скорость обычно мала, и в практических расчетах вторым членом уравнения можно пренебречь.
Анализ уравнения (7-30) показывает, что при заданных значениях х, Х2, pjp0 и скорость в выходном сечении горловины определяется неоднозначно: уравнению (7-30) удовлетворяют два значения Х3, связанные зависимостью
![]()
Физический смысл неоднозначности определения Д,3 очевиден, если учесть, что в прямом скачке уплотнения скорости перед скачком и за ним связаны таким же соотношением. Поскольку в скачке импульс, расход газа и температура торможения не изменяются, основное уравнение ступени эжектора (7-30) остается справедливым независимо от того, возникает ли или не возникает скачок в горловине. При достаточно длинной горловине, обеспечивающей выравнивание смешанного потока, обычно осуществляется дозвуковое решение уравнения (7-30). Переход к дозвуковому течению происходит при этом в системе скачков в горловине.
Уравнение (7-30) служит для определения основной геометрической характеристики ступени эжектора F*JF,c или, если эта величина известна, уравнение (7-30) может быть использовано для определения газодинамических параметров х и pj Ра или х и pjpo в условиях переменного режима. В последнем случае необходимо использовать еще одно уравнение — неразрывности, которые позволяет определить давление торможения в сечении 3.
Уравнение неразрывности Для выходного Сечения горло* вины представим в виде:
После деления на G1 находим:
' i ' F,c р„ ач
Так как
то
/1 I \ ^*д Р*з д*з
Замечая, что
_и_Лз 146 +х и ^__/т_. /* + *'ci
Р* /?0 ^2 Ро 'Л^1 2 V 1+х ’
окончательно получаем:
к-Ы1'<'+г-н'+™‘>- (7'3,)
Из уравнения (7-31) следует, что давление торможения в выходном сечении горловины зависит от скорости b3(q3), X, X, и F.JF.C.
Статическое давление /?4 за диффузором связано с давлением полного торможения /?04 и безразмерной скоростью Я4 на выходе из диффузора очевидным соотношением:
к
Е*. —
Ро*
Обычно скорость Xt невелика и в первом приближении можно считать, что рг = p0i. Если в расширяющейся части диффузора потери невелики, то давление торможения в сечениях 3 и 4 приближенно можно принять одинаковыми, т. е. ‘считать
Роз ^ Pov
Таким образом, предполагая, что скорость Я4 мала и потери в расширяющейся части отсутствуют, мы можем ¦определить давление за диффузором pi —роз По формуле (7-31). Если скорость Я4 не может рассматриваться как величина пренебрежимо малая, то р4 определяется по формуле (7-32).
Полученные в предположении простейшего одномерного характера процесса в эжекторе уравнения (7-30) и (7-31) оценивают только потери смешения, которые являются в рассматриваемой задаче основными. Однако наряду с потерями смешения необходимо учитывать и другие потери в отдельных элементах эжектора: потери в сопле, во входной части диффузора и в горловине', а также потери в расширяющейся части. Кроме того, процесс во входной части диффузора в действительности может отклоняться от изобарического процесса, принятого ,при выводе уравнения (7-30). Изменение давления в общем случае начинается не точно во входном сечении горловиньи 2, а выше или ниже по потоку в начальном участке диффузбра. Далее, основное уравнение количества движения необходимо дополнить членом, выражающим воздействие сил давления от стенки входного участка диффузора. Вместе с тем, даже при значительной длине горловины, следует учитывать неравномерность поля потока в сечении 3, которая существенно сказывается на эффективности диффузора.
Учет всех перечисленных факторов, характеризующих действительный процесс в ступени эжектора, осуществляется на основании следующих соображений.
Потери в сопле учитываются коэффициентом скорости фс. Действительная скорость истечения из сопла равна:
Коэффициент фс~ У1—?с определяется с помощью кривых, представленных на рис. 6-31.
Потери в расширяющейся части диффузора, учитываемые коэффициентом е0д, можно принимать по графику на рис. 7-4 в зависимости от скорости Х3 в выходном сечении горловины.
Силовое воздействие стенки входной части диффузора на поток учитывается введением в уравнение количества движения иМпульса ot стенок /ст. При Этом подсчитывается удельный импульс от стенок начального участка диффузора, равный:
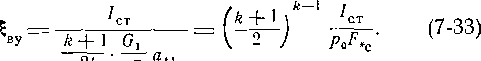
2k ' g ач
Абсолютное значение ?ау зависит от режима работы и геометрических параметров ступени, прежде всего от коэффициента эжекции х, отношения pjp0, угла конусности входной части диффузора, расстояния от выходной кромки сопла до начала горловины диффузора и отношения FtJF,c% Опытное исследование влияния неравномерности потока в выходном сечении горловины показывает, что и этот фактор должен быть учтен при расчете ступени.
При этом установлено, что неполное выравнивание потока в горловине приводит к перераспределению работы сжатия между горловиной и расширяющейся частью диффузора. С увеличением неравномерности в сечении 3 работа сжатия и потери в горловине уменьшаются, а в расширяющейся части растут. Детальный анализ показывает, что в основные уравнения эжектора должны быть введены коэффициенты, учитывающие влияние неравномерности.
С учетом всех потерь и неравномерности поля в сечении 3 уравнения ступени эжектора принимают вид:
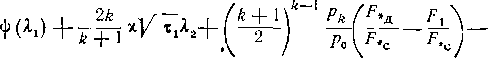
(7-34)
(7-35)
![]()
с it-T?cxu •
(7-36)
¦ИМ=?А.+;ггг.
ti(^s)—'Рн^з + ;
где
9Н — коэффициент, учитывающий неравномерность ноля в выходном сечении горловины; он мо»ет быть подсчитан, если известен профиль скорости.
Опытом установлено, что в предельном режиме (см. ниже) при определенной (оптимальной) длине горловины средняя скорость смешанного потока в выходном сечении горловины диффузора достигает критического значения,а профиль скоростей приближается к квадратичной параболе. Это позволяет для частного случая подсчитать этот коэффициент и принять <рн= 1,22-г-1,26. По опытным данным значения коэффициента <рн на переменных режимах колеблются в среднем в пределах <рн = 1,0 -г- 1,3. Меньшие значения <р соответствуют более равномерному полю скорйстей. Все коэффициенты: е0л~^, <рс, <рн и меняются при изменении режима работы ступени и профиля проточной части ступени (формы сопла и диффузора) и пока могут быть получены только опытным путем.
Расчет ступени для х — 0 производится по аналогичным уравнениям. Уравнение импульсов для этого случая имеет вид:
ф(А1)+*/т1ф(Я>)=ф1(Я,)/ (1-М(1+ -О- (7-37)
где
?с2^21 '
<рс2—коэффициент скорости сопла пассивного газа.
Уравнение (7-37) не содержит основного геометрического параметра ступени FtJF^. Связь между FtJFtc и коэффициентом эжекции по-прежнему выражается уравнением (7-35).
7-6. СТУПЕНЬ ЭЖЕКТОРА ПРИ ПЕРЕМЕННЫХ РЕЖИМАХ;
ПРЕДЕЛЬНЫЙ РЕЖИМ
В условиях эксплуатации ступень эжектора часто работает на режимах, отличающихся от расчетного. Причинами отклонений от расчетного режима могут быть изменения начальных параметров (следовательно, и расхода) эжекти-рующего газа, параметров и расхода эжектируемого газа и давления смешанного потока за диффузором.
Количество независимых параметров, определяющих режим ступени, и связь между этими параметрами устанавливаются уравнениями (7-34) и (7-35), которые при /%д/7%с = const являются основными уравнениями переменного режима ступени.
Согласно уравнениям (7-34) и (7-35) к числу определяющих безразмерных параметров режима ступени относятся:
а) коэффициент эжекции * =
б) степень сжатия (повышения давления) в ступени гд =
= PjP*>
в) располагаемый перепад давлений pjp0\
г) отношение температур торможения смешиваемых потоков т1 = ^.
* 01
При изменении режима ступени меняются условия работьи отдельных ее элементов: сопла, камеры смешения и диффузора. При этом происходит перераспределение потерь в указанных элементах ступени. В условиях эксплуатации возможно одновременное изменение всех четырех параметров. При этом все элементы ступени работают в нерасчетных условиях.
Проанализируем поведение ступени при отклонениях режима, вызванных изменением давления за диффузором р4 или изменением давления в камере смешения рк, предполагая, что давление эжектирующего газа перед соплом ро и отношение %\ остаются неизменными
При постоянном давлении 1перед соплом изменение давления в камере смешения рн или давления за ступенью р4 приводит к изменению количества эжектируе-мого газа Очевидно, что при этом изменяется и степень сжатия в диффузоре &K=pJph-
По уравнениям (7-34) и (7-35) между коэффициентом эжекции и и степенью сжатия ед существует определенная зависимос1ь, которую называют характеристикой ступени или диаграммой режимов. Вид этой характеристики определяется тем, какой из двух основных параметров (pk или pi) изменяется при изменении режима.
1. Работа ступени при постоянном давлении всасывания. Проследим характер изменения основных параметров режима при увеличении коэффициента эжекции от к — 0 (холостой ход) до максимального значения х=хпр147 при рь = const.
При к = 0 задвижка на линии всасывания закрыта полностью и давление за диффузором достигает максимального значения р^ = рш при данном рк- Для увеличения у. необходимо уменьшать противодавление р4, т. е.
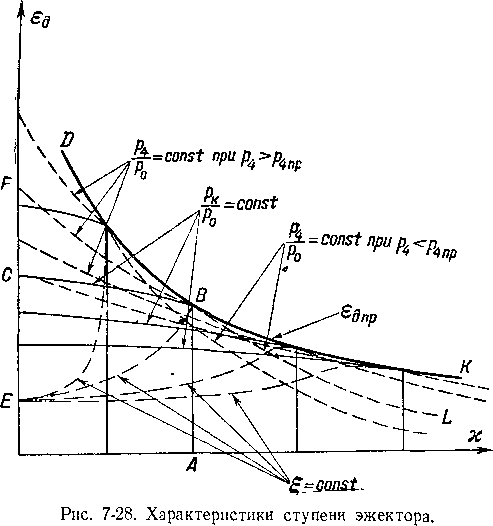
сопротивление проточной часги, сохраняя рк неизменным; при этом степень сжатия в ступени снижается. На участке СВ рассматриваемой характеристики (рис. 7-28) скорости в сечениях 2 и 3 (^ и А.з), показанных на рис. 7-27, увеличиваются (из условия неразрывности).
При некотором значении коэффициента эжекции х = хпр скорость в начальном участке горловины диффузора достигает максимального значения, а скорость в выходном сечении горловины близка к критической
(Л,з~ 1) - Отношение давлений Р3/Р04 в расширяющейся части диффузора также близко к критическому. Дальнейшее уменьшение противодавления не приводит к изменению коэффициента эжекции. На этом участке характеристика ступени бд=/(х) располагается параллельно оси ед (отрезок АВ). Это означает, что на рассматриваемом режиме производительность ступени не зависит от степени сжатия и коэффициент эжекции равен предельному (х=хпр).
Предельным называется максимальный для данного значения pufpo коэффициент эжекции; соответствующее противодавле-• ние называется предельным противодавлением. Этот режим, отвечающий на диаграмме точке В, называется предельным. Механизм наступления предельного режима представляется следующим. По мере увеличения х в некотором сечении входного участка диффузора средняя скорость потока становится сверхзвуковой. Пристеночный дозвуковой слой в этом сечении имеет минимальную поперечную протяженность и не способен передавать возмущение против потока. Поэтому снижение противодавления (р4<р4пр) не влияет на условия в камере смешения и коэффициент эжекции сохраняется постоянным. Он может быть увеличен только за счет повышения, плотности потока, т. е. давления в камере смешения рп. Поэтому на участке ВА характеристика ри — const параллельна оси ординат. Процесс в ступени эжектора на этом участке характеристики принципиально отличается, как видно из дальнейшего, от процесса на участке СВ; вслед за зоной максимальной скорости, расположенной в начальном участке горловины диффузора, смешанный поток тормозится в горловине, пересекая сложную систему скачков уплотнения, до дозвуковой скорости во входном сечении (если длина горловины соответствует оптимальной), после чего осуществляется дальнейшее (уже плавное) торможение в расширяющемся участке. Описанная «сартина иллюстрируется графиком распределения давлений вдоль контура диффузора на рис. 7-29. Если длина горловины меньше той, при которой обеспечивается торможение потока до дозвуковой скорости, то в расширяющейся части диффузора поток разгоняется, а затем в системе скачков, переходит в дозвуковой (расширяющаяся часть диффузора работает, как сопло Лаваля в нерасчетных условиях). По мере снижения pi система скачков смещается к выходному сечению диффузора.
Возвращаясь к кривым изменения давления оо контуру диффузора (рис. 7-29) на предельном (pilpia9=\) и запредельном (pdp4np<\) режимах, видим, что возмущения от снижения р± не передаются выше определен-
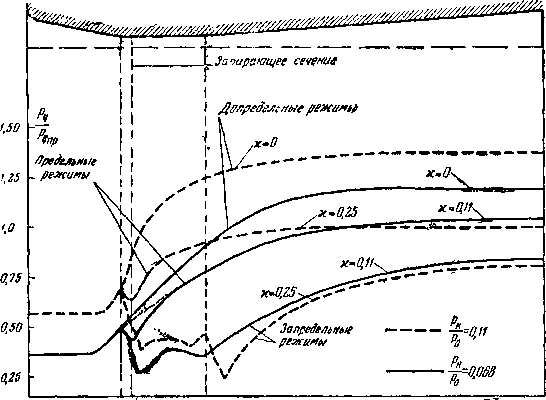
Рис 7-29. Распределение давлений по контуру диффузора при различных режимах работы ступени эжектора; 1*д =4; х — 6. Опыты МЭИ.
ного сечения, расположенного в начальном участке диффузора. Это сечение (точнее, зона, прилегающая к нему), как указывалось выше, является запирающим. На рис. 7-30 можно видеть, что при переходе от предельного режима к запредельному профиль скорости в начальном участке диффузора и коэффициент эжекции % практически не измегодатся. В то же время в выходном сечении горловины при неизменном коэффициенте эжекции средняя скорость увеличивается. Опыты показали, что на предельном режиме профиль скоростей в выходном сечении горловины приобретает форму, близкую к параболической, что характерно для течения в трубе, когда средняя скорость близка к критической (гл. 5).
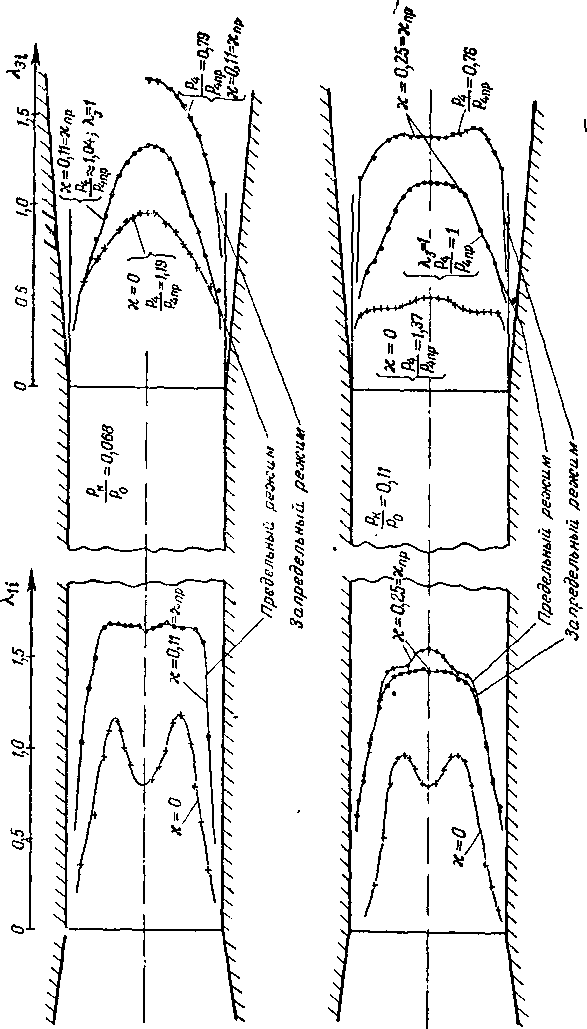
Рис. 7-30 Распределение безразмерных скоростей Л( во входном и выходном сечениях горловины длиной I, при различных режимах. Расстояние между соплом и диффузором х = 6. Опыты МЭИ.
Ма рис. 7-31 показан «универсальный профиль» относительных средних скоростей Х3Д0 (Л,о — скорость на оси диффузора), полученный в результате наложения скоростных полей в выходных сечениях горловин различных диффузоров на предельных режимах148. Как видно,
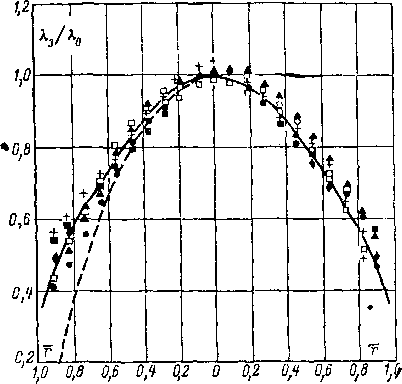
a Pf 0,107; х=0,25 'i • frOflN,
? рн= 0,042, к= 0,083 Ч’Х Ь“ ф р^ 0,042, х = 0 )
в р =0,037; л- 0,1*д=Ч, X =7,9 4 р- 0,067, х = 0,12, X =1,4
Рис. 7-31 Универсальный профиль скорости в выходном сечении горловины на режимах, близких к предельным.
все кривые практически совпадают и мало отличаются от квадратичной параболы независимо от относительной длины горловины ^,д = ^дЛ^д- Такая перестройка профиля скорости при околозвуковых скоростях объясняется влиянием вязкости в околозвуковом потоке, весьма чувствительном к любому внешнему воздействию.
дится по уравнениям (7-34) и (7-35). Для предельного режима (х = хпр и ед = едпр) после подстановки Я3=1 и <7з = 1 эти уравнения принимают вид (скорость Я2 ^ 0):
янное значение для всех точек данной кривой pkjp0= const.
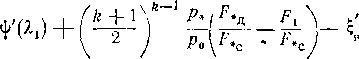
=(?а+1)/(1 + v) (1 + V*); (7-39)
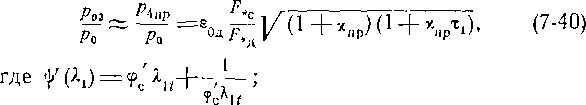
Ус ’ Ъ Ку— коэффициенты, характеризующие рассматриваемые предельные режимы, причем ср^ сохраняет посто-
По уравнению (7-39) при заданном значении pjp0 определяется предельный коэффициент эжекции хпр, а по формуле (7-40) — предельное противодавление р4пр. С помощью этих зависимостей могут быть построены кривые
![]()
Значения f3 (pjp0) Для холостого хода легко могут быть получены из выражений (7-34) и (7-35) после подстановки х = 0.
Характеристики е (х) при pk/p0 = const, как правило, весьма пологи и поэтому с достаточной для практики точностью могут быть построены по двум точкам: х = 0 и х = хпр. Отметим, что с уменьшением pjp0 диапазон регулируемой производительности ступени снижается [участок характеристики, соответствующий допредельным режимам, Pt^> PtПр ) сокращается (рис. 7-28)]. При этом предельный коэффициент эжекции уменьшается, а предельная степень сжатия возрастает. При х = 0 и ед = едпр участок характеристики pk/p0 = const, соединяющий точки ч = 0 и х = хпр, превращается в точку.
Линия DBK на диаграмме режимов ступени, Соответствующая предельным значениям ед = едпр и * = *пр для различных pjp0, называется предельной линией. Во всех точках этой линии при правильном выборе длины горловины скорость 1.
2. Характеристики ступени при постоянном давлении за эжектором = с on s t. Так же как
и на режимах pk = const, характеристики /?4 = const имеют две ветви: допредельную и запредельную, отвечающие соответственно условиям j04Ssj04np и р^< /?4пр. Проследим протекание процессов в эжекторе при изменении давления всасывания рк.
Пусть в точке F (рис. 7-28) Л>/»4пр; здесь гд<вдпр, рк >/7,пр. Чтобы увеличить коэффициент эжекции при заданном противодавлении, необходимо увеличить давление перед диффузором, т. е. в камере смешения рк. Степень сжатия ед при этом уменьшится, а .средняя скорость смешанного потока возрастет. Так будет продолжаться по мере увеличения х, пока средняя скорость потока в запирающем сечении не достигнет максимального значения Я,=1.
При дальнейшем возрастании % процесс в эжекторе меняется. Увеличение коэффициента эжекции по-прежнему достигается за счет повышения давления перед диффузором pk, но скорости в запирающем и выходном сечениях увеличиться не могут и производительность аппарата возрастает только за счет повышения плотности потока.
Статическое давление и давление полного торможения в сечении 3 р3 и р03 также увеличиваются. В расширяющейся части диффузора поток приобретает сверхзвуковые скорости. В результате здесь возникает скачок (или система скачков), положение которого зависит от противодавления р4. При снижении pt скачок смещается к выходному сечению диффузора.
Точки рассматриваемого участка характеристик pjp0— = const со скачками в расширяющейся части лежат на вертикальных участках соответствующих характеристик pjp0 = const. На режимах со скачками уплотнения потери в расширяющейся части диффузора возрастают вследствие уменьшения давления торможения в скачках и отрыва потока. Рассматриваемые режимы сопровождаются возрастанием pk, и степень сжатия ед продолжает снижаться.
Таким образом, характеристики ступени, соответствующие условию /?4/Ро const, изображаются линиями, форма которых показана пунктиром на рис. 7-28 (линия FBL), причем на участке FB противодавление ptt>Pinp>а на участке BL противодавление р4 < /?4пп.
Расчет характеристик pjp0 = const осуществляется с помощый уравнений (7-34) и (7-35), если известны гео-
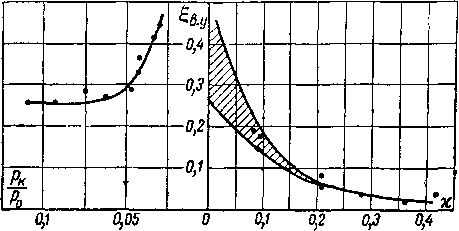
Рис 7-32 Изменение коэффициента входного участка диффузора в зависимости от рк1р1> и х.
метрические параметры эжектора (FtJFfc, FJF^) и два параметра режима (например, pjpk и у). В этом случае по
формуле (7-35) определяется величина х ^в предположе-л), а по уравнению (7-34) значение pjp0.
Рог
Ро ' Ро)
Графики распределения давлений на рис. 7-29 позволяют установить характер изменения удельного импульса ?ву в зависимости от у. и pjp0. На рис. 7-32 приведена такая зависимость для входной части с углом конусности 20°. Отсюда можно заключить, что при больших значениях х, отвечающих условиям заполнения свободной струей входного сечения горловины, величина ?ву близка к нулю. С уменьшением х возрастает давление за диффузором и во входном сечении горловины (на стенке входного участка). Повышение давления от pk до давления во входном сечении горловины (рассматриваются режимы pkjp0 = const) осуществляется во входном участке диффузора.
НИИ, что
При уменьшенных х во входном сечении горловины возникают обратные токи: излишек газа, вошедшего в активную струю, выбрасывается вблизи входного сечения горловины. Часть струек при этом притормаживается и затем ускоряется в направлении, обратном движению основного потока. Торможение и поворот отдельных струек не могут, очевидно, произойти без повышения давления в направлении движения основного потока. Отсюда вытекает, что независимо от формы профиля проточной части эжектора уменьшение х всегда приводит к интенсификации сжатия в начальном участке смешения.
Давление в камере рк влияет на величину ZBy лишь при существенных отклонениях режима от расчетного. Уменьшение давления приводит к возрастанию ?ву. Этот факт объясняется увеличением подсоса в струю и соответствующей интенсификацией обратных токов.
3. Режимы с переменным противодавлением при неизменном положении задвижки на линии всасывания149 (т. е. при одновременном изменении pk и /74). Очевидно, что при /?4</>4пр такая характе-
ристика ступени совпадает с характеристикой —= const.
Р °
При /74 > /74пр с увеличением pt коэффициент эжекции уменьшается, так как pk резко возрастает (кривая АВЕ на рис. 7-29). При этом одновременно падает и степень сжатия. Чем больше открыта задвижка на линии всасывания, тем менее интенсивным оказывается изменение степени сжатия. Все линии \ = const сходятся в точке х = 0 (точка Е), где давление pk равно давлению внешней среды 150.
Область, заключенную между предельной линией и осью х, будем называть диаграммой режимов ступени. Диаграмма режимов, полученная опытным путем, показана на рис. 7-33. Следует подчеркнуть, что расчет, произведенный с помощью опытных (переменных) коэффициентов fc , 9J, , удовлетворительно совпадает с дан
ными эксперимента.
До сих пор мы предполагали, что давление активйо?б 1аза перед соплом сохраняется постоянным. По опытным данным изменение ро оказывает весьма большое влияние на эффективность ступени, так как при этом меняются расход и располагаемая энергия активного газа.
В ступени заданных размеров расход активного газа «прямо пропорционален ро. Если давление за ступенью р4
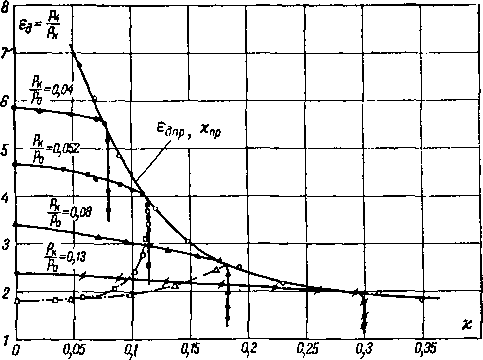
Рис. 7-33. Экспериментальная диаграмма режимов ступени эжектора.
и положение задвижки на линии всасывания сохраняются неизменными, то с ростом рг, давление в камере смешения рк уменьшается, а расход эжектируемого газа увеличивается. При достижении некоторой оптимальной величины! ро давление рк приобретает минимальное значение.
Дальнейшее увеличение ро приводит к возрастанию рк и уменьшению расхода эжектируемого газа.
Распределение давлений по диффузору позволяет объяснить влияние ро (рис. 7-34). При ро>р'о заметно резкое увеличение давления во входной части диффузора, которое вызывается появлением системы скачков. Поток в суживающейся части за скачками становится дозвуковым и ускоряется, приобретая критическую скорость в горловине. В расширяющейся части диффузора
продолжается ускорение потока, заканчивающееся системой скачков.
Предельное противодавление пропорционально начальному давлению [уравнение (7-39)]. При заданном открытии задвижки и /?4=const по мере увеличения ро эжектор от допредельного режима (/?4>Р4пр) приближается к предельному (р4=Р4пр). Поэтому степень сжа-
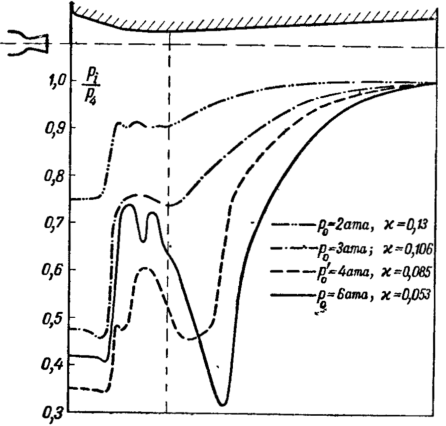
Рис. 7-34. Распределение давления по контуру диффузора при различных начальных давлениях активного газа,
тия возрастает, а рк уменьшается. При дальнейшем увеличении р0(р4пр>р4) рн увеличивается, т. е. эжектор 'переходит на запредельный режим.
Визуальные исследования потока в ступени эжектора отчетливо показывают, что, на всех режимах с завышенным начальным давлением (/?„> р') в расширяющейся части возникают скачки (рис. 7-35,а). Аналогичная картина, как мы видели, наблюдается и на режимах х=хпр при р4 < р4пр. Скачки приводят к отрыву вихреобразованию в расширяющей части диффузора (рис. 7-35,6).
В ступени с малым расстоянием между соплом и диффузором (л: = 0), кроме рассмотренного первого пред ель-
Рис. 7-35. Спектры потока в ступени эжектора.
а — скачок уплотнения в расширяющейся части диффузора; р0 =
=. 5,02 ата; р? = 0,81 ата\ б — отрыв потока в диффузоре (визуализация потока парами нашатыря, опыты МЭИ).
ного режима (критическая скорость достигается в выходном сечении горловины: 23 = 1), может возникнуть и второй предельный режим, соответствующий критической скорости пассивного газа в сечении 2 (Я2 = 1).
7-7. ВЫБОР ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ СТУПЕНИ
ЭЖЕКТОРА
При расчете ступени эжектора заданными, как правило, являются: параметры и расход активного газа (/?0, Т01, G,), параметры и расход пассивного газа (p0k, pk, Т02, *) и необходимая степень сжатия е . Тогда по уравнениям (7-34) и (7-35) определяется основной геометрический параметр ступени F JF с (при условии Я3=1). Как нетрудно заметить, увеличение расчетных коэффициентов эжекции приводит к росту параметра F,JF,c, возрастание расчетных
степеней сжатия — к уменьшению этогс) параметра.
Перед определением Ft /F,c необходимо рассчитать сопло. При заданных значениях рй, pk, <рс расчет сопла элементарно производится по таблицам газодинамических функций. При этом давление в выходном сечении на расчетном режиме следует выбирать несколько большим рут Для низконапорных эжекторов можно применять суживающиеся сопла.
Влияние всех основных геометрических параметров эжектора, не поддающихся расчету, можно оценить по опытным данным. Различные варианты ступени сопоставляют при наивыгоднейших условиях: при оптимальном расходе эжектирующего газа (оптимальном начальном давлении) и при оптимальном расстоянии между соплом и диффузором. Сравнение исследуемых вариантов целесообразно производить по предельным характеристикам ступени едпр =
= /(Хпр)-
^Характер зависимости давления в камере смешения от л; при постоянном давлении р4 показывает, что pjp0 меняется периодически при изменении x = x/d1 (dx—диаметр выходного сечения сопла), если поток на входе в диффузор сверхзвуковой (рис. 7-36). При больших значениях х давление р& непрерывно увеличивается с ростом л; (в этом случае скорость на входе в диффузор дозвуковая). Периодический характер зависимости рк от х при М,> 1 объясняется волновой структурой потока. Если при перемещении сопла относительно диффузора на стенку входной части попадают скачки, импульс от стенки уменьшается (снижается ? ) и давление в камере увеличивается. Наоборот, если на входе в диффузор расположены волны разрежения, давление в камере смешения возрастает. Изменение коэффициента эжекции при этом происходит по характеристике ступени, соответствующей постоянному давлению за диффузором (pjp0 = const).
Как показывают опыты, хопт соответствует такое положение сопла, когда смешанная струя приблизительно вписывается в горловину диффузора; однако при этом должно быть удовлетворено основное требование: поверхность смешения активной струи должна быть достаточной для присоединения заданного количества пассиЕДогд газа.
Можно приближенно рассчитать расстояние между соплом и горловиной диффузора151 по эмпирической формуле
5V * '
и затем для контроля определить диаметр струи на расстоянии л; от выходного сечения сопла ??стр =5= 1 -f- 0,35х.
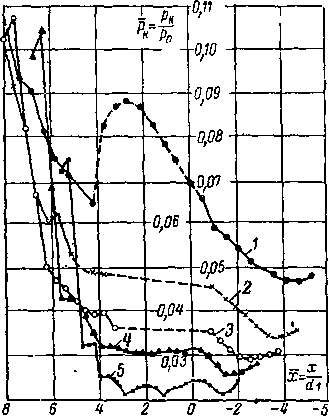
Рис 7-36. Зависимость давления в камере смешения Рь1Ро = Рк от Рас' стояния между соплом и диффузором х = xjdt.
5 / — 1, 2 — М,= 1,59; 3 — Mi— 1,94; 4—М,=
= 2,31; 5 —М,= 2,95.
При проектировании эжектора для заданного коэффициента эжекции диаметр струи должен несколько превышать (примерно на Ю°/0) диаметр горловины диффузора.
Представленные на рис. 7-37 кривые иллюстрируют влияние основного геометрического параметра F.JFtc_ (при F, — const). По мере увеличения /%с (или при прочих
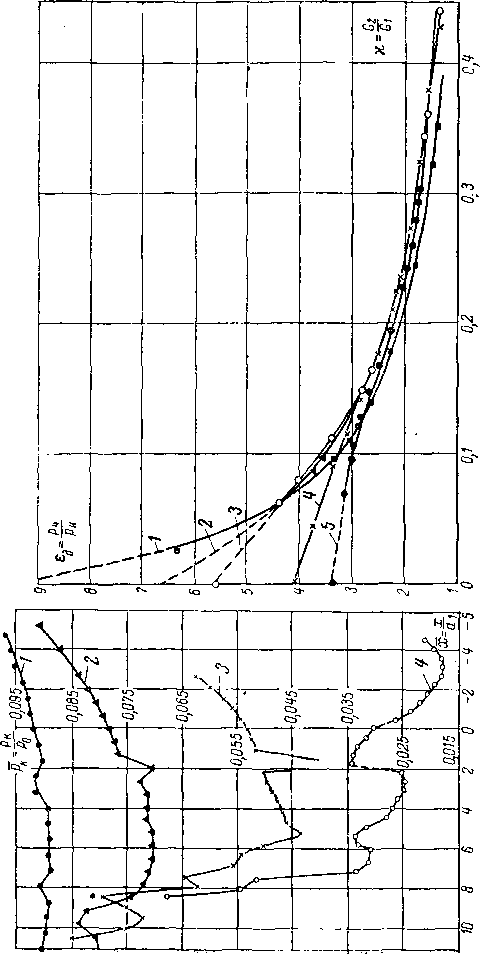
ft. [ft.
lN
с
s
>>
ftjft.
I
I *
к
9 *°
s?^
Л
4
<L>
I!
if I * ft, к
a,
03
с
p i ^ r* * ft, к
s
CQ
J* * * ft, I ft. i
s
равных условиях кривые рк(х) снижаются. Объяснение этого факта дает анализ уравнения неразрывности (7-40). Так как на предельном режиме при оптимальной длине горловины скорость Я3 Г, а следовательно, и <73~1, то для Xj = 1 имеем (полагая, что р03 = /?4):
А Пр = Л (! + *)•
1 *д
С увеличением расхода активного газа Glt т. е. отношения 7%с/7\д, растет и р (при р0 и % постоянных). Следовательно, при постоянном противодавлении рх разность — /?4пр будет уменьшаться, пока р4 не станет равным /?4 ". При дальнейшем увеличении отношения
Л с
-=— pi — р4 становится меньше нуля, т. е. аппарат пере-
I' г д
ходит на запредельные режимы, что должно сопровождаться уменьшением и ростом pk (/?4 = const).
Влияние отношения (или Мх) на величину давления
* I
в камере смешения можно проследить по рис. 7-37,6. С ростом числа М, минимальное давление в камере смешения уменьшается и при М1 = Ммакс = 2,95 достигает наименьшей величины. При этом давление в камере смешения и давление на срезе сопла сближаются, потери в струе уменьшаются.
Характерно, что с увеличением х влияние параметра Ft/Ffс резко снижается и при значениях * = 0,1 почти не обнаруживается; кривые ®д(*) на этом участке практически сливаются.
Опыты показали также, что оптимальные значения углов раствора сопла составляют ус = 12-=-24°.
На эффективность ступени эжектора большое влияние оказывает длина горловины. При всех расходах эжекти-руемого газа увеличение длины горловины от 1*л= 0 до /п=4 приводит к резкому повышению предельной степени сжатия (рис. 7-38). Дальнейшее удлинение горловины не вызывает заметного изменения предельной характеристики при заданном значении FtJFtc. Величина /,д опт меняется при изменении основного геометрического параметра сту-
эжекторы с изобарическим участком смешения, длину горловины следует выбирать в пределах 4—8 диаметров горловины. Для ступеней с /»Д0Пт увеличивается до
10—12.
Диффузоры эжекторов с короткой горловиной плохо работают на переменных режимах. В этом случае поток
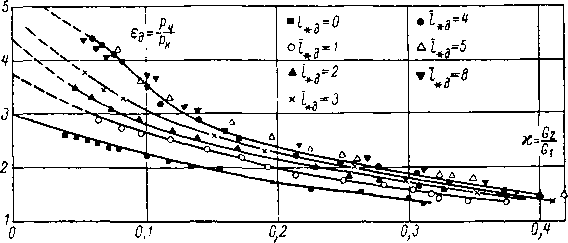
Рис. 7-38. Влияние длины горловины диффузора на предельную характеристику эжектора.
на входе в расширяющуюся часть может быть сверхзвуковым, что приводит к образованию скачков и резкому возрастанию потерь в расширяющейся части.
При взаимодействии струи со стенкой входного участка последняя воспринимает часть скоростного напора, которая тем больше, чем больше угол конусности входного участка. Поэтому желательно выполнение входного участка с небольшим, около 20°, углом сужения. Однако при этом длина входного участка увеличивается.
В тех случаях, когда эжектор стабильно работает на режимах, близких к расчетным, можно допускать угол у ( до 50°, обеспечивая плавное сочленение входного участка с горловиной.
При нормальной горловине (/ =4^#д) лучшая характеристика получена с коротким входным участком и углом Y , = 19°. При /,д = 0 хорошие результаты показал удлиненный входной участок.
Результаты исследования различных выходных участков диффузора показали, что лучшими оказались выходные участки с углами раствора 5 и 8°. Меньшие углы конус-
ности уд1 и ~(д2 целесообразно выбирать при малой длине горловины; в этом случае во входной и выходной частях диффузора происходит частичное выравнивание смешанного потока.
