Глава третья плоское движение газа при постоянной энтропии
ГЛАВА ТРЕТЬЯ
ПЛОСКОЕ ДВИЖЕНИЕ ГАЗА ПРИ ПОСТОЯННОЙ ЭНТРОПИИ
3-1. ПОТЕНЦИАЛЬНОЕ ДВИЖЕНИЕ ЖИДКОСТИ
Условие безвихревого движения можно получить из уравнении (1-6). Для пространственного безвихревого потока («1^,= % = тг = 0) из (1-6) следует:
dw dv
ду дг
ди_dw
(3-1)
dz дх
dv_ди
дх ду
Имея в виду механический смысл частных производных в уравнениях (1-6), можем заключить, что формулы (3-1) действительно выражают условие отсутствия вращательного движения жидйой частицы. С другой стороны, равенства (3-1) математически выражают тот факт, что существует некоторая функция координат Ф(х, у, г), частные производные от которой по координатам равны проекциям скорости на соответствующие оси координат, т. е.
![]()
![]()
(3-2)
![]()
)
Действительно, подстановка (3-2) в (3-1) приводит к тождествам.
Функция Ф(х, у, z) называется потенциалом скорости.
Понятие потенциала скорости в аэрогидромеханике тождественно понятию потенциала сил в механике твердого тела. Из механики известно, что производная потенциала сил по какому-либо направлению дает проекцию потенциальной силы, действующей в этом направлении. По аналогии интенсивность изменения потенциала скорости в направлении координатных осей определяет проекции скорости на соответствующие 'оси [формулы (3-2)].
Изложенное выше показывает, что потенциальное движение газа в изолированной системе является изоэнтро-пическим, т. е. если поток безвихревой и адиабатический, то изменение энтропии по любому направлению в потоке равно нулю и течение газа- описывается некоторой функцией координат Ф(х, у, г).
Ограничиваясь в этой главе рассмотрением только плоских потенциальных течений газа, мы можем получить уравнение потенциала скоростей с помощью уравнений Эйлера.
Для плоского установившегося потока в предположении X = Y = 0 уравнения (1-12) и (1-16) дают:
ди , ди 1 др
U --h- V -j— —---г— *
дх 1 ду рдх
![]()
дх ду р ду
(3-3)
)
Градиенты давления и можно выразить следующим образом:
![]()
![]()
(3-4)
Из третьего уравнения (3-3) после дифференцирования получаем:
![]()
После подстановки (3-4) в (3-3) будем иметь: dp р / ди , ди \
d7—~^~{ud7 + v^) ;
dp р / dv I dv \
Подставляя производные плотности в (3-5), получаем:
Имея в виду (3-2), перепишем (3-6) в виде:
и2 j d2<I> \ f л у2 \ д2Ф 2uv д2Ф _„ /о -7\
1 — — х _ о
^ydi/2 ~aF'dxdy
а2 ) дх2
Уравнение (3-7) является нелинейным дифференциальным уравнением потенциала скоростей в частных производных второго порядка.
Введение потенциала скорости позволило систему трех уравнений (3-3) свести к одному (3-7), уменьшить число неизвестных с шести до пяти и оЛавить в уравнении только кинематические параметры.
Если в исследуемом поле потока известен потенциал скорости Ф (х, у), то при заданных граничных условиях могут быть определены все параметры течения. Потенциал скорости позволяет определить скорости потока (и, v) по формулам (3-2). С помощью уравнения энергии совместно с уравнением изоэнтропического процесса легко определяются давление р, плотность р и температура газа Т.
Таким образом, при исследовании потенциальных движений газа основная задача сводится к определению потенциала скоростей Ф(х, у) для данного вида движения, т. е. к нахождению решения уравнения (3-7). Если потенциальная функция Ф(х, у) определена, то кинематическая часть задачи решена. Далее без особых затруднений решается и динамическая часть задачи. Однако уравнение (3-7) в общем виде не интегрируется.
Заметим, что потенциальная функция должна удовлетворять определенным начальным и граничным условиям данной конкретной задачи. В качестве кинематических начальных условий должно быть задано распределение параметров течения в определенной—начальной—области потока, а также должны быть известны условия на границе обтекаемого тела. При решении конкретных задач обтекания тел чаще всего задаются параметры течения невозмущенного потока на бесконечном удалении от тела (начальные условия) и условия непротекаемости — нормальная составляющая скорость у поверхности тела равна нулю (граничные условия).
Так, например, если плоский поток в бесконечности параллелен оси х, то потенциал скорости должен отвечать
следующим условиям:
![]()
![]()
При этом известными должны быть также и остальные параметры:
Роо’ ^оо’ ^00’
На границе обтекаемого тела физические условия обтекания диктуют распределение скоростей. Предполагая безотрывное обтекание, мы можем записать, что нормальная составляющая скорости на поверхности обтекаемого тела должна быть равна нулю и, следовательно,
![]()
Рассматривая идеальную жидкость (при отсутствии сил вязкости), мы должны допустить, что частицы жидкости скользят вдоль обтекаемой поверхности тела и, следовательно, касательные составляющие скорости
![]()
(при этом рассматривается подвижная система координат, расположенная таким образом, что направление оси х в каждой точке совпадает с направлением касательной к поверхности тела; ось у нормальна к поверхности тела и, следовательно, к линиям тока).
Более подробное рассмотрение уравнения (3-7), по которому определяется потенциальная функция Ф(х, у), однако, показывает, что оно обладает различными свойствами в зависимости от соотношения между составляющими скорости и и v и скоростью звука а. Действительно,
и V
допустим, что величины — и — весьма малы и ими
можно пренебречь, т. е. допустим, что скорость газового потока мала по сравнению со скоростью звука. Тогда из (3-7) следует:
<Э2Ф
*?- + -^ = 0- (3'8) Уравнение (3-8) характеризует потенциальное течение идеальной несжимаемой жидкости.
При больших дозвуковых скоростях, когда влиянием сжимаемости пренебречь нельзя, нелинейное дифференциальное уравнение (3-7) значительно упрощается в случае^ если поток можно считать слабо возмущенным0(§ 3-3).
Изучение установившихся плоских и некоторых осесимметричных течений газа можно также упростить введением другой функции координат — функции тока Ч?\ Обращаясь к третьему уравнению системы (3-3), видим, что оно удовлетворяется, если положить
дЧГ дФ'
рЫ==__ и tv = -dx-
или
Р ' ду ’
— _ _!_
р ’ дх
Для того чтобы функция тока и потенциал скорости имели одинаковую размерность, коэффициент при производных целесообразно привести к безразмерному виду. Тогда в случае потенциального потока уравнения для и и v запишутся в следующем виде:
— Ji. ^ = .
р ’ ду дх ’
(3-9)
— _ дФ
V р ' дх ду
В 'простейшем случае движения несжимаемой жидкости в уравнениях (3-9) величину относительной плотности
_i_
+ =1 + 4-М2 + ^М4+. .. (3-10)
можно положить равной единице.
При этом уравнения (3-9) принимают вид:
ду
дЧ!
(3-11)
н дх
Нетрудно заметить, что в случае безвихревого потока [условия (3-1)] функция ’F(i удовлетворяет уравнению
д2Фн д2Фн дх2 ду2
Если во всей области течения газа скорости изменяются незначительно и можно принять = const, то переход к уравнениям (3-11) достигается подстановкой 11гн = =-^- W. При такой подстановке скорость газа просто равна скорости несжимаемости жидкости: и = ии; v = vH.
Таким образом, указанные простейшие случаи перехода от дозвуковых течений газа к течениям несжимаемой жидкости являются по существу просто пренебрежением влиянием сжимаемости. Возможности такого пренебрежения, обусловленные зависимостью плотности от числа М, являются весьма ограниченными. В самом деле, если потребовать, чтобы величина отличалась от единицы не более
чем на 2°/0, то в соответствии с (3-10) число М должно быть не больше 0,20.
Физическое значение функции тока ’F выясняется при определении расхода газа через элементарный незамкнутый контур в плоском потоке. Можно показать, что функция тока численно равна объемному расходу газа через такой элементарный контур. Отсюда следует, что функция тока сохраняет постоянное значение вдоль линий тока плоского течения.
Действительно, проведем в плоскости потока некоторый контур LLl (рис. 3-1) и подсчитаем секундный объемный
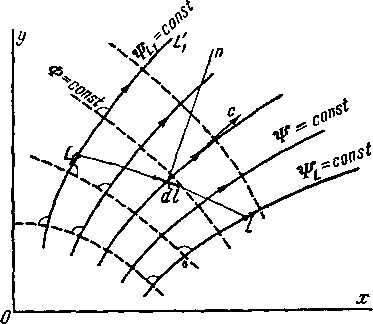
Рис. 3-1. К выводу условия безвихревого движения.
расход V через этот контур. В соответствии с обозначениями на рис. 3-1 получим94:
hx Ls L1
V = \сп^ = J [иcos(x, n)-j-&cos (y, n)]dl = \^{udy — vdx),
так как и
Но
тогда
udl cos (х, п) = udy vdl cos (у, n) = vdx. udy - vdx -- dxV;
V = f«'f=j:(" dy + ^dx'r4!L-VL.
Область потока, ограниченная линиями тока 4^ = const и = const, является трубкой тока. Следовательно, разность значений функции тока ^ ^ равна объемному
расходу жидкости через сечение трубки тока, ограниченной линиями тока, прохо-Реэулыпирующий дящими через точки L и Lt.
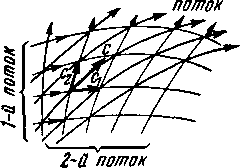
Рис. 3-2. Сложение плоских поступательных потоков.
Из уравнений (3-11) следует, что для несжимаемой
(3-12)
|
жидкости | |
|
дфн | . |
| дх | ду ’ |
| дФн |
д*„ |
| ду |
дх |
Придавая функции Ф различные постоянные значения, мы получим семейство изопотенциальных линий. Пользуясь условиями (3-12), можно показать, что линии тока (линии 'FH = const) и изопотенциальные линии (линии Фн = const) взаимно ортогональны, т. е. пересекаются под прямым углом (рис. 3-1).
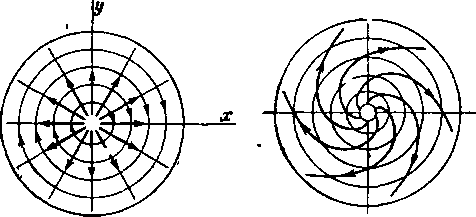
Рис. 3-3 ЧВихреисточник (вихресток).
Уравнение потенциала скоростей плоского потока несжимаемой жидкости (3-8) позволяет развить широко применяемый метод наложения потенциальных потоков. Из теории дифференциальных уравнений эллиптического типа известно, что если функции Фн|, Фн2, ... Фнл являются решениями такого уравнения, то и сумма Фн = Фн1 + -j-Ф -|-... -f-Ф является также решением этого уравнения. Отсюда следует, что, складывая потенциалы скорости Ф и функции тока Ч' простейших потоков, можно получить характеристики более сложного движения. При этом потенциалы скоростей и функции тока складываются алгебраически, а векторы скоростей — геометрически.
Метод наложения потенциальных потоков при некоторых условиях может быто использован также для построения сложных течений сжимаемой жидкости.
На рис. 3-2 приведен простейший случай сложения двух плоских поступательных потоков, понятный без пояснений.
Другой пример сложения потенциальных потоков показан на рис. 3-3. Сложение плоского источника (стока) и циркуляционного течения дает более сложное движение, называемое вихреисточником (вихрестоком), линии тока которого имеют форму спиралей.
4
3-2. КОЭФФИЦИЕНТЫ ДАВЛЕНИЯ. КРИТИЧЕСКОЕ ЧИСЛО М
Остановимся на некоторых простых понятиях, имеющих существенное значение при рассмотрении конкретных теоретических и экспериментальных задач газовой динамики и используемых нами в дальнейшем.
Поместим в газовой поток дозвуковой скорости некоторый криволинейный профиль и рассмотрим изменение параметров элементарной струйки, охватывающей такой профиль (рис. 3-4).
Создаваемые профилем возмущения потока при дозвуковых скоростях будут распространяться во всех направлениях, в том числе и против течения. Под влиянием этих возмущений элементарные струйки, движущиеся к профилю, будут деформироваться. У носика профиля центральная струйка расширяется; скорость течения при этом падает и в точке разветвления А обращается в нуль. В этой точке параметры будут равны параметрам полного торможения потока. На передней части профиля сечение струйки уменьшается, вследствие чего скорость увеличивается, а давление падает. На верхней и нижней поверхностях профиля продолжается поджатие струйки с соответствующим нарастанием скорости. В некоторой точке сечение струйки минимально. В этом месте скорость будет максимальной. Далее, на задних поверхностях профиля струйка вновь расширяется, скорость ее падает, а давление растет.
Таким образом, в результате деформации струек, характер которой определяется формой обтекаемого тела, вдоль поверхности профиля давление меняется. Распределение давлений обусловливает возникновение аэродинами-
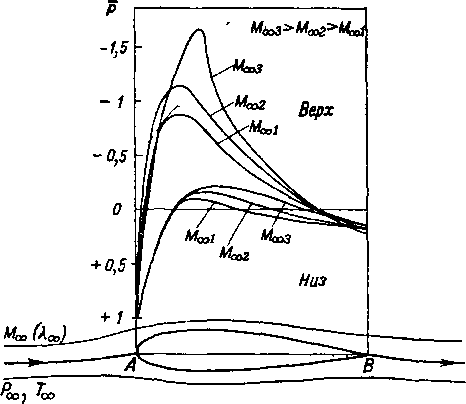
Рис. 3-4 Распределение коэффициентов давления по профилю.
ческих сил, действующих на профиль: подъемной силы, вызванной разностью давлений на верхней и нижней поверхностях профиля, и силы лобового сопротивления, вызванной разностью давлений на переднюю и заднюю части профиля и силами трения95.
Распределение давлений вдоль обтекаемой поверхности характеризуется безразмерной величиной — коэффициентом давления, который определяется как отношение разности давлений в данной точке на поверхности и статического в бесконечности к скоростному напору невозмущенного потока:
Р =
![]()
(3-13)
2
Скоростной напор можно выразить через безразмерную скорость Мм или А , воспользовавшись формулами (2-21) и (2-55).
• Тогда
Р=-
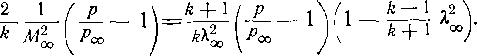
(3-14)
В некоторых случаях распределение давлений вдоль
поверхности характеризуется безразмерным давлением р, которое представляет собой отношение давления в данной точке ? давлению торможения невозмущенного потока:
![]()
Очевидно, что связь между коэффициентом давления р и относительным давлением р выражается формулой
![]()
(3-15)
![]()
k
![]()
•)
При малых скоростях набегающего потока более удобно для подсчета коэффициента давления пользоваться формулой (3-13).
На рис. 3-4 показано примерное распределение р вдоль поверхности профиля. До тех пор, пока скорость с^ значительно меньше скорости звука, характер деформации струек, а вместе с тем и картина распределения коэффициентов давления по профилю при изменении скорости невозмущенного потока сохраняются практически неизменными. Однако по мере увеличения влияние сжимаемости сказывается все более ощутймо; распределение р по профилю начинает меняться особенно сильно
там, где местные скорости в струйке (на поверхности профиля) велики. В минимальном сечении струйки скорость наибольшая. Найдем зависимость между безразмерной скоростью и скоростью в некоторой точке на профи
ле М.г.
С этой целью воспользуемся формулой (3-14), заменив в ней отношение давлений через соответствующие числа М:
k к—1
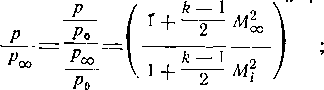
получим
k ft—1
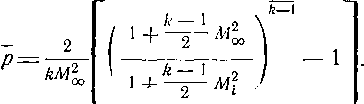
При некотором значении М„=М, в минимальном се-
О .
(3-16)
чении трубки тока устанавливается критическая скорость
М.= 1. Соответствующая величина коэффициента давления будет:
2
к
ft—!
ft ft—1
![]()
Величина М, называется критическим числом М набегающего потока; оно определяет то значение безразмерной скорости набегающего потока, при котором максимальная местная скорость на контуре тела становится равной местной скорости звука. Из определения критического числа М, следует, что эта величина разграничивает дозвуковые режимы обтекания тела на две группы. Первая группа докритических режимов (М^^М.) характеризуется тем, что во всех точках поля потока местные скорости дозвуковые (М;<1). Ко второй группе (М^^М.) относятся режимы обтекания с местными сверхзвуковыми скоростями.
При исследовании плоских движений сжимаемой жидкости, относящихся как к первой, так и в особенности ко второй группе режимов, необходимо учитывать влияние сжимаемости. Эта задача решена в работах ряда советских ученых. Еще в 1902 г. С. А. Чаплыгин в своей работе ,0 газовых струях* опубликовал метод учета сжимаемости для плоского потока. Эта работа приобрела особенно большое значение в настоящее время и явилась отправной для большинства современных исследований го определению влияния сжимаемости при обтекании тел потоком газа. Советские ученые С. А. Христианович, Л. И. Седов и др., плодотворно развивая идеи С. А. Чаплыгина, разработали надежные методы учета влияния сжимаемости. Эти методы находят широкое распространение и при решении задач, связанных с течением газа в проточной части турбомашин.
Наряду с относительно сложными методами учета влияния сжимаемости рядом авторов предложены приближенные методы, позволяющие ценой тех или иных допущений упростить задачу и путем сравнительно простых вычислений оценить влияние сжимаемости на обтекание тела. К числу таких методов относятся методы Л. Пран-дтля, С. Г. Нужина, Г. Ф. Бураго, А. Н. Шерсткка и др.
3-3. УЧЕТ ВЛИЯНИЯ СЖИМАЕМОСТИ ПО МЕТОДУ МАЛЫХ ВОЗМУЩЕНИЙ
Рассматриваемый ниже простейший метод оценки рлия-ния сжимаемости в плоском дозвуковом течении применим в тех случаях, когда возмущение потока можно считать слабым.
Выберем систему координатных осей так, чтобы ось х была направлена по скорости невозмущенного потока, а ось у — нормально к скорости.
Обозначив через с' и соответственно и' и х/ добавочные скорости, вызванные , тем или иным возмущением потска (так, например, влиянием обтекаемого тела), представим скорость в некоторой точке возмущенного течения в таком виде:
с=соо-)-с', или u — u’; v = vf.
При этом мы считаем, что а =0, так как поток на бесконечности параллелен оси х(со;) = и^). Полагая далее, что и' и у' являются малыми величинами порядка Д, приходим к заключению, что производные
ди ди'. ди ди'. dv . dv
дх дх ’ dy ду ’ дх ’ di/
имеют тот же порядок Д. Оценив члены, входящие в уравнение (3-6), найдем:
Т2 и-V Т д ¦
аоо
где Д и Д2-—малые величины, имеющие порядок Д или Д2.
Оценка членов, входящих в уравнение (3-6), позволяет упростить это уравнение, если пренебречь членами,
порядок малости которых выше Д. После указанных упрощений получим:
или для потенциального течения
= (3-19)
Таким образом, излагаемый метод, предложенный
JI. Прандтлем, основывается на предположении, что отклонение скорости возмущенного течения от скорости невозмущенного потока соа = иао настолько мало, что степенями указанного отклонения выше первой можно пренебречь. Уравнение для потенциала скорости (3-19) в отличие от (3-7) является линейным дифференциальным уравнением, поэтому метод малых возмущений вызывается также методом линеаризации. Рассматриваемый метод может дать удовлетворительные результаты при расчете обтекания тонких слабо изогнутых профилей, расположенных под небольшими углами к направлению скорости невозмущенного течения, а также при исследовании потока в каналах с малой кривизной ограничивающих стенок. Отметим, что вблизи точек разветвления потока (критические точки на поверхности обтекаемого тела) основное допущение метода не оправдывается, так как в этих областях поток тормозится и величина изменения скорости соизмерима со скоростью на бесконечности.
Уравнение (3-19) при дозвуковых скоростях можно привести к уравнению (3-8), определяющему потенциал скорости потока несжимаемой жидкости. Действительно, сравним рассматриваемый дозвуковой поток газа с потоком несжимаемой жидкости, полагая, что скорость и плотность обоих потоков на бесконечности будут одинаковыми. Допустим, что потенциалы скоростей сравниваемых потоков связаны соотношением
Ф = оФн. (3-20)
Обозначим координаты точек потока несжимаемой
жидкости хн и уи. Предположим далее, что между координатами х, у и хн, ун существует зависимость следую
щего вида:
yJ^ = ^XJL.
У X
Для упрощения мояно принять x — xtt\ тогда
УН = Ц. (3-21)
Подставим теперь соотношения (3-20) и (3-21) в уравнение (3-19):
„ дгФ д2Ф
<1-"“,sf’+9’^f3=0'
Отсюда следует, что если принять
-=0=|/l -Ml, (3-22)
yJL
У
то уравнение (3-19) преобразуется к виду: д2Ф дф
-г^+т^ = 0- (3-8а)
дхн дуи
Уравнение (3-8а) в новых переменных совпадает с уравнением (3-8). Используя полученные соотношения, нетрудно найти связь между параметрами двух сравниваемых потоков.
Рассмотрим обтекание одного и того же тела потоком несжимаемой жидкости и потоком газа. Обозначим через а и а{ углы наклона малых отрезков линий тока (рис. 3-5). Имея в виду, что в соответствии с основным допущением метода эти углы малы, найдем:
, dy , dyн
(3-23)
В идеальной жидкости одна из линий тока совпадает с контуром тела. На граничной линии тока должно выполняться условие
tg а = tg ан,
или согласно (3-23)
dy _dyH
dx dx
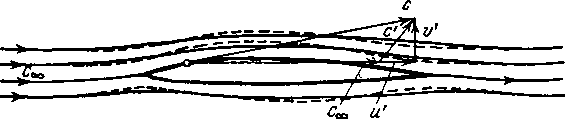
Рис 3-5 Линии тока при обтекании профлля потоком газа (пунктир) и несжимаемой жидкостью.
Учитывая, что скорости на бесконечности одинаковы, находим, что указанное условие соблюдается, если v = vh дф_дФи ду ~дуа
или — — ; на основании соотношений (3-20) и (3-22)
устанавливаем, что в рассматриваемом случае о&=1, или
Отношение продольных составляющих скорости в двух сравниваемых потоках равно:
1
и _дф дх _ _
(3-24)
' дФн — 3 — Y\ -М2
Для сравнения распределения давлений достаточно сопоставить градиенты давления в обоих потоках, так как ранее принято было, что х = хн и, следовательно, отношение конечных разностей давлении равно отношению градиентов
dp dx__Ар
dx dpH Д рн
На основании уравнения импульсов (2-1) градиенты давления в сжимаемой и несжимаемой жидкости будут:
— — dJL — _ *±-
dx ^нСн ах dx РС ах ’
тогда
Ар_ рс dc
или с учетом формулы (3-14)
Р с dc Ссс + с' d (см + с')
Рн сн dcH Cqo + с'и d (Cqo + ^
где с', с'н — как и ранее, добавочные скорости (малые величины), вызванные возмущением, вносимым обтекаемым телом.
После соответствующих преобразований окончательно получаем:
~Р____1
(3-25)
Рн |Л -м,
Из формул (3-24) и (3-25) следует, что при обтекании одного и того же тела газом скорость и разность давлений больше, чем в случае обтекания несжимаемой жидкостью.
Это различие между течениями газа и несжимаемой жидкости можно объяснить зависимостью плотности газа от скорости (§ 2-4). На рис. 3-5 показаны линии тока при обтекании тела сжимаемой и несжимаемой жидкостью при одинаковых параметрах и скорости с невозмущенного потока.
Другое упрощение исходных уравнений, основанное также на предположении о слабом возмущении потока, дано А. Н. Шерстюком, развившим упрощенный, но более точный метод учета влияния сжимаемости.
Для оценки влияния сжимаемости в слабо возмущенном плоском потоке с докритическими скоростями
(М00<М.) воспользуемся уравнением неразрывности (1-12), записав его для плоского установившегося движения газа:
![]()
а также условием отсутствия вихрей (3-1) для плоского течения.
В этом случае из формул (1-6) получаем:
![]()
(3-1а)
Рассмотрим обтекание плоским потоком газа крылового профиля, показанного на рис. 3-5.
Следуя за А. Н. Шерстюком, перейдем в уравнениях (3-26) и (3-1а) от скоростей и, v потока сжимаемой жидкости к скоростям в потоке несжимаемой жидкости ин’ин’ положив
![]()
(3-27)
Здесь показатель степени 0 определяется на основании упрощенных связей, соответствующих предположению
о малой возмущенности потока; р — плотность потока в данной точке; р^ — плотность невозмущенного потока.
Как уже отмечалось выше, в соответствии с методом малых возмущений можно принять:
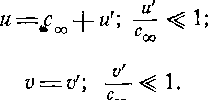
'ОО
(3-28)
(3-28а)
Для несжимаемой жидкости справедливы аналогичные упрощения:
Используя эти соотношения, подставляя (3-28) в уравнения (3-27) и (3-5а) и отбрасывая члены второго порядка малости, нетрудно получить:
<4 .>4
V)v I А„ У>
. 62М2дх ' ди
00 \ (3-30)
1 <4 д0_3 = () ?
1 — бМ^, дУ дх
Для того чтобы уравнения (3-30) привести к уравнениям неразрывности и отсутствия вихрей для несжимаемой жидкости, достаточно принять, как и ранее, связь между координатами в сжимаемой и несжимаемой жидкости (3-22):
1 -К
и, кроме того, положить:
- 1Л - м*
(3-31)
Действительно, после подстановки (3-22) и (3-31) в уравнения (3-30) находим:
дп dv„ дин dv„
Отсюда следует, что скорости ин и vH действительно являются местными скоростями в потоке несжимаемой жидкости при обтекании того же тела при том же угле атаки.
Для определения скоростей при обтекании тела сжимаемой жидкостью необходимо вначале рассчитать поле скоростей в потоке несжимаемой жидкости при той же величине и том же направлении скорости невозмущенного потоки (сноо=соо)- ПРИ этом местная безразмерная скорость Я в произвольной точке потока будет:
Зависимость 6 = /(Яоо) представлена на рис. 3-6. Из этого графика следует, что коэффициент 9 можно приближенно считать постоянным при числах Яот<;0,7 ч- 0,8. Резкое возрастание 6 при больших Я^ обусловливает непригодность рассматриваемого метода в этой области.
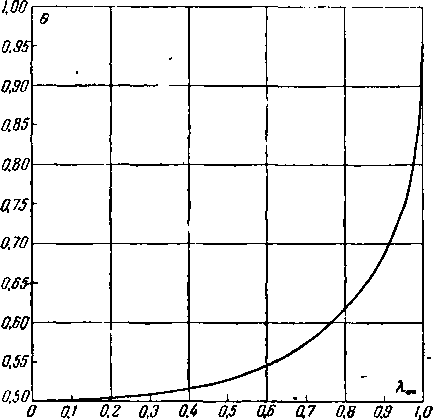
Рис. 3-6. Зависимость показателя степени 0 от безразмерной скорости .
Связь между скоростями в сжимаемой и несжимаемой жидкостях по формуле (3-27а) для различных скоростей набегающего потока показана на рис. 3-7. С увеличением *оо скорость в потоке сжимаемой жидкости в данной точке
обтекаемого тела интенсивно возрастает по сравнению со скоростью в несжимаемой жидкости.
Установим теперь связь между коэффициентами давления в несжимаемой и сжимаемой жидкостях.
Из уравнения Бернулли для несжимаемой жидкости
... (3-33,
Для сжимаемой жидкости коэффициент давления определяется по формуле (3-16). Выражая р через безразмерные скорости Я и Я , находим (табл. 2-1):
Рс0
к к—1
• (3-34)
X2
' k+ 1
'k+1
Пользуясь формулами (3-27а), (3-33) и (3-34), можно получить связь между коэффициентами давления в сжимаемой и несжимаемой жидкостях р и ра. Эта связь представлена на рис. 3-8 и 3-9. Здесь показана зависимость
0,7
0,6
0,5
о А
0,3
|
К | |||||||
| л | jUzt- | ||||||
| 1 |
|||||||
|
JF | |||||||
|
У/ // / |
Я |
0,2 0,3 0,Ь 0.5 0,6 0,7 0,8 • 0,3 1,0
Рис. 3-7. Зависимость между безразмерными скоростями в сжимаемой и несжимаемой жидкостях по А. Н Шерстюку.
между р и рн для различных значений Я^. Кривые на рис. 3-8 пригодны для пересчета положительных значений рн. В этом случае давление в рассматриваемых точках на поверхности теда выше давления набегающего потока.
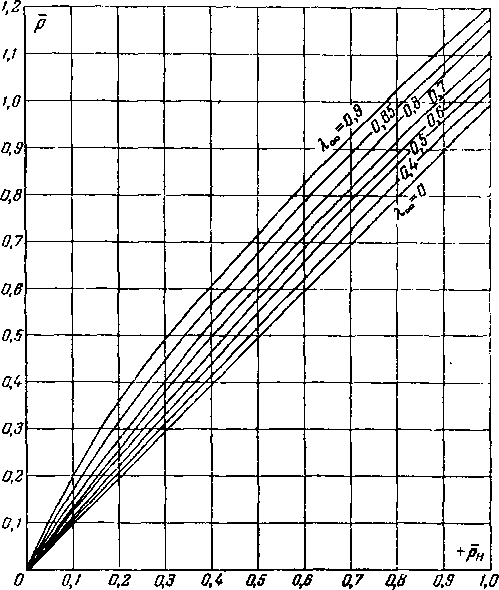
Рис. 3-8. Зависимость между положительными коэффициентами давления в сжимаемой (р) и несжимаемой (рп) жидкостях при различных Х^.
Для пересчета отрицательных значений рн служит график на рис. 3-9. Пунктирная линия, ограничивающая диаграмму p=f(pj сверху, соответствует значениям р„ при которых А = 1. Другими словами, эта линия определяет критические значения безразмерной скорости набегающего потока Моо = М» в зависимости от р или от ра и тем самым ограничивает ту область величин Моо<М» = /(/7н), для которой может быть произведен учет влияния сжимаемости рассматриваемым методом.
На рис. 3-10 приведена кривая по данным развитой теории, устанавливающая зависимость между минимальным коэффициентом давления в точке обвода тела при обтекании его несжимаемой жидкостью р мин и критическим числом Я* набегающего потока. Кривая на рис. 3-10
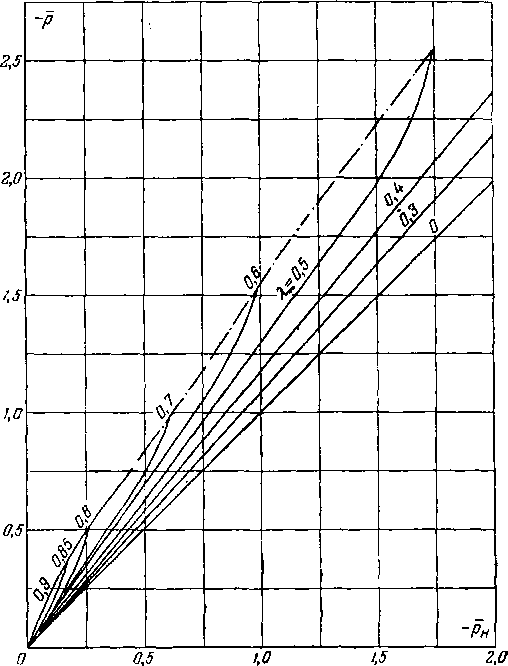
Рис. 3-9. Зависимость между отрицательными коэффициентами давления для сжимаемой р и несжимаемой рн жидкостей при различных .
в координатах (ра мин, Я ) воспроизводит граничную линию Я = 1 на рис. 3-10.
Формула для расчета этой кривой может быть полу<-чена из (3-33) с помощью (3-27а). Действительно, из этих соотношений имеем:
'К \2 / > \2 / Р~\20
(3-35)
(табл. 2-1), получим:
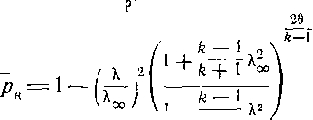
k + 1
Положив Я=1 и Я = Я,, находим:
29
/г-1
Заменив отношение
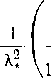
2
!+ 1
Рп.
1
’ft + 1
(3-36)
~!,5
-0,5
| Рнмт \ |
i | |||
|
\ | ||||
| \ | ||||
0J5 ав 0,7 Ofl 0,3 1,0
Рис. 3-10. Зависимость между коэффициентами давления рп и безразмерной критической qkq-ростыо X*
зуясь кривыми на рис. 3-8 и 3-9, легко мо» но найти распределение давлений и при больших дозвуковых скоростях с учетом сжимаемости. Как видно из графиков, влияние сжимаемости сказывается в том, что в области положительных значений р коэффициенты давления для сжимаемой жидкости будут выше, а в области отрицательных значений—ниже, чем для несжимаемой жидкости. Следовательно, благодаря сжимаемости увеличиваются абсолют-
Таким образом, если известно распределение давлений по обводу тела при малых скоростях, когда влиянием сжимаемости можно пренебречь (распределение рн), то, поль-
-2,0
-t,o
ные значения коэффициента давления. При этом области минимальных давлений становятся более крутыми и вытягиваются (рис. 3-4)96. Из рассмотрения рис. 3-4 видно, что с ростом М увеличивается площадь, заключенная между кривыми давлений для верхней и нижней поверхностей
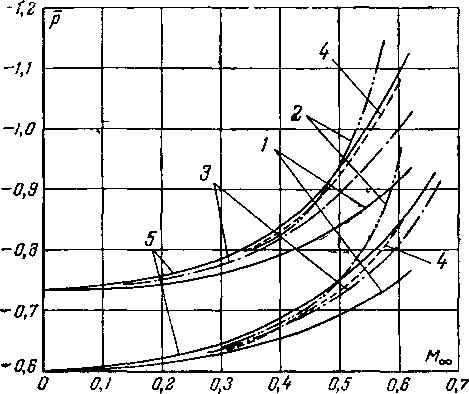
Рис. 3-11. Сравнение опытных и расчетных коэффициентов давления.
/ — по Л. Прандтлю; 2—по С. А Христианович};
3—по формуле Кармана —Цзяна (3 37), 4—по А. Н Шерстюку; 5 — опыт
профиля. При этом, очевидно, подъемная сила с увеличением Мм возрастает.
Все выводы рассматриваемого метода хорошо подтверждаются опытными данными.
Сопоставление опытных и расчетных значений р в точке верхней поверхности крылового профиля, расположенного в потоке под небольшим углом атаки, показано на рис. 3-11. Профиль имеет относительно большие толщину и кривизну.
Для сравнения на рис. 3-11 приведены также расчет-
ные кривые, соответствующие формуле (3-25) Л. Прандтля и по более точной формуле Кармана — Цзяна:
(3-37)
Рн
РиМ0
2(1 + V 1 -M2J
Совпадение расчета по 'формулам (3-27а)—(3-34) и по формуле^ (3-37) ,с опытом является вполне удовлетворительным. Значительно худшие результаты получены при использовании формулы (3-25).
3-4. ТЕОРЕМА Н. Е. ЖУКОВСКОГО
Теория силового воздействия потока идеальной жидкости на обтекаемые тела основывается на известной теореме Н. Е. Жуковского. Н. Е. Жуковский установил вихревое происхождение силы взаимодействия и нашел простую связь между этой силой и интенсивностью циркуляционного те-
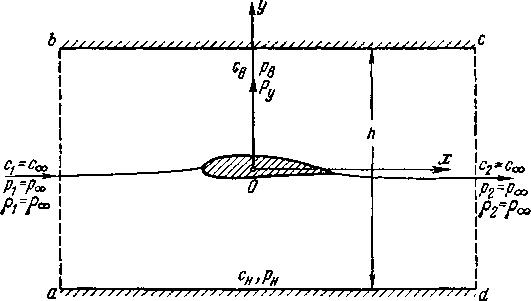
Рис. 3-12. К доказательству теоремы Н. Е. Жуковского.
чения, возникающего при обтекании тела. Эта задача была решена Н. Е. Жуковским в 1906 г.
Для доказательства97 теоремы Жуковского воспользуемся схемой, показанной на рис. 3-12. Расположим крыловой профиль в плоском потоке между двумя непроницаемыми плоскими контрольными поверхностями, ориентированными по потоку и удаленными друг от друга на расстояние h. Систему координат хОу разместим так, чтобы направление оси х совпадало с направлением вектора скорости невозмущенного потока с^. На бесконечном удалении от профиля проведем сечения ab и cd, нормальные к направлению потока.
Предполагая, что профиль обтекается безотрывно, и применяя теорему об изменении количества движения к массе жидкости, заключенной внутри объема abed, найдем, что сила, направленная против течения и называемая лобовым сопротивлением профиля, определяется формулой98
рх = S (А — Рг) dy ~ [ Pici (Сх — с3) dy.
(ft) (ft)
Так как скорости и давления в сечениях аЪ и cd одинаковы, то
Р= 0.
Приведенный результат был получен впервые Л. Эйлером в 1745 г. и независимо от него в более общем виде Даламбером. Он может показаться парадоксальным, так как противоречит опыту. Однако следует иметь в виду, что этот результат получен в предположении отсутствия вяз-"кости и отрыва потока от поверхности обтекаемого контура. В действительности всегда в какой-то степени оба эти фактора имеют место.
В практическом отношении можно сделать вывод, что следует стремиться добиваться таких форм контура, при которых обеспечивались бы безотрывное обтекание и наименьшие воздействия сил вязкости; в этом случае, по-видимому, сила сопротивления будет наименьшей.
Найдем теперь величину силы Р нормальной к вектору скорости с . Эту силу называют подъемной силой. Обозначив через ри давление на нижней контрольной поверхности и через рв давление на верхней контрольной поверхности, получим:
ОО
— Ру+ { (PH-PB)dx = 0,
так как проекция скоростей у непроницаемых контроль-, ных поверхностей на ось у равняется нулю. Следовательно,
— СО
Увеличивая расстояние между стенками /г, в предельном случае (при & -»- оо) получим обтекание тела безграничным потоком. При этом поток у стенок будет слабо возмущенным. Скорости такого течения, как известно, можно представить в виде [формулы (3-28)]:
сн=соо+сн'; Св = Соз + Св’
(3-286)
где сн, с'ъ — малые добавочные скорости у стенки, вызванные влиянием обтекаемого тела.
Давление в произвольной точке возмущенного потока связано с давлением на бесконечности уравнением Бернулли:
Р Рса , k — I
которое при принятом допущении (слабо возмущенный поток) на основании (3-286) преобразуется к виду:
ИЛИ
Р=Рт— РооСооС'- (3‘39а)
Уравнение (3-39) или (3-39а) справедливо для линеаризованного течения и называется линеаризованным уравнением Бернулли. Уравнение (3-39а) можно записать для сечений на верхней и нижнеи контрольных поверхностях:
Р = р~ — Р с с
rH t'co ~со <х> и
И
Г
Р = Р~ — Р с с .
“в "оо гоо оо в
Подставляя рн и рв в уравнение (3-38), находим:
+°°
Р = р с [(с' — с )dx. у «ОО ОО J V в Н'
—00
Нетрудно видеть, что интеграл ^ (сл — dx
-8
можно выразить через циркуляцию скорости по замкнутому контуру (рис. 3-12). Действительно,
Г = Г 4- Г 4- Г 4- Г •
abcda ab be cd daf
так как
+ 00 ^ +00
= j (Соо~Ь О ^ da= j (Соо"Ь Ch) dx, 1 ab — 1 cd,
TO
-f-OO
l\bcd = \(Cl~Cl)dX-—00
Следовательно,
Формула (3-40) выражает теорему H. Е. Жуковского, являющуюся основной теоремой аэродинамики. Теорему Жуковского можно сформулировать так: при обтекании тела плоскопараллельным безграничным потоком идеальной сжимаемой жидкости на тело единичного размаха действует сила, равная произведению циркуляции скорости Г на скорость ст и на плотность невозмущенного потока. Направление этой силы нормально к направлению скорости невозмущенного потока с . При этом, как следует из вывода, если циркуляция скорости, вычисленная при обходе по часовой стрелке, окажется положительной, то и Р будет положительной. Подъемную силу Ру часто называют силой Жуковского. Для определения Ру необходимо знать величину циркуляции скорости, которая вычисляется на основании постулата Жуковского—Чаплыгина (§ 1-2).
3-5. ПЛОСКОЕ ДОЗВУКОВОЕ ПОТЕНЦИАЛЬНОЕ ТЕЧЕНИЕ ГАЗА В КРИВОЛИНЕЙНЫХ КАНАЛАХ
Рассматривая плоское или осесимметричное потенциальное движение газа по криволинейным траекториям, выберем в качестве независимых переменных расстояние вдоль линий тока (S) и вдоль эквипотенциальных линий (п) (рис. 3-13).
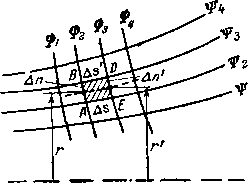
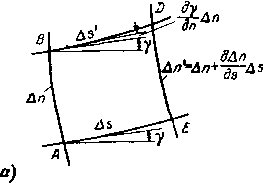
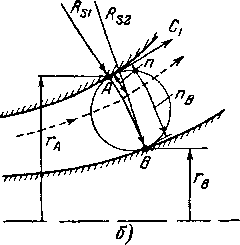
Рис. 3-13 К выводу уравнений движения в криволинейном канале.
Преобразуем уравнения неразрывности (1-14) и отсутствия вихрей [третье уравнение системы (3-1)] в новых координатах. Для элементарного объема, ограниченного в плоскости чертежа отрезками линий тока AS и ДS', и экви потенциальных линий Ап и Ап' условие неразрывности запишется в такой форме:
(per Ап) —О,
д In (per) j 1 дЛn _ p.
as- ~Т~Гп ~dS — ’
где r — радиус центра тяжести сечения Ап (рис. 3-13,а). Далее, так как
дАп ду * oS дп
(Т — Угол наклона линии тока), представим уравнение неразрывности в такой форме:
д |п foffi -L = р. (3-41)
= 0.
(3-41а)
as-
Полученные уравнения позволяют наиболее простыми способами рассчитать течение газа в плоских или осесимметричных криволинейных каналах1. С этой целью необходимо найти распределение скоростей вдоль эквипотенциальных линий в канале.
Для приближенного определения длины эквипотенциальных линий в канал вписываются окружности (рис. 3-13,6), касающиеся стенок в точках А и В. Через точки касания проводится дуга окружности, нормальная к стенкам канала, которая приближенно дает длину эквипотенциальной линии.
Такой способ определения линий Ф = const справедлив только при малой их кривизне.
Уравнения неразрывности (3-41) и (3-41а) показывают характер изменения угла наклона вектора скорости в поперечном сечении канала, а уравнение отсутствия вихрей позволяет сформулировать условие, которому должна удовлетворять эпюра скоростей на любой линии тока, в том числе и на стенках канала:
i
где --кривизна линии тока.
Ks
Тогда
Левая часть этого выражения обращается в нуль при п — 0; постоянную Д" можно выбрать таким образом, чтобы производная
±[c(Rsl+n + Kn2)}
была равна нулю и при RSI = RS2 (рис. 3-13,6). В этом случае она мало отличается от нуля и во всех точках линий Ф = const. Это условие означает, что закон изменения скоростей вдоль линии Ф = const будет:
с (Rsl + и + Кпг) = const,
или
(3-43)
SI
Изменение скоростей вдоль границ канала устанавливается с помощью формулы (3-43), справедливой и для сжимаемой жидкости. Исходным служит условие постоянства расхода через канал.
При малых числах М <[ 0,4, когда влиянием сжимаемости можно пренебречь, объемный расход жидкости через плоский канал будет:
«в
Q = | cdn.
о
С помощью формулы (3-43) после интегрирования получим:
8 = -5-=-^ =
с1пВ
Здесь ст — средняя скорость в сечении канала; с, — скорость в точке на выпуклой стенке.
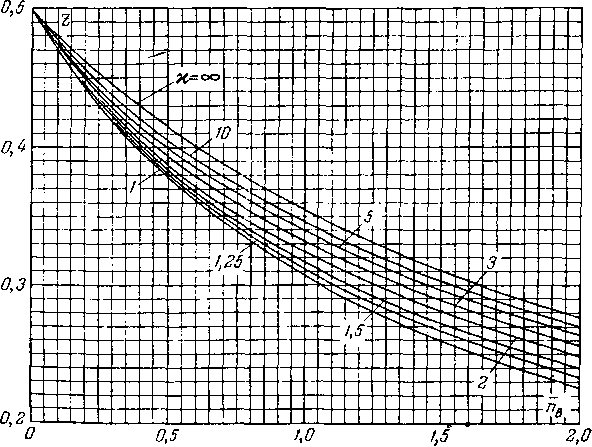
Для удобства расчетов на рис. 3-14 представлен график зависимости b = f(ng, -/.), выражаемой формулой (3-44).
В случае осесимметричного канала объемный расход жидкости определяется по формуле
пв
Q — 2% J Rscdn.
Ь
Рис. 3-14. График зависимости 8 от пв и х.
Упрощая решение задачи, можно принять линейную связь между Rs и п:
п в
По аналогии с формулой (3-44) можно получить99:
8о — 2 кЯ^спв =д — (3-45)
Расчет осесимметричных каналов существенно упрощается применением графиков, представленных на рис. 3-15.
Приведенные выше формулы (3-44) и (3-45) справедливы для малых чисел М (несжимаемой жидкости). Однако закон распределения скоростей, выражаемый формулой (3-43), может быть принят и для сжимаемой жидкости в такой же форме:
(3-43а)
1 + п — кjrt2
Слабое влияние сжимаемости на эпюру скоростей в поперечном сечении объясняется тем, что условие безвихревого движения, использованное для получения (3-43), не содержит плотности.
Заметное изменение кривизны линий тока и закона распределения скоростей в поперечном сечении отмечается только при больших безразмерных скоростях и значитель-
ных градиентах скоростей вдоль канала. В широком диапазоне дозвуковых скоростей (М<М*) расчет канала с учетом сжимаемости может быть произведен путем введения средней плотности в данном сечении. На основании метода малых возмущений А. Н. Шерстюком было показано, что средний приведенный расход в сечении, равный:
![]()
где G — весовой и G* — критический расходы газа через ' данное сечение, связан со средними скоростью и плотностью соотношением
(рш, — средние для сечения плотность и безразмерная скорость). Средняя плотность РШ = ?ШР*4~ легко может
быть определена по qm с помощью таблиц газодинамических функций. Скорости с учетом сжимаемости могут определяться по простой формуле: ~=— (с и ст — ско-
т ст т
рости, определенные без учета сжимаемости).
Метод, изложенный выше, пригоден для расчета различных каналов, например, каналов решеток1 турбоманиш.
3-6. ПЛОСКИЙ СВЕРХЗВУКОВОЙ поток
Перейдем к изучению основных свойств плоского сверхзвукового течения. С этой целью рассмотрим простейший случай установившегося равномерного сверхзвукового потока, движущегося с постоянной скоростью вдоль стенки ВА (рис. 3-16). Допустим, что по нормали к стенке ВА скорости также не меняются. В точке А этой стенки возникает возмущение потока, обусловленное поворотом стенки на малый угол. Вследствие малости угла db возмущение в точке А, выражающееся в изменении параметров потока (давление и температура уменьшаются, скорость возрастает), можно считать слабым.
Легко видеть, что в сверхзвуковом потоке возмущение может распространяться только в направлении течения, так как скорость движения частиц газа больше скорости
распространения слабых возмущений (с1 >а,). Возмущение, возникшее в точке А, сносится по потоку, причем некоторая линия Ат служит границей между двумя различными областями потока: слева от линии Ат располо
жена невозмущенная область течения, а справа от этой линии поток возмущен поворотом в точке А. Таким образом, линия Ат является границей, отделяющей невозмущенную часть потока от возмущенной. Так как в рассматриваемом случае речь идет о линию называют гр а н и ц е й слабых или звуковых возмущений, слабой волной, характеристикой или линией Маха.
слабом возмущении, то эту
т
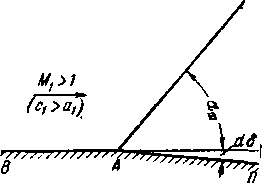
Рис 3-16. Обтекание сверхзвуковым потоком угловой точки.
При этом имеется в виду, что любые слабые возмущения потока распространяются со скоростью звука (гл. 2).
Механизм распространения слабых возмущений можно проанализировать более ' подробно, рассматривая другой непрерывно действующий источник возмущения в плоском безграничном сверхзвуковом потоке. Таким источником слабых возмущений может служить остроконечное тонкое тело бесконечного размаха с весьма малым углом раствора переднего клина (рис. 3-17). Создаваемые телом небольшие изменения параметров потока распространяются со скоростью звука аи тогда как скорость набегающего на тело потока с,
Волны возмущения представляют собой круговые бесконечные цилиндры, радиус которых легко определяется как a,At, где At — отрезок времени, исчисляемый от момента зарождения рассматриваемой волны в точке А. За этот же отрезок времени частицы проходят путь, равный CyAt. Следовательно, центр наблюдаемой волны перемещается в новое положение А,. При непрерывном обтекании тела в точке А последовательно образуется бесконечное количество волн, движущихся по направлению потока. Так как скорость течения с1'^>а1, то позднее образовавшиеся волны отстают от предыдущих» причем все семейство волн имеет две общие касательные: Ат и Amlt исходящие из точки А.
В этом легко убедиться, найдя соотношение между радиусами волны и перемещениями ее центра:
г3 _ гг ____ 1
М
:sma
где am — угол наклона касательной к направлению вектора скорости ct.
Появление линий Ат, Атг можно рассматривать как результат непрерывных слабых (звуковых) возмущений потока; они стационарно связаны с источником возмущений (носиком тела).
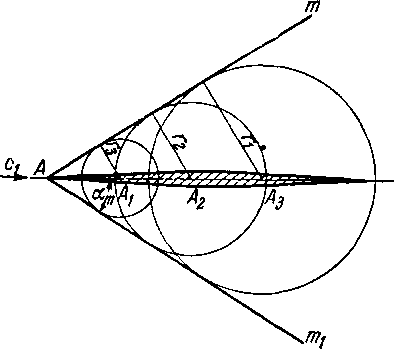
Рис. 3-17. Обтекание тонкого остроконечного тела сверхзвуковым потоком.
При пересечении такой волны частицы газа испытывают изменения всех параметров: *давления, плотности, температуры и скорости. Однако в связи с малостью возмущения эти изменения бесконечно малы. В рассматриваемом случае обтекания острого носика тела происходит незначительное уплотнение потока и давление за волнами Ат, Атх увеличивается на малую величину dp, а скорость соответственно падает на dc. Поэтому волны Am, Amt называют слабыми волнами уплотнения.
В тех случаях, когда переход через волну сопровождается расширением потока и, следовательно, уменьшением давления на dp, волну называют слабой волной разрежения. Звуковые волны разрежения возникают, например, при обтекании сверхзвуковым потоком внешнего тупого угла (рис. 3-16).
Из рассмотрения обтекания тонкого клина можно заключить, что в сверхзвуковом течении образуются характеристики двух семейств, расположенные под углом ±а к вектору скорости в данной точке.
Из формулы
следует, что в ускоряющемся сверхзвуковом потоке углы характеристик в направлении течения уменьшаются, а
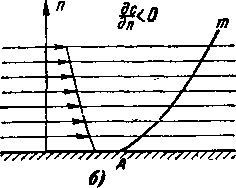
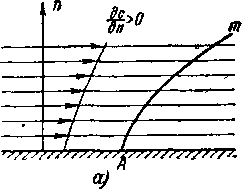
Рис. 3-18. Слабые волны в плоском потоке с неравночер ным полем скорости.
в диффузорном потоке — увеличиваются. Отсюда можно также заключить, что при изменении скоростей в поперечном направлении к потоку характеристики приобретают криволинейную форму.
Так, если по нормали к линиям тока скорости увеличиваются, характеристика обращена выпуклостью к невозмущенной области течения (рис. 3-18). Если, наоборот, скорости в направлении нормали к стенке падают, то характеристика обращена выпуклостью к возмущенной области потока. При сложном неравномерном распределении скоростей в потоке характеристики могут приобретать и более сложную форму.
Перейдем теперь к изучению конечных возмущений сверхзвукового потока. При этом рассмотрим вначале только такие возмущения, которые вызывают непрерывное изменение параметров течения.
Предположим, что вдоль стенки ВА движется равномерный сверхзвуковой поток (рис. 3-19). За точкой А газ попадает в область с пониженным давлением (/?2<СЛ)-При этом поток отклоняется от направления стенки ВА, поворачиваясь на некоторый угол относительно точки А в сторону^ пониженного давления. Возмущение, создавае-
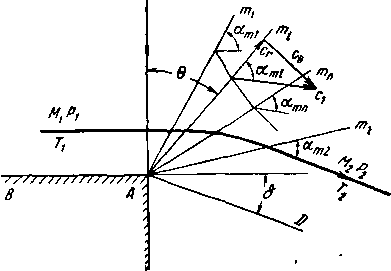
Рис. 3-19. К образованию волны разрежения при обтекании угла сверхзвуковым потоком.
мое точкой А, распространяется в сверхзвуковом течении вдоль характеристик Лот1; Amt,..., Атг, образующих стационарную волну разрежения т1Ат3. Возмущение сверхзвукового потока начинается на характеристике Ат{, угол наклона волны Атх к направлению невозмущенного
течения определяется по формуле ami = arcsin^-. Возмущение заканчивается на линии Атг; положение этой характеристики может быть определено, если известна скорость возмущенного потока:
Между характеристиками Ат.! и Ат2 происходит расширение газа от рх до рг. При пересечении волны разрежения линии тока соответственно искривляются, так как при обтекании точки А поток расширяется: скорость по
тока увеличивается, а температура и плотность падают. Промежуточным точкам линии тока в пределах волны разрежения отвечают характеристики Amv Атп и т. д.; вдоль каждой характеристики параметры течения остаются неизменными. Углы между характеристиками и касательными к линиям тока в направлении течения уменьшаются:
а а ~> а '
т! ^ т, тп
Рассматривая постепенный переход к параметрам возмущенного потока М2 и р2 с бесконечно малыми интервалами ДМ и Д/7 в пределах между Ат^ и Атг, можно провести бесчисленное множество характеристик, составляющих стационарную волну разрежения конечной интенсивности. Интенсивность волны m1Atn2 меняется при изменении давления рг. При этом, если параметры невозмущенного потока остаются неизменными, характеристика Атх сохраняет прежнее положение, а характеристика Ат2 перемещается в зависимости от изменения рг. С ростом рг характеристика Атг приближается к Атх и при /?8=/?! обе характеристики совпадают (слабое возмущение потока).
Установим зависимости между параметрами потока на границах волны разрежения. С этой целью воспользуемся основными уравнениями плоского изоэнтропического течения — уравнениями Эйлера. Имея в виду, что параметры потока вдоль характеристик не меняются, указанные уравнения используем в цилиндрических координатах.
""Для плоского установившегося движения газа уравнения (1-17а) и (1-14) в координатах (г, 0) принимают вид100:
| дсг сй дс, с - 1 г дг ^ г дв | СЧ О» . u 1 1 | _ 1 дР р дг ’ |
| dcs С„ дсв |
СГ св |
*>\ 1 |
| 'Г дг Г г дб 1 | г | р гдв |
| д(?гсг) дг "Т | д(? с„) дО | — 0. |
Рассматривая простейший случай, когда невозмущенный поток перед волной разрежения имеет равномерное поле скоростей и характеристики, образующие волну разрежения, прямолинейны, можно считать, что параметры потока сохраняют постоянные значения вдоль любого ра-радиуса в пределах волны.
др дс др
дг дг дг
![]()
Тогда в уравнениях (3-46) можно перейти к полным производным. После упрощений получаем:
![]()
(3-46а)
![]()
(3-466)
![]()
(3-46в)
Уравнение (3-46в) выражает в полярных координатах условие плоского безвихревого течения.
Действительно, из третьего уравнения (1-19), полагая о>г = 0, легко получить формулу (3-46в).
Отсюда приходим к заключению, что при обтекании угловой точки А поток остается потенциальным и безвихревым, а следовательно, и энтропия потока, пересекающего волну разрежения, сохраняется неизменной.
Совместное решение уравнений (3-466) и (3-46в) позволяет установить еще одно важное свойство сверхзвукового потока.
Подставим в (3-466) производную плотности:
2 dp ![]() d%
'
d%
'
Исключая из (3-466) и (3-46в) ^ , получаем:
с, = а.
Последнее означает, что отклонение потока в волне разрежения происходит таким образом, что составляющая скорости, нормальная к радиусу-вектору, равна скорости звука в данной точке.
Этот вывод можно получить также из анализа картины распространения слабых возмущений в сверхзвуковом потоке (рис. 3-19). Отсюда следует, что принятое допущение о постоянстве параметров течения вдоль радиуса позволяет рассматривать возникновение волны разрежения конечной интенсивности как результат последовательного расширения потока в системе бесконечного множества слабых (звуковых) волн разрежения.
Установим теперь, как меняются скорость и давление вдоль линии тока, пересекающей волну разрежения. Для этой цели воспользуемся уравнением энергии:
, k + 1 2 к — 1 ,
а ~1Г~ а,--2— ;
имея в виду, что
2 2 I 2
с=сr ; с0 = а,
получим:
А + 1 2 & + 1 2 k — 1 2
—2~ с0 _Т~ а, 2“ сг •
n dc -
Подставим в это уравнение — тогда получим
дифференциальное уравнение для определения радиальной составляющей с :
Л'
к -j- 1
Интегрируя последнее выражение, приходим к уравнению
Q
arc sin т — = т (0 -j- К),
® *
где
I А— 1
Постоянная интегрирования К. определяется из граничного условия. Примем, что при 6 = 0 радиальная составляющая скорости сг = 0; это значит, что мы рассматриваем расширение невозмущенного потока, имеющего скорость, равную скорости звука (Я-j =1); отсюда К=0.
Окончательно получаем:
Составляющая скорости cQ определяются по уравнению
Сл ct"^r
ге = ^ = Ж=СО8(т0)-
Безразмерная скорость X в произвольной точке волны разрежения
+ х] = ^ sin2 (mb) + cos2 (mb),
или
Для определения давления в той же точке воспользуемся уравнением
ft—1
1
(?П-
1
Я2 = ,
т
Отсюда после подстановки X из (3-47) получим:
- cos (2от9)
Т+1
_Р__.
Ро
(3-48)
Пользуясь формулой (3-47) или (3-48) и имея в виду,
что в волне разрежения процесс изоэнтропический, можно
также подсчитать изменение плотности и температуры
макс = V
k — \=~m отвечает
пРеДельное значение угла о:
*П*(1И0и1ПЮ) = 1,
или
п ж/k + 1 2 V k—Y
В этом случае при обтекании угла поток приобретает давление рг — 0 (истечение в пустоту). Заметим, что при таком режиме направление граничной характеристики Атсовпадает с направлением линии тока отклонившегося течения, так как
Необходимо подчеркнуть, что рассматриваемый режим течения (А = Д.макс) является теоретическим — предельным— режимом.
Второй предельный режим обтекания угловой точки отвечает значению скорости Х = \. При этом 0 = 0 (звуковой поток с бесконечно малым изменением давления у точки А).
Уравнения (3-47) и (3-48) применимы и для других сверхзвуковых значений скорости перед волной разрежения, больших единицы, но при этом начальный угол отсчета определяется по формуле
Qi = ~йГ arcsin }/(Я1 — ^
и линия отсчета располагается не перпендикулярно направлению невозмущенного потока, а под углом —|— <х к нему.
Большой практический интерес представляет возможность определения формы линии тока в пределах волны разрежения. Для решения этой задачи можно воспользоваться дифференциальным уравнением линий тока плоского течения в полярных координатах
dr _rdQ
~т Н'
Используя формулы для Хг и X , получаем: d In г = tg (mb) dQ.
После интегрирования приходим к выражению
г — r0 [cos (mO)] *+l , (3-50)
где г0 — радиус-вектор линии тока при 0 = 0.
Из уравнения (3-50) следует, что все линии тока в пределах волны разрежения представляют собой систему подобных кривых; расстояние между соседними линиями тока в соответствии с основными свойствами сверхзвукового потока увеличивается в направлении течения.
Как уже указывалось, обтекание угловой точки сверхзвуковым потоком является потенциальным. Составляющие
_дФ . _<ЭФ
°г ~д7 ’ се гб9-
Отсюда после подстановки сг или с0 и интегрирования получаем:
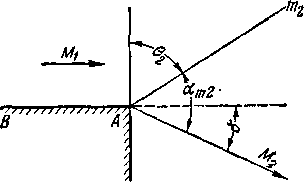
Рис. 3-20. К определению yrjia отклонения в волне разрежения.
Остановимся в заключение на способе расчета угла отклонения потока 8. Из рис. 3-20 следует, что при известном положении граничной характеристики Атг угол отклонения определяется по формуле
+ (3-52)
Имея в виду, что
1 / (*+1)_(*_1)Х|
a = arcsm\ .
т2 \ Л?
KV 2 /
и согласно (3-47)
2
получим:
-i/T+T . (ЛГ (/е— l)Xj —(*— 1)'
Применяя известные тригонометрические преобразования, из (3-53) найдем:
8= |/"arcsin [k — (k — 1)^2 ]-j~
(3-53a)
-j- arccos k — (k -j- 1) —
зависимости от M2 8 для трех различ-
Величину 8 можно представить в или pjра. Соответствующие значения ных показателей /г=1,135; 1,3 и 1,4 приведены на рис. 3-21 и в таблице функций изоэнтропического потока (см. при ложение).
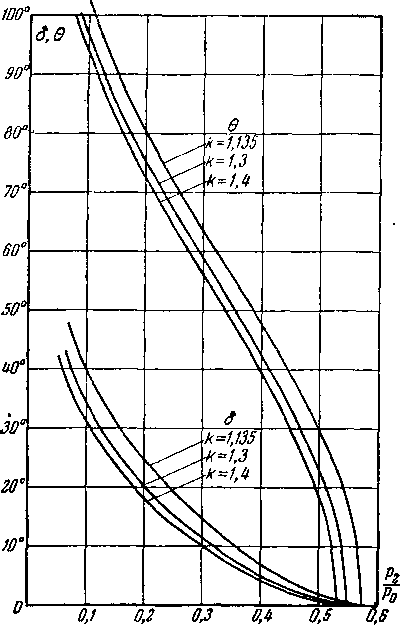
Максимальный угол отклонения 8ыакс отвечает максимальной скорости течения Амакс (или р2/р0 = 0). В этом случае, как уже указывалось, ат^ = 0 и, следовательно,
8 =0 — — макс макс 2 ’
или с учетом (3-49) получим:
(3-54)
3-7. ДИАГРАММА ХАРАКТЕРИСТИК
Пользуясь уравнением (3-53), рассмотрим изменение скорости вдоль некоторой линии тока EFH (рис. 3-22). Допустим, что скорость невозмущенного течения перед угловой точкой A Aj = 1. За угловой точкой давление рг = 0. Таким образом, вдоль линии тока EFH происходит непрерывное расширение потока от рг = /?* до /?2 = 0;
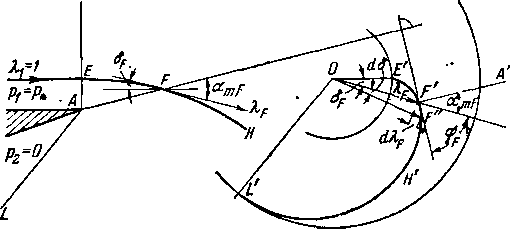
Рис. 3-22. Годограф вектора скорости при обтекании угла сверхзвуковым потоком.
при этом скорость потока увеличивается от = 1 до А2 = Амакс. В каждой точке линии тока можно определить величину и направление вектора скорости А. Отложим эти векторы из некоторого центра 0. Тогда концы векторов опишут кривую—годограф скорости для данной линии тока.
Заметим, что точки годографа скорости E'F'H' соответствуют точкам EFH линии тока. Отсюда следует, что
отрезок ОЕ'= 1, а отрезок OL'=^Уравнение (3-53), 116 выражающее функцию § (Я), является уравнением годографа скорости в полярных координатах. Согласно (3-53) годограф скорости представляет собой эпициклоиду.
Остановимся более подробно на некоторых свойствах годографа скорости. Проведем в .плоскости потока характеристику AF, пересекающую линию тока EFH в точке F (рис. 3-22), и найдем в плоскости годографа соответствующую ей точку F'. Это можно сделать, проведя из точки О линию вектора скорости Хр под углом bt к направлению потока ОЕ'. Направление вектора 1р совпадает с направлением касательной к линии тока в точке F. При перемещении в бесконечно близко расположенную точку F" скорость потока меняется на dXp (угол отклонения изменился на db). Угол между касательной к годографу в точке F и вектором скорости можно найти по уравнению
Xj dti
![]()
Л р
Величину -г— определяем дифференцированием уравне-
hF
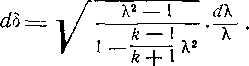
ния (3-53); получим:
Следовательно,
Очевидно, что
Угол между нормалью к годографу F'A' и направлением невозмущенного потока OF' равен:
Следовательно, нормаль к годографу скорости F'A* является характеристикой в плоскости потока, так как угол этой нормали с направлением вектора скорости рав'ен углу наклона характеристики amF. Отсюда следует очевидный
вывод о взаимной ортогональности характеристик и касательных к годографу скорости (рис. 3-22). Линию годографа скорости E'F H'L называют характеристикой течения в плоскости год ографа (плоскостьы, о). Следует подчеркнуть, что все линии тока имеют общий годограф скорости, т. е. форма характеристики в плоскости годографа не зависит от характера течения и одинакова для всех плоских сверхзвуковых потоков газа с данными физическими свойствами.
Так же как и в поле потока, в плоскости годографа можно построить две характеристики, симметричные относительно оси, которые относятся к двум различным семействам. Для решения ряда практических задач удобно использовать сетку характеристик первого .и второго семейств. Совокупность характеристик двух семейств в плоскости годографа называется диаграммой характеристик. Диаграмма характеристик может быть построена по уравнению (3-53) или графическим способом.
Графический способ основывается на следующих соображениях. Установим характер зависимости между вектором скорости X и углом наклона характеристики ат. Заметим, что в плоскости годографа сверхзвуковая область заключена в кольцевой области между двумя окружностями (рис. 3-23). Радиус внутренней окружности равен Х= 1.
1 Г k 4- 1
Внешняя
окружнэсть имеет радиус, равный у _j .
Как уже ука-
/ЩП
угол нате
клона характеристики меняется в пределах от ат = до ат = 0. Учитывая, что
(As + 1) —(As— 1)Х*
Sin'
2Х2
и I? = \2r + Xjj, где = X sin ат, приходим к уравнению
k ~ 1 j2 , j2 _ < k + 1 \ + h - L
Таким образом, зависимость ат (X) в полярных координатах (X, ат) выражается уравнением эллипса. Длина малой полуоси эллипса
равна 1, длина большой полуоси равна ^^TT“f -
Расположим эллипс в плоскости годографа (рис. 3-23).
Отрезок, соединяющий центр О с некоторой точкой на дуге эллипса F, определяет в масштабе построения вектор скорости X. Угол между вектором X и большой полуосью эллипса равен ат.
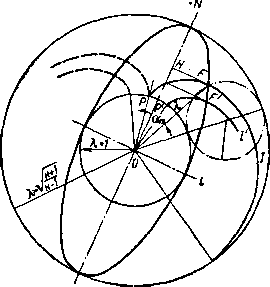
Рис. 3-23. К построению характеристик в плоскости годографа.
Очевидно, что большая полуось ON при этом дает направление характеристики в поле потока, а малая полуось OL — направление характеристики в плоскости годографа. Следовательно, отрезок FH, параллельный OL, является касательной к характеристике в плоскости годографа в точке F.
Проведя в нескольких точках эллипса отрезки, параллельные малой оси, и поворачивая эллипс вокруг центра О, мы можем построить группу характеристик первого семейства в плоскости годографа PFJ, P'F'J' и т. д.
Так как при повороте эллипс проходит через каждую точку кольцевой области дважды, то легко нанести и другую группу эпициклоид, составляющих второе семейство характеристик (пунктирные кривые на рис. 3-23). Характеристики второго семейства являются зеркальным отображением характеристик первого семейства.
Годограф скорости можно также получить путем качения без
1 (i/k + 1
скольжения окружности радиусом I \ дГПГ} — 1) .по внутренней
окружности кольцевой области (штрих-пунктирная окружность на рис. 3-23).
Диаграмма характеристик в плоскости годографа используется для приближенных расчетов плоских сверхзвуковых течений. С этой целью в плоскости годографа наносят отрезки характеристик двух семейств на одинаковом и достаточно малом расстоянии друг от друга. Для практического использования достаточна часть кольцевой области, расположенная в секторе с углом 70°. Каждой эпициклоиде присваивается определенный номер.
Заметим, что любая окружность в плоскости годографа представляет собой линию постоянного модуля скорости, а любой луч, идущий из центра О, определяет направление
вектора скорости в данной точке (рис. 3-24). Внутренняя окружность разбивается на градусы; отсчет угла ведется от горизонтальной оси плоскости годографа (положительные углы, откладываются вверх, а отрицательные — вниз).
Каждой эпициклоиде приписывается номер, показывающий угол луча, продолжением которого служит рассматри-
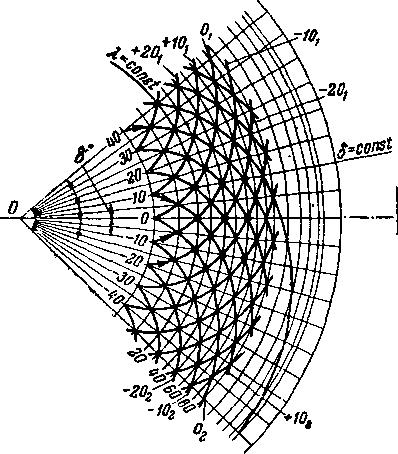
Рис. 3-24. Обозначения характеристик и окружностей (линий X = const) в диаграмме характеристик.
ваемая эпициклоида (рис. 3-24). Эпициклоиды первого семейства, идущие вверх, имеют индекс 1 (101;20t, и т. д.),
идущие вниз обозначены соответственно индексом 2 (102, 20г, 302 и т. д.).
Окружности (линии Я = const) также обозначены определенным номером. При ускорении от Я = 1 до заданного значения Я поток отклоняется на определенный угол 8, который можно найти наложением двух лучей, пересекающих характеристику на окружности радиуса Я = 1 и на окружности радиуса Я (рис. 3-24). Вдоль окружности угол отклонения 8 сохраняет постоянное значение; он равен полусумме номеров эпициклоид двух семейств, пересекающихся на данной окружности. Если номера эпициклоид"
обоих семейств уменьшаются или увеличиваются на одну и ту же величину, то соответствующая им точка в плоскости годографа перемещается вдоль окружности.
Каждая окружность в диаграмме характеристик обозначена номером, показывающим сумму номеров эпициклоид [имеющих разный знак (±)] или разность номеров эпициклоид [имеющих одинаковый знак (-|- или —)], пересекаю-
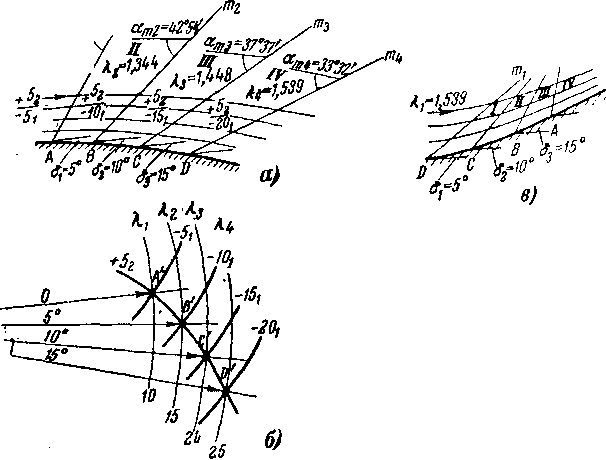
Рис. 3-25. Пример расчета сверхзвукового потока вдоль криволинейной стенки методом характеристик. а и в—плоскость потока; б — плоскость годографа скорости.
Omrstrsf/ kfljtt7.
,щихся на данной окружности, и равным удвоенному углу отклонения потока при расширении от А = 1 до Я, отвечающему рассматриваемой окружности.
Ниже приводятся примеры, иллюстрирующие методику пользования диаграммой характеристик.
Так, на рис. 3-25,а показано обтекание выпуклой криволинейной стенки плоским сверхзвуковым потоком. Для приближенного расчета потока заменим плавную линию стенки ABCD ломаной линией; каждый отрезок этой линии (АВ, ВС, CD) поворачивается на одинаковый угол, равный, например, 5°. Перед характеристикой Атх известны скорость потока = 1,227 и соответствующий угол лт1 =
= 50°37\ В плоскости годографа (рис. 3-25,6) этой характеристике отвечает точка А', которая в диаграмме характеристик может быть выбрана произвольно на окружности 10, соответствующей скорости Я1 = 1,227. Возьмем эту
точку на пересечении характеристик -ЦА .
При переходе в область II поток отклоняется на угол 5°. Следуя вдоль характеристики —в плоскости годографа, находим окружность, проходящую через точку В' (номер окружности равен 15—сум-ме 5 и 10), и соответствующие скорость в области IIЯ2 = 1,344 и угол ат = 42э54'. Переходя в область III и далее в область IV, последовательно находим в диаграмме характеристик точки С' и D’ и соответствующие скорости потока Я3 и Я4, а также ат и а .
rtii
Совершенно аналогично может быть произведен расчет течения около вогнутой стенки (рис. 3-25,в). Если скорость перед Dml равна Яг = 1,539, а углы поворота отрезков DC, СВ, ВА одинаковы и, как и в случае «а», приняты равными 5°, то изменения скорости и направления потока в областях I, II, III и IV находим по диаграмме характеристик, переходя вдоль эпициклоиды-}- 5г от точки D' к точке А'.
3-8. ПЕРЕСЕЧЕНИЕ И ОТРАЖЕНИЕ ВОЛН РАЗРЕЖЕНИЯ
На рис. 3-26 представлена схема пересечения двух волн разрежения, образующихся благодаря поворотам стенок канала на углы Sj и соответственно 82.
Так как угол б2 8г, то волна BCD имеет меньшую интенсивность по сравнению с волной АСЕ. Если принять, что во всех точках области I скорости одинаковы, то первые характеристики АС и ВС имеют одинаковый угол наклона к линиям тока невозмущенного течения. В области
II устанавливается давление, которое может быть определено по формулам § 3-6. Правее характеристики АЕ давление р3 будет меньше, чем р2, так как поток проходит более интенсивную волну разрежения АСЕ. В зонах II и
III линии тока принимают направление, параллельное стенкам ДЛ1 и BBt. Вслед за тем линии тока еще раз пересекают участки волн разрежения DIKF и EFGH, которые являются продолжением волн АСЕ и BCD. При этом давление потока снижается до /?4, а скорость соответственно увеличивается (Я1У>Д.Ш
При пересечении волн D1KF и EFGH линии тока отклоняются в противоположных направлениях, при этом линия тока а—а поворачивается на больший угол, чем линия тока Ь—Ь. Правее KFG линии тока имеют одинаковое направление и отклонены на угол Д§ = — 82 от пер
воначального направления, так как пересекающиеся волны
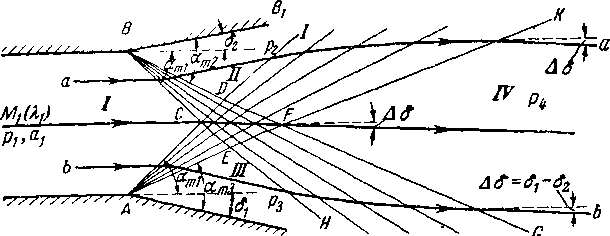
G
А
а)
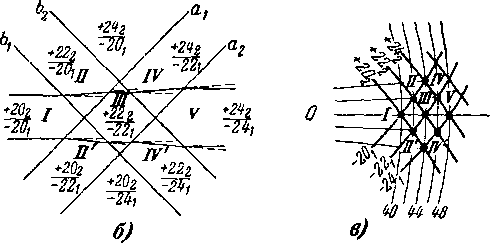
Рис. 3-26. Взаимодействие двух волн разрежения.
имеют различную интенсивность. Результативное отклонение потока происходит в том направлении, которое диктуется более мощной волной, в данном случае волной AJKA.
Параметры потока за системой пересекающихся волн (область IV) могут быть определены по формулам, приведенным в предыдущих параграфах. Построение спектра течения и определение параметров в зоне пересекающихся волн можно осуществить с помощью диаграммы характеристик.
Рассмотрим пересечение двух пар характеристик (рис. 3-26,6), причем параметры и направление потока в области I будем считать заданными. Величина и направление скорости в этой области определяются в той точке плоскости годографа, в которой пересекаются эпициклоиды двух семейств. Пусть для рассматриваемого примера число X в области / равно 1,522 и соответствующие эпициклоиды
имеют номера -\-20г и —201 (~(номер окружности 40).
Направление потока в области / совпадает с направлением луча О (см. диаграмму характеристик). При переходе в область II поток пересекает характеристику blt причем мы предполагаем, что при переходе через эту характеристику угол отклонения потока составляет 1°. Тогда, перемещаясь вдоль эпициклоиды 20, находим в плоскости годографа точку, отвечающую состоянию потока в области II
![]()
Аналогично находим величину и направление ско-
рости в зоне III после пересечения характеристики ах. Соответствующие эпициклоиды имеют* номера -j- 222 и
![]()
переходе в область IV отклонение по-
тока происходит в противоположном направлении на ту же величину (1°). В этом случае, перемещаясь вдоль эпициклоиды — 22u находим величину скорости в зоне IV, которая определяется суммой номеров эпициклоид -\-24г и —¦22j. Переход в область V из области IV связан с поворотом потока на угол 1° в противоположном направлении. Одновременно происходит дальнейшее расширение потока и сумма номеров эпициклоид увеличивается. Этой
зоне отвечают эпициклоиды Скорость потока здесь
2.4\
составляет Яу = 1,558. Последовательный переход через характеристики разрежения в диаграмме характеристик показан на рис. 3-26,в. Здесь точки Г, II', III' и т. д. соответствуют областям I, II, III... на рис. 3-26,6. Рассмотренный метод построения потока в зоне пересекающихся звуковых волн является приближенным. В основу метода положено допущение, что при пересечении каждой характеристики поток поворачивается и расширяется на одинаковые величины, т. е. все волны имеют одинаковую интенсивность. В пределах между соседними характеристиками параметры потока считаются неизменными.
Указанным способом можно рассчитать поток в четырехугольнике CDFE (рис. 3-26,а), в пределах которого происходят интенсивное расширение газа и деформация линий тока. В этой области характеристики криволинейны. Если обе взаимодействующие волны разрежения обладают одинаковой интенсивностью, то четырехугольник CDFE является симметричным и отклонения нейтральной линии тока в зоне IV не происходит.
Таким образом, мы видим, что в результате взаимодействия волн разрежения происходят расширение и ускорение потока.
Практический интерес представляют случаи отражения волн разрежения от стенки или свободной границы струи. Первый случай показан на рис. 3-27,а. При пересечении
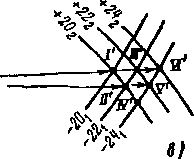
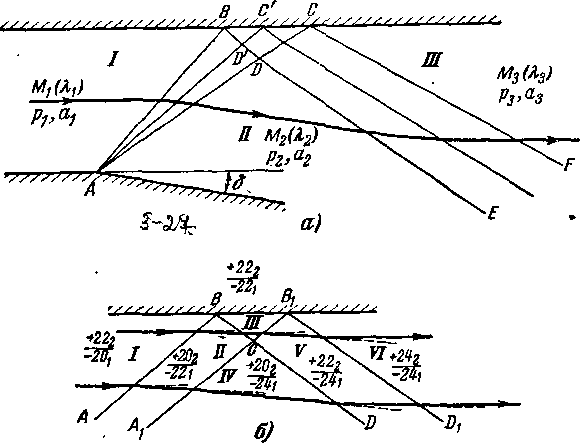
Рис. 3-27 Отражение волны разрежения от плоской твердой стенки,
первичной волны разрежения ABC линии тока, деформируясь, поворачиваются на угол 8. Первая характеристика АВ отражается от стенки, причем элемент отраженной волны BD пересекает первичную волну разрежения. Следовательно, вдоль BD давление должно падать, а скорость— увеличиваться. К такому же выводу мы приходим, рассматривая поведение линий тока непосредственно у стенки: здесь при безотрывном обтекании линии тока параллельны стенке и, следовательно, повернуты на угол 8 к линиям тока, расположенным за характеристикой AD. Такой поворот означает разрежение сверхзвукового потока. Отсюда заключаем, что волна разрежения отражается от плоской стенки в форме волны разрежения, т. е. сохраняет знак воздействия на поток.
Легко видеть, что отраженные характеристики составляют с направлением стенки угол, меньший угла соответствующих первичных характеристик, так как скорость за точкой падения.увеличивается.
С удалением от стенки угол отраженной характеристики уменьшается в связи с тем, что характеристика пересекает область разрежения (на участке BD) и вдоль характеристики скорость увеличивается. Отсюда следует, что отрезки характеристик, лежащие в пределах первичной волны разрежения, будут криволинейными. Лишь за последней характеристикой DC отраженные характеристики становятся прямолинейными. Аналогичный вывод можно сделать и для участков первичных характеристик AD' и др.
При переходе через первичную и отраженную волны разрежения поток расширяется: давление падает, а скорость соответственно увеличивается. Параметры потока в зоне II определяются по известным значениям Хг, рх, ai, 8. Параметры зоны III можно найти, учитывая, что угол поворота потока в отраженной волне EBCF равен 8. Тогда после определения Хг, р2, а2 по тем же формулам находим А3, р3, а3.
Построение отраженной волны можно выполнить, пользуясь методом характеристик. Так, например, допустим, что при переходе через характеристику АВ, падающую на стенку в точке В (рис. 3-27,6), направление скорости изменилось на 1°. Если скорость перед АВ составляет Аг =
= 1,522 ^эпициклоиды i--\ то в зоне ABC А, номера соответствующих характеристик в плоскости годографа равны i|^(An== 1,535). При пересечении отраженной
волны ВС поток возвращается к первоначальному направлению и, следовательно, в этой области величина и направление скорости определяются в точке диаграммы характеристик ±-^-(2ш = 1,558).
Переход из зоны II в зону IV приводит к новому изменению величины и направления скорости, отвечающих
характеристикам^—- (Я[у = 1,558).
В результате пересечения отраженной волны BD поток отклоняется в противоположном направлении (волна разре-
) 22
жения) и его характеристики будут (Яу=1,575). На
конец, за второй отраженной волной B1D1 величина и на-
24
правление
скорости отвечают характеристикам _
(Яу1 — = 1,595). Положение
соответствующих точек в диаграмме
характеристик можно видеть на рис.
3-27,в.
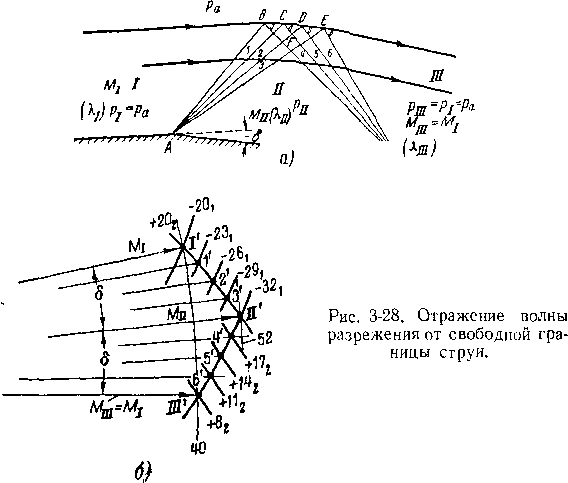
Аналогично можно рассмотреть отражение от свободной границы струи волны разрежения АВЕ, образующейся при обтекании внешнего угла (рис. 3-28). Характеристики, не проникая во внешнюю среду, отражаются от границы, причем линии тока и граница струи искривляются. Вдоль первой волны АВ давление равно давлению внешней среды ра\ за последней волной рп<с.ра. Однако непосредственно на границе струи с внешней стороны давление, температура и скорость не меняются. Следовательно, если вдоль отрезка характеристики BF давление падает, то вдоль FE оно растет. Но отрезок FE пересекает отраженную волну. Это означает, что при переходе через отраженную волну давление повышается до значения ра.
Отсюда заключаем, что волна разрежения от свободной границы струи отражается, как волна сжатия. Характеристики отраженной волны сходятся. Это очевидно, так как угол между отраженными характеристиками и границей остается одинаковым (в точках В, С, D, Е давление, скорость и температура одинаковы).
В отраженной волне сжатие газа происходит постепенно (не скачкообразно) и изменение состояния является изоэн-тропическим.
Построение процесса в волнах разрежения и сжатия в диаграмме характеристик показано на рис. 3-28,6. Точки Г, 1', 2' и т. д. позволяют определить величину и направление скорости в областях потока 1,1,2 и т. д. (рис. 3-28,а). Пересекая обе волны, поток поворачивается на угол, равный 28.
Таким образом, мы видим, что отражение волн разрежения от свободной границы происходит с изменением знака воздействия на поток. В результате взаимодействия волны разрежения с границей происходит отклонение струи.
Принципиальное различие между свойствами отраженных волн от стенки и свободной границы объясняется в конечном итоге тем, что вдоль обтекаемой стенки распределение параметров потока диктуется самим потоком, тогда как на свободной границе оно задано внешней средой.
Рассмотренные примеры взаимодействия волн отнюдь не исчерпывают того круга задач в этой области, с которым приходится сталкиваться в практике эксперимента и в теоретических исследованиях. Однако эти примеры могут быть положены в основу изучения и других, более сложных случаев.
