Глава вторая одномерное движение газа
ГЛАВА ВТОРАЯ ОДНОМЕРНОЕ ДВИЖЕНИЕ ГАЗА
Значительное число технических задач газовой динамики можно решать, предполагая движение одномерным, т. е. таким, в котором все параметры течения меняются только в одном направлении. Этим условиям отвечает течение газа вдоль слабо искривленных линий тока или в трубках тока.
Одномерным можно считать течение газа в трубе с мало изменяющимся поперечным сечением и малой кривизной оси. В ряде случаев результаты исследования одномерного течения могут быть применены и к потокам с неравномерным распределением параметров по сечению.
2-1. ОСНОВНЫЕ УРАВНЕНИЯ ОДНОМЕРНОГО ТЕЧЕНИЯ. СКОРОСТЬ ЗВУКА
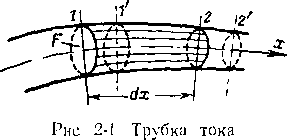
Для получения основных уравнений одномерного движения рассмотрим течение газа в трубке тока. Направление оси выберем так, чтобы оно совпадало с осью трубки (рис. 2-1). Воспользуемся первым уравнением системы (1-16). Пренебрегая для газа влиянием массовых сил, полагаем
X = Y = Z = 0.
Имея в виду, что для рассматриваемого одномерного течения и = с, v = w — 0 и перейдя в уравнении (1-16) к полным производным, получим:
cdc+l_dP= о dx 1 р dx
или
Уравнение изменения количества движения (уравнение импульсов) (2-1) справедливо только для таких’ течений, в которых отсутствуют силы трения, т. е. для обратимых течений. Легко показать, что в этом случае если система адиабатична, изменение параметров состояния совершенного газа подчиняется изоэнтропическому закону:
-^ = const. (2-2)
Следует заметить, что формулируя обстановку процесса течения, считая, что поток непрерывен, энергетически изолирован и трение отсутствует, мы тем самым определили его изоэнтропичность, так как в таком потоке отсутствуют необратимые преобразования механической энергии в тепло и, следовательно, энтропия потока не меняется. Поэтому мы можем непосредственно проинтегрировать уравнение (2-1), предполагая очевидной связь (2-2).
Действительно, проинтегрировав уравнение (2-1) и имея в виду (2-2), получим:
^cdc -f- |^y- = ~-f-const^ | pk~2dp =
= 4+&^lf- = const- M
Эхо уравнение, известное под названием уравнения Бернулли для сжимаемой жидкости, выражает закон сохранения энергии для адиабатического течения. После простой подстановки
тА-1 —= c T==i
k — 1 р k — 1e р
оно преобразуется к виду:
i + -у- = const. (2-4)
Здесь энтальпия газа i и теплоемкость газа при постоянном давлении с отнесены к единице массы и измеряются в механических единицах90.
Уравнению энергии (2-4) можно дать простое газокипе-
Г2
тическое толкование. Член в этом уравнении выражает
энергию направленного движения частиц, а энтальпия /, пропорциональная температуре, определяет энергию движения молекул. Следовательно, уравнение (2-4) выражает факт взаимного превращения энергии направленного движения частиц и тепловой энергии.
Таким сбразом, мы установили, что при изоэнтропи-ческом течении газа интеграл уравнения изменения количества движения совпадает с уравнением энергии1.
Следует отметить, что уравнения (2-3) и (2-4) можно непосредственно получить и из интеграла (1-26), записанного для сжимаемой жидкости (газа). Пренебрегая влиянием массовых сил, т. е. полагая f/ = 0, из (1-26) легко получаем уравнение (2-3), принимая связь между р и р по формуле (2-2)91.
Уравнение неразрывности для одномерного установившегося потока можно получить, рассматривая движение газа в трубке тока переменного сечения (рис. 2-1). Предполагая, что по сечению струйки параметры течения не меняются* рассмотрим часть потока, заключенную между сечениями 1-1 и 2-2. По определению трубка тока представляет собой замкнутую поверхность, образованную линиями тока. Через ее боковую поверхность частицы газа не проникают, так как векторы скорости касательны к этой поверхности. За 1 сек через сечение 1-1 внутрь рассматриваемой части трубки втекает масса газа, равная р1с1/г1; вытекающая через сечение 2-2 масса газа равна р2c2F2. По условию неразрывности течения эти количества должны быть одинаковыми, т. е.
Pici^ 1 — ?2СгР (2~5)
или
m = pcF== const, (2-5а)
где т — секундная масса газа.
Уравнение неразрывности можно получить в дифференциальной форме. После логарифмирования и дифференцирования под знаком логарифма формула (2-5а) принимает вид.
= (2'6>
Заметим, что для струйки постоянного сечения уравнение неразрывности (2-5) дает:
рс = -^-=const. (2-7)
Произведение рс = ~ определяет удельный расход массы газа в данном сечении (расход массы
через единицу площади сечения).
Выражение (2-7) для удельного расхода можно было также получить непосредственно из дифференциального уравнения неразрывности (1-12) для пространственного потока, полагая и = с и v = w — 0. Тогда, полагая движение установившимся и перейдя к полным производным, полу-
Отсюда, интегрируя, получаем (2-7). Очевидно, что по смыслу вывода уравнение неразрывности (1-12) при переходе к одномерному потоку может дать только условие рс -- const.
Для 0/fH0MepH0r0 течения несжимаемой жидкости (р = = const) уравнение неразрывности (2-5) принимает такой вид:
схРх = сгРг, (2-8)
или
cF — const.
Формула (2-8) выражает условие постоянства секундного объемного расхода жидкости, протекающей через сечения трубки Fx и Ft. Эта формула применима к газовым потокам только в тех случаях, когда на рассматриваемом участке трубки 1-2 изменением плотности можно пренебречь. Для газов это условие выполняется, если скорость движения мала по сравнению со скоростью звука.
Скоростью звука, как известно, называют скорость распространения малых возмущений в физической среде. Скорость звука имеет особенно большое значение при анализе процессов течения сжимаемой жидкости. Многие свойства потока, в том числе и характер изменения параметров течения вдоль трубки заданной формы, при различных условиях взаимодействия с окружающей средой существенно зависят от того, в каких пределах лежит отношение скорости к скорости звука.
Влияние сжимаемости в газовом потоке становится ощутимым в том случае, когда в результате изменения давления объемная деформация частицы и изменение скорости течения соизмеримы.
Воспользуемся уравнением неразрывности одномерного потока, записав его в таком виде:
dAV I _rfp_n
AV ' f ’
dAV * 1 n
где --относительное изменение объема элемента 1—2
(рис. 2-1), переместившегося в новое положение 1’ — 2’.
Умножив это равенство па dp, после преобразований получим:
Из уравнения импульсов (2-1) следует: dp = — pcdc.
Сопоставляя два последних выражения, получаем:
dAV с2 dc
AV (dP\ с
(Индекс s свидетельствует об изоэнтропичности процесса.) Обозначим
<2'9>
тогда
dAV __ с2 dc AV а* с
Таким образом, мы видим, что если с и а величины одного порядка, то относительная объемная деформация элемента будет такого же порядка, как и изменение скорости. При ~ 1 даже значительные изменения скорости
не приводят к большим изменениям объема частиц.
Из курса физики известно, что величина а, определяемая по формуле (2-9), является скоростью распространения волн малых возмущений. Характерным примером Таких волн могут служить звуковые волны.
Для совершенного газа скорость звука равна:
a = V b-*-=VbgRT. (2-9а)
' Р
Для воздуха (k = 1,4) скорость распространения звука а = 20,1]/Т. (2-96)
Следовательно, скорость звука в совершенном газе зависит только от физических свойств и абсолютной температуры газа. Этот вывод находится в полном соответствии с газокинетическими представлениями о процессе распространения малых возмущений в среде, состоящей из движущихся молекул. Скорость распространения возмущения должна зависеть от скорости движения молекул, которая определяется температурой. Хорошо известно, что средняя скорость движения молекул газа близка к скорости звука.
В этой связи необходимо подчеркнуть, что отношение
квадратов скоростей является мерой отношения сред
ней кинетической энергии направленного движения к средней кинетической энергии беспорядочного движения частиц.
2-2. РАЗЛИЧНЫЕ ФОРМЫ УРАВНЕНИЯ ЭНЕРГИИ
Уравнение Бернулли - устанавливает баланс энергии адиабатического течения газа в трубке тока. Выше мы познакомились с двумя формами этого уравнения: (2-3) и (2-4).
Постоянная в правой части уравнения энергии может быть выражена различным образом. Применяя это уравнение к двум сечениям трубки тока, в одном из которых скорость уменьшается до нуля и, следовательно, поток тормозится, можно уравнения (2-3) и (2-4) записать в следующем виде:
4~ + ‘ = '.: (2-Ю)
где 10 = срТ0 — энтальпия заторможенного потока;
А>> Ро> Т, — параметры заторможенного потока или параметры торможения.
В результате полного торможения потока вся кинетическая энергия направленного движения переходит в тепловую энергию. Заметим, что при полном торможении потока совершенного газа температура торможения Т0, так же как и энтальпия, может иметь только одно вполне определенное значение, в то время как давление торможения рй и плотность р0 могут принимать любые значения, но
Рв
такие, при которых отношение -у- остается постоянным.
Параметры торможения имеют весьма большое значение при рассмотрении как теоретических, так и экспериментальных задач газовой динамики.
Таким образом, мы видим, что правая часть уравнения энергии, выражающая полную энергию частицы, может быть представлена через параметры торможения.
гии.
Вспомним, что
a* = k-?-.
9
Тогда уравнение (2-11) приобретает вид:
2
^2 л 2 Лл
где а0 — скорость распространения звука в полностью заторможенной среде.
Если применить уравнение энергии к двум сечениям трубки тока, в одном из которых давление р уменьшается до нуля, то скорость течения с будет стремиться к некоторой максимальной величине счакс, которую будем называть максимальной скоростью. В соответствии с рассмотренными условиями эта скорость отвечает истечению газа в пустоту (/ = 0; р — 0; Т — 0). Следовательно, правая часть уравнения (2-12) может быть выражена через максимальную скорость:
2 2
с \ а . Siane {г, юч
2 ~Т k—\ 2 '
При максимальной скорости течения, равной сшкс, вся тепловая энергия молекул преобразуется в энергию направленного движения. Практически максимальная скорость течения недостижима и является известным теоретическим пределом для скорости газа.
Следует иметь в виду, что с приближением скорости течения к максимальной разрежение газа становится весьма большим и поэтому к рассматриваемому потоку нельзя применять уравнения состояния совершенных газов и уравнение энергии в известной нам форме (2-10) или (2-11).
Из формулы (2-12) может быть получено еще одно выражение для постоянной в правой части уравнения энергии.
Согласно (2-12) вдоль оси трубки тока с.увеличением скорости с скорость звука а падает. Совершенно очевидны при этом пределы возможных изменений с и а~
Скорость течения может изменяться от нуля до с
J МЯКС»
а скорость звука — от а0 до нуля. В одном из сечений трубки тока скорость движения газа с может стать равной местной скорости звука, т. е.
с = а~а,.
В этом случае уравнение (2-12) запишется таким образом:
2 9 9
2. at _ k + ! at
2 ' k— 1 k— 1 2 •
Следовательно, постоянная в правой части уравнения энергии может быть выражена через скорость а, и уравнение энергии примет тогда вид:
Скорость течения, равную местной скорости звука а, называют критической скоростью.
Из уравнения энергии, записанного в различных формах, следует, что между характерными скоростями и параметрами торможения существует определенная связь.
Приравнивая правые части уравнений (2-10) — (2-14), можем получить такое соотношение:
![]()
к_ Ро_
2
Отсюда получаем выражения для характерных скоростей потока через параметры торможения.
Так, максимальная скорость будет равна:
/2i0 = \/2cpT0 = Y
![]()
С,
макс
Критическая скорость
![]()
(2-17)
Кроме того,
![]()
Из формул (2-16) и (2-17) следует:
Смакс 1 / k + 1 /п 1о\
Таким образом, мы видим, что максимальная и критическая скорости зависят от физических свойств газа (по
казателя изоэнтропы k) и температуры торможения.
Для воздуха при А = 1,4 и # = 287,1 м*/сек2-град
а, = 18,У/ Т0 M-jceK.
Для перегретого водяного пара при k = 1,3 и R = 462,0 м*!секг-град
По формуле (2-18) можем получить:
/*
макс л л г"
для воздуха -= 2 До;
с*
Смакс п 77
для перегретого водяного пара -=2,77.
2-3. ПАРАМЕТРЫ ТЕЧЕНИЯ В ПРОИЗВОЛЬНОМ СЕЧЕНИИ ТРУБКИ ТОКА
Пользуясь уравнением энергии, выразим параметры течения в некотором сечении трубки тока через параметры торможения и скорость в этом сечении.
С этой целью, преобразовав формулу (2-14), получим:
Сг , аг rk + 1 а _ Сманс (9-Ыя\
2 ‘ k — 1 k — 1 2 2 •
Деля все члены на с2, получим:
1 j 1 Я2 k -f- 1 _ 1 ^макс
Тk—\ с2"- 2(k—\) ~с:
Введем следующие обозначения для безразмерных скоростей:
с
Af =
А = -
а *
с
(2-19)
а*1
с
тогда уравнение (2-146) будет иметь вид:
(2-20)
2>k — 1 /И2 2(k—1)' X2 2 ?2
Уравнение (2-20) устанавливает связь между безразмерными скоростями. После простых преобразований получаем:
2 Р (2-21)
М1
ft—I 1— ?2'
k— 1
k +
Воспользуемся теперь формулой (2-10). Выразим температуру торможения в таком виде:
(2-10а)
2с.
Разделим левую и правую части на Т0 и определим отношение температур:
L—ii — 1
так как
: + 1 а•
то
^ = 1 т
1 о
fe—l k 1
Я3= 1 — Е3.
Кроме того, определив из (2-10а) отношение
и заменив в правой части
^ _ аг _ аг
~~ kR~cP(k —
получим:
Для изоэнтропического течения
JL=(P-'\ =Ш*“' (2-24)
т<S \ Рв J \ Ро/
Пользуясь формулами (2-22) и (2-23) можно представить относительные давление и плотность газа в произвольном сечении трубки тока в зависимости от безразмерных скоростей М, Я и & (табл. 2-1).
Таким образом, зная параметры полного торможения потока и одну из безразмерных скоростей, по уравнениям (2-22) и (2-23) можно определить температуру, а по формулам, представленным в табл. 2-1, — плотность и давление газа в данном сечении трубки тока.
Из основных уравнений легко получить связь между параметрами в двух произвольно выбранных сечениях трубки тока.
Из формул (2-22) и (2-23) выразим температуру торможения в таком виде:
о—* I * I 9 *•* ) ,i-е*-
k + 1
Для двух сечений изоэнтропического потока (1-1 и 2-2) можем записать уравнение энергии для совершенного газа в такой форме:
Т = Т ¦
(2-25)
2
1+ — M2 i-j+T*
В предположении изоэнтропического течения, используя соотношения (2-24), получим формулы для отношений давлений и плотностей (табл. 2-1).
Отношение плотностей
Отношение давлений
Легко также поЛу^йть отношение абсолютных скоростей в этих сечениях:
С 2 _ММ2 щУ Т%
(2-26)
И См3кс П°-
Заметим, что уравнения (2-22) — (2-26) и формулы, представленные в табл. 2-1, являются модификациями уравнения энергии, полученные путем преобразования уравнения (2-10) и введения безразмерных скоростей.
В практических расчетах газовых течений может быть использована любая форма уравнения энергии и параметры р, р и Т могут быть выражены через любую из безразмерных скоростей М, Я, ?.
Однако в зависимости от рассматриваемой задачи оказывается целесообразным применять ту безразмерную скорость, которая обеспечивает максимальную простоту окончательных уравнений.
Если в рассматриваемой области скорости меньше критической, т. е. если
0
то
0<М^1;
0< 1;
Если скорости течения больше критической,* т. е.

В первом случае течение называется дозвуковым или докритическим; а во втором — сверхзвуковым или сверхкритически м. Следовательно, значение безразмерных скоростей
М = 1=1
разделяет области течений с дозвуковыми (докритиче-скими) скоростями и со сверхзвуковыми (сверхкритиче-скими) скоростями. Можно видеть, что безразмерные скорости i и Ё имеют конечные предельные значения, причем скорость I — 1 при с = <2„, в некоторых случаях более удобна для пользования.
Следует подчеркнуть, что безразмерные скорости имеют определенный физический смысл.
В § 2-2 было установлено, что в зависимости от соотношения с и а в большей или меньшей степени проявляется сжимаемость потока и, следовательно, М=-^-в каждой точке течения определяет степень влияния сжимаемости. Кроме того, физическое значение числа М выявляется при рассмотрении величины
С'
![]()
![]()
откуда следует, что квадрат числа М
пропорционален отношению кинетической энергии потока к его потенциальной энергии в данной точке.
Зная, что квадрат критической скорости может быть выражен через энтальпию торможения:
![]()
_k + 1 _
к 1
Таким образом, квадраты безразмерной скорости Я, а также ? пропорциональны отношению кинетической энергии потока к его полной энергии i0.
При течениях газа без энергетического обмена с окружающей средой полная энергия потока i0 является в каждой точке величиной постоянной. Соответственно постоянными являются и скорости а„ аа и смакс, зависящие только от i0 (при k = const). В этом случае Я и ? дают нам скорость течения, отнесенную к различным, но постоянным для всего потока масштабам.
В энергетически, неизолированном течении, когда имеет место теплообмен с окружающей средой (dQ=fc 0) или обмен механической работой (dLT=/= 0), полная энергия меняется от точки к точке. В соответствии с изменениями
i0 меняются скорости а„ а0 и ?макс.
Следует подчеркнуть, что формулы (2-23), (2-24) и др., связывающие параметры торможения с параметрами потока (табл. 2-1), справедливы и для течений с энергетическим обменом, но, однако, в этом случае связь между параметрами торможения, статическими параметрами и безразмерными скоростями является локальной, т. е. относится только к данной точке или данному сечению трубки тока, причем под р0 и р0 понимаются параметры изоэнтропического торможения в данной точке. Эти уравнения не могут быть применены к двум различным сечениям трубки, так как на участке между сечениями меняется полная энергия потока. Следовательно, формулы для статических параметров, указанные в табл. 2-1, и формулы (2-25) и (2-26) для таких течений неприменимы.
Отметим, что безразмерная скорость М является одним из основных критериев в теории подобия при рассмотрении процессов движения с большими скоростями1, так как коэффициент сопротивления в основном зависит от отно-с
шения —. а
2-4. ИЗМЕНЕНИЕ СКОРОСТИ ВДОЛЬ ТРУБКИ ТОКА.
ПРИВЕДЕННЫЙ РАСХОД ГАЗА
Подвергнем более подробному исследованию характер изменения скорости вдоль трубки тока. Для этой цели воспользуемся уравнениями одномерного течения:
cdc -(- у- = 0;
dF ,df I dc _q
F ' $ ‘ с
Простые преобразования позволяют получить: отсюда
-/>'!-_—^
с F
(2-2 7)
Разделив обе части уравнения на агйх и выразив логарифмическую производную скорости, получим:
1 dF
1 dc _F 'dx . (2-28)
с dx M2— 1
Выразив с помощью (2-21) М2 через Я2, получим:
ft—I г
1 d\ 1 dF _ 9р,
\ dx~ \г — 1 F dx- ^ '
Уравнения (2-28) и (2-29) являются дифференциальными уравнениями распределения скоростей вдоль оси
трубки тока. Они могут быть проинтегрированы, если известен вйд функции F (х). Вместе с тем эти уравнения весьма удобны для качественного анализа изменения ско
рости потока в трубках тока различной формы.
Из уравнения (2-29) следует, что 4^ = 0 при
dx
а) Я = 0;
’ Г k — 1 N
\ dF А
в) 55 = °-
Случай „а“ отвечает неподвижному газу и поэтому интереса не представляет. Случай „б“ соответствует максимальной скорости течения и вполне очевиден: при X — = Ямакс дальнейшее возрастание скорости невозможно.
Наконец, случай „в“ приводит к 0 только при Хф\.
Легко видеть, что при этом в рассматриваемой точке = функция F (х) имеет максимум, минимум или точку перегиба. Следовательно, в таких сечениях трубки тока скорости также имеют экстремальные значения.
По уравнению (2-29) можно заключить, что производная скорости ^~ = сх) при Я = 1 и 0. Однако такое
решение, означающее наличие разрыва скорости, физически невозможно (мы рассматриваем непрерывно изменяющееся движение газа).
Рассмотрим качественную картину течения газа в трубке тока, имеющей в х = х, максимум или минимум сечения (рис. 2-2). Пусть функция F (л:) имеет в этой точке ма-
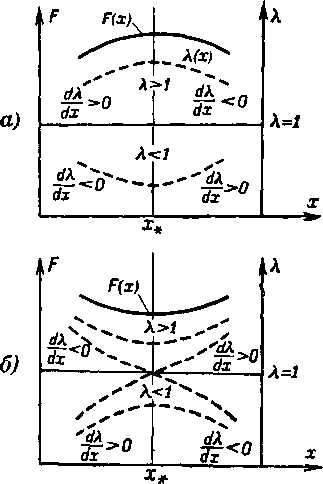
ксимум (рис. 2-2,а). Допустим, что слева от F (х) = f4aKc скорость Я<^1. Тогда из (2-29) следует, что так как ^->0, то т- е- скорость в трубке тока к /7макс
убывает. Справа О и >0 — скорость течения возрастает.
Аналогично при X > 1 будем иметь слева ~ > 0 и
(t~h. , Л
справа < 0-
Если функция F (х) имеет минимум в рассматриваемой
dF
точке, то слева от Р (x) = FKm при Я<1 и скорости будет возрастать, так как > 0 (рис. 2-2,6). При
Я>1 будет слева ^-<С0, справа ^->0.
Таким образом, мы показали, что в максимальном сечении трубки тока дозвуковой поток приобретает минимальную скорость, а сверхзвуковой — максимальную. В расширяющейся части трубки тока скорость дозвукового течения падает, а в суживающейся — растет. Сверхзвуковой поток в расширяющейся части ускоряется, а в суживающейся — тормозится. При любых значениях Я на входе кривая скорости в этом случае (F (х) = Рмакс) имеет экстремум. Отсюда следует весьма важный вывод: характер изменения скорости вдоль трубки тока принципиально различен для дозвуковых и сверхзвуковых течений. В первом случае поток газа с качественной стороны ведет себя так же, как и поток несжимаемой жидкости, а во втором случае кривая скорости Я(х) имеет характер, аналогичный кривой сечений /7(;с). Очевидно, что в трубке тока, имеющий максимум сечения, невозможен переход из области дозвуковых в область сверхзвуковых скоростей и наоборот.
В трубке тока с минимумом сечения скорость как дозвукового, так и сверхзвукового течения приближается к значению Я=1 в минимальном сечении. Если скорость течения в минимальном сечении будет Я=1 и rfX =7-0, то переход через критическую скорость, очевидно, осуществляется.
/
Рассмотрим теперь изменения давления, температуры и плотности газа в трубке тока. Непосредственно из формулы (2-13) и др. следует, что, там, где скорость увеличивается, температура, плотность и давление при изоэн-тропическом течении газа падают, и наоборот.
Таким образом, в суживающейся струйке при дозвуковом течении температура, давление и плотность уменьшаются, а при сверхзвуковом — растут. В расширяющейся струйке картина будет обратной.
Параметры, отвечающие сечению трубки тока, в котором Я = 1, будем называть критическими параметрами. Они легко определяются по формуле (2-22) и формулам для — и —, представленным в табл. 2-1, после Ро Ро
подстановки Я =1:
-Т ¦
1 1 о>
(2-31) (2-32) (2-33)
к +
= (^)'
= (т+т)
Р,
1_
А—1
Ро-
Мы видим, что критические параметры зависят от физических свойств газа (показатель k) и параметров полного торможения.
В табл. 2-2 приведены значения относительных критических параметров (отнесенных к соответствующим параметрам торможения) для различных показателей k.
Таблица 2-2
Критические отношения параметров для различных газов
|
k | 1,67 | 1,4 | 1,33 | 1,30 |
1,25 | 1,20 | 1,15 |
1,1 |
| Т. Т, |
0,7491 | 0,8333 |
0,8584 | 0,8696 | 0,889 | 0,9091 | 0,9292 |
0,9524 |
| р* Ро |
0,6498 | 0,6339 |
0,6296 | 0,6276 | 0,624 | 0,6209 | 0,6173 |
0,6139 |
| Р. Ро | 0,4867 | 0,5282 | 0,5404 | 0,5457 |
0,555 | 0,5645 |
в 0,5746 | 0,5847 |
Полученные выше основные закономерности, определяющие изменения параметров течения в трубке тока, физически могут быть понятны из рассмотрения уравнения постоянства расхода в трубке тока [формула (2-7)]. С помощью уравнения
![]()
(табл. 2-1) определим удельный расход газа:
/га=-^ = рс = р0а*Я^1 — '• (2-34)
Секундный массовый расход т для каждого сечения трубки тока будет одним и тем же. Интенсивность изменения плотности р и скорости с будет различной в дозвуковой и сверхзвуковой областях. В дозвуковой области с ростом с плотность р падает медленее, чем растет скорость, поэтому трубка тока должна суживаться, сечение F — уменьшаться. При сверхзвуковых скоростях, наоборот, падение плотности будет более интенсивным, чем возрастание скорости, и трубка тока будет расширяться.
Как видно из формулы (2-34), функция т(Х) = 0 при
![]()
и, следовательно, при некотором X
имеет экстремальное значение. Для определения этого зна иения X продифференцируем (2-34):
2—*
![]()
Отсюда следует, что максимальное значение удельного расхода соответствует X=1, т. е. критическому значению
скорости, так как обращается в нуль при X = 1. Следовательно,
Приведенным расходом назовем отношение
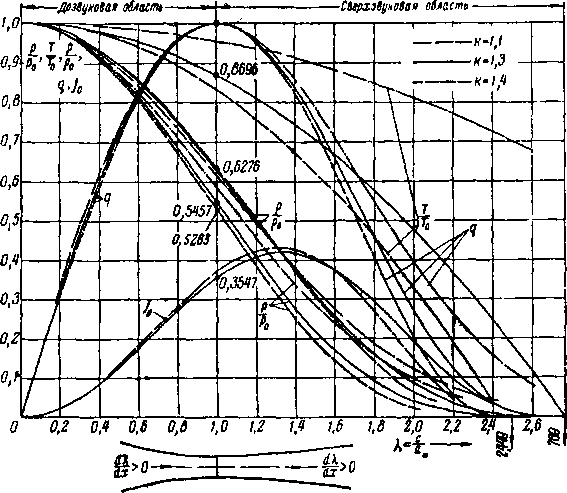
На рис. 2-3 представлены зависимости параметров те
А ’ Ро
- и приведенного расхода q от безраз-
чения
о
мерной скорости (для различных k).
Здесь приведена соответствующая схема изменений сечений трубки тока, вдоль оси которой скорость непрерывно возрастает. Нетрудно видеть, что при максимальной
скорости Я = ^MaKc=:|/A|-i-| приведенный расход q —
F
= -jr = 0, т. е. F = оо. Физически это понятно, так
как при Я = Ямакср = 0 (истечение в абсолютную пустоту) и р = 0.
||Т ИГ
Рис 2-3 Газодинамические функции одномерного и’оэнтропического потока if, р/f,, Т/Т„, р/р, , /0 1Д 1,4).
Таким образом, мы установили, что в трубке тока, имеющей минимальное сечение, может происходить переход через критическую скорость. Необходимыми и достаточными условиями для такого перехода являются условия 2 = 1 и dX/йхфО в минимальном сечении. Приведенный расход газа при этом приобретает максимальное значение.
Если скорость в минимальном сечении достигает кри
тического значения, а второе условие
няется, то перехода через, критическую скорость не произойдет. Этот случай соответствует появлению критических скоростей в трубке тока и является важным как в теории сопла Лаваля, так и в задачах внешнего обтекания тел.
2-5. НЕКОТОРЫЕ ГАЗОДИНАМИЧЕСКИЕ ФУНКЦИИ ОДНОМЕРНОГО АДИАБАТИЧЕСКОГО ПОТОКА
Выше (§ 2-3 и 2-4) мы познакомились с некоторыми важными безразмерными характеристиками одномерного потока газа, которые выражаются в виде простых функций безразмерных скоростей М, Я или 5. Эти газодинамические функции играют важную роль при выполнении различных газодинамических расчетов, а также при обработке результатов эксперимента.
Кроме уже известных, нетрудно получить и другие газодинамические функции, встречающиеся в преобразованиях уравнений сохранения расхода, количества движения и энергии.
С помощью приведенного расхода q легко определяется полный весовой расход газа через заданное сечение:
G = gF?c = gFqa* р„ (2-37)
или после подстановки
и преобразований находим:
G = KF(2-38)
не выпол-
где
*+i
fc-i
Расход можно выразить и через статическое давление потока в данном сечеиии. С этой целью разделим и умножим правую часть формулы (2-38) на р:
где
' (2-40)
— новая функция безразмерной скорости Я, зависящая также только от k и Я.
Уравнения расхода в форме (2-38) и (2-39) могут быть использованы для расчета адиабатического потока в изолированной системе (без энергетического обмена с внешней средой) при наличии трения. Действительно, условие постоянства расхода (2-38) для двух произвольно выбранных сечений канала можно записать в такой форме:
р Ръ\Я\ р РаъЯъ
Так как для изолированной системы Та1 = Тм = Та, то
Ъ; (2-41)
Pt 1 Рг Яг
для каналов постоянного сечения
Eb. = Rl.' (2-41а)
Рч Яг
Формулы (2-41) и (2-41 а) позволяют найти изменение
давления торможения, обусловленное необратимыми изме
нениями состояния движущегося газа и, в частности, потерями, вызванными внутренними силами трения.
Аналогично с помощью (2-39) можно получить (Т01 =
— Т —ТУ
- 1 02 - 1 0)'
FiPiai == F ъРгг*з.'>
откуда
Рг _
(2-42)
Р1 ^г °2
или для цилиндрического канала
Рг _°i
Соотношения (2-42) можно использовать для определения статического давления в одном из сечений потока, если известны скорости в двух сечениях (^ и Я2) и статическое давление в одном из них.
Введем еще одну функцию, которая характеризует импульс потока, равный
J=±c + pF. (2-43)
Учитывая, что
перепишем (2-43а) в виде;
у=т (с+?)- (2'43а)
Из (2-17) и (2-22) имеем:
и с = Ял*; тогда уравнение (2-43) можно записать в виде: J=^c + pF (2-44)
где
Ф = * + Х (2-45)
— некоторая новая функция безразмерной скорости Я,.
Уравнение для импульса газового потока (2-44) было впервые получено Б. М. Киселевым. Оно широко используется в различных задачах и, в частности, для расчета энергетически неизолированных потоков (расчет течений с подводом или отводом тепла при наличии сил трения, расчет внезапного расширения канала, процесса смешения и др.).
Исходное уравнение импульса (2-43а)
нетрудно преобразовать к другому виду, используя новую важную функцию безразмерного статического давления
*=—=dr*=-4--r-- (246)
Р се. Рс ра, *
Заменив здесь -y=gRT и а, по формуле (2-17) получим92:
<93-46а>
Следовательно, импульс потока выражается через функцию тс по формуле
а связь между ф и it устанавливается соотношением
*=Чг*-х- ^248)
Воспользуемся теперь формулами (2-38) и (2-39) и заменим величину расхода G в уравнениях (2-44) и (2-47).
После несложных преобразований находим:
J=ke.Fpaq(l + r)=^Fp0q<1? (2-49)
и
/= kstFp<s (X -j- T^ — p'Fp'sty. (2-50)
k
Здесь s. = ^ k —критическое отношение давле
ний;
l
- / 2 \A-1
P “(fe+r) —критическое отношение плот
ностей.
С помощью формул (2-40) и (2-50) легко устанавливается связь между газодинамическими функциями q, о, фин.
В некоторых расчетах удобно ввести также функции
1
Т = Р.^Ф = Лв.<7(ЯН-*) = (Я*+ 1)'1 — (2-51)
> —*+Тхя
Тогда
•!=ЧРРо = ЬРр. (2-53)
Функция безразмерного статического давления it встречается также при использовании уравнения энергии. Выразим из (2-14) скорость звука:
- ft -f1 1 2 k 1 ,
аг = -^—а,--2~° ¦
Разделив это уравнение на а, получим:
Если воспользоваться уравнением энергии в форме (2-11),
ос ^
то нетрудно найти отношение скоростного напора к статическому давлению р:
После подстановки значений и — получим:
(2'55)
Скоростной напор, отнесенный к давлению торможения, можно найти по формуле
1
: _рс2_P?l_iL_JL- Л—_ ^ j 2 Л_ft * х2 к~1
0 2pa 2Р Р» 2п Ро ft +1 \ ft +1 ) *
Таким образом, ряд характеристик одномерного газового потока выражается в виде функций безразмерной скорости Я и показателя изоэнтропического процесса k. Наиболее важные из функций сведены в таблицы газодинамических функций, построенные для различных постоянных значений k (приложение 1). Пользование такими таблицами существенно упрощает газодинамические расчеты, что и определило широкое распространение таблиц.
Вместе с тем анализ изменения некоторых газодинамических функций позволяет сделать важные выводы о свойствах газового потока. Так, например, на рис. 2-4, дополняющим рис. 2-3, приведены функции я, о, Д, у и j(k = = 1,4). Функция /0 показана на рис. 2-4.
Функция тс монотонно убывает с ростом скорости Я и при Я = 1 принимает критическое значение, равное [формула (2-46а)]:
Вспоминая выражение для критического отношения дав лений, легко находим:
k
е* /9 ^—*
Обращаясь к рис. 2-4, можно отметить, что функция у слабо меняется в широком диапазоне скоростей 0<Я<1,5. Имея в виду смысл этой функции [формула (2-51)], нетрудно прийти к выводу, что при постоянном давлении торможе ния импульс потока слабо зависит от безразмерной скорости при Я < 1,5. При постоянном статическом давлении
/
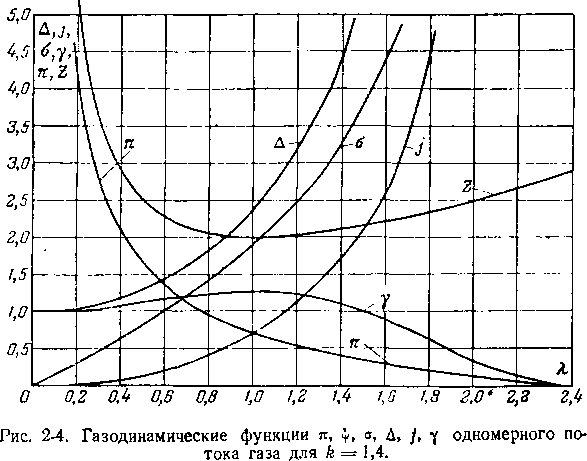
импульс в данном сечении интенсивно возрастает с ростом Я, так как функция Д резко увеличивается от единицы при Я = 0 до бесконечности при Я -> Ямакс.
Расход газа через заданное сечение F меняется весьма интенсивно при изменении Я, если статическое давление
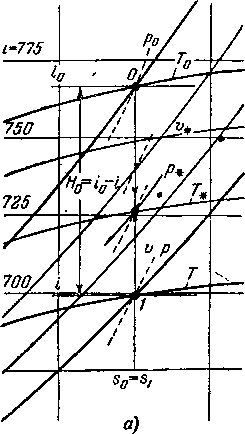
ккал/иг кг/м2сен
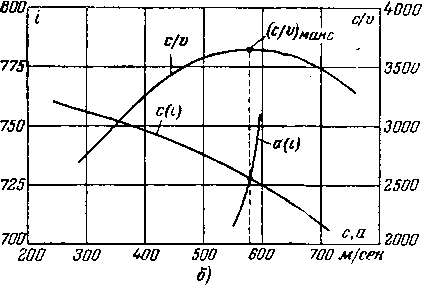
Рис. 2-5 Изоэнтропическин процесс расширения в тепловой диаграмме (а) и определение критических параметров для реального газа (б).
/
сохраняется постоянным, что характеризуется поведением функции о (рис. 2-4).
В выведенные выше формулы входят постоянные, зависящие только от k. Значения некоторых постоянных приведены в табл. 2-3.
Таблица 2-3
| к | 1,67 |
1,6 | 1,5 | ! ,4 |
1,35 | 1,3 | 1,25 | 1.2 | 1.1 |
| Г k+x уЧ-тгг | 0,7268 | 0,7164 | 0,7011 |
0,685 | 0,676 | 0,667 |
0,658 | 0,6486 |
0,6285 |
| *(^Г |
0,8128 | 0,7947 | 0,7680 | 0,7393 | 0,725 |
0,7095 | 0.6938 | 0,6895 | 0,6432 |
2-6. ОСОБЕННОСТИ РАСЧЕТА ОДНОМЕРНОГО ПОТОКА РЕАЛЬНОГО ГАЗА
Уравнение энергии (2*10) позволяет широко использовать диаграммы состояния для расчета газовых течений, что особенно важно при исследовании потоков реальных газов, изменение состояния которых не подчиняется уравнению (1-1), а теплоемкость является функцией давления и температуры.
В практике расчетов тепловых двигателей (паровых и газовых турбин, компрессоров и др.) наибольшее распространение находят тепловые диаграммы, в которых по осям координат отложены либо температура и энтропия, либо энтальпия и энтропия (диаграммы Ts и is). Такие диаграммы строятся по экспериментальным данным и позволяют с достаточной точностью рассчитывать различные процессы изменения состояния газов, в том числе в области влажного пара и вблизи линии насыщения.
Диаграммы состояния Ts и is могут быть широко использованы и при исследовании газовых течений.
Действительно, выразим* из уравнения энергии (2-10) скорость течения:
c=V2 (ia — i).
После подстановки i (к кал j кг) получим:, с=|/^(г'„ —«).
с = 91,53 (/" (г0 — г). (2-106)
Формула (2-106) показывает, что для определения скорости течения необходимо знать разность энтальпий i0 — г, которая легко определяется по диаграмме is, если известны параметры полного торможения газа (рй, Т0) и статические параметры течения (р, Т).
На рис. 2-5,а представлена часть диаграммы is для водяного пара. Если нам известны два любых параметра полного торможения (р0 и Т0), то на диаграмме is легко находится точка О, определяющая состояние заторможенного потока. Эта точка может быть'найдена и по другим параметрам состояния (например, i0 и sa). Проведя вертикальную линию до точки пересечения с изобарой статического давления р, изотермой Т или изохорой v, определим состояние движущегося газа (точка /) и прежде всего его энтальпию г; тогда скорость течения легко может быть определена по уравнению (2-106).
Входящую в это уравнение разность энтальпий Н0 = = i0 — i называют изоэнтропическим перепадом энтальпий.
Тепловые диаграммы могут быть использованы и для расчетов необратимых течений (см. ниже). В этом случае, однако, для определения скорости течения трех параметров состояния недостаточно.
Рассматривая изоэнтропическое движение вдоль трубки тока переменного сечения в диаграмме i — s, нетрудно
найти удельный расход газа в различных сечениях и построить эту величину, а также и другие параметры в зависимости от скорости с (рис. 2-5,6). Максимум удельного расхода соответствует критическому сечению трубки, определяемому по уравнению расхода:
Параметры в критическом сечении находятся из условия с^а,. С этой целью можно построить кривые изме-
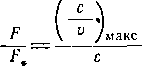
V
нений скорости звука a(i) и скорости потока с (/) в зависимости от энтальпии; точка пересечения указанных кривых дает значения а и г в критическом сечении. Перенеся эту точку в диаграмму i—s, можно найти и другие параметры в этом сечении (рис. 2-5,6).
