Глава первая основные понятия и уравнения газовой динамики

Глава первая

Основные понятия и уравнения газовой динамики

5-5. Потери на трение в цилиндрической трубе (опытные данные) 217 5-6. Пограничный слой. Основные понятия и уравнения .... 229 5-7. Условные толщины и интегральное соотношение для пограничного слоя......................235

5-8. Общее выражение для коэффициента сопротивления трения

7-7. Выбор геометрических параметров ступени эжектора .... 443

Глава восьмая Течение газа через решетки турбомашин

8-1 Геометрические и газодинамические параметры решеток.

9-6.    Осевая ступень с малым изменением    реакции    по    радиусу. . 611

Глава десятая'

Методы экспериментального исследования газовых потоков и проточной части турбомашин

10-1.    Экспериментальные стенды для исследования проточных

ОСНОВНЫЕ ПОНЯТИЯ И УРАВНЕНИЯ ГАЗОВОЙ ДИНАМИКИ

1-1. ПАРАМЕТРЫ ТЕЧЕНИЯ

Состояние неподвижного газа, как известно, характеризуется давлением, плотностью и температурой — параметрами состояния. Связь между параметрами состояния устанавливается в термодинамике. Для совершенного газа эта связь выражается в простой форме уравнением состояния:

у^8йТ,    (1-1)

где g — ускорение силы тяжести, м/сек²;

R— газовая постоянная⁸⁸, имеющая в технической системе единиц размерность к Г м(кГ-град.

Для воздуха газовая постоянная

R = 29,27 кГм/кГ-град,

Для перегретого водяного пара (приближенно)

= 47,1 к Гм) к Г -град.

Вместо плотности р в уравнение состояния может быть введен удельный вес или удельный объем газа.

Между плотностью, удельным весом и удельным объемом существует очевидная зависимость

S gv '

(1-16)

где у — удельный вес; v — удельный объем.

При движении газа параметры состояния являются не только физическими, но и динамическими характеристиками потока. В общем случае они меняются при переходе от одной точки пространства к другой, от одного момента времени к другому. Следовательно, р, р и Т зависят от положения точки и от времени и должны быть определены как точечные параметры.

В каждой точке движущегося совершенного газа параметры состояния связаны между собой уравнением состояния (1-1). Во многих практически важных случаях связь между параметрами р, р и Т выражается в более сложной форме. При рассмотрении физических свойств реальных газов иногда нельзя пренебрегать собственным объемом молекул и силами взаимодействия между ними. Эти факторы сказываются особенно существенно, если давления газа велики и, следовательно, концентрация молекул в определенном объеме велика.

Таким образом, в общем случае неустановившегося течения газа параметры состояния зависят от координат и времени:

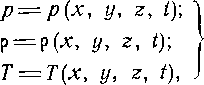
(1-2)

где л*, у, 2 — координаты точки; t — время.

Для решения задачи о течении сжимаемой жидкости, которая в конечном счете сводится к установлению силового взаимодействия между обтекаемым телом и жидкостью (внешнее обтекание) или — в случае внутреннего течения (трубы и каналы) — к установлению энергетического баланса потока, необходимо определить кинематическую картину течения, т. е. найти скоростное поле потока. Это значит, что наряду с зависимостями (1-2) должны быть найдены составляющие скорости частицы как функции координат и времени. Скорость газовой частицы меняется при переходе от точки к точке и с течением времени. Следо-

вательно, проекции скорости на оси координат могут быть представлены уравнениями:

и — и(х, у, 2, t);

(1-3)

v = v(x, у, 2, t); w = w (х, у, г, t), ,

где и — проекция вектора скорости с на ось х, a v, w— соответственно на оси у и г.

К числу параметров течения реальной (вязкой) жидкости относится также вязкость, которую необходимо определять как параметр в точке.

Известно, что коэффициентом вязкости называют отношение

дп

(1-4)

где х — сила трения, отнесенная к выделенной поверхности, кГ/м²;

дс

^--градиент скорости по нормали к выделенной по

верхности трения в данной точке

Коэффициент вязкости имеет размерность в технической системе единиц кГ-сек/м².

В общем случае для реального газа коэффициент вязкости зависит от температуры и давления. Однако зависимость от давления в широком диапазоне изменений давления оказывается весьма слабой и ею можно пренебречь. Таким образом, коэффициент вязкости может быть выражен в зависимости только от температуры. Соответствующие формулы для различных газов устанавливаются экспериментально.

Отметим, что закон трения в газах, выражаемый формулой (1-4), принадлежит Ньютону и справедлив только для ламинарных течений. При турбулентных режимах течения коэффициент трения приобретает совершенно новое содержание в соответствии с другим, значительно более сложным механизмом внутреннего трения.

Для решения указанной выше основной задачи необходимо определить и, v и w, а также р, р и Т как функции координат и времени. В дальнейшем будут рассмотрены только установившиеся течения газа и перечисленные параметры течения должны быть определены только в зависимости от координат л*, у и г.

Для этой цели мы располагаем шестью основными уравнениями: уравнениями количества движения в проекциях на оси координат, уравнением сохранения массы, уравнением сохранения энергии и уравнением состояния.

1-2. НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ АЭРОГИДРОМЕХАНИКИ t

Прежде чем перейти к выводу основных уравнений движения, остановимся на некоторых понятиях аэрогидромеханики, необходимых для дальнейшего.

Рассмотрим в движущейся жидкости ряд точек, каждая из которых лежит в направлении вектора скорости

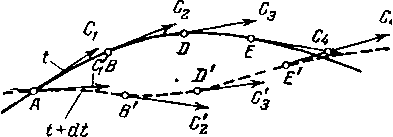
Рис. 1-1. К определению линий тока.

предыдущей точки. Уменьшая расстояние между соседними точками до нуля и проведя через эти точки линию, получим линию тока. В каждый момент времени векторы скорости будут касательными к этой линии. Следовательно, движение жидких частиц в данный момент времени происходит вдоль линии тока.

Если движение неустановившееся, то, очевидно, скорость в точке А в следующий момент времени будет отличной от с_г по величине и направлению (рис. 1-1). В результате линия тока займет новое положение в пространстве. Отсюда следует, что при неустановившемся движении линии тока меняют форму и положение в пространстве.

Для установившегося движения величина и направление вектора скорости не меняются во времени; в этом случае линии тока сохраняют неизменное положение в пространстве и форму.

¹ В § 1-2 весьма кратко излагаются некоторые основные понятия аэрошдромеханики, встречающиеся в специальных главах книги.

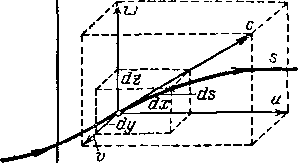
На линии тока 5 (рис. 1-2) выделим элементарный отрезок ds и спроектируем его на координатные оси (отрезки dx, dy, dz) Найдем углы между элементом ds и вектором —>

скорости с .с осями координат:

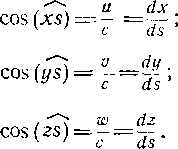
dx  dy  dz  ds

a    v    w    с

Отсюда получим:

Следовательно, дифференциальное уравнение линий тока имеет вид:

dx  dy  dz

(1-5)

и    v    w

Выделим в движущейся жидкости некоторый бесконечно малый замкнутый контур, через каждую точку которого проходит линия тока (рис. 1-3). Совокупность всех линий тока образует некоторую замкнутую поверхность—т рубку тока. Жидкость, движущаяся внутри трубки тока, называется элементарной струйкой.

z

X

Рис. 1-2. К выводу дифференциального уравнения линий тока.

Возвращаясь к понятию линии тока, отметим, что в установившемся движении, она совпадает с траекторией частицы. Траектория представляет собой линию, изображающую путь, пройденный в пространстве частицей за некоторый отрезок времени. Линия же тока является мгновенной линией, вдоль которой в данный момент движется совокупность частиц. Очевидно, что только при установившемся движении эти понятия могут совпадать, так как в этом случае траектории всех частиц, проходящих через какую-либо определенную точку пространства, будут одинаковыми

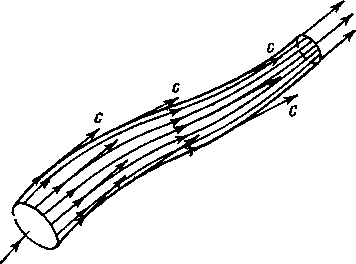
Рис 1-3. К определению трубки тока и элементарной струйки.

и, следовательно, в каждый момент времени все частицы, которые лежат на траектории, будут образовывать и линию тока.

В общем случае движение жидкой частицы является сложным. Наряду с поступательным движением вдоль некоторой траектории частица может вращаться относительно собственных осей и в процессе этого движения деформироваться.

Благодаря неодинаковым скоростям на различных гранях частица испытывает линейную деформацию и деформацию скашивания или сдвига. Если в первоначальный момент движения частица имела форму параллелепипеда, то с течением времени вследствие деформации форма ее изменяется. В случае сжимаемой жидкости меняется также и объем частицы.

Обращаясь к рис. 1-4, проанализируем вращение и деформацию одной из граней параллелепипеда, показанного на рис. 1-2. Если в точке D (рис. 1-4) проекция скорости

на ось л; будет и, то в точке А она будет u\-\-pdy. Под

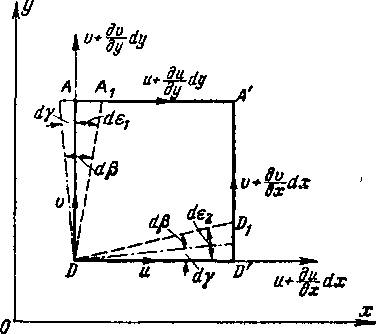
Рис. 1-4. Деформация грани частицы жидкости в процессе движения.

« ди ,

действием разности скоростей в этих точках, равной щау,

ребро DA повернется на некоторый угол de_x, переместившись относительно точки D за элемент времени dt в положение DA_t. Величина отрезка AA_t определяется по формуле

AA^Pydydt.

За рассматриваемый элемент времени точка U сместится по оси у на величину

UDl=p_xdxdt.

¦ При этом ребра DA и DU повернутся на малые углы de_t и ds₂, которые определяются по очевидным уравнениям:

.    ,    . D'D. dv ,,

ds₂—tg ofs₂ — —j-_xdt.

Рассматриваемые перемещения ребер DA и DU вызваны как вращением плоского жидкого элемента (грани параллелепипеда), так и его деформацией. Заметим, что если бы грань только деформировалась, без вращения, то ребра DA и DD' поворачивались бы на одинаковый угол навстречу друг другу или в противоположных направлениях. Наоборот, если бы грань совершила только вращательное движение (как абсолютно твердое тело), то ребра DA и DU поворачивались бы на одинаковый угол в одном направлении.

Движение элемента в сбщем случае можно рассматривать как сумму деформационного и вращательного движений и таким путем определить углы ds_t и ds₂. Принимая, что в результате вращения (против часовой стрелки) ребра DA и DD' повернулись на угол с/у, а в результате деформации—дополнительно на угол оф, найдем:

ds₁~d^ — dy,

ds₂ = d$ -J- dy.

Из этих двух уравнений получим:

2afy = <is₂ — ofsj.

Угловая скорость вращения грани будет равна:

= — !—^г —Л

dt 2 (л    dt у

Подставив значения производных ~_t и ^с-~ , находим угловую скорость вращения грани в таком виде:

_dt 1 /dv _ди\

⁰⁾³    dyj’

где (о_г — составляющая вектора угловой скорости вращения, параллельная оси г (индекс г указывает направление оси, относительно которой происходит вращение). Заметим, что («_г является угловой скоростью вращения биссектрисы угла в точке D. Аналогичные рассуждения приводят нас к заключению, что угловые скорости вращения двух дру-

гих граней, расположенных в плоскостях хог и уог, выражаются через соответствующие значения частных произ-

ди dw dv dw

водных    -щ,    причем    вращение    каждой грани па

раллелепипеда определено двумя угловыми скоростями.

Таким образом, уравнения для всех трех составляющих вектора угловой скорости вращения будут иметь вид:

_ 1 /dw_ctoy 1

2 уду с>zj’

1 / ди dw v

% = 2^Тг-Тх/ 1    I¹'⁶)

1 ,dv ди .

со •— — I----

г 2 и* ду;‘

Уравнения (1-6) выражают компоненты вектора угловой скорости вращения жидкой частицы ю, величина которого определяется как геометрическая сумма i»_x, и ш_г:

ш = 1/ш²_л4- U>J + (D* .    (1-7)

Формулы (1-6) определяют в дифференциальной форме связь между составляющими угловой скорости вращения и составляющими скорости поступательного движения.

Вращательное движение частицы вокруг осей, проходящих через частицу, называют вихревым движением. Опыт показывает, что во всех случаях движения реальной (вязкой) жидкости все поле потока или часть его являются вихревыми. В тех областях течения, где вихревое движение частиц    отсутствует, угловая    скорость    вращения    равна

нулю    (о) =    0).    В    этих областях    частицы    жидкости    могут

двигаться по траекториям любой формы, деформируясь при этом, но не вращаясь относительно своих осей.

Если в частном случае при ш = 0 траектории частиц являются замкнутыми кривыми, то такое движение будет частным случаем циркуляционного движения. Следует подчеркнуть, что при таком движении частицы совершают вращение вокруг некоторой оси, расположенной вне траектории, но не вращаются относительно собственных осей.

Понятия вихревого и циркуляционного движений жидкости играют большую роль в гидромеханике. В этой связи ₍ остановимся на одной весьма важной характеристике потока — циркуляции скорости. Рассмотрим еще один

пример циркуляционного течения. При обтекании несимметричного профиля крыла (рис. 1-5) плоскопараллельным потоком линии тока в области потока у крыла искривлены,

так как крыло возмущает поток. Характер возмущения, вносимого крылом в поток, можно выяснить, определяя скорости в различных точках поля у крыла. Сравнивая локальные значения скоростей со скоростью набегающего потока, нетрудно установить, что течение у крыла можно представить как сумму поступательного невозмущенного потока и течения по замкнутым траекториям. Интенсивность потока у крыла можно характеризовать величиной циркуляции скорости, которая определяется по уравнению

Циркуляционное

р '__I течение у

~~~ ^крыла

Рис. 1-5. Схема обтекания крылового профиля.

Т=фс/11,    (1-8)

/

где c_t-—проекция вектора скорости на направление элемента контура I.

В общем случае произвольно выбранный контур / может не совпадать с линией тока циркуляционного течения.

Формулу (1-8) можно записать в таком виде:

Г=<|с cos (с, /) dl.    (1-9)

/

Таким образом, циркуляционным движением можно назвать такое движение, при котором циркуляция скорости отлична от нуля. Если Г = 0, то движение называется бесциркуляционным⁸⁹.

При вычислении циркуляции скорости по формуле (1-9) необходимо условиться о направлении обхода контура интегрирования. Положительным направлением обхода, как пра-ёило, считают такое направление, при котором заключенная внутри контура область потока остается справа (рис. 1-5).

Понятие циркуляции весьма широко используется при исследовании вихревых движений газа. В теории вихревого движения доказывается ряд фундаментальных теорем, связывающих циркуляцию скорости с основными характеристиками вихря. Остановимся прежде всего на основных понятиях вихревого движения: вихревой линии, вихревой трубки и вихревого шнура.

Эти понятия близко совпадают с приведенными выше понятиями линии тока, трубки тока и элементарной струйки.

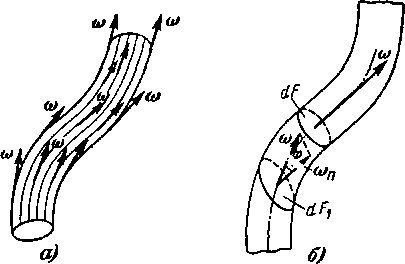
Рис. 1-6. Вихревая трубка и вихревая нить.

Вихревой линией называют такую-линию в потоке, в каждой точке которой направление вектора угловой скорости совпадает с направлением касательной к этой линии. Напомним, что вектор угловой скорости направлен перпендикулярно плоскости вращения. Следовательно, вихревая линия представляет собой мгновенную ось вращения частиц жидкости, которые располагаются на этой линии.

Вихревой трубкой называют замкнутую поверхность, состоящую из вихревых линий, построенную на элементарном контуре (рис. 1-6,а). Жидкость, заполняющая вихревую трубку, образует вихревую нить. Если вихревая трубка имеет сечение конечных размеров, то частицы, заполняющие ее и находящиеся во вращательном движении, образуют вихревой шнур.

Рассмотрим вихревую нить (рис. 1-6,6). Проведем сечение, нормальное к оси нити. Интенсивность или напряжение вихревой нити характеризуется удвоенным произведением вектора угловой скорости вращения со на площадь сечения ннти dF:

dJ=2mdF.

В общей случае рассматриваемое сечение нити может быть проведено произвольно под некоторым углом к ее оси (рис. 1-6,6); тогда интенсивность dJ определяется по формуле

dJ =2w dF_t ,

П ¹ ’

где т_п — проекция вектора угловой скорости на направление оси вихревой ннти:

о>_л = о> cos 9.

Таким образом, напряжение вихревой нити определяется как удвоенное произведение площади произвольного сечения нити на проекцию вектора ш на направление нормали к выбранному сечению.

В теории вихревого движения доказывается, что циркуляция скорости по замкнутому контуру, охватывающему вихревую нить, равна интенсивности вихревой нити, т. е.

dT = dJ — 2ш dF.

П

Для контура, охватывающего вихревой шнур конечного сечения, состоящий из бесчисленного множества вихревых нитей, циркуляция скорости определяется криволинейным интегралом

Г = 2 §®_ndF.

1

Это выражение, полученное Стоксом, позволяет сформулировать одну из основных теорем вихревого движения: циркуляция скорости по любому замкнутому контуру, проведенному в жидкости, равна сумме интенсивностей вихрей, охватываемых контуром, если этот контур путем непрерывной деформации можно стянуть в точку, не выходя за пределы жидкости. Если контур охватывает твердое тело (например, профиль лопатки), то непосредственно применить рассматриваемую теорему в этом случае нельзя, так как контур невозможно стянуть в точку, не выходя за пределы жидкости. Однако если замкнутый контур провести так, как это показано на рис. 1-7 (контур ЛВСОА), то согласно уравнению Стокса получим:

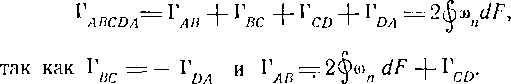
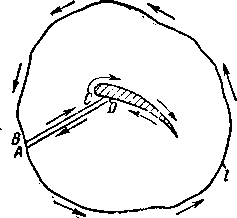
Рис. 1-7. К определению циркуляции скорости по замкнутому контуру, охватывающему профиль.

Формула Стокса приводит к заключению, что ядро прямолинейного вихря постоянного сечения вращается, как твердое тело, с постоянной угловой скоростью. Действительно, на основании указанной теоремы для прямолинейного бесконечно длинного вихря можно записать, что циркуляция по контуру, охватывающему вихрь,

F = 2u)/^:' = const.

При F = const в произвольной точке ядра вихря <в = const. Линейная скорость в ядре будет:

с_и = а>г,

где г — радиус рассматриваемой точки.

Следовательно, распределение скоростей в поле вихря будет линейным. На внешней поверхности ядра скорость имеет максимальное значение:

^Си макс^=и)Го

(г₀ — радиус вихря).

В гидромеханике доказывается также теорема о Неизменности циркуляции во времени в идеальной невязкой жидкости (теорема Томсона).

Согласно теореме Томсона для идеальной жидкости вне вихря циркуляция сохраняет постоянное значение по любому контуру, охватывающему вихрь. Циркуляционное течение около бесконечно длинного прямолинейного вихря (вне его) имеет гиперболическое поле скоростей (рис. 1-8), так как

Г = 2пшГ² = 2тсС _и г

и

q _ ^си мзкс^го _ Г

¹¹ ~ г ' 2тт г'

Легко видеть, что в соответствии с теоремой Томсона в идеальной жидкости вращательное вихревое движение частиц возникнуть или исчезнуть не может. Это и физи-

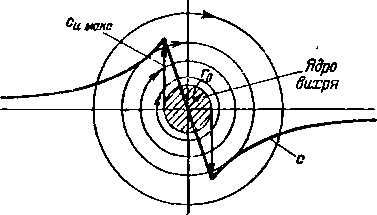
Рис. 1-8 Поле скоростей в ячре вихря и во внешнем потоке

чески понятно, так как в такой жидкости отсутствует механизм передачи вращательного движения и торможения.

Наблюдая течения реальной вязкой жидкости, можно указать большое число примеров возникновения и затухания вихрей. При этом условие постоянства циркуляции, которое является важнейшим свойством движения идеальной жидкости, не сохраняется.

Различия в свойствах идеальной и реальной жидкостей можно проследить при рассмотрении спектра несимметричного обтекания тела. Если задняя кромка тела выполнена острой (тело крылового профиля), то безотрывное обтекание такой кромки идеальной жидкостью должно привести к тангенциальному разрыву скоростей за профилем (рис. 1-9). В реальной вязкой жидкости наличие такого разрыва приводит к тому, что при сходе с задней кромки поток завихривается (рис. 1-9,6).

Таким образом, возникновение вихрей, а следовательно, и циркуляции вокруг профиля объясняется влиянием вязко-

Рис. 1-9 Образование вихрей при сходе потока с крылового профиля.

•

сти. В начальный момент времени поток у крыла бесциркуляционный. В точке схода в силу свойства вязкости зарождается начальный вихрь (рис. 1-9,6), который создает циркуляцию. Опыт показывает, что при не очень большой несимметрии этот вихрь возникает у задней кромки. Соответствующее условие в потоке идеальной жидкости, согласно которому точка схода должна находиться на задней кромке, носит название постулата Жуковского— Чаплыгина: при безотрывном несимметричном обтекании идеальной жидкостью профиля вокруг него образуется такая циркуляция Г, которая обеспечивает сход потока с задней кромки.

Это условие, сформулированное Н. Е. Жуковским и

С. А. Чаплыгиным, позволяет вычислять циркуляцию Г и вместе с тем подъемную силу крыла.

1-3. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ

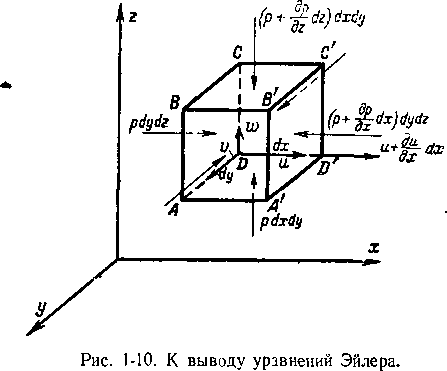
Выделим в движущемся газе элементарный объем в форме параллелепипеда (рис. 1-10) и запишем условие неизменяемости массы во времени для этого элемента. Это условие будет выражать закон сохранения массы; оно может быть представлено в таком виде:

d( _PAV)__n

dt

где ДУ — объем элемента;

р — средняя плотность элемента.

Дифференцируем, имея в виду, что р и ДУ- переменные величины:

ду^_|_р^К—о.

Разделив это уравнение на рДV. Получим уравнение неразрывности в виде:

1 ^Р_1_J_ dbV __п р dO ДУ dt

(1-10а)

Здесь производная выражает скорость изменения

объема или, следовательно, скорость объемной дефор^ма*

и 1 dbV    „    „

ции жидкои частицы. Член ^    представляет    собой

скорость относительной объемной деформации.

В частном случае несжимаемой жидкости, когда р = =const, последнее уравнение принимает весьма простую форму:

<ш ₌

at

выражающую условие постоянства объема элемента:    скорость объемной деформации элемента

равна нулю. Отсюда следует, что частица несжимаемой

жидкости деформируется в процессе движения так, что объем ее сохраняется неизменным.

Определим величину скорости относительной объемной деформации частицы, выразив ее через соответствующие проекции скорости и, v и w.

Подсчитаем линейную деформацию частицы в направлении оси л; (рис. 1-10). Эта деформация будет происходить в связи с тем, что скорости граней ABCD и A'B'C'D' неодинаковы. Если скорость левой грани равна и, то скорость правой будет и -f- ^ dx.

Предположим, что в пределах каждой из рассматриваемых граней параллелепипеда скорости постоянны. За элемент времени dt левая грань ABCD переместится на расстояние udt вправо. За тот же отрезок времени грань A’B’C'D'

переместится в том же направлении на расстояние ^u-f-

-{-^dx^jdt. Следовательно, объем элемента изменится,

так как скорости этих двух граней различны. Подсчитав абсолютное изменение объема частицы по направлению оси л:, получим:

(иdx^j dy dz dt — udy dz dt = ^ dx dy dz dt.

Рассуждая аналогично, для других двух пар граней можно получить приращения объема частицы по осям у и 2 в следующем виде:

dxdydzdt;

^ dxdydzdt.

Полное изменение объема частицы определяется как -сумма этих приращений.

Следовательно, скорость относительной объемной деформации определяется весьма просто:

1 dkV_ди . dv . dw    ..    ,

Д!’ dt    '    '

так как объем элемента Д1/ = dxdydz.

1 dp /да    ,    dv |    dw\    _{п    /л 1п}^_ч

Jdt    (^Ь106)

р

Заметим здесь, что входящие в уравнение (1-11) пря-

ди dv dw

мые    частные    производные    ^^    имеют    конкретный

механический смысл. Из предыдущих рассуждений очевидно, что эти производные определяют величины скоростей    относительных линейных    деформаций    граней    парал

лелепипеда. Рассмотрим, например, линейную деформацию грани DCCD' в направлении оси л:. Так как скорость

ребра CD равна и, а ребра C'D' u-^pdx, то удлинение грани по л: будет:

(^w %с ^^л:) ^ “ ^и^ ⁼ Тх ^^Х1^-

Относительное удлинение составляет ^ dt, а скорость

ди

относительного удлинения .

Преобразуем теперь уравнение (1-106). Так как р =

— P(x,y,z,t), то полная производная плотности равна:

dр dp dx I dp dy , dp dz ,dp

dt dx dt dy dt'dz dt ""^d^ ‘

t,    dx    du    dz

Имея в    виду,    что ^г = «; ~ft^=zV’    di~^w’    ^полУ^чим:

dt    дх>    dy'    dz    i dt'

Подставив    p    в уравнение    (1-106)    и    преобразовав,    будем

иметь:

dp . д (ри) _|_ д (ри) | d(pa>)__n dt'~dx*dy~^t' dz •    К¹'¹*)

Если движение является установившимся, то ^—0.

Для несжимаемой жидкости (р = const) легко получить из уравнения (1-12):

fe+S+5I = °-    (^М3)

Уравнение (1-12) является уравнением неразрывности газового потока в дифференциальной форме. Это уравнение было впервые получено Эйлером в 1659 г. Мы видим, что оно связывает изменения плотности с изменениями составляющих скорости и, v и w. Имея в виду

ди dv dw механическим смысл частных производных ^    ^    и

выражающих скорости относительной линейной деформации жидкой частицы в направ-? лении осей х, у иг, можно на основании уравнения неразрывности заключить, что деформация такой частицы подчиняется определенной закономерности и не может быть произвольной. Для несжимаемой жидкости уравнение (1-13) показывает, что частица не-

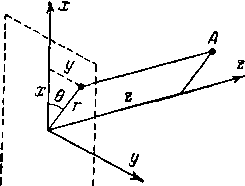
сжимаемой жидкости в про- Рис. 1-11. Положение точки в цессе движения деформирует- прямоугольной    и    цилиндрической

ся с сохранением объема.    системах    координат.

Для сжимаемой жидкости деформация частицы происходит с изменением объема. В этом случае уравнение неразрывности связывает изменения объема и плотности частицы.

Уравнение (1-12) записано в прямоугольной системе координат. Во многих случаях, в особенности при изучении процессов, протекающих в турбомашинах, удобно пользоваться цилиндрической системой координат.

Положение некоторой точки А в цилиндрических координатах определяется радиусом-вектором г, полярным углом 0 и аппликатой г (рис. 1-11). Давая указанным координатам бесконечно малые приращения dr, db и dz, выделим в массе жидкости частицу ABCDA’B'C'U (рис. 1-12).

Движение точки в рассматриваемых координатах задано, если известны составляющие скорости:

dr

^c_r — ^f_t — радиальная составляющая;

dd ,

—    —тангенциальная составляющая (нормальная к ра

диусу-вектору);

Составим уравнение неразрывности в цилиндрических координатах. Подсчитаем скорость относительной объемной деформации .движущейся жидкой частицы, показанной на рис. 1-12. Изменение объема этой частицы за элемент времени dt в направлении радиуса-вектора можно вырасить так:

или, оставляя члены одного порядка

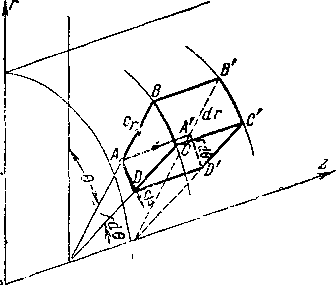
Рис. 1-12. К выводу уравнений Эйлера в цилиндрической системе координат.

й

Изменение объема в направлении, нормальном к радиу-су-вектору, будет:

?( c₀-f-    —    _e,l    dzdrdt    =    Y    ^-dzdrdbdt.

По оси z объем меняется на величину

Суммарное изменение объема за рассматриваемый отрезок времени составляет:

/ с. дс_г 1 дс₀ г),м\

7^+^j) rdzdrdbdt.

Тогда скорость относительной объемной деформации будет:

dAV __

Д1/ dt г I dr I г 60 I^- д_г '

Подставив это выражение в уравнение неразрывности (1-1 Оа) и выразив полную производную плотности в цилиндрических координатах, после преобразований окончательно получим:

Й+Г+да+^-О- О-Н)

1-4. УРАВНЕНИЯ КОЛИЧЕСТВА ДВИЖЕНИЯ

Ниже рассматривается движение газа без внутреннего теплообмена при отсутствии теплопроводности и трения.

Такое движение является, конечно, идеализированной моделью действительного движения, в котором проявляются силы трения, возникают градиенты температуры и совершается внутренний теплообмен между соседними частицами.

Принимаемая упрощенная схема потока сжимаемой жидкости, однако, играет весьма важную роль в газовой динамике, так как она служит известным эталоном при анализе действительных процессов течения. Многие практически важные реальные случаи течения газа весьма близки по своим свойствам к рассматриваемому идеализированному течению, закономерности которого в этих случаях могут быть использованы для расчетов. Получаемые при указанных упрощениях зависимости широко используются для анализа физических свойств потока, энергетически изолированного от окружающей среды.

Установим основные закономерности, которым подчиняется такая схематизированная модель течения.

Выделим в потоке жидкости элементарный параллелепипед. Внутри замкнутой говерхности параллелепипеда заключена масса жидкости. Применим к рассматриваемому элементу теорему количества движения.

Изменение количества движения массы газа, сосредоточенной внутри поверхности, происходит в общем случае вследствие того, что каждая частица, перемещаясь, занимает с течением времени новое положение и приобретает новую скорость, а также потому, что в каждой точке пространства скорость изменяется во времени. При установившемся движении количество движения меняется только в связи с изменением положения частиц.

В соответствии с известной теоремой механики изменение количества движения массы, заключенной в выделенном элементе, равно импульсу внешних сил. Составим уравнения импульсов в проекциях на координатные оси (рис. 1-10).

На грань ABCD в направлении оси л: действует сила давления pdyd2, импульс которой будет:

pdydzdt.

Импульс сил давления, действующих на грань А'В'СЧУ, равен:

— (p-\-^d?dx^ dydzdt.

Заметим, что, кроме сил давления, на элемент могут действовать массовые силы (гравитационные, магнитные и электростатические). Из них чаще всего необходимо учитывать гравитационную силу — силу тяжести. Для газов вследствие относительно малой их плотности сила тяжести по сравнению с силами давления оказывается малой и ею обычно можно пренебречь.

Однако в некоторых задачах влияние массовых сил должно быть учтено. Обозначим через X, Y и Z проекции единичной массовой силы (отнесенной к массе жидкости) на оси координат х, у и 2. Тогда проекции полной массовой силы на координатные оси будут:

Xpdxdydz, Ypdxdydz и ZpdxdydZ.

Введем импульс массовых сил в проекции на ось л:, равный Xpdxdydzdt. Тогда суммарный импульс равен изменению количества движения:

Xpdxdydzdt — dxdydzdt ~ pdxdydzdu_xгде рdxdydz — масса элемента.

du у 1 др

dt    f дх '

Аналогичные уравнения получим в проекции на оси у иг:

(1-156)

(1-15b)

dw

dt

= Z —

dv у  ¹' др.

dt    р ду ’

1 др

р dz

Имея в виду, что приращения скорости равны:

^d-=^dT_x^dx+%^dy+fz^dz+%^dt>

^dv=^+%^dy+fz^d2+%^dt’

, dw , I dw .    , dw , i dw ,,

dw = — dx-{-^ dy+^ dz-\-_w dt,

dx

для проекции ускорения на координатные оси получим из (1-15):

da ди , ди , ди i ди _v= 37 +^lld-_X + ^V?y+^Wrz = ^X-

1 dp. p 6л’

L

P

1 dp p 6*

dt dt

(1-16)

dx

dw

dw

’^JdF

J

dv dv . dv

dt    dt ‘ ^U Л*

dw

dt

dv . dv ,,

¦»ГТ*Г='-dy ¹ dz

dw

%

r-г    du dv dw

Производные ^    ^ и ^ выражают проекции полного

ускорения движущейся частицы. Уравнения (1-16) показывают, что ускорение жидкого элемента вызывается соответствующими изменениями сил давления, действующих на этот элемент, и массовыми силами. Уравнения (1-16) были также получены Эйлером.

Составим теперь уравнения импульсов в цилиндрических координатах. С этой целью найдем составляющие ускорения в новой системе координат. Полное ускорение вдоль радиуса-вектора выражается как сумма относитель-

dc_r

dt

——. Следовательно, радиальное ускорение равно:

'    о

dc, ci

dt

Полное ускорение в направлении, нормальном к радиусу-вектору, складывается из тангенциального ускорения Г ^ „ „    о dr d%

dt²

и кориолисова ускорения 2 —¦ — , т. е.

dt dt 1 d (rc₈) dc_%

d²0 . n dr dQ ^rriii-T^Z:

'dt

dt dt

dt

Тогда уравнения импульсов (1-15) можно записать в такой форме:

dc__r dt dc_e dt ' dw

W'

--У-

r

cr.

-R

(1-17)

Z —

)

-ft    ^{1 c}^-

— ^y--P rdV

1 dp .

7 Tr^;

1 dp p dz '

где R, 0 и Z — проекции единичной массовой оси координат г, 6 и г.

силы на dc_r

Ж

Подставив в (1-17) значения полных производных ,

dc д    d_w

и — через частные, окончательно находим:

1

1 dp . р гдд’

(l-17a)

—'4_г ^0.1» ^ dt г дг т~ г

^8, ?fe, ^св ^дс°

dt ‘ ^ г dr г

<30

^дсг ^С1    г> I dp.

^u2Jdz~ г    р dr ’

dc_a с_гс_й

¦и_г‘4-—^е=0-dz¹ г

dw .    dw    .    ^се    dw    . dw ~    1    dp

+    -Wjt — Z--

dt ¹    r Q_r    i    _r    fig    i d_z    о

)

1-5. УРАВНЕНИЯ ДВИЖЕНИЯ В ГИДРОМЕХАНИЧЕСКОЙ ФОРМЕ. УРАВНЕНИЯ И. С. ГРОМЕКО

Уравнения движения в форме Эйлера являются общими уравнениями механики. Особенности движения жидкой среды могут быть отражены введением специфических элементов движения — компонентов вихря, кинетической и потенциальной энергии — в уравнения Эйлера.

Компоненты угловой скорости вращения а>_х, ш_у и <»_г могут быть непосредственно введены в уравнения движения (1-16) и (1-17а). Если к левой части первого из уравнений (1-16) добавить, а затем отнять    то после

несложных преобразований получаем:

да    . ди    , до    . до»    /ду да \    , /да да) \

~dt    ^U дх    ^V~дх    дх ~    [дх~ду    \дг~Ш)

= L ZL.

р дх

Имея в виду, что

и учитывая формулы (1-6), представим первое из уравнений движения (1-16) в такой форме:

Аналогично можно преобразовать и два других' уравнения движения. В результате получим:

Аналогично можно преобразовать уравнения (1-17а) в цилиндрической системе координат. Компоненты угловой скорости вращения в этой системе координат выражаются уравнениями:

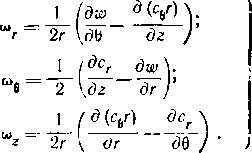
0-1‘О

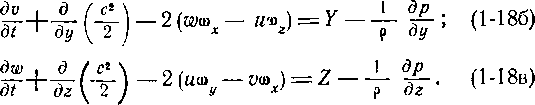
Пользуясь известными формулами перехода от прямоугольных к цилиндрическим координатам, нетрудно выразить компоненты угловых скоростей со_Л, ы_у и ы_г через ш_г, и со_г. Угловая скорость вращения ш может быть выражена через составляющие <л_г, со^ и ш_г по уравнениям (1-19), так как

⁼ “х + “у + “г ⁼ “г + “е + "г •

Смысл величин ь>_г, и ь>_г поясняется на рис. 1-13. Составляющая <?>_г определяет такое вращение частиц, осью которого является радиус-вектор (радиальный вихрь); компонента характеризует вращение частиц относительно оси, имеющей форму окружности (кольцевой вихрь); ш_г представляет собой угловую скорость вращения вокруг оси z.

dw

Введем в левую часть первого уравнения (1-17а) члены:

dw

— ^с9 ~дг ’ ^тогда

*?¦•    “•²⁰>

аналогично преобразуются второе и третье уравнения (1 17а).

Преимущества уравнений количества движения (1-18)— (1-20)    очевидны.    В    отличие    от    уравнений Эйлера они содержат    в    явной    форме    величины, характеризующие особенности    движения    жидкости — легко деформируемой среды.

Эти уравнения включают компоненты угловой скорости вращения частиц, т. е. члены, характеризующие вихревое движение жидкости, кинетическую энергию и потенциальную энергию давления, а также потенциальную энергию

массовых сил.

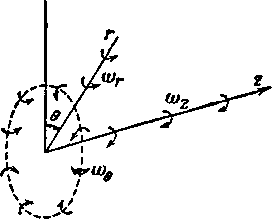
Рис. 1-13. К определению компонентов вихря в цилиндрической системе координат

Введение этих величин существенно упрощает анализ многих сложных видов движения жидкости и, в частности, облегчает исследование некоторых свойств потока в проточной части турбомашин.

В некоторых частных случаях уравнения (1-18) или (1-20) легко интегрируются. Для этой цели уравнениям движения мож-

но придать еще более простую и наглядную форму, вводя некоторую функцию давления

(1-21)

Кроме того, влияние массовых сил учитывается путем введения потенциальной функции U, частные производные от которой по координатам выражают проекции ускорения массовых сил на оси координат:

dU ^ dU

У  ___#    у  _ у

^Л~~ дх'    ду'    ~~~ dz •

Тогда уравнения (1-18) принимают вид:

'+я-(т-+¹'+^р)=²(^“"’"»)'

, ( "j-

(1-22)

(1-23)

Уравнения (1-23) были получены профессором Казанского университета И. С. Громеко в 1881 г.

Для установившегося движения    — ^

после умножения обеих частей уравнения (1-23) соответственно на dx, dy и dz и суммирования нетрудно получить:

¦<*(4 + У + Р)=2

dx dy dz

и V W <D СО Ш

(1-24)

Определитель (1-24) равен нулю в следующих частных случаях:

а) при отсутствии вихрей в жидкости, т. е. когда

: to = CD =0; у г ’

б) при условии

_dy_z ~ V

dx

и

условия „б“ и ,в“ являются дифференциальными урав

нениями линий тока и соответственно вихревых линий [см. уравнение (1-5)]; следовательно, согласно условиям „б" и ,в“ определитель (1-24) равен нулю для линий тока и вихревых линий;

г) при

Via =доа» ; w<a = и,’л_\ цю    ,

2    уХ    у    X

ИЛИ

и

V

со

СО

У

X

г

(1-25)

Во всех перечисленных случаях из (1-24) получаем:

или после интегрирования

(1-26)

Интеграл (1-26) является уравнением энергии для струйки, т. е. выражает баланс энергии жидкой частицы: сумма кинетической и потенциальной энергии, т. е. полная энергия частицы является величиной постоянной. Следует вспомнить, что функция U выражает потенциальную энергию массовых сил, а Р — потенциальную энергию сил давления. Первый член (1-26) дает величину кинетической энергии жидкой частицы. Все указанные составляющие полной энергии отнесены к секундной массе протекающей жидкости.

Несмотря на то, что интеграл (1-26) имеет одинаковую форму для всех рассмотренных случаев, смысл его и область применения различны в зависимости от условий, для которых интеграл был получен.

Для безвихревого установившегося движения жидкости (случай ,а“) интеграл (1-26) справедлив для всех точек потока.

При выполнении условий ,6“ или „в“ полная энергия частицы сохраняется постоянной только вдоль линии тока

или соответственно вдоль вихревой линии. При переходе от одной линии тока к другой или от одной вихревой линии к соседней величина постоянной в правой части (1-26) может меняться.

Условие „г“ пропорциональности линейных и угловых скоростей (1-25) приводит к интегралу (1-26), т. е. к постоянству полной энергии- жидкой частицы, справедливому для всех точек потока. Следовательно, в рассматриваемом частном случае вихревого движения полная энергия сохраняется неизменной для всех вихревых линий. Особенность этого вида движения состоит в том, что каждая частица вращается вокруг оси, вдоль которой она движется. Действительно, условие (1-25) означает, что направления векторов линейной и угловой скоростей совпадают, так как пропорциональность этих векторов указывает на то, что эти векторы ориентированы под одинаковыми углами к осям координат. В рассматриваемом движении линии тока и вихревые линии совпадают. Заметим, что во всех изучаемых случаях при адиабатическом течении в точках, связанных между собой интегралом (1-26), энтропия остается постоянной.

Интеграл (1-26) можно преобразовать для практически важного случая, когда из массовых сил действует только сила тяжести; при этом

X = Y = 0; Z = -g

(ось 2 направлена вертикально вверх).

Следовательно,

dU    ,,

_Tz=g и U = gZ.

После подстановки [этих величин уравнение (1-26) приобретает вид:

-у +8^z + ^y = const-    (1-27)

Для несжимаемой жидкости (р = const) находим: ^ + ² +    = const.    (1-28)

Последнее уравнение получено Д. Бернулли. Величина г в этом уравнении характеризует потенциальную знергию

положения, обусловленную движением в однородном поле земного тяготения жидкой частицы, и называется нивелирной высотой. Величина — представляет собой потенциаль-

с²

ную энергию давления (пьезометрическая высота), а -=--

кинетическую энергию; все члены уравнения (1-26) отнесены к секундному весу протекающей жидкости.

Глава вторая одномерное движение газа  »

Библиотека »