§ 6. зависимость проницаемости от пористости и размера пор

§ 6. ЗАВИСИМОСТЬ ПРОНИЦАЕМОСТИ ОТ ПОРИСТОСТИ И РАЗМЕРА ПОР

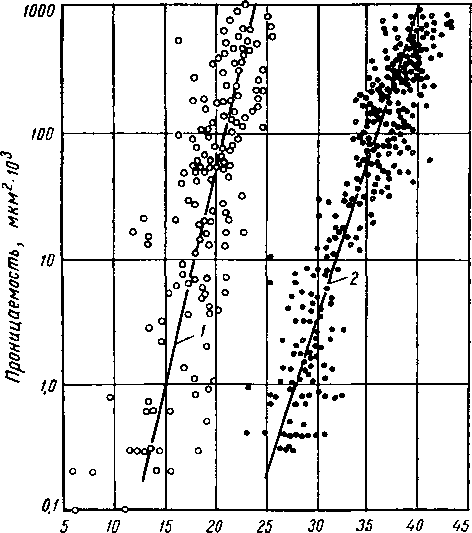
Прямой зависимости между проницаемостью и пористостью горных пород не существует. Например, трещиноватые известняки, имеющие малую пористость, часто обладают большой проницаемостью и, наоборот, глины, иногда характеризующиеся высокой пористостью, практически непроницаемы для жидкостей и газов, так как их поровое пространство слагается каналами субкапилляр-ного размера. Однако на основании среднестатистических данных можно сказать, что более проницаемые породы часто и более пористые ⁴⁵ (рис. 1.10).

Проницаемость пористой среды зависит преимущественно от размера поровых каналов, из которых слагается поровое пространство. Поэтому изучению структуры, строения и размеров пор уделяется большое внимание.

Зависимость проницаемости от размера пор можно получить путем приложения законов Дарси и Пуазейля к пористой среде, которую представим в виде системы трубок одинакового сечения. По закону Пуазейля расход Q жидкости через такую пористую среду составит

<!•“>

где п — число пор, приходящихся на единицу площади фильтрации;

R — радиус поровых каналов (или средний радиус пор среды);

(1.15)

V,

т -

пор

nFnR*L

' Обр

FL

¦¦ nnR².

Пористость, %

Рис. 1.10. Зависимость между проницаемостью и пористостью пород двух коллекторов (по А. И. Леворсену). / — песчаник эоценового возраста; 2 — тонкозернистый песчаник мелового возраста.

F — площадь фильтрации;

Ар — перепад давления; ц — динамическая вязкость жидкости; L — длина пористой среды. Коэффициент пористости среды

Подставляя в формулу (1.14) вместо п nR² значение пористости т, получим

_п mR^F Др

(1-16)

8(iL

По закону Дарси расход жидкости через эту же пористую среду

kApF (.i L

Q =

Здесь к — проницаемость пористой среды. 28

Приравнивая правые части формул (1.17) и (1.16), получим

, тД2

Откуда

R =

Если выразить проницаемость в дарси, то радиус поровых каналов R (в м) будет равен

О-¹⁹)

Или, если R выразить в мкм, то

* = 2,86/4- (1.20)

Величина Л, определенная по формуле (1.19), представляет собой радиус пор идеальной пористой среды, обладающей пористостью т и проницаемостью к. В приложении к реальной пористой среде величина R имеет условный смысл и не определяет среднего размера пор, так как не учитывает их извилистость и сложное строение.

По предложению Ф. И. Котяхова лучше вычислять средний радиус пор реальных пористых сред по эмпирической формуле

R

7 • 10⁶

где ф — структурный коэффициент, характеризующий отличительные особенности    строения порового    пространства    реальных коллекторов.    Величину    ф    можно оценить    путем    измерения    электросо

противления пород. Для керамических пористых сред при изменении пористости от 0,39 до 0,28 по экспериментальным данным ф изменяется от 1,7 до 2,6. Структурный коэффициент для зернистых пород можно приблизительно определить также по эмпирической формуле

0,5035    /_{Т оох}

=    (^L22>

Другим широко применяемым методом исследования структуры и строения высокодисперсных пористых тел является экспериментальная порометрия — измерение размеров и характера распределения пор по размерам.

§ 7. распределение пор по размерам.  »

Библиотека »