Часть 2. лопастные насосы и гидродинамические передачи глава 12. основы теории лопастных насосов

часть 2. ЛОПАСТНЫЕ НАСОСЫ

И ГИДРОДИНАМИЧЕСКИЕ ПЕРЕДАЧИ

Глава 12. ОСНОВЫ ТЕОРИИ ЛОПАСТНЫХ НАСОСОВ

2.1. Введение

! Гидравлическими машинами называются машины, которые сооб-щают протекающей через них жидкости механическую энергию ¹ (насос), либо получают от жидкости часть энергии и передают ее ¦ рабочему органу для полезного использования (гидравлический

1 двигатель). Насосы являются одной из самых распространенных разновидностей машиы. Их применяют для различных целей, начиная от водоснабжения населения и предприятий и кончая подачей топлива в двигателях ракет. Гидродвпгатели имеют большое значение в энергетике. В настоящее время в Советском Союзо около 20 % всей электроэнергии вырабатывается на гидроэлектростанциях. Для использования гидравлической энергии рек и преобразования ее в механическую энергию вращающегося вала генератора на гидроэлектростанциях примепяют гидротурбины, являющиеся одной из разновидностей гидродвагателей. Мощность современных гидротурбин доходит до 650 тыс. кВт. Турбины используют и при бурении скважин.

Насосы и гидродвигатели применяют также в гидропередачах, назначением которых является передача механической энергии от двигателя к исполнительному рабочему органу, а также преобразование вида и скорости движения последнего посредством жидкости. Гидропередача состоит из насоса и гидродвигателя. Насос, работающий от двигателя, сообщает жидкости энергию. Пройдя через насос, жидкость поступает в гидродвигатель, где передает механическую энергию исполнительному рабочему органу. Назначение гидропередач такое же, как и механических передач (муфты, коробки скоростей, редукторы и т. д.), однако но сравнению с последними они имеют следующие преимущества.

4. Большая плавность работы. Люфты, неизбежные в элементах механической передачи, а также неточность ее изготовления приводят к вибрациям. Включение и выключение механической передачи или изменение ее передаточного числа сопровождается толчками.

2. Возможность получения бесступенчатого изменения передаточного числа. В механических передачах изменение передаточного числа обычно производится ступенями. Механические передачи, допускающие бесступенчатое изменение передаточного числа (например, фрикционные), недостаточно надежны и могут применяться только при малой мощности.

3.    Возможность получения меньшей зависимости момента на ведущей валу от нагрузки, приложенной к исполнительному органу. Это упрощает обслуживание машин н предохраняет двигатель и трансмиссию от перегрузки.

4.    Возможность передачи больших мощностей.

5.    Малые габаритные размеры и масса.

6.    Высокая надежность.

Эти преимущества привели к большому распространению гидропередач, несмотря на их несколько меньший, чем у механических передач КПД.

В современной технике применяется большое количество разновидностей гядромапшн. Наибольшее распространение получили объемные я лопастные насосы и гидродвигатели. Объемные гидро-ыашшга (поршневые, шестеренные, аксиально-поршневые и т. д.) работают за счет изменения объема рабочих камер, периодически соединяющихся с входным и выходным патрубками- Рабочим органом лопастной машины является вращающееся рабочее колесо, снабженное лопастями. Энергия от рабочего колеса жидкости (лопастный насос) или от жидкости рабочему колесу (лопастный двигатель) передается путем динамического взаимодействия лопастей колеса с обтекающей пх жидкостью. К лопастпым насосам относятся цеятробежпые и осевые.    '    .

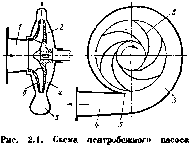
копсольпого типа:

- раСочсе кодсео; i

На рис. 2.1 изображена простейшая схема центробежнояр насоса. Проточная часть насоса состоит из трех осповвых элементов — подвода 1, рабочего колеса 2 и отвода 3. По подводу жидкость подается в рабочее колесо нз подводящего трубопроьода. Назначением рабочего колеса является передача жидкости энергии от двигателя. Рабочее колесо центробежного насоса состоит из ведущего а и ведомого (обода) б дисков, между которыми находятся лопатки в, изогнутые, как правило, в сторону, противоположную направлению вращения колеса. Ведущем диском рабочее колесо крепится на валу. Жидкость движется через колесо из центральной его части к периферии. По отводу жидкость отводится от рабочего колеса к напорному патрубку или, в многоступенчатых насосах, к следующему колесу.

К наиболее распространенный лопастным гидродвнгателям относятся радиально-осевые и осевые гидротурбины. Радпальяо-осевая гидротурбина принципиально не отличается по конструкции от центробежного насоса. Направление движения жидкости в вей и направление вращения колеса противоположны движению в центробежном насосо. Радиально-осевая турбина и центробежный насос являются обратимыми машинами и могут работать как в турбинном, так и в насосном режимах.

Рассмотрим подробнее механизм передачи энергии в лопастной гидромашиие. При обтекании потоком крылового профиля (например, крыла самолета) на его верхней и нпншей поверхностях образуется перепад давления и, следовательно, возникает сила Р (рис. 2.2), которая называется подъемной силой. Аналогично этому возникает подъемная сила на лопатках рабочего колеса лопастпой гидромашины при движении их в жидкости. У лопастного насоса направление момента подъемных сил противоположно направлению вращения рабочего колеса. Преодолевая этот момент при вращении, колосо совершает работу. Для этого к колесу от двигателя подводится энергия, которая, согласно закону сохранения энергии, передается жидкости и увеличивает ее удельную энергию. В дальнейшем удельная энергия жидкости частично Рис. 2.2. Сила, действующая на врыло- превращается в тепло ыз-за тре-вои профиль    _{пия и0Ж}ду слоями жидкости в

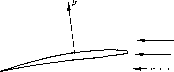
насосо и, следовательно, теряется, частично остается в форме механической удельной энергии, составляя полезный папор насоса. Насос конструируют так, чтобы потери энергии были возможно малыми.

У лопастного двигателя (гидротурбины) направление момента подъемных сил совпадает с направлением вращения колеса. Воздействуя на лопатки, жидкость вращает рабочее колесо, передавая ему энергию.

Лопастные насосы бывают одноступенчатыми и многоступенчатыми. Одноступенчатые насосы имеют одно рабочее колесо, многоступенчатые — несколько последовательно соединенных рабочих колес, закрепленных на одпом валу. На рис. 2.1 изображен одноступенчатый насос консольного типа. Рабочее колесо у этих пасосов закреплено на конце (консоли) вала. Вал не проходит через область всасывания, что позволяет применить простейшую форму подвода в виде прямоосного коифузора.

На рис. 2.3 изображен одноступенчатый насос двустороннего входа. Он имоег раадваивающийся спиральный подвод (ем. рис. 2.47). Жидкость входит в рабочее колесо с двух сторон двумя потоками. В рабочем колесе эти потоки соединяются и выходят в общий отвод.

Одноступенчатые насосы сообщают жидкости ограниченный напор ³⁶. Для повышения напора применяют многоступенчатые насосы, в которых жидкость проходит последовательно через несколько

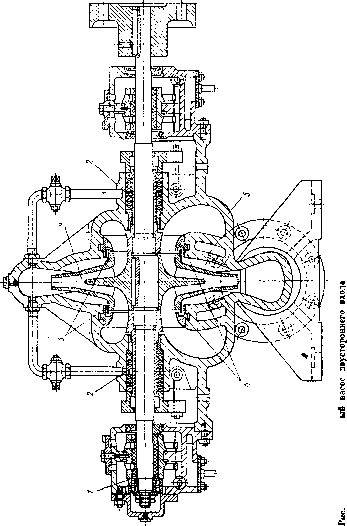
2.3. Одноступенчат!

рабочих колес, закрепленных на одном валу (рис. 2.4). При этом пропорционально числу колес увеличивается напор насоса.

Осевые насосы будут рассмотрены в п. 2.8.

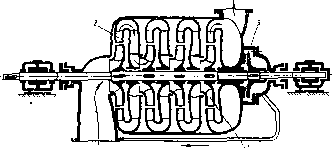
Рве. 2Л. Схема многоступенчатого секционного центробежного насоса: . 1 — рабочее нодесо; s — насравлпкмцнЗ аппарат; s — гидравлическая пята

2.2. Подача, напор н мощность насоеа

Работа насоса характеризуется его подачей, напором, потребляемой мощностью, КПД и частотой вращения. Подачей насоса называется расход жидкости через напорный (выходной) патрубок. Так же как и расход, подача может быть объемной (<?) и массовой (Q_m). Напор Н представляет собой развость анергий единицы веса жидкости в сечении потока после насоса г_в + р_а/ (Р?) *1“ щ! (2g) и перед ним z_a + р_в/ (pg) + v\! (2g):

(2.1)

Я = г_и - 2_В + (р_в - Pb)l(pg) + (Ун - »1)/(2 g)

а выражается в метрах.

Мощностью насоса (мощностью, потребляемой насосом) называется энергия, подводимая к нему от двигателя за единицу времени. Мощность можно определить из следующих соображений. Каждая единица веса жидкости, прошедшая через насос, приобретает энергию в количестве Н, за единицу времена через насос протекает жидкость весом Qpg. Следовательно, энергия, приобретенная за единицу времени жидкостью, прошедшей через пасос., иле полезная мощность насоса

(2.2)

Nn^QpgH.

Мощность насоса N больше полезной мощвоети N_n па величину потерь в насосе. Эти потери оцениваются КПД насоса tj, который равен отношению полезной мощности насоса к потребляемой:

(2.3)

4i = Nu/N.

Отсюда мощность, потребляемая насосом,

JV = gp_Sff/ri.    (2.4)

По этой мощности подбирается двигатель. Найденные по уравнениям (2.2) и (2.4) мощности выражаются в единицах СИ с ваттах, в технической системе единиц — в кгс-м/с.

2.3. Баланс энергии в лопастном насосе

На рнс. 2.5 изображен баланс энергии в лопастном насосе. К насосу подводится мощность N. Часть этой мощности теряется (превращается в тепло). Потери мощности в насосе делят на механические, объемные н гидравлические.

Механические потери. Механическими являются потери на трение в подшипниках, в уплотнениях вала л па трение наружной    ,,

поверхности рабочих колес о жид-    Нехани- Объемные ческие

кость (дисковое трение).    веские

Н _я,    ГидраI

Мощность, остающаяся за ви-    Потери

четом механических потерь, передается рабочим колесом жидкости.

Ее принято называть гидравли-ческой. Энергия, переданная рабочим колесом единице веса проходящей через него жидкости, называется теоретическим напором Я_т. Он больше напора Я насоса на величину гидравлических потерь йд при течении жидкости в рабочих органах насоса:

Величина механических потерь оценивается механическим КПД, который равен отношению оставшейся после преодоления механических сопротивлений гидравлической мощности N? к мощности N, потребляемой насосом

Чмех = N_e/N.    (2-7)

Объемные потери. Рассмотрим объемпые потери в одноступенчатом насосе. Жидкость, выходящая из рабочего колеса в количестве Q„, в основном поступает в отвод (Q) и, следовательно, в напорный патрубок насоса, и частично возвращается в подвод через зазор в уплотнений 1 между рабочим колесом и корпусом насоса (уточка q_H, рис. 2.6). Энергия жидкости, возвращающейся в подвод, теряется. Эти потери называются объемными. Утечки обусловлены тем, что давление па выходе из рабочего колеса больше, чем в подводе.

Утечки той значительное, чем больше зазор в уплотцеппи 1 между рабочим колосом и корпусом насоса. Для того чтобы уменьшить утечки, следует уменьшить этот зазор до минимума, допускаемого технологией изготовления и деформацией вала и корпуса насоса при их нагрузке во время работы.

Кроме рассмотренных утечек жидкости имеют место утечки через уплотнения вала. Они обычно малы и при рассмотрении баланса мощпости ими можно пренебречь.

Объемные потери оценивают объемным КПД, равным отношению мощности N', оставшейся за вмчетом мощности, затрачиваемой на объемные потери, к гидравлической мощпости N_T (см. рис. 2.5): т)₀ = N'/Nr = (N_r - jV₀)/iV_r>    (2.8)

где N о — мощноыь, затрачиваемая на объемные потерн.

Каждая единица веса жидкости, протекающей через уплотнение -рабочего колеса, уносит энергию Я_т. Следовательно, мощность, эатрачинаемая на объемные потери N₀=q_KpgH_T.

Так как расход через колесо Q_K = Q -f q_K (см. рис. 2.6),

N' = N_r — N₀ = Q_ePgH, - g_K9gH, =QpgII,.    (2.9)

Подставив выражения (2.9) и (2.6) в уравнение (2.8), получим

4^Q/Q« = Ql(Q+q«).    (2.10)

В многоступенчатых насосах секционного типа (см. рис. 2.4) также имеются утечки жидкости через зазоры между валом и перегородками — диафрагмами, разделяющими ступени, и через гидравлическую пяту 3. Потери энергии, обусловленные утечками через уплотпения дцафрагм, относятся к гидравлическим и механическим потерям, а через гидравлическую пяту — к объемным. Для многоступенчатых секционных насосов объемный КПД определяется также по уравнению (2.10), однако при этом под q_K следует понимать не утечку через уплотнение рабочего колеса одной ступени, а сумму этой утечки и утечки q_a в гидравлической пяте.

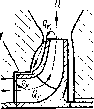
Рис. 2.6. Утечки о лощении рабочего леса

Гидравлические потери. Третьим видом потерь энергии в насосе являются потери иа преодолеппо гидравлического сопротивления подвода, рабочего колеса и отвода, или гидравлические потери. Они оцениваются гидравлическим КПД rj_г, который равен отношению полезной мощности насоса N_n к мощности N' (см. рис. 2.5). Согласно уравнениям (2.2), (2.5) и (2.))

Ч, = NJN' = tf/tf_т = Н/(Н -f h_B).

(2.11)

Как было указано в п. 2.2, КПД насоса tj = N_U/N.

Умножив и разделив правую часть уравнения на jV_riV', получим JVn iV'

t]= -Jjr 7^7 “Ту" ⁼ ^(-'По'Чмех»    (2.12)

т. е. КПД насоса равен произведению гидравлического, об-ьемного и мехашгаеского КПД.

2.4. Основное уравнение лопастных насосов

Основное уравнение лопастпых насосов можно вывести на основании уравнения (f .187) моментов количества цвтхснин

ДО,

примененного для жидкости, находящейся в рабочем колесе насоса, которое представляет собой систему каналов. Рассматриваемый объем жидкости ограничен изнутри и ио периферии поверхностями вращения, образующими которых явлпготся входные й выходние кромки лопаток. Момент сил давления на эти границы равеп нулю, так как нормали к поверхностям вращения проходят через ось колеса. Силы трения яа указанных грапицах пренебрежимо малы. Поэтому момент М, действующий на жидкость в колесе, обусловлен только воздействием на нее стенок каналов колеса (лопаток и внутренних поверхностей ведущего и ведомого дисков). Под величиной Q_m в уравнении (1.187) следует понимать массовый расход <2_mK = Q_K р жидкости через колесо.

Умножим последнее уравнение на угловую скорость ш рабочего колеса. Произведепие Мо~> есть секундная работа, которую совершает рабочее колесо, воздействуя яа находящуюся в нем жидкость. Эта работа равна энергии, передаваемой рабочим колесом жидкости за единицу времени, или гидравлической мощности N_r. О^юда Nr = Qm*® (^v_u2^2 — V_tM.

Согласно уравнению (2.6) с учетом того, что <?„р — Q_ml{,

N_r = Q_mKgH_T.

Следовательно,

= Qm»ш (t>_u2-fts —

Я_т = Я/r_1г = (оi/g) (»_uZR_a - v_ulR,).    (2.13)

Полученвое осиовпое уравнение лопастпых насосов было впервые выведено Эйлером. Оно связывает напор насоса со скоростями движения жидкости, которые зависят от подачи и частоты вращения насоса, а также от геометрии рабочего колеса и подвода. Поток на входе в колесо создается предшествующим колесу устройством — подводом. Следовательно момент скорости v_nlRi на входе в колесо определяется конструкцией подвода и практически не зависит от конструкции колеса. Поток на выходе из колеса создается самим колесом, поэтому момент скорости v_ulR₂ определяется конструкцией колеса, особенно геометрией его выходных элементов (наружным дваметром, шириной лопаток, углом установки их на выходе). Основное уравнение дает возможность по заданным напору, частоте вращения н подаче насоса рассчитать выходные элементы рабочего колеса.

Подводы многих конструкций, например прямоосный конфузор, ле закручивают поток и момент скорости у_и1Дх = 0. В атом случае теоретический напор

Я_т = (о>?g)v_u2R₂.    (2.14)

2.5. Движение жидкости в рабочем колесе центробежного насоса

В рабочем колесе пасоса частицы жидкости движутся относительно рабочего колеса и, кроме того, они вместе с ним совершают переносное движение. Сумма относительного и переносного движений

дает абсолютное движение жидкости, т. е. движение ее относительно неподвижного корпуса насоса. Скорость абсолютного движения v (абсолютная скорость) равна геометрической сумме скорости w жидкости относительно рабочего колеса (относительной скорости) и окружной скорости и рабочего колеса (переносной скорости):

v — w-\-u.    (2.15)

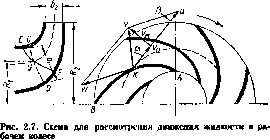
Для упрощения рассуждений допускаем, что поток в рабочем колесе осесимметричный. При этом траектории всех частиц жидкости в относительном движении одинаковы. Примем, что они совпадают с кривой очертания допаткв АВ (рис. 2.7). Относительные скорости частиц жидкости, лежащих на одной окружности, одинаковы и направлены но касательной к поверхности лопатки в рассматриваемой точке. Указанные допущения часто называют схемой бесконечного числа лопаток. В действительности поток жидкоств в рабочем колесе не является осесимметричным. Давление на лицевой еторопе ло-ватки (передняя сторона лопатки по отношению к направлению ее движения) больше, чем на ее тыльной стороне. Согласно уравнению Бернулли, чем больше давление, тем меньше скорость. Поэтому относительная скорость частиц, движущихся вдоль лицевой стороны лопатки, меньше относительной скорости частиц, движущихся вдоль ее тыльной стороны. Относительные траектории частиц, непосредственно примыкающих к лопатке, совпадают по форме с лопаткой. Траектории же остальных частиц отличаются от вее,

Из уравнения (2.15) следует, что скорости v, и> и и образуют треугольник скоростей. На рис. 2.7 изображено сложение скоростей для произвольной точки К внутри колеса. Согласно схеме бесконечного числа лопаток, относительная скорость w направлена по касательной к лопатке. Окружная скорость и направлена по касательной к окружности, на которой расположена рассматриваемая точка, в сторону вращения рабочего колеса.

Разложим абсолютную скорость v на две взаныно перпендикулярные составляющие: v_u — окружную составляющую абсолютной скорости и у_м — меридиональную скорость — проекцию абсолютной скорости на плоскость, проходящую через ось колеса и рассматриваемую точку. Эта плоскость называется меридиональной.

Введем следующие обозначения:

а — угол между абсолютной v и перепосной и скоростями жидкости;

j} — угол между относительной скоростью w и отрицательным направлением переносной скорости и жидкости;

р_я — угол между касательной к лопатке и отрицательным направлением переносной скорости и жидкости.

Введем также индекс 1 для обозначения скоростей и углов на входе в рабочее колесо и индекс 2 для обозначения тех же величин на выходе из него.

Построим треугольник скоростей для точки G входной кромки EF рабочего колеса (см. рис. 2.7). Меридиональную скорость t?_M1 определим из уравнения расхода. Принимая распределение меридиональных скоростей по ширине рабочего колеса равномерны^ получим p*ji = Qk/S i = Q}{ По? i),    (2.16)

где Q_H — расход жидкости, протекающей через колесо; S_t — площадь нормального сечения меридионального потока.

Меридиональным называют воображаемый поток, движущийся через рабочее колесо со скоростями, равными меридиональным. Иными словами, меридиональный ноток есть поток, протекающий без окружной скорости через полость вращения, образованную ведомым и ведущим дисками рабочего колеса. Нормальное сечение меридионального потока имеет форму поверхности вращения. Она образована вращением вокруг оси колеса линии CD, пересекающей под прямыми углами линии тока меридионального потока, и проходящей через точку G. Согласно теореме Гюльдена, площадь S„ этой поверхности вращения равна произведению длины Ь_х образующей CD на длину окружности, описываемой центром тяжести ли-

ш

еии CD при ее вращении вокруг оси насоса:

5_в = 2яД_ш&1,    (2.17)

где П\ц — радиус, на котором расположен цсптр тяжестп личин CD-

Часть поверхности вращения занята телом лопаток, поэтому искомая площадь нормального сечепия меридионального потока = i_:|:₁jS^,₀, где ifj < 1 — коэффициент стеснения на входе в рабочее колесо.

Величина !(>! определяется из следующих соображении. Площадь 5i=2nR_ul6, —

где <У₁ — толщина лопатки ]

гдо s, — толпцша лопатки иа входе, измеренная по нормали к ее поверхности.

Отсюда ty =

= (2пЯ_и1-_г01)/(2я/?,_;1).    (2.18)

У наиболее распространенных насосов вели* чипа колеблется от 0,75 (малые колеса) до 0,88 (большие колеса). Окончательно получим

^ы1 ~ (?/(2nfl_lllb₁ii;₁r|o)-    (2.19)

В п. 2.4 было отмечено, что момент скорости v_ulR₁ и, следовательно окружная составляющая v_ul абсолютной скорости на входе определяются конструкцией подвода. Многие разновидности подвода не закручивают поток, при этом v_ul — 0. Окружная составляющая абсолютной скорости на входе пе равна нулю для спиральпого подвода (см. рис. 2.47) и часто для обратных каналов направляющего аппарата (см. рис. 2.49), служащих подводом промежуточных ступеней секционных насосов.

Окружная скорость рабочего колеса

^ = 0)/?!, (2.20) где со — угловая скорость рабочего колеса; R_t — радиус, па котором расположена точка G входной кромки колеса (см. рис. 2.7).

Зная величины i>_Ml, i>_ul и «_ь можно построить треугольник скоростей па входе (рве. 2.9) и, следовательно, определить относительную скорость и»! и углы а, и

Направление входного элемента лопатки следует выбирать близким к направлению относительной скорости w_v В противном случае получается отрыв потока от лопатки с образованием вихревой боны (см. рис. 2.12, б), сильно увеличивающей потери на входе в рабочее колесо. Опыт показывает, что как КПД, так и высота, на которую насос способен засосать жидкость (высота всасывания), увеличиваются, если входной элемент лопатки рабочего колеса установить по отцогаепшо к окружности не под углом |3_lt получающимся из треугольника скоростей входа, построенного для расчетной подачи насоса, а под углом |3_1Л, большим угла |3, на 3—8^Э. При таком небольшом отклонении входною элемента лоначки от направления относительной скорости отрыва потока от лопатки не получается. Назовем угол между направлением относительной скорости и направлением входного элемента лопатки углом атаки.

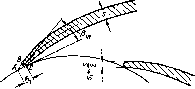
Начальпый участок лопатки утоняют по направлению к входной кромке примерно в 2 раза (см. рис. 2.8) па длине, равной 1/3—1/4 длины лопатки, причем входную кромку лопатки скругляют. Благодаря этому улучшаются условия обтекания входной кромки и уменьшаются гидравлические потери на входе жидкости на лопатки рабочего колеса.

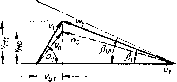
Рис. 2.9. Треугольник скоростей аа входе в рабочее колесо (штрих-пушггир-пяд ляпил показывает направленно входного элемепта лопатки)

Кроме того, при этом увеличивается высота всасывания насоса.

При построении треугольника скоростей входа было учтено стеснение потока лопатками.

Следовательно, треугольник скоростей построен для точки, расположенной непосредственно за входом на лопатки рабочего колеса. Для некоторых расчетов необходимо знать относительную и абсолютную скорости потока непосредственно перед входом на лопатки, т. е. потока, не возмущенного лопатками, Введем индекс О для обозначения скоростей этого потока, Учитывая уравнение (2.17), получим меридиональную скорость

к.. = де.Г|о) = <?/(2лЯ„Аг|о>-    '    (2.21)

Стеспение потока лопатками не может сказаться на величине окружной составляющей абсолютной скорости. Следоиагеяьно, y_u0 = i>_ul.

Треугольник скоростей перед входом в рабочее колесо изображен па рис. 2.9 штриховой линией.

Жидкость выходит из рабочего колеса через цилиндрическую поверхность площадью

S₂ = 2л/?гМ)2,

где R₂ — наружный радиус рабочего колеса (см. рис. 2.7); Ь₂ — ширина капала рабочего колеса на выходе; ij>₄ — коэффициент стеснения на выходе ил рабочего колеса,

Коэффициент 1|)₈ определяется по уравнению

ifj = (2n/?₂ — zcs)/(2rcfl₂),    (2 22)

где Cj — толщкна лопатки на выходе, намеренная в окружной направления: (Tj=j_s/8in p_sn.    (2.23)

У наиболее распространеппых насосов величина колеблется от

0,9 {малые пасосы) до 0,95 {большее насосы).

Меридиональная скорость на выходе

Vm = <?/<2я^_гМъЛо)-    (2.24)

Окружная скорость рабочего колеса на выходе Ui — aRz.    (2.25)

Окружпая составляющая скорости жидкости на выходе из рабочего колеса v_u2 определяется из уравнения Эйлера (2.13) по известному папору пссоса. Зная величины v_m, и_г и f_uS можно построить треугольник скоростей на выходе пз колеса (рис. 2.10, треугольник ADC) и определить из него величину и направление относительной скорости w_z. Опыт показывает, что направление относительной скорости w₂пе совпадает с направлением выходного элемента лопатки, что не соответствует схеме бесконечного числа лопаток. Причина этого отклонения относительного потока жидкости от выходного элемента лооаток в инерции жидкости. Рабочее колесо закручивает жидкость, увеличивая момент абсолютной скорости v_uR. Инерция препятствует этому изменению момента скорости. При бесконечном числе лопаток траектории относительного движения предопределены формой лопаток, которые препятствуют иному движению жидкости. При конечном числе лопаток проходы между ними широки, и траектории относительного движения частичек могут отличаться от формы лопаток. В этом случае из-за инерции, препятствующей увеличению момента v_uR абсолютной скорости, траектории частиц изменяются так, что момент скорости возрастает в меньшей степени. Следовательно, действительное значение окружной составляющей t»_u2 абсолютной скорости на выходе при конечном числе лопаток меньше, чем это следует согласно схеме бесконечного числа лопаток: v_ui < u_u2oo.

Рис. 2.10. Треугольник скоростей на выходе нз рабочего колеса

«Недокрутка» потока из-за конечного числа лопаток, т. е. указанное выше уменьшение окружной составляющей абсолютной скорости тем больше, чем шире канал между лопатками рабочего колеса, в, следовательно, тем больше, чем меньше число z лопаток, и больше угол р_л между лопаткой и окружностью {см. рис. 2,16).

Для большинства центробежных пасосов «недокрутка» потока из-за конечного числа лопаток может быть приближенно найдена

do формуле Стодолы—Маазеля

Вычислив по уравнению (2.26) окружную составляющую абсолютной скорости Р_и2от, можно построить треугольник скоростей ABC, соответствующий схеме бесконечного числа лопаток. В этом треугольнике скоростей относительная скорость w_i<a направлена по касательной к выходному элементу лопаткн. Иэ треугольника скоростей определяем угол р_2>1 установки выходного элемента лопаткн. Зная углы р_1Л и р_2П, получаем очертание лопатки в плане колеса. Следует отмстить, что чаще при расчете рабочего колеса центробежного насоса значением угла р_гл задаются на основании соображений, изложенных в п. 2.7, и определяют такой диаметр колеса D₂, при котором обеспечивается задапныи напор. Более подробно расчет проточной полости центробежного насоса будет изложен в п. 2.23.

При бесконечном числе лопаток согласно уравнению (2.13) теоретический напор насоса

Н_тоо - («/§)    — v^RJ.    (2.27)

Этот папор больше, чем напор при конечном числе лопаток, определяемый по уравнению (2.13), вследствие большей величины окружной составляющей абсолютной скорости на выходе (v_u2X > У_и2).

При прохождении жидкости через рабочее колесо повышается как ее кинетическая, тан и потенциальная энергия (давление). Скорость жидкости на выходе из рабочего колеса равна щ, на входе в него у₁. Следовательпо, прирост кинетической энергии единицы веса жидкости, или динамический напор, Ядвн-ОД-^)/(2*)-

Квадрат абсолютной скорости равен сумме квадратов меридиональной и окружной составляющих. Следовательно,

Г,    ^vu2~^vu\ , ^рм2 ^—Ри1

вд„.--5—+ 2Г -¦

Меридиональные скорости v_MS и с_М1 сравнительно малы и рааностыо их квадратов можно пренебречь по сравнению с квадратом скоростями». По этол же причине часто можно пренебречь квадратом окружной составляющей абсолютной скорости па входе р_и1. Тогда

H_am~vh/(2g).    (2.28)

Прирост энергии давления единицы веса жидкости лрн ее прохождении чорез рабочее колесо, или потенциальный напор,

2.6. Характеристика центробежного насоса

Рабочие органы насоса рассчитывают для определенного сочетания подачи, напора и частоты вращения, причем размеры и форму проточной полости выбирают так, чтобы гидравлические потери при работе на этом режиме были минимальными. Такое сочетание подачи, напора в частоты вращения называется расчетным режимом. При эксплуатации насос может работать на режимах, отличных от расчет-пого. Так, прикрывая задвижку, установленную на напорном трубопроводе пасоса, уменьшают подачу. При этом также изменяется напор, развиваемый насосом, Для правильной эксплуатации насоса необходимо зпать, как изменяются напор, КПД и мощность, потребляемая насосом, при изменении его подачи, т. е. знать характеристику насоса, под которой понимается зависимость папора, мощности и КПД от подачи пасоса при постоянной частоте вращения.

Ограничимся рассмотрением случая подвода жидкости к рабочему колесу без момента скорости (v_ul = 0). При этом теоретический папор при бесконечном числе лопаток, согласно уравнению (2.27)

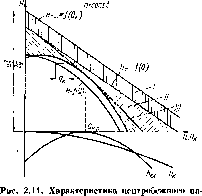
I — уменьшение напора из-аа коночного числа лопаток; II — потери и каналах иасоса Л • III — иотсри

H_lca — (<a/g) y_u2cci?2 =

= «2l>„2=o/?-    (2.30),

Из треугольника скоростей на выходе из рабочего колеса (см. рио. 2.10) и уравнения (2,24) находим

г\,2со = и₂ — v_M2 ctg р₂л =

—и₂ — ctg ргл(!к/(2л/?₂6_?1{)₂).

(2.31)

Подставив это выражение в уравнение (2.30), получим H^-uVg-

— щ ctg РалйдаяДЛЪ).

(2.32),

Из уравпепия следует, что зависимость теоретического напора при бесконечном числе лопаток от расхода Q_K через колесо линейная (рис. 2.11). При подаче, равной нулю (задвижка на напорном трубопроводе закрыта полностью),

Ятос “«!/?¦

При конечном чпсле лопаток зависимость теоретического напора Н_Т от расхода через рабочее колесо тоже линейная. Так как па одинаковых подачах теоретический напор при конечном числе лопаток меньше, чем при бесконечном, прямая Н_Т — / (Q_H) расположена ниже прямой Я_тео = / ((?„). Из уравнений (2.26) и (2.13) следует, что приближенно прямые Я_тс0 = / (<3к) и Н, = / (0к) параллельны.

Напор, развиваемый насосом, меньше теоретического на величину гидравлических потерь:

Я = Я_т — h_a.

Эти потери состоят из потерь fe_BX при входе в рабочее колесо и в отвод и потерь h_K в каналах подвода, рабочего колеса и отвода (потери в каналах насоса).

Потери в каналах насоса приближенно пропорциональны скорости жидкости во второй степени и, следовательно, расходу во второй степени: hf, = kQji,

где к — сопротпплеппо каналов.

На рис. 2.11 изображена ниже оси абсцисс кривая k_K — f (Q„), являющаяся параболой с вершиной в начале координат.

Рассмотрим потери при входе в рабочее колесо. На рис. 2.12, а изображен треуюльник ABC скоростей входа при расчетном режиме. Поскольку рассматриваем случай отсутствия закрутки па входе и рабочее колесо (v_ul = 0), треугольник скоростей является прямоугольным. Направление входного элемента лопатки при расчетном режиме

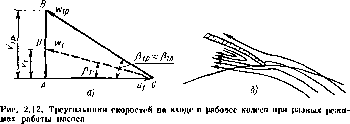
вьтбираем близким к направлению относительной скорости жидкости w_lp. Следонательпо, при расчетном режиме р_1Р « р_1Л и noiepst па входе в рабочее колесо практически отсутствуют. При уменьшении подачи меридиональная скорость уменьшается. Направление абсолютной скорости определяется конструкцией подвода % от подачи вс зависит, поэтому в данном случае закрутка потока па входе равна нулю иезависимо от подачи = 0). Таким образом, при уменьшении подачи получаем треугольник ADC скоростей. Из рис. 2.12, а видно, что при нерасчетной подаче направление относительной скорости w_x не совпадает с направлением входного элемет я лопатки (pj ф р_1Л). При этом поток отрывается от лопатки и образуется вихревая зона (рис. 2.12, б), наличие которой ведет к дополнительным потерям энергии.

Причина потерь у входа в отвод следующая. Сечения отвода рассчитывают так, чтобы при расчетном режиме момент скорости жидкости в отводе был равец моменту скорости па выходе из рабочего колеса. При этом никакого изменения скоростей у входа в отвод пет, и потеря при входе равны нулю. При уменьшении подачи насоса через то же сечение отвода проходит меньший расход жидкости. Следовательно, скорости в отводе и их момент при уменьшении подачи умень-гоаются пропорционально последней, скорости же па выходе из рабочего колеса возрастают. Для бесконечного числа лопаток это хорошо видно из рис. 2.13. То же получается и при конечном числе лопаток. Таким образом, при подачах, мелыпнх расчетной, момепт скорости жидкости на выходе из рабочего колеса больше, чем в отводе, Аналогично при подачах, больших расчетной, момент скорости жидкости в отводе больше, чем иа выходе из рабочего колеса.

Следовательно, при подачах, отличных от расчетов, потоки вытекающей из рабочего колеса и текущей по отводу жидкости имеют разные моменты скорости. При слияния этих потоков в отводе наблюдаются вихреобразов&ине и дополнительные потери.

Рис. 2.13. Треугольники скоростей на выходе вз рабочего колеса при разных режимах работы насоса

На рис. 2.11 ниже оси абсцисс изображена кривая /г_рх = / (<?„). При расчетном расходе <?_кр потери как у входа в рабочее колесо, так и у входа, в отиод равны нулю. При отклонении подачи от расчетной эти потери быстро увеличиваются. Вычтя из ординат линии

= f (ф_к) ординаты кривых потерь в каналах пасоса и у входа в рабочее колесо и в отвод, получим кривую Н = } (фв) зависимости напора насоса от расхода жидкости через колесо,

Подача насоса отличается от расхода через рабочее колесо на величину утечек:

<? = !?»-»«¦

Учет утечек приводит к сдвигу кривой вапоров влево па величину утечек q_K.

Из уравнения (2.13) следует, что теоретический напор не зависит от рода жидкости [в уравнении (2.13) отсутствуют величины, характеризующие физические свойства жидкости]. Гидравлические потери являются функцией Re и, следовательно, зависят от вязкости жидкости, Однако, если Re велико и имеет место турбулентная автомодельность потоков в рабочих органах насоса, то гидравлические потери и, следовательно, напор насоса от рода жидкости но зависят, поэтому график напоров характеристики лопастного насоса одинаков для разных жидкостей, если потоки в рабочих органах насоса авто-модельны.

Построим кривую мощности, Иа уравнения (2.6) гидравлическая мощность

Nv = QvpgH_lf.

Зависимость теоретического напора #_т от расхода через рабочее колесо линейна (си. рас. 2,11) а может быть выражена уравнением Я_т = 4-В<?к.

Отсюда гидравлическая мощность

N_f = pg(AQ_B~BQl).

Это уравнение является уравнением параболы, пересекающей ось абсцисс в точках <2н = 0 и Q„ = А/В [рис. 2.14, кривая N_r = = /(&)!•

Механические поте-    H=f(n)

ри мало зависят от по- ^ дачн насоса. Прибавив мощность механических потерь к гидравлической мощности, получаем кривую N = } (Он) зависимости мощности на валу насоса от расхода жидкости через рабочее колесо. Для получения кривой мощности характеристики пасоса остается учесть объемные потери, при этом кривую N = / (Он) надо сместить влево са. на величину утечек q_a.

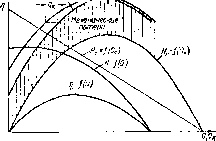
Рис. 2.14. Характеристика центробежного насоса, подучепная теоретически

Я = / (Q), построим кривую КПД

Имея кривые N — } (Q) по уравнению’

r\ = QpgS/N.

N.kBt

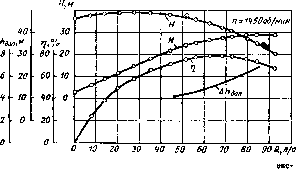
Рис. 2.15. Характеристика центробежного насоса, полученная

При С = ОиЯ = 0т|=0. Следовательно, кривая КПД пересекает ось абсцисс в начале координат (Q — 0) и в точке, где ее пересекает кривая напора.

Приведенные вышо рассуждения являются приближенными, так как они не учитывают ряда факторов, влияющих на напор и мощность. В частности они ие учитывают вторичных токов, возникающих при малых подачах, поустановившегося движения жидкости в каналах колеса при нерасчетных реяшмах и т, д. Поэтому характеристика насоса, гозтроенная теоретически на основании описанных рассуждений, плохо согласуется с данными опыта. Характеристика насоса можот быть получена лишь опытным путем.

Па рис. 2.15 изображена характеристика центробежного насоса. На пей папесепы кроше зависимости напора II, мощности N, КПД г| ж допустимого кавитационного запаса АА_Д0П (см. п. 2.19) от подачи Q.

2.7. Выбор угла установки лопатки на выходе

На выходе из рабочего колеса лопатки могут быть изогпуты по направлению вращения паэад ф_2Л < 90^а) или вперед (р_гп > 90°), либо оканчиваться радиалыю ({1_аЛ = 90°) (рис. 2.16).

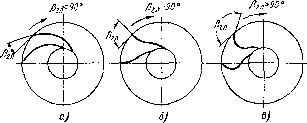
Рас. 2.16. Формы лонаюк центробежного насоса

На ряс. 2.17 изображены треугольники скоростей ва выходе из рабочего колеса с бесконечным числом лопаток, соответствующие этим трем формам лопаток. Из треугольников скоростей слеяуег, что при увеличении угла р_гЯ

Рис. 2.17. Треугольники скоростей на пмходе длл лопаток различных форм

окружная составляющая абсолютно» скорости и ^ увеличивается. Следовательно, согласно уравнению (2.27), напор насоса при увеличении р_8Л повышается. Это делает, на первый взгляд, выгодным применение лоиаток, изогнутых по ходу вперед. Тем не менее рабочие колеса цептробежных насосов выполняют, как правило, с лопатками, иэогиутшш но ходу назад. Причины этого слс-

1.    Из рис. 2.16 следует, что у рабочих колес с радиальными и изогнутыми вперед лопатками канал между последними получается коротким и с большим углом расширения, вследствие чего гидравлические потери в них значительно больше, чем в колесах с лопатками, изогнутыми назад.

2.    Найдем отношение потенциального напора Я пот к теоретическому Н?< Согласно уравнениям (2.29), (2.28), (2.14)

Я_П0Т Я_Т-//_ДШ1 , vl_s!(2g) _л v_ui

Я_т “ Hi ^_1    2и,‘

Коэффициент р называется коэффициентом реакции. При бесконечном числе лопаток с учетом уравнения (2.31) получим

Из этого уравнения видпо, что чем больше угол р_2Л, тем мепыле коэффициент реакции. Таким образом, при увеличении угла р_2Л установки лоиатки на выходе повышается доля скоростного

напора, который должеп быть преобразован в пьезометрический в диффузорной части отвода, что сопровождается большими гидравлическими поте-

3. На рис. 2.18 изображены теоретические характеристики насоса с бесконечным числом лопаток при различных углах установки лопатки аа выходе. Из уравнения (2.32) следует, что при Рал > 90“ и

ctg В_2Л < 0 напор увеличи-    ____

вается ири увеличении подачи;    q

яри р._4Л = 90° и ctg р_гл = О

напор не зависит от подачи;    Рис. 2.18. Характеристики центробежного

при р_2Л < 90° и ctg р_2Л > 0 пасоса для различных форм лопаток напор уменьшается при увеличении подачи- Форма характеристики, получающейся при р_гл ^ 90°, приводит к неустойчивой работе насоса в установке (см. п. 2.15).

4. Из рис. 2.18 следуст, что гидравлическая мощность N_rm = Q_KpgH_TCO а следовательно, и потребляемая мощность пасосов с лопатками, изогнутыми иаззд, изменяется с изменением иодачц сравнительно мило. Эго создаст благоприятные условия для работы приводного двигателя, который при изменения подачи пасоса в довольно широких пределах работает почтп в постоянном режиме. Круто поднимающаяся кривая мощности насосов, имеющих лопатки, изогнутые по ходу вперед, приводит к тому, что незначительные изменения подачи ведут и большому изменение мощности и, следовательно, к необходимости выбирать двигатель повышенной мощности.

В современных насосах угол устаповки лопаток на выходе выбирают в пределах р₂л = 16 4- 40°.

2.8. Осевые насосы

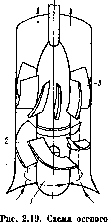
Рабочее колесо осевого насоса похоже на гребной випт корабля (рис. 2.19). Оно состоит из втулки 1, на которой закреплено несколько допастей 2. Мехапизм передачи энергии от рабочего колеса жидкости тот же, что и у центробежного насоса. Отводом насоса служит осевой направляющий аппарат S, с помощью которого устраняется закрутка жидкости и кинетическая энергия ео преобразуется в энергию давления. Осевые насосы применяют при больших подачах и малых напорах.

В осевом насосо жидкость движется по цилиндрическим поверхностям, соосным с валом насоса. Следовательно, радиусы, на которых жидкость входит в колесо и выходит из него, одинаковы, скорости

и, = i/j = и и основное уравнение принимает вид

На рис. 2.20 изображена характеристика осевого насоса. Напор максимален при подаче Q — 0. При малых подачах кривая II ~ / (Q) круто падает вниз, имея характерный перегиб в точке А '. В отличие от центробежных насосов мощность осевых насосов понижается при увеличении подачи и имеет наибольшее значение при подаче, равной пулю.

насоса

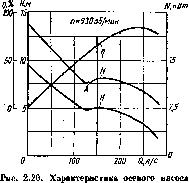
Резкое возристалие иаиора и мощности осевого насоса прп малых подачах обусловлено тем, что ири нерасчетных подачах напор, сообщаемый колесом жидкости на разпых радиусах, различен. Вследствие этого при малых подачах на части колеса возникает обратное движение жидкости из отвода в рабочее колесо. Многократное прохождение >ьидкости через колесо цриводит к дополнительной передаче ей энергии от лопастей. Однако этот процесс сопровождается уволнчеппымл гидравлическими потерями.

В осевом насосе можно расширить диапазон рабочих подач и напоров, в котором насос работает экономично, применив поворотные лопасти. С изменением угла установки лопасти характеристика касоса сильно изменяется при незначительном снижении оптимального КПД.

Глава 13. эксплуатационные расчеты лопастных насосов  »

Библиотека »