Глава 8. истечение жидкости через отверстия и насадки
Глава 8. ИСТЕЧЕНИЕ ЖИДКОСТИ ЧЕРЕЗ ОТВЕРСТИЯ И НАСАДКИ
1.37. Истечение через малые отверстия
в тонкой стенке при постоянном напоре
Рассмотрим различные случаи истечения жидкости из резервуаров, баков, котлов через отверстия и насадки (короткие трубки разной формы) в атмосферу или в пространство, заполненное газом или той же жидкостью. Этот случай движения жидкости характерен тем, что в процессе истечения запас потенциальной энергии, который обладает жидкость в резервуаре, превращается с большими или меньшими потерями в кинетическую анергию свободной струи или капель.
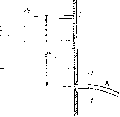
Рис. 1.78. Истечение яз резервуара через малое отверстие
Основным вопросом, который интересует в данном случае, является определение скорости истечения и'расхода жидкости для различных форм отверстий и насадков.
Рассмотрим большой резервуар с жидкостью под давлением р0, имеющий малое круглое отверстие в стенке на достаточно большой глубине Я0 от свободной поверхности (рис. 1.78). Через это отверстие жидкость вытекает в воздушное (газовое) пространство с давлением pv
Пусть отверстие имеет форму, показанную на рис. 1.79, а, т. е. выполнено в виде сверления в тонкой стенке без обработки входной
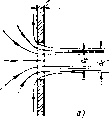
Рис. 1.79. Истечение через круглое отверстие
кромки или имеет форму, показанную на рис. 1.79, б, т. е. выполнено в толстой стенке, но с заострением входной кромки с впешпей стороны. Условия истечения жидкости в зтих двух случаях будут совершенно одинаковыми: частицы жидкости приближаются к отверстию из всего прилежащего объема, двигаясь ускоренно по различны»! плавным траекториям (см. рис. 1.79, а). Струя отрывается от стенки у кромки отверстия и затем несколько сжимается. Цилан-доическую форму струя принимает на расстоянии, равном примерно одному диаметру отверстия. Сжатие струи обусловлено необходимостью плавного перехода от различных направлений движения жидкости в резервуаре, в том числе от радиального движения по стенке, к осевому движению в струе.
Так как размер отверстия предполагается малым по сравнению с напором Н0 и размерами резервуара, и следовательно, его боковые стенки и свободная поверхность жидкости не влияют на приток жидкости к отверстию, то наблюдается совершенное сжатие струи, т. е. наибольшее сжатие в отличие от несовершенного сжатия, которое рассмотрено ниже.
Степень сжатия оценивается коэффициентом сжатия е, равным отношению площади сжатого поперечного сечения струи к площади отверстия
г = Sc/Sq = (dc/d0)2.
(1.123)
Запишем уравнение Бернулли для движсипя жидкости от свободной поверхности в резервуаре (сеченне О — О на рис. 1.78), где давление а скорость можно считать равной пулю, до одного из сечений струи (сечение 1 — /) в той ее части, где она уже приняла цилиндрическую форму, а давление в пой. следовательно, сделалось равным давлению рг окружающей среды. Б^дси иметь
![]()
где ? — коэффициент сопротивления отверстия.
Вводя расчетпый напор Я = Я0 -j- (р0 — Р\)!{ (>g), получаем
отсюда скорость истечения
(1.124)
V а-К
где <р — коэффициент скорости:
(1.125)
В случае идеальной жидкости ? = О, а = 1, следовательно, ф = 1 н скорость истечения идеальной жидкости
(1.126)
Из рассмотррттия формулы (1.124) можно заключить, что коэффициент спорости ф есть отношение действительной скорости истечения к скоросш идеальной жидкости
Ф = vj\ 2gH = v/v„.
(1-127)

Действительная скорость истечения v всегда несколько меньше идеальной из-за сопротивления, следовательно, коэффпциеш скорости всегда меньше единицы.
Распределение скоростей по сечению струи янляется равномерный лишь в средней части сечения (в ядре струи), наружный же слой жидкости несколько заторможен из-за трения о стейку (см. рис. 1.79, б). Как показывают опыты, скорость в ядре струи практически равпа идеальной (уи = ]/2gH), поэтому введенный коэффициент скорости ф следует рассматривать как коэффициент средней скорости. Если истечение происходит в атмосферу, то давление по всему сечению цилиндрической струи равпо атмосферному.
Подсчитаем расход жидкости как произведение действительной скорости истечения па фактическую площадь сечения струи, а затем, используя соотношения (1.123) и (1,124), получим
Q = Scv = eSu(fY2^JI, (1.128)
Произведение коэффициентов е и (р принято обозначать буквой ц, и называть коэффициентом р а с х о д а, т. е. ц = ?ср.
Тогда формулу (1,128) можно окончательно записать так ^> = jj50 \/r‘2.gH или
р = и.50 |А2Лр/о, (1.129)
где Др — расчетная разность давлений, вод действием которой происходит
ИСЮЧС1!!Г>.
При помощи выражения (1.129) решается основная задача — определяется расход. Оно применимо для всех случаев исгечепия, рассмотренных и том п следующих параграфах. Трудность использования этого выражения заключается в достаточно точной оценке коэффициента расхода |i.
Из уравнения (1.129) следует, что
Эю значнт, что коэффициент расхода есть отношение действительного расхода к тому расходу который имел бы место при отсутствии сжатия с 1 руи и сопротивления. Величина Q'a не является расходом цри истечении идеальной жидкости, так как сжатие струи будет иметь место и при отсутствии гидравлических потерь.
Действительный расход всегда меньше теоретического, и, следовательно, коэффициент (i расхода всегда меньше единицы вследствие влияния диух факторов: сжатия струи и сопротивления. В одних случаях больше влияет первый фактор, в других — второй.
Введенные в рассмотрение коэффициенты сжатия е, соиротивле-ния ?, скорости ф и расхода jx зависят в первую очередь от типа отверстия и насадка, а также, как и все безразмерные коэффициенты в гидравлике, от основного критерия гидродинамического подобия — числа Не,
На рис. 1.80 показаны зависимости 31 коэффициентов е, ср и [j, для круглого отверстия от Re^, подсчитанного но идеальной скорости истечения, т. е.
Из графика видно, что с увеличением Re,,, т. е. с уменьшением влияния сил вязкости, коэффициент (р возрастает в связи с уменьшением коэффициента сопротивления 'С, а коэффициент е уменьшается вследствие уменьшения торможепия жидкости у кромки отверстия и увеличения радиусов кривизпы поверхности струи на ее участке от кромки до начала цилипдрнческой части. Значения коэффициентов ф и е при этом асшш-тотичееки приближаются к их значениям, соответствующим истечению идеальвой жидкости, т. е. при Reu со значения |р^1 И 8 ->0,6. Это близко к теоретически найденному Кирхгофом значению е ври истечении идеальной жидкости через плоскую щель е„= л/(2 + я).
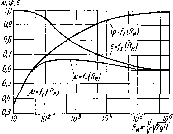
Рис. 1.80. Зависимость е, <р в ц от Пеи для круглого отверстия d тонкой стопке
Коэффициент расхода ц, определяемый произведением е па <р, с увеличением Re сначала увеличивается, что обусловлено крутым возрастанием ср, а затем, достигнув максимального значения ((*,„ах “ 0,60 при Р>е„ = 350), уменьшается в связи со значительным падением е и при больших Re„ практически стабилизируется на значении, равном ц = 0,60 -s- 0,61.
В области весьма малых ReH (R^a С 25) ролi. вязкости настолько велика, а торможение жидкости у кромки столь значительно, что сжатие струи отсутствует (е — 1) и <р = ц. В этом случае мЛшо пользоваться формулой, вытекающей из теоретического решения Вюста [2]:
^ = ф = Ro,i/(25 + и Кеи). откуда
р = У 156/Rch +1 - 12,5/Re*. (1.130)
Для маловязких жидкостей (воды, бензина, керосина и др.), истечение которых обычно происходит при достаточно больших числах Re, коэффициенты истечения изменяются в небольших пределах. В расчетах обычно принимают следующие их осрсдпенныс значения: е =* 0,64; <р = 0,97; ц = 0,62; ? = 0,065.
При истечении маловязких жидкостей через круглое отверстое в топкой стейке имеет место значительное сжатие струи и весьма небольшое сопротивление, поэтому коэффициент расхода р. получается значительно меньше единицы, главным образом, за счет влияния сжатия струи.
1.38. Истечение при несовершенном сжатии
Несовершенное оцэтис струп наблюдается в том случае, кот да на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых степок резервуара. Ограничимся рассмотрением частного случая, когда отверстие расположено иа одипаковых расстояниях от ятих стенок, т. е.
на оси симметрии резервуара {рис. 1.81). Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, струя по пыходо из отверстия сжимается в мепьшетт степени, чем при истечении из резервуара неограниченных размеров, как это рассматривалось вцше ¦ для совершенного сжатия. Вследствие уменьшения сжатия струн возрастает коэффициент езкатия, а следовательно, и коэффициент расхода.
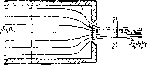
'i
Рпс. 1.81. Схема несовершенного сжатия струи
При истечении жидкостей нэ цилиндрического резервуара круглого сечения через круглое отверстие, расположенное в центре торцовой стенки, при больших числах Re коэффициент сжатия % можно находить по следующей формуле, соответствующей теоретическому решению данной задачи [f. Е. Жуковским для идеальной жидкости
-0.57 + 0,043/(1, t-n). (1.131)
где п = 5s/,S’1 — отношение площади отверстия к площади поперечного сечения резервуара.
Коэффициент ? сопротивления отверстия, а также коэффициент <р скорости при несовершенном сжатии можно считать не зависящими от соотношения п плош,адсй (если п не слишком близко и единице) в приближенно равными их значениям по графику на рис. 1.80. Поэтому коэффициент расхода ^ = е,ф, а расход Q=\iiSa Y2glf, где напор Н нужно находить с учетом скоростного наиора в резервуаре:
а-'1—+ -§. (1.132)
1.39. Пстечение под уровень
Часто приходится иметь дело с истечением жидкости пе в атмосферу и не в газовую среду, а в пространство, заполненное этой же жидкостью (рис. 1.82). Такой случай называют истечением под уровень, или истечением через затопленное отверстие.
В этом случае вся кинетическая анергия струн теряется на вихре-образование, как при внезапном расширении. Поэтому уравнение Бернулли для сечений О — О и 2 — 2, где скорости считаем равными иудвэ, запишем в следующем виде (с учетом коэффициента а)-.
где U — расчетный напор; ? — коэффициент сопротивления отверстия, имеющий примерно то >г<е значение, что и при истечении в атмосферу; v — скорость истечения в сжатом сеченпи струя.
Отсюда
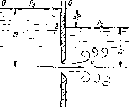
q = vSc — etp?0J/ 2gH — ц5„ у 2§Н.
Таким образом, имеем те же расчетные формулы, что и лри истечении в воздух (газ), только расчетный напор И в данном случае представляет собой разность гидростатических напоров ио обе стороны степки, т. е. скорость и *’кс- 1-8<г- Детечепвс под уро« расход не зависят от высоты расположения отверстия.
Коэффициенты сжатия и расхода лри истечении под уровень можно принимать те же, что и при истечении в воздушную среду.
1.40. Истечение через насадки при постоянном напоре
Внешним цилиндрическим насадком называется короткая трубка длиной, равной нескольким диаметрам без закруглепия входной кромки (рис. 1.83, а). На практике такой насадок часто получается

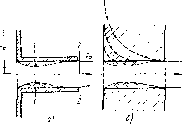
Рис. 1.83. Истечение через ввешпий цилиндрический насадок
в тех случаях, когда выполняют сверление в толстой стопке и по обрабатывают входную кромку (рис. 1.83, б). Истечение через такой насадок в газовую среду может происходить двояко. Схема течения, соответствующая первому режиму, показана па рис. 1.83, с и б. Струя после входа в пасадок сжимается примерно так же, как и пря истечении через отверстие в тонкой стоике. Затем вследствие взаимодействия сжатой части струи с окружающей со завихренной жидкостью, струя посюпешго расширяется до размеров отверстия и из насадка выходит полным сечением. Этот режим истечения называют безотрывным.
Так как па выходе из насадка диаметр струи равен диаметру отверстия, ю р =• 1 и, следовательно, (X = ф.
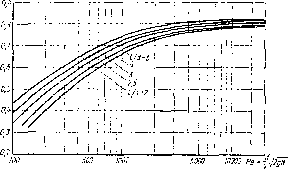
Рис. 1.(44. Зависимость коэффициента расхода ввешпего цилиндрического васадка от Пе
Осредиснные значения коэффициентов для этого режима истечения маловязких жидкостей (большие Re) следующие:
Сравнение с отверстием в тонкой стенке показывает, что при безотрывном истечении через цилиндрический насадок (первый режим) расход получается больше, чем при истечении через отверстие из-за отсутствия сжатия струи па выходе из васадка. Скорость же оказывается меньше вследствие значительно большего сопротивления.
Коэффициент |я расхода цилиндрического насадка при описанном (первом) режиме истечения жидкости в газовую среду зависит от относительной длипы насадка lid и числа Re. На рис. 1.84 приведены опытные кривые зависимости [А от Не для разных lid, на осповаиии которых может быть рекомендована эмпирическая формула для коэффициента ^ при первом режиме истечения:
(1.133)
Из формулы следует, что при Яэ —со (J. = щ1т = 0,813. Минимальная относительная длина насадка Ud, при которой может реализоваться первый режим истечения, равна приблизительно
единице. Однако и при достаточном зпачеиии I'd пе всегда возможен этот режим.
Найдем давление внутри насадка и условие, при котором возможен первый, безотрывный режим истечения.
Пусть истечение жидкости происходит под действием давления ра в среду газа с давлением р2. Расчетный напор при совершенном сжатии (это понятие применимо и для насадков) в этом случае

Так как в струе на выходе из насадка давление равно р2, в суженном месте струи внутри насадка, где скорость увеличепа, давление рх понижено по сравнению с рг. При этом чем больше напор, под которым происходит истечение, а следовательно, и расход через пасадок, тем меньше абсолютное давление в суженном месте струи внутри насадка. Разность давлений р2 — р, растет пропорционально напору Я. Покажем ото, составив уравнение Ьсрнуллп для сечепип 1 — 1 и
2 — 2 (см. рис. 1.83, а):
SL + "J. = _1_ е!
Pg ’2g ^ 2g ^ 2^
Последний член уравнения представляет собой потерю напора па расширение потока, ногорое в данном случае происходит примерно так же, как и при внезапном расширении русла, и, следовательно, определяется формулой (1.105). Сжатие струи внутри насадка оценивается тем же коэффициентом сжатия е, что и в случае отверстия! поэтому на основании уравнения расхода —1/е.
Исключив с помощью этого соотношения скорость vt оз ранее записанного уравнения Бернулли а заменив в нем скорость и,г ее
выражением через коэффициент скорости насадка, т. е. у2 — ср 2§Н>
найдем падение давлонпя внутри насадка: ^
й-Р1-ф'(,1 -1 - = ljpgff.
Подставляя сюда <р = 0,8 и е =» 0,63, получаем Pt — Pi^OJoffpg. (1.134)
При некотором критическом паооре Я1ф абсолютное давление внутри насадка (сечепио 1—1) становятся равным нулю (или точнее давлению насыщенных паров), и поэтому ЯН1,^р*/(0,75р-). (1.135)
Следовательно, при Я > 7/вр давление рх должно было бы стать отрицательным, но отрицательных давлений в жидкости практически не бывает, поэтому и первый реяшм истечения при Я > Якр делается невозможным. Опыт ото подтверждает и показывает, что при Я « Якр происходит внезапное изменение режима истечения, переход от первого режима ко второму см. рис. 1.83. в).
Второй режим истечения характеризуется тем, что струя после сжатия уже не расширяется, а сохраняет цилиндрическую форму и перемещается внутри насадка, пе соприкасаясь с его стевкамя. Истечение становится точно таким же, как и иа отверстия в тонкой стенке, с теми же значениями коэффициентов. Следовательно, при переходе от первого режима ко второму скорость возрастает, а расход умепыпается благодаря сжатию струи.
Если через описанный насадок происходит истечение воды в атмосферу, то
Нцр = pa/(0,75pg) = 10,33/0,75 ;=« 14 м.
Когда давление рнп насыщенных паров истекающей жидкости соизмеримо с давлением рг среды, в которую происходит истечение, в пренебречь величиной рн0 нельзя, в формуле (1.134) следует принять pj = рп п. В результате вместо формулы (1.135) для критического напора нолучим Якр = 0?2 - рн. n)/(0,75pg).
Если после перехода от первого режима истечения ко второму уменьшить напор Н, то второй режндс будет сохраняться вплоть до самых малых Н. Это значит, что второй режим истечения возможен при любых напорах, и, следовательно, при П < Нкр возможны оба режима.
— При истечении через цилиндрический насадок под уровень первый режим истечения не будет отличаться от описанного выше. Но когда абсолютное давление внутри насадка благодаря увеличению Н падает до давлепия насыщенных паров, перехода ко второму режиму не происходит, а начинается кавитационный режим, при котором расход перестает зависеть от противодавления р2, т. е. получается эффект стабилизации, оппсанный выше (см. п. 1.23). При этом чем меньше относительное противодавление р2(р0 =: рпых/pBi = р, которое является критерием кавитации, тем шире область кавитации внутри насадка и тем меньше коэффициент расхода |i.
Таким образом, при истечении жидкости через пгтешний цилиндрический насадок под уровень коэффициент |х является функцией трех безразмерных критериев, а именио

Результаты новых экспериментальных исследований этого случая истечения, проведенных В. М. Фомичевым и др., представлены в безразмерных координатах на рис. 1.85. На рис. 1,85, я дапы зависимости ц от Re при lid = 3 для ряда значений р, начиная от р » 0 и до р > рВр, где рцр — критическое значение р, соответствующее началу навигации и, следовательно, критерию янр (см. п. 1.23). На рис. 1.85, 6 показаны области кавитапионных и безкавитационных режимов истечения через насадки с lid = 3; 5 и 10. Увеличение ркр при возрастании Re объясняется уменьшением коэффициента е сжатия струи внутри насадка, т, е. увеличением степени сжатия, а умень-шепие ркр °РИ увеличении lid происходит из-за возрастания давления; в сзкатом сечении вследствие увеличения потерь на треки© ио длипе насадка.
Таким образом, внешний цилиндрический насадок имеет существенные недостатки: ла персом режиме — большое сопротивление
0 недостаточно пысокпй коэффициент расхода, а на втором — очень низкий коэффициент расхода. Недостатком является также двойственность режима истечения в газовую среду при 11 •< Явр, а следовательно, двузначность расхода при данном Н и возможность кавитации при истечении под уровень.
При использовании цилиндрического насадка (сверления в толстой стенке), напрпмер, в качество жиклеров, дросселей или форсунок эти недостатки следует учитывать иди улучшать насадок.
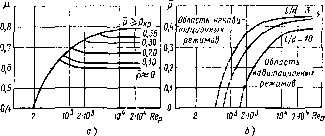
Рис. 1.85. Зависимости дня вяешпего аваппдрвчсского насадка при не* течении под уроиень
Внешний цилиндрический насадок может быть значительно улучшен путем закругления входной кромки (см. штриховые лийш на рис. 1.83) или устройства конического входа с углом црнусности около 60° (см. жиклер на рис. 1.-75). Чем больше радиус закругления, тем выше коэффициент расхода и ниже коэффициент сопротивления. В пределе при радиусе кривизны, равном толщине стенки, цилиндрический насадок приближается к коноидальному насадку, влв соплу.
Коноидальный насадок, или сопло, (рис. 1.86) очерчивается приблизительно по форме естественно сжимающейся струи и благодаря этому обеспечивает безотрывпость течения внутри насадка и парал-лельноструйность в выходном сечепии. Это весьма распространенный насадок, так как он имеет коэффициент расхода, близкий к единице, в очепь малые потери (коэффициент сжатия е — 1), а также устойчивый режим течения без кавитации.
Зпачеппя коэффициента сопротивления те же, что и при плавном сужении (см. п. 1.32), т. е. ? = 0,03 -ь 0,1 (большим Re соответствуют малые ? и наоборот). В соответствии с етим ц = q> = 0,99 -*•
0,96.
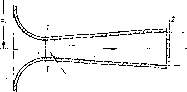
Дпффузориый насадок представляет собой комбинацию сопла и диффузора (рнс. 1.87). Приставка диффузора к соплу влечет за собой снюиецае давления в узком месте насадка, а следовательно, увеличение скорости и расхода жидкости через него. При том же
Кавитация ,
Рис. 1.87. Доффузорвып пасадок
диаметре узкого сечения, что и у сопла, п том же яапоро ъ пый насадок может ладь значительно больший расход (увеличение до 2,5 раза), чем сопло.
Рис. 1.86. Сопло
Такие насадки применяют в том случае, когда заданы диаметр уэкого сечения и папор и требуется получить возможно больший расход. Однако использовать диффузорный насадок можно лишь при
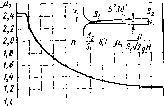
О 2 4 6 8 10 12 К 16 18 201ZH#
Риг. 1,88. Зависимость коэффициента расхода Hi от вапора Я
Рис. 1.89. Внутренний цидц ский пасадок
небольших напорах [Н — 1 -г* 4 м), так как ипаче в узком месте насадка возникает кавитации. Следствием кавитации являются увеличение сопротивления а уменьшение пропускной способности насадка.
На рис. 1.88 показано падение коэффициента расхода диффузор-ного насадка с увеличением папора вследствие кавитации, возникающей в узком месте иасадка при истечении воды в атмосферу.
Коэффициент расхода отнесен к площади узкого сечения, т. е. =
Приведется кривая получена r результат испытания Диффу-зорного насадка, обладающего паивыгоднейшпыи углом и степенью расширения, которые обеспечивают наибольший коэффициент расхода.
Внутренний цилиндрический насадок, или насадок Борда, изображен па рас. 1.89. 'Гам жо скехттически цоказапы два режима истечения, аналогичное режимам истечения через внешний цилиндрический пасадок; очертания струи ори первом режиме показаны сплошными линиями, а при втором — штриховыми. Так как частица жидкости приближаются к входпому отверстию насадка из всего прилежащего объема, а некоторые из них, попадающие на периферию струи, изменяют направление своего движения иа 180°, то степень сжатия струн в даппом насадке больше, а коэффициент е меньше, чем во внешнем цилиндрическом насадке. Значение е в этом Случае при истечении идеальной жидкости может быть получено на основании теоремы Эйлера об изменении количества дважепия (см. п. 1.15). Применим эту теорему к фиксированному объему н виде кругового цилиндра ABCD, сооспого с насадком, и с основанием CD, достаточно удаленным от насадка (где v = 0). Пренебрегая толщипой стоики насадка, на основапии указаппой теоремы при втором режиме истечения получим
pSq — pScv®,
где р — давление в центре осиопания СП; S0a Sc — площади отверстия насадка и сечения струи (силы давления жидкости па кольцевые площади основапий цялипдра A BCD уравновешиваются, а избыточное давление по площади SQ в плоскости АВ равно нулю).
С другой стороны, д«к скорости истечения имеем v = V 2/VP-
После подстановки второго уравнения в первое и обращения, на р и р получим
е = 5с/50 — 1/2.
Этому зиачонию е соответствуют значения коэффициентов расхода (х = 0,71 и потерь ? =1, что подтверждается опытами при первом режиме истечения и больших числах Рейнольдса.
1.41. Истечение через отверстия и насадки
при переменном напоре (опорожнеиие сосудов)
Рассмотрим опорожнеиие открытого в атмосферу сосуда произвольной форми через донное отверстие или насадок с коэффициентом р, (рис. 1.90). В этом случае истечение будет происходить при переменном, постепенно уменьшающемся иапоре, т. с., строго говоря, течение является пеустаиовивишмся.
Однако если напор, а следовательно, п скорость истечения изменяются медленно, то движение в каждый данный момент времени можно рассматривать как установившееся, и для решения задачи применить уравнепие Бернулли (квазистациопарпое течение). Обозначив переменную высоту уровня жидкости в сосуде, отсчитываемую от дна, через h, площадь сечення резервуара па этом уровне S, а площадь отверстия S0 и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнепие объемов
= — dt,
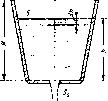
S dh — — Q dt
Рис. 1.90. Схема опорожнения резервуара
где dh — пзмепепио уровня жидкости в сосуде за время At.
Знак минус обусловлен тем, что положительному приращению dt соответствует отрицательное приращение dh.
Отсюда время полного опорожнения сосуда высотой Н найдем Следующим путем (считая ц = const)
, dh
(1.136)
Интеграл можно подсчитать, если известен закон измепепия площади S по высоте h. Для призматического сосуда S = const, следовательпо,
¦ГГ 2SII
ун
(1.137)
' ps,V2g
' 1ьг. Vie ! Vh
Числитель этой формулы равен удвоенному объему сосуда, а знаменатель представляет собой расход в начальный момент опорожнения, т. е. при напоре Н. Следовательно, время полного опорожнения сосуда в 2 раза больше времени истечения того же объема жидкости при постоянном папоре, равном первоначальному.
Г л а в а 9. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТРУБОПРОВОДОВ
1.42. Простой трубопровод постовпмого сечения
Трубопровод называют иростым, если он не имеет ответвлений. Простые трубопроводы могут быть соединены между собой так, что они образуют последовательное соединение, параллельное соединение или разветвленный трубопровод. Трубопроводы могут бьггв сложными, содержащими как последовательные, так я параллельные соединения или ветви разветвления.
Жидкость движется по трубопроводу благодаря тому, что ев энергия в начале трубопровода больше, чем в конце. Этот перепад (разность) уровней энергии может быть создан тем или иным способом: работой насоса, благодаря разности уровней жидкости, давлением газа. В машиностроении приходится иметь дело глааным обра-80м с такими трубопроводами, движение жидкости в которых обусловлено работой васоса. В некоторых специальных устройствах применяется газобаллонпая подача жидкости, т. е. используется давление газа. Течение жидкости за счет разности уровней (разности геометрических высот) осуществляется во вспомогательных устройствах, а также в гидротехпике и водоснабжении.
Пусть простой трубопровод поеюяппого сечения расположен произвольно в пространстве (рис.
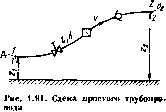
1.91), имеет общую длину I и диаметр d и содержит ряд местных сопротивлений. В начальном сечении (1 — 1) геометрическая высота равна zt и избыточное давление ри а в конечном (2 — 2) — соответственно г2 и рй. Скорость потока в этих сечениях вследствие постоянства диаметра трубы одинакова и равна v.
Запишем уравнение Бернулли для сечепий 1 — 1 и 2 — 2. Считая ctj = ctg и исключая скоростные напоры, получаем
Zi4- — = r»4-—
1Т('г г~ 98 ^ ^
или
? = *-* + * + 2*. „ (1.138)
Пьезометрическую высоту, стоящую в левой части уравнения (1.138) назовем потребным напором Наотр. Если же эта высота задана, то будем называть ее располагаемым напором Я раса- Как видно из формулы, этот напор складывается из геометрической высоты Дг — = z2 — zb па которую поднимается жидкость в процессе движения по трубопроводу, пьезометрической высоты в конце трубопровода и суммы всех потерь напора в трубопроводе.
Сумма двух первых слагаемых Az + pj{ рg) есть статический напор, и его можно представить как некоторую эквивалентную геометрическую высоту #ст подъема жидкости, а последнее слагаемое
— как степенную функцию расхода, тогда
+ + (1-139)
где величина К, вазываеман сопротивлением трубопровода, и показатель т имеют разные значения в зависимости от режима течения.
Для ламинарного точения при замене местных сопротивлений эквивалентными дллпами со формулам (1.121) л (1.122) получим ?й=128 v/paci!<?/(^d’).
Следовательно,
Я — 128\’/Расч/(л?^4) и т = 1, (1.140)
г^е ^расч = ^ • ^экгг
Для турбулентного течения [см. формулы (1.57) и (1.59)1, выражая скорость через расход, получаем
следовательно,
^ = (2 ? + 5^ и tn — 2. (1.14!)
Формула (1.139), дополненная выражениями (1.140) и (1.141), является основной для расчета простых трубопроводов. По пей можно
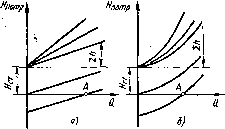

Рве. 1.92. Зависимости потребных напоров от Рпс. 1.93. Схема самогеч-расхода жидкости в трубопроводе ноги трубопровода
построить кривую потребного напора, т. е. его зависимость от расхода жидкости в трубопроводе. Чем больше расход, который необходимо подавать по трубопроводу, тем больше потребный напор. При ламинарном течении эта кривая изображается прямой линией (или близкой к прямой при учете зависимости 1ЭИп от Rc), при турбулентном — параболой с показателем степени, равным двум (при Ат = const) или близким к двум (при учете зависимости Ат от Re). Величина ffCT положительна в том случае, когда жидкость поднимается или движется в полость с повышеппым давлением, и отрицательна при опускании жидкости или движении в полость с разрежением.
Крутизна кривих потребного напора для ламинарного (рис. 1.92, а) и турбулеитиого (рис. 1.92, б) режимов течения зависит of сопротивления трубопровода К и возрастает с увеличением длины трубопровода и уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений. Кроме того, при ламинарном течении наклон кривой (которую для этого течения можно считать прямой) изменяется пропорционально вязкости жидкости.
Точка пересечения кривой потребного напора с осью абсцисс при НС1 = Дг = 0 (точка А) определяет расход при движении жидкости самотеком, т. е. за счет лишь разности геометрических высот Дг. Потребный напор в этом случае равен нулю, так как давление и начале и в конце трубопровода равно атмосферному (за начало трубопровода считаем свободную поверхность в верхнем резервуаре); такой трубопровод условимся называть самотечным (рис. 1.93). Если в конце самотечного трубопровода происходит истечение жидкости в атмосферу, то в уравнении (1.139) для потребпого напора к потерям напора следует добавить скоростной напор.
Иногда вместо кривых потребного напора удобнее пользоваться характеристиками трубопровода.
Характеристикой трубопровода называется зависимость суммарной потери напора (или давления) в трубопроводе от расхода:
? h = f{Q).
Таким образом, характеристика трубопровода представляет собой кривую потребпого напора, смещенную в начало координат. Характеристика трубопровода совпадает с кривой потребного нанора при НС[ = 0, например, когда трубопровод лежит в горизонтальной плоскости, а .противодавление р2 отсутствует.
Рассмотрим возможные задачи па расчет простого трубопровода.
Задача 1. Исходные данные: расход Q, давление р2, свойства жидкости (р и V), размеры трубопровода, а также материал я качество поверхности трубы (шероховатость). Найти потребпмй напор Лпотр-
Решение. По расходу и диаметру d трубопровода находят скорость течения v] по v, d и v определяют Re и режим течения. Затем по соответствуют#»! формулам (или опытным данным) оценивают местные сопротивления (^Kb/d или $ при ламинарном И 'Q при турбулентном точении); по Be и шероховатости определяют коэффициент А в, наконец, решают основное уравнение (1.139) относительно Лппт1,.
При хаынпарном течении рассчитывать ). не обязательно, можно сразу определить К по формуле (1.140).
Задача 2. Исходные данные: располагаемый напор //расп. свойства жидкости, все размеры и шероховатость трубопровода. Найти расход Q.
Решение. Задаются режимом течения, основываясь па вязкости жидкости 32, тая как решение существенно различцо для ламинарного и турбулентного точение.
1. При ламнварном течении и замене местных сопротивлений эквивалентными длинами задача решается ироето: из уравнения (1.139) с учетом формулы (1.140) ваходп'/ расход <?; ори этом вместо ЯВотр подставляют //pilclI.
2. При турбулентпом течении задачу надо решать методом последовательных приближений или 1рафически.
В первом случае имеют одно уравнение (1.130) с двумя неизвесгнтп) Q и Я.Т. Для решения задачи задают значение коэффициента Хт с учетом шероховатости. Так как этот коэффициент изменяется в сраввительно узких пределах = 0,015 ч-0,04), большой ошибки при erost не будет, теи более, что при дальнейшем определении С33 коэффициент А,т оказывается под корней.
Решая уравнение () .139) с учетом выражения (1.141) относительно Q, находят расход в первом приближении. По найденному Q определяют Re в сер-вом приближении, а ао Re — уже боясе точвое значение \х. Спова подставляют полученное значение и то же основное уравнение и решают его относительно '>¦ Найдя расход во втором приближении, получают большее или меньшее расхождение с первый приближением. Если расхождение велико, то расчет продолжают в том же порядке, рааница между каждым иоедедуюшдм значением Q м предыдущим будет делаться все меньше и меньше.
Обычно бывает вполне достаточно двух нни грек приблажрцни для получения приемлемой точности.
Для решения той же задачи графическим способом строят кривую погребного напора для данного трубопровода с учетом переменности Хт, т. е. для ряда значений Q подсчитывают и, Be, \т и, наконец, ЯПогр по формуле (1.139). Злтем, построив кривую Ясотр 01 Q и зная ординату Яиотр = tfpacn, находят соответствующую ей абсциссу, т. ©. Q,
Задача 3. Исходные данные: расход Q, располагаемый напор //рас», свойства Жидкости и все размеры трубопровода, кроме диаметра. Найти диаметр трубопровода.
Решение- Основываясь па свойствах жидкости (\), задают режим течет»! *.
Для ламинарного течения задача решается просто на основе уравнения (1,139) с учетом выражения (1.140), а именно;
![]()
(.1142)
Оиределнв d, выбирают ближайший большой стандартный диаметр и по тому >пи .уравнению уточняют значение напора при заданном Q или наоборот.
При турбулентном течении решение уравнения (1.139) с учетом выражения (1.141) относительио d лучше всего выполнить следующим образок-, .задать ряд стандартных значений d и для заданного Q подсчитать ряд значений Яиотр, аатем построить график зависимости Япотр от d и по заданному Ярасп по кривой определить d, выбрать ближайший большой стандартный диаметр и уточпить #погр-
1.43. Соединения простых трубопроводов
Последовательное соединение. Возьмем несколько труб, например, 1, 2 и 3 различной длины, разного диаметра и содержащих различные местные сопротивлениями соедивим их последовательно (рис. 1.94, а). В результате получим простой трубопровод перемен-аото сечения.
Очевидно, что при подаче жидкости по такому трубопроводу расход во всех последовательно соединенных трубах один и тот же, а полная потеря напора между точками М и N равна сумме потерь напора во всех последовательно соединенных трубах, т. о. имеем следующие основные уравнения:
2bn-iv-2'>,+ 2*2 + 2^. (1,Ш)
Эти уравнения определяют правило построения характеристик последовательного соединения труб. Пусть даны характеристики трубопроводов 1, 2 и 3 (рис. 1.94, б). Чтобы построить характеристику всего последовательного соединения М — N, следует в соответствии с выражением (1.143) сложить потери напора прв одинаковых расходах, т. е. сложить ординаты всех трех кривых прн равных абсциссах.
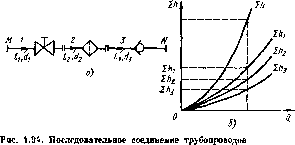
Так как в рассматриваемом более общем случае скорости в начале М и конце N трубопровода различны, то выражепие потребного напора для всего трубопровода М — Л'’ н отличие от формулы (1.139) должно содержать разность скоростных напоров в конце и начал©
трубопровода. Принимая а = 1, имеем •.
н„п = I» - * м + + 2 Лм - ~ Яс» + С<?> + К (1.144)
Параллельное соединение. Такое соединепне песколышх простых трубопроводов (например 1, 2 и 3) между точками М и N показано на рис. 1.95, а. Для простоты допустим, что трубопроводы расположены в горизонтальной плоскости.
Обозначим полные напоры в точках М и N соответственно через Нм и Нк, расход в основной магистрали (т. с. до разветвления и после слияния) — через Q, а в параллельных трубопроводах через Qij Qi 11 Q*', суммарные потери напора в этих трубопроводах через 2//,, Zh2 и 2йя.
Пре;кде всего запишем следующее очевидное уравнение
Затем выразим потери папора в каждом из трубопроводов через нолпыо лалоры в точках М и N:
2 — — НКг ? ^2 — X Ья = Яц — lift.
Отсюда делаем следующий важный вывод:
2Ai=»2Ae=S/tj, (1.146)
т. е. потери папора в параллельных трубопроводах равны между собой. Их можно выразить в общем виде через соответствующие расходы следующим образом
Zki=I<iQ?; Zh = K%Qt\ %ht =к.?™,
где К и т — определяются в зависимости от режима течения формулами (1.140) или (1.141).
Следовательно, в дополнение к уравнению (1.145) получаем на основании равенств (1.146) еще два уравиения:
Кх0Г = **<?”; (1-147) (1.148)
Система уравнений (1.145), (1.147) и (1.148) позволяет решать, например, следующую типичную задачу: даны расход в основной магистрали Q и все размеры трубопроводов; определить расходы в параллельных трубопроводах <?t, ()г и Qy
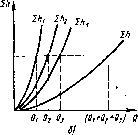
| а м | г аг |
Л" |
| 3 Ь |
Рис. 1.95. Параллельное соединение трубопровода!!
Пользуясь выражениями (1.145) и (1.146),, можно составить столько уравнений, сколько параллельных трубопроводов между точками М в N.
Из уравнений (1.145) и (1.146) вытекает следующее важное правило: для построения характеристики параллельного соединения нескольких трубопроводов следует сложить абсциссы (расходы) характеристик этих трубопроводов при одинаковых ординатах (Zh). Пример такого построения дан па рис. 1.95, 6.
Изложенные соотношения и правила для параллельных трубопроводов справедливы, разумеется, также в том случае, когда трубопроводы 1,2,3 и т. д. (см. рис. 1.96) но сходятся в одной точке N, а подают жидкость в разные места, но с одинаковыми давлениями и равными иивелираыми высотами. Если я;е последнее условие не соблюдается, то рассматриваемые трубопроводы нельзя считать параллельными, а следует относить к разряду разве! влеппых трубопроводов.
Разветвленное соединение. Условимся называть разветвленным соединением совокупность нескольких простых трубопроводов, имеющих одно общее сечение ~ мссто разветвления (или смыкания) труб.
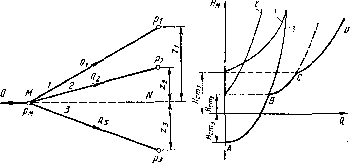
Рис. 1.96. Разветвленный трубопровод Рис. 1.97. Построение кривой потребного иапора для разветвлеиного трубопровода
Пусть основной трубопровод имеет разветвление в сечении М — М, от которого отходят, например, три трубы I, 2 и 3 разных размеров, содержащие различные местные сопротивления (рис. 1.96). Геометрические высот Zj, z2 и z3 конечных сечений и давления рг, p.t и рз в них пусть будут также различными. ^
Найдем связь между давлением рм =* Нщ PS в сечении М — М в расходами Qv Qxi и Q3 в трубопроводах, считая направление течения в пих заданным.

Так же как и для параллельных трубопроводов,
Записав уравнение Бернулли для сечепия М — М и конечного сечения, нанример первого трубопровода, получим (пренебрегая разностью скоростных высот)
Нм — Zi + Pi/(P?) + ?
Обозначая сумму двух первых членов в правой части уравнения через Нст и выражая третий член через расход (как это делалось выше), получаем
09К
Аналогично для двух других трубопроводов можно записать = Нм = ястз+K.,Q?-
Таким образом, получаем систему четырех уравнений с четырьмя пеизвестиыми: Qv Q2, Q3 и Нм-
Осповной задачей по расчету разветвленного трубопровода является следующая: даны расход в точке М, все размеры ветвей (иклю-чая геометрические высоты г), давления в конечных сечениях и все местные сопротииленпя; определить расходы Qt, Q2 и Q3, а также потребный напор Нм — Ндотв. Возможны и другие варианты постановки задачи, решаемой на основе той же системы уравнений.
Построение кривой потребного напора для разветвленного трубопровода выполняется сложением кривых потребных напоров для ветвей по правилу сложения характеристик параллельных трубопроводов (рис. 1.97) — сложением абсцисс (Q) при одинаковых ординатах (Нм)- Кривые потребных напоров для ветвей отмечены цифрами
1, 2 и 3, а суммарная кривая, т. е. кривая потребного напора для всего разветвления, обозлачепа буквами ABCD. Из графика ясно, что условием подачи жидкости во все ветви является неравенство Нм > Н сх1.
1.44. Сложные трубопроводы
Сложный трубопровод в общем случае составлен из простых трубопроводов с последовательным и параллельным их соединением (рис. 1.98, а) или с разветвлениями (рис. 1.98, 6).
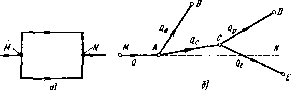
Рис. 1.98. Схемы сложных трубоироводов
Рассмотрим разомкнутый сложный трубопровод с разветвлениями и с раздачей жидкости в конечных сечениях (точках) ветвей. Магистральный трубопровод разветвляется в точках А и С. Жидкость подается к точкам (сечениям) В, D и В с расходами Qb, Qd и Qb.
Пусть известны размеры магистрали и всех ветвей (простых трубопроводов), заданы все местные сопротивления, а также геометрические высоты конечных точек, отсчитываемые от плоскости М — N и избыточные давления в конечных точках ро, Ро и Ре-В этом случае могут быть следующие основные задачи по расчету указанного трубопровода, соответствующие двум первым задачам, рассмотренный в п. 1.42.
/ее
Задача i. Дан расход Q в основной магистрали МА. Определить расходы в каждой ветви — Qb, Qd, Qe, а также потребный напор в точке М: Япотр = Нм — рмПё р)-
Задача 2. Дан напор в точке М — Нм- Определить расход в маги
страли Q и расходы в каждой веши.
Обо. задача решают иа основе одыой в той же системы уравнений, число которых еа единицу больше числа конечных ветвей,
а именно:
уравнение расходов
Q = Qb + Qd + Qe;
равенства потребных напоров для ветвей CD и СЕ Нет d + KcdQd = Нет е + Ксе(Уё<
равенства потребных напоров для ветви АВ и сложного трубопровода ACED
HCi в -\г ~ НСт d+KcdQ^d + Кас (Qd + Фе)"1;
выражение для потребного напора в точке М
Ям — Км aQ™-^-Нет в -Ь KabQb-
Здесь, как и выше, физический смысл статических напоров в ко-* печпых точках В, D и Е тот же, что и в формуле (1.139), а сопротивления ветвей К и показатели степени тп определяются в зависимости от режима течения (см. п. 1.42).
Расчет сложных трубопроводов часто выполняют графоаналитическим способом, т. е. с применением кривых потребного напора или характеристик трубопроводов. Кривую потребного напора Наотр для всего сложного трубопровода можно построить следующим образом:
1) сложный трубопровод разбить на ряд простых;
2) построить кривые потребных напоров для каждого вз простых трубопроводов, причем для ветвей с конечной раздачей — с учетом /7СТ, а для промежуточных участков (например, АС и МА) — без учета НСт;
3) сложить кривые потребных напоров для ветвей (и параллельных линий, если они имеются) по правилу сложения характеристик параллельных трубопроводов;
4) полученную кривую сложить с характеристикой последовательно присоединенного трубопровода по соответствующему правилу (см. п. 1.43) и т. д.
Таким образом, при расчете нужно идти от конечных точек сложного трубопровода к начальной его точко, т. е. против течения жидкости.
Руководствуясь этим правилом, можно построить кривую потребного папора для любого сложного трубопровода как при ламинарном, так и при турбулентном режиме течеяик.
Выполнив описанное построение и получив график Япотр = / ((?), можно с его помощью решать рассмогрепвые выше задачи 1 и 2 в различных вариантах, Кроме того, кривая потребного напора Н„отр необходпма для расчета сложного трубопровода с насосной подачей.
Сложный кольцевой трубопровод представляет систему смежных замкнутых контуров — колец с отбором жидкости в узловых точках или с непрерывной раздачей ее на отдельных участках.
Рассмотрим простейший случай, когда трубопровод состоит из двух колец О ABC н ADEB (рис. 1.99). Точка О является первичной точкой (узлом), из которой жидкость подается в сеть с расходом Q0 и где, следовательно, напор имеет наибольшее значение. В точках Л, В, С, D и Е происходит отбор жидкости с расходами, которые обозначены соответственно Qa, Qb, Qc, Qd и Qe-
Различные задачи расчета такого и более сложных кольцевых трубопроводов обычно решают аналитическим методом последовательных приближений или па ЭВМ с применением электроаналогий. При атом основываются на двух обязательных условиях, аналогичных требованиям к расчету электрических сетей. Первое условие — баланс расходов, т. е. равенство притока и оттока жидкости для каждой узловой точки, что соответствует первому закону Кирхгофа в электротехнике (сила тока аналогична расходу). Второе условие — баланс напоров, т. е. равенство нулю алгебраической суммы потерь напора для каждого кольца (контура) при подсчете по направлению движения часовой стрелки или против нее, что соответствует второму закону Кирхгофа (падение напряжения аналогично потере напора). Потери напора считаются положительными, если направление подсчета совпадает с направлением движения жидкости, и отрицательными, если направление подсчета противоположно направлению движения жидкости.
- йо о f а, АS Qs лу^Од
|
1, | h | |||
| 4 | h г | lL | 6 |
*¦6 |
| в* |
tj j | Qi I | 7 | h |
Рис. 1.99. Схема сложного кольцевого трубопровода
Наиболее типичной для расчета сложных кольцевых трубопроводов (сетей) является следующая задача, которую рассмотрим на примере показанной на рис. 1.99 схемы двухкольцевого трубопровода. Даны максимальный напор в начальной точке (узле) 0 — Н0, минимальный напор в наиболее удаленной точке Е — Не, расходы во всех шести узлах (от Q0 до Qe) и длины семи учасФков I—7 (линий) (от 1г до 1-). Требуется определить диаметры трубопроводов па всех семп участках.
Особенностью данной задачи, как и других задач расчета сложных кольцевых трубопроводов, является то, что неизвестными будут расходы на отдельных участках, в данном примере — расходы от Qlдо Q-, и напори в четырех узлах Л, В, С и D. Таким образом, пссго имеем 18 неизвестных. Кроме того, неизвестно направление движения жидкости во втором участке {АВ).
Для нахождения этих неизвестных имеются следующие уравнения: шесть уравнений баланса расходов для шести узлов; два уравнения баланса напоров для двух колец и семь уравнений, связывающих потерю напора с расходом для каждого из семи участков. Таким образом, число уравнений (15) меньше числа неизвестных (18), поэтому при решеиии задачи в первом приближении надо задать диаметры некоторых уча«ков. Проще всего это сделать для участков 6 и 7, подающих жидкость к конечной точке Е, так как для них известен суммарный расход (Qe = Qe + Q:)-
Решение системы уравнений'приходится выполнять неоднократно пе только потому, нто выбранные диаметры оказались неудачными, но и потому, что окончательно принятые диаметры труб па всех участках должны соответствовать ГОСТам.
Удобным расчетным приемом, применяемым нри небольшом числе колец, является следующий. Сложный кольцевой трубопровод мысленно разрывают в наиболее удалепной точке Е и л одной из точек участка 2 на два сложных разветвленных трубопровода OADE и ОСВЕ. Тогда расход па участке О А будет a Q0, а на участке ОС — (1 — a) Q0. Значение коэффициента а можно приблизительно оценить, так как известны расходы Qa и Qz> в одном из указанных трубопроводов и Qc и QB — в другом; неизвестны лишь Qs и (?7, •из которых складывается Qe-
Далее выполняют расчет каждого из двух сложных разветвленных трубопроводов так, как ото было описапо выше. Если в этом расчете определяются диаметры, то при окончательном их выборе нужно соблюсти равенство потерь папора в линиях OADE и ОСВЕ.
1.45. Трубопроводы с насосной подачей жидкости
Выше рассмотрены, по существу, лишь отдельные уч^тки простых и сложных трубопроводов, а не вся система подачи жидкости (кроме простейшей самотечной системы). В машиностроении, как уже отмечалось, основным способом подачи жидкости является принудительная подача насосом. Рассмотрим совместную работу трубопровода с насосом и принцип расчета трубопровода с пасоспой подачей жидкости.
Трубопровод с насосной подачей может быть разомкнутым, т. е. таким, по которому жидкость перекачивается из одной емкости в другую (рис. 1.100, а) или замкнутым (кольцевым), в котором циркулирует одно и то же количество жидкости (рис. 1.100, б).
Рассмотрим вначале разомкнутый трубопровод, по которому насос перекачивает жидкость, папример, из нижнего резервуара с давлением р0 в другой резервуар (или в камеру) с давлением р3. Высота расположения оси насоса относительно нижнего уровня Нх называется геометрической высотой всасывания, а трубопровод, по которому жидкость поступает к пасосу, всасывающим грубо-проводом, или линией всасывания. Высота расположения конечного сечения трубопровода, или верхнего уровня жидкости Нг, называется геометрической высотой нагнетания, а трубопровод, по которому жидкость движется от насоса, напорным, иди лилией нагнетания.
Составим уравнение Бернулли для потока жидкости во всасывающем трубопроводе, т. е. для сечений 0—0 и 1—1 (принимая а — 1):
Уравнение (1.149) является основным для расчета всасывающих трубопроводе в. Оно показывает, что процесс всасывания, т. е. подъем
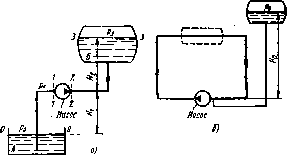
Рис. 1.100. Трубопроводы с насосной подачей
жидкости ва высоту П1, сообщение ей кинетической энергии и преодоление всех гидравлических сопротивлений происходит за счет использования (с -помощью насоса) давления р0. Так как это давление обычно бывает весьма ограниченным, то расходовать его следует тан, чт&бы перед входом в насос остался некоторый запас давления plf необходимый для его нормальной бескавитацыонной работы.
Возможны следующие задачи на расчет всасывающего трубопровода.
Задача I. Даны все размеры н расход и требуется пайтн абсолютное давление неред входом в насос.
Решение этой задачи представляет собой поверочный расчет всасывающего трубопровода. Абсолютное давление plt полученное по уравнению (1.149), сравнивают с тем, которое является минимально допустимым для данного случая.
Задача 2. Дано минимально допустимое абсолютное давление перед входом в пасос р1 и требуется найти одну из следующих предельно ДОПУСТИМЫХ веЛаыИН. Яцпал» Оглат^ ИЛИ рощ1й'
Запитом уравнение Бернулли для движения жидкости по напорному трубопроводу, т. е. для сечений 2—2 а 3—3:
![]()
(1.150)
Левая часть уравнения (1.150) представляет собой энергию жидкости на выходе из насоса, отиесениую в единице веса.
Аналогичная энергия жидкости перед входом в насос может быть вычислена но уравнении (1.14У):
Л т = Ро Pg "Г 2g pg
Найдем приращение энергии жидкости в насосс, т. е. определим ту энергию, которую приобретает, проходя через насос, каждая единица веса жпдкости. Эта энергия сообщается жидкости насосом, поэтому опа носит название напора, создаваемого насосом, и обозначается обычно //нас-
Для нахождения Нвас вычтем последнее уравнение из уравнения (1.150):
(1.151)
Н„ВС
![]()
Ям, = Да + й=?2 + КО",
нас i pg х
илц
где Ai — полная геометрическая высота подъема жидкости (см. рис. 1.100, а); KQm — сумма гидравлических потерь во всасывающем и напорном трубопроводах.
Если в действительной разности Дз уровней добавить разность пьезометрических высот (pa — р0)/( pg), то можно рассматривать как бы увеличенную разность уровней
“ Pg
и формулу (1.151) переписать так: Ниас = Не т 4“ KQm.
(1.151')
Сравним полученное выражение (1.151') с формулой (1.139) для потребного напора. Очевидно, что
(1.152)
Это равенство можно распространить на все случаи устойчивой работы васоса, соединенного с трубопроводом, и сформулировать в веде следующего правила: при установившемся течении жидкости в трубопроводе насос развивает напор, равный потребному.
На равенстве (1.152) основывается метод расчета трубопроводов, питаемых насосом, который заключается в совместном построение, в одной и том же масштабе в па одном графике двух кривых: напора Яцотр = f\ (0 и характеристики пасоса Янас = /а (ф) и в нахождении их точки пересечения (рис. 1.101).
В дальнейшем (во второй и третьей частях) будет достаточно подробно сказано о характеристиках насосов. Здесь яге пока дадим лишь определение: характеристикой насоса называется зависимость напора, создаваемого насосом, от его подачи (расхода жидкости) при постоянной частоте вращения вала насоса. На рис. 1.101 дано два варианта графика: а — для турбулентного режима течения в трубопроводе и центробежного насоса и б — для ламинарного режима и объемного пасоса.
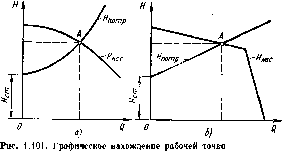
В точке пересечения кривой потребного напора и характеристики насоса имеем равенство между потребным напором и напором, создаваемым насосом, т. е. равенство (1.152). Эта точка называется рабочей точкой, так как всегда реализуется режим работы пасоса, ей соответствующий. Чтобы получить другую рабочую точку, необходимо или изменить открытие регулировочного крана (вентиля, задвижки), т. е. изменить характеристику трубопровода, или изменить частоту вращения вала насоса.
Указанный расчетный прием для нахождения рабочей точки применим в том случае, когда частота вращения привода насоса не зависит от мощности, им потребляемой, т. е. от нагрузки на валу насоса. Это имеет место, например, при соединении насоса с электродвигателем переменного тока или с иным двигателем, мощность которого во много раз больше мощности насоса.
Для замкнутого трубопровода (рис. 1.100, б) геометрическая высота подъема жидкости равна пулю (Дг = 0), следовательно, при = v2:
•^потр = ?h = (р2 — Р\)/(Рё),
т. е. между потребным напором и напором, создаваемым насосом, справедливо то же равенство.
Замкнутый трубопровод обязательно должен иметь расширительный, или компенсационный бачок, соединенный с одним из сечений трубопровода, чаще всего с сечением у входа в насос, где давление имеет минимальное значение. Без этого бачка абсолютное давление внутри замкнутого трубопровода было бы неопределенным, а также переменным в связи с колебаниями температуры и утечками через неплотности.
При наличии расширительного бачка, присоединенного к трубопроводу, как показано на рис. 1.100, б, давление перед входом в насос
Pi — Ро + HaPg‘
По величине pi можно подсчитать давление в любом сечении замкнутого трубопровода. Если давление в бачко р0 изменить па некоторую величину, то во всех точках данной системы давление изменится ца ту же самую величину.
Бачок можно включить также в замкнутый трубопровод, как показапо па рис. 1.100, б штриховой линией (трубопровод внутри бачка при этом должен иметь разрыв).
1.46. Основы расчета газопроводов
При установившемся движении вязкого газа по трубе постоянного сечепия в силу постоянства вдоль потока массового расхода можно записать
QtnjS = vlp1=svilpi’=vp=‘Con$t (вдоль потока). (1.153)
Так как движение газа сопровождается трением, давление его падает вдоль потока, газ расширяется, следовательно, плотность его р уменьшается, а скорость v, как это впдио из формулы (1.153), увеличивается.
При полном отсутствии теплообмена с внешней средой процесс расширения при движении газа будет адиабатным, а при интенсивном теплообмене температура газа вдоль трубы остается постоянной, т. е. происходит изотермический процесс. Чем короче газвпровод
и, следовательно, чем меньше время прохождения ег^ частицами газа, тем ближе процесс к адиабатному. И наоборот, чем больше относительная длина газопровода, тем ближе процесс к изотермическому. Именно его и будем предполагать в газопроводах и рассмотрим основы их расчета применительно к изотермическому движению газа в трубах.
Выразим число Рейнольдса для потока газа и трубе через массовый расход газа и динамическую его вязкость:
Re = vd/v =4<2т/(лф).
Отсюда видно, что число Рейнольдса может изменяться вдоль потока в трубе постоянного диаметра лишь за счет изменения вязкости jj.. Но вязкость газов jj. пе зависит от давления, а определяется лишь температурой, поэтому при изотермическом процессе движения газа по трубе число Рейнольдса будет оставаться постоянным вдоль потока. Следовательно, коэффициент X потерь на трение по длине также будет величиной постоянной вдоль трубы по-стояииого диаметра, несмотря на возрастание скорости потока rasa.
Двумя бесконечно близкими друг к другу сечениями выделим элемент трубы длиной dx (рис. 1.102). Пренебрегая неравномерностью распределения скоростей по сечению, обозначим скорость в левом сечении трубы р, в пра-. . dx bom v -I- dv, а давления — соот-
| - . ^ *1,1 I ветственно р и р + dp.
р у \ j р Г"\p-ntp \р„ Применим к выделенному эле-
1 1—*~ *---eO-L*—-—1_ ментарному объему теорему ыеха-
fy+dv наян об изменении количества
-*4
движения. Приращение за ? цу времени количества движения в направлении потока Ряс. 1.102. Схема дая расчета raw л dv = pSv dv
провода <т г
где S = .4^/4.
Это приращение получается в результате импульса внешних сил; давления и трения за ту же единицу времени. Секундный импульс равнодействующей силы
dR = [р — (р 4- dp)] тР/А — т0яd dx = — ltd? dp/4 — x^nd ¦ dx, где т0 — касательное напряжение на степке трубы.
Приравнивая секундный импульс сил приращению количества движении, подучаем
~ dp — xndx — p ^vdv ш dp+pd^j-^-~-dx = 0.
Используя формулу (1.61), вместо предыдущего выражения
запишем
Умножив уравнепие на р2, будем иметь р<гр+рч(|)+л?9|? = 0. (1.154)
Так как в соответствии с уравнением (1.153) (ру)1 = -const,
то
pad(ua) =— v*d (ра),
поэтому уравнение (1.154) можно переписать в виде п J г, _ у (РР)*
р аР- — -р- — * г —
Используя уравнения состояния р = p/(RT), вместо последнего выражения получим
Р<*Р _ Щ d (^)__. dx {{шр
ИТ 2 р» ~~ А d 2 ‘
Так как по условию Т = const, можно выполнить интегрирование вдоль газопровода, т. в. в пределах от р± до р а соответственно от х = 0 до х = I. Будем иметь
Отсюда определяем массовый расход газа
В длинных трубопроводах при движении газа со скоростями^ значительно меньшими звуковых,
В этих условиях выражением 2 In (pjp) в формуле (1.156) можно пренебречь и получить упрощенную формулу
(Р*-Рг)d .. 1Г_>
URT • ( '
Коэффициент X, входящий в формулы (1.156) и (1.157), определяется так же, как и для несжимаемых жидкостей по числу Re и относительной шероховатости.
Приведем некоторые дополнительные сведения об изотермическом течения гага по трубопроводам.
С помощью формулы (1.453), а также уравнения состояния я уравнения изотермы исключим из формулы (1.155) давления, введя в нее скорости, и приведен к виду
Г=1,'-=Вт(±-±)-2Ь°-. (1.158)
Полученное уравнение перепишем в безразмерных величинах; вводя отношенае скорости потока к скорости звука, т. е. число Ыаха *
где х — извостпыи из термодинамики показатель адиабаты, для воздуха и двухатомных газов н = 1,4.
Тогда вместо выражения (1.158) будем иметь
1Ч(щ--м.)-21пй-- (1Л59)
Продифференцировав уравнение (1.159) по М, считая Мх = const, в определив <й!, получим
Анализируя это уравнение, пряходим к выводу, что в случав изотермического течения прн значении № <; 1/х в цпляидричо-ской трубе скорость вдоль потока возрастает (при dl > 0 и dM > 0), а ври значениях Ма > 1/к скорость вдоль потока уменьшается. Следовательно, значение М —1 iVу. для изотермического движения газа в трубе является критическим. Перейти через это значение М, которое равно Мкр = 0,845, сохраняя изотермическое движение, невозможно, так как малейшее отклонение числа М от Мкп в сторону увеличения меняет знак приращения <ЗМ и возвращает поток вновь к критическому состоянию.
Заметим, что при адиабатном процессе движения газа таким критическим числом Маха является число М = 1.
