Глава 7. местные гидравлические сопротивления

Глава 7. МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ

*

1.31. Общие сведения о местных сопротивлениях

Выше указывалось (см. п. 1.17), что гидравлические потери энергии делятся на местные потери и потери на трение по длнно. Потери на трение в прямых трубах постоянного сечения рассмотрены при ламинарном (см. гл. 5) ц турбулентном (см. гл. 6) течениях. Рассмотрим потери, обусловленные местными гидравлическими сопротивлениями, т. е. такими элементами трубопроводов, в которых вследствие изменения роз.меров пли конфигурации русла происходит изменение скорости потока, отрыв транзитного потока от стенок русла и возникают впхреобразованпя.

В п. 1.17 былп приведены примеры некоторых местных сопротивлений п дана как эмпирическая общая формула снязи местной потерн напора п скорости потока, т. е. формула (1.57) Всйсбаха:

Простейшие местные гидравлические сопротивления можно разделить на расширения, сужения и повороты русла, каждое из которых может быть внезапным или ностепеицым. Более сложные случаи местных сопротивлений представляют собой соединения шш комбинации перечисленных простейших сопротивлений. '1'ак, например, при течении жидкости через вентиль (см. рис. -1.28, ?) поток искривляется, меняет свое направление, сужается и, наконец, расширяется до первоначальных размеров; при этом возникают ин1енсивпые вихреобразования.

Рассмотрим простейшие местные сопротивления при турбулентном режиме течения в трубе. Коэффициенты потерь t ^ПР^П турбулентном течении определяются в основном формой местных сопротивлений и очень мало изменяются с изменением абсолютных размеров русла, скорости потока и вязкости v жидкости, т. е. с изменением числа Re, поэтому обычно принимают, что опи пе зависят от Be, что означает квадратичный закон сопротивления, или автомодельность. Местные сопротивления при ламинарном течении рассмотрим в конце главы.

1.32, Внезапное расширение русла

Значения коэффициентов местных потерь в большинстве случаев получают из опытов, на осповании которых выводят эмпирические формулы или строят графики. Однако для внезапного расширения русла при турбулентном течении потерю напора можно достаточно точно найти теоретическим путем.

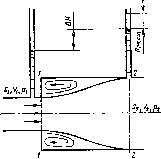
Рис. 1.03. Внезапное расширение трубы

При внезапном расширении русла (грубы) (рис. 1.63) поток срывается с угла и расширяется не внезапно, как русло, а постепенно, причем в кольцевом пространстве между потоком и стенкой трубы образуются вихри, которые и являются причиной потерь энергии. При этом, как показывают наблюдения, происходит непрерывный обмен частицами жидкости между основным потоком и завихренной его частью. Кроме того, основной впхрь порождает другие, более мелкие вихри, которые уносятся потоком и при этом распадаются ка еще более мелкие вихри. Таким образом, поторя энергии происходит не только в основном вихре, но и по длине следующего за ним участка потока.

Рассмотрим два сьчеиия горизонтального потока: 1 — 1 — в плоскости расширении трубы и 2 — 2 — в том месте, где поток, расширившись, заполнил все сечение широкой трубы. Так как поток между рассматриваемыми сечениями расширяется, то скорость его уменьшается, а давлеппе возрастает. Поэтому второй пьезометр до-казывпет высоту, па АН большую, чем первый; по если бм потерь напора в данном месте не было, то иторой пьезометр показал бы высоту большую еще па Л_расш. Эта высока и есть местная потеря напора на расширение.

Обо?.наи:м давление, скорость п площадь потока в ссчскии 1 — 1 соответственно через р,, у, п 6',, а в сечении 2 — 2 — через р._г, с„ и <?₂.

Прежде чем составлять исходные уравнения, сделаем тр» допущения:

1)    распределение скоростей в сечениях 1 — 1 и 2 — 2 равномерное; т. с. cc_t— а_г = {, что обычно и принимается при турбулентном режиме;

2)    касательное напряжение на стейке трубы между сечениями 1 — 1 и 2 — 2 равно нулю, т. е. пренебрегаем силой трения, малой по сравнению с сп.тами давления;

3)    давление Рх в ссчепии 1 — 1 действует но всей площади S₂ потому, что, хотя труба п расширилась, поток в сечении 1 — 1 еще сохранил свой поперечный размер, следовательно, ни скорость, ни давление еще не изменились'.

Запишем для сечений 1 — 1 и 2 — 2 уравнение Берпулли с учетом потери напора /г_раСш на расширение, и принимая z_x = i₂ = О, получим

Pi < ^vi _ Ра ] vl < и

Pg    Рg ⁺ 2g т^ст-

Затем применим теорему Эйлера об изменении количества движения (см. п. 1.20) к фиксированному цилиндрическому объему, ааключенному между сечениями 1 — 1, 2 — 2 и степкои трубы. Для этого определим равнодействующую внешних сил, действующих на рассматриваемый объем в направлении движения, т. е. сил давления.
Учитывая, что площади оснований цилиндра    слева и    справа одинаковы п равны S₂, а также считая, что    в    сечении    1    — 1    давление р_г

равномерно распределено по всей площади S₂, получим равнодействующую силу, численно равную секундному импульсу

Соответствующее этому импульсу изменение количества движения пайдем как разность между секундным количеством движения, выносимым из рассматриваемого объема о вносимым в него; нри равномерном распределении скоростей но сечениям эта разность равна

<?р(?>₂ — 1>i).

Приравнивая одно к другому, получим

Разделим полученное уравнение на S₂pg\ учитывая, что Q = = v₂S₂, преобразуем правую часть уравнения

Сгруппировав члены, получим

fi <    »*    _ Рг_ г    j    {vi — Vi)*

P« "^r 2g    i>g ^ 2ц ^    2g

Сравнение последнего уравпеипя с ранее записанным уравнением Бернулли показывает полную их аналогию, откуда делаем вывод, что

(1.105)

врасти — (^yi^{— у}г)²/(2?)»

т. о. потеря напора при внезапном расширении русла равпа скоростному напору, определенному по разности скоростей. Это положение часто называют теоремой Борда в честь французского ученого, который в 1766 г. вывел эту формулу.

Если учесть, что согласно уравнению расхода

i>i«S’* = v₂S\,

то получепный результат можно записать еще в виде, соответствующем общему способу выражения местных потерь:

(1.105')

Следовательно, для внезапного расширения русла коэффициент потерь

(1.106)

Доказанная теорема, как и следовало ожидать, хорошо подтверждается опытом при турбулентном течении и широко используется в расчетах.

Когда площадь дУ₂ весьма велика но сравнению с площадью S_i и, следовательно, скорость v_% можно считать равной нулю, потеря на расширение

йрасш = V[/(2g),

т. е. в этом случае теряется весь скоростной напор (вся кинетическая энергия, которой обладает жидкость); коэффициент потерь ? = 1. Такому случаю соответствует, например, подвод жидкости по -грубо к резервуару достаточно больших, размеров.

Рассмотренная потеря напора (анергии) прн внезапном расширении русла расходуется, можно считать, исключительно на вихре-образовапие, связациоо с отрывом потока от стенок, т. е. па под-дер-каппе непрерывного вращательного движения жидких масс с постоянным их обновлением (обменом). Поэтому этот вид потерь энергии, пропорциональных скорости (расходу) во второй степени, называют потерями на вихрообразование. В конечном счете они расходуются на работу сил трения, но не непосредствепно, как в прямых трубах постоянного сечения, а через ввхреобразоианио, как это было указано в начало параграфа.

Постепенно расширяющаяся труба называется диффузором. Течение жидкости в диффузоре сопровождается уменьшением скорости и увеличением давления, а слсдовательпо, преобразованием кинетической эпергии жидкости в энергию давления. Частицы движущейся жидкости преодолевают нарастающее давление за счет своей кинетической энергии, которая уменьшается вдоль диффузора и, что особенно важно, в направлении от оси к стенке. Слои жидкости, прилежащие к стенкам, обладают столь малой кинетической энергией, что иногда оказываются не в состоянии преодолевать повышенное давление, они останавливаются или даже начпнатот двигаться обратно. Обратное движение (противоток) вызывает отрыв основного потока от стенки и вихреобразования (рис. 1.64). Интенсивность этих явлений возрастает с увеличением угла расширения диффузора, а вместе с этим растут и потери на вихреобразования в ней.

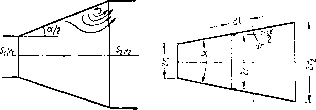
Рис. 1.0‘5. Расчетная схема диффузора

Рис. 1.64. Вихреобразования диффузоре

Кроме того, в диффузоре имеются обычные потери па трение, подобные тем, которые возникают и трубах постоянного сечения.

Полную потерю напора А_ДИф в диффузоре условно рассматриваем как сумму двух слагаемых:    *

Адиф = Атр4"^расш)    (1.107)

где fc_Tp в йрасш — потери напора на трение и расширение (еа внхреобразова-оис).

Потерю напора на трение можно приближенно подсчитать следующим способом. Рассмотрим круглый диффузор с прямолинейной образующей и с углом а при вершине. Пусть радиус входного отверстия диффузора равен выходного г₃ (рис. 1.65). Так как радиус сечения и скорость движения жидкости являются величинами переменными вдоль диффузора, то следует взять элементарный отрезок диффузора длиной вдоль образующей dl и для него выразить элементарную потерю напора на трение по основной формуле

где v — средняя скорость в произвольно взятом сечении, радиус которого г.

Из элементарного треугольника следует: dl = dr / sin (а/2). Далее, на основании уравнения расхода можио записать v = v_t (Vr)²,

гдо v_t — скорость в начале диффузора.

Подставил эти выражения в формулу для dh_Tp и щлголнщг интегрирование в пределах от до т, с. вдоль всего диффузора, считая при этом коэффициент L, постоянным:

Ж

(1.108)

^тр 8siu (а/2) V «² I 2g ’ где п — (S₂/S,) — (r₂/r₁)² — степень расширения диффузора.

Второе слагаемое — цотеря напора па расширенно (на вихрообразование) — имеет в диффузоре ту жо природу, что и при внезапном расширении, но мепынес значение, поэтому опо обычно выражается по той жо формуле (1.103) пли (1.106), но с поправочным коэффициентом к, меньшим единицы,

W - ^ki^r^L -^к (¦¹ ¦-%)' -¦i¹- i)' i-¦    (' •¹⁰⁹⁾

Так как в диффузоре по сравнению с внезапным расширением торможение потока как бы смягченное, коэффициент к называют коэффициентом смягчения. Его численное зизчение для диффузоров с углами конусности а = 5 — 20° можпо определить по приближенной формуле

/, = sin а.    (1.110)

Учитывая полученные формулы (1.108) и (1.109), можно исходное выражение (1.107) переписать в ьп"о

а коэффициент сопротивления диффузора можпо выразить формулой

Последнее выражение показывает, что коэффициент зависит от угла а, коэффициента Я_т и степепи расширения п.

Важно выяснить характер зависимости ?диф от угла а. С увеличением угла а при заданных Ьг и и первое слагаемое в формуле (1.112), обусловленное трением, уменьшается, так как диффузор становится

короче, а второе слагаемое, обусловленное вихреобразовапием и отрывом потока, увеличивается. При уменьшении ;:;е угла а вихреобрэ-зованпе уменьшается, но возрастает трение, гак как при заданной степени л расширения диффузор удлиняется, и поверхность его трения увеличивается.

Функция ?дыф = / (а) имеет минимум при некотором нанвыгоднейшем оптимальном значении угла а (рис.

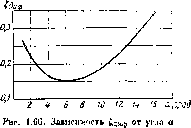
1.60).

Значение этого угла можно приближенно найти следующим способом: в формуле (1.112) заменим sin (а'2) через sina/2, продифференцируем полученное выражение по а, приравняем нулю и решим относительно а. Найдем ^диф    1т    Г    '1

- cos a ! 1 -

: =0,

откуда оптимальное значение a

. , / пЦЛ~\ a_01ir = arcsm I/ -~^_₁ -

При подстановке в эту формулу ^ = 0,015 + 0,025 и п = 2 -т- 4 получим а опт — fi°, что соответствует экспериментальным данным. На практике для сокращения длины диффузора при заданном п обычно принимают несколько большие углы а, а именно а = 7    9°.

Эти же значения угла а можно рекомендовать и для квадратных диффузоров.

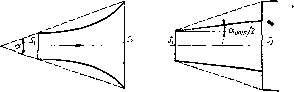
Рис. 1.67. Диффузор е состо-    Рис. 1.68. Ступенчатый

явдым градиентом давления    диффузор

Для прямоугольных диффузоров с расширением в одной плоскости (плоские диффузоры) оптимальный угол больше, чем для круглых а квадратных, и составляет 10 — 12°.

Если габариты не позволяют установить углы а, близкие к оптимальным, то при а > 15 + 25° целесообразно отказаться от диффузора с прямолинейной образующей и применить один из специальных диффузоров, например, диффузор, обеспечивающий постоянный градиепт давления вдоль осы (dpldx = const) и, следовательно, приблизительно равномерное нарастание давления (при прямой образующей градиент давления убывает вдоль диффузора) (рис. 1.07).

Уменьшение поп ери энергии в таких диффузорах по сравнению с обычными будет тем больше, чем больше угол а, и при углах 40 — 60° доуодпт до 40 % от потерь в обычных диффузорах. Кроме того, поток в криволинейном диффузоре отличается большей устойчивостью, т. е. в нем меньше тенденций к отрыву потока.

Хорошие результаты дает также ступенчатый диффузор, состоящий из обычного диффузора с оптимальным углом и следующего за ним внезапного расширения (рис. 1.68). Последнее не вызывает больших потерь энергии, так как скорости в этом месте сравнительно малы. Общее сопротивление такого диффузора значительно меньше, чем обычного диффузора такой же длины, и с той же степенью расширения, показанного ста рисунке штриховыми линиями.

Более подробные сведения о специальных диффузорах даны в спе-цпальпой литературе 110, 11].

1.34. Сужение русла

Внезапное сужение русла (трубы) (рнс. J.69) всегда вызывает меньшую потерю энергии, чем внезапное расширение с таким же соотношением площадей. В этом случае потеря обусловлена, во-первых, трением потока при входе в узкую трубу и, во-вторых, потерями па впх ре образование. Последние вызываются тем, что поток не обтекает входной угол, а срывается с него и сужается; кольцевое же пространство вокруг суженной части потока заполняется завихренной жидкостью.

В процессе дальпейшего расширения потока происходит потеря напора, определяемая формулой Борда (1.105). Следовательно, полная потеря папора

(1.113)

где — коэффициент потерь, нбуеловлеииый тревием потока при входе в уз-трубу и зависящий от SjS₂ и По; и_х — скорость потока в суженном месте; ?гуж — коэффициент сопротивления внезапною сужепня, ьависящий от степеви сужения.

Для практических расчетов можно пользоваться полуомнирнче-ской формулой И. Е. Идельчика:

?_С7)„= (1-5,/5₁);2 = (1 - 1/л)/2,

(1.114)

где п = SrfSz — степень сужении.

Из формулы следует, что в том частном случае, когда могкно считать S₂/Sj = 0, т. е. при выходе трубы из резервуара достаточно больших размеров и при отсутствии закругления входного угла, коэффициент сопротивления

Scym = U = 0,5.

Закруглением входного угла (входной кромки) можно значительно уменьшить потерю напора при входе и трубу.

Постепенное сужение трубы, т. е. гномическая сходящаяся труба, называется конфузором (рис. 1.70). Течение жидкости б копфузоре сопровождается увеличением скорости и падением давления; так как давление жидкости в начале коифузора вшпо, чем в конце, причин к возникновению цпхреобразоваиий и срывои потока (как в диффузоре) нет. В конфузоре имеются лишь потери на тренио. В связи с от им сопротивление коифузора всегда меньше, чем сопротивление такою же диффузора.

Рпс. 1.69. Внезапное сужспие Put-. 1.7lt. Конфузор трубы

Потерю irauopa на грегше в кокфузоре можно подсчитать гак же, как ото делали для диффузора, т. е. сначала выразить потерю для элементарного отрезка, а затем выполнить интегрирование. В результате получим следующую формулу:

(1.115)

Небольшое вихреобразовапие и отрыв но-тока от стенки с одновременным сжатием но-    -»-—

тока возникает лишь на иыходе из коифузора в месте соединения коипческой трубы с цилиндрической. Для ликвидации вихреобразовдпия ^^ис- 1.71. Соило л связанных с ним потерь рекомендуется ко-    Ч

ничсскую часть плавно сопрягать с цилиндрической или коническую часть заменять криволинейной, плавно переходящей к цилиндрическую (рис. 1.71). При этом можно допустить значительную степень сужения п при небольшой длине вдоль оси и пеболыщк потерях.

Коэффициент сопротивления такого плавного сужения, называемого соплом, изменяется примерно в пределах ? = 0,03 ¦+¦ 0,1 в зависимости от степени и плавности сужения и Re (большим Re соответствуют малые значения ? и наоборот).

1.35. Поворот русла

Внезапный поворот трубы, или колено без закругления (рис. 1.72), обычно вызывает значительные потери энергии, так к.'к в нем происходят отрыв потока и вихреобразование, причем эти г. )-тори тем больше, чем больше у гот б. Потерю папора рассчитывают

по формуле

л = ил»'/(2г).

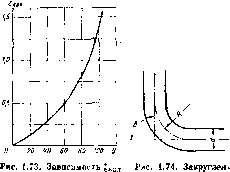
Коэффициент сопротивления колена круглого сечения ?_ВОл возрастает с увеличением 6 очень круто (рис. 1.73) и при б = 90° достигает единицы.

Постепенный поворот трубы, или закругленное колено (рис. 1.74), называется также отводом. Плавность поворота значительно уменьшает интенсивность вихреобразования, а следовательно, и сопротивление отвода по сравнению с коленом. Это уменьшение тем больше,

Рис. 1.72. Колено

от угла (>

ное колело

чем больше относительный радиус кривизны отвода R/d, и при достаточно большом его значении срыв потока и связанное с ним вихре-образование устраняется полпостьк». Коэффициент сопротивления отвода ?_01В зависит от отношения Rid, угла б, а также формы поперечного сечения трубы.

Для отводов круглого сечения с углом б = 90° и R/d i при турбулентном течении можпо пользоваться эмпирической формулой:

Соть = 0,051 +0,19<³⁰/Д.    (1.116)

Для углов 6 < 7О³ коэффициент сопротиалеакя

Ссп-О.ЭвГлб&га.    (1.117)

а при б > 100^е

Е.,,= (о ,1 + 4‘⁰'³⁵)^&'"*-    <^1Л18)

Потеря напора, определяемая приведенными коэффициентами Соты учитывает лишь дополнительное сопротивление, обусловленное кривизной русла, поэтому при расчете трубопроводов, содержащих отводы, следует длины этих отводов включать в общую длину трубопровода, по которой подсчитывается потеря на трение, а затем к это» потере на трение нужно добавить дополнительную потерю от кривизны, определяемую коэффициентом ?_ота.

1.36. Местные сопротивления при ламинарном течении

Изложенное в предыдущих параграфах данной главы относилось к местным гидравлическим потерям при турбулентном режиме течения в трубопроводе. При ламинарном режиме, во-первых, местный сопротивления обычно играют малую роль по сравнению с сопротивлением трепня и, во-вторых, закон сопротивления является более сложным и исследован в меньшей степени, чем при турбулентном течении.

Если при турбулентном течении местные потери напора можно считать пропор- ““'

циональными скорости (расходу) во второй степени, а коэффициенты потерь ? определяются в основном формой местного сопротивления и практически не зависят от Re, ___L

то при ламинарном течении потерю напора

следует рассматривать как сумму

Рис. 1.75. Схема жиклера

й_мА_тр -j- Авир,    (1.119)

где Ь_Тр — потеря ванора, обусловленная непосредственным действием сил трения (вязкости) в данном местном сопротивлении и пропорциональная вязкости жидкости и скорости в первой степени; Авихр — потеря, связанная с отрывом потока и вихреобразованием в самом местном сопротивлении или за нам и пропорцновальная скорости во второй степени.

Так, например, прп течении через жиклер (рис. 1.75) слева от плоскости расширения возникает потеря напора на трение, а справа — на вихреобразованяе.

Учитывая за коя сопротивления при ламинарном течении [см. выражении (1.83) и (1.84)1 с поправкой на начальный участок, а также формулу (1.57), выражение (1.119) можно представить в виде:

^,,Ы“"П"2«+^В 2?'

где А и В — безразмерные константы, зависящие в основном от формы местного сопротивления.

После делепия уравнения (1.119) на скоростной напор получим общее выражение для коэффициента местного сопротивлепия при ламинарном течении в трубопроводе *

С* = A/Re + Д.    (1.120)

* Получено А. Д. Альштулсм и автором одновременно,

т

Соотношение ме;рду первым и вторым членами в формулах (1.119) и (1.120) зависит от формы местного сопротивления и числа Re.

В таких местных сопротивлениях, где имеется узкий канал, длина которого значительно превышает его поперечный размер, с плавными очертаниями входа в выхода, как, например, показано на рис. 1.76, а, а числа Re малы, потеря напора определяется в основпом трепием,

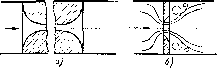
Рас. 1.76. Местное сопротивление

и закоп сопротивления близок к линейному. Второй члеи в формулах (1.110) и (1.120) в этом случае ранен нулю ели очень мал по срав-пелию с первым.

Если же в местном сопротивлении трение сведено к минимуму, например, благодаря острой кромке (как ыа рис. 1.76, б), и имеются отрывы потока п впхреобразование, а числа Re достаточно велики, то потери папора пропорциональны скорости (и расходу) ирибли-зительпо во второй степени.

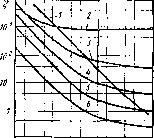
При Широкове диапазоне изменения числа Re в одном и том же местном сопротивлении возможеп как линеппый (при малых Re), так и квадратичный (при больших Re) закон сопротивления, а также переходная между ними область сопротивления при средних Не.

Типичная для такого широкого диапазона Re зависимость ? от Re в логарифмических коорди-

0    1 j W W² Ю³^ ю* Re    натах дапа на рис. 1.77, где пока-

Рие. 1.77. Зависимость ? от числа Rc:    ^заны результаты испытаний шести

1 — Фстропый фильтр, и — диафрагма (п=    МШрОТИВЛвшш. Наклонные прр-

= 0.06); 3 — шщювой клапан; 4 — разъем-    МЫС соответствуют линейному 88-

^U "    }Г0Льнш>, треншик _копу сопротивления (козффиди-

ен-г ? обратно пропорционален Re), криволинейные участки — переходной области, а горизонтальные прямые — квадратичному закону или автомодельности (коэффициент ? не зависит от Re). Такие графики для конкретных местных сопротивлений обычно строят на основе опытных данных.

Иногда вместо двучленной формы выражения месшых гидравлических потерь применяют стеленной одночлен кц •** kQ^m.

Ш где к — размерная величина; т — показатель степени, зависящий от формы местного сопротивления и Re и изменяющийся d пределах от 1 до 2.

Для местных сопротивлений и Re, при которых закон сопротивления близок к линейному, часто применяют выражение местных гидравлических потерь через эквивалентные длины Z„_KB трубопровода, т. е. фактическую длипу ^_вк трубопровода увеличивают па длину, эквивалентную по своему сопротивлению .местным Сопротивлениям.

Таким образом,

W = W + A«сп    (J-121)

и

_{(l j22)}

Численные значения эквивалентных длин (отнесенных' к диаметру трубопровода) для различных местных сопротивлений обычно находят опытпым путем.

Доказаппая в п. 1.32 для турбулентного режима теорема о потере напора при внезапном расширении русла при ламинарном режиме неприменима. Дело в том, что в зтом случае уже неприемлемы то допущения, которые делались при доказательстве этой теоремы, а именно, предположения о равпомеряом распределении скоростей в сечениях 1 — 1 и 2 — 2, о постоянстве давления по всей ujio-щадя S₂ в сечении 1 — 1 и о равенстве нулю касательных напряжений.

Кан показывают повые экспериментальные исследования [2], коэффициент потерь для внезапного расширения при очень малых Re (Re < 9) слабо зависит от соотношения площадей и в основном определяется числом Re по формуле вида ? -= Л/Re. Это значит, что течение является безотрывным, и потеря на расширение Лропорцио-нальпа скорости в первой степени. Прн 9 < Re < 3500 коэффициент потерь зависит как or числа Re, так а от отношения площадей. При Re > 3500 можно считать вполне справедливой теорему Борда, т. е. формулу (1.105) (число Re определяется по диаметру ы скорости до расширения).

Когда по трубе подводится жидкость со скоростью v_x к резервуару больших размеров, где v₂ = 0, то можно считать, что теряется вся удельная кинетическая энергия жидкости, которая для стабилизированного ламинарного потока в круглой трубе равна

f² = a_nvl/2g = vj/g.

Если же поток не является стабилизированным (длипа трубы

I < (,,_ач), то коэффициент а_л следует оцределять по графику, данному на рис. 1.46.

Глава 8. истечение жидкости через отверстия и насадки  »

Библиотека »