Глава 1. введение. свойства жидкостей 1,1. предмет гидравлвки
Глава 1. ВВЕДЕНИЕ. СВОЙСТВА ЖИДКОСТЕЙ 1,1. Предмет гидравлвки
Раздел механики, в котором изучают равновесие и движение жидкости, а также силовое взаимодействие между жидкостью и обтекаемыми ею телами или ограничивающими ее поверхностями, называется гидромеханикой. Если же помимо жидкостей изучают движение газов и обтекание ими тел, то науку называют аэрогидродинамикой.
Науку о законах равнонссия и движения жидкостей и о способах приложения этих законов к решению практических задач называют гидравликой. В гидравлике рассматривают, главным образом, потоки жидкости, ограниченные и направленные твердыми стенками, т. е. течения в открытых и закрытых руслах (каналах). В понятие «русло» или «канал» включают поверхности (стенки), которые ограничивают и направляют поток, следовательно, не только русла рек, каналов и лотков, во и различные трубопроводы, насадки, элементы гидромашин и других устройств, внутри которых протекает жидкость.
Таким образом, можно сказать, что в гидравлике изучают в основном внутренние течения жидкостей и решают так называемую внутреннюю задачу в отличие от внешней, связанной с внешним обтеканием тел сплошной средой, которое имеет место при движении твердого тела в жидкости или газе (воздухе). Внешнюю задачу рассматривают в аэрогидромеханике. Она получает значительное развитие в связи с потребностями авиации и судостроения.
Термину «жидкость» в гидромеханике часто придают более широкий смысл, чем это принято в обыденной жизни. В понятие «жидкость» включают все тела, для которых свойственна текучесть, т. е. способность сильно изменять свою форму под действием сколь угодно малых сил. Таким образом, в это понятие включают как жидкости обычные, называемые капельными, так и газы. Первые отличаются тем, что в малом количестве под действием поверхностного натяжения принимают сферическую форму, а в большом — обычно образуют свободную поверхность раздела с газом. Важной особенностью капельных жидкостей является то, что опи ничтожно мало изменяют свой объем при изменении давления, поэтому их обычно считают несжимаемыми. Газы, наоборот, могут значительно уменьшаться в объеме иод действием давления и неограниченно расширяться при отсутствии давления, т. е. они обладают большой сжимаемостью-if
Несмотря на это различие, законы движения капельных жидкостей и газов при определенных условиях можно считать одинаковыми. Основным из этих условий является малая скорость течения газа по сравнению со скоростью распространения в нем звука.
В гидравлике изучают движения, главным образом, капельных жидкостей, причем в подавляющем большинстве случаев последние рассматривают как несжимаемые. Внутренние течения газа относятся к области гидравлики лишь в тех случаях, когда их скорости значительно меньше скорости звука и, следовательно, сжимаемостью газа можно пренебречь. Такие случаи движения встречаются в практике довольно часто {например, течение воздуха в вентиляционных системах, в системах кондиционирования воздуха и некоторых газопроводах). В дальнейшем изложении под термином «жидкость» будем понимать капельную жидкость, а также газ, когда его можно считать несжимаемым.

Историческое развитие механики жидкостей шло двумя различными путями.
Первый путь — теоретический, нуть точного математического анализа, основанпого па законах механики. Он привел к созданию теоретической гидромеханики, которая долгое время являлась самостоятельной дисциплиной, непосредственно не связанной с экспериментом. Метод теоретической гидромеханики является весьма эффективным средством научного исследования. Однако на пути чисто теоретического исследования движения жидкости встречается множество трудностей, и методы теоретической гидромеханики не всегда дают ответы на вопросы, выдвигаемые практикой.
Второй путь — путь широкого привлечения эксперимента и накопления опытных равных для использования их в инженерной практике — привел к созданию гидравлики; он возник из насущных задач практической, инженерной деятельности людей. В началйшц период своего развития гидравлика была наукой чисто эмпирической. В настоящее же время в ней, где это возможно и целесообразно, все больше применяют методы теоретической гидромеханики для решения отдельных задач, а теоретическая гидромеханика все чаще начинает прибегать к эксперименту как к критерию достоверности своих выводов. Таким образом, различие в методах этих двух направлений одной и той же науки постепенно исчезает.
Метод, используемый в современной гидравлике при исследовании движения, заключается в следующем. Исследуемые явления сначала упрощают и к ним применяют законы теоретической механики. Затем полученные результаты сравнивают с данными опытов, выясняют степень расхождения, уточняют и исправляют теоретические выводы и формулы для приспособления их к практическому использованию. Целый ряд явлений, крайне трудно поддающихся теоретическому анализу из-за сложности, исследуют экспериментальным путем, а результаты представляют в виде эмпирических формул.
Гидравлика дает методы расчета и проектирования разнообразных гидротехнических сооружений (плотна, каналов, водосливов, трубопроводов для подачи всевозможных жидкостей), гидромашин (насосов, гидротурбин, гидропередач), а также других гидравлических устройств, применяемых во многих областях техники. Особенно велико значенле гидравлика в машиностроении, где приходится иметь дело с закрытыми руслами (например, трубами) ,и напорными течениями в них, т. е. с потоками без свободной поверхности в с давлением, отличным от атмосферного.

Гидросистемы, состоящие из насосов, трубопроводов, различных гидроагрегатов широко используют в машиностроении в качестве систем жидкостного охлаждения, топливоподачи, смазочных и др.
На различных современных машинах все более широкое применение находят гидропередачи (гидроприводы) в гидроавтоматика.
Гидропередачи представляют собой устройства для передачи механической энергии и преобразования движения посредством жидкости. По сравнению с передачами других видов (зубчатыми и т. п.) гидропередачи имеют ряд существенных преимуществ: простота преобразования вращательного движения в возвратно-поступательное, возможность плавного (бесступенчатого) изменения соотношения скоростей входного и выходного звеньев, компактность конструкций и малая масса гидромагаин при заданной мощности по сравнению, папример, с электромашинами и др.
Гидропередачи, снабженные системами автоматического или ручного управления, образуют гидроприводы, которые благодаря перечисленным преимуществам широко используют в рааличпых металлообрабатывающих станках, на летательных аппаратах (самолетах, вертолетах, ракетах), на сухопутных транспортных машинах (колесных и гусеничных), в строительно-дорожных и подъемно-транспортных машинах, в прокатных станах и прессах и т. п.
Гидроприводы, гидроавтоыатика и различпые гидравлические устройства являются весьма перспективными для комплексной автоматизации н механизации производства.
Для расчета и проектирования гидроприводов, их систем автоматического регулирования и других устройств с гидромашинами и гидроавтоматикой, а также для правильной их эксплуатации, ремонта и наладки нужно иметь соответствующую подготовку в области гидравлики и теории гидромагаин.
1.2 Силы, действующие на жидкость.
Давление в жидкости

Жидкость в гидравлике рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т. е. отвлекаются от молекулярного строения жидкости и ее частицы, даже бесконечно малые, считают состоящими из большого числа молекул.
Вследствие текучести (подвижности частиц) в жидкости действуют силы не сосредоточенные, а непрерывно распределенные по ее объему (массе) или поверхности. В связи с этим силы, действующие на объемы жидкости и являющиеся по отношению к ним внешними, разделяют па массовые (объемные) и поверхностные.
Массовые сады в соответствии со вторым законом Ньютона пропорциональны массе жидкости или, для однородной жидкости, — ее объему. К ним отпосятся сила тяжести а сила инерцин переносного дввженвя, действующая на жидкость при относительном ее покое в ускоренно движущихся сосудах или при относительном движении жидкости в руслах, перемещающихся с ускорением.
Поверхностные силы непрерывно расцределены по поверхности жидкости и при равномерном их распределения пропорциональны площади этой поверхности. Эти силы обусловлены непосредственным воздействием соседних объемов жидкости ва данный объам или же воздействием других тел (твердых или газообразных), соприкасающихся с данной жидкостью. Как следует из третьего закона Ньютона, с такими же силами, но в противоположном направлении, жидкость действует на соседние с нею тела.
В общем случае поверхностная сила ДЛ, действующая па площадке ДS, направлена иод некоторым углом к ней, и ее можно разложить на нормальную AF и тангенциальную Д Т составляющие (рис. 1.1). Первая называется силой давления, а вторая — силой трения.
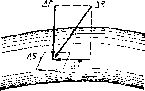
Как массовые, так и поверхностные силы в гидромеханике рассматривают обычно в виде единичных сил, т. е. сил, отнесенных к соответствующим единицам. Массовые силы относят к единице массы, а поверхностные — к единице площади.
Так как массовая сила равна произведению массы па ускорение, следовательно, единичная массовая сила численно равна соответствующему ускорению.
Единичная поверхностная сила, называемая напряжением поверхностной силы, раскладывается на нормальное и касательное напряжения.
Нормальное напряжение, т. е. напряжение силы давления, называется гидромеханическим (в случае покоя — гидростатическим) дешением, или просто давлением, и обозначается буквой р.
Если сила давления AF равномерно распределена по площадке AS, то среднее гидромеханическое давление определяют по формуле
p = AF/AS. (1.1)
В общем случае гидромеханическое давление в данной точке равно пределу, к которому стремится отношение силы давления к площади AS, па которую она действует, при уменьшении AS до нуля, т. ?>. при сгягиваылл ее к точке
р = Um AF/AS. (1.2)
iS-»0
Если давление р отсчитывают от абсолютного нуля, то его называют абсолютным, а если отсчитывают от атмосферного давления ра, т. е. от условного нуля, то его называют избыточным (pUec) иля манометрическим. Следовательно, абсолютное давление
Рабс = Ра + Риэб-
За единицу давления в Международной системе единиц (СИ) принят паскаль — давление, вызываемое силой 1Н, равномерно распределенной по нормальной к пей поверхности площадью 1 м2. Наряду с этой единицей давления применяют укрупненные единицы: килопаскаль (кПа) и мегапаскаль (МПа):
1 Па = 1 Н/м8 = 10-3 кПа= 10-9 МПа.
В технике в настоящее время продолжают применять также систему единиц МКГСС (метр, килограмм-сила, секунда), в которой за единицу давления принимается 1 кгс/м8. Используют также внесистемные единицы — техническую атмосферу и бар
1 ат=1 кгс/сма = 10 ООО кгс/м2;
1 бар = 10® Па =*1,02 ат.
Соотношение между единицами давления в системах СИ и МКГСС следующеэ:
1 Па = 0,102 кгс/м2 или 1 кгс/м2 = 9,81 Па.
Касательное напряжение в жидкости, т. е. напряжение трения, обозначается буквой т и выражается подобно давлению пределом
х— lim А77Л.?,
(1.3)
Д8-.0
а размерность его та же, что и размерность давления.
1.3. Основные свойства капельных жидкостей
Одной из основных механических характеристик жидкости является ее плотность.
Плотностью р (кг/м8) называют массу зкидкости, заключенную в единице объема; для однородной жидкости
р = mfV,
(1.4)
где т — масса жидкости в объеме V.
Удельным весом у (Н/м3) называют вес единицы объема жидкости, т. е.
у — G/V,
(1.5)
где G — вес яшдкссто в объеме V.
Например, для воды при 4 °С имеем -у =1000 кгс/мз = 0,001 кгс/см8 = 9,81 • 10® Н/м3,
Связь между удельным весом у и плотностью р легко пайти, села учесть, что G — gms
Р = Gi(gV) = yJg. (1.6)
Если жидкость неоднородна, то формулы (1.4) и (1.5) определяют лишь среднее звачепие удельного веса или плотности в данном объеме. Для определения истицного значения у и р в данной точке следует рассматривать объем, уменьшающийся до нуля, и искать предел соответствующего отношения.
Применяют еще относительную плотность жидкости б, равную отношению плотности жидкости к плотности воды при 4 5С:
3 = рш/рвад. (l-'O
Коротко рассмотрим основные физические свойства капельных жидкостей.
1. Сжимаемость, или свойство жидкости изменять свой объем под действием давления, характеризуется коэффициентом |5Р (м2/Н) объемного сжатия, который представляет собой относительное изменение объема, приходящееся на единицу давления, т. е.
--CdK/dp) C1/V). (1.8)
Знак минус в формуле обусловлен тем, что положительному приращению давления р соответствует отрицательное приращение (т. е. уменьшение) объема V.
Рассматривая конечные приращения Др = р — рх и AF = V — — Vj и считая рр постоянным, получаем
V «а К, (1 —РрДр),
или, учитывая равенство (1.4), находим приближенную формулу для определения плотности
P^PJil-PpAp), .(1-9)
где pf и р — плотности лрв давлениях р, и р. ^
Величина, обратная коэффициенту рр, представляет собой объемный модуль упругости К.
Через модуль К и конечные разности формулу (1.8) можно переписать в виде зависимости
ДГ/К=--Д р/К, (1.8')
которую называют обобщенным законом Гука.
Выразив объем через плотность, вместо формулы (1.8) получим К = — tfp/[pd(l/p)] = р dp/dp или К/р — dp/dp = с2, (1.10)
Для капельных жидкостей модуль К несколько уменьшается с увеличением тешгерагуры в возрастает с повышением давления. Для воды он составляет при атмосферном давлении приблизительно 2000 МПа. Следовательно, при повышении давления на 0,1 МПа объем воды уменьшается всего лишь на 1/20 000 часть. Такого же порядка модуль упругости и для других капельных жидкостей, например для минеральных масел он равен приблизительно 1200 МПа.
Как следует из формулы (1.9), при повышении давления воды, например, до 40 МПа ее плотность повышается лишь на 2 %, а масла — па 3 %. Поэтому в большинстве случаев капельные жидкости можно считать практически несжимаемыми, т. е. принимать их плотпость не зависящей от давления. Но при очень высоких давлениях и упругих колебаниях сжимаемость жидкостей следует учитывать.
Различают адиабатный и изотермический модуль упругости. Первый больше второго приблизительно в 1,5 раза и проявляется при быстротечных процессах сжатия жидкости без теплообмена. Приведенные выше значения К являются значениями изотермического модуля.
2. Температурное расширение характеризуется коэффициентом (5т объемного расширения, который представляет собой относительное изменение объема при изменении температуры Т па 1 °С и постоянном давлении, т. е.
Pr^Q/VdldVldT). (1.11)
Рассматривая конечные приращения AF — V — Vx и ДТ = = Т — 7\ и принимая Рг постоянным, получаем
V = Vi{1+Pt№),
а учитывая равенство (1.4), находим приближенную формулу
P-PiAl + РгДГ). (1.12)
где pi и р — плотности при температурах Тх и Т.
Для воды коэффициент (5г возрастает с увеличением давления и температуры от 14 • 10_6 при 0 °С и ОД МПа до 700 • 10-8 при 100 "С и 10 МПа. Для минеральных масел в диапазоне давлений от 0 до 15 МПа {5т можно в среднем принимать равным 800-10'6.
3. Conpomue.ienue растяжению внутри капельных жидкостей но молекулярной теории может быть весьма значительным. При опытах с тщательно очищенной и дегазированной водой в ней были получецы кратковременные напряжения растяжения до 23—28 МПа. Однако технически чистые жидкости, содержащие взвешенные твердые частицы и мельчайшие пузырьки газов, не выдерживают даже незначительных напряжений растяжения. Поэтому в дальнейшем будем считать, что напряжения растяжения в капельных жидкостях невозможны.
4. На поверхности раздела жидкости и газа действуют силы поверхностного натяжения, стремящиеся придать объему жидкости сферическую форму и вызывающие некоторое дополнительное давленье. Однако это давление заметно сказывается лишь при малых объемах жидкости и для сферических объемов (капель) определяется 10
формулой р — 2а/г,
где 0 — коэффициент поверхностного натяжения жидкости; г_радиус сферы.
Коэффициент сг имеет следующие значения (Н/м) для разных жидкостей, гравичащих с воздухом при температуре 20 °С: для воды 73‘а, спирта 22,5‘3, керосина 27'8, ртути 460-10-8. С ростом температуры поверхностное натяжение уменьшается.
В трубках малого диаметра дополнительное давление, обусловленное поверхностным натяжением, вызывает подъем (или опускание) жидкости относительно нормального уровня, характеризующий .капиллярность жидкости.
Высоту подъема смачивающей жидкости (или опускание несмачивающей жидкости) в стеклянной трубке диаметром d определяют по формуле для полусферического мениска
has4o/(dy) = k]d, (1-13)
где к (мы8) имеет следующие значения; для воды +30, ртути —10,1; спирта +11,5.
С явлением капиллярности приходится сталкиваться при использовании стеклянных трубок в приборах для измерения давления, а также в некоторых случаях истечения жидкости. Большое значение приобретают силы поверхпост-ного натяжения в жидкости, находящейся в условиях невесомости.
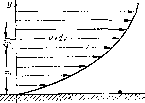
Рае. 1.2. Профиль скЭ^остей при ' течении вязкой жидкости вдоль стенки
5. Вязкость представляет собой свойство жидкости сопротивляться Сдвигу (скольжению) ее слоев. Это свойство проявляется в том, что в жидкости при определенных условиях возникают касательные напряжения. Вязкость есть свойство, противоположное текучести: более вязкие жидкости (глицерин, смазочные масла и др.) являются менее текучими, и наоборот.
При течении вязкой жидкости вдоль твердой стенки происходит торможение потока, обусловленное вязкостью (рис. 1.2). Скорость v уменьшается по мере уменьшения расстояния у от стейки вилось до v = 0 при у = 0, а между слоями происходит проскальзывание, сопровождающееся возникновением касательных напряжений (напряжений трения).
Согласно гипотезе, высказанной впервые Ньютоном в 1680 г., а затем экспериментально обоснованной проф. Н. П. Петровым в 1883 г., касательное'напряжение в жидкости зависит от ее рода и характера течения и при слоистом течении изменяется прямо пропорционально тан называемому поперечному градиенту скорости. Таким образом
x<=Hdv/dy, (1-14)
гдо ц — коэффициент пропорциональности, получивший название динамической вязкости жидкости; dv — приращение спорости, соответствующее приращению координаты dy (см. рис. 1.2).
Поперечный градиент скорости dv/dy определяет измепение скорости, приходящееся па единицу длины в направлении нормали к стецке и, следовательно, характеризует интенсивность сдвига жидкости в данной точке (точнее dv/dy — это модуль градиента скорости; сам градиент ~ вектор).
Из закона трения, выражаемого уравнением (1.14), следует, что напряжения трения возможны только в движущейся жидкости, т. е. вязкость жидкости проявляется лишь при ее течении. В покоящейся жидкости касательпые напряжения будем считать равными нулю 17.
Изложенное позволяет сделать вывод, что трение в жидкостях, обусловленное вязкостыо, иодчинепо закону, принципиально отличному от закона трения твердых тел.
Если течение жидкости таково, что имеется еще градиент скорости в направлении, нормальном к плоскости рисунка (см. рис. 1.2), то полную производную в формуле (1.14) надо заменить частной производной dv/dy.
При постоянстве касательного напряжения по поверхности S полная касательная сила (сила трения), действующая по этой поверхности
Т = Ц {dv/dy) S.
(1.15)
Для определения размерности вязкости ц (Па-с) решим уравнение (1.14) относительно ji, в результате ¦чего получим = т dy/dv.
В системе СГС за единицу вязкости принимается пуаз:
1 П = 1 дин-с/см2.
Так как 1 дин = 10~5 II = 1,02-10"а кге, а 1 ма = Ю4 см2, то
1 П = 0.1 Па-с = 0,0Ю2 кгс-с/ма.
Наряду с динамической вязкостью [i применяют кинематическую
(1.16)
Единицей измерения кинематической вязкости является стокс:
1 Ст =* 1 см2/с.
Сотая доля стокса называется сантистоксом (сСт).
Вязкость капельных жидкостей зависит от температуры и уменьшается с увеличением последней (рис. 1.3). Вязкость газов, наоборот, с увеличением температуры возрастает. Объясняется это различием природы вязкости в жидкостях и газах. В жидкостях молекулы расположены гораздо ближе друг к Другу, чем в газах, и вязкость вызывается силами молекулярного сцепления. Эти силы с увеличением температуры уменьшаются, поэтому вязкость падает. В газах же вязкость обусловлена, главным образом, беспорядочным тепловым движением молекул, интенсивность которого увеличивается с повышением температуры. Поэтому вяэкость газов с увеличением температуры возрастает.
Влияние температуры на вязкость жидкостей можно оценить формулой
ц = ИоС-*(Г-аУ, (U7)
где ц и |j.0 — вязкости при температуре Г и Тп\ (5 — коэффициент, значение которого для масел изменяется в пределах 0,02—0,03.
Вязкость жидкостей зависит также от давления, однако эта зависимость существенно проявляется лишь при относительно больших изменениях давления (в несколько десятков МПа). С увеличением давления вязкость большинства жидкостей возрастает, что может быть оценено формулой fi — (1.18) где ц и (i0 — вязкости при давлении р и р0; а — коэффициент, значение которого для минеральных масел изменяется в пределах 0,02—0,03 (ннЖ' вий предел соответствует высокий температураи, а верхний — низким).
^.см^с
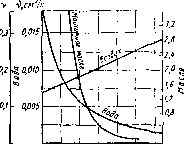
Рис. 1.3. Зависимость кинематической вязкости от температуры
в so too WT,°C
Приближенная зависимость относительной вязкости (я/[10 от давления для минеральных масел ноказаЛ па рис. 1.4 для продельных значений коэффициента а. %
Вязкость жидкостей измеряют при помощи вискозиметров. Наиболее распространенным является вискозиметр Энглера, который представляет собой цилипдрический сосуд диаметром 106 ми, с короткой трубкой диаметром 2,8 мм, встроенной в дно. Время t истечения 200 см3 испытуемой жидкости из вискозиметра через эту трубку под действием силы тяжести, деленное на время fBOn истечения того же объема дистиллированной воды при 20 0 С выражает вязкость в градусах Энглера: 1 °Е = t/tgoa, где *вол = 51,6 с.
Для пересчета градусов Энглера в стоксы в случае минеральпых масел применяют формулу
v = 0,073" Е-
6. Испаряемость свойственна всем капельным жидкостям, однако интенсивность испарения неодинакова у различных жидкостей и зависит от условий, в которых они находятся.
Одним из показателей, характеризующих испаряемость жидкости, является температура ее кипения при нормальном атмосферном давлении; чем выше температура кипения, тем меньше испаряемость жидкости. В гидросистемах нормальное атмосферное давление является лишь частным случаем; обычно приходится иметь дело с испарением, а иногда и кипением жидкостей в замкнутых объемах при различных температурах и давлениях. Поэтому более полной характеристикой испаряемости является давление (упругость) насыщенных ?аров рн. п, выраженное в функции температуры. Чем больше давление насыщенных паров при данной температуре, тем больше испа- -ряемость жидкости. С увеличением температуры давление рн ц увеличивается, однако у разных жидкостей в разной степени (рис. 1.5).
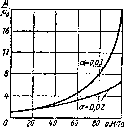
Рис. 1.4. Зависимость относительной вязкости минерального масла от давления
Если для простой жидкости рассматриваемая зависимость является вполне определенной, то для сложных жидкостей, представляющих собой многокомпонентные смеси (например, для бензина и др.), давление рн п зависит не только от физико-химических свойств и температуры, но и от соотношения объемов жидкой и паровой фаз. Давление насыщенных паров возрастает с увеличением части объема, занятого жидкой фазой. Обычно значения упругости паров сложных жидкостей даются для отношения паровой и жидкой фаз, равного 4 :1.
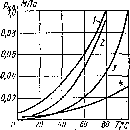
Рис. 1.о. Зависимость давления насыщенных паров жидкостей от температуры:
7. Растворимость газов в жидкостях характеризуется количеством растворенного газа в единице объема жидкости, различна для разных жидкостей н изменяется с увеличением давления.
Относительный объем газа, растворенного в жидкости до ее полного насыщения, можно считать по закону Генри прямо пропорциональным давлению, т. е.
Vr!Vm=-kplpa,
где VT — объем растворевпого газа, приведешшй к нормальным условиям (р0, Та)\ Vm — объем жидкости; к — коэффициент растворимости; р — давление жидкости.
U
Коэффициент к имеет следующие значения при 20 °С: для воды 0 016, керосина 0,13, минеральных масел 0,08, жидкости АМГ-10 — ОД.
При понижении давления выделяется растворенный в жидкости газ, причем интенсивнее, чем растворяется в ней. Это явление может отрицательно сказываться па работе гидросистем.
Г л а в а 2. ГИДРОСТАТИКА
1.4. Гидростатическое давление и его свойство
Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практические приложения.
Как следует из гл. 1, жидкости практически не способны сопротивляться растяжению, а в неподвижных жидкостях не действуют касательные силы. Поэтому на неподвижную жидкость из поверхностных сил могут действовать только силы давления; причем на внешней поверхности рассматриваемого объема жидкости силы давления всегда направлены по нормали внутрь объема жидкости и, следовательно, являются сжимающими. Под внешней поверхностью жидкости поиимают не только поверхность раздела жидкости с газообразной средой или твердыми стенками, но и поверхность объема, мысленно выделяемого из общего объема жидкости.
Таким образом, в неподвижной жидкости возможен лишь один вид напряжения — напряжение сжатия, т. е. гидростатическое давление.
Рассмотрим основное свойство гидростатического давлення:-в любой точке жидкости гидростатическое давление не зависит от ориентировки площадки, на которую опо действует, т. е. от углов 1е наклона по отношению к координатным осям. *
Для доказательства этого свойства выделим в неподвижной жидкости элементарный объем в форме тетраэдра с ребрами, параллельными координатным осям и соответственно равными dx, dy и dz (рис. 1.6). Пусть внутри выделенного объема на жидкость действует единичная массовая сила, составляющие которой равны X, Y и Z. Обозначим через рх гидростатическое давление, действующее на грапь, нормальную к оси Ох, через pv — давление на грань, нормальную к оси Оу, и т. д. Гидростатическое давление, действующее на наклонную грань, обозначим через рп, а площадь этой грани — через dS.
Составим уравнение равновесия выделенного объема жидкости сначала в направления оси Ох, учитывая при этом, что все еллы направлены по нормалям к соответствующим площадкам ввутрь объема жидкости. Проекция сил давления на ось Ох
Рх dy dz/2 — рп dS cos (гг, х).
Масса жидкости в тетраэдре равна произведению ее объема на плотность, т. е. dxdydz/6, следовательно, массовая сила, действующая па тетраэдр вдоль оси Ох, составляет dx dy dzpX/Q.
Уравнение равновесия тетраэдра запишем в виде: dy dz pj2 — рп dS cos (гс, x) 4- dx dy dz pX/6 = 0.
Разделив это уравнение па площадь dydz/2, которая равна нло-'щади проекция наклонной грани dS на плоскость уОг, т. е. dydz/2 = = dS cos (п, х), получим ХР/3 = 0.
При стремлении размеров тетраэдра к нулю последний член уравнения, содержащий множитель dx, также стремится к пулю, а давления рх и рп остаются величинами конечными. Следовательно, в пределе получим Рх~Рп = 0 или рх=рп.
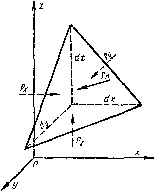
Рис. 1.6. Схема для доказательства свойства гидростатического давленая
Аналогично составляя уравнения равновесия вдоль осей Оу и Oz, находим
Ри = Рп< Рг = Рп ИЛИ
px=Pv=Pi = Pn- (1-19)
Так кап размеры тетраэдра dx, ¦ dy и dz взяты произвольно, то и наклон площадки dS произволен
и, следовательно, в пределе при стягивании тетраэдра в точку дав18 ление в этой точке по всем направлениям будет одинаково.
Ото положение можно легко доказать, основываясь на формулах сопротивления материалов для напряжений при сжатии цо двум и трем взаимно перпендикулярным направлениям *. Для этого положим в указанных формулах касательное напряжение равным пулю, в результате чего получи?!
Oj = Оу = аг = — р.
Рассмотренное свойство давления в неподвижной жидкости имеет место также при движении невязкой жидкости. При движении же реальной жидкости возникают касательные напряжения, вследствие чего давление в реальной жидкости указанным свойством, строго
говоря, не обладает.
Рассмотрим распространенный частный случай равновесия жидкости, когда на нее действует лишь одна массовая сила — сила тяжести, в получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Если этот объем весьма мал по сравнению с объемом Земли, то свободную поверхность жидкости можно считать горизонтальной плоскостью.
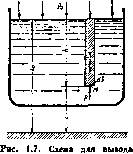
Пусть жидкость содержится в сосуде (рис. 1.7) и на ее свободную поверхность действует давление р0. Найдем гидростатическое давление р в произвольно взятой точке Л/, расположенной на глубине h.
основного уравнения гидроста-
Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиид* рический объем высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на ниж« нее основание цилиндра теперь будет виеганим и направлено по нормали внутрь объема, т. е. вверх.
Запишем сумму сил, действующих яа рассматриваемый объем в проекцни на вертикаль:
pdS — p0dS — pgh dS = 0. ,
Последний член уравнения представляет собой вес жидкости в указанном объеме. Силы давления по боковой поверхности цилиндра в уравнение не входят, так как она нормальны к вертикали. Сократив выражение на dS и перегруппировав члены, найдем ,
P=Po + hpg = p0 + hy. % (1.20)
Получепноо уравнение называют основным уравнением гидростатики; по нему можно подсчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления р0 на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.
Величина р0 является одинаковой для всех точек объема жидкости,'поэтому, учитывая свойство гидростатического давления, можно сказать, что давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково. Это положение известно под названием закона Паскаля *.
Давление жидкости, как видно из формулы (1.20), возрастает с увеличением глубины по закону прямой и на данной глубине есть величина постоянная.
Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня. В данном случае поверхностями уровня являются горизонтальные плоскости, а свободная поверхность является одной из поверхностей уровня.
Возьмем на произвольной высоте горизонтальную плоскость сравнения, от которой вертикально вверх будем отсчитывать координаты z. Обозначив через г координату точки М, через г0 — координату свободной поверхности жидкости и заменив в уравнении
(1.20) h па г0 — г, получи»
z + p/(pg) = zo + poj{pg). (1-21)
Так как точка М взята произвольно, можно утверждать, что для всего рассматриваемого неподвижного объема жидкости *-bp/(p?)~const.
Координата г называется геометрической высотой. Величина р/( pg) имеет линейную размерность и называется пьезометрической высотой. Суммач г-t-р/( pg) называется гидростатическим напором.
Таким образом, гидростатический напор есть величина постоянная для всего объема неподвижной жидкости.
Те же результаты можно получить путем интегрирования дифференциальных уравнений равновесия жидкости, которые рассмотрены в следующем параграфе.
1.6. Дифференциальные уравнения равновесия жидкости н их интегрирование для простейшего случая
Получим дифференциальные уравнения равновесия жидкости в общем случае, когда на нее действуют пе только сила тяжести, по и другие массовые силы, например, силы инерции переносного движения при так называемом относительном покое (см. пп. 1.10 и 1.11).
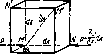
Рис. 1.8. Схема для вывода дифференциальных уравнений равно, весая жидкости
В неподвижной жидкости возьмем произвольную точку М с координатами х, у и z и давлением р (рис. 1.8). Систему координат будем считать жестко связанной с сосудом, содержащим жидкость. Выделим в жидкости элементарный объем а форме прямоугольного параллелепипеда с ребрамп, параллельными координатным осям и соответственно равпыми dx, dy и dz. Пусть точка М будет одной из вершин параллелепипеда. Рассмотрим условия равновесия выделенного объема жидкости. Пусть внутри параллелепипеда на жидкость действует равнодействующая массовая сила, составляющие которой, отнесенные к единице массы (см. п. 1.2), равны X, Y и Z. Тогда массовые силы, действующие па выделенный объем в направлении координатных осей, будут раины этим составляющим, умноженным на массу выделенного объема.
Давление р есть функция координат х, у и z, но вблизи точки М по всем трем граням параллелепипеда оно одинаково, что вытекает из доказанного выше свойства гидростатического давления (см. п. 1.4). При переходе от точки М, например, к точке N изменяется лишь координата х па бесконечно малую величину dx, в связи с чем функция р получает приращение, равное частному дифференциалу {др/дх) dz, поэтому давление в точке N равно p-\.{dpldx)dx,
где др/дх — градиент давления вблизи точки М в направления оси х.
Рассматривая давления в других соответствующих точках граней, нормальных к оси х, например в точках N' и М', видим, что они отличаются на одинаковую (с точностью до бесконечно малых высших порядков) величину
![]()
Ввиду этого разность сил давления, действующих на параллелепипед в направлении оси х, равна указанной величине, умноженной
на площадь грани: — pdxdydz.
Аналогичным образом, но через градиенты давления др/ду и dp/dz выразим разности сил давления, действующие на параллелепипед в направлении'двух других осей.
На выделенный параллелепипед действуют лишь указанные массовые силы и силы давления, поэтому уравнения равновесия параллелепипеда в направлениях трех координатных осей заицшем*в следующем виде: V
Хр dx dy dz — ^ dx dy dz = 0; I
Yp dx dy dz — dx dy dz = 0; }•
(1.22)
Zn dr. dn dz — fir dii dz — fl. I
Zp dx dy ds — dx dy dz = 0. I
Разделим эти уравнения на массу pdxdydz параллелепипеда и перейдем к пределу, устремляя dx, dy и dz к нулю, т. е. стягивая параллелепипед к исходной точке М- Тогда в пределе получим уравнения равновесия жидкости, отнесенные к точке Afi
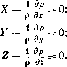
(1.23)
Система (1.23) дифференциальных уравнений гидростатики называется уравнениями Эйлера 19.
Для практического пользования удобнее вместо системы уравнений (1.23) получить одно эквивалентное им уравнение, не содержащее частных производных. Для этого умножим первое из уравнений
(1.23) на dx, второе — на dy, третье — на dz и, сложив все три уравнения, получим
х «ь+у dy +z dz - j (g dt+g. dy+% dz) = o.
Трехчлен, заключенный в скобках, представляет собой полный дифференциал давления, т. е. функции р (х, у, г), поэтому предыдущее уравнение можно переписать в виде:
X dx-{-Y dy-\~Z dz — dp/p = 0
ЕЛИ
dp = p(X dx-\-Y dy-\-Zdz). (1-24)
Полученное уравнение выражает приращение давления dp при измепеыии координат па dx, dy и dz в общем случае равновесия жидкости.
Если предположить, что на жидкость действует только сила тяжести, и паправить ось г вертикально вверх, то X = Y = 0, Z = —g и, следовательно, вместо уравнения (1.24) для этого частного случая равновесия жидкости получим
dp = —pgdz. (1.25)
После интегрирования будем иметь Р = — Pgz + C-
Постоянную интегрирования пайдем, подставив параметры свободной поверхности, для которой при г = z0 р = р0 (см. рис. 1.7). Получим
С = ра-\~ pgz0.
При этом
P = Po-\-{zo-z)pg (1-26)
или
* + Pl(f>g) = za + Po/iPg) — const.
Заменяя в уравнении (1.26) разность z0 — z на h — глубину расположения точки М, найдем p = p0+pgh.
Получили то же основное уравнение гидростатики [(1.20) или
(1.21)], которое было выведено в предыдущем параграфе иным путей.
Интегрирование уравнения (1.24) для других случаев равновесия будет рассмотрено ниже (см. пп. 1.10 и 1.11).
1.7. Пьезометрическая высота. Вакуум.
Измерение давления
В данном параграфе, а также в пп. 1.8 и 1.9 продолжим рассмотрение важнейшего частного случая равновесия жидкости — равновесие в поле лишь одной массовой силы — силы тяжести.
Пьезометрическая высота, равная p/{pg), представляет собой высоту столба данной жидкости, соответствующую данному давле* нию р (абсолютному или избыточному). Пьезометрическую высоту, соответствующую избыточному давлению, можно определить пй пьезометру — простейшему устройству для измерения давления. Пьезометр представляет собой вертикальную стеклянную трубку, верхний конец которой открыт в атмосферу, а нижний присоединен к емкости, в которой измеряется давление (рис. 1.9).
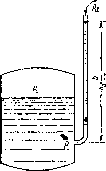
Рис. 1.9. Пьезометр, присоединенный к баку
Применяя формулу (1.20) к жидкости, заключенной в пьезометре, получим
Рабе = Pa-{~Pghp,
где рабе •— абсолютное давление в жидкости на уровне присоединения пьезометра; ра — атмосферное давлепие.
Отсюда высота подъема жидкости в пьезометре
hp = (ра0о - Ра)/<Р?) = ризб/(р?), (1 -27)
где Разб —• иабиточноо давление на уровне при-соединения пьезометра.
Очевидно, что если на свободную поверхность покоящейся жидкости действует атмосферное давление, то пьезометрическая высота для любой точки рассматриваемого объема жидкости равна глубине расположения этой точки.
Часто давление в жидкостях или газах численно выражают в виде соответствующей этому давлению пьезометрической высоты по формуле (1.27).
Например, одной технической атмосфере соответствуют Л1 = Р/(Рвод?) = Р/7оод = 10 000/1000= Ю м вод. ст. ht — PliPpTg) = p/Урс = 10000/13600 = 0,735 м рт. ст.
Если абсолютное давление в жидкости или газе меньше атмосферного, то говорят, что имеет место разрежение, или еакуум. За величину разрежения, или вакуума, принимается недостаток до атмосферного давления!
Рван = Ра — Рабе ИЛИ heail = (pa — pac0)/(pg).
Возьмем, например, трубу с плотно пригнанным к ней поршнем, опустим нижний ее конец в сосуд с жидкостью и будем постепенно поднимать поршень (рис. 1.10). Жидкость будет следовать за поршнем и вместе с ним поднимется на некоторую высоту h от свободной
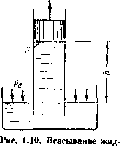
коста поршвем
поверхности с атмосферным давлением. Так как для точек, расположенных под поршнем, глубииа погружения относительно свободной поверхности отрицательна, согласно уравнению (1.20), абсолютное давление жидкости под поршнем
а вакуум
Рвак = Ра - р = pgh или Аван = (ра “ р)!{pg)=h.
По мере подъема поршпя абсолютное давление жидкости под ним уменьшается. Нижним пределом для абсолютного давления в жидкости является пуль, а максимальное значение вакуума числецпо равпо атмосферному давлению, поэтому максимальную высоту всасывания Лтах жидкости можно определить из уравнения (1.28), если в нем’положить р = 0 (точнее р = рн п). Таким образом, без >чета давления рн,н насыщенных паров
При яормальвоч атмосферном давлении (0,1033 МПа) высота hmах равна для воды 10,33 м, для бензина (р = 750 кг/м3) 13,8 м, для ртути 0,760 м и т. д.
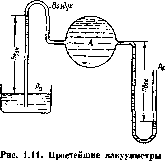
Простейший устройством для измерения вакуума имеет служить стеклянная трубка, показанная на рис. 1.11 в двух вариантах. Вакуум в жидкости А можно измерять при помощи U-образноя трубки (см. рисунок справа) или перевернутой U-образной трубки, один конец которой опущен в сосуд с жидкостью (см. рисунок слева).
Для измерения давления жидкостей и газов в лабораторных условиях помимо пьезометра пользуются жидкостными и механическими манометрами.
На рис. 1.12 показаны схемы жидкостных манометров. Так называемый U-образцый манометр (рис. 1.12, а) представляет собой изогнутую стеклянную трубку, содержащую ртуть. Прн измерении небольших давлений газа вместо ртути применяют спирт, воду и
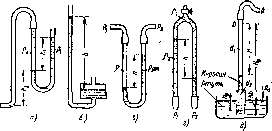
Рис. 1.12. Схемы жидкостных манометров
иногда тетраброиэтан (б = 2,95). Если измеряется давление жидкости в точке М, и соединительная трубка заполнена этой же жидкостью, то следует учитывать высоту расположения манометра над точкой М. Так, избыточное давление в точке М »
pM^'hPig + fhpzg. «*
Чашечный манометр (рис. 1.12, б) удобнее описанного выше тем, что при пользовании им необходимо фиксировать положение лишь одного уровня жидкости (при достаточно большом дпаметре чашки по сравнению с диаметром трубки уровень жидкости в чашке можно считать неизменным).
Для измерения разности давлений в двух точках служат дифференциальные манометры, простейшим из которых является U-образ-ный манометр (рис. 1.12, в). Если при помощи такого манометра, обычно заполняемого ртутью, измерена разность давлений рг и р2 в жидкости плотностью р, которая полностью заполпяст соединительные трубки, то
Pi~ Рг — hg (ррт — р)-
Для измерения малых перепадов давления воды применяют двухжидкостный микроманометр, представляющий собой перевернутую
U-образеую трубку с масломиликоросиномв верхней части (рис. 1.12, г). Для этого случая
Pi—P3~kg (ра — pi).
Двухжидкоствый чашечный манометр (рис. 1.12, д) предназначен для измерения давлений или разрежений воздуха в интервале от 0,01 до 0,05 МПа, т. е. для того случая, когда спиртовой или водяной манометр дает чрезмерно высокий столб спирта или воды, а потому неудобен для пользовании, а ртутный манометр не дает необходимой точности из-за недостаточной высоты столба ртути. Таким манометром, например, пользуются при опытах в скоростных аэродинамических трубах. В чашку заливают ртуть, а в трубку — спирт, керосин или иную жидкость. Соответствующим подбором диаметров верхнего dj и вгоквего участков трубки можно получить любую условную плотность РуС> входящую в формулу P — HpjCg,
где р — измеряемое давление (или разрежение); II — показание манометра.
Найдем выражение для руС из следующих уравнении-.
уравнение равновесия столбов ртутя и керосина ври р ~ Р& Hopug—hoppig',
уравнение равновесия при р > ра р + {Нй— Н -f Mi) pKg =* (Ad 4- Щ ppTg,
уравнение объемов {объем керосина, переместившегося из верхней трубки диаметром dj в нижнюю трубку диаметром ds, равен объему вытесненной ртути) /W‘r= Ш1
где рн и ррт — плотности керосина и ртути соответственно.
Произведя подстановки и преобразования, получим Рус = (il'i/di) Ррт + (1 — d'i/dl) рк.
Например, при = 2d, имеем рус = 0,25-13 600 4- 0,75-800 = 4000 кг/м*.
Для измерения давлений более 0,2—0,3 МПа применяют механические манометры — пружинные или мембранные. Принцип их действия основан на деформации полой пружипы или мембраны под действием измеряемого давления. Через механизм эта деформация передается стрелке, которая показывает величину измеряемого давления па циферблате.
Наряду с механическими манометрами применяют электрические манометры. В качестве чувствительного элемента (датчика) в электроманометре используют мембрану. Под действием измеряемого давления мембрана деформируется и через передаточный механизм перемещает движок потенциометра, который вместе с указателем включен в электрическую схему.
1.8. Сила давления жлдкостя еа плоскую стенку
Используем осаовное уравнение гидростатики (1.20) для нахождения полной силы давления жидкости на плоскую стенку, наклоненную к горизонту под произвольным углом а (рис. 1.13). Вычислим силу F давления, действующую со стороны жидкости на некоторый участок рассматриваемой степки, ограниченный произвольным контуром и имеющий площадь^ равную S.
Ось Ох направим по линии пересечения плоскости стенки со свободной поверхностью жидкости, а ось Оу — перпендикулярно к этой линии в плоскости стенки.
Выразим сначала элементарную силу давления, приложенную к бесконечно малой площадке dS:
dF = dS — pbdS + pgk dS,
где p0 — давление на свободпой поверхности; h — глубина расположения площадки dS.
Для определения полной силы F проинтегрируем полученное выражение по всей площади S:
F = p0\dS-\-pg^kdS = PqS + Pg sin a j у dS, где у — координата площадки dS.
Последний интеграл представляет собой статический момент площади S относительно оси Ох и равен произведению этой площади на координату ее центра тяжести (точка С), т. е.
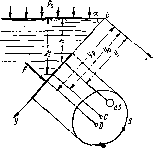
$ J/dS = ус-S*-Следовательно,
F — рцЗ -f- Pfsin aycS = pyS+pghcS
(здесь he — глубина расположения центра тяжести площади S), или
F = (p0 + pgkc)S=pcSi (1-29) т. е. полная сила давления жидко• сти на плоскую стенку равна Про- рис- 1.13, Схема для определения изведению площади стенки на вид-’ силы давления жидкости на плоскую ростатическое давление рс в цент- стенку ре тяжести этой площади.
В частпом случае, когда давление р0 является атмосферным и действует также с другой стороны стенки, сила F„Вб избыточного давления жидкости на плоскую стенку равна лишь силе Рж давления от веса жидкости, т. е.
Fизб ' F)JS = pghcS = рс взб&•
В общем случае давление р0 может существенно отличаться от атмосферного, поэтому полную силу F давления жидкости на стенку будем рассматривать как сумму двух сил: F0 от внешнего давления р0 и силы Fm от веса жидкости, т. е.
Рассмотрим вопрос о точках приложения этих сил, называемых центрами давления 20.
Так как внешнее давление р0 передается всем точкам площади S одинаково, то его равнодействующая F0 будет приложена в центре тяжести площади S• Для нахождения точки приложения силы давления FiK от веса жидкости (точка D) применим теорему механики, согласно которой момент равнодействующей силы относительно оси Ох равен сумме моментов составляющнх сил, т. е.
где yD — 1\Оор^ипата точки приложения силы ?ж.
Выражая Fm и dFm через Ус и у и определяя jjd, получаем siu a \y2dS
Уп ~ pg&iaaycS ~~ ycS '
где Jx — j y2dS — момент инарцки площади S относительно оси Ох.
(/то — момент инерции площади .S’ относительно центральной оси, параллельной Ох)х находим Уо = yc + JxaKVcS). (1.30)
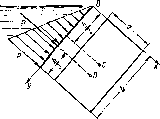
Таким образом, точка приложения силы Fsk расположена ниже центра тяжести площади стенки; расстояние между ними Ьу=*Мс8).
Если давление г>р равпо атмосферному, то точка V и будет центром давления. При р0 выше атмосферного центр давления находят по правилам механики как точку приложения равнодействующей двух сил: Fb и fш,; чем больше первая сила по сравнению со второй, тем, очевидно, центр давления ближе к центру тяжести площади S.
В частном случае, когда стенка имеет форму прямоугольника размерами а х Ъ (рис. 1.14) и одна из его сторон а лежит на свободной поверхности с атмосферным давлением, центр давления D находится на расстоянии 6/3 от нижней стороны.
1.9. Сила давления жидкости ва криволинейные стенки.
Плавание тел
Нахождение силы давления жидкости на поверхности произвольной формы в общем случае приводится к определению трех составляющих суммарной силы и трех моментов. Чаще всего рассматривают цилиндрические или сферические поверхности, имеющие вертикальную плоскость симметрии. Сила давления жидкости в этом случае сводится к равнодействующей силе, лежащей в плоскости симметрии.
Возьмем цилиндрическую поверхность АВ с образующей, перпендикулярной к плоскости чертежа (рис. 1.15), и определим силу давления жидкости на эту поверхность в двух случаях: 1) жидкость расположена сверху (рис. 1.15, а); 2) жидкость расположена спизу (рис. 1.15, б).
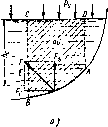
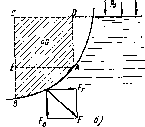
Рис. 1.15. Схема для определения силы давления жидкости ва цилиндрическую поверхность
В первом случае выделим объем жидкости, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями, проведенными через границы этого участка, и свободной аоЙйрхпостыо жидкости, т. е. объем ABCD, и рассмотрим условия его равновесия в вертикальном н горизонтальном направлениях. Если жидкость действует на стенку АВ с силой F, то стенка АВ действует на жидкость с силой F, направленной в обратную сторону. На рис. 1.15 показана эта сила реакции, разложенная на две составляющие: горизонтальную Fr и вертикальную FB.
Условие равновесия объема ABCD в вертикальном направлении имеет вид
F*=PvSr+G, (1-31)
где р0 — давление на свободной поверхности жидкости; 5Г — площадь горизонтальной проекции поверхности АВ\ G — вес выделенного объема жидкости.
Условие равновесия того же объема в горизонтальном направлении запишем с учетом того, что силы давления жидкости па поверхности ЕС и AD взаимно уравновешиваются и остается лишь сила давления на площадь BE, т. е. на вертикальную проекцию поверх-нооти АВ — S„. Тогда
Fp — SDpgkc + p0SB.
Определив но формулам (1.31) и (1.32) вертикальную и горизоп-тальную составляющие полной силы давления F, найдем
Когда жидкость расположена снизу (см. рис. 1.15, б), гидростатическое давление во всех точках поверхности АВ имеет те же значения, что а в первом случав, но направление его будет противоположным, и суммарные силы FB и FT определятся темп же формулами (1.31) и (1.32), но с обратным знаком. При этом под величиной G следует понимать так же, как и в первом случае, вес жидкости в объеме ABCD, хотя этот объем и не заполнен жидкостью.
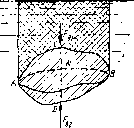
Рис. 1.16. Схема для доказательства закона Архимеда
Положение центра давлепия на цилиндрической стенке можно легко найти, если известны силы FB a FTa определены цептр давления на вертикальной проекции стенки и центр тяжести выделенного объема ABCD. Задача значительно облегчается в том случае, когда рассматриваемая цилиндрическая поверхность является круговой. Равнодействующая сила при этом пересекает ось поверхности, так как любая элементарная сила давления нормальна к поверхности, т- е. направлена по радиусу.
Изложенный способ определения силы давления на цилиндрические поверхности применим и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии.
Описанный выше прием нахождения вертикальной составляющей силы давления жидкости па криволинейную стенку используют для доказательства закона Архимеда.
Пусть в я{идкость погружено тело произвольной формы объемом V (рис. 1.16). Спроектируем его па свободную поверхность жидкости и проведем проектирующую цилиндрическую поверхность, которая касается поверхности тела ло замкнутой кривой. Эта кривая отделяет верхнюю часть поверхности тела АС’В от нижпей ее части ADB. Вертикальная составляющая Fu силы избыточного давления жидкости на верхнюю часть поверхности тела направлеяа вниз и равна весу жидкости в объеме АА'В'ВСА. Вертикальная составляющая F„a силы давления жидкости на нижнюю часть поверхности тела направлена. вверх и равна весу жидкости в объемо AA'B'BDA. Отсюда следует, что вертикальная равнодействующая сил давления жидкости S8 на тело будет направлена вверх и равна весу жидкости в объеме, равном разности указанных двух объемов, т. е.
F\ — FBi — Fbi — Gacbd — Vp8-
В этом и заключается закон Архимеда, обычно формулируемый так: на тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх, численно равная весу жидкости, вытесненной телом, и приложенная в центре тяжести объема погруженной части тела.
Сила Fa называется архимедовой си.гой, или силой поддержания, а точка ее приложения, т. е. центр тяжести объема V, — центром водоизмещения.
В зависимости от соотношения веса G тела и архимедовой силы Fк возможны три случая: 1) G > FA — тело тонет; 2) G < Fa — тело всплывает и плавает на поверхности жидкости в частично погруженном состоянии; 3) G =* Fa — тело плавает в полностью погруженном состоянии.
Для равновесия плавающего тела кроме равенства сил G — Fa должен быть равен нулю суммарный момент. Последнее условие соблюдается тогда, когда центр тяжести тела лежит на одной вертикали с центром водоизмещения. Условие устойчивого равновесия тела, плавающего в полностью погруженном состоянии заключается в следующем: центр тяжести тела должен находиться ниже центра водоизмещения. Устойчивость равновесия тел, плавающих на поверхности жидкости, здесь не рассматривается.
1.10. Прямолинейное
равноускоренное движение сосуда с жидкостью
Ранее было рассмотрено в основном равновесие жидкости нод действием лишь одной массовой силы — ее веса. Этот случай; имеет место тогда, когда жидкость покоится в сосуде, неподвижном относительно Земли, а также в сосуде, движущемся равномерй* и прямолинейно. Если же сосуд с жидкостью находится в неравномерном или непрямолинейном движении, то на частицы жидкости кроме силы тяжести действуют еще силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
При относительном покое свободная поверхность жидкости и прочие поверхности уровня (см. п. 1.5) могут существенно отличаться от поверхностей уровня при покое жидкости в неподвижном сосуде, т. е. от горизонтальной плоскости. При определении формы и положения свободной поверхности жидкости, находящейся в относительном покое, следует руководствоваться основным свойством всякой поверхности уровня, которое заключается в следующем: равнодействующая массовых сил всегда действует нормально к поверхности Уровня. В самом деле, если бы равнодействующая массовая спла действовала под некоторым углом к поверхпости уровня, то касательная составляющая этой силы выаывала бы перемещение частиц жидкости вдоль поверхности уровня. Однако в состоянии относительного покоя отсутствуют какие-либо перемещения частиц жидкости как относительно Степок сосуда, так и друг относительно друга. Следовательно, единственно возможным направлением равнодействующей массовой силы является направление, нормальное к свободной поверхности, а таюко и к другим поверхностям уровня.
Поверхности уровня не могут между собой пересекаться, иначе по линии пересечения двух таких поверхностей был бы получен ряд точек, давление в которых в одно и то же время имело бы два разных значения, что невозможно.
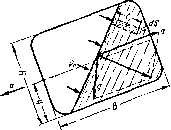
Рис. 1.17. Силы, действующие при относительном покое жидкости я яря-молниейшш равноускоренном движение сосуда
Рассмотрим два характер-ных случая отпосительного покоя жидкости: в сосуде, движущемся прямолинейно и равноускоренно и в сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью.
Пусть сосуд с ЖИДКОСТЬЮ движется прямолинейно с постоянным ускорением а. Б этом случае результирующую массовую силу, действующую на жидкость, найдем как сумму векторов силы инерции, направленной в сторону, обратную ускорению а и силы тяжести (рис. 1.17).
Обозначив вектор равнодействующей массовой силы, отнесенной к единице массы, через /', получим /“<*+ g,
где а и { — векторы единичных сил инерцпи и тяжести.
Для всех частиц рассматриваемого объема жидкости равнодействующие массовые силы параллельны друг другу, а поверхности уровня перпендикулярны к этим силам, поэтому все поверхности уровня, в том числе свободная поверхность, являются плоскостями, параллельными друг другу. Угол наклона этих плоскостей к горизонту определяется из условия перпендикулярности их к силе /.
Для определения положения свободной поверхности жидкости в сосуде, движущемся прямолинейно равноускоренно, необходимо к предыдущему условию добавить уравнение объемов, т. е. вужно знать объем жидкости в сосуде и выразить его через размеры сосуда В и Н и первоначальный уровень жидкости h.
Уравнение, позволяющее находить давление в любой точке рассматриваемого объема жидкости, можно получить аналогично тому, как это сделано в п. 1.5. Возьмем, например, около точки М площадку dS, параллельную свободной поверхности, и на этой площадке по^Р0™ цилиндрический объем с образующей, нормальной к свебодвой поверхности. .Условие равновесия указанного объема жидкости в направлении- нормали к свободной поверхности будет яметь вид
pdS =*p0dS 4- jpl dS,
где последний член представляет собой полную массовую силу, действующую на выделенный объем жидкости, а I — расстояние от точки М до свободной поверхности.
После сокращения на dS получим
p = pa + jpl‘ (1.33)
В частном случае, когда а = 0 и соответственно ] — g, формула (1.33) превращается в осповпое уравнение гидростатики (1.20).
То же уравнение (1.33) можно получить интегрированием дифференциального уравнения (1.24). Для этого одну из координатных осей удобнее направить вдоль линии действия результирующей массовой силы /. Приняв такое направление, например, для оси г, будем иметь
' X — У = 0; Z = /; dz=dl.
Следовательно, вместо уравнения (1.24) можно записать dp — р/ dl
или после интегрирования и определения постояпаой подставовкоЙ параметров свободной поверхности
Р = P# + Ро-
Полученное уравнение совпадает с формулой (1.33).
1.11 Равномерное вращение сосуда с жидкостью
Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью и вокруг его вертикальной оси. Жидкость постепенно приобретет ту же угловую скорость, что и сосуд, а свободная поверхность ее видоизменится; в центральной части уровень жидкости понизится, у стенок — повысится, и вся свободная поверхность жидкости станет некоторой поверхностью вращепия (рис. 1.18).
На жидкость в этом случае будут действовать две массовые силы — сила тяжести и центробежная сила, которые, будучи отнесенными к единице массы,- соответственно равны g и о>2г.
Равнодействующая массовая сила } увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидкости, поэтому ваклон этой поверхности с увеличением радиуса возрастает. Найдем уравнение кривой АОВ в системе координат гиг © началом в центре дна сосуда. Учитывая, что сила } является нор-малт.ю к кривой ЛОВ, из чертежа находим
tg а = dz/dr = (a2r/g,
откуда dz = cu2r dr/g,
или после интегрирования
В точке оерееечения кривой ЛОВ с осью вращения г = 0, z = k — “ С, поэтому окончательно будем иметь
* (1.34)
т. е. кривая АОВ является параболой, а свободная поверхность жидкости — параболоидом. Такую же форму имеют н другие поверхности уровпя.
Пользуясь уравнением (1.34), можно определить положение свободной поверхности в бОсу'де, например максимальную высоту Н подъема жидкости и высоту h расположения вёрпшны параболоида при данной угловой скорости а. Для этого необходимо использовать еще уравнение объемов: объем неподвижной жидкостй равен ее объему во время вращения.
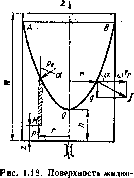
сги ори вращении открытого туда вокруг вертикальной
Для определения закона изменения давления во вращающейся жидкостй в функции радиуса и высоты поступим аналогично тому, как ато сделано в п. 1.5. Выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе г и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (1.34) будем иметь
р dS - [h - z + шгга/(2^)] рgdS-
— Ри {dS/cos ос) cos а = 0.
После сокращений получим р = p<! + [h — z-\-(a2r3/{2g)]pg. (1.35)
Это значит, что давление возрасгает пропорционально радиусу
¦ уменьшается пропорционально высоте z.
Если сосуд, вращающийся вокруг вертикальной оси, имеет крыш-¦у и заполнен жидкостью доверху, то ее форма измениться не может, шо изменяется давление в соответствии с выражением (1.35). На рас. 1.19 показана эпюра давления по крышке, стснке п дну сосуда.
На практике часто рассматривается вращение сосуда с жидко-етыо, когда угловая скорость со столь велика, что силой тяжести Можно пренебречь но сравнению с центробежными силами. При атом вакон измепения давления в жидкости легко получить из формулы 92 {1.35), в которой следует принять z = h = 0- Угол, образуемый осью вращения сосуда с вертикалью, значения не имеет, а поверхности уровня можно считать круглыми цилиндрами с общей осью — осью вращения сосуда. Если к тому жо давление р0 действует не в центре, а при г = г0, то очевидно, что вместо выражения (1.35) будем иметь
Часто бывает необходимо определить силу давлепия вращающейся вместе с сосудом жидкости на его стенку, нормальную к оси вращения (или на кольцевую часть этой степки). Для этого необходимо выразить сначала силу давления, приходящуюся на элементарную кольцевую площадку радиусом г и шириной dr:
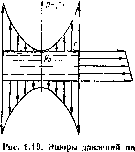
крышку, стейку и дно враща-
dF = pdS = !р0 -j- pro2 (г8 — r,*)/2] 2лr dr,
а затем выполнить интегрирование в требуемых пределах.
При большой угловой скорости жидкости можно получить весьма значительную суммарную силу давления на стенку. Это используется в некоторых фрикционных муфтах, где для осуществления сцепления двух валов требуется создание больших сил нормального давления. Способ, указанный вы
ше, применяют для определения силы осевого давления жидкости на рабочие колеса центробежных пасосов, а также па крышки центрифуг.
Те же формулы для рассмотренного случая относительного покоя можно вывести путем интегрирования дифференциального уравнения (1.24) равновесия жидкости. Поместив начало координат в центре дна сосуда и направив ось z вертикально вверх, получим
X ~ огг cos (г, х) = со8#; Y =<a2r cos (г, у) — ыгу, Z = — g.
Подставляя эти величины в уравнение (1.24), находим ъ%х dx -f <агу dy — g dz = dp/p, или
'dp ~ ри2 {x dx + у dy) - pg dz.
Если учесть, чго xdx + ydy = d{r'/2), то после итерирования получим
р = p©V*/2 - pgz + С.
При г = 0 и г — h, р = р0, следовательно,
В результате окончательно получим р = Ро + Р? Ф ~ г) + р(02Г2/ 2.
Уравнение свободной поверхности жидкости можно найти, если положить р = р0. После сокращений и преобразований будем иметь z — a>srsl(2g) -j- h,
что совпадает с ранее полученными формулами (1-34) и (1.35).
Г л а в а 3. КИНЕМАТИКА И ДИНАМИКА ЖИДКОСТИ
Кинематика жидкости существенно отличается от кинематики твердого тела. Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жвдкой среде такие связи отсутствуют; эта среда состоит из множества частиц, движущихся одна относительно другой.

Скорость в данной точке пространства, занятого движущейся жидкостью, является функцией координат этой точки, а иногда и времени. Таким образом, задачей кинематики жидкости является определение скорости в любой точке жидкой среды21 т. е. нахождения поля скоростей.
Сначала рассмотрим движение так называемой идеальной жидкости, т. е. такой воображаемой жидкости, которая совершенно лишена вязкости, а затем перейдем к изучению реальных потоков. В такой невязкой жидкости, так же как и в неподвижных реальных жидкостях, возможен лишь один вид напряжений — нормальные напряжения сжатия, т. е. гидромеханическое давление, или просто давление.
Давление в движущейся идеальной жидкости обладает теми же свойствами, что и в неподвижной жидкости, т. е. на внешней поверхности жидкости оно направлено по внутренней нормали, а в любой точке внутри жидкости — по всем направлениям одинаково.*
Течение жидкости может быть установившимся (стационарным) или неустановпвншмся (нестационарным).
Установившимся называется течение жидкости, неизменное по времени, при котором давление и скорость являются функциями только координат, по не зависят от времени. Давление и скорость могут изменяться ори перемещении частицы жидкости из одного положения в другое, по в данной неподвижной относительно русла точке давление и скорость при установившемся движении не изменяются по времени, т. о.
dgldt — Q; dvx(dt — 0; diyd*=0; dvjdt — 0,
где индексы у скорости означают ее проекции на соответствующие оси, жестко связанные с руслом.
В частном случае установившееся течение может быть равномерным, когда скорость каждой частицы не изменяется с изменением ее координат, и поле скоростей остается неизменным вдоль потоьа.
Неустановившимся называется течение жидкости, все характеристики которого (или некоторые из ннх) изменяются по времени в точках рассматриваемого пространства.
В общем случае пеустановившегося течения давление и скорость завысят как от координат, так и от времени:
p — F1(x, у, г, г); v = F2(x, у, z, t).
Примерами пеустановившегося течения жидкости могут слук;нть быстрое опорожнение сосуда через отверстие в дне пли движение во всасывающей или напорной трубе поршневого насоса, поршень которого совершает возвратно-поступательное движение. Примером установившегося течения может служить истечение жидкости из сосуда, в котором поддерживается ностояпный уровень, или движение жидкости в трубопроводе, создаваемое центробежным насосом с постоянной частотой вращения вала.
Исследование установившихся течений гораздо проще, чем не-установнвшихся. В дальнейшем будем рассматривать, главным образом, установившиеся течения и лишь некоторые частные случаи неустановившегося течения.
Траектории частиц жидкости при установившемся течении являются неизменными по времени.
Лрп неуст&яовившеыся течения траектории различий* частиц, проходящих через данную точку пространства, могут иметь разную форму. Поэтому для рассмотрения картины течения, возникающей в каждый данный момент времени, вводится понятие линии ч ока.
Линией тока называется кривая, в каждой точке которой векюр скорости в данный момент времени направлен по касательной (рис. 1.20).
Очевидно, что в условиях установившегося течения линяя юка совпадает с траекторией частицы и не изменяет своей формы с течением времени.
Если в движущейся жидкости взять бесконечно малый замкнутый коптур и через все его точки провести линии тока, то образуется трубчатая поверхность, называемая трубкой тока. Часть потока, ааключенная внутри трубки тока, называется элементарной струйкой (ряс. 1.21). При стремлении поперечных размеров струйки к нулю она в пределе стягивается в линию тока.
В любой точке Трубки тона, т. о. боковой поверхности струйки, векторы скорости направлены по касательной, а нормальные к этой поверхности составляющие скорости отсутствуют, следовательно, при установившемся двпжешш ии одно часгпца жидкости ни в одлой точке трубки тока не может проникнуть впутрь струйки л.'ш вынш наружу. Трубка юка, таким образом, является как бы непроницаемой стедкой, а плсментарпак струйка гтрсдстаБ.чг.м ссСий самостоятельный элементарный поток.
Потеки конечных размеров будем сначала рассматривать как совокупность элемспгарпых струек, т. е. будем предлолакт. течение струйным. Из-за различия скоростей соседние струйки будут сколь-алть одла г;о другой, по но будут перемеипгоатьгн одды. с другой.
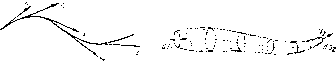
Ряс. 1.20. Лшшл тока Рис. 1.21. Сгруцца
Живим сечением, или просто сечением потока, пизырпется в общем случае поверхность в пределах потока, проведенная нормально к линиям тона. Далее будем рассматривать в потоках такие участки, в которых струйки можно считать параллельными п., сдедооатекьво, живые сечения — плоскими.
Различают напорные и безнапорные течепия жидкости. Напор-пыли называют течения в закрытых руслах без свободной поверхности, а безнапорными — течения со свободной поверхностью. При наиорпых течениях р.аил.еиие вдоиь. шлоко. обычно ври
безнапорном — постоянное (на свободной поверхности) и чаще всего атмосферное. Примерами напорного течения могут служить течения в трубопроводах с повышенным (или пониженным) давлением, в гид-ромашпиах или других гидроагрегатах. Безнапорными являются аечсиия в реках, wrapwmx канала-х я лотках. Н да яшм курсе рассмотрены напорные течения.
1.13. Расход. Уравнение расхода
Расходом называется количество жидкости, протекающее через живое течение потока (струйки) в единицу времени. Это количество можно измерить в единицах объема, в весовых единицах или в единицах массы, в связи с чем различают объемный Q, весовой Qg и массовый Qm расходы.
Для элементарной струйки, имеющей бесконечно малые площади сечений, можно считать истинную скорость v одинаковой во всех точках каждого сеченая. Следовательно, для этой струйки объемный 36
(м8/с), весовой (Н/с) и массовый (кг/с) расходы dQ^vdS; (1.36) dQa-PgdQ; (1.37)
dQm~ pdQ=:pvdS,
гдо dS — площадь сечения струйки.
Для потока конечных размеров в общем случае скорость имеет различное значение в разных точках сечения, поэтому расход или о определять как сумму элементарных расходов струек
Q=^vdS.
(1.39)
s
Обычно в рассмотрение вводят среднюю со ссчепию скорость
1>ор = <?/*?. откуда Q = VCVS.
(1.40)
Основываясь на законе сохранения вещества, па предположении
о сплошности (неразрывности) течения и на указанном выше свойстве трубки тока, заключающемся в ее «непроницаемости», для установившегося течения несжимаемой жидкости можно утверждать, что объемный расход ко всех сечениях элементарной сгруйкз (см. рис. 1.21) одип и тот же:
dQ = d$i = vz dSz = conpt (вдоль струйки) (1-41)
Это уравнение называется уравнением объемного расхода для элементарной струйки.
Аналогичное уравнение можно составить и для потока конечных размеров, ограниченного непропицаемыми стенками, только вместо истинных скоростей следует ввести средние скорости. В результате Q — vcplS = vCJ,2Sz= const (вдоль потока). -(1-42)
Из последнего уравнения следует, что средние скорости в потоке несяшмаомол жидкости обратно пропорциональны площадям сечений: 4»
Vcy i/t’cp а= •
Уравнение расхода является следствием общего закопа сохранения вещестиа для частных условий, в частпости для условий сплошности (неразрывности) течения.
1.14. Уравнение Бернулли для элементарной струйки идеальной жидкости
Рассмотрим установившееся течение идеальной жидкости, находящейся под действием лишь одной массовой силы — силы тяжести, и выведем для этого случая основное уравнение, связывающее между собой давление в жидкости и скорость ее движения.
Возьмем одну из элементарных струек, составляющих поток, и выделим сечениями 1 а 2 участок этой струйки произвольной длины (рис. 1.22). Пусть площадь первого сечения равна dSскорость в нем Vj, давление рг, а высота расположения центра тяжести сечепстя, отсчитанная от произвольной горизонтальной плоскости сравнения, гг. Во втором сеченкн соответственно dS2, и2, р2 и гг.
За бесконечно малый отрезок времена dt выделенный участок струйип перемесился в положение Г—2'.
Применим к массе жидкости в объеме учястка струйки теорему механики о том, что работа сил, приложенных к телу, равна приращению кинетической энергии этого теле. Такими силами в данном случае являются силы давления, действующие нормально к поверхности рассматриваемого участка струйки, н сила тяжести. Подсчитаем работу сил давления, силы тяжести и изменение кинетической энергии участка струйки за время dt.
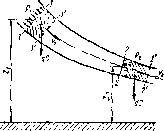
Рис. 1.22. Схема для вывода уравнения Ьеряудав
Работа силы давления в первом сечения положительна, так как направление силы совпадает с направлением перемещения, и выражается как произведение силы pjdS на путь гуй: pidSxvj dt.
Работа силы давления во втором сечсник имеет 8нак минус, так как направление силы прямо противоположно направлению перемещения, и определяется выражением
Силы давления, действующие по боковой поверхности отрезка струйки, работы не производят, так как они нормальны к этой поверхности, а следовательно, нормальны и к перемещениям.
Итак, работа сил данления будет равна
piVi dS1di — pzvi dSa dt. (1-43)
Работа силы тяжести равна изменению потенциальной энергии положения участка струйки, ноэтому надо из энергии положения яшдкости в объеме 1—2 вычесть энергию положения жидкости в объеме 1' — 2'. При этом энергия положения промежуточного объема 1' — 2 сократится, и останется лишь разность энергий элементов 1 — 1', 2 —2'. Если учесть уравнение расхода (1.41), то нетрудно заметить, что объемы, а следовательно, и силы тяжести заштрихованных элементов 1 — 1' и 2 — 2' равны между собой:
dG =pgvldS1di = pgv,dSidt. (1.44)
Тогда работа силы тяжести выразится как произведение разности высот на свау тяжеста dG:
"Чтобы подсчитать приращение кинетической энергии рассматриваемого участка струйки за время dt, необходимо из кинетической энергии объема 1' — 2' вычесть кинетическую энергию объема 1 — 2. При вычитании кинетическая энергия промежуточного объема 1' — 2 совратятся, и останется лишь разность кинетических энергий элементов 2 — 2' и 1 — 1', сила тяжести каждого из которых равна dG.
Такам обрезом, приращение кинетической энергии равно
Сложив работу сил давления {си. уравнение (1-43)] с работой силы тяжести [си. уравнение (1.45)1 в приравняв огу сумму приращению кинетической энергии 1см. уравнение (1.46)5, получим Pi dt — ps dSzvз dt -f (zx — za) dG — (y| — wj) dG/(2g). (1.46')
Разделим это уравпение на dG {см. формулу (1.44)1, и произведя сокращения, получим
Сгруппируем члены, относящиеся к первому сечению, в лезоа .части уравпепия, а члены, относящиеся ко второму сечевию, в правой:
*+&+?-*+$+%' <и7> где z — геометрячзския высота, или геометричг-скнй наоор; p/(pg) — пьезометрическая высота, или пьезометрический пааор; vi/(2gj — скоростная высота, или скоростной даиор.
Полученное уравнение назынается уравнением Бернулли для элементарной струит идеальной несжимаемой жидкости. Оно-был© выведено Дапиилом Бернулли * в 1738 г.
Трехчлен вида *
‘+&+%-нназывается полным напором.
Уравнение Бернулли (1.47) записано для двух произвольно взятых сечений струйки и выражает равенство полных напоров Н в этих сечениях. Так как сечения взяты произвольно, следовательно, а для любого другого сечения этой же струйки полный напор будет иметь то же значение:
а JL -j- — Н = const (вдоль струйки).
•Д. Бернулли (1700—1782 гг.) — швейцарский учепчй, сын известного математика Иогляна Берзулли, с 1725 по J733 гоп жил в России, являясь профессором, а затем почетным членом Петербургской академии наук; с 1733 г. — профессор Базельскою университета. В своем труде «Гидродц? шика» осветил ряд гидравлических вопросов и в том числе вывел указанное выше уравнение. Считается одним из основоположников гидравлики как пауки,
Итак, для идеальной движущейся жидкости сумма трех напоров (высот,): геометрического, пьезометрического и скоростного есть величина постоянная вдоль струйки.
Это положение иллюстрируется графиком, приведенным на рие. 1.23, где показано изменение всех трех высот вдоль струйки. Линия изменения пьезометрических высот называется пьезометрической линией, ее можно рассматривать как геометрическое место уроьной в пьезометрах, установленных вдоль струйки.
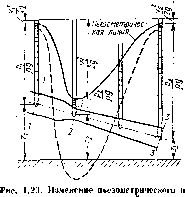
Для горизонтального участка струйки из уравнения Бернулли и уравнения расхода следует, что если площадь поперечного сечения струйки уменьшается, х. е. струйка сужается, то скорость течения жидкости увеличивается, а давление уменьшается, и наоборот, если струйка расширяется, то скорость уменьшается, а давтеиие возрастает.
На рис. 1.23 в виде примера показана струйка, площадь поперечного сечения которой от сечения 1 — 1 к сечоппю 2 — 2 уменьшается в 4 раза, в связи с чем скоростной напор увеличивается в 10 раз, а сечение 3 — 3 имеет ту же площадь, что и сечение 1 — 1. Штриховой линией показана пьезометрическая лпнпя при увеличении расхода в У2 раз, вследствие чего скоростпые высоты увеличиваются в 2 раза, а в узкой части струйки давление становится меньше атмосферною.
Уравнение Бернулли можно записать в двух других формах.
Разделим уравнение (1-40') на массу dm отрезка, равную pv-^lS^dt = = pVidS-ifU и преобразуем уравнение подобно предыдущему. Тогда вместо выражения (1.47) будем иметь
Рассмотрим энергетический смысл уравнения Бсрпулли, записанный в форме (1.48). Условимся называть удельной энергией жидкости виергито, отнесенную к единице массы 22.
Нетрудно показать, что члены этого уравнения являются различными формами удельной механической энергии жидкости, а цмеиио: gz — удейьпая энергия положения, так как частица жидкости массой Ат, паходясь на высоте г, обладает энергией положения, равной Atngz, а на единицу массы приходится энергия gAmzlAm — = gz\ р/р — удельная энергия давления движущейся жидкости, так как частица жидкости массой Дт при даилеиин р обладает способностью подняться на высоту р/ pg и приобрести энергию положения Amgp/(pg) (после деления на Ат получаем р/р); gz р/р — удельная потенциальная энергия жидкости; v2/2 — удельная кинетическая энергия жидкости, так как для той же частицы Ат кинетическая энергия, отпесенная к единице массы, Amv2/2 i Ат = у2/2; }Jg — zg -)- p/p -f v*/2 — полная удельная механическая энергия движущейся жидкости.
Таким образом, энергетический смысл уравнения Бернулли для элементарной струйки идеальной жидкости заключается в постоянстве вдоль струйки подпой удельной энергии жидкости. Следовательно, уравнение Бернулли выражает закон сохранения механической энергии в идеальной жидкости. Механическая энергия движущейся жидкости может иметь три формы: энергия положения, давления и кинетическая энергия.
Первая и третья формы механической энергии известны из механики п они в равной сюпепи свойстнеппы твердым и жидким телам. Энергия давления является специфической для движущихся жидкостей. В процессе движения идеальной жидкости одна форма энергии может превращаться в другую, однако полная удельная анергия при этом, как следует из уравнения Бернулли, остается без изменений.
Энергию давления легко преобразовать в механического работу. Простейшим устройством, с помощью которец о осуществляют такое преобразование, является цилиндр с поршнем (рис. 1.24). Покажем, что при этом преобразовании каждая единица массы ги^дкости совершает работу, численно равную р/р.
Пусть площадь поршня раопа S, его ход L, избыточное давление жидкости, подводимой к левой полости цил/тдра р, избыточное давление по другую сторону поршня равно нулю. Тогда суммарная сила давления жидкости, равная силе F, преодолеваемой при перемещении поршня из левого положения в правое: F = pS, а работа этой силы А =; pSL. Масса жидкости, которую необходимо подвести к пплпндру для совершения этой работы, равна массе жидкости в объеме цилиндра, т. е. т = SLp.
Следовательно, работа, приходящаяся на 1 кг массы,
е = А/т = pS Lf(SLp) = p/p.
Уравнение Бернулли часто пишут еще и в третьей форме. Разделив все члены уравнения (1.46') на объем dV — dG/(pg), после преобразований получим
pgzj + Pi+pvl/2 = р gZi + рг4- pv\jZ. (1.49)
Теперь члены уравнения Бернулли смеют размерность давления (1Га) и называются так: рgz — весовое давление; р — гидромеханическое давление (или просто давление); pfV2 — динамическое давление 23.
Члены уравнения (1.49) представляют собой различные виды механической энергии жидкости, отнесенные к единице ее объема, а члены уравнения (1.47) —ie же виды энергии, отнесенные к единице веса.
1.15. Вывод дифференциальных уравнений дапжения идеальной жидкости и ох интегрирование
В потоке идоальяоп жидкости возьмем произвольную точку М с координатами х, у, z (pi;o. 1.25) и выделим у этой точки элемент жидкости в форме прямоугольного параллелепипеда так, чтобы точка М была бы одной из его вершин. Пусть ребра этого параллелепипеда будут параллельны координатным осям и соответственно равны Ьх, Ьу и бг.
РП
Ji
P'-S-to
Составим уравнение движения выделенного элемента жидкости массой рб2'6г/бз. Так же, как и при рассмотрение равновесия подобного объема жидкости (см. п. l.ti), будем считать, что внутри этого объема на жидкость действует результирующая массовая сила, составляющие которой, отнесенные к единице массы, равны X, Y и Z. Тогда массовый силы, действующие на выделенный объем в направлении координатных осей, будут равны этим составляющим, умноженным на массу выделенного объема. Если давление в точно М обозначить через р, то, рассуждая так же, как в п. 1.6, получим, что разность сил давления, действующих на параллелепипед, папример, в направлении оси х, составляет
Рис. 1.25. Схеаа для вывода дифференциальных уравнений движения идеальной жаднеет
-fc6*6»62-
Скорость движения жидкости в точке М обозначим через v, -а ее компоненты — через vx, vy и vt. Тогда проекции ускорения, с которым движется выделенный объем, будут равны! dvjdt, dvv!dt в dvs/dt, а силы, которые необходимо ввести в уравнения движения по принципу Д’Аламбера, определяются как произведения этих ускорений на массу параллелепипеда.
Уравнения движения выделенного объема жидкости в проекциях на координатные оса будут иметь вид
р bxbybzd-^ = Хр бх bybz—^ Ьх 6 у б г; рбхУрЬхЦЫ - ^ pbxbybz Zpbxbybz — ^ bxb'jbz.
Разделим эти уравнения почленно иа массу элемента рбхбуЬг в перейдем к пределу, устремляя одновременно Ьх, by и бг к пулю, т. е. стг.п'вая параллелепипед к исходной точке М. Тогда в пределе получим уравнения движения жидкости, отпесенные к точке Мх
dvx , i_ Ьр_, j
dt p dt ’
dvy i л"
ИГ=яУ~~'
![]()
(1.50)
^рг ^ t др
dl р dz '
Полученная система дифференциальных уравнений движение идеальной жидкости носит название уравнений Эйлера. Члены 9ТИХ уравнений представляют собой соответствующие ускорения, а смысл каждого из уравнений заключается в следующем: полное ускоренве частицы вдоль координатной оси складывается из ускорения от массовых сил и ускорения от сил давления, ч»
Уравнения Эйлера в таком виде справедливы как для несжимаемой, так и для сжимаемой жидкости, а также для случая, когда из числа массовых сил действует лишь сила тяжести, и для общего случая относительного движения жидкости (см. п. 1.18) При этом в величины X, У в Z должны воёти компоненты ускорения переносного (или поворотного) движения. Так как прп выводе уравнений (1.50) не накладывались условия стационарности движения, то она справедливы в для неустановившегося движения.
Рассматривая установившееся движение жидкости, умножим каждое из уравнений (1.50) на соответствующие проекции элементарного перемещения, равные dx = vxdt; dy — Vydt, dz = vzdt, и сложим уравнения. Будем иметь
Xd, + y^ + Z*_l(&* + ^dy + &*)=.
—vx dvx -J- Vg dvy -f vt dvz.
(1.51)
43
Учитывая, что выражение и скобках является полным дифференциалом давления, а также, что
vxdvx — vu dvy — =
уравнение (1.51) можно переливать в следующем воде»
X dx-]-Y d’j 4-Z dz = * (1.52)
пли
dV='-ip+i{$),
гдо V — силовая функция.
Интегрирование этого уравнения выполним для основного част* ного случая установившегося движения идеальной жидкости, когда па жидкость действует лишь одна массовая сила — сила тяжести, При направлении оси z вертикально вверх
Х = 0; у= 0; Z=~g.
Подставляя эти зваченпя в уравнение (1.52) получим
«*+?+«'(т)-° "лп i*+s?+d[?)-a-
Так как для несжимаемой жидкости f> — const, предыдущее уравнение можно переписать в виде
Это уравнение означает, что нриращеиио суммы трек члрвов, заключенных в скобки, ири перемещении частицы жидкости вдоль линии тока (траектории) равно пулю, Следова1ельно, указанный трехчлеп есть величина постоянная вдоль линии тока, а следовательно, и вдоль эломонтариой струйки, т. е.
Таким образом, получили уравнение Бернулли для струйки идеальной жидкости, найденное в предыдущем параграфе другим способом.
Если записать это уравнение для двух сечений струйки 1—1 в 2—2, оно примет вид выражения (1.47).
1.16. Уравнение Бернулли
для потока реальной (вязкой) жидкости
При переходе от элементарной струйки идеальной жидкости к потоку реальной (вязкой) жидкости, имеющему копечнне размеры и ограниченному степками, необходимо учесть неравномерность распределения скоростей по сечепию, а также потери энергии (напора). То и другое является следствием вязкости жидкости.
При движении вязкой жидкости вдоль твердой стенки, например, в трубе, происходит торможение потока вследствие влияния вязкости, а также из-за действия сил молекулярного сцеплеиия между жидкостью п стенкой. Поэтому наибольшего значения скорость достигает в центральной части потока, а по мере приближения к стенке она уменьшается практически до нуля. Получается распределение скоростей, подобное тому, которое показано на рис. 1.2(

Неравномерное распреде.чс пие скоростей означает сколь жение (сдвиг) одних слоов пл частей жидкости ио лругт вследствие чего возникают ка сателыше напряжения (напря жения трепия). Кроме того, движение вязкой жидкости ча- Рис. 1.20. Распределение скоросчей в сто сопровождается вращением Реальном потоке частиц, ьпхреобраэоваппем и
перемешиванием. Все это требует затраты энергии, поэтому удельная анергия движущейся вязкой жидкости не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следонательно, уменьшается вдоль потока.
Из-за неравномерного распределения споростей приходигея вводить в рассмотрение среднюю по сечеыш скорость vCp (см. п. 1.13), а также среднее значение удельпой энергии жидкости в данном сече-
Прежде чем приступить к рассмотрению уравнения Бернулли для потока вязкой жидкости, сделаем следующее допущение: будем считать, что в пределах рассматриваемых поперечных сечеций потока справедлив основной закоп гидростатики, например в форме
(1,21), т. е. гидростатический яапор в пределах сечений есть величина, одинаковая длн всех точек данного сечения:
т. е. предполагаем, что при движении жидкости отдельные струйки оказывают одна на другую в поперечном направлении такое же давление, как слои жидкости в неподвижном состоянии. Это соответствует действительности и может быть доказано теоретически в том случае, когда течение в данных поперечных сечениях является параллельпоструйным. Поэтому именно такие (или близкие к ним) поперечные сечения и будем рассматривать.
Введем понятие мощности потока. Мощностью потока в данном сечепин будем называть полную энергию, которую проносит поток через это сечение в единицу времени. Так как в различных точках донеречиого сечения потока частицы жидкости обладают различной энергией, сначала выразим элементарную мощность (мощность эле-иеитарной струйки) в виде произведения полной удельной энергия жидкости в дайной точке на элементарный массовый расход: dN — gH dQn = (gz -f pip r2/2) pi? dS.
Мощность всею нотока найдем как интеграл от предыдущего выражения по всей площади S:
¦W = Р $ iSz + PlP -Ь b,2/2) v dS,
з
или, учитывая сделанное допущение,
![]()
Найдем среднее по сечению значение полной удельной энергии жидкости делением полной мощности потока на массовый расход. Используя выражение (1.39), получаем
![]()
Умножив о разделав последний чдеи na получим (пераходя к напорам)
![]()
(1.53)
где а — безразмерный коэффициент Кориолпса, учитывающий [^равномерность распределения скоростей и равный
![]()
(1.54)
Если умпожпть числитель и знаменатель выражения (1.54) на р/2, то нетрудно убедиться, что коэффициент а представляет собой отношение действительной кинетической энергии потока а данном сечетши к кинетической энергии того же потока и в том же сечении, но при равномерном распределении скоростей.
Для обычного распределения скоростей (см. рпс. 1.26) коэффициент а всегда больше единицы 24, а при равпомерном распределении скоростей ранен единице.
Возьмем два сечения реального иотпка, первое и второе, и обо-значим средние значения полного папора жидкости в этих сечениях соответственно Нср1 и Нср1- Тогда •^ерг ^ ^ср2 Ч" 2АД,
где Х*»п — суммарная нотеря полного напора па участке между рассматриваемыми сеченииии.
Исподьэуя формулу для #ср, предыдущее уравнение можно пв* реписать так:
![]()
(1.55)
Это и есть уравнение Бернул,ги для потока вязкой жидкости. От аналогичного уравневия для элементарной струйки идеальной жидкости полученное уравнение отличается членом, представляющим собой потерю полного напоре, и коэффициентом, учитывающим неравномерность распределения скоростей. Кроме того, скорости, входящие в ото уравнение, являются средними по сечениям.
Умножив уравнение (1.55) на g, получим форму записи уравнения Бернуллп, соответствующую формуле (1.48), где члены выражают виды энергии, отнесенной к единице массы, а член пред
ставит собой потерю удельной энергии жидко- |&j
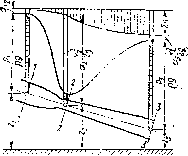
Умножение уравнения
(1.55) на pg даст третью форму записи уравнения Бернулли для потока вязкой жидкости, соответствующую формуле (1.49), но член рgSftn выражает потерю энергии, отвесеп-иуш к единице объема жидкости.
Уравнение Бернулли
(1.55) и его формы применимы не только для
Жидкостей, ио и для газов при условии, что ско- рнс< 1.27. Графвческая иллюстрация урагае* рость их движенхя зла- пия Бернулли доя рсазыюго лофка чительно меньше скорости
авука.
Графически это ypaFneuue можно представить диаграммой подобно тому, как это делали для идеальпей жидкости, но с учетом потери напора. Последняя является некоторой высотой, которая веукловво возрастает вдоль потока (рве. 1.27).
Бела для струйки идеальной жидкости уравнение Бернулли представляет собой закон сохранения механической энергии, то для потока реальной жидкости оно является уравненном баланса энергии с учетом потерь. Энергия, теряемая жидкостью на рассматриваемом участке течения, разумеется, не исчезает бесследно, а лишь превращается в другую форму — тепловую. Так как удельная теплоемкость жидкостей обычно велика по сравнению с потерями удельной энергии, а также ввиду того, что тепловая энергия непрерывно рассеивается, повышение температуры часто бывает практически малозаметным. Этот процесс преобразования механической энергии ъ тепловую является необратимым, т. в. таким, обратное течение которого (превращение тепловой энергии в механическую) невозможно.
Уменьшение среднего значения полной удельной энергии жидкости вдоль потока, отнесенное к единица его длины, называется гидравлическим уклоном. Изменение удельной потенциальной энергии жидкости, отнесенное к единице длины, называется пьезометрическим уклоном. Очевидно, что в трубе постоянного диаметра с неизменным распределением скоростей указанные уклоны одииа-колы.

1.17, Гидравлическое потери (общие сведения)
Потери удельной энергии (напора), или, как их часто называют, гидравлические потери, зависят от формы, размеров русла, скорости течения и вязкости жидкости, а иногда и от абсолютного давления в ней, Вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину.
Как показывают опыты, во многих, но не во всех случаях гидравлические потери приблизительно пропорциональны скорости течения жидкости во второй степени, поэтому в гидравлике нрппят следующий общий способ выражения гндраилических потерь полного папора в линейных единицах:
или в единицах давления Ра = pgha — ?рг>ср/2.
Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности ?, называемый коэффициентом потерь, или коэффициентом сопротивления, значение которого для давпого русла в первом грубом приближении постоянно.
Коэффициент потерь ?, таким образом, ость отношение потерянного напора к скоростному напору.
Гидравлические потери обычно разделяют на местные потери и потери на трение do длипе.
Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями, т. е. местными изменениями формы и размера русла, вызывающими деформацию потока. Пра протекании жидкости через местные сопротивления изменяется ее скорость и обычно возникают крупные вихри. Последние образуются за местом отрыва потока от стенок и представляют собой области, в которых частицы жидкости движутся в основном по замкнутым кривым или близким к ким траекториям.
Примерами местных сопротивлений могут служить устройства, изображенные на рис. 1.28. Там же показаны отрывы потока и ви-хреобразования.
Местные потери напора определяются по формуле (1.56) следующим образом:
Л„ = ^/(2г), (1.57)
. яли в единицах давления
Ря = ?мР&25/2.
(Далее в п. 1.32 эта формула для важнейшего случая будет получена теоретически.)
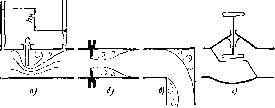
Рис. 1.28. Схемы местных гидравлических сопротивлений:
а — зопопжьа; б — диафрагма; в — колено; г — вситиль
Выражепие (1.57) часто называют формулой Вейсбаха. В пой v — средпяя по сечению скорость в трубе, в которой установлено данное местное сопротивление *. Если же диаметр трубы и, следовательно, скорость в пей изменяются по длине, то за расчетную скорость удобнее принимать большую из скоростей,
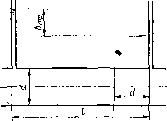
*. е. ту, которая соответствует меньшему диаметру трубы.
Каждое местное сопротивление характеризуется своим значением коэффициента сонротив-лепия ?, которое но многих случаях приближенно можно считать иостоянньш для данной формы местного сопротивления.
Более подробно местные гидрав- Ряс. 1.29. Потери напора на трение по яические сопротивления будут Длипе трубы рассмотрены в гл.. 7.
Потери на трение по длине, — зто потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, Т- ©• при равномерном течении, и возрастают пропорционально длине трубы (рис. 1.29). Рассматриваемые потери обусловлены внутренним тревнем в жидкости, а потому имеют место пе только в шероховатых, но и в гладких трубах.
Потерю напора на трение можно выразить по общей формуле (1.56) для гидравлических потерь, т. е.
(1.58)
однако удобнее коэффициент ? связать с относительной длиной трубы l/d.
Возьмем участок круглой трубы длиной, равной ее диаметру, и обозначим его коэффициент потерь, входящий в формулу (1.58), через Тогда для всей трубы длиной I и диаметром d коэффициент потерь будет в lid раз больше:
tip = tdjd,
В результате формула (1.58) примет вид
(1.59)
![]()
. I v*
Ртр — Л •? ~2~Р-
или в единицах давления
(1.60)
(Далее в пп. 1.24 и 1.30 эта формула для основных режимов течения жидкости будет получена теоретически.)
Формулу (1.59) обычно называют формулой Вейсбага — Дарси. Безразмерный коэффициент пазьтвают коэффициентом потерь на трение по длине, или коэффициентом Дарси. Его можно рассматривать как коэффициент пропорциональности между потерей напора на трепке, и произведением относительной длины трубы на скоростной напор..
Нетрудно выяснить физический смысл коэффициента Я, если рассмотреть условие равномерного движения в трубе цилиндрического объема длиной I и диаметром d (см. рис. 1.29), т. е. равенство нулю суммы сил, действующих на объем: сил давления и силы трения. Это равенство имеет вид
яdaРгр/А — я dir,, — 0,
где т0 — напряжение трения па стенке трубы.
Если учесть формулу (1.{Ю), то легко получить
![]()
т. е. коэффициент к есть величина, пропорциональная отношению напряжения трения на стенке трубы и динамическому давлению, определенному во сродней скорости.
Ввиду постоянства объемного расхода песжвмаемой жидкости вдоль трубы постоянного сечения скорость и удельная кинетическая энергия также остаются постоянными, несмотря па наличие гидрав-50 яячесяв! сопротавлений и потерь напора. Потеря напора в этом Случае определяются рааностыо показаний двух пьезометров (см. рве. 1.28 и 1.29).
Нахождение численных значений коэффициента I. потерь на тре-няе для различных конкретных случаев течения жидкости подробно рассмотрено в гл. 5 и 6,
1.18. Уравнение Бернулли для относительного движения
' Уравнение Бернулли в формулах (1-47) и (1.55) справедливо в тех случаях установившегося течения жидкости, когда из массовых сил ва гпидкость действует лешь сила тяя;ести. Однако иног да приходится рассматривать такие течения, при расчете которых кроле силы тяжести следует учитывать силтл инерции переносного движения (папример, когда русло, по которому движется жидкость, перемещается в пространстве с ускорением). Если иперциовлая сила постоянна ло времена, то течение жидкости относительно стенок русла может быть установившимся, и для вето можно выиеств урдииепг.о Бернулли так же, как это
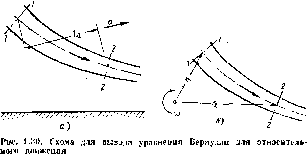
делали и п. 1,14. Различие заключается лишь в юм, что в левую чЛгь уравнения (1.46') к работе сил давлении и тяжести следует добавить работу силы инерции, действующую иа элемент струйки весом dG при его перемещении из сечения 1—1 в сечение 2—2 (см. рис. 1.22). Затем ату работу, как к другое члены уравнения (1.46') делил па dG, т. е. отпосим к единице веся* и, получив вското-рый напор, перопосим его в правую часть уравпеши. Получим уравнение Бернулли для относительного движения, которое в случае реального потока принимает вид
%+*•+*, g-h+A+t,j}+a.+a*m. <1*9
где ЛЯ ан — так называемый инерционный напор, который представляет собой работу силы инерции, отнесенную к единице веса и взятую с обратным знаком '(обратный знак обусловлен тем, что эта работа перенесена из левой части урав-вевня в прав>ю).
Рассмотрим определение инерционного напора для двух основвых случаев относительного движения жидкости.
1. Прямолинейное равноускоренное движение русла. Если русло, ио которому течет жидкость, движется прямолинейно с постоянным ускорением а (рис. 1.30, а), то на все частицы жидкости действует одинаковая и постоянная по времени сила инерции переносного движения, которая может способствовать или препятствовать течению. Если эту силу отнести к единице массы, то она будет равна соответствующему ускорению а и направлена в сторону, обратную ему, а на каждую единицу веса жидкости будет действовать сила инерции a/g. Работа этой силы при перемещении жидкости из сечепия 1—1 в сечение 2—2 (так же, как п работа силы тяжести) не зависит от формы пути, а определяется лишь разностью координат, отсчитываемых в направлении ускорения а, следовательно,
(1.63)
где 1а — проекция рассматриваемого участка русла ва направление ускорения а.
Чтобы не ошибиться в знаке, с которым всличива Д//ив должна быть записана в правой части уравнения Бернулли можно руководствоваться следующим правилом, непосредственно вытекающими из физиии явления. Если ускорение а направлено от сечепия 1—1 к сечевию 2—2, а сила иперции — наоборот, то эта сила препятствует течению жидкости, и инерционный напор должен иметь анак плюс. В этом случае инерционный напор уменьшает напор в сечении 2—2 во сравнению с напором в сечении 1—1 и, следовательно, аналогичен гидравлическим потерям 2 hu, которые всегда входят в правую часть уравнения Бернулли со знаков! плюс. Если же ускорение а направлено от сечения 2—2 к сечению 1—1, то сила аиерции способствует течению и инерционный напор должен иметь знак минус. В атом случае инерционный напор будет увеличивать напор в ссчошш 2—2, т. е. будет кап бы уменьшать 1идравличе«'кие потерп.
2. Вращение русла вокр>г вертикальной оси. Пусть русло, 1,о которому дяижется жидкость, вращается вокруг вертикальной оси с постоянной угловой скоростью ш (рис. 1.30, б). Тогда на жидкость действует енла инерцвп вращательного движения, являющаяся функцией радиуса. Поэтому для подсчета работы этой силы или изменения потенциальном энергии, обусловленной ео действием, необходимо применить интегрирование.
На единицу веса будет действовать сила инерции afr/g. Работа этой силы ори перемещении вдоль радиуса на расстояние аг равна afirdr/g, а ори перемещении от радиуса тг до радиуса г2 (по любой кривой) работу находят интегрированием етого выражения в пределах от rt до г2. Выполнив и итерирование, найдем инерционный напор, только знак следует изменить на обратный (как указывалось выше):
![]()
ДЯИВ
(1.64)
Знак инерционного напора, который получается при подсчете по этой формуле, соответствует указанному выше правилу званов.
1.19, Примеры использования уравнения Бернулли в технике
Расходомер Вентури представляет собой устройство, устанавливаемое в трубопроводах и осуществляющее сужение потока — дросселирование (рис. 1.31). Расходомер состоит из двух участков — плавно сужающеюся (сопла) и постепенно расширяющегося (диффузора). Скорость потока в суженном месте возрастает, а давление надает. Возникает раавость (перепад) давлений, которая измеряется двумя пьезометрами иди дифференциальным U-обраапым манометром и определенным образом связана с расходом. Найдем эту связь. Допустим в сечении 1—1 потока непосредственно перед сужением скорость пою ка равна давление pit площадь сечения S-i, а в сечении 2—2, т. е. в самом узком место потока, соответственно щ, р2 и St. Разность показаний пьезометров, нрисоо-дипеввых к указанным сечениям, АН.
Запишем для сечений 1—1 и 2—2 потока ураппепио Бернулли и уравнен ю расхода {считан распределение скоростей равномерным):
?1-4- ^ = Р- + Д+V «Л —^г. pg + 2g Pg + 2S ^ "
где hu — потеря напора между сечениями 1—1 а 2—2.
Учитывая, что
найдем из этой системы ураиненпй одпу из скоростей, например,
к-]/" JZ
-(ад)2-К ’
отсюда объемный расход
TV Ш
(1.05)
(1.66)
или Q-
=сУТн,
где С — величина, постоянная для даппого расходомера.
Зная величину С и наблюдая за показанием пьезометра, можяо найти расход в трубопроводе для любого момепта времени по формуле (1.66). Константу С можно определить теоретически, но точнее ее можно найти экспериментально, т. е. в результате градуирования расходомера.
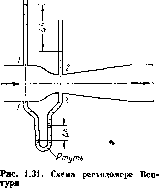
Связь между АП в Q получается параболической, а если по оси абсцисс откладывать расход во второй степе-ни, то график этой аависимости будет представлять собой прямую.
Очень часто вместо пары пьезометров дяя измерения перепада давлении в расходомере применяя» дифференциальный ртутный мапометр. Учитылан, что над ртутью в трубках находится та же жидкость плотностью р, можно записать
Д// = ДЛ {Ррт—р)/р. .
Карбюретор поршневых двигателей внутреннего сгорания служит для подсоса бензина и смешения его с потоком воздуха (рис. 4.32). Поток воздуха; засасываемого в двигатель, сужается в Том место, где установлен распылитель бензина (обрез трубки диаметром d). Скорость воздуха в этом сечении возрастает, а даплепие но закону Верпулли падаит.^Благодаря понижеииому давлению бензин вытекает в поток воздуха.
Найдем соотношение между массовыми расходами бензина Qr, и воздухи <)в при заданных размерах D и d и коэффициентах сопротивления воздушного канала (до сечения 2—2) и жиклера ?>в (сопротивлением бепзотрубкп пренебре
гаем).
Записав уравнение Берпулли для потока воздуха (сечение О — О и 2—2), « аатеы для потока бензина (сёчооие 1—1 и 2—2), получим (при zt = zt и а =¦ 1):
Ы
Рв (1+св)-Рб W) (1+с«).
Учитывая, что массовые расходы фв={я?>2/4) е2врв и Q0 = (nrf2/4)‘,20P6. получим
Таким образом обеспечивается постоянство соотношения расходов бсязвва и воздуха. Однако следует иметь в виду приближенный характер данного решения.
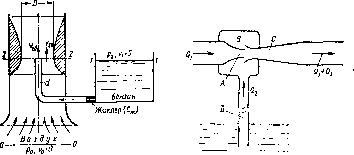
Рве. 1.32. Схема карбюратора
Рис. 1.33. Схема эжектора
Струйный насос (эжектор) состоит из плавво сходящегося изсадва Л (рис. 1.33), осуществляющего сжатие потока, и постепенно расширяющейся офубки С, установлеоноп на некотором расстоянЕи от насадка в камере В. Вследствие увеличения скорости потока давление в струе ва выходе из насадка
'У//УУУУ//УЛ У/у///
: %__
М'
W0 [
Рнс. 1.34. Схема трубки полного напора
Рве. 1.35. Схеиа васадка для намерения скорости
в по всей камере В значительно понижается. В расширяющейся трубке скорость уменьшается, а давление возрастает приблизительно до атмосферного (если жидкость вытекает в атмосферу), следовательно, в камере В давление обычно меньше атмосферного, т. е. возникает разреженно (вакуум). Под действием раэ-режевия жидность из нижнего резервуара псасыняется ио трубе D в камеру В, где происходят елнянве и дальнейшее перемепшоаяие дпух потоков,
"ГиШа пвдного ваворв (яла трубка Пито) служит для измерения скорости, *Шпгп~Г в трубе {рис. 1.34). Если установить в этом потоке трубку, нзогау-"*5ю под углом 90°, отверстием навстречу потот.-у и пьезометр, то жидкость в этой ;’5м«ке поднимается над уровнем в пьезометре на высоту, равпую скоростному напору. Объясняется это тем,-что скорость v частиц жидкости, попадающих в отверстие трубки, уменьшается до нуля, а давление, гледовательно, увеличивается на величину скоростиого папора. Измерив разность высот подъема жид-¦встя в трубке Пито и пьезометре, легко определить скорость жидкости в давкой точке.
На этом жо прииципе основано измерение скорости полета самолета. На вив. 1.35 показана схема самолетпой скоростной трубки (насадка) для иэыере-пя'ыалых во сравнению со скоростью звука скоростей полета.
Запишем уравнение Берпулли для струйки, которая наоегаэт на трубку вдоль ее оси, а затем растекается по ее поверхности. Для сечений 0—0 (невоз-нущеяншг поток) и 1—1 (где v = 0), получаем
Л>+Ро«/2
Так как боковые отверстия трубки приближенно воспринимают давление невозмущеяного потока, р2 == р9, следовательно из предыдущего писем
v9^V2(p1— Рг)/Р-
1.20. Применение уравнения количества движения к жидкости
В некоторых случаях в гидравлике удобно применять уравнения количества движения (импульса сил), например когда надо .найти силу воздействия потока на преграду или русло, не рассматривая процессы, происходящие внутри потока жидкости.
Для материального тела массой т, движущегося со скоростью v, изменение количества движения за время dt вследствие действия силы F выразится векторным уравнением mdv = Fdt,
где mdv — приращение количества движения, обусловленное импульсом Fdt.
Применим эту теорему механики к участку потока с расходам Q между сечениями 1—1 и 2—2 в условиях установившегося течения (рис. 1,36). За время dt этот участок переместится в^золоже-ние, определяемое сечениями 1'—Г и 2'—2'. Чтобы выразить при-ращенпе количества движения рассматриваемого участка, нужно нз количества движения объема между сечениями 1—1 и 2—2 вычесть количество движения объема между сечениями V —1' и 2'—2'. Пр. вычитании количество движения промежуточного объема, ограниченного сечениями 1'—Г и 2—2, сократится и останется лишь разность количеств движения элементов 2—2' и 1—Г, которые на рис. 1.36 заштрихованы. Объемы этих элементов 6F, а следовательно, и их массы Ьт — pQdt одинаковы, поэтому приращение количества движения будет равно pQ (vt — v^) dt.
Это приращение количества движения обусловлено импульсом всех внешних сил, действующих па объем жидкости между сечениями 1—1 и 2—2, — сил давления в первом и втором сечениях P,Si и рг52, силы тяжести всего объема G, а также реакции стенок русла R, которая складывается из сил давления и трения, распределенных по боковой поверхности объема. Обозначим вектор равнодействующих всех сил через F. Тогда pQ (i>3 —f]) dt=F dt, или после сокращения на dt
(1.67)
Таким образом, при установившемся движении вектор равнодействующей всех внешних сил, действующих на жидкость в фиксированном объеме, равен геометрической разности количеств движения жидкости, вытекающей из этого объема и втекающей в оого за единицу времени. В этом заключается теорема Эйлера об изменеяии количества движения жидкого объема.
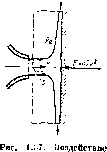
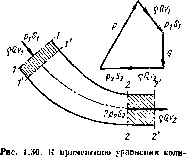
чества движения к жидкости струи на преграду
Уравнение (1.67) можно записать в виде pQ?j —pQv:2+>{+pli'1+^3:2+C = 0 (1.68)
зя в соответствии с этим построить замкнутый треугольник (или многоугольник) векторов, как показано па рис. 1.36. В связи с тем что в уравнении (1.68) вектор (>Qv2 имеет аиак «минус», при построении он направлен в сторону, обратную действительному его направлению.
То же уравнение (1.68) можно записать и в проекциях на ту или иную ось.
В качество примера оаределим силу воздействия потока жидкости на преграду. Пусть жидкость вытекает в атмосферу и наталкивается на без1 ранпчпую стенку, установленную нормально к потоку- В результате жидкость растекается по стенке, изменяя направление своего течения на 90° (рис. 1.37). Известим площадь сечения потока S, скорость истечения v и плотность жидкости р.
Для решения данной задачи берем фиксированный объем, показанный штриховой линией, и применяем теорему Эйлера. Так как
¦ давление ввутри струи 0 по поверхности жидкости равно атмосферному, т. е. избыточное давление равно пулю, уравнение, выражающее теорему Эйлера, для направления, совпадающего с веКторои скорости истечения г, будет иметь вид'
^.p^—pvSv или F=piAS’. (i,69)
Это и есть сила воздействия потока гкидкости на преграду. При другом угле установки стенки или других ее форме и размерах в правую часть формулы (1.69) вводится безразмерный коэффициент, отличный от единицы, по пропорциональность силы F произведению рSi? сохраняется.
Г д а в а 4. ГИДРОДИНАМИЧЕСКОЕ ПОДОБИЕ
И РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТИ В ТРУБАХ
1.21. Основы гидродинамического подобия
При изучении движения реальных жидкостей встречается много трудностей потому, что на характер движения и происходящие при атом процессы влияют ъгаотие факторы. Важный этап этого изучения — отбор тех факторов, которые являются определяющими для изучаемого процесса. Так, например, в п. 1.17 уже былп перечислены факторы, определяющие потери энергии при течении вязкой жидкости. Одпи нз них влияют болыдо, другие меньше, а есть и такие, влияние которых в обычных условиях пренебрежимо мало.
Следующий этап изучения — это установление зависимости интересующей величины от системы выбранных определяющих факторов. Этот этап может выполняться двумя путями: аналитическим, основанным па законах механики и физики, и экспериментальным. Первый путь применим лишь для ограниченного числа задач и при том обычно лишь для упрощенных моделей явлений.
Другой путь, экспериментальный, в принципе может учесть многие факторы, но он требует научно обоснованной постайЬвкп опытов, планирования эксперимента, ограничения его объема необходимым минимумом и систематизации результатов опытов. При этом должно быть обосновано моделирование явлений.
Эти задачи позволяет решать так называемая теория гидродинамического подобия, т. е, подобия потоков несжимаемой жидкости.
Гидродинамическое подобие складывается из трех составляющих: геометрического подобия, кинематического и динамического.
Геометрическое подобие как известно из геометрии, представляет собой пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимают подобие тох поверхностей, которые ограничивают потоки, т. е. подобие русел (или каналов) 26.
Отношение двух сходственных размеров подобных русел назовем линейным масштабом и обозначим через Эта величина одн-вакова (idem) для подобных русел I и II, т. е.
&?, = ?i/?ii — idem.
Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках в равенство углов, характеризующих направление этих скоростей:
.И = Us. = JiL = -22- = fc„ = idem,
VU bxII vyll
где fcv — масштаб скоростей, одинаковый Ери кизематаческом подобии.
Так как v = L/Т, кр = kjkr (где Т — время, кт — масштаб времени).
Из кинематического подобия вытекает геометрическое подобие линий тока. Очевидно, что для кинематического подобия требуется геометрическое подобие русел.
Динамическое подобие — это пропорцпональнреть сил, действующих на сходственные объемы в кинематически подоб-еых потоках и равенство углов, характеризующих направление этих сил.
В потоках жидкостей обычно действуют разные силы: силы давления, вязкости (трения), тяжести и др. Соблюдение их пропорциональности означает полное гидродинамическое подобие. Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому обычно имеют дело с частичным (неполным) подобием, прн котором соблюдается пропорциональность лишь основных, главных спл.
Для напорных течений в закрытых руслах, т. е. для потоков в трубах, в гидромашинах и тому подобных, таками силами, как показывает анализ, являются силы давления, вязкости в силы инерции. На жидкость действует также сила тяжести, но в напорных потоках ее действие проявляется через давление, т. е. оно сводится к соответствующему изменению давления. Поэтому, рассматривая так называемое приведенное давление = р pgz, тем самым учитываем силу тяжести.
Силы инерции определяются произведением массы на ускорение, т. е. F = та, а их отношение в подобных потоках, равно масштабу
*11 (me)ll
где kj, — масштаб плотностей.
Таким образом, силы инерции пропорциональны плотности, скорости во второй степени и размеру L во второй степени, который, в свою очередь, пропорционален площади S:
. 5аы&Твм, что этому же произведению р?у2 пропорциональны 'й>ды> Ь которыми поток воздействует (пли способеп воздействовать) на преграды (см. п. 1.20), лопасти гидромашин, обтекаемые тела.
Примем силы инерции за основу и будем другие силы, действующие на жидкость, сравнивать с инерционными, т. о. с выражением pSi?.
Таким образом, для гидродинамически подобных потоков I и II Вкеен
^ = f-snVi =idem. (1-70)
Ото отношение, одинаковое для подобных потоков, называют числом Ньютона и обозначают No. Здось под F подразумевается освовн&я сиза: сила давления, вязкости, тяжести илп др. Следовательно, соотношение (1.70) представляет собой общий вид закона гидродинамического подобия. Рассмотрим три характерных случая воздействия па движущуюся жидкость основных сил п найдем условия подобия потоков.
1. На жидкость действуют лишь силы дазленпл п инерции. Тогда F = ApS ~ АрЬг и условие (1.70) првиет вид
-B,=u"m- <l71> где Др — Hej-:oTopja разность давлений (или просто давление); Ей — безразмерный критерий, называемый числом Эйлера.
Следовательно, -условием гидродинамического подобия геомет? рически подобных потоков в данном случае является равенство для них чисел Эйлера.
Из предыдущего ясоп физический смысл числа Эйлера: ото есть величина, пропорциональная отношению сил давления к силам
5ерции.
1 На ;
i жидкость действуют силы вязкости, давления и инорции. Тогда
F — ц (dv/dy) S ~ vp (v/L) L2 ~ \pvL *
в условие (1.70) после деления последнего выражения на рv2L* примет вид
(п-).“(д)„ (4-)I = (if)„ = E«=№“. (‘-72)
где Re — безразмерный критерий, называемый числом Рейнольдса *.
Следовательно, условием гидродинамического подобия 'геометрически подобных потоков в рассматриваемом случае является равенство чисел Рейнольдса, подсчитанных для сходственных сечений вотоков.
•О. Ройнольдс (1842—1912 гг.) — известный английский физнк и инженер. Помимо установления важнейшего критерия, названного его именем, исследовал ряд других вопросов гидравлики с позиций инженера: режимы те-_ чения жидкости, теорию наиболее сложного турбулентного режима течений, теорию смазки, течение с парообразованием (кавитацию) в др.
Последнее условие является особенно важным в даппом курсе, так как им устанавливается основной критерий подобия напорных потоков — число Рейиолт.дса. За характерный размер L при подсчете числа Рейнольдса должен приниматься поперечный размер потока, например, диаметр сечения.
Из предыдущего ясен физический смысл числа Рейнольдса: это есть величина, пропорциональная отношению сил вязкости к силам инерции.
3. Па жлдкостт. действуют силы тяжести, давления и инерции. Тогда F ~ рgL? и условие (1.70) принимает вид /grin lpgL»\ /в*_\ = (*\ =
Ь-). =Гр-Иош,
(1-73)
^pi2!3/1! II ' \gL )\ \gL)n
гдо Fr — безразмерный критерий, называемый числом Фруда.
Следоватодьпо, услозпем гидродинамического подобия геометрически подобных потоков в данном случае является равенство чисел Фруда. Из предыдущего ясно, что число Фруда — это величина, пропорциональная отношению сил инерции к силам тяжести.
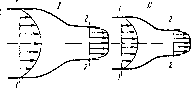
Рис. 1.38. Подобные потоки
Критерий Фруда является важным при рассмотрении безнапорных течений в открытых руслах, для напорных течений его можно по учитывать.
Для установления связи между гидродинамическим подобием в основным уравнением гидравлики — уравнением Бернулли — рассмодрнм два напорных потока I и II, которые подобны друг другу гидродинамически (рис. 1.38), и отметпм па пих сходствешшо сече-Вия 1—1 и 2—2.
Запишем сначала для указанных сечений одного из потоков уравнение Бернулли в предположении, что жидкость идеальная. Это будет соответствовать первому из рассмотренных выше случаев движения, так как на жидкость, можно считать, будут действовать лишь силы давления и инерции. Будем иметь
" = -& + ?»
Pg ~Г 2g
~ 2г og ~ 2l ’
где рj и р.с — прнпедеиные давления.
Используя уравнение расхода = vtSг, исключим скорость vx и, перегруппировав члены уравнения, приведем его к безразмерному виду. Для этого разделим уравнение на v\! (2g), после чего получим
2(р1-й)/(р»8 = 1-да:. (1.74)
Правая часть уравнения (1-74) одипакова для подобных потоков вследствие геометрического подобия, а левая часть, представ-яяющая собой удвоенное число Эйлера 2Еи, одинакова вследствие динамического подобия, и всо уравнеине (1.74) одинаково для подобных потоков идеальной гладкости. Таким образом, для обеспечения гидродинамического подобия напорных потоков идеальной жидкости достаточно одного геометрического подобия.
Теперь запишем ^раьнешгс Бернулли для тех же сечонлй 1—1
и 2_2 одного из напорных потоков вязкой гкидкост, подобных
гидродинамически. Будем иметь
где ?_коаффициепт потерь энергии между рассматриваемыми сечепиями.
После приведения этого сравнения к безразмерпому виду подобно предыдущему получпм
2 (pi — jJs)/(Pbi) = 2Eu = СС2 ~ ai$il+ ?¦ (1 -75}
Число Еп одрнпкопо для рассматриваемых подобных потоков вследствие их дипампчсского подобия; коэффициенты Кориолиса ctj и сг2 одинакова из-за кинематического подобия, следовательпо, одинаковым будет п коэффициент потерь а гакже все уравнение.
Если жо рассматривать подобные потокп в трубах постоянного сечения, то одинаковом будет коэффициент потерь на трение по длине (Я).
Итак, в подобных нзньриых потоках пмеем равенство безразмерных коэффициентов п чисел а, С, Я, Eu, Rc и некоторых других, которые будут введены в рассмотрение ниже. Изменение числа Re означает, что изменяется соотношение основных сил в потоке, в связи с чем указанные коэффициенты могут также несколько измениться. Поэтому все коэффициенты следует рассматривать как функции основного и определяющего критерия для папорных потоков вязкой жидкости —числа Рейнольдса Re (хотя в некоторых интервалах числа Re эти коэффициенты могут оставаться постоянными). При экспериментальных исследованиях и моделпровапии напорных течений в лабораторных условиях необходимо, во-пермлх, обеспечить геометрическое подобие модели (I) и натуры (П), включая условия вдода и выхода, и, во-вторых, соблюсти равенство чисел Рейнольдса: Re( — Reu. Из второго условия получаем необходимую скорость потока при эксперименте Si-UnZnV^ZiVi,).
В частном случае, при vj \ц скорость при эксперименте должна быть больше натурной в Zu/Zj раз. Применяя моиее вязкою жидкость (или ту же жидкость, по прп повышенной температуре) можно
СНИЗИТЬ CKOpOCTI, Vi-
Помимо перечисленных основных критериев подобия (Eu, Re, Fr), в гидравлике применяют и другие критерии для особых случаев течения жидкости. Так, при рассмотрении течений, связанных с поверхностным натяжением (например, при распаде струи на капли, распиливании топлива в двигателях), вводят критерий Вебера (We),
равный отношению сил поверхностного натяжения к силам инерции. Для этого случая условно (1.70) принимает вид We = crZ./(pr27?*) ¦ о/(руа?) = idem.
При рассмотрении неустановившихся (нестационарных) периодических течений с периодом Т (иапрлмер, течений в трубопроводе, присоединенном к поршневому насосу) вводят критерий Струха-ля (Shj, учитывающий силы инерции от нестационарности, называемые локальными. Последние пропорциональны массе (pi-3) и ускорению dv/dt, которое, в свою очередь, пропорционально и!Т. Следовательно, условие (1.70) для этого случая принимает вид pL3v/{pviLiT) — L/(vT) = idem или Sk = vT/L = idem.
При рассмотрении движений жидкости с учетом ее сжимаемости (например, движений эмульсий) вводят критерий Маха (М), учитывающий силы упругости. Последние пропорциональны площади (L1) и объемному модулю упругости К — рс2 [см. формулу (1.10)]. Поэтому силы упругости пропорциональны pc2L3 п условие (1.70) принимает вид
pcB?a/(pi^2i2) = сг/(рг) = idem или М = и,'с — idem.
Критерий Маха имеет о^епь большое значение при рассмотрении движений газа. Чем ближе число М к единице, тем больше влияние сжимаемости газа нри его движепия *.
1.22. Режимы течения жидкости в трубах
Опыты показывают, что возможны два режима или два вида течения жидкостей и газов в трубах: ламинарный и турбулентный.
Указанные течения жидкости можно наблюдать на приборе, представленном на рис. 1.39. Он состоит из резервуара А с водой, от которого отходят стеклянная труба В с краном С на конце, щ сосуда D с водным раствором той или иной краски, которая может по трубке вводиться тонкой струйкой внутрь стеклянной трубы В.
Если несколько приоткрыть кран С и дать возможность воде протекать н трубе с небольшой скоростью, а затем с помощью крана Е впустить краску в поток воды, то увидим, что введенная в трубу краска не будет перемешиваться с потоком воды. Струйка краски будет отчетливо видимой вдоль всей стеклянной трубы, что указывает на слоистый характер течения жидкости и на отсутствие перемешивания. Пьезометр или трубка Пито, присоединенные к трубе, показывают неизменность давления и скорости по времени, отсутствие колебаний (пульсаций). Это так называемое ламинарное (слоистое) течение.
При постепенном увеличении скорости течения воды в трубе путем открытия крана С картина течения иначале не меняется,
ВО затем при определенной скорости течения наступает быстрое ее дамевенве. Струйка краски по выходе из трубки начинает колебаться, затем размываться и перемешиваться с потоком воды, причем становятся заметными вихреобразовапия и вращательное движение »шдкости. Пьезометр и трубка Пито показывают непрерывные пульсации давления и скоростей в потоке воды. Течение становится, как его принято называть, турбулентным (см. рнс. 1.39, вверху).
Если уменьшить скорость потока, то восстановится ламинарное течение.
Итак, ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсаций скоростей и давления. При таком течении все линии тока вполне определяются формой русла* до которому течет жидкость. При ламинарном течении ясидкостн
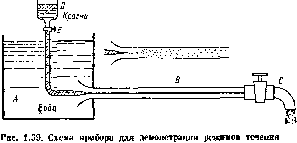
в прямой трубе постоянного сечения все линии тока направлены параллельно оси трубы, т.- е. прямолинейно; отсутствуют поперечные перемещения жидкости. Ламинарное течение является вполн# упорядоченным и при постоянном напоре строго установившаяся течением (хотя в общей случае может быть и неустаповившимся). Однако его нельзя считать безвихревым, так как в нем хотя и нет видгмых вихрей, но одновременно с поступательным движением имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров с некоторыми угловыми скоростями.
Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. Движение отдельных частиц оказывается подобным хаотическому, беспорядочному движению молекул газа. При турбу-лентном течении векторы скоростей имеют не только осевые, но и нормальные к оси русла составляющие, поэтому наряду с основным продольным перемещением жидкости вдоль русла происходят поперечные перемещения (перемешивание) и вращательное движение отдельных объемов жидкости. Этим и объясняются пульсации скоростей и давления.
Режим течения данной жидкости в данной трубе измеияется примерно при определенной среднем до сечстю скорости течения vw, которую называют критической. Как показывают опыты, значение этой скорости прямо пропорционально кинематической вязкости v и обратпо пропорционально диаметру d трубы, т. е.
^нр — kv(d.
Входящий в эту формулу безразмерный коэффициент пропорциональности к одинаков для всех жидкостей и газов", а также для любых диаметров труб. Это означает, что измепепие режима течения происходит при определенном соотношении между скоростью, диаметром и вязкостью v: к — укр d/v.
Полученное безразмерное число называется критическим числом Рейпольдса и обозначается
Векр =» ь’кр d/v. (1.76)
Этот результат согласуется с изложенной вьтше теорией гидродинамического подобия, и вполне закономерно, что именно число Рейнольдса является критерием, определяющим режим течения в Трубах.
Как показывают опыты, для труб круглого сечения ReBp sss 2300.
Таким образом, критерий подобия Рейнольдса позволяет судить о режиме течения жидкости в трубе. При Re < ReKp течение является ламинарным, при Re > Покр — турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re « 4000, а при Be — 2300 -ь 4000 имеет место переходная, критическая область.
Зная скорость движения жидкости, ее вязкость и диаметр трубы, можно расчетным путем найти число Re и, сравнив его с Векр, определить режим течения жидкости.
На практике имеют место как ламинарное, так и турбулентное течения, причем первое наблюдается в основном в тех случаях, когда по трубам движутся весьма вязкие жидкости, например смазочные масла, второе обычно происходит в водопроводах, а также в трубах, по которым перетекают бензин, керосин, спирты, кислоты п другие маловязкие жидкости.
Смена режима течения при достижении Пскр обусловлена тем, что одна течение теряет устойчивость, а другое — приобретает. При fie < fle„p ламинарное течение является вполне устойчивым: всякого рода искусственная турбулчзация потока и его возмущения (сотрясения трубы, введение в поток колеблющегося тела и пр.) погашаются влиянием вязкости и ламинарпое течение восстанавливается. Турбулептное течение при этом неустоцчино. При Re > Ве,ф, наоборот, турбулентное течение устойчиво, а ламинарное — нсустой-Ч08О.
В связи с этим число Relip, соответствующее переходу от лама-парного течения к турбулентному, может получиться несколько больше, чем ReKp для обратного перехода. В особых лабораторпых условия к при полком отсутствия факторов, способствующих тур-булизации потока, можно получить ламинарное течение при Не, значительно превышающем Re1;p. Однако в утих случаях ламинарное течение оказывается настолько неустойчивым, что достаточно небольшого возмущения (толчка), чтобы оно перешло в турбулентное. На практике обычно имеются условия, способствующие 'гур-булизации, — вибрация труб, местпыё гидравлические сопротивления, неравномерность (пульсация) расхода и прочее, а потому указанное обстоятельство имеет в гидравлике скорее принципиальное, чем практическое, значение.
1.23. Кавитация
В некоторых случаях при движении жидкости в закрытых руслах происходят явления, связанные с изменением агрегатного состояния жидкости, т. с. с превращением со в пар, а также с выделением рз жидкости растворенных в ней газов. Например, при течении жидкости через местное сужение трубы увеличивается скорость и падает давление. Если абсолютное давление при этом достигает значения, равного давлению насыщенных паров этой жидкости при данной температуре, или давлению, при котором начинается выделение из нее растворенных газов, то в данном месте потока начинается интенсивное парообразование (кипение) и выделение газов. В расширяющейся части скорость потока уменьшается, а давление возрастает, и выделение паров и газов прекращается; выделившиеся пары конденсируются, а газы постепенно вновь растворяются.
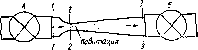
Рис. 1.40. Схема трубки для демонстрации кавитации
Это местное нарушение сплошности тсчония с образованием паровых и газовых пузырей (каверн), обусловленное местным падением давления в погоко, называется кавитацией¦
Наглядно это явление можпо продемонстрировать на простом устройстве (рис. 1.40). Вода или иная жидкость под давлением в несколько атмосфер подводится к регулировочному крану (вентилю) А и далее протекает через прозрачную трубку Вентури, которая сначала плавпо сужает иоток, затем еще более плавно расширяет и через кран В выводит в атмосферу.
При небольшом открытии регулировочного крапа и, следовательно, при малых значениях расхода и скорости жидкости падегтпе давления в узком месте трубки незначительно, поток вполне прозрачен, и каяигадия отсутствует. При ггостепешгом открытии крема происходит увеличение скорости жидкости в трубке и падение абсо-дютного давления.
При некотором зиачрппи атого давления, которое можно счит?тт> равным давлению насыщенных парии (рАг,е3 = р„ 0), в узком месте трубки появляется отчетливо икдимая зона кавитации, ыредставляю-гцая собой область местного кипения жидкости и последующей коп-денсации паров. Р;;нмеры золи ка шпации возрастают по мере дальнейшею открытия крана, т. е. при увеличении давления в сечении 1—1, а следовательно, о расхода. Однако как бы при этом пл возрастал расход, давление в узком сеченпп 2—2 сохраняется строго постоянным потому, что постоянно давление насыщенных napGB.
Кавитация сопровождается характерным шумом, а при длительном ео воздействии также эрозионным разрушением металлических стенок. Последнее объясняется тем. что конденсация пузырьков пара (и сжаше пузырьков газа) происходит со значительной скоростью, частицы жидкости, заполняющие полость конденсирующегося пузырька, устремляются к его центру и в момент завершепия конденсации (схлопывания пузырька) вызывают местные удары, т. е. значительное повышение давления в отдельных точках. Материал прн кавитации разрушается ые там, где выделяются пузырьки, а там, где они конденсируются.
При возникновении кавитации значительно увеличивается сопротивление трубопроводов н, следовательно, уменьшается их пропускная способность, потому что каверны уменьшают живые сечения потоков, скорость в которых резко возрастает.
Кавитация в обычных случаях является нежелательным явлением, и ее не следует допускать в трубопроводах и других элементах гидросистем. Опа может возникать во всех местных гидравлических сопротивлениях, где поток претерпевает местное сужение с последующим расширением, например в кранах, вентилях, задвижках, диафрагмах, жиклерах и др. В отдельных случаях возникновение кавитации возможно также и без расширения потока вслед за его сужением, а также в трубах постоянного сеченая при увеличения геометрической высоты и гидравлических потерь.
Кавитация может иметь место в гидромаптпах (насосах и гидротурбинах), а также па лопастях быстро вращающихся гребных винтов. В этлх случаях следствием кавитации является резкое снижение коэффициента полезного действия машипы и затем постепенное разрушение ее деталей, подверженных воздействию кавитации.
В гидросистемах кавитации может возникать в трубопроводах низкого давления— во всасывающих трубопроводах. В этом случае ее область распространяется на значительную часть всасывающего трубопровода пли даже па всю его длину. Поток в трубопроводе при эточ делается двухфазным, состоящим из яшдкой и паровой фаз.
В начальной стадии иаровыдсления паровая фаза может быть в виде иелких пузырьков, приблизительно равномерно распределенных по объему движущейся жидкости (рис. 1.41, а). 11рп дальнейшей па рога зовы деле нии происходит укруппеппе пузырьков, которые при горизонтальном расположении трубы движутся преимущественно в верхней части ее сечеппя (рис. 1.41, б).
Очевидно, что при столь значительной парогазовой фазе портальная подача жидкости по зрубопроводу нарушается. Кокдекса-дия выделившихся паров (частичная или полная) и растворение газа Происходят в насосе, где давление значительно повышается, и в па-дерпом трубопровод?, оо которому жидкость движется под высоким давлением от насоса к потребителю.
Навигация, обусловленная выделение:! пироп жидкости, происходит по-разному в однокомпонентных (простых) н многокомпонентных (сложных) жидкостях. Для одпокомпоцентнон жидкости давление, соответствующее началу кавитации, вполне определяется давлением насыщенных паров, зависящим только от температуры, я кавитация протопает так, как было описано вт>шс. Мпоюкомио-яептпая жидкость сосгомг из так называемых легких п тяжелых фракций. Первые обладают большие упругостью паров, чем вторые,
![]()
а) 5)
Рис. 1.41. Схемы двухфазных г.отокоо
поэтому при кавитации сначала вскипают легкие фракции, а затем тяжелые. Конденсация же паров происходит в обратном порядке — сначала выпадают тяжелые фракции, затем — легкие. Паровая фаза в многокомпонентных жидкостях удерживается дольше, и процесс кавигацин выражен менео резко, чем в одпокомпонентных жидкостях.
Для характеристики местных гидравлических сопротивлений в отношении кавитации применяется безразмерный критерий, называемый числом кавитации: •*
' (1.77)
где Pi п i>i — абсолютное давление и скорость потока в сечении тру'ы п?р?,д местный сопротввлсписм.
Очевидно, что по своему смыслу число кавитация аналогично числу Эйлера Ей (см. п. 1.21), опо используется как критерий подобия течений с кависацией. Значение к, при котором в местном сопротивлении начинается кавитация, называется критический числом кавитации хкр.
Число кКр определяется в основной формой местного сепрогнв.г\> ния, хотя в некоторой степени на него может влиять ц число Рей-¦ояьдса. Для такого простого устройства, как показанная вшиа трубка Вентури, значение х приближенно можно определить щ.о-•Шм расчетом. Запишем уравнение Бернулли для сечений 1—1
Ч 2—2 {си. рве. 1.40), считая, что сс1=а2 = 1и?=0 (потеря эпе;>-гин незначительна):
Pi/P + v]/2 = р.,/р -I- vi'2.
Оаределии отсюда ри подставим его в формулу (1-77):
где iSt п S,± — площади сечений 1—1 я 2—2.
Экспериментальные кавптаг.конные характеристики местных гидравлических сопротивлений получают при постоянном расходе н постепенном уменьшении давления, а затем представляют в безразмерном виде ? = / (к). Прп к < х„р коэффициент потерь ? от х це зависит, а ори х — х1ф — резко возрастает. На рис. 1.42 показаны кривые для сопротивлений 1 и 2 при > 12 и krpi > ИцРг.
Отя кривые справедливы лишь для определенно го значения числа Re или для той обласш чисел Re, где ? от Re но зависит.
Обычно стремятся к тому, чтобы кавитацию в гидросистемах не допускать. По иногда это явление может оказаться полезным. Например, опо используется в кавитационном регуляторе расхода, принцип действия которого показан па схеме, приведенной на рис. 1.40. Предположим, что давление в сечении 1— —I (р1 = рвх) является постоянным (степень открытия крана А неизменная), а давление в сечеппи 3—3 (р3 = р^ых) постепенно уменьшаем, увеличивая степень открытия крапа В. В результате расход через трубку увеличивается, а давление рг в узком сечении 2—2 уменьшается.
*крг *кр! *
Рис. М2. Зависимость коэффициента потерь от числа кавитации
Так будет происходить до тех пор, пока давление р,абе не ста-цет равным значению рв а, при котором в сечении 2—2 возникнет кавитация. При дальнейшем увеличении степени открытия крана В область кавитащш в узком месте трубки будет увеличиваться, а давление ргаСо будет оставаться равным />н.ц- Расход при этом будет сохраняться практически постоянным, несмотря на падение давления р3.
Таким образом удается стабилизировать расход жидкости через регу.гятор в условиях, когда противодавление р3 изменяется от критическою р,)Кр, соответствующею началу кавитации, до нуля. Результаты испытаний подобного кавитационного регулятора расхода показывают, что точность стабилизации расхода получается очень высокой (рис. 1.43).
Из графиков, изображенных на рис. 1.43, можно сделать два вывода. Во-первых, олп наглядно показывают преимущество использования безразмерных величин по сравнению с размерными: несколько кривых на рис. 1.43, а заменяются единой кривой на рисЛЛЗ, б. Во-вторых, критерий рВых/рах = P-JP\ гак же, как и х, можно считать критерием кавитации. Действительно, так как обычно pi^pu.n, в формуле (1.77) можно принять = 0. а знаменатель заменить пропорциональной ему величиной ?piq.-:2 — р, — р3,
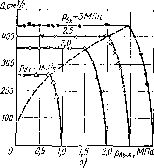
Рис. 1.43. Зависимость расхода жидкости через кавитационную трубку от давлений на «ходе и выходе
которая при у, = v3 {dx = d3) представляет собой потерю давления между сечепиямн 1—1 и 3—3 (см. рис. 1.40). Тогда получим число кавитации к', пропорциопальнос я:
В некоторых случаях критерий ръых/рих оказывается удобнее, чем х, он будет использован далее (см. и. 1.40).
Г л а в а 5. ЛАМИНАРНОЕ ТЕЧЕИИЕ
1.24. Теория ламинарного течения в круглых трубах
Как указывалось в п. 1.22, ламинарное течеппе является строго упорядоченным, слоистым течением без перемешивания жидкости. Теория ламинарпого течения жидкости основывается на законе трения Ньютона (см. п. 1.3). Это трение между слоями движущейся жидкости является единственным источником потерь анергии в данном случае.
Рассмотрим установившееся ламинарное течение жидкости в прямой круглой цилиндрической трубе с внутренним Диаметром d — 2/•„• Чтобы исключить влияние силы тяжести и этим упростить вывод, Допустим, что труба расположена горизонтально. Достаточно далеко от вуода в нее, где поток уже вполне сформировался (стабилизировался), выделим отрезок длиной I между сечениями 1—1 и 2—2 (рнс. 1.44).
Пусть в сечении 1—1 давление равно рг, а в сечении 2—2 — р3. Ввиду постоянства диаметра трубы, скорость жидкости будет постоянной, а коэффициент а будет неизменным вдоль потока вследствие его стабильности, поэтому уравнение Бернулли для выбранных сечений примет вид
МР?) —Р*/(Р?)+* тр,
где hTp — потери напора ва трение по длине.
Отсюда
/гтр = {pi ~ Pt)l{P8) = prrfipg),
что и показывают пьезометры, установленные в этих сеченплх.
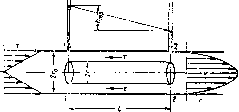
Рис. 1.44. К теории ламинарного течения жидкости в трубе
В потоке жидкости выделим цилиндрический объем радиусом г, соосный с трубой и имеющий осповапия в выбранных сеченпях. Запишем уравнение равномерного движения выделенного объема жидкости в трубе, т. е. равенство пулю суммы сил, действующих на объем: сил давления и сопротивления. Обозначая касательное напряжение па боковой поверхности цилиндра через т, иолучпи
(Pi — Рг) лг2 — 2яг/т = О,
откуда
т=РтСг/(2/).
Из формулы следует, что касательные напряжения в поперечной сеченип трубы изменяются по линейному закону в функции радиуса. Эйтора касательного напряжения показана на рис. 1.44 слева (эта jnwpa не зависит от режима течения).
Выразим касательное напряжение т по закону трения Ньютона через динамическую вязкость и поперечный градиент скорости 1см. формулу (1.14)1; при этом заменим переменное у (расстояние от стенки) текущим радиусом г:
Знак минус обусловлен тем, что направление отсчета г (от оси К стенке) противоположно направлению отсчета у (от стеякв). Подставляя значение т в предыдущее уравнение, получаем
Ртр/(20 = — iidv/dr.
Найдем отсюда приращение скорости dv — — pJVr drl{2[il).
При положительном приращегши радиуса получается отрицательное приращение (умецыпепие) скорости, что соответствует профилю скоростей, показанному па рпс. 1.44.
Выполнив интегрирование, получим
![]()
Постоянную интегрирования С найдем из условия, что па стенко при г = r„ v = 0:
С = pip^o/(4jiZ).
Скорость по окружности радиусом г
(1.78)
v = p-n{rl-ry{ip.l).
Это выражение является законом распределения скоростей по сечению круглой трубы при ламинарном течении. Кривая, изображающая эпюру скоростей, является параболой второй степени.
Максимальная скорость, имеющая место в центре сечения (при г = 0),
Pjnax = Ртр^о/^М-О- (^'79)
Входящее в формулу (1.78) отношение ртр/1 (см. рпс. 1.44) представляет собой гидравлической (пьезометрический) уклон, умноженный па pg. Эта величиаа является постоянной вдоль прямой трубы постоянного диаметра. *
Применим полученный закон распределения скоростей, описываемый уравиепием (1.78) для расчета расхода. Для этого выразил сначала элементарный расход через бесконечно малую площадку dS: dQ = vdS.
Здесь v есть функция радпуса, определяемая формулой (1.78), а площадку dS целесообразно взять в виде кольца радиусом / и шириной dr, тогда
dQ— Prp (/¦« — r}) 2nrdrt{A\xl).
После интегрирования по всей площади иоперечпого сичепия, f. е. от г — 0 до г = га
![]()
Сродшою по селению скорость пайдем делением расхода па площадь. С учетом выражения (1.80) получим
fcp = Q!{nrl) — pTprJ/(8^).
(1.81)
Сравнеппс этого выражения с формулой (1.79) показывает, что средняя скорость при ламинарном течении в 2 раза меньше максимальной: fcp = 0,5l’mox-
Для получения закона сопротивления, т. е. выражения потери напора hTр па трение через расход и размеры трубы, определим ртр из формулы (1.80):
Pip —fyiZ(?/(nrJ).
Разделив это выражение на pg, заменив j.t на vp и р1Р на hTppg, а также перейдя от г0 к d = 2гс, найдем
(1.82)
Кх> - Ihv'ipg) — i2ivlQl{ngdi).
Полученный закон сопротивления показывает, что при ламинарном течении в трубе круглого сечепия потеря наиора на трение пропорциональна расходу и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закоп, обычно называемый законом Пуазейля, используется для расчета трубопроводов с ламинарным течением *.
Ранее (и. 1.17) условились выражать Еотери напора на трение через среднюю скорость по формуле (1.59). Приведем закон сопротивления (1.82) к виду формулы Вейебаха—Дарси:
![]()
Для этого в формуле (1.82) заменим расход произведением ла2г>Ср/4; умножив и разделив па i?cp и перегруппировав множители, после сокращепий получим
![]()
или, приведя к виду формулы (1.59), окончательно найдем
(1.83)
(1-84)
где ?.л — коэффициент потерь на трение для ламинарного течения: Я, = 64/Пс.
Потеря напора на трение по длине при ламинарном течении пропорциональна скорости в первой степени [квадрат скорости в формуле (1.83) для ламинарного течения получен искусственно умножением и делением па а коэффициент обратно пропорционален Re
и, следовательно, скорости уср.
'* Ж. II у а з е й л ь (1799—1809 гг.) — фраапуземш ученый, получивший формул) (1.82,1 экспериментальным путем в 1840 г.
Зпая закон распределения скоростей по сечению трубы, легко определить коэффициент Кориолиса а, учитывающий неравномерность распределения скоростей в уравнении Берлудли, для случая стабилизированного ламинарного течения жидкости в круглой хрубе. Для этого в выражении (1.54) заменим скорость по формуле (1.78) и среднюю скорость по формуле (1.81), а также учтем, что S = л/^о и dS = 2nrdr. После подстановок и сокращений получим
![]()
Обозначав переменную 1 — га/>о через г, найдем
а = — 8 jj г3 dz = 21 г4= 2.
Итак, действительная кинетическая энергия ламинарного потока с параболическим распределением скоростей в 2 раза превышает кинетическую энергию того же потока, но при равномерном распределении скоростей.
Таким же путем можно показать, что секундное количество движения ламинарного потока с параболическим распределением скоростей в р раз больше количества движения того же потока, но при равномерном распределении скоростей, причем коэффициент р, называемый коэффициентом Буссинсска, в данном случае равен 4/s.
Изложенная теория ламинарного течения жидкости в круглой трубе хорошо подтверждается опытом, и выведенный закон сопротивления обычно не нуждается в каких-либо поправках, за исключением следующих случаев:
1) при течения в начальном участке трубы, где происходит постепенное формирование параболического профиля скоростей (этот вопрос рассмотрен в следующем параграфе);
2) при течении с теплообменом;
3) при течении в капиллярах и зазорах с облитерацией;
4) при течения с большими перепадами давления (пи. 2—4 рассмотрены в п. 1.27).
1.25. Начальный участок ламинарного течения
Если жидкость из какого-либо резервуара поступает в прямую трубу постоянного диаметра и Движется по ней ламинарным потоком, то распределение скоростей по сечению трубы вблизи входа получается практически равномерным, особенно, если вход выполнен с закруглением (рис. 1.45). Но затем под действием сил вязкости происходит перераспределение скоростей по сечениям: слои жидкости, прилежащие к стенке, тормозятся, а центральная часть потока (ядро), где еще сохраняется равномерное распределение скоростей, движется ускоренно, чю обусловлено необходимосидо прохода через неизменную площадь определенного расхода жидкости.
При атом толщина слоев заторможенной жидкости постепенно увеличивается, пока не станет равной радиусу трубы, т. е. пока слои, прилегающие к противоположным стенкам, не сомкнутся на оси трубы. После этого устанавливается характерный для ламинарного течения параболический профиль скоростей.
Участок от начала трубы, на котором формируется (стабилизируется) параболический профиль скоростей, называется начальным участком течения (/нач). За пределами этого участка имеем стабилизированное ламинарное течение, параболический профиль скоростей остается неизменным, как бы ци была длппиа труба, при условии сохраиеиия ее прямолинейности и постоянства сечения. Изложенная выше теория ламинарного течения справедлива именно для этого стабилизированного ламинарного течения и неприменима в пределах начального участка.
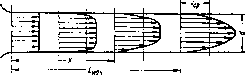
Рис. 1.45. Формирование профиля скоростей на начальном участке
Для определения длины начального участка можпо пользоваться приближенной формулой Шиллера, выражающей эту длину, отнесенную к диаметру трубы, как функцию числа Re;
U/d-0,029Rc. (1.85)
Сопротивление на начальном участке трубы получается больше, чем на последующих участках. Объясняется это тем, что значение производной dvjdy у стенки трубы па начальном участке больше, чем на участках стабилизированного течения, а потому больше и касательное напряжение, определяемое законом Ньютона, и притом тем больше, чем ближе рассматриваемое сечение к началу трубы, т. е. чем меньше координата х.
Потеря нанора на участке трубы, длина которого I «S /нач1 определяется по формулам (i-82) или (1.83) и (1.84), но с поправочным коэффициентом к, большим единицы. Значения этого коэффициента могут быть найдены ио графику (рпс. 1.46), на котором он изображен как функция безразмерного параметра х• 10s/ (dRe). С увеличением этого параметра коэффициент к уменьшается и при зпачеиии x/(d Не) = ?нач/(^ Re) =0,029,
т. с. при х = 1иач, становится равиым 1,09. Следовательно, сопротивление всего начйльпого участка трубы па 9 % больше, чем сопротивление такого же участка трубы, взятого в области стабилизированного ламинарного течения.
Для коротких труб значения поправочного коэффициента к как видно из графика, весьма существенно отличаются от единицы.
Когда длина I трубы больше длины !,1ач начального участка, потеря налоря складывается яз иоте]ш на печальном участке и на участке стабилизированного течения:
![]()
Учитывая формулы (1.84) и (1.85) и выполняя соответствующие преобразования, получаем
![]()
• Если относительная длияа I'd трубопровода достаточно велика, то дополнительный член в скобках, равиый 0,165, ложно
Рис. 1.46. Зависимость коэффициенте»» к и а от параметра s.lO-VfdRe)
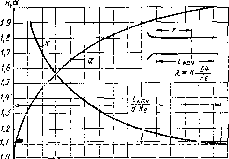
,0\___1 1 ! J- 1 1......J—)__!—
’ 0 г * В 8 '.0 11 !Ч /V 1S 20 22 Z* 2S
Гб^О3
ввиду ка.юсти не учитывать. Од;гз .\о up я уточпо/шых расчетах труб, длина которых соизмерима с 1пач, этот член следует у’црын;!'! г,.
Для начального участка труби с плавным входом коэффициент Кориолиса а возрастает от единицы до Двух (см. рпс. 1.4В).
1.26. Ламинарное течение в зазоре
между двумя стенками п в прямоугольных трубах
Рассмотрим ламинарное течение в зазоре, образованном Двумя параллельными плоскими стейками, рассюяпие между которыми равно а (рис. 1.47). Начало коор;',пнат поместим н ссредпгге зазора, нанравоъ ось Ох вдоль точешгя, а ось Оу — по нормали к стенкам.
Возьмем два нормальных поперечник сеченпя потока на расстоянии I одно от другого и рассмотрим поток шириной, равной единице. Выделим объем жидкости в форме прямоугольного параллелепипеда, расположенного симметрично относительно оси Ох м^жду выбранными поперечными ссчеппяни потопа и имеющего размеры сторон I X 2у X 1.
Запишем условие равномерного движения выделеппого объема вдоль оси Ох:
2//Ртр--|i (dv/dy) 21,
где ртр •— р1 — pz — разность давлений (перепад) в рассматриваемых сечелинх.
Знак минус обусловлен тем, что производная dv/dy отрицательна .
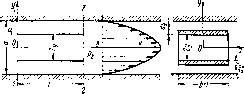
Рис. 1.47. Схема для рассмотрения ламинарного течения в зазоре
Из предыдущего найдем приращение скорости dv, соответствующее приращению координаты dy:
После интегрирования получим /’гр „ п
Так как при у — а/2 v = 0, находим С=
откуда
/’гр ( \
~ 2ц/ ( 4 У )'
(1.87)
Далеэ подсчитаем расход q, приходящийся па единицу ширины иотока, для чего возьмем симметрично относительно оси Oz две элементарные площадки размером 1 х dy п выразим элементарный расход
dq = vdS =
t)2dy.
2ц1
(l.S
12 nZ 1
Выразим потерю давления на трение через полный расход Q = qb в зазоре шириной Ъ Ф 1; получим
Pip = i2\\lQ/(a3b). (1.89)
Когда одна из стенок, образующих зазор, перемещается в направлении, параллельном другой стойко, а давление в зазоре постоянно вдоль длины, подвижная степка увлекает за собой жидкость, и возникает так называемое фрикционное безнапорное движение. Выделим в таком потоке элемент, как показано на рис. 1.48, в рассмотрим действующие на него силы. Так кап давления р, приложенные к левой и правой граням элемента, одинаковы, то для равновесия сил необходимо, чтобы касательные напряжения на нижней и верхней гранях были бы также одинаковы, т. е. т = const.
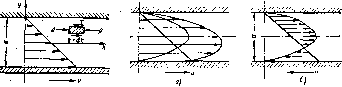
Рис. 1.48. Профиль скоро- Рис. 1.49. Профили скоростей в зазоре с двд-. стен в зазоре с движущей- гнущейся стойкой в с перепадом давления ся степной
Применив для этого случая закон Ньютона получим т = = —\idvlldy — С (знак минус взят потому, что при dy > 0 dv < 0) и после интегрирования
— №) 3/-Непостоянные С и Сх найдем, учитывая, что на границах потока при у — й/2 v — 0 и при у = —а/2 v = и, где и — скорость стенки. Отсюда
Стщ!а и С1 = и/2.
После подстановки С и Сх в последнее уравпепие получим закон распределения скоростей *
* (1.90)
v = (i/2—y/a)u.
Расход q жидкости, приходящийся на единицу ширины зазора, определится по средпей скорости
(1.91)
Если же указанное перемещение стенкя происходит прп перепаде давленпя в жидкости, заполняющей зазор, то закон распределения скоростей в пем найдем как сумму (пли разность в зависимости от направления движения стенки) вырагкепии (1.87) а (1.90):
![]()
Распределение скоростей в зазоре доказано на рис. 1.4? в двух вариантах: я) направление движения стенкн совпадает с набавлением течения жидкости под действием перепада давлений; б) направление движения стопки противоположно течению жадности.
Расход жидкости чгрез зазор единичной ширины в этих случаях определится как сумиа расходов, выражаемых формулами (1.S8) и (1.91), т. о. д - РтРя3/( 12^1?) ± {и/2) а.
Первое слагаемое формулы называется расходом напорного течения, а второе — фрикционным расходом.
Приведенным выражением можпо также пользоваться в том случае, когда зазор образован двумя цилиндрическими поверхностями, паирпмер поршнем и цилиндром, при условии, что зазор между
?ими мал по сравнению с диаметрами поверхпостей, я поверхности расположены соосио
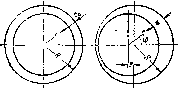
(рис. 1.50, а).
а) 6)
Рис. 1.50. Схемы концентричного в эксцентричного зааорои
Если поршень расположен в пнлиндро с некоторым эксцентриситетом (рис. 1.50, 6), то зазор а между ними будет переменной величиной:
а — R + е cos <р — г —
= a0(l-!-ecosqj),
где й0 = R — г и е — в/а^. Рассматривая элемент зазора шириной rdip как плоскую щель, получим следующее выражение для элементарного расхода:
![]()
Интегрируя по окружности, пайдем поллый расход
24
/>тр2п г
гдо Qo=—^ ^ - af) —
расход при сооспом располоя(спяп поршня в
цилиндра (при концентричной щели).
Из этого выражения следует, что при максимальном эксцентриситете (е = 1) расход Q = 2,5Q0.
При расчетах течений жидкости в грубах с некруглым поперечным сечением используют так называемый гидравлический радиус, равный отшшеппю площади сечения к его смоченному периметру П: Вг = 5/11, или гидравлическим диаметром Dt = 4RP (для круглого сэчеппя гидравлический диаметр равен геометрическому: Dr = d).
При ламинарном течении в этом случае расчеты ведут по обобщенной формуле Вейсбаха—Дарси (1.59), в которую вместо d подставляют Dr, а вместо X — = кХД, т. е.
![]()
(1.92)
где к — поправочный коэффициент, зависящий от формы сечения.
Для прямоугольного сечения {а х Ь) Д = 2ab!{a -Ь Ь). о к =* = /(№):
«/а ..........1 1.5 2 3 4 5 10 со
k ............0,89 0,92 0,97 1,07 1,14 1.19 1.32 1,50
Для сечсиня в форме равностороннего треугольника е,> сторонами а к = 0,83.
1.27. Особые случаи ламинарного течения
Течение с теплообменом. В рассмотревших выше случаях лалпгнарвого гечепип не учитывалось изменение температуры и, следовательно, изменение вязкости жидкости как в пределах поперечного сечения, так и вдоль потока, т. е. предполагалось постоянство температуры го всех точках потока. Подобное течение в отлично от течений, сопровождающихся изменением температуры жидкости, называют изотермическим.
Если по трубопроводу движется жидкость, температура которой значительно выше температуры окружающей среды, то такое течение сопровождается теплоотдачей через стенку трубы во внешнюю среду и, следовательно, охлаждением жидкости. Когда же температура движущейся жидкости пюче температуры окружающей среды, то происходит приток тепла через стенку тр^бы, в результате жидкость в процессе течения нагревается.

Рис. 1.51. Распределение скорости! «три изотермическом (/) в неизотсрмическом {2 я 3) течениях
В обоих указанных случаях при течепии жидкости происходит теплообмен с внешней средой, следовательно, температура жидкости, а также ее вязкость пс сохраняются постоянными, и течеаие не является изотермическим. Поэтому формулы (1.88) и (1.89), получепные в предположении постоянства вязкости по сечению потока, при течении жидкости со значительным теплообменом нуждаются в поправках.
I
При течении, сопровождающемся охлаждением жидкости, ее слои, непосредственно прилегающие к стенке, имеют температуру более низкую, а вязкость более высокую, чем в основном ядре потока. Вследствие этого происходит более интенсивное торможение пристенных слоев жидкости и снижение градиеЕт^сиорости у стенки. При течении, сопровождающемся нагреванием жидкости, обусловленным притоком тепла через стенку, пристенные слои жидкости имеют более высокую температуру и пониженную вязкость, вследствие чего [радиент скорости у стенки более высокий. Таким образом, вследствие теплообмена через стенку трубы между жидкостью и внешней средой парутпаетсн рассмотренный выше параболический закон распределении скоростей.
На рис. 1.51 показаны сравнительные графики распределения скоростей: при изотермическом точении (Ij, при течении с охлаждением (2) и с вагрсва-ваем (3) жидкости, по при одинаковом расходе и примерно одинаковой вязкости жидкости в ядре потока. Из рисунка бидно, что охлаждение жидкости влечет 8а собой увеличение неравномерности распределения скоростей (а > 2), a n,i-греванпе — уменьшение этой иеравномерностк (а < 2) по сравнению с обычным параболическим распределением скоростей (а = 2).
Изменение профиля скоростей при отклонении от изотермического течения вызывает изменение закона сопротивления. При ламинарном течении вязких жидкостей в трубах с теплоотдачей (охлаждением) сопротивление «случается больше, а при течении с притоком теплоты (нагреванием) — меньше, чем при изотермическом течении.
Ввиду того что точное решение задачи о течении жидкости с теплообменом Представляет большую сложность, так как приходится учитывать перемеппость температуры я вязкости жидкости по поперечному сотспгтго и вдоль трубы, а таток? рлстк'лтрпвли, тч'шюйые потоки и ранних сечениях труби, пользуются ирт'лижешюл формулой для коэффициента Хл, предложенной академиком М. Л. Михеевым:
где Неж — число Рейнольдса, подсчипнгто но средней вялкопи жидкости; \\.т — вязкость я>ядкостп, соотнегопукпцая средней темпорл t j ре стснии; \'я, — средняя еяjhocti, жидкост п.
Течение при больших мереиа.зпх давления. Опыт показывает. что при яамп-1».|р::ом течении л зазорах и труба*, пропеходртчем ппд действием больших иеооиадов давления (около гесколькнх десятгов мегапаскалей), падение напора вдоль ноюяа оказывается существенно ислил&ниым, т.е. пьелометричогкдя ли:а:!( дли потока постоянного сечения заметно искрипляетсп, а закоп 1!jаяоПтп даст зпачтедмтуго ногрегпаосчк Объясняется jto том, то при любом режима потеря онергнп на единицу расхода я>идкосгн растет пропорционально персноду давдешш, чю впечет за собой пагревапио жидкости при больших перепадах давления и уменьшение со вязкости.
С другой стороны, так как вязкость жидкости возрастает с упелпчелшем давления, в начале потока она будет ловытпетшой, а вдоль потока будит уменьшаться вследствие тдаиия давлении. Таким образом, вязкостт> переменна вдоль потока, п, кап результат одновременного действия на нее температуры и давления, продольный градишт давлении dp/dx, Обуслонлцнный трением, сказывается в начале потока больше, а в конце потока меньше, чем то следует из закона Пуазе шш.
Что |?,к;;>ется расхода, то повышение температуры уменьшает вязкость п, следопателмю, способствует увеличению расхода, а высокое давление в жидкости шпглппет вязкость и уменьшает расход по сравнению с его значением по Пуа.юй.по при том же перепаде давления, т. е. влияние этих двух факторов на расход является ирокиюттоложным.
С описанным видом ламинарного течения приходится сталкиваться особенно часто в высокшсшорнь’х гидромпптинах, г^с под действием больших пере-па; ion давления происходит перетекание вязкой жидкости через малые зазоры.
Рассмотрим задачу о ламинарном точении в зазоре величиной а, длипон ! н шяриной b с учетом влинния на вязкостг, давления и температуры. При оточ допустим, что плотность жидкости не зависит от давления и температуры, а соотношение размеров зазора а/Ь-+ 0.
Для одновременного учета влияния на вязкость жидкости давления и температуры принимаем в соответствии с формулами (1.17) и (1.18)
l е(Р —Р,>«—(!—Т<>0_
(1.93)
Здесь индекс 1 отпосптся к величинам в начале uoiokci. Примерные значения ве.линн аир были приведены н и, 1.3.
Воспользуемся ьолученноп п п. 1,26 формулой (1.89), но применил со пе к конечной длине I зазора, а к его элементу dl = dx. Определив из этой формулы расход Q, будем иметь
![]()
(1.94)
(знак минус вводим потому, что положительному гтрпращевню х соответствует отрицательное приращение р).
Полученное выражение отличаеюя от формулы (1,89) том, что в нем dp/de и (1 являются переменными величинами, зависящими от х, При этом, если Q — = const вдоль потока (жидкость абсолютно несжимаема), то одно неремеипоа пропорционально другому.
Запишем теперь уравнение энергии, т, е. равенство между потерей энергия па трение, перешедшей в шило, и приростом тепловой энергии жидкости за единицу времени: г,1,0 с — теплоемкость жидкости; к — коэффициент, учитывающий долю работы сил ппакостн, которая идет па нагревание жидкости; р — давление в конце участка.
При к — 1 теплоотдача в стенку отсутствует и вся теряемая энергия, обу-словленили ня.жосгыи, идет па нагревание ;кидкости. Ион к = О происходит столь интенсивная теплоотдача в стенку, что температура жидкости не повышается (изотермическое [ечеине).
Из выражения (1.95) имеем Т — Т1=-к(р1 — р)‘рс.
Поело 1Юдс1апов!Я1 тфодидущою выражения в формулу (1.93) получим , '¦S'
li = |i,e ''' ^ Н (1.36)
Используем найденную связь между ц и р для интегрирования уравнения (1.91). После разделения нёремеппцх вместо уравнения (1.94) будем иметь
Постояпнуго интегрирования С найдем из условий в начальном сечепии, где при х = 0 р = pi. Следовательно, с__
ct + pfc/(pc) •
Пусть в конечном сечепии потока при х = I р = ривб — 0. В результате
v 12ц,/ a+fc(5/(pc)
Входящая в формулу (1.97) величина является вязкостью в начальном сечении потока, т. е. при р = р, я Т =• Т0; она может быть выражена черав щ» — вязкость при р = рцэб = 0и Т = Т„ по формуле (1.86), т. е.
|i, = u,Jeaf’1- *
Для изотермического точения в формуле (1.97) следует положить к — 0. С учетом предыдущего в этом случае получим
Найдем относительный расход Q, равный отношению расхода при переменной вязкости к расходу при ц = ц0 — const, Для этого разделим уравнение (1.97) на
Qo — Pi<isb/(l2nol) и получим
_ о с-«р, Ы«+М) \
О _S._ U ' Р«/ 1 Л (1.99)
V Qo М« + Р*/<Р«>Г 1 U'
На рис. 1.52 представлены зависимости Q от р, по формуле (1.99) для трех жидкостей: керосина (1), трансформаторного масла (2) и жидкости АМГ-10 (3), причем для двух случаев к = 1 (отсутствие теплообмена) и i = 0 (изотермическое течение). Кривые соответствую ио двум крайний режимам расходятся гг'гольно существенно. Реальные процессы описываются кривыми, которыо располагаются между этим» предельными криш.гап. В связи с тем что скорости течения жидкости и зазорах при столь высоких перепадах давления отель велики и каждая частпца пребывает в зазоре весьма везпачвтелъное время, более вероятным представляется режим течения, ври котором fc= 1, т. е. теплообмен играет незначительную роль. Это предположение подтверждается новыми экспериментальными исследованиями пепзотермнческого течепия в зазорах, проведенными Ю. А. Содипым. Однако эти же исследования показывают, что при увеличении относительной длины зазора На п числа Прандтли, равною Рг = цсД (с — теплоемкость, Я — коэффициент теплопроводности), а также npii уменьшении числа Re роль теплообмена возрастает, и процесс течения может приблизиться к изотермическому.
Изложенная теория позволяет получить зависимость p;pt от х/l и построить соответствующие кривые, т. е. безразмерные апюры давления вдоль потока (рис. 1.53). Как видно из графика, чем выше давление рг, тем больше отклоне-иие кривых от прямой, соответствующей закону Пуаасйля.
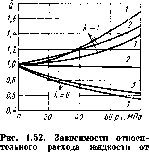
_Р_
Р>
0,6 ОА 0,2
О
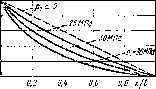
Рис. 1.53. Изменение давления вдоль зазора с уютом псрснсвпостп вязкости
Течение с облитерацией. Иногда пря течении через капилляры и малые зазоры наблюдается явление, которое ие может быть объяспепо законами гидравлики, Оно заключается в том, что расход жидкости через капилляр или зазор с течением времени уменьшается, несмотря на то что перепад давлении, под которым происходит движение жидкости, и ее физические свойства остаются неизменпыми. В отдельных случаях движение жидкости но истечении некоторого времени может прекратиться полностью. Это явление носит название облитерации, и его причина кроетсв в том, что при опрепелеппых условиях уменьшается площадь поперечного сечения канала (зазора, капилляра) вследствие адсорбции (отложения) полярпоактивпых молекул жидкости па ого стенках.
Толщина адсорбционного слоя для масел составляет несколько микрометров, поэтому при течении через капилляры и малые зазоры этот слой может существенно уменьшить площадь поперечного сечевпл или даже полностью перекрыть его.
Г л а в а 6. ТУРБУЛЕНТНОЕ ТЕЧЕНИЕ
1.28. Основные сведения
В п. 1.22 было указано, что для турбулентного течения характерно перемешивание жидкости, пульсации скоростей и давлений. Если с помощью особо чувствительного прибора-самописца измерить и записать пульсации, например, скорости по времеып в фиксированной точке потока, то получим кзр'шку, подобную показанной на рис. 1.54. Скорость беспорядочно колеблется около некоторого осредненного иаср но времепи значения, которое в данной случае остается постоянным.
Траектории частиц, проходящих через данную неподвижную точку пространства в разныо моменты времени, представляют собой кривые линии различной формы, несмотря на прямолинейность трубы. Характер линий тока в трубе в данный момент времени также отличается большим разнообразием (рис. 1.55). Таким образом,

Рис. 1.54, Пульсация скорости в тур. Рпс. 1.55. Характер лпппй тока в булентвом потоке турбулентном потоке
строго говоря, турбулентное течение всегда является неустановив-ппгмея, так как значения скоростей и давлений, а также траектории частиц, изменяются по времени. Однако его можно рассматривать как установившееся течение при условии, что осредиенные по времени значения скоростей и давлений, а также полпый расход потока не изменяются со временем. Такое течение встречается на практике достаточно часто.
Распределение скоростей (осредненных по времени) % поперечном сечении турбулентного потока существенно отличается от того, которое характерно для ламинарного течения. Если сравним кривые распределения скоростей в ламинарном и турбулентном потоках в одной и той же трубе и при одном и том же расходе (одинаковой средней скорости), то обнаружим существенное различие (рис. 1.36). Распределение скоростей при турбулентном течении более равномерчос, а нарастание скорости у стенки более крутое, чем при ламипарцом течении, для которого характерен параболический закоп распределения скоростей.
В свягп с этим коэффициент Корполиса а, учитывающий неравномерность распределения скоростей в уравнении Бернулли (см. п. 1.1G), irpif 1урбулеит1гом течения значительно меньше, поясе ла при ламинарном. В отличие от ламинарного течения, где а не зависит от Re и равен 2 (см. п. 1.24), здесь коэффициент а является функцией Re и уменьшается с увеличением последнего от 1.13 при Re = ReKp до 1,025 при Re = 3-106. Как видно из графика, приведенного па рис. 1.57 28, кривая а при возрастании числа Re приближается к единице, поэтому в большинстве случаев при турбулентном течении можно принимать а — 1.
Так как при чурбулеитпом течении отсутствует слоистость потока и происходит перемешивание жидкости, закон трения Ньютона в атом случае выражает лишь малую часть полного касательного напряжения. Благодаря перемешиванию жидкости и непрерывному перекосу количества движения в поперечном направлении касательное напряжение х„ на степке трубы в турбулентном потоке значительно больше, чем в ламинарном, при тех же значениях числа Re и динамического давления pv2/2, подсчитанных по средней скорости
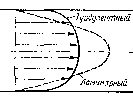
Рис. 1.56. Профили скоростей в .чймлкарпом и турбулентном по-
С,8
’ 3fl 3,6
Рис. 1.57. Зависимость коэффициента а от Ig Re
В связи с этим потери энергии прп турбулентном течении жидкости » трубах такжо получаются иными, нежели при ламинарном. 13 турбулентном потоке при Не > ReKp потери напора на трение по длине значительно больше, чем при ламинарном течении при тех же размерах трубы, расходе и вязкости жидкости, а следовательно, при одинаковых числах Re (ламинарный режим прз этом неустойчив).
Если при ламинарном течении потеря напора на трение возрастает пропорционально скорости (расходу) в цервой степени, то при переходе it турбулентному течению заметны некоторый скачок сопротивления и затем более круюе нарастание величины Лтр по кривой, близкой к параболе второй степени (рис. 1.58).
Ввиду сложности турбулептпого течения и трудностей его аналитического исследования до настоящего времени для пего пе имеется достаточно строгой и точной теории. Существуют полуомпириче-окио, приближенные теории, например теория Ирандтля 29 п другие, которые здесь не рассматриваются.
В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей и трубах, пользуются экспериментальными данными, система 1 тированными на основе теории гидродинамического подобия.
Основной расчетной формулой для потерь папоум при турбулентном течении и круглых трубах является уже приводившаяся выше кая эмпирическая формула (1.59), называемая формулой Всйсбаха— Дарси п имеющая следующий вид:
где Кт — коэффициент потерь на треяле при турбулентном течении, или коэффициент Дарси.
В следующем параграфе будет показано получение формулы Вейсбаха—Дарси методом анализа размерностей.
Эта основная формула применима как при турбулентном, так и при ламинарном: течении (см. п. 1.24); различно заключается лишь в значениях коэффициента Я.
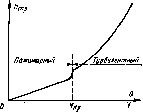
Так как при турбулентном течении потеря наиора на трение приблизительно пропорциональна скорости (и расходу) во второй степени, коэффициент потерь иа трение в формуле (1.59) в цервой приближении для данной трубы можно считать величиной постоянной.
Однако из закона гидродинамического подобия (см- п. 1.21) следует, что коэффициент Ят так же, как Рис. 1.58. Зависимость ftT(, от о и Яп, должен быть функцией основ- и Q ного критерия подобия напорных
потоков — числа Рейнольдса Re, а также может зависоть от безразмерного геометрического фактора — относительной шероховатости внутренней поверхности трубы, т. е. Ят = / (Re, a/d), где Д — средняя высота бугорков шероховатости, d — диаметр трубы.
Когда шероховатость трубы не влияет на се сопротивление (на Ят), трубу называют гидравлически гладкой. Для этих случаев коэффициент Я* является функцией лишь числа Рейпольдса: Ят = = /; (Кс). Существует ряд эмпирически? и полуэмпирических формул, выражающих эту функцию для турбулентного течения в гидравлически гладких трубах; одной из наиболее удобных и употребительных яиляется формула П. К. Конакова Я? — 1/(1,8 lg Re — 1,5)2, (1.100)
применимая прп числе Re or Re,!p до Re, равного нескольким миллионам.
При 2300 < Rc < 105 можно пользоваться также формулой Блазиуса
Отсюда видно, что с увеличением Re коэффициепт Ят уменьшается, однако это ^уменьшение гораздо менее значительно, чем при ламинарном течении (рис. 1.59). Это различие в законах изменения коэффициента А связано с тем, что непосредственное влияние вязкости жидкости на сопротивление в турбулентном потоке гораздо меньше, чей в ламинарном. Если в последнем потери папора на трение прямо пропорциональны вязкости (см. п. 1.22), то в турбулентном потоке, как это следует из формул (1.59) и (1.101), они пропорциональны вязкости в степени V4. Основную роль в образовании потерь энергии при турбулентном течения играют перемешивание и рассеивание кинетической энергии завихренных частиц.
К числу гидравлически гладких труб можно без большой погрешности отнести цельнотянутые трубы из цветных металлов (включая и алюминиевые сплавы), а также высококачественные бесшовные стальные трубы. Таким образом, трубы, употребляемые в качестве топливопроводов и гидросистем, в обычных условиях можно считать гидравлически гладкими и для их расчета пользоваться приведенными формулами. Водопроводные стальные и чугунные трубы гладкими нельзя считать, так как они обычно дают повышенное сопротивление, и формулы
| Ал Re | |||||||||||
| 1 (1,81дйе-1,5)г | |||||||||||
| Г4* | |||||||||||
| Дт |
|||||||||||
| к-. | |||||||||||
| 2 3 4 Ь | 6 7 8 9 10 11R8- | ||||||||||
Рис. 1.59. Зависимость Хл в ki от числа Re
(1.100) и (1.101) для них не справедливы.
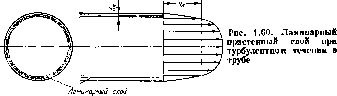
Вопрос о сопротивлении шероховатых труб рассмотрен ниже.
Как показывают опыты ряда исследователей (II. И. Никурадзе, Г. Г. Гуржиенко, Рейхардта и др.), при турбулентном течепии жидкости пепосредственно па степке трубы обычно имеется ламинарный слой (рис. 1.60). Это очень топкий слой жидкости, движение в котором является слоистым и происходит без перемешивания. В его пределах скорость круто нарастает от пуля па стенке до некоторой конечной величины ул на границе слоя. Толщина бл ламинарного слоя крайне невелика, причем оказывается, что число Re, подсчитанное по толщине 5Л, скорости v„ и кинематической вязкости v, есть величина постоянная, т. е.
Рдбд/V —const.
Эта величина в соответствии с теорией гидродинамического подобия имеет универсальное постоянное значение подобно тому, как постоянно ReKp для течения в трубах. Поэтому ори увеличении скорости потока и, следовательно, Re растет также скорость t>„, а толщина <3Л ламинарного слоя уменьшается.
1.29. Турбулентное течение в шероховатых и некруглых трубах
Если для гидравлически гладких труб коэффициент потерь на тресте вполне определяется числом Re, то для шероховатых труб Я, зависит еще и от шероховатости внутренней поверхности трубы. При этом важен не абсолютный размер Д бугорков шероховатости, а отношение этого размера к радиусу (или диаметру) трубы, т. е. так называемая относительная шероховатость Дid. Одна и та же абсолютная шероховатость может совершенно не оказывать влияния па сопротивление трубы большого диаметра, но способна значительно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости. Простейшим случаем будет тот, когда все бугорки шероховатости имеют один и тот же размер Д и одинаковую форму, т. е. при так называемой равномерно распределенной зернистой шероховатости.
Таким образом, в этом случае коэффициент Я, зависит как qt Rc, так и от отношения Aid (или Д/г0):
Ат = / (Re, Дid).
Характер влияния этих двух параметров па сопротивление труб отчетливо виден из графика, который является результатом опытов И. И. Никурадзе.
И. И. Никурадзе испытал на сопротивление ряд труб с искусственно созданной шероховатостью на их внутренней поверхности. Шероховатость была получена путем приклейки песчинок определенного размера, полученного просеиванием песка через специальные сита. Тем самым была получена равномерно распределенная зернистая шероховатость. Испытания были проведены при широком диапазоне относительных шероховатостей^-^- = ’ а также чисел
Re (Re = 500 10е). Результаты этих испытаний представлены на
рис. 1.61, где построены кривы© зависимости lg (1000А.) от lg Re для ряда значений Д/г0.
Наклонные прямые Л и В соответствуют законам сопротивления гладких труб, т. е. формулам (1.100) и (1.101). После умножения на 1000 и логарифмирования получим уравнения прямых
lg (1000ЛЛ) = lg 64 000 - lg Re; lg(10001,) = lg316- [ IgRo.
Штриховыми линиями показаны кривые для труб с различной относ ятельной шероховатостью А/г0.
Из рассмотрения графика можно сделать следующие основные выводы.
1. При ламинарном течении шероховатость на сопротивление во влияет; штриховые кривые, соответствующие различным шероховатостям, практически совпадают с прямой А.
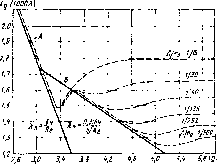
Рис. 1.61. Зависимость lg (1000 Ji) от lg Re для труб с искусственной шероховатостью
2. Критическое число Re от шероховатости практически пе зависит; штриховые кривые отклоняются от прямой А приблизительно при одном и том же Кекр.
3. В области турбулентного течения, но при небольших Re и Д!г0 шероховатость на сопротивление не влияет; штриховые линии на некоторых участках совпадают с прямой В. Однако гри увеличении Re ато влияние начинает сказываться, и кривые для шерохо-иатых труб начинают отклоняться от прямой, соответствующей закону сопротивления гладких труб.
4. При больших Re и больших относительных шероховатостях коэффициент Хт нерестает зависеть от Re и становитст постоянным для дайной относп1ельной шероховатости. Это соответствует тем участкам штриховых кривых, где они после некоторого подъема располагаются параллельно осп абсцисс.
Таким образом, для каждой из кривых, соответствующих шероховатым трубам при турбулентном течении, можно отметить следующие три области значений Re п Д;Г0, отличающиеся друг от друга характером изменения коэффициента А.т.
Первая область — область малых Ro и Д/г0, где коэффициент Ят от шероховатости не зависит, а определяете:! лишь числом Re; эго область гидравлически гладких труб. Она ле гмеет места для максимальных значений шероховатости в опытах И. И. Никурадзе.
Во второй области коэффициент ?.т зависит одновременно от двух параметров — числа Re и относительной шероховатости.
Третья область — область больших Re и А/гп, тде коэффициент Хт ис зависит от Re, а определяется лишь относительной шероховатостью. Оту область называют областью автомодельности или режимом квадратичного сопротивления, так как независимость коэф-фициепта JiT от Re означает, что потеря напора пропорциональна скорости во второй степени [см. формулу (1.59)].
Чтобы лучше уяснить эти особенности сопротивления шероховатых труб, необходимо учесть наличие ламинарного слон (см. п. 1.28).
Как указывалось выше, при увеличении Re толщина ламинарного слоя 6Л уменьшается, поэтому Для турбулентного потока при малых Re толщина ламинарного слоя больше высоты бугорков шероховатости, последние находятся внутри ламинарного слоя, обтекаются плавно (безотрывно) и на сопротивление не влияют. По мере увеличения Rc толщина 6Л уменьшается, бугорки шероховатости начинают выступать за пределы слоя и влиять на сопротивление. При больших Re толщина ламинарного слоя становится весьма малой, а бугорки шероховатости обтекаются турбулепшьш потоком с вихре-образованиями за каждым бугорком; этим и объясняется квадратичный закон сопротивления, характерный для дапной области.
График И. И. Никурадзе позволяет построить примерную зависимость от Re допустимой шероховатости, т. е. такого максимального значения, при котором шероховатость трубы еще не влияет на ее сопротивление. Для этого следует взять те точки на графике (см. рис. 1.61), в которых кривые для шероховатых труб начинают отклоняться от прямой В для гладких труб. Очевидно, что с увеличением Re значение допустимой шероховатости умепыпается.
Опыты Никурадзе проводились на трубах, снабженная искусственной, равпомерпо распределенной зернистой шероховатостью. Для натуральных шероховатых труб закон изменения L, от Ro получается несколько иным, без подъема кривых после отклонения их от закона для гладких труб. На рис. 1.62 в полулогарифмических координатах даны результаты опытов, поставленных во Всесоюзном теплотехническом институте Г. Л. Мурпным. Коэффициент Ят для натуральных шероховатых труб на графике указан в зависимости от Re для разных значений dl Дэ, где Аэ — абсолютная шероховатость, эквивалентная по сопротивлению зернистой шероховатости в опытах И. И. Никурадзе. Для новых стальных бесшовных труб рекомендуется принимать при расчетах значение Лэ = 0,1 мм; для труб, бывших в употреблении, Аэ = 0,2 мм.
Различие в характере кривых, представленных па рис. 1.61 и 1.62, объясняется тем, что в натурной трубе (см. рпс. 1.62) бугорки шероховатости имеют различную высоту и нри увеличении числа Re начинают выступать за пределы ламнпарцого слоя но одновременно, а при разных Re. Ввиду этого переход от лстпии, соответствующей сопротивлению гладких труб, к горизонтальным прямым, соответствующим квадратичному закону, происходит для натурных труб более нлавпо, без провала кривых, характерного для графика И. И. Никурадзе.
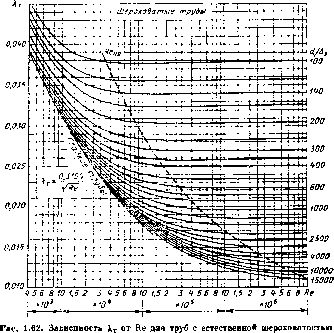
Для практических расчетов по определепию сопротивления реаль-пых шероховатых труб можно рекомендовать также универсальную формулу Л. Д. Алмшуля [2]:
Ят-ОДЦДэ/^-ЪОДе)1/4, (1.102)
где Дэ — эквивалентная абсолютная шероховатость; d — диаметр трубы.
Характерные значения Да (в мм) для труб из различных мате
риалов приведены ниже
Сгекло ................................... О
Трубы, тянутые из латуни, евннца, меди..............................0—0,002
Высококачественные бесшовные стальпые трубы......................0,06—0.2
Стальные трубы...............................0,1—0,э
Чугунные асфальтированные трубы....................................0,1—0,2
Чугунные трубы............................................................0,2—1,0
При Re < 20 tf/Д, формула (1.102) переходит в приведетгаую г..;ште формулу (1.101) Блазиуса для гладких труб, а при Re > >¦ 500 dlДэ — в формулу для вполне шероховатых труб, т. е. длл режима квадратичною соиротиЕлепия (антомодельностп):
Я1 = 0,11(Дв/й)1/*.
(1.103)
Таким образом, путем сравнения численного значения отношения dlД, с числом Re можно установить границы указанных выше областей (режимов) турбулентного течения в шероховатых трубах.
Иа практике часто приходится иметь дело с турбулентным течением в пекруглых трубах, применяемых, например, в охлаждающих устройствах {радиаторах, теплообменниках, охлаждающих трактах двигателей и др.). Рассмотрим расчет потерь на трение при турбулентном течении в трубе с поперечным сечением произвольной формы. Суммарная сила трешзя, действующая на внешнюю поверхность потока длиной I,
Т — Штц,
где П — периметр сечения; т0 — касательное напряжение на стенке, зависящее в основном от динамического давления, т, е. от средней скорости течения и няотпостн жидкости (см. п. 1.16).
Итак, при заданной площадп сечепия S и данном расходе жидкости, а следовательно, и при данной средней скорости сила трения пропорциональна периметру сечения. Поэтому для уменьшения силы трепия, а также потерь энергии на трение следует уменьшать периметр сечения. Наименьший периметр при заданной площади имеет круглое сечепие, которое поэтому является наивыгоднейшим с точки зрения получения минимальных потерь энергии (напора) еа трение в трубе.
Для количественной оценки влияния формы сечения на потерю напора при турбулентном течении так же, как и при ламинарном, в расчет вводят гидравлический радиус 7?г или диаметр Дг (см. п. 1.26).
Можно пользоваться так же, как и при ламинарном реЛвмс, обобщенной формулой Вейсбаха—Дарси, причем в отличпе от ламинарного реяшма в первом приближении поправочный коэффпппент к принимают равным единице. Таким образом, Для любой формы сечения
k
![]()
(1.104)
При этом коэффициент Кт подсчитывают по тем же формулам
(1.100) — (1.103), но число Re выражают через D{ : Re = Z)ru/v.
1.30. Применение метода анализа размерностей
Формулы Вейсбаха — Дарсп и Вейсбаха и некоторые другие соотношения гидравлики могут быть получены ш апалпза размерностей. В основе пгого ме-*ода лежит так называемая Пц-георема, пли теорема Бакингема, которая заключается в следующем: функциональная зависимость между п физическими размерными полтинами всегда может быть преобразована в уравнение, содержя-щее m безразмерных комбинаций тех я,о физических величин (так называемых чисел я), причем т всегда меньше п. Газностт. п — т = г представляет собой число нервичпых (осиоииых) единиц, паириис-р в мехапцко и гидромеханике — единицы длппы, времени п массы, i. с. z = В, а п теплотехнике i( перечисленным единицам добавляется еще температура, следовательно, z — 4,
В п. 1.21 был рассмотрен такой случаи, ко1да уравнение Бернулли, записанное п размерных величинах, спязыплло мги;ду собой пять размерных переменных; рь р(< ц,, р2 и йм. Д после приведения этого уравнения к безразмерному виду в ием остались лишь дне безраамерпыо переменные: число Эллера Еа и коэффициент потерь I.
Рассмотрим получение формулы Войсбах.! — Дарси.
Очевидно, что на потерю давления на трение в трубе рТр = 7iTp pg влияют (или могут влиять) следующие факторы: длипа I и диаметр d трубы, средняя скорость течения v, свойства жидкости р н |л и средняя высота бугорков шероховатости Д на стенках трубы.
Запшчем интересующую функцию в виде Ртр=к (г. d, v, р, ц, Л).
Число перемепных п = 7, следовательно, в соответствии с Пи-тсоречой т = п — г = 7 — 3 = 4, и вместо предыдущего можем записать я = Ф(--Ч, я2, я3),
где гс, гс1, я2 н тт3 — безразмерные комплексы, вид которых найдем следующим путем.
Из числа п переменных выберем три с независимыми размерностями, включающими в себя три осповпых единицы (длкпы L, времепп Г и массы М), например d, v и р; их размерпости в системе LTM таковы:
\d] = L\ [v] = LT~'\ [pJ=i/L-3,
Выразим числа л, ль ла и л3 делением на выбранные три переменпие в некоторых степенях х, у и г (с соответствующими индексами) остальных четырох переменных, а именпо: ;чр, I, ц в 4, которые имеют следующие размерности: [p] = M/LT2; ll] = L; [\i\-MlLT-, [AJ=L.
Таким образом, будем иметь
d*vY ’ 1 dxKv‘рг‘
Паттдсч псе 12 показателей cTeneueii пч условия бсзразмерпостл всех чисел л, т. е. сравнением размерностей ирп L, Т и М во всех четырех выражениях. а именно:
показатели степени при L:
— i=x + y — Зг; 1 = <Е, + ух— 3zj;
— 1 = хг + уа — 3za; 1 = jv-\- уг — ?. г3;
показателя стапеля при Т:
-2=—у, о—— j/i; — 1=— г/а: о=— г/зГ
показатели стопсни ири М:
1 = г; 0 = ri; 1 = гг; 0 = г,.
Решая совместно иолучиппые равнения, получаем х=0; у = 2; z = 1; iri = l; j/j~0; z, = 0; х2— 1; у^= 1 ’ 3^ = 1;
*¦*=!; Уз = 0; г3 = 0,
где Ax = (f, (Re, ДIII).
Таким образом, получили формулу Вейсбаха — Дарси, а также информацию о том, какими факторами определяется ьоаф-фпционт Дарси Хт.
Таким образом, теперь вместо выражении (1.105) 5 Ртр _( 1 , V Д \ pi."2 “ ^d ’ dvo ’ d j ’ впя прс
1Х0ДИМ
Pip
К тому же результату можно прийти, если вместо решения системы из 12 уравнении соиташпь таблицу. содержащую первоначальные размерные Ееременпмс, их размерности, затем делители, подобранные из условия получения безразмерных псрсменпых, и, наконец, новые безразмерные переменные (табл. 1.1).
Обращение в едннипу трех новых переменных л и влечет за собой уменьшение числа переменных на три.
I можем записать
:сти:о числа Рей-Т о б л ип а 1.1
| Размер- менные | Размерность в единицах СИ | Дели |
Uotwir безразмерная пере- |
|
Л Р | кг/(м • с2) |
ро» | Pip/(P^2) |
| 1 | , |
d | Hd |
| ¦ | |||
|
» | м/с | ||
| Р | кг/и3 |
9 | |
|
Р | кг/(м • с) |
dv р | м/(Л>р) |
| д | d |
A/d |
