Глава 2 расчет трубопровода на прочность
Глава 2
РАСЧЕТ ТРУБОПРОВОДА НА ПРОЧНОСТЬ
2.1. ТРЕБОВАНИЯ, ПРЕДЪЯВЛЯЕМЫЕ К ТРУБАМ И МАТЕРИАЛАМ
Утечки перекачиваемых нефти или газа даже через небольшие трещины, образующиеся в трубопроводе, загрязняют окружающую среду и приводят к экономическому ущербу. Разрывы трубопроводов больших диаметров могут нанести значительный экономический и социальный ущерб. Поэтому к трубам предъявляются жесткие требования (к качеству материала, поверхности, точности размеров труб, качеству сварных швов).
Качество материала характеризуется механическими свойствами: временным сопротивлением, пределом текучести, относительным удлинением, ударной вязкостью. Весьма существенное значение имеют пластичность и свариваемость. Для труб, соприкасающихся с агрессивной средой, имеет значение коррозионная стойкость. Стойкостью против коррозии отличаются трубы из алюминия или из неметаллических материалов. Но механические свойства этих материалов невысоки. Изготовленные из них трубы имеют ограниченное применение. Трубы магистральных газопроводов и нефтепроводов изготовляют из стали. Сталь — экономичный, прочный, хорошо сваривающийся и надежный материал. По способу изготовления трубы для магистральных трубопроводов подразделяются на бесшовные, сварные с продольным швом и сварные со спиральным швом. Бесшовные трубы применяют для трубопроводов диаметром до 426 мм. Обычная область применения сварных труб — трубопроводы диаметром 530 мм и выше. Трубы диаметром до 530 мм изготовляют из спокойных и по-луспокойных углеродистых сталей. Для изготовления труб диаметром до 1020 мм применяют спокойные и полуспокойные низколегированные стали. Трубы больших диаметров изготовляют из низколегированных сталей в термически или термомеханически упрочненном состоянии.
Сталь должна удовлетворять требованиям СНиП. Например, отношение предела текучести к временному сопротивлению должно быть не больше 0,75 для углеродистых сталей, 0,8 —для низколегированных, 0,85—для термически упрочненной стали. Металл труб не должен иметь трещин, расслоений, закатов.
Серьезные требования предъявляются, как уже было сказано, к самим трубам. Так, согласно СНиП овальность труб не должна превышать 1 %, кривизна труб не должна быть больше 1,5 мм на 1 м длины. Длина поставляемых заводом труб должна быть в пределах 10,5—11,6 м. Концы труб должны быть обрезаны под прямым углом и иметь разделку кромок под сварку. Сварные швы должны быть рав-44
| Марка стали | Предел прочности, МПа, не менее |
Предел текучести, МПа. не менее |
Относитель ное удлинение, . не менее | Наружный диаметр трубы, мм |
| 14ХГС | 500 | 350 |
19 | 530, 720, 1020 |
| 17ХГС | 520 | 360 | 20 |
630, 720, 820 |
|
17Г1С | 520 |
360 | 20 | 1020, 1220 |
| 17ГС |
520 | 360 |
20 | 530, 720, 820 |
| 14Г2САФ | 550 | 380 | 20 |
1020 |
|
14Г2САФ | 570 |
400 | 20 | 1020; 1220 |
| (для экспандиро-ваниых труб) 16Г2САФ |
600 | 420 |
20 | 1020 |
|
10Г2СД (МК) | 500 |
350 | 18 |
530, 630 |
нопрочными основному металлу трубы; переход от шва к телу трубы должен быть плавным.
Марки и прочностные характеристики сталей, применяемых для прямошовных труб, приведены в табл. 2.1.
2.2. КРАТКИЕ СВЕДЕНИЯ ОБ
ИЗГОТОВЛЕНИИ ТРУБ
Прокатка бесшовных труб состоит из следующих основных операций.
Сначала из раскаленной заготовки получают толстостенную трубу (гильзу). Эта операция называется прошивкой. Она осуществляется на стане винтовой прокатки, оснащенной расположенными под углом друг к другу конусными валками. Чтобы придать получающемуся отверстию правильную круглую форму, между валками устанавливают оправку. Затем следует операция раскатки: уменьшение толщины стенки до близкой к требуемой и одновременно удлинение трубы. Она выполняется на станах продольной прокатки с круглыми калибрами. Прокатка ведется на оправке. Следующая операция — калибровка. На калибровочном стане труба получает нужные размеры и форму правильного круга. Далее труба направляется на охлаждение и отделку.
Сварные трубы для магистральных трубопроводов изготовляют, как уже было сказано, с прямым продольным или спиральным швом. Для прямошовных труб заготовки — стальные листы, для спиральношовных — полосовая сталь, свернутая в рулон. Прямошовные трубы получают вальцеванием или холодным прессованием. Последний метод — более производительный. Сначала стальные листы очищают от окалины и ржавчины, обрабатывают кромки. Затем на специальном стане кромки подгибают, в результате чего заготовка приобретает корытообразный вид. Следующая операция — придание корытообразной заготовке U-образной формы. Эта операция выполняется на гидравлическом прессе при помощи круглого штампа, диаметр которого равен диаметру будущей трубы. Далее U-образная заготовка поступает в более мощный пресс, имеющий два штампа в виде полых полуцилиндров. При схождении штампов металл заготовки обжимается по периметру трубы. Затем окончательно сформованную трубу переводят на установку для сварки.
Сваренную трубу калибруют. В оба конца трубы вставляют заглушки — конусы силовых головок. Через одну головку в трубу подают воду, через другую выходит воздух. Под давлением воды труба расширяется и ее наружный диаметр становится равным диаметру обоймы. Процесс расширения трубы называется экспандированием. Степень экспандирования не должна быть слишком большой (не рекомендуется превышать 1,2 %), так как при экспандировании возникает наклеп и свойства стали ухудшаются.
После экспандирования каждую трубу подвергают гидравлическому испытанию (на прочность и герметичность). Качество сварных швов проверяют рентгенографически или другими неразрушающими способами.
Процесс изготовления спиральношовных труб протекает так. Стальная лента из рулона направляется (разматывателем) в правильную машину. Затем следует обработка кромок (вплоть до снятия фасок под сварку), после чего подающая машина вводит ленту в формовочно-сварочное устройство. Формовочный элемент этого устройства представляет собой втулку, продольная ось которой находится под углом (угол формовки) к оси поступающей стальной ленты. При прохождении через втулку лента сворачивается в спираль. При помощи сварочных головок, расположенных внутри и снаружи формовочной втулки, непрерывно смыкающиеся кромки ленты свариваются: получается спиральный шов. Диаметр выходящей из формовочно-сварочного устройства трубы зависит от угла формовки. Спиральношовные трубы имеют преимущества перед прямошовными. Стальная полоса, из которой изготовляют спиральношовные трубы, дешевле листов для изготовления прямошовных труб того же диаметра, так как ширина ее меньше. Спиральное расположение волокон в трубе более благоприятное, чем продольное. К недостаткам спиральношовных труб следует отнести большую протяженность шва, затрудненность контроля качества сварки, а также качества свернутой в рулон полосовой стали.
2.3. РАСЧЕТ ТРУБОПРОВОДА НА ПРОЧНОСТЬ
Уложенный в грунт трубопровод испытывает вызванные целым рядом силовых воздействий напряжения: кольцевые, продольные и радиальные (рис. 2.1).
Кольцевые напряжения стк возникают от внутреннего давления и определяются котельной формулой ак = pD/(26), где р — давление; D—внутренний диаметр; S—толщина стенки трубопровода.
Продольные напряжения стпр создаются:
под действием внутреннего давления аГф = |лак = npD/(26), где ц — коэффициент Пуассона, для стали р = 0,3; если трубопровод может свободно перемещаться^вдоль оси, то апр = pD/(48);
при изменении температуры апр =
= —EaAt, где Е — модуль упругости; а — коэффициент линейного расширения; At = t—ty—температурный перепад; t и ty — температура стенки трубопровода соответственно в рассматриваемый момент времени и в момент укладки; для стали Е — 206 ООО МПа, а = 12-10-6 1/°С.
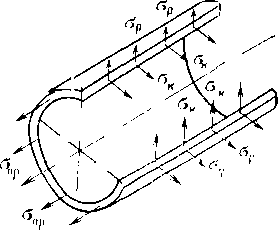
Рис. 2.1. Схема {напряжений, возникающих в трубопроводе
при изгибе сг„р = + EDJ{2р), где D„ — наружный диаметр трубопровода; р — радиус изгиба; знак плюс относится к растягивающим напряжениям, а знак минус — к сжимающим; напряжения изгиба возникают при укладке трубопровода на поворотах трассы, а также на переходах'через повышенные и пониженные точки.
Продольные напряжения различного происхождения складываются:
pD п 4 j , ED
- -р
-EaAt
-*пр
26
2р
Радиальные напряжения ар малы и в расчетах не учитываются.
Не принимается во внимание при расчете трубопровода на прочность давление грунта, а также подвижные нагрузки, которые могут действовать на трубопровод (тракторы, сельскохозяйственные машины, автомобили). Эти внешние нагрузки незначительны и, кроме того, компенсируются внутренним давлением. Не принимаются в расчет также силовые воздействия случайного характера (от оползневых явлений, от массы трубопровода, при размыве основания, на котором он лежит). Определение усилий, которые может выдержать трубопровод, или, наоборот, определение толщины стенки трубопровода при заданной нагрузке — цель расчета на прочность.
Магистральные трубопроводы рассчитывают по методу предельных состояний. Предельным состоянием называют такое, при достижении которого нормальная эксплуатация рассчитываемой конструкции становится невозможной. Различают первое, второе и третье предельные состояния. Первым предельным состоянием называется такое, при достижении которого рассматриваемая конструкция теряет несущую способность, или, что то же самое, способность сопротивляться приложенным к ней усилиям, т. е. разрушается. Второе предельное состояние характеризуется чрезмерными, недопустимыми при эксплуатации остаточными деформациями или колебаниями. Третье предельное состояние определяется чрезмерными, недопустимыми при эксплуатации трещинами. Ни при достижении третьего предельного состояния, ни при достижении второго конструкции не грозит разрушение, ее прочность и устойчивость сохраняются. По третьему предельному состоянию рассчитывают, например, железобетонные резервуары, по второму предельному состоянию — междуэтажные перекрытия зданий, расстояния между опорами для трубопроводов при надземной прокладке, когда регламентируется стрела прогиба и т. д. Уложенные в грунт магистральные трубопроводы рассчитывают по первому предельному состоянию, т. е. принимают, что наибольшее усилие, испытываемое трубопроводом, не должно превышать его несущей способности.
Для уложенного в грунт трубопровода достижение предела текучести не означает потерю работоспособности. Трубопровод может успешно эксплуатироваться до тех пор, пока напряжения в нем не достигнут предела прочности. При расчете, трубопровода на прочность считают, что он идеально круглый. Овальность труб не принимают во внимание, так как под действием внутреннего давления она выравнивается. Учитывают лишь внутреннее давление (основное воздействие). Таким образом, условие прочности может быть выражено в виде npD < ^]2б, где п — коэффициент надежности по нагрузке и Rx — расчетное сопротивление. В левой части этого выражения — действующее расчетное усилие (стремящееся разорвать трубопровод по образующей). В правой — несущая способность трубопровода.
Заменив в условии прочности D на Д,—26, получаем, что толщина стенки трубопровода
6 ¦:= npDJ{2 (Rx J пр)\.
Согласно СНнП 2.05.06—85 расчетное сопротивление Rl следует определять по формуле Rt = R'fm/(k1kn), где R” — нормативное сопротивление, принимается равным временному сопротивлению, Rni = ствр; т — коэффициент условий работы трубопровода; kx — коэффициент надежности по материалу; kn — коэффициент надежности по назначению трубопровода. Числовые значения этих коэффициентов надо брать по СНиП.
При наличии продольных осевых сжимающих напряжений толщину стенки следует определять из условия S = = npDJ[2 (грг^! + пр)\, где — коэффициент, учитывающий двухосное напряженное состояние труб.
^ = лЛ^0.75(|<тпрЛ,|/Я,)2 —0,51 спр N HR,.
Полученное расчетное значение толщины стенки трубы округляется до ближайшего большего значения, предусмотренного государственными стандартами или техническими условиями. Продольные осевые напряжения onp N определяются от расчетных нагрузок и воздействий с учетом упругопластической работы металла. Расчетная схема должна отражать условия работы трубопровода и его взаимодействие с грунтом.
В частности, для прямолинейных и упругоизогнутых участков при отсутствии продольных и поперечных перемещений
сгПр -olEM-t \inpD/(2S„),
где At — расчетный температурный перепад; бн — номинальная толщина стенки трубы.
2.4. ТРУБОПРОВОДЫ С ПЕРЕМЕННОЙ ТОЛЩИНОЙ СТЕНКИ
Если толщина стенки будет переменная, изменяющаяся в соответствии с изменением давления по длине, то для нефтепроводов может быть достигнута существенная экономия металла. Для газопровода давление в конечной точке перегона может быть равно среднему (при остановке г.^рекачки). Поскольку различие между давлением в начале перегона и средним невелико, газопроводы обычно не сооружают с переменной толщиной стенки.
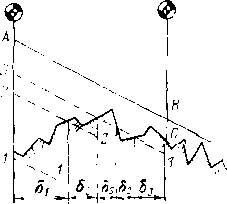
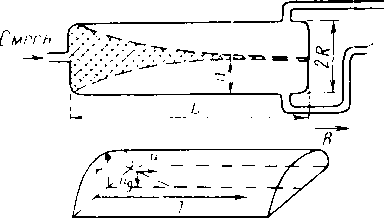
Рис .‘22. Схема раскладки труб на перегоне между станциямм
Уменьшение толщины стенки нефтепровода осуществляется ступенчато. Число ступеней для каждого перегона обычно принимают равным трем.
Размещение труб с различными толщинами стенок но длине перегона называется раскладкой труб. Она может быть осуществлена следующим образом: сначала надо на профиле трассы для каждого перегона построить линии гидравлического уклона. Эти линии должны соответствовать наименьшему расходу, возможному при эксплуатации (перекачка через станцию, начальный период при вводе в строи нефтеперекачивающих станций по очередям.) Далее измеряе\л расстояние от точки на профиле в конце перегона до линии гидравлического уклона (напор). На рис. 2.2 — это отрезок ВС. Затем вычисляем давление, соответствующее напору ВС, и определяем толщину стенки трубопровода. Округлив полученную величину в большую сторону до ближайшего значения по ГОСТ, получим наименьшую толщину стенки 6а, которая должна быть принята для раскладки труб на рассматриваемом перегоне. После этого определяем напор, который может выдержать труба с такой толщиной стенки. Отложим этот напор от точки А по вертикали вниз (отрезок АЗ). .Между толщинами стенок для начального участка (бх) и 6а выбираем по ГОСТ промежуточное значение 62. Определяем напор, соответствующий 62, и откладываем напор А2, соответствующий 62. От точек 3, 2 и 1 проводим линии 33, 22 и 11, параллельные линии гидравлического уклона АВ. В точках пересечения линии <33 с профилем напор будет равен АЗ. На участках, где линия профиля расположена выше линии 33, напор будет меньше АЗ. Здесь надо укладывать трубы с толщиной стенки бя. На участках, где линия профиля находится между линиями 33 и 22, толщина стенки должна быть равна 62. На участках, где линия профиля проходит ниже линии 22 (т. е. между линиями 22 и 11), должна быть наибольшая толщина стенки, т. е. б,.
ПОДГОТОВКА НЕФТИ И ГАЗА К ТРАНСПОРТУ1
Начальный период разработки нефтяных месторождений, как правило, характеризуется безводной добычей нефти из фонтанирующих скважин. Однако на каждом месторождении наступает такой период, когда из пласта вместе с нефтью поступает вода сначала в малых, затем все в больших количествах. Примерно 60—75 % всей нефти добывается в обводненном состоянии.
Пластовые воды, поступающие из скважин различных месторождений, могут значительно отличаться по составу и концентрации растворенных в них минеральных солей, содержанию газа и наличию микроорганизмов. При извлечении смеси нефти с пластовой водой образуется эмульсия, которую следует рассматривать как механическую смесь двух нерастворимых жидкостей (нефти и воды), одна из которых распределяется в объеме другой в виде капель различных размеров. Наличие воды в нефти приводит к удорожанию транспорта в связи с возрастающими объемами транспортируемой жидкости и увеличением ее вязкости. Присутствие в нефти даже 0,1 % воды приводит к интенсивному ее вспениванию в ректификационных колоннах нефтеперерабатывающих заводов, что нарушает технологические режимы переработки и, кроме того, загрязняет конденсационную аппаратуру.
Легкие фракции нефти (углеводородные газы от этана до пентана) являются ценным сырьем, из которого получают такие продукты, как спирты, синтетический каучук, растворители, жидкие моторные топлива, удобрения, искусственное волокно и другие продукты органического синтеза, широко применяемые в промышленности. Поэтому необходимо стремиться не только к снижению потерь легких фракций из нефти, но и к сохранению всех углеводородов, извлекаемых из нефтеносного горизонта, для последующей их переработки.
Качество вырабатываемой продукции во многом зависит от качества исходного сырья, т. е. нефти. Если в недалеком прошлом на технологические установки нефтеперерабатывающих заводов шла нефть с содержанием минеральных солей (100—500 мг/л), то в настоящее время требуется нефть с более глубоким обессоливанием, а зачастую перед переработкой нефти приходится полностью удалять из нее соли.
Наличие в нефти механических примесей (частиц песка и глины) вызывает абразивный износ трубопроводов, нефтеперекачивающего оборудования, затрудняет переработку нефти, повышает зольность мазутов и гудронов, образует отложения в холодильниках, печах и теплообменниках, что приводит к уменьшению коэффициента теплопередачи и быстрому выходу их из строя. Механические примеси способствуют образованию трудноразделимых эмульсий. Наличие мине-
| Показатель | 1 |
Группа нефти II | III |
| Содержание воды, %, не более | 0,5 | 1 | 1 |
| » хлористых солей, мг/л, не бо |
100 | 300 |
1800 |
| лее |
|||
|
Содержание механических примесей, %, | 0,05 |
0,05 | 0,05 |
| не более | |||
| Давление насыщенных паров при темпера | 66 650 |
66 650 | 66 650 |
| туре нефти в пункте сдачи, Па, не более |
ральных солей в виде кристаллов в нефти и раствора в воде вызывает усиленную коррозию металла как нефтеперерабатывающего, так и нефтеперекачивающего оборудования и трубопроводов, увеличивает устойчивость эмульсий, затрудняет переработку нефти.
При соответствующих условиях часть хлористого магния и хлористого кальция, находящихся в пластовой воде, гидролизуется с образованием соляной кислоты. В результате разложения сернистых соединений при переработке нефти образуется сероводород, который в присутствии воды вызывает усиленную коррозию металла. Хлористый водород, растворенный в воде также разъедает металл. Особенно интенсивно идет коррозия при наличии в воде сероводорода и соляной кислоты.
Причины, приведенные выше, указывают на необходимость подготовки нефтн к транспорту. Собственно подготовка нефти включает: обезвоживание и обессоливание нефти и полное или частичное ее раз-газирование.
Качество подготовки нефти к транспорту регламентирует ГОСТ. Основные требования к качеству приведены в табл. 3.1.
Природный газ, получаемый с промыслов, содержит посторонние примеси: твердые частицы (песок и окалину), конденсат тяжелых углеводородов, водяные пары и часто сероводород, углекислый газ и инертные газы. Присутствие твердых частиц в газе приводит к бы-строму износу соприкасающихся с газом деталей компрессоров. Твердые частицы засоряют и портят арматуру газопроводов и контрольно-измерительные приборы; скапливаясь на отдельных участках газопровода, они сужают его поперечное сечение, ухудшают работу газо-горелочных устройств. Жидкие частицы, оседая в пониженных участках трубопровода, также вызывают уменьшение площади его поперечного сечения. Они, кроме того, оказывают корродирующее действие на трубопровод, арматуру и приборы. Влага в определенных условиях приводит к образованию гидратов, выпадающих в газопроводе в виде твердых кристаллов. Гидратные пробки могут полностью закупорить трубопровод.
Сероводород — весьма вредная примесь. В количествах, больших 0,01 мг на 1 л воздуха рабочей зоны, он ядовит. При промышленном использовании газа содержащийся в нем сероводород отрицательно сказывается на качестве выпускаемой продукции. В присутствии влаги сероводород вызывает сильную коррозию металлов. Углекислый газ вреден главным образом тем, что он снижает теплоту сгорания газа. Перед поступлением в магистральный газопровод газ должен быть осушен и очищен от вредных примесей. Кроме того, газ подвергают одоризации, т. е. вводят в него компоненты, придающие ему резкий и неприятный запах. Одоризация позволяет более быстро обнаружить утечки газа.
Подготовка газа к транспортировке проводится на специальных установках, находящихся на головных сооружениях газопровода. Газ после подготовки к транспортировке должен соответствовать требованиям отраслевого стандарта (ОСТ 5140—83) на природный газ, транспортируемый по магистральным газопроводам, с учетом климатических условий.
3.1. ОБРАЗОВАНИЕ НЕФТЯНЫХ ЭМУЛЬСИЙ И ИХ ОСНОВНЫЕ СВОЙСТВА
Для правильного выбора способов обезвоживания нефти (деэмульса-ции) необходимо знать механизм образования эмульсий и их свойства. Образование эмульсий уже начинается при движении нефти к устью скважины н продолжается при дальнейшем движении по промысловым коммуникациям, т. е. эмульсии образуются там, где происходит непрерывное перемешивание нефти и воды. Интенсивность образования эмульсий в скважине во многом зависит от способа добычи нефти, которая, в свою очередь, определяется характером месторождения, периодом его эксплуатации и физико-химическими свойствами самой нефти. В настоящее время любое месторождение эксплуатируется одним из известных способов: фонтанным, компрессорным или глубиннонасосным.
При фонтанном способе, который характерен для начального периода эксплуатации залежи нефти, происходит интенсивный отбор жидкости нз скважины. Интенсивность перемешивания нефти с водой в подъемных трубах скважины увеличивается из-за выделения растворенных газов, что приводит к образованию эмульсий уже на ранней стадии движения смеси нефти с водой.
При глубиннонасосной добыче нефти эмульгирование происходит в клапанных коробках, самих клапанах, в цилиндре насоса, в подъемных трубах при возвратно-ностунательном движении насосных штанг. При использовании электропогружных насосов перемешивание воды с нефтью происходит на рабочих колесах насоса и в подъемных трубах.
В компрессорных скважинах причины образования эмульсий те же, что и при фонтанной добыче. Особенно отрицательно влияет воздух, закачиваемый иногда вместо газа в скважину, который окисляет часть тяжелых углеводородов с образованием асфальтосмолистых веществ.
В эмульсиях принято различать две фазы — внутреннюю и внешнюю. Внешнюю фазу — жидкость, в которой размещаются мельчай-52
шие капли другой жидкости, называют дисперсионной, внешней или сплошной средой. Внутреннюю фазу — жидкость, находящуюся в виде мелких капель в дисперсионной среде, принято называть дисперсной, разобщенной или внутренней фазой.
По характеру внешней среды и внутренней фазы различают эмульсии двух типов: нефть в воде (н/в) и вода в нефти (в/н). Тип образующейся эмульсии в основном зависит от соотношения объемов двух фаз; внешней средой стремится стать та жидкость, объем которой больше. На практике наиболее часто (95 %) встречаются эмульсии типа в/н. Реже, чем эмульсии типа н/в, встречаются эмульсии третьего типа — вода в нефти в воде.
На способность эмульгирования нефти и воды кроме соотношения фаз оказывает влияние присутствие эмульгаторов, т. е. веществ, которые способствуют образованию эмульсии. Они понижают поверхностное натяженне на границе раздела фаз и создают вокруг частиц внутренней фазы прочные адсорбционные оболочки. Эмульгаторы, растворимые в воде, способствуют созданию эмульсии нефть в воде. К таким гидрофильным эмульгатором относятся щелочные мыла, желатин, крахмал и др. Гидрофобные эмульгаторы (растворимые в нефти) способствуют образованию эмульсий типа в/н. К ним относятся хорошо растворимые в нефти щелочноземельные соли органических кислот, смолы, мелкодисперсные частицы сажи, глины и других веществ, которые легче смачиваются нефтью, чем водой.
Нефтяные эмульсии характеризуются вязкостью, дисперсностью, плотностью, электрическими свойствами и стойкостью. Вязкость нефтяной эмульсии изменяется в широких диапазонах и зависит от собственной вязкости нефти, температуры образования эмульсии, соотношения количеств нефти и воды и температуры эмульсии.
Нефтяные эмульсии, являясь дисперсными системами, при определенных условиях обладают аномальными свойствами, т. е. являются неньютоновскими жидкостями. Как и для всех неньютоновских жидкостей, вязкостные свойства нефтяных эмульсий характеризуются кажущейся (эффективной) вязкостью.
Аномалия вязкости эмульсий усиливается, если сами нефти обла-лают аномальными свойствами, особенно при низких температурах. Аномальность нефтяных эмульсий объясняется образованием пространственных структурных решеток из частиц внутренней фазы, которые могут состоять как из капель воды, так и из кристаллов парафина. Наличие структурной решетки в эмульсии вызывает появление как динамического, так и статического напряжения сдвига. Существование аномалии вязкости в нефтяных эмульсиях определяется температурными условиями и содержанием воды. Каждой нефтяной эмульсии соответствует свое предельное значение температуры, выше которой реологические характеристики эмульсий соответствуют ньютоновской жидкости, т. е. вязкость эмульсии становится постоянной величиной при всех градиентах скорости.
С повышением содержания воды в нефти увеличивается кажущаяся вязкость эмульсии, что наблюдается до перехода эмульсии из типа в/н в тип н/в, а затем резко снижается. Содержание воды в нефти, при которой вязкость эмульсии снижается, называется точкой инверсии.
Для измерения реологических параметров эмульсий применяют известные методы исследования неньютоновских жидкостей. Имеющиеся зависимости, полученные эмпирическим путем, для определения вязкости эмульсий в общем случае универсальными не являются:
уравнение Эйнштейна
|i0 = м- (1 +2,5ф),
где ц0—динамическая^вязкость эмульсии; р,—динамическая вязкость дисперсионной среды; ср — отношение объема диспергированного вещества к общему объему эмульсии;
уравнение Гатчека
[10 = ji л] A tsj А — 1 ,
где А — отношение объема эмульсии к объему внутренней фазы;
уравнение Тейлора
М-о = И- 11 + 2’5Ф [(Hi f 0,4р,)/(рх -f p.)J |,
где —динамическая вязкость внутренней фазы.
Дисперсностью эмульсии принято называть степень раздробленности капель внутренней фазы во внешней среде. Дисперсность характеризуется одной из трех взаимосвязанных величин: диаметром капель d\ обратной величиной диаметра капель D = 1 id, обычно называемой дисперсностью; удельной межфазовой поверхностью, которая является отношением суммарной поверхности частиц к их общему объему.
В зависимости от физико-химических свойств нефти и воды, а также от условий образования эмульсий размеры капель могут быть самыми разнообразными и колебаться в пределах от 0,1 мкм до нескольких десятых миллиметра. Критические размеры капель, которые могут существовать в потоке при данном термодинамическом режиме, определяются скоростью совместного движения воды и нефти, поверхностным натяжением на границе раздела фаз и масштабом пульсации потока.
Нефтяная эмульсия, проходя по промысловым коммуникациям, оказывается в различных гидродинамических условиях, при которых может происходить как дробление, так и укрупнение капель. Наличие дополнительных факторов (нагрев, введение деэмульгаторов и др.) при определенных гидродинамических условиях может привести к разделению фаз эмульсии, транспортируемой по трубопроводам.
Плотность нефтяных эмульсий определяется по формуле для смеси нескольких жидкостей
_1_
(I — 0,01^)/fiH + 0,01g'pB
где рэ, рв, Рп — плотность эмульсии, воды и нефти при заданной температуре соответственно; q — содержание воды и растворенных солей в нефти, q = qj( 1—0,01 qc), где qB — содержание чистой воды в эмульсии; qc — содержание растворенных в воде солей.
Электропроводность чистых нефтей колеблется от 10"9 до 10-14 См/м, а электропроводность воды в чистом виде — от 10° до 10~? См/м, т. е. смесь из этих двух компонентов является хорошим диэлектриком. Однако при растворении в воде незначительного количества солей или кислот резко увеличивается электропроводность воды, а следовательно, и эмульсии. Электропроводность нефтяных эмульсий увеличивается в несколько раз при нахождении их в электрическом поле. Это объясняется различной диэлектрической проницаемостью воды и нефти и ориентацией капель воды в нефти вдоль силовых линий электрического поля.
Стойкость (устойчивость) эмульсий, т. е. способность в течение определенного времени не разделяться на составные компоненты, является самым важным показателем для водонефтяных смесей. Чем выше устойчивость эмульсии, тем труднее процесс деэмульсации. Нефтяные эмульсии обладают различной стойкостью. На устойчивость водонефтяных эмульсий значительное влияние оказывают следующие факторы: дисперсность системы; физико-химические свойства эмульгаторов, образующие оболочки вокруг капель воды; наличие на глобулах внутренней фазы электрического заряда; температура эмульсии; состав пластовых вод.
При всех прочих равных условиях устойчивость эмульсий тем выше, чем больше дисперсность. Устойчивость эмульсий в большой степени зависит от состава компонентов, входящих в защитную оболочку, которая образуется на поверхности капли. На поверхности капли также адсорбируются, покрывая ее бронирующим слоем, стабилизирующие вещества, называемые эмульгаторами. В дальнейшем этот слой препятствует слиянию капель, т. е. затрудняет деэмульсацию и способствует образованию стойкой эмульсии. В процессе существования эмульсий происходит упрочнение бронирующей оболочки, так называемое «старение» эмульсии. Установлено, что поверхностные слои обладают аномальной вязкостью, и со временем вязкость бронирующего слоя возрастает в десятки раз. Так, после суток формирования поверхностные слои эмульсий приобретали вязкость, соответствующую вязкости таких веществ, как битумы, которые практически по своим реологическим параметрам приближаются к твердым веществам.
Наличие электрических зарядов на поверхности глобул увеличивает стойкость эмульсий. Чем больше поверхностный заряд капель, тем труднее их слияние и тем выше стойкость эмульсии. В статических условиях дисперсная система электрически уравновешена, что повышает устойчивость эмульсии.
С повышением температуры уменьшаются вязкость нефти и механическая прочность бронирующего слоя, что снижает устойчивость эмульсии. Особенно резко прослеживается влияние температуры на устойчивость эмульсий высокопарафинистых нефтей. С понижением температуры в нефти выпадают кристаллы парафина, которые легко адсорбируются на поверхности капель воды, создавая высокопрочную бронирующую оболочку.
Существенно влияет на устойчивость нефтяных эмульсий состав пластовой воды. Пластовые воды разнообразны по химическому составу, но все они могут быть разделены на две основные группы: первая группа — жесткая вода содержит хлоркальциевые или хлоркаль-циево-магниевые соединения; вторая группа—щелочная или гидро-карбонатно-натриевая вода. Увеличение кислотности пластовых вод приводит к получению более стойких эмульсий. Уменьшение кислотности воды достигается введением в эмульсию щелочи, способствующей снижению прочности бронирующих слоев.
Основными из указанных факторов, влияющих на устойчивость эмульсий, являются: соотношение плотностей фаз, вязкость нефти, а также прочность защитных слоев на каплях воды. Свежие эмульсии легче поддаются разрушению, поэтому обезвоживание и обессолива-нне целесообразно производить на промысле.
3.2. ОСНОВНЫЕ СПОСОБЫ ОТДЕЛЕНИЯ ВОДЫ ОТ НЕФТИ
Процесс обезвоживания нефти можно условно разделить на два этапа: первый — укрупнение капель, т. е. сближение и флокуляция капель, разрушение бронирующей оболочки на каплях воды и их коагуляция до размеров, достаточных для их дальнейшего слияния, и второй — осаждение укрупненных капель. Скорость оседания взвешенных частиц может быть определена по формуле Стокса и? = dr (рв—()„)?/ (18 p,i), где иА — скорость оседания капель; d — диаметр оседающих капель; pD и р„ — плотность соответственно воды и нефти; fiH — динамическая вязкость нефти; g— ускорение свободного падения.
Формула Стокса не учитывает влняние стенок отстойника, а также вязкости осаждаемых частиц и характеризует осаждение или всплытие капель в неподвижной бесконечной среде.
Адамар и Бонд предложили поправку, учитывающую влияние вязкости жидкости внутренней фазы,
ug d2 (рв—рн) gK (18цн),
К 3 (р.,, -|- цв)/(2^ц -f- 3[хв).
Приведенные формулы применимы для движущейся капли с Re <L 2. Скорость осаждения при режимах 2 < Re <500 можно определять по формуле
при Re >500
![]()
число Рейнольдса Re = dugpj\in. Из приведенных формул очевидно, что скорость осаждения капель возрастает: с увеличением диаметра частиц; со снижением вязкости жидкостей, составляющих эмульсию; 56 с увеличением вязкости и плотности воды и нефти; с увеличением диаметра частиц; с увеличением ускорения движения частиц, которое в поле естественного тяготения равно ускорению свободного падения.
Однако чаще всего не скорость осаждения капель воды играет решающее значение при обезвоживании нефти, а время разрушения защитных оболочек и слияния капель в крупные, способные преодолеть вязкость внешней среды и осаждаться с образованием слоя свободной воды.
Выявление указанных факторов и характера их влияния позволяет наметить технические приемы повышения эффективности разделения эмульсий. Принципиальными основами этих приемов являются: повышение температуры обрабатываемых эмульсий, которое снижает вязкость жидкостей, составляющих эмульсию, и уменьшает поверхностное натяжение на границе раздела фаз (на этом принципе основаны термические методы обезвоживания нефти);
увеличение размеров частиц выделяемой диспергированной жидкости за счет различных приемов деэмульсацип, в частности, деэмуль-сации при помощи химических реаген.. в и электрического поля (на этом принципе основаны химические и электрические методы обезвоживания нефти);
увеличение скорости движения частиц дисперсной фазы путем замены естественной силы тяжести более мощной центробежной силой; плотность воды и механических примесей выше плотности нефти, и частицы под действием центробежной силы прижимаются к стенке и, коагулируя, стекают вниз; метод центрифугирования низкопроизводителен, сложен, дорог и широкого применения на промыслах не нашел;
уменьшение высоты отстаивания без увеличения общей площадки отстойника; на этом основано применение параллельных пластин в горизонтальных отстойниках и разделительных дисков в сепараторах.
Эффективность разделения эмульсий снижается при наличии в них взвешенных частиц, плотность которых мало отличается от плотности сплошной фазы. Не поддаются очистке механическими методами стойкие стабилизированные мелкодисперсные эмульсии. Отрицательное влияние на разделение эмульсий оказывают неблагоприятные гидравлические условия отстаивания, такие, как турбулентность, конвекция потоков, перемешивание и др. Значительное повышение эффективности разделения нефтяных эмульсий достигается путем комбинированного использования гравитационного отстаивания в сочетании с термическими, химическими и электрическими методами обработки нефти в процессе ее обезвоживания.
При проектировании сооружений обезвоживания нефти для конкретных производственных условий необходимо иметь экспериментальные данные об обводненности, качественном и количественном составе примесей, ожидаемом состоянии эмульсии. Одновременно с обезвоживанием нефти происходит и ее обессоливание, поскольку вода отделяется от нефти вместе с растворенными в ней минеральными примесями. При необходимости, для более полного обессоливания, можно дополнительно в нефть подавать пресную воду, которая растворяет кристаллы минеральных солей, и при последующем отделении минерализованной воды происходит углубленное обессоливание нефти.
Механическое обезвоживание нефти
Основная разновидность приемов обезвоживания нефти — гравитационное отстаивание. Применяют два вида режимов отстаивания — периодический и непрерывный, которые соответственно осуществляются в отстойниках периодического и непрерывного действия.
В качестве отстойников периодического действия обычно применяют цилиндрические отстойники — резервуары (резервуары отстаивания). Сырая нефть, подвергаемая обезвоживанию, вводится в резервуар при помощи распределительного трубопровода (маточника). После заполнения резервуара вода осаждается и скапливается в нижней части, а нефть собирается в верхней части резервуара. Отстаивание осуществляется при спокойном (неподвижном) состоянии обрабатываемой нефти. По окончании процесса обезвоживания нефть и вода отбираются из отстойного резервуара. Положительные результаты работы отстойного резервуара достигаются только в случае содержания воды в нефти в свободном состоянии или в состоянии крупнодисперсной нестабилизированной эмульсии.
Различают горизонтальные и вертикальные отстойники непрерывного действия (рис. 3.1). Горизонтальные отстойники подразделяются на продольные и радиальные. Продольные горизонтальные отстойники в зависимости от формы поперечного сечения могут быть прямоугольные и круглые. В гравитационных отстойниках непрерывного действия отстаивание осуществляется при непрерывном потоке обрабатываемой жидкости. На рис. 3.2 изображена принципиальная схема горизонтального цилиндрического отстойника непрерывного действия. Эмульсия жидкости В, диспергированная в жидкости Н, вводится в резервуар отстойника и расслаивается под действием силы тяжести. Разделившиеся жидкости выходят из отстойника по трубопроводам Я и В. На схеме рис. 3.2 заштрихована область эмульсии, которая разделяет зоны жидкостей Н (вверху) и В (внизу). Здесь а — уровень раздела фаз. При достаточной длине отстойника L в выходной его части происходит полное разделение фаз, составляющих эмульсию. Капля жидкости 5, движущаяся в однородной жидкости Н, находится под действием силы потока жидкости Я, которая увлекает каплю вдоль отстойника, it архимедовой силы, возникающей в результате различия плотности капли жидкости В (рп) и жидкости Н (р„).
Капля движется вдоль отстойника с постоянной скоростью потока Ui и опускается также с постоянной скоростью ug. Скорость падения капли ий может быть определена по закону Стокса, представленному в виде формулы Адамара. Капля, которая начинает движение с уровня г, находящегося выше поверхности раздела (уровня а), достигает этой поверхности в течение времени падения: tg = г!ий. Достигнув поверхности раздела, капля сохраняется у этой поверхности в течение времени tK, которое представляет собой время до коалес-

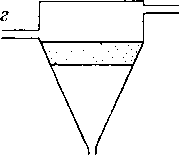
Рис. 3.2. Принципиальная схема горизонтального отстойника
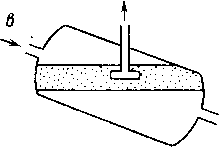
Рис. 3.1. Отстойники непрерывного действия: а — горизонтальный; 6 — вертикальный; н — наклоненный; ft — конический; / — поверхность
раздела; 2 — перегородка
ценции. В целом до коалесценции капля пройдет расстояние вдоль оси отстойника 2 ut (te ! tK) = uL (r/ug -f- Время коалесценции tк учитывать очень трудно. Задача решается относительно просто, если время коалесценции tK значительно меньше времени падения tgи им можно пренебречь.
Скорость потока определяется как uL -- Q/S, где Q — расход потока; 5 — площадь поперечного сечения потока. Если уровень раздела фаз Н и В находится посередине отстойника, то 5 -- л/?'2/2, где R — радиус цилиндрического отстойника.
При Rut/itf, < L диаметр капель, выделившихся в отстойнике:
f_3G
я
do
(3.1)
r'Kp,\p RL
где К --- (3/2) [(|1в 4- |1и)/(2рн + 3[,iB) ] — поправка к закону Стокса по Адамару и Бонду;
Ар — рв р„
Если ввести понятие поверхности отстойника' Sg = 2RL, то формула (3.1) примет вид
я Kg&p Sg
Капли в отстойнике, для которых d ^dn, выделяются из эмульсии. Полученная формула имеет существенное ограничение из-за того, что не учитывается время коалесценции капель дисперсной фазы. Эта формула при заданной степени очистки, определяемой предельной крупностью отделяемых частиц d для заданного отстойника, который характеризуется площадью поверхности отстаивания в нем Sg, позволяет найти максимальную производительность отстойника Q. Для общего расхода Q0c очищаемой эмульсии требуемое число отстойников определяется из выражения N = QodQ.
Термическое обезвоживание нефти
Одним из основных современных приемов обезвоживания нефти является термическая, или тепловая, обработка, которая заключается в том, что нефть перед отстаиванием нагревают. Вязкость вещества бронирующего слоя на поверхности частицы воды при повышении температуры уменьшается и прочность оболочки снижается, что облегчает слияние глобул воды. Кроме того, снижение вязкости нефти при нагреве увеличивает скорость оседания частиц при отстаивании. Термическая обработка нефти редко осуществляется только для отстаивания, чаще такая обработка применяется как составной элемент более сложных комплексных методов обезвоживания нефти, например в составе термохимического обезвоживания (в сочетании с химическими реагентами и отстаиванием), в комплексе с электрической обработкой и в некоторых других комбинированных методах обезвоживания.
Нагревание нефти осуществляется в специальных нагревательных установках, которые располагают в технологической линии обезвоживания нефти после отделения (сепарации) из нефти газов, но ранее ввода нефти в отстойник. Температура нагревания устанавливается с учетом особенностей водонефтяных эмульсий и элементов принятой системы обезвоживания.
Химическое обезвоживание нефти
В нефтяной промышленности весьма широко применяют химические методы обезвоживания нефти, основанные на разрушении эмульсий при помощи химических реагентов. Эффективность химического обезвоживания нефти в значительной степени зависит от типа применяемого реагента. Выбор эффективного реагента, в свою очередь, зависит от вида водонефтяной эмульсии и свойств нефти, подвергаемой обезвоживанию. Выбор реагентов-деэмульгаторов в каждом конкретном случае производится на основе специальных лабораторных и промысловых исследований. Химическое обезвоживание, как и прочие комбинированные методы обезвоживания нефти, включает гравитационное отстаивание после обработки реагентов водонефтяной эмульсии. В эмульсию, подвергаемую разрушению, вводится реагент-деэмульгатор и перемешивается с ней, после чего создаются условия для выделения воды из нефти путем отстаивания. Можно применять как периодическое, так и непрерывное разрушение эмульсий, но предпочтение отдается непрерывным процессам.
Существуют три метода химического обезвоживания нефти: обезвоживание, основанное на деэмульсации, которая осуществляется в нефтяной скважине («внутрискважинная деэмульсация»), когда реагент вводится в эмульсию непосредственно в скважине;
обезвоживание, основанное на деэмульсации, которая осуществляется в нефтесборном трубопроводе («путевая деэмульсация»), когда реагент вводится на начальном участке нефтесборного коллектора;
деэмульсация и обезвоживание нефти непосредственно в отстойных резервуарах, когда реагент вводится в резервуар после его заполнения эмульсией, подвергаемой обработке.
Первые два метода имеют некоторые преимущества и являются более эффективными.
Фильтрация
Для деэмульсации нестойких эмульсий применяют метод фильтрации, основанный на явлении селективной смачиваемости веществ различными жидкостями. Материалом фильтрующего слоя могут служить обезвоженный песок, гравий, битое стекло, стекловата, древесная стружка из осины, клена, тополя и других несмолистых пород древесины, а также металлическая стружка. Особенно часто применяют стекловату, которая хорошо смачивается водой и не смачивается нефтью. Фильтры из стекловаты долговечны. Фильтрующие вещества должны обладать следующими основными свойствами: хорошо смачиваться водой, благодаря чему глобулы воды прилипают к поверхности фильтрующего вещества, коагулируют и стекают вниз; иметь высокую прочность, которая обеспечивает длительную работу фильтра; иметь противоположный, чем у глобул, электрический заряд. Тогда при прохождении глобулами воды фильтра электрический заряд с поверхности капли снимается, чем снижаются отталкивающие силы между ними. Капли укрупняются и стекают вниз, а нефть свободно проходит через фильтр.
Фильтрующие установки обычно выполняют в виде колонн, размеры которых определяются в зависимости от вязкостных свойств эмульсии и объема обезвоживаемой нефти. Обезвоживание нефти фильтрацией применяют очень редко из-за малой производительности, громоздкости оборудования и необходимости частой смены фильтрующего материала. Фильтрация более эффективна в сочетании с процессами предварительного снижения прочности бронирующих оболочек.
Теплохимические процессы снижают прочность бронирующих оболочек или полностью их разрушают, что ускоряет и удешевляет разделение нефтяной эмульсии. В настоящее время более 80 % всей обводненной нефти проходит обработку на теплохимических установках. Такое широкое применение этот метод получил благодаря возможности обрабатывать нефти с различным содержанием воды без замены оборудования и аппаратуры, простоте установки, возможности менять деэмульгатор в зависимости от свойств поступающей эмульсии без замены оборудования. Однако теплохимический метод имеет ряд недостатков, например большие затраты на деэмульгаторы и повышенный расход тепла. На практике обессоливание и обезвоживание ведутся при температуре 50—100 °С.
По воздействию на нефтяные эмульсии все существующие деэмульгаторы делятся на электролиты, неэлектролиты и коллоиды. Деэмульгаторами-электролитами могут быть некоторые органические и минеральные кислоты (серная, соляная и уксусная), щелочи и соли (поваренная соль, хлорное железо, нефтенат алюминия и др.). Электролиты могут образовывать нерастворимые осадки с солями эмульсии, снижать стабильность бронирующей оболочки или способствовать разрушению эмульгаторов бронирующей пленки. Электролиты как деэмульгаторы применяют крайне ограниченно из-за их высокой стоимости или особой коррозионной активности к металлу оборудования. К неэлектролитам относятся органические вещества, способные растворять бронирующую оболочку и снижать вязкость нефти. Такими деэмульгаторами могут быть бензин, ацетон, спирт, бензол, четыреххлористый углерод, фенол и др. Неэлектролиты в промышленности не применяются из-за высокой их стоимости. Деэмульгаторы-кол-лоиды — это поверхностно-активные вещества (ПАВ), которые в эмульсии разрушают или ослабляют защитную оболочку капли.
Существующие ПАВ делятся на анионоактивные, катионоактивные, неионогенные. Анионоактивные ПАВ в водных растворах диссоциируют на отрицательно заряженные ионы углеводородной части молекулы и положительно заряженные ионы металла или водорода, Представителями этой группы являются карбоновые кислоты и их солн, сульфокислоты, алкилсульфонаты и др. Катиопоактивные ПАВ в водных растворах распадаются на положительно заряженный радикал и отрицательно заряженный остаток кислоты. Как деэмульга-торы этп ПАВ в промышленности не применяются. Неионогенные ПАВ в водных растворах не распадаются на ионы. К этой группе относятся оксиэтилированные алкилфенолы (деэмульгаторы ОП-4, ОП-7, ОП-Ю, ДБ-4, УФЭ-8, Кауфэ-14 и др.), оксиэтилированные органические вещества с подвижным атомом водорода (дипроксамин-15,7, проксамин-385, проксанол-305 и др.).
Деэмульгаторы должны хорошо растворяться в одной из фаз эмульсии (в воде или нефти), т. е. быть гидрофильными или гидрофобными, иметь поверхностную активность, достаточную для разрушения бронирующих слоев оболочек глобул, быть инертными по от-С2
ношению к металлам, не ухудшать качества нефти, быть дешевыми н, по возможности, универсальными по отношению к эмульсиям различных нефтей н вод. Чем раньше деэмульгатор вводится в смесь воды и нефти, тем легче происходит дальнейшее разделение эмульсии. Однако для разделения эмульсии еще недостаточно одного введения деэмульгатора, необходимо обеспечить полный контакт его с обрабатываемой эмульсией, что достигается интенсивной турбулизацией и подогревом эмульсий.
Электрическое обезвоживание
Электрическое обезвоживание и обессоливание нефти особенно широко распространено в заводской практике, реже применяется на нефтепромыслах. Возможность применения электрического способа в сочетании с другими способами (термическим, химическим) можно отнести к одному из основных его достоинств. Правильно выбранные режимы электрической обработки практически позволяют успешно провести обезвоживание и обессоливание любых эмульсий.
Рассмотрим механизм обезвоживания нефтяных эмульсий в электрическом поле.
В результате индукции капли воды вытягиваются вдоль цепи электрического поля с образованием в вершинах электрических зарядов. Под действием основного и индивидуального полей капли приходят в упорядоченное движение и сталкиваются, что приводит к их коа-лесценции. При прохождении эмульсии через электрическое поле, создаваемое переменным по величине и направлению током, так же как и при постоянном токе, капли, имеющие заряд, стремятся к электродам. Однако вследствие изменения напряжения и напряжения поля капли воды начинают двигаться синхронно основному полю и поэтому все время находятся в колебании. При этом форма капель непрерывно меняется. В связи с этим происходит разрушение адсорбированных оболочек капель, что облегчает их слияние при столкновениях. Установлено, что деэмульсация нефти в электрическом поле переменной частоты и силы тока в несколько раз эффективней, чем деэмульсация при использовании постоянного тока.
На эффективность электродеэмульсации значительно влияют вязкость и плотность эмульсии, дисперсность, содержание воды, электропроводность, а также прочность адсорбированных оболочек. Однако основным фактором является напряженность электрического поля. В настоящее время электродеэмульсаторы в основном работают на токах промышленной частоты (50 Гц), реже — на постоянном токе и совсем редко — на токах высокой частоты. Напряжение на электродах деэмульсаторов колеблется от 10 ООО до 45 ООО В.
3.3. СТАБИЛИЗАЦИЯ НЕФТИ
Добываемые нефти могут содержать в различных количествах растворенные газы (азот, кислород, сероводород, углекислоту, аргон и др.) и легкие углеводороды. При движении нефти от забоя скважины до нефтеперерабатывающего завода из-за недостаточной герметизации систем сбора, транспорта и хранения часто полностью теряются растворенные в ней газы и происходят значительные потери легких нефтяных фракций. При испарении легких фракций, таких, как метан, этан и пропан, частично уносятся и более тяжелые углеводороды (бутан, пентан и др.).
Предотвратить потери нефти можно путем полной герметизации всех путей движения нефти. Однако некоторое несовершенство существующих систем сбора и транспорта нефти, резервуаров, технологии налива и слива не позволяет доставить нефть на переработку без потерь легких фракций. Следовательно, необходимо газы и легкие фракции нефти отобрать в условиях нефтепромысла и направить их для дальнейшей переработки.
Основную борьбу с потерями нефти необходимо начинать с выхода ее из скважины. Ликвидировать потери легких фракций нефти можно в основном применением рациональных систем сбора нефти и попутного нефтяного газа, а также сооружением установок по стабилизации нефти для ее последующего хранения и транспорта. Под стабилизацией нефти следует понимать извлечение легких углеводородов, которые при нормальных условиях являются газообразными, для дальнейшего их использования в нефтехимической промышленности. Степень стабилизации нефти, т. е. степень извлечения легких углеводородов, для каждого конкретного месторождения зависит от количества добываемой нефти, содержания в ней легких углеводородов, возможности реализации продуктов стабилизации, технологии сбора нефти и газа на промысле, увеличения затрат на перекачку нефти за счет повышения вязкости после стабилизации из-за глубокого извлечения легких углеводородов, влияния стабилизации на бензиновый фактор нефти.
Существует два различных метода стабилизации нефти — сепарация и ректификация.
Сепарация—отделение от нефти легких углеводородов и сопутствующих газов одно- или многократным испарением путем снижения давления (часто с предварительным подогревом нефти).
Ректификация — отбор из нефти легких фракций при одно- или многократном нагреве и конденсации с четким разделением углеводородов до заданной глубины стабилизации.
Процесс сепарации может начинаться сразу же при движении нефти, когда из нее отбирается газ, выделившийся в результате снижения давления или повышения температуры. При резком снижении давления в сепараторе значительно увеличивается количество тяжелых углеводородов, уносимых свободным газом. При быстром прохождении нефти через сепаратор возрастает количество легких углеводородов в нефти.
Многоступенчатая система сепарации позволяет получить на первых ступенях метан, который направляется па собственные нужды или потребителям, а на последующих ступенях — жирный газ, содержащий более тяжелые углеводороды. Жирный газ отправляется на газобензиновые заводы для последующей переработки.
При наличии газобензинового завода (с учетом затрат на содержание и эксплуатацию установок многоступенчатой сепарации) экономически целесообразно применять двухступенчатую систему сепарации. При этом на первой ступени отбирается в основном метан, направляемый потребителям, а на второй ступени — жирные газы, идущие на газобензиновые заводы.
Для стабилизации нефти на промыслах используют в основном метод сепарации. Сосуд, в котором происходит отделение газа от нефти, называют сепаратором. В сепарационных установках происходит и частичное отделение воды от нефти. Применяемые сепараторы можно условно подразделить на следующие основные типы: по принципу действия — гравитационные, центробежные (гидроциклонные), жалюзийные, ультразвуковые и др.; по геометрической форме и положению в пространстве — сферические, цилиндрические, вертикальные, горизонтальные и наклонные; по рабочему давлению — высокого давления (более 2,5 МПа) среднего (0,6—2,5 МПа), низкого (0—0,6 МПа), вакуумные; по назначению — замерные и рабочие; по месту положения в системе сбора — I, II, концевой ступеней сепарации.
В сепараторах любого типа по технологическим признакам различают четыре секции: I — основную сепарационную, в которой происходит отделение газа от нефти; II —осадительную, предназначенную для выделения пузырьков газа, увлеченных нефтью из сепара-ционной секции, III — секцию отбора нефти, служащую для сбора и отвода нефти из сепаратора; IV — каплеуловительную, находящуюся в верхней части аппарата и служащую для отвода газа и улавливания капельной нефти, уносимой потоком газа.
Эффективность работы аппаратов характеризуется количеством жидкости, уносимой газом, и количеством газа, оставшегося в нефти после сепарации. Чем ниже эти показатели, тем более эффективна работа аппарата.
Конструктивные особенности промысловых сепараторов
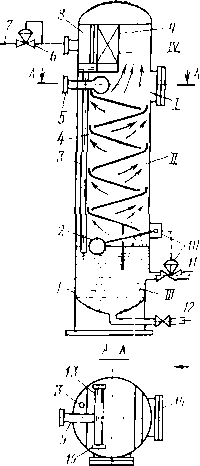
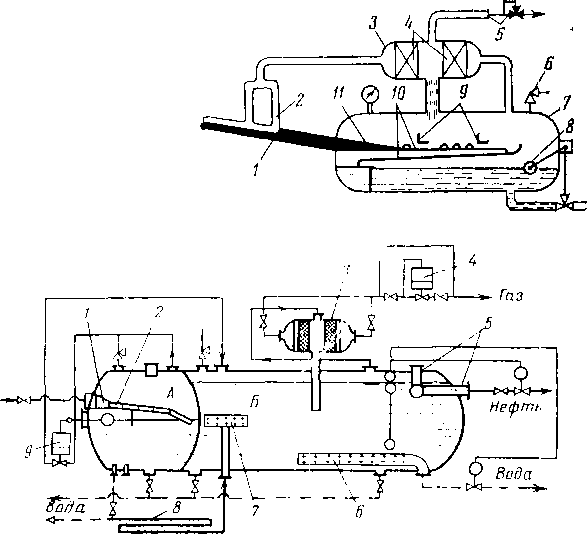
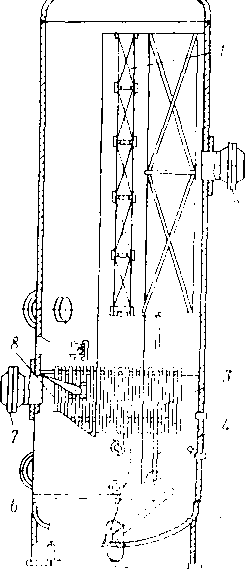
В вертикальном цилиндрическом гравитационном сепараторе (рис. 3.3) газонефтяная смесь через патрубок поступает в раздаточный коллектор и через щелевой выход попадает в основную сепарационную секцию. В осадительной секции из нефти при ее течении по наклонным плоскостям происходит дальнейшее выделение окклюдированных пузырьков газа. Разгазированная нефть поступает в секцию сбора нефти, из которой через патрубок отводится из сепаратора. Газ, выделившийся из нефти на наклонных плоскостях, попадает в каплеуловительную секцию, проходит через жалюзийную насадку и по трубопроводу выходит из сепаратора. Капли нефти, захваченные потоком газа и неуспевающие осесть под действием силы тяжести, в жа-люзийных решетках прилипают к стенкам и стекают по дренажной трубке в секцию отбора нефти.
Гидроциклонный двухъемкостный сепаратор (рис. 3.4) применяют на промыслах для работы на I ступени сепарации. Газонасыщенная
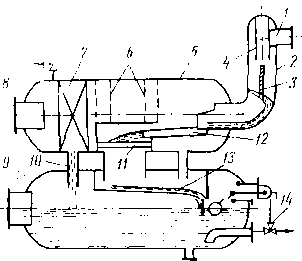
Рис .3 4 .Гидроциклонный двухъемкост-ный сепаратор:
1 — тангенциальный ввод газонефтяной смеси; 2 — головка гидроцнклона; 3 — отбойный козырек газа; 4 — направляющий патрубок; 5 — верхняя емкость сепаратора; 6 — перфорированные сетки для улавливания ка-пильной жидкости; 7 — жалюзийная насадка; 8 — отвод газа; 9 — нижняя емкость гидродиклона; 10 — дренажная трубка; 11 — уголковые разбрызгиватели; 12 — направляющая полка; 13 — перегородка; 14 — исполнительный механизм
Дитчпь 8
ООООО
ОоооО
ТО о о
ОоооО
о о о о
ОоооО
ООООО
иПирчиг
iemamiS •ЛААЛА--ЛЛЛЛЛ--ЛАЛАЛ- --ЛЛЛЛЛ-^\ДЛАЛ-
Рис. 3.3. Вертикальный сепаратор:
1 — корпус; 2 — поплавок; 3 — дренажная трубка; 4 — наклонные плоскости; 5 — патрубок для ввода газожидкостной смеси; 6 — регулятор давления «до себя»; 7 — выход газа; 8 — перегородка для выравнивания скорости газа; 9 — жалюзийная насадка; 10 — регулятор уровня; 11 — патрубок для сброса нефти; 12 — сброс грязи; 13 — раздаточный коллектор; 14 — люк; 15 — заглушка; секции: 1 — сепарационная; II — осадительная; 111 — отбора нефти; IV — каплеуловительнап
нефть через тангенциальный ввод поступает в гидроциклонную головку, где за счет центробежных сил происходит разделение нефти и газа на самостоятельные потоки. В верхнюю емкость нефть и газ поступают раздельно. Нефть по направляющей полке стекает на уголковый разбрызгиватель, в котором поток нефти разбивается на отдельные струи и происходит дальнейшее выделение газа. По сливной полке разгазированная нефть собирается в нижней емкости гидроциклона. При достижении определенного объема нефти в нижней емкости поплавковый регулятор уровня через исполнительный механизм, направляет дегазированную нефть в отводной трубопровод. Газ, отделившийся от нефти в дегазаторе, проходит в верхней емкости перфорированные перегородки, где происходит выравнивание скорости газа и частичное выпадание жидкости. Окончательная очистка газа происходит в жалюзийной насадке 7. Отделенная от газа жидкость по дренажной трубке 10 стекает в нижнюю емкость 9.
Падение давления в сборных коллекторах в результате движения по ним газонефтяной смеси может приводить к частичному выделению газа из нефти. В этом случае в сепарационную установку можно подавать разделенными потоками газ и нефть. Такой принцип использован на блочных сепарационных установках с предварительным отбо-
Рис. 3.6. Технологическая схема установки УПС-3000/6
Рис. 3.5. Сепаратор с предварительным отбором газа и жалюзийными насадками:
Продукция
снбажин
Горячая
/ — подводящий трубопровод; 2 — вилка для предварительного отбора газа; 3 — каплеуловитель (сепаратор газа); 4 — жалюзийные насадки; 5 — газопровод с регулятором давления «до себя*; 6 — предохранительный клапан; 7 — корпус сепаратора; 8 — поплавок; 9 — пе-ногасители; 10 — наклонные пол* ни; // — диффузор
ром газа (рис. 3.5). Газожидкостная смесь от скважин поступает в устройство предварительного отбора газа, которое расположено на наклонном участке подводящего трубопровода. Устройство предварительного отбора газа представляет собой отрезок подводящего трубопровода значительно большего диаметра, чем основная подводящая линия, установленный под углом 3—4° к горизонту, с приваренной вертикально газоотводной вилкой, соединенной трубопроводом с каплеуловительной секцией. Предварительно отобранный газ проходит через каплеуловитель, где в жалюзийных насадках отделяется от капельной влаги. Нефть вместе с газом, не успевшим выделиться из нефти и не попавшим в газоотводную вилку, поступает в технологическую емкость, в которой па диффузоре и наклонных полках скорость потока снижается и происходит интенсивное разга-зирование. Выделившийся в технологической емкости газ также проходит через каплеуловитель.
Разработано и применяется большое число аппаратов для разга-зирования и частичного обезвоживания нефти перед подачей ее на установку товарной подготовки нефти. Такие установки позволяют уменьшить объем воды, поступающей в сепараторы-деэмульгаторы, что приводит к снижению затрат на подогрев и обработку водонефтяной эмульсии.
Рассмотрим работу установок предварительного сброса воды на примере УПС-3000/6 (рис. 3.6). Продукция скважины поступает в отсек А через сопло 1, и на нефтеразливной полке 2 происходит выделение основного объема газа из жидкой фазы. Газ из отсека А через регулятор уровня 9 перепускается в отсек Б. С помощью регулятора давления 4 поддерживается перепад давления (до 0,2 МПа) между отсеками А и Б, благодаря которому водонефтяная эмульсия после смешения в каплеобразователе 8 с горячей водой поступает через входной распределитель 7 в отсек Б. Горячая вода поступает после установок термохимической подготовки нефти и содержит остаточный деэмульгатор. Из отсека Б газ отводится через каплеотстойник 3, нефть — через штуцер 5, вода — через перфорированный трубопровод 6.
3.4. ТЕХНОЛОГИЧЕСКИЕ СХЕМЫ УСТАНОВОК ПОДГОТОВКИ НЕФТИ
Сбор и подготовка нефти и попутного газа, начинающиеся вблизи устья скважин и заканчивающиеся на установках подготовки нефти и газа, являются единой технологической системой. К системам сбора и подготовки предъявляются следующие основные требования: высокая экономичность, полная ликвидация потерь нефти и газа в процессе сбора и подготовки, возможность ввода в эксплуатацию участков промысла до окончания строительства всего комплекса сооружений, надежность и эксплуатация, возможность автоматизации и телемеханизации всей системы в целом.
Существует^много технологических схем по подготовке нефти, которые следует рассматривать совместно с системами сбора нефти и газа. Рассмотрим две из них.
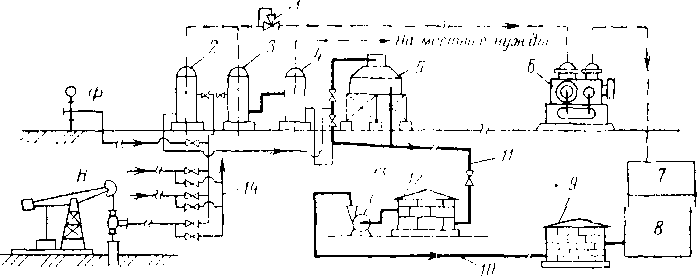
Рис. 3.7. Двухтрубная самотечная система сбора нефти, газа и воды:
/ -* регулятор давления на входе; 2 — замерный трап; 3 и 4 — трапы первой и второй ступеней соответственно; 5 — мерник; С — компрессорная; 7 — газобензиновый завод; 8 — установка подготовки нефти; 9 — сырьевой резервуар; 10 — сборный коллектор (вода и нефть); II — самотечный сборный коллектор (нефть и вода); 12 — у'/астковьсГг резервуар; 13 — центробежный насос; 14 — распределительная батарея; Ф и И — фонтанная н насосная скважины
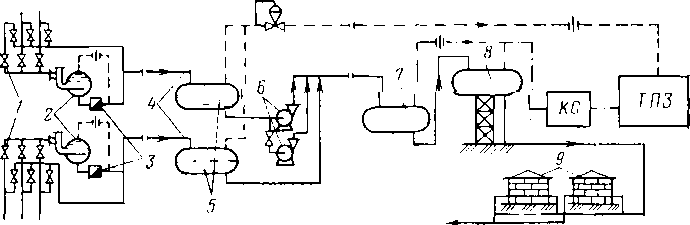
Рис. 3.8. Напорная система сбора нефти, газа и воды:
J — выкидные линии; 2 — гидроциклоиные сепараторы; 3 — расходомеры жидкости; 4 — сборные напорные коллекторы; 5, 7, 8 — сепараторы ncpnofi, второй и третьей ступеней соответственно; 6 — центробежные насосы; 9 — сырьевые резервуары; КС — компрессорная станция; ГПЗ — газоперерабатывающий завод
Г Двухтрубная самотечная система сбора (рис. 3.7) наиболее распространена на промыслах Советского Союза. Нефть из скважин поступает в трап первой ступени, где поддерживается давление 0,6 МПа, затем в трап второй ступени. Газ под собственным давлением транспортируется до компрессорной станции и далее на газобензиновый завод. Газ из второй ступени используется на собственные нужды или сжигается в факеле. Нефть с водой и оставшимся газом после трапа второй ступени через мерник поступает в резервуары участковых пунктов сбора, откуда подается насосом в сырьевые резервуары центральной установки подготовки нефти. Резервуары на участковых сборных пунктах и на центральной установке подготовки нефти не герметизированы. Распределительная батарея позволяет поочередно измерять дебит скважин в замерном трапе или мернике. В самотечной системе сбора транспорт нефти обеспечивается за счет перепада высот в начале (мерник) и конце нефтепровода. Следовательно, отсутствуют энергозатраты на транспорт нефти до участковых сборных пунктов. Однако, как и все самотечные системы трубопроводов, данную систему сбора требуется значительно реконструировать при повышении дебита скважин или при увеличении вязкости нефти. Для иредотвращення образования газовых пробок в трубопроводах необходима глубокая сепарация нефти и газа. Из-за низких скоростей движения возможно запарафинивание трубопроводов, что приводит к снижению пропускной способности системы. Потери легких фракций нефти и газа вследствие негерметичности резервуаров и мерников и невозможности доставки газа от трапов второй ступени достигают
2—3 % от общей добычи нефти. Самотечная система сбора нефти применяется ограниченно.
Напорная система сбора (рис. 3.8) действует следующим образом. Из скважины нефть под давлением поступает на автоматическую групповую замерную установку, где поочередно замеряется дебит всех скважин, а затем вся нефть подается на участковую сепарационную установку. Дебит скважины замеряется жидкостным расходомером с предварительным отделением газа в циклонном сепараторе. После прохождения расходомера нефть и газ снова смешиваются и подаются на участковую сепарационную установку, где на сепараторе первой ступени при давлении 0,4—0,5 МПа газ отделяется и подается на газоперерабатывающий завод. Нефть с пластовой водой и оставшимися растворенными газами насосами перекачивается на центральный сборный пункт, где проходит вторую ступень сепарации через кольцевые сепараторы и подается на установку комплексной подготовки или в сырьевые резервуары. Газ второй ступени сепарации компрессорной станцией направляется на газоперерабатывающий завод. Данная напорная система сбора полностью герметизирована, что исключает потери газа и легких фракций нефти. Она позволяет производить подготовку нефти на центральном пункте нескольких месторождений, расположенных на расстоянии до 100 км. Однако длительный совместный транспорт нефти и воды может привести к созданию стойких эмульсий, и при высокой обводненности нефти могут увеличиться эксплуатационные расходы на транспорт. Тем не менее это одна из перспективных систем сбора нефти.
Существует сравнительно большое число технологических схем по подготовке нефти, газа и воды. Сами установки по подготовке могут размещаться в любом пункте системы сбора, начиная от скважины и кончая головными сооружениями магистральных нефтепроводов. Целесообразность размещения установок подготовки нефти в том или ином пункте определяется в каждом конкретном случае технико-экономическим анализом возможных вариантов. Установлено, что наименьшие капитальные вложения и эксплуатационные затраты на подготовку нефти возможны при размещении установок в местах наибольшей концентрации нефти (сборные пункты, товарные парки, головные сооружения). Оптимальной технологической схемой подготовки нефти к транспорту следует считать такую, которая при наименьших затратах в отведенное технологическое время позволяет получать нефть с допустимым содержанием воды, солей и необходимой глубиной стабилизации.
В настоящее время проводят комплексную подготовку нефти в районах промыслов, поэтому на основных нефтяных месторождениях созданы комплексные установки по подготовке нефти, которые объединяют процессы обезвоживания, обессоливания и стабилизации. На рис. 3.9 изображена принципиальная технологическая схема установки комплексной теплохимической подготовки нефти. Нефть на скважины после групповых замерных установок подается по коллектору в концевую совмещенную сепарационную установку (КССУ) 2, в которую через смеситель 1 поступает горячая вода из отстойника 6, содержащая отработанный деэмульгатор. Под действием тепла пластовой воды и остатков деэмульгатора, поступающих из отстойника 6 в КССУ 2, происходит частичное разделение эмульсии на нефть, воду и газ. Отделившаяся вода подается в нефтеловушки 20, а выделившийся газ поступает на газобензиновый завод. Нефть из КССУ 2 вместе с оставшейся водой насосом 3 прогоняется через теплообменники 4 и пароподогреватели 5, затем нагретая нефть поступает в от-
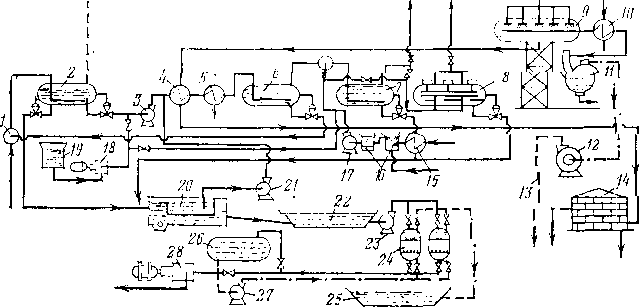
Рис. 3.9. Теплохимнческая установка по обезвоживанию, обессоливанию и ста* билизации нефти:
; — смеситель; 2 — КССУ; 3 — сырьевой насос; 4, 15 — теплообменники; 5 — пароподогреватель; 6, 7 — отстойники; 8 — электродегидратор; 9 — вакуумный сепаратор; 10 — холодильник; 11 — сепаратор; 12 — вакуумный компрессор; 13 — газовая линия на газофракв ционирующую установку; 14 — резервуар товарной нефти; 16 — емкости для обескислороживания воды; 17 — насос для подачи пресной воды; 18 — дозировочный насос для подачи деэмульгатора; 19 — емкость для деэмульгатора; 20 — нефтеловушка; 21 — насос для «ло-вушечной нефти»; 22 — пруд-отстойник для сточной воды; 23 — насос для подачи сточной воды на фильтры; 24 — фильтр; 25 — хранилища для промывания воды; 26 — емкость дли очищенной сточной воды; 27 — насос для промывки фильтров; 28 — поршневой насос дли подачи сточной воды в нагнетательные скважины
![]()
-------------^„п ц,:<
стойник 6 для окончательного отделения нефти от воды. Отделенная вода уносит с собой основное количество солей из нефти. Для более полного обессоливания нефть из отстойника 6 направляется на смешение с горячей пресной водой, которая подается насосом 17 с предварительным подогревом в теплообменнике 15 и обескислороживанием в емкости 16. После тщательного перемешивания пресной воды с нефтью, содержащей соли, эмульсия направляется в отстойник 7, где доводится до требуемой кондиции по содержанию солей. После обессоливания и отделения воды нефть при необходимости может быть направлена из отстойника 7 на дополнительное обессоливание и обезвоживание в электродегидратор 8, а если содержание воды и солей в пределах нормы, то нефть, минуя электродегидратор 8, подается прямо в вакуумный сепаратор 9. Вакуумные компрессоры 12 забирают из сепаратора 9 газ, из которого при прохождении холодильника
10 и гидроциклонного сепаратора 11 выделяется основное количество легких углеводородов. Конденсат из сепаратора 11 отправляется на газобензиновый завод, а газ поступает на специальные установки для полной деэтанизации. Перед теплообменником 4 в нефть вводится деэмульгатор, воздействующий на поверхностные свойства пограничных слоев двух фаз эмульсии. Деэмульгатор также вводится вместе с подачей пресной воды перед отстойником 7. Данной системой предусмотрена очистка сточных вод с последующей подачей их на нагнетательные скважины для закачки в пласт.
К механическим примесям относятся частицы породы, выносимые газовым потоком из скважины, строительный шлам, оставшийся после окончания строительства промысловых газосборных сетей и магистральных трубопроводов, продукты коррозии и эрозии внутренних поверхностей и жидкие включения конденсата и воды.
По принципу работы аппараты для очистки газа от механических примесей подразделяются на следующие:®
работающие по принципу «сухого» отделения пыли; в таких аппаратах отделение пыли происходит в основном с использованием сил гравитации и инерции; к ним относятся циклонные пылеуловители, гравитационные сепараторы, различные фильтры (керамические, тканевые, металлокерамические и др.);
работающие по принципу «мокрого» улавливания пыли; в этом случае удаляемая из газа взвесь смачивается промывочной жидкостью, которая отделяется от газового потока, выводится из аппарата для регенерации и очистки и затем возвращается в аппарат; к ним относятся вертикальные и горизонтальные масляные пылеуловители и др.;
использующие принцип электроосаждения; данные аппараты почти не применяют для очистки природного газа.
Наиболее широко используют аппараты «мокрого» и «сухого» пылеулавливания. Очистка газа по пути следования его от месторождения до потребителя производится в несколько ступеней. Для ограничения выноса из месторождения породы призабойную зону оборудуют фильтром.
Вторую ступень очистки газ проходит на промысле в наземных сепараторах, в которых сепарируется жидкость (вода и конденсат) и газ очищается от частиц породы и пыли. Промысловые очистные аппараты работают по принципу выпадения взвеси под действием силы тяжести при уменьшении скорости потока газа или по принципу использования действия центробежных сил при специальной закрутке потока. Поэтому промысловые аппараты очистки делятся на гравитационные и циклонные. Гравитационные аппараты бывают вертикальные и горизонтальные. Вертикальные гравитационные аппараты рекомендуют для сепарации газов, содержащих твердые частицы и тяжелые смолистые фракции, так как они имеют лучшие условия очистки и дренажа. На рис. 3.10 изображен гравитационный односекционный сепаратор. Он имеет тангенциальный подвод газа (скорость газа в нем достигает 15—20 м/с), что способствует выпадению в сепараторе твердой взвеси и капельной влаги. В основном он работает по принципу выпадения взвеси при малых скоростях восходящего потока газа. При выборе пулеуловителя оценивают допустимую скорость в свободном сечении по формуле
w = V4gd (рч — pr)/(3prfe),
где d — диаметр сепаратора, м; р„ и р, — плотность соответственно частицы и газа, кг/м3; k — коэффициент сопротивления среды.
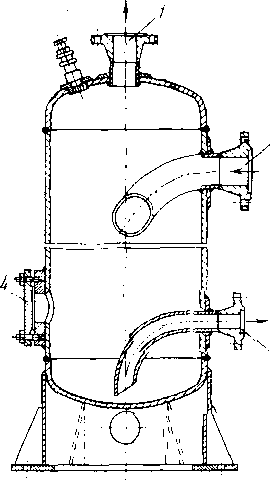
Рис. 3.10. Гравитационный односек- Рис. 3.11. Схема движе-
циоиный сепаратор при рабочем да- ния газов в циклоне:
влении: / — пыход газа; 2 — пход
] — выходной патрубок для газа; 2 — газа; 3 удаление продук-
входноп патрубок; 3 — люк; 4 — патрубок тов очистки
для продувки сепаратора
При малых Re обычно принимают /е = 24/Re. Для горизонтальных сепараторов с жалюзийными насадками рекомендуется использовать газ со значительным количеством влаги.
Вертикальные сепараторы изготовляют диаметром 400—1650 мм, горизонтальные—диаметром 400—1500 мм при максимальном давлении 16 МПа. При оптимальной скорости газа w0 эффективность сепарации достигает 70—80 %. Опыт эксплуатации показал, что wa не должна превышать 0,1 м/с при давлении 6 МПа. При пересчете скоростей пользуются зависимостью w1^w2^P1/P2. Из-за большой металлоемкости и недостаточной их эффективности гравитационные сепараторы применяют редко.
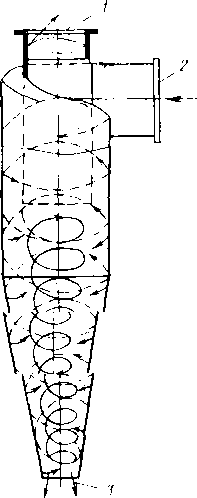
На рис. 3.11 схематически изображена работа циклонного сепаратора. Корпус циклона и патрубок для выхода газа образуют внутреннее кольцевое пространство. В нижней части имеется отверстие для отвода осадка из циклона.
При тангенциальном вводе газ в сепараторе приобретает в кольцевом пространстве и конусе вращательное движение, вследствие чего из газа выпадают механические взвеси (твердые и жидкие) и опу-
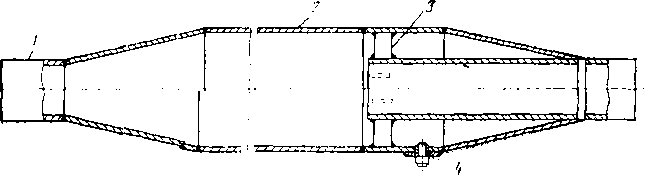
Рис. 3.12. Конденсатосборник типа «расширительная камера»:
J — газопровод; 2 — расширительная камера; 3 — ребра жесткости; 4 — конД(;нсатоотвод-ная трубка
скаются в сборный бункер. Газ с уменьшенной скоростью выходит через выходной патрубок.
Третья ступень очистки газа производится на линейной части газопровода и компрессорных станциях. На линейной части устанавливают конденсатосборники, так как в результате несовершенной сепарации на промысле газ может иметь жидкую фазу.
Наибольшее распространение получил конденсатосборник типа «расширительная камера» (рис. 3.12). Принцип работы основан на выпадении из потока газа капелек жидкости под действием силы тяжести из-за местного снижения скорости газа при увеличении диаметра трубопровода. Длина траектории осаждения капелек жидкости, оценивается по формуле
/: w\z--1»------1.
L D\gt (1 — Рг/Рж) J
где
Т = d2 (Рж—Рг)/(18|х),
w — скорость газа на входе в конденсатосборник; D — диаметр газопровода; Du — диаметр расширительной камеры; рж — плотность жидкости; ц — вязкость газа.
При эксплуатации газопроводов с системой «расширительных камер» бывают затруднения, связанные с пропуском устройств для очистки внутренней полости трубопровода. Для этого необходимо предусматривать специальные направляющие для беспрепятственного прохождения через них очистного устройства. Для очистки газа от механических примесей на отечественных газопроводах применяют установки с масляными пылеуловителями (рис. 3.13). Природный газ Г, пройдя пылеуловители 1, направляется в компрессорный цех. Пылеуловители заполнены маслом. По мере загрязнения масло М3 передавливается из пылеуловителей 1 в отстойники 7. Свежее масло МС поступает в пылеуловители самотеком из масляного аккумулятора 2. Предварительно в аккумуляторе и пылеуловителях выравнивают давление. В масляный аккумулятор масло подается насосом 3 из мерного бака 5 или из бака свежего масла 4. При этом аккумуля*
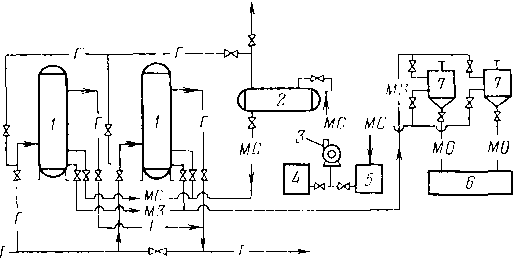
Рис. 3.13. Схема установки пылеуловителей
тор отключают от пылеуловителей и находящийся в нем газ выпускают в атмосферу. В мерный бак масло поступает самотеком из отстойников 7. Отбросное масло МО вместе со шламом, накапливающимся в нижней части отстойников, спускают в сборную емкость 6.
Вертикальный масляный пылеуловитель (рие. 3.14) представляет собой вертикальный стальной цилиндр со сферическим днищем, рассчитанным на рабочее давление в газопроводе. Диаметр пылеуловителя 1080—2400 мм. Внутри пылеуловителя находятся устройства, обеспечивающие контактирование масла с газом и отделение частиц масла от газа при выходе его из аппарата. Газ поступает в пылеуловитель через входной патрубок 7. Благодаря отбойному козырьку 8 газ меняет свое направление и движется к поверхности масла, находящегося в нижней части аппарата. Крупные посторонние частицы при этом сразу же выпадают и оседают на дно. Уровень масла устанавливается на расстоянии 25—30 мм от концов вертикальных трубок 3. При этом газ устремляется вверх, захватывая е собой частицы масла. В трубках 3, а далее в средней свободной части пылеуловителя газ интенсивно перемешивается е маслом, которое поглощает содержащиеся в газе частицы, а также поступающий вместе с газом конденсат тяжелых углеводородов. При этом уровень масла повышается. По выходе газа из вертикальных трубок скорость его резко уменьшается. Более крупные частицы жидкости при этом выпадают и по дренажной трубке 4 стекают вниз. Из свободной средней части пылеуловителя газ и масляный туман поступают в верхнюю его часть, а оттуда в жа-люзийное сепарационное устройство 1, в которое отбирается мелкозернистая взвесь. Очищенный газ выходит через патрубок 2. Загрязненное масло удаляется из поддона через дренажную трубку 5. Полная очистка пылеуловителя производится 3—4 раза в год через люк 6. Количество заливаемого масла в пылеуловитель диаметром 2400 мм не превышает 1,5—2 м3.
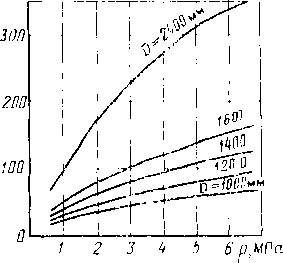
Пропускная способность масляного пылеуловителя (м3/сут) может быть рассчитана по формуле
Рис. 3.15. Зависимость пропускной способности Q масляного пылеуловителя от давления р и диаметра D:
а — для одного пылеуловителя; б — дли нескольких пылеуловителей п
а
Q тыс. м з)ц
QtMb/C.
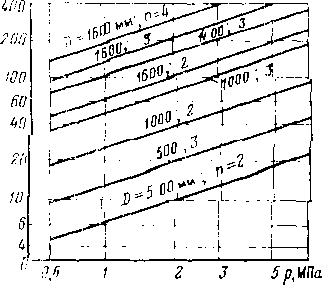
Рис. 3.16. Циклонный пылеуловитель пропускной способностью 20 млн. м^/сут и рабочим давлением 7,5 МПа:
1 — выходной патрубок для газа; 2 — входной патрубок;

3 — циклоны; 4 — люк; 5 — штуцеры контролирующих приборов; 6 — дренажный штуцер
где D — внутренний диаметр пылеуловителя, м; р—давление газа, МПа; рж и рг — плотность смачивающей жидкости и газа при рабочих условиях, кг/м:!; Т - -температура газа, К.
Для выбора пылеуловителей можно использовать графические зависимости, представленные на рис. 3.15.
Чтобы обеспечить нормальную работу пылеуловителей, необходимо поддерживать постоянный уровень масла. Пропускная способность вертикальных масляных пылеуловителей при заданном давлении ограничивается скоростью потока газа в контактных трубках, которая не должна превосходить 1—3 м/с.
Преимущество вертикального масляного пылеуловителя по сравнению с другими конструкциями пылеуловителей заключается в высокой степени очистки (общий коэффициент очистки достигает 97—98 %); недостатки —большая металлоемкость, наличие жидкости и ее унос (допускается не более 25 г на 1000 ма газа), большое гидравлическое сопротивление (0,035—0,05 МПа), чувствительность к изменениям уровня жидкости и др.
Циклонный пылеуловитель (рис. 3.16) представляет собой сосуд цилиндрической формы с встроенными в него циклонами. Газ поступает через боковой верхний входной патрубок в распределитель, к которому приварены своими входными патрубками звездообразно расположенные циклоны, которые закреплены неподвижно на нижней решетке. Отсепарированная жидкость и твердые частицы по дренажному конусу циклона попадают в грязевик. Для автоматического удаления собранного шлама имеется дренажный штуцер. Качество очистки повышается с уменьшением диаметра циклона. Поэтому созданы батарейные циклоны, объединяющие в общем корпусе группу циклонов малого диаметра. Закручивание потока осуществляется в циклонах типа «розетка» или «улитка» (рис. 3.17).
При работе по системе «газ — твердая взвесь» пропускная способность батарейных циклонов обычно рассчитывается, исходя из допустимых скоростей газа, обеспечивающих достаточно полное удаление твердой взвеси из газового потока. При большом расходе газа наблюдаются чрезмерный эрозионный взнос и повышенный перепад
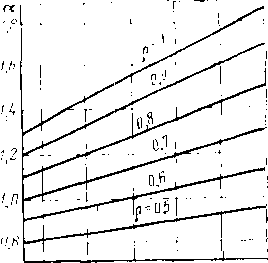
I_I_!-1-1-L-
263 273 293 313 333 3S3 Г, К
OB «розетка» Рис. 3.18. График для определения поправочного коэффициента газа: з — уст в зависимости от температуры и
плотности газа
вность очистки газа батарейными циклонами 85—98 % и уменьшается с увеличением его
широко применяются циклонные пылеулови-на рабочее давление до 7,36 МПа. Пропускная > пылеуловителя Q при заданной степени min ДО Qmax (р = 0,65 кг/м3, Т = 283 к. ;обности при иных рабочих параметрах ве-ного коэффициента а, зависящего от темпера-а (рис. 3.18).
max
3.6. ГИДРАТЫ ПРИРОДНЫХ ГАЗОВ И МЕТОДЫ БОРЬБЫ С НИМИ
Природные газы в определенных термодинамических условиях вступают в соединение с водой и образуют гидраты, которые, скапливаясь в промысловых и магистральных газопроводах, существенно увеличивают их гидравлическое сопротивление и, следовательно, снижают пропускную способность. Особое значение вопрос борьбы с образованием гидратов приобретает при разработке месторождений Западной Сибири и Крайнего Севера. Низкие пластовые температуры и суровые климатические условия этих районов создают благоприятные условия для образования гидратов в скважинах и газопроводах.
Гидраты представляют собой соединения молекулярного типа, возникающие за счет Ван-дер-Ваальсовых сил притяжения. Молекулы воды при образовании гидратов как бы раздвигаются молекулами газа. Образующиеся при этом полости между молекулами воды полностью или частично заполняются молекулами газа. Гидраты природных газов представляют собой неустойчивые соединения, которые при повышении температуры или понижении давления разлагаются
Z?J 253 273 293 313
333 353 373 393 М3 4.TJ Т К
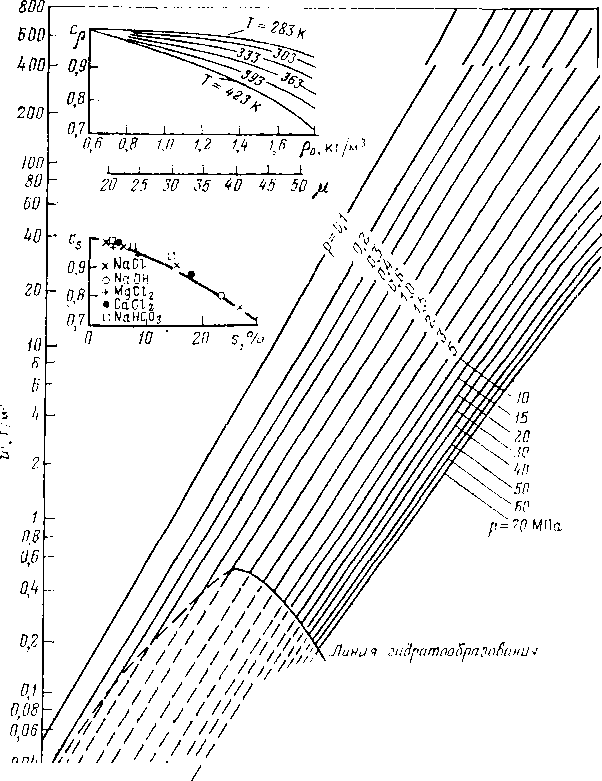
002
/ // ////// // / /////
/' //////
/ l V / t/f_L
001
l
Рис. 3.19. Номограмма влажности природных газов
на газ и воду. По внешнему виду — это белая кристаллическая масса, похожая на лед или снег.
Природные газы часто содержат углекислоту, сероводород, азот и редкие газы. Наличие кислых газов резко усиливает процесс гидратообразования.
Процесс гидратообразования обычно происходит на границе газ — вода при условии полного насыщения природного газа влагой. Для прогнозирования места образования и интенсивности накопления гидратов в системах газоснабжения необходимо знать изменение влажности газа в различных термодинамических условиях.
В практике часто пользуются абсолютной влажностью w, выраженной массой паров воды в единице объема газа, приведенной к нормальным условиям (273 К (О °С) и 0,1013МПа). Относительная влажность — это выраженное в процентах или долях единицы отношение количества водяных паров, содержащихся в газовой смеси, к количеству водяных паров в том же объеме и при тех же температуре и давлении при полном насыщении. На практике влажность газов чаще всего определяют по номограмме (рис. 3.19), которая получена в результате обработок большого числа измерений влажности природного газа относительной плотности по воздуху А = 0,6 прямыми методами. На номограмме нанесена равновесная кривая гидратообразования, ограничивающая определенную область, в которой влажность газов должна определяться из условия равновесия паров воды над гидратами. Из номограммы видно, что влажность природного газа растет с повышением температуры и снижается с увеличением давления. Влажность природных газов уменьшается также с увеличением их молекулярной массы р, и солености воды s. На рис. 3.19 приведены два вспомогательных графика для определения поправочных коэффициентов на молекулярную массу (плотность р0) газа ср и соленость воды cs. При определении влажности газа, проходящего по газопроводам, в которых газ находится в контакте с пресной водой, можно считать cs — 1. Температура, при которой газ становится насыщенным при данных давлении и влажности, называется точкой росы газа.
Рис. 3.20. График изменения влажности газа по длине газопровода
Изменение влажности природного газа при его движении по газопроводу зависит от характера изменения давления и температуры и начальной влажности газа (рис. 3.20). Влажность газа в состоянии полного его насыщения w„ac меняется по длине газопровода I по кривой abed. На начальном участке газопровода температура газа Т быстро падает (при значительной разности температур газа и окружающего грунта), а давление р снижается весьма медленно (скорость движения газа сравнительно невелика). Поэтому влажность газа в состоянии полного его насыщения снижается. На конечном участке картина обратная. Температура газа приближается к температуре окружающего грунта и изменяется по длине газопровода весьма незначительно, а давление резко падает (вследствие расширения газа скорость его движения в трубопроводе возрастает). В связи с этим влажность газа, соответствующая состоянию насыщения при температуре и дав-80
268 273 Z7S 283 288 298 Г, К
Рис. 3.21. Кривые гидратообразования для природных газов различной плотности Д
DBS -
283 ГК,
' р.чс. 3.32. Графики „упругости пчрюв воды в равновесии с водой (1) и гидратами (2)
лении газа в газопроводе, увеличивается ио длине последнего. При поступлении в газопровод газа с начальной влажностью wt = wx нас на начальном участке будет происходить конденсация паров воды, а влажность газа будет изменяться по кривой ас. Количество воды, которая сконденсируется на этом участке газопровода, AW = = (и»! „ас — ^min) Q, где w± пас — влажность газа в состоянии насыщения при начальном давлении и температуре газа в газопроводе; K'min — минимальная влажность газа в состоянии насыщения при движении его по газопроводу в точке с\ Q —пропускная способность газопровода.
На конечном участке газопровода (после точки с) влажность газа остается неизменной и равной wmin (линия се). При этом относительная влажность газа (степень насыщенности его водяными парами) будет постепенно снижаться. При поступлении в газопровод газа влажностью tt>min < wk < ш1Нас на начальном участке она остается постоянной, хотя степень насыщенности газа водяными парами будет возрастать и, наконец, достигнет максимума (точка Ь). После этого в газопроводе начнется конденсация влаги (линия Ьс). На конечном участке влагосодержание будет оставаться неизменным (линия се). Количество воды, которая сконденсируется в этом случае в газопроводе на участке Ьс, AW = (wh — aymin) Q-
Наконец, при поступлении в газопровод газа влажностью wf <.wmin конденсации влаги не происходит (линия fg).
Таким образом, во избежание конденсации водяных паров в газопроводе влажность подаваемого в него газа не должна превышать wmin.
Это условие является основным при проектировании установок осушки газа перед подачей его в газопровод.
Условия образования гидратов газа могут быть представлены равновесными кривыми гидратообразования в координатах температура Т—давление р (рис. 3.21). Графики гидратообразования получены из условия равновесия пар—жидкость. Упругость паров воды над гидратом при данной температуре ниже упругости насыщенного пара над водой. Эксперименты показывают, что условия образования и разложения гидратов неидентичны. Давление начала разложения гидратов значительно ниже давления начала образования гидратов при одной и той же температуре. Такое снижение равновесного давления разложения по отношению к давлению образования гидратов происходит в результате уменьшения упругости паров воды над образующимися гидратами. Для определения условий образования и разложения гидратов пользуются графиками, характеризующими упругость паров воды в равновесии с водой /?01 и гидратами р± (рис. 3.22). Так, при температуре 7\ гидраты могут образоваться только при влажности газа, соответствующей упругости паров воды р01, т. е. при р >poi- При образовании гидрата часть паров воды, соответствующая снижению упругости паров с р01 до ри переходит в гидрат. Таким образом, при образовании гидрата влагосодержание газа после гидратной пробки уменьшается в соответствии со снижением упругости паров воды до рх.
Рис. 3.23. Зона образования гидратов в магистральном газопроводе
В газопроводе очень важно определить место образования гидратов. Для этого необходимо знать (так же как и для определения самой возможности образования гидратов) состав и начальную влажность газа, а также изменение его давления и температуры в газопроводе. Пусть давление р в газопроводе (рис. 3.23) меняется по кривой АВ, а температура Т — по кривой CD. На основании равновесных кривых гидратообразования (см. рис. 3.21) и линии падения давления АВ строим кривую MN равновесной температуры гидратообразования ТГИдр для данного газопровода. Точки тип пересечения кривых, показывающих изменение в газопроводе температуры и равновесной температуры гидратообразования газа, определяют участок возможного образования гидратов при условии полного насыщения газа водяными парами (участок тп). Однако зона выпадения гидратов в газопроводе фактически будет зависеть от начальной влажности газа, подаваемого в газопровод, т. е. в конечном счете от точки росы газа. Если последняя оказывается выше температуры газа в точке, соответствующей, например, точке к, то гидратообразование начнется в точке т. Как отмечалось ранее, па конечном участке газ недонасы-щен парами воды, поскольку при практически неизменной температуре давление в газопроводе быстро падает и, следовательно, гидра-тообразование на этом участке невозможно (начало этого участка па рис. 3.23 отмечено точкой /). Таким образом, зона гидратообразования данного газопровода определяется участком mf. Однако гидраты могут образовываться не на всем протяжении участка inf. Это объясняется тем, что в результате образования гидратов в точке т упругость паров воды уменьшается, что соответствует снижению точки росы газа от т до tnl. В дальнейшем по мере снижения температуры газ все больше насыщается парами воды, и в точке г он будет снова полностью насыщен, что приведет к образованию второй гидратной пробки. После этого точка росы газа снижается до гг и оказывается ниже минимальной температуры газа в газопроводе, что исключает образование третьей гидратной пробки.
jTaKHM образом, в газопроводе в зависимости от характера изменения температуры н давления газа и его начальной влажности (точки росы) могут образоваться несколько локальных гидратных пробок.
Методы предупреждения образования гидратов
Предупреждение образования гидратов подогревом газа заключается в том, что при сохранении давления в газопроводе температура газа поддерживается выше равновесной температуры образования гидратов. В условиях транспорта газа по магистральному газопроводу этот метод неприменим, так как связан с большими затратами энергии. Как показывают расчеты, при больших объемах транспортируемого газа целесообразнее охлаждать его (с учетом увеличения затрат на более глубокую осушку газа), поскольку это позволяет заметно увеличить пропускную способность газопроводов, особенно газопроводов с большим числом компрессорных станций (КС). Метод подогрева применяется на газораспределительных станциях (ГРС), где при больших перепадах давления вследствие дроссельного эффекта температура газа может значительно снижаться, в результате чего обмерзают редуцирующие клапаны, краны, диафрагмы и др.
Предупреждение образования гидратов снижением давления заключается в том, что при сохранении температуры в газопроводе снижается давление ниже равновесного давления образования гидратов. Этот метод применяют и при ликвидации уже образовавшихся гидратов. Ликвидация гидратных пробок осуществляется путем выпуска газа в атмосферу через продувочные свечи. После снижения давления необходимо некоторое время (от нескольких минут до нескольких часов) для разложения гидратов. Очевидно, что этот метод пригоден только для ликвидации гидратных пробок при положительных температурах. Иначе гидратная пробка перейдет в ледяную. Поскольку минимальная температура газа в магистральных газопроводах близка к нулю, а равновесное давление при этом для природного газа находится в пределах 1 —1,5 МПа, применение данного метода для предупреждения гидратообразования в магистральных газопроводах оказывается неэффективным (оптимальное давление транспортируемого газа 5—7 МПа). Метод снижения давления применяется в аварийных
CK
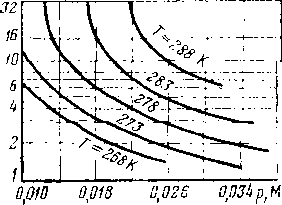
Рис. 3.24. Зависимость коэффициента а от давления и температуры в точке образования гидратов
случаях для^разложения гидратов в газопроводе в сочетании с ингибиторами, так как в противном случае после повышения давления гидраты появляются вновь.
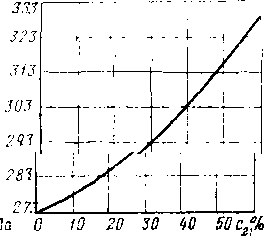
Рис. 3.25. График снижения температуры гидратообразования при вводе в газовый поток метанола
Ингибиторы, введенные в насыщенный водяными парами поток природного газа, частично поглощают водяные пары и переводят их вместе со свободной водой в раствор, который совсем не образует гидратов или образует их, но при более низких температурах. В качестве ингибиторов применяют метиловый спирт (метанол), растворы этиленгликоля (ЭГ), диэтиленгликоля (ДЭГ), триэтиленгликоля (ТЭГ), хлористого кальция, этилкарбитола (ЭК) и др. Удельный расход ингибитора для предупреждения процесса гидратообразования
qH = К -
?». _|_
io-»ctf2,
Су — С'2
где wx и w2 — влажность газа в точке соответственно ввода и вывода ингибитора; сх, с.2 — массовая концентрация соответственно вводимого и выводимого ингибитора; а — коэффициент, определяющий отношение массового содержания ингибитора в газовой фазе к массовой концентрации ингибитора в водном растворе, контактирующем с газом (рис. 3.24). Величина с2 определяется по графику на рис. 3.25 в зависимости от требуемого снижения температуры гидратообразования АТ = Тр—7Y, где 7’р — равновесная температура гидратообразования газа; Тг — температура газа в газопроводе. Для уменьшения расхода метанола его необходимо вводить в начале зоны возможного гидратообразования в газопроводе. Экономически метанол выгодно применять при небольших расходах газа, когда из-за высоких капиталовложений нерационально использовать другие методы. Этот способ целесообразно применять также там, где гидраты образуются редко и в небольших количествах. Метанол можно вводить в сочетании с другими средствами, например с осушкой газа (при нарушении технологии осушки) или с понижением давления (с целью разложения уже образовавшихся в газопроводе отложений гидратов). Использование метанола для предупреждения образования гидратов в газопроводе при больших объемах транспортируемого газа экономически невыгодно. Ввод ингибиторов в газовый поток широко применяют на промыслах для предупреждения образования гидратов в сепараторах, теплообменниках и других дегидраторных аппаратах, а также в скважинах. При этом предпочтение следует отдать диэтиленгли-колю, так как возможность его регенерации и сравнительно небольшие потери и в большинстве случаев делают этот ингибитор наиболее экономичным.
При больших объемах транспортируемого газа его осушка является наиболее эффективным и экономичным способом предупреждения образования кристаллогидратов в магистральном газопроводе. При промысловой подготовке газа к дальнему транспорту его осушают сорбционным способом или охлаждением газового потока. В результате осушки газа точка росы паров воды должна быть снижена ниже минимальной температуры при транспортировке газа (влажность должна составлять не более 0,05—0,1 г/м3).
3.7. СОРБЦИОННЫЕ СПОСОБЫ ОСУШКИ ГАЗА
Осушка газа абсорбентами
Жидкие сорбенты — абсорбенты, применяемые для осушки природных и нефтяных газов, должны иметь высокую растворимость в воде, низкую агрессивность, стабильность по отношению к газовым компонентам, простоту регенерации, малую вязкость, низкую упругость паров при температуре контакта, слабое поглощение углеводородных компонентов газа, пониженную способность к образованию пены или эмульсий. Большинству этих требований наилучшим образом отвечают диэтиленгликоль (ДЭГ) и триэтиленгликоль (ТЭГ) и в меньшей степени этиленгликоль (ЭГ).
Диэтиленгликоль получают реакцией соединения двух молекул ЭГ с образованием молекулы воды. В химически чистом виде это бесцветная жидкость с молекулярной массой 106,12, относительной плотностью (по воде) 1,117 н температурой кипения при р = 0,1013 МПа, равной 518 К.
Как показали эксперименты в лабораторных и промышленных условиях, максимальное понижение точки росы газа при осушке ДЭГ обычно не превышает 308 К, что довольно часто оказывается недостаточным. В связи с разработкой газовых месторождений с высокой пластовой температурой газа потребовался более сильный влагопо-глотитель — ТЭГ. Его получают соединением трех молекул ЭГ с образованием воды. Молекулярная масса ТЭГ — 150,17, относительная плотность (по воде) 1,1254 и температура кипения 560,4 К при р — = 0,1013 МПа.
Гликоли хорошо отбирают влагу из газов в большом интервале концентраций. Вследствие низкой упругости паров потери поглотителя незначительные (5—18 г на 1000 м3 газа у ДЭГ и 2—4 г на 1000 м3/газа у ТЭГ). Температура кипения и упругость паров воды и гликолей сильно различаются, что облегчает регенерацию поглотителя, а небольшая вязкость поглотителя облегчает работу циркуляционных насосов. Обводненные гликоли неагрессивны в коррозионном отношении. Растворимость природного газа в них незначительная: при давлениях до 15 МПа она не превышает 6 л на 1 л гликоля. При атмосферном давлении ДЭГ начинает распадаться при 437 К, а ТЭГ при 478 К- В соответствии с этим в производственных условиях степень их регенерации может достигать 96—99 %. ТЭГ имеет склонность к ценообразованию, для борьбы с этим применяют различные присадки, например моноэтаноламин.
Интенсивность процесса осушки газа гликолями находится в прямой зависимости от давления, температуры контакта газ — сорбент и концентрации сорбента.
Как было показано ранее, в газе при повышенном давлении уменьшается содержание влаги, что, естественно, приводит к снижению количества циркулирующего раствора сорбента, необходимого для осушки газа до заданной точки росы. Повышение температуры контакта газ —¦ сорбент приводит к увеличению парциального давления водяных паров над сорбентом, снижению поглотительной способности последнего и повышению точки росы осушки газа. Понижение температуры контакта газ — сорбент оказывает обратное действие, т. е. снижает точку росы осушенного газа. Однако при осушке газа жидкими сорбентами не рекомендуется применять температуру ниже 303 К в связи с повышением вязкости сорбентов и значительной трудностью их перекачки. При увеличении вязкости сорбента одновременно несколько снижается его поглотительная способность.
На поглотительную способность сорбента паров воды из газа большое влияние оказывает его концентрация: чем концентрация выше, тем ниже точка росы осушенного газа. Концентрация сорбента обычно колеблется в зависимости от требуемой степени осушки в пределах 90—99 %. Зависимость точки росы газа Тр.г от концентрации раствора сорбента сс и температуры контакта Т графически изображена на рис. 3.26.
При сравнении ДЭГ и ТЭГ необходимо иметь в виду, что ДЭГ более дешевый. Однако при использовании ТЭГ можно получить большее снижение точки росы газа. Потери ТЭГ при регенерации значительно меньше, чем потери ДЭГ, вследствие более низкой упругости паров ТЭГ.
На рис. 3.27 изображена схема установки осушки газа жидкими сорбентами, получившая широкое распространение на газовых месторождениях. Поступающий с промысла газ проходит сепаратор /, где осаждается капельная влага, и поступает в нижнюю часть абсорбера 2. Сначала газ идет в нижнюю скрубберную секцию 3, в которой дополнительно очищается от взвешенных капель влаги благодаря большой поверхности контакта с насадками. Затем газ последовательно проходит через тарелки 4, поднимаясь вверх. Число колпачковых тарелок в абсорбере 4—12. Навстречу потоку газа протекает 95—97 %-ный раствор ДЭГ, вводимый в абсорбер насосом 10. Осушенный вследствие контакта с раствором газ проходит через верхнюю скрубберную секцию 5, где освобождается от захваченных капель раствора и направляется в газопровод. Насыщенный раствор, содержащий 6—8 % влаги, с нижней глухой сборной тарелки абсорбера поступает в теплообменник 7, в котором нагревается встречным потоком регенерированного раствора, а далее проходит через выветриватель 8, где из него выделяется растворенный газ, который идет на собственные нужды. Из выветривателя насыщенный ДЭГ насосом 9 закачивается в выпарную колонну (десорбер) 12, где осуществляется регенерация раствора. Выпарная колонна состоит из двух частей: собственно колонны тарельчатого типа, в которой из насыщенного раствора ДЭГ, стекающего вниз, выпаривается влага встречным потоком острого водяного пара и паров ДЭГ; кипятильника-испарителя 11, в котором происходит нагревание раствора гликоля и испарение воды. В кипятильнике поддерживается температура раствора гликоля в предела.. 423—433 К, а в верхней части выпарной колонны 378—380 К- Это достигается за счет орошения верхней части колонны водой с температурой 303 К, что позволяет сконденсировать пары ДЭГ и уменьшить его потери. Водяной пар из десорбера поступает в конденсатор 16, где основная часть пара конденсируется и собирается в сепараторе 15. Отсюда газ отсасывается из конденсата вакуумным насосом 14 и направляется на сжигание. Часть полученной воды, содержащей ДЭГ, подается в верхнюю часть колонны насосом 13 для орошения и поддержания температуры 105—107 °С. Регенерированный раствор ДЭГ насосом 10 прокачивается через теплообменник 7 и холодильник 6, где его температура снижается, и вновь поступает на верхнюю тарелку абсорбера. Если необходимо получить высокую концентрацию насыщенного раствора ДЭГ (98—99 %) для достижения более низких точек росы газа, то регенерацию гликолей производят под вакуумом, который создается вакуумным насосом 14.
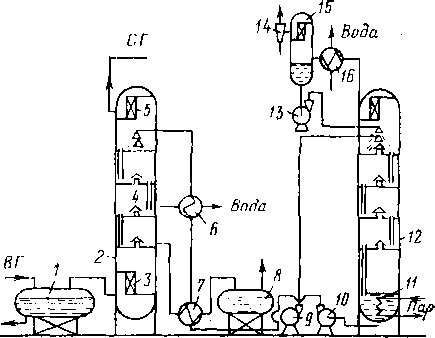
Рис. 3.27. Схема установки осушки газа жидкими сорбентами
ГР.Г
333
322
Сг:=0%
300
277
273
255
233
|
______Г е | А |
|||
| 811. | ||||
| N | сс ^ | 99 *!>< | ||
253
313
Рис. 3.26. Зависимость точки росы осушаемого газа от температуры контакта и концентрации водного раствора ДЭГ
Экономичность работы абсорбционных установок в значительной степени зависит от потерь сорбента. Для их снижения в первую очередь необходимо строго поддерживать расчетный температурный режим десорбера, тщательно сепарировать газ и водяной пар на выходе соответственно из абсорбера и десорбера и по возможности исключить пенообразование при контакте газа с абсорбентом за счет специальных добавок.
Количество концентрированного раствора абсорбента, подаваемого в поглотительную колонну, определяется из материального баланса по воде по формулам:
Wi = G(\—кг), Wi = (G + bW)(l — к2), (3.2)
где — массовый расход воды в концентрированном растворе абсорбента; G — массовый расход концентрированного раствора абсорбента; kx — количество гликоля в концентрированном растворе; W2 — массовый расход воды в насыщенном растворе абсорбента; G + AW — массовый расход насыщенного раствора абсорбента; k2 — количество гликоля в насыщенном растворе; AW — массовое количество влаги, отбираемой из газа,
bW=Wi — W1 = Q(w1—wJ\ (3.3)
Q — объемный расход газа через абсорбер, приведенный к 273 К и 0,1013 МПа; и w2 — влажность газа соответственно на входе и выходе абсорбера.
Решая совместно уравнения (3.2) и (3.3), находим
G=Q(w1—w2) k2l{k!—&2).
Теоретическое число тарелок в абсорбере обычно определяется графическим методом путем построения ступенчатой линии между оперативной (рабочей) линией и кривой равновесия.
Для построения оперативной линии воспользуемся уравнением материального баланса всего абсорбера:
V(y1—yi) = L(x2—x1), (3.4)
где V — число молей сухого газа, выходящего из абсорбера; уг и у2 — число молей воды на 1 моль сухого газа соответственно на входе в абсорбер и на выходе из него; L — число молей чистого сорбента, подаваемого в абсорбер; xt и х2 — число молей воды на 1 моль чистого сорбента соответственно на входе в абсорбер и выходе из него.
Из (3.4) следует
= (У\ — УЖХ* — *i)-
Это уравнение оперативной линии абсорбера; оно показывает, что наклон линии в координатах х—у определяется отношением количе-88 ства чистого абсорбента к количеству подаваемого сухого газа L/V. Таким образом, для построения оперативной линии (рис. 3.28) достаточно двух крайних точек с координатами: верхняя точка — выход насыщенного раствора абсорбента и вход влажного газа (х2, уг) и нижняя точка — выход сухого газа и концентрированного раствора абсорбента (*bу2).
В то же время в абсорбере система газ—раствор абсорбента проходит через несколько равновесных состояний, число которых и будет определять необходимое теоретическое число тарелок абсорбера.
Рис.ЩЗ.28. График^ определения теоретического числа тарелок в абсорбере:
1 — оперативная прямая; 2 — кривая равновесия
В соответствии с законом Дальтона парциальное давление любого компонента в газовой фазе равно произведению его молярной концентрации на общее давление
Рв^У'Р, (3.5)
где рй — парциальное давление водяных паров в газовой фазе; у' — молярная концентрация водяных паров в газовой фазе; р — общее давление над жидкостью.
Для жидкой фазы в первом приближении можно применить закон Рауля: рв = х'ру. в, где х' — молярная концентрация водяных паров в жидкой фазе (в долях единицы); руь — упругость паров воды в чистом виде при данной температуре.
При равновесном состоянии двухфазной системы у'р = х'ру, в. Для практических расчетов вводят понятие константы равновесия, представляющей собой отношение упругости паров ру. в к общему давлению р, т. е. k = ру. Jp. Константа равновесия k определяется в зависимости от температуры и давления по таблицам или графикам, составленным на основе экспериментальных данных. Тогда уравнение равновесия системы примет вид
y' = kx'. (3.6)
Это уравнение позволяет по концентрации компонента в одной фазе равновесной системы определять его концентрацию в другой фазе. Чтобы получить уравнение кривой равновесия в координатах х—у, переведем молярные концентрации х' и у' в долях единицы в концентрации х и у, выраженные в молях воды на 1 моль абсорбента и сухого газа соответственно: х = mjm^c, х = + тгвс), где
та — число молей воды; табс — число молей абсорбента.
Отсюда
х = х'1{\~х'У, х'=х/( 1+*).
Из (3.6), (3.7) и (3.8) получаем уравнение кривой равновесия
y = kx'l{\—kx') = kx/[[ +л:(1—?)].
Для определения числа теоретических тарелок между оперативной линией и равновесной кривой (см. рис. 3.28) строят ступенчатую линию, изображающую переход смеси водяных паров, газа и абсорбента из состояния, характеризуемого начальными координатами (x2i */i)> к состоянию с координатами (хг, г/2)- Число теоретических тарелок птеор равно числу горизонтальных участков линии перехода (у ¦¦= idem). На рис. 3.28 это число равно 3,7. Рабочее число тарелок принимают равным праб = птсор/г], где т] — к. п. д. тарелок, зависящий от их конструкции.
Аналогичным образом рассчитывается десорбция (регенерация) раствора.
Диаметр абсорбера и размеры скрубберных секций назначают в зависимости от допустимой скорости в свободном сечении абсорбера и в скрубберных секциях, а также от расхода осушаемого газа. Указанные допустимые скорости газа определяются по данным опыта в зависимости от требуемой степени сепарации взвешенных капель раствора абсорбента. Они могут быть определены и по эмпирическим формулам. Так, допустимая скорость газа в свободном сечении абсорбера и = 0,82/д/р, где р — плотность газа в рабочих условиях, определяемая из уравнения состояния реального газа, р = p/(zRT). Насосы и диаметры трубопровода для циркуляции раствора, теплообменные аппараты и кипятильники подбирают и рассчитывают по известным формулам применительно к избранному режиму работы установки осушки газа.
Осушка газа адсорбентами
В качестве твердых поглотителей влаги в газовой промышленности широко применяют активированную окись алюминия и боксит, который на 50—-60 % состоит из А1203. Активизируется боксит при температуре 633 К в течение 3 ч без доступа воздуха. Поглотительная способность боксита составляет 4—6,5 % от массы. Преимущества метода: низкая точка росы осушенного газа; простота регенерации поглотителя; компактность, несложность и низкая стоимость установки. Боксит поставляется в зернах (гранулах) диаметром 2—4 мм. Насыпная масса равна 800 кг/м3. Глубина осушки зависит от степени насыщения боксита, уменьшаясь с увеличением последней. Продолжительность работы бокситовой загрузки больше года. Скорость прохождения газа через активированный боксит равна 0,5—0,6 м/с. Загрузка боксита определяется в зависимости от количества газа и содержания в нем влаги по формуле G = Qwr/a, где Q — объемный расход газа через адсорбер, приведенный к 273 К и 0,1013 МПа; х —
Рис. 3.29. Схема осушки газа твердым поглотителем:
1 и Я — сепараторы; 2 и 3 — адсорберы; 4 — холодильник; 6 — газодупка; 1 — подогреватель; К — конденсат; ГВ — газ влажный; ГС — газ сухой; ГН — газ нагретый; ГНИ — газ нагретый насыщенный*, PJI — регулятор давления
влажность газа; т — продолжительность цикла поглощения; а — коэффициент активности боксита.
Схема осушки газа твердым поглотителем изображена на рис. 3.29. Влажный газ через сепаратор поступает в адсорбер, где проходит через несколько слоев активированного боксита, насыпанного на тарелки с перфорированным основанием (толщина одного слоя не превышает 60 см). Проходя через боксит, газ освобождается от влаги и направляется в газопровод. После определенного промежутка времени в зависимости от загрузки твердого поглотителя и объемной скорости газа (этот промежуток времени обычно равен 12—16 ч) адсорбер переводят на восстановление (регенерацию). Газ же переключают на второй адсорбер, который уже прошел регенерацию. Боксит регенерируют (осушают), продувая через него горячий газ. При этом из боксита выделяется вся влага, поглощенная им из газа в процессе осушки. Регенерацию боксита проводят следующим образом (на рис. 3.29 на регенерацию боксита переведен правый адсорбер 3). При пуске адсорбера на регенерацию определенное количество газа, требуемого для заполнения системы регенерации, отводят от линии сухого газа через регулятор давления РД (при давлении несколько более 0,1 МПа). Этот газ поступает сначала в холодильник и далее в сепаратор. Газодувкой под давлением не более 3 кПа газ подается в подогреватель, где он нагревается до температуры 473 К, и далее поступает в адсорбер, в котором регенерируется боксит. По выходе из адсорбера нагретый насыщенный газ поступает в холодильник, а затем в сепаратор, где отделяется влага, поглощенная в адсорбере. В результате повторных циклов регенерирующего газа (газодувка — подогреватель -адсорбер—холодильник—адсорбер—сепаратор — газодувка) боксит осушается и может снова поглощать воду из газа.
Осушка газа молекулярными ситами
Для глубокой осушки применяют молекулярные сита, обычно называемые цеолитами. Цеолиты представляют собой сложные неорганические полимеры с кристаллической структурой. Форма кристалла цеолита—куб. На каждой из шести сторон его имеются щели, через которые влага проникает во внутреннее пространство. Каждый цеолит имеет свой размер щелей, образованных атомами кислорода (от
3-10—7 до 10-10-7 мкм). Благодаря этому цеолиты способны резко избирательно сорбировать в основном мелкие молекулы, т. е. при адсорбции происходит как бы отсеивание более мелких от более крупных молекул. Мелкие молекулы проникают во внутреннее пространство кристалла и застревают в нем, а крупные молекулы не проходят и, следовательно, не будут адсорбироваться. Цеолиты, применяемые в виде порошка или гранул размером до 3 мм, обладают высокой пористостью (до 50 %) и огромной поверхностью пор. Их активность (поглотительная способность) достигает 14—16 г на 100 г цеолитов при парциальном давлении 50 Па и превышает активность силикагеля и окиси алюминия почти в 4 раза. Необходимо отметить высокую поглотительную способность цеолитов при низкой относительной влажности газа или при малом парциальном давлении водяных паров, что обеспечивает осушку газа до очень низкой точки росы (до 173 К).
Преимуществом молекулярных сит является их хорошая поглотительная способность при высоких температурах (до 373 К она уменьшается весьма незначительно). В то же время поглотительная способность силикагеля и боксита уже при температуре 311 К снижается в несколько раз, а при температуре 373 К практически равна нулю.
Для регенерации молекулярных сит используют сухой газ, нагретый до 473—573 К, который пропускают через слой цеолита в направлении, обратном движению газа при осушке. При глубокой осушке газа с большой начальной влажностью возможна двухступенчатая схема с применением обычных осушителей (гликолей и бокситов) и молекулярных сит. Цеолиты выдерживают до 5000 циклов, теряя при этом около 30 % своей поглотительной способности.
3.8. ОСУШКА ГАЗА ОХЛАЖДЕНИЕМ
Охлаждение широко применяется для осушки газа, выделения конденсата из газа газоконденсатных месторождений на установках низкотемпературной сепарации, а также при получении индивидуальных компонентов газа, выделении из природного газа редких газов, сжижении газов и т. д. Низкотемпературный способ разделения газов позволяет в зависимости от глубины охлаждения извлекать от 80 до 100 % тяжелых углеводородов и осушать газ при транспортировке однофазного компонента до необходимой точки росы по влаге и углеводородам. На практике применяют низкотемпературную сепарацию (НТС), при которой получают относительно невысокие перепады температур как за счет использования пластового давления (путем дросселирования газа), так и искусственного холода. Детандер (поршневой или турбинный) позволяет получить более глубокое охлаждение газа, а также продлить срок службы установок НТС. Применение искусственного холода (холодильных машин) в установках НТС позволяет обрабатывать газ до конца разработки месторождения, но прн этом капитальные вложения в обустройство промысла увеличиваются примерно в'1,5—2,5 раза.
Принципиальная технологическая схема НТС изображена на рис. 3.30. Сырой газ из скважины поступает на установку комплексной 92
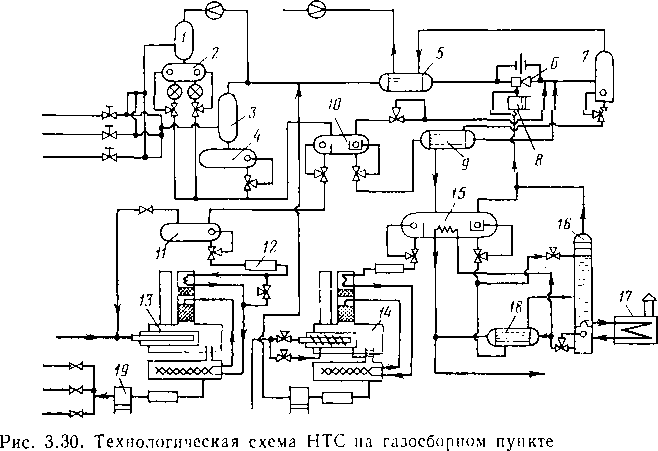
подготовки, где после предварительного дросселирования (или без него) направляется в сепаратор первой ступени 3 для отделения от капельной жидкости. Затем газ направляется в теплообменник 5 для охлаждения газом, поступающим в межтрубное пространство из низкотемпературного сепаратора 7. Из теплообменника газ поступает через эжектор 6 или штуцер в низкотемпературный сепаратор 7, в котором за счет понижения температуры в теплообменнике и на штуцере (эжекторе) выделяется жидкость. Осушенный газ поступает в теплообменник 5, охлаждает продукцию скважины и направляется в промысловый газосборный коллектор. Нестабильный конденсат и водный раствор ингибитора (например, диэтиленгликоля ДЭГ), предотвращающий гидратообразование, из сепаратора первой ступени 3 поступают в конденсатосборник 4 и далее в емкость 10. Здесь происходит разделение конденсата и водного раствора ДЭГа. Затем конденсат через теплообменник 9 подается в поток газа перед низкотемпературным сепаратором, а водный раствор ДЭГа направляется через емкость 11 и фильтр 12 для очистки от механических примесей в регенерационную установку 13, после чего регенерированный гликоль из установки с помощью насоса 19 подается в шлейфы для предотвращения образования гидратов в них. Поток нестабильного углеводородного конденсата и водного раствора ДЭГа направляется в разделительную емкость 15 через межтрубное пространство теплообменников, где охлаждает нестабильный конденсат, поступающий из емкости 10 для впрыскивания в газовый поток. Водный раствор гликоля через фильтр поступает в установку регенерации 14, после чего насосом 19 подается в газовый поток перед теплообменником 5. Конденсат из разделительной емкости 15 направляется через межтрубное пространство теплообменника 18 в деэтанизатор 16. Установка деэтанизации состоит из тарельчатой колонны, печи 17 и теплообменника 18. Заданная температура в нижней части деэтанизатора поддерживается с помощью теплообменника 18, в котором стабильный конденсат (нижний продукт деэтанизатора), подогретый в печи 17 до температуры 433 К, отдает тепло насыщенному конденсату, поступающему из емкости 15. Охлажденный стабильный конденсат подается в конденсатопровод. По схеме предусматривается также ввод части холодного нестабильного конденсата на верхнюю тарелку стабилизатора. В этом случае деэтанизатор работает в режиме абсорбционно-отпарной колонны.
Если предусматривается транспортировка конденсата в железнодорожных цистернах, то стабилизация его проводится в ректификационной колонне, работающей в режиме либо частичной, либо полной дебутанизации. Газ выветривания (дегазации) из емкости 15 и газ деэтанизатора 16 через штуцер поступает в общий поток. Если давление недостаточно, то предусматривают компрессор 8. Газ дегазации из емкости 10 также возвращается в общий поток. Периодический контроль за дебитами газа и жидкости осуществляется с помощью сепаратора 1, на выкидной линии которого установлены замерная диафрагма и конденсатосборник-разделитель 2 со счетчиками. Если на устье скважины температура газа достаточно высока и на его пути до газосборного пункта гидраты не образуются, то схеме подготовки газа упрощается. На период добычи, когда требуются дополнительные источники холода на установке НТС для обеспечения требуемой точки росы газа, в схеме вместо штуцера устанавливают турбодетандер, использование которого дает эффект по снижению температуры, больший в 3—4 раза, чем при обычном дросселировании. В этом случае в схеме предусматривается сепаратор второй ступени, предназначенный для отделения жидкости от газа, поступающего в турбодетандер. Осушенный газ из межтрубного пространства теплообменника 5 поступает на прием компрессора, установленного ¦ а одном валу с турбодетандером, и далее в промысловый коллектор.
Возможны модификации описанной схемы в соответствии с конкретными условиями. В частности, дополнительно к теплообменнику 5 устанавливают воздушный или водяной холодильник. По мере снижения пластового давления для поддержания постоянной температуры сепарации газа на установках НТС требуется последовательное увеличение поверхности теплообменников, что приводит к необходимости перестройки установки. Однако наступает такой период, когда это становится нерациональным. В таком случае вводят холод извне либо применяют другие способы подготовки газа.
Эффективность работы НТС любого типа существенно зависит от технологического режима эксплуатации скважины. В проектах разработки за оптимальное давление сепарации на газоконденсатных месторождениях принимается давление максимальной конденсации, которое для каждого состава газа определяется экспериментальным путем. Для обеспечения однофазного движения газа по магистральным трубопроводам температура сепарации выбирается с учетом теплового режима работы газопровода.
Природный газ, очищенный от сероводорода, не имеет ни цвета, пи запаха. Поэтому обнаружить утечку газа довольно трудно. Чтобы обеспечить безопасность транспорта и использования газа, его одорируют, т. е. придают ему резкий и неприятный запах. Для этой цели в газ вводят специальные одоранты, и продукты их сгорания должны быть физиологически безвредными, достаточно летучими (низкая температура кипения), не должны вызывать коррозию, химически взаимодействовать с газом, поглощаться водой или углеводородным конденсатом, сильно сорбироваться почвой или предметами, находящимися в помещениях. Одоранты должны быть недорогими. Этим требованиям в наибольшей степени удовлетворяет этилмеркаптан. Однако при использовании этилмеркаптана следует учитывать присущие ему недостатки. Так, по токсичности он равноценен сероводороду; если газ идет на химическую переработку, то необходимо очищать его от меркаптана, так как последний отравляет катализаторы. Этилмеркаптан химически взаимодействует е окислами металла, поэтому при транспорте одорированного газа запах его постепенно ослабевает.
Кроме этилмеркаптана также используют сульфан, метилмеркап-тан, пропилмеркаптан, калодорант, пенталарам и др. В качестве одоранта также применяют смесь меркаптанов, получаемых при очистке природного газа с высоким содержанием серы и сернистых соединений. Одоризацию газа проводят на головных сооружениях газопровода и газораспределительных стаициях.
Концентрация паров одоранта в газе должна быть такой, чтобы резкий запах ощущался при объемной концентрации газа, не превышающей 1/5 от нижнего предела взрываемости. Среднегодовая норма расхода этилмеркаптана составляет 16 г на 1000 м3 газа. В летнее время расход одоранта примерно в 2 раза меньше, чем зимой.
одоризатор с ди-
2 — фильтр-отс гоii • поплавковая каме-тон* У —
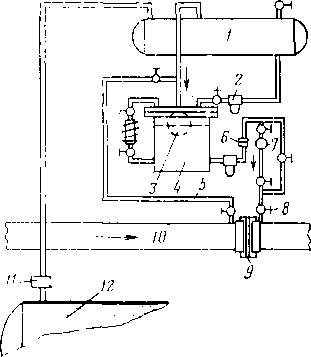
Рис. 3.31. Капельный афрагмой:
I — бачок для одоранта; пик; «3 — поплавок; 4 — ра; 5, 8 — соединительные трубки; в -кая диафрагма; 7 — смотровое стекло; диафрагма в газопроводе; 10 — газопровод;
II — ручной насос; 12 — запасная емкость
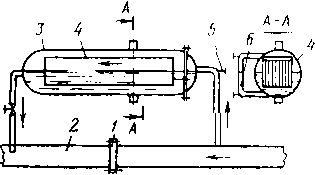
Рис. 3.32. Испарительный (фитильный) одоризатор:
1 — диафрагма; 2 — газопровод; 3 — рс-ЭсрВуНр! 4 — ВСрТИКаЛЬНО ПОДВбШСМПЫС фитили; 5— регулировочный вентиль; 6 — мерное стекло
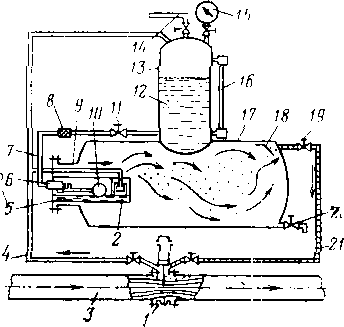
Рис. 3.33. Барботажный одоризатор;
J — диафрагма; 2 — барботажиая камера; 3 — газопровод; 4 — трубка, подводящая газ под давлением; 5 — тарелка; 6 — клапан; 7 — питательная трубка; 8 — фильтр; 9 — трубка, подводящая газ в барботажную камеру; 10 —поплавок регулятора уровня; 11 — вентиль; 12 — этилмеркаптан; 13 — расходный бак; 14 — трубка, подводящая этилмеркап-тан со склада; 15 — манометр; 16 — стеклянная трубка указателя уровня; 17 — емкость одоризатора; 18 — отбойник брызг; 19 — регулировочный вентиль; 20 — сливноА кран; 21 — трубка, отводящая газ
?? Устройства, при помощи которых одорант вводится в поток газа, называются одоризаторами. Они бывают капельные, испарительные и барботажные. Капельными одоризаторами одорант вводится в газопровод каплями или тонкой струей (рис. 3.31). Одоризатор действует за счет перепада давления, создаваемого диафрагмой. Одорант из поплавковой камеры проходит через диафрагму, смотровое стекло и по трубке поступает в газопровод. В поплавковой камере все время сохраняется постоянный уровень. Расход одоранта можно изменять при помощи сменной диафрагмы.
Наибольшее распространение имеют испарительные (фитильные) и барботажные одоризаторы (рис. 3.32). В резервуар с одорантом частично погружены фланелевые полосы. Над поверхностью одоранта между полосами фланели проходит газ и насыщается одорантом. Резервуар снабжен подогревателем (на схеме не показан). Температура одоранта, от которой зависит интенсивность испарения (а следовательно, и степень одоризации), поддерживается терморегулятором.
Барботажный одоризатор изображен на рис. 3.33. Из газопровода 3 часть газа попадает в барботажную камеру 2, в которой происходит насыщение газа одорантом, поступающим из расходного бака 13. При помощи поплавкового регулятора в барботажной камере поддерживается постоянный уровень. Отсюда газ проходит через емкость одоризатора 17, входит в газопровод сзади диафрагмы 1, создающей перепад давления для прохождения газа через одоризатор. Капли не-испарившегося одоранта, захватываемые газом из барботажной камеры, оседают на дно емкости 17. Накапливающийся там одорант 96
о
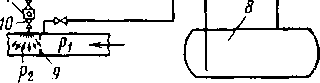
сливается через кран 20. Регулирование степени одоризации осуществляется вентилем 19.
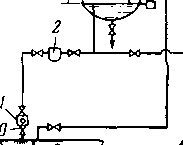
Однако для рассмотренных одоризаторов характерно отсутствие прямой пропорциональной зависимости расхода одоранта от расхода газа, так как ввод одоранта происходит под действием меняющегося столба жидкости, не зависящего от количества проходящего газа. При колебании расхода в течение суток часто приходится менять режим работы установки. Регулировку выполняют вручную игольчатым вентилем, поэтому точность дозирования зависит от опытности обслуживающего персонала.
На некоторых газораспределительных станциях внедрены полуавтоматические установки одоризации газа, которые просты по конструкции, надежны в работе и обеспечивают практически полную пропорциональную зависимость расхода одоранта от расхода газа. Установка работает следующим образом (рис. 3.34). На пути газового потока в газопроводе установлена диафрагма 9, на которой создается определенный перепад давления в зависимости от расхода газа. Газ с давлением рх до диафрагмы поступает в бачок 3 с одорантом и создает давление на столб одоранта, равное рг—H$g. Одорант из бачка 3 через фильтр 2 и калибровочное сопло 1 впрыскивается в газопровод за диафрагмой с давлением р2. Давление впрыскивания меняется в зависимости от количества газа, проходящего через диафрагму, н этим достигается пропорциональность расхода одоранта и газа. Уровнемерное стекло 4 используется для наблюдения за расходом одоранта. Емкость 8, предназначенная для заполнения бачка деодорантом, снабжена предохранительным клапаном 5. Давление заполнения бачка поддерживается редуктором 7 и контролируется по манометру 6. При монтаже фланец с соплом крепится к фланцу задвижки 10, что позволяет заменять и чистить сопла. Диаметр сопла подбирается по формуле
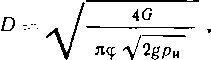
где G — расход одоранта на 1000 м3; <р — коэффициент истечения, Ф = 0,82; р„ — давление истечения одоранта.
Изменение степени одоризации достигается за счет изменения диаметра сопла. Степень одоризации определяется хроматографическими методами.
3.10. ОЧИСТКА ПРИРОДНЫХ ГАЗОВ ОТ СЕРНИСТЫХ СОЕДИНЕНИЙ И УГЛЕКИСЛОГО ГАЗА
Природные газы многих месторождений содержат в своем составе сернистые компоненты и углекислый газ, так называемые кислые газы. Сернистые соединения отравляют катализаторы в процессах переработки газа, при сгорании образуют S02 и S03, высокое содержание которых в воздухе опасно для человека и окружающей среды. Сероводород H2S и углекислый газ С02 в присутствии воды вызывают коррозию стальных труб, оборудования трубопроводов, компрессорных машин и пр. Их присутствие ускоряет гидратообразование. Требования к газу, подаваемому потребителям, по содержанию сернистых компонентов постоянно возрастают. В настоящее время допускается содержание H2S в природном газе не более 5,7 мг/м3, общей серы не более 50 мг/м3, углекислого газа С02 —до 2 %. Сернистые компоненты природного газа и в первую очередь H2S служат отличным сырьем для производства серы. Из сероводорода природного газа получается наиболее чистая и дешевая сера. Современные процессы очистки сернистого природного газа связаны с производством серы и обеспечением чистоты воздушного бассейна.
Ю YL i-lllllflllb
ж
ж
У
10
Т
Ш
Рис. 3.35. Схема очистки природного газа методом химической абсорбции:
/ — сырьевой газ; 11 — очищенный газ; /// — насыщенный абсорбент; IV — регенериро^ ванный абсорбент; V — газ выветривания; VI — кислый газ; 1 — входной сепаратор; 2 — абсорбер; 3 — гидравлическая турбина; 4 — насос; 5 — выветриватель; 6 — промежуточная емкость; 7 — теплообменник; 8 — фильтр; 9 — десорбер 10 — воздушный холодильник
11 — сепаратор рефлюкса
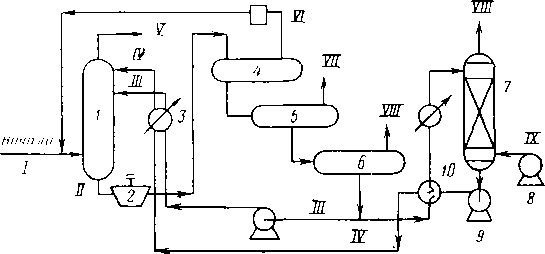
Рис. 3.36. Схема процесса физической абсорбции:
/ — исходный газ; // — насыщенный абсорбент; III — груборегенернрованный абсорбент; JV — тонкорегенерированный абсорбент; V — очищенный газ; VI — рецикловый газ; VII — газ выветривания среднего давления; VIII — кислый газ; IX — воздух или инертный газ; I — абсорбер; 2 — турбина снижения давления; 3 — холодильник; 4, 5 и 6 — первая, вторая и третья ступени выветривания соответственно; 7 — отпарная колонна; 8 — воздуходувка; 9 — насос; 10 — теплообменник
Традиционные схемы очистки больших объемов газа включают процессы извлечения кислых компонентов (производство очищенного газа), переработку кислых газов в серу, очистку или сжигание отходящих газов и очистку газов сгорания.
Для извлечения кислых компонентов из природного газа применяют главным образом абсорбционные регенеративные процессы. В процессе химической или физической абсорбции из газа извлекаются кислые компоненты. При регенерации насыщенного абсорбента получается поток кислого газа, направляемый на установку производства серы.
В процессах химической абсорбции применяют водные растворы поглотителей, которые вступают в обратимую реакцию с кислыми компонентами газа. В качестве химических поглотителей используют моноэтаноламин, диэтаноламин, диизопропаноламин, дигли-кольамин, растворы солей^щелочных металлов, растворы солей аминокислот и др. Схема процесса, типичная для химической абсорбции, изображена на рис. 3.35.
В частности, часто применяют моноэтаноламиновый процесс, характеризующийся высокой реакционной способностью поглотителя, его хорошей химической устойчивостью и небольшими капитальными вложениями. Реакцию взаимодействия моноэтаноламина с H2S и СОа можно представить уравнениями
2C2H5ONH2 + H2S^ [(QHbONFy Н|2 S,
2c2h6onhs + н2о+co2 [(c2h5onh2):hi3;co3.
Во избежание коррозии оборудования концентрация моноэтаноламина в растворе с водой не превышает 15—20 %.
При физической абсорбции кислых газов из потоков природного газа используются органические растворители: метанол, пропилен-карбонат, диметиловый эфир полиэтиленгликоля и др. Процессы физической абсорбции характеризуются высокой степенью насыщения
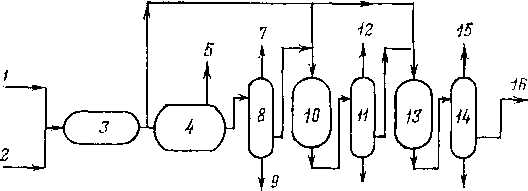
Рис. 3.37. Схема установки Клауса с однопоточным процессом:
/ — кислый газ; 2 — воздух; 3 — горелка и реакционная камера; 4 — котел-утилизатор; 5, 15 — пар (высокое давление); 6 — обводная линия горячего газа; 7, 12 — пар (низкое давление); 8, ft, 14 — конденсаторы; 9 — сера; 10 и /3 — первый и второй каталитические конверторы соответственно; 16 — «хвостовой* газ
абсорбента кислыми газами и соответственно низкими скоростями циркуляции поглотителя, низкими энергозатратами, небольшими габаритами оборудования и его простотой. Схема, типичная для процесса физической абсорбции, изображена на рис. 3.36.
Выбор растворителя основывается на составе, температуре и давлении исходного газа, последующей его обработке и требований к качеству очищенного газа.
Вторая операция при очистке природного газа — получение серы из сернистых соединений. При обработке больших потоков природного газа чаще всего используются различные модификации процесса Клауса, основанного на каталитической реакции кислорода воздуха с сероводородом, поступающим из регенерационной колонны абсорбционных процессов, при повышенной температуре. Реакция Клауса протекает в две стадии по уравнениям
2H2S + 302 ч=ь 2Н20 -f 2S03 + 520 кДж;
4H2S -f- 2S02 4Н20 -f- 6S + 105 кДж; 1
6H2S + 302 6Н40 + 6S + 625 кДж.
Для увеличения выхода серы процесс проводится в соответствии с двумя стадиями реакции. Сначала в печи Клауса при высокой температуре сжигается часть H2S с получением S02. В результате очень высокой температуры и некаталитического сжигания H2S с воздухом получается непосредственно сера с выходом около 60 %. После высокотемпературного сжигания и утилизации теплоты продуктов горения устанавливается один или несколько каталитических конвертеров Клауса (рис. 3.37), где оставшийся H2S взаимодействует с S02. Снижение температуры каталитической реакции способствует повышению выхода серы. При очистке отходящих с установок Клауса газов возможны два варианта. В одном случае газы, отходящие с установок Клауса, подаются непосредственно в установку доочистки, в другом — они предварительно сжигаются до превращения всех сернистых соединений в S02 и только после этого поступают на установку доочистки.
ТЕХНОЛОГИЧЕСКИЙ РАСЧЕТ МАГИСТРАЛЬНЫХ НЕФТЕПРОВОДОВ
В технологический расчет нефтепровода входит решение следующих основных задач:
определения экономически наивыгоднейших параметров нефтепровода (диаметр трубопровода, давление на нефтеперекачивающих станциях, толщина стенки трубопровода и числе нефтеперекачивающих станций);
определения местонахождения станций на трассе нефтепровода;
расчета режимов эксплуатации нефтепровода.
Экономически наивыгоднейшие параметры определяют сравнением конкурирующих вариантов нефтепровода по рекомендуемым для заданной пропускной способности диаметра трубопровода. При нескольких значениях диаметра выполняют гидравлический и механический расчеты, определяющие (для каждого варианта) число нефтеперекачивающих станций и толщину стенки трубопровода. Наилучший вариант находят по приведенным затратам, т. е. экономическим расчетом.
Расположение нефтеперекачивающих станций определяют графически на сжатом профиле трассы. В расчет режимов эксплуатации входит определение давлений на станциях, подпоров перед ними и пропускной способности нефтепровода при условиях перекачки, отличающихся от расчетных; решается вопрос о регулировании работы нефтепровода.
4.1. ИСХОДНЫЕ ДАННЫЕ ДЛЯ ТЕХНОЛОГИЧЕСКОГО РАСЧЕТА НЕФТЕПРОВОДА
Для расчета нефтепровода необходимы следующие данные: пропускная способность; зависимость вязкости и плотности нефти от температуры; температура грунта на глубине заложения трубопровода; механические свойства материала труб; технико-экономические показатели и чертеж сжатого профиля трассы.
Пропускная способность нефтепровода дается в задании на проектирование.
Пропускная способность—основной фактор, определяющий диаметр трубопровода и давление на станциях. В нормах технологического проектирования даются значения диаметра трубопровода и давления на нефтеперекачивающих станциях в зависимости от пропускной способности.
Плотность и вязкость нефти определяют лабораторными анализами. Плотность р измеряют обычно при 293 К. При других температурах Рт-= р—? (Т—293), где ?— температурная поправка, ? = = 1,825—0,001317 р (плотность р должна быть выражена в кг/м3).
Зависимость вязкости от температуры может быть представлена в виде графика. При отсутствии такового кинематическая вязкость vT при нужной (расчетной) температуре Т может быть определена по формуле
vT = v0exp f — и (Т—Т0)],
где v0 — кинематическая вязкость при температуре Т0; и — показатель крутизны вискограммы. Для определения величины и кроме v0 и Т0 достаточно иметь еще одно значение вязкости при какой-либо другой температуре.
Расчетной температурой считают наинизшую температуру, которую принимает поток нефти в трубопроводе. Эта температура определяется наинизшей температурой грунта на глубине заложения трубопровода с учетом самонагревания потока в результате трения. Температура грунта на глубине заложения трубопровода определяется по материалам изысканий.
Механические свойства материала труб указываются в соответствующем ГОСТе.
В капитальные затраты на линейную часть входит как стоимость труб, так и стоимость всех работ по сооружению трубопровода (сварка, изоляция, рытье траншей и т. д.). В капитальные затраты на станции входит стоимость оборудования, трубопроводных коммуникаций, зданий и т. д., а для головных станций, кроме того,— стоимость резер-вуарного парка. На линейную часть приходится около 80 % суммарных капитальных затрат. Около 45—50 % от капитальных затрат на линейную часть составляет стоимость труб.
Эксплуатационные расходы состоят из следующих основных статей: отчислений на амортизацию, текущий ремонт, расходов на электроэнергию, смазку, воду, отопление, электроэнергию на собственные нужды, зарплаты, содержания охраны, управления, прочих расходов. Первые три статьи расходов — главные. На амортизацию и текущий ремонт приходится 30—40 % всех расходов. Затраты на электроэнергию составляют 40—60 %.
Суммарные эксплуатационные расходы определяют себестоимость перекачки — важнейший показатель, характеризующий экономичность работы нефтепровода.
При определении эксплуатационных расходов для выбора экономически наивыгоднейшего варианта можно идти обратным путем: их можно вычислить по себестоимости перекачки, указанной в нормах технологического проектирования: Э = CQL, где С — себестоимость перекачки; Q — пропускная способность; L — протяженность нефтепровода.
Профиль трассы (рис. 4.1) используют при определении расчетной длины трубопровода и разности геодезических высот. На профиле ведется расстановка нефтеперекачивающих станций (НПС). Профиль— чертеж, на котором отложены и соединены между собой характерные точки трассы. Расстояния от начального пункта и геодезические высоты этих точек — их координаты. Таким образом, расстояние между какими-либо двумя точками определяется не длиной соединяющей
Рис. 4.1. Профиль трассы
их линии, а ее проекцией на ось абсцисс. Иными словами, расстояния на профиле откладываются по горизонтали. Это очень важно иметь в виду.
Профиль трассы вычерчивается сжатым: масштаб по вертикали крупнее, чем по горизонтали. Поэтому все возвышенности и впадины на трассе выступают резко, чертеж получается наглядным.
4.2. ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ТРУБОПРОВОДА
Установившееся движение жидкости в трубопроводе описывается уравнением
где p —давление; p — плотность жидкости; X — коэффициент гидравлического сопротивления; х — длина; D — диаметр трубопровода; w — средняя скорость движения жидкости; g — ускорение свободного падения; г — нивелирная высота.
Величина dpiр представляет собой работу перемещения жидкости на участке dx, отнесенную к единице массы. Эта работа расходуется на преодоление сил трения [A, (dx/D) (w2/2) ], на изменение кинетической энергии жидкости (dw2l2) и на подъем жидкости на высоту dz. Учитывая, что р = idem (капельная жидкость) и что в этом случае при постоянном диаметре трубопровода dw2/2 = 0, после интегрирования получаем
где L — расстояние между точками 1 и 2, т. е. длина трубопровода; Аг = г2—z! — разность геодезических высот конца и начала трубопровода.
![]()
В уравнении (4.3) каждый член представляет собой работу, отнесенную уже не к единице массы, а к единице веса жидкости, т. е. высоту. Величина рг (рg) представляет собой высоту Ни на которую жидкость поднимается в пьезометре под действием избыточного давления рх в начальной точке трубопровода, р2 (pg) — высоту Я.2. Произведя замену
=Н1 — Нг=Н,
Р В
получим
(4.4)
![]()
H = hx + Az.
или
В общем случае величину Н (или pf(pg)) называют напором (единица напора — метр). Смысл этого уравнения такой. Разность напора в начальной и конечной точках трубопровода Н — общая (суммарная) потеря напора. Она складывается из потери напора на трение
(формула Дарси — Вейсбаха) и разности геодезических высот Дг.
Коэффициент гидравлического сопротивления X является функцией числа Рейнольдса Re = wD/v и относительной шероховатости k/D; k — эквивалентная абсолютная шероховатость, характеризует влияние состояния внутренней поверхности трубопровода на гидравлическое сопротивление.
При ламинарном и турбулентном течениях в зоне сравнительно небольших Re выступы шероховатости плавно обтекаются потоком жидкости, шероховатость не влияет на потерю напора и коэффициент гидравлического сопротивления зависит только от числа Рейнольдса. С увеличением Re коэффициент X уменьшается. Область, в которой X — X (Re), называется областью гладкого трения. Увеличение числа Рейнольдса приводит к тому, что от бугорков шероховатости начинают отрываться вихри. Это явление наступает тем раньше, чем больше шероховатость. Теперь сопротивление течению жидкости зависит не только от числа Рейнольдса, но и от шероховатости.
Область, в которой X = X (Re, k/D), называется областью смешанного трения. Здесь с увеличением Re его влияние на X постепенно уменьшается, а влияние k/D возрастает (увеличивается интенсивность вихреобразования у выступов шероховатости).
При большом числе Рейнольдса коэффициент X перестает зависеть от него.
Область, в которой к = к (k/D), называется областью совершенно шероховатого трения или областью квадратичного режима движения, так как здесь к — постоянная величина и потеря напора прямо пропорциональна квадрату скорости.
При ламинарном течении (Re <2000) коэффициент гидравлического сопротивления находят по формуле Стокса: к = 64/Re. Ламинарный режим бывает при перекачке вязкой нефти. Для вычисления к при турбулентном режиме (Re >3000) в зоне гладкого трения служит
эмпирическая формула Блазиуса: к = 0,3164/>/Re. Обычно этой формулой пользуются при расчете нефтепроводов для нефти средней вязкости.
При расчете трубопроводов для перекачки светлых нефтепродуктов в ряде случаев приближенно можно считать, что режим течения квадратичный. При квадратичном законе трения А. Д. Альтшуль рекомендует пользоваться формулой Шифринсона: Я, = 0,11 (k/D)0'25.
Для определения коэффициента гидравлического сопротивления в зоне смешанного трения применяют «универсальные» формулы. Их структура такова, что при малых числах Рейнольдса они обращаются в формулы к = к (Re), а при больших — переходят в формулы к = = к (k/D). Впервые такого типа формула была предложена Кольбру-ком и Уайтом:
Результаты вычислений к по формуле Кольбрука и'Уайта хорошо совпадают с опытными данными, полученными на технических трубопроводах. Но эта формула имеет существенный недостаток: при вычислении к необходимо прибегать к методу последовательных приближений.
От этого недостатка свободны аналогичные формулы (дающие практически такие же результаты), предложенные Н. 3. Френкелем
И. А. Исаевым
LV 3,7D J T Re J
Особой простотой отличается формула Альтшуля
\D Re /
А. Д. Альтшуль указывает, что при Re k/D <10 она практически совпадает с формулой Блазиуса, а при Re k/D >500 — с формулой Шифринсона. Таким образом, Re k/D — 10 можно считать границей между областями гладкого и смешанного трения, Re k/D = 500 —
105
границей между областями смешанного и совершенно шероховатого трения.
А. Д. Альтшуль рекомендует следующие значения эквшзалентной шероховатости: для новых бесшовных стальных труб k = 0,01 — —0,02 мм, после нескольких лет эксплуатации k = 0,15—0,3; для новых сварных стальных труб k = 0,03—0,1, с незначительной коррозией после чистки — k = 0,1—0,2.
Для магистральных нефтепроводов диаметром до 377 мм принято, что k = 0,125 мм, а для труб большего диаметра k = 0,1 мм.
Формулы Стокса, Блазиуса и Шифринсона имеют следующий общий вид:
X=.4./Rem, (4.6)
где А и т — постоянные величины, т называется показателем режима движения жидкости.
Поставив (4.6) в уравнение Дарси—Вейсбаха (4.5) и учитывая Re = 4Q/(nDv), получим обобщенную формулу Лейбензона
Л2—mvm
hx = р-5--— L,
т r D5-m
где
8 А
г 4тя2-mg
Формула Лейбензона применяется в тех случаях, когда зависимость hx от Q должна быть выражена в явном виде.
Величины т, А и р приведены в табл. 4.1.
На графике lg X = / (lg Re) зависимость (4.6) для указанных в таблице режимов течения выглядит в виде прямых линий, тангенс угла наклона которых к оси lg Re равен т. В области смешанного трения, где X зависит не только от Re, но и от относительной шероховатости kID, линия lg X — / (lg Re) оказывается плавной кривой. Показатель режима течения т в этой области — переменная величина. Последнее обстоятельство исключает возможность использования формулы Лейбензона в области смешанного трения. Это большой недостаток, так как область смешанного трения охватывает широкий
Таблица 4.1
| Режим | т |
А | 0, С5/м |
| Ламинарный | 1 | 64 | 128 -4,15 ng |
| Турбулентный в зоне Блазиуса | 0,25 | 0,3164 | 0,241 - 0,026 g |
|
Область квадратичного закона трения | 0 | X | - 0,0827b n2g |
Рис. 4.2. График зависимости lg А, =
= f (lg Re)
интервал чисел Рейнольдса, при которых обычно ведутся перекачки маловязких нефтей и светлых нефтепродуктов. Однако ценой некоторой потери в точности расчетов этот недостаток может быть устранен.
Отметим на графике lg к = f (lg Re) (рис. 4.2) цифрой 1 точку на прямой Блазиуса, где Rex = 10 (k/D)~l, и цифрой 2 точку на прямой Шифринсона, где Re2 = 500 (k/D)~l (границы области смешанного трения). Подставив Rej в формулу Блазиуса, a Re2 в формулу Шифринсона, найдем Ig^j и lg/Ц — ординаты точек 1 и 2. Теперь проведем через точки 1 и 2 прямую. Ее уравнение приводится к виду
lg к = 0,127 lg k/D—0,627 — 0,123 lg Re.
Приняв 100'127 */-0—0.627 = получим
к~- /4/Re0,123. (4.7)
Очевидно, замена кривой lg к = / (lg Re) прямой 1—2 равносильна замене формулы Альтшуля формулой (4.7). Это дает возможность распространить формулу Лейбензона и на область смешанного трения. Для этой области в соответствии с (4.7) т — 0,123. Коэффициент fi будет зависеть от k/D (так как от k/D зависит Л).
Его нетрудно вычислить по формуле
8 =-—-= 0,0802 • 10°'1271* ыо-0,627
r 4mn2~mg
4.3. ГИДРАВЛИЧЕСКИЙ УКЛОН В МАГИСТРАЛИ И НА УЧАСТКАХ С ЛУПИНГАМИ И ВСТАВКАМИ
Отложим вверх по вертикали от начальной и конечной точек профиля трассы напоры Н1 = pJipg) и #2 = pt/(pg) (рис. 4.3). Концы полученных отрезков Нг и Я2 соединим прямой. Тангенс угла наклона этой прямой называется гидравлическим уклоном г. Предполагается, что диаметр трубопровода — одинаковый по всей длине, местных сопротивлений нет, расход по длине не изменяется. Из чертежа видно, что i = (Hl—H2—Az)/L. Но в соответствии с (4.4) Нг—Я2—Дг = /гт. Следовательно, физический смысл гидравлического уклона — по-
Рис. 4.3. Схема к определению Рис. 4.4. Гидравлический уклон на раз-гидравлического уклона личных участках трубопровода
теря напора на трение, приходящаяся на единицу длины трубопровода:
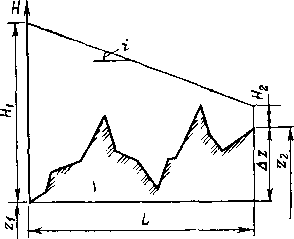
i = X-
D 2g
или по Лейбензону
q2-mvm
; = р
Удобно пользоваться следующей компактной формулой: i = /Q2""1, где / = $vm/Db~m.
Прямая, соединяющая концы отрезков Нt и //2, называется линией гидравлического уклона. Она показывает распределение напоров (а следовательно, и давлений) по длине трубопровода. Если на каком-либо участке трассы проложен параллельный трубопровод (лупинг) или трубопровод другого диаметра (вставка), то гидравлический уклон на нем будет отличаться от гидравлического уклона магистрали. Найдем соотношения между гидравлическими уклонами лупинга, вставки и магистрали. Будем считать, что режимы движения нефти в них одинаковы.
Пользуясь обозначениями рис. 4.4, имеем: гидравлический уклон магистрали
a‘Q2~mvm
1 ~ Р-— •
гидравлический! уклон луиингованного участка
g2-mvm ^2-mvm
Р-
гл = ico,
[1 + (0л/0)5—m/2—m ]2—m
Если Бл = D, то со = 1/22_/п. В этом случае при ламинарном режиме со = 0,5, при турбулентном режиме в зоне Блазиуса и = 0,297, для квадратичной области и = 0,25.
Аналогично для вставки
Потеря напора на трение для трубопровода с лупингом будет складываться из потерь напора на одиночном и сдвоенном (лупингован-ном) участках: /ц = i (L—х) + i„x, где * — длина лупинга.
Учитывая (4.8), можно также написать, что hx = i [L—х (1—со)]. Полная потеря напора для трубопровода с лупингом
Н = i\L —x(l — со)] + Az.
(4.9)
Для трубопровода со вставкой выражение для потери напора имеет аналогичный вид.
Далее для краткости вместо (4.9) будем писать Н — iL + Дг, имея в виду, что при необходимости всегда L можно заменить на L—л; (1—со) или на L—х (1 — Q).
Если надо потерю напора выразить в зависимости от Q, то будем пользоваться формулой
|2—ni vm
![]()
\L + Az
(4.10)
или
H = fQ2~mL + Az.
(4.11)
Лупинги или вставки прокладывают в тех случаях, когда необходимо уменьшить гидравлическое сопротивление трубопровода. Очевидно, что для действующего нефтепровода реальной оказывается лишь прокладка лупинга. При проектировании же требуемый эффект может быть достигнут как при помощи лупингов, так и при помощи вставок. Наилучший вариант может быть определен сравнением капитальных затрат на сооружение. Специальные расчеты позволили сделать следующий вывод. По металлозатратам во всех имеющих практическое значение случаях вставки оказываются выгоднее лупингов. При этом расход металла на вставки уменьшается с уменьшением их диаметра.
4.4. ВСАСЫВАЮЩИЙ УЧАСТОК- ПЕРЕВАЛЬНЫЕ ТОЧКИ И РАСЧЕТНАЯ ДЛИНА НЕФТЕПРОВОДА
Участок нефтепровода, подводящий нефть к насосу, называется всасывающим. Основное требование, предъявляемое к всасывающему трубопроводу, состоит в том, что ни в одной его точке давление не должно быть ниже упругости паров перекачиваемой нефти. В противном случае в точках с низким давлением нефть закипает, образуются паровые пробки, сильно затрудняющие перекачку. Пониженное давление в конечной точке всасывающего трубопровода, т. е. во входном патрубке насоса, может вызвать кавитацию. При кавитационном режиме из протекающей в насосе жидкости выделяются пузырьки паров и затем разрушаются, схлопываются (закипание и затем конденсация). В результате появляется шум, возрастает износ, снижается к. п. д., уменьшается подача. Но повышение давления на всасывающей стороне насоса (насосной станции) приводит к возрастанию давления на нагнетательной стороне, т. е. к ничем не оправданному увеличению механической нагрузки на трубопровод. Из сказанного следует, что давление во всасывающем патрубке насоса должно быть предельно низким, но при этом обеспечивающим режим работы без кавитации.
Очевидно, что соответствующий этому давлению допускаемый напор во входном патрубке насоса (принято обозначать его Hs) может быть выражен в виде Hs = py/(pg) + ДhAon. Здесь ру — давление насыщенных паров перекачиваемой нефти (упругость паров); А/гдоп — допускаемый кавитационный запас; определяется экспериментально. Он включает в себя потерю напора от входного патрубка до области пониженного давления в насосе и напор в этой области, гарантирующий отсутствие кавитации. Кривые зависимости Д/гд0п от расхода совмещают с характеристиками насосов Н = Н (Q).
Возвышенность на трассе, от которой нефть приходит на конечный пункт нефтепровода самотеком, называется перевальной точкой. Таких точек может быть несколько (рис. 4.5). Расстояние от начального пункта нефтепровода до ближайшей из них л называется расчетной длиной нефтепровода Ьрасч. При гидравлическом расчете длина нефтепровода принимается равной расчетной, разность отметок Дz — равной превышению перевальной точки над начальным пунктом трассы. Для нахождения перевальной точки проведем от конечного пункта трассы К линию гидравлического уклона / до пересечения ее с профилем. Затем вычертим параллельную линию 2 с расчетом, чтобы она касалась профиля, нигде его не пересекая. Место касания линии гидравлического уклона 2 с профилем трассы — перевальная точка л, определяющая расчетную длину нефтепровода. Если линия гидравлического уклона, проведенная из конечной точки трассы, нигде не пересекается с профилем и не касается его (на рис. 4.5 — пунктир ная линия), перевальная точка отсутствует и расчетная длина равна полной длине нефтепровода. Перевальная точка может оказаться не только между последней станцией и конечным пунктом нефтепровода, но и на перегоне между промежуточными НПС. При соответст
вующем профиле перевальная точка может появиться при изменении режима работы нефтепровода: при отключении какой-либо станции или при изменении вязкости перекачиваемой нефти.
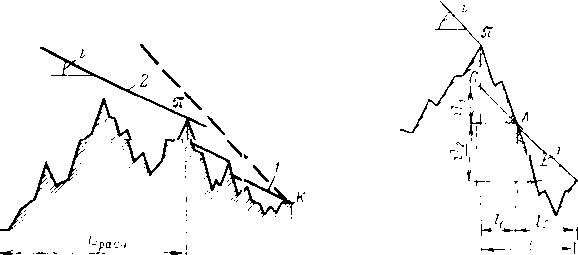
¦К
Рис. 4.6. Схема течения нефти за перевальной точкой
Рис. 4.5. Схема к определению перевальной точки
Рассмотрим движение нефти за перевальной точкой. В промежутке трассы от перевальной" точки до конечного пункта выделим два участка: пА длиной 11 и АК длиной /2 (рис. 4.6). На последнем из них самотечное движение нефти обеспечивается разностью высот точек А и К'. = Агл_к. На участке пА, как видно из чертежа, Агя._л>г71
на величину я С. Но это противоречит условию баланса потерянного Иг и активного Аг„_л напоров. Следовательно, на участке я А гидравлический уклон должен быть больше i. Это возможно только в случае увеличения скорости движения нефти на участке пА. Из уравнения сплошности Q = wF видно, что с увеличением скорости живое сечение потока F должно уменьшаться. Следовательно, от перевальной точки до пункта А (см. рис. 4.6) нефть будет течь при частичном заполнении поперечного сечения трубопровода. При этом (Агл_к—Иг) Qpg представляет собой мощность, расходуемую непроизводительно. Пространство, свободное от нефти, будет занято выделившимися из нее парами и растворенными газами. Во избежание разрыва сплошности потока на конечном пункте (или на НПС, куда приходит нефть с перевальной точки) следует поддерживать давление, обеспечивающее некоторый запас напора на перевальной точке. Обычно этот запас принимают равным 10 м.
4.5. ХАРАКТЕРИСТИКА ТРУБОПРОВОДА.^
ХАРАКТЕРИСТИКА НАСОСА И НАСОСНОЙ СТАНЦИИ,
СОВМЕЩЕННАЯ ХАРАКТЕРИСТИКА 1
Характеристикой трубопровода называется зависимость потери напора от расхода. Уравнение (4.10) или (4.11) — аналитическое выражение этой зависимости. Характеристика трубопровода изображена
/ наго течения
/Область
"гпурбдлент
t:
Область
Ламинарного
течения
Q
на рис. 4.7. Начальная точка характеристики — конец отрезка Az, откладываемого по оси Я вверх, если z2>2г или вниз, если z2 <Zi. Величины v, L и D определяют крутизну характеристики. Чем больше вязкость перекачиваемой жидкости, протяженность трубопровода и чем меньше его диаметр, тем характеристика круче. При расчетах нет нужды вычерчивать характеристику от начальной точки, соответствующей Q = 0. Вполне достаточно построить характеристику трубопровода по трем или даже двум точкам, находящимся в узком диапазоне расходов, ожидаемых при эксплуатации рассчитываемого трубопровода.
Характеристикой насоса называется зависимость развиваемого им напора Я от подачи Q. Для центробежных насосов, применяемых на магистральных нефтепроводах, характеристики имеют вид пологопадающих кривых. Участок характеристики, соответствующий наиболее высоким значениям к. п. д.,— рабочая область. Для этой области зависимость Я от Q очень удачно аппроксимируется выражением
(4.12)
Я = а—bQ2.
Однако, когда бывает необходимо совместно решать уравнения характеристик насоса (насосной станции) и трубопровода, целесообразно вместо (4.12) принять
Я = а—bQ2~™.
(4.13)
В формулах (4.12) и (4.13) а и b — постоянные величины, определяемые обработкой координат точек, взятых в рабочей области характеристики. По смыслу в (4.12) или (4.13) а — напор при Q = 0; коэффициент b свидетельствует о крутизне характеристики. В формуле (4.13) величина т та же, что и в формуле Лейбензона для потери напора в трубопроводе.
Характеристики насосов получают опытным путем при работе на воде. При работе на нефти (вязкая жидкость) характеристика Q—Я снижается, становится более крутой. Методику пересчета характеристики «с воды на нефть» можно найти в специальных руководствах.
Плотность не влияет на характеристику Q—Я: напор, развиваемый насосом, не изменяется при изменении плотности перекачиваемой жидкости.
Изменением диаметра колеса насоса D, а также частоты вращения п изменяют характеристику. Известно, что
DJD = QJQ; = (4.14)
(При изменении частоты вращения — аналогичные равенства.) Звездочкой обозначены новые, измененные условия. При обточке колес (Z)# <.D) или при уменьшении частоты вращения (п* <п) характеристика Q—Н снижается.
Характеристика насоса после обточки колеса до диаметра D* может быть получена на основании прежней характеристики при помощи формул (4.14). При этом нельзя перестраивать характеристику, пользуясь лишь одной из этих формул.
Если необходимо, чтобы характеристика насоса проходила через точку с координатами Q+, Н*, находящуюся под характеристикой, соответствующей диаметру колеса D, то диаметр колеса после обточки может быть найден по формуле
VH 4-bQ2
’-а
. (4-15)
Эта формула выводится из (4.12) и (4.14). Входящие в нее а и b — те же, что и в формуле (4.12).
Характеристику группы соединенных между собой насосов (суммарную характеристику) получают сложением характеристик насосов, входящих в эту группу. При последовательном соединении складываются напоры при одинаковых расходах, а при параллельном — расходы при одинаковых напорах (рис. 4.8). Уравнение суммарной характеристики имеет такой же вид, как (4.12) или (4.13).
Теперь перейдем к основному технологическому элементу нефтепровода, включающему в себя нефтеперекачивающую станцию (НПС) и примыкающий к ней трубопровод (перегон). Для этого элемента характеристикой трубопровода принято считать зависимость напора в начальной точке трубопровода от расхода, а характеристикой нефте-
® б
Рис. 4.8. График построения суммарной характеристики двух насосов, соединенных последовательно (а) и параллельно (б)
|
»ст< | ||||
|
AHi | Н6 | АН | ||
| 1 | il+Az | |||
| nIh | ||||
| i^lgUflJLQl | ||||
|
НПС |
Перегон | |||
Рис. 4.9. Схема основного технологического элемента нефтепровода
перекачивающей станции —зависимость напора на выходе из блока регуляторов давления от расхода. Выход из блока регуляторов давления принимают за начальную точку трубопровода (перегона). Конечной точкой будем считать точку врезки в магистраль всасывающего участка, подводящего нефть к первому насосу следующей станции.
На рис. 4.9, изображающем схему НПС и перегона, указаны гидравлические сопротивления отдельных участков, а также напоры в характерных точках. Обозначено: hBC — потеря напора во всасывающем участке; /гкал — потеря напора в коллекторе, т. е. в трубопроводной обвязке насосов и блока регуляторов давления; А„ач — потеря напора на участке от блока регуляторов до магистрали;
il + Az — потеря напора на трение и преодоление разности геодезических высот для перегона между станциями; Яст — напор на выходе из блока регуляторов давления (в начальной точке перегона); Яв — напор во всасывающем патрубке первого насоса; АН — напор на входе в НПС (или в конечной точке перегона).
Очевидно, что
ДЯ = /гвс + Я„. (4.16)
Напор Яв называют подпором. Этот же термин применяют и для АН.
В соответствии с рис. 4.9 и принятыми обозначениями для перегона между двумя промежуточными станциями
Нст Анач -j- il -)- Az АН. (4,17)
Для перегона, на котором имеется перевальная точка,
Нет = Анач -Ь Ип “Н Azn -f- Яп. (4.18)
Здесь 1п и Дz„ относятся к перевальной точке, а Нп — напор на перевальной точке, гарантирующий сплошность потока. Для перегона между промежуточной НПС и конечным пунктом
НСт = Аная “Ь il “Н Az -j- Як, (4.19}
где Як = Лк + ЯРез — напор в конце магистрали, учитывающий потерю напора hK в трубопроводах конечного пункта и высоту уровня Ярез в заполненном резервуаре.
114
Рис. 4.10. Совмещенные характеристики
Формулы (4.17), (4.18) и (4.19) — аналитические выражения характеристики трубопровода; в них, за исключением Аг и Яя, все слагаемые являются функциями расхода.
Аналитическое выражение характеристики НПС напишем в виде
Яст=Яв + Яднф-АкоЛ (4.20)
или, если учесть (4.16),
Яст = АЯ—hBc//диф—hKon, (4.21)
где //диф — дифференциальный напор, развиваемый основными насосами; определяется по заводским характеристикам Я = Я (Q) (при необходимости пересчитанным «с воды на нефть»).
Для головной НПС Яв = Н„—hn и поэтому
Яст — Я п-^п“4“//диф-^кол» (4.22)
где Нп — напор на выходе из подпорной насосной; /гп — потеря напора в трубопроводе, соединяющем подпорную насосную с основной.
Если на головной НПС подпор Яв создается подпорной насосной, то на промежуточной НПС его источником является предыдущая станция. И в том, и в другом случае подпор Яв не должен быть меньше допускаемого наименьшего значения Hs. В противном случае перекачка окажется невозможной (кавитация).
Характеристика НПС, построенная в соответствии с формулами (4.20), (4.21) или (4.22), называется полной. Характеристика НПС, построенная при условии, что при всех значениях расхода Яв = Я5, называется исходной. Полная характеристика располагается выше исходной на Яв—Hs.
Полная характеристика НПС и характеристика трубопровода (примыкающего к НПС перегона), построенная на одном чертеже (рис. 4.10, линии / и //), образуют совмещенную характеристику. Координаты точки пересечения этих характеристик определяют пропускную способность системы НПС — перегон и напор на выходе из блока регуляторов давления. На совмещенной характеристике проводят горизонтальные линии, показывающие ограничения напора для магистрали //маг.доп и для коллектора //кол.доп- Высота расположения этих линий соответствует напорам, допускаемым из условия прочности. Точка пересечения характеристики НПС с линией ограничения давления для коллектора определяет наименьшую пропускную способность, с которой может работать станция. На рис. 4.10, а это точка 1. При меньшем расходе срабатывает защита и станция отключается. Точка пересечения характеристики НПС с линией ограничения давления для магистрали (точка 2 на рис. 4.10, а) определяет наименьшую пропускную способность, при которой станция может работать без регуляторов давления. При меньших расходах включаются регуляторы, поддерживающие после себя давление на постоянном допускаемом уровне. Таким образом, линия 1—2—3 на рис. 4.10, а представляет собой рабочий участок полной характеристики НПС (ограниченный расходами Qmin и Стах), а линия 4—2—3 — рабочий участок характеристики (учитывающий действие регуляторов давления). Если линия ограничения давления в магистрали 4—2 проходит ниже точки 3, как это показано на рис. 4.10, б, то максимальный расход будет определяться точкой пересечения этой линии с характеристикой трубопровода. Рабочий участок полной характеристики НПС в этом случае показан линией 1—2, а с учетом работы регуляторов давления—отрезком 4—2. Выражения (4.17), (4.18) и (4.19), представленные на графике в виде характеристики трубопровода, определяют «требуемый напор», т. е. необходимый для реализации заданного расхода. Разность между напором, определяемым полной характеристикой НПС, и требуемым напором, называют «свободным напором». На совмещенной характеристике он изображается вертикальным отрезком между полной характеристикой НПС и характеристикой трубопровода. Свободный напор полностью передается на следующую станцию, если давление на выходе из НПС меньше или равно допускаемому из условия прочности магистрали. Если линия ограничения давления для магистрали пересекает вертикальный отрезок, определяющий свободный напор, и, таким образом, делит его на две части, то на следующую НПС передается напор, соответствующий лишь нижней части этого отрезка. Остальная часть свободного напора (верхняя часть отрезка) подлежит дросселированию в блоке регуляторов.
4.6. УРАВНЕНИЯ БАЛАНСА НАПОРОВ. ОПРЕДЕЛЕНИЕ|ЧИСЛА НЕФТЕПЕРЕКАЧИВАЮЩИХ СТАНЦИЙ
Напор на выходе из нефтеперекачивающей станции и напор в начальной точке трубопровода (перегона между станциями) равны друг другу. Для головного (первого) участка нефтепровода, состоящего из НПС и примыкающего к ней перегона, это условие на основании (4.22) и (4.17) выражается в виде:
Нп —Ядиф — Ькол = ^нач "Ь Ml "t-
Приняв hn = Лв и обозначив hB+h
кол ~Н ^нач — ^ст
(гидравлическое сопротивление всех коммуникаций станции), получим
Нл Ядиф—Аст := (7Х-(- Azt -)- АЯ2.
Для второго участка, для участка, имеющего номер с, и для последнего п-го участка будем иметь
АЯ2 -f- Ядиф—Лст — il2 -j- Az2 -f- АЯ3; A Hc -f- Ядиф1—h„ = ilc -f- A zc 4"
(4.24)
АЯ„ -f- //диф—Аст — iln Azn -f- Я к.
Сложив первые ? выражений, получим уравнение баланса напоров для участка от головной НПС до станции с + 1, а сложив все п — уравнение баланса напоров для всего нефтепровода:
Яп “Ь С (Ядиф — Act) ¦= l‘Lc+1 Azc+i -f- АЯ?+i>
Яп -f- /1 (Ядиф—Аст) = iL -f- Az -)- Я к. (4.25)
Здесь Lc+1 — расстояние от начальной точки нефтепровода до станции с + 1, a L—длина всего нефтепровода. Разности геодезических высот Azc+1 и Az соответствуют /с+1 и L. Предполагается, что
все НПС однотипные, оборудование станций одинаковое. Принимается
также, что перекачка идет без регулирования.
Если считать, что границами НПС являются точки врезки в магистраль всасывающего трубопровода и трубопровода, идущего от блока регуляторов давления, то ЯДИф —hcт будет представлять собой напор, развиваемый нефтеперекачивающей станцией (с учетом сопротивления внутренних коммуникаций /гст). Смысл уравнений (4.24) и (4.25) будет следующий: напор, развиваемый станциями, равен потере напора в трубопроводе. Очевидно, что зависимость ЯДИф — h„ от расхода тоже можно считать характеристикой НПС. В ряде случаев ее удобно выражать в виде (4.13): ЯДИф— Лет = а—6Q2-m.
Уравнение баланса напоров (4.25) примет вид:
Яп -f n (a—bQ2~m) = iL + Аг + Як.
(4.26)
Здесь Q — конкретная величина.
Считая Яп и Як постоянными, из (4.26) можно получить:
q__ I / Яп -j- tin (Az -f- //к)
К nb + fL
где Q — расход в системе насосные станции — трубопровод.
Баланс напоров и равенство подачи насосов расходу в трубопроводе (материальный баланс перекачки) дают основание для следующего важного вывода: трубопровод и нефтеперекачивающие станции составляют единую гидравлическую систему.
Изменение режима работы какой-либо одной насосной станции (например, отключение части насосов) нарушит режим работы остальных станций и трубопровода. Работу трубопровода и насосных станций всегда надо рассматривать как совместную.
Уравнения (4.24) и (4.25) действительны, как уже было сказано, при однотипных станциях, работающих без дросселирования. В тех случаях, когда расход следует считать строго заданной величиной, согласование напора, развиваемого станциями, и потери напора в трубопроводе (соблюдение баланса напоров) регулируют подбором диаметров колес насосов и при необходимости при помощи дросселирования. Уравнение баланса напоров (4.25) позволяет получить формулу для определения числа станций п проектируемого нефтепровода.
Удобно, чтобы эта формула была связана с условием прочности трубопровода. Для этой цели введем в уравнение (4.25) напор Яст, соответствующий толщине стенки трубопровода. Имеем: ЯДИф = ~ Яст “f- Икол Я В.
Приняв здесь Яв = Я8 и учитывая (4.23), напишем
Яд„ф—/гст= Яст—Д/г, (4.27)
где
Ah — /гнач + /гвс + Я5. (4.28)
Вместо (4.25) теперь получим
Ни т- п (Яст — Д/г) = iL + Дг + Як.
Отсюда число НПС
Если на перегоне между последней НПС и конечным пунктом есть перевальная точка, то в этих формулах L — расстояние от начальной точки нефтепровода до перевальной точки и Az — соответствующая разность геодезических высот.
Перевальные точки на перегонах между промежуточными НПС не оказывают влияния на уравнение баланса напоров и, следовательно, на число НПС (если, разумеется, нет необходимости в дросселировании на участке между перевальной точкой и следующей станцией).
При вычислении п напор Яст следует находить по исходной характеристике НПС, построенной для роторов наибольшего диаметра. Если этот напор окажется больше допускаемого по условию прочности магистрали (Ятах). то расчетное значение Яст принимается равным Я max-
Величину Ah называют передаваемым напором. Это не совсем точно. На самом деле «передаваемым» (на следующую НПС) напором является /гвс + Hs, т. е. лишь часть Ah. Остальная часть (hHS4) от-118
носится к потерям напора на рассматриваемой НПС и, следовательно, не может считаться «передаваемой». Напор Ah можно назвать передаваемым лишь условно, если считать, что напор Яст относится не к выходу из блока регуляторов давления, а к начальной точке магистрали (перегона между НПС). Это все равно, что поднять линию гидравлического уклона на высоту h»aч.
Дробное число станций п, полученное по формуле (4.29) или (4.30)г округляют в большую сторону. При этом баланс напоров соблюдается за счет соответствующего подбора диаметров колес насосов на станциях. Если число п округлить в меньшую сторону до целого л0, то недостаток напора, развиваемого станциями, равный (п—п0)
(//ст —A/i), должен быть компенсирован уменьшением гидравлического сопротивления трубопровода при помощи лупинга (или вставки). Лупинг длиной х уменьшает гидравлическое сопротивление на IX—inx — ix (1—со). Величина х может быть определена из равенства
(п—п0)(Н ст — A h) = u(l-—о). Получаем
x-=(HCT—Ah)
п~пл- .
[' (1 — (О)
4.7. РАССТАНОВКА НЕФТЕПЕРЕКАЧИВАЮЩИХ СТАНЦИЙ
Задача о расстановке нефтеперекачивающих станций впервые была решена В. Г. Шуховым. Идея состоит в том, что станции должны находиться в точках, где линии гидравлического уклона пересекаются с профилем трассы. Будем учитывать, что, поскольку в комплект каждого насоса входит несколько (до четырех) рабочих колес различного диаметра, имеется возможность работы НПС с различными напорами (при одной и той же заданной пропускной способности). Возможность изменения напора дает свободу выбора мест нахождения НПС. Они могут находиться не в строго фиксированных точках трассы, а на некоторых участках, называемых зонами возможного расположения станций. Определение границ этих зон связано с выполнением следующего требования: напор на выходе любой НПС не должен выходить за пределы Ятах и Hmin, соответствующие наибольшему и наименьшему диаметру рабочего колеса и условию прочности трубопровода.
Процедура нахождения зон возможного расположения НПС может быть показана наиболее просто для трубопровода с горизонтальным профилем (рис. 4.11). От начальной точки профиля трассы, где должна быть расположена первая станция, откладываем по вертикали вверх напоры Ят,п —Ah и Нтгх —Ah (напомним, что Ah включает в себя потерю напора в коммуникациях НПС от магистрали до первого насоса и от блока регуляторов давления до магистрали, а также минимально допускаемый напор на входе в первый насос). От концов отрезков НтХ„ —Ah и Нтах—Ah проводим линии гидравлического уклона до пересечения с профилем. Получим точки а2 и Ь2. Если вторую
----icjj 2f
"1 d3~---' cj
п = Л
.-----lCi ---I „^4
¦*¦---i Cj 2 3 4 [*
Рис. 4.11. Схема расстановки нефтеперекачивающих станций
станцию поставить в точке а2, то напор на первой НПС будет равен Hmin. При перемещении второй НПС вправо напор на первой станции будет возрастать и по достижении точки Ь2 он станет равным Ятах. Очевидно, что ни слева от точки а2, ни справа от точки Ь% вторую станцию ставить нельзя. Далее от точки а2 откладываем по вертикали вверх напор #min —АЛ, а от точки Ь2 — напор Ятах—А Л. Затем снова проводим линии гидравлического уклона до пересечения с профилем, получаем точки а3 и Ь3, ограничивающие расположение третьей НПС, и т. д.
Нетрудно заметить, что индекс последней точки Ь, полученной на ¦профиле, означает наименьшее число станций п, при котором может быть обеспечена расчетная пропускная способность. Оно равно округленному в большую сторону числу НПС, полученному по приближенной формуле
n = (iL-\- Az)/(//maI— АЛ). (4.31)
Наибольшее число НПС, обеспечивающее расчетную пропускную способность, соответствует индексу предпоследней точки а. Это число получается и по формуле (4.31), если вместо Ятах взять Нт1п и полученный результат округлить до целого числа в меньшую сторону. 120
При достаточной протяженности трассы наибольшее и наименьшее числа НПС могут отличаться друг от друга больше чем на единицу. Наилучший вариант определяется экономическим сравнением.
Для нахождения границ зон возможного расположения станций недостаточно получить точки а и Ь, откладывая напоры Нт\п —А к и Ятах —Д/г и вычерчивая линии гидравлического уклона, начиная от начальной точки трассы.
Необходимо также удовлетворить и другому требованию: линия гидравлического уклона от последней НПС должна прийти к конечному пункту и при этом напор последней станции не должен выходить за пределы #min и Ятах. Чтобы выполнить это требование, надо найти границы зон возможного расположения при построении линий гидравлического уклона и напоров от конечного пункта к начальному. Удобно эти построения выполнять «под профилем». От конечной точки профиля по вертикали вниз откладываем напоры Нт\п —Д/г и Ятах —АЛ и по-прежнему вычерчиваем линии гидравлического уклона до пересечения с профилем, как показано на рис. 4.11. Полученные точки —¦ границы зоны возможного расположения последней НПС удовлетворяют указанному второму требованию. Обозначим их буквами си d. Индексы — номер последней НПС. Далее аналогично описанному выше от точек с и d откладываем вниз напоры Нт\„ —Aft и Нтлх —Ah, проводим линии гидравлического уклона, получаем точки cud для предпоследней станции и т. д.
Зонами возможного расположения станций будут части участков ab и cd, перекрывающие друг друга, т. е. оказавшиеся общими, имеющие одинаковые индексы. На рис. 4.11 по индексам у точек b и а находим, что наименьшее число станций равно трем, а наибольшее — четырем. Приняв п — 3, маркируем точки cud. Ближайшие к концу трассы будут иметь индексы 3, следующие — 2 и т. д. Для наглядности точки а, Ь, с и d перенесены вниз под профиль и попарно соединены горизонтальными отрезками. Оказалось, что участки а3Ь3 и c3d3, а также аф2 и c2d2 частично перекрывают друг друга. Отсюда находим, что третья станция может быть помещена между точками Ь3 и d3, а вторая — между точками Ь2 и d2¦ На рисунке эти зоны возможного' расположения показаны горизонтальными отрезками 3 и 2.
Если принять число станций п = 4, то индексы у точек cud надо-будет изменить. Так, точки с3 и d3 должны быть обозначены сх и d4, а точки Со и d2 будут теперь с3 и da. Зона возможного расположения четвертой НПС, как видно из рисунка, будет находиться между точками я4 и с.1, третьей — между точками а3 и с3 и второй — между точками а2 и с.,.
Число станций, полученное по формуле (4.31), округляется, как было сказано, в большую сторону. Поэтому вычисленный по этой формуле средний напор Яср, приходящийся на каждую из принятых п станций, оказывается меньше Ятах. От разности Ятах—Яср зависит протяженность зон возможного расположения. Чем эта разность, меньше, тем меньше протяженность этих зон. При Яср = Ятах, т. е. когда найденное по формуле (4.31) число станций п оказывается целым, протяженность зон возможного расположения равна нулю..
Станции должны будут располагаться в точках пересечения линий гидравлического уклона с профилем при напоре на станциях, равном Ятах (точки Ь). Аналогично получается и при Яср = Hmin. Места расположения станций в этом случае — точки а.
В зонах возможного расположения могут быть места или участки, на которых сооружение НПС нежелательно или даже запрещено. Нельзя, например, помещать станцию перед водной преградой, на болотистой местности и т. д. Протяженность зоны возможного расположения в таких случаях может резко сократиться.
После того как в зоне возможного расположения второй станции выбрано место, где она должна находиться, зоны возможного расположения остальных станций не могут оставаться прежними. Теперь вторую НПС считают первой и зоны возможного расположения остальных станций определяют заново. Процедура их определения такая же.
4.8. РАСЧЕТ РЕЖИМОВ РАБОТЫ СТАНЦИЙ
Расчет режимов работы станций выполняется после того, как выявлены зоны их возможного расположения и выбраны точки, где они будут находиться. Цель расчета — подбор диаметров рабочих колес насосов, определение напоров на входе и выходе НПС, а также напоров, подлежащих дросселированию.
Предварительно должны быть определены гидравлический уклон i, потери напора в коммуникациях НПС /гвс, Лнач и hK0л и напор в конечном пункте Як, а также дифференциальные напоры станций Ядиф при расчетном значении расхода для всех диаметров рабочих колес насосов, имеющихся в наборе. Расчет ведется по участкам (НПС и примыкающий к ней перегон). Удобно начинать с последнего участка.
Процедура расчета может быть следующей.
1. Ищем перевальную точку на последнем перегоне. Для «подозреваемых» точек вычисляем напор Я' = Az'—il', где Az' —¦ разность высот перевальной точки и конечного пункта и V — расстояние от перевальной точки до конечного пункта. Перевальная точка есть, если Я' >ЯК.
2. Определяем требуемый напор на выходе из НПС. Если нет перевальной точки, то Я „тр = йнач + il + Az + Як. Если перевальная точка есть, то ЯСттР = Кгч + Ип + Агл + Я„.
3. Определяем требуемый дифференциальный напор ЯДИф. Тр =
— ЯСТТр 4- Лкол — Яв. Здесь подпор Яв на входе в первый насос, получаемый от предыдущей НПС, пока еще не известен. Примем его равным наименьшей допускаемой величине Я5.
4. Для всех диаметров, имеющихся в наборе колес насосов по характеристике Q—Я, находим дифференциальные напоры ЯДНф, соответствующие расчетной пропускной способности. Выбираем из них наиболее близкий к ЯДИф. тр-
5. Избыток напора подлежит дросселированию /гдр =
— Ядиф Ядиф. тр.
6. Если ЯДИф < Ядиф. тр, то подпор на входе в первый насос дол-
жен быть увеличен на Ядн ф. тр—//ди ф. Получим: Нв —
= Нs ~\- Ндиф. тр ЯдИф.
7. Этот подпор может оказаться еще большим, если на предыдущем (предпоследнем) перегоне имеется перевальная точка. Для выявления перевальной точки следует вычислить значение Н'. В рассматриваемом случае Н' = А г'—il'— hBC, где А г' — разность геодезических отметок перевальной точки и последней НПС; V — соответствующая длина трубопровода. Если окажется, что Н' больше Нв, то-рассматриваемая точка — перевальная. В этом случае подпор на входе в первый насос последней НПС следует считать равным //', и все расчеты, начиная с п. 3, придется выполнить заново.
8. Далее аналогичные расчеты выполняются для всех остальных участков.
4.9. УВЕЛИЧЕНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ НЕФТЕПРОВОДА
На совмещенной характеристике Н = Н (Q) (рис. 4.12) увеличение пропускной способности означает перемещение рабочей точки вправо. Чтобы это произошло, необходимо либо «поднять» характеристики НПС, либо сделать более пологими характеристики перегонов. Отсюда — два способа увеличения пропускной способности: сооружение дополнительных станций на перегонах между существующими (удвоение числа НПС) и прокладка лупингов. Очевидно, что коэффициент увеличения пропускной способности % = QJQ (отношение увеличенной пропускной способности к прежней) при удвоении числа НПС есть фиксированная величина, а при прокладке лупингов коэффициент % может иметь различные значения в зависимости от длины и диаметра лупинга. В обоих случаях напор на выходе из станции уменьшается (//ст* С Н„). Поэтому несущая способность трубопровода окажется недоиспользованной. Эффективность удвоения числа НПС или прокладки лупингов увеличится, если давление будет поднято до величины, близкой к допускаемой по условию прочности. Это может быть осуществлено подбором диаметров колес насосов, заменой
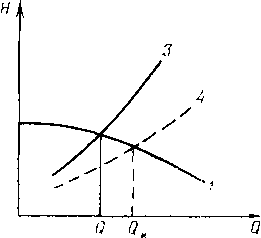
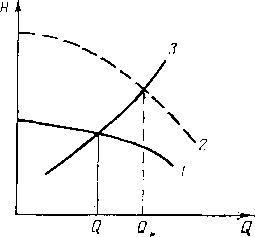
Рис. 4.12. Совмещенные характеристики Н = Н (Q):
— существующей НПС; 2 — существующей и дополнительной НПС; 3, 4 — трубопровода к после прокладки лупинга
существующих насосов на другие, параметры которых ближе к необходимым, установкой дополнительных подпорных насосов или даже сооружением на той же площадке второй магистральной насосной, включаемой параллельно.
Будем считать, что до и после увеличения пропускной способности давления на выходе из НПС одинаковые (ЯСТ;(. = Яст).
Определим коэффициент % = QJQ, получающийся при удвоении числа станций.
Для существующей станции с и примыкающего к ней перегона напишем следующие уравнения баланса напоров.
До увеличения пропускной способности в соответствии с (4.24) и (4.27) имеем:
АНс + (Яст—Ah) == ilc -f Azc + ЛЯ,:+1.
После удвоения числа станций
АНс 4- 2 (ЯСт— АН) = i^lc -|- Azc -j- АЯс+1.
Разделим второе уравнение на первое. Приняв, что АНС == АЯс+1, получим
( Q* \*~т 2—т 2 (Ист ДА) — AZc it оо\
*¦ “ V О ) ~ ~ (НСТ - ДА) - д2 *
Если пренебречь величиной Az, то ^ = 22-ni.
Теперь рассмотрим увеличение пропускной способности прокладкой лупинга.
Из уравнения баланса напоров для станции с и соответствующего перегона
АНс + (Яст— Ah.) =- ilc “Н Azc -)- AHc+i и уравнения
А Не + (Я ст— Ah.) -= i^ [1С—х (1 —со)] Azc -(- AHc+i, учитывающего прокладку лупинга длиной х, получаем
г* [/—дс(1—co)] = i7 (индекс с опущен) и далее
i" l — x( 1 — ш)
Отсюда длина лупинга, обеспечивающего заданное увеличение пропускной способности
![]()
(4.33)
Нетрудно увидеть, что прокладка лупингов целесообразна при сравнительно небольшом увеличении пропускной способности (Х<21/(2~т'). Если требуется увеличить пропускную способность в число раз, близкое к 21/2_т (при турбулентном течении в зоне дейст-
вия формулы Блазиуса 2|/2~т = 1,486), то это можно сделать удвое
нием числа станций. Но можно такой же эффект получить и прокладкой лупинга. Если же % >2|/2_т, то может оказаться выгодным комбинированный способ: удвоение числа НПС с одновременной прокладкой лупингов.
Вопрос о предпочтительности того или иного способа решается сравнением приведенных затрат П. Для участка нефтепровода, состоящего из одной НПС и примыкающего к ней перегона, выразим их в следующем виде:
при удвоении числа станций
/7 удв = Кст (Е н осст) 4~ Зудв 4" 3; при прокладке лупинга Пл = Кл (?н 4" ал) х 4~ Эл,
здесь Кст — капитальные затраты на вновь сооружаемую (дополнительную) станцию; Кл — капитальные затраты на единицу длины лупинга; Ен — нормативный коэффициент эффективности; аст и ал — отчисления на амортизацию и текущий ремонт для станции и линейной части; Зудв и Эл —расходы на электроэнергию; 3—другие эксплуатационные расходы на вновь сооружаемой НПС (зарплата, стоимость смазки, воды и т. д.).
Длина лупинга х и расходы Эудв и Эл подлежат специальному определению. Остальные величины справочные. Длина лупинга может быть найдена по формуле (4.33). Расходы на электроэнергию ЭУАВ и Эл определяются по формулам:
g _ о °^диф i О Д/ .
‘-'удв -- ‘Ээ ^ JycT'V ,
Jb/T]
Q _ О ^^диф
Jjl--LJ3 *
367r]
где 5Э —стоимость электроэнергии, руб/(кВтч); G — требуемая пропускная способность, т/год; ЯДИф — дифференциальный напор (при вычислении Эл — это напор, развиваемый существующей станцией; при вычислении Эудв — напор, развиваемый двумя станциями, т. е. существующей и дополнительной); т) — к. п. д. насосных агрегатов; Sуст — плата за установленную мощность, руб/кВт в год; N — номинальная мощность, кВт.
Расчеты, определяющие наивыгоднейший способ увеличения пропускной способности, необходимо выполнять для каждого перегона между существующими станциями. После этого следует расчет режимов работы всех НПС.
4.10. ИЗМЕНЕНИЕ ПОДПОРОВ ПЕРЕД СТАНЦИЯМИ ПРИ ИЗМЕНЕНИИ ВЯЗКОСТИ ПЕРЕКАЧИВАЕМОЙ НЕФТИ
Вязкость перекачиваемой нефти в течение года не остается постоянной. Она изменяется вслед за сезонными колебаниями температуры грунта на глубине заложения трубопровода. Изменяется режим работы трубопровода, т. е. расход и напоры на выходе из станций и на приеме (подпоры). Рассмотрим физическую картину изменения подпора перед насосной станцией с + 1. Будем считать, что ни на одной из станций нет нужды ни в дросселировании, ни в других видах регулирования. Подпор перед насосной станцией с + 1 определим из следующего уравнения баланса напоров для участка 4+i (между первой и с + 1 станциями):
Яп + с(а— bQ ) = fQ lc+i -Ь Azc+i + AHC+1.
Учитывая (из уравнения баланса напоров для всего нефтепровода),
что
__Нп Ч~ па — (Ag ~Ь Д к)
nb + fL
получим
'AHc+1 = Ha +
ca — Azc+1—[Hn + na—(Az + HK)\ —
b +
.
п b-\-fL!n
(4.34)
В этом уравнении от вязкости нефти зависит лишь величина / = = Pvm/D6_m. Таким образом, изменение подпора АНс+1 при изменении вязкости определяется значением (b -f flc+1/c)/(b + fLlri), где lc+i/с представляет собой среднее расстояние между нефтеперекачивающими станциями на участке le+1, a L/n — то же для всего нефтепровода.
Если lc+1/oL/n, то при увеличении вязкости нефти дробь (b -f flc+1lc)l(b + fL/n)возрастает и, следовательно, уменьшается подпор АНс+1. Для случая lc+1/c<L/n—наоборот, при увеличении вязкости нефти подпор перед станцией АНс+1 увеличивается.
И наконец, если lc+1/c = L/n, то изменение вязкости нефти не оказывает влияния на подпор, так как при любом значении f в этом случае (b + flc+i/c)/(b -f fLlri) = 1.
Изменение подпоров перед станциями при изменении вязкости иллюстрируется рис. 4.13. Вертикальные пунктирные линии отсекают на профиле трассы одинаковые расстояния Lin (на чертеже L/3); L— расчетная длина нефтепровода. Сплошные и пунктирные линии гидравлического уклона i и i* соответствуют вязкостям v и v*; v* >v. Отрезки аАх = АгА 2 = А 2А3 и аАы = AXifA2i( = A2lfA.^ представляют собой напоры Яд„ф и Ядиф*, развиваемые насосными станциями при вязкости нефти v и v* соответственно; отрезок 1а — подпор перед первой станцией (Яп). Примем точку 1 за начало координат. Тогда линии гидравлического уклона, идущие от точек А и А#, будут описываться уравнениями
Я = Яп + сЯдИф—И и Н% = Яп -1- сЯдиф * —
где / — расстояние от начальной точки трассы I, а Я и Я, — соответствующие им ординаты.
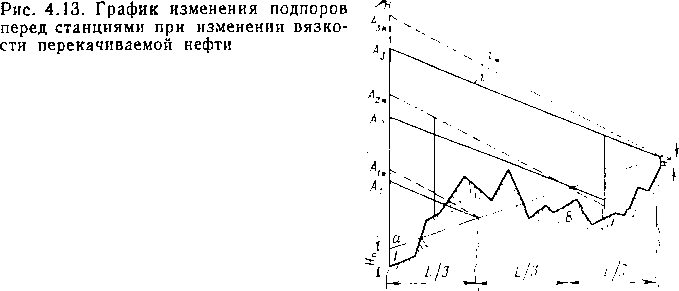
В точках пересечения этих линий Н = Нт. е.
С//диф-/ I = С//диф *
Учитывая, что
; - (Дг+//К) • Яп + ^Ядиф* - (A2 4"^k)
t = - И i* — -%
L L
нетрудно убедиться, что линии гидравлического уклона при вязкостях v и v* пересекаются на расстояниях I = cLIn, где с — целое число, равное 1, 2, 3 и т. д.
Если бы третья станция находилась в точке В, над которой пересекаются линии I и I*, т. е. на расстоянии, кратном Lin, то при любом увеличении или уменьшении вязкости нефти подпор остался бы неизменным (условие lc+Jc = L/n). Но эта станция расположена дальше точки пересечения гидравлических уклонов i и i'*, для нее lc+1/c ~>Un. Поэтому подпор перед третьей станцией при увеличении вязкости понижается, что и показано на чертеже. Нефтеперекачивающая станция 2 находится левее точки пересечения линий i и i'*; для нее lc+1/c <LLln. Поэтому подпор перед ней при вязкости v* больше, чем при вязкости v.

4.11. НЕФТЕПРОВОДЫ СО СБРОСАМИ И ПОДКАЧКАМИ
Нередко для снабжения потребителей, расположенных вдоль трассы, производится отбор перекачиваемой нефти из нефтепровода (сброс). Сбросы бывают непрерывные и периодические. Непрерывный сброс может быть организован, например, для снабжения нефтью нефтеперерабатывающего завода, расположенного вблизи от трассы нефтепровода. Периодические сбросы обычно бывают на нефтепродукто-проводах (для пополнения запасов близлежащих нефтебаз). Если в каком-либо месте нефтепровод проходит близ промыслового района, то может быть организована подкачка; добываемую на этих промыслах нефть направляют в тот же нефтепровод. В зависимости от мощности месторождения подкачка также может быть непрерывной или периодической.
Расчет нефтепровода с непрерывными сбросами или подкачками можно вести по участкам, разграниченным пунктами сбросов или подкачек. При незначительных сбросах или подкачках нефтепровод рассчитывается без учета их. Но следует иметь в виду, что при периодических сбросах (подкачках) изменяется технологический режим перекачки; обычно эго ведет к необходимости регулирования работы насосных станций.
Рассмотрим режим работы нефтепровода при периодических сбросах и подкачках. Участок нефтепровода от начальной точки до пункта сброса (подкачки) будем называть левым, а от пункта сброса (подкачки) до конечной или перевальной точки — правым. При сбросе количество нефти, поступающей в правый участок нефтепровода, уменьшится. Насосные станции, работающие на этом участке, начнут «высасывать» нефть из трубопровода. В результате возрастет расход в левой части нефтепровода и уменьшатся подпоры перед всеми промежуточными станциями.
Из уравнений баланса напоров для левой части нефтепровода
АЯп -\~е (a bQ2—‘n) = flc+iQ*~m + Az,+1 + А Н(с+1и (индекс * означает «при сбросе») и уравнения
А Я п -f с (a-bQ*-’») = flc+lQ2~m + А гс+1 + А Я,+1 (перекачка без сброса) найдем уменьшение подпора
б Яс+1 = АЯс+1 АЯ((.+1)*
перед станцией с -f- 1 (где расположен пункт сброса):
6Hc+l = (cb + //,+]) (Q2_«_Q2-«).
Такой же формулой определяется изменение подпора перед станцией с' + 1, находящейся левее станции с + I:
бЯС'+1 = {cb + iU'+i)
(здесь Q* имеет прежнее значение).
Поскольку с'<е, 6ЯС-+ 1<6ЯС4.|. Следовательно, по длине левого участка нефтепровода подпоры перед станциями (начиная со второй) убывают: наименьший подпор — у станции с + 1, где ведется сброс. Подпоры по длине правого участка нефтепровода возрастают; это можно показать аналогичным рассуждением. Изменение подпоров перед станциями при сбросе иллюстрируется рис. 4.14. При подкачке расход в левой части нефтепровода Q, а расход в правой части Q* + q >Q. С увеличением подкачки q расход Q* убывает. Подпор перед станцией с + 1 с увеличением подкачки увеличивается. Распределение подпоров перед станциями будет следующим: у станции, расположенной близ пункта подкачки,— наибольший подпор; по мере удаления от нее (в обе стороны подпоры уменьшаются.
Сброс и расход в левой части нефтепровода, при которых подпор перед станцией с + 1 (у пункта сброса) достигает наименьшего допустимого значения АЯд = hBC + Я8, будем называть критическими:
<?кр И фкр-128
Рис. 4.14. Линии изменения режима работы нефтепровода при сбросе
Напишем уравнение баланса напоров для левой части нефтепровода при критическом сбросе:
АЯП + ‘; (я—bQ2Kpm) = fU+iQup"1 + AZc+i + АЯД.
Отсюда находим критический расход
QKp = ( ЬН„ + са-Агс+1-ЬНл У/2~т (4.35)
\ cb -f- //<7+1 /
Уравнение баланса напоров для правой части нефтепровода
АЯд + (п—с) [а—b (QKp—9кР)2_т] = / (L—lc+1) (QKp—<7кР)2“т + Az позволяет получить формулу, определяющую критический сброс:
to=g.„-r
д"*+(|,,т??~(д;+¦Г""'
• «-зд
(здесь Az — разность высот между конечным пунктом и станцией с + 1).
Если сброс q >(7кр, то появляется необходимость искусственно поднимать подпор перед станцией с + 1, для обеспечения бескавита-ционной работы он должен быть не меньше АЯд. Подпор может быть повышен увеличением гидравлического сопротивления правой части трубопровода или уменьшением напора, развиваемого расположенными там (после пункта сброса) станциями. Это осуществляется регулированием.
Выясним, каково должно быть увеличение сопротивления, или, что то же самое, какой напор Н' должен быть погашен регулированием. Поскольку при помощи регулирования перед станцией с + 1 поддерживается подпор АЯД| расход в левой части нефтепровода равен QKp; в правой — он будет равен QKp—q. Напор Я', который должен быть поглощен регулирующим устройством, может быть определен из уравнения
АЯД + (л-с) [а—b(QKp—qf~m\ - / (L-lc+1) (QKP-qf~m +
Az “Ь Як + Н'.
Если Я' = КНЛас + Л', где Я„ас — напор, развиваемый одним насосом при расходе QKp—q, К — целое число и h' < Янас, то целесо-
образно отключить К насосов, а напор ti погасить дросселированием.
Критической подкачкой (<7«р) будем называть такую, при которой напор на станции с + 1 достигает максимально допустимого значения Яд. Расход в правой части нефтепровода при критической подкачке также будем называть критическим (QKp). Критический расход найдем из уравнения баланса напоров для правой части нефтепровода:
Яд -1 (п-с-\)(а - bQtpm) /(/. -1елл) (&~т + Az + Як
(подкачка по-прежнему перед станцией с 1).
Получим
Q = Г
яд + - 1*1
+/yJiL]1 2~m
(4.37)
Теперь напишем уравнение баланса напоров для левой части нефтепровода при критической подкачке:
АЯп-|-с[а— b (QKр — qKp) ]=— [Ic+i{Qkp—<7кр) Н-
-I- Azc+1 + Яд — (а — bQlpm).
Отсюда находим, что критическая подкачка
- Q«p" I
АН" + а~ -
К - (^Д1 р
I cb + flc+i )
При подкачке q >qKp необходимо регулирование. Цель регулирования — снижение расхода в левой части нефтепровода до величины Qкр—<?¦ Это достигается тем же путем — отключением части насосных агрегатов или увеличением гидравлического сопротивления.
Напор Я', который должен быть снят регулированием в левой части нефтепровода, определяется из уравнения
АЯГ, + с [а—b(QKp—qf~m\ = flc+1 {Q«P-q?~m + Azc+1 + Яд-
-(а-Ь<ЙЛ+Я'.
4.12. РЕЖИМ РАБОТЫ НЕФТЕПРОВОДА ПРИ ОТКЛЮЧЕНИИ НАСОСНЫХ СТАНЦИЙ
Временное отключение какой-либо станции может быть вызвано неполадками в системе энергоснабжения, аварией, необходимостью проведения ремонтных работ и т. д. Выход из строя насосной станции резко меняет режим работы нефтепровода (расход, давление, подпоры перед станциями). Чтобы лучше понять изменение режима перекачки, будем считать, что нефтепровод может работать при любых напорах и давлениях, возникающих в результате отключения станции. Независимо от того, какая станция вышла из строя — вторая, третья и т. д. или последняя, из уравнения баланса напоров для всего нефтепровода следует, что
q2—/Л Нц -f- (п 1) Д (Az -|- //к)
(л-1)М IL
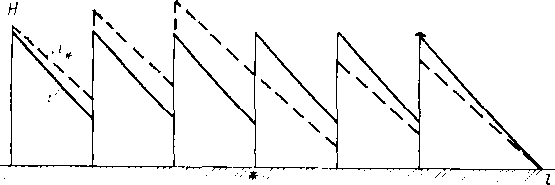
Рис. 4.15. Линии изменения работы режима нефтепровода при отключении одной из станций
Расход Q* устанавливается автоматически, в результате саморегулирования. Очевидно, что он меньше расхода Q, который был до отключения станций.
Выясним, как изменяются подпоры перед станциями при отключении станции с. Из уравнений баланса напоров для левой части нефтепровода (участок lc+i)
Нп-\-(с—1) (а—bQt ) //,. iQ. 4 Azt4_i-I- Л//(C+1>
(станция с отключена) и
Н\\-\-с{а—bQ ) = flc+1Q Azc+i~\- hHc+i
(работают все станции) имеем, что при отключении станции с подпор перед станцией с + 1 уменьшится на величину
б Нс+1 = АНс+1-АН(с+т = (а—bQ2~m)— (cb +flc+1)(Q2-m-(fm).
Из этого выражения видно, что чем ближе отключенная станция находится к головной, тем больше будет снижение подпора перед станцией с -Ь 1.
Аналогично из уравнений
Нп -f (с-2) (a-bQ2,-m) = fL^Ql-m + Az^ + AH<c_1)t
и
Нп + (с—2) {a-bQ2~m) = flc_iQ2~m + Azc^ АНс_хследует, что перед станцией с—1 подпор возрастает:
6Яе_1 = АН<С_1Н~АНС^ = 1(с-2)Ь + flc^\ (Q2__m—Q2~m)-
Очевидно, что подпор перед станцией с—2 также возрастает, но в меньшей степени, перед станцией с—3 в еще меньшей и т. д.
Также можно показать, что в правой части нефтепровода иодпоры будут возрастать от станции к станции, но останутся меньшими, чем были до отключения станции с. Изменение подпоров перед станциями при отключении одной из них изображено на рис. 4.15.
Если окажется, что ЛЯ(С+и;|;-<ЛЯд, т. е. подпор в точке врезки всасывающего трубопровода в магистраль меньше допускаемого, (АЯд
— Лес
+ Я5), то на станции с + 1 возникает кавитация. Ка-5* 131
витации не будет, если подпор Аподнять до АЯд. Это может быть достигнуто регулированием работы станций (снижением развиваемого ими напора), находящихся в правой части нефтепровода, т. е. за вышедшей из строя.
Напор Я', который должен быть погашен регулированием, найдем из уравнения баланса напоров для правой части нефтепровода
АЯд + (п—с) (а — bQ2~m) = / (L — lc+1) Q.2~m + Az + Як + Я',
где расход Q* определяется из уравнения баланса напоров для левой части нефтепровода:
Яп + (с— 1) (a-bQl~m) = flc+\Q2~m + Azc+1 + А Яд
(он будет меньше расхода, определяемого формулой (4.39)).
Поскольку подпоры перед станциями в левой части нефтепровода возрастут, давление нагнетания на станции с—1 может оказаться больше допустимого Яд. Снижение напоров до Яд достигается регулированием на станциях левой части нефтепровода. При этом расход Q* будет определяться из уравнения
Яд = flQl~m + А г + АЯд, (4.40)
где I — расстояние между станциями с—1 и с + 1; Az— разность нивелирных высот конца и начала участка /.
Величина Я', на которую должен быть снижен напор, развиваемый станциями левой части нефтепровода, может быть найдена из уравнения
Яп -\~(с—1)(я—bQ, ) ~/4-iQ, -f- Azc_i -f- Яд -f- Я
или
Яп + (с—1)(а—bQtm)= flc+iQ. + Azc+1АЯд + Я .
Если Я' превосходит напор Нтс, развиваемый одним насосом, то, округлив Я'/Янас До целого числа К (в меньшую сторону), найдем число насосов К, подлежащих отключению. Напор Я — Л7/„ас должен быть погашен дросселированием.
Режим работы нефтепровода при выходе из строя той или иной станции можно рассчитать графически, пользуясь профилем трассы и характеристикой насосной станции. Покажем это на следующем примере.
На нефтепроводе с горизонтальным профилем трассы расположены четыре станции 1—4, на каждой из них — по три рабочих насоса. Линии гидравлического уклона при нормальном режиме работы изображены сплошными (рис. 4.16). Пусть вышла из строя станция 3. Отложим от точки на профиле, где находится станция 2, напор Яд, а от точки расположения станции 4 — АЯд. Соединив концы этих отрезков (а, b), получим линию гидравлического уклона i*, соответствующую уравнению (4.40) и определяющую расход Q*, с которым должен работать нефтепровод после отключения станции 3. Теперь по характеристике насосной станции найдем напор Яднф* (с учетом потерь в коммуникациях) при расходе Q* и отложим его от началь-
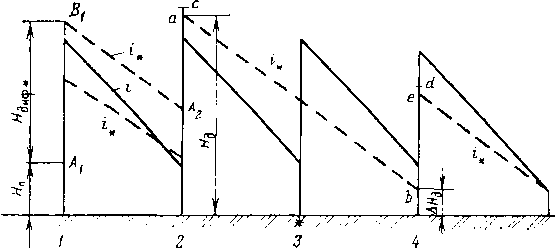
Рис. 4.16. Схема для расчета режима работы нефтепровода при отключении станции
ной точки профиля после #„ (отрезок А^В^. Из точки Вх проводим линию гидравлического уклона L*. Отложив от точки А 2 напор Ядиф* (отрезок Л2В2), увидим, что на станции 2 необходимо отключить один насос и лишний напор ас снять дросселированием. Но лучше отключить один насос на станции 1, а на станции 2 погасить напор ас, тогда перегон между станциями 1 и 2 будет испытывать меньшее давление (см. линию гидравлического уклона ниже линии 8^%)- Далее, вычертив линию i* на последнем перегоне, найдем, что на станции 4 следует отключить один насос (отрезок bd равен напору, развиваемому двумя насосами при расходе Q*) и снять дросселированием напор ed. Графическим способом расчета режима удобно пользоваться для контроля аналитического расчета.
4.13. СПОСОБЫ РЕГУЛИРОВАНИЯ РАБОТЫ НАСОСНЫХ СТАНЦИЙ
Изменения условий перекачки в процессе эксплуатации (изменения расхода, временный выход из строя какой-либо станции и т. д.) могут привести к нарушению нормального режима работы нефтепровода: к кавитации на одних станциях и давлениям, превышающим предельное, на других. Это означает, что пропускные способности отдельных участков нефтепровода окажутся неодинаковыми. Согласование работы насосных станций (или, что то же, выравнивание пропускных способностей участков нефтепроводов) достигается регулированием. В результате регулирования подпоры перед станциями должны быть не меньше допустимых АЯД, а напоры не должны превосходить предельного значения Яд.
При регулировании изменяется напор на насосной станции и одновременно расход. Регулирование может быть ступенчатое (отключение насосных агрегатов) и плавное, осуществляемое изменением частоты вращения двигателя или насоса, перепуском части потока нефти
Рис. 4.17. График к расчету регулирования работы насосной станции
? 2''
",
![]()
из нагнетательного коллектора во всасывающий и дросселированием потока.
Регулирование отключением одного или нескольких агрегатов — наиболее экономичный способ. Он применяется в тех случаях, когда необходимо уменьшить напор на величину, близкую к напору, развиваемому по крайней мере одним насосом. Чтобы точно установить нужные напор и расход, ступенчатое регулирование должно быть дополнено плавным регулированием. Регулирование изменением частоты вращения двигателя не получило распространения, так как существующие схемы пока еще сложны, громоздки и дороги (имеются в виду электродвигатели). Регулирование изменением частоты вращения насоса может осуществляться при помощи специальных магнитных муфт или гидромуфт.
Рассмотрим способы регулирования дросселированием, перепуском и при помощи муфт и сравним их по к. п. д. Пусть расход должен быть равен Q* и по характеристике трубопровода этому расходу соответствует напор Я*. Напор Яст* на выходе из станции при расходе Q* больше Я* на величину Н' (рис. 4.17). Чтобы получить расход Q*, надо, очевидно, погасить напор Я'. Определим к. п. д. регулирования дросселированием. Выразим полезную и затраченную мощности в виде Q*H#Pg и @*^ст*Р? соответственно. Тогда к. п. д.
Т)др — Я*/Яст* ИЛИ Т)др — 1 Я'/Яст*.
(4.41)
При регулировании перепуском подача насосной станции равна Q0, поток нефти с расходом Q0—Q* должен циркулировать по обводной линии. Следовательно, при перепуске к. п. д. г]п = QJQ0. Выразим т]п через величины Я' и Н„^. Если уравнение характеристики насосной станции написать в виде Я = а—bQ2, то сящиеся к валу двигателя, а /V* и п.? — соответственно мощность и частота вращения, относящиеся к валу насоса.
Q* = V(a—^ст*)/6 И Qo= V(a—H*)lb •
Учитывая также, что Я# =¦ ЯСТ4. —Я', получим
(4.42)
При регулировании с помощью муфты крутящий момент на валу двигателя передается на вал насоса без изменения ,т .е. А^да/ядв=/V*/л*, где МцВ и ЛдВ — соответственно мощность и частота вращения, отно-134
Следовательно, к. п. д. при этом способе регулирования равен nJnAB. Это — полный к. п. д. (г]ПОЛн). Он включает к. п. д. при отключенном регулирующем устройстве муфты, т. е. максимальный к. п. д. t]max = njtiw, когда ведомый вал вращается с наибольшей частотой пъ и к. п. д. регулирующего устройства муфты r]M = njni-Таким образом, цПОдн n.JnAB = г|тахт|м.
_ Максимальный к. п. д. 1]тах для магнитных муфт находится в пределах 0,93—0,95, а для гидромуфт — в пределах 0,97—0,98; к. п. Д. г|м выразим в зависимости от Я' = //ст* —Я*. Из известных соотношений njn — Q*/Q и ti2ln2 -= II.JH имеем т]„ — QJQх и
H--^H*Q2/Ql (4.43)
Уравнение (4.43) — уравнение параболы подобных режимов работы насоса (на рис. 4.17 — пунктирная кривая). Расход Qlt соответствующий частоте вращения пг, найдем совместным решением уравнения (4.43) и уравнения характеристики насосной станции. В результате будем иметь ^ai{b -\-HJQl). Далее, произведя замену
Q2 = (а—Н„^)/Ь и Я* = Яет* — Я', получим
т|м = V1 — Я'/а . (4.44)
Из формул (4.41), (4.42) и (4.44) следует, что i]M >r|Ap и rjM >г)п.
Однако это не означает, что регулирование при помощи муфт всегда выгоднее. При сравнении регулирования при помощи муфт с остальными способами надо пользоваться не к. п. д. rjM, а полным к. п. д. т|м полп, который учитывает потери энергии при регулировании и постоянные потери. Последние имеют место не только во время регулирования, но и при работе нефтепровода, когда регулирование не ведется. Чем меньше частота и продолжительность периодов регулирования, тем менее выгодным оказывается регулирование при помощи муфт.
Сравним теперь способы регулирования дросселированием и перепуском. Из формул г]др = С*Я*/«?*Яет*) и г)п = QtHJ(Q0H*) следует, что если Q0H* >ф*Я„*, то г|„ < т]др. Иными словами, если мощность, потребляемая насосом (насосной станцией), с увеличением расхода возрастает, то регулирование дросселированием выгоднее регулирования перепуском, и наоборот.
Насосы, применяемые на магистральных нефтепроводах, имеют пологие характеристики Q—Я; для них зависимость N — N (Q) — возрастающая функция. Поэтому на магистральных нефтепроводах регулирование дросселированием выгоднее регулирования перепуском.
ТЕХНОЛОГИЧЕСКИЙ РАСЧЕТ МАГИСТРАЛЬНЫХ ГАЗОПРОВОДОВ
5.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И СВОЙСТВА ГАЗОВ
Количество газа, как и любого другого вещества, естественно выражать в единицах массы. Однако принято определять не массу газа, а его объем, приведенный к стандартным условиям. Стандартные условия— это давление, равное 0,1013 МПа, и температура 293 К (20 °С). Не следует путать стандартные условия с нормальными, (0,1013 МПа и 273 К).
Расход газа выражают как в единицах массы, так и в единицах объема. Массовый расход, если нет путевых отборов или подкачек, не изменяется по длине газопровода. Объемный расход возрастает, так как давление по длине газопровода снижается. Объемный расход на входе в газоперекачивающий агрегат, т. е. при условиях всасывания, называют объемной подачей. Объемный расход, приведенный к стандартным условиям, называют коммерческим. Коммерческий расход — аналог массового: по длине газопровода он остается неизменным.
Плотность газа р зависит от давления и температуры. Поэтому данные о плотности должны сопровождаться указанием условий (давление и температура). Однако, когда речь идет о плотности при стандартных условиях, указание на эти условия часто опускают.
Удельный объем — величина, обратная плотности: v = 1/р.
Часто пользуются относительной плотностью газа по воздуху А =
= р/рвозд.
Вязкость газа — свойство, являющееся причиной внутреннего трения, а следовательно, и сопротивления при движении в трубопроводе. Вязкость газа динамическая определяется главным образом количеством движения, переносимым молекулами при переходе их из одного слоя в другой. При увеличении температуры возрастает скорость движения молекул и, следовательно, переносимое количество движения. Поэтому при повышении температуры вязкость возрастает. Зависимость динамической вязкости т} от температуры Т описывается формулой Сатерленда tj== т]0(77273)''5 (273 + С)/(Т + С), где т)0 — вязкость при 273 К; С — постоянная величина.
Теплоемкость (массовая удельная) есть количество тепла, необходимое для нагревания единицы массы газа на один градус: с =
= dq/dT. Теплоемкость зависит от природы газа и от происходящего процесса. Если газ нагревается изохорически, то подводимое тепло q идет на увеличение внутренней энергии и; теплоемкость при постоянном объеме cv ~ dqldT — du/dT. Е!сли же газ нагревается изобарически, то подводимое тепло идет также и на совершение работы; теплоемкость при постоянном давлении
с — d{l — d(u + pv) _ dt
p dT dT dT
Функция i = w + pv называется энтальпией.
Эффект Джоуля — Томсона — это изменение температуры реального газа при дросселировании. Дросселированием в газопроводе можно считать распределенное по длине падение давления. При обычных для газопроводов давлении и температуре дросселирование сопровождается охлаждением газа. Снижение температуры газа при движении его по трубопроводу из-за эффекта Джоуля — Томсона можно объяснить так. Считается, что дроссельный процесс энергетически изолирован. В этом случае внутренняя энергия остается неизменной. Внутренняя энергия включает в себя кинетическую энергию
молекул и потенциальную энергию их взаимодействия. Газ при движении по газопроводу расширяется. В результате увеличивается расстояние между молекулами и, следовательно, возрастает потенциальная энергия их взаимного притяжения. Но поскольку внутренняя энергия, как было сказано, остается неизменной, увеличение потенциальной энергии сопровождается уменьшением кинетической энергии молекул, т. е. снижением температуры газа. Эффект снижения температуры газа при дросселировании характеризуется коэффициентом Джоуля—Томсона D-, (дТ/др);.
Газовые смеси. Любой природный газ — смесь газов. Состав смеси может быть выражен в объемных, мольных и массовых долях. Объемная, мольная и массовая концентрации г-го компонента в смеси будут соответственно vt — Кг/2Кг; у\ = Л/,/2Л/,; yt = mJ'Zm^ здесь t/; — объем г-го компонента; Nt — число молей в объеме Imt — масса г-го компонента. Учитывая, что VJNiy т. е. объем одного моля, согласно закону Авогадро, для всех газов одинаковый, из выражений для Vi и y'i находим, что у\ = vh т. е. мольные и объемные концентрации совпадают. Связь между мольной (объемной) и массовой концентрациями найдем из очевидных равенств: mt = р;Л/; и где р.; — молекулярная масса г-го компонента; р — молекулярная масса газовой смеси. Разделив первое равенство на второе, получим yt = (р^/р) y'i. Отсюда, если учесть, что 2г/г — 1, получается формула для определения молекулярной массы газовой смеси: р = или,
поскольку у\ = vh р =
Уравнение состояния. Состояние газа определяется зависимостью между давлением р, объемом V и температурой Т. Графически эта зависимость может быть изображена семейством изотерм (рис. 5.1). Линии ТА (Т^!, Т^Аг и т. д.) показывают изотермическое сжатие в газовой фазе. По достижении объема vA начинается конденсация. Горизонтальные участки Аф^ А2Б2 характеризуют двухфазное состояние. В точках Би Б2 конденсация заканчивается; очень крутые ветви 5^!, Б2Т2 относятся к жидкой фазе. С увеличением температуры участок двухфазного состояния сокращается. Температура Ткр, при которой линии Б1А1 и Б2А 2 сливаются в точку К, называется критической. Давление ркр, объем Ккр и плотность ркр, соответствующие точке К, тоже называются критическими. Когда газ при по-
Рис. 5.1. График зависимости между р, V и Т
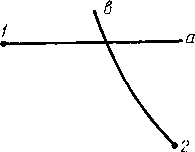
Рис. 5.2. График изобарического /—а и изотермического 2—в процессов
v
Р
стоянной температуре Ткр будет сжат до объема vKp (при этом давление будет равно ркр), его плотность достигнет плотности жидкости. Газ нельзя будет отличить от жидкости. Однородность вещества при этом не нарушится. Но малейшее уменьшение температуры вызовет расслоение на жидкую и паровую (газовую) фазы. При температуре выше критической газ не переходит в жидкость ни при каких давлениях. Аналитическая зависимость между р, V и Т (уравнение состояния) наиболее простой вид имеет для идеального газа, т. е. для газа, подчиняющегося законам Гей-Люссака и Бойля—Мариотта.
Представим себе некоторое количество газа при состоянии 1 и такое же количество газа при состоянии 2 (рис. 5.2, точки 1 и 2). Газ, находящийся в состоянии 1, начнем нагревать, сохраняя давление рхнеизменным. Газ будет расширяться и, согласно закону Гей-Люссака, его объем при температуре Т2 будет V = УгТ^Тг. Газ, находящийся в состоянии 2, будем сжимать при постоянной температуре Т2. Когда давление окажется равным р1г в соответствии с законом Бойля—Мариотта будем иметь V = V., р21рх. Поскольку в обоих случаях V — одна и та же величина (на рис. 5.2 она соответствует точке пересечения изобары 1—а и изотермы 2—в), получим VXT2ITX-- V«p<Jp\ и далее p1VlIT1 = p2VJT2 или pVIT = const. Постоянная величина зависит от количества газа, содержащегося в объеме V, и от его физической природы. Если взять один моль газа, то, поскольку объем его V для всех газов один и тот же, одинаковой для всех газов будет и величина R. Это — универсальная газовая постоянная. Так получается уравнение состояния для одного моля идеального газа (уравнение Клапейрона)
pV = RT. (5.1)
Физический смысл универсальной газовой постоянной R — работа 138
изобарического расширения одного моля газа при нагревании его на один градус.
Подставив в (5.1) значения р, V и Т, соответствующие нормальным условиям, т. е. р0 = 101 325 Па, V0 = 22,4135 м3/кмоль и Т0 — = 273,15 К, получим, что R = 8314 Дж/(кмоль• К).
Если разделить (5.1) на молекулярную массу ц, то получим уравнение состояния для единицы массы газа. Поскольку V7[x = 1/р, это уравнение будет иметь вид р!р = RT, где R — газовая постоянная для единицы массы газа (Дж/(кг-К). Физический смысл R аналогичен физическому смыслу R. В отличие от R численное значение R зависит от состава газа. Таким образом, наряду с молекулярной массой р, газовая постоянная R есть, параметр, характеризующий физическую природу газа. К таким параметрам относятся также плотность газа р (при стандартных или нормальных условиях) и относительная плотность по воздуху Д.
Молекулярную массу определяют, как уже было сказано, по составу газа: р, = остальные упомянутые параметры — по фор
мулам R Я/ц; р = [х/К; Д = ц/цВочД = р/рпо^.
Законы идеального газа не дают существенных ошибок лишь при небольших давлениях. При давлениях и температурах, обычных для магистральных газопроводов, заметное влияние на зависимость между р, р и Т оказывают Ван-дер-Ваальсовы силы: природный газ сжимается больше, чем это следует для идеального газа (силы притяжения между молекулами превосходят силы отталкивания). Эффект «сверхсжимаемости» усиливается при понижении температуры. В таких случаях уравнение состояния должно учитывать реальное поведение газа. Существует очень много уравнений состояния для реальных газов. Но использование их при расчетах газопроводов почти всегда приводит к весьма громоздким выкладкам. Поэтому обычно пользуются скорректированным уравнением Клапейрона: р!р — zRT, в котором отклонения от законов идеального газа учитываются множителем 2, называемым коэффициентом сжимаемости (или сверхсжимаемости, это точнее). Коэффициент z зависит от давления и температуры. При обычных для магистральных газопроводов условиях z <1 (сверхсжимаемость). Коэффициент сжимаемости зависит от состава газа: чем газ тяжелее, тем z меньше. Однако если г взять в зависимости от р/ркр и Т/Тцр, то влияние состава газа исчезает (закон соответственных состояний). Безразмерные давление и температура р/ркр и 77Ткр называются приведенными (рпр и Тпр). Для смеси газов они берутся по отношению к средним критическим давлению и температуре, которые определяются по формулам ркр = Еу,ркр1-; Гир ¦= = 2UjTVp j.
Коэффициент сжимаемости газа любого состава можно определять по графику г = 2 (р„Р, Тир) (рис. 5.3). В нормах технологического проектирования рекомендована следующая формула: z ~
= 1-0,4273 рпрГ-3-668.
5.2. ОСНОВНЫЕ ФОРМУЛЫ ДЛЯ ГИДРАВЛИЧЕСКОГО РАСЧЕТА ГАЗОПРОВОДА
Движение газа в трубопроводе описывается, как известно из газодинамики, уравнениями:
![]()
д (poi) _ _ф
дх dt
(5.2)
(5.3)
Первое из них называется уравнением движения, второе — уравнением неразрывности.
Обозначения: х — координата, совпадающая с осью трубы и направленная по течению газа; р, w и р — соответственно плотность, скорость и давление газа в сечении х (средние значения); t — время; 1 -f р — поправочный коэффициент на неравномерное распределение скоростей по сечению; за малостью влияния его можно не учитывать (при турбулентном течении р = 0,02—0,03); z — высота, на которой находится центр сечения х\ g — ускорение свободного падения; X — коэффициент гидравлического сопротивления; D—диаметр трубопровода, принимаемый постоянным, не зависящим от х.
Уравнение движения выводится из закона изменения количества движения для потока сжимаемой среды. Первый член в левой части этого уравнения характеризует интенсивность изменения количества движения по длине трубопровода, определяется разностью между выносимым через сечение х + dx, и вносимым через сечение х количествами движения (через сечение х в единицу времени поступает количество движения Fpww = Fpw2, а через сечение х -f dx выносится Fpw2 + д/дх (Fpw2) dx\ F — площадь поперечного сечения трубопровода). Второй член характеризует скорость изменения количества движения в объеме Fdx во времени и указывает на нестационарность процесса.
Члены, стоящие в правой части уравнения, определяют проекции на ось х сил, действующих на элементарную массу газа рFdx: сил
давления --pFdxj, тяжести —pg~~Fdx^ и трения
|~--kpw j
знак МИНуС у этих сил
обусловлен тем, что
градиент
давления dp/dx —отрицательная величина, так как давление по длине трубопровода уменьшается, а сила трения и проекции на ось х силы тяжести действуют в направлении, противоположном направлению оси х.
В левой части уравнения неразрывности представлена разность между количествами газа, прошедшего за единицу времени через сечения х + dx и х, а в правой — накопление газа за то же время в элементарном объеме Fdx. Если через сечение х -f dx вышло больше газа, чем поступило через сечение х, то накопление в объеме Fdx должно быть отрицательным. Этим объясняется знак минус в правой части уравнения неразрывности. К уравнениям (5.2) и (5.3) добавляется еще уравнение состояния / (р, р, Т) =¦¦= 0, где Т — температура. Решение этой системы уравнений, определяющее р, р, w и Т в зависимости от х и t, сопряжено с громадными трудностями. Поэтому прибегают к упрощениям, к линеаризации уравнений.
Рассмотрим установившееся течение газа в трубопроводе. Такой режим движения газа принимают при решении целого ряда практических задач, в том числе и при технологическом расчете магистрального газопровода. Для установившегося течения уравнения (5.2) и
(5.3) упрощаются, так как пропадают члены, содержащие время. Получим
![]()
dx dx ^ dx 2D ’
(5.4)
d (pm) _ q dx
(5.5)
Из (5.5) видно, что рш — постоянная величина. Поэтому d (рw*) = = pwdw = pdw2/2. Учитывая это, приходим к известному уравнению
Это уравнение говорит о том, что падение давления в трубопроводе складывается из падения давления на трение, на подъем газа по вертикали и на возрастание скорости. Уравнение (5.6) — исходное для вывода основных формул гидравлического расчета газопроводов. Чтобы получить эти формулы, следует из (5.6) исключить переменные р и w. Это достигается при помощи уравнения неразрывности, которое запишем в виде
Fpw == М, (5.7)
(М — массовый расход), и уравнения состояния
plp = zRT. (5.8)
Температуру Т принимают постоянной. Коэффициент г, учитывающий отклонение от законов идеального газа, также считают постоянным, поскольку он в диапазоне обычных для газопроводов условий изменяется мало.
Заменив в (5.6) согласно (5.7) и (5.8) р на p/(zRT) и w на MzRTl(Fp) и пренебрегая членом рgdz (его следует учитывать лишь для газопроводов, проходящих по сильно пересеченной местности), получим
f 2Г'1 V D р )
и далее после интегрирования МЪЯТ /. L
" к z72 \ D рк )
где L — длина расчетного участка газопровода, начало и конец которого обозначены индексами «н» и «к». Второе слагаемое в скобках (2 In pJpK) учитывает возрастание кинетической энергии по длине трубопровода. Для магистральных газопроводов эта величина по сравнению с XLID весьма мала. Пренебрегая ею и заменив F на nD2/4, получим
= (5.9)
По этой формуле можно определить падение давления в трубопроводе, если задан массовый расход М.
Если расход М — искомая величина, то из (5.9) получаем
=-л/—
А \ zR
М=—Л/^——Db. (5.10)
- Х/ zRTKL v '
Здесь должны быть заданы давления ри и рк. Разумеется, что остальные величины, входящие в (5.9) или (5.10), также должны быть известны. Формулу (5.10) называют уравнением или формулой расхода, формулу (5.9) — формулой падения квадрата давления. В проектных и эксплуатационных организациях определяют, как уже было сказано, коммерческий расход Q, т. е. объемный расход, приведенный к стандартным условиям.
Заменим в (5.10) М на Q: М = Qp„. Плотность при стандартных условиях выразим в виде рст = pcJRTcr, а газовую постоянную R — через газовую постоянную воздуха и относительную плотность А : R = Rвоэд/А. После таких замен получим, что коммерческий расход
<5Л'>
V 2Т
где
к = я_ у _
4 Рст
Формула для разности квадратов давлений примет вид
р2 — р1 =-.—
гПХА Q2.
(5.12)
I и к Кг Dr,
Входящие в эти формулы г, Т п А, подлежат предварительному определению. Вычислим, чему равен коэффициент Л^. Имеем: температура Гст = 293 К, давление рст = 101,3-103 Па, газовая постоянная воз-духа /?[юзд 287 м2/(с2-К). Следовательно,
^ = 3,14-293 -sJW 0 0385 м2 с-A:0,5
4 101,3-103
5.3. ТЕМПЕРАТУРНЫЙ РЕЖИМ ГАЗОПРОВОДА
Температура движущегося в трубопроводе газа зависит от физических условий движения и от теплообмена с окружающей средой. Для решения задачи привлечем уравнение первого начала термодинамики. Имеем dq = da -f- pdv, где dq — количество подведенной теплоты; du — изменение внутренней энергии газа; р — давление; v —¦ удельный объем газа; pdv — работа, совершаемая газом. Количество теплоты dq складывается из подведенной теплоты извне (dqBn) и выделившейся в результате трения (dqTp). Для газа, движущегося в трубопроводе, теплота, подведенная извне на участке dx,
dqBn= —knD(T—T0)dx/M,
где k — коэффициент теплопередачи от газа в окружающую среду; D —диаметр трубопровода; Т — температура газа в сечении х; Т0 — температура окружающей среды; М — массовый расход.
Представив работу pdv в виде d (р/р) — dpiр, где р — плотность газа, получим
-
J?9JT-To)dX_ +
= du { d/ _рч_
ор_
М V р ) р
и далее, поскольку и + р!р = i (энтальпия), knD (Т — Т0) dx i_(Uhf = di_dp__
М р
Заметим здесь, что теплота dqTР, выделившаяся на участке dx, равна Xdx/D (w2l2) и что этой же величине равно и — dp!р (если пренебречь изменением кинетической энергии и влиянием силы тяжести). Следовательно, dqTp и — dpiр сократятся. Это формально. Физический смысл здесь в том, что работа, затраченная газом на преодоление трения, тотчас же возвращается газу в виде теплоты dqTр. Компенсация работы трения выделившейся теплотой — внутренний процесс, а рассматриваемое уравнение выражает собой баланс энергии между газом и окружающей средой. Поэтому в нем не должно быть ни работы трения, ни теплоты трения. Итак, получим
— knD(T — T0)dx!M=-di. (5.13)
Теперь учтем, что энтальпия — функция температуры и давления i ~ i (Т, р) и, следовательно,
di
Вспомним, что (дИдТ)р — ср — теплоемкость при постоянном давле-нии. Что представляет собой (дИдр)т, выясним, предположив, что i — постоянная величина. В этом случае
Отсюда получаем, что
\ др )т V дТ )р \ др Ji
Но (dT/dp)i = Dt — коэффициент Джоуля — Томсона. Следовательно, (дИдр)т = —CpDi и, далее, di = cpdT—cj^idp. Введем это в (5.13) и разделим (5.13) на ср:
knD (Т — Тв) dx
dT-Didp.
McD
Теперь представим dp в виде dx и примем, что градиент паде-
dx
ния давления dp/dx == — (рн—pK)/L (линейный закон распределения давления). Затем, обозначив для краткости knD/(Mcp) = а, будем иметь
- а (Т — Т„)dx dT + Di
Ри ~ Рк dx и
далее
dT
После интегрирования получаем следующую формулу, определяющую температуру газа на расстоянии х от начальной точки газопровода:
Рис. 5.4. Кривые изменения температуры газа по длине газопровода:
/ — по Шухову; 2 — с учетом эффекта Джоуля — Томсона
.7
Т = Т0 +
(Т„-Т0) ехр
(—ах)—?>, Рн
~'Рк [1—ехр (-ах)].
(5.14)
aL
Если здесь отбросить последнее слагаемое, то получим знаменитую формулу Шухова
Т=Т0 +(Г„ — Т0)ехр( —ах). (5.15)
Формула Шухова описывает распределение температуры по длине трубопровода, обусловленное теплопередачей в окружающую среду. Согласно (5.15) при Тн >Т0 температура газа Т в любой точке газопровода больше Т0. Лишь при х = оо Т = Т0. В формуле (5.14) последнее слагаемое учитывает понижение температуры из-за эффекта Джоуля —Томсона. Этой формулой следует пользоваться, когда требуется повышенная точность расчета.
На основании (5.14) и (5.15) получаются следующие формулы для вычисления средней температуры газа по длине трубопровода:
Тс р = Т0 + (Т„
- Т0)
-L-exP(~aL)
aL
Рн — Рк Л I — ехр ( — al)
—
^1--еХР^ )
(5.16)
¦D.
aL
Тср =: Т„
+ (Т„- То) ' exp (.--^L- .
(5.17)
aL
Температура газа, входящая в формулы для гидравлического расчета газопровода, принимается равной Тср. На рис. 5.4 изображен график, показывающий характер изменения температуры по длине газопровода.
5.4. КОЭФФИЦИЕНТ ГИДРАВЛИЧЕСКОЮ СОПРОТИВЛЕНИЯ ДЛЯ ГАЗОПРОВОДОВ. КОЭФФИЦИЕНТ ЭФФЕКТИВНОСТИ
Природа гидравлического сопротивления для газа и капельной жидкости одна и та же. Поэтому нет принципиальных различий между формулами, определяющими коэффициент гидравлического сопротивления для газопроводов и нефтепроводов. Однако при расчете магистральных газопроводов обычно пользуются специальными формулами. До 60-х годов весьма широко применялись эмпирические формулы, в которых коэффициент гидравлического сопротивления X выражен в зависимости от числа Рейнольдса и диаметра трубопровода:
X = X (Re) и X = X (D). Число таких формул велико, и порой было трудно решить, какой из них следует отдать предпочтение. После появления универсальных формул X - - X (Re, k/D), учитывающих как число Рейнольдса, так и относительную шероховатость труб (k/D), стали пользоваться формулой
X = 0,067 (158/Re -| - 2 k/D)0-2, (5.18)
аналогичной по своей структуре формуле Альтшуля
Я. = 0,11 (68/Re-! -k/D)°&.
При режиме гладкого трения, когда 158/Re ; - 2к/D, она переходит в X —- 0,1844/Re0-2, а при квадратичном режиме, когда 158/Re ^ 2k/D, переходит в
к = 0,067 (2/e/D)0'2 (5.19)
и в частном случае, когда к =¦--- 0,03 мм (по данным ВНИИгаза — среднее значение эквивалентной шероховатости для новых газопроводов) X = 0,03817/D0'2.
Квадратичный режим движения газа — обычный для магистральных газопроводов. Режим смешанного трения бывает при неполной загрузке газопровода. Режим гладкого трения характерен для распределительных газопроводов в населенных пунктах. Считается, что переход от режима смешанного трения к квадратичному происходит при числе Рейнольдса
Renep-U(2k/D)~'*. (5.20)
Если Re >Reriep, то режим квадратичный. Число Рейнольдса удобно представить в следующем виде:
-- __ 4 Аряолд(?
яОг| п!)ц
и далее, выразив Q в млн. м:|/сут, D — в мм и г] — в Па-с,
Re — 17,75- 10я. (5.21)
Di]
Из (5.20) и (5.21) получается выражение для расхода, соответствующего Re„cp: <?псг> “• 0,219-10~:,D2'5)]/(AI',’A) пли при k ^ 0,03 мм Qnep = 0,0422D2-5 г]/Д. Режим считается квадратичным, если Q >- 0„ер. Щ
Коэффициент гидравлического сопротивления с течением времени изменяется.
Если газ сухой и не содержит сероводорода, то находящиеся в нем твердые частицы шлифуют стенки трубопровода, шероховатость, а следовательно, и коэффициент гидравлического сопротивления постепенно уменьшаются. И наоборот, наличие в газе влаги и особенно сероводорода (внутренняя коррозия) приводит к постепенному возрастанию шероховатости и коэффициента гидравлического сопротивления. Сильное влияние па гидравлическое сопротивление оказывают скопления п пониженных точках трассы конденсата и влаги. К значительному увеличению гидравлического сопротивления приводит образование гидратов. Изменение гидравлического сопротивления трубопровода по сравнению с проектным характеризуется коэффициентом эффективности ф, где Хг — теоретическое значение
коэффициента гидравлического сопротивления, определяемое обычно по формуле (5.19); Яф— фактический коэффициент гидравлического сопротивления. Коэффициент находят из формулы, определяющей пропускную способность газопровода. Входящие в нее значения Q, рн, рк и А берут по фактическим, опытным данным, Т и 2 предварительно вычисляют, использовав средние значения давлений и температур, измеренных в начальной и конечной точках рассматриваемого участка трубопровода. Измерения делают в дни, когда режим наиболее близок к стационарному.
Коэффициент эффективности свидетельствует также об изменении пропускной способности трубопровода: Е = Qj,/Qr, где Q, — фактическая пропускная способность-, QT — пропускная способность , вычисленная при коэффициенте гидравлического сопротивления Хт и при значениях рп, рк, А, Т и г, полученных по опытным данным. Коэффициент эффективности определяют периодически для каждого участка (перегона между станциями). По величине Е судят о загрязненности трубопровода. Низкие значения Е указывают на необходимость очистки трубопровода. Скопления конденсата и воды удаляют продувкой. Если это не приводит к нужному эффекту, то прибегают к очистке трубопровода специальными скребками.
5.5. ПАДЕНИЕ ДАВЛЕНИЯ ПО ДЛИНЕ ГАЗОПРОВОДА.
СРЕДНЕЕ ДАВЛЕНИЕ
Распределение давления по длине трубопровода можно получить из (5.12), заменив L на х:
, , 1 гТХД
р- == р„-------Qх
у п к* D5
или
если принять для краткости 1 гТ). А К2 D6
Это уравнение падения квадрата давления.
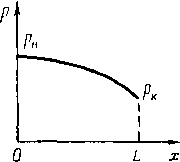
Рис. 5.5. Кривые распределения давлений и квадратов давлений по длине газопроводов
Для магистральных газопроводов можно считать, что с не изменяется по длине трубопровода и, следовательно, зависимость р2 от х — линейная (рис. 5.5). Из (5.22) получаем уравнение распределения давления по длине газопровода
Р = Vp2h-cQ2*. (5.23)
Замечая, что согласно (5.11) cQ2 = (р2н—pfylL, представим уравнение 5.23) в другом виде:
График р = р (х) — отрезок ветви параболы, ограниченной точками
О, /?н и L, рк (см. рис. 5.5).
Воспользовавшись формулой (5.24), найдем среднее давление в газопроводе:
2 2
Рн-Рк xdx
L
После интегрирования получаем Рср -
2 Рн - Pi
3 Р2„-Р2к
или
з V Ри + Рк /
Среднее давление устанавливается в газопроводе после остановки перекачки. По среднему давлению находят коэффициент г, учитывающий отклонение от законов идеального газа, а также определяют количество газа, содержащегося в трубопроводе. Положив в (5.24) P — Рср, найдем расстояние, на котором давление равно среднему: , -Лео —
Рв-Рк
Из этой формулы видно, что расстояние хср зависит от отношения давлений pJpK. При изменении pJpK от 1 до оо xcpIL изменяется от 0,5 до 5/9.
Газопроводы, отличающиеся от простых, т. е. однониточных постоянного диаметра, будем называть сложными. Таковыми являются многониточные газопроводы, газопроводы с лупингами, газопроводы, состоящие из последовательно соединенных участков различного диаметра. К сложным будем относить также газопроводы, имеющие путевые отборы или подкачки. Цель расчета сложных газопроводов такая же, как и для простых: определение либо пропускной способности, либо давлений в узловых пунктах (начальная или конечная точки, точки отборов или подкачек).
Основные расчетные формулы — те же, что и для простых газопроводов, т. е. (5.11) и (5.12). Эти формулы можно применять либо для отдельных ниток рассчитываемого сложного газопровода, либо в том случае, когда газопровод приведен к простому.
Представим упомянутые формулы в более компактном виде. Входящие в них г, Т и Д определяются отдельно, и их можно считать заданными. Включив эти величины в состав постоянного коэффициента А0, получим
Pl-Pl- ВафШО\
(5.25)
(5.26)
где Ао~К/л/гТА-, Во—1/At.
При квадратичном режиме течения, если постоянные величины, содержащиеся в (5.19), ввести в коэффициент А0, формулы (5.25) и
(5.26) примут вид
(5.27)
![]()
![]()
(5.28)
Однониточный газопровод с путевыми отборами и подкачками
Пусть газопровод состоит из участков, границами которых служат пункты отборов (подкачек). Будем считать, что эти участки —простые трубопроводы (рис. 5.6). Отборы (подкачки) qlt q2, qa и т. д. заданы, известны, следовательно, расходы на участках будут Qx, Q2, Q3 и т. д. Требуется определить давления в узловых точках газопровода. В соответствии с (5.26) и рис. 5.6 имеем:
для первого участка pl—p\ = Для второго участка
р\—р\ = B(lQp.2L2/Df, для т-го р2т_—р2т = B0Q2mXmLJD5m; для конечного pi-1—рк = B0QlKLJDl. Сложив эти уравнения, получим
k
| 1 | *1 |
Чг | Ь | Jm- t |
Jm | I K-t |
| Ь г |
L3 Qj |
Qm | Я ^ |
PH ft Рг Рз Рт-1 Рт /V/ Рк
Рис. 5.6. Схема сложного однониточного газопровода
Давление в конце участка т может быть найдено из формулы
т
' Pl-Pl-^QPlL.lD] (5.29)
м
или
j=m+l
в зависимости от того, какое давление известно — рн или рк.
Предварительно, разумеется, должны быть определены коэффициенты гидравлического сопротивления X,-. Это не вызовет затруднений, поскольку Qi и Di известны. Если отборы (подкачки) невелики, то целесообразным оказывается трубопровод постоянного диаметра. Будем иметь
1=1
Приняв, что режим течения газа квадратичный и, следовательно, коэффициенты гидравлического сопротивления на всех участках одинаковы, получим
п2_р2 ^ В _А_ у Q2L
“н г к 0 ?)й i
откуда легко определяется диаметр D, поскольку коэффициент гидравлического сопротивления А, есть функция диаметра. При необходимости можно воспользоваться формулой (5.29) или (5.30) и определить давления в узловых точках.
Далее речь пойдет о сложных газопроводах, не имеющих путевых отборов или подкачек. Режим течения будем считать квадратичным.
Способы приведения сложного газопровода к простому
Сложный газопровод может быть приведен к простому заменой его на эквивалентный или при помощи специальных коэффициентов. Эквивалентным газопроводом называют однониточный постоянного диаметра, равноценный по пропускной способности рассчитываемому. Очевидно, что для любого газопровода можно подобрать целый ряд эквивалентных, различающихся по диаметру и длине. Их может быть столько, сколько существует значений внутренних диаметров труб, выпускаемых промышленностью. Чтобы задача была определенной, одна из указанных величин — либо диаметр, либо длина — должна быть задана. Вторая должна определяться специальным расчетом. Ясно, что эквивалентной может быть названа лишь эта вторая, т. е. подлежащая определению величина. Если считать заданной длину эквивалентного газопровода (естественно принять ее равной фактической длине L), то пропускная способность рассчитываемого газопровода будет определяться формулой, аналогичной (5.27):
![]()
(5.31)
А если заданным считать диаметр эквивалентного газопровода D0 (произвольная величина), то
(5.32)
В первом случае определению подлежит эквивалентный диаметр Д,, а во втором — эквивалентная длина L3. Привести сложный газопровод к эквивалентному — значит определить специальным расчетом либо D3, либо L3. Оба эти способа равноправны. Расчет состоит в том, чтобы выразить D3 или 1э сложного газопровода через D3 или L3 простых трубопроводов, входящих в его состав. Для простого трубопровода эквивалентный и фактический диаметры совпадают, т. е. D9 = D, а эквивалентная длина L3 = L (D0/D)5’2 следует из сопоставления формул (5.27) и (5.32). Приведение сложного газопровода к эквивалентному при помощи D3, как видно, несколько проще, чем при помощи L3. Отдадим ему предпочтение.
Теперь рассмотрим приведение сложного газопровода к простому при помощи специальных коэффициентов. Введем в рассуждение «эталонный газопровод». Диаметр эталонного газопровода (обозначим его D0) — произвольная величина. Удобно принять D0 = 1000 мм. Пропускная способность эталонного газопровода
![]()
(5.33)
Умножим и разделим правую часть (5.31) на D^6. Получим, что пропускная способность сложного газопровода
![]()
(5.34)
Сомножитель kp называется коэффициентом расхода газопровода: kv — (D3/Z)0)2’6. Из сопоставления (5.34) и (5.33) следует, что kp =
- Q/Qo, откуда и происходит название этого коэффициента.
Для простого трубопровода диаметром D kp — (D/D0)2-6, поскольку в этом случае, как уже было показано, D3 = D.
При рг:счете сложных газопроводов, содержащих блоки с параллельными трубопроводами различной длины, весьма удобным оказывается коэффициент, включающий в себя не только эквивалентный диаметр D „ но и длину газопровода L. Обозначим этот коэффициент я и назовем его «коэффициентом приведения». Формула пропускной способности теперь будет иметь вид
Из формул (5.35), (5.34) и (5.31) следует связь к с Ар и Da:
к = Do,6Wr = DY/^L.
Как и D3, коэффициенты kp и и учитывают особенности конструкции рассчитываемого газопровода. Поэтому определение kp или х сложного газопровода, как и определение D3, означает приведение его (газопровода) к простому. Итак, чтобы рассчитать сложный газопровод (вычислить Q или pi—р^), необходимо прежде всего определить D3 или kp или и этого газопровода.
В большинстве случаев сложный газопровод можно представить состоящим из отдельных блоков трубопроводов, соединенных друг с другом параллельно или последовательно. В свою очередь, каждый из этих блоков может состоять из более мелких блоков, соединенных тоже параллельно или последовательно вплоть до отдельных ниток.
Рассмотрим, как определяются D3, kp и х при параллельном и последовательном соединении трубопроводов (или блоков).
Параллельные газопроводы
Пропускная способность газопровода любой конструкции, в том числе и системы параллельных трубопроводов, как уже было показано, может быть выражена формулами (5.31), (5.34) или (5.35).
Пропускная способность t'-ro трубопровода, входящего в эту систему, Qc выражается такими же формулами. Следует лишь D3, kp
П
или к приписать индекс i. Учитывая, что Q=?Qj, где п — число
1=1
параллельных трубопроводов, получаем
^•6 = iz?321; /fep = 2>Pi; * = (5.36)
i=i i=i ;=i
Очевидно, что первые два равенства действительны лишь при условии, что L, = L, т. е. все параллельные трубопроводы имеют одну и ту же длину. Последнее равенство свободно от этого ограничения; оно справедливо также и при неодинаковых длинах параллельных трубопроводов. В этом — некоторое преимущество приведения сложного газопровода к простому при помощи коэффициента н.
Последовательно соединенные газопроводы Напишем формулы разности квадратов давления;
L
и к иi
Эти формулы пригодны для газопроводов любой конструкции, в том числе и для рассматриваемой.
Аналогично (5.37) напишем, чему равны разности квадратов давлений р2—р\, р2—р\, р\—р2, .... р\_х—р2 для последовательно соединенных участков. Сложив эти равенства, будем иметь
к к ¦ р2 = BQ2 V ; Р2 — Р2 = —!— Q2V
р2-Г Н
k
(=|
Теперь сопоставим (5.37) и (5.38). Получим, что при последовательном соединении трубопроводов (или трубопроводных блоков)
= \ _L_. (5.39)
5,2
D
p
.=i [=j
Газопроводы, состоящие из параллельно и последовательно соединенных блоков
Процедура приведения таких газопроводов к простому или, что то же, определение их D3, kp или х прежде всего состоит в том, чтобы выделить (начала самые крупные блоки, из которых состоит газопровод, затем более мелкие блоки и так далее до отдельных ниток. Помня, что при параллельном соединении складываются D2&, kpi или хе, а при последовательном — LjD^, Ьс/к2 или 1/х2, составляются в той же последовательности выражения, определяющие эти параметры. Следующий этап — определение численных значений D3, kp или х отдельных трубопроводов (ниток) затем блоков и, наконец, всего газопровода Способы приведения сложного газопровода к простому при помощи D3, kp или х, очевидно, равноценны. Однако при неодинаковых длинах параллельных трубопроводов в каком-либо блоке коэффициент х оказывается предпочтительным.
Газопроводы с лупингами\ увеличение пропускной способности газопроводов
Лупинги предназначаются либо для увеличения пропускной способности, либо для повышения давления в конечной точке газопровода, либо для снижения давления в начальной точке. Цель расчета — определение длины лупинга, при которой обеспечивается требуемый эффект. Газопровод с лупингом — один из простейших видов сложных
газопроводов. При расчете газопроводов с лупингами удобно пользоваться коэффициентами расхода.
Определим коэффициент расхода газопровода, схема которого изображена на рис. 5.7. Газопровод состоит из участков L—х и х. Первый из них — однониточный, диаметром коэффициент расхода этого участка — kpl. Участок х —двухниточный; диаметры ниток— Dj и D2, коэффициент расхода kpi2. Участки L—х и х соединены последовательно. Поэтому в соответствии с (5.39) будем иметь
где kp — коэффициент расхода всего газопровода; коэффициент расхода kpi следует считать известной величиной; коэффициент расхода ?Р12 подлежит определению. Поскольку трубопроводы / и 2 соединены параллельно, согласно (5.36) kpl2 = kpl + kP2 (как и kpl, коэффициент kP2—тоже известная величина). Получим
L L — х х
откуда
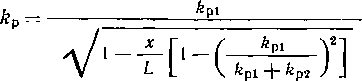
(5.40)
Теперь сравним пропускную способность газопровода с лупингом (Q) с пропускной способностью газопровода без лупинга (Qx). При условии, что давления р„ и рк до и после прокладки лупинга одинаковые, на основании формулы (5.34) можно написать, что коэффициент увеличения пропускной способности х = Q/Qx = kp/kpi. Учитывая (5.40), получим, что
(5.41)
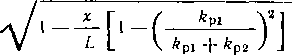
Из (5.41) находим, что длина лупннга, необходимая для увеличения пропускной способности в % раз,
Теперь найдем длину лупинга, для случая, когда необходимо повысить давление р.< до рк* (при неизменной пропускной способности Q).
В частном случае, когда диаметры магистрали и лупинга и D2 одинаковые, кр.г ----- kvl и формулы (5.41) и (5.42) примут вид
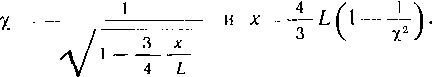
(5.43)
Из уравнений
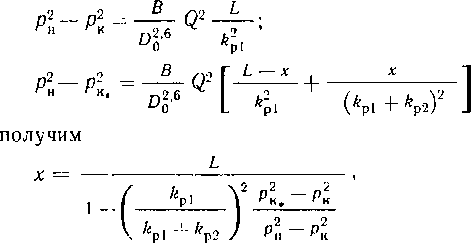
(5.44)
а при одинаковых диаметрах лупинга и магистрали (Z)a = Dt)
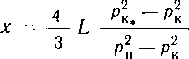
Если же лупинг прокладывается для снижения давления ра до то, поступив аналогично, найдем
L
х
\-( fepl V Рн“Рк
V ^р1 Ч" k р2 )
и при D2 == Dv
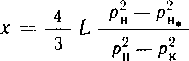
Второй способ увеличения пропускной способности газопровода — удвоение числа компрессорных станций. Считая, что это равносильно сокращении) расстояний между станциями вдвое, напишем: до удвоения числа станций
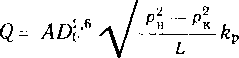
и после удпоения
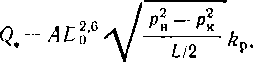
Отсюда следует, что коэффициент увеличения пропускной способности
x=Q*/Q = V2 .
Многониточный газопровод с лупингом
Рассмотрим n-ниточный газопровод с лупингом. Начальная точка лупинга соединена со всеми п трубопроводами (рис. 5.8). По-прежнему будем считать, что рассматриваемый газопровод состоит из двух последовательно соединенных блоков: L—х и х. Блок L—х составлен из л, а блок х — из n + 1 параллельно идущих ниток. Очевидно, что формулы для х и для х будут иметь вид, аналогичный (5.41) и (5.42).
п я-}-1
Достаточно лишь заменить в них kpl на ?/гр* и kpl~\-kp2 на ^kpi.
i=i i=i
Получим, что коэффициент увеличения пропускной способности при прокладке лупинга длиной л:
Х=--'
" -:---.
(5.45)
а длина лупинга при заданном значении %
Из трех последних формул видно: чем больше число ниток п, тем меньше эффективность лупинга — коэффициент увеличения пропускной способности % уменьшается, длина лупинга, обеспечивающая заданные х или Л**, возрастает.
Эффективность перемычек
Если лупинг соединен лишь с частью параллельных ниток (рис. 5.9) или лишь с одной из них, то линия падения квадратов давления у ниток, связанных с лупингом, будет с изломом (в точке подключения лупинга), а у «свободных» ниток — без излома. Давление в свободных нитках будет выше, чем в лупингованных. Если теперь соединить перемычкой все нитки, то давления сравняются и линия падения квадратов давления будет для всех ниток одна и та же (на рис. 5.9 — пунктирная). Произойдет перераспределение расходов, в результате чего пропускная способность газопроводной системы увеличится. Отношение пропускной способности газопровода с перемычкой к пропускной
156
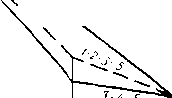
J-4 -S
р,
Рис. 5.8. Схема многониточного газопровода с лупингом
L — х и х после соединения всех ниток ь*------------------[-*---
способности до включения перемычки будем называть эффективностью перемычки. Перемычки эффективны не только в местах присоединения лупингов, но и в точках, где изменяются диаметры трубопроводов. В этих точках изменяется угол наклона линии падения квадрата давления, и соединение перемычкой таких ниток с другими приведет к перераспределению расходов и, следовательно, к увеличению пропускной способности. Очевидно, что с увеличением числа ниток эффективность перемычки уменьшается. Очевидно также, что эффективность перемычки уменьшается с уменьшением различия в диаметрах участков. Если диаметры параллельных ниток не изменяются по длине и если отсутствует лупинг, то перемычки как средство, увеличивающее пропускную способность газопровода, оказываются бесполезными (в этом случае линия падения квадрата давления будет одна, общая для всех параллельных ниток). Однако это не означает, что для таких газопроводов перемычки не нужны. Перемычки позволяют, например, уменьшить снижение пропускной способности при аварийных или планово-предупредительных ремонтах трубопровода. Эти работы ведутся не на всей поврежденной нитке, а на сравнительно небольшой ее части. При помощи кранов ремонтируемый участок отключается. Пропускная способность газопровода при этом снижается. Очевидно, что чем меньше длина ремонтируемого участка
и, следовательно, чем большее число перемычек имеет система трубопроводов, тем меньше будет снижение пропускной способности. Определим число перемычек, при котором пропускная способность уменьшается до заданного предела. Обозначив длину ремонтируемого участка L—х, получим, что число перемычек
![]()
Пусть общее число ниток газопровода равно п. Тогда при отключении на участка L—х одной нитки на ремонт газопровод можно считать
157
(п—1)-ниточным с лупингом длиной х. Далее поступим аналогично тому, как это было при определении коэффициента увеличения пропускной способности /2-ниточного газопровода прокладкой лупинга. Отличие состоит лишь в том, что сейчас требуется определить не коэффициент увеличения пропускной способности, а коэффициент ее уменьшения t|) = Q„_i/Qn, где Q„_j — расход при отключении участка L—х одной из ниток на ремонт и Qn — расход, когда все нитки загружены полностью. В результате будем иметь:
л —I
Отсюда находим относительную длину перемонтируемой части газопровода xlL и подставляем в (5.46). В результате получаем формулу, определяющую число перемычек в зависимости от заданного снижения пропускной способности:
и формула числа перемычек будет выглядеть проще:
т == ^(l+W - 1 .
1 — г|>2
5.7. РАСЧЕТ ГАЗОПРОВОДА С УЧЕТОМ РЕЛЬЕФА ТРАССЫ
Согласно нормам технологического проектирования газопроводов рельеф следует учитывать в тех случаях, когда на трассе имеются точки, расположенные выше или ниже начального пункта газопровода более чем на 200 м. Представим себе, что такой газопровод состоит из соединенных друг с другом прямолинейных наклонных участков. Начало и конец каждого из них — характерные точки трассы, геодезические отметки которых существенно различные. Микрорельефом участков пренебрегаем. Для любого из этих участков
| mlZ. (5.47)
Привлечем сюда уравнение состояния piр — zRT и сделаем замены:
4 М 4MzRT . dz ,
где Az — р;зность высот конца п начала участка; 1 — длина участка. Кроме того, умножим (6.47) на р. В результате получим:
Az
J/)- ^M-h |-a—^-p^dx
где
11 л aAz
(индексы «н» и «к» означают начало п конец наклонного участка).
Далее целесообразно индекс «п» присвоить началу первого участка, а индекс «к» — концу последнего. Первый, второй, третий и т. д. участки, составляющие рассматриваемый газопровод, обозначим соответствующими цифрами. Этими же цифрами будем обозначать конечные точки участков. Таким образом, для первого участка
Умножим второе уравнение па ехр (aAz^, третье на ехр [а (Дг.2 I Az,) I, четвертое па ехр \а (Az3 I Аг3 + Дгх) 1 и т. д. и учтем, что
аД?! ~ о (z, — г„); а (Az3 -|- Az,) а (г,— z„); а (Лг3 f Лг2 | Дг,) ¦ a (z3 — ?„) и т. д.
Затем сложим уравнения для всех участков. Приняв гн = 0, получим
Pl~ р\чЩ) К) - М2Ь У /. гх: (!г- :) . (5.48)
V ^ afa-Zi-j)
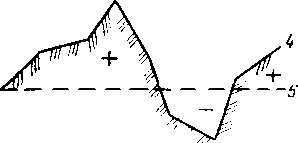
3
Теперь воспользуемся формулой
![]()
и примем exp (azt) ж 1 -f azi -f . Отсюда
![]()
(агг-х)8
2
]
![]()
a (21 —
“ 1 + ~(г1 +;ri-l)-
a (Zi — 2<_!)
1 + агг_ 1 +
Примем также exp (azK) ж 1 + azK. Подставив это в (5.48), получим
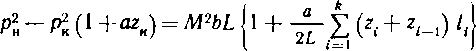
(5.49)
и далее
(5.50)
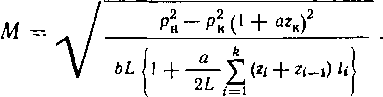
Здесь azK учитывает влияние разности высот конечной и начальной точек газопровода на его пропускную способность. Чем выше расположена конечная точка по отношению к начальной (чем больше zK), тем пропускная способность меньше, и наоборот.
а к
Слагаемое - У (Zj-fZj-i)/,- учитывает влияние на пропуск-
i=i
ную способность геодезических отметок промежуточных точек, т. е. влияние характера профиля трассы. Заметим, что
1 к
— ^(zt + zi_1)li = F представляет собой алгебраическую сумму
2 i=i
площадей, заключенных между линией профиля трассы и горизонтальной линией, проведенной из начальной точки трассы (рис. 5.10). Там, где линия профиля проходит выше горизонтальной линии, площадь F имеет знак плюс, а где ниже — минус. Пропускная способность, как это видно из (5.50), будет больше у того газопровода, у ко-160 торого при прочих равных условиях суммарная площадь /• меньше.
Например, пропускная способность топронодч / Я......3 4 меньше
пропускной способности горизонтального газопровода 1-5 такой же протяженности и такого же диаметра не только из-за того, что г4 _>zB, по и потому, что = 0, а /•'/_2...,;--/;>0. Влияние вида профиля трассы на пропускную способность обусловлено тем, что в начале трубопровода плотность газа больше, чем в конце. Если
а к
azK и —- (Zi -hzi-i)ti отбросить, то (5.49) и (5.50) обратятся в уже
известные нам формулы для расчета газопроводов, проходящих по равнинной местности.
5.8. ХАРАКТЕРИСТИКИ НАГНЕТАТЕЛЕЙ
Характеристикой центробежного компрессора называется зависимость отношения давлений (степени сжатия) г, политропического коэффициента мощности (к. п. д.) т)пол и внутренней мощности от расхода при различной частоте вращения ротора. Известно, что
ляяраь
Ппол) Ni — fit2, з (Qb> рв» Рв> w)) (5.51)
где Qa — расход; рв — давление; рв — плотность газа при условиях всасывания, называемых обычно начальными-, D ., —диаметр рабочего колеса; ш — угловая скорость.
На основании теории подобия зависимость (5.51) представляют в критериальной форме:
PbD2u V ®2и2 -\JzaRTв)
где и2 = Dto) —окружная скорость; QJ(D%ui) — коэффициент расхода; u^/^JzbRTв — число Маха.
Согласно (5.52) можно построить графики зависимости безразмерной мощности Ni/pBD'iul от безразмерного расхода QJ(D\u2) при различных числах Маха. Но поступают иначе. Поскольку D2 — заданная величина, заменяют окружную скорость иг частотой вращения ротора п и переходят к следующему выражению:
е, Л-«и., “ /i ,-2 ,з (^~ , V (5 • 53)
Pb«j V п л/znRTu)
где AVpBrt3, Qb/п и h/'s/zbRTb -размерные величины, пропорциональные соответствующим безразмерным параметрам в (5.52).
Чтобы характеристики были пригодны для природных газов различного состава, их приводят к фиксированным, целесообразно выбранным условиям. Параметры приведения: Rllp = 490 Дж/(кг-К); Тъ. пр = 288 К; 2В. пр = 0,91 и ппр — пи (номинальная).
В результате получаем
Е, т1пол, Г-^1 =/i,a,3rQ..p, f—) . (5-54)
L Рв Jnp L \ tin /пр
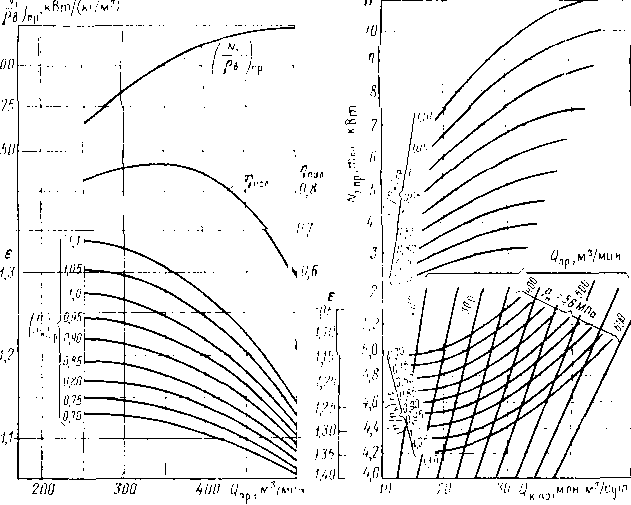
Рис. 5.11. Приведенные характеристики нагнетателя 370-14-1. Условия приведения: Тв. пр = 288 К; Rnp = 500 Дж/(кг-К); 2D.np =40.9i; n„= 5300 i/мин
где
п н п
pRunT
иpJ в. пр
(5.55)
ZbRT d
V; Qa
V pH /пр Рв V П /
/_«_Ч =_П_ /г^
V п„ /пр п„ V
Такие характеристики, называемые приведенными, были разработаны во ВНИИгазе. В итоге широко поставленнв1х натурных испытаний центробежных нагнетателей ВНИИгазом изданы специальные альбомы приведенных характеристик.
На рис. 5.11, а изображены приведенные характеристики для нагнетателя 370-14-1. Порядок расчета следующий: по формулам (5.55) определяют приведенный объемный расход на всасывании Qnp и приведенную относительную частоту вращения («/«н)пР; при этом рабочий расход Qnp должен быть больше наименьшего, от которого начинаются кривые характеристики, не менее чем на 10 %; наименьший расход соответствует границе помпажа;
в зависимости от Qnp по соответствующим кривым находят поли-тропический к. п. д. т]ПОл и приведенную внутреннюю мощность 162
(AVp„)r,P, а в зависимости от Qnp и (п/и,,),,Р — степень сжатия; по найденной величине (AVpB)nP вычисляют согласно (5.55) и, прибавив сюда мощность jVMex, затрачиваемую на механические потери, получают мощность на муфте привода.
При расчете режимов работы нагнетателей можно пользоваться также характеристиками второго типа, построенными не по объемному, а по коммерческому расходу. Такие характеристики нагнетателя изображены на рис. 5.11,6.
Порядок расчета следующий:
вычисляют приведенный коммерческий расход QK. „р и приведенную относительную частоту вращения:
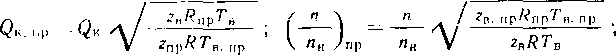
в нижнем поле кривых находят точку с координатами QK. щ>, ра\ от этой точки движутся по линии приведенного объемного расхода Qnp до пересечения с нужной линией (nlnu)uP; на шкале е находят, чему равна степень сжатия;
далее по вертикали переходят на верхнее поле кривых; в точке пересечения вертикали с (п/пн)ир — значение приведенной внутренней мощности A^jnp; по формуле
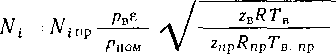
вычисляют внутреннюю мощность Л/,, и затем находят мощность на валу привода N ~ /V; -[- NMex.
Характеристики компрессоров могут быть представлены аналитически. Из известных зависимостей наилучшей считается
(5.56)
![]()
Это уравнение характеристики первого типа. Если заменить
![]()
![]()
получим уравнение характеристики второго типа
(5.57)
![]()
здесь
Ь = Ь0(ра2вТв1Т„),
(5.58)
а и Ь0 — опытные коэффициенты, зависящие от состава газа (R, гв), температуры газа перед входом в нагнетатель Тв и частоты вращения ротора (п).
Для поршневых компрессоров (станций) достаточно точным оказывается следующее эмпирическое уравнение характеристики: где а и Ь — коэффициенты, получаемые обработкой опытных кривых зависимости объемного расхода при условиях всасывания (QB) от степени сжатия е; а -= Qa (при е ----- 1, b — учитывает влияние мертвого пространства).
Если объемный расход Qu заменить коммерческим QK, то из (5.59) получается уравнение такого же вида, как и для центробежных компрессоров:
![]()
![]()
Это уравнение, как в (5.59), весьма удобно при совместном решении с уравнением характеристики трубопровода.
5.9. СОВМЕСТНАЯ РАБОТА ГАЗОПРОВОДА И КОМПРЕССОРНЫХ СТАНЦИЙ
Режимы работы трубопровода и компрессорных станций (КС) связаны между собой: расход в трубопроводе равен подаче КС, давление нагнетания соответствует давлению в начале перегона между станциями, а давление всасывания следующей КС. равно давлению в конце перегона. Любые изменения режима работы КС приводят к изменениям режима работы трубопровода, и наоборот. Поэтому нельзя определить пропускную способность газопровода при помощи одной только формулы расхода. Пропускную способность газопровода также нельзя найти, пользуясь только характеристиками нагнетателей или только аналитическими выражениями этих характеристик.
Трубопровод и КС следует рассматривать как единое целое, и в технологическом расчете газопровода режимы работы трубопровода и КС должны быть согласованы. Это согласование может быть осуществлено совместным решением уравнений характеристик КС и характеристики перегонов между станциями. Уравнение характеристики КС возьмем в виде р* — ар\—bQ2, а уравнение характеристики трубопровода (перегона между КС) удобно выразить так: р\ = р2 + clQ2, где с — постоянный коэффициент; I - длина перегона.
Рассмотрим простейший магистральный газопровод с одной промежуточной КС (рис. 5.12). Требуется рассчитать режим работы газопровода как единой газодинамической системы, а именно определить пропускную способность газопровода Q и давления всасывания ря и нагнетания р,п КС при известных (и постоянных) значениях давления в начале и в конце рк газопровода. Это можно сделать, решив совместно уравнения характеристик двух перегонов и КС газопровода
![]()
| V |
||
| кг. А |
Г» | \ |
|
......: | 9 |
......h________ |
При этом предполагается, что коэффициент с, равный
|6Р стгсрГсри
(5.61)
rt2rLo5
практически одинаков для первого и второго перегонов. Для его определения необходимо задаться в первом приближении значениями zcp, ГСр и X. После определения Q, рв и ра1, а также в процессе теплового расчета перегонов их значения могут быть уточнены. Отметим, что принятие различных значений коэффициента с для каждого из перегонов газопровода не осложнило бы решение задачи.
Решая систему уравнений (6.50), находим
Q
(5.62)
+ Ь + с12
При неработающей КС уравнение (5.62) превращается в известное уравнение расхода участка газопровода
Q
поскольку в этом случае а = 1, а b 0. Из уравнения (5.62) следует очень важный практический вывод: при прочих равных условиях (неизменных значениях давлений в начале и конце газопровода и заданной характеристике КС) пропускная способность газопровода как системы тем больше, чем ближе КС будет размещена к началу газопровода. Очевидно, что при этом одновременно будут возрастать давления на входе и выходе КС. Увеличение пропускной способности газопровода при смещении КС к его началу объясняется повышением степени сжатия КС вследствие уменьшения объемной производительности на ее всасывании (растет давление рв), а также некоторым повышением среднего давления для обоих перегонов, что вызывает расход энергии на преодоление сил трения при движении газа по трубопроводу (снижается средняя скорость движения газа на перегоне).
Для газопровода с п компрессорными станциями имеем ph-aipli-bfi-2’
PI2 = а2Р2в2 - b,fi2\ P2h2 - P% + c2/2Q2; (5.63)
Pln^anPln-bnQ'2’ Pin /'к : c,irR2-
Обозначив ijt = bi + Ci lt и найдя из первой пары уравнений pt2,
из второй р\-л и т. д., получим, что для КС, номер которой равен х
Р{^ах • ¦ • +!/x-i)Q2:
= • • • й,р2в. (!>, ¦ • • а^-1 -I й,)Q2- (5-64)
Для конечной точки газопровода
Pi = ВД, - (? пЛ-14 «/„) Q2-
где П; = . . . ап.
Отсюда расход в системе КС — трубопровод
(5.65)
Если станции однотипные и перегоны между ними одинаковые (за исключением последнего, длина которого зависит от давления рк), т. е. если
то
| аг = а2 = . . | а II с в II |
| bi = ь.г = . . | • bn b\ |
| 1! II sj | ¦ = cn = c\ |
| |j II iH |
¦ — I n -1 = U |
| II II | ii a 1 1 |
|
2 П/f/j—i — |
(ап~{ + an~‘ |
. о , ч а" — а . . .+а? + а)уг=-—у
1=2 а — 1
и формула (5.65) станет проще
Q= д/(anPS, —Рк)/(-7ТГу + ' (5’66)
Если начальной точкой газопровода считать не всасывающий, а нагнетательный коллектор головной компрессорной станции, где дав-166 ление равно то из системы (5.63) надо будет исключить первое уравнение. Тогда
Q д/ У Л a*~'cl -I Уп)- (5-67)
Из (5.65), (5.66) и (5.67) видно, что пропускная способность газопровода в первую очередь зависит от давления в начальной точке газопровода (рВ1 или р,п)', даже незначительное снижение этого давления приводит к ощутимому уменьшению пропускной способности газопровода (а » !)¦
Давление в конечной точке газопровода, напротив, оказывает незначительное влияние на его пропускную способность; оно может изменяться в довольно большом диапазоне, и на пропускной способности газопровода это существенно не отразится. Влияние рл на Q тем меньше, чем больше число станций п; влияние начального давления на пропускную способность газопровода с увеличением п, наоборот, возрастает.
Из (5.65), (5.66) и (5.67) также следует, что на пропускную способность газопровода влияет расположение компрессорных станций: чем меньше расстояния между ними, тем меньше у и, следовательно, тем больше Q. Но при сближении станций возрастут давления рв и рн. Это — ограничение: давление в любой точке газопровода не должно превышать допустимого из условия прочности.
При однотипных станциях и одинаковых перегонах между ними упрощаются также выражения, определяющие давления всасывания и нагнетания: для произвольно взятой компрессорной станции х вместо (5.64) получаем
(5.68)
Отсюда следует, что давления всасывания и нагнетания даже при однотипных КО и при перегонах одной и той же протяженности практически не бывают одинаковыми на всех станциях. Одинаковыми эти давления будут при расходе, который получается из первой пары уравнений (5.63):
Q = /)BiV(a—!)/«/¦ (5.69)
Если это подставить в (5.68), то на любой станции х окажется, что
Рв — Ръ\ и рн = Phi-
Из последней пары уравнений (5.63) нетрудно найти давление рк, при котором все это может быть обеспечено. Получается, что р^ =
= Pbi [а (1 —уп /у) + yjy 1-
Изменения давления рк вызывают изменения давлений всасывания и нагнетания (рв и р„) на КС. Рассмотрим, как это происходит. Пусть давление рк повысилось на Дрк. Если бы расход оставался
неизменным, то для перегона между последней КС и конечным пунктом газопровода р2пi A pi,)- (р к i А/;к)-. Отсюда следует,
ЧТ('
(5.70)
АрнСАр,
т. е. прирост давления в начале перегона меньше величины, на которую повысилось давление в конце перегона.
На компрессорной станции повышение давления всасывания (Арв) по сравнению с повышением давления нагнетания (Д/;„) определяется из сопоставления отношений давления (степеней сжатия). При неизменном расходе (ра ч Ари)/(рв -(¦ Д/;и) -- pjpa. Отсюда следует, что
(5.71)
ApB<A/;„.
Однако в действующем газопроводе изменения давления рк связаны с изменением отбора газа в конечном пункте газопровода; увеличение рк происходит при уменьшении отбора. Если это учесть, то неравенства (5.70) п (5.71) усилятся.
Таким образом, на участке последняя КС — конечный пункт газопровода Арв <Д/?Н <Д/?к.
Такой же вывод следует и для остальных станций и перегонов между ними. Но заметными изменения р„ и рв при изменении рк бывают лишь на последних двух — трех станциях. На последней КС Арн и Арв — самые большие, на предпоследней они значительно меньше, а на остальных КС давления ра и рв практически не изменяются. Теперь рассмотрим, как будут изменяться давления рв и р„ на КС при изменении давления в начальной точке газопровода. Пусть давление pBJ возросло на АрВ1. Считая сначала, что расход не изменился, получим, как и прежде из сравнения степеней сжатия, что Л/?,,! > Арв1, а из равенства разностей квадратов давлений для перегона между первой и второй станциями Л/?в2^>Арн1.
Для второй станции окажется, что Арн2у>Арв2, для перегона между второй и третьей станциями Дрви > Д/?н2 и т. д. Но, как уже было сказано, изменение давления рвл сопряжено с изменением подачи газа в газопровод, при этом чем больше число КС, тем больше увеличивается расход при повышении давления рвХ. Увеличение расхода приведет к уменьшению степени сжатия, а это, как нетрудно понять,— к уменьшению Ари. В результате неравенства Арн >Арвокажутся либо ослабленными, либо знак у них переменится на обратный. То же получается и с неравенствами для перегонов между станциями. Таким образом, в общем случае нельзя сделать вывод о том, что больше — Ари или Арв и как эти величины будут изменяться от станции к станции — увеличиваться или уменьшаться. Можно лишь сказать, что при увеличении подачи газа в газопровод давления рв и рл повысятся, линии падения давлений поднимутся, а при уменьшении подачи газа — наоборот.
Для сравнения заметим, что при увеличении отбора газа давления рв и р„ уменьшатся и линии падения давлений на перегонах между станциями снизятся.
5.10. РЕЖИМ РАБОТЫ ГАЗОПРОВОДА ПРИ ОТКЛЮЧЕНИИ КОМПРЕССОРНЫХ СТАНЦИЙ ИЛИ АГРЕГАТОВ
Нередко случается, что часть КС по тем или иным причинам не работает. Это бывает, например, в периоды слабого потребления газа (летом) на газопроводе, не имеющем подземных хранилищ, при авариях, в начальный период эксплуатации газопровода, когда станции вводятся в действие по очередям.
Рассмотрим сначала простейший случай: на газопроводе с однотипными и расположенными на одинаковых расстояниях станциями одна из них (х) вышла из строя. Очевидно, что пропускная способность их уменьшается. Ее можно найти из той же системы уравнений (5.63), но при этом надо учесть, что в точке х р„х = рвх и поэтому в уравнении plx = axplx — bxQ2, входящем в систему (5.63), следует принять ах = 1 и Ьх = 0. Тогда получим
Qx==yil—^^LA--------------------(5.72)
—-— у + an~xcl + уп
а — 1
или, если первой станции нет и давление газа, поступающего в начальный пункт газопровода, обозначить р„Л, то
Q Л /-- —^—--------. (5.73)
1П
2
~а у +
(а«-> + fl»-*) cl +
уп
а — 1
Формула (5.72) или (5.73) позволяет сделать вывод, что чем меньше номер вышедшей из строя станции (х), тем сильнее снижается пропускная способность газопровода. Больше всего она снизится при отключении первой станции. Разделив (5.67) на (5.72) при х = 1, найдем, во сколько раз уменьшится пропускная способность газопровода при отключении первой станции:
= / о" Ун|-Рк
Л
<?i
Если ап~1рвх > рк, то Q/Qt « рн1/рв1 = ex.
Выход из строя последней КС не оказывает существенного влияния на пропускную способность газопровода. В этом нетрудно убедиться. Положив в (5.72) х — п, при достаточно большом п, когда an~lp2Bi > р2к
получаем, что Qrl ж рВ1 л/{а — 1 )1у. Это — расход при условии, что давления рв и р„ па всех станциях одинаковые. Помимо формального вывода, вытекающего из (5.72) или (5.73), можно дать следующее объяснение снижению пропускной способности газопровода в зависимости от номера отключенной станции. Будем считать, что станция х -f 1 делит газопровод на два участка: левый и правый. На левом участке снижение пропускной способности происходит из-за уменьшения числа действующих КС. При этом очевидно, что это уменьшение числа станций будет тем ощутимей, чем меньше их находится на рассматриваемом участке, т. е. чем меньше х.
Причина снижения пропускной способности газопровода на правом участке — уменьшение давления всасывания на станции х -|- 1. Влияние уменьшения давления всасывания на снижение пропускной способности газопровода согласно (5.66) возрастает с увеличением числа станций. В рассматриваемом случае (на правом участке) число станций увеличивается при уменьшении левого участка, т. е. при уменьшении х. Следовательно, как и для левого участка, пропускная способность газопровода снижается тем сильнее, чем меньше х.
При отключении двух станций хх и х2 по аналогии с (5.72)
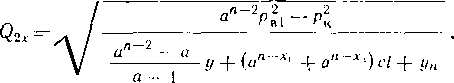
Таким же путем получаются формулы, определяющие расход при выходе из строя любого числа станций. Если на какой-либо КС работают не все, а лишь часть компрессорных агрегатов, то, обозначив для этой станции а — ах и b — Ьх, из системы уравнений (5.63) можно получить
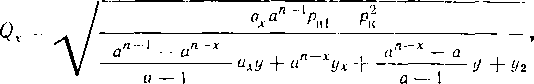
где ух — bx + с/.
Теперь рассмотрим, как после отключения части или всех агрегатов на станции х изменятся давления ръ и рп на предыдущих и последующих станциях. Примем всасывающий коллектор станции х (точка х) за конечный пункт левого участка газопровода. Линия падения давления, идущая от станции х—1, вследствие уменьшения расхода будет более пологой. Поэтому давление в точке х возрастет. Получается аналогия с рассмотренным выше увеличением давлений при уменьшении отбора газа. Поэтому давления рн и рв на станции л-—1 увеличатся; на станции х—2 они возрастут в меньшей мере и т. д. Для пра-ного участка, начинающегося от станции х |- 1, аналогия будет со случаем уменьшения подачи газа на головную станцию: линия падения давления будет более пологой, давления на станциях понизятся. Давления р„ и рв можно определить, переходя от станции к станции. Зная давление в конце газопровода, по формуле р\ — р\j + c/Q2 находим давление р„ на последней станции. Затем по формуле р1к — = ар\—bQ или при помощи приведенных характеристик нагнетателей находим давление Далее таким же путем можно вычислить 170 давления на всех остальных станциях. Пели при нормальной работе газопровода давления рн близки к допустимому ра, то при отключении станции .V необходимо провести регулирование, снижающее давление рп на станции х—1 до допустимого давления рл.
Возьмем участок, начинающийся от станции х—1. Вторая станция на этом участке отключена. Расход при условии, что давление на первой станции х—1 равно рА, может быть определен по формуле (5.73), в которой сначала следует принять х = 2, а затем п надо будет заменить на п — (х—2). Получим, что наибольшее допустимое значение расхода при отключении станции
Д/ JL—ziiL у+ 2ап ~х а + Уп
у а — 1
После определения расхода QxPi решается вопрос о том, каким образом на станции х—1 может быть достигнуто давление ря т. е. решается вопрос о регулировании. Наиболее экономичные способы регулирования — отключение агрегатов и изменение частоты вращения роторов.
Число агрегатов, которые должны быть отключены на станциях от первой до х—1 включительно, и частоту вращения роторов можно определить по приведенным характеристикам. При этом возможен целый ряд режимов работы, обеспечивающих на станции х—1 давление, равное рд. Наилучшим из них будет тот, при котором давления поддерживаются на возможно более высоком уровне. В этом случае линии падения давления будут пологими, степени сжатия на станциях, а следовательно, и мощности, затрачиваемые на компримиро-вание,— наименьшими.
5.11. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ МАГИСТРАЛЬНОГО ГАЗОПРОВОДА
Определение экономически наивыгоднейших параметров магистрального газопровода (диаметр D, рабочее давление рг и степень сжатия компрессорных станций е) — одна из основных задач технологического расчета. В качестве критерия при выборе оптимальных параметров газопроводов принимаются приведенные затраты 5 ~
^ КЕ + Э , где 5 — приведенные годовые затраты; К — капитальные затраты; Е— нормативный коэффициент эффективности капитальных вложений (при расчете объектов транспорта и хранения нефти и газа он принимается равным 0,12 1/год); Э— эксплуатационные расходы. Для расчета наивыгоднейших параметров магистральных газопроводов используют методы графоаналитический, сравнения конкурирующих вариантов, а также аналитический. В практике проектирования наибольшее распространение получили первые два метода.
Этот метод расчета оптимальных параметров в конечном счете сводится к определению рациональной области применения труб различного диаметра и рабочего давления, а также к обоснованию области использования газоперекачивающих агрегатов (ГПА), выпускаемых промышленностью в данный период. С этой целью для каждого из вариантов с постоянным диаметром труб, рабочего давления, типа ГПА и степени сжатия строят графическую зависимость удельных приведенных затрат Syд от пропускной способности газопровода Q. Удельные затраты — затраты на единицу длины и пропускной способности газопровода. При построении такой зависимости для выбранного сочетания основных параметров (D, р и е), а также для определенного типа ГПА используют укрупненные нормативные технико-экономические показатели, разрабатываемые проектными институтами, в частности В НИПИтрансгазом.
Удельные приведенные затраты находят из следующего выражения: 5УД = SKC/(IQ) + Sj,. JQ, где SKC — приведенные затраты на одну КС, зависящие от ее типоразмера, т. е. от типа, числа и схемы работы ГПА; 5Л. ч — приведенные затраты по линейной части газопровода в расчете на единицу длины, зависящие от его диаметра и рабочего давления; / — расстояние между КС, зависящее от диаметра и рабочего давления газопровода, а также от степени сжатия КС. На рис. 5.13 приведено несколько подобных графических зависимостей 5уД = / (Q) для газопроводов диаметром 1020—1620 мм с рабочим давлением 5,6 МПа и двухступенчатым компримированием. Подобные графические зависимости, построенные для всех практически возможных и целесообразных сочетаний диаметра и рабочего давления газопровода и степени сжатия КС, позволяют при проектировании
Рис. 5.13. График рациональной области применения газопроводов различного диаметра
конкретного газопровода наметить сравнительно небольшое число конкурирующих вариантов для выбора его экономически иаивыгод-иейшнх параметров. При этом конкурирующие варианты назначаются с учетом стандарта па трубы, а также типов ГПА, выпускаемых промышленностью для магистральных газопроводов. Следует отметить, что подобные графические зависимости обычно строят для каких-то средних условий строительства газопроводов без учета таких важных показателей, как сроки ввода в эксплуатацию газопровода в целом, уровень замыкающих затрат на газ в районе строительства газопровода и т. д. Поэтому при проектировании конкретных газопроводов обычно используют метод сравнения конкурирующих вариантов.
Метод сравнения конкурирующих вариантов
В соответствии с этим методом и в зависимости от пропускной способности газопровода намечается ряд конкурирующих вариантов по диаметру, рабочему давлению газопровода и степени сжатия КС. При этом используют известные рекомендации о рациональной области применения труб различного диаметра и рабочего давления, а также различных типоразмеров КС. Применительно к газопроводам достаточно большой пропускной способности (более 5 млрд. м3/год) с учетом выпускаемого промышленностью оборудования для магистральных газопроводов для сравнения следует рассматривать варианты с рабочим давлением 5,6 и 7,6 МПа, а в отношении степени сжатия КС — схемы одно- и двухступенчатого компрнмирования. Для выбора оптимального диаметра обычно достаточно сравнить 2—3 варианта.
По каждому из
намеченных вариантов проводят комплекс
механических, тепловых, гидравлических и
экономических расчетов для определения
приведенных затрат на строительство и
эксплуатацию газопровода. К строительству
обычно принимается вариант с наименьшими
приведенными затратами. Если какие-либо
варианты оказываются по приведенным
затратам примерно равноценными (разница
приведенных затрат не превышает 5 %),
то для выбора наивыгоднейшего варианта
может быть использован дополнительный
критерий, например величина
металловложений, капитальных затрат и т.
д.
Аналитический метод
При проектировании реальных газопроводов рассмотренные методы являются наиболее целесообразными и рациональными, вместе с тем при общем исследовании вопроса об оптимальных параметрах магистральных газопроводов, в частности при изучении зависимости оптимальных значений диаметра и рабочего давления газопровода и степени сжатия КС от его пропускной способности, более рациональным становится аналитический метод. Хотя этот метод и является менее точным в результате использования приближенных аналитических выражений для приведенных затрат, тем не менее он позволяет получить более четкую зависимость оптимальных параметров газопровода от его пропускной способности, применяемого оборудования, материа-
лов, условий строительства и т. д. Аналитический метод позволяет обеспечить научный подход к разработке стандарта на трубы н нормального ряда ГПА для магистральных газопроводов.
Аналитический метод расчета оптимальных параметров магистральных газопроводов предполагает использовать приближенные аналитические зависимости для приведенных затрат как функции пропускной способности газопровода, его диаметра и давления, а также степени сжатия КС. Выбор указанных аналитических зависимостей определяется требованиями достаточно точного совпадения расчетных значений экономических показателей с нормативными и необходимой простоты исследования поставленной задачи, поскольку в противном случае аналитический метод лишается всех своих преимуществ.
Исследуем сначала зависимость оптимальной степени сжатия КС от пропускной способности газопровода. Удельные приведенные затраты на КС газопровода в расчете на единицу его длины можно представить следующим образом 5уд. кс -= 5КС//. Величина SKC может быть достаточно точно представлена в виде
^кс ;= Ь AnQ. (е 0’
где А о — приведенные затраты на одну КС, не зависящие от ее мощности; An — коэффициент, характеризующий приведенные затраты на одну КС, зависящие от ее мощности; т — показатель политропы. Расстояние между КС газопровода определяется из уравнения расхода
РР5
I
cQ2
Тогда выражение удельных приведенных затрат на КС газопровода принимает следующий вид:
с Uo+,4wQ(em |т— 1)1 cQ2 к2 /к -7ЛЧ
-ЬУД КС ^5 72—Г- (5-74)
Оптимальную степень сжатия найдем, приравняв нулю частную производную от выражения удельных приведенных затрат по степени сжатия. После преобразований получаем
С
AnQ
Таким образом, оптимальная степень сжатия КС газопровода не зависит от его диаметра и рабочего давления. При увеличении пропускной способности газопровода правая часть стремится к двум, поэтому степень сжатия должна стремиться к единице. Это объясняется тем, что при повышении пропускной способности газопровода уменьшается доля приведенных затрат на КС, не зависящих от ее мощности, и, наоборот, увеличиваются затраты, пропорциональные рабочей мощности КС. Последние же с понижением степени сжатия уменьшаются. Значения отношения AJAN для КС с агрегатами ГТК-Ю
О 20 40 60 80 100 2 k в 8 10
Q^ мг-ti M3/cij гл
Рис. 5.14. График зависимости оптимальной степени сжатия газотурбинных (а) и газомоторных (б) КС магистральных газопроводов от пропускной способности:
/ — при Л0Л4д'~ 1 млн. м'/сут; 2 — 0,8 мли. м:,/сут; 3 — 0,4 млн. м'/сут
и ГТК-16 соответственно равны (при m -- 1,31) 0,97 и 0,94 млн. м3/сут при рабочем давлении 5,6 и 0,8 МПа и 0,86 млн. м3/сут при давлении 7,6 МПа.
На рис. 5.14 изображена зависимость оптимальной степени сжатия е газотурбинных и газомоторных КС газопровода от его пропускной способности Q при m = 1,31 и различных значениях отношения А0!АЫ. Приведенные графические зависимости е0пт = / (Q) в определенной степени носят качественный характер, однако они дают достаточно четкое представление о характере изменения оптимальной степени сжатия КС при изменении их пропускной способности и определяют область, где необходимо искать оптимальную степень сжатия более точными методами.
При проектировании большинства магистральных газопроводов отдают предпочтение даже при больших расходах (15—20 млрд. м3/год) вариантам со степенью сжатия 1,4—1,5, хотя это менее выгодно как по приведенным затратам, так и по всем остальным экономическим показателям. Преимуществом такого решения можно считать несколько большую надежность, более широкий диапазон регулирования пропускной способности, большую устойчивость системы КС — газопровод вследствие более крутой газодинамической характеристики КС, возможность более быстрого ввода в эксплуатацию всех КС газопровода (меньшее число строительных площадок). Однако в каждом конкретном случае необходимо детально обосновать выбор той или иной схемы компримирования КС.
Перейдем к исследованию зависимости оптимального диаметра и рабочего давления газопровода от его пропускной способности. Анализ нормативных экономических показателей позволяет рекомендовать следующую интерполяционную формулу, аналитически выра-
жающуго зависимость приведенных затрат линейной части газопровода от диаметра и рабочего давления:
(5.75)
где S0 — приведенные затраты на единицу длины газопровода, не зависящие от его диаметра и рабочего давления; Sp — приведенные затраты на единицу длины газопровода, пропорциональные массе трубопровода; SD — приведенные затраты на единицу длины газопровода, зависящие только от диаметра трубопровода. Выражение (5.75) достаточно точно аппроксимирует нормативные приведенные затраты по линейной части газопроводов в широком диапазоне изменения диаметра (от 530 до 1420 мм) и рабочего давления. Максимальная погрешность расчетных данных по отношению к нормативным не превышает 3—4 %, что следует считать вполне допустимым для проводимых исследований.
Для приведенных затрат на одну КС с газотурбинным приводом весьма удобна следующая приближенная аналитическая зависимость:
5кс *^окс Н~ SqQ 4 Sp kcPiQ,
(5.76)
где 50КС — приведенные затраты на одну КС, не зависящие от ее типоразмера; SQ — приведенные затраты на одну КС, зависящие только от ее подачи; SpKC — приведенные затраты на одну КС, зависящие от ее рабочего давления и подачи.
С учетом выражений (5.74), (5.75) и (5.76) уравнение удельных приведенных затрат на единицу длины газопровода при фиксированной степени сжатия КС (считается, что выбор оптимальной степени сжатия КС уже сделан) принимает следующий вид:
(¦SqKC + SqQ -\- Sp KCPlQ) Q'
[ S0 + SpPiD* + SdD\
![]()
где
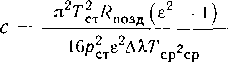
Оптимальные значения рабочего давления и диаметра газопровода найдем, приравняв к нулю частные производные от приведенных затрат по давлению и диаметру:
g (-SqKC 4- SqQ -|- Sp kcPiQ) Q2cp\D6
<)S
<)D
2SlplD -\ ‘2SuU - 0; (5.77)
2 ¦SqKC + SqQ___Sp kcQ3 |
cp\D5 cp^D1'
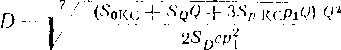
OS др l
1SpD* = 0;
Решая совместно два последних уравнения, находим
(5.78)
0 2 | ( Sqkc + sqq _2Sd_\р _л s_p__s0KC + SqQ ;Q ^5 80)
+ l SpKCQ Sp )Pl Sp SD kcQ
Анализ полученных уравнений позволяет сделать выводы.
1. Оптимальное давление газопровода в основном зависит от соотношений SD/SP и SQ/SP кс, повышаясь с их ростом. Другими словами, оптимальное давление тем выше, чем меньше при прочих равных условиях составляющие приведенных затрат линейной части и КС, зависящие от рабочего давления. В частности, если SpKC = О, т. е. приведенные затраты на КС не зависят от рабочего давления, то оптимальное давление р1 = 4Sd/Sp.
2. Применение высокопрочных сталей приводит к увеличению оптимального рабочего давления газопровода, так как при этом отношение SD/SP увеличивается.
3. Оптимальное рабочее давление весьма слабо зависит от пропускной способности газопровода, особенно в области больших расходов, когда уравнение (5.80) принимает такой вид:
Sq _ 25р ^ п _ А Sд _Sq_ _ q
+ ---S )Pl_4'
SP SpKC
V jpKc /
4. Оптимальный диаметр газопровода, как видно из уравнения (5.79), в первую очередь зависит от пропускной способности газопровода. При больших значениях Q оптимальный диаметр газопровода примерно пропорционален пропускной способности в степени 7/3.
5. Удельные приведенные затраты в расчете на единицу длины и пропускной способности газопровода уменьшаются с ее ростом. Поэтому удельные приведенные затраты однониточного газопровода всегда меньше, чем многониточного равной пропускной способности. Однако необходимо отметить, что существует другой подход к выбору оптимальных параметров магистральных газопроводов, составляющих вместе с газовыми промыслами и потребителями единую систему. Наличие сезонной неравномерности газопотребления и условие бесперебойной подачи газа потребителям накладывают отпечаток на экономику трубопроводного транспорта газа. В частности, обработка статистических данных об отказах на магистральных газопроводах показывает, что их общая продолжительность за год существенно возрастает с увеличением диаметра газопровода. Поэтому с увеличением диаметра газопровода возрастают (для обеспечения одного уровня надежности газоснабжения) затраты на создание необходимых резервов газообразного или другого вида топлива в районе газопотребления. В первую очередь это возможно за счет увеличения мощности подземных хранилищ газа. На случай перерыва подачи газа по газопроводу следует предусмотреть возможность увеличения суточного отбора газа из подземного хранилища, что даже при его неизменной полезной емкости приводит к значительному увеличению затрат на его сооружение и эксплуатацию. Поэтому с учетом обеспечения необходимой надежности двухниточный газопровод может оказаться более экономичным, чем однониточный газопровод большего диаметра с такой же пропускной способностью. Приведенные аналитические исследования оптимальных параметров в значительной степени носят качественный характер. В таком виде аналитический метод для проектной практики вряд ли представляет большой интерес. Однако в несколько упрощенном виде аналитическая методика может быть применена и к решению целого ряда задач в проектной практике. В частности, при определении рациональной области применения труб различного диаметра вместо графоаналитического метода более удобен следующий упрощенный аналитический метод.
Для заданных значений рабочего давления и диаметра газопровода, а также типа ГПА и схемы компримирования уравнение удельных приведенных затрат в расчете на единицу длины и пропускной способности имеет вид
(Sa -1- SqQ) Q
S
УД -
где 5Л. ч — удельные приведенные затраты па единицу длины газопровода диаметром D и рабочим давлением рг. Если, например, необходимо определить пропускную способность, выше которой трубопровод диаметром D2 будет выгоднее трубопровода диаметром Dj (при Dj <CD2), достаточно решить равенство
(Vi-SQ<?)C , _ (s„ I SqQ)Q s
л. 4
где 5л.ч и 5л! ч — удельные приведенные затраты на линейную часть газопроводов соответственно диаметром ?), и D 2, принимаемые по нормативным источникам.
Аналогичным образом может быть найдена пропускная способность, при которой, например, двухниточный газопровод будет выгоднее однониточного и т. д.
Для практики определенный интерес представляет оптимальная пропускная способность газопроводов различных диаметров, соответствующая минимальным удельным приведенным затратам.
Приравнивая к нулю производную от удельных приведенных затрат по расходу, получаем
dSya ___2SqQ Sa (| q
dQ ср\оГз QJ
о тсюда
2Q3 + Q2---cp\Dri ^ 0.
Sq Sq
Из последнего уравнения определяется оптимальная пропускная способность газопровода заданного диаметра и рабочего давления.
5.12. РЕЖИМ РАБОТЫ ГАЗОПРОВОДА ПРИ СБРОСАХ И ПОДКАЧКАХ
Характерной особенностью магистральных газопроводов является наличие значительного числа сбросов попутным потребителям. Эти сбросы могут производиться как в течение всего года (будучи, как правило, переменными по времени), так и периодически (например, сбросы буферным потребителям). Для протяженных магистральных газопроводов нередко также наличие подкачек газа по трассе. Эти поступления газа возможны из других магистральных газопроводов по специальным перемычкам или с недалеко расположенных газовых месторождений и подземных хранилищ газа.
В связи с созданием Единой системы газоснабжения страны любой крупный магистральный газопровод, как правило, имеет значительное число сбросов и подкачек, которые, будучи переменными во времени, могут существенно влиять на режим работы газопровода в целом. Расчет режима работы протяженного магистрального газопровода с переменными сбросами и подкачками представляет весьма сложную инженерную задачу, требующую применения совершенного математического аппарата и вычислительной техники.
Здесь даются лишь качественный анализ режима работы магистрального газопровода с переменными сбросами и подкачками и на основе этого некоторые общие рекомендации по регулированию его режима работы.
На рис. 5.15, а изображен график изменения режима работы газопровода при периодическом сбросе. Как видно из графика, при периодическом сбросе линия депрессии давления (пунктирная линия) снижается на всем протяжении газопровода, но особенно заметно на участке после сброса. Это объясняется тем, что при сбросе пропускная способность на участке после сброса уменьшается, а это, в свою очередь, при неизменных конечном давлении газопровода и характеристиках КС приводит к снижению линии депрессии давления за сбросом. Отсюда же следует, что на участке до сброса пропускная способность должна несколько возрасти. С увеличением пропускной способности степени сжатия КС, расположенных до сброса, уменьшаются, что приводит к снижению линии депрессии давления и на этом участке.
Очевидно, чем больше сброс, тем в большей степени снижается линия депрессии давления. На основе сделанного ранее анализа также следует, что чем ближе к началу газопровода будет расположен сброс, тем в большей степени при прочих равных условиях будет изменяться режим работы газопровода. Таким образом, при периодических сбросах давления на всех КС газопровода понижаются, а подача газа конечному потребителю уменьшается (при неизменных характеристиках КС). Такая же картина получается при увеличении сброса. Последнее очень характерно для зимнего периода работы газопровода, когда из-за сезонной неравномерности газопотребления сбросы газа попутным потребителям заметно увеличиваются. При этом давления на выходе последних станций заметно снижаются, а эффективность их работы падает вследствие снижения их степеней сжатия.
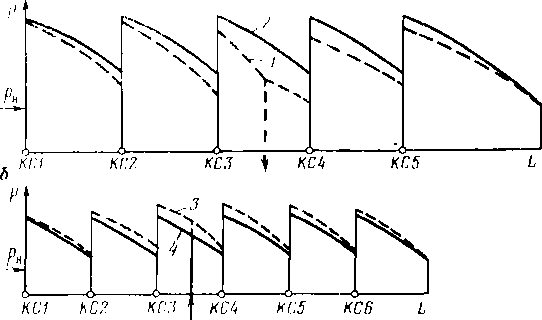
Рис. 5.15. Графики изменения режима работы газопровода при периодических сбросе (а) и подкачке (б):
/и 2 — линии депрессии газопровода соответственно со сбросом и без сброса; 3 и 4 — линии депрессии газопровода соответственно с подкачкой и без подкачки
Снижение степеней сжатия на КС, расположенных за сбросом, объясняется увеличением объемной подачи, отнесенной к условиям всасывания КС этого участка. В некоторых случаях эта подача может снизиться настолько, что возникает необходимость регулирования, поскольку она не должна быть меньше минимально допустимой, указанной в паспорте нагнетателя (здесь рассматривается лишь КС с центробежными нагнетателями). Повышения рабочих давлений на участке за сбросом можно добиться за счет отключения части агрегатов на одной или двух последних КС газопровода или снижения частоты вращения ротора нагнетателей на тех же КС. При отключении части агрегатов на последней или двух последних КС пропускная способность протяженного газопровода с большим числом станций практически не изменяется, в то же время заметно повышается эффективность работы остальных КС за сбросом (повышаются их степень сжатия, мощность и к. п. д.).
График изменения режима работы газопровода при периодической подкачке изображен на рис. 5.15, б. Как видно из графика, при подкачке (пунктирная линия) наблюдается повышение давления на всех КС газопровода. Поэтому если давление на какой-либо КС превышает максимально допустимое, то возникает необходимость регулирования отключением части агрегатов или снижением частоты вращения ротора агрегатов на этой станции или на станциях, расположенных до нее.
Компрессорные станции на трассе газопровода размещают с учетом как чисто технологических, так и экономических соображений. В частности, необходимо стремиться к тому, чтобы размещение КС отвечало требованиям удобства их строительства и эксплуатации. Кроме того, следует помнить, что расположение КС по трассе существенно влияет на пропускную способность отдельных участков и газопровода в целом, а также на суммарную мощность КС. Как было показано ранее (см. уравнение (5.65)), при прочих равных условиях пропускная способность газопровода тем больше, чем ближе к его началу расположены КС. Физически увеличение пропускной способности газопровода при смещении КС к началу газопровода объясняется двумя причинами. Во-первых, при приближении КС к началу газопровода (рис. 5.16, а) увеличиваются давления на входе станций, а следовательно, уменьшается подача КС, отнесенная к условиям всасывания. Это, в свою очередь, приводит к увеличению степени сжатия КС, а значит, и пропускной способности газопровода. Во-вторых, при смещении КС к началу газопровода повышается среднее давление на участках между станциями, что приводит к уменьшению затрат энергии (при прочих равных условиях) на преодоление сил трения при движении газа по трубопроводу, так как снижается скорость движения газа. Максимально возможная пропускная способность газопровода при заданном числе КС с учетом ограничения давления нагнетания, следовательно, будет достигнута при таком расположении КС по трассе, когда на всех станциях давление нагнетания будет равно максимально допустимому ртах- Так, при однотипных КС и отсутствии сбросов и подкачек по трассе газопровода оптимальное расположение КС на трассе, обеспечивающее максимально возможную пропускную способность газопровода, может быть найдено из следующей системы уравнений характеристик участков трубопровода и КС:
![]()
-\- С (L — П.1) Qmax
Отсюда находим максимально возможную пропускную способность газопровода Qmax при п промежуточных КС
а затем расстояние между КС
I = (а ~ 1} р™ах ~ ас^шах
и давление всасывания КС
![]()
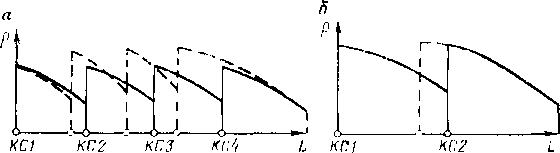
Рис. 5.16. График изменения режима работы газопровода при смещении КС (а) и промежуточной КС (б) к началу газопровода:
1 \\ 2 ¦— линии депрессии газопровода еоотпететпенпо после смещения и до смещения КО
Давление нагнетания головной КС также принято равным ртах. Следует подчеркнуть, что давление нагнетания головной КС необходимо во всех случаях (в том числе и в процессе надения пластового давления на промысле) поддерживать на уровне за счет ввода
дополнительных мощностей (увеличения числа ступеней сжатия), так как это позволяет максимально использовать пропускную способность газопровода в целом и уменьшить затраты энергии на перекачку газа.
При строительстве крупных магистральных газопроводов в несколько очередей возникает задача определения очередности ввода в эксплуатацию КС газопровода. Минимально возможное число КС, которые должны быть введены в эксплуатацию на том или ином этапе развития газопровода с заданной пропускной способностью, может быть найдено из системы уравнений (5.81). При этом необходимо лишь учитывать, что на КС к этому времени могут быть в эксплуатации не все газоперекачивающие агрегаты, что отразится на коэффициентах а и b в уравнении характеристик КС.
В некоторых случаях размещение КС на трассе газопровода может проводиться из условия минимальных энергозатрат на перекачку заданного количества газа. Это, в частности, возможно в том случае, когда при расстановке КС в соответствии с системой уравнений (8.51) пропускная способность газопровода окажется больше необходимой подачи газа или возможностей промысла.
Так, при одной промежуточной КС и постоянном начальном давлении газопровода рН1 (рис. 5.16, б) мощность этой КС при неизменной (заданной) пропускной способности газопровода будет существенно зависеть от ее положения на трассе газопровода. Чем ближе она расположена к началу газопровода, тем меньше будет ее степень сжатия (при постоянной пропускной способности газопровода) и тем меньше будет ее рабочая мощность. Следовательно, для уменьшения энергозатрат на перекачку газа надо КС располагать как можно ближе к началу газопровода, т. е. размещать их на трассе таким образом, чтобы давления нагнетания на них были равны ртах.
С энергетической точки зрения при поэтапном вводе в эксплуатации протяженного газопровода с большим числом КС предпочтителен одновременный пуск возможно большего числа КС, что позволит при заданной пропускной способности на первых этапах развития газопровода уменьшить расход энергии на перекачку газа (за счет снижения степеней сжатия отдельных КС) по сравнению с вариантом, где та же самая пропускная способность обеспечивается строительством меньшего числа КС (с большей степенью сжатия и, следовательно, большим числам газоперекачивающих агрегатов). Так, если при полном развитии газопровода все его КС будут работать по схеме двухступенчатой) компримирования, то уже на первом этапе строительства, когда пропускная способность его будет меньше проектной, может оказаться целесообразным ввести в эксплуатацию большую часть КС (а возможно, и все КС) па режиме одноступенчатого компримирования, так как это может уменьшить энергозатраты на перекачку газа. Однако в этом случае увеличивается фронт строительно-монтажных работ, поскольку их необходимо вести на большем числе площадок, что имеет свои минусы. Очевидно, в каждом конкретном случае необходим детальный технико-экономический расчет для выбора оптимального варианта наращивания мощности газопровода в целом.
Характерной особенностью работы магистральных газопроводов является наличие сезонной и суточной неравномерности газопотребления. В частности, для покрытия часовых пиков газопотребления используется аккумулирующая способность самого газопровода и прежде всего его последнего участка. Аккумулирующая способность последнего участка зависит, очевидно, от его геометрических размеров (диаметра и длины) и рабочего давления, а следовательно, и от расположения последней КС.
Исследуем, как зависит аккумулирующая способность последнего участка газопровода от его длины. Для определения аккумулирующей способности последнего участка воспользуемся методом последовательной смены стационарных состояний, считая, что дважды в сутки, когда расход газа в начале и конце участка становится равным среднечасовому, режим движения газа и распределение давления на последнем участке близки к стационарному. Тогда в конце периода накопления газа в последнем участке среднее давление можно выразить следующим образом:
(5 82)
)•
где рутах—максимальное давление в начале последнего участка газопровода; оно определяется прочностью газопровода или возможностями последней КС-,р0_1тпх— максимальное давление в конце последнего участка.
С учетом сделанных допущений из уравнения для последнего участка
![]()
('о .83)
В конце периода выдачи накопленного в последнем участке, газа в нем будет среднее давление
Рис. 5.17. Зависимость аккумулирующей способности последнего участка (Vлкк!Уакк max) газопровода от его длины (/к//к тах)
Рсртт - 4- (Pimin Н--™--) ; (5.84)
«J V pi min “Г Р2 min /
Pi min 1=7 д/р2 min Ч~ С1к Qcp t (5.85)
где р2т\п — минимальное допустимое давление в конце последнего участка.
Тогда аккумулирующую способность последнего участка, приведенную к стандартным условиям, запишем таким образом:
Уакк
-= Рср тах ~ Рср mil1
—1—L. (5 .86)
Подставив в уравнение (5.86) выражения (5.82), (5.84) и (5.85), после преобразования получим
т / TtD" Тс-т ( 3 2 j 2 /°»21 ,
^акк 7:т:; ~ ~ \Plmax Pi max \ Pi max CQ /к Ч~
о рст1 Ср2Ср
i cQ /кЛ/pimax /к '[~P2min' cQ /к д/ргт in cQ lK —
¦—P2min д/р2т1П+cQ2/K ) CQ2 (5.87)
Оптимальную длину последнего участка газопровода, при которой обеспечивается максимальная аккумулирующая способность участка, найдем из условия dVaKJdlK = 0. После преобразования получим
2 2
I Р Imax P2m\n /Р ооч
I к — -—--¦ (о.оо)
2с(?2 V ’
Таким образом, максимальная аккумулирующая способность последнего участка достигается в том случае, если его длина будет равна половине максимально возможной:
2 2
/ _ РI mnx ~ ^2inin
fKinax —
cQ*
Величину Какк max найдем из (5.87), подставив в него (5.88),
где k — постоянный коэффициент.
На рис. 5.17 изображена зависимость аккумулирующей способности последнего участка газопровода от его длины. При малой длине аккумулирующая способность мала, поскольку мал геометрический объем участка. При большой длине участка мала разность р ершах—Рсргпщ- Таким образом, чтобы использовать аккумулирующую способность последнего участка, КС газопровода необходимо несколько еднннуть к концу газопровода по отношению к оптимальной расстанопке, при которой обеспечивается максимальная пропускная способность газопровода, если режим потребления постоянный. Вопрос об оптимальной расстановке КС должен, следовательно, находиться в каждом конкретном случае с учетом всех перечисленных факторов, а также с учетом нестационарное™ работы последнего участка и газопровода в целом. Критерием выбора оптимального варианта расстановки КС, как уже говорилось, может быть максимум подачи газа или минимум энергозатрат при заданной пропускной способности.
ПОСЛЕДОВАТЕЛЬНАЯ ПЕРЕКАЧКА НЕФТИ И НЕФТЕПРОДУКТОВ
6.1. ОСОБЕННОСТИ ТЕХНОЛОГИИ И ПРЕИМУЩЕСТВА ПОСЛЕДОВАТЕЛЬНОЙ ПЕРЕКАЧКИ
Магистральные трубопроводы широко применяются для транспорта нефтепродуктов массового потребления, главным образом автомобильных бензинов, дизельных и реактивных топлив от нефтеперерабатывающих заводов (НПЗ) до районов их потребления.
Метод последовательной перекачки позволяет решить проблему транспорта по одному и тому же нефтеиродуктопроводу с НПЗ до перевалочных и распределительных нефтебаз различных нефтепродуктов массового потребления, и в первую очередь бензинов и дизельных топлив различных сортов. При последовательной перекачке различные нефтепродукты поступают с НПЗ в резервуары начального пункта нефтепродуктопровода, а перекачка их происходит последовательно (отсюда и название метода) — в виде отдельных, следующих друг за другом партий разных нефтепродуктов. Так, вслед за партией бензина А-72 закачивается в нефтепродуктопровод партия бензина А-76, затем партия дизельного топлива и т. д.
В нефтепродуктопроводе большой протяженности при определенных условиях одновременно может находиться несколько партий различных нефтепродуктов. В период закачки в нефтепродуктопровод очередной партии нефтепродукта поступающие с НПЗ другие нефтепродукты принимаются в резервуары начального пункта нефтепродуктопровода. В период поступления из нефтепродуктопроводов на нефтебазы его конечного или промежуточных пунктов очередной партии определенного нефтепродукта снабжение потребителей нефтепродуктами других сортов осуществляется за счет созданных за это время запасов соответствующих нефтепродуктов в резервуарах нефтебаз.
Преимущества последовательной перекачки нефтепродуктов — это возможность использовать для перекачки различных нефтепродуктов один нефтепродуктопровод, а не сооружать несколько нефтепродуктопроводов для каждого нефтепродукта; обеспечить наиболее полную загрузку нефтепродуктопровода при перекачке по нему нескольких нефтепродуктов; применить для перекачки разных нефтепродуктов один более крупный нефтепродуктопровод (большого диаметра, большей пропускной способности) и тем самым снизить себестоимость перекачки, которая уменьшается с ростом диаметра и пропускной способности.
Применение последовательной перекачки на разветвленных нефте-продуктопроводах позволяет доставлять моторные топлива разных сортов от НПЗ непосредственно на распределительные нефтебазы дан-186
иого района. При этом отпадает необходимость в перегрузке нефтепродуктов на железнодорожный и автомобильный транспорт.
Особенностью последовательной перекачки является образование некоторого количества смеси в зоне контакта двух следующих друг за другом нефтепродуктов вследствие неравномерности осредненных местных скоростей по сечению трубопровода, а также при переключении системы задвижек перед резервуарами начального пункта при смене нефтепродуктов, закачиваемых в нефтепродуктопровод (смесь, образующуюся при таком переключении, называют первичной).
Количество смеси нефтепродуктов, образующейся при последовательной перекачке, при турбулентном режиме течения находится [1 пределах 0,5—1 от объема исфтопродуктокровода. Для контроля за прохождением зоны смеси и ее своевременного приема на конечном пункте нефтепродуктопровод оборудуют специальными приборами. Чтобы уменьшить количество смеси, иногда применяют различные разделители, помещенные в зону контакта разносортных нефтепродуктов и двигающиеся вместе с ними по нефтепродуктопроводу. При последовательной перекачке должны быть предусмотрены мероприятия но исправлению и реализации получающейся смеси нефтепродуктов, а объем резервуарных парков па начальном, промежуточном и конечном пунктах нефтепродуктопровода определяется с учетом создания необходимых запасов нефтепродуктов.
Последовательную перекачку очень вязких нефтепродуктов (масел, некоторых мазутов и др.) при ламинарном режиме течения без специальных разделителей (с непосредственным контактом нефтепродуктов) обычно не применяют, так как в этом случае количество смеси может в 4—5 раз превысить объем нефтепродуктопровода.
Последовательная перекачка бензинов и дизельных топлив разных сортов практически применяется на всех магистральных нефте-продуктоироводах. Г1о некоторым из них последовательно перекачиваются по 8—]0 различных сортов нефтепродуктопроводов, бензин А-72, А-76, дизельные топлива с температурой вспышки 40 и 65 °С и различным содержанием серы.
Большие преимущества имеет последовательная иерекачка различных нефтей по одному и тому же нефтепроводу. Очень часто в одном и том же районе добываются нефти разного состава. Обычно такие нефти перекачиваются на НПЗ по нефтепроводу совместно, в виде смеси, и перерабатываются по одной технологической схеме.
В ряде случаев при последовательной перекачке разных по составу нефтей и раздельной переработке их на НПЗ по различным схемам можно получить дополнительное количество очень нужных нефтепродуктов (масел, строительных битумов и т. и.) пли упростить процесс переработки.
В СССР имеется положительный опыт последовательной перекачки обессоленной и «сырой» нефти с наличием воды и солей по магистральному нефтепроводу. Освоена последовательная перекачка сернистой и малосернистой нефтей по нефтепроводу диаметром 1220 мм, протяженностью около 1000 км. Последовательная перекачка нефтей с различным содержанием солей, механических примесей или воды обычно имеет ряд отличий от последовательной перекачки таких нефтепродуктов, как бензины и дизельные топлива, обусловленных меньшими числами Рейнольдса, возможностью образования отложений солей или механических примесей на стенках труб при перекачке одной из нефтей и смыва этих отложений при перекачке другой нефти.
При последовательной перекачке возникает необходимость в определении конфигурации и гидравлическом расчете разветвленных нефтепродуктоироводов, оптимизации их параметров, выборе средств контроля последовательной перекачки, в определении количества ожидаемой смеси и выборе способа ее реализации. Важной проблемой является уменьшение количества смеси при последовательной перекачке.
6.2. ОБЩИЕ ПРИНЦИПЫ ПРОЕКТИРОВАНИЯ СИСТЕМ НЕФТЕПРОДУКТОПРОВОДОВ
Все системы нефтепродуктопроводов условно можно разделить на две основные группы. Первая группа включает магистральные нефтепро-дуктопроводы относительно больших диаметров (350—700 мм). Для таких трубопроводов характерно задание основного направления потока нефтепродуктов и сравнительно небольшое число промежуточных отводов. К трубопроводам первой группы относится большинство систем, построенных до 60-х годов. Вторая группа включает распределительные системы нефтепродуктопроводов с высокой степенью разветвленное™ (трубопроводы типа «дерева») и наличием большого числа подключенных потребителей (распределительных нефтебаз) с относительно небольшими объемами потребления. Такие разветвленные системы нефтепродуктопроводов сооружают в последние годы.
На первом этапе проектирования НПЗ как поставщиков прикрепляют к пунктам сосредоточенного потребления нефтепродуктов. В качестве критерия на этом этапе может быть использован минимум грузовой работы, который позволяет приближенно определить основные направления потоков нефтепродуктов на территории СССР или отдельных экономических районов страны. В масштабах всей страны в качестве сосредоточенных потребителей удобно рассматривать столицы союзных республик и областные центры. В пределах отдельного экономического района, при более детальной проработке, сосредоточенными потребителями являются распределительные или перевалочные нефтебазы. Исходными данными являются план производства нефтепродуктов (по объему и номенклатуре) на НПЗ и схема размещения пунктов сосредоточенного потребления. Данная задача решается при условиях, что каждый сосредоточенный потребитель был бы полностью обеспечен требуемыми нефтепродуктами (автобензином, дизельным топливом), а весь объем выработки каждого НПЗ был бы полностью распределен между потребителями.
Введем обозначения: п — число пунктов потребления; т — число поставщиков (НПЗ); х,-, yj — координаты пунктов потребления на карте (/ = 1, ri)\ 2[, Wi — координаты НПЗ на карте (i ~ 1, tn)\ bj — объем потребления /-го потребителя; а; — объем производства /-го НПЗ; VtJ — объем нефтепродуктов, планируемых к доставке от г-го 188
НПЗ к /-му потребителю. С учетом формулы, определяющей расстояние между двумя точками на плоскости, заданными координатами, задача ставится следующим образом. Найти минимум выражения
т п
? ? V(zi— XjY + iWi—у if V ц min
?= I / = 1
при ограничениях: объем нефтепродуктов, поставляемых с любых НПЗ к каждому потребителю, соответствует его объему потребления
![]()
Vtj= bj I и объем доставки нефтепродукта ко всем потребителям
![]()
сданного НПЗ не превышает его объема
Таким образом определяется приближенное распределение потоков нефтепродуктов по направлениям.
Следующим этапом проектирования является определение оптимальной конфигурации системы разветвленных нефтепродуктопрово-дов в данном экономическом районе, исходя из определенных ранее направлений потоков нефтепродуктов, расположения НПЗ и распределительных нефтебаз с известным объемом потребления для каждой из них.
Известно, что стоимость сооружения линейной части трубопроводов составляет до 80 % от общих капитальных затрат. Эксплуатационные затраты также зависят от длины трубопровода. Поэтому минимум суммарной длины трубопровода является важным критерием, характеризующим его экономическую эффективность, и используется при отыскании оптимальной конфигурации системы разветвленных нефтепродуктопроводов. Эта задача формулируется следующим образом: на карте местности заданы пункты производства и потребления нефтепродуктов, которые необходимо связать сетью нефтепродуктопроводов минимальной протяженности, чтобы приведенные затраты на ее сооружение и эксплуатацию были бы минимальными. Для этого на топографическую карту местности наносятся возможные трассы нефтепродуктопроводов, связывающих источники нефтепродуктов с их потребителями. При этом источники и потребители находятся в вершинах связанного графа, и возможные трассы трубопроводов являются его ребрами. Исходя из условий местности оценивается стоимость сооружения трубопровода по каждой такой трассе (по каждому ребру графа), и в результате получают цифровую модель местности (ЦММ). Топографические карты местности обновляются с интервалом в 10—15 лет, поэтому реальное состояние местности может не соответствовать зафиксированному на карте, кроме того, составление ЦММ по карте является трудоемкой ручной работой.
Существенно облегчить составление ЦММ с получением реального плана и вертикального профиля возможных трасс можно, используя космические фотоснимки, каждый из которых позволяет получить стереоскопическую модель участка земной поверхности размером до 100 X 180 км. Обрабатывая эти снимки на стереокомпараторах, снабженных ЭВМ и графопостроителями, можно получить вертикальный профиль и план возможных трасс со степенью точности 10—15 м.
Отыскание оптимальной трассы разветвленного нефтепродуктопровода формулируется как задача поиска кратчайшего пути на графе, соединяющем источники с потребителями, и осуществляется на ЭВМ с использованием алгоритмов, основанных на решении задачи Штейнера о кратчайшем пути, связывающем точки на плоскости, с учетом метода .Лаунгардта, учитывающего количество нефтепродукта, перекачиваемого от источника к каждому потребителю. В результате решения такой задачи путем направленного перебора получают схематическое изображение «дерева» разветвленной системы трубопроводов, координаты точек разветвления, характеристики участков (объем перекачки, диаметр трубопровода, длины участков) и другие необходимые данные для оптимального варианта с минимальными приведенными затратами и минимальной суммарной протяженностью. Затем по этой трассе может быть произведено аэрофотографирование с обработкой аэроснимков на стереокомпараторах, что позволяет сделать окончательную привязку трассы на местности с погрешностью определения планово-высотных координат не более 2—3 м.
Эксплуатационные затраты по каждому участку сети длиной /? определяют по формуле Эс = (Э„г + Qt /;), где ЭпД,ср постоянная и переменная части эксплуатационных расходов-,Q-,— расход по данному участку.
Суммарные приведенные затраты по рассматриваемому варианту системы нефтепродуктопроводов складываются из приведенных затрат на каждом участке их сети
1 = I
где Е„ — нормативный коэффициент эффективности капитальных затрат; Kl — капитальные затраты.
Полученная система разветвленных нефтепродуктопроводов может быть сопоставлена с уже имеющимися видами транспорта в данном экономическом районе (железными и автомобильными дорогами), что позволит определить участки, где трубопроводный транспорт экономически более выгоден, исходя из соотношений приведенных затрат.
Все расчеты по определению оптимальной конфигурации разветвленных нефтепродуктопроводов производят на ЭВМ по специально разработанным программам.
6.3. ПРИБЛИЖЕННАЯ ТЕОРИЯ СМЕСЕОБРАЗОВАНИЯ В ТРУБОПРОВОДЕ ПРИ ПОСЛЕДОВАТЕЛЬНОЙ ПЕРЕКАЧКЕ НЕФТЕПРОДУКТОВ
При последовательной перекачке в зоне контакта двух нефтепродуктов образуется некоторое количество из смеси. Предположим, что в начальный момент времени перекачиваемые последовательно нефтепродукты соприкасаются по плоскости, перпендикулярной к оси трубы, 190
Рис. 6.1. График изменения концентрации замещающего нефтепродукта и зоне смеси
Рис. 6.2. Эпюра вклинивания замещающего нефтепродукта Б п замещаемый нефтепродукт А при ламинарном режиме последовательной перекачки

а концентрация замещающего нефтепродукта Б в этой плоскости изменяется скачкообразно от единицы до нуля (рис. 6.1, линия /). После начала последовательной перекачки в процессе движения нефтепродуктов по трубопроводу будет происходить перемешивание обоих нефтепродуктов в месте их контакта, в результате чего образуется зона смеси этих нефтепродуктов. Концентрация нефтепродуктов по длине зоны смеси при этом будет изменяться от сБ = 0 в ее начале до сБ — 1 в конце (см. рис. 6.1, линия 2). Причиной образования зоны смеси в месте первоначального контакта нефтепродуктов при ламинарном режиме последовательной перекачки является неравномерность местных осредненных скоростей по поперечному сечению трубы, а при турбулентном режиме перекачки — неравномерность местных осредненных скоростей и турбулентное перемешивание жидкости в поперечном сечении трубы. Вблизи оси трубопровода скорость течения жидкости больше, чем около стенок. Поэтому при ламинарном режиме последовательной перекачки замещающий нефтепродукт Б будет вклиниваться в замещаемый нефтепродукт А в соответствии с профилем скоростей (рис. 6.2, а). Одновременно с этим из-за различия плотностей этот клин нефтепродукта Б будет всплывать к верхней образующей трубы, если рл > ps, или опускаться к нижней образующей, если Рл<Рб> а на всей поверхности раздела этих нефтепродуктов будет взаимная молекулярная диффузия (рис. 6.2, б, в).
При ламинарном режиме последовательной перекачки замещающий нефтепродукт Б будет вклиниваться в замещаемый нефтепродукт А в соответствии с профилем местных осредненных скоростей и в некоторый момент этот клин подойдет к конечному сечению трубопровода и начнется «вымывание» нефтепродукта А из трубопровода, при котором в приемный резервуар будет поступать смесь нефтепродуктов А и Б (рис. 6.2, г). Этот процесс «вымывания» достаточно длительный. В результате объем смеси, образующейся при ламинарном режиме последовательной перекачки, достигает 4—5 объемов всего нефтепровода. Вследствие значительного объема смеси последова-
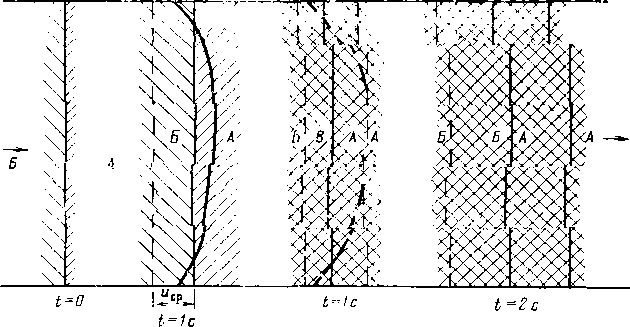
Рис. 6.3. Схема смесеобразования при турбулентном режиме последовательной перекачки
тельная перекачка при ламинарном режиме с непосредственным контактом перекачиваемых нефтепродуктов не применяется. Для уменьшения образования смеси при последовательной перекачке высоковязких нефтепродуктов (масел, мазутов) при ламинарном режиме необходимо проводить ее с разделительными устройствами, помещаемыми в зону контакта перекачиваемых нефтепродуктов и препятствующими «вклиниванию» нефтепродукта Б в нефтепродукт А, что позволит существенно уменьшить количество смеси.
При турбулентном режиме последовательной перекачки одновременно с вклиниванием нефтепродукта Б в нефтепродукт А в соответствии с профилем местным осредненных скоростей происходит турбулентное перемешивание этих нефтепродуктов по поперечному сечению трубы и это уменьшает количество образующейся смеси. В связи с этим механизм образования смеси при турбулентном режиме последовательной перекачки, обусловленный неравномерностью скоростей по сечению трубопровода и турбулентным перемешиванием, можно упрощенно представить в следующем виде.
В момент времени t = О, соответствующий началу последовательной перекачки, нефтепродукты А и Б соприкасаются по плоскости, перпендикулярной к оси трубопровода (рис. 6.3, а). За первую се-кунду (/ = 1 с) нефтепродукт Б вклинивается в нефтепродукт А в соответствии с профилем местных осредненных скоростей, а первоначальная плоскость раздела этих нефтепродуктов переместится на расстояние, равное средней (по расходу) скорости потока иср (рис. 6.3, б). Одновременно с этим за тот же промежуток времени под воздействием турбулентной диффузии будет происходить перемешивание вклинившейся части нефтепродукта Б с нефтепродуктом А в поперечном направлении, и к исходу первой секунды в трубопроводе образуется
некоторый объем, занятый смесью нефтепродуктов А и Б примерно в равных количествах (рис. 6.3, в). В течение второй секунды (t = 2 с) часть уже образовавшейся смеси (а не чистый нефтепродукт Б) будет вклиниваться в чистый нефтепродукт А, одновременно перемешиваясь с ним под воздействием турбулентной диффузии. В головной части зоны смеси она будет смешиваться с чистым нефтепродуктом А и в хвостовой части — с чистым нефтепродуктом Б, а плоскость первоначального раздела этих нефтепродуктов, двигаясь со средней скоростью потока, будет оставаться примерно в середине зоны смеси (рис. 6.3, г).
Таким образом, по мере продвижения зоны смеси по трубопроводу ее объем будет увеличиваться, причем влево от плоскости первоначального раздела нефтепродуктов, где их концентрации примерно одинаковы, увеличивается концентрация замещающего нефтепродукта Б, а в право от этой плоскости концентрация уменьшится.
При турбулентном режиме последовательной перекачки в результате турбулентного перемешивания вклинившийся нефтепродукт Б будет перемешиваться с нефтепродуктом А и будет происходить выравнивание концентраций смеси по поперечному сечению трубы. В результате воздействия турбулентного перемешивания (турбулентных пульсаций) «вытягивания» жидкостного клина не происходит. В результате количество смеси при турбулентном режиме значительно меньше, чем при ламинарном, и находится в пределах от 0,5 до 1 % от объема нефтепродуктопровода. При этом по мере увеличения числа Рейнольдса распределение скоростей по сечению трубы становится более равномерным и объем смеси в результате последовательной перекачки уменьшается. В результате такого перемешивания по мере движения зоны контакта нефтепродуктов по трубопроводу будет происходить продольное распространение зоны смеси по обе стороны от первоначальной границы их раздела. При этом протяженность зоны смеси будет увеличиваться с течением времени пропорционально величине (Dt)0'5, где D — эффективный коэффициент диффузии, характеризующий интенсивность распространения зоны смеси под воздействием конвективной диффузии при ламинарном режиме течения и под воздействием конвективной диффузии в сочетании с турбулентным перемешиванием в поперечной плоскости при турбулентном режиме.
Эффективный коэффициент диффузии имеет различную величину для разных режимов течения: большую при ламинарном режиме и меньшую при турбулентном режиме. Интенсивность продольного распределения смеси (скорость ее диффузии в продольном направлении) можно определить в соответствии с законом Фика по формуле
IJ dC,i , (6.1)
dx
где v — скорость диффузии; D —эффективный коэффициент диффузии; dCE/dx — градиент концентрации замещающего нефтепродукта.
Чтобы получить уравнение, описывающее процесс образования смеси нефтепродуктов, поместим начало координат в середину зоны смеси, двигающейся по трубопроводу со средней скоростью потока
Рис. 6.4. График распределения концентраций относительно подвижного начала координат
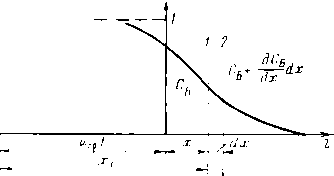
(рис. 6.4), где концентрации замещающего и замещаемого нефтепро-дуктов равны: СА = СБ = 0,5. Тогда продольная координата х в подвижной системе координат будет связана с той же координатой xt в неподвижной системе (с началом координат в начале трубопровода) соотношением хт-= хх—ucpt. Двумя сечениями 1 и 2 на расстоянии х и (х + dx) от подвижного начала координат выделим в трубопроводе элементарный объем Fdx и составим уравнение бгланса замещающего нефтепродукта Б в этом объеме в процессе последовательной перекачки. Пусть средняя по поперечному сечению концентрация замещающего нефтепродукта в сечении 1 равна СБ, а в сечении 2 (на расстоянии dx) она составит
Cs + -^-dx.
ах
Тогда на основании зависимости (6.1) можно записать, что через сечение 1 за промежуток времени dt в выделенный объем в процессе продольного распространения смеси войдет нефтепродукт Б в количестве
В (6.2) и (6.3) берутся частные производные потому, что концен
трация СБ изменяется не только вдоль зоны смеси, но и во времени. Вследствие переноса через сечения 1 и 2 в выделенном объеме за время dt накопится следующее количество нефтепродукта Б:
tl* Вполне очевидно, что уравнение баланса нефтепродукта Б в вы
веденном объеме имеет вид
Подставим в (6.5) значения слагаемых из (6.2), (6.3) и (6.4)
п дСв с At I п ( дСв . дгСк
дх V дх дхг J
dt
и после упрощения получим дифференциальное уравнение, описывающее изменение концентрации нефтепродуктов в смеси вдоль зоны смеси и во времени с постоянным эффективным коэффициентом диффузии
dt дх3
Уравнение (6.6) — линейное уравнение второго порядка в частных производных, часто называемое уравнением теплопроводности.
Рассмотрим решение уравнения (6.6) на трубопроводе условно бесконечной длины с известным начальным условием в месте контакта нефтепродуктов (см. рис. 6.1): при t = О
( 0 для л: > 0.
Решение уравнения (6.6) на бесконечной прямой имеет вид
оо
СБ(х, t) =-±—
Г / (?) ехр Г — (* -п;)2 1 fifS,
(6.7)
2 л/nDt L 4Dt J
где / (?) — начальное распределение концентраций замещающего нефтепродукта.
Чтобы убедиться, что при t = 0 выполняется начальное условие
I/=о = / (*). достаточно в (6.7) произвести замену
тогда
r 1 “
Б~ /— j f{х—2ri^/D^)exp( — r\2)dr\
V ТС —оо
и при t — 0 из этого выражения следует
оо
С в I /=о = —l— f (х) | exp (— if) dr] f (х).
л/п
В соответствии с начальным распределением концентрации (см. рис. 6.1, линия /) интеграл (6.7) будет отличаться от нуля лишь на отрезке — оо <0, где f (х) = 1, и примет вид
о
СБ(х, t)=-Г ехр Г - 1 (6.9)
2 л/nDt ^ ADt -*
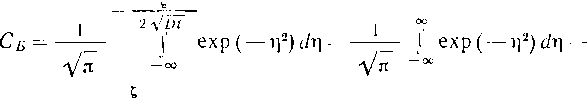
2 VDt
—~ j' ехр (— r\2)dr\ =
¦\ Л 0
S
![]()
2 л/Dt
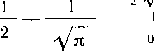
Функция
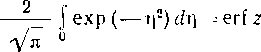
называется интегралом вероятности, и для нее составлены подробные таблицы, поэтому решение (6.10) можно записать в виде (имея в виду, что переменная ? — аналог координаты х)
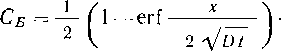
Поскольку рассматривается изменение концентрации в конечном сечении трубопровода длиной хх = L, можно записать я = L—ucpt, где uCpt — путь, который прошла подвижная система координат за время t со средней скоростью «ср. Следовательно,
L — ucpt
2 л/Dt 2-yjDt
Обозначим через t0 время, в течение которого середина зоны смеси с концентрацией СА = СБ = 0,5 дойдет до конца трубопровода длиной L. Тогда L = ucpt0 и
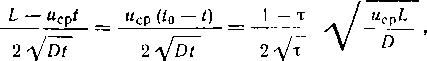
где т = tlt0.
Величина под знаком радикала в (6.12) является безразмерной и получила название диффузионного параметра Пекле, Ре</ = == UcpL/D.
Поскольку протяженность зоны при турбулентном режиме не превышает 1 % от длины трубопровода L, моменты прохождения смеси через концевое сечение трубопровода t мало отличаются от ta
и, следовательно, величина л/х ж 1. Поэтому в интересующем ин-
Рис. 6.6. Схема к определению объема смеси в пределах граничных концентраций Свх (для z,) и СБ2 (для 2 г)
тервале времени, определяемом продолжительностью прохождения зоны смеси через концевое сечение трубопровода, можно принять
Рис. 6.5. Вид функции Св (г) при различных значениях числа Пекле
(Ре<*)
±-LsJj&L = J_(i— т)д/Ре^ =2. (6.13)
2'У'С
При условии (6.13) уравнение, определяющее изменение мгновенной концентрации замещающего нефтепродукта в концевом сечении трубопровода, может быть записано в виде
•¦[l-erf^-l^-PeS’5)] (6.14)
сБ= 2
ИЛИ
СБ ;=-L(l_erfz).
График функции (6.14) при разных значениях числа Пекле изображен на рис. 6.5. Формула (6.14), выражающая зависимость мгновенной концентрации смеси от времени, позволяет получить методику определения количества смеси, образовавшейся в трубопроводе. Объем смеси, прошедшей через концевое сечение трубопровода в промежуток от tr до 12, определяется выражением
Vcm = Q(/2-*i), (6.15)
где Q — пропускная способность, которая предполагается постоянной в период прохождения зоны смеси.
На основании (6.15) относительный объем смеси (отнесенный к объему трубопровода Утр можно записать следующим образом:
1'С“ - Q (t^U) ^ :=-—(ti-t1) = T2~-X1. (6.16)
^тр ^тр LF t О
Но из соотношения (6.12) следует, что
|
СБ 1 |
СБ2 | 2 | СБ1 |
СБ2 | г |
| 0,01 | 0,99 |
1,645 | 0,1 | 0,9 | 0,906 |
| 0,02 |
0,98 | 1,452 | 0,15 | 0,85 | 0,733 |
| 0,03 | 0,97 | 1,33 | 0,2 | 0,8 |
0,595 |
| 0,04 |
0,96 | 1,238 | 0,25 |
0,75 | 0,477 |
|
0,05 | 0,95 | 1,163 |
0,3 | 0,7 | 0,371 |
| 0,06 | 0,94 |
1,099 | 0,35 | 0,65 | 0,272 |
| 0,07 |
0,93 | 1,044 | 0,4 | 0,6 | 0,18 |
| 0,08 | 0,92 | 0,994 | 0,45 | 0,55 |
0,089 |
| 0,09 |
0,91 | 0,948 | 0,5 |
0,5 | 0 |
Примечание. Для всех С ^ < 0,5 значения erf z и г положительные, а для осох С ? > 0,5 — отрицательные.
поэтому, подставив в (6.16) значения тх и т2 в соответствии с (6.17) получим формулу для определения объема смеси
VcM/Vxp-2(21-22)Pe7°'5. (6.18)
Значения г1 и z2 в (6.18) можно определить следующим образом. На основании формулы (6.14) для заданных значений концентраций СБ1 (для zj и СБ2 (для z2), в пределах которых определяют искомый объем смеси (рис. 6.6), находят соответствующие значения интеграла вероятностей erf и erf z2 из соотношений erf zx = 1—2 СБ1, erf z2= == 1—2 СБ2 и затем по таблицам интеграла вероятностей определяют соответствующие значения аргументов гх и z2. Значения аргумента z для некоторых значений концентраций смеси приведены в табл. 6.1. Если объем смеси определяют в пределах симметричных концентраций, дающих в сумме единицу, например, СБ1 = 0,01 и СБ2 = 0,99, то Zj—z2 = 2z и формула для объема смеси (6.18) упрощается:
VcuIVTp = 4z Ре7°'5’ (6.19)
где знак аргумента z всегда положительный, а само значение одинаково для любого из двух симметричных пределов концентраций СБ1 и СБ2. Если заданы граничные концентрации не замещающего СБ, а замещаемого нефтепродукта СА, то формула (6.19) не изменяется, а в формуле (6.18) аргументы zx и z2 поменяются местами.
Для эффективного коэффициента смещения в уравнении одномерной линейной диффузии (6.6). Тейлор аналитически получил следующее выражение (без учета различия вязкостей и плотностей смешивающихся жидкостей):
-i
di]
(6.20)
D = 2 Я2
Т)е (11)
\их&)-иср\Ж
где R — радиус трубы; их (?) — функция распределения местных ско-198
ростей по I оперечному сечению трубы; е (т]) — радиальный коэффициент турбулентной диффузии,
«д—динамическая скорость, ия = иср -\Д/8; X— коэффициент гидравлического сопротивления; duldr\ — градиент скорости; иср— средняя скорость потока.
Эффективный коэффициент диффузии D на порядок больше коэффициента радиальной турбулентной диффузии е (т]), так как неоднородность поля скоростей по сечению трубы является основной причиной увеличения длины зоны смеси.
Формула (6.20) позволяет при известном распределении скоростей их (?) вычислить эффективный коэффициент диффузии D. Так, для ламинарного режима течения с распределением скоростей
М?) = 2«ср(1-?2).
где t = r!R; г — переменный радиус; R — радиус трубы.
Принимая радиальный коэффициент диффузии е (г|) равным коэффициенту молекулярной диффузии х, из (6.20) получим
Д1ам=--/?2ис Р/(48х). (6.21)
Для турбулентного режима течения Тейлор в 1954 г. в результате обработки опытов Никурадзе по измерению профиля скоростей по поперечному сечению трубы на основе выражения (6.20) получил следующую формулу для эффективного коэффициента диффузии:
D - Ю.ЫцЯ = 3,57ысрЛ л/Т. (6 22)
Формулы (6.21) и (6.22) позволяют сравнить эффективные коэффициенты диффузии при ламинарном и турбулентном режимах перекачки. Принимая R = 0,25 м, иср = 1 м/с, X = 0,02, % = 10~8 м2/с, получим
Dj,aMiDryvc = Rucp/(\72%X) та 10е.
Из формулы (6.18) и полученного соотношения эффективных коэффициентов диффузии при ламинарном и турбулентном режимах последовательной перекачки следует
Уем лам/V,m турб -- л]DjjaMIDTyp6 та 103 .
Таким образом, если при турбулентном режиме Ус ~ 0,005 Утр, что подтверждается опытными данными и расчетами, то при ламинарном режиме следует ожидать объема смеси, достигающего 5 Утр, т. е. в 5 раз большего, чем объем всего трубопровода. Это означает, что надо прокачать пять объемов трубопровода, чтобы вытеснить оставшийся вблизи стенок замещаемый нефтепродукт А вследствие вклинивания замещающего нефтепродукта Б. Это подтверждает, что последовательная перекачка при ламинарном режиме с непосредственным контактом нефтепродуктов нецелесообразна из-за очень большого количества смеси. В формуле (6.22) для эффективного коэффициента диффузии при турбулентном режиме использовано распределение скоростей однородного потока в трубе, и эта формула не всегда подтверждается опытными данными по последовательной перекачке разносортных нефтепродуктов. В связи с этим предложен ряд других формул для вычисления эффективного коэффициента диффузии при турбулентном режиме, полученных в результате экспериментальных данных:
формула Асатуряна
D/v —- 17,4 Re2/3; формула Нечваля—Яблонского D/v = 28,3 (Re
Кинематическую вязкость в этих формулах следует вычислять для смеси с 50 %-ной концентрацией по формуле
¦v5o = ("Vi + 3v2)/4,
где и v2 — кинематическая вязкость компонентов смеси (всегда
vi >v2).
Удобной для вычислений является формула Съенитцера
![]()
Используя это выражение, можно получить формулу для подсчета объема смеси в нефтепродуктопроводе в пределах симметричных концентраций в виде
![]()
где Ях, Я2 — коэффициенты гидравлического сопротивления в потоке соответственно менее вязкого и более вязкого нефтепродуктов; СБ1 — концентрация отсечки смеси в нефтепродуктопроводе (СБ1 + СБ2 =1); d, L — соответственно диаметр и длина нефтепродуктопровода; A (Cbi) — коэффициент для разных значений концентраций отсечки.
Изменение концентрации СБ в концевом сечении трубопровода при этом описывается, по В. С. Яблонскому, формулой
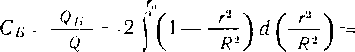
о
![]()
где QB — расход жидкости Б в концевом сечении.
Для объема смеси при ламинарном режиме В. С. Яблонский предложил формулу
![]()
где tx и t2 — моменты времени, соответствующие прохождению через концевое сечение смеси с концентрациями СА1 и СА2¦ Из этой формулы следует, в частности, что в пределах граничных концентраций СА1—СА 2 = 0,99—0,01 объем смеси при ламинарном режиме составит
Уем = (0,01-0.5-о,99-0,5) = 4j5i/Tp,
а при СА1—СА2 = 0,991—0,009 объем смеси VCM = 4,8 VTp.
Как это было найдено позднее (В. И. Черникиным, В. Ф. Новоселовым, В. И. Харламенко и др.), различие вязкостей существенно влияет на объем смеси и продолжительность фазы вытеснения при ламинарном режиме последовательной перекачки. Однако при турбулентном режиме расчет объема смеси только по различию местных осредненных скоростей и без учета турбулентного перемешивания дает чрезмерно завышенные результаты по сравнению с наблюдаемым на практике.
6.4. ВЛИЯНИЕ РАЗЛИЧНЫХ ФАКТОРОВ НА ПРОЦЕСС СМЕСЕОБРАЗОВАНИЯ ПРИ ТУРБУЛЕНТНОМ РЕЖИМЕ
Влияние первичной смеси. При смене нефтепродукта, закачиваемого в трубопровод на его начальном пункте, перекачка не прекращается. Поэтому закрытие задвижки у резервуара с нефтепродуктом А и открытие у резервуара с нефтепродуктом Б производится одновременно при работающем трубопроводе. Таким образом, в трубопроводе в течение некоторого периода времени, определяемого быстрым действием задвижек, поступают нефтепродукты одновременно и на его начальном участке образуется так называемая первичная смесь нефтепродуктов А и Б.
Концентрация нефтепродуктов СБ по длине первичной зоны смеси изменяется от 0 до 1 по произвольному закону, определяемому интенсивностью открытия и закрытия задвижек, уровнем нефтепродукта в резервуарах и пропускной способностью трубопровода.
При продолжительности переключения задвижек всего лишь 5 мин и скорости перекачки 2 м/с протяженность зоны первичной смеси составляет 600 м, что при диаметре трубопровода 0,5 соответствует 120 м3 смеси.
При наличии первичной смеси первоначальный скачок концентрации (см. рис. 6.1, линия 1) отсутствует и смесеобразование нефтепродуктов Л и ? при их движении по трубопроводу, обусловленное различием местных осредненных скоростей и турбулентного перемешивания, начинается при наличии между ними первичной смеси с некоторым распределением концентраций замещающего нефтепродукта / (х) по ее длине (рис. 6.7). Подсчитать общее количество смеси, образующейся в трубопроводе, с учетом первичной смеси можно следующим образом.
Условно увеличим длину данного трубопровода на величину LAon, на которой в результате последовательной перекачки тех же нефте-
Рис. 6.7. График влияния первичной смеси на распределение концентраций и общее количество образующейся смеси:
/ — без учета первичной смеси; 2 — с учетом первичной смеси
продуктов образуется то же самое количество первичной смеси Vn, что и в результате переключения задвижек. Тогда формулу (6.19) для этого объема первичной смеси можно записать в виде
V-
V-
DLa
D
= 4 Ftdz
uLn
V п — 4 F xpiLnonZ
откуда эта дополнительная длина определяется в виде Vn и
(6.23)
D
1 ^ с > >
16/V~
Чтобы определить общий объем смеси (с учетом первичной Vu), достаточно в формуле (6.19) увеличить длину трубопровода L на величину ?доп и записать ее в виде
VCM = 4 -FTpz откуда получаем
L
доп ,
sV'+
= 4г Ре 7°
" тр
Подставляя в (6.24) значение Адоп отношение объемов смеси:
(6.24)
из (6.23), получим следующее
Vn,
где Упем и Vm —объем смеси в данном трубопроводе с учетом и без учета первичной смеси соответственно.
Из последнего выражения видно, что влияние первичной смеси сильно сказывается лишь на коротких трубопроводах. Поэтому мероприятия по уменьшению первичной смеси наиболее эффективны на коротких трубопроводах.
Смесеобразование при переменной скорости перекачки
Скорость перекачки может изменяться скачкообразно в местах изменения диаметра трубопровода и в местах промежуточного отбора части нефтепродуктов или изменяться плавно вследствие регулирования расхода и его постепенного изменения в процессе замещения нефтепродуктов, различающихся по вязкости и плотности. Кроме того, в местах изменения диаметра трубопровода зона смеси будет «сжиматься», если <C.d2, и «вытягиваться», если dj >d2 (рис. 6.8). Таким образом, скорость перекачки в процессе движения зоны смеси может меняться с течением времени.
| \ | |||
| J, | \ \ \ _b | s. |
dZ |
|
. | |||
Рис. 6.8. Схема деформации зоны смеси в трубопроводе с участками разного диаметра
Уравнение, описывающее процесс смесеобразования при произвольном изменении скорости перекачки и (t) и зависящего от нее эффективного коэффициента диффузии D (t), будет иметь вид (при условии, что неподвижное начало координат расположено в начальном пункте трубопровода)
_2?в_ + и(*) (6.25)
dt dxi дх*
После перехода к подвижной системе координат по условию х =
= хг—и (t) t и замены независимой переменной по условию г| = г
= | D(t)dt уравнение (6.25) примет вид дСБ/дк] = д2СБ/дх2. Ре-
о
шение этого уравнения для трубопровода с п участками разного диаметра и, кроме того, с монотонным изменением скорости перекачки будет следующим:
tj, t2, . . . , tn —моменты подхода зоны смеси к tn границам соответствующих участков трубопровода.
Предположим х = L и записав L для рассматриваемого случая в виде
L= \ щ (t) dt + \ ux(t) dt + . . . + \ un(t) dt,
о i, tn
/о t
Хп = I un(t) dt —j un (t) dt.
ln ln
Объем смеси в конце трубопровода в пределах граничных концентраций СБ1 и СБ 2 для рассматриваемого случая можно определить по формуле
4
где dn — диаметр последнего участка трубопровода; г± и г, — аргументы интеграла вероятности для граничных концентраций СБ j и СБ2.
Влияние различия вязкостей на процесс смесеобразования
При последовательной перекачке нефтепродуктов, существенно отличающихся по вязкости, вязкость смеси по ее длине будет изменяться в соответствии с изменением концентрации в ней нефтепродуктов.
Вследствие изменения вязкости смеси будет происходить деформация профиля местных осредненных скоростей и это, в свою очередь, приведет к изменению эффективного коэффициента диффузии D по длине зоны смеси. Эффективный коэффициент диффузии D можно считать пропорциональным коэффициенту гидравлического сопротивления, также определяемого профилем местных осредненных скоростей.
При последовательной перекачке нефтепродуктов, существенно отличающихся по вязкости, количество смеси увеличивается, а концентрация СБ = 0,5 не совпадает с координатой z -= 0. Расчеты и практические наблюдения свидетельствуют о том, что на количество смеси и распределение концентраций по ее длине влияет порядок следования нефтепродуктов разной вязкости: если замещающий нефтепродукт имеет меньшую вязкость, чем замещаемый, то объем смеси на 10—15 % больше, чем при обратном порядке следования этих же нефтепродуктов. Физически это можно объяснить трудностью «смывания» высоковязкого нефтепродукта, например дизельного топлива, маловязким нефтепродуктом, например бензином, вблизи стенок трубы, где интенсивность турбулентного перемешивания снижается. Объем смеси при последовательной перекачке различающихся по вязкости нефтепродуктов в пределах симметричных концентраций можно определить по формуле
Кс„/Ктр=2г РеБ°'5[\ +{DA/DBf%
где D4, Об, Рев — соответственно эффективные коэффициенты диффузии и числа Пекле для нефтепродуктов А и Б.
Влияние плотностей и остановок последовательной перекачки
Различие плотностей последовательно перекачиваемых нефтепродуктов оказывает гораздо меньшее влияние иа объем смеси, чем различие вязкостей, и им можно пренебречь при нормальных условиях перекачки. Однако в случае остановки зоны смеси в трубопроводе при аварийном прекращении последовательной перекачки различие плотностей может привести к существенному увеличению количества смеси, особенно если рельеф местности пересеченный и нефтепродукт большей плотности находится выше по склону нефтепродукта меньшей плотности. Если при остановке перекачки нефтепродукт большей плотности находится выше по склону нефтепродукта меньшей плотности (наиболее опасный случай), то происходит существенное увеличение смеси вследствие растекания более плотного нефтепродукта вниз по склону.
Заметное увеличение количества смеси происходит и в том случае, если остановка зоны смеси происходит в горизонтальном трубопроводе большого диаметра. Если же при остановке перекачки более плотный нефтепродукт находится ниже по склону, чем менее плотный нефтепродукт, то заметного увеличения смеси не происходит. На количество смеси оказывают также влияние тупиковые ответвления от основного трубопровода и лупинги на его трассе, например, при пересечении рек. Тупиковые ответвления остаются заполненными замещаемым нефтепродуктом А, который постепенно вымывается замещающим нефтепродуктом Б и ухудшает его качество. При наличии большого числа тупиковых ответвлений на трубопроводе ухудшение качества нефтепродукта Б вследствие вымывания из этих ответвлений нефтепродукта А может оказаться заметным.
При наличии на трубопроводе лупинга поток на этом участке раздваивается и при несовпадении скоростей в основной магистрали и лупинге уже образовавшаяся смесь попадает в поток чистого нефтепродукта в месте соединения лупинга с магистралью. При одинаковом диаметре и скорости течения в лупинге и основной магистрали оценка влияния лупинга на увеличение смеси вследствие раздваивания потока может быть приближенно определена ио формуле
VfM.JVm = ^/l +7LJL,'
где 1/См. л и — соответственно объем смеси с учетом лупингов и длина лупингов; УСм и L — объем}|смеси без лупингов и длина трубопровода.
6.5. ГИДРАВЛИЧЕСКИЙ РАСЧЕТ НЕФТЕПРОДУКТОПРОВОДА ПРИ ПОСЛЕДОВАТЕЛЬНОЙ ПЕРЕКАЧКЕ
Предполагаются заданными количество и номенклатура нефтепродуктов, получаемых от «источника» — НПЗ, и годовая потребность потребителей — распределительных нефтебаз для разветвленной системы трубопроводов или конечного пункта «стволового» магистрального трубопровода. На основе этих данных определяют среднегодовую пропускную способность отдельных расчетных участков нефтепродуктопровода Gr:
П
Gr = I Gri,
где Gri — годовое количество г'-го нефтепродукта; п — число перекачиваемых последовательно нефтепродуктов.
Для найденного значения Gr по табл. 6.1 для разветвленных или по нормам технологического проектирования для «стволовых» нефтепродуктопроводов определяют рекомендуемый диаметр данного участка, берут для расчета еще два соседних диаметра и ведут дальнейший расчет по этим трем вариантам. При расчете «стволового» нефтепродуктопровода определяют расчетную часовую пропускную способность по формуле
П
8400
![]()
i = l
Затем для всех рассматриваемых вариантов выполняется гидравлический расчет с определением потерь напора на всех расчетных участках, определением числа насосных станций, подбором насосов. Если на нефтепродуктопроводе по расчету должны быть промежуточные насосные станции, то расчет потерь напора следует вести по нефтепродукту с наибольшей вязкостью, так как при последовательной перекачке партия наиболее вязкого нефтепродукта на участке между двумя соседними насосными станциями будет «лимитировать» пропускную способность всего нефтепровода. Если нефтепродуктопровод по расчету не имеет промежуточных насосных станций, то его пропускная способность будет плавно меняться по мере замещения нефтепродукта одной вязкости нефтепродуктом другой вязкости. Поэтому при подборе насосов в этом случае должна быть обеспечена возможность их работы при перекачке каждого нефтепродукта в зоне максимального коэффициента полезного действия. По совмещенным характеристикам для каждого варианта определяют фактическую часовую пропускную способность Q4 i и продолжительность (в сутках) перекачки каждого из нефтепродуктов Nt:
где Гр — расчетное число суток работы нефтепродуктопровода в течение года. Если это условие не выполняется, то подбирают насосы с большей подачей.
В качестве оптимального принимают вариант нефтепродуктопровода с минимальными приведенными затратами (на сооружение и эксплуатацию линейной части и насосных станций), определяемыми по 206 нормативным показателям в соответствии с нормами технологического проектирования.
Для оптимального варианта «стволового» нефтепродуктопровода определяют оптимальное число циклов исходя из следующих соображений. На начальный пункт нефтепродуктопровода с НПЗ практически одновременно поступает несколько разных нефтепродуктов. Поэтому в период закачки в нефтепродуктопровод одного из нефтепродуктов все остальные должны поступать в предназначенные для них резервуары.
Снабжение потребителей на конечном пункте нефтепродуктопровода разными нефтепродуктами также практически происходит одновременно. Поэтому в период поступления на конечный пункт из нефтепродуктопровода одного из перекачиваемых последовательно нефтепродуктов для бесперебойного снабжения потребителей нефтепродуктами других сортов должны быть созданы запасы их в выделенных для этого резервуарах конечного пункта. Если нефтепродукты перекачивать последовательно очень большими по объему партиями, то в течение года на конечный пункт нефтепродуктопровода поступит небольшое количество смеси этих нефтепродуктов. Следовательно, затраты на исправление смеси и убытки от пересортицы окажутся незначительными. Однако при этом на начальном и конечном пунктах нефтепродуктопровода потребуется соорудить резервуарные парки большого объема, что приведет к большим капиталовложениям и расходам на их эксплуатацию. Если перекачивать нефтепродукты большими по объему партиями, то расходы на сооружение и эксплуатацию резервуаров окажутся небольшими, зато значительно увеличится количество смеси на конечном пункте и, следовательно, возрастут затраты на исправление смеси и убытки от пересортицы. Таким образом, по мере увеличения числа циклов последовательной перекачки и уменьшения объема партий нефтепродуктов затраты на резервуары будут снижаться, а затраты на исправление и реализацию смеси возрастать, поэтому должно существовать некоторое оптимальное число циклов, которому соответствует минимум суммарных затрат на резервуары и исправление смеси.
Число разных нефтепродуктов, перекачиваемых последовательно по существующим магистральным нефтепродуктопроводам, колеблется от 3 до 10 видов и более. При этом сами нефтепродуктопроводы могут иметь путевые сбросы и подкачки нефтепродуктов, а объем потребления отдельных нефтепродуктов претерпевает сезонные изменения.
Оптимальное число циклов последовательной перекачки для рассматриваемого случая может быть определено из условия минимума приведенных затрат на резервуары для создания запасов нефтепродуктов и на реализацию получаемой смеси.
В настоящее время по отечественным магистральным нефтепродуктопроводам последовательно перекачиваются в основном бензины и дизельные топлива различных марок.
Если в каждом цикле необходимо последовательно перекачивать разные по своим свойствам и назначению нефтепродукты, то число отдельных партий в цикле и число зон контакта разных нефтепродук-
1 2 . п-1 п п-1 . 2 1
' Цикл
Рис. 6.9. Схема к определению числа партий нефтепродуктов в цикле последовательной перекачки (с учетом совместимости нефтепродуктов)
тов, т. е. зон образования смеси (как это следует из рис. 6.9), при соблюдении условия наименьшего различия физико-химических свойств будет п = 2 (т—I). Если /; — продолжительность закачки в нефте-продуктопровод i-го нефтепродукта, а в каждом цикле перекачиваются т нефтепродуктов, то общая продолжительность одного цикла составит
т—1
+ 21-2 2tm—i + tm -- t% + 2 У] Ui 4~ tm-
i=2
Предположим, что нефтепродуктопровод имеет г сосредоточенных путевых отборов в определенных пунктах трассы с суточными расходами ^сут 1, Чсут 2. • • • . <7сутг и s подкачек нефтепродуктов от расположенных вдоль трассы нефтеперерабатывающих заводов с суточным расходом qni, qn2, . . . , qns- При перекачке всех нефтепродуктов
ТП—\
в цикле, кроме первого, в течение времени Tll — t1 = 2 ti + tm на
i=2
начальном пункте и в местах подкачки будет накапливаться первый нефтепродукт, а на конечном пункте и в пунктах сброса тот же первый нефтепродукт из созданных ранее запасов, который будет поставляться потребителям. Если q1H — суточное поступление нефтепродукта с завода на начальный пункт, то необходимый для его хранения объем резервуаров будет V1П = <7m (Ta—tj, а в местах подкачек на трассе необходимо иметь объем
^1П / + Л <?1П / (Тц /ц),
/=1 /=1
где 71П/- — суточное поступление первого нефтепродукта на /-м пункте подкачки.
Объем резервуаров для создания необходимых запасов первого нефтепродуктопровода на конечном пункте составит VK = qjh (Тц -tx), а в местах отбора (сброса) на трассе
? Z <7ю i(Tu-/Л,
1=1 i=i
где q 1С1- — суточное потребление первого нефтепродукта на i-м пункте отбора; 91К — суточное потребление первого нефтепродукта на конечном пункте нефтепродуктопровода.
Таким образом, для создания необходимых запасов перекачиваемых нефтепродуктов всех сортов требуется следующий объем резервуаров:
Общий объем резервуарных парков всего нефтепродуктопровода определится из суммы этих выражений
Ц Lp=l
-S /71 Г ГП
+ ? Е?рп/(^о-^)+Е Е<7рс^0-лд +
/=1 р==1 i=l р=1
+ ? <7„к(лг0-лд1 = -?-. (6.26)
р = 1 J ц
где ip -- Np/Ц] Тц = Nq/Ц-, Np — число дней в году для перекачки р-го нефтепродукта; yv0 — число дней работы нефтепродуктопровода в течение года; Ц — число циклов последовательной перекачки в году.
Суммарные приведенные затраты П на сооружение и эксплуатацию резервуаров и на реализацию смеси можно представить в виде соотношения
где Ей — нормативный коэффициент эффективности капиталовложений для нефтяной промышленности; /( и Э — соответственно удельные капиталовложения и эксплуатационные расходы на единицу полезного объема резервуара; А — убытки от смешения нефтепродуктов
П
за цикл, Л = ? ait п — число контактов разных нефтепродуктов
i = 1
в одном цикле; УСм — объем резервуаров для приема смеси нефтепродуктов на конечном пункте.
Необходимый объем резервуаров для смеси Усм можно определить из следующего соотношения: Усм = (Ус. ц —Vp. ц) //, где 1/с. ц — объем смеси, принятый на конечном пункте за один цикл; Vp. „ — объем смеси, реализованный в течение одного цикла.
Для определения минимума функции ее первую производную по числу циклов приравняем к нулю с учетом (6.26)
[т s т
йП
ЛЦ
I q^Wo-NJ+'Z ^qpniiNo-N,)-]-р = \ / = 1 р== I
г т т т
+ 1 ? 17г /( V,, .V..) • ZqpK(N0-Np) \ ^—+ А+
.¦=1р=‘ р-i J ^пт
+ (^с.ц-^р.и)(?,Л+Э) ч.
Решая это уравнение относительно оптимального числа циклов Z/опт, получаем следующую расчетную формулу
В (ЕиК + Э)
I__yj.5
нК + Э) J
А -{-(Усц-Ури) (Е
Зная Z/опт, можно по формуле (6.26) определить оптимальный объем резервуарных парков всего нефтепродуктопровода и распределение этого объема между начальным, конечным и промежуточным пунктами нефтепродуктопровода. Затем определяют продолжительность перекачки каждого нефтепродукта в период одного цикла, а с учетом формулы рассчитывают объем партий нефтепродуктов в каждом цикле.
Гидравлический расчет разветвленного нефтепродуктопровода (типа «дерево») при большом числе отводов производится при помощи ЭВМ для различных сочетаний включений отводов. Методика гидравлического расчета разветвленных нефтепродуктопроводов разработана в отраслегой лаборатории гидродинамических исследований кафедры
транспорта и хранения нефти и газа а [ МИНГ им. И. М. Губкина.
На рис. 6.10 изображены две схемы разветвленных нефтепродуктопроводов, имеющих структуру простого а и сложного б дерева. Из комбинаторики известно, что для трубопровода с п отводами, имеющего структуру простого дерева, число N возможных способов включения отводов равно 2П. Если разветвленный трубопровод имеет структуру сложного дерева, каждое из ответвлений которого характеризуется Nu N г ... Nn способами включений, то общее число N возможных сочетаний включения отводов будет равно произведению этих чисел: N = N3 . . . Nn. Рис. 6.10. Схемы разветвленных Для схемы, изображенной на рис. нефтепродуктопроводов 6.10, а, число возможных включений составляет 8, а для случая рис. 6.10, б— 1024. Поэтому разветвленный нефтепродуктопровод будет иметь не одну, а N гидравлических характеристик «расход — напор», каждая из которых относится к определенному варианту включения отводов. Вначале выполняется гидравлический расчет системы для всех возможных комбинаций включения отводов для определения расходов в отводах и основной магистрали при различных вариантах. Для этого решается система уравнений баланса напоров и расходов в каждом узле системы нефтепродуктопроводов. Эти уравнения для г-го узла варианта включения отводов имеют вид
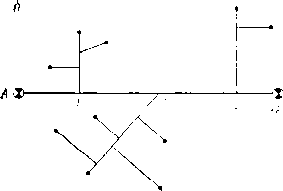
тг 11 ikhk г\ 2 .гг lt klia, k 2 ,
Н i — 1, k H i, к— , r n Ik H io K 4ikt
nzd°ikg я d^g
Qik =- -; Qik~Q(i+l)k + Qik^
4
где Hik — напор в i-м узле; со* — максимально допустимая скорость потока жидкости в отводе; Xlk, hi0y k — коэффициенты гидравлического сопротивления г-го участка и г-го отвода; lik, dik — соответственно длина и диаметр г-го участка; Qik — расход на участке между (г—1) и i-м включенными отводами; g— ускорение свободного падения; Hi0 — расчетный напор в конце каждого отвода; li0, di0 — соответственно длина и диаметр г-го отвода; qlk — расход в i-м отводе.
В результате такого расчета определяют расходы qlk, qik, . . . . . . , qnk при всех «?» вариантах включения, а также транзитные расходы qok.
Запланированные объемы поставки нефтепродуктов на i-ю нефтебазу Vi за время Т, продолжительность работы tk при k-м варианте включения отводов связаны с расходами qt выражениями:
п N
'L 4iktk==V1-,
i=0 k = \
Решение этой системы ищут при условии, что транзитный расход
N
через рассматриваемый участок будет равен плановому ^ q^kh
k=i
— У план-
Задачу решают на ЭВМ подбором различных сочетаний расходов в отводах, диаметров магистрали, отводов и напоров. В результате уточняют параметры разветвленного нефтепродуктопровода, размещение насосных станций и оптимальную схему включения отводов, обеспечивающую доставку нефтепродуктов на нефтебазы в минимальные сроки. Число циклов и объем партий нефтепродуктов для разветвленных нефтепродуктопроводов определяют исходя из мощности НПЗ, потребности нефтебаз, наличия резервуарной емкости на нефтебазах с учетом принятой схемы эксплуатации разветвленной системы. При этом может оказаться, что на отдельных нефтебазах потребуется установка дополнительного числа резервуаров, чтобы обеспечить снабжение потребителей при соблюдении оптимального числа циклов последовательной перекачки.
6.6. РАСЧЕТ ИЗМЕНЕНИЯ ПРОПУСКНОЙ СПОСОБНОСТИ НЕФТЕПРОДУКТОПРОВОДА ПРИ ПОСЛЕДОВАТЕЛЬНОЙ ПЕРЕКАЧКЕ НЕФТЕПРОДУКТОВ С РАЗНОЙ ВЯЗКОСТЬЮ
В трубопроводе большой протяженности с промежуточными насосными станциями обычно находится несколько чередующихся партий нефтепродуктов, так как объем каждой партии в несколько раз меньше объема всего трубопровода. Так, в магистральном нефтепродуктопроводе протяженностью 1000 км могут одновременно находиться 5—6 партий разнородных нефтепродуктов, например бензин и дизельное топливо. Пропускная способность такого трубопровода будет ограничиваться (лимитироваться) пропускной способностью одного из участков, занятого партией более вязкого нефтепродукта. И хотя на участках, занятых менее вязким нефтепродуктом, будет при этом оставаться неиспользуемый напор, передать его на участки с более вязким нефтепродуктом полностью не удается из-за ограничения максимального давления в трубопроводе прочностью труб. По мере перемещения партий нефтепродуктов по трубопроводу лимитирующая пропускная способность может изменяться.
Определить максимальную пропускную способность трубопровода с промежуточными насосными станциями в этом случае можно методом последовательных приближений, который заключается в следующем. При известном расположении партий нефтепродуктов, полагая включенными все насосы на насосных станциях, из уравнения баланса давлений определяют пропускную способность трубопровода (нулевое приближение). Затем при найденной таким образом пропускной способности проверяют выполнение ограничений по максимальному давлению нагнетания после каждой насосной станции и по минимальному давлению подпора перед каждой насосной станцией, начиная с первой.
При первом же невыполнении этих ограничений давление на данной насосной станции принимают равным предельно допустимому и определяют новое значение пропускной способности, после чего повторяют процедуру проверки ограничений. В результате расчета определяют «лимитирующий» участок трубопровода, где давления нагнетания и подпора равны предельно допустимым и определенная для этого случая пропускная способность всего трубопровода будет максимально возможной при данном расположении партий нефтепродуктов.
Предлагаемая методика расчета максимальной пропускной способности нефтепродуктопровода путем последовательных приближений позволяет определить «лимитирующую» пропускную способность и «лимитирующий» участок на каждом шаге перемещения партий нефтепродуктов.
Продолжительность движения Т по нефтепродуктопроводу любой «отмеченной» границы раздела нефтепродуктов в этом случае может быть определена суммированием продолжительности замещения на каждом шаге расчета Att при известной и постоянной на этом шаге максимальной пропускной способности Q*.
При последовательной перекачке бензина, дизельного топлива разных сортов можно ограничиться рассмотрением двух групп нефтепродуктов, существенно различающихся по вязкости и плотности. Если перекачивается один нефтепродукт или несколько нефтепродуктов с одинаковыми вязкостями и плотностями или нефть одного сорта по нефтепродуктопроводу, то эта методика позволяет определить его максимальную пропускную способность.
Пропускную способность на каждом шаге расчета при известном расположении партий нефтепродуктов с разными вязкостями определяют из уравнения баланса давления для «стволового» трубопровода с п насосными станциями, на которых установлено по kt насосов, включенных последовательно:
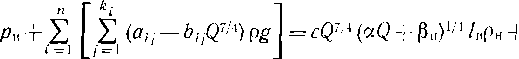
О
+ Z cQ7/4 (aQ + p,)i;i IrP, + cQ7/i («Q 4- pK)1/4Lp, +
П
+ ? РдР i ~Г P2 + Put
(6.27)
4=1
где ац, btj — коэффициенты; р„ — соответственно протяженность начальной партии нефтепродукта, закачиваемого в трубопровод, и его плотность; /к, рк — соответственно протяженность конечной партии нефтепродукта, принимаемой из трубопровода в резервуар, и его плотность; рдрj—дросселируемое давление на t-м участке; с — = 0,88l(n2d6); а = kjd, Р == ndv, къ — эффективная шероховатость труб.
Потерю давления на преодоление разности геодезических отметок для участка трубопровода с равномерным уклоном при перекачке двух нефтепродуктов с разными плотностями можно записать следующим образом (рис. 6.11):
Pz=-- Ipб1б + Рл (L — h)] g tg сс — рAgSz + (рв — Рл) Az/b/L.
Если профиль трассы трубопровода более сложный, то он может быть условно разделен на участки с примерно равномерными уклонами и величина р2 такого трубопровода при известном расположении партий нефтепродуктов определится суммой потерь давления на отдельных участках.
Ограничения на давления до и после Уе-й насосной станции можно записать в следующем виде:
k—l
Ри + ? Рст i ? Pn i ' ? Рдр i S? Pmim
= 1
ft ft—I ft
Pn + ? Per i ? Pn i ? Рдр i ^ Ртах>
(6.28)
где i — давление, развиваемое t-й насосной станцией; рni— потери давления на t-м участке трубопровода.
Рис. 6.11. Схема, иллюстрирующая вычисление величины р2
0 Р 5
В качестве нулевого приближения принимается пропускная способность Q0, определяемая по уравнению (6.27) при давлении в начале первого линейного участка ри, при давлении в конце трубопровода (в конце последнего линейного участка) pn+i == Рк и при отсутствии дросселирования давления. Затем при определенной таким образом пропускной способности Q0 проверяют выполнение ограничений (6.28) по давлению перед &-й насосной станцией и давлению после k-ii насосной станции, начиная с первой насосной станции. Если давление подпора перед какой-либо насосной станцией pt <Срт\п и не удовлетворяет ограничению (6.28), то оно принимается равным pmin(р{ = ртin) и вновь определяется пропускная способность на участке от первого линейного участка до этой насосной станции. Если давление нагнетания после k-й станции больше ртах, то оно принимается равным ртаи и по уравнению (6.27) определяется новое значение пропускной способности Qr для участка от этой насосной станции до конца трубопровода и в дальнейших расчетах учитывается лишь меньшее значение.
Если нефтепродуктопровод без промежуточных насосных станций, то различие вязкостей нефтепродуктов будет влиять на изменение пропускной способности в период замещения нефтепродуктов и продолжительность этого замещения (рис. 6.12). Когда нефтепродукт вязкостью и плотностью рл замещается в начале нефтепродуктопровода с одной насосной станцией, оборудованной центробежными насосами, другим нефтепродуктом вязкостью vB и плотностью QB, то по мере перемещения зоны раздела этих нефтепродуктов пропускная способность последовательной перекачки будет изменяться от QA в момент начала замещения до QB в момент окончания замещения (рис. 6.13). Такое изменение пропускной способности будет происходить из-за неодинаковых потерь напора на преодоление гидравлического сопротивления на участках, занятых перекачиваемыми нефтепродуктами. При этом если vA >vfi, то пропускная способность перекачки будет увеличиваться, а если vA Од — уменьшаться. Уравнение баланса давлений для этого случая (только одна головная насосная станция) имеет вид
k
Рн+ Е (aj — bjQ7li)psg = cQ7/*(a0Q \-$s)'/-ip5lB +
+cQ7/4 (a0Q + Рл)1/4 Рл (L—1Б) + рдр + р2 + рк
где рл = l7ndvA; = 17ndvE. 214
режимов перекачки бензина и дизельного топлива ошибка в определении пропускной способности последовательной перекачки и продолжительности замещения достигает 15 %.
6.7. ПРИЕМ И РЕАЛИЗАЦИЯ СМЕСИ НЕФТЕПРОДУКТОВ НА КОНЕЧНОМ ПУНКТЕ НЕФТЕПРОДУКТОПРОВОДА
Образующаяся в нефтепродуктопроводе смесь перекачиваемых последовательно нефтепродуктов принимается, как правило, в конечном пункте нефтепродуктопровода и реализуется одним из следующих способов: добавляется в допустимых количествах к соответствующим нефтепродуктам; отправляется на ближайший НПЗ в качестве сырья для переработки совместно с нефтью.
Нефтепродукты, поступающие с НПЗ, имеют, как правило, некоторый «запас качества» по отдельным показателям, например, по температуре конца кипения и октановому числу для бензинов, по температуре вспышки для дизельного топлива и т. п. Этот «запас качества» необходим для компенсации возможного ухудшения качественных характеристик топлив при их транспорте и хранении.
Поскольку с конечного пункта нефтепродуктопровода нефтепродукты поступают в большинстве случаев к потребителям, оказывается возможным использовать имеющийся у них «запас качества» для добавления к ним смеси соответствующих нефтепродуктов в небольших количествах, определяемых допустимыми концентрациями примеси одного нефтепродукта к другому, которые предполагаются известными в результате проведенных анализов нефтепродуктов и их смесей или в результате предварительных расчетов.
Технология приема смеси из нефтепродуктопровода в резервуары конечного пункта определяется свойствами компонентов смеси, запасом качества и количеством нефтепродуктов в резервуарах.
При большом объеме резервуаров с нефтепродуктами и значительном «запасе качества» у них иногда можно всю смесь прямо из нефтепродуктопровода распределить по резервуарам с перекачиваемыми нефтепродуктами.
Смесь разносортных нефтепродуктов, например бензина и дизельного топлива, обычно делят на две части и принимают в два отдельных резервуара (рис. 6.15). Та часть смеси, в которой меньше бензина, получила название легкого дизельного топлива, а другая часть смеси, в которой больше бензина,— тяжелого бензина.
Тяжелый бензин добавляют затем в допустимых количествах к товарному бензину за счет запаса качества у него по концу кипения и другим показателям. Легкое дизельное топливо добавляют к дизельному топливу, используя запас качества у него по температуре вспышки и другим показателям. При этом в зависимости от состава смеси и запаса качества в резервуарах соответствующих товарных нефтепродуктов составляется карта смешения с указанием, сколько и какой смеси можно добавить в резервуар с конкретным нефтепродуктом. При подходе зоны смеси к конечному пункту ее головная часть направляется в резервуар с замещаемым нефтепродуктом, хво-
Рис. 6.14. Графики для сопоставления расчетов продолжительности замещения по уравнениям (6.31) (/) и (6.32) (2) при перекачке бензина и дизельного топлива в трубопроводе диаметром 359 мм
Начальное условие для уравнения (6.31) имеет вид у (0) = 0. Уравнение (6.31) позволяет определить изменение расхода в трубопроводе без промежуточных насосных станций и продолжительность замещения в нем нефтепродуктов с разными вязкостями и плотностями. Уравнение (6.31) допускает параметрическое решение, так как не зависит в явном виде от аргумента т. Если замещаемый и замещающий нефтепродукты перекачиваются в зоне гидравлически гладких труб по горизонтальному трубопроводу (Дг = 0), то (6.31) принимает более простой вид
![]()
(6.32)
где
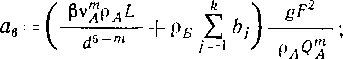
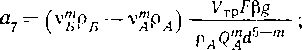
т = 0,25; р --Х
Уравнение (6.32) имеет аналитическое решение
![]()
откуда следует
![]()
I —1/(3—т)
Из сопоставления расчетов по «точному» уравнению (6.31) и упрощенному уравнению (6.32) для случая последовательной перекачки бензина и дизельного топлива по трубопроводу диаметром 359 мм и длиной 170 км (рис. 6.14) видно, что при расчете без учета различия 2)6
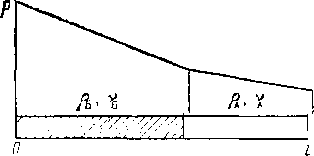
Рис. 6.12. Схема замещения нефтепродуктов в трубопроводе без промежуточных насосных станций
Рис. 6.13. Совмещение характеристик насосной станции и трубопровода при последовательной перекачке:
/ — насосной станции; 2 —• трубопровода при перекачке нефтепродукта Б\ 3 — трубопровода при перекачке нефтепродукта А: 4 — переменная характеристика трубопровода при замещении нефтепродуктов
Перейдем в (6.29) к относительному расходу с/ и времени т по условиям
QaHV
(6.30)
тр-
q~QIQA\
С учетом (6.30) величину 1Б (/) в уравнении (6.29) представим в виде
VT
Q (t) dt
q( т) dx =Ll/(t),
h(t)
nd'2 b
а относительный расход
dr
С учетом этих замен исходное уравнение (6.29) запишем в виде
at — а2у П4/7
г b
У’ = \— L a.i
(6.31)
+ а4 (ау' + ря)1/4 у + аъ (ay' + Рл)1/4 (1 — У) J где у' (т) — относительный расход в трубопроводе;
f}F*
Р Л<?Л
h - Г Рн + Z а/Р?
L / = 1
-(Агрл + р к)
q AzF-Р А® А
а3==
0,11/-2 QUM
а г, - ¦
ai ~ (Рв —Рл) О, llp?L
2р
Рб^2 Е Ь,
_ /=1
ап
Функция г/ (т) в уравнении (6.31) представляет собой относительный объем трубопровода, заполненный к моменту времени т замещающим нефтепродуктом, и изменяется в пределах 0 < у < 1.
Рис. 6.15. Схема приема смеси разносортных нефтелродук-_ тов — бензина и дизельного топлива:
1 — дизельное топливо; 2 — «легкое» дизельное топливо; 3 — «тяжелый» бензин; 4 — бензин (^бенч — концентрация бензина в смеси; г,, t2 — моменты начала и конца приема смеси соответственно; tQ — момент разделения смеси)
стовая часть — в резервуар с замещающим нефтепродуктом, а остальная основная часть смеси принимается в отдельный резервуар. Допустимое количество нефтепродукта Б, которое можно принять вместе со смесью в резервуар с нефтепродуктом А, определяется исходя из «запаса качества» замещаемого нефтепродукта и его количества в резервуаре с нефтепродуктом А. Момент переключения задвижек у резервуаров для отсечки головной части смеси от остальной ее части определяют по графику изменения концентрации смеси по ее длине, измеряемой прибором контроля. Аналогично поступают и при отсечке хвостовой части смеси в резервуар с нефтепродуктом Б.
На конечном пункте устанавливают обычно два прибора контроля, измеряющих концентрацию нефтепродуктов в зоне смеси: первый в 10—15 м от конечного пункта, а второй — на конечном пункте. Зная допустимые количества примеси в резервуарах с нефтепродуктами А и Б, по графику изменения концентрации по длине зоны смеси, измеренной первым прибором, определяют графическим интегрированием моменты отсечки головной и хвостовой частей смеси и соответствующие им значения мгновенной концентрации смеси. Как только второй прибор контроля в момент прихода смеси на конечный пункт зарегистрирует эти значения концентраций отсечки, переключают задвижки перед соответствующими резервуарами и ведут прием смеси в соответствии с принятой схемой ее реализации. Если режим перекачки соответствует расчетному и можно ожидать, что распределение концентраций по длине зоны смеси будет следовать формуле (6.27), то концентрации отсечки головной и хвостовой частей смеси можно определить следующим способом.
Если известно время (t2—/2), в течение которого в резервуар с нефтепродуктом А будет поступать головная часть смеси, то количество нефтепродукта Б, попавшего в этот резервуар вместе со смесью, определится интегралом
л
где Q — пропускная способность трубопровода, принимается постоянной в период приема смеси.
Подставив в (6.33) значения СБ (t) из формулы (6.27) и проинтегрировав, получим
f erf г] ~ z erf
zexP ( ~f_) — 1
t
и у Jl
после интегрирования получим для концентрации нефтепродукта Б в резервуаре с нефтепродуктом А следующие выражения:
СБра= [Ф (Zl) “ Ф (Za)1 ’ (6'34)
VPA VpAPe0.5
где VPA — количество нефтепродукта в резервуаре А;
Ф(21,2) = = 2ll2(l— erf zlt 2)--^ ехр ( —z?i2);
V л
ix — момент начала прохождения смеси, определяемый точностью прибора; t., — момент отключения резервуара с нефтепродуктом А.
Поскольку СБ (zx) близко к нулю, по абсолютной величине функция Ф (Zj) < Ф (z.,) и ею можно пренебречь. Так, при СБ (Zj) = = 0,5 % и СБ (z2) = 10 % Ф (Zj) = 0,0001 и погрешность при ее отбрасывании составляет всего лишь 0,1 %. При этом допущении получим
Г ехр ( — г?) 1
СБРл=?л[---z2(l — erf z2)j , (6.35)
где
Ia^VtAV рдРе0'5).
Если известно время (/4—/3), в течение которого в резервуар с нефтепродуктом Б будет поступать хвостовая часть смеси, то количество нефтепродукта А , попавшего в этот резервуар вместе со смесью, определится интегралом
VV=Qf[l-CB(t)\dt, (6.36)
t:
где t:i — момент отсечки хвостовой части смеси в резервуар с нефтепродуктом А\ /4 — момент окончания прохождения смеси по показанию прибора контроля.
Произведя в (6.36) интегрирование по аналогии с (6.33), получим
где
?B = VTP/(VPBPe°-s);
(г3,4) == г3,4 (1 + er f z3,4)-J--p^exp ( —Z3,4);
V л
VPB — количество нефтепродукта Б в резервуаре.
Поскольку в момент окончания прохождения смеси величина СБ (z4) близка к единице, по абсолютному значению гр (z4) гр (za) и ею можно пренебречь. При этом
С л р в = + 2з (1 + erf га)] • (6.37)
Из формулы (6.27) следует, что
СБ (z2) =-^-{\—^\z2)\ С б (гя) =-у (1—erf za).
Функции (6.35) и (6.37) представлены на рис. 6.16 в виде семейства кривых с параметрами t,A и ?,Б. Зная допустимые концентрации примеси к нефтепродуктам СБРА и САрБ, а также параметры Z,A и можно с помощью графика на рис. 6.16 определить значения мгновенных концентраций смеси в трубопроводе СБ2 и Свя, при которых следует переключать резервуары. На оси ординат находят точки,
соответствующие заданным значениям СБРА и САРБ, и проводят го
ризонтальные линии до пересечения с соответствующими кривыми
ДЛЯ ЪА И 1Б.
Затем из точек пересечения проводят вертикальные прямые до пересечения с кривой СБ (г) и сносят эти точки пересечения на ось
ординат, находят точки, соответствующие концентрациям смеси в трубопроводе СБ2 и СБа, при достижении которых следует переключать резервуары. Если окажется, что СБ2<.СБа, то часть смеси между этими концентрациями не может быть принята в резервуары с нефтепродуктами А и Б и ее следует принимать в резервуары для смеси. При этом объем смеси можно подсчитать по формуле VcJVjp = = 2 (z,2—zs) Ре-0'5, а значения z2 и 23 определить по графику на рис. 6.16 путем сноса точек пересечения на ось абсцисс. Если окажется, что С б г >?/;?, то вся смесь может быть принята в резервуары с нефтепродуктами А и Б, а переключать эти резервуары МОЖНО гри любом значении концентрации смеси в трубопроводе в диапазоне СБ2—СБа. В этом случае СБ2 = СБЗ = СБ и г2 = z4 = г. Если равны и объемы резервуаров 220
СБ' САрб 'L fipA
Рис. 6.16. Обобщенный график для расчета приема смеси
Урб ~ VPA, то t,A — и система расчетных уравнений упрощается
С а р и ~ р А ----- 2?z;
С с : - ~ (1— erf г)
и может быть преобразована в одно уравнение, связывающее допустимые концентрации примеси в резервуарах и концентрацию смеси в трубопроводе в момент ее разделения по резервуарам с нефтепродуктами Ли Б:
СБ j- [ 1 - erf (
^р_б_-СБрА
.
При разделении смеси разносортных нефтепродуктов на две части, например на тяжелый бензин и легкое дизельное топливо, при последовательной их перекачке в расчетах иногда учитывается относительное количество одного нефтепродукта, попавшего в другой, при помощи критерия качества смеси /.
Критерии качества смеси / определяется суммой двух интегралов (рис. 6.17)
1 (z0) = ~Va\1~
Vh = .1 t1 — сб (г)]
dz-4- J СБ (г) dz,
*тр —оо
где VА и VB — объем нефтепродуктов соответственно А и Б, попавших в смесь; г„ — координата сечения деления смеси на две части.
Если г0 ¦= 0 и СБ (г0) = 0,5, то критерий качества смеси имеет минимальное значение
/ . — Dp-о..ч
1 mi л — /— ГС •
V л
Критерий качества позволяет оценивать по характеру кривой распределения концентраций по длине зоны смеси влияние количества примеси одного нефтепродукта к другому при разделении всей смеси на две части. Он также позволяет сравнивать количества товарных нефтепродуктов, необходимое для реализации смеси. Так, из рис. 6.18 видно, что критерий качества смеси для распределения концентраций для случая 1 меньше, чем для случая 2, хотя суммарный объем смеси 17см в обоих случаях одинаков. Поэтому для реализации смеси, разделенной на дне части, путем подмешивания в случае 1 потребуется меньше товарных нефтепродуктов, чем в случае 2. Допустимые концентрации примеси одного нефтепродукта к другому определяются, как правило, по результатам анализа нефтепродуктов и их смесей в лаборатории конечного пункта. Ориентировочные значения допустимых концентраций для некоторых нефтепродуктов приведены в табл. 6.2.
Рис. 6.17. Схема, иллюстрирующая критерий качества смеси
Рис. 6.18. Схема сопоставления критериев качества смеси при различном характере распределения концентраций по длине зоны смеси
Примесь бензина к дизельному топливу ограничивается допустимым снижением его температуры вспышки, а примесь дизельного топлива к бензину — допустимым повышением конца кипения бензина.
Определить допустимую концентрацию примеси бензина к дизельному топливу по температуре вспышки можно по эмпирической формуле
Р (16,7/jo-
'-'бенз -
~ 32) jg in. ф
tn, ф + 55 tв
где tl0 — температура выкипания 10 % бензина; U. ф —фактическая температура вспышки чистого дизельного топлива; tBCп — минимально допустимая температура вспышки дизельного топлива.
Определить допустимую концентрацию примеси дизельного топлива к бензину по температуре конца кипения можно из эмпирического соотношения
с (<к- 124)»-(<к.ф- 124)2
Д Т ~ (Рас — 0,753) 28 10:)где tK — максимально допустимое значение конца кипения бензина; tv., ф — фактическая температура конца кипения чистого бензина; р20 — плотность дизельного топлива.
Таблица 6.2
| Товарный нефтепродукт |
Ориентировочные максимально допустимые концентрации примеси. | ||||
| Бензин А-72 |
Топливо ТС-1 |
Дизельное топливо |
Керосин трактор ный | ||
| Л | 3 | ||||
|
Бензин А-72 | ЛК |
3 | 0,5 |
1 | 1 |
|
Топливо ТС-1 | 0 |
лк | 1 |
5 | 0 |
|
Дизельное топливо летнее (Л) |
0 | 1 |
лк | 0,5 |
0,6 |
| Дизельное топливо зимнее (3) | 0,5 | 6 | 55 |
лк | 16 |
| Керосин тракторный |
3 | лк |
1,5 | 3 |
лк |
Примечание. ЛК — любое количество примеси.
6.8. МЕРОПРИЯТИЯ ПО УМЕНЬШЕНИЮ КОЛИЧЕСТВА СМЕСИ ПРИ ПОСЛЕДОВАТЕЛЬНОЙ ПЕРЕКАЧКЕ
Количество смеси, образующейся в каждой зоне контакта последовательно перекачиваемых нефтепродуктов, составляет 0,5—1 % от объема трубопровода при турбулентном режиме перекачки, а для трубопровода большой протяженности достигает нескольких сотен кубических метров. При остановках перекачки, большом объеме первичной смеси и малой скорости перекачки количество смеси может в 2—,3 раза превысить номинальное ее количество для конкретного трубопровода.
Для уменьшения количества смеси на магистральных нефтеиро-дуктопроводах предусматривают организационные мероприятия, а также применяют разделители для полного или частичного разобщения последовательно перекачиваемых нефтепродуктов.
Организационные мероприятия по уменьшению количества смеси предусматривают перекачку при нормальных и повышенных скоростях турбулентного потока нефтепродуктов (при Re >10 ООО), чтобы уменьшить эффективный коэффициент диффузии; правильный выбор порядка следования партии нефтепродуктов, обеспечивающего меньшие затраты на прием и реализацию смеси: максимально возможное увеличение партий нефтепродуктов (исходя из возможностей резер-вуарного парка), что позволяет уменьшить общее количество физических смесей в течение квартала, года; применение быстродействующих задвижек для уменьшения количества первичной смеси; предотвращение остановок последовательной перекачки, особенно при неблагоприятном рельефе местности.
Перечисленные организационные мероприятия следует применять при проведении последовательных перекачек, так как они позволяют свести количество смеси к некоторому минимуму, определяемому гидродинамикой процесса смешения контактирующих жидкостей в процессе перекачки.
Дальнейшее уменьшение количества смеси ниже этого минимума можно обеспечить, лишь применяя разделители, помещаемые в зону последовательно перекачиваемых нефтепродуктов. Разделители могут быть жидкостные и твердые. Жидкостный разделитель представляет собой буферную жидкость, помещаемую между последовательно перекачиваемыми нефтепродуктами. В качестве жидкого разделителя применяют какой-либо нефтепродукт или образовавшуюся ранее смесь последовательно перекачиваемых нефтепродуктов. Так, между бензином и дизельным топливом можно поместить буферную партию реактивного топлива (или керосина). В этом случае бензин и дизельное топливо будут смешиваться с реактивным топливом, и эту смесь легче реализовать, чем смесь бензина с дизельным топливом. Объясняется это тем, что допустимые концентрации реактивного топлива к бензину и дизельному топливу в несколько раз больше (см. табл. 6.2) и для реализации смеси потребуется меньше «чистых» нефтепродуктов. В качестве разделителей стали чаще применять загущенные жидкости (так называемые полужидкие или гелеобразные разделители). Полужидкие разделители получают загущением некоторого количества одного из перекачиваемых нефтепродуктов или с помощью специальных студнеобразных полимеров. Применение полужидкого разделителя особенно целесообразно в том случае, если эффективный коэффициент диффузии его материала на несколько порядков меньше, чем у последовательно перекачиваемых нефтепродуктов. Расчеты показывают, что при последовательной перекачке бензина А-72 и дизельного топлива по трубопроводу диаметром 350 мм и длиной 180 км для надежного их разделения при помощи жидкой пробки требуется 20 м3 реактивного топлива ТС-1 или 3,2 м3 полужидкого разделителя.
Твердые разделители представляют собой механические устройства, которые находятся между перекачиваемыми нефтепродуктами и перемещаются вместе с ними по трубопроводу. Эти устройства должны касаться внутренней поверхности стенок труб и предохранять тем самым перекачиваемые нефтепродукты от смешения. Эффективность действия твердых разделителей в значительной степени зависит от надежности такого контакта с поверхностью трубопровода в течение всего времени движения.
Хотя конструкций твердых разделителей к настоящему времени предложено много, их можно разделить на два основных вида: манжетные и сферические. Манжеты у разделителей первого типа и сами разделители второго типа изготовляют из эластичного износостойкого материала, в основном из маслобензостойкой резины или полимерных материалов.
При последовательной перекачке нефтепродуктов широко применяют шаровые резиновые разделители, а при последовательной перекачке нефтей — манжетные (рис. 6.19). Внутренняя полость шарового разделителя заполняется водой (зимой антифризом) до определенного давления, чтобы обеспечивать достаточно плотный контакт с внутренней поверхностью трубопровода. Запуск шаровых разделителей в трубопровод и прием их из трубопровода производятся при помощи специальных устройств (рис. 6.20). Камера запуска разделителей 4 приподнята под углом до 20° и заканчивается концевым затвором 3. Второй конец камеры 4 соединен с тройником 1. Последовательный ввод шаровых разделителей в тройник 1 осуществляется отсекающим механизмом 5, после чего они под действием силы тяжести (или под напором жидкости из линии, показанной пунктиром) попадают в основной трубопровод и их проход в него фиксируется сигнализатором 2. Приемная камера 6 опущена под углом 10° и имеет одну или две отводящие линии. Жидкость из камеры 6 после поступления туда разделителя откачивается насосом 7. Приход разделителя в камеру фиксируется сигнализатором.
На промежуточных насосных станциях производится смена разделителей: прием перед станцией и запуск после станции другого разделителя. Для более лучшего разделения нефтепродуктов в одну и ту же зону их контакта помещают до трех разделителей, в том числе чтобы отделить зону первичной смеси от чистых нефтепродуктов.
Опыт применения шаровых разделителей при последовательной перекачке показал, что они позволяют уменьшить количество смеси 224
о - сферически'!,' С> млпл'отиыл; 1 -'•>л;1стн‘л1ия сф'ра; 2 - штуцер; 3 ни у трен м 'л 'л полость; -I -- эластичные уилитп птсуьиы манжеты1. 5 —octoii разделителя; 6 — трубопровод
Рис. 6.20. Устройство для запуска и приема сферических разделителей
Рис. 6.19. Механические разделите л и:
J
на 20 -40 %. Износ разделителей от трепня о стенки труб, а также, наличие в трубопроводе участков с разной толщиной стенок труб, поперечных сварных стыков и нервнчной смеси являются причинами неполного разделения перекачиваемых нефтепродуктов.
Эффективность перекачки с разделителями может быть определена по формуле
•^р ’ 1 Iрачд/Л| . к |
где /ралд — критерий качества смеси при перекачке с разделителями; /н. к — критерий качества при перекачке с непосредственным контактом нефтепродуктов.
Целесообразность последовательной перекачки с разделителями определяется в каждом конкретном случае путем сопоставления приведенных затрат при перекачке с разделителями и с непосредственным контактом нефтепродуктов.
6.9. ОСОБЕННОСТИ ПОСЛЕДОВАТЕЛЬНОЙ ПЕРЕКАЧКИ НЕФТЕЙ
Количество смеси при последовательной перекачке нефтей обычно бывает несколько увеличенным но сравнению с количеством смеси при перекачке светлых нефтепродуктов вследствие большой вязкости нефтей и увеличенного эффективного коэффициента диффузии. При последовательной перекачке нефтей с разным содержанием воды, а также механических примесей или солей объем смеси дополнительно увеличивается из-за смывания солей, отложений или механических примесей со стенок трубопровода партией нефти с меньшим содержанием этих примесей. Например, при последовательной перекачке обессоленной и сырой нефтей головная часть партии обессоленной нефти будет насыщаться солями, смываемыми со стенок трубопровода, где они скопил): сь в период прохождения партии сырой нефти.
Вследствие значительного объема смеси последовательную перекачку сыры ( и обессоленных нефтей проводят с твердыми разделите
лями. При^последовательной перекачке нефтей применяются манжетные разделители с манжетами из полиэтилена. Диаметр и форма манжет подобраны таким образом, что между ними^и^стенкой трубы остается пленка нефти и^онн работают в зоне полужидкостного трения, что позволяет существенно уменьшить износ манжет. В^пастоящее время применяют манжетные разделители подобного типа диаметром 500—1200 мм. Использование разделителей при последовательной перекачке сырых и обессоленных нефтей позволяет уменьшить в 5 раз (с 15 до 3 % объема нефтепровода) количество потерь обессоленной нефти.
Имеется опыт последовательной перекачки сернистых и малосернистых нефтей по одному из отечественных магистральных нефтепроводов большого диаметра на расстояние около 1000 км. Контроль последовательной перекачки в этом случае осуществляется но содержанию серы при помощи специальных приборов, основной частью которых является датчик содержания серы. Работа датчика серы основана на различии характеристик поглощения радиоактивного излучения в зависимости от содержания серы. Радиоактивное у-излуче-ние от источиика проходит через поток нефти, содержащей серу, и попадает в ионизационную камеру. Сила тока ионизационной камеры зависит от количества серы и плотности жидкости. Для компенсации изменения плотности в приборе имеется вибрационный плотномер. Как показал опыт последовательной перекачки сернистой и малосернистой нефтей, отложения серы на поверхности трубы и связанного с этим значительного увеличения объема смеси не наблюдается.
6.10. КОНТРОЛЬ ПОСЛЕДОВАТЕЛЬНОЙ ПЕРЕКАЧКИ НЕФТЕПРОДУКТОВ
При последовательной перекачке надо иметь надежные средства контроля за прохождением зоны смеси через определенные пункты нефтепродуктопровода и для определения концентраций нефтепродуктов по длине зоны смеси. Это необходимо, чтобы своевременно принимать меры для приема чистых нефтепродуктов и их смеси в разные резервуары на конечном пункте нефтепродуктопровода, определять заранее ожидаемое количество смеси.
Эффективное управление процессами транспорта, приема и распределения по резервуарам разносортных нефтепродуктов и их смесей зависит от точности, чувствительности и быстродействия применяемых методов и приборов аналитического контроля, которые должны обеспечивать: автоматический контроль границ раздела смеси для исключения возможности попадания смеси в резервуары с товарными нефтепродуктами; непрерывное измерение концентрации одного нефтепродукта в другом во всей зоне их смешения.
Большинство известных методов и приборов контроля последовательной перекачки нефтепродуктов основано на различии их физических свойств: плотности, вязкости, диэлектрической постоянной, цвета, скорости распространения ультразвуковых колебаний и т. п. По изменению физических свойств нефтепродуктов, определяемых соответствующими приборами, судят о составе (концентрации) емееи и определяют границы раздела последовательно перекачиваемых нефтепродуктов
Приборы контроля размещают как правило, на конечном пункте нефтепродуктопровода, где принимают смесь нефтепродуктов. При этом используют два однотипных прибора, один из которых размещен непосредственно на конечном пункте перед приемными резервуарами, а второй в виде выносного блока — в 10—15 км от конечного пункта. Это необходимо для получения предварительной информации о подходе емееи и распределении концентраций нефтепродуктов по ее длине, чтобы можно было за 1,5—2 ч до подхода емееи выполнить необходимые расчеты по ее приему.
Наибольшее распространение на нефтепродуктопроводах получили методы и приборы, основанные на измерении плотности, скорости распространения ультразвуковых колебаний, диэлектрической постоянной п оптической плотности в ультрафиолетовой области спектра. Представляется возможным и применение вискозиметров непрерывного действия, производство которых освоено в настоящее время промышленностью. Для повышения селективности и точности методов контроля последовательной перекачки продуктов возможно использование и комбинированного метода, когда измеряются два физических показателя нефтепродуктов и их смесей (например, плотность и цвет или диэлектрическая постоянная и цвет).
Рассмотрим принцип действия отечественных промышленных ана -литических приборов, наиболее перспективных для применения на нефтепродуктопроводах, в системах контроля последовательной перекачки нефтепродуктов.
Приборы контроля плотности по принципу измерения подразделяются на поплавковые, весовые, гидростатические, вибрационные, радиоизотопные и ультразвуковые плотномеры.
Действие плотномеров е погруженным поплавком основано на непрерывном уравновешивании выталкивающей силы, действующей на чувствительный элемент — поплавок, помещенный в специальной камере, в которой находится контролируемая жидкость. К плотномерам с погруженным поплавком относится датчик удельного веса етемпературной компенсацией типа ДУВ-П-ТК-104. Датчик представляет собой пневматический компенсационный прибор, предназначенный для непрерывного на потоке измерения удельного веса жидкости. Контролируемой жидкостью могут быть светлые нефтепродукты.
Принцип действия радиоизотопных плотномеров основан на изменении интенсивности пучка -\>-лучей после прохождения их через измеряемую жидкость в зависимости от изменения плотности этой жидкости. Интенсивность Jy однородного пучка у-лучей, прошедшего через слой жидкости, определяется соотношением Jv - J0v ехр (— up/) где /„v — интенсивность ^-излучения на поверхности слоя; — массовый коэффициент ослабления пучка у-лучей; р — плотность емееи нефтепродуктов; I — толщина слоя жидкости.
Основное преимущество радиоактивного метода измерения плотности — беоконтактность, что позволяет применять его при опреде-
!/
=шга
J 2
/
Tltn
Щ
X3=
F=\_
/-/
4 5 в 7 8 0 10
Рис. 0.21. Принципиальная схема плотномера АИП
лении плотности агрессивных и вязких сред, а также жидкостей, находящихся при высоких давлениях и температурах, где использование приборов других типов практически невозможно.
Значительное повышение точности измерения плотности достигается при использовании вибрационных плотномеров. Их действие основано на зависимости собственной частоты колебаний механических резонаторов от плотности жидкости, находящейся внутри них. Наиболее распространенными являются проточные вибрационные датчики плотности с трубчатыми резонаторами, внутри которых протекает контролируемая жидкость.

Жидкость, помещенная внутри колеблющейся трубки, движется вместе с ней практически как единое целое. В этом случае влияние вязкости очень незначительно и им можно пренебречь. Таким образом, поперечные колебания заполненной жидкостью трубки постоянного сечения можно рассматривать как колебания упругого тела с массой, зависящей от плотности жидкости. В СССР3 выпускается автоматический измеритель плотности типа ЛИП (рис. 6.21). Контролируемый продукт поступает на вход вибрационного преобразователя 1 и через распределитель 4 разветвляется на два потока, проходя по трубкам 9 чувствительного элемента. На распределителях установлены платиновые термометры сопротивления 5, введенные в поток распределителя 4 для коррекции показаний при изменении температуры контролируемого продукта. Между распределителями и трубками расположены сильфоны 2, устраняющие температурный напряжения и влияние вибрации корпуса 1 на вибратор. На корпусе вибрационного преобразователя предусмотрен влагопоглотитель 6, предотвращающий конденсацию влаги на трубках при понижении температуры продукта. Трубки соединены между собой системой упругих перемычек 7,8 и образуют вместе с ними механическую колебательную систему — вибратор. Механическая колебательная система вибрацион-228
I_______!
Рис. 6.22. Структурная схема ультразвуковой системы контроля типа УК.П-2
вых волн в нефтепродуктах влияют изменение температуры и давления анализируемой среды, содержание механических примесей, свободной воды и газовых включений в нефтепродуктах. Скорость распространения ультразвуковых волн в нефтепродуктах уменьшается при повышении их температуры, а повышение давления среды вызывает рост их скорости приблизительно по линейному закону.
Для повышения точности ультразвуковых приборов необходимо включать в схему системы контроля соответствующие устройства коррекции показаний по температуре и давлению.
Принцип действия диэлькометрнческих приборов контроля основан на зависимости диэлектрических свойств от концентрации смеси. Измерение концентрации смеси нефтепродуктов при использовании этого метода сводится к определению емкости конденсатора, между обкладками которого протекает смесь нефтепродуктов, выполняющая роль диэлектрика.
В СССР разработан диэлькометрический прибор СК-2, позволяющий контролировать границы раздела смеси и измерять концентрацию нефтепродуктов в зоне их смешения (рис. 6.23). Он состоит из двух вмонтированных в трубопровод / емкостных датчиков 2 и 3. Измерительный датчик 2 имеет форму цилиндра с кожухом. Благодаря отверстиям в кожухе датчик имеет хороший контакт с анализируемым нефтепродуктом. Компенсационный датчик 3, имеющий герметический кожух-стакан, заполнен очищенным трансформаторным маслом, служит для коррекции показаний прибора при измене-230 нии температуры анализируемого нефтепродукта. С повышением температуры нефтепродуктов значениями.* диэаектрической проницаемости уменьшаются. Датчики соединены с блоком сопоставителя емкостей 4, состоящего из двух генераторов. Сопоставитель емкостей 4 осуществляет непрерывное сравнение частот двух генераторов, формируя на выходе разностный частотный сигнал, который зависит ОТ значении электрических емкое- Рис. (i.23. Принципиальная схема тей измерительного и компенсаци- диэлькометрического прибора типа онного датчиков. Сигнал сопостави-теля емкости 4 поступает на частотно-аналоговый преобразователь 5, соединенный с вычислительным блоком 6 и регистрирующим прибором 7.
Достоинством диэлектрических и ультразвуковых приборов является то, что их чувствительные элементы могут встраиваться непосредственно в нефтепродуктопровод, исключая устройства отбора пробы с использованием насосов.
Ограничением для широкого применения на нефтепродуктопровода х приведенных методов и приборов контроля являются их недостаточная селективность и разрешающая способность при контроле пар нефтепродуктов с близкими характеристиками по химическому составу (например, смеси различных марок бензинов и разных сортов дизельных топлив).
В этих условиях представляют интерес спектрофотометрический и индикаторный методы контроля последовательной перекачки нефтепродуктов. Спектрофотометрический метод контроля основан на связи между поглощением оптического излучения и концентрацией, определяемой законом Бугера—Ламберта—Бера Jx = J ох, ехр (— Н\с1), где Jx — интенсивность излучения, прошедшего через слой вещества толщиной I и концентрацией с\ Jох — интенсивность падающего на вещество излучения; — молярный коэффициент поглощения, определяемый свойствами молекул растворенного вещества и длиной волны света Я оптического излучателя.
На практике чаще пользуются не понятием интенсивности, а понятием оптической плотности D = lg которая прямо
пропорциональна концентрации.
Спектрофотометрический метод измерения концентрации нефтепродуктов для различных парных сочетаний последовательно перекачиваемых продуктов (бензин—бензин, бензин—дизтопливо, дизтопливо—дизтопливо) построен на различии оптических плотностей D разных марок нефтепродуктов, измеренных в ультрафиолетовой области спеетра, где D является параметром, с помощью которого можно различать близкие по составу нефтепродукты.
нкп
MKfl
menc-mlmti' ' \ СмсГь 1'! | Н !i i* ' Н^твпроЗуктм ¦
__ 'j-J |—Jj liii-н [jj,'.
b||i» j_¦ j-—
Рис. 6.24. Структурно-функциональная схема ИИС «Компаунд»:
хтсктропрпиодом; .? фильтр самоочищающийся ФС; 4 — фо-6 — устройство телемокамики TM-800 li; 7 - устронстпи контроля управления, обработки информации н индикации марок нефтепродуктом УКУ
1 — насос; ‘2 падпнжкл тоабеорбциометр ФА* I
«Компаунд», в которую входят: два ультрафиолетовых абсорбционных фотометра 3 типа ФА-1, разнесенных по нефтепродуктопроводу на расстояние 10—15 км, т. е. превышающее удвоенную длину потока смеси нефтепродуктов, и устройство контроля, управления и обработки информации 7 типа УКУ. На выносном и местном контролируемых пунктах (ВКП и МКП) устанавливаются фотометры ФА-1, элементы отбора и подготовки пробы 1, 2,3, а в операторной резервуар-ного парка — устройство контроля, управления, и обработки информации. Управление и получение информации с ВКП осуществляются по каналам связи через устройство телемеханики 5, 6 типа ТМ-800В.
Определение концентраций СЛ и Сп нефтепродуктов производится следующим образом: при прохождении смеси нефтепродуктов через кюветы фотометра ФА-1 (ВКП) на диаграмме регистрирующего прибора типа КСП-4 записывается график, показывающий качественный характер изменения концентрации смеси. Значения оптической плотности снимаются оператором с графика смеси на В К ГТ и вводятся в блок обработки информации 7, что приводит к установлению в устройстве 7 диапазона измерения по массовой концентрации 0—100 %. При прохождении этой смеси через кюветы фотометра ФА-1, установленного на М1<П, происходят автоматическое измерение оптической плотности смеси DCM и вычисление СЛ и СГ/ с записью их значений на диаграмме прибора.
ОСОБЫЕ СЛУЧАИ ПЕРЕКАЧКИ НЕФТЕЙ, НЕФТЕПРОДУКТОВ И ГАЗА ПО ТРУБОПРОВОДАМ 3
В настоящее время добывается значительное количество высоковязких и высокопарафинистых нефтей, застывающих при сравнительно высоких температурах. Перекачка таких нефтей обычным способом нерациональна, так как при температуре окружающей среды велико гидравлическое сопротивление трубопроводов. Снижение гидравлического сопротивления трубопроводов обеспечивается различными способами повышения текучести нефтей: смешение вязких и застывающих нефтей и нефтепродуктов с маловязкими и совместная их перекачка, смешение и перекачка с водой, термическая обработка застывающих парафинистых нефтей и нефтепродуктов и последующая их перекачка, перекачка газонасыщенных нефтей, использование при-садок-депрессаторов в нефти и др. В каждом случае выбор способа перекачки должен быть обоснован технико-экономическим расчетом.
7.1. РЕОЛОГИЧЕСКИЕ СВОЙСТВА ВЯЗКИХ И ЗАСТЫВАЮЩИХ НЕФТЕЙ
Реология —- наука, занимающаяся изучением текучести жидких, газообразных и пластических веществ, а также процессов, связанных с остаточными деформациями твердых тел. Свойства жидкости, от которых зависит характер их течения, называются реологическими. В трубопроводном транспорте реологические характеристики нефтей оцениваются следующими параметрами: вязкостью (ньютоновской), пластической вязкостью, эффективной вязкостью, начальным (статическим) напряжением сдвига, предельным динамическим напряжением сдвига и температурой застывания.
Характер течения жидкости определяется видом зависимости напряжения сил трения на поверхности соприкосновения слоев жидкости или напряжения сдвига т от градиента скорости по радиусу или скорости сдвига dw/dr. Графическое напряжение этой зависимости называется кривой течения жидкости.
Для светлых нефтепродуктов, нефтей с низким содержанием парафина и парафинистых нефтей при высокой температуре справедлива полученная Ньютоном зависимость, которую он сформулировал следующим образом: «Сопротивление, которое возникает из-за недостаточного проскальзывания частиц жидкости, при прочих равных
Рис. 7.1. Зависимость напряжения сдвига т от скорости сдвига dw/dr для различных жидкостей
условиях, пропорционально скорости, с которой частицы жидкости перемещаются друг относительно друга», или
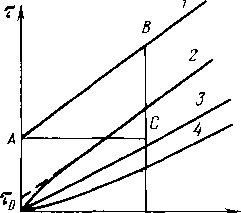
D dm
dr
т= —(X
47.1)
dr
где р. — коэффициент динамической вязкости.
Жидкости, для которых справедлива приведенная зависимость т от dw/dr при постоянной величине р,, называются ньютоновскими, а вязкость таких жидкостей — ньютоновской.
Поведение многих жидкостей, в частности парафинистых нефтей и нефтепродуктов, при температурах, близких к температуре их застывания, не подчиняется закону Ньютона. Такие жидкости называются неньютоновскими. Существует несколько классов неньютоновских жидкостей, различающихся по виду кривой течения (рис. 7.1). Кривые течения описывают поведение жидкостей: пластичных, или бин-гамовских /, псевдопластичных 2, ньютоновских 3 и дилатантных 4. Как видно из рис. 7.1, кривые течения псевдопластичных, ньютоновских и дилатантных жидкостей проходят через начало координат, следовательно, их течение начинается при малейших перепадах давлений. Течение бингамовских жидкостей начинается только после создания определенного напряжения т0. При меньших, чем т„, напряжениях такие жидкости ведут себя как твердые тела, а при больших — как жидкости. Реологическое уравнение бингамовской жидкости было получено из сочетания двух уравнений — уравнения Ньютона и реологического уравнения пластического тела (т = т0) — и может быть записано следующим образом:
![]()
dr
Оно содержит два коэффициента: предел текучести т0 и вязкость г)пл, которая называется пластической вязкостью.
Для псевдопластичных и дилатантных жидкостей в широком диапазоне изменения скорости сдвига в технических расчетах можно применять степенную зависимость напряжения от скорости сдвига
dw \п- I dm
dr | dr
где | dw/dr — безразмерный модуль скорости сдвига; п и k — постоянные для данной жидкости коэффициенты. Коэффициент п называется индексом течения, а коэффициент к — характеристикой кон-систентности. Для ньютоновской жидкости п — 1 и k == |х,для псев-допластичных жидкостей п <С 1 и для дилатантных 1.
Течение парафинистых нефтей и нефтепродуктов при температурах, близких к температуре их застывания и ниже, может быть описано кривыми / или 2 (см. рис. 7.1). Иначе говоря, они могут быть отнесены к пластичным или 'лсевдопластичным жидкостям, а при достаточно высоких температурах — к ньютоновским жидкостям. Эта особенность связана с высоким содержанием парафина в таких нефтях. При высокой температуре основное количество парафина, содержащегося в нефти, находится в растворенном состоянии. В этих условиях нефть является ньютоновской жидкостью.
При снижении температуры из нефти начинает выкристаллизовываться парафин, что влечет за собой изменение структуры жидкой фазы нефти. Сущность этого изменения заключается в упорядоченности расположения молекул растворенного вещества за счет снижения их теплового движения. По мере охлаждения раствора способность молекул растворителя удерживать в рассеянном и изолированном состоянии молекулы парафина снижается, т. е. снижается растворяющая способность растворителя. При дальнейшем снижении температуры концентрация парафина в углеводородной среде достигает такого уровня, при котором раствор становится насыщенным. Однако кристаллизация парафина при этом не начинается, и необходимо некоторое перенасыщение раствора, которое создает возможность появления достаточно крупных кристаллов парафина.
При приближении температуры охлаждения к температуре застывания Та число и размеры кристаллов настолько увеличиваются, что они образуют пространственную структурную решетку по всему объему нефти, иммобилизуют жидкую фазу нефти. Нефть приобретает свойства псевдопластичных, а затем и пластичных жидкостей.
Некоторые высокопарафинистые нефти (например, мангышлак-ские) обладают еще и свойствами тиксотропных жидкостей. Тиксот-ропия — это свойство тел, благодаря которому отношение касательного напряжения к скорости деформации (сдвига) временно уменьшается за счет предшествующих деформаций. Иными словами, тиксот-ропия — это способность жидкости с течением времени восстанавливать разрушенную ранее структуру.
Вязкость (ньютоновская). При перекачке вязких жидкостей влияние вязкости на гидравлические потери весьма существенны, поэтому в каждом реальном случае надо определять вязкость с наиболее возможной точностью. Если нет возможности получить в лаборатории вязкостно-температурную кривую нефти, то ее вязкость при интересующей температуре можно рассчитать по эмпирическим формулам. Наибольшее распространение получили следующие формулы:
Американского общества испытания материалов (ASTM) кретном случае начальное напряжение сдвига тн определяется экспериментальным путем.
Предельное динамическое напряжение сдвига. Одним из реологических параметров, характеризующих пластические свойства парафинистых нефтей, является предельное динамическое напряжение сдвига т0.
Для определения т0 необходимо снять реологическую кривую нефти; продление прямолинейного участка реологической кривой до оси т отсекает на ней отрезок, который характеризует предельное динамическое напряжение сдвига данной нефти (см. рис. 7.1). Следует отметить, что на реологические параметры как ньютоновских, так и неньютоновских нефтей большое влияние оказывает то, каким температурным воздействием подвергалась нефть перед определением того или иного реологического параметра.
7.2. ПЕРЕКАЧКА ВЫСОКОВЯЗКИХ НЕФТЕЙ С РАЗБАВИТЕЛЯМИ
В последнее время все шире применяется перекачка высоковязких нефтей, обладающих высокой температурой застывания, в смеси с углеводородными разбавителями. Введение в парафннистую нефть углеводородного разбавителя позволяет в некоторых случаях добиться значительного улучшения ее реологических свойств.
В качестве разбавителей целесообразнее всего использовать маловязкие нефтн. Если в одном районе добываются парафинистые и маловязкие нефти, то целесообразно смешивать их на головных сооружениях нефтепровода и совместно транспортировать. При разбавлении вязкой нефти увеличивается объем перекачиваемой жидкости, но вязкость смеси уменьшается. Это обстоятельство позволяет решать различные оптимизационные задачи. В результате исгользования разбавителя может быть увеличена загрузка нефтепровода, перекачано дополнительное количество вязкой нефти, минимизирован расход электроэнергии и т. д. Смешение высокопарафинистых нефтей с маловязкими позволяет не только удешевить перекачку, но и эффективнее использовать добываемые нефти. Смешивая нефти в разных соотношениях, можно получить нефтяные смеси заранее определенного состава, что позволит стабилизировать работу нефтепровода и установок нефтеперерабатывающих заводов. Кроме того, смешение нефтей позволяет иногда значительно улучшить их качество. Так, например, смешение высокопарафинистых, но малосернистых нефтей с малопарафинистыми, но высокосернистыми нефтями дает возможность получить смесь с умеренным содержанием парафина и серы. Примером этому может служить высокопарафинистая мангышлакская нефть, которая с п-ова Мангышлак перекачивается в подогретом состоянии в район г. Куйбышева, где часть ее перерабатывается, а часть смешивается с маловязкими сернистыми нефтями 11оволжья п поступает в систему нефтепровода «Дружба».
Механкзм действия углеводородного разбавителя можно объяснить следующим образом. Во-первых, при добавлении разбавителя к парафинистой нефти уменьшается концентрация парафина в смеси и понижается "смпература насыщения раствора и появления кристаллов парафина. Следовательно, снижается температура застывания системы, Во-вторых, при использовании в качестве разбавителей маловязких нефтей, содержащих асфальтосмолистые вещества, последние препятствуют образованию парафиновой структурной решетки в нефти и тем самым снижают температуру застывания и эффективную вязкость civecn. Следует иметь в виду, что растворимость парафинов в большой степени зависит от свойств разбавителя. Как правило, чем меньше плотность и вязкость разбавителя, тем эффективнее его действие. Кроме того, чем ниже температура смеси, тем лучше реологические свойстза парафинистой нефти при добавлении разбавителя.
7.3. ПЕРЕКАЧКА ВЫСОКОЗАСТЫВАЮЩИХ НЕФТЕЙ С ПРИСАДКАМИ
Перспективным способом трубопроводного транспорта высокопарафинистых нефтей и нефтепродуктов является перекачка их с полимерными денрессорнымн присадками, незначительная добавка которых существенно улучшает (снижает) их реологические характеристики. Известно много соединений, обладающих в той или иной мере депрес-сорной активностью. Особенно часто применяют соединения полимерного типа, среди которых найдены наиболее эффективные депрессор-ные присадки к парафинсодержащим нефтепродуктам, газовому конденсату и нефтям.
Депрессорные присадки эффективно использовать при температурах ниже температуры застывания нефти. Температура помутнения (температура массовой кристаллизации парафинов) считается наивысшей, при которой заметно воздействие присадки на высокопарафи-нистую нефть. Депрессоры пе являются растворителями кристаллического парафина и не уменьшают его количества в нефти. Они изменяют размеры, форму и строение частиц дисперсной фазы. Эффективность действия присадок зависит от физико-химических свойств парафинистых нефтей пли их смесей с маловязкими нефтями, и в первую очередь от содержания в них парафинов и естественных поверхностно-активных веществ —смол и асфальтенов.
Необходимая концентрация депрессора в нефти зависит от цели и конкретных условий применения. Так, для успешной перекачки нефти по магистральному трубопроводу в нее достаточно ввести присадку с массовой концентрацией 0,1—0,2 %. В случае транспорта смеси высокозастывающей нефти с маловязкими эта концентрация может быть снижена. Хранение парафинистой нефти с массовой концентрацией присадки до 0,03 % в значительной мере уменьшает пара-финизацию оборудования и может исключить дорогостоящую ручную зачистку резервуаров нефтебаз, танкеров и т. д. Рассмотрим влияние депрессорной присадки, представляющей собой 20 %-ный раствор сополимера этилена с виинлацетатом в дизельном топливе на нефти, содержащей до 10 % парафиновых углеводородов. Присадка вводилась в нефти при температуре 50 "С.
Рис. 7.3. Зависимость т — т (dw/dr) при постоянной скорости деформации г const:
/ — ДЛЯ ИСХОДНОЙ П.'Д рафии ИСТОМ
/,: Г
нефти при температуре зпетыплиия;
2 - • для нефти, обработанной стимулятором потока при roii (же температур?
О механизме воздействия присадок для высокопарафииистых нефтей можно судить но изменению деформационно-прочностных свойств структуры парафиновых углеводородов нефти в зависимости от условия ее формирования (в присутствии добавки или без нее). Изучение кинетики развития напряжений сдвига при постоянной скорости деформации в дисперсных системах позволяет исследовать механизм возникновения и характер структуры. Физико-химическая обработка системы, изменяющая условия возникновения частиц и число контактов между ними, проявляется в изменении хода деформационного процесса.
На рис. 7.3 изображена диаграмма, характеризующая развитие течения‘гв высокозастывающей нефти, предварительно нагретой до 323 К (50 °С). Процесс разрушения структуры парафиновых углеводородов включает в себя собственно разрушение кристаллической решетки, высвобождение жидкой среды, находящейся внутри структурной сетки, изменение ориентации частиц. Нисходящая ветвь кривой 1 (см. рис. 7.3) отражает завершение сложного процесса изменения структуры и перехода на установившийся режим течения. По характеру разрушения структуры парафина высокозастывающие нефти относятся к упругопластическим телам.
В присутствии депрессора, массовая концентрация которого составляет 0,2 %, коренным образом изменяется картина развития деформации в парафиннстой нефти. Здесь имеет место пластическое течение при напряжениях значительно меньших, чем к исходной нефти (кривая 2 на рис. 7.3).
Снижение прочности и увеличение пластичности нефти с депрессором следует объяснить образованием комплексов из молекул присадки и парафина, создающих пространственное препятствие формированию контактов кристаллического геля и уменьшающих их упорядоченность.
Основным в механизме действия добавки является сокристаллиза-ция молекул присадки и парафинистьгх углеводородов нормального строения нефти в период их выкристаллизовывания. В этом случае образуются смешанные кристаллы депрессор -парафин , что мешает объединение частиц в пространственную сетку.
Присадки необходимо вводить в нефть при температурах, при которых ее парафиновые углеводороды растворены и она представляет собой истинный раствор. Обычно депрессоры вводятся в нагретую до 323—333 К (50—60 °С) нефть. Для обеспечения нормальной перекачки парафинистой нефти при изотермическом режиме по трубопроводу значительной длины достаточно ввести добавку лишь один раз, например на головных сооружениях нефтепровода. Способы ввода присадок потока могут быть различными. Основным условием является обеспечение высоком степени перемешивания депрессора и нефти. Нели присадка представляет собой пасту или твердые гранулы, то она предвари'елыго растворяется в заданном соотношении в нефти или другом углеводородном растворителе в специальном резервуаре и уже в виде концентрата впрыскивается через форсунку дозировочным насосом в нефтепровод. В месте ввода депрессора режим течения нагретой нефти должен быть турбулентным, что создает хорошие условия для распределения присадки по всему объему перекачиваемой нефти.
Реологические свойства нефтей с присадкой определяются струк-турообразованием несвязанными молекулами депрессора и парафиновых углеводородов. Это подтверждают реометрические исследования, которые показали, что высокопарафинистые нефти, обработанные депрессорами, сохраняют неныотоновский характер течения.
Депрессорнаа активность присадки увеличивается с уменьшением содержания в нефтях парафиновых углеводородов, а степень улучшения их текучести зависит от концентрации добавки. Наиболее эффективными являются первые доли добавки. Максимальное снижение реологических характеристик достигалось при массовой концентрации депрессора, равной 0,2 %. Применение депрессорной присадки наиболее эффективно при изотермическом ламинарном режиме течения высокопарафинистых нефтей. В области турбулентного течения нефти с присадкой наблюдается снижение коэффициента гидравлического сопротивления по сравнению с необработанной в среднем на 20 %.
Для уменьшения расхода депрессора предложена другая технология его применения, при которой присадка вводится только в пристенный кольцевой нагретый слой нефти. Основные количество нефти не нагревается, и она течет при ламинарном (структурном) режиме. На трубопроводах с несколькими нефтеперекачивающими станциями присадка вводится после каждой промежуточной станции, так как после прохождения насосов депрессор распределяется по всему объему нефти. Эта технология позволяет при практически неизменных гидравлических характеристиках нефтепровода сократить в 7—10 раз расход присадки и энергозатраты на нагрев нефти при ее добавлении. Однако приведенный способ их использования ограничен структурным режимом течения высокопарафинистых нефтей. К настоящему времени имеется опыт по применению депрессорных присадок в промышленных условиях. Различные присадки использовались при пуске в эксплуатацию нефтепровода Узень—Куйбышев, при перекачке африканских нефтей по европейским трубопроводам. С их помощью можно увеличить пропускную способность без дополнительных капитальных вложений на расширение основного оборудования или на усиление тепловой изоляции; облегчить пуск трубопровода и перекачку нефти пр i температурах ниже температуры ее застывания; уменьшить или полностью исключить смешение с низкозасчитываю-240 щими нефтями и тем самым повысить использование на перерабатывающих заводах парафинистых нефтей.
В случае применения присадок на горячих нефтепроводах возможно снизить температуру подогрева или вообще от него отказаться. Последнее особо важно при прокладке нефтепроводов в вечной мерзлоте, где подогрев отрицательно влияет на внешнюю среду и требуются специальные мероприятия по сохранению несущей способности грунта.
7.4. ПЕРЕКАЧКА ТЕРМИЧЕСКИ ОБРАБОТАННЫХ НЕФТЕЙ
При нагревании нефти до определенной температуры и последующем охлаждении реологические параметры нефти претерпевают значительные изменения. Термообработка — один из способов улучшения реологических свойств нефти с целью повышения эффективности трубопроводного транспорта парафинистых нефтей и нефтепродуктов. Термообработка позволяет получить нефть с непрочной парафиновой структурой, не способной удерживать в своих ячейках весь объем нефти.
Процесс термообработки заключается в нагреве нефти до температуры, при которой растворяются содержащиеся в ней твердые парафиновые углеводороды, и охлаждении с заданной скоростью в определенных условиях (в движении или покое). Степень снижения реологических характеристик термически обработанной нефти зависит от температуры нагрева, содержания^парафииов и асфальто-смолистых веществ и условий охлаждения.
Исследования вопросов термообработки парафишстых нефтей и нефтепродуктов позволили выявить ряд закономерностей.
1. Для парафинистых нефтей существует оптимальная температура подогрева, при которой эффект термообработки наибольший. Эта температура всегда выше температуры плавления парафинов, находящихся в нефти. С ростом температуры нагрева (рис. 7.4) температура застывания сначала увеличивается, затем уменьшается, становясь минимальной при определенной температуре термообработки. Эти особенности влияния температуры термообработки на реологические параметры можно объяснить следующим образом. На поверхности кристаллов парафина адсорбированы асфальтосмолистые вещества, входящие в состав нефти. При нагреве нефти до невысокой температуры часть кристаллов парафина растворяется и освободившиеся асфальтосмолистые вещества адсорбируются на поверхности нераст-воренных кристаллов парафина. Последующее охлаждение приводит к образованию из выпадающего парафина прочной мелкокристаллической структуры, повышающей эффективную вязкость и температуру застывания нефти. Следовательно, термообработка высокозастывающих парафинистых нефтей при температуре подогрева 3S3—333 К (несколько ниже температуры плавления парафинов) резко ухудшает реологические свойства нефти. При повышении температуры подогрева увеличивается количество растворенного в жидкой фазе нефти парафина и остающиеся кристаллы тугоплавких парафинов адсорбируют все меньшее количество асфальтосмолистых веществ. При охлаждении за счет достаточного количества неадсорбированных асфальтосмолистых веществ, являющихся повер хностно-активными веществами, способствующими дендритной кристаллизации, образуется небольшое число крупных кристаллов парафина. При подогреве до температуры 363—368 К, когда весь парафин растворен, создаются наиболее благоприятные условия для дендритной кристаллизации парафина с образованием наименее прочной структуры. При еще большей температуре термообработки содержащиеся в нефти асфальтосмолистые вещества, которые благоприятно влияют на образование крупнозернистой структуры, необратимо разрушаются, тем самым снижается эффект термообработки.
2. На свойства термообработанных нефтей большое влияние оказывают условия охлаждения нефти. Размер, число и форма кристаллов парафинов зависят от соотношения двух скоростей: скорости возникновения центров кристаллизации парафиновых углеводородов и скорости роста уже выделившихся кристаллов. Если скорость возникновения центров кристаллизации выше скорости роста кристаллов, то получается система с большим числом мелких кристаллов, в противном случае в системе образуются крупные кристаллы и прочность такой структуры значительно меньше мелкокристаллической. Для высокопарафинистой нефти Мангышлака оптимальный темп охлаждения в статических условиях составляет 10—20 °С/ч. При этой скорости создается благоприятное соотношение скорости возникновения центров кристаллизации и скорости роста образовавшихся кристаллов парафина, и большая часть парафина идет на построение небольшого числг крупных кристаллов, образующих рыхлые скопления. В результате достигается значительный эффект улучшения свойств текучести нефти. Так, например, при 293 К начальное напряжение сдвига узеньской нефти снижается до нуля.
Рис. 7.4. Характер влияния температуры термообработки Тх на температуру застывания Т3 высокопарафинистой нефти
3. С увеличением содержания асфальтосмолистых веществ по отношению к содержанию парафиновых углеводородов нефти эффект термообработки увеличивается. При недостатке асфальтосмолистых веществ они полностью адсорбируются на поверхности первых порций появившихся кристаллов парафина. Образовавшиеся впоследствии кристаллы парафинов создают прочный гель. При относительно большом содержании естественных поверхностно-активных веществ — смол и асфальтенов в нефти их хватает на блокирование значительного числа образующихся кристаллов и процесс протекает по пути дендритной кристаллизации. Исследование реологических характеристик термообработанных нефтей показали их нестабильность. Повторный нагрев до температуры 303—323 К снимает в значительной сте-242 пени эффект термообработки. Реологические параметры нефти, улучшенные в результате термообработки, со временем принимают свои первоначальные значения. Срок восстановления реологических параметров нефти необходимо учитывать при эксплуатации трубопроводов, перекачивающих термообработанную нефть.
Таким образом, если термообработка высокопараоинистой нефти дает хорошие результаты и термообработанная нефть имеет длительный срок восстановления реологических свойств, то такую нефть после термообработки можно перекачивать, как обьчную маловязкую.
7.5. ГИДРОТРАНСПОРТ ВЫС0К03АСТЫВАЮЩИХ И ВЯЗКИХ НЕФТЕЙ И НЕФТЕПРОДУКТОВ
Существенного улучшения транспортабельности вязких или высоко-застывающих нефтей можно достичь добавлением в поток нефти воды. При совместной перекачке воды и нефти потоку можно придать разные структуры, например, коаксиальную, эмульсионную, раздельную и т. п. Коаксиальная структура получается, когда вода образует вокруг нефти, у внутренней поверхности трубы, концентрическое кольцо. Чтобы нефть не всплывала в воде и не прилипала к верхней стенке трубы, в трубе делают нарезку, которая придает потоку вращательное движение. При этом вода, как более тяжелая жидкость, отбрасывается к стенке трубы. При работе по такой технологии на экспериментальном трубопроводе длиной в 40 км и диаметром 200 мм было получено увеличение пропускной способности в 12 раз. Разделение воды и нефти производится на конечном пункта трубопровода одним из известных способов (отстой, термический способ и др.). Широкого распространения гидротранспорт высоковязких нефтей по трубопроводам с внутренней нарезкой не получил по следующим причинам:
при остановке перекачки происходит расслоение воды и нефти; нефть прилипает к верхней образующей трубы, забивает спираль и из-за этого резко снижается эффективность гидротранспорта;
применение этого метода возможно только при передачке нефти по трубопроводу без промежуточных насосных станций; эри попадании воды и нефти в насос образуется стойкая эмульсия, которая за насосной станцией уже не распадается и препятствует образованию водяного кольца у стенок трубы;
сложность изготовления винтовых нарезок на внутренней поверхности труб. : <
При образовании эмульсии нефть в воде (н/в) происходит значительное снижение вязкости системы. Такая система состоит из частиц нефти, окруженных пленкой воды, и контакта нефти с поверхностью трубы практически не происходит. В результате этого по всей внутренней поверхности трубы образуется водяное кольцо, по которому скользит нефть. Однако при транспорте водонефтяных эмульсий по трубопроводам при некоторых скоростях перекачки, температурах и концентрациях воды в нефти образуется эмульсия воды в нефти (в/и).
Вязкость таких эмульсий может быть больше вязкости чистой нефти. Для улучшения условий образования и повышения стабильности эмульсий типа н/в в водонефтяную смесь добавляют различные поверхностно-активные вещества (IIAB).
Поверхностно-активное вещество, растворенное в воде, гидрофи-лизирует стенки трубопровода, значительно уменьшает силы прилипания нефти к стенкам, создает условия для образования дисперсной системы типа и/в. Все это приводит к резкому уменьшению гидравлического сопротивления при перекачке. Технология совместной перекачки нефти с водным раствором ПАВ направлена на создание в трубопроводе устойчивой системы типа и/в и на предотвращение инверсии фаз, т. е. перехода системы из прямой в обратную (в/н). На устойчивость системы типа н/в в значительной степени влияют вид и концентрация Г1АВ, температура, интенсивность перемешиваиия, соотношения фаз.
Используемые для приготовления водонефтяных эмульсий Г1АВ должны отвечать следующим основным требованиям: хорошо эмульгировать нефть — создавать оболочку на поверхности глобул нефти, достаточно прочную и способную легко восстанавливаться при ее прорывах; быть нетоксичными; не вызывать коррозии трубопровода и резервуаров. Одним из I1AB, наиболее отвечающим перечисленным требованиям, является сульфанол HI 1-1.
Увеличение концентрации воды в смеси улучшает устойчивость эмульсии, но снижает экономические показатели данного вида гидротранспорта. В результате экспериментальных исследований было установлено, что оптимальное содержание воды должно составлять около 30 % общего объема транспортируемой смеси.
7.6. НЕФТЯНОЙ ГАЗ. ПЕРЕКАЧКА ГАЗОНАСЫЩЕННЫХ НЕФТЕЙ
Газ, который выделяется из нефти в процессе ее добычи и промысловой подготовки, называется нефтяным. В пластовых условиях вследствие высоких давлений легкие углеводороды и сопутствующие газы N2, H2S, Не, СО2 И другие находятся в нефти в растворенном состоянии. Однако при снижении давления сопутствующие газы и отдельные парафиновые углеводороды полностью или частично переходят в газообразное состояние. Поскольку при движении нефти в пласте по стволу скважины и в нефтепромысловых коммуникациях давление падает постепенно, количество и состав выделяющегося газа непрерывно изменяются.
Важной характеристикой пластовой нефти является компонентный состав, позволяющий производить оценку физико-химических свойств как самой нефти, так и выделяющегося из нее нефтяного газа. Компонентный состав пластовой нефти различен для разных месторождений и площадей. Содержание головных (СН4—С6Н12) парафиновых углеводородов в нефтях различных пластов и месторождений изменяется в широких пределах, в соответствии с этим изменяется и молекулярная масса пластовой нефти. Содержание в пластовой нефти головных углеводородов и определяет потенциальные ресурсы нефтяного газа, а также его углеводородный состав.
Ресурсы нефтяного газа определяются как произведение объема добытой нефти на газовый фактор. Под газовым фактором понимается объем выделившегося газа, отнесенный к 1 т или 1 м3 добытой нефти.
Разгазирование (дегазация) — это процесс выделения газа из нефти посредством изменения термодинамических условий. Процесс разделения двухфазной смеси на два самостоятельных потока (сепарация) — жидкостный и газовый осуществляется в сепараторах.
Существенное влияние на газовый фактор и углеводородный состав нефтяного газа, отделившегося в сепараторах, оказывает характер разгазирования пластовой нефти (контактное, ступенчатое, дифференциальное). При контактном разгазировании газ, выделившийся из нефти, не удаляется из системы, а все время остается в контакте с жидкой фазой. Идеального контактного разгазирования можно достичь только в лабораторных условиях. Именно такое разгазирование применяют при определении полного пластового газового фактора нефти. Выделившийся при этом газ отделяют только после полного разгазирования нефти. В промышленных условиях контактным разгазирова-нием с достаточной точностью можно считать разгазирование нефти при движении ее в трубопроводных коммуникациях системы «бора. При ступенчатом разгазировании разделение газожидкостной смеси на две самостоятельные фазы происходит в несколько лриемов по мере разгазирования системы. В качестве примера ступенчатого разгазирования можно привести разгазирование на промыслах с двух-, трех-и четырехступенчатой сепарацией нефти. Давление на каждой последующей ступени сепарации снижается. Отделившийся на каждой ступени газ отводится по газопроводу потребителю. При ступенчатом разгазировании нефти правомерно говорить о газовом факторе на каждой ступени сепарации. При дифференцированном разгазировании газ по мере его выделения отводится от нефти. Дифференциальное разгазирование является предельным случаем ступенчатого, когда число ступеней стремится к бесконечности.
В промысловых условиях приходится встречаться с контактным и ступенчатым разгазированием нефти. Контактное разгазирование нефти происходит в трубопроводах между ступенями сепарации, ступенчатое разгазирование — в целом на месторождении с двумя и большим числом пунктов отбора газа со ступенчатым изменением давления от пластового до атмосферного.
Опыт эксплуатации показал, что в течение первых десяти лет разработки нефтяных месторождений нефтяной газ в основном не утилизируется (сжигается в факелах). Это обусловлено следующим. С одной стороны, нефтяной газ, являясь неизбежным спутником нефти, извлекается из недр земли в объемах, пропорциональных объемам добытой нефти, независимо от возможностей использования его в народном хозяйстве. С другой стороны, отсутствие потребителей газа на местах его добычи и отставание строительно-монтажных работ по сооружению объектов сбора и подготовки газа осложняют подачу газа в индустриальные центры, где он может быть испэльзован. Дело
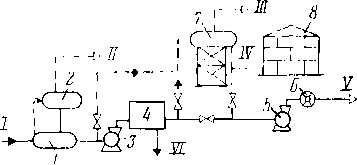
Рис. 7.5. Принципиальная схема КСП:
/ — узел нерпой ступени сепарации, 2 — каплеуловитель для тонкой очистки газа; 3 — технологический насос; 4 — УПН; 5 — насос внешнем перекачки; 6 — замерный узел; 7 — аварийная сепарациониая установка; 8 — аварийные резервуары. Технологические линии: I — сырая нефть (газожидкостная смссь) с промысла; II — газ потребителю; III — газ па факел; IV — раэгазироваплая нефть; V — газонасыщенная нефть на головные сооружения магистрального нефтепронода; V! пода па очистные сооружения
в том, что транспортировка сырого (неотбензиненного и неосушенного) газа по газопроводам сопровождается интенсивным выпаданием конденсата, а при компримировании — и образованием кристаллогидратов, которые приводят к частичной или полной закупорке газопровода, увеличивают гидравлические сопротивления, ведут к потерям пропан-бутановых и пентановых фракций, резко снижают транспортабельность газа и сокращают дальность его подачи.
Одним из перспективных направлений в успешном решении проблемы полного и рационального использования нефтяного газа в народном хозяйстве является его транспортировка совместно с нефтью в однофазном (растворенном) состоянии на большие расстояния к пунктам газопотребления.
Получение газонасыщенных нефтей должно идти за счет сохранения газа в нефти в процессе ее добычи и промысловой подготовки. В соответствии с этим дальнейшее совершенствование герметизированных схем сбора и подготовки нефти должно идти по пути создания таких технологических схем, которые позволяют перекачивать нефть в газо-насыщенном состоянии ие только по внутрипромысловым, но и по межпромысловым и магистральным нефтепроводам. Промышленная реализация такой схемы в настоящее время уже осуществлена на многих месторождениях Западной Сибири.
В состав комплексного сборного пункта (КСП) (рис. 7.5) входят первая ступень сепарации нефти, установка подготовки нефти (УПН), на которой газснасыщенная нефть обезвоживается, аварийная сепара-ционная установка и узел учета нефти. Давление на первой ступени сепарации выбирается исходя из возможности бескомпрессорной подачи выделившегося газа потребителю. Для обеспечения однофазно-сти потока газонасыщенной нефти на всем пути движения через установку подготовки и создания бескавитационного режима работы насосов внешней перекачки следует использовать технологические насосы, развивающие давление, необходимое для предотвращения раз-газирования нефти при нагреве в печах. При обосновании выбора давления на первой ступени сепарации следует также исходить из того факта, что от этого давления существенно зависят количество и состав свободного и растворенного в нефти газа.
Растворенный газ существенно влияет на физические свойства нефти, которые должны учитываться в технологии ее перекачки на большие расстояния, а также при выборе технологаеского оборудования насосных станций. При фиксированной температуре давление, при котором начинается процесс выделения свободного газа, называется давлением насыщения газонасыщенной нефти. Это давление определяется экспериментально с помощью прибора, позволяющего при плавном снижении давления улавливать момент появления первого пузырька газа в объеме пробы нефти. Давление насыщения можно принимать с некоторым приближением, равным давлению сепарации нефти. Хотя эти давления в общем случае могут быть различными.
Вязкость и плотность газонасыщенной нефти должны определяться экспериментально на специально разработанных приборах, в которых исследуемая проба нефти находится под давлением, обеспечивающим ее однофазное состояние. Эти параметры можно описать эмпирическими зависимостями.
Для плотности газонасыщенной нефти справедливо выражение
где (>0 — плотность дегазированной нефти при фиксированных температуре и давлении; b — эмпирическая константа; — количество растворенного в нефти газа.
Для аналитического описания динамической вязкости газонасыщенной нефти р,* можно предложить эмпирическую зависимость
Н-* (Т, ГР) = р-о ехр [(Гд — Т)и--(с— dT) Гр], (7.3)
где fi0 —динамическая вязкость дегазированной нефти при температуре Т0; и, с, d — эмпирические константы. Константа ихарактеризует крутизну вискограммы дегазированной нефти.
При фиксированном значении количества растворенного газа выражение (7.3) позволяет получить зависимость вязкости газонасыщенной нефти от температуры:
М-* (7') = Р* (Тп) ехр [и* (Т0—Г)1, (7.4)
где ц* (Г0) — вязкость газонасыщенной нефти при температуре Т„; и* — крутизна вискограммы газонасыщенной нефти.
'При постоянной температуре Т и переменном значении Гр выражение (7.3) принимает простой вид:
ц* = цгехр(—аГр), (7.5)
где (хг вязкость дегазированной нефти при температуре Т', а =
с Td. Влияние растворенного газа на вязкость неоти можно проследить но графику на рис. 7.6. При построении графгка использовалась безразмерная вязкость и (отнесенная к вязкости дегазированной
Рис. 7.6. Зависимость вязкости газонасыщенной нефти ц от количества растворенного газа Гр при разных температурах Т
Рис. 7.7. Схема сооружения нефтепровода при перекачке газонасыщенной нефти:
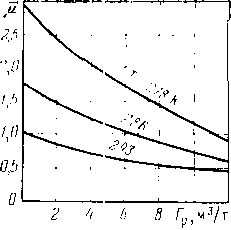
гнс
/ — аварийная сепарационная установка; 2 — резервуарный парк; 3 — фильтр; 4 — замерный узел; 5 — подпорная насосная; 6 — перекачивающая насосная; 7 — узел регулятора давления; 8, 9, 12 — узлы пуска, пропуска и приема скребка соответственно; 10 — буферная емкость; И — установка сглаживания волн давления; 19 — концевая сепарационная установка
| о | о | о | о |
| о | о |
о | о |
| о | о | о | о |
| о | о |
о | о |
| о | о | о | о |
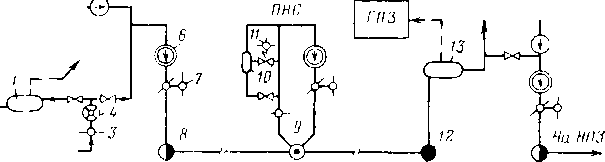
Нефть С промысла
| о | о | о | о | о | о |
| о | о |
о | о | о |
о |
| о | о | о | о | о | о |
нефти при температуре 293 К). Степень влияния растворенного газа различна в зависимости от температуры и его количества. С уменьшением температуры эффект снижения вязкости возрастает. Именно поэтому перекачка газонасыщенных нефтей, кроме решения проблемы доставки потребителю нефтяного газа низкого давления, в ряде случаев позволяет увеличить пропускную способность нефтепровода. Особенно перспективна эта перекачка в условиях месторождений Крайнего Севера с участками вечной мерзлоты, где возникает новая проблема — предотвращение растепления грунта. В этих условиях такие способы, как горячая перекачка, термообработка, и другие могут оказаться неприемлемыми. При низких же температурах даже легкие нефти имеют высокую вязкость и становятся плохотранспортабельными.
Трубопроводный транспорт нефти в газонасыщенном состоянии предполагает осуществлять на территории промысла только первую ступень сепарации. Конечные ступени сепарации (одна, а при необходимости и несколько) переносятся с промысла на концевые сооружения (рис. 7.7), которые должны содержать концевую сепарацион-ную установку, узел замера количества газа и резервуарный парк, объем которого выбирают исходя из требования обеспечения надежности нефтеснабжения потребителя, например, нефтеперерабатывающий завод (НПЗ) на случай остановок нефтепровода. Площадки концевых сооружений следует располагать вблизи к потребителю нефтяного газа для обеспечения более полной утилизации его. Подача газа на газоперерабатывающий завод (ГПЗ) может осуществляться как вакуум-компрессорами, так и эжекторами.
Технологические схемы перекачивающих станций и используемое на них оборудование должны обеспечивать перекачку нефти с высоким давлением насыщения. Это возможно только при полной герметизации пути движения газонасыщенной нефти с промысла до концевых сооружений магистрального нефтепровода и при поддержании в любой точке_системы давления, обеспечивающего однофазность потока нефти. Поэтому при перекачке газонасыщенной нефти технологические схемы как головной, так и промежуточных насосных станций будут отличаться от соответствующих схем, применяемых при перекачке дегазированных нефтей. При перекачке газонасыщенной нефти головная насосная станция (ГНС) должна иметь следующие дополнительные сооружения: аварийную сепарационную установку, буферную емкость, установку сглаживания волн давления, систему аварийного сброса газа на факел. При ГНС должен быть резервуарный парк, основное назначение которого — обеспечение бесперебойной работы нефтепромысла при аварийных и плановых остановках нефтепровода. При нормальном режиме работы нефтепровода наполнение резервуар-ных емкостей парка должно быть минимальным. При прекращении перекачки поступающая на головные сооружения газонасыщенная нефть подается в аварийные сепараторы для полного разгазирования, а затем самотеком поступает в резервуары. Отделившейся в сепараторах газ подается на факел. Для обеспечения самотечного движения дегазированной нефти сепараторы устанавливают на эстакадах. Высоту поднятия сепараторов определяют в результате гидравлического расчета отводящего трубопровода.
Основное назначение буферной емкости — предотвратить попадание свободного газа на прием центробежных насосов, тем самым обеспечить бескавитационный режим их работы. Буферная емкость может одновременно выполнять функции резервуара-сборника для сброса нефти при появлении гидравлического удара.
Появление свободного газа в трубопроводе возможно при его остановках, связанных с нарушением герметичности линейной части. Падение давления в трубопроводе приводит к разгазированию нефти. Выделившийся газ скапливается в повышенных участках трассы. После устранения аварии поднятием давления в трубопроводе удается только уменьшить объем газовой пробки, которая выносится потоком нефти в буферную емкость. В соответствии с этим должен определяться объем буферной емкости
V6 ^ nD'2l,J(4k),
где D —диаметр нефтепровода; /п —длина газовой пробки; к — коэффициент наполнения буферной емкости (к = 0,3 -т-0,8).
Давление в буферной емкости задается, исходя из бескавитацион-ного режима работы насосов:
Р ~Ps 4' А рК з -)- А Ряс “Ь Л Рдоп, (7-6)
где ps—давление насыщения нефти; Арк з — кавитационный запас магистральных насосов; Дрйс — потери давления в подводящих коммуникациях насосной станции; Дрдоп — дополнительный запас давления, учитывающий возможные колебания температуры (можно принять равным 0,1—0,2 МПа).
Поддержание этого давления обеспечивается регулятором давления — «до себя», установленным на газоотводящий линии буферной емкости. Необходимый уровень нефти в буферной емкости обеспечивается автоматически с помощью регулируемой задвижки на выходе насосной станции.
При пуске магистрального нефтепровода или при возобновлении перекачки после его остановки должны выполняться операции в следующей последовательности. Сначала пускают головную насосную станцию, для чего стравливают газ из мест возможного его скопления (из насосов, всасывающего коллектора) открытием кранов на газоотводящей линии. Включают подпорные насосы, которые забирают дегазированную нефть из резервуаров товарного парка или из сепараторов и поднимают давление в системе трубопроводов, подводящих нефть к магистральным насосам, до значения, обеспечивающего беска-витационный режим их работы на газонасыщенных нефтях. Затем включают в работу основные насосы. Далее производится напрессовка трубопровода до тех пор, пока давление в буферной емкости на следующей насосной станции не достигнет величины в соответствии с формулой (7.6). После этого аналогичным способом пускают промежуточную насосную станцию (ПНС). После выхода на нормальный режим все насосные станции, в том числе и головная, переводятся на работу по схеме «из насоса в насос», минуя буферные емкости. Подпорные насосы на ГНС подкачивают дегазированную нефть из резервуарного парка. После высвобождения резервуаров они отключаются. Таким образом, подпорные насосы на ГНС необходимы только в моменты пусков нефтепровода и для откачки дегазированной нефти из резервуаров.
В случае перекачки газонасыщенной нефти очень важным становится отыскание перевальных точек. При этом понятие «перевальная точка» можно обобщить на случай нестабильной нефти. Под перевальной точкой понимается такая точка трассы нефтепровода, давление в которой равно или меньше давления насыщения нефти. Если такая точка существует, то в ней происходит разгазирование нефти. Поскольку процесс растворения в нефти газа происходит значительно хуже, чем разгазирование, и требует высоких давлений и времени, то за перевальной точкой имеет место двухфазный поток. Существование перевальной точки снижает пропускную способность нефтепровода, а в отдельных случаях и ведет к прекращению перекачки. Это объясняется тем, что потери давления на участке двухфазного потока резко возрастают и может случиться, что запаса давления окажется недостаточно для преодоления гидравлических сопротивлений конечного участка трубопровода. Для обеспечения условий пуска нефтепровода и нормального режима его работы необходимо выявить наличие перевальных точек и устранить их путем поднятия давления в этих точках выше давления насыщения нефти.
При гидравлическом расчете трубопровода, предназначенного для транспортировки газонасыщенной нефти, а также пря построении напорной линии можно пользоваться формулой Лейбензона, в которой плотность и вязкость следует брать в соответствии с формулами (7.2)—
(7.5).
7.7. ТРУБОПРОВОДНЫЙ ТРАНСПОРТ КОНДЕНСАТА И ШИРОКОЙ ФРАКЦИИ ЛЕГКИХ УГЛЕВОДОРОДОВ
Продукция газовых, газоконденсатных и газонефтяных месторождений рассматривается как комплексное сырье для многих отраслей народного хозяйства. Поскольку природный и нефтяной газы представляют собой широкую гамму углеводородов, рациональное их использование предусматривает их переработку, которая осуществляется на ГПЗ. Основной продукцией ГПЗ является сухой отбензиненный газ, состоящий в основном из метана, который используется в качестве высокоэффективного топлива, и жидкие продукты—этан, пропан, бутан, пропан-бутановая смесь. В зависимости от условий сбыта и требований потребителя на ГПЗ можно получать и смеси различных компонентов, таких, как нестабильный и стабильный газовые бензины, широкая фракция легких углеводородов (ШФЛУ). Если перерабатываемый газ содержит редкие и ценные химические элементы, то на ГПЗ должно предусматриваться и их извлечение.
Отдельные жидкие продукты ГПЗ образуют так называемые сжиженные углеводородные газы (СУГ), которые используются в качестве энергетического топлива и сырья для нефтехимических производств.
Кроме жидких углеводородных смесей, получаемых в процессе переработки нефтяных и природных газов, следует особо рассмотреть конденсат, который добывается вместе с газом из газоконденсатных месторождений. Этот продукт является высокоэффективным аналогом нефти, содержащим значительное количество жидких углеводородов. Фракционный состав конденсата может существенно отличаться для различных месторождений. Температура конца кипения большинства конденсатов составляет 420—570 К. Под сырым (нестабильным) конденсатом подразумевается смесь углеводородов, находящихся при давлениях выше давления насыщенных паров компонентов в виде жидкости. Его компоненты при понижении давления ниже давления насыщенных паров выделяются в виде газов и конденсат переходит в двухфазное состояние.
После специальной подготовки, в том числе деметанизации и де-этанизации, можно получить стабильный конденсат, который практически состоит только из жидких углеводородов.
Рассмотрим основные параметры конденсатов и смеси жидких углеводородов, характеризующие их физические свойства.
Плотность жидких углеводородных смесей можно определять экспериментально или, если известен их компонентный состав (по данным хроматографического анализа), по формуле
Yj yrfPi i = l
где — массоЕ;ая концентрация i-й компоненты, имеющей соответствующую плотность р;.
Вязкость можно также определять экспериментально. Для продуктов с повышенными значениями давления насыщения необходимо при этом пользоваться вискозиметрами высокого давления. Если известен компонентный состав, то можно подсчитать динамическую вязкость
П
(температура фиксирована) по формуле lgfx = ? (*ilgM-;)> гДе xi —
t=i
объемная концентрация г-й компоненты, имеющей вязкость р,;.
Динамическая вязкость г-й компоненты при любой температуре Т вычисляется по уравнению Андраде
|хг = а{ехр(сг/Т),
где at и С; — змпирические константы [5].
Давление насыщенных паров жидких углеводородных смесей определяется экспериментально в бомбе pVT. Для приближенного вычисления можно пользоваться формулой ps = Exipsi, где xt — объемная концентрация i-й компоненты в смеси; psi—давление насыщенных паров t'-й компоненты. Для расчета psi можно применять формулу Антуана
lg Psi = Ai — Bi/(t + Ci),
где ЛBh С,- — коэффициенты для индивидуальных углеводоро дов [5].
Особенности технологических расчетов трубопроводов для транспортировки нестабильного конденсата и широкой фракции легких углеводородов обусловлены способностью продукта переходить в газообразное состояние. Если в процессе эксплуатации давление в какой-либо точке трубопровода упадет ниже давления насыщенных паров, соответствующего данной температуре, то перекачиваемая среда переходит в газообразное состояние. Последнее приводит к резкому возрастанию гидравлических сопротивлений, тем самым ухудшая условия перекачки, а в отдельных случаях влечет за собой и полную остановку перекачки. Поэтому необходимость создания условий, при которых давление в любой точке трубопровода обеспечивает однофазное состояние перекачиваемой среды, является одним из главных отправных положений при гидравлическом расчете трубопроводов, р Минимальное давление pmin в трубопроводе должно удовлетворять условию pmin > ps + рлоп. Дополнительное давление pRon принимается равным 0,5 МПа. Давление насыщенных паров транспортируемой среды определяется для максимально возможной по длине трубопровода температуры перекачки. Потери давления на гидравлические сопротивления можно определять по формуле Дарси— Вейсбаха.
7.8. ОСОБЕННОСТИ ДВИЖЕНИЯ ГАЗОЖИДКОСТНЫХ СМЕСЕЙ ПО ТРУБОПРОВОДАМ
Совместное движение жидкости и газа ио трубопроводу значительно сложнее движения однофазных сред и характеризуется наличием различных структурных форм течения, а именно двухфазных потоков. К двухфазности потока может привести падение давления в трубопроводе ниже давления насыщенных паров компонентов перекачиваемой жидкости (например, нестабильного конденсата, газонасыщенной нефти). Под структурой газожидкостного потока понимается характер распределения по объему каждой из фаз. Структурные формы течения и границы их существования могут изучаться только экспериментально с использованием визуальных методов. М югочисленные исследования показали, что структурные формы потокое весьма разнообразны и зависят от соотношения расходов жидкой и газовой фаз, их физических свойств, а также от диаметра и угла наклона трубопровода. Все многообразие структурных форм сводят к нескольким, характерным для вертикальных (рис. 7.8) и горизонтальных (рис. 7.9) потоков.
Пузырьковая структура. При таком характере те-тени я газовая фаза в виде отдельных пузырьков распределена по все? массе жидкости более или менее равномерно. Однако при горизонтальном и малонаклонном течении наблюдается тенденция концентрации пузырьков в верхней части трубы. Это объясняется действием сил гравитации. Пузырьковая структура наблюдается при малых концентрациях газа, например, когда давление в системе снижается до давления насыщения, и по всему объему нестабильной жидкости происходит зарождение газовой фазы.
Пробковая структура. По мере дальнейшего снижения давления ниже давления насыщения (в случае транспорта нестабильной нефти или конденсата) происходит увеличение объема газовой фазы как за счет перехода из растворенного состояния, так и за счет расширения объема выделившегося ранее газа. При этом отдельные лузырьки сливаются, образуя пробки. Пробковая структура характеризуется последовательным чередованием пробок газа и жидкости. В случае вертикальных потоков газовые пробки имеют пулеобразную форму и занимают почти все поперечное сечение, располагаясь практически осесимметрично, поэтому эту структуру (для вертикальных течений) часто называют еще снарядной или четочной. В случае горизонтальных потоков газовые пузырьки концентрируются в верхней части трубы. При пробковой структуре наблюдается пульсация давления, характеризующаяся тем, что давление в любом фиксированном течении трубы колеблется. Амплитуда этих колебаний зависит от разных факторов, например от соотношения объемных расходов жидкой к газовой фаз, абсолютного давления, профиля трубопровода и т. д.
Расслоенная структура. Эта структура газожидкостного потока может встречаться только в трубах горизонтальных или с относительно небольшими значениями угла наклона, когда под действием сил гравитации поток расслаивается: жидкость течет в нижней части,
Рис. 7.8. Структурные формы газожидкостных потоков в вертикальных трубах:
а — пузырьконаи; 6 — пробковая или снарядная; в -- вспененная , :• --- кольцевая или дисперсно-кольцевая
Рис. 7.9. Структурные формы газожидкостных потоков в горизонтальных и слабонаклонных трубах:
а — пузырьковая; б — пробковая; л — расслоенная с гладкой границей раздела', г — расслоен -пая с волновой границей раздела; д — расслоенная со шквальными волнами; е — ггробкопо-вспе-пепная; ж — мелкодиспергироваиная или эмульсионная; ч — кольцевая или дисперсно-кольцевая структуры потоков
смачивая только часть поверхности трубы, а газ — в верхней. При этом граница раздела жидкость — газ может быть гладкой и плоской, может иметь небольшую рябь или волны значительной длины и амплитуды. Расслоенная структура может быть получена из пробковой посредством увеличения объемного расходного содержания газа, когда отдельные пробки газа сливаются. Дальнейшее увеличение расхода газа приводит к образованию сначала небольших, затем больших и, наконец, шквальных волн, которые могут перекрывать все сечение трубы, и, следовательно, создавать пробковую структуру, но уже на другом уровне — резко выраженными пульсациями давления, появлением пены и т. д.
Вспененная или мелкодиспергироваиная структура. В вертикальных восходящих потоках увеличение скорости двухфазной смеси приводит к смене пробковой (снарядной) структуры на вспененную. Эта структура является переходной от пробковой к кольцевой. Причем с уменьшением диаметра трубы переход от пробковой к кольцевой структуре происходит более плавно и область существования вспененной структуры уменьшается. Появление вспененной структуры объясняется распадом пробок на более мелкие из-за турбулентных пульсаций скорости и давления. Иными словами, происходит диспергирование газовой фазы до очень малых размеров. Отдельные глобулы газа разделяются между собой тонкой пленкой жидкости, прочность которой зависит от физических свойств жидкости, в том числе и от поверхностного натяжения. В случае горизонтальных течений вспененную структуру часто называют еще мелкодиспергированной или эмульсионной.
Кольцевая или дисперсно-кольцевая структура. Такое течение, газожидкостного потока характеризуется тем, что на стенках трубы имеется слой жидкости, в центральной же части движется газ, содержащий мелкие капли жидкости. Кольцевая структура существует при очень больших содержаниях газа и высоких скоростях движения газожидкостной смеси. Граница раздела жидкость — газ представляет собой волнистую поверхность, с которой происходит отрыв и унос капель жидкости. С ростом скорости смеси количество распыленной жидкости в газовом ядре потока и степень дисперсности увеличиваются.
Особенность течений двухфазных смесей заключается в том, что они всегда имеют не только фиксированные внешние ограничивающие поверхности (стенки труб), но и внутренние поверхности раздела фаз, положение которых меняется во времени и в пространстве. Через поверхности раздела происходит взамодействие фаз (гидродинамическое, тепловое, фазовые переходы, химические реакции и т. д.). Все это осложняет математическое описание и изучение двухфазных потоков, относит их к классу неустановившихся движений. При расчете газожидкостных потоков вводятся специфические понятия и определения, которые так или иначе характеризуют движение и рассматриваются как осредненные величины по пространственно-временным координатам. Принято считать движение газожидкостной смеси установившимся, если массовые (Сж, Gr) и объемные (QM, Qr) расходы жидкой и газовой фаз постоянны. Постоянными будут также массовый и объемный расходы смеси: GCM = Сж + Gr; Qcu = Q*. + Qr.
Одним из определяющих критериев двухфазных потоков является объемное расходное газосодержание р, под которым понимается отношение объемного расхода газа Qr к объемному расходу смеси QCM:
Р = Qp/Qcm -<2г/(<2ж -h Qr).
Следует подчеркнуть, что объемный расход газа пересчитывается на те термодинамические условия (давление и температуру), которые имеют место в рассматриваемом сечении потока. Если рассматривать достаточно длинный трубопровод, в котором давление заметно изменяется, то Qг, а следовательно, и р не являются постоянными величинами.
В соответствии с объемным расходным газосодержг нием вводится понятие плотности газожидкостной смеси
рем = GCM/QCM = рж (1 — р) -|- ргр,
где рж, рг — плотности соответственно жидкости и газа в условиях трубы.
Другим важным критерием подобия газожидкостнь х потоков является число Фруда смеси FrCM, определяемое формулой
FrCM= w2cJ(gD), где wcм — средняя по сечению скорость смеси,
wCM = QCJF = 4 (Q,- + Q*)/(nD2),
F — площадь сечения трубопровода; D — диаметр трубы.
Число Фруда представляет собой отношение сил инерции газожидкостного потока к силе тяжести.
При течении газожидкостных смесей, как правило, наблюдается относительное движение фаз, которое приводит к изменению объемного соотношения фаз на рассматриваемом участке трубопровода. Так, при восходящем течении газожидкостной смеси происходят торможение и задержка жидкой фазы, что ведет к увеличению плотности смеси. При нисходящем течении — наоборот, происходит торможение газовой фазы. Чтобы учесть это явление, вводится понятие истинного (объемного) газосодержания <р, которое связано с расходным газосо-держанием р соотношением
Ф = -- FJF —: Fr/[ Fr - j Fк),
где wc — истинная скорость движения газа, представляющая собой отношение объемного расхода газа к площади сечения, занятого им, т. е. wT -- Qr/Fe; FK, Fr —доля сечения трубы, занятая жидкой и газовой фазами соответственно.
Физический смысл истинного газосодержания — это отношение доли сечения трубы, занятого газовой фазой, ко всему сечению трубы.
В соответствии с явлением относительного движения фаз вводится понятие истинной плотности газожидкостной смеси ри, которую определяют но формуле ри -¦ рж (1—ф) I ргф-
Многолетний опыт эксплуатации промысловых трубопроводов показал, что при движении газонефтяных и газоконденсатных смесей по трубопроводам диаметром более 0,2 м в практическом диапазоне скоростей течения основными структурами являются расслоенная и пробковая. Причем при нисходящих и горизонтальных потоках может быть как расслоенная, так и пробковая структуры. При восходящих газожидкостных потоках с углом наклона более 2° всегда наблюдается пробковая структура. Каждая структура потока характеризуется своими значениями относительной скорости движения фаз, своими закономерностями гидравлических сопротивлений. Именно поэтому важно правильно определить структуру газожидкостного потока. При этом определяющим критерием подобия является число FrCM. Если FrCM < FrKp, то течение газожидкостной смеси расслоенное, если FrCM > Fri(p, то течение пробковое.
Критическое значение числа Фруда вычисляется по формуле
(7.7)
![]()
![]()
(1 _р)([ -1-72 Ю-4^*)2 [1 +210-4(pD/o)0,bj
где а — угол наклона трубопровода к горизонту; р.ж — относительная вязкость; р,ж = (Хж/Нч-; и рг — динамическая вязкость соответственно жидкой и газовой фаз; р -- среднее давление на рассматриваемом участке трубопровода; а поверхностное натяжение на границе жидкость — газ.
Из формулы (7.7) видно, что на границу перехода из расслоенной структуры потока в пробковую существенно влияют объемное расходное газосодержание, угол наклона трубопровода, давление в нем, а также вязкость жидкой фазы.
ВНИИгаз рекомендует определять критическое значение числа Фруда по формуле
![]()
где кж — коэффициент гидравлического сопротивления безнапорного течения жидкости в наклонном трубопроводе под действием сил тяжести. Значение Кж определяется методом последовательных приближений. Сначала по заданному значению геометрического уклона Az/Al = sin а и приближенному значению Яж,*о (принятому по интуиции) определяется скорость безнапорного течения жидкости ^
ш* = ^2gD sin а/кж< 0.
Полученное в первом приближении значение скорости используется для определения числа Рейнольдса течения жидкости с последующим вычислением значения Хж' в первом приближении по одной из известных формул, например по формуле Аль'чпуля Хж = = 0,11 (68/ReK-b K/D)0’25. Далее процесс вычислений повторяется, но уже за исходное значение принимается новое значение. И так до тех пор, пока значения Яж, полученные в двух последующих вычислениях, не окажутся достаточно близкими.
Гидравлический расчет при пробковой структуре потока. В основе гидравлического расчета трубопровода при пробковой структуре потока лежит обобщенное уравнение Дарси—Вейсбаха
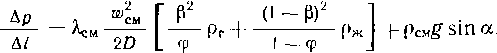
где Ар — перепад давления на участке длиной А/; Ясм — коэффициент гидравлического сопротивления для газожидкостной ;меси;
(7.8)
истинный динамический напор газожидкостного потока.
Входящие в (7.8) параметры ducm, |3, рг, рж находятся в соответствии с приведенными формулами с учетом термодинамических условий (р и Т) на рассматриваемом участке трубопровода /диной А1. Угол наклона а имеет положительное значение для восходящего и отрицательное — для нисходящего потоков.
Для вычисления Ясм используется эмпирическая зависимость
^СМ г—
ap^(ReCM, k), где ^
1 — 0,78ft [ 1 — схр ( — 2,2 VFpl — 0,22 [l — ехр ( — I5p)] ft
1-Р
р — относительная плотность газа, р = рг/рж. Коэффициент X (ReCM, k) вычисляется как для однофазного потока, но с условными параметрами
![]()
ReCM = ьУсм f — -+¦ -^—1 D; V vr v* J
vr и v* — кинематическая вязкость соответственно газовой и жидкой составляющих потока.
Для истинного газосодержания <р, входящего в (7.8), существует несколько формул, каждая из которых справедлива при определенных условиях газожидкостного потока с пробковой структурой. В случае восходящих и горизонтальных потоков, когда вязкость жидкой фазы находится в пределах 1 • 10_e < v ==с 25 ¦ Ю_в, справедлива формула
Ф^= 0,8р [l —ехр (—2,2
д/FrrM )1 1 + *’5 Vp .
Для нисходящих потоков ф определяется по формуле ф — 0,81 р.
Основные расчетные зависимости при расслоенной структуре потока. Расслоенная структура представляет собой два самостоятельных гомогенных потока (жидкостный и газовый), имеющих подвижную границу разде/а. Поскольку давление представляет собой непрерывную функцию координат, в любом фиксированном сечении оно имеет одинаковое значение как для жидкой, так и газовой составляющих потока. Поэтому перепад давления Ар = рг—р2 в трубопроводе на участке длиной АI равносилен перепаду давления в каждом из составляющих потока, например в газовом потоке
—~г — V Рг + Prg sin а, (7.9)
ДI 2 L'p
где — коэффициент гидравлического сопротивления газового потока; Dr — гидравлический диаметр газового потока.
Если учесть, что истинное газосодержание связано с центральным углом 0 соотношением
Ф = (0 — sin 0 cos 0)/л, а гидравлический диаметр DT выражается через ф, 0 и D формулой
D -= г 0 -)- sin (я — 0)
то равенство (7.9) можно представить в виде Др я [0 + sin (я — 0)1 Q?
~ТГ - гРг---— ---[ Prg sin а. (7.10)
М n3(f3D-‘
Значение А,г определяется по одной из известных формул гидравлики (например, по формуле Альтшуля), в которой при вычислении числа Рейнольдса для газового потока необходимо использовать понятие гидравлического диаметра.
258
Для вычисления потерь давления на гидравлические сопротивления при расслоенной структуре газожидкостного потока требуется правильно определять истинное газосодержание. В :лучае нисходящих потоков с углом наклона а от 1 до 10° можно воспользоваться следующими эмпирическими зависимостями, полученными во ВНИИгазе:
<р= 1— X0,4 при 0< х< 0,18; (7.11)
Ф === 0,615(1 — х) при 0,18<х< 1-
Если расслоенное течение неустойчивое, приближается к пробковому, что наблюдается в области изменения параметров |3 и FrCM'-
0 Ср <10,16; [(1 —sin а) ехр (—9,4sin a) I2 <С FrCM/ FrKp <1, то истинное газосодержание определяется по формулам
ф= —7— (1— X0'4) при 0г? х < 0,18; (7.12)
0,18
ф-~- —77--(l— X)0,615 при 0,18 <х<1-
0,1 о
Значение параметра %, входящего в выражения (7.11), (7.12), находится по формуле
% = 0l705-^^-- (7-13)
л 2sina
Следует отметить, что при малых значениях а (от 0 до 1°) выражениями (7.11) и (7.12) пользоваться нельзя. При а = 0 (случай горизонтального трубопровода) параметр % вообще теряет смысл, так как стоящий в знаменателе sin а обращается в нуль. Поэтому в диапазоне изменения а от 0 до 1° производить гидравлический расчет по методике ВНИИгаза не представляется возможным. Однако в указанном диапазоне изменения а можно применять другой мето;,, который основан на том, что расслоенное течение представляет собой два гомогенных потока, для каждого из которых можно записать уравнение движения. Для газового потока им является выражение (7.10). Для жидкостного потока, если воспользоваться понятием гидравлического диаметра, можно записать аналогичное уравнение
Др 8<&(я-в) .
где Хж — коэффициент гидравлического сопротивления по длине жидкостного потока, определяемый по известным формулам гидравлики однофазных потоков, в которых вместо диаметра трубы следует подставить значение гидравлического диаметра Ож
Рж = —(¦' ~
ф)D. п — 0
Рассматривая (7.10) и (7.14) как систему алгебракческих уравнений с двумя неизвестными, можно в результате решения ее одновременно найтн истинное газосодержание гр и перепад давления А/?. Указанная система уравнений имеет единственное решение.
Следует отметить, что приведенные методы определения Ар при расслоенном газожидкостном потоке в случае значительного волнообразования на границе раздела фаз дают заниженные значения перепада давления. Объясняется это тем, что одна из фаз, движущаяся с большей скоростью, представляет поток, частью границы которого является подвижная волновая поверхность с эквивалентной шероховатостью большей, чем шероховатость внутренней поверхности трубы. Этот факт никак не учитывается при определении Я по известным фор-мулзм.
заложения (hJDN >2) коэффициент си можно вычислять по формуле Форхгеймера
&2 ~ %Kp/(DNa0).
Коэффициент теплоотдачи от нефти к стенке трубы представляет собой отношение теплового потока в данном сечении трубы к разности между средней температурой нефти и температурой внутренней стенки трубы. Для определения коэффициента теплоотдачи от движущейся нефти (нефтепродукта) используют критериальные уравнения М. А. Михеева:
при ламинарном режиме (Ref <2000)
Nu = 0,17 Ref0’33 Pr?-43 Gr?’1 (Pr,/ PrJ0'25; при турбулентном режиме (Re^ > 104)
Nu = 0,021 Re/’8 Pr°’43 (Prf/PrJ°'25.
В области 2000 <Re <104 коэффициент теплоотдачи находят интерполяцией. В приведенных формулах величины с индексом / определяют при средней интегральной температуре нефти, а с индексом w— при средней интегральной температуре внутренней стенки трубы. Средняя интегральная температура внутренней стенки трубы связана со средней интегральной температурой нефти соотношением
гр _ Т O' - Т'ср f) 1 /®1
/=1
где /?,, — внутренний радиус трубопровода; Rj — наружный радиус /-го слоя.
.. Параметры Рейнольдса (Re), Прандтля (Рг), Грасгофа (Gr) и Нус-сельта (Nu) равны соответственно
К
где ш — средняя по сечению скорость течения нефти; v — коэффициент кинематической вязкости нефти; g — ускорение свободного падения; р„ — коэффициент объемного расширения нефти.
При учете сопротивления теплоотдачи на границе групт — воздух можно применять формулу
принята равной 2,1 кДж/(кг-К). Удельная теплоемкость углеродистых сталей и отложений парафина равна 0,5 и 2,9 кДж/(кг-К) соответственно.
Коэффициент теплопроводности нефти X в зависимости от параметров перекачки—0,1—0,16 Вт/(м2-К). Для уточненных расчетов применяют формулу Крего—Смита
_0Л37_ (J —0,54. 10-37).
Средние значения коэффициентов теплопроводности стали и парафина составляют соответственно 46—50 и 2,5 Вт/(м2-К).
Полный коэффициент теплопередачи К от нефти в окружающую среду зависит от режима движения жидкости и ее теплофизических свойств, термического сопротивления передаче теплоты в окружающую среду через антикоррозионную тепловую изоляцию, стенку трубы, отложения парафина и т. д.:
KDa oti^i / i Di—i a.2Dj\:
/=i
где D0 и DN — внутренний и наружный диаметр трубопровода соответственно; otj — внутренний коэффициент теплоотдачи (от нефти к внутренней поверхности отложений или трубы); X-t — коэффициент теплопроводности /-го цилиндрического слоя (отложений, металла трубы, изоляции и т. д.); Z), — наружный диаметр /-го цилиндрического слоя; а2 — коэффициент теплоотдачи от внешней поверхности нефтепровода в окружающую среду. Для трубопроводов большого диаметра (DN >500 мм) величину К можно определить приближенно по формуле
/=1
где 8 j — толщина /-го цилиндрического слоя.
Коэффициент теплоотдачи от внешней поверхности подземного трубопровода в окружающую среду характеризует термическое сопротивление грунта и теплоотдачу от его поверхности в атмосферу
Ф ___2ХГр В ij__
D n (1 «о В i 2)
где Ягр — коэффициент теплопроводности грунта; Bi2 = ан c/krp — критерий Био; ав — коэффициент теплоотдачи от поверхности грунта
в воздух; с^дАо -(0,5DW)2 ; h0 — глубина заложения трубопровода до его оси;
ae=In[2VDw + y(2V0w)-I ]¦
В условиях высокой интенсивности теплоотдачи с поверхности грунта (большие значения Bia), а также при значительной глубине
ПЕРЕКАЧКА ВЫСОКОЗАСТЫБАЮЩИХ И ВЫСОКОВЯЗКИХ НЕФТЕЙ С ПОДОГРЕВОМ
Перекачка высоковязких и высокозастывающих нефтей и нефтепродуктов с подогревом является самым распространенным способом трубопроводного транспорта этих продуктов. Трубопроводы, по которым перекачиваются подогретые нефти, называются горячими. Нефть подогревают на станциях или вдоль всей трассы трубе провода.
В первом, наиболее распространенном варианте гоэячих трубопроводов на них устанавливают станции трех видов: насосно-тепловые (НТС)—для подогрева и перекачки продукта, тепловые (ТС) — только для подогрева и насосные (НС) — только для перекачки продукта. Подогрев продукта производится как в резервуарах (на головной станции), оборудованных змеевиковыми или секционными паровыми подогревателями, так и в подогревателях (на станциях), которые могут быть паровыми или огневыми (печи).
Во втором варианте рядом с нефтепроводом укладывают греющий трубопровод-спутник, по которому перекачивается теплоноситель; этот же вариант подогрева можно осуществить с помощью электроэнергии.
Сокращение потерь теплоты на горячих трубопроводах может быть достигнуто нанесением теплоизоляционного покрытия на трубы.
8.1. ИСХОДНЫЕ ДАННЫЕ ДЛЯ ТЕПЛОВОГО РАСЧЕТА ГОРЯЧИХ НЕФТЕПРОВОДОВ
При проведении теплового расчета нефтепровода неоСходимы следующие исходные данные: физические и теплофизические характеристики нефти, тепловой изоляции, грунта, климатические данные.
Сведения о климатических данных (средние месячные температуры воздуха, грунта на глубине заложения трубопровод^ в естественном тепловом состоянии, уровень солнечной радиации, толщина снежного покрова) принимают по климатическим справочникам для района прохождения трассы трубопровода. Физические и теплофизические характеристики нефти, тепловой изоляции, грунта определяют опытным путем или рассчитывают по соответствующим эмпирическим формулам.
Удельную теплоемкость нефти определяют по формуле Крего c=r. -L__ (1,687+ 3,39-10-3/).
V p!s
где р‘б — относительная плотность нефти по воде при i - 288 К. Удельная теплоемкость нефти и нефтепродуктов лежит в пределах от 1,6 до 2,5 кДж/(кг- К) и для ориентировочных расчетов может быть
где an — коэффициент теплоотдачи от поверхности грунта в воздух, равный 10—18 Вт/(м2-К).
Чаще всего высокозастывлющие нефти перекачивают при турбулентном режиме. Для подземных магистральных трубопроводов, эксплуатирующихся при турбулентном режиме, коэффициент оц изменяется от 50 до 300 Вг/(м2-К). Он значительно превышает коэффициент а2, который изменяется от 1,5 до 7 Вт/(м2-К). Следовательно, с малой погрешностью величиной i/(ctj) можно пренебречь. Если трубопровод не имеет тепловой изоляции, то для турбулентного режима можно принять, что К та ссо.
Определение теплофизических характеристик грунта является наиболее сложной и ответственной задачей, так как их значения изменяются и по глубине массива, и по длине трассы трубопровода. Кроме того, значения теплофизических характеристик грунта меняются в течение года в результате сезонной миграции влаги в грунте , вызываемой весенними паводками, дождями, колебанием температур. Свойства верхних слоев почвы, кроме того, могут изменяться даже на протяжении суток из-за конденсации влаги в порах грунта в ночные часы и ее испарения с повышением температуры днем. Наряду с этими факторами на теплофизические свойства грунта значительное влияние оказывает тепловое действие самого трубэпровода. Эго связано с перемещением влаги в области теплового влияния трубы, возникающим из-за температурного градиента между стенкой трубопровода и близлежащими слоями грунта. Теплофизические характеристики грунта — коэффициент теплопроводности ЯГр, коэффициент температуропроводности avp и удельную теплоемкость сгр — определяют в результате специальных изысканий в полевых условиях или в лаборатории. Число точек измерения теплофизических характеристик грунта по трассе трубопровода и их повторяемость определяются требованиями к точности нахождения ЯГр> агр, сгр.
Для ориентировочных расчетов на стадии технико-экономического обоснования средние значения коэффициента теплопроводности грунта Хгр при температуре 273 К можно принимать но табл. 8.1.
Таблица 8.1
|
Грунт | Степень н;п жпос.ти | ¦ П t/(mj 'К) | Грунт |
Степень пла жностн |
V Вт/(М-- К) |
| Глина | Сухая | 1 1 |
Песок | Сухой |
0,4 |
|
Умеренно | 1,9 |
Умеренно |
1,6 | ||
|
влажная | 1 влажный | ||||
|
Влажная | 2,7 |
Влажный | 2 | ||
| Суглинок |
Сухой | 0,8 |
Грунт насып | Сухой | 0,2 |
|
Умеренно | 1,8 |
ной | |||
| влажный |
Грунт скалfa | По сухой пес | 0,35 | ||
| Влажный |
2,4 | il ый |
чаной подуш | ||
|
Супесь | Сухая |
0,6 | ке |
||
| У мерен но | 1,7 | Грунт на под | Сильно обвод |
3 | |
|
влажная | водных пере | пенный | |||
| Влажная |
2,2 | ходах |
Теплофизические характеристики тепловой изоляции определяют опытным путем или принимают по паспортным данным. В тепловых расчетах используют значение теплофизических характеристик теплоизоляции, равное полусумме значений, соответствующих температуре внутренней и внешней поверхности теплоизоляционного покрытия. Значения коэффициента теплопроводности для некоторых изоляционных материалов, используемых при сооружении горячих нефтепроводов, следующие (в Вт/(м2-К): 0,018—0,022 для пенополиуретана, 0,03 для пенополистирола, 0,033 для стекловолокна, 0,051 для пеностекла.
8.2. ТЕПЛОВОЙ РЕЖИМ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
Цель теплового расчета при проектировании магистральных трубопроводов — определить распределение температуры по его длине и оценить тепловые потери. С учетом данных теплового расчета определяют пропускную способность трубопровода, шаг насосных (тепловых) станций, рассчитывают трубопровод на прочность и устойчивость, выбирают тип и толщину теплоизоляции.
В процессе эксплуатации нефтепроводов результаты теплового расчета используют для оперативного диспетчерского управления работой трубопровода: нахождения безопасного времени остановки горячей перекачки высоковязких нефтей, выбора способа выталкивания застывшей нефти из остановленного трубопровода, оценки оптимального варианта пуска горячего нефтепровода в эксплуатацию, определения безопасного времени отключения тепловых станций.
Режимы работы горячего нефтепровода в условиях пуска в эксплуатацию, остановок перекачки, изменения пропускной способности и температуры подогрева нефти называются переходными. Они характеризуются изменением пропускной способности и температуры нефти при переходе от одного стационарного состояния к другому. Процесс течения нефти по трубопроводу и его тепловой режим в этих условиях являются неустановившимися. Причиной возникновения переходных режимов работы горячих нефтепроводов может явиться плановое или аварийное отключение отдельных насосных агрегатов или НС, тепловых печей или теплообменников ТС, заполнение трубопровода нефтью при его пуске, остановка перекачки и ее возобновление, последовательная перекачка нефтей с различными физическими свойствами, подключение или отключение отборов и подкачек нефти по трассе трубопровода, сезонное колебание температуры воздуха и теплофизических характеристик грунта. Указанные причины приводят к изменению параметров перекачки: температуры, давления, пропускной способности. Причем отклонение любого из этих параметров от стационарного состояния, если не производится специального регулирования системы, приводит к соответствующему изменению всех остальных. Так, например, при аварийном отключении станции подогрева в трубопровод начинает поступать холодная нефть, имеющая более высокую вязкость по сравнению с подогретой нефтью. По мере заполнения участка трубопровода холодной нефтью и вытеснения подогретой повышается потеря напора на трение. Для трубопровода с НС, оборудованными центробежными насосами, это автоматически приводит к уменьшению подачи и росту давления, причем последнее может превысить допустимое давление, назначаемое из условия прочности труб. Одновременное изменение температуры, давления и пропускной способности происходит из-за изменения тепловых потерь трубопровода в окружающую среду, возникающего на участках, заполненных холодной нефтью. Всякое изменение скорости перекачки, в свою очередь, влияет на распределение температуры нефти по длине трубопровода и во времени. Переходный режим работы нефтепровода продолжается до тех пор, пока теплообмен в системе «трубопровод — грунт» не достигнет нового установившегося состояния. Продолжительность переходных тепловых процессов может достигать нескольких месяцев. Принимая во внимание сезонное колебание температуры воздуха и грунта, необходимо отметить, что горячие нефтепроводы практически всегда работают в условиях переменных режимов. Однако, поскольку число и характер переходных процессов носят случайный характер, проектирование горячих нефтепроводов ведут для средних условий стационарных режимов эксплуатации. Для этих условий производится выбор основных технико-экономических показателей, строительных и технологических решений. Результаты расчетов переходных режимов работы учитывают в процессе эксплуатации при определении безопасного отклонения параметров перекачки от номинальных значений, выборе оптимальных условий транспортировки нефти при выходе из строя отдельных насосных агрегатов и печей и т. д.
В связи с разработкой и внедрением автоматизированных систем управления работой магистральных трубопроводов (АСУТ) расчеты переходных режимов эксплуатации горячих нефтепроводов все чаще проводят на стадии проектирования. В данном случае результаты таких расчетов используют для определения параметров системы автоматики и телемеханики нефтепроводов, являющейся составной частью АСУТ, при определении алгоритма управления работой насосных и тепловых станций.
Рассмотрим порядок теплового расчета нефтепроводов при стационарных гидравлическом и тепловом режимах. Пусть в трубопровод через его начальное сечение поступает нефть, подогретая до температуры Тп- Тогда на некотором расстоянии х от начала трубопровода вследствие теплообмена с окружающей средой температура нефти понизится до Т (рис. 8.1). Для определения температуры в сечении л: выделим элементарный участок длиной dx и рассмотрим его тепловой баланс. Согласно основным законам теплопередачи, количество теплоты, теряемой нефтью, заключенной в данном элементарном объеме
0,25 nD20dx, прямо пропорционально температурному перепаду АТ = = Т—Т0, поверхности теплообмена лD0dx и обратно пропорционально термическому сопротивлению окружающей среды. Следовательно, количество теплоты, получаемое окружающей средой с температурой Тп от элементарного объема нефти составит
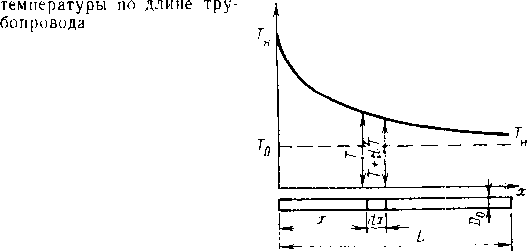
(kh KnD0(T—T0) dx.
(8.2)
(8.3)
Потеря нефтью части теплоты в окружающую среду dq., -¦ —GcdT,
где G — массовый расход.
Если пренебречь теплотой трения и не учитывать фазовые переходы, связанные с кристаллизацией парафина в нефти, то, согласно закону сохранения энергии, величины dql и dq% должны быть равны между собой, т. е.
KnD0 (Т- 7'0) dx - - —Gcdt. (8.4)
Разделяя переменные и интегрируя, получаем KkDq | Т н Tq
Gc
ИЛИ
(8.5)
При * — L значение температуры нефти в конце трубопровода
КпРд
Gc
)
L
7V -То-l (7Y-¦ Го) ехр ( ¦
При значительной протяженности нефтепровода (теоретически при х -* оо) согласно (8.5) температура нефти приблизится к температуре окружающей среды, равной температуре грунта на глубине заложения трубы в естественном тепловом состоянии в случае подземной прокладки и температуре воздуха при надземной прокладке. Это уравнение впервые получено В. Г. Шуховым и носит его имя. Оно дает практически удовлетворительные результаты для значительного диапазона режимов работы трубопроводов, и поэтому его широко используют при тепловых расчетах. Точность расчетов по формуле (8.5) в значительной степени зависит от достоверности определения полного коэффициента теплопередачи.
В. Г. Шухов предлагал определять значение К экспериментально на действующих трубопроводах и эти результаты распространить на проектируемые системы. Такой подход допустим, если К определяют непосредственно для уже эксплуатирующегося трубопровода или проектируемого трубопровода, находящегося в аналогичных с эксплуатирующимся трубопроводом условиях, например, при укладке его параллельно действующему трубопроводу на небольшом расстоянии от него. Тогда., используя эксплуатационные данные, коэффициент теплопередачи можно определить но выражению, которое следует из (8.5):
К =- 1п —i •
nD0L 7’к - То
В общем же случае К следует определять по формуле (8.1).
При транспортировке нефти с высоким содержанием парафина необходимо учитывать эффект кристаллизации парафина. От начальной температуры 7’,, до температуры начала кристаллизации парафина Тн.п охлаждение нефти происходит по закону Шухова. При дальнейшем охлаждении потери теплоты частично компенсируются выделяющейся теплотой кристаллизации парафина. Если принять, что количество кристаллизующегося парафина пропорционально снижению температуры, то количество теплоты, выделяющейся за счет кристаллизации, для элементарного участка dx
где в — концентрация парафина (в долях единицы), выделяющегося из нефти при понижении температуры от 7Y п до Те; Те — любая температура, для которой известно е; к — скрытая теплота кристаллизации парафина.
Тогда, записывая тепловой баланс для элементарного участка и решив исходное уравнение, получим для /] < х L (1Х — плина участка на котором нефть охлаждается от температуры Тп до 7„. п)
Т—Т0 { (7\,п -Т0)ехр (х-/*)],
где сх — с + ех/(Тпл—Те).
При перекачке вязких нефтей в подогретом состоянии возможны случаи, когда на начальном участке трубопровода имеет место турбулентный режим, а на конечном из-за остывания нефти — ламинарный.
Переход из одного режима в другой происходит при критическом числе Рейнольдса ReKp. Установлено, что для подогретых нефтей, ReKp = 1000 -^2000, причем для высокопарафинистых нефтей ReKp ближе к нижнему значению, а для вязких нефтей с малым содержанием парафина ближе к верхнему пределу. Так как ReKp-^ 4Q/(nD0vKp), то vKp = 4QAtD0ReKp. Величина vKp определяет критическую температуру Ткр, при которой происходит смена режима течения. Используя формулу Филонова—Рейнольдса, получаем
Ш Ут Ткр —Г„
Следовательно, на участке 0 < х ^ хкр режим течения нефти турбулентный, а при хКр < х < L — ламинарный. Температуру на обоих участках рассчитывают по формуле (8.5), в которой величину К определяют соответственно для условий ламинарного и турбулентного режимов течения.
Зная длины участков с различными режимами течения жидкости, можно оценить потерю напора в трубопроводе суммированием потерь напора hs == hT f- h„, где hT и h„ — потери напора при турбулентном и ламинарном режимах.
При учете выделения теплоты за счет трения тепловой баланс участка трубопровода запишется в виде
KnD0 (Т—Т0) dx =- GcdT [- Gidx,
где i — гидравлический уклон.
Разделяя переменные, получим
1 Тн — Tq — ь
In —----= ах
Т-Та-Ь
или
Т = Т0 + Ь + (ТЛ— Т0 — 6) ехр ( — ах), (8.8)
где а = KnD0/(GcM)\ b — Gi/(KnD0).
Сравнивая полученное выражение с формулой В. Г. Шухова, видим, что при учете теплоты трения прирост температуры нефти А = Ь (1—ехр (— ах)). Максимальный прирост при х -> оо Дта1С = ь.
Для нефтепровода с разными значениями коэффициентов теплопередачи Ki на отдельных участках длиной можно на основании
(8.5) записать
In -я—0Kill-
TKt-T0 Gc
Замечая, что Тщ+i "= TV* и Тн; == Тk;_i, и складывая почленно, получаем
In TH1-_r„_=jtPo_ ?
Kilt,
Т к n — То GcM i =i
Где i — порядковый номер участка; п —¦ число участков.
Гидравлический режим горячих нефтепроводов в значительной степени определяется условиями его теплообмена с окружающей средой. С увеличением температуры транспортируемой нефти снижается ее вязкость и уменьшается потеря напора. При понижении температуры наблюдается обратная картина. Температурный режим нефтепровода зависит от пропускной способности, условий передачи тепла от нефти в окружающую среду и других факторов. Используя зависимость изменения температуры нефти, а следовательно, и ее вязкости по длине трубопровода, можно найти распределение давления по длине нефтепровода, транспортирующего высоковязкие нефти в подогретом состоянии, и оценить потери напора на ее перекачку.
Для определения потерь напора используем уравнение Дарси— Лейбензона в дифференциальной форме
cLH = Р—--Ardx\-dz, (8.9)
D 5—71 u0
откуда
Q2-m? L
H=^ ~гл5-~т j ¦v'” (х) А г (х) dx + Az, (8.10)
ио L о
где Az — разность геодезических отметок начала и конца трубопровода.
Величина Аг представляет собой поправку на неизотермичность потока в радиальном направлении. Если коэффициент Аг считать постоянным по всей длине трубопровода, то интеграл в правой части последнего выражения имеет смысл средней интегральной вязкости нефти
vm =-( vm (х) dx.
ср Li w
Тогда потери напора составят
02-mvra
Н = Р—--- ArL + \z.
nb-m
иа
Это выражение при Ar = 1 совпадает с формулой Дарси—Вейсбаха для определения потерь напора на перекачку нефти с вязкостью vcp в изотермических условиях.
Значение vcp определяется температурными условиями транспорта и вязкостно-температурной зависимостью данной нефти. Примем распределение температуры нефти по формуле В. Г. Шухова, а зависимость v = v (Т) по формуле Филонова—Рейнольдса. Тогда
Vm L
v'?p = —— f ехр (— umT0) ехр [ — ит (Тн — Т0) ехр (— ах)\ dx.
L о
Г ехр(^)_=Ё|Ы
J У
*1
получим
ут
vcp = —— ехр [ит (Т„ — Т0)\ {Е i [ — um(TH— Т0)| — aL
— Ei [¦— urn (Tн — Т0) ехр (— aL)\\,
где Ei (х) — интегральная показательная функция.
Умножим правую часть последнего выражения на vH/[v0exp (— иТн)] = 1, найдем
vm
v"1 = —-ехр [um(TH—T0)\ (Ei [ —um(TH —T0)J —
Lp aL
— Ei \ — um(T„ — TK)]\,
где v„ — вязкость нефти при начальной температуре подогрева. Обозначим
Д / =
ехр (Г., - _-Гд)Х j Еj
( _шп (Тн_ То)( _
Ej { _ ит (Гн _ Тк)](
t
O.L
тогда V™ = v™At. Коэффициент At характеризует отклонение вязкости нефти, а следовательно, и гидравлических потерь от значений, соответствующих изотермическим условиям при Т = Тп. С учетом полученных результатов потери напора на перекачку подогретой высоковязкой нефти составят
02~mvm
Я=В —-H—LArAt + Az. (8.11)
п 5-т и0
Анализ последней формулы показывает, что график распределения напора по длине нефтепровода имеет вид параболы, в то время как в изотермических условиях он линейный. Отклонение от линейного распределения связано с повышением вязкости нефти из-за ее охлаждения. Темп падения напора возрастает на конечном участке. При больших величинах (Т„—Т0) и малых (Тк—Т0)
Ei [ — ит(ТЛ — Т0)] «0.
В этом случае основное сопротивление движению потока создается на холодном конце трубопровода.
У капельных жидкостей не все физические свойства зависят от температуры одинаково. Наиболее сильно зависит вязкость, гораздо слабее — плотность, теплопроводность и теплоемкость. Изменение температурных напоров (tw — tf) в сечении трубопровода в первую очередь приводит к изменению профиля скоростей, так как наиболее сильно меняется вязкость и, как следствие этого, к дополнительному изменению профиля температур. Изменения профиля скоростей будут большими в ламинарных потоках и меньшимн в турбулентных. Обычно зависимость потери напора от неоднородности потока по диаметру сводят к учету изменения вязкости и искажение полей температур и скоростей вследствие теплопередачи учитывают множителем ЛЛ. Для Аг принимают зависимость
Ar = e (vJvf)Z,
где е и ? — коэффициенты (при практических расчетах принимают для ламинарного потока е = 0,9 и ? = 1/3 ч-1/4, а для турбулентного потока е == 1 и ? == 0); — вязкость нефти при средней тем
пературе стенки трубопровода Тш ср, Тш ср = 7)ср — (7)ср—Т0) аХ//С; vI — вязкость нефти при средней температуре потока 7)с.р,
Гр Т1 I Гц ^к
/ f cd“ -* о i---»
f Р In [(Гн - То) (Гк - Го)]
Гк определяют по формуле (8.5).
Учитывая изменение температуры нефти по длине трубопровода по В. Г. Шухову, а изменение вязкости по Филонову—Рейнольдсу, получим
Л, = = ехр J JL (Г„ - 70) [ 1 4- ехр (— aZ)}) =
vcp 18а! I
= ехр(т ~ КГ.-Т.) I (Тк - То)]} ¦
Ранее коэффициент ЛЛ определялся для средней по длине нефтепровода температуры. Если величину Аг относить к элементарному участку, то в соответствии с (8.10) получим
Л _ д,д, - jEi [ _ „ _L i) (Г. - Т.)] -
_Ei[-u(/n--^-^-)(7\«-7’0)]}. (8.12)
В тех случаях, когда в трубопроводе наблюдаются два режима течения — турбулентный в начале и ламинарный в конце, определяют отдельно потери для обоих участков. Длины участков находят по формулам, приведенным ранее.
Достоверность расчетных данных в значительной степени зависит от точности аппроксимации вязкостно-температурной зависимости v (t). Поэтому для расчетов повышенной точности наиболее обоснованным является численный метод определения потерь напора на перекачку подогретых нефтей. В этом случае трубопровод разбивают на М участков (/ = 1, 2, . . . , М), в пределах которых вязкость нефти
272
Рис. 8.3. Напорная характеристика горячего трубопровода
с заданной точностью считается постоянной и равной ее среднему значению. Тогда можно записать
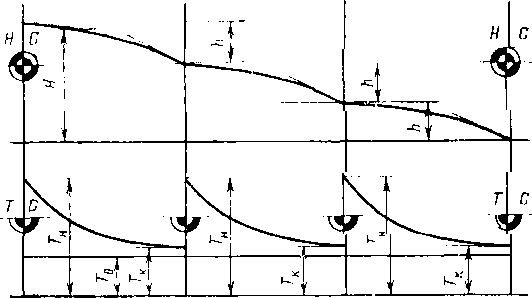
Рис. 8.2. Кривые падения напора и температуры по перегонам
м
1=1
п2-т т
где индекс i означает, что данная величина относится к /-му участку
ДЛИНОЙ /j.
При решении технико-экономических задач целесообразно использовать аналитические зависимости, например, для исследования гшия-ния различных факторов на технологические и энергетические показатели систем транспортировки нефти.
Кривые падения температуры и напора изображены на рис. 8.2. При этом каждой температуре нефти соответствует вполне определенный гидравлический уклон. Число насосных станций лимитируется максимальным напором, который могут выдержать трубы и перекачивающие насосы, а число подогревательных станций — максимальной допустимой температурой подогрева.
Графическая напорная характеристика горячего трубопровода, описывающая зависимость Q—Н согласно полученной формуле потерь напора на трение, изображена на рис. 8.3. Напорную характеристику можно разделить вертикальными прямыми на три зоны. В зоне малых расходов / медленно движущаяся нефть успевает охладиться еще на начал!:,ном участке трубопровода до температуры, близкой к температуре окружающей среды, и на оставшейся большей части трубопровода движется холодная нефть с практически постоянной высокой вязкостью. Графически в этой зоне напорная характеристика имеет вид прямой линии с большим углом наклона к оси абсцисс из-за высокой вязкости. В зоне больших расходов III нефть, двигаясь с большой скоростью, успевает пройти до конца трубопровода, сохранив еще высокую температуру. Поскольку средняя температура потока в этой зоне высока, напорная характеристика близка к прямой линии (ламинарный режим), с гораздо меньшим углом наклона к оси абсцисс, чем в зоне /, из-за малой вязкости нефти. Как в /, так и в /// зоне потери напора с увеличением расхода возрастают. В зоне II потери напора возрастают с уменьшением расхода. Это объясняется тем, что с уменьшением расхода в этой зоне (зоне средних расходов), а следовательно, и с уменьшением скорости движения нефти каждая ее порция дольше находится в трубопроводе и успевает остыть. В результате снижается средняя температура и возрастает средняя вязкость нефти, причем относительный рост вязкости в этой зоне больше, чем относительное уменьшение расхода, что приводит к росту потери напора при уменьшении расхода. Рабочей является только III зона со сравнительно большими расходами; / зона является нерабочей, так как при тех же напорах на станции расходы здесь будут в несколько раз меньше, чем в третьей зоне. Если потери напора в точке перехода из зоны I в зону III превышает максимальный напор, развиваемый насосной станцией, то при попадании рабочей точки системы насосная станция — трубопровод во II зону, являющуюся неустойчивой, расход будет самопроизвольно сокращаться и в конце концов рабочая точка перейдет в / зону. Это означает практически остановку трубопровода, поскольку расход становится очень малым. Если по каким-то причинам рабочая точка горячего трубопровода приблизилась к границе зоны II или уже перешла в эту зону, то возвратить ее в рабочую III зону можно одним из следующих способов: быстро повысить температуру нагрева нефти; быстро увеличить напор на станциях подключением дополнительных насосов; начать закачку в трубопровод менее вязкого продукта, не снижая температуру нагрева нефти. Если насосная станция может развивать напор, превышающий максимальные потери напора на границе / и II зон, причем эти потери не превышают допустимый напор из условий прочности трубопровода и оборудования на станции, то возвращение из / зоны в III не представляет трудностей.
8.4. ОБОРУДОВАНИЕ ДЛЯ ПОДОГРЕВА НЕФТИ
Для подогрева нефти и нефтепродуктов на насосно-тепловых и тепловых станциях используют подогреватели различных конструкций. Резервуары головной станции оборудуют трубчатыми подогревателями (змеевиковыми или секционными) для предварительного подогрева нефти. Цель этого подогрева — снизить вязкость нефти до уровня, достаточного для выкачки ее из резервуара с заданным расходом; на-274 грев в резервуаре до температуры перекачки по трубопроводу нецелесообразен из-за больших потерь тепла от стенок резервуара в окружающую среду и увеличения потерь легких фракций за счет усиленного испарения при подогреве. В качестве теплоносителя применяется обычно водяной нар. Для снижения потерь теплоты резервуары можно оборудовать тепловой изоляцией.
Подогрев до температуры перекачки производится в паровых или огневых подогревателях. Наибольшее распространение получили многоходовые теплообменники с плавающей головкой. Нефть в них проходит по трубам, а пар пропускают через затрубное пространство. Такое распределение потоков повышает коэффициент теплопередачи и уменьшает габариты теплообменника. Обычно на станции устанавливают несколько теплообменников, которые можно включать последовательно и параллельно.
При подогреве нефти в теплообменниках наряду с контролем температуры нефти необходимо вести тщательный контроль за чистотой выходящего из подогревателей конденсата. Попадание в него нефти свидетельствует о неисправности теплообменника и следует немедленно прекратить подачу в теплообменник нефти. На горячих нефтепроводах широко применяют и огневые подогреватели (впервые в СССР — на нефтепроводе Узень—Гурьев—Куйбышев). Они представляют собой печн, топливом для которых может быть газ, перекачиваемый продукт или нефть. Рассмотрим принципиальную схему радиантно-конвекционной печи для подогрева нефти (рис. 8.4). Все пространство печи, смонтированной в металлическом каркасе 1, разделено на две зоны: радиантную I и конвекционную II. Радиантная зона в свою очередь разделена на две части стенкой 2 из огнеупорного кирпича, размещенной вдоль оси печи. В нижней части печи установлено по шесть форсунок 5 с воздушным распылением топлива. Топливом на нефтепроводе Узень—Гурьев —Куйбышев является транспортируемая нефть. Однако форсунки являются газомазутными, что позволяет сжигать с их помощью и газообразное топливо. Воздух к форсункам подается по воздуховоду 6. Для предотвращения разрушения печи от«хлопка», возникающего при возобновлении подачи топлива после кратковременного перерыва, в печи имеются хлопушки 3, у которых при ударной волне вылетают крышки 15. В радиантной зоне печи на кронштейнах 4 уложены трубы 11 змеевика, по которому течет нефть. Нагрев нефти в этой зоне осуществляется в основном за счет лучистой энергии факела. Продукты сгорания проходят затем в конвективную зону, где передача теплоты текущей по трубам нефти осуществляется за счет конвекции. Из конвективной зоны печи продукты сгорания через дымовую трубу 8 выбрасываются в атмосферу. Регулирование разрежения (тяги) в печи осуществляется с помощью шибера 7. Змеевиковьте трубы в конвективной камере закреплены в средней 9 и торцовой 10 трубных решетках. Стены печи покрыты изнутри огнеупорной обмуровкой 13, а снаружи тепловой изоляцией 12. Для обслуживания печи, высота которой без дымовой трубы достигает 10,5 м, установлена лестница 14. Для наблюдения за состоянием конвективных труб и их очистки при накоплении на них сажи, сущест-
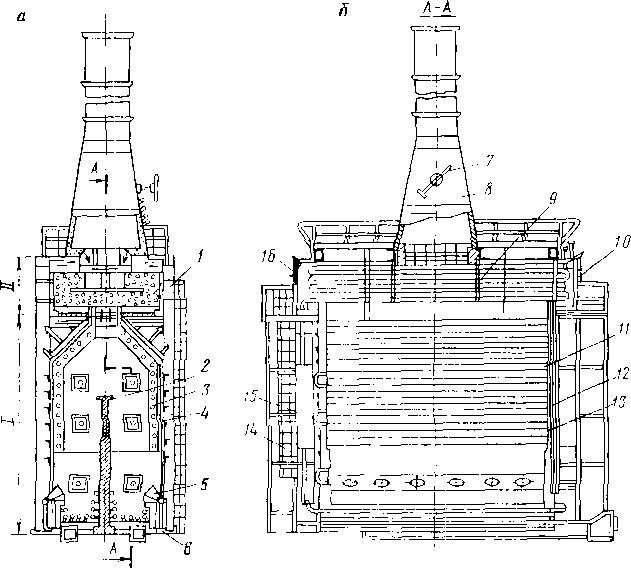
Рис. 8.4. Принципиальная схема радиантно-конвекционной печи
венно снижающей коэффициент теплопередачи, предусмотрены люки с крышками 16.
Система приборов контроля и автоматики позволяет оператору следить за ходом процесса подогрева нефти и обеспечивает автоматическую защиту печи при нарушении заданного технологического режима. Присутствие обслуживающего персонала во время работы печи обязательно. Пропускная способность одной печи составляет 600 м3/ч, при этом нефть нагревается от 30 до 65 °С. Максимальное рабочее давление нефти на входе в змеевик не должно превышать 6,5 МПа. Мощность печи составляет 10 500 кВт, а к. п. д. достигает 0,77, что свидетельствует о высокой тепловой эффективности печи.
Подогрев нефти на насосно-тепловых и тепловых станциях накладывает ограничения на конструкцию и эксплуатационную гибкость горячих трубопроводов. Так, из-за ограничения температуры подогрева нефти условиями нормальной работы теплообменных аппаратов в ряде случаев расчетное расстояние между тепловыми станциями может оказаться небольшим, что вынуждает увеличивать их число и соответственно приводит к повышению капитальных затрат. Длительная остановка перекачки может привести к застыванию нефти в трубопроводе, и в этом случае возобновление перекачки связано с
Рис. 8.5. Схема системы для подогрева трубопровода с ‘помощью скин-эффекта
большими затратами. Указанные недостатки могут быть устранены применением иутевого подогрева горячего нефтепровода. Для коротких трубопроводов получил распространение путевой подогрев с помощью трубопроводов-спутников, представляющих собой трубопроводы малого диаметра, уложенные параллельно нефтепроводу и прилегающие к нему (на нефтепровод и горячий водопровод накладывается общее для них теплоизоляционное покрытие); по ним перекачивается горячая вода.
А
Г
Перспективным является электроподогрев трубопровода с использованием скин-эффекта. Как известно, при пропуске переменного тока по стальной трубе он не распределяется равномерно ио поперечному сечению стенки трубы, а концентрируется из-за скин-эффекта ближе к внутренней поверхности трубы. Глубина концентрации тока зависит от частоты последнего. Однако благодаря высокой электропроводности стали в ней даже при промышленных частотах переменного тока в высокой степени проявляется скин-эффект. Так, при частоте 50 Гц глубина скин-эффекта (основной показатель интенсивности этого явления, показывающий, какой толщиной металла, измеряемой от его поверхности, ограничена зона прохождения тока) составляет для стали всего 1 мм.
Система для подогрева трубопровода с помощью скин-эффекта включает нефтепровод 1 (рис. 8.5), к которому вплотную прилегает нагревательная труба 2 диаметром от 6 до 40 мм; внутри трубы проходит медный кабель 3 с поперечным сечением проводников от 8 до 60 мм2. Кабель имеет теплостойкую изоляцию. Источник переменного тока промышленной частоты присоединен с одной стороны к внутреннему кабелю и с другой — ко второму кабелю 4, конец которого присоединен к нагревательной трубе. Второй конец внутреннего кабеля присоединен к противоположному от источника тока концу нагревательной трубы. Поскольку электрический ток концентрируется в очень малой по площади поперечного сечения зоне трубы, сопротивление трубы возрастает и выделяется большое количество теплоты. Обычно 80—90 % общего количества теплоты, выделяемой в контуре, генерируется в нагревательной трубе, а остальное — во внутреннем кабеле. Нефтепровод и нагревательная труба покрыты общей теплоизоляцией. Нагревательный трубопровод приварен к нефтепроводу и теплота, генерируемая в нагревательном трубопроводе, свободно переходит в нефтепровод. В то же время, поскольку ток проходит только по внутренней поверхности нагревательного трубопровода, он может быть заземлен.
Такая система путевого подогрева обладает высоким к. п. д., так как теплота от нагревательной трубы и внутреннего кабеля идет на нагрев нефтепровода. По данным испытаний разность температур нагревательной трубы и нефтепровода не превышает 283 К, выход теплоты составляет от 15 до 150 Вт на 1 м для одной нагревательной трубы. На трубопроводах большого диаметра можно укладывать несколько нагревательных труб.
8.5. ТЕПЛОИЗОЛИРОВАННЫЕ ТРУБОПРОВОДЫ
В некоторых случаях для повышения экономичности эксплуатации горячего трубопровода может оказаться целесообразным покрыть его теплоизоляцией. Изоляция снижает потери теплоты перекачиваемым продуктом, что позволяет сократить число тепловых станций. Правильный выбор материала, конструкции и толщины тепловой изоляции играет важную роль в повышении экономичности горячего трубопровода. Вначале выбирают материал и конструкцию тепловой изоляции, а затем переходят к определению ее толщины. Решение последней задачи зависит от принятого критерия оптимальности или условия, которому должно удовлетворять решение (экономические критерии, недопущение застывания продукта при остановках определенной продолжительности, заданные потери теплоты).
Материалы, применяемые для тепловой изоляции, должны обладать следующими свойствами: низким коэффициентом теплопроводности, малой гигроскопичностью, малой плотностью, отсутствием химического взаимодействия с поверхностью трубопровода, негорючестью, биологической инертностью по отношению к плесени, паразитам и грызунам, термостойкостью, способностью многократно выдерживать охлаждение и нагревание, прочностью, долговечностью и однородностью. Кроме того, при выборе теплоизолирующего материала следует стремиться удовлетворить ряд дополнительных требований. Так, например, затраты на изоляцию должны быть невысокими и быстро окупаться, монтаж изоляции должен быть удобен. Обычно не удается удовлетворять все упомянутые требования. Многим требованиям, предъявляемым к изоляции трубопроводов, удовлетворяет тепловая изоляция из пенополиуретана, покрытая синтетическими пленками.
Определение оптимальной толщины изоляции является техникоэкономической задачей, и в общем случае весьма сложной, поскольку приходится оптимизировать кроме толщины изоляции еще несколько параметров: температуры на выходе и входе тепловых станций, число подогревательных и насосных станций и т. п. Однако на практике с учетом опыта проектирования и эксплуатации горячих нефтепроводов задача оптимизации может быть упрощена. Во многих случаях температура нагрева Тн нефти на тепловых станциях принимается
на основании опыта эксплуатации аналогичных трубопроводов или максимально допускаемой технологическими ограничениями (начало разгонки нефти, закоксовывание труб теплообменных аппаратов и т. п.); конечная температура Тк в конце перегона между тепловыми станциями принимается для высокозастывающих нефтей на (3—5) °С выше температуры застывания, а для высоковязких нефтей — на основании опыта эксплуатации аналогичных трубопроводов. Следовательно, на перегоне между тепловыми станциями должны быть заданы потери теплоты. Исследования показали, что минимальным расход (масса) изоляции будет, если толщина ее на всей длине перегона постоянна. С увеличением толщины изоляции растут капитальные и эксплуатационные затраты на изоляцию, но одновременно снижаются теплопотери и соответственно уменьшается необходимое число тепловых станций и затраты на эти станции. Уменьшение толщины изоляции соответственно уменьшает затраты на изоляцию, но одновременно из-за увеличения потерь теплоты растут число тепловых станций и затраты на них. Оптимальным будет вариант, для которого сумма приведенных затрат на теплоизоляцию и тепловые станции будет минимальной.
В соответствии с формулой В. Г. Шухова для трубопровода длиной L и диаметром D0 необходимое число тепловых станций
п ^ KnDgL Qpc Ш у
![]()
где Шу = In l(Tu—T0)/(TK~T0)l и
![]()
Яи и Яиз — коэффициент теплопроводности соответственно металла трубопровода и изоляции; D0 и DN — соответственно внутренний и наружный диаметры трубопровода; DH3 == DN -f- 26из; б„а — толщина изоляции.
Для подземных трубопроводов внешний коэффициент теплоотдачи может быть определен с некоторыми упрощениями по формуле
2Х| р
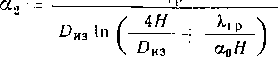
(8.14)
Тепловое сопротивление на границе нефть—труба и сопротивление металла трубы незначительны по сравнению с тепловым сопротивлением изоляции и грунта, поэтому первыми двумя членами (8.13) пренебрегаем и после подстановки (8.14) в (8.13) получаем
А В In D„з,
А
In 4Н--In Dw;
п =
Qpc Шу А -f В In Dиз
Расход тепла на нагрев перекачиваемой нефти на каждой тепловой станции фт = Qpc (Т„ — Тк).
Поверхность нагрева тепловой установки F = <2т/(р/(<7тТ]т), гДе /Ср —¦ коэффициент резерва теплового оборудования; qT — тепловое напряжение поверхности нагрева; rjT — к. п. д. тепловых установок. Стоимость сооружения тепловых станций
nLKp (Тн Тк) Ст__1__
<М1т Шу А + В In D„з
где Ст — стоимость сооружения тепловых установок, отнесенная к единице поверхности нагрева установки.
Эксплуатационные расходы для тепловых станций
Qpc (Гн - Гк)
Эст = а'Кст + а-\П -\-а2п
где а' — годовые отчисления на текущий ремонт и амортизацию в долях единицы; аг — годовая заработная плата, приходящаяся на одну тепловую станцию; а2— расходы на воду, топливо, смазку и т. д. на единицу тепловой мощности станции.
Тогда приведенные затраты по тепловым станциям
где Е — нормативный коэффициент эффективности капитальных вложений;
![]()
Далее учтем затраты на изоляцию. Капитальные затраты представим в виде
![]()
где Унз — объем изоляции; ри:, — плотность изоляции; Сиз — стоимость единицы массы изоляции, включающая затраты на ее сооружение.
Эксплуатационные расходы на содержание изоляции Э„3 = = РЛиз + Ьи где Р! —отчисления на амортизацию и текущий ремонт тепловой изоляции; — затраты, не зависящие от параметров трубопровода.
5Из — (Е -j- Pi) — (D„3 — Dn) ^-РизСиз -\-b\ .
4
Суммарные приведенные затраты
2S = ——™---f-MiDls + M?,
f- M iDK 3 М2,
A -(- В ln D„3
где
M, = -5- (E + p,) — LpH3CH3
4 4
/И.2 — остальные слагаемые, не зависящие от толщины изоляции.
Приравняв <325/(дОиз) к нулю, получим алгебраическое уравнение относительно Da3:
![]()
которое решается численно или графически.
Из анализа уравнения следует, что оптимальная толщина тепловой изоляции не зависит от длины трубопровода и вязкости перекачиваемой жидкости, уменьшается при увеличении глубины заложения, диаметра, пропускной способности трубопровода, стоимости изоляции и увеличивается при увеличении коэффициентов теплопроводности грунта и изоляции.
В случаях если предусматривается циклическая эксплуатация горячих трубопроводов, то необходимо выполнить проверочный расчет для того, чтобы либо выбрать изоляцию такой толщины, которая позволила бы после остановки на заданное время начать перекачку без осложнений, либо оценить время возможной остановки трубопровода при данной толщине изоляции, при котором нефтепродукт по всей длине не охладится ниже заданной температуры.
8.6. ПЕРЕКАЧКА НЕФТЕЙ, ЯВЛЯЮЩИХСЯ НЕНЬЮТОНОВСКИМИ жидкостями
Как упоминалось в гл. 7, течение парафинистых нефтей и нефтепродуктов может быть с некоторым приближением описано уравнением
![]()
(8.15)
Такие нефти являются неныотоновскими жидкостями и относятся к классу бингамовских жидкостей. Для цилиндра в потоке жидкости, ось которого совпадает с осью трубопровода, можно записать следующую зависимость между силой, действующей на цилиндр, и напряжением на поверхности цилиндра (рис. 8.6):
уже построенного горячего трубопровода также возникает задача выбора оптимальной температуры подогрева нефти. При проектировании оптимизацию параметров трубопровода выполняют для каких-то заданных условий: определенной температуры воздуха и грунта, заданной пропускной способности, свойств подлежащей транспортировке нефти и т. п. При эксплуатации трубопровода многие из этих условий меняются. В частности, в течение года меняется температура окружающей среды, возможно изменение объемов перекачки, характеристик перекачиваемой нефти. В этих случаях проектная температура подогрева нефти на станциях перестает быть оптимальной, и ее надо в каждом отдельном случае определять заново.
Оптимальная температура подогрева нефти на станциях определяется из следующих соображений. С повышением температуры нагрева возрастают затраты на разогрев нефти; одновременно снижается вязкость нефти, а значит, и потери напора в трубопроводе и соответственно затраты на перекачку нефти. Оптимальная температура нагрева нефти соответствует минимуму суммы затрат на подогрев и перекачку нефти. При введении некоторых упрощений задача оптимизации температуры нагрева может быть решена аналитически, однако более наглядным является графоаналитическое решение этой задачи.
Стоимость затрачиваемой в единицу времени энергии на перекачку нефти
5м== _0Яря Стм, (8 23)
Ям
где г)м — к. п. д. насосного агрегата; <тм — стоимость единицы механической энергии.
Стоимость затрачиваемой в единицу времени энергии на подогрев нефти
ST= Qpc (Т" ~
Гк> <тг,
(8.24)
Я7-
где г)7 — к. п. д. подогревательных устройств; ат — стоимость единицы энергии (например, топлива).
Если на перегоне между НТС имеются ТС, то полученное по формуле значение ST надо умножить на число пунктов подогрева на перегоне (предполагается, как это обычно бывает, что на НТС и всех ТС разность температур нефти на выходе и входе в станцию одинакова). Потеря напора Н, определяемая по формуле (8.11), зависит от температуры Т„ на выходе из НТС. Температура Тк в конце перегона между НТС также может быть определена по формуле (8.5) как функция Т„. Задаваясь рядом значений Т„, определяем соответствующие им значения 5„ и S/ и строим кривые SM = / (Тн) и ST = / (Т„), (рис. 8.7). Оптимальной является температура (ТоптМ соответствующая минимуму функции SM + ST = f (Т„).
Несмотря на то, что структура формулы (8.24) свидетельствует, казалось бы, о линейной зависимости Sr = f (Тн), в общем случае эта зависимость выражается кривой линией, так как с увеличением температуры подогрева Тн изменяется соотношение длин участков
Расход для структурного потока может быть определен из уравнения
Это уравнение было выведено Букингемом в 1921 г. Из (8.19) следует, что чем меньше перепад давлений в трубопроводе, тем больше радиус ядра г0. При некотором перепаде давлений радиус ядра становится равным внутреннему радиусу трубопровода R — это минимальный перепад давлений, при котором жидкость еще движется. Этот перепад давлений
Ар0 = 2lr0/R.
(8.21)
Из (8.20) и (8.21) получим другой вид уравнения Букингема
q nhpR* г ^__4 Лро 1 / Ар0 уп
8цпд1 L 3 Др 4 3 V Ар ) У
Уравнение Букингема связывает расход с перепадом давления для бингамовской жидкости в горизонтальном трубопроводе. Обычно задается расход, и надо определить соответствующий перепад давления, что по формуле Букингема можно сделать только путем нескольких итераций. Поскольку во многих случаях Ар0 значительно меньше Ар, третьим членом в скобках в этих случаях можно пренебречь, что несколько упрощает определение перепада давления Ар.
При т0 =¦= Ара = 0 уравнение Букингема превращается в расчетную формулу для ламинарного режима — уравнение Пуазейля:
![]()
8.7. ОПТИМАЛЬНАЯ ТЕМПЕРАТУРА ПОДОГРЕВА
В отличие от изотермических нефтепроводов, где при проектировании надо оптимизировать только диаметр трубопровода и давление на выходе из насосной станции, при проектировании горячего трубопровода надо оптимизировать и другие параметры: температуру на входе и выходе из подогревателей, число насосно-тепловых, тепловых и насосных станций и т. п. Решить эту задачу в общем виде, аналитически, с получением зависимостей, с помощью которых можно было бы вычислить значения параметров, пригодных для практического использования, не представляется возможным. В каждом конкретном случае эта задача должна решаться сравнением по экономическим показателям всего комплекса практически осуществимых вариантов. В связи с большим объемом вычислений, а также значительным числом вариантов для выбора оптимальных параметров целесообразно использовать электронно-вычислительные машины.
Температура подогрева нефти на станциях горячих трубопроводов является одним из проектных параметров, связанных с другими конструктивными параметрами трубопровода. Однако при эксплуатации
Рис. 8.6. Эпюры касательных напряжений и скоростей в поперечном сеченип потока бингамовской жидкости
где Ар — перепад давления, действующий на торцы цилиндра; г — радиус цилиндра; / — длина цилиндра, откуда
т = Apr 1(21).
(8.16)
Подставив значение т в (8.15), после преобразования получим вы. ражение для скорости потока на расстоянии г от оси трубопровода
![]()
Постоянная интегрирования С определяется из условия прилипания жидкости к стенке (отсутствие скольжения), т. е. при г = R и w = 0:
![]()
Подставив значение С в (8.17), получим
![]()
(8.18)
На рис. 8.6, а изображена построенная в соответствии с (8.16) эпюра касательных напряжений по поперечному сечению потока. Эти напряжения уменьшаются от максимального значения на стенке трубопровода до нуля на оси. Когда эти напряжения равны или меньше предела текучести т0, не происходит сдвига между концентрическими слоями потока и, следовательно, ядро потока движется как твердое тело. Радиус г0 этого ядра определяется подстановкой в (8.16) т — т0:
(8.19)
На рис. 8.6, 6 изображена эпюра скоростей потока бингамовской жидкости, в которой ядро движется как твердое тело, а жидкость, окружающая ядро, течет в ламинарном режиме. Такой поток называется структурным.
Рис. 8.7. График определения $ г, оптимальной температуры по- "д’ т догрева

с турбулентным и ламинарным потоками; рост Тн приводит к увеличению длины турбулентного участка, росту средневзвешенного коэффициента теплопередачи на перегоне и, как следствие, увеличению разности температур Тп и Тк.
Значения Т„ должны приниматься с учетом технологических ограничений. Температура подогрева нефти Т„ не должна превышать величины, при которой происходит закоксовывание трубок теплообменного аппарата или начинается разложение нефти. В то же время температура нефти в конце перегона Тк должна не менее чем на 3—5 °С превышать ее температуру застывания для высокозастывающих нефтей; следовательно, по формуле (8.5) при известном минимальном значении Тк определяем нижнюю границу возможных значений Тн. Для высоковязких нефтей нет технологического ограничения по нижнему пределу Тк.
8.8. РАССТАНОВКА СТАНЦИЙ НА ГОРЯЧЕМ НЕФТЕПРОВОДЕ
На горячем трубопроводе, как уже говорилось в начале гл. 8, уста-наливают станции трех видов: ТС, НС и НТС. При этом практически возможны сочетания станций на трубопроводе в трех вариантах: 1) только НТС; 2) НТС и ТС и 3) НТС и НС. Рассмотрим, как размещают станции на трубопроводе во всех упомянутых вариантах.
1. На трубопроводе нужно установить только насосно-тепловые станции (рис. 8.8, а). На вертикали, проведенной на профиле из начала трассы, откладываем подпор Ah, создаваемый подпорными насосами, и напор Н, развиваемый магистральными насосами. По формуле Шухова определяем пункт, где температура Т опустится до значения ТКр, соответствующего переходу режима течения из турбулентного в ламинарный. Разбив участок с турбулентным потоком на несколько участков (желательно с одинаковыми грунтами на каждом из этих участков, что позволит для каждого из них брать свое значение полного коэффициента теплопередачи), определяем потери напора на каждом из них (т = 0,25) и по полученным значениям строим кривую пьезометрических напоров. Если эта кривая пересекает профиль трассы, значит, на всем перегоне до следующей НТС будет наблюдаться турбулентный режим. Если же кривая не пересечет профиль трассы, то от пункта, где турбулентный режим переходит в ламинарный, определяем потери напора на небольших участках, пользуясь той же формулой, но при т -= 1, последовательно до тех пор, пока расстояние между кривой пьезометрического напора и профилем не станет
Рис. 8.8. Схемы расстановки иа трассе нефтепровода станции: а — НТС; б — НТС и ТС; в — НТС и НС
равно необходимому противокавитационному подпору Ah для насосов. Затем откладываем от кривой пьезометрических напоров напор Н, развиваемый магистральными насосами устанавливаемой в этом пункте НТС, и продолжаем построения так же, как и для перегона между первой и второй НТС.
2. На трубопроводе нужно установить НТС и ТС (рис. 8.8, б). Как и в предыдущем случае, откладываем на профиле из начала трассы трубопровода напор на головной НТС. Определяем с учетом возможного изменения коэффициента теплопередачи вдоль трассы расстояние от НТС до пункта, где температура опускается до конечного значения Тк (Lk), и до пункта где температура опускается до Ткр (/кр). Разбиваем расстояние LK на участки с постоянными коэффициентами теплопередачи К, и если LK -< /кр, то расчет с построением кривой пьезометрических напоров ведем только для трубулентного режима (,пг = 0,25), а если LK > /кр — для двух режимов — до 1кр для турбулентного и от /кр до LK\ — для ламинарного (m = 1). Если кривая пьезометрических напоров пересечет до LK профиль трассы, то на данном перегоне между НТС не надо ставить ТС, а вторую НТС размещаем так же, как и в предыдущем случае. Если же пьезометрическая кривая не пересечет профиль трассы, то в месте, где кончается кривая, т. е. на расстоянии LK от головной НТС, надо поставить ТС, которая снова поднимает температуру нефти до Т„. Далее определяем расстояние L* до пункта, где температура снизится до Тк, а также расстояние Гкр. Расчеты повторяют до тех пор, пока расстояние между пьезометрической линией и профилем не станет равно противокавитационному запасу. В этом: пункте размещаем НТС. Дальнейшие расчеты и построения для размещения ТС] и НТС аналогичны описанным.
3. На трубопроводе нужно установить НТС и НС (рис. 8.8, в). По формуле Шухова определяем расстояние LK от начала трубопровода, на котором температура опустится от Тц до Тк. При этом в случае существенного различия коэффициентов теплопередачи на разных участках трассы расчет падения температуры ведется по участкам. На расстоянии LK от начала трубопровода устанавливается вторая НТС (первая — в начале трубопровода). Подставив значение LK[ в формулу (8.11), находим потерю напора на этом участке Н (в случае двух 286 режимов на участке — турбулентного и ламинарного — вычисляем потери на каждом участке и суммируем их). На профиле трассы из ее начала проводим вертикаль, на которой откладываем подпор, создаваемый подпорными насосами, и к нему добавляем напор Н, равный рассчитанной потере напора. Напор Н делим на равное число частей так, чтобы каждая часть была равна или несколько меньше допустимого из условия прочности напора на станции (точки В и С). Проводим построение условной кривой пьезометрических напоров от точки А. Эта кривая пересечется с вертикалью, проведенной из места расположения второй НТС, на высоте Ah от линии профиля, соответствующей противокавитационному подпору, передаваемому на вторую НТС. Из точек В и С проводим линии, эквидистантные профилю трассы, до пересечения с условной кривой пьезометрических напоров (В1, С'). Точки на пересечениях вертикалей, проведенных через В' и С и линией профиля трассы, соответствуют пунктам размещения насосных станций. Если из С и В" провести линии, эквидистантные соответственно линиям АВ' и В'С', то получим линии пьезометрических напоров на перегонах между станциями.
Возможны и другие сочетания станций: НТС с НС и ТС, НС и ТС; принципы построения для размещения станций в этих случаях аналогичны описанным. Во всех случаях при расстановке станций необходимо наиболее полно использовать несущую способность трубопровода.
8.9. УВЕЛИЧЕНИЕ ПРОПУСКНОЙ СПОСОБНОСТИ ГОРЯЧИХ НЕФТЕПРОВОДОВ
Как и на изотермических трубопроводах увеличения пропускной способности горячих трубопроводов можно достичь тремя способами: прокладкой лупинга, увеличением числа станций, комбинацией этих двух способов. Но поскольку на горячем трубопроводе можно установить станции всех трех видов, соответственно увеличивается и число способов: 1) прокладка лупинга, 2) увеличение числа НТС, 3) увеличение числа ТС, 4) увеличение числа НС.
Кроме того, увеличить пропускную способность можно комбинированием упомянутых способов. Рассмотрим каждый из этих способов.
1. Увеличение пропускной способности прокладкой лупинга. При разных диаметрах лупинга и основного трубопровода тепловые режимы в этих двух нитках на параллельных участках будут неодинаковы, что окажет влияние на распределение расходов. Поэтому формулы изотермической гидравлики для расчетов лупингов на горячих трубопроводах неприменимы. Для определения длины лупинга, необходимой для достижения заданного увеличения пропускной способности, составляют систему уравнений:
а) баланс напоров на перегоне между станциями
б) условие равенства потерь напоров в лупинге и параллельном ему участке основного трубопровода
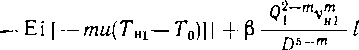
exp[mu(rHj-r0)] ^
x
X {Ei [ — mu(TH1 — T0)\ — Ei [ -mu (TK1
ailn
-T0)])+AA; (8.25)
![]()
р5__от
lEi [~mu(Tul — T0)}~ Ei ( —
mu(TK1 —T0)]j =
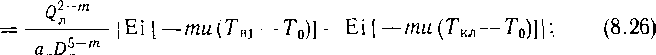
в) уравнения падения температуры по длине трубопровода
7V- Т0-\-{Тц — Т0) exр ( ali)',
(8.27)
(8.28) (8.29)
Тki-- т0 + (ТП1 — То)ехр (—aj/л); Ткл - Т0 + (Тщ — Т0) ехр (—ал1л)\
г) уравнения баланса длин и расходов
(8.30)
(8.31)
L — li /л; Q* Qi 4 Q-
В этих уравнениях: L, /х и /л — соответственно длины всего участка, участка до лупинга и лупинга; <2Л, Qi и Q* — соответственно расходы в лупинге, в параллельной лупингу нитке и суммарный; Т„, ТН1, Ткл, ТК1 — соответственно температуры в начале перегона, в начале лупинга, в конце лупинга и в конце параллельной лупингу нитке трубопровода.
Совместным решением приведенных уравнений определяется длина лупинга 1Л заданного диаметра йл, обеспечивающего увеличение пропускной способности трубопровода до заданного значения Q*.
Во всех приведенных формулах предполагается, что режим потока на всем протяжении трубопровода одинаковый. Можно получить решение и для случая разных режимов на участках трубопровода.
Ввиду большого числа однородных вычислений рассчитывать длину лупинга целесообразно на ЭВМ.
В отличие от изотермических трубопроводов местоположение лупинга на горячем трубопроводе влияет на общую потерю напора. Лу-пинги надо располагать на холодных концах перегонов; при этом теплопотери будут меньше, чем при укладке лупинга на горячем конце, и соответственно при том же расходе будет меньше общая потеря напора.
2. Увеличение числа НТС (рис. 8.9). Рассмотрим перегон между двумя НТС с равномерным подъемом или спуском трассы и одинаковыми теплофизическими характеристиками грунтов вдоль трассы. Тогда вторую НТС с тем же напором и температурой подогрева, что
г
Рис. 8.9. ГрафишГраспределения напоров Я и температур Т по длине горячего нефтепровода до удвоения НТС (/) и после (2)
г
на первой НТС, надо устанавливать в серединеЪерегона, и напор И каждой НТС будет расходоваться на преодоление сопротивления в 1/2 длины перегона, т. е. Н = / (Qr, 1/2). Следовательно, в соответствии с (8.11) получим
![]()
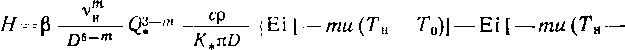
![]()
(8.32)
где /С* и Ar*—значение коэффициентов К и А г после увеличения пропускной способности.
Методом последовательных приближений или графическим интерполированием из (8.32) определяется значение Q*.
^ При пересеченном профиле трассы, неодинаковых теплофизических свойствах грунтов вдоль трассы или смене режимов течения на перегоне до установки дополнительной НТС последнюю надо размещать не в середине перегона; положение дополнительных НТС определяется в этом случае так же, как и при расстановке на вновь проектируемом трубопроводе. Следует отметить, что при пересеченном профиле и разных теплофизических свойствах грунтов вдоль трассы число дополнительных НТС на разных перегонах для достижения заданного увеличения пропускной способности может оказаться неодинаковым. На рис. 8.9 показаны падение напора и распределение температур нефти вдоль трассы до и после установки дополнительной НТС. Более высокая температура на подходе к дополнительной НТС, чем до ее установки, объясняется увеличением расхода при установке дополнительной НТС.
3. Увеличение числа ТС (рис. 8.10). При одинаковых теплофизических свойствах грунтов вдоль трассы и одинаковом режиме потока на всем перегоне дополнительную ТС надо устанавливать в середине перегона. Напор насосов И будет расходоваться на преодоление сопротивлений двух одинаковых по тепловому режиму участков длиной
Рис. 8.10. Графики распределения напоров Н и температур Т по длине горячего нефтепровода до удвоения ТС (/) и после (2)
1/2, где I — длина перегона между НТС, т. е. Н = 2/ (Q*, 1/2). Подставив эти обозначения в формулу (8.11), получим
v"1 f
Я =
2Р-5— СР Ei
[•—mu(TH—7"0)] — Ei [—mu(T„
—
Г ?>5-m [ 1 v H о/l V
-7'»>exK-JvL-^)]}A,*+"' <8-зз>
Значение Q*, как и в предыдущем случае, определяется итеративным методом.
4. Увеличение числа НС (рис. 8.11). При установке дополнительной насосной станции на преодоление сопротивлений на перегоне между НТС будет расходоваться удвоенный напор станции, т. е. 2Н = = / (Q*, 0 или
Vя1 f
2Н = $~— Ql~m
-KCPnD |Ei [—mu(T„ —
TQ)\ — Ei [—mu(TH —
_Г0)ехр(—^--^-)]jAr* + AA.
(8-34)
Дополнительную НС надо располагать ближе к концу перегона, чтобы преодолеваемые каждой станцией потери напора были одинаковы. Местоположение дополнительной НС можно определить ана-
Рис. 8.11. Графики распределения напоров Я и температур Т по длине горячего нефтепровода до удвоения НС (/) и после (2)
литически, но удобнее это сделать графоаналитически. Для этого на профиле трассы в начале перегона откладываем по вертикали подпор и удвоенный напор магистральных насосов станции. Подставляя в формулу (8.34) разные значения I, определяем соответствующие значения потерь напора и строим условную пьезометрическую кривую. Из точки А, соответствующей напору одной станции, проводим линию, эквидистантную профилю трассы; ее пересечение с условной пьезометрической линией определяет положение дополнительной НС.
8.10. ОСОБЫЕ РЕЖИМЫ РАБОТЫ ГОРЯЧИХ ТРУБОПРОВОДОВ
Горячие трубопроводы значительную часть времени работают в нестационарном тепловом и гидравлическом режимах. Тепловая неста-ционарность, связанная с медленным прогревом или охлаждением окружающей трубопровод среды, может привести к остановке трубопровода из-за чрезмерного повышения потерь напора в трубопроводе— «замораживанию» его.
Одной из наиболее ответственных операций является пуск вновь построенного горячего трубопровода. Перед вводом в эксплуатацию трубопровод заполнен холодной водой после опрессовки. Если вытеснять эту воду горячей высокозастывающей или вязкой нефтью, для перекачки которой предназначен трубопровод, то нефть, особенно часть ее, контактирующая с холодной водой, будет быстро остывать, вязкость ее сильно повысится или она застынет и закупорит трубопровод, остановив поток.
При небольшом расстоянии между тепловыми станциями и сравнительно небольшой вязкости или температуре застывания нефти иногда можно осуществить пуск закачкой в холодный трубопровод подогретой вязкой или высокозастывающей нефти. Однако в большинстве случаев таких условий нет, и перед закачкой подлежащей транспорту нефти трубопровод надо разогреть. Нужно создать соответствующее тепловое поле в грунте вокруг трубопровода. Такое поле перед пуском в эксплуатацию создается прокачкой через трубопровод разогретой маловязкой нефти, нефтепродуктов пли воды. Для определения длительности прогрева (прокачки греющей жидкости) П. И. Тугунов предложил упрощенную формулу
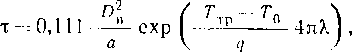
(8.35)
где т — длительность прогрева маловязким нефтепродуктом; 1)„ ¦— наружный диаметр трубы; а и X — соответственно коэффициенты температуропроводности и теплопроводности грунта; Ттр —температура наружной стенки трубопровода, принимаемая равной температуре греющей жидкости в конце перегона между тепловыми станциями; Т0—температура грунта в ненарушенном тепловом состоянии на глубине заложения трубопровода; q — теплоотдача с единицы длины трубопровода в единицу времени, q « Gc (Т„—Тк) 1 !L\ G — массовый расход греющей жидкости; с — теплоемкость жидкости; Тк и Тк— соответственно начальная и конечная температура греющей жидкости; L — расстояние между тепловыми станциями.
Температура стенки трубы ниже температуры потока, поэтому, принимая в (8.35) температуру стенки трубы Ттр, равной температуре потока Тк, несколько завышаем время прогрева, т. е. обеспечиваем некоторый запас но времени. Объем греющей жидкости тогда определится из формулы V Ст/р.
Значение Тгр ~ Тк принимается таким, чтобы полная потеря напора на участке между насосными станциями при заполнении его подлежащей транспорту нефтью не превышала максимально допустимого напора на станциях и в то же время поток был либо турбулентным, либо находился в третьей зоне характеристики при ламинарном течении. Это позволит выводить трубопровод на стационарный тепловой режим уже при перекачивании транспортируемой нефти. Прогрев можно ускорить, используя для этого вместо маловязкого нефтепродукта подогретую воду, обладающую примерно в два раза большей теплоемкостью, чем нефтепродукты. Время прогрева водой тв при известном времени прогрева нефтепродуктом т„ определяется по приближенной формуле
![]()
где Св и сш — соответственно массовый расход и теплоемкость воды.
При прогреве водой технико-экономическим расчетом можно определить, до какого теплового уровня (выше минимального, определяемого максимально допустимыми потерями напора иа перегоне между насосными станциями при перекачке подлежащей транспорту нефти) целесообразно подогревать трубопровод перед закачкой нефти.
Приведенные ранее формулы следует применять для предварительных расчетов времени прогрева трубопровода. Из-за неточности в определении коэффициентов температуропроводности, теплопроводности и других параметров, а также неточности математической модели фактическое время прогрева может существенно отличаться от расчетного. Поэтому закачку транспортируемой нефти надо начинать, когда замеренная приборами температура греющей жидкости в конце перегона между подогревательными станциями достигнет заданного значения Тк.
При эксплуатации горячего нефтепровода неминуемы его остановки на более или менее длительный период. Они могут быть вызваны аварией на одном из участков, необходимостью выполнения ремонтных работ, перебоями в подаче нефтн па головную станцию, принятой технологией циклических перекачек и т. п. Чтобы по возможности предотвратить «замораживание» трубопровода, необходимо знать так называемое безопасное время остановки трубопровода, т. е. время, за которое высокозастывающая нефть в остановленном трубопроводе еще не застынет, а вязкость высоковязкой не достигнет того значения, при котором потеря напора превысит допустимый напор на насосной станции.
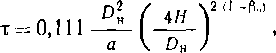
где Н — глубина заложения трубопровода; р = (Т—Т0)/(ТН—Т0); Ти — начальная температура стенки трубы (сразу после прекращения перекачки); Т — температура стенки трубы, при которой еще возможно без каких-либо осложнений возобновление перекачки.
Приближенно безопасное время т остановки трубопровода можно вычислить по формуле
В некоторых случаях горячий трубопровод обладает пропускной способностью, значительно превышающей количество поступающей для транспортировки нефти. Так бывает в начальный период разработки месторождения, когда объем добычи еще недостаточен для загрузки рассчитанного на полное развитие промысла магистрального трубопровода, или в период падающей добычи на истощающемся месторождении. В этих случаях возможны два варианта эксплуатации трубопровода: с непрерывной перекачкой при пониженных расходах и с циклической перекачкой, при которой часть времени трубопровод работает с полной загрузкой, а на остальное время перекачка прекращается.
Для выявления, какой из вариантов эксплуатации выгодней, надо предварительно определить оптимальное число циклов (циклом называется в данном случае период времени, включающий длительность одного интервала непрерывной перекачки и одного интервала простоя) при циклической перекачке.
Чем больше циклов перекачки, тем меньше должны быть вместимость дополнительных резервуаров для накапливания нефти на обоих концах трубопровода и связанные с ними затраты, но зато больше будут затраты на разогрев и замещение маловязким продуктом основного транспортируемого продукта на время простоев трубопровода. И обратно — сокращение числа циклов вызывает увеличение затрат на дополнительную емкость и уменьшение затрат на замещение нефти в трубопроводе маловязким продуктом. Задаваясь разными числами циклов, можно определить сумму приведенных затрат на дополнительную емкость и вытеснение нефти для каждого варианта. Оптимальным будет число циклов, соответствующее варианту с минимальными приведенными затратами.
Теперь сопоставим варианты с непрерывной и циклической перекачкой. При непрерывной перекачке с пониженным расходом температура нефти между тепловыми станциями будет падать больше, чем при номинальном расходе, что может привести к чрезмерному увеличению потери напора или застыванию нефти. Следовательно, при уменьшении расхода по сравнению с нормальным проектным придется построить определенное число дополнительных ТС, что связано с дополнительными затратами на их строительство и эксплуатацию. При циклической же перекачке возникнут дополнительные затраты на резервуары и вытеснение нефти маловязким продуктом при остановках перекачки. Вариант с минимальными приведенными затратами будет лучшим,
При остановке перекачки нефти по горячему трубопроводу на длительный срок для предотвращения его замораживания нефть должна быть вытеснена маловязкой нефтью или нефтепродуктом. В некоторых случаях нефть к началу вытеснения успевает застыть. Если вытесняемая нефть является ньютоновской, т. е. у нее нет статического напряжения сдвига, то вытеснение ее из всего перегона между насосными станциями возможно насосами станции. Если же нефть неньютоновская, то такое выталкивание возможно, если давление р, развиваемое станцией, достаточно для преодоления статического напряжения сдвига тст, т. е. если удовлетворяется условие (для горизонтальных трубопроводов)
pnD2/4 < itD/TCT, откуда
р > 4/тст/1>,
где D и / — соответственно диаметр и длина перегона трубопровода между станциями. Если это условие не удовлетворяется, то вытеснение нефти надо производить меньшими участками.
Рассмотрим поршневой процесс вытеснения нефти, который реализуется при размещении разделителя перед вытесняющим продуктом или при структурном течении вытесняемой нефти.
Для ускорения процесса вытеснения нефти его целесообразно вести при максимально возможном расходе. Ограничениями в этом случае являются либо максимально допустимый из условия прочности трубопровода и оборудования напор на выходе из насосной станции, либо максимальная подача насосов станции. В общем случае процесс вытеснения нефти можно разбить на два периода (рис. 8.12, а). В течение первого периода (/) напор насосов ограничивают максимально допустимым значением hmaT, а расход Q по мере увеличения длины участка, занятого маловязким продуктом, возрастает. Наконец, расход достигает максимально возможной подачи насосов при данных условиях, т. е. ограничение напора к этому времени полностью снято. Тогда наступает второй период (//) — в связи с дальнейшим увеличением длины участка, занятого маловязким продуктом, потеря напора, а с ней и напор на станции снижаются, а расход в трубопроводе медленно возрастает за счет перемещения точки пересечения напорных характеристик центробежной насосной станции и трубопровода в направлении увеличения расходов (при оборудовании станций поршневыми насосами расход в течение второго периода будет постоянным).
Возможны два частных случая. Если при полной подаче насосов в самом начале вытеснения развиваемый насосами напор равен или меньше максимально допустимого (рис. 8.12, б), то напор на станции будет все время снижаться, а расход будет медленно расти. Если же потери напора в трубопроводе, соответствующие максимальной подаче насосов станции при достижении выталкивающим продуктом конца перегона между насосными станциями, превышают максимально
Рис. 8.12. Графики вытеснения застывшей нефти из трубопровода
допустимый на станции напор /гтах, то напор на станции все время надо поддерживать равным hmRX, а расход будет все время увеличиваться (рис. 8.12, в).
Для первого периода (см. рис. 8.12, а) при вытеснении ньютоновской нефти потери напора в трубопроводе в любой момент выражаются так:
-j2—mlvm2
(L
(P2
^maxPi — Pi
(8.36)
ср»
где индексы 1 и 2 относятся соответственно к вытесняющей и вытесняемой жидкостям; Дг — разность отметок конца и начала перегона; рср — средняя плотность жидкостей в трубопроводе.
Разбив трубопровод на участки небольшой длины, подставляем соответствующие значения х в (8.36) и определяем значения Q при разных режимах течения двух жидкостей. По значениям Q на участках определяем время прохождения границей раздела каждого участка и, суммируя их, находим время —длительность первого периода вытеснения.
При ламинарном режиме течения обеих жидкостей выражение (8.36) упрощается:
128Qi
^maspi =
Kpi* -4 v2p2(Z—x)] 4- Агре
(8.37)
ngD4
откуда
Q_ ngD* (Pl^max ~ Агрср)
(8.38)
128 [Vipix — v2p2(L — x))
Подставив в уравнение неразрывности я D3
Qdr ¦
-dx
(8.39)
значение Q из (8.38), после интегрирования получим длительность первого периода вытеснения
32 / ,_ p2v2 -- pivt
2
(v2 Lx,pt —
«?)¦
(8.40)
т,=
gD1 (pihniax Д2Рер)
Значение длины участка xlt соответствующего первому периоду вытеснения, определяется и а (8.37) подстановкой значения Q, соответствующего напору hm,is по напорной характеристике насосной станции.
Для второго периода можно записать уравнение баланса давлений
gPt
(a -bQ) - 12-^ lp^-1 p2v2
(L --x)l + AzpCpg\
(8.41)
откуда
Q ___JtffD4 (ap, — Агрср)_ _
128 [piVxj; + p2v2(L — x)j + bngDipj
После подстановки (8.42) в уравнение (8.39) и интегрирования получим
sdhJ-^
[(V’ift+ ”S"
ьЬчРУ1—*)-
lp_ л
Здесь a и b — коэффициенты интерполяционной формулы вида Н ~ a—bQ2, описывающей напорную характеристику центробежной насосной станции. Полное время вытеснения т = Tj + т2.
Если выталкиваемая нефть течет в структурном режиме, то общую потерю давления рс в трубопроводе можно представить так:
128vi<*jcp1 , 128v2Q (L — х) р2 ( 16 т0 (L — х)
Рс— т
яО4 яD* 3 D
Здесь первое слагаемое представляет собой потерю давления на участке х, занятом толкающей жидкостью, движущейся при ламинарном режиме; второе и третье слагаемое — это потеря давления на участке L—х, занятом вытесняемой жидкостью, движущейся в структурном режиме, в соответствии с упрощенной формулой Букингема. Подставляя в это уравнение вместо рс максимально допустимое давление Amaxpig Для первого периода и a—bQ2 для второго периода и решая это уравнение совместно с уравнением неразрывности (8.39), аналогично предыдущему случаю определяем время вытеснения нефти, текущей при структурном режиме.
Если выталкиваемая нефть при температуре вытеснения является ньютоновской жидкостью, то выталкивающий ее продукт (при ламинарном течении обеих жидкостей) будет вклиниваться в нее (при отсутствии разделителя на границе раздела жидкостей) и вершина клина достигнет конца перегона раньше, чем остальная масса продукта. В связи с этим весь процесс вытеснения нефти можно разделить на две фазы: фазу выталкивания, заканчивающуюся достижением вершиной клина вытесняющей жидкости конца перегона, в фазу вымывания в течение которой практически полностью вытесняется из перегона вся выталкиваемая нефть. Предполагая, что при выталкивании в потоке сохраняется профиль скоростей, характерный для ламинарного режима, т. е. осевая скорость в два раза больше средней скорости, можно приближенно определить длительность первой фазы выталкивания, которая будет в два раза меньше определенной по выделенным ранее формулам. Длительность второй фазы — вымывания определяется по формулам для аналогичной операции последовательной перекачки при ламинарном режиме.
ЭКСПЛУАТАЦИЯ МАГИСТРАЛЬНЫХ ТРУБОПРОВОДОВ
9.1. ОСНОВЫ УПРАВЛЕНИЯ МАГИСТРАЛЬНЫМИ ТРУБОПРОВОДАМИ
Сущность управления магистральным трубопроводом, как и любым другим производством, заключается в принятии решений в процессе эксплуатации трубопроводного, резервуарного, энергетического и другого хозяйства, входящего в комплекс трубопроводного транспорта нефти и газа.
Правильное решение может быть принято лишь тогда, когда лица, принимающие его, обладают достаточно полной, достоверной и своевременно полученной информацией об управляемом ими магистральном трубопроводе. Полнота информации оказывает большое влияние на эффективность принимаемого решения, так как она позволяет найти рациональный вариант решения исходя из анализа конкретной производственной обстановки и накопленного опыта.
Для своевременного сбора необходимой, полной и достоверной информации и подготовки управленческого решения в структуре нефтегазопроводных и нефтепродуктопроводных управлений создается управленческий аппарат. На основе материала, подготовленного аппаратом, руководители принимают решения, организуют мероприятия по выполнению принятого решения и устанавливают контроль за его выполнением.
Взаимосвязанный комплекс месторождений, хранилищ, нефтегазо-перерабатывающнх заводов, районов потребления совместно с разветвленной сетыо магистральных трубопроводов может быть представлен в виде единой технологической системы нефтегазоснабжения.
Для диспетчерского управления функционирующими нефтегазоснабжающими системами характерна сложная информационно-управленческая надстройка. Развивающаяся трубопроводная система обладает еще большим числом многомерных экономических, материальных, энергетических и информационных связей.
Система нефтегазоснабжения, если исходить из современных теорий управления,— целенаправленный развивающийся комплекс взаимосвязанных технологических объектов (реально существующих и имитируемых) добычи, транспорта, хранения и распределения нефти, нефтепродуктов и др. Этот комплекс также включает энергетические, материальные и информационные потоки, объекты машинной переработки и передачи данных. В нем заняты большие коллективы для сбора, анализа и преобразования информации на различных иерархических и временных уровнях управления, проектирования и планирования.
Постоянное усложнение взаимосвязей между отдельными маги-
стральными, во многих случаях многониточными трубопроводами, жесткая технологическая связь с добывающими комплексами и многочисленными потребителями, рост комплекса средств регулирования, резервирования и переработки нефти и газа привели к формированию сложнейшей транспортно-энергетической системы страны, ядром которой являются системы магистрального транспорта газа, нефти и нефтепродуктов. Взаимодействие, взаиморезервирование между магистральными трубопроводами создают гибкость в маневрировании потоками нефти, газа и нефтепродуктов, повышают надежность нефтегазоснабжения промышленных центров страны и населения из различных нефтегазодобывающих районов и районов нефтепереработки, способствуют максимальному использованию производственных мощностей нефтяных и газовых промыслов и систем магистральных трубопроводов.
Основной чертой современных систем нефтегазоснабжения является их масштабность. Второй важной особенностью является динамичность, связанная с темпами развития нефтяной и газовой промышленностей и систематическим повышением удельного веса газа в топливно-энергетическом балансе. Третья особенность состоит в последовательной концентрации мощностей. Четвертая особенность — систематическая централизация нефтегазоснабжения, повышение уровня централизации. Вместо отдельных изолированных систем возникли единые взаимосвязанные системы нефтегазоснабжения.
Отличительная черта систем нефтегазоснабжения по сравнению с другими энергетическими системами — это изменение ее ресурсной части. Перемещение добычи нефти и газа из одних районов в другие, причем существенно отдаленные от центров потребления, чрезвычайно осложняет размещение нефтегазотранспортных магистралей, ухудшает экономические показатели, тормозит освоение ресурсов. Однако это — объективная реальность, с которой нельзя не считаться, а при развитии необходимо своевременно предвидеть.
Еще одна отличительная черта — значительная замедленность технологических процессов. Эта особенность нефтегазоснабжающих систем приводит к тому, что, например, для них в целом не существует совмещенного графика в суточном и недельном периодах. Совмещенные графики возможны лишь для месячных или сезонных периодов.
Специфика нефтегазоснабжающих систем как больших систем проявляется также в следующем.
1. Их создание преследует цель обеспечить плановые поставки нефти, нефтепродуктов и газа при минимуме народнохозяйственных затрат с учетом возможности перестраивать поведение системы в случае изменения плановых объемов нефтяных и газовых ресурсов, ограничений по металловложениям, ввода новых потребителей, колебания нефтегазопотребления. Кроме того, должны быть предсказаны параметрическое изменение элементов (скопление гидрата, изменение характеристик агрегатов, пласта, скважин, установок и т. д.), температурное влияние на их работу.
2. Сложность иерархической структуры управления. Организация управления осуществляется на основе сочетания централизованных и децентрализованных принципов. Между технологическими объектами и функциональными подсистемами, а также между развиваемой структурой и плановыми подразделениями имеются многофакторные технологические и информационно-управленческие связи, с помощью которых на основе накопленного опыта в различных иерархических уровнях проявляются самоорганизация и адаптация.
3. Системность. Данное свойство больших систем проявляется как между подзадачами различного уровня одной и той же задачи, так и между различными по своему существу задачами. Напримгр, можно обособить задачу оптимального управления компрессорными станциями, не теряя основных связей с задачами по системе газопроводов, задачу оптимизации добычи газа от задачи но транспорту и т. д. Задачи оперативного управления н текущего оптимального планирования, регулирования неравномерности газопотребления и надежности, текущего и перспективного планирования также находятся во взаимосвязи.
4. Размерность систем нефтегазоснабжения. Ввиду чрезвычайно большого числа элементов, звеньев, подсистем, их входов и выходов, разнообразия выполняемых функций, многопараметричности и распределенности параметров, особенно при условии более точного их воспроизведения, их размерность достигает очень большой величины.
5. Целостность, Существующие системы нефтегазоснабжения обладают целостностью в технологическом смысле , т . е . объекты объединены в технологические подсистемы «промысел—трубопровод—потребитель», что проявляется и в организационно-управленческой сфере деятельности. Однако наряду с этим имеются достаточно обособленные технологические объекты. В ближайшем будущем намечен быстрый рост степени целостности; появляются магистральные трубопроводы — перемычки, контурные трубопроводы , многониточные межсистемные магистрали, гз целом образующие сеть трубопроводов высокой плотности. Целостность систем и их основной части — системы магистрального транспорта нефти и газа не противоречит искусственному делению на автономные подсистемы. Как правило, такое деление облегчает решение проблемы оптимизации, так как позволяет применить принципы построения поуровневых и пообъектных решений. Однако нельзя забывать того, что абсолютно обособить подсистемы невозможно. Главной причиной этого является то, что глобальное оптимальное решение по всей системе в целом нельзя получить, суммируя изолированно найденные оптимальные решения по отдельным подсистемам. Это вытекает из того, что системы нефтеснаб-жения в целом и отдельные ее подсистемы относятся к открытым большим системам.
6. Изменение планов материально-технических ресурсов. Из-за возможных некоторых диспропорций в народном хозяйстве, температурных и параметрических колебаний, аварийных состояний возможны существенные изменения планов по ресурсам. Кроме того, неточность исходной информации приводит к неопределенности состояния системы, возникновению зоны равноэкономических решений, что в значительной мере ухудшает условия принятии окончательных решений.
Согласно технологическому принципу системы нефтегазоснабже-иия делятся на подсистемы добычи, транспорта, храпения и использования газа и нефти. Для систем нефтегазоснабжения характерны тесные технологические связи, и поэтому ее деление в большей степени условное. Точно так же, как и для других энергетических подсистем, для них нельзя получить глобальное оптимальное решение на верхнем иерархическом уровне по решениям, полученным на различных уровнях в отдельности. Таким образом, для них же характерно деление по территориальному признаку согласно следующей иерархии: страна—район—предприятие. Связи между технологическими подсистемами в энергетике принято называть горизонтальными связями, а связи между иерархическими уровнями согласно территориальному признаку — вертикальными связями. Можно сказать, что системы нефтегазоснабжения представляют единый комплекс иерархически построенных, вертикально и горизонтально расположенных и автономно функционирующих подсистем.
Иерархическая система оперативно-диспетчерского управления системами нефтегазоснабжения формировалась с основными этапами их развития: с созданием магистральных систем возникла необходимость организации диспетчерских служб; образование объединений обусловило создание объединенного диспетчерского управления (ОДУ); с дальнейшим развитием потребовалось создание высших ор -ганов диспетчерского управления —- центрального диспетчерского управления (ЦДУ). При последовательном переходе от одного этапа к другому происходило резкое усложнение объекта управления, возникали новые особенности режима, специфические трудности и задачи, что требовало развития научных исследований в области управления режимами, создания новых средств оперативного управления, применения более совершенных средств для планирования и анализа режимов, повышения уровня управлении нормальными и аварийными процессами.
В основе построения системы диспетчерского управления трубопроводным транспортом лежат следующие принципы: разграничение оперативно-диспетчерского управления (в пределах ее функций) от административно-хозяйственного руководства системами; иерархическое построение системы с прямым подчинением дежурного оперативного персонала каждой ступени персоналу более высокой ступени иерархии; предоставление персоналу каждой ступени максимальной самостоятельности в выполнении всех оперативных функций, не требующих вмешательства оперативного руководителя более высокой ступени; четкое разграничение функций гг ответственности оперативного персонала всех ступеней управления по ведению нормальных режимов и ликвидации аварийных нарушений; строжайшая диспетчерская дисциплина.
Основным принципом ведения режимов при оперативном управлении является подчинение режима каждого низшего звена (части) требованиям обеспечения оптимального режима высшего звена (це-
Лого). Так, например, режим каждого газоперекачивающего агрегата (ГПА) подчинен требованиям режима КС, режим КС — требованиям режима магистрального газопровода (МГ), режим МГ требованиям режима производственного объединения по транспорту (ПО), а режимы ПО, а следовательно, и всех низших звеньев подчинены требованиям обеспечения режима для ЕСГ СССР в целом. Тем самым достигается наиболее рациональное функционирование систем нефтегазо-снабжения в увязке с общими интересами народного хозяйства, т. е. с общегосударственными интересами. В этом проявляется одна из основных особенностей социалистического хозяйства, заключающаяся в подчинении местных интересов общим интересам народного хозяйства.
Иерархическая (централизованно-ступенчатая) система диспетчерского управления имеет следующие ступени: ЦДУ отрасли, ОДУ ПО, центральные диспетчерские службы (ЦДС) МГ, пункты оперативного управления КС.
Общая задача управления режимами систем нефтегазоснабжения заключается в обеспечении потребности в нефти, нефтепродуктах и газе с наибольшим экономическим эффектом для народного хозяйства в целом. Строго говоря, экономический оптимум должен определяться по минимуму суммарных расчетных затрат, включающих как издержки на производство и распределение нефти, нефтепродуктов и газа, так и зависящие от функционирования нефтегазотранспортных систем затраты в других отраслях народного хозяйства, т. е. должны быть учтены тесные связи с обеспечивающими отраслями по энергоснабжению, использованию водных ресурсов и т. д., а также влияние надежности снабжения нефтью, нефтепродуктами и газом на функционирование всех отраслей народного хозяйства и социальных структур.
Основными вопросами при управлении нефтегазотранспортными системами является повышение пропускной способности, снижение энергетических затрат на транспорт нефти, нефтепродуктов и газа, стабилизация режимов во времени, оптимальное управление при неустановившихся, в том числе аварийных, режимах.
Оперативное диспетчерское управление режимом систем нефтегазоснабжения предусматривает функции контроля и регулирования потребления и распределения нефти, нефтепродуктов и газа и обеспечения технологического режима транспорта и распределения заданных количеств нефти, нефтепродуктов и газа при минимальных затратах (энергетических и стоимостных) с учетом технологических ограничений и фактора надежности.
При оперативном управлении достигаются основные параметры линейных участков (баланс и количество нефти, нефтепродуктов и газа, коэффициенты гидравлического сопротивления и эффективности, зоны возможного гидратообразования и др.) и перекачивающих станций (фактическая мощность, удаленность от помпажной зоны, резерв мощности и др.).
При технологическом контроле режима сравниваются фактические и расчетные величины для оперативного принятия решения в случае отклонений. Для систем нефтегазоснабжения за сутки определяется баланс и количество нефти, нефтепродуктов и газа, коэффициент загрузки, коэффициент использования мощности, технико-экономические показатели и др.
При управлении системами нефтегазоснабжения важна диагностика состояния ее элементов. Она необходима при решении задач оперативного управления, планирования, обслуживания и ремонта, в особенности прогнозирования аварийных ситуаций.
Управление работой систем нефтегазоснабжения, регулирование межсистемных перетоков, ведение режимов КС различных типов подчинены единой цели — обеспечению наиболее экономичной их работы в целом при рациональном расходовании энергоресурсов и удовлетворении требований надежности снабжения нефтью, нефтепродуктами и газом.
Исключительная сложность задачи диспетчерского управления, при решении которой режимы каждого из большого числа звеньев в каждый данный отрезок времени должны быть подчинены требованиям обеспечения оптимального режима системы в целом для длительного периода (цикла) управления, обусловливает необходимость разделения (декомпозиции) этой комплексной задачи на ряд более простых взаимосвязанных задач, решаемых на всех ступенях системы диспетчерского управления и относящихся к различным временным уровням управления. Наряду с декомпозицией в территориальном аспекте (в соответствии с иерархической структурой системы диспетчерского управления) необходима декомпозиция во временном и ситуационном аспектах.
Декомпозиция во временном аспекте заключается в разделении общей задачи управления, решаемой на каждой из основных ступеней территориальной иерархии, на задачи, относящиеся к четырем различным временным уровням управления: долгосрочное планирование режимов на месяц — год; краткосрочное планирование режимов на сутки — неделю; оперативное управление текущими режимами, осуществляемое дежурным оперативным персоналом; автоматическое управление нормальными и аварийными режимами по ходу технологических процессов. Обеспечение оптимального режима системы нефтегазоснабжения при декомпозиции задачи управления достигается подчиненностью каждой ступени управления и временного уровня более высоким ступени и уровню с широким использованием принципа оптимальности. На основе этого принципа задание, вырабатываемое на высшей ступени (уровне), определяется оптимизацией режима с использованием эквивалентных характеристик (моделей) управляемых объектов, а это задание соответственно отрабатывается оптимальным образом на каждой более низкой ступени.
На высшем уровне временной иерархии решаются стратегические задачи долгосрочной оптимизации режимов. При этом осуществляются (в увязке с требованиями структура других отраслей народного хозяйства) прогнозирование потребления нефти, нефтепродуктов и газа и характерных графиков нагрузки, разработка балансов топливно-энергетического комплекса, оптимизация планов использования энергоресурсов и проведения капитальных ремонтов оборудования.
К этому же временному уровню относятся: разработка схем и режимов на характерные периоды года (осенне-зимний максимум, период паводка и др.), а также в связи с вводом новых объектов; решение всего комплекса вопросов повышения надежности нефтегазоснабжения, внедрения и совершенствования средств оперативно-диспетчерского управления и систем автоматического управления нормальными и аварийными режимами; разработка диспетчерских инструкций и т. д.
Оптимальные долгосрочные планы регулярно корректируются по мере изменения и уточнения условий работы. Результаты долгосрочного планирования играют роль основных ограничений, которые должны быть наложены на краткосрочные планы (недельные или суточные расходы, ремонтные мощности и т. д.). Оптимизация краткосрочных планов осуществляется с учетом указанных ограничений на основе более полной и точной информации об условиях работы в этом цикле управления; при разработке краткосрочного режима ряд ограничений, связанных с требованиями надежности, подлежит уточнению.
Оперативное управление — ведение текущего режима оперативным персоналом — осуществляется на основе суточных планов-графиков; при отклонениях от плана (по топливному газу, потребляемой мощности, состоянию оборудования и др.) производится необходимая корректировка режима в целях обеспечения требований надежности, качества и экономичности.
9.2. УЧЕТ ПЕРЕКАЧИВАЕМЫХ НЕФТИ И ГАЗА
Магистральные трубопроводы как наиболее современный вид транспорта нефти, нефтепродуктов и газа должны обеспечить нормальный производственный режим работы нефтегазопромыслов, нефтеперерабатывающих заводов, систем снабжения нефтепродуктами промышленного и городского газоснабжения. В обязанности дежурного диспетчера трубопровода входит непрерывное наблюдение за приемом нефти и газа от промыслов и нефтепродуктов от нефтеперерабатывающих и газобензиновых заводов для перекачки их по трубопроводам.
Подготовленные к подаче в трубопровод среды принимает оператор трубопровода, который следит, чтобы качество принимаемого продукта соответствовало условиям поставок, действующим ГОСТам и их техническим условиям. Обеспечение ритмичной работы трубопровода с минимальными энергетическими условиями требует четкой работы диспетчерской службы и невозможно без точного учета количества перекачиваемых нефти, нефтепродуктов и газа.
Расходом вещества обычно называют количество вещества (массы или объема), проходящее через определенное сечение канала (трубопровода) в единицу времени, а приборы или комплекты приборов, определяющие расход вещества в единицу времени, называют расходомерами. Расходомер может быть снабжен интегратором, показывающим массу или объем вещества, прошедшего через прибор за ка-кой-либо промежуток времени, в этом случае он называется счетчиком количества,
В зависимости от принципа действия наиболее часто применяемые в промышленности приборы для измерения расхода перекачиваемой среды можно разделить на следующие группы.
1. Расходомеры переменного перепада давления, принцип действия которых основан на зависимости от расхода вещества перепада давления, создаваемого неподвижным устройством, устанавливаемым в трубопроводе. Наибольшее распространение получили расходомеры с сужающим устройством, работа которых основана на зависимости от расхода перепада давления, образующегося на сужающем устройстве в результате частичного перехода потенциальной энергии потока в кинетическую.
2. Расходомеры постоянного перепада давления, принцип действия которых основан на зависимости от расхода вещества вертикального перемещения тела (поплавка), изменяющего при этом площадь проходного отверстия прибора так, что давление по обе стороны поплавка остается постоянным. Из расходомеров постоянного давления наибольшее распространение получили-.
ротаметры с поплавком, перемещающимся вдоль длинной конической трубки; характерными признаками большинства конструкций ротаметров являются значительная длина трубки, обычно не менее чем в 10 раз превышающая его диаметр, и значительный ход поплавка и связанного с ним стержня;
поплавковые расходомеры с поплавком обычно конической формы, перемещающимся внутрь' отверстия; характерными признаками большинства конструкций поплавковых расходомеров являются дистанционная (электрическая или пневматическая) передача положения поплавка, незначительный ход поплавка, обычно не превосходящий его диаметр.
3. Тахометрические расходомеры и счетчики количества, действия которых основаны на измерении частоты вращения тела в потоке измеряемой среды. Тахометрические расходомеры бывают вертушечные, камерные объемные, шариковые. Для измерения количества жидкости широкое применение получили турбинные и объемные счетчики количества. Тахометрический способ измерения является одним из наиболее точных методов измерения расхода в широких диапазонах от 5- 10-1 до 2 м3/с, они обладают малой инерционностью.
4. Электромагнитные (индукционные) расходомеры, принцип действия которых основан на измерении з. д. с., возникающей при движении электропроводной жидкости в магнитном поле.
Существует также большое число расходомеров, действие которых основано на других принципах: например, тепловые, ультразвуковые парциальные и др.
Л При приеме нефти и нефтепродуктов в трубопровод, сдаче на конечном пункте и передаче из одного управления в другое требуется определять их количество. В предыдущие годы количественный учет осуществлялся по резервуарам, резервуар заполняли продуктом, отстаивали, измеряли уровень и температуру и по калибровочным таблицам рассчитывали количество нефти и нефтепродуктов. Такая система учета требовала больших затрат ручного труда, плохо поддава-
Рис. 9.1. Схема объемного счетчика с овальными шестернями:
7 — измерительная камера
лась механизации и автоматизации, не обеспечивала требуемой точности и достоверности измерения. Применение счетчиков дает возможность осуществить учет нефти непосредственно на потоке, повысить точность измерения, автоматизировать получение результатов измерения, сократить персонал, выполняющий приемно-сдаточные операции. В настоящее время счетчики являются основным средством количественного учета и исходным звеном внедрения автоматизированных систем управления технологическими процессами.
Широкое распространение нашли объемные счетчики. Для измерения количества жидкости поток разделяется на отдельные порции механическим способом при помощи эксцентрично укрепленных вращающихся лопастей или шестерен, движимых ротором. В процессе движения в определенный момент создается измерительная камера, размер которой вымерен с достаточной точностью. Количество порции в единицу времени, пропущенное через камеру, определяется частотой вращения ротора. Построенные на этом принципе шестеренчатые (рис. 9.1) и лопастные объемные счетчики повсеместно применяют для учета нефтепродуктов при малом расходе. Большие размеры корпуса, высокое гидравлическое сопротивление, увеличение протечек из-за истирания стенок корпуса ограничивают их применение для трубопроводов с большой пропускной способностью.
Для измерения количества нефти и нефтепродуктов в трубопроводах с большой пропускной способностью применяют турбинные счетчики. Поскольку вращение создается за счет передачи энергии потока на лопасти ротора, счетчик» называются турбинными. Частота вращения турбинки счетчика непосредственно зависит от скорости потока, что позволяет определить расход в трубопроводе. Для преобразования частоты вращения ротора в потоке используют магнитные или магнитоиндукционные преобразователи. В последнем случае при прохождении лопасти турбинки вблизи магнитоиндукционного датчика в соленоиде наводится э. д. с. и изменение количества перекачиваемой среды сводится к подсчету электрических импульсов с помощью счетчика импульсов. В серийно выпускаемом счетчике «Турбоквант» (рис. 9.2) ротор счетчика 4, помещенный в корпус 1, вращается 300
Рис. 9.2. Турбинный счетчик «Турбоквапт»
в подшипниках 2 и 3, крепящихся в опорном кольце 8. На ступице ротора смонтирован зубчатый диск из ферромагнитного материала. В головке счетчика [укреплены] постоянный электромагнит 7 и катушка индуктивности 5 с сердечником 6. При прохождении зубцов диска вблизи катушки в ней происходит изменение поля, создающего импульс в соединительной линии с прибором. Счетчик «Турбоквант» в диапазоне измерения расходов имеет следующие характеристики: погрешность — 0,5%; повторяемость 0,1%. Допускаемая кратковременная перегрузка не превышает 125 % от номинального расхода.
Ультразвуковые методы основаны на изменении скорости распространения ультразвуковой волны в жидкости при наличии потока (рис. 9.3). При распространении волны по направлению потока скорость возрастает, а против потока — уменьшается. Этот эффект проявляется в изменении времени распространения ультразвука от излучателя к приемннку в том случае, если ультразвуковая волна распространяется в жидкости под некоторым углом к оси трубопровода. Использующие ультразвуковые методы счетчики разделяются на типы в зависимости от схемы измерения. Приборы, измеряющие скорость
Таблица 9.1
| Счетчик |
Типовые диа метры, мм |
Макси мальный расход, м:,/ч | Диапазон измене ния расходов |
Погреш ность, | Повто ряемость, | Макси мальное давление, МПа |
Максимальная вязкость, 10-“ ма/с |
| Объемный |
25—250 | 1200 |
1 : 10 | 0,25 |
0,1 | 5 |
100 |
| Турбинный | 8—600 | 6500 | 1 : 15 | 0,25 |
0,05 | 25 |
50 |
| Ультразву ковой | 25—600 |
8000 | 1 : 15 |
0,5 | 0,1 |
2 | 50 |
|
Вихревой | 50—150 |
2500 | 1 : 10 | 0,5 | 0,2 |
10 | 50 |
Рис. 9.4. (Схема установки счетчика:
/ — задвижка; 2 — манометр; 3 — фильтр; 4 — струевыпрямитель; .5 — счетчик; б — термометр; 7 — кран для контроля утечек; 8 — задвижки для подключения к контрольному счетчику или устройства для лронерки счетчика; 9 — контрольный кран
Рис. 9.3. Принципиальная схема ультразвукового расходомера типа РУЗ-1: / _ трубопровод; 2 — измеряемая жидкость; И, и /7а — излучающие ультразвук пьезоэлементы; /7, и Пг — приемные ультразвука льеяоэлементы; Г — высокочастотный генератор; ФЛ — фазовый детонатор; ФР — фазорегулятор; АРУ — авторегулятор усиления; РП — регистрирующий прибор; У — усилитель
распространения ультразвука только в одном направлении, называются одноканальными, а в двух направлениях — двухканальными. Время прохождения расстояния между излучателем и приемником по направлению потока Т] и против потока т.2 определяется формулами: тх = Ы(с + и); т2 = U{c—v), где L —длина пути между излучателями; с — скорость ультразвука в среде; v — скорость потока.
В табл. 9.1 приведены основные параметры счетчиков, а в табл. 9.2 — влияние различных факторов на показания счетчиков, используемых для измерения расхода нефти и нефтепродуктов.
Таблица 9.2
| Счетчики | ||||
|
Факторы | турбиннЫН |
ультра звуковой |
вихревой | объемный |
| Градуировочная характеристика |
Практически линейная |
Линейная | Линейная | Линейная |
|
Дополнительная потеря на |
Значитель | Отсутст | Незначи |
Значитель |
|
пора | ная |
вует | тельная |
ная |
| Наличие прямого участка трубопровода |
Требуется |
Требуется |
Требуется | Не требуется |
|
Изменение плотности и вязкости жидкости | Не влияет в ограниченных пределах |
Влияет | Не влияет | Не влияет |
| Изменение температуры | Влияет |
Влияет | Влияет |
Влияет |
|
Изменение давления | Не влияет | Влияет |
Не влияет | Не влияет |
| Направление по потоку | Двухсто | Двухсто |
Односто | Односто |
| роннее |
роннее | роннее | роннее | |
Рис. 9.5. График изменения давления в трубопроводе при внезапном закрытии запорной задвижки
При установке счетчика необходимо создать условие, обеспечивающие правильную работу (рис. 9.4). При наличии в жидкости механических примесей, больших, чем допускает конструкция счетчика, в начале участка должны быть установлены дополнительные фильтры. Размер ячеек фильтрации указывается в инструкции и обычно составляет 1,5—4 мм. Потери давление на фильтре зависят от степени его загрязнения и меняются от 0,025 до 0,06 МПа. Перед счетчиком и после него должны быть обеспечены прямые участки необходимой длины для создания равномерного потока по сечению трубопровода. Для снятия счетчика или при поверке с обеих сторон его должны быть установлены задвижки. При любом обводе вокруг счетчика устанавливаемые задвижки должны обеспечивать герметичное перекрытие и иметь устройство для проверки герметичности. Аналогичные условия должны соблюдаться при параллельной установке нескольких счетчиков. При компоновке узла следует обращать внимание на достаточный запас давления для преодоления потерь па счетчике и фильтре. При обычных условиях длина прямого участка перед счетчиком рекомендуется примерно в 20 диаметров. Нормируемая длина прямого участка сокращается с уменьшением скорости потока, плотности жидкости и увеличением его вязкости. Прямой участок после счетчика принимается около пяти диаметров. Для сокращения прямого участка применяют струевыпрямители, представляющие собой набор труб более мелкого диаметра, устанавливаемых внутри трубы. При больших расходах рекомендуется применять несколько параллельно устанавливаемых счетчиков.
Отметим косвенный метод оценки расхода, основанный на относительно быстром перекрытии трубопровода. В этом случае в трубопроводе наблюдается повышение давления за счет инерционного воздействия внезапно остановленной массы жидкости. Если при этом зафиксировать изменение давления в сечении трубы, находящемся на расстоянии L перед вентилем или задвижкой, то полученная кривая будет иметь вид, изображенный на рис. 9.5. На рисунке р0 и д — начальное и конечное статические давления в контрольном сечении . Точка Л соответствует началу закрытия задвижки, а точка В — окончанию. Затухающие колебания после закрытия задвижки (по истечении времени А/) характеризуют лишь инерционные свойства прибора, применяемого для записи изменения давления в трубопроводе. Линия АВ характеризует изменение давления, связанное с явлением гидравлического удара, а линия АС — изменение давления, связанное с из-
менением гидравлического сопротивления задвижки при ее закрывании.
По площади диаграммы /д, ограниченной линиями А В и АС, определяют импульс ударной силы массы остановленной жидкости /д = At
= j Apdt. Закон количества движения жидкости при гидравличе-
о
At
ском ударе имеет вид р LQ = F j A pdt, где р — плотность жидкости;
о
F — площадь трубопровода. Тогда искомый объемный расход Q = = FfRl(pL). Таким образом, планиметрируя диаграмму (см. рис. 9.5) и зная F, р и L, можно определить расход Q.
Данный метод применяют для измерения больших расходов жидкости в трубопроводах значительных диаметров (свыше 500 мм) при испытаниях гидравлических турбин или мощных насосов. Косвенная (расчетная) градуировка метода делает его пригодным для этих условий. Учет количества газа в газотранспортной системе необходим для ведения технологического процесса перекачки газа, коммерческих расчетов с потребителями, оптимизации потоков и режимов работы магистральных газопроводов. Получили широкое распространение расходомеры с сужающими устройствами для измерения расхода газа. Существенным является то, что характеристика стандартных сужающих устройств может быть определена расчетным путем.
Сужающие устройства могут быть нормальными и специальными. К нормальным сужающим устройствам относятся нормальные диафрагмы и сопла, сопла Вентури, для которых коэффициенты расхода достоверны и воспроизводимы, поэтому они рассчитываются и не требуют индивидуальной градуировки. К специальным сужающим устройствам относятся трубки Вентури, применяемые, когда необходимо обеспечить очень малые потери давления, сегментные диафрагмы с эксцентрично расположенным круглым проходным отверстием при изменении расхода сильно загрязненных газов.
Комплекс приборов для измерения расхода методом переменного перепада состоит из сужающего устройства (преобразователя переменного перепада), дифференциального манометра (измерительного прибора и передающего преобразователя), измеряющего перепад давления на сужающем устройстве, и вторичного прибора, подключаемого к дифманометру, если результаты необходимо передавать на расстояние.
Из приведенной на рис. 9.6 схемы распределения давления в трубопроводе при установке диафрагмы диаметром d видно, что сжатие потока начинается перед сужающим устройством за сечением 7 (до этого сечения еще нет влияния диафрагмы на поток) и под действием сил инерции достигает наибольшего значения на некотором расстоянии за ней; далее после сечения II струя начинает расширяться до полного сечения трубопровода. До сужающего устройства давление в трубопроводе будет р\. Непосредственно перед сужающим устройством давление возрастает до значения рг за счет подпора и понижается до р'2 за диафрагмой. Далее, по мере расширения струи, давление
Рис. 9.6. Схема распределения давления в трубопроводе при установке диафрагмы
В трубопроводе выравнивается и становится равным р3, меньшим, чем ри на значение безвозвратных потерь рп на сужающем устройстве. Перепад давления на сужающем устройстве Ар = р1—р2 зависит от расхода протекающего по трубопроводу вещества и может служить мерой расхода.
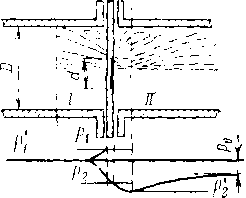
Рз
Перепад давления на сужающем устройстве измеряют непосредственно у его торцов, а вместо площади сечения потока F г пользуются площадью отверстия сужающего устройства F0. Основные расчетные уравнения имеют вид: для объемного расхода, м3/ч,
Qo = 12,76аemDa<\jАр/р ; для массового расхода, кг/ч,
GM — l2,76aemD2 д/Дрр ,
где а — коэффициент расхода; е — поправка на расширение измеряв" мой среды; т — модуль сужающего устройства; D — внутренний диаметр трубопровода; р — плотность измеряемой среды. Коэффициент расхода а учитывает неравномерное распределение скоростей по сечению потока, обусловленное влиянием вязкости реальной жидкости и трения ее о трубопровод и сужающее устройство, а также то, что практически перепад давления измеряют непосредственно у торцов сужающего устройства, а вместо площади сечения потока используют площадь отверстия сужающего устройства. Коэффициент расхода а зависит в основном от типа и модуля сужающего устройства, от числа Рейнольдса и не зависит от рода протекающего вещества. Модулем сужающего устройства т называется отношение площадей отверстий сужающего устройства F0 и трубопровода Fх при температуре измерения.
Наиболее простыми и получившими широкое распространение являются диафрагмы. Диафрагмы бывают камерные типа ДК, когда отбор давлений осуществляется из кольцевых камер, и бескамерные типа ДБ, когда отбор давлений осуществляется через отдельные отверстия. Камерные диафрагмы удобны и более точны, но более трудоемки в изготовлении.
Диафрагма — тонкий стальной диск с круглым концентрическим отверстием со стороны входа потока. Кромка отверстия диафрагмы рстрая (нескругленная), а далее расточена под углом 30—45°; при
больших диаметрах трубопроводов диафрагмы могут изготовляться без расширения.
Согласно действующим государственным стандартам камерные диафрагмы изготовляются на условные давления ру, равные 0,6; 1,6; 2,5; 4 или 10 МПа, для технологических трубопроводов с условными проходами Dу, равными 50; 65; 80; 100; 125; 150; 200; 250; 300; 350; 400; 500 мм, а бескамерные па ру, равные 0,25; 0,6; 1; 2,5 и 4 МПа, для трубопроводов с Dу, равными 400; 500; 600; 800; 1000; 1200 и 1400 мм.
Измерение расхода диафрагмами производится с соблюдением следующих требований:
сужающее устройство (диафрагма) устанавливается только на прямом участке газопровода, длина которого после диафрагмы должна быть не менее пяти внутренних диаметров трубопровода;
при установке диафрагмы должно быть обеспечено точное совпадение геометрического центра ее с центром трубопровода, поскольку несоосность диафрагмы и трубопровода приводит к значительным погрешностям при измерении расхода;
диафрагму разрешается устанавливать на трубопроводе диаметром не менее 50 мм при одновременном соблюдении условия 0,05 < т < 0,7, где т --- модуль сужающего устройства;
перепад даЕ;ления следует измерять через кольцевые камеры, обеспечивающие вэфавнивание давления;
входная кромка отверстия диафрагмы должна быть острой; у диафрагм, диаметэ отверстия которых не превышает 125 мм, падающий на кромку луч света не должен отражаться; у диафрагм с отверстием более 125 мм луч может отражаться, но кромка не должна иметь заметного притупления;
внутренняя поверхность участка трубопровода длиной 2D (два диаметра трубопровода) перед диафрагмой и за ней не должна иметь никаких уступов, а также заметных невооруженным глазом неровностей и наростов;
не допускается установка диафрагм непосредственно у местных сопротивлений (краны, угольники, повороты, задвижки и т. д.); минимально необходимая длина прямого участка трубопровода перед диафрагмой определяется в зависимости от типа местного сопротивления и диаметра трубопровода;
регулирующие краны и задвижки предпочтительно устанавливать после диафрагмы; при установке их перед диафрагмой должно соблюдаться расстояние не менее ста диаметров трубопровода;
рабочую температуру газа необходимо измерять перед диафрагмой; гильза термометра должна входить внутрь трубопровода на глубину 0,5 диаметра; наименьшее расстояние от диафрагмы до диаметра гильзы термометра d' должно составлять 5 D при d' < 0,03 D и 20 D при 0,03 D <С d’ ^ 0,13 D\
линии, соединяющие диафрагму с дифманометром-расходомером, должны быть проложены по кратчайшему пути вертикально или с уклоном к горизонтали 1 : 10; уклон па всем протяжении должен быть односторонним; для поплавковых манометров расстояние от места замера давления не должно превышать 50 м, так как в противном случае возможно чрезмерное запаздывание показаний прибора;
внутренний диаметр импульсных трубок должен быть не менее 8 мм;
соединительные линии подключаются к верхней половине диафрагмы и должны быть герметичны.
Поплавковые диафманометры работают по принципу обычных U-образных манометров (измерительная система и механизм для передачи измерительного сигнала на стрелку регистрирующего прибора). Измерительная система состоит из двух герметичных сосудов: поплавкового (*f) и сменного (—). К первому сосуду подводится давление до диафрагмы, а ко второму после диафрагмы. Сосуды соединяются между собой U-образной трубкой. Уровень жидкости в сосудах будет устанавливаться в зависимости от перепада давления на диафрагме Положение уровня жидкости в сосудах регистрируется поплавком который механически связан с регистрирующим устройством. Первый сосуд является одинаковым для всех перепадов давления, а второй должен меняться в зависимости от измеряемых перепадов давления.
Широко применяются расходомеры, которые представляют собой поплавковые самопишущие диафрагмы от часового механизма. Ei мембранных дифманометрах измеряемый перепад давления на диафрагме преобразуется в электрический сигнал, который регистрируется вторичным прибором. Действительное количество газа определяется независимо от типа дифманометра-расходомера:
Уд QKrKrK
рА р,
где Q — расход газа, определяемый по диафрагме расходомера при рабочих параметрах; Кр, Кт. ЛГР — поправочные коэффициенты, учитывающие соответственно отклонения фактических давлений, температуры и плотности газа от расчетных величин.
Поправочные коэффициенты определяются по следующим формулам:
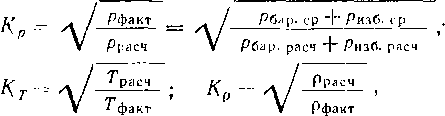
где уОфакг — среднесуточное фактическое абсолютное давление газа перед диафрагмой; /?расч — расчетное абсолютное давление перед диафрагмой; раР. Ср—-среднесуточное барометрическое давление; Р«зб. ср — среднесуточное избыточное давление перед диафрагмой; уОбар. расч — расчетное барометрическое давление; р„3с. расч — избыточное расчетное давление; Трасч — расчетная температура; 7"факт — среднесуточная температура газа, замеренная у диафрагмы; ррасч — расчетное значение плотности газа; РфаКт — среднесуточная фактическая плотность.
Рис. 9.7. Схема измерения расхода парциальным методом:
/ — обводная трубка; 2 — расходомер; 3 — диафрагма, установленная в трубопровода
Установка диафрагм в трубопроводах большого диаметра с диаметром 700 мм и более сопряжена со значительными трудностями. Поэтому для измерения расхода газа по трубопроводам большого диаметра применяют разветвление потока по нескольким трубопроводам меньшего (до 700 мм) диаметра.
Для газопровода большого диаметра целесообразно также использовать парциальный метод измерения расхода (рис. 9.7). Часть потока отводится н обводную трубку при помощи сужающего устройства, установленного в трубопроводе. Для измерения расхода в обводной трубке может применяться любой из рассмотренных расходомеров. Если между расходом Q в основном трубопроводе и расходом q в об* водной линии существует стабильная функциональная зависимость Q ~ f (я)> то по результатам измерения q можно в каждом конкретном случае определить Q. Для этого необходимо лишь определить зависимость между Q и ц при непосредственной или расчетной градуировке. Погрешность измерения расхода парциальным методом будет складываться из погрешностей градуировочной зависимости Q ~ f (q) и измерения расхода в обводной линии.
Единственным, но в ряде случаев немаловажным достоинством парциального метода является принципиальная возможность измерять сколь угодно большие расходы в трубопроводах сколь угодно большого диаметра.
9.3. ОЧИСТКА НЕФТЕПРОВОДОВ ОТ ОТЛОЖЕНИЙ ПАРАФИНА, УДАЛЕНИЕ МЕХАНИЧЕСКИХ ПРИМЕСЕЙ И ВОЗДУХА
Многие нефти, особенно нефти восточных районов, парафинистые. Так, нефти Поволжья содержат парафина от 2 до II %, нефти Туркмении до 16 %, озексуатская нефть (Ставропольский край) —24 % и ман-гышлакские нефти (Казахстан) до 29 %.
В пластовых условиях парафин растворен в нефти. При подъеме на поверхность и при перекачке по нефтепроводам температура нефти снижается, раствор становится насыщенным и из него при определенных условиях выпадает парафин, отлагаясь на стенках нефтепровода. Отложения парасЬина уменьшают поперечное сечение труб и, следовательно, снижают пропускную способность. Так, запарафинивание некоторых нефтепроводов в Башкирской АССР снижало их пропускную способность до 50 %. Как показали исследования, отложения состоят из тугоплавких парафинов и цезерина (до 50 %), асфальтосмолистых веществ (до 20 %), механических примесей и масел.
Основными факторами, влияющими на отложение парафина, являются физико-химические свойства перекачиваемой нефти, изменение температурного режима (охлаждение) нефти во время ее перекачки по трубопроводу, изменение содержания растворенных газов, характер режима перекачки (изменение давления, остановки и др.) Парафин выделяется из нефти в виде кристаллов, которые, соединяясь между собой, образуют парафиновую массу. Она представляет собой пористый скелет, поры которого заполнены нефтью и водой. Температура плавления такой массы зависит от ее состава и колеблется от 40 до 50 °С. Вязкость и температура застывания парафинистой нефти зависят от количества находящегося в ней парафина и температуры. Чем больше содержание парафина и ниже температура нефти, тем больше увеличивается ее вязкость и тем меньше ее текучесть. Так, нефть с содержанием парафина 8 % уже при температуре около 273 К теряет свою подвижность. Перекачка такой нефти в зимнее время по магистральным трубопроводам затруднительна, особенно если она проводится периодически При охлаждении такой нефти увеличивается ее вязкость, а следовательно, повышается давление перекачки или же понижается пропускная способность (при постоянном давлении). При дальнейшем охлаждении нефть может образовать парафиновые пробки и гызвать серьезное повреждение, в результате чего нефтепровод надолго выводится из строя. Освобождение нефтепровода от застывшей нефти — тяжелая операция, на выполнение которой требуются длительное время и большие затраты труда.
Отложения располагаются вдоль нефтепровода неравномерно. На начальном участке нефтепровода, где температура выше температуры начала выпадения парафина, его отложения незначительны. Далее, где температура ниже, парафин интенсивно выделяется и отложения его существенны. Затем толщина отложений парафина по длине нефтепровода уменьшается, так как нефть движется уже с почти постоянной температурой, равной температуре грунта, а основная масса парафина, выпадающего при этой температуре, уже отложилась на предыдущем участке. Особенно интенсивное отложение парафина происходит в период остановки перекачки, когда нефть в трубопроводе начинает застывать. Процесс застывания начинается у стенок трубы и постепенно распространяется к центру, причем скорость образования застывшего слоя будет больше у верхней образующей трубы, т. е. наиболее холодной части. В период перекачки застывший слой парафина не смывается потоком нефти и остается в нефтепроводе до летнего сезона, когда температура трубы и перекачиваемой нефти повысится до величины, достаточной для размягчения и смывания застывшего слоя. В этот период нефтепровод очищается сам.
Отложение парафина по диаметру трубопровода также происходит неравномерно. Как показал опыт эксплуатации восточных магистральных нефтепроводов, в нижней части трубопровода парафина откладывается меньше, чем в верхней. Это объясняется тем, что пластовая вода, содержащаяся в нефтях, препятствует отложению парафина, а механические примеси (песок и глинистый раствор), попадающие в нефть, сдирают со стенок трубопровода отложившийся парафин.
Однако сле/.ует отметить, что как погодные условия, влияющие на температуру окружающего нефтепровод грунта, так и свойства нефти могут вносить существенные коррективы в описанную картину распределения отложений парафина в нефтепроводе.
Для поддерживания пропускной способности нефтепровода на близком к проектному уровню необходимо очищать его от отложений парафина. Наибо/ее эффективным способом очистки внутренней поверхности нефтепроЕ:ода является в настоящее время механическая очистка с помощью скребков. Разработано много конструкций металлических скребков, в которых чистящим элементом являются диски, ножи и проволочные щетки. Скребки разных конструкций различны по эффективности удаления отложений со стенок труб, по износостойкости и проходимости. Последнее качество очень важно для нефтепроводов, имеющих хотя бы незначительные препятствия во внутренней полости в виде подкладных колец, грата и сужений в запорной арматуре. При регулярной очистке нефтепровода металлические скребки могут без чрезмерного износа проходить до 100 км.
По мере движения скребка по трубопроводу на его частях налипает парафин, поэтому трение ножей и щеток о стенки трубопровода становится слабее. Для облегчения контроля за продвижением скребка применяют переносный звукоуловитель, состоящий из микрофона, усилителя и наушников. Дежурный диспетчер следит за давлением перекачки и количеством откачанной нефти, чтобы обеспечить заданную скорость, необходимую для продвижения скребка. Она должна быть не менее 1,2—1,5 м/с. Хорошей проходимостью обладают резиновые шаровые разделители, которые могут использоваться и для очистки нефтепроводов от отложений парафина. Лучше применять резиновые шары, оплетенные металлической стальной цепью, или шаровой резиновый скребок типа СШ, изготовленный из износоустойчивой резиновой смеси с пластмассовыми и металлическими резцами круглой формы, запрессованными в его оболочку с внешней стороны.
Скребок имеет клапан, через который закачивают заданную порцию рабочей жгдкости, в результате чего наружный диаметр соответственно увеличивается и резцы несколько выступают над поверхностью. Резцы расположены так, что скребок, находящийся в любом положении в полости трубопровода, очищает всю его внутреннюю поверхность.
Оптимальная периодичность пропуска скребков (или шаровых разделителей) по нефтепроводу определяется исходя из следующих соображений. Запарафиннвание нефтепровода вызывает снижение пропускной способности и соответствующие убытки, причем чем больше интервал между пропусками скребков, тем больше будут эти убытки. С другой стороны, чем меньше интервал между пропусками скребков, тем больше затраты на скребки (а также убытки из-за остановок станций при пропуске мимо них скребков, если такие остановки требуются применяемой технологией очистки). Оптимальная периодичность пропуска скребков соответствует варианту, когда сумма убытков от за-парафинивания нефтепровода и приведенных затрат на пропуск скребков минимальна.
При эксплуатации трубопроводов, транспортирующих парафини-стые нефти, необходимо проводить профилактические мероприятия по предотвращению образования отложений парафина. К важнейшим из них относятся:
исключение закачки в трубопровод накопившейся в резервуарах парафинистой взвеси (шлака); в соответствии с ГОСТ 1510—84 металлические резервуары должны периодически подвергаться очистке (не менее двух раз в год для авиационных нефтепродуктов, не менее одного раза для светлых нефтепродуктов и Fie менее одного раза в два года для нефти и темных нефтепродуктов);
термообработка высокопарафпнистой нефти, которая заключается в подогреве нефти до определенной для каждого сорта температуры и охлаждении. При этом термообработанную нефть для большего эффекта рекомендуется смешивать с маловязкой нефтью;
механическое перемешивание и перекачка переохлажденной нефти; они целесообразны, когда кристаллы парафина вместе с адсорбированными на них смолами теряют способность цементироваться друг с другом и прилипать к стейкам трубопровода и поэтому уносятся потоками нефти; при этом необходимо поддерживать критическую скорость перекачки, когда указанные частицы находятся в потоке нефти во взвешенном состоянии;
разбавление парафинистой нефти малопарафинистой, как это практикуется при перекачке озексуатской парафинистой нефти, разбавленной малгобекской нефтью, или разбавление такой нефти газолином, при этом надо учитывать, что добавки, вводимые в перекачиваемые нефти для понижения их вязкости, не должны уменьшать долю транспортируемого нефтесырья в общей пропускной способности трубопровода, а также иметь в виду, что вводимые разбавители в некоторых случаях могут способствовать более интенсивному выпадению парафина;
добавка к высокопарафинистой нефти специальных присадок, сжижающих нефть, т. е. уменьшающих вязкость и отложение парафина на стенках трубопровода.
Скопление воздуха в трубопроводе, засорение его песком, образование ледяной пробки, отложение парафина можно определить по излому фактической линии гидравлического уклона (рис. 9.8). Линия гидравлического уклона строится на профиле трубопровода по показаниям манометров, установленных в колодцах линейных задвижек. На участке трубопровода, где произошло засорение, гидравлический уклон имеет большую величину. На рис. 9.8, судя по излому линии гидравлического уклона i, засорение произошло между 64-м и 70-м километром и, вероятнее всего, в овраге. Воздух, скапливаясь в наиболее высоких местах трассы, суживает живое сечение трубопровода. В суженных местах создается большое сопротивление, на преодоление которого расходуется значительный напор, развиваемый насосами. Если на перегоне между перекачивающими станциями много таких воздушных «мешков», то они могут погасить большую часть развивае-
Рис. 9.8. Профиль трубопровода с нанесенной на нем линией гидравлического уклона
мого насосами напора. Иногда потери настолько велики, что на преодоление их не хватает давления насосов и нефть или нефтепродукт не поступает на соседнюю перекачивающую станцию. Для удаления воздуха из трубопровода на всех повышенных местах трассы в трубопровод обычно монтируют патрубки с кранами или вентилями, называемыми вантузами. Вантуз служит также для выпуска из трубопровода воды. Диаметр вантуза d зависит от диаметра трубопровода D, на котором он монтируется d~ D -\Jmvlui, где т — коэффициент объема выпускаемого воздуха, равный 0,9—1; v — скорость выдавливания воды; со — скоэость воздуха, проходящего через вантуз.
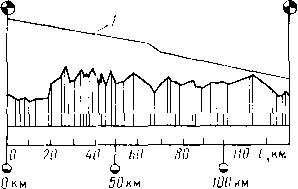
Скопившийся воздух в трубопроводе можно удалить также путем создания определенной скорости перекачки жидкости, при которой пузырьки воздуха захватываются ею и уносятся на конечный пункт трубопровода — в резервуары. Выносную скорость потока жидкости, необходимую для удаления воздуха из трубопровода для средних его уклонов, равных примерно 40° на нисходящих участках, при турбулентном движении маловязких нефтепродуктов можно определить
по формуле, предложенной В. К. Касперовичем: = /\jgD7lr'd^7,
где g— ускорение свободного падения; d„ —- диаметр воздушного пузыря, равный примерно 0,2 см.
Для трубопровода диаметром 250 мм —¦ 78 см/с, диаметром
500 мм — 86 см/с и диаметром 1000 мм —- 95 см/с.
В настоящее время для удаления из трубопровода одновременно воды, механических примесей и воздуха перед закачкой нефти и нефтепродукта по трубопроводу пропускают механический разделитель в виде поршня или шара из бензостонкон резины. Резиновые шаровые разделители и поршни изнашиваются, пройдя примерно 80—120 км в зависимости от шероховатости внутренней поверхности трубопровода.
Ориентировочно местонахождение поршня I можно оценить, зная объем нефти V3, закачиваемой в трубопровод после пуска скребка-.
/ == VJV — Q&rJV, где V — объем нефти в единице длины трубопровода; Q — пропускная способность трубопровода; Ат— отрезок времени после г:апуска поршня.
9.4. ОЧИСТКА ВНУТРЕННЕЙ ПОВЕРХНОСТИ ГАЗОПРОВОДА БЕЗ ПРЕКРАЩЕНИЯ ПЕРЕКАЧКИ ГАЗА
При эксплуатации магистрального трубопровода происходит загряз ' нение его внутренней поверхности частицами породы, окалиной, от' слоившейся от труб, конденсатом, водой, метанолом и т. д. Это приводит к увеличению коэффициента гидравлического сопротивления и соответственно к снижению пропускной способности газопровода. Внутреннюю поверхность газопровода от загрязнений очищают следующими способами: периодически очистными устройствами без прекращения перекачки газа; разовым использованием очистных устройств с прекращением подачи газа; установкой конденсатосборников и дренажей в пониженных точках газопровода; повышением скоростей потоков газа в отдельных нитках системы газопроводов и последующим улавливанием жидкости в пылеуловителях КС. Наиболее эффективный способ очистки — без прекращения подачи газа при помощи очистных устройств. Этот способ позволяет постоянно поддерживать коэффициент гидравлического сопротивления газопровода, равным первоначальному значению. Периодичность пропуска очистных устройств можно оценить по увеличению гидравлического сопротивления газопровода.
В качестве очистных устройств применяют очистные поршни, скребки, поршни-разделители. В зависимости от вида загрязнений (твердые частицы, жидкость) применяют и определенные очистные устройства. Основное требование к ним: быть износостойкими, обладать хорошей проходимостью через запорные устройства, простыми по конструкции и дешевыми.
Наиболее часто применяют очистные устройства типа ДЗК-РЭМ, ОПР-М, позволяющие одновременно очищать полость газопровода от твердых и жидких веществ. Для очистки газопроводов больших диаметров применяют поршни-разделители ДЗК-РЭМ-1200, ДЗК-РЭМ-1400, ОПР-М-1200, ОПР-М-1400. Поршень-разделитель
ОПР-М-1400 представляет собой полый металлический корпус, на котором расположены кольцевые очистные элементы, конструктивно подобные автомобильной покрышке. Они поджаты распорными втулками с установленными на них поролоновыми кольцами. Поршень монтируют с двумя, тремя и более очистными элементами.
Для движения поршня по газопроводу на нем создается определен* ный перепад давления, который зависит в основном от его конструкции. Создаваемый перепад давления на поршне в среднем равен 0,03—0,05 МПа. Скорость движения поршня в газопроводе зависит от скорости движения газа, наличия загрязнений в нем, герметичности соприкасающихся поверхностей. Она составляет 85—95 % скорости газа в газопроводе. На всех проектируемых и вновь вводимых магистральных газопроводах предусматривают устройства по очистке внутренней полости газопровода от загрязнения при помощи пропуска очистных поршней. В состав устройства входят узлы пуска и приема очистных поршней, система контроля и автоматического управления процессов очистки. Узлы пуска и приема очистных поршней распола-
Рис. 9.9. Схема узла пуска и приема очистных устройств (изображена камера пуска)
гают вблизи пунктов подключения КС, а чаще их совмещают. На начальном участие магистрального газопровода монтируют узел пуска очистных порпней, на конечном участке — узел приема, а на всех промежуточных пунктах (на КС) совмещенные узлы приема и пуска. Предусматривают устройства для очистки полости газопровода и на наиболее сложных и ответственных участках трассы газопровода, например на переходах через водные препятствия. При этом на первом берегу по ходу газа монтируется узел пуска очистных поршней, а на втором — узел приема. В зависимости от технологических схем газопровода и составов перекачиваемого газа места расположения очистных устройств могут быть самыми различными.
Совмещенный узел пуска и приема очистных устройств (рис. 9.9) представляет собой комплексное устройство, состоящее из установленных один напротив другого па бетонных опорах узлов пуска и приема поршней. Узел пуска / включает в себя: обечайку с приваренными к ней опорами 15, патрубки 2 диаметром 500 и 50 мм, концевой затвор 3 с заслонкой и устройством для занасовки поршня, контрольной рейки 5. Узел приема аналогичен по конструкции камере пуска, но в отличие от нее имеет амортизатор. Заслонки узла пуска и приема закреплены в шаровых опорах 4 тележек 11, на которых установлены пульты управления гидросистемой затвора. Тележки передвигаются по двум участкам рельсового пути 10 с помощью механизма перемещения, состоящего из двух лебедок 14, четырех кронштейнов с блоками 8 и тросов 9, которые крепятся к рымболтам тележек при помощи металлических иланок и наматываются па барабаны лебедок 14 с левой 12 и правой 13 навивкой для обеспечения реверсивного движения
Рис. 9.10* Схема устройства концевого'затвора узла пуска
тележек. Для погрузки и выгрузки очистных поршней с кареток узлов пуска и приема предусмотрено подъемное устройство 6 с ручной талью 7.
Наиболее ответственная часть узлов пуска и приема —¦ концевой затвор. Отечественная промышленность выпускает узлы пуска и приема с концевым затвором, изображенным на рис. 9.10. Он выполняется в виде массивной крышки 6, по поверхности которой в направляющих 15 и 16 под действием гидравлических цилиндров 17, через шток и толкатели 12 движутся четыре запирающихся сектора 9, оканчивающихся самотормозящимися клиновыми поверхностями, входящими в зацепление с внутренней клиновой поверхностью фланца 8. Уплотнение проводится кольцевой прокладкой 7. Запирающие секторы 9 снабжены фиксаторами 13 и зажимными штурвалами 14. Гидравлические цилиндры 17 приводятся в действие через кольцевую гидравлическую систему 18. Для перемещения заслонку закрепляют на шаровой опоре тележки, входящей в полость 10 и закрывающейся крышкой 11. На заслонке концевого затвора имеется захват 1 для поддона, на который укладывают очистное устройство. Кроме того, на заслонке узла пуска предусмотрен гидравлический толкатель 4 с подпятником 5, который приводится в действие через гидравлическую систему 2,3 и служит для запасовки очистного устройства.
Заслонка концевого затвора узла приема аналогична описанной ранее, только вместо толкателя на ней установлен амортизатор.
Узлы пуска и приема очистных поршней изготавливают на рабочее давление 7,5 МПа и температуру рабочей среды от — 60 до 60 °С. После 100 циклов (открытие-закрытие) проводят ремонт прокладок и бы-строизнашивающихся деталей. Общий ресурс составляет 1000 циклов. Конструктивно узлы пуска и приема, а также участки газопровода длиной по 100 м, примыкающие к ним, выполняются в соответствии
Рис. 9.11. Технологическая схема запуска и приема очистных поршней
с требованиями, предъявляемыми к участкам первой категории. Их испытание проводят гидравлически с давлением, равным 1,25 ррвй-Чтобы обеспечить возможность периодической очистки полости газопровода, необходимо предусмотреть выполнение следующих требований, которые позволяют поршню беспрепятственно пройти на всем очищаемом участке узла запуска до камеры приема:
диаметр газопровода для пропуска очистных поршней должен быть по всей длине одинаковым;
запорная линейная арматура должна быть равнопроходной; в тройниках на отводах, если их диаметр более 30 % диаметра газопровода, предусматривается установка направляющих планок для предотвращения заклинивания очистного поршня;
внутренняя поверхность труб не должна иметь выступающих деталей, кроме сигнализаторов, рычаг которых утопает при проходе очистного устройства;
отводы, компенсаторы должны быть с радиусами изгиба не менее пяти диаметров очищаемого газопровода;
конденсатосборники типа «расширительная камера» оборудуются направляющими планками для беспрепятственного прохода очистного поршня, причем они не должны мешать нормальной работе кон-денсатосборника;
переходы через естественные и искусственные препятствия должны выполняться с учетом дополнительных нагрузок от массы поршня и газоконденсатной смеси.
Очистные поршни запускают в следующей последовательности (рис. 9.11). Закрывают краны 2, 3, 5, 7 (краны 8 и 10 — закрыты, а краны 9, 11 — открыты) и открывают краны 4, 6 для выпуска газа из узла пуска в атмосферу. После освобождения узла пуска от газа открывают концевой затвор, и тележка с заслонкой отводится до тех пор, пока из узла не выйдет каретка (поддон), на которую с помощью подъемного устройства загружают поршень. Тележку вместе с заслонкой и кареткой подводят к узлу пуска до полного закрытия заслонки и ручным насосом в гидросистеме создают избыточное давление для закрытия концевого затвора. Затем затвор фиксируют фиксаторами и зажимными штурвалами. Очистной поршень толкателем вводят в газопровод. Далее узел продувают через открытые краны 4 и 6 путем открытия кранов 3 и 5. После продувки и закрытия кранов 4 и 6 выравнивают давление по обе стороны поршня, затем открывают краны 2, 7, 8, закрывают кран 11, после чего поршень начинает двигаться к следующей КС, на которой перед пуском поршня обязательно на узле приема должен быть открыт кран 16. Выход очистного поршня из узла пуска контролируют сигнализатором 1. После запуска поршня собирают первоначальную схему: кран 11 открывают, а краны 2, 7, 8 закрывают. При неработающей КС на запасованный поршень подают газ путем открытия кранов 7,9 и закрытия крана 10.
При движении очистного устройства по газопроводу благодаря его плотному прилеганию к стенке трубы происходит ее очистка. Продукты очистки (твердые частицы, жидкость) собираются перед очистным устройством и движутся вместе с ним. От герметичности между поршнем и стенкой трубы во многом зависит степень очистки последней. На узле приема открывают краны 12, 13, 16, а затем при подходе жидкости и кран 15. Проход поршня в узел приема контролируют по двум сигнализаторам: после срабатывания первого сигнализатора по ходу поршня закрывают краны 15, 16 и открывают кран 14, после срабатывания вторично—закрывают краны 12, 13, 14 и краном 6 на свече регулируют заход поршня в камеру. Закрытию крана 15 должно предшествовать открытие крана 14. Жидкость и грязь отводятся в приемный колодец или емкость. После освобождения узла приема от газа через кран 6 открывают концевой затвор. Тележку с заслонкой, а вместе с ней коробку с поршнем отводят от камеры. Поршень с помощью подъемного устройства убирают с каретки, проводят осмотр, очистку концевого затвора и приводят все в первоначальное состояние.
Для контроля за прохождением очистных устройств по газопроводу в отдельных его точках стоят анализаторы прохождения поршня. По принципу действия они бывают механическими, гидравлическими и электрическими. По способу установки на газопроводе их можно разделить на два типа: установка с нарушением герметичности трубы и установка без нарушения герметичности.
Разработан комплекс «Волна-1», предназначенный как для сигнализации прохождения очистных устройств по газопроводу, так и для отыскания их в случае застревания в нем. Принцип действия его основан на использовании низкочастотных магнитных волн для передачи сигнала через стенку трубопровода. На очистном поршне устанавливают генератор низкочастотных магнитных волн, которые улавливает приемник. В состав комплекса «Волна-1» входят: передатчик, пять 11* 323
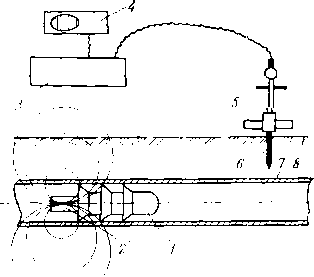
Рис. 9.13. Схема сигнализации прохождения очистного устройства:
1 — очистное устройство; 2 — пере* датчик; 3 — сигнализатор; 4 — устройство звуковой сигнализации; 5 — антенна; 6 — штатив; 7 — газопровод;
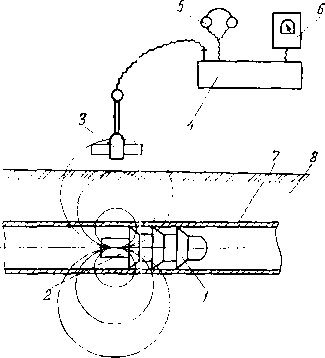
Рис. 9.12. Схема отыскания очистного устройства:
1 — очистное устройство; 2 — передатчик; 3 — антенна; 3 — сигнализатор (приемник); 5 — головные телефоны; 6 — стре> лочный индикатор; 7 — газопровод; 8 — грунт
8 — грунт
сигнализаторов (приемщиков), зарядное устройство, зажим для крепления передатчика на очистном устройстве.
При отыскании очистного устройства, застрявшего в газопроводе, оператор передвигается, держа над газопроводом антенну сигнализатора так, чтобы ось антенной катушки была параллельна оси газопровода (рис. 9.12). При попадании антенны в зону переменного магнитного поля, создаваемого генератором, установленным на поршне, в телефонах появляется звуковой сигнал, свидетельствующий о местонахождении очистного устройства.
Для сигнализации прохождения очистного устройства (рис. 9.13) через фиксированную точку на трассе газопровода катушку антенны располагают параллельно оси газопровода на специальном штативе, закрепленном в грунте в том месте, где стенка газопровода ближе всего к поверхности земли. Вместо головных телефонов к сигнализатору подключают устройство звуковой сигнализации. Сигнал приемника, поступающий на вход устройства звуковой сигнализации, преобразуется в импульсы, которые включают генератор звуковой частоты с громкоговорителем. Передатчик выполнен в виде трубы с размещенными в ней генератором, электромагнитным индуктором, батареей аккумуляторов и устройством включения. Передатчики в герметичном взрывозащищенном исполнении закрепляют специальным зажимом, прикрепленным к поршню шестью болтами. Включают его через стенку трубы магнитным ключом.
fl.6. ЗАЩИТА НЕФТЕПРОВОДОВ ОТ ЧРЕЗМЕРНО ВЫСОКИХ ДАВЛЕНИЙ
При внезапной остановке одной из промежуточных насосных станций возникает волна повышенного давления, которая со скоростью звука в нефтепродукте движется к предыдущей насосной станции и суммируется с развиваемым ею давлением. При этом суммарное давление в трубопроводе вблизи предыдущей насосной станции может значительно превысить рабочее, что является недопустимым по условию прочности труб. Как показывает опыт эксплуатации магистральных трубопроводов, разрыв труб из-за чрезмерно высокого давления, возникающего при внезапной остановке промежуточной насосной станции, в большинстве случаев происходит на расстоянии 20—40 км после предыдущей насосной станции, где суммарное давление может превысить допустимую величину, прежде чем волна повышенного давления достигнет предыдущей насосной станции и на ней сработает система защиты по максимальному давлению.
Предотвратить возможность возникновения в магистральном трубопроводе с промежуточными насосными станциями чрезмерно высокого давления при внезапном отключении промежуточной насосной станции можно при их работе из насоса в насос следующими способами:
созданием волны пониженного давления, идущей навстречу волне повышенного давления:
гашением волны повышенного давления в месте ее возникновения или уменьшением крутизны фронта такой волны.
Волна пониженного давления создается путем посылки сигнала по линии связи с остановленной насосной станцией на предыдущую насосную станцию для отключения на ней одного или нескольких насосных агрегатов. При этом от предыдущей насосной станции навстречу волне повышенного давления будет двигаться волна пониженного давления, и при встрече эти волны давления будут взаимно гаситься. В результате такого взаимодействия на участке нефтепровода перед предыдущей насосной станцией опасного повышения давления не произойдет. Однако при этом необходимо отключить отдельные насосные агрегаты на нескольких предыдущих насосных станциях, так как отключение агрегатов на одной из них создаст волну повышенного давления по направлению к ближайшей предыдущей станции и опасность чрезмерного повышения давления на ней.
Система создания встречной волны пониженного давления включает:
устройство для формирования сигнала при возникновении опасных возмущений давления (например, при внезапной остановке насосной станции или отказе системы дросселирования);
линию связи с предыдущей и последующей насосными станциями; устройство для отключения одного или нескольких насосных агрегатов при поступлении сигнала.
Система создания волны пониженного давления (система «Волна») применена на отдельных участках нефтепровода «Дружба». Для формирования сигнала в этой системе был использован специально разработанный датчик опасных возмущений, который выдает сигнал лишь при большой скорости нарастания давления (на 1—1,2 МПа за 5—6 с).
Сигнал по специальной линии связи поступает на предыдущую опасную станцию в систему местного автоматического управления, которая отключает один или несколько насосных агрегатов. Сигнал на отключение насосной станции может передать также диспетчер при наличии на нефтепроводе соответствующей системы телемеханики.
При проектировании и эксплуатации системы, создающей волну пониженного дазления для защиты нефтепроводов от чрезмерно высоких давлений при внезапной остановке промежуточных насосных станций, необходимо уметь рассчитать число насосных агрегатов, которые надо отключать на предыдущей насосной станции, чтобы не допустить опасных давлений, а также определять, как при этом изменится пропускная способность нефтепровода и на каких еще насосных станциях может потребоваться отключение насосных агрегатов. Ответить на эти вопросы можно на основании изложенных методик расчета неустановившегося течения в магистральных нефтепроводах с промежуточными насосными станциями. Рассмотрим нефтепровод с т промежуточными станциями, которые включаются в момент t = 0, в момент >0 отключается k-я насосная станция, а для создания волны пониженного давления на (k—1)-й насосной станции отключается часть насосных агрегатов в момент t2 (например, один из трех последовательно включенных насосов). Требуется рассчитать изменение давления в нефтепроводе при таком переходном процессе и, в частности, изменение давления на выходе (k—1)-й насосной станции, чтобы оценить опасность для прочности нефтепровода. Промежуток времени (t2—tL) составляет 15—20 с и обусловлен продолжительностью формирования сигнала и его передачи по линии связи.
Для рассматриваемых условий давление, развиваемое (k—1)-й насосной станцией, удобнее записать в виде двух слагаемых:
PcTjk-~\) Рст —]1) ^ PqtIIi— 1) ’ ^Де р—-jj,
где Рст(л-1) —давление, создаваемое насосными агрегатами, которые продолжают работать и после момента t2\ р“ — давление, соз-даваемое насосными агрегатами, которые отключаются в момент t2 для создания волны пониженного давления.
Рассчитывая режим работы при разных значениях р** для наиболее опасных точек нефтепровода, например, для выхода из (А—1)-й насосной станции, можно определить необходимое число отключенных агрегатов и степень дросселирования давления на (k—1)-й станции при внезапном отключении k-й станции, полагая & = 2, 3, . . ., пг, и предельную продолжительность срабатывания системы «Волна», при которых обеслечивается надежная защита всего нефтепровода от давлений выше допустимых по условиям прочности, а также опреде-
Рис. 9.14. Кривые изменения давления на расстоянии 25 км от предыдущей насосной станции
лить вероятность и длительность снижения давления подпора перед (к + 1)-й насосной станцией ниже допустимого по условиям кавитации.
На рис. 9.14 изображены рассчитанные по описанной методике кривые изменения относительного давления (р/ри)1 на расстоянии 25 км после первой промежуточной насосной станции нефтепровода длиной 300 км с двумя промежуточными насосными станциями, после остановки второй промежуточной станции (кривая 1) и после отключения одного насоса из трех на первой промежуточной насосной станции (кривая 2) при срабатывании системы защиты «Волна». В данном случае достаточно было отключить один насос из трех на предыдущей насосной станции, чтобы созданная таким образом волна пониженного давления предотвратила опасное увеличение давления выше рабочего (пунктирная линия).
Недостатком системы защиты путем создания волны пониженного давления является необходимость обеспечения помехоустойчивости и высокой надежности линии связи. Кроме того, часть нефтепровода остается незащищенной от волны динамического давления с бэльшой крутизной фронта.
Гашение волны пониженного давления непосредственно в месте ее возникновения позволяет исключить динамическую перегрузку линейной части нефтепровода. При этом достаточно снизить скорость нарастания давления у остановленной насосной станции до допустимых пределов. Для этого надо, чтобы уменьшение расхода через остановленную насосную станцию происходило постепенно за время, соизмеримое с временем пробега ударной волной участка между насосными станциями. Это может быть достигнуто увеличением махового момента насосных агрегатов, установкой на линии всасывания насосных станций воздушных колпаков и автоматическим сбросом части перекачиваемой нефти в месте возникновения волны повышенного давления в специальный резервуар. Для увеличения махового момента требуется существенное изменение конструкции насосных агрегатов, в том числе и уже установленных. Воздушный колпак для современных магистральных нефтепроводов с большой пропускной способностью должен быть объемом до 300 м3, чтобы обеспечить требуемое снижение скорости нарастания давления, и должен работать при давлениях до 6 МПа. Это связано с большими металлозатратами и созданием специальной системы пополнения запаса воздуха, который частично растворяется в перекачиваемой нефти.
Рис. 9.15. Шланговый клапан типа «Флекс-Фло» для гашения волны давления
Способ автоматического сброса части нефти в резервуар применяется на магистральных нефтепроводах вследствие простоты конструкции и эксплуатации. Объем резервуара для сброса нефти, составляющий 300 м3, обеспечивает несколько срабатываний системы защиты. В качестве автоматических устройств для сброса применяются так называемые шланговые клапаны, называемые иногда регуляторами скорости изменения давления. Шланговый клапан типа «Флекс-Фло» (США) (рис. 9.15) состоит из корпуса 1 с входным 4 и выходным 6 патрубками. Входная / и выходная II полости клапана разделены перегородкой с боковыми прорезями, закрытыми цилиндрическим шлангом 5 из бензостойкой резины. Шланговые клапаны устанавливают на каждой промежуточной станции, полость / соединена с нефтепроводом на линии всасывания станции, и давление в этой полости равно давление подпора перед насосной станцией. Полость // соединена с резервуаром для сбрасываемой нефти. Полость III заполняется воздухом или инертным газом. Полости / и III соединены с разделительным сосудом 3, внутри которого имеется эластичная мембрана. В разделительный сосуд из полости / поступает нефть, а из полости III — инертный газ (или воздух). При установившемся режиме работы нефтепровода давление в полостях I м III одинаковое и равно давлению в нефтепроводе. При этом резиновый шланг плотно принимается к боковым стенкам цилиндрической части корпуса и герметично перекрывает боковые отверстия, разобщая при этом полости / и II. На линия, соединяющей полость / с разделительным сосудом, установлен дроссель 2 (местное сужение потока), поэтому изменение давления в разделительном сосуде всегда несколько запаздывает по сравнению с изменением давления в полости /. При плавном повышении давления во всасывающей линии насосной станции (например, при регулировании давления) давления в полостях / и III успевают своевременно выравняться и шланговый клапан не открывается. При резком повышении давления в нефтепроводе и соединенной с ним полости /, например при внезапном отключении промежуточной насосной станции, создается разность давлений под резиновым шлангом и полостью III, достаточная для преодоления жесткости шланга. При этом шланг отходит от боковых прорезей, и часть нефти из полости / попадает в полость II, а из нее — в резервуар для сброса. Сброс нефти из нефтепровода при срабатывании шлангового клапана обеспечивает полное или частичное гашение волны повышенного давления, и волна давления распространяется по нефтепроводу с небольшой крутизной фронта, благодаря чему на предыдущей станции и остальных насосных станциях успевает срабатывать система регулирования давления, опасного повышения давления не произойдет и нефтепровод плавно перейдет на новый установившийся режим работы с уменьшенным расходом и без одной промежуточной насосной станции. Подбирая степень закрытия дросселя 2 клапана, жесткость клапана и объем воздуха в полости III, можно при помощи шлангового клапана обеспечить заданную минимальную скорость повышения давления при остановке промежуточной насосной станции.
При проектировании и эксплуатации устройств для гашения волн давление путем сброса части нефти из нефтепровода возникает необходимость в определении параметров работы клапана для сброса нефти из нефтепровода (расход жидкости через клапан, продолжительность работы и другие), обеспечивающих снижение скорости увеличения давления до требуемых пределов.
Зависимость изменения давления в нефтепроводе от расхода через клапан, длительности его включения и места установки определяется уравнениями (5.2), (5.3), которые следует видоизменить применительно к рассматриваемому нефтепроводу; при этом сброс нефти через шланговый клапан рассматривается как сосредоточенный отбор жидкости из нефтепровода.
Рассмотрим нефтепровод с т промежуточными насосными станциями, на которых установлены шланговые клапаны. В момент / = О все насосные станции включаются, а в момент t >0 k-я промежуточная станция останавливается. В момент (t1>t1) включается шланговый клапан (с расходом Mk), установленный на этой станции для гашения волн повышенного давления, и работает до момента времени tз (ht Из решения уравнений (5.2), (5.3) можно определить, как
будет изменяться давление в любом сечении нефтепровода при внезапной остановке одной из промежуточных насосных станций и срабатывании на ней шлангового клапана. При этом, изменяя моменты открытия, расход шлангового клапана и продолжительность его работы, можно определить требуемый режим работы шлангового клапана, при котором будет обеспечиваться гашение волны давления, а скорость его изменения будет в требуемых пределах, обеспечивающих безаварийную работу нефтепровода.

Примеры расчета по формулам показаны на рис. 9.16 в виде графика изменения давления на выходе предыдущей насосной станции при различных режимах работы шлангового клапана для нефтепровода диаметром 1000 мм и длиной 3000 км с двумя промежуточными насосными станциями при остановке второй из них и сбросе части жидкости через шланговый клапан, установленный на этой же насосной станции (решение без учета инерционного слагаемого). При отсутствии предохранительного устройства для сброса части жидкости из трубопровода давление на выходе первой промежуточной насосной станции быстро увеличивается на 32 % (кривая /). При этом скорость увеличения давления на выходе первой промежуточной насосной станции в первые 100 с изменяется от 0,3 до 0,015 МПа/с. Кривые 2, 3 и 4 характеризуют изменение давления на рассматриваемой насосной станции при работе предохранительного устройства с расходом, соответственно равным 0,5; 0,1 и 0,15 от расхода жидкости в основном трубопроводе, при работе предохранительного устройства в течение 273 с (от I ¦¦¦= 0 до t = 270 с). В этом случае увеличение давления замедляется уже при расходе Мк = 0,05. При М к = 0,1 увеличение давления не превышает 9 % от первоначального, а при Мк = 0,15 после первоначального увеличения давления на 6 %, в дальнейшем оно уменьшается до 98 % от первоначального. После прекращения работы предохранительного устройства (при t = 270 с) давление при всех трех значениях отбора постепенно увеличивается, но со значительно меньшим градиентом. Кривая 5 соответствует прекращению сброса жидкости через предохранительное устройство с расходом Мк =0,1 через 82 с после его срабатывания. Во всех рассмотренных случаях предполагалось,, что предохранительное устройство срабатывает одновременно с остановкой второй промежуточной насосной станции. Расчет показал, что задержка в срабатывании предохранительного устройства на At = 13,5 с лишь незначительно влияет на характер изменения увеличения давления на первой промежуточной насосной станции (кривая 6 при Мк = 0,1, t = 0 и кривая 7 при Mk = 0,1 и t = 13,5 с).
Анализ решения уравнений (5.2), (5.3) для конкретных условий работы магистрального трубопровода позволяет выбрать требуемые расходы через предохранительные устройства и время их срабатывания таким образом, чтобы изменение давления в различных сечениях трубопровода было в пределах безопасного по условию прочности труб. При известных параметрах работы предохранительных устройств {расходе и времени работы) уравнения (5.2), (5.3) позволяют оценить характер изменения давления в трубопроводе при различных случаях неустановившегося движения жидкости в нем.
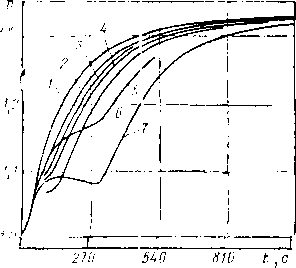
Рис. 9.16. График изменения давления на предыдущей насосной станции при срабатывании предохранительного шлангового клапана на отключенной насосной станции
9.6. ОБНАРУЖЕНИЕ И ОПРЕДЕЛЕНИЕ МЕСТОНАХОЖДЕНИЯ УТЕЧЕК НЕФТИ И ГАЗА
Важное значение в регулировании режимов работы магистральных трубопроводов имеет своевременное обнаружение утечек из магистральных трубопроводов. Утечки подразделяются на малые (не превышающие 3—5 % от номинального расхода), средние (до 10 %) и большие (свыше 10 %). Причины возникновения утечек могут быть самые разнообразные. Так, малые утечки (или так называемые свищи) обычно возникают при коррозионном разрушении материала трубы окружающей средой. Другой причиной появления утечек может быть наличие повреждении металла труб при заводском изготовлении или строительстве, которые не удалось выявить при испытаниях трубопровода. Такие повреждения в виде небольших трещин под действием внешних и внутренних сил давления в трубопроводе постепенно развиваются и могут привести к появлению свищей или разрывам. И наконец, нарушение технологических режимов, превышение рабочих давлений в трубопроводе, возникновение волн давления могут вызвать повреждения, и разрывы металла трубопровода. Аварии на магистральных нефтепроводах являются особенно опасными, так как кроме ущерба от потерь нефти могут возникнуть взрывы и пожары. Большой вред связан с попаданием нефти в почву и особенно в реки. При этом происходит загрязнение среды и гибель животных и растительных организмов.
Для определения величины и места утечек транспортируемого продукта целесообразно использовать сочетание пассивных (по данным слежения за ведением технологического процесса перекачки) и активных (путем пропуска диагностирующих устройств) методов.
Пассивные методы — по балансу перекачки; сопоставление давлений вдоль трассы с давлением при нормальном режиме эксплуатации трубопровода; сопоставление расходов по участкам трубопровода; анализ прохождения ударных волн. Активные методы —¦ пропуск диагностирующих зондов с использованием акустических, электромагнитных и других методов; запуск в поток и фиксация различного типа сред — «меток», контроль акустических шумов, внешних признаков утечки при осмотре трассы с поверхности земли; использование различного типа излучений (инфракрасного, ультразвукового и т. д.) для контроля утечек как с воздуха, так и с поверхности земли.
Для нефтепроводов место повреждения методом «по балансу перекачки» определяется расчетным или графическим путем по разности гидравлических уклонов в начале и конце поврежденного трубопровода.
Метод сопоставления давлений вдоль трассы трубопровода с давлениями до повреждения позволяет определить только крупные повреждения. Вместе с тем для определения места повреждения необходимо иметь значение давлений вдоль трассы трубопровода.
Мзтод сопоставления расходов по участкам трубопровода применяется при использовании расходомеров класса точности 0,2—0,5 %.
L - /л; — "гг ’> ,i 2
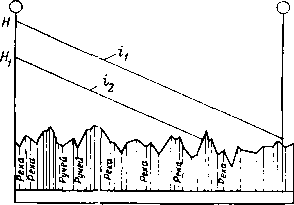
Рис. 9.17. Схемы определения места повреждения трубопровода: а — по падению напора; С, и i, — линии гидравлического уклона до и после повреждения трубопровода соответственно; 6 — по изменению расхода; t; и ?а — линии гидравлического уклона, определенные по количеству откачанного и поступившего на конечный пункт нефтепродукта соответственно
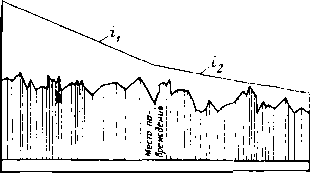
Такой метод чаще всего используется для определения наличия уте* чек, так как нахождение поврежденного участка требует значительного числа расходомеров высокого класса точности.
Полные разрывы стыков труб, а также разрывы продольных и спиральных швов определяются по падению напора и увеличению расхода (при центробежных насосах). Если напор до разрыва был Н (рис. 9.17, а), то ему соответствовала линия с гидравлическим уклоном гх. После разрыва трубопровода напор снизился до Нъ теперь ему соответствует линия с гидравлическим уклоном г2, которая наносится на профиль трубопровода через точку Нх параллельно Точка пересечения новой линии гидравлического уклона с линией профиля является наиболее вероятным местом разрыва. Сюда и следует направлять обходчиков или подвижные ремонтные бригады.
Если через разрывы вытекает только часть перекачиваемого нефтепродукта, а остальная поступает на конечный пункт трубопровода, то новая линия гидравлического уклона определяется по количеству откачанного нефтепродукта с головной перекачивающей станции и количеству поступившего нефтепродукта на конечный пункт (рис. 9.17, б). До повреждения трубопровода с головной перекачивающей станции откачивалось Q нефтепродукта и столько же поступало на конечный пункт. После повреждения количество откачанного нефтепродукта Q осталось прежним (при поршневых насосах, работающих при постоянной частоте вращения электропривода) или несколько возросло до С}г (при цетробежных насосах, способных увеличивать свою подачу при уменьшении сопротивления перекачки). Поступление нефтепродукта на конечный пункт в обоих случаях стало меньше откачанного. На профиль наносят линии гидравлических уклонов
и i2. Точка пересечения их указывает наиболее вероятное место повреждения трубопровода.
Один из методов определения мест утечки газа основывается на том, что в этом месте х0 происходит скачок массового расхода. Интегрируя уравнения стационарного движения газа от нуля до х0 и от х0 до I и сравнивая их, получаем выражение для определения места утечки газа:
м1~ М.\ L Р J
где х0 — координата места утечки газа; Мн и Мк — массовые расходы газа в начале и конце расчетного участка; ри и рк — давление в начале и конце участка; |3 = 16А,фzRT/^D6), —фактический
коэффициент гидравлического сопротивления; D—диаметр трубопровода; I—-длина расчетного участка.
Зная дисперсии ошибок измерения давления ст^' и расхода а2м и считая их некоррелированными, получаем дисперсии определения xoi, i — порядковый номер замера параметров режима работы газопровода:
, 2 2
о? =--- -" +
Рк- в* -Ь I Ml (I —хЛя
+ М х*\ о2
‘ (Ml-Ml) \ Р1 Р 1 Д °j н 01 '
Считая расчетное значение места утечки газа х01 случайной величиной, подчиненной нормальному закону распределения ее среднего значения х0, и применяя метод максимума правдоподобия, получим оптимальную оценку места утечки:
/V
*01
I
Метод обнаружения и оценки малой утечки газа с последующей ее локализацией целесообразно основывать на непрерывном автоматическом измерении расхода и давления газа на концах контролируемого участка, используя теорию выделения слабого сигнала из помех большой интенсивности, значительно большей величины полезного сигнала. Тогда обнаружение утечки основано на автоматическом вычислении за интервал наблюдения т отношения расходов газа в начале и конце участка газопровода и сравнении его с заданным порогом. Оценка местоположения утечки газа определяется формулой, аналогичной (9.1):
р\ — р\ — AlQl
х0 = —-=-г- . (9.2)
Aqo (Ql + О2)
где рн, рк, Q,, Q2 — измеряемые давления и расходы газа в течение времени т в начале и конце участка соответственно; q0 — усредненная за время т утечка газа; А — коэффициент пропорциональности между квадратом давлений и расходом газа по участку. Коэффициент А регулярно рассчитывается и усредняется по интервалу т, достаточному для получения необходимой точности.
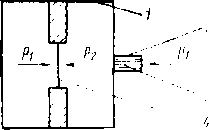
Рис. 9.19. Схема чувствительного элемента датчика давления:
/ — корпус; 2 — входные патрубки; 3 — демпфер; 4 — мембрана
F?
Но
TWlF
Рис. 9.18. Схема оборудования участка газопровода контрольной аппаратурой:
] — место разрыва трубы; 2 — две образо* вавшиеся волны давления; 3 — датчики давления; 4 — усилитель-преобразователь;
- — управляющий блок клапана; 6 — клапан-отсекагель
ой
-;
Разработанный метод хорош для квазпстационарных режимов газоперекачки. При существующих изменениях режимов транспортировки газа увеличивается время измерения исходных данных, т. е. возрастает время определения места утечки с момента ее возникновения.
Экспериментальная проверка метода была проведена на участке газопровода протяженностью 60,1 км с внутренним диаметром 300 мм. В течение пяти часов непрерывно измерялись расход и давление газа на концах участка. Утечка имитировалась отбором газа с относительной величиной 4 % на седьмом километре трассы. Разработанным способом бы/о определено местоположение отбора — 7,7 км. Относительная погрешность, как видно, составила 10 %. Теоретическая максимальная погрешность равна 12 %. Отсюда видно, что фактическая погрешность определения х0 лежит в пределах максимально допустимой.
К достоинствам предложенного метода следует отнести практически полное устранение влияния неточности измерительной аппаратуры на результаты расчетов. Простота его технической реализации, относительно высокая оперативность расчетов позволяют легко автоматизировать процесс обнаружения и поиска малых утечек газа.
Другой способ обнаружения мест утечек газа требует минимума исходной информации: необходимо наличие датчиков давления только в начален коице контролируемого участка (рис. 9.18). Поясним сказанное. В момент местного разрыва трубы образуется ударная волна пониженного давления. От места разрыва х0 в противоположных направлениях движутся две волны со скоростью с распространения звука в среде. Найдя разность времени прихода волн (tx, U) на концы контролируемого участка протяженностью /, нетрудно определить местоположение утечки:
где уср — средняя скорость движения газа. 334
Погрешность определения места аварии этим методом не превышает 0,1 %. Схема чувствительного элемента датчика давления, измеряющего весьма малые высокочастотные возмущения давления (0,1—0,001 МПа) на фоне значительных, медленно меняющихся давлений (3—7,5 МПа), изображена на рис. 9.19. Сигнал из трубопровода в месте измерения подается одновременно на два входных канала чувствительного элемента, т. е. одно и то же давление действует на мембрану с двух сторон. В одном из каналов имеется многоканальная или резьбовая демпфирующая вставка, которая гасит высокочастотные колебания давления, т. е. является низкочастотным фильтром. При такой схеме включения прибора мембрана будет реагировать только на измеряемую величину, поскольку медленно меняющийся большой фон компенсируется. Показания прибора преобразуются в электрический сигнал, который интегрируется, и результат сравнивается с известным пороговым значением. В качестве преобразователей используются емкостные или тензометрические датчики. Когда датчик на одном конце участка зафиксирует момент прихода волны возмущения давления, включается счетчик времени, который останавли вается в момент прихода другой волны к датчику на другом конце участка.
Оценка времени прихода волн осуществляется методом максимального правдоподобия, другими словами, происходит фильтрация высокочастотных возмущений давления от помех большой интенсивности и оценка их времени прихода. Описанный метод позволяет регистрировать аварийные утечки газа весьма малой величины (менее 1 %) вдоль участков газопроводов протяженностью 30 км с точностью не ниже 0,1 % (неопределенность Ах < 30 м). Для эффективного применения этого метода диагностики аварийных утечек газа предложена дифференциальная схема измерения давления. Следует отметить, что разработанный автоматический способ поиска аварийных утечек газа является весьма эффективным и точным, точность локализации утечек в основном зависит от погрешности определения средней скорости газа при предложенном способе фиксации волн давления.
Акустический метод обнаружения утечек заключается в следующем. Для обнаружения малых утечек при наличии значительных помех в трубопроводе появляется необходимость детального и всестороннего анализа информации, характеризующей состояние трубопровода. Существующие в настоящее время магнитные головки, обеспечивающие запись на малой скорости, и источники питания большой удельной емкости позволяют использовать регистраторы с непрерывной записью.
Разработанный экспериментальный образец автоматического регистратора утечек (АРУ) осуществляет непрерывную запись информации на контролируемых участках магистральных трубопроводов. Принцип действия АРУ основан на регистрации акустических шумов, возникающих при истечении жидкости через отверстие в месте повреждения трубопровода. АРУ состоит из зондового устройства с аппаратурой для обнаружения и регистрации утечек (АОР), магнитного датчика и поискового прибора для определения местоположения зондо-
вого устройства в трубопроводе и устройства воспроизведения записанной информации (рис. 9.20). Зондовое устройство представляет собой парусную четырехосную тележку 7, в которую встраиваются контейнер 3 с аппаратурой АОР и контейнер 2 с магнитным датчиком. Парус 1, установленный на конце тележки, перекрывает 80 % сечения трубопровода, что обеспечивает движение зондового устройства по трубопроводу под действием потока перекачиваемой жидкости. Для обеспечения лучшей проходимости по трубопроводу ось тележки смещена относительно оси трубы. Эксцентрично установленный на основании паруса груз 8 обеспечивает неподвижность паруса при возможном повороте тележки вокруг своей оси. Для того чтобы устройство свободно проходило задвижки, колеса 6 тележки как спереди, так и сзади располагаются в два ряда (по три колеса в каждом ряду). На передней поверхности контейнера 3 установлены включающее устройство 5 и гидрофон 4.
При разработке зондового устройства особое внимание было уделено вопросу уменьшения шума от перемещения носителя устройства по трубопроводу. С этой целью колеса тележки выполнены из мягкой резины и закреплены на подпружиненных рычагах. В состав АОР входят пьезоэлектрический гидрофон, электронный блок, магнитофон и включающее устройство. Электронный блок состоит из двух плат, одна из которых предназначена для приема сигнала от пьезоэлектрического гидрофона 4 и преобразования его для записи на магнитную пленку, а другая управляет работой магнитофона. Сигналы от гидрофона поступают на вход предварительного усилителя. Последующее усиление входного сигнала осуществляется с помощью фильтра-усилителя, представляющего собой активный фильтр верхних частот на 35 кГц.
Для записи акустических шумов на магнитный носитель сигналы на магнитную головку поступают через амплитудный детектор и усилитель низкой частоты. Таким образом, на магнитную пленку записывается огибающая амплитудно-модулированного входного сигнала.
_i_
Oh
J_L
100 200 .WO 400 500 HOO 700 800 900 i,с
/], I la
L. km
Рис. 9.21. Диаграмма акустических шумов
На рис. 9.21, а изображена диаграмма акустических шумов в узле запуска скребка от утечки в трубопроводе через отверстие диаметром
hi! 80 170 I fill Ш! 2чО Ш 320 JhO i ,C
P,ria 1 -
0.8
ll/i
0,8 мм при давлении 6 МПа, скорость утечки равна 150 л/ч. Диаграмма акустических шумов от утечки на линейной части трубопровода через отверстие диаметром 1 мм изображена на рис. 9.21, б, скорость утечки составляет 210 л/ч. Шумы, сопутствующие перемещению устройства по трубопроводу на разных участках, имеют различный характер. В моменты прохождения зондовым устройством подкладных колец возникают удары, которые четко видны на диаграмме, изображенной на рис. 9.21, в. Время между импульсами на диаграмме соответствует расстоянию между подкладными кольцами. Эти шумы легко отличить от шумов утечки.
Для привязки записанной информации к длине трубопровода необходимо в определенных точках трассы установить на трубопроводе акустические реперы пути (излучатели), при прохождении которых гидрофон выдает сигналы, фиксируемые магнитным носителем АОР. Как уже отмечалось, в устройстве осуществляется непрерывная запись информации, причем скорость протяжки пленки стабилизирована. В этом случае длина пленки между записанными на ней сигналами от реперов пути соответствует длине реперного участка. Подсчитав число записанных на пленке реперов пути, а также оценив местоположение утечки внутри записанного на пленку реперного участка (временной отсчет по пленке), можно с погрешностью 2,5 % от длины реперного участка определить место утечки.
9.7. УПРАВЛЕНИЕ ТРУБОПРОВОДАМИ ПРИ ОБНАРУЖЕНИИ АВАРИЙ И ПОВРЕЖДЕНИЙ И ВО ВРЕМЯ ПРОВЕДЕНИЯ РЕМОНТНЫХ РАБОТ
При обнаружении аварий и повреждений, в зависимости от сложившейся ситуации, принимают незамедлительные меры к остановке перекачки или находят другие решения. В том и другом случае действия должны быть направлены на минимизацию ущерба от аварий или повреждения.
На ритмичную работу магистрального трубопровода большое влияние оказывают как внутренние аварии и повреждения, так и аварии и повреждения у поставщиков и потребителей.
При полном прекращении или уменьшении объемов поставок или потребления диспетчер связывается с поставщиками и потребителями и уточняет сроки возвращения нефтепровода к доаварийиому режиму. В зависимости от характера повреждения и ожидаемой продолжительности простоя поставщиков или потребителей, а также с учетом объемов перекачиваемой среды в хранилищах и емкостях принимается решение о переводе нефтепровода на другие, оптимальные в данных условиях режимы работы или его остановку. При авариях и повреждениях на стороне потребителей на конечных пунктах и наличии промежуточных пунктов увеличивают объемы сброса на эти пункты.
Вынужденная остановка перекачки может быть использована для проведения предупредительно-профилактических и ремонтных работ. Аварии и повреждения оборудования собственно нефтепроводов в зависимости от их места и характера подразделяются на следующие группы: аварии и повреждения оборудования линейной части; аварии и повреждения основного оборудования, повреждения каналов связи, средств автоматизации и телемеханики; аварии и повреждения в резервуарах парка.
Аварии и повреждения оборудования линейной части могут произойти в районах водных переходов, населенных пунктов или в удалении от них. Серьезные последствия могут иметь аварии в районах населенных пунктов и особенно тяжелые в районах водных переходов. При авариях и повреждениях линейной части с выходом нефти и нефтепродуктов все станции до аварийного участка отключаются не-338
медленно. Станции, размещенные после аварийного участка, остаются в рабочем состоянии. Аварийный участок отсекают линейными задвижками, даются указания аварийно-ремонтным бригадам о выезде на место аварии.
Аварии и повреждения с выходом нефти и нефтепродуктов в районах водных переходов ликвидируют по планам, которые разрабатываются и составляются заранее на перекачивающих станциях, обслуживающих эти участки. Диспетчерский персонал должен быть знаком с этими планами и при обнаружении аварии действовать в строгом соответствии с ними.
Наиболее часто режимы работы магистральных трубопроводов нарушаются в результате аварий и повреждений оборудования. Сюда относятся повреждения основного и вспомогательного оборудования, неисправность систем энергоснабжения.
Аварии и повреждения оборудования могут быть с нарушением герметичности и без него. При больших объемах утечек нефтепродуктов на территорию станция обесточивается, при небольших — отсекается от магистрали закрытием общестанционных задвижек. При нарушении герметичности насосного агрегата, например сальниковых уплотнений, станция может быть сохранена в рабочем положении. Неисправный агрегат отсекается от схем технологической обвязки закрытием агрегатных задвижек.
Аварии и повреждения оборудования, как правило, приводят к изменениям установившихся режимов работы магистрального трубопровода. В одних случаях, например, при больших объемах утечек, диспетчерский персонал отключает все работающие станции. В других случаях, например при отключении агрегата или станции при отсутствии нарушения герметичности схем технологической обвязки, магистральный нефтепровод переводится на другие режимы работы. Диспетчерский персонал должен хорошо ориентироваться в таких ситуациях, своевременно и правильно принимать необходимые решения по оперативному управлению нефтепроводом.
Ремонтные работы без остановки трубопровода ведутся по заранее разработанному плану и в основном заключаются в заварке одиночных коррозионных каверн, приварке латок на групповые каверны и планок, хомутов муфт на сварные стыки. Для проведения указанных работ остановки перекачки не требуется, для этого достаточно на ремонтируемом участке трубопровода снизить рабочее давление. Тогда
А/г„ = hH j- (2Н Zj)---- -- -\- (zi zK) — Ahx\,
l — /j
где A fin — необходимое снижение напора на подающей станции; Л„ — напор на станции; zu — нивелирная отметка перевальной точки профиля трассы на ремонтируемом участке; 1г — расстояние от насосной станции до ремонтируемого участка трубопровода; I — общая длина перегона трубопровода, на котором производится ремонт; 1гг — фактический напор в трубопроводе на ремонтируемом участке до производства работ; zlt zK —¦ нивелирные отметки ремонтируемого и конечного участков перегона; Ahx—снижение напора в трубопроводе на ремонтируемом участке до производства работ.
Основными мероприятиями, направленными на снижение потерь газа, являются:
сокращение потерь в атмосферу при ремонтах участков газопровода благодаря совершенствованию технологии и применению устройств для утилизации газа;
сокращение потерь газа при продувках и испытаниях вновь вводимых и отремонтированных газопроводов благодаря применению высоконапорных передвижных воздушных компрессорных установок;
внедрение прогрессивных методов ремонта газопровода — ремонт газопроводов без остановки перекачки газа, врезка отводов в действующий газопровод под давлением, внедрение безогневых методов ремонта на оснэве клеевых композиций и соединений для повышения и восстановления несущей способности газопроводов;
повышение эксплуатационной надежности газопровода и его сооружений путем качественного и современного проведения плановопредупредительного ремонта (ППР);
исключение повреждений газопровода сторонними организациями благодаря соблюдению порядка ведения работ в охранной зоне газопровода.
Большинство из перечисленных мероприятий в настоящее время внедрено или внедряется в практику эксплуатации магистральных газопроводов. Перспективными способами сокращения потерь газа при ремонтах линейной части газопровода являются утилизация газа при опорожнении ремонтируемого участка газопровода и внедрение ремонта газопровода без остановки перекачки газа.
Утилизацию газа при опорожнении ремонтируемого участка газопровода можно осуществить следующими способами:
перепуском газа из подлежащего ремонту участка газопровода с повышенным давлением через существующие или временно проложенные технологические перемычки в газопровод с более низким давлением газа;
подключением к ремонтируемому участку потребителей газа через газопроводы-отводы;
перекачкой газа из ремонтируемого участка газопровода в соседний прилегающий участок данного газопровода или в параллельно проложенный газопровод передвижными компрессорными установками.
Первые два способа применимы в тех случаях, когда режим работы и технологическая схема газопровода позволяют провести соответствующие переключения. Чаще всего провести их не представляется возможным. Поэтому в настоящее время ведутся работы по разработке и внедрению различных схем по опорожнению ремонтируемого участка с использованием различных устройств. Разработана эжекторная схема опорожнения участка многониточного газопровода с помощью поршневого устройства.
Для утилизации газа при ремонтах одно- и многониточных систем газопроводов рекомендуется применять универсальные газоперека-
Рис. 9.22. Схема опорожнения ремонтируемого участка газопровода с помощью МГПА
чивающие устройства — мобильные газоперекачивающие агрегаты (МГПА). В схеме подключения МГПА к однониточному газопроводу отбираемый газ из опорожняемого участка разделяется на две части, одна из которой направляется в нагнетатель, а другая эжектируется с помощью давления газа после нагнетателя (рис. 9.22). Установка состоит из газоперекачивающего агрегата, включающего в себя приводной двигатель 3 и нагнетатель 4, на входе которого установлен регулятор давления 5. На выходе из нагнетателя расположены холодильник газа 2 и эжектор /, всасывающая камера которого через обратный клапан 6 соединена с выходным трубопроводом нагнетателя. На топливопроводе двигателя установлен детандер 7, имеющий на своем валу электрогенератор 8 для выработки электроэнергии для собственных нужд. Установку подключают к обводной линии (свечевой обвязки) линейного крана 11, с одной стороны которого расположен ремонтируемый участок 10. Этот участок отключают от газопровода 12 крапами 9 п 11. Трубопровод к обводной линии подключают при помощи фланцевых соединений 13. После подготовки технологической схемы и выполнения предпусковых операций запускают МГПА. Газ сжимаемый нагнетателем, охлаждается в холодильнике газа 2 и направляется к высоконапорной камере эжектора 1. Вторая часть газа через обратный клапан 6 подается к низконапорной камере эжектора, где его эжектируют высоконапорным потоком газа после нагнетателя. Общий поток газа эжектора направляется в газопровод 12. Эжектор отключается автоматически после того, как давление газа в опорожняемом участке упадет ниже допустимого. Постоянство параметров газа на входе в нагнетатель обеспечивается регулятором давления 5. В указанную схему можно подключить несколько эжекторов, работа которых может осуществляться как параллельно, так и последовательно.
Компоновка МГПА выполнена так, что его можно разместить на одном подвижном трейлере. В конструкции МГПА используют газотурбинный привод многоступенчатого центробежного нагнетателя. Такие установки имеют ряд преимуществ перед поршневыми МГПА: высокая производительность, минимальные вибрации при работе.
Значительно сокращаются потери газа благодаря своевременному обнаружению и быстрому оперативному устранению утечек газа на линейной части газопровода. Этому способствует ремонт трубопровода безогневым методом без остановки перекачки по нему газа.
9.8. ЗАДАЧИ АВТОМАТИЗИРОВАННОГО ДИСПЕТЧЕРСКОГО УПРАВЛЕНИЯ СИСТЕМАМИ ТРУБОПРОВОДНОГО ТРАНСПОРТА НЕФТИ И ГАЗА
Системам трубопроводного транспорта свойственны разнохарактерные жесткие внутренние (технологические, экономические, информационные) и внешние (с топливно-энергетическим комплексом и нефтеперерабатывающими отраслями, системами снабжения нефтепродуктами и газом) связи. Технологическая связь обусловлена непрерывностью процессов добычи, подготовки нефти и газа к дальнему транспорту, транспорта, переработки нефти и газа, распределения газа среди потребителей. Экономические и информационные связи тесно переплетаются при решении задач проектирования, планирования, управления. Внешние связи с народным хозяйством выражаются в широком использовании нефтепродуктов и газа почти всеми отраслями.
Жесткая и чрезвычайно экономичная с народнохозяйственной точки зрения технологическая связь с трубопроводными системами имеет и существенный недостаток: ограничение возможности маневра потоками. Вследствие малых скоростей транспортировки сред по трубопроводам возникает высокая вероятность нарушения режимов для отдельных потребителей. Соблюдение режимов у потребителя — обязательное условие функционирования систем — ставит в разряд первоочередных задач переоценку взглядов на роль резервных мощностей по всем звеньям системы.
Непрерывный характер производства, ограниченные возможности создания резервов в непосредственной близости от потребителя повышают требования к надежности оборудования, так как у протяженных трубопроводных систем с высокими единичными параметрами (диаметры, мощность перекачивающих агрегатов и т. д.) возрастают отрицательнее последствия отказов оборудования и аварийных ситуаций. Устранить или ослабить эти отрицательные последствия можно при оперативной и достаточной информации о происшедшем рациональным изменением режимов.
Обеспечение бесперебойного снабжения многочисленных потребителей различных отраслей народного хозяйства нефтью, нефтепродуктами и газом требует разработки и последующей реализации ком-342 нлекса взаимосвязанных задач регулирования. Постоянно возрастающее требование к качеству и надежности нефтегазоснабжения народного хозяйства, необходимость снижения издержек и потерь делают насущными четкое выделение подсистемы регулирования и ее максимальную оптимизацию внутри отрасли. Методологическое единство народнохозяйственного подхода к решению этой задачи состоит в согласовании совокупности критериев выбора решения в подсистемах добычи, транспорта, регулирования и использования нефти и газа с требованиями отрасли, а для отраслевых критериев — в согласовании с народнохозяйственным критерием.
Задачи регулирования в трубопроводных системах нефтегазоснабжения решаются как на стадии оптимального проектирования и планирования развития систем трубопроводного транспорта, так и в процессе функционирования.
Непрерывный характер технологического процесса добычи, очистки и осушки, дальнего транспорта и использования газа, масштабность и высокий уровень концентрации определяют принципы организации и структуру диспетчерского управления трубопроводными системами.
На верхней ступени иерархии (на уровне ЦДУ) являются актуальными и подлежат реализации совокупности задач: оперативного прогнозирования потребления; прогнозирования режимов трубопроводного транспорта; планирования режимов трубопроводного транспорта; диспетчерского контроля за соблюдением запланированных режимов трубопроводного транспорта; анализа фактических режимов работ трубопроводных систем; выявления «узких» мест в системе и способов оперативной их ликвидации; обеспечения экономичной работы трубопроводных систем; получения, обработки, анализа и выдачи информации об основных технико-экономических показателях.
На уровне объединенного диспетчерского управления (ОДУ) реализуется совокупность региональных или межрегиональных задач, входящих в сферу деятельности всесоюзных промышленных объединений.
Взаимоувязка задач осуществляется за счет соблюдения принципа иерархичности, т. е. результаты расчета на уровне ЦДУ являются исходными для расчета на уровне ОДУ.
Применительно к трубопроводным системам критерием оптимальности служит минимум суммарных затрат при условии удовлетворения потребности народного хозяйства в нефти, нефтепродуктах и газе с учетом ограничений по запасам и возможностям освоения в данные календарные сроки природных ресурсов, а также по капитальным вложениям, трудовым ресурсам и лимитированной продукции других отраслей.
Автоматизированная система диспетчерского управления (АСДУ) трубопроводными системами предназначена для автоматизации следующих процессов:
оперативного планирования потоков газа и режимов работы с целью максимального удовлетворения потребностей в нефти, нефтепродуктах и газе при условии минимизации энергозатрат на собственные нужды (периодичность — месяц);
оперативного управления основными объектами трубопроводного транспорта с целью обеспечения плановых режимов и локализации аварийных возмущений (периодичность — неделя);
развития и реконструкции объектов систем трубопроводного транспорта с целью обеспечения заданных уровней добычи и транспорта газа (периодичность — месяц);
сбора, обработки и воспроизведения режимно-технологической информации о фактических режимах работы трубопроводных систем в целью контроля технического состояния и анализа эффективности режимов функционирования (периодичность — час);
сбора, обработки и воспроизведения планово-учетной информации
о фактическом выполнении планов добычи, транспорта и потребления нефти и нефтепродуктов (периодичность — сутки);
создания и ведения отраслевого информационного банка данных, содержащего сведения о структуре, технических характеристиках, плановых и режимных показателях объектов систем трубопроводного транспорта.
В соответствии с назначением АСДУ решает пять функционально-ориентированных и информационно взаимосвязанных комплексов задач для систем трубопроводного транспорта: оперативного планирования режимов работы; диспетчерского контроля и анализа режимов работы; оперативного управления режимами работы; оптимального развития и реконструкции структуры; контроля и учета выполнения планов добычи, транспорта и распределения.
Оперативное планирование режимов дальнего транспорта газа призвано обеспечивать выбор оптимальных решений по заданному критерию с применением современных экономико-математических методов и вычислительной техники. Результатом оптимального оперативного планирования является эталонная диспетчерская режимная карта работы магистрального газопровода, содержащая данные о давлении, пропускной способности и расходе в узловых точках, схемы работы перекачивающих станций, энергетические показатели транспорта.
Отраслевая база данных содержит обобщенную информацию по элементам трубопроводных систем. В частности, нецелесообразно предусматривать конфигурацию линейного участка; отражать его гидродинамические свойства обобщенным параметром, который описывает как состояние труб, так и их геометрию. Необходимость такого подхода диктуется практической невозможностью собрать детальную информацию о системе и систематически ее обновлять с существенным возрастанием времени расчетов при детализации расчетной схемы. Кроме того, использование обобщенных характеристик оборудования позволяет провести унификацию соответствующих паспортных данных, в противном случае неоправданно возрастает объем информации.
Изменения обобщенной информации можно разбить на следующие руппы.
1. Изменения, отражающие новые свойства объекта, находящегося ] ведении соответствующего органа управления. Например, появле-I i t нового крупного узла притока или отбора, изменение возможных (хем обвязки перекачивающих станций, парка машин, геометрии литейного участка и т. д. Соответствующие изменения вносятся в базу данных, которая ведется на нижнем уровне управления и передается г главный вычислительный центр (ГВЦ), где также вносятся коррективы в отраслевой банк данных.
2. Изменения, важные для объектов, находящихся в ведении дру-I их органов управления, в соответствии с принципом унификации. с тс в основном изменения, требующие корректировки действующих классификаторов: появление нового оборудования, характеристики которого не представлены в соответствующих массивах паспортов в отраслевом банке данных, появление новой схемы и т. д. В этом случае определенная информация передается на верхний уровень управления, где она формализуется (вносятся соответствующие дополнения в классификаторы, уточняются паспортные данные нового оборудования и т. д.) и заносится в отраслевой банк данных. Формализованная и унифицированная информация передается на более низкий уровень управления, где также вносятся необходимые изменения в классификаторы и банк данных.
Отклонение указанных параметров от проектных существенно уменьшает пропускную способность магистральных трубопроводов, ухудшает показатели энергозатрат на транспорт. Сравнительные расчеты на базе проектных и фактических параметров позволяют дать своевременные рекомендации по очистке линейных участков трубопровода, ремонту перекачивающих агрегатов и т. д.
Трубопроводную систему как большую систему можно разбить на подсистемы таким образом, что состояние каждой из них будет характеризоваться множествами внешних и внутренних параметров, при этом взаимодействие между подсистемами в рамках системы осуществляется лишь через внешние параметры, часть которых может быть не привязана к подсистемам.
Систему ограничений можно разбить на две части: первая — это ограничения на внешние параметры, вторая — ограничения на внешние и внутренние параметры каждой подсистемы.
Задача оптимизации решается в несколько этапов.
Этап 1. Построение допустимых областей изменения для внешних параметров. Область изменения внешних параметров для каждой подсистемы строится так, чтобы для каждого набора значений внешних параметров существовал набор значений внутренних параметров, причем внутренние и внешние параметры должны удовлетворять системе ограничений второго плана для данной подсистемы. При этом не должно существовать допустимого, т. е. удовлетворяющего ограничениям второго плана, набора внешних и внутренних параметров, при котором внешние параметры не входят в построенную допустимую область. Для случая, когда в качестве подсистемы рассматриваются гтерекачивакщие станции, допустимая область может быть трехмерной в координатах: давление на входе, давление на выходе, подача. Она включает те значения давлений и подачи, реализация которых возможна без нарушения технологических ограничений на КС.
Этап 2. Построение агрегированных характеристик (АХ) подсистем. Агрегированная характеристика есть функция, ставящая в соответствие каждому вектору внешних параметров подсистемы из допустимой области оптимальное значение составляющей критерия по данной подсистеме, причем оптимизация ведется по всем значениям внутренних параметров с учетом технологических ограничений.
Для случая, когда в качестве подсистемы принята перекачивающая станция, агрегированная характеристика представляет собой функцию, отражающую минимальные режимно-допустимые затраты при различных наборах давлений на входе и выходе перекачивающих станций и их подачи.
Этап 3. Решение оптимизационной задачи верхнего уровня. Задача заключается в определении оптимального набора внешних параметров, исходя из интересов системы в целом. Она сводится к оптимизационной задаче, где в качестве критерия выступает сумма функций — АХ по подсистемам, а в качестве ограничений — ограничение первого плана и построенные допустимые области для внешних параметров подсистемы.
Этап 4. Восстановление оптимальных значений внутренних параметров. На этапе 3 получено оптимальное значение внешних параметров. Для каждой подсистемы им соответствуют внутренние параметры, что вытекают из принципа построения допустимой области. Восстановление (в случае, если они не сохранились) этих значений — содержание задачи этапа 4. В частности, для подсистемы КС задачей этапа 4 может быть восстановление режима работы перекачивающей станции, реализующего заданные давления на входе и выходе станции при заданной подаче.
Отметим, что в случае, когда критерий выбора решения для системы не зависит от внутренних параметров, последовательность решения задачи модифицируется. При этом отпадает необходимость построения агрегированных характеристик подсистем.
Комплекс задач оптимального развития и реконструкции структуры трубопроводных систем предназначен для определения и уточнения оптимальных планов размещения ввода мощностей: перекачивающих сташщй, лупингов и участков трубопроводов на действующих и развивающихся магистральных трубопроводах. Иерархические связи его строятся на той же основе, что и для оперативного планирования режимов.
Комплекс задач диспетчерского контроля и анализа режимов работы трубопроводных систем предназначен для автоматического сбора и обработки технологической информации по фактическим режимам работы. Он позволит дать диспетчерам ЦДУ и ОДУ ВПО объективные сведения из одного источника и в удобной форме для контроля фактического состояния объектов и принятия решений по устранению отклонений от технологической карты режима, а также осуществлять оперативный контроль за выполнением принятых решений. При этом реализуются следующие функции:
автоматизация сбора, обработки оперативных сведений и регистрации их в диспетчерских журналах;
выдача концентрированной информации в удобном для использования виде;
автоматический контроль за параметрами режимов с выдачей диспетчеру предупредительных и аварийных сведений; расчет фактических параметров работы системы; обслуживание стандартных запросов работников ЦДУ и руководителей отрасли.
Комплекс задач учета и контроля выполнения планов добычи, транспорта и распределения нефти, нефтепродуктов и газа предназначен для совершенствования учета и контроля выполнения планов добычи, транспорта и распределения с целью повышения качества и оперативности управления трубопроводными системами путем применения современных средств сбора и обработки данных.
В рамках АСДУ трубопроводным транспортом работа может проводиться по следующим основным направлениям:
автоматическое ведение журналов оперативного суточного учета фактической добычи, транспорта и потребления нефти, нефтепродуктов и газа;
разработка новых форм документов, отражающих динамику развития систем трубопроводного транспорта;
сравнительный анализ работы отдельных объектов и трубопроводных систем в целом за отчетный период с соответствующим периодом прошлых лет;
увязка математического и информационного обеспечения по всем уровням управления отраслью с организацией интегрированной системы обработки данных на базе АСУ ВПО и АСУ ПО.
ТЕХНИЧЕСКАЯ ДИАГНОСТИКА ТРУБОПРОВОДНЫХ СИСТЕМ
10.1. ЗАДАЧИ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ ТРУБОПРОВОДНЫХ СИСТЕМ
Эффективным направлением в интенсификации трубопроводных систем (ТС) и повышении надежности его оборудования является использование прогнозирующего диагностического обеспечения, в том числе таких составляющих, как основное и управляющее оборудование, базирующееся на современных автоматизированных средствах получения информации о фактическом состоянии оборудования и эффективных средствах ее обработки. Для этого необходимо располагать методами построения диагностического обеспечения, в которых могли бы сочетаться как существующие разрозненные и недостаточно используемые средства диагностирования, так и новые перспективные решения. Эта методология должна включать методы и средства построения диагностических моделей, оценки степени их достоверности и эффективности, рекомендации по использованию и размещению на объектах средств диагностирования.
Все используемые и перспективные методы и средства объединяются и концентрируются в рамках единой отраслевой системы диагностирования ТС с единой целью и едиными задачами. Наличие такой системы позволит обоснованно планировать сроки вывода оборудования в ремонт, сократить его продолжительность, улучшить качество, уменьшить стоимость, сэкономить материальные ресурсы, своевременно обеспечить снабжение запчастями. При этом сокращается число вынужденных остановок за счет раннего обнаружения дефектов и их устранения. Получения своевременной информации можно достигнуть только автоматизацией процессов диагностирования, совместным использованием средств вычислительной техники и методов прогнозирующего диагностирования.
Такая постановка задачи, в свою очередь, требует разработки общей процедуры создания систем диагностирования ТС и его оборудования. Наличие научно обоснованной последовательности действий при разработке систем диагностирования позволит в значительной степени формализовать и автоматизировать процесс их создания.
Система технического диагностирования (СТД) содержит следующие элементы: объект диагностирования (ОД), технические средства диагностирования (ТСД) и человека-оператора. Диагностическое обеспечение включает в себя перечень оцениваемых показателей, методы их оценки, условия работоспособности, признаки наличия дефектов и алгоритмы, программы и ТСД. Диагностическое обеспечение можно получить в результате анализа одной или нескольких диагностических моделей трубопроводной системы. Диагностическая модель является формальным представлением объекта, учитывающим возможные изме-
нения его состояний. Параметры, которые характеризуют существенные свойства трубопроводной системы, называют определяющими, которые и используются в соответствующих определенному технологическому режиму транспорта газа моделях.
Определение и классификация диагностических параметров — достаточно сложный и неформализованный процесс, который выполняют в несколько этапов. На первом этапе предварительно назначаются существенные и диагностические параметры. Для этого используются знания и опыт специалистов. На втором этапе уточняют предварительно выбранные параметры путем использования различных формальных методов. Если определяющие параметры выделены, то составляют и выбирают диагностические модели, число которых определяется спецификой трубопроводной системы и условиями ее эксплуатации. По выбранным моделям назначают (определяют) прямые и косвенные показатели (параметры), которые предстоит оценить с помощью ТСД. После того как выбрана диагностическая модель трубопроводной системы, используют принципы теории идентификации — наблюдаемость, управляемость и различимость.
В общем случае в ходе анализа процессов взаимодействия элементов трубопроводных систем можно определить максимальное значение выбранного критерия (прямые задачи) или значения показателей, характеризующих трубопровод и его оборудования и ТСД, которые обеспечивают достижение заданного критерия (обратные задачи).
В процессе проектирования системы диагностирования ТС на первом этапе исходят из ситуаций, складывающихся на практике, и которые, например, могут быть сведены к следующим задачам.
Первая задача. Определить значение выбранного критерия при заданных показателях, характеризующих свойства ТСД трубопроводов, процессы диагностирования и режим работы трубопроводов.
Вторая задача. Для заданных ТС и технических средств в предположении, что режим работы трубопровода строго регламентирован, определить значения показателей, характеризующих процесс диагностирования, которые обеспечат заданный показатель организации СТД. Подобная задача возникает в том случае, когда назначение трубопровода, его конструктивные особенности и специфика использования строго регламентируют показатели его работы и ТСД.
Третья задача. Для заданных ТС и ТСД наилучшим образом (в каком-то смысле) организовать процесс использования и диагностирования. Задача такого рода возникает тогда, когда в отличие от предыдущего случая имеется возможность перестроить или повлиять на организацию диагностирования с целыо достижения наибольшего эффекта в смысле принятого критерия организации СТД для объектов периодического использования. При этом разработчики СТД могут обоснованно рекомендовать целесообразные периодичности диагностирования и использования объекта.
Четвертая задача. Для заданной трубопроводной системы, у которой строго регламентированы режимы работы и процессы диагностирования, определить показатели ТСД при определенном значении критерия организации СТД. Такая задача возникает, как правило, когда ТСД являются внешними, а принятая организация использования и технического обслуживания трубопроводной системы не определяется жесткими условиями извне (технологическим процессом, техническими возможностями, численностью обслуживающего персонала и пр.)
Пятая задача. Для строго регламентированных режимов работы ТС и процессов диагностирования определить показатели ТС и ТСД, обеспечивающие заданные значения организации СТД. Здесь, исходя из назначений ТС и внешних условий, влияющих на режим ее работы, определяется организация СТД и техническое обслуживания, а в ходе разработки СТД определяют соответствующие требования к ТСД и добиваются их удовлетворения.
10.2. МЕТОДЫ ДИАГНОСТИРОВАНИЯ ОБОРУДОВАНИЯ ТРУБОПРОВОДНЫХ СИСТЕМ
По назначению диагностирование ТС можно разделить на текущее и прогнозное. При текущем диагностировании определяют состояние ТС в какой-то определенный момент времени функционирования. Цель текущего диагностирования — определение правильности и возможности выполнения объектом определенных функций до следующего диагностического воздействия. При прогнозном диагностировании необходимо получить исходные данные для прогнозирования возможных изменений объекта или процесса и предсказания возможных неисправностей, могущих возникнуть при работе объекта. Поэтому прогнозное диагностирование ТС всегда выполняют в большем объеме, чем текущее.
Функциональное диагностирование ТС дает возможность на работающем магистральном трубопроводе выявить нарушения правильности функционирования отдельных узлов и немедленно реагировать путем включения резерва, повторного выполнения операций, перехода на другой режим и т. п. Функциональное диагностирование во многих случаях обеспечивает нормальное или частичное выполнение магистральным трубопроводам возложенных на него функций даже при наличии неисправности в нем. Недостаток функционального диагностирования в том, что оно выявляет правильность функционирования только в данный момент и только в данном режиме. При этом могут быть не выявлены неисправности, мешающие работе ТС в другом режиме.
Тестовое диагностирование ТС дает возможность получить полную информацию о техническом состоянии ТС, дать оценку его работоспособности и исправности, однако его применение возможно только при ^проведении профилактики или ремонте объекта.
Комбинированное диагностирование ТС представляет собой сочетание функционального и тестового и дает наиболее точное представление о техническом состоянии объекта как при эксплуатации, так и ремонте. При комбинированном диагностировании проверяют не только правильность функционирования, но и исправность и работоспособность объекта.
И тестовые, н функциональные методы применяют при текущем диагностировании, например, при температурном контроле за режимом металла. Для прогнозного диагностирования ТС используют тестовые методы, например: осмотры, проверки, испытания и исследования в период ремонта объекта. Следует отметить, что для получения правильного прогноза, кроме данных диагностирования, следует учитывать ретроспективные данные.
По режиму работы методы диагностирования ТС можно разделить на постоянно действующие (непрерывные), периодически действующие и разовые. Постоянно действующие методы характеризуются постоянным контролем за выбранными параметрами в процессе работы объекта, поэтому этими методами выполняется только функциональное диагностирование. При периодически действующих методах контроль рабочих параметров ТС при функциональном или тестовом диагностировании осуществляется через определенные, строго повторяющиеся промежутки времени, определенные производственными инструкциями. Разовые методы применяют только при необходимости получения дополнительной информации, когда информация от постоянного и периодического контроля недостаточна.
Неавтоматизированное диагностирование отдельных элементов ТС, основанное на правилах эксплуатации, инструкциях, на интуиции обслуживающего персопала, существует и функционирует давно, например: проверка механической прочности элементов оборудования, дефектоскопия элементов насосных агрегатов и трубопроводов и др. Остановка оборудования персоналом из-за изменения вибрации, шума, температуры — это пример интуитивного диагностирования.
В настоящее время разработано значительное число методов технического диагностирования, основанных на различных физических, механических, химических и др.
По степени автоматизации методы диагностирования ТС можно разделить на автоматические, автоматизированные, ручные. Автоматические обеспечивают диагностирование ТС, включая и выдачу заключения, без участия человека. В этих случаях автоматически реализуется весь алгоритм технического диагностирования, задающий совокупность элементарных проверок, последовательность их реализации, правила обработки и анализа информации. При решении задач диагностирования автоматизированными методами человек не исключается из процесса диагностирования — он реализует часть алгоритма, например, обработку или анализ результатов элементарных проверок, контроль за выдерживанием параметров работающего энергоблока, когда средства контроля только дают информацию об отклонении параметров от заданных, а анализ информации и поиск дефекта должен выполнять оперативный персонал. К таким методам относят, например, виброакустический, предусматривающий диалог «человек—машина». При ручном методе диагностирования весь алгоритм технического диагностирования выполняет человек.
Накопленную и постоянно поступающую информацию о состоянии эксплуатируемого оборудования следует систематизировать и целенаправленно подбирать. Информация должна характеризовать такие параметры, которые в максимальной мере определяют состояние диагностируемых элементов. Очень перспективна система диагностирования и прогнозирования состояния, основанная на сравнении параметров математической модели с фактическими параметрами реального объекта, например, на каждой насосной станции имеется выделенная группа узлов и элементов оборудования, определенная как наиболее ответственная и представительная с точки зрения надежности и лимита ресурса для них.
Эксплуатационное обслуживание современных ТС предполагает расчет и определение параметров технической эксплуатации и подготовку необходимой технической документации. Схема организации эксплуатационного обслуживания включает следующие постановки задач:
оценка фактического уровня надежности и прогнозирование на ее основе межремонтного цикла; используют следующие параметры — время между отказами, время восстановления, коэффициент готовности и др; выходная документация — формы сбора и методы обработки информации;
планирование технического обслуживания; используют параметры — период и время проверки и ремонта; выходная документация — план-график и инструкция по проведению проверок',
планирование запасных деталей, материалов, механизмов; основные параметры — число элементов каждого типа, время ремонта, число восстанавливаемых и невосстанавливаемых элементов с привязкой их к существующей организации ремонта; выходная документация — ведомости, маршрутные карты;
расчет численности персонала, определение специализации, распределение на диспетчерский и ремонтный; выходная документация — проект штатного расписания.
Средства технической диагностики можно использовать как во время ремонтов для проверки его качества, так и в оперативном режиме, они, выполняя роль предвестников отказа, позволяют более эффективно использовать оборудование и сократить потери.
Ремонт современного оборудования трубопроводных систем характеризуется большим объемом подготовительных работ, ограниченными размерами ремонтной площадки. Плановые ремонты проводят для ответственных, сложных блоков, требующих больших трудозатрат.
Сокращение потерь идет прежде всего за счет сокращения времени ремонта, снижения недопоставки нефти и газа. Необходимо совмещать анализ, причины появления дефектов с контролем технологических режимов эксплуатации и другими компонентами, нарушение которых приводит к дефектам.
Для высокой достоверности установления видов и механизмов дефектов необходимо знать и условия, в которых возникают дефекты. Поэтому важной задачей является организация и выбор запоминающих индикаторов, фиксирующих различного рода воздействия.
10.3. СТРУКТУРА СИСТЕМЫ ТЕХНИЧЕСКОЙ ДИАГНОСТИКИ 1 РУБОПРОВОДНЫХ МАГИСТРАЛЕЙ
I систему технического диагностирования (СТД) ТС обычно включают объект диагностирования (сам трубопровод), диагностическое обеспечение, технические средства диагностирования и, в общем случае, человека-оператора.
Диагностическое обеспечение ТС включает перечень оцениваемых показателей, методы их оценки, условия работоспособности, признаки дефектов, и, наконец, алгоритмы, программы и аппаратные средства диагностирования. Оно может быть получено в результате анализа одной или нескольких диагностических моделей трубопроводной системы, которая является формальным ее представлением, учитывающим возможные изменения состояний ее элементов.
Технические средства СТД реализуют процесс диагностирования. Существует два принципа проведения диагностирования — тестовый,
I ри котором на элементы трубопровода подается специальное тестовое Еоздействие и по искажению выходных переменных делается вывод ( его исправности, и функциональный, когда для заключения о состоянии трубопровода используются только имеющиеся внешние воздействия.
Информация о техническом состоянии трубопровода и его оборудовании обеспечивается соответствующими измерительными и вычислительными устройствами, поэтому точность их имеет важное значение для построения адекватных моделей. При этом могут применяться прямые и косвенные методы проведения измерений: давления, расхода, температуры и т. д.
При синтезе структуры системы диагностирования ТС необходимо выбрать: состав контрольных точек для подключения системы диагностирования и принятия решения, состав технических средств, методы [еализации проверочных функций и согласования их с целями, общими для системы, распределить проверочные функции по узлам и блокам.
Процесс диагностирования, в котором определенные функции выполняет человек—оператор, предполагает тесную взаимосвязь магистрального трубопровода и технических средств диагностирования. При этом действие оператора определяется принятой степенью автоматизации процесса трубопроводного транспорта. Высокая эффектив-костьСТД трубопроводного транспорта может быть достигнута только ]том случае, когда в процессе диагностирования будет максимально учтена специфика процесса транспорта нефти. Это требует тщательного проектирования СТД для различных объектов трубопроводного транспорта. Разработана достаточно обоснованная последователь-юсть действий при создании СТД различного назначения, которую хегко автоматизируется с использованием современной вычислитель-: ой техники. Эта последовательность включает три этапа. На первом усматривается процесс диагностирования и на основе выбранного критерия организации с учетом специфики использования и эксплуатации трубопроводов определяются требования ко всем элементам
СТД. На втором этапе осуществляется параллельное во времени создание технических средств диагностирования и планирования деятельности оператора. На этом этапе могут участвовать различные организации, проектирующие и эксплуатирующие трубопровод, разрабатывающие технические средства диагностирования и планирующие деятельность операторов. Наконец, на третьем этапе должны быть оценены эффективность диагностирования СТД, ТС.
Разработка систем диагностирования — процесс сложный. В результате проектирования должны быть разработаны в принципе различные элементы (магистральный трубопровод, технические средства и оператор), которые тесно взаимодействуют между собой при диагностировании. Это обстоятельство обусловливает необходимость в согласовании действий организаций, проектирующих объект, технические средства диагностирования и деятельность оператора.
Планирование деятельности оператора предусматривает корректировку, принимаемых технических решений при эксплуатации объекта и технических средств диагностирования. Подробное рассмотрение функции оператора в процессе диагностирования позволяет предъявить обоснованные требования к его профессиональной подготовке и квалификации.
"Достоверность результатов прогнозирующего диагностирования зависит от следующих факторов: достоверности исходной информации (точность и отсутствие случайных и систематических ошибок при измерении давлений а расходов); вероятности исключения или исправления случайных ошибок, возникающих в центральном процессоре СТД при расчете показателей диагностирования; надежности работы устройств и каналов ввода—вывода; соответствия моделей, заложенных в основу функционирования устройства, реальным процессам, происходящим в ТС при его эксплуатации; точности определения начальных показателей диагностирования (предела длительной и кратковременной прочности, структуры и фазового состава металла , наличия микротрещин, пор и их параметров).
Достоверность исходной информации о трубопроводе обеспечи -вается блоком измерений. Для этого в его состав вводится микропроцессорный блок, связанный с системной магистралью через блок сопряжения. Избыточность измеряемых микропроцессорным блоком измерений параметров трубопровода позволяет повысить достоверность определения и прогнозирования показателей диагностирования. Эффективность работы блока измерений зависит от рациональности выбора точек контроля и общего уровня контролепригодности трубопровода. Блок измерений позволяет не только измерять и сравнивать показания нескольких датчиков, измеряющих один и тот же параметр , но и определять этот параметр косвенным путем, по результатам измерений других параметров. Фактическая измеряемая величина определяется после до пускового контроля, группировки и сглаживания. Кроме того, блок измерений, входящий в состав СТД прогнозирующего диагностирования, позволяет проводить предварительнную статистическую обработку измерительной информации для повышения ее достоверности.
Надежность функционирования СТД и исключение случайных ошибок, возникающих в системе при вычислении показателей работоспособности трубопровода, достигается путем введения в структуру СТД блока диагностирования, представляющего собой специализированный микропроцессорный блок, иод контролем которого находится вся работа системы, и надежность которого превышает надежность всех других блоков системы. Блок диагностирования осуществляет функциональный и тестовый контроль отдельных узлов и решает следующие задачи: своевременное обнаружение неисправностей и ошибок в работе СТД, анализ ошибок и сбоев, поиск дефекта с заданной точностью, принятие решения на устранению последствий неправильной работы и обеспечение работы СТД.
Диагностическая информация (например, остаточный ресурс насосного агрегата) носит интегральный характер, поэтому даже незначительный сбой в работе СТД, приводящий к изменению результата диагностирования, не может быть исправлен. При этом может быть сведен на нет результат всей работы системы в течение длительного периода времени. Для исключения этого применяют методы резервирования долгосрочно хранящейся информации и ее периодическое обновление. Это позволяет уменьшить влияние возможных сбоев СТД, при которых возможна утрата результирующей интегральной информации. Для этого резервируются накопители результирующей" и некоторой промежуточной информации (накопители на магнитных дисках или кассетных лентах).
• ......Общая методика получения диагностированного обеспечения трубо
проводных систем может состоять из следующих основных этапов: составление математического описания магистрального трубопровода и его элементов;
получение диагностической модели технологических процессов транспорта нефти;
анализ диагностической модели и выбор совокупности контролируемых показателей процесса транспорта нефти;
оценка достоверности выбранных показателей работы магистрального трубопровода;
разработка алгоритмов и программ тестирования СТД; разработка средств для подготовки процесса диагностирования; разработка средств проведения процесса диагностирования, в том числе выбор точек контроля на трубопроводе и средств связи.
Каждый из перечисленных этапов в свою очередь состоит из ряда операций. Так, этап осуществления процесса диагностирования текущего состояния трубопровода включает такие операции: выработку входных воздействий на трубопровод, подачу входных воздействий; управление магистральным трубопроводом при его диагностировании; съем выходных переменных (давления, расхода и др.); анализ выходных переменных и принятие решений но дальнейшей эксплуатации
трубопровода.
Этап подготовки средств диагностирования, например, тестовых, состоит из подготовки тестовых воздействий (стимулирующих воздействий и эталонных реакций); составление словаря; оценки их качества;
перенесения на носители автоматических установок контроля.
Все перечисленные этапы тесно связаны между собой. Особо важное значение имеет этап составления и анализа диагностических моделей трубопровода к его оборудования, ибо неверное составление моделей приводит к созданию неэффективных средств проверки, к напрасным затратам материальных ресурсов на процесс контроля, г Диагностическое обеспечение магистрального трубопровода получают в результате анализа его диагностической модели. Любой элемент трубопровода или трубопровод в целом может быть описан математической моделью с той или иной степенью адекватности. Параметры, характеризующие какие-либо его существенные свойства, считаются определяющими, им соответствуют адекватные математические модели. Диагностическая модель представляет собой формализованное описание трубопровода, учитывающее возможность изменения его состояния. Строится модель на основе анализа состава сооружений, условий использования и эксплуатации и может быть аналитической, графической и графоаналитической.
Определение и классификация диагностических параметров магистральных трубопроводов достаточно сложный и неформализованный процесс. В настоящее время при создании систем диагностирования используют в связи с этим несколько этапов. На первом этапе предварительно назначаются существенные и диагностические параметры трубопровода и его оборудования, обычно для этого используются знания и опыт специалистов. На втором этапе производится уточнение предварительно выбранных параметров путем использования различных формальных методов.
Если выделены определяющие параметры магистрального трубопровода, то производится составление и выбор его диагностических моделей, число которых определяется спецификой трубопровода и условиями его эксплуатации. По выбранным моделям назначаются (определяются) показатели (параметры) прямые и косвенные, которые предстоит оценивать с помощью технических средств. После того, как выбрана диагностическая модель трубопровода, используются принципы общей теории идентификации — наблюдаемость, управляемость и различимость.
Выбор оцениваемых прямых и косвенных показателей работы ТС, методов их оценки, осуществляемой в результате анализа диагностической модели, с одной стороны, определяют его контролепригодность, а с другой — влияет на технические решения, принимаемые при проектировании технических средств диагностирования. Технические возможности разработчиков СТД во многом определяют решения, принимаемые при разработке диагностического обеспечения магистрального трубопровода по выбору оцениваемых показателей и методов их оценки. С другой стороны, условия работоспособности трубопровода и признаки наличия дефектов в нем, определяемые при разработке диагностического обеспечения трубопровода, существенно влияют на технические решения при разработке ТСД, поскольку являются основой для получения метрологического обеспечения трубопровода и характеризуют методическую достоверность диагностирования процесса транспорта нефти.
Алгоритмы и программы диагностирования элементов 'ГС используются при построении алгоритмов, реализуемых автоматическими средствами диагностирования или оператором. При разработке алгоритмов и программ диагностирования транспорта нефти существенной является оценка их по выбранным критериям с целью обеспечения требуемой эффективности диагностирования. Диагностическое обеспечение трубопроводных систем включает перечень оцениваемых показателей, методов их оценки, условия работоспособности, признаки наличия дефектов, алгоритмы и программы диагностирования.
Эффективность диагностирования транспорта нефти, определяемая в ходе разработки диагностического обеспечения, позволяет оценить результаты, получаемые специалистами в ходе эксплуатации магистрального трубопровода. Вероятностная оценка результатов диагностирования с учетом вероятностных показателей всех составляющих процесса дает возможность объективно судить об эффективности диагностирования. На основе учета влияния всех составляющих процесса диагностирования можно дать обоснованные рекомендации по ужесточению требований, предъявляемых к отдельным компонентам ТСД.
Оценка эффективности системы диагностирования трубопроводных систем, осуществляемая на последнем этапе создания системы диагностирования, дает возможность оценить целесообразность затрат, связанных с ее применением в период эксплуатации ТС.
Разработка технических средств диагностирования (ТСД) выполняется в два этапа. На первом этапе определяются задачи, решаемые ТСД, вид средств (внешние, встроенные) и требования по безотказности, предъявляемые к ТСД; выбираются методы диагностирования; разрабатывается метрологическое обеспечение. В качестве критерия для оценки системы диагностирования при решении задач на первом этапе можно использовать экономические показатели. Содержание действий на первом этапе тесно связано со спецификой задач, решаемых СТД. Выбор метода диагностирования целесообразно осуществлять из библиотеки апробированных методов, причем каждый метод может характеризоваться двумя подмножествами показателей: показателями процесса диагностирования (время, достоверность, глубина поиска, стоимость и др.) и показателями объекта (вид объекта, число входов и выходов, необходимость тестового воздействия и др.). Это обстоятельство предопределило целесообразность их специального рассмотрения.
На втором этапе строятся алгоритмы и программы ТСД и с учетом определенной степени автоматизации принимаются решения по выбору элементной базы, построению структуры, принципиальных схем и конструкций. В заключение второго этапа определяется инструментальная достоверность, которая является одной из составляющих при определении эффективности диагностирования.
При наблюдении за процессом эксплуатации оборудования ТС можно отметить сочетание как бытропротекающих, так и медленно меняющихся процессов изменения технического состояния. В первом случае это — разрушение определенных частей установок, например, лопаток ГПА, во втором снижение мощности, производительности и т. п. И в том и другом случае задача сводится к скорейшему обнаружению момента разладки. К задаче обнаружения момента разладки могут быть отнесены задачи обнаружения также отказов и управляющего оборудования, например, датчиков, преобразователей и др. Для обнаружения разладки имеется возможность не обязательно следить только за абсолютными значениями случайных процессов, а только за определенными функционалами датчиков трубопроводной системы.
10.4. ОРГАНИЗАЦИЯ ОТРАСЛЕВОЙ СИСТЕМЫ ДИАГНОСТИЧЕСКОГО ОБЕСПЕЧЕНИЯ ТРУБОПРОВОДНЫХ СИСТЕМ
Повышение надежности работы основного технологического оборудования ТС необходимо осуществлять путем коренного улучшения ремонтного обслуживания на базе системы технической диагностики. При этом важное значение имеют обоснованные графики ремонтов с оптимальными, определенными автоматизированными СТД, объемами ремонтных и реконструктивных работ. Рассмотрим принципы организации отраслевой системы автоматизированного диагностического обеспечения; трубопроводных систем (ОСДО).
При формировании ОСДО целесообразно придерживаться иерархического принципа построения, предполагающего локальные системы нижнего уровня, сформированные непосредственно на оборудовании, подсистемы диагностирования технологических объединений и систему диагностирования всей отрасли, в которой и содержится центральный банк определяющих данных. Второй принцип организации ОСДО — максимальная унификация информации для всех уровней для снижения требований к средствам вычислительной техники (ВТ).
ОСДО имеет три уровня и охватывает все виды оборудования ТС и все технологические процессы трубопроводного транспорта.
I уровень с соответствующим контуром управления — локальная СТД уровня объектов диагностирования, который охватывает основные виды технологического оборудования, функционирующего в управлениях по транспорту нефти и газа.
II уровень со своим контуром управления — подсистема технического диагностирования производственных управлений по транспорту нефти и газа.
III уровень — уровень отрасли, на котором целесообразнее всего вести прогнозирование, оптимизацию средств замера параметров и определение их представительности, распределение объектов прогнозирования по иерархическим уровням, распределение функций между различными по уровню и средствами диагностирования, создание и применение научно обоснованных методов планирования объемов ремонтных работ на основе прогнозирующего диагностирования и оптимизацию технического обслуживания отрасли в целом. Эти задачи являются достаточно сложными и их решение невозможно без широкого применения ВТ и средств автоматизации.
Принципы организации ОСДО, обладающей функциями достоверного определения фактического состояния оборудования магистральных трубопроводов и своевременного выявления элементов с дефектами в заданном диапазоне времени, базируются на использовании системного подхода к решению поставленных задач, в частности методов декомпозиции, агрегирования, унификации, эквивалентирования.
Построение подсистемы I уровня предусматривается в три этапа. Первый этап включает следующие операции: контроль режимов работы оборудования и выдача информации об отклонениях от нормальных режимов оперативному персоналу с их фиксацией; сжатие информации и передача на II уровень ОСДО функциональных параметров для определения технического состояния и остаточного ресурса работы оборудования. Второй этап — анализ режимов работы и выдача рекомендаций оперативному персоналу по коррекции режимов с учетом технического состояния оборудования; сжатие информации, определение технического состояния оборудования и его остаточного ресурса и передача на II уровень; учет результатов тестового диагностирования при определении остаточного ресурса оборудования; диагностирование технической и психофизической готовности оперативного персонала и правильности его действия. Третий этап — управление всеми средствами автоматики, технологических защит и блокировок на базе микропроцессорной техники.
Рассмотрим более детально организацию подсистемы перекачивающих станций ТС. Первый этап — подготовка и обучение персонала и формирование организационных структур — осуществляется в рамках региональной системы подготовки персонала по специальным программам с использованием ВТ. Обучению подлежат все группы персонала с проверкой усвоения. Организационное оформление административных структур определяется распорядительным документом по министерству, управлению и предприятию и предусматривает создание отдела технического диагностирования в главном информационном вычислительном центре, подотделов в службах ВТ управлений с подчинением главному инженеру системы, групп технического диагностирования в производственно-технических отделах предприятий без увеличения численности за счет перераспределения обязанностей. Ответственность за создание подсистем технического диагностирования перекачивающих станций возлагается непосредственно на главных инженеров предприятий и объединений. Второй этап — классификация оборудования перекачивающих станций. Оборудование делится на механическое, электротехническое, теплотехническое, средства управления и др.
Основная задача, стоящая перед подсистемой перекачивающих станций, — интенсифицировать энергетическое производство путем повышения надежности, т. е. определить для каждого элемента структуру, наиболее перспективную с точки зрения прогнозирования (по надежности), установить интегральный критерий, по которому вести прогноз и выдавать информацию по прогнозирующему диагностированию в вышестоящую по иерархии структуру системы диагностирования отрасли.
Инструментальное обеспечение подсистемы базируется на штатных :амерах необходимых параметров с возможной оптимизацией и уточ-кением объемов и мест замеров. Возможны новые дополнительные средства технического диагностирования.
На II уровне управлений по транспорту нефти и газа должны [ыполняться следующие функции. На первом этапе — определение технического состояния и остаточного ресурса оборудования; выдача информации о техническом состоянии оборудования оперативному персоналу и техническим службам насосных станций. На втором этапе — определение технического состояния и остаточного ресурса работы оборудования; выдача рекомендаций диспетчерскому персоналу по ведению режимов работы с учетом технического состояния оборудования; выдача информации техническим службам ПЭО о сработанном ресурсе оборудования; планирование объемов и сроков ремонтов основного оборудования с учетом его технического состояния; определение потребностей в материально-техническом снабжении ремонтов оборудования; диагностирование технической и психофизической готовности диспетчерского персонала и правильности его действий. На третьем этапе — контроль и управление важнейшими перетоками мощности; контроль автоматики и релейной защиты; выполнение типовых простейших противоаварийных диспетчерских функций.
j На III уровне отрасли должны выполняться следующие функции. Ра первом этапе — выдача данных о техническом состоянии оборудо-гания управлениям по транспорту нефти; определение остаточных ресурсов оборудования и передача этой информации в управления по техническому обслуживанию и ремонту материально-технического снабжения для определения сроков и объемов ремонтов. Второй и третий этапы не рассматриваются.
Пользователями информации ОСДО могут быть: на I уровне — сперативный персонал перекачивающих станций; руководящий персонал (директор, главный инженер); производственно-технический стдел; руководящий ремонтный персонал; на II уровне — руководство управления по транспорту нефти и газа; диспетчерская служба; служба наладки, надежности, испытаний и ремонтов механического, электротехнического и другого оборудования, ремонтные предприятия; централизованный отдел материального снабжения; на III уровне — руководство министерства.
Таким образом, отраслевая система диагностирования должна строиться по иерархическому принципу с центром системы и использованием разнородных вычислительных средств. Только они в состоянии обеспечить учет противоречивых требований по надежности, стоимости, объемам памяти и другим показателям.
Методика создания ОСДО содержит следующие этапы: подготовка j обучение персонала и формирование организационных структур; классификация оборудования отрасли (электрическое, механическое теплотехническое), которое в свою очередь представляется совокупностью объектов; определение необходимых иерархических уровней для каждого вида оборудования при формировании подсистем диагностирования; определение (параметров ) ОД по видам оборудования и его определяющим элементам; определение параметров, по которым можно и нужно прогнозировать фактическое состояние оборудования и изменение которых влияет на прогнозируемые элементы; определение оптимальных объемом измерений ио количеству и месту путем составления диагностических моделей для выбранных конструкций и их обработки на ЭВМ, уточнение критериев диагностирования; определение инструментального обеспечения измерений выбранного параметра, выбор состава вычислительных средств (средств автоматизации) и их программного обеспечения; распределение задач прогнозирования по располагаемым вычислительным средствам; проведение процедур сжатия информации для разных иерархических уровней; выбор или построение модели прогноза для каждой подсистемы прогнозирования и проведение отраслевого прогноза в целом на заданный этап времени; автоматизированное составление планов и объемов ремонтных и реконструктивных работ по результатам прогнозирующего диагностирования с помощью вычислительных средств. Реализация этих принципов осуществляется в сочетании как формальных, так и эвристических процедур с привлечением различных способов математического моделирования трубопроводных систем.
Эффект от применения ОСДО достигается за счет значительной интенсификации технологических режимов ТС вследствие повышения надежности работы оборудования и прежде всего снижения числа вынужденных остановок блоков; научно обоснованного графика ремонтов и оптимального объема ремонтных и реконструктивных работ с целенаправленной концентрацией финансовых, трудовых и материальных ресурсов; оптимизации технологического обслуживания всех объектов отрасли в целом.
1. Агапкин В. М., Кривошеин Б. Л., Юфин В. А. Тепловой и гидравлический расчеты трубопроводов для нефти и нефтепродуктов. М., Недра, 198].
2. Александров А. В., Яковлев Е. И. Проектирование и эксплуатация систем дальнего транспорта газа. М., Недра, 1974.
3. Березина И. В., Ретинский В. С. Оперативное управление системами газоснабжения. М., Недра, 1985.
4. Гидродинамика трубопроводного транспорта нефти и нефтепродук-тов/А. X. Мирзаджанзаде, А. К. Галлямов, В. И. Марон, В. А. Юфин. М., Недра, 1984.
5. Гуревич Г. Р., Брусиловский А. И. Справочное пособие по расчету фазового состояния и свойств газоконденсатных смесей. М., Недра, 1984.
6. Гусейнзаде М. А., Юфин В. А. Неустановившееся движение нефти и газа в магистральных трубопроводах. М., Недра, 1981.
7. Нечваль М. В., Новоселов В. <#>., Тугунов П. И. Последовательная перекачка нефтей и нефтепродуктов по магистральным трубопроводам. М., Недра, 1976.
8. Оптимизация последовательной перекачки нефтепродуктов/М. В. Лурье, В. И. Марон, Л. А. Мацкин и др. М., Недра, 1979.
9. Сложные трубопроводные системы/В. В. Грачев, М. А. Гусейизаде, Б. И. Ксенз, Е. И. Яковлев. М., Недра, 1982.
10. Трубопроводный транспорт газа/С. А. Бобровский, С. Г. Щербаков, Е. И. Яковлев и др. М., Наука, 1976.
11. Тугунов П. И. Нестационарные режимы перекачки нефтей и нефтепродуктов. М., Недра, 1984.
12. Харламенко В. И., Голуб М. В. Эксплуатация насосов магистральных нефтепродуктопроводов. М., Недра, 1978.
13. Чарный И. А. Неустановившееся движение реальной жидкости в трубах. М., Недра, 1975.
14. Щербаков С. Г. Проблемы трубопроводного транспорта нефти и газа . М., Наука, 1982.
15. Эксплуатация газопровода в Западной Сибири/Г. В. Крылов, А. В. Матвеев, О. А. Степанов, Е. И. Яковлев. Л., Недра, 1985.
Авогадро закон 137 Альтшуля формула 105
Бингама уравнение 236 Блазиуса формула 106 Букингема уравнение 283
Вставка 307
Высоковязкие нефти 233, 237, 261 Высокозастывающие нефти 243, 261 Вытеснение нефти 294 Вязкость газа 136
— нефти 102
кинематическая 102, 236
ньютоновская 233, 235
•--эффективная 236
— смеси газов 136
Газ нефтяной 244 Газовая постоянная 138 Газопроводы многониточные 156
— сложные 149
— с лупингами 153
— с подкачками 149
— с путевыми отборами 149 Гидравлический уклон 108
— вставки 109
-- лупинга 108
Гидраты 78
— методы предупреждения образования 83
— состав 78
Горячий нефтепровод 261
--безотказное время остановки
293
---особые режимы работы 291
Грасгофа параметр 263
Давление критическое 140
— приведенное 140
— среднее в газопроводе 148 Дальтона закон 89
Дарси—Вейсбаха формула 104 Депрессаторы 238
Деэмульсация нефти теплохимическая 55, 62
---фильтрацией 61
----электро- 63
Джоуля—Томсона эффект 137 Диффузии коэффициент 193 Диэтиленгликоль 84
Жидкости бингамовские 236
— дилатантные 234
— ньютоновские 234, 236
— пластичные 234
— псевдопластичные 234
Задание на проектирование 21 Затраты капитальные 15, 171 --на линейную часть трубопровода 176
---компрессорную станцию 172
— приведенные 16
-- при водном транспорте 19
---железнодорожном транспорте 18
--- трубопроводном транспорте
Изыскания 33
— геологические 39
— геофизические 39
— гидрогеологические 39
— гидрометрические 40
— климатологические 40
— по водоснабжению 41
— по выбору трассы 33
— по канализации 41
— по организации работ 41
— по энергоснабжению 40
— топографо-геодезические 33 Ингибиторы гидратообразования 84
Клапейрона уравнение 138 Концентрация массовая 137
— объемная 137
Коэффициент гидравлического сопротивления 104, 146
— сжимаемости газа 140
—эффективности газопровода 147 Кривая течения жидкости 235
Ламинарное течение 105, 191 Лейбензона формула 106, 146 Лупинг на газопроводе 154 ---- нефтепроводе 108
Метанол 84
Нагнетатели 12
— характеристики 161 Насоспо-тепловые станции 261
—--расстановка 285
--- увеличение числа 288
Насосные станции 12
вспомогательное оборудование
мощность 134
основное оборудование 12
расстановка 119
увеличение числа 123
Нефтепроводы классификация 8 Нуссельта параметр 263
Обезвоживание нефти 56
механическое 58
термическое 60
химическое 60
—• — электрическое 63 Обессоливание нефти 56 Одоранты 95
Одоризаторы барботажные 96
— капельные 95
— фитильные 96 Одоризация газа 95 Окупаемости срок 16 Оптимальное число циклов 210 Оптимальные параметры газопровода 171
Осушка газа 85
--абсорбционная (жидкими поглотителями) 85
--адсорбционная (твердыми поглотителями) 90
— — молекулярными ситами 91 --низкотемпературной сепарацией 92
-- охлаждением 92
Отвод земель 42
Отключение насосных станций 130 Отстой нефти 58
Очистка газа от механических примесей 72
-- сероводорода 98
-- углекислого газа 98
Парафинистые нефти 235 Пекле параметр 196 Перевальная точка 110 Перемычки 156 Плотность газа 136
— нефти 101
Поверхностно-активные вещества 62, 244
Подготовка к транспорту газа 52
—-----нефти 50
Подкачки 127, 179 Подогреватели 275
— огневые 275
Последовательная перекачка 186 Прандтля параметр (критерий) 263 Присадки — стимуляторы потока 238
Профиль трассы 110, 158 Пуазейля уравнение 283 Пылеуловители 72
— масляные 75
— циклонные 77
Рабочие чертежи 23 Разбавители 237 Разделители 223
— манжетные 224
— шаровые 224
Расстановка станций компрессорных 181
--нефтеперекачивающих 119
Расхода коэффициент 151 Рауля закон 89
Регулирование насосных станций 133
---дросселированием 134
---отключением насосов 134
--- перепуском 135
---- при помощи муфт 135
Рейнольдса формула 236, 270
— число 104, 146, 263 Реологические свойства нефтей 233
Сбросы 127
Сбора нефти система 68
---- напорная 69
----самотечная 68
Свсрхсжимаемость 140 Сдвига напряжение 233
-- начальное 233
--предельное динамическое 233
— скорость 233
Сепаратор гидроциклонный 65
— гравитационный 65
— жалюзийный 65
— типа «расширительная камера» 74 Сепарация нефти и газа 65 Скип-эффект 277 Смесеобразование 191
Смесь первичная 191 Смета сводная 21 Стабилизация нефти 63 Станция газораспределительная 13
— компрессорная 12
— насосная 12
-- головная 12
----промежуточная 12
— насосно-тепловая 274
— перекачивающая 12 -----состав сооружений 12
— теплота 274 Стокса формула 56, 105
Тейлора формула 199 Температура критическая 140
— приведенная 140
Тепловой режим газопровода 143
--- нефтепровода 265
Тепловые станции 264
--расстановка 285
--- увеличение числа 288
Теплоемкость газа 136
— нефти 261
Теплоизолированные трубопроводы 279
Теплоотдачи коэффициент 262 Теплопередачи коэффициент 262 Теплопроводность грунтов 264
— тепловой изоляции 279
— нефти 262
Теплофизические характеристики грунтов 264
--- тепловой изоляции 278
Термообработка нефти 241 Технико-экономическое обоснование 20
Технический проект 21 Технологический расчет нефтепровода 102 Точка росы 80
Транспорт нефти автомобильный 15
— водный 19
— железнодорожный 18 трубопроводный 18
Триэтиленгликоль 84 Трубопроводы, классификация 8
— расчет на прочность 46
— состав сооружений 9 Трубопровод с переменной толщиной стенки 49
Трубы бесшовные 45
— прямошовные 45
— спиралыюшовпые 46 Турбулентное течение 192
Увеличение пропускной способности газопровода 153, 155
--- нефтепровода 123
Удвоение числа станций 123, 155 Удельный объем газа 136 Уравнение движения 140
— неразрывности 140
— состояния 138 Условия нормальные 136
— стандартные 136
Френкеля формула 105
Характеристика насоса 110
---- пересчет на нефть 112
-----сложение 112
—трубопровода 112
Цеолиты 91
Шероховатость стенок труб 104, 146
Шпфрппсоиа формула 107 Шухова формула 145, 267
Электронодогрев 277 Эмульгаторы 53 Эмульсии 52 Этиленгликоль 84 Эффективности коэффициент 147
УЧЕБНИК
Алиев Рустам Аббасович Белоумов Владимир Дмитриевич Немудрое Анатолий Георгиевич и др.
ТРУБОПРОВОДНЫЙ ТРАНСПОРТ НЕФТИ И ГАЗА
Заведующий редакцией Н. Е. Игнатьева Редактор издательства Н. В. Сергеева Технический редактор Е. С. Сычева Корректор Н. А. Громова
ИБ № 6516
Сдано u набор UI.I0.87. Подписано в печать 3l.U5.88. T-0599G. Формат (iOX'JO'/u;. Бумаги книжно-журнальная. Гарнитура Литературная. Печать высокая. Уел. печ. л. 23,0. Уел, кр.-отт. 23,0. Уч.-изд. л. 25,4. Тираж 5340 экз. Заказ 3090/923—5. Цена 1 ]>. 20 к.
Ордена «Знак Почета» издательство «Недра», 125047, Москва, пл. Белорусского вокзала, 3.
Ленинградская типография № 4 ордена Трудового Красного Знамени Ленинградского объединения «Техническая книга» им. Евгении Соколовой Союзполиграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли. №1126, Ленинград, Социалистическая ул., 14.
ПИвЛРеНБЛАТТ В WXHTGB. ам«*жж
ТЕОРИЯ
НЕСТАЦИОНАРНОЙ
ФИЛЬТРАЦИИ
И ГАЗА
ТЕОРИЯ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ ЖИДКОСТИ И ГАЗА
Г. И. БАРЕНБЛАТТ, В. М. ЕНТОВ, В. М. РЫЖИК
те
178174
ИЗДАТЕЛЬСТВО „НЕДРА" Москва 1972
УДК 622.32
Баренблатт Г. П., Ентов В. М., Рыжик В. М. Теория нестационарной фильтрации жидкости и газа. М., «Недра», 1972, с.288-
В книге дана краткая характеристика пористых сред, в которых происходит фильтрация жидкости.
Основное внимание уделено решению задач по нестационарной фильтрации жидкости, газа и многокомпонентных систем. Рассматриваются теоретические предпосылки фильтрации в пористых, трещиноватых и трещиновато-пористых средах. Описаны законы фильтрации смесей различных физических свойств, зависимости вытеснения одних жидкостей другими.
Все задачи решаются применительно к разработке нефтяных, газовых н газоконденсатных месторождений.
Книга предназначена для инженерно-технических работников нефтедобывающей промышленности. Особый интерес она представит для научных работников научно-исследовательских и проектных институтов.
Таблиц 7, иллюстрации 89, список литературы — 162 названия.
0382—031 -
Б

Теория фильтрации изучает движение газов, жидкостей и их смесей в пористых средах, т. е. в твердых телах, пронизанных системой сообщающихся между собой пустот (пор), что делает их проницаемыми для жидкостей
Движение жидкостей и газов в пористой среде имеет ряд особенностей. Пористая среда состоит из огромного числа случайно расположенных зерен различной формы и величины. Поэтому пространство, в котором движется жидкость, представляет собой систему пор, непрерывно переходящих одна в другую. Для пористой среды характерно свойство сообщаемостн пор, ее нельзя представлять себе в виде совокупности капилляров, расположенных обособленно один от другого. Некоторое представление о пористой среде дает фотография шлифа нефтеносного песчаника (рис. 1.1). Характер связи пор между собой виден на фотографии слепка порового пространства (рис. 1.2), заимствованной из книги [58].
Нерегулярный характер структуры порового пространства не позволяет изучать движение жидкости и газов, в нем прямым применением обычных методов гидродинамики, т. е. путем решения уравнений движения вязкой жидкости для области, представляющей собой совокупность всех пор. Такое решение (собственно, даже запись граничных условий зтой задачи), очевидно, связано с непреодолимыми трудностями. Однако в таком решении и нет необходимости: с увеличением числа отдельных мпкродвижеиий, составляющих макроскопическое фильтрационное движение, начинают проявляться суммарные статистические закономерности, характерные для движения в целом и не справедливые для одного порового канала пли нескольких каналов. Возникающая ситуация характерна для систем с большим числом элементов (см. § 1 книги [66]), слабо связанных между собой. Такие системы могут быть описаны как некоторые сплошные среды, свойства которых не выражаются непосредственно через свойства составляющих элементов, а являются осредненными характеристиками достаточно больших объемов среды.
Подобно этому в гидродинамике не рассматривается движение отдельных молекул, а вводятся некоторые осредиенные динамические характеристики жидкости как сплошной среды. При таком подходе гидродинамикой рассматриваются только объемы жидкости, размеры которых достаточно велики по сравнению с межмолекулярными
расстояниями, чтобы в любом объеме находилось достаточно большое число молекул и было бы возможно осреднение 4.
Аналогично теория фильтрации строится на представлении о том, что пористая среда и заполняющая ее жидкость образуют сплошную среду. Это означает, что физически бесконечно малые элементы системы жидкость— пористая среда все же достаточно велики по сравнению с размерами пор и зерен пористой среды; только для объема, в котором заключено большое число пор и зерен, достаточно представительны вводимые осредненные характеристики. В применении к меньшим объемам выводы теории фильтрации теряют силу.
С точки зрения теории фильтрации значение твердого скелета пористой среды прежде всего геометрическое: он ограничивает ту область пространства, в которой движется жидкость. Лишь в более специальных случаях, о которых будет сказано ниже, приходится непосредственно учитывать силовое взаимодействие между скелетом и прилежащими к нему слоями жидкости. Поэтому свойства пористой среды в теории фильтрации описываются некоторым набором геометрических характеристик. Из-за нерегулярности строения поро-вого пространства его нельзя полностью описать никаким конечным набором параметров; для целей теории фильтрации, однако, достаточно небольшого числа осредненных характеристик.
Важнейшая характеристика пористой среды — ее пористость т. равная отношению объема, занятого в выделенном элементе порами, к общему объему элемента:
m = VJV. (1.1.1)
Соотношение (1.1.1) определяет среднюю пористость данного элемента. Выбрав некоторую точку пористой среды, окружая ее элементами все меньшего объема, мы можем определить локальную пористость как предел пористости при стягивании объема. При этом необходимо иметь в виду, что при «стягивании» элемента он все время должен оставаться большим по сравнению с микромасштабом пористой среды (размером пор или зерен). Ситуация здесь вполне аналогична положению в других разделах механики сплошной среды; так, при определении локальной плотности газа размер контрольного объема всегда выбирается большим по сравнению с межмолекулярными расстояниями [см., напр., 95].

Рис. 1.2.
При определении пористости обычно различают полную пористость, в которой учитываются все поры, и активную пористость, при определении которой учитываются лишь те поры, которые входят в единую систему соединенных между собой пор и, следоватёльно, могут
быть заполнены жидкостью извне. Для наших целей важна, естественно, лишь активная пористость; поэтому в дальнейшем под пористостью понимается именно она. Наряду с пористостью т иногда вводится понятие «просветности» п, определяемой для каждого сечения, проходящего через данную точку, как отношение площади пор в сечении ко всей площади сечения. Легко убедиться, что про-светность в данной точке не зависит от выбора направления сечения и равна пористости т [94].
Пористость характеризует форму и взаимное расположение пор и одинакова для геометрически подобных сред. Наряду с пористостью для описания пористой среды необходимо указать также некоторый характерный размер порового пространства d0. Имеется много по существу равноценных способов определения этого размера.
Естественно, например, за характерный размер <f0 принимать некоторый средний размер порового канала d или отдельного зерна пористого скелета I. Чтобы подсчитать эти средине размеры, в каждом конкретном случае исследуется микроструктура пористой среды в некотором достаточно представительном элементе (объема или сечения). Вначале тем или иным способом определяют размер отдельной поры или отдельного зерна. Этот размер меняется при переходе от одной поры к другой или от одного зерна к другому. Поэтому результаты измерений представляются в виде кривой распределения выбранного случайного размера; среднее значение получается как результат некоторого осреднения кривой распределения.
Сами по себе кривые распределения размеров пор или зерен дают значительно больше информации о микроструктуре пористой среды, чем одни средние значения. Поэтому предпринимались многочисленные попытки определения всех геометрических и гидродинамических характеристик пористой среды на основе кривых распределения. Однако зависимости характеристик пористой среды от параметров кривых распределения не могут быть универсальными. Действительно, вводя, например, тонкие непроницаемые перегородки, можно коренным образом изменить гидродинамические характеристики среды, слабо изменив вид кривых распределения. В то же время можно указать ряд процессов (в первую очередь процессы переноса в пористой среде), для которых существенна степень неоднородности составляющих пористой среды — пор и зерен. В этом случае наряду со средним значением размера существенна и его дисперсия, характеризующая степень отклонения от среднего значения; обычно предполагается, что кривая распределения имеет некоторый стандартный вид (например, является логарифмически нормальной) и ее можно полностью охарактеризовать, задав два параметра. Подробные сведения по этому вопросу можно найти в книге |3].
§ 2. ЗАКОН ФИЛЬТРАЦИИ ОДНОРОДНОЙ ЖИДКОСТИ
Фильтрация представляет собой движение жидкости в пористой среде под действием перепада давления Основной характеристикой фильтрационного движения является вектор скорости фильтра-
—^
ции и, определяемый следующим образом. Выберем точку М пористой среды и проведем через нее элементарную площадку AS. Через выделенную площадку в единицу времени протекает масса
жидкости AQ. Тогда проекция вектора и на нормаль к выделенной площадке равна lim AQ/(p AS), где р — плотность жидкости. Под-
as -о
черкнем, что масса жидкости делится на полную площадь AS, а не на ее часть, занятую порами.
Основное соотношение теории фильтрации — закон фильтрации — устанавливает связь между вектором скорости фильтрации и тем полем давления, которое вызывает фильтрационное движение. Некоторые сведения о законе фильтрации можно получить, исходя из самых общих представлений.
Окружим точку цористой среды некоторой малой окрестностью; поле скоростей фильтрации в этой окрестности можно считать непрерывным, а все параметры пористой среды и насыщающей ее жидкости — постоянными. Нельзя пренебречь лишь изменением давления, как бы мало оно ни было, поскольку при постоянном по пространству давлении движение полностью отсутствует (по существу это утверждение является основной гипотезой). Поскольку изменение давления в окрестности данной точки определяется градиентом давления, основное предположение при установлении вида закона фильтрации состоит в том, что вектор скорости фильтрации в данной точке пористой среды определяется свойствами жидкости и пористой среды и градиентом давления grad р. Пористая среда характеризуется геометрическими параметрами — характерным размером d и некоторыми безразмерными характеристиками: пористостью т, безразмерными параметрами кривой распределения и др. Закоп фильтрации должен являться следствием уравнении количества движения жидкости в поровом пространстве, поэтому в систему определяющих величин следует включить также те характеристики жидкости, которые входят в эти уравнения, т. е. плотность р и вязкость |i. Таким образом, предполагается, что существует зависимость градиента давления grad р от вектора скорости
фильтрации и, геометрических характеристик пористой среды т, d и т. д. и характеристик жидкости р и |i. Среди величин, от которых
зависит grad р, только скорость фильтрации и является вектором. В силу изотропии среды (т. е. независимости ее свойств от вращений
и отражений системы отсчета) зависимость grad р от и должна быть инвариантной относительно вращения вокруг направления век-
тора и.
Поэтому вектор grad р должен быть направлен по одной прямой с вектором и. В самом деле, предположим обратное, т. е. пусть вектор grad р составляет некоторый угол с направлением вектора и. Если повернуть выбранную произвольную систему координат отно-
сительно направления вектора и на некоторый угол, то ни вектор и, ни какой-либо другой из определяющих параметров не изменится. Следовательно, не должен измениться и вектор grad р, зависящий только от этих параметров. Но если grad р составляет некоторый
угол с направлением вектора и, то при повороте его направление относительно координатных осей обязательно изменится. Отсюда вытекает, что вектор grad р может быть обращен только по напра-вленпю вектора и, так что
gradp =—си, (1.2.1)
.где с — некоторая скалярная величина, зависящая от модуля вектора скорости и, а также величин d, т, р, р.
Рассмотрим сначала такие фильтрационные движения, для которых несущественны силы инерции. К числу подобных безынерционных движении принадлежит, в силу их крайней медленности, большинство фильтрационных движений, встречающихся иа практике При этом плотность р, характеризующая инерционные свойства жидкости, несущественна и исключается из числа определяющих параметров. Таким образом, при безынерционных движениях величина с зависит только от и, d, т п и. Выпишем размерности интересующих нас величии:
М = -^г; [и]=^; [d]=L\ [р] = -^г; М-1- (1.2.2)
Из пяти величин (1.2.2) можно выбрать три с независимыми размерностями (например, и, р и d). Тогда, согласно зт-теореме, анализа размерностей искомая зависимость будет связывать две безразмерные комбинации указанных величин. В качестве одной из безразмерных величин удобно взять пористость т, в качестве другой выберем cd2/[i. Таким образом, имеем
cd2/p = /(m), c — ^d~2f(m). (1.2.3)
После этого уравнение (1.2.1) может быть представлено в виде:
^ к d% gradp = — nd-zf(m)u или и= — — gradp; & = (1.2.4)
Это соотношение называется законом фильтрации Дарси (по имени французского ученого, установившего его экспериментально в 1856 г.). Величина к = d'2/f(tn), вводимая уравнением (1.2.4), носит название проницаемости. Проницаемость имеет размерность площади; она не зависит от свойств жидкости и является чисто геометрической характеристикой пористой среды.
В физической системе единиц проницаемость измеряется в см2. Однако проницаемость большинства горных пород выражается при этом весьма малыми числами. Так, проницаемость крупнозернистых песчаников составляет 10~8—10_асм2; проницаемость плотных песчаников — около 10“10 см2. Ввидуг этого в нефтепромысловой практике получила распространение единица проницаемости 1 д (дарси) = = 1,02 -10-8 см2.
В практике гидротехнических расчетов вместо давления обычно используется напор Н = p/pg, и закон Дарси записывается в виде:
и=—Cgradff. (1.2.5)
Величина С, имеющая размерность скорости, называется коэффициентом фильтрации.
Напомним, что функция / в выражении (1.2.3) зависит не только от пористости, но и от других безразмерных характеристик геометрии порового пространства. Были сделаны многочисленные попытки представить проницаемость в качестве функции пористости и характерного размера для типичных пористых сред как путем рассмотрения простейших моделей, так и путем обработки опытных данных. Эти вопросы подробно рассмотрены в книге [71]. Все полученные результаты носят частный характер и имеют узкую область применимости. Наибольшей известностью из формул этого рода пользуется уравнение Козени — Кармана, полученное на основе аналогии между пористой средой и системой параллельных трубок, выражающее проницаемость через удельную поверхность 2 и пористость in:
Постоянная К определяется из опыта и оказывается разной для пористых сред различной структуры. Формула (1.2.6) используется главным образом при расчетах 'фильтрационных сопротивлений искусственных пористых сред, применяемых в химических аппаратах; ею пользуются также при определении удельной поверхности порошков.
Как видно из приведенного вывода, закон Дарси является следствием предположения о безынерционности движения жидкости. Фильтрационное течение, следующее закону Дарси, является частным случаем ползущего течения (широко известным примером ползущего течения является стоксовское обтекание сферы). Течепия такого типа характеризуются преобладанием вязких сил над инерционными, т. е. очень малыми числами Рейнольдса (Re «С 1)- Поэтому представляются нецелесообразными многочисленные попытки получить закон Дарси путем осреднения уравнений Навье — Стокса. Ясно, что любой такой вывод будет сводиться в конечном счете к попытке вычислить проницаемость по известной геометрической структуре пористой среды.
Закон Дарси имеет весьма широкую область приложения и на его основе получены основные результаты теории фильтрации. Существуют, однако, случаи, когда линейный закон фильтрации Дарси не применим. Эти случаи, необходимые обобщения закона Дарси и возникающие при этом нелинейные задачи теории фильтрации будут рассмотрены ниже (гл. VIII). Пока же будем считать все рассматриваемые движения подчиняющимися закону Дарси.
До сих пор предполагалось, что пористая среда изотропна. Если пористая среда нс является изотропной, то из общих соображений можно утверждать, что в произвольной ортогональной декартовой системе координат х2, х-л
компоненты вектора grad р выражаются через компоненты и, вектора и следующим образом L:
(1-2.7)
где с/j — некоторый тензор. В случае ‘безынерционных движений компоненты тензора сц могут зависеть только от вязкости жидкости ц, тех или иных геометрических характеристик пористой среды и модуля вектора скорости фильтрации и.
Аналогично выводу формулы (1.2.7) можно показать, что сц = |хгц, где тензор гц зависит только от геометрических характеристик пористой среды и называется тензором удельных фильтрационных сопротивлений; компоненты тензора гц имеют размерность обратной площади. Выражая, наоборот, компоненты вектора скорости через компоненты вектора градиента давления, получаем
с-2-8'
где тензор является обратным тензору гц. также зависит только от геометрических характеристик пористой среды, имеет размерность площади и называется тензором проницаемости. Эта зависимость представляет собой закон Дарси для анизотропной пористой среды.
Покажем теперь, что тензор сопротивлений гц и тензор проницаемости кц являются симметричными, т. е. гц = rjj, кц = Ау/. В самом деле, на пористую среду со стороны фильтрующейся жидкости действует объемная сила, пропорциональная градиенту давления; безразмерный множитель пропорциональности зависит только от геометрических характеристик пористой среды. Удельная работа этой силы, т. е. работа за едиющу времени на единицу объема системы жидкость — пористая среда, равная удельной диссипации энергии жидкостью в пористой среде, равна скалярному произведению
(grad р, и) = -JL и? = - (12-9)
н
Очевидно, что удельная работа спл взапмоденсвия жидкости с пористой средой не должна зависеть от выбора осей координат .тt, х2, х3. Но для того чтобы квадратичная форма r^yiijiy, пропорциональная этой удельной работе, не зависела от выбора системы координат, необходимо и достаточно, чтобы га? = Аналогично можно показать, что А-г3 - к?л.
В приложениях особую роль играет анизотропии естественных пористых сред, связанная с осадконакоплением. В этом случае проницаемости вдоль слоев имеют одно значение, а в перпендикулярном направлении — другое, обычно значительно меньшее. Поэтому одна из главных осей тензора проницаемости — хх перпендикулярна плоскости напластования, а две другие — х1 и х2 можно выбрать произвольно в плоскости напластования. Система .гх, хг. xs будет главпой системой в каждой точке пористой среды; в этой системе имеем
кц = к22 = к: кзз — кц, = *21 = А'зг = А-23 = А31 = к13 = 0. (1.2.10)
Закон Дарси в выбранной системе координат записывается в силу соотношений (1.2.10) следующим образом:
к др _ к др _ t0 др
(1.2.11)
(-1 ’ - II дх2 ' ft (9.!;,
§ 3. ЗАВИСИМОСТЬ ПАРАМЕТРОВ ЖИДКОСТИ И ПОРИСТОЙ СРЕДЫ ОТ ДАВЛЕНИЯ
Поскольку движение жидкости в пористой среде вызывается перепадом давления, окончательная формулировка большинства задач теории фильтрации заключается в составлении дифференциальных уравнений для распределения давления и в установлении соответствующих начальных и граничных условий. Как при составлении зтих уравнений, так и при решении их необходимо знать, как зависят от давления характеристики пористой среды п насыщающей ее жидкости.
1. Рассмотрим прежде всего влияние давления на свойства жидкости — ПЛОТНОСТЬ Р И ВЯЗКОСТЬ |1.
Для капельных жидкостей — воды и нефти — изменения плотности обычно невелики. Встречающиеся в фильтрационных движениях перепады давления (десятки кгс/см2) весьма малы по сравнению с модулями объемного сжатия К9 капельных жидкостей (5-103— 2 • Ю4 кгс/см2). Поэтому для приложении достаточно ограничиться линейной зависимостью
Р<Р) = Ро(1 + ^). (I-3-1)
Следует, однако, иметь в виду, что хотя сжимаемость капельных жидкостей и мала, она играет значительную роль в тех случаях, когда возмущения давления захватывают обширные области (здесь существенно то, что нефтяные залежи обычно граничат с пластовой водой, суммарный объем которой значительно больше объема нефти в залежи; в результате этого расширение воды при снижении давления может полностью компенсировать извлекаемый объем нефти). Зависимостью вязкости капельных жидкостей от давления при изменении давления в тех же пределах можно обычно пренебречь 5.
Фильтрационные движения газа характеризуются тем, что при их исследовании, с одной стороны, почти всегда можно пренебречь изменениями температуры, считая их малыми, а с другой, — тем, что ввиду больших абсолютных значений давления и перепадов считать газ идеальным можно лишь с большой натяжкой. Уравнение состояния газа обычно записывают в виде:
Преимущества такой записи связаны с тем, что для функции s (р, Т), называемой коэффициентом сверхсжимаемости, составлены таблицы и графики, охватывающие ряд практически важных случаев, и имеются простые способы приближенного вычисления ее для газовых смесей [27]. Температуру в этом уравнении обычно можно считать постоянной и рассматривать как параметр. Отклонение г от единицы (газа от идеальности) значительнее для более тяжелых углеводородных газов.
Согласно элементарной кинетической теории газов, вязкость газа не должна зависеть от давления. Это утверждение также не применимо к условиям, характерным для газового пласта. При фиксированной температуре вязкость газа может изменяться на десятки процентов при изменении давления на десятки атмосфер.
2. Рассмотрим теперь вопрос, как зависят от давления жидкости свойства пористой среды — ее пористость т и проницаемость к.
Обе эти величины характеризуют структуру порового пространства, и их изменение в любой точке определяется давлением жидкости и тензором напряжений, действующих в скелете пористой среды. При этом следует отметить, что в опытах определяется их зависимость не от истинных напряжений, действующих в скелете, а от некоторой их части, которую мы назовем фиктивными напряжениями. Для выяснения этого обстоятельства разберем следующую элементарную схему опыта. Пусть (рис. 1.3, а) в цилиндрическом сосуде с площадью поперечного сечення, равной единице, находится некоторый объем пористой среды, в котором содержится жидкость под давлением р. На верхней грани этого объема лежит непроницаемый поршень, по другую сторону которого находится жидкость под тем же давлением р. В силу известного принципа гидростатики — принципа отвердевания — эта система находится в состоянии равновесия. Для выяснения зависимости пористости от нагрузки приложим к поршню дополнительную нагрузку q. Вычислим сжимающее нормальное напряжение, действующее в сечении объема порпстой среды плоскостью, параллельной поршню; для этого составим уравнение равновесия части рассматриваемого объема, ограниченной поршнем и плоскостью сечения (рис. 1.3, б). Пренебрегая силами трения

Рис. 1.3.
о стенки вмещающего сосуда п собственным весом среды и жидкости, получаем
a-f/np=g- р; o=q-i-p(l — т), (1.3.3)
где о — истинное напряжение, действующее в пористой среде (в расчете на единицу площади общего сечения) и, очевидно, не равное приложенной нагрузке q. Изменение пористости в зависимости от давления прн фиксированной нагрузке в целом мало существенное, учитывается отдельно (это изменение обусловливается сжимаемостью материала зерен, составляющих пористую среду, которая мала сравнительно со сжимаемостью пористой среды в целом, так как изменение иористости происходит в основном за счет более плотной упаковки зерен и лишь в очень небольшой мере — за счет их сжатия; если вообще не учитывать сжимаемость материала зерен, составляющих пористую среду, то пористость при фиксированной нагрузке не будет зависеть от давления жидкости). Можно показать также, что при фиксированных напряжениях сг изменение давления жидкости вообще не будет приводить к изменению объема скелета, независимо от того, какова сжимаемость его материала. Таким образом, рассматриваемый опыт дает нам зависимость пористости от нагрузки q, составляющей лишь часть истинных напряжений, действующих п скелете пористой среды:
q = of~ с — р{\ — т). (1.3.4)
Величину of будем в дальнейшем называть фиктивным напряжением.
Важная особенность пористой среды, отмеченная выше, заключается в том, что изменения занятого ею объема могут происходить при весьма малых изменениях собственного объема твердого скелета, почти исключительно за счет его перестройки. Простейшей моделью подобной системы рис. 1.4 может служить пружина, погруженная в воду (рис. 1.4). Объем цилиндрического тела, ограниченного пружиной, практически не изменяется при изменении давления жидкости и может сильно измениться, если приложить по концам противоположно направленные силы. В формулу для вычисления осадки пружины следует подставлять величину истинных напряжений за вычетом слагаемого, обусловленного давлением жидкости.
Аналогичные соображения применимы и в более общих случаях. Таким образом, опыт, поставленный в условиях произвольного нагружения, даст нам зависимость пористости не от тензора истинных напряжений, действующих в скелете пористой среды, а от тензора фиктивных напряжений. Ввиду того что при действии на пористую среду одного гидростатического давления касательные напряжения в пористой среде не возникают, касательные компоненты тензора истинных напряжений и тензора фиктивных напряжений совпадают, а нормальные компоненты отличаются на величину р (1 — т), имеем
Oij = a?i—p(i — m)6iJ (»,/=!, 2,3...), (1.3.5)
где alj — компоненты тензора фиктивных напряжений; a?i — компоненты тензора истинных напряжений; 6t;- = 1 при / = г, 6ц = О при i 4= 7-
Будучи величинами скалярными, пористость и проницаемость могут зависеть только от инвариантов тензора фиктивных напряжений. Следуя Н. М. Герсеванову [37], зависимостью их от второго
гают *, откуда
т~т (©,/?); к = к(©,р); 0
f
^22 С33
Oi-i-OqH-O;
где о{, сг|, ofs — главные нормальные фиктивные напряжения, а 0 — среднее напряжение.
Величину 0 можно связать с давлением р, если рассматривать напряженное состояние в пласте. Пусть Н — глубина залегания пласта, h — его мощность, а р0 — средняя плотность горных пород. Обыкновенно нефтяные пласты располагаются па значительной глубине под дневной поверхностью и их мощность мала сравнительно с глубиной залегания, т. е. h Н. В этом случае удается связать изменение величины 0 с измепепием давления р. В самом деле, лежащие над пластом горные породы поддерживаются скелетом пласта и насыщающей пласт жидкостью, так что вес вышележащих горных пород уравновешивается системой напряжений в пористой среде и гидродинамическим давлением жидкости. Составляющую пласт систему жидкость — пористая среда можно представить себе как некоторую деформируемую систему, касательные напряжения в которой совпадают с касательными напряжениями в пористой среде, а нормальные напряжения равны сумме истинных нормальных напряжений, действующих в пористой среде, и доли нормальных напряжений, воспринимаемых жидкостью (эта доля равняется, очевидно, произведению пористости на давление жидкости). Имеем, таким образом, выражение для компоненты суммарного напряжения СГ; у!
°ij = аЬ 'г mp8if = of,- -f (1 — m) pb4 + тр8и = afy + рб(/. (1.3.7)
Пусть р — суммарная плотность системы жидкость — пористая среда, а gt- — компонента вектора ускорения силы тяжести по оси Тогда уравнение равновесия системы жидкость — пористая среда имеет вид:
, dfyt„ | г\ /т о
•taf - Рй = - + жг = °* (L3-8)
Считая жидкость слабосжимаемой, можно положить в уравнении (1.3.8) р = р*, где р* — постоянное исходное значение суммарной плотности. Таким образом, суммарное уравнение равновесия системы жидкость — пористая среда окончательно записывается в виде:
¦^ + Prfi = 0 (1-3.9)
и, как видно, это уравнение не зависит от времени. Покажем теперь, что и суммарные напряжения на кровле и подошве пласта (т. е. на верхней и нижней ограничивающих пласт поверхностях) можно с большой степенью точности считать постоянными. Физически объяснение этого факта сводится к следующему: упругое смещение, обусловливаемое изменением давления жидкости, насыщающей породу пласта, пропорциональное, очевидно, мощности пласта, распределяется на всю огромную толщину Н вышележащего массива горных пород, так что соответствующие относительные деформации в этом массиве малы и, следовательно, малы возникающие в нем дополнительные напряжения, в частности дополнительные напряжения на кровле и подошве пласта.
Поясним это несколько подробнее. Предположим, что давление жидкости, насыщающей пласт, изменилось по сравнению с исходным моментом на величину бр. Обозначим величину изменения давления жидкости в том месте, где оно максимально, через 6рма1(С. Для поддержания вышележащих горных пород необходимо, чтобы напряжение в скелете пористой среды внутри пласта изменилось также на величину порядка бр. Соответствующая относительная деформация в пласте составила величину порядка бр/Е, где Е — некоторый эффективный модуль Юнга системы, а полное вертикальное смещение точки, например кровли пласта, — величину порядна v — /16р/Е, где h — мощность пласта. Заметим теперь, что, закрепив точки свободной поверхности, т. е. обеспечив на свободной поверхности равенство нулю упругих смещений, а также заменив во всех точках пласта бр на брыакс, мы можем лишь увеличить возникающие дополнительные напряжения. Таким образом, если на свободной поверхности вышележащего массива смещение равно нулю, а на глубине Н оно имеет величину порядка г;накс = h6pMaKC/E, то, очевидно, соответ-ствуюin.ee. напряжение (Тмакс имеет величину порядка сгмаке = = vMSKCE/H. Отношение этого дополнительного напряжения к действующему на глубине Н вертикальному напряжению сжатия *, имеющему порядок р0gH (р0 — средняя плотность горных пород — величина, примерно равная 2,5 г/см3), равно по порядку величины
^Рмакс ^
(1.3.10)
Значение &pkiaKCf(>ogH обычно не превышает одной-двух десятых; величина h/H исчезающе мала, так что изменение напряжения во
всем вышележащем массиве и, в частности, на его границах мало сравнительно с исходным напряжением. Поэтому можно считать, что при изменении давления жидкости в пласте напряжения, действующие на кровле и подошве пласта, остаются постоянными.
Предыдущее рассуждение существенно основано на том, что модуль Юнга системы жидкость — пористая среда Е и модуль вышележащего массива горных пород Ех имеют одинаковый порядок величины (что обычно имеет место в действительности). Если бы эти модули Юнга сильно отличались между собой, то выражение (1.3.10) содержало бы дополнительный множитель EJE и при Ег^> Е отношение напряжений могло бы и не быть малым. Физически это означает, что в случае, когда вышележащая толща сложена из очень жестких пород, могут образоваться своды, и при изменении давления жидкости напряжения на кровле и подошве пласта будут меняться.
Если теперь пренебречь влиянием таких границ области фильтрации, как стенки скважин (зти границы имеют сравнительно очень малую протяженность; их влияние будет оценено ниже), то из независимости от времени уравнений равновесия системы жидкость — пористая среда (1.3.9) и напряжений на кровле и подошве пласта следует важный вывод о независимости суммарного напряженного состояния в системе жидкость — пористая среда от времени, так что
![]()
6(a[j + pbjj) _ G
откуда
(1.3.11)
et
Свертывая уравнения (1.3.11) (т. е. полагая i, ) = 1, 2, 3 и суммируя получающиеся уравнения), имеем
-Щ- (°11 + °22 + °33 + ЗР) ~ 0
откуда вытекает важное соотношение
д(в + р) _ п дв
др_
dt
dt ’ dt
ОСНОВНЫЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ
§ 1. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ
Рассмотрим баланс массы жидкости в произвольном элементе объема пористой среды V, ограниченном поверхностью S. За бесконечно малое время dt приток жидкости внутрь элемента равен согласно определению скорости фильтрации
— dt f рundc=—dt f p (un)da (II.1.1)
s s
(n — единичный вектор нормали; за положительное направление нормали принято направление внешней нормали к поверхности; ип — нормальная к поверхности составляющая скорости фильтрации). Приращение массы жидкости внутри этого элемента равняется
( nwdv^j dt = ^ dv^ dt. (II.1.2)
Приравнивая выражения (II.1.1) и (II.1.2) и используя формулу преобразования поверхностного интеграла в объемный
f рundc = J div (ри) dv,
s V
находим
V
откуда в силу произвольности элемента V и вытекает уравнение неразрывности
-т- 6 div ры^О. (II.1.3)
dt
1. Самым простым и наиболее изученным случаем нестационарной фильтрации является фильтрация слабосжимаемой жидкости в упругодеформируемом пласте (в технических приложениях эти задачи получили название задач упругого режима фильтрации). В основу исследования кладется система уравнений закона фильтрации и уравнения неразрывности:
+ divpu = 0; и=— -^-gradp. (II.2.1)
Для того чтобы получить замкнутую систему уравнений, нужно воспользоваться тем, что свойства жидкости (плотность р и вязкость ц), так же как и пористость и проницаемость пористой среды, являются функциями давления (мы предполагаем движение изотермическим).
В силу (1.3.12) имеем
бр _ 6(i др дт dm дв . dm (>р _/ дт дт \ др
dt др dt ’ dt дв dt * др dt \ др дв / dt
Исходя из предположения о слабой сжимаемости жидкости и пористой среды, можно считать относительные изменения величин р п т малыми и коэффициенты при dp/df в предыдущих формулах постоянными:
др _ Ро <)т дт т0 д (1:/\л) /,-0 . _ 0
др Kf ’ др дв Кт ’ др ц0Лк ' ^
Опытные данные показывают, что в реальных случаях (р — Ро)/Кт<? U (Р — Ро)/кр€ 1 и т. д.
Подставляя второе уравнение (II.2.1) в первое и преобразуя получающееся соотношение с учетом (II.2.2), находим, пренебрегая малыми величинами,
и°р« (4г+тВ-^+^[^рЧ^+лЬ+^)<Bradp)!] - °-
Если др — характерное изменение давления, a L — характерная длина, то первый член в скобках имеет, очевидно, порядок 8p/L2, а второй (6p)2/L2K. Отсюда следует, что вторым членом в принятом приближении также следует пренебречь *. Таким образом, имеем
где коэффициент
ко
Цо'»о
носит название коэффициента пьезопроводности. Уравнение (II.2.3) обычно называется уравнением упругого режима или, по предложению В. Н. Щелкачева, уравнением пьезопроводности. Оно совпадает с хороню известным классическим уравнением теплопроводности.
Постановка задачи об упругом режиме пласта была дана в работах Тейса [160], Джекоба [138] и независимо В. Н. Щелка-чевым [123].
2. Рассмотрим постановку основных задач теории упругого режима. Определим распределение давления р в некоторой замкнутой области пространства D на протяжении промежутка времени 0 ^ t ^ Т. Из теории уравнения теплопроводности известно, что если задать на границе Г области/) линейную комбинацию давления и его производной по нормали к границе области
ар+Р J г = / (^, У, z, t) (II.2.5)
и задать начальное распределение давления в области D
р(х, у, z, 0) = ф(ж, у, z), (II.2.6)
то существует распределение давления р (х, у, z, /), и притом единственное, удовлетворяющее уравнению (II.2.3), непрерывное в замкнутой области D, включая границу, и удовлетворяющее условиям
(II.2.5) и (II.2.6).
Сформулированная задача охватывает почти все основные задачи теории упругого режима фильтрации.
Рассмотрим подробнее физический смысл тех или иных дополнительных условий.
Область, в которой ищется распределение давления жидкости, обычно представляет собой пористый пласт, частично имеющий непроницаемые границы, а частично сообщающийся с другими пластами и вскрывающими его скважинами. На непроницаемых границах должно удовлетворяться очевидное условие отсутствия потока — равенство нормальной компоненты скорости фильтрации нулю:
= 0,
-откуда, используя закон Дарси, получаем
(gradp)„ = -g- = 0. (II.2.7)
На участках границы с областями, в которых перераспределения давления практически не происходит («области питания»), давление можно считать постоянным и известным, так что
Такое условие справедливо, если, например, рассматриваемый пласт граничит с высокопроницаемой областью, запас жидкости в которой весьма велик. Давление на границе такой области близко к среднему давлению в ней и ввиду ее большого объема мало зависит от процессов, происходящих в исследуемой области. Характерным примером является нефтяная залежь, окруженная со всех сторон обширной водоносной областью.
При рассмотрении нестационарных процессов в залежи давление в водоносной области можно считать постоянным. Следует, однако, отчетливо представлять себе, что понятие области постоянного давления не является абсолютным. Чем более длительный характер носят изменения давления, тем на большую область они распространяются.
Часть границы области фильтрации обычно образована стенками скважины или дренажных галерей. На этой части границы чаще всего задается либо давление жидкости, либо поток ее через стенки скважины. Выбор того или иного условия зависит от режима работы скважины или галереи. Могут быть и более сложные условия, когда задается связь давления с расходом жидкости. Задание потока жидкости согласно закону Дарси эквивалентно заданию нормальной производной от давления.
Условия этого типа выполняются на тех участках, границы, через которые может происходить обмен жидкости с соседними пластами через сравнительно слабопроницаемые перемычки. Если толщина перемычки А мала, а давление р' за ней можно считать постоянным, то расход вытекающей жидкости через участок перемычки
площадью ds составит
¦- ¦ ^P~J>
^ds ¦ Это количество
жидкости
г' ^
должно оыть равно
urds = —^Ads.
11 цсм
где ип — нормальная проекция скорости фильтрации на рассматриваемом участке границы. Отсюда имеем
т. е. условия третьего рода.
Все три типа условий являются частными случаями общего условия (II.2.5). Таким образом, задавая начальное распределение давления и указанные условия на границе, получаем однозначно разрешимую задачу.
§ 3. УРАВНЕНИЯ БЕЗНАПОРНОЙ ФИЛЬТРАЦИИ НЕСЖИМАЕМОЙ ЖИДКОСТИ
Рассмотрим безнапорное движение в однородной и изотропией пористой среде, область течения будем предполагать ограниченной снизу непроницаемой и криволинейной поверхностью — водоупором.
Закон Дарси в рассматриваемом случае можно записать в виде:
и=—Cgrad&; h — z-i-p/pg. (11.3.1)
Величина С, имеющая размерность скорости, называется коэффициентом фильтрации, h — напором, а функция С к — фильтрационным потенциалом. Заметим, что для безнапорного движения изменения давления обычно настолько малы, что пористую среду можно считать недеформпруемой, а жидкость несжимаемой, так что С = const, pg = const.
В точной постановке исследование безнапорного фильтрационного движения представляет исключительные трудности математического характера; относящиеся сюда постановки задач и результаты можно найти в книге П. Я. Полубариновой-Кочиной [94]. Поэтому приходится обращаться к некоторым упрощенным постановкам.
Большое значение имеет приближенная постановка задачи о безнапорной фильтрации, соответствующая случаю движения, которое будем называть пологи м. Под пологим фильтрационным движением понимается движение, происходящее в пластах с конечной глубиной водоупора, в котором вертикальная компонента скорости фильтрации иг мала сравнительно с горизонтальной компонентой. Так как характерной скоростью в безнапорном фильтрационном движении является скорость С, то горизонтальная компонента скорости фильтрации может быть либо порядка С, либо малой сравнительно с С. В обоих случаях ясно, что вертикальная компонента игмала сравнительно с С, т. е.
Это неравенство можно переписать еще так:
Но представляет собой ту часть вертикальной компоненты
градиента давления, которая обусловлена фильтрацией жидкости. Неравенство (II.3.3) показывает таким образом, что вертикальная компонента фильтрационного градиента давлепия мала сравнительно с гидростатическим градиентом давления. Поэтому распределение давления по вертикали можно в случае пологих движений считать гидростатическим.
Выведем важное для дальнейших рассуждений соотношение. Рассмотрим объем V, ограниченный свободной поверхностью жидкости и некоторой цилиндрической поверхностью с вертикальными образующими. Обозначим через h расстояние от свободной поверхности жидкости до водоупора. а через Н — расстояние от свободной поверхности до горизонтальной плоскости z — О (рис. II.1); очевидно, dhjdt = dHjdt. Объем жидкости, заключенной в объеме V, равен
J mhdS,
(II.3.4)
где площадка S представляет собой проекцию объема на горизонтальную плоскость (см. рис. II.1). Изменение количества жидкости
в объеме V за бесконечно малый промежуток времени dt равно поэтому
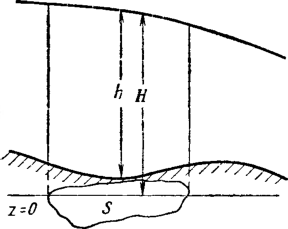
\s ' s
Вместе с тем это изменение равно притоку жидкости в объем V извне за время dt, равному
н
— dt \ dl j" undz= —dt | wndl,
V II -h V
Рис. II.1
где у — замкнутый контур, ограничивающий площадку S, а ип -нормальная компонента скорости и; wn — нормальная компонента вектора потока и>, определяемого соотношением
и
w = I udz. н-ъ
(II.3.7)
Приравнивая (II.3.5) и (II.3.6) и используя формулу преобразования контурного интеграла в интеграл по площади
§wndl = fdivu?d,S,
V S
получаем
i +Aiyw)ds = 0,
(11.3.8)
откуда, пользуясь произвольностью площадки S, находим уравнение
dh , п т. — -f- div w = 0. at
(II.3.9)
Согласно закону Дарси, скорость фильтрации определяется соотношением (II.3.1).
Поскольку, по предыдущему, давление распределяется по вертикали с точностью до малых величин по гидростатическому закону, величина h вдоль каждой вертикали будет постоянна и равпа Н:
h(x, у, z, t) — Н(х, у, z, t)+0(uJC); и= —С grad #-j-0 (i/z).
->¦
Таким образом, скорость и можно, пренебрегая малыми величинами, вынести из-под знака интегрирования по вертикали в соотно-
тении (II.3.7), определяющем вектор w. Тогда получаем
W——CTtgrad Н. (II.3.10}
Подставляя (II.3.10) в (II.3.17), имеем
^- = -?- div (h grad Н). (11.3.11)
В это уравнение следует подставить соотношение
Н {х, у, t) = h (х, у, t) hQ (х, у),
определяющее вертикальную координату свободной поверхности Н через ее расстояние h до водоупора и расстояние h0 от водоупора до плоскости отсчета z = 0; получим окончательное уравнение для определения h. В частности, если поверхность водоупора представляет собой горизонтальную плоскость, то ее можно принять за
плоскость отсчета и, следовательно, h0 (х, у) можно считать равным нулю. Тогда Н = h, и уравнение (II.3.11) принимает вид:
«=|г=-?г- <П-3',2>
Уравнения (II.3.11) и (II.3.12) были даны Бусспнеском [133].
§ 4. ОСНОВНЫЕ УРАВНЕНИЯ ФИЛЬТРАЦИИ ГАЗА
При исследовании фильтрации газа основное значение имеет тот факт, что сжимаемость газа обычно на несколько порядков превышает сжимаемость пористой среды. С учетом этого обстоятельства в уравнении неразрывности
дтр
dt
изменением пористости т во времени можно пренебречь, так что получим
т ~ -{- div ри = 0. (II.4.2)
Для того чтобы получить замкнутую систему уравнений, снова
нужно использовать связь плотности газа р с его давлением р п тем
пературой Т:
поэтому в задаче появляется новая переменная Т, и для замыкания системы уравнении нужно добавить еще одно уравнение — уравнение энергии. Однако, если в среде отсутствуют источники выделения пли поглощения энергии, то изменения температуры в процессе движения газа к > айне малы, и при расчете поля давления газа ими можно пренебречь. Это обстоятельство легко понять, если учесть, во-первых, крайнюю малость скорости фильтрации и, во-вторых, наличие теплового балласта — скелета пористой среды, эффективно, подавляющего изменения температуры. Будем поэтому считать, что
9 = Р(р,То) = р(р), (ПАЛ)
где Т0 — постоянная температура.
Присоединяя к уравнениям (II.4.2) и (II.4.4) уравнение закона фильтрации (предполагаемого линейным)
и= — у grad р, (II.4.5)
получаем замкнутую систему уравнений. Исключая скорость фильтрации, имеем
m-~- = A'div gradp^. (II.4.6)
В уравнении (II.4.6) р — известная функция давления. Аналогично и вязкость газа, зависящая в общем случае от давления и тем
пературы, может быть представлена в виде:
И = М>(Р, T0) = ii(p). (И-4.7)
Таким образом, п вязкость может считаться известной функцией одного лишь давления.
Введем теперь функции
О
Уравнение (II.4.6) принимает при зтом вид:
^- = х(Р)АР. (II.4.9)
Можно показать, что уравнение для давления сохранит форму (II.4.9) п в случае, если учитывается деформируемость пористой среды, т. е. зависимость от давления пористости и проницаемости (среда по-прежнему считается однородной).
В простейшем случае, когда газ можно считать термодинамически идеальным, с вязкостью, не зависящей от давления,
![]()
(II.4.12)
![]()
и уравнение (II.4.9) преобразуется к виду:
или
(II.4.13)
Уравнения (II.4.12) и (II.4.13) выведены в предположении постоянства температуры газа Т0. Поэтому их обычно называют уравнениями изотермической фильтрации газа.
Уравнение (II.4.13) — основное для теории фильтрации газа — получено впервые J1. С. Лейбензоном [70], а затем, несколько позднее, в работе Маскета и Ботсета [148]. Преобразование (II.4.8) также берет свое начало от работ J1. С. Лейбензона. Поэтому будем называть функцию Р (р) функцией Лейбензона. Далее уравнение
(II.4.13) совпадает с уравнением Буссинеска (II.3.12) для напора при пологих безнапорных фильтрационных движениях. Эта аналогия, впервые обнаруженная Л. С. Лейбензоном, позволяет рассматривать исследование изотермической фильтрации газа и пологих безнапорных движений несжимаемой жидкости как одну задачу.
§ 1. ОДНОМЕРНОЕ ПРЯМОЛИНЕЙНО-ПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ
Под упругим режимом фильтрации, как уже упоминалось выше, понимается фильтрация упругой слабосжимаемой жидкости в упругой пористой среде. В этих условиях распределение давления описывается классическим уравнением теплопроводности (II.2.3). Хорошо разработанная техника решения этого уравнения при различных начальных и краевых условиях применима и к задачам теории упругого режима. Разнообразные конкретные решения могут быть заимствованы, например, из руководства Карслоу и Егера {54] и из других источников. Однако задачи теории фильтрации имеют свою специфику, связанную с наличием некоторых малых параметров (например, отношения радиуса скважины к размеру пласта), которая в ряде случаев существенно упрощает решения. Поэтому приводимые ниже примеры предназначены не только проиллюстрировать постановку и способы решения основных задач, но и обратить внимание на эту специфику, отличающую эти задачи от задач теплопроводности.
Читатель, заинтересованный в ознакомлении с другими аспектами теории упругого режима, может обратиться к книгам [124, 125, 3, 38], где рассмотрено большое число задач, от самых простых до весьма сложных задач движения в неоднородных пластах.
1. Рассмотрим движения жидкости, для которых скорость параллельна оси х и не зависит от координат у и z. Давление при этом удовлетворяет уравнению
* = <)=:*«?. (III.1.1)
Наиболее интересны случаи, для которых в начальный момент движение в пласте стационарно. Поскольку стационарное распределение давления также удовлетворяет уравнению (III.1.1), удобно отсчитывать давление в каждой точке от стационарного значения ро (х). Введенная таким образом разность Р — р — р0 удовлетворяет уравнению (III.1.1) с нулевым начальным условием
Р(х, 0) = 0. (III.1-2)
Предположим, что в плоскости х = L давление сохраняет постоянное значение, равное начальному:
Р (L, f) = 0. (III. 1.3)
Такое условие выполняется, если, например, рассматриваемая область граничит с обширным хорошо проницаемым водоносным пластом. Обозначим через / (t) функцию, описывающую изменение давления в начальном сечении х = 0. Чтобы получить решение уравнения (III.1.1) при указанных начальных и краевых условиях, применим к нему преобразование Лапласа [42, 43, 63]:
ОО
L {Р{х, 0} = Р(х, о)= J е~,сР (х, t)dt, (III.1.4)
о
в результате чего для трансформанты Р получим уравнение
при граничных условиях
P(0) = L{f(t)}=F(o), P(L) = 0. (III.1.6)
Искомое решение уравнения (III.1.5) имеет вид:
P = F (a) ib
• (III.1.7)
sh (L У а/у.)
Кроме распределения давления в пласте для приложений обычно важно знать также поток жидкости через начальное сечение пласта
х = 0 и через удаленную границу (контур питания L).
Расход жидкости, приходящийся на единицу площади, равен
Используя (III.1.7), получаем для трансформанты Q выражения W (О) Ctb(?/!);
Соотношения (III.i.7) и (ITT.1.9) дают решение поставленной задачи, если воспользоваться общей формулой обращения для преобразования Лапласа:
у—i со
Р (х, t) = J P(x,o)ealde, Y>0. (III. 1.10)
У~г оо
2. Применение такого операционного метода к задачам упругого режима удобно в том отношении, что позволяет легко исследовать асимптотическое поведение полученного решения при больших н малых значениях времени, даже не выписывая его полностью. Это обстоятельство особенно важно применительно к сложным задачам, для которых эффективное осуществление обратного преобразования затруднено. Кроме того, око дает значительные упрощения при решении обратных задач, когда речь идет об определении гидродинамических характеристик пласта по данным измерений давлений п расходов (ср. § 4).
Из формул преобразования Лапласа (III.1.4) и (III.1.10) непосредственно видно, что поведение решения при малых значениях времени t определяется асимптотикой изображения при больших о \ и обратно — поведение преобразованной, функции при малых и | определяет асимптотику оригинала при больших t.
Различные приемы определения асимптотик и их обоснование можно найти в книгах [42, 631.
Конкретизируем теперь вид функции / (t), приняв ее равной постоянной р°. При этом предполагается, что в начальпый момент давление на границе пласта принимает новое фиксированное значение; при этом F = р°!а. Из (III.1.7) и (III. 1.9) имеем

(Ш. 1.;11)
Рассмотрим вначале поведение решений при малых временах, т. е. будем рассматривать (III. 1.11) при больших |а|. Выразим в (III. 1.11) гиперболические функции через показательные и, считая
![]()
2Ьу ^ > 1, разложим эти выражения в ряды по степеням е
Тогда
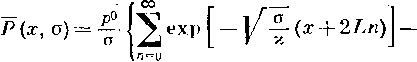
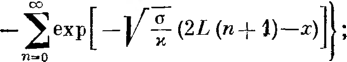
Q (U) = ~ {2 [exp( “ 2Ln Vt) + exp ( - 2L (n -M) Y-?-)]J .
(III.1.12)
Производя почленное обращение рядов (III.1.12) (соответствующие формулы обращения выводятся, например, в книге М. А. Лаврентьева и Б. В. Шабата [63], гл. 6, § 1), имеем
СО
р (х, о=р°2 [erfc -erfc ' (1пллз)
¦» — п -*
ОО
Q (0) = - кр°
V -я уЛ
п-1
3. Полученные ряды, как нетрудпо убедиться, сходятся при всех t и х. Допустим вначале, что рассматриваются малые времена
L~
и 1. Тогда в выражении для Р (х, t) можно все значения erfc
заменить их предельными erfc 00 = 0, за исключением члена ряда
erfc ——=-. Аналогичным образом в выражении для Q (0) все члены 2 V xt
ряда обращаются в нуль. Имеем
Р(х, f) = p«erfc—$=-; Q (0)=--к^=. (III.1.14)
2 I xf (I V яуЛ
Полученные формулы имеют двоякий смысл. С одной стороны, они описывают распределение давления в пласте конечной длины L при малых временах v.t L2. С другой стороны, они дают распределение давления в произвольный момент времени в пласте «бесконечной» протяженности L -*¦ оо. Дело в том, что конечное (не бесконечно-малое) изменение давления распространяется за заданное время лишь на конечное расстояние, и, если рассматриваются малые времена, можно считать пласт бесконечным. Решение задачи для бесконечного пласта автомодельпо: независимые переменные х и t входят в решение не порознь, а лишь в комбинации xj~\fnt. Автомодельность решения является простым следствием отсутствия в постановке задачи постоянных, из которых можно образовать величины размерности длины или времени. Автомодельные решения будут подробно рассмотрены ниже (гл. IV).
Уравнение теплопроводности (III.1.1) является линейным и в силу этого допускает суперпозицию решений. Это позволяет, используя приведенное выше решение для скачкообразного изменения давления в начальном сечении пласта, построить решение, отвечающее произвольному граничному условию
и обращающееся в нуль при / — О и зс = L (интеграл Дюамеля):
t
t-j)dj. (III.146)
О
В частности, для бесконечного пласта
t t d> <т> ___* .. w,. п -__к _ С df <т> dT
О ‘ о
(1114.17)
Если задано не давление, а расход через концевое сечение бесконечного пласта
<?(0) =<?(<), (III.148)
то решение, как нетрудно показать тем же способом, имеет вид:
о
4. Решение (III444) представляет «тепловую волну», распространяющуюся с момента t = 0 из точки х — О в положительном направлении оси х. Поэтому выражение (III. 143) можно рассматривать как результат суперпозиции тепловых волн той же амплитуды рп, распространяющихся из точек х = —2Ln вправо и из точек х — = 2Ln влево, начиная с того же момента времени, причем волны, распространяющиеся влево, имеют обратный знак. Такому толкованию можно придать простой физический смысл. Попытаемся удовлетворить уравнению (III. 1.1) и поставленным краевым условиям при помощи решений типа тепловой волны. Очевидно, все такие решения удовлетворяют начальным условиям. Чтобы удовлетворить условию при х = L, добавим к решению (III. 1.14) тепловую волну, исходящую из точки х = 2L в отрицательном направлении осп и имеющую обратный знак:
Afc, f) = -P°erlc^=^. (III4.20)
2 \ ytt
В силу симметрии очевидно, что суммарное решение обращается в нуль прн х — L. Однако при х = 0 построенное решение уже не равно точно р°. Чтобы скомпенсировать невязку, вызванную второй тепловой волной, добавим третью волну того же знака и направления, что и первая, п исходящую из точки х — —2L. При этом возникает невязка в граничном условии при х = L, для компенсации которой придется добавить обратную волну пз точки х = 4L и т. д. Нетрудно видеть, что таким путем мы придем к решению (1114.13). Отсюда ясно, что пока рассматриваемые значения времени не слишком велики, достаточно ограничиться учетом волн от нескольких ближайших к рассматриваемой точке источников [зто, конечно, легко увидеть и непосредственно из (III.1.13)]. Таким путем можно получить простые выражения для достаточно длительного начального периода движения.
5. Рассмотрим теперь противоположную асимптотику: t
В этом случае выражение (III.1.13) неудобно тем, что приходится суммировать много членов ряда. Чтобы получить решение в более удобной форме, обратимся вновь к соотношению (III.1.7), полагая в нем опять / = р°. Используя формулу обращения (III.1.10), имеем
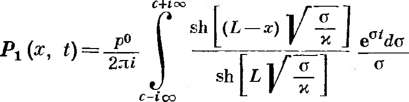
; С> 0. (III.1.21)
Подынтегральное выражение убывает при | а оо. Это позволяет обычным приемом перейти к интегрированию по прямой, параллельной мнимой оси, но лежащей левее ее, добавив вклады от полюсов подынтегрального выражения, лежащих между прямыми. Полагая поэтому л2у.Ь~2 < —сг < 4jt2xL~2, имеем
Рг(х, 0 = p°(l—J-)--^Sin[«(l—J-)]exp(—^) +
![]()
Первый член выражения (III.1.22) представляет собой стационарное решение, отвечающее заданным краевым условиям; второй член выражает основную, при больших временах, часть поправки к этому стационарному решению; наконец, последний член мал даже по сравнению с первым поправочным членом. Таким образом, приближение к стационарному режиму происходит экспоненциально, причем характерное время выхода на стационарный режим — порядка '
r — L2x 1 2.
(III.1.23)
Оценим это время для систем различных размеров. При этом для х примем характерное значение х = 104 см2/сек. В результате имеем: при L = 1 м (переходный процесс в одном куске-блоке породы) т = 0,1 сек; при L = 300 м (порядка расстояния между скважинами) т = 104 сек 3 ч; L = 10 км (порядка размеров месторождения) т = 107 сек = 100 суткам; L = 100 км (порядка размеров крупной водонапорной системы) т = 109 сек = 30 лет. В практических задачах часто приходится рассматривать нестационарные процессы в сложных системах, в которые входят элементы с различными собственными временами. Оценивая время установления (стационарного течения) для каждого элемента по его размерам, мы упростим задачу, отделив те элементы, движение в которых уже можно считать стационарным, и те, в которых нестационарный процесс находится в начальной стадии.
§ 2. ОСЕСИММЕТРИЧНЫЕ ЗАДАЧИ И ЗАДАЧИ ИНТЕРФЕРЕНЦИИ СКВАЖИН ПРИ НЕУСТАНОВИВШЕЙСЯ ФИЛЬТРАЦИИ
1. Рассмотрим теперь одномерное осесимметричное (плоско-ра-диальное) движение при упругом режиме. Распределение давления определяется при этом как решение уравнения теплопроводности в полярных координатах (г, ©):
удовлетворяющее начальному условию
р(г, 0) = /(/¦) (III.2.2)
и граничным условиям при г = р и г = R.
По-прежнему основной интерес представляют решения, отвечающие стационарному начальному распределению давления / (г) = = Сх In г + С*. В силу линейности уравнения (III.2.1) отклонения распределения давления от стационарного также удовлетворяют уравнению (III.2.1), но уже с нулевым начальным условием. Поэтому примем далее / (г) = 0, понимая иод р отклонение давления от стационарного распределения.
Переходя в уравнении (III.2.1) к лапласовым изображениям, получаем уравнение
общее решение которого имеет вид:
P(r, o) = C1/0(rj/‘^-) + Cg/i:0(r|/'-2-), (IH.2.4)
где /„ и К0 — модифицированные функции Бесселя от мнимого аргумента нулевого порядка. Задавая два граничных условия, мы можем определить постоянные Съ С2, а вместе с ними и решение.
2. В приложениях особое значение имеет задача, в которой на скважине задается не постоянное давление, а постоянный дебит. Решение этой задачи используется в наиболее распространенных способах определения параметров пласта по наблюдениям нестационарного притока к скважине. Положим таким образом
где р* — постоянная размерности давления. Удовлетворяя граничным условиям, получим для изображения распределения давления
Р(о)
| А'о| |
)'°(г | |||||||
| м | 4 | 'Ю |
Ко (л | *] | ('] | 1-^) | ||
рС
(III.2.6)
Рассмотрим «промежуточную асимптотику»
\ xt V xt
что позволяет упростить выражение (III.2.6), полагая
Прп больших значениях аргумента z модифицированные функции Бесселя имеют асимптотические выражения {26, 129]
/0(s)~-|=-e‘; A^(z)=]/'^e-z. (Ш.2.7)
г 2л2 f Zz
В зтом случае граничное условие на внешнем контуре оказывается несущественным, и мы имеем решение для неограниченного пласта:
Р*Ух к°(г /т)
Р(г, о)=—ЧЛ—-гЩ-. (III.2.8)
ра/2 А’
Упростим теперь выражение (III.2.8), используя неравенство Vу, t и асимптотические формулы для Кг (z) и К{] (г) при г -> 0:
К0(2)=- (с + 1и|) “ (III.2.9)
(С = 0,7772 — постоянная Эйлера).
Подставляя (III.2.9) в (III.2.8), получаем
Р(г, о)= —(г]/-?-), (ш.2.10)
в частности, для давления в скважине
Р(Р, a)=-^(c + lnp^). (III.2.11)
Отметим важное обстоятельство: в соотношения (III.2.10)
и (III.2.11) не входит радиус скважины р. Это означает, что в области применимости условия p2/y,t 1 распределение давления не зависит от радиуса скважины.
3 Заказ 1865 33
Используя таблицу преобразований Лапласа (см., например, [26, формула 5.16 (35)], имеем
(1/сет) ^>-А-ехр(-^-). (III.2.12)
Отсюда, используя связь между преобразованиями Лапласа функции и ее производной [формула (С. 3) приложения], получим
t оо
J^exp(-^)dT = l J e-s-^ =
0 aj it
Полагая теперь в соответствии с (III.2.10) а = г2/х, получим
р(г, !) = ip.Ei(-?r)-iat-Ei(-?r). (Ш.2.14)
Выражение для давления в скважине р (р, t) можно непосредственно получить из выражения (III.2.11), по таблицам преобразования Лапласа или используя известную асимптотику интегральной показательной функции
Ei( — х) = С - 1пж ... (III.2.15)
При этом получим
(III.2.16)
Последнее выражение широко используется при интерпретации результатов исследования скважин (см. § III.4).
3. Рассмотрим теперь простейшие задачи интерференции скважин при неустановившемся движении. Интерес к этим задачам связан с тем обстоятельством, что на любом месторождении имеется большое число скважин, объединяемых в более или менее правильно расположенные группы (батареи), причем режимы всех скважин в батарее обычно являются примерно одинаковыми. При расчете удобно заменять батарею однотипных скважин дренажной галереей или укрупненной скважиной: группа дискретных стоков (источников) заменяется одним распределенным.
Пусть имеется бесконечная цепочка скважин, расположенных на расстоянии 2а друг от друга вдоль прямой, которую мы примем за ось х. Предположим, что вначале движения не было, а при t = О из всех скважин начинается отбор с одинаковым дебитом q. Рассмотрим изменение давления в точке с координатами х, у, где для определенности считается, что \х \ <L а. у >0и что одна из скважин расположена в начале координат. Считая, что радиус скважины мал по сравнению с расстоянием между соседними скважинами 2 а, воспользуемся упомянутым в предыдущем пункте выражением для давления, получаемым из автомодельного решения.
Имеем
оо
П*=—со
Практический интерес обычно представляют два вопроса: темп снижения давления в скважинах цепочки и темп снижения давления на большом удалении от цепочки. Положим поэтому сначала у с. Вычислим давление в точках, лежащих на оси у. Имеем
ОО
рл •)-**• 2н(-.й2*-)-
/2=-СО
00 оо
1 п= 1
Последнее выражение можно преобразовать, используя тождество [41, № 552, 61:
оо СО
Имеем
P(0,V)=-jP* $ехр(-^)-^
а2
nnt
СО CXJ
-P* 1ехр(-^)2ехр(-^)т7;• (IH.2.20)
O* ft=l
31 v.t
В последнем интеграле, в силу быстрой его сходимости на нижнем пределе, можно интегрирование вести от нуля, После этого результат почленного интегрирования ряда может быть найден достаточно просто. Имеем (например, непосредственно по таблицам преобразо вания Лапласа)
о
В результате второй интеграл в уравнении (III.2.20) представляется в виде интеграла от геометрической прогрессии. В первом же интеграле удобно выделить не убывающие при f -> оо члены. После указанных преобразований имеем
Р (0, 0) = Р*[ - + ^ + In (1 -emj!a) + о (1)].
(III.2.22)
Напомним, что формула (III.2.22) описывает распределение давления вдоль линии, проходящей через ось одной из скважин и перпендикулярной оси батареи, при достаточно больших временах 4xt у2, 4х< > а2.
Мы видим, что вдали от скважипы (при у а) последний член выражения (II 1.2.22) несуществен, первые же два члена этого выражения, если учесть условие у2 4уЛ, совпадают с выражением для падения давления при пуске галереи с дебитом д/4а в расчете на единицу площади галереи. Практически этим выражением можно пользоваться уже начиная с у = а.
Представляет интерес выяснение того, каким образом давление меняется вдоль линий, параллельных оси галереи. Непосредственно очевидно, что
Р(0, У)^Р(х, у)^р{а, у),
(III.2.23)
откуда легко получить величину колеоания давления вдоль линии у = const. Имеем
[СО СО “I
ft—-СО ft—-СО J
Если обозначить временно через р'а распределение давления, определяемое формулой (III.2.22), то
+
+f-+m
0(1)
(III.2.24)
Р(а, У) = р’с_~р'а = р*
| 1 —ехр | | с»**: |
), |
| 1 — ехр | |
- j |
V ml
Сравнение выражений (III.2.22) и (III.2.24) дает
1-е а
Таким образом, по мере удаления от батареи скважин различие давлений между отдельными точками прямой у = const быстро исчезает и уже при у = а им можно пренебречь.
Полученные результаты показывают, что вне полосы |у|^а движение можно с высокой степенью точности считать одномерным; напротив, внутри этой полосы существенна неодномерность движения, связанная с наличием точечных стоков (скважин) вместо распределенных.
Вычислим, используя формулу (III.2.22), давление в скважине, положив у = р (р а — радиус скважины). Имеем
Р( О, Р) = -Р* (-^ - In -f- +...). (III.2.26)
Выражение (III.2.26) показывает, что давление в скважине отличается от давления на галерее с тем же дебитом на единицу площади
сечения пласта лишь постоянным слагаемым р* Это обсто
ятельство позволяет вести расчет батарей скважин так же, как и рас-счет галерей, добавляя к перепаду давления величину р* In •
Соответствующий метод («метод фильтрационных сопротивлений») разработан Ю. П. Борисовым [33] первоначально для стационарного движения; его применение к нестационарным процессам дано в работе [113]. Метод сводится к тому, что сопротивление притоку к скважинам разбивается на два соединенных последовательно: внешнее сопротивление, отвечающее движению вне галереи, и внутреннее, определяющее разность давлений между скважиной и фиктивной галереей. Применительно к нестационарному движению особо важное упрощение достигается благодаря тому, что нестационарность следует учитывать лишь для внешнего давления; добавочное сопротивление при переходе от скважины к галерее можно считать постоянным.
§ 3. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ЗАДАЧИ УПРУГОГО РЕЖИМА
Рассмотрим теперь несколько более сложных задач, имеющих существенное значение для приложений.
1. Предположим, что плоский пласт состоит из двух областей с различными свойствами (проницаемостью, пористостью и т. д.), разделенных прямолинейной границей (рис. III.1). Пусть в момент t — 0 первоначально стационарное состояние возмущается в результате пуска скважины в точке (а, 0) с постоянным расходом д. Тогда распределение давления в каждой из областей описывается уравнениями
На границе х — О выполняются условия непрерывности давлений и потоков:
р(*-0,
Й-Мх+О, у)-,
К°1М±±Л=К»<*-<>.
¦».
дх
(III.3.2)
Во втором уравнении (III.3.1) в правую qaCTb непосредственно введен точечный источник интенсивностью q. Через б, как обычно, у обозначена дельта-функция, опреде
ляемая условиями (см., например. [106])
-вГ-Н со
\ kt,x, ) 6(t)f(t)dt = f(0); б(5) = 0;
-•-— СО
Т X
(III.3.3)
а + о).
Применив к уравнениям (III.3.1) косинус-преобразование Фурье и преобразование Лапласа, получим
Рис. III.1
(Ш"+^)Р = С; (КО);
dx2 d-P dx'1
(III.3.4)
где
P(x, to, a)= Jcos asy dy I e p(x, y, t) dt.
(III.3.5)
Наличие в правой части уравнения второго порядка (III.3.4) величины ^ ^ ё (х — а) означает, что Р удовлетворяет одиород-
, dP
ному уравнению при х Ф а, а при х = а производная-^- претерпевает скачок величиной тогда как сама величина Р непре
рывна.
Учитывая это, легко выписать решение уравнении (III.3.4), удовлетворяющее условиям сшивки при х = 0 и стремящееся к нулю при х -*¦ ±оо. Это решение имеет вид:
Р (х, ш, о) = С ?ch sxx + ~ sh sxxJ; (0<^<Ся);
Р (х, м, a) = 4e_s‘a'; (а<Сж<С°°);
Р{х, со, o) = CeS2X; (ж<<0);
С= - ^ е
2A'i0 fc-2s2
®1 +
ch sxa 4-
^2S2 sh И9 «1
Л= -
2/,'lCT /,' 1S1 - j A’2 ¦'’2
Проанализируем теперь полученное решение. Определим сначала давление в точке х = а + р, у = 0 (р а).
Имеем
р <« ¦+ р>:= [< +тИтйге"”'] ¦ <ш-3-8)
Пусть оа2/х 1 > 1 (т. е. рассматриваются малые времена; t <? <Z a2/x1). В этом случае
Чтобы вычислить лапласово изображение давления, необходимо выполнить обратное косинус-преобразование:
ОО
р (х, у, о) — ~ ^ Pcosay da), (III.3.10)
О
откуда
оо
р(а~г р, 0, о) = -|- J (а + р)йш. (III.3.11)
Подставляя (III.3.9) в (III.3.11), имеем
-pf/~ (02Н———
р (а + р,
О, о) =- С JL г. _ йсо
=
о2-)—— щ
I/ - оо -up I/ ---
-р
Me
ы-P- f
”__- du= - -^-кМ j-p). (III.3.12)
2nhiO J уи(и_^_2) 2\т щ )
о
Используем известное соотношение
Т огда
Полученный результат, конечно, вполне очевиден; он означает, что для достаточно малых времен (t- ffl2/Ki) влиянием второй зоны можно пренебречь, и давление распределено так же, как и в однородном пласте.
Пусть теперь имеется обратное неравенство: t- а2/хх, так 410 о xja2. При этом вклад первого члена (III.3.8) не изменится; вклад же второго члена уже не будет пренебрежимо малым. Представим его в виде:
цд ехр [ — (2fl + р) si] ( кх — к2 , 2кхкг (sj — s2)
— ко ¦__2к1к2 (&i—s2) \ ттт о
>'1 + *2"Г (*1 + *2)(*1«1 + Мг) >'
4&10
Первый член (III.3.14) подобно выражению (III.3.9) отвечает течению от источника, помещенного в точке (—а, 0) и пущенного
в момент t ---- 0 с
дебитом q f1 , f2; его вклад
может быть легко
«1 + «2
вычислен. Второй член (III.3.14) дает после обращения
А С¦+ о.'">¦-- -swk)- ? fsb&tPJal*. (ш.з.is»
О
j
Интеграл (III.3.15) принимает при о = 0 конечное значение — А0.
к\
Это означает, что при больших временах распределение давления имеет весьма простой вид, причем опущенные члены стремятся к нулю при t -> оо;
Р <*. V. I)= 4^ [Ei ( - w) +тЫгЕ‘ (
![]()
В табл. III.1 приведены значения интеграла Д0 для случая {52 -= kjk^.
Таблица III-1
| ftl/*2 |
До | кг / fc2 | До |
| 0,01 |
—0,022 | 1 | 0 |
| 0,1 | -0,195 |
2 | 0,267 |
|
0,2 | -0,120 | 3 |
0,534 |
| 0,333 |
-0,123 | 5 | 1,030 |
| 0,5 | -0,106 |
10 | 2,080 |
| 100 | 11,400 |
П. Я. Полубаринова-Кочина [94]
рассмотрела аналогичную стационарную
задачу и показала, что распределение
давления п той части пласта, где находится
источник, совпадает с распределением
давления в однородной среде при действии
двух источников интен-синпостью q и t.q
( где А — f1 . -^-Л,
расположенных симметрично
\ Л'1 - Г '>'2 /
относительно границы раздела. Как мы видели выше, то же имеет .место и для движения при упругом режиме. При этом следует иметь i; виду, что появление дополнительного члепа Д0 не противоречит сказанному, поскольку при стационарном движении давление определено с точностью до постоянной; при нестационарном же движении такого произвола уже нет, так как естественным началом отсчета служит давление в невозмущенном пласте. Рассмотренную задачу впервые изучил В. А. Максимов [75, 3].
Приведенная упрощенная форма решения удобна при анализе решения для участка пласта вблизи скважины. Для удаленных участков пласта решение может быть представлено по-другому. Выполним это для точек, расположенных на оси у, считая у а. При этом Р (0, о, о) = С и
CO
о
При у а и a2‘Gjy.x 1 главный член выражения (III.3.17) имеет вид:
ОО
—v tic С cos сf}yd(a
О
__оо
__т ТТ [-\Г G_ \__Mh f cos toy (Si—s2)tfo
~ яа (ki -)- kv) 0\r Kx У J k^Tio (kL + k2) J «х («х + ^/Мг)
0
- - «fer
{Vi») - ¦?№&
CO
fTfr, ft *• /* \ — f__COBT^Jv_
-2. l) J y'\+y2 (Vl-I vS +V'P2+v2)(V'l + v2
((0 = V Vcjx1 ; - Р2 = х1/и2; tj = у У о/щ ). (III.3.18)
Полученная асимптотика имеет простой смысл. Если точка, в которой рассматривается решение, удалена от начала координат на расстояние, большее по сравнению с а, то точное положение скважины уже не имеет значения. В частности, можно в первом приближении считать скважину расположенной непосредственно на границе пластов. В видоизмененной таким образом задаче уже отсутствует характерный размер, и она имеет автомодельное решение вида:
где ? = —у-—; г и © — полярные координаты.
2 У xi i
Приведенное выше выражение (III 3.18) отвечает значению 0 — я/2.
Можно уточнить рассмотренную асимптотику, учитывая следующие члены разложения.
Чтобы понять смысл последующих членов разложения, заметим, что, «сдвигая» источник в начале координат (т. е. полагая а = 0), мы вносим ошибку, которую можно компенсировать, добавив «пару»
| «гоД | |
| . \кг,хг |
|
| Рис. |
III.2 |
из стока в начале координат и источника в точке (а, 0). Действие этой пары можно приближенно заменить действием «диполя» интенсивностью до, расположенного в на-! Аг, .г2 чале координат. Отвечающее ему решение также автомодельно. Подобным же образом может быть произведен учет высших поправок. В результате решение для больших г окажется представленным в виде наложения автомодельных решений сравнительно простого вида.
2. Рассмотрим теперь аналогичную задачу о влиянии неоднородности пласта, считая, что неоднородность имеет круговую форму (рис. III.2). Имеем
(III.3.20)
| 1 | dp _ 1 | д | (г др \ | , 1 &р |
м |
| Г-1 |
dt г | дг |
V дг ) | 1 г2 902 |
/Г]Г |
6 (г-а) б(©) (г<Д);
a на границе r = R выполняются условия сшивки:
p(R-0, ©, t) = p{R + 0, 0, t)\
dp(R —0, 0, t) dp(R-f-0, 0, t)
«1 -dr —к2— dr -
(III.3.21)
Представив решение рядом Фурье, получим для коэффициентов
Рп (r> °) = “ J § e~at P(ri 0 cos dt dQ (И 1.3.22)
о о
выражения
Рп = С1п(Ус/>11 г) (г < a); (III.3.23)
Рп - -- BIn (УQiv.x г) + DKn (Уо/х, г) (а </¦< ft);
Рп = АКп {VС/Ул г) (Г > Н).
Здесь
цд
В
Кщ (ро) \Кп+\ (Рро) Н~ К п-i (ppo)i —РАл+i (ро) К п (Рро) Р Кп (ро) К п-i (Рро) _ In (Ро) [A/hi (PPo) + ^n-i (РРо)] + Р^п(РРо) [^п+1 (Po)+^n-i (Ро)] ’
х
м
sik\G
с^в-
Л — r> (Ро) ' Г) Kn (po) ¦
Kn (Ppo) ‘ A'n(PPo) '
Выберем точку г = a — 6,0 <6 С «¦ Имеем
Pn (a - 6) = BIn (p) -^Kn (a) /„ (p).
(III.3.25)
Соответствующий второму члену разложения (III.3.25) ряд Фурье суммируем. Тогда
M
2nkxeK°^' (III.3.26)
л/fja
р(р, 0, o) = yPo + 2^nCosn0 =
П= 1
ОО \
¦§¦ ^0 (“) h (р) + 2 ^^In ^C0S R0 n-l
(о = V P2 + о2 — 2ap cos 0
(cm. [26, формулы 7, 45, 351), что отвечает течению от источника в однородном пласте. Если а и р0 велики (о велики, т. е. времена малы), то, как легко убедиться, вклад первого члена формулы
(III.3.25) экспоненциально мал, так что решение совпадает с решением для однородного пласта. Это имеет место, очевидно, до тех пор, пока возмущение давления не достигнет круговой границы г — R.
Рассмотрим подробнее противоположный случай, когда а, р0 и Ррр малы. Тогда выражение (III.3.24) для В можно упростить, используя известные формулы для малых значений аргумента:
(п — 1)! 2n_1
Кп(а)>
2пп\
(n>0). , (III.3.27)
В результате при п ф 0 в (III.3.24) можно пренебречь членами, содержащими Ки /п+1, и получить после некоторых упрощений
В =--м ¦¦¦ -3~~*L2п(п— I)1 ( —У* п 2пкха *2-Ь*1 ' \Р?/ ‘
(III.3.28)
При п = 0 имеем
D __ №
(Ш.3.29)
0 пкга
ОО
2/ сер \ncos пВ
к\ — к% jig
-j- к% 2zih\0
ы (1-^-008 0 + ^.) (II 1.3.30)
ki~k2 № к\~\~к2 4зтк\0
(см. [40, формула I.448.2J).
Таким образом, отвечающее большим значениям времени изображение распределения давления имеет вид:
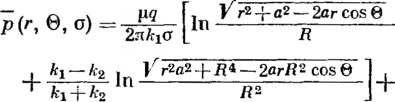
![]()
(III.3.3J)
В формуле (III.3.31) выражение в квадратных скобках с точностью до постоянной совпадает с выражением для распределения давления в соответствующей стационарной задаче; член, содержа-
![]()
обратном преобразовании дает логарифми-
ческий рост давления во времени, так что формула (III.3.31) обнаруживает в целом следующую картину: давление во внутренней кольцевой зоне распределено стационарно, т. е. разность давлений между любыми двумя точками области имеет то же значение, что и при стационарном движении, а средний уровень давления медленно (логарифмически) изменяется с ростом времени. При этом давление лишь постоянной величиной отличается от давления вблизи одиночной скважины, пущенной с постоянным отбором q в однородном пласте проницаемостью к2 и пьезопроводностью >с2.
3. Рассмотрим теперь приток жидкости к вертикальной трещине длиной 2L, которую будем считать поверхностью постоянного давления. Положим, что полный отбор жидкости через трещину сохраняет известное постоянное значение. Примем, как и раньше, начальное давление в пласте за нуль. При этом, учитывая симметрию относительно осей х и у, имеем
![]()
(00<оо; 0<(/< со); (Ш.3.32)
![]()
L
![]()
О
Р(*); fp (x)dx=^. (III.3.33)
-L
Считая величину р (я:) заданной, можно, применяя к задаче (III.3.32) преобразование Лапласа по t и косинус-преобразование Фурье по х, найти для преобразованного по Лапласу давления Р (х, у, о) выражение
со - j/"ш3+ -2- у L
Р(х,у,о)~—Г costoa:—- —Г p(|)coso)|d| dco. (III.3.34)
о г х о
Это выражение есть общее решение задачи (III.3.32), удовлетворяющее всем дополнительным условиям, кроме условия постоянства
давления на отрезке О <Г х < L, у = 0. Это условие дает
оо L
Р(х, 0, а) — Р0(о)~-~^- Г Гр(|)со8со|й1. (III.3.35)
и о
Меняя в этом выражении порядок интегрирования и вычисляя внутренний интеграл
СО __._
У 0)2 + —
О Г X
приведем это уравнение к виду:
Л»И= —^P(E.o)^0[(*-E)/-j]dE, 1*1<Ь
-ь
(здесь дополнительно учтена четность величины р по непосредственно следующая из симметрии задачи). Удобно ввести здесь безразмерные переменные и = ж/L, rj = ?/L, %= При этом имеем
1
^oW=-4Jp(4,^)^o[(»-4)MrfTif |и|<1. (III.3.36)
-1
Формула (III.3.36) представляет собой интегральное уравнение для определения неизвестной функции р (rj, Я). Мы ограничимся отысканием его приближенного решения для малых Я.
Используя асимптотическое выражение для К0 при малых значениях аргумента, имеем
j
р0(>.)--41рКя>[1г|• • -]dn (hi.з.з7) -l
или, учитывая (III.3.33), г
AJp(n,X)ln|u-n|dr1==P0-^(ln^fc). (III.3.38) -i
Заметим, что если бы вместо задачи (III.3.32) мы рассматривали такую же задачу для стационарного движения, то, действуя тем же способом, получили бы интегральное уравнение вида:
1 1
—г]\d4 = const; J р0 (ri)dri = -Ц- - (III.3.39) -i -i
При этом постоянная в уравнении (III.3.39) не определена, поскольку в соответствующей стационарной задаче давление определяется лишь с точностью до постоянной. Стационарную задачу можно легко решить, рассматривая ее как краевую задачу теории функций, и применяя формулу Келдыша — Седова ([63, гл. III, § 31).
Искомое решение имеет вид:
р0(г,)=—(II 1.3.40)
nkL V 1-г)2
Уравнения (III.3.38) и (III.3.39) эквивалентны, так что функция
— р0 (т}) дает в рассматриваемом приближении также и решение
исходной задачи. Иначе говоря, при Я 1, что отвечает большим временам (t L2jу.), распределение скоростей фильтрации по по
верхности трещины можно считать стационарным. Подставляя
в (III.3.38) р = —р0 (rj), получим
(III.3.41)
Формула (III.3.41) определяет асимптотику давления в трещине при больших временах. Сопоставляя ее с формулой (III.2.27), видим, что давление изменяется так же, как в скважине радиусом г* =
= yL, т. е.
Эхо обстоятельство позволяет определить размер трещины по наблюдениям нестационарного притока к ней (см. § 4).
4. Приведенные примеры позволяют сделать некоторые выводы общего характера относительно нестационарных течений со сложной геометрией. В большинстве случаев рассматриваемые задачи сводятся к изучению поведения системы при локализованном воздействии достаточно простого вида (например, при скачкообразном изменении дебита в одной из скважин).
Из получаемых таким образом решений при желании можно, пользуясь принципом суперпозиции, найти результат более сложных воздействий. Такая сосредоточенность изменений во времени и в пространстве приводит к тому, что асимптотические свойства соответствующих решений оказываются весьма простыми. В большинстве задач удается выделить три основные области. Первая из них — удаленная от места возмущения область, которая к данному моменту еще сохраняет свое исходное состояние и условия в которой еще не успели повлиять на поведение решения. Вторая область — непосредственно прилегающая к месту возмущения; движение здесь в известном смысле близко к стационарному (например, если возмущение заключалось в скачкообразном изменении расхода через трещину (п. 3), то поле скоростей вблизи трещины близко к стационарному полю скоростей). Наконец, в третьей, сравнительно узкой и имеющей простую геометрическую форму переходной области и происходит собственно нестационарное движение. Такая простая структура решения (присущая к тому же не только задачам упругого режима, по и нелинейным нестационарным задачам) позволяет в ряде случаев легко устанавливать основной ход решения, используя известные стационарные решения для «внутренней» части области движения и простые (например, автомодельные) нестационарные решения для внешней области.
§ 4. ОБРАТНЫЕ ЗАДАЧИ ЛИНЕЙНОЙ ТЕОРИИ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ
В вопросах геологии, особенно геологии нефти, широко используются решения обратных (стационарных и нестационарных) задач теории фильтрации. Общий принцип исследования пластов при нестационарном течении заключается в том, что путем изменения работы скважин в пласте искусственно создается нестационарный режим фильтрации и измеряется давление в зависимости от времени в одной или нескольких скважинах. На основе данных об изменении дебитов скважин и об изменении давления в определенных точках пласта могут быть получены сведения о параметрах пласта — проницаемости, пьезопроводности, о расположении границ пласта и др.
1. Самым простым и наиболее употребительным способом создания нестационарного течения является остановка одной из скважин. Кривая зависимости давления от времени, при помощи которой проводится исследование пласта, может быть снята либо в самой остановленной скважине, либо в другой — неработавшей скважине (пьезометрической). При этом предполагается, что во время исследования дебиты остальных скважин меняются незначительно. Типичный вид кривой изменения давления в остановленной скважине (кривой восстановления давления) изображен на рис. III.3 в координатах р, In t (кривая 1).
Решение задачи об изменении на постоянную величину давления в бесконечном пласте после измепепия дебита скважины было приведено в § 2. С точки зрения анализа кривых восстановления давления прежде всего представляет интерес асимптотический участок кривой р (In t) при больших t, описываемый формулой (III.2.28). Изменение давления в скважине, остановленной после того как она
Рис. Ш.з
работала на стационарном режиме с дебитом д0, может быть записано в виде:
Р(Р.О-Р(Р,0)=--йг(1п< + 1л^.). <111.4.1)
Формула (III.4.1) определяет прямую в координатах р, In t. При построении кривой восстановления давления в остановленной скважине такой прямолинейный участок часто устанавливается через непродолжительное время (кривая 2). Пусть уравнение асимптоты есть р — A In t + В. Тогда сравнение с формулой (III.4.1)
показывает, что А = В — A In Поскольку значение о0
4nkh VP
известно, то, измерив по графику параметры А и В, можно найти
Ус
гидропроводность пласта и отношение .
Следует иметь в виду, что радиус скважины, входящий в формулы для притока к скважине, обычно не равен истинному радиусу вследствие того, что, во-первых, скважина вскрывает пласт не на всю мощность, и, во-вторых, не вся поверхность скважины открыта для движения жидкости (несовершенство скважины по степени и характеру вскрытия). Поэтому, зная величину нельзя по отдельности
определить и и р7. Для определения пьезопроводности пласта удобнее использовать метод гидропрослушивания, т. е. исследовать изменение давления в другой скважине, не работавшей к моменту пуска «возмущающей» скважины. В этом случае характерным размером является не радиус скважины, а расстояние между скважинами, которое известно достаточно точно.
Воспользуемся для анализа кривой изменения давления формулой, описывающей распределение давления в бесконечном пласте при работе скважины-источника, пущенного при t = 0 с дебитом д0:
p(r, t)-p(r, 0)= - (Ш.4.2)
После несложных преобразований формулу (III.4.2) можно записать в виде:
t Г2
р (г, t) - р (г, 0) = Др = -g- J е' ^ ^ . (III.4.3)
о
Обычный способ обработки кривых изменения давления в реагирующей скважине заключается в том, что на кривой фиксируется время появления каких-либо характерных точек — точки перегиба, точки касания и др. Удобно фиксируется, например, точка касания с кривой р (() прямой, проведенной из начала координат. Пусть в этой точке t — tu Ар = (Др),:
др _ (Ар)! dt
Подставляя сюда значения и Ар из формул (III.4.2)
и (III.4.3), можно легко найти,' что tx определяется из уравнения
7*2 _ 7*2
Корень этого уравнения
равен ^ = 0,44, откуда
я =0,57 — .
Таким образом, протяженность прямолинейного участка на кривой р (In t) ограничена. Вместе с тем фактически в силу ряда технических трудностей скважина не может быть остановлена мгновенно. Скважина обычно закрывается не на забое, т. е. на границе пласта, а на поверхности. Из-за упругости жидкостей и газов, заполняющих скважину, приток из пласта продолжается еще некоторое время после закрытия. Время до выхода на асимптоту, очевидно, должно превышать время дополнительного притока. Поэтому возможны условия, особенно в скважинах, расположенных близко от границ пласта, когда прямолинейного участка на кривой р (In t) не существует.
Кроме того, дополнительный приток в скважину значительно увеличивает продолжительность исследования.
Способ обработки кривых восстановления давления, свободный от указанных недостатков, был предложен в работе [15]. В этом методе непосредственно используются преобразования Лапласа кривых восстановления давления, поэтому он пригоден при произвольном изменении дебита скважин.
Изложенные выше методы обработки кривых восстановления давления могут быть получены как частный случай общего метода. Использование преобразования Лапласа позволяет также во многих случаях определять по кривым восстановления давления характер неоднородности пласта (радиус зоны пониженной проницаемости вблизи скважин, расстояние до непроницаемых границ и т. д.).
Предположим, что в результате измерений в скважине известны
, 2nhh др ...
зависимости р (г, t) и —-—• р — q (t).
Рассмотрим пласт, неоднородный и произвольной конфигурации, в котором при t = 0 начинает работать скважина на нестационарном режиме. Изменение давления p(r, 0, z, t), отсчитываемое от начального стационарного уровня, удовлетворяет уравнению пьезопроводности
-§!—= О, (III.4.4)
и начальному условию р — 0. Пусть скважина (г = р) удовлетворяет условию р\г=? = р 1 (t). Кроме того, на внешних границах пласта
должны выполняться условия вида р — 0 на контурах питания
и др/дп 0 на непроницаемых участках границы. Переходя к преобразованию давления по Лапласу Р (г, z, 0, о), получим, что Р удовлетворяет уравнению
ницах. На скважине U=l. По этим условиям может быть найдена функция U (г, z, 0, о), не зависящая от режима работы скважины. Пусть дебит скважины будет q (t). Имеем
Q(P)= f q(t)e-^dt = ^y-p J e-’1 ^^dtdl = -^~-^(o) §^rdl,
0 0 I I
(III.4.6)
где интегрирование производится по длине вскрывшей пласт части ск важины.
Из формулы (III.4.6) следует, что отношение
i
. . -Pi (о)
(III.4.7)
Ф(о)^-
зависит только от вида функции U и, следовательно, не зависит от режима работы скважины. Вид функции ij) (о) полностью определяется параметрами пласта. Когда функции ру (t) и q (t) известны, функции (о) и Q (о) могут быть найдены без затруднений каким-либо методом численного интегрирования. По виду функции ij) (о) в ряде случаев удается определить некоторые параметры пласта.
Для случая мгновенной остановки скважины Q (о) = следовательно, —Рг (а) = Р° (о) — . Таким образом, функция
ij) (а) равна аР° (о), где Р° (а) — преобразование Лапласа изменения давления р° (t) при мгновенной остановке скважины.
Из формулы (III.4.7) следует (см. также § 1), что функция р (t) в общем случае может быть выражена через Р° (t) при помощи интеграла Дюамеля, если q (t) известно:
t
P{t) = l^P°{t-T)dT. (111-4.8)
О
В § 2 и 3 настоящей главы были получены решения ряда задач о распределении давления вблизи скважины при скачкообразном изменении дебита. Приведенные там функции Р (х, у, а) можно непосредственно использовать для определения функции ij) (о) =
= -^- Р, не находя отдельно U (х, у, а). Функция U для некоторых
из этих задач была получена в работах Г. И. Баренблатта и В. А. Максимова {22] и В. А. Максимова {75, 76, 3].
Рассмотрим простейший пример — скважину, работающую в однородном бесконечном пласте. Функция U имеет вид (см. § 2):
и = (Ш-4.9)
2лр-д—
откуда
<?r Jl
При практическом построении преобразования Лапласа от /> (t) и 9 (0 Удобно вместо а использовать параметр т = —, т. е. писать
СО 1_
Р (т) = J Р (О е т с?т. Интегралы вычисляются для нескольких
о
значений параметра т. Фактически из-за наличия множителя е -используется только участок кривой р (I) или q (t), для которого t не превосходит 6а. Очень малые значения т (меньше 1—2 мин) брать нельзя, так как на начальном участке кривая р (t) определяется
очень неточно. Поэтому значения р во всех практи
чески интересных случаях достаточно малы для того, чтобы можно было использовать представления функций К0 (z) и Кг (г) для малых значений аргумента (III.3.27). Отсюда
V (t) = 4J)(<t)=--Н— 1н-^ = 74т1пт + гт11п"ТТ- (III-4.il)
W 2лkh 2 Vxx 4лkh ' 4лkh Y2P2 V '
Параметры пласта на основе формулы (III.4.11) определяются
по графику от In т точно так же, как параметры по графику
р, In t при мгновенной остановке скважины. Тот факт, что зависимость ф (In т) прямолинейна, позволяет ограничиться вычислением функции при очень небольшом числе значений т.
В § 3 было приведено решение задачи о притоке к скважине в пласте с неоднородностью круговой формы. Из формулы (III.3.25) следует, что при небольших временах (больших о) функция Р (х, у. о), а следовательно, и ij) (о) имеет тот же вид, что и для однородного пласта с параметрами внутренней зоны. При малых о (больших т) для определения ij) (о) можно воспользоваться формулой (III.3.31), которая дает в точках, где г = а 4- р (р R, 0 ««0):
+
2nk‘>h |
Формулу (III.4.12) можно записать иначе:
feg fe2 fej-fe* Kl+fe*
В простейшем случае, когда скважина расположена в центре зоны радиусом В,
fes
(р* — приведенный радиус скважины). Сравнивая формулы {III.4.11) и (III.4.13), видим, что формула (III.4.13) представляет преобразованную кривую восстановления давления в однородном пласте с параметрами внешней зоны, но в скважине, радиус которой равен р*. Нетрудно убедиться, что р* — эквивалентный радиус скважины для стационарного притока в круговом пласте с теми же зна-
kh гч и •>
чениями —. Эквивалентный радиус определяется как радиус такой Iх
совершенной скважины, стационарный приток к которой в пласте с параметрами внешней зоны равен притоку к действительной скважине в неоднородном пласте при том же перепаде давления между скважиной и круговым контуром.
Рассмотренный случай пласта, проницаемость которого вблизи скважины (в призабойной зоне) отличается от проницаемости во внешней областй, представляет большой практический интерес. Процесс бурения и оборудования нефтяной или газовой скважины и ее последующая работа изменяют проницаемость в призабойной зоне, чаще всего уменьшают ее. Для восстановления и увеличения проницаемости призабойной зоны производятся различные обработки ее: промывка кислотой, образование трещин путем закачки жидкости под высоким давлением (гидравлический разрыв пласта) или взрывом (торпедирование) и др. Исследование скважин методом восстановления давления позволяет выяснить необходимость проведения таких выработок, т. е. определить снижение проницаемости в призабойной зоне по сравнению с проницаемостью остальной части пласта, а впоследствии — оценить эффективность проведенных работ.
Существование вертикальных и горизонтальных трещин вблизи скважины приводит к тому, что течение не является радиальным. Однако, как отмечалось в § 3, спустя некоторое время после начала возмущения движение жидкости вблизи скважины близко к стационарному. Нестационарность притока сказывается только на больших расстояниях, где поток можно считать радиальным. Поэтому кривые восстановления давления при больших значениях т имеют асимптотический прямолинейный участок типа, описываемого формулой (III.4.13). Входящий в эту формулу приведенный радиус р* определяется из решения задачи о стационарном притоке к скважине в пласте с заданным распределением трещин. Например, для
вертикальной трещины длиной 2Lp* = как это следует из решения, приведенного в § 3, п. 3. Ряд других задач о притоке к скважине с трещинами в призабойной зоне решен В. А. Максимовым (75].
Если значение и2 известно, например, по кривым гидропрослушивания, то по кривым восстановления давления можно определить р* — наиболее важный параметр для расчета дебита.
Анализ кривых восстановления давления позволяет также обнаружить существование неоднородности пласта на больших расстояниях от скважины. Важнейшей задачей такого рода является определение расстояния до прямолинейной границы, разделяющей области разной проницаемости.
Решение соответствующих задач о притоке к скважине приводится в § 3. При малых т, т. е. больших о, функция (т) имеет вид, соответствующий однородному пласту. Поскольку всегда а р, то на кривой Чг (In т) имеется начальный прямолинейный участок, соответствующий формуле (III.4.11) для однородного пласта. Для малых а можно воспользоваться формулами (III.3.8), (III.3.12) — (III.3.15), из которых следует
Р(а+р.ст)= - До] •
Пользуясь асимптотическими выражениями для К0, получим
¦ф (а) = — - —
- Г -
In о -j-
In —(- ~
*2 In + Л0"]
Q 4. L /' [ L кх -|- Л’2 /.'1 I А'2 J
(111.4.16)
или
где приведенный радиус р* равен
h2
p* = /2pa(^r)ft,+Vo.
Из формулы (III.4.17) следует, что при больших т кривая ? (In т) имеет асимптотический прямолинейный участок, наклон которого к оси абсцисс в 2к1/(к1 + к2) раза больше, чем наклон асимптоты для однородного пласта. Расстояние до границы раздела зон разной проницаемости может быть определено по второму слагаемому формулы (III.4.17), если известно отношение Если
неизвестная граница непроницаема, то можно положить к2 = 0. При этом наклон асимптоты в два раза больше, чем в однородном
пласте, а р* = j/2pa.
Таким образом, сравнивая два прямолинейных участка преобразованной кривой восстановления давления, можно найти вели-
чины — и ejели известны значения х или р по отдельности,
то может быть найдено искомое значение а.
Рассмотренные до сих пор методы исследования относились главным образом к случаю монотонно изменяющегося дебита скважины. Иногда представляет интерес исследование скважин при периодическом изменении дебита. Такой метод был предложен С. Н. Бузиновым и И. Д. Умрихиным [35]. При зтом в пласте возникают волны давления, аналогичные тепловым волнам.
Предположим, что дебит скважины в однородном бесконечном пласте, начиная с t —- 0, изменяется по закону
q = q0 sin соt.
Таким образом, требуется найти решение уравнения (III.2.1), удовлетворяющее нулевым начальным условиям, а также условию
2nhhp ( др
Используя преобразование Лапласа Р (г, о), получим, что Р должно удовлетворять уравнению (III.2.3) при граничном условии
(III.4.19)
JX ^ dr I г=р (72 + (1)2 '
|
QepKO1 | ['Vi |
) . | |||
| 2лА-/гр j | *1 | | ы2 -j- ст2 | |||
Тогда, используя формулы, полученные в § 2, имеем
Р (г, а) =---¦ (III.4.20)
Для больших времен, когда р VI <? 1, выражение для Р (г, о)
упрощается:
Для определения оригинала по изображению (III.4.21) воспользуемся теоремой о свертке, которая дает
(III.4.22)
Нас, однако, интересует изменение давления в скважин е при г = р. Во всех практически интересных случаях период колебания
55
значительно превышает характерное время. Тогда функцию Ф (о) можно приближенно представить в следующем виде:
Ф (°):= - т ^ i 'ln VO -1 ^ In Jg-. -(111-4.23)
^ Vp2
Оригинал второго слагаемого естьInsin со L Для вычисления оригинала первого слагаемого снова воспользуемся теоре-
1
мой о свертке и формулой L [In t] = — — In уо. Тогда t
lnrcosc»(? — r)dr — 1н-~sinco?, (III.4.24)
о
откуда можно получить
P(Pi 0 — С8111 (0t Cj М)— coscof Si (of)—sincof In ,
(111.4.25)
где Ci (cat) и Si (cat) — интегральные косинус и синус (см. [401).
Функции Ci (сat) и Si (сof) при больших значениях соt (превышающих 1) могут быть выражены асимптотическими формулами:
(111.4.26)
Из (III.4.26) видно, что с течением времени изменение давления в скважине становится синусоидальным с периодом 2л/со. Последним членом в скобках, выражающим влияние начальных условий, можно пренебречь уже через 2—3 периода. По изменению давления в скважине можно в соответствии с формулой (III.4.26) по амплитуде и сдвигу фаз колебания давления (по сравнению с фазой колебания дебита) найти значения гидропроводности и параметра р2/х.
НЕЛИНЕЙНЫЕ ИНВАРИАНТНЫЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ ЖИДКОСТЕЙ И ГАЗОВ
§ 1. ОБЩАЯ ХАРАКТЕРИСТИКА ИНВАРИАНТНЫХ ЗАДАЧ ТЕОРИИ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ.
АВТОМОДЕЛЬНЫЕ ПОЛОГИЕ БЕЗНАПОРНЫЕ ДВИЖЕНИЯ ПРИ НУЛЕВОМ НАЧАЛЬНОМ УРОВНЕ ЖИДКОСТИ
1. Общая характеристика инвариантных задач теории нестационарной фильтрации. В главе II было показано, что основные задачи гидродинамической теории нестационарной фильтрации приводят к краевым, смешанным или начальным задачам для нелинейных, как правило, дифференциальных уравнений в частных производных параболического типа. Нелинейность вообще характерна для многих актуальных задач современной гидродинамики: газодинамики, теории волн, теории движений вязкой жидкости и т. д. В настоящее время не существует сколько-нибудь общих эффективных аналитических методов решения достаточно широких классов нелинейных задач математической физики; это в полной мере относится и к теории фильтрации. Поэтому в теории фильтрации (как и во многих других разделах математической физики вообще и механики сплошных сред, в частности) уже давно привлекли внимание своеобразные частные решения, которые выражаются через функции одной переменной. Вначале эти решения обратили на себя внимание только потому, что их получение сводилось к решению обыкновенных уравнений и представлялось (особенно в домашинную эру) более простым, чем решение уравнений в частных производных в общем случае. При построении различных приближенных методов решения, более общих, эти решения часто использовались как эталоны, позволяющие оценить точность • метода. (Приближенные методы аналитического решения сохраняют, особенно в теории фильтрации, свое значение и сейчас, при широком внедрении машин, поскольку эти методы дают аналитические формулы, позволяющие наглядно проследить влияние различных параметров, а высокая точность в теории фильтрации не представляет особого интереса. Эти методы будут рассмотрены в следующей главе.) В ряде случаев задачи, описываемые такими решениями, представляют и самостоятельный интерес.
Однако главная ценность таких решений была осознана позднее. Оказалось, что они представляют собой асимптотические представления решений весьма широких классов задач именно там, где детальная структура граничных и начальных условий перестает быть существенной, а эти области часто бывают наиболее интересными (например, спустя некоторое время после начала отбора из скважины, пока воронка депрессии не достигла области влияния соседней скважины и т. д.). Поэтому, зная такие решения, мы фактически получаем возможность судить, по крайней мере качественно, о поведении очень широкого класса фильтрационных движений.
Важным свойством рассматриваемых ниже решений является их инвариантность: для одних из этих решений — «автомодельных» — распределение давлений, напоров, плотностей и т. п. оказывается все время подобным самому себе, для других — перемещается как твердое тело с постоянной скоростью и т. д. Это свойство связано с особым характером задач, приводящих к таким решениям. Выполнение определенных преобразований зависимых и независимых переменных оставляет уравнения, граничные и начальные условия задачи неизменными. Как говорят в математике, зти задачи инвариантны относительно некоторой группы непрерывных преобразований. Такие задачи называются инвариантными, они рассматриваются ниже.
2. Автомодельные пологие безнапорные движения при нулевом начальном уровне жидкости. Ниже будут рассмотрены точные решения некоторых нелинейных задач нестационарной фильтрации, характеризующихся нулевым начальным условием. Исследование этого класса движений представляет, помимо непосредственного, также принципиальный интерес, поскольку в подобных задачах наиболее сильно проявляется существенно нелинейный характер рассматриваемой проблемы и обнаруживаются некоторые свойства нелинейных движений, резко отличающие их от соответствующих линейных задач и неизбежно утрачиваемые при линеаризации.
Для определенности при исследовании задач с нулевым начальным условием будем рассматривать безнапорные пологие фильтрационные движения в первоначально сухом грунте, имея в виду, что в силу обнаруженной JI. С. Лейбензоном аналогии (см. гл. II) все результаты непосредственно переносятся на задачи изотермической фильтрации газа. Излагаемые ниже в этом параграфе решения были получены Г. И. Баренблаттом [4, 5, 9].
Рассмотрим полубесконечный пласт, имеющий снизу плоскую горизонтальную непроницаемую границу — водоупор, а со стороны канала — плоскую вертикальную границу (рис. IV.1), перпендикулярную оси х и проходящую через точку х = 0.
Пусть начальный напор жидкости в пласте равен нулю, а напор на вертикальной границе пласта изменяется по степенному закону, начиная с исходного момента t = t0:
где о >0, а а — некоторая константа, которую будем выбирать
Л
в пределах--— <С°°- В частности, константа а может рав
няться нулю; в этом случае напор на границе мгновенно принимает некоторое значение о и остается постоянным.
В случае фильтрации газа сформулированная задача отвечает
закачке газа в первоначально не заполненный однородный пласт
постоянной мощности при изменении давления газа в начальном сечении пласта х = 0 по закону (IV.1.1). Линиями равных напоров будут линии х = const, параллельные границе пласта. Таким образом, напор h (ж, t) удовлетворяет уравнению
__ „ d2fo2 . __ С _ kpg
dt дх* ' 2т 2тц ’ ^ 8'
получающемуся из общего уравнения Рис. IV.1
Буссинеска (II.3.20) для данных геометрических условий задачи, а также граничному условию (IV. 1.1), начальному условию и условию на бесконечности:
h(x, tv) = h(oo, f) = 0. (IV.1.3)
Напор в некоторой точке пласта h зависит от следующих аргументов: координаты х, времени, прошедшего от начала процесса t — <0 (в силу однородности уравнения (IV.1.2) по времени напор будет зависеть только от разности t — t0, а не от значений t и t0 в отдельности], коэффициентов а и а и константы а. Вводя для удобства независимую размерность напора (это возможно, так как для рассматриваемой задачи несущественно, что размерности длины и напора одинаковы) J, получим размерности этих аргументов в следующем виде:
la) = \h]-WT-i- \t-t0\ = T; [а] = [й]Т-“, (IV-1-4)
где через [/г], L и Т обозначены соответственно размерности напора, длины и времени; константа а безразмерна. Из аргументов, от которых зависит напор жидкости, можно составить только две независимые безразмерные комбинации:
В силу я-теоремы анализа размерностей выражение для напора можно представить в виде произведения комбинации определяющих параметров, имеющей размерность напора [в качестве нее можно взять о (t — f0)“], на безразмерную функцию от безразмерных комбинаций (IV. 1.5). Имеем таким образом
h = o(t-t0ffa,k); Ь = <*/(1 + а), (IV.1.6)
где / — безразмерная функция, а параметр Я введен вместо параметра а для удобства последующего изложения. Очевидно, что 7, лежит в интервале —1 < 1. Имеем, далее, в силу (IV. 1.6)
d*h2 __ a2 (t- t0)2' (a i 1) d”-p
dx2 <30 (< — <o)'/+1
Подставляя эти соотношения в уравнение (IV.1.2) и упрощая, получаем для функции / обыкновенное дифференциальное уравнение:
После подстановки выражения (IV.1.6) в граничное условие (IV. 1.1) и условие (IV.1.3) получаем для функции / (?, К) краевые условия:
/(О, К) = ь (IV. 1.8)
/(ооД) = 0. (IV.1.9)
Напор и объемный поток (расход) грунтовых вод должны быть
непрерывными функциями х и t. Используя закон Дарси, имеем
для расхода, приходящегося на единицу ширины пласта, выражение
— Ch^- = --=
~СС h) 2 -/a + l4r-
дх 2 дх 2 а ' dg
(IV.1.10)
Таким образом, из требования непрерывности расхода следует непрерывность функции df/dt,.
При непрерывной функции / (?) и / =^= 0 требование непрерывности функции df2/db, = 2fdf/di, совпадает с требованием непрерывности производной df/dОднако при / — 0 из непрерывности dp/di, непрерывность df/db, не вытекает. Напротив, как увидим далее, искомая функция / (|, X) имеет в точке, где / обращается в нуль, разрыв первой производной.
Условие (IV. 1.9) удобнее привести к другому виду. Умножим обе части основного уравнения (IV. 1.2) на ж и проинтегрируем по х от нуля до бесконечности. В результате получим
оо со со
j x'Wdx=='It J xh{x,t)dx = a j X dx =
0 0 0
= a{xl&)Z.7 + aIft2(°’ t) — h2(oo, t)].
Очевидно, что dh2/dx стремится к нулю при х —*- °° быстрее, чем аг1, в противном случае h не стремилось бы к нулю при х —> оо. Используя это обстоятельство и условие на бесконечности (IV. 1.3), получаем
ОО
“ J xh(x, t)dx = ah2 (0, t). о
Интегрируя это соотношение в пределах от t = t0 до t и используя граничное условие (IV. 1.1) и представление решения (IV. 1.6), имеем
оо оо
j xh(x, t)dx=
°°г +1 |
lf(l,%)dl =
о о
t
Г 1.2 /п ао2 (t — *o)2ct+1
#0
(напомним, что считаем а удовлетворяющим неравенству —Vs < <a < сю), откуда получаем искомое условие в форме
ОО
о
В интересующей нас области изменения а и Я правая часть (IV. 1.11) конечна и положительна.
3. Исследование интегральных кривых обыкновенного дифференциального уравнения. Итак, решение рассматриваемой задачи свелось к решению обыкновенного дифференциального уравнения второго порядка (IV.1.7) при условиях (IV.1.8) и (IV.1.11), непрерывного и имеющего непрерывную производную от квадрата. Заметим, что уравнение (IV.1.7) инвариантно относительно группы преобразований
Ф(1,Ц) = Г2/ИД), (IV.1.12)
т. е. если / (|, fi) удовлетворяет уравнению (IV.1.7), то и Ф (?, ц.) удовлетворяет этому уравнению при произвольном положительном (л.
Это свойство уравнения дает возможность понизить его порядок. Положим по общему правилу (см., например, [53, стр. 93])
/ (?, Л.) = 6»ф (ч, X), ч] = In ?, (IV. 1.13)
тогда уравнение (IV.1.7) сведется к уравнению второго порядка
относительно функции ср (г)), не содержащему независимой переменной rj:
ФФ" -Ь 6ф2 + 7фф'+ф'2 + -|-(1 -1) ф +1 ф' = О, (IV. 1.14)
Полагая далее
%=* (IV.J.15)
и принимая ф за независимую переменную, получим для функции ч|з уравнение первого порядка:
W=_^[6^+7^+*24'V^+t’15]- <IV116>
Исследование этого уравнения проводится обычным образом (см., например, книгу В. В. Степанова [111]). Поскольку, очевидно, напор заведомо неотрицателен, функция / и, следовательно, функция ф также неотрицательны, так что интересующая нас область плоскости ф'ф представляет собой правую полуплоскость (см. рис. IV.2).
Вблизи оси ч|з (т. е. там. где ф мало и я|) ф) уравнение (IV.1.16) записывается следующим образом:
Стало быть, при малых ф и^>—интегральные кривые имеют
большой отрицательный наклон, при я]э <С--1 — большой положи
тельный наклон. Интегрируя уравнение (IV.1.17), получим, что вблизи оси я]з интегральные кривые представляются формулой
Ф = |—Х + 0(ф), (IV.1.18)
где С — константа интегрирования, различная для разных интегральных кривых. Для исследования поведения интегральных кривых в окрестности начала координат проведем через начало прямые ф — = пкр и рассмотрим поведение интегральных кривых на этих прямых вблизи начала. Имеем на прямой яр = тф вблизи начала
4S» •”*+ 2 ci - i)J - 0 ci). (IV.).»)
так что при т > т0 = — 2 (1 — Я,) = —2/(1 + а) наклон интегральных кривых велик и отрицателен, при т < т0 — велик и положителен. Как нетрудно видеть, при положительных <ри я);, т. е. в первом квадранте, наклон интегральных кривых отрицателен. Вблизи оси ф, т. е. при малых -ф ф, уравнение (IV.1.16) представляется в виде:
поэтому вблизи этой оси наклон интегральных к ривых меняет знак, обращаясь в бесконечность. Таким образом, интегральные кривые уравнения первого порядка (IV.1.16) имеют вид, изображенный на рис. IV.2 В зависимости от того, положительно С или отрицательно, эти интегральные кривые разбиваются на два класса: I и II. Уравнение (IV. 1.18) показывает, что ни одна из интегральных кривых I класса (С > 0) и ни одна пз интегральных кривых II класса (С <0) не пересекает ось я|з в конечной точке. Кривые I класса вблизи начала координат стремятся к совпадению с пря-
„ , 2ф мои линиеи ч|з =
т0ф = —Q , ; , так
что
вблизи начала координат плоскости ф1|) эти кривые удовлетворяют уравнению
Интегрируя это уравнение, получаем
1п<р== _^тгТ]+1п?'+*--== ~‘ег|г1п^+1п?'+-**’
(IV.1.22)
2
где D — константа интегрирования, а многоточия означают неучитываемые малые величины.
Из (IV.1.22) видно, что при подходе вдоль рассматриваемой интегральной кривой к началу координат, т. е. при ф -> 0, ? стремится к бесконечности. Возвращаясь к переменным / и получаем, что интегральные кривые уравнения второго порядка (IV.1.7), соответствующие интегральным кривым I класса уравнения первого порядка, при ? -»- оо удовлетворяют соотношению
f = + о(Б*«). (IV. 1.23)
Далее, при малых ф для интегральных кривых II класса имеем
Ф3 = 2Сг} -|- -Е + 0 (ф2),
которое показывает, что г) остается конечным при ф -> 0, т. е. при f 0 для соответствующих интегральных кривых уравнения второго порядка | остается конечным. Имея это в виду и переходя в соотношении (IV.1.24) к переменным /, |, получаем, что при малых / соответствующие интегральные кривые II класса уравнения второго порядка (IV.1,7) удовлетворяют соотношению
Интегральные кривые I и II классов уравнения первого порядка (IV. 1.16) разделяются интегральной кривой, соответствующей С = О,
которая вблизи оси ч]з представляется уравнением
Ф = -^-=-4 + 0(ф). (IV. 1.26)
Переходя к переменным / и получаем, что разделяющая кривая при малых / удовлетворяет соотношению
Рис- IV-3 -g = _ { | - 0 (/). (IV.1.27)
Системы интегральных кривых уравнения второго порядка (IV. 1.7), принимающих различные значения при g = 0, получаются одна из другой преобразованием подобия (IV. 1.12). Таким образом, резюмируя все сказанное, получаем, что интегральные кривые уравнения (IV. 1.7), удовлетворяющие условию (IV.1.8), располагаются следующим образом (рис. IV.3). Кривые I класса при ? -*¦ °о изменяются по закону / = D g2X(D 0 — константа, различная для различных кривых), причем ни одна из этих кривых ни в одной точке не касается и не пересекает оси абсцисс. Очевидно, что ни одна из этих кривых не является искомой, поскольку ни одна из них не удовлетворяет условию (IV.1.И) — для каждой из них интеграл
ОО
j |/( ?, X) dg расходится. Исключением является случай а —О
о
(рассматриваемый ниже), для которого все кривые I класса имеют горизонтальные асимптоты. На рис. IV.3 изображен случай а > 0. Остальные интегральные кривые (кривые II класса) пересекают ось абсцисс в конечных точках, причем они подходят к оси абсцисс под прямым углом, поскольку для каждой из этих кривых соотношение (IV.1.25) дает при малых /
Здесь С < О — константа, соответствующая рассматриваемо!! интегральной кривой Н класса, пересекающей ось абсцисс в точке с координатой go Разделяющая кривая подходит к оси абсцисс в точке | = = |0 под некоторым углом v. В силу (IV. 1.27) этот угол определяется соотношением
Поскольку напор жидкости по физическим соображениям не может быть отрицательным *, ясно, что искомая функция / (|, Я) должна каким-то образом комбинироваться из интегральных кривых уравнения (IV.1.7), не принадлежащих к I классу, в той их части, где эти кривые располагаются над осью абсцисс, и из самой оси абсцисс. Однако, если мы составим функцию / (?, Я) таким образом, чтобы она представлялась отрезком некоторой кривой II класса вплоть до точки |с пересечения этой кривой с осью абсцисс, и далее самой осью абсцисс, то полученная функция в точке ? = |с будет иметь разрыв производной от квадрата! В самом деле, при приближении к точке пересечения | — ?с справа, где функция / (|, Я) представляется осью абсцисс, получаем, что (df2/dt,)%^%c+о = 0, так как при df2jd | тождественно равно нулю | > |с. При приближении же к точке пересечения | = |с слева, где функция /(?, Я) представляется некоторой кривой II класса, получаем в силу соотношения (IV. 1.25)
Разрыв величины df2/d?, соответствует разрыву потока жидкости, что противоречит постановке задачи. Поэтому ни одна из функций / (|, Я), получающихся указанной выше комбинацией интегральных кривых II класса при С Ф 0 и оси абсцисс, не годится.
Искомой кривой уравнения (IV.1.7), удовлетворяющей условию (IV. 1.8), непрерывной и обладающей непрерывной производной от квадрата, будет кривая, состоящая из отрезка интегральной кривой, разделяющей кривые I и II классов, вплоть до пересечения ее с осью абсцисс в некоторой точке ?0, н отрезка оси абсцисс | ^
Сама функция непрерывна по построению; проверим непрерывность производной от квадрата в точке пересечения | = |0 (в остальных точках эта непрерывность не вызывает сомнений, поскольку интегральная кривая состоит из двух участков гладких кривых). При подходе к точке ? = справа, где интегральная кривая представляется осью абсцисс, предел (df2[d|)|=$„+о равен нулю. При подходе к точке | слева предел равен (df2/'d |)?==о-0
= 2 (fdf/d и в силу (IV. 1.27) равен - V4 ( = О.
Таким образом, для построенной кривой производная df9/dt непрерывна.
Покажем теперь, что построенная функция удовлетворяет условию (IV.1.11). Умножим обе части уравнения (IV.1.7) на ? и проинтегрируем в пределах от 6 = 0 до | = °о (или, что то же, до 6 == = 10, так как при | ^ ?0 / (6, К) ~ 0). Получим
- Я 6/ © dt + ± j Б» dt + J 6 = 0 (IV. 1.30)
о оо
откуда и из (IV. 1.30) получаем
со |о
j 6/(6, я) <*6 =^6/(6,^=ттг' (IV.1.31)
о о
т. е. функция / (6, Я) удовлетворяет условию (IV. 1.11), что и требовалось доказать.
Таким образом, функция / (6, Я) отличается от нуля лишь при 6 <С ё„, а ПРИ ? 5= 10 °на тождественно равна нулю. Разумеется, величина |0 зависит от параметра Я. В точке 6 = 10 ФункЧия / ( ?, Я) имеет разрыв первой производной г.
Из требования непрерывности / и dp/d ? и теоремы единственности решения дифференциального уравнения следует, что при составлении функции / (6, Я) склеивание различных интегральных кривых уравнения (IV.1.7) можно производить только в точках, где / = 0, откуда непосредственно вытекает единственность построенной нами функции, т. е. единственность автомодельного решения 2.
4. Эффективное вычисление функции / (?, Я). Для эффективного вычисления функции / ( ?, Я) нецелесообразно обращаться к интегрированию уравнения первого порядка (IV.1.16). Удобнее поступить следующим образом.
Построим решение Ф (?, Я) уравнения второго порядка (IV.1.7), обращающееся при ? = 1 в нуль и имеющее в этой точке конечную первую производную, т. е. соответствующее разделяющей интегральной кривой, проходящей через точку ? = 1. В силу равенства (IV. 1.27), независимо от того, выполняется условие (IV. 1.8) или нет, эта производная равна —¦ 1/4.
При | < 1 решение Ф (|, Я) представляется быстро сходящимся рядом
Ф (?, Я) = 4 (1 - 5) + Сх (1 - If + С2 (1 ¦— If+ ..(IV. 1.32)
где
(IV.1.33)
Ряд (IV.1.32) достаточно быстро сходится на всем отрезке 0 ss =g: Е 1, однако для вычисления Ф (?, к) при малых ? удобно воспользоваться методом. Адамса — Ш тер мер а (см. об этом методе, например, в книге А. Н. Крылова [611), вычисляя при помощи ряда (IV. 1.32) необходимые при применении этого метода начальные значения Ф ( ?, Я) в точках, близких к | = 1. Суммируя ряд (IV.1.32) при | = 0 или вычисляя Ф (0, Я) методом численного интегрирования, можно получить Ф (0, к) = N (Я), где N (Я) представляет собой положительное число, не равное единице. Таким образом, функция (?, Я), равная Ф (|, Я) при ? ^ 1 и тождественно равная нулю при ? > 1 непрерывна и имеет непрерывную производную от квадрата. удовлетворяет уравнению (IV 1.7) и условию на бесконечности (IV.1.9), а условию (IV,1.8) не удовлетворяет.
Для получения искомого решения вспомним, что функция
/(?, Я)=^гЧЧр?, к) (IV. 1.34)
также удовлетворяет уравнению (IV.1.7) при произвольном ji > 0 и обладает нужными свойствами непрерывности. Выберем теперь
jx = jx0 таким образом, чтобы функция / (|, К) удовлетворяла также и условию (IV.1.8), тогда полученная функция f Ц будет удовлетворять всем условиям, налагаемым на искомое решение. Имеем
/(О, Ь) = 1 = -^Ф(0, K) = ±N(\),
(IV. 1.35) (IV.1.36)
Мо го
откуда получаем
Значение |0 (начиная с которого/(|, ^) = 0) получается в случае, если учесть, что ? (р0 |, К) 0 при р0 ? 1, откуда, а также из
(IV. 1.34) следует, что
= (IV.1.37)
Функция Ф (|, К) и, следовательно, Т (|, Я) определяются суммированием ряда (lV.1.32) или численным интегрированием; зная [1 -- р0, можно таким образом вычислить / (|, Я)
| \ к Е/6*\ | 0,00 |
0,05 | 0,10 |
0,15 | 0,20 |
0,25 | 0,30 |
0,35 | 0,401 |
0,45 | |
| 0.1 |
0,9257 | 0,9222 |
0,9190 | 0.9161 | 0,9133 | 0,9107 | 0,9083 |
0,9060 | 0,9034 | 0,9019 | |
| 0,2 |
0,8161 | 0,8399 | 0,8341 | 0.8288 | 0,8239 |
0,8192 | 0,8149 | 0,8108 | 0,8070 | 0,8034 | |
| 0,3 | 0,7610 |
0,7528 | 0,7452 | 0,7382 | 0,7316 | 0,7255 |
0,7198 | 0,7144 | 0,7093 | 0.7045 | |
|
0,4 | 0,6702 | 0,6608 |
0,6521 | 0,6440 |
0,6365 | 0,6294 | 0,6228 | 0,6166 | 0,6107 |
0,6052 | |
| 0.5 |
0,5738 | 0,5639 |
0,5547 | 0,5463 | 0,5383 | 0,5309 | 0,5240 |
0,5174 | 0,5113 | 0,5055 | |
| 0,6 |
0,4714 | 0,4618 | 0,4530 | 0,4448 | 0,4372 |
0,4300 | 0,4232 | 0,4169 | 0,4110 | 0,4053 | |
| 0,7 | 0,3629 |
0,3545 | 0,3468 | 0,3395 | 0,3328 | 0,3265 |
0,3205 | 0,3149 | 0,3097 | 0,3047 | |
|
0:8 | 0,2483 |
0,2419 | 0,2359 | 0,2304 | 0,2252 | 0,2203 |
0,2158 | 0,2115 | 0,2074 | 0,2036 | |
|
0,9 | 0,1273 | 0,1237 |
0,1204 | 0,1172 |
0,1143 | 0,1115 | 0.1090 | 0,1065 | 0,1042 |
0,1021 | |
| ?*(*) |
2,286 | 2,250 | 2.216 | 2,185 | 2,154 |
2,126 | 2,098 | 2,072 |
2,047 | 2,023 |
по формуле (IV.1.34). Результаты вычислений / (|, Я) для ряда значений Я сведены в -табл. IV. 1 и ГУ.2 и приведены на рис. IV.4, а на рис. IV.5 представлены функции Е0 (Я) и М (к) = —df2 (0, K)/d |.
Мы видим, что кривые /(|, Я), соответствующие обра
щены вогнутостью вверх; кривая, соответствующая Я = г/2, является ломаной, составленной из двух прямых; при Я V2 кривые / (|, Я) обращены вогнутостью вниз, причем вплоть до функции, соответствующей Я = —1/2, производная /' (О, Я) отрицательна. Значению Я = —х/2 соответствует функция
4 2/ 1 о (E3S/8),
имеющая /' (0, —V*) = 0- При Я <[ —х/а /'(О, Я) положительно.
Таблица IV.1
| 0,50 |
0,55 | 0,60 |
0,65 | 0,70 |
0,75 | 0,80 |
0,85 | 0,90 |
0,95 | 1,00 | |
| 0.9000 | 0.8982 |
0,8965 | 0,8949 | 0,8933 | 0,8918 | 0,8904 |
0,8890 | 0.8876 | 0,8863 | 0,8850 | |
|
0,8000 | 0,7968 | 0,7937 | 0,7908 | 0,7880 |
0.7853 | 0,7828 | 0,7803 | 0,7779 | 0,7756 |
0,7735 | |
| 0,7000 |
0,6957 | 0,6916 |
0,6878 | 0,6841 | 0,6806 | 0,6772 | 0,6739 |
0,6708 | 0,6677 | 0,6647 | |
| 0.6000 |
0,5951 | 0,5904 | 0.5859 | 0,5816 | 0,5776 |
0.5737 | 0,5699 | 0.5663 | 0,5628 | 0,5594 | |
| 0,5000 | 0,4948 |
0,4899 | 0.4852 | 0,4807 | 0,4764 | 0,4723 |
0,4683 | 0,4645 | 0,4609 | 0,4573 | |
|
0,4000 | 0,3950 | 0,3902 | 0,3856 | 0.3812 |
0,3771 | 0,3731 | 0,3693 | 0,3656 | 0,3621 |
0,3586 | |
| 0,3000 |
0,2955 | 0,2913 |
0,2873 | 0,2834 | 0,2797 | 0,2762 | 0,2728 |
0,2696 | 0,2665 | 0,2634 | |
| 0,2000 |
0,1966 | 0,1933 | 0,1902 | 0,1872 | 0,1843 |
0.1817 | 0,1791 | 0,1765 | 0,1742 | 0,1718 | |
| 0.1000 | 0,0980 |
0,0962 | 0,0944 | 0,0927 | 0,0911 | 0,0896 |
0,0881 | 0,0867 | 0,0853 | 0,0840 | |
|
2,000 | 1,978 | 1,957 |
1,936 | 1,916 |
1,897 | 1,879 | 1,861 |
1,844 | 1,827 |
1,810 |
| М(Х) |
ДГ(Я-) | К |
МШ | ||
| 0,00 | 0,6276 | 0,35 |
0,9010 | 0,70 |
1,120 |
| 0,05 |
0,6714 | 0,40 |
0,9349 | 0,75 |
1,149 |
| 0,10 |
0,7134 | 0,45 |
0,9680 | 0,80 |
1,176 |
| 0,15 |
0,7538 | 0,50 |
1,0000 | 0,85 |
1,203 |
| 0,20 |
0,7925 | 0,55 |
1,031 | 0,90 |
1,229 |
| 0,25 |
0,8299 | 0,60 |
1,062 | 0,95 |
1;255 |
| 0,30 |
0,8661 | 0,65 |
1,091 | 1,00 |
1.280 |
Функция |0 (Я) монотонно возрастает с убыванием Я, стремясь к бесконечности при Я, стремящемся к —1 (решение, соответствующее Я = —1, будет рассмотрено ниже).
f
П
0,5
| ^;т 4-0 N. | ||
| I |
/^XN10 |
1 г
Рис. IV.4
ренблатта и М. И. Вишика [16] было дано доказательство конечности скорости распространения передней границы возмущенной области для задач пологих безнапорных движений (а также широкого класса более общих задач), соответствующих начальным распределениям напора жидкости, тождественно равным нулю вне некоторой конечной области.
Координата движущегося переднего фронта жидкости для рассматриваемых автомодельных движений выражается формулой
Mt) =
l,VaG{tUT+1
(IV.1.39)
(поскольку передний фронт соответствует 6 = ?0» напомним, что параметры а и Я, связаны между собой соотношением Я = а/(а 1)). Скорость распространения переднего фронта v0 представляется соотношением
Vo = \toVao {t — to)*-1 (а + 1).
В частности, когда напор на границе пласта постоянен, т. е. а = 0, то
z0 (0=2,286 Vao(t-t0y, vq = 1,143 -т—• (IV.1.40)
Г t- IQ
Далее, для суммарного объемного количества жидкости
в пласте М на основе уравнений (IV.1.5) и (IV.1.6) получается следующее выражение:
00 ЗС& 1
м== \ mh(x, ?)dx~-77==--/ (S,
J у a 4-1 J
(IV.1.41)
а для потока жидкости при х = 0, т. е. для скорости притока жидкости в пласт, в силу (IV. 1.10) — выражение
за__1_
Интегрируя обе части уравнения (IV. 1.7) по 6 от ? = 0 до ? = °о или, что все равно, до ? = поскольку / ( ?, Я) = 0 при ? ?0,
получаем
так что формула (IV. 1.41) приводится к виду:
за+1
_ 2та1/!а’1! (t — t0) 2 V1
1+2а
Таким образом, предыдущие соотношения показывают, что решения, соответствующие 0 < а < сю, т. е. 0<^Я<^1, отвечают возрастанию напора жидкости на границе и общего количества жидкости в пласте; для решения, соответствующего а — Л, = 0, напор жидкости на границе постоянен в ходе всего процесса, количество жидкости в пласте возрастает. При —11/3 < а <; 0, т. е. —7 2 < Я < 0, напор на границе в начальный момент бесконечен и убывает с течением времени до нуля; количество жидкости, первоначально равное, как и во всех предыдущих случаях, нулю, со временем увеличивается. При а = —1/3, т. е. Я = —1/2, напор на границе в начальный момент бесконечен и с течением времени убывает до нуля; общее количество жидкости в пласте постоянно в течение всего процесса — жидкость через границу х = 0 в пласт не поступает. Во всех указанных случаях на границе пласта х = 0 во всякий момент времени достигается максимальное для этого момента значение напора. При —1/2 < а < <[ —7з, т. е. —1 <С ^ <Z —1/2, напор жидкости на границе в начальный момент бесконечен и с течением времени убывает до нуля. Общее количество жидкости в начальный момент бесконечно велико и с течением времени убывает, стремясь к нулю, так что на границе пласта жидкость уже не втекает в пласт, как в предыдущих случаях, а вытекает из пласта. Тогда на границе пласта напор жидкости уже. не будет максимальным; максимальная величина напора достигается в некоторой внутренней точке пласта, различной для разных моментов времени.
6. Линейное возрастание со временем напора жидкости на границе пласта. Рассмотрим теперь частный случай, соответствующий линейному возрастанию напора жидкости на границе пласта, т. е. когда а = 1. Здесь
А (0, <) = а (<-*„); (IV. 1.45)
I аа(< — f0)
и уравнение (IV. 1.7) принимает вид:
/=°- (IV-1/l6>
Как нетрудно проверить, функция
удовлетворяет уравнению (IV. 1.46) и всем условиям задачи; отсюда получается
А (х, t) =
o(t —10) —
лгХ—г=-;
0 «? х У 2 аа (t —
/,,);
I 2а/а
Координата переднего фронта жидкости xQ (t) выражается следующим образом:
x0(t) =VlZmy(t—10), (IV.1.49)
а постоянная скорость распространения переднего фронта
v0 = V2ao. (IV.1.50)
Таким образом, график распределения напора жидкости в пласте представляется отсекаемым осями координат отрезком прямой линии, перемещающейся параллельно самой себе с постоянной скоростью.
Этот качественный результат был экспериментально проверен В. М. Шестаковым [122] на щелевом лотке, часто применяемом для моделирования безнапорных движений жидкости в пористой среде (с теорией щелевого лотка можно ознакомиться по книге В. И. Аравина и С. Н. Нумерова [2]). Щелевой лоток представляет собой две близко поставленные вертикальные стеклянные пластинки; щель между этими пластинками имеет непроницаемое горизонтальное дно и соединена с сосудом достаточно большого объема. Движение вязкой жидкости в щели подчиняется тем же закономерностям, что и безнапорное движение жидкости в пористой среде; место соединения щели с сосудом соответствует границе пласта. Равномерно поднимая уровень'глицерина в сосуде, В. М. Шестаков [122] получил распределение уровней глицерина в лотке, хорошо согласующееся с приведенным выше теоретическим результатом.
§ 2. ПОЛОГИЕ БЕЗНАПОРНЫЕ ДВИЖЕНИЯ С НУЛЕВЫМ НАЧАЛЬНЫМ НАПОРОМ:
ПРЕДЕЛЬНЫЕ АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ, ОСЕСИММЕТРИЧНЫЕ АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ
Составим полный список аргументов, от которых зависит это решение. Помимо координаты х и времени t, в этот список войдут также величины h0, у. и а. Тогда размерности всех определяющих параметров решения представляются в виде:
[x\ = L\ [t] = T-, [с] = [Л0] = [/*]; [и] = 2п'1,
(IV.2.4)
где по-прежнему символы L, Т ш [h\ означают соответственно размерности длины, времени и напора. Из пяти аргументов (IV.2.4) с тремя независимыми размерностями можно составить две независимые безразмерные комбинации, которые удобно взять в виде:
отсюда на основе л-теоремы решение рассматриваемой задачи будет
\ V ah0/x ]
где <р — безразмерная функция.
Положим теперь t = t' -f- т, где х — произвольная константа. При этом условие (IV.2.1) и уравнение (IV.2.3), как нетрудно проверить, записываются через новую переменную t’, гак же как и через прежнюю переменную, а условие (IV.2.2) принимает вид:
h (О, О = h’0eKl'; h'0 = htle*\ (IV.2.6)
Таким образом, сдвиг во времени влияет лишь на некоторое преобразование величины hQ, и постановка задачи оказывается инвариантной по отношению к группе преобразований переноса по времени; для определения h в переменных х, t’, а, у, h'n получается та же задача, что и для определения h в переменных (IV.2.4). Стало быть, на основе соотношений (IV.2.5) и (IV.2.6) имеем
= е-Л0ф (х Y —г-, та - их) • (I V .2.7)
Отсюда следует, что при любом х имеет место тождество
y{xVik’ xt)=evMxV^' *-**)• (iv-2-8)
Положим теперь х = t п получим
y[xVik' Kt)=eMxV^’ °)=е^(*/^)-
(I V.2.9)
Итак, функция h, зависящая от пяти аргументов (IV.2.4), представляется через функцию одного аргумента:
h =
h0e?«f<?y, 1= y'^ho '
(IV.2.10)
Подставляя (IV.2.10) в основное уравнение (IV.2.3), получаем для функции / (?) обыкновенное дифференциальное уравнение
Ж + = (1УЛШ)
Подставляя выражение (IV.2.10) в условие на бесконечности (IV.2.1) и граничное условие (IV.2.2), имеем граничные условия для функции / (?):
/(0) = 1; / (оо) = 0. (IV.2.12)
В силу непрерывности напора жидкости и потока жидкости функция / (?) по-прежнему должна быть непрерывной и иметь непрерывную производную от квадрата df2/d Мы получили, таким образом, для определения функции / (?) граничную задачу того же типа, что и граничные задачи для автомодельных решений, рассмотренных в предыдущем параграфе, и соответствующую значению параметра а, равному бесконечности, т. е. Л = 1. Эффективное вычисление функции / (?) выполняется способом, указанным в п. 4 предыдущего параграфа; результаты вычислений были приведены в табл. IV. 1 и на рис. IV.4. Функция /(?) = /(?, 1) тождественно
равна нулю при ? > ?0 = 1,810; передний фронт х0 (t) переме
щается, таким образом, по закону
х0 (t) = 1,810 У , (IV.2.13)
а скорость его перемещения равна
1>о(0 = 0,905/айМ55- (IV.2.14)
Полученное решение является в некотором смысле предельным для автомодельных решений, рассмотренных в предыдущем параграфе. В самом деле, положим в формуле (IV.1.6)
где h0 — некоторая константа размерности напора; т — константа размерности времени, причем, очевидно, эти константы выбираются с точностью до некоторого постоянного множителя. Решение (IV. 1.6) принимает при этом вид
Будем неограниченно увеличивать в этом решении ос при начальном моменте t0 ——сю по закону
t0 = —ат. (IV.2.17)
Раскрывая неопределенность, получаем, что при а -> °о
(t—t0\a t ога ft — г0 \а+1 f i л
(-М ехр—• —— (--М ехр —• К 1.
\ ат ) т ’ а+1\ т / т ’
Уравнение (IV. 1.7) в пределе при а -> со переходит в уравнение (IV.2.11), а условия (IV. 1.8) и (IV. 1.9) совпадают с условиями
Обозначая т через 1/и, получаем, что при а -> сю решение (IV.2.16) стремится к решению (IV.2.10). Поэтому решение (IV*2.10) было названо предельным автомодельным решением. Это решение было получено в работе Г. И. Баренблатта [8]. Предельные автомодельные решения представляют и принципиальный интерес в том отношении, что для доказательства автомодельности этих решений уже недостаточно соображений анализа размерности, т. е. недостаточно инвариантности постановки задачи относительно группы преобразования подобия величин с независимыми размерностями, как это было в ранее рассмотренных автомодельных задачах, а требуется дополнительно воспользоваться инвариантностью постановки задачи относительно еще одной группы — группы преобразований переноса по времени.
Приведенные при рассмотрении предельной автомодельной задачи рассуждения носят общий характер и могут применяться во многих других задачах. Очевидно, что предельные автомодельные движения существуют всегда, если система основных уравнений рассматриваемой задачи имеет автомодельные решения обычного степенного типа с произвольным показателем степени (который может принимать сколь угодно большие значения) и инвариантна относительно преобразования переноса соответствующей координаты. Как пример можно указать задачу пограничного слоя в несжимаемой жидкости, а также задачу одномерных неустановившихся движений газа. Полученные для этих задач автомодельные решения, содержащие степенные функции независимых переменных [136, 103], при предельном переходе, аналогичном проделанному в рассматриваемой задаче теории фильтрации *, дают предельные автомодельные решения, полученные Гольдштейном и Станюковичем [137, 109] путем формальной постановки.
Задача. На границе х = 0 полубесконечного пласта с непроницаемым горизонтальным водоупором задастся поток (расход) жидкости как степепная функция времени
Начальный напор во всем пласте равен нулю.
1 См. статью Г. И. Баренблатта [8] и книгу JI. И. Седова [102].
Г баг2 (< *o)Sj3+1 T/.f \ГЖМ(к)ф+2)*У1* А п
где М (А) = —df2 (О, A)/d? (см. рис. IV.5 и табл. IV.2), а координата переднего фронта жидкости хв (t) — в виде:
'¦«-s-wElsffiSfJ"' <iv-2'2i>
2. Осесимметричные автомодельные движения. При осесимметричных пологих безнапорных движениях жидкости напор жидкости h удовлетворяет уравнению
д {„дк2\ „ с kPS /тлг о 9o^
аТ = аТаг(г-аг)- а==2^Г=21Гт- (IV-2.22)
где г — расстояние рассматриваемой точки пласта от оси симметрии.
Рассмотрим следующую задачу.
Пусть (рис. IV.6) в бесконечный пласт, ограниченный снизу непроницаемой горизонтальной поверхностью — водоупором, через скважину, радиус которой пренебрежимо мал, начинается закачка жидкости. Предположим, что начальный напор жидкости в пласте рис jy g
равен нулю, так что начальное условие и условие на бесконечности имеют вид:
h(r,t0) = 0; Л(оо, г) = 0. (IV. 2.23)
Предположим далее, что расход закачиваемой жидкости изменяется со временем по степенному закону. Выражение для полного расхода жидкости, закачиваемой через скважину радиусом R, имеет вид:
По предположению, радиус скважины пренебрежимо мал (ниже мы остановимся на причинах, по которым это допущение можно делать для большинства реальных движений), поэтому можно принять R = 0; так как расход жидкости, закачиваемой в скважину, меняется по степенному закону, граничное условие на скважине принимает вид:
— лС =т(< — <0)?, (IV.2.25)
где т > 0 и р > —1. В частности, случай {5 = 0 соответствует закачке жидкости в пласт с постоянным расходом. Таким образом, решение задачи удовлетворяет уравнению (IV.2.22) и условиям (IV.2.23) и (IV. 2.25). Пс-прежнему, используя л-теорему анализа размерности, можно показать, что это решение является автомодельным и представляется в виде:
h “\ic & *)¦ (IV.2.26)
Здесь
g — r /in2r ~ 1оУ+2 . P (IV 2 27)
ё У яС(Р + 2)а * P + 2 V-4.^«)
представляют собой две независимые безразмерные комбинации определяющих параметров решения: других независимых комбинаций этих параметров не существует. Постоянный множитель снова введен в формулу для t с Целью удобства последующего изложения. Как и прежде, искомая функция должна быть непрерывной и иметь непрерывную производную от квадрата. Подставляя выражение (IV.2.26) в уравнение (IV.2.22) и условия (IV.2.23) и (IV.2.25), находим, что функция /j (Я) удовлетворяет уравнению
при условиях
l-Щ | Е_0 -1; U (ОО, Ч = 0. (IV.2.29)
Исследование этой граничной задачи проводится аналогично предыдущему; также единственным образом строится функция /1(6, Я.), отличающаяся от нуля лишь при 0 t sg ti (Я), где (Я) — некоторая функция ?, а при t ^ ?i (Я) тождественно равная нулю. Функция /j (t, Я) при | 0 имеет особенность, как
нетрудно видеть из первого условия (IV.2.29):
Второе условие (IV.2.29) может быть приведено к другой форме: умножая уравнение (IV. 2.28) на t и интегрируя в пределах от ? = 0 до g = °°, получаем, используя оба условия (IV.2.29) и условия
(g^f)?_ = 0; 1?/i(?.*)]!-o=0, (IV.2.31)
следующее интегральное соотношение:
со Ъ (Я)
j tu а, я) dt=J т а, я) dt=^. (iv.2.32)
о о
Первое условие (IV.2.31) непосредственно следует из условия, которому удовлетворяет функция /г (|, Я) на бесконечности, так как
если бы предел Е при | -> °о не был равен нулю, то функ-
ция fl (?, Я) не стремилась бы к нулю при ? -»- оо. Второе условие (IV.2.31) непосредственно следует из (IV.2.30).
Эффективное вычисление функции /г ('?, Я) удобно проводить следующим образом. Строим решение задачи Коши Ф5 (?. Я) для уравнения (IV.2.28). обращающееся в нуль при ? = 1 и имеющее в этой точке конечную первую производную. Исследование, в точности аналогичное приведенному в п. 3 § 1, показывает, что эта производная равна —1/4. Строить решение задачи Коши удобно так: вблизи ? = 1 можно представить решение в виде ряда, при помощи которого находится надлежащее число начальных значений, после чего применяется метод численного интегрирования Адамса — Штермера. Далее численно вычисляется величина
Величина N (Я) не раина единице, поэтому функция, равная ПРИ ? <С 1 и тождественно равная нулю при ? 22= 1, удовлетворяет всем условиям граничной задачи (IV.2.28)—(IV.2.29), кроме первого условия (IV.2.29). Воспользуемся теперь тем, что, как нетрудно показать, уравнение (IV.2.28) и второе граничное условие (IV. 2.29) инвариантны относительно - группы преобразований:
Ф2(|, Я)=-^-Ф1 (|р, Я), (IV.2.33)
Г
поэтому при произвольном положительном и функция Ф2 (?, Я) удовлетворяет уравнению (IV.2.28) и второму граничному условию (IV. 2.29). Но
Выбрав р = р.* = У N (К) так, что ^ ) о ~ П°~
лучим, что функция
у=~ Ф, (еКлгЩ; я); [0 ^ § ss (Я)] = [N (Я)]-1/-
h (I. Я) -
(IV.2.35)
удовлетворяет всем условиям граничной задачи (IV.2.28)— (IV.2.29).
В табл. IV.3 представлены полученные в результате проведенных таким способом вычислений значения функции /г (?, Я) для К в пределах от нуля до единицы через 0,1. Для удобства вычисления расхода жидкости на рис. IV.7; а, б даны соответствующие
| *=0,00 |
Л=0,05 | *. = 0,19 |
*=0,15 | 1=0.20 |
* = 0,25 | ||
| ? |
0,01119 | 0,01096 | 0,01075 | 0,01056 | 0,01037 | 0,01020 | |
| h |
2,534 | 2,525 |
0,517 | 2,510 |
2 502 | 2,497 | |
| ? | 0,01758 |
0,01722 | 0,01689 |
0,01659 | 0,01630 |
0,01603 | |
|
11 | 2,412 | 2,402 | 2,394 |
2,387 | 2,379 |
2,373 | |
| E | 0,02557 | 0,02505 | 0,02457 | 0,02413 | 0,02371 | 0,02331 | |
| /1 |
2,307 | 2,296 |
2,287 | 2,280 |
2,272 | 2,265 | |
| с | 0,03836 |
0,03758 | 0,03686 |
0,03620 | 0,03556 |
0,03497 | |
| Л | 2,186 |
2,176 | 2,166 |
2,158 | 2,149 |
2,142 | |
| 1 | 0,05754 | 0,05637 | 0,05529 | 0,05-430 | 0,05334 | 0,05246 | |
| /l |
2,059 | 2,047 |
2,037 | 2,029 |
2,020 | 2,012 | |
| 0,08950 |
0,08769 | 0,08601 |
0,08446 | 0,08298 |
0,08160 | ||
| л |
1,911 | 0,898 | 1,887 | 1,878 |
1,868 | 1,860 | |
| 0,1279 |
0,1252 | 0,1229 |
0,1207 | 0,1185 |
0,1166 | ||
| л |
1,782 | 1,769 | 1,757 | 1,747 |
1,737 | 1.728 | |
| с | 0,1918 | 0,1879 | 0,1843 | 1,1810 | 0,1778 | 0,1749 | |
|
/i | 1,624 |
1,609 | 1,597 |
1,586 | 1,574 |
1,565 | |
| 5 | 0,2685 | 0,2631 |
0,2580 | 0,2534 |
0,2489 | 0,2448 | |
| /1 | 1,480 |
1,464 | 1,451 | 1,439 | 1,427 |
1,417 | |
| ё | 0,3580 |
0,3507 | 0,3440 |
0,3378 | 0.3319 |
0,3264 | |
| Л |
1,345 | 1,329 | 1.315 | 1,302 |
1,289 | 1,278 | |
| ? | 0,4731 | 0,4635 | 0,4546 | 0,4464 | 0,4386 | 0,4313 | |
|
Л | 1,202 |
1,185 | 1,170 |
1,156 | 1,143 |
1,132 | |
| ? | 0,6137 | 0,6013 |
0,5898 | 0,5792 |
0,5216 | 0,5596 | |
| /j | 1,054 |
1,036 | 1,021 | 1,006 | 1,045 |
0,9809 | |
| - | 0,7416 |
0,7266 | 0,7127 |
0,6998 | 0 6638 |
0,6761 | |
| л |
0,9347 | 0,9170 | 0,9012 | 0,8868 | 0,8962 | 0,8610 | |
| I |
0,8950 | 0,8769 |
0,8601 | 0,8446 |
0,7824 | 0,8160 | |
| /1 | 0,8042 |
0,7868 | 0,7713 |
0,7571 | 0,7855 |
0,7318 | |
| ?. |
1,048 | 1,027 | 1,008 | 0,9894 |
0,9246 | 0,9559 |
|
| /1 |
0,6830 | 0,6665 |
0,6517 | 0,6381 |
0,6639 | 0,6139 | |
| 1 | 1,227 | 1,203 | 1,180 |
1,158 | 1,043 |
1.119 | |
| h |
0,5494 | 0,5344 | 0,5211 | 0,5087 | 0,5693 | 0,4867 | |
| 1 | 1,381 | 1,353 |
1,327 | 1,303 |
1,185 | 1,259 | |
| h | 0,4394 | 0,4262 | 0,4146 | 0,4037 | 0,4621 | 0,3845 | |
|
ё | 1,509 |
1,478 | 1,450 |
1,424 | 1,304 |
1.376 | |
| fx | 0,3498 |
0,3386 | 0,3288 |
0,3193 | 0,3768 |
0,3029 | |
| ? |
1,637 | 1,603 | 1,573 | 1,544 |
1,422 | 1,492 | |
| Л | 0,2616 | 0,2527 | 0,2450 | 0,2373 | 0,2946 | 0,2242 | |
|
6 | 1,739 |
1,704 | — |
1,641 | 1,541 |
— | |
| /l | 0,1917 | 0,1848 |
— | 0,1730 |
0,2147 | — | |
| ё | 1,841 | 1,804 | 1,769 |
1,737 | 1,660 |
1,679 | |
| /i | 0,1221 | 0,1175 |
0,1134 | 0,1096 |
0,1368 | 0,1029 | |
| 1,943 |
1,904 | 1,868 |
1,834 | 1,802 |
1,772 | ||
| /i | 0,05233 | 0,05030 | 0,04845 | 0,4677 | 0,04520 | 0,04377 | |
| 1 |
2,046 | - 2,004 |
1,966 | 1,931 |
1,897 | 1,865 | |
| Л=С,30 |
* = 0,35 | Л=0,40 |
*.= 0,45 | Л = 0,50 | |||
| i |
0,01004 ¦ | 0,009885 |
0,009740 | 0,009603 |
0,009472 | ||
|
п | 2,491 |
2,486 | 2,481 |
2,477 | 2,472 | ||
| 0,01577 |
0,01563 | 0,01531 |
0,01509 | 0,01488 |
|||
|
Я=0,30 |
Кг 0,35 |
Я=0,40 | Я— 0,45 |
Я=0,50 | |
| h | 2,367 | 2,361 |
2,356 | 2 351 |
2,347 |
|
0,02294 | 0,02259 |
0,02226 | 0,2195 |
0,02165 | |
| А |
2,259 | 2,253 |
2 248 | 2,243 |
2,238 |
| 1 |
0,03442 | 0,03389 |
0.03340 | 0,3292 |
0,03247 |
| h | 2,136 | 2,130 |
2,124 | 2,119 |
2,114 |
| 1 |
0,05163 | 0,05084 |
0,05009 | 0,04939 |
0,04871 |
|
h | 2,005 |
1,999 | 1,992 |
1,987 | 1,982 |
| I | 0,08031 |
0,07908 | 0,07792 |
0,7682 | 0,7577 |
| h | 1,852 | 1,845 | 1,839 |
1,833 | 1,827 |
| I | 0,1147 | 0,1130 | 0,1113 | 0,1097 | 0,1082 |
| h |
1,720 | 1,712 |
1,705 | 1,699 |
1,692 |
| ¦I | 0,1721 | 0,1808 | 0,1670 | 0,1646 | 0,1624 |
|
h | 1.556 |
1,520 | 1,540 |
1,532 | 1,526 |
| I | 0,2409 |
0,2372 | 0,2332 |
0,2305 | 0,2273 |
| h | 1,407 | 1,398 | 1,390 |
1,382 | 1.375 |
| s | 0,3212 |
0,3163 | 0,3117 |
0,3073 | 0,3031 |
| /i | 1,268 |
1,259 | 1,250 |
1,242 | 1,234 |
| I | 0,4245 |
0,4180 | 0,4119 |
0,4061 | 0,4005 |
| h | 0,1121 | 1,111 | 1,102 |
1,093 | 1,085 |
| 0,5507 |
0,5423 | 0,5343 |
0,5268 | 0,5196 | |
| X | 0,9698 |
0,9695 | 0,9498 |
0,9409 | 0,9325 |
| I | 0,6654 |
0,6553 | 0,6457 |
0,6585 | 0,6278 |
| h | 0.8498 | 0,8394 | 0,8297 | 0,7982 | 0.8122 |
| t | 08031 | 0,7908 | 0,7792 | 0,7682 | 0,7о77 |
| h |
0,7208 | 0,7105 |
0,7009 | 0,6920 |
0,6837 |
| I | 0,9407 | 0,9264 | 0,9128 | 0,8999 | 0,8876 |
|
fl | 0,6033 |
0,5935 | 0,5843 |
0,5758 | 0,5678 |
| I | 1,101 |
1,085 | 1,069 |
1,054 | 1,039 |
| fl | 0,4771 |
0,4682 | 0,4599 |
0,4521 | 0,4448 |
| I | 1,239 | 1,220 | 1,202 |
1,185 | 1,169 |
| fl | 0,3760 | 0,3682 | 0,3608 | 0,3540 | 03476 |
| 1,330 |
1,311 | 1,291 |
1.273 | 1,256 | |
| /l | 0,3115 |
0,3046 | 0,2981 |
0,2920 | 0,2863 |
| I | 1,468 |
1,446 | 1,425 |
1,404 | 1,386 |
| fl | 0,2184 |
0,2131 | 0,2081 |
0,2034 | 0,1990 |
| I | 1,560 | 1,536 | 1,514 |
1,493 | 1,472 |
| h | 0,1585 | 0,1543 | 0,1505 | 0,1469 | 0,1435 |
| I |
1.652 | 1,627 |
1,603 | 1,580 |
1,559 |
| fl | 0,09992 | 0,09716 | 0,09459 | 0,09219 - | 0,08993 |
|
I | 1,744 |
1,717 | 1,692 |
1,668 | 1,645 |
| /l | 004245 |
0,04121 | 0,04006 |
0,03899 | 0,03798 |
| ii | 1,836 |
1,808 | 1,781 |
1,756 | 1,732 |
| Я=0,55 | Я=0,60 * | Я~0,65 |
Я = 0,70 | Я=0,75 | |
| i | 0,009347 |
0,009232 | 0,009114 |
0,009009 | 0,008901 |
| h | 2,468 | 2,466 | 2,463 | 2,460 | 2,455 |
| I |
0,01469 | 0,01451 |
0,01432 | 0,01416 |
0,01399 |
| h | 2,343 | 2,341 |
2,337 | 2,334 |
2,329 |
| I | 0,02137 | 0,02110 | 0,02083 | 0,02059 | 0,02034 |
|
fi | 2,233 |
2,232 | 2,227 |
2,224 | 2,219 |
|
| *=0,55 | Я=0,60 |
Л = 0,65 | Л= 0,70 |
*=0,75 | |
| 1 |
0,03205 | 0,03165 |
0,03125 | 0,03089 |
0,03052 |
|
h | 2,109 |
2,107 | 2,102 |
2,099 | 2,093 |
| 0,04807 | 0,04748 | 0,04687 | 0,04633 | 0,04577 | |
|
)х | 1,976 |
1,974 | 1,969 |
1,965 | 1,960 |
| 6 | 0,07478 |
0,07386 | 0,07291 |
0,07208 | 0,07120 |
| /l | 1,822 |
1,818 | 1,813 |
1,809 | 1,803 |
| I | 1,1068 |
0,1055 | 0,1042 |
0,1030 | 0,1017 |
| fx | 0,687 |
1,683 | 1,678 |
1,673 | 1,667 |
| I | 1,1602 |
0,1583 | 0,1562 |
0,1544 | 0,1526 |
| fx | 1,520 | 1,516 | 1,509 |
1,505 | 1,499 |
| I | 0,2243 | 0,2216 | 0,2187 | 0,8162 | 0,2136 |
| h |
1.368 | 1,363 |
1,357 | 1,352 |
1,345 |
| % |
0,2291 | 0,295/i | 0,2917 | 0,2883 | 0,2849 |
|
h | 1,227 |
1,221 | 1,215 |
1,209 | 1,202 |
| I | 0,3953 |
0,3904 | 0,3854 |
0,3810 | 0,3764 |
| h | 1,077 | 1,071 | 1,065 |
1,058 | 1,052 |
| t 'Zj |
0,5128 | 0,5065 |
0,5000 | 0,4942 |
0,4883 |
| fx | 0,9246 | 0,9181 | 0,9111 | 0,9047 | 0,8977 |
|
I | 0,6196 |
0,6120 | 0,6041 |
0,5972 | 0,5900 |
| fx | 0,8042 | 0,7975 | 0,7905 | 0,7839 | 0,7769 |
| 0,7478 |
0,7386 | 0,7291 |
0,7208 | 0,7120 | |
| fx | 0,6758 |
0,6691 | 0,6621 |
0,6556 | 0,6488 |
| I | 0,8760 | 0,8652 | 0,8541 | 0,8443 | 0,8341 |
| fl |
0,5603 | 0,5538 |
0,5472 | 0,5409 |
0,5345 |
| 1,026 |
1,013 | 1,000 |
0,9885 | 0,9765 | |
| fx | 0,4380 |
0,4320 | 0,4259 |
0,4202 | 0,4144 |
| I | 1,154 | 1,140 | 1,125 |
1,112 | 1,099 |
| fx | 0,3416 | 0,3362 | 0,3309 | 0,3260 | 0,3209 |
| 9- 5 |
1,239 | 1,224 |
1,208 | 1,194 |
1,180 |
| /i |
0,2810 | 0,2762 |
0,2715 | 0,2671 |
0,2626 |
| 6 |
1,368 | 1,351 |
1,333 | 1,277 |
1,261 |
| h |
0,1949 | 0,1912 |
0,1875 | 0,2111 |
0,2073 |
| i | 1,453 | 1,435 |
1,417 | 1,359 |
1,343 |
| h | 0,1403 | 0,1375 | 0,1346 | 0,1578 | 0.1547 |
|
l | 1,538 |
1,519 | 1,500 |
1,442 | 1,424 |
| fx | 0,08782 |
0,08591 | 0,08396 |
1,099 | 0,1047 |
| I | 1,624 | 1,604 | 1,583 |
1,565 | 1,546 |
| h | 0,03703 | 0,03617 | 0,03529 | 0.03453 | 0,03374 |
| Ix |
1,709 | 1,688 |
1,667 | 1,647 |
1,628 |
| Я= 0,80 | * = 0,85 |
*=0,90 | Я=0,95 |
*=i,oo | |
| I | 0,008800 | 0,008707 | 0,008610 | 0,08522 | 0,008434 |
|
fx | 2,453 |
2,452 | 2,448 |
2,447 | 2,444 |
| I | 0,01383 |
0,01368 | 0,01230 |
0,01096 | 0,01084 |
| fx |
2,327 | 2,326 |
2,319 | 2,318 |
2,314 |
| I |
0,02011 | 0,01990 |
0,01968 | 0,01948 |
0,01928 |
|
h | 2,216 |
2,216 | 2,211 |
2,210 | 2,206 |
| I | 0,03017 |
0,02985 | 0,02952 |
0,02922 | 0,02892 |
| fx |
2,091 | 2,090 |
2,085 | 2,083 |
2,080 |
| I |
0,04526 | 0,04478 |
0,04428 | 0,04383 |
0,04338 |
| * = 0,80 |
*=0,85 | *=0,90 |
* = 0,95 | *=1,00 | |
| fx | 1,957 |
1,955 | 1,950 | 1,948 | 1,945 |
| I |
0,07040 | 0,06965 |
0,06888 | 0,6818 | 0,06747 |
| /г | 1,800 |
1,798 | 1,793 | 1,791 | 1,787 |
|
0,1006 | 0,09951 | 0,09840 | 0,09740 | 0,09639 | |
| h | 1,664 |
1,661 | 1,656 | 1,654 | 1,649 |
|
I | 0,1509 |
0,1493 | 0,1476 | 0,1461 | 0,1446 |
|
fx | 1,495 |
1,492 | 1,486 | 1,483 |
1,479 |
| I |
0,2112 | 0,2090 |
0,2066 | 0,2045 | 0,2024 |
| h | 1,341 | 1,338 | 1,332 |
1,329 | 1,324 |
|
I | 0,2816 |
0,2786 | 0,2755 | 0,2727 | 0,2699 |
|
h | 1,198 |
0,194 | 1,188 | 1,184 |
1,179 |
| I | 0,3721 | 0,3682 |
0,3641 | 0,3604 | 0,3470 |
| fx |
1,046 | 1,042 | 1,036 |
1,032 | 1,043 |
|
I | 0,4827 |
0,4777 | 0,4723 | 0,4675 | 0,4627 |
|
fx | 0,8923 |
0,8876 | 0,8816 | 0,8772 | 0,8720 |
|
0,5833 | 0,5772 | 0,5707 | 0,5649 | 0,5591 | |
| /i | 0,7714 | 0,7666 | 0,7606 | 0,7560 |
0,7508 |
| 0,7040 |
0,6966 | 0,6888 |
0,6818 | 0,6747 | |
|
/l | 0,6433 | 0,6384 |
0,6326 | 0,6280 |
0,6230 |
| 0,8046 |
0,7961 | 0,7872 |
0,7792 | 0,7711 | |
|
fx | 0,5474 |
0,5426 | 0,5370 | 0,5325 | 0,5277 |
|
I | 0,9253 |
0,9155 | 0,9053 | 0,8961 | 0,8868 |
|
fx | 0,4424 |
0,4379 | 0,4328 | 0,4285 | 0,4240 |
|
i | 1,086 |
1,075 | 1,023 | 0,9740 | 1,002 |
|
fx | 0,3166 |
0,3127 | 0,3381 | 0,3647 | 0,3302 |
|
I | 1,207 |
1,154 | 1,181 | 1,052 |
1,080 |
| fx | 0,2311 | 0,2553 |
0,2242 | 0,3047 | 0,2724 |
| ? | 1,287 |
1,234 | 1,260 | 1,130 | 1,195 |
|
fx | 0,1777 |
0,2010 | 0,1720 | 0,2482 | 0,1920 |
|
I | 1,368 |
1,314 | 1,338 | 1,247 |
1,272 |
| fl | 0,1271 | 0,1496 |
0,1226 | 0,1694 | 0,1424 |
| I | 1,408 | 1,393 | 1,417 |
1,364 | 1,388 |
|
fx | 0,1027 |
0,1009 | 0,07594 | 0,09730 | 0,07326 |
|
г | 1,529 |
1,513 | 1,496 | 1,481 |
1.465 |
| h | 0,03302 | 0,3237 |
0,03169 | 0,03109 | 0,03048 |
| lx |
1,609 | 1,592 | 1,575 |
1,558 | 1,542 |
значения/j (|) и ( — |-тгЛ при X = 0 (скачкообразное изменение
расхода). На рис. IV.8 построен график функции (А).
Координата г0 движущегося переднего фронта жидкости выражается соотношением
.. г 4fl2T(t-i0)9+2 4/- Сх(f-<0)P+* /IV “ЯЮ
r° = W V ,яГ(р + 2)*--У лтЧРН Wim • (! V-2-3b)
В частности, в. случае постоянного расхода закачиваемой жидкости q (t) = т, т. е. при (3=0, выражение для напора жидкости представляется в виде:
_Ст_ У '* ¦.г- ’
(IV.2.37)
01.
. 4л7П- ) t г°
Координата переднего фронта жидкости в этом случае выражается как
Рис. IV.7
Го (0 = 1,537 (~уиХ
X у7^Г0= 1,087 (^-У/4У7=Т0.
(IV.2.38)
§ 3. АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ ЖИДКОСТИ И ГАЗА ПЛОСКИМИ ВОЛНАМИ В ПОЛУБЕСКОНЕЧНОМ ПЛАСТЕ ПРИ НЕНУЛЕВОМ НАЧАЛЬНОМ ДАВЛЕНИИ ГАЗА ИЛИ УРОВНЕ ЖИДКОСТИ
1. Автомодельные пологие безнапорные движения при ненулевом начальном уровне жидкости. Рассмотрим снова пологие безнапорные движения несжимаемой жидкости в полубесконечном пласте, ограниченном снизу горизонтальным водоупором, а сбоку — вертикальной плоской границей, по другую сторону которой располагается резервуар, заполненный жидкостью. Предположим, что начальный уровень жидкости в пласте над водоупором постоянен и равен некоторому значению hQ, отличному от нуля (случай h0 — 0 был рассмотрен выше). Предположим, далее, что в начальный момент уровень жидкости в резервуаре внезапно изменяется, достигает некоторой величины hv большей или меньшей h0 (но сначала не равной нулю; случай hx = О будет рассмотрен особо) и затем остается постоянным. Очевидно, что возвышение hx свободной поверхности жидкости зависит только от времени t и координаты х, отсчитываемой по нормали к плоской границе; самой этой границе мы придадим значение координаты х, равное нулю, так что уравнение для h имеет вид:
dh й2й2 kpg ,TV о м
В силу постоянства начального уровня жидкости начальное условие и условие на бесконечности представляются в виде:
h (х, 0) =* ft0; h (оо, t) = h0, (IV.3.2)
а условие на границе пласта х — 0 принимает форму
h(0,t) = h1' (IV.3.3)
Таким образом, возвышение h свободной поверхности зависит от следующих величин:
х, t, а, й0, fh, (IV.3.4)
имеющих размерности
[*] = ?; Ш = {a] = {h]-'L*T-\ [Л0] = [/11] = [/1]
(L — размерность длины, Т — размерность времени, [й] — размерность напора, которую мы вправе принять независимой от размерности длины). Из величин (IV.3.4) можно, очевидно, составить две независимые безразмерные комбинации, в качестве которых удобно выбрать
* Ь = -г^, (I \г .3.5)
«1
так что рассматриваемое движение оказывается автомодельным и функцияJi представляется в виде:
h = h1F(Z>1X). (IV.3.6)
Подставляя это представление функции h в уравнение (IV.3.1) и условия (IV.3.2) и. (IV.3.3), получаем для определения функции F (?, к) уравнение
(IV-3-7)
и граничные условия
F (О, X) = 1, F (оо, К) = X. (I V.3.8)
В зтом случае ни одно из граничных условий (IV.3.8) уже не инвариантно относительно группы преобразований
хотя уравнение (IV.3.7) по-прежнему инвариантно относительно этой группы. Из-за этого обстоятельства определение функции F (|, К) не удается привести к задаче Коши, что сильно осложняет ее эффективное вычисление. Поэтому вычисления были проведены на быстродействующей электронной счетной машине (руководил вычислениями
Н. П. Трифонов).
Значения функции F (?, Ц представлены для различных А, (от О до 2 с шагом 0,1) на рис. IV.9, здесь же изображен предельный случай Я -=¦= 0, соответствующий h0 = 0 и рассмотренный выше. На рисунке IV. 10 приведены
Рис. IV.9
Рис. IV. 10
значения функции g (К) = ^ - определяющие поток жид
кости череа границу пласта д согласно соотношению
q 2М V^r- I1'-3*9)
Представим
в уравнении (IV 3.7) член
12/g—в виде
-|-?—f
умножим обе его части на ? и проинтегрируем это уравнение от 1 = 0 до 1 = 0°; получим
СО ОО
f Наг'Я+Н Е‘зг|У(ЕД)_ч‘'6"[ЕжЕ’-
0 0
СО со
Исследование, которое мы здесь опускаем, показывает, что функция F (6, Я) стремится к своему предельному значению при ? ->-00 очень быстро, по показательному закону. Поэтому, а также учиты-
вая, что при 6 = О F (X) и —щ - конечны, получаем
Поскольку, очевидно,
ОО
= (ОО, %)-F*(О, Я),
О
выражение (IV.3.10) дает интегральное соотношение, которому удовлетворяет функция F (Я):
ОО
J i[F(i, я)-я1^ = 1-я2. (iv.3.11)
о
Рассмотренные выше автомодельные решения задачи о пологой безнапорной фильтрации жидкости при ненулевом начальном уровне были найдены П. Я. Полубариновой-Кочиной [92, 93]. На существование автомодельных решений такого типа в задачах нестационарной фильтрации жидкости и газа было указано в работах Бус-синеска [133] и Лейбензона [72], однако ни их качественного исследования, ни численного расчета в этих работах проведено не было.
2. Фильтрация жидкости из полубесконечного пласта в пустой резервуар. Случай hx = О нуждается в отдельном рассмотрении. Здесь из оставшихся определяющих параметров можно составить только одну безразмерную комбинацию ? = #/"[/ah0t, так что возвышение свободной поверхности h представляется в виде:
= <p(g). (IV.3.12)
Функция h по-прежнему удовлетворяет уравнению Буссинеска (IV.3.1), начальному условию и условию на бесконечности (IY.3.2), а также граничному условию
h (О, 0 = 0, (IV.3.13)
откуда получается, что функция ф (|) удовлетворяет уравнению
^+{|Ц=0 (IV.3.M)
при условиях
ф(0) = 0; ф(оо) = 1. (IV.3.15)
В этом случае уравнение (IV.3.14) и первое условие (IV.3.15) инвариантны относительно группы преобразований /(?) = ц-2ф.
Поэтому, если ср(?) удовлетворяет уравнению (IV.3.14) и первому условию (IV.3.15), то и / (?) удовлетворяет этим соотношениям при любом ц > 0. Это дает возможность свести определение функции ф к решению задачи Коши для уравнения (IV.3.14). Однако в данном случае нет даже необходимости решать задачу Коши ввиду того, что рассматриваемая задача оказывается в точности математически эквивалентной основной задаче теории пограничного слоя —
о пограничном слое на плоской пластине.
В самом деле, положим в уравнении (IV.3.1) z (х, t) ~ — Л2.
Тогда это уравнение сводится к виду:
![]()
(IV.3.16)
а условия (IV.3.2) и (IV.3.3) перепишутся так:
0,5
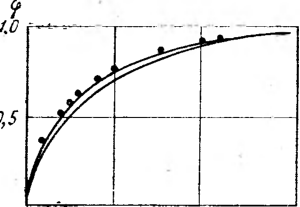
0 0,5 1,0 1,5 %
Рис. IV. 11
- (°°! t) = 0; z(0, t) = hl;
z (x, 0) = 0. _ (IV.3.17)
Но уравнение (IV.3.16) и условия (IV.3.17) совпадают с основным уравнением в форме Мизеса и условиями упомянутой задачи теории пограничного слоя 159], если заменить t на продольную коорди-
нату х, х — на функцию тока ф, 2а — на вязкость жидкости v, й0 — на скорость набегающего потока U, причем z выражает величину U2 — и'2, где и — продольная скорость потока. Таким образом, возвышение свободной поверхности h соответствует продольной скорости потока и в задаче пограничного слоя. Заметим теперь, что мы определяем зависимость функции ф, равной h/h0, от переменной \ ~х /|/ah0t, которая в терминах пограничного слоя соответствует
зависимости функции ujU от переменной я]; ¦ Как известно
из теории пограничного слоя.
![]()
(IV.3.18)
где I (т]) — затабулированная функция Блазиуса, таблица значений производной от которой имеется в каждом руководстве по гидро
![]()
динамике, а г] — безразмерная переменная Блазиуса, равная у
(у — поперечная координата в пограничном слое). Таким образом, мы
должны найти зависимость от переменной ]/2? и затем, полагая U — ф, ]/2? = 5, получим искомую функцию ф (|).
На рис. IV. 11 приведены полученные таким образом значения функции ф (?).
Определим теперь поток жидкости, вытекающей в резервуар из пласта. Имеем
kpgh% Ар2
2ji Vahtf
kpg dh22ц дх
4 =
5=0
Но согласно предыдущему ф = (]/2?), так что
dtp2
~Ж
Как известно из теории пограничного слоя, величина ?" (0), через которую выражается коэффициент трения пластины, равна 0,332, откуда получаем окончательно выражение для потока жидкости, вытекающей в резервуар, в виде:
hpgm
И'
(IV.3.19)
0,332
II V2ah0t
,332 hy*Y
Рассмотренное решение было найдено II. Я. Полубариновой-Кочиной [92—94].
§ 4. ОСЕСИММЕТРИЧНЫЕ АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ В БЕСКОНЕЧНОМ ПЛАСТЕ ПРИ НЕНУЛЕВОМ НАЧАЛЬНОМ ДАВЛЕНИИ ГАЗА ИЛИ УРОВНЕ ЖИДКОСТИ
1. Автомодельное изотермическое движение термодинамически идеального газа с постоянной вязкостью, возникающее при закачке или отборе газа через скважину. Рассмотрим бесконечный горизонтальный пласт мощностью II, вскрытый по всей мощности цилиндрической скважиной, направление которой перпендикулярно направлению простирания пласта. В начальный момент пласт насыщен газом, находящимся под давлением Р. Через вскрывающую пласт скважину в начальный момент начинает закачиваться газ с постоянным массовым расходом q. Рассмотрим возникающее при этом фильтрационное движение газа.
Поскольку картина движения симметрична и одинакова во всех плоскостях, перпендикулярных оси скважины, распределение давления газа зависит только от времени t и расстояния г рассматриваемой точки пласта от оси скважины г = 0 и удовлетворяет уравнению
Начальное давление газа в пласте постоянно и равно Р, так что начальное условие и условие на бесконечности имеют вид:
Р (>', 0), — Р, p(oo,t)=P. (IV.4.2)
89
Через скважину, радиус которой равен R, в пласт закачивается газ с постоянным массовым расходом q:
=q. (IV .4.3)
fip0 V dr /г=11 3 ’
Будем считать радиус скважины пренебрежимо малым (ниже мы приведем оценки, оправдывающие это допущение). Тогда условие (IV.4.3) перепишется в виде:
Итак, искомое распределение давления в пласте, удовлетворяющее уравнению (IV.4.1) и условиям (IV.4.2) и (lV.4.4), зависит
от определяющих параметров г, t, а2, ¦ ¦ размерности которых
следующие: [rl — L; Ш = Т\ [<г2] = [р]~гЬ2Т~г\ = f/?]2;
[PI = I/?] ([p] — размерность давления). При помощи анализа размерности можно убедиться в автомодельности рассматриваемого движения. Распределение давления при этом представляется в виде:
Подставляя (IV.4.5) в уравнение (IV.4.1) и условия (IV.4.2) и (1V.4.4), получим, что функция (|, К) является интегралом уравнения
diF* j J —1__(IV46)
т | -t- 2 dg и (IV.4.0)
при граничных условиях
^(°°’ X)==1* (IV-4-7) Качественная картина расположения интегральных кривых уравнения (IV.4.6) исследуется аналогично тому, как описано в § 1: точно так же порядок уравнения (IV.4.6) понижается до первого, затем исследуется картина интегральных кривых уравнения первого порядка, после чего результаты переносятся на интегральные кривые уравнения (IV.4.6). Это исследование показывает, что интегральные кривые уравнения (IV.4.6), удовлетворяющие второму условию (IV.4.7), распадаются на два класса, разделенные между собой интегральной кривой Fi(?, 0) = 1, соответствующей, как легко видеть, К = 0 (рис. IV.12). Кривые первого класса, располагающиеся над кривой Fi (|, 0) = 1, беспредельно близко подходят к оси ординат, асимптотически уходя в бесконечность при уменьшении | до нуля. При | -*¦ 0 функция F i (?, медленно возрастает по закону так что каждой из интегральных кривых первого класса соответствует свое значение параметра Я, монотонно возрастающее от нуля до бесконечности по мере удаления от кривой F^ (|, 0) = 1.
При 6 -> 00 ординаты кривых обоих классов быстро стремятся к единице по закону
Л(6, Я) = 1 + о[-|-ехр(— -f-)]. (IV.4.9)
Кривые второго класса, располагающиеся под интегральной кривой Ft (6, 0) = 1, не доходят до оси ординат, а заканчиваются, подходя под прямым углом к оси абсцисс [которая является особой линией уравнения (IV.4.6), поскольку на этой линии обращается в нуль коэффициент при старшей производной в этом уравнении]. При этом вместо первого условия, которому удовлетворяют все интегральные кривые первого класса, соответствующие Я >0, эти кривые удовлетворяют условию •
где 6 (Я.) — координата точки пересечения рассматриваемой кривой с осью абсцисс. Каждой q кривой соответствует определенное значение Я, монотонно убывающее по мере удаления кривых Pnc.IV.12 от интегральной кривой Fi (|, 0) = 1 от нуля до —оо.
Интегральные кривые второго класса описывают автомодельные движения, в процессе которых происходит не нагнетание газа в пласт, как в случае движений, отвечающих интегральным кривым первого класса (Я >0), а отбор газа из пласта с расходом, определяемым соответствующей этой кривой величиной Я:
ХякНРгро
(IV.4.H)
* ИР о
(в этой формуле массовый расход q считается отрицательным).
Следует отметить, что, создавая достаточный перепад давления, можно, в принципе, закачивать газ в пласт с любым большим расходом через скважину сколь угодно малого радиуса. Однако отбирать газ из пласта можно лишь прн расходах, не превышающих того расхода, который соответствует установлению у стенки скважины нулевого давления. Дальнейшее увеличение расхода отбираемого газа возможно только при условии расширения скважины. Таким образом, в отличие от случая закачки газа, нельзя ставить задачу об отборе газа через скважину пренебрежимо малого радиуса. Кривые Ft (|, Я) при Л >0 (кривые второго класса) соответствуют автомодельным движениям, в которых отбор газа с постоянным расходом, определяемым формулой (IV.4.11), происходит через расширяющуюся скважину, радиус которой растет по закону
R = H%)Va*Pt,
(IV.442)
причем у стенки этой расширяющейся скважины давление постоянно и равно нулю. Заметим, что это расширение отбирающей скважины ни в коей мере не препятствует применению рассматриваемых решений к практическим задачам, поскольку для значений параметра к, представляющих практический интерес, эта фиктивная скважина, как показывают проведенные расчеты (см. ниже), всегда будет находиться внутри настоящей скважины.
Далее, если взять часть любой интегральной кривой Ft (|, к), принадлежащей к первому или второму классу, от некоторого | = = т) > 1 (Я) А» ? = ©о, то формула (IV.4.5) будет представлять собой автомодельное решение задачи, соответствующей постоянному начальному давлению и отбору или нагнетанию газа (в зависимости от знака к) через расширяющуюся скважину. При этом у стенки скважины поддерживается постоянное давление, равное
(IV.4.13)
PFi(4, Ц.
Радиус R расширяющейся скважины увеличивается по закону
R = f\ У a2Pt.
(IV.4.14)
Для дальнейшего изложения полезно выяснить, какой порядок величины к = gpp0 [nkpfflP2]'1 встречается в практических задачах. Возьмем в качестве примера случай, для которого величина % будет весьма высокой, этим самым определится порядок верхнего предела значений к. Пусть через скважину отбирается
1 ООО ООО м3 газа в сутки (имеется в виду объем при атмосферных условиях); такой расход является достаточно высоким. Пусть, далее, вязкость газа р равна 0,01 спз, проницаемость пористой среды к —
— 1 д == 10“8 см2, мощность пласта Н — 10 м, начальное пластовое давление Р = 30 кгс/см2 (относительно небольшое давление для столь высокого отбора газа); за величины р0 и р0 возьмем соответственно
1 кгс/см* и плотность газа при давлении 1 кгс/см2, так что величина qjр0 представляет собой заданный объемный расход газа, отбираемого через скважину. Переходя к одинаковым единицам измерения и подставляя приведенные величины параметров в выражение для к, примем к «=* 0,04. Стало быть, в реальных случаях параметр к равен 0,01—0,02 и менее.
На рис. IV.13, а, б изображены кривые Fid, Я), отвечающие нескольким значениям параметра к, как положительным, так и отрицательным, а также соответствующие кривые — |dF*/d|. Эти кривые показывают, что в довольно значительной области вблизи точки | = 0 (соответственно вблизи | == | (/.) для кривых, отвечающих к < 0) функция — \dF\ld | близка к своему значению при | = 0
(соответственно при | | (Я)), т. е. к К. При этом основное измене
ние функции (|, Я), т. е. основное изменение давления газа, сосредоточивается именно в этой области. При тех же значениях для которых функция —уже существенно отклоняется по величине от X, функция F i (|, X) оказывается достаточно близкой к единице. В практически наиболее интересной области значений параметра X, равных по абсолютной величине одной сотой и менее,
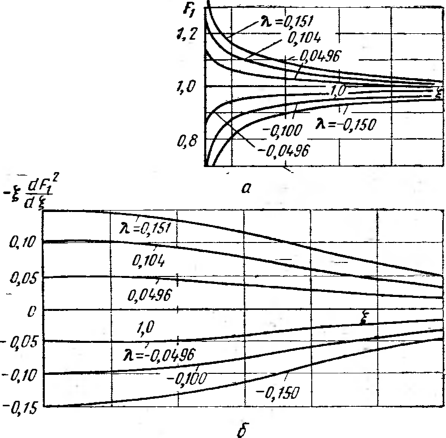
Рис. IV.13
это свойство постоянства функции —-\dF\ld % в области, где Ft (|, X) существенно отличается от единицы, выражено еще более резко. В табл. IV.4 приведены результаты численного расчета кривых (S, X), соответствующих X = —0,009999 и X = —0,004994. Через обозначено значение аргумента |, обладающее тем свойством, что при | < 1* значения — ^,dF\/d | отличаются от X меньше, чем на 0,01%. Стало быть, при ? ^ с этой же степенью точности выполняется соотношение
откуда при | имеем с той же степенью точности, с которой
вычислены таблицы,
| Я | = -0,009989 | К |
= -0,004994 | ||
|
1 | i?i (I, Я) |
dF* | 6 | Fl (1, Я) | dF‘ |
|
5* = 0,005787 | 0,9701 |
0,009999 | |«= 0,003886 |
0,9842 | 0,004994 |
|
0,01157 | 0,9737 | 0,009999 | 0,01555 | 0,9877 |
0,004994 |
| 0.01929 |
0,9763 | 0,009999 | 0,03109 | 0,9894 | 0,004993 |
| 0,03472 | 0,9793 |
0,009998 | 0,06218 | 0,9912 | 0,004992 |
| 0,06558 | 0,9825 | 0,009994 |
0,1244 | 0,9929 | 0,004984 |
| 0,09645 | 0,9845 | 0,009987 | 0,2487 |
0,9947 | 0,004955 |
|
0,1582 | 0,9870 | 0,009968 | 0,4974 | 0,9964 |
0,004841 |
| 0,2816 |
0,9899 | 0,009899 | 0,9949 | 0,9980 | 0,004412 |
| 0,5285 | 0,9930 |
0,009653 | 1,492 | 0,9988 | 0,003779 |
| 0,7754 | 0,9948 | 0,009270 |
2,487 | 0,9996 | 0,002305 |
| 1,269 | 0,9970 |
0,008167 | 3,482 |
0,9999 | 0,001098 |
|
1,763 2,751 3,738 | 0,9982 0,9994 0,9999 | 0,006770 0,003879 0,001743 |
Поэтому значения i?1 (|, X) при 1 < 6* в табл. IV.4 не приводятся. Проведенные численные расчеты показывают, как это видно из табл. IV.4, что при |Я|<0,01 величина F4 (^, Я) отличается от единицы менее чем на 0,03, так что при. 6 справед
ливо неравенство 1 >/’, (6, Я) >0,97. Отсюда следует, что с практически вполне достаточной точностью в этой области уравнение (IV.4.6) для функции Ft(6, Я) можно заменить линейным относительно F* (6, Я) уравнением
± A g dFl . J_ in =0 (IV 4 17)
| dl S ^ 4 dl V
[в последнем слагаемом уравнения (IV.4.6) добавлен множитель Fi (6, Я), согласно предыдущему мало отличающийся от единицы I. Это линейное уравнение легко интегрируется и дает
| (IV.4.18)
где С — константа интегрирования. Определим эту константу иа
dF^
условия, что при 6=1* величина 6 ~т€ - = —Имеем
“Ь
С = — Яехр(~ VgiD-
Так как для рассматриваемой практически интересной области |Я]<0,01 значение 6* весьма мало (< 0,01) и е"‘,,5‘ отличается от единицы не более чем в шестом десятичном знаке, то можно полагать С = —Я.
Fl(l, K)^D-K J-j- (IV.4.19)
Константа интегрирования D находится из условия, что при 1=5* величина f t (I,., X), соответствующая решению линейного уравнения (IV.4.17), совпадает с величиной f\(|, А), полученной численным интегрированием. Это дает при | 5=
Fid, X) = F*(U, ?,) + AEi(__|.)__*iEi(—|-), (IV.4.20)
где Ei — интегральная показательная функция.
При 5 -v оо функция, определяемая уравнением (IV.4.20), строго говоря, не удовлетворяет второму условию (IV.4.7) — при | —°о эта функция стремится не к единице, а к величине
Однако оказывается, что зта величина очень мало отличается от единицы, — отличие для практически наиболее интересной области f X f < 0,01 находится в пределах 0,01%. Так при К = —0,009999
имеем: ?* = 0,005787; -i-Ei(| |*) = 5,905; Fj( g*, К) = 0,9701;
S = 1,00007. Для меньших по абсолютной величине К это отличие еще меньше, так что величина S для этого диапазона значений Я может быть принята равной единице. Таким образом, построенное нами решение линейного уравнения удовлетворяет с вполне достаточной степенью точности второму условию (IV.4.7).
Итак, при Е I* функция Ft (5, X) с точностью до 0,01% представляется в виде:
FAl, M = /l--^Ei(—f-) . (IV.4.21)
Заметим теперь, что так как в рассматриваемом интервале | к | < <0,01 величина I* весьма мала, для функции Ei ^^ j при
с большой точностью выполняется асимптотическая формула
(см., например, Янке и Эмде [129]). Поэтому при | ^ I* с точностью, большей 0,01 %, имеет место равенство
Подставляя это соотношение в формулу (IV.4.16), получаем, что при | ^ с точностью до 0,01%
Но это выражение точно совпадает с соотношением (IV.4.20), которому функция •/'’id, X) удовлетворяет при | ^ I*. Кроме того, выше было показано, что первые два слагаемых правой части предыдущей формулы в сумме с большой точностью равны единице. Отсюда следует весьма существенный вывод о том, что в практически наиболее интересном интервале значений параметра К, | К | < 0,01. функция Fid, Я) представляется в виде (1V.4.21) при всех значениях
Переходя от функции jFi(1, "к) к давлению р по формуле (1.4.5), получаем, что для
распределение давления с весьма высокой степенью точности пред-ставляется для всех значений г и t в виде:
Шй)- <IV-4-'22>
Именно таким получилось бы решение задачи, если бы мы заменили в уравнении (IV.4.1), которое можно представить в форме
множитель р во втором члене на значение р — Р этого множителя при г = оо, т. е. если бы от уравнения (IV.4.1) при тех же граничных и начальных условиях перешли к линейному относительно р2 уравнению
Такой способ линеаризации уравнения (IV.4.1) был впервые предложен J1. С. Лепбензоном [711. Приведенные расчеты показывают практически точное совпадение решения рассматриваемой нелинейной осесимметричной задачи с решением линеаризованной задачи. Успех линеаризации объясняется в данном случае тем, что в случае осесимметричных движений область движения разбивается на две части: 1) область квазистационарного
движения, соответствующая малым значениям |, в которой сосредоточивается основная часть всего перепада давления, но ноток газа почти постоянен, и 2) — область малых д е п р е с -с и й (перепадов давления), в которой поток газа сравнительно медленно уменьшается, а перепады давлений малы.
В области квазистационарного движения не только разность вели-
др2 0 2 д др2 чин г и Ли р г равна нулю, как это следует из уравнения
(1V.4.1),ho и каждая из этих величин сама по себе исчезающе мала (сравнительно со значениями этих величин в тех точках, где они макси-
мальны). Поэтому в зтой области поток газа, равный — —»
почти постоянен, а величина множителя при втором члене уравнения (IV.4.1) несущественна, и с большой степенью точности можно заменить в этом множителе р (г, t) на Р (г, t). В области же малых депрессий, в определенной части которой оба члена уравнения (IV.4.1) существенно отличаются от нуля, возможность такой замены обусловливается малостью разности р (г, t) — Р.
Обнаруженная допустимость линеаризации при описании нелинейных осесимметричных движений вне зависимости от величины возникающего перепада давления позволяет сделать важные выводы применительно к более общим классам движения.
Заметим теперь, что в реальных задачах задается поток газа через скважину хотя и малого, но конечного фиксированного радиуса, так что граничное условие на скважине на основании выражения (IV.4.3) имеет вид:
Покажем, что построенное выше автомодельное решение удовлетворяет с большой степенью точности этому условию уже спустя несколько секунд после начала процесса.
В самом деле, на основании (IV.4.5) имеем
Числеппые расчеты, проведенные для кривой Я = —0,009999, показывают (см. табл. IV.4), что уже при ? = 0,1582 значение функции gcLFf/d| равно 0,009968, т. е. отличается от —/, менее чем на
0,5% и еще менее при меньших |.
При радиусе скважины R «=< 10 см, проницаемости к ^ 1 д = = 10“8 см2, пористости т0,2, вязкости р ^ 104 г/см-сек, ве-кР
личина а2Р — имеет порядок 103 -?¦ Ю1 см2/сек, и тогда уже ири t = 3 сек
l=,RlYa2Pt <0,19.
Поэтому можно с весьма высокой степенью точности полагать при t > 3 сек
Чэ dl J^R/Va*Pt
Используя это обстоятельство в соотношении (IV.4.25), получаем, что спустя несколько секунд после начала движения автомодельное
решение (TV.4.5) с большой степенью точности удовлетворяет уравнению
![]()
л/г//р0 ’
WPo
т. е. граничному условию (IV.4.24).
Как было показано выше, встречающиеся на практике значения параметра Я по модулю значительно меньше, чем рассмотренное только что значение, примерно равное —0,08. Поэтому для меньпгнх Я условие (IV.4.24) будет удовлетворяться еще быстрее.
Выше было отмечено, что автомодельные решения при Я < 0 соответствуют отбору газа из пласта через расширяющуюся со вре-менем скважину. Покажем теперь, что зто неестественное, на первый взгляд, свойство решений не препятствует применению их к реальным задачам, поскольку для представляющего практический интерес времени расширяющаяся (фиктивная) скважина всегда остается внутри настоящей скважины. Для этого определим порядок величины | (Я) — координаты точек подхода кривой /^(1, Я) при Я<0 к оси абсцисс. Как было отмечено выше, при | ^ т. е. в частности, при S = S (Я), функция FЯ) с высокой степенью точности удовлетворяет соотношению (IV.4.16):
Полагая в этом соотношении | = |(Я), Я) = 0, получаем
Я) = Я1п-^; |(Я)=1*е
_ При Я = — 0,08, Fi (Я) 0,72 значение — 0,0050, откуда | (Я) 0,005 е-6>5 = 0,75 -Ю-5. Как показывает формула (IV.4.12),
промежуток времени Т, за который расширяющаяся внутренняя скважина достигает размеров настоящей скважины, составляет
что в силу предыдущих оценок для |, а2Р и R дает примерно Т — = 2-10® сек — около шести лет. Отметим, что значение Я — —0,08 очень велико сравнительно со значениями, встречающимися на практике. При уменьшении Я величина Т резко возрастает: так, при Я = —0,01 Т 1075 лет. Таким образом, для реальных задач расширяющаяся (фиктивная) скважина всегда остается внутри настоящей.
Приведенные выше оценки показывают, что рассматриваемое автомодельное решение является вполне пригодным для реальных задач.
Автомодельность рассматриваемой в настоящей рубрике задачи была отмечена JI. С. Лейбензоном [721 и П. Я. Полубариновой-Ко-чиной [94]. Изложенное выше решение згой задачи дано Г. И. Ба-ренблаттом [12, 9]. Численные расчеты были выполнены под руководством Н. П. Трифонова [24].
§ 5. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ
В этом параграфе будут изложены решения некоторых автомодельных задач нестационарной фильтрации, представляющих специальный интерес. В связи с тем, что методическая сторона построения подобных решений достаточно выяснена в предыдущих параграфах, изложение здесь будет более кратким; читатель, интересующийся подробностями вычислений, сможет найти их в цитируемой литературе.
1. Подъем уровня жидкости при прекращении фильтрации в пустой резервуар и при набегании переднего фронта жидкости на препятствие. Пусть начальному моменту t — 0 соответствует стационарное распределение уровня жидкости, отвечающее пологому безнапорному истечению жидкости из пласта в пустой резервуар. Если вторая граница пласта находится достаточно далеко, то пласт можно считать полубескоиечным; начальное распределение уровня жидкости hn(x), удовлетворяющее уравнению (IV.3.1) и условию h0 (0) — 0, представляется в виде:
![]()
(IV.5.1)
где q — постоянный поток жидкости, вытекающей из пласта. Заметим, что возвышение свободной поверхности с увеличением х безгранично возрастает; однако это не имеет значения, поскольку, рассматривая бесконечный пласт, мы интересуемся только начальной стадией движения, когда возмущения стационарного режима, производимые вблизи границы х = 0, несущественно сказываются вблизи второй границы^
Предположим теперь, что в начальный момент времени граница пласта х — 0 внезапно изолируется, так что истечение жидкости через нее прекращается. Рассмотрим последующий процесс подъема уровня жидкости. Поток жидкости на границе при х = 0 равеп нулю; это дает условие
![]()
(IV.5.2)
Как следует из анализа размерности, решение уравнения (IV.3.1) при условиях (IV.5.1) и (IV.5.2) автомодельно и представляется и виде:
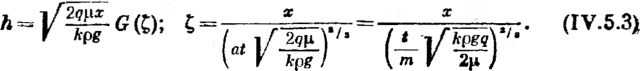
Положим G (Q — ? !’g(Z,); ? = t, У Тогда в соответствии
с уравпеписм (IV.3.1) и условиями (IV.5.1) и (IV.5.2) функция g (g) удовлетворяет уравпению
совпадающему с уравнением (IV.1.7) при % == 3/4, при краевых условиях
Построим функцию g„ (|) — решение задачи Коши для уравпения (IV.5.4), удовлетворяющее условиям go(0) = l, go (0) = 0.
Как показывает исследование, приведенное в § 1, при | оо для функции gо (?), принадлежащей к иптегральным кривым I класса уравнепия (IV.5.4), справедливо соотношение lim g0 (?)/]/ ? = const;
согласно вычислению константа равпа 0,7772, и фупкция g0 (%) удовлетворяет уравнепию (IV.5.4) и первому условию (IV.3.5), но не удовлетворяет второму условию (IV.3.5). Поскольку фупкция \i2g0 ([х g) удовлетворяет уравпению (IV.5.4) и первому условию (IV.5.5) при любом (х, то, выбирая |i = ji^ = 0,8763, получаем, что функция g (|) = H*2g0 (И* i) удовлетворяет всем условиям задачи, и решение представляется в виде:
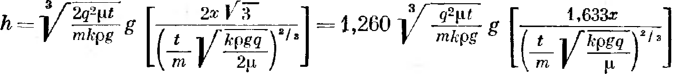
(А / J
(IV.5.6)
Зпачения фупкции g(|) приведепы па рис. IV.13. В частпости, при х = 0, т. е. на грапице пласта, уровень жидкости возрастает со временем по закону
Рассмотренные выше примеры автомодельпых движений показывают, что передний фронт жидкости распространяется по сухому водоунору с конечной скоростью, причем свободная поверхность подходит к точке своего соприкосновения с водоупором под острым углом и вблизи этой точки имеет форму наклонной плоскости.
Следующее рассуждение, принадлежащее Я. Б. Зельдовичу и А. С. Компапейцу [50], показывает, что . это обстоятельство имеет место и в общем случае движения жидкости в сухом групте. В самом деле, уравпепие (lV.3.1), описывающее распределение уровня жидкости, можпо переписать следующим образом:
Но в точке xn(t) —на переднем фронте области, занятой жидкостью, выполняется соотношение h\x0 (/), t] = 0. Для определенности иудея считать, что фронт движется справа налево. Тогда, дифференцируя последнее соотношение, находим
dh , / dh \ dx0 _dh _/ dh \
dt ' \ dx )x=xt dt ’ dt \ dx )x=x0V°’
где v0 — абсолютная мгновенная скорость перемещения границы этой области (сама скорость отрицательна). Подставляя эти соотношения в уравнение (IV.5.8), находим
Отсюда получается, что вблизи переднего фронта распределение уровня жидкости имеет вид:
Лг=-^ (IV.5.10)
причем в теченйе непродолжительных промежутков времени можно скорость перемещения переднего фронта считать постоянной.
Таким образом, приходим к следующей постановке задачи. В пачальпый момент распределение уровпя жидкости при х > 0 выражается, как
h(x, 0) = -^-. (IV.5.11)
На границе х = 0, соответствующей непроницаемому препятствию, поток жидкости равен пулю:
Распределение уровня жидкости h (х, t), удовлетворяющее уравнению (IV.3.1) и условиям (IV.5.11) и (IV.5.12), автомодельно и может быть представлено в виде:
A = 1 = (IV.5.J3)
Функция и (?) удовлетворяет уравпению
| 1 с &U \ /л ./ттт рг л / \
при граничных условиях
(-S’) =°! lim — (IV.5.J5)
V dl /5-0 Е-*со ? V2
Решепие u(?) краевой задачи (IV.5.14)—(IV.5.15) выражается, как и в предыдущем случае, через решепие задачи Коши для
101
уравнепия (IV.5.14), удовлетворяющее условиям и0 (0) = 1, и0 (0) =0. Значения функции м(|) приведены на рис. IV.14. В частности, уровень жидкости на самом препятствии, т. е. при х — 0, возрастает по закону
-А(0, = (IV.5.16)
2. Напорно-безнапорное движение при нулевом начальном уровне жидкости. Рассмотрим однородный пласт копечной мощпости Н. Пусть вначале пласт был заполнен неподвижпой жидкостью до уров -ня йоо-< Н; в момент t — 0 на границе пласта х = 0 создается напор
h0 > II. Распределение напора в последующие момспты врс-мепи будет, очевидпо, иметь вид, показанный на рис. IV.15. В части пласта, непосредственно примыкающей к начальному сечению х = 0, напор превысит величину Н. Поэтому пласт будет заполнеп жидкостью
Рис. IV.14
т
I
И I
I
Рис. IV.15
целиком, и движение на этом участке будет напорным. В некоторой точ^е х ~ «j напор сравняется с Н и при х ^>х1 движепие станет безнанорпым. Если пласт вначале не содержал жидкости (hm= = 0), то зона движения распространяется с конечной скоростью; если начальный уровепь отличается от пуля, то движепие сразу захватывает весь пласт. Сформулироваппая задача имеет автомодельное решепие:
(IV.5.17)
При зтом'от | = 0 до 6i = *i) Сдвижениеявляетсянапор-
ным, а от 6 = ? i и Далее — безнапорным. При нулевом начальном уровне жидкости область безнапорпого движения простирается до некоторого копечпого значения
Р = ? (- тУ У1г
5 ?2 ^ kHpgt ) •
Читатель легко закончит иостроеиие автомодельного решения задачи о напорно-безнапорном движепии при нулевом начальном уровпе жидкости, используя для аффективного построения решения автомодельиые решения § 1.
3. Решения типа мгновенных источников для задач политропи-ческой фильтрации термодинамически идеального газа. Пусть п бесконечном объеме пористой среды происходит фильтрация газа при политропической связи плотпости и давления фильтрующегося гаэа. Предполагая движение одномерным, имеем уравнение для плотности газа в виде:
![]()
![]()
где г — пространственная коордипата, т. е. расстояпие рассматриваемой точки пористой среды от плоскости отсчета при движении газа плоскими волнами, расстояние этой точки от оси симметрии движе-пия — при осесимметричном движении газа и расстояние ее от центра симметрии — при центральпо-симметричном движении газа, a s соответственно равно нулю, единице или двум для этих трех типов симметрии движепия. Начальное давление и плотность газа предполагаем пренебрежимо малыми во всей области пористой среды, так что начальное условие и условие па бесконечности имеют для рассматриваемой группы задач вид:
(IV.5.19)
Излагаемые ниже решения соответствуют «мгновенным» источникам. Для движения газа плоскими волнами это означает, что в начальный момент некоторая масса газа сосредоточена вблизи плоскости начала отсчета г = 0. Для осесимметричных и централь-но-симметричных движений это озпачает, что некоторая масса газа сосредоточена в начальный момепт вблизи оси или, соответственно, центра симметрии, которым также соответствует значение г = 0. Поскольку во время движепия не происходят никакие процессы, приводящие к исчезновению или появлению газа, должны выполняться некоторые соотношения, выражающие сохранение полной массы газа во всем объеме пористой среды; эти соотношения записываются в виде:
СО
со
оо
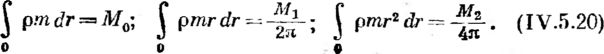
Рассматриваемые решения представляют, например, для случая движения газа плоскими волнами, удобную схематизацию реальных движений, возникающих в пористой среде, когда определенная масса газа сосредоточивается под большим давлением, значительно превышающим давление в остальпых точках пористой среды, а затем растекается по пласту.
Умножая обе части уравнения (IV.5.18) на г® и интегрируя от г = 0 до г = оо, пользуясь условиями (IV.1.3) и тем, что ноток газа
на бесконечности,
пропорциональный (^/s ^
получаем
frs дРП+1
V ~0г
- —\
¦) =0-/г-0
(IV.5.21)
Используя соображения размерпости, получим следующие выражения для плотности газа при осесимметричном и цептрально-сим-метричном движении его плоскими волнами:
!/о
V а2т‘Ч )
/ М^са; V тп
(IV.5.22)
I--' , I
1 / MyCfit \ 2П+2 I
L\ (2яm)n J J
2 Г 7T-_ТГ
I ( Mza2t \ 3U+3 |_ \ (4гш)п )
(IV.5.23)
(_ Jji
\(4яш)
(IV.5.24)
Здесь функции /s (|) [ ? обозначает в каждом случае свой безразмерный аргумент функции fsв формулах (IV.5.22) — (IV.5.24)] удовлетворяют уравнению
d/Г12
dp
и условиям
CO
J/s(S)^ = l; (^f"+1)|=o^° (* = 0,1,2). (IV.5.26)
Из непрерывности плотности газа р и потока газа ри =
*р»« grad рп+|
следует, что функции р и grad р”
— yPgradp =
(X (п + 1)
должны быть непрерывными. Для одномерных движений это влечет за собой непрерывность р и дрп+1/дг, а для рассматриваемых нами авто-модельпых задач — непрерывность fs (|) и dj"+l/d g.
Умпожив обе части уравнения (IV.5.25) на c,s, получим в левой части этого уравпения полную производную. Интегрируя, найдем первый интеграл в виде:
__1__?s+l/ =с
(IV.5.27)
dl ^ sn + 2~ ls
Заметим теперь, что 6?+1/s (I) стремится к нулю при ?->-0, ипаче интегралы в условиях (IV.5.26) расходились бы при ? —0. Поэтому, полагая в уравнении (IV.5.27) ? = 0 и используя условие (IV.5.26), получим С0 — Ci = С2 = 0. Имея это в виду и интегрируя еще раз соотношения (IV.5.27), легко найдем выражения для /,(?) в виде:
2<n + i)(sn+2)
(IV. 5.28)
где es—постояпная интегрирования. Как петрудио видеть, эти решения удовлетворяют сформулированпым выше требованиям непрерывности fs и dfs+1/d
Из первого соотношения (IV.5.2G) получаем
| ( 2 (ft-j-1) (w -j-2)\n+2 | ’2r(' + f)r(i)l |
| V ‘ п ) | Чт+i) J |
Г». X ILTA
ех = (2
[ ffr+Jj!= [2 (1
J-n)JrTrTn-b (IV.5.30)
2 п П+2
(IV.5.29)
2 (n-f 1) (3« + 2) ""|зп+2 n I
| 2Г | |
(i+40 | 1 | |||
| Г| | 0+40 |
1 г | | (i |
Ь) | |
21t
3»+2
(IV.5.31)
где Г — гамма-функция Эйлера. Окончательно имеем выражения для распределений плотности газа в виде:
\1/п
\е _г2 ( ¦ то—- Г+2)
L 0 \муч) J)
0 ^ г ^ г0 (*);
1
|я+2
Г Д/g у
2 (и4-1) (п+2)
Ро
(IV.5.32)
Г_>+l (- П Го _ м2 ( (2пт)п\
|_2afl2/nfJ [ 4(п+1)2|_ 1 V М^аЧ )
Pl=
M\la~t \ i+n
| 3 Г му* 1зп+2 |
п | [с |
г2 11 |
| [ (4ят)г1‘аЧ J | 2(в + 1)(Зв + 2) | 2 |
1(4яп)п } |
1 In
p.
0^r^r2(<); (iv.5.34)
Как • видпо, эти решения непрерывны и обладают непрерывной производной дрп+1/дг. Однако производная др/дг имеет в точке г —
— rs(0 разрыв, так что построенные решепия не относятся к классическим решениям уравпения в частпых производных (IV.5.18) и являются его обобщенными решепиями.
Интереспо проследить, как при стремлении п к нулю решения (IV.5.32)—(IV.5.34) переходят в известные решепия типа мгновенного источника классического линейного уравнения теплопроводности. Рассмотрим это на примере решения (IV.5.32). Имеем при г sS r0(t)
(z»l) (IV.5.35)
и тем, что Г (7г) = получим при п -+¦ 0 известное выражение для решения типа мгповеипого источпика классического линейпого уравнения теплопроводности:
г1 4 аЧ
М0
I Vcfint
(IV.5.36)
(отсутствие обычной двойки в знаменателе объясняется тем, что мы приняли полную массу газа равной 2М0, а не М„).
На рис. IV.16 изображены распределения плотности газа в некоторый момент времени, соответствующие различным зпачениям п при одинаковых значениях всех прочих параметров. Как видно
из рисунка, при п > 1 кривая распределения плотпости подходит к границе области, занятой газом, под прямым углом. При п — I эта кривая подходит к границе области, запятой газом, под острым углом. При 0 < п < 1 кривая распределения плотности газа подходит к грапице области, занятой газом, под нулевым углом, касаясь оси абсцисс в конечной точке, координата которой возрастает с уменьшением п. Во всех этих случаях имеет место конечная скорость распространения переднего фронта области, занятой газом. Предельпому случаю п — 0 (классическое линейное уравнение теплопроводности) соответствует, как известно, бесконечная скорость распространения переднего фронта.
Рассмотреппые выше движения были впервые исследовапы в работе Я. Б. Зельдовича и А. С. Компанейца [50] применительно
7777777//Z/7777777/77777777- х Рис. IV.17
0,5
|
n=ls0'' - f |
1 I \ |
|
1 | г з |
| Рис. | IV.16 |
к математически аналогичной задаче теории теплопроводности и независимо — применительно к задаче теории фильтрации в работе Г. И. Баренблатта [5].
4. Задача о растекании бугра жидкости на непроницаемом горизонтальном водоуноре. Полученпые в предыдущей рубрике решения могут быть использованы, благодаря апалогии между пологими безнапорпьтми движениями несжимаемой жидкости и изотермической фильтрацией термодинамически идеальпсго газа (см. гл. II), для построения решепия некоторых интересных задач пологих безнапорных движений.
Предположим, что в пласте бесконечной мощпости, лежащем на непроницаемом водоуноре, тем или иным способом создается бугор жидкости, который затем растекается под действием силы тяжести по всему во до упору (рис. IV. 17). Рассмотрим две простейшие схемы. В первом случае предположим, что бугор жидкости сильно вытянут в одном направлении, так что картину движения можно считать не зависящей, от коордипаты, отсчитываемой в этом направлении; обозначим ее через j/. Таким образом, возвышение свободпой поверхности над водоупором h зависит только от времепи t и координаты х, отсчитываемой в перпендикулярном направлении, и удовлетворяет уравнению
/т2 # 2 __
dt № ' 2 пцх •
Предполагая, далее, что бугор жидкости в начальный момент сосредоточен в очепь узкой области вблизи линии ж — 0, получаем начапьпое условие и условие па бесконечности в виде h (ж, 0) = 0 (ж ф 0); h (со, t) = 0. Далее, суммарное количество жидкости, приходящееся на единицу ширипы бугра в процессе движения, постоянно, так что
СО
hdx=,~b. (IV.5.38)
Эта задача в точности аналогична рассмотренной ранее задаче о мгновенном источнике при изотермической фильтрации газа плоскими волнами (п — 1), причем вместо плотности газа фигурирует высота h свободной поверхности. Переписывая решение (IV.5.32) при п — 1 в повых термипах, получим решение задачи о растекапии сосредоточенного плоского бугра в виде:
и h = 0 при x^x0(t).
Во втором случае предположим, что форма начального бугра жидкости симметрична относительно некоторой вертикальной оси. Тогда и все последующее движение будет обладать симметрией отпот сительно этой оси, и возвышепие свободной поверхности будет удовлетворять уравпению
— —а2 1 8 г g2 (TV 5 40}
dt ~а г дг г вг • а 2тц '
где г — расстояние от оси симметрии.
Если считать, что начальный бугор сосредоточен в малой окрестности оси симметрии, то начальное условие и условие на бесконечности имеют вид h (г, 0) = 0, (г ф 0); k (°°, t) = 0. Условие постоянства всей массы жидкости в пласте М t имеет вид:
СО
2ят§ h(r, t)rdr^Mlm (IV.5.41)
о
Эта задача в свою очередь в точности аналогична задаче о мгновенном источнике при изотермической осесимметричной фильтрации газа, только вместо плотности газа в задаче учитывается высота свободной поверхности.
Полагая в решении (IV.5.33) п = 1 и переписывая его в обозначениях повой задачи, получаем решение этой задачи в виде:
h~[ arf4i] j)7g р ~ Jfitfi yTrji (IV.5.42)
и fe = 0 при r^srt(t).
5. Решение типа диполя. Рассмотрим политропическую фильтра-цию термодинамически идеального газа в полубесконечном пласте с плоской границей. Предположим, что до начала движения давление и плотность газа в пласте пренебрежимо малы. В начальный момепт в пласт через границу мгновенно внедряется некоторое количество газа, после чего давлепие и плотность газа па границе стаповятся равными нулю. Исследуем процесс растекания газа по пласту. Фильтрация газа происходит плоскими волнами, так как все характеристики движепия зависят только от времепи t и координаты х, отсчитываемой но нормали к плоскости границы пласта, которой приписывается зпачение координаты х = 0. Плотность газа удовлетворяет при этом уравпению
_йР. = я2_Ё!р^1. а2=_ЬИЁ*___(IV 5 43)
dt дх* > а ут(п+ !)(%'
Поскольку внедрение газа в пласт происходит, по предположению, мгновенно, а начальпая плотность газа пренебрежимо мала, начальное условие и условие на бесконечности для рассматриваемой задачи имеют вид:
р(д:, OJesO (хф0)\ р(оо, <)=0. (IV-5.44)
Умпожив теперь обе части уравпения (IV.5.43) па жи проинтегри-тв от х = 0 яо х— получим
ровав от х = 0 до х = получим
оо со СХЭ
A j рxdx = a?Jx dx — а? (х igi) J dx=
х ~^~)\х 0 i «2Р”+1(0, t) — fl2pn+1 (°°, t).
= а2[а
Но выражение (zdp"+1/frr)Ae(M равно пулю в силу условия на бесконечности р (°°, t) = 0; если бы эта величипа была не равна нулю, то условие равенства пулю плотности на бесконечности пе было бы выполнено. Далее, величина (ж дрп+1/дх)х„0 равна нулю, так как иначе плотность при х = 0 была бы бесконечной. Так как по условию в течение процесса плотность газа на границе аг = 0 равна нулю, предыдущее соотношение дает
со оо
J pxdx = 0-, J рх dx .— Q~ const, (IV-5.45)
dt
о
причем постоянная Q характеризует в некотором смысле количество газа, мгновенно поступившего в пласт в начале процесса. Таким образом, рассматриваемый процесс характеризуется постоянством «статического момента» распределения плотности.
Из анализа размерности видно, что решепие рассматриваемой задачи, т. е. решение уравнения (IV.5.43) при условиях (IV.5.44) и (IV.5.45), является автомодельным и представляется в виде:
Р = (^Р/(|); | =-Ъп- (IV.5.46)
(aZQnt)2 <и+1>
Подставляя выражение (IV.5.46) в уравнение (IV.5.43) и условие (IV.5.45), получаем для определения функции / (|) краевую задачу
&Г13 ¦ 1 г df ,__1_#_п. плт^/.ъ
dp + 2(н + 1) * dl + га |1 /~0’ (IV.5.47)
причем по-прежнему в силу необходимой непрерывности плотности и потока газа функция / (?) должна быть непрерывной и иметь непрерывную производную djn+ fd%.
Искомое решение этой краевой задачи имеет вид:
т)
где
(IV .5.48)
(IV.5.49)
(В — В-функция Эйлера).
Координата х* (t) переднего фронта области, давление газа в которой отличается от нуля, изменяется согласно соотношению
я* (t) = go {a?Qnty <»+». (IV.5.50)
Аналогично предыдущему можно показать, что при п 0 полученное решение стремится к известному решению типа диполя классического линейного уравнения теплопроводности.
Заметим, что построенное нами решение является предельным случаем для решений, рассмотренных в гл. IV, § J, и соответствующим п — 1, а — —у?, к = —1. .
При п — 1 полученное решение можно интерпретировать с точки зрения задачи безнапорной фильтрации. Пусть на плоской границе х — 0 полубесконечного пласта, расположенного на горизонтальном водоупоре и не содержащего жидкости, внезапно создается очень высокий напор жидкости, а затем напор на границе вновь падает до нуля х.
Возвышение свободной поверхности h удовлетворяет при этом уравнению (IV.5.37) и условию
f° h(x, t) xdx = Q, (IV.5.51)
о
которое получается из уравнения (1V.5.37), аналогично.тому, как было получено условие (IV.5.40) из уравнения (IV.5.43).
Константа Q определяет количество внедренной в пласт в начале процесса жидкости. Полагая в соотношениях (IV.5.46) и (IV.5.48) п — 1 и переписывая эти соотношения в терминах рассматриваемой задачи безнапорного движения, получаем решение этой задачи в виде:
h = VJ,t[~?u} <IV-5S2>
о i З3 ?о~ 2уА5,
так что координата передней границы области, занятой жидкостью, изменяется со временем по закону
z* (t) = 2V^Qt =|/¦ (IV.5.53)
Координата точки x**(t), соответствующей максимальному возвышению свободной поверхности, определяется соотношением
ж** (<)=---—л/
bk^gQt- -
(IV.5.54)
(1+6V5)" V 2mfl
На рис. IV.18 изображена форма свободной поверхности жидкости, соответствующая рассмотренному движению, для нескольких моментов времени (т0 — некоторый произвольно выбранный момент времени). Рассмотренное выше решение было получено в работе Г. И. Ба-ренблатта и Я. Б. Зельдовича [191.
6. Автомодельные движения при произвольном уравнении состояния. Аналогия между безнапорной фильтрацией несжимаемой жидкости и фильтрацией термодинамически идеального газа может быть распространена на случай фильтрации газа с вроизвольным уравнением состояния и произвольной зависимостью вязкости от давления. При безнапорной фильтрации этому отвечает часто встречающийся случай движения в слоистом грунте, свойства которого переменны по высоте.
| / < Г/ *?f \ | |
| И |
|
Рис. IV.18
Рассмотрим пологое безнапорное фильтрационпое движение несжимаемой жидкости в грунте, проницаемость к и пористость т которого зависят от расстояния от горизонтального водоупора z. Если уровень жидкости в данном вертикальном сечепии будет h, то в элементарпом слое толщиной dx и шириной Ъ содержится объем жидкости
Н* dx ~ ^ J m(z)b (z) dz j dx. (IV.5.55)
В то же время расход жидкости через это сечение составляет
(z)k(z)d\fx, (IV.5.56)
где р — плотность жидкости.
Составляя обычным образом уравнение неразрывности, получим для напора h дифференциальное уравнение
dh
(IV.5.57)
дх
где
ф (h) = j к (z) Ъ (z) dz о
— неубывающая функция. Вводя функцию
h
легко привести уравнение (IV.5.57) к стандартному виду:
дР *»к(р) S. (IV.5.59)
v __Ф (ро) pg . к ,п\ ^Ц(ро)т(ро)Ь (Рр) /Tv г
К° цт(Р0)Ъ(Ра)’ А ^ V(P0)m(P)b(P0) 1 '
(очевидно, ср, m и b можно считать известными функциями Р). Решепие уравнения (IV.5.59) при условиях
^(0,*) = РЮ; />(г,0) = Ро (IV.5.61)
автомодельно. Будем рассматривать фильтрацию в сухой грунт, для которой jP00= 0. Искомое решение представится в виде:
/>(i,*) = i>0/(i); ^-=-4=-, (IV.5.62)
2 г x-of
где функция / (5) удовлетворяет уравнению
К (P0f) /" (Q f ИГ = 0. (IV.5.63)
Можно доказать, что если k (z) и те (z) принимают при малых z конечные значения, то, как п в задаче изотермической фильтрации газа, движение за конечное время охватывает лишь ограниченный участок пласта. Поэтому при ? ^ ?0 Р = 0. Кроме того, из условия
непрерывности расхода следует, что /' (|0) = 0.
Мы видим, что задачи, отличающиеся конкретным видом функций т (z), Ь (z) и к (z), сводятся к одинаковой краевой задаче для уравнений, отличающихся между собой лишь видом коэффициента К. Поэтому желательно, не решая уравнения (IV.5.63), составить представление о том, как меняется решение с изменением коэффициента К. Приведем следующий наиболее простой пример. Пусть функция fi удовлетворяет тем же краевым условиям, что и /, и уравнению вида (IV.5.63), но с некоторым другим коэффициентом К (. Предположим также, что функция К (Р) монотонно возрастает и что Ki (Р) ^ К (Р). Тогда при всех ?
U (0^/(6). (IV.5.64)
Доказательство этого утверждения дано А. М. Пирвердяном [90], который использовал его также для оценки одних решении при помощи других, допускающих элементарное выражение.
Задачи к § 5.
1. Рассмотреть осесимметричные автомодельные решения задачи Коши для уравнения изотермической фильтрации термодинамически идеального газа
др „19 др2
-гт=«2 — -г-г - —, (IV. 5.65)
удовлетворяющие начальным условиям:
Р {г, 0) = ar!<; a = const>0; а = const>0
Ответ. При 0 < а < 2 решение задачи существует для любого значения времени и выражается в виде:
Р (г, t) = a (я2аг)2-а[л*2Ф
(IV. 5.66)
У 1 — а/2 (с2а<)1/(2 а)
где Ф (I) — решение уравнения (IV.2.39) при к = а/2, удовлетворяющее начальным условиям
Ф(0) = 1, Ф'(0)-0.
1
![]()
(IV.5.67)
При а = 2 решение выражается в конечном виде:
(IV.5.68)
Это решение существует лишь на конечном интервале значений времени t: О ==? г === Т, где Т — 1/16а*о.
При t = Т оно обращается в бесконечность одновременно для всех значений г.
При а 2 решение рассматриваемой задачи Коши не единственно, поэтому при а > 2 такая постановка задачи оказывается физически бессмысленной.
2. Рассмотреть автомодельные решения задачи Коши для движения газа плоскими волнами р = р (х, t) в бесконечном пласте при начальных условиях:
Р (ж, 0) = скха1 (я>0); р (х, 0) = а2 ( — х)и* (х^О).
3. Рассмотреть случай выравнивания скачка давления (c>i = Pi; о2 = Р2фР1, «! —а2 = 0).
По аналогии между безнапорной фильтрацией и фильтрацией газа решение этой задачи н то же нремя описывает выравнивание уровнен ht и подземных вод при безнапорной фильтрации. При ht ]> Н, h2 = О этот случай отвечает распространению, первоначально вертикальной границы между жидкостью и газом в пласте мощностью И. Задача о таком движении границы возникает при проектировании подземного хранения газа [34].
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ
Если не считать линейных задач, получение эффективного точного решения задач нестационарной фильтрации окажется скорее исключением, чем правилом. Однако и решения линейных задач, в принципе всегда доступные, не всегда удовлетворяют требованиям простоты и обозримости. В еще большей мере это относится к решениям (в этой книге не рассматриваемым), получаемым при помощи электронно-вычислительных машин.
Разнообразные технические задачи необходимо решать в сравнительно простой аналитической форме, допускающей качественный анализ решения в зависимости от параметров задачи. В связи с зтим широкое применение получили приближенные методы. Большинство этих методов не имеет строгого обоснования, и их использование оправдывается главным образом тем, что при сопоставлении результатов с известными точными решениями получается удовлетворительное совпадение.
Прежде чем перейти к конкретному рассмотрению вопроса, укажем специфические особенности задач нестационарной фильтрации, которые во многом обусловливают успех применения приближенных методов.
1. Большинство задач нестационарной фильтрации сводтися к уравнениям параболического тина, для которых характерно сглаживание возмущений со временем и по мере продвижения их внутрь области, для которой рассматривается решение.
2. В ряде задач, представляющих интерес для техники, решение имеет в некоторых точках области движения известные особенности, а вне окрестностей этих точек состояние системы близко к невозмущенному или к стационарному. Это обстоятельство имеет тем большее значение, что нелинейность многих задач проявляется лишь при значительном отклонении системы от стационарного состояния.
3. Практический интерес представляют интегральные характеристики решения.
Отмеченные особенности задач нестационарной фильтрации определяют и характер приближенных методов. В основном они состоят в том, что вначале ставится задача, близкая к данной и имеющая эффективное решение, а затем ищутся малые поправки к этому решению. В тех случаях, когда исходная задача имеет особенности, естественно ставить и вспомогательную задачу с теми же особенностями. Приближенные методы различаются в зависимости от того, какие задачи используются в качестве «близких» и каким образом в решение вносятся дополнительные поправки.
Применение приближенных методов к конкретной задаче имеет свою специфику, особепно в связи с требованием эффективности. Поэтому, не пытаясь дать готовые рецепты для каждого метода, приведем примеры, из которых будет ясна и техника применения метода, и возможные осложнения при использовании его в иных обстоятельствах.
§ 1. СХЕМА МЕТОДА ИНТЕГРАЛЬНЫХ СООТНОШЕНИЙ.
ПРИТОК К ГАЛЕРЕЕ В БЕСКОНЕЧНОМ ПЛАСТЕ ПРИ УПРУГОМ РЕЖИМЕ
Рассмотрим прежде всего несколько одномерных задач теории упругого режима. При этом, как известно, распределение давления описывается линейным уравнением теплопроводности
![]()
и использование приближенных методов связано не с невозможностью получения точных решений, а с их сложностью. Кроме того, решение ряда задач имеет чисто методическое значение.
1. Ранее (см. гл. Ill, § 1) было уже приведено решение задачи
(V.1.2)
о пуске галереи в бесконечном пласте, которое имеет вид:
Р = Ро — (Ро~ Pi) erf
где р6 — начальное давление в пласте; рг — давление на галерее.
Разность между начальным давлением и его мгновенным значением быстро убывает.
Используя определение функции ошибок в виде интеграла, легко показать, интегрируя по частям, что
![]()
Поэтому естественно ввести понятие об области влияния галереи, т. е. области, в которой давление заметно отличается от своего первоначального значения. Из предыдущей формулы и из соображений размерности ясно, что размер области влияния где с — постоянная порядка единицы, значение которой зависит от того, как определена область влияния.
Будем теперь искать приближенное решение задачи. Предположим, что вне области влияния галереи движения нет, а внутри нее давление распределено так же, как при стационарной фильтрации, т. е. линейно. Примем далее, что давление непрерывно. Тогда
р(х, 0 = Pi+(Po — Pi) -f [0 ==? ж ss Z (01; (у ! 4)
Р (*> 0 = Ро [x^^l (?)].
Теперь достаточно определить вид зависимости I (t), чтобы завершить построение приближенного решения. Выбор соотношения для определения I (t) является в известной мере произвольным, так как нельзя указать то единственное соотношение, удовлетворив которому, можно достичь наилучшего соответствия между приближенным решением (V.1.4) и точным решением поставленной задачи. Поскольку для большинства приложений основное значение имеет правильное определение количества отбираемой из пласта жидкости, обычно границу I (t) находят из условия материального баланса для пласта в целом. За время dt через участок сечения пласта шириной b и мощностью Н проходит объем жидкости bHudt, причем в соответствии с законом фильтрации
/с Pi-Po (V.1.5)
к др
и —---х-
I
ц дх
За время t с начала движения через сечение х — 0 проходит объем жидкости
о
Этот объем жидкости высвободился (будем для определенности считать, что из пласта отбирается жидкость и <Ср0) за счет снижения давления в области движения. В предположении, что деформация пласта и жидкости происходит упруго, имеем
I I (О
Q — тЪН ^ dx — j (Po — Pl) -l) dx. (V.1.7),
0 0 Приравнивая выражения (V.1.6) и (V.1.7), получаем
jbH - *°> f m=nr ¦- ¦p°> К1 —т)dx
или
1 = 2 Via (V.1.9)
(постоянная с в уравнении (V.1.3) равна в данном случае 2).
Таким образом, окончательное выражение для давления будет
р(х, t) = p1 + ±-(p0-p1)-~ (0<*^21^);(уЛЛ0)
p(x,t) = p0 (хгэ=21fvS).
Согласно уравнению (V.1.5) скорость фильтрации па Гранине пласта меняется по закону
ц(0,0 = -
Р17- • (V.1.11)
Из точного решения (V.1.2) для скорости фильтрации получается выражение
“о (0, 0 = (V.1.12)
— ц V nxt
Таким образом, полученное решение, давая качественно верное описание движения, является все же лишь грубо приближенным. Тем не менее проиллюстрированный выше метод, называемый методом последовательной смены стационарных состояний, получил достаточно широкое применение в практических расчетах. Не останавливаясь на дальнейших примерах из теории упругого режима, которые можно найти в книгах И. А. Чарного [118, 119], В. Н. Щел-качева и Б. Б. Лапука [126], А. М. Пирвердяна [91] и др., сформулируем общую схему метода.
Предполагается, что при наложении возмущения весь пласт отчетливо разбивается на две области — область невозмущенного состояния и область возмущения и что давление в области возмущения распределено так, как если бы движение в этой области было стационарным, а вне области возмущения — возмущение отсутствовало бы вовсе. Наконец, при помощи некоторого дополнительного условия, в качестве которого чаще всего выбирается уравнение материального баланса, определяется закон разрастания области возмущения.
Таким образом, метод последовательной смены стационарных состояний основан на трех допущениях: 1) существует конечная область возмущенного движения; 2) движение внутри этой области стационарно; 3) размер области возмущения определяется из условия материального баланса.
Первое из этцх трех допущений само по себе не вносит значительной погрешности, поскольку, как известно из примеров, возмущенное движение весьма быстро затухает с удалением от места возмущения. Второе допущение связано с тем, что движение жидкости вблизи источника возмущения сравнительно быстро стабилизируется. Однако
здесь произвольным является предположение о том, что стабилизация происходит -сразу во всей области возмущенного движения. Третье предположение вполне естественно, хотя выбор именно этого дополнительного условия вовсе не обязателен.
2. Приведенные рассуждения показывают, что возможные уточнения метода последовательной смены стационарных состояний связаны в первую очередь с заменой второго допущения иным, более отвечающим истинному положению дел, и с соответствующим изменением тех дополнительных условий, на основании которых определяется размер области возмущения.
Последовательное проведение этой программы приводит к методу «интегральных соотношений», представляющему собой унифицированный метод, который позволяет получить решение ряда задач нестационарной фильтрации с достаточной для практики точностью.
Пусть р (х, t) — решение уравнения (V.1.1) в случае прямолиней-по-параллельного движения:
![]()
Г д2р
дх2 '
(V.1.13)
Умножив это уравнение на произвольную функцию / (х, t) и проинтегрировав по а; в пределах от Lx (t) до L2(t), получим равенство
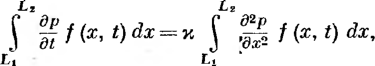
(V.1.14)
справедливое при любых Lu L2, f (х, t) и t.
Пусть при этом имеется семейство таких функций /„ (х, t) (п =
— О, 1 . . .), что при любом t это семейство полно (как семейство функций от х) на отрезке [(Ь1(г), L2(t)]. Пусть, далее, соотношение (Y.1.14) выполняется для всех /„. Тогда, если производные dpjdt и д2р!дхъ непрерывны, то функция р (х, t) удовлетворяет уравнению. (V.1.13) при L^t) ^ х L2 (t). Таким образом, между системой ин
тегральных равенств (V.1.14). записанных для полной системы функций, и дифференциальным уравнением (V.1.13) существует эквивалентность, и вместо решения уравнения (V.1.13) можно искать решение системы уравнений вида (V.1.14).
Возьмем простейшую полную систему функций — последовательные степени пространственной переменной
![]()
Xnd^dx (п = 0,1,...). (V.1.15)
Из (V.1.14) имеем и (О
![]()
Lt (О
и (О
L, (О
Левую часть этого уравнения можно представить, используя формулу дифференцирования определенного интеграла, в виде:
?2 (О и «)
J xn-%-dx^± J ptrdx-p(L„l)Ll^-+
Г 1 (О Li(О
В правой части можно провести интегрирования по частям. В результате после несложных вычислений получим из (V.1.15)
Lг (<)
dt
U «)
— Y,nL'lr1p (L.-,, t) + KnL1~1p(Ll, I) f
(n — 1) к J p (a:, i) a;"-2 dx~p (i2, f) Z,?
dt
При построении приближенного решения удобнее пользоваться -системой интегральных соотношений (V.1.6), чем исходным дифференциальным уравнением, поскольку в выражение (V.1.16) не входят производные неизвестпых функций.
3. Рассмотрим вновь задачу о возмущении первоначально стационарного движения в пласте. Пусть в момент t = 0 давление распределено по закону
p(x,0) = P + Gx, (V.1.17)
отвечающему отбору жидкости из пласта с расходом — kbHG/yi (в частности, G = 0 соответствует отсутствию движения в невозмущенном пласте). Пусть, далее, возмущение возникает вследствие некоторого изменения условий на границе х 0. Тогда, очевидно, в каждый момент изменение давления в удаленных точках пласта мало. Поэтому, естественно, при отыскании приближенного решения вновь ввести представление о конечной области влияния 0^
5S I (t), предполагая, что на границе х = I (t) давление и расход жидкости не успели измениться и сохраняют первоначальные значения (в случае конечного пласта протяженностью L область влияния, начинал с некоторого момента t*, охватывает пласт целиком, и I (t) = L, t ^ f*).
Будем искать приближенное решение задачи в виде многочлена
р (х, t) = Р0 (t) + Рг (0 х/1--. . . -]- Рп (t) х"/1п (О SS х ^ I)] р(х, t) = p(x, 0) (x^l).
Выражение (V.1.18) полностью определяется п + 2 неизвестными функциями времени — коэффициентами />0> рп ы положе
нием границы области влияния I.
Для определения этих п + 2 неизвестных можно составить
систему уравнении, включающую некоторое число интегральных соотношений (V.1.16), граничное условие при х = 0, определяемое постановкой задачи, и условия при х — I.
Первое из этих условий — непрерывность давления
Аналогичным образом условие непрерывности расхода дает
Наконец, эта система условий может быть дополнена условиями определенной гладкости решений на границе возмущенной области
Основной вопрос при применении метода интегральных соотношений состоит в том, какие из бесконечного числа условий следует использовать для определения неизвестных. Ясно, что необходимо использовать хотя бы одно из интегральных соотношений, так как в противном случае совершенно не будет использовано уравнение (V.1.13). Обязательно также должно быть использовано граничное условие при х = 0, поскольку оно отражает специфику задачи. По тем же соображениям должно быть принято условие непрерывности давления и расхода при х = I. Значительно сложнее дать какие-либо рекомендации по выбору остальных определяющих соотношений. Отметим лишь, что каждое интегральное соотношение добавляет одно дифференциальное уравнение, а каждое условие гладкости при х — I — одно конечное соотношение. В то же время условия при х — I, будучи локальными, могут не обеспечить хорошего приближения решения в основной области. Болес того, принятие слишком большого числа таких условий может привести к качественному искажению решения — появлению колебаний и т. д. С этой точки зрения использование интегральных соотношений в качестве дополнительных определяющих условий при повышении порядка приближения — более оправдано, хотя и более сложно.
4. Применим эти общие соображения к сформулированной выше задаче о пуске галереи. В этом случае
МО. t) = p1-, р(х,0) = ро = 0 (V.1.22)
(удобно принять начальное значение давления за нуль).
Распределение давлепия будем искать в виде (У. 1.18). Используя условие (V.1.22), получаем
Полагая в (V.1.16) L, (t)-—0, L2(t) = I (/). находим интегральные соотношения в виде:
о
/
О
I
40
dt
^ pxkdx = vJt(k—I) ^ р(х, t)xk~2dx (к^2). (V.1.26)
Если выбрать п = 1 и использовать в качестве единственного недостающего условия интегральное соотношение (V.1.24), то мы вернемся к решению методом последовательной смены стационарных состояний. Будем теперь уточнять решение, используя приближение многочленами более высокого порядка. Положим п = 2 и добавим еще одно условие.
Возьмем сначала в качестве этого дополнительного условия
дР (I, О
= 0. х**1- 0
дх
Тогда
*\> = Pi; Л, 1-Л + ^О; /\!-2Р2-0, (V .1.27)
а из (V.1.24) следует соотношение
Отсюда находим
Po=Pi, Pt = - 2Pi, Р,*=Ри Z2-12Kf. (V.1.28)
Соответственно для скорости фильтрации на границе и (0, <) получаем
(VX29)
что уже весьма близко к точному выражению (V.1.12). Посмотрим
теперь, что получится, если в качестве дополнительного условия
использовать второе интегральное соотношение (V.1.25).
Имеем систему уравнений
d_
dt
| 1 p/l- | xPl |
| 3 J | I |
Интегрирование последнего соотношения дает Г- (GjDj -f 4Рг -f 3 Ро) = 12v.pxt. Выражая Р2 через Pt, получаем систему
I2 (ЗА + Pi) = 12xpx?;
В данном случае очевидно, что
l — c\fy,t\ с —const, (V.1.32)
так что решение задачи упрощается. Из (V.1.32) следует
Рг — Ю1. _ 3pt — const
и
Следовательно, решение, найденное таким способом, совпадает с решением (V.1.28)—(V.1.29).
Рассмотрим теперь, что может дать следующее приближение (п = 3).
Согласно общей схеме имеем решение в виде:
р (х, t) — Р0-\- Ргх/1 + Р2х2/12 + Psx3/l3; х<С I-
Если принять в качестве дополнительных условий
p(fi,t)=p1; р{1, 0 = 0; dp(l,t)/dx = 0
и первые два интегральных соотношения (V.1.24), то получим систему уравнений
Po = Pi, Po + Pi + P2 + P3 = 0; Р1 + 2Л + ЗР3 = 0;
[р,<+1 Р.г+1 ^+{ p,i] - X ;
ТГ [1р‘1‘ + т Р>'*+ Т Р‘Р+ Т ¦*V‘]'- “Л-
Решение этой системы нами фактически уже найдено. Оно, очевидно, дается выражениями
Р0=тА; Pi=-2Pi, ра = Рй ^s = 0; 12к*.
так как удовлетворяет и системе (V.1.27)—(V.1.27а), и системе (V.1.30). '
Таким образом, найденное третье приближение совпадает со вторым.
Выберем теперь другую систему определяющих условий. Потребуем выполнения условий
p(o, <)=Pi; р(М)=о
и трех первых интегральных соотношений. Тогда для определения Рг, Р2, Р3 и Р0 имеем следующую систему:
Р.=Рх; 1\ !Л: Ра-0;
1 |>г+4 Р./+4 iV+? Р»г] = — у [4 р.р+j р,р+4 ЛР+4 р=р] - *д; Шр"г’+4р>,'+4^+4р>гз]“
=-2к[/у I 4 Л'+4Р*г+4Р»;]• (V.J.33)
И в данном случае, решение облегчается тем, что из соображении размерности I — c\/~Kt, а все Рг могут быть только константами. Поэтому уравнения (V.1.33) сводятся к алгебраической системе
Ро -Рй р0 I-Pi -! Р% + Рз = 0;
^[/,о + у^1 + |-Р2 + {Рз]=-2Р1;
с2[| Р^ \Р^\Р> + \РзУ^[Рй + ±Р1 + \Р* + {Р*~\.
Исключая неизвестные Ри Р2 и Ря, приходим к следующему кубическому уравнению для с2:
с6 — 84 с4-! 1440с2 - 9600 -= 0,
единственный действительный корень которого
с2 я» 63,78.
Для остальных неизвестных имеем
Po~Pi', P1=~ifi7pt; Р% — 6,79/^; Р3=-Ъ,12р1.
Для скорости фильтрации на границе
w(0, о = _ A _]ч
4 ’ llZ И Vvt Ц 1^2,93at

Рис. V.1
г *=.
гш
Сопоставим теперь первые три приближения:
первое
Р(х, 0 = {x^2V>u);
второе
(¦««
третье
Р (*, 0 = Pi (1 - 0,583 + 0,107 ~ + 0,0061
(х^7,98\Гм). pjh
Результаты расчета для трех приближений показаны на рис. V.1 вместе с точным решением (цифры у кривых соответствуют номеру приближения, ноль отвечает точному решению).
Из приведенного примера понятпа схема применения метода интегральных соотношений к задачам упругого режима. Ясно также, что построение приближений многочленами высокого порядка наталкивается на трудности не только вычислительного, но и принципиального характера. Прежде всего нет сколько-нибудь обоснованных правил для выбора того или иного из нескольких возможных дополнительных условий. Вторая трудность связана с тем, что приближение многочленами может дать решения физически недопустимого вида (например, отрицательные на некотором участке, см. среднюю кривую на рис. V.1) при попытке повысить точность приближения.
§ 2. РЕШЕНИЕ ЗАДАЧ УПРУГОГО РЕЖИМА МЕТОДОМ ИНТЕГРАЛЬНЫХ СООТНОШЕНИИ
Приведем еще несколько примеров использования метода интегральных соотношений для решения задач упругого режима. Из сопоставления получаемых решений с соответствующими «точными» решениями очевидны преимущества ясности и обозримости, достигаемые при помощи метода интегральных соотношений.
1. Осесимметричная задача о пуске скважины в бесконечном пласте. Рассмотрим еще одну автомодельную задачу — пуск скважины нулевого радиуса в безграничном пласте.
Выведем сначала те интегральные соотношения, которым должно удовлетворять распределение давления в осесимметричной задаче. Из основного уравнения распределения давления
после умножения на r*+I и интегрирования в пределах от Rx до получим, по аналогии с соотношением (V.1.16), тождества: при к = 0 (уравнение материального баланса)
Ri
при k^>0
A f, - НЯГ (t -
Ii,
— vkR\p (/?,, t) -f KkR\p (Rltt) -f к/с2 J /> (г, ?) r*-1 c?/ -f
Ri
+ js(/?2, 0 (fll, 0 7?i11 (V.2.2)
Воспользуемся этими соотношениями для того, чтобы получить приближенное решение задачи о пуске скважины — основной задачи для многочисленных методов исследования скважин.
Примем первоначальное (постоянное) давление в пласте за нуль. Будем считать, что в момент t -¦- 0 начинается отбор жидкости из пласта через скважину пренебрежимо малого радиуса. Предполагая, что отбор происходит в постоянном темпе, имеем дополнительные условия:
Р('.С)-0; (V.2.3)
Точное решение этой задачи, как было показано в § 2, гл. IIT, имеет вид:
2. Приближенное решение задачи. Введем вновь увеличивающийся во времени радиус I (f) и предположим, что при г > I (t)
р (г, t) = 0.
При этом интегральные соотношения (V.2.2), записанные для отрезка 0 <г <с ? (t), принимают вид:
I (О
A j гр (г, О dr = -Klim (г -g-) = -xg; (V.2.5)
о
i (о г
i (о
^ j /-fc+1 р (г, f) dr - vk* J р (r, 0 /-*-1 dr (Л 561) • (V. 2.6)
О
О
Как следует из граничного условия при г -»- 0 [второе условие (V.2.3)], искомое решение обладает при г —*¦ 0 той особенностью, что др/дг я» qjr. Поэтому и приближающую функцию выберем так, чтобы она имела ту же особенность, т. е. примем
![]()
Так же, как и при плоско-параллельном движении, наиболее грубое приближение получается при допущении, что
![]()
Из условия непрерывности давления при г = I имеем также Р0 = = 0, поэтому остается лишь одна неизвестная функция I (t), которая определяется при помощи одного интегрального соотношения. Б качестве этого соотношения возьмем уравнение материального баланса (V.2.5). Несложный подсчет дает
(V.2.8)
Z2 = Ак1,
так что в нулевом приближении
Pofr. t)~ q\n
r (rz=:2Vxt)',
2 r vd
(V.2.9)
Нулевое приближение, полученное таким образом, вновь совпадает с решением методом последовательной смены стационарных состояний (напомним, что давление в стационарном плоско-радиальном потоке линейно зависит от In г).
При отыскании приближений высшего порядка для определения неизвестных нужны дополнительные условия. Б качестве них можно использовать либо последующие интегральные соотношения, отвечающие к ф 0, либо дополнительные условия для производных от давления по радиусу. Действительно, так же как и в плоско-параллельном течении, систему определяющих условий можно дополпить условиями сопряжения
![]()
Поэтому для определения неизвестных коэффициентов в формуле (V.2.7) наряду с интегральными соотношениями можно пользоваться и выражениями (V.2.10).
Ограничимся первым приближением:
/>(/¦, t) = gln-~ + P0 (t) + Pt (О
(V.2.И)
l(t)
и будем определять неизвестные так, чтобы выполнялись интегральное соотношение (V.2.5) и условия р (I, t) = др (I, t)/dr — 0. Тогда
/'« ! l\ U: Ч--1У,
2 ?
и p(r, t)~
= a In -7=^=- — а 4- а .
\\2v.t V \2v.l
(V.2.12)
На рис. V.2 дано сопоставление точного решения (V.2.4) — точки — с двумя приближениями решения: (V.2.9) — пунктирная кривая и (V.2.12) — сплошная кривая. Как видно, уже первое приближение обе-Рис. V.2 спечивает довольно высокую
точность.
3. Достоинства метода интегральных соотношений еще яснее выступают при решении задач нестационарного движения в ограниченном пласте, когда нельзя пренебречь влиянием границ. Конечно, и для этих задач можно без особых затруднений написать решения, пользуясь обычными методами математической физики. Однако решения эти представляются в виде рядов Фурье (плоско-параллельное движение) или Фурье — Бесселя (плоско-радиальное движение) и потому трудно обозримы. Трудности усугубляются тем, что даже простейшие монотонные решения разлагаются по осциллирующим функциям, и для получения хорошего приближения приходится брать большое число членов ряда.
При применении метода интегральных соотношений к ограниченному пласту исследуемый промежуток времени разбивается на две части. На протяжении первой из них происходит распространение возмущения (например, области, охваченной движением) от того места, где оно возникло, до границ пласта. При этом зге границы, до которых возмущение еще не дошло, не оказывают влияния на решение. Так, при пуске галереи, расположенной
на некотором расстоянии L от непроницаемой границы пласта, приближенное решение ничем не будет отличаться от соответствующего решения для неограниченного пласта, пока I (t) <Г L. Принято называть промежуток времени, в течение которого не сказывается влияние границ, первой фазой фильтрации. Под второй фазой фильтрации понимается движепие начиная с того момента, когда граница области влияния доходит до удаленной границы пласта, и решение начинает зависеть от условий на этой границе. Естественно, что такое разделение на фазы условно, а продолжительность первой фазы существенно зависит от того, какое приближенное решение используется. Так, при решении упомянутой выше задачи методом последовательной смены стационарных состояний (первое приближение метода интегральных соотношений) I = 2|fv,t и продолжительность первой фазы В то же время в третьем приближении I nt
и ty L2/6Ax. Однако это различие незначительно сказывается на распределении давления.
Ограничимся здесь лишь одним примером, достаточно хорошо иллюстрирующим возможности метода.
Рассмотрим круговой пласт, на контуре которого (г = R) поддерживается постоянное давление, равное начальному давлению R пласте. Давление это мы по-прежнему будем принимать за нуль. В начальный момент производится пуск скважины пренебрежимо малого радиуса, расположенной в центре пласта. Расход жидкости, отбираемой из скважины, по-прежнему считается постоянным. Тогда вплоть до момента t = tx = R\j\1xt для распределения давления справедливо, в первом приближении, соотношение (V.2.12). При t > tj необходимо учитывать условие на контуре питания:
p(R, t) = 0. (V.2.13)
Примем далее, что при t > t± I (t) = R*\ Тогда представление (V.2.11) примет вид:
р (г, t) = д In + Р0 (t) + Pt (t) -L-, (V.2.14)
причем из условия р (R, t) = 0 следует Р0 — —Рг.
Для определения единственной оставшейся неизвестной функции P0(t) воспользуемся первым интегральным соотношением (V.2.2). Полагая здесь Rx = 0, = R и учитывая (V.2.14), получим
о
*> Часто встречаются «обоснования» этого допущения, связанные с той или иной физической интерпретацией «радиуса влияния» I (г). Такая интерпретация вовсе необязательна. С таким же успехом можно было бы п дальше пользоваться представлением (V.2.11) при I > R, но рассматривать решение лишь прп г < R, записывать интегральные соотношения только для этого участка и учитывать дополнительные условия при г = R.
Полученное дифференциальное уравнение для Р0 должно решаться при условии Р01 — —g, которое следует из требования
непрерывности давления при t = /х и соотношений (V.2.11) и (V.2.14). Соответствующее решение имеет вид:
Ро (0 = — g ехр [—
6к-^)-].
(V.2.15)
Таким образом, приближенное выражение для распределения давления будет
p(r, t) = q In ~ — q (l - exp [ — ¦ (V.2.16)
Как видно, распределение давления быстро стремится к стационарному.
4. Прежде чем перейти к более сложным задачам, рассмотрим вопрос о том, каким образом, не имея точного решения, оценить степень приближения, достигаемого при помощи метода интегральных соотношений. Трудность здесь заключается в том, что пет критерия, позволяющего определить заранее, сколько нужно взять приближений, чтобы получить решение с заданной точностью. Более того, лишь в исключительно редких случаях удается определить, насколько построенное решение отличается от точного. При зтом так же, как и во многих других задачах, связанных с отысканием эффективного приближенного решения, обычно используются два критерия точности приближенного решения: первый — проверка на близких по постановке задачах, допускающих точное решение (как это делалось выше); второй — решение задачи с последовательным увеличением числа членов приближающего многочлена. Расчет ведется до тех пор, пока разность двух приближенных решений не станет меньше заданного значения. Что касается практических расчетов, то в них почти всегда ограничиваются тремя членами в приближенном выражении для давления.
Рассмотренный в последних двух параграфах метод интегральных соотношений был предложен для решения нестационарных задач теории фильтрации Г. И. Баренблаттом [10] и многократно применялся рядом исследователей. До сих пор широко используется также более грубый, но более простой метод последовательной смены стационарных состояний [120] и его видоизменение, данпое А. М. Пир-вердяном [90].
Наряду с рассмотренными выше методами последовательной смены стационарных состояний и интегральных соотношений часто применяется также метод осреднения производной по времени в соответствующем уравнении. Этот метод аналогичен методу Слезкина — Тарга [105] в теории пограничного слоя; в гидродинамическую теорию фильтрации он введен работами Ю. Д. Соколова [108] и Г. П. Гусейнова [39].
Так же, как и в рассмотренных выше методах, весь пласт разбивается на область движения (возмущенную область) и область покоя;
в области движения производная по времени заменяется ее средним по области значением. После этого распределение давления в зоне движения определяется путем решения обыкновенного дифференциального уравнения второго порядка. Решение содержит в качестве параметров среднее значение временной производной и протяженность зоны движения. Для их определения обычным образом используются краевые условия сопряжения и интегральные соотношения. Таким образом, как и в теории пограничного слоя, этот метод является вариантом метода интегральных соотношений.
§ 3. РЕШЕНИЕ ЗАДАЧ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ ГАЗА
1. Для задач фильтрации газа, равно как и для близких к ним задач фильтрации в неупруго-деформируемой среде, приближенные методы составляют практически единственное средство эффективного аналитического исследования, если не считать немногочисленных автомодельных случаев.
Самую широкую область применения имеет метод, указанный еще JI. С. Лейбепзоном [71]. Этот метод заключается в том, что вместо нелинейного дифференциального уравнения
![]()
(V .3.1)
рассматривается линейное (относительно рг) уравнение
![]()
(V.3.2)
где р0 — некоторое постоянное давление. Очевидно, это уравнение получается из выражения (V.3.1), если умножить это уравнение па р, а затем заменить в множителе перед скобкой р па р0. В качестве р0обычно берется некоторое характерное давление. Л. С. Лейбензон впервые ввел такое преобразование в связи с задачей об изменении давления в первоначально невозмущенном пласте, и под р0оы понимал давление в невозмущенной части пласта. Такой способ сведения нелинейного уравнения (V.3.1). к линейному (V.3.2) называется линеаризацией по Л. С. Лейбензону.
К линейному уравнению (V.3.2) применим весь хорошо разработанный аппарат теории теплопроводности (и теории упругого режима). Важнейшее достоинство метода состоит в том, что оп имеет весьма широкую область применения — как при решении одномерных, так и многомерных задач, при любом законе изменения граничных значений давления и расхода жидкости и т. д. Это определило широкое применение метода линеаризации в теории разработки газовых месторождений. Однако этот метод имеет и недостаток: при его применении специфика задачи, отличающая ее от задач упругого режима, правильно учитывается лишь в тех областях, где движение можно считать стационарным [действительно, в таких областях dpjdt =
— dp^/dt — O и уравнения (V.3.1) и (V.3.2) совпадают].
К настоящему времени имеется уже довольно значительный опыт применения метода Л. С. Лейбепзона. Он оказался весьма эффективным при решении задач, в которых первоначально неподвижный газ начинает двигаться под влиянием локальных возмущений. Типичной в этом отношении является задача о пуске газовой скважины в бесконечном пласте.
После линеаризации можно воспользоваться готовым решением из гл. III, § 2. Имеем
![]()
(V.3.3)
где г — расстояние точки от оси скважины; р0 — начальное давление в пласте, a q — объемный дебит скважины на единицу мощности, пласта, приведенный к начальному пластовому давлению р0.
Метод линеаризации обладает еще одним достоинством, особенно существенным с логической точки зрения, — его можно включить в общую схему метода малого параметра. Именно так понимал этот метод Л. С. Лейбензон [71].
Детальное изложение метода малого параметра в теории нестационарной фильтрации и примеры его применения можно найти в книге П. Я. Полубариновой-Кочиной [94]; последовательное применение метода малого параметра к задачам исследования скважин приведено в книге [35].
2. Линеаризация и метод малого параметра отличаются громоздкостью, особенно применительно к исследованию движения в ограниченной области. Чтобы обойти зто затруднение, так же как и в задачах упругого режима в фильтрации газа, можно искать приближенное решение методом интегральных соотношений. Рассмотрим для примера задачу об истощении газовой залежи радиусом R, эксплуатируемой одиночной центрально расположенной ск валенной. В обычных предположениях задача сводится к решению уравнения
![]()
(V.3.4)
при условиях
![]()
Из последнего граничного условия (V.3.5) следует, что при приближении к скважине изменение давления может быть асимптотически представлено выражением 14
(V.3.6)
где / (г, t) не имеет особенности при г —0.
^=-^[1пТ7*Г+во{0 + Я1(0 W+- '
p2 = r?{R) (r^l). (V.3.7)
Движение, как обычно, подразделим на две стадии: на первой стадии I (t) < В (возмущение еще не дошло до границ пласта) и р (I, t) — jр0; на второй стадии I (t) = R.
Умножим уравнение (V.3.4) на Г'1 и проинтегрируем от г0 до 1 (t). При п = 1 после несложных преобразований имеем
Га
(уравнение материального баланса); при п >1
Kt) nt)
i
ra
Обычно эти выражения можно существенно упростить, учитывая,
что в представляющих интерес случаях rjl 1. Поэтому г0 можно
к др2 (jv|, t) о
всюду положить равным нулю, имея в виду, что —— r0 — -V--—- = ,
-1
а произведение rjjp (/¦ 0, f) мало. Отсюда получим вместо (V.3.9)
I (о
d
dt
к (л-1)2
2m|J.
J rn-Y-dr-lnp0^. (V.3.10)
Найдем решение в первом приближении, полагая aL (t) = О (г = 2, 3, . . ., п). Из условий р (1, t) — р0, др (I, t)jdr— 0 определим
ч Де
для первой фазы движения а0 (t) = Ро~^-+ 1> а1 (0 = — и искомое решение имеет вид:
W ]п_Г__LJ'fLtzJi
пк Цг)^ nld(t) ‘
р1-р
Из (V.3.8) имеем Ко
I '• ]f P* -u-i (Inf+4-T)dr= ~ 2^“^o
d
dt
dl
dt
| 1 o,ss | ||
|
<7,54 | ||
| 1 L 1 1 > | V, , | |
| 2,0 -1,6 -1,2 |
-0,8 -0^ | |
Рис. V.3
He делая значительной ошибки, можно заменить в интеграле г0 на 0*>. Тогда
dl
Pol^- (V.3.12)
(1пи+1 — u^du
2я т
j^spo j и Y
на протяжении первой фазы движения.
Таким образом, на протяжении первой фазы движения имеем для I (<):
kPo
nkpl -
VI + д* (In ы-1-1 -и) - Va j = -^ <?*; q
Зависимость интеграла / в (V.3.12) от безразмерного параметра q* показана на рис. V.3. Таким образом,
1=сУ*; к = ^; c=Vq^/(2I-l),
*> Возникающую при этом малую мнимую добавку мы отбрасываем.
где постоянная с зависит от единственного оезразмерного параметра q* (см. рис. V.3). При t >Л2/с2х положим I = R, и таким образом
Здесь pR — давление на контуре пласта. Ясно, что это давление должно меняться во времени за счет истощения пласта.
Чтобы найти закон изменения pR, воспользуемся вновь уравнением материального баланса. Полагая в нем I = R, получим
~R2lu]/ p'k \ ^ir(lnu+i-u)du=~^rn-
или
1
Ро
1
— J и 1 /л + -р- д* (In и-\-1 — и) du-
is ' н
- j и VI + д*(1п и~-1 - и) du-~ . (V.3.14)
о
Здесь 11 — момент окончания первой фазы движения. Зная зависимость интеграла
1
1 (q*) — | и V1 -г Q* (1п и + 1 — и) du (V.3.15)
»
от параметра д* (см. рис. V.3), можно, используя уравнение (V.3.14), построить зависимость pR/pn от t. Для практики, однако, достаточную точность дает самое грубое приближение, когда интеграл (V.3.15) просто полагается равным 1/2: Физически это равносильно приравниванию среднего давления в пласте давлению на контуре. Как следует из рис. V.3, для реальных значений безразмерного дебита скважины q* (порядка сотых долей) это допустимо с ошибкой менее 2%. При этом
и
Если не стремиться к точному удовлетворению условия непроницаемости при г — Я, то можно отбросить последние члены в выражениях для давления (т. е. положить at (t) = 0). Получающееся при этом выражение отвечает решению методом последовательной смены стационарных состояний. Оно впервые было получено Б. Б. Лапу-ком [67, 68] и широко применяется в практических расчетах.
Можно попытаться построить, придерживаясь обычной техники применения метода интегральных соотношении (см. предыдущие параграфы), последующие приближения. При этом, однако, для неан-томодельных движений коэффициенты в,- и радиус области влияния I приходится находить из сложной нелинейной системы уравнений. Попытка избавиться от трудностей путем замены корня в подынтегральном выражении (V.3.15) первыми двумя членами его разложения фактически означает переход к линеаризованной теории движения газа. Многочисленные работы выполнены этим методом Лан Чжан-Синем [64, 65].
3. Из приведенного примера ясно, что применение метода интегральных соотношений к задачам фильтрации газа оправдано либо когда допустим переход к линеаризованным уравнениям, либо когда требуемая точность достигается уже в первом приближении. Иначе говоря, выгоднее осуществлять приближение более сложными функциями, но ограничиваться минимальным числом свободных параметров.
Один из способов такого приближения заключается в использовании автомодельных решений по аналогии с тем, как в теории пограничного слоя используются автомодельные решения Фокнера — Скэн (метод Кочина — Лойцянского [60]), другой способ излагается в следующем параграфе.
В гл. IV были приведены (применительно к эквивалентной задаче фильтрации грунтовых вод) автомодельные решения одномерных задач изотермической фильтрации совершенного газа, описываемой уравнением
д> 02 д-т^ (V.3.18)
dt Xs дх дх
(s = 0; 1; 2 — соответственно для плоских, осесимметричных и цен-трально-симметричных движений). Эти решения строились для случая, когда на границе пласта (при х = 0) задано либо давление
что возможно только в случае плоско-параллельного движения, либо поток газа
Движения автомодельны при определенном сочетании начальных и граничных условий. В частности, если происходит заполнение пласта, в котором вначале давление газа было весьма малым, так что его можно считать равным нулю, то задача автомодельна прн
произвольных степенных функциях Ф (t) или ? (t):
Ф (t) = сГ; ?(г) = т**, (V.3.21)
где а, т, а и р — некоторые постоянные.
В общем случае, когда начальное давление в пласте не равно нулю, движение автомодельно лишь при а — 0 и [> — 3/2 — !)•
Общая схема применения автомодельных решений для приближенного решения иелипейпой задачи заключается в том, что берется однопараметрическое семейство автомодельных решений, отвечающих данным начальным и граничным условиям, а затем этот параметр полагается равным некоторой функции времени, причем вид этой функции выбирается так, чтобы, дифференциальное уравнение задачи удовлетворялось в среднем. Иначе говоря, нужно, чтобы выполнялось некоторое интегральное соотношение, являющееся следствием исходной задачи.
Очевидно, существует много способов введения параметра в автомодельное решение и варьирования этого параметра. Каждый из этих способов приводит к тому или иному приближенному решению задачи. Обычно нельзя заранее сказать, какой способ решения окажется более удачным.
Рассмотрим сначала процесс плоской одномерной фильтрации газа в пустой пласт [уравнение (V.3.18) при s— 0 с нулевым начальным условием]. Пусть на границе х = 0 задан закон изменения давления [уравнение (V.3.19)]. Если Ф (t) = тf“, то решение автомодельно и может быть представлено в внДе:
р (х, ~t) = arf (t, Я); 1 = -тУ-Щ-, (V.3.22)
где / (|, а) — решение краевой задачи
к=^тг: o.(v.3.23>
Решение тождественно равно нулю вне конечного промежутка О ^ | ^ и удовлетворяет интегральному соотношению
?*
J \f{i, a.)dg = i/(i-i %).
о
В табл. 1 гл. IV (см. также рис. IV.4) были приведены величины
функций / (|, л) для значений Я, равных 0,00; 0,05; . . ,; 1,00 и зна
чений аргумента |, равных 0,1 |*; 0,2 и т. д.
В общем случае произвольной функции Ф (t) соответствующее интегральное соотношение принимает вид:
X* (t)
J хр(х, t)dx = а2Ф2 (t). (V.3.24)
о
Здесь ж* (t) — координата переднего фронта продвижения газа.
Будем искать приближенное решение сформулированной задачи в виде:
р т - Ф <0 1 • Ч<>];' МО = . (V.3.25)'
При Ф (t) = ct*, а = const выражение (V.3.25) переходит в точное автомодельное решение. Поэтому естественно ожидать, что при функциях Ф (t), близких к степенным, выбранное представление будет обеспечивать хорошее приближение. После того как принято выражение (V.3.25), решение задачи сводится к определению единственной функции К (t). Определяя ее из интегрального соотношения (V.3.24), находим
|^Ф2 (t) —$Ф2 (0 й«1 К (t) = 1-5-A- (V.3.26)
|^ф2 (t) — |Фг (f) dt J
После этого по формуле
«<¦>- таг <v'3-27)
находим a (О и, пользуясь формулой (V.3.25) и табл. IV.1, находим искомое решение. Координата переднего фронта продвижения газа определяется при этом соотношением
ж* (t) = а|* [Я (01 УФЩ - Я (01- (V.3.28)
Рассмотрим пример решения задачи по положенной методике.
Положим Ф (i) = cmtm + Gntn, т <[ п. Тогда из формул (V.3.26) и (V.3.27) находим
... 1 / 2o,nOntm+n+1 A-clr2,1+1
^ ^ о / л
1^ГТ°™<2т+1 + —г Г7 отоп(т,п,1 + тГЦ<А*1“+1
\ 2т+1 ' m+n+t 2и+1 /
Из этого выражения непосредственно видно, что прн малых t a. (t) ^ т, а при больших ( о (() ^ п. Это означает, что то мере движения происходит переход от одного автомодельного движения к другому.
При расчете конкретного примера положим а = 1, т = 0, п = 1, ат = = ап — 1. Тогда
Используя таблицу функций / (Е,, а) , можно вычислить распределение давления р (ж, f) в различные моменты времени. Результаты вычислений нока-заны на рис. VA.
Рассмотрим теперь задачу о заполнении пласта в предположении, что задан поток газа через скважину пренебрежимо малого радиуса:
Если V (t) — тfi, то решение задачи авгомодельно и может быть представлено в виде (см. гл. IV, § 3):
2),;
(V.3.29)
-1.
р{х, *) = TVsfB/2/1(c, Я.); Я=р/(р g=r[4a4TfP+3]-,/4(p4-2),/,;
АЦ
/, (оо) = 0; lim i ¦
l-o
Функция ft (s, X) обращается в нуль при ? ряет интегральному соотношению (IV.2.32):
(л) И УДОВЛСТВО-
(V.3.30)
SJ а)
i+x *
Найдем приближенное решение сформулированной задачи в виде:
Рис. V.4
'Г 0) <111 , i.(0j
(V.3.31)
Как нетрудно видеть, такое приближенное представление решения удовлетворяет начальному условию и условию на бесконечности при любом X (<), функцию же X (t) мы считаем подлежащей определению. Для ее нахождения воспользуемся интегральным соотношением
г* (О
J гр (г, t).dr = а2Ч)‘ (t),
й
dt
(V.3.32)
где г* (t) — граница области проникновения газа; р (г, t) ^ 0 при r^r* (t); р (г, f) = 0 при г is г* (t). После некоторых вычислений получаем
(V.3.33)
Lo
Формулы (V.3.31) и (V.3.33) позволяют выразить приближенное решение через затабулированную функцию ft (?, X). В тех случаях, когда задача допускает точное автомодельное решение, приближенное решение совпадает с точным.
Есть две причины, по которым мы ограничились использованием автомодельных решений только для приближенного решения задач с нулевым начальным давлением газа. Во-первых, только в этом случае решение автомодельно при любых (постоянных) а и р, т. е. имеется однопараметрическое семейство решений. Во-первых, именно задачи
о фильтрации с нулевым начальным давлением газа представляют особую сложность для методов линеаризации и малого параметра, поскольку разложение по параметру v=l — (р Jp (|)2 становится при этом неправомерным.
§ 4. ВИДОИЗМЕНЕНИЕ МЕТОДА ИНТЕГРАЛЬНЫХ СООТНОШЕНИЙ ДЛЯ СЛУЧАЯ БЕСКОНЕЧНОГО ПЛАСТА
При решении нелинейных задач различного вида последовательное применение метода интегральных соотношений по стандартной схеме приводит к громоздким вычислениям, тем более сложным, чем больше число неизвестных коэффициентов в приближенном выражении. Заметного упрощения можно достигнуть таким подбором приближающих функций, чтобы нужная точность получалась уже в одном из
первых приближений (а практически — в первом приближении). Иными словами, задача состоит в том, чтобы почти «угадать» решение. Большую помощь при этом может оказать предварительное качественное исследование. Такое исследование уже было описано в § 4 гл. IV для автомодельной задачи о притоке газа к скважине, пущенной
Ч-(Щ)
Рис. V.5
о
в эксплуатацию с постоянным дебитом. При этом оказалось, что движение вблизи скважины быстро стабилизируется, так что массовый расход газа
через соосную со скважиной цилиндрическую поверхность практически не меняется вплоть до некоторого расстояния от скважины (рис. V.5). Там же, где расход начинает меняться значительно, изменения давления газа по отношению к начальному значению невелики, и уравнения движения можно линеаризовать. Это позволяет но существу считать, что расход газа зависит от расстояния и времени так же, как и в соответствующей линеаризованной задаче, причем близость истинного и «линеаризованного» распределений расхода обусловлена малостью обычно встречающихся значений дебита (малостью значений к в обозначениях гл. IV). Методом инте-гра льных соотношений с учетом указанных соображений можно получить простые и достаточно точные решения ряда задач.
1. Рассмотрим осесимметричное движение сжимаемой жидкости в деформируемой среде, следующее закону Дарси. Для наших целей будет удобно ввести в ясном виде величину массового расхода жидкости в данный момент через поверхность г const единичной высоты:
![]()
Уравнение (V.4.1) вместе с уравнением неразрывности д(тр) i dg dt ' г дг
Р = Р(Р), ~к~к(р), р = ^(р), т = т(р) (V.4.3)
составляет замкнутую систему уравнений движения. Вводя функцию
р(Р) (V .4.4)
о
являющуюся аналогом функции Лейбензона в теории фильтрации газа, можно привести систему (V.4.1), (V.4.2) к стандартному виду:
дР . м(Р) dq . дР ,лг , -
где
(V.4.6)
| / d (mp) | ~ d (mp) "j-i | |
| V dP j | I n i |
-dp J |
— переменный коэффициент пьезопроводности.
Система (V.4.5) может быть записана в виде одного уравнения для Р. В таком виде можно записать систему уравнении движения при упругом режиме уравнения изотермической фильтрации газа и уравнения фильтрации в нелинейно деформируемой среде, так что система (V.4.5) описывает достаточно общую ситуацию.
Предположим, что рассматривается некоторое возмущение стационарного режима, возникающее на внутренней границе системы (в скважине). Чаще всего такое возмущение состоит в том, что задается определенный закон изменения отбора из скважины. Поэтому будем считать, что задача для уравнений (V.4.1) имеет вид:
q (г, 0) = <70—const; q(a, t) = Q(t)
-(я. /• < со, 0<^<С°°)- (V.4.7)
Условия (V.4.7) соответствуют важнейшей для приложений задаче
о нестационарном притоке к скважине (а — радиус скважины).
Наиболее простым является случай, когда расход в скважине изменяется скачком. При этом от скважины начинает распространяться волна изменения расхода, и распределение q (г, /) принимает вид, показанный для последовательных моментов времени на рис. V.5. Характерно при этом, что расход сохраняет постоянные значения вблизи скважины и на удалении от нее и лишь в некоторый промежуточной области происходит его резкое изменение.
Такой характер изменения q (г, t) имеет место при всех представляющих интерес видах зависимости к (Р). В простейшем случае при у. (Р) — у. — const, Q — const имеем
Естественно поэтому попытаться найти приближенное решение задачи (V.4.1) — (V.4.2), полагая
q{r, t) = q0+{Q— g0)exp ( — -J-), (V.4.9)
где 1=1 (I) — параметр, выбираемый так, чтобы наилучшим образом удовлетворить некоторому дополнительному условию, которое будет приведено ниже. Если желательно учесть также конечность радиуса скважины и изменение во времени дебита скважины Q (<), то удобно принять
Q
(г, t) = q0 + (Q — q0) ехр
—~^-г- . (V.4.10)
В отличие от (V.4.9) выражение (V.4.10) не является точным даже для случая упругого режима. Оно, однако, удобно в том отношении, что позволяет значительно упростить вычисления, обеспечивая достаточно хорошее приближение.
Для определения функции I (I) воспользуемся интегральным соотношением
ОО СО
-ГЗН к (Р) -f?- dr. (V.4.11)
а а
Выражение (V.4.10) удобно в том отношении, что после его подстановки уравнение (V.4.11) принимает достаточно простой вид.
Прежде чем перейти к рассмотрению примеров, сделаем одно общее замечание. Выбор расхода q (г, t) в качестве функции, для которой задается распределение относительно простого вида, не случаен. Можно показать, что в задачах, в которых на границах области движения фиксируются значения q, распределение расхода сравнительно мало зависит от вида уравнений движения, оставаясь качественно таким же, как и для задач упругого режима. По этой причине распределение расхода q (г, t) достаточно легко «угадать» с требуемой точностью. Здесь мы воспользуемся этой возможностью только для движения в однородном бесконечном пласте, однако тот же подход применим к неоднородным пластам и пластам конечной протяженности.
2. В качестве первого примера возьмем задачу из области теории упругого режима, рассмотренную еще Маскетом [78], о притоке к скважине конечного радиуса, пущенной с постоянным дебитом. В этом случае Р — рkp/\i; у. — у.0 = kK/m\i — const; Q — const; q (r, 0) = 0. Подставляя для q выражение (V.4.10), из (V.4.11) получаем
4[т + -т"(-?)]-*. (V.4.12)
ИЛИ
'=?.[*+-?е°'',,к(-4)]- <у-4'13)
Интегрирование первого уравнения системы (V.4.1) с учетом условия р (со, t) = р (г, 0) = 0 дает
|Л(>
P{r, t)
Ei
кр
(V.4.14)
Выражения (V.4.14) и (V.4.13) представляют в параметрическом виде искомую зависимость р (г, t). На рис. V.6 показана зависимость отношения l2/(4xt) и безразмерной депрессии в скважине Р —
— р (a, t) от безразмерного времени vX/ar — т; полученное решение хорошо согласуется с точным решением Маскета (78]. Рассмотрим теперь несколько задач фильтрации газа.
Примем, что в начальном состоянии движения нет вовсе, q (г, 0) = = 0, а начальное значение функции Лейбензона Р (г, 0) — Р0 одинаково во всех точках, Р (г, 0) = Р0 — const. В этом случае, используя первое уравнение системы (V.4.5) и соотношение (V.4.11) и ограничиваясь поправкой пер-вого порядка на изменение
Рис. V.6
*(Р)
x(P) = K{P0)[i + v\AP-P0)}\ (V.4.15)
легко представить интегральное соотношение (V.4.11) в виде:
dt
- *»{ 9+ Ч,?! [«”'"¦ Ei ( —?) - Ei ( - т)]}. (V.4.16)
В свою очередь для Р (г, t) из (V.4.1) и (V.4.8) получается выражение
a!/l2
-Qe
(V.4.17)
Е
P(r, t)=P0-
В практически интересных случаях выражение (V.4.16) удается без особого труда упростить.
Если рассмтривать лишь достаточно большие времена, 1~{а~ 2> li то уравнение (V.4.16) представится в виде:
143
При выводе этого выражения учтено также, что практически во всех случаях r)0(? <? 1. Из (V.4.18) следует выражение для времени:
J2_-a2 1n(J2/n2)
![]()
4жо?1 —i/г Чо<? Ь2]’
а из (V.4.17) — формула
P(r, t) = P0+±-QeatfP Ei (V.4.20)
При больших временах можно, пренебрегая'членами порядка (а2/^2) (l2la~)i представить (V.4.20) в виде:
р (Г, 0 = р.¦+
4-QЕ1 ( -
^,|,,,';г%(,1п-2Г).
(V.4.21)
Эта формула весьма близка к аналогичной формуле теории упругого режима и совпадает с ней, если пренебречь величиной произведения УгПоФ In 2 но сравнению с единицей. Поэтому, наблюдая изменение функции Лейбензона при пуске газовой скважины с постоянным дебитом, можно определять параметры пласта таким же образом, как при упругом режиме определяются параметры пласта по изменениям давления. Тот же результат получится, если исходную систему (Y.4.5) линеаризовать по методу Л. С. Лейбензона, т. е. заменив переменный коэффициент пьезопроводности к (Р) постоянной величиной к0 = я (Р0). Слагаемое '/VloC^ In 2 представляет собой поправку к линеаризованной теории.
3. Для определения параметров пласта по испытаниям газовой скважины на нестационарный приток в соответствии с формулой (V.4.21) необходимо, чтобы дебит скважины на протяжении испытаний оставался постоянным. Поскольку давление на забое скважины при этом сильно изменяется, для поддержания постоянного дебита необходимо принимать специальные меры, не всегда осуществимые. Значительно проще вести эксперимент, оставляя гидравлическое сопротивление скважины постоянным. В этом случае дебит скважины оказывается функцией забойного давления
Q = Q(Pa). (V.4.22)
Эта функция — расходная характеристика скважины — может быть определена независимо, и ее можно считать известной. Более
того, в одном случае она может быть без труда подсчитана — если
в непосредственной близости к забою скважины в ней установлена диафрагма достаточно малого проходного сечения, то истечение газа в скважину носит критический характер; при этом расход приблизительно пропорционален давлению на забое
Q = cPa. (V.4.23)
Можно получить приближенное решение, позволяющее определять характеристики пласта по наблюдениям за изменением давления в случае, если дебит также изменяется в соответствии с соотношениями (V.4.23) или (V.4.22).
Рассмотрим достаточно большие значения времени: Г- а2. Тогда уравнение (V.4.18) примет вид:
= (t) [l - j- 4oQ (0 In 2]. (V/i.24)
Используя (V.4.22), можно связать значение функции Лейбензона в скважине Р (a, t) с дебитом Q. Тогда из (V.4.17) следует.уравнение
Р(а, t) = P0 v\Q[P{a,t)]Ei(—-fj-). (V.4.25)
Систему уравнений (V.4.25) и (V'.4.24) легко решить приближенно, предполагая, что изменение дебита Q (t) происходит достаточно медленно. Заметим прежде всего, что Q (t) монотонно убывает от значения
= Q (0), отвечающего моменту пуска
Qo = Q(P0)- (V.4.26)
Учитывая это обстоятельство и используя уравнение (V.4.24), можно легко получить оценку:
[1 -4ч 1-ЛЛ.1П2. (V.d.27)
Из (V.4.27) следует, что с малой относительной ошибкой определения 12/а2 — порядка In IQJQ (*)]Дп (4in0t,/a2) — можно положить
«L. (?.4.28)
а- а- '
Если подставить выражение (V.4.28) в (V.4.25), то получится уравнение, определяющее Р (a, t) как неявную функцию времени. Это уравнение удобно преобразовать к виду:
(V-4-29>
где
Х(Р0)-=-р~0--W(M)J (\.4.dU)
— безразмерная функция забойного давления, определяемая зависимостью функции Лейбензона и дебита скважины от давлепия; зависимость % (ра) может быть заранее определена для данной скважины. Формула (V.4.29) показывает, что в экспериментах с критическим истечением величина % так же зависит от времени, как безразмерное давление в условиях упругого режима. Поэтому, представляя экспериментальные данные в координатах % (ра) — In t, можно определять параметры пласта по обычной методике (см. гл. III, § 4).
При желании полученные выражения можно уточнить, вводя поправки в уравнение (V.4.28) для 1г. На практике, однако, при обычно встречающихся значениях дебита в такой поправке нет необходимости.
ФИЛЬТРАЦИЯ НЕОДНОРОДНЫХ ЖИДКОСТЕЙ § 1. ФИЛЬТРАЦИЯ МНОГОФАЗНЫХ ЖИДКОСТЕЙ
1. В связи с проектированием и анализом разработки нефтяных и газовых месторождений приходится рассматривать совместное движение в пористой среде нескольких жидкостей, чаще всего воды, нефти и газа, представляющих собой обособленные фазы, не смешивающиеся между собой.
Чтобы описать фильтрацию многофазной жидкости применительно к модели сплошной пористой среды, нужно ввести характеристики осредненного движения. Масштаб осреднения в данном случае должен быть велик пе только ио сравнению с характерным размером пор, но и с размером частиц каждой из фаз. Существенно, что наименьший размер частиц может значительно превышать размер порового канала, поэтому масштаб осреднения определяется характером распределения фаз в порах и может быть различен в зависимости от постановки задачи. Подробнее об этом будет сказано ниже, пока же допустим, что существует такой линейный размер г, при котором характеристики каждой из фаз, осредненные по шару радиусом R, имеют при R —>- г асимптотические предельные значения, а размер г намного меньше характерных масштабов рассматриваемых задач. Главными характеристиками фильтрации многофазной жидкости являются насыщенность и скорость фильтрации каждой фазы.
Доля объема пор в элементарном макрообъеме в окрестности данной точки, занятая i-й фазой, называется местной насыщенностью порового пространства этой фазой и обозначается s?. Очевидно,
j=i
где п — число отдельных фаз. Таким образом, в системе п фаз имеется п — 1 независимая насыщенность. В частности, при исследовании
фильтрации двухфазной жидкости достаточно рассматривать лишь одну насыщенность. Движение каждой из фаз можно охарактеризо-
—>
вать вектором скорости фильтрации данной фазы щ. Аналогично
¦скорости фильтрации однофазной жидкости, ut определяется как вектор, проекция которого на некоторое направление равна объемному потоку данной фазы через единичную площадку, перпендикулярную указанному направлению.
Характерные особенности движения многофазной жидкости связаны с влиянием поверхностного натяжения. Как известно, на искривленной границе двух фаз возникает скачок давления, равный
![]()
(VI4-2)
{формула Лапласа), где а — межфазное натяжение, и — главные радиусы кривизны поверхности раздела фаз в данной точке. В пористой среде граница двух фаз разбивается на множество отдельных участков. Радиус кривизны каждого из них близок по порядку величины к размеру порового канала *. Капиллярный скачок давления, особенно в малопроницаемых средах, может играть существенную роль в процессе фильтрации. Например, при проницаемости пористой среды около 10 мд радиус пор песчаника составляет примерно 10-4 см и капиллярное давление на границе газ — вода имеет порядок 0,5 кгс/см2.
Влияние капиллярных сил на фильтрационные процессы сказывается двояким образом. Движение каждой из фаз многофазной системы зависит от сил давления, вызывающих движение, и от взаимного расположения фаз в поровом пространстве. Распределение фаз в порах определяет форму области течения каждой из фаз и тем самым величину сопротивления, испытываемого этой фазой при движении, так же как структура порового пространства определяет гидравлическое сопротивление при однофазном течении. Капиллярные силы влияют как на распределение давления в фазах, так и на взаимное расположение фаз в поровом пространстве. Соответственно и процессы фильтрации многофазной жидкости идут по-разному в зависимости от характерного времени фильтрационного процесса и от размеров области течения. Капиллярные силы создают в пористой среде перепад давления, величина которого ограничена и не зависит от размера области. Перепад внешнего давления, создающего фильтрационный поток между двумя точками, пропорционален скорости фильтрации и расстоянию между этими точками. Если размеры области малы, то при достаточно медленном движении капиллярные силы могут превзойти внешний перепад давления. Поэтому в такой области время
1 Мы не касаемся случая, когда одна из фаз находится в другой в виде эмульсии, радиус пузырьков которой намного меньше размера поровых каналов. В этом случае жидкость можно рассматривать как квазиоднородную; теория фильтрации таких эмульсий для случая системы газ — жидкость была развита •Л. С. Лейбензоном [73].
установления равновесного распределения фаз значительно меньше, чем время, за которое происходит заметное изменение средней насыщенности под действием фильтрационного потока. Таким образом, при исследовании локальных процессов, т. е. процессов, происходящих в элементарном макрообъеме, распределение фаз в порах обычно можно считать равновесным. Такой подход допустим, если насыщенность не меняется заметным образом на расстояниях порядка размера поровых каналов. Иначе говоря, безразмерная величина ]/ к | grad s| должна быть мала. Напротив, если рассматривается движение в очень большой области (например, в целой нефтяной залежи), то влияние капиллярных сил на распределение давления незначительно и их действие сказывается косвенно, через локальные процессы перераспределения фаз, вызывающие изменение местных гидравлических сопротивлений. Наконец, в ряде задач приходится рассматривать течение в областях таких промежуточных размеров, что длительность процессов перераспределения, вызываемых капиллярными силами, сравнима с характерным временами фильтрации. Задачи такого рода встречаются, например, при исследовании процессов вытеснения нефти или газа водой из неоднородных или трещиноватых пород.
Поскольку нас интересуют локальные характеристики крупномасштабного движения, будем рассматривать равновесное распределение фаз, не исследуя процесс его установления. Однако и равновесное распределение фаз при одной и той же насыщенности может быть различным. Хотя распределение фаз не зависит от средней скорости фильтрации, оно существенно зависит от того, как возникла данная насыщенность.
В ряде случаев одна или несколько фаз могут находиться в порах в виде изолированных пузырьков или капель, не связанных между собой и остальной частью данной фазы. Такие изолированные пузырьки или капли возникают либо при выделении фазы, растворенной в другой фазе, либо в конце процесса вытеснения одной фазы другою, когда частицы вытесняемой фазы разрываются ка отдельные капли. Подвижность отдельной капли, окруженной другими фазами, в пористой среде весьма мала и может быть равна нулю при тех градиентах внешнего давления, которые существуют в основном фильтрационном потоке. Для примера типичное положение отдельной капли смачивающей фаяы'в порах показано на рис. VI.4. Для того чтобы протолкнуть эту каплю через сужение поры радиусом г, требуется приложить перепад давления одного порядка с избыточным капиллярным давлением, которое составляет около oJr. Поэтому при длине капли в несколько норовых каналов движение начнется только при условии, если градиент давления превысит ~а/г2, что. как нетрудно подсчитать, намного превышает обычные градиенты давления в фильтрационных потоках в нефтяных и газовых пластах. Поэтому несвязная часть каждой фазы обычно является неподвижной. Заметим также, что несвязная насыщенность может составлять лишь небольшую долю порового пространства.
Для описания равновесного распределения фаз с порах используется понятие капиллярного давления. В состоянии равновесия граница раздела фаз в порах имеет сложную разветвленную форму. Рассмотрим равновесие двух фаз в пористой среде. Если каждая фаза в окрестности некоторой точки пористой среды является непрерывной, то можно ввести понятие среднего давления в этой фазе, которое в пределе, при стягивании поверхности осреднения может рассматриваться как давление в данной точке. Таким образом, при равновесии двухфазной смеси в пористой среде в каждой точке определяются дна давления: рi и р2- Разность между этими давлениями называется
капиллярным давлением в данной точке пористой среды. В соответствии с формулой Лапласа (VI.1.2) капиллярное давление пропорционально средней кривизне поверхности раздела фаз в окрестности данной точки. Давление больше со стороны жидкости, хуже смачивающей твердую фазу скелета пористой среды. По-видимому, основная часть жидкости не может находиться в виде пленки на поверхности твердой фазы, а имеет границы пина менисков (см. работу М. М. Куса-кова и Л. И. Мекеницкой [62]). Средняя кривизна этих менисков, очевидно, зависит прежде всего от искривленности порового пространства, т. е. от среднего радиуса пор среды. Далее, кривизна менисков, а следовательно,и капиллярное давление зависяг от насыщенности порового пространства более смачивающей фазой, которая имеет тенденцию занимать более мелкие поры.
Состоянию равновесия соответствует минимум термодинамического потенциала, что сводится при неизменном давлении к минимуму поверхностной энергии, т. е. минимальной величине поверхности раздела фаз в данном объеме. Сложное строение порового пространства приводит к тому, что при данной насыщенности существует ряд локальных минимумов поверхностной энергии, и равновесное распределение является неоднозначным. В результате капиллярное давление зависит при данной насыщенности от пути насыщения. Тем не менее, если рассматривать только процессы вытеснения (без фазовых переходов), то можно считать, что капиллярное давление, кроме насыщенности смачивающей фазой, зависит лишь от того, увеличивается или уменьшается насыщенность для достижения заданного ее значения.
Если отвлечься от этой неоднозначности, то из соображений размерности следует, что капиллярное давление рс в равновесном состоянии может быть представлено в виде:
где г — характерный линейный размер пор; 0 — статический краевой угол смачивания; зависимость (VI. 1.3) называется капиллярной кривой.
Если рассматривать пористые среды, структуры которых подобны, то в качестве характерного линейного размера удобно принять (в соответствии со сказанным в гл. I) величину Vк/т.
Влияние угла смачивания 0 на форму капиллярных кривых экспериментально изучено недостаточно. По аналогии с равновесием жидкости в капиллярной трубке принято включать в формулу для капиллярного давления вместо а «натяжение смачивания», равное a cos 0, и считать, что зависимость рс от © этим исчерпывается. Тогда равенство (VI.3.1) преобразуется следующим образом:
рс=
2a™le-J(s).
(VI. 1.4)
V т
Представление (VI. 1.4) было впервые предложено Левереттом [143], и безразмерная функция / (s) носит название функции Леве-ретта. Разумеется, в реальных условиях не может существовать двух сред, микроструктуры которых полностью подобны. Тем не менее экспериментально установлено, что фупкция / (s) сохраняет свой вид с достаточной точностью для целых классов сходных по структуре пористых сред (нанример, для отдельных групп песчаников, песков и др.).
Равновесное распределение фаз в поровом пространстве зависит не только от конечной насыщенности, но и от того, каким образом достигнута эта насыщенность. Учесть всю предысторию насыщения, конечно, невозможно. Однако в приложениях наиболее интересны процессы постепенного замещепия одной жидкости другой, когда изменение насыщенности происходит монотонно. Для анализа таких процессов можно использовать один из двух типов экспериментальных кривых J (.s), различающихся способом их получения. Если в исследуемом процессе возрастает насыщенность менее .смачивающей фазой, то используются «кривые вытеснения», получаемые в условиях, когда менее смачивающая жидкость (или газ) очень медленно вытесняет из образца пористой среды более смачивающую жидкость. Напротив, для процессов, в которых возрастает насыщенность более смачивающей фазой, используются «кривые пропитки», получаемые при самопроизвольном капиллярном вытеснении менее смачивающей жидкости (или газа) смачивающей жидкостью в вертикальной колонке пористой среды.
После окончания пропитки жидкости находятся в гидростатическом равновесии, и капиллярное давление в каждом сечении определяется по формуле рс = Apgz, где Дрg — разность плотностей жидкостей, z — высота данного сечения над уровнем свободной смачивающей жидкости. Измеряя насыщенность в каждом сечении s, можно построить кривые рс (s) и J (s).
Рпс. VI.2
Кривые вытеснения и пропитки заметно отличаются друг от друга (рис. VI.2), но практически не зависят от свойств жидкостей, применяемых для исследования, и каждая из них может быть описана однозначной функцией насыщенности.
Отмстим еще, что та часть жидкости, которая находится в виде отдельных капель (несвязная насыщенность), не используется в определении капиллярного давления. Если вся жидкость находится в несвязном состоянии, то понятие капиллярного давления теряет смысл. Поэтому, например, кривые вытеснения J (s) на рис. VI.2
Рис. VI.3
фактически обрываются при некотором s = s, и не имеют смысла при s < s#.
2. При фильтрации двух жидкостей в пористой среде по крайней мере одна из них образует связную систему, граничащую с пористым скелетом и частично с другой жидкостью (рис. VI.3). Из-за эффекта избирательного смачивания твердой фазы одной из жидкостей площадь контакта каждой из жидких фаз со скелетом пористой среды значительно превышает площадь контакта фаз между собой (выше уже упоминалось, что существование одной из фаз в виде пленки на поверхности твердого скелета маловероятно). Это означает, что в первом приближении можно принять, что каждая фаза движется в занятом ею пространстве под действием «своего» давления независимо от других фаз, т. е. так, как если бы она была ограничена только твердыми стенками. Закон фильтрации каждой из жидкостей двухфазной системы можно записать в следующем виде:
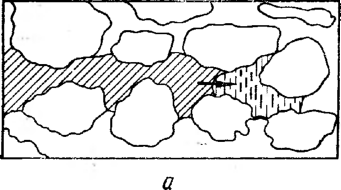
Рис. VI.4
Безразмерные величины /,• принято называть относительными проницаемостями. Относительные проницаемости являются важнейшими характеристиками двухфазного течения 15. Если не учитывать инерционных эффектов, то каждая функция зависит только от безраз-
А-1 grad р I Ui
мерных параметров s, —- -— , —, т.
СС jig
Большой экспериментальный материал, накопленный к настоящему времени [127], показывает, что вид кривых относительной проницаемости для данной пористой среды мало зависит от природы жидкостей и определяется главным ооразом преимущественной смачиваемостью. В.частности, из большинства экспериментальных данных следует, что относительные проницаемости не зависят от отнояте-ння вязкостей фаз. Это служит подтверждением сделанного выше предположения о том, что течение каждой жидкости в занятом ею пространстве происходит независимо от движения соседней фазы L.
Параметр л.г/ = А’| grad р \/а характеризует отношение перепада внешнего давления на расстояниях порядка размера поровых каналов к капиллярпому давлению. Выше уже отмечалось, что для обычных достаточно медленных движений это отношение мало, и градиент внешнего давления не может существенно повлиять на распределение фаз в порах. Поэтому в этих условиях относительные проницаемости можно считать функциями только насыщенности.
Если считать, что сопротивление движению каждой фазы определяется только структурой занимаемой ею части порового пространства, то величина kji является для данной фазы проницаемостью (иногда А/, называют фазовой проницаемостью) в обычном понимании. Очевидно, что с ростом насыщенности данной фазой от нуля до единицы функция /г также возрастает от нуля до единицы. Выше было показано, что распределение фаз в порах зависит фактически только от того, какая из жидкостей обладает преимущественной смачиваемостью, но не от индивидуальных свойств жидкостей. Отсюда следует, что вид функций f-t (s), так же как и / (s), определяется структурой порового пространства.
Из того, что более смачивающая фаза занимает при той же насыщенности более мелкие поры, чем менее смачивающая, следует, что и относительная проницаемость при той же насыщенности для менее смачивающей жидкости больше, чем для более смачивающей. Поэтому кривые зависимости относительной пропицаемости от насыщенности одною из фаз (например, более смачивающей) имеют обычно несимметричный вид типа, изображенного на рис. VI.5.
Характерно, что для каждой фазы существует предельная насыщенность (s* и 1 — %*) — такая, что при меньших насыщенностях эта фаза неподвижна, т. е. находится в несвязном состоянии (индекс
1 на рис. VI.5 относится к более смачивающей жидкости, индекс 2 — к менее смачивающей).
При увеличении скорости фильтрации на распределение фаз в порах начинает влиять градиент внешнего давления. Согласно данным Д. А. Эфроса [127], это влияние начинает сказываться на относительных проницаемостях при параметре л а = к | grad р |/а, большем 10'5 (т. е. Лд = г21 grad р\/а ^ 10" 3.
Применение условий равновесия к задачам фильтрации двухфазной жидкости значительно усложняется ввиду,-неединственности распределения фаз при заданной насыщенности. Дополнительные осложнения возникают из-за гистерезиса смачивания, капиллярного гистерезиса, изменения свойств твердого скелета под действием длительного контакта с жидкостью и других аналогичных физикохимических явлений. Поэтому вид кривых относительной проницаемости, как и кривых J (s) (см. рис. VI.2), зависит от того, повышается или попижается насыщенность в данном процессе, или в более общем случае — от всей предыстории процесса. Однако для наиболее практически интересных процессов, в которых насыщенность изменяется монотонно, относительные проницаемости, точно так же как и функция J (s), могут рассматриваться как однозначные функции насыщенности.
Кривые относительной проницаемости, как и J (s), разделяются по способу их получения на «кривые вытеснения» и «кривые пропитки», которые могут заметно различаться (см. рис. VI.5 — «кривые пропитки» отмечены пунктиром).
Область несвязной насыщенности (s < s* па рис. VI.5) также зависит от пути насыщения пористой среды и в процессе вытеснения различна в зависимости от того, возрастает или убывает насыщенность данной фазой. Если данная фаза является вытесняющей, то неподвижной (несвязной) может быть только та часть этой фазы, которая первоначально насыщала пористую среду. Например, в случае вытеснения нефти водой вытесняющая вода полпостью подвижна, но вода, находившаяся ранее в пласте при малой начальной водонасыщенности (погребепная вода), может быть неподвижной в той части пласта, куда не дошла нагнетаемая вода. Это объясняется тем, что погребенная вода находится в пласте в виде отдельных капель и становится подвижной, только соединившись с основной массой вторгающейся в пласт воды.
Наиболее существенное отклонение кривых относительных проницаемостей от равновесных, связанное как с различными гистере-зисными явлениями, так и с разрывностью фаз, отмечено при фильтрации газированной жидкости. Распределение газа и жидкости в поровом пространстве при одной и той же пасыщенности существенно различно в случаях, когда газ появился в порах «извне», вытесняя жидкость, и когда растворенный ранее газ выделился из жидкости. Газ, пришедший «извне», движется как непрерывная фаза, находясь в капиллярном равновесии с жидкостью. Для газа в таком состоянии величины относительных проницаемостей зависят только от насыщенности и совпадают с обычными относительными проницаемостями для несмачивающей фазы. В то же время газ, выделившийся из раствора, находится в порах в виде отдельных пузырьков. Как отмечено в экспериментах Д. А. Эфроса [127], относительные проницаемости для газа в таком состоянии при той же насыщенности во много раз меньше, чем для непрерывной газовой фазы. Отклонение от капиллярного равновесия проявляется также и в том, что относительные проницаемости в этом случае зависят от отношения вязкостей. Относительные проницаемости для газа, выделившегося из раствора, в большей степени, чем обычные относительные проницаемости, зависят от предыстории процесса выделения газа и последующего его движения, так как эти процессы влияют на величину и количество пузырьков. Д. А. Эфрос показал, что в качестве первого приближения можно считать относительные проницаемости зависящими от насыщенности и от приведенного давления, т. е. от отношения давления в газе к давлению насыщения нефти растворенным газом.
§ 2. ВЫТЕСНЕНИЕ НЕСМЕШИВАЮЩИХСЯ ЖИДКОСТЕЙ.
ЗАДАЧА БАКЛЕЯ-ЛЕВЕРЕТТА
Извлечение нефти из пласта в большинстве случаев происходит путем вытеснения ее водой или газом. Общая схема такого процесса изображена на рис. VI.6. Вода либо поступает в нефтенасыщенную
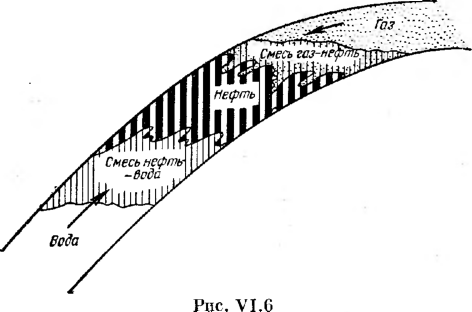
часть пласта, перемещаясь из водонасыщенных зон того же пласта (краевая зона), либо искусственно закачивается в пласт через специальные нагнетательные скважины. Таким же вытесняющим агентом может быть газ, находящийся в пласте или специально нагнетаемый. Нефть извлекается через эксплуатационные скважины, причем в ряде случаев вместе с нефтью извлекается и вода или газ, прорвавшиеся к эксплуатационным скважинам. Хотя обычно природный газ отбирается из пласта за счет его расширения при снижении давления, в некоторых, случаях и газовые пласты раоотают на режиме вытеснения газа водой, насыщающей внешние области того же пласта. Для анализа эффективности вытеснения нефти или газа несме-шивающейся с ней жидкостью необходимо знать, как изменяется распределение насыщенности в пласте. В связи с этим вытеснение несмепшвающихся жидкостей должно рассматриваться как процесс двухфазной фильтрации.
Выведем систему уравнений двухфазной фильтрации в однородной пористой среде без фазовых переходов. При записи закона фильтрации будем предполагать, что в любой точке каждая из фаз находится целиком лишь в одном из двух крайних состояний: а) связном и подвижном и б) несвязном и поэтому неподвижном. В соответствии со сказанным в предыдущем параграфе, в областях медленного термодинамически равновесного течения для тех жидкостей, которые можно считать связными, можно ввести в расчет зависящие только от насыщенности относительные проницаемости ft(s) и капиллярное давление рс (s).
Кроме того, не касаясь гистерезисных явлепий, будем рассматривать только однонаправленные процессы, которые наиболее интересны для приложений.
В результате сделанных предположений закон фильтрации можно записать в виде:
и{=—A/.(S)grad# (i = 1, 2). (VI.2-1)
В равновесном однонаправленном течении разность давлений в фазах равна капиллярному давлению, определяемому формулами (VI.1.3) или (VI.1.4):
рг — pj =pe(s)^.a|/-^-cos07(s). (VI.2.2)
Для определенности будем индекс 1 относить к более смачивающей фазе, насыщенность которой равна s. В задачах совместной фильтрации нефти или газа и воды более смачивающей фазой обычно является вытесняющая вода.
Для получения замкнутой системы уравнений необходимо записать уравнения сохранения массы для обеих фаз. Выделим в фильтрационном потоке некоторый объем Т. Масса первой фазы в нем равна
jmpjrfr (dx — элемент объема Т). Приток первой фазы за время dt
т
через поверхность S, ограничивающую объем Т, составляет
— dt f рiUindo- (п — вектор нормали к поверхности S, da — элемент
s
поверхности S). Полагая, что в объеме Т нс содержится источников массы, имеем
d
г s
откуда, преобразуя поверхностный интеграл в объемный и учитывая, что объем Т произволен, а границы его неподвижны, получим окончательно
— (mpjs) + div (рЛ) =- 0. (VI.2.4)
Аналогично выводится уравнение сохранения массы для второй фазы:
~ [тор, (1 — s)] — div (p2w2) =-0. (Vl.2.5)
Таким образом, мы получаем замкнутую.систему уравнений для Pi и s, поскольку pi и р2 являются функциями давлений р | и р2,
а изменение пористости в однородном пласте зависит только от изменения среднего давления р —P\S +/>2 — 8) (ср- гл. II), а не давле
ния компонентов.
Если вытесняемая и вытесняющая фазы — слабосжимаемые капельные жидкости, влиянием сжимаемости на распределение насыщенности можно пренебречь. Действительно, характерное время нестационарного перераспределения давления за счет сжимаемости имеет порядок ?1 = L2/k, где и — коэффициент пьезопроводности, L — характерный размер. Характерное время вытеснении — порядка t2 = L/u, где и — средняя скорость фильтрации. Обычно скорость фильтрации — около 10 3 см/сек, L *=» 104 -f-106 см, 101 см2/сек.
Поэтому 10* 2, откуда видно, что нестационарные процессы
упругого перераспределения давления заканчиваются в начале хода вытеснения.
Если жидкости и пористую среду можно считать несжимаемыми, имеем вместо (VI.2.4) и (IV.2.5)
тп -|^-+divw1 = 0, m — divM2 = 0. (VI.2.6)
Решение системы уравнений (VI.2.1), (VI.2.2), (VI.2.6) для двух-или трехмерных случаев весьма сложно. Для анализа общих, свойств поля насыщенности при вытеснении применим асимптотический подход, основанный на малости некоторых безразмерных параметров, входящих в условия задачи (см. работу Г. И. Баренблатта [26]).
В систему уравнений и граничные условия входят следующие размерные определяющие параметры: Ар — перепад давления между скважинами или галереями; L — характерный размер области течения; коэффициенты /г/[л4 и к/ц2, а также pl = a'\f m/k cos 0. Перейдем в уравнениях (VI.2.1), (VI.2.2), (VI.2.6) к безразмерным переменным:
Pi п . Т _ и‘ ( _ к Ар \ ^ х
U1=-f1 (s) grad Р2 + е/, (s) J (s) grad s;
u г = - Mo/a (s) &rad Pz, Mo =" Mi /М2
(оператор grad выполняется здесь в переменпых X, Y, Z):
m ds , dUlx , pUiy ( SU1Z
dx dX “* dY dZ ’
= 0. (VI.2.8)
dz dX dY dZ
Уравнения (VI.2.7) записаны через P2, так как только вытесняемая жидкость остается непрерывной во всей области течения, а вытесняющая может в целых областях, куда еще не дошел фронт вытеснения, находиться в виде отдельных капель.
Параметр е = мал в большинстве интересных для приложении
задач, так отмечалось в § 1. Поэтому члеп Uc — efi (s)J'(s) grad s может быть существен лишь в узких областях, где велик градиент насыщенности. Самый факт существования таких областей будет установлен позже, пока же отметим, что их протяженность должна быть мала по сравнению с основной внешней областью именно потому, что в них велик jgrad s|, a s — ограниченная величина. Это позволяет применить для анализа системы (VI.2.7), (VI.2.8) метод асимптотического сращивания [36а], который заключается в использовании разных масштабов при рассмотрении движения в основной области и в узких зонах резкого изменения насыщенности. Подобно этому течение в пограничном слое вязкой жидкости вблизи стенок имеет иной пространственный масштаб, нежели внешнее течение.
Разделим область фильтрации на внешнюю зопу, где Uc — малая величина, и узкую внутреннюю зону или зоны, где вследствие больших значений |grad я| значением Uc пренебречь нельзя.
Малость параметра е приводит к естественной попытке исследовать течение во внешней зоне, разлагая искомое решение в степенной ряд по этому параметру (внешнее разложение). Первый член впешнего разложения мы получим, полагая е = 0. Исследование структуры внутренней зоны (внутреннее разложение) будет рассмотрено в следующем параграфе.
Общие свойства внешнего разложения рассмотрим вначале на примере одномерной задачи, решение которой получается в замкнутом виде.
В одномерном случае (плоском, радиальном или сферическом)
уравнения (VI.2.8) с учетом (VI.2.7) при е — 0 запишем, возвращаясь к размерным переменным, в виде:
ds к 1 а { , . др
т ¦
dt jij дх
(VI.2.9)
mTS'+i А ? (*"Ч‘(!) ?) ='0 ~ Р- “Р>
(v = 1, 2, 3 соответственно для линейного, радиального или сферического течения).
Вычитая второе уравнение (VI.2.9) из первого и интегрируя, получим
1Ы»-1 МЛОИ-М---рг (!*.-?-)• (у1'210)
Это равенство выражает постоянство суммарного расхода вдоль трубки тока в силу несжимаемости жидкостей. Определяя др/дх из (VI.2.10) и подставляя в любое из уравнений (VI.2.9), получим одно уравнение для s:
t Я (0 F (s) дь q (VI ? 11)
dt i,
где q (t) ---— С (I) — суммарный расход жидкости через трубку
Hi
тока, а
р (s) —_____
./l (s)H-Mo/z (-я)
Функция F (s) равна отношению скорости фильтрации (или расхода) вытесняющей фазы к суммарной скорости фильтрации (или к суммарному расходу). Функцию F (.?) принято называть функцией распределения фаз.
Введем новые
независимые переменные: Q — ^ ~'т^~
^
to
Величину W можно рассматривать как объем трубки тока между сечениями .т0 и х (в частности, при v = 1 и q (?) = const переменная Q пропорциональна времени, a W = х). Тогда вместо (VI.2.11) имеем
= (VI.2.12)
Этому уравнению в частных про из и одних первого порядка соответствует следующая система характеристических уравнений:
dQ ____ds /л/i 9 14^
1 F(s) ~ 0 * ( '
Общее решение системы (VI.2.13) представляется в виде:
s = Ci; (VI.2.14)
W=~QF‘ (.s) \-С.л.
Таким образом, вдоль характеристик уравнения (VI.2.12) s —
— const и в плоскости (W, Q) характеристики представляют собой прямые линии. Физически ато означает, что каждое значение насыщенности «распространяется со «скоростью» dW/dQ, пропорциональной F' (s). В случае движения плоскими волнами v — 1, а есть
истинная скорость распространения данного значения насыщенности.
На основании равенств (VI.2.14) общее решение уравнения (VI.2.12) можно формально записать в виде:
W = QF' (s) 4- W0 (*), (VI.2.15)
где функция Wo (s) соответствует начальному распределению насы-щеппости (при Q — 0, т. е. t = t0).
На скважинах (или галереях), через которые нагнетается вытесняющая жидкость, должны быть заданы условия, определяющие состав нагнетаемой жидкости. Если пагнетается одна (вытесняющая) жидкость, то такое условие записывается в виде:
0. (VI.2.1G)
Поскольку др/дх =j= 0, так как не равен нулю суммарный расход, то из (VI.2.5) следует /2 (s) =0, я s**. Пусть в начальный момент везде в пласте насыщенность вытесняющей фазы ниже, чем s** (s** — насыщенность, при которой вытесняемая фаза становится неподвижной). Это условие выполняется почти во всех задачах, имеющих физический смысл. Тогда при I 0 на границе будет выполняться условие
s-s**. (VI.2.17)
Действительно, если предположить, что в некоторой точке границы s > то в силу непрерывности насыщенности вблизи этой
точки границы должна существовать целая область конечных разме
ров, в которой s^>s** и ы2=0. В силу уравнения неразрывности для вытесняемой фазы (VI.2.6) отсюда следует ds/dt — 0. Это противоречит условию s sc s** при t — 0. Если же задано отношение расходов двух фаз на поверхности нагнетания А, то условие на границе имеет вид:
= (VI.2.18)
откуда также определяется насыщенность на границе, поскольку относительные проницаемости /1 (s) и /2 (s) известны.
Вернемся к анализу общего вида решения (VI.2.15).
На рис. VI.7, а, б изображены типичные кривые F (s) и F' (s). Функция F' (s) имеет максимум в некоторой точке sm. Поэтому в соответствии с формулой (VI.2.15) два различных значения насыщенности могут иметь одинаковую скорость распространения. В связи с этим получаемая по формуле (VI.2.15) зависимость насыщенности от W может статт. неоднозначной — большие значения «обгоняют» меньшие, как это показано на рис VI.8.
Неоднозначность формального решения, получаемого из (VI.2.15), означает, что непрерывных решений задачи о вытеснении при заданном начальном условии не существует. Чтобы получить решение, имеющее физический смысл, необходимо вводить разрывы (скачки) насыщенности, т. е. поверхности, на которых значение насыщенности меняется скачком. Такие скачки могут существовать и в начальных условиях.
а 6
Рис. VI.7
С ростом Q начальное гладкое распределение насыщенности деформируется, как это видно на рис. VI.8. В некоторый момент (т. е. при некотором Q) касательная к кривой s {W) становится вертикальной. Начиная с этого момента, возникает и распространяется скачок насыщенности. Положение скачков насыщенности заранее неизвестно и должно быть найдено в зависимости от времени из решения задачи. На скачках (поверхностях разрыва) должны выполняться условия непрерывности давления и сохранения массы каждой из движущихся фаз.
Выведем условия па скачках для общего случая неодномерного двухфазного течения. Первое из этих условий записывается в виде:
p(D = p(2). (VI-2.19)
Рассмотрим теперь условия сохранения массы каждой из фаз при прохождении поверхности разрыва (скачка) через некоторым элемент объема пористой среды (рис. VI.9), вырезанный по норуали к поверхности разрыва. В силу непрерывности давления сжимаемость жидкостей для условий на скачке несущественна. Применим к этому элементу уравнение сохранения массы (VI.2.3). Имеем
^ J msdx'j = mVn (s*1) — s<2>) A -j- о (T),
d_
dt
где A — площадь поперечного сечения элемента (индексом 1 сверху обозначены величины за скачком, индексом 2 — перед скачком); F„ — скорость перемещения скачка по нормали к нему; о (Г) —
величина, стремящаяся к нулю быстрее, чем Т.
Поток жидкости через сечения, параллельные поверхности разрыва, равен (ы$ —
— u<in) A (uin — проекция скорости фильтрации первой фазы на нормаль к поверхности скачка). Поток, связанный с касательной составляющей скорости, исчезающе мал по сравнению с и1пА при стремлении Ап к нулю в силу условия (VI.2.19).
Условие сохранения массы первой жидкости примет тогда вид:
mVn (sW — s<2>) = — и[*>.
(VI.2.20)
Равенство (VI.2.20) можно переписать в виде:
ит ищ
(VI.2.21)
” m(s^—s^)
Условие сохранения массы второй жидкости также сводится к выражению (VI.2.20), поскольку
^ + = “$+“$• (VI.2.22)
Вернемся к исследуемой одномерной задаче. Из определения функции q (t) и F (s) можно записать выражения для скоростей фильтрации вытесняющей фазы позади и впереди скачка:
где индекс 1 относится к величинам за скачком, индекс 2 — перед скачком. Тогда получим следующее выражение для скорости скачка Vn — V = dx/dt:
dx g(0 fL(s(1)) —f (s(2))
(VI.2.24)
(VI.2.25)
-Jf— тхУ-1 - s(!)"(?)
Переходя к переменным W и Q, получим
dW F(s(1))-F(s(2>) dQ — S(D_S<2)
Распределение насыщенности по обе стороны скачка описывается формулой (VI.2.15). Положение скачка Wc и насыщенность на скачке sc = s(1) можно определить вычислением последовательными шагами, исходя из начального положения скачка (т. е. места появления вертикальной касательной), по формуле (VI.2.25).
Выведем дифференциальное уравнение, описывающее изменение насыщенности на скачке в зависимости от Q. Для насыщенности на скачке, как и для любого значения насыщенности, выполняется соотношение (VI.2.15):
Wc = QF‘(sc)-W0(se). (VI.2.26)
Очевидно, согласно (VI.2.26), sc — s(1) меняется с изменением Q (т. е. со временем). Дифференцируя (VI.2.26) по Q, имеем
^ F' (sc) -г- [F" (sc) Q 4- W'o (Sf)] -g . (VI.2.27)
Приравнивая выражения для скорости распространения скачка насыщенности (VI.2.25) и (VI.2.27), придем к следующему уравнению для sc:
dfc F (sc) — F (s(2)) — F' (яе) (sc— s(3)) CVT 2 98^
dQ' (SC-S<^)IF"(SC)Q + W'C(SC)]
Значение s<2) в уравнении (VI. 2.28) является функцией Q и sc.
Оно определяется из условия W (s<2))= IV (sc) = Wc в соответствии
с формулой (VI.2.15):
0F>C) + (О = (*<*>)+ (*<*>). (VI.2.29)
Для решения уравнения (VI.2.28) начальные значения sc и Q определяются в той точке, где dlV/ds, соответствующее формуле (VI.2.15), впервые обращается в нуль.
Из уравнения (VI.2.28) следует, что на скачке насыщенности, по обе стороны которого sc и s0— s(2) постоянны (стациопарный скачок), должно выполняться условие
F
(!с) -РЫ ^р’ (sc).
(VI.2.30)
sc— s0
Это условие (полученное впервые в работе Баклея и Леверетта [134]) означает, что скорость распространения скачка равна скорости распространения насыщенности на скачке sc.
Рассмотрим отдельно случай, когда начальная насыщенность s (IV, 0) = s0 постоянна во всем пласте. Тогда W0 (s) = 0 при s > s0 и W0 (s) неопределенно при s О0- Из формулы (VI.2.15) имеем в данном случае
W = QF'(s) (s>s0).
Предположим, что s0 < sm (см. рис. VI.7, б), и скачок возникает. При заданных условиях в уравнении (VI.2.28) переменные разделяются.
Обозначим sc — s0 = у, F (sc) — F (s0) = -ф (у). Тогда из уравнения (VI.2.28), интегрируя, получим
= с = const. (VI.2.31)
Поскольку при Q -у 0 (в начальный момент), левая часть равенства (VI.2.31) остается ограниченной, С должно обращаться в нуль. Следовательно, скачок является стационарным. Возвращаясь к переменным sc и s0, получаем, что на скачке при любых Q выполняется соотношение (VI.2.30).
Пусть начальное распределение насыщенности таково, что Wo (s) <0 при всех s, а при W -у ос s (VF, 0) -> s0. Тогда рассмотренное выше решение для случая .<>0 = const будет выполняться асимптотически при Q -*¦ 00, поскольку W'o (sc) ограничено.
Рассмотренное решение и условие (VI.2.30) было получено Бак-леем и Левереттом [134]. Исследование движения скачков насыщенности выполнено С. Н. Бузиновым и И. А. Чарным [36].
В общем случае неодномерной задачи системы (VI.2.7) и (VI.2.8) даже при е — 0 уже не сводятся к одному уравнению для насыщенности. Необходимо определять р и s совместно. При этом граничные и начальные условия для р те же, что и в задачах фильтрации однородной жидкости.
Условия для s имеют вид (VI.2.17) или (VI.2.18). Кроме того, на скачках, положение которых заранее неизвестно, должны выполняться условия (VI.2.19), (VI.2.22) и (VI.2.23). Решения неодномерных задач могут быть получены лишь численно на ЭВМ.
§ 3. СТРУКТУРА СКАЧКА НАСЫЩЕННОСТИ.
УРАВНЕНИЕ РАПОПОРТА - ЛИСА.
СТАБИЛИЗИРОВАННАЯ ЗОНА
На примере решения Баклея — Леверетта видно, что если в задаче о вытеснении нефти водой ограничиться первым членом внешнего разложения, т. е. не учитывать капиллярной разности давлений, то необходимо вводить поверхности, па которых насыщенность терпит разрыв.
Чтобы описать распределение насыщенности в узких областях, вблизи скачка, .нужно получить «внутреннее разложение» решения задачи о вытеснении на основе полной системы уравнений (VI.2.7), (VI.2.8). Для построения первого члена внутреннего разложения введем в окрестности некоторой точки поверхности разрыва (т. е. скачка насыщенности) локальную мгновенную декартову систему координат с центром в точке 0 поверхности разрыва. Ось х направим по нормали к поверхности разрыва и введем вдоль этой оси масштаб I =eL,
т. е. положим X — у, сохраняя
вдоль других осей масштаб L (рис. VI. 10). Масштаб времени примем равным ti — 1/и0 и положим т = t/tj. В остальном сохраним те же безразмерные параметры и пере менные, что и в уравнениях (VI.2.7) и (VI.2.8).
Запишем систему уравнения в безразмерном виде. Обобщенный закон Дарси:
1 * /-ч вРг
9Р 2 дХ
7i(«)
U
ах
2Х
ЭР 1 dY
и1Г=~Ш
V
(Vl.3.1)
дР2
dZ
M-о/з (s)
1 z
И
Из
Со'
Уравнения неразрывности:
dU,x ~дХ + 6 dU„
аи
аи
ds
дх
1У
1Z
;0;
т
az
dY
(VI.3.2)
Подставляя (VI.3.1) в (VI.3.2) и отбрасывая члены порядка г и е2 получим
as 1 а
е ах
дх
m-w~w v* (*>F ^ r <s> -?г)=°- <VL3-4>
где
Ит) - —^"2 (*) + М^о/а (*)] + И0/2^ (s) -gj =
= ^х + ^- (VI.3.5)
Система (VI.3.1) — (VI.3.2) свелась к одномерному уравнению (VI.3.4), потому что радиус кривизны поверхности разрыва имеет порядок L , и в принятом масштабе I эта поверхность, как и поверхности s = const, заменяется плоскостями. Равенство (VI.3.5) означает, что в пределах зоны скачка, где движение можно считать одномерным, суммарная скорость фильтрации обеих фаз вдоль оси х, w есть величина, зависящая только от времени, как при движении в цилиндрической трубке тока.
Значение w в уравнении (VI.3.4) находится из внешнего разложения, как безразмерная суммарная скорость фильтрации через поверхность разрыва в точке 0. Уравнение (VI.3.4), описывающее одномерное вытеснение несмешивающихся жидкостей, называется уравнением Рапопорта — Лиса [152].
Поскольку масштаб времени во внутреннем разложении tx намного меньше, чем во внешнем, а скорость w определяется внешним разложением, то при исследовании внутреннего разложения можно считать w (т) = const. Ввиду различия масштабов времени во внешнем и внутреннем разложении достаточно воспользоваться стационарным решением задачи Копти для уравнения (VI.3.4), т. е. положить
s=s(x), х = Х — У°т (у°=—V (VI.3.6)
' ии /
Иными словами, в масштабе времени внутреннего разложения процесс вытеснения продолжался весьма долго, и его . можно счи тать установившимся в системе координат, связанной со скачком. При этом в силу различия масштабов I и L должны выполняться граничные условия
s (—oo) = s<1) = sc; s (-j- 00) = s<2) = s0, (VI.3.7)
где s(1> = sc и s(2) = s0 — насыщенности за и перед скачком, определяемые из внешнего разложения [в задаче Баклея — Леверетта они связаны соотношением (VI.2.30)]. Параметр V0 в равенстве (VI.3.6) есть, очевидно, скорость распространения поверхности разрыва, определяемая формулами (VI.2.21) или (VI.2.24).
Используя (VI.3.6), получим вместо (VI.3.4) уравнение
_mV0 -р-и, -ЁПЭ- + A U (s)F (s) (S) ^1 = 0. (VI.3.8)
dx dx ox [ dx J
— mV°s — wF (s) + И0/2 (s) J* (s) — c = const. (VI.3.9)
dx
Из условия s=sc при x -*¦ — oo, учитывая, что при зтом ds/dx =0, имеем
с = — mV°sc — wF (sc). (VI .3.10)
Заметим, что, поскольку значение V определяется формулой (VI.2.24), второе условие (VI.3.7) будет выполнено автоматически. Подставляя значение с из (VI.3.10) в (VI.3.9) и разрешая относительно dx/ds, получим
dx _ w\i012 (s) F (s) J' (s) __/VI 4 11^
ds V°(s-*o)-lF(s)~F(s0)]w ' (M.o.ll)
Если проинтегрировать уравнение (VI.3.11) no s, принимая начало отсчета так, чтобы при х = xt было s — su где s0 <$i <se, получим,
используя для F° формулы (VI.2.24) и (VI.3.5) при s(1) = sc, s(S) = s0:
/ у _ ЦрЩ F (sc) — F(s0) _ y0 _ ]?_ F(sc) — F(s0) \ ^
\ m sc — s0 • m Sg Sq j »
/2 (s) F (s) J (.?) d?______ (VI 3 12)
IF (%) - F (*„)] --F(s) -[ F (s„)
SC—*0
Если справедливо предположение о стационарности скачка насыщенности и V определяется из формулы (VI.2.24), получим иную запись для х (s):
~ ~ Г h (s) F (s) J' (s) ds
*1
Интегралы (VI.3.12) и (VI.3.13) описывают переходную зону бесконечной протяженности, что является следствием принятой аппроксимации. Фактически для определения ширины зоны нужно брать по формулам (VI.3.12) и (VI.3.13) расстояние между точками с насыщенностями s0 -f 8 и s0 — 6, где 6 — малая, но конечная величина. Тогда безразмерная ширина переходной зоны будет порядка несколь-
7 Рст «Ка
ких единиц, а размерная
ширина — порядка I, т. е. L или ^
.
Типичная кривая распределения насыщенности в переходной зоне приведена на рпс. VI. 11.
Проанализируем распределение насыщенности в переходной зоне в зависимости от вида функций F (s) и J' (s) и значений sc и s0.
При s, близких к sc, знаменатель подынтегрального выражения имеет порядок
F(sc)-F(s0)
F' («с)}+«1 (S “«с)2.
тт F lsc) — F (sn)
а числитель есть конечная величина. Поэтому, если——¦-- --- =±=
_ _
Ф F'
(sc), то для . больших отрицательных
х имеем х ^ В In (s — sc). Если же
—F fa) _ р, ^
(СЛуЧай Баклея — Леверетта),
то
_ sc —
х^С (sc — s)-1 (а,, В, С
постоянные).
Рис. VI.11
dj
Если s0 и F (s0) не обращаются в нуль и при s = se конечно.
то из (VI.3.12) для s, близких к s0, следует х — xt ^ A In (s — s0).
Пусть теперь F (s0) = 0 и, следовательно, ^ s0 ^ 0. Тогда вместо (VI.3.12) получим
(s) П _h(*)F(s)J'
ds (V1.3.14)
F(sc) F(s)
-Sq J S-Sq
~s0
Функция fi (s) при s, близком к s*, имеет вид b (s — s*)?, где P >2, F (s) M (s — s,)p, b и M — постоянные. Тогда при s, близких к s*, если s* ф s0, то
х~ х% — N J (s — s*)P/' (s) ds.
(VI.3.15)
При s ->¦ s% величина J' (s) растет медленнее, чем (s — s*) (^+1) ’ интеграл (VI.3.15) сходится, и значение s = s* достигается при конечном значении х (рис. VI.12), а от s* до s0 возникает скачок насыщенности. На этом скачке, как и на всяком скачке насыщенности, должно
выполняться условие (VI.2.12). Проверим его выполнение. В нашем случае Vn = V, s(1) = s*, s(s) = s0, u[2J = 0. Тогда условие (VI.2.12) примет вид:
(VI.3.16)
Сравнивая формулы (VI.3.3) и (VI.3.4), можно получить
и1 = ыв[1Р/'(в)-Ио/а(*)^(«)^(«)-^-] • (VI.3.17)
Теперь нетрудно убедиться, что с учетом (VI.3.17) из уравнения (VI.3.11) при s = s* следует условие (VI.3.16).
Если s0 — s*, то вместо формулы (VI.3.15) имеем при s, близких к Sjj.:
S
x — x^Ni l(s-s*)V-iJ'(s)ds. (VI.3.18)
Величина s обращается в s* при конечном значении х в том случае, если интеграл (VI.3.18) сходится.
Рис. VI.12
Существование решений вида (VI.3.12) и (VI.3.13) показывает, что при постоянной скорости вытеснения распределение насыщенности в переходной зоне является стационарным. Экспериментально такая стациопарная переходная зона при вытеснении нефти водой в трубах, заполненных песком, была обнаружена Тервиллигером и др. [158] и впоследствии подробно исследована в работах Рапопорта и Лиса [152] и Д. А. Эфроса и В. П. Оноприенко [128]. В связи со стационарностью распределения насыщенности эта зона получила название стабилизированной зоны. Фильтрация в стабилизированной зоне исследовалась в работах Джонс-Парра и Колхауна [141], а также В. М. Рыжика, И. А. Чар-ного, Чень-Чжун-Сяна [99а].
Распределение насыщенности в стабилизированной зоне устанавливается в результате совместного действия сил вязкого сопротивления, гравитации и капиллярных сил. Все эти силы находятся в равновесии при постоянной скорости вытеснения. Здесь имеется аналогия с гидростатическим равновесием жидкости в пористой среде, когда граница раздела фаз бывает размытой под действием капиллярных сил из-за разницы в размерах поровых каналов. Грубо оценивая величину сил, действующих на жидкость в переходной зоне, можно сказать, что капиллярное давление, вызывающее размывание фронтов,
имеет порядок а (—---—V где г(вг( — минимальный и максималь-
\ гс ri 1
ный «радиусы пор» среды. Перепад давления, необходимый для преодоления вязкого сопротивления, и силы тяжести в зоне длиной I пропорциональны I. Поэтому при постоянной скорости размер зоны, в которой «срабатывается» капиллярный перепад, остается постоянным.
Возможность описания процесса вытеснения в большом масштабе при помощи внешнего разложения (напримвр, с использованием решения Баклея — Леверетта) связана только с малостью параметра
е = . Если граничные условия внешней задачи таковы, что пара
метр в мал, то он остается малым даже в том случае, если капиллярное давление зависит, кроме насыщенности, it от других параметров, поскольку капиллярное давление связано в основном с распределением фаз в порах и при любом распределении остается ограниченным. Напротив, при анализе структуры переходной зоны в настоящем параграфе учитывалось, что капиллярное давление и относительные проницаемости являются функциями только насыщенности.
Г. И. Баренблатт [26] отметил, что во внутренней переходной зоне использование предположения о фазовых проницаемостях и капиллярном давлении как универсальных функциях мгновенной насыщенности неправомерно из-за неравновесных процессов перераспределения фаз в порах. Вместо этого предполагается, что в каждый момент при каждой насыщенности s существуют объемы вытесняющей и вы-
„ у ds
тесняемои фаз, равные т„ не принимающие участия в движении
(здесь т0 — некоторый параметр, имеющий размерность времени, зависящий от свойств пористой среды). Эти объемы захвачены процессами перераспределения, в связи с чем поры, где они находятся, как бы «заперты». Тогда в первом приближении можно полагать, что
U = fl (s — т0/2 = Л (s + гДе /“ («) и /I (s) - обычные
«равновесные» относительные проницаемости. В работе [26] были получены выражения для распределения насыщенности в стабилизированной зоне при сделанных предположениях о «запаздывании» относительных проницаемостей.
Как показывают эксперименты, стабилизированная зона при постоянной скорости вытеснения всегда образуется через достаточно большое время. Измерения распределения насыщенности в стабилизированной зоне может помочь выяснить, в каких продолах справедливы предположения, сделанные при выводе формул (VI.3.12) и (VI.3.13), т. е. предположения об однозначной зависимости функций /? (s) и J (s) от насыщенности и о независимости их от скорости фильтрации.
Такие эксперименты были проведены В. М. Рыжиком совместно с. В. Н. Мартосом. Из горизонтальных труб длиной 170 см, заполненных кварцевым песком с проницаемостью 10 д и пористостью 0,40, вытеснялся воздух водой при атмосферном давлении с постоянной скоростью. Распределение насыщенности измерялось методом электросопротивления. Скорость вытеснения и0 менялась в пределах от 0,0011 до 0,020 см/сек. Начальная насыщенность s0 равнялась 0,21.
Эксперименты показали, что при вытеснении с постоянной скоростью изменение насыщенности в различных точках по длине модели практически повторяется со сдвигом во времени, пропорциональным скорости вытеснения, т. е. образуется стабилизированная зона. Типичные кривые s (t) в точках, отстоящих друг от друга на 58 см, при скорости фронта 0,013 см/сек показаны на рис. VI. 13.
Если относительные проницаемости и капиллярное ^0^0.свдгсм давление являются функциями только насыщенности, то
80 160 2Ь0 з го 1/v, сек/смь
Рис. VI.14
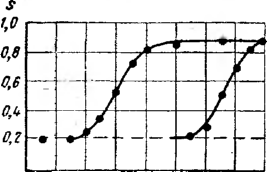
50 SD 130 по t,mn Рис. VI.13
в соответствии с формулами (VI.3.12) и (VI.3.13) безразмерная длина стабилизированной зоны 6 не зависит от скорости. Это означает, что размерная длина этой зоны, равная d = Ы, обратно пропорциональна скорости, т. е.
d =
= = —У
кт cose.
(VI.3.19)
Ар и0ц
На рис. VI.14 показана зависимость длины стабилизированной зоны d от 1/F (V — скорость фронта вытеснения), получеппая в описанных выше опытах (кривая 1)\длина стабилизированной зоны определялась как расстояние между точками с насыщенностями 0,40 и 0,80. Из графика видно (кривая 2), что при больших 1/У (малых скоростях) d приблизительно пропорциональна 1/У, как и следует из формул (VI.3.12) и (VI.3.13). Однако при значении 1/У около 100 сек/см имеется минимум d, а далее снова наблюдается рост стабилизированной зоны. По-видимому, этот рост d связан с неравно-весностыо течения и запаздыванием процессов перераспределения фаз в порах. По схеме «запаздывающих» относительных проницаемостей, как показано в работе [26], получается именно такая зависи-
1 ds
мость а от скорости, когда величина т0 -т— становится сравнимой с s.
Из формул (VI.3.12) и (VI.3.13) можно получить также выражения для dpc/ds, которые позволяют, зная из эксперимента распределение насыщенности, найти «динамическую» зависимость капиллярного давления от насыщенности (при этом приходится предполагать, что относительные проницаемости мало зависят от скорости. Это предположение справедливо, если вытесняющей фазой является вода, а вытесняемой — воздух, вязкость которого пренебрежимо мала). Оказалось, что при малых скоростях динамические кривые совпадают со статической кривой, а при больших — лежат тем ниже ее, чем больше скорость.
§ 4. КАПИЛЛЯРНАЯ ПРОПИТКА И АВТОМОДЕЛЬНЫЕ ЗАДАЧИ ВЫТЕСНЕНИЯ НЕСМЕШИВАЮЩИХСЯ ЖИДКОСТЕЙ
В предыдущем параграфе было рассмотрено действие капиллярных сил вблизи фронта вытеснения несмешивающихся жидкостей из пористой среды. Капиллярные силы становятся существенными и в других случаях, когда в пористой среде в силу ее собственной неоднородности или под влиянием неоднородности потока создаются значительные местные градиенты насыщенности. При этом под действием капиллярных сил происходит перераспределение фаз, поскольку градиент капиллярного давления может быть близким к градиенту внешнего давления, а в ряде случаев значительно превосходить зтот градиент. Процессы перераспределения (роль которых в вытеснении несмешивающихся жидкостей будет более подробно рассмотрена в главах VII и X) проще всего проследить на примере капиллярной пропитки, т. е. фильтрации, происходящей под действием только капиллярных сил.
Можно выделить два идеализированных процесса, в которых капиллярные силы являются единственными движущими силами [99, 100].
1. Пусть цилиндрический образец пористой среды имеет непроницаемую боковую поверхность. Первоначально образец заполнен газом (имеющим пренебрежимо палую вязкость). В начальный момент один из концов образца приводится в соприкосновение со смачивающей жидкостью, которая начинает впитываться в образец. Далее будем предполагать, что давление в газе (начальное давление в образце) и давлепие в жидкости вне пористой среды одинаковы.
Как ив § 3, считаем, что жидкость является непрерывной вытесняющей фазой и фильтрация происходит в одном направлении. По уже упоминавшимся соображениям жидкость, движущуюся в пористой среде под действием капиллярных сил, можно рассматривать как несжимаемую. Фильтрация непрерывной фазы описывается обобщенным законом Дарси в виде:
Поскольку вязкость газа мала по сравнению с вязкостью жидкости, для газовой фазы можно положить р2 — р0 ~ const. Для рассматриваемого одномерного движения непрерывной жидкой фазы выполняется соотношение
P2 — Pi^Pc(s) (Vl.4.2)
или
(оставляем пока в стороне неравновесные эффекты).
Подставляя это выражепие для pt в равенство (VI.4.1), получаем
"1 =?/.<«)*(«> (VI.4.4)
где
_. s
с2 —
К
J (s) — функция Леверетта [см. формулу (VI. 1.4)]
Уравнение неразрывности для жидкости в рассматриваемом одномерном случае имеет обычный вид:
= CVI.4.S)
Подставляя сюда выражение (VI.4.4), получим следующее уравнение для s:
Ыа кривых J (s), полученных путем пропитки (например, путем впитывания жидкости в вертикальную колонку пористой среды), всегда существует такое значение s = s* 1, что J (s*) = 0. В силу непрерывности давления в жидкости при переходе через границу пористой среды и так как давление в свободной жидкости равно р(1, то на границе пористой среды должно выполняться условие р t = = р0, откуда рс — 0 и J (s) — 0. Следовательно, во входном сечении (где примем х — 0) будет s — s* (если пренебречь сжимаемостью). В выходном сечении, очевидно, вытесняющая жидкость неподвижна, поскольку истечение жидкости из порового канала не может происходить под действием одних лишь капиллярных сил (для вытекания жидкости должно произойти оборачивание мениска на выходе, что приведет к изменению знака капиллярного давления и прекращению движения). В соответствии с формулой (VI.4.4) равенство нулю скорости фильтрации означает, что в выходном сечении (х = I)
поскольку dpc/ds в нуль не обращается.
Первое из условий (VI.4.7) выполняется до подхода жидкости к выходному сечению, когда &¦ s* (где s* — «неподвижная» насыщенность), а второе после подхода.
Рассмотрим случай, когда I оо. Тогда единственным размерным определяющим параметром для распределения насыщенности оказывается а2. Размерность этого параметра есть LP/T. Если, кроме того, начальная насыщенность s0 — const, задача становится автомодельной и s является функцией переменной ? = x/a\rt. Уравнение (VI.4.6) обращается в обыкновенное дифференциальное уравнение вида
Зависимости относительной проницаемости для смачивающей фазы /1 (s) и функции Леверетта J (s) можно аппроксимировать формулами
к (s) = b (s — s*)p. (/i (s) = 0 при s < s*),
/(s)=C1—fii(s — «*)“' или J(s)~B2(s — s*)®2 — C,
причем P>2, l>at>0, 1>а2>0. Таким образом, функция H (s) представляется в виде A (s — s*)", где п = РЧ-а^ или р — а2.
Если в качестве автомодельной переменной выбрать ? = t,
где = Аа2, уравнение (VI.4.8) приводится к виду:
dSan . | da _ /тгт /
Это уравнение относится к типу, рассмотренному в гл. IV.
Рассмотрим по отдельности три возможных варианта начальных условий: s0 = s*, я0<>* и s0^>s%. Пусть сначала s0 = s%. Как показано выше (см. гл. IV), если ге>1, решения уравнения (VI.4.9) обращаются в нуль при некотором конечном значении ? = с, т. е. существует «фронт пропитки», скорость которого конечна: При малых значениях s — s* и т] — с — ? решение уравнения (VI.4.9) асимптотически представляется в виде:
с-?= -П°Г-..
do. (VI.4.10)
о I
Чтобы определить постоянную си потребуем дополнительно, чтобы при s —> s% и с — ? -> 0 оставалось конечным отношение и i/m (к — s*), где ut — скорость фильтрации жидкости. Это отношение представляет собой среднюю скорость частиц подвижной (непрерывной) части впитывающейся жидкости на фронте в момент ее слияния с неподвижной жидкостью, находящейся впереди фронта.
Из формулы (VI.4.4) имеем
щ ___/_?1___ii_\
m{s — s*) /7 V s-s* 2 / '
Следовательно, чтобы отношение ujm (s — s*) было конечным, необходимо, чтобы ct — 0. Тогда (VI.4.10) приводит к асимптотиче- ' скому выражению
c(n=ir^-16*)n_1-
(VI.4.12)
Аналогично автомодельной задаче для фильтрации газа решение задачи в случае s0 =s* будем искать в виде ряда
1 1
S — S* = (у ^ п-1 (l+fllT14 а2if-U ...). (VI.4.13)
Коэффициенты ряда д(- при заданном значении с находятся путем подстановки в уравнение (VI.4.9). Меняя с, будем получать различные значения Sj = s (0).
Обратимся к случаю, когда s0< s*. При этом, очевидно, фронт пропитки может распространяться только с конечной скоростью. Поскольку за фроптом вытесняющая фаза везде подвижна, на фронте должно быть s = s* и от s* до s0 возникает скачок насыщенности, аналогичный скачку на передней кромке стабилизированной зоны, описанному в § 3. На скачке должно выполняться условие (VI.2.21). При этом ^‘’определяется по формулам (VI.4.10) и (VI.4.11) при s = = s0, 7/'s>— 0, а скорость скачка Vнайдется из условия хс= ra0|/V, откуда
п-1
С
С1 (s~s*)
cftQ _а0т 2
V t s*~s0
Таким образом, из (VI.2.21) имеем
или —(s* —S0). (VI.4.14)
ca0__«о _ с
2 У't V J s* so
При s0 = s* снова имеем условие cl — 0, эквивалентное условию конечной скорости движения впитывающейся жидкости.
Если s* — s0, а следовательно, и ct не равны нулю, разложение (VI.4.13) имеет вид:
среды может находиться лишь в одном из двух крайних состояний — полностью связном и подвижном или полностью несвязном и поэтому неподвижном. Это приводит к однозначной зависимости относительной проницаемости от насыщенности характерного вида, изображенного на рис. VI.5, с точкой s*, где /х (s*) = 0, а при s<^s% жидкость является неподвижной. Более детальное исследование показывает, что фактически лишь часть жидкости находится в каждом из состояний, причем между связной и несвязной частями происходит обмен жидкостью до достижения некоторого равновесного распределения. В этом случае скачок насыщенности на фронте капиллярной пропитки заменяется узкой зоной плавного перехода от s0 к s*.
Как и для фильтрации газа, конечная скорость распространения фронта позволяет использовать полученнное решение не только для бесконечных, но и для конечных областей, до подхода фронта к удаленному концу.
Пусть теперь s0^>s%. Уравнение (VI.4.12) можно переписать в виде:
n(s — '+|“|г = 0 y=(s — s*)n- (VI.4.16)
Если s0>s*, уравнение (VI.4.16) не имеет особенностей, так как коэффициент при старшей производной не обращается в нуль. Кроме того, из общих свойств уравнений параболического типа следует, что s меняется монотонно от Sj до s0 при изменении ? от 0 до сю. Поэтому v — v0, а следовательно, и s — s0 не может обратиться в нуль ни в какой конечной точке и s -> s0 лишь асимптотически при Решение для этого случая можно получить численно,
задаваясь при данном значении Sj = s (0) некоторым значением ds/сЩ 1—0). Тогда, решая задачу Коши, получим решение, соответствующее определенному значению s0=s(oo). Меняя ds/dt, можно найти решение, соответствующее заданному значению s0.
Зависимость sl (с) при s0 s* можно найти в явном виде, используя тот легко проверяемый факт, что если некоторая функция s —
- s* = ф0 (?) удовлетворяет уравнению (VI.4.9), то функция
s — s* = (p(?)=-c"~1(p()(!-) (VI.4.17)
также будет решением этого уравнения. Пусть ф0 (t) есть решение уравнения (VI.4.9) такое, что ср0 (1) = 0, представляемое формулой (VI.4.13) или (VI.4.15) для с = \.
Условие (VI.4.14) будет соблюдаться и для всех функций ф (?), выражаемых формулой (VI.4.17). Таким образом, зная решение поставленной задачи при некотором значении или с, можно получить все решения для заданного s0. Из'формулы (VI.4.17) получим связь между Si и с в виде:
я п~1
На рис. VI.15 изображены вычисленные при помощи ряда (VI.4.13)
3 5
кривые ф0( I) Для п—-^ и п = у.
Полученное решение можно использовать для определения параметров пористой среды по результатам экспериментального измере
ния скорости капиллярной пропитки. Если скорость «фронта пропитки» конечна, то это можно сделать, измеряя координаты фронта хс в различные моменты времени.
Вследствие автомодельности задачи хс выражается по формуле
хс ~ ca0Vt.
Пользуясь соотношением (VI.4.18), хс можно выразить в виде:
хг — Nst
(VI.4.19)
%
0,5
| “ *4. | п-5/Z 31 |
0,5 Рис. VI.15
J_ д-l
где N = А 2 [ф0 (0)] а .
Измеряя экспериментально отношение хс/\/Т и значение s4, можно найти показатель степени п и коэффициент N, характеризующий структуру порового пространства. Эксперименты такого рода описаны в работе [77].
2. Другой процесс, в котором фильтрация происходит под действием только капиллярных сил, — противоточная капил-
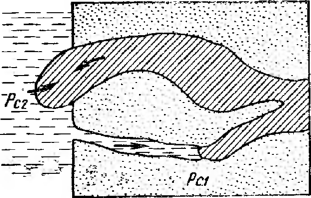
Рис. VI.17
\
Рис. VI.16
лярная пропитка, — возникает в том случае, когда участок пористой среды, занятый менее смачивающей фазой, оказывается полностью окруженным другой, более смачивающей жидкостью (рис. VI.16). В таких условиях более смачивающая жидкость по мелким порам впитывается в образец, вытесняя менее смачивающую фазу по соседним крупным порам. Проще всего механизм зтого явления иллюстрируется на примере двух соседних поровых капалов, соединенных на концах (рис. VI.17). Противоточная пропитка возникает, например,
в нефтяных пластах, разбитых трещинами на отдельные блоки (трещиноватые пласты), когда продвигающаяся вода быстрее движется по трещинам и блоки оказываются окруженными водой. После этого вода впитывается в блоки, а нефть выходит из них через ту же поверхность.
Исследуем противоточную капиллярную пропитку для линейного случая. Рассмотрим, как и в предыдущем пункте, цилиндрический образец пористой среды, боковые поверхности которого непроницаемы. Первоначально образец заполнен несмачивающей фазой. Если один из торцов цилиндра также непроницаем, а другой приводится в соприкосновение со смачивающей жидкостью, то начнется противоточная капиллярная пропитка. Это означает, что смачивающая фаза будет впитываться, а несмачивающая выходить через единственную открытую торцовую поверхность. Описанный линейный образец можно рассматривать как элемент блока более сложной формы, например прямоугольного.
Как показывают эксперименты по противоточной капиллярной пропитке прозрачных образцов, фильтрация во встречном направлении происходит равномерно по всему сечению, т. е. «каналы», по которым движется каждая из фаз, как и при обычном двухфазном течении, сравнимы по размерам с диаметром пор. Поэтому противоточную фильтрацию можно рассматривать в рамках представлений, принятых для прямоточной двухфазной фильтрации, и записывать закон фильтрации в виде:
00^; P-i — Pi = P*c (s) (« = 1,2). (VI.4.20)
Следует только учитывать, что до сих пор относительные проницаемости мы рассматривали лишь для случая, когда обе фазы движутся в одну сторону. Противоточное движение фаз повлияет, конечно, на распределение фаз в порах, и вид кривых относительной проницаемости и капиллярного давления изменится. В настоящее время нет прямых опытных данных о кривых относительной проницаемости при противоточном движении. Для качественного исследования будем принимать их такими же, как и раньте, т. е. примем
ft (s) = ft (S), Pc (s) = Pc (.v).
Уравнения неразрывности для каждой из фаз сохраняют обычный вид:
![]()
(VI.4.21)
Для противоточного движения из уравнений (VI.4.21) следует
(VI.4.22)
и x —| - JjL .) — 0.
![]()
Исключая dpi/dx из системы (VI.4.20)—(VI.4.22), получаем
¦-5Т----=0 >
dt дх-
где
к_
fi0 Т m
Ф (.9) = - f /, (s)/¦ (s) Г (s)ds, а* =
. Но
Уравнение (VI.4.24) является частным случаем уравнения Ра попорта — Лиса при w — 0. Это уравнение совпадает по виду с урав нением (VI.4.6), только функция Н (s) заменяется на Ф (s). Граничные условия также одинаковы для капиллярной пропитки газонасыщенного образца и для противоточной капиллярной пропитки, т. е" условие равенства нулю капиллярного давления на входе (sj — s*, J (s*) = 0) и равенства нулю расхода на закрытом конце. И точно так же задача о пропитке становится автомодельной, если закрытый конец бесконечно удален и начальная насыщенность постоянна вдоль образца. При этих условиях можно вместо х и t ввести автомодельную переменную ? =
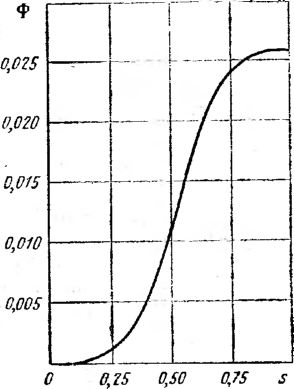
Рис. VI.18
= х/а ]/1.
Уравнение для насыщенности в случае пропитки имеет в автомодельных переменных следующий вид:
F-Ф ? ds dt? + 2 <?? :
(VI.4.25)
= 0,
т. е. совпадает с уравнением (VI.4.8). Полагая, что качественно кривые относительной проницаемости для противотока таковы же, как и при одинаково направленной фильтрации, воспользуемся теми же представлениями для /, (я) и J (s), что и в предыдущем пункте (т. е. fl(s) = b(s— s*)13, J (s) — В (s — %)_Г4-С), и получим, что при малых s — s* функция Ф представляется в виде:
Ф (s) л* N (s — s*)n n> 1
(/2 (s) остается не равным нулю).
Типичный вид функции Ф (s) показан на рис. VI.18.
Таким образом, При малых s — s* уравнение (VI.4.25) совпадает по виду с уравнением (VI.4.9). Поэтому качественные выводы о характере решений уравнения (VI.4.9) при различных значениях начальной насыщенности s0, в том чнсле и вывод о конечной скорости «фронта пропитки» при s0 s* и условия на скачке при <' s* сохраняются и для решения уравнения (VI.4.25). В частности, поскольку скорость фильтрации первой фазы выражается формулой (VI.4.23), сохраняются и асимптотические выражения (VI.4.13) и (VI.4.18) для малых значений s — s*.
Решение уравнения (VI.4.25) можно, как и ранее, найти, задаваясь значением | = с таким, чтобы s (с) = s*. Вблизи точки (с, 0) это решение может быть представлено в виде ряда (VI.4.16) или
(VI.4.18), а при больших значениях s — найдено каким-либо численным методом. Решение для заданного S! = s (0) = s* опре-
Рис. VI.19 Рис. VI.20
деляется подбором путем изменения с, поскольку требуемая точность невелика.
Если s0 больше неподвижной насыщенности то, как и для задачи предыдущего параграфа, s — s0 только при | ->¦ оо. Семейство решений находится путем численного решения задачи Коши при заданном Si = s (0) с различными значениями ds/d%|g_0. Каждому из этих решений соответствует некоторое значение s0. Искомое решение для заданного s4 = s (0) снова определяется подбором.
В качестве примера на рис. VI.19 и VI.20 приводятся кривые s (|), найденные при следующем выборе относительных проницаемостей и функции Леверетта:
Л = *4; /,=(1-: *)(!-*)’; /(®) = *-I/*-i;
|ij/|i2 = р0 было принято равным 1. На рис. VI.19 показаны кривые, соответствующие случаю s0 = 0 и различным с. Видно, что при с > 0,38 кривые s (|) пересекают линию s = 1 при ? > 0. Следовательно, физический смысл имеют только те кривые, для которых с <[
< 0,38.
На рис. VI.20 изображены кривые s (?), соответствующие разным значениям s0 при Sj = 0,75. Заметим, что количество жидкости Q, впитавшейся в пласт через единицу площади сечения к моменту времени t, равно
Q = ma]/rtK(slt s0), (VI.4.26)
где
СО
0
На рис. VI.21 построены кривые зависимости К (s0) для st = 0,7 при различных отношениях вязкостей (р0 = 0,5; 0,1 и 0,01).
Для того чтобы использовать данные о противоточной капиллярной пропитке в задачах вытеснения не-смешиванщихся жидкостей из неоднородных и трещиновато-пористых сред (см. гл. VII, § 3), необходимо иметь кривую зависимости средней насыщенности образца конечной длины от времени. Если начальная насыщенность образца s0 несвязная или равна нулю, скорость «фронта пропитки» конечна. Поэтому решение для образца конечной длины до подхода фронта к закрытому концу совпадает с автомодельным. При этом из формулы (VI.4.26) следует, что средняя насыщенность образца выражается формулой
зс
Рис. VI.21
s = s04-^VtK(sbs0). (VI.4.27)
Чтобы получить зависимость s от времени, следует решать дифференциальное уравнение в частных производных (VI.4.24). Для качественного исследования ограничимся тем, что найдем приближенное решение. Проинтегрируем уравнение (VI.4.24) по х от 0 до I, предполагая, что фронт пропитки уже подошел к закрытому концу и s(l)^> s*. Тогда, используя граничные условия, имеем
t для последующих моментов
i
В
Учитывая условие ds/dx = 0 при х — I, будем искать распределение s в виде:
Поэтому
* = Sl-f(Sl-^)(2-f)-f. (VI.4.31)
Подставляя в уравнение (VI.4.28) выражения м J sc^x’
О
полученные из формулы (VI.4.31), найдем
ds
IF
Рис. VI.22
д. (VI.4.32)
Уравнение (VI.4.32) нужно решить при начальном условии, выражающем непрерывность средней насыщенности в момент подхода фронта к концу образца: при t — t0 s = = s„, где s„ получается из формулы (VI.4.27), т. е.
So = «о + К/с’ к = iz/cza2.
Искомое решение имеет вид:
s = Sl - (Sl - 6-0 - 4-) ехР [ ¦- ЗФ' (si) (¦1? - ^)] • ( VI.4.33)
Таким образом, при t <С t0 средняя насыщенность выражается
формулой (VI.4.27), а при t >- t„ — формулой (VI.4.33). Общий вид
— a2f u
зависимости s (т), где т = показан на рис. VI.22 для условий
рассмотренного выше примера.
3. В обозначениях, использованных в п. 2, уравнение Рапопорта — Лиса (VI.3.4) примет вид:
ds ГгЛ ds „2 52Ф — П
(VI.4.34)
I--* (s) “Н--& ТТ ~ "
1 т v ' дх Я.г2
dt
при этом для скоростей фильтрации каждой из фаз имеем в соответствии с (VI.3.17)
щ = uF (s) — а2тФ' (s)
ds
dx '
(VI .4.35)
(Суммарная скорость и (t) есть функция времени и должна быть задана или определена из граничных условий для давления. Если
имеет автомодельное решение вида s = s (|), | = x/a\f t. Для существования автомодельного решения требуется также, чтобы s (х, 0) = = s0 — const и иг (0, t) = 0. Тогда получим вместо (VI.4.34) уравнение
Ж + [т+и"<»]#“° (*=*)- <VIA3e>
При 1 = 0 должно выполняться условие (равносильное условию иг — 0)
— —-?v|'" - (VI.4.37)
dl /i (s)/'(«)'
Это следует из формул (VI.4.24) и (VI.4.35). Кроме того, при | -> оо s—>¦ s0. Вблизи фронта, т. е. при s, близком к s0, уравнение (VI.4.36) асимптотически переходит в уравнение (VI.4.25), так как | 2KF' (s),
либо потому, что | очень велико (при s0 > s*), либо потому, что F' (s) -»- 0 (при s0 sg s*). В связи с этим условия на фронте вытеснения при различных значениях s0 сохраняются теми же, что и в случае капиллярной пропитки. При s0 ^ s* скорость фронта конечна, и для численного счета при малых г) = с — | можно использовать разложения (VI.4.13) или (VI.4.18). Выполнения условия (VI.4.37) можно добиться, меняя значение | = с, при котором s обращается
В S,|..
В качестве примера на рис. VI.23 приводятся решения уравнения (VI.4.36), удовлетворяющие условию (VI.4.37) при Я = 0,25 и X = = 1,0. Функции f i (s) и / (s) были использованы те же, что и в примере в п. 2. Характерно, что при изменении начальной насыщенности s0 в весьма широких пределах конечная насыщенность sf меняется незначительно. Так, при Я = 0,25 изменению s0 от 0 до 0,90 соответствует изменение st от 0,89 до 0,93. В случае Я = 1 изменение еще меньше: 0,992 << Sj < 0,998 при 0 < s0 < 0,98.
Полученное решение задачи о вытеснении несмешивающихся жидкостей с учетом капиллярных сил интересно сравнить с решением той же задачи в постановке Баклея — Леверетта. В обозначениях настоящего параграфа решение Баклея — Леверетта (VI.2.21) имеет вид:
1-2 hF'(s) (VI. 4.38)
(поскольку в начальный момент при 1 —> оо [t = 0) s=s0 = const).
При | = %с в решении Баклея — Леверетта вводится скачок насы
щенности, положение которого можно найти по формуле
1С - 2%F’ (Sq) =- 2X—(Sc)~F {so\, (VI.4.39)
sc s0
По формулам (VI.4.39) можно найти sc и зная se.
На рис. VI.23, а, б вместе с решениями уравнения (VI.4.36) (кривая /) приводятся также кривые 2 для s (1), рассчитанные по формуле (VI.4.38) с условием (VI.4.39) для тех же значений X (т. е. Л = 1
а
s
Рис. VI.23
и Я = 0,25). Из приведенных кривых видно, что при X = 1 решение Баклея — Леверетта очень близко к точному. В частности, для решения Баклея — Леверетта | (sc) = 2,45, а для точного решения с =
— 2,49. В случае X = 0,25 расхождение более существенное.
НЕУСТАНОВИВШАЯСЯ ФИЛЬТРАЦИЯ В ТРЕЩИНОВАТО-ПОРИСТЫХ СРЕДАХ, СРЕДАХ С ДВОЙНОЙ ПОРИСТОСТЬЮ И СЛОИСТЫХ ПОРОДАХ
§ 1. ФИЛЬТРАЦИЯ ОДНОРОДНОЙ ЖИДКОСТИ В ТРЕЩИНОВАТО-ПОРИСТОЙ СРЕДЕ
Наряду с зернистыми пористыми средами, в которых жидкость содержится и движется в мсжзернопом пространстве, встречаются также трещиноватые горные породы, в которых существует развитая система трещин, полностью или частично обусловливающая фильтрационные свойства среды. Важность изучения таких сред опре деляется тем, что ряд крупнейших месторождений нефти приурочен к породам, в которых имеются многочисленные трещины.
Специфика трещиноватой среды обусловлена тем, что трещина — это (схематически) узкая щель, два измерения которой в тысячи раз больше третьего, в отличие от пор, все размеры которых одного порядка. В результате этого даже при самом незначительном объеме трещин в общем объеме пустот в твердом скелете они могут оказывать определяющее влияние на характер движения жидкости. В этом проявляется общее для всей теории фильтрации свойство ее объектов: гидродинамические характеристики могут существенно зависеть от таких элементов структуры, статистический вес которых пренебрежимо мал.
Обычно различают чисто трещиноватые и трещиновато-пористые среды. Первые из них представляют собой блоки горной породы, между которыми имеются трещины, причем сами блоки непрони цаемы и не обмениваются жидкостью с трещинами (например, трещиноватый грапит); в трещиновато-пористой среде блоки представляют собой куски обычной пористой среды, обладающей конечной пори стостыо и проницаемостью (трещиноватый известняк). Во всех случаях объем трещин пренебрежимо мал по сравнению с общим объемом, занятым твердым скелетом и пустотами; в большинстве случаев
он мал и по сравнению с общим объемом пустот, складывающимся из объема порового пространства пористых блоков и объема самих трещин. Лишь в тех случаях, когда собственная пористость блоков практически равна нулю (например, у трещиноватых изверженных пород), приходится принимать в расчет объем собственно трещин.
Напротив, в большинстве случаев гидравлическая проводимость системы трещин во много раз больше гидравлической проводимости блоков. Поэтому можно сказать, что в трещиновато-пористой среде жидкость «хранится» в пористых блоках, а перемещается по трещинам. При.стационарном движении жидкости это не приводит к существенным отличиям от обычной пористой среды. Однако при нестационарных процессах и в ходе вытеснения одной жидкости другой
проявляется ряд особенностей, еще пе изученных до конца. Фильтрация в чисто трещиноватых средах происходит качественно так же, как в обычных пористых средах, лишь с небольшими количественными отклонениями. Поэтому в дальнейшем основное внимание уделяется трещиновато-пористым средам.
1. Для ламинарного движения вязкой жидкости в щели с параллельными стенками справедлива формула Буссинеска
Здесь Q — расход жидкости; b — ширина щели в сечении, перпендикулярном оси х; h — раскрытие щели; [i — вязкость жидкости; р — давление.
Существование такой простой формулы движения в отдельной трещине побудило многих исследователей к поискам выражений, описывающих движение в упорядоченной системе трещин. Однако этот подход оказался менее плодотворным, чем описание течения в трещиновато-пористой породе методами механики сплошной среды.
Допустим, что трещиновато-пористая среда состоит из системы блоков, отделенных друг от друга трещинами, причем форма и расположение блоков нерегулярны (рис. VII.1). Возьмем в качестве элементарного макрообъема (ср. гл. I) объем, размеры которого велики по сравнению с размерами отдельного блока, а следовательно, и интересующие нас процессы происходят в масштабе значительно более крупном, чем размер блока *. Рассмотрим вначале наиболее существенный случай, когда проницаемость блоков мала настолько, что при описании макроскопического движения жидкости ею можно пренебречь. Считая движение в трещинах медленным (безынерцион-
1 Размеры блоков (и, следовательно, длина трещин I) бывают самыми различными. Излагаемый подход основан на предположении, что d < Z L, т. е. блоки всликп по сравнению с размером пор ri, но малы по сравнению с размером пласта L.
ным), можно записать для него закон Дарси, который выводится из анализа размерности так же, как и в гл. I. При зтом, учитывая возможную анизотропию системы трещин и то, что каждая трещина характеризуется двумя размерами — длиной I и раскрытием h, закон фильтрации удобно представить в виде:
<VIU'2)
Здесь щ — компоненты вектора скорости фильтрации, определяемого обычным образом; симметричный тензор кц называется тензором трещинной проницаемости; h — среднее раскрытие трещин; I — характерный размер блока. Конкретный вид безразмерного тензора проницаемости /$,- определяется геометрией системы трещин; для среды, состоящей из непроницаемых блоков и нескольких систем плоских регулярно расположенных трещин, он сможет быть получен на основании формулы Буссинеска (VI 1.1.1).
В общем случае трещиновато-пористой среды закон фильтрации также имеет тензорный вид (VII.1.2). Однако расчет компонент тензора проницаемости в этом случае невозможен, и их определяют, исходя из данных наблюдений. Соответствующим выбором системы координат тензор ktj можно привести к главным осям. Если вектор градиента давления направлен вдоль одной из главных осей, то вектор скорости фильтрации направлен так же.
2. Как уже упоминалось, характерная особенность трещиновато-пористой среды состоит в том, что движение жидкости в такой среде происходит в основном по трещинам, в то время как объем трещин мал, и основные запасы жидкости заключаются в пористых блоках. Предположим, что мы пренебрегли движением жидкости в блоках, и на границе трещиновато-пористого пласта, жидкость в котором первоначально находилась под давлением Р0, происходит снижение давления до некоторого иного значения Pt. Пренебрегая проницаемостью блоков, можно использовать для описания движения в трещинах обычные соотношения теории фильтрации в пористой среде (например, в случае слабосжимаемой жидкости и упруго-деформируе-мого пласта — соотношениями теории упругого режима). После некоторого переходного процесса в трещинах установится новое стационарное распределение давления, причем по крайней мере вблизи границы пласта давление окажется значительно ниже первоначального. Поскольку давление в блоках в силу предположенной их непроницаемости не могло измениться, то между жидкостью в блоках и жидкостью в трещинах создается значительная разность давлений — порядка Р0 — Рь а следовательно, в блоках Возникают локальные градиенты давлений (Р0 — Р \)/1, значительно превосходящие существующий в пласте градиент давления в трещинах ~ (Р0—
— Pt)/L. В этих условиях в пласте даже при самой незначительной проницаемости блоков возникают локальные фильтрационные потоки, обусловливающие приток жидкости из блоков в трещины и выравнивание местных разностей давлений между блоками и трещинами.
Тот факт, что в трещиновато-пористой среде могут в нестационарном процессе возникать местные разности давлений и местные перетоки между блоками и трещинами, мы положим в основу описания трещиновато-пористой среды, состоящей из малопроницаемых пористых блоков и трещин, суммарный объем которых мал.
Введем вместо одного среднего давления жидкости в данной точке среды два давления — давление в трещинах pt и давление в порах блоков р2- В предположении, что проницаемость блоков к2 очень мала, мы можем для определения фильтрационного потока жидкости через некоторую площадку среды использовать уравнение (VI 1.1.2), подставляя в него значение давления в трещинах pt.
Составим теперь уравнения баланса жидкости в трещинах и блоках. Обозначая через т t трещинную пористость (отношение объема трещин к полному объему среды), имеем
![]()
(VII.1.3)
где q — количество жидкости, перетекающее за единицу времени из блоков в трещины в единице объема среды.
Для блоков можно пренебречь непосредственным фильтрационным потоком, так что уравнение неразрывности имеет вид:
![]()
(VII.1.4)
где т2 — пористость блоков (в расчете на общий объем среды).
Для того чтобы замкнуть полученную систему уравнений, нужно, помимо уравнения состояния жидкостей и уравнений, связывающих изменения пористости т, и т2 с давлением, дать и выражение для потока q. Это выражение может быть получено из анализа размерностей. Заметим прежде всего, что поскольку движение жидкости в пласте считается безынерционным, то безынерционным должно быть и движение Жидкости в блоках. Далее, поток q может зависеть от давления'в блоках р2 и в трещинах ри размера блоков I, проницаемости блоков к2, вязкости жидкости р, ее плотности р и должен обращаться в нуль при равенстве давлений р 4 и р2. Предположим вначале, что плотность р и вязкость |.i жидкости мало зависят от давления в промежутке р i<^ р<СР2 и их можно считать постоянными, равно как и проницаемость блоков к2¦ Тогда выражение для q должно быть инвариантным относительно выбора начала отсчета давления и может зависеть лишь от разности pt—р2. Таким образом, величина q зависит от размерных величин р2 — ри р, |Л, к2, I.
Заметим теперь, что вследствие безынерционности движения размерности проницаемости, давления и вязкости могут быть выбраны независимо, при одном лишь условии
помимо зтого можно считать, что размерность массы М не связана с размерностью давления или вязкости.
где а — безразмерная постоянная, характеризующая геометрию среды. Соотношение (VII.1.5) должно быть уточнено в случае, если плотность жидкости р и вязкость ее р зависят от давления. Предполагая, что закон фильтрации в блоках может быть представлен в виде:
_ ^2Ро df(p)
1 Ро 8хс ’
где р0 и р0 — характерные постоянные значения р и р, а / (р) — функция размерности давления, соотношение (VI 1.1.5) можно переписать так:
д =
a(;t2
/(Pa)~/(Pl) ¦
(VII.1.6)
Ро
Например, при фильтрации термодинамически идеального газа / = р2/2р0, и выражение (VII.1.6) дает
где р0 — давление, отвечающее плотности р0.
Трещинная пористость tni обычно мала и ею в большинстве случаев можно пренебречь, если среда является трещиновато-пористой (но не чисто трещиноватой), а пористость блоков т2 считать функцией обоих давлений р 4 и р2- Ограничиваясь линейным приближением, имеем соотношение
где величины p2i> Р22 и т2о ПРИ малых изменениях пористости можно считать постоянными.
Изменение пористости, как обычно, следует учитывать лишь в тех выражениях, где пористость дифференцируется; кроме того, поскольку она входит в произведение с величиной плотности жидкости р, изменения пористости существенны лишь в случае слабосжимае-мой (капельной) жидкости; при фильтрации газа изменениями пористости можно пренебречь. Ограничиваясь случаем капельной жидкости, имеем
где р — р 1, pz — в зависимости от того, рассматривается ли жидкость в трещинах или в блоках.
Подставляя выражения (VII.1.2), (VII.1.8) и (VII.1.9) в уравнения (VII.1.3) и (VII.1.4) и полагая тi =0, имеем систему уравнений
кро^'г Рг — Pi п.
/2 .. и’
I2 ц
![]()
0. (VII.1.10)
Ро 9 (, дрх \ (I dx'i V Ч- dxj j
Чаще всего рассматривается случай, когда среда однородна и изотропна и трещинная проницаемость выражается шаровым тензором *,-¦ = kfiij. При этом система (VII.1.10) принимает простой вид:
![]()
(VII.1.11)
__. о__Р21
где
ак-2
l'l2m0 (Р22 + Р*) ’ t*mo(P22 + P*) ’ Р22+Р*
Из системы (VII.1.11) можно исключить одно из давлений; определив из второго уравнения рг и подставив полученное значение в первое уравнение, имеем
(VII.1.12)
дР1 д\Г~ ~0t ^
![]()
![]()
кА-, (1- fi) ‘
В пределе при rj->0, что соответствует беспрепятственному обмену жидкостью между блоками и трещинами, уравнение (VII.1.12) переходит в обычное уравнение упругого режима с коэффициентом пьезопроводности */(1 — Р); нетрудно видеть, что этот коэффициент пьезопроводности отвечает проницаемости системы трещин, но пористости и сжимаемости блоков.
3. Уравнение (VII. 1.12) и система (VII.1.11) обладают рядом особенностей, которые на первый взгляд кажутся необычными и причина которых лежит в вырожденном характере системы (VII.1.11), относящейся к среде с пренебрежимо малыми трещинной пористостью и проницаемостью блоков. В связи с этим представляет интерес исследование свойств решений этой системы.
Заметим, что уравнению вида (VII. 1.12) удовлетворяет не только давление рг, но и давление р2 и, следовательно, любая линейная комбинация этих давлений. Чтобы убедиться в этом, достаточно второе уравнение (VII. 1.12) умножить на $[А и продифференцировать по t, а затем прибавить к исходному уравнению. После этого из системы (VII.1.11) легко исключается рг. Это показывает, что обоим давлениям и любой их комбинации присущи те свойства, которыми должно обладать любое решение уравнения (VII. 1.12) (см. ниже). Вместе с тем, как нетрудно убедиться, не все эти линейные комбинации равноправны. Среди них есть одна, а именно р = р2 — Ррц которая должна быть непрерывной по времени в замкнутой области определения решения, включая и границу t = 0. Действительно, пусть надо найти ограниченное решение системы уравнений (VII.1.11) в пространственной области D при 0 ^ t sc Т; заданы начальные распределения давлений рг и р2. Интегрируя первое уравнение (VII.1.11) по малому промежутку времени 0 =? t^r. е и устремляя е к нулю, находим lim р (х, t) = р (х, 0). Представим теперь второе f-o
уравнение системы (VII.1.11) в виде:
— Лр - (1 — Р) Арх -pxV2/?i = 0.
Если выбирать достаточно малые моменты времени, то первый член этого выражения будет стремиться к своему начальному значению р (х, 0). Следовательно, к такому же значению с обратным знаком будет стремиться и сумма двух других членов. Поэтому для того, чтобы давление рг (х, I) было непрерывным при t0, необходимо, чтобы начальное распределение рг (х, 0) удовлетворяло уравнению
+ (l-^Ap^Apix, 0) (VII.1.13)
при соответствующих граничных условиях. В противном случае давление в трещинах рг (х, t) при t — 0 скачкообразно изменяется в соответствии с уравнением (VII. 1.13). При этом, если Р =р 0 и поэтому р =р р2, происходит также и мгновенное перераспределение давления в порах р2 при неизменном давлении р.
Такое поведение решения имеет простой физический смысл. Изменение давлений ^ к р2 вызывает изменение массы жидкости, заполняющей пористые блоки. Всякое такое изменение приводит к перетоку некоторого количества жидкости из блоков в трещины или обратно. Если изменение массы жидкости конечно (не бесконечно мало), оно требует конечного времени, так как происходит под действием ограниченных сил давления, которые не могут вызвать бесконечно больших скоростей перетока. Это показывает, что мгновенное изменение массы заключенной в блоках жидкости невозможно, а следовательно, невозможно и мгновенное изменение приведенного давления р = рг — однозначно связанного с этой массой.
Если же давления рг и одновременно изменяются скачком таким
образом, что приведенное давление р не меняется, то перемещения жидкости не происходит, и такое согласованное мгновенное изменение давлений возможно. Если учесть также собственный объем трещин, то появится также и другая независимая комбинация давлений р', определяющая изменение эффективного объема трещин. При этом оба давления рг и ръ окажутся непрерывными при t — 0, и необходимо будет задавать их начальные значения отдельно.
Другая особенность системы (VII.1.11) заключается в том, что в ней исключен за малостью поток жидкости непосредственно по пористым блокам. Поэтому выравнивание разности поровых давлений рг между двумя соседними точками среды может происходить лишь посредством обмена жидкостью между блоками и трещинами и перемещения жидкости по трещинам. В результате этого в трещиноватопористой среде, описываемой уравнениями (VII.1.11), скачки порового давления не исчезают мгновенно (как это бывает, например, при упругом режиме), а затухают во времени по экспоненциальному закону. Чтобы убедиться в этом, установим условия на скачках, которые должны выполняться для решений системы (VI 1.1.11).
Рассмотрим изолированную поверхность разрыва 2- При выводе условий на скачках ее можно считать плоской и принять за плоскость х = 0.
Проинтегрируем второе уравнение (VI 1.1.11) по г в пределах
d2pi д2Рх
от
—е до е. В силу ограниченности р2,
ри и
~^-2-
при
е—vO имеем
-? -?
Таким образом, производная dpjdx, а вместе с ней и само давление в трещинах р1 непрерывны на поверхности 2-
Запишем теперь первое уравнение системы (VII.1.11) для точек впереди поверхности разрыва (х = +0) и для точек за этой поверхностью (х = —0), обозначая соответствующие значения значками +
и “, и вычтем полученные уравнения друг из друга. Имеем
llEtzPlL^. Р
d(Pt-PT) +
А [(р| _р+) _
(й-рТ)] = 0.
По доказанному [pj = р{ — р\ ~ 0, так что для скачка давления [р2] = pi —pi имеем
-^Г^-М[р2] = 0. (VII.1.14)
Таким образом, скачки порового давления р2 должны удовлетворять уравнению (VII. 1.14), или после интегрирования
[/>2] = [Р2]ое-л'. (VII.1.15)
Здесь через [р21о обозначен начальный скачок в момент t = 0.
Допустим теперь, что вблизи поверхности 2* (являющейся или не являющейся поверхностью разрыва давления р2) производная dpjdx непрерывна. Тогда первое уравнение (VILl.il) можно вне поверхности 2# (принимаемой за плоскость х — 0) продифференцировать по х, получив при этом
Применяя к этому уравнению те же рассуждения, что и выше, и используя непрерывность производной др Jdx на поверхности 2\ получим
4. Отмеченные в предыдущем пункте особенности решений уравнения (VII.-1.12) и системы (VII.1.11) порождают соответствующие особенности в постановке граничных и начальных условий, которым должны удовлетворять эти решения.
Прежде всего, как уже было сказано ранее, нельзя требовать, чтобы при стремлении t к нулю оба давления (в порах и трещинах) принимали заранее заданные значениярх (0, х, у, z); р.2 (0, х, у, г). Обязательным условием должна быть лишь непрерывность приведенного давления
Р = А-РРь (VII.1.18)
а давление в трещинах рх должно затем определяться из уравнения (VII.1.13). Таким образом, начальное условие будет иметь вид:
р (0, х, у, z) — р2 (0, х, у, z) (О, х, у, z)=f (х, у, z). (VII. 1.19)
В свою очередь при стремлении к границе области лишь давление в трещинах рг должно быть непрерывно вместе со своими производными. Как обычно, будем рассматривать условия трех типов: когда на границе заданы значения давления жидкости и потока жидкости или их комбинация, т. е. условия вида:
или'
Pi (t, S) +
hap^;/) =y. (S).
(VI1.1.20)
Здесь S обозначает точку граничной поверхности, а п — направление нормали к ней.
Описание трещиновато-пористой среды как «двойной» пористой среды или системы вложенных друг в друга пористых сред, способных обмениваться жидкостью, дано в работах Г. И. Баренблатта, Ю. П. Желтова и И. Н. Кочиной [17, 18]; там же рассмотрены некоторые примеры. Постановка краевых задач для уравнения (VI 1.1.12) уточнена в работе [14].
Иной подход к описанию трещиновато-пористых сред, связанный с рассмотрением регулярно расположенных трещин, принадлежит Е. С. Ромму с jсоавторами (см., например, [97]).
§ 2. ОСНОВНЫЕ ЗАДАЧИ НЕУСТАНОВИВШЕЙСЯ ФИЛЬТРАЦИИ ОДНОРОДНОЙ ЖИДКОСТИ В ТРЕЩИНОВАТЫХ И СЛОИСТЫХ ПЛАСТАХ
1* Задачи неустановившейся фильтрации в трещиновато-пористой среде сложнее соответствующих задач теории упругого режима, потому что описывающие их уравнения (VII. 1.12) имеют не второй, а третий порядок и не допускают автомодельных решений, так как содержат характерное время т]/х. Рассмотрим здесь две простейшие задачи, представляющие наибольший практический интерес, — задачи притока к дренажной галерее и пуска скважины.
Предположим, что первоначально давление во всем трещиноватопористом пласте, занимающем полупространство х ^ 0, постоянно и равно нулю, а в момент t = О граница пласта х = 0 сообщается с областью постоянного давления р = Рг. Задача определения давления в пористых блоках р2 сводится к решению уравнения (принято р = 0)
(VII.2.1)
при дополнительных УСЛ0ВИЯХ1
р.г (0, х) = 0 (0 SS ?< сю);
Рг (*, +0) = Pi (1 -е-*Л). (VII.2.2)
Вид краевого условия при х = 0 связан с законом затухания разрывов распределения порового давления, подробно рассмотренным в предыдущем параграфе.
Преобразуя уравнение (VII.2.1) по Лапласу и учитывая начальное условие, получаем
--ЗЕ*-=0, (VII.2.3)
dx* arj-J-x v 7
где
со
р., = pz (а, х) = J e~atp2 (t, х) dt. (VII.2.4)
о
Преобразование краевых условий (VII.2.2) дает
+0) = -^^р-) ; р2(о, оо) = 0. (VII.2.5)
Удовлетворяющее этим условиям решение уравнения (VII.2.3) имеет вид:
Рг (о, *) = с-(р^;-х)- ехр [ х У ^—\ ¦ (VII.2.6)
Используя формулу обращения, получаем
c+ico { ¦ о
c-ioo
При вычислении интеграла (VII.2.7) удобно свести его к интегралу по контуру, охватывающему отрицательную часть действительной оси. При этом, как легко убедиться, интегралы по участку (—°о, — х/т]) взаимно уничтожаются и остается лишь интеграл по контуру, охватывающему отрезок (—х/т], 0). Тогда
Р2 (t, х) = Р, ^1 - ± j e-atx/i) sin [у j
(VII.2.8)
(внеинтегральный член здесь получается в результате интегрирования по малому контуру, охватывающему точку о = 0).
Положим, а/( 1 — о) = v2T], Имеем
CO
у, ч п 2Р\ С sin vz [ v2rJ \ J
Р-2 (*> х) = Pi--—7-exp(-TT^)dv =
О
со
= Pi_2^J^eip(__^_)d,.5 = _?5.. (vn29)
О
Отсюда при т] = 0 получается распределение давления при пуске галереи в однородной пористой среде
СО
p(t,x)^Pl-^± J —^exp(--^|-)du = P1(l-erf|).
(VII.2.10)
Для того чтобы вместо (VII.2.9) можно было пользоваться обычным соотношением (VII.2.10), необходимо выполнение неравенства
г]/и*<1. (VII.2.11)
Действительно, при этом член т]ц2/хг сравнивается с Iя только при и2 |2, когда экспоненциальный мнойштель в (VII.2.9) уже пренебрежимо мал. Если, напротив, заменить неравенство (VII.2.11) на обратное, то показатель экспоненты мал при всех и, и уравнение (VII.2.9) дает
оо'
р2 (х, t) ъ Рг - Ц±- j ^ du = 0. (VII .2.12)
О
Таким образом, при временах, больших сравнительно с характерным временем г\/х, давление в блоках трещиновато-пористого пласта меняется так же, как в обычном пористом пласте. При временах же малых сравнительно с г]/х давление в блоках не меняется вовсе. Возникающее таким образом запаздывание характерно для трещиновато-пористой среды.
Вычислим теперь закон изменения потока жидкости через границу пласта х = 0. Поскольку поток пропорционален производной от давления в трещинах plt необходимо прежде всего вычислить это давление. Для этого удобно воспользоваться первым уравнением основной системы (VII. 1.11). Полагая 0=0, получаем
в - D л. Л Pi — Pn> х dt
(VII.2.13)
При любом t Ф 0 дифференцирование в (VII.2.9) можно производить под знаком интеграла. Имеем
п - п -L 4 др*
-Рх~
Pl р* 1 к 1Г
_2Р\ Г sin \х
J V(l+V2>]) Х.
Из (VII.2.14), в частности, следует(0, t) = Plt
з if ft
как это и должно было быть в соответствии со сказанным ранее. Чтобы вычислить поток жидкости через границу х — 0, нужно продифференцировать выражение (VII.2.14) по х при х — 0. Дифференцируя под знаком интеграла, имеем
др
дх
о
В условиях упругого режима q = q0 = —P-J\f• Таким образом,
Х_/^Мр(_Лг)/0(?-) = ф(А). (VH.2.16)
На рис. VII.2, а показаны распределения давления в порах для различных значений параметра r|/xt и на рис. VII.2, б — функ
196
ция ф (r\/xt). Как и следовало ожидать, при t -> оо 0) все ре
шения стремятся к соответствующим решениям для пористой среды.
2. Неустановившееся движение вблизи скважины, работающей с постоянным расходом. Рассмотрим теперь осесимметричную задачу, предполагая, что в пласт, находящийся при постоянном давлении р0 = 0, начинается закачка жидкости с постоянным расходом Q через скважину пренебрежимо малого радиуса.
В цилиндрических координатах рассматриваемая задача сводится к решению уравнения
ай (VH.2.17)
dt
при условиях
Pi (0> г) = 0; Pl (t, оо) = 0; ^
-P..
(VII.2.18)
Задача (VII.2.17—18) формулируется для давления в трещинах Pi, при желании ее можно сформулировать для давления в пористых блоках р2- Тогда краевое условие при г = 0 примет вид:
а остальные условия и основное уравнение останутся без изменения.
Переходя в соотношениях (VII.2.17—18) к лапласовым изображениям, имеем
~~7ГГ --—Pi = 0; (г -р) Pi (°°) — 0.
г dr dr K + rja \ дг /г=о о ' ' '
(VII.2.20)
Этим условиям удовлетворяет решение
<УП'2-21>
так что по формуле обращения
с+гсо _
а(<.0=т1Н ir4Vir-v^r)da- (v,,'2'22)
С-2 ОО
Этот интеграл может быть сведен к интегралу по вещественной переменной таким же образом, как это было сделано в предыдущем пункте. Мы, однако, проанализируем лишь асимптотическое поведение полученного решения при малых значениях параметра р = = г/2|/"xf. Представим выражение (VII.2.20) в виде:
с+гоо
йМНЙ Т*»(^Т+Й7«И (VII.2.23)
и будем считать р 1.
При т]/х? 1 рассматриваемое выражение переходит в известное
выражение теории упругого режима (ср. §2гл. III). Если же r\/x.t ^>1, то выражение, стоящее под знаком функции Макдональда, равномерно мало, так что для нее можно воспользоваться приближенным представлением
К0 (х) = — (С 4- In х/2) 4-о(1).
В результате получаем
(r/V^€ 1» **/*]< О-
![]()
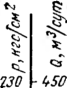
220 - Ш 2/0 ¦ 350 2D0 - 300 190 - 250 180 - 200 170 - ISO 1Б0 - 100 150 » 50
---1
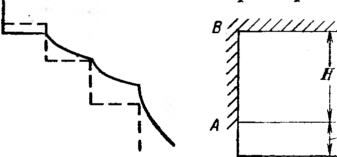
И А,
tk k 1
1_J_I___1_Il
юо гоо зео ш t, мин ?пс. VI 1.3
х=0
![]()
П
'7У:г /7-Г'-7777^у: 'Уу//у/.
тL о
a-=L
Рпс. VII.4
Смысл соотношения (VI 1.2.24) прост: оно означает, что если собственное время трещиновато-пористой среды т)/х не слишком мало, существует промежуточный квазистацио-нарный режим, когда жидкость,
В ///////////////////////////С
Смысл
поступающая из скважины, поглощается ближайшими к ней блоками. Лишь тогда, когда давление в блоках в окрестности скважины сравняется с давлением в трещинах (т. е. по истечении времени -—-rj/j<), начинает сказываться обмен жидкостью с более отдаленными участками пласта г.
3. Близкие по характеру задачи возникают при исследовании фильтрации в слоистых пластах. Например, если движение происходит в двух лежащих друг над другом пластах, отделенных слабопроницаемой перемычкой, то давление в каждом из пластов следует
1 Отметим еще одно обстоятельство. Соотношение (VII.2.24) показывает, что существует некоторый промежуток времени г2/у, <g t т]/к, на протяжении которого давление в скважине не меняется. Если временем r2jy, можно пренебречь (обычыо это сотые доли секунды и менее), то из (VII.2.24) следует, что при скачкообразном изменении дебита скважины давление в ней изменяется скачком, а затем сохраняет постоянное значение на протяжении времени /и. Такое поведение давления действительно наблюдается на практике. На рис. VI1.3, заимствованном из работы [80], показано ступенчатое изменение давления (несколько, правда, искаженное влиянием побочных факторов).
уравнению упругого режима с интенсивностью перетока между пластами в правой части; эту интенсивность в большинстве случаев можно считать пропорциональной разности давлений в соответственных точках пластов. Сходство возникающей задачи с задачей фильтрации в «двойной» пористой среде очевидно.
Из всего разнообразия задач этого цикла мы рассмотрим здесь лишь одну — задачу об истощении пласта, граничащего с пластом большой мощности, но малой проницаемости. Эта задача представляет большой интерес в связи с оценкой запасов нефти и газа некоторых месторождений.
Предположим, что область фильтрации имеет вид, приведенный на рис. VII.4. Допустим, что пласты / и II сложены породами одинаковой пористости, но существенно различной проницаемости, так что kh кгН, хотя Н h.
Будем рассматривать истощение системы, предполагая, что вначале она находилась под давлением Р0, а с момента t = 0 начинается отбор жидкости через нижний пласт в сечении х = О, причем давление на всей линии х = 0 одинаково, а отбор жидкости Q сохраняется постоянным. Система считается замкнутой, т. е. границы АВ, ВС и CD — непроницаемы. При этом задача сводится к решению совокупности уравнений
i?. = v ( ^E.jl^EJ\ ( — h^y^O);
= V ( (— fcsSysSf
at Л v а** “Г йг/2 ) (0 ^ а: ^ L);
&•-*.(-3-+Ц-) <0«1Г«Я). (VI 1-2.25)
При условиях
= (VII.2.26)
О
е p(0,y,t) = 0; k^\xJy = Q-, fo>°)- (VII.2.27)
ду
-ft
При сделанных предположениях (тонком нижнем и слабопроницаемом верхнем пластах) постановку задачи можно упростить.
Заметим прежде всего, что в силу равенства граничных значений давления в обоих пластах при у = 0 производные по х от давления в этих пластах — одного порядка, а следовательно, скорость фильтрации в направлении оси х в верхнем пласте пренебрежимо мала (по условию кхН « kh). Вместе с тем скорости фильтрации в направлении оси у совпадают при у =.0, что может быть только в случае, если изменение давления в направлении оси у в верхнем пласте происходит быстрее, чем в нижнем.
Отсюда следует
д'2р ду2 д1р дх1.
Таким образом, второе уравнение (VII.2.25) можно записать в виде:
Первое уравнение, относящееся к нижнему пласту, можно осред-
о
нить по мощности. Полагая Р = ~ J pdy, имеем
-ft
дР __ SW . у. / др \ _ д*Р , v.kv ( др \
dt ~Х дх2 ' h \ ду )у=-о — Х 8x2 i hk ^ ду )у=+о
^ здесь использовано граничное условие к у о= о)-
Наконец, заменим условие р\у=к> ~ р \у=-ъ условиемр |у_+0 — = Р. Совершаемая при этом ошибка мала при малой толщине h нижнего пласта.
Таким образом, возникает следующая упрощенная задача:
lfT = xilw lp^-p(x,y,t); у>0];
др 02 Р y_k
01 — = р(*.*)]; (VII.2.28)
Р (ж, у, 0) = Р (ж, 0) = Р0; р (ж, 0, t) - Р (х, t); (VII.2.29)
= X
др I _л. kh 8Р_ ду \у=Н~ ’ И дх
Решение этой задачи легко получить операционным методом. Не приводя его полностью, выпишем формулу для'изображения р0 от давления на галерее р0 = Р (0, ?).
Имеем
| И | {"Уй |
“ __?о дУк '
а с
(VII. 2.31)
Отсюда легко получить несколько простых выражений, отвечающих различным временам с момента пуска галереи.
Пусть прежде всего время t настолько мало, что возмущение, возникшее на галерее, не достигло непроницаемых границ системы:
t^rj/K^HyKx. (VII.2.32)
При этом в уравнении (VII.2.32) можно ограничиться асимптотикой о > х/Г2 > у.1Н~й. Для таких значений о гиперболические тангенс и котангенс в (VII.2.31) можно заменить их предельными значениями при о -*¦ сю, равными единице, откуда
Учитывая еще, что в данном случае —~^L=- <<' \^ имеем
kh у ах.!
<vn'2'33)
следовательно,
д,(0~я.- 2/4 <Н |t|J/i«9 + ... (VII.2.34)
Таким образом, на первой стадии движения влияние верхнего слабопроницаемого пласта сказывается лишь в добавлении малых членов, порядка Vt, по сравнению с главными.
Рассмотрим теперь промежуточный диапазон времен, которому отвечает разложение формулы (VII.2.31) при xL~2 о и1Я“2. В этом
случае вновь можно положить thH]/— 1, a cth^Z/j/^—К - .j ,
используя второе неравенство для ст, можно представить разложением при малых значениях аргумента. Имеем
Р= 1Г--7-f—r=\ + •'' (VII.2.35)
Отсюда, используя таблицу изображений Лапласа, получаем
(VII. 2.36)
| _ р | Г №К1УЛ |
ехр( | kW f |
| ~l° L |
L уЩ | ||
| { *kl V~t\ | 2 Vtx1 |
kh | 1 |
| \ kh Уv.\) | VH | mi J |
Последнее выражение можно упростить, если величина
мала или велика сравнительно с единицей. В первом случае, разлагая первый член в скобках по степеням аргумента, получим
РоМ^Ро-1*?- + ¦•; (VII.2.37)
что совпадает с решением для случая непроницаемого верхнего пласта. Если же k^Vt/kh 1, то для упрощения первого члена можно использовать асимптотику erfc а: при больших значениях аргумента
erfc х е-*2.
Имеем
Л(‘>--f(l 2V^ + “<«) + р- <VII-2-38>
Таким образом, изменение давления в эхом случае определяется уже в основном притоком из верхнего пласта. Наконец, при еще больших временах, t Я2/к1, начинается вторая фаза фильтрации в верхнем пласте (истощение верхнего пласта). Разлагая гиперболические тангенс и котангенс при малых значениях аргумента, получаем
Ро=^----7—-Г7ГТ-= —--Т*Л—к—Т> (VII .2.39)
С c*L ( 1 +^тг) С 02L (h j II—-1 )
\ KjA/i / \ K^m I
откуда
(VII.2.40)
Таким образом, для двухслойного пласта рассматриваемого вида отчетливо выделяются два периода движения при работе на истощение. На протяжении первого периода происходит истощение первого пласта, а движение в малопроницаемом верхнем пласте незначительно, на второй стадии пижний пласт практически полностью истощен, и происходит истощение верхнего пласта.
Если по данным о падении давления по мере отбора на первой стадии подсчитать запасы жидкости или газа в пласте, то подсчет даст лишь запасы, заключенные в нижнем пласте (F0 = mhbL), что значительно меньше истинных запасов V = (tnh + m1H) ЪЬ. Это обстоятельство оказывается существенным для ряда месторождений; в частности, так обстоит дело на крупнейшем Шебелинском месторождении газа. Как показал М. А. Бернштейн [28а], первоначальные запасы Шебелинского месторождения оказались заниженными, так как не были учтены запасы газа в слабопроницаемых ангидритах. Проницаемость этих пород настолько мала, что пробуренные в них скважины не имеют промышленного значения, однако переток из ангидритов в расположенный ниже хорошо проницаемый пласт оказался весьма существенным.
§ 3. ДВУХФАЗНАЯ НЕСТАЦИОНАРНАЯ ФИЛЬТРАЦИЯ И ВЫТЕСНЕНИЕ НЕСМЕШИВАЮЩИХСЯ ЖИДКОСТЕЙ В СРЕДАХ С ДВОЙНОЙ ПОРИСТОСТЬЮ
При совместном движении в неоднородной пористой среде двух несмешивающихся жидкостей возникают дополнительные факторы, обусловливающие обмен жидкостью между участками разной проницаемости. Прежде всего за счет различия насыщенности в разных областях пористой среды меняются фильтрационные сопротивления, что вызывает перераспределение давления и перетоки жидкости между высоко- и малопроницаемыми участками. Другая причина, вызывающая обмен жидкостью между высокопроницаемой средой и малопроницаемыми включениями при вытеснении несмешива-
Ю1ЦИХСЯ жидкостей, заключается в действии капиллярных сил. Вначале вытесняющая жидкость (вода) быстро прорывается по высокопроницаемой среде, а малопроницаемые включения оказываются окруженными водой. Поэтому содержащаяся в них нефть может быть извлечена только путем иротивоточной капиллярной пропитки если вытесняющая фаза является и более смачивающей.
Для описания вытеснения несмешивающихся жидкостей из сред с двойной пористостью может быть применен общий подход, изложенный в предыдущих параграфах. Будем рассматривать вытеснение несмешивающихся жидкостей в среде, которая состоит из области с проницаемостью кг, имеющей малопроницаемые включения с проницаемостью к2 кг. Общая схема такой среды изображена на рис. VII.5, а. Поскольку kz кх, фильтрацией в малопроницаемых Рис. VII.5
участках за счет общего
градиента давления в пласте будем пренебрегать. Частными случаями рассматриваемой схемы являются пласт, состоящий из двух слоев разной проницаемости, и трещиновато-пористый пласт (рис. VI 1.5, б).
Процессы перераспределения давления за счет сжимаемости жидкости и пористой среды, особенно в трещиновато-пористой среде, происходят значительно быстрее, чем перераспределение жидкости, вызываемое капиллярными силами, так как пьезопроводность пористых сред, как уже отмечалось в гл. II, имеет порядок 104 см2/сек,
а параметр а2 = ~ |/"определяющий скорость капиллярных процессов, почти никогда не превышает 1 см2/сек. Поэтому в большинстве случаев можно ограничиться исследованием вытеснения несжимаемых жидкостей в несжимаемой пористой среде. Один случай вытеснения сжимаемых жидкостей в среде с двойной пористостью будет рассмотрен в конце настоящего параграфа.
Как и для описания нестационарной фильтрации однородной жидкости в среде с двойной пористостью, введем в каждой точке сплошной среды по два значения каждой характеристики движущейся жидкости — одно для малопроницаемой среды, другое — для высокопроницаемой. Таким образом, будем использовать две
скорости фильтрации каждой из фаз Uf1' и Uj™, две насыщенности su> и s<2> 0 два давления рш и р(2> (верхние индексы 1 и 2 отно
сятся соответственно к высокопроницаемой и малопропицаемой средам, нижние 1 и 2 — к вытесняющей и вытесняемой жидкостям). Каждая из указанных характеристик получается путем осреднения по объему, охватывающему большое число блоков Или малопроница емых включений. При слоистой среде осреднение производится по мощности каждого слоя.
В соответствии с условием кг к2 будем рассматривать только случай, когда вся фильтрация происходит в высокопроницаемой
среде, т. е. U\n считаются равными нулю. Обобщенный закон Дарси для движения в высокопроницаемой среде можно записать в виде:
—— 7i1)gradp<1>;
U<P = —^ /^grad (VII.3.1)
Ц2
В формулах (VII.3.1) давление принято одинаковым в обеих фазах, т. е. влиянием капиллярных сил непосредственно на фильтрацию пренебрегается. Их действие учитывается, далее, только через скорость обмена жидкостью между участками разной проницаемости. Такое упрощение справедливо, если зона, где существенно меняется насыщенность, включает большое число блоков (в слоистой среде эта зона должна значительно превышать мощность каждого из ?лоев). Тогда градиент насыщенности в «продольном» направлении в высокопроницаемой среде мал, и влиянием капиллярных сил на фильтрацию можно пренебречь. Это условие выполняется при достаточно малом значении параметра a\{Uh, определяющего отношение скорости капиллярной пропитки к скорости фильтрации.
Относительные проницаемости fl11, входящие в формулы (VI 1.3.1), могут существенно отличаться от относительных проницаемостей, входящих в уравнения обобщенного закона Дарси для однородных пористых сред (при одинаковых насыщенностях). Последние относятся к квазистатическим распределениям насыщенности, которые в макромасштабе Однородны, а в микромасштабе определяются действием поверхностных сил (см. гл. VI). В неоднородной среде из-за неправильной формы малопроницаемых включений и под влиянием других причин распределение насыщенности при нестационарном течении заметно отличается от квазистатического. В высокопроницаемой среде могут образовываться области, в которых насыщенность резко отличается от средней, — «языки» воды, целики нефти. Естественно, что при этом преимущественное расположение частиц более смачивающей фазы в мелких порах нарушается, и форма осредненных кривых относительной проницаемости приближается к прямолинейной (прямолинейные относительные проницаемости соответствуют полностью случайному распределению фаз в порах).
Вид кривых относительной проницаемости в неоднородной среде зависит от характера неоднородности. Сравнительно равномерным в макромасштабе будет распределение фаз по мощности высокопроницаемого слоя в слоистом пласте, если эта мощность меньше мощности малопроницаемого слоя. В этом случае кривые относительной проницаемости сохраняют обычный вид. Напротив, в трещиноватопористой среде относительные проницаемости при движении фаз в трещинах можно в большинстве случаев считать линейными функциями насыщенности, так как распределение фаз в трещинах не зависит от капиллярных сил и каждая фаза движется свободно (экспериментально этот факт проверялся Е. С. Роммом [97]). Относительные проницаемости в высокопроницаемой среде являются также функциями безразмерных параметров вида a2/Uh, где U — скорость вытеснения, h — характерный размер включения. Однако зта зависимость пока не исследована. Далео предположим, что осред-ненные относительные проницаемости зависят только от средней насыщенности соответствующей среды.
Уравнения неразрывности можно выписать для каждой фазы в каждой из составляющих сред аналогично тому, как это было сделано в § 1 для однородной жидкости, т. е. предполагая, что в каждой точке происходит обмен жидкостью между соответствующими средами с интенсивностью qr
Имеем для течения в высокопроницаемой среде
mi 0 — п) + div [ 1 — п) V^\ -f qx = 0;
„1 (VI 1.3.2)
~т1 (1 — п) + div [(1 - п) U?' ] + q2 = 0.
Здесь qi и дг — интенсивности перетока каждой фазы из более проницаемой среды в менее проницаемую; п — объемная плотность включений, зависящая от пространственных координат. Если предположить в соответствии со сказанным выше, что в малопроница-
—V-
емых включениях скорости фильтрации Z7f2) равны нулю, то уравнения неразрывности в малопроницаемой среде примут вид:
gsis)
— 9 = 0;
91=*-Я» = 9, (VIT.3.3)
т. е. перетоки каждой из фаз равны по величине и противоположны по направлению.
Для замыкания полученной системы уравнений нужно найти связь интенсивности перетоков q с другими переменными. Как п в случае однофазной жидкости, перетоки возникают вследствие разности давлений в составляющих средах, однако при двухфазном течении эти разности различны для каждой из фаз. Большая величина капиллярного давления в малопроницаемых включениях создает в них зону пониженного давления в водной фазе. Вода является одновременно и вытесняющей и более смачивающей фазой. Напротив, в вытесняемой фазе давление во включениях выше, чем в высокопроницаемой среде. Вследствие этого и возникает переток воды во включения, а вытесняемой фазы — в противоположном направлении. Если отношение проницаемостей kjk* очень велико, капиллярное давление в малопроницаемых включениях намного больше, чем в высокопроницаемой среде. Тогда можно рассматривать обмен жидкостью между средами за счет капиллярных сил как результат капиллярной пропитки малопроницаемых включений. Поэтому интенсивность перетоков q может быть определена на основе исследования противоточной капиллярной пропитки.
Исследовать ход пропитки, учитывая истинную форму включений или блоков, практически невозможно; кроме того, за редкими исключениями форма блоков бывает неизвестна, поэтому приходится исходить из анализа пропитки линейного образца.
В гл. VI, § 4 было получено, что когда начальпая насыщенность s = s0 постоянна, то при малых t насыщенность является функцией переменной ? = x/a\f t, а скорость фильтрации каждой из фаз v при х = 0 по абсолютной величине выражается формулой
v=ac (s-j, (VII.3.4)
При этом скорость впитывающейся фазы равна а извлекаемой
После подхода фронта вытеснения к закрытому концу образца средняя насыщенность в нем стремится к постоянному значению s — Sj в соответствии с приближенным выражением (VI.4.39)
s=-- Sj (1 —ke-a,'/T«).
В то же время значение v убывает со временем по экспоненциальному закону
у= (VII.3.5)
где А на — постоянные, а т0 = Р/а2. Для приближенного описания хода пропитки постоянную А нужно выбрать гак, чтобы скорость v была непрерывна при пекотором значении t = tu так что при t < tx справедлива формула (VII.3.4), а при t > tx — формула (VII.3.5).
В целом ход пропитки линейного образца иллюстрируется приведенными выше на рис. VI.22 графиками зависимости средней насыщенности s от времени. При малых t значение s линейно зависит от [/i, a v — обратно пропорционально у t. При больших t s стремится к s1? a v убывает по экспоненциальному закону.
Если проницаемость кг достаточно велика, то с момента подхода воды к малопроницаемым включениям или блокам в трещиноватопористой среде на границе их сразу устанавливается максимально
возможное значение насыщенности s = s*. В таких условиях, если начальная насыщенность блоков постоянна, можно считать, что продвижение воды, впитывающейся в блок, и, следовательно, интенсив-ность перетоков зависят только от времени нахождения данного блока или элемента в обводненной зоне.
Введем новую неизвестную функцию t0 (х, у, г) — время прохождения фронта вытеснения в высокопроницаемой среде или в трещинах через точку с координатами х, у, z. Разумеется, это возможно только в том случае, если можно выделить такой фронт, т. е. поверхность, с одной стороны которой в трещинах (или в высокопроницаемой среде) появилась вытесняющая жидкость, а с другой стороны ее насыщенность равна начальному значепию. При перечисленных условиях интенсивность перетоков является функцией времени нахождения блока в зоне, охваченной вытесняемой жидкостью (обводненной). Это время равно t — tQ (х, у, z) = т.
Вид функции д (т) может быть выбран, исходя из выражений для скорости пропитки одного элемента (VII.3.4) и (VII.3.5).
Чтобы перейти от скорости пропитки одного элемента к интенсивности перетоков в единице объема среды с двойной пористостью, нужно скорость пропитки v умножить на удельную поверхность малопроницаемых блоков и на некоторый коэффициент, зависящий от формы этих блоков. При этом следует учесть, что пропитка в данной точке пласта начинается лишь после подхода к ней фронта вытеснения. Удельную поверхность из соображений размерности можно выразить в виде рГ"1, где р — постоянная, I — характерный размер блока. Тогда из равенства (VII.3.4) получим, что при малых значениях xq(x) можно принимать в виде:
q= (т0т)-'/., (VII.3.6)
где т0 = — характерное время пропитки блока; Nt — безразмерная постоянная. Для больших т из (VII.3.5) следует формула
e=Arsf-exp(-^). (VII.3.7)
Удобной аппроксимацией для q (т) при всех значениях т является функция вида:
д(х ) = А^=-. (VII.3.8)
Эта функция при малых т совпадает с выражением (VII.3.6), а при больших т убывает таким образом, что полный впитавшийся
СО
объем в единице объема среды, равный J q (т) dx, является конеч-
о
ным. Постоянные А и Ь в формуле (VII.3.8) нетрудно подобрать так, чтобы при малых т уравнение (VII.3.8) совпадало с (VII.3.6), а при больших т s,2,CTpeMiMOCb к предельной насыщенности блока после пропитки sL. Тогда
Выражение вида (VII.3.8) было предложено Э. В. Скворцовым [104].
Интенсивность перетоков можно ввести в уравнения (VII.3.2) — (VII.3.3) и по-иному, предположив, что q зависит от насыщенности каждой из среды. При этом можно принять, что q пропорционально с (sl5s.2) [формула (VII.3.4)3. Зависимость с (sx, s2), как показывают расчеты автомодельных решений, приближенно представляется в виде:
с (slt s2) = К (.\) (Sj — s2). (VII.3.10)
Вместо sx и s2 в выражение (VII.3.10) следует подставить s'1’ и некоторую функцию s(2), выбранную с учетом того, что пропитка происходит до выравнивания капиллярных давлений в обеих средах. Такой способ введения интенсивности перетоков был использован в работе В. М. Рыжика [98].
Для описания вытеснения в трещиноватой среде в уравнениях
(VII.3.2) и (VII.3.3) следует положить п — 1, (1 — п) U\l)~ и\ исходя
из того, что объем трещин мал по сравпепию с объемом пор. wt представляют собой средние по всему объему скорости фильтрации фаз. Обозначив, далее, s<2) = s и т2 = т, получим
¦+¦ ->¦ Яо
divi^j-]-5 = 0; div (wt 4-ц>2) == 0; ?n —y=0. (VII.3.11)
Рассмотрим одномерные задачи о вытеснении в трещиноватопористом пласте. Система (VII.3.11) приведется к виду:
-^-+9 = 0; m~—д = 0; w1~tw2 = w(t). (VII.3.12)
Пусть начальная насыщенность блоков постоянна и интенсивность перетоков может быть выражена формулой вида q = q (т).
Проинтегрируем первое из уравнений (VII.3.12) от входного сечения (ж = 0) до «фронта» вторгшейся воды. Учитывая, что при х = 0 движется только вытесняющая фаза и = w (t), получим
w (t) = ^ q (t—T (x)) dx. (VII.3.13)
0
Из (VII.3.13) можно получить интегральное уравнение для перемещения фронта вытесняющей жидкости в трещинах х0 (() = / (/). Введем в уравнении (VII.3.13) новую переменную интегрирования Т, полагая х = / (Т). Получим
1
w{t)-= | q(t — T)f (T)dT. (VII.3.14)
о
Определив из интегрального уравнения (VII.3.14) функцию / (t) или обратную функцию Т (х) = t0 (х), из второго уравнения системы (VII.3.12) можем найти распределение насыщенности блоков s в любой момент времени:
i-T (дг)
s — s® = 4~ J q (т~7’(ж)) dx J Q(^)dx. (VII.3.15)
T (JT) о
Правая часть уравнения (VII.3.14) имеет вид свертки и оно может быть решено методом преобразования Лапласа. Пусть
ОО СО
J w(t)e'’aidt = W(a); J q (t) e~stdt = Q (a); (VH.3.16)
о о
CO
| f (t) e °‘ dt = Ф (a).
о
Пользуясь теоремой о свертке и начальным условием / (0) = О, получим из (VII.3.14)
W (о) --= оф (о) Q (a). (VII.3.17)
откуда
Рассмотрим некоторые частные случаи. Для начальных моментов
времени, когда q (г) выражается формулой (VII.3.6), имеем
откуда
Nx V яа
В частности, если скорость вытеснения w (?) меняется по степенному закону w = w0 ft, то
Що) = ^±11
ф(<у) = _.,^Г(Р+1) .
-шогг(р + 1) ?+
\ ' (VI
1.3.20)
r-J*т' NiaVn г(р+|)
JL * ЛТ|Я У л а 2
Для случая постоянной скорости р = 0 и
При р ¦< —решение (VII.3.20) не имеет физического смысла, так как не удовлетворяет условию / (0) = 0.
14 Заказ 1865 209
Полное описание вытеснения из трещиновато-пористой среды удобно провести с использованием зависимости q (т) в виде (VII.3.8). Функция вида (VII.3.8) хорошо аппроксимирует ход пропитки в линейном случае, а ее преобразование по Лапласу имеет сравнительно простой вид, что позволяет решить уравнение (VII.3.14) в конечном виде для ряда важных случаев зависимости и: (t).
При q (t), выражающейся формулой (VII.3.8),
Q(a) = ^2?, (VII.3.22)
откуда
ф (а) =
WJa)VoJ± (VII.3.23)
АУ а а
Рассмотрим снова случай w (t) = w0 — const. Тогда
Ф(',)-^='!ТГ±- (VII.8.24)
Из таблиц преобразования Лапласа можно найти / (t) в виде: / (t) = (1 + 2Ы) ег! (УЩ + (1 - е-«); (VII.3.25)
f (t) = erf (УЫ). (VII.3.26)
АУ n
Из формулы (VII.3.26) видно, что при t -> оо скорость перемещения фронта становится постоянной п равной
у-_ 2 woVb aVh
В соответствии с формулой (VII.3.15) пасыщенность блоков s, если f (t) = Vt, выражается в виде:
‘"V , ___
s==s®',_"^ 1 ?(T)dT = s0-f (si—s0)erf (у b(t — -f-)). (VII.3.27)
О
т. e. s является функцией x — Vt. Таким образом, в пределе получаем решение типа, описанного в § 3 гл. VI, т. е. решение типа
бегущей волны. При больших значениях I--насыщенность
блоков стремится к постоянному предельному значению s — s2. Все изменение насыщенности от s0 до Sj происходит в зоне, протяженность которой имеет порядок • (2 -f- 3). Эта зона no аналогии со случаем вытеснения в однородной среде (см. гл. VI, § 3) получила название стабилизированной. Внутри стабилизированной зоны фактически осуществляется весь процесс пропитки блоков.
Зависимость / (t), соответствующая уравнению (VII.3.25), показана на рис. VII.6 [1041. Видно, что стабилизированная зона обра-
зуется за время порядка у (2 -f- 3), т. е. приблизительно в 2 ^3
раза больше времени пропитки одного блока. При малых t функция
/ (t) имеет порядок ]/Т, т. е. ход вытеснения таков же, как в случае
Точно так же, как и рассмотренный случай линейного вытеснения, можно исследовать радиальные задачи. При радиальном течении, когда вытесняющая жидкость нагнетается через скважину,
центр которой принимается за начало координат, первое из уравнений (VII.3.11) запишется к виде:
рез скважину на единицу мощности пласта:
Т (г) = t„ (г) — время появления фронта жидкости на окружности радиусом г. Пусть функцией, обратной Т (г), будет R (Т). Примем в качестве искомой функции ф (I) = пП2 (t) — площадь, охваченную продвигающимся фронтом. Тогда из (Vll.3.29) получается следующее интегральное уравнение для (р (?):
/
G (t) = f q (t - T) ф' (T) dT. (VII.3.30)
0
Это точно такое же уравнение, как и (VII.3.14), только вместо
скорости фильтрации w (t) в него входит расход G (<). Все приведен
ные решения уравнения (VII.3.14) могут быть перенесены на радиальное течение. Для определения насыщенности в блоках из (VII.3.12) получим аналогично (VII.3.5)
l-Т (г)
s — sD= | 9(x)dx. (VII.3.31)
о
Заметим, что в случае G (t) = const, если q определяется по формуле (VII.3.8), то из формул, аналогичных (VII.3.6) или (VII.3.18), получим при больших t
Полученное решение кроме трещиновато-пористой среды может быть использовано также для описания вытеснения в двухслойном пласте, когда мощность малопропицаемого слоя очень велика и к2/к1 весьма мало, и высокопроницаемый слой можно рассматривать как щель (аналогично случаю, описанному в § 2). При этом условии, если пренебречь пропиткой в продольном направлении, каждый элемент малопроницаемого слон (вырезанный перпендикулярно оси
С
х) пропитывается по автомодельному закону, т. е. д ~ —- . Реше
V т
ние для перемещения 'фронта по щели сохраняет вид (VII.3.20),
только постоянная iVj-j- заменяется на С — ас [см. (VII.3.4)].
Если мощность малопроницаемого слоя конечна, то следует использовать те же выражения д (т),что и для трещиновато-пористой среди.
Изложенный выше подход к задачам вытеснения несмешива-ющихся жидкостей в трещиновато-пористой среде развивался в работах В. М. Рыжика [98, 3], А. А. Боксермана, Ю. П. Желтова, А. А. Кочегакова, В. JI. Данилова [30, 31].
До сих пор мы рассматривали задачи вытеснения, в которых обмен жидкостью между трещинами и блоками (или между" участками разной проницаемости) вызывался действием капиллярных сил. Однако в специфических условиях сред с двойной пористостью ход вытеснения может существенно измениться также за счет нестационарных процессов обмена, вызвашшх упругим перераспределением давления между блоками и трещинами. Этот фактор используется в процессе циклического заводнения, который применяется в „условиях резко неоднородных и трещиноватых коллекторов. При циклическом заводнении расход закачиваемой в пласт воды (или другой жидкости) периодически изменяется. Это изменение вызывает периодический обмен жидкостью между трещинами и блоками за счет упругого перераспределения давления. В ходе обмена происходит постепенное обогащение блоков вытесняющей жидкостью, которая, очевидно, быстрее перемещается по трещинам. Выходящая из блоков жидкость всегда поэтому имеет меньшую насыщенность вытесняющей фазой, чем жидкость, находящаяся в трещинах и входящая в блоки. Капиллярные силы интенсифицируют зтот процесс, поскольку более смачивающая вытесняющая жидкость (вода) удерживается в блоках за счет «концевых эффектов». Но и в случае, когда жидкости — полностью смешивающиеся и капиллярные эффекты отсутствуют, циклический режим приводит, к обмену жидкостями между блоками и трещинами и постепенному извлечению вытесняемой жидкости. Излагаемая ниже упрощенная схема цикли ческого процесса вытеснения в пластах с двойной пористостью была предложена А. А. Боксерманом и Б. В. Шалимовым [321.
В простейшей постановке для анализа принципиальных свойств циклический процесс вытеснения можно рассмотреть на примере вытеснения из трещиновато-пористого пласта жидкостей, равных плотности, вязкости и сжимаемости (разноцветные жидкости).
В этих условиях попе давлении в блоках и трещинах описывается системой уравнений (VII.1.11) и не зависит от распределения насыщенности.
Для рассматриваемой системы динамически одинаковых жидкостей относительные проницаемости как для течения в трещинах, так и в блоках равны соответствующим насыщенностям. Уравнения неразрывности /-Й фазы в трещинах и блоках соответственно имеют вид:
A (wijps}1’) + div (рUj) = -рqf, (VII.3.33)
д
~gf (тгРsfZ)) = Р9/.
где s/1’ — насыщенность в трещинах; sj2) — насыщенность в блоках. Здесь сделаны те же предположения, что и при выводе уравнений
(VII.1.11). В соответствии со сказанным выше V= S;1}6\ где
U = иг + U2 — суммарная скорость фильтрации в трещинах. Имеем:
Г sll)q q > 0;
т. е. если переток идет из трещин в блоки, то перетекающая жидкость имеет тот же состав, что и жидкость в трещинах, и наоборот. Если принять функцию q согласно формуле (VII. 1.5), то из системы (VI 1.3.33) может быть получена система (VI 1.1.11) и, кроме того, следующие уравнения для насыщенности:
as«>
—j- -f U grad sm
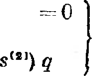
q> 0; (VII.3.35)
at
dst*1
~W
ds<i>
dt
f- U grad s'1’ = (s(1) — s(*>) q
= 0
q< 0. (VII.3.36)
dt
Уравнения (VII.3.35) и (VII.3.36) показывают, что в той из сред, из которой происходит переток, насыщенность не меняется в соответствии с предположением, что состав перетекающей жидкости тот же, что и в той среде, откуда происходит переток (фактически под влиянием капиллярных сил в выходящей из блоков жидкости будет преобладать вытесняемая фаза, что ускорит процесс обмена).
Если рассматривать вытеснение несмешивающихся жидкостей с учетом истинного вида относительных проницаемостей, то насыщенности будут меняться при любом знаке q.
В рассматриваемой постановке задачи поля давлений и насыщенностей могут быть определены поочередно путем решения уравнений
(VII.1.11) и (VII.3.35) — (VII.3.36). Для дальнейшего упрощении задачи надо учесть, что переток жидкости из трещины в блок и обратно за время одного цикла невелик по сравпению с общим объемом жидкости в блоке, поскольку этот переток происходит только за счет сжимаемости. Поэтому изменение насыщенности происходит намного медленнее, чем изменение давления. Это позволяет осреднить все параметры в уравнениях (VII.3.35) и (VII.3.36) по промежутку времени, равному одному периоду, т. е. ввести осредненные переменные вида:
г
< s(i) > = ± j s(0 dt. (VII.3.37)
о
Считая отклонения от средних значений малыми, получим для средних значений насыщенности систему уравнений
s(i)' дГ
т2 lAlp. = ( < SU, > _ < scS, > } (VII.3.38)
dt
где
<7<Г
Для того чтобы определить вид функции qt) (х), следует найти соответствующие периодические решения уравнения (VII.1.11) и осреднить их по времени. Для случая одномерного течения между галереями будем искать периодические решения уравнения (VII.1.11) с периодом Т = 2я/со:
Решение ищем в виде:
Pi = Ро (я) + (VI1.3.40)
так, чтобы оно удовлетворяло уравнению (VII.3.39) и периодическим граничным условиям
k\h dpi
Hi дх
-§Г L =Qo ^ Qi 008 И + 6г)- (VII.3.41)
Из уравнения (VII.3.39) следует, что р”0 (х) — 0 и р0 (х) = А + + Вх. Значение А представляет собой несущественную постоянную, а
D . Hl(>o kxh •
откуда определяются два корня: а.1 и а2.
Полагая ах = + iy2, «2 = Yi — имеем
Рг (*, *) = Ро (*) + [С^ + С2е-Ъ*] = р0 (х) 4 Р0 (х) еш.
(VII.3.43)
Подставляя выражение (VII.3.43) в условие (VII.3.41) и выделяя действительную часть, можно найти значения постоянных Сх и С5. После того как найдена функция рх (х, t), вид функции перетока может быть определен из второго уравнения (VII.1.11), т. е.
Определение постоянных в приведенном выше решении довольно громоздко и мы не будем приводит!, окончательных формул.
Как показали многочисленные расчеты, проведенные А. А. Бок-серманом и Б. В. Шалимовым [32], при обычных значениях периодов — порядка нескольких часов — амплитуда давления практически не зависит от координаты х. Следовательно, и амплитуда интенсивности перетоков qv может быть принята не зависящей от х. Для постоянного qD решение системы (VII.3.38) в одномерном случае может быть получено в замкнутом виде при начальном условии
(VII-3.45)
< s<8> > — 0. В одномерном случае уравнения (VII.3.38) можно записать, опуская знаки осреднения:
Введем новые независимые переменные
1 = х; x=t~^ = • (VII.3.46)
Тогда вместо (VII.3.45) получим систему
(VII-3.47)
Система (VII.3.47) должна быть решена при граничных условиях s(1) = l при | = 0 и s<2) = 0 при т=0. (VII.3.48)
Применяя преобразование Лапласа по т и учитывая второе условие (VII.3.48), получим вместо (VII.3.47) уравнения
f (Sa> — S(2,)a--0;
dS'J>
dl
(VII.3.49)
где ?(1) и Sw — преобразования Лапласа от s(l1 и a — пара
метр преобразования Лапласа; а — р =
Из граничных условий следует, что при ? — 0 5(1> =
0,75
0,50
0,25
| — |
---ч | що/п _500 | |
| N V |
'''4v | ||
| \ ч \ . V |
j Г 400 | ||
| sm-W0 | |||
| 1 1 |
5 1___ |
О
0,25 0,50 0,75 X
Решение уравнений (VII.3.49) имеет вид:
(VII.3.50)
c(s>_ Р«ф(-с?) / «Р5 \
* ~ a exP(^-jTpj
Используем формулу
°° ___а_
] /0 (V2at)e-3ldt^e*°
Рис. VII.7
(VII.3.51)
(см. {431, формула (9.3.42)]. Пользуясь формулой (VII.3.51) и теоремой умножения для преобразования Лапласа, получим следующие
выражения для sa> и sli):
s,1* = exp(—a|—Рт)/0(2 Vap|r)-{-
Т
-f Pexp( -ag) Jexp(-pX)/0(2]Zapp)<iZ;
0
(VII.3.52)
s*%) = (5 exp (—a|) j exp (—0Я) /„ (2 VaPS*-) dk.
Из формул (VII.3.52) следует, что на фронте продвижения воды в трещинах (при т = 0) имеет скачок, интенсивность которого равна ехр (—а|).
Графики зависимости sa> и s(2) от х при разных значениях t приведены на рис. VII.7.
$ 1. ОТКЛОНЕНИЯ ОТ ЗАКОНА ДАРСИ.
НЕЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
Во всех рассмотренных до сих пор задачах мы предполагали выполненным закон Дарси. Объясняется это тем, что закон Дарси достаточно точно описывает основной круг фильтрационных движений. Вместе с тем в ряде случаев нелинейность закона фильтрации становится существенной, а иногда п определяющей.
В основу вывода закона Дарси в гл. I, § 2 были положены два основных предположения: 1) движение является безынерционным («ползущим»); 2) жидкость вязкая пьютоновская, не взаимодействующая с твердым скелетом пористой среды 1.
Последующие уточнения связаны с отказом от этих предположений.
1. Как видпо из самого вывода закона Дарси (см. гл. I, § 2), он должен нарушаться в области достаточно больших скоростей, при которых уже нельзя не учитывать инерционной составляющей сопротивления движению жидкости.
Добавляя к числу определяющих параметров (1.2.2) плотность с размерностью ML'3, получим уже шесть величин, из которых можно образовать три безразмерные комбинации. Повторяя рассуждения гл. I, § 2, получаем
![]()
(возникающая здесь комбинация udp/ц играет роль числа Рейнольдса фильтрационного микродвижения). Допуская возможность
1 Т. е. влияние скелета сказывается лигпт. в том, что на его поверхности выполняется обычное для вязкой жидкости условие прилипания. В то же время предполагалось, что скелет не создает действующего на жидкость силового поля, не адсорбирует сколько-нибудь заметную часть жидкости, не образует с ней коллоида и т. д.
разложения функции / в ряд Тейлора и ограничиваясь первыми двумя членами разложения, получаем
(здесь учтено, что d2 к, см. гл. I, § 2).
Выражение (VIII.1.1) носит название двучленного закона фильтрации. Впервые двучленный закон был предложен Форхгеймером [117].
Как показывают опыты, это простое выражение хорошо описывает данные наблюдений. Наряду с часто цитируемыми данными Фенчера, Льюиса и Бернса [115], отметим еще опыты Линдквиста, воспроизведенные в работе [149]. Эти опыты показывают, что соотношение (VIII.1.1) представляет собой нечто большее, нежели простую эмпирическую формулу, поскольку оно хорошо выполняется даже для весьма больших значений скорости фильтрации. Физический смысл этого заключается в том, что при больших скоростях быстропеременное движение в порах сопряжено с появлением значительных инерционных составляющих гидравлического сопротивления.
Выяснению физического смысла - соотношения (VIII. 1.1) посвящен ряд работ, из которых необходимо отметить работы Е. М. Минского [82—84].
Появление квадратичного члена в уравнении закона фильтрации иногда связывается с турбулизацией течения. Однако уже порядок чисел Рейнольдса (1—10), рассчитанных по диаметру зерен или пор пористой среды, при которых сказываются отклонения от линейности, указывает на неправильность такого утверждения [149, 126]. В последнее время отсутствие турбулентности (т. е. флуктуаций скорости во времени) доказано также прямыми опытами [457].
В задачах теории фильтрации (в отличие, например, от задач химической технологии) приложения двучленного закона фильтрации ограничены главным образом движением газа вблизи высоко-дебитных газовых скважин или движением вблизи скважин в трещиноватых средах. В последнем случае особое значение имеет то обстоятельство, что истинная скорость жидкости в трещинах значительно больше скорости фильтрации.
2. Двучленный закон фильтрации (VIII.1.1) учитывает отклонения от закона Дарси при больших скоростях. Иной характер носит уточнение, рассматриваемое ниже. Будем рассматривать только безынерционные движения. Допустим, что кроме сил вязкого сопротивления существуют также силы сопротивления, величина которых не зависит от скорости фильтрации (хотя зависит от ее направления — силы сопротивления всегда направлены против скорости относительного перемещения). Простейшим случаем системы с такими свойствами является неньютоновская вязко-пластическая жидкость, для которой касательные напряжения связаны с градиентом скорости du/dn соотношением Бингама [85, 861:
(VIII. 1.2)
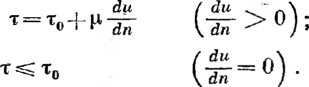
В это соотношение, кроме вязкости р, входит также постоянная т0, называемая начальным напряжением сдвига.
Допустим теперь, что происходит фильтрация жидкости, характеризуемой двумя постоянными: вязкостью р и характерным напряжением т0. Из соображений размерности, так же как и в гл. I, § 2, получаем
![]()
(VIII.1.3)
Предположим, что движущаяся r пористой среде жидкость обладает тем свойством, что с увеличением скорости деформации значение вязких напряжений становится преобладающим. Тогда при увеличении скорости фильтрации влияние параметра тп должно асимптотически уменьшаться. Это означает, что функция / должна иметь конечный предел при стремлении аргумента к нулю:
(VlII.l/i)
Постоянная к представляет собой проницаемость среды в обычном смысле. Пусть теперь фильтрующаяся жидкость обладает тем свойством (присущим, например, вязко-пластическим жидкостям), что при малых скоростях деформации напряжения не зависят от величины скорости и не стремятся к нулю с уменьшением скорости сдвига до нуля. Очевидно, что при малых скоростях фильтрации в выражении (VIII. 1.3) скорость должна исчезать. Это означает, что
(VIII.1.5)
(u 0).
В результате при снижении скорости фильтрации до нуля градиент давления стремится к конечному (ненулевому) пределу:
(grad p)0 = — Y = — “T
(VHI-1.6)
Это предельное значение у определяет ту величину градиента давления, по достижении которой начинается движение жидкости; при меньших значениях градиента движение отсутствует. Величина у называется предельным (начальным) градиентом; если для рассматриваемого случая такое предельное значение существует, то говорят о фильтрации с предельным (начальным) градиентом. Наиболее простой вид закона фильтрации с предельным градиентом получается в предположении, что функция / представляется двучленным выражением
(VIII.1.7)
к ци
удовлетворяющим соотношениям (VIII.1.4) и (VIII.1.6). При этом уравнение (VIII.1.3) дает (рис. VIII.1)
gradp = — — Y-j- («>?>);
(VIII.1.8)
Igradpj^v (u = 0).
Закон фильтрации с предельным (начальным) градиентом использовался в гидротехнике [96, 116] и в нефтепромысловой механике, в первую очередь в работах А. X. Мирзаджанзаде с сотрудниками {85, 86, 112].
1 2 3 Ь Рис. VIII.2
Надо, однако, заметить, что соотношение (VIII. 1.8) необязательно выполняется точно даже для фильтрации вязко-пластической жидкости. Это легко объяснимо. Суммарная, сила сопротивления складывается из сил сопротивления, действующих в отдельных порах. При этом в каждом элемепте жидкости соотношение между «вязкой» (|i du./dn) и «пластической» (т0) составляющими напряжения зависит не только от величины средней скорости (скорости фильтрации), но и от перераспределения скоростей между отдельными поровыми каналами.

Рис. VIII.1
Подобное явление происходит и при движении вязко-пластиче-ской жидкости в одном капилляре (здесь перераспределение происходит между отдельными слоями жидкости). В результате связь между перепадом давления и средней скоростью для капилляра радиусом R имеет вид (рис. VIИ.2):
Движение в капилляре прекращается при перепаде давления
(VIII.1.10)
Асимптота к линейному участку кривой Дp/l — v пересекается с осью Др/l при Ар = &/3t0l/R.
Пусть теперь мы имеем пористую среду, состоящую из множества микрокапилляров различных радиусов. При снижении перепада давления начинается постепенное «закупоривание» капилляров. В соответствии с формулой (VIII.1.10) вначале движение прекращается в наиболее мелких капиллярах, а по мере снижения давления происходит закупоривание все больших и больших капилляров. Ясно, что чем сильпее разброс размеров пор, тем больше растянут переход к полному прекращению движения и тем сильнее отличается истинный вид закона фильтрации от идеализированного соотношения (VIII. 1.8).
Однако выражение это может иметь также асимптотический смысл, описывая движение при относительно больших скоростях фильтрации (и T0d/[x). При таком понимании закон фильтрации с предельным градиептом (VIII.1.8) описывает широкий класс нелинейных фильтрационных движений. При этом естественно различать истинный предельный градиент у0, отвечающий полному прекращению движения, и предельный градиент у, отвечающий асимптотическому участку закона фильтрации. Имеем по порядку величины
¦Vo(VIII.1.11)
°макс а
где duaKC и d — соответственно максимальный и средний размеры иоровых каналов. Для сред с сильно неоднородным строением эти величины могут различаться во много раз.
Как уже было установлено из соображений размерности, d <=« я» с/Поэтому для сред однотипной структуры 7 ^ rj]/~k. Это соотношение установлено и экспериментально проверено Б. И. Султановым [112] (в его опытах величины y0 и у не различались).
3* Проиллюстрируем сказанное некоторыми экспериментальными данными. На рис. VIII.3, а — в приведены данные по фильтрации: а — воды в глине [132]; 6 — воды в глинизированном песчанике [162]; в — нефти в песке [1]. Как видно из графиков, выражение (VIII.1.8) достаточно хорошо описывает движение во всех этих случаях в области сравнительно больших скоростей; при малых же скоростях различные системы ведут себя по-разному.
В основе нелинейного поведения систем в этих случаях лежат различные физические механизмы. Важно, однако, что эти эффекты проявляются при малых скоростях фильтрации и в средах с малым размером пор (зерен), т. е. с малой проницаемостью. Относительная роль нелинейных эффектов определяется параметром
? = -1! или = (VIII.1.12)
(AU [XU v 7
Это обстоятельство определяет особенности нелинейной фильтрации в неоднородных пластах. Области малой проницаемости оказываются областями максимального проявления нелинейных эффектов, что способствует дополнительному затруднению движения в этих областях. Рассмотрим это на примере тонкого слоистого пласта. Этот практически важный случай приведет нас также к некоторым новым постановкам задач.
4. Тонкий слоистый пласт мощностью ht сложен N пропластками проницаемостью к{. Предположим, что для каждого пропластка справедлив закон фильтрации с предельным градиентом
(| grad p | > Y/); u = 0 (| gradp| < y,)- (VIII. 1.13)
и, см]сен-10s
a, cmfсен
| уРю%н /5°/о№ | аС1 :ь | |||
| ^Вада | ||||
| 0 0,05 0,10 0,15 \gradp |
picfcM 2 | |||
\дгайр\,нгс]?м$
_i_[__
0,01 0,02 0,03
a, CMjcen-/C~3
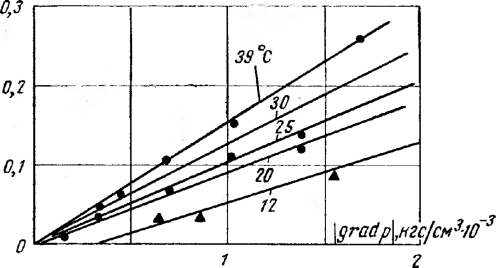
В
Рис. VIII.3
Примем, что пропластки занумерованы в порядке возрастания проницаемости. В соответствии со сказанным выше это означает также, что значения убывают с увеличением номера i.
Уточним теперь, что понимается под тонким пластом. Будем считать нласт топким настолько, что можно пренебречь изменением давления по толщине (тем самым предполагается, что возникающие между отдельными прослойками разности давлений быстро выравниваются за счет обмена жидкостью между пропластками). Определим
в этом предположении вектор w —¦ среднюю скорость фильтрации жидкости через площадку, высота которой равна мощности пласта, а ширина равна единице. Имеем
w^±- J Zdz= -^["jM-gradp-^Yi-iSlT
(VIII.1.14)
О 1-1 l-l
Здесь номер 0 ^ j ^ N, до которого ведется суммирование, определяется очевидным условием
V/ < grad р sg Y/+i- (VIII.1.15)
При |grad р | < Vi имеем w = 0. Нетрудно видеть что движение однородной жидкости в слоистом пласте можно рассматривать так
же, как движение в однородном пласте со скоростью фильтрации w
6
Рис. VIII.4
и в соответствии с законом фильтрации (VIII.1.14) (рис. VIII.4, а). Таким образом, наряду с законом фильтрации с предельным градиентом (VIII.1.8) имеет смысл рассматривать кусочно-линейные законы фильтрации, описываемые выпуклой книзу ломаной линией (рис. VIII.4, а). Отсюда нетрудно перейти к непрерывно изменяющейся по мощности пласта проницаемости. При этом получается закон фильтрации, описываемый произвольной выпуклой книзу кривой (рис. VIII.4, б). Наконец, рассматривая простейший случай двухслойного пласта, в котором один из прослоев обладает пренебрежимо малым предельным градиентом, получаем простой кусочнолинейный закон фильтрации (рис. VIII.4, в), на котором можно проследить ряд особенностей движения жидкости в слоистых пластах. Во всех перечисленных случаях закон фильтрации в области больших скоростей имеет прямолинейный асимптотический участок.
В нефтепромысловой литературе обычно разделяют случаи нелинейной фильтрации и выключепия отдельных прослоев пласта с изменением градиента давления. Такое разделение, по-видимому, нерационально: изменение эффективной мощности пласта не только является одним из проявлений нелинейности закона фильтрации, но и может быть описано тем же математическим аппаратом.
В дальнейшем мы не будем этого оговаривать особо, но следует помнить, что все сказанное ниже о нелинейной фильтрации допускает непосредственную интерпретацию применительно к движению в слоистых тонких пластах.
5. Дополняя уравнение закона фильтрации уравнением неразрывности и уравнением состояния жидкости, получим нелинейную теорию упругого режима, или теорию нелинейной фильтрации газа, подобно тому как это было сделапо в гл. II.
Наряду с рассмотренной кусочно-линейной аппроксимацией нелинейного закона сопротивления часто встречается также аппроксимация степенным выражением вида:
(VIII.1.16)
“= -/(Ig^d р |)gradр.
где / — степенная функция;
f (| grad р |) С | grad р \а.
(VIII.1.17)
Вначале такая аппроксимация использовалась для описания закона фильтрационного сопротивления в переходной области между линейным и квадратичным законом сопротивления; при этом а < 0. Впоследствии, однако, такая аппроксимация почти везде уступила место двучленной аппроксимации, рассмотренной выше. В последнее же время степенной закон фильтрации вновь приобретает самостоятельное значение, поскольку он хорошо описывает движение ряда пеныотоновских жидкостей, в том числе растворов и расплавов полимеров, в пористой среде. Для таких жидкостей характерно «псевдо-пластическое» поведение, когда эффективная вязкость жидкости падает по мере увеличения скорости деформации и показатель а положителен.
§ 2. АВТОМОДЕЛЬНЫЕ РЕШЕНИЯ ЗАДАЧИ ФИЛЬТРАЦИИ ЖИДКОСТИ ПРИ НЕЛИНЕЙНОМ ЗАКОНЕ СОПРОТИВЛЕНИЯ.
ФИЛЬТРАЦИЯ С ПРЕДЕЛЬНЫМ ГРАДИЕНТОМ
Автомодельные решения задач фильтрации с нелинейным законом сопротивления, если он не является степенным, существуют лишь при узко специальном выборе начальных и граничных условий. Однако автомодельные решения важны в том отношении, что позволяют выяснить особенности возникающих нелинейных задач.
1. Прямолинейно-параллельное движение упругой жидкости. Кусочно-линейпый закон фильтрации. Рассмотрим фильтрационное движение при нелинейном законе сопротивления в условиях упругого режима. Выразим скорость из уравнения закона фильтрации через градиепт давления в виде:
![]()
Здесь к — проницаемость среды; ^ — вязкость жидкости; у — характерное значение.градиента давления; Ч? — безразмерная функция, описывающая закон фильтрации.
При такой записи предполагается, что у закона фильтрации имеется линейный участок, для которого можно определить отношение к/ц (очевидно, это требование выполнено для всех рассмотренных в § 1 законов фильтрации, кроме степепного). Подставляя выражение (VIII.2.1) в уравнение неразрывности (II.1.3) и считая жидкость и пласт упруго-деформируемыми, придем к уравнению упругого режима при закопе фильтрации (VIII.2.1):
Здесь к — пьезопроводность, рассчитанная обычным образом но определенным выше величинам к и ц:
кК (VIII .2.3)
туi
а величины К и т имеют обычный смысл..
В частности, для одномерного движения в направлении оси х имеем
dt
Пусть рассматривается полу бесконечный пласт и начальное распределение давления в ном липейпо, а на границе пласта поддерживаются постоянный отбор или закачка жидкости, так что
|}\х_о = В- p(0,x) = Ax. (VIII.2.5)
Легко убедиться, что задача с такими условиями автомодельна и имеет решение вида:
P — yxf (?); ? = 1/2x/Vxt- (VIII.2.6)
Для функции / получается уравнение
-2124l = ~k'?(f + t%-) (VIII.2.7)
при условиях
/М = у = «; Ит(/4^)=|. = р. (VIII.2.8)
Будем рассматривать кусочно-линейный закон фильтрации (см. рис. VIII.4, в):
У(у) = еу (|*м<1; е < I): (VIII.2.9)
XV (y) = esgay-\-y — sguy (I УI > 1)-15 Заказ i865 225
Особый интерес представляет продельный случай е —*¦ 0, когда получается закон фильтрации с начальным градиентом, рассмотренный выше.
При законе фильтрации вида (VIII.2.9) представленная задача может быть решена в явном виде. Уравнение (VIII.2.7) распадается на дна линейных уравнения:
sr+ 2(1 + 1®)/'=о (1/+1Л > 1); ,v„T9im е1/" Ч 2 (е +12) /' = О (1/Ч-1ГК1). ( 4)
Область значений аргумента 0 < 1 < °° разбивается на несколько участков (lh li+1) таким образом, что на каждом из них выполняется одно из уравнений (VIII.2.10), причем на смежных участках решение удовлетворяет разным уравнениям. Число и характер расположения участков легко установить из соображений непрерывности, если учесть, что решения уравнений (VIII.2.10) и их производные монотонны.
1. Если градиенты А и В (будем называть их исходным н конечным соответственно) — одного знака и по абсолютной величине больше критического градиента у (|а|>1,| Р|> 1, сф >0), то во всем пласте градиент превосходит критический по абсолютной величине. На всей прямой 0 < 1 < °° выполняется первое уравнение (VIII.2.11), и задача сводится к известной линейной задаче.
2. Если исходный и конечный градиенты по модулю меньше критического, то на всей прямой выполняется второе уравнение (VIII.2.10), и задача вновь сводится к линейной.
3. Если |а |]> 1, | р|< 1, то на примыкающем к границе пласта участке [0, Л, где I — неизвестная граница, подлежащая определению, градиент давления меньше критического, и выполняется второе уравнение; в интервале (Z, оо) — первое.
4. Если | а | < 1, [ р |> 1, тона участке [0, I] вблизи границы пласта выполняется первое уравнение (VIII.2.10), а на остальной полупрямой — второе.
5. Наконец, если исходный и конечный градиенты, превосходя по модулю критический, имеют разные знаки (| а |>1,| Pl> 1, сф < 0), то область движения разбивается на три участка: на (0, 1г) и (12, оо) удовлетворяется первое уравнение (VIII.2.10), а на (1Х, 12) — второе.
Для каждого участка решение может быть выписано в явном виде:.
/ (1) = С, Ч- А []/я" erf 14-ехр (—12)1;
1 х\ * * , (viii.2.11)
/ (1) = С2 ч D2 [V^ erf (l/V8 ) + tl Vг exp (-?*/«0]
— соответственно для первого и второго уравнений (VIII.2.10). Поэтому для того, чтобы решить задачу, достаточно найти постоянные С и D и границы /,• для всех участков. Уравнения для постоянных получаются нз дополнительных условий (VIII.2.8) и условий сопряжения на границах. Эти условия состоят в том, что давление и расход непрерывны на границах участка, прячем положение этих границ определяется из дополнительного требования равенства градиента критическому. Таким образом, имеем:
/(Z + 0) = /(Z-0); (/+У')|+о = (/ + ЕЛ|-о= ±1- (VIII.2.12)
Знак в последнем условии (VIII.2.12) определяется из соображений непрерывности. Нетрудно проверить, что условия (VIII.2.12) вместе с краевыми условиями дают столько же уравнений, сколько неизвестных имеется в задаче.
Рассмотрим теперь последовательно те три из перечисленных выше пяти возможностей, при которых задача не переходит в линейную. Для случая 3 решение, удовлетворяющее краевым условиям (VIII.2.5), имеет вид:
/ (Б) = Р - А,[/я erf (g/1/i) + Г1 У« ехр (- /е)] (0 ^ *);
/ (I) =a+/)i|/n — A [jAierfg + l'iexp (-?2)] (Z < ? < оо)
(VIII.2.13)
а из условий (VIII.2.12) следует система алгебраических уравнений для Dt, D2 и I:
a -| A Уп erfc Z = sgn a;
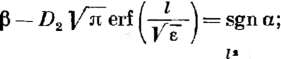
(VIII.2.14)
Система (VIII.2.14), как легко убедиться, однозначно разрешима. Аналогичным образом, в случае 4 решение определяется выражениями
/ (|) = р - Dx [Уп erf ? + | le -i (0 ^ ^ I);
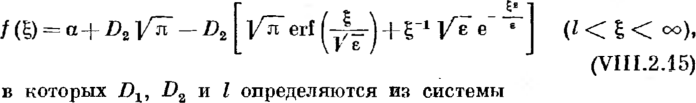
![]()
Р — Уп erf Z = sgn Р;
(VIII.2.16)
D2 У г е е = D^e1'.
Перейдем теперь к пределу при е —0. При этом в соответствии с выражением (VIII.2.9) закон фильтрации принимает в пределе вид:
?(г/)=о V(y) = y — sgnjr
(I г/1 ^ 1);
(M^D;
соответствующий фильтрации с предельным, градиентом, когда движение жидкости начинается лишь но достижении критического значения градиента давления. Такой закон фильтрации является вырожденным и для него сама постановка задачи с заданием докри-тического значения градиента давления является сомнительной. Как будет видно из дальнейшего, правильная формулировка задачи
0 фильтрации с начальным градиентом требует, чтобы на границе области задавался не градиент давления, а скорость фильтрации.
Рассмотрим вначале случай 3. Из системы (VIII.2.14) следует, что
1 0 при е-^0. Действительно, пусть I остается больше б > 0. Тогда D2 остается ограниченным и из последнего уравнения -> 0, что противоречит первому уравнению (VIII.2.14).
Чтобы понять смысл полученного результата, рассмотрим следующий частный случай разбираемой задачи. Пусть первоначально стационарный фильтрационный поток, градиент давления в котором превосходит критический, мгновенно останавливается в результате того, что-градиент давления на границе становится меньше критического. Можно было бы ожидать, что вблизи границы возникает застойная зона, в которой движения нет, а затем, по мере удаления от нее, скорость движения будет постепенно увеличиваться. Решение показывает, что это не так. Застойной зоны нет, и движение происходит во всем пласте, причем скорость движения монотонно уменьшается по мере приближения к границе пласта и обращается в нуль на самой границе, так что градиент давления здесь равен критическому.
Распределение давления в области движения определяется вторым уравнением (VIII.2.13), в котором нужно положить
Z)1 = (sgna— а)/1/л), (VIII.2.18)
как это получается из формулы (VIII.2.14) при 1 = 0. Нетрудно видеть, что этот результат не зависит от того, каким задавалось значение градиента давления на границе (|3). В качестве примера на рис. VIII.5 приведены результаты решений для |3 = 0, a = 2 и трех значений е \р° = |/(|)Ь
В случае 4 переход к пределу при е -> 0, очевидно, дает ограниченную область движения, примыкающую к границе пласта, причем остальная часть пласта занята застойной зоной. Такой характер решения усматривается также непосредственно из выражений (VIII.2.15) и системы (VIII.2.16), в которой можно перейти к пределу при 6 —*• 0, считая I конечным. Решения для {3 = 2, a = 0 и трех значений е приведены на рис. VIII.6.
В случае 5 область движения разбивается на три зоны, и для определения неизвестных границ и коэффициентов уравнений приходится рассматривать систему шести уравнений, аналогичную по своей структуре системам (VIII.2.14) и (VIII.2.16). Переходя в этой системе к пределу при е -*- 0, можно убедиться, что область, в которой градиент давления меньше критического, уменьшается до нуля, так что в пределе пласт разбивается на две части, в которых движение происходит навстречу друг другу. Распределение давления для случая а = 2, р = —2 показано на рис. VIII.7.
Все полученные в пределе при е 0 распределения имеют угловую точку в месте сшивки двух решений. Если движения первона-
0,5 1,0?
Рис. VIII.Л
Рнс. VII 1.6
чально не было (случай 4), то возмущение, вносимое граничным условием, охватывает лишь конечную, расширяющуюся со временем область пласта. Поэтому решение, полученное для бесконечного пласта, применимо без вся-к их оговорок и к пласту к о-нечных размеров для ограниченных интервалов времени.
Рис. VIII.7
Если же движение в пласте существовало с самого начала (случаи 3 и 5), то возмущение мгновенно охватывает весь пласт, как и в соответствующих задачах упругого режима.
2. Осесимметричное одномерное движение в условиях упругого режима. Степенной закон фильтрации. В осесимметричном случае движение автомодельно при произвольном законе фильтрации, если рассматривается задача о пуске скважины пренебрежимо малого радиуса при дебите, изменяющемся пропорционально квадратному корню из времени, отсчитываемому от момента пуска скважины
При таком законе изменения дебита скважины можно найти решение, в частности, при законе фильтрации с предельным градиентом [49]. Однако искусственность постановки задачи снижает ее практический интерес, и в этом случае приходится ограничиваться приближенными решениями. В то же время при степенном законе фильтрации (VIII.1.17) осесимметричное движение автомодельно при изменении дебита скважины после пуска по произвольному степенному закону:
Q(t) = QtK (VIII.2.20)
В наиболее общем виде такие движения рассмотрены в работе
[5]; ниже мы ограничимся основным для приложений случаем
(3 = 0, что отвечает мгновенному пуску скважины с постоянным дебитом ' Q. Имеем для распределения давления р (г, t) с учетом (VIII.1.17) уравнение
которое должно быть решено при условиях
р(г,0) = 0; . (VIII.2.22)
Нетрудно видеть, что решение задачи автомодельно и его можно искать в виде:
01 / га+1
0С+ 2
А =-Цт-Г-^У^а^. (VIII.2.23)
(Зсс+2)1/С1 Vе/
Подставляя (VIII.2.23) в (VIII.2.21), получаем уравнение
^{1[/'(1Г+1Н 11(0+1)1/'(9-а/(91 = 0. (VIII.2.24)
Уравнение (VIII.2.24) должно быть решено при условиях
а+1
lim 1 [/' (1)]a+1 ~ const = (3a + 2) « . (VIII.2.25)
Далее, очевидно, что при 1 -> со (г -> оо) функция / (1) должна стремиться к нулю вместе со своими производными, причем таким образом, чтобы интеграл
СО
М= J 1/(1) dt (VIII.2.26)
о
оставался конечным.
При а > 1 (случай, который нас сейчас интересует) производная /' (?) интегрируема вблизи ? — 0, так что существует конечный предел
/(0) —lim/(|). (VIII.2.27)
Это означает, что при степенном законе фильтрации (VIII.1.17) с показателем а ^>0 имеет смысл постановка задачи об отборе жидкости через скважину нулевого радиуса при конечном давлении в скважине.
Далее из (VIII.2.27) и (VIII.2.23) следует, что
Pc = P(0, t) = Af(0)tP; р = а/(3« + 2), (VIII.2.28)
т. е. давление в скважине изменяется по степенному закону, причем показатель степени этого закона |3 однозначно связан со степенью закона фильтрации а:
р = а/(За + 2), (VIII.2.29)
а коэффициент А пропорционален дебиту скважины Q в степени (а + 2)/(За + 2).
Таким образом, полученное автомодельное решение открывает возможность экспериментального определения как показателя а, так и коэффициента С закона фильтрации. Подробнее об этом сказано в § 3, где закон фильтрации представлен в виде зависимости градиента давления от скорости .фильтрации и показатель п = - 1/(а + 1).
§ 3. ПРИБЛИЖЕННОЕ РЕШЕНИЕ ЗАДАЧ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ ПРИ НЕЛИНЕЙНОМ ЗАКОНЕ СОПРОТИВЛЕНИЯ
Выше уже рассматрргвались простейшие (автомодельные) движения с нелинейным законом фильтрации. Однако наиболее важная для приложений задача об осесимметричном притоке к скважине, пущенной с постоянным дебитом, в условиях нелинейного закона фильтрации неавтомодельна; ниже эта задача рассматривается приближенно.
1* Предполагая, что фильтрующаяся жидкость и пласт упруго сжимаемы, запишем основную систему уравнений задачи в виде:
Здесь q = ru; U = ук/ц — характерное значение скорости фильтрации; у — характерное значение градиента давления.
Уравнения (VIII.3.1) должны быть решены при дополнительных условиях, отвечающих пуску скважины в пласте, в котором первоначально движения не было.
Принимая начальное давление за нуль, имеем
р(г, 0) = 0; q(a, t)~Q= const. (VIII.3.2)
Здесь a — радиус скважины.
Примем вначале для закона фильтрации выражение, отвечающее фильтрации с начальным градиентом (см. рис. VIII.1):
|ф(/)|^1 (/ = 0); ф»-»+«./ ч.фоь (VI11-3-3»
Достаточная точность достигается, если приблизить функцию д (г, t) параболой
Соответствующее выражение для давления имеет вид:
Р{г, *) = -^-[ln7 + 6(y — 1) + Tc(li—l)l+Y(r — О, (r^l);
р (г, 0 = 0, {r^l). (VI11.3.5)
Из условия q (I, t) следует с ~ —1 — Ъ. Для определения оставшихся неизвестных Ъ (<) и I (I) используем два первых интегральных соотношения, получающихся из второго уравнения системы (VIII.3.1) после умножения его на г и г2 соответственно и интегрирования от 0 до I. При этом во всех промежуточных расчетах пренебрегаем отношением а/l по сравнению с единицей (тем самым мы ограничиваемся
рассмотрением лишь достаточно больших времен). Имеем после простых выкладок
ут
|>(8 + 3fc) +15-^] = -^^±^-. (VIII.3.6)
А dt
Исключая из системы (VIII.3.6) переменное Ъ (t) и вводя безразмерные переменные
1 1 1/212 Кт * ПТ TFT4 74
*=12"^: т = (VIII.3.7)
Искомое решение этого уравнения должно удовлетворять очевидным условиям
Я(0) = 0; Х(оо)=оо; К'(т)^0 при т>0. (VIII.3.9)
Условия (VIII.3.9) выделяют единственное решение уравнения (VIII.3.8). Заметим прежде всего, что точка (0,0), через которую должно проходить решение, является для уравнения (VII 1.3.8) особой. Исследуя ее по первому приближению (см., например, [87]), легко убедиться, что это седло, и две его сепаратрисы, aw б, проходящие в первом квадранте, имеют касательные с угловыми коэффициентами 1 и 10/3. Вторая из этих сепаратрис, как можно проверить, выходит из первого квадранта во второй, а сепаратриса с начальным угловым коэффициентом (<й./йт)т_0 — 1 удовлетворяет всем условиям (VIII.3.9). Это легко установить, используя фазовую диаграмму уравнения (VIII.3.8), показанную на рис. VIII.8. Индексами 0 и со здесь отмечены изоклины нуля и бесконечности [на которых обращаются в нуль соответственно числитель и знаменатель выражения (VIII.3.8)].
Найдем для функции X (т) асимптотическое выражение для больших значений времени. Если предположить, что А, (т) возрастает быстрее или медленнее, чем тг'\ то из (VIII.3.8) получим противоречие. Отсюда
Х(т) = ст*/» + о(т’/’). (VIII.3.10)
Подставляя это выражение в (VIII.3.8), находим с = (48)'1'*. Продолжая процесс последовательного выделения членов, можно получить более точное выражение:
Начальный участок зависимости Л (т) можно найти численным интегрированием уравнения (VIII.3.8) с учетом известного значения
V (0) = 1. Сопоставление вычисленных таким образом значений со значениями, даваемыми асимптотической формулой (VIII.3.11), показывает, что уже при т = 1 эта формула верна с точностью в несколько процентов. Зависимость А (т) показана на рис. VIII.9 [начальный участок кривой получен численным интегрированием; начиная с х = 1 — по формуле (VIII.3.11)].
Зная X (т), можно найти Ъ и с из исходных уравнений. Из (VIII.3.6) после перехода к безразмерным переменным имеем
Ъ=
2т~8* -3; с = — 1 —
Ь. (VIII.3.12)
При малых т из X (т) т следует Ъ <=» —1, 0. При больших
т, используя асимптотическую формулу (VIII.3.10), имеем
Если рассматривается изменение давления для достаточно больших значений времени в точке, близкой к скважине, так что rjl 1, rUJQ 1, то формулу для распределения давления после отбрасывания малых членов можно представить в виде:
p(r, <) = ^-(ln|-fc—(VI11.3-14)
Подставляя сюда значения коэффициентов и возвращаясь к исходным переменным, имеем окончательно
р(г, 0 = - V^W-ж'"-р-+1г (VIII.3.15)
2. При помощи метода интегральных соотношений можно найти также решение задачи о пуске скважины при нелинейном законе фильтрации вида:
Ф (/) = (//«Г (/««);
<Р (/)=/—П + Sgnj (i^n), (VIII.3.16)
который в пределе при п -> 0 переходит в закон фильтрации с предельным градиентом. В этом случае давление в скважине р (a, t) меняется во времени по закону
1—п 2(1-п)
р(а, t) — const-13~п -Q 3 71 -| . . . (VIII.3.17)
3* Применим теперь полученные результаты к анализу некоторых данных по исследованию скважин на нестационарный приток.
Сделаем вначале следующее замечание. Пусть рассматривается изменение давления р (t) в некоторой фиксированной точке пласта, движение жидкости в котором вызвано пуском скважины с постоянным дебитом (в частности, может рассматриваться давление в самой скважине). Пласт будем считать однородным и неограниченным. Выберем некоторый промежуток времени At и рассмотрим величину
Ap(t) = p(t 1 Д t) — p(t). (VIII.3.18)
Тогда изменение величины Ар (t) при больших t зависит исключительно от вида закона фильтрации в области малых скоростей (тем меньших, чем больше рассматриваемые времена). Это утверждение достаточно очевидно: в прилегающей к скважине области движение стабилизируется и распределение давления оказывается таким же, как и при стационарном движении (см. также гл. III и IV). В результате значение этой области в отклонении давления в скважине от начального уровня перестает меняться и уже не сказывается на величине Ар. Та область, в которой происходит основная перестройка потока и которая дает основной вклад в значение Ар (t), оказывается удаленной от скважины. Чем больше время t, тем дальше эта область и тем меньше поэтому достигаемые здесь скорости фильтрации. Этим и доказывается сформулированное утверждение.
Рассмотрим теперь приток к скважине в условиях нелинейной фильтрации, но с тем дополнительным условием, что при скоростях фильтрации, меньших некоторой и < и0, закон фильтрации может быть приближенно представлен прямой (как на рис. VIII.4, а, б, в). Тогда, как показано выше, характер изменения давления в скважине при больших временах будет таким же, как и в случае линейной фильтрации. В частности, изменение давления будет пропорционально дебиту скважины Q и будет линейно зависеть от логарифма времени, так что
(при этом сама величина С может нелинейно зависеть от Q).
Предположим теперь, что мы анализируем серию снятых при различных дебитах Q кривых изменения давления в скважинах. Тогда при достаточно больших временах все кривые в координатах Ар — 1м t будут иметь прямолинейные участки, по которым обычным способом определится гидропроводность пласта khj\i, очевидно, не зависящая от Q (в то же время величина приведенного радиуса скважин аг/у. окажется, возможно, зависящей от Q). Напротив, изменение гидропроводносги khj\i с изменением Q указывает на нелинейность закона фильтрации при малых скоростях (в этом случае мы будем называть закон фильтрации существенно-нелинейным Или нелинеаризуемым; случай, рассмотренный выше, назовем линеаризуемым) .
4- Рассмотрим с этой точки зрения данные работы [56] (табл. VIII.1), которые ясно показывают увеличение гидронроводности с ростом дебита. Особенно важно, что этот эффект свойствен как нагнетательным (где его можно было бы объяснить раскрытием трещин прп увеличении давления), так и эксплуатационным скважинам. Согласно сказанному выше, эти данные свидетельствуют о действии в пластовых условиях нелинеаризуемых законов фильтрации. Более того, такого рода нелинейность проявляется не непосредственно вблизи скважины (где нелинейные эффекты изменения эффективной мощности пласта обнаруживаются прямым наблюдением [29]), а вдали от скважины, в области медленного движения жидкости.
Таблица VIII.1
| Нагнетательные скважины |
Эксплуатационные скважины | ||||
| Дебит, |
Гидропро- |
Дебит, | Гидропро- | ||
| -V, скважины | • водность. | № скважины |
водность. | ||
|
ж*/сутки | 0-см | м/сутки |
д-см | ||
| 514 |
793 | 838 | 1529 | 153 | 951 |
| 757 | 839 | 140 | 950 | ||
| 540 | 760 |
85 | 875 | ||
|
360 | 693 | 65 | 832 | ||
| 1246 |
745 | 575 |
40 | 670 | |
|
511 | 485 | 23 | 620 | ||
| 323 | 314 | 16 |
473 | ||
| 367 |
1364 | 1111 | 1608 |
216 | 3200 |
| 1333 | 1007 |
208 | 2910 | ||
|
1182 | 964 | 154 | 2350 | ||
|
1106 | 984 | 93 | 1700 | ||
| 742 | 676 | 51 |
1070 | ||
| 561 |
567 | 1288 | 149 | 843 | |
| 553 | 527 | 115 101 88 | 770 730 555 |
||
Попытаемся теперь количественно Охарактеризовать наблюдаемую нелинейность на основе рассмотренных в пп. 1 и 2 модельных законов фильтрации. При этом будем исходить из предположения
о том, что данные работы [56] правильно отражают зависимость приращения давления Ар за сопоставимые отрезки времени от дебита скважины Q (так что наблюдаемая величина khj\i <=>Q/Ap; подробнее см. [461). Вместе с тем, предполагая, что имеет место закон фильтрации (VIII.3.3) или (VIII.3.16), можно установить, что ему отвечает зависимость вида:
(?Ш'3'20)
причем п ~ 0 отвечает закону (VIII.3.3).
Представим теперь данные табл. VIII.1 в координатах lg kh —
— lg Q (рис. VIII.10). Согласно формуле (VIII.3.20) точки, отвечающие определенной скважине, должны лежать на одной прямой с угловым коэффициентом /, удовлетворяющим неравенству
Угловые коэффициенты прямых, приведенных на рис. VIII.10, показаны в табл. VIII.2 вместе с отвечающими им значениями п. Как видно из таблицы, результаты подсчета для скважин 367 и 1246 указывают на необъяснимо быстрый рост гидропроводности с увеличением дебита. Возможно, это связано с тем, что для обеих этих скважин (нагнетательных) проницаемость может также увеличиваться с ростом давления на забое скважины.
3,5
3,0
2,5
I 3 IgQ
Рие. VIII.10
Таблица VII 1.2
| К" скважины | 1608 | 1 529 |
1288 | 514 | 367 |
1246 |
| Угловой коэффициент........ | 0,67 | 0,28 | 0,36 |
0,24 | 0,74 |
0,84 |
| Показатель п.......... | 0 |
0,68 | 0,56 |
0,73 | — |
— |
Для остальных скважин получаются физически допустимые значения показателя п. Однако результаты эти ни в коем случае не являются окончательными. Из них можно сделать лишь один достоверный вывод: в исследованном диапазоне скоростей фильтрации эффективная проницаемость пласта с уменьшением скорости монотонно убывает до нуля (с рассматриваемой точностью). Естественно, такое затухание фильтрации может иметь фундаментальное значение и нуждается в глубоком исследовании.
Изложенные результаты были получены в работе В. М. Ен-това [45, 46].
СПЕЦИАЛЬНЫЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ ОДНОРОДНОЙ ЖИДКОСТИ
§ 1. НЕИЗОТЕРМИЧЕСКОЕ ФИЛЬТРАЦИОННОЕ ДВИЖЕНИЕ
До сих пор предполагалось, что температура жидкости или газа при движении их в пористой среде остается постоянной. Представление это связано с тем, что изменения температуры, возникающие при изменении давления в ходе движения, в значительной мере компенсируются теплообменом со скелетом пористой среды. Большинство же задач, в которых рассматривается изменение температуры в пласте вследствие закачки в пласт теплоносителя, например горячей воды, может быть отнесено к теории стационарной фильтрации.
Однако даже малые изменения температуры могут быть в принципе измерены и использованы для анализа вызывающих их гидродинамических процессов [121]. Поэтому мы рассмотрим здесь общую постановку задачи о неизотермическом движении сжимаемой жидкости и приведем решение для случая пуска скважины с постоянным дебитом.
1. Отказываясь от требования изотермичности, мы должны добавить к числу искомых функций еще и температуру жидкости. Можно было бы, используя уравнение сохранения энергии применительно к жидкости, составить уравнение для температуры жидкости. При этом, однако, мы столкнулись бы с необходимостью учитывать теплообмен, происходящий между жидкостью и вмещающей ее пористой средой. Описание такого теплообмена требует исследования, учитывающего закономерности движения и теплообмена в отдельных норовых каналах.
Чтобы избежать связанных с этим трудностей, воспользуемся тем, что теплообмен между жидкостью и пористой средой происходит по огромной поверхности (или, что равнозиачно, глубина прогрева очень мала), так что существующая в некоторый момент разность температур между жидкостью и скелетом исчезает весьма быстро. Характерное время выравнивания температур составляет по порядку величины Р/а, где а — коэффициент темнературопровод-
ности наименее теплопроводящей из контактирующих сред, а / — характерный размер структуры порового пространства. Полагая
I ^ 10"1 см, а 10“а см2/сек, имеем 12/а «=10 сек. Таким образом, время выравнивания температурных различии (сейунды и менее) несравнимо меньше времен, характерных для фильтрации. Поэтому, не интересуясь кратковременными эффектами, будем считать температуры жидкости и скелета равными. В результате в каждой точке будет определена единая температура, вводимая, как и все другие характеристики фильтрационного потока, путем осреднения по элементарному макрообъему .(ср. § 1.1).
2. Выделим теперь некоторый объем V пористой среды, ограниченный поверхностью S, и составим для него уравнение энергетического баланса. Обозначая через е удельную внутреннюю энергию жидкости, а через ех — удельную внутреннюю энергию вещества твердого скелета, получим
J[emp-f &iPi(l — m)\dV — W + Q — O. (IX. 1.1)
v
Здесь объемный интеграл определяет полный запас энергии в выделенном объеме (кинетической энергией в силу ее малости пренебрежено); Q — количество тепла, выносимого через поверхность S; W — работа, производимая внешними силами над данным объемом.
Перенос тепла через границу обусловлен двумя механизмами. Первый из них — механизм теплопроводности — не связан с перемещением макроскопических объемов (не отдельных молекул) вещества; второй механизм — конвективный — определяет перенос тепла с макрообъемами вещества. Однако такое разделение является чересчур грубым. В ряде случаев, типичными примерами которых являются турбулентное движение и движение жидкости в пористой среде, возможно некоторое промежуточное положение, когда в переносе тепла существенны, помимо тепловых флуктуаций и переноса со средним движением, еще и перенос со случайными мелкомасштабными отклонениями от среднего движения. При рассмотрении одних лишь осредненных характеристик движения удобно объединять все флуктуационные механизмы одним общим термином — теплопроводность. Чтобы подчеркнуть отличие от обычного (молекулярного) механизма переноса, вводят понятия конвективной диффузии и теплопроводности в пористой среде. Поток тепла за счет такого объединенного механизма теплопроводности определяется выражением
Наличие в уравнении (IX.5.2) тензорного коэффициента теплопроводности вместо одного скалярного коэффициента теплопроводности связано с гем, что процесс теплопроводности при фильтрации обладает анизотропией, поскольку тензор теплопроводности уже не является тензором материальных констант жидкости, а зависит также и от характеристик фильтрационного потока (в первую очередь от скорости фильтрации). Это вполне аналогично тому, что имеет место при конвективной диффузии [3, 58]. Однако в отличие от случая диффузии коэффициент теплопроводности насыщенной пористой среды сравнительно мало зависит от скорости фильтрации [471. Поэтому достаточная точность достигается и при использовании простейшего соотношения
![]()
Учитывая вышесказанное, можем записать
s
Здесь первый член выражает конвективный перенос энергии со средним движением.
При определении работы внешних сил W не будем учитывать силу тяжести, поскольку дальше не встретятся задачи, в которых ее значение существенно, тогда все сведется к подсчету работы сил, действующих по поверхности S. При этом оказывается, что следует учитывать лишь работу нормальных напряжений (давления), а работой касательных напряжений можно пренебречь. Действительно, работа сил давления в единицу времени составляет
W" — — J рпи dS = — J у (ри) dV = — ^и\pdV — J ру« dV.
S V V V
При фильтрации несжимаемой жидкости у и = 0. При этом,
IX ^
используя закон фильтрации Дарси ур = — ~и, получаем
В то же время для работы касательных напряжении т имеем следующую простую оценку: W" <=& xuS. Но т pu/Z, где I — характерный размер порового пространства. Поэтому W" ^ \xu'2S/l, так что W"/Wr kS/IV. Но к I* (в действительности даже к 12), отношение V/S — порядка L (характерного размера рассматриваемой области). Таким образом, согласно основным предположениям W"/W ^ IJL 1. Для газа такой подсчет не применим, поскольку величина W' близка к нулю, но и в этом случае можно убедиться, что W пренебрежимо мало.
Подставляя полученные выражения в уравнение (IX.1.1), переходя от поверхностных интегралов к объемным и используя произвольность выбора объема V, получаем
[етр + Елр^! —пг)] + у (емр —ХуГ) + у (рм) = 0. (IX. 1.5)
3. Если рассматривается движение однородной жидкости, то уравнение анергии (IX.1.5) может быть упрощено. Пользуясь тем, что по определению е + р/р = г и в силу уравнения неразрывности
—
у(цр) =_—д (mp)/dt, имеем
тР [i !- fiPi (1 — т)1 + ри V* — -Jf (mP) — V (*- VD.
Удобно выразить в этом уравнении энтальпию i через температуру и давление. Тогда
dl = Ср (dT — 6 dp)
(Ср — теплоемкость при постоянном давлении; 6 — коэффициент Джоуля — Томсона). Отсюда получим
„ дТ , „ ОТ . ¦*-, „
mPСр-Qf-{-Ci -ЬриСр\Т —
= + mpCpb + риСрЬ ур -f V (Ь у Т). (IX .1.6)
В тех областях, где движение жидкости отсутствует, это уравнение переходит в обычное уравнение теплопроводности
(mpCp ! <^i) ~^- = V V^)-
Фильтрационное движение стабилизируется значительно быстрее, чем тепловое поле. Поэтому возникает задача, в которой следует учитывать лишь нестационарность теплового поля, — задача о тепловой конвекции при стационарной фильтрации:
(mpCp — Cj) — 4-рСрм \Т = риСр8 ур + у(Я,уГ). (IX.1.7)
Сопоставляя вторые члены правой и левой частей уравнения (IX.1.7), легко убедиться, что уже при сравнительно небольших скоростях фильтрации теплопроводностью в направлении движения жидкости можно пренебречь всюду, кроме областей резкого изменения температуры. Действительно:
(L — характерный размер; Ар — перепад давления на расстоянии L; а — температуропроводность). При а 10_3 сма/сек; р = 10 спз = = 0,1 пз; к = 10-9 см2 — 0,1 д; Ар — 10 кгс/см® = 107 дин/см* имеем
Из приведенной оценки следует, что теплопроводность обусловливает лишь локальное перераспределение температуры, а перенос
тепла на большие расстояния связан с конвекцией. В силу этого обстоятельства теплопроводностью в направлении фильтрационного потока обычно пренебрегают, учитывая лишь теплопроводность в направлении, перпендикулярном движению.
4. Рассмотрим теперь задачу о пуске газовой скважины с постоянным дебитом, учитывая возникающие при этом изменения температуры. Основная система уравнений может быть, прн пренебрежении теплопроводностью, представлена в виде:
![]()
8 (mp) \ dq
dt г дг ’
![]()
Величины р, 6 и (.1 являются известными функциями давления и температуры, в частности
(IX. 1.9)
Р=~ z(p, T)RT ’
Положим 6 = Т/Т(), р° = р/р0, где р0 и Т0 — начальные давления и температура, после чего система (IX.1.8) приведется к виду:
р° др° _ Q д / р° \_ х SQ
цОг 0 дг г 1 dt \ Z& ) г дг *
![]()
(1X4.10)
z© dt 1 1 r dr
Здесь
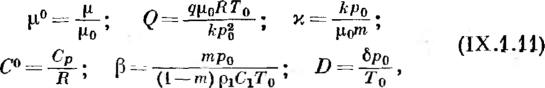
а нижний индекс нуль означает, что соответствующие величины берутся при р = р0, Т = Т 6.
Система (IX.1.10) должна быть решена при следующих дополнительных условиях:
P° (>', 0) = 1; 0 (r, 0) = 1; <?(0, t) = QB. (IX.1.12)
Легко убедиться, что сформулированная задача автомодельна и имеет решение вида:
P°=p°(I); e = 0(|); Q=Q{t)- l = 'UxiVy.t, (1X443)
где pf>, © и Q удовлетворяют системе обыкновенных дифференциальных уравнении:
ОС2 d ( Р° \ . dQ ¦
-dl \ Z& ) dl '
gpo dpO _ „
t,0ze d| (IX.1.14)
[2|2 (1 -f ^g0) + PC°?<?]-§- =
= [2P?2 (1 + + PC0 /)<?] |f-;
p0(oo)=1. 0(oo) = 1; <?(+()) = &•
Система (IX.1.14) может быть проинтегрирована численно.
Задача (IX.1.14) допускает также достаточно простое приближенное решение, основанное на том, что искажение поля скоростей под влиянием изменений температуры мало. Действительно, рассматривая изменение температуры частицы газа вдоль ее траектории, можно показать, что температура отклоняется от своего первоначального значения на величину, не превосходящую величину интегрального эффекта Джоуля — Томсона при изменении давления от начального р0 до существующего в данной точке пласта давления р:
(IX.1.15)
j* 6 dp
|Д Т
Ро
Для природных газов коэффициент Джоуля — Томсона б ^
0,4 -т- 0,5 °С/(кгс/см2). Поэтому вне непосредственной окрестности газовой скважины изменения температуры весьма малы. Вблизи же скважины распределение массовых скоростей фильтрации стабилизировано и является таким же, как и при стационарном движении. Поэтому без особой погрешности можно принять, как и для изотермического движения,
<? = <?0ех р( —?2). (IX.1.16)
Предположим теперь, что параметры задачи позволяют подобрать такое значение 1, что
Ql In2 Е* < 1 (IX.1.17)
и в то же время
(IX.1.18)
Первое из зтих неравенств обеспечивает малость отклонений давлений, а следовательно, и температур от их начальных значений; второе позволяет упростить третье уравнение (IX.1.14). Обычное значение рС°я«10_г. Поэтому системе неравенств (IX.1.17) и (IX.1.18) можно без труда удовлетворить уже при Q 0 ^ 0,05 (что является весьма большим для практики значением).
При выполнении неравенства (IX. 1.17) для ? > имеем
= 1 +72z0C„Ei(- I2)- (IX.1.19)
После этого распределение температуры может быть определено непосредственным интегрированием третьего уравнения системы (IX.1.14); тогда оно приобретает вид (в пренебрежении малыми членами):
В области | в
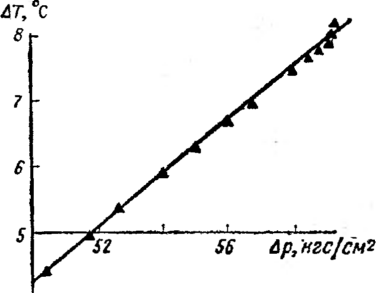
Рис. IX.1
силу неравенства (IX.1.18) последнее уравнение
(IX.1.14) упрощается и принимает вид:
![]()
откуда
е=0*+д (Р°~Р1У,
(IX.1.22)
Подставляя сюда выражение (IX.1.20) и учитывая (IX.1.18), получаем
е =-1 — D (1 -Р°) -z0<?0 Ei ( - . (IX.1.23)
Это выражение показывает, что в рассмотренном автомодельном решении изменения температуры при малых 1 (т. е. достаточно больших временах) повторяют в соответствующем масштабе изменения давления.
С учетом зависимости температуры от давления (IX.1.23) плотность р и вязкость р. газа в близкой к скважине области, где отклонения давления от начального значения велики, оказываются известными функциями одного лишь давления. Поэтому можно определить распределение давления в области малых Вводя безразмерную функцию Лейбензона
1
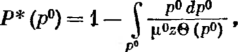
(IX.1.24)
имеем для нее приближенно
(IX.1.25)
Строя зависимость Р* (р°) от In t, можно определить обычным образом (подобно тому, как это делалось в § 4, гл. V) параметры пласта с учетом поправки на неизотермический характер движения.
Полученное выше простое приближенное решение хорошо согласуется с результатами численного интегрирования системы (IX.1.14), которое было выполнено для нескольких значений параметров' задачи. Вывод о линейной связи между изменениями давления и температуры подтверждается экспериментальными данными [811, полученными на скважинах Шебелинского газового месторождения. Как видно из рис. IX.1, экспериментальные точки хорошо лозкатся на прямую, угловой коэффициент которой [0,41° С/(кгс/см2)] близок к значению коэффициента Джоуля — Томсона, рассчитанному по термодинамическим функциям газа. Изложенные здесь результаты получены в работе В. М. Ентова [48].
§ 2. УПРУГО-ПЛАСТИЧЕСКИЙ РЕЖИМ НЕФТЯНОГО ПЛАСТА [20. 21]
1. При выводе основных уравнений теории упругого режима мы предполагали, что деформация скелета пористой среды при изменении давления в пласте является упругой (т.е. обратимой при снятии нагрузки) и более того — линейно-упругой. Казалось бы, для этого есть все основания, поскольку изменения давления в процессе разработки пласта малы по сравнению с модулями упругости жидкости и материала пористого скелета, а сам материал скелета обычно является вполне хрупким телом, деформирующимся упруго вплоть до разрушения.
Тем не менее имеются определенные указапия [159] на то, что изменение пористости пород, слагающих нефтяной пласт, с изменением давления жидкости носит неупругий характер. Такой вид не-упругости типичен для пластического состояния материала. Характер связи между деформациями и напряжениями существенно зависит от направления процесса деформирования и даже от всей его предыстории.
Типичная диаграмма деформирования пластического материала показана на рис. IX.2. Материал подвергается нагружению, начиная от недеформированного состояния. Если, достигнув некоторого состояния, начать разгружать материал, то вместо возврата к первоначальному состоянию будут получаться некоторые новые состояния. Разгрузка происходит так, как если бы модуль упругости материала увеличился. При новой нагрузке материал деформируется по кривой разгрузки до тех пор, пока не приобретет прежде не достигавшегося состояния.
Качественно сходная картина обнаруживается при деформации пористой среды. На рис. IX.3 показана зависимость пористости от нагрузки для песка [159], однако аналогичная зависимость имеет место и для других пористых сред. Причиной того, что изменение пористости носит «пластический» характер, являются, естественно, не пластические деформации отдельных зерен скелета, а необратимые изменения их взаимного расположения (переупаковка зерен). Возможность переупаковки частиц пористой среды качественно отличает €е поведение от поведения материала скелета, не содержащего пор.
2. Рассуждая так же, как и при выводе уравнений упругого режима, примем, что пористость является функцией одного лишь давления и первого инварианта тензора фиктивных напряжений в скелете:
т (р, 0)
(IX.2.1)
т-
«==-§<
€-
т
1-т
Нагрузка, иге j с у.2Рис. IX.3
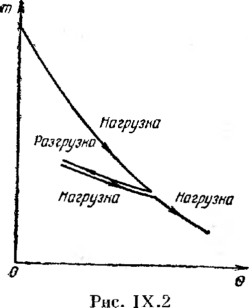
В соответствии с этим
дв
дг
дт
~дг~
(IX.2.2)
_/ дт \ др . / дт \
_\~др )в~дГ‘\~д?)
(производная по р берется при постоянном ©, а производная по © — при постоянном р)-
Как это было уже показано при выводе уравнений упругого режима (см. гл. II, § 2), изменение давления компенсируется изменением напряжений в скелете, так что
д(6+р)
= 0.
dt}
(IX.2.3)
Иначе говоря, сумма давления и первого инварианта тензора фиктивных напряжений постоянна — она уравновешивается массой вышележащих пород, которая практически не меняется.
Изменение пористосгн среды с изменением давления жидкости при постоянном 0 вызывается исключительно упругими деформациями материала скелета. Поэтому независимо от направления деформирования можно производную (дт/др)о — 1/К3 считать постоянной.
В противоположность этому зависимость пористости от первого инварианта тензора фиктивных напряжений 0 является существенно
необратимой. Положим, что она описывается зависимостью, подобной приведенной на рис. IX.2 зависимо.сти т от напряжений. Предположим далее, что в пласте происходит однократное увеличение фиктивных напряжений, возможно с последующим их уменьшением. В силу равенства (IX.2.3) это соответствует первоначальному снижению давления с последующим частичным его увеличением. Такая схема представляет значительный интерес в связи с тем, что на первой стадии разработки нефтяного месторождения вначале обычно происходит снижение давления на месторождении в целом, затем следует период частичного восстановления пластового давления при помощи вторичных методов — в основном законтурного и внутриконтурного заводнения.
В соответствии с изложенным предположим, что первоначальное давление в пласте р0 сначала монотонно снижается: dp/dt < 0. При этом dQJdt > 0, и можно считать производную (дт/дО)р постоянной и равной некоторому значению —1/К t. При повышении давления (dO/dt) «С 0, а производная (дт/д@)р принимает некоторое другое значение —1/KZ. Разгрузка является «более жесткой» — обычно модуль разгрузки К2 больше модуля нагрузки К Новое нагружение участка, уже подвергнутого разгрузке, происходит с тем же значением модуля А,.
Таким образом, для характеристики зависимости т от © достаточно задать два значения модулей: К1 и К2 и указать, каким из них следует пользоваться в каждый данный момент. Это легко сделать, если ввести понятие о максимальном за всю историю нагружения значении 0.
Положим:
0* (х, t) = max 0 (х, т).
о s' г < (
Тогда, очевидно, можно записать
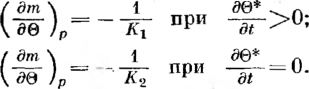
(IX.2.4)
Если перейти к давлению, то с учетом (IX.2.3) можно ввести функцию
(IX.2.5)
о < т < (
и переписать соотношение (IX.2.4) в виде:
(IX .2.6)
р*(х, tf)— min р(х, т)
Теперь можно выписать полную систему уравнений теории упруго-пластического режима нефтяного пласта.
Будем считать жидкость упругой, а фильтрацию — следующей закону Дарси. Тогда, поступая аналогично выводу уравнений упругого режима, придем к следующей системе соотношений:
-f—хЛр, (IX.2.8)
где
(IX.2.9)
| х = их = | kRt jim | при | др* dt ^ ’ |
| ус — к |
hK* | прн | др* _ п. dt ’ |
| цт | |||
| 1 | 1 | | 1 1 | , 1 . |
| А? | К ж ' | m К1 | 1 mKa ' |
| L | 1 | | 1 , | 1 » |
|
к; | А» 1 |
тК2 1 | тА'з * |
р+ (х, t) определяется соотношением (IX.2.5).
Несмотря на сходство с уравнением упругого режима, уравнение (IX.2.8) с учетом (IX.2.9) является нелинейным. Общих методов решения его не существует. Практически приходится разбивать область движения на несколько зон, для части которых справедливо уравнение (IX.2.8) с у. — а для остальных — то же уравнение с х = и2- Для каждой зоны уравнение является линейным. Поэтому нелинейность задачи проявляется лишь в существовании неизвестных границ зон действия разных форм уравнения (IX.2.8).
Постановка основных задач для уравнений упруго-пластического режима совпадает в основном с постановкой задач для уравнений упругого режима. Некоторая особенность имеется лишь в том, что при разбивке области движения на зоны нужно дополнительно указать условия для «сшивки» решений, полученных для различных зон. Условия эти имеют обычный физический смысл: равенство давлений и потоков жидкости по обе стороны границы зон, откуда получаем
р+(х, 0 —
Р-(х> 0=0; -л?
др-? 0 = 0 (ix.2.10)
(здесь учтено, что зоны различаются лишь приведенным модулем объемного сжатия).
3. Рассмотрим в качестве примера задачу о восстановлении давления в пласте при прекращении эксплуатации галереи в бесконечном пласте.
Пусть начальное давление в пласте, на границе которого (х = 0) имеется дренажная галерея, постоянно и равно Р. Пусть, далее, в начальный момент t — 0 давление на галерее падает до некоторой величины р0 < Р и остается постоянным в теченне времени Т, после
чего отбор ишдкости через галерею прекращается, и давление в пласте начинает восстанавливаться.
В рассматриваемом одномерном движении давление удовлетворяет уравнениям
др д2р
1П дх*
°т (# «о);
(|f >о) . (IX.2.11)
д‘р
1 дх-
др
— К
dt
при условиях
Р(Х, 0) = Р; Р(0,
t) = p0 (0</ < Г); jp(0,
t)д0
(IX.2.12)
дх
Очевидно, что плоскость переменных х, t разбивается на две области линией х — jx (t), на которой
Рис. IX.4
д*Р
dx-
др_
dt
О.
Линия эта, изображающая фронт волны разгрузки, начинается в точке смены граничных условий х = 0, t = Т и перемещается с ростом t в глубь пласта.
Положение этой линии должно быть определено в ходе решения задачи.
Будем искать приближенное решение задачи, используя метод интегральных соотношений (см. гл. V). В соответствии с общей схемой метода введем область влияния начального изменения режима [границу ее обозначим через I (t)] и область влияния смены режима в момент t — Т [граница Я (?)]. В отличие от имеющей ясный физический смысл границы ц (/) обе эти границы являются условными, возникающими в связи с применением приближенного метода. На рис. IX.4 они показаны пунктиром.
На начальной стадии (/ < Т) давление в пласте убывает, и распределение давлении определяется первым уравнением (IX.2.11). Принимая для распределения давления приближенное выражение
- +
I)
= *).
(IX.2.13)
Р
для которого первые две производные обращаются в нуль при х = I, и используя первое интегральное соотношение (уравнение материального баланса), найдем
(IX.2.14)
Рассмотрим теперь собственно процесс восстановления давления (f > Т). Предполояшм, что область влияния изменения режима
10 <; x <Z A (?)] будет захватывать лишь часть возмущенной области [0 < х < I (?)], так что при К < х <Ц распределение давления сохраняет прежний вид. определяемый соотношениями (IX.2.13) и (IX.2.14).
Для распределения давления в области 0 < х < X (t) примем приближенное выражение
P^L+m? + n?, (IX.2.15)
удовлетворяющее краевому условию при х — 0, а коэффициенты L, М и N определим так, чтобы при х — К выражение (IX.2.15) непрерывно сопрягалось с выражением (IX.2.13) при сохранении непрерывности первых двух производных. Условия сопряжения дают систему трех уравнений, разрешая которую, получим выражения для L, М и N в функции от К/1:
L = p0-r (Р—Ро)у;
М-3(Р-р0)у(1-у); jVr=-(P_p0)l( 1-^). (IX.2.16)
Положение волны разгрузки [х (t) определяется тем обстоятельством, что при х — [X (t) распределение давления, рассматриваемое как функция х, имеет точку перегиба, д2р{дх2 = 0. Дважды дифференцируя выражение (IX.2.15) и используя формулы (IX.2.16), получаем
Таким образом, распределение давления будет полностью известно, если определить функцию К (t). Для нахождения % (t) воспользуемся интегральным соотношением, следующим из уравнений (IX.2.11). Интегрируя эти уравнения — первое от ^ (г) до К (t), а второе от 0 до |х (г) и складывая полученные соотношения, получаем
A I1/
J Р(х> t)dx — p[k(t), tl — = (х2 — 3c=(1(0 + ><i(“to');c=x(,)*
Потребуем, чтобы распределение (IX.2.15) удовлетворяло интегральному соотношению (IX.2.18). Используя полученные выше выражения для L, М, N и [х через К и обозначая %/l= z, получим, учитывая выражение (IX.2.14) для I (t), уравнение первого порядка для функции z (/). Это. уравнение можно привести к виду:
dt 4z(l + z)<?z
Т" _ {.(1 — 2) [1+0-Z2+Z2 (н z)(5-3z)]
— безразмерное отношение, характеризующее степень необратимости деформаций среды.
Имеем далее
Интегрируя уравнение (IX.2.19) с учетом этого условия, получаем
Ф (z, о) = 4 j + Р (нТ) (5= 3^)Г = 1п ~Т ¦ <1Х-2-22)
О
Z
Таблица значений функции Ф (z, а) приведена в работе [11]. Используя эту таблицу, легко найти значение z, отвечающее данному значению t (рис. IX.5), а затем найти распределение давления, подставляя в (IX.2.15) значение z и соответствующие ему значения L, М и N, определяемые формулами (IX.2.16).
Из соотношения (IX.2.22) ясно, что при всех Т ^ t <[ 00 величина 0 < z < 1; при t -*¦ оо z -> 1, откуда в соответствии с (IX.2.17) следует, что jx/Z -»- Уг- Таким образом, при больших tволна разгрузки делит возмущенную область примерно пополам.
Заметим, что в соответствии с выражениями (IX.2.15) и (IX.2.16)
= (IX .2.23)
* Ро
Таким образом, графики рис. IX.5 описывают повышение давления на галерее после ее закрытия.
1. Пусть р (х, t) — распределение давления в полубесконечном пласте, удовлетворяющее при 0 < г < i (() второму уравнению (IX.2.11), а при I •< оо — первому, причем р (х, I) Р0 при х -> со.
Получить интегральное соотношение
I ОО
о I
,)P°Ti-- (¦?¦)«• (,x'2-21,
Получить также последующие интегральные соотношения по аналогии с теорией упругого режима и задачами фильтрации газа (см. гл. V).
Каков физический смысл соотношения (IX.2.24)?
2. Решить, используя метод интегральных соотношений, задачу о восстановлении давления вблизи скважины, работавшей на протяжении времени
О < t < Т с постоянным отбором в первоначально невозмущенном пласте, а затем остановленной.
Изложешше выше результаты были получены в работах Г. И. Баренблатта я А. П. Крылова [20] и Г. И. Баренблатта [11].
4« В теории упруго-пластической фильтрации нетривиальным оказывается вопрос об автомодельных решениях. Казалось бы, решение задачи о мгновенном источнике для упруго-пластического режима фильтрации должно в соответствии с § IV.5 представляться в виде:
,1Х-2'25)
где /(Е) удовлетворяет уравнениям
/"(!) + !/'(!)+/ = 0 (О^Е<|0); (IX.2.26)
О/'(?) + !/'<?)+/ = о .(&,*? Е<ео), а = х1/х? и условиям
f (0) — 0, lira f(l) -0, (1Х.2.27)
? ->со
причем [I (?) = |0l/2xjt — координата волны разгрузки.
В самом деле, уравнения упруго-пластического режима фильтрации не содержат ни одной новой величины с независимой размерностью (xi и я2 имеют одинаковую размерность). Поэтому, полагая
СО
| ]Р — р(х, 0)]cte=(); р(х, 0) = 0 (а-=?0) (1Х.2.28)
-со
и используя обычные соображения размерности, мы должны получить решение в форме (IX.2.25). Легко показать, однако, что решения в форме (IX.2.25) не существует. В самом деле, решение уравнений (IX.2.26) при условиях (IX.2.27) имеет вид, соответственно, А ехр (—1/г12). 4texp (~12/2а) при ? < X и ? Если теперь
записать условия непрерывности / и /' при ? — т0 ПРИ любом
X ф 0 для А и A j получается система уравнений, несовместная при ct Ф 1.
Этот результат представляется странным, потому что, казалось бы решение задачи Коши спустя достаточно большое время после начала движения должно «забывать» о деталях, связанных с начальным условием, и становиться автомодельным. Рассмотрим решение неавтомодельной задачи Коши [уравнения (IX.2.11)], соответствующей начальному условию
Р-р(х, 0) = (<?//)ч>(х/l), (IX.2.29)
где I — некоторый параметр размерности длины, а функция «р (х/1) — непрерывная вместе со своей производной по х, монотонно убывающая, и притом такая, что
J Ф(?)<2?:
1. (IX.2.30)
В силу теоремы, доказанной С. JI. Каменомостской [51, 52], решение этой задачи Коши существует и единственно. Согласно д-теореме оно представляется в виде:
Р-р(х, t) = -?=F (-??=, -Д=-, (IX.2.31)
Vnjt \ I 2y.it \ 2y.it v-z J v
Обычное рассуждение состоит в том, что при достаточно малых I второй аргумент функции F несуществен, откуда й получается представление (1Х.2.25).Нетривиальность положения, возникающего в теории упруго-пластического режима фильтрации, объясняется тем, что при ¦»! — I (к i?)_1/2 -»- 0 функция F (|, tj, а) в случае а Ф 1 не стремится к конечному пределу, а стремится к нулю или бесконечности (в зависимости от величины а = ~лi/x2) и притом так, что существует такое число р, что
lim
F& 4J± = f(zt a).
(IX.2.32)
г,-* 0 rf
Подставляя это выражение в (IX.2.31), получаем, что главный член асимптотики решения задачи Коши при / —>- 0 (или, что то же, t -*¦ оо) имеет вид:
Р-р(х, 0 = 4(M)-*/»<1+p>/(S, а), (IX.2.33)
где А = Q№, что и наводит на мысль искать автомодельное решение задачи Коши в форме (IX.2.33), причем параметр р должен быть найден в ходе решения задачи. Подставляя (IX.2.33) в (IX.2.11), находим для функции / уравнения:
-^-+&-5? + (1 + Р)/=о в|- + 5| + (1 + Р)/ = ° (lo^Koo).
Из граничных условий и условий непрерывности давления нп волне разгрузки находим
/' (0) = 0; /(?о_0) = /(!„ + 0), (IX.2.35)
откуда и из определения волны разгрузки
d2f (ip—0) _ dif(lо+О) _ n dl2
получается условие непрерывности f (|) на волне разгрузки. Из этих условий и условия быстрого убывания функции / на бесконечности находим
/ (I, р)=Ле^ф (1 1 , .(0^1^ 1о);
. ' (IX.2.36)
/ (I, Р) = (/«?) (g0 ^ К оо),
(где Ф, D — соответственно вырожденная гипергеометрическая функция и функция гиперболического цилиндра, см. [129]) и систему из двух трансцендентных уравнений, которая однозначным образом определяет Е0 (а) и р (а). Естественно, что р = 0 при а = 1. Полученное автомодельное решение интересно в том отношении, что показатель размерности автомодельной переменной в нем не определяется из соображений размерности, а находится из условия существования решения задачи в целом. Такие автомодельные решения называются автомодельными решениями второго рода. Исследование этой задачи было выполнено в работе Г. И. Баренблатта и Г. И. Сивапшнского [23], в которой можно найти детали вычислений и результаты численных расчетов.
СПЕЦИАЛЬНЫЕ ЗАДАЧИ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ НЕОДНОРОДНОЙ ЖИДКОСТИ
§ 1. ВЫТЕСНЕНИЕ ВЗАИМОСМЕШИВАЮЩИХСЯ ЖИДКОСТЕЙ
В настоящем параграфе будет рассмотрена совместная фильтрация двух полностью взаиморастворимых жидкостей, образующих нрн движении одну фазу. Такого рода фильтрационные течения осуществляются, например, при вытеснении нефти из пласта растворителями, при исследовании нефтеносных и водоносных пластов при помощи меченых частиц, а также в некоторых процессах химической технологии.
1. Рассмотрим процесс изотермической фильтрации однофазной двухкомпонентной смеси. Свойства такой смеси (плотность и вязкость) определяются двумя параметрами — массовой концентрацией одного из компонентов с и давлением р. При вытеснении смешивающихся жидкостей главной особенностью фильтрации однофазной двухкомпонентной смеси является сложный механизм переноса массы, связанный с перемешиванием частиц обоих компонентов вследствие различия скоростей в разных точках пористой среды. Влияние перемешивания на теплопередачу в пористой среде отмечалось уже в § 5 гл. IX. Из-за хаотического расположения поровых каналов движение жидкости при фильтрации происходит по сложным траекториям п на расстояниях порядка размеров пор скорость каждой отдельной частицы жидкости может значительно отличаться по величине и направлению от средней скорости, равной и/т, (где и — скорость фильтрации, т — пористость). Поэтому при движении в пористой среде двухкомпонентной смеси частицы каждого компонента рассеиваются относительно начального положения, несмотря па равенство средней скорости для всех частиц. При этом первоначально резкая граница двух полностью смешивающихся жидкостей оказывается «размытой». Размывание границы происходит, конечно, и под влиянием молекулярной диффузии, но эксперименты показывают [153], что в пористой среде при фильтрации перенос массы в результате отклонения скоростей от средних значений может происходить
во много раз (иногда на несколько порядков) быстрее, чем перенос, вызванный молекулярной диффузией.
Чтобы учесть влияние перемешивания на перенос компонента, имеющего концентрацию с, следует к вектору конвективного переноса
реи добавить дополнительный член, связанный с изменением концепт-
рации от точки к точке. Дополнительный вектор переноса qD может быть записан в форме
Возможность использования вектора переноса в указанной форме подтверждается обработкой данных экспериментов по перемешиванию в пористой среде. Тензор Atj обычно называется тензором дисперсии, иногда также тензором конвективной диффузии. Из условий симметрии следует, что в изотропной среде одна из главных осей тензора Ац совпадает с направлением скорости фильтрации, а две другие могут быть выбраны произвольно в плоскости, перпендикулярной
--V-
вектору и. Компоненты тензора А{]- в главных осях Кг = Ац и Кг = А 22 = Ааз называются соответственно коэффициентами продольной и поперечной дисперсии.
Коэффициенты Kin К2 определяются описанным выше механизмом перемешивапия и поэтому являются функциями средней скорости движения (скорости фильтрации и) и свойств пористой среды (/, тп, . . .) и жидкости (|х, р, D):
Ki = fi(u, D, р, р, I, m), (i=l, 2), (Х.1.2)
где D — коэффициент молекулярной диффузии.
Размерность коэффициентов дисперсии Ki и Кг есть L2jT. Поэтому
Ki = ийр,- (Ре, N. Oj, а2, . . .), (ХЛ.З)
где Ре = (число Пекле); N = аь аг> • • • представляют собой
безразмерные параметры структуры порового пространства; ф, —
безразмерная функция.
Из формулы. (ХЛ.З) следует, что зависимость коэффициентов дисперсии от скорости фильтрации проявляется через их зависимость от числа Пекле. На рис. Х.1 приведена зависимость безразмерного коэффициента продольной дисперсии К/D от Ре. Этот график получен в результате обработки большого числа экспериментов по исследованию распределения концентрации нейтральной примеси в однородной жидкости при фильтрации в несцементированных песках [58]. В качестве характерного размера I принимался средний диаметр зерен.
Заметим, что эксперименты проводились при различных значениях параметра N) но заметного влияния этого параметра на К 4 не обнаружено. В области самых малых скоростей фильтрации, когда ul <? D, механическое перемешивание несущественно по сравнению с молекулярной диффузией и
Kt — aD, (Х.1.4)
где а — постоянная, зависящая от структуры порового пространства. Б диапазоне 1 <С Ре < 100 располагается переходная область, в которой существенны оба процесса — молекулярная диффузия и механическое перемешивание.
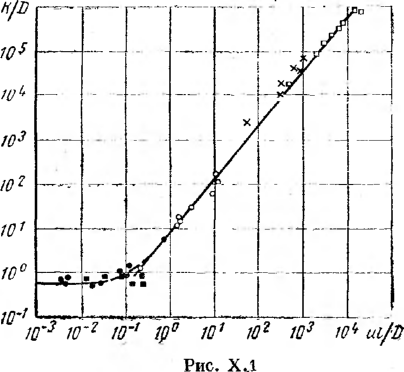
Накопец, в области Ре >> 100 влияние молекулярной диффузии на коэффициенты дисперсии незначительно и — const.
При числах Ре >105 величина К Jul начинает уменьшаться с ростом Ро.
Б этом диапазоне уже сказывается влияние инерционных сил на распределение скоростей в порах. , 1
Зависимость коэффициента поперечной дисперсии К 2 от числа Пекле в принципе аналогична зависимости Aj(Pe). Однако влияние скорости на К2 начинает проявляться при значительно больших числах Пекле, чем для Kt. Поэтому при больших числах Пекле
Ki К2, как это видно из рис.Х.2, заимствованного из работы Марль и Потье [147]. Подробный анализ зависимости тензора дисперсии от скорости приводится в гл. II книги А. Бан и др. [3], на-иисанной В. Н. Николаевским, а также в книге Коллинза [58]. Там же имеется и подробная библиография.
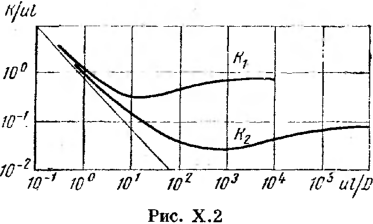
Запишем теперь уравнения совместной изотермической фильтрации двух взаиморастворимых несжимаемых жидкостей. Уравнения неразрывности каждого компонента выводятся в точности так же, как уравнение (VI.2.4), и имеют вид:
гДе Qx — поток данного компонента, который может быть выражен в виде:
Подстановка выражений (Х.1.6) в (Х.1.5) приводит к системе нелинейных уравнений для с — и р:
= (ХЛ.7)
dt * dxi
дс
При исследовании потоков жидкости в пористой среде при помощи меченых частиц вытесняющая жидкость (содержащая нейтральную примесь) имеет те же физические свойства, что и вытесняемая. Поэтому система (X.1.7)—(Х.1.8) разбивается па два независимых уравнения, одно из которых определяет поле скоростей, а второе служит для определения концентрации. При этом второе уравнение будет линейным. В большинстве задач, связанных с движением меченых частнц, фильтрацию можно считать установившейся. Тогда уравнение (Х.1.7) переходит в уравнение Лапласа.
При исследовании собственно вытеснения смешивающихся жидкостей, например вытеснения нефти растворителями, задача упрощается в связи с тем, что скорости фильтрации в пласте вдали от скважин невелики и изменяются незначительно. Так, например, при а = 350 м/год 10“3 см/сек и I = 0,01 см (что соответствует проницаемости около id) Ре 1 (так как D обычно порядка — 10“5 см2/свк). Поэтому коэффициенты дисперсии можно считать не зависящими от скорости, а при достаточно малых скоростях (при Ре< 10) и равными между собой (приблизительно равными коэффициенту молекулярной диффузии). Вблизи скважин течение можно считать одномерным (радиальным), однако распределение концентрации может и не быть одномерным.
2. Рассмотрим некоторые одномерные задачи вытеснения смешивающихся жидкостей.
В случае одномерного прямолинейного вытеснения несжимаемых жидкостей в несжимаемой пористой среде уравнение (Х.1.7) дает и = и0 — const. Если не учитывать возможной зависимости коэффициента К4 от отношения вязкости, уравнение (Х.1.8) примет вид:
(Х.1.9)
Поскольку и0 — const, ТО И К i(ti0) = const.
Пусть жидкость 1 нагнетается в полубесконечный пласт, первоначально заполненный жидкостью 2. Тогда имеем следующие граничные и начальные условия: с (0, t) — 1, с (©о, t) = 0, с (х, 0) = 0. Приме-ния преобразование Лапласа к уравнению (Х.1.9), имеем для с* =
СО
= J с (х, I) e_D/dt
Граничные условия для с* запишутся в виде: с* (0) = ~ J с*(оо) = 0.
Соответствующее решение уравнения (Х.1.10) имеет вид:
С* \ ехр | — уж (V'а2-1 о а)|, (Х.1.11)
где а
Для отыскания оригинала по изображению (Х.1.11) используем известную формулу (см. гл. III)
4-сх (Х.1.12)
Кроме того, известно, что если преобразование Лапласа функции ф (/.) есть F (а), то преобразование функции ехр (—<Л)ф (t) будет F (д.2 -f- о). Используя эти соотношения, а также теорему умножения для преобразования Лапласа, найдем после некоторых преобразований
с<*. ()-=|erfc(i=^-)+iexp(f.)erfc(^). (Х.1.13)
Фронту вытеснения, очевидно, соответствует окрестность точки х — Vt. При х, близком к Vt, и при больших t второе слагаемое в формуле (Х.1.13) пренебрежимо мало и
2
Формула (Х.1.14) представляет решение уравнения (Х.1.9), удовлетворяющее следующим начальным условиям: с (х, 0) — 1 при х <С 0 и с (х, 0) = 0 при х > 0.
Из формулы (Х.1.14) следует, что через достаточно большое время переходная зона, в которой концентрация меняется от некоторого малого значения е до 1 — е, со временем расширяется пропорционально У Kt. Если принять е = 0,005, то половина ширины переходной зоны равна 4|/Kt.
Для случая радиального вытеснения уравнение (Х.1.7) дает и = qjr, где q0 = const. Из уравнения (Х.1.8) получим
Если молекулярной диффузией можно пренебречь, то Kt = Ки или К j — Тогда вместо (Х.1.15) имеем
(Х.1.16)
dt 1 г дг г дг2 ' '
Уравнения (Х.1.15) или (Х.1.16) могут быть решены только численно. Для приближенной оценки роста переходной зоны заменим в уравнении (Х.1.15) переменные г2 — 2q0t = ?, t' — t. Зависимость К ,(«) приближенно примем в виде К , — К 0 + Я и. Тогда уравнение (Х.1.15) запишется как
дс
dt
Если в пласт, содержащий только вытесняющую жидкость (с — 0), закачивается жидкость с концентрацией с = 1, то фронт вытеснения (без учета дисперсии) перемещается по закону г — |/2q0t. Для оценки распределения концентрации вблизи фронта при больших t можно полагать, что ширина переходной зоны намного меньше, чем г, т. е. | ?| 2q0t. Тогда выражение в квадратных скобках при
мет вид: 2K0q0t + /2(q0t) 1г К и может быть вынесено за знак производной по Z,. Полагая
о l/о* К
Т = 4q0 (*2 — *о) + —д — 7^ 1ШУ/г - Шо)v*l
(где t0 — некоторая постоянная), приведем уравнение (Х.1.17) к виду:
(ХЛЛ8)
Чтобы оценить скорость роста переходной зоны, рассмотрим автомодельное решение уравнения (Х.1.18), имеющее вид, аналогичный (Х.1.14):
с
Это решение описывает в переменных т распросранение первоначально «ступенчатого» распределения концентрации (т. е. так, что при т — 0 с — 1, если Z, < 0, н с — 0, если ? >0). В переменных г, t эти условия выразятся так: при t — t0 с — 1, если г'2 —
— 2g0i0 < 0, и с = 0, если г2 — 2q0t0 >0. При этом, разумеется, остается в силе предположение, что | т2 — 2g0i0| < 2q0t0. Подставляя в (Х.1.19) вместо |итн выражения через г и t, получим
с= 4-erfcf—р-:---Т.гЬ (Х.1.20)
12 (*2-Ф + ((?о'о)’/2-(?<A>)'/sJ ’ )
Для оценки ширины переходной зоны используем условие е =
= 0,005, откуда —?=- < 2, или 2 V Я0т
_=---тт77^2- (Х.1.21)
2|4?<До(*2-г8)+
8 32Х
(fooOV2-(9o'o)*/2)j
При сравнительно небольших временах, когда второй член в квадратных скобках значительно превышает первый (т. е. дисперсия преобладает над молекулярной диффузией), из условия (Х.1.21), пользуясь также тем, что |r2 — 2g0# | <С 2q0t, легко установить для ширины переходной зоны асимптотическое выражение
г- V2qj ~ 4 j/| X (2^о0,/а~ 4 Кг. (X. 1.22)
Для больших времен, когда значения г таковы, что К0
r — V2qBtt**2V2Kotf*2Y-^r. (Х.1.23)
Как показывает экспериментальная проверка (Бентсен, Нильсен, [131]), формула, аналогичная (Х.1.20), сравнительно хорошо описывает распределение концентрации при радиальном вытеснении.
§ 2. УСТОЙЧИВОСТЬ ВЫТЕСНЕНИЯ НЕСМЕШИВАЮЩИХСЯ И СМЕШИВАЮЩИХСЯ ЖИДКОСТЕЙ ИЗ ПОРИСТОЙ СРЕДЫ
При изучении вытеснения жидкостей в пористой среде существенны вопросы устойчивости полученных решений. Физически возможность возникновения неустойчивости связана с тем, что при проникновении (за счет случайных возмущений) частицы более подвижной жидкости в область, занятую менее подвижной жидкостью, она оказывается под действием больших градиентов давления, чем действовавшие на нее в невозмущенном состоянии, и движение частицы ускоряется. Если более подвижная жидкость является вытесняющей, это приводит к разрастанию возмущений. В результате такого элементарного подхода (см. И. А. Чарный [119]) получаются те же условия устойчивости, что и при использовании более строгой теории.
Общий способ анализа устойчивости какой-либо системы состоит в исследовании ее поведения после наложения на основное состояние малых возмущений.
1. Рассмотрим вначале простейший случай —- вертикальное движение с постоянной скоростью плоской границы раздела двух жидкостей, имеющих различные плотности и вязкости. Такая схема является предельной как для вытеснения смешивающимися, так и несмешивающимися агентами, если препебречь шириной переходных зон.
Фильтрация каждой из жидкостей описывается следующими уравнениями (ось х направлена вертикально вверх):
Ъ~1 / др , \ !ci др др
йЬ^+р*); vi=-jjW'
ди; ди: dWj
Величины, относящиеся к каждой из фаз, здесь обозначены индексом 7 = 1, 2; проницаемости kj приняты различными по обе стороны границы раздела, чтобы учесть возможную неполноту вытеснения несмешивающихся жидкостей; в последнем случае по обе стороны границы различны насыщенности в, следовательно, различны относительные проницаемости.
На границе раздела должны выполняться условия (см. гл. VI, § 2) (VI.2.19) и (VI.2.21):
A = Pi’
где unj — проекции скорости фильтрации на нормаль, к границе раздела; Vn — скорость перемещения границы по нормали к ней.
Система (Х.2.1) с условиями (Х.2.2) имеет следующее решение, соответствующее равномерному перемещению плоской границы раздела :
w1 = w2 = w0; ^ = ^ = 0; щ^и>2 = 0;
Р1 - М0) - Ро — (тг>о + Рхg) (х - Vt) (х — Vt < 0);
/?2 = Ря0) = /,о-(-^-«о + Р2^) (х~Vt) (z — Vt >0). (Х.2.3)
При зтом V„ = V — Уравнение невозмущенной границы раздела имеет вид х — Vt.
Рассмотрим решение системы (Х.2.1), отличающееся от (Х.2.3) малыми возмущениями. Для этого положим
Uj = u0+Bu*; Vj = rv*; Wj=--&w*\ рг р<°> -+ ejpJ; ft —p?0)-f epl,
(X.2.4)
где e — малая величина.
Уравнение границы раздела имеет вид:
х = х0 (у, z, f) = Vt + sx* {у, 2, t). (Х.2.5)
к; др* к/ др* kj др*
---i- • Vi = —--5---W: =---*
И/ дх > ' |i/ ду > I Hj dz *
в»? dw*,
—L_J--L.J--L — 0.
dx dy ‘ dz
Пользуясь малостью искажения границы, можно отнести условия (Х.2.2) на невозмущенную границу раздела х = Vt. Тогда с точностью до малых порядка е условия на границе принимают вид:
дх*
* * С/л*
при x = Vt;
К условиям (Х.2.7) следует присоединить также услопия затухания всех возмущений при х -» ±°°, так как предполагается, что возмущение возникает вблизи границы раздела.
Произвольное возмущение может быть разложено в интеграл Фурье по у и z. Позтому для исследования устойчивости достаточно рассмотреть развитие элементарного синусоидального возмущения. Для этого представим х* и р* в виде произведений
х* =- X (t) ехр (iy^j + iy2z) (i = V~A)\
p*i — Pj(x, t) exp (iyxy -f iy2z) (/=-1, 2), (X.2.8)
где X (t) и Р,(х, t) — амплитуды возмущений х* и р*.
Подставляя выражения (Х.2.8) в уравнение (Х.2.6), получим, что функция Pj(x, t) должна иметь вид:
Р{(:с, t) = Р<.'> (г) охр {ух’)-\ Р<2> (t) ехр ух) (v = VH + Та);
(x = x — Vt).
Условия затухания возмущений на бесконечности дают:
Рх = Ра' (t) ехр {ух’)\ Р2 = Pw (t) ехр ( — 'I’-z')- (Х.2.10)
Подставляя эти выражения в условия (Х.2.7) и исключая Рш и Р(2), получаем следующее уравнение:
dX
dt
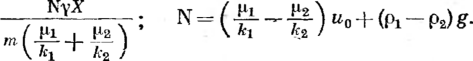
(Х.2.11)
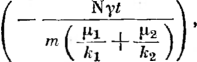
где Z0 — начальная амплитуда возмущения. Поэтому, если
N
то начальные возмущения со временем затухают, в противном же случае — возрастают. Поскольку в условие (Х.2.12) не входит параметр возмущения -у, это условие справедливо для возмущений произвольной формы. Таким образом, перемещение границы раздела устойчиво, когда выполняется условие (Х.2.12). Если условие (Х.2.12) не выполняется, граница раздела становится неустойчивой и разбивается на отдельные «языки» сложной и случайной формы (рис. Х.З). Когда действие силы тяжести несущественно, неравенство (Х.2.12) означает, что граница раздела устойчива в тех случаях,
когда вытесняющая жидкость обладает большей вязкостью, чем
вытесняемая, и неустойчива в противном случае. Действие силы тяжести способствует устойчи-У__________j______вости границы, если вытес
нение идет снизу вворх и вытесняющая жидкость Dena
li „ дает большей плотностью. г В случае несмешивающихся жидкостей рассмотренная граница раздела представляет собой факти-Рпс. Х.З чески предельное положение
скачка насыщенностей, когда насыщенности но обе стороны скачка различны, но постоянны. В общем случае насыщенность вытесняющей фазы впереди фронта и насыщенность вытесняемой фазы за фронтом не равны нулю. С каждой стороны границы различны не только вязкости, но и проницаемости каждой из фаз. Поэтому в случае несмешивающихся жидкостей устойчивость определяется не соотношением вязкостей, а соотношением подвижностей, т. е. величин Д^/цу. Отношение подвижностей может быть рассчитано по кривым относительной проницаемости, исходя из насыщенностей по обе стороны скачка, которые в свою очередь определяются по формулам (VI.2.29) и зависят от отношения вязкостей. С ростом отношения вязкостей
Л/ = — отношение подвижностей М* — также растет, но М*
Г1 «2^1
становится больше единицы, т. е. устойчивость нарушается только когда М значительно превышает единицу. При обычной форме кривых относительной проницаемости типа изображенных на рис. VI.5 отношение вязкостей, при котором наступает неустойчивость, составляет около 10—15. Типичная зависимость М* от М показана на рис. Х.4.
Эксперименты по вытеснению нефти водой, проведенные Б. Е. Ки-силенко [55] на прозрачных моделях пласта с насыпной пористой средой, показали, что неустойчивость наступает при отношении вязкостей фаз около 12—13. Если плоская граница раздела неустойчива, то с течением времени она разбивается на большое число отдельных «языков» неправильной формы (см. рис. Х.З).
Если за счет неоднородности потока насыщенность в некоторой точке изменяется на малую величину, то такое возмущение распространяется, не затухая и не разрастаясь. Действительно, уравнения неразрывности при плоском двухфазном течении имеют вид (см. гл. VI):
диг , dvi
ds_
dt
ди
дх
+ #=0; 1 ду
(Х.2.13)
-т
дх
Зу
Кроме того, исходя иэ обобщенного закона Дарси (VI.2.1), можно записать
M
Рис. X.4
ил = uF (s); i?! = vF (s);
/i<*)
1
fi (s) + -jf /2 (s)
(X.2.14)
Тогда вместо первого из уравнений (Х.2.13) имеем
(Х.2.15)
dt
дх
тТГ + иР' (*) ? + vF' (s) -?r=°-
By
Для невозмущенного течения и = и0, s = s0, причем скорость распространения скачка, согласно условию Баклея — Леверетта
(VI.2.30), равна V = ~F' (s0). Вводя значения возмущения скорости
и насыщенности, получим из (Х.2.15)
ds*
«о
(Х.2.16)
= 0.
os ' . т/ as~
~dt •" дх
Из этого уравнения видно, что возмущения насыщенности вблизи скачка распространяются, не затухая, со скоростью, равной скорости скачка. Таким образом, учет возмущений насыщенности не приводит к изменению условия устойчивости.
2. Выше была рассмотрена устойчивость резкой границы раздела фаз, на которой действуют только силы тяжести и вязкого сопротивления. Однако при вытеснении несмешивающихся жидкостей на устойчивость могут оказать влияние поверхностные силы, а в случае смешивающегося вытеснения — дисперсия и молекулярная диффузия. Выравнивающее действие капиллярных сил в пористой среде в общем случае связано с процессами перераспределения насыщенности, и для исследования устойчивости необходимо рассматривать
возмущения течения в переходной зоне. Ограничимся условиями, когда длина волны возмущения велика по сравнению с шириной переходной зоны, чтобы действие капиллярных сил можно было учитывать только в граничных условиях. В этом случае для исследования вне узкой переходной зоны можно использовать уравнения (Х.2.1). Этот подход, как мы увидим далее, связан с довольно существенными ограничениями. Для простоты выкладок ограничимся случаем плоской горизонтально!! фильтрации. Исходя из формул
(VI.2.1) гл. VI, уравнения двухфазной фильтрации в переходной зоне запишем в виде:
А- 4 / \ 8Pi A* j / \ '-др>
(Х.2.17)
Примем, что разность давлений в фазах равна капиллярному давлению — известной функции насыщенности (см. Рис. Х.5 гл. VI, § 3):
Уравнения неразрывности имеют обычный вид (Х.2.13). Комбинируя уравнения (Х.2.17) и (Х.2.13), можно получить систему для и — иу + u2, v = vx + v2 и s:
ds - . . ds - . ds „ / й2Ф (s) . д-Ф (s) \ A
(X-2,9)
(обозначения см. гл. VI, § 4); ф (s) — f1 (s) -j-
Чтобы получить граничные условия для возмущений, проинтегрируем уравнения (Х.2.19) по х вдоль переходной зоны, считая, что граница раздела слабо искривлена (рис. Х.5). При этом пренебрежем членами порядка ширины зоны и квадратами производных по у. Тогда вместо первого уравнения (Х.2.19) получим
т (si — sa) 4- uWF (si) — ull'F (s^
\vn)F Kb v2F (s2)] ^ - a*m (Ф, - Ф,)-^- = 0. (X.2.20)
Здесь индексом 2 обозначены величины справа, от переходной зоны, а индексом 1 — слева от нее. Интегрирование двух других уравнений (Х.2.19) дает
рП> t-(2)
(—---~)-PL- (Х.2.21)
= - гг'2’
V Ф1 Фг / ду
ф1 ф2 \ ф!
Переходя к возмущениям, примем, как и ранее,
х0 — Vt-\-bx*',
«7 = и о + eu*; v}= еу*.
Тогда для возмущений получим из (Х.2.20)
дх* _и*^ V —
a2-1- Фг- 4гг~ = О
(Х.2.22)
5/ к0 sx — s2 di/2
и из (Х.2.21)
«1 = и; = ы*; --—(Х.2.23)
12 фл Ч>2 ' 7
Второе из уравнений (Х.2.23), очевидно, эквивалентно последнему из уравнений (Х.2.7) при = р2 и может быть переписано в виде:
р\ - Pi - «« (-g— -g-) X*; Л, = Лф#-. (Х.2.24)
Условие (Х.2.22) заменяет второе равенство (Х.2.7). Поскольку, как и ранее, предполагается, что по обе стороны границы течение потенциальное, р* и х* снова могут быть выражены формулами (Х.2.8)—(Х.2.10).
Используя условия (Х.2.7) и (Х.2.22) и исключая Pa\t) и Pw (t), получим для X (t) уравнение
Таким образом, граница раздела несмешивающихся жидкостей в пористой среде может стать устойчивой под действием капиллярных сил даже, если 1 — М* <' 0, т. е. условие (Х.2.12) не выполняется. Пусть М* > 1 ,т. е. без учета капиллярных сил граница неустойчива.
._-J у
Тогда условие (Х.2.26) все же выполняется, если у .
Это означает, что если длина волны возмущения границы Х= меньше критического значения Яс, то граница остается устойчивой. Критическая длина волны Яс определяется формулой
2п 2па2 Ф1—Ф2
(X.2.27)
Yc ~ V Si —S'2 ~M* — T'
![]()
В работе Чуок и др. [135] была исследована устойчивость границы раздела жидкостей в плоской щелевой модели, где действие поверхностных сил при искривлении границы приводит к возникновению разности давлений по обе стороны ее. Эта разность давлений направлена таким образом, что способствует выравниванию границы.
Предлагаем читателю самостоятельно исследовать устойчивость границы раздела в этом случае, воспользовавшись формулой Лапласа для разности давлений
![]()
где а — поверхностное натяжение; h — половина ширины щели. В этом случае критическая длина волны возмущения имеет вид:
(Х.2.29)
Эксперименты Чуока [135] и Б. Е. Кисиленко [55] подтверждают, что граница раздела остается устойчивой даже при неблагоприятном соотношении подвижностей, если скорость вытеснения достаточно Мала и вследствие этого ширина модели меньше критической длины волны возмущения.
3- Вывод формул (Х.2.26) и (Х.2.27) был сделан в предположении, что ширина переходной зоны намного меньше длины волны возмущения. В соответствии с результатами § 3 гл. VI ширина переходной зоны пропорциональна а2 IV. Поэтому указанное выше предположение справедливо только при М*, близком к единице, и большой величине (М* — I)-1. Существует значительный диапазон величин М, при которых М* близко к единице (см. рис. Х.4).
Тем не менее формулы (Х.2.26) и (Х.2.27) верны лишь для «слабой» неустойчивости, т. е. для М*, близкого к единице, и являются в этом смысле асимптотическими. Чтобы исследовать устойчивость во всем диапазоне изменения отношения вязкостей, следует использовать полную систему уравнений (Х.2.26). Эта задача пока до конца не решена.
Критическая длина волны возмущения Яс, разделяющей области устойчивого и неустойчивого вытеснения, в общем случае является
функцией параметров с2, У и М — Из соображений размерности
тогда следует
Если М близко к тому значению Мс, при котором М* становится равным единице, то выражение (Х.2.30) должно приближаться к зависимости (Х.2.27).
Рассмотрим отдельно устойчивость границы раздела по отношению к одномерным возмущениям насыщенности при учете капиллярных сил, т. е. исследуем устойчивость стабилизированной зоны. Распределение насыщенности в стабилизированной зоне представляет собой решение уравнения Рапопорта — Лиса (VI.3.4) вида s = ф0(а: — Vt) — ф0(х) и выражается формулой (VI.3.12). Перейдем в уравнении Рапопорта — Лиса, записанном в форме (VI.4.34), вместо х и t к новым независимым переменным x0(s) и (и новой искомой функции х — Vt = х; тогда это уравнение примет вид:
Ф’ (s) -J-
дх0
Введем теперь малые возмущения положения точки с насыщенностью s в стабилизированной зоне: х — z0(s) + ex*.
Для х* имеем уравнение
-ТГ'+ [- F+% F‘ w] ТГ+W ж “ <x-2-32>
где F^x) = F'(s)-, F2(x) = Ф'(*)-?-
dx
Учитывая формулу (VI.3.12), связывающую x с s, уравнение (X.2.32) можно записать в иной форме:
При малых t можно искать х*(х, t) в виде:
х*=Х{х)е~иш (Х.2.34)
Тогда уравнение (Х.2.33) сведется к следующему:
Яф1 (х) + а*А (f2 ф = 0. (Х.2.35)
ах \ ах )
Чтобы исследовать устойчивость, нужно таким образом решать задачу о собственных значениях для уравнения (Х.2.35) при граничных условиях .У = 0 при х — ± А. Если Я < 0, — течение неустойчиво, если Я > 0, — устойчиво.
Из приведенного в гл. VI, § 3 описания распределения насыщенности в стабилизированной зоне нетрудно убедиться, что
ах ах
В соответствии с общей теорией наименьшему собственному значению Я в поставленной граничной задаче соответствует собственная функция, обращающаяся в нуль только на концах рассматриваемого интервала. Тогда, интегрируя уравнение (Х.2.35) по х от —А до I А , легко получить что Ямнн ^ 0 при любых А. Это означает, что по отношению к одномерным возмущениям в любом конечном интервале стабилизированная зона всегда устойчива. Если рассматривать бесконечный интервал, то Я = О также может быть собственным значением, которому соответствует собственная функция X = Х0 = = const. Очевидно, возмущение подобного вида, т. е. сдвиг но оси х, не нарушает устойчивости стабилизированной зоны (см. аналогичную задачу об устойчивости пламени — Г. И. Баренблатт и Я. Б. Зельдович [19]).
В процессе вытеснения смешивающихся жидкостей стабилизирующее влияние на движение границы раздела оказывает перемешивание жидкостей в переходной зоне, т. е. дисперсия и молекулярная диффузия, поскольку перемешивание приводит к сглаживанию случайных возмущений насыщенности. Учесть влияние перемешивания на устойчивость границы раздела изменением условий на границе невозможно хотя бы потому, что ширина переходной зоны при вытеснении смешивающихся жидкостей неограниченно возрастает со временем (пропорционально ]/"t, см. § 1). Таким образом, для исследования устойчивости необходимо рассматривать полную систему уравнений для насыщенности (Х.1.8).
Полностью эта задача пока не решена, однако было получено несколько приближенных решений [130,142], каждое из которых связано с рядом довольно существенно ограничивающих предположений.
4. Чтобы описать вытеснение после потери устойчивости, можно действовать двумя способами. Первый из них заключается в том, чтобы проследить за формированием симметричной системы языков, образующихся в результате малого начального искажения границы (например, синусоидальном). Описание развития языка для случая, когда вязкость вытесняющей жидкости пренебрежимо мала, было сделано с Саффманом и Тейлором [155]. Впоследствии появился еще ряд работ, в которых учитывалась вязкость вытесняющей фазы. Однако этим способом можно проанализировать только начальную стадию развития языков как из-за математических трудностей, так и потому, что правильная форма языков не может сохраняться неограниченно долго. Последнее вызвано тем, что на боковой поверхности удлиненных языков возникают вторичные искажения, когда длина языка превосходит критическую длину волны возмущения.
Для упрощенного описания совместной фильтрации двух жидкостей при таком хаотическом движении рассмотрим случай плоского течения, когда протяженность языков в продольном направлении намного больше их ширины (см. рис. Х.З). Предположим, что в среднем течение является одномерным, т. е. скорость фильтрации каждой из жидкостей, осредненная по сечению, содержащему большое число языков, направлена вдоль оси х. Примем также, что насыщенности (или концентрации) s, и s2 постоянны по обе стороны границы (т. е. в областях 1 и 2). Тогда, пренебрегая фильтрацией и обменом в поперечном направлении, можем записать
<»*> =--^<-?>4 (* = 1.2), - (Х.2.36)
Н
где h — суммарная высота сечения, занятая первой (вытесняющей) жидкостью.
Рис. Х.6
ности для осредненного течения имеют вид:
dt
д < 1*2 >
Н
дх
¦т (1
Исключая из уравнений (Х.2.37) <; ) и учитывая, что (1-
— s2) < ы 1 > f Sj < щ > = и0, где и0 рации, получим одно уравнение для т] = было получено уравнение (VI.2.11):
-средняя скорость фильт-
h
Н
аналогично тому, как
(Х.2.38)
-О,
дх И-* -
dt
где
Т1 + М*(1-Ч) ’ ^ AiMl —*2) ‘
Решение уравнения (Х.2.38) получается точно так же, как решение уравнения Баклея — Леверетта (VI.2.И):
1
х(ч) -F' 0l)J МтМт + ЯоСП^С^'М + ЖоОп). (Х.2.39)
О
Зависимость ij (Q), соответствующая формуле (Х.2.39), представлена на рис. Х.6. Поскольку функция /'’'(t]) является монотонной, скачков средней насыщенности г] при зтом не образуется.
Решение вида (Х.2.39) рассматривалось А. М. Пирвердяном 191] и И. А. Чарным [119] применительно к образованию языка обводнения в наклонном пласте и А. Шейдеггером [156] для общего случая неустойчивого течения. Для вытеснения смешивающихся жидкостей близкие схемы были предложены Перрином [151] и Ковалем [140].
В книге использованы некоторые простейшие формулы и понятия векторного анализа. Ниже приводятся определения этих величин. Более подробные сведении можно найти в учебниках.
1. Скаляру (числовой функции) ф (л:и х2, х3) ставится в соответствие вектор градиента:
![]()
(А1)
2. Вектору а с компонентами at, a2, a3 соответствует скаляр div а (диверген-
ция а):
(А2)
![]()
Обозначим ii, i2; i3 — единичные векторы в направлении осей х1, х% и х3 и введем оператор Гамильтона (набла) у:
(АЗ)
С оператором Гамильтона можно формально производить действия, как с вектором, по правилам векторной алгебры. Имеем при этом
grad ф = уф;
(А4)
div а = уа.
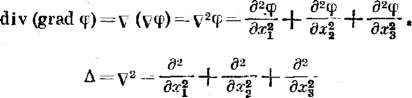
(AS)
(А6)
(А7)
Оператор
Наконец,
называется оператором Лапласа. В цилиндрических координатах (г, ф, г) его выражение имеет вид;
Наконец, часто используется формула преобразования поверхностного интеграла и объемный (формула Остроградского — Гаусса):
![]()
(А9)
Здесь а — некоторый вектор, заданный в объеме V, окруженном поверхностью S;
ап — проекция вектора а в некоторой точке поверхности S на направление нормали к этой поверхности.
В. Обозначения некоторых специальных функций
Интегральная показательная функция
СО
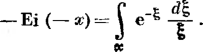
Функция ошибок
со
X
![]()
j e-S* d%. (В2)
О
X
Функция Бесселя n-го порядка первого и второго рода:
•М*); y„(x).
Модифицированные функции Бесселя n-го порядка первого и второго рода: /„(ж), Кп(х), функция Кп(х) называется также функцией Макдональда.
Функции Бесселя удовлетворяют дифференциальному уравнению Бесселя:
Х2у" — ту' -J- (z2 — /?2) У = О,
(ВЗ)
а модифицированные функции Бесселя — такому же уравнению, но только со знаком (+) перед п2. Необходимые свойства перечисленных специальных функций можно найти в книге [74] или в справочнике [26].
С. Некоторые сведения из операционного вычисления
В операционном исчислении каждой функции / (/,) переменной t, определенной при 0 sg г< оо, ставится в соответствие изображение
оо
![]()
о
(С1)
Соотношение (С1) носит название преобразования Лапласа; переменная а — параметр преобразования Лапласа. Если применить преобразование Лапласа к производной /'(t) и выполнить интегрирование по частям, то получим
L {/' (0) = oF (а) — / (0). В частности, если / (<) = 0 при ? — 0, то
(С2)
(СЗ)
Таким образом, функциональной операции дифференцирования для функций соответствует алгебраическая операция умножения на параметр а. Поэтому,
применяя преобразование Лапласа к некоторому дифференциальному уравнению, содержащему дифференцирование по времени, можно прийти к новому уравнению, в котором вместо аргумента t входит аргумент а уже в качестве параметра [ср. уравнения (III.1.1) и (III.1.5)]. Решая это уравнение, находим изображение F (а). Наконец, завершающим этапом является нахождение оригинала / (I) по изображению F (о). В настоящее время имеются обширные таблицы преобразований Лапласа, позволяющие в ряде случаев непосредственно найти необходимое изображение и соответствующий ему интеграл. Если это не удается сделать, то зачастую возможно свести рассматриваемый случай к табличному (приемы такого сведения также излагаются в справочниках). Например, пусть необходимо найти оригинал, отвечающий изображению
^(a)=-[(a + a)a]-i.
Ио таблице находим
[а + а]'1 — е~а>. (С4)
Учитывая, далее, что умножение изображения на а соответствует дифференцированию оригинала [формула (С2)], получаем
1
/' « - е-к(; / (7) = f е-“т А = 1 {1 - е'*1].
J а
0
Тот же результат можпо получить по-другому. Представим F (о) в виде:
F(rr) =_1 _ 1 Г 1 1 1
a(o-j-a) а L° а-{-а_Г
Отсюда, используя линейность преобразования Лапласа, по формуле (С4) получаем выражение для f (t).
Наконец, в общем случае оригинал находится по изображению по формуле обращения:
¦уf со
Y-^oo
Здесь F (а) рассматривается как функция комплексного переменного о — = Е; -j- i\], и интеграл берется по прямой, параллельной мнимой оси т) и расположенной иранее нее. Формула обращения (Со) является одновременно и наиболее сложным, и наиболее универсальным средством анализа решения, полученного методами операционного исчисления. Согласно теории функций комплексного переменного, путь интегрирования в комплексной плоскости можно при определенных условиях деформировать, не изменяя значения интеграла. Это позволяет в ряде случаев либо явным образом вычислить интеграл (С5), либо исследовать его свойства. В частности, установлена следующая связь между видом функции F (а) и асимптотическим поведением функции / (/) при I. -> оо.
Рассмотрим все особые точки функции F (а) (а0, а j, а.,, . . .), считая их занумерованными в порядке убывания веществспиых частей (Re а0 > Re at > >• Re а2 >•. . .). Тогда пмеет место теорема [42].
Если изображение F (а) можно разложить в окрестности точки о0 в степенной ряд
ОО
F(o) = 2cv(a-a0)Xj (--V<X0<X1<...) (СО)
v-0
с произвольными показателями (необязательно целочисленными), то оригинал / (!) при t ->- оо можно представить в виде асимптотического разложения:
ОО
/(*>~е’-'2т(=г^- гЛ,'1‘ (С7)
V-0
в котором необходимо положить 1,/Г ( A.v) = 0, если к.ы принимает значения О! 1; 2;----
В частности, отсюда следует, что если разложение (С6), начиная с некоторого члена, содержит лишь целые положительные степени, то соотношение (С7) превращается в конечную асимптотическую формулу. Поэтому разность
CO
V=0
стремится к нулю быстрее (или возрастает медленнее), чем е^°0_Е^1, где е — достаточно малое число.
Можно показать, что асимптотическое поведение/,(?) при t -*¦ оо определяется поведением F (а) вблизп особой точки о о1 таким же образом, каким асимптотика / (*) определяется поведением F (а) вблизп точки а = а0.
В случае, если несколько особых точек изображения имеют одинаковые веще ствениые части, асимптотическое поведение оригинала оказывается более сложным. Соответствующие результаты приводятся также в литературе [42].
D. Анализ размерностей и подобия
В теории фильтрации анализ размерностей н подобия играет существенную роль. Соображения анализа размерностей и подобия просты, но не тривиальны; они осповапы па нескольких определениях и фактах, которые предсталляется целесообразным изложить здесь без доказательств.
1. Все физические величины выражаются числами, получающимися путем их сравнения с единицами измерения. Единицы измерения разделяются на основные (например, единица массы — 1 г, единица длины — 1 см и т. д.) и производные, которые получаются из основных единиц на основе определения соответствующих величин (единица скорости — 1 см/сек, единица силы — 1 гсм/сек2 и т. д.). Системой единиц измерения называется совокупность единиц измерения, достаточная для измерепия характеристик рассматриваемого класса явлений. Например, для класса механических явлений стандартной системой является система СИ, наряду с которой применяются системы СГС (см. г, сек), МКС (м, кге (сила), сек). Классом систем единиц измерения называется совокупность систем единиц измерения, отличающихся только величиной основных единиц измерения. Например, из спстемы СИ получается класс систем
кг м сек ..
лГ> Т> -Т ’ (Ш)
в котором основные единицы массы. длины и времени получаются соответственно уменьшением в М, L, Т раз произвольно выбранных единиц массы, длины и времени: килограмма, метра и секунды. Класс систем единиц измерения обозначается заглавными буквами величин, единицы измерения которых приняты
за основные; одновременно эти буквы означают, во сколько раз уменьшается
основная единица при переходе от одном системы к другой внутри даппого класса. Например, класс (1) обозначается MLT. Размерностью данной величины называется выражение, которое показывает, во сколько раз изменяется единица измерения данной величины при переходе от одной системы к другой внутри данного класса. Естественно, что размерность существенно зависит от класса систем единиц намерения, например в классе MLT— размерность скорости LТ~1, силы MLT'2 и т. д. Если размерность величины в данном классе тождественно равна единице, величина называется безразмерной. Размерность некоторой величины / обозначается символом [/].
2. В приведенных выше примерах размерность всегда представлялась степенным одночленом. Можно показать, что это — общий факт, поскольку все системы внутри данного класса равноправны. Равноправие означает, что размерность зависит только от того, во сколько раз изменяются основные единицы системы единиц измерения при переходе от одной системы к другой внутри данного класса систем единиц измерения, но не зависит от того, какая именно система единиц измерения была исходной.
3. Величины ctj, а2, . . ., ад. имеют независимые размерности, если ни для одной из них нельзя нредстанить размерность в виде произведения степеней размерностей остальных. Например, плотность р, сила f и скорость vимеют независимые размерности ML~3, MLT~Z, LT_1. Напротив, размерности длины I, скорости v и ускорения w зависимы.
4. Физическую закопомерпость можно представить в виде одной или нескольких зависимостей:
о = /(а ......ak, ак+ъ . . ап.) (D2)
Функция / зависит от п переменных, в качестве которых должны быть выбраны все величины, определяющие характеристики рассматриваемого явления. Если известна математическая постановка задачи, то величины в1, . . ., а^, а?+1, . . ., ап представляют собой независимые переменные н параметры, входящие в уравнения и в дополнительные условия (начальные и граничные), определяющие единственное решение уравнения. Если математическая постановка задачи неизвестна, выбор величин ах, . . ., ап—вопрос интуиции исследователя.
Предположим, что величины аи .... а* имеют независимые размерности, а размерности величин а*+1, . . ., ап выражаются через размерности величин “д.....в ak:
............................(D3)
= . . . [а*]’"-*.
Размерность величины а заведомо выражается через размерности величин а 1, . . ., а^:
N = [^1* . . . [а*]«. (D4)
В противном случае это означало бы, что список величин а1г . . ., пп, опре
деляющих величину а, неполон: изменяя основные единицы измерения так, чтобы величины а„ . . ., ад,, а следовательно, и afe+1, . . ., ап оставались неизменными, мы могли бы изменять величину а, не меняя величин а1( . . ., ап.
Введем величины
п=-—-----• Я! =-а——— , . . nn-k=-—--• (D5)
л» лх J 1 гу. X, * ’ " й а. .¦ v... . ' '
л®1 /7*1 " ^п—У Щг-Ь
а1 ¦ ¦ ¦ ak а\ ... а* К
Нетрудно проверить, что эти величины безразмерны. Можно доказать следующий факт. Зависимость (D2), выражаемую через функцию п переменных, можно представить через функцию п — к переменных:
Jl = f (я*, Л2, • ¦ Ял-fc). (D6)
Такая зависимость носит название л-теоремы; л-тсорсма отражает независимость физических законов от выбора основных единиц измерения. Она имеет фундаментальное значение, поскольку позволяет уменьшить число параметров, определяющих искомые характеристики задачи.
5. Фундаментальное значение имеет также понятие подобия явлений. Явления называются подобными, если они отличаются между собой только величиной определяющих параметров alt . . ., ап и притом так, что величины л |, . . ., для этих явлений одинаковы.
Важность понятия подобия явлений определяется следующими соображениями. Рассмотрим два подобных явления, одно иа них условно назовем моделью, другое — натурой; соответствующие значения величин будем обозначать индексами (м) и (н).
В силу jx-теоремы и равенства величин п15 . . ., величины я для этих
двух явлений равны:
Ш7)
откуда и из (D5) имеем
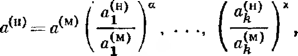
так что значение а(н) в натуре при обеспечении подобия простым пересчетом получается по результатам определения величины а,м) на модели (в ряде случаев более дешевой, проще изготовляемой и т. д.). Величины jilt . . ., яп_?, равенство которых обеспечивает подобие явлений, называются поэтому параметрами подобия, или критериями подобия.
1. Алишаев М. Г., Вахитов Г. Г., Глумов И. Ф., Фоменко И. Е. Особенности фильтрации пластовой девонской нефти при пониженных температурах. «Теория и практика добычи нефти». Ежегодник. М., изд-во «Недра», 1966.
2. Аравин В. И., Нумеров С. Н. Теория движения жидкостей и газов в не-деформируемой пористой среде. М., Гостехтеориздат, 1953.
3. Бан А., Богомолова А. Ф., Максимов В. А., Николаевский В. Н-, Оган-джаиянц В. Г., Рыжик В. М. Влияние свойств горных пород на движение в них жидкостей. М., Гостоптехиздат, 1962.
4. Бареиблатт Г. И. О некоторых неустановпвшихся движениях жидкости и газа в пористой среде. «Прикладная математика и механика», т. 16, выи. 1, 1952.
5. Баренблатт Г. И. Об автомодельных движениях сжимаемой жидкости в пористой среде. «Прикладная математика и механика», т. 16, вып. 6, 1П52.
6. Баренблатт Г. И. Об одном классе точных решений плоской одномерной задачи нестационарной фильтрации газа в пористой среде. «Прикладная математика и механика», т. 17, вып. 6, 1953.
7. Баренблатт Г. И. О приближенном решении задач одномерной нестационарной фильтрации в пористой среде. «Прикладная математика и механика», т. 18, вып. 3, 1954.
8. Баренблатт Г. И. О предельных автомодельных движениях в теории нестационарной фильтрации газа в пористой среде н теории пограничного слоя. «Прикладная математика и механика», т. 18, вып. 4, 1954.
9. Баренблатт Г. И. О некоторых задачах неустановившейся фильтрации, Изв. АН СССР, ОТН, № 6, 1954.
10. Бареиблатт Г. И. О некоторых приближенных методах в теории одномерной неустановившейся фильтрации жидкости при упругом режиме. Изв. All СССР, ОТН, № 9, 1954.
11. Баренблатт Г. И. О некоторых задачах восстановления давления и рас-просграиенин волны разгрузки прп упруго-пластическом режиме фильтрации. Изв. АН СССР, ОТН, № 2, 1955.
12. Баренблатт Г. II. О возможности линеаризации в задачах нестационарном фильтрации газа. Изв. АН СССР, ОТН, № 11, 1956.
13. Баренблатт Г. И. Об автомодельных решениях задачи Коши для нелинейного параболического уравнения нестационарной фильтрации газа d пористой среде. «Прикладная математика и механика», т. 20, вып. 6, 1956.
14. Баренблатт Г. И. О некоторых краевых задачах для уравнений фильтрации жидкости в трещиноватых породах. «Прикладная математика и механика», т. XXVII, вып. 2, 1963.
15. Барепблатт Г. П., Борисов Ю. А., Каменецкий С. Г., Крылов А. П. Об определении параметров нефтеносного пласта по данным о восстановлении давления в остановленных скважинах. Изв. АН СССР, ОТН, № 11, 1957.
16. Баренблатт Г. И., Вишик М. И. О конечной скорости распространения в задачах неустановившейся фильтрации жидкости и газа в пористой среде. «Прикладная математика и механика», т. 20, вып. 3, 1956.
17. Баренблатт Г. И., Желтов Ю. П. Об оснонных уравнениях фильтрации однородных жидкостей в трещиноватых породах. ДАН СССР, т. 132, вып. 3, 1960.
18. Баренблатт Г. И., Желтов Ю. П., Кочина И. Н. Об основных представлениях теории фильтрации однородных жидкостей в трещиноватых породах. «Прикладная математика и механика», т. 24, вып. 5, 1960.
19. Баренблатт Г. И., Зельдович Я. Б. О решении типа диполя в задачах нестационарной фильтрации газа при политропическом режиме. «Прикладная математика и механика», т. 21, вып. 5, 1957.
20. Баренблатт Г. И., Крылов А. П. Об упруго-пластическом режиме
фильтрации. Изв. АН СССР, ОТН, № 2, 1955.
21. Баренблатт Г. И., Крылов А. П. Об упруго-пластическом режиме
нефтяного пласта. Доклады на IV Международном нефтяном конгрессе н Риме. Изд-во АН СССР, М., 1955.
22. Баренблатт Г. И., Максимов В. А. О влиянии неоднородностей на
определение параметров нефтеносного пласта по данным нестационарного
притока жидкости к скважинам. Изв. АН СССР, ОТН, № 7, 1958.
23. Баренблатт Г. И., Сивашинский Г. И. Автомодельные решения второго рода в нелинейной фильтрации. «Прикладная математика н механика», т. 33, вып. 5, 1969.
24. Баренблатт Г. И., Трифонов Н. П. О некоторых осесимметричных задачах неустановившейся фильтрации жидкости и газа в пористой среде. Изв. АН СССР, ОТН, 1956.
25. Барепблатт Г. И., Шестаков В. М. О фильтрации в сухой грунт. «Гидротехническое строительство», 1955, № 1.
26. Баренблатт Г. И. Фильтрация двух несмешивающихся жидкостей в однородной пористой среде. Изв. АН СССР, серия «Механика жидкости и газа», № 5, 1971.
27. Бейтмен Г., Эрдейи А. Высшие трансцендентные функции, т. 1—3 (нер. с англ.). М., изд-во «Наука», 1965—1967.
28. Берчик Э. Свойства пластовых жидкостей. Гостоптехиздат, 1960.
28а. Бернштейн М. А. Анализ разработки газовых месторождений и установление реальных запасов газа на примере Ижма-Омринских месторождений Коми АССР. Дисс. на соиск. уч. степ. канд. техн. наук, МИНХ и ГП, М., 1964.
29. Блинов А. Ф., Зайнуллии Н. Т. Об изменении параметров пласта в нагнетательных скважинах. Тр. ТатНИИ, вып. 10. М., изд-во «Недра», 1967.
30. Боксерман А- А., Данилов В. Л., Желтов Ю. П., Кочешков А. А.
К теории фильтрации несмешивающихся жидкостей в трещиновато-пористых породах. «Теория и практика добычи нефти», Ежегодник ВНИИНефть. М., изд-во «Недра», 1966.
31. Боксерман А. А., Желтов Ю. П., Кочешков А. А О движении несмешивающихся жидкостей в трещиновато-пористой среде. ДАН СССР, т. 155, № 6, 1964.
32. Боксерман А. А., Шалимов Б. В. О циклическом воздействии па пласты с двойной пористостью при вытеснении нефти водой. Изв. АН СССР, серия «Механика жидкостей и газа», 1967, № 2.
33. Борисов Ю. П. Определение дебита скважин при совместной работе нескольких рядов скважин. Тр. МНИ им. Губкина, вып. 11. М.. Гостоптехиздат, 1951.
34. Бузинов С. Н. Теоретические и экспериментальные исследования движения двухфазной системы жидкостей в пористой среде. Дисс. на соиск. уч. степ. канд. техн. наук, МИНХ и ГН, 1958.
35. Бузинов С. Н., Умрихин И. Д. Исследование пластов и скважнн при упругом режиме фильтрации. М., Гостоптехиздат, 1964.
36. Бузинов С. Н., Чарный И. А. О движении скачков насыщенности при вытеснении нефти водой. Изв. АН СССР, ОТН, № 7, 1957.
36а. Ван-Дайк М. Методы возмущений в механике жидкости. М., изд-во «Мир», 1967.
37. Герсеванов Н. М. Основы динамики грунтовой массы. М., Госстрой-нздат, 1933.
38. Гусейн-Заде М. А. Фильтрация в неоднородных пластах. М., Гостоптехиздат, 1963.
39. Гусейнов Г. П. Некоторые вопросы гидродинамики нефтяного пласта. Баку, Азернешр, 1961.
40. Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. М., Физматгиз, 1962.
41. Двайт Г. Таблицы интегралов. М., ИИЛ, 1948.
42. Деч Г. Руководство к практическому применению преобразования Лапласа. М., Физматгиз, 1958.
43. Диткин В. А., Прудников А. П. Интегральные преобразования и операционное исчисление. М., Физматгиз, 1961.
44. Ентов В. М. О приближенном решении плоско-радиальных задач нестационарной фильтрации. Изв. АН СССР, серия «Механика и машиностроение» № 4, 1964.
45. Ентов В. М. Об одной задаче нелинейной нестационарной фильтрации. Изв. АН СССР, серия «МехГаника и машиностроение», № 5, 1963.
46. Ентов В. М. Об исследовании скважин на нестационарный приток при нелинейном законе фильтрации. Изв. АН СССР, серия «Мехапика и машиностроение», № 6, 1964.
47. Ентов В. М. Об эффективном коэффициенте теплопроводности насыщенной пористой среды при наличии фильтрационного движения. «Прикладная механика и техническая физика», 1965, № 5.
48. Ентов В. М. Нестационарные задачи нелинейной фильтрации. Дисс. на соиск. уч. степ. канд. техн. наук, МИНХ и ГП, 1964.
49. Ентов В. М-, Сухарев М. Г. Автомодельный случай плоско-радиальпой нестационарной фильтрации при нелинейном законе сопротивления. Изв. вузов, «Нефть и газ», № 4, 1965.
50. Зельдович Я. Б., Компанссц А. С. К теории распространения тепла при теплопроводности, зависящей от температуры. Сб. к 70-летию А. Ф. Иоффе, М., изд-во АН СССР, 1950.
51. Каменомостская С. Л. Об одной задаче теории фильтрации. ДАН СССР, т. 116, № 1, 1957.
52. Каменомостская С. Л. Некоторые задачи для уравнений параболического типа с неизвестной границей. Дисс. на соиск. уч. степ. канд. физ.-ыат. наук, МГУ, 1958.
53. Камке Э. Справочник по обыкновенным дифференциальным уравнениям. М., Физматгиз, 1961.
54. Карслоу Г., Егер Д. Теплопроводность твердых тел (пер. с англ.). М., изд-во «Наука», 1964.
55. Кисиленко Б. Е. Экспериментальное изучение характера продвижения водо-нефтяного контакта в пористой среде. Изв. АН СССР, серия «Механика и машиностроение», № 6, 1963.
56. Кисляков Ю. П., Демин Н. В., Русских В, И. Влияние градиентов давления на величину параметров пласта на Туймазинском месторождении. «Нефтяное хозяйство», 1964, As 2.
57. Коджасв Ш. Я., Кочешков А. А. Экспериментальное исследование поведения стабилизированной зоны при заводнении трещиновато-пористой среды. Научно-тсхн. сб. по доб. нефти, ВНИИНефть, вып. 26. М., изд-во «Недра», 1965.
58. Коллинз Р. Течения жидкостей через пористые материалы. (Пер. с англ.). М., изд-во «Мир», 1964.
59. Кочин Н. Е., КиС1е.1ь И. А., Розе Н. В. Теоретическая гидромеханика, т. 1. М., Гостехтеориздат, 1955; т. II, Физматгиз, 1963.
60. Кочин Н. Е., Лойцянский Л. Г. Об одном приближенном методе расчета ламинарного пограничного слоя. ДАН СССР, т. 36, вып. 9, 1942.
61. Крылов А. Н. Лекции о приближенных вычислениях, изд. 4-е, М., Гостехиздат, 1950.
62. Кусаков М. М., Мекеницкая Л. И. Толщина тонких слоев связанной воды. Тр. IV Международного нефтяного конгресса, т. III, М., изд-во АН СССР, 1956.
63. Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. М., Физматгиз, 1958.
64. Лан Чжан-Синь. Решение задачи о нестационарной фильтрации газа в пласте переменной мощности. «Газовая промышленность», 1961, № 7.
65. Лан Чжан-Синь. Расчет истощения газового пласта, дренируемого батареей скважин. Изв. вузов, «Нефть и газ», № 3, 1962.
66. Ландау Л. Д., ЛифшицЕ. М. Статистическая физика. М., изд-во «Паука»,
1964.
67. Лапук Б. Б. Теоретические основы разработки месторождений природных газов. М., Гостоптехиздат, 1948.
68. Лапук Б. Б. Приближепное решение задач о неустановившейся радиальной фильтрации газов. ДАН СССР, т. 58, вып. 1, 1947.
69. Лебедев Н. Н., Скальская И. С., Уфлянд Я. С. Сборник задач по математической физике. М., Гостехтереотиздат, 1955.
70. Лейбензон Л. С. Движение газа в пористой среде. «Нефтяное хозяйство», 1930, № 8—9.
71. Лейбензон Л. С. Подземная гидравлика воды, нефти и газа. Собр. трудов, т. II. М., изд-во АН СССР, 1953.
72. Лейбензон Л. С. Движение газированной жидкости в пористой среде. Изв. АН СССР, серия геогр., № 4—5, 1941.
73. Лейбензон Л. С. Движение природных жидкостей и газов в пористой среде. М., Гостехиздат, 1947.
74. Лебедев Н. Н. Специальные функции и некоторые их приложения, изд. 2-е. М., Физматгиз, М., 1963.
75. Максимов В. А. О влиянии неоднородностей на определение параметров нефтеносного пласта по данным нестационарного притока жидкости к скважинам. Изв. АН СССР, серия «Механика и машиностроение», Л» 3, 1959.
76. Максимов В. А. О влиянии неоднородностей на определение параметров нефтеносного пласта, по данным нестационарного притока жидкости к скважинам. Случай двухслойного пласта. Изв. АН СССР, серия «Механика и машиностроение», № 3, 1960.
77. Мартос В. Н., Рыжик В. М. Исследования капиллярной пропитки пористых сред применительно к моделированию процесса вытеснения газа водой. АН СССР, серия «Механика жидкости и газа», № 1, 1967.
78. Маскет М. Течение однородных жидкостей в пористой среде (пер. с англ.). М., Гостоптехлздат, 1949.
79. Маскет М. Физические основы технологии добычи нефти (пер. с англ.). М., Гостоптехиздат, 1953.
80. Медведский Р. И. Определение давления в остановленной скважине пористо-трещиноватого коллектора. Сб. «Гидродинамические методы исследования иластов и скважин». Баку, АзИНТИ, 1967.
81. Мельпичук Я. Г., И па то та М. М. Применение термометрии в исследовании нефтяных и газовых скважин и пластов. Тр. Укр. НИГРИ, вып. 3. Гостоптехиздат, 1963.
82. Минский Е. М. О турбулентной фильтрации в пористых средах. ДАН СССР, т. 78, № 3, 1951.
83. Минский Е. М. О турбулентной фильтрации газа в пористых средах. Тр. Всес. н.-и ин-та природных газов. «Вопросы добычи, транспорта и переработки природных газов». М., Гостоптехиздат, 1951.
84. Минский Е. М. Статистическое обоснование уравнений фильтрационного движения. ДАН СССР, т. 118, № 2, 1958.
85. Мирзаджанзаде А. X. Вопросы гидродинамики “вязко-пластических п вязких жидкостей в применении к пефтедобыче. Баку, Азернефть, 1959.
86. Мирзаджанзаде А. X., Мирзоян А. А., Гевинян Г. М., Сеид-Рза М. К. Гидравлика глинистых п цементных растворов. М., изд-во «Недра», 1966.
87. Нсмыцкий В. В., Степанов В. В. Качественная теория дифференциальных уравнений. М., Гостехиздат, 1947.
88. Николаевский В. Н. Некоторые задачи распространения меченых частиц в фильтрационных потоках. Изв. АН СССР, серия «Механика и машиностроение», № 5, 1960.
89. Нумеров С. Н. О неустаповившейся фильтрации в полосообразном иласте к прямолинейной цепочке совершенных скважин. Изв. АН СССР, ОТН, № 1, 1958.
90. Пирвердян А. М. Приближенное решение задач о фильтрации жидкости цри упругом режиме. ДАН АзССР, т. 6, № 1, 1950.
91. Пирвердян А. М. Нефтяная подземная гидравлика. Баку, Азнефте-издат, 1956.
92. Полубаринова-Кочнна П. Я. Об одном нелинейном уравнении в частных производных, встречающемся в теории фильтрации. ДАН СССР, т. 63, № 6, 1948.
93. Полубаринова-Кочина П. Я. О неустановивпгихся движениях грунтовых вод при фильтрации из водохранилищ. «Прикладная математика п механика», т. 13, № 2, 1949.
94. Полубаринова-Кочина П. Я. Теория движения грунтовых вод. М., Гостехиздат, 1952.
95. Прандтль JI. Гидроаэромеханика (пер. с нем.). М., ПИЛ, 1949.
96. Роза С. А. Осадки гидротехнических сооружений на глинах с малой
влажностью. «Гидротехническое строительство». 1950, № 9.
97. Ромм Е. С. Фильтрационные свойства трещиноватых горных пород. М., изд-do «Недра», 1966.
98. Рыжик В. М. О вытеснений нефти водой в пористой среде с малопроницаемыми включениями. Изв. АН СССР, серия «Механика и машиностроение», № 1, 1964.
99. Рыжик В. М. О капиллярной пропитке водой нефтенасыщснного гидрофильного пласта. Изв. АН СССР, серия «Механика и машиностроение», № 2, 1960.
99а. Рыжик В. М., Чарный И. А., Чень Чжун-Сян. О некоторых точных решениях уравнений нестационарной фильтрации двухфазной жидкости. Изв. АН СССР, серия ^Механика и машиностроение», № 1, 1961.
100. Рыжик В. М. О механизме капиллярной пропитки пористой среды. Изв. АН СССР, серия «Механика и машиностроение», № 6, 1959.
101. Рыжик В. М. Некоторые задачи взаимного вытеснения несмешивающихся жидкостей из пористой среды. Дисс. на соиск. уч. степ. канд. физ.-мат. наук, МГУ, 1962.
102. Седов Л. И. Методы подобия и размерности в мехаиике. М., Гостех-теориздат, 1957.
103. Седов Л. И. О неустановившихся движениях сжимаемой жидкости. ДАН СССР, т. 48, № 2, 1945.
104. Скворцов Э. В. К одномерной задаче вытеснения нефти водой в тре-щиновато-иористой среде. Изв. АН СССР, серия «Механика жидкости и газа», № 5, 1967.
105. Слезкин Н. А., Тарг С. М. Обобщенные уравнения Рейнольдса. ДАН СССР, т. 54, 1946.
106. Снеддон И. Преобразования Фурье (пер. с англ.). М., ИИЛ, 1955.
107. Соболев С. Л. Некоторые применения функционального анализа в математической физике. Л., изд-во ЛГУ, 1950.
108. Соколов Ю. Д. Об одной задаче теории неустаповившихся движений грунтовых вод. «Укр. математич. журнал», № 5, 1951, № 2.
109. Станюкович К. П. Об автомодельных решениях уравнений гидродинамики, обладающих центральной симметрией. ДАН СССР, т. 48, вып. 5, 1945.
110. Станюкович К. П. Неустановивпшеся движепия сплошной среды. М., Гостехиздат, 1955.
111. Степанов В. В. Курс дифференциальных уравнений. М., Гостех-теориздат, 1953.
112. Султанов Б. И. О фильтрации вязко-пластических жидкостей в пористой среде. Изв. АН СССР, серия физ.-мат. и техн. наук, № 5, 1960.
113. Сухарев М. Г. Метод приближенного расчета интерференции скважин при упругом режиме фильтрации. Изв. вузов, «Нефть и газ», № 6, 1959.
114. Уиттекер Э. и Ватсон Дж. Курс современного анализа, т. I и II (пер. с англ.). М., Физматгиз, 1963.
115. Фенчер Д., Льюис Д., Бернс К. Физические испытания пород нефтяных и газовых пластов и их свойства. «Инотехника», вып. 105. Баку — М., 1935.
116. Флорин В. А. Уплотнение земляной среды и фильтрация при переменной пористости с учетом влияния связанной воды. Изв. АН СССР, ОТН, № 11, 1951.
117. Форхгеймер Ф. Гидравлика. М. — Л., ОНТИ, 1935.
118. Чарный И. А. Подземная гидромеханика. М., Гостехиздат, 1948.
119. Чарный И. А. Подземная гидрогазодинамика. М., Гостоптехиздат, 1963.
120. Чарный И. А. Метод последовательной смены стационарных состояний. Изв. АН СССР, ОТН, № 3, 1949.
121. Чекалюк Э. Б. Термодинамика нефтяного пласта. М., изд-во «Недра», 1965.
122. Шестаков В. М. Вопросы моделирования. Сб. «Вопросы фильтрационных расчетов». М., Стройиздат, 1956.
123. Щелкачев В. Н. Основные уравнения движения уиругой жидкости в упругой пористой среде. ДАН СССР, т. 52, № 2, 1946.
124. Щелкачев В. Н. Упругий режим пластовых водонапорных систем. М., Гостоптехиздат, 1948.
125. Щелкачев В. Н. Разработка нефтеводоносных пластов при упругом режиме. М., Гостоптехиздат, 1959.
126. Щелкачев В. Н., Лапук Б. Б. Подземная гидравлика. М., Гостоптехиздат, 1949.
127. Эфрос Д. А. Исследование фильтрации неоднородных систем. М., Гостоптехиздат, 1963.
128. Эфрос Д. А., Оноприенко В. П. Моделирование линейного вытеснения пефти водой. Тр. ВИИИНефть, вып. 12. М., Гостоптехиздат, 1958.
129. Янке Е., Эмде Ф. Таблицы функций с формулами и кривыми (пер. с нем.). М., Физматгиз, 1959.
130. Benham О. L., Olson R. W. A model study of viscous fingering. Soc. Petr. Eng. Joum. June, N 3, p. 138, 1963.
131. Bentsen R. G., Nielsen R. E. A study of plane radial miscible displacement in a consolidated porous medium. Soc. Petr. Eng. Joum., vol. 6, N 1, March 1966.
132. Bondarenko N., Nerpin S. Proprictes rhcologiques de l’eau dans les milieux poreux. Colloque RILEM, 1964.
133. Boussinesq I. Rech.erch.es theoriques sur l’ecoulement des nappes d’eau infiltrees dans le sol. J. de math, pure et appl., ser. 5, vol. X, 1904.
134. Buckley S., Leverett М. C. Mechanism of fluid displacement in sands. Trans. AIME, vol. 146, 1942.
135. Chuoke B. L., van Meurs P., van der Poel C. The instability of slow irnmicible viscous liquid-liquid displacement in permeable media. Trans. AIME, vol. 216, 1959.
136. Falkner V. М., Skan S. W. Some approximate solutions of the boundary layer equations. Aeron. Res. Comm. Rep. and Mem., N 1314, 1930.
137. Goldstein S. A note on the boundary layer equations. Proc. Cambr. Phil. Soc., vol. 35, 1939.
138. Jacob С. E. On the flow of water in an elastic artesian aquifer. Trans. Amer Geophys. Union, 1940, p. 11.
139. Koch H. A., Slobod R. L. Miscible slug process. Journ. Petrol. Techo-logy, N 2, Febr. 1957.
140. Koval E. J. A method for predicting the performance of unstable mls-eible displacement in heterogeneous media. Soc. Petr. Eng. J., 1963, vol. 3, N 2.
141. Jone*-Parra J., Colhoun J. Computation of a linear flood by the stabilized zone method. Trans AIME, vol. 198, 1953.
142. Kyle C. R., Perrine R. L. Experimental studies of miscible displace
ment instability. Soc. Petr. Eng. J., 1965, N 3, N 5.
143. Leverett М. C. Capillary behaviour in porous solids. Trans. AIME, vol. 142, 1941, p. 151.
144. Leverett M. Flow of oil water mixtures through unconsolidated sands.
Trans. AIME, vol. 132, 1939.
145. Mattax C., Kyte J. Imbibition oil recovery from fractured water-drive
reservoir. Soc. Petr. Eng. Journ. June 1962, N 2.
146. Miller С. C., Dyes A. B., Hutchinson C. A. The estimation of permeabi
lity and reservoir pressure from bottom-hole pressure build-up characteristics. Joum. Petr. Techn., vol. 2, N 4, 1950.
147. Marie C., Pettier J. Aspects theoriques du deplacement miscible en milieux poreux pour la recuperation du pctrole. Rev. de l’lnst. Franc, de petrole,
l965, vol. 20, N 2.
148. Muskat М., Botset M. Flow of gases through porous materials. «Physics», vol. 1, N 1, 1931.
149. Nemenyi P. Uber die Gultigkeit des Darcyschen Gesetzen und deren
Grenzen. Wasserkraft u. Wasserwirtschaft, 29(14), 157—159, 1934.
150. Odeh A. S. Effect of viscosity on relative permeability. J. Petrol. Techn., К 12, 1959.
151. Perrine R. L. A unified theory for stable and unstable miscible displacement. Soc. Petr. Eng. J., 1963, vol. 3, N 3.
152. Rapoport L. A., Leas W. J. Properties of linear waterfloods. Trans. AIME, vol. 198, 1953.
153. Von Rosenberg D. V. Mechanics of steady singlephase fluid displacement from porous media. AIChE Journal, 1956, vol. 2, N 1.
154. Saffman P. G. A theory of dispersion in a porous medium. Journ. Fluid Mech., vol. 6, N 3, 1959.
155. Saffman P., Taylor G. The penetration of a fluid into a porous media or Hele — Shaw cell containing a more viscous fluid. Proc. Roy. Soc., N 1242, A-245, 1958.
156. Scheidegger A. E. Growth of instabilities on displacement fronts in
porous media. Phys. Fluids., 1960, vol. 3, N 1.
157. Schneebeli G. Experiences sur la limite de validite dc la loi de Darcy et l’apparition de la turbulence dans un ecoulement de filtration. Houille Blanche, Mars-Avril 1955, N 2.
158. Terwilliger P. L. An experimental and theoretical investigation of gravity drainage performance. Trans. AIME, vol. 192, 1951.
159. Terzaghi K. Erdbaumechanik auf bodenphysikabischen Grundlage 1'. Denticke. Leipzig, 1925.
160. Thciss Ch. V. The relation between the lowering of the piezometric sur
face and the rate and duration of discharge of a well using ground-water storage. Trans, am. geophys. union, 1935, v. 16, pt. 2, p. 519—524.
161. VVyckoff R. D., Botset H. F. Flow of gas-liquid mixtures through
unconsolidated sands. «Physics», vol. 7, 1936.
162. Engelhardt W. v., Tium YV. Uber das Stromen von Fliissigkeiten durcli Sandsteine. Heidelberger Beirtriige zur Mineralogie und Petrographie. Bd. 4, H. 1/2, 1954.
Григорий Исаакович. Баренблатт, Владимир Мордухович Ентов, Виктор Михайлович Рыжик
ТЕОРИЯ НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ ЖИДКОСТИ И ГАЗА
Редактор Н. Д. Дуб-роеина Технический редактор В. В. Соколом
Корректор М. П. Курылееа
Сдано в набор 13/VII 1972 г. Подписано в печать 17/Х 1972 г. Т-17124.
Формат 60X90*/i«. Бумага JSS 2. Печ. л. 18.0. Уч.-изд. л. 18,51.
Тираж 1500 экз. Заказ № 1865/72-6. Цепа 2 р. 08 к.
Издательство «недра», 103633, Москва, К-12, Третьяковский проезд, 1/19. Ленинградская типография Mt 6 Главполиграфпрома Государственного Комитета Совета Министров СССР по делам издательств, полиграфии и книжной торговли.
Московский пр., 91-
Настоящая книга предназначена в качестве учебника для студентов машиностроительных специальностей вузов, в учебных планах которых предусмотрен общий курс гидравлики, гидромашин и гидроприводов. Такой же объединенный курс читается и для других специальностей в связи с тем, что гидрооборудоваиие, гидропривод и гидроавтоматика широко применяются в производственных процессах разных отраслей: при разработке месторождений полезных ископаемых, в энергетике, металлургии, лесной промышленности, на транспорте, строительстве и т. д.
Книга написана в соответствии с учебной программой указанного курса, утвержденной Министерством высшего и среднего образования СССР, и содержит все основные разделы этой программы.
Второе издание книги отличается от первого тем» что оно частично переработано и дополнено некоторым новым материалом. Несколько повышен теоретический уровень изложения.
Так, в первой части введены дифференциальные уравнения движения жидкости, теорема о количестве движепия в применении к жидкости, понятие о п-теореме н методе размерностей и др.
Во второй части не только неснолько изменена методика изложения, но и внесены дополнительные материалы особенно по теории подобия лопастных насосов, кавитации в них, а также даны современные примеры использования гидродинамических (лопастных) передач.
В третью часть введены следующие иовые вопросы» общие свойства объемных гидромашин, рабочий процесс насосных и регулирующих клапанов, учет сжимаемости жидкости в гидромашвиах, кавитация в поршневых и роторных насосах, конструктивные схемы современных роторно-поршневых и других роторных гид-ромашин, характеристики и КПД различных типов гидроприводов, сравнение способов регулирования гидроприводов и др.
Первая часть написана проф. д-ром техн. науи Б. Б. Некрасовым, вторая часть — проф. С. С. Рудневым, проф. д-ром техн. наук О. В. Байбаковым и доц. канд. техн. наук Ю. Л. Кирилловским, третья часть — проф. д-ром техн. наук Т. М. Баштой при участии Ю. Л, Кирилловского и Б. Б. Некрасова.


