Специальные модели движения газа
Глава II
Специальные модели движения газа
Основные проблемы теоретического исследования движений газа связаны с отысканием решений полученной в главе I системы дифференциальных уравнений с условиями на сильных разрывах и дополнительными начальными и граничными условиями. Большие математические трудности, возникающие на пути решения таких проблем вследствие сложности самой модели движения, вынуждают к поиску более простых моделей, для которых можно было бы продвинуть исследование дальше, чем в общем случае. Не будет преувеличением, если сказать, что современный прогресс в решении многих проблем газовой динамики достигнут благодаря успешному использованию упрощенных постановок ее задач. В данной главе намечаются методы построения и приводится некоторый список таких упрощенных моделей и, коротко говоря, подмоделей.
Всякое движение газа неразрывно связано с идущим в нем термодинамическим процессом. При этом возможны такие ситуации, когда этот процесс является однопараметрическим. Отсюда возникают термодинамические подмодели, среди которых наиболее важной и часто эксплуатируемой является модель изэнтропического движения. Далее, большое место в газовой динамике занимает теория установившихся течений (в том числе безвихревых). В этой подмодели пространство событий отходит на второй план, каждое событие является «вечным», застывшим во времени. В пространстве течения процесс утрачивает, вообще говоря, свойство детерминированности, что влечет целый ряд новых эффектов. К ним относится, например, переход через скорость звука и связанное с ним изменение типа основных дифференциальных уравнений.
Очевидно, что упомянутые выше и многие другие случаи подмодели-рования сводятся к выделению и описанию тех или иных классов точных решений уравнений газовой динамики. При этом естественна постановка вопроса о наиболее широком раскрытии возможностей, предоставляемых Для этой цели самой исходной моделью. Здесь решающим является ее групповое свойство, возможности которого иллюстрируются многочисленными примерами классов инвариантных и частично инвариантных решений.
В газовой динамике, особенно при решении конкретных практических задач, широко используются также различные методы приближенного под-моделирования. Здесь характерно сочетание предварительного физического анализа (учитывающего экспериментальные данные) с надлежащим формально-математическим введением малого параметра и последующим предельным переходом.
Конечно, приведенный в этой главе список упрощенных моделей далеко не исчерпывает всех случаев точного и тем более приближенного подмо-делирования уравнений и задач газовой динамики. Цель главы — дать общее представление о богатстве множества конкретных подмоделей и о некоторых основах и методах их построения.
Вынесенное в заголовок название специального класса математических моделей газовой динамики означает, что в таких моделях делаются дополнительные предположения о характере термодинамического процесса в газе. В простейшей форме они сводятся к условию постоянства в рассматриваемом движении какой-либо из термодинамических величин. Эти предположения в действительности обычно выполняются приближенно, в зависимости от конкретных условий движения газа. Использование таких предположений на практике требует каждый раз тщательного анализа и экспериментального подтверждения. Привлекательной стороной применения различных термодинамических моделей является то, что в них обычно достигается определенное упрощение описания движения газа и облегчается получение результирующих аналитических формул и выполнение численных расчетов. Здесь в сжатой форме рассматриваются некоторые из таких моделей с целью показать основные особенности в получаемых уравнениях движения газа.
Изэнтропическое движение. Движение газа называется изэнтропи-ческим, если в этом движении энтропия S тождественно постоянна
5 = const. (1)
Основание для изучения изэнтропических движений дает следующий, уже отмеченный в § 3 факт: энтропия сохраняется в частице газа. Поэтому, если в некоторой массе газа в какой-то момент времени распределение энтропии по частицам газа было постоянным, то оно будет постоянным в этой массе газа и в последующее время. Конечно, это утверждение безоговорочно справедливо лишь для непрерывных движений. Если же по массе газа пройдет ударная волна, то, согласно выводам §5, энтропия в ней изменится и может стать уже не постоянной по частицам. В случае ударных волн малой интенсивности можно, однако, принимать свойство сохранения энтропии приближенно, учитывая, что скачок энтропии есть величина третьего порядка малости по сравнению с силой разрыва (теорема 5.2).
В случае изэнтропического движения уравнение DS ~ 0 выпадает из системы дифференциальных уравнений (3.11). Кроме того, при этом будет Vp = c2Vp согласно определению 2.3. Поэтому дифференциальные уравнения изэнтропических движений газа принимают вид
Dp + pdivu = О, pDu + c2V р = О,
(2)
где с2 = с2(р) рассматривается как заданная функция.
Модель изэнтропического движения особенно проста для политропно-го газа, в котором в силу (2.5) и (2.18) справедливо соотношение
dc = 7 ~ldp с 2 Р '
(3)
позволяющее исключить плотность р из системы (2). В результате получаются уравнения изэнтропического движения политропного газа
![]()
Du Н—rcVc = О,
7-1
где 7 - показатель адиабаты.
Уместно отметить, что в ряде работ по газовой динамике встречается термин «баротропный газ». Обычно под этим подразумевается, что давление р является однозначной функцией плотности р, и пишется «уравнение состояния» вида р — f(p). Однако необходимо помнить, что уравнение р = = f(p) отражает не свойство газа как физической среды, а лишь свойство движения газа, при котором такая связь давления с плотностью реализуется. Но эта связь и есть следствие предположения об изэнтропичности исследуемого движения газа, который в других условиях вполне может проявлять и те свойства, которые связаны с изменением энтропии (например при прохождении сильных ударных волн).
При решении задач об изэнтропическом движении газа с относительно слабыми ударными волнами, когда изменением энтропии в ударных волнах пренебрегается, уравнения ударного перехода (4.12) и (4.13) остаются прежними, а вместо уравнения адиабаты Гюгонио (4.14) или (4.18) к ним Добавляется уравнение адиабаты Пуассона S = So = const. Последнее при
записи исходного уравнения состояния в виде р = /(р, 5) равносильно уравнениям
Pl=/(Pl,S0), P2 = /(P2.S0). (5)
При этом необходимо допускать только такие ударные переходы, для которых скачки давления и плотности положительны, т.е. (если (pi,pi) — состояние перед волной)
Ы = Р2 - Pi > 0, [р\ = Р2 - р\ > о,
хотя здесь эти неравенства уже не следуют из закона возрастания энтропии.
Изотермическое движение. Движение газа называется изотермическим, если в этом движении температура Т тождественно постоянна
Т = const.
Если рассматривать давление как термодинамическую функцию от температуры и энтропии, то для изотермического движения р = p{S), в силу чего давление должно сохраняться в частице. Тем же свойством должна обладать и плотность р. При этих предположениях из (3.11) получится система уравнений
Dp — 0, div и = 0, pDu 4- c2Vp = 0 (6)
(где с2 = с2(р)), которая оказывается переопределенной. В ней имеется пять скалярных уравнений для четырех искомых функций и, v, w, р. Хотя эта система и не противоречива, ее общее решение до настоящего времени не получено.
Использование модели изотермического движения можно связать с возможностью сохранения температуры за счет подвода (отвода) некоторой энергии к каждой частице газа извне, например за счет действия какого-либо излучения (см., например, [6]). Конечно, в получаемой модели энтропия в частице сохраняться не будет и уравнение энергии должно принять другой вид, связанный с учетом механизма внешнего притока энергии. Обычно, однако, уравнение энергии отбрасывается и предполагается просто, что давление есть однозначная функция плотности, р = /(р), как это имело бы место при условии Т = const без учета подвода энергии.
При этом соглашении дифференциальные уравнения снова приводятся к (2), однако с другим характером связи с2 = ( {(>)¦ Например, для идеального газа согласно (2.3) получается, что давление просто пропорционально плотности, откуда следует постоянство скорости звука:
Условие (7) можно рассматривать как предположение, эквивалентное изотермическому характеру движения газа. В этом случае связь давления с плотностью имеет вид
Р = с2р. (8)
где постоянная с называется изотермической скоростью звука.
Система основных дифференциальных уравнений здесь снова имеет вид (2), но с постоянным коэффициентом с2. Что же касается условий на ударной волне, то в них также отбрасывается уравнение адиабаты Гюгонио, которое заменяется вытекающим из (7) и (8) уравнением изотермы
Р2У2 =p\V\. (9)
Здесь возможен также учет изменения изотермической скорости звука при переходе через ударную волну, но тогда скачок [с] = сг - с\ должен либо быть задан непосредственно, либо определяться из других соображений (например из точных уравнений ударного перехода).
Изобарическое движение. Движение газа называется изобарическим, если в этом движении давление р тождественно постоянно:
р = const. (10)
Для нормального газа в таком движении должно быть р = p(S) (заданная функция) и потому плотность должна сохраняться в частице. Следовательно, система дифференциальных уравнений изобарического движения имеет вид
Dp = 0, Dm = 0, div и = 0. (11)
Таким образом, в изобарическом движении все газодинамические величины сохраняются в частицах и потому полностью определяются их распределениями в некоторый момент времени, например при t = 0. Для описания таких движений удобно ввести лагранжевы координаты ? = (?, Т]. Q как значения координат частиц газа в момент t = 0. Тогда решение первых двух уравнений (11) дается равенствами
Р = Р{?). u=u(?). (12)
В силу (12) каждая частица ? движется по своей траектории с постоянной скоростью, и потому ее траектория есть прямая линия
х = ? + и (?)#. (13)
Однако получаемое этим путем поле скоростей должно удовлетворять еще и последнему уравнению (11). Несложное вычисление показывает, что это
уравнение будет выполнено, если и только если входящие в (12) компоненты вектора скорости и = (и, v, w) удовлетворяют системе уравнений
и.? + vv + w<; = 0.
|
щ | Uг) |
+ | щ | + | Vr, |
Ч | |
| Ч |
vv | Щ |
Wjj | U)( |
W-n
0.
0,
(14)
Это означает, что изобарическое движение возможно только при некотором специальном начальном распределении скоростей. Уравнения (14) интегрируются; их общее решение зависит от трех произвольных функций двух независимых переменных. Выделение класса изобарических решений уравнений газовой динамики полезно, такие решения часто встречаются при изучении других классов подмоделей. Примером служат решения с линейным полем скоростей и = А? с постоянной матрицей А.
Существенным обобщением изобарических являются барохронные движения газа, выделяемые зависимостью давления только от времени:
Р = P(t)
(15)
В настоящее время барохронные движения также достаточно хорошо изучены [16].
Изохорическое движение. Движение газа называется изохорическим, если в этом движении плотность р тождественно постоянна:
(16)
р = const.
Предположение (16) в дифференциальных уравнениях законов сохранения массы и импульса (3.11) приводит к системе уравнений движения
идеальной несжимаемой жидкости
(17)
div и = 0. pDu 4- Vp = 0.
При изохорическом движении нормального газа должно быть, кроме того, Dp = fsDS = 0, т. е. давление должно сохраняться в частице. Добавление к (17) уравнения Dp = 0 приводит к системе уравнений изотермического движения газа (6).
Тем не менее модель несжимаемой жидкости можно использовать для приближенного описания движений газа. Эта модель должна быть хороша
в тех случаях, когда малые изменения плотности вызывают конечные изменения давления. Так как Dp = с?Dp, то это означает, что величина Dp мала по сравнению с величиной рс2. В частности, для политропного газа из соотношений (2.20) вытекают равенства
Dp 1 Dp Dp ~рс? = 7 ~Т= ~Р~'
Поэтому движение несжимаемой жидкости можно трактовать как предельное для движения политропного газа, когда 7 —> сю. Если исходные уравнения взяты в форме (3.14), то и для произвольного нормального газа модель (17) формально получается как предельная при условии, что
Dp/pc2 —» 0.
Уместно заметить, что если при этом не предполагать р = const, то останется еще уравнение Dp = 0. С этим дополнительным уравнением система (17) описывает движение неоднородной несжимаемой жидкости.
На практике приближение, связанное с использованием модели идеальной несжимаемой жидкости, широко применяется в аэрогидромеханике, например при решении задач обтекания тел стационарным потоком. Здесь применимость обсуждаемой модели определяется малостью величины отношения скорости потока к скорости звука по сравнению с единицей. Для ориентира можно напомнить, что скорость звука в воздухе (при нормальных условиях) с и 340 м/с, а в воде с ~ 1500 м/с.
Движение газа называется установившимся (или стационарным), если основные величины не зависят от времени:
ut - 0, pt=0, Pt = 0, St = 0, (1)
и являются, таким образом, функциями только точки х пространства /?3(х).
В литературе принято называть установившиеся движения также установившимися (стационарными) течениями газа. Этот термин хорошо отражает свойство неизменности во времени, «вечности» таких движений и будет также использоваться в дальнейшем изложении.
Модель установившегося течения систематически используется при решении конкретных задач благодаря тому, что она приближенно описывает широкий класс реальных движений газа. Типичным примером приближенно установившегося течения газа является движение, реализуемое при истечении газовой струи из большого сосуда через относительно малое отверстие. Установившееся течение получается в пределе, когда размеры сосуда бесконечны и параметры газа в нем (на бесконечности) фиксированы, а процесс истечения длится неограниченно долго.
Другой важный пример дает равномерно-поступательное движение твердого тела в безграничном, покоящемся на бесконечности газе. Возникающее при этом неустановившееся движение газа сводится к установившемуся с помощью преобразования Галилея (см. §8) так, как это описано в § 7 (см. «Задача обтекания»). В системе координат, движущейся вместе с телом, последнее неподвижно. Равномерный на бесконечности и имеющий там заданную скорость поток газа обтекает это неподвижное тело и, в силу неизменности граничного условия на теле, может рассматриваться как установившееся течение.
Исходные уравнения. Установившиеся движения естественно рассматривать безотносительно к времени, только на пространстве течения Я3(х). Оказывается, что при этом их уравнения приобретают особые свойства, которые необходимо учитывать при постановке и решении краевых задач. Описанию и анализу специфики уравнений установившихся течений и посвящено последующее изложение. При записи различных соотношений в декартовых координатах будут, как всегда, использоваться представления х = (х, у, z) и и = (м, v, iv).
Исходные интегральные законы сохранения, взятые в балансовой форме (1.4), принимают вид уравнений нулевых суммарных потоков массы, импульса и энергии через границу -у любой области а> С Д3(х):
JJ ри • n d'y = 0,
7
JJ{pn + pu{u-n))d'y = 0, ^
7
7
Р + Р (j>q2 + ")) U ’ ndl = °'
Дифференциальные уравнения гладких установившихся течений могут быть взяты в прежней форме, например (3.11), но с заменой оператора производной в частице (3.3) «укороченным» оператором
Следовательно, система дифференциальных уравнений установившихся течений такова:
D' р + р div и = 0, pD'n 4- Vp = 0, (4)
D'S = 0.
Линии тока. Специфика кинематики установившегося течения отражается следующим фундаментальным понятием.
Определение 1. Линии в пространстве Я3(х), определенные как интегральные кривые системы обыкновенных дифференциальных уравнений
dx _ dy _ dz u(x, у, z) v(x, у, z) w(x, y, z) ’
называются линиями тока установившегося течения с вектором скорости и = (и, v, w). В дальнейшем линии тока обозначаются символом
Сравнение (5) с уравнениями траекторий (1.1) показывает, что линии тока являются траекториями частиц в Вг(х). Однако необходимо иметь в виду, что, в отличие от общих движений газа, когда траектории частиц образуют трехпараметрическое семейство кривых, совокупность линий тока установившегося течения является лишь двухпараметрическим семейством.
В силу определения 1 оператор D' является оператором дифференцирования вдоль линий тока. Это позволяет получить два важнейших интеграла системы уравнений (4).
Первый из них есть интеграл энтропии, вытекающий из уравнения D'S = 0 и означающий, что энтропия вдоль линии тока постоянна:
S = S0(2). (6)
Величина Sq(%) зависит только от линии тока для каждой фиксированной линии тока она постоянна, но, вообще говоря, меняется с изменением if.
Интеграл Бернулли. Второй интеграл есть следствие (6) и уравнения импульсов. Для его получения уравнение импульсов в форме Громеки-Лэмба (3.19)
V + iVp = ихш
скалярно умножается на вектор скорости и. В силу (3) и известного свойства векторного произведения это дает
Но из уравнения первого закона термодинамики (2.1), в котором надо положить d-= D' и ввести удельную энтальпию i = z -V pV, следуют равенства
D'i = TD'S — V D'p — ±D'p.
где принято во внимание, что D!S = 0 и У = 1 /р. Поэтому предыдущее уравнение переписывается в виде
D'{q2 + 2i) - 0.
Отсюда, аналогично интегралу (6), и следует искомый интеграл
q2-\-2i = 2i0(f?), (7)
где величина i.o(J?) зависит только от линии тока 1?.
Соотношение (7) называется интегралом Бернулли. Следует иметь в виду, что в общем случае установившегося течения интеграл Бернулли (в отличие от интеграла энтропии) не равносилен дифференциальному уравнению импульсов (и потому не может полностью заменить это уравнение); он представляет собой лишь необходимое следствие уравнений энергии и импульсов. Тем не менее интеграл Бернулли является ключевым для понимания основных закономерностей установившихся течений газа.
Удобно записать интеграл Бернулли в несколько иной форме. Так как в нормальном газе удельная энтальпия дается формулой (2.14), то можно определить величину
р
о
которая отличается от 2г самое большее постоянным слагаемым (зависящим от S).
Утверждается, что (при постоянной S) величина (8) есть однозначная
возрастающая функция от квадрата скорости звука, / = и такая, что
1(с2)0, (с2 —> 0), I(с2) —> эо (р —> ос). (9)
Действительно, в силу (2.24) справедлива формула
Далее, согласно Лемме (2.1) / —> 0 при р —> 0, что равносильно первому соотношению (9). Наконец, из неравенства fpp > 0 следует, что с некоторым р 1 > 0 при р > pi будет с2 = /р > а > 0 (а — const), откуда р
I > ai + 2У 'j^dp = ai + 2aln —> ос (р —*¦ ос),
pi
Максимальная и критическая скорости. С функцией (8) интеграл
Бернулли записывается в виде
где qm = Ят\^?) есть максимально возможная скорость на данной линии тока !? (всегда q < qm). Значение q — qm достигается, в силу (9), лишь в состоянии вакуума, когда с2 = 0 и р = 0.
Определение 2. Критической скоростью называется величина с* > 0, определяемая как корень уравнения
Очевидно, что при любом данном q~n уравнение (11) имеет единственный корень с'1, так как его левая часть возрастает вместе с с2 и принимает,
в силу (9), все положительные значения.
Для политропного газа эти соотношения сильно упрощаются. Из (2.20)
сразу следует, что /(с2) = 2с2/(7 — 1), так что интеграл Бернулли имеет
вид
Ч2 + = Яш- (12)
а критическая скорость дается выражением
с* = (13)
До- и сверхзвуковые течения. Наиболее важные динамические свойства установившихся течений связаны с различением их по следующему признаку.
Определение 3. Установившееся течение газа в области П с Я3 называется дозвуковым, если всюду в Q
оно называется сверхзвуковым, если всюду в О.
q>c. (15)
Важно заметить, что дозвуковой или сверхзвуковой характер течения можно обнаружить путем сравнения модуля скорости q только с критической скоростью с». Это следует из того, что если q Ф с, то величина с* всегда лежит внутри интервала (q,c.). Действительно, если q < с, то в силу монотонности функции Цсг) и определения (11)
q2 + I(q2) <q2- I(c2) = <?m = ? + I (с2) < c2 + I(c2).,
откуда q < с» < с. Если q > с, то все знаки неравенств заменяются на противоположные. Это свойство легко усматривается из рис. 1, на котором качественно показана зависимость c(q), определяемая интегралом Бернулли.
Установленное с помощью интеграла Бернулли различение дозвуковых и сверхзвуковых течений не является формальным. На самом деле оно связано с зависимостью типа системы дифференциальных уравнений (4) от характера установившегося течения, когда это течение рассматривается не в пространстве событий Д4(х, t), а лишь в «своем» про-q с - странстве /?3(х). Такое рассмотрение оправ-
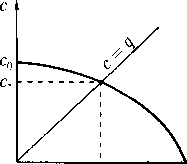
С’ 9 дано постановкой краевых задач стационар-
рис j ного обтекания или стационарного течения со
свободными границами, для которых каждое событие является «вечным». Поэтому вместо характеристик общих уравнений на решениях-установившихся течениях необходимо изучить поведение характеристик самих уравнений (4) в пространстве Я3(х).
Характеристики. С этой целью удобно взять исходные уравнения в виде, соответствующем матричной записи (3.17), с учетом того, что для установившихся течений отсутствует слагаемое с А*, так как Ut = 0. В отличие от общего случая (6.14), нормальные характеристические векторы ищутся в Я3(х):
Тогда характеристическая матрица А(?) снова будет иметь вид (6.15), но с укороченным выражением вспомогательной величины х> а именно с величиной
Здесь, не нарушая общности анализа, можно считать ? единичным вектором, |?; = 1. Тогда величина - и ¦ ? будет равна проекции вектора скорости на направление ?. Но вектор ? совпадает с нормалью п к характеристике C(t), которая па самом деле неподвижна в /?л(х). Поэтому просто
х' ~ и • п = ип.
Далее, выражение для определителя характеристической матрицы (6.17) здесь будет тем же самым (с заменой х на х') и ег0 корни даются равенствами х' = 0 или х' = ±с-
Итак, для уравнений установившегося течения возможны два типа характеристик: контактные, на которых ип = 0, и звуковые, на которых
ип = ±с. (16)
Уравнение ип = 0 означает, что вектор скорости ортогонален нормали к характеристике, т. е. является касательным к характеристической поверхности. Так как это верно в любой ее точке, то вместе с каждой точкой Р данной характеристике принадлежит целая линия тока, проходящая через Р. Следовательно, всякая контактная характеристика является геометрическим местом линий тока.
Уравнение (16) означает, что ортогональная проекция вектора и на нормаль п равна (по абсолютной величине) скорости звука. Но величина проекции \Un\ вектора и не может быть больше его модуля q = |и . Поэтому равенство (16) возможно, только если выполнено неравенство (15), т. е. если течение сверхзвуковое. Следовательно, звуковые характеристики существуют только в сверхзвуковых течениях. Для них всегда абсолютная величина проекции вектора скорости на нормаль к характеристике равна скорости звука.
В соответствии с определением 6.2 эти выводы показывают, что система уравнений установившихся течений является гиперболической, только если течение сверхзвуковое. На дозвуковых течениях существуют лишь контактные характеристики.
Интересно взглянуть на эту ситуацию с точки зрения пространства событий Я4(х,?) на примере постоянного решения u = Uo, c. = со, которое описывает установившееся течение. На этом решении в Д4(х, t) существует характеристический конус (6.32), внутренность которого (при t > to), согласно рассмотрениям § 7 (см. текст после теоремы 7.3), является областью влияния его вершины Р(х0До)- Здесь характеристики C(t) С Я3(х) суть сферы, центр которых перемещается со скоростью qo = |uo|, а радиус растет со скоростью Со- Поэтому, если qo < со, то вершина Р во все моменты времени t > to остается внутри сферы C(t) (рис. 2, а). Если же qo > со, то сферы C(t) не содержат точку Р и огибают прямой круговой конус Ко с Я3(х) с вершиной Р и углом раствора 2а, определяемым из соотношения (рис. 2, б)
sin а = со/до.
Таким образом, если течение дозвуковое, то его возмущение в точке Р ео временем охватит все пространство Я3(х). Если же течение сверхзвуковое, то возмущение в точке Р локализуется внутри конуса Ко- Из рис. 2, б непосредственно видно, что проекция вектора ио на нормаль к конусу Ко равна скорости звука со. Следовательно, Ко — характеристический конус рассматриваемого сверхзвукового установившегося течения.
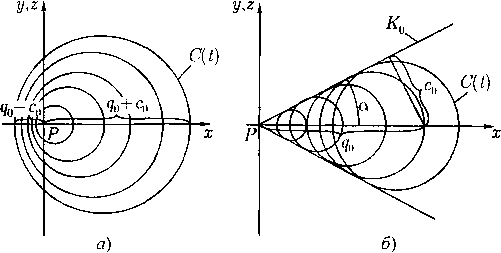
Рис. 2
Определение 4. Величина
М = ц/с (17)
называется числом Маха.
Для дозвуковых течений число Маха М < 1, а для сверхзвуковых течений М > 1.
Трубки тока. Следующая особенность установившихся течений связана с понятием трубки тока. Этот объект формируется так. Берется некоторая трубообразная область Тг, образованная линиями тока, проходящими через некоторый «начальный» диск Кг малого радиуса г с центром в некоторой точке Р ? Я3, перпендикулярный вектору скорости u(Р). Пусть К — какое-нибудь сечение Т'г, и пусть ? — боковая поверхность отрезка области Тг, заключенного между Кг и К (рис. 3). Ясно, что ? образована линиями тока, т. е. является контактной характеристикой. Поэтому и • п = О на ? и применение интегрального закона сохранения массы (2) к области с границей 7 = Kr + Е + К дает соотношение
Q{Tr) = JJ pu-nd'y = J J pu ¦ nd'y, (18)
Kr к
если нормаль n выбрана так, чтобы было u-n > 0. Следовательно, входящий в (18) интеграл не зависит от выбора сечения К. Поэтому величина Q(Tr) называется расходом газа через сечения трубообразной области Тг. Пусть !? есть линия тока, проходящая через точку Р, и пусть сечение К выбрано плоским, перпендикулярным к 1?. Площадь сечения диска Кт обозначается через су, а площадь сечения диска К — через а. Предполагается, что отношение ст/су имеет конечный предел
lim cr/crr = F. (19)
г—»0
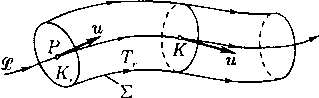
Рис. 3
Тогда будет существовать также конечный предел
Q = lim Q(Tr)/ar = pqF, (20)
г—»0
называемый расходом вдоль линии тока !?. Предельный переход в (18) с учетом (19) и (20) дает объект (J?, Q, р, q, F), который и называется
(абстрактной) трубкой тока. Он состоит из линии тока с расходом Q
и распределенных вдоль нее значений плотности р, скорости q и площади сечения F, связанных соотношением
pqF = Q = const. (21)
Произведение pq называется удельным расходом. Говорят о расширяющейся (сужающейся) трубке тока, если ее площадь сечения F растет (убывает) при перемещении вдоль линии тока в направлении вектора скорости и. Оказывается, что поведение течения в трубке тока существенно зависит от до- или сверхзвукового характера течения. Это поведение описывается следующим утверждением.
Теорема 1. В расширяющейся трубке тока дозвуковая скорость убывает, а сверхзвуковая скорость возрастает; в сужающейся трубке тока, наоборот, дозвуковая скорость возрастает, а сверхзвуковая убывает. Равносильная формулировка: при замедлении дозвукового течения трубки тока расширяются, а при замедлении сверхзвукового течения — сужаются; при ускорении дозвукового течения трубки тока сужаются, а при ускорении сверхзвукового течения — расширяются.
Доказательство. Изменение удельного расхода pq в зависимости от q вдоль линии тока 1? описывается легко выводимым из (8) и (9) соотношением
d(pq)/dq = р( 1 - М2), (22)
где использовано обозначение (17). В силу (22) дифференцирование соотношения (21) приводит к равенству
^ - (М2 - 1)^. (23)
Из (23) вытекает следующая таблица, строки которой дают все возможные сочетания знаков:
| dF |
> | o' | M |
< | 1, |
dq | < | 0: |
| dF |
> | о, | M |
> | 1, |
dq | > | 0; |
| dF |
< | 0. | M |
< | 1, |
dq | > | 0; |
| dF |
< | о, | M |
> | 1, |
dq | < | 0, |
равносильная совокупности всех утверждений о свойствах трубок тока. ¦
Ударные волны. В установившемся течении поверхность ударной волны необходимо должна быть неподвижной в пространстве Д3(х). Такую «стоячую» ударную волну принято называть скачком уплотнения. Так как скорость перемещения скачка уплотнения Dn = 0, то теорема Цемпле-на 5.4 для состояния «1» перед скачком и состояния «2» за скачком дает неравенства
|«П1|>гь |и„2|<с2. (24)
Тем более должно быть q\ > гСледовательно, перед скачком уплотнения всегда находится сверхзвуковое течение. Другими словами, скачки уплотнения могут существовать только в сверхзвуковых течениях. При этом течение за скачком может быть как сверхзвуковым, так и дозвуковым.
Следующее свойство скачков уплотнения связано с интегралом Бернулли. Из последнего уравнения (4.9) или, что равносильно, из уравнений (4.14) и (4.13) следует соотношение
![]()
q+ ? + pV - 0
или, с удельной энтальпией г = ? + pV,
[q2 + 2 г] = 0.
Сравнение этого соотношения с (7) показывает, что [го] = 0, т. е. константа в интервале Бернулли при переходе через скачок уплотнения меняется непрерывно. В силу (10) это свойство справедливо и для максимальной скорости:
[<7m] = 0.
(25)
Для критической скорости с» аналогичное свойство, вообще говоря, неверно, так как интеграл (8) зависит также и от энтропии S, скачок которой всегда отличен от нуля. Можно заметить, однако, что в случае политроплого газа, в силу прямой связи (13) критической скорости с максимальной, из (25) следует также, что [с,] = 0.
Различают прямые и косые скачки уплотнения. Скачок уплотнения называется прямым, если вектор скорости ортогонален поверхности скачка. При переходе через прямой скачок направление вектора скорости не меняется, линия тока проходит через точку скачка гладко.
Скачок уплотнения называется косым, если вектор скорости образует ненулевой угол с нормалью к поверхности скачка. При переходе через косой скачок вектор скорости скачкообразно меняет свое направление, линия тока в точке скачка имеет излом. Эти эффекты регулируются условием сохранения касательной к поверхности скачка составляющей вектора скорости (4.15). Более подробно они будут рассмотрены в § 25.
В заключение следует отметить, что предположение об изэнтрогшчно-сти установившегося течения существенных изменений, отличных от уже обсуждавшихся в § 9, не вносит. Наибольшие упрощения получаются в тех случаях (например в задаче обтекания), когда свойство изэнтропичности дополняется свойством независимости константы в интеграле Бернулли от линии тока. Установившиеся течения с единой для всего потока константой Бернулли иногда называют изоэнергетическими. Свойство изоэнергетич-ности сохраняется при переходе через скачки уплотнения, хотя при этом изэнтропичность течения может нарушаться.
Преобразование Мунка — Прима. Замечательное свойство симметрии установившихся течений газа состоит в том, что для широкого класса уравнений состояния «с разделенной плотностью» такие течения эквивалентны изэнтропическим. Эти уравнения состояния задаются заменяющим первое (2.7) соотношением
p = a(S)b(p) (26)
с функциями a(S) > 0 (a'(S) < 0) и Ь(р) > 0 (Ь'(р) > 0). Легко проверить, что в результате преобразования (и,р,р) —> (tti,pi,pi) по формулам
щ = у7a(S)u , pi = p/a(S) , р\ = р (27)
система (4) останется неизменной, а уравнение состояния (26) примет вид р\ = Ь(р]), т. е. давление р\ будет зависеть только от плотности р\. При этом, в силу (5), линии тока исходного и преобразованного течений будут одни и те же. В частности, классу (26) принадлежит и политропный газ (2.5).
Класс уравнений состояния (26) обнаружили М. Munk и R. Prim еще в 1947 г. Преобразование (27) (и даже более общее свойство симметрии) есть следствие того, что система (4) при уравнении состояния (26) допускает бесконечномерную группу преобразований с оператором
где /i(x) — любая функция, удовлетворяющая уравнению ГУ р = 0. В частности, можно взять р = Ф(В, S) с произвольной функцией Ф, где В есть левая часть интеграла Бернулли (10), т. е. В = ц2 + 1(с2) (сообщение Ю. А. Чирку нова, 1990г.).
Здесь обсуждается поведение важной кинематической характеристики поля скоростей — его вихря и рассматривается специальная модель движения, когда вихрь равен нулю. Эта модель заслуживает внимания благодаря сильному упрощению основных уравнений, особенно в соединении с другими предположениями об изэнтропичности, стационарности и т. д.
Вихрем вектора скорости и называется вектор ш = rot и.
В декартовых координатах х = (х, у, z) и и = (и. v, w) вихрь может быть записан в форме символического определителя:
\ . j k
rotu= д/дх д/ду d/dz ,
где i, j, к — орты осей х, у, г, или в компонентах:
ш = rotu = (wy - vz, uz - wx, vx - Uy). (1)
Движение газа называется безвихревым, если в этом движении вихрь и> равен нулю:
rotu = 0. (2)
Условия безвихревого движения. Необходимое условие безвихревого характера движения дается следующим предложением.
Лемма 1. При непрерывном безвихревом движении нормального газа выполняется соотношение
Vp х VS = 0. (3)
Доказательство. К уравнению импульсов в форме Громеки-Лэмба (3.19) применяется дифференциальная операция rot, и используются формулы векторного анализа
rot(/a) = / rot а + V/ ха, rot(a х Ь) = (Ь • V)a — (а • V)b + adivb - bdiva.
В результате для вектора ш = rot и с учетом тождества div ш = 0 получается уравнение
Du) — (ш ¦ V)u — из div u + p-2Vp x Vp. (4)
Здесь последнее слагаемое, в силу равенства Vp = c2Vp+ fsVS, пропорционально векторному произведению Vp х VS. Поэтому, если и) = 0, то из (4) следует (3). ¦
Движение газа, при котором верно соотношение Vp х Vp = 0, называется баротропным. Оно характерно тем, что в нем поверхности уровня плотности и давления совпадают. Для нормального газа свойство баротроп-ности движения равносильно выполнению соотношения (3).
Так как уравнение (4) справедливо для любых движений газа, то для баротропных движений (4) превращается в уравнение вихря:
Du = (u> • V)u - u> div u. (5)
Замечательно, что это уравнение может быть проинтегрировано вдоль траекторий частиц в R4 (х, t). Если принять обозначения (1.2) и ввести значение вихря при t = О
то решение дается формулой
w(x0,f)
![]()
которая проверяется прямой подстановкой в уравнение (5) с учетом уравнения (3.4) и формулы Эйлера (3.5) для производной от детерминанта 5 — det(cbc/cbc0). Этот факт приводит к следующей формулировке условия, при котором движение является безвихревым.
Теорема (Лагранжа). Если движение газа непрерывно и баротропно и если в некоторый момент времени в какой-либо частице (в какой-либо массе газа) вихрь равен нулю, то он будет равен нулю в этой частице (в этой массе газа) во все моменты времени.
Доказательство следует из формулы (6). ¦
Соотношение (3) всегда справедливо для изэнтропического движения. Кроме того, оно может быть выполнено в силу специальной геометрии движения газа, когда поверхности уровня плотности и энтропии или давления совпадают (например, в одномерных движениях с плоскими, цилиндрическими или сферическими волнами).
Предположение (2) о безвихревом характере движения равносильно факту существования потенциала скоростей tp = ^(х, ?.), т. е. такой функции, что
(7)
u = Vy>.
Поэтому безвихревое движение называется также потенциальным движением. Необходимо иметь в виду, что равенством (7) потенциал определен лишь с точностью до постоянного слагаемого, которое может зависеть от времени t.
Интеграл Коши-Лагранжа. Основная особенность модели безвихревого изэнтропического движения состоит в том, что в ней уравнение импульсов может быть проинтегрировано. Действительно, в силу определения удельной энтальпии (2.19), при S —- const уравнение первого закона термодинамики (2.1) превращается в соотношение
(8)
dp — р di
с любым дифференцированием d. В частности, если взять d = V, то будет Vp = pVi и с учетом (7) уравнение Громеки-Лэмба (3.19) может быть записано в виде
Отсюда и получается интеграл Коши -Лагранжа
где постоянная интегрирования Ь = b(t) может произвольной функцией времени. Так как потенциал сам определен лишь с точностью до слагаемого, зависящего от t, то без нарушения общности можно записывать интеграл Коши - Лагранжа (9) с правой частью b — 0.
Очевидно, что при S = const иы = 0 уравнение (9) равносильно векторному уравнению импульсов (с учетом определения (7)). Поэтому безвихревое изэнтропическое движение газа описывается системой, состоящей из уравнения неразрывности и интеграла Коши-Лагранжа для двух неизвестных функций — плотности р и потенциала скоростей <р. С учетом равенства (7) и определения оператора Лапласа
эти уравнения таковы:
pt. + Vy? • Vp + рА‘^> = О,
'•ft + ;j!V<p|" + i(p) — 0.
Уравнение для потенциала скоростей. Из уравнений (10) можно исключить плотность р и получить одно независимое уравнение для потенциала ip. С этой целью используется справедливое при S = const равенство Dp — c2Dp, в силу которого из (8) при d = D следует
c2Dp = pDi.
Поэтому первое уравнение (10) после умножения на с2 переписывается в виде
Di + c2Atp = 0.
Наконец, применение оператора D ко второму уравнению (10) и исключение Di дает требуемый результат:
D^( + i|V*>|2) -с2Д*> = 0. (11)
Это уравнение называется уравнением для потенциала скоростей безвихревого изэнтропического движения. В нем через первые производные от потенциала выражаются как оператор
гак и входящая в определенную уравнением состояния газа зависимость с2 = с2(г) энтальпия г, значения которой даются вторым уравнением (10). С расшифровкой оператора D согласно (12) уравнение для потенциала скоростей (11) принимает вид
<pt, +• 2Vp> • Vy>f + Vv? ¦ V ^|Vy>|2^ - c2Aifi = 0. (13)
Наконец, в декартовых координатах, когда ц> = ip(x, у, z, #,), уравнение (11) в подробной записи выглядит так:
<Ptt + 2uipxt + 2vipyt 2wipzt +
+ (u2 - c2)(pxx 4- (v2 - c2)ipyy + (w2 - c2)(pzz+ (14)
+2uvipxy + 2uw<pxz + 2mmpyz = 0,
где (и, v, w) -- (tpx, ipz). Уравнение (14) является квазилинейным дифференциальным уравнением с частными производными второго порядка.
Характеристики уравнения (14) определяются через нормальные характеристические векторы аналогично тому, как это делалось для системы уравнений газовой динамики в § 6. Роль характеристической матрицы (6.15) здесь играет характеристическая квадратичная форма, которая составляется по следующему правилу: берется вектор ? = (т, ?, г), Q, и в уравнении (14) каждая производная второго порядка заменяется произведением соответствующих координат этого вектора, например, на место iptt подставляется г2, на место ~рх1 подставляется ?т и т. д. В результате для уравнения (14) характеристическая квадратичная форма оказывается такой:
Q(0 =r2 + 2и?т + 2 vrjT + 2 wC,t 4- (и2 — с2)?2+
4- (v2 - c2)rf 4- (w2 — с2)?2 4- 2uv?r) + 2+ 2vwqC,.
Очевидно, что ее можно записать компактно:
Q(i) = x2-c2(e + v2 + С2), (15)
где х = т + и€ + Щ + w-'C ~ Уже встречавшееся выражение (6.16). Нормальные характеристические векторы ? определяются как векторы, обращающие в нуль форму Q(?). Из (15) видно, что они совпадают с теми, которые определялись равенствами (6.19), т. е. дают две звуковые характеристики разных семейств. Это означает, что уравнение (14) на любом решении имеет гиперболический тип. Отыскание самих характеристических поверхностей путем задания их уравнением вида h(x,t) = const выполняется так же, как это делалось для общих уравнений в § 6.
Из этого построения следует одна из особенностей описания безвихревых изэнтронических движений с помощью уравнения для потенциала: здесь не получаются контактные характеристики. Это означает, что слабый разрыв решения уравнения для потенциала (14), определяемый, естественно, как разрыв некоторых производных второго порядка от потенциала ip, может иметь место только на звуковых характеристиках. Так как тем не менее контактные характеристики существуют (они есть на любом решении уравнений газовой динамики), то отсюда следует важный вывод.
В безвихревом изэнтропическом движении газа слабый разрыв на контактных характеристиках невозможен. Другими словами, всякий разрыв на контактной характеристике необходимо является сильным разрывом.
Необходимо заметить, что этот вывод справедлив, только если непрерывное движение является безвихревым изэнтропическим по обе стороны контактной характеристики. Если же по одну сторону движение безвихревое, а по другую — вихревое, то на такой контактной характеристике обязательно будет слабый разрыв. Это следует, например, из формулы вихря (6). Поэтому в общем случае область безвихревого изэнтропического движения всегда отделена от области, в которой этот характер движения нарушен, некоторым сильным или слабым контактным разрывом.
Другая замечательная особенность уравнения для потенциала скоростей (14) состоит в том, что оно является уравнением Эшера для экстремалей функционала над 'р вида
(16)
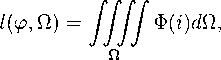
где вместо удельной энтальпии i надо подставить ее выражение из (10), интеграл берется по любой области ft с Д4(х, t), а функция Ф есть решение дифференциального уравнения (штрихами обозначены производные по г)
с2(г)Ф"(г) + Ф'(г’) - 0.
(17)
В частности, для политропного газа с2 - (7 - 1 )г, уравнение (17) легко интегрируется и функция Ф, с точностью до несущественных постоянных, оказывается такой:
7-2
Ф(г) = г7' 172 (7 ф 2), Ф(?) - In г, (7 = 2).
(18)
Вывод отмеченной связи уравнения (14) с функционалом (16) для функции Ф, определенной формулами (18), выполняется стандартным методом.
Это свойство уравнения (14) позволяет рассматривать некоторые краевые задачи газовой динамики для безвихревых изэнтропических движений как задачи вариационного исчисления.
Модель установившегося течения. Модель безвихревого изэнтро-пического установившегося течения ввиду ее относительной простоты получила широкое применение на практике, особенно при решении задач аэродинамики летательных аппаратов. Ес особенности вытекают из объединения тех фактов, которые установлены выше в данном параграфе и в § 10.
Здесь потенциал скорости не зависит от времени t, т.е. ip = у>(х) = = tp(x, у, г). Поэтому константа Ь в (9) также не зависит от ?, в силу чего интеграл Коши-Лагранжа совпадает с интегралом Бернулли
q2 + 1(С2) = q2m. (19)
Следовательно, в этой модели интеграл Бернулли (19) равносилен уравнению импульсов и максимальная скорость qm не зависит от линии тока, а является характерной константой всего движения в целом. То же самое верно и для критической скорости с, (в области непрерывного течения). Уравнение для потенциала скоростей (14) укорачивается до следующего:
(и2 - с2)<рхх + (V2 - C2)iPyy + {w2 - С2)<ргг+ ^
-г-2uvipxy + 2uwipxz + 2vwipyz ••= 0.
Соответствующая характеристическая квадратичная форма (15) для единичного вектора ? = (?, г], Q, |?| — 1, принимает вид
СМ) - (и • ?)2 - (21)
Так как и • ? = qcos(u, ?), то всегда !и ¦ ? < q. Поэтому характеристическое уравнение Q(?) = 0 при q < с не имеет вещественных корней, причем форма Q(i•) является (отрицательно) определенной. Это означает, что в области дозвуковых скоростей уравнение (20) имеет эллиптический тип.
Если же q > с, то характеристическое уравнение Q(?) = 0 имеет два вещественных корня, соответствующих двум различным характеристическим направлениям. Это означает, что в области сверхзвуковых скоростей уравнение (20) имеет гиперболический тип.
Корни характеристического уравнения в случае q > с можно наглядно представить геометрически, если (в данной точке пространства) ввести в рассмотрение угол а между характеристическим направлением и вектором скорости и (рис. 1). Так как cos(u, ?) = sin а, то положительный корень характеристического уравнения дается формулой где М — число Маха (см. § 10). Второй корень получается из (22) заменой а на —а. Определенный формулой (22) угол а(0 < а < 7г/2) называется углом Маха.
Итак, характеристические направления сверхзвукового течения в каждой точке наклонены к вектору скорости под углом Маха.
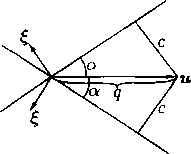
В общем случае течение рассматриваемого вида может содержать как области дозвуковых, так и области сверхзвуковых скоростей. Переход через скорость звука осуществляется на звуковой поверхности, характеризуемой равенством q = с или М = 1. Такие течения называются смешанными до- и сверхзвуковыми или трансзвуковыми. В об- Рис. 1
ласти трансзвукового течения уравнение для потенциала скоростей (20) имеет смешанный (эллиптико-гиперболический) тип.
Специальный интерес представляют течения, в которых величина |М — 1| мала по сравнению с единицей. Такие течения называются околозвуковыми; некоторые их особенности будут рассмотрены в § 26.
Течение типа источника. Как и в несжимаемой жидкости, существуют чисто радиальные течения газа, когда па каждой из семейства концентрических сфер плотность, давление и модуль скорости постоянны, а частицы движутся по радиусам (аналог источника или стока). В таком течении вектор скорости имеет представление вида
и --- ya(r,t) (г - \/х2 + у2 + z2). (23)
Легко проверяется, что векторное поле вида (23) всегда безвихревое, причем его потенциал зависит только от переменных (г, t). Очень простым оказывается описание непрерывного изэнтропического установившегося течения типа источника, которое сводится к анализу конечных (алгебраических) уравнений.
В этом случае 9 — ~р(г) и вектор скорости имеет вид
u = 7 4>'{г). (24)
Знак производной р'{г) указывает направление течения: если ^ > 0, то течение от центра (источник); если 9' < 0, то течение к центру (сток). Анализ обоих случаев, по существу, одинаков, и для определенности далее предполагается, что v'{r) = q > 0.
Разными способами можно убедиться в том, что уравнение (20) для потенциала = ср(г) имеет интеграл
где 47tQ есть расход газа через сферу радиуса г. Итак, дело сводится к совместному анализу двух уравнений: интеграла Бернулли (19) и уравнения расхода (25), определяющих функцию q(r). Для этого достаточно заметить, что в силу (19) характер зависимости удельного расхода pq от q определяется соотношениями
d(pq)/dq ¦= р{ 1 - М2), pq(0) = 0, pq(qm) = 0. (26)
Поэтому получаемый из (25) график зависимости r(q) имеет вид, показанный на рис. 2, где
г* ¦= VQ/p*c(27)
Следовательно, возможны два вида непрерывного течения типа источника: чисто дозвуковое и чисто сверхзвуковое. В случае дозвукового источника скорость течения q убывает с ростом г и стремится к нулю, когда г —+ ос. В случае сверхзвукового источника скорость q возрастает с ростом г и стремится к максимальной qm, когда г > эс; при этом на бесконечности достигается состояние вакуума.
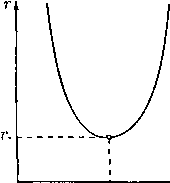
Важной особенностью газового источника является то, что он не может иметь точечный ха-рис 2 рактер: по данным значениям величин Q и qm од
нозначно определяется минимальный радиус (27) той сферы, из которой еще может «бить» источник газа с расходом Q при данном qm.
Возможны также течения рассмотренного типа с сильными разрывами. Анализ возможных здесь ситуаций для источника или стока предоставляется читателю.
§ 12. Классы инвариантных решений
Рассматривается широко распространенный частный случай инвариантно-групповых решений, в котором добавление дополнительных соотношений вида (8.16) к исходной системе не влечет переопределенности результирующей системы дифференциальных уравнений, а сразу приводит к определенной факторсистеме. Приводимое ниже построение применимо для любых систем дифференциальных уравнений; здесь оно обсуждается применительно к системе (8.1). Временно, для краткости записи формул, используются сокращенные обозначения независимых переменных (X, у, Z, t) = (Х\, х2. Хз, Х4) = х и искомых функций (и, V, W, р,р) = = («I, U2, U3, U4, «=>) = и.
Инвариантные решения. Предполагается, что базис инвариантов группы Я состоит из скалярных инвариантов двух видов. Первый составляют инварианты-функции только от независисмых переменных. Число к таких (функционально независимых) инвариантов может быть не более четырех; пусть это будут
Условие (3) позволяет разрешить уравнения (2) относительно всех искомых Uj и записать (2) в равносильной форме
Щ г) (j'=l, ...,5)
с конкретными известными функциями /,-. Тем самым из (4) следует представление Я-решений.
Uj = fj(x,U( Л)) 0 = 1,..., 5). (5)
В результате подстановки выражений (5) в систему (8.1) получается факторсистема из уравнений первого порядка для искомых Г//(Л) , содержащая только величины Ui, переменные А, и производные OUi/dXi. Доказательство этого факта, справедливого для любых исходных систем дифференциальных уравнений, допускающих группы II с требуемым базисом инвариантов, можно найти в [5].
Определение 1. Решения, получаемые вышеописанным построением, называются инвариантными Н-решениями ранга к. Соответствующая факторсистема называется инвариантной подмоделью ранга к исходной «большой модели» (8.1).
Специфика инвариантной подмодели состоит в том, что в ней участвуют лишь А: < 4 независимых переменных. Поэтому инвариантные решения находить и анализировать, вообще говоря, проще, чем решения исходной системы (8.1).
Замечание 1. В случае к = О инвариантов J; нет, и тогда в представлении (5) величины ?/» считаются искомы,ми константами, а уравнения подмодели (факторсистема) сводятся к системе конечных соотношений для этих констант,
ЗАМЕЧАНИИ 2. Для произвольных исходных систем дифференциальных уравнений возможна такая ситуация, когда факторсистема оказывается противоречивой (т. е, не имеет решений). Однако, для системы (8.1) эта ситуация встречается только при отыскании инвариантных //-решений ранга нуль.
Итак, для построения инвариантных Я-подмоделей системы (8.1) надо выполнить четыре операции: (а) выделить те подгруппы Я допускаемой группы, для которых существует базис инвариантов со свойствами (1)-(3); (б) вычислить эти инварианты; (в) сформировать представление решений вида (5) и (г) выполнить подстановку этого представления в систему (8.1). Методы выполнения пунктов (я) и (б) с достаточной подробностью изложены в Приложении, а пункты (в) и (г) выполняются автоматически.
Далее в этом разделе перечисляются все инвариантные подмодели ранга 3 для случая общего уравнения состяния газа и рассматриваются примеры подмоделей меньших рангов.
Подмодели ранга три. Эти помодели порождаются однопараметрическими подгруппами. Для группы Gn в оптимальной системе ее подгрупп (см. Приложение) содержится всего 13 представителей классов подгрупп Я = G1. Они порождают 13 различных подмоделей, описывающих все неэквивалентные классы инвариантных движений газа ранга три. В нижеследующем перечне этим классам движений присвоены названия (не всегда традиционные) и указаны представления соответствующих решений вида [5]. При этом, наряду с обычными декартовыми координатами (D) = (t. х, у, г, и, v, w) используются также цилиндрические координаты (С) = (t, х. г, 9, ис. vc, wc), вводимые следующими соотношениями:
х = х: у = rcosO. z = v sin O', г = \fy2 + г2, О = arctg(z/y),
ис = и, vc — vcos О + losing, wc = —vsin О -f и: cos 0, (6)
и = ис, v ~ vc cos О — wc sin в, w = vc sin 0 -f wc cos 0,
где vи wc — радиальная и окружная компоненты вектора скорости ис —
— (ис, vc, wc). В координатах (С) исходная система уравнений газовой
динамики имеет вид
Dcuc -г р 1Vcp = r'1(0,w2,-vcwc),
Dcp pdivcttc = 0. Dcp + perdivcuc = 0,
где Dc - dt + ис ¦ Vc, Vc ¦= (дх. дг, г~1дв), divcuc = исх + vcr + r~lvc + + r"lwcg.
Перечень подмоделей идет в порядке, обратном указанному в таблице П. 1 (см. Приложение). Инвариантный вектор скорости всюду обозначается символом U — (U, V, W). Так как подмодели рассматриваются только для уравнения состояния газа общего вида, то плотность р и давление р — инварианты любой подгруппы Я С G11 и потому здесь явно не указываются; они должны быть функциями тех же независимых переменных, что и вектор U.
13°. Двумерные движения (V): и — U(t, у, z). При U — 0 получается подмодель плоскопараллельных движений.
12°. Галилеево-инвариантные движения (V):
и = (x/t + U, V, W)\ U = U(t, у, z).
11°. Сдвиговые движения (Т>)\
u = (z + U,V,W)\ U = U(t, А, у); A = x-tz.
10°. Установившиеся течения (V): u = U(x,y,z).
9°. Стационарные течения в однородном поле
u = {t + U,V,W); U = U(t,\,z): X = x-t2/2.
8°. Конические дв и ж е н и я (D):
7°. Обобщенные конические движения (V):
и = (x/t + U, V, W); U ---- U(XU А2, Аз); Х\= x/t —pint, A 2 = y/t, Аз = z/t.\
/3 / 0 - произвольный параметр.
6°. Вращательные движения (С): ис = U(X, х, г), X — t-~B. 5°. Обобщенные вращательные движения (С):
Uc = (t. + и, V, wy. и = U(Xi, X2,г);
Ai t - 30, А2 = х - t1 /2, ft /--- 0 -¦ произвольный параметр.
4°. Винтовые движения (С): ис = U(t, А, г), А = х - в.
3°. Вращательно-симметричные движения (С):
ис = U(?, х, г).
2°. Обобщенные вращательно-симметричные движения (С):
wc = (ДО + U, V, W); U = U(t, А, г)А = х — в ф 0— произвольный параметр.
1°. Квазиконические спиральные движения (С):
ис = [0в + U, V, W); и = Щ\и А2, Аз);
А] = .т/t-вв. Xy — r/t,, \я = в — а_11п?;
а Ф 0, /3 — произвольные параметры. При /3 = 0 получается подмодель конических спиральных движений.
Вывод уравнений соответствующих подмоделей (факторсистем) делается просто подстановкой указанных представлений для (V) в систему (8.1) или для (С) в систему (7).
Подмодели 1°—13° остаются в силе и для политропного газа, когда рс2 = 7р. Однако следует иметь в виду, что в этом случае есть 30 подходящих подгрупп G1, порождающих подмодели ранга три, и среди них имеются не эквивалентные приведенным в данном списке.
Подмодели ранга два. Порождаются двухпараметрическими подгруппами Н2. В группе G11 имеется всего 27 классов таких подгрупп (см. Приложение). Все 27 соответствующих инвариантных подмоделей ранга два описаны и изучены их общие свойства. К ним относятся, в частности, подмодели одномерных движений, подробно рассматриваемые в главах III и IV, а здесь обсуждается лишь происхождение этих подмоделей.
Подмодель одномерных движений газа с плоскими волнами порождается подгруппой переносов (в системе координат (V)) по каким-либо двум координатам, например Я2{/2. /3}. Инвариантами являются независимые переменные t, х и искомые и, р, р. Уравнения факторсисгемы имеют вид
ut + иих + р~ 1рх = 0,
Ut ! uvx = 0, wt + uwx = 0, (8)
pt + ирх + рих = О,
Решения, в которых v = w — 0 описывают одномерные движения с плоскими волнами, перепендикулярными оси х.
Подмодель одномерных движений газа с цилиндрическими волнами порождается подгруппой переносов вдоль одной из осей и вращений вокруг этой оси, например Я2{/1, /7}. Инвариантами (в координатах (С)) являются независимые переменные t, г и искомые ис = U, р, р. Уравнения факторсистемы имеют вид (см. (7))
Vt + VVr + p~lpr = r~lW2,
Pt + V pr + p(Vr + r~lV) = 0,
Pt + Vpr + pc2(Vr + r~lV) = 0.
Её решения описывают подкласс вращательно-симметричных движений (см. 3°) и получаются, если искомые величины не зависят от х. Решения, в которых U = W =- 0 описывают одномерные движения с цилиндрическими волнами с осью х (осесимметричные движения).
Подмодель одномерных движений газа со сферическими волнами порождается подгруппой всех вращений Я3{/7, /8, /°}. Это - особая инвариантная подмодель ввиду того, что для нее не выполняется условие (3). Действительно, группа Я3 имеет базис инвариантов всего из шести скалярных величин: независимые переменные t, г = \х\ и зависящие от искомых р, р, q — |u| и s = х ¦ и. Однако на особом инвариантном многообразии этой группы (см. Приложение), заданном уравнением х х и - 0, инвариантов хватает, так как добавляется соотношение вида и - цх, где р, = q/r, и получается представление инвариантного Я3-решения
u-fq{t,r), p-p(t,r), p = p{t.r). (10)
Прямая подстановка выражений (10) в уравнения (8.1) дает факторсистему (три уравнения импульсов сводятся к одному)
Pt + <IPr p{qr + 2r~lq) =0, (11)
Pt + ЧРг + pc2{qr + 2 r~lq) = 0.
Решения этой системы описывают одномерные движения газа со сферическими волнами (сферически симметричные движения).
Замечание 3. Если в факторсистемах (8), (9) оставить только радиальную часть, положив v — w = 0 в (8) и U - W = 0 в (9), а также ввести единое
обозначение скорости и = q в (8) и V = q в (9), то все три полученные подмодели
запишутся единообразно в виде
qt г Иг - р~'рг = О,
Pt-г ЯРг 1 p{qr — vr~lq) = (12)
Pi + qPr + pc2{<jr + vr~1 q) = 0
с параметром геометрии и, имеющим значение v ^ 0 для плоских волн, v — 1 для цилиндрических волн и v = 2 для сферических волн.
Подмодели ранга один. Порождаются, как правило, трехпараметрическими подгруппами Я3. В группе G11 содержатся всего 47 классов таких подгрупп (см. Приложение). В этих подмоделях все искомые функции-инварианты зависят от одного независимого переменного-инвариан-та, а факторсистема является системой обыкновенных дифференциальных уравнений.
Пример. Берется подгруппа Я3{/4, /7, /п} совместных преобразований галилеевых переносов /4 вдоль оси х, вращений /7 вокруг этой оси и растяжений /п всех независимых переменных. Базис инвариантов этой группы образуют (в координатах (С)) независимый переменный инвариант А = г ft и набор инвариантов ис - x/t, vc, wc, р, р. Подстановка представления Я3-решения
ис = x/t. 4- (7(A), vc = К(А), wc = ЩА), р = р{ А), р ¦= р( А); А = г ft в систему (7) приводит к факторсистеме
(V - \)W ¦= -X~lVW, (13)
(V - \)р + [V 4 А-1V + 1 )р - 0.
(V - A)S' = 0.
где пятое уравнение записано через энтропию S = S(А), а штрихом обозначены производные по А. Физически содержательными будут только такие решения, в которых V ф А, а тогда S -- const. Значит эта подмодель описывает класс изэнтропических движений. Полный анализ всех возможных видов решений системы (13) весьма не прост. Уместно заметить лишь, что есть решения с U = W = 0, отыскание которых для политропного газа сводится к одному автономному уравнению первого порядка и квадратурам.
Замечание 4. Оказывается, что большинство классов подгрупп Н3 С G'11 не удовлетворяет условию (3). Более плодотворным является массив инвариантных подмоделей ранга один в случае политропного газа, для которого в группе G13 содержится 207 серий классов подгрупп IIя. Однако обсуждение всего массива возможных здесь подмоделей выходит за рамки данных «Лекций».
Некоторые частные случаи инвариантных решений ранга один (в основном — автомодельные решения) рассматриваются в главах III, IV.
Подмодели ранга нуль. Порождаются, как правило, четырехмерными подгруппами Н4. В G11 имеется 50 различных классов таких подгрупп. В подмоделях ранга нуль независимых переменных-инвариантов нет, все искомые величины-инварианты являются константами, а факторсистемы сводятся к системе конечных (алгебраических) уравнений. Ясно, что в случае уравнения состояния газа общего вида все подмодели ранга нуль описывают изобарические движения.
Простейшим примером является подмодель постоянного решения, когда все искомые и, р, р суть константы; она порождается подгруппой переносов по всем независимым переменным t, х, у, z. По аналогии с этим решения инвариантных подмоделей ранга нуль называются «простыми» решениями. Для политропного газа массив классов подалгебр Н С G13 состоит из 290 представителей и имеется много нетривиальных «простых» Н4-решений, причем все они найдены. В качестве примера не изобарических решений здесь выбран следующий.
Пример. Одна из серий подгрупп Н4(а) с Gu, зависящих от параметра а и представляющих собой комбинацию галилеевых переносов по осям ?/, л и растяжений имеет инварианты
tu/x, (tv — y)/x. (tw - z)/x, t~°~2xa+2p, t~axap.
Соответствующее представление «простых» решений таково:
и = Ux/t, v = (у 4 Vx)/t, и; = (z + Wx)/t, р = (x/t)-a~2R, р = (:x/t)~aP,
где U, V, W, Я, Р — некоторые константы. Подстановка в систему (8.1) в случае политропного газа, когда рс2 — *ур, приводит к факторсистеме
U2 -U = «P/Я, UV = 0, UW - 0, а( 1 - U) = U - 4, а(1 - U) = -7{U + 2).
Возможность U = 0 дает изобарические решения. Наряду с этим есть решение с V = W = 0. В этом случае для констант a,U и Р/R получаются выражения через показатель адиабаты 7
а =--, U --- 2(2
(2-7)- (15)
7-1 7 + 1 R \7 I- !/
Следовательно, здесь физически осмысленные не изобарические «простые» решения получаются при 7 < 2. Легко проверить, что эти решения описывают изэнтропические движения газа.
Частично инвариантные решения. Теория группового анализа позволяет выделять и изучать в качестве упрощенных моделей не только классы инвариантных решений. Одно из возможных обобщений понятий инвариантного решения достигается за счет отказа от полной инвариантности и использования частичной инвариантности многообразия относительно группы преобразований основного пространства. Это приводит к понятию и алгоритму отыскания так называемых частично инвариантных решений.
Такие решения возможны либо когда базис инвариантов группы Н (Определение 8.2) не удовлетворяет условию (12.3), либо когда ищутся решения ранга большего, чем число к в (12.1). Применительно к уравнениям газовой динамики это означает, что получается меньше пяти независимых инвариантных соотношений вида (8.16). Поэтому инвариантов нехвагает для выражения из этих соотношений всех пяти искомых величин (и, v, w, р, р) • - среди них есть «лишние». Последние должны считаться функциями от всех независимых переменных (t. х). Требование совместности соотношений (8.16) с уравнениями газовой динамики в этом случае приводит к объединению фактор-сиегемы (связывающей только инварианты группы Я) с дополнительной системой уравнений для «лишних» функций. Число независимых переменных — инвариантов в факторсистеме и здесь называется рангом подмодели (и также рангом класса искомых решений). В результате анализа совместности этой объединенной системы и получаются искомые решения. Общая теория частично инвариантных решений изложена в [5].
Число существенно различных классов частично инвариантных решений значительно больше, чем инвариантных, так как они зависят не только от выбора подгруппы Я основной группы, но также и от выбора «лишних» функций. В полном объеме совокупность всех классов частично инвариантных решений уравнений газовой динамики пока еще не изучена. Ниже рассматривается один из простейших классов таких решений, дающий пример хорошо известной и полезной модели.
Кратные волны. В качестве Н берется группа Я5, порожденная всеми переносами fl, /2, /3,/10 и растяжением /п (см. (8.5)). Ее базис инвариантов состоит только из всех искомых величин
J = (и, V, W, р, р), (3)
а число к = 0. Инвариантное Я°-решение ранга нуль есть «простое» постоянное решение
и = и0 , р = ро , Р~Ро ¦ (4)
Нетривиальными могут быть лишь частично инвариантные Я°-решения ранга п, где 0 < п < 4.
Определение 1. Частично инвариантные Яг’-решения уравнений газовой динамики (3.11) ранга п называются п-кратпыми волнами. При этом 1-кратная волна называется простой волной, 2-кратная волна — двойной волной и 3-кратная волна — тройной волной.
Представление n-кратной волны должно состоять из 5 — п соотношений между величинами (3). Законченные результаты удается получить лишь для простых волн, описание которых приводится ниже.
Отыскание простых волн. Простая волна описывается 5 — 1=4 независимыми соотношениями между величинами (3). Путем разрешения таких соотношений можно получить выражения четырех из переменных (3) через одну из них. Для более симметричной записи получаемых выражений удобно ввести вспомогательный параметр простой волны а, назначив величины (3) функциями от этого параметра. Тогда этот параметр и будет играть роль той «лишней» функции, которая определяет дефект инвариантности (5 = 1 простой волны. Итак, всякая простая волна описывается следующим представлением решения системы (3.11):
u = и(«), р = р(а), р р(п), S — 5(a), (5)
где а = а(х. t) — новая неизвестная функция, подлежащая определению вместе с функциями (5).
Область пространства R4(x,t), в которой определена простая волна, покрыта однопараметрическим семейством гиперповерхностей а = const, вдоль каждой из которых все основные величины постоянны. Эти гиперповерхности называются поверхностями уровня простой волны.
-я В результате подстановки представления (5) в систему уравнений (3.11), с учетом соотношений вида
Du = и'Da. div u = u' • Vq, Vp = p'Va, i^c штрихом обозначены производные по а, эта система примет вид
pDa + ри' • Vq = О, ри'Da + p'Va — 0, (6)
S'Da = 0.
Пять уравнений этой системы содержат четыре производных первого порядка от «лишней» функции а. Их исключение приведет к уравнениям, связывающим только инвариантные величины и их производные; это будет часть инвариантной факторсистемы. Кроме того, полученные выражения для производных от а должны быть совместны. Очевидно, что условия совместности породят новые соотношения между инвариантными величинами и их производными. Эти соотношения составят вторую часть инвариантной факторсистемы. Что же касается теперь уже совместных выражений для производных от а, то они образуют дополнительную пассивную (т. е. не порождающую каких-либо новых уравнений) систему Р. Весь этот путь реализации представления системы (6) в виде объединения инвариантной факторсистемы и пассивной системы Р фактически будет проделан при доказательстве нижеследующей теоремы, дающей описание основных свойств простых волн.
Последнее из уравнений (6) является классифицирующим, так как приводит к альтернативе: либо S' Ф 0, и тогда Da = 0, либо S' = 0.
Если в простой волне Da = 0, то поверхности уровня являются контактными характеристиками. Так как при этом Vq Ф 0 (иначе получилось бы, что а = const тождественно, т. е., согласно (5), просто постоянное решение), то из (6) следует, что р' = 0 или р = const. Следовательно, простая волна этого типа представляет собой изобарическое движение (см. § 9).
Основные свойства простых волн. Простая волна, в которой Da = 0, будет называться вырожденной, а простая волна, в которой Da ф 0, будет называться невырожденной простой волной.
Теорема 1. Невырожденная простая волна есть изэнтропнческое безвихревое движение. Поверхности уровня такой волны являются звуковыми характеристиками и представляют собой гиперплоскости в Л4(х, t).
Доказательство. В невырожденной простой волне должно быть S' = 0, откуда S = const. Далее, здесь р' ф 0, так как в противном случае из (6)
получилось бы, что и' = 0 и р' = 0, т. е. постоянное решение. Поэтому в результате векторного умножения второго уравнения (6) на и' получается равенство
u'xVq = 0. (7)
Но в силу представления (5) справедливо выражение
rotu = —и' х Va.
Поэтому равенство (7) равносильно rot и = 0. Далее, в результате скалярного умножения второго уравнения (6) на Va и использования первого уравнения (6) получается соотношение
p'(Da)2 — p'jVa|2 = 0,
откуда с учетом равенства р' = с? р’, следует уравнение
(Da)2 - c2|Va|2 = 0. (8)
Сравнение этого уравнения с (6.27) показывает, что гиперповерхности а = const являются звуковыми характеристиками. Далее, в результате скалярного умножения второго уравнения (6) на и' и исключения величины и' ¦ Va с помощью первого уравнения (6) получается равенство
р2\и'\2 = р'р'. (9)
Теперь надо заметить, что равенство (7) равносильно соотношению
Va = Jfcu' (10)
с некоторой функцией к = к(х, t) -ф 0. Так как Da = at + u ¦ Va, то исключение из первого уравнения (6) величины Va дает выражение для производной а<:
p’at = —к(р и ¦ u' + pju'j2).
Это выражение, с учетом равенства (9) и того, что с модулем вектора скорости <7 — | и| верна формула и ¦ и' = qq', упрощается до следующего:
«t = -к (qq! -f . (11)
Из (10) и (11) следует, что нормаль к каждой данной гиперповерхности a = const имеет одно и то же направление для всех ее точек. Поэтому каждая поверхность уровня невырожденной простой волны есть гиперплоскость в i?4(x, /). ¦
Здесь инвариантная факторсистема образована уравнениями S' — 0 и (9), а пассивная система Р — уравнениями (10) и (11) для «лишней» функции а. Легко проверить, что в силу совокупности этих уравнений исходные уравнения (6) удовлетворяются тождественно.
Параметр простой волны а находится путем интегрирования системы уравнений (10), (11). Для этого надо заметить, что дифференцирование вдоль любой кривой, лежащей на поверхности уровня а -- const, дает соотношение
da = Va ¦ с/х + oct.dt = 0, откуда, в силу (10) и (11), следует уравнение
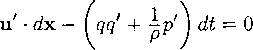
с постоянными коэффициентами при дифференциалах еЬс и dt. Поэтому оно просто интегрируется в виде
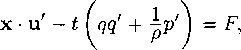
где постоянная интегрирования F может быть произвольной функцией а (впрочем, несущественной, так как сам параметр а определен с однофункциональным произволом). Видно, что (12) есть уравнение однопараметрического семейства (с параметром а) гиперплоскостей — поверхностей уровня простой волны. При заданных функциях и(а), р(а), р(п) и F(a) уравнение (12) неявным образом определяет параметр как функцию переменных х, t.
В уравнении (12) величины и, р, р, как функции переменного а, связаны только с уравнением состояния р — f(p, S) при S = const и уравнением (9). Поэтому совокупность всех простых волн зависит от трех произвольных функций одного независимого переменного.
Для двойных и тем более тройных волн — решений уравнений газовой динамики (3.11) — такого простого описания не получается. Симметричное параметрическое представление двойных волн имеет вид
u = u(a,/3), р = р(а,0), р — р(п,0), S = S(a,0), (13)
где параметры а и 0 — «лишние» искомые функции переменных х, t. Здесь факторсистема оказывается очень сложной и исчерпывающему анализу не поддается. Тем не менее теория частично инвариантных решений позволяет доказать, что двойные волны общего (в определенном смысле) характера являются изэнтропическими решениями (см. [5]).
Автомодельные кратные волны. Уместно обратить внимание на
специальный случай кратных волн, которые сводятся к инвариантным решениям. Например, если в представлении простых волн (12) положить F = О и v = w — 0, то в качестве параметра волны можно взять а = x/t. Это приводит к частным инвариантным решениям подмодели конических движений 12,8°. В общем случае решения, описываемые подмоделью 12,8°, можно рассматривать как тройную волну, которая сама себе подобна в том смысле, что все искомые величины остаются неизменными при равномерном растяжении пространства /?4(х, t). Для установившихся течений также возможны аналогичные подмодели, в которых все искомые зависят только от отношений x/z, y/z или х/у/у2 -г z2, описывающие стационарные двойные или простые волны. Такие сами себе подобные решения принято называть автомодельными.
Существование таких кратных волн является типичным для любых дифференциальных уравнений, допускающих группу G1 равномерных растяжений всех независимых переменных (аналогично группе (8.8). Этот важный класс кратных волн заслуживает выделения специальным термином.
Определение 2. Решение дифференциальных уравнений, допускающих группу равномерных растяжений пространства независимых переменных, инвариантное относительно этой группы, называется коническим автомодельным решением.
Данный термин отражает тот факт, что в коническом автомодельном решении все искомые функции постоянны на лучах, выходящих из фиксированной точки (центра). Поэтому характерными областями определения таких решений являются внутренности прямолинейных конусов с общей вершиной в центре. В краевых задачах дополнительные данные, определяющие коническое автомодельное решение, должны задаваться на поверхности таких конусов и быть постоянными вдоль образующих.
Особенно важно обратное свойство: граничные значения в краевой задаче, заданные на поверхностях конусов с общей вершиной и постоянные вдоль образующих, совместимы с предположением о конической автомодельности искомого решения. Поэтому краевые задачи, в которых данные обладают указанными свойствами, называются конически автомодельными задачами.
Итак, если задача конически автомодельна, то можно искать ее коническое автомодельное решение. Конечно, вообще говоря, ниоткуда не следует, что такое решение существует. Этот вопрос связан с корректностью постановки краевой задачи в неограниченной области и должен решаться индивидуально для каждой конкретной задачи. На практике обычно используется именно возможность построения решения, которое ищется в надлежащем виде, с последующей проверкой всех граничных условий и, если это возможно, доказательством единственности решения.
В важном частном случае уравнений с двумя независимыми переменными, например х и у, коническое автомодельное решение имеет вид (для любой искомой величины F)
и тем самым постоянно на лучах х = Ху (А = const). Такое решение изображается на плоскости В?(х, у) в виде «веера» лучей А = const, разбивающих эту плоскость на ряд угловых областей (плоских конусов), в которых решение F( А) меняется непрерывно (в частности, может быть постоянным). Эти области примыкают друг к другу вдоль некоторых особых лучей (которые могут быть носителями дополнительных условий, линиями сильного или слабого разрыва).
Следовательно, если граничные значения величин F заданы и постоянны вдоль некоторых лучей А = const, то решение такой краевой задачи можно искать в классе конических автомодельных решений вида (14). При этом для искомых функций F(А) получится система обыкновенных дифференциальных уравнений. Примеры такого построения для различных конкретных уравнений и задач газовой динамики рассматриваются в главах III и IV.
Предыдущие специальные математические модели газовой динамики давали точные решения исходных уравнений. Здесь будут рассмотрены некоторые случаи такого упрощения уравнений, которое приводит к приближенным решениям. Этот метод заслуживает внимания, так как он широко применяется в приложениях при решении сложных практических задач.
Основой приближенного моделирования является глубокое изучение особенностей поведения движения газа, направленное на выяснение определенных закономерностей, которые могут быть достаточно просто описаны в аналитической форме. С точки зрения исходных уравнений, эти закономерности принадлежат точным решениям, а приближенные решения выступают как их упрощенные асимптотические описания. Общая схема такого подхода состоит в том, что в уравнения и в решение вводится некоторый малый параметр S, от которого описание рассматриваемой особенности не зависит, и учитываются порядки малости членов уравнений при 8 —> 0. Если в уравнениях возникают слагаемые с различными степенями S, то в каждом уравнении удерживаются только те из них, которые имеют наинизшую степень малого параметра 6. Это и дает искомые приближенные уравнения.
Понятно, что указанная процедура является в значительной мере формальной. Математический идеал требует доказательства того, что решение полных уравнений при 6 —* 0 действительно имеет решение приближенных уравнений в качестве главного члена (хотя бы асимптотически).
На самом деле этот идеал достигается в весьма редких случаях; обычно исследователи ограничиваются формальным построением приближенной модели. Обоснование же предоставляется физической интуицией, для которой тем самым открывается широкий простор. Ясно, что при этом сильно возрастает роль критерия практики.
В этом параграфе метод формального приближенного моделирования иллюстрируется на четырех примерах. Последний из них (теория мелкой воды) интересен тем, что вскрывает несколько неожиданную связь между волнами на воде и газодинамическими процессами.
Линеаризация. Пусть известно некоторое основное движение, т. е. точное решение уравнений газовой динамики (3.11):
u = u0(x,i), p = p0{x,t), p = po{x,t): S = So(x, t). (1)
Ищется другое, мало отличающееся от (1), решение вида
u = uo + <5u', р = ро + Sp', р = ро + Sp', S = So + SS', (2)
где штрихом обозначены новые неизвестные функции (добавки к основному решению или его возмущения) переменных х и t, а (5 — некоторый параметр. При подстановке выражений (2) в уравнения (3.11) надо учесть, что оператор D производной в частице примет вид
D = D0 + 5и' ¦ V, D0 = dt + u0 • V
и что функции (1) образуют решение системы (3.11). После подстановки и сокращения на общий множитель д получаются уравнения
Dop' + и' • Vpo + р' div ио + ро div и' + ди' • Vp'+
+5р' div и' = О,
?>0и' + и' • Vu0 ~
Р ,-^ЧРо
+-rT7VP'+
+(5и' • Vu' = О,
DoS' + и' • VS0 + ди' • VS' = О,
р' = + V, So + SS') - /(ро, So))-
Ясно, что на самом деле возмущения и', р' и т.д. должны зависеть не только от переменных х, t, но также и от параметра 6. Главная трудность дальнейшего анализа состоит в оправдании следующего предположения: функции и', р', р', S' как решения точных уравнений (3), а также входящие в эти уравнения их производные имеют конечные предельные значения при 5 —» 0.
Если это предположение оправдано, то переход к пределу при (5 —> 0 в уравнениях (3) приводит к следующей системе уравнений для возмущений основного движения:
Dqp' + р' div u0 + u' • Vpo + Po div u' = 0,
D0n' - u' • Vu0 + TjrVp' + ~Vp0 = 0,
Po Po (4)
D0S' + u' • VS0 = 0,
p' = c2op' + fs„S'.
где /s(i —• fs (po, So).
Описанная процедура вывода уравнений (4) называется линеаризацией исходных уравнений (3.1), так как уравнения (4) являются линейными дифференциальными уравнениями относительно искомых u', р', р', S'. Необходимо иметь в виду, что при рассмотрении краевых задач дополнительные условия также подвергаются аналогичной процедуре линеаризации.
Важный частный случай системы (4) получается тогда, когда в качестве основного движения взято следующее постоянное решение (покоящийся газ):
и0 = 0, Ро const, Ро = const, So - const.
В этом случае Dq = dt.. Пусть ищутся только изэнтропические возмущения, т. е. S' = 0. Тогда система (4) примет вид
p't + ро div и' = 0, pou't + Vp'=0 {р' = с2ор')-
Это — классическая система уравнений акустики (для однородной среды). В частности, из (5) легко выводится одно уравнение для возмущения давления: где А - оператор Лапласа. Волновому уравнению (6) удовлетворяет также возмущение плотности р', а в случае безвихревых возмущений (т. е. когда rot и' = 0) — и вектор возмущения скорости и'.
Околозвуковое приближение. Ради простоты рассматривается случай безвихревого установившегося движения, описываемого интегралом Бернулли (11.19) и уравнением для потенциала скоростей (11.20). Околозвуковое приближение предназначено для упрощенного описания течений, возникающих при малых возмущениях звукового потока, в котором
и-с», vw - 0, с = с». (7)
Если выполнить изложенную в предыдущем пункте операцию линеаризации с основным движением (7), то легко убедиться в том, что полученная модель оказывается неудовлетворительной. Формально правильное описание возмущений звукового потока получается, если принять следующие представления координат, потенциала и скорости звука:
х = 81+кх\ у = 5ку\ z — 8кz \
с/з = с»х + 83+к<р\ с = с* + 82с'
при любом выборе значения вещественного параметра к. С использованием обозначений
После подстановки величин (10) и выражения для скорости звука (8) в интеграл Бернулли (11.19) последний принимает вид
с2 + 252с*у' + 54и'2 + 86(v'2 -г и/2) + Т(с2 +- 2d2c*c + 54с'2) = q2t. Использование разложения по формуле Тейлора
l{cl + r1) = I{ci) + (2/m,)i1 ! 0(г/2)
(где т* = т(р») есть величина (2.22)), справедливого в силу (2.24), и учет соотношения с2 г /(с2) = приводят после сокращения на 2$2, к уравнению
с,и' + (2с*/тп.)с' + 0(82) - 0. (11)
Теперь делается предположение, аналогичное тому, которое использовалось при линеаризации: функции и', г/, w', с', как решения соответствующих точных уравнений, а также входящие в эти уравнения производные при фиксированных конечных значениях переменных х'. у\ z' имеют конечные предельные значения при S —> 0. Выделенные здесь курсивом слова акцентируют внимание на нетривиальности данной ситуаций, так как согласно (8), например, у/х = И"1у'/х' и при фиксированном отношении у'/х' будет у/х —> оо при S - > 0. Качественно это означает, что околозвуковое движение слабо меняется в направлениях, перпендикулярных основному звуковому потоку, и потому для правильного описания этого изменения надо сокращать расстояния (как бы сжимать поток) в этих направлениях так, как предписывают формулы (8)—(10). Обоснование этого предположения для одного вида околозвукового течения дано в § 26.
В пределе при S --> 0 из (11) получается соотношение
т*и' + 2с' = 0, (12)
заменяющее интеграл Бернулли в околозвуковом приближении.
В уравнении для потенциала скоростей (11.20) представления отдельных слагаемых в силу (8), (9) и (10) имеют вид
(и2 - С2)рхх = 25*-kc,(u' - J)<p'x,x, \ 0(5ъ~к),
(v2 ~ с2У-Руу + (го2 - с2)?» = -53-кс1(ч/у.у. + <р'г.г, + 0(S5~k), 2uvipxy + 2 uwipxz = ()(5°~к), 2vwipyz = 0(S9~k).
Следовательно, после деления на 53~ к и предельного перехода 5 —> 0 подучается уравнение
2с*(и — С )<рх'х' ~ с*(''Ру'у‘ 'Pz’z') г~ О-
Наконец, использование соотношения (12) и равенства и' = ip'x, привода! это уравнение к окончательному виду
тп* + 2 / ^ j / _ . ..
(;'PXt^X'X> 'fiy'y' ''Рzf z' * (13)
Выполненное моделирование показывает, что возмущения звукового потока приближенно описываются нелинейным уравнением, а именно квазилинейным уравнением (13). Этот нетривиальный факт делает теорию околозвуковых течений газа очень трудной, но вместе с тем и очень интересной для математического исследования.
Гиперзвуковое приближение. Рассматриваются сверхзвуковые, равномерные в бесконечности вверх по потоку плоскопараллельные установившиеся течения газа. Пусть qi есть значение скорости в бесконечности и Ci — соответствующее значение скорости звука. Течение называется гиперзвуко-вым, если число Маха Mj = cji/ci является очень большим (по сравнению с единицей). Ясно, что если в такой поток вносятся относительно малые возмущения, то число Маха М будет большим и во всем потоке. Гипер-звуковое приближение предназначено для описания течений, получаемых относительно малыми возмущениями поступательного течения, в котором
и = <7i, v = 0, с = С\
(14)
при условии, что д = с\/ц\ мало.
Правильное описание возмущений гиперзвукового течения получается при следующем представлени величин (подробности даны в § 27):
х = х', у = 5у', и = <ji + 52и', v = St/,
(15)
В результате подстановки представления (15) в уравнения (3.11) последние принимают вид
^2(<?i + SVK, + S2v'u‘+ <52-^р'х, -- 0.
р
S(qi + 52u')v'x, + Sv'v'yl + S^jp'y, = 0,
(16)
(?! + 52u')p'x, + v'p'y, + p'{52u'x, + v'y,) ~ 0, (<?, + 52u')S'x, + v'S'y. = 0.
Далее делается стандартное предположение: функции и\ г/, р'. р', S' и их производные по х', у' имеют при фиксированных конечных значениях переменных х', у' конечные предельные значения при 5 —> 0. Здесь ситуация аналогична случаю околозвуковой модели. В этом предположении в результате сокращения второго уравнения (16) на 5 и последующего предельного перехода при 6 -> 0 из (16) получается система уравнений
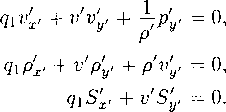
(17)
После замены х' = q\t и переобозначения г/ —> и. у' —> х система (17) в точности совпадает с системой уравнений одномерного движения газа с плоскими волнами. В этом приближении величина и' остается неопределенной; она может быть вычислена в более высоком приближении, например из интеграла Бернулли.
Теория мелкой волы. Здесь дается вывод приближенных уравнений, описывающих динамику волнового движения идеальной несжимаемой жидкости на поверхности водоема конечной глубины при условии, что толщина слоя жидкости мала по отношению к характерному горизонтальному размеру (например к длине волны). Оказывается, что получаемая модель этой задачи, казалось бы не имеющей отношения к динамике, в точности совпадает с уравнениями движения политропного газа с показателем адиабаты 7 = 2. Возникающая при этом гидродинамическая аналогия не только дает замечательный пример единства природы волновых явлений, но может быть полезной и при анализе конкретных движений.
Исходная задача ставится так: требу-Щ стоя определить потенциальное движение
идеальной несжимаемой жидкости, на которую действует равномерное поле сил тя-
___ жести, в тонком слое над горизонтальным
У q h.(x,t) ровным дном с постоянным давлением на
х верхней свободной поверхности (рис. 1), возникающее под действием некоторого на-Рис- * чального возмущения. Для простоты будет
рассмотрена двумерная задача, хотя все почти дословно справедливо и для трехмерной задачи. Пусть Ф = Ф(х, у, t) есть потенциал скорости, д — ускорение сил тяжести, вектор которых направлен по оси у, дно водоема есть у = 0 и у ¦--- h(x,t) — уравнение
свободной границы. В области П = {-ос < х < оо, 0 < у < h(x,t)j
потенциал Ф удовлетворяет уравнению Лапласа
Кроме того, для Фи h задаются некоторые начальные значения при t = 0.
Для анализа удобно ввести в рассмотрение значение потенциала на свободной границе
Тогда входящие в уравнения (20) и (21) производные от Ф могут быть выражены через производные от <р и производную Фу. Последняя же может трактоваться как значение определенного оператора N над парой (<р, h), действующего по правилу: в области fi решается смешанная краевая задача для уравнения (18) с граничными условиями (19) и (22), после чего находится N = $y\y=h = N(<p, h). При этом N, очевидно, линеен относительно ip, но нелинеен относительно h.
Приближенное моделирование этой задачи выполняется путем введения малого параметра 5 согласно формулам
х = х'. у = 8у'. t = 5~l^2t', h = 8hr,
Г231
Ф = 81/2Ф\ у = S1/:У.
Вначале приближенно решается краевая задача в области С1. В силу (23) уравнение (18) переходит в уравнение
S2Ф', , + Ф', , = 0.
w ^х'х' ' у у Его решение ищется в виде ряда по степеням 5
Ф' = Ф0 + <?2Ф 1 + ..., для членов которого получается рекуррентная система Ф()у'у' — 0, Ф]у’у> + Фоаг'а:' = 0, . . .
Решение этой системы с граничным условием (19) имеет вид
Фо Ф1 = -\Ах,х.(х'Л')у'2,---
и дает представление потенциала
Ф' — А — ^5~ АХ1Х’у'~ + ...
Функция А находится из граничного условия (22), которое дает А = р' +¦ + S-\i> + ... В итоге получается представление решения краевой задачи (с точностью до членов порядка 8А)
Уравнения (20) и (21) в результате подстановки (23) принимают вид
h't, 4- К'К' - S 2ф;„ Ф'(, 4 |(ФЗ - 6~2Ф$) t gh' = О. (25)
При обычном предположении о предельных значениях всех штрихованных величин при S —> 0 из (24) находится предел
1ш1(<Г2ф;,|у,=/1,) = -h'(p'x,x,. (26)
В силу (26) формальный предельный переход S —> 0 в уравнениях (25) с учетом (24) приводит к уравнениям
К1 + '-Рх'^'х' + ^ф'х'х’ = 0, 4s'v +• 7j?42/ + = 0- (27)
Наконец, если ввести скорость и' = <р'х, и продифференцировать второе уравнение по х', то получится система уравнений (штрихи опущены)
ht + uhx + hux = О,
(zs)
щ 4 иих 4- ghx = 0.
Это есть система уравнений одномерного с плоскими волнами изэнтропического движения газа (роль плотности р играет h) с уравнением состояния р = ^gh2. Легко показать, что начальным данным в исходной задаче соответствуют некоторые начальные данные для системы (28). Теория волновых движений несжимаемой жидкости, основанная на приближенной модели (28), получила название теории мелкой воды.
Задачи и упражнения к главе II
1. Доказать, что изобарическое движение является безвихревым, если и только если вектор скорости u = const.
2. Показать, что матрица Л определяет изобарическое движение с линейным полем скоростей (9.15), если и только если Л3 = 0.
3. Показать, что уравнения изэнтропического движения имеют решения, в которых плотность р зависит только от времени t (обобщение изобарических движений). Установить, что в этом классе решений удельный объем необходимо имеет вид (а, — постоянные)
4. Показать, что в установившемся движении политропного. газа приведенная скорость А = q/c, выражается через число Маха М = q/c по формуле
5. Пусть при установившемся обтекании тела политропным газом давление в точке торможения (q = 0) имеет значение ро. Вывести формулы
i = (. _ . Л +
6. Выяснить, до каких скоростей полета вблизи земли можно считать воздух несжимаемой жидкостью при определении давления в критической точке с точностью 1% (скорость звука 1200 км/ч, 7 = 1,4).
7. Показать, что установившееся сверхзвуковое течение типа источника возможно со скачком уплотнения, расположенным на любом заданном расстоянии го > г«.
8. Вычислить инварианты группы G1 с оператором (8.10). Найти представление решения, инвариантного относительно этой группы.
9. Восстановить преобразования, образующие группу G1 с оператором
С ¦ д = t2dt -f- txdx + tydy + (х — tu)du + (У - tv)dv - 2tpdp - 4tpdp.
Показать, что система уравнений плосконараллелыюго движения политропного газа (12.17) допускает эту группу только при 7 — 2.
10. Доказать, что для системы уравнений (12.29) при и > 0 простые волны необходимо являются автомодельными решениями, т. е. имеют вид
и = и{ А), р = р{ А), р = р{ А),
где А = r/t с точностью до преобразования переноса по t.
11. Вычислить характеристики системы уравнений стационарных конических движений газа (12.25). Дать описание класса решений, на которых эта система имеет гиперболический тип.
12. Найти характеристическую форму уравнений акустики (5) в случае одномерных движений с плоскими волнами. Использовать ее для решения задачи Коши с произвольными начальными данными при t = 0.
13. Найти преобразования растяжения, допускаемые уравнением (13) для потенциала скоростей в околозвуковом приближении.
14. Показать, что уравнения теории мелкой воды на непрерывных решениях равносильны интегральным законам сохранения
<j)(hdx — hudt) = 0, <j> ^hudx — ^hu2 + dtj = 0,
I" г
где Г — произвольный замкнутый контур на плоскости R2(x, t).
15. Найти уравнения сильного разрыва в теории мелкой воды исходя из интегральных законов сохранения предыдущей задачи.
Одномерные неустановившиеся движения
Модель одномерного неустановившегося движения представляет собой одну из наиболее полно изученных газодинамических подмоделей. Исторически начало теоретического изучения движений этого класса восходит к Риману, почти 150 лет тому назад заметившему наиболее важные особенности явления распространения волн конечной амплитуды. Это явление сопровождается такими существенно нелинейными эффектами, как градиентная катастрофа, образование ударных волн, распад произвольного разрыва и рядом других.
Предположение об одномерном характере движения является привлекательным и полезным по ряду причин. Прежде всего, оно приближенно оправдывается для многих случаев реальных движений газа. Даже если некоторое движение в целом и не одномерно, отдельные ег о пространственно-временные подобласти часто могут быть описаны в рамках одномерного движения. Таковы движения в трубах, при взрывах и ударах и т. д. Далее, уравнения и задачи этой модели являются сравнительно доступными для качественного анализа и численного расчета благодаря тому, что здесь основные величины зависят лишь от двух независимых переменных. При этом не последнюю роль играет также и возможность предельно наглядного изображения различных газодинамических ситуаций на плоскости событий. Далее, многие выявленные в рамках одномерного приближения особенности движения оказываются качественно присущими и более сложным движениям, позволяя изучать последние на основе оправданной аналогии. Очень важно и то, что в теории одномерных движений имеется много до конца решенных конкретных задач, образующих, в их совокупности, «золотой фонд» теоретической и прикладной газовой динамики.
Несомненно, что значение фактов и эффектов, выявленных при изучении одномерных движений, выходит за рамки этой теории. Они послужили отправным пунктом для развития ряда направлений современной математической физики. Например, прогресс в теории квазилинейных гиперболических систем дифференциальных уравнений во многом обусловлен представлениями и результатами, почерпнутыми из области одномерной газодинамики.
Настоящая глава и предназначена для ознакомления читателя с основными свойствами и методами исследования одномерных неустановившихся движений газа.
§ 15. Плоские, цилиндрические и сферические волны
Основные уравнения и их характеристики. Дифференциальные уравнения одномерного движения с плоскими, цилиндрическими или сферическими волнами уже были получены в виде (12.12). С заменой обозначения скорости q на и эти уравнения таковы:
Щ + uur + ipr = О,
Pt + ирт \ риг + ури -- о, Pt -Ь ирг 4 рс2иг + урс2и = О,
(1)
где с2 = с2(р, р) рассматривается как заданная функция. Параметр геометрии v имеет значение и = 0 для плоских волн, и = 1 для цилиндрических волн и v — 2 для сферических волн. В случае и = 0 координата г = х меняется на всей оси (—оо,оо), а если v > 0, то координата г меняется лишь в интервале (О.эс). Первое из уравнений (1) есть уравнение импульса, второе — уравнение неразрывности и третье - одна из форм уравнения энергии.
Общие качественные свойства гладких решений системы (1) выясняются с помощью се характеристик. Хотя для этой цели и можно было бы воспользоваться выводами § 6 и перенести их на систему (1) с учетом того, что она описывает лишь класс частных решений уравнений газовой динамики, моделируя уравнения (3.14), однако здесь уместно провести независимый анализ. Для системы (1) пространством событий является плоскость B?(r,t). На этой плоскости событий и рассматривается картина одномерного движения газа, «частицы» которого можно считать перемещающимися по оси г. Здесь характеристики будут просто линиями на плоскости Я2(г. t).
Нормальные характеристические векторы ищутся в виде ? — (?, г). С величиной х =- Т + характеристическая матрица (см. § 6) системы (1) такова:
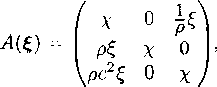
и ее определитель равен
det А(?) = х(х2 ~ с2(2)-
Очевидно, что характеристическое уравнение dctA(?) = 0 здесь всегда имеет три вещественных корпя: ^ = 0 и \ соответствующих
контактной и звуковым характеристикам. Следовательно, система (1) является гиперболической. Разыскивая уравнения характеристик на плоскости Д2(гЛ) в виде г — r(t), удобно взять в качестве задающей их функции h(r,t) = г - r(t). Тогда нормальный характеристический вектор запишется в виде ? — (1, -r'(t)), а величина х будет равна х = и ~ г,(0>
где r’(t) = dr(t)/dt. Отсюда получаются следующие дифференциальные
уравнения характеристик системы (1):
(С+) dr/dt —и + с, (2)
(С_) dr/dt. = и — с.
Всюду в дальнейшем будет использоваться именно эта, указанная в (2), маркировка характеристик: Со для контактных и С± для звуковых.
Для получения условий на характеристиках находятся соответствующие левые собственные векторы А матрицы А(?). Они оказываются такими: Ао = (0, —с, 1) для характеристик Со и А± = (±рс, 0, 1) для характеристик С±. По правилам, изложенным в § 6, это дает следующие условия на характеристиках:
(Со) Pt + ирг - c2(pt -Г ирг) = О,
(С±) pc(ut + (и ± с)иг) ± (Pt + (и ± с)рг) ± урс2и = О,
где одновременно берутся верхние или нижние знаки. Более компактно эти условия записываются с помощью операторов дифференцирования вдоль характеристик
в следующем виде
(Со) D0p = с2D0p (D0S - 0),
(С+) D+u+ jfiD+p = -jcv, (4)
(C_) D-u-^?Lp=?cu.
Совокупность соотношений (4) образует характеристическую форму системы уравнений (1) и равносильна этой системе.
Как и в § 3, гладким движением газа здесь называются такие решения U = (и, р, р) системы (1), в которых все искомые функции непрерывно дифференцируемы. В области гладкого движения через каждую точку М е В~(г, I) проходит одна и только одна характеристика каждого семейства. При этом, как это видно непосредственно из уравнений (2), в силу положительности скорости звука с направление характеристики Со всегда разделяет направления характеристик С+ и С_ (если все направления берутся в одну и ту же сторону: dt > 0 или dt < 0).
Лемма о плотности. Для дальнейшего анализа полезна следующая лемма (которая на самом деле верна для произвольных, а не только для одномерных непрерывных движении газа).
Лемма 1. Если движение гладкое и если р = 0 в некоторой точке М (в которой г ф 0 при v > Q), то р — 0 вдоль всей характеристики С'о(М) (траектории), проходящей через точку М.
Доказательство. Уравнение неразрывности (1) с использованием оператора Dq переписывается в виде обыкновенного дифференциального уравнения для величины р вдоль Со:
![]()
Так как коэффициент при р в правой части этого линейного однородного уравнения непрерывен, то из р(М) = 0 следует р(Со(М)) = 0 в силу
единственности решения.
В нормальном газе аналогичное свойство справедливо для скорости звука с и для давления р. Из него вытекает также, что если какая-либо из величин р, с, р отлична от нуля в точке М, то все они будут отличны от нуля вдоль всей линии Со(М). Если назвать точкой вакуума такую точку, в которой р = с = р = 0, то на основании предыдущего можно сделать вывод: линией вакуума может быть только характеристика Со (траектория). Кроме того, из уравнений (2) следует, что вдоль линии вакуума характеристика Со сливается с характеристиками С+. Поэтому никакая звуковая характеристика С+ или С_, сама не являющаяся линией вакуума, не может пройти через точку вакуума.
Теорема единственности. Пусть гладкое движение определено в полу полосе П = {0 ^ t ^ Т, г>0},и пусть точка А/ € П не есть точка вакуума и выбрана так, что все проходящие через М характеристики достигают оси t — 0. Тогда образуется (криволинейный) характеристический треугольник АМВ (рис. 1) с основанием АВ. При v > 0 предполагается, что замкнутый треугольник AM В лежит в области г > 0.
Утверждается, что в треугольнике AM В нет точек вакуума. Действительно, в противном случае в нем содержалась бы некоторая линия вакуума Со, которая непременно пересекла бы одну из боковых сторон AM или ВМ. Это означало бы, что эта боковая сторона — звуковая характеристика — достигает точки вакуума. По предыдущему она должна совпадать с Со, а тогда лежащая на ней точка М была бы точкой вакуума, в противоречии с предположением. Пусть U — (и, р, р) есть то решение системы (1), для которого построен характеристический треугольник АМВ. Справедлива следующая теорема единственности решения U.
Теорема 1. Если решение U непрерывно дифференцируемо и если другое, непрерывно дифференцируемое в характеристическом треугольнике АМВ решение U' совпадает с U на основании АВ, то U' = U во всем треугольнике АМВ.
Доказательство. Систему уравнений (1) можно заменить равносильной ей симметрической системой, аналогичной (3.16):
рщ + puur + Рг = о,
bpt + bupr + ur = -ju (5)
St + uSr = 0.
В равносильной (5) матричной записи (здесь U = (и, р, S))
A1 U, + ArUr = A0U (6)
матрицы А1 и Аг симметричны. Так как в замкнутом треугольнике АМВ,
в силу сделанных предположений, справедливы равномерные оценки снизу вида
р > ра > 0, b > Ьо > 0, г > г0 > 0
с некоторыми постоянными ро, Ьо и го, то матрица А1 положительно опре
делена, а матрица Д0 непрерывна. С учетом этих замечаний доказательство проводится по схеме доказательства теорем 7.2, 7.3 (правая часть в (6) существенного влияния не оказывает). ¦
Как и в § 7, важным следствием теоремы единственности является существование областей определенности, зависимости и влияния. Характерные примеры таких областей показаны на рис. 2.
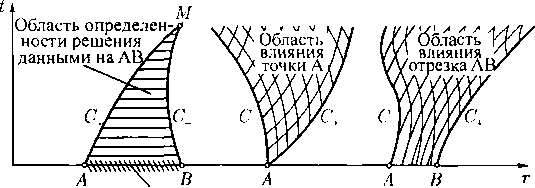
Область зависимости для точки М
Рис. 2
Теорема 1 допускает различные обобщения. Одно из них заключается в отказе от требования непрерывной дифференцируемости решения. Ее утверждение остается справедливым и для решений, в которых функции и, р, р предполагаются лишь удовлетворяющими условию Липшица. Это дает возможность использовать теорему единственности применительно к движениям со слабыми разрывами.
Времени и пространству подобные направления. Другое обобщение, тесно связанное с корректностью постановок краевых задач для системы (1), состоит в рассмотрении случаев совпадения значений двух решений не только на прямых t = const. Можно указать широкий класс таких кривых в плоскости R2(r,t), что совпадение двух решений на какой-либо из этих кривых влечет совпадение этих решений в соответствующей области определенности. В следующем определении характеристики рассматриваются на некотором данном решении U.
Определение 1. Направление / в точке М 6 R2(r,t.) называется времени подобным, если I разделяет направления касательных к характеристикам С+{М) и С-(М), выходящих из М в сторону dt. > 0. Направление называется пространству подобным, если I не разделяет (оставляет по одну сторону) направлений касательных к характеристикам С+(М) и С-(М), выходящих из М в сторону dt > 0. Кривая называется времени подобной (пространству подобной), если во всех ее точках направление касательной к Jz? является времени подобным (пространству подобным) (рис. 3).
подобна
подобна
Рис. 3
Вышеупомянутое обобщение теоремы 1 состоит в следующем. Пусть на решении U дана пространству подобная кривая !?, и пусть характеристики С+ и С , проведенные из некоторой не лежащей на !? точки М, отсекают на !? лугу АВ, образуя криволинейный треугольник AM В. Тогда, если решение U' определено в AM В и U' = U на АВ, то U' — U во всем треугольнике AM В.
Уместно отметить, что любая прямая t = const является пространству подобной и что любая контактная характеристика, не являющаяся линией вакуума, времени подобна.
Теорема существования решения задачи Коши, поставленной для системы (1) с начальными данными на гладкой пространству подобной кривой, справедлива (в малом, т. е. в некоторой окрестности начальной кривой), если начальные данные непрерывно дифференцируемы.
Слабые разрывы. Характеристическая форма (4) исходных уравнений удобна для анализа поведения и распространения слабых разрывов вдоль характеристик (теорема 6.2). Согласно определению 6.4 характеристика С является линией слабого разрыва, если решение всюду непрерывно и по каждую сторону от С (включая саму линию С) непрерывно дифференцируемо, но на С некоторые производные основных величин терпят разрыв первого рода — при переходе через С меняются скачком. В этих условиях при переходе через С производные по касательному направлению к С меняются непрерывно. Поэтому разрывными могут быть только производные по направлениям, трансверсальным к С (образующим с касательной к С ненулевой угол).
Очевидно, что в условиях слабого разрыва на плоскости R2(r,t) для описания скачков производных по любому направлению достаточно знать величину скачка по какому-нибудь одному трансверсальному направлению. Для уравнений (4), учитывая уравнения характеристик (2), в качестве универсального трансверсального направления можно взять, например, направление оси г (скорости и и с предполагаются конечными). Тогда слабый разрыв будет полностью описываться величинами разрыва значений производных иг, рг, 5Г. Более удобно, как это будет видно из дальнейшего, взять равносильный этому набору производных набор их комбинаций
Я = ыг + ^рг, L = Ur- j^Pr, М - Sr. (7)
Для каждого семейства характеристик выполняются свои условия на слабом разрыве. Для вывода этих условий полезны соотношения между дифференциальными операторами (3)
D+ = D0 + cDr, D_=D0-cDr,
D+ + D_ = 2D0; Df - D_ = 2c.D0, ' >
где Dr = д/дг. Ниже используется также символ скачка [/] = /2 — /i для записи величины разрыва любой функции / при переходе через линию слабого разрыва. В частности, по условию [и] = [р] = \р\ = [5] = = [cj = 0. Операция взятия скачка линейна, т. е. для любых непрерывных функций f(u, p. S) и д(и. р, S) справедливы формулы вида
Кроме того, необходимо учитывать, что для характеристики Со касательным дифференцированием является Do, и потому для любой функции f(u, р, S) на Со будет [D0f] = 0. Для характеристики С+ касательным дифференцированием является D+, следовательно, на С+ всегда [D+f] = 0. Аналогично, на С_ всегда [D_/] = 0.
С учетом этих замечаний и соотношений (8) применение операции взятия скачка к уравнениям (4) даст для каждой из характеристик (2) следующие условия на слабых разрывах:
Транспортные уравнения. Итак, на слабом разрыве для каждого типа характеристик две из комбинаций трансверсальных производных (7) меняются непрерывно. Что же касается той комбинации производных, которая имеет ненулевой скачок, то для нее из уравнений (4) может быть получено так называемое транспортное уравнение, которое представляет собой обыкновенное дифференциальное уравнение, описывающее эволюцию этой величины вдоль соответствующей характеристики. Для величины М дифференцирование Dr первого уравнения (4) дает соотношение DqM = = —игМ, которое, с учетом вытекающего из (7) равенства 2ur = R + L, записывается в виде
Это и есть транспортное уравнение вдоль характеристики Со для производной Sr = М. Его принципиальная особенность состоит в том, что коэффициент при М в правой части (10) при переходе через Со меняется непрерывно, как это следует из (9).
Для получения транспортного уравнения величины R вдоль характеристики С+ надо применить оператор Dr ко второму уравнению (4). С учетом формулы коммутации
DrD+ = D.i-L)r 4' I)r(v, 4- c)Dr
это дает
D+R+Dr(u+cyR+Dr(^j-D±p-Dy ^ Drp = -Dr (?cu) . (11)
Здесь величины рис следует рассматривать как функции термодинамических параметров р и 5. Если уравнение состояния газа взято в виде р = f(p,S), то легко найти, что производные от функций сг(р, S) и рс(р, 5) выражаются через функцию / по формулам
от
С учетом формул (12), после выражения всех производных по г через величины (7), окончательно транспортное уравнение для величины R вдоль характеристики С+ приводится к виду
D+R = ^n^2R2^n_2L _ Ъп*пгсМ_
~^;(2c+mu^R - ^ — c-LM J +n2)cuM +
-rj^(2c: - mu)L - (13)
где величина m определена в (2.22) и введены обозначения
Транспортное уравнение для величины L выводится аналогично, дифференцированием Dr последнего из уравнений (4). Формально оно может быть получено из (13) просто заменой с на -с и L на R, a R на L:
Непосредственно видно, что коэффициенты при степенях R в правой части уравнения (13) при переходе через характеристику С+ меняются непрерывно. Поэтому, если на С.есть слабый разрыв, то эволюция вдоль С+ комбинации R, производных с каждой стороны от С+ описывается одним и тем же уравнением (13), но, вообще говоря, с разными начальными данными. В частности, если в некоторой точке слабый разрыв отсутствует, то его не будет и вдоль всей характеристики С+. Другая важная особенность уравнения (13) состоит в том, что оно нелинейно, точнее, является уравнением Риккати. Из теории уравнения Риккати известно, что его решение может обращаться в бесконечность на конечном интервале изменения независимого переменного. Этот факт имеет большое значение для понимания структуры решений уравнений газовой динамики. В более простой ситуации он будет подробно изучен в § 16.
D-L = -
![]()
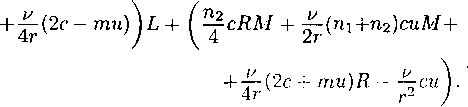
(15)
Задача о распаде слабого разрыва. С помощью уравнений (9) можно решить задачу о распаде произвольного слабого разрыва. Как задача Коши для системы (1) с начальными данными при t — О
и(г, 0) - и0(г), р(г, 0) = ро{г). 5(г. 0) - S0(r) (16)
эта задача ставится так. Пусть начальные данные всюду непрерывно дифференцируемы, кроме точки г = г'о > 0, в которой первые производные функций (16) имеют разрыв первого рода. Вдоль характеристик Со, С+ и С-, выходящих из точки (го,0), решение задачи Коши с такими данными (16) будет иметь, вообще говоря, слабый разрыв. Требуется определить начальные значения величин (7), распространяющиеся вдоль каждой из трех характеристик.
Для решения задачи о распаде слабого разрыва удобно ввести показанную на рис. 4 нумерацию областей, на которые характеристики разбивают полуокрестность точки (го,0), лежащую со стороны / > 0. В каждой из этих областей первые производные основных величин непрерывны и потому имеют конечные предельные значения, когда точка (r,t) стремится
к точке (г'о. 0). Для величин (7) эти предельные значения отмечаются соответствующим нижним индексом. Например, из начальных данных (16) сразу находятся значения
Ri = u'Q(r0 - 0) + p^Poiro ~ 0),
U - u'0(r0 - 0) - т^г-Ро(го - 0), Mi = 5ц(г0 - 0);
(17)
Й2 = Uo(r0 -Г 0) ^ —Po(r0 + 0),
L2 = «о(го + 0) (го т 0), М2 — So(ro + 0),
где штрихом обозначены производные по г и роСо есть значение рс в точке
разрыва (го,0). Остается заметить, что из условий (9) следуют равенства
Ri = R3 = R4, L2 — L3 = L4, М{ А/3. М2 ~ M/i, (18)
которые и решают поставленную задачу. Действительно, в каждой серии равенств (18) есть величина, известная из начальных данных (17). Поэтому в совокупности формулы (17) и равенства (18) дают выражения всех искомых величин. Кроме того, из соотношений (17) и (18) легко находятся предельные значения всех производных иг, рг и SV в точке (го,0)
для каждой из областей, показанных на рис. 4.
Уравнения в лагранжевых координатах. Для одномерных движений газа принимается следующее определение лагранжевой координаты.
Определение 2. Лагранжевой координатой ? называется дифференцируемая функция ?(r, t), удовлетворяющая уравнению
it + и$г = 0 (19)
и условию монотонности по г для любого фиксированного t. В более слабой форме это условие выражается неравенством
Из этого определения вытекает характерное свойство лагранжевой координаты: она сохраняется в каждой частице газа и отличает частицы одну от другой. В частности, если энтропия S(r,t) удовлетворяет условию (20), то ее можно взять в качестве лагранжевой координаты. Очевидно, что во всех случаях энтропия зависит только от лагранжевой координаты, т. е. справедлив интеграл энтропии
Доказательство. Дифференцирование уравнения (19) по г дает уравнение для производной ?г:
“Ь — 0.
В силу этого уравнения и уравнения неразрывности (1) справедливы равенства
D° = ~vr~V~Xu% + (Р“г + TpU) ~ r~UUrT =
Отсюда следует, что г_1/р_1?г = ф(?), т. е. первая из формул (22). Вторая формула (22) вытекает из уравнения (19) в силу первой. Если удовлетворяющая содержащемуся в определении 2 условию монотонности функция (23) задана, то известна и ей обратная функция г = ?о *(?)¦ Тогда функция ip дается вытекающей из (22) при t = 0 формулой
= (€о_1ю)",,(р(й'1(о,о))"Чо(ео1(0).
где штрихом обозначена производная функции (23) по г. Я
Лемма 2 показывает, что на данном движении лагранжева координата определена с точностью до замены ? на F(?) с любой монотонной функцией F. Если устранить этот произвол путем конкретизации функции 9 в (22), например, положить ip = 1, то уравнениями (22) функция ?(r, t)
будет определена однозначно (с точностью до несущественного постоянного слагаемого). В этом случае ?,{r,t) называется массовой лагранжевой
координатой.
С другой стороны, если лагранжева координата ?,(r,t) задана, то при ip = 1 формулы (22) определяют величины
Р = г-^г, и = -?(/?г. (24)
Следовательно, при заданной функции (21) движение газа полностью определено, гак как давление дается уравнением состояния
P = f(p,S). (25)
Однако построенное по формулам (21), (24), (25) движение автоматически удовлетворяет лишь уравнениям неразрывности и энергии. Требование того, чтобы это движение удовлетворяло также и уравнению импульсов (1), приводит к уравнению относительно функции ?(r.t):
Ф(|)-If .5(0). (26)
Для данного уравнения состояния (25) это уравнение является универсальным — оно описывает всевозможные лагранжсвы координаты, которые можно ввести на каком-нибудь движении газа. После выполнения дифференциальных операций и введения скорости звука согласно формуле с2 = fp(p, S) уравнение (26) переписывается в следующей форме:
- VUiZrt + (tf - c2%.r -V = trfsS'. (27)
Итак, система уравнений (1) одномерных движений газа сводится к одному квазилинейному дифференциальному уравнению с частными производными второго порядка (27) для лагранжевой координаты ? — ?(г, /), содержащему произвольное распределение энтропии (21).
Класс точных решений. Лемма 2 имеет также интересное применение для построения одного класса частных решений системы уравнений (1) в случае политропного газа. Этот класс выделяется предположением о линейной зависимости лагранжевой координаты от геометрической координа-
В силу (28), соотношения (22), в которых для упрощения дальнейших формул сделана замена функции </з ~ 1 /'ф, дают следующее представление скорости и плотности:
u=^r = a'i, р = = а (29)
где р, — v 4-1 и штрихом обозначена производная по t. В политропном газе уравнение состояния дается соотношением (2.5) и для давления справедлива формула вида р = В(^)ру или, в силу (29),
Р = а-^Г">7(0В(0, (30)
где функция В(?) определяет распределение энтропии по частицам газа. Необходимо заметить, что в силу соотношения (28) для производных по г и ? справедлива формула связи д/д? — ад/дг. Поэтому в результате подстановки выражений (29) в уравнение импульсов (1) оно приводится к следующему:
и интегрируется:
с константой Bq, которая предполагается не зависящей от t. Сравнение формул (30) и (31) показывает, что переменные (?,?) разделяются. Это приводит к соотношениям
Что же касается уравнения (33), то его решение сводится к квадратуре. Если принять в качестве начальных условий значения то решение можно представить в виде равенства
а(«)
/
a^-]>/2da , 2
yjboa}1^1 Ч — ао
где введена константа
Ьо =' ао - |м(7 - 1)а?.
Формулы (28), (29), (32), (35) и (36) дают семейство частных решений уравнений (1) одномерного движения газа. Решение зависит от одной произвольной функции ф{?) и нескольких произвольных постоянных. При различном выборе констант ао и 6о это решение может описывать разлет газа от центра, его схождение к центру или определенного вида пульсации. Полная классификация получаемых типов движения приведена в [7]. Особый интерес представляет решение, соответствующее выбору ф(?,) = S,1'. Оно описывает разлет в вакуум массы газа, в которой давление и температура распределены по параболическому закону (с максимумом в центре), а плотность постоянна по пространству и убывает со временем.
§16. Изэнтропические движения с плоскими волнами
Изэнтропические одномерные движения газа е плоскими волнами представляют собой одну из простейших моделей неустановившихся движений газа. Она наиболее богата как конкретными фактами, так и разнообразными до конца решенными задачами. Исторически на этой модели отрабатывались не только многие понятия и аналитические построения нестационарной газовой динамики, но также и алгоритмы численного расчета ее основных краевых задач. Условие изэнтропичности, конечно, является сильно ограничительным, так как оно не позволяет во всей общности рассматривать движения с ударными волнами, в результате прохождения которых по газу энтропия меняется и, вообще говоря, становится переменной по частицам. Однако и здесь возможно искусственное моделирование сильных разрывов, на которые надо наложить определенные условия устойчивости (см., например, [6]).
Исходные уравнения. В этом параграфе будут рассматриваться только гладкие движения. Пространственная координата обозначается через х и принимает значения на всей оси, -ос < х < +эо. Поэтому плоскостью событий здесь является вся плоскость R2(x.t). Исходные дифференциальные уравнения можно взять в виде (15.1), где надо положить и = 0, г = х
и отбросить третье уравнение, которое есть следствие второго ввиду того, что условие S = So = const влечет равенство dp = c2dp с любым дифференцированием d. Итак, в качестве исходных берутся уравнения
Ut ИНх -\~ ~р Рх — 0.
где с2 = с2(р) = fp(p,S0).
Уравнения (1) могут быть преобразованы ко многим равносильным формам, удобным для анализа различных ситуаций. Например, в координатах (?,<), где лагранжева координата ? = ?(x,t) вводится уравнениями (частный случай (15.22))
= Р! & = -ри,
для скорости и и удельного объема V = 1/р легко получается равносильная (1) простейшая сильно нелинейная (см. [6]) квазилинейная система из двух уравнений:
Ut + W))z =0, Ц - u€ = 0, (2)
где функция p(V) связана с уравнением состояния газа р = g(V. S) формулой p{V) = д(V, Sq). При этом существенно, что ее производная удовлетво
ряет условию
так как согласно (2.23) она равна —р2с2. Система (2) с условием (3) была предметом многих тонких математических исследований, начало которым положил еще Б. Риман в середине XIX столетия. Эти исследования привели к созданию современной математической теории разрывных решений квазилинейных гиперболических систем дифференциальных уравнений, особенно сильно продвинутой за последние 30 лет.
Инварианты Римана. Наиболее ценную информацию о поведении решений системы (1) дает ее характеристическая форма, которая может быть получена из (15.2) и (15.4) при и — 0. В силу условия S — const здесь исчезают контактные характеристики и остаются только звуковые. Это не значит, конечно, что исчезают траектории частиц — они есть в любом движении газа; пропадает лишь свойство траекторий быть возможными линиями слабого разрыва. Кроме того, условия (15.4) на звуковых характеристиках здесь интегрируются. Действительно, при любом дифференцировании d для величины dp/рс можно написать представление
где интеграл можно рассматривать как стандартную функцию а скорости звука с. Итак, с функцией
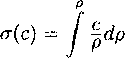
(4)
при любом дифференцировании d выполнено равенство
dp = pcda(c).
Если уравнение состояния р = f(p. S) таково, что при S = So интеграл (4) не сходится, то можно заменить нижний предел интегрирования любым фиксированным значением р0 > 0. В силу предыдущего равенства соотношения (15.4) на звуковых характеристиках принимают вид
(5)
D+(u + (г(с)) = 0, D-(u - <т(с)) = 0.
Определение 1. Величины и ± а{с) называются инвариантами Ри-мана. Для них вводятся обозначения
(6)
г — и + а(с.), I = и — <т(с).
В этих обозначениях и в силу (5) характеристическая форма системы (1) принимает вид
(С+) dx/dt = u + c, г = и + а(с) ~ const; (С..) dx/dt = и - с, I = и - ег(с) = const.
(7)
Другими словами, вдоль каждой характеристики С+ сохраняет постоянное значение инвариант Римана г и вдоль каждой характеристики С . сохраняет постоянное значение инвариант Римана /.
В случае политропного газа функция (4) вычисляется на основании уравнения состояния р = Ар1 (Л = const) и оказывается такой:
![]()
Следовательно, инварианты Римана в политропном газе даются формулами
В общем случае справедливо выражение для производной а'(с) = 2/то с величиной т, определенной в (2.22). Поэтому для нормального газа а'(с) > 0 и функция а имеет обратную, обозначаемую ст-1. С ее помощью скорость и и скорость звука с находятся из уравнений (6) и выражаются через инварианты Римана:
На каждом движении газа инварианты Римана являются функциями переменных (х, t), т.е. г = r(x,t) и I = l(x,t). Условие их сохранения вдоль соответствующих характеристик может быть записано, в обозначениях (15.3), в виде равенств D+r = 0 и D .1 =0 или, в развернутой форме,
П + (и + с)гх = 0,
lt + (u- с)1х гг. 0. 1 Л)
Так как величины и ± с выражаются, согласно (10), через переменные г и I, то равенства (13) образуют систему дифференциальных уравнений с двумя искомыми функциями, r(x.t) и l(x.t). Ясно, что система (13) равносильна исходной (1). Поэтому система (13) называется системой уравнений в инвариантах Римана одномерных изэнтропических движений газа.
Простые волны. В терминах инвариантов Римана явно описываются простые волны как специальные типы рассматриваемых движений газа. Непосредственный перенос результатов § 13 дает лишь следующую информацию о простой волне: это такое движение, в котором основные величины зависят от одной функции а(х, t) — параметра простой волны, причем линии уровня а(х, t) = const являются прямыми и образуют семейство характеристик на плоскости R2(x,t). Однако здесь о простых волнах можно сказать больше.
Теорема 1. В каждой простой волне, если она не есть постоянное движение, один и только один из инвариантов Римана, г или I, сохраняет тождественно постоянное значение. Если в простой волне г = const, то ее линиями уровня являются прямолинейные характеристики семейства С-. Если в простой волне I = const, то ее линиями уровня являются прямолинейные характеристики семейства С _. Обратно, если в некоторой области движение не постоянно и один из инвариантов Римана тождественно постоянен, то движение в этой области есть простая волна.
Доказательство. По определению простой волны и в силу формул (7) инварианты Римана должны быть функциями одного параметра — функции cv = а(х, t)y т. е.
означает, что оба инварианта, г и I, одновременно тождественно постоянны, что в силу формул (10) дает не простую волну, а постоянное движение. Предположение
D+a = О, D-а = 0
также не годится, так как оно равносильно равенствам at = 0 и их ах = 0, т. е. приводит к тому, что а = const тождественно. В этом случае величина а не может быть параметром простой волны. Поэтому остаются только две возможности. Первая из них
г'(а) = 0. D~a = 0
означает, что в простой волне г = const тождественно и что параметр волны а постоянен вдоль характеристик С_. Но так как вдоль каждой характеристики CL всегда постоянен инвариант Римана I, то вдоль каждой характеристики С_, в силу формул (10), постоянны также величины и и с, а с ними и угловой коэффициент (7) этой характеристики dx/dt = и — с. Это означает, что характеристика С- есть прямая линия. Аналогично, последняя возможность
приводит к такому же заключению с заменой г на I и С_ на С+. Тем самым первая часть теоремы доказана. Обратно, пусть в некоторой области непостоянного движения тождественно постоянен один из инвариантов Римана, например г = tq. Тогда инвариант I не тождественно постоянен и обе величины и и с являются, в силу формул (10), функциями только от /. Согласно определению движение в рассматриваемой области есть простая волна. ¦
Простая волна, в которой тождественно постоянен инвариант Римана г (соответственно I), называется коротко r-волной (соответственно 1-волной).
Уравнения прямолинейных характеристик для простых волн легко интегрируются. Например, в случае г-волны в уравнении характеристик С-
dx — (и - c)dt = 0
коэффициент и - с на С_ постоянен, в силу чего вдоль этих характеристик а;— (u—c)t = const. При переходе от одной характеристики С- к другой константа интегрирования может меняться и потому должна рассматриваться как функция параметра волны а. Вместо этого ее можно считать функцией любой непостоянной величины, например и, с или инварианта I, — все эти предположения равносильны. Для определенности эта константа итерирования будет считаться функцией скорости и. Аналогично интегрируется уравнение характеристик С+ в простой /-волне. Итак, уравнения простых волн могут быть записаны в следующем виде.
Уравнения г-волны:
г = и~ а (с) = го = const, х — (и — c)t = F(u). (16)
Уравнения /-волны:
I = и - а (с) = /о = const, х - (и 4- c)t = F(u). (17)
Отсюда следует, в частности, что совокупность всевозможных простых г-волн (а также /-волн) зависит от одной произвольной функции. В качестве таковой может рассматриваться, например, функция F(u) в уравнениях (16) и (17).
Теорема о примыкании. В связи с понятием простых волн возникает важная задача об их распознавании, т. е. о формулировке таких признаков, по которым можно было бы судить о том, что в некоторой области движения газа есть простая волна. Общее достаточное условие существования простой волны дается в нижеследующей теореме, в которой одномерное движение с плоскими волнами заранее не предполагается изэнтропическим.
Теорема 2. Если в непрерывном (одномерном, с плоскими ватами) движении газа есть характеристика С+ (соответственно С-), не являющаяся линией вакуума, вдоль которой величины и, р, р постоянны, то в окрестности этой характеристики, с каждой ее стороны, данное движение является изэнтропическим и либо постоянным, либо простой 1-волной (соответственно r-волиой). В частности, непостоянное изэнтропическое движение, непрерывно примыкающее к постоянному, всегда есть простая волна.
Доказательство. Пусть вдоль характеристики С+ величины и, р, р постоянны. Тогда вдоль нее также постоянна и энтропия S. Пусть Оо С R2(x,t) есть множество, состоящее из точек всех траекторий Со, пересекающих данную характеристику С+. Так как С+ не есть линия вакуума, то По является областью. Ясно, что в области Оо энтропия тождественно постоянна. Пусть с R2(x,t) есть множество, состоящее из точек всех характеристик С_, пересекающих данную характеристику С+. Ясно, что Q_ тоже является областью. Так как инвариант Римана I постоянен вдоль данной С+ и постоянен вдоль каждой С_, то он тождественно постоянен в области И-. Следовательно, если на пересечении областей По и Q_ движение не постоянно (хотя бы с одной стороны от С+), то в силу теоремы 1 это движение есть простая /-волна. Аналогично рассматривается случай, когда величины и, р, р постоянны вдоль некоторой характеристики С_.
Если не постоянное изэнтропическое движение примыкает к постоянному движению вдоль некоторой линии !?, то вдоль этой линии должен быть слабый разрыв. По теореме 6.2 линия должна быть характеристикой. В силу изэнтропичности движения линия !? может быть только звуковой характеристикой, например С+. Так как она принадлежит находящемуся по одну сторону от нее постоянному решению, то вдоль этой характеристики С+ все величины и, р, р постоянны. Согласно первой части теоремы по другую сторону от С+ движение есть простая волна . ¦
Если во второй части теоремы отказаться от требования изэнтропичности непостоянного движения, примыкающего к постоянному, то утверждение будет, вообще говоря, неверным. Действительно, нримыкание может происходить вдоль траектории (характеристики Со), а не постоянное движение может быть изобарическим (см. § 9). Однако если дополнительно предположить, что примыкание происходит по звуковой характеристике, то вторая часть теоремы будет верна и без требования изэнтропичности (впрочем, в этом случае она фактически совпадает с первой частью теоремы).
Центрированные простые волны. Выделяется важный специальный тип простых волн.
Определение 2. Простая r-волна (или Z-волна) называется центрированной в точке (xo- to), если все ее прямолинейные характеристики С_ (соответственно С+) пересекаются в точке (хо, to).
Пусть простая r-волна центрирована в точке (xo,to)- Тогда в ее уравнении (16), переписанном в виде
х - х0 - (и - c)(t - t0) = F(u),
(18)
коэффициент и — с и правая часть постоянны вдоль любого принадлежащего r-волне луча с уравнением х - xq = k(t — to). Но если вдоль этого луча (x,t) —> (xq, to), то левая часть в (18) стремится к нулю. Следовательно, на каждом таком луче F(u) = 0, т. с. функция F равна нулю тождественно. Аналогичный вывод справедлив и для /-волны, центрированной в точке (xo,to). Таким образом, из уравнений (16) и (17) получаются следующие уравнения центрированных простых, волн (для простоты записи в качестве центра взята точка (xo,to) = (0,0)).
Уравнения центрированной г-волны:
г = и + а(с) = го — const, и —с = j. Уравнения центрированной /-волны:
(19)
(20)
I -¦ и — сг(с) = /о = const, U + С = J.
Очевидно, что величины и и с, определенные уравнениями (19) (или уравнениями (20)) как функции переменных (х, t), зависят только от отношения А = x/t. Это означает, что каждая центрированная простая волна описывается автомодельным решением уравнений (1). Из определения простых волн (см. § 13) следует, что, и обратно, любое автомодельное решение системы уравнений одномерного движения с плоскими волнами с автомодельной независимой переменной А = x/t, должно быть простой волной. Используя уравнения (13), легко показать, что любое их автомодельное решение этого типа является либо постоянным, либо дается формулами (19) или (20). Следовательно, совокупность всех автомодельных решений упомянутых уравнений (в частности, уравнений (1)) с параметром автомодельности А = x/t описывается соотношениями (19) и (20).
В случае политропного газа с помощью выражений (9) решение находится в явном виде, а именно для центрированной г-волны
и для центрированной /-волны
![]()
Простые волны, центрированные в произвольной точке (?о, ^о). описываются теми же формулами (21) и (22) с заменой дроби x/t дробью (х -x0)/(t. ¦¦¦¦ to).
Центрированные простые волны дают пример решений с особенностью. Из формул (19), (20) видно, что в «центре» волны (точка (0,0)) основные величины разрывны, а область существования решения есть некоторый сектор, не содержащий оси х. Пример следующей задачи поясняет, что центрированные простые волны образуются тем не менее вполне естественно.
Задача об истечении газа в вакуум. Пусть левая часть цилиндрической трубы заполнена покоящимся газом, удерживаемым заслонкой в сечении х = 0, справа от которой находится вакуум (рис. 1). В момент времени t = 0 заслонка мгновенно убирается, и начинается процесс истечения газа в вакуум. Требуется найти возникающее одномерное, с плоскими волнами движение газа, в частности, определить скорость истечения, если известна скорость звука со в покоящемся газе и его уравнение состояния (функция <j(c)).
Г аз
Вакуум
Рис. 1
Решение этой задачи основано на использовании предыдущих результатов. Для области х < 0 начальные данные при t = 0 к уравнениям (1) имеют вид и ~ 0, с = со- В силу теоремы единственности 15.1 в области определенности решения этими начальными данными, ограниченной справа характеристикой CL с уравнением х = —cot, газ покоится и с = со при всех t > 0. Непостоянное движение, примыкающее к этой области покоя вдоль указанной характеристики С_, должно быть простой волной, а именно г-волной (теорема 2). Однако в области х > 0 при t = 0 находится вакуум и в ней с = 0. Поэтому никакая прямолинейная характеристика С-, не будучи линией вакуума, не может достичь полуоси {? = 0, ж > 0} и; имеется единственная возможность: простая r-волна должна быть центрированной в точке (0,0). Поэтому решение должно даваться формулами (19), в которых величина г0 определяется условием на граничной характеристике С_, где и = 0. Отсюда получается значение го = сг(со). Следовательно, решение задачи дается соотношениями
и Ь а (с) = сг(со), и - с = x/t.
На границе истекающего газа с вакуумом должно быть с = 0, и из первого соотношения находится скорость истечения ит — сг(со).
В случае политропного газа г о в явном виде:
со и формулы (21) дают решение
7 - 1
(c»+f)
(23)
и
С =
7 + 1 С° 7+U
- 1
В частности, скорость истечения политропного газа в вакуум оказывается равной
2
rn
; co
7
Картина течения на плоскости событий показана на рис. 2.
В задаче об истечении газа в вакуум интересен и важен тот факт, что начальные значения разрывны в точке х = 0, так как скорость звука с — = со > 0 при х < 0 и с = 0 при х > 0. Таким образом, эта задача дает пример того, как из разрывных начальных данных при t = 0 может вырабатываться движение газа, непрерывное при t > 0.
Волны сжатия и разрежения.
Процесс распространения простой волны по частицам газа приводит к тому, что плотность р в каждой частице увеличивается (возрастает, растет) или уменьшается (убывает, падает). Ясно, что направление изменения плотности в частице со временем характеризуется знаком производной D0p-
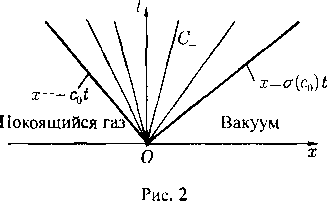
Определение 3. Простая волна называется волной сжатия (соответственно волной разрежения), если плотность р в частице с течением времени возрастает, т. е. Dop > 0 (соответственно убывает, т. е. D^p < 0).
Оказывается, что простые волны сжатия и разрежения можно различать с помощью их наглядного изображения в виде картины соответствующих прямолинейных характеристик на плоскости событий Er(x,t). Так как наклон этих прямых при переходе от одной из них к другой изменяется, то все семейство прямых образует как бы «веер». При этом «ручка веера», т. е. та его часть, где прямые характеристики расположены теснее, ближе друг к другу, может быть как сверху, со стороны больших значений времени, так и снизу, со стороны меньших значений времени. В общем случае простая волна может состоять из различных участков, как с «ручкой веера» сверху, так и с «ручкой веера» снизу. Ясно, что расположение «ручки веера» может
быть однозначно описано направлением изменения, с ростом координаты х, величины углового коэффициента
к = u i с
(25)
наклона соответствующего семейства прямолинейных характеристик к оси t. Именно, очевидно, что если кх > 0, то «ручка веера» находится снизу, а если кх < 0, то сверху.
Теорема 3. Простая волна является волной сжатия (соответственно волной разрежения), если и только если «ручка веера» ее прямолинейных характеристик находится сверху (соответственно снизу).
Доказательство. Для производной от углового коэффициента наклона (25) прямолинейных характеристик простой волны, с величиной т из (2.22), справедлива формула
![]()
(26)
Так как в нормальном газе всегда т > 0, то из этой формулы, с учетом предыдущих замечаний, следуют все утверждения теоремы. Для вывода формулы (26) в случае простой r-волны, когда прямолинейны характеристики семейства С- с угловым коэффициентом k = и -• с, используется уравнение (16), из которого следует равенство
рих + срх = 0.
Далее, так как в силу определения (2.22) величины т
2ссх --= (с2)х = (fp)x = fppPx = (тс2/р)рх,
то с помощью предыдущего равенства находится
![]()
Это дает выражение для производной кх = их — сх:
2кх - (т + 2)их.
(27)
С другой стороны, непосредственно из уравнения неразрывности (1) следует равенство
Dop = -рих.
(28)
Исключение величины «х из соотношений (27) и (28) и дает формулу (26) для простых /’-волн. В случае простой /-волны тс же выкладки опять дают выражение (27) для величины кх = их + сх, откуда снова вытекает форму -
Иллюстрация к теореме 3 дана на рис. 3. В частности, построенное выше решение задачи об истечении газа в вакуум, согласно рис. 2, есть волна разрежения.
Рис. 3
Градиентная катастрофа. В простых волнах сжатия непрерывное движение газа, возникающее из сколь угодно гладких начальных данных (скажем, заданных при t = 0), не может существовать как угодно долго (при всех t > 0). Действительно, при «ручке веера» сверху сближающиеся с ростом t прямолинейные характеристики должны пересечься при конечном значении t. Тогда предположение о непрерывной дифференцируемости и даже вообще о непрерывности решения в окрестности точки пересечения приходит в противоречие с теоремой единственности решения обыкновенных дифференциальных уравнений характеристик. Из соотношений типа (27) видно, что при сближении характеристик (когда необходимо |кх\ —» оо) происходит неограниченный рост градиентов основных величин — абсолютных значений производных их, рх, и т.д., которые в точке пересечения характеристик обращаются в бесконечность. Существование таких решений типично вообще для нелинейных гиперболических уравнений.
Явление неограниченного роста градиентов основных величин называется градиентной катастрофой.
Разумеется, градиентная катастрофа может произойти не только в простой волне, но и в гладком движении общего характера. Для выяснения этого вопроса надо обратиться к транспортным уравнениям, как раз и описывающим эволюцию трансверсальных производных (градиентов основных величин) вдоль соответствующих характеристик.
Полученные в § 15 для любых одномерных движений транспортные уравнения (15.13) и (15.15) в случае изэнтропических движений существенно упрощаются и, как оказывается, могут быть проинтегрированы. Прежде всего, из сравнения формул (15.7) и (6) видно, что здесь величины R и L просто равны производным по х от инвариантов Римана:
R = г*. L - 1Х. (29)
Кроме того, в уравнении (15.13) надо положить v -- 0, а также, в силу постоянства энтропии, М =- 0. В результате транспортное уравнение для величины R вдоль характеристики CV принимает вид
D+R = R2 + LR. (30)
Аналогично выглядит транспортное уравнение для величины L вдоль характеристики С-; оно может быть получено из (30) заменой D+ на D_ и R на L, a L на R. Конечно, уравнение (30) (и ему аналогичное для L) нетрудно получить и непосредственно, применив оператор Dx к уравнению D+r = 0 (или D.-1 = 0).
Уравнение Бернулли (30) приводится к линейному подстановкой R —
D^z = -T±^Lz+T^l. (31)
Для его интегрирования следует заметить, что коэффициент при z может быть записан в виде
T-^—~L —- D+ In (32)
Действительно, во-первых, из формулы 2cDx = D+ — D- и того, что D-J, = = 0, следует равенство 2cL = D ^1. Кроме того, определение (6) и соотношение D+r = 0 влекут равенства
D+l = D+(l - г) = -2D+a(c) = ~jD+p.
Вместе с предыдущим это дает другое выражение для величины L (аналогично получается и выражение для R):
L = ~j)D+P, R=-\D-p. (33)
Во-вторых, в силу определения (2.22) величины гп справедливы равенства
Теперь очевидно, что из (33) и (34) следует (32). С помощью выражения (32) уравнение (31) легко приводится к следующему:
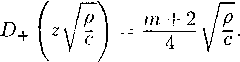
При решении этого уравнения необходимо помнить, что производная D+ берется вдоль характеристики Сц.. Без потери общности можно считать, что интегрирование вдоль Сл. по t начинается от точки t — 0. Пусть значения величин при t = 0 отмечаются индексом нуль. С этим соглашением интегрирование уравнения (35) дает соотношение
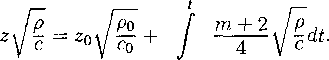
0(С+)
Наконец, возвращение к величине R = l/z дает окончательно следующую явную формулу для решения транспортного уравнения (30):
(36)
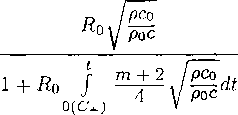
Я =
Формула (36) описывает изменение трансверсальной производной R = гх инварианта Римана г вдоль любой характеристики С+. Аналогичная формула справедлива для описания изменения трансверсальной производной L = 1Х инварианта Римана I вдоль любой характеристики С-:
(37)
1
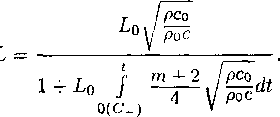
Формулы (36) и (37) показывают, что если Rq > 0 и L0 ^ 0, то при всех t > 0 будет также R ^ 0 и L > 0. Значит, если начальные распределения инвариантов Римана
г{х, 0) = г0{х), 1,{хЛ)) = /о(-г)
(38)
удовлетворяют неравенствам то в решении задачи Коши с такими начальными данными градиентная катастрофа невозможна. Если же в некоторой точке xq будет, напрнмер, г,(жо) ~ Н-о(хо) < 0, то вдоль выходящей из точки (.Го,0) характеристики С+ все время будет R < 0 до тех нор, пока знаменатель в (36) не обратится в нуль. Там, где это случится, и произойдет градиентная катастрофа. Момент наступления градиентной катастрофы tK определяется уравнением
(До<0). (40)
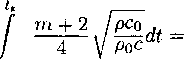
По
0(С„ )
Для моментов времени t ^ tK непрерывное движение невозможно. В действительности оно продолжается, но уже как движение с сильными разрывами. Отсюда становится понятной одна из важнейших особенностей движения газа: в первоначально непрерывном движении со временем могут возникать сильные разрывы.
Применение этих выводов к простым волнам дает особенно красивые результаты. Например, в простой /-волне вдоль прямолинейных характеристик семейства С+ подынтегральное выражение в (36) сохраняет постоянное значение, равное его значению при Z = 0, в силу чего эта формула упрощается до следующей:
R=-. (41)
1 f Ro^—^t
Здесь при Ro < 0 градиентная катастрофа неизбежна, причем в момент времени, определяемый непосредственно по начальным данным:
№<0)- (42) Этот результат согласуется с выводами о поведении простых волн, полученными вслед за теоремой 3. Неравенство R = гх < 0 в простой /-волне равносильно неравенству (гг + с)х < 0. В силу теоремы 3 это означает, что характеристика С+, на которой в момент времени (42) наступает градиентная катастрофа, принадлежит волне сжатия. Аналогичные результаты справедливы для простых г-волн.
Плоскость инвариантов Римана. При изучении гладких изэнтро-пических движений газа с плоскими волнами, носящих общий характер, иногда с успехом используется метод перехода в уравнениях (13) к независимым переменным - инвариантам Римана. Это возможно, если на данном (или на искомом) решении из системы уравнений
Г — r(;X. t), I = l(x. t)
можно однозначно выразить величины х и t как функции переменных г и I:
х = x(r, I), t = t(r,l). (43)
В таких случаях говорят о преобразовании плоскости событий R2(x,t) в плоскость инвариантов Римана R2(r, I):
R2(x, t) —> R2(r,l). (44)
Достаточным условием локальной взаимной однозначности преобразования (44) является отличие от нуля якобиана
д(г.1) j ~ д{хЛ)
Гх ПI
Lx Lt I
В силу уравнений (13) для этого якобиана получается выражение
j = 2с7х/х. (45)
Отсюда видно, что на данном движении газа при с ф 0 тождественное равенство j = 0 возможно для трех типов движения. Если гх = 0, то из (13) следует, что также г* = 0, в силу чего инвариант г тождественно постоянен. По теореме 1 непостоянное движение этого типа есть простая г-волна. Аналогично, если 1Х = 0, то непостоянное движение есть простая /-волна. Наконец, если одновременно гх = 0 и 1Х = 0, то движение является постоянным. Эти выводы согласуются с тем, что область на плоскости событий, занятая простой r-волной, изображается на плоскости инвариантов Римана линией г = го, область простой /-волны — линией / = /о, а область постоянного движения — одной точкой (г, I) = (го, /о). За исключением этих особых случаев, преобразование (44) отображает область движения на некоторую область плоскости П2(г,/).
Вывод уравнений для функций (43) можно выполнить разными способами. Проще всего заметить, что так как вдоль характеристики С ( меняется только инвариант Римана I, то ее уравнение dx = (и + e)dt равносильно уравнению .х/ = (и + с)/.;. Аналогично, вдоль С- меняется только г и
получается уравнение хг — (и - c)tr. Следовательно, искомые уравнения движения на плоскости инвариантов Римана таковы:
(46)
хт = (и — cjtr,
где индексами обозначены частные производные по г и I, а величины и и с являются, согласно (10), известными функциями независимых переменных (г, I). Так как система уравнений (46) линейна, то тем самым установлен важный факт: уравнения одномерных изэнтропических движений с плоскими волнами допускают точную линеаризацию; она достигается преобразованием на плоскость инвариантов Римана.
После исключения величины х (путем перекрестного дифференцирования и вычитания) система (46) сводится к специального вида линейному однородному дифференциальному уравнению с частными производными второго порядка — уравнению Дарбу:
Здесь существенно то, что в силу последней из этих формул уравнение (47) записывается в самосопряженной форме:
Взаимодействие центрированных волн. Рассматривается задача о взаимодействии, дающая пример применения метода расчета движения газа путем решения уравнения (52). Простейшая постановка задачи такова. При t = 0 на интервале х\ ^ х хо задано постоянное решение и =¦ uq. с со; простые волны, которые согласно теореме 2 должны примыкать к этому постоянному движению, предполагаются центрированными в точках А(х\,0) и В(х2,0). Требуется описать движение газа после того, как эти центрированные простые волны вступят во взаимодействие.
Качественная геометрическая картина движения на плоскости событий показана на рис. 4. Характеристики AM и ВМ с уравнениями, соответственно,
х = х\ + (и0 + ca)t, х = Х2 4- (ио - c.o)t
ограничивают область постоянного решения. В области АМР находится простая Z-волна, центрированная в точке Л, а в области BMQ — простая г-волна, центрированная в точке В. В этих областях решение описывается формулами вида (19), (20). Областью взаимодействия является криволинейный четырехугольник PMQR, в котором и надо найти решение. Так как характеристики МР и МQ и распределения вдоль них искомых величин известны из описания центрированных волн, то рассматриваемая задача сводится к задаче Гурса (см. § 7).
Рис. 4 Рис. 5
Для ее решения необходимо построить образ движения при отображении (44) на плоскость инвариантов Римана. Координаты точки M(roJo) таковы:
r0 = UQ + a(c0). lo = и0 - (t{c.q).
Вдоль МР справедливы равенства и так как эта характеристика принадлежит волне разрежения («ручка веера» снизу), то скорость звука с, а потому и инвариант г убывают при перемещении от М к Р. Аналогично, вдоль MQ
г = г0, 1 = Го- 2 сг(с),
и по тем же соображениям при перемещении от М к Q инвариант I возрастает. Кроме того, г — const вдоль PR, так как это — характеристика С+, и I — const вдоль QR, так как это — характеристика С_. Следовательно, образ области PMQR на плоскости R2(r, I) есть прямоугольник, показанный на рис. 5.
Граничные условия для функции t = !\r. I) определены на характеристиках МР и MQ, вдоль которых искомое решение примыкает к известному. В точках пересечения линии МР с характеристиками С+ простой /-волны
х = Xi 4- (и 4- c.)t.
Дифференцирование этого уравнения вдоль МР по переменному г с учетом того, что МР есть характеристика С- и вдоль нее хг =- (и — c)tr, дает уравнение
(г/ - c)tr = (и 4- c)tr 4 t.(u 4 с)т, которое в силу (51) упрощается до следующего:
2tr — — t -ф In h,
dt
и с начальным условием t = to при г = г о интегрируется явно:
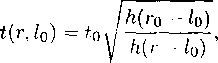
(53)
где to = ?(го, /о) есть значение t в точке М. Аналогично, вдоль МQ
х = хо 4 (и - c)f. и Х[ = (и 4 с)?/, так что после дифференцирования по I (¦и + c)tt = (и - c)ti *-t(u- ¦ c)t.
и в результате упрощения с использованием (51) получается уравнение
которое с начальным условием t = to при I = Iq тоже интегрируется яв-
(54)
но:
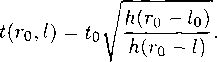
Метод Римана. Итак, требуется найти решение уравнения (52) в прямоугольнике PMQR, если значения решения заданы на двух его сторонах — характеристиках этого уравнения: значения (53) на характеристике МР и значения (54) на характеристике MQ. Следовательно, задача свелась к задаче Гурса для линейного уравнения (52). Решение этой краевой задачи следует из общей теории линейных уравнений второго порядка гиперболического типа и может быть получено, например, методом Римана, ссли для уравнения (52) известна функция Римана.
Оказывается, что в данном случае решение задачи (53), (54) просто совпадает с функцией Римана уравнения (52) с точностью до постоянного множителя. Действительно, функция Римана W(r, I; го, 1о) должна быть, как функция переменных (г, /), решением того же уравнения (52) в силу его самосопряженности и должна удовлетворять следующим краевым условиям: на характеристике г — го — условию
2hWi + htW =¦¦ О и на характеристике I = 1о — условию
2hWT + hrW =--- 0.
Эти условия легко интегрируются и, если еще принять во внимание условие
нормировки IV(го, 1о\ го, lo) — I, то дают значения
(55).
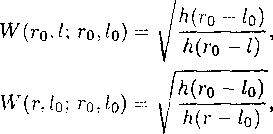
которые совпадают, с точностью до множителя to, соответственно с (54), (53). Поэтому в силу единственности решения задачи Гурса функция
t{r.l) = tQW(r,l: r0,lo)
(56)
дает решение поставленной задачи о взаимодействии центрированных волн.
Конечно, функцию Римана еще надо построить. Для этого существуют различные методы, изложение и применение которых выходит за рамки данных лекций. Полезно отметить лишь то, что в случае политропного газа, когда основное уравнение имеет вид (50), функцию Римана можно найти в явной аналитической форме:
для которых функция Римана, а потому и решение задачи о взаимодействии выражаются через элементарные функции.
§17. Распад произвольного разрыва
Возникновение градиентной катастрофы в неравномерных движениях газа является скорее правилом, чем исключением. Как было выяснено в предыдущем параграфе, для ее предотвращения должны выполняться специальные ограничения, связанные со знаками градиентов инвариантов Римана. Так или иначе, в момент наступления градиентной катастрофы основные величины становятся разрывными и при дальнейшем продолжении движения оно будет, вообще говоря, содержать сильные разрывы. Тем самым возникает необходимость изучить и описать обобщенные движения газа (см. определение 4.1), определяемые разрывными начальными данными. В ее полном объеме эта большая задача газовой динамики на решена до настоящего времени даже для одномерных движении с плоскими волнами.
Простейшая из такого сорта задач — когда в начальных данных имеется всего одна точка разрыва первого рода основных величин, которые по обе стороны от точки разрыва постоянны, различны и не связаны априори никакими соотношениями. В связи с тем, что сложное движение, возникающее из таких начальных данных, содержит несколько распространяющихся в разные стороны сильных и слабых разрывов, эта задача получила название задачи о распаде произвольного разрыва. Следует отметить, что эта простейшая задача интересна не только сама по себе. На самом деле, исторически (ссылки можно найти, например, в [6]) она послужила тем элементом, на основе которого были созданы высокоэффективные методы численного расчета произвольных одномерных движений газа и развиты качественные математические методы доказательства теорем существования и единственности более широких классов обобщенных решений. Ниже дается полное решение этой задачи для одномерных движений с плоскими волнами.
Постановка задачи. Для уравнений одномерного движения газа е плоскими волнами задаются при t = 0 начальные данные вида
и(х, 0) = и\, р(х, 0) = рь р(х, 0) = pi {х < 0);
w(x,0) = it2, р(х,0) = рг, р{х,0)=р2 (х>0),
где иь Рь Рь U2, рг, Р2 — заданные постоянные. При этом допускается, что газ в состоянии «1» (х < 0) и газ в состоянии «2» (х > 0) имеют различную физическую природу, т. е. разные уравнения состояния. Предполагается, что оба газа являются нормальными (определение 2.2). Требуется найти решение (вообще говоря, обобщенное) при t > 0.
Задача (1), очевидно, конически автомодельна (см. § 13). Поэтому ее можно решать в классе автомодельных решений (см. § 13 и § 20), имеющих представление
и = и{ А), р = р( А), р = р(А); А = x/t. (2)
Согласно (2) распределения основных величин по пространству (по координате х) в любой момент времени t > 0 получаются из одного такого распределения при t = 1 простым изменением масштаба по оси х (растяжением координаты х). Так как в решении вида (2) основные величины
постоянны вдоль каждого луча А = const, то его изображение на плоско
сти событий R2(x,t) должно состоять из секторов с вершиной в начале координат, определяемых неравенствами вида А' < А < А", внутри которых движение гладкое, а границы представляют собой линии сильного или слабого разрыва. При этом, если гладкое движение в некотором секторе не постоянно, то оно должно быть простой волной, линиями уровня которой являются лучи х = At. Следовательно, такой сектор с необходимостью образован центрированной (в точке (0.0)) простой волной разрежения. Один из возможных типов решения показан на рис. 1.
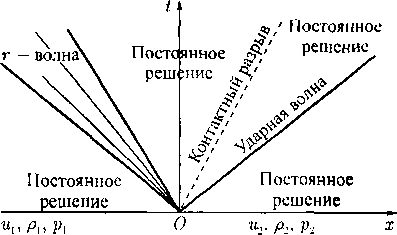
Рис. 1
Направление обращения волн. В связи с тем что решение может включать простые и ударные волны, бегущие в разных направлениях, для дальнейшего анализа целесообразно фиксировать некоторые конкретные правила и термины, учитывающие специфику одномерного движения. Прежде всего, ось х считается расположенной горизонтально и направленной слева направо. Нормаль к фронту ударной волны (в пространстве Я3 — к плоскости, перпендикулярной оси х) выбирается раз навсегда направленной в положительном направлении оси х. Поэтому в уравнениях ударного перехода всегда будет ип = и и Dn = D. Если состояние перед фронтом находится справа (соответственно, слева) от него, то говорят, что ударная волна обращена вправо (соответственно, обращена влево). Далее, так как через любую звуковую характеристику газ течет, то у нее также есть передняя сторона и задняя сторона и можно различать состояния перед характеристикой и за характеристикой, вполне аналогично ударным волнам. Говорят, что характеристика обращена вправо (обращена влево), если состояние газа перед характеристикой находится справа от нее (соответственно, слева от нее). Очевидно, что всякая характеристика С+ всегда обращена вправо, а всякая характеристика С_ всегда обращена влево. Простая волна называется обращенной вправо (обращенной влево), если ее прямолинейные характеристики обращены вправо (соответственно, влево). Согласно предыдущему выводу, всегда простая 1-волна обращена вправо, а простая г-волна обращена влево. Ввиду того, что каждая простая волна имеет конечную протяженность в направлении оси х, говорят также о состоянии движения перед простой волной и о состоянии движения за простой волной.
Метод (и, р)-диаграмм. При решении задачи о распаде разрыва (а также и в некоторых других вопросах) используется специальный метод построения и анализа так называемых (и,р)-диаграмы как для простых, так и для ударных волн. Эти диаграммы описывают состояния движения (и, р), в которые может перейти данное состояние движения (i/о, Ро) в результате прохождения какой-либо волны, в предположении, что фиксировано также некоторое значение энтропии So- При этом плоскость /?2(и,р) называется плоскостью состояний движения.
Определение 1. (и, р)-диаграммой простых воли, с центром (щ,ро) называется геометрическое место точек плоскости состояний движения, изображающих всевозможные состояния (и,р) за простыми волнами, имеющими состояние {щ,ро) перед волной.
Уравнения простых волн (16.16) и (16.17) показывают, что (и, р)-диаграмма простых волн есть некоторая линия, уравнение которой получается, если величину а рассматривать как функцию давления р, т. е. а = о-(р).
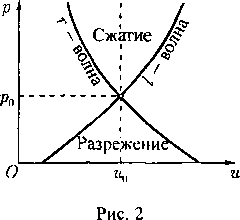
Тогда уравнение (и, р)-диаграммы с центром (t/,0, ро) простых г-волн запишется в виде
и +а{р) ~ и0 4 сг{р0), (3)
а для простых Z-волн — в виде
и - а{р) =и0~ сг(ро). (4)
Полная (и, р)-диаграмма простых волн показана на рис. 2. Ветви, на которых р > ро, соответствуют волнам сжатия, а ветви, на которых р < ро, — волнам разрежения. Ясно, что эта диаграмма симметрична относительно прямой и = ио- Важные для дальнейшего выражения первой и второй производных от и по р легко вычисляются исходя из определения (16.4) и,
с величиной т из (2.22), даются формулами
du _ _1_ d2u _ т -Н 2
dp ~ PC dP2~ 2р2с3'
Определение 2. (и, р)-диаграммой ударных волн с центром (щ,ро)
называется геометрическое место точек плоскости состояний движения, изображающих всевозможные состояния (и, р), в которые состояние (г/о, Ро) (при фиксированном значении энтропии So) может перейти в ударных волнах. При этом не предполагается, что состояние (мо,Ро) находится перед волной.
Уравнения (и, р)-диаграммы ударных волн вытекают из уравнения ударного перехода (4.17) и уравнения адиабаты Гюгонио. В уравнении (4.17) надо индекс «1» заменить индексом «0», убрать индекс «2» и заметить, что v — vo = и — и о в силу определения (4.11), после чего это уравнение примет вид
Входящая сюда величина V является функцией р, определяемой адиабатой Гюгонио с центром (Vo, ро). Эта функция, введенная равенством (5.1) и исследованная в § 5, здесь имеет вид
Подстановка выражения (6) в предыдущее уравнение и дает уравнение (и, р)-диаграммы ударных волн
(и - ио)2 = (р- Ро)(И) - W(р; У0, Ро))- (7)
Входящая сюда величина Vo однозначно определяется значением ро из уравнения состояния ро = g{Vo- So), так как значение So предполагается закрепленным.
Необходимо иметь в виду, что (и, р)-диаграммы простых волн и ударных волн с данным центром (щ,ро) меняются при изменении энтропии So (или удельного объема Vo) и, следовательно, образуют однопараметрическое семейство (с параметром So или Vo).
Непосредственно из (7) видно, что (и, р)-диаграмма ударных волн симметрична относительно прямой и = щ. Дифференцирование уравнения (7) один и два раза дает соотношения
2 (и - гю)& = Vo-W-(p- р0)~, (В)
Соотношение (9) в точке («о, ро) приводит к формуле
где последнее равенство следует из (5.7). Это дает два различных, отличающихся знаком, значения для производной du/dp в центре (ио,Ро)- Поэтому (и, р)-диаграмма (7) состоит из двух ветвей, пересекающихся в ее
центре подгконечным углом. Далее, в силу (7), из (8) получается неравенство
(и - и0)(р - ро)^ > о.
(И)
Отсюда и из теоремы 5.1 следует, что каждая из ветвей есть монотонная кривая, вдоль которой принимаются все значения давления, 0 < р < ос. Кинематическое различие этих ветвей выясняется с помощью закона сохранения массы в ударном переходе
(« - D)\о = (uo - D)V, (12)
который можно преобразовать к следующему виду:
(¦и - uq)Vq - (D - U0){V0 - V).
Отсюда следует, что знак произведения (и — щ)(р — ро) совпадает со знаком величины D — Uq, который определяется тем, куда обращена ударная волна. Именно, всегда D > и о для волн, обращенных вправо, и D < uq для волн, обращенных влево. В силу неравенства (11) это означает, что ветвь (и, р)-диаграммы, на которой du/dp > 0, соответствует волнам, обращенным вправо, а ветвь du/dp < 0 — волнам, обращенным влево. Полная (и, р)-диаграмма ударных волн показана на рис. 3.
Значение производной d2u/dp2 в центре (uq,pq) вычисляется путем дифференцирования соотношения (9) и после преобразований с учетом формулы (5.7) и обозначения (2.22) оказывается таким (для ветви с du/dp > 0):
(13)
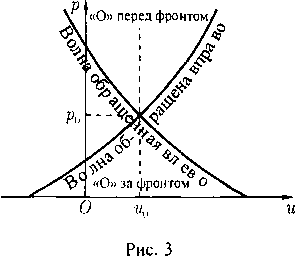
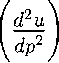
тпо ¦
Сравнение формул (10) и (13) с (5) показывает, что (и, р)-диаграммы простых и ударных волн с общим центром (щ,ро) имеют в точке (ио-ро) одинаковый наклон и одинаковую кривизну, т. е. имеют касание второго порядка.
В политропном газе, в силу уравнения (4.21), функция (6) такова:
Ь -1 )р -t Ь + i)po (7 + 1 )р 4- (7 - 1)ро
Поэтому в политропном газе (и, р)-диаграмма ударных волн описывается элементарными уравнениями каждой из ветвей
и=щ±{р-рв)^1}р2^_1)к, (15)
где знак «4 » берется для волн, обращенных вправо, и знак «-» для волн, обращенных влево.
Существование и единственность автомодельного решения. Основной качественный результат формулируется в виде следующей теоремы.
Теорема 1. Задача о распаде произвольного разрыва в нормальном газе при любых начальных данных (1) имеет одно и только одно автомодельное решение вида (2).
Доказательство. Согласно теореме единственности 15.1 в некоторой окрестности полуоси х < 0 решение постоянно: и = и\, р = р\, р = р\. Это решение может измениться либо непрерывным образом в некоторой центрированной г-волне разрежения, либо через ударную волну, обращенную влево. Этим изменениям соответствуют (и.р)-диаграммы, состоящие из правой нижней ветви на рис. 2 и левой верхней ветви на рис. 3. Их совмещение на одном чертеже дает (и, р)-диаграмму возможных состояний, в которые может перейти состояние 1 (рис. 4). Аналогично строится (и, р)-диаграмма возможных состояний, в которые может перейти состояние
2 посредством волн, обращенных вправо (рис. 5). Если обе эти диаграммы совместить на одном чертеже, то они обязательно пересекутся, и притом только в одной точке. Этот факт вытекает из свойств нормального газа и адиабаты Гюгонио (теорема 5.1), в силу которых эти диаграммы определены в интервале 0 < р < ос и монотонны, причем вдоль (и, р)-диаграммы ударных волн Ы —> оо при р —> оо. Исключением является лишь тот случай, когда точка а\ оказывается лежащей левее точки а>. Всего имеется 10 типов случаев в зависимости от того, на какие части (ударного У или непрерывного П перехода) (и.р)-диаграмм возможных состояний попадает точка пересечения.
Утверждается, что точка пересечения (мз.рз) дает решение. Действительно, оба газа после переходов 1-3 или 2-3 имеют в состоянии 3 одинаковую скорость из и одинаковое давление рз. Поэтому их можно связать контактным разрывом, идущим по лучу х = u^t, вдоль которого могут претерпевать разрыв плотность р и энтропия S. Полный перечень всех 10 возможных типов конфигураций распада произвольного разрыва дан на рис. 6-15, где пунктиром на плоскости R2(x,t.) показана траектория х = »з?. Необходимо доказать еще, что луч А = из всегда идет в секторе между задними фронтами волн, осуществляющих переходы 1-3 и 2-3.
и
Ударные
волны
Рис. 4
Простые / - волны
Рис. 5
Это проверяется непосредственно для каждого из типов распада разрыва. Например, в случае, показанном на рис. 7, ударная волна обращена влево и потому для нее D < щ. Поэтому из соотношения p\(D — U\) — pz(D — из) следует, что D < щ. Далее, на задней стороне центрированной /-волны Аз — из — сз > ы3, и этот случай исчерпан.
В предыдущих рассуждениях предполагалось, что р\ > 0 и р2 > 0. Однако, если pi — 0, то состояние 1 есть состояние вакуума, и тогда решение дается правой половиной рис. 15. Аналогично, если ро = 0, то решение дается левой половиной рис. 15 (пунктиром показаны граничные линии вакуума). Тем самым существование решения доказано.
Доказательство единственности автомодельного решения основано на замечании, что в таком решении не может быть двух различных характеристик Cq (траекторий) в виде лучей х = At. Точнее, две контактные характеристики этого вида возможны только в том случае, если между ними находится область вакуума (рис. 15). Действительно, если х = X't и х = A"t — две траектории и А' < А", то заключенная между ними масса равна
t
А"
![]()
А Ч
А'
Согласно интегральному закону сохранения массы (1.3) эта величина не должна зависеть от t, что возможно, только если интеграл равен нулю, т. е. р(А) = 0 в интервале А' < А < А". Но если есть лишь одна Co-характеристика х = щЬ, то состояния по каждую ее сторону (различные, если вдоль нее есть сильный контактный разрыв) могут получиться из состояния 1 только с помощью волн, обращенных влево, а из состояния 2 — только с помощью волн, обращенных вправо. Утверждается, что в автомодельном решении не может быть двух последовательных волн (простых
|
у\ | t |
> | |
| 3'/ |
|||
| 1 |
/у | ' 2 | |
| О | X | ||
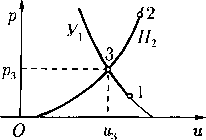
Рис. 7
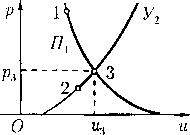
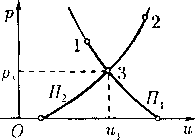
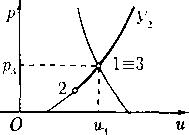
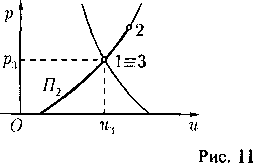
| р |
уг\/ | \У, t | ; | |
|
Р.Ч | ......-Д2=3 | \ 2=3' | / | |
|
у !\ | ||||
| ; \ | 1 \ |
< | 2=3" | |
|
0 | щ “ |
О | X |
|
Рис. 12
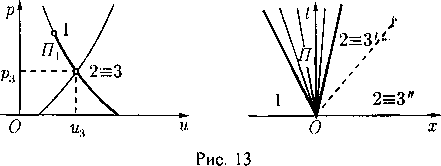
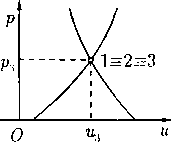
Рис. 14
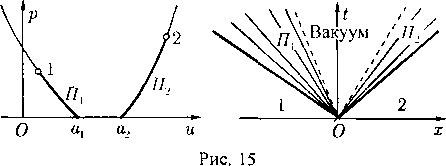
или ударных), обращенных в одну сторону. Например (рис. 16), если бы существовали две ударные волны, обращенные вправо, идущие со скоростями D\ > D\, то должны были бы выполняться неравенства
D\ > и\, D\ > и\.
Тогда в силу теоремы Цемплена (теорема 5.4) было бы
D\ - и\ < с\, D\ — и\ > с\,
откуда D\ < D\, что противоречит предположению. Остальные возможные комбинации рассматриваются аналогично. Но если с каждой стороны от траектории х = u-^t возможна лишь одна волна, то она должна определяться точкой 3 пересечения (и,р)-диаграмм переходов из состояния 1, обращенных влево, и из состояния 2, обращенных вправо. В противном случае были бы нарушены условия на контактном разрыве х — Поэтому нет никаких других, кроме перечисленных выше, конфигураций распада произвольного разрыва. ¦
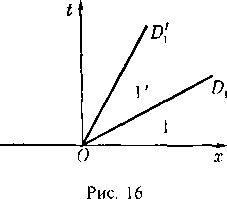
Фактически расчет распада разрыва выполняется с помощью уравнений (и, р)-диаграмм (3), (4) и (7). С этой целью рассматриваются функции, описывающие соответствующие ветви (и.р)-диаграмм: для переходов из состояния 1 (рис. 4)
\/(р -P\){V\ -W{p- vuPl)) (p^pi).
Ui +ct(p,Vi)-сг(рь Vi) (p<pi)
и 1
Fi{p)
и для переходов из состояния 2 (рис. 5)
^ / “2 +¦ \/(P ~ P2XV2 - W(p: V2,p2)) (p ^ p2),
\ U'2 — ст(р, Vo) + cr(p2, V2) (P Рз)-
Тогда значение p — рз определяется как единственный корень уравне
ния
F,(p) = F2(p).
после чего находится величина U3 — Fi(p3).
Акустическое приближение. Метод {и,р)-диаграмм применим для анализа и решения многих конкретных задач с сильными разрывами. При относительно небольших значениях скачков [и], (р] и [р| на практике успешно используется акустическое приближение. Оно состоит в том, что кривая (и, р)-диаграммы заменяется прямой — касательной к ней в ее центре. При этом важно, что (и,р)-диаграммы простых и ударных волн касаются друг друга, в силу чего угловой коэффициент аппроксимирующих прямых одинаков для обоих типов волн. В акустическом приближении с величиной
импеданса h = рс уравнения (м. р)-диаграмм с центром (щ,ро), в силу
формул (5) или (10), записываются в следующем виде: для волн, обращенных вправо,
р - h0u = ро - houo (17)
и для волн, обращенных влево,
р + h0u = ро + h0u0, (18)
где ho = росо есть значение импеданса в центре (и, р)-диаграммы.
Одномерное движение с плоскими волнами можно, интерпретировать как модель движения газа в цилиндрической трубе, в каждом сечении которой в любой фиксированный момент времени основные величины постоянны по сечению. С точки зрения ее практического использования такая интерпретация, конечно, нуждается в оговорке насчет трения о стенки трубы, которого нет в модели невязкого газа, но которое есть в природе. Эксперимент показывает, что для быстропротекающих процессов и на коротких участках трубы это приближение является удовлетворительным. Так или иначе, принятая в данном параграфе трактовка одномерного движения газа как его движения в трубе может рассматриваться как формальная, вводимая для большей наглядности получаемых результатов.
Здесь дается анализ и решение простейших задач с участием распадов разрывов, объединяемых общим понятием задач о взаимодействиях. Описываемые в них ситуации часто встречаются на практике в качестве элементов более сложных газодинамических процессов. Используется развитый в § 17 метод (?/,р)-диаграмм. Без дальнейших оговорок труба предполагается расположенной горизонтально, вдоль оси х, а все газы — нормальными, с известными уравнениями состояния.
Работа ударной трубы. Два покоящихся газа разделены заслонкой в сечении х = 0. Газ 1 с параметрами pi,pi находится под высоким давлением, а газ 2 с параметрами Р2,Р2 — под низким, так что pi > P2 (рис. 1).
В момент времени t = О заслонка мгновенно убирается. Требуется описать последующее движение газов и дать расчет его параметров для t > 0.
В этой постановке задача об ударной трубе является частным случаем задачи о распаде произвольного разрыва. Соответствующие (и, р)-диаграмма и возникающая на плоскости со-
![]()
X
я бытий конфигурация волн аналогичны случаю рис. 17.8 и в уточненном виде показаны на рис. 2. Расчет должен дать скорость ударной волны D, идущей по газу низкого давления, скорость щ и
О
Рис. 1
давление рз в постоянном движении за этой ударной волной, а также плотности газов р'3 и /?з в этой области по разные стороны контактного разрыва.
Согласно (и,р)-диаграмме рис. 2 точка (г*з,Рз) находится из уравнений (17.3) и (17.7), точнее, в результате решения системы конечных уравнений
из + 0-(р3) = o-(pi),
из - V(рз - Р2)(У2 - И^(рз; V2,P2))-
Затем по адиабате Пуассона для состояния 1 определяется удельный объем Уд и по адиабате Гюгонио с центром (V^,p2) — удельный объем V3':
(2)
Рз = sKK.Si), V'g" = Щрз; V2,р2).
Наконец, скорость ударной волны находится из закона сохранения массы (17.12), который в данном случае приводит к формуле
![]()
t
Ударные трубы широко применяются в газодинамических экспериментах для создания высокоскоростного потока, который получается в области 3. В акустическом приближении с помощью уравнений (17.17) и (17.18) для скорости и, получается значение
и3 = (pi - P2)/(/ll + /12),
где hi и /12 — импедансы (17.16) газов 1 и 2. Увеличение скорости потока за счет повышения давления pi затрудняется тем, что с ростом рь вообще говоря, растет и импеданс h\. Однако влияние этого фактора может быть уменьшено, если в состоянии 1 одновременно с повышением давления газ сильно охлаждать.
Задача о поршне. В сечении х = О труба перекрыта поршнем, справа от которого находится покоящийся газ с параметрами рьр\ (рис. 3). В момент времени t — О поршень начинает двигаться с постоянной скоростью U. Требуется описать последующее движение и дать расчет его параметров для t > 0.
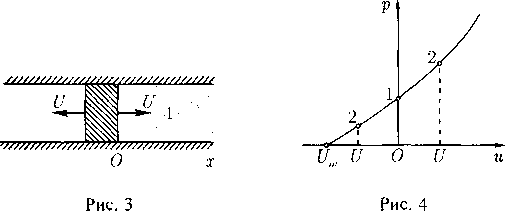
Эта задача, в отличие от рассмотренных ранее, является задачей с граничным условием, так как скорость частиц газа, прилегающих к поршню, должна быть равна скорости поршня (см. §, 7):
u{Ut,t) = U. (4)
Здесь постоянное значение (4) задано на прямой х = Ut, в силу чего задача конически автомодельна (см. § 13) и ее решение можно искать в виде и — и(А), р = р(А), где А = x/t. Единственность такого решения доказывается с помощью тех же соображений, которые были использованы в доказательстве теоремы 17.1.
Так как переход из состояния 1 в составе 2 должен осуществляться волнами, обращенными вправо, то (и, р)-диаграмма этого перехода будет такой, как на рис. 4. Характер возникающего движения определяется знаком величины U. Если U > 0 (поршень движется в сторону газа), то в газ идет опережающая поршень ударная волна, за которой образуется область постоянного движения газа со скоростью, равной скорости поршня U. Если же U < 0 (поршень выдвигается, отходя от газа), то газ переводится из состояния покоя в состояние постоянного движения со скоростью поршня посредством центрированной /-волны разрежения. Плоскость событий для обоих вариантов показана на рис. 5.
Рис. 5
Для расчета первого варианта используется уравнение (и, р)-диаграммы ударных волн (17.7), в котором надо положить щ = 0, и = U, СИьРо) = (Vi.Pi) и рассматривать его как уравнение для р = Р2 > Pi•'
По известному р2 термодинамические величины находятся из уравнения состояния газа:
Если скорость поршня \U\ достаточно велика, то, как это видно на (и, р)-диаграмме рис. 4, поршень оторвется от газа. Движение газа будет таким же, как при истечении в вакуум (см. § 16). Максимально возможная скорость поршня, не теряющего контакта с газом, равна
Um = (9)
В случае политропного газа уравнение (5) в силу (17.14) сводится к квадратному и решается явно, что дает возможность детально проанализировать зависимости давления на поршень и скорости ударной волны от скорости поршня. В варианте выдвигающегося поршня также можно получить достаточно простые окончательные формулы.
На практике задача о поршне находит применение в вопросах, связанных с предварительным быстрым сжатием газа, а также с явлениями удара и откола.
Отражение ударной волны от жесткой стенки. По трубе, заполненной покоящимся газом с параметрами р\, рi и закрытой справа (в сечении х — 0) жесткой стенкой, идет ударная волна, перемещающаяся слева направо с постоянной скоростью D (рис. 6). В момент времени t -- 0 ударная волна достигает закрытого конца. Требуется описать и рассчитать движение газа для t > 0.
////I//////////////////////,
У/////}////////, 7.7////////////77ZW
V///7/777
О X
Рис. 6
Это также задача с граничным условием. Предположение о наличии жесткой стенки означает, что на ней должно быть выполнено условие
Здесь в состоянии 2 за ударной волной можно считать известными все основные величины, т. е. и•>. ро и р2 (теорема 5.5). Поэтому для t ^ 0 снова получается конически автомодельная краевая задача (см. § 13) с граничным условием на контактной характеристике х = 0, имеющая единственное автомодельное решение. Здесь (г/, р)-диаграмма и конфигурация на плоскости событий будут такими, как показано на рис. 7. Характерными элементами решения являются падающая на стенку и отраженная от стенки ударные волны.
Поскольку состояние 2 известно, то за основу расчета можно взять (ц.р)-диаграмму ударных волн с центром (м2, р2). Тогда оба давления, Р\ и рз, должны быть корнями одного и того же уравнения (вытекающего из (17.7))
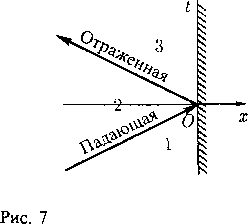
При этом величина р\ удовлетворяет уравнению (11) автоматически, причем р\ < Р2, так как состояние 1 находится перед падающей ударной волной, которая, по предположению, рассчитана по состоянию 1 и ее скорости D. Поэтому уравнение (11) служит для определения давления рз > рг. После того как рз найдено, остальные величины определяются обычным путем. В частности, для скорости Do отраженной ударной волны с помощью уравнения сохранения массы (17.12) выводится формула
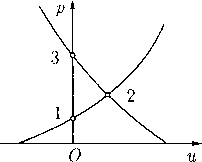
D0 = -1-
D. (12)
РЗ Р2
Наиболее существенная особенность явления отражения ударной волны от жесткой стенки состоит в том, что действие падающей волны после отражения усиливается. Коэффициент усиления характеризует отношение избыточного давления Дрз = р3 — рь получаемого после отражения, к избыточному давлению Дрг = рг — Pi в падающей ударной волне:
к — Дрз/Арг- (13)
Если падающая волна слабая, т. е. в ней относительное изменение давления а = Дрг/pi мало, то для отыскания величины (13) можно воспользоваться акустическим приближением (см. § 17). В этом приближении криволинейный треугольник 1 —2—3 на (и, р)-диаграмме рис. 7 аппроксимируется равнобедренным прямолинейным треугольником (с равными сторонами 1
2 и 2-3). Это означает, что рз - Р2 = Р2 — Р\ и формула (13) дает значение к = 2. Следовательно, при отражении слабой ударной волны избыточное давление удваивается.
Оказывается, что если падаюшая волна очень сильная, т. е. а — Дрг/pi велико, то коэффициент усиления (13) может быть значительно больше двух. Оценка легко выполняется для политропного газа, когда уравнение (И) в силу (17.15) принимает вид
(РЗ -Р2)2
(Р2 -Pi)2
(7 + 1)рз + (7 - 1)Р2 (7 + -1 )Pi + (7 - 1)Р2
и после элементарного решения относительно рз дает величину коэффициента усиления
(З7 — 1)а + 47
Др2 \ Р1 ¦
(14)
к =
(7 - 1 )а + 27
Из (14) следует, что к = 2 при а = 0 и возрастает с ростом а. При а —> ос предельное значение кж коэффициента усиления есть
7 + 1 7-1'
(15)
2 +
/////////////////////////////////////////
V77777777777777777777777777777777777777777-
X
О
Рис. 8
Например, для воздуха 7 = 1,4 и формула (15) дает возрастание избыточного давления после отражения в fcoo = 8 раз. Этим объясняется известное из практики большое разрушительное действие сильных ударных волн.
Преломление ударной волны. В трубе, заполненной двумя покоящимися газами 1 (при х < 0) и 2 (при х > 0) с данными значениями р\ и р2 и с одинаковыми давлениями pi = рг, по газу 1 слева направо идет ударная волна с заданной постоянной скоростью D (рис. 8). В момент времени t = 0 эта ударная волна достигает границы раздела сред в сечении х = 0. Требуется дать описание и расчет последующего движения газа для t > 0.
Ясно, что в момент времени t — 0 в сечении ,т = 0 образуется произвольный разрыв, в силу чего задача сводится к задаче о распаде разрыва со следующими начальными данными:
(х < 0); (ж > 0),
и3 > 0, и = 0,
Р = Р з, р = р2-
Р = Р 3 Р =Р2
в которых состояние 3 может считаться известным (теорема 5.5).
Как показывает (и,р)-диаграмма рис. 9, в результате распада этого разрыва в газ 2 всегда пойдет ударная волна, соответствующая переходу 2-4. Ее можно назвать преломленной, получаемой в результате преломления пришедшей на границу раздела падающей ударной волны. Остающийся позади
преломленной ударной волны контактный разрыв между данными газами всегда приходит в движение со скоростью г/,4. Преломленная ударная волна будет сильнее или слабее падающей в зависимости от того, какую ветвь (м, р)-диаграммы с центром (из.рз) пересечет (гг,^-диаграмма ударных переходов с центром (О ,р2).
В акустическом приближении, когда падающая ударная волна слабая (отношение (рз — pi)/pi), эти две возможности различаются величиной импеданса (17.16) исходных состояний газов. Если газ 2 является более жестким, чем газ 1, т. е. импеданс hi > hi, то на (и, р)-диаграмме линия перехода 2-4 пойдет выше линии 1-3. В этом случае после преломления ударная волна усиливается, скорость потока за ней уменьшается, а по левому состоянию газа 3 идет отраженная от границы раздела ударная волна. Если же газ 2 более мягкий, чем газ 1, т. е. импеданс hi < hi, то после преломления ударная волна ослабевает, скорость потока за ней увеличивается, а по левому состоянию газа 3 распространяется простая r-волна разрежения. Конфигурации на плоскости событий для этих двух случаев аналогичны тем, которые изображены, соответственно, на рис. 17.6 и рис. 17.8.
Рис. 9
Критерий для точного различения двух возможностей выводится на основании (гг,р)-диаграммы рис. 9. Пусть известна скорость за падающей ударной волной. Тогда можно вычислить вспомогательную величину р» как больший корень уравнения
(P*-Pi№-W(p«: V2,p2))=--ul (17)
равный давлению за фиктивной ударной волной, которая шла бы по состоянию 2 со скоростью из, за фронтом. Сравнение величины р* с рз приводит к следующим выводам. Неравенство р* > рз соответствует случаю усиления ударной волны после преломления, когда назад по газу 3 идет отраженная от границы раздела ударная волна. Неравенство р* < рз соответствует случаю ослабления ударной волны после преломления, когда назад по газу 3 идет волна разрежения.
Взаимодействие ударных волн. По трубе, заполненной покоящимся газом с параметрами pi, pi идет ударная волна с постоянной скоростью Di.
Имеется вторая ударная волна, которая перемещается также с постоянной скоростью D3 (рис. 10). Требуется дать описание и расчет движения после момента встречи этих волн.
| 111 | А, . ./>' | ///{/////:, ;1|1Й |
|
| у/Шш | Р) | г ! |
Рис. 10
Возможны два случая: а) ударные волны движутся навстречу друг другу и, значит, обе идут по состоянию 1, и б) ударные волны движутся в одну и ту же сторону, например слева направо, и значит, ударная волна Dj идет по состоянию 2 за ударной волной Di- В обоих случаях встреча этих двух волн неизбежна, что в случае б) следует из теоремы Цемплена 5.4, в силу которой в области 2 справедливы неравенства
Dz > U2 + ci > Do.
Ясно, что в момент встречи (скажем, в точке х = 0 при t = 0) в распределении основных величин образуется произвольный разрыв с известными параметрами при х < 0 и при х > 0. Дальнейшее движение для t > 0 будет распадом этого разрыва, который определяется (и, р)-диаграммами, показанными на рис. 11 сплошными линиями для случаев а) и б).
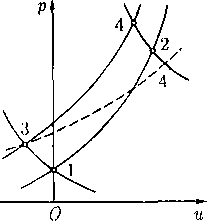
Рис. 11
В действительности может оказаться, что положение точки 4 на (и, р)-диаграмме будет другим, например положением 4' (пунктирная линия на рис. 11, а). Здесь также можно дать критерий различения разных возможностей (которых на самом деле больше, чем показано на рис. 11), опираясь на тот же принцип, с помощью которого был получен критерий (17) в задаче о преломлении ударной волны. Если положение точки 4 на (гг.р)-диафамме определено, то дальнейший расчет процесса взаимодействия выполняется по стандартной методике расчета распада произвольного разрыва (см. § 17).
При решении задачи в акустическом приближении для слабых ударных волн ?>2 и Д> адиабата Гюгонио заменяется касательной к ней в точке (PbPi):
Теперь для решения задачи о распаде разрыва между состояниями (20)
и (21) необходимо найти состояние 4 путем совместного решения уравнений (и, р)-диаграмм переходов 2-4 и 3-4, которые, соответственно, таковы (здесь предполагается, что изменениями импеданса можно пренебречь):
Р4 + P1C1U4 = Р2 + PlClU2, ^
Р4 - P1C1U4 = РЗ - Plf'iU3-
В результате решения этой системы, в силу формул (20), (21) и (18), определяется состояние 4:
u4 = D2 + D3, р4 =pi +pi^i(D2 - Аз — 2ci), p,\ — pi{D2 - Di - ci)/ci.
Итак, в случае лобового столкновения двух слабых ударных волн, в результате их взаимодействия, в обе стороны пойдут ударные волны, между которыми образуется область постоянного движения с параметрами (23).
Тем же способом исследуется в акустическом приближении случай б), когда одна волна догоняет другую. Оказывается, что если изменением импеданса пренебречь, то в этом случае после взаимодействия остается просто одна ударная волна, которая идет по газу 1 со скоростью D3. Другими словами, догоняющая ударная волна как бы поглощает Ударную волну, идущую впереди нее в том же направлении.
Взаимодействие ударной и простой волн. По трубе, заполненной покоящимся газом С параметрами р\, р\ слева направо идет ударная волна с постоянной скоростью D. Навстречу ей распространяется простая 7'-волна конечной протяженности с заданным распределением параметров (рис. 12). В некоторый момент времени to в сечении х = хц ударная волна приходит в контакт с простой волной. Требуется дать описание и расчет процесса взаимодействия ударной и простой волн для t > to.
|
//////////////, 2 |
///////////////////////////. 0^ j ^ с. |
ШИ /¦= roust | 3 |
| //////?/////// |
////////////////////////Л х{) |
/7V7//////K | X |
Рис. 12
Качественное отличие этой задачи от предыдущих состоит в том, что возникающее при t > tо движение уже не состоит только из ударных и простых волн. Процесс взаимодействия ударной и простой волны происходит в течение конечного промежутка времени и в конечной массе газа. За время взаимодействия по этой массе проходит ударная волна переменной интенсивности, оставляя за собой энтропийный след — область с переменной энтропией. В итоге вырабатывается движение, элементами которого являются идущая вправо преломленная ударная волна и идущая влево преломленная простая волна.
На основании изложенных в § 15 общих соображениях об областях определенности, влияния и зависимости решения вырабатывается качественное представление о возникающей конфигурации на плоскости событий, показанной на рис. 13.
На отрезке взаимодействия МР линия ударной волны искривляется, а характеристики С- простой r-волны претерпевают излом. Выше линии МР образуется область переменной энтропии, которая показана на рис. 13 семейством траекторий Со, нанесенных пунктиром. Область QMFR представляет преломленную простую волну, идущую по газу в состоянии 2 с энтропией S = S2. В областях 1, 2, 3 и 5 движение является постоянным, а область 4 с границей KPFG представляет собой энтропийный след.
Рис. 13
На рис. 14 показана (и, р)-диаграмма этого процесса, где линия 1-3 изображает данную простую r-волну, а линия 2-4 есть геометрическое место состояний движения за ударной волной на участке взаимодействия МР.
Эта линия отнюдь не совпадает с (и, р)-диаграммой возможных переходов из состояния 2; на самом деле она заранее неизвестна. Поэтому здесь для расчета процесса взаимодействия надо непосредственно решать довольно сложную задачу Коши с начальными данными при t — to, постоянными при х < хм, разрывными в точке М и известными, но не постоянными на интервале MN. Решение этой задачи уже не сводится к алгебраическим уравнениям и может быть найдено только численным расчетом (см. также [6]). Возможные здесь приближенные методы связаны с предположенном о том, что ударная волна слабая.
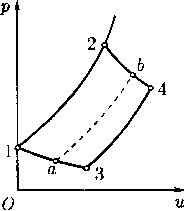
Рис. 14
Акустическое приближение. В этом приближении решение строится элементарно. Здесь предполагается, что ширина простой r-волны мала и она изображается на плоскости событий одной характеристикой С-, а область взаимодействия сводится к одной точке (см. рис. 14). Основными малыми величинами можно считать изменение скорости в простой волне из = U и отклонение скорости ударной волны от скорости звука D — с.\. Состояние 2 определяется формулами (20), где надо положить D2 — D, а давление в состоянии 3 - из перехода 1-3 в простой
волне:
Решение уравнений (и. р)-диаграмм переходов 2-4 и 3-4, которые имеют, соответственно, вид
Первое из них, в силу теоремы Цемплена 5.4, показывает, что в газ 3 всегда идет ударная волна. Из второй формулы (27) следует, что взаимодействие сохраняет характер простой волны: если до взаимодействия была волна разрежения, для которой U > 0 (или волна сжатия, для которой U < 0), то и после взаимодействия простая волна останется волной разрежения ввиду неравенства < р? (соответственно, волной сжатия ввиду неравенства Р4 > Рг)-
Задача о безударном сжатии. Этой задаче посвящен большой цикл работ А. Ф. Сидорова [14]. Здесь она рассматривается в классе одномерных изэнтропических движений политропного газа с плоскими волнами. В этом случае задача решается в явном виде.
Постановка такова: пусть на отрезке 0 ^ х < а находится покоящийся политропный газ с известными параметрами р0, cq и пусть в момент времени t = 0 в этот газ из положения х - 0 начинает вдвигаться поршень с пулевой начальной скоростью. На плоскости событий (х, t) из точки О выходит прямолинейная характеристика ОВ, разделяющая области возмущенного и покоящегося газа, которая приходит в точку В в момент времени Ь = а/cQ. Требуется найти такой закон движения поршня х -- X(t), чтобы его траектория соединяла точки О и В и чтобы в области ОЛВ не возникала градиентная катастрофа (см. рис. 15).
Оказывается, что при заданном значении а > 0 эта задача имеет единственное решение. Действительно, из теоремы 10.2 следует, что область ОАВО должна покрываться простой /-волной, т. е. в ней скорость газа и и скорость звука ссвязаны (см. (16.9)) соотношением (7 — 1)и — 2с = — 2со, откуда
Рис. 15
Возникающая /-волна необходимо должна быть центрирована в точке В, так как иначе не будет выполнено либо условие безударности движения (отсутствие градиентной катастрофы), либо условие направленности движения поршня в сторону газа (детальная проверка предоставляется читателю).
В /-волне, центрированной в точке В, для любой (прямолинейной!) характеристики С+ типа АВ (рис. 15) с уравнением dx/dt. = и -т с выполнено равенство (с учетом (28) и а cob)
7 + 1
cob - х b — t
и + с = —-—и + Со,
которое в точке А поршня переписывается в виде дифференциального уравнения для искомой функции X(t)
cob - X(t) 7 + 1 ~b-t “ = ^XW + co.
Интегрирование с начальным условием Х(0) -= 0 приводит к искомому результату
Полезно отметить, что после растяжения переменных х, t формула (29) приобретает стандартный вид
УМ = 1 + ^(1-'0-^(1-'07?т . (30)
дающий решение «эталонной» задачи о безударном сжатии для значений параметров а = b = cq = 1.
В результате движения поршня по закону (29) вся масса газа т = аро, первоначально распределенная по отрезку (0, а), при t = Ь сжимается (коллапсирует) в одну точку х - а, где достигается бесконечная плотность.
Аналогичные одномерные задачи о цилиндрическом или сферическом безударном сжатии также решались, но лишь численными методами.
§ 19. Асимптотическое поведение ударных волн
В приложениях часто встречается такой вид движения, когда под действием некоторого локализованного во времени и пространстве возмущения покоящегося газа с данными параметрами рьр\ формируется ударная волна, которая затем распространяется до бесконечности. При этом ввиду прекращения внешнего воздействия движение ударной волны происходит так, что ее амплитуда, вообще говоря, убывает и стремится к нулю при t —¦> ос. Например, такое движение может быть произведено поршнем, который, начиная с момента времени t. = 0, движется с постоянной скоростью, а затем в момент времени > 0 внезапно останавливается и покоится при t. > t0. Оно может быть вызвано также взрывом, когда при t ~ 0 в области г < г0 возникает высокое давление р0 > рь которое при t > 0 производит, в результате распада разрыва на границе г = г0, уходящую от центра взрыва ударную волну.
Итак, воздействия на газ, вызывающие ударную волну, могут быть различны и начальные условия не являются строго фиксированными. Тем не менее оказывается справедливым замечательный факт, имеющий большое познавательное и практическое значение, состоящий в том, что при предположениях достаточно общего характера асимптотическое поведение одномерной ударной волны при t —> ос оказывается, с точностью до одной постоянной, вполне определенным. Здесь будет дан вывод этого закона «затухания» для плоских, цилиндрических и сферических ударных волн.
Амплитуда слабых ударных волн. Вначале выводятся формулы Ударного перехода, удобные для анализа слабых ударных волн. Пусть индекс «1» обозначает постоянное состояние перед фронтом и индекс «2» - со-
стояние на задней стороне фронта ударной волны. Вводится безразмерная величина
_ Р2 ~ Р1
Р\с\
называемая амплитудой ударной волны. Если амплитуда 2 задана, то согласно теореме 5.5 все остальные величины на задней стороне фронта однозначно определены. Для вывода асимптотики достаточно найти их разложения по степеням 2 до определенного порядка. В дальнейшем будет использовано обозначение часто встречающейся величины (2.25)
Удельный объем V> находится с помощью адиабаты Гюгонио с центром В силу теоремы 5.2 в разложении функции V = W(p) по
формуле Тэйлора две первые производные достаточно вычислить вдоль из-энтропы S = 5Ь что дает (см. аналогичные формулы (5.7))
Следовательно,
V2 = V1-V1z + -^z2 + 0{z3). (5)
Скорость и о находится из уравнения (4.17) и дается формулой
U2 = \/{р2 ~ Pl)(V\ ~ Vh), откуда в силу (3) и (5) следует представление
КромеИКх), полезно найти инвариант Римана l2 = и2 — а(с2). Так как
Другими словами, скачок инварианта Римана I = и—а(с) есть величина третьего порядка малости по сравнению с амплитудой ударной волны, когда амплитуда стремится к нулю.
Наконец, скорость перемещения ударной волны D находится из уравнения (4.12), т.е. здесь (и2 — D)V\ = -DVo, и после подстановки выражений (5) и (6) оказывается такой:
Постоянство энтропии и инварианта Римана. Для вывода асимптотики на плоскости R2(r,t) рассматривается область Q = = {го < г < гф, t >0}, где постоянная г0 > 0 и г = r$(i) есть уравнение ударной волны (фронта), причем гф(0) == г о. Вывод основан на приближении, связанном с отбрасыванием, ввиду их относительной малости, величин 0(z3) в соотношениях (4) и (8), а также с условием конечности суммарного расхода через границу г = го. Эти соглашения формулируются ниже как предположения А и В.
Предположение А. Всюду в области П энтропия S и инвариант Римана I постоянны, S = S\ и I = l\ = — a(ci), или
и = а(с) - а(с\). (10)
Кроме того, считается, что движение в Q непрерывно и все величины мало отличаются от их значений перед фронтом.
Из предположения А следует, что все газодииамические величины в области Я являются функциями одной из них, т. е. движение в Q есть простая волна. При этом уравнение (15.4) вдоль характеристик С- можно отбросить (оно заменяется соотношением (10)) и движение описываетэдяМН00 уравнениями характеристик С+:
![]()
щ(и + (т{с)) + (и + c)j^{u + а {с)) = -JCU.
(П)
Оказывается, что при условии (10) уравнения (11) интегрируются точ-но. Для этого вводится дифференциальный оператор
и (11) переписывается в виде
(и -4- с)д+(и + <т(с)) + vr~lcu — 0.
Применение оператора к тождеству (10) дает pdj = с9+ р, в силу чего
(и + с)дг (и + а(с)) = ид? и+и^дг р + сд* и + р =
=2и^д+р + 2сд?и = 2^д+ (ри).
Поэтому предыдущее уравнение равносильно уравнению
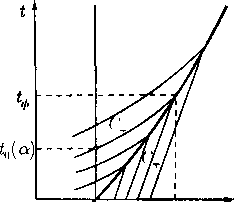
о Угл
Рис. 1
2 гд* (ри) + vpu = 0,
интегрирование которого дает
г^^ри = а
(12)
где величина « постоянна вдоль С+-характеристик и является параметром, отличающим одну характеристику от другой.
Каждая из этих характеристик соединяет некоторую точку to(a) на прямой г = г о с точкой (гф,?ф), лежащей на ударной волне
(рис. 1). Интегрирование первого из уравнений (11) вдоль С+ дает
Дифференцирование этого соотношения по а с учетом того, что dtф/da = = D~ldr<f,/dci, приводит к уравнению
i ~ й+с) ж ~ +/ (&;гЬ)*• (13)
ГО
В силу предположения А величины D и и 4- с можно рассматривать как функции от ри. С помощью формул (5), (6) и (9) получаются достаточные для вывода асимптотики приближенные выражения
7) = к~\^ри' гГ+Ъ = ^ ~ ^зри' (14)
D ci 2 picj и + с Cl picf
второе из которых можно считать справедливым не только на фронте, но и всюду в области Q. Если положить к = B\j(2picf), то в результате подстановки (14) и использования (12) уравнение (13) упростится до следующего:
Гф
ГО
Гф
Пусть J(a) = f r~l/‘/2dr; тогда это уравнение перепишется так:
Го
kctj'(a) + 2 kJ(a) — t'0(a),
или равносильно:
= ato(a)>
и проинтегрируется в виде
а
Ото
где предполагается, что г$ = го при а = ао, т.е. ^o(Qo) = 0. Последний интеграл можно преобразовать с учетом соотношения (12):
a to
J 0t'o(0)dP = J pu{r0,t)dt.
Пр!|$положение В. Интеграл
ОС
J pu(ro,t)dt = Q (16)
о
конечен и положителен.
Асимптотические формулы. В силу предположения полу
чается асимптотическое представление интеграла J(a):
J(a)=rvQ/2%± (17)
к а
С-другой стороны, интеграл J(a) берется явно, и для различных значений v получаются формулы
(i'= 0) J(a) = Гф — го;
(и = 1) J(a) = 2(^/гф — у/го); (18)
(и> = 2) J(a) = 1п(гф/г0).
Сравнение (17) с (18) дает асимптотическую зависимость Гф(а) или а(гф), а значит, и величины (ри)ф в зависимости от гф в силу (12).
В заключение надо заметить еще, что в силу формул (5) и (6) справедливо соотношение
piui = piciz + 0(z2), позволяющее представить амплитуду 2 асимптотической формулой
2 = (ри)ф!р\СХ. (19)
Отсюда и получается искомое асимптотическое представление амплитуды 2 через при Гф —» оо. При этом в формулах (18) слагаемыми г о и ^/го
можно пренебречь. Окончательно, с учетом (2) и выражения В\ = 2кр\с\, асимптотика амплитуды z записывается через относительный радиус ударной волны ? = гф/го и дается следующими формулами:
(v — 0, плоские волны) 2 =#?-1//2;
(и = 1, цилиндрические волны) 2 =—^=Я?~3/4; (20)
V ^
(и = 2, сферические волны) z =.//?-l(ln?)-:1/2,.
где безразмерны!; величина Н дается формулой
1/2
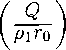
2
JLf „ _?___
v^7T2 v^ir°
(21)
На основе асимптотики (20), (21) и предыдущих выводов легко получаются формулы, описывающие асимптотическое поведение на ударной волне величины давления (3), плотности (5), массовой скорости (6) и скорости ударной волны (9) для каждого значения параметра симметрии у.
Термин «автомодельность» уже встречался в § 13 для описания частных случаев кратных волн, обладающих конической автомодельностью. В более широкой трактовке, применительно к физическому содержанию решаемых задач, автомодельными принято называть решения, которые получаются путем анализа размерностей всех участвующих величин. С точки зрения теоретико-группового подхода это равносильно использованию допускаемых уравнениями групп растяжений. Однако свойство некоторой группы преобразований быть группой растяжений зависит от выбора системы координат в пространстве основных переменных. На самом деле единственным инвариантным характеристическим свойством групп растяжений является то, что они абелевы (коммутативны). Поэтому рационально использовать термин «автомодельный» применительно к любым решениям, инвариантным относительно абелевых подгрупп основной группы. При этом представление решения в той системе координат, в которой группа является группой растяжений, удобно называть автомодельным в узком смысле.
Уравнения автомодельных движений. В этом параграфе речь пойдет об автомодельных в узком смысле решениях уравнений одномерных движений политропного газа (12.12). Эти решения выделяются тем, что они полезны и часто используются в приложениях; кроме того, они наиболее хорошо изучены (см. [7]). Общее представление таких решений и соответствующая факторсистема имеют следующий вид:
q=jU( А), Р = t^R(X), р = ^-2г2Р(Л); А = гГа; (1)
здесь аир — показатели автомодельности, а функции U, R, Р удовлетворяют системе обыкновенных дифференциальных уравнений (штрихом
(U - a)XU' + А^ - U + U2 + 2^ = О, {U - а)ХR' + RXU' + {ци + 0)R = О, (U - а)АР' + т<PXU' + ((м7 + 2)U + 0 - 2)Р = О,
обозначены производные по А)
где положено ц, = 1 + и, так что ц = 1 для плоских волн, р = 2 для
цилиндрических волн и // = 3 для сферических волн.
Замечательная особенность системы (2) состоит в том, что она сводится к одному независимому уравнению первого порядка и двум квадратурам. Этот факт не случаен, он имеет групповую природу и связан с тем, что исходные уравнения (12.12) допускали трехпараметрическую группу растяжений, а для определения решений вида (1) использована только одна ее однопараметрическая подгруппа; оставшиеся два независимых растяжения должны допускаться системой (2). Здесь эти преобразования видны непосредственно: _ _ _
(о) А = аХ¦ (6) R = bR, Р = ЪР. (3)
Преобразование (3, а) позволяет избавиться от явного вхождения неза
висимого переменного А за счет замены ? = In А, а преобразование (3, Ь) показывает, что единственным независимым уравнением должно быть уравнение, связывающее инварианты этого преобразования U и Z = Р/R. Вывод последнего требует лишь выполнения ряда тождественных преобразований, в итоге которых получается уравнение
dZ Z М
(4)
dU и-a N'
где
М = (2jU—(j - 1)(2а + 0) - 2)Z—
— (U - q)((w - 7 + 1 )U2 + (7 -- aui - 3)U + 2a), (5)
N = (n-yU+2a + 0-2 )Z - {U - a)(U2 - U),
и введено обозначение ш = /2(7 — 1) t- 2. По известной зависимости Z(U) функция U (А) находится квадратурой из уравнения
dU (^U + 2а + 0 - 2)Z - (U - a){U2 - U)
(6)
![]()
(U - a)2 - 7Z
после чего еще одной квадратурой находится R(А) из второго уравнения (2): A dR At/' + fiU + 0 .
Наконец, функция Р находится из определения Z:
Р = ZR.
Полезно заметить еще, что для скорости звука из формулы с2 = ~/р/р
(газ политропный) в силу представления (1) и определения (8) получается выражение
c=JC(A), С2 = 7Z.
О)
Линии уровня. Линии А = const называются линиями уровня решения (1); на плоскости R2(r,t) они имеют уравнение г = r\(t) = Ata. Картины расположения линий уровня для q > 0 показаны на рис. 1. Скорость движения точки вдоль линии уровня дается формулой
![]()
г
0<а<1
а>1
г
О
Рис. 1
О
Поэтому из формул (1) и (9) следует вывод: линия уровня является траекторией частицы, если и только если на ней U = а; линия уровня есть С+(С_ ^характеристика, если и только если на ней U + С = о (U — С = а). Кроме того, в решениях с ударными волнами, движущимися по закону г = Гф(?), участвует скорость волны D, которую удобно здесь
представить в виде D — -j-Dф(А); тогда ударная волна является линией
уровня, если и только если Иф = а.
С помощью уравнений (4)-(9) могут быть рассмотрены задачи об автомодельном разлете газа, о вытеснении газа поршнем, о движении в результате сосредоточенного в точке г = 0 воздействия на газ путем приложения мгновенного импульса или путем мгновенного выделения энергии и т. п. В таких задачах необходимо учитывать различные особенности исследуемого движения, связанные с заданием тех или иных дополнительных условий. Такие условия следует интерпретировать, в первую очередь,
как дополнительные к ключевому уравнению (4). Эти условия могут быть связаны с отысканием интегральных кривых, проходящих через его особые точки. Так как характер и расположение особых точек уравнения (4) зависят от четырех параметров -- показателей автомодельности q и 0, размерности пространства \х и показателя адиабаты 7, то в общем виде нарисовать поле интегральных кривых этого уравнения затруднительно. Это приходится делать в каждой конкретной задаче после того, как все или хотя бы некоторые из параметров фиксированы. При этом следует иметь в виду, что иногда показатели автомодельности удается определить только на основе очень глубокого качественного анализа искомого решения. В этом вопросе могут оказаться полезными выводимые ниже интегральные законы сохранения, которые для автомодельных решений принимают специальную форму.
Интегральные законы сохранения. Рассматривая объем ш, ограниченный поверхностями го = const и г = const (при v > 0 надо взять в качестве и> соответствующий сектор слоя (го, г)), можно привести балансовые уравнения (1.4) для одномерных движений к следующим интегральным законам сохранения массы, импульса и энергии
Г
ГО
г г
^ j pqrv dr + [ip + pq2)rv)rTQ = v j -prv~l dr; (11)
ГО Го
I/ + ^V‘),'dr+
1 \р<? +
= 0.
ГО
где символ [/]?0 означает разность /(г) — /(го). Здесь в законе сохранения энергии принято во внимание выражение (2.6) для внутренней энергии политропного газа.
Для автомодельных движений (1) все выражения и интегралы (после замены переменных г —» А = rt~a) в (11) принимают вид произведения некоторой степени t на функцию от А, например
г Л
\pqru}rra = t0+ati-l[\u=lRU]l0 , J pr11 dr = t0+ati J XVR dX
ro Ao
U i. д. Так как в (11) производные берутся при постоянном г, то для произ-дрдных по t от tmf(X) = tm f(rt~a) справедливо выражение
Применение формулы (12) в уравнениях (11) дает следующую систему интегральных законов сохранения для автомодельных движений (1):
Закон сохранения массы
А
{Р + ац) J X»~1RdX + [АМД({/ - <*)]?, = 0 ; (13)
Закон сохранения импульса
л
(Р + а{ц+ !)-!) J X»RU dX + [AM+1 (Р + RU(U - ct))]=
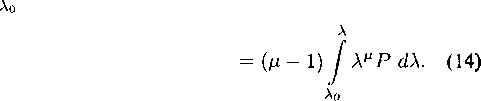
Закон сохранения энергии
л
(Р + a(ji + 2) - 2) J A^+1 (^RU2 + :^-1P^j dX+
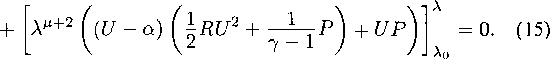
Дифференцирование по А соотношений (13)—(15) дает систему уравнений для U, г, р, эквивалентную (2). Если параметры а, Р, ц обращают в нуль какой-набудь из коэффициентов при интегралах, то соответствующий закон сохранения дает конечный первый интеграл системы уравнений (2). Например, при Р + ац = 0 из (13) получается интеграл массы
Xi*R(U-a) = AM;
при p + a(ц + 2) = 2 из (15) получается интеграл энергии
Конечный интеграл импульса получается из (14) только при р, = 1 (плоские волны) и /3 + 2а = 1
\2{Р + RU(U - а)} =АХ
(18)
Здесь Л\[. Ле . А\ — константы, равные значениям левых частей при А = Ао.
Свойства примыкания. При решении конкретных задач существенно знать, с какими другими решениями можно сопрягать автомодельное решение непрерывным образом или через сильный разрыв. В общей постановке этот вопрос очень сложен и конструктивно не решается. Однако если ограничиться случаем примыкания двух автомодельных решений, то можно заметить следующее. Во-первых, такое примыкание возможно, только если показатели автомодельности а ив для обоих решений одни и те же. Во-вторых, во всех случаях сопряжения линия примыкания должна быть линией уровня А = const. Действительно, в противном случае возникли бы два дополнительных тождественных соотношения между величинами U, R, Р, не вытекающих из законов сохранения, а диктуемых только формой линии примыкания. Вообще говоря, такие соотношения несовместимы с системой уравнений (2) ввиду того, что ее общее решение зависит лишь от трех произвольных постоянных, подбором которых удовлетворить «лишнему» тождественному соотношению невозможно.
Далее, если примыкание осуществляется по линии уровня Л{А = const}, то эта линия должна быть либо характеристикой (в случае непрерывного примыкания), либо линией сильного разрыва (ударной волной). В первом случае на Л необходимо выполняется одно из соотношений
U = a, U + C = a, U — С = а,
(19)
в зависимости от того, является ли Л траекторией или характеристикой семейства С+ или С_. Во втором случае на Л выполнено соотношение для скорости перемещения ударной волны
![]()
Полезно заметить, что точки, в которых выполнено одно из соотношений (19), являются, вообще говоря, особыми для уравнений (2); это видно непосредственно из уравнений (6) и (7), если учесть соотношение (9).
Простейший случай сопряжения разных решений — примыкание к постоянному решению. В силу предыдущего возникает вопрос, является ли автомодельным постоянное решение
Из представления (1) видно, что решение (21) может быть автомодельным только при значениях параметров а = 1 и /3 — 0 (при этом исключается случай вакуума, когда ро = Ро = 0). Следовательно, здесь А = r/t и полученные из (1) выражения
-1
-2
(22)
U = (?о А
R = p0. Р = р0\
должны удовлетворять системе (2). Простая проверка показывает, что (22) есть решение только в двух случаях: (a) q0 ф 0, v = 0 и (Ь) до = 0, v произвольно. Итак, можно сформулировать следующий вывод.
При скорости (jo ф 0 постоянное решение автомодельно только в одномерном движении с плоскими волнами; если же qo = 0, то постоянное решение всегда автомодельно; во всех случаях показатели автомодельного постоянного решения имеют значения а — 1, (3 = 0.
Соотношения на ударной волне. В случае политропного газа соотношения (4.12)-(4.14) могут быть записаны в виде
(23)
DY
= 0,
где [...] — символ скачка. В предположении, что показатели а и (3 в формулах представления (1) и (20) по обе стороны ударной волны одни и те же, соотношения (23) могут быть переписаны в терминах величин U, Л, Р:
\R(U - а)] = 0, [Р + R(U - а)2} = 0,
(24)
7 Р , \,тт \2 7 - 1 R 2^
0.
Введение величины Z согласно (9) дает возможность выделить мы (24) два уравнения, связывающие только U и Z\
систем
+ U -а
= 0, = 0.
U
(25)
i^iz + hu
Уравнения (25) удобны тем, что они позволяют интерпретировать ударный переход на той же плоскости R2{U, Z), где расположены интегральные кривые основного уравнения автомодельных решений (4).
В важном частном случае, когда рассматриваются автомодельные ударные волны, идущие по неподвижному газу с постоянными параметрами состояния =0, pi, pi, второе и третье соотношения (23) принимают вид
(26)
Как уже было отмечено выше, соотношениям (26) можно удовлетворить вдоль линии уровня rt~a = const, только если 0 — 0 и q = 1.
Случай сильной ударной волны. Здесь возможна приближенная постановка для очень сильных ударных волн, когда значение давления перед волной pi много меньше давления за волной р2. В предельном случае pi /рг —> 0 это приводит к приближению, уравнения которого получаются из (26), если просто положить pi = 0. Следует заметить, что, строго говоря, состояние политропного газа с рх — 0 и рх ф 0 достигается, только если в нем обращается в нуль температура Т\. Хотя реально абсолютный нуль недостижим, как приближение такое предположение является приемлемым. В приближенной постановке, когда pi = 0 и р\ ф 0, соотношения (26) могут быть удовлетворены при (3 = 0 и при произвольном а. Следовательно, для очень сильных автомодельных ударных волн (с показателями автомодельности [3 = 0 и любым а), идущих по неподвижному газу с плотностью pi, приближенно справедливы следующие соотношения:
Решение этих уравнений относительно величин с индексом «2» находится элементарно:
(27)
Третье из равенств (27) показывает, что в рассматриваемой постановке за ударной волной достигается предельное сжатие. Очевидно, что этот факт находится в полном соответствии с исходным предположением.
Д2(^2 - а) = -ар 1,
7
7 - 1
![]()
Лг + #2(^2 - о)2 = a2pi.
Общие соображения и подходы к изучению одномерных автомодельных движений газа развиты в монографии JI. И. Седова [7], где приведен также подробный анализ и дано решение многих конкретных задач. Две из них рассматриваются более подробно в следующем параграфе.
§21. Задачи о поршне и о сильном взрыве
Задача о поршне, уже рассмотренная в § 18 для одномерных движений с плоскими волнами, представляет интерес и для движений с цилиндрической или сферической симметрией. В этих случаях сравнительно простое — автомодельное — решение существует лишь тогда, когда поршень вдвигается в покоящийся газ, расширяясь из точки (начала координат) с постоянной скоростью; для других краевых условий задача о поршне неавтомодельна. Тем не менее исследование решения задачи о поршне полезно для понимания общей методики отыскания таких решений.
Постановка задачи о поршне. В неподвижный политропный газ с показателем адиабаты 7 и с постоянными параметрами состояния pi, pi, заполняющий все пространство Я3, в момент времени t = 0 из точки г = 0 начинает вдвигаться с заданной скоростью qo поршень, форма которого соответствует цилиндрической или сферической симметрии. Впереди поршня возникает ударная волна, идущая по покоящемуся газу. Требуется определить скорость перемещения ударной волны, а также движение газа между ней и поршнем в предположении автомодельности; в частности, представляет интерес величина давления на поршень.
Из результатов § 20 следует, что автомодельность движения газа за ударной волной возможна только для показателей автомодельности а = 1 и Р — 0. В этом случае представление решения (20.1) таково:
q=rjU(А), р -- Я(А), Р=^Р(А); А=?. (1)
Здесь основное дифференциальное уравнение (20.4) упрощается до следующего:
dZ _Z27Z~ (U — l)(xU — 2)
dU U /i7Z - (U - l)2 M
где
*={(*- 1)(7 - 1) + 2
и величина Z дается формулой (20.9). Если уравнение (2) имеет решение Z = Z(U), удовлетворяющее граничным условиям на поршне и на ударной волне, то зависимость U(А) находится квадратурой из уравнения (20.6), которое здесь упрощается и может быть записано в виде
(3)
A M7Z- (U- l)2 U '
Граничные условия на поршне и на ударной волне дают начальные данные для решения уравнений (2) и (3). На поршне, закон движения которого есть г = qot, известно значение А = <jo и, согласно (20.19), должно выполняться условие
U(4o) = !•
Так как точка (A, U) = (qQ, 1) не является особой для уравнения (3), то условием (4) его решение определено однозначно.
Условие на ударной волне вытекает из (20.25). Пусть индекс «ф» отмечает значения величин на фронте (за волной). Тогда с учетом того, что скорость перед фронтом U\ = 0 и а = 1 уравнения (20.25) упрошаются и равносильны следующим:
где Z\ есть значение величины Z перед фронтом. Эти уравнения легко решаются относительно величин за фронтом и дают
(5)
При переменном Z\ формулы (5) определяют на плоскости R2(U,Z) линию — геометрическое место всевозможных состояний за фронтом. Эта линия ударной волны после исключения из (5) параметра Z\ дается явным уравнением
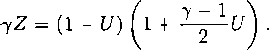
Значение параметра Z\, определяющего положение точки (5) на линии ударной волны (6), связано с постоянной (в силу (20.20)) скоростью ?>ф перемещения ударной волны через соотношения (20.9). Именно, так как закон
§ 21. Задачи о поршне и о сильном взрыве движения фронта есть г = D$t, то из (20.9) следует равенство
7Z1 =
(7)
где ci есть скорость звука в покоящемся газе.
Структура плоскости (?/, Z). Картина расположения особых линий уравнений (2) и (3) на плоскости R2{U, Z) (нули числителя и знаменателя) и линии ударной волны (6) показана на рис. 1. Из нее следует, что в области полосы 0 < U ^ 1, лежащей выше линии ударной волны (6), производная dZ/dU в (2) непрерывна и всюду положительна. Поэтому каждая интегральная кривая уравнения (2), выходящая в этой области из какой-либо точки Ф линии ударной волны, необходимо достигает линии поршня U — 1 в некоторой точке П. Эта интегральная кривая и дает искомую зависимость Z от U, в которой еще присутствует неопределенный параметр Zi, т. е. на самом деле функцию Z — Z(U, Z\). В частности, определяется значение величины Z = Z„ на поршне.
7Z
Линия ударной
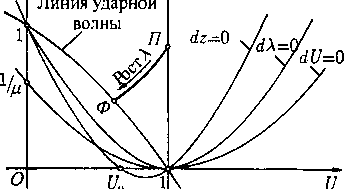
Ц1Г\ и
Рис. 1
После этого зависимость С/(А) находится квадратурой из уравнения (3) и оказывается однозначной, так как в рассматриваемой области всюду dX/dU < 0. Интеграл от (3), взятый по всему промежутку (С/ф, 1), позволяет учесть условие (4) и, в силу равенства Аф = ?>ф, дает соотношение pa Z\. Соотношение (8) можно также рассматривать как уравнение, неявно определяющее зависимость вида
1
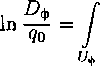
(8)
1Z(U,Z1)-(U-l)2 dU li^ZiU, Z\) — (U — I)2 и '
Это соотношение, с учетом выражений (5) и (7), следует рассматривать как уравнение относительно оставшегося до сих пор неопределенным парамет-
Мф = F(M„) (9)
между числом Маха поршня Mo = qo/ci и числом Маха ударной волны Мф = D$/c\. Входящая сюда функция F определяется расчетом, включающим численное интегрирование уравнения (2) и выполнение квадратуры (8). Очевидно, что функция F является стандартной, зависящей только от показателя адиабаты 7 и размерности пространства р.. Выполненные расчеты (см. [7]) показывают, что при прочих равных условиях порожденная поршнем сферическая ударная волна перемещается медленнее, чем плоская.
Давление на поршень. Для определения давления на поршень необходимо обратиться к уравнению (20.7), которое в данном случае после комбинирования с уравнением (3) принимает вид дифференциальной связи Я с U:
Интегрирование уравнения (10) вдоль всей кривой ФП (см. рис. 1) с учетом
условия (11) приводит к формуле
1п0
п" и^-*[ 7<nTT)dn
гл2’ (12) pi{l-uф) J
n-yZ{U, Zi) -
(1 -
uy
С/ф
которая определяет значение плотности рП на поршне. Так как значение Znвеличины Z на поршне известно (оно уже получено при интегрировании уравнения (2)), то давление р„ на поршне определяется вытекающей из соотношений (20.9) формулой
Р„ = QoPnZn.
Учитывая, что 7р\ = cjpi, ее можно записать в безразмерной форме:
Рп 7 |и|2 Рп -=^Z„M0-.
Очевидно, что правая часть формулы (13) зависит только от числа Маха поршня Мо- Расчет показывает (см. [7]), что, при прочих равных условиях, давление газа на сферический поршень меньше, чем на плоский.
Следует заметить, что хотя наиболее интересными значениями параметра ц здесь являются /и = 2 и р = 3, приведенное решение задачи о поршне годится и для ц = 1. Тогда получаются результаты, которые уже обсуждались в § 18. Проверка этого факта предоставляется читателю.
Задача о сильном взрыве представляет большой интерес не только в связи с практической возможностью оценивать энергию взрыва, например при атомных взрывах в воздухе или в воде, но также ввиду достигаемого здесь изящного описания сложного неустановившегося движения газа посредством относительно простых конечных формул.
Постановка задачи о сильном взрыве. В покоящемся политропном газе с показателем адиабаты 7 и параметрами состояния р\, р\, заполняющем все пространство Я3, в момент времени t = 0 в точке г = 0 мгновенно выделилась большая (по сравнению с внутренней энергией газа) конечная энергия Eq (произошел взрыв). При t > 0 в газ распространяется ударная волна, вызывающая одномерное движение с плоскими, цилиндрическими или сферическими волнами. Требуется найти закон перемещения ударной волны и движение газа за ее фронтом.
На основании рассмотрений § 20 легко устанавливается, что точное автомодельное решение этой задачи не существует. Действительно, так как фронт ударной волны должен быть поверхностью уровня А = Аф, то выражение для полной энергии, заключенной в шаре радиуса Гф = Аф?“, дается формулой (см. (20.12), (20.15):
![]()
о
E(t) = ^+(*'+3)“-2 Iru2 + \u+2d\. (14)
Если здесь показатель степени при t отличен от нуля, то при t —> 0 для E(t) в пределе получится либо значение нуль, либо бесконечность. Ясно, что это противоречит постановке задачи, так как при t —> 0 должна получиться конечная энергия Eq. Поэтому необходимо
(3+(v + 3)а -2 = 0.
(15)
С другой стороны, ударная волна идет по покоящемуся газу и потому показатели автомодельности должны быть а = 1 и (3 = 0. Однако при этих значениях соотношение (15) не выполняется ни при каком и > 0.
По этой причине автомодельное решение задачи о сильном взрыве возможно лишь в приближенной постановке, которая уже обсуждалась в § 20.
Она годится как приближение для очень сильных ударных волн, что хорошо согласуется с предположением о большой величине выделенной энергии Eq. Так как эта постановка возможна при 13 = 0 и любом значении а, то требование (15) конечности энергии E(t) является уравнением, определяющим величину показателя автомодельности а. Он необходимо должен быть равен
Следовательно, приближенное автомодельное решение задачи о сильном взрыве можно получить только с показателем автомодельности (16), а именно а = 2/3 для плоских волн, а = 1/2 для цилиндрических волн и а = 2/5 для сферических волн. Ниже излагается решение этой задачи для сферического случая.
Для сферической ударной волны, когда а = 2/5, значения основных величин на фронте, согласно формулам (20.27), таковы:
Интеграл Седова. Как было замечено впервые JL И. Седовым (см. ссылки в [7]), эта задача имеет конечный интеграл энергии. Он следует из интеграла (20.17) при Ао = 0; тогда будет Ае = 0 и получится равенство
PU + (±RU2 + (и - f) = 0. (18)
Это и есть интеграл Седова. После деления на R и введения, согласно (20.8), величины Z равенство (18) принимает вид
uz+{lu'! + ^hz){u-f)=°-откуда получается простое выражение Z через U:
57
Посколфсу соотношение (19) есть точное следствие законов сохранения, то .опрсдешемая им функция Z(U) должна быть точным решением соответ-
ствующего уравнения (20.4). В этом нетрудно убедиться прямой подстановкой выражения (19) в уравнение с учетом значений показателей автомодельности (3 = 0. Q = 2/5 и числа ц = 3. Легко проверить также, что интегральная кривая (19) проходит через нужную точку на фронте (С/ф, 2ф), координаты которой даются формулами (17).
Следует заметить, что интеграл Седова (18) является частным интегралом соответствующего дифференциального уравнения (20.4): он не содержит произвольных постоянных.
Анализ решения. Имея интеграл (19), можно найти зависимость U(А). Соответствующее уравнение (20.6), после подстановки в него функции (19), принимает вид
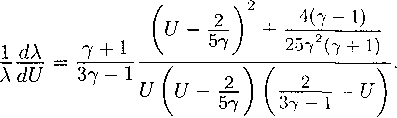
Для того чтобы разобраться в ходе искомой интегральной кривой, необходимо заметить, что для положительности величины Z согласно (19) требуется, чтобы величина U менялась в интервале (с учетом того, что всегда 7 > 1)
Нетрудно убедиться в том, что точка Щ из (17) при любом 7 > 1 лежит в интервале (21). Но уравнение (20) имеет еще одну особую точку С/* = 2/(37 — 1). Сравнение ее с С/ф показывает, что при 7 < 7 справедливо неравенство ?/ф < ?/*, а при 7 > 7, наоборот, U* < Щ. При этом всегда 2/5-7 < U*.
Пусть сначала 7 < 7. Тогда из (20) следует, что d\/dU > 0 в интервале 2/57 < U < U,ф, в силу чего величина U возрастает с ростом А. При этом А —> 0, когда U —> 2/57- Отсюда вытекает качественный график зависимости U(А), показанный на рис. 2,а. Этот график описывается аналитически после взятия квадратуры в (20), которая выполняется явно и дает
т
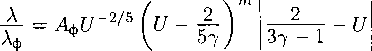
— п
7-1 1З72 -77+12
где а константа Афзависит только от 7 и получается из (22) при А = Аф и U = t/ф. Получаемое здесь решение определено во всей области, от центра г = 0 до фронта ударной волны гф = \$t2/5.
Рис. 2
Если же 7 > 7, то в окрестности и справа от точки (Уф будет d\/dU < О, т.е. с убыванием А величина U растет. Отсюда вытекает качественный
график зависимости U( А), показанный на рис. 2,6. Этот график описывается аналитически той же зависимостью (22), но теперь в интервале Щ < U < 2/5. При этом, когда U = 2/5, то А = А* >0. Это означает, что получаемое здесь решение не определено вплоть до центра г = 0. Так как при U — 2/5 из (19) получается, что Z = 0, то все эти факты приводят к следующему выводу. Если 7 > 7, то область движущегося газа заключена между сферами /¦* = А*?2//5 и Гф = Афt?^, а внутри сферы г — г* находится состояние вакуума.
Вытекающее из этих рассмотрений поведение величин Z, U и А показано на рис. 3, где дан график зависимости (19) и стрелками обозначено направление изменения этих величин от фронта ударной волны к центру для случаев 7 < 7 и 7 > 7. При 7 = 7 в области за фронтом величины U и Z постоянны; анализ этого решения предоставляется читателю.
Вычисление зависимости ЩА) выполняется с использованием функции (22) и соответствующего уравнения (20.7). При этом фактически получается функция R(U), которая выписывается явно, аналогично (22). Наконец, зависимость Р(А) находится просто по формуле Р = ZR.
Расчет движения фронта. В полученном решении остается один неопределенный параметр — входящее в (22) значение Аф. Эта величина определяется условием заданной энергии взрыва Eq. Действительно, в силу (15) в формуле (14) следует положить E(t) = Ео- Кроме того, необходимо заметить, что, как это следует из (22), на самом деле величины U, R, Р зависят только от отношения А/Аф. Поэтому после подстановки
U=U(S), R = PlR(S), P = PlP(?), € = А/Аф, (23)
и перехода к переменной интегрирования ? равенство (14) примет вид
(24)
где величина
(25)
1
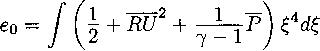
о
зависит только от показателя адиабаты 7.
Тем самым задача о сильном взрыве полностью решена. Закон движения фронта ударной волны дается уравнением
Формулой (24) и определяется искомое значение
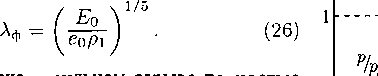
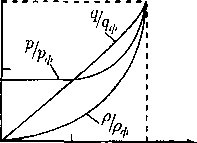
Рис. 4
Гф = Аф/2/о,
(27) О
а распределение параметров газа за фронтом формулами
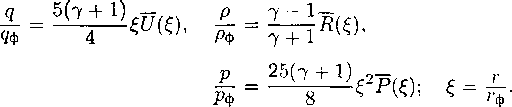
Качественный характер распределений скорости, плотности и давления за ударной волной, описываемых формулами (28), показан на рис. 4.
Можно заметить еще, что если выразить скорость фронта ударной вол-йы 1)ф через его радиус Гф и использовать значение (26), то получится формула
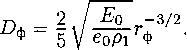
(29)
Сравнение (29) с асимптотикой (19.19) показывает, что при сильном взрыве скорость распространения ударной волны с ростом ее расстояния от места взрыва убывает быстрее, чем в случае слабых ударных волн. Поэтому область применимости формул (28) решения задачи о сильном взрыве ограничена теми расстояниями, на которых ударная волна остается достаточно сильной.
Задачи и упражнения к главе III
1. Показать, что стационарные решения уравнений одномерного движения (15.1) описывают течения типа источника (см.§ 11).
2. Показать, что с массовой лагранжевой координатой ? (см. § 15) система (15.1) в лагранжевых координатах (?,t) имеет вид (V = 1 / р)
Ut + rupt: = 0, Vt — = у Vu, St = 0.
3. Найти характеристическую форму уравнений одномерного движения газа в лагранжевых координатах (см. задачу 2).
4. Для уравнений одномерного изэнтропического движения с плоскими волнами политропного газа при 7 = 3 найти класс точных решений, для которых массовая лаграижева координата имеет вид ? = ?(А), где А = r/t.
5. Найти явные окончательные формулы и дать анализ точного решения вида (15.29), (15.30) системы (15.1) в случае -ф(?) = для показателя адиабаты 7 =
6. Поршень, занимавший в момент времени t = 0 положение х = 0, выдвигается по закону х = at2 (а < 0) из трубы, заполненной покоящимся политропным газом (при х > 0), в котором скорость звука равна со- Описать движение газа в классе простых волн.
7. При условиях предыдущей задачи поршень вдвигается в трубу 110 закону х = at (а > 0). Показать, что момент наступления градиентной катастрофы дается формулой
tx = со/(7 + 1)а.
8. Найти закон движения свободного поршня массы М в неограниченной трубе с площадью сечения F иод действием давления расширяющегося политропного газа, первоначально находившегося в состоянии покоя, если по другую сторону поршня давление равно нулю (вакуум).
9. Показать, что если при отражении простой волиы от жесткой стенки получается снова простая волна, то падающая и отраженная волны являются одновременно либо волнами сжатия, либо волнами разрежения.
10. Показать, что для политропного газа с -у = 3 уравнение Эйлера - Пуассона (16.50) имеет общее решение вида
г — I
где F и G— произвольные функции. Используя этот факт, найти явное решение задачи о взаимодействии центрированных волн разрежения (см. § 16).
11. Закрытая с двух концов труба длины L заполнена покоящимся политроп-иым газом с 7 = 3. В момент времени t = 0 один конец открывается и через него начинается истечение в вакуум. Найти распределение основных величин в трубе для всех t > 0.
12. Ударная волна падает на контактный разрыв, разделяющий два состояния покоя одного и того же политропного газа. Найти условия, при которых контактный разрыв исчезнет в результате взаимодействия.
13. Поршень, вдвигающийся с постоянной скоростью в покоящийся политроп-ный газ, внезапно останавливается. Показать, что давление на поршне положительно (т. е. что газ не отрывается от поршия).
14. Доказать, что в политроппом газе после встречи ударных волн, идущих навстречу друг другу, всегда образуются две ударные волны.
15. Показать, что при столкновении одинаковых политропных газов с параметрами со, То, двигавшихся навстречу со скоростью qo каждый, образуется область с температурой
![]()
где
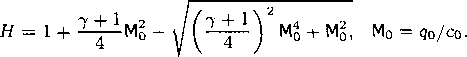
16. Построить графики распределения (функции от х) основных величин (и, р, р. S) для некоторого момента времени t > 0 при распаде произвольного разрыва (10 конфигураций).
17. Вывести формулы для решения задачи о распаде произвольного разрыва в акустическом приближении.
18. Проинтегрировать дифференциальное уравнение траекторий dx/dt = и в центрированной простой волне при одномерном движении политропного газа с плоскими волнами.
19. При условиях предыдущей задачи проиитегрировать дифференциальное уравнение характеристик ненрямолинейного семейства.
20. Показать, чго при определении результата преломления ударной волны на контактном разрыве (см.§ 18) в случае, когда по обе с тороны разрыва находя гея политропные газы с одинаковым показателем адиабаты, будет р, > рз, если рг > pi ир«< рз, если р2 < pi.
21. Вывести формулу для отношения плотностей рз/Pi при отражении ударной волны от жесткой стенки в случае политропного газа (см. § 18). Показать, что предельное значение этого отношения ири Р2/Р1 —+ оо таково:
lim?3 = 7(l±i)
Pi (?- I)2
22. Найти и проанализировать точное решение системы (20.2) при /3 = -1,
23. Показать, что точное решение (20.18) совместимо с условиями на автомодельной ударной волне (20.24) в том смысле, что оио может описывать движение по обе стороны от разрыва.
24. Бесконечная труба с площадью сечения F заполнена покоящимся полит-ропным газом с известными параметрами и разделена па две части невесомым поршнем. Найти силу, которую надо приложить к поршню для того, чтобы мгновенно привести его в движение с заданной скоростью U.
25. Построить решение задачи о сильном сферическом взрыве в газе с показателем адиабаты 7 = 7.
26. Дать анализ решения задачи о сильном взрыве для одномерного движения с плоскими волнами.
27. Показать, что решение задачи о поршне в случае одномерного движения с плоскими волнами, описанное в §21, совпадает с решением, полученным в § 18.
