Лекции по основам газовой динамики
Лекции по основам газовой динамики. — Москва-Ижсвск: Институт компьютерных исследований, 2003, 336 стр.
Книга предназначается для ознакомления с математическими основами теоретической газовой динамики. Излагаются принципы построения разнообразных газодинамических моделей — от интегральных законов сохранения до конкретных формул, описывающих то или иное движение газа. Даются теоретико-групповые основы вывода дифференциальных уравнений, описывающих классы частных решений. Методами качественного анализа разбирается решение многих конкретных задач. Для облегчения восприятия материала текст снабжен графическими иллюстрациями.
Книга предназначена для студентов математиков и механиков, аспирантов и преподавателей, научных работников в области "4inniimtiv ''г,яп
ISBN 5-93972-201-6
© Л. В. Овсянников, 2003 © Институт компьютерных исследований, 2003
Нормальные характеристические векторы; гиперболичность (51). Условия на характеристиках (54). Задача Коши (55). Слабый разрыв (55). Характеристики уравнений газовой динамики (57). Классификация характеристик (59). Бихарактеристики (60). Характеристический коноид (61). Характеристическая форма уравнений газовой динамики (62).
§ 7. Краевые задачи............................... 63
Задача Коши (63). Теорема об оценке решения (65). Единственность решения задачи Коши (68). Обобщения задачи Коши (69). Задача о поршне (70). Задача обтекания (71). Задача со свободными границами (71). Задача Гурса (72). Задачи с особенностями (73).
Исходные уравнения (90). Линии тока (91). Интеграл Бернулли (91). Максимальная и критическая скорости (93). До- и сверхзвуковые течения (93). Характеристики (94). Трубки тока (96). Ударные волны (98). Преобразование Мунка - Прима (100).
Основные уравнения и их характеристики (133). Лемма о плотности (135). Теорема единственности (135). Времени и пространству подобные направления (137). Слабые разрывы (138). Транспортные уравнения (139). Задача о распаде слабого разрыва (141). Уравнения в ла-гранжевых координатах (142). Класс точных решений (144).
§ 16. Изэнтропические движения с плоскими волнами............146
Исходные уравнения (146). Инварианты Римана (147). Простые волны (149). Теорема о примыкании (151). Центрированные простые волны (152). Задача об истечении газа в вакуум (154). Волны сжатия и разрежения (155). Градиентная катастрофа (157). Плоскость инвариантов Римана (160). Взаимодействие центрированных волн (163). Метод Римана (165).
§17. Распад произвольного разрыва......................166
Постановка задачи (167). Направление обращения волн (168). Метод («,р)-диаграмм (168). Существование и единственность автомодельного решения (172). Акустическое приближение (177).
§ 18. Семь задач .................................177
Работа ударной трубы (177). Задача о поршне (179). Отражение ударной волны от жесткой стенки (181). Преломление ударной волны (183). Взаимодействие ударных волн (184). Взаимодействие ударной и простой волн (187). Акустическое приближение (188). Задача о безударном сжатии (189).
Постановка задачи о поршне (205). Структура плоскости (U, Z) (207). Давление на поршень (208). Постановка задачи о сильном взрыве (209).
Ин теграл Седова (210). Анализ решения (211). Расчет движения фронта (213).
Плоскопараллельные и осеснмметричные течения (218). Линии тока (219). Функция тока (220). Изэнтропичность безвихревых течений (222). Основные уравнения (225). Потенциал скоростей (226). Метод годографа (227). Простые волны осесимметричных течений (228). Уравнения на плоскости годографа (229). Уравнения С. А. Чаплыгина (231). Групповое свойство (234). Течение Прандтля - Мейера (235). Обтекание выпуклого угла (237). Течения Буземаиа (238).
§23. Дозвуковые течения............................241
Задачи о струях (242). Истечение симметричной струи (244). Струйное обтекание клипа (248). Свободные струи (250). Задачи обтекания (252). Циркуляция (253). Аналог теоремы Жуковского (254). Некоторые качественные результаты (257).
§ 24. Характеристики и простые волны ....................258
Исходные уравнения. (258). Характеристики (259). Транспортные уравнения (262). Качественные свойства (264). Простые волны (266). Волны сжатия и разрежения (269). Плоскость инвариантов Римаиа (272). Задача об истечении струн (273).
§ 25. Косые скачки уплотнения.........................275
Ударная поляра (276). Аналитическое представление (277). Обтекание вогнутого угла (280). Отражение косого скачка от стенки (282). Осесимметричное обтекание конуса (285).
§ 26. Околозвуковые течения..........................287
Звуковая линия (287). Теорема А. А. Никольского и Г’. И. Таганова (288). Примыкание простой волны (289). Местная сверхзвуковая зона (290). Окрестность центра течения (291). Трехлистность годографа (295). Замечание о моделировании (297). Прямая звуковая линия (298). Сопло Лаваля (302). Истечение сверхзвуковой струи (304).
Предисловие ко второму изданию
Необходимость в переиздании этого учебника возникла по ряду причин. За 20 лет его использования в преподавании основ газовой динамики в университетах он стал библиографической редкостью даже в библиотеках. У специалистов в этой области знания возникли замечания о его недостатках, связанных с некоторыми неточностями в формулировках, пояснениях, формулах и выкладках. Наконец, за это время в научном сообществе существенно вырос объем понимания разнообразных нелинейных газодинамических процессов благодаря систематическому учету влияния свойства симметрии уравнений газовой динамики (УГД) на построение точных решений этих уравнений.
Последние 10-15 лет коллективно разрабатывалась научно-исследовательская программа «Подмодели газовой динамики» по использованию симметрии (группового свойства) УГД [13]. Главной целью этой программы является исчерпывающее описание классов точных решений УГД в виде инвариантных и частично инвариантных подмоделей. Для этого были разработаны аналитические алгоритмы отыскания наиболее широкой допускаемой УГД локальной группы Ли G преобразований базового пространства, групповой классификации УГД по входящим в них произвольным функциям и параметрам, построения нормализованных оптимальных систем 0G подгрупп конечномерной группы Ли G, использования аппарата алгебр Ли операторов. В частности, с уравнением состояния газа общего вида УГД допускает 11-мерную группу G11, для политропного газа — группу G13, а в случае показателя адиабаты 7 = 5/3 — группу С14. Вычисленные для них нормализванные оптимальные системы подгрупп состоят из 223 представителей в 0G11, 1342 в QG13 и 1826 в 0(7 . Каждая подгруппа Н допускаемой группы порождает класс Н-решений, описываемый упрощенной системой дифференциальных уравнений — факторсистемой УГД по группе Я. Для возникающих массивов Я-решений введен ряд классификационных признаков, позволяющих описать подмножества Н-решений в более компактной форме. Найдены существенно новые, подчас обладающие неожиданными свойствами, Н-решения, ранее не упоминавшиеся в классической литературе. Несомненна необходимость хотя бы беглого ознакомления с этими достижениями всех, кому нужны и полезны сведения о симметрии УГД и ее использовании — читателям, слушателям курса лекций,
преподавателям и студентам, практикам-вычислителям, научным работникам. В первом издании сведения о симметрии УГД и ее использовании содержались в § 8, 12 и в Приложении, но сообщались там лишь выборочно.
В предлагаемом издании подвергнуты переработке разделы, относящиеся к понятию гиперболичности возникающих систем дифферециальных уравнений, интегральным законам сохранения для автомодельных движений, описанию примеров осесимметричных и околозвуковых течений газа. В § 18 добавлена задача о безударном сжатии. Заново написаны § 8, где дано общее представление о свойстве симметрии УГД и принцип его использования для построения классов точных решений (подмоделей) и § 12, где приведен полный список всех инвариантных подмоделей с тремя независимыми переменными (ранга 3), получившими свои названия, а также примеры подмоделей рангов 2, 1,0.
Полностью изменено добавленное к основному тексту Приложение, которое теперь содержит краткое описание понятий и алгоритмов, связанных с использованием алгебр Ли дифференциальных операторов. Здесь также приведена нормализованная оптимальная система подалгебр (223 представителя) всех размерностей 11-мерной алгебры Ли, допускаемой УГД в случае уравнения состояния газа общего вида.
Немного расширен список рекомендуемой литературы. Ввиду временного отсутствия единой монографии по симметрии УГД и ее использованию даны ссылки на несколько основополагающих журнальных статей.
Автор благодарит д.ф.-м.н. В. М. Тешукова, д.ф.-м.н. Л. II. Чупахина и к.ф.'М.н. С. В. Головина за содействие и ценные замечания, послужившие улучшению текста, а также инж. Э. 3. Боровскую за помощь при подготовке рукописи к печати.
Современная газовая динамика представляет собой обширную физико-математическую дисциплину, занимающую прочное место в фундаменте системы знаний о поведении сплошных легкоподвижных сред. Ее объектами являются не только непосредственно наблюдаемые газообразные и жидкие тела, но и твердые при обычных условиях материалы, если оеш находятся под воздействием больших температур и давлений. Собственно газовая динамика выделяет и изучает свойство сжимаемости среды. Вместе с тем в реальных условиях проявление сжимаемости сопровождается другими, во многих случаях не менее важными эффектами, такими как вязкость, теплопроводность, способность к химическим реакциям и т. д. Однако если изменение состояния среды происходит достаточно быстро, за времена много меньшие характерных времен протекания диссипативных процессов, то свойство сжимаемости оказывается определяющим и может быть выделено и изучено независимо. Поэтому газовую динамику следует рассматривать как науку, изучающую быстропротекающие процессы в сжимаемых средах.
Область практических приложений результатов и выводов газовой динамики весьма широка. Она охватывает процессы и явления, происходящие при движении в газе (воздухе) летательных аппаратов, снарядов и ракет, при истечении газовых струй, при протекании газа через газовые турбины и компрессоры, при взрыве и детонации взрывчатых веществ, при распространении ударных волн и их воздействии на препятствия, при формировании кумулятивных струй, при волновых движениях на поверхности водоемов, при формировании погоды в атмосфере Земли и т.д.
Как и во всякой физико-математической дисциплине, в газовой динамике выделяются экспериментальное и теоретическое направления. Опираясь на результаты экспериментов но прямому наблюдению и регистрации параметров газодинамических процессов, теоретическая газовая динамика имеет своей основной целью предсказание хода явления путем анализа его математической модели и применения подходящего расчетного метода. Необходимость в охвате широкого круга газодинамических явлений привела к тому, что теоретическая газовая динамика образовала самостоятельную научную область со своей разветвленной системой понятий, с оригинальными методами исследования и конструкциями решений классов конкретных задач. Богатство теоретической газовой динамики заключено в большом
количестве различных математических моделей и подмоделей, в разнообразии применяемых математических методов, в многочисленных до конца решенных задачах, в ценности ее выводов для практических приложений.
Исторически становление теоретической газовой динамики послужило не только пониманию и описанию общей структуры происходящих в сжимаемых средах физических процессов. Газовая динамика оказала также заметное влияние на развитие математики, главным образом ее части, связанной с теорией дифференциальных уравнений. Она вдохнула жизнь в целые математические направления — теорию разрывных решений дифференциальных уравнений, теорию уравнений смешанного типа, теорию квазиконформных отображений. Она стимулировала развитие теории сингулярных интегральных уравнений, группового анализа дифференциальных уравнений, функционально-аналитических и топологических методов исследования краевых задач. Она обогатила математику рядом важных понятий, таких как вырождение типа дифференциальных уравнений, сильный и слабый разрывы в решениях, градиентная катастрофа, сильная и слабая нелинейности, инвариантное и частично инвариантное решения, автомодельное решение и т. п.
Основоположниками теоретической газовой динамики следует считать немецкого математика Б. Римана (1826 1866), впервые давшего теорию явления образования и распространения сильного разрыва в решениях дифференциальных уравнений газовой динамики, и замечательного русского учепого-механика С. А. Чаплыгина (1869-1942), разработавшего носящий ныне его имя метод исследования установившихся течений газа. Важные экспериментальные данные по эффектам сжимаемости при течении газа, послужившие основой для последующих теоретических обобщений, были получены еще в XIX веке многими исследователями, в частности, французскими учеными-инженерами Сен-Венаном, Гюгонио и Жу-ге, русским ученым-артиллеристом Н. В. Маиевским, австрийским физиком Э. Махом. Развитие теоретической газовой динамики в текущем столетии связано с целым рядом имен выдающихся ученых, математиков и механиков, таких как Л. Прапдтль, Т. Карман, А. Буземан, Г. Гудерлей, К. Фридрихе, М. А. Лаврентьев, Л. И. Седов, С. А. Хрисгианович, М. В. Келдыш, А. А. Дородницын, Ф.И.Франкль и многих других, внесших признанный вклад в методологию исследования и конструктивные подходы к решению актуальных газодинамических задач.
Принципиальной особенностью газодинамических процессов, создающей значительные трудности для теоретического исследования, является их нелинейность, проявляющаяся в весьма разнообразных и иногда неожиданных формах. Отсюда и идет многообразие методов анализа и конкретных закономерностей, которые не укладываются в какую-либо одну стандартную схему. В теоретической газовой динамике особенно остро стоят проблемы адекватности модели явлению. Для большинства практически важных газодинамических задач до сих пор нет теорем существования, единственности и устойчивости решения. Поэтому и численные методы, получившие теперь с развитием быстродействующих ЭВМ новые возможности их применения, во многих конкретных случаях оказываются не обеспеченными надлежащим обоснованием и часто связаны с затратой больших усилий и средств при их разработке и реализации.
Все это вместе — многообразие явлений, фактов и методов, и трудности анализа — привело к тому, что в газовой динамике сложился целый ряд самостоятельных направлений со своими школами, литературой и преемственностью. Несомненно, что это обстоятельство накладывает определенный отпечаток и на преподавание газовой динамики в различных университетах. Здесь явно ощущается отсутствие достаточно простого и вместе с тем единого учебного пособия, опираясь на которое можно было бы развивать и надстраивать дальнейшие этажи стройного здания газовой динамики.
В настоящих лекциях делается попытка восполнения этого пробела. Лекции посвящены систематическому изложению основных математических моделей, конструкций и методов исследования, служащих для теоретического анализа газодинамических явлений. Как учебное пособие, они составляют содержание обязательного или специального годового курса лекций, который вместе с упражнениями должен быть изложен за 60-70 учебных часов. Это жесткое требование наложило отпечаток и на отбор материала, и на способ изложения.
В первую очередь, это выразилось в том, что предпочтение было отдано точным математическим результатам, которые возможно получить в рамках строго сформулированной математической модели газовой динамики. Приближенные методы, как правило, лишь намечены, и потому для обоснования получаемых выводов экспериментальный материал не привлекался. При прочих равных условиях, за основу взята дедуктивная манера изложения, позволяющая не только избежать многих повторов, но и выдвинуть на первое месш предмет исследования при смещении его методов на второй план. Отбор фактически излагаемого материала опирался на принцип фундаментальной универсальности, согласно которому от каждого рассматриваемого факта требуется, чтобы он содержал новый элемент знания с достаточно широкой областью применения.
О предметном содержании настоящих лекций можно судить по оглавлению книги. Почти весь преподносимый материал можно найти в ряде известных учебников и монографий, приведенных в списке литературы. Нетрадиционными являются, пожалуй, лишь фрагменты, касающиеся тео-ретико-группового подхода к точному моделированию и построению классов частных решений. В связи с этим уместно заметить, что в настоящее время совершенно ясна необходимость включения элементов группового анализа в преподавание прикладных дисциплин. Польза этого заключается не столько в возможности продемонстрировать тсоретико-грушювой метод исследования на конкретном материале (хотя и это довольно важно), сколько в выработке у изучающего острого ощущения ценности свойства инвариантности рассматриваемых объектов при предельно возможной рационализации их изучения. При этом существенно подчеркнуть, что всякое упрощающее моделирование бывает полезно именно в силу того, что оно придает объекту дополнительную инвариантность и тем самым позволяет исследовать его более простыми средствами. Что же касается основной массы фрагментов, то данный в лекциях их перечень, конечно, не исчерпывает всего богатства фактов газовой дииамики. Очевидно, однако, что удовлетворить все претензии по этому поводу в указанных выше рамках лекционного курса невозможно; тем не менее автор выражает готовность прислушаться к любым рекомендациям этого рода.
При использовании настоящих лекций как основы для фактического чтения лекционного курса можно ориентироваться на то, что материал каждого парафафа приблизительно соответствует содержанию одной-двух лекций. Отклонения возможны как за счет более детального и, значит, более длительного изложения отдельных вопросов, так и за счет сокращения некоторых элементов, которые могут быть уже известны аудитории. Этой схеме автор следовал как лектор в течение ряда лет в Новосибирском университете, где обязательный для специальности «прикладная математика» годовой курс газовой динамики предваряется небольшим (полугодовым) общим введением в механику сплошных сред. Конечно, подобная пропедевтика не обязательна, так как настоящие лекции содержат все необходимое для независимого изучения основ теоретической газовой динамики.
От изучающего газовую динамику в рамках настоящих лекций требуется определенная общая математическая культура и навыки в математическом анализе, развиваемые на первых двух курсах механико-математических и физических факультетов. Все специфические для газовой динамики понятия, термины и обозначения разъяснены непосредственно в тексте. Небольшое количество упражнений и задач, приведенных в конце глав, имеет целью проверку усвоения материала и возможностей самостоятельного решения изучающим частных вопросов, органически примыкающих к основному тексту.
При подготовке настоящих лекций к изданию существенную помощь автору оказали сотрудники кафедры гидродинамики НГУ В.М.Тешуков и В. М. Меньшиков, читающие курс лекций по газовой динамике в течение нескольких последних лет. Они внимательно просмотрели весь текст и приняли конструктивное участие в отшлифовке отдельных мест, а также в отборе упражнений и задач. Значительную работу по оформлению рукописи выполнила Э. 3. Боровская. Всем упомянутым товарищам автор выражает свою искреннюю благодарность.
| t |
время |
| X |
— радиус-вектор |
|
х, у, г | — координаты вектора х |
| и | — вектор скорости |
| и, V, W | — координаты вектора и |
|
Q = 1ч| | — модуль скорости |
| V |
— давление |
|
Р | — плотность |
| V = 1 /р |
— удельный объем |
|
S | энтропия |
| ? | - удельная внутренняя энергия |
|
i | — удельная энтальпия |
| с | — скорость звука |
| М | — число Маха |
| VF |
— градиент функции F |
| diva | -- дивергенция вектора а |
| det-А |
- определитель матрицы А |
Векторы выделяются полужирным шрифтом. Символ а • b обозначает скалярное произведение векторов а и Ь. Символ Rn для любого п = = 1, 2, 3,... обозначает n-мерное евклидово аффинное векторное пространство. Символ Rn(а) обозначает пространство Rn с общим вектором а. Координатное представление вектора а в ортогональном базисе записывается равенством а = (а1, .... ап); в этом случае вместо Rn(a) пишется также Я" (а1, .... а”). Конец доказательства обозначается знаком. ¦
Внутри каждого параграфа исиользуется независимая нумерация формул, определений, теорем, рисунков и т. д. При ссылках на формулы, определения и г. д. из другого параграфа впереди номера формулы добавляется номер этого параграфа. Например, ссылки «теорема 4.5», «уравнение (11.14)» или «рис. 17.10» отсылают к теореме 5 из §4, уравнению (14) из § 11 или рис. 10 из § 17. Ссылки на литературу даются в квадратных скобках.
Математическая модель газовой динамики
Согласно общим физическим представлениям всякий ограниченный объем газа и состоит из конечного числа движущихся молекул (г --
- 1,2,..., N). Каждая молекула имеет массу 1щ, вектор скорости иг, импульс (количество движения) т^пг, кинетическую энергию (l/2)mi|uj|2 и внутреннюю энергию Ei. При неизменности массы каждой молекулы ее импульс и энергия изменяются в результате столкновений (соударений) с другими молекулами, что придает движению молекул в ансамбле и) свойство некоторой хаотичности.
Основной задачей газовой динамики является изучение движения газа как целого и его взаимодействия с другими физическими телами.
«Лобовой» способ математического описания этого движения и взаимодействия, состоящий в использовании дифференциальных уравнений движения всех молекул, неприемлем не только из-за очень большого их числа (в 1 см3 воздуха при нормальных условиях содержится 2, 7 • 1019 молекул), но также ввиду невозможности указать точные начальные данные. Поэтому в газовой динамике используется оередненное описание движения и взаимодействия. При таком подходе наиболее изученными являются две математические модели - газокинетическая и феноменологическая.
В кинетической теории газов используется модель, основанная на статистическом (вероятностном) описании поведения совокупности молекул. Основную роль в этой модели играет уравнение Больцмана для функции распределения молекул по их положениям в пространстве и по скоростям. Газокинетическая модель существенна и уснешно применяется для описания поведения сильно разреженных газов.
В механике сплошных сред используется феноменологическая модель, связанная с представлением о средних величинах, непрерывно распределенных по занимаемому газом объему, а законы изменения средних величин устанавливаются на основе дополнительных предположений, согласующихся с общими физическими законами. Эта модель всесторонне апробирована практикой и приемлема для описания поведения достаточно плотных газов. Она и принимается за основу в настоящих лекциях.
Процедура формирования средних величин такова. Основными физико-математическими характеристиками совокупности молекул в объеме и> являются масса газа
N
т — т,.
1=1
импульс (количество движения)
N
К = ]Г тг\1г
г — 1
и полная энергия
'ср ~ jTTj y2m^Ui ~ Ucp^ ?i) '
Отсюда масса, импульс и полная энергия газа в объеме и выражаются через средние величины по формулам
т = |о>|рСр- К = Мрсриср,
Г . | (\ | ,9 \ (*)
1 +?ср)-
Феноменологическая теория отождествляет любой достаточно малый (но все еще содержащий достаточно большое число молекул) физический объем газа и; с «материальной точкой», постулируя, что при стягивании к точке объема и) введенные средние величины имеют конечный предел и тем самым порождают сплошные распределения плотности, вектора скорости и внутренней энергии. Получаемые распределения и являются предметом изучения в математической модели газа как сплошной среды. Эта модель основана па том, что в пределе формулы (*) для любого конечного объема и дают выражения основных физико-математических характеристик в виде интегралов по объему ш от указанных средних величин.
Целью первой главы является установление и общий предварительный анализ основных законов, управляющих упомянутыми распределениями.
§ 1. Интегральные законы сохранения
Движение газа происходит в трехмерном пространстве К3(х) точек (векторов) х, причем состояние движения в точке х зависит от времени t. Поэтому пространством событий газовой динамики является четырехмерное пространство Л4(х, t).
Основные величины. Основными величинами, описывающими движение газа, являются
вектор скорости u - и(х, t),
плотность р = р(х, t),
давление р = р(х, f),
удельная внутренняя энергия г =- s(x. ?).
Величина u(x, t) есть скорость частицы газа, занимающей положение х е Я3 в момент времени t. С другой стороны, само положение х частицы зависит от времеии и скорость его изменения равна производной dx/di. Поэтому описание движения частиц газа дается дифференциальным уравнением
dx/dt = u(x,t). (1)
В координатной форме, когда в одной и той же декартовой системе координат х = (х, у, z) и и =• (и, V, ш), уравнение (1) может быть записано в виде системы обыкновенных дифференциальных уравнений
dx/dt = и(х, у, г, t.), dy/dt = v(x, у, z, t). dz/dt = w(x, y, z, t).
Если векторное поле u задано в некоторой области Пс Д4, непрерывно в П и удовлетворяет условию Липшица по х, то область Q однократно покрыта семейством интегральных кривых уравнения (1). Эти кривые являются, таким образом, «мировыми линиями» частиц газа в пространстве событий Их проекции на пространство /?3(х) называются тра
екториями частиц. Следует иметь в виду, что термин «траектории» часто употребляется и для самих мировых линий частиц, что обычно не приводит к недоразумениям.
Каждая интегральная кривая однозначно определена условием прохождения через заданную точку Хо С О. в момент времени t = 0, т. е. начальным условием х(0) = хо. Поэтому решение уравнения (1) зависит от начального значения хо и должно записываться в виде
Это описание позволяет дать абстрактное определение понятия «частица газа»: этим термином называется точка х е Я3, зависящая от времени t по формуле (2) при фиксированном хо. При этом (2) истолковывается как уравнение движения частицы но ее траектории. Значения хо отличают одну частицу от другой и являются, таким образом, лагранжевыми координатами.
Движущийся объем. Область u)(t) С Я3, состоящая при всех t из одних и тех же частиц, называется движущимся объемом (иногда говорят — материальным объемом).
Абстрактное понятие частицы газа является математическим эквивалентом представления о том достаточно малом физическом объеме газа, с помощью которого еще можно сформировать средние значения скорости, плотности и т.д. Движущийся объем есть конечный объем, содержащий в процессе движения все время одну и ту же порцию газа.
В феноменологической теории каждый движущийся объем рассматривается как единое физическое тело, снабженное следующими физико-механическими характеристиками:
![]()
At)
импульс
![]()
Ul(t)
энергия
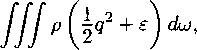
АП
где q = |u| есть длина (модуль) вектора скорости. Импульс называется также количеством движения объема u>(t). Под энергией здесь понимается полная энергия, равная сумме кинетической и внутренней энергий.
Законы сохранения массы, импульса и энергии. В основу вывода уравнений, определяющих законы изменения этих характеристик, можно положить следующий принцип отвердевания: изменение массы, импульса и энергии любого движущегося объема uj(t) в каждый данный момент времени происходит (за счет воздействия извне) так же, как для твердого тела, занимающего объем uj(t) и имеющего те же самые физико-механические характеристики. Приняв этот принцип, можно написать законы изменения массы, импульса и энергии в следующей форме.
Масса неизменна, т. е. производная по t от массы движущегося объема равна нулю:
![]()
¦At)
Импульс меняется за счет приложенных сил; его производная по t равна сумме (главному вектору) F всех сил, приложенных к объему u>(t):
![]()
u(t)
Энергия меняется за счет работы внешних сил и дополнительного притока энергии; ее производная по t равна мощности W, развиваемой действующими силами, плюс скорость притока дополнительной энергии Q:
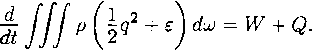
w(t)
В настоящих лекциях будет рассматриваться модель невязкого нетеплопроводного газа, движущегося в отсутствие внешних силовых полей и внешних источников энергии. В этой модели силами, действующими на объем uj{t), будут только поверхностные силы давления, направленные по нормали к поверхности этого объема. Следовательно, если 7 (t) — поверхность и п — единичный вектор внешней нормали к 7(t), то принимается, что
![]()
¦y(t)
Кроме того, в этой модели Q = 0, a W есть мощность, развиваемая силами давления — рп на 7, т. е.
где точка обозначает скалярное произведение в R3.
![]()
lit)
Итак, исходные интегральные законы сохранения массы, импульса и энергии в рассматриваемой модели имеют вид
pdu> = О,
Ш
w(t)
— (3)
u(t) 7 (J)
u>(t) l(t)
Необходимо помнить, что уравнения (3) должны выполняться для любого движущегося объема u>(t) (с достаточно гладкой границей 7(t)) и в любой момент времени t.
Балансовые уравнения. Возможен и другой подход к получению исходных интегральных законов сохранения, когда рассматривается изменение во времени массы, импульса и энергии в фиксированном (не зависящем от времени) объеме ш. В этом случае необходимо оперировать со скоростями притока основных физических количеств в данный объем. Тогда основные законы изменения массы, импульса и энергии принимают вид уравнений баланса этих количеств.
Скорость изменения массы в объеме и равна скорости потока массы через его границу 7:
//
ри • n dj.
Скорость изменения импульса в объеме ы равна действующей силе плюс скорость потока импульса через границу 7:
//
(рп -г pu(u ¦ n))d7.
Скорость изменения энергии в объеме ы равна мощности действующих сил плюс скорость потока энергии через границу 7:
-//(
Р + Р ( \ч2 +? ) ) u - n flh
Это даст интегральные законы сохранения в виде следующих балансовых уравнений:
& IIIPn<liJ = ~ II^РП ^ PU^U dl' (4)
и> 7
« III " + -") ^ “// (!> + Р (|«2 +
w 7
Введенное здесь обозначение оператора дифференцирования d/dt (вместо d/dt) подчеркивает, что ввиду независимости л от 1. этот оператор может быть внесен под знак интеграла именно как оператор частной производной по t.
Очевидно, что обе системы законов сохранения (3) и (4) равносильны, так как они выражают одни и те же физические законы. Этот факт легко проверяется и путем вычислений, показывающих, что каждая из систем (3) и (4) равносильна одной и той же системе дифференциальных уравнений на гладких решениях и одной и той же системе соотношений на сильных разрывах. Система (4) удобна и часто используется на практике, например при анализе стационарных движений, когда левые части в равенствах (4) обращаются в нуль.
Из основных физических законов в систему (3) не вошел явно закон сохранения момента импульса, имеющий вид
dt- Ilf P^U Х ^^ = ~ II Х Х^7' ^
'-'(О 7 Ш
Оказывается, однако, что соотношение (5) не является независимым и есть следствие первых двух законов сохранения (3). Проверка этого факта, которая должна быть выполнена отдельно для гладких и для разрывных движений, предоставляется читателю.
Система (3) содержит всего пять скалярных законов сохранения и связывает шесть искомых основных величин (три компоненты вектора скорости, плотность, давление и внутреннюю энергию). Следовательно, эта система уравнений является недоопределенной. Для ее пополнения требуется привлечение термодинамических свойств газа, обсуждаемых в следующем параграфе.
§ 2. Термодинамические свойства
При термодинамическом рассмотрении статистически равновесных процессов в газах, наряду с введенными выше параметрами состояния p. р, s, используются еще два основных параметра состояния: абсолютная температура Т и удельная (отнесенная к единице массы) энтропия S. В дальнейшем предполагается, что газ как термодинамическая система является двухпараметрической средой. Это означает, что его состояние вполне определяется заданием каких-либо двух параметров. Следовательно, упомянутые пять параметров должны быть связаны тремя соотношениями.
Первый закон термодинамики. Фундаментальное свойство эквивалентности тепловой и механической энергии выражается в виде первого закона термодинамики:
где V — 1/р — удельный объем (объем единицы массы газа). Левая часть равенства (1) равна количеству тепла, сообщаемому единице массы, а правая — приращению внутренней энергии плюс работа расширения этой порции газа. На самом деле, для двухнараметрических сред соотношение (I) является определением энтропии S.
Если рассматривать внутреннюю энергию как функцию удельного объема и энтропии, т. е. положить е = E(V, S), то (1) эквивалентно двум соотношениям:
р = -Ev(V, S), T = Es(V,S). (2)
Следовательно, задание функции E(V, S) полностью описывает всю термодинамику двухпараметрической среды. Однако на практике такое задание не всегда удобно и термодинамические свойства газа описываются другими соотношениями, рассматриваемыми ниже.
Идеальный газ. Газ называется идеальным (иногда говорят — совершенным), если выполнено уравнение Клапейрона, вытекающее из фундаментальных законов Бойля-Мариотта и Гей-Люссака:
где R — газовая постоянная, определяемая химическим (молекулярным) составом газа.
Внутренняя энергия идеального газа зависит только от температуры Т. Действительно, если предположить, что е = §(V', Т) и S = S(V,T), то из (1) получатся два соотношения, которые в силу (3) имеют вид
Исключение энтропии S перекрестным дифференцированием приводит к соотношению 8у = 0, т. с. ? = §(Т). Если функция 8(Т) известна, то интегрирование предыдущих уравнений даст выражение (с точностью до произвольного постоянного слагаемого)
S = R\nV - J S'(T)d\nT. (4)
Следовательно, описание термодинамики идеального газа сводится к заданию функции ? = §{Т).
Политропный газ. Величина су = &р называется удельной теплоемкостью газа при постоянном объеме. Очевидно, что для идеального газа су зависит только от Т. Особенно важен частный случай, когда су — const.
Определение 1. Идеальный газ называется политропным, если функция $ линейна по Т, т. е. 8 — суТ(су = const).
Для политропного газа формула (4) даст
S — R In V + су In7’ г So {Sq = const),
откуда
и из (3) получается соотношение
p = A(S)p\ (5)
где
Безразмерная константа у является важной характеристикой политропного газа и называется показателем адиабаты (или показателем политропы). Так как R > 0 и су > 0, то всегда -> > 1. Для внутренней энергии ? политропного газа из предыдущих соотношений получается выражение
Модель политропного газа благодаря ее сравнительной аналитической простоте и подтвержденному опытом хорошему приближению к действительности получила широкое распространение в прикладных исследовани
ях.
Нормальный газ. Оказывается, что качественное исследование фундаментальных закономерностей в газовой динамике может быть выполнено без окончательной конкретизации основных уравнений состояния газа при условии, что участвующие в этих уравнениях функции удовлетворяют некоторым естественным требованиям. Такая обобщенная трактовка была впервые предложена Вейлем и затем повторялась в ряде монографий (см. [4, 61). Формулируемое ниже определение понятия «нормального» газа несколько отличается от упомянутого прототипа в сторону сужения класса сред, но зато дает возможность описать более широкий класс процессов без каких-либо дополнительных предположений.
Уравнениями состояния называются зависимости
р = f(p, S) = g{V, S), с = е(К р) - E(V, S) , (7)
где V -- 1 /р, удовлетворяющие уравнению (1).
Определение 2. Газ называется нормальным, если функции (7) обладают следующими свойствами 1° и 2°.
1°. Функция / определена, трижды непрерывно дифференцируема в области {0 < р < оо, St < S < S*} (может быть 5, -- —оо. S* = -гоо), всюду в этой области удовлетворяет неравенствам
V~*0 V —*oc
Легко проверяется, что политропный газ является нормальным. Свойства функции д в области {0 < V < ос, S, < S < S*} аналогичны свойствам функции / с очевидными изменениями, вытекающими из того что V = 1 /р. Дифференцирование тождества f{l/V, S) = g(V. S) по V и S дает соотношения в силу которых из (8) следуют неравенства
(а) д > 0 , (b) 3V < 0 , (с) gvv > 0 , (d) gs> 0 . (12)
Видно, что неравенство (8,с) сильнее, чем (12,с). Условия (12) определяют «газ Вейля». Данное выше определение 2 несколько сужает класс рассматриваемых сред, но зато расширяет совокупность закономерностей, которые, будучи справедливы для политропного газа, распространяются также и на нормальный газ. В частности, это относится к свойству взаимно однозначного соответствия между плотностью р и скоростью звука с (см. ниже определение 3), которое для «газа Вейля», вообще говоря, не имеет места.
Из соотношений (2) для нормального газа вытекает ряд важных свойств, которые указаны ниже.
Лемма 1. В нормальном газе функция f(p,S) при любом фиксированном S ? (S*,S*) и функция e(V,p) обладают следующими свойствами:
(a) / -> 0, fp 0 при р —» 0;
(b) интеграл I ---ар конечен;
о
(c) ер > 0, 2e,v + р > 0.
Доказательство. Первая формула (2) равносильна интегральному равенству (зависимость от S явно не указана, т. к. S = const)
E{V) — E(Vi) ~ Jg{V') dV' . (*)
к
Из него, в силу второго условия (11), при V\ —¦ ос следует сходимость
ОС
интеграла Jg(V') dV', что влечет свойство g(V) 0 при V ос,
равносильное первому (а). Ввиду монотонного убывания g с ростом V из (*) при V\ > V получается неравенство E(V) — E(Vi) > (Vi — V)g(Vi). Если в нем положить Vi = 2V и перейти к пределу при V —> оо, то
получится также, что Vg(V)—¦ 0 при V —¦ оо. Далее, интегрирование по частям в (*) дает равенство
Vi
E(V) - E(Vi) = VlS(Vl) - Kg(V) - jgv(V')V' dV’ . (**)
V
Так как | gy\ убывает с ростом V, то отсюда при V\ > V получает-
ся неравенство E(V) - E(Vi) > Vig[V{) - Vg(V) + ±(Vf - V2)gv{V{).
Снова положение V\ = 2V и переход в полученном неравенстве к пределу при V —у оо с учетом предыдущего приводит к свойству V2gy —> О при V —¦ оо, равносильному второму свойству (а). Кроме того, переход к пределу в (**) при Vj —> ос дает равенство
ОС
E(V) + Vg(V) = - Igv(V')V' dV (13)
с конечным несобственным интегралом в правой части, который равен интегралу (Ь). Первое неравенство (с) следует из соотношения epgs = Т и (12,d). Далее, дифференцирование равенства e{V, g{V)) — E(V) дает соотношение еу + ерду = ~Р, из которого, в силу (10,Ь) следует неравенство еу+р > р~1(ду)е. Наконец, функция G(V) = 2дуЕ + д2 —» 0 при
V —> эо и Су = 2дууЕ > 0. Значит всюду G(V) < 0, что равносильно неравенству 2|<?к|е > Р2> которое вместе с предыдущим дает второе неравенство (с) ¦
Формулу (13), в силу (Ь), можно переписать в виде
р
о
где интеграл берется при постоянной 5.
Указанные в Лемме 1 свойства позволяют ввести понятие вакуума путем доопределения функций / и е их предельными значениями при /9 —> 0. Состояние вакуума нормального газа определяется любым из следующих равенств (при S, < S < S*), влекущим выполнение остальных:
р = 0 , У = эо, р = 0 , е = ()
bits
Свойства адиабат. Последующее изучение термодинамических соотношений проводится на плоскости R2{V, р) в квадранте Q = {0 < V < оо,
О < р < оо}. Кривые 5 = const называются адиабатами (или адиабатами Пуассона, или изэнтропами). Адиабата, вдоль которой S = So, обозначается a(So). Для каждого So из интервала (S*, S*) рассматривается область Q(So), определенная неравенством S > So; ее границей является адиабата a (So).
Лемма 2. Семейство адиабат {a(S)} обладает следующими свойствами:
(a) через любую точку (V0, щ) е Q проходит одна и только одна адиабата a(So);
(b) Si < S2, если и только если a(S2) С Q(S\);
(c) для любого So область Q(Sq) строго выпукла:
(d) любая адиабата a(So) имеет асимптоты V = О (при р —> оо) и р = О (при V —» ос).
Доказательство. В силу (12, d) и (9) при фиксированном V значение р = g(V,S) монотонно возрастает вместе с S, пробегая весь интервал (0. оо), откуда следует (а). Итак, существует определенная на Q функция S = cr(V,p), с которой выполнено тождество g(V,a(V.p)) = р. Его дифференцирование дает соотношения
9v + 9sGv = 0, gS(Jp = 1, (16)
откуда, в силу (12), а у > 0 и ор > 0. Значит, градиент S в точках адиабаты a(So) направлен строго внутрь области Q{Sq), что влечет свойство (Ь). Да;1се, строгая выпуклость области Q(.S'o) гарантируется неравенством (12, с). Наконец, из (8, Ь, с) и определенности / при всех р, S следует, что р —* ос равносильно р > ос, откуда, вместе с (9), вытекает свойство (d). ¦
Прямая с уравнением р — kV + 6 называется прямой типа i_, если к ^ 0, и прямой типа если к < 0. Из леммы 2 следует, что вдоль любой прямой типа /+ энтропия S меняется монотонно, возрастая с ростом р (или V) от S, до S*. Напротив, для каждой прямой типа I- существует единственное значение So, при котором оиа является опорной прямой для выпуклой области Q(So), т. с. касательной к адиабате a(So). Пусть (Vo,po) — соответствующая точка касания. В этом случае поведение энтропии S, рассматриваемой на /_ как функция от V согласно выражению S — о(V. kV 4 6), описывается следующим утверждением.
dS/dV > О (V < К0), dS/dV < О (V > VQ).
Доказательство. Из леммы 2 следует, что адиабата a(S") при S" > So не пересекает I- и что любая адиабата a(S') при 5' < So пересекает /_ ровно в двух точках 1 и 2, причем Vj < Vo и Vi > Vo (рис. 1). Дифференцирование формулы S = a(V,kV + 6) по V дает dS/dV = оу + кар, или, в силу (16),
Лемма 3. На прямой типа /_ энтропия S имеет единственную стационарную точку V = Vq, в которой S достигает максимума, приче.ч
(17)
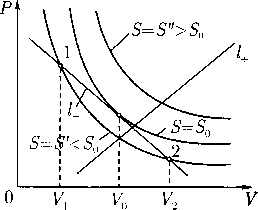
Рис. 1
dS/dV = {к - gv)/gs-
Так как gs > 0 (см. (12, d), то неравенства (17) являются следствием свойства строгой выпуклости адиабаты a(S'), гарантирующего, что {gv)\ < к и {gv)2 > к. Действительно, если бы было, например, (gv)i — к, то точка 1 была бы точкой перегиба для a(S'), в которой необходимо должно выполняться равенство gvv{Vi, S') = 0, противоречащее (12, с). ¦
Термодинамические функции. В дальнейшем будут играть важную роль некоторые термодинамические функции, определяемые заданными уравнениями состояния нормального газа (7).
Определение 3. Скоростью звука (термодинамической) называется величина с > 0, заданная формулой
= UP,S) :
(18)
S=const
удельной энтальпией (или теплосодержанием) называется величина, заданная формулой
i = e(V,p) + pV . (19)
Из (18) и условия нормального газа (8,с) следует, что д(с2)/др — ~ fpp > 0, т. е. выполнено свойство взаимно однозначного соответствия между скоростью звука с и плотностью р. Состояние вакуума (15) также определяется равенством с = 0.
Для политропного газа явные выражения этих функций легко находятся из уравнений (5) и (6) и имеют вид
di I
: S=const
§ 3. Дифференциальные уравнения
С точки зрения рассматриваемой математической модели движением (или течением) газа в области О. С Я4(х. t) называется набор функций u, р, р, е, определенных в Г! и удовлетворяющих уравнениям (1.3).
Определение 1. Движение газа называется гладким в области С Я4, если функции и, р, р, е непрерывны вместе с первыми производными всюду в П.
Дифференцирование интеграла no движущемуся объему. Гладкие движения удовлетворяют системе дифференциальных уравнений, равносильной системе законов сохранения (1.3). Для вывода этих уравнений удобно ввести абстрактный закон сохранения
JJJ fduj + JJ ip ¦ nd'y = °, (1)
j(t) 7(t)
где функции f и ip определены в области ft. Здесь предполагается, что движущийся объем tu(t) определен с помощью векторного поля вектора скорости и так, как это описано в § 1.
Лемма 1. Производная интеграла по движущемуся объему дается формулой
ffJJJfdu> = JJJ(Df + fdivu)cLj1 (2)
u>(i) uj(t)
где D есть дифференциальный оператор:
D = Ft + "v-~-m+ui+vfy+wi- <3>
Доказательство. Закон движения (1.2) позволяет сделать в интеграле по u>(t) замену переменных интегрирования х на Хо. Если при этом область и>{1) перейдет в область с^'о, то интеграл преобразуется по формуле
где S — det(dx/0xo) есть определитель матрицы Якоби из производных от старых переменных по новым. Теперь надо заметить, что если вектор и непрерывно дифференцируем, то решение (1.2) уравнения (1.1) также непрерывно дифференцируемо по хо- При этом производная <9x/cbco (в координатах — матрица Якоби) удовлетворяет уравнению «в вариациях», выводимому из (1.1) дифференцированием по Хц:
А ( ) = ( дп \ ( Эх\ (4)
Отсюда для определителя d(f,xo) получается формула Эйлера:
Кроме того, для любой функции F(x, t) в силу уравнения (1.1) справедлива формула дифференцирования
JjF(x(*,xo),i) = Ft + u • VF = DF,
где символом Ft обозначена частная производная (d/dt)F(x,t). Теперь дифференцирование интеграла по движущемуся объему с использованием (5) выполняется автоматически:
U>(t) W()
= Ш (i/+/divu)^° =
///
{Df + / div u) duj.
4*1 u>(t)
Применение формулы Остроградского - Гаусса к входящему в (1) интегралу по поверхности дает
JJ <р ¦ n d-у = JJJ div ip du.
7 (t) w(t)
Кроме того, полезно заметить еще, что
Df + / div u = ft + div(/u).
Предыдущие соотношения и лемма показывают, что если и, / и ip имеют непрерывные производные, то закон сохранения (1) оказывается равносильным следующему:
![]()
W(t)
{ft + dW{fu + (p))dui = 0. (6)
Отсюда, в силу произвольности объема u{t), следует, что подынтегральное выражение равно нулю, т. е. что (6) равносильно дифференциальному уравнению
ft + div(/u + tp) = 0. (7)
Вывод основных дифференциальных уравнений. Теперь можно обратиться к конкретным законам сохранения (1.3) и заметить, что все они
имеют вид (1) при специальных значениях / и <р. Для закона сохранения массы надо принять / = р, tp = 0. Здесь (7) дает дифференциальное уравнение
pt + div(pu) = 0, (8)
которое называется уравнением неразрывности. Для закона сохранения импульса удобно ввести его проекции согласно представлению и = (и, v, w). рассматривая проекцию на ось х, следует положить / = ри и = (р, 0, 0), и тогда из (7) получится уравнение
{pu)t + div(puu) + рх = 0.
После преобразования с учетом равенств (pu)t = рщ + upt, div(puu) = = и div(pu) + pu • Vu и уже найденного соотношения (8) это уравнение упрощается до следующего:
put + pu • Vu + рх = 0,
где индексом х обозначена частная производная д/дх. Аналогичное преобразование двух других проекций (на оси у и z), после свертывания полученных трех скалярных уравнений в одно векторное, приводит к уравнению
ut + и • Vu + |Vp = 0. (9)
которое называется уравнением импульсов (или уравнением количества движения). Наконец, для последнего из законов сохранения (1.3) следует
взять / = P^q2 + ? j и ip = ри. В этом случае (7) дает уравнение
(p(!<72+s)) +div (p(f<724-?^ u+puj = 0,
которое в силу (8) и (9) упрощается до следующего:
?t + и • Ve 4- ^ div и = 0.
Дальнейшие преобразования связаны с использованием вытекающего из (8) выражения
div u = - ^Dp,
после подстановки которого и замены V = 1/р получается
Но в частице газа, движущейся по траектории, выполняется первый закон термодинамики:
TDS - Ds + pDV.
благодаря которому оказывается, что дифференциальное уравнение закона сохранения энергии вместе с (8) и (9) равносильно уравнению
DS = 0. (10)
Из формулы (3) для оператора D видно, что он имеет смысл оператора дифференцирования по времени вдоль траектории частицы. Поэтому его называют оператором дифференцирования в частице (иногда говорят — оператор полного дифференцирования) по t.
Свойство движения газа, выражаемое уравнением (10), можно сформулировать так: при гладком движении газа энтропия сохраняется в частице.
Окончательно для гладкого движения получается следующая система дифференциальных уравнений газовой динамики:
Dp 4- р div и = 0,
Du-fiVp = 0, (11)
DS = 0,
которая замыкается уравнением состояния р -- f(p, S).
Уравнения (11) записаны в инвариантных векторных операциях. Для их подробной скалярной записи в декартовых координатах х = (х, у, z),
и = (и, v, w) используются, кроме (3), выражения операторов
Vp = {рх, Ру, pz), divu = их + Vy + wz.
Поэтому в декартовых координатах система (11) имеет вид
Pt Ь ирх + иру -г- wpz + р{их + vy -J- wz) 0, щ. + иих + vuy -f иmz + Jjpx = 0,
vt + uvx + uvy + wvz + - 0, (12)
wt + uwx + vwy + wwz + ip, = 0.
St + uSx + vSy + wS2 = 0,
где индексами обозначены частные производные по соответствующим координатам, например: pt = dp/dt, их = ди/дх и т.д.
В различных вопросах газовой динамики система (11) может быть представлена в других равносильных формах. Например, можно исключить энтропию S, заметив, что Dp = fpDp + fsDS. Так как /р = с2, то уравнение DS = 0 равносильно уравнению
или, с учетом первого уравнения (11), уравнению Dp = —рс2 div и. В этом представлении система принимает вид
Dp + /э div u = 0,
Dp -г pc2 div u — О,
где величину рс? следует рассматривать как функцию от р и р. Это представление особенно удобно в случае политронного газа, когда рс2 = -ур.
Симметрическая форма. В общей качественной теории уравнений (11) (исследование характеристик, краевых задач и т. п.) целесообразна специальная запись системы с искомыми функциями u, р, S. С этой целью из первого уравнения (11) с помощью соотношения (13) исключается Dp, что приводит к равносильной системе
pDu + Vp = О, bDp + div u = О

Здесь величины р и 6 рассматриваются как функции от р и S. Важное свойство системы (15) состоит в том, что она является симметрической. Этот термин означает, что в матричной записи системы (15) участвуют симметричные матрицы. Для перехода к матричной записи система (15) расписывается в декартовых координатах:
p(ut + иих + VUy + wuz) + рх = О, p(vt + uvx -f VVy + WUZ) + Py - 0, p{u>t -I- UWX + VWy -I- wvuz) + pz = 0, (16)
b(pt -I- upT + vpy + wpz) + ux - Vy + wz - 0, St + uSx 4 vSy -r vuSz = 0,
и вводится вектор-функция U - (u, v, w, ps S) (рассматриваемая как век-тор-столбсц). Тогда с матрицами AJ(j = t, х, у, г), элементами которых служат коэффициенты системы (16), эта система записывается в виде
,4fU, AXUX 4 AvVy -j- AZVZ --¦= О, (17)
где нижними индексами при U обозначены частные производные этого вектора по t, х, у, г и каждая матрица умножается на вектор-столбец по обычному правилу. Конкретный вид матриц А* таков:
|
(р 0 | 0 | 0 |
f ри 0 0 1 | 0N\ | ||||||
| 0 р | 0 |
0 | 0 | 0 ри 0 0 | 0 | |||||
| = | 0 о |
р | 0 | 0 |
Ах - |
0 0 ри 0 | 0 | |||
| 0 0 | 0 |
ь | 0 | 1 0 0 Ьи | 0 |
|||||
| \0 0 |
0 | 0 | У |
V о о о о |
и) | |||||
| ( pv 0 | 0 | 0 | °\ | ё о о | 0 | ON | ||||
| 0 | pv |
0 | 1 | 0 | 0 ри> 0 |
0 | 0 | |||
| 0 | 0 | pv |
0 | 0 | , Az = | 0 0 pw |
1 | 0 | ||
| 0 | 1 | 0 |
bi | 0 | 0 0 1 | bw |
0 | |||
| \0 |
0 | 0 | 0 | VJ | \ 0 0 0 | 0 | W / | |||
Непосредственно видно, что все матрицы А] симметричны, причем Аь — положительно определенная.
Форма Громеки-Лэмба. Еще одна форма записи получается с использованием вектора вихря и = rot и, который в декартовых координатах имеет компоненты
и) — (wy - vz, uz - wx. vx — uy). (18)
Переход к новой форме основан на тождестве
и • Vu = V ^2^) U Х
где х — знак векторного умножения. С помощью этого тождества уравнение импульсов (второе из уравнений (11) записывается в форме Громеки -Лэмба:
В приложениях возникает необходимость в изучении классов движений, более широких по сравнению с классом гладких движений. Математическая модель таких движений может быть построена на основе интегральных законов сохранения (1.3). Вначале рассматривается абстрактный закон сохранения (3.1). В предыдущем параграфе было показано, что если величины и, / и if обладают непрерывными производными, то (3.1) равносильно (3.6), откуда вытекало дифференциальное уравнение (3.7). Здесь (3.6) будет обобщено в другом направлении.
Обобщенные движения. Пусть $1 С R] есть ограниченная область с кусочно-гладкой границей Г и сечениями uin(t) гиперплоскостями t = const. В соотношении (3.6) полагается u(t) = и>n(t), и оно интегрируется по t в интервале (t\, i2), на который проектируется область (Л. Это даст
J JJJ(ft + div(/u + ip))dudt =- О
11 -Jn(t)
Здесь подынтегральное выражение есть дивергенция четырехмерного вектора (если if = (ifi, ip2, <рз))
g = (/¦. fu -i-'fi, fv + '~P2, fw + ?>з).
Поэтому согласно теореме Остроградского-Гаусса предыдущее соотношение равносильно следующему:
(1)
![]()
г
где и — орт внешней нормали к Г. Если 1 — орт оси t и п — орт внешней нормали к сечению Г гиперплоскостью t = const, то
v = 1cos(ia/) fnsin(iM)
(2)
и, следовательно,
g • и — f cos(i/, t) (/u <f) ¦ n sin(i/, t). Поэтому соотношение (1) принимает вид
![]()
Итак, для непрерывно дифференцируемых функций и. /. ip из выполнения (3.6) для любого объема сo(t) С R3 следует выполнение (3) для любой замкнутой гиперповерхности Г С RA. Ясно, что, и обратно, специализируя Г как цилиндрическую поверхность с образующими, параллельными оси t в Я4, и сечением и С R3, легко вывести (3.6) из (3).
Однако если не предполагать функции и, /. ip непрерывно дифференцируемыми, то из (3) указанным путем уже не удастся вывести (3.6). В частности, такой вывод невозможен, если величины и, /. ip сами разрывны. В этом смысле закон сохранения (3) является обобщением закона сохранения (3.6).
Определение 1. Набор функций и. р, р, г, определенных в R4(x,t), называется обобщенным движением газа, если для любой замкнутой кусочно-гладкой гиперповерхности Г с Д4(х, t) эти функции удовлетворяют соотношениям
JJJ(pcos(u, t) + ри ¦ nsin(i/, t)) dT = О, г
JJJ (ри cos(v, t) + (p(u • n)u -I- pn) sm(b>, t)) dr - 0, ^
г
/1f (p(^q2+?) +(K^2+?)+p)u'nsin(i'>t))rfr=°-
Соотношения (4) получаются из абстрактного (3) путем специализации функции f и ip соответственно законам сохранения (1.3). В силу предыдущего они равносильны дифференциальным уравнениям (3.11) в классе гладких движений газа.
Движение с сильным разрывом. Класс всех обобщенных движений газа до настоящего времени полностью не изучен. Фактически исследован только (во всяком случае, для многомерных движений) некоторый подкласс обобщенных движений, а именно класс движений с сильным разрывом.
Определение 2. Если в области определения обобщенного движения существует гиперповерхность Е С R4, на которой величины и, р. р, ? имеют разрыв первого рода и вне которой это движение гладкое, то такое движение называется движением с сильным разрывом, а сечение U(t,) гиперповерхности Е гиперплоскостями t — const называется поверхностью сильного разрыва.
Итак, поверхность сильного разрыва B(t) есть двумерная поверхность в пространстве Л3(х), которая перемещается с течением времени и на которой функции и, р, р, г имеют разрыв первого рода, оставаясь гладкими с каждой стороны от B(t). Оказывается, что величины разрывов (или, как говорят, скачков) этих функций не могут быть произвольными, но с необходимостью удовлетворяют некоторым соотношениям, которые и называются уравнениями сильного разрыва.
Вывод соотношений на сильном разрыве. Удобно вывести уравнение сильного разрыва сначала для абстрактного закона сохранения (3). С этой целью на гиперповерхности Е выделяется некоторая (малая) область а с гладкой границей 7 и строится замкнутая гиперповерхность Г = <Ti + <т2 + аз, где <7з есть «боковая поверхность» цилиндра с направляющей 7, a <7i и <72 — куски «параллельных» к Е поверхностей, находящихся на расстоянии h от Е (рис. 1), вырезанные этим цилиндром. В соотношении (3) с так построенной гиперповерхностью Г интеграл разобьется на сумму трех интегралов — по <7i, <72 и <73. Затем выполняется предельный переход при h —> 0. Так как при этом мера |<7з| подынтегральная функция ограничена, то интеграл по <73 в пределе дает нуль. Что же касается интегралов по ст\ и <72, то они в пределе перейдут в интегралы по разным сторонам <7 с противоположными направлениями нормалей и\ —
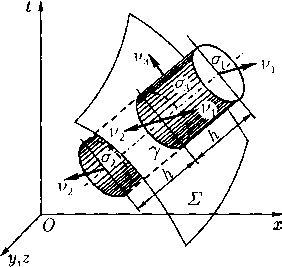
Рис.
0 и
Пусть v — одно из этих направлений, и пусть символ скачка [а] = аг — а i дает разность предельных значений на Е какой-либо величины а, которые существуют с каждой стороны Е. При этих соглашениях в пределе получится соотношение
///
[/ c.os(i/, t) + (fun + <рп) sin(i/, t)]da = 0,
где un = u • n и <pn = ip ¦ n. Отсюда, ввиду произвольности области сг С Е и непрерывности подынтегрального выражения на Е, получается абстрактное уравнение сильного разрыва
Некоторое неудобство этого уравнения состоит в том, что в него входит четырехмерная нормаль v к гиперповерхности Е. Однако нормаль и можно исключить с помощью понятия скорости перемещения поверхности B(t) и тем самым получить описание сильного разрыва в терминах только пространства Я3(х).
Берется точка М 6 B(t) и находится точка N пересечения нормали в М к B(t) с поверхностью B(t + At). Пусть H(At) есть длина отрезка MN, взятая со знаком «плюс», если вектор А/N направлен так же, как
орт нормали п к B(t) в точке М, и со знаком «минус», если вектор MN направлен противоположно п.
Определение 3. Скоростью перемещения поверхности B(t) в направлении нормали п называется предел
П I- Н<Д‘>
Связь Dn с четырехмерной нормалью v обнаруживается, если заметить, что вектор (рис. 2)
где 1 — орт оси t, лежит в касательной плоскости к Е и потому ортогонален вектору (2). Следовательно, искомая связь такова:
Dn sin(i/, t) + cos(u, t) = 0. (7)
В силу соотношения (7) уравнение (5) можно записать в виде
[/(u„ - Dn) 4 <рп] s'm{v, t) = 0.

Рис. 2
Естественно считать, что скорость перемещения Dn поверхности B(t) конечна. Тогда из (7) следует, что sin{и ,t) Ф 0, и окончательно получается равносильное (5) абстрактное уравнение сильного разрыва
[/(^71 Dn) ! tpnj 0.
(8)
Применительно к конкретным уравнениям (4), в результате надлежащей специализации функций / и уз, из (8) получаются следующие уравнения сильного разрыва в газовой динамике (уравнения Гюгонио):
\р(ип Dn)i 0, [pu(un - Dn) -Lpnj - 0,
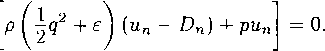
Классификация разрывов. Пусть ист есть ортогональная составляющая вектора и, лежащая в касательной плоскости к поверхности разрыва B(t). Проектирование на эту плоскость второго из уравнений (9) дает соотношение
р(ип - Dn)\IV] = 0,
(10)
которое позволяет дать следующую классификацию сильных разрывов (предполагается, что р ф 0).
Первый тип разрыва: ип = Dn. В этом случае скорость течения газа в направлении нормали п к B(t) равна скорости перемещения самой поверхности B(t) в том же направлении. Следовательно, через такой разрыв газ не течет. Из (9) следует, что на таком разрыве необходимо [р] 0
и [unj = 0. Однако, вообще говоря, может быть [р] ф 0, [е] Ф 0 и [ист] ф 0. Сильный разрыв этого типа называется контактным разрывом.
Второй тип разрыва: ип ф Dn. В этом случае juCTj = 0, но, вообще говоря, [«„] ф 0, [р] ф 0, [р] ф 0, [sj ф 0. Через такой разрыв газ течет. Сильный разрыв этого типа называется ударной волной.
Основное качественное различие двух указанных типов разрывов состоит в том, что контактный разрыв разделяет области, каждая из которых состоит все время из одних и тех же частиц газа, а ударная волна распространяется по частицам газа.
Ударные волны. Поверхность ударной волны принято также называть фронтом ударной волны.
Определение 4. Та сторона фронта ударной волны, с которой газ натекает на нее, называется передней стороной (или стороной перед фрон-том) ударной волны. Противоположная сторона фронта называется задней стороной (или стороной за фронтом) ударной волны.
В дальнейшем (если не сделано специальных оговорок) принимается следующее соглашение: нормаль п к фронту ударной волны направлена в переднюю сторону (в область перед фронтом) ударной волны. Пусть индекс «1» отмечает значения газодинамических величин на передней стороне, а индекс «2» — на задней стороне ударной волны. Наконец, вводится скорость течения газа относительно фронта в направлении нормали п:
I) = ип - Dn. (11)
В последующих формулах используется также обозначение удельного объема V = 1/р.
После небольших преобразований исходные уравнения сильного разрыва для ударных волн принимают вид
Они выражают соответственно законы сохранения массы, импульса и энергии в ударных волнах. Эти уравнения связаны с изменением вектора скорости в направлении нормали к фронту; кроме ннх еще выполнено уравнение сохранения касательной к фронту составляющей вектора скорости:
Из определения 4 и соглашения о направлении нормали п в сторону перед фронтом следует, что v\ < 0; в силу (12) и положительности плотности р также Vo < 0. Кроме того, из (16) и (18) следует, что все скачки
[р}=р2-р1, \Р\=Р2-Рг,
имеют один и тот же знак.
Адиабата Гюгонио. При исследовании ударных волн ключевым является уравнение (18), так как оно связывает только термодинамические величины. Более того, в силу уравнения состояния (2.7) верны выражения ?\ — e(Vi,Pi) и ?2 = e(V9, Р2), благодаря чему уравнение (18) определяет термодинамическое состояние (V2,P2) газа за ударной волной только по термодинамическому состоянию (Vi,pi) перед волной.
Определение 5. Функция переменных (V,p)
Я = H(V,p\ V\,pi) = e(V,p) - e(Vi,pi) + |(V - Vi)(p 4- p,) (19)
называется функцией Гюгонио. Кривая на плоскости R2(V,p), заданная уравнением
H{V,p\ Vbpi) = 0,
(20)
называется адиабатой Гюгонио с центром (Vj,pi).
Иногда вместо термина «адиабата Гюгонио» употребляется синоним «ударная адиабата». С функцией Гюгонио (19) уравнение (18) записывается в виде H(Vo,p2', Vi,pi) = 0.
Для политропного газа, в силу выражения (2.6), уравнение адиабаты Гюгонио (20) приводится к виду
р_ _ Ь ~j~ 1)^1 ~ (7 - 1)У П ~ (7 + 1)1/ — (7 — l)Vi '
(21)
Этому уравнению соответствует уравнение ударного перехода (18), записанное вместо удельных объемов V, через плотности рг:
Р2 = (7 + 1)/>2 - (7 - 1)/>1 п (7 + 1)Р1 - (7 - 1)Р2
(22)
§ 5. Основные свойства ударных волн
Здесь собраны фундаментальные свойства ударного перехода, т. е. изменения основных величин при переходе через ударную волну. Эти свойства являются общими и верны для любого нормального газа (определение 2.2). Ниже они фиксируются в виде ряда теорем и их следствий.
Форма адиабаты Гюгонио. Вначале устанавливается общая форма адиабаты Гюгонио (4.20) на плоскости R2(V.p).
Теорема 1. Для любой точки (VbPi) € Q уравнение адиабаты Гюгонио с центром (Vj,Pi) может быть записано в виде
(1)
V = W(p) = W(p: Vupi)
с трижды непрерывно дифференцируемой функцией W (р), которая однозначно определена и является строго убывающей для всех р е (0, ос).
Доказательство. В силу леммы (2.1, с) справедливо неравенство
2dH/dV = 2ev{V,p) t-p + pi> 0.
Кроме того, поведение функции Я при фиксированном р таково, что
Я +-ОС при V ¦-> ос и, в силу (2.11), Я —» — e(Vi,pi) - ^V\{p + р\) < О
при V —* 0 . Поэтому для каждого р 6 (0, ос) существует единственное значение V -- W(p), при котором И = 0, т. е. справедливо представление адиабаты Гюгонио (1). Гладкость функции W следует из условия 2° определения 2.2 для нормального газа.
Далее, дифференцирование тождества H(W(p),p: V\,p\) -= 0 по р дает соотношение
(2ev + Р -r Pi)^~ (2ep + W{p) - 1^) = 0,
(2)
позволяющее установить знак производной dW/dp. Первая скобка в (2), как отмечено выше, строго положительна. Для оценки второй скобки используется неравенство (2.10,Ь), в силу которого вдоль Я = 0 справедливы соотношения
2ep f W(p) - V\ = 2ep - 2
e(V,p) - e(Vi,pi) >
p + p\

Поэтому из (2) следует, что для р G (0, оо) всюду dW/dp < 0.
Следствие 1. Вдоль адиабаты Гюгонио существуют предельные значения
У0 - lim W(p) > Vi, Voc = lim W(p) < Vb
p- *0 p—>oc
Можно показать, что в нормальном газе всегда Vq < ос.
Поведение вблизи центра. Следующие факты относятся к поведению адиабаты Гюгонио вблизи ее центра. Пусть S(p) = a(W (р),р) — значения энтропии вдоль адиабаты Гюгонио. В последующих формулах индексом «1» обозначаются значения величин в центре (V\,p\), например: S\ = S(p\) и т. п.
Теорема 2. Справедливо предельное соотношение
lim ^ - к\ > 0, (4)
Р-Рг (р-рi)3 W
и в центре (Vi.pi) адиабата Гюгонио имеет с изэнтропой a(S\) касание второго порядка.
ДОКАЗАТЕЛЬСТВО. Пусть е(р) = e(W(p), р). Дифференцирование тождества H(W(p),p-, Vi,pi) = 0 по р приводит к выражению
2? = -(p + pi)W' - {W - Vi)
(здесь и ниже штрихами обозначены производные по р). С другой стороны, если в уравнении (2.1) взять производные всех величин по р вдоль адиабаты Гюгонио, то оно примет вид TS' ¦= <? + pW. Исключение величины е' с помощью предыдущего выражения приводит к соотношению
Отсюда следует, что S[ = 0. Дифференцирование (5) дает
откуда S" = 0. Наконец, еще одно дифференцирование приводит к равенству
2T"S' + 4T'S" + 2TS'" = W" -г (p - pi)W",
из которого получается, что 2TiS[" = W". Для вычисления значений W[ и W{' используется тождество g(W(p),S(p)) = р, дифференцирование которого один и два раза дает
gvW' + gsS' = 1, gvvW2 + 2gvsW'S' + gssS'2 + gvW" + gsS" = 0.
В силу предыдущего в точке (Vi, р\) эти равенства принимают вид <jv W[ = 1, yvvW'\ +fjvW" — 0. Итак, получаются следующие выражения для производных:
5(=о S7 =-- о, s;" = —
(6)
![]()
где значения правых частей взяты в центре (Vi,pi). Теперь ясно, что формула (4) следует из (6), причем к\ = (1 /6)5"'. Кроме того, для производных функции V(p), определенной уравнением g(V, Si) = р и задающей изэн-тропу a(Si) в виде V = V(p), справедливы соотношения
gvV'= 1, gvvV,2 + gvV" = 0, из которых в силу (7) следует, что -= V{ и W" — V".
(8)
Следствие 2. Для ударных волн справедливы следующие предельные соотношения при р2 —> рЛ вдоль адиабаты Гюгопио:
lim = с?, lirn !uni - Dnj = lim |utl2 - D2\ = cb
(9)
![]()
Равенства (9) легко получаются с помощью (4) из определения (2.3) и формул (4.16), (4.17).
Величину скачка р2 — рх = [р] в ударной волне называют (абсолютной) силой разрыва. Предыдущие результаты можно описать, сказав, что скачок энтропии в ударной волне есть величина третьего порядка малости, а скачки плотности и нормальной составляющей вектора скорости (а также и внутренней энергии) суть величины первого порядка малости по сравнению с силой разрыва, когда последняя стремится к нулю. Второе соотношение (9) означает, что при этом относительная скорость движения газа по нормали к поверхности ударной волны стремится к скорости звука. Другими словами, «бесконечно слабые» ударные волны распространяются по газу со скоростью звука.
Возрастание энтронии. Соотношение (4) показывает, что локально, вблизи центра (Vi,pi), энтропия S(p) монотонно возрастает с ростом р. Оказывается, что это свойство справедливо и в целом.
§ 5. Основные свойства ударных векш Теорема 3. Вдоль адиабаты Гюгонио всюду
Доказательство. В силу теоремы 2 неравенство (10) выполнено в окрестности точки р\. Пусть S'(p2) = 0 в некоторой точке р2 Ф р\-Тогда определена прямая 1у> на плоскости R2(V,p), проходящая через точки (Vi,pi) и (V2,p2), где V2 = \V(p2). В силу теоремы 1 прямая 1\2 является прямой типа /_, причем ее угловой коэффициент равен к = dV/dp -= (V2 — ^i)/(P2 — Pi)- С другой стороны, из соотношения (5) в точке р> следует, что в этой точке W'(p2) = {W{p2) — Vi)/(p2 ~Р\)- Следовательно, прямая 1\2 касается адиабаты Гюгонио в точке (Vo, р2).
Теперь надо заметить, что наклон касательной к адиабате Гюгонио может быть вычислен дифференцированием тождества a(W(p),p) = S(p), т.е. из уравнения ayW'(p) + <тр = S’(p), которое, согласно сделанному предположению, в точке р2 принимает вид (TvW{p2) ор = 0. Наклон же касательной к изэнтропе a(S2) вычисляется дифференцированием тождества <r(V(p),p) = S2, что дает ovV'(p2) + ор = 0. Сравнение этих соотношений показывает, что V'(p2) W'{p2), т. е. что изэнтропа а(52) касается
адиабаты Гюгонио, а значит, и прямой 1у> в точкй (Vo, ро) ¦ Согласно лемме 2.3 это означает, что энтропия S вдоль прямой 112 имеет в этой точке максимальное значение.
Однако если рассмотреть изменение функции Гюгонио (4.19) вдоль какой-нибудь прямой I, проходящей через точку (Vi , р:) (например ^2), то для ее дифференцирования получится выражение
dH = ds + ±(V V,)dp + I (p + Px)dV = ds+pdV,
где последнее равенство выполнено в силу уравнения V = V] + к(р - р\) прямой I. Сравнение этого выражения с уравнением (2.1), в котором дифференциалы взяты вдоль прямой I, приводит к соотношению
TdS = dH,
(П)
справедливому, в частности, вдоль 1\2- Функция Н на прямой I\2 обращается в нуль в точках (Ц,р0 и (Vo. р->) . По теореме Ролля в интерва-ле (Pi • Р2) найдется точка рз, в которой dH = 0. Но тогда из (11) получится, что dS(p^) = 0. Так как рз / ро, то последнее равенство противоречит
лемме 2.3.
Следствие 3. Адиабата Гюгонио звездна относительно своего центра. Это означает, что каждый луч, выходящий из центра (V'i,pi). либо вообще не пересекает адиабату Гюгонио, либо пересекает ее только в одной точке. Образно выражаясь, можно сказать еще, что вся адиабата Гюгонио «видна» из своего центра. Свойство звездности вытекает непосредственно из соотношения (11) и леммы 2.3.
Уместно отметить, что звездность адиабаты Гюгонио следует только из условий 1° определения 2.2, более того, она справедлива и при выполнении лишь условий (2.12) для «газа Вейля». Условия 2° определения 2.2 использовались лишь для установления свойства монотонности адиабаты Гюгонио.
Из полученных фактов следует качественная картина расположения адиабаты Гюгонио среди семейства изэнтроп, показанная на рис. 1.
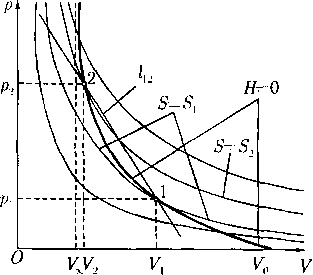
Рис. I
Итак, вдоль всей адиабаты Гюгонио энтропия строго возрастает с ростом давления. Важность этого результата обусловлена тем, что с его помощью можно однозначно установить знаки скачков давления и плотности в ударной волне. Для этой цели привлекается второй закон термодинамики, согласно которому энтропия теплоизолированной системы не убывает. Так как в рассматриваемой здесь модели газовой динамики процессом теплопроводности пренебрегастся, то каждую частицу газа следует считать теплоизолированной. Согласно предыдущему, если такая частица прошла через ударную волну с ненулевой силой разрыва, то в ней энтропия обязательно изменилась. В силу второго закона термодинамики это изменение должно быть возрастанием. Поэтому если состояние 1 находится перед фронтом ударной волны, то обязательно должно быть S-> > Sь и тогда из теоремы 3 следует, что р2 > Р\ и р2 > Р\. Если же состояние 1 находится за фронтом, то в том состоянии 2, из которого путем ударного перехода получилось состояние 1, необходимо должно быть 5’г < Si и, соответственно, р2 < Pi и р2 < рх. Итак, справедлив следующий вывод.
Следствие 4. Ударная волна всегда вызывает повышение давления и сжатие (уплотнение) газа; ударные волны разрежения невозможны.
Теорема Цемплена. Выражаемое следующей теоремой свойство ударного перехода фактически равносильно свойству возрастания энтропии вдоль адиабаты Гюгонио. В дальнейшем на него будут делаться ссылки как на теорему Цемплена.
Теорема 4. Абсолютная величина нормальной составляющей скорости движения газа относительно ударной волны больше скорости звука перед фронтом и меньше скорости звука за фронтом, т. е. если состояние 1 — перед фронтом, то
|!ini Dn\ > С], | Un2 Dn\ < С2.
(12)
Доказательство. Рассматривается изменение энтропии S вдоль прямой р - р 1 = k(V — Vi) типа проходящей через центр (Vi,pi) адиабаты Гюгонио и какую-либо ее точку (Vb.pa), где рг > рь так что к =
— (Р2 ~ Pi)/(V2 — Vi) < 0. Из соотношения (11), справедливого вдоль такой прямой, следует, что dS = 0 в некоторой точке, лежащей строго внутри интервала с концами (Vj,pi) и (Иг,рэ). В силу леммы 2.3 в этой точке S достигает максимума. Поэтому па концах интервала должно быть
(dS/dV)i < 0, {dS/dV)2 > 0.
(13)
Дифференцирование по V уравнения р = g(V.S) вдоль прямой I- даег соотношение к = gy + gs{dS/d.V), откуда в силу того, что д$ > 0, и неравенств (13) следуют неравенства
gvi > к > .
Но формулы (2.13) и (2.18) дают выражение ду - -р2с2, в силу которого эти неравенства равносильны следующим:
![]()
Наконец, подстановка V* = 1 / р\ (г = 1, 2) и учет уравнений сильного разрыва (4.16) приводят к неравенствам
r2 . Р1 РЗ ~ РI 2 „2 ^ Р2Р2- Р1
UO ^ — Уо, Cl Ч — -
P2p2-pi 2’ 1 Р1Р2-Р1
которые равносильны (12).
¦
Свойство определенности. Следующий факт, называемый свойством определенности ударной волны, нуждается в небольшом пояснении. Уравнения сильного разрыва для ударной волны (4.11)—(4.14) связывают семь величин
Uni,pupuUn2,P2,P2,Dn. (14)
Говорят, что ударная волна определена, если все эти величины известны. Так как для них имеется всего три уравнения —(4.12), (4.13), (4.14), то четыре из семи величин (14) могут быть заданы, а оставшиеся три должны находиться их этих уравнений. Возникает вопрос, можно ли такое определение осуществить. В сущности, это есть вопрос о существовании и единственности ударного перехода при различных заданиях четырех из параметров (14).
Здесь будет рассмотрено лишь такое задание четырех параметров, когда движение по одну сторону от ударной волны известно, т. е. когда заданы параметры
uni,p\:pi- (15)
и, разумеется, фиксировано некоторое направление нормали к поверхности ударной волны. Ниже принимается, что нормаль п направлена в ту сторону, с которой находится заданное состояние (15). При этом не предполагается, что движение (15) находится перед фронтом. Вопрос ставится так: будет ли ударный переход определен, если кроме значений (15) задать еще одну из оставшихся величин (14)? В частности, можно ли определить, на какой стороне фронта находится движение (15)?
При такой постановке вопроса на величины (15) надо наложить некоторые необходимые ограничения. Данные (15) определяют адиабату Гюгонио с центром (V\,pi), где V\ = 1/р\. В силу (3) значение р2 не может быть задано произвольно. Именно, если движение (15) находится перед фронтом, то должно быть
Р\ < Р2 <Poc=z 1/^оо, (16)
а если движение (15) — за фронтом, то
Далее, так как точка (Ц>,р2), в силу (4.16), лежит на прямой
Р-РХ = -p\vl{V -Vx). (18)
хо в случае рг < Рь т е. когда движение (15) находится за фронтом, значение v\ (связанное с заданием ?>„) не может быть очень мало. Его нижняя
грань определяется из условия прохождения прямой (18) через точку (Vo, 0) пересечения адиабаты Гюгонио с осью р = 0. Следовательно, в этом случае должно быть
v?>Pi/Pi(VV-V,). (19)
Теорема 5. Для любого заданного движения (15) существует один и только один ударный переход, в котором одна из величии р2, Р2 или Dn имеет произвольно заданное значение (с ограничениями (16), (17), (19), причем этим заданием определяется и сторона фронта, с которой находится движение (15). Если же к движению (15) дополнительно задача величина иП2, то соответствующий ударный переход всегда существует, но, в зависимости от абсолютной величины скачка [urt], возможны одно или два решения. В последнем случае единственное решение выделяется указанием стороны фронта, с которой находится движение (15).
Доказательство. Пусть дополнительно к данным (15) задано р2-Сравнение рд с р\ и учет того, что ударные волны ведут к повышению давления, определяет, с какой стороны фронта находится движение (15). В обоих случаях по адиабате Гюгонио (4.20) однозначно определяется значение V2 = 1/рг, после чего можно найти Dn из уравнения (4.16), а именно:
Г% „ I lP2P2~Pl ,Г,ПЛ
п - П| -fc у Р1 Р2 - рг ( )
В силу соглашения о направлении нормали п в сторону движения (15), в формуле (20) следует взять знак «+», если движение (15) находится перед фронтом, и знак «•-», если (15) — за фронтом. Наконец, иП2 определяется из уравнения P2V2 = piV\, что дает
иП2 = Dn + ^(u„, - Dn), (21)
и тем самым случай заданного рг исчерпан.
Если дополнительно к (15) задано рг, то сравнение рг с р\ определяет сторону фронта для движения (15), а по адиабате Гюгонио находится соответствующее значение рг (всегда существующее при выполнении ограничений (16) или (19)). После этого все делается так же, как и в первом случае.
Пусть дополнительно к (15) задана скорость перемещения ударной волны ?>„. Тогда можно сравнить v\ — иП] — Dn со скоростью звука с\ в движении (15), которая вычисляется по формуле
и применить теорему 4. При j?;i' > с\ движение (15) находится перед фронтом, а при |«]| < ci — за фронтом. В последнем случае надо проверить условие (19), и если оно выполнено, то, без дальнейших ограничений, можно утверждать, что система уравнений (18) и H{V,p\ V\,p\) 0
имеет единственное решение (V>,p2), отличное от {V\,p\). Справедливость этого утверждения вытекает из следствия теоремы 3 (звездности адиабаты Гюгонио). После этого величина иП2 определяется по формуле (21).
Наконец, пусть задана величина иП2. Здесь для определения величин Vi,р-2 имеется система из двух уравнений: (4.17) и (4.18) или
(Р “ Р\){У\ - V) — (иП2 - г/П1 )'2. H(V,p; V\.p\) ¦- 0. (22)
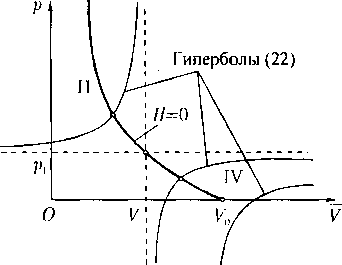
Рис. 2
Если начало координат на плоскости R2(V,p) поместить в точку (, pi), то ветви гиперболы, описываемой первым уравнением (22), расположатся в тех же квадрантах II и IV, в которых лежит адиабата Гюгонио. Из свойств адиабаты Гюгонию (теорема 1) следует, что во II квадранте всегда есть одна и только одна точка пересечения ее с гиперболой (22), а в IV квадранте — или одна такая точка, или ни одной (рис. 2).
Ясно, что точки пересечения в IV квадранте нет при достаточно больших значениях (иП2 — иП1 )2 и что нижняя грань таких значений определяется прохождением гиперболы через точку (Vo-0). Итак, в IV квадранте есть решение, если
К ~ Unf ^ Pl(V0 - V0, (23)
и нет решения в случае неравенства противоположного знака. В случае (23) указание стороны фронта для движения (15) определяет единственное решение, а именно решение, лежащее во II квадранте (если движение (15) находится перед фронтом), или решение в IV квадранте (если движение (15) находится за фронтом). В противоположном случае есть всего одно решение во II квадранте, соответствующее расположению движения (15) перед фронтом. ¦
§6. Характеристики и слабые разрывы
Уравнения газовой динамики (3.16) образуют систему квазилинейных дифференциальных уравнений первого порядка из пяти уравнений для пяти искомых функций от четырех независимых переменных. Фундаментальное свойство этой системы состоит в ее гиперболичности и описывается с помощью характеристик. Поэтому вначале уместно напомнить ряд общих фактов, связанных с понятием характеристик.
Нормальные характеристические векторы; гиперболичность.
Рассматривается система из т квазилинейных дифференциальных уравнений первого порядка для т искомых функций и = (и1, .... ит) от п независимых переменных х •- (гг1. ..., хп):
пт .
i=1*=i их
где коэффициенты 4, и правые части /; являются заданными функциями переменных (х, и). С помощью квадратных гп х m-матриц А7 с элементами агк1(к — номер столбца, I — номер строки) и обозначения щ = ди/дх1систему (1) можно записать в матричной форме:
г=1
Здесь введен вектор-столбец / = (/ь • • •, /т) и предполагается, что каждая матрица А1 умножается на вектор-столбец с элементами (и].....и™) по обычному правилу «строки на столбцы». Пусть ? -- (?ь ..., ?п) есть вспомогательный «.-мерный вектор. Системе (1) или (2) сопоставляется ее характеристическая матрица
П
при этом направление (п — 1)-мерной гиперплоскости в пространстве Л"(х), заданной уравнением
П
'У'&хг = const,
t=1
называется характеристическим направлением для системы (I) в точке (х, и). Уравнение (5) относительно вектора ? называется характеристическим уравнением.
С нормальным характеристическим вектором ? ранг г матрицы Л(?) меньше т. Значит между ее строками есть линейная зависимость: существует хотя бы один левый собственный вектор А, с которым справедливо равенство
В общем случае для данного ? определено векторное подпространство (пространства Rm) векторов Л, удовлетворяющих (6). В этих терминах формулируется фундаментальное понятие гиперболичности системы (1). Пусть г] = (щ,..., rjm) есть фиксированный единичный вектор, |т7| = 1. Тогда ? может быть разложен на две составляющие: по направлению г) и по направлению, ортогональному г), т. е. представлен в виде
? =rjz + cr (г/ • а = 0).
В результате подстановки этого выражения det Д(?) становится многочленом от л степени т с коэффициентами, зависящими от <т, а харктеристи-ческое уравнение принимает вид
det A(r}z -)- or) = 0 . (7)
Определение 2. Система (1) называется гиперболической, если существует такой вектор г), что при любом векторе <т уравнение (7) имеет т вещественных корней (считаемых с их кратностью) и если в пространстве Лт существует базис из левых собственных векторов, соответствующих всем этим корням. Система (1) называется эллиптической, если ни при каком векторе г/ уравнение (7) не имеет вещественных корней.
Замечании I. Симметрические системы (I), в которых все матрицы А1 симметричны и некоторая линейная комбинация OiA1 с вещественными 9г является положительно определенной матрицей, являются гиперболическими.
Необходимо учитывать, что для нелинейных систем вида (1) свойство гиперболичности может зависеть от решения. Пусть набор функций
ufc = /(x) (fc=l,...,m) (8)
образует некоторое решение системы (1). Оно будет кратко называться «решением Ф». На решении Ф точка (х, и) = (х, <р(х)) определяется точкой хе Я", В соответствии с этим очевидным образом определяются понятия нормального характеристического вектора, характеристического направления и гиперболичности системы (1) в точке х на решении Ф.
Определение 3. Пусть дано некоторое решение Ф. Гиперповерхность Г С Rn(x), в каждой точке которой касательная гиперплоскость имеет характеристическое направление на решении Ф, называется характеристической поверхностью (кратко: характеристикой) системы (1) на решении Ф.
Отыскание характеристик основано на том, что гиперповерхность Г с уравнением h(x) = const является характеристикой на решении Ф, если и только если вектор ? = V7t удовлетворяет характеристическому уравнению (5), т. е. уравнению
det A(Vh) = 0, (9)
в котором сделана подстановка (8). Само по себе уравнение (9) есть дополнительное уравнение с частными производными первого порядка (вообще говоря, нелинейное) относительно одной неизвестной функции h. Если на каком-нибудь решении Ф вещественные нормальные характеристические векторы существуют для целой области точек х, то уравнение (9) также имеет решения h(x).
дик
дх1
(10)
а к
ы
Замечание. Если коэффициенты системы (1) не зависят от переменных и, то в предыдущих формулировках можно опустить слова «на решении Ф». В этом случае характеристики определяются независимо от решения.
Условия иа характеристиках. Пусть Л — (Л1,____Ат) есть левый
собственный вектор матрицы A(Vh). В результате умножения /-го уравнения (1) на Аг и суммирования по I получается соотношение
т / п т
ЕЕ Е*‘
к=\ \г=1 г= 1
Оказывается, что это соотношение обладает следующим важным свойством.
Теорема 1. Если функция /г(х) удовлетворяет уравнению (9) на некотором решении Ф и если в (10) положить А = A(V/i), то каждое из выражений в круглых скобках равенства (10) есть производная от функции ик вдоль некоторой кривой, лежащей на поверхности /i(x) = const.
Доказательство. Производная от uk вдоль кривой, заданной параметрически уравнениями х1 = xl(t) (г = 1, ..., п), дается формулой
d.uk _ dx1 duk
dt ^ dt dxi'
2=1
Поэтому достаточно показать, что для каждого фиксированного к криваяк определяемая системой дифференциальных уравнений
т
^ = X>‘a‘w (г = 1-----п)
1=1
и проходящая чрез точку Хо, принадлежащую поверхности /г(х) = const, лежит на этой поверхности целиком. Но вдоль такой кривой
j;/ \ п пт
Соотношения (10), получаемые для некоторой харакгеристи-ки h(x) = const со всевозможными векторами А = A(V/i), определяемыми из (6), называются условиями на характеристике.
Важность факта существования условий на характеристиках обусловлена тем, что в условиях (10) дифференциальные операторы, действующие на каждую из искомых функций и , являются операторами внутреннего дифференцирования на характеристике Г(/i(x) = const). Это означает, что результат действия этих операторов (круглые скобки в (10) может быть вычислен, если искомые функции ик заданы только на гиперповерхности Г. Это свойство может быть положено в основу следующего определения понятия характеристик, эквивалентного определению 3.
Определение 3'. Гиперповерхность Г С i?"(x) называется характеристикой системы (1) (на решении Ф), если существует такая линейная комбинация уравнений (1), в которой дифференцирования всех искомых функций являются внутренними по отношению к Г.
Задача Коши. Характеристики играют важную роль в качественной теории дифференциальных уравнений, в частности, при постановке, анализе и решении краевых задач. Например, задача Коши для системы (1) ставится так: на некоторой «начальной» гиперповерхности Г задаются значения искомых функций (данные Коши)
ик = фк(х) (к = 1, ..., тп; х ? Г), (11)
и требуется найти решение (7) в окрестности Г, принимающее эти значения на Г. Существование условий на характеристике означает, что данные Коши (11) нельзя задавать произвольно, если Г является характеристикой системы (1). Эти данные должны быть связаны соотношениями (10). Кроме того, даже если данные (11) удовлетворяют соотношениям (10) на характеристике Г, то решение задачи Коши, вообще говоря, не единственно. Действительно, если бы этими данными решение определялось однозначно, то по ним из системы (1) можно было бы найти значения производных по направлению нормали к Г. Но это невозможно, так как в системе (1) имеется всего m уравнений и m — г > 0 из них равносильны уравнениям вида (10), в которых, согласно теореме 1, содержатся производные от всех ик только вдоль Г. Эти соображения показывают, что задача Коши с данными вида (11) на характеристике является недоопределенной.
Слабый разрыв. Развивая предыдущее рассуждение, можно рассмотреть следующую ситуацию. Пусть на некотором решении Ф существует характеристика Г, делящая (локально) пространство Лп(х) на две части, 1 и 2, и пусть сужение данного решения на часть 1 есть Ф,. Спрашивается, можно ли восстановить решение Ф в части 2, зная только Ф]? Следует учесть, что решение Ф удовлетворяет условиям на характеристике Г, и потому по данным на Г все производные по нормали к Г в части
2 найти нельзя. Поэтому возможно, что в части 2 существует другое реше-нис Ф2 / Ф, непрерывно примыкающее на Г к решению Фь Отличие Ф2 от Ф в точках Г будет в том, что некоторые производные по нормали к Г будут на Г различными для Ф2 и Ф. Образно говоря, решение, составленное из Ф1 и Фг, вдоль характеристики Г имеет как бы излом. Это приводит к понятию слабого разрыва.
Определение 4. Гладкая гиперповерхность Г С Д”(х) называется поверхностью слабого разрыва решения Ф, если это решение, а также первые производные от него по касательным направлениям к Г всюду непрерывны (включая Г), а некоторые первые производные по нормали к Г, будучи непрерывны вне Г и односторонне непрерывны на Г, имеют в точках Г разрыв первого рода.
Предшествующее рассуждение показывает, что характеристика может быть поверхностью слабого разрыва (но может и не быть таковой). Обратное утверждение является точным.
Теорема 2. Если гиперповерхность Г является поверхностью слабого разрыва решения Ф, то Г — характеристика на решении Ф.
Доказательство. Пусть ? — единичный вектор нормали к Г. Рассуждая от противного, достаточно показать, что если в точках Г на решении Ф будет det А(?) / 0, то из системы (1) можно найти единственным образом первые производные всех функций ик но направлению ?, выразив их через значения самих функций и и их производных по касательным направлениям к Г. Это будет означать, что на Г разрыва нормальных производных нет, в противоречии с условием теоремы.
Пусть д/Ь\ есть дифференцирование по направлению нормали ? к Г. Для каждого направления 1 дифференцирование д/д1 можно разложить в сумму
где д/д.ч — дифференцирование в направлении, перпендикулярном ?, т. е. касательном к Г. В частности, для д/дх1 в качестве 1 надо взять орт оси хг, так что ? • 1 --- ?*, и это разложение дает
«-1.....">¦ <“>
В результате подстановки выражений (12) в уравнения (1) с учетом формул (4) получаются уравнения
В силу определения 4 правые части равенств (13) являются функциями, непрерывными всюду, в том числе и на Г. Так как матрицей из коэффициентов при дик/дА является характеристическая матрица А(?), то неравенство det А(?) / 0 позволяет определить все нормальные производ-
ные дик/дА однозначно.
Задача об отыскании характеристик сводится к построению решений уравнения (9) для одной искомой функции h(x), которое само есть уравнение с частными производными первого порядка. Общая теория таких уравнений (см. напр. [9]) устанавливает возможность их решения методом характеристик. В свою очередь, характеристики уравнения (9) называются бихарактеристиками системы (1) (в общем случае — на решении Ф) и описываются системой обыкновенных дифференциальных уравнений. Существенное свойство бихарактеристик состоит в том, что вдоль них, по определенным законам, распространяются слабые разрывы (скачки производных) решений гиперболических систем вида (1). Законы распространения слабых разрывов задаются специально выводимыми транспортными уравнениями; они имеют большое значение для понимания и анализа структуры решений системы (1). Некоторые детали упомянутых здесь построений будут изложены ниже на ряде примеров различных газодинамических моделей.
Характеристики уравнений газовой динамики. Предыдущие понятия и факты существенны для понимания качественных закономерностей движения газа и должны учитываться при анализе уравнений газовой динамики. Для отыскания характеристик исходную систему удобно взять в виде системы (3.15) или (3.16), для которой соответствующая форма записи (2) уже получена в виде (3.17). Из нее следует, что система уравнений газовой динамики является гиперболической. Для вычисления вводится следующая запись искомого нормального характеристического вектора;
(14)
соответственно обозначениям независимых переменных (?, х, у, z). Характеристическая матрица А'т + Ах? 4- Луг) + А2 С такова:
(РХ о 0 ? 0\
(15)
? г/ С Ьх О
здесь введено обозначение
Вычисление определителя с учетом обозначения (3.15) дает
подразделяются на два типа. Для наглядного представления об отличительных свойствах разных типов характеристик удобно вернуться в пространство R3(x) и представить каждую характеристику Г как двумерную поверхность C(t), перемещающуюся со временем в Л3(х). Пусть п есть орт нормали к C(t) и Сп — скорость перемещения поверхности в направлении нормали п (см. определение 4.3). Считая ? единичным вектором, можно написать формулу, аналогичную (4.2):
? = lcos(?,?) + nsin(?,?),
в силу которой для величины (16) получается выражение
X = cos(?,?) ¦+¦ u„sin(?,?).
С другой стороны, так же как и в § 4 (см. (4.7), для скорости перемещения Сп справедливо соотношение
¦ Сп = sin(?,t) + cos(?,i) = 0.
Следовательно,
Кроме того, из представления ? следует равенство
?2 + rj1 -f С2 = siir(?,0- (22)
Классификация характеристик. Предполагая скорость перемещения Сп конечной, можно дать следующую классификацию типов характеристик.
Первый тип: х = О или ип = Сп. Через такую характеристику газ не течет. Она отделяет одни частицы от других и, следовательно, в пространстве Л4 является геометрическим местом траекторий частиц. Характеристика этого типа называется контактной характеристикой (иногда говорят — энтропийной характеристикой).
Второй тип: х дается формулой (19). В силу (21) и (22) эта формула равносильна такой:
ип-Сп = ±с. (23)
Через такую характеристику газ течет, причем относительно характеристики по нормали к ней — со скоростью звука. Характеристики этого типа называются звуковыми характеристиками. Ясно, что скорость распространения звуковой характеристики, в направлении нормали к ней, по частицам газа равна скорости звука.
Слабый разрыв возможен как на контактной, так и на звуковой характеристике. Из предыдущего следует, что если слабый разрыв распространяется по частицам газа (т. е. если через поверхность слабого разрыва газ течет), то его скорость относительно частиц газа (по нормали к поверхности разрыва) всегда равна скорости звука.
Для отыскания уравнений характеристик в виде h(t, х) = const следует, согласно общей теории, подставить выражение (20) в уравнения (18) и (19). В случае контактных характеристик это дает уравнение
ht 4- uhx 4- vhy 4- whz = 0. (24)
В случае звуковых характеристик соответствующее уравнение таково:
ht + uhx 4- vhy 4- whz = ±cyjh\ 4- ti* 4 fi*. (25)
Каждое из этих уравнений, в которых г/„ и. w. с надо считать известными функциями переменных (х, t) (характеристики ищутся на данном решении!), представляет собой дифференциальное уравнение с частными производными первого порядка для одной искомой функции h. Для этих уравнений можно поставить задачу Коши: найти решение h(t, х), если задана функция
/t(0,x) =- /io(x). (26)
Из общей теории дифференциальных уравнений этого вида следует, что если функции и, v, w, с являются достаточно гладкими, то для любой непрерывной начальной функции (26) существует единственное решение (во всяком случае, в малом по t). С геометрической точки зрения задание начальных данных (26) эквивалентно заданию начальной двумерной поверхности в /?'5(х) с уравнением /io(x) = const, через которую и пройдут характеристики h.(t. х) = const. Для одной и той же начальной поверхности таких характеристик будет три: одна контактная — решение уравнения (24) и две звуковые — решения уравнения (25) для разных знаков в правой части.
Полезно отметить, что уравнения (24) и (25) компактно записываются с помощью оператора дифференцирования в частице (3.3):
Dh= 0, Dh ± е:j VЛ| = 0. (27)
В дальнейшем контактные характеристики будут обозначаться символом Со, а звуковые -- символами С л. или С- соответственно выбору знака в (27).
Бихарактеристики. Решение задачи Коши (26) может быть построено методом характеристик применительно к каждому из уравнений (27). Характеристики этих уравнений называются бихарактеристиками исходных уравнений газовой динамики. Соответственно типам характеристик уравнений газовой динамики различаются контактные и звуковые бихарактеристики. Согласно общей теории они представляют собой кривые в пространстве Д4(х, /,), вдоль которых координаты точки и производные функции h удовлетворяют определенным обыкновенным дифференциальным уравнениям, которые называются уравнениями бихарактеристик.
Уравнение (24) линейно относительно h. Поэтому его характеристики определяются просто как интегральные кривые системы
dx/dt = и.
Следовательно, контактные бихарактеристики совпадают с траекториями частиц в Я4(х, ?).
Для уравнения (25) характеристик С+ соответствующие уравнения бихарактеристик имеют вид
dx/dt ~~~ и + cV/i/|V/i;; dhj/dt = —Uj ¦ Vh — Cj'.Vh] (j — t, x, y, z),
где символами с нижним индексом j обозначены частные производные по указанным аргументам. Для характеристик С- в этих уравнениях следует заменить с на —с.
При отыскании бихарактеристик путем интегрирования их дифференциальных уравнений следует учитывать, что начальные данные для системы (28), включающие задание начальных значений всех производных hj, должны быть согласованы с исходным уравнением (25) и с условием /го(х) = const.
Характеристический коноид. Особый вид характеристической поверхности получается, если образовать геометрическое место всех бихарактеристик, выходящих из данной точки Р(хо,^о)- Чтобы представить совокупность всех таких бихарактеристик, необходимо учесть начальные данные к системе (28):
х(*о) = Хо, М*о) = hjO {j = t,x,y,z). Условие согласования (25) в этом случае имеет вид
(29)
![]()
где uo- wo, wo, со — значения известных функций в точке Р. Следовательно, если точка Р фиксирована, то в начальных данных (29) есть всего три свободных параметра, например hx„, hyu, hZu. Однако если задавать искомую характеристическую поверхность уравнением h(x, t) = 0, то функцию h достаточно определить с точностью до постоянного множителя. Можно заметить, кроме того, что замена h на ah (а = const) не меняет ни уравнений (28), ни условий (30). Это означает, что на самом деле в начальных данных (29) один из трех свободных параметров несуществен. Поэтому в результате решения задачи (28), (29) получится семейство кривых в R , зависящих от двух параметров, например г и s, с уравнениями вида
х = X(t, г, ,s), у — Y(t, г, s), г = Z(t, г, а).
(31)
Исключение из этих уравнений параметров (г, ,s) и дает искомую характеристическую поверхность /г(х, t) = 0.
Полученная этим построением характеристическая поверхность называется характеристическим коноидом с вершиной Р и будет обозначаться символом К(Р). Вблизи точки Р этот коноид имеет вид искривленного конуса с вершиной Р и состоит из двух полостей; одна из них, К+(Р), раскрывается в сторону dt > 0, а другая, К- (Р), — в сторону dt < 0. В целом форма характеристического коноида зависит от решения и может сильно искажаться вдали от его вершины Р.
В качестве примера легко построить характеристический коноид на постоянном решении, когда и uo -- const и с = со = const. В этом случае вторая серия уравнений (28) принимает вид dhj/dt = 0, откуда вдоль бихарактеристик hj h]0 = const для всех j. Поэтому первая серия
уравнений (28) интегрируется тривиально и дает в качестве (31) семейство прямых
х = х0 (и0cQVh0/\V/i0 )(t - to).
Исключение V/iq приводит к уравнению характеристического коноида на постоянном решении
jx — х0 uo(t - to)!2 = cl(t - to)2. (32)
На самом деле (32) есть уравнение характеристического конуса в пространстве R4{x, t) с вершиной Р(хо,*о). Сечение конуса (32) гиперплоскостями t = const представляет собой сферу в Д3(х), центр которой движется со скоростью uo по прямой х = хо + uo(t - to), а радиус растет (с ростом t) пропорционально времени и равен co\t — fo|. Эта сфера и представляет собой перемещающуюся в R3(x) характеристику C(t). Можно показать, что конус (32) аппроксимирует вблизи вершины Р характеристический коноид К(Р) на любом гладком решении уравнений газовой динамики.
Характеристическая форма уравнений газовой динамики. Для
определенности получаемых ниже условий на характеристиках уравнений газовой динамики уравнение характеристик Со будет записываться в виде h°(x,t) — const, а уравнения характеристик Cj- — в виде h^(x,t) = =¦- const.
На контактной характеристике (18) ранг матрицы Л(?) равен двум. Соответствующие левые собственные векторы Л — (Л1, Л2, А3, Л'1, Л5) оказываются такими:
Л (О, О, О, 0, 1), и еще два независимых вектора Ао и Аз определяются соотношениями
-г- r/A2 I (А3 =0, А4 = Аг> = 0.
Вектор Ai дает в качестве условия на С'о уравнение DS 0 (поэтому характеристики Со и называются «энтропийными»). Два оставшихся условия должны выражать факт коллинеарности вектора (?, q, Q - Vh° вектору pDu+Vp, что может быть записано в виде равенства нулю их векторного произведения. Следовательно, условия на контактных характеристиках Со таковы:
Dh° = 0, DS 0, V/i° х (pDu + Vp) = 0. (33)
Здесь последнее векторное условие на самом деле содержит лишь два независимых скалярных соотношения.
На звуковой характеристике С+ (соответствующей знаку «минус» в (19)) ранг матрицы Л(?) равен четырем. Соответствующий левый собственный вектор может быть взят в виде
Dh+ 4- c|V/i+1 = 0.
pc(V/i+ • Du — dV/)*, divu) — (|V/i+!Dp - cV/i+ • Vp) = 0.
Аналогичный вывод для характеристик С_ дает условия, получаемые из (34) заменой с на -с:
Dh~ - c|V/i” I = 0.
. _ (35)
pc(V/i -Du + c\Vh j divu) + (jV/i [Dp + cVh • Vp) = 0.
Полученная система из восьми (скалярных) дифференциальных уравнений (33), (34) и (35) для восьми искомых функций hP, /г4', /г~, и, и, го, р, S вместе с уравнением состояния р = f(p, S), образует характеристическую форму уравнений газовой динамики.
Каждое конкретное движение газа происходит в определенной обстановке, в некотором окружении газового потока другими физическими телами. Эта обстановка влияет на движение, формируя дополнительные условия, которым оно должно быть подчинено. С точки зрения дифференциальных уравнений это означает наложение соответствующих условий на искомое решение. К таким условиям предъявляется требование, чтобы с ними задача об отыскании конкретного решения была поставлена корректно: в определенном функциональном пространстве решение задачи должно существовать, быть единственным и непрерывно зависеть от дополнительных условий.
Особенно широко распространен способ задания дополнительных условий путем предписания значений искомых функций и их производных на некоторых границах, «краях» той области независимых переменных, в которой желательно определить решение. Такие задачи получили название краевых задач.
Ниже дается краткое описание постановок наиболее важных краевых задач для уравнений газовой динамики. Необходимо иметь в виду, что в полном объеме корректность большинства таких постановок, несмотря на всю их физическую естественность, к настоящему времени доказана лишь в очень редких случаях.
Задача Коши. Так называется задача, в которой дополнительное условие состоит в задании движения в некоторый начальный момент времени t. =¦ to (без ограничения to — 0). Состояние движеиия при t — 0 описывается набором функций — начальных значений основных величин
и(х, 0) = и0(х), р(х, 0) ^ Ро(х), р(х, 0) = Po(x), (1)
которые можно считать заданными на всем пространстве Я3(х). Задача Коши называется еще задачей с начальными данными (начальными условиями). В этих терминах формулируется следующая постановка задачи Коши: найти такое решение уравнений газовой динамики, которое при t = 0 принимает заданные начальные значения (1).
Задачу Коши можно рассматривать в различных функциональных классах, например (в порядке усложнения) в классе Сд аналитических функций, в классе бесконечно дифференцируемых функций, в классах Ck (или Нк) функций конечной гладкости, в классе С непрерывных функций, в классе измеримых ограниченных функций, наконец, в классах обобщенных функций.
Для того чтобы уравнения газовой динамики можно было рассматривать в классе С а, необходимо предположить, что входящая в термодинамическое уравнение состояния функция J(p, S) является аналитической. Кроме того, для простоты формулировки результатов удобно считать значения плотности в начальном условии (1) ограниченными от нуля положительной константой, а именно:
inf р0{х) - ро > 0. (2)
х? /¦?*
При этих условиях к системе (3.14) применима теорема Коши-Ковалев-ской, гарантирующая корректность постановки задачи Коши в классе аналитических функций.
Теорема 1. Для любых аналитических данных (1) существует единственное аналитическое решение системы уравнений (3.14), удовлетворяющее начальным условиям (1). Это решение определено в области вида Q = {х € Я3, j?j < а(х)}, где а(х) > 0 для любого х е Я3, и непрерывно зависит от начальных данных (1) в метрике пространства аналитических функций.
Доказательство теоремы Коши-Ковалевской можно найти, например, в [9]. ¦
В этой теореме можно заменить пространство Я3 любым множеством М С Я3, лишь бы данные (1) были аналитичны в окрестности М. Недостатком теоремы 1 является то, что она гарантирует существование решения задачи Коши только, как говорят, в малом по t в смысле ограничения |t < ci(x). Однако, как выяснится в дальнейшем, та-
кое ограничение необходимо присутствует даже при рассмотрении задачи в классе С. Это обстоятельство вызывает принципиальные трудности доказательства разрешимости задачи Коши в целом по t, которые для уравнений газовой динамики до настоящего времени не преодолены.
В классах функций конечной гладкости справедлив аналог теоремы 1, утверждающий корректность постановки задачи Коши в малом по t. Для приложений этих результатов к конкретным задачам особенно важно свойство единственности решения. Оно позволяет выяснить существенные структурные особенности движений газа.
Теорема об оценке решения. Пусть U = (и, v, w, p. S) есть некоторое решение системы (3.16), определенное при t > 0. Рассматривается ограниченная область О. С R4, граница которой состоит из трехмерной области и;о, лежащей в гиперплоскости t — 0, и из расположенной при ? > 0 кусочно-гладкой гиперповерхности Г, имеющей общую границу с областью шо- Пусть ? = (?, г/, (, т) есть вектор внешней нормали к Г. Утверждение о единственности решения U в области Q теено связано со свойством гиперболичности системы (3.16), которое проявляется в следующем наиболее существенном дополнительном предположении: в каждой точке гиперповерхности Г выполнено неравенство
г + + VI] -Г > С\/€2 + Г)2 + С2-
(3)
Требуемая для доказательства единственности решения оценка связана с рассмотрением сечений u)(t) области Q гиперплоскостями t = const > 0 (не путать с движущимся объемом!) и с введением для любой заданной на П вектор-функции W = {IV,) ее L-2-нормы !|W:fjj по таким сечениям, а именно:
![]()
U>(t)
где \W\2 В обозначении нормы j|W;i|| явно указывает
ся на ее зависимость от времени ?; как функция переменного t эта норма определена при t > 0. Следующая теорема формулирует основной результат в виде сравнительной оценки разности двух решений. Как и в теореме 1, здесь для простоты предполагается, что плотность р отграничена от нуля положительной константой (на самом деле, для решений класса С\ достаточно потребовать выполнения этого условия при t = 0), т. с. что
Теорема 2. Если решение U 6 С\ (Q) и область Q удовлетворяют условиям (3) и (5), то для любого другого решения U' ? С\ (Q) найдется Нонстанта к > 0, с которой для разности W = U' — U справедлива оценка
\\W-t\\ <fcl|W;0!| (t> 0). (6)
Доказательство, Для сокращения записи удобно ввести символический индекс j, принимающий значения t, х, у, г, и матричный дифференциальный оператор (здесь и ниже dt = d/dt и т. д.)
А ¦ д = A^dj = A*dt + Ахдх + Ауду + Агдг,
с которым система (3.16) или (3.17) переписывается в виде одного уравнения A(U) ¦ dU = 0. В результате вычитания этого уравнения из ему аналогичного для U' = U -f W получается уравнение вида
A(U) ¦ dW = B'W (7)
с матрицей В', определенной соотношением
B'W = {A{U) - A(U + W)) ¦ dU'.
Уравнение (7) умножается скалярно на вектор 2 W, и его левая часть преобразуется согласно тождеству
2W ¦ (AjdjW) = dj(W ¦ AjW) - 2W ¦ (djAJW),
справедливому благодаря симметричности всех матриц АК Получается соотношение
где В — 2В1 — 2OjA3. Это соотношение интегрируется по области fit, остающейся после отсечения от области Q. гиперплоскостью t = const, той ее части, которая лежит выше этой гиперплоскости. Применение теоремы Гаусса -Остроградского к интегралу в левой части полученного соотношения приводит к равенству
где Г(?) — часть гиперповерхности Г, заключенная между гиперплоскостя
ми t = const и t = 0. Здесь
есть матрица (6.15), введенная при вычислении характеристик системы (3.16).
Утверждается, что в силу условия (3) подынтегральная квадратичная форма W ¦ A(?)W неотрицательна, т. е. что
W-A(t)W\r>0 (9)
для любого вектора W = (а, 0, 7, 5, г). Действительно, вычисление дает
W • A(?)W = рХ(а2+02 + }
+2(а? + 017 + ~iQ)5 + Ьх52 + хе2,
где х = т + + VT) + WC- Но всегда (неравенство Коши)
а? + 0г) + 7С ^ - \/ос2 + 02 4- 72 • у/%2 + г)2 + С2,
и так как согласно (3) ? >cv^T г]2 -f С2 на Г, то
W ¦ А(€)И^|г > Ьу/Р + г,2 + С2{(рСу/а2 + /З2 + 72 - <5)2 + /?с3-2] ^ 0.
Далее, утверждается, что с некоторыми положительными константами М, m, N равномерно по области П справедливы неравенства
M\W\2 > W- А1\?^т\\У\2, \W ¦ BW\^N\Wf. (11)
Здесь первые два справедливы в силу ограниченности (ввиду условия (5)) и положительной определенности матрицы А1, а последнее — в силу того, что элементы матрицы В равномерно ограничены на Q (ввиду свойств нормального газа и принадлежности решений U и U' классу Ci(fi)).
Теперь видно, что благодаря неравенствам (9) и (11) из (8) следует неравенство (с учетом обозначения (4))
t
тгсНИ';*!!2 < M\\W:0\i2 + N J\\W:tn.'2dt\ (12)
справедливое для любого t ? (0,7 ), где Т = supi. Если положить
а
t
о
то (12) перепишется в равносильной форме
nvp'(t) < Mtp'(0) -+ Nip(t). (13)
Для решения этого дифференциального неравенства вводится функция y.’(t) — f(t)e\p( — tN/m), с которой оно принимает вид
^(0 < ЦУ(0)ехр (-Щ-)
и интегрируется с начальным условием ф{0) = 0:
< 77^(0) (l-exp^-^j .
Следовательно, Nip(t) < Л/-р' (0) (схр (/Л’/т) - 1), откуда видно, что правая часть в (13) удовлетворяет неравенству
М(р'(0) + Nip(t) < M'~p'(0)cxi>(tN/m).
Наконец, так как <p'(t) = ||W: t\\2 и ^'(0) — IjW; 0||2, то (6) следует из (13) с константой
к = (М/т)1/2 ехр(ТN/2т).
Я
Единственность решения задачи Коши. Из этой теоремы вытекает ряд важных фактов. Прежде всего, надо заметить, что если дано решение U класса Ci(t. ^ 0), то для фиксированной области uJo, в пространстве Л3(х) существует бесконечное множество областей с «основанием» uIq типа той области Q, которая рассматривается в теореме 2, т. е. таких, что на их границе Г выполнено неравенство (3). Пусть fi(u>o) есть объединение всех таких областей. Справедлива следующая теорема единственности решения задачи Коши.
Теорема 3. Если равенство U' = U выполнено на uJq при t — 0, то это равенство верно в любой точке (х, t) ? f2(u;o).
Тем самым единственность решения задачи Конги для системы (3.16) установлена в классе Ci. Область Q(luq) называется областью определенности решения задачи Коши начальными данными на uiq.
Можно показать, что если граница Г(а>о) области Щшо) является гладкой гиперповерхностью (класса Ci), то на ней (3) выполнено со знаком равенства, т. е. она есть характеристика системы (3.16) на решении U. В частности, если для некоторой точки Р = (х, t), где t > 0 существует характеристический коноид К...(Р), направленный в сторону dt < 0 (см. §6) и пересекающий гиперплоскость t, = 0 по области u)q, то этот коноид совпадает с областью f2(wo).
В этом случае область uiq = uiq(P) называется областью зависимости точки Р. Этот термин понимается в том смысле, что значение решения U (Р) определяется только его начальными значениями на области uJq(P) и не зависит от значений начальных данных вне этой области (для решений класса С\).
С другой стороны, если при t -= 0 взято некоторое множество Mq и в каждой точке Pq G Mq построен характеристический коноид К + [Pq), направленный в сторону dt > 0, то объединение К (Л/о) всех таких (открытых) коноидов будет таким, что значение решения в каждой точке Р е К (Mq) необходимо зависит от значений начальных данных на множестве Mq. Поэтому К (Л/о) называется областью влияния множества Л/о. В частности, область влияния точки Pq сеть коноид K+(Pq).
Существование конечных областей определенности, областей зависимости и областей влияния открывает возможность предсказывать во многих задачах газовой динамики качественный характер движения без его детального построения или расчета.
Обобщения задачи Коши. Начальные данные, т. е. значения всех искомых функций, можно задавать не только на гиперплоскости t — const. Если носителем начальных значений является некоторая гиперповерхность Е, то говорят о постановке общей задачи Коши. Корректность такой краевой задачи можно гарантировать в том случае, когда Е всюду пространству подобна, т. е. когда на Е выполняется строгое неравенство вида (3). Если же некоторые бихарактеристики лежат в гиперповерхности Е или даже только касаются ее, то общая задача Коши может быть некорректной. В каждом конкретном случае этот вопрос требует дополнительного исследования.
В смешанной задаче Коши наряду с начальными данными (например при t = 0) задаются граничные условия на некоторой времени подобной гиперповерхности Е, примыкающей к гиперплоскости t = 0. При задании дополнительных данных на Е необходимо принимать во внимание расположение Е не только относительно звуковых бихарактеристик, но также и относительно контактных бихарактеристик, т, е. траекторий частиц. В общем случае вопрос о корректности постановки таких задач довольно сложен и во многом до настоящего времени остается открытым. Один из важных частных случаев рассматривается ниже
Задача о поршне. Так называется специальная смешанная задача Коши, когда гиперповерхность Е является контактной характеристикой, т. е. когда всюду на Е выполнено равенство х = 0 или
(14)
т 4- -г vr] + г«С = 0,
где ? = (?, г), С) т) — вектор нормали к Е. В этом случае через ? газ не течет. Совокупность сечений a(t) гиперповерхности Е гиперплоскостями t= const можно интерпретировать как движущуюся в пространстве Я3(х) непроницаемую поверхность, которая оттесняет газ, расположенный от нее с одной стороны. Следовательно, a(t) действует на газ, как «поршень», форма которого меняется со временем.
Задача о поршне поставлена корректно, в частности, она разрешима в классах функций конечной гладкости (в малом по t) при выполнении некоторых условий согласования начальных данных с формой гиперповерхности Е вблизи поверхности <т(0), по которой Е пересекается с гиперплоскостью t — 0. Эти условия связаны с тем, что область определенности решения начальными данными при t = 0 в задаче

о поршне всегда отделена от Е звуко
Рис,
вой характеристикой Г, проходящей через <т(0) (рис. 1). Условия согласования нулевого порядка состоят в равенстве значений скорости и](Т(0) и скорости перемещения поверхности Е в точках <т(0) в направлении вектора и|(Т(о).
Условия согласования первого порядка состоят, сверх того, в равенстве
первых производных от этих скоростей (дифференцировать надо только вдоль Е) и т.д. При этом характеристика Г будет, вообще говоря, поверхностью слабого разрыва. Именно, если выполнены условия согласования только нулевого порядка, то вдоль Г могут быть разрывны первые производные основных величин; если выполнены условия согласования только первого порядка, то первые производные на Г непрерывны, но могут быть разрывны производные второго порядка и т. д.
Если же на <т(0) условия согласования нулевого порядка не выполнены, то непрерывного в замкнутой области решения задачи о поршне не существует и вместо него реализуется движение с особенностями типа ударных волн и центрированных волн разрежения.
Теорема единственности решения в классе С\ (с возможным слабым разрывом на Г) и здесь доказывается с помощью теоремы 2 об оценке разности двух решений, которая для задачи о поршне верна дословно. Для проверки этого утверждения достаточно показать, что квадратичная форма (10) неотрицательна на Е. Но ввиду (14) на Е верно равенство
W ¦ A(?)W = 2(q? + /Зг? + 70* + 52 / рс2,
и остается заметить, что компоненты а, /3, 7 вектора W имеют значения а = и' - и, /3 = v' - v, 7 = го' - го. Поэтому, если для решения U' на Е верно равенство — 0. то равна нулю и разность х! ~ X — + Р*) + 7С
на Е.
Задача о поршне является одной из наиболее распространенных краевых задач, встречающихся в приложениях. Например, ее частным случаем является задача о движении газа, формирующемся в результате перемещения в нем твердого тела или системы тел (вообще — твердых непроницаемых границ). При заданном законе движения тела положение его поверхности известно в любой момент времени. Эта поверхность является, таким образом, поверхностью типа ar(t), следовательно, контактная характеристика Е полностью задана.
Задача обтекания. Это частный случай задачи о поршне, выделяемый условием независимости сечения <j(t) от времени t. В этом случае границей является неподвижная непроницаемая поверхность а С Д (х), или, как говорят, обтекаемая потоком газа неподвижная твердая стенка. Если уравнение а есть Л(х) = 0, то граничное условие (14) записывается в виде
и • VAU = 0. (15)
К задаче обтекания сводится анализ течения, возникающего прн равномерном поступательном движении ограниченного тела в безграничной массе газа, покоящейся на бесконечности. Если скорость движения тела равна uo, то можно применить преобразование Галилея, перейдя в систему координат, движущуюся со скоростью uo. Тогда, в силу инвариантности уравнений газовой динамики (см. §8), система (3.16) не изменится, а тело станет неподвижным. Для определения движения газа получится задача обтекания данного неподвижного тела с дополнительным условием
| X \ —*'Xj
Задача со свободными границами. Контактная характеристика Е называется свободной границей, если на ней заданы значения давления р.
Такое задание делает смешанную задачу Коши переопределенной и для восстановления «равновесия» необходимо одно из условий снять. С точки зрения описания реальных движений газа естественно считать неизвестной саму гиперповерхность Е. Тогда задающая ее уравнение Л(х, t) = О функция h становится новым искомым элементом задачи.
Задачу со свободной границей можно интерпретировать как задачу
о поршне, форма которого заранее не задана, но на нем предписаны значения давления. Наиболее распространенной является такая постановка, когда заданное давление постоянно. В этом случае на искомой гиперповерхности Е с уравнением /г(х, t) = 0 должны быть выполнены граничные условия
/ii + uhx + vhy + whz =0, p = const. (17)
Пример такой постановки дает задача о волнах на поверхности водоема. Задачи со свободными границами очень трудны для анализа и к настоящему времени, за исключением простейших случаев, изучены слабо.
Задача Гурса. Существует несколько вариантов постановок краевых задач, когда все граничные данные задаются на характеристиках. Такие задачи называются задачами Гурса. Необходимость анализа задач Гурса возникает в вопросах примыкания решений, получаемых в разных областях с общей границей. При постановке какой-либо задачи Г’урса существенно учитывать условия на характеристиках (см. §6), которые накладывают ограничения на задаваемые значения основных величин. Ниже приводится пример такой постановки.
Пусть задана гладкая поверхность <то С /?3(х), расположенная на гиперплоскости /, = 0, и две гиперповерхности Г+ и Г_, содержащие (в качестве границы) поверхность <то и расположенные при t ^ 0. На Г+ и на Г_ заданы наборы U— (и+, р+, р+) и U" = {U~, р~, р~) значений основных газодинамических величин как функции класса Ci(T±). Предполагается, что со значениями U+ и U~ гиперповерхности Г+ и Г- являются звуковыми характеристиками, причем разных семейств (см. §6), и что условия на характеристиках Г± выполнены. Требуется определить решение в области ft, заключенной между Г+ н Г_.
Если решение этой задачи Гурса существует и принадлежит классу G'i(Q), то в области ft необходимо содержится контактная характеристика Е, проходящая через поверхность со и делящая ft на две части ft+ и ft_ так, что ft^ примыкает к Г+, a ft_ — к Г_. На Е, вообще говоря, образуется слабый разрыв, характер которого зависит от выполнения условий согласования граничных данных на поверхности сто- Здесь ситуация аналогична той, которая была описана при рассмотрении задачи о поршне.
Если условия согласования нулевого порядка не выполнены, то решение класса Ci(ft) не существует; в решении такой задачи Гурса необходимо должны быть особенности. С условиями согласования нулевого порядка задача Гурса поставлена корректно (в малом по t), причем вдоль Е может иметь место разрыв первых производных и т. д.
Задачи с особенностями. Нели начальные данные (1) в задаче Коши не являются непрерывными, то в сколь угодно малой окрестности момента t = 0 в решении могут появиться особенности, характер и поведение которых зависят от структуры функций (1). Разрывные начальные данные могут порождать движение с сильными разрывами -- ударными волнами или контактными разрывами. К этому приводят задачи о взаимодействиях различных движений газа между собой или с внешними телами (например, задача о воздействии ударной волны на твердое тело). Сюда же относятся модельные задачи о последствиях сосредоточенных воздействий на газ, когда в некоторых точках, на линиях или поверхностях задаются интегральные характеристики движения газа — поток массы (расход), сосредоточенный импульс или мгновенно выделившаяся энергия (например задача о сильном взрыве). Особенностью является также поведение параметров движения газа в бесконечно удаленной точке пространства Я3(х) или при t —> оо.
При анализе задач с особенностями необходимо опираться на общие закономерности, определяющие характер движения газа вдали от особенностей, учитывать области определенности, влияния и зависимости решения. В таких задачах зачастую бывает полезно обращаться к исходным интегральным законам сохранения, которые справедливы без ограничений для всех физически осмысленных движений газа.
Фундаментальную основу исследования какой-либо физической системы составляют ее свойства инвариантности относительно некоторых преобразований. В частности, в терминах инвариантности соответствующих объектов могут быть выражены основные законы природы (однородность и изотропность пространства-времени). Вообще, следует заметить, что свойства инвариантности используются в приложениях гораздо чаще, чем может показаться на первый взгляд.
Пусть, например, некоторый физический процесс однороден во времени; тогда можно искать его состояния равновесия. На языке дифференциальных уравнений процесса это означает, что уравнения не содержат явно времени t (оно участвует только в дифференцированиях типа du/dt; состояние равновесия не должно зависеть от времени t, и его уравнения получаются из исходных путем приравнивания нулю производных типа du/dt. В частности, так определяются стационарные точки в фазовом пространстве динамических систем. Теперь надо сделать важный шаг: заметить, что в этом описании стандартной процедуры содержится элементарный алгебраический факт, состоящий в инвариантности уравнений относительно группы переносов по времени, т. е. совокупности преобразований t —>t + а, где а — произвольный вещественный параметр, причем функции, описывающие состояние равновесия, образуют инвариантное решение исходных дифференциальных уравнений. Этот факт можно было бы игнорировать, как тривиальный (что часто и делается), если бы не возникал естественный вопрос: можно ли с помощью какого-то алгоритма распознать групповое свойство заданных дифференциальных уравнений? Ответ оказывается положительным, причем в его общей форме далеко не тривиальным.
Надлежащее обобщение ряда фактов, аналогичных упомянутому выше, привело к созданию теории группового анализа дифференциальных уравнений, основы которой были заложены более 100 лет тому назад норвежским математиком Софусом Ли. Эта весьма общая и, в известном смысле, законченная теория дает алгоритмы выявления в полном объеме свойства инвариантности любых дифференциальных уравнений и использование этого свойства для отыскания классов частных решений путем упрощения исходных уравнений за счет понижения размерности (уменьшения числа независимых переменных).
Группа Галилея. В данном параграфе описывается групповое свойство инвариантности уравнений газовой динамики; его применение к построению классов частных решений излагается в § 12. Исходные уравнения газовой динамики здесь удобно взять в следующем виде:
ut + и • Vu + ^Vp pt + u • Vp + pdivu pt-r u • Vp + pc2 div u
0,
0,
0,
(1)
где pc2 рассматривается как заданная функция переменных р, р, а именно:
рс2 = а(р,р). (2)
Групповым свойствам системы (1) называется ее свойство оставаться неизменной (инвариантной) при некоторых преобразованиях всех участвующих в (1) переменных
<т — (f, х, у, z, и. V, w, р. р).
рассматриваемых как координаты точки пространства Z = Я9(<т). Если / : Z —> Z есть такое преобразование, то образ точки а е Z дается формулой а' = f{cr). Еслн при преобразовании / система (1) не меняется,
то говорят, что (1) допускает преобразование /. Задача описания группового свойства системы (1) состоит в определении всех допускаемых ею преобразований.
Эта задача имеет алгоритмическое решение, сводящееся к отысканию однопараметрических локальных групп JJu G1 преобразований пространства Z. Каждая группа G1 задается законом преобразования
классу Соо • Согласно (4) групповой операцией является композиция преоб
разований; при этом обратный элемент есть преобразование, обратное к (3), а именно; а = /(V, -а). В полном объеме решение задачи об определении всех групп G1, допускаемых системой (1), изложено в [5], а здесь приводится лишь окончательный результат, который можно проверить непосредственной подстановкой. Группа G1 преобразований (3) будет обозначаться символом G1{f)
Система (1) инвариантна относительно следующих групп G1(fl) (штрихом обозначены координаты преобразованной точки а'; переменные, которые явно не написаны, в каждом случае преобразуются тождественно, например: х' = х, р' = р и т. д.):
/1 : х' = х + а :
/3 : z' = г + а ;
f4,.x' = x + at, и' = и + а ;
/° : у1 = у + at, v' = v + а;
( I
/6 : z = г + at, w' — w + а\
f7:y' + iz' = (у + iz)eta, v' + iw' = (г» + iw)em\
/8 : z’ -(¦ ix' = (z + ix)eta, w' + in' = (w + iu)ela:
fg : x’ -(- iy = (:r 4- iy)ela, u' -+- iv' = (u + iv)eia\
Каждое из преобразований f1, /2. f'K /10 называется переносим (говорят также трансляцией или сдвигом), а именно fl — перенос по х, f~ — по у и т. д. Преобразования /4. /°, /6 называются галилеевыми переносами, /4 -- по х и т.д. Преобразования /7, /8, /9 называются вращениями, причем /' — вращение вокруг оси х, /8 — вокруг оси у и /® - вокруг оси г. Для краткости здесь они записаны в комплексной форме и для получения формул преобразования каждой координаты надо сравнить действительные и минимые части.
Если взять два каких-либо преобразования (5) с разными значениями параметров, например /х с а и /' с 6 и составить их композицию, то получится некоторое комбинированное преобразование, точнее, двухпараметрическое семейство преобразований, также допускаемых системой (1). Неограниченное продолжение такого комбинирования приводит к группе Ли преобразований пространства Z, порожденное преобразованиями (5). Она называется группой Галилея. Общий элемент группы Галилея есть преобразование вида (3), где скалярный параметр а заменен векторным а = (а1, .... а10). Поэтому группа Галилея является 10-параметриче-ской группой преобразований и обозначается символом G10. Итак, система (1) допускает группу Галилея G10, порожденную однопараметрическими группами (5).
Для построения общего группового преобразования (общего элемента группы Галилея) достаточно взять каждое из преобразований (5) со своим значением параметра, например 1° -•¦ с параметром а1, 2° — с параметром а2 и т.д., 10° - с параметром а10, и составить компо
зицию этих десяти преобразований. В результате получится преобразование вида (3^, но в нем уже параметр а будет векторным параметром а — (а1, а2, ..., аш). Следовательно, группа Галилея является 10-па-раметрической группой преобразований и потому обозначается символом Сю- Итак, система (1) допускает группу Галилея Сю, порожденную одиопараметрическими группами (5).
Преобразования растяжения. Кроме того, система (1) может допускать преобразования растяжения всех переменных, которые следует искать в виде
t1 = at. х' = 6х. u' - mu, р' = кр, р = 1р. (6)
где положительные параметры а, Ь, т, к, I подлежат определению. При преобразовании (6) первые производные преобразуются по простому правилу: каждая производная умножается на частное от деления параметра-множителя функции на параметр-множитель независимой переменной, например:
= р'х, = 1-рх,. ¦.
Требование инвариантности системы (I) относительно преобразования (6) сводится к сравнению множителей, появляющихся в отдельных слагаемых левой части каждого уравнения. В результате получается система уравнений относительно параметров а, ..., I и требуется найти ее общее решение.
Для первого уравнения (I) эта процедура дает соотношения
т _ а ~~ b kb'
откуда b = am и I = кт2. С учетом этих соотношений второе уравнение (1) оказывается инвариантным без дополнительных ограничений. Наконец, третье уравнение инвариантно, если и только если функция (2) удовлетворяет функциональному уравнению
а(крЛр) = 1а(р,р) (7)
при любых значениях параметров /си/. Ясно, что функция а общего вида может удовлетворять соотношению (7), только если к = I = 1. В этом случае будет т = 1 и Ь — а. Поэтому с функцией а общего вида система (1) допускает только одну группу G1 растяжений:
/п : = at, х' = ах. (8)
Добавление к (5) преобразований (8) расширяет группу Галилея до 11-параметрической группы G11. Итак, группа G11 допускается системой уравнений газовой динамики для любого нормального газа.
Возможные дальнейшие расширения допускаемой группы связаны с решениями функционального уравнения (7). В частности, ему удовлетворяет при всех к и / функция а = ур с любой постоянной В этом случае из (2) получается с2 = 7р/р, г. е. известное соотношение (2.20) для политропного газа. При этом пять параметров а. ..., I связаны только предыдущими двумя соотношениями и, следовательно, три из них свободны, например а, т, к. Это дает еще две независимые от (8) допускаемые группы растяжений:
j»12 i / f 2 f : х = ах, и -- аи, р -- а р\
,13 , (9)
/ : р = ар р ¦- ар.
Тем самым в случае политропного газа допускаемая группа расширяется до 13-параметрической группы G13.
Необходимо учитывать, что в записи (8) и (9) групп G1 растяжений групповой параметр меняется в интервале (0,-(-ос) и что групповое свойство, вместо соотношений (4), описывается соотношениями /(<т, 1) = сг, /(/(сг, a),b) = f(a,ab). Для возвращения к описанию вида (4) достаточно сделать в (8) и (9) замену параметра а —> ехр а.
Замечательно, что для политропного газа с ¦у = 5/3 система (1) допускает еще одну группу G1, которую трудно «угадать» или найти путем общих рассуждений; для этого надо применить технику группового анализа, изложенную в [5],
/14;*' = Т^ x' = T^t' =
р' = (1 — at)3p, р = (1 - at)5p.
Этот результат справедлив для размерности физического пространства п = 3. Для уравнений вида (1) произвольной размерности п аналогичное преобразование допускается при 7 = (п + 2)/п. В частности, для плоскопараллельных движений оно существует при 7 = 2 и для одномерных движений с плоскими волнами — при 7 = 3.
Максимально широкая группа. Возникает вопрос: нет ли других, не сводящихся к комбинациям перечисленных выше, групп G1, допускаемых системой (1)? Оказывается, что нет: приведенными выше преобразованиями групповое свойство уравнений газовой динамики исчерпывается.
Теорема 1. Максимально широкая локальная группа Ли преобразований, допускаемая сист&иой уравнений газовой дииа,хшки (1), совпадает с G11 в случае произвольной функции (2), совпадает с G в случае политропного газа при любом показателе адиабаты 7 и совпадает с G14 в случае 7 = 5/3 (для трехмерных движений).
ДОКАЗАТЕЛЬСТВО этой теоремы можно найти в [5]. ¦
Действие на множестве решений. Групповое свойство вносит в множество всех решений системы (1) алгебраическую структуру, определяемую следующим фактом: под действием любого допускаемого преобразования вида (3) каждое решение системы (1) переходит в некоторое решение этой же системы. Другими словами, допускаемая группа, например G11, действует на множестве решений системы (1).
Этот факт позволяет производить новые решения из уже известных. Алгоритм преобразования решений в решения состоит в следующем. Пусть
U = u0(x, t), р = Ро(х. t), р -- ро(х. ?) (11)
есть некоторое решение. Его надо записать с преобразованными (штриховыми) переменными:
и' = и0(х',?')> Р' = Ро(х',0. Р' = А)(х',0,
сделать подстановку выражений для штрихованных переменных согласно формулам преобразования вида (3) и затем разрешить полученные соотношения относительно переменных и, р, р. В результате получится набор функций
U = Ua(X,f), p = pa(x,f), p = pa(-X,t), (12)
которые образуют новое решение, зависящее от параметра а.
Например, с помощью галилеева переноса /4 решение (11) преобразуется в решение
и = u0(x + ae\t, t) - аеь р = ро(х + ae\t, t), р = p0(x4-aeit,t):
где ei — орт направления оси х.
Подгруппы и инварианты. Допускаемые группы эффективно используются для построения классов точных (частных) решений. Идея состоит в присоединении к системе (1) дополнительных соотношений, вводимых с помощью инвариантов подгрупп Н С G.
Напомним, что подмножество Я С G называется подгруппой группы G, если вместе с любыми преобразованиями / и /', принадлежащими Я, обратное преобразование /_1 и композиция /о/' также принадлежат Я. Ясно, что любая подгруппа Я группы G, допускаемой системой (1), является группой, допускаемой (1) и что любая группа Я, допускаемая системой (1), необходимо есть подгруппа наиболее широкой группы G, допускаемой этой системой.
Определение 1. Не тождественно постоянная функция J(cr) называется инвариантом группы Я преобразований вида (3), если для всех / 6 Я выполняется равенство
J(f(a)) = J(a) . (13)
Вообще говоря, группа Я имеет бесконечное множество инвариантов, так как любая функция от инвариантов есть снова инвариант. Это множество описывается понятием базиса инвариантов.
Определение 2. Набор инвариантов J = .... Jq) называется ба
зисом инвариантов группы Я, если функции Jfc(cr) в совокупности функционально независимы и если любой инвариант 1С(а) группы Я является функцией от инвариантов J\, .... Jq:
K(a) = F(.h(a),...Jq(a)) . (14)
Если ввести координаты вектора а 6 Z, положив а = (сг1, ..., as) (для системы (1) s — 9), то всегда будет q < s, а условие функциональной независимости инвариантов выразится через q х ,ч-матрицу Якоби (dJk/dtji) равенством
с некоторыми, заранее не фиксированными функциями Fp. В результате дифференцирования соотношений (16) по всем независимым переменным t, х (при этом и, р, р считаются функциями от t, х) получается дополнительная к (1) система дифференциальных уравнений, связывающая производные ut,ux, ..., рг, присоединением которой к (1) образуется переопределенная система Е дифференциальных уравнений для искомых и, р, р. Для того чтобы система Е имела решения, функции Fp, в свою очередь, должны удовлетворять некоторым новым дифференциальным уравнениям (условиям совместности уравнений Е), совокупность которых называется факторсистемой.
С любым решением факторсистемы уравнения системы Е совместны и, тем самым, имеют решения. Такие решения называются инвариантно-групповыми решениями, произведенными группой Н или, коротко, Н-решения-ми. Ясно, что это будут не все решения системы ( I), они образуют лишь определенный класс решений, характеризуемый тем, что в нем искомые функции связаны инвариантными соотношениями (16).
Тем самым групповое свойство уравнений газовой динамики (1) открывает широкую возможность построения классов точных частных решений системы (1), гак как допускаемые ею группы G11- Gl i имеют бесконечное множество подгрупп.
1. Поле скоростей задано формулой
u — x/t + a. (а = const).
Найти форму и положение при любом t того движущегося объема, который при t — 1 является шаром радиуса R с центром х — хо.
2. Показать, что в непрерывном движении г аза справедлив интегральный закон сохранения энтропии движущегося объема
ш(()
3. Исходя из абстрактного закона сохранения в форме (4.3), дать строгий вывод балансовых уравнений (1.4).
4. Доказать справедливость закона сохранения момента импульса (1.5) для непрерывных движений и для движений с сильным разрывом.
5. Показать, что в идеальном газе квадрат скорости звука выражается через внутреннюю энергию е = %(Т) формулой
с2 = RT{\+ R/g'{T)).
6. Показать, что внутренняя энергия е = ?(V,T) имеет вид
${V,T) = gl(V) + g-2{T),
если и только если давление р = p(V,T) есть линейная функция температуры Т.
7. Доказать формулу Эйлера (3.5).
8. Показать, что в лагранжевых координатах (хо,<)> введенных согласно (1.1) и (1.2), система уравнений газовой динамики (3.11) принимает вид
д(рб) _ п м*ди , ij?P=n dS-n дМ _ ди dt ’ dt Р 9х0 dt ’ dt <Эх0
с матрицей М — дх/дхо, сопряженной матрицей М* и rt — ciet М.
9. Показать, что скорость перемещения в направлении нормали п поверхности, заданной уравнением F(x,t) = 0, равна
Dn = Fl
n-VF'
10. Пусть функция е = e(V.р) удовлетворяет неравенству ер ^ bV (b — const
для всех р и V < Vo- Показать, что вдоль адиабаты Гюгонио будет lim V =
р — СО
11. Показать, что скорость перемещения ударной волны Dn строго монотонно
возрастает вместе с силой разрыва [р], причем D„ —» оо при [р) —* ос.
12. Пусть Н1 — адиабата Гюгонио с центром (V'i, pi). и пусть точ-
ка (V2,p2) е Я,. Выяснить взаимное расположение кривой Hi адиабаты S = S2, хорды с концами (Ц,pi) и (Уг.рг) и адиабаты Гюгонио Н-2 с центром (И^рг).
13. Выяснить, когда достигается большая плотность: при сжатии одной ударной волной, повышающей давление от pi до рз, или при последовательном сжатии двумя ударными волнами, если в первой давление повышается от pi ло pi < рз, а во второй — от Р2 до рз.
14. Показать, что в случае слабой ударной волны справедлива оценка (предполагается, что Dn > un,)
Ищ "Ь (-1 11п2 т- ^2 ~ 0([р] ).
15. Проверить, что в уравнениях (6.33)-(6.35) характеристической формы уравнений газовой динамики искомые фуикпии u, р, S дифференцируются только в касательном направлении к соответствующей характеристике.
16. Пусть начальные значения при t = 0 некоторого непрерывного решения уравнений плоскопараллельного движеиия (12.7) (см. пример 12.2) постоянны в квадрате {|ж| ^ 1, \у\ ^ 1}. В пространстве событий R3(x, у, t) найти область, в которой решение постоянно.
17. Для уравнений плоскопараллельного движения (12.17) (см. пример 12.2) построить характеристические поверхности С± на решении и = 0, с = со (покой), проходящие через кривую, образованную лучами {ж = —1, 0 ^ у < оо}, {0 ^ х < ос, у = —1} и дугой окружности {х2 у2 —¦ 1, X ^ 0, у ^ 0}.
18. Показать, что величины Vp и div и при переходе через слабый контактный разрыв меняются непрерывно.
19. Непосредственной подстановкой (заменой переменных) проверить, что система уравнений (8.1) допускает каждое из преобразований (8.5) /’ -/ °.
20. Проверить, что функции
х ¦+- F(y) 1 с с
и=---, v = w = 0, Р=у. S = So,
где So = const и F(y) — произвольная функция, дают точное решение уравнений газовой динамики (3.11). Найти общий вид решения, получаемого из данного преобразованиями группы G2, порожденной преобразованиями (8.5) /9 и (8.8) /п.
21. Показать, что система уравнений (8.1) в случае нолитронного газа допускает преобразование (8.10) только при -у — 5/3.
