Поток через нкт и выкидные линии
Течение жидкости в пласте и заканчивании обсуждалось в предыдущих главах. Тем не менее оценка производительности скважины не закончена до тех пор, пока не принято во внимание влияние НКТ и выкидных линий совместно с эффектами, рассмотренными в предыдущих главах. В данной главе рассматривается течение жидкости в системе трубопроводов скважины. Нашей целью является рассчитать потери давления в НКТ или выкидных линиях как функцию притока разных фаз. В большинстве нефтяных и газовых скважин имеет место двух- и трехфазный (нефть, газ, вода) поток по системе труб. Поэтому ниже приведено несколько основных положений теории многофазного потока в трубе. Данная теория является продолжением теории однофазного потока.
Уравнение градиента давления при установившемся потоке для однофазной несжимаемой жидкости может быть записано следующим образом:
psin0+——нр———. (4Л)
4cd zMdL)
где dp/dL- падение давления по единице длины трубы (psi/фут),
р - плотность жидкости (фунтов/фут3),
0 - угол наклона трубы,
v - скорость движения жидкости (футов/сек),
/- коэффициент трения, d - внутренний диаметр трубы (футов),
а - поправочный коэффициент для компенсации колебаний скорости по сечению трубы. Он изменяется от 0,5 при ламинарном течении до 1,0 при полностью турбулентном течении.
Данное уравнение применяется для любой жидкости на установившемся течении жидкости. Необходимо отметить, что градиент давления в данной формуле является суммой трех составляющих.
Гидростатический градиент (р sin 0).
Градиент трения
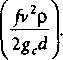
( j Л pv dv
Градиент ускорения „ м
\ оС /
Коэффициент трения/при ламинарном одно фазном течении рассчитывается с использованием следующей аналитической зависимости:
где Nrj- число Рейнольдса, определяемое как
![]()
где \1 - вязкость текущей жидкости.
При турбулентном течении, когда число Рейнольдса превосходит 2000, отношение между коэффициентом трения и числом Рейнольдса носит эмпирический характер. Данное отношение очень чувствительно к характеристикам стенок трубы и является функцией относительной шероховатости Eld, где е определяется как абсолютная шероховатость трубы. Наиболее распространенный метод расчета коэффициента трения при турбулентном течении - это формула Колербрука (Colerbrook, 1938):
f
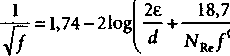
¦оз '
/
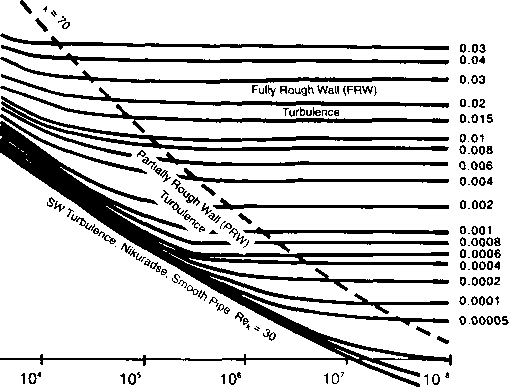
Заметьте, что коэффициент трения/присутствует в обеих частях уравнения, что требует применения метода подбора. По этой причине, решение этих уравнений, предложенное Муди (Moody, 1944) в графической форме (диаграммы Муди), широко применяется при расчете коэффициента трения. Диаграммы Муди представлены на рис. 4.1. Формула, предложенная Джейном (Jain, 1976) воспроизводит уравнение Колербрука,по существу, на всем спектре чисел Рейнольдса и интересующих нас значений относительной шероховатости в следующей форме:
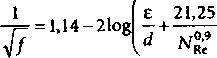
г 0,9 Re У
Выбор абсолютной шероховатости трубы часто является трудной задачей, так как шероховатость зависит от материала трубы, процесса изготовления, возраста, типа жидкостей, текущих через трубу. Стеклянные трубы, а также большое количество пластиковых труб могут считаться гладкими трубами. Для скважинных НКТ обычно используется шероховатость 0,00005 фута. Для выкидных линий шероховатость лежит в пределе от 0,00015 фу-
та для новых, чистых труб до 0,00075 фута для очень грязных труб. Многими исследователями применяется вполне приемлемая процедура, целью которой является подогнать абсолютную шероховатость для совпадения с измеренным градиентом давления.
| 0.025 ¦ | |
|
0.0225 ¦ | |
| 0.020 * | |
| 0.0175 * | |
| 0.015 - | |
|
0.014 • | |
| 0.013 . | |
| 0.012 • | |
| 0.011 - | |
|
О 0.010 - | ¦ Л |
| 3 0.009 - | |
| « 0.008 * | % |
| ? 0.007 * | \ |
| ? 0.0065 • | |
| .Я 0.006 • | |
| и" 0.0055 ¦ |
|
| 0.005 • | |
| 0.0045 • | |
|
0.004 * | |
| 0.0035 - |
|
| 0.003 • | |
| 0.0025 * | |
|
0.00225 " 0.002 | —1— |
103
о
с
-С
О)
3
о
сс
«
ф
(Г
Число Рейнольдса, Re =
DVP
0.00001
k
o’ 0 000005 O' O-OOOOOJ
Коэффициент трения труб при турбулентном течении (Modified after Moody L.F., Trans. ASME, 66, 671, 1944)
Рис. 4.1.
Однофазный поток газа по трубе
Для потока газа или сжимаемой жидкости плотность жидкости есть функция давления и температуры. Уравнение 4.1 энергетического баланса может быть модифицировано, чтобы принять во внимание зависящую от давления и температуры плотность. Уравнение энергетического баланса для установившегося течения записывается как
Потеря давления, возникающая вследствие трения, использует фактор трения Муди f Слагаемым кинетической энергии (vdv) / gc можно пренебречь для всех случаев потока газа, как было показано Азизом (Aziz, 1963). Применяя закон реального газа, выражение для плотности газа р принимает следующий вид:
/ \ фунтов фут3
Из.
zT
53,24Tz dp . ajI fv2dL Л (4.3)
Перепишем уравнение 4.2:
-- +smOdL +--= 0.
Скорость газа при соответствующих давлении и температуре:
Tzq
v = 0,4152—7, pd2
где q - дебит газа, млн футов3/день,
v - скорость газа в трубе, футов/сек, d - диаметр трубы, фут,
- плотность газа (воздух = 1). Подставляем выражение для скорости в уравнение 4.3:
53,24-Гг
^+sin8 dL +0,002679^
Это наиболее практичная форма уравнения энергетического баланса, используемая при расчетах течения газа. Коэффициент трения рассчитывается с использованием диаграмм Муди (рис. 4.1) или любой формулы из представленных ранее как функции числа Рейнольдса и относительной шероховатости. Для установившегося течения газа число Рейнольдса определяется как
N«‘=1671-^>
где вязкость газа (i. дается в сантипуазах. Для диаметра, данного в дюймах
АЛ, =20050—^
Определение статического забойного давления
(4'4)
Пренебрегая потерями из-за трения и интегрируя соответственно по давлению и длине, получим
![]()
Pbh Pwh^
(4.5)
- статическое забойное давление, psia, pwl, - статическое давление на устье, psia,
где
Т - средняя температура между поверхностью и забоем, z - фактор сжимаемости при средних давлении и температуре.
Уравнение 4.5 широко используется при расчетах веса колонны газа. Решение данной формулы ищется методом итерации, так как z является функцией давления. Чтобы рассчитать забойное давление при известном на поверхности давлении и температуре, его необходимо предположить. Потом при известном геотермальном градиенте считаются среднее давление и температура, откуда определяется z-фактор. Теперь, используя уравнение 4.5, считается новое значение забойного давления. Если рассчитанное таким образом рьи не совпадает с предположенным забойным давлением, то итерационная процедура повторяется до совпадения предполагаемого и рассчитываемого значений.
Определение динамического забойного давления
Календер и Смит (Cullender, Smith, 1956) предложили простой метод расчета динамического забойного давления по формуле 4.4. Календер и Смит перегруппировали уравнение 4.4 и проинтегрировали давления по всей длине трубы:
/ \

(4.6)
Уравнение 4.5 может быть решено при помощи любого численного метода интегрирования, такого, например, как правило Симпсона. В уравнении 4.6 использован коэффициент трения Муди и диаметр в футах. Краткий вывод формулы 4.6 приведен в Приложении Д.
Уравнение энергетического баланса для многофазного потока очень
похоже на уравнение для однофазного потока. Различие в том, что при многофазном потоке используется скорость и свойства смеси вместо одной фазы. Однако определение смеси становится сложным. Качественный состав смеси меняется по диаметру трубы в связи с наклоном трубы, температурой, давлением и т.д., главным образом вследствие проскальзывания между фазами. В отсутствие проскальзывания свойства смеси задаются как средневзвешенная часть смеси по объему компонента в смеси. Например, если смесь содержит 50% нефти и 50 % газа на входе в трубу, тогда средняя плотность смеси
Pm = ро*0,5 + р/0,5
Тем не менее такое осреднение практически неприменимо в случае многофазного потока в трубах. Когда газ и жидкие фазы текут в трубах, вследствие плавучести или разницы плотностей между фазами, газовая фаза стремится приобрести направленную вверх относительно жидкой фазы скорость. Таким образом, в случае направленного вверх двухфазного потока (добыча) газ набирает скорость по направлению движения, в то время как жидкость скользит вниз или теряет скорость. Для удовлетворения закона сохранения массы сечение трубы, занятое газом или жидкостью, постоянно меняется. Часть сечения трубы, занятая жидкостью в любой точке мультифазного потока по эксплуатационной колонне называется объемным содержанием жидкости (Hi). Оставшаяся часть сечения трубы, занятая газом, называется газовой полостью. В мультифазном потоке действительные свойства смеси считаются как взвешенная сумма свойств разных фаз в объеме жидкости. Так объемное содержание жидкости в трубе постоянно меняется, то и скорости фаз меняются. В данном разделе представлено определение некоторых важных свойств потока (таких как объемное содержание жидкости) и разных значений скоростей, используемых при расчетах многофазных потоков.
В двухфазном потоке газ/жидкость вследствие разности плотностей фаз газ стремится двигаться вверх, в то время как жидкость стремится двигаться вниз относительно газовой фазы', вызывая проскальзывание между фазами. Как результат при течении, направленном вверх, жидкость теряет скорость, что приводит к увеличению доли сечения, занимаемой жидкостью при постоянной объемной скорости потока. Подобный феномен проскальзывания приводит к тому, что текущая жидкая составляющая в трубе отличается от объемного содержания жидкости на входе в трубу. Текущая жидкая составляющая называется объемным содержанием жидкости (ОСЖ). ОСЖ определяется как отношение объема сегмента трубы, занимаемого жидкостью, к полному объему сегмента трубы:
объем жидкости в сегменте трубы 1 объем сегмента трубы
ОСЖ изменяется от нуля при однофазном течении газа до единицы при однофазном течении жидкости. Наиболее распространенным методом измерения ОСЖ является изоляция сегмента трубы двумя клапанами и физическое измерение пойманной жидкости. Существуют различные механистические и эмпирические модели для прогнозирования ОСЖ. Оставшийся объем сегмента трубы занят газом, объемное содержание газа (ОСГfHg)
Hg=l-HL.
ОСЖ6П иногда называют содержанием жидкости на входе в трубу, определяется как отношение объема жидкости в сегменте трубы к объему сегмента трубы, который существовал бы, если бы жидкость и газ двигались со скоростями, которыми они обладали на входе в трубу, отсутствие проскальзывания. ОСЖ6П может быть рассчитано напрямую из известных дебитов газа и жидкости:
где qinqg- дебит жидкости и газа на поверхности соответственно. ОСГбП определяется как п
\=\-К =
Очевидно, что разность между ОСЖ и ОСЖ6П является мерой степени проскальзывания между жидкостью и газовой фазой. Так как ОСбП - параметр, определенный аналитически, он часто используется как независимая переменная для определения важных параметров двухфазного потока, таких, как ОСЖ.
Многие соотношения для двухфазного потока основываются на таком параметре, как приведенная скорость (ПС). ПС жидкой фазы определяется как скорость, которую имела бы жидкая фаза, если бы она текла по всему сечению трубы.
Таким образом, приведенная скорость жидкости а газа
^SG =
tr~.----
f тде qLuqg- дебит жидкости и газа соответственно, А - поперечное сечение трубы. Действительные скорости фаз определяются как:
I Vi,=—,
"1'' ”’F1-
V.
н
S
где VLHVg- скорости жидкости и газа при их течении в трубе.
Смешанная скорость vm, используемая в расчетах двухфазного потока: vm ~ VSL + VSG-
Это очень важный корреляционный параметр при двухфазных расчетах.
СП определяется как разность между действительными скоростями газа и жидкости: vs = vg-vL
Суммарная плотность жидкости может быть рассчитана по известным плотностям нефти и воды и их дебитам, если предположить, что нет проскальзывания (скольжения) между фазами:
РL ~ Рofo ^ Рwfw*
где
у Чо ч'0в„ _1
Чо +4w ЧоВо +ЧоК j + WOR
fw ~ 1 — fo>
WOR = отношение - вода/нефть = (q'w) / (q'„), q'(0iW) = дебит нефти и воды (СТБ/день)
Для расчета плотности двух фаз необходимо знать ОСЖ. При двухфазном потоке для расчета плотности двух фаз различными исследователями используются три различные формулы:
Ps=PiW/.+PA,
Pn=PiA?.+PA’
РлЛ1 Pg^g
P‘-"ST н, •
ps используется большинством исследователей для определения градиента давления, возникающего из-за изменений при подъеме. Некоторые корреляции основаны на предположении отсутствия скольжения и, таким образом, используют р„ как плотность двух фаз. р*. используется рядом исследователей, например Даклером (Dukler, 1969), для определения плотности смеси, используемой в слагаемом потерь на трение и числе Рейнольдса.
Вязкость водонефтяной смеси обычно считается с использованием водонефтяного отношения в качестве весового множителя:
M-L ~ №-ofo + Ци'/и"
Следующие уравнения используются для расчета вязкости двухфазной смеси,
Ц„ = ц.? Xi + [ig Xg, вязкость смеси без скольжения,
M-s= вязкость смеси со скольжением.
Корреляции для межфазных напряжений на границе раздела вода/газ при различных давлениях и температурах получаются на основе лабораторных измерений или PVT-корреляций. Межфазное напряжение между газом и нефтью зависит от плотности нефти, температуры и растворенного газа наравне с другими параметрами.
Когда жидкая фаза содержит воду и нефть, используются те же весовые множители, что и при расчете плотности и вязкости:
&L ~ G0f0 + Owfw где О0 - поверхностное напряжение нефти,
Ow - поверхностное напряжение воды,
fo ,fw ~ фракции нефти и воды соответственно.
Уравнения градиента давления при многофазном потоке
Уравнение градиента давления для однофазного потока может быть расширено для многофазного потока путем замены свойств потока и жидкости на свойства смеси. Таким образом,
V sine + + PmVm(dVm
], (4.7)
dL
где g - витационная постоянная,
gc - гравитационный переводной коэффициент, dp /dL - перепад давления (градиент давления), т - свойства смеси,
0 - угол наклона, считаемый от горизонтали.
Г
r
>
Чаще всего уравнение адаптируется к двухфазному путем предположения, что смесь газ/жидкость считается однородной в конечном объеме трубы. Гидростатический перепад давления при двухфазном потоке
—p5sin0,
gc
где р* - плотность смеси газ/жидкость на отрезке трубы.
Если предположить, что элемент трубы содержит жидкость и газ, то плотность смеси можно рассчитать следующим образом:
ps = PLHL + pgHg,
Компонент потерь на трение принимает вид
ftpP fvm 2 gcd
где /,р и Pf определяются по-разному разными исследователями, такими, как Дане и Рос (Duns, Ros, 1963),Хейгедорн и Браун (Hagedorn, Brown, 1965) и т.д.
Ранее, мы показали, что слагаемое (dp / dL)f представляет потери дав-
ления, вызванные трением, когда газ и жидкость текут в трубе одновременно. Данное слагаемое не просчитывается аналитически, за исключением случая ламинарного однофазного потока. Таким образом, оно должно определяться по экспериментальным данным или по аналогии с однофазным потоком. Метод, которому уделено наибольшее внимание, заключается в выведении двухфазного коэффициента трения. Существует несколько выражений для расчета двухфазного градиента трения:
/
dp
dL
V
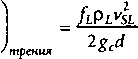
(используется при пузырьковом режиме),
dp _ /gP
трения
(используется
при кольцевом режиме потока),
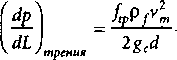
В общем, методы расчета коэффициента трения при двухфазном потоке различаются только путем определения коэффициента трения и с большой натяжкой от структуры потока. Например, при эмульсионном режиме чаще используется формула, основанна> на газе, в то время как при пузырьковом режиме используется формула основанная н; жидкости. Определение рf может сильно различаться в зависимости от исследователя как мы и говорили раньше.
Большинство корреляций пытается связать коэффициент трения с числом Рейнольдса Вспомните, что число Рейнольдса для одной фазы определяется следующим образом:
р vd Ц '
NRe=J
Стандартный, используемый в расчетах числа Рейнольдса набор единиц: р - плотность, фунт/фут3, v - скорость, футов/сек, d - диаметр трубы, фут,
(X - вязкость, фунт/фут*сек.
Так как вязкость чаще выражается в сантипуазах, то число Рейнольдса с вязкостью в сантипуазах:
N„-1.448^.
Из формул градиента давления для одно- и двухфазного потока становится очевидно, что подъемный компонент исчезает при горизонтальном течении. Тем не менее подъемный, или гидростатический, градиент, безусловно, самый важный из трех компонентов при вертикальном или наклонном потоке. Это принципиальный компонент, вызывающий перегрузку скважин и их остановку. Перегрузка газовой скважины -типичный пример, когда гидростатический градиент в скважине постоянно возрастает из-за проскальзывания жидкости и превышения пластового давления, уменьшая таким образом приток газа.
Данный компонент обычно превалирует при горизонтальном течении. Помимо этого при вертикальных и сильно наклонных газовых, газоконденсатных либо в многофазных потоках с высоким газожидкостным фактором потери на трение могут стать доминирующими. В скважинах, работающих на газлифте, закачивание с превышением оптимального газожидкостного фактора вызывает реверсию градиента НКТ из-за очень больших потерь на трение по отношению к гидростатическим потерям. Другими словами, путем увеличения закачки газа можно потерять дебит нефти в скважинах с газлифтом.
Компонент ускорения, который иногда называют кинетической энергией, составляет слагаемое со скоростью в квадрате (ур. 4.7) и основывается на изменении скорости, имеющем место между различными точками в трубе. В 98% случаев, в полевых условиях, данное слагаемое стремится к нулю, но в отдельных случаях может быть значительным и составлять до 10% суммарных потерь давления. В подобных случаях при низких давлениях и соответственно низких плотностях и при больших объемах газа или высоких газонефтяных факторах имеют место быстрые изменения скорости и компонент ускорения может принимать большие значения. Он должен включаться в любые компьютерные расчеты.
Данный компонент полностью игнорируется некоторыми исследователями, а другими исследователями игнорируется при некоторых режимах тока. Когда его принимают во внимание, делаются различные предположения, касающиеся относительных величин используемых в расчетах, чтобы получить некоторую упрощенную процедуру определения падения давления вследствие изменения кинетической энергии. Данный компонент градиента давления имеет большое значение близко к поверхности в скважинах с высоким газожидкостным фактором.
Из обсуждения влияния различных компонентов на суммарный градиент давления ясно видно, что методы определения ОСЖ и коэффициента трения в двух фазах были разработаны.
Одновременное течение двух жидкостей, обладающих различными физическими свойствами, в трубе приводит к образованию самых различных структур потока. Структура потока обозначает геометрическое распределение каждой фазы в трубе относительно другой фазы. Многие исследователи, такие, как Мукерджи и Бриль (Mukherjee, Brill, 1985), предпринимали попытки предсказать структуру потока в зависимости от различных условий. Это имеет особое значение, так как было обнаружено, что ОСЖ различно при разных структурах потока. В наиболее поздних исследованиях было подтверждено, что структура потока зависит от наклона трубы и направления потока (другими словами, добыча это или закачка). В результате наиболее надежные корреляции зависят от аккуратности прогноза структуры потока.
Существуют четыре основные структуры потока:
• Пузырьковый режим (как в нисходящем, так и в восходящем потоке)
• Пробковый режим (как в нисходящем, так и в восходящем потоке)
• Эмульсионный режим (как в нисходящем, так и в восходящем потоке)
• Расслоенный режим (только в нисходящем потоке)
Рис. 4.26.
0.01 0.10 1.0 10.0 Приведенная скорость нефти, Vso, ft/sec
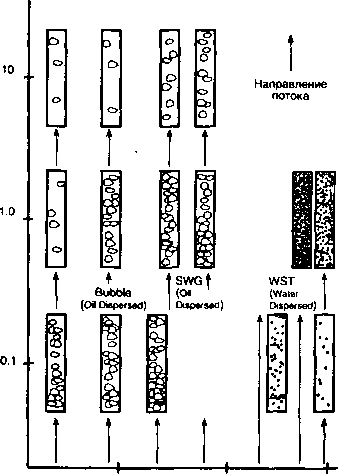
Рис. 4.2а. Структура потока нефти вязкостью 20,09 сантипуаза, относительной плотностью 0,851 в смеси с водой в трубе
диаметром 1,04 дюйма,
по наблюдениям Говьера
(Sullivan, Woods, 1961)
¦с
ф
а
=1
ся
I
Профиль скорости
жидкости
при нисходящем
потоке
Пузырьковый режим газожидкостного двухфазного потока определяется как режим тока, при котором две фазы почти равномерно перемешаны или когда газовая фаза в виде маленьких пузырьков движется в сплошной жидкой среде. Пробковый режим, с другой стороны, определяется как режим тока, при котором размер пузырей газа превышает диаметр трубы и поток в трубе движется дискретными порциями жидкости и газа. Вследствие постоянного разделения фаз по направлению потока пробковый режим приводит к постоянным колебаниям давления. Это создает проблемы при добыче, такие, как переполнение сепараторов (заводнение), неправильное функционирование газлифтных клапанов и т.д. Эмульсионный режим определяется как режим тока, при котором газовая фаза течет внутри трубы, а жидкая фаза движется в виде тонкой пленки, прилегающей к
стенкам трубы. Это происходит при очень высоких скоростях движения газа. Расслоенный режим имеет место только в нисходящем двухфазном потоке. Данный тип структуры потока характеризуется расслоением жидкости по сечению трубы. Более тяжелые жидкости текут в нижней части сечения трубы, в то время как более легкие жидкости/газы занимают верхнюю часть сечения трубы. На рис. 4.2 представлена геометрическая конфигурация контрольных объемов жидкости и газа при различной структуре потока. В двухфазном газожидкостном потоке уравнение сохранения количества движения (4.7) зависит от структуры потока. Прогноз структуры потока возможней с использованием методов, предложенных Макерджи и Брилем (Mukherjee, Brill, 1979), Барнеа (Barnea et al., 1982), Тайтэлем (Taitel et al., 1980). На рис. 4.3 - 4.5 показаны некоторые карты структуры потока для восходящих и горизонтальных потоков. Карты структуры потока даются с использованием скоростей жидкости и газа как независимых переменных. Они определяются следующим образом:
число скорости жидкости
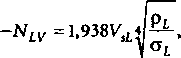
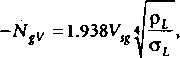
число скорости газа
VsL - приведенная скорость жидкости, фут/сек,
где
VSg - приведенная скорость газа, фут/сек, рi - фунт/фут3,
Ol - поверхностное напряжение жидкости, дин/см.
1 10 102 103 Число скорости газа (NVG)
1 10 102 ю:
Число скорости газа (NVG)
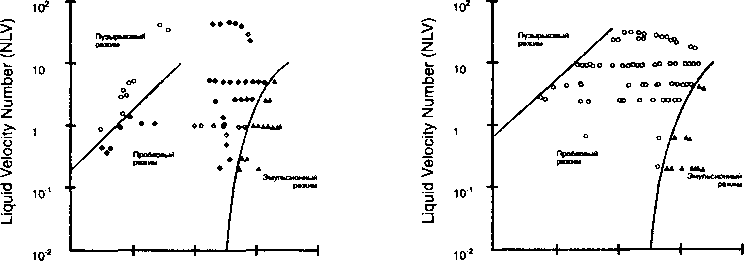
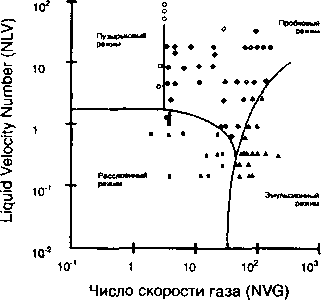
Рис. 4.3.
Расчетные границы перехода структуры потока, нанесенные на наблюдаемую карту структуры потока керосина в вертикальном восходящем потоке.
Расчетные границы перехода структуры потока, нанесенные на наблюдаемую карту структуры потока керосина в вертикальном восходящем потоке 30°.
Рис. 4.5.
Расчетные границы перехода структуры потока, нанесенные на наблюдаемую карту структуры потока керосина в горизонтальном потоке
Дано:
Пример 4.1.
Внутренний диаметр НКТ = 2,441 дюйма (2 7/8 дюйма),
API плотность = 30°,
поверхностное натяжение нефти = 26 дин/см, дебит нефти = 250 СТБ/день, газовый фактор = 56 СКФ/СТБ.
Определить структуру потока по вертикальной добывающей скважине.
141,5 141,5
Относительная плотность нефти .. - гтгт—гг = 0,88.
Решение:
Xj 1)D < iii i 13г 3U
nd2 n( 2,441 n2 ~12~
= 0,0325 футов2.
Площадь сечения трубы
Приведенная скорость жидкости, фут/сек: 250*5,615
0,5 фут/сек.
VSL=-
86400*0,0325 Число скорости жидкости
Nlv
= 1,938*0,5?/-,8в 62,4 = 1,938*0,5* 1,2055 =
1,2.
V 26
Приведенная скорость газа 250*56
= 5 фут/сек.
Число скорости газа NgV= 1,938 * 5 * 1,2055 = 11,7.
По рис. 4.3 при Nlv= 1,2 и NgV = 11,7 ожидаемая структура потока ¦ пробковый режим.
Существует несколько методов расчета потерь давления, когда газ и жидкость текут в трубе одновременно. Данные методы представляют способ предсказывать структуру потока для данных потока и свойств жидкости, таких, как дебиты отдельных фаз, свойства жидкостей, размеры насосных систем и одно из конечных давлений (устье/сепаратор). Для предсказанной структуры потока рассчитываются ОСЖ и коэффициент трения для определения гидростатического градиента и градиента трения. Более детально один из этих методов рассмотрен Брауном и Беггсом (Brown, Beggs, 1977).
Программы NODAL/GLAD и STAR/WPT, установленные на компьютерных системах «Шлюмберже Уаирлайн Сервисес» (Schlumbrger Wireline Services), представляют в наше распоряжение следующие корреляции:
Duns, Ros, 1963 Orkiszewski, 1967 Hagedorn, Brown, 1965 Beggs, Brill, 1973 Mukherjee, Brill, 1985 Dukler, 1964.
Первые три корреляции разработаны для вертикального потока либо для добывающих скважин. Только корреляции Beggs, Brill и Mukherjee, Brill разработаны для наклонных многофазных потоков и подходят как для добывающих, так и для нагнетательных скважин совместно с трубопроводами, проходящими по пересеченной местности. Они также применимы для горизонтальных одно- и многофазных потоков. Корреляция Dukler подходит только для горизонтального течения. Все эти корреляции также могут применяться для однофазного потока газа или жидкости. Только программа Mukherjee, Brill из всех представленных выше предсказывает изменения структуры потока при наклонном двухфазном потоке. ^
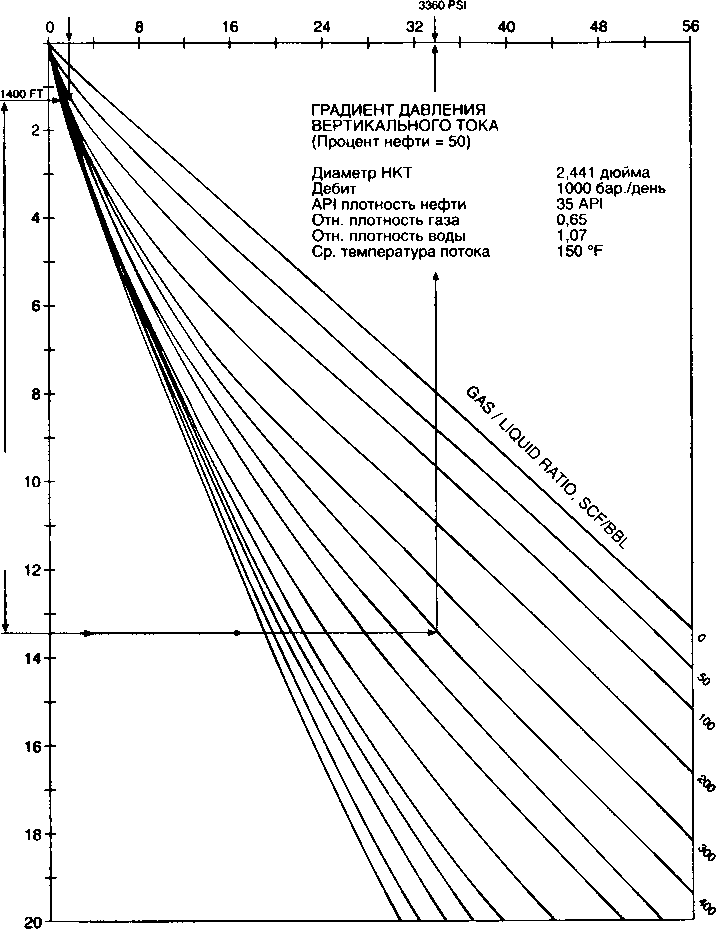
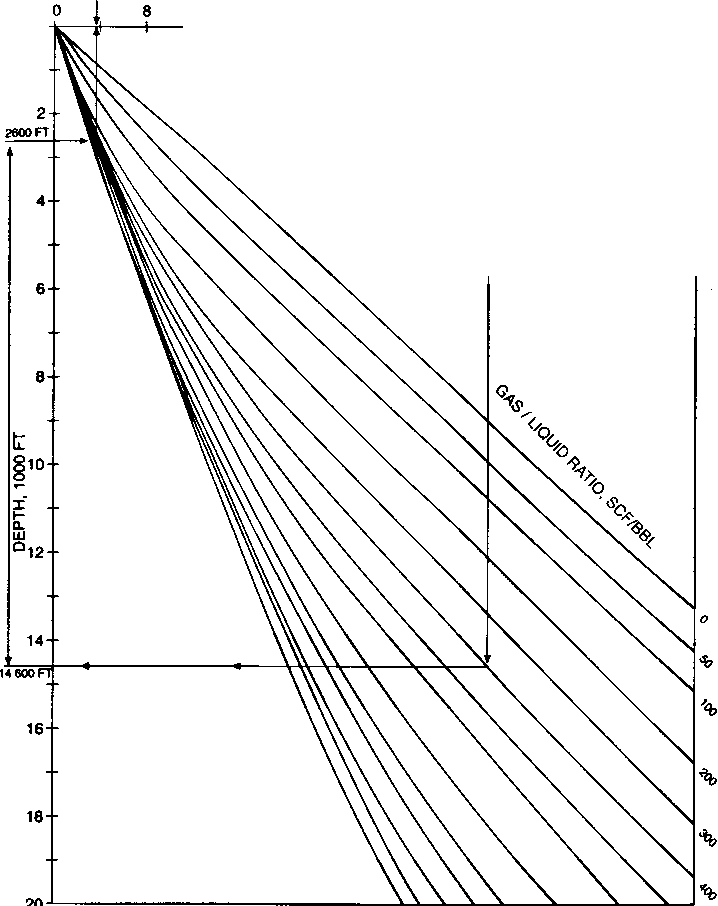
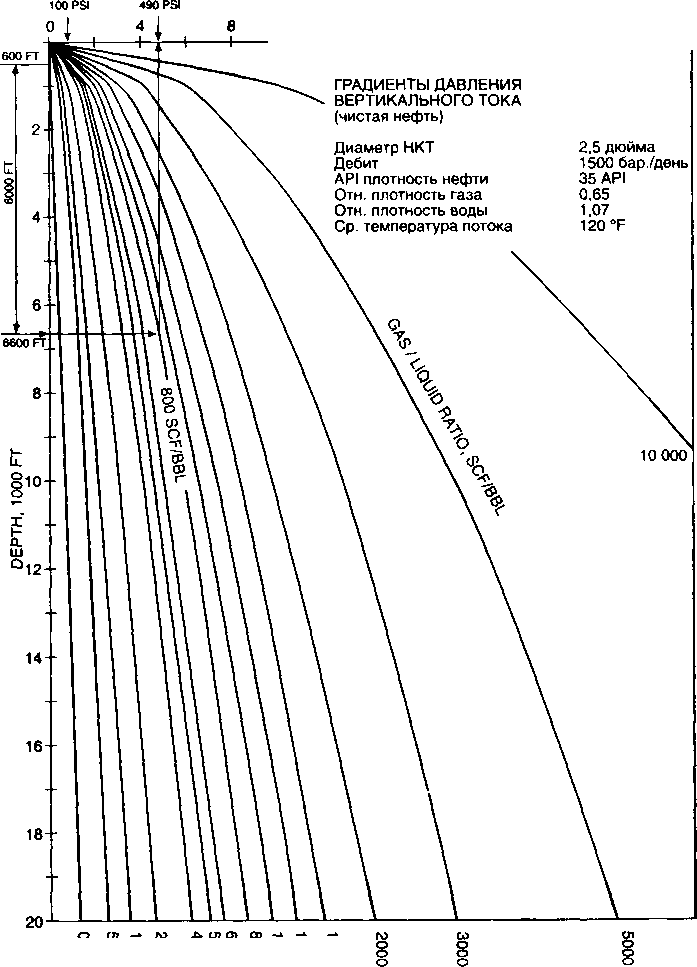
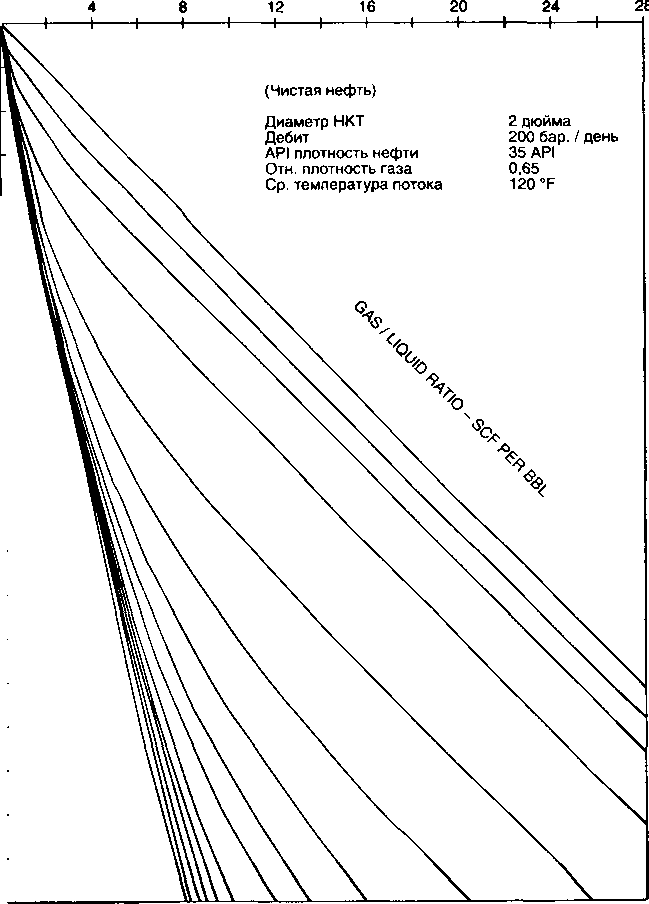
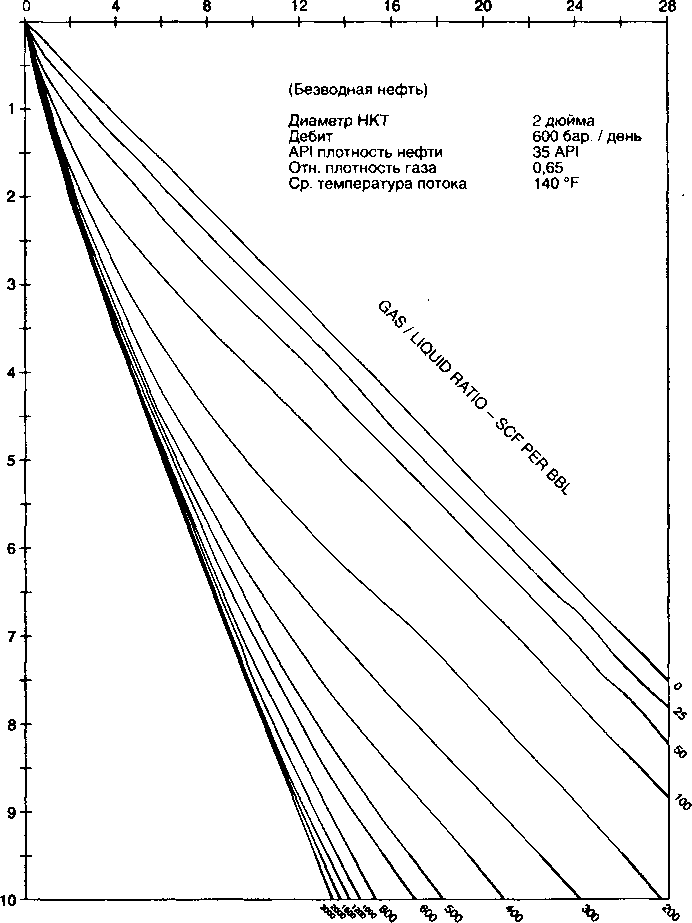
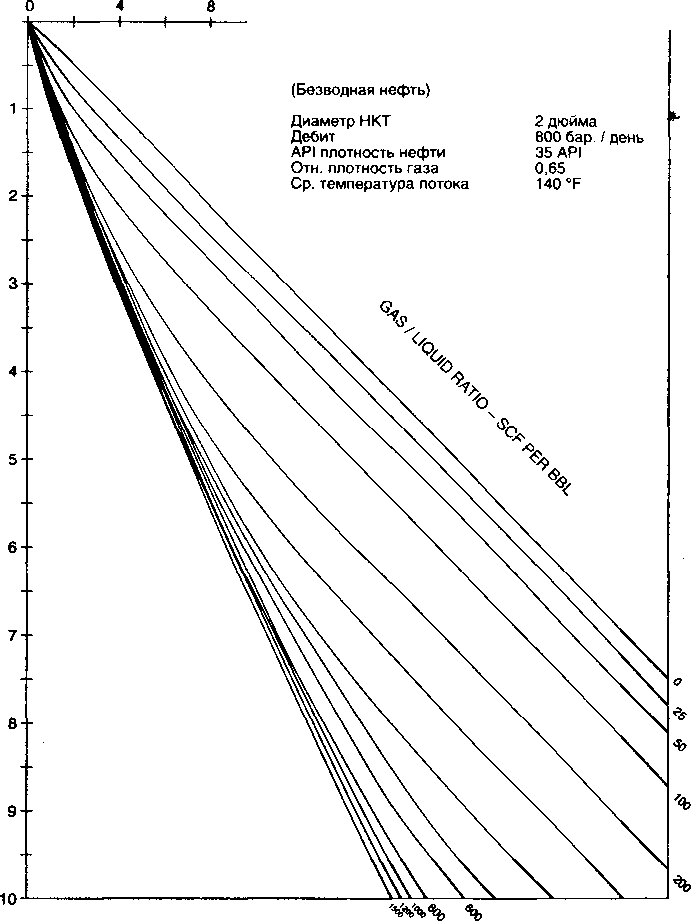
Градиентные кривые - это графическое представление распределения давления по длине или глубине НКТ или выкидной линии для постоянных параметров жидкости потока. На рис. 4.6 представлены типичные градиентные кривые для НКТ -
2 7/8 дюйма, дебита 1000 баррелей в день и обводненности 50%. Постоянные свойства, такие как относительная плотность газа и т.д., указаны в верхнем правом углу графика. На каждом графике представлено семейство градиентных кривых для различных газожидкостных факторов. Эти кривые строятся компьютером и используются для расчетов при отсутствии компьютера под рукой. Градиентные кривые используются для расчета одного из конечных давлений, когда другое конечное давление, а также соответствующие свойства потока и жидкости известны.
Браун и др. (1980) представили ряд градиентных кривых для широкого диапазона размеров НКТ и различных дебитов, используя корреляцию Хагедорна-Брауна (1965). Часть из них используется в приведенных примерах. На рис. 4.6 - 4.9 приведен ряд градиентных кривых, представленных Брауном. Градиентные кривые для горизонтального потока (Рис. 4.8) и вертикального потока в НКТ (рис. 4.6 и 4.7) начинаются при атмосферном давлении на нулевой отметке длины или глубины. Чтобы использовать эти кривые для неатмосферного сепаратора или устьевого давления, применяется концепция эквивалентной длины. Использование градиентных кривых проиллюстрировано в примере 4.2.
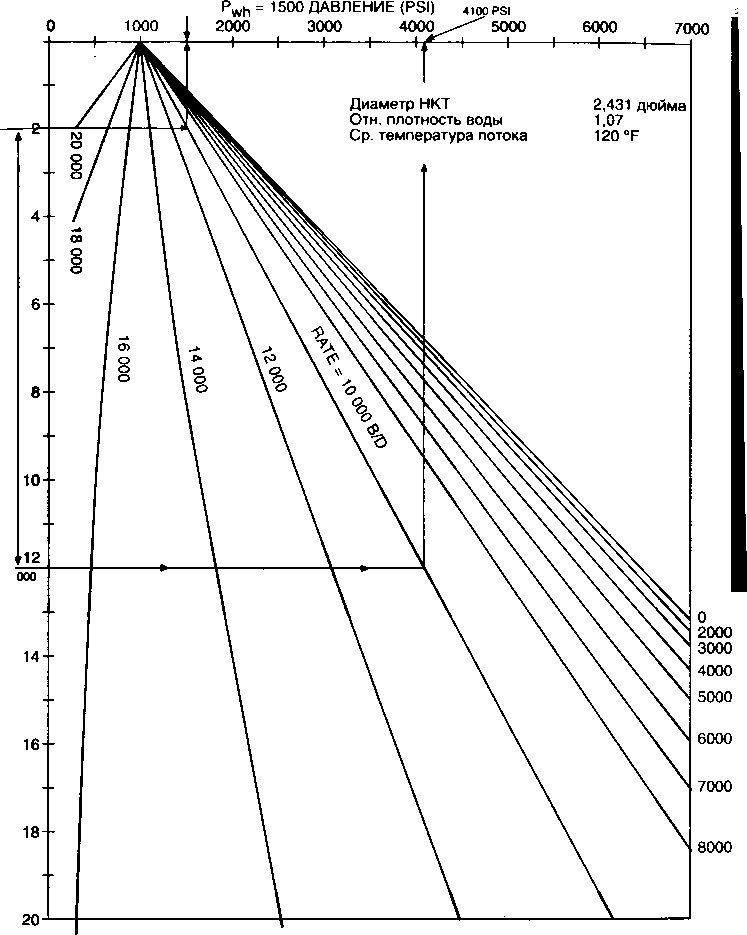
Пример 4.2. Дано:
Pwh = 100 psig Температура на устье = 70°F
ГЖФ = 400 СКФ/баррель Tns = 140°F
yg = 0,65 Глубина = 5000 футов (сер. перф.)
НКТ = 2 дюйма Плотность API = 35° API
Рассчитать и построить кривую приема НКТ.
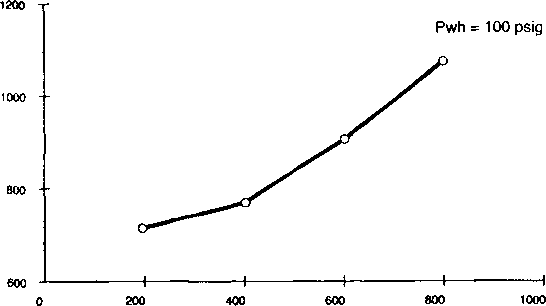
Решение: График зависимости забойного давления от дебита строится на осно
вании градиента давления в трубах.
Используя корреляцию вертикального многофазного потока, по рис. 4.10-4.13 предполагаются разные дебиты и определяется давление на приеме НКТ. Строим следующую таблицу:
| Предполагаемый дебит q, баррелей/день |
pwh psig |
| 200 | 730 |
| 400 | 800 |
|
600 | 910 |
|
800 | 1080 |
| Пример расчетов |
|
Используя рис. 4.10, начинаем в вершине градиентной кривой при давлении 100 psig. Двигаемся по вертикали вниз до газонефтяного фактора 400 СКФ/баррель. Далее по вертикали считываем значение эквивалентной глубины, равное 1600 футов. Складываем значение эквивалентной глубины и глубины скважины в середине перфорации. Полученное значение 6600 футов берем по вертикальной оси и далее по горизонтали до кривой ГЖФ 400 СКФ/баррель. От этой точки двигаемся по вертикали вверх и считываем значение давления на приеме НКТ при 200 баррелях в день, равное 730 psig.
Повторяем эту процедуру для дебитов 400,600 и 800 баррелей/день, используя графики с 4.11 по 4.13 соответственно.
Откладываем значения, представленные в таблице, на графике зависимости Pwf от q, как показано на рис. 4.14, для завершения построения графика давления на приеме НКТ.
DEPTH 1000 FT
%%%% % % % %
ДАВЛЕНИЕ, 100 PSI 16 24 32
-1-1-1-1-(_
3800 PSI
40
ГРАДИЕНТ ДАВЛЕНИЯ ВЕРТИКАЛЬНОГО ТОКА (процент нефти = 50)
Диаметр НКТ Дебит
API плотность нефти Отн. плотность газа Отн. плотность воды Ср. температура потока
2,441 дюйма
1000 бар./день
35 API
0,65
1,07
150 °F
%%%%% % *Ъ %
ДАВЛЕНИЕ, 100 PSI 12 16 Ч-1-н
> сл о> а> -»¦ -»¦ -*¦
ООО о о м сл
ООО ООО о
о о о
DEPTH 1000 FT SI 10 000

LENGTH in 1000 FEET
LENGTH in 1000 FEET
% % %
Рис. 4.14.
На графике
представлена
рабочая
характеристика
давления
на приеме или
на выкиде при
давлении
на устье,
равном 100 psig
а.
ф
Дебит (бар. / день)
1. Colebrook C.F. «Turbulent Flow in Pipes with Particular Reference to the Transition Region Between the Smooth and Rough Pipe Laws», J. Inst. Civil Engrs. (London), 11,(1938-1939), 133 - 156.
2. Moody L.F. «Friction Factor for Pipe Flow», Trans. ASME 66, (Nov. 1944), 671 - 684.
3. Jain A.K. «Accurate Explicit Equation for Friction Factor», J.Hydraulics Div., ASC, 102 (-HY5),
(1976), 674.
4. Aziz K. «Ways to Calculate Gas Flow and Static Head», Handbook Reprint from Pet. Eng. (1963), Dallas. TX.
5. Cullender M.H. and Smith R.V. «Practical Solution for Gas-Flow Equations for Wells and Pipelines with Large Temperature Gradients», Trans., AIME, 207,281 - 287.
6. Dukler A.E. et al. «Gas-Liquid Flow in Pipelines», I.Research Results, AGA - API Project NX-28 (May 1969).
7. Duns H. Jr. and Ros N.C.J. «Vertical Flow of Gas and Liquid Mixtures in Wells», Proc. Sixth World Pet. Congress, (1963), 451.
8. Mukherjee H. and Brill J.P. «Empirical Models to Predict Flow-Patterns in Two-Phase Inclined Flow», Int. J. Multiphase Flow, Vol. 11, No. 3, pp. 299-315,1985.
9. Barnea D., Shoham O. and Taitel Y. «Flow Pattern Transition for Downward Inclined Two Phase Flow; Horizontal to Vertical», Chem. Engr. Sci. (1982) 37,735-740.
10. Taitel Y., Barnea D. and Dueler A.E. «Modeling Flow Patter Transitions for Steady Upward Gas-Liquid Flow in Vertical Tubes», AIChEJ. (1980) 2,3,345-354.
11. Brow K.E. and Beggs H.D. «The Technology of Artificial Lift Methods», Penn Well Publishing,
(1977), 1.
12. Orrkizhewski J. «Predicting Two-Phase Pressure Drops in Vertical Pipes», JPT (June 1967), 829-838.
13. Hagedorn A.R. and Brown K.E. «Experimental Study of Pressure Gradients Occuring During Continuous Two-Phase Flow in Small Diameter Vertical Conduits», JPT (April 1965), 475-484.
14. Beggs H.D. and Brill J.P. «А Study of Two-Phase Flow in Inclined Pipes», JPT (May 1973), 607-617.
15. Mukherjee H. and Brill J.P. «Liquid Holdup Correlations for Inclined Two-Phase Flow», JPT (May 1983).
16. Dueler A.E., Wicks М., Ill and Cleveland R.G. «Frictional Pressure Drop in Two-Phase Flow: B. An Approach Through Similarity Analysis», AIChEJ. (1964) 10,1.
17. Brown K.E. «The Technology of Artificial Lift Methods», Penn Well Publishing (1980), 3.
