Пластовая система
2.
Глава
Рис. 2.1. Типичная индикаторная кривая (IPR)
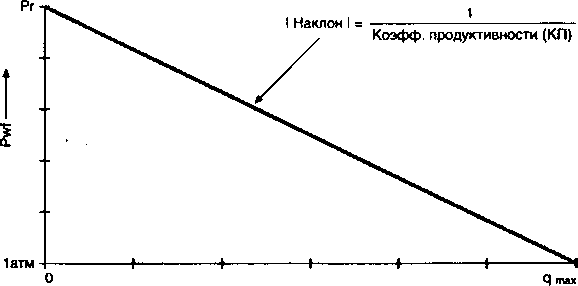
q (СТБ / д)-*
q max = теоретический дебит скважины (AOFP)
Соотношение забойного давления с дебитом (индикаторная кривая / IPR) определяется как функциональная зависимость между производительностью и давлением на забое. Гилберт (1954) первым предложил анализировать скважины с использованием данной зависимости. IPR определена на отрезке между средним пластовым давлением и атмосферным давлением. Производительность, соответствующая атмосферному давлению на забое, обозначается AOFP - теоретический дебит скважины, тогда как производительность при забойном давлении, равном среднему внутрипластовому давлению, равна нулю. Типичная индикаторная кривая представлена на рис. 2.1.
Соотношение забойного давления с притоком
Для однофазной нефти или жидкостей индикаторная кривая, представленная на рис. 2.1, определяется законом Дарси для радиального потока следующим образом:
Мс
приток нефти к скважине, stb/D (стандартных баррелей/день),
объемный коэффициент нефти, bbl/stb (баррелей/станд. баррель),
Во
Но
К
h
Рг
Kf
Dq0 ~
вязкость нефти, сантипуаз, проницаемость породы о нефти, миллидарси, эффективная мощность пласта, фут, среднее пластовое давление, psia (пи эс ай), гидродинамическое забойное давление, psia, радиус дренирования, фут,
где А - это площадь круга дренирования, кв.
Я
*’ А,
фут,
радиус ствола скважины, фут, суммарный скин,
псевдоскин, возникающий из-за турбуленции. В нефтяных скважинах это слагаемое незначительно, особенно для низкопроницаемых коллекторов.
Можно показать, что при re = 1.466 фут, rw = 0,583 фут, st = 0 и отсутствии турбуленции закон Дарси принимает следующую упрощенную форму:
Чо
КВ,
Эта простая формула часто применяется для оценки дебита скважин.
Соотношение забойного давления с дебитом, основанное на законе Дарси, является прямой линией. Как показано на рис. 2.1 теоретический дебит скважины (AOFP) - это максимально возможный дебит скважины при забойном давлении, равном атмосферному. Коэффициент продуктивности (PI) - абсолютное значение наклона индикаторной кривой. Таким образом,
7,08* 10~3itJi
М<
| / \ | ||
|
In | ii. | -0,75 + s, |
| \ rw ) |
ьы
psi - D
Чо
iPr-P*f)
Исходя из закона Дарси
Pi о,1=-
Концепция коэффициента продуктивности (PI) не применяется для газовых скважин, так как соотношение забойного давления и дебита в этом случае является не прямой линией, а кривой.
Коэффициент относительной продуктивности (КОП)
КОП определяется как отношение действительного коэффициента продуктивности к идеальному коэффициенту продуктивности (s, =0)
КП(действительный) КЩидеальный, s( = 0)
КОП =
|
Г (г \ | |
| In -*¦ | -0,75 |
|
L Vг» у |
| ( г Л | |
| И |
— 0;75 + 5( |
Р, Pwf bPskin
Р, -Pwf
ДPAi„ =0,87ms,
.0,87(-Г}„
где
т - наклон однолагорифмической прямой (Хорнер или MDH).
КОП также называют эффективность дебита, показатель повреждения пласта законченной скважины или степень повреждения пласта.
Пример 2-1. Закон Дарси является, возможно, самым главным уравнением в раз
работке месторождений. Эта зависимость связывает дебит с депрессией и часто применяется при принятии решений по стимуляции. Следующий пример иллюстрирует подобный случай:
Нефтяная скважина
WPe-Pyf)
ч=-
( \ In i+s
141,2цВ
г
\ 'w J
h (эффективная мощность пласта) = 50 футов,
Ре (начальное пластовое давление) = 3000 psi,
Р^забойное давление) = 1000 psi,
В (объемный коэффициент) = 1,1 resbbl/stb,
(i (вязкость) = 0,7 сантипуаза,
ге(радиус контура питания)
rw (радиус скважины) = 0,328 фута (7-7/8( дюйма).
1. Влияние площади контура питания
| А (акров) | ге (футов) | InWrJ |
Падение дебита (s=0) |
|
40 | 745 |
7,73 | |
| 80 | 1053 | 8,07 |
4% |
| 160 |
1489 | 8,42 |
9% |
| 640 |
2980 | 9,11 |
16% |
Увеличение площади контура питания в 16 раз приводит к максимальному падению дебита - 16%. Другими словами, для скважины на установившемся режиме площадь контура питания не оказывает большого влияния на дебит. В то же время площадь контура питания имеет огромное влияние на величину накопленной добычи скважины.
2. Влияние проницаемости и скина.
920к
Для заданных
ранее значений q = ^
'
|
5=0 | 5=10 | |
| к (миллидарси) q (ст. баррелей/день) к (миллидарси) q (ст. баррелей/день) | ||
| 10,0 1190 | 10,0 |
519 |
| 1,0 119 |
1,0 | 52 |
|
0,1 12 | 0,1 |
5 |
| 0,01 1,2 |
0,01 | 0,5 |
Если к = 10 миллидарси, снижение скина с 10 до 0 приводит к увеличению дебита более чем на 600 баррелей/день (т.е. эта скважина - кандидат для кислотной обработки материнской породы).
Если к = 0,1 миллидарси, устранение скина приведет к увеличению дебита всего на 7 баррелей/день.
Пример 2.2.
Рис. 2.2.
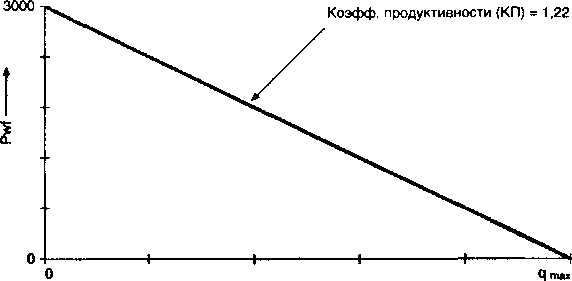
Q них = теоретический дебит скважины (AOFP) = 3672 СТБ / д
Индикаторная
кривая
для примера
Для следующих данных по нефтяной скважине рассчитать
а) теоретический дебит скважины и построить индикаторную кривую,
б) коэффициент продуктивности.
Проницаемость к0 = 30 миллидарси
Дано:
Эффективная мощность h = 40 футов
Среднепластовое давление Рг = 3000 psig
Температура пласта Т = 200 °F (по Фаренгейту)
Расстояние между скважинами А = 160 акров (43 560 футов2/акр) Диаметр ствола скважины D = 12-1/4 дюйма (без обсадной колонны)
Объемный коэффициент В0 = 1,2 (баррель /ст. баррель)
Вязкость нефти ц0 = 0,8 сантипуаза
(предположим скин = 0 и отсутствие турбулентности)
Решение:
А* 43560
(а) Радиус контура питания ге = -—-=1490 футов
Радиус скважины, rw = 0,51 фута
Применяем закон Дарси для радиального притока
7,08* 10~3fc„/»(Pr —P„f)
|
г | ||
| Mo | In—-0,75 т« |
= 3,672
Чо=-
, 1490
In--0,75
0,51
7,08 * 10-3 (30 * 40) (3000 - 0) 26550
7,23
(0,8* 1,2)1
ст. баррелей / день.
(б) Коэффициент продуктивности (PI) Ч_
7,08*10 }kh
КП=-=-
= 1,22
In-0,75
Ги,
ц В
Г-о о
1. Интерпретация тестирования неустановившегося режима, к.т. восстановление давления, снижения давления и интерференция дают следующие данные
kh -~,pr,st.
Примечание:
В нагнетательных скважинах тест восстановления давления называется тестом резкого снижения, а тест снижения давления называется тестом на приемистость.
2. Специальные исследования скважин, т.е. расширенный тест на снижение давления или определение границ пласта, применяются для определения контура питания и ге.
3. Данные каротажа и исследования керна применяются для определения kuh.
Довольно часто при правильном проведении и интерпретации методы интерпретации исследований скважин приносят самые типичные значения таких параметров пласта, как kh/[i, Рг и др. Эти значения являются среднеобъемными значениями в радиусе проведения исследований, в то время как каротаж и исследования керна определяют значение к в отдельных точках вокруг ствола скважины.
Рис. 2.3.
Закон Дарси для линейного потока
А
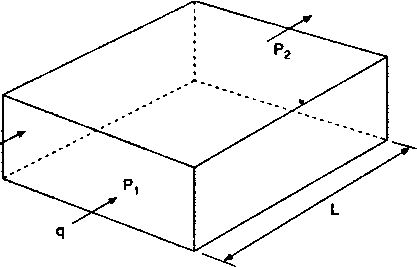
Проницаемость (к): способность горных пород пропускать сквозь себя жидкость и газы. В простейшей форме закон Дарси, применяемый к прямоугольному образцу породы, имеет вид
кА{рх -р2)
Я~~ „т »
q - объемный расход жидкости, см3/сек,
где
Ц - вязкость жидкости, сантипуаз,
к - проницаемость породы, дарси,
L - длина образца, см,
А - площадь фильтрации, см2,
Р1-Р2 - перепад давлений на образце, атмосфер.
Из этой формулы проницаемость пористой среды, равная одному дарси, определяется для однофазного потока вязкостью один сантипуаз, полностью заполняющего пустоты среды и текущего через образец, при условии вязкого потока объемом один кубический сантиметр в секунду через поперечное сечение в один квадратный сантиметр при падении давления в одну атмосферу на один сантиметр. Данное определение применимо в основном к материнской породе. В карбонатах, некоторых песках, углях, а также в других породах, в которых часто присутствуют растворенные каналы, естественные или наведенные трещины, эти каналы или трещины изменяют эффективную проницаемость всей горной породы. Можно показать, что в материнской породе с низкой проницаемостью несколько трещин могут привести к значительному изменению эффективной проницаемости породы. Также можно показать, что проницаемость (в дарси) трещины шириной w (в дюймах) на единицу высоты рассчитывается по следующей формуле
к = 54.44 06иЛ
Следовательно, трещина шириной 0,01 дюйма в куске породы будет соответствовать проницаемости породы 5440 дарси. Заметьте, что наличие всего нескольких таких трещин в породе с низкой проницаемостью может существенно увеличить эффективную проницаемость породы.
Эффективная мощность пласта (h): средняя толщина пласта в зоне дренирования, через которую жидкость поступает в скважину. Под эффективной мощностью пласта понимается не только высота зоны перфорации или толщина пласта, встречающаяся в скважине.
Среднепластовое давление (Рг): если заглушить все скважины месторождения, стабилизированное давление в пласте называется среднепластовым давлением. Лучшим способом получения приблизительного значения этого давления является тест на восстановление давления.
I
Рис. 2.4. j
Положительный j
скин =
'"¦¦'Г................................1
................................................———
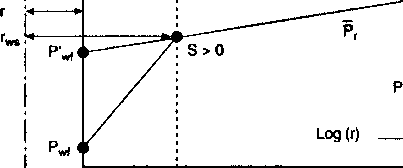
поврежденная !
скважина
или уменьшенный радиус скважины
Скин-фактор (st): В процессе бурения и заканчивания скважины проницаемость породы вблизи ствола скважины может быть изменена. Эта зона измененной проницаемости называется поврежденной зоной. Вторжение бурового раствора, частичек глины, фильтрационной корки бурового раствора и цемента, а также наличие высокой газонасыщен-ности в зоне вокруг ствола скважины - вот некоторые из 1|ричин, вызывающих снижение проницаемости. Тем не менее удачная стимуляция, такая, как кислотная обработка или ГРП, приводят к значительному улучшению проницаемости вблизи скважины, таким образом, уменьшая скин, возникший вследствие повреждения породы. Скин-фак-тор, определяемый при исследовании скважины, отражает любой физический или механический феномен, ограничивающий приток в скважину. Наиболее часто встречающиеся причины таких ограничений помимо повреждения породы, - это частичное проникновение скважины в пласт, ограниченная перфорация, закупоривание перфорационных отверстий и турбуленция (Dq). Весь этот скин, возникающий помимо повреждения породы, чаще всего называется «псевдоскин». Необходимо отметить, что суммарный скин, включая турбуленцию, может составлять 100 или даже больше в плохо законченных скважинах. Тем не менее минимальный скин в скважинах после интенсивной стимуляции составляет приблизительно 5.
Скин-фактор (st) - это константа, связывающая падение давления в прискважинной зоне, дебит и гидропроводность породы (Рис. 2.4). Таким образом, »
s, = АР$кт / (141,2/ kh)
&Pskin = 0,87 ms, = (p’wf - pwf) на рис. 2.4.
где m - наклон полулогарифмической прямой из Хорнера или Миллера,
Дайса и Хатчинсона, полученной из исследований на восстановление или падение давления соответственно (psi/логарифмич. цикл) s, = s + sp + Spp + sturb + s0 + ss + ...;
где st - суммарный скин-эффект,
sj - скин-эффект вследствие повреждения породы (+ve),
spp - скин-эффект вследствие частичного проникновения скважины
в пласт (+ve),
Sp - скин-эффект из-за перфорации (+ve) (Приложение Д),
sturb ~ Dq> скин эффект вследствие турбуленции или скин, зависящий
от темпа отбора (+ve),
s0 — скин-эффект вследствие наклона скважины (-ve),
ss - скин-эффект, возникающий вследствие стимуляции (в основном
-ve).
Только положительный скин можно рассматривать с данной точки зрения. Необходимо заметить, что Sj в лучшем случае может быть уменьшен до нуля кислотной обработкой. Тем не менее искусственные трещины могут накладывать отрицательный скин (ss) в дополнение к сведению скина из-за повреждения породы (sj) к нулю.
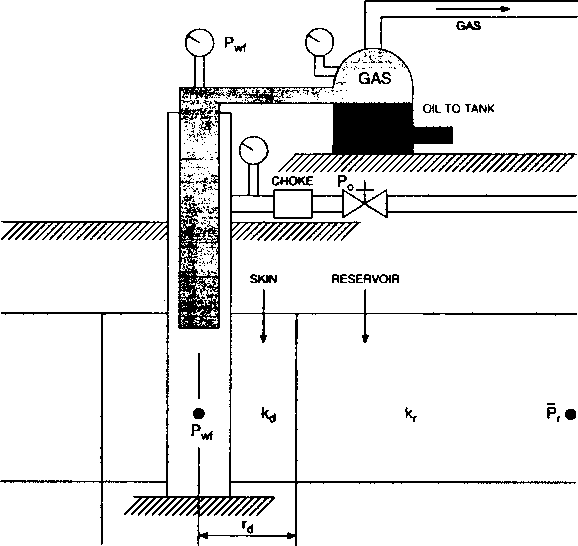
Используя концепцию скина как кольцеобразной зоны вокруг скважины с измененной проницаемостью, Хокинс построил модель скважины, как показано на рис. 2.5:
s,= (kr/kd-1) In rd/rw,
где кг - проницаемость коллектора,
kd - проницаемость измененной или поврежденной зоны, rd - радиус измененной или поврежденной зоны, rw - радиус скважины.
Исходя из данной формулы видно, что, если скин s, равен нулю, т.е. скважина не повреждена, проницаемость измененной зоны кд равняется проницаемости коллектора кг или rw равен rj. Положительный скин служит признаком поврежденной скважины, в то время как отрицательный подразумевает стимуляцию.
и поврежденная
зона,
или зона
измененной
проницаемости
Формула Дарси для однофазного газа имеет следующий вид:
7,03*10 ^kgh(Pr2-P^)
| / \ Г | |||
|
\igzT | In |
-0,75+s, +Dqg |
qg - дебит газа, млн ст. куб. футов/день,
где
kg - проницаемость для газа, миллидарси,
z - коэффициент сжимаемости газа, определенный при средней
температуре и среднем давлении, доля (Приложение А),
Т - средняя пластовая температура (градусов Ранкина),
- вязкость газа,сантипуаз (Приложение А),рассчитана при средней температуре и среднем давлении.
Все остальные параметры в формуле 2.1 известны. Обратите внимание, что скин уменьшается только при стимуляции, турбуленция уменьшается путем увеличения плотности перфорации или комбинацией обоих методов.
z = 1, = 0/02ср, t = 200°F, или 660°R,
ln(rJrw)-0,75 = 7,03,
4g ~ 77*10'7 kh (Pr2-Pwf2),
получаем
где
qg - дебит газа, млн ст. куб. футов/день,
к - проницаемость, мдарси,
h - эффективная мощность пласта, футов.
Данная формула применяется для быстрой оценки дебита газа из скважины. Турбулен-ция Dqg в формуле 2.2 называется скином, возникшим из-за турбуленции. В газовых скважинах он может быть весьма значительным и требовать дополнительной оценки для принятия решения о путях его снижения. В высокопродуктивных нефтяных скважинах данный член также может иметь большое значение. Для оценки скина из-за турбуленции формулу Дарси можно переписать в следующей форме:
(Рг Pwf ) “ &0 Чо ^0 Чо^'
![]()
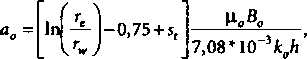
где
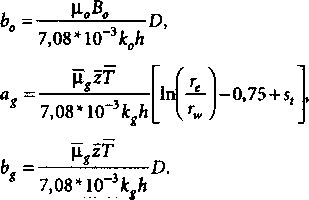
Обе эти формулы можно привести к линейной форме, разделив обе части выражения на дебит:
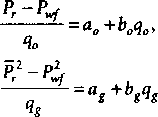
Рис. 2.6а.
График, построенный на исследованиях по четырем точкам
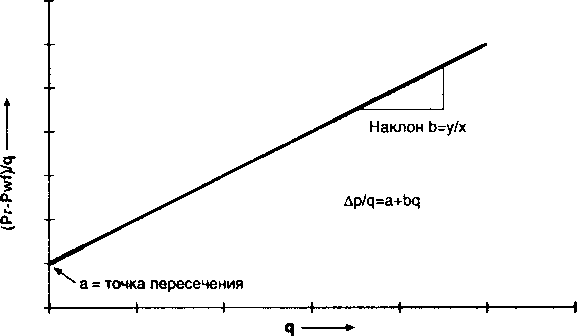
Беря за основу четырехточечный тест (КВД), где забойное давление фонтанирования Pwf рассчитывается для четырех установившихся дебитов q, на картезианской бумаге строится график, показанный на рис. 2.6а. Точка пересечения графика с осью ординат и наклон кривой на рис. 2.6а дают значения констант а и Ь, определяющих прямую линию. Коэффициент турбуленции может быть рассчитан, зная Ь. Диагностика четырехточечного теста приведена на рис. 2.66. Необходимо отметить, что данные со скважины, представленные в случае 1, не показывают наличия какой-либо турбуленции, так как наклон графика равен нулю, соответственно значение b также равно нулю. В то же время турбулен-ция или скин, возникающий из-за турбуленции, увеличиваются по мере увеличения наклона прямой, как показано в случае 2 и 3.
Джоунс, Блоунт и Глэйз модифицировали формулу Дарси для радиального притока путем аналитического выражения коэффициента турбуленции D как функции интервала перфорации и коэффициента турбуленции газа или нефти в породе р. Данные формулы приведены в Приложении А (секции 1Д и 2Б).
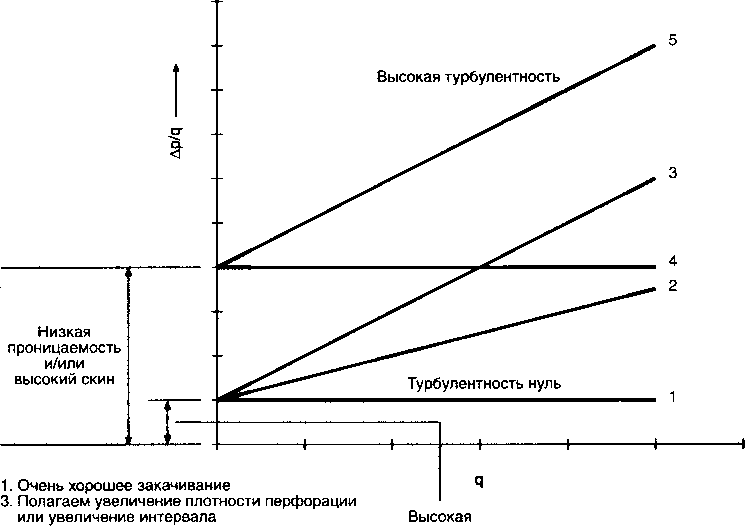
проницаемость, низкий скин
4. Стимуляция для уменьшения скина
5. Стимуляция и перфорация
Оценка данных теста по четырем точкам, по Джонсу, Блонту, Глэйзу (Jones, Blount, Glaze)
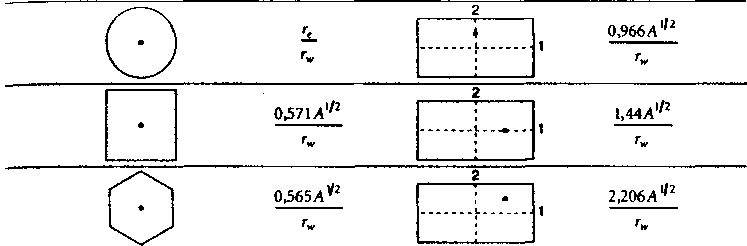
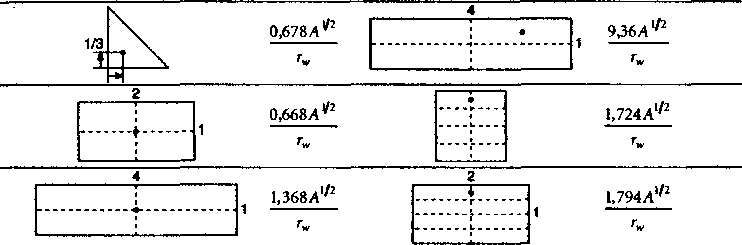
Таблица 2.1. Граничные факторы для различных контуров питания и положений
скважин в контуре питания, где А - площадь контура питания и А ^2/ге — безразмерный коэффициент
К
Система
Система
0,604А112
1,925Л1/2

0,610 л'12
42
6,59 А
2,066Л1,2
4,072А1,2
н—У—
9,523 А*2
0,884А1/2
Большинство расчетов при резервуарном инжиниринге предполагает радиальную геометрию притока. Радиальная геометрия подразумевает, что контур питания скважины круглый и добывающая скважина располагается в центре дренируемого круга. Во многих случаях контур питания скважины имеет прямоугольную или какую-либо другую, не круглую форму. Применение формул, основанных на радиальной геометрии к нерадиальным контурам питания может привести к значительным ошибкам. Формула Дарси может быть модифицирована для различных форм радиуса контура питания следующим образом -
7,08*10 ~*ЩРГ-Р^) q° BoHo[ln(jc)-0,75+s] ’
703*10~*ЩРгг-Р^)
Ц .Tz[ln(x) -0,75+s+Dq, ] ’
для нефти и газа соответственно, PI = =-q° -
7,08*10“3 JWi
Рг-Р*4 Boiio[\n(x)-0J5+s}' где даётся в Таб. 2.1 для различных форм контура питания и расположения скважин.
а) На скважине с установившимся дебитом q0 = 1000 баррелей/день тест КВД показывает следующее: kh/\l = 20 мдарси-футов/сантипуаз; s( = 2.
Пример 2-3.
Рассчитать падение давления из-за скина для В0= 1.
^.=141,2.ffib4=141,2.i52,
Решение:
2 = 1412psi
б) Построить IPR (индикаторные кривые) по следующим скважинным данным и представить таблицу зависимости теоретического дебита (AOFP) от скина.
Нефтяная скважина: к = 5 мдарси h = 20 футов Ц0 = 1,1 сантипуаза сетка = 80 акров Радиус контура питания
Дано:
рг = 2500 psig s = -5,-1,0,1,5,10,50 Я0=1,2 пластовых барреля/баррель rw = 0,365 футов
Решение:
80*43560 г„ = ,|-= 1053 футов,
In—-0,75+s г...
М.
7,08*10 *5*20*2500
1341
lni^l-0,75+s
7,97-0,75+s
1,1 *1,2
0,365
| Скин (s) |
AOFP (стандартных баррелей (СТБ) / день) |
| -5 |
604 |
| -1 |
216 |
| 0 |
186 |
| 1 |
163 |
| 5 |
по |
| 10 |
78 |
| 50 |
23 |
Исходя из того, что КП (PI) прямая линия, для нефтяных скважин рг и AOFP определяют индикаторную кривую.
с) Нарисовать индикаторную кривую для газовой скважины со следующими параметрами. Рассчитать теоретический дебит скважины (AOFP):
к = 1 мдарси h = 200 футов
Т = 200°F Ц = 0.019 сантипуаза
z=l,l рг= 3,500 psig
сетка = 80 акров rw = 0.365 фута
скин = 1 Из раздела (б)
Решение:
Inf—1—0,75 = 7,22.
Из закона Дарси
(без учета турбуленции)
гл-4 .
7,03* 10 Щрг~ptf)
| ( \ | |||
| llgzT |
In | ге \rw ) | -0,75+s |
7,03 * 10"4 * 1 * 200(35002 - )
0,019*1,1*660(7.22 + 1)
| p».f(psig) |
Дебит (млн ст. куб. футов/день) |
| 3500 | 0 |
| 3000 | 4030 |
| 2500 | 7440 |
| 2000 | 10 230 |
| 1500 | 12 400 |
| 1000 | 13 950 |
| 500 |
14 880 |
| 0 |
15190 |
д) Рассчитать теоретический дебит скважины для примера (б) для квадратной зоны дренирования вместо радиальной и скина, равного нулю.
Пример 2-4.
Решение:
| \огг 1341 |
1341 | притока неф- |
| AUl'l — , — lnx-0,75+s Из таб. 2.1 0,571-^80* 43560 х --= rw 1341 | lnx-0,75' Ю66 -= 2920. 0,365 1341 IOC If' ТГ1-----\ | |
| 1п2920-0,75 7,98-0,75 Представленные данные получены в ходе измерения тяной скважины. | ||
| Номер измерения |
q (СТБ/день) |
pwf( psia) |
| 1 | 400 |
2820 |
| 2 |
1000 | 2175 |
|
3 | 1340 |
1606 |
| 4 |
1600 | 1080 |
рг =3000 psia.
Используя метод Джонса, Блонта, Глэйза, рассчитайте:
1) а и Ь,
2) AOFP.
Строим график зависимости q от (pr- pwj)lq в декартовых координатах, основываясь на представленных данных. Для этого подготовим следующую таблицу:
Решение:
| q (СТБ/день) | P«f (psia) |
(pr-pwf)/q |
| 400 |
2820 | 0,45 |
| 1000 | 2175 |
0,825 |
| 1340 |
1606 | 1,0403 |
| 1600 | 1080 |
1,2000 |
Через полученные точки проводим прямую, получая таким образом точки пересечения с осями и наклон. Уравнением прямой является
(Pr - pwf)!q = 0,1997+0,000625q в = 0,1997, b = 0,000625,
AOFP = q(pwf= 14,7 psia).
Решаем квадратное уравнение относительно q:

0,000625<j2 + 0,1997q—2985,3 = 0,
-0,1997±/(0,1997)2+(4*0,000625*2985,3) q~ 2*0,000625
-0,1997 ±475
q=-г—
1,25* 10“3
Выбираем положительное решение уравнения
-0,1997+7^5 _ ч
q =-;— = 2031
(СТБ/день). ![]()
Теоретический дебит скважины составляет 2031 (СТБ/день).
Закон Дарси распространяется только на однофазный поток в пласте. В случае нефтяного пласта однофазный поток имеет место при забойном давлении выше давления насыщения пластовой жидкости при пластовой температуре. В течение разработки месторождения пластовое давление продолжает падать, если не применяется закачка жидкости или заводнение. Следовательно, в течение истощения залежи забойное давление падает ниже давления насыщения, что приводит к совместному однофазному и двухфазному потоку в пласте. Для расчетов в этом случае требуется композитная индикаторная кривая. Перед тем как перейти к обсуждению композитной индикаторной кривой, кратко обсудим фазовые превращения.
Образцы пластовых жидкостей, взятые при пластовом давлении, анализируются в PVT-бомбах для построения фазовых диаграмм. Типичная фазовая диаграмма для тяжелой нефти представлена на рис. 2.7 и показывает физическое состояние флюида. Исходя из среднего пластового давления, забойного давления и соответствующих им температур можно определить состояние пластового флюида, т.е. одну фазу, две фазы или комбинацию. Данная информация используется при определении формулы для построения индикаторной кривой.
A BLACK OIL В COMPOSITE С WET GAS D DRY GAS
E SOLN. GAS DRIVE OIL
Критическая точка
Рис. 2.7.
Типичная фазовая диаграмма дегазированной нефти
ш
СЕ
э
со
(Л
ш
СС
а_
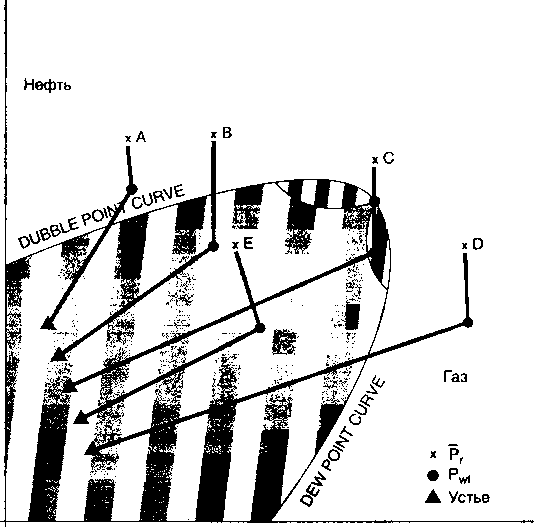
Температура (°F) •
В случае двухфазного потока в пласте, когда пластовое давление рг ниже давления насыщения, рекомендуется применять отношения Вогеля для определения притока (рис. 2.8)
Данную индикаторную кривую можно построить либо если мы знаем теоретический дебит скважины q0 max и пластовое давление либо пластовое давление рг и дебит при известном забойном давлении. В любом случае нам потребуется КВД для определения рг и измерение притока с забойным датчиком.
Рис. 2.8.
Различные формы отношения дебита к забойному давлению (IPR)
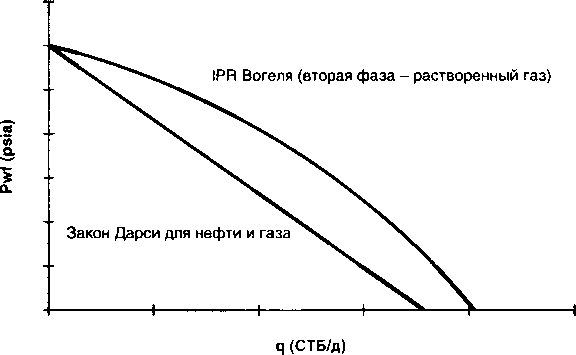
Композитная индикаторная кривая
Композитная индикаторная кривая является комбинацией коэффициента продуктивности (КП/PI), основанного на формуле Дарси для давления выше давления насыщения и соотношения Вогеля ниже давления насыщения. Данная конкретная индикаторная кривая используется, когда пластовое давление ргвыше давления насыщения рь, а забойное давление - ниже (рис. 2.9).
Рис. 2.9. Композитная индикаторная кривая Вогеля
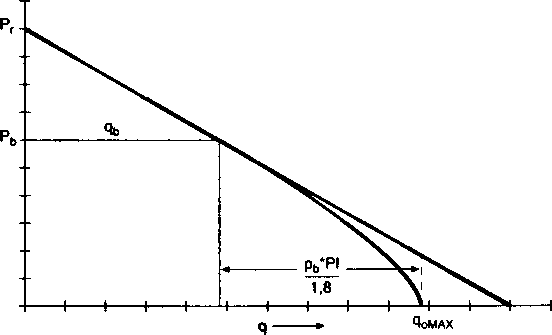
г
CL
![]()
![]()
ДЛЯ pwf<pb-
Таким образом, q0 = Pl*(pr-pwf) для pwf> рь
и
где qb = РГ(рг - рь) - дебит при pwf = рь.
Необходимо отметить, что индикаторная кривая Вогеля не зависит от скин-фактора и поэтому может применяться только для неповрежденных скважин. Стэндинг [11] ввел поправку индикаторной кривой Вогеля для поврежденных или простимулированных скважин.
Поправка Стэндинга для индикаторной кривой Вогеля
Стэндинг скорректировал индикаторную кривую Вогеля для учета эффекта скина и вывел концепцию фактора эффективности притока (ФЭП/FE). Если p’wf (рис. 2.4) - забойное давление неповрежденной скважины, а, соответственно забойные давления поврежденной и стимулированной скважины соответственно, тогда
Г’Г’ Рг ~
FE = —- — поврежденная скважина,
Pr ~ Pwf 1| *>0
FE = 1 неповрежденная скважина,
стимулированная скважина.
Pr Pwf2\s<Q
Таким образом, ФЭП (FE) может быть рассчитан, используя методы испытания скважин. Индикаторные кривые Вогеля для различных значений ФЭП (FE) представлены на рис. 2.10:
*DM ln(tD)-0,80907
FE = -
PD|s ln(fD)—0,80907 + 2s
Pd 141,2qp.|3 ’
0,000264itf
Значения pD и tD берутся с графиков соответствия или из данных исследований, таких, как kh/[L и s, а также других доступных параметров скважин и пластов.
Из определения ФЭП (FE)
P’wf=P,-FE(pr-Pwfi)-Таким образом, индикаторная кривая Вогеля может быть записана как
|
-а о И 0 1 О N>_ | ( \ Pwf |
-0,8 | Pwf |
|
ЯОтах | 1л J | 1 р' ) |
Для больших отрицательных значений скин-фактора или фактора эффективности притока (ФЭП/FE) и низких давлений эти индикаторные кривые предсказывают более низкие дебиты, чем достигаемые в реальности.
Эффективность притока
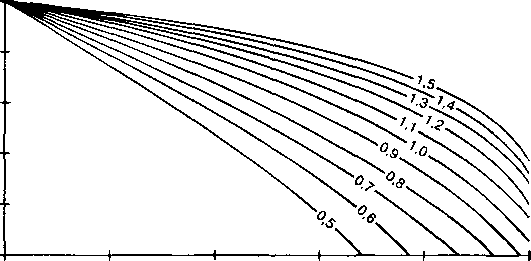
О 0,2 0,4 0,6 0,8 1,0
Отношение дебита к максимальному дебиту без повреждений qo / (qo) max [FE = 1.0]
| Рис. 2.10. | 1.0 |
|
Корреляция | |
|
Стэндинго для | 0,8 |
| скважин | |
| с ФЕП, | 0.6 |
| отличным | |
| от единицы |
0.4 |
| 0.2 | |
| 0 |
Многоступенчатое исследование газовых скважин методом противодавления является стандартной процедурой построения кривой производительности или производительности газовой скважины. Феткович применил данные исследования на нефтяных скважинах при пластовом давлении выше и ниже давления насыщения. Основной вывод из этих исследований состоит в том, что, как и в газовых скважинах, соотношение дебита и забойного давления в нефтяной скважине, или индикаторная кривая нефтяной скважины, имеет следующую формулу:
4o=C(p2-p2wf)n.
Данная формула также называется формулой нефтяной и газовой производительности. Показатель степени п лежит между 0,5 и 1,0 для нефтяных и газовых скважин. Значение п меньше чем 1,0 часто является следствием не Дарси-эффектов. В таких случаях может использоваться не Дарси-множитель притока. Коэффициент С представляет коэффициент продуктивности залежи. Следовательно, данный коэффициент увеличивается с ростом кики уменьшается с увеличением скина.
Индикаторные кривые Фетковича являются частными случаями индикаторных кривых скважин и получаются как результат многоступенчатых исследований скважин методом противодавления, таких, как изохронные испытания.
Многоступенчатый тест или исследование скважин методом противодавления (испытания на неустановившемся притоке при переменных дебитах)
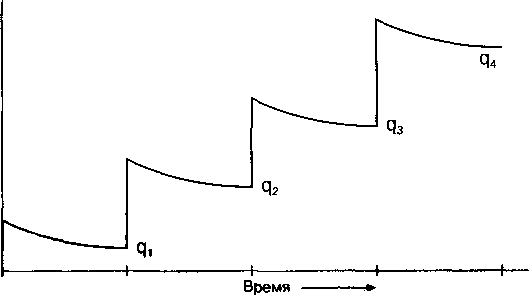
Такие исследования производятся в остановленных скважинах, достигших установившегося давления во всем контуре питания. Данные исследования также называют тестом производительности, так как они используются для предсказания производительности или дебита скважины при различных значениях забойного давления pwf (противодавления на пласт). Обычно данный тест представляет собой серию, состоящую минимум из трех дебитов и значений забойного давления как функции времени в течение этих интервалов притока. Результаты исследований представляются в логарифмических координатах как log(р^ - ) от log q. Типичные последовательности представлены
на рис. 2.11 и 2.12.
Рис. 2.11.
Различные притоки, прямая ?
последовательность ® (по Фетковичу) о-
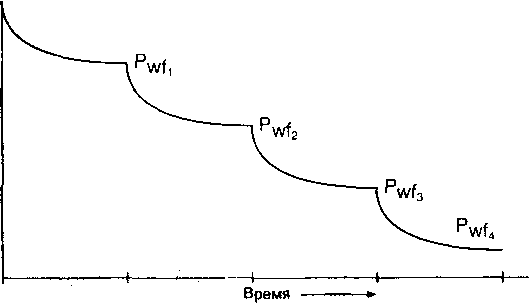
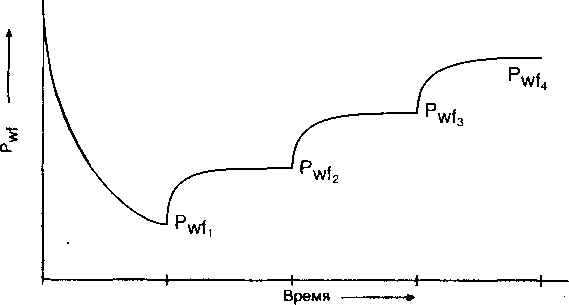
| Рис. 2.12. | |
|
Различные | |
|
притоки, | |
|
обратная | |
|
последовательность |
;о о |
| (по Фетковичу) | СЛ сг |
Пример. Многоступенчатый тест
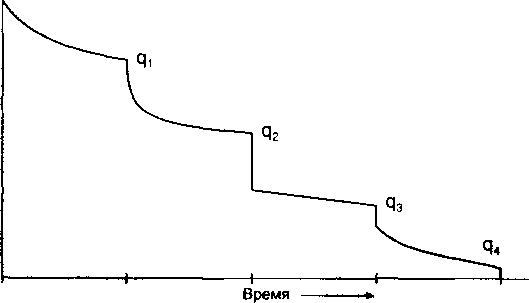
Цель данного упражнения - рассчитать С, п, AOF, используя общепринятые формулы.
Дано: рт= 201 psia
| Продолжительность (часов) | Pwf (psia) | m(p) (ММр$1а2/сантипуаз) |
Дебит (млн куб. фут./день) |
| 0 | 201 | 3,56 | 0,00 |
| 3 | 196 |
3,38 | 2,73 |
| 2 | 195 |
3,35 | 3,97 |
| 2 | 193 |
3,28 | 4,44 |
| 4 | 190 |
3,18 | 5,50 |
После проведения испытаний на приток коэффициенты формулы фильтрационных свойств, такие, как Сип рассчитываются по графику зависимости (pr2-Pwf2) от Ч- После того как эти точки нанесены на график, через них проводится прямая линия. Полученная линия называется фильтрационным графиком, где
log(рг -p<2)-log(рг2 -рЧ1) Ч
С =
рассчитываются для любого q и соответствующего ему pwf, полученного с фильтрационного графика.
Подобные исследования проводятся в низкопроницаемых коллекторах, где необходимое время для достижения установившегося забойного давления чрезмерно велико. Это случается в очень низкопроницаемых нефтяных или коллекторах, требующих стимуляции. В стандартный тест входит запуск скважины на нескольких различных дебитах с периодами остановки между ними. Длительность периодов работы скважины остается постоянной, а время остановок скважины - достаточно продолжительным для достижения пластовым давлением в контуре питания уровня среднепластового давления в пласте. Исследование заканчивается продолжительным периодом добычи на одном дебите (рис. 2.13).
q4
Рис. 2.13. Изохронный тест, дебит
и диаграмма давления
Стабилизировавшийся
дебит
Рз
41
Время
Рис. 2.15. Зависимость
log С от log t
при изохронном тесте
Pr2-P2wfsот дебита q, изохронный тест
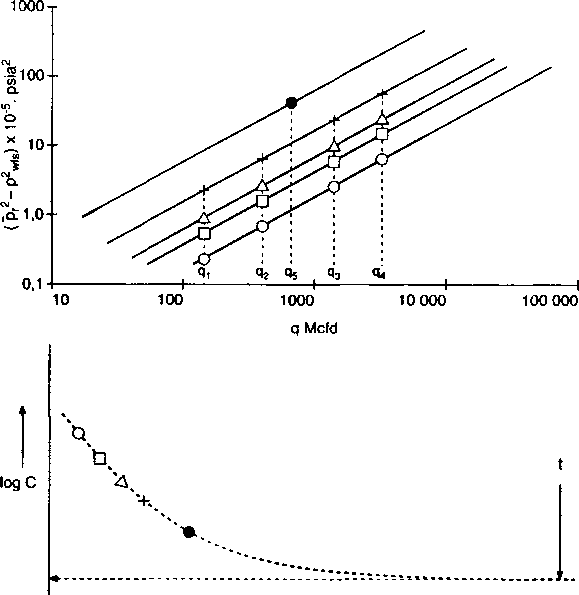
Для анализа данных исследований строятся графики зависимости log(pr2~Pwfs2) от l°g <?> как показано на рис.2.14, для каждого периода работы скважины на определенном дебите. Далее проводятся прямые линии через полученные точки, по одной для каждого дебита. Угол наклона п всех кривых должен быть одинаков, прямые должны быть параллельны. С увеличением времени эти прямые должны располагаться все ближе и ближе друг к другу. Угол наклона п рассчитывается для любой из этих прямых по формулам, используемым при испытаниях на неустановившемся притоке при переменных дебитах. Коэффициент С рассчитывается, основываясь на прямой с наклоном п, проведенной через точку, соответствующую последнему стабилизировавшемуся дебиту продленного периода в конце испытания.
Более точным методом определения С является метод, приведенный на рис. 2.15, где построен график зависимости log С от log t. Плавная кривая проведена через все точки. Значение С в точке, где график становится асимптотичен оси времени, считается действительным значением С. Часто необходимо проэкстраполировать кривую для определения действительного значения С.
Стабилизировавшийся
дебит
Чз
Qsc
Р2
qi
Время
Рис. 2.16. Модифицированный изохронный тест. Дебит
и диаграмма давления
| Рис. 2.17. | |
| Зависимость | |
| Рг2~Р Ifs от дебита q, | см «100-- <л О. |
|
модифици | •О О |
| рованный | 10 - |
|
изохронный тест |
J Q. I CM ,0.1,0-- |
В коллекторах с очень низкой проницаемостью, при проведении подобных исследований длительность остановки скважины, необходимой для достижения установившегося давления, становится слишком большой. В подобных случаях производится модифицированный изохронный тест, как показано на рис. 2.16 и 2.17. При модифицированных исследованиях длительность остановки скважины равна длительности периода замера дебита. В этом случае на графике с логарифмической шкалой откладывается разность площадей начального и конечного давлений для каждого периода. И через полученные точки проводится прямая линия. Далее строится график (pr2-p ?ys) против конечного продолжительного дебита и проводится прямая через эту точку параллельно начальной. Теоретический дебит скважины (AOFP) рассчитывается по этой прямой при забойном давлении, равном нулю. (Более детально данный вопрос рассматривается в книге «Теория и практика исследования газовых скважин», глава 3. Energy Resources Conventional Board, Калгари, Канада, 1975.)
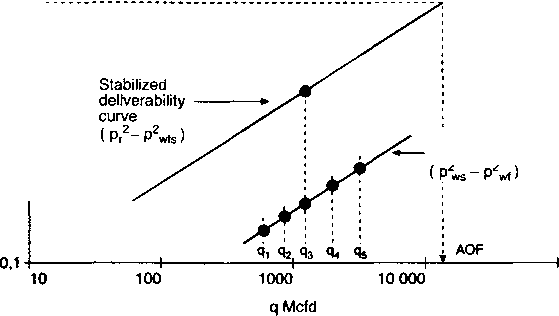
Transent
dellverability curve
100 000
Закон Дарси предполагает, что толщина или эффективная мощность пласта прямо пропорциональна производительности скважины. Продуктивная длина горизонтальной скважины может быть значительно больше. В горизонтальных скважинах производительность напрямую не зависит от длины. С увеличением длины горизонтальной скважины ее производительность увеличивается очень медленно. Тем не менее горизонтальные скважины могут быть очень длинными. Их длина ограничивается только экономическими показателями. В неоднородных пластах или пластах с естественной трещиноватостью подобные скважины могут быть пробурены перпендикулярно плоскости естественных трещин с целью значительного увеличения производительности. На месторождении Роспо Мэа в Италии горизонтальная скважина дает в 10 раз больше соседних вертикальных. В маломощных низкопроницаемых пластах это менее вероятно.
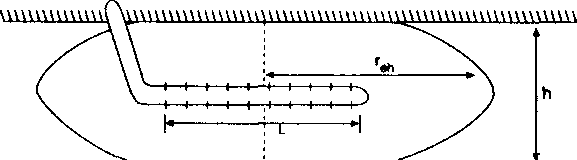
Рис. 2.18.
ГПТГТТШ! 111111ITI111111111111111111111111IIП111111 ml II1111111111111II1111111
Модель дренирования горизонтальной скважины
Соотношение между притоком и забойным давлением для горизонтальной скважины, пробуренной по центру пласта (рис. 2.18), определяется уравнением
7,0840-ъкф(р,-р^)
Qo=-
НА
In
для L>$h и (L/2)<0,9reh, где
т0,5
0,5 +
полудлина большей оси эллипса дренирования в горизонтальной плоскости (Рис. 2.18).
где индексы h и v относятся к горизонтальной и вертикальной плоскости соответственно. Все переменные в данной формуле даны в нефтепромысловых единицах, и она может быть применена в газовой скважине в соответствии с формулой Дарси для газа.
Сетка 160 акров
Горизонтальная проницаемость, к/, 0,06 мдарси
Вертикальная проницаемость, kv 0,06 мдарси
Среднепластовое давление, рт 800 psia
Забойное давление, pwf 400 psia
Радиус скважины, rw 5 дюймов
Пластовая температура, Тт 800°F
Относит, плотность газа, yg 0,65
Мощность пласта, h 1600 футов
Длина горизонтального участка, L 2770 футов
Решение: г = 0,9 (по корреляции Стэндинга),
= 0,0123 сантипуаза,
703*10^ ktffi-plf)
4iC - '
p/,
In
L \(P +
l)rw
= 0,19,
x = -
0,79+0,58P ln(l920p) qx = 1057 (млн ст. куб. футов/день)
Плотные породы
d/2)
703*10703 *10^ *1600 Tfigz ~ 540*0,0123*0,9 -2 *2
x = x(pf -pwf) = 0,19(800 - 400 ) = 91200, 912001
a+ja*-(Lf2)2
= 1057,
rpj
В резервуарах с очень низкой проницаемостью (меньше 0,1 мдарси) очень тяжело разработать поддающийся интерпретации тест. Самая большая проблема в этом случае это время, необходимое для достижения радиального притока бесконечного размера, что делает подобные тесты непрактичными. Следовательно, становится очень сложно получить такие характеристики пласта, как (kh/ц), s, рг и т.д., для установления КП (коэффициента продуктивности). Многоступенчатые исследования для определения индикаторных кривых также становятся достаточно сложными из-за времени, необходимого скважине для стабилизации на каком-либо дебите, если в скважине вообще есть приток. К сожалению, на большинстве таких низкопроницаемых скважин был произведен ГРП. После ГРП эффективный радиус скважины значительно увеличивается. В этом случае становится еще сложнее получить радиальный приток, чтобы можно было применить типовой анализ Хорнера для исследования скважин после ГРП. Данные тесты после ГРП дают свойства трещин ГРП, такие, как проводимость трещины, полудлина трещины и т.д.
Очень часто, когда стандартный анализ (Хорнер/полулогарифмический анализ и т.д.) не подходит для интерпретации результатов теста, применяется техника наложения на типовую кривую для определения параметров пласта, таких, как (kh/^i), s и т.д.
После определения параметров пласта типовые кривые могут использоваться для построения притока на неустановившемся режиме. Плотные формации остаются в неустано-вившемся режиме в течение длительного времени после запуска скважины. В течение этого неустановившегося периода, типовые кривые (ТК) могут быть использованы для построения индикаторных кривых неустановившегося режима (ИКНР). ИКНР позволяют рассчитывать накопленную добычу в этот период в дополнение к дебитам, рассчитываемым по индикаторным кривым установившегося режима.
Типовые кривые (ТК) являются графическим представлением решения уравнения проводимости для постоянного падения дебита и различных граничных условий. Уравнение проводимости является математическим описанием феномена течения жидкости в пласте к скважине. Каждая типовая кривая (ТП) допускает следующие типы коллекторов и скважин:
• однородные пласты со скважинами и скином или без;
• однородные пласты с индуцированными трещинами в скважине;
• пласты с двойной пористостью или естественной трещиноватостью;
• пласты с большим количеством пропластков и т.д.
Три переменные по осям х, у и z типовой кривой являются соответственно безразмерным давлением, безразмерным временем и переменной, представляющей условия в присква-женной зоне или форму границы. В зависимости от условий в стволе скважины (освоение скважины) переменная z может быть
• дополнительным скважинным притоком (с) или скином (s) в случае однородного пласта;
• проводимостью трещины (FCD) в случае скважин с индуцированными трещинами.
Все ТК строятся на логарифмической бумаге, таким образом, форма кривых напрямую зависит от замеров времени и давлений, полученных при исследовании на неустановившемся режиме. Другие параметры, такие, как kh, Ц, q, ф и др., влияют на совпадение графика данных исследования и ТК. Объяснение данного факта может быть дано при помощи ТК для однородного пласта с дополнительным скважинным притоком и скином.
Типовая кривая однородного пласта
ТК для однородного пласта с дополнительным скважинным притоком и скином представляет pD как функцию fo/Cp для различных Ср?25 на Рис. 2.19 (Gringarten et al Flopetrol Johnston Schlumberer). Эта ТК широко известна как типовая кривая Флопетрол Джонстон (Flopetrol Johnston). Периоды, в которых доминирует дополнительный скважинный приток для всех значений Cpe2s ложатся на одну линию (с одним наклоном). Конец участка графика линии с одним углом наклона для различных значений Сре25 отмечен на ТК. Начало участка кривой, представляющего бесконечный радиальный приток, отмечено на графике. Данная кривая не показывает эффект границ, а посему не может строго применяться к бесконечному резервуару. В реальности, как только скважина чувствует влияние границ, данные типовые кривые смещаются вверх. Безразмерное время при влиянии граничных условий зависит от того, насколько эти границы далеко от скважины. Типичная типовая кривая для скважины без границы контура питания представлена позже для скважины после ГРП (рис. 2.20).
Преимуществом ТК Флопетрол Джонстон (Flopetrol Johnston) является простота совмещения и ясное определение режимов притока, таких, как конец периода дополнительного притока скважины, начало периода бесконечного радиального притока и т.д. На данной типовой кривой безразмерные переменные определяются следующим образом:
kh
Ри = 141
2qB~ii ~ безразмерное
давление
___khAp „ 0.8936С
fD/CD=0,000295—-f, CD=—-
И С фцС,г*
Рис. 2.19. Типовая Кривая для однородного
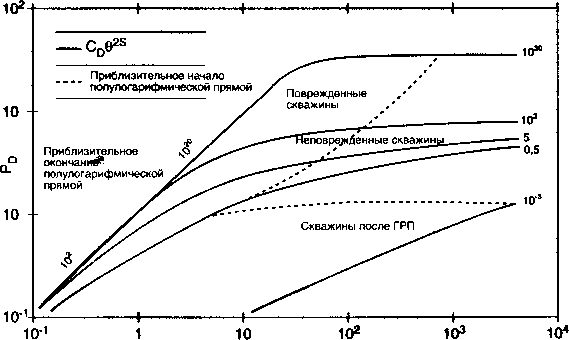
Данные безразмерные группы представляют универсальную шкалу давления и времени. На самом деле ТК представляют глобальную реакцию давления по времени на различные уровни дебитов и закачки. Представление этих переменных в логарифмических координатах делает возможным совмещение их с графиком зависимости давления от времени, полученным при испытании скважины. Логическое обоснование данного факта заключается в следующем:
!°gpD =logAp + Iog
kh
\4l,2qB\l
= log Др +logy,
где у - константа для данного конкретного пласта. Подобным же образом
kh
0,000295-I = log At + log x,
l°S(f d ICD) = log At + log
где x =fl.k, h, p., С)- константа для системы скважина-пласт. Следовательно, log рр и log tD фактически являются log ApD и log Af соответственно, переведенными некими константами, определяемыми характеристиками пласта. Таким образом, если используется правильная типовая кривая, представляющая модель пласта, реальный и теоретический графики зависимости давления от времени совпадают по форме но смещены по масштабу при построении в логарифмических координатах.
Соотношение для расчета притока при неустановившемся режиме
Бесконечный однородный пласт
Индикаторные кривые неустановившегося режима для бесконечного пласта могут быть построены с использованием типовых кривых Флопетрол Джонстон (Flopetrol Johnston) как показано в примере.
Дано:
Пример 2.6.
k = 1 мдарси h = 20 футов = 1 сантипуаз В„ = 1,0 РБ/СтБ рг = 000 psia rw = 0,5 фута
Расчет:
tn kh At
~P~ = 0,000295--= 5,9At,
ц С
Ct = 10'5 psf1
С = 0,001 барреля/psi
время = 0,1,1,10,100 часов
S= 1,21
0.8936С <t>HC,rI
CD =
= 89,36,
Сое25 = 89,36*е242 = 1000.
По типовой кривой рис. 2.19 для CDe2s = 1000 значения pD получаются для различных значений (д/Сд как функция времени. В этом случае, теоретический дебит скважины
kh Pr 141,2BjiepD’
| At, час |
tc/Cp | pD, из ТК |
Теоретический дебит, баррелей/день |
|
0,1 | 0,59 |
0,56 | 506 |
| 1 | 5,9 |
3,15 | 90 |
|
10 | 59 |
5,9 | 48 |
|
100 | 590 |
7,2 | 39 |
Для однородных пластов широко известное бесконечное полулогарифмическое приближение для скважин со скином, работающих на постоянном дебите после ослабевания эффектов дополнительного притока скважины, дается в следующем виде:
pD = l/2(ln tD + 0,80907 + 2s).
Данная формула представляет типовую кривую однородного пласта до тех пор, пока неустановившееся давление не достигает границы радиуса дренирования. Это время зависит от радиуса контура питания и может быть рассчитано, основываясь на некоторых свойствах коллектора:
‘(часы) =94^
Уравнение для ро упрощается до следующего вида: kh(Pr~Pwf)
%
| ( ( , ^ | 1 | ||
|
162,6|!0В0 |
jl°R | к |
-3,23+0,78sUlog(f) |
|
LI1 | J J |
||
Соотношение для расчета притока при неустановившемся режиме газовых скважин приведено в Приложении А, секция IV.
То же, что и в предыдущем примере, ге = 2000 футов.
Время до окончания псевдобесконечного радиального притока, в часах:
246 log t + 4,3
0,2* 10-5 *0.52
-3,23+0,87sf + log(f)
| f, час |
q0 (теоретический дебит скважины) |
| 0,1 |
74,55 |
| 10 |
46,42 |
| 100 |
39,05 |
| 1000 |
33,70 |
| 7584 | 30,07 |
Обратите внимание на отклонение значения теоретического дебита на отрезке времени менее 100 часов. Это происходит по причине того, что полулогарифмическая аппроксимация не учитывает влияния дополнительного притока скважины.
162,6 {log
Однородный пласт с искусственными вертикальными трещинами
Мэнг и Браун (Meng & Brown) представили типовые кривые для скважин с наведенными вертикальными трещинами в центре пласта с зоной дренирования различной прямоугольной формы. В расчетах принято, что жидкость слегка сжимаема и обладает постоянной вязкостью ц. Для расчета притока газа используется функция приведенного давления Аль-Хусаини (Al-Hussainy et al., 1966) для оценки свойств газа при начальном пластовом давлении. Безразмерные переменные, используемые при построении этих ТК, определяются следующим образом:
безразмерное скважинное падение давления
(нефть),
141,2 qpB
(газ),
(нефть),
(газ),
Pd :
1,424qt безразмерное время 0,000264fcf
lDxf ~
ф \LC,xj 0,000264kt
krW
Fcd = ---безразмерная проводимость трещины.
hcf
Часть этих типовых кривых представлена на рис. 2.20. Необходимо отметить, что на начальной стадии отношение времени от давления зависит от FCD; тогда как в позднее время или после того, как начинается истощение, основное влияние на реакцию давления оказывает форма и размер контура питания.
Как и в случае однородного пласта, индикаторные кривые неустановившегося режима пласта после ГРП могут быть построены с использованием соответствующих типовых кривых, представленных на рис. 2.20. Эти ТК могут использоваться как для однофазной нефти, так и для однофазного газа. В случае газа вместо давления используется т(р). Для нефтяных скважин при давлениях ниже давления насыщения используются индикаторные кривые Вогеля. Ниже приведена пошаговая процедура расчета притока при неуста-новившемся ре
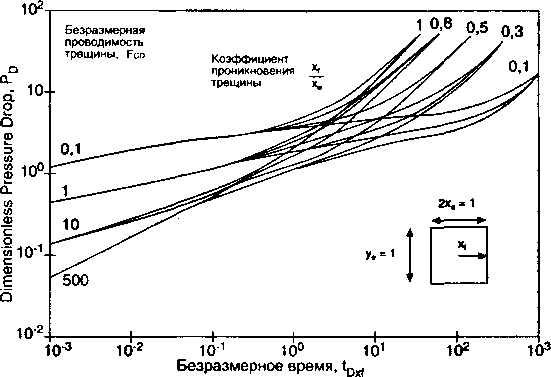
жиме.
Рис. 2.20.
Типовая кривая
установившегося
дебита трещины
конечной
проводимости
закрытой
квадратной
системы
1. Рассчитать безразмерную проводимость трещины, определенную раньше.
2. Геометрия контура питания хе/ уе предполагает замкнутый коллектор, рассчитать отношение глубины проникновения трещины xf/xe.
3. Рассчитать безразмерное время tDxf для любого произвольного времени и известных параметров к, ф, С, Xf и т.д.
4. По типовым кривым определить безразмерное давление рд( tDj, FCD, Xj! х^ хе /уе).
5. Рассчитать и коэффициент продуктивности (PI) при давлении насыщения:
_kh(p,pb)_
l4l,2B0[lpD(tDxf,FCD,xf/xe,xe / у,)'
Чь =
Р/ =
Чь
Pi-Pb
где pf,- давление насыщения, qj, - дебит при давлении насыщения.
6. Рассчитать q\/0Seh где
л -hlfi qvogel 18 •
7. Рассчитать зависимость дебита от забойного давления pwf vs, q, используя формулу Вогеля
| / \ | / N |
2 | ||
| 1-0,2 |
Pwf | -0,8 |
Pwf | |
|
< Рь , |
1 ft J |
Для газовых скважин для построения индикаторных кривых используйте шаги с 1 по 5. Поправка притока (Не-Дарси)
Все представленные ранее в этом разделе формулы расчета притока основаны на притоке, определенном Дарси; предполагается, что градиент давления в направлении притока прямо пропорционален скорости потока. Для линейного притока математически это может быть выражено следующим образом:
dp _ цу
dx~T’
где dp / dx - градиент давления в направлении притока, ц - вязкость жидкости, к - проницаемость пористой среды, v - скорость потока. В ходе лабораторных исследований, проведенных рядом ученых, было замечено, что данная формула неприменима, если скорость превышает пороговое значение. Поведение потока при скорости выше пороговой называется потоком, не определенным Дарси, что является эквивалентом турбулентного течения в трубе. Форхаймер (Forcheimer, 1901) описал это отклонение от притока Дарси:
где Р - фактор притока не определенного Дарси, р - плотность жидкости, все остальные переменные определены в предыдущем параграфе. Обратите внимание, что эта формула становится формулой Дарси для притока, когда второе слагаемое очень мало. Подобное случается, когда один из или комбинация параметров Р, р и v становится нулем или значением, близким к нулю. Таким образом, если скорость потока или плотность жидкости (в случае разреженного газа) становятся незначительными - можно применять формулу -Дарси для описания градиента давления. В газовых скважинах высокого давления и нефтяных скважинах с большими дебитами либо многофазовым потоком в пористой среде доминирует приток, не определяемый формулой Дарси.
Ваттенберг и Рэми (Wattenberg & Ramey, 1969) обнаружили эффекты потока, «не определенного Дарси», в пластах с искусственными (наведенными) трещинами. Они пришли к выводу, что этими эффектами можно пренебречь, если трещина достаточно длинная. Тем не менее они заметили, что эти эффекты могут быть довольно значительными в самой трещине. Холдич и Морс (Holditch & Morse, 1976) изучали эти эффекты более детально и обнаружили большое падение проводимости трещины при преобладании потока, «не определенного Дарси». Эти авторы не предлагали какого-либо конкретного метода корректировки проводимости трещины при потоке «не определенном Дарси». Гаппи и др. (Guppy et at 1982) представил метод корректировки проводимости трещины. Они использовали корреляцию Кука (Cook, 1973) для определения {J как функции проницаемости трещины kf( мдарси) и размера пропанта:
(30,48 *106)*Ь
ка
kf
где а и b - константы получаемые из табл. 2.2, р измеряется в футах"1.
Таблица 2.2. Константы я и Ь формулы Кука
| Размер пропанта (мэш) | а |
Ъ |
| 8-12 |
1,24 | 17423,61 |
| 10-20 | 1,34 |
27539,48 |
| 20-40 |
1,54 | 110470,39 |
| 40-60 | 1,60 | 69405,31 |
Таким образом, если для трещины рассчитан фактор турбулентности Р, Гаппи предлагает следующую корреляцию для потока, не определенного Дарси для проводимости трещины, определенной по типовым кривым Кинко (Cinco):
Видимая Fqy) (с типов°й кривой) 1 + 031(<2гт>)/
Fcd -
1,027336 *10~15/t,
wh\L
4,64 * 10-16к уррМд
где, для нефтяных скважин, в промысловых единицах,
/Р
(^dnd) ~ для газовых скважин
(<?dnd) =
где Hi - вязкость в начальных пластовых условиях.
Другими параметрами, используемыми в данной формуле, являются р - плотность жидкости, w - ширина трещины, И - эффективная мощность пласта (при условии полного вскрытия пласта), ц - вязкость жидкости, q - суммарный приток жидкости в скважину, kf-проницаемость трещины.
Необходимо отметить, что безразмерный приток (дозаявляется функцией притока. Приток, в свою очередь, определяется значением безразмерного давления pD, которое в случае скважины после ГРП является функцией Fcd¦ Следовательно, каждый раз, когда корректируется безразмерная проводимость трещины, необходимо рассчитать новое значение притока q, и данная итерация производится до тех пор, пока два соседних значения притока не будут настолько близки, чтобы не вызывать сколь-либо значительной разницы в корректированной проводимости. Также при расчете падения дебита проводимость трещины должна корректироваться в каждый момент времени, в котором рассчитывается дебит, используя ту же процедуру итерации.
Примеры (5 и 6) расчета падения дебита при притоке не определенном Дарси по программе FracIPR представлены в конце главы 5.
Упражнения. 1. Дано (нефтяная скважина)
Проницаемость пласта, к Мощность пласта, h Пористость пласта, ф Полная сжимаемость системы, С Объемный фактор нефти, В0 Вязкость нефти, Ц0 Начальное пластовое давление, р,
0,2 мдасри 30 футов 0,15
1,14*10'5 psi"1
1,44 пластовых баррелей/СТБ 0,35 сантипуаза 5200 psi 3500 psi 40 акров 500 футов
Давление насыщения, р;,
~ Площадь зоны дренирования, А
Расчетная полудлина трещины, Xj Расчетная проводимость трещины, kf, w 2000 мдарси - футов Расчетное время, tp 5,10,30,365 дней
Подсказка: постройте индикаторные кривые неустановившегося режима для различных значений времени.
2. По следующим данным газовой скважины рассчитайте теоретический дебит скважины: kg = 0,1 мдарси рг = 3000 psi h = 300 футов
Пластовая температура = 200°F yg = 0,7
Сетка = 160 акров
Диаметр скважины = 12,25 дюйма
Скин = 1
Пренебречь турбуленцией.
6000т
Рис. 2.21.
IPR
неустановившегося режима скважины после ГРП с закрытым квадратным контуром питания
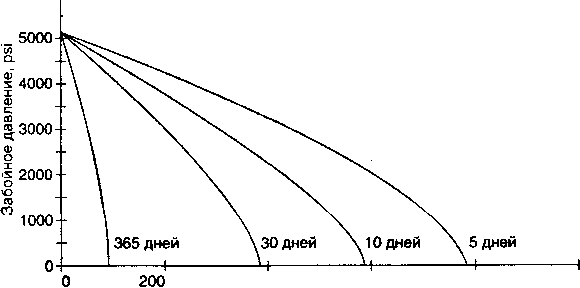
400 600
Дебит, СТБ / д
3. Рассчитать ln(re / rw) при rw = 7 дюймов для различных контуров питания площадью 20,40,80,160 и 320 акров.
Подсказка: постройте таблицу
In (те / rw)
Площадь контура питания, акры
_20_
_40_
_80_
_160_
320
4. Построить индикаторную кривую для следующей скважины: к = 50 мдарси Глубина = 5000 футов
/* = 100 футов
рг = 2000 psia 100%-ная нефтяная скважина.
Определить теоретический дебит скважины.
1. Evinger Н.Н. and Muskat М. «Calculation of Theoretical Productivity Factor», Trans., AIME (1942) 146,126-139.
2. Gilbert W.E. «Flowing and Gas-Lift Well Performance», Drill, and Prod. Prac., API (1954) 126.
3. Govier G.W., et al. «Theory and Practice of the Testing of Gas Wells», Energy Resources
Conservation Board, Alberta, Canada, 3rd Ed, 1975.
4. (ones L.G., Blount E.M. and Glaze D.H. «Use of Short Term Multiple Rate Flow Test to Predict-
Performance of Wells Having Turbulence», paper SPE 6133,1976. ~
5. Cinco-Ley H. and Samaniego-V F. «Transient Pressure Analysis for Fractured Wells», JPT (Sept. 1981)1749-1766.
6. Ginger F.M., Reiss L.H., and Jourdan A.P. «The Reservoir Engineering Aspect of Horizontal
Drilling», paper SPE 13024,1984. *
7. Joshi S.D. «Augmentation of Well Productivity With Slant and Horizontal Wells», paper SPE \ 15375 (1986); JPT, (June 1988) 729-739.
8. Meng H-Z. and Brown K.E. «Coupling of Production Forecasting, Fracture Geometry ^ Requirements and Treatment Scheduling in the Optimum Hydraulic Fracture Design», paper SPE 16435,1987.
9. Muskat M. «The Flow of Homogeneous Fluids Through Porous Media», IHRDC, Boston, 1982. -
10. Prats M. «Effect of Vertical Fractures on Reservoir Behavior - Incompressible Fluid Case», SPEJ (June 1961) 105-118.
11. Standing M.B. «Inflow Performance Relationship for Damaged Wells Producing by Solution Gas Drive Reservoirs», JPT (Nov. 1970) 1399-1400.
12. Fetkovich M.J. «The Isochronal Testing of Oil Wells», paper SPE/AIME 4529,1973.
13. Vogel J.V. «Inflow Performance Relationships for Solution Gas Drive Wells», JPT (Jan. 1968), 7 83-93.
14. Horner D.R. «Pressure Buildup in Wells», Third World Petroleum Congress, Sec. II, 503-521.
15. Agarwal R.G., AI-Hussainy R., and Ramey H.J.: «An Investigation of Wellbore Storage and Skin Effect in Unsteady Liquid Flow: 1 .Analytical Treatment», SPE Trans. (Sep. 1970) 279-290
16. Al-Hussainy R., and Ramey H.J.: «Application of Real Gas Flow Theory to Well Testing and ~ Deliverability Forecasting», JPT (May 1966) 637-642.
17. Brown K.E. «Technology of Artificial Lift Methods» Vol. 1, Tulsa, OK, Penn Well Publishing. :
18. Mukherjee H. and Economides M.J. «А Parametric Comparison of Horizontal and Vertical J
