Фракционная перегонка
ГЛАВА XIV
XIV. 39, XIV. 41]. Целью данной главы является изложение некоторых принципов перегонки, а не систематизация всех соотношений, характеризующих работу ректификационных колонн.
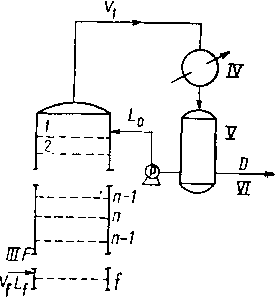
Ректификационную колонну [рис. XIV. 1] можно рассматривать как сочетание абсорбционной и выпарной колонн. Внизу ректификационной колонны имеется подо-греватель-рибойлер, где за счет частичного испарения флегмы образуется паровая фаза и отгоняются те компоненты, которые должны быть извлечены из нижнего
продукта. На верху колонны находится конденсатор, обеспечивающий орошение или избирательную абсорбцию тех компонентов, которые подлежат удалению из верхних продуктов, Ферро, Легатский и Гахмут (Ferro, Legatsti and Hachmuth) [XIV, 18] установили, что в рек-тификационной колонне одновременно происходят абсорбция и десорбция, и на этой основе разработали свой метод расчета колонны, основанный на вычислении коэффициентов поглощения и отпаривания.
т-1
т
т+1
35 °С
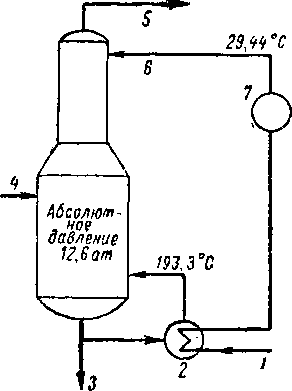
Рис. XIV. 2. Схема потоков деэта-низатора насыщенного сорбента.
1 — из колонны: 2— кипятильник; 3 — деэтанизированный сорбент; 4 — насыщенный сорбент при 71° С; 5 — сухой газ; 6 — тощий сорбент; 7 — холодильник.
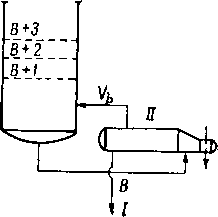
Рис. XIV. I. Схема фракционирующей колонны с вспомогательным оборудованием и обозначением потоков,
/ —> нижний целевой продукт; II — рибойлер (кипятильник); III— питание', IV — конденсатор*, V — сборник орошения, VI —• дистиллят.
Поскольку теоретически перегонка может осуществляться без каких-либо необратимостей, т. е, поскольку полезная работа теоретически может быть сведена до уровня, термодинамически необходимого для разделения, Бенедикт (Benedict) [XIV. 3] охарактеризовал перегонку как потенциально обратимый, процесс. Практически же ректификационные колонны строятся с конечными: числом тарелок, площадями теплообмена в конденсаторах и рибойлерах, что связано с введением некоторых необратимостей.
Если верхний погон нельзя сконденсировать при температуре охлаждающей воды, процессы абсорбции и десорбции объединяют. Примером подобного гибридного процесса является колонна, в которой осуществляется отгон этана из насыщенного сорбента (рис. XIV. 2). Извлечение тяжелых углеводородов, которые должны остаться в нижнем продукте, осуществляется с помощью орошения таким сорбентом; в рибойлере образуются пары, что необходимо для извлечения из нижнего продукта летучих компонентов [XIII. 10]. Допускается
Твпливныи газ & тровыемтльри на бытовтнужов еаводского поселка
/ Изопенщн н-пентан Гек сан Пропан Бутан-
уменьшение диаметра колонны над питающей тарелкой, поскольку объем потока жидкости в верхней части колонны значительно меньше, чем в нижней, выпарной части. В некоторых случаях десорбционные пары, вырабатываемые рибойлером, дополняют парообразными углеводородами, вводимыми под тарелку, находящуюся где-то между рибойлером и питающей тарелкой.
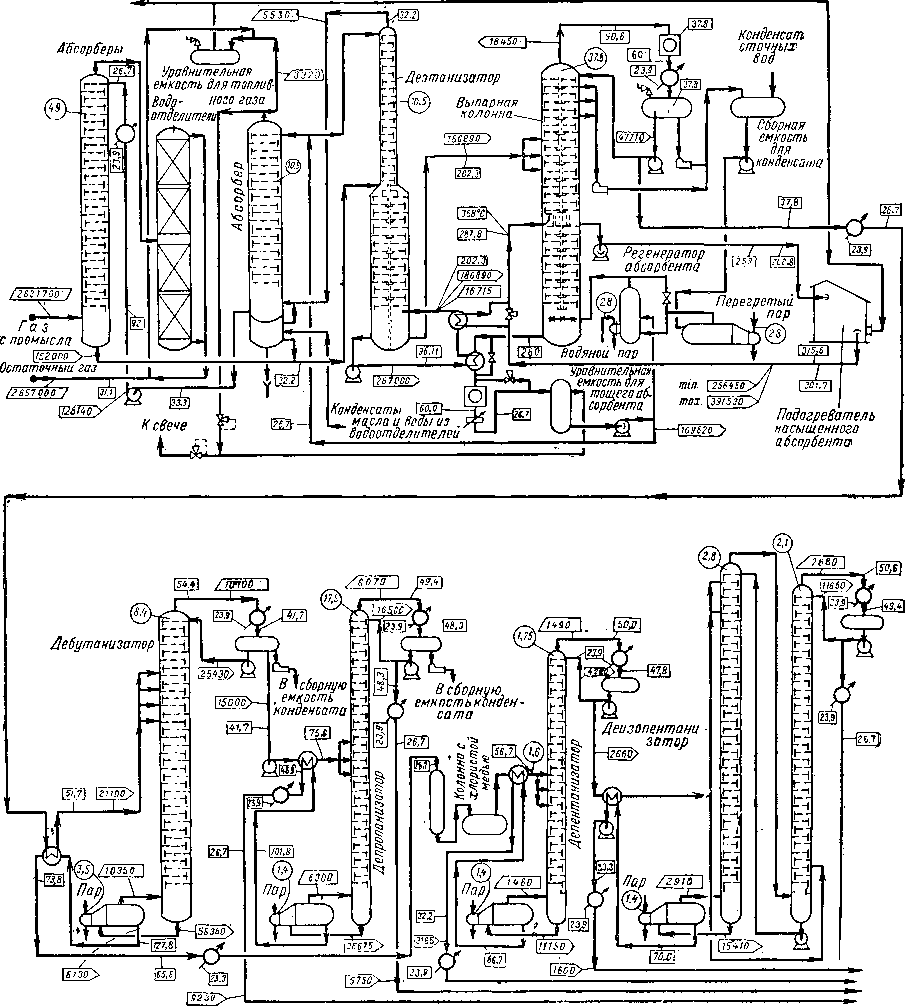
На рис. XIV. 3 схематически показано сочетание процессов в типовом газобензиновом заводе [XIV. 37а]. На этой схеме обозначены главные производственные установки и указаны условия их работы (температура и давление). На рис. XIV. 4 показан общий вид того же. завода.
Главным предварительным условием разделения жидкой и парообразной фаз путем массообмена является благоприятное соотношение равновесия этих фаз. Относительная летучесть компонентов, подлежащих разделению, должна быть достаточно высокой, чтобы обеспечить разделение без чрезмерных затрат тепловой энергии и значительного увеличения числа тарелок. Коэффициенты распределения и другие термодинамические свойства углеводородов уже были рассмотрены в главах III—VI.
§ 1. ПЕРЕГОНКА ДВУХКОМПОНЕНТНЫХ СМЕСЕЙ
Ниже излагаются три. основных метода расчета числа равновесных ступеней в ректификационной колонне: 1) графический метод Мак Кэба — Тиле (McCabe — Thele), в котором не используются непосредственно соотношения энергии; 2) метод Поншона — Савари (Роп-chon — Savarit), в котором фазовое поведение и термическое поведение объединены в единую графическую процедуру, и 3) аналитический метод.
1. ГРАФИЧЕСКИЙ МЕТОД МАК КЭБА —ТИЛЕ
Метод Мак Кэба — Тиле [XIV. 33] позволяет быстро, хотя и не совсем точно, определить соотношения важнейших переменных параметров для расчета равновесных ступеней при перегонке двухкомнонентных систем. Несмотря на простоту этого метода, единственное допущение, которое при этом приходится делать,—это то, что соотношение между жидкостью и паром в адиабатической части колонны остается неизменным.
Как показано на рис. XIV. 1, общий материальный баланс по верхней части колонны охватывает потоки I'nJ-i, и D, что дает следующее уравнение материального баланса:
f Dxl Dxd
V
п + \Уп + 1 ' L„
У/г + 1
I/
я+ 1 v п + 1
где Vn + i — число молей пара на выходе с тарелки п+1; уг+1—мольная доля наиболее летучего компонента в
+ Ln — число молей жидкости на выходе с тарелки п\ хп—мольная доля наиболее летучего компонента в L„\ D — число молей верхнего продукта, отбираемого из колонны; xD — мольная доля наиболее летучего компонента в верхнем продукте.
Поскольку мы исходим из предположения о наличии в колонне стационарных условий, величины V, L и D можно считать показателями как массовой скорости потока, так и самого массопотока. Уравнения (XIV. 2а) и (XIV. 26) характеризуют составы смежных противо-точных потоков пара и жидкости в показателях расходов жидкости и пара в данной точке колонны и выхода дистиллята.
Уравнение (XIV. 26) часто называют уравнением рабочей линии. Чтобы упростить построение рабочей линии, предположим, что соотношение LjD для потока жидкости постоянно. Тогда
L , D Уп+1 = у хп+ yXD-
(XIV. 2а) (XIV. 26)
(XIV. 3)
¦хп +
\в
Мольная концентрация метана в жидкости з:
Рис. XIV. 5. Построение диаграммы Мак Кэба Тиле для полной колонны.
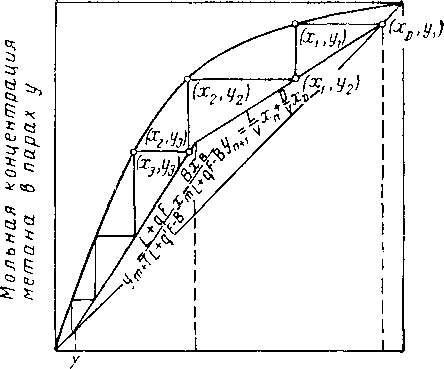
Следовательно, для колонны, работающей при стационарном режиме, зависимость состава пара от со-сгава жидкости в мольных долях будет представлять прямую линию (рис. XIV. 5).
При подстановке в уравнение (XIV. 3) xn=xD y^ + i=xD. Значит, точка (xD, У\) будет находиться на линии, проходящей под углом 45° через точку начала координат (х = 0; у = 0) и точку (* = 1; у=1). Построение рабочей линии с наклоном L/V, т. е. линии, соответствующей составам контактирующих потоков, показано на рис. XIV. 5.
(XIV. 6)
Разрыв рабочей линии вызван введением в колонну питания. Компонентный баланс по нижней части колонны дает стоянного молекулярного переноса во всех частях колонны. Это будет показано в дальнейшем при рассмотрении точного метода расчета перегонки двухкомпонентных смесей, предложенного Понтоном — Савари.
Чтобы увязать между собой уравнения (XIV. 3) и (XIV. 5), вводим параметр q', определяющий состояние питания:
где„ У' — числ° молей насыщенной жидкости, образующейся на питающей тарелке при вводе 1 моля питания; F—число молей питания.
Из диаграммы энтальпия — концентрация видно, что
^sv — hF HSV~ hSL
(XIV. 4)
Г =
(XIV. 7a)
1 + 1 Ут + 1
где Ут_|_1 — число молей пара на выходе из тарелки m-bl, расположенной ниже питающей тарелки; ym + i — мольная доля наиболее летучего компонента в Vm + \\; Lm — число молей жидкости на выходе из тарелки т, расположенной ниже питающей тарелки; В — число молей в нижнем продукте; хв— мольная доля наиболее летучего компонента в нижнем продукте.
При неизменном мольном соотношении жидкости и пара в отгонной части колонны
Если указанное выше требование 2 оказывается удовлетворенным при составе, близком к составу питания, то
н
- hc
•SI/
Я' =
(XIV. 76)
^SV — hSL
где HSv—энтальпия насыщенного пара в ккал/кмоль\ hr энтальпия питания в ккал/кмоль\ hsL —энтальпия насыщенной жидкости в ккал/кмоль.
Из уравнения (XIV. 76):
V Вхь Ут + I — угхт — ~уТ
(XIV. 5)
hF — Hsv> то я' = 0;
если
Требованию о неизменном соотношении между жидкостью и паром в каждой части колонны удовлетворяет колонна, в которой:
1) нет теплообмена с окружающей средой, кроме как в кипятильнике-рибойлере и конденсаторе-холодильнике верхнего продукта;
2) мольная теплота испарения остается постоянной по всему интервалу содержания компонентов, который охвачен перегонкой.
Если пренебречь такими факторами, как унос, нетрудно убедиться, что эти условия вполне достаточны для сохранения постоянного соотношения L/V или по-
hF = hSL, то q' = 1,0;
hF > Hsv, то q' < 0;
если
hF < hsu to q' >1,0.
Поскольку V' = U—В, уравнение (XIV. 5) можно выразить в другой, более удобной форме:
I, ^ . L + q'F— х„. — _—И___(XIV. 8)
m+1 L+q'F—B т L — q’F — B
Это и будет уравнение рабочей линии отгонной секции колонны.
Другое выражение для V' можно получить, написав материальный баланс по питающей тарелке:
L + V' + F = L' + У;
V = L + q'F+V — L — F = F (q’ — \) + V. (XIV. 9)
Другой способ определения рабочей линии для одной части колонны по рабочей линии другой части и по концентрации и состоянию питания заключается в совместном решении уравнений (XIV. 3) и (XIV. 8) при условии, что точки пересечения удовлетворяют требованию
В результате решения [XIV. 2, XIV. 11] получаем уравнение линии q, которая является геометрическим местом точек пересечения рабочих линий верхней и нижней секций колонны:
У = • (XIV. 10)
Ч 1 q — 1
Наклон q'Kq'—1) кривой для этого уравнения определяется исключительно состоянием q' питания. Линия, соответствующая уравнению (XIV. 10), проходит через точку (у = у г, х = xF), лежащую на прямой равного состава, угол наклона которой равен 45°.
На рис. XIV. 6 показано влияние состояния питания q’ на пересечение рабочих линий отгонной и укрепляющей секций колонны при неизменных прочих условиях. Влияние качества питания на потребное число равновесных ступеней можно определить посредством расчета по отдельным ступеням.
При нанесении на диаграмму у—х результатов весьма точных расчетов по отдельным тарелкам рабочие линии могут представлять собой кривые. Однако метод Мак Кэба — Тиле позволяет получить достаточно точный расчет перегонки с использованием диаграмм «энтальпия — концентрация» (XIV. 40, XIV. 44).
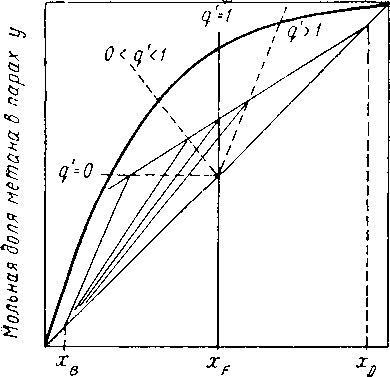
Мольная доля метана в жидкости х
Рис. XIV. 6. Влияние состояния питания q' па положение рабочей линии отгонной секции колонны для бинарной системы метан — этан при 35 ат.
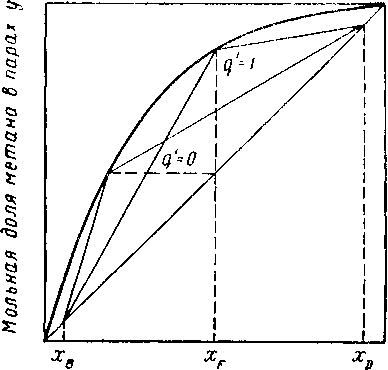
Мольная доля мешана в жидкостих
Рис. XIV. 7. Влияние состояния питания на коэффициент минимального орошения для бинарной смеси метан — этан при 35 ат.
Метод Мак Кэба — Тиле был успешно применен и для приближенных расчетов перегонки многокомпонентных смесей (XIV. 22, XIV. 23, XIV. 25).
Важными теоретическими параметрами для данной степени разделения являются коэффициент минимального внешнего орошения (L0/D)m[n и минимальное число теоретических тарелок. Коэффициент минимального орошения соответствует коэффициенту орошения, необходимому для данного разделения при бесконечно большом числе теоретических тарелок. Коэффициент минимального орошения соответствует также минимальным теоретическим затратам энергии, при которых может быть проведена данная перегонка. Рабочие линии, соответствующие коэффициенту минимального орошения при неизменном составе, но различном состоянии питания, показаны на рис. XIV. 7. По наклону рабочих линий можно непосредственно определить (L/V) min- Зависимость коэффициента минимального внешнего орошения (Lq/D)min от коэффициента минимального внутреннего орошения (L/V) min выражается соотношением
= (Lo/P)min (XIV. 11)
V/min (Lo/O)min+1
Из рис. XIV. 7 видно, что сила, побуждающая мас-
сообмен в местах пересечения рабочими линиями рав
новесной линии, уменьшается до нуля. Зона нулевой побудительной силы известна под названием зоны бесконечного числа тарелок, в пределах которой при переходе от одной тарелки к другой разделение не происходит. При разделении двухкомпонентных смесей легких углеводородов вследствие правильной формы равновесной линии можно ожидать совпадения зоны бесконечного числа тарелок с пересечением линии q и
равновесной линии. Это может, однако, не происходить, если жидкая фаза обнаруживает серьезные отклонения от идеального раствора [XIV. 7].
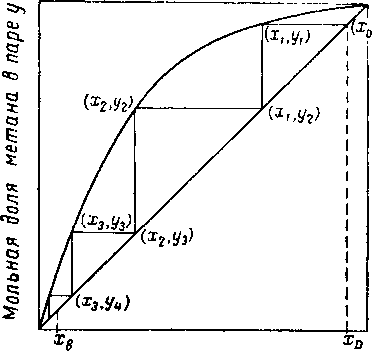
Минимальное число теоретических тарелок соответствует условию полного орошения: L/V = 1,0 или
Lc/D->-°o-В этих условиях рабочая линия совпадает с прямой равного состава. Расчет минимального числа равновесных ступеней для данного разделения приве-
ден на рис. XIV. 8. При данном давлении минимальное число равновесных ступеней зависит только от состава продукта и константы равновесия.
4500
¦о
с;
с>
5:
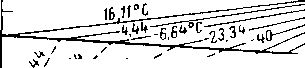
- 56,65 ~73,3°L
3000
с;
о
i:
i:
of
3
с:
о
с;
0
Е
1
1500
1500
2775
о 0,20 0,40 0,60 0,80 1,00
Мольная концентрация метана
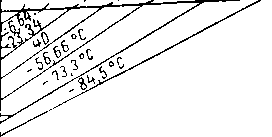
Рис. XIV. 9. График энтальпия — концентрация для системы метан — этан, находящейся под абсолютным давлением 35 кГ/см2.
X или у
F.Xf
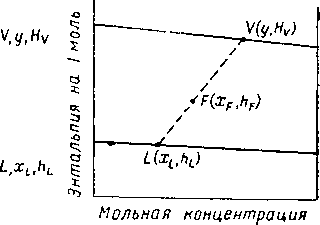
Рис. XIV. 10.
Схема одноступенчатого разделения сырья.
'6
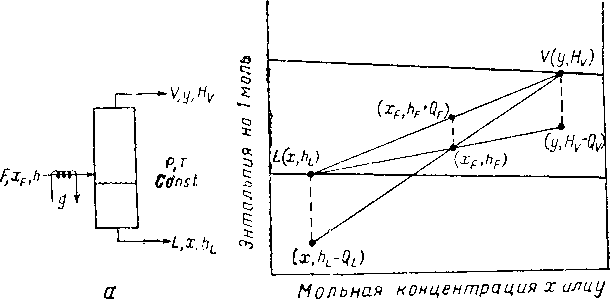
Рис XIV. 11.
одноступенчатое разделение с дополнительным подогревом сырья; 6-ние материального и теплового баланса ч схеме а.
¦ построе-
Мольная доля метана 6 жидкости х
Рис. XIV. 8. Расчет минимального числа теоретических тарелок для бинарной системы метан — этан при 35 ат.
2. МЕТОД ПОНШОНА — САВАРИ
(PONCHON— SAVARIT) С ИСПОЛЬЗОВАНИЕМ ДИАГРАММ ЭНТАЛЬПИЯ —КОНЦЕНТРАЦИЯ
В этом разделе излагается метод поступенчатого расчета перегонки двухкомпонентных смесей, разработанный Понтоном [XIV. 40] и Савари [XIV. 44]. В литературе имеются многочисленные указания о применении этого метода и для расчета перегонки других смесей [XIV. 43, XIV. 56, XIV. 57, XIV. 59]. Этот метод основан на применении диаграмм энтальпия—концентрация и констант равновесия, При надлежащем выборе таких параметров, как энтальпия и масса, тепловые и материальные потоки можно складывать или вычитать линейно графическим путем.
На рис. XIV. 9 показана характерная диаграмма энтальпия — концентрация для смеси метан — этан, находящейся под абсолютным давлением 35 кГ/см2. Геометрические места энтяльпий насыщенной жидкости и пара показаны вместе с несколькими равновесными изотермами. Величины энтальпии смесей метана и этана экспериментально не установлены, но были вычислены при допущении идеальности растворов как в парообразной, так и в жидкой фазах. Показано несколько изотерм в зонах перегретого пара и переохлажденной жидкости.
Координатами графика могут быть или ккал/кг-моль— мольная концентрация, или ккал/кг—весовая концентрация.
Точное определение материальных и тепловых балансов для двухкомпонентных смесей может быть выполнено по диаграмме энтальпия—концентрация. Применим этот метод для технологических схем, изображенных на рис. XIV. 10 и XIV. II. На рис.
XIV. 10 показан адиабатический
Процесс, а на рис. XIV. 11 — неадиабатнческий, при котором к смеси добавляют определенное количество тепла q. Составы потоков F, V и L выражаются соответственно х F, у и х.
Уравнения материального и теплового балансов для схемы, представленной на рис. XIV. 10, таковы: общий материальный баланс
рассматривается равновесное разделение, применять этот метод анализа можно не только для фаз, находящихся в равновесии.
Неадиабатическое состояние (рис. XIV.11, а) дает следующие уравнения баланса: общий материальный баланс
где Hv—энтальпия пара на единицу массы; hL—энтальпия жидкости на единицу массы; hf— энтальпия питания на единицу массы.
Исключив F из уравнений (XIV. 12) и (XIV. 13), а также (XIV. 12) и (XIV. 14), получим
(XIV. 24)
Общее количество теплоты q можно представить на диаграмме энтальпия — концентрация следующим образом:
FQp = VQy=LQL,
hF—hL
V
I
(XIV. 15)
НI,
¦hF у — хр
При исключении L получим
hF — hL Hu — h,
V
F :
(XIV. 16)
У — х
где Qf, Qv и Ql— количество теплоты, поглощенной системой извне на единицу массы F, V и L соответственно. Эти определения позволяют сочетать теплопо-ток q с любым из массопотоков. Преобразования, подобные проделанным в отношении системы (рис. XIV. 10, а и б), дают следующие уравнения:
(V+Qf) — hL Н у —(hp+ Qf) Ну — hL
(XIV. 25)
У — хр
а после исключения V L
F ~ Н
Hp — (hL — Ql) ^ Ну — hp хр — х ~ у — хр Ни —
Hv-hF
¦ А,
(XIV. 17)
У — х
v ~~ {hL — Ql)
(XIV. 26)
v) — hF
(XIV. 27)
(XIV. 18)
У-
Hy-hL
F F —
По этим уравнениям видим, что три точки с координатами
(xF, hp), (х, h?) и (у, Ну)
должны лежать на прямой линии (рис. XIV. 10,6).
Так как L н V, находящиеся в равновесии, приходятся на концы соединительной линии, F расположено в точке (xF, hF) между ними.
Направление V или L можно изменить, чтобы показать, что точка, изображающая разность между двумя потоками, также лежит на изотермах, соответствующих двум данным потокам. В этом случае точка, выражающая разность между двумя потоками, находится вне двухфазного парожидкостного участка изотермы. Расположение точки разности устанавливается приложением правила плеча рычага к соотношениям величин потоков. Следует подчеркнуть, что, хотя в данном случае
Уравнения (XIV. 15) — (XIV. 17) показывают, что соотношения величины потоков могут быть получены по координатам величин энтальпии или концентрации. Правые члены уравнения (XIV. 15) можно преобразовать:
Комбинация уравнений (XIV. 18) и (XIV. 19) дает
(XIV. 20)
Н у — hp hp h^
У — Хр ~ Хр — X
(XIV. 19)
У — х
У — х
Точно так же из уравнения (XIV. 17) получим
Н ж/ — hp Ну — hr
Эти зависимости представлены на рис. XIV. 11, б. Здесь для определения соотношения величин массопотоков применяется правило плеча рычага. Уравнения (XIV. 25) — (XIV. 27) получены сочетанием тенлопотока q с F, V и L.
Эффект смешивания тепла с частным потоком вызывает вертикальное отклонение от точки, действительно характеризующей свойства этого массопотока. Отклонение определяется направлением массопотока, а также направлением q (q считается положительным, когда теплота поглощается извне). Направление смещения можно характеризовать так:
1. Массопоток направлен внутрь, q внутрь: смещение вверх или +
2. Массопоток направлен наружу, q наружу: смещение вверх или +
3. Массопоток направлен внутрь, q наружу: смещение вниз или —
4. Массопоток направлен наружу, q внутрь: смещение вниз или —
На рис. XIV. 11,6 показан четвертый случай, когда q сочетается с L либо V, и первый случай, когда q сочетается с F. Величина смещения равна q, деленному на массу потока, с которым происходит сочетание.
Тремя основными определениями, производимыми при расчетах по методу Понтона — Савари, являются:
У — хр (Ну — Qy) — hL У — х
hp hL (Ну Q

Состав,мольные или весовые доли
Точна разности
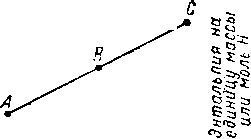
Состав, мольные ила весовые доли
lA+9}4
I
I
I
I
*А
ез -о
* Йз: aU
о = з Ё э ^
Составг мольные или. весовые доли
Рис. XIV. 12. Три основные операции, проводимые на диаграмме энтальпия — концентрация. а — сложение; б — вычитание; в — совмещение тепловых и массопотоков.
Яс
D
Я,.
lL i
1) определение суммы двух потоков для получения качества и количества третьего потока (так называемая точка суммы);
2) определение разности двух потоков для получения третьего потока или сочетания потоков (так называемая точка разности);
3) совмещение чисто теплового потока с одним из потоков массы.
Эти схемы расчетов показаны на рис. XIV. 12. Рассчитывать по методу Понтона—Савари можно и аналитически [XIV. 35]. Однако аналитический расчет менее удобен по сравнению с предыдущим методом.
3. РАСЧЕТ РАВНОВЕСНЫХ СТУПЕНЕЙ ДЛЯ ОПРЕДЕЛЕННОГО КОНЕЧНОГО КОЭФФИЦИЕНТА ОРОШЕНИЯ
Полная ректификационная колонна (рис. XIV. 1) связана с пятью внешними потоками: F, В, D, q0 и q,, где qc — тепло, переданное в конденсаторе; qs — тепло, переданное в ректификационной колонне.
Сочетая
1) qs с В, qc с D;
2) qa с F, qc с D;
3) qc с F, qa с В,
получаем три различные линии общего теплового и материального баланса. Эти три линии (рис. XIV. 13) показывают, как теплопотоки совмещаются с различными массопотоками.
Хотя на рис. XIV. 13 показано, каким образом можно построить линии общего материального и теплового баланса, предстоит еще уяснить взаимосвязь внутренних потоков. При наличии полного конденсатора состав дистиллятного продукта не отличается от состава у\ пара, выходящего с верхней тарелки. До ввода питания разность между D и qdD по массе и энергии точно равна разности по массе и энергии между любыми двумя потоками, проходящими в контакте по колонне. Изобразим это при помощи следующих обозначений:
(XIV. 28)
Но (hD—qdD) должно дать определенную точку, лежащую выше точки с координатами (хв, hD) на расстоянии qc/D от нее, а именно точку, характеризующую сочетание qJDnD. Это — точка (xD, НЛг) на рис. XIV. 14. Таким образом, все линии разности, идущие сверху вниз до питающей тарелки, сходятся в верхней точке
= \Hv,-bLt
Hv1~hL,
обходимой подготовки питания обычно находится на пересечении соединительной линии с линией общего теплового и материального баланса.
Переход с одной точки разности на другую равнозначен введению питания. Расчеты продолжают, как показано на рис. XIV. 14 (используя в отгонной части колонны нижнюю точку разности хв, Н^г), пока не будет достигнут состав нижнего продукта хв. Общее число теоретических тарелок в колонне можно получить, сосчитав число изотерм или соединительных линий, начерченных во время построения. Фракционные равновесные ступени можно вычислить путем интерполяции вдоль линий насыщенного пара или насыщенной
разности (xD, НЛ). Пар Vi состава у\ находится в равновесии с (xi,hLl) на линии насыщенной жидкости (точка К). Точка {угНу2) находится на пересечении линии разности (xithLl) (xD, #д ) с линией насыщенного пара. При ином возможном построении линий равновесия и разности потоки рассматриваются снизу вверх до точки, где вводится питание. Оптимальное место ввода питания с точки зрения числа потребных тарелок и не-
Рис. XIV. 13. Совмещение теплопото-ков с различными .массопотоками в полной колонне.
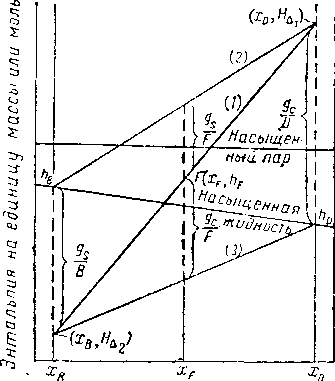
Концентрация 'Мол. или бес доли
Рис. XIV. 14. Расчет полной фракционирующей колонны при определенном конечном коэффициенте орошения.
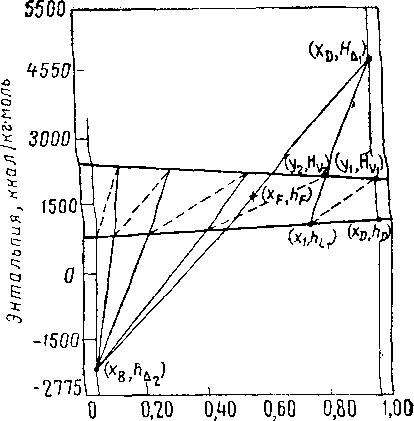
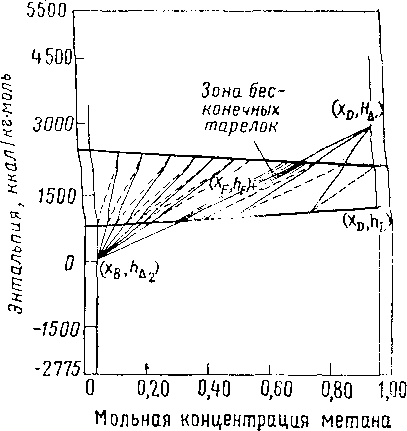
Рис. XIV. 15. Определение минимального коэффициента орошения для системы метан — этан, находящейся под абсолютным кГ(см?.
жидкости. Коэффициент наружного орошения L0/D для рис. XIV. 14 характеризуется отношением величин линий
5. МИНИМАЛЬНОЕ ЧИСЛО РАВНОВЕСНЫХ СТУПЕНЕЙ
Минимальное число равновесных ступеней, необходимое для проведения данного разделения, соответствует состоянию полного орошения:
(Уъ Н V7,) (*?>¦ (#!’ HVl) (XD’ ЛD)•
р ->¦ оо или -у = 1,0
4. МИНИМАЛЬНЫЙ КОЭФФИЦИЕНТ ОРОШЕНИЯ
5550
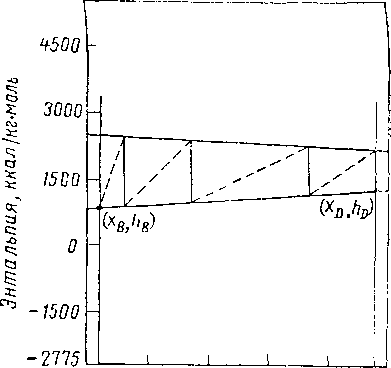
Минимальным коэффициентом орошения, необходимым для данного разделения, будет наивысший коэффициент орошения, для которого изотерма и линия разности совпадут. При определении минимального коэффициента орошения представим, что все изотермы являются линиями разности; изотермы, лежащие над питанием, продолжаются до пересечения с линией x = xDla лежащие под линией питания — до пересечения с линией х — хв. Представляют интерес наивысшая точка пересечения над линией питания и наинизшая — под этой линией, поскольку они характеризуют наивысшие коэффициенты орошения, удовлетворяющие критерию минимального коэффициента орошения.
Наконец, проводят линии через эти две точки и через точку питания, чтобы установить наивысший коэффициент орошения из двух. Графический метод определения минимального коэффициента орошения показан на рис. XIV. 15. Обычно для двухкомпонентных углеводородных смесей и для систем, характеризующихся правильным равновесным поведением, изотерма, проведенная через точку питания и продолженная, соответствует минимальному коэффициенту орошения, который дает зону постоянного состава у питающей тарелки. Для таких систем, как этанол — вода, которые значительно отклоняются от идеальных систем в жидкой фазе, зона бесконечных ступеней может быть расположена и в другом месте.
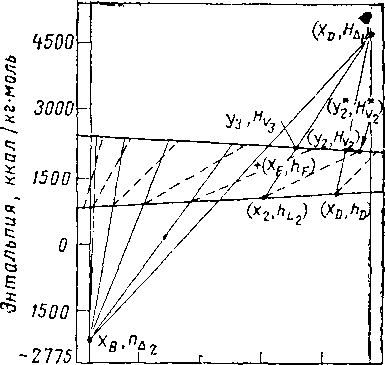
Рис. XIV. 16. Определение минимального числа ступеней равновесия для системы метан — этан, находящейся под абсолютным давлением 35 кГ/см2.
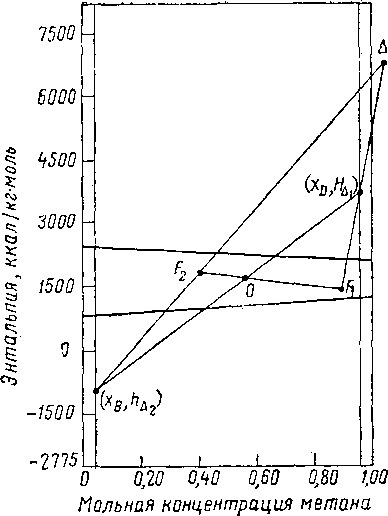
Рис. XIV. 17. Определение расположения точки разности для колонны с двойным питанием, фракционирующей двойную систему метан — этан с абсолютным давлением 35 кГ/см2.
Этому требованию удовлетворяет диаграмма энтальпия— состав, когда верхняя и нижняя точки разности расположены соответственно в + °о и — оо. Построение по таким точкам разности показано на рис. XIV. 16. Линии разности теперь стали вертикальными, поскольку потоки, проходящие рядом, имеют одинаковый состав.
В литературе имеются сведения о применении графического метода Поншона—Савари и для других расчетов. Для колонны с двойным питанием имеются три точки разности. Положение точки О для суммы питаний F1 и Ft определяют приложением принципа плеча рычага:
Масса Fx _ 0F2 Масса F2 OF^
Построение точек разности для колонны с двумя потоками питания показано на рис. XIV. 17.
Коэффициент полезного действия одной тарелки по пару (коэффициент Мерфри)
(XIV. 29)
¦По =•
где уп, Уп + i — действительный состав пара, а уп — состав пара, который был бы в равновесии со средним составом жидкости хп.
Это уравнение передает эффективность контакта на одной тарелке на основе состава паровой фазы.
О .0.20 0,40 0,60 0.80 1,00
Рис. XIV. 18. Ввод точечной эффективности (по Мерфри) по паровой фазе в уравнение Поншона—Савари.
Поскольку эффективность для одной тарелки может не быть равна общей эффективности для всей колонны [XIV. 36], иногда необходимо включить эффективность тарелки в расчеты, производимые по отдельным ступеням равновесия. На рис. XIV. 18 приведен пример расчетов для нескольких ступеней.
Когда кривые энтальпии—концентрации для парообразной и жидкой фаз, построенные на мольной основе, параллельны, результаты вычислений по методам Поншона—Савари и Мак Кэба—Тиле совпадают. При отсутствии термодинамических показателей той или иной смеси достаточно правильную взаимозависимость между энтальпией и составом для углеводородных систем можно вывести на основе скрытой теплоты испарения чистого компонента, исходя из предположения, что раствор идеальный.
К числу других многоступенчатых колонн, которые были успешно рассчитаны при помощи метода Поншона—Савари, относятся колонны с многократной подачей питания [XIV. 59], отводом боковых погонов [XIV. 59], парциальным конденсатором [XIV. 59], промежуточным нагревом или охлаждением между ступенями [XIV. 30], использованием сочетания рибойлера и острого пара [XIV. 30], использованием острого пара, полностью смешивающегося с жидкой фазой [XIV. 7], разгонкой смеси, имеющей две жидкие фазы [XIV. 30], двойными колоннами типа Линде [XIV.43, XIV. 59].
Большое число различных технологических вариантов колонн, рассчитанных по этому методу, свидетельствует о его универсальности.
7. АНАЛИТИЧЕСКИЙ МЕТОД РАСЧЕТА ФРАКЦИОННОЙ ПЕРЕГОНКИ ДВУХКОМПОНЕНТНЫХ СМЕСЕЙ
Аналитические методы расчета фракционной перегонки на основе принципа ступеней равновесия были разработаны для многокомпонентных смесей при допущении постоянной относительной летучести и постоянного мольного перетока [XIV. 37, XIV. 55]. Общие уравнения были получены из принципов; положенных в ос-
нову аналитических методов расчета фракционировайий диухкомпонентных [XIV. 52] и трехкомпонентных смесей [XIV. 53, XIV. 54].
Аналитические расчеты фракционирования двухкомпонентных смесей применяют в тех многочисленных случаях, когда производится фракционная перегонка двух компонентов одного гомологического ряда, с близкими интервалами выкипания.
хп У — У\
У =¦
Данный метод [XIV. 7], как и другие [XIV. 48,
XIV. 62], предполагает, что относительная летучесть и мольный переток во всех частях колонны постоянны. Вследствие неточностей, неизбежно присущих графическим методам, аналитический метод может быть сравнительно точен и удобен для расчета фракционирования, требующего большого числа ступеней. Хотя очевидно, что основными уравнениями, используемыми для ступенчатых расчетов, являются уравнения конечной разности [XIV. 51], разработанная методика строится исключительно на алгебраических уравнениях [XIV. 7].
Из предположения о постоянной относительной летучести вытекает, что
= У
(XIV. 30)
а = = const,
У =
где Ка = у/х — константа более летучего компонента а; Кь = у/х — менее летучего компонента Ь.
Уравнение (XIV. 30) можно записать через мольную долю у компонента а в парообразной фазе и мольную долю х компонента а в жидкой фазе:
(XIV. 36)
У = х
(XIV. 31)
У = '
1 + (а — I) х
(XIV. 33)
гДе (*i, У\) и (*ц, уи) — координаты соответственно нижнего и верхнего концов равновесной линии, выраженной уравнением (XIV. 31), и первоначальной рабочей линии в ректификационной части. Следует обратить внимание на то, что если х = *п, х' = 1,0, а у — уи, то у' =1,0. Преобразуя уравнения (XIV. 31) и (XIV. 33) и исключая у, получим
| 1 + (а — 1) * |
1 + (а — 1)лг, |
|
ахи | ах. |
| 1 + (а — 1) |
1 + (а — 1)*, |
| для У, получим | |
|
X | *1 |
|
l + (ot—1)* | 1 + (а — 1)х, |
| *1 | |
|
1 + (а — 1) хи | 1 + (а — 1) х1 |
| Х — Х\ и — . . |
1 + (а — 1) хп |
(XIV. 34)
(XIV. 35)
Хц — Х1 1 + (а — 1) *
t 1 + (а — 1) *[[
(XIV. 37)
1 + (а — 1)*
Пользуясь уравнением (XIV. 32) и исключив х из уравнения (XIV. 37), получим
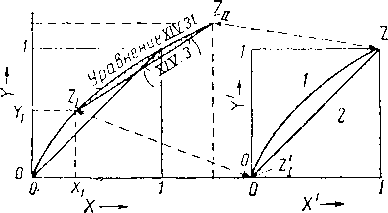
После линейного преобразования координат (рис. XIV. 19) угол наклона рабочих линий равен 45°. Заштрихованная полоса, представляющая участок
г'п
Рис. XIV. 19. Преобразование координат, необходимое для аналитического расчета фракционирования двойных систем.
/ — уравнение (XIV. 31), преобразованное в (XIV. 40); 2 — уравнение (XIV. 3), преобразованное для у n+i~ х п .
[1 + (os — I)*!!]*7
(XIV. 38)
1 + (а — 1) + (а — 1) — *,) х1
Разделив числитель и знаменатель (XIV. 38) на 1 + (а — 1)* и вводя
уравнения (XIV. 39)
с — 1 + (ст~ 0 *н I + (а — 1)*, ’
получим следующую формулу для равновесной линии в плоскости х? — У:
сх
(XIV. 40)
1 + (с-1)*
Рабочая линия преобразована в линию, проходящую под углом 45° в координатах х' — г/', т. е.
1 —
1 + (с-1)*'
-1 + (с-1)*' Для любой тарелки г У1+1
между рабочей линией в ректификационной части и равновесной линией, может после преобразования находиться между линией с углом наклона 45° и преобразованной равновесной линией в новой плоскости х' — if. При этом рабочая линия упрощается, но новая равновесная линия отличается несколько большей сложностью. Необходимые преобразования таковы:
Поскольку ступенчатое соотношение между контактирующими потоками в координатах х' — у' таково, что
(XIV. 44)
xi = У1+ v
ТО МОЖНО ИСКЛЮЧИТЬ y'i+ll
(XIV. 45)
1 - xi+1
l-Xt
Для ступеней i + 1 и < + 2
*f+l _
(XIV. 46)
1 —
Решая совместно уравнения (XIV. 45) и (XIV. 46), получим
*г+2
1 — X,
1 — ХЦ-2
Вообще зависимость между составом жидкости, поступающей с тарелки О и выходящей с тарелки п, можно выразить следующим образом:
уравнений (XIV. 5) и (XIV. 31). Эти величины можно определить, заменив в уравнении (XIV. 49) L на U, V на V", D на В и xD на хв- Взаимозависимость между потоками, находящимися выше и ниже питающей тарелки, выражается уравнениями
V = L + qF,
V'=F(q-l)+V.
При полном орошении (поскольку D — О, L/V = 1,0) *i, *11 = 0,1.
После подстановки этих значений в уравнение (XIV. 49) получим с = а. Вследствие этого уравнение (XIV. 48) сведется к уравнению Фенске—Андервуда. По уравнению (XIV. 48), примененному для расчетов ректификационной и отгонной частей колонны, получим число ступеней равновесия, необходимое для разделения.
8. ГРАФИЧЕСКОЕ ИЗОБРАЖЕНИЕ РАСЧЕТОВ
ФРАКЦИОНИРОВАНИЯ ТРЕХКОМПОНЕНТНЫХ СМЕСЕЙ
fxn 1 —
1 — хп
№[xe{l-x’n)/x'n{\-x0)\
D
V XD
*1,11 = 1-
±
d(«-d}V2)
где п — число равновесных ступеней, необходимых для фракционирования от х' = х0 до xf — хп.
По форме уравнение (XIV. 48) абсолютно тождественно уравнению Фенске—Андервуда (Fenske—Under—Wood) (XIV. 17, XIV. 52) для расчета минимального числа ступеней при. 100%-ном орошении. В уравнении Фенске—Андервуда lg с заменен lga.
Интервал концентрации компонентов смеси в различных частях фракционирующей колонны можно вычислить по уравнению ((XIV. 32), если только х\ и хц известны, xi и Хц — это точки пересечения равновесной линии, выраженной уравнением (XIV. 31), и рабочей линии, выраженной уравнением (XIV. 3).
Координаты х можно получить, исключив у из уравнений (XIV. 31) и (XIV. 3) и решив уравнение второй степени, в результате чего
где xi > хц.
Величины xi и хц, находящиеся ниже десорбцион-нсй части, определяются при одновременном решении
у — а + (а — 1)
2 (а — 1)-
(XIV. 49)
(XIV. 48)
lgc
V
__ а+ (а — 1) — xD
— —г LDx
2 (а - 1).
(XIV. 47)
Применению диаграмм энтальпия—концентрация к расчетам перегонки трехкомпонентных смесей препятствует необходимость использования трех измерений для выражения энтальпии и двух независимых переменных параметров состава при постоянном давлении. Для обычных расчетов применять построения Понтона—Савяри в трех измерениях практически нецелесообразно, однако они могут помочь для уяснения расчетов фракционирования многокомпонентных смесей.
Диаграмма энтальпия—концентрация для расчета минимального числа ступеней, необходимого для разделения, показана на рис. XIV. 20. Верхняя поверхность представляет собой геометрическое место точек, отображающих насыщенный пар, а нижняя поверхность—¦ геометрическое место точек насыщенной жидкости. Равновесные соотношения между паром и жидкостью для многокомпонентных смесей углеводородов лучше всего выразить при помощи констант равновесия К. Насыщенный пар в данной точке (на верхней поверхности) связан с равновесной с ней жидкой фазой при помощи расчета температуры росы, а данная точи в нижней поверхности увязывается с равновесной с ней паровой фазой посредством расчета температуры начала кипения. В трех измерениях линия разности становится семейством линий в пространстве, а точка разности— точкой в пространстве. Зная точку разности и точку на геометрическом месте точек насыщенной жидкости (или пара), моокно установить расположение третьей точки как точки прокола на геометрическом месте точек насыщенного пара (или соответственно жидкости).
Точки разности на рис. XIV. 20 расположены в ± поскольку разделение производится при полном орошении. Следует обратить внимание на то, что в этих условиях все линии разности проходят вертикально. При полном орошении, поскольку D = 0, составы и количества контактирующих потоков находятся на вертикальных линиях разности в местах, соответствующих энтальпиям.
При фракционировании многокомпонентной смеси не всегда ясно, какие параметры необходимо знать, чтобы прийти к определенному решению. В примере расчета перегонки с полным орошением (рис. XIV. 21) берутся такие параметры, как давление смеси или давление в колонне, состав питания и содержание наиболее летучего компонента в нижнем продукте и наименее
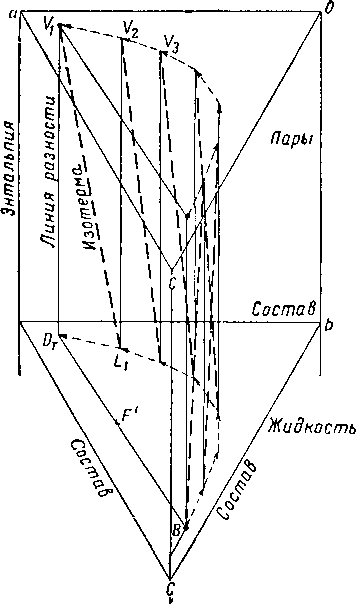
Рис. XIV. 20. Расчет минимального числа ступеней по диаграмме энтальпия — состав для тройной смеси.
а
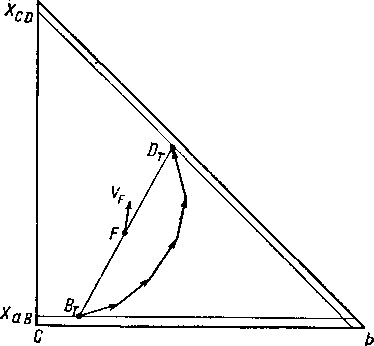
Рис. XIV. 21. Расчет минимального коэффициента орошения [XIV-58].
летучего компонента — в верхнем продукте. Ограничения в отношении верхнего и нижнего продуктов передаются линиями xcd и хаЬ на рис. XIV. 21. Для определения остальных зависимых величин концентрации компонентов в верхнем и нижнем продуктах необходимы вычисления по методу повторных попыток. Величину DT определяют по принятой величине Вт с учетом того, что Вт, F и DT находятся на одной прямой. Но по принятой Вт можно получить DT и путем ступенчатого расчета вверх по колонне. Если Вт определена верно, то DT, вычисленная из материального баланса, и Dт, найденная при ступенчатом расчете, должны совпадать. Минимальное число ступеней (не обязательно целое) получают, подсчитывая число изотерм.
При расчете перегонки трехкомпонентной смеси изотермы и линии разности можно спроектировать на плоскость состава, несколько снизив этим наглядность построения, особенно, если рассматриваемая смесь имеет постоянную мольную скрытую теплоту испарения по всему интервалу. Предложенный Уайтом метод расчета [XIV. 58] для полной колонны показан на рис. XIV. 22.
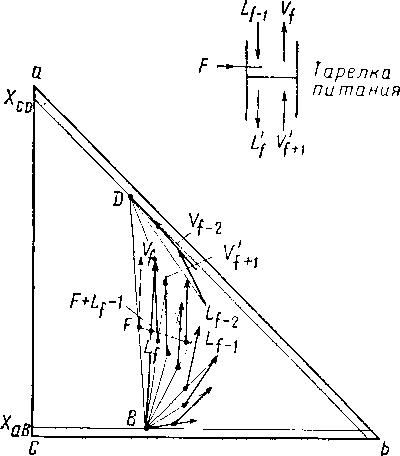
Рис. XIV. 22. Поступенчатый расчет полной колонны при определенном конечном коэффициенте орошения [XIV. 58].
Для полной колонны, работающей с промежуточным коэффициентом орошения при фракционировании трехкомпонентной смеси можно указать следующее число необходимых переменных:
1) давление в колонне (одна переменная);
2) состав и характеристика питания (три переменные) ;
3) состав нижнего продукта (две переменные);
4) состав верхнего продукта (две переменные);
5) число теоретических ступеней (одна переменная);
6) расположение питающей тарелки (одна переменная);
7) коэффициент орошения в одной точке колонны (одна переменная);
8) состояние дистиллята и орошения (одна переменная).
Из этих переменных пусть будут даны давление в колонне,'состав и состояние питания, состав наиболее летучего компонента в нижнем продукте, состав наименее летучего компонента в верхнем продукте, коэффициент орошения (Vs/B или Lo/D) и расположение тарелки питания. Vs/B — это соотношение между числом мдлей в десорбцирнном паре и числом м^й а шик* нем продукте. Чтобы получить другие зависимые переменные, необходимо произвести вычисления по методу повторных расчетов. Предположительно берут концентрацию остальных компонентов в нижнем продукте, предварительно устанавливая расположение В. По материальному балансу находят предварительно А поскольку В + D — F. Тарелку питания следует располагать так, чтобы подача питания в колонну осуществлялась в оптимальной точке. Для проверки предположительно взятых показателей состава нижнего продукта необходимо произвести ступенчатый расчет вверх по колонне. Количество пара Vs, находящегося в равновесии с В, определяют по температуре начала кипения при предварительно взятом составе нижнего продукта. Поскольку l/s + В = Lb + u по известному соотношению Vs/B можно установить LB +1. Теперь tB + i находится в равновесии с Ув-и и Ув-и + В = Ьв+2.
При предположении о постоянном мольном перетоке
(XIV. 49а)
расположение точек состава жидкости можно установить после каждого подсчета температуры начала кипения. Вычисление продолжают вверх по колонне, пока соотношение между ключевыми компонентами в жидкой части питания не будет примерно равно соотношению между этими же компонентами в жидкости, уходящей с питающей тарелки.
Величину L/V над тарелкой питания, соответствующую величине Vs/B под ней, получают при помощи теплового баланса по всей колонне:
FhP+qs = (V1H1 - VxhD) + Вкв + DhD, (XIV. 50) что позволяет установить расположение ?/_ь По температуре начала кипения получаем V/_i, после чего можно установить расположение Lf_2, Расчет продолжают вверх по колонне до пересечения с линией тех нических условий хсв. Допущенная величина В будет правильна лишь в том случае, если изотерма пересечет линию технических условий х •= xzD так, чтобы величина D находилась на прямой линии BFD. Если же это не случится, берут предположительно новую величину В и снова повторяют вычисления. Окончательное решение получают в результате очень кропотливых, трудоемких и громоздких вычислений.
где/7 — количество массы питания; hF — энтальпия на единицу массы питания; qs — общее тепло, поступающее в десорбер; Vi — масса пара, выходящего с верхней тарелки, L0 + D; Hi— энтальпия Vi на единицу массы; hD — энтальпия дистиллята или орошения на единицу массы; В — масса нижнего продукта; hB — энтальпия единицы массы нижнего продукта.
При помощи уравнения (XIV. 50) можно найти решение для V1 и, следовательно, для коэффициента орошения L/V над тарелкой питания. По рис. XIV. 22 видно, что разность потоков над тарелкой питания составляет Vf — Lf_ 1 =¦ D или
vp
-7-1
(XIV. 50а)
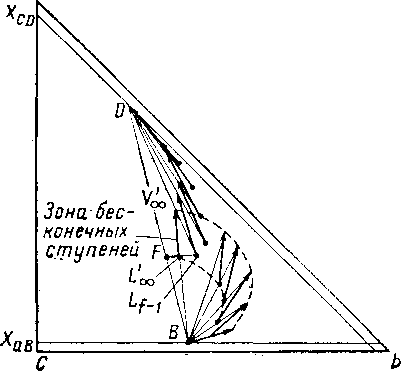
Рис. XIV. 23. Расчет зоны бесконечного числа теоретических тарелок для тройной смеси [XIV. 58].
Минимальным коэффициентом орошения будет такой коэффициент, при котором изотермы и линии разности совпадут в какой-либо части колонны. Это совпадение равнозначно возникновению зоны бесконечных тарелок. На рис. XIV. 23 приведено построение расчета минимального коэффициента орошения для случая, когда сырье подается (расчет ведется вверх по колонне) до тех пор, пока ниже тарелки пнтания не возникнет зона бесконечных тарелок. При этом следует обратить внимание на то, что при изменении точек разности или вводе питания можно исключить зону бесконечных тарелок.
§ 2. МЕТОДЫ СТУПЕНЧАТОГО РАСЧЕТА ФРАКЦИОНИРОВАНИЯ МНОГОКОМПОНЕНТНЫХ СМЕСЕЙ
Методы ступенчатого расчета фракционирования многокомпонентных смесей были разработаны и описаны Льюисом и Матесоном (Lewis and Matheson) [XIV. 32], Тиле и Геддесом (Thille and Geddes) [XIV. 50] и Макинтайром (Mclntire) [XIV. 34]. При первом методе число теоретических ступеней определяют, исходя из известного состава конечного продукта посредством одновременного расчета с обеих сторон колонны по направлению к тарелке питания. Второй метод также основан на таком расчет©, но в этом случае определяют состав продукта, исходя из данного числа теоретических тарелок.
Третий метод основывается на повторных пробных вычислениях, позволяющих проверить правильность допущенного соотношения L/V и кривой температуры по колонне. Вычисления продолжают до тех пор, пока перепад температур, градиент объема паров, число теоретических тарелок в абсорбционной и десорбционной частях не перестанут изменяться по сравнению с результатами предшествующих пробных вычислений.
1. МЕТОД ЛЬЮИСА—МАТЕСОНА (LEWIS-MATHESON)
Из всех перечисленных методов рассмотрим только метод Льюиса—Матесона, при котором допускается, что распределяются только смежные ключевые компоненты. Расчеты разделений, в которых распределяется более двух компонентов, можно производить при допущении постоянной относительной летучести и постоянного мольного орошения [XIV. 55] или же при помощи электронных цифровых счетно-решающих машин, как это было описано Боннером (Bonner) [XIV. 5].
Если предположить, что в нижнем и верхнем продуктах распределяются только смежные ключевые компоненты, то, зная количество компонента в потоке каждого продукта, можно рассчитать полный компонентный материальный баланс разделения. Затем, учитывая известные параметры: давление в колонне, составы питания, верхнего и нижнего продукта, состояние питания, коэффициент орошения и состояние орошения, по методу Льюиса—Матесона можно определить число равновесных ступеней, производя вычисления по отдельным последующим тарелкам.
По температуре точки росы верхнего продукта получают температуру верхней тарелки Т\ и состав равновесной жидкой фазы. Вычислив температуру начала кипения нижнего продукта, получаем температуру начала кипения нижнего продукта и состав паров Vв, находящихся в равновесии с ним. Поскольку известиы число молей в У,, 1о и А и состояние этих потоков, можно вычислить /HVl — hLo/ или разность энтальпии в потоках, проходящих рядом друг с другом в ректификационной части колонны.
Для расчета вниз по колонне состав L известен, но его количество неизвестно. Поэтому Li задаемся, определяя предварительную величину количества и состава V2 по формуле материального баланса. По вычисленной температуре точки росы для V2 определяют температуру потока V2. Итак, по формуле теплового баланса можно проверить необходимое тождество
Если же это тождество не соблюдается, принимаем новую величину L\ и повторяем вычисление. Обычно тепловой баланс удается получить после двух-трех попыток установить эмпирически L\. Для расчета следующей, второй ступени используют величину концентрации жидкости L2, полученную при предшествующем вычислении точки росы для Vs. Истинную величину L определяем методом повторных расчетов, используя для проверки разность энтальпий / — Эти вы
числения вниз по колонне продолжают до тех пор, пока не станет очевидно, что соотношения между ключевыми компонентами в жидкости и в жидкой части питания идентичны или почти идентичны.
Для нижней части колонны разность между энтальпиями контактирующих потоков можно получить при помощи теплового и материального балансов по реакти-фккационной части колонны, включая тарелку питания. Разность между энтальпиями контактирующих потоков десорбционной части также можно получить при помощи теплового баланса по нижней части колонны, если известно отношение Vs/B, а не коэффициент орошения Lo/Vu
О 0,10 0,20 0,30 0,40 0,50 0,50 0,10 0,80 Состав жидкости , мольные доли
По температуре начала кипения нижнего продукта определяется состав Vgi но не его количество. Искомое количество VD должно удовлетворять требованию
14$ — кв! = !HvB — hLB+\!'
т. е. разность между теплотой в рибойлере и теплотой в нижнем продукте должна быть равна разности между энтальпиями контактирующих потоков пара и жидкости. Найдя правильную величину VB и правильную температуру потока Ls+ь начинают расчет следующей ступени, исходя из эмпирически допущенного количества Vb + i и т. д. Ступенчатые вычисления продолжают до тех пор, пока соотношение между главными компонентами при расчете вверх по колонне не будет примерно равно соотношению между главными компонентами в жидкой части питания.
До этого момента при расчетах не учитывались компоненты легче самого легкого из ключевых компонентов в десорбционной части и компоненты тяжелее самого тяжелого из ключевых компонентов в ректификационной части. Но эти компоненты оказывают некоторое влияние на кривые жидкости, пара и концентрации в соответствующих частях колонны и поэтому в любом претендующем на точность расчете их необходимо должным образом учитывать.
Чтобы получить окончательный результат, необходимо учитывать добавление небольших количеств нераспределенных компонентов и снова произвести вычисления до тарелки питания с обеих сторон колонны. Если количества допущенных и добавленных нераспределенных компонентов были взяты неправильно, составы компонентов на общей ступени и ступени питания не совпадут. После учета этих нераспределенных компонентов кривая концентрация главных компонентов несколько изменится.
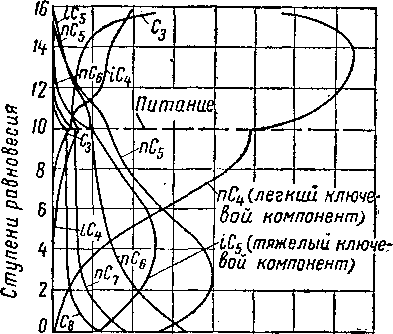
Способ расчета, основанный на совпадении искомых параметров на тарелке питания, при вычислениях, проводимых по направлению к этой тарелке с обеих сторон колонны, подробно описан Брауном [XIV. 7]. Окончательные кривые концентрации, температуры и пара для промышленного дебутанизатора, работающего под абсолютным давлением 8,4 кГ/см2, приведены на рис. XIV. 24— XIV. 26 [XIV. 46].
Характерные относительные максимумы концентрации ключевого компонента находятся на какой-либо промежуточной ступени.
В настоящее время в литературе имеются примеры использования электронных цифровых счетно-решающих машин для точного ступенчатого расчета фракционных колонн [XIV. 5, XIV. 34, XIV. 47].
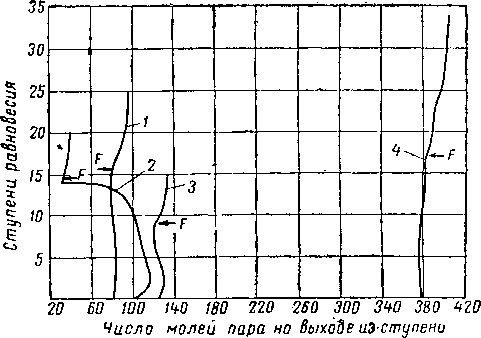
Рис. XIV. 26. Количество пара для четырех фракционирующих колонн [XIV. 46].
1 — депропанизатор; 2 — деэтанизатор; 3 — дебутанизатор; 4 •-* колонна для фракционирования изобутана-бутана.
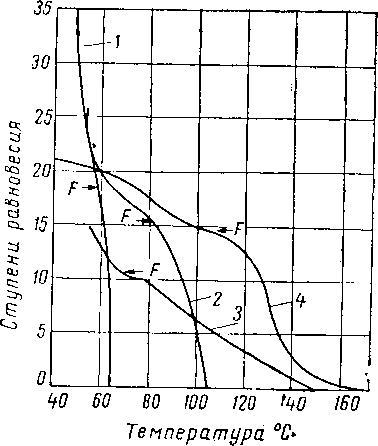
Рис. XIV. 25. Перепады температур для четырех фракционных колонн [XIV. 46].
1 — колонна для разделения изобутана и бутана;
2 — депропанизатор: 3 — дебутанизатор; 4 — де-
этанизатор.
§ 3. УПРОЩЕННЫЕ МЕТОДЫ РАСЧЕТА ФРАКЦИОННЫХ КОЛОНН
'-пл-п, F .
п-ч, D
-ф
+ I.
+
'min
Расчеты фракционирования многокомпонентных смесей можно ускорить путем применения быстродействующих электронных цифровых счетно-решающих машин и упрощенных методов расчета.
Упрощенные методы не бесполезны и при подготовке к расчетам с использованием электронных машин. Исходя из упрощенных методов, можно составить программу для цифровых электронных машин, получив таким образом основу для предварительного суждения, прежде чем приступить к более точным, но и более сложным расчетам.
Последовательность вычислений в одном из упрощенных методов следующая.
1. Определение минимального коэффициента орошения.
2. Определение минимального числа теоретических тарелок.
3. Вычисление действительного числа теоретических тарелок по минимальному коэффициенту орошения и минимальному числу тарелок.
4. Установление расположения тарелки питания.
5. Пересчет числа теоретических тарелок в действительное число тарелок.
где а—величины относительной летучести; х — величины молярных концентраций; индекс F — компоненты в питании; индекс D — компоненты в дистилляте; q' — число молей насыщенной жидкости, образующейся на тарелке питания при вводе 1 моля питания = = (tfsi,— h,)l(Hsv— hSL); Ф—параметр обогащения, определяемый уравнением (XIV. 51); Rmin — минимальный коэффициент орошения Lo/D.
Уравнение (XIV. 51) получают, исключая коэффициенты орошения из (XIV. 52) и аналогичного ему урав-нения для выпарной колонны:
г1х1 ,В а2х2,В ”3*3,
(XIV. 52)
а2
а„х,
-Ф
а2х2, D кз*3, D I I
Fi г* <Ti
(XIV. 51)
а„ —Ф
Ф
I. ВЫЧИСЛЕНИЕ МИНИМАЛЬНОГО КОЭФФИЦИЕНТА ОРОШЕНИЯ ПО МЕТОДУ АНДЕРВУДА (UHDERWOOD)
’¦п п, В
• S,
Для случая, когда относительная летучесть и мольное орошение постоянны, Андервуд [XIV. 15] получил следующие уравнения, позволяющие вычислить минимальный коэффициент орошения:
«1*1 р . <*2*2, F ¦ а->*’
П-Ч, F
*3 3, F
-Ф
(XIV. 53)
-Ф
где Ф — параметр выпарной колонны, примененный для упрощения алгебраических действий;
S=(RD + q'F-B)/B.
Уравнения (XIV. 51) и (XIV. 52) можно решить для общего случая с любым числом компонентов и для специальных случаев: 1) когда разделение между смеж-
(под тарелкой питания),
(над питанием), (XIV. 54)
(под питанием). (XIV. 55)
(XIV. 56)
(XIV. 57)
Ктхт т Kd
(хс !xd)n (хс lxd)m
(1 —sc,
Уп + \
*л+1
ными ключевыми компонентами (компонентами, концентрацию которых желательно контролировать) не резкое; 2) когда, помимо ключевых компонентов, распределяются еще один или несколько компонентов.
Для получения минимального коэффициента орошения, когда распределяются только ключевые компоненты, примыкающие один к другому, из величин относительной летучести смежных ключевых компонентов нужно выбрать сначала величину Ф, удовлетворяющую требованиям уравнения (XIV. 51). Эта величина Фиспользуется для вычисления минимального коэффициента орошения Rmin по уравнению (XIV. 52). Для такого решения все показатели концентрации компонентов в дистилляте известны, ибо распределяются только ключевые компоненты. Для случая, когда помимо ключевых компонентов распределяются и другие, все составы дистиллят-ного продукта неизвестны и для вычисления Rmm требуются дополнительные уравнения. Если между двумя ключевыми компонентами распределяется еще один компонент, две величины Ф , находящиеся между величинами относительной летучести ключевых компонентов, дают два уравнения (XIV. 52), при одновременном решении которых получают неизвестную концентрацию в дистилляте и минимальный коэффициент орошения Rmin.
Применять уравнения минимального коэффициента орошения для практических расчетов разделения многокомпонентных смесей следует с учетом того, что исходные допущения о постоянном мольном орошении и постоянных величинах относительной летучести могут не соответствовать действительности.
Рекомендуется, в частности, брать величины относительной летучести при средней температуре колонны или средней из температур зоны бесконечного числа тарелок. Вычисление последней рассматривается в следующем разделе.
2. УРАВНЕНИЕ КОЛБЕРНА (COLBURN)
ДЛЯ ВЫЧИСЛЕНИЯ МИНИМАЛЬНОГО КОЭФФИЦИЕНТА ОРОШЕНИЯ
Минимальный коэффициент орошения учитывает наличие в колонне хотя бы одной зоны бесконечного числа тарелок. Число и расположение таких зон при фракционировании систем, которым свойственно определеннее равновесное поведение (например, смеси углеводородов), можно характеризовать так:
1. При полном распределении каждого компонента между верхним и нижним продуктами зона бесконечного числа ступеней находится у тарелки питания.
2. Если в верхнем продукте отсутствует один или несколько компонентов, зона бесконечного числа ступеней находится в ректификационной части колонны.
3. При отсутствии одного или нескольких компонентов в нижнем продукте зона бесконечного числа тарелок находится в десорбционной части колонны.
4. При отсутствии одного или нескольких компонентов и в верхнем и в нижнем продуктах имеются две зоны бесконечного числа тарелок: одна в ректификационной, а другая в десорбционной части колонны.
Во втором, третьем и четвертом случаях возникновение зоны бесконечного числа тарелок связано с полным устранением одного или нескольких компонентов из потока продукта.
Для зоны бесконечного числа тарелок напишем следующие системы уравнений (условные обозначения — см. рис. XIV. 1):
^'п-\-\Уrt-fl ^*пхп ^XD^
Кх„
(над тарелкой питания),
где с означает более летучий ключевой компонент; d — менее летучий ключевой компонент; п — верхняя зона бесконечного числа тарелок; т — нижняя зона бесконечного числа тарелок; х — мольные доли.
Колберн [XIV. 10] предложил эмпирическое соотношение между составами в обеих зонах бесконечного числа тарелок, возникающих в четвертом случае, которое может служить для проверки правильности принятых величин минимального коэффициента орошения в уравнениях (XIV. 54) и (XIV. 55). Принятую температуру для данного коэффициента орошения проверяют тем, отвечает ли она требованию температуры начала кипения Ех = 1,0. Эмпирическое уравнение Колберна записывается следующим образом:
где е Ст(Ктхт/Ка) — сумма Cm(K.mxmlxd) для всех компонентов менее летучих, чем наименее летучий ключевой компонент d\ ZC„xn — сумма Спхп всех компонентов более летучих, чем наиболее летучий ключевой компонент С. Величины Сп и Ст берут по рис. XIV. 27. Если левый член уравнения (XIV. 58) меньше правого, допущенный минимальный коэффициент орошения (L/D)min слишком завышен, поэтому необходимо повторить расчет снова.
Представляет интерес детальный поступенчатый расчет минимального коэффициента орошения, выполненный Брауном и Холкомбом [XIV. 6].
Следует обратить внимание на то, что уравнения (XIV. 54) и (XIV. 55) должны удовлетворять также условию температуры начала кипения — 1,0. Уравнение (XIV. 54) или (XIV. 55) в сочетании с условием температуры начала кипения Хх = 1 не разрешимо, даже если известен состав потока продукта. Уравнения (XIV. 54) и (XIV. 55) можно также выразить в величинах относительной летучести или в соотношениях констант равновесия
[(*/*„)„- ЧМтЬГ _
¦ (К/Ко)» (Xd, Dlxd, п)’
ХВ {^с1^й)т
п KD + L (К - 1)
_ Вхв т KB-\-L'{\—K)
_ХВ (Kc/Kd)m_
+ (K/K(l)m (хс. в/хс, m)
[(^c/^d)m — [KlKd)m] (L°/B)m!n +
(1-Жпха), (XIV. 58)
Ут+1 ~ Кхт+1
что ведет к
*/П+1
Dxr
01
| 1 | |||||||||||||||||
| 1 L | J- | ||||||||||||||||
|
Cm {КМ’ЦК/Кб |
(KclKd-t)KclK | ||||||||||||||||
| У | /1 |
||||||||||||||||
| ? | |||||||||||||||||
| / |
/ | ||||||||||||||||
|
/ | / | / | |||||||||||||||
| i ( |
/ / | / / / / ! | |||||||||||||||
•' 0,030,040,060,08 OJ5 0,2 0,3 0,40,50,8 0,8 iJJ 1,5 20 ЗП 4-05,0 °J WcPd-VH/fywufaw-Wcl/ij "
!,0 с 0,8
* °А6
5 is % ОА ^ 0,3
02
Рис. XIV, 27. Эмпирические функции Колберна для определения минимального коэффициента орошения [XIV. 10].
3. МИНИМАЛЬНОЕ ЧИСЛО ТЕОРЕТИЧЕСКИХ ТАРЕЛОК
Минимальное число ступеней равновесия можно вычислить при помощи уравнения Фенске — Андервуда
Поэтому потоки жидкости и газа, проходящие мимо друг друга, имеют одинаковый состав и одинаковую массу. Поступенчатые расчеты выполняются с использованием указанных выше допущений.
4. СООТНОШЕНИЕ МЕЖДУ МИНИМАЛЬНЫМ ЧИСЛОМ ТЕОРЕТИЧЕСКИХ ТАРЕЛОК, МИНИМАЛЬНЫМ КОЭФФИЦИЕНТОМ ОРОШЕНИЯ, ДЕЙСТВИТЕЛЬНЫМ КОЭФФИЦИЕНТОМ ОРОШЕНИЯ И ДЕЙСТВИТЕЛЬНЫМ ЧИСЛОМ ТЕОРЕТИЧЕСКИХ ТАРЕЛОК
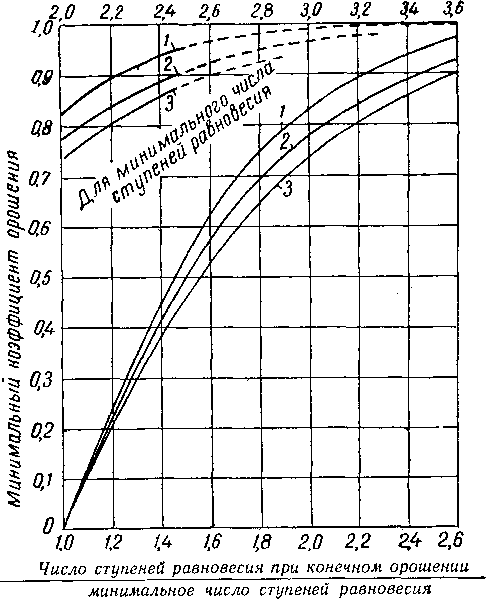
Мартин и Браун (Martin and Brown) [XIV. 8] и Джиллиленд (Gilliland) [XIV.21] установили эмпирические соотношения, которыми можно воспользоваться при вычислении действительного числа теоретических тарелок, необходимого для данного разделения с данным коэффициентом орошения, исходя из известного минимального числа ступеней и известного минимального коэффициента орошения. Эмпирические соотношения Мартина и Брауна представлены кривыми на рис. XIV. 28. Ордината Р (минимальный коэффициент орошения) определяется по формуле
'Ы(Й)
I II к LJitHH. орош
(XIV. 58а)
L'V
V'L ^действ
Р =
= ?я
хп, - х„
где га—число теоретических тарелок, необходимое для фракционирования от тарелки 0 до тарелки га, при котором состав ключевых компонентов в жидкой фазе меняется с (хс, xd)o на (хс, xd); хс — мольная доля легкого ключевого компонента; xd — мольная доля тяжелого ключевого компонента; Кс, Ка — константы равновесия ключевых компонентов.
Следует напомнить, что уравнение (XIV. 58а) было получено, исходя из допущений, что фракционируемая смесь состоит из двух компонентов, а относительная летучесть = Kd К а остается неизменной по всей колонне.
Для многокомпонентной смеси ни одно из этих допущений не соответствует действительности, поэтому при применении уравнения (XIV. 58а) это следует учитывать. В этом случае поступают следующим образом.
1. Разделяют продукт.
2. Начиная с паров, выходящих с верхней тарелки, ведут расчет на несколько ступеней вниз, вычисляя последующие температуры точки росы, пока изменение температуры от одной тарелки к другой не станет незначительным или постоянным.
3. Начиная с жидкости, выходящей из колонны, ведут расчет на несколько ступеней вверх, вычисляя последующие температуры начала кипения, пока изменение температуры от одной тарелки к другой не станет незначительным или постоянным.
4. Применяют уравнение Фенске — Андервуда к интервалу с почти постоянным или низким перепадом температур, используя среднюю относительную летучесть.
5. Подсчитанное число ступеней будет представлять минимальное число тарелок.
Для поступенчатых расчетов при 100%-ном орошении, когда 0 = 0, В = 0, уравнения материального баланса сводятся к виду:
lg[(*c)o(^V(*0„(V)0l lg(*c l^d)
^+1 Уп+\ Ут+1
Рис. XIV. 28. Соотношение между минимальным числом ступеней и минимальным коэффициентом орошения и действительным числом ступеней и действительным коэффициентом орошения [XIV. 8].
I — больше 8; J = c 6 до 8; 3 — меньше 6.
где t — средний расход жидкости над тарелкой питания в молях; V — средний расход пара над тарелкой питания в молях; L' — средний расход жидкости под тарелкой питания в молях; V—редний расход пара под тарелкой питания в молях.
Эмпирические соотношения были выведены первоначально на основании расчетов фракционирования двухкомпонентных систем и впоследствии были проверены на многокомпонентных системах. Там, где состав питания приближается к составу одного из конечных продуктов, и там, где система имеет неидеальные характеристики равновесия и энтальпии, эти эмпирические соотношения следует применять с осторожностью. Отметим также, что первоначальное уравнение было выведено для насыщенного жидкого питания и поэтому его следует корректировать в тех случаях, когда питание находится в ненасыщенном состоянии [XIV. 8].
5. РАСПОЛОЖЕНИЕ ТАРЕЛКИ ПИТАНИЯ
Оптимальное место ввода во фракционирующую колонну питания, находящегося при температуре начала кипения, можно приближенно определить по эмпирическому уравнению [XIV. 27]
п_ [В xd I хсВ \21
lg т = 0,206 lg [д г - J > (XIV. 59)
где п — число идеальных ступеней выше тарелки питания; т — число идеальных ступеней ниже тарелки питания; хс—мольная концентрация легкого ключевого компонента в питании; ха — мольная концентрация тяжелого ключевого компонента в питании; Xd,D — мольная концентрация тяжелого ключевого компонента в верхнем продукте; хс, В — мольная концентрация легкого ключевого компонента в нижнем продукте; В/D — мольное отношение между нижним и дистиллятным продуктами.
Так как нельзя предсказать колебания в составе питания, фракционная колонна должна иметь несколько сопел или иных устройств для подачи питания. Если мольное орошение и относительная летучесть постоянны, оптимальное расположение тарелки питания можно определить по уравнениям Андервуда [XIV. 55].
§ 4. СООТНОШЕНИЕ МЕЖДУ ЧИСЛОМ ТЕОРЕТИЧЕСКИХ И ДЕЙСТВИТЕЛЬНЫХ ТАРЕЛОК
Для получения основных соотношений между числом теоретических тарелок или идеальных ступеней равновесия и числом действительных (реальных) тарелок необходимо знать законы массообмена. Однако были предложены приближенные эмпирические соотношения для абсорбции и фракционирования, в основу которых (соотношений) положены только физические качества системы [XIV. 15, XIV. 38].
1. МЕТОД,
ОСНОВАННЫЙ НА ФИЗИЧЕСКИХ КАЧЕСТВАХ ФРАКЦИОНИРУЕМОЙ СИСТЕМЫ
Первая эмпирическая зависимость общей эффективности тарелки была предложена на основе заводских испытаний Дрикамером и Бредфордом (Drickamer and Brodford) [XIV. 15]. Общая эффективность тарелки в колонне где п * — число идеальных ступеней равновесия; п — число действительных тарелок, была выражена как эмпирическая функция средней мольной вязкости питания при средней температуре колонны.
Считая, что эти переменные параметры не подходят для вывода корреляционной зависимости эффективности тарелки в абсорбере, О’Конелл (O’Connell) [XIV. 38] предложил выражать общую эффективность абсорбции как функцию растворимости поглощенного газа (выраженной в константах уравнения Генри), общего давления и вязкости (рис. XIV. 29). Следует отметить, что при выводе этого соотношения были использованы и показатели эффективности тарелки по Мерфри (в интервале очень низкой эффективности). Для фракционных колонн была предложена вторая корреляционная зависимость, в которой общая эффективность ставится в зависимость от относительной летучести ключевого компонента, умноженной на среднюю мольную вязкость питания при средней температуре колонны (рис. XIV. 30).
Хотя эти корреляционные зависимости позволяют быстро установить общую эффективность тарелки, бы-
| О пО | |||||||||||
|
О ^ |
и | ||||||||||
| О | |||||||||||
| °оЧ | > |
> | |||||||||
| о |
Оо | ||||||||||
| о | — | ||||||||||
| о | |||||||||||
0,1 0,2 0,3 ол 0,6 0,81,0 2 3 4 6 8 10
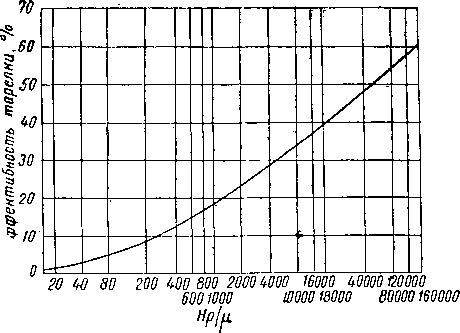
Н — константа закона Генри в кмоль/м3 ат\ р — давление в ат: р- »— вязкость в спз.
100 Ч 90 180 § 70 % 60 s 50 § 4 0 30 | 20
О- о
Относительная летучесть главного компонента х Вязкость питания (сС=1)
Рис. XIV. 29. Общая эффективность тарелки [XIV. 38].
Рис. XIV. 30. Зависимость общей эффективности тарелки от произведения относительной летучести ключевого компонента на вязкость питамия [XIV. 38].
Jio показано, что эффективность зависит также от переменных параметров массообмена, определяемых конструкцией тарелки, уносом жидкости и перемешиванием ее на тарелках [XIV. 19, XIV, 28].
2. МЕТОД,
'100
80
50
40
20
0.
ОСНОВАННЫЙ НА ФИЗИЧЕСКИХ КАЧЕСТВАХ ФРАКЦИОНИРУЕМОМ СИСТЕМЫ И ДИНАМИКЕ ТАРЕЛОК
При выводе теоретических корреляционных зависимостей эффективности тарелок сначала определяют корреляционную эффективность в определенной точке (по Мерфри), затем общую эффективность по тарелке и соизмеряют общую эффективность отдельной тарелки с общей эффективностью колонны.
Герстер (Gcrstcr) с сотрудниками [XIV. 20] установили следующее соотношение между сопротивлением индивидуальной пленки и эффективностью в определенной точке ЕР по Мерфри:
mV
I/
1
(XIV. 60)
1п(1 -Ер) -ZKGa ZKLa
ЕР = {Уп ~ Уп+\)/{'Л ~ Уп+1>
где V расход газа на единицу активной поверхности тарелки в кмоль/ч на 1 м2 сечения колонны, Кг,а. — коэффициент массопередачи через пленку газа в кмоль/ч ¦ м3 на единицу разности в мольной концентрации газа; Z — вертикальное расстояние контакта между жидкостью и газом на тарелке в м; Кьа — коэффициент массопередачи через пленку жидкости в кмоль/ч • м3 на единицу разности в мольной концентрации жидкости.
Для определения эффективности по уравнению [XIV. 60] недостаточно данных о коэффициентах массообмена пленок.
Другой метод определения местной эффективности основан на использовании показателей эффективности тарелок по малым колоннам. По методу О’Коннелла получают более удовлетворительные результаты, если применяют не общие показатели эффективности. На рис. XIV. 31 показана эффективность тарелки как функция произведения вязкости иа отношение летучести легкого компонента к летучести более тяжелого ключевого компонента.
Лыоис (Lewis) [XIV. 31] изучил взаимоотношение общей эффективности отдельной тарелки с точечной эффективностью по Мерфри для случая, когда на тарелке не происходит перемешивание жидкости. Им были рассмотрены три варианта.
1. Пар однородного состава поступает на тарелку, жидкость несмешанная.
I
2. Пар поступает на тарелку не смешанным, несмешанная жидкость течет в том же направлении на последующих тарелках.
3. Пар поступает на тарелку не смешанным, несмешанная жидкость течет в противоположном направлении на последующих тарелках.
На всех трех моделях обнаруживают значительное превышение эффективности всей тарелки над локальной или точечной (по Мерфе) эффективностью. Разность эффективностей наиболее велика для второго варианта. Самая большая разность имеет место, когда точечная эффективность сама по себе уже достаточно высока, и для ректификации, когда величина mV/Ii превышает 1,0. Здесь т—наклон dy*/dx линии равновесия; V—расход газа в моль/ч; L—расход жидкости в моль/ч.
Фактический избыток эффективности тарелки вследствие поперечного течения жидкости становится существенным только в колониях больших размеров. По-
I
Q_>
<5
В
=3
Б
Qj
S-
&
съ
| N |
N | |||||||||||||
| V | ||||||||||||||
| ь s | ||||||||||||||
| \ | ||||||||||||||
| г |
V | |||||||||||||
| V | ||||||||||||||
| '•ч | ||||||||||||||
| 1 |
Относительная летучесть * Вязкость, спз
Рис, XIV. 31. Эффективность тарелки как функция произведения относительной летучести на вязкость [XIV. 19].
1 —* общая эффективность (рассчитанная по уравнению О’Коннелла); 2 — локальная эффективность (умозрительная).
скольку величина избытка в колоннах намного меньше, Льюис заключает, что на тарелках происходит значительное перемешивание смеси.
Зависимость между точечной эффективностью и общей эффективностью отдельной тарелки была рассмотрена Готро и О’Коннеллом (Gautreaux and O’Connell) [XIV. 19] в работе, где анализируется влияние поперечного течения жидкости и учитывается перемешивание жидкости на каждой тарелке. Следуя первоначальному анализу Киршбаума (Kirschbaum) [XIV. 28], Готро и О’Коннелл принимают, что жидкость на тарелке разделяется на ступени, каждая из которых состоит из «ванночек», полностью перемешанных. Готро и О’Коннелл делают следующие упрощающие допущения.
1. В каждую ступень поступает постоянная нагрузка жидкости и пара.
2. Пары, поступающие в каждую ступень, однородно перемешаны.
3. Уравнение равновесия имеет вид:
у* — тх + Ь;
4. Локальная эффективность по тарелке постоянна.
5. Унос и другие факторы настолько малы, что ими можно пренебречь.
Гостро и О’Коннелл [XIV. 19] выводят следующее уравнение общей эффективности по отдельной тарелке:
(XIV. 61)
где Ео — общая эффективность отдельной тарелки, определяемая по уравнению
(Уп) ср Уп-1-1
(XIV. 62)
Уп Уп-1-1
где п — число теоретических ступеней.
Соответственно можно ожидать, что число ступеней увеличивается: 1) по мере увеличения пути, проходимого жидкостью; 2) по мере увеличения расхода жидкости; 3) по мере уменьшения расхода паров; 4) по мере увеличения значения таких факторов конструкции тарелки, которые доводят до минимума перемешивание жидкости.
На основании результатов испытаний, проведенных на колоннах больших размеров, и вычисленных величин точечной эффективности было получено по уравнению (XIV. 48) число п ¦ теоретических ступеней. Полученные величины п показаны на рис. XIV. 32.
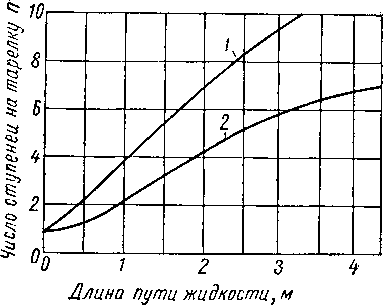
Рис. XIV. 32. Зависимость числа ступеней на тарелку от длины пути жидкости [XIV. 19].
/ —г высокий расход жидкости*. 2 — низкий расход жидкости.
О 1,2 1Л
Мерсрри.) на
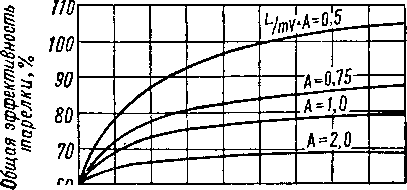
Рис. XIV. 33. Влияние числа ступеней на общую эффективность тарелки при локальной эффективности, равной 60% [XIV. 19].
Влияние числа ступеней на общую эффективность тарелки при локальной эффективности, равной 60%, представлены на рис. XIV. 33. Результаты указывают на то, что по мере того, как h становится очень большим, общая эффективность отдельной тарелки приближается к постоянной величине, получающейся из уравнения Льюиса для первого из перечисленных ранее вариантов.
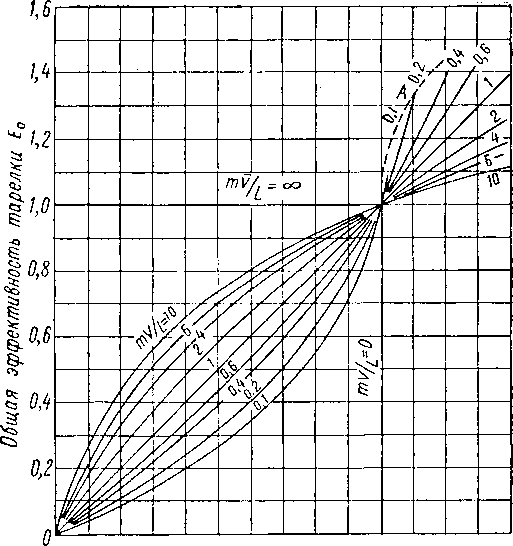
Часто допускают, что общая эффективность колонны равна общей эффективности отдельной тарелки. Это, однако, не всегда верно. Маршалл и Пигфорд (Marshall and Pigford) [XIV. 36] показали следующее: если параметр
Общая эффективность по пару (по отдельной тарелке
Рис. XIV. 34. Общая эффективность по пару (по Мерфри) на отдельной тарелке [XIV. 36].
А —' огибающая кривая, соответствующая точечной эффективности, равной 100% (пар перемешивается под каждой тарелкой).
mV/L значительно отличается от единицы, как это часто бывает в абсорберах, оба показателя эффективности не идентичны. На рис. XIV. 34 приведена зависимость общей эффективности отдельной тарелки по пару (по Мерфри) от общей эффективности всего абсорбера, найденная Маршаллом и Пигфордом.
До настоящего времени не имеется серьезных исследований вопроса о влиянин уноса на эффективность разделения. Было установлено, что унос является главной переменной величиной, влияющей на соотношение эффективности разделения по мере приближения к максимальной производительности колонны.
§ 5. КОНСТРУКЦИЯ ТАРЕЛОК И ИХ РАБОТА
Колпачковая тарелка является одним из видов оборудования, предназначенного для осуществления тесного контакта между газом и жидкостью. В данном случае контакт осуществляется с главной целью — способствовать массообмену между двумя фазами (теплообмен рассматривается как побочный процесс).
На рис. XIV. 35 показан изометрический чертеж двух верхних тарелок фракционирующей колонны, на котором видны колпачки, сливные стаканы и их затворы. На чертеже показаны прямоугольные затворы, но они могут быть и круглыми. Схематический разрез колпачковой тарелки при работе показан на рис. XIV. 36.
Тот же разрез, но с условными обозначениями конструктивных элементов и эксплуатационных параметров тарелки, изображен на рис. XIV. 37. Следует подчеркнуть, что на рис. XIV. 36 и XIV. 37 передана фактическая динамика только в условиях низкого расхода газа.
Для анализа динамики тарелок элементы тарелки можно разделить на три функциональные группы.
1. Колпачок и связанные с ним детали, которые обеспечивают тесный контакт между газом и жидкостью.
2. Затворные перегородки, которые обеспечивают распределение жидкости на тарелке.
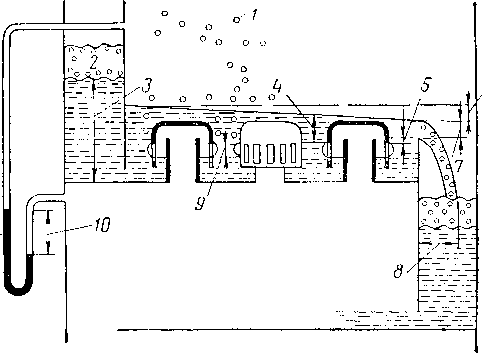
Рнс. XIV. 36. Схематический разрез колпачковой тарелки при работе [XIV. 4].

Рис. XIV. 35. Изометрический чертеж двух верхних тарелок колпачковой колонны.
/-^ выход верхних паров; 2— сливной стакан — выходная перегородка; 3 — входная перегородка и затвор; 4 — вход орошения; 5 — колпачок.
/ — унос; 2 — пена; 3 — высота жидкости в сливном стакане;
4 — динамический затвор прорезей; 5 — статический затвор;
6 — гидравлический перепад; 7 — высота над перегородкой; 8 — горизонтальная проекция жидкости над перегородкой; 9 — от-* верстие прорези; 10—перепад давления но тарелке.
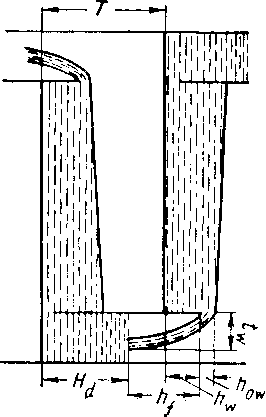
Рис. XIV. 37. Разрез колпачковой тарелки с условными обозначениями конструктивных элементов [XIV. 4].
Т — расстояние между тарелками в мм; — горизонтальная проекция жидкости иад перегородкой в мм; hw — высота перегородки в мм; hqw — высота чистой жидкости, перетекающей через перегородку; Нd — высота чистой жидкости в сливном стакане в мм; h j— зазор в мм.
17
15
12
^ 9
CL
r\j
Сэ
5:
СЬ
I
| \ | S' | ||||||||
|
щ § ^ Ci ^ г-j СЪ С\3 UJ с; о; § * 3 ^ ? 5-Ni Qj ? |
hмерн | э нагр | у wen |
\ ные | \ npope | 3U | са S X). D; С) е о ? *сь- 5: | ||
| "У/А | ////. |
'//s | __ / | Ос / о СУ* о <-%¦ V / | |||||
| 9 | m Удов, '/// | m | purne та// |
Ш льная y/y. |
/^// |
cP Ун Д-7^ /\<ъ У До" | |||
|
f} | P |
Ш w |
'flk w |
рл | |||||
| i |
ьсацс | <я na, |
ю^У, | w |
Y | 4 | Uj § > 1 fcs to | ||
| 1 1 1 1 | 4 $/ | jj— |
/i | V — |
|||||
500 1000 1500 2000 2500 3000 3500 WOO 4500 Нагрузка по жидкости, л/мин
Рис. XIV34.38. Пределы удовлетворительной работы тарелки при определенном сочетании условий на тарелке определенной характеристики потоков [XIV.4].
релки данной конфигурации и данных качеств жидкости и газа. Для низких расходов паров неудовлетворительная динамика тарелки характеризуется пульсацией пара, сбрасыванием жидкости вниз по стаканам для прохода паров или неравномерным распределением паров. При высоких расходах паров излишняя нагрузка прорезей приведет в конечном счете к захлебыванию вследствие того, что перепад давления по тарелке становится слишком высоким; жидкость не успевает перетекать с вышележащей тарелки вследствие уноса или
вследствие сочетания этих факторов. С другой стороны, при низких расходах жидкости данная высота затворных перегородок может не обеспечивать удовлетворительного контакта между жидкостью и газом. Высокие расходы жидкости способствуют захлебыванию при среднем или высоком расходе пара, но могут вести к недостаточному распределению паров при их низком расходе. В интервале, ограниченном этими крайними случаями, работа тарелки будет обычно удовлетворительной.
Представим себе, что при данном расходе жидкости перепад давления газа по тарелке постепенно увеличится. При некоторой величине перепада давления, равной гидростатическому столбу над прорезью, начнется барботаж через прорезь. В горизонтальной тарелке бар-ботаж начнется на выходном конце, поскольку перепад вызван сопротивлением потоку по тарелке. По мере увеличения перепада давления начнется барботирова-ние через прорези на колпачках, находящихся выше по течению потока; скорость барботирования через прорези, где оно началось в первую очередь, будет увеличиваться. Поскольку прорези имеют ограниченную высоту, нижняя их часть будет закупорена жидкостью до тех пор, пока перепад давления по прорези не станет равен ее высоте. При перепаде давления, при котором в действие вступают все имеющиеся на тарелке прорези, тарелка, как говорят, становится «стабильной».
При удовлетворительных рабочих условиях энергичный барботаж через прорези вызывает сильное разбрызгивание над более плотной смесыо газа и жидкости, находящейся на дне тарелки. В этих условиях на тарелке через гетерогенную смесь газа и жидкости бар-ботируготся не отдельные пузырьки, а непрерывная Цег1Ь ггузырьков. Далее перепад давления снаружи прорези до свободного газового пространства над ней не равен перепаду давления, определяемому гидростатическим столбом чистой жидкости. Жидкость, перетекающая через затворную перегородку, связана со значительным количеством газа, который должен быть отделен от жидкости в сливном стакане.
Допустимый предел увеличения перепада давления оказывается исчерпанным, когда перепад давления по тарелке настолько высок, что жидкость уже не может стекать на нее с вышележащей тарелки. Это состояние называется «захлебыванием». Высота разбрызгивания или пены повышается по мере увеличения перепада давления по тарелке или увеличения расхода газа. Множество мельчайших капелек жидкости уносится по стакану, вследствие чего капельки поднимаются на вышележащую тарелку. Но размеры этих капелек слишком невелики, чтобы унести значительное количество жидкости. Резкое увеличение уноса имеет место, когда брызги достигают дна вышележащей тарелки. Однако этот унос объясняется в основном не увлечением частиц жидкости газовой фазой, а просто попаданием сравнительно больших капелек, обладающих высокой кинетической энергией, на вышележащую тарелку [XIV. 241. Унесенная жидкость вызывает внутреннюю рециркуляцию, которая увеличивает жидкую нагрузку в колонне и в конечном счете вызывает захлебывание. В правильно рассчитанной тарелке захлебывание, вызванное задержкой жидкости в сливном стакане, объясняется в значительной степени перепадом давления и уносом.
§ 6. РАСЧЕТ КОЛПАЧКОВЫХ КОЛОНН
Выбор критериев для расчета колпачковых колонн должен быть основан на физическом характере происходящих в них явлений. Проведенные в последние годы исследования процессов, происходящих во фракционном оборудовании, способствовали появлению новых представлений о механизме фракционирования в колпачковых колоннах и разработке более совершенных критериев расчета этих колонн..
У
(XIV. 64)
Данный раздел преследует цель объяснить динамику работы колпачковой тарелки.
Были предложены упрощенные методы определения габаритов колонны [XIV. 49, XIV. I], которые можно применять для предварительных расчетов (в том числе экономических). Практический расчет и сооружение колпачковых колонн производятся на основании более детализированных методов [XIV. 4, XIV. 14].
(XIV. 65)
1. УПРОЩЕННЫЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ ГАБАРИТОВ КОЛОНН
Упрощенные методы определения габаритов колонн основываются на эмпирическом применении формулы уноса капель. Для данной капли диаметром d, только что подхваченной поднимающимся потоком пара, действующая сила тяжести равна сопротивлению самой капли:
В этих условиях скорость газа
Рж рг Рг
где
-if-W—
Выразив в единицах массовой скорости (массопоток в единицу времени на единицу площади поперечного сечения [XIV. 49] уравнение (XIV. 64), получим
“ = с/ Рг(Рж-Рп),
где и — массовая скорость паров в кг/чна 1 мг поперечного сечения колонны; с — эмпирически найденный параметр в м/ч\ рж—плотность жидкости в условиях колонны в кг/м3', рп — плотность паров в условиях колонны в кг/м3.
Уравнение (XIV. 65) применяли, чтобы определить с в экспериментальных и промышленных колпачковых колоннах, работающих в различных условиях расхода жидкости и газа, плотности газа и расположения и конструкции тарелок и т. п. Для первого приближения величина с, как показали Соудерс и Браун (Souders and Brown) [XIV. 49], является функцией расстояния между тарелками, плотности жидкости и газа и поверхностного натяжения (рис. XIV. 39). Очевидно, эта корреляция построена на чрезмерном упрощении действительной картины, но она обеспечивает возможность быстрого вычисления поперечного сечения колонн, давая величину, составляющую 60—80% предельной или максимальной паропропускной способности. Поверхностное натяжение берется одним из параметров, так как можно полагать, что дисперсия жидкости на мельчайшие капельки увеличивается по мере уменьшения поверхностного натяжения. Однако Киршбаум (Kirschbaum) [XIV. 28] обнаружил, что поверхностное натяжение очень незначительно влияет на допускаемую скорость, паров.
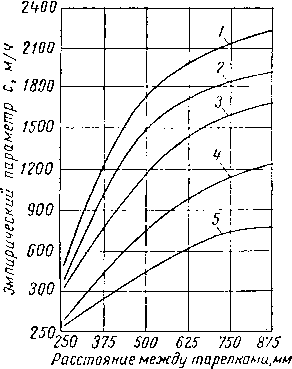
Рис. XIV. 39. Корреляция Со-удерса — Брауна для приближенного определения габаритов колонн.
/ — поверхностное натяжение
20 дин/см и выше; 2 — 10 дин/см',
3 — 5 дин1см; 4— 1,0 дин!см (рекомендуемое поверхностное натяжение для углеводородных абсорберов);
5 — 0.5 дин/см.
Киршбаум систематически изучал значение расстояния между тарелками для расчета колонн, особенно для расстояний меньше 300—400 мм. При большем расстоянии между тарелками (рис. XIV. 40, а и б) дальнейшее увеличение расстояния дает очень небольшое увеличение предельной скорости паров, за исключением случаев большой плотности газа. По соотношению Киршбаума максимально допускаемая скорость, паров
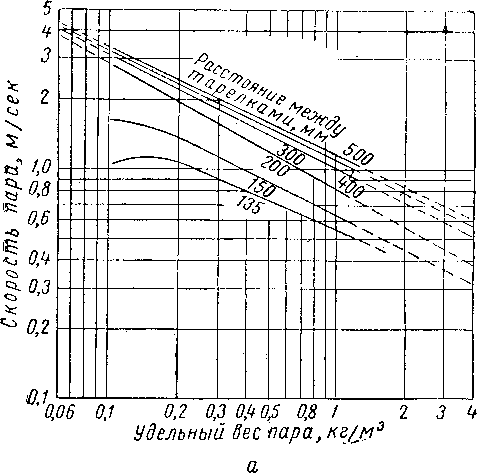
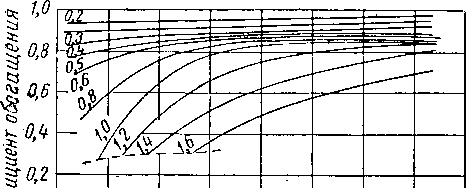
i>=c'(Pn)ft, (XIV. 66)
где о — максимально допускаемая скорость паров; рп— плотность паров; Ь — функция расстояния между тарелками; колеблется от —0,425 до —0,545; с'— эмпирическая функция расстояния между тарелками.
Уравнение (XIV. 66) можно получить из (XIV. 64), если рж принять больше рп и если УРж—Рп считать константой, которую включает в себя с'.
Удобный метод установления габаритов колонн для фракционирования углеводородов был предложен Эткинсом и Вильсоном (Atkins and Wilson) [XIV. 1]. Уравнение того же типа, что и уравнение Соудерса — Брауна, применяется для активной поверхности тарелки, т. е. поверхности, занятой колпачками. Приводятся критерии для определения пропускной способности колонны по жидкости и пару.
2) ЮО 150 200. 250 300 350 -400 450 500
Рдсстояние>между тарелками, мм
Рис. XIV. 40.
а —• допускаемая скорость пара при различной плотности пара и различном расстоянии между тарелками; б — зависимость коэффициента обогащения от расстояния между тарелками при различной скорости пара в м!сек.
2. НЕКОТОРЫЕ КРИТЕРИИ РАСЧЕТА КОЛПАЧКОВЫХ ТАРЕЛОК
При рассмотрении рис. XIV. 40 мы уже обращали внимание на то, что небольшое расстояние между тарелками приводит к низкой предельной пропускной способности по пару. Это можно объяснить уносом, задержкой жидкости в сливных стаканах вследствие перепада давления на тарелке или ограниченной пропускной способностью сливных станков по жидкости.
Здесь уносом именуется образование на тарелке обильного разбрызгивания жидкости, которая достигает вышележащей тарелки. Обычно следует располагать тарелки на расстоянии 450—600 мм одна от другой.
Влияние уноса на увеличение потребного числа идеальных ступеней было рассмотрено в предыдущем разделе. Влияние уноса на эффективность действительной тарелки может быть вызвано повторным смешением жидкостей. Резкое снижение эффективности тарелок в интервале, непосредственно предшествующем предель-

Рис. XIV. 41. Влияние уноса на эффективность.
2,0 7 1,65
\2Ч
0,83
0,62
0,41
-с
.л
ОЩ
+
Условия построения кривой: сетчатая тарелка с отверстиями диаметром 3,2 мм, расположенными в вершинах равносторонних треугольников со стороной 9,5 мм, свободная поверхность — 6,7%. ^ср — 38,1 мм. А — экспериментальная кривая для тарелки без уноса (отдельная тарелка); В — экспериментальная кривая эффективности для трех тарелок, расположенных на расстоянии 300 мм одна от другой; С — экспериментальная кривая уноса для трех тарелок. Кружками обозначена эффективность для трех тарелок, находящихся на расстоянии 300 мм одна от другой, вычисленная по кривым Л и О [XIV. 25а].
ной пропускной способности по пару, может быть вызвано уносом. Это подтверждает рис. XIV. 41, где расходы пара, при которых наблюдалось увеличение уноса и снижение эффективности тарелок, совпадают.
Поскольку очевидно, что унос в значительной степени зависит от расстояния между тарелками, Хант, Хансон и Вилке (Hunt, Hanson and Wilke) [XIV. 24] определили, что успокоение, наоборот, не оказывает большого влияния на унос. Симкин, Стренд и Олни (Simkin, Strand and Olney) [XIV. 45] разработали эмпирическую зависимость уноса жидкости в колпачковых колоннах. Эта зависимость, представленная на рис. XIV. 42, хотя не вполне универсальна, но характеризует некоторые главные переменные, определяющие унос жидкости, и ясно свидетельствует о экспоненциальной зависимости между уносом и расходом пара.
Высота, до которой прорези колпачка залиты жидкостью, должна быть достаточной для обеспечения надлежащего контакта между газовой и жидкой фазами. Эффективность тарелки в зависимости от глубины затопления прорези для системы этанол — вода показана на рис. XIV. 43 [XIV. 9, XIV. 28]. Очевидно, что эффективность тарелки уже весьма значительная, когда глубина затопления прорези или расстояние между вершиной прорези и уровнем жидкости без течения пара рав-
а 0,207 с 0,165 0,124
| / / | г /— / |
t t | ||||||||||
| ? f | ||||||||||||
| А — | Т | |||||||||||
|
/ | / | |||||||||||
| i |
/ | / / |
||||||||||
|
/ | / | |||||||||||
| V |
) | <2 | ||||||||||
| - / V- | * | t |
||||||||||
|
* / | -А- / | |||||||||||
|
-4- | ||||||||||||
| / | • | / | ||||||||||
| -4 | / |
/ / |
Рп
695
35,2ц
Рп
Рис. XIV. 42. Эмпирическая зависимость уноса жидкости [XIV. 45].
Cs — массовая скорость уноса жидкости на активную поверхность в кг/мин-m‘J; h$w—высота гребня жидкости над перегородкой в мм; — статический затвор прорези в мм; hs — перепад давления через прорезь в мм; иf — скорость паров на активной поверхности в м1сек; Т — расстояние между тарелками в мм; рж. рп — плотность жидкости и пара в Кс!м3. I — поверхностное натяжение 30 дин/см; 2 — 70 дин/см.
ны нулю. При увеличении глубины затопления свыше
2.5 см эффективность разделения этой системы изменяемся очень мало. Глубина затопления прорези в 2,5 см и выше благоприятствует фракционированию легких углеводородов. Регулировка высоты затворной перегородки позволяет контролировать глубину затопления прорези. Затворная перегородка высотой 5—7,5 см обычно обеспечит глубину затопления прорези, достаточную для сохранения активности тарелки.
На рис. XIV. 44 показана зависимость между величиной отверстия прорези и горизонтальным расстоянием перемещения потока и скоростью пара [XIV. 28,
XIV. 42]. Горизонтальное расстояние течения достигает асимптотической величины около 2,5 см при высоких скоростях пара. Чтобы избежать взаимного столкновения между потоками пара, выходящими из смежных колпачков, минимальное расстояние между колпачками должно в 2 раза превышать максимальное расстояние течения и быть равным примерно 5 см. При равной скорости пары высокой плотности могут проходить большее расстояние по горизонтали, чем пары низкой плотности. Минимальное расстояние между прямоугольными колпачками при прохождении потока жидкости параллельно ряду колпачков должно составлять не менее 10 см. Вследствие большого расстояния между кол-пйчками образуются сквозные потоки жидкости, что нежелательно, поэтому следует обеспечивать достаточно высокую и равномерную плотность колпачков на тарелке. либо применять распределительные перегородки, направляющие поток жидкости но тарелке.
Для данного диаметра колпачка и данного расхода газа соотношение по площади между стаканами для подъема паров возвратным и кольцевым пространством должно обеспечивать наименьший перепад давления по всей тарелке.
_1-1-1-Т--1-!-1-1-
Действие колпачка по Киршбауму
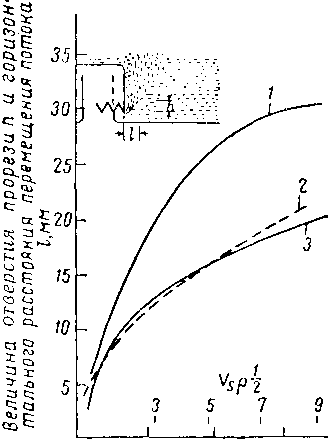
_L
г m
га
&
Cl
Qj
¦?:
Q
t
*
<=;
Qj
Ci.
CJ
?
100
90
| 80 CO
I,
s-
съ
11
I
SO
Влияние изменения соотношения между площадью кольцевого пространства и площадью пароподъемного стакана на перепад давления по этим конструктивным элементам для уравнения Дофина [XIV. 4, XIV. 12] показано на рис. XIV. 45.
Стабильной является тарелка, на которой активно действуют все колпачки. Пределом стабильности является такой расход пара, при котором как раз становятся активными все колпачки на тарелке.
Для определения стабильности тарелки нет простого критерия, поскольку она зависит от размера и формы колпачка, расстояния между колпачками, высоты затворных перегородок, качеств жидкости, жидкой и парообразной нагрузки и длины пути, проходимого жидкостью. Общая методика предварительного определения перепада жидкости была предложена Дэвисом (Davies) [XIV. 13] и усовершенствована Бол-лесом (Bolles) [XIV. 4].
Гидравлический перепад по колонне в нормальных условиях ее работы вызывается в основном сопротивлением, оказываемым газовым потоком потоку аэрированной массы, и перепадом аэрированной массы под действием трения при движении ее по тарелке. При
Рис. XIV. 43. Эффективность тарелки по Мерфри как функция гидравлического затвора.
1 — данные Киршбаума; 2—данные Кэри и других.
| Н аименование | По Киршбауму | По Кэри и другим |
| Диаметр колонны, мм....... | 110,0 |
152,4 |
| Площадь прорезей, %....... | 4.55 | 3.53 |
| Соотношение жидкость—пар . . . | 0,5 | 1,0 |
| Ширина прорези, мм........ |
Треугольная | 6,4 |
| Высота прорези, мм........ |
5,0 | 12,7 |
| 1 м/сек с |
||||
| f |
||||
|
Г |
М1сен | |||
|
' . | /fi //$ Г/ <ь / Ч* | о / • 2 | ||
| // |
{ // ¦" | |||
| j / |
0 10 20 30 40 50
Высота гидравлического затвора, мм
3 6 Э 12
Скорость пара при прохождении через прорезь, м/сек
Рис. XIV. 44. Зависимость между величиной отверстия прорези и горизонтальным расстоянием перемещения потока и скоростью пара [XIV. 28, XIV. 42].
1—горизонтальное расстояние истечения; 2 — теоретическая кривая — уравнение Роджерса и Тиле; 3 — данные Киршбаума.
Диаметр колонны 400 мм, поверхность прорези 14,1%; система этанол — вода, треугольные прорези, высота прорези 15 мм, зазор между колпачком и тарелкой 7 мм.
расчетах гидравлический перепад важен лишь постольку, поскольку он вызывает неустойчивость тарелки при низком расходе газа. Но когда тарелка становится стабильной, то хотя гидравлический перепад увеличи-
' 0 U 0,8 1,2 1,6 2,0 JJS
Отношение площадей кольцевой межтрубнои части и пароподъемного стакана
Рис. XIV. 45. Определение оптимального соотношения между площадью межтрубной части ih пароподъемноро стакана [XIV. 4].
1 — всего — пароподъемный стакан, возвратная трубка н межтрубная часть; 2 — пароподъемный стакан; 3 — возвратная трубка и межтрубная часть.
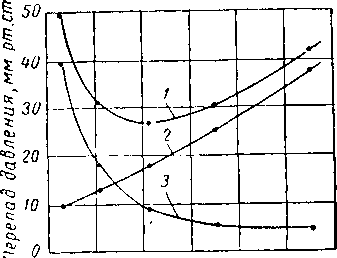
вается по мере увеличения расхода газа, но уже не оказывает вредного влияния на работу тарелки.
По-видимому, наиболее важным фактором, определяющим гидравлический перепад, является гидростатический напор на выходной стороне тарелки и высокие затворные перегородки на выходе могут весьма эффективно противодействовать возникновению нестабильности тарелки при большом расходе жидкости [XIV. 29].
Для предотвращения нестабильности тарелки в колоннах среднего размера достаточен перепад давления по тарелке, существующий при разнице в уровне жидкости в 5—7,5 см. Более обстоятельно этот вопрос рассмотрен в работах Дэвиса [XIV. 14], Боллеса [XIV.4] и Кемпа и Пайла (Kemp and Pyle) [XIV. 26].
Сливные стаканы обеспечивают некоторое время отстоя для окончательного разделения жидкой и парообразной фаз, подают жидкую фазу на нижележащую тарелку и создают гидравлический затвор на пути паров, поднимающихся с нижней тарелки.
По рекомендации Дэвиса [XIV. 14] минимальное время отстоя при стекании жидкости вниз должно составлять 5 сек. Эткинс и Вильсон (Atkins and Wilson) [XiV. I] считают, что скорость при стекании жидкости вниз должна составлять от 6,3 до 10,5 см!сек, а при расстоянии между тарелками 600 мм — 8,4 см/сек; это дает около 7 сек времени отстоя. Для обеспечения эффективного разделения газа и жидкости в сливных стаканах высота жидкости, сброшенной через затворные перегородки, должна быть меньше ширины перегородки.
Для отдельной тарелки с поперечным потоком это требование оказывается удовлетворенным, когда
h>VKJ’ (XIV. 67)
где Ь, — средняя ширима сливного стакана в мм; t — расстояние между тарелками в мм; hHn— высота чистой жидкости над затворной перегородкой в мм.
Для центрального сливного стакана затворной перегородки с двойным поперечным потоком
bs>2VKJ’ (XIV. 68)
поскольку оба потока встречаются у центрального сливного стакана. Уравнения (XIV. 67) и (XIV. 68) выведены с учетом горизонтальной составляющей скорости жидкости, текущей через затворную перегородку, и максимально возможной высоты, с которой падает жидкость.
В этих условиях значительная часть площади сливного стакана остается для выделения паров, если только жидкости не отличаются высокой способностью к пенообразованию.
Одним из наиболее важных моментов расчета яи-ляется высота столба чистой (без пены) жидкости в сливном стакане. Она зависит от гидростатического напора на тарелке, перепада давления на тарелке и сопротивления течению в сливных стаканах. В современной практике расчета принято предусматривать примерно 50% свободной высоты в сливных стаканах фракционирующих колонн и даже до 60% свободной высоты в системах с более вязким абсорбентом. С каждым днем накапливается все больше данных, позволяющие вычислять уровень пены в сливном стакане по расчетной высоте столба чистой жидкости. Коэффициент аэрации в сливном стакане
высота столба чистой жидкости
Л —— .....
f высота слоя пены
изменяется в зависимости от характера системы газ— жидкость и динамики тарелки. Для данного сливного стакана величина Л/ уменьшается по мере увеличения расхода жидкости и газа и повышения вязкости жидкости.
1,18
/
Р»
и = К.
28
Р„Ю3
Рж —Рг h wsdh
Ниже рассматриваются последовательные этапы расчета тарелок, начиная от расчета перепада давления по колпачкам и кончая расчетом столба чистой жидкости в сливных стаканах. Приводятся только некоторые из описанных в литературе формул расчета [XIV. 4, XIV. 14, XIV. 27].
1. ПЕРЕПАД ДАВЛЕНИЯ В КОЛПАЧКАХ
Перепад давления в колпачках определяют, суммируя перепады давления по каждому элементу колпачка. Перепад давления в пароподъемной трубке по определению Дофина [XIV. 12]
d,
где hr — потеря напора в пароподъемной трубке в мм вод. ст.; йт — внутренний диаметр пароподъемной трубки в мм; рж—плотность жидкости в кг/м3; рп — плотность пара в кг/м3; V — общая паровая нагрузка на тарелку в условиях потока в м3/сек; Аг — общая поверхность зоны пароподъемной трубки на тарелку в м2.
Перепад давления по обратной и межтрубной зонам передается полуэмпирическим выражением
р / _ т/ 2/42 \1,71
^га — 0,275 — (У^рп -j— -—~ 0,827 j . (XIV. 70)
(XIV. 69)
2. ПЕРЕПАД ДАВЛЕНИЯ ЧЕРЕЗ ПРОРЕЗИ
Следующим этапом является вычисление перепада давления газа при прохождении его через прорези. Боллес [XIV. 4] применил метод Роджерса и Тиле [XIV. 42] для определения размера отверстия прорези и отсюда перепада давления в трапецоидальных прорезях, к которым относятся и треугольные и прямоугольные прорези. Следующие расчеты заимствованы из статьи Боллеса [XIV. 4].
Чтобы получить расход пара, нужно применить к площади dA уравнение диафрагмы
где hra — потеря напора в возвратном и межтрубном пространстве в мм вод. ст.; рв — плотность воды в кг/м3; Аи — площадь пароподъемного стакана на тарелку в м2; Ат — меньшая из двух площадей Аа и АТ; Л„ —площадь межтрубного пространства в м2; Ас — общая внутренняя площадь поперечного сечения колпачков на тарелку в м2.
(XIV. 71)
Тогда
¦Р nh
где Va — паровая нагрузка иа прорезь в м3/сек; и — скорость прохождения потока через прорезь в м/сек; Ks — коэффициент отверстия прорези; g— гравитационная постоянная в м/сек2; ря,—плотность жидкости в кг/м3; рг—плотность газа в кг/м3-, ws — ширина прорези в мм; h — высота прорези в мм.
Ширина w действительного элемента потока для трапецоида определяется размерами элементов по следующему соотношению:
vst
wsb ~*Г wst 1 +
wst
Rs = — . (XIV. 80)
Поскольку
R<
(XIV. 81)
К
(XIV. 73)
' = wst + {ь
s Ь ¦
(XIV. 82)
wsb +Ws t 1 + Rs
Уравнение (XIV..79) будет иметь следующий вид:
где wst — ширина прорези наверху в мм-,—ширина прорези внизу в мм; ha — отверстие или перепад давления прорези в мм; Нs — высота прорези в мм.
Совмещая уравнения (XIV. 72) и (XIV. 73), получаем
¦ASV* +
I' = 0258
3 1 + R
Н,
^?_l/ %тРж— Рг[
"10е К L
hs — ft]
vst + (wsb - wst) “777 h'^dh.
(XIV. 74)
dV
(XIV. 83)
+
15 1 + Rs Hs
Решить уравнение (XIV. 83) точно для отверстия прорези невозможно, но решение, где отношение отверстия прорези к высоте прорези определяется в зависимости от отношения паровой нагрузки к максимальному расходу пара, можно представить графически, как это сделано на рис. XIV. 46. Следует обратить внимание, что максимальный расход пара или расход, соответствующий полностью раскрытой прорези, равен
Общий расход пара через отверстие прорези h, выряжается интегралом
hs hs
$wsthl/*dh+ j (ffi>sb - x
0 0
— л / 2g Рж-Рг
¦10°]/ юз Рг XWsh'hdh~l
sb ¦
-R,
tiudh
. (XIV. 75)
х
Vm - 0,258 \3 j + ^ -г 15 j + ^
xv
+ •
н/ж_
Рглс
Интегрируя, получаем
,, / 2 g Рж-Рг I2
vs- 10» у To*—
(XIV. 84)
Рг
2 wsb~wstwsA +“-”-X
поскольку в данных условиях h„ = Hs.
На рис. XIV. 46 показаны три кривые, соответствующие треугольным прорезям (Rs—0,00), трапецои-дальным прорезям (Rs = 0,50) и прямоугольным прорезям (Rs = 1,00).
3 Hs
(XIV. 76)
9 W U — W 4 V А»/2__?_Ё-S1 hV:
x "s 5 ns
Применив величину Ks = 0,51, получаем объем пара для всей тарелки:
100
*2 80
^ Qj
* ё
53 ^ ип
<о ^
оо<с. 20 о S'
V = 1,29- 107/VSNc у P-2L^X
'I fcV, j. 1 (w*b-w«) h>,«
3 wsths + 15 ( /7 j hs~
, (XIV. 77)
X
где Ns — число прорезей в колпачке; Nc— число колпачков на тарелке.
w и -4- w 4 Ач = NNH4 - s6-^ st, s s 0 s 2 x 10е
(XIV. 78)
| — | |||||||||
| $ |
\у | И | |||||||
| Л / V У/ | ^ ма S.V про п нос |
ксимальная \ ценная способ пь прорези | _ | ||||||
| 1/ | V | ||||||||
|
1 |
•*S ^5 0,00 0.63 0,50 0.7Ц 1,00 1 0.79 | | ||||||||
| 1 |
|||||||||
рг V 3 wsb + wst
Я.
wsb ~ wst hs2
Ч& + wst hs
0 20 «7 60 80 100
Паровая нагрузка.,
°/о от максимальной пропускной способности прорезей
Рис. XIV. 46. Общая корреляция для трапецеидальной прорези [XIV, 4].
Дэвис [XIV. 13] предложил полутеоретический подход к проблеме вычисления гидравлического перепада в колпачковой колонне. Схематическое изображеиие тарелки, работающей в условиях, приближающихся к нестабильным, показано на рис. XIV. 47. Барботаж в D можно бражены перепад давления при нулевом гидравлическом затворе и геометрическое место точек стабильности тарелки.
Хотя метод предсказания гидравлики тарелок, предложенный Дэвисом [XIV. 13], только качественно согласуется с экспериментально установленными фактами [XIV. 26], это единственный систематический подход
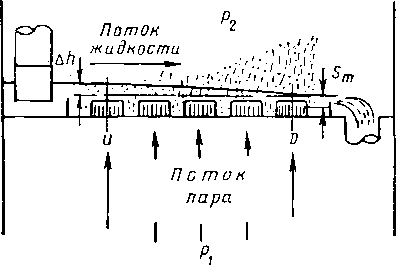
Рис. XIV. 47. Схематическое изображение тарелки, работающей в условиях, близких к нестабильным [XIV. 26].
считать нормальным, а барботаж в U так незначителен, что сопротивление потоку можно приравнять сумме перепада и глубине затопления прорези. С другой стороны, перепад давления в D равен перепаду давления через прорези плюс напор, создаваемый аэрированной жидкостью. Оба перепада давления можно выразить так:
(XIV. 85)
где hT — перепад давления в пя.роподъемном стакане; hra — перепад давления через возвратный и межтруб-ный слой; hs — перепад давления через прорези; фу— часть глубины затопления прорези, характеризующая потери давления у выходного ряда колпачков U; Sm — глубина затопления; Д —гидравлический перепад.
Если фу = 1,0, тогда hr + hra. + h„ для барбо-тажа в том ряду колпачков, который обозначен U на рис. XIV. 47. При этом барботаж начинается лишь тогда, когда hr + hra + ha = Д . Фактически, как свидетельствуют данные Кемпа и Пайла (Kemp and Pyle) [XIV. 26], величины фу для активных колпачков меньше единицы, когда другая часть колпачков нестабильна, поэтому мы можем написать
hr + Ка + hs + - I) Sm = д- (XIV.86)
Это указывает на то, что, когда тарелка начинает становиться нестабильной, гидравлический перепад может быть несколько меньше перепада давления через колпачок.
Но гидравлический перепад Д в колпачковой колонне является сложной функцией большого числа следующих переменных [XIV. 13]: 1) расхода жидкости;
/Д
I +
2) плотности жидкости; 3) расхода паров; 4) плотности паров; 5) минимальной величины гидравлического затвора; 6) характеристики работы колпачка, включая перепад давления в колпачке; 7) расстояния между колпачками; 8) числа рядов колпачков; 9) зазора между дном колпачка и тарелкой.
Суммирующая кривая гидравлического перепада как функции коэффициента F, для данной тарелки приведена на рис. XIV. 48. На той же диаграмме изо-
X \hlt + S(a — 1)
(XIV. 87)
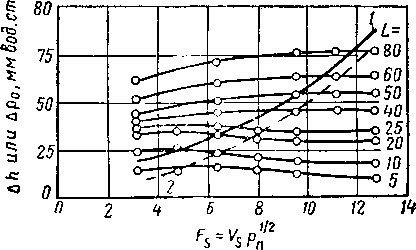
Рис. XIV. 48. Зависимость перепада давления от Fa, использованная при построении диаграмм пропускной способности по жидкости. Для 16 рядов колпачков диаметром 76 мм, утопленных заподлицо в тарелку и расположенных в вер-шинах равносторонних треугольников (длина стороны 114 мм). Минимальный постоянный гидравлический затвор равен 25 мм [XIV. 26]*
/ — перепад давления при нулевом затворе; 2 — кри* оая стабильности.
к данной проблеме, имеющийся в литературе. Уравнение Дэвиса было выведено на основе следующих допущений и условий.
1. Поперек тарелки течет только чистая жидкость, уровень которой выше диа колпачка, но не выше вершины колпачка.
2. Колпачки и пароподъемные стаканы круглые.
3. Колпачки расположены на тарелке по принципу равнобедренных треугольников.
4. Барботируют все колпачки.
5. Расположение и расстояние между колпачками повсюду одинаково.
6. Тарелка горизонтальна.
7. Ряд колпачков перпендикулярен направлению потока жидкости.
8. Тарелки относятся к типу тарелок с поперечным течением, потоки жидкости идут параллельно друг Другу.
9. Основное сопротивление трения создается колпачком.
10. Стационарные условия потока.
Используя формулу погруженной диафрагмы для вычисления потерь трения, возникающих при движении потоков через колпачки, и экспериментальные данные
о гидравлическом перепаде, Дэвис [XIV. 14] вывел конечное уравнение, показывающее зависимость гидравлического перепада Д' от других переменных параметров тарелки:
+ 3Wr X
N3/2 V Г+ V-ф-' Q 2,4 C^lc
УК
=0,0025-;
,(XIV.
где Nr — число рядов колпачков, перпендикулярных к направлению потока; h — глубина чистой жидкости на тарелке в мм; hla — глубина чистой жидкости у пе-реточной перегородки в мм; 1С — общая свободная ширина между колпачками, перпендикулярными к направлению потока, в мм; S — зазор между дном колпачка
Боллес [XIV. 4] делает дальнейшие допущения о том, что колпачки расположены в вершинах равносторонних треугольников, а диаметр пароподъемного стакана составляет примерно 0,7 диаметра колпачка. Тогда
1,6ДГ + 3 1й| +
ох
и тарелкой в мм; Са—коэффициент гидравлического перепада; Lw — общая ширима потока по тарелке, перпендикулярной к направлению потока; Q — нагрузка жидкости на тарелку или часть тарелки в л/мин; а — отношение расстояния между пароподъемными стаканами к расстоянию между колпачками; а' — гидраЕ)-лический перепад между колпачками, не скорректированный на паровую нагрузку, в мм; Д^_—гидравлический перепад на один ряд колпачков, не скорректированный на паровую нагрузку, в мм;7 — отношение расстояния между колпачками к диаметру колпачка; [j — отношение расстояния между колпачками, находящимися на параллельных потоках жидкости, к расстоянию между колпачками на наклонных потоках жидкости.
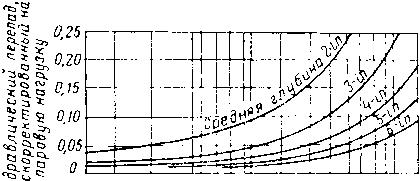
757 10 15 20 30 40 ВО 80 100 120 ISO 200
t Нагрузка no жидкости наО,30^8 п средней ширины тирепни ,л/«
Рис. XIV. 51. Типовой рабочий график для вычисления гидравлического перепада (Болес [XIV. 4]).
I'd
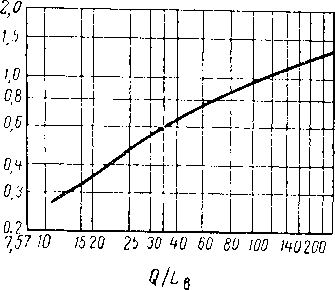
На рис. XIV. 49 приведена кривая коэффициента гидравлического перепада, которую можно использовать вместе с уравнением [XIV. 88] для составления рабочих диаграмм с целью определения гидравлических перепадов на колпачковых тарелках. Наконец, истинный гидравлическим перепад получаем, если умножим нескорректированный перепад на поправочный коэффициент (на расход пара), полученный по рис. XIV. 50. Типовой рабочий график, составленный Боллесом [XIV. 4], показан на рис. XIV. 51.
Рис. XIV. 49. Кривая коэффициента гидравлического перепада [XIV. 13].
Нагрузка жидкости на 0,3048 м средней ширины тарелки о л/мин.
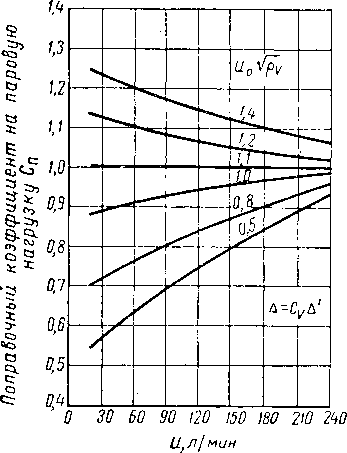
Рис. XIV. 50. Корреляция гидравлического перепада для па розой нагрузки [XIV. 13].
Нагрузка по жидкости на фут средней ширины грелки в л/мин.
4. ПОТЕРИ ДАВЛЕНИЯ ПРИ ПРОХОЖДЕНИИ ПАРОВ ЧЕРЕЗ ЗОНУ БРЫЗГ ЖИДКОСТИ
Давление паров, вышедших из прорезей, снижается также при прохождении их через зону обильных брызг, выбрасываемых над колпачками. Действительный перепад давления при прохождении через эту зону
(XIV. 89)
hA^ hw + hotu + Д — ht-
где: hА — действительный перепад давления паров при прохождении через фонтанирующую жидкость; hw — высота затворных перегородок; Ло» — высота чистом жидкости, переливающейся через затворную перегородку-Д —гидростатический напор, вызванный гидравлическим перепадом, в определенной точке тарелки; hta— высота от дна тарелки до верхней части прорези. Коэф фициент аэрации на тарелке
si
Фг = h 4- h -4- Д — fi, 1
niu i now “ is
его также можно определить по экспериментально по лученным данным, поскольку
“to ~ ош ‘ “ts
где Л( — замеренный общий перепад давления по тарелке. Достаточно полных данных для вычисления нет. Кемп и Пайл [XIV. 26] нашли, что коэффициент аэрации для системы воздух—вода колеблется от 0,50 до 0,80. Высокий уровень жидкости и высокий расход пара повышают величину <ЬТ. Для системы воздух— абсорбент равно от 0,4 до 0,6. Коэффициенты аэрации, встречающиеся при фракционировании газового бензина, неизвестны, но можно без риска применять при расчетах величину 0,6. Коэффициент аэрации зависит от многих переменных, но наиболее важными из них являются расход пара, глубина затопления прорези и качество фракционируемой системы. В предварительном порядке можно использовать для пересчета статического погружения Sm в действительный перепад давления.
ha = К
5. ПОТЕРИ НАПОРА В ОБРАТНОЙ ПЕРЕГОРОДКЕ
Потери гидравлического напора, происходящие при движении жидкости в обратной перегородке, приближенно вычисляются по формуле
hd = 4,6-10~8 (jy) . (XIV. 91)
где hd — потеря напора в мм вод. ст.\ Q—нагрузка жидкости на тарелку или часть тарелки в л/мин', Ad — минимальная площадь под сливным стаканом в ж2.
6. ВЫСОТА СТОЛБА ЖИДКОСТИ В СЛИВНОМ СТАКАНЕ
Исходным пунктом для вычисления высоты столба жидкости в сливных стаканах является высота жидкости на входе в тарелку, выражаемая как
(XIV. 92)
где hn — высота жидкости на входе в тарелку, а другие переменные — те же, что и в уравнении (XIV. 89). Общая высота чистой жидкости в сливном стакане
Hd = hit-\- hd + hr + hra + hs-\- <)JTSm. (XIV. 93)
Фактически высота жидкости в сливном стакане вследствие аэрации значительно больше указанной. Коэффициент аэрации в сливном стакане
(XIV. 94)
где Н/ — фактическая высота пены в сливном стакане. Экспериментальные данные о А/ в сливных стаканах немногочисленны. Коэффициент аэрации системы воздух—вода примерно равен 0,8, а точнее 0,75. С другой стороны, для системы воздух—абсорбент получены величины 0,5—0,7 (точнее, 0,5). Для расчетов фракционирования газового бензина можно без риска применять величину 0,45. Когда уровень жидкости в сливном стакане дойдет до верха переточкой перегородки, колонна, как можно предполагать, захлебнется.
Фактически принято при расчетах предусматривать 60%-ное заполнение сливных стаканов.
