Промысловая сепарация и масляная абсорбция газа
ГЛАВА XIII
ПРОМЫСЛОВАЯ СЕПАРАЦИЯ И МАСЛЯНАЯ АБСОРБЦИЯ ГАЗА
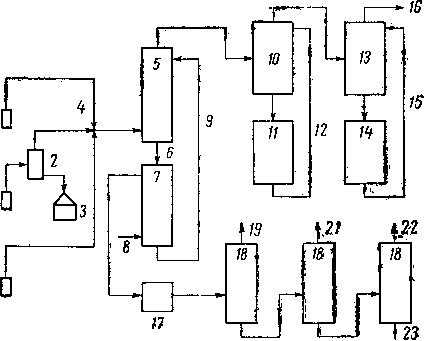
Газ высокого давления, выходящий из скважин, поступает в промысловые сепараторы, где отделяются углеводородный конденсат и вода. Природный газ многих месторождений содержит пропан, бутан и газовый бензин в количествах, оправдывающих использование специальных установок для извлечения этих компонентов (рис. XIII. 1). Наиболее широко применяемым методом извлечения является абсорбция в тарелочных колоннах. Насыщенный абсорбент, содержащий большое количество легких углеводородов, десорбируют для удаления пропана, бутана и газового бензина, после чего охлаждают и вновь возвращают В абсорбер.
методы, не получившие широкого применения, но тем не менее пригодные для специальных целей.
Отбензиненный природный газ, если только он не содержит сероводород, пригоден для поставки потребителям. Газ, содержащий H2S, очищают путем промывки растворами этаноламина. Чтобы предотвратить образование гидратов в трубопроводах, газ обычно осушают при помощи жидких или твердых поглотителей.
Жидкие углеводороды, выделенные из газа, во фракционирующих колоннах разделяют на стабильные продукты: жидкий газ (пропан и бутан) и газовый бензин или стабилизированный конденсат.
Извлечение конденсируемых углеводородов из газа может быть достигнуто и путем низкотемпературной сепарации. При этом используется холод, получаемый в результате редуцирования избыточного давления газа.
В настоящее время многими исследователями изучается вопрос о полном сжижении природного газа с целью перевозки его в танкерах, если невозможно транспортировать газ по трубопроводам.
Процессы массо- и теплообмена и движения жидкости подробно описаны в литературе по химической технологии. Здесь эти вопросы рассматриваются в основном для объяснения физических основ распространенных методов очистки и подготовки газа. Описываются и некоторые
Рис. XIII. 1. Принципиальная схема переработки газа.
/ — скважины; 2 — промысловый сепаратор; 3 — промысловый конденсат; 4 — промысловая газосборная система;
5 — абсорбер; 6 — обогащенное масло; 7 — выпарная колонна; 8 — пар; 9 — возврат масла; 10— очистка от сероводорода; 11 — регенерация раствора этаноламнна: 12 "возврат этаноламнна; 13 — осушка; 14 регенерация раствора гликоля; 15 — возврат гликоля; 16 — газ к потребителю; 17 — сырой бензин; 18 — фракционная перегонка; 19 — топливный газ; 20 — продукт для фракцноннровкн; 21 -1 пропан; 22 — бутаны; 23 — газовый бензнн нлн конденсат.
Продукция нефтяной или газовой скважины содержит обычно газ, несколько жидких компонентов и часто небольшое количество твердых примесей. Наряду с жидкими углеводородами обычно имеется соленая или пресная вода. Разделять эти компоненты желательно, как правило, у скважины. Ниже рассматриваются факторы, которые должны быть учтены при определении оптимальных условий извлечения жидких углеводородов в промысловых сепараторах. С целью увеличения выхода конденсата и осушки газа в конструкцию стандартных сепараторов были внесены изменения [XIII. 3, V. 66, XIII. 5,
XIII. 6, XIII. 7, XIII. 14, XIII. 15, XIII. 27, XIII. 34,
XIII. 40]. Принципиальные схемы процесса сепарации нефтей, содержащих растворенный газ, и газоконденсатных смесей показаны на рис. I. 19 и 1.20. Углеводородный состав газа и конденсата на выходе из сепаратора приведен в табл. VI. 4.
Схема потоков при трехступенчатой сепарации показана на рис. XIII. 2. Перед сепаратором I ступени из потока удаляется вода. Если происходит образование гидратов, то для предотвращения этого либо подогревают газ у устья скважины, либо вводят соответствующие ингибиторы. К числу факторов, определяющих эффективность улавливания углеводородов, относятся фазо-
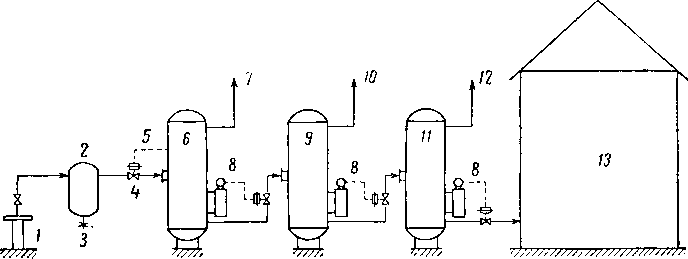
Рис. XIII. 2. Схема трехступенчатого промыслового сепаратора.
/— устье скважины; 2 — удаление воды; 3— вода; 4 — задвижка № 1; 5 — регулятор давления; 6 — сепаратор первой ступени; 7 — газ высокого давления; 8 — регулятор уровня; 9—сепаратор второй ступени; 10 — газ среднего давления; —сепаратор третьей ступени; 12 — газ низкого давления; 13 — резервуар для конденсата.

Рис. XII. 3. Промысловые сепарационные установки.
вое поведение Движущейся смеси, давление и температура в каждой ступени сепарации и число ступеней. Без учета этих факторов найти оптимальную технологию сепарации невозможно. Иногда серьезное значение могут иметь второстепенные факторы (вспенивание, эмульгирование и наличие посторонних веществ). Промысловые сепарационные установки показаны на рис. XIII. 3 и XIII. 4.
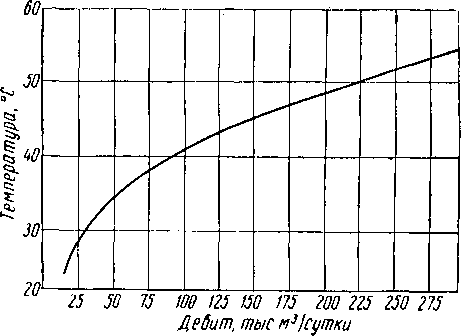

Рис. XIII. 5. Температура у устья скважины в зависимости от дебита для скважин южной Луизианы [V. 66].
Рис. XIII. 4. Промысловая установка ратурной сепарации.
низкотемпе-
Давление и температура газа на устье скважин определяются параметрами пласта, дебитом газа и характером движения газа вверх по эксплуатационной колонне. Например, температура на устье скважины, как видно из рис. XI11. 5 [V. 66], изменяется в широких пределах в зависимости от дебита. Состояние потока на пути в сепаратор изменяется вследствие теплообмена с окружающей средой и перепада давлений в трубопроводе. Тем не менее состав и состояние потока у устья скважины являются исходными параметрами для расчетов
сепарации. Для последующих расчетов необходимо иметь данные об изменении температуры газа на устье в зависимости от дебита. При этом следует иметь в виду, что температура газа при работе скважины с постоянным дебитом в процессе эксплуатации повышается.
Зная состав выходящего из скважины газа и константы равновесия, можно вычислить состав газожидкостного потока и выход жидкости (см. гл. VI). Во многих случаях состав потока, выходящего из скважины, определяют методом рекомбинации проб газообразных и жидких продуктов при замеренном дебите. Однако иногда желательно определять составы газа и жидкости в сепараторах при различных температурах и давлениях сепарации. Может потребоваться также определение составов
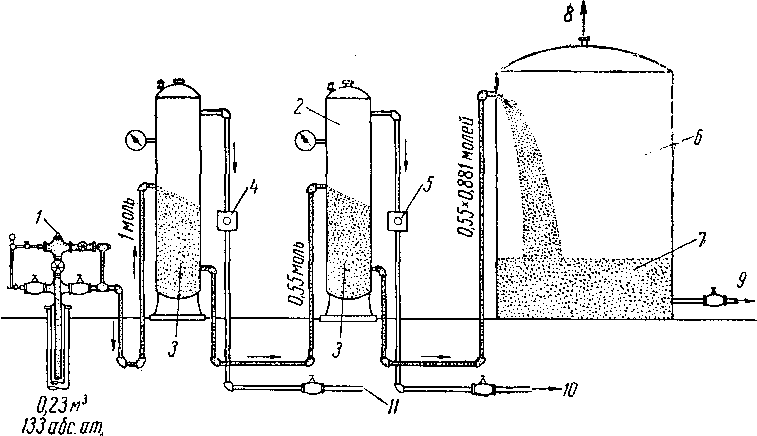
Рис. XIII. 6. Вычисленные составы и выходы для отдельных сепараторов.
/ — устье скважины; 2 — газ (избыточное давление в первом сепараторе 7 ат, температура 15,5° С; избыточное давление во втором сепараторе 0,7 ат, температура 15,5° С); 3 — жидкость: 4 газовый счетчик первого сепаратора (0,45 моль нли 17,7 м3) 5 — газовый счетчик второго сепаратора (0,55Х Х0,П9 моль или 2,58 жЗ); 6 — резервуар; 7 — сырая нефть (0,55ХС,8Р1Х0,969 моль или 0,159 мя иефти 7=0,813); <9 — выпускается в атмосферу 0,59 мя газа или 0,55X0,881X0,081 моль\ 9 — в нефтепровод;
10 — газ в газосборную систему низкого давления; II —таз в газосборную систему высокого давления
|
Компонент | Мольная кон* Нентрация углеводородов в газе скважины 2 | К при абсолютном давлении 8,05 am и 15,5е С | Г] редположим, V = 0,40 | Предположим, V = 0,500 | Предположим. V = 0,4 61 | ||||
| К + 1,5 |
2 | Я + 1 |
2 | К + 1,17 |
г | ||||
| К + 1,5 |
К +1 | К + 1,17 | |||||||
| Метан............. Этан.............. Пропан............. Изобутан............ н-Бутан............ Изопентан ........... н-Пентан............ Гексаны............ Гептаны и более тяжелые фракции | 0,303 0,131 0,094 0,018 0,049 0,020 0,025 0,038 0,322 | 30,0 3,7 0,98 0,400 0,285 0,120 0,094 0,032 0,0022 | 31,5 5,2 2,48 1,90 1,785 1,62 1,994 1,532 1,5022 | 0,0096 0,0252 0,0379 0,0095 0,0272 0,0123 0,0157 0,0248 0,2140 | 31,0 4,7 1,98 1,40 1,285 1,12 0,094 1,032 1,0022 |
0,00976 0,0279 0,0475 0,0129 0,0381 0,0179 0,0228 0,0368 0,3210 |
31,17 4,87 2,15 1,57 1,455 1,29 1,264 1,202 1,1722 |
0,00972 0,0269 0,0437 0,0115 0,0336 0,0155 0 0198 0,0316 0,2745 | |
| Всего. . . | 1,000 | — | — |
0,3762 | — |
0,5346 | — |
0,4668 | |
Решение: V е= 0,4 5.
164 39
Плотность = ’
= 0,813
г/см*
По даннвм рис. XIII. 6 н мольным количествам, испарившимся в процессе трех испарений, количество товарной нефти, прихо
на 1 л8 товарной нефти
Мольная концентрация углеводородов в продуктах сепаратора II ступени
Предположим, V = 0,03571
Предположим, V = 0,0400
Компоненты
пар
жидкость (новое г)
К при абсолютном давлении 1 ат и 15,5* С
К. + 24
К + 24
К + 27
К + 27
| Метан............. |
0,1692 | 0,00118 |
230 | 254 |
0,000004 | 257 |
0,00000 |
|
Этан.............. | 0,3474 | 0,0193 | 29 |
53 | 0,000364 |
53 | 0,00036 |
| Пропан............. |
0,2910 | 0,0673 |
6,2 | 30,2 |
0,002238 | 33,2 |
0,00203 |
| Изобутан ........... | 0,0411 |
0,0223 | 3,2 |
27,2 | 0,000819 |
30,2 | 0,00074 |
| н-Бутан............ |
0,0921 | 0,00692 |
2,2 | 26,2 |
0,002641 | 29,2 |
0,00236 |
|
Изопентан........... |
0,0197 | 0,0350 |
0,94 | 24,94 |
0,001403 | 27,94 |
0,00125 |
|
н-Пентан............ | 0,0230 | 0,0450 | 0,72 |
24,72 | 0,001826 |
27,72 | 0,00162 |
| Гексаны............ |
0,0100 | 0,0753 |
0,22 | 24,22 |
0,003109 | 27,22 |
0,00276 |
| Гептаны и более тяжелые фракции |
0,0065 | 0,6652 |
0,0138 | 24,0138 |
0,02770 | 27,0138 |
0,02462 |
| Итого. . . | 1,0000 |
1,0000 | — |
— | 0,040108 |
— | 0,03574 |
Решение: V = 0,031.
потока после прохождения его через сепараторы низкого давления или хранения в резервуарах [III. 27, XIII. 34]. Пример подобного расчета приведен в табл. XIII. 1 и на рис. XIII. 6. Об использовании электродно-вычислительных машин для подобных расчетов было сказано в главе VI.
Изменение состава фаз потока в результате резкого снижения давления в задвижке 4 (см. рис. XIII. 2) можно рассчитать. Явление, создаваемое адиабатическим расширением, при котором не производится полезная работа, называется «свободным расширением» или расширением Джоуля — Томсона. Ясно, что хотя при этом газ не производит полезной работы, наблюдается падение температуры при абсолютных давлениях менее 350 ат (см. гл. IV). Количество жидкости, содержащейся в потоке после расширения, может быть вычислено методами, описанными в главе IV. При использовании кривых энтальпии — энтропии для определения перепада температур газа вследствие расширения получают несколько завышенные величины, поскольку образование жидкости сопровождается выделением скрытой теплоты,
Для обеспечения оптимального извлечения жидких углеводородов из газоконденсатных систем необходимо учитывать в основном те же переменные факторы, что и для системы газ — нефть. Но оптимальные условия сепарации в данном случае значительно больше зависят от характера конкретной смеси. Оптимальные условия сепарации можно определить эмпирически или же при помощи расчетов, основанных на использовании констант равновесия.
| Мольная концентрация углеводородов в продуктах сепаратора I ступени | К при абсолютном давлении 1,7 ат и 15,5° С |
Предположим, V = 0,119 |
Предположим, V = 0,145 | Предположим, V =0,10 | |||||
| пар |
жидкость (новое г) |
К + 7,4 | г | К + 5,9 | 2 |
К + 9,0 | 2 | ||
| К + 7,4 | К + 5,9 |
К. + 9,0 | |||||||
|
0,6158 | 0,0208 |
140 | 147,4 |
0,00014 | 145,9 |
0,00014 | 149 |
0,00014 | |
|
0,2150 | 0,0575 |
17,5 | 24,9 |
0,00231 | 23,4 |
0,00246 | 26,5 |
0,00217 | |
|
0,0916 | 0,0936 |
4,2 | 11,6 |
0,00807 | 10,1 |
0,00927 | 13,2 |
0,00708 | |
|
0,0098 | 0,0246 |
1,80 | 9,2 |
0,00267 | 7,7 |
0,00320 | 10,8 |
0,00227 | |
|
0,0205 | 0,0720 |
1,30 | 8,7 |
0,00827 | 7,2 |
0,01000 | 10,3 |
0,00699 | |
|
0,0398 | 0,0332 |
0,55 | 7,95 |
0,00418 | 6,45 |
0,00515 | 9,55 |
0,00348 | |
|
0,0040 | 0,0425 |
0,50 | 7,90 |
0,00538 | 6,40 |
0,00665 | 9,50 |
0,00448 | |
|
0,0022 | 0,0677 |
0,131 | 7,531 |
0,00899 | 6,031 |
0,01122 | 9,131 |
0,00742 | |
|
0,0013 | 0,5881 |
0,0096 | 7,4096 |
0,07937 | 5,9096 |
0,09951 | 9,0096 |
0,03448 | |
|
1,000 | 1,000 |
— | — |
0,11938 | — |
0,14760 | — |
0,09851 | |
Решение: V = 0,119.
при 15,5° С, и 1 атп.
дящейся на 1 моль товарной смеси, равно С,55 X 0,881X0,969 =0,47 моль жидкости. Число молей смеси, поступающей d I сепаратор,
813
РаВВ° 0.47 X 164~
= 10'5
М°ЛЬ'
Продолжение табл, XIII. 1
| Предположим, V = 0,0303 | Мольная концентрация углеводородов в продукте, хранимом в резервуаре | Молекулярный вес | Количество жидкости | |||||
| К+ 32 | 2 | пар |
жидкость |
г/моль |
г/см* | см33/моль | ||
| К+ 32 | ||||||||
| 262 | 0,00000 |
0,0340 | 0,0001 |
16 | 0,0016 |
0,35 | 0,005 | |
| 61 | 0,000316 | 0,0300 | 0,0104 | 30 | 0,312 |
0,50 | 0,62 | |
| 38,2 |
0,001769 | 0,3600 |
0,0584 | 44 |
2,57 | 0,508 |
5,06 | |
| 35,2 | 0,000633 | 0,0665 | 0,0208 | 58 |
1,21 | 0,563 |
2,15 | |
| 34,2 | 0,002023 | 0,1462 | 0,0667 | 58 |
3,87 | 0,584 |
6,64 | |
| 32,94 | 0,001062 | 0,0330 | 0,0351 | 72 |
2,53 | 0,625 |
4,05 | |
| 32,72 | 0,001375 | 0,0327 | 0,0454 | 72 |
3,26 | 0,631 |
4,16 | |
| 32,22 | 0,002337 | 0,0170 | 0,0771 | 86 |
6,64 | 0,664 |
10,0 | |
|
32,0138 | 0,02078 |
0,0096 | 0,6860 |
210 | 144,00 |
0,850 | 169,5 | |
| — | 0,030295 | 0,999 | 1,000 |
— | 164,3936 |
— | 202,185 |
|
Газ из I сепаратора: 0,45 х 3,67 X 10,7= 17,7 мя.
Газ нз II сепаратора: 0,55 X 0,119 х 3,67 X 10,7 = 2,58 Л8.
Газ нз резервуара: 0,55 X 0,881 X 0,031 X 3,67 X 10,7 = 0,59 мг.
q.Looxtfn>i<;
а
гг
з
*8
) o*
’ о
; °o
q.LDOHtfH>K
CO
Фракционный состав образцов газа и жидкости, находящихся в равновесных условиях (III. 11)
qIDOM'D'H>K
338 * 300
д
\ 250 <>
Е=
чхэояЬ'и^
'S
5i
*
qiDOW’D'H^
qi.Doa'tfH>K
qi30M'n'H>|(
5. I I
(J
о
LO
ш ю
3
4
а>
, к
3 к
J3
4 о s
У. « ?
5 -о М В! О) н
ч о 2, 4 sic
O §
ЕИ
о
05 ____
05
NCO — оо со
05
eg о ’—1 с-4 со со cd —« о ^ со 05 о оо^>-0^гсо^ооо5С75едо^05^;о со* г-* со* со еГ —* со* со ~ о* — ^
Tf — о
CN
iOOegcONCO(?)LOOMON,nO cD^cxDco^cD^LOcooieg г-сою ^ —¦
со co* cd* —* eg* eg* o* ^r* ю со со’ co* —1 ^
_ <4J
— eji-ot'-cot"—гоа51_оюед1Ло Tf t'- Tf CD^ Г- CD 1-0 — со ю —
Ю ю el ю co -¦ tJ 50’t cn - ^
oiOonolo — Nco — egoi-*, 0^c^cdl0(^-l0cd lo oeg oo ^
^ со co eg* eg* cd* cd*
eg co
CD CN CO l-O — CO M lO CO CO CO I I I CO 0\ <N CO —^ 0_ — | | |
lO(n6666o’6
05
-lO^OnOtNOGOCOcO't-,
eg co cd^ lo co eg о —_ — ^ J
crT lO eg* eg" о lo cd* ^ lo eg •
eg со eg — 05
05 О 05 ю — — , I
союь--ооо | delddcddd
05
LO со ¦''f со 05
Tf — CD CD Г-
—1 cd eg 05 co cd — ООО ccT ef о о о о о о
t'-. Tf — CO
'f 05 со co eg о oo ьо о о о о со* eg о о о о’ о
05
I и • ,27 oi <и * ^CS uS aiuuO
eg
CJi
Фазовая диаграмма потока, выходящего из скважины, приведена на рис. III. 26. Состав этого потока (на основе данных о фракционном составе газа и жидкостт при абсолютном давлении 70 ат и температуре 25° С приведен в табл. III. I. На рис. XIII. 7 показаны выхо ды конденсата из сепаратора скважины. Кривые на этои рисунке характерны для систем, обнаруживающих изобарную и изотермическую ретроградную конденса цию. Фазовая диаграмма этого типа, составленная Эй лером и другими, представлена на рис. XII. 46. В коя денсате, выводимом из сепаратора при высоком давле нии, растворено еще большее количество метана, эта на и пропана. Если этот конденсат стабилизировать пу тем многоступенчатого снижения давления, произойде значительная усадка жидкости. Эта усадка тем больше, чем выше давление в первом сепараторе.
Барри и Паркс (Barry and Parks) [XIII. 3] показали (рис. XIII. 8), что давление, обеспечивающее максимальную конденсацию в сепараторе I ступени, не соответствует максимальному конечному выходу углеводородов. Оптимальное давление в сепараторе I ступени находится значительно ниже давления максимальной конденсации в сепараторе. Однако выбор давления в сепараторе I ступени может диктоваться другими факторами, например стоимостью повторного компримирова-ния или же гидратообразованием. Низшие пределы давления, до которых можно расширять газ без образования гидратов, показаны на рис. V, 48—V. 50.
Барри и Паркс рекомендуют удалять свободную воду непосредственно перед снижением давления в I сту-
Факторы, влияющие на получение конденсата из газоконденсатных скважин, были изучены Хантингтоном (Huntington) и другими [XIII. 18, XIII. 80]. Бакли и Лайтфутом (Buckley and Lightfoot) [III. 11]. Эйлером (Eilerts) и другими [III. 19]. Чтобы доказать наличие условий оптимальной конденсации при температуре сепаратора I ступени, изменяли давление в этом сепараторе при постоянной температуре. Удельный вес газовой фазы, характеризующий ее состав, минимален при давлении максимальной конденсации жидкости.
Бакли и Лайтфут [III. II] изучали влияние давления и температуры на конденсацию углеводородов из природного газа, используя экспериментальный промысловый сепаратор. Составы фаз при различных условиях в сепараторе приведены в табл. XIII. 2.
ISO
I 7 00
I I-1 ?
JO
| ~Ь5,56°С | |||
| / / |
7777П | ||
|
/ / ^ / / | г ю°с\ | ||
| / | ------ |
—-- | |
| Ц 78°С | \ \ \ | \ \ \ | |
| _ |
0
JO
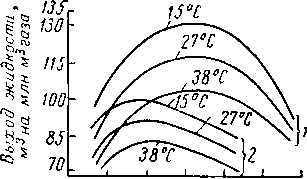
Рис. XIII. 7. Влияние температуры сепарации на общий выход жидкости при различном давлении [III. II].
WO 150 Щ8 избыточное даВление В сепараторе, am
Избыточное давление В сепараторе, первой ступени ,ат
Рис. XIII. 8. Оптимальное давление, обеспечивающее максимальный выход товарной жидкости ниже давления, обеспечивающего максимальный выход жидкости в сепараторе [XIII. 3].
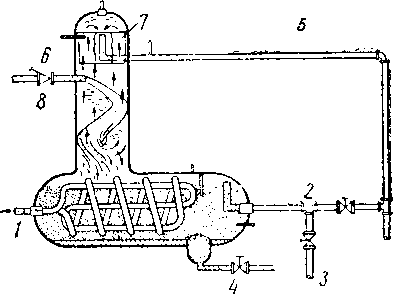
1 — жидкость, отделенная в сепараторе при давлении сепарации; 2 — товарная жидкость при давлении в складском резервуаре.
пени (рис. XIII. 2), чтобы воспользоваться преимуществами низкого влагосодержания в газе высокого давления. В многоступенчатых сепарационных установках предусмотрены автоматические приборы для контроля давления и уровня жидкости в сепараторах каждой ступени.
2. НИЗКОТЕМПЕРАТУРНАЯ СЕПАРАЦИЯ
Низкотемпературная сепарация позволяет увеличить выход конденсата и снизить влажность газа с помощью эффекта Джоуля — Томсона. При достаточно высоком давлении на головке скважин для осушки газа преднамеренно образуют гидраты углеводородов в соответствии с равновесными условиями газ — гидрат при низкой температуре [V. 66, XIII. 40, XIII. 6]. Температуры, которые могут быть достигнуты при охлаждении газа путем расширения, обеспечивают также значительное повышение выхода газового бензина.
Рис. XIII. 10. Низкотемпературный сепаратор [V. 66].
I — поток из скважины; 2 — выпуск конденсата; 3 —¦ в резервуар; 4— выпуск воды: 5 — выпуск газа; 6 — регулируемый штуцер: 7 — каплеотбой-ник: 8 — вход газа.
50 Щ0 150 200 250 300 350 400 Ш
Первоначальное изёытоинпе Вавление,ат
На рис. XIII. 9 показана технологическая схема одного из вариантов низкотемпературной сепарации '[XIII. 5]. Поток газа высокого давления из скважины поступает в змеевиковый теплообменник, находящийся внизу низкотемпературного сепаратора, где происходит
Г“
-s
Рис. XIII. 9. Технологическая схема низкотемпературной сепарации [XIII. 5].
/ — газ высокого давления из скважины; 2 — сепаратор; 3 — конденсат на стабилизацию; 4 — вода; 5 — сухой газ в газопровод; 6 — регулятор давления; 7 — регулятор уровня жидкости; 5 — отбойник свободной воды.
теплообмен между газом и твердыми гидратами и холодной жидкостью. Затем охлажденный газовый поток проходит через теплообменник, где он подвергается дальнейшему охлаждению (если это возможно с точки зрения гидратообразования) путем противоточного теплообмена с холодным газом из низкотемпературного сепаратора. Вода, сконденсировавшаяся в процессе охлаждения, удаляется в водоотделителе. Из водоотделителя поток проходит через дроссельный штуцер сепаратора, где происходит расширение газа. Газ, освобожденный в сепараторе от жидкости и твердых частиц, выходит сверху. Специальный регулятор температуры обеспечивает отвод части холодного и осушенного газа, помимо теплообменника, если охлаждение газа в сепараторе превышает технологически необходимое. Жидкий конденсат и воду удаляют через самостоятельные выпускные отверстия в днище сепаратора. Жидкие углеводороды можно направить в резервуары.
Рекорде и Сили (Records and Seely) описали работу сепаратора, в котором образуются гидраты при расширении газа (рис. XIII. 10). Перепад температуры газа
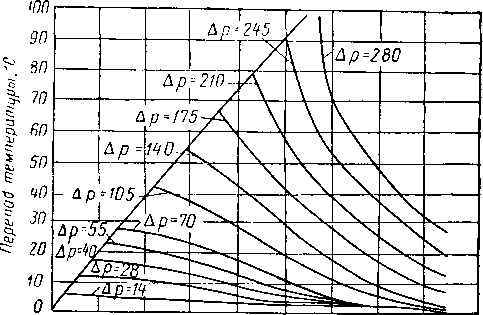
Рис. XIII. II. Перепад температуры, сопровождающий перепад давления при расширении природного газа относительного удельного веса 0,64.
Др —р первоначальное — р конечное.
| то | |
| 1000 | |
|
800 | |
| 600 | «*> |
| ш | о |
| 200 | |
| м | |
|
100 | |
| 80 |
г? |
| 60 |
* |
| ио | |
| го |
I
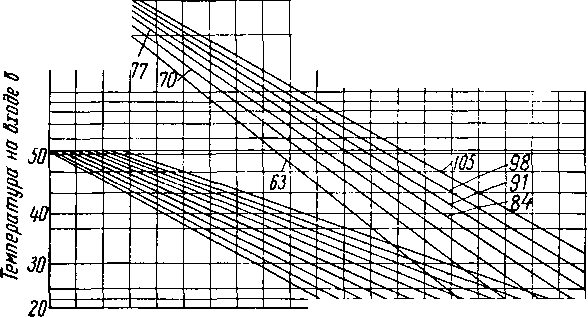
избыточное даВление 6 сепараторе, am
15516618319721122523925226Т280 Избыточное даВление на Входе В сепаратор, ат
Рис. XIII. 12. Эксплуатационные кривые низкотемпературного дегидратора при работе на газе удельного веса 0,64 [V. 66].
при расширении показан на рис. XIII. 11. График составлен на основе экспериментов с газом, состав которого приведен в табл. XIII. 2а, а кривые влажности — на рис. XIII. 12. Для определения содержания влаги в газе при выходе из низкотемпературного сепаратора гидратов на рис. XIII. 12 находим точку, соответствующую давлению и температуре на входе в сепаратор. Из этой точки проводим вертикальную линию до пересечения с линией, соответствующей давлению на выходе из сепаратора и на правой вертикальной оси находим ответ.
Температуры точек росы по воде ниже температуры в сепараторе, так как точка росы для воды является метастабильным равновесием системы «вода—газ», а не системы «газ — гидрат» (см. гл. V), Технические условия на газ, транспортируемый по газопроводам, допускает содержание воды 0,095—0,128 г на 1 м3 газа при
15,5° С и 1,03 ат. При достаточно
высоком давлении газа на устье скважины можно установить та
кие технологические условия сепарации, которые обеспечат выполнение этого требования по
влажности газа. Процесс низко
температурной осушки непрерывный и ограничивается лишь доступным перепадом давления. Однако в работе установки низкотемпературной сепарации могут возникнуть перебои вследствие парафинообразования.
Кемпбелл (Campbell) [XIII. б] дает следующие рекомендации применения процессов низкотемпературной сепарации при использовании в нем охлаждения за счет расширения потока. Рекомендуемая область применения — в тех случаях, где перепад давления обеспечивает не меньшее снижение температуры точки росы, чем при других методах
осушки. Необходимый перепад составляет обычно около 105 кГ/см2. При введении в схему установки необходимых теплообменников процесс можно вести в широком интервале температур.
Преимущества
Таблица XIII. 2а
Фракционный состав газа удельного веса
0,64 на устье скважины [V. 66]
|
Наименование компонентов |
Мольная концентрация, % |
|
Двуокись углерода...... |
0,20 |
| Метан............ | 92,80 |
|
3,47 | |
| Пропан........... | 1,16 |
| Изобутан ......... | 0,39 |
|
н-Бутан........... | 0,35 |
| Изопентан.......... |
0,14 |
| н-Пентан......... | 0,11 |
| Гексаны и более тяжелые углеводороды ........ |
1,38 |
| Всего. . . | 100,00 |
Например, газ, выходящий из скважины с давлением в 211 ат и температурой 38° С, при абсолютном давлении в сепараторе 70 ат будет содержать цоды
0,15 г/м3 газа.
1. Если схема переработки предусматривает низкотемпературную сепарацию, основанную на дросселировании давления, то эта схема является самой дешевой.
2. Увеличивается выход конденсата из природных газов.
3. При достаточном перепаде давления обеспечиваются низкие температуры точки росы.
4. Обеспечивается простое автоматическое регулирование процесса при минимальном обслуживании.
Недостатки
1. Процесс применим лишь в тех случаях, когда возможен большой перепад давления.
2. Эффективность процесса уменьшается при снижении давления газа. В этом случае потребуется установка дополнительного оборудования, работающего по иному принципу.
3. Хрупкость малоуглеродистой стали и опасность разрывоп оборудования, работающего при температуре ниже —29° С.
4. Необходимость в некоторых случаях тщательного контроля с целью предотвращения гидратообразования перед низкотемпературным сепаратором.
Низкотемпературная сепарация, если она применяется лишь для осушки газа, как правило, не может быть оправдана.
____I —
/
п
D-h
"25
г*
г г
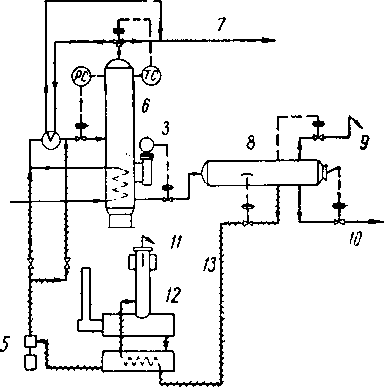
Рис. XIII. 13. Технологическая схема процесса низкотемпературной сепарации с инжекцией гликоля [XIII. 6].
/ — газ высокого давления из скважины; 2 — водоотбойный сепаратор (близ скважины): 3 — регулятор уровня; 4 — необязательная инжекция гликоля;
5 — насос для подачи гликоля; 6—сепаратор высокого давления; 7 — сухой газ в трубопровод; S — сепаратор низкого давления: 9 — свеча; 10 —* конденсат в резервуар; // — вода; 12 — регенерация гликоля; 13 — гликоль.
сравнительно низкой упругостью паров и небольшой растворимостью в конденсате. Процесс осушки больших объемов газа и экономические показатели различных методов осушки будут рассмотрены в разделе, посвященном осушке газа. Кемпбелл [XIII. 6] дает следующую общую характеристику системы низкотемпературной сепарации с инжекцией гликоля.
Расход гликоля
Обычно 2,6—5,3 л гликоля на 100 000 м3 газа в час.
3. НИЗКОТЕМПЕРАТУРНАЯ СЕПАРАЦИЯ С ПРИМЕНЕНИЕМ ДИЭТИЛЕНГЛИКОЛЯ
Процесс низкотемпературной сепарации, рассмотренный в предыдущем разделе, может быть также осуществим с применением инжекции в поток газа непосредственно перед теплообменником 70—80%-ного (по весу) раствора диэти-ленгликоля. Этот технологический вариант применим в тех случаях, когда можно ожидать значительных колебаний давления в скважине и при давлении, недостаточно высоком, чтобы обеспечить необходимую осушку газа путем одного лишь охлаждения. Схема процесса с применением инжекции гликоля показана на рис. XIII. 13 [XIII. 6].
Она отличается от схемы, рассмотренной выше, тем, что инжекция гликоля в поток газа происходит после водоотделителя. Кроме того, вводится дополнительный сепаратор для отделения гликоля — конденсата и предусматривается регенерация диэтиленгликоля. Теплообменник обычно располагают непосредственно перед сепаратором, предназначенным для отделения гликоля от конденсата, благодаря чему сепарацию можно осуществлять при температуре около 21° С, получая сравнительно стабильный конденсат.
Потребное количество гликоля зависит от влажности сырого газа, перепада давления и требуемой техническими условиями степени осушки газа. При выборе поглотителя необходимо учесть и такой фактор, как потери гликоля вследствие его испарения и растворения в жидких углеводородах.
Величина потерь гликоля вследствие испарения [XIII. 29, XIII. 32] и растворения изучена. При наличии в газе жидких углеводородов в качестве поглотителя чаще всего применяют диэтиленгликоль, отличающийся

Рис. XIII, 13а, Промысловая низкотемпературная сепарационная установка.
70—85%-ный раствор диэтиленгликоля. При использовании такого раствора содержание гликоля в извлеченной углеводородной жидкости теоретически не должно превышать 0,04% по весу.
Преимущества
1. Процесс эффективен при меньшем перепаде давления, поскольку обеспечивается более значительное снижение температуры точки росы, чем при одном лишь охлаждении за счет перепада давления.
2. Возможность получения высокого выхода конденсата из природного газа.
3. Компактность установки.
4. Более дешевая стабилизация полученных жидких углеводородов.
5. При пропускной способности установки выше 48 ООО м3/сутки первоначальная стоимость ее ниже соответствующего показателя для установки низкотемпературной сепарации, работающей без инжекции гликоля.
Недостатки
1. При пропускной способности менее 48 000 м3/сутки первоначальная стоимость установки выше соответствующего показателя для установки низкотемпературной сепарации без инжекции гликоля.
2. Повышенные эксплуатационные расходы и ремонтные работы.
3. Необходимость регенерации и возврата раствора гликоля к пункту инжекции. Общее количество раствора, однако, невелико.
На многих промыслах давление добываемого газз недостаточно для того, чтобы организовать выделение углеводородов и осушку сепараторами у скважин. В то же время содержание пропана и бутана в этих газах может быть достаточно высоким, чтобы оправдать затраты на их извлечение. Эти газы поступают обычно на газобензиновые заводы, где их перерабатывают, отбирая из них жидкие углеводороды. Основной производственной установкой газобензинового завода является масляная абсорбция, с помощью которой из газа извлекаются желательные компоненты.
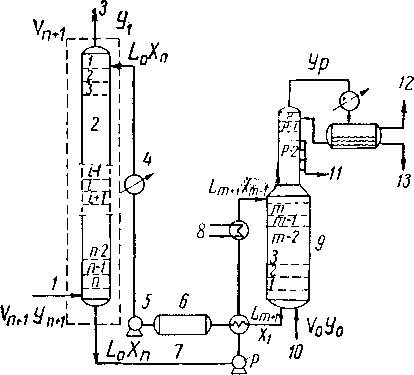
Рис. XIII. 11. Технологическая схема аб-сорбции и десорбции.
/ — сырой газ; 2 — абсорбер; 3 — выход газа;
4 — холодильник; 5 — насос; 6 — тощее масло; 7 — насыщенное масло; 8 — нагреватель; 9 — вы. парная колонна; 10 — пар; 11 — отвод воды; 12 — газ, возвращаемый на переработку; 13 — сырой бензин на стабилизацию.
Абсорбционно-десорбционный цикл улавливания жидких углеводородных газов и газового бензина (рис. XIII. 14) нашел широкое применение в промышленности. При этом целевые компоненты поглощаются из газа в абсорбере абсорбентом и затем выделяются из него р десорбере.
Абсорбция — это противоточное многоступенчатое контактирование потоков газа и жидкого поглотителя (обычно в колоннах с колпачковыми тарелками). Процесс абсорбции основывается на том физическом явлении, что различные газы обладают различной растворимостью в жидкостях. Поэтому в абсорбере необходим тесный контакт между фазами, что обеспечивается многократным барботированием газа через жидкость на тарелках абсорбера.
Основные затруднения этого процесса обусловлены присутствием в насыщенном абсорбенте метана и этана, полное отделение которых от углеводородов, получаемых в виде жидких продуктов, сравнительно сложно.
Абсорбция применяется для выделения тяжелых фракций газа и осушки его от влаги без снижения температуры с таким расчетом, чтобы была достигнута требуемая точка росы. Обычно для получения газового бензина в качестве абсорбента используют фракцию газойля, выкипающую в сравнительно узком интервале (205—315° С).
Для газа данного состава поглощенная сорбентом молярная доля каждого компонента, первоначально присутствовавшего в сыром газе, зависит от равновесного фазового отношения между компонентами газа и поглощающим маслом, от соотношения между расходом жидкости и расходом газа и от числа ступеней равновесного контакта. Равновесное фазовое отношение в свою очередь зависит в основном от температуры и давления, но также и от фракционного состава фаз и содержания ароматики в сорбенте [VI. 31].
После поглощения легкие углеводороды выделяются из абсорбента путем десорбции или выпаривания.
На рис. XIII. 14 показан цикл абсорбции — десорбции и даны обозначения, которые будут применяться при дальнейшем рассмотрении этого вопроса. Приведенные на схеме цифры означают равновесные или идеальные теоретические тарелки, а не фактическое число тарелок в колонне.
Равновесная или идеальная ступень — это воображаемая тарелка, выходящие из которой газы находятся в равновесии с покидающей ее жидкостью.
Десорбция углеводородов облегчается при низких давлениях и высоких температурах и впуске острого пара в нижнюю часть выпарной колонны. Равновесные фазовые соотношения показывают, что низкое давление и высокая температура уменьшают растворимость легких углеводородов в сорбенте. Пар служит для снижения парционального давления легких углеводородов в газовой фазе, что равнозначно снижению рабочего давления на этапе десорбции.
У/ =
L,
А, =
А,
< -KtVt • -/-I -K^V^ Подставляем (XIII. 7) в (XIII. 6), получаем
+ ^-1^-1 I + Ai
Y, =
(XIII. II)
о' о — у
(XIII. 12)
(XIII. 13)
(XIII. 2)
Vi ~ '
X,L о
В следующем разделе описано несколько методов расчета абсорбционных и десорбционных колонн в порядке увеличения их точности и объясняется причина того, что более простые методы расчета оказываются бессильными точно предсказать абсорбцию и десорбцию, имеющую место в фактических рабочих условиях. Все вычисления основываются на концепции теоретической тарелки, которую следует отличать от фактической контактной ступени (тарелки). Эта концепция позволяет использовать константы равновесия, рассмотренные в главе VI.
Как уже указывалось, десорбция является процессом, в основном противоположным абсорбции. Для уменьшения потерь сорбента с отдельным продуктом в выпарной колонне применяется орошение (рис. XIII. 14). В некотором отношении работа абсорбера и работа де-сорбсра в достаточной мере сходны, что позволяет параллельное аналитическое рассмотрение обеих колонн.
1. РАСЧЕТ КОЭФФИЦИЕНТА ИЗВЛЕЧЕНИЯ ПО МЕТОДУ КРЕМСЕРА — БРАУНА (Kremser — Brown)
Кремсер [XIII. 26] модифицировал метод теоретического анализа процесса абсорбции Соудерса и Брауна (Souders and Brown) [XIII. 38, XIII. 4]. В соответствии с этим аналитическим 'методом доля поглощенного или десорбированного компонента рассматривается в зависимости от числа равновесных тарелок (или ступеней), соотношения жидкость — газ и константы равновесия этого компонента. Влияние давления, температуры и состава газовой и жидкой фаз на константы равновесия были рассмотрены в предшествовавшей главе.
Ниже выводятся модификация Кремсера расчета, предложенного Соудерсом и Брауном [VII. 9, XIII. 12].
Материальный баланс по любой тарелке i абсорбера с числом тарелок п выражается уравнением
h (xi~xi-1) = l/n+i (Yn+i -YiY (XIII. 1)
где L0 — число молей свежего абсорбента, поступающего в абсорбер; V п+\ — число молей сырого газа, поступающего в абсорбер; Xj — число молей компонента в жидкости, покидающей тарелку г, на I моль свежего абсорбента, поступающего в абсорбер; Y— число молей компонента в паре, покидающем тарелку г, на 1 моль сырого газа, поступающего в абсорбер; Xi_i — число молей компонента в жидкости, поступающей на тарелку ?, на 1 моль свежего абсорбента, поступающего в абсорбер; Vi + i — число молей компонента в паре, покидающем тарелку i + 1 (или поступающем в тарелку г), на 1 моль сырого газа, поступающего в абсорбер.
Действительные молярные доли пара и жидкости, покидающих тарелку г, равны соответственно
где уi—молярная доля компонента в паре, покидающем тарелку г; xt — молярная доля компонента в жидкости, покидающей тарелку г; V,¦ —число молей пара, покидающего тарелку г; L,- — число молей жидкости, покидающей тарелку ?.
Вводим константу равновесия К(.
Yl V„+i V,
(XIII.3)
L;
Исключая У1 и находя Y2 по уравнениям (XIII. 12) и (XIII. 13), распространяем уравнение (XIII. 9) на двухтарелочный абсорбер:
(^ + 1)^3 +^0*0/^!(ХШЛ4)
2~ А^Аг+ А2+1 ( '
Точно так же получаем для трехгарелочного абсорбера
(А]А2 + А2 + 1) У4 + /4 j Л 2L0X0/Vn+i AiA2A3 + Л2Л3 + Аа + 1
где Y2 — число молей компонента в поступающем сыром газе на 1 моль поступающего сырого газа; Уо—число молей компонента в газе, находящемся в равновесии с поступающим свежим абсорбентом, на 1 моль поступающего сырого газа; У0 = 0 для всех компонентов, отсутствующих в свежем сорбенте, А о, А\ — коэффициенты поглощения для теоретических тарелок при i = 0 и i = 1 соответственно.
Подставляя в уравнение (XIII. 5.) i = 0, получаем
Подставляя в уравнение (XIII.1) для Xi и Xi— i значения, полученные по уравнению (XIII. 5), находим
V _ У'+1 + (*7-1/*/-1^-1)^-!
' I +LijKlVi ‘ <ХШ- 6)
Коэффициент поглощения (абсорбционный фактор) определяется как
-. (XIII.7)
+ A,Yt 1 + Л2
1 Li 1'л+1
(XIII. 10)
(XIII. 9)
(XIII. 8)
AnYn =
1 + Аг
Vo
X,..
п+1
о‘ о
или
i— 1
Для однотарелочного абсорбера (г=1) уравнение (XIII. 8) приобретает следующий вид:
Используем уравнение (XIII. 11) для исключения A0Y0 из уравнения (XIII. 9). Тогда
Пары, выходящие из второй тарелки, можно определить с помощью уравнения (XIII. 8);
У 2 + ^Q^o/^n+l I + Aj
Ч+l
Зависимость между содержанием данного компонента в газовой фазе, уходящей с п-й тарелки, коэффициентом поглощения этого компонента на каждой тарелке, количество свежего сорбента, содержанием данного компонента в свежем сорбенте, и количеством сырого газа может быть представлена соотношением
(А\А2А3 . . . Ап_х + А2А3 . . •Л„_1 + . . . + Ап—j +
_ + О Yn+j + AtA2 ... L0Xn/Vn+1
n — А\А2Аг . . . An + A2A3 . . . An-\-. . . + An-\- 1
(XIII. 16)
Так как удобнее сопоставлять между собой составы пара вне абсорбера, объединяем уравнение
Ап+1
h(Xn-X0) = Vn+I(Ya+1-Y1) (ХШ. 16а)
п+1
с уравнением Хп = 1р~т~тгУ п (XIII. 166)
“я о vп
щенном абсорбенте, поступающем в выпарную колонну, на 1 моль насыщенного абсорбента, поступающего в выпарную колонну; Lm + i — число молей насыщенного абсорбента, поступающего в выпарную колонну; Vo— число молей десорбирующего агента, обычно водяного пара, поступающего в выпарную колонну; Уо— число молей компонента в десорбирующем агенте на 1 моль десорбирующего агента, поступающего в выпарную колонну.
Уравнения (XIII. 18) и (XIII. 19) требуют упрощения.
Для упрощения уравнения (XIII. 18) принимаем абсорбционный фактор для каждой тарелки постоянным и равным средней величине А. В этих условиях поскольку
i«+i — А
п+1
(XIII. 21)
л+1
= An + An~l+... + A* + A, (XIII. 22)
и получаем
у -- "+*-1 -г о о п+1 _ (ХШ. 17)
- л = Ап +
Ап+1 + ... + а*+А
+ 1. (XIII. 23)
Используем уравнение (XIII. 17) для исключения Y в уравнении (XIII. 16) и вводим конечный состав У nJr\. Тогда
Yп , [ — Ух АгА2А3 . . . Ап + А2Аз ¦ ¦ ¦ А п + . . . +
я-Н____
Уп+1 АгА2А9 ¦ .. Ап + А2А3 . . . Л„ + .. . +
+ Л« / LoXo ) х
+ ^„+1 '^n+l^n+l'
/ А2А3 . .. Ап + Л3Л4 . . . Ап + . . . + Ап + 1 \
х \ A iA2A3 . . . Ап + А2А3 . .. Ап + . . . Ап + 1/
(XIII. 18)
Следует отметить, что левый член уравнения (XIII. 18) выражает долю компонента в сыром газе, которая будет поглощена, если свежий сорбент абсолютно лишен этого компонента. Соответствующее уравнение для десорбции можно написать так:
Хт+\
Хт+1 ~ -^i S^2^3 .. . Sm -f S2S3 . . . Sm +
¦хп
sm+\
Xm+l SlS2S3 ¦ ¦ ¦ Sm + S2S3 ¦ ¦ • Sm +
+ • • • + Sm
X
/ S2S3 ¦ ¦ ¦ Sm + Sa ¦ ¦ - Sm + • • • + Sm + 1 \
\S,S2S3 • • • Sm + ^2^3 • • • Sm + • • ' + Sm + *' ’
(XIII. 19)
где S — коэффициент отпаривания (фактор десорбции) выражается как
(XIII. 20)
Xi — число молей компонента в отпаренном тощем абсорбенте, выходящем снизу выпарной колонны, на 1 моль насыщенного сорбента, поступающего в выпарную колонну; —число молей компонента в насы-
После преобразования получим
дп+1
(XIII. 24)
где A — средний абсорбционный фактор; Y и ^„ + 1 были определены ранее; Уо— число молей компонента в паре, находящемся в равновесии с тощим абсорбентом, на 1 моль поступающего сырого газа; п — число теоретических тарелЪк в абсорбере.
Так как Yп ц — У1 равно числу молей поглощенного компонента на 1моль поступившего газа и
равно числу молей, которое было бы поглощено, если бы можно было привести выходящий газ в равновесие с поступающей жидкостью, левая часть уравнения (XIII. 24) выражает долю компонента, поглощенную при прохождении через абсорбер с числом тарелок п.
Соответствующее уравнение для десорбционной секции выпарной колонны составляет
sm+! .
(ХШ. 25)
где S—средний фактор десорбции, равный KV/L; A'i, X были определены ранее; Х0 — число молей компонента в жидкости, находящейся в равновесии с десорбирующим агентом, на 1 моль поступающего насыщенного сорбента; т — число теоретических тарелок в десорбционной секции выпарной колонны.
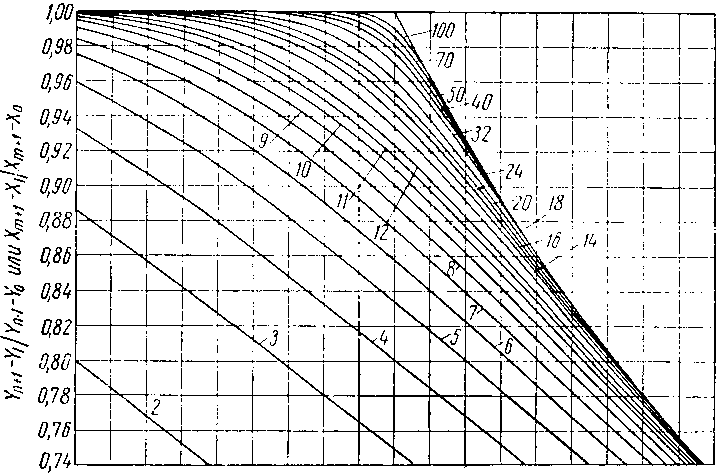
Решение уравнений (XIII. 24) и (XIII. 25) может быть выполнено графически в виде семейства кривых, приведенных на рис. XIII. 15 и XIII. 16. Преимуществом графического способа Кремсера — Брауна является его простота.
Пример
Из природного газа указанного в таблице состава необходимо абсорбировать углеводороды при абсолютном давлении i4 ат и температуре 32,2° С при помощи соляра молекулярного веса 210 и удельного веса 0,3063. Найти количество каждого компонента, которое будет абсорбировано при расходе соляра 2670 л на 1000 м3 газа, замеренных при 15,5° С и 1,03 ат при использовании восьми теоретических тарелок.
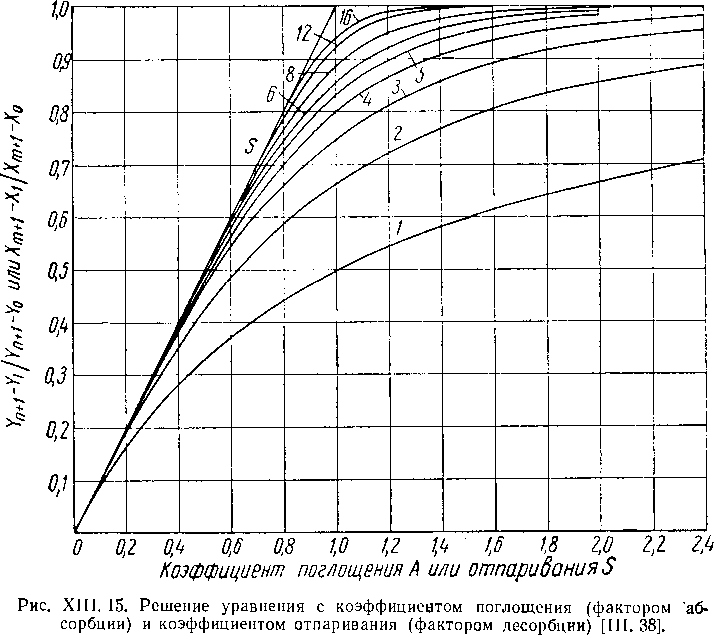
Цифры на кривых обозначают число теоретических тарелок.
OJSk од
Рис, XIII. 16. Решение уравнения с коэффициентом поглощения и коэффициентом
отпаривания [XIII. 4].
Цифры на кривых обозначают число теоретических тарелок.
| Компонент | Моль ный состав | К при 33,2® С и 14 абс. ат | * СО CS о* |
Абсорбирова-но, %** | л/100 абсор биро вано | 0 Jи3 остает ся в газе | |
| Метан .... | 0,8319 | 18,2 |
0,0133 | 1,33 | |||
| Этан..... |
0,0848 | 2,85 | 0,085 | 8,5 |
|||
| Пропан .... | 0,0437 | 0,85 |
0,286 | 28,6 | 47 | 116,5 |
|
| Изобутан . . . |
0,0076 | 0,375 | 0,648 | 64 |
22,0 | 12,20 | |
| н-Бутан . . . |
0,0168 | 0,282 | 0,861 | 81 |
59,0 | 13,9 | |
| Изопентан . . |
0,0057 | 0,131 | 1,85 | 99,6 |
27,7 | 0,134 | |
| н-Пентан . . . |
0,0032 | 0,105 | 2,31 | 99,9 |
15,40 | 0,000 | |
| Гексаны . . . |
0,0063 | 0,038 | 6,40 | 99,9+ |
34,8 | 0,000 |
|
L = 2670XMOM=IO;25 ммЬ' V = igpf- = 42,2 моль.
= 0,243.
* Л = — , KV
** По рис. XIII. 15.
Недостаток этого способа заключается в том, что температура не является постоянной величиной, a L/V колеблется в зависимости от поглощения компонентов жидкой фазой.
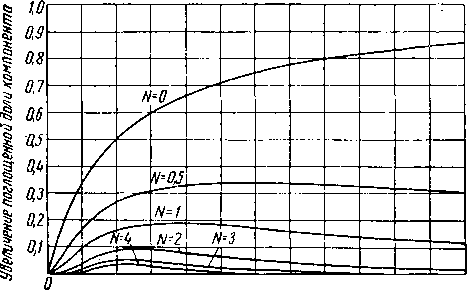
0,5 10 1,5 2,0 2,5 3,0 3,5 и,0 \5 5,0 5,5 В,О Коэффициент поглощения А
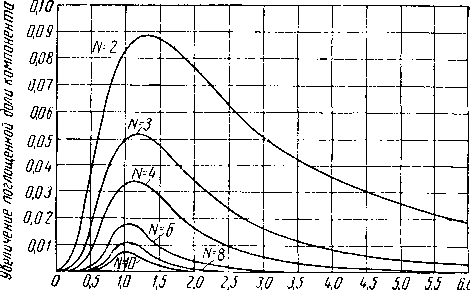
1,5 2.0 2,5 3,0 3,5 k,0 4,J 5,1
Коэффициент поглощения А
Рис. XIII. 18. Влияние добавления одной теоретической тарелки к абсорберу с п теоретическими тарелками.
Предположение о том, что имеется средняя величина коэффициентов поглощения или отпаривания, дающая точное решение уравнения (XIII. 24), является более серьезным, чем это может показаться на первый взгляд.
Метод Кремсера — Брауна не позволяет вычислить средние коэффициенты сорбции. Кроме того, можно предполагать, что для различных компонентов число теоретических тарелок п различно, поскольку, очевидно, эффективность тарелок для различных компонентов не одинакова [XII. 33].
Метод Кремсера — Брауна весьма точен для таких случаев, при которых соотношение между жидкостью и газом L/V остается по существу постоянным по всей высоте колонны. Это значит, что данный метод больше всего подходит для расчетов абсорбции малорастворимых газов в условиях давления и температуры, при которых уменьшение газовой фазы, а также увеличение жидкой фазы относительно невелики, ибо тогда средний коэффициент поглощения легко определить по количеству и состоянию наружного потока. Средний коэффициент поглощения (L/KV)C р можно вычислить, произведя отдельный подсчет константы равновесия К и соотношения жидкость — газ L/V. Большая часть абсорберов, в которых происходит поглощение углеводородов, имеет температурный профиль, напоминающий показанный на рис. XIII. 19. Форма кривой зависит в основном от количества газа, поглощенного 1 кг раствора, и количества скрытой теплоты, воспринятой или потерянной
Рис. XIII. 17. Влияние добавления одной теоретической тарелки в абсорбере с п теоретическими тарелками.
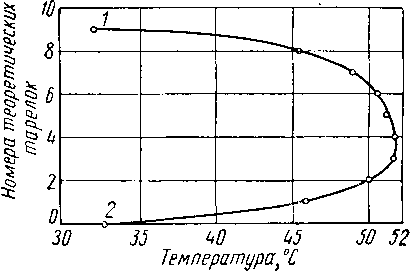
Рис. XIII. 19. Кривая температуры в абсорбере [XIII. 13].
/ — свежий сорбент; 2 —сырой газ.
Первая производная уравнений (XIII. 24) или (XIII. 25) по л (или т) выражает увеличение абсорбированной (или соответственно десорбированной) доли для данного увеличения числа теоретических тарелок. На рис. XIII. 17 и XIII. 18 показаны кривые зависимости абсорбированной (или десорбированной) доли от коэффициентов А или S. Эти кривые свидетельствуют о наличии относительного максимума для каждого первоначального числа тарелок. Там, где первоначальное число тарелок больше 2, относительный максимум находится близ А (или S), равного 1,0. Как показано на рис. XIII. 18, увеличение числа теоретических тарелок в абсорбере, имеющем уже и без того большое число теоретических тарелок, очень незначительно увеличивает выход целевых компонентов.
газовым потоком. Как показывает корреляция, рис.
XIII. 20 применим к абсорберам низкого (меньше
10,5 кГ/см2) давления, в которых производится извлечение легких углеводородов.
Однако в абсорбере высокого давления, обеспечивающем значительно большую абсорбцию, повышение температуры вследствие существенного снижения теплоты абсорбции по мере увеличения давления может быть не так велико [ХШ. 37]. Неизотермическое состояние, возникающее вследствие теплоты абсорбции, может привести к перемене направления массообмена и вызвать где-то в колонне вместо абсорбции десорбцию.
На рис. XIII. 21 показана зависимость числа теоретических тарелок от величины обратной константе равновесия l/К, L/V, и от коэффициента поглощения — для такой же колонны, что и на рис. XIII. 19. Мы видим, что кривая поглощения имеет по меньшей мере такой же характер, что и кривые для 1/К или L/V, поскольку первая кривая является продуктом двух последних.
Уравнения Кремсера — Брауна можно решить методом последовательных приближений с учетом колебания температуры и изменения L/V. Отдельные этапы вычисления общего числа молей легких углеводородов, поглощенных на данном числе теоретических тарелок, перечислены ниже. При этом эффективность всех тарелок принята одинаковой, абсорбент—соляр—полностью десорбированным, а поглощенная доля ключевого компонента и расход газа при определенной температуре и давлении известны.
1. От точки, соответствующей поглощенной доле ключевого компонента, на оси ординат на рис. XIII. 15 или
XIII. 16 проводим горизонтальную линию до пересечения с линией данного числа теоретических тарелок.
2. Узнаем необходимый коэффициент поглощения для ключевого компонента.
3. По вычисленной температуре определяем константу равновесия К ключевого компонента.
4. Вычисляем по этой константе равновесия К и А ключевого компонента L/V.
5. Используя соотношение L/V и константы равновесия прочих компонентов, определяем поглощенную долю этих компонентов по рис. XIII. 15 или XIII. 16.
6. Умножение поглощенной доли на число молей каждого компонента в поступающем в абсорбер газе, дает число поглощенных молей каждого компонента.
7. Определяем общее число поглощенных молей газа. Находим новую температуру по рис. XIII. 20.
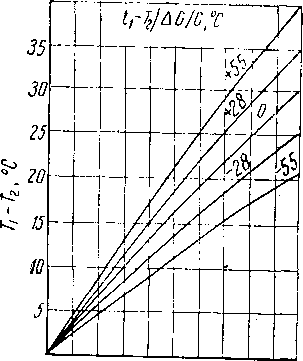
Количество газа,поглощенного сорбентом, кг/кг
Рис. XIII. 20. Повышение температуры вследствие поглощения легких углеводородов при давлении до 10,5 кГ/см2 [XIII. 37].
t температура пара на выходе из колонны; ТI — температура жидкости на выходе; Тг — температура жидкости на входе; AG/G — количество кг абсорбированного пара на | кг поступающего пара.
8. Используя коэффициент поглощения ключевого компонента и его константу равновесия К, пересчитанные на новую температуру, вычисляем соотношение L/V для ключевого компонента и получаем новые константы равновесия К и коэффициенты поглощения для остальных компонентов.
9. Уточняем количество поглощенных прочих компонентов на основе пересчитанных коэффициентов поглощения.
10. Повторяем вычисления, пока величины, выражающие повышение температуры и количество поглощенных компонентов, не будут совпадать при двух последующих расчетах.
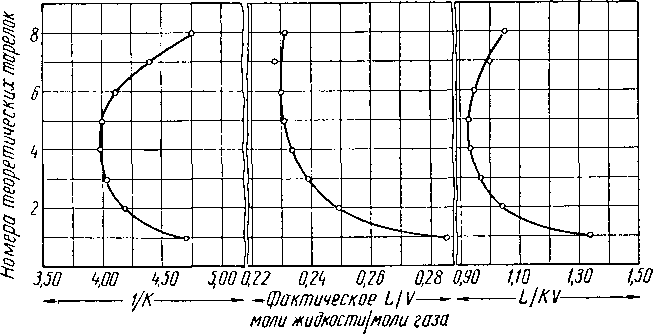
Рис. XIII. 21. Изменения -параметров в абсорбере при давлении 28 кГ/см2
[XIII. 18].
{УаЬ_
(Xa)i
(Kah.
Уш-
Y;:
Y = КХ
(ХШ. 35)
SK-* 1.0,
2. ГРАФИЧЕСКИЙ МЕТОД РАСЧЕТА АБСОРБЦИИ И ДЕСОРБЦИИ ПО ЛЮИСУ—ШЕРВУДУ
Чтобы наглядно показать отношение одного компонента к другим, остановимся на методе графического расчета абсорберов, предложенном Люисом и модифицированном Шервудом [XIII. 37]. Этот метод позволяет также определить массообмен, происходящий по высоте абсорбера.
Аналитические уравнения, определяющие характер графических построений, рассматриваются ниже. Уравнение (XIII. I) можно представить следующим образом:
Его можно интерпретировать как уравнение прямой, в котором показатели концентрации вычисляются по характеристике наружных потоков. Таким образом, на графиках все рабочие линии величин концентрации равновесных потоков, контактирующих друг с другом, являются прямыми линиями, поскольку они имеют одинаковый наклон L0/Vп+ [, который остается неизменным до тех пор, пока не меняется соотношение между свежим абсорбентом и сырым газом.
Для данного компонента а истинная мольная доля на тарелке iвыражается как
(XIII. 26)
Л+1
1 + Ел
где 1У—сумма всех величин У ,• для компонентов, находящихся в паровой фазе; %Х— сумма всех величин Х( для поглощенных компонентов, находящихся в жидкой фазе.
Аналогичные рассуждения дают следующее уравнение линии равновесия во время десорбции:
Легко увидеть, что уравнение кривой равновесия приобретает значительно более сложный вид, чем когда оно выражено в мольных долях. Уравнение (XIII. 34) на модифицированной системе координат упрощается до прямолинейного, когда
Окончательный вид, который примет уравнение для линии равновесия, это
У КХУ х'
1 + YY I + ЪХ'
(XIII. 36а)
(ХШ. 33)
(XIII. 34)
(XIII. 27)
где va — число молей компонента а в паре, покидающем тарелку (в данном случае тарелку <); »а+ + Vb + ..--общее число молей пара, покидающего тарелку (в данном случае тарелку i).
Разделив числитель и знаменатель уравнения (XIII. 27) на Vполучаем
п+1
.(XIII,28)
(»a)t
EX-0. (XIII. ЗбЬ)
Условие (XIII, 36а) выполняется при очень незначительной усадке газовой фазы, а (XIII. ЗбЬ), когда концентрация растворенного компонента в жидкой фазе невелика. Установлено, что эти условия имеют место при абсорбции малорастворимых газов и верхней части абсорбера или в той части десорбера, где происходит по существу полная десорбция.
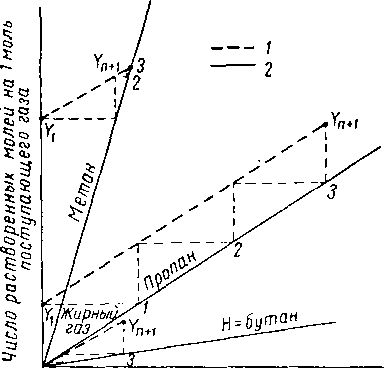
Рис. XIII. 22 схематически иллюстрирует применение метода Люиса — Шервуда к абсорбции метана, пропана и бутана соляровым маслом. Главным компонентом, т. е. компонентом, абсорбцию которого желательно контролировать, является пропан, н-бутан
+
+ '
п+1
п+1
п+\
(ХШ. 29)
(ya)i
Аналогичное выражение для жидкости *(, покидающей тарелку ?, можно получить, написав
(*")' = (l0 +/0 ++ (ХШ. 30)
(х°>‘ \Lq/L0 + la/L0 + lbIL0 + IJL0 +...)’
(XIII. 31)
где la — число молей жидкости а, покидающей тарелку (в данном случае тарелку ?); la + 1ь + ... — общее число молей поглощенных углеводородов, покидающих тарелку (в данном случае тарелку i); 20 - число молей свежего сорбента, поступающего в абсорбер, принимаемое за постоянное по всей колонне.
В сокращенном виде
(Xah I + ix( ¦
^ X,число растВоренных молей на 1 моль ненасьщенного газойля
Рис. XIII. 22. Метод Люиса—Шервуда.
/^рабочая линия; 2 — лнння равновесия.
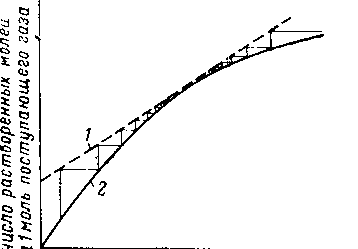
х, число растворенных молей на 1 моль ненасыщенного газойля
с; <у
'Сэ (Ъ
? с> ? 5 5;« §¦§, 00 к
в!
S *5
~J >«*
х, число растворенных молей на i моль ренчсыщенного- газойля
Рис. XIII. 23. Возникновение зон бесконечного числа тарелок в абсорберах. /—рабочая линия; 2— равновесная лниия.
поглощается почти полностью, а абсорбция метана относительно невелика. Предполагается, что линии равновесия прямые, хотя на деле это может быть и не так. Следует отметить, что метан поглощается в верхней части абсорбера, пропан — по всей высоте колонны, а бутан — наиболее интенсивно в низу колонны.
Горизонтальные линии «ступенчатой» функции будут выражать общую диффузию жидкой фазы (включая вихревую диффузию), а вертикальные линии — общую диффузию газовой фазы. В абсорберах высокого давления, где константы равновесия метана приближаются к величине, меньшей 10,0, абсорбция метана близ верхней тарелки вызывает значительное повышение температуры. Перепад температур близ нижней тарелки колонны вследствие абсорбции более тяжелых углеводородов также относительно велик. Это явление, т. е. то, что абсорбция углеводородов из газовых смесей происходит неравномерно, послужило основой для предложенной Хортоном и Франклином (Horton and Franklin) модификации метода расчета коэффициента извлечения [XIII. 17].
Если мы имеем дело с малорастворимыми газами, построить линии равновесия нетрудно, однако жирные газы могут придать линиям равновесия значительную кривизну. Линию равновесия можно упростить для верха абсорбера, поскольку там ? X = 0; тогда уравнение (XIII. 34) упростится:
(XIII. 37)
где KL и L —для верха абсорбера; XY L нужно будет определить путем пробных вычислений, производимых по данному или другому методу, например методу Кремсера — Брауна. Величина К ^ должна отражать температуру верхней тарелки, поэтому она берется при температуре, несколько более высокой, чем температура свежего сорбента. Один из методов, которым можно получить примерно правильное представление о форме равновесной линии, заключается в вычислении воображаемой величины X, обозначаемой Хц и соответствующей составу сырого газа.
Для этого делят величину мольной доли каждого компонента уя в перерабатываемом газе на константу равновесия этого компонента при температуре и давлении потока сырого газа, получая мольный состав х% воображаемой равновесной жидкости. Разность между
и 1,0 должна быть отнесена за счет поглотителя.
По данному (или принятому) мольному расходу сорбента вычисляют общее количество в потоке R, откуда в свою очередь высчитывают число молей каждого компонента. Затем вычисляют величины ХдИ Yкоторые дают точку на каждой равновесной линии, а также наклон линии для условий верха абсорбера. По точке и наклону можно приближенно построить линию равновесия.
Можно взять столько переменных, сколько нужно для вычисления числа теоретических тарелок для одного компонента. Затем постепенно уточняют положение рабочей линии, сохраняя параллельность всех рабочих линий, пока число расчетных теоретических тарелок для различных компонентов не совпадает с первоначально взятым.
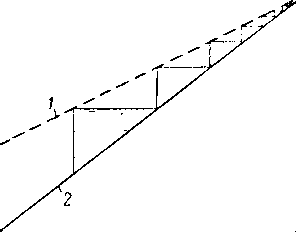
«Минимальный расход сорбента» — это расход, при котором может быть достигнуто данное извлечение при бесконечном числе теоретических тарелок. Минимальный расход сорбента, как и при фракционной перегонке, происходит при возникновении зон бесконечного числа тарелок. На рис. XIII. 23 показаны два случая возникновения зоны бесконечного числа тарелок в абсорбере. В колонне, в которой равновесная линия прямая, можно ожидать возникновения такого состояния либо в низу, либо на верху колонны (рис. XIII. 23, а). В колоннах, где равновесные линии кривые (рис. XIII. 23, б), зоны бесконечного числа тарелок могут появиться где-то посреди колонны.
Метод Люиса — Шервуда не дает точных решений, поскольку точно предсказать равновесную линию невозможно. Графические построения для многокомпонентных систем очень громоздки, в связи с чем этот метод не нашел широкого применения. Однако только вычисления, произведенные для каждой тарелки, могут лучше, чем метод Люиса — Шервуда, показать массообмен в абсорбционной колонне.
3. МЕТОД КОЭФФИЦИЕНТА ЭФФЕКТИВНОГО ПОГЛОЩЕНИЯ ПО ХОРТОНУ —ФРАНКЛИНУ (HORTON — FRANKLIN)
Метод расчета абсорбции по Хортону — Франклину [XIII. 17] основан на том факте, что абсорбция углеводородов из смеси происходит не равномерно по всей колонне. Как показано на рис. XIII. 22, это является следствием различий в константах равновесия разных компонентов. По рис. XIII. 22 поглощение метана происходит в основном на верху колонны, поглощение пропана— относительно равномерно по всей высоте колонны, а бутана — в нижней части абсорбера.
Хортон и Франклин считают, что коэффициент поглощения следует определять для интервала колонны, в котором располагается наибольшее число тарелок, связанных с поглощением данного компонента, или где происходит в основном абсорбция данного компонента. К такому же заключению приводит изучение пределов правого члена уравнения (XIII. 24) для очень малых коэффициентов поглощения и коэффициентов поглощения, значительно превышающих 1,0. Относительное положение коэффициента эффективного поглощения (или отпаривания) для различных величин А (или S), найденное эмпирически [XIII. 17], приведено в табл. XIII. 3.
Таблица XIII. 3 Определение порядкового номера тарелки, для условий которой должны подсчитываться коэффициенты эффективного поглощения или отпаривания
| Величина А (или S) | Соотношение 1: п (или 1 : ш) |
|
0—0,1 | 1,0 |
| 0,1—0,4 | 0,9 |
| 0,4—1,0 |
0,8 |
|
1,0—4,0 | 0,7 |
| 4,0 |
0,6 |
Здесь I номер эффективной тарелки, считая с верхнего конца колоииы: п или т — общее число теоретических тарелок в абсорбере или десорбциоииой части выпарной колонны [XIII. 171.
Для определения коэффициентов эффективного поглощения и отпаривания нужно определить нагрузку по газу и жидкости и температуру на тарелках эффективной сорбции. Предполагается, что изменение количества паров от тарелки i к тарелке i + 1 происходит по уравнению
Vi— = ( У±Л, (XIII. 38)
где Vt — общее число молей пара на полезной тарелке i; Vi + | — общее число молей пара, уходящих с полезной тарелки i; Vt— общее число молей пара, уходящего с верхней тарелки; V„ + i — общее число молей сырого газа, поступающего в абсорбер; п—число теоретических тарелок в абсорбере.
Принимая за основу 1 ноль сырого газа, уравнение (XIII. 38), связывающее условия тарелок 1 и i, можно записать следующим образом:
I/. = И" + 1 — ‘,/n . (XIII. 39)
В качестве первого приближения Vi можно вычислить более простым методом Кремсера — Брауна. Материальный баланс по верхней части колонны и эффективной тарелке
L, =^0+ l7i + i — I'i. (XIII. 40)
где L; — общее число молей жидкости, уходящей с эф
фективной I арелки i\ Lq — число молей ненасыщенного сорбента.
Вычислив по уравнению (XIII. 38) Vi + i, можно при помощи уравнения (XIII. 40) определить поток жидкости с эффективной тарелки.
При предположении, что изменение температуры приблизительно пропорционально общему объему поглощенного газа, т. е.
Tn~Ti _Vn+i~Vi+ l, (XIII. 41) Т*-Т0 V' + x-V,
можно определить температуру на эффективной полезной тарелке i.
Для этого пробного вычисления коэффициент эффективного поглощения каждого компонента можно рассчитать по константе равновесия К для условий эффективной полезной тарелки, общему количеству пара Vi, покидающего ее, и общему количеству жидкости Li, уходящей с этой тарелки. Число молей каждого компонента можно тогда рассчитать по уравнениям Кремсера — Брауна при помощи коэффициентов эффективного поглощения.
4. МЕТОДЫ РАСЧЕТА ПО КОЭФФИЦИЕНТУ КОНЕЧНОГО ПОГЛОЩЕНИЯ (ОТПАРИВАНИЯ)
Следует упомянуть два метода вычисления сорбций по установленным величинам коэффициентов конечного поглощения и отпаривания (на верхней и нижней тарелках) [XIII. 12, XIII. 13]. Оба метода построены на предположении, что коэффициент эффективного поглощения (или отпаривания) можно вычислить по конечным показателям работы колонны.
По методу Эдмистера (Edmister) для того, чтобы получить коэффициент эффективного поглощения как функцию коэффициента конечного поглощения, решают уравнение (XIII. 24) для двухтарелочного абсорбера. Этот коэффициент эффективного поглощения используют в уравнении Кремсера — Брауна как средний эффективный коэффициент поглощения отдельного рассматриваемого компонента. Чтобы легче было применять уравнения коэффициента эффективного поглощения для расчета абсорбции, десорбции и фракционной перегонки, решения их даются в графической форме [XIII. 12]. Примеры их применения приведены там же [XIII. 12].
Метод Ферро (Ferro) и других [XIII. 13] также основан на концепции коэффициента конечного поглощения, но для определения точек колонны, характерных для коэффициентов поглощения и отпаривания, применяют алгебраические зависимости (геометрическая или арифметическая прогрессия). При этом на одной и той же тарелке могут происходить абсорбция и десорбция различных компонентов. Решения прогрессий представлены графически. В том же источнике [XIII. 13] приводятся многочисленные примеры расчета, которые сопоставляются с точным (аналитическим) расчетом от тарелки к тарелке.
5. ТОЧНЫЙ МЕТОД РАСЧЕТА АБСОРБЦИИ
Критерием оценки точности упрощенных методов расчета являются расчеты, включающие составление теплового и материального балансов для последующих тарелок с использованием точных показателей работы абсорберов. Упрощенные и точные методы расчета редко сопоставляются в литературе [XIII. 13, XIII.23]. Применению точного метода расчета к абсорберам высокого давления препятствовал недостаток достоверных данных по теплоте растворения легких углеводородов при высоких давлениях.
Применению точных методов расчета может способствовать использование быстродействующих электронных вычислительных машин [XIII. 11]. Точные расчеты абсорберов производятся на основе известных составов, объема и состояния поступающего потока, числа теоретических тарелок и предполагаемого состава выходящего потока (обогащенное масло или отбензиненный газ). Вычисления производятся для каждой тарелки колонны. На основе предполагаемых и вычисленных показателей абсорбции получают новый «пробный» состав выходящего потока и повторяют вычисления. При совпадении вычисленного и предположенного составов потока дальнейшие вычисления прекращают.
Другой метод, который, по-видимому, быстрее приводит к точному ответу, связывают с именем Харберта (Harbert) [XIII. 16]. Этот метод основан на прямом вычислении состава жидкости и пара, уходящих с каждой тарелки, по предполагаемым соотношениям между жидкостью и паром (L/V) и температурам на всех тарелках колонны. По вычисленным соотношениям L/V судят о правильности предположительно взятых величин L/V, а тепловой и материальный балансы по каждой тарелке позволяют проверить предположительно взятые температуры. Совпадение вычисленных и предположительно взятых величин L/V и температуры на каждой тарелке показывает, что решение найдено. Для этого метода нужно знать константы равновесия и тепловые показатели конкретных смесей жидкости и пара при условиях, существующих в абсорбере.
6. ВЫВОД УРАВНЕНИЙ ДЛЯ МЕТОДА ХАРБЕРТА
(XIII. 52) (XIII. 53)
Материальный баланс для каждого компонента на отдельно взятой тарелке i в абсорбере
(Vy)i + , + (Lx)t _ , = (Vy)i + (Lx),. (XIII. 42)
(Lxh
. (XIII. 56)
Тепловой баланс для каждого компонента
(VyH}!+ i + {Lxh)[_ | = (VyH)i + {Lxh)it (XIII. 43)
где n — число теоретических тарелок в абсорбере; i — любая теоретическая тарелка; V — общее число молей пара; L— общее число молей жидкости; х — мольная доля данного компонента в жидкости; у — мольная доля данного компонента в паре; Н—парциальная энтальпия компонента (относительно принятого уровня or-счета) в парообразном состоянии при условиях абсорбера в ккал/кГ • моль; h — парциальная энтальпия компонента в жидком состоянии в ккал/кГ • моль', К = у/х— константа равновесия.
(Lx)i
Таким образом (Lx)\—число молей компонента в жидкости, выходящей из тарелки 1, т. е. верхней тарелки; (Vy)n +i — число молей компонента в паре, поступающем в абсорбер. Уравнение равновесия для каждого компонента на тарелке i таково:
yi = K[Xlt (XIII. 44)
Умножая каждые части уравнения (XIII. 44) на L(V? , получаем
lKV\
(XIII. 45)
Принимая At — Lt/V.К., получаем
А^’у); = (Lx),. (XIII. 46)
Запишем уравнение (XIII. 46) для тарелки i—I, затем из уравнения (XIII. 42) получим
(Lx){ = (Vy)i + l + A,_y (Vy), _ , _ (Vy)l. (XIII. 47)
Следует напомнить, что уравнение (XIII. 46) можно написать для каждого компонента на каждой тарелке. Так, для трехтарелочного абсорбера можно написать следующий ряд уравнений для данного компонента — первые три для балансов по каждой тарелке абсорбера и последнее —для общего баланса по всему трехтарелочному абсорберу:
(Lxk = (Vy)n + , + (Lxh - (Vy)3, (XIII. 48)
(Lx)2 = (Vy)3 -|- (Lx)r — (Vy)2, (XIII. 49)
(?*)! = (ty),+ Lx)a-(Vy)lt (XIII. 50)
Формулировка уравнения (XIII. 46) для каждой тарелки дает
(Lx)3 — (VУ)3'
(Lx)2 = А2 (Vy)2,
(Lxh^A^Vy)^ (XIII. 54)
Для свежего сорбента, из которого десорбированы те компоненты, для которых были сформулированы уравнения,
(Lx)о=0. (XIII. 55)
Одновременное решение уравнений (XIII. 48) — (XIII. 55) дает уравнение, выражающее соотношение между числом молей данного компонента на данной тарелке и числом молей того же компонента в сыром газе, а также его коэффициентом поглощения на каждой тарелке. Соответствующее уравнение для тарелки 3 таково:
(V У)п + 1 Из + А3А2 + А3А2Аг) 1 + А3 + А3А2 + А3А2АХ
Для абсорбера с п теоретическими тарелками число молей компонента на тарелке i может быть выражено как
(Vy)n + 1 (^1 + AlAl — 1 + AlAi — lAi — 2 +
I -h An~h AnAn — ! + ••• +
+ AnAn - 1 - • • A 2A1
(XIII. 57)
Состав пара определяют по уравнениям (XIII. 57) и (XIII. 46). Число молей каждого потока в колонне вычисляется на основе предположительных соотношений между жидкостью и паром L/V, предположительной температуры на каждой тарелке колонны и скорости подачи данного компонента. Это дает исправленные величины L/ V.
Четырем потокам, уходящим с любой данной тарелки абсорбера, соответствуют три температуры, поскольку два из представленных потоков находятся в равновесии. Поэтому при составлении тепловых балансов удобнее вести расчеты с верха колонны вниз или снизу вверх; один из четырех потоков будет определенно известным на тарелке 1 или тарелке п. Представим себе, что тепловой баланс составляется по верхней тарелке. Температура потока свежего сорбента известна, а температура на верхней тарелке берется предположительно. Итак, на верхней тарелке будет один поток, температура которого неизвестна, а именно, поток пара, поступающий с нижележащей тарелки. Для вычисления температуры этого потока составляют тепловой баланс по тарелке 1. Следует отметить, что тепловой баланс используется для проверки температуры потока (в данном случае — газа), поступающего на тарелку с соседней тарелки, а не для проверки предположительно взятой температуры на этой тарелке.
Расчет ведут, составляя тепловой баланс по каждой тарелке и, наконец, пс всей колонне, используя вычис ленные и известные составы потоков для проверки об щего теплового баланса- При втором пробном вычисле нии соотношения жидкости и газа и температуры та релок, которые были вычислены при первой пробе, слу жат критерием для проверки новых допущенных нам} соотношений жидкости и пара и температур тарелок
Для примера приводим расчет трехтарелочного аб сорбера.
¦V»
(XIII. 59)
(Х111. 60)
V
Ki
Вычислить по методам Хортона — Франклина и Хар-берта извлечение компонентов из газов известного состава, поступающего при температуре 28° С в количестве 8,15 млн. м3/сутки (приведенных к абсолютному Давлению 1,03 ат и температуре 15,5° С) в абсорбер с тремя теоретическими тарелками. Абсорбер работает при абсолютном давлении 106,5 ат. Свежий сорбент — соляровое масло молекулярного веса 200 и удельного веса 0,8411—поступает в абсорбер при температуре 32° С в количестве 3420 л/мин.
где V „-J-1—число молей сырого газа, принимаемое за единицу.
По материальному балансу
где L;—общее число молей жидкости на эффективной тарелке; L0 — число молей свежего масла:
Tn-Ti_Vn+
Li — Ln -|- V _
¦Т0
| Состав сырого газа | Константы равновесия при абсолютном давлении 106,5 am | ||
| компонент | мольная доля | 29,4* С, | 32° С |
|
Метан............ | 0,9302 | 3,80 | 3,36 |
| Этан ............ |
0,0373 | 0,78 |
0,835 |
|
Пропан........... | 0,0163 | 0,36 | 0,385 |
| Изобутан.......... |
0,00444 | 0,19 |
0,020 |
|
н-Бутан........... | 0,00448 | 0,15 | 0,165 |
| Изопентан.......... |
0,00279 | 0,083 |
0,0905 |
|
н-Пентан.......... | 0,001375 | 0,068 | 0,076 |
| Гексаны........... |
0,001563 | 0,035 |
0,0385 |
| Гептаны и более тяжелые уг | |||
| леводороды ........ | 0,00147 | 0,005 | 0,0056 |
| 0,999918 | | |||
Решение.
А. Метод Хортона — Франклина Расход свежего сорбента
3420 х 60_Х 0,8413 = 862 200
Расход сырого газа 8150000 24 X 23,7
14400 моль/ч.
Соотношение между свежим сорбентом и сырым газом равно
862
j-^qq = 0,060 моль/моль.
Изменение величин констант равновесия в интервале температур абсорбера выражается прямыми в координатах lgfe — t. Величины констант при температурах 29,4° С и 32° С приведены выше.
Расчет состава отбензиненного газа при наличии в абсорбере грех теоретических тарелок приведен в табл. XIII. 4. Для расчета нужны следующие данные:
1) состав сырого газа — колонка 1 табл. XIII. 4;
2) молярное соотношение между свежим сорбентом и сырым газом (дано): в нашем случае—0,06 моль свежего сорбента на 1 моль сырого газа;
(XIII, 61) (XIII, 62) (XIII, 63)
3) таблица соотношения ijn, т. е. номера эффективной тарелки к общему числу тарелок в зависимости от коеффициента эффективного поглощения (см. табл. XIII. 3);
(Lx)2 =
(L*)i =
4) число теоретических тарелок (здесь произвольно принято три);
5) эмпирические уравнения Хортона—Франклина [уравнения (XIII. 39) и (XIII. 41)]
VI
(Vl/Vn-где Тп — температура нижней тарелки в °С; Гг—температура эффективной тарелки в °С; То — температура свежего сорбента в °С.
l)l/n
Необходимо задаться предположительно числом молей поглощенного газа на 1 моль поступающего сырого газа. В данном случае на 1 моль сырого газа с насыщенным сорбентом уходит 0,0545 моль газа (см. табл. XIII. 4). Табл. XIII. 4 строится следующим образом.
Колонка 1. Дана.
Колонка 2. Берется эмпирически.
Колонка 3. Вычисляется по колонке 2 для п = 3,
Колонка 4. Вычисляется по уравнению (XIII. 39) и колонке 3.
Колонка 5. Вычисляется по уравнению (XIII. 58) и колонке 4.
Колонка 6. Вычисляется по уравнению (XIII. 59) и мольному соотношению между свежим сорбентом и сырым газом (в данном случае 0,06).
Колонка 7. Вычисляется по уравнению (XIII. 60) и предположительно взятой температуре 29,4° С для нижней тарелки и 32° С для свежего сорбента.
Колонка 8. Константы равновесия для температур, указанных в колонке 7.
Колонка 9. Вычислена по колонкам 4, 6 и 8 (А — =>L/KV).
Колонка 10. Поглощенная доля компонента по кривой коэффициента поглощения (рис. XIII. 15 или XIII. 16) для величин А (колонка 9) и трех теоретических тарелок.
Колонка 11. Колонка 10, умноженная иа колонку 1, число поглощенных молей.
Колонка 12. Колонка 1 минус колонка 11,
Б. Метод Харберта
В табл. XIII. 5а — XIH. 5г приведены результаты расчета трехтарелочной колонны по методу Харберта.
В табл. XIII. 5а перечислены известные данные, а также предположительно принятые температуры и соотношения L/V. Для каждого компонента на каждой тарелке по L/V и /( и соответствующей принятой температуре находят А.
Чтобы решить уравнение (XIII. 57) для трехтарелочной колонны, находят три состава жидкости при помощи следующих уравнений, записанных для каждого компонента:
(VУ)п -|- 1 {Аз + AsA2 + ЛзЛг/1,)
' + + АяА2 АзА2А1
1 “h A3 + Л3Л2 + AgA^A!
(Vy)n+lA, _
1 -|- Л3 -j- A3A2 + A3AsAi
Следует отметить, что знаменатели во всех трех уравнениях одинаковые, В табл. XIII. 5а знаменатель вычислен для каждого компонента.
Для абсорбера с тремя теоретическими тарелками. Предположительно принятая абсорбция составляет
0,0545 моль на 1 моль газа
|
Компонент | Мольная фракция газа жирного гп+ 1 |
Пред- поло- жи- тельно взятое соотно шение i/n | ДЛЯ п = 3 |
Число молей пара и а по* лезной тарел* ке V't | Мольная фра к-Ция V‘+l | Число молей жидкости иа полезной та релке Li | Температура полезной та релки, Т iy °С |
Коистаи* та равновесия при Т[ К | А | X + с X | § О et К Ж — х 1 & + 3 с о х g | х" 1 + с X | Число молей ненасыщенного газа, У |
| 1 |
2 | 3 | 4 |
5 | 6 | 7 |
8 | 9 | 10 | 11 | 12 | ||
|
Метан......... | 0,9302 |
1,0 | 3,0 | 0,9815 |
1,0000 | 0,1145 |
29,44 | 3,30 | 0,0354 |
0,0354 | 0,0329 |
0,8973 | |
| Этан ......... |
0,0373 | 0,9 | 2,7 | 0,9760 | 0,9944 |
0,1089 | 29,75 | 0,783 | 0,1415 | 0,1414 |
0,00528 | 0,03202 | |
| Пропан........ | 0,0163 |
0,9 | 2,7 | 0,9760 |
0,9944 | 0,1089 |
29,75 | о;зб2 | 0,308 | 0,298 | 0,00486 |
0,01144 | |
| Изсбутан ....... | 0,00444 | 0,8 |
2,4 | 0,9706 | 0,9889 | 0,1034 | 30 |
0,191 | 0,559 |
0,514 | 0,02228 | 0,00216 | |
| н- Бутан........ |
0,00448 | 0,8 | 2,4 |
0,9706 | 0,9889 |
0,1034 | 30 | 0,152 |
0,701 | 0,606 |
0,00272 | 0,00176 | |
|
Изопентан ....... | 0,00279 |
0,7 | 2,1 | 0,9652 |
0,9834 | 0 0979 |
30,15 | 0,084 | 1,208 |
0,815 | 0,00227 |
0,00052 | |
| н-Пентан ....... | 0 001375 | 0,7 |
2,1 | 0,9652 | 0,9834 |
0,0979 | 30,15 |
0,069 | 1,47 |
0,872 | 0,0012 | 0,000175 | |
| Гексаны........ Гептаны и более тяже | 0,001563 |
0,7 | 2,1 | 0,9652 |
0,9834 | 0,0979 |
30,15 | 0,036 | 2,82 |
0,969 | 0,00152 |
0,000043 | |
| лые углеводороды . . | 0,00147 | 0,6 |
1,8 | 0,9598 | 0,9779 | 0,0924 | 30,55 |
0,00506 | 19,00 |
1,000 | 0,00147 | ||
| Всего. . . | 0,999918 |
- | - | 1 - | 1 | 0,05450 | 0,945418 | ||||||
Таблица XIII, 5а
Пример расчета по методу Харберта
Даны: состав жирного газа, температура жирного газа 28° С, соотношение между ненасыщенным сорбентом и жирным газом 0,060 моль/моль, температура ненасыщенного сорбента 32,2° С Эмпирические допущения:
|
1 | 2 |
3 |
| 0,1025 |
0,104 | 0,114 |
| 35,5 | 34,4 |
31,6 |
№ тарелки .......
Принятое L/V ......
Принятая температура, °С
Коэффициенты поглощения для каждого компонента на каждой тарелке:
|
Компонент | Тарелка 1 | Тарелка 2 |
Тарелка 3 | |||
| ^35,5 |
А | ^34,4 |
А | К31,6 |
А | |
|
Сх................ |
3,36 | 0,0305 |
3,35 | 0,0311 |
3,33 | 0,0342 |
| С2................ |
0,835 | 0,123 |
0,825 | 0,126 |
0,800 | 0,1425 |
| С3................ |
0,385 | 0,266 |
0,380 | 0,274 |
0,369 | 0,309 |
| 0,200 | 0,513 | 0,199 | 0,523 |
0,192 | 0,595 | |
| 0,165 |
0,621 | 0,161 |
0,646 | 0,155 |
0,736 | |
|
0,0905 | 1,13 |
0,089 | 1,17 |
0,086 | 1,318 | |
| 0,076 | 1,35 | 0,074 | 1,41 |
0,0705 | 1,62 | |
| С6........;....... |
0,0385 | 2,66 |
0,038 | 2,74 |
0,036 | 3,17 |
| 0,0056 | 18,30 | 0,0055 | 18,90 |
0,0052 | 21,95 |
|
Продолжение табл. XIII, 5а
Знаменатель уравнения (XIII, 57) для каждого компонента:
| с, | С„ | Сз | 1-С, | п-С4 |
1- с. | п-С, | С, | С,+ | |
| 1+^3 А3А2 AsA2Ai |
1,0342 0,00106 0,0000325 |
1,1425 0,0180 0,00221 | 1,309 0,0846 0,0225 | 1,595 0,311 0,160 | 1,736 0,476 0,296 | 2,318 1,54 1,74 | 2,62 2,28 3,08 | 4,17 8,69 23,10 | 22,95 415,00 7460,00 |
| Сумма | 1,03529 | 1,1627 | 1,4161 | 2,066 |
2,508 | 5,598 |
7,98 | 35,96 |
7898,00 |
В табл. XIII, 56 расчеты числителя для каждого компонента на тарелке / приводятся в такой форме, что аналогичный расчет колонны с большим числом тарелок сведется к введению дополнительных обозначений и, следовательно, не составит труда. Решение уравнения (XIII. 63) представляет собой просто соотношение между числителем и знаменателем и дает (Lx) I или число молей каждого компонента в жидкости, выходящей с верхней тарелки. Состав пара или газа, выходящего с верхней тарелки, определяется по составу жидкости и следующему уравнению
Ai(Vy)l = (Lx)t. (XIII. 64)
Мольные доли — это (Lx) i или (Vy)\, деленные на общее число молей.
Подобный же расчет состава пара и жидкости на второй и третьей тарелках приведен соответственно в табл. XIII. 5в и XIII. 5г. Таким образом, нами определены составь! всех потоков в трехтарелочном абсорбере.
В табл. XIII. 56 — XIII. 5г приведен также расчет теплового баланса. Сумма произведений молярных долей у компонентов пара на их молекулярный вес дает молекулярный вес пара. Молекулярный вес, деленный на 28,9, дает удельный вес газа относительно воздуха. Зная его, можно при помощи рис. XIII. 24 определить энтальпию пара. Для определения энтальпии жидкости необходимо знать плотность последней, вычисляемую методом Стендинга и Катца [IV. 88]. Величины кажущейся плотности метана и этана отсчитываются по рис. IV. 31. Величины энтальпии на кг/моль при нулевом давлении и температуре тарелки берутся по рис. IV. 72, Мольная доля х в жидкости, умноженная на мольную энтальпию h, дает парциальную энтальпию для каждого компонента. Общую энтальпию нужно скорректировать при помощи рис. IV. 73 и плотности жидкости.
Таблица ХШ, 56
Расчет по методу Харберта (тарелка 1)
Числитель уравнения (XIII. 63) для каждого компонента, тарелка 1
| С, |
Сг | С, |
1-С. | п- С4 | 1-С, | п-С, | С, | С ч~\- | |
|
(Vy) 4 ^1 (VyhA i |
0,42193 0,0305 0,01288 |
0 016919 0,123 0,0020819 | 0,007394 0,266 0,001968 | 0,002014 0,513 0,001030 |
0,002032 0,621 0,001261 |
0,001266 1,13 0,001429 | 0,0006237 1,35 0,0008437 | 0,0007089 2,66 0,001887 |
0,0006668 18,30 |
|
Компонент | Решение уравне- | Уравнение (XIII.63) | Мольная доля на тарелке 1 | Моле куляр | Жидкость | Пар | ||||||
| (XIII.63) (Z. х), | ненне (XIII.64) (Vy)t | X |
У | ный вес |
х X молекулярный вес |
весо вая доля |
плот ность, г/см3 |
объем, см3 |
й35,5 | *й35,5 |
у х молекулярный вес | |
| Сх | 0,01243 |
0,40778 | 0,281 |
0,949 | 16,04 |
4,51 | 0.0340 | 549,9 | 154,42 | 15,24 | ||
|
с2 | 0,001792 |
0,01456 | 0,0405 |
0,0339 | 30,07 |
1,22 | 0,0092 | 805,47 | 32,77 | 1,02 | ||
|
С3 | 0,001388 |
0,005216 | 0,0314 |
0,01215 | 44,09 |
1,39 | 0,0105 |
0,510 | 0,0206 |
994,35 | 31,11 |
0,536 |
|
г-С4 | 0,000499 | 0,000977 | 0,0113 | 0,00226 | 58,12 | 0,66 | 0,005 |
0,565 | 0,0089 |
1133,2 | 12,78 |
0,131 |
| п- С5 | 0,000503 |
0,0008119 | 0,0114 |
0,00189 | 58,12 |
0,66 | 0,005 |
0,585 | 0,0085 |
1183,22 | 13,33 |
0,110 |
| /-Се |
0,0002558 | 0,0002263 |
0,0058 | 0,00053 |
72,15 | 0,42 |
0,0032 | 0,625 |
0,0051 | 1333,2 |
7,78 | 0,038 |
| п-С5 |
0,0001057 | 0,0000785 |
0,0024 | 0,000183 |
72,15 | 0,17 |
0,0013 | 0,631 |
0,0021 | 1388,8 |
3,33 | 0,013 |
| Сорбент— | 0,000053 | 0,000195 | 0,0012 | 0,000454 | 86,17 | 0,11 | 0,0008 |
0,664 | 0,0012 |
1555,4 | 1,67 |
0,004 |
| газойль С7 + | 0,02721 | _ | 0,615 |
_ | 200 127 | 123,2 | 0,931 |
0,841 0,782 |
1,107 | 3249,7* |
2005,3 | |
|
0,044239 | 0,42984 |
1,0000 | 1,00037 |
— | 132,34 |
1,000 | — |
1,1534 | — |
2262,6 | 17,092 |
|
Вычисленное
0,044239
0,42984
= 0,1029. Удельный вес =
Энтальпия жидкости на тарелке 2262,6 + 304,3 =
= 2566,9 ккал/кмоль.
17,092 ~z2,4X1^29
= 0,591. И35 55 = ккал/кмоль.
* Энтальпия сорбента при 35,5° С и 0 абс. ат = 200 х х (35,5) х 0,457 = 3260 ккал/кмоль.
0.9568 1 .1534 :
1,0000 — 0,0340 — 0,0092 1,1534
Удельный вес C3_j_ = 0,829 г/см*.
Удельный вес C2_j_ = 0,825 г/см3.
Удельный вес Ci_j_ = 0,790 г/см3 прн 15,55° С и 1 ат.
Энтальпия, пересчитанная на абсолютное давление 106,05 ат = 2,3 ккал/кг, нлн 132,3 х 2,3 = 304,3 ккал/кмоль.
Тепловой баланс по тарелке 1 для достижения температуры V2.
Выделение тепла hLt = 0,044239 х 2566,9 = 113,5 ккал.
HVt = 0,42984 X 1075 = 462,1 ккал.
Сумма: 113,5 -|- 4 62,1 = 575,6 ккал.
Поступление тепла
h сорбент = 0,02721 х 3396.6 — 92,5 ккал жирного газа.
HV2 х 0.4465 = 485 ккал/моль жирного газа.
HV2 — 4 92 ккал/моль• V2.
Прн удельном весе 0,600 по табл. XIII. 5в н рис. XIII. 24 температура У.г — + 33.89° С,
Эмпирически принятая температура равна 34,4° С.
| С, | С2 | С3 | i-С. | /г-С4 | «¦•с. | п-Съ | С, | С7 + | |
|
(Vy) 4 | 0,42193 |
0,016919 | 0,007394 |
0,002014 | 0,002032 |
0,001266 | 0,0006237 |
0,0007089 | 0,0006668 |
|
Аг | 0,0311 |
0,126 | 0,274 | 0,523 |
0,646 | 1,17 | 1,41 | 2,74 | 18,90 |
| A2Ai | 0,00095 |
0,0155 | 0,073 | 0,268 | 0,402 | 1,32 |
1,90 | 7,30 | 346 |
| Сумма | 0,03205 |
0,1415 | 0,347 | 0,791 | 1,048 | 2,49 |
3,31 | 10,04 | 364,9 |
| (Vy)4X сумму |
0,013517 | 0,0023995 |
0,0025627 | 0,0015921 |
0,0021318 | 0,00315246 |
0,0020638 | 0,0071213 |
0,24312 |
| Жидкость | Пар | ||||||||||
| (Lx)2 |
(Vy)2 | X |
У | X X мо-леку-ляр-ный вес | весо вая доля | удель ный вес | объем, см3 | й34,4 |
xft34,4 | У X мо-леку-ляр* ный вес | |
|
Сх | 0,013063 |
0,42002 | 0,279 | 0,941 | 4,49 | 0,0352 |
— | — | 527,7 |
147,21 | 15,10 |
|
с2 | 0,002059 |
0,016329 | 0,044 | 0,0365 | 1,32 | 0,0103 |
— | — | 777,7 |
34,44 | 1,098 |
|
С3 | 0,001810 |
0,006622 | 0,0386 | 0,0148 | 1,71 | 0,0134 |
0,510 | 0,0263 | 949,9 | 36,66 | 0,653 |
| г-С4 | 0,000771 |
0,001470 | 0,0165 | 0,00329 | 0,96 | 0,0075 |
0,565 | 0,0133 | 1105,4 | 18,33 | 0,191 |
| л-С4 | 0,0008482 |
0,001315 | 0,0181 | 0,00294 | 1,05 | 0,0082 |
0,585 | 0,0140 | 1144,3 | 20,55 | 0,171 |
| i-С5 | 0,0005624 |
0,000481 | 0,0120 | 0,00108 | 0,87 | 0,0068 |
0,625 | 0,0109 | 1283,2 | 15,55 | 0,078 |
| л-С5 | 0,0002585 |
0,0001833 | 0,0055 |
0,00041 | 0,40 | 0,0031 | 0,631 | 0,0049 |
1338,8 | 7,22 | 0,030 |
| св | 0,0001996 | 0,0000721 | 0,0043 |
0,00016 | 0,37 | 0,0029 | 0,664 | 0,0044 |
1499,9 | 6,67 | 0,014 |
| С, | 0,0000318 |
— | 0,0007 | — | 0,09 | 0,0007 |
0,782 | 0,0009 | 2333,1 | 1,67 | |
|
Сорбент | 0,0227215 |
— | 0,5813 | — |
116,3 | 0,912 | 0,841 | 1,083 | 3144,1 |
1830,37 | |
| Сумма | 0,046811 | 0,446498 |
1,0000 | 1,00018 | 127,56 | 1,000 | — |
1,1577 | — | 2118,68 | 17,335 |
0,46811
= 0,1049. Удельный вес =
Выделение тепла
hL = 0,0468 х 241.3,68 = 112.96 ккал
Ну = 0,4465 X 1090 = 486,9 ккал
599,86 ккал
Поступление тепла
hj^i по табл. XIII, 56 — 113,5
х 0,4483 = 486 ккал,
486
492 ккал/кмоль.
Вычисленное
з 0,4483
V 0,4465
1090 ккал/кмоль.
= W-5=°’600- "34,4
* Энтальпия сорбента прн 34,4° С н 0 ат = 200 х 34,44 х X 0,457 = 3110 ккал/кмоль.
1,000 — 0,0352 — 0,0103 0,9545
Удельный вес Сэ_|_ =
0,825 г/см3.
Удельный вес С2_|_ = 0,819 г/смъ> Удельный вес Cj_|_ = 0,784 г/см%>
1,1577
1,1577
ИI
Поправка на давление прн 34,4° С и 106,05 ат =
= 2,32 ккал/кг, или 127,6 х 2,32 = 295 ккал/кмоль.
Энтальпия жидкости на тарелке 2: 21 18,68 + 295 =;
= 2413,68 ккал/кмоль.
Тепловой баланс по тарелке 2.
По рис, XIII. 24 при удельном весе 0,605, взятом по табл. XIII. 5г.
Температура V3 = — 32.7° С.
Эмпирически принятая температура равна 31,6° С.
Однако расхождение составляет ~ 5 ккал из 492 и им можно пренебречь, как находящимся в пределах неточности графиков и расчетов*
|
С, | С2 |
с3 |
i-Ct | п-СА | 1- С, |
Л-с, | С. | Су + | |
| (yy)i Л3 А3А2 A3A%Ai | 0,42193 0,0342 0,00106 0,0000325 |
0,016919 0,1425 0,0180 0,00221 | 0,007394 0,309 0,0846 0,0225 |
0,002014 0,595 0,311 0,160 | 0,002032 0,736 0,476 0,296 |
0,001266 1,318 1,54 1,74 | 0,0006237 1,62 2,28 3,08 |
0,0007089 3,17 8,69 23,10 | 0,0006668 21,95 415 7460 |
| Сумма (vy)4 X сумму | 0,0353 0,014877 | 0,1627 0,002753 | 0,4161 0,003048 | 1,066 0,002145 | 1,508 0,003062 | 4,598 0,0005806 | 6,98 0,004354 | 34,96 0,024766 | 7897 |
|
Жидкость | Пар | |||||||||||
| (Lx), |
(Vy) s | X |
У | X х мо-леку-ляр-ный вес |
весо вая доля |
удель ный вес | объем, см3 |
Л3 1,6 |
xh3l,6 | у х мо* леку* ляр-ный вес | ||
|
Сг | 0,014379 |
0,42003 | 0,280 | 0,9369 | 4,49 |
0,0370 | — |
— | 483,29 |
136,65 | 15,02 | |
| с2 | 0,002363 |
0,016601 | 0,0461 |
0,0370 | 1,39 | 0,0114 | — |
— | 705,49 |
32,77 | 1,115 | |
| С3 |
0,002155 | 0,006967 |
0,0420 | 0,0155 |
1,85 | 0,0152 |
0,510 | 0,0298 |
877,69 | 36,66 |
0,685 | |
| г- С4 | 0,001039 |
0,001746 | 0,02025 |
0,0039 | 1,18 | 0,0097 | 0,565 |
0,0172 | 999,9 |
19,99 | 0,227 | |
| л-С4 |
0,001220 | 0,001660 |
0,0238 | 0,0037 |
1,38 | 0,0113 |
0,585 | 0,0193 |
1049,9 | 25,0 |
0,215 | |
| i~ С5 | 0,001039 |
0,0007893 | 0,02025 | 0,00176 | 1,46 |
0,0120 | 0,625 |
0,0192 | 1177,66 |
23,89 | 0,127 | |
| п- Сь |
0,000544 | 0,0003357 |
0,0106 | 0,00075 |
0,76 | 0,0062 |
0,631 | 0,0098 |
1222,1 | 12,78 |
0,054 | |
| Q |
0,0006895 | 0,0002177 |
0,0134 | 0,00049 | 1,15 | 0,0091 |
0,664 | 0,0137 |
1383,2 | 18,33 |
0,042 | |
|
С7 + |
0,0006668 | — |
0,0130 | — |
1,65 | 0,0136 |
0,782 | 0,0174 |
2110,9 | 27,22 | ||
| Сорбент |
0,0272 | — |
0,531 | — |
106,2 | 0,8745 |
0,841 | 1,04 |
2894,16* | 1538,7 | ||
| 0,051310 |
0,448343 | 1,004 |
1,0000 | 121,51 |
1,000 | — |
1,1664 | 1872 |
17,485 | |||
L 0,0513 „ 17,485
Вычисленное -р = Q
44-33 = 0,1143. Удельны;! вес = 2g-y
=
Выделение тепла
0,605. Яз] у г= Ю85 ккал/кмоль.
hr = 0,0513 х 2155= 110,6 ккал
* Энтальпия сорбента прн 31,6* С и 0 ат — 220 х 3167 X х 0,456 = 2892 ккал/кмоль.
Иуз = 0,4483 х 1085 = 486 ккал596,6 ккал
1,0000 — 0,0370 — 0,0114 0,9516
Удельный вес С3+ = -----=
= 0,816 kzJcm*.
Удельный вес С8_|_ = 0,809 г/см*. Удельный вес C*_j_ — 0,773 г/см*.
Поправка на давление при 31,6° С и 106,05 абс. ат— = 2,33 ккал/кг, или 121,5 х 2,33 = 283 ккал/кмоль.
Энтальпия жидкости иа тарелке 3: 1872 4- 283 =
=г 2155 ккал/кмоль ед. моль.
Теплово.1 баланс по тарелке 3.
Поступление тепла hL = 112,96.
И жирного газа х 0,4536 = 483,3 ккал.
По рис. XIII. 24 при удельном весе 0,62 температура жир* ного газа 27,7° С.
Была взята температура 27,7° С.
Энтальпия тощего сорбента, поступающего с температурой 32,2° С, равна 200Х (32,2—0) X0,457 =
. = 2940 ккал/кмоль при абсолютном давлении, равном нулю.
Поправка на давление 106,5 ат (абс) при 32,2° С равна 2,25 ккал/кг, или 200 X 2,25 = 450 ккал/кмоль. Энтальпия тощего сорбента равна 2940 + 450 ~
= 3390 ккал/кмоль.
Тепловой баланс по всему абсорберу
Поступление тепла
Свежий сорбент при температуре 32,2° С: 3400 X 0,06 = 204 ккал
Сырой газ при температуре
27,8° С (удельный вес 0,62) 1065 ккал
1269 ккал.
Выделение тепла
Насыщенный сорбент при температуре 31,7° С: 0,1131 х 2153 =
= 243,6 ккал
отбензиненный газ при 1020 ккал.
температуре 35,5° С 1263,6 ккил
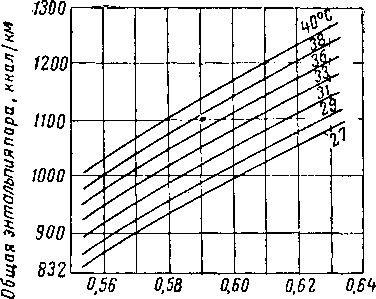
Удельный Вес пара относительно Воздуха
Рис. XIII. 24. Энтальпия углеводородных паров при абсолютном давлении 106 ат над жидкостью с температурой 0° С и с нулевым давлением [XIII. 23].
Прежде чем приступить к расчету энтальпии на тарелке 2, составляют тепловой баланс (или баланс энтальпии) по первой тарелке, получая энтальпию пара, выходящего со второй тарелки. Если температура, соответствующая этой энтальпии, отличается от первоначально ориентировочно принятой для второй тарелки, для определения энтальпии жидкости на тарелке 2 пользуются вычисленной температурой, а не эмпирически допущенной. Эта энтальпия в свою очередь дает температуру паров, выходящих с тарелки 3, При абсолютно правильном решении балансы, составленные для последующих тарелок, должны совпадать с тепловым балансом по всей колонне.
| Число равновесных тарелок | 3 | 12 | |
|
2 | 3 |
4 | |
| Абсорбция, %: | |||
|
метан............ | 3,41 |
3,56 | 3,56 |
| этан............ |
13,96 | 14,7 |
14,8 |
| пропан ........... | 29,1 |
31,0 | 31,4 |
| изобутан .......... |
51,6 | 56,0 |
57,8 |
|
н-бутан........... | 60,0 | 66,4 | 69,7 |
| изопентан .......... |
82,1 | 92,2 |
97,9 |
| н-пентан .......... | 87,4 |
96,0 | 99,4 |
| гексаны .......... |
97,1 | 99,8 |
100,0 |
| гептаны и более тяжелые уг | |||
| леводороды ........ | 100,0 | 100,0 |
100,0 |
|
Температура, °С; | |||
| свежего сорбента...... | 32,2 |
26,7 | 32,2 |
| сырого газа......... |
27,8 | 26,7 |
27,8 |
| верхней тарелки (расчетная) , |
35,5 | 34,4 |
37,2 |
| нижней тарелки (расчетная) , |
31,7 | 28,9 |
31,7 |
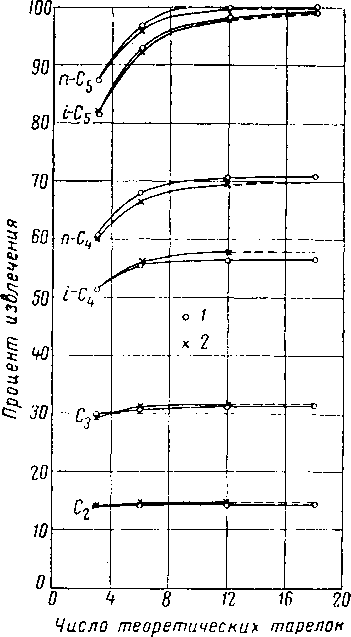
Рис. XIII. 25. Процент извлечения различных компонентов, вычисленный по методу Харберта и методу Хортона — Франклина (Катц и Жа-са) [XIII. 23].
I —. метод Хортона — Франклина; 2 — метод Харберта.
| 12 теоретических тарелок |
...... | |||||||||||||
| / | \ | |||||||||||||
| \ | V | |||||||||||||
| I- | \ | У | ||||||||||||
|
\ | / |
|||||||||||||
| ^2 | ||||||||||||||
| 1 |
1 | |||||||||||||
131 0,090
0,094 0,098
0,102 0.106 LJU
О,ПО
21—28_29 30 31_32 33 34 35 36 31 38 39 40 41 42°С бента обычно характеризуют как процесс, прямо
С помощью метода Харберта были произведены расчеты для 6- и 12-тарелочных абсорберов. Результаты этих расчетов приведены в табл. XIII. 6. Процент абсорбции графически изображен на рис. XIII. 25, где для сравнения приведены также результаты, полученные методом Хортона и Франклина. Соотношения L/V и температуры, полученные при расчетах 12- и 3-тарелочных абсорберов, приведены на рис. XIII. 26.
0
1 2 3
* *
0
? 5
О)
1 5
§ 7 CJ ?5
9
10 11 12
7. ВЫПАРКА ЛЕГКИХ УГЛЕВОДОРОДОВ ИЗ СОРБЕНТА
Абсорбция легких углеводородов из природного газа сорбентом составляет первый этап их извлечения. Абсорбированные углеводороды необходимо выделить из сорбента путем процесса, известного под названием выпарки. Выпарка (десорбция)— это выделение целевого продукта из жидкой в паровую фазу. Массообмену при этом способствуют высокая температура и низкое парциальное давление выпариваемых компонентов. Высокая температура создается предварительным нагревом питания, а низкое парциальное давление десорбируемых газов над жидкой фазой обеспечивается низким давлением в выпарных колоннах и подачей инертного газа (обычно водяного пара) в нижнюю часть колонны.
Хотя выпарку легких углеводородов из сор-
о.т от
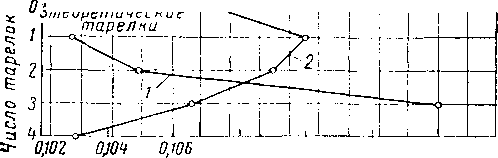
о.т
0,108 0,ПО
LJV
противоположный абсорбции, в ней есть все же свои особенности. Например, для облегчения разделения выпаренных легких углеводородов и сорбента в промышленных десорберах предусматривают зону орошения (рис. XIII, 14). Следует упомянуть и такие проблемы, как поглощение водяного пара горячим сорбентом и частичная конденсация легких парообразных углеводородов при охлаждении целевых компонентов.
При расчете десорбции, как и при расчете абсорбции, достаточно знать коэффициент отпаривания одного компонента, чтобы получить соответствующие показатели для всех других. Углеводороды низкого молекулярного веса, как например бутаны, отпариваются полностью; поэтому выходы в десорбере обычно определяют процентом извлеченных гексанов (или гептанов) и соответственно более тяжелых углеводородов. При двухступенчатой десорбции, когда последовательно используются колонны высокого и низкого давления, в первой колонне получают за счет снижения четкости десорбции, больший выход газов высокого давления.
26. Кривые температуры и соотношения для абсорбера [XIII. 23].
1 — в зависимости от числа тарелок (второй расчет); 2 — температура в зависимости от числа тарелок.
Если вычисленные соотношения L/V не совпадают с ориентировочно принятыми, повторяют расчет, решая уравнения (XIII. 61) — (XIII. 63). Для этого нужны новые температуры, их берут предположительно на основе расхождений, обнаруженных между тепловыми балансами по отдельным тарелкам и общим балансом.
Для успешного применения метода Харберта решающее важное значение имеет выбор температуры верхней тарелки. Если тепловые балансы, составленные по последующим тарелкам колонны, дают температуру нижней тарелки, отличную от полученной при расчете общего теплового баланса по колонне, то выбирают новую температуру верхней тарелки, предполагая при этом, что иривая перепада температур по колонне остается почти постоянной.
Если же вычисленные соотношения LJV близки к принятым, а температуры значительно отличаются, можно вычислить для температур, взятых при втором приближении, тепловые балансы (по последующим тарелкам и по всей колонне), не входя в расчеты составов. Однако в конце концов необходимо рассчитать составы и баланс энтальпии по всей колонне подобно тому, как это было сделано для трехтарелочного абсорбера.
Рис. XIII.
Расчеты абсорбции, охарактеризованные выше, можно использовать и для определения десорбции. При двухступенчатой десорбции в колонне высокого давления можно принять давление максимум 14 кГ/см2, а при одноступенчатой — 7 кГ/смг. Насыщенный сорбент перед подачей в десорбер подогревают (например, при помощи огневого подогревателя) до температуры 175— 260° С в зависимости от желательной глубины извлечения и давления десорбции. Для этого нужно установить состав и количество жидкости и паров, поступающих в ректификационную зону выпарной колонны. Константы равновесия для высоких температур можно взять по данным из главы VI.
Для установления степени десорбции, получаемой при определенном числе равновесных тарелок и определенном соотношении между жидкостью и газом L/V, можно воспользоваться расчетом по коэффициентам
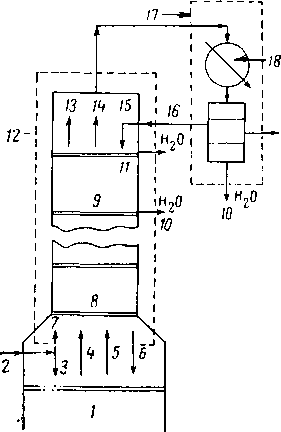
Рис. X111. 27. Ректификационная зона выпарной колонны (показан состав потоков):
1 — питающая тарелка; 2 — питание;
3 — неиспарившееся питание; 4 — от-бензиненный сорбент и извлеченный углеводород; 5 — десорбционный водя-ной пар; 6 — орошающий сорбент; 7 — испарившееся питание; 8 — нижняя та-релка ректификатора; 9 — вторая та-релка: 10 — отвод воды; // — верхняя
тарелка ректификатора; 12 — граница ректификационной части колонны; 13 — водяной пар; 14 — углеводородное орошение и целевой продукт; 15 — углеводородное орошение; 16 — орошение;
17 — граница конденсационной части;
18 —. конденсатор: 19 — целевой про
дукт,
отпаривания. Фактически для определения коэффициента извлечения в стационарном состоянии нужно произвести несколько циклов расчетов, В результате применения орошения и вследствие разницы между температурами водяного пара и горячего сорбента можно ожидать наличия в десорбционной зоне выпарной колонны перепада температур порядка 2,8—8° С.
Определив количество водяного пара, в том числе и количество растворенного водяного пара [XIII. 13], выходящего с низа колонны вместе с остаточным продуктом, можно установить примерное количество паров, поступающих в ректификационную зону десорбера. Можно без риска ошибки предположить, что в десорбционной зоне свободная вода не образуется. Метод определения потребного орошения в ректификационной секции предложен Хатчинсоном (Hutchinson) [XIII. 20]. Для упрощения анализа ректификационной секции расчеты можно вести по отдельным потокам (см. рис. XIII. 27). Пары, поднимающиеся в ректификатор с питающей тарелки, состоят из следующих компонентов: 1) испарившейся части питания; 2) отбензиненного сорбента и извлеченных углеводородов; 3) десорбцион-ного водяного пара, не растворенного в тощем сорбенте.
Жидкость на выходе с нижней тарелки ректификационной части колонны состоит в основном из используемого для орошения сорбента и некоторых легких углеводородов. Пары, выходящие с верхней тарелки ректификационной зоны колонны, можно разделить на: I) водяной пар, который при температуре на верхней тарелке около 93° С смешан с парообразными углеводородами; 2) углеводородное орошение плюс целевой продукт.
Сконденсировавшаяся вода отводится с верхних тарелок ректификационной части колонны. Как показано на рис. XIII. 27, на верхнюю тарелку возвращается в виде орошения лишь сорбент, поскольку отделение его от целевого продукта не представляет трудности.
Для вычисления углеводородного орошения можно воспользоваться тепловым балансом по границе 12 (рис. XIII. 27) при условии, что все другие потоки можно вычислить или определить иным способом. Для определения нагрузки конденсатора можно применить тепловой баланс по границе 17. Чтобы определить с помощью теплового баланса по границе 12 коэффициент орошения, необходимо установить количество каждого потока следующим путем.
1. Испарившееся питание — путем расчета мгновенного испарения.
2. Отбензиненный сорбент — путем расчета десорбции.
3. Извлеченные углеводороды — путем расчета десорбции.
4. Десорбционный водяной пар — путем расчета десорбции.
5. Количество орошающего сорбента — исходя из общего количества сорбента, поступающего на нижнюю тарелку ректификатора.
6. Водяной пар, выходящий из верхней тарелки ректификатора, вычисляется как неизвестное (количество орошения), деленное на сумму орошения и целевого продукта.
7. Вода, отведенная с тарелок, определяется вычитанием количества шестого потока из четвертого.
Тепловой баланс можно тогда сформулировать с одним неизвестным—количеством орошения и, таким образом, определить это количество. Величину шестого потока можно выразить как
W = (R +0) Pw ... ,
P — Pw
где W — число кмоль воды на выходе с верхней тарелки ректификатора; R—число молей углеводорода, возвращаемого для орошения; О — число молей углеводорода, отбираемого в качестве верхнего продукта; рш — парциальное давление водяного пара при температуре верхней тарелки; р — суммарное давление на верхней тарелке.
Тепловую нагрузку конденсатора можно определить по балансам энтальпии в пределах границы 17. Количество каждого потока в пределах границы 17 следует определять по уравнениям теплового и материального балансов.
При расчете маслосорбционной установки стационарные количества потоков, поступающих в абсорбер и де-сорбер, в том случае, когда пары из частичного конденсатора возвращают в абсорбер, приходится определять путем последующих приближений. Вследствие сезонных и эксплуатационных колебаний в составе газа можло ожидать значительных изменений в загрузочной части десорбера, коэффициент запаса, применяемый при расчетах, должен быть высоким [XII. 20]. Поскольку для выпарных колонн характерно высокое соотношение между потоками жидкости и газа, в этих колоннах тарелки и сливные стаканы, расположенные ниже питающей тарелки, должны быть спроектированы с таким расчетом, чтобы они могли справиться с большим количеством жидкости.
Фракционная перегонка, как и процесс абсорбции — десорбции, является наиболее широко применяемым методом разделения углеводородов. В этой главе рассматриваются расчеты фракционной перегонки двух-, трех-и многокомпонентных систем, а также вопросы массо-обмена и гидравлического режима работы колпачковых тарелок и колонн. Более подробно эти вопросы трактуются в [XIV, 2, XIV. 4, XIV. 7, XIV. 11, XIV. 16, XIV. 28,
