Двумерные установившиеся течения
Глава IV
Двумерные установившиеся течения
Теория двумерных — плоскопараллельных и осесимметричных — установившихся течений составляет обширный и богатый конкретными фактами раздел газовой динамики. Исторически эта теория выросла из потребностей аэродинамики самолета и снаряда. При этом ограничение двумерной моделью оправдано примерно теми же соображениями, которые уже высказывались в начале главы III по поводу одномерных движений.
Внешне модель двумерных установившихся течений имеет много общего с моделью одномерных движений газа. Их роднит, например, наличие лишь двух независимых переменных и возможность наглядного изображения газодинамических ситуаций на плоскости течения. Кроме того, сверхзвуковые установившиеся течения обладают определенным свойством эво-люционности и для них плоскость течения (точнее, плоскость потенциала) может трактоваться как плоскость событий.
Для двумерных установившихся течений газ с уравнением состояния «с разделенной плостностью» (10.26), в частности — для политропного газа, справедливо преобразование Мунка-Прима (10.27). В этом случае можно ограничиться рассмотрением изэнтропических течений.
Радикальное отличие от модели одномерных движений состоит в том, что основные дифференциальные уравнения уже не являются гиперболическими для всех возможных течений. Это влечет подразделение установившихся течений на дозвуковые (эллиптический тип уравнений), сверхзвуковые (гиперболический тип) и трансзвуковые или околозвуковые (смешанный тип). Для каждого типа течения характерны свои постановки корректных краевых задач и свои методы исследования.
До определенного предела теория развивается одинаково для плоскопараллельных и осесимметричных течений. Однако более богатая результатами (за счет более широкого группового свойства) теория плоскопараллельных течений излагается в этой главе и более детально. Для нее развивается один из основных методов изучения и решения конкретных задач о безвихревых течениях — метод годографа. Разработанный еще в начале текущего столетия С. А. Чаплыгиным метод годографа и сегодня остается наиболее эффективным в этой области газовой динамики. Его ценность не только в том, что он позволяет получать аналитические решения ряда конкретных задач, но также в возможности выявления с его помощью качественных закономерностей течений.
Одним из наиболее ярких достижений современной газовой динамики явилось познание закономерностей перехода через скорость звука. Трансзвуковая газодинамика дала толчок развитию новой области математической физики — теории уравнений смешанного типа. Вместе с тем модели околозвуковых, а также гиперзвуковых течений особенно тесно примыкают к практическим задачам. Однако сегодня их разработку вряд ли можно считать законченной. Теоретическая газовая динамика еще далеко не разрешила всех своих проблем и нуждается в дальнейшем развитии.
§ 22. Уравнения безвихревого течения
Плоскопараллельные и осесимметричные течения. Изучаемые в этом параграфе плоскопараллельные и осесимметричные течения газа обладают общими свойствами. Основными величинами здесь являются компоненты вектора скорости u = (u,v), плотность р, давление р и энтропия S, причем последние связаны уравнением состояния р = f(p, S) и газ предполагается нормальным (см. § 2). Основные величины рассматриваются как функции декартовых координат (х,у). При этом некоторого разъяснения требует изображение осесимметричных течений. Прежде всего, безоговорочно принимается, что ось симметрии совпадает с прямой у = 0. Далее, физическая картина осесимметричного течения восстанавливается в трехмерном пространстве R3 путем вращения меридиональной полуплоскости у > 0 вокруг оси у — 0. При повороте на угол 180° эта полуплоскость становится продолжением исходной, а любое изображение — зеркально симметричным исходному. Ясно, что этим же свойством обладает преобразование симметрии
х' = х, у' = -у, и' = и, г/ = -v, (1)
причем остальные основные величины сохраняются. Следовательно, условие симметрии (1) является необходимым для правильного описания осесимметричных течений на всей плоскости R2(x,y). Во всех случаях плоскость R2(x, у) называется плоскостью течения. Используется координатная форма записи различных соотношений, причем частные производные обозначаются соответствующими индексами.
Исходные дифференциальные уравнения для основных величин следуют, например, из уравнений (12.17), (12.19):
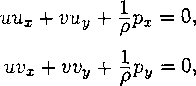
![]()
uSx + vSy = 0,
где параметр и = 0 для плоскопараллельных течений и v — 1 для осесимметричных течений. Здесь первые два уравнения описывают закон сохранения нмпульса, третье есть уравнение неразрывности и последнее — одна из форм закона сохранения энергии (см. § 3). Легко проверяется, что уравнения (2) допускают преобразование (1). Поэтому требование выполнения условия симметрии (1) означает, что в случае и = 1 рассматриваются только такие решения, которые инвариантны относительно этого преобразования. Следовательно, если область непрерывного осесимметричного течения содержит ось у — 0 (или некоторый ее интервал), то необходимо должно выполняться условие
(3)
v(x, 0) =0, {v — 1).
Линии тока. Основным качественным элементом при анализе и графическом наглядном представлении решений системы (2) являются линии тока, которые для любых установившихся течений уже были введены определением 10.1. С учетом специфики двумерности течения они определяются здесь как интегральные кривые дифференциального уравнения
dx dy
(4)
u{x,y) v(x,y)'
Это определение равносильно тому, что в каждой точке вектор скорости и = (и, v) направлен по касательной к линии тока, проходящей через эту точку. В симметричной записи (4) не предопределяется, какая из переменных, х или у, является независимой, а какая — зависимой. Область течения, в которой вектор скорости удовлетворяет условию Липшица по обеим переменным и и2 ~ v2 Ф 0, однократно покрыта семейством линий тока. Их изображение на плоскости Л2 (ж, у) дает наглядное представление
о течении газа, частицы которого как раз и движутся вдоль линии тока.
В дальнейшем анализе используются операторы дифференцирования вдоль линий тока Di и по нормали к линиям тока Dn:
Di = u-Q- + v-@-, Ox ay
(5)
Dn — ~v~n~ + и~к~-ox ay
Функция тока. С линиями тока тесно связан другой важный элемент описания течения — так называемая функция тока. Ее определение основано на том, что уравнение неразрывности (2) допускает равносильную запись в виде дифференциального закона сохранения:
(6)
(;уири)х + {yupv)y = 0.
Соотношение (6) показывает, что выражение —y^pv dx + уи pudy есть полный дифференциал некоторой функции ф = ф(х, у), в силу чего ее частные производные даются формулами
(7)
Эта функция ф и называется функцией тока. Итак, для любого течения газа существует функция тока ф, которая определена уравнениями (7) с точностью до произвольного постоянного слагаемого. Если и = 1 и в области непрерывного течения содержится интервал оси у 0, то из (7) следует, что фх(х, 0) = 0. В этом случае принимается соглашение об однозначном определении функции тока дополнительным условием
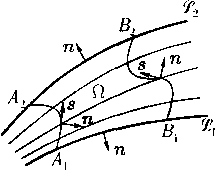
Рис. 1
ф(х, 0) = 0.
(8)
Первое свойство функции тока состоит в том, что она постоянна вдоль каждой линии тока. Это очевидно, так как непосредственно из определения (7) следует равенство Dt ф = 0.
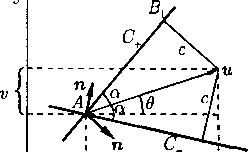
Второе свойство функции тока связано с расходом газа между двумя линиями тока. Пусть линии тока и !?¦> расположены в области непрерывного течения, и пусть А\ Л2 и BiB2 — гладкие кривые (сечения), ограничивающие вместе с и У2 область Q С R2(x,y) (рис. 1). Согласно интегральному закону сохранения массы (1.4), записанному для плоскопараллельных или осесимметричных движений, в установившемся течении выполняется
где п — внешняя нормаль к границе Г области Q. Здесь граница Г состоит из четырех кривых: сечений AiA2 и В\В2 и отрезков линий тока А\В\ С !?\ и А2В2 С i?2- Очевидно, что в силу определения линий тока и • п = = 0 на А\В\ и А2В2. Пусть s — касательный вектор к Д1Д2 или В1В2, указывающий направление перемещения от А\ к Лг или от В\ к В2. Удобно изменить направление орта нормали п, выбрав его так, чтобы оно после поворота на 90° против часовой стрелки совпадало с направлением s. При таком выборе нормали п равенство (9) принимает вид
![]()
Л1Л2
ВгВ2
Величина 1,-^2) называется расходом газа между линиями тока !?\
и Равенство (10) показывает, что это определение корректно, так как в силу (10) расход Q(i?i,i?2) не зависит от выбора сечения.
Ясно, что благодаря принятому соглашению о направлении нормали п из представления из da = (dx, dy) следует представление nds = (dy, —dx). Значит, u • nds = —vdx + udy и в силу определения (7) подынтегральное выражение в (10) оказывается совпадающим с дифференциалом функции тока:
у”ри ¦ nds = yvp(~vdx + udy) — xjjxdx + ipydy = dtp. Поэтому равенство (10) равносильно следующему:
(П)
Соотношение (11) и выражает второе свойство функции тока: расход газа между двумя линиями тока равен приращению функции тока. Из него следует, что в области непрерывного течения функция тока различает линии тока в том смысле, что на разных линиях тока она необходимо имеет разные значения.
В § 10 уже были получены два интеграла, (10.6) и (10.10), основных дифференциальных уравнений движения газа, справедливые для любого установившегося течения. В силу свойств функции тока, для уравнений (2) они могут быть записаны в уточненной форме, подчеркивающей зависимость констант интегрирования от ф. Это интеграл энтропии
и интеграл Бернулли
(13)
Вектор вихря ш в случае двумерных течений легко подсчитывается по формуле (11.1). При этом в случае v = 1 надо перейти к полярным координатам в плоскости (у, z) и принять во внимание, что в настоящем параграфе v обозначает у-компоненту вектора скорости в той меридиональной плоскости, в которой w = 0. Вычисление показывает, что во всех случаях и> имеет только одну ненулевую компоненту, равную (в обозначениях данного параграфа) величине и = vx - иу.
Изэнтропичность безвихревых течений. Дальнейший анализ двумерных течений связан с предположением о безвихревом характере движения (см. § 11). При этом система (2) дополняется уравнением и> = 0 или
vx ~ Uy = 0. (14)
В таком течении, согласно лемме 11.1, должно выполняться соотношение (11.3), которое здесь сводится к одному скалярному и переписывается в виде
рх^у Ру^Х - 0- (^5)
Очевидно, что соотношение (15) может быть справедливо лишь в следующих трех случаях: (a) S = const тождественно; (b) р = const тождественно; (с) функции р и S связаны функциональной зависимостью р — p(S). Предположение (а) об изэнтроппчности течения является основным; такие течения в дальнейшем будут изучаться подробно. Предположение (Ь) приводит к классическим уравнениям безвихревых течений несжимаемой жидкости, которые в газовой динамике играют роль приближенной предельной модели (см. § 9). Что же касается случая (с), то он требует специального исследования, результаты которого приводятся ниже.
Если S ф const и р = p(S), то все термодинамические параметры становятся функциями только энтропии S. В силу интеграла (12) это равносильно тому, что все они являются функциями только величины функции тока ик Но тогда из интеграла Бернулли следует, что и модуль скорости q тоже является функцией только и. Кроме того, в силу равенства Dip = p'( ip)Diip = 0 уравнение неразрывности (2) упрощается до следующего:
их ^ Vy ¦+ JjV = 0. (16)
Для удобства дальнейшего анализа вместо ф вводится новая величина ?, определяемая интегралом
t
а ее производные получаются из формул (7):
ix = -yl'v, ty^y^u. (18)
В силу представления модуля скорости q = <?(?) дифференцирование соотношения и2 + v2 = q2 по х и по у с учетом равенств (14) и (18) дает уравнения
uux + vuy = -yvqq'v,
V /
uvx -I- vvy = у qq u,
равносильные уравнениям импульса (2). Здесь штрихом обозначена производная по ?. Итак, для трех функций, и(х,у), v(x,y), и ?(ж, у), получилась система из шести дифференциальных уравнений первого порядка (14), (16), (18) и (19), в которые еще входит пока неопределенная функция <?(?). Так как из этой системы получаются выражения для всех производных первого порядка (для функции ? они даются формулами (18)), то при данной функции q(?) ее общее решение может зависеть самое большее от двух произвольных постоянных. Однако вопрос о существовании решений этой системы нетривиален, так как получаемые выражения для производных должны удовлетворять условиям совместности. Легко заметить только, что всегда существует постоянное решение
и = Щ = const, V = Do = const, причем в случае v = 1 в силу (3) должно быть г>о = 0.
Теорема 1. Всякое осесимметричное безвихревое течение с переменной энтропией есть поступательное движение в направлении оси симметрии. Не постоянное пл о с ко п ар ал л ел ь но е безвихревое течение с переменной энтропией описывается формулами
и - -ayq2, v2 = q2 - a2y2q4. q = exp«), (20)
где a = const, причем линии тока этого течения образуют семейство концентрических окружностей.
Доказательство. Если ? = ?(у), то v = 0 и и.х — иу -- 0, что приводит к постоянному решению. В противном случае можно взять у и ? в качестве независимых переменных. Тогда, если временно положить и = й(у. ?), v = v(y,i), то уравнения (19) приведутся к виду
иу = -yvqq'< vvy = у”qq и.
Интегрирование по у дает выражения
U =
y~
Vh)2
V2 =
Ы
y +
У‘ ' •
~VTTqq r/(^’
W ,.2 2 yv+x
jW f(0 + h(0>
где / и h — произвольные функции только ?. По построению найденные функции и и v удовлетворяют уравнениям (19). Легко проверить, что с этими функциями обращается в тождество также и уравнение (14). Остается удовлетворить уравнению (16). После подстановки в него найденных из (21) производных от и и v и сравнения членов с одинаковыми степенями у получаются следующие результаты. В случае v = 1 необходимо h — 0 и либо / = 0, либо q' = 0 и / = const. Обе возможности приводят к постоянному решению. В случае v = 0 существует нетривиальное решение
h - q'2 - /2, / = bq2, q' = aq
с постоянными а и Ь. Отсюда, с точностью до несущественного переноса по переменной у, получаются формулы (20). В силу этих формул дифференциальное уравнение линий тока (4) принимает вид
\/(Г2 - a2y2dx = —aydy
и сводится к квадратуре, так как q = const вдоль линии тока. В интеграле этого уравнения
(ах - х0)2 + а2у2 = q~2(0 (22)
константа интегрирования хо, вообще говоря, может зависеть от переменной Однако дифференцирование соотношения (22) по у с учетом формул (18) и (20) приводит к равенству х'0(?) = 0, т.е. х0 = const. Следовательно, уравнение (22) описывает семейство концентрических окружностей, радиус которых зависит от ¦
Этот результат означает, что достаточно широкий класс двумерных установившихся безвихревых течений образуют лишь течения с постоянной энтропией. Однако необходимо помнить, что если в течении присутствует скачок уплотнения (см. § 10), то за ним образуется, вообще говоря, вихревое течение с переменной энтропией. В оставшейся части данного параграфа течение предполагается безвихревым и изэнтропическим.
Замечание 1. Каждое безвихревое изэнтропическое течение является изо-энергетическим (см. § 10), т.е. в нем константа q^ в иитырале Бернулли (13) не зависит от ф. Этот факт легко проверяется непосредственно, дифференцированием соотношения (13) по х и у с использованием уравнений (2) и (14).
Основные уравнения. Важное свойство рассматриваемых течений состоит в том, что они описываются системой из двух уравнений для компонент вектора скорости. Первое из них есть уравнение (14), а второе выводится путем исключения производных рх и ру, из уравнения неразрывности (2). Для этого используются выражения этих производных, из уравнении импульса (2) в силу равенства dp = с2dp:
с2рх = -р(иих + VUy), с2ру = -p(uvx + VVy).
Окончательно получается следующая система уравнений двумерных безвихревых изэнтропических течений:
иу vx — О,
(23)
(и2 - С2)их + 2UVUy + (v2 - c2)vy = 7jC2V,
где квадрат скорости звука с2 выражается через q2 = и2 + v2 из интеграла Бернулли
q2 + 1{с2) = q2m (24)
с постоянной, в силу замечания 1, величиной q^.
В случае политропного газа интеграл Бернулли (10.12) удобно записывать с критической скоростью (10.13):
Уместно вспомнить, что анализ типа уравнений любых установившихся течений уже был выполнен в § 10. Он легко повторяется для системы (23) и показывает, что она имеет эллиптический тип на дозвуковых течениях и гиперболический тип на сверхзвуковых течениях (см. определение 10.3). Это различие существенно, оно с необходимостью влечет различие в постановках, методах исследования и решениях краевых задач. Более подробный анализ каждого типа течений и соответствующих задач будет проводиться в следующих параграфах. Здесь же внимание концентрируется на тех фактах, которые априори с типом системы (23) не связаны.
Уравнениям (23) можно придать множество равносильных форм, каждая из которых имеет свои преимущества при анализе тех или иных конкретных задач об отыскании газовых течений. Дальнейшее изложение посвящено выводу и предварительному изучению наиболее важных эквивалентных форм записи основных уравнений (23).
Потенциал скоростей. Первое из уравнений (23) равносильно существованию функции = <р(х,у), производные которой даются формулами
'-Рх = u, ipy- V. (26)
Эта функция называется потенциалом скоростей. Ясно, что данным безвихревым полем скоростей (u,v) его потенциал определен единственным образом с точностью до постоянного слагаемого. Из сравнения определений (7) и (26) вытекает следующая связь функции тока с потенциалом скоростей:
Vx = У = У Р^Рх, (27)
где плотность р выражается через q2 = р2 + ц>2 с помощью интеграла Бернулли (24). Поэтому соотношения (27) образуют независимую систему из двух дифференциальных уравнений первого порядка для искомых потенциала скоростей р и функции тока ф, равносильную системе (23).
При наглядном графическом изображении течений на плоскости R2(x,y) наряду с линиями тока полезны также линии равного потенциала ip(x.y) — const, или эквипотенциали. Так как |Vy>! = q, то расстояния между двумя эквипотенциалями характеризуют величину скорости течения q. Кроме того, из (27) следует равенство Уф ¦ V'-p — 0, а это значит, что в любой точке плоскости течения проходящие через нее эк-випотенциаль и линия тока взаимно ортогональны. Следовательно, линии тока и эквипотенциали всегда образуют на плоскости течения ортогональную сеть. Вытекающее из (27), в силу определения операторов (5), равенство
дает представление о соотношении сторон прямоугольных ячеек этой сети.
После подстановки выражений для и и г) из (26) во второе уравнение (23) последнее становится уравнением для tp. Разумеется, оно должно совпадать с уравнением (11.20), которое надо только взять в соответствующем двумерном варианте. Любым из этих двух способов получается следующее уравнение для потенциала скоростей:
(и — с Урхх "t~ 2uvipXy -г (и — с )^Руу = уС ру, (28)
которое, конечно, надо рассматривать одновременно с интегралом Бернулли (24). В частности, в случае политропного газа уравнение для потенциала
у;хх + 2ш^13/+
S^yy =
(u2 + v2) .
(2Щ
-I»
7 + 1/2 2\ 7 — 1-2
-J~(u -с») + -Ly-^2 +
7+1,2 7_1/..2 I „.2
-гг +
-с; -
Метод годографа. Существует специальный метод исследования двумерных безвихревых изэнтропических течений газа, имеющий большое теоретическое и практическое значение, — так называемый метод годографа. Он основан на том, что описание таких течений сводится к отысканию отображения В?(х,у) —» R2(u,v), определяемого формулами
и = и(х,у). v = v(x,y). (30)
Определение 1. Плоскость R2(u,v) называется плоскостью годографа. Для каждого течения, заданного формулами (30), годографом любого, содержащегося в области течения, множества точек плоскости R2(x,y) называется образ этого множества при отображении (30) на плоскость R2(u,v). В частности, определен годограф любой точки, линии или области.
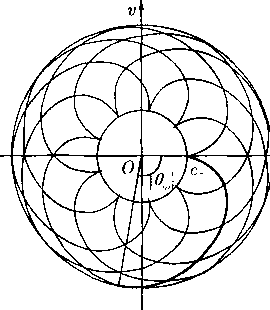
На плоскости годографа вектор скорости и изображается радиус-вектором точки (u,v), приложенным в начале координат. Ясно, что в силу интеграла Бернулли (24) годограф любого течения содержится внутри круга радиуса qm с центром в начале координат (рис. 2). При этом все дозвуковые течения попадают внутрь круга радиуса с», а все сверхзвуковые течения — в кольцо с» < q < qm (см. замечание после определения 10.3). Окружность q = qm является годографом состояний вакуума.
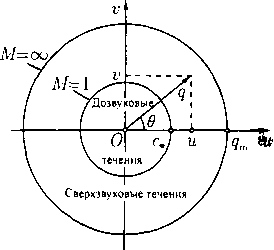
Отображение (30) будет взаимно однозначным не для любого течения. Например, каждая область постоянного течения имеет своим годографом одну точку. Исследование локальной взаимной однозначности этого отображения сводится к выяснению того, обращаете» ли якобиан
T_d{u,v)_.........
ч UxVy UyVx (31)
д(х, у)
в нуль или нет. Как известно, тождество J — 0 равносильно существованию функциональной зависимости между функциями (30). Но если в некотором течении и = F(v) (или v = F(u)), то согласно определению 13.1 это течение есть простая волна. Поэтому важно найти и исследовать все решения — простые волны системы (23). В случае v = 0 множество простых волн достаточно обширно и будет подробно изучено в § 24.
Простые волны осесимметричных течений. В случае v = 1 система (23) имеет точное решение и = 0, v = v(y), принадлежащее классу простых волн. Оно описывает двумерный источник газа и получается с помощью интеграла уравнения неразрывности (2) в виде соотношения, аналогичного (11.25), а именно, ypv -- Q = const, Качественная картина течения в двумерном источнике такая же, как и для сферического (см. рис. 11.2).
Все остальные простые волны описываются следующей теоремой, в которой предполагается, что решение не является постоянным или решением типа источника.
Теорема 2. Всякая осесимметричная простая волна есть автомодельное решение системы (23) и, с точностью до переноса по координате х, дается формулами
и = и(Л), v v(\): \ = х/у. (32)
Доказательство. Пусть простая волна определена зависимостью и = F(v). Тогда, после подстановки в систему (23) получаемых из этого равенства выражений для производных, она примет следующий вид:
vx = F'vy,
[(и2 — c2)F'2 + 2uvF’ +- (гг - c2)\yvy — c2v. ^ ^
где штрих обозначает производную функции F по и. Выражение в квадратной скобке не может быть тождественно равно нулю, так как иначе получилось бы, что v = 0 и и = F(0) = const, т. е. постоянное течение. Поэтому из второго уравнения (33) можно найти величину yvy как функ-
Тогда соотношение yvtJ = G(v) преобразуется в соотношение угиу 4- w = О, которое интегрируется и дает интеграл yw = ?{х), где ?(х) — некоторая, пока произвольная функция. Но ясно, что для величины w, так же как и для ъ\ справедливо уравнение вида первого уравнения (33), а именно:
шх = —a(w)wy
цию только v, например yvv = G(v). Здесь удобно заменить переменную v вспомогательной переменной п,\ определив последнюю формулой
![]()
Подстановка сюда найденного выше выражения w = ?{х)/у дает соотношение с разделенными переменными ?'(х) = wa(w), которое, в силу независимости переменных х и ш, может быть справедливым, только если ?'{х) = Ъ и wa(w) = Ъ с постоянной Ь ф О (при 6 = 0 получается двухмерный источник). Поэтому, с точностью до переноса по х, будет ?(х) = Ьх, и, значит, w = Ьх/у. ¦
Ясно, что во всех случаях годограф области, занимаемой простой волной, на плоскости течения есть линия на плоскости годографа. Поэтому в области простой волны отображение (30) не однолистно. Следовательно, за исключением постоянных течений и простых волн, течение общего характера отображается на плоскость годографа локально взаимно однозначно. В таких течениях величины и и v могут быть приняты в качестве независимых переменных.
Уравнения на плоскости годографа. Метод годографа и состоит в рассмотрении определяющих течение величин как функций переменных годографа (u.v). Существует несколько вариантов получения преобразованных уравнений (23) на плоскости годографа, каждый из которых имеет свои преимущества и недостатки. Ниже излагаются два наиболее часто используемых варианта такого преобразования.
Имея в виду охват единым анализом как плоскопараллельных, так и осесимметричных течений, целесообразно принять в качестве искомых величин координаты точки (х, у). Использование свойств якобианов позволяет выполнить преобразование производных с помощью цепочки равенств вида
_ д{и, у) _ д(и, у) д{и, у) _ д{х,у) d{u,v)d{x,y) Vv'
где использовано обозначение (31). Аналогично преобразуются остальные производные, что приводит к стандартным формулам перемены ролей зависимых и независимых переменных:
"U,x — JVvi 'Му — vx Jyu'. Vy — Jxu. (34)
В результате подстановки выражений (34) в систему (23) и п0Я$еде$СЯ>ИС-комая система уравнений на плоскости годографа:
Уи — 0,
(it2 - C2)yv - 2uvxv + (г)2 - c2)xu = ^c2v{xuyv - xvyu).
Непосредственно видно, что система дифференциальных уравнений (35) в случае и — 0 является линейной, но остается нелинейной, если г/ - L В этом факте коренится принципиальное различие описания плоскопараллельных и осесимметричных течений.
Введение потенциала Лежандра Ф = Ф(и, г;) с помощью соотношений
х = Фи, у = Ф„ (36)
позволяет удовлетворить первому из уравнений (35). При этом второе принимает форму уравнения Монжа-Ампера:
{и2 - с2)ФУХ1 - 2иьФиу + (v2 - с2)Фии = !~{Фии®м - О- (37)
Дифференцированием по а: и у легко проверяется, что потенциал Лежандра Ф связан с потенциалом скоростей <р соотношением
ip = хи + yv — Ф. (38)
Переход от к Ф согласно равенству (38) называется преобразованием Лежандра.
Особенно простую форму принимает уравнение (37) в случае плоскопараллельных течений (когда и = 0) после перехода к полярным координатам (q,9) на плоскости годографа (см. рис. 2):
u — qcos9. v = qsin9. (39)
После небольших вычислений уравнение для потенциала Лежандра Ф = ф(д, 9) плоскопараллельных течений оказывается таким:
(м2 - 1)Фвв - <г2Ф„ -г (М2 - 1)9ф, = о, (40)
где использовано обозначение числа Маха М = g/с. Важное свойство уравнения (40) состоит в том, что оно не только линейно, но в нем переменные q и в разделяются. Это дает возможность строить его решения методом разделения переменных. Очевидно также, что уравнение (40) имеет гиперболический тип, если М > 1 (сверхзвуковое течение), и эллиптический тип, если М < 1 (дозвуковое течение). Рассматриваемое для всевозможных скоростей 0 ^ М < ос, т. е. в максимально широкой области плоскости годографа (см. рис. 2), уравнение (40) является уравнением смешанного типа. Кроме того, это уравнение вырождается (в смысле его типа) также на окружности вакуума М = ос, где с = 0.
В случае политропного газа, в силу вытекающей из интеграла Бернулли (25) формулы
(41)
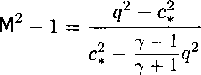
уравнение для потенциала Лежандра таково:
(<72 - с;) Фев ~ ~ <72фте + {Я2 ~ cl)q= 0. (42)
Уравнения С. А. Чаплыгина. Другой вариант преобразования системы (23) на плоскость годографа состоит в том, что в качестве искомых величин берутся потенциал скоростей р и функция тока ip. Это преобразование особенно эффективно в случае плоскопараллельных течений, для которых оно и дается ниже.
Непосредственно из определения потенциала скоростей (26) и функции тока (7) следуют равенства (для и = 0)
dip = и dx + v dy, dф = —pv dx + pu dy.
После разрешения относительно dx и dy и перехода к полярным координатам (39) эти равенства принимают вид
![]()
Если считать q и в функциями переменных у> и ф, то условие полного дифференциала для dx
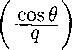
d_
dip
JL
дф
sin 9
pq
в раскрытой форме приводится к соотношению
Аналогично, условие полного дифференциала для dy дает
d
А. п -Le
„2 Яф pq
1
cos в
— sin в
<??>
dq \РЯ
Совместное рассмотрение этих соотношений показывает, что выражение в каждой квадратной скобке должно равняться нулю. Входящая сюда вели-, чина d(l/pq)/dq вычисляется с помощью интеграла Бернулли (24) и оказывается такой (фактически она уже вычислена в (10.22)):
М2 - 1 pq2
А ±
dq \РЯ
(44)
Поэтому из предыдущих соотношений следуют уравнения о - м2-! Яо
^ ~ pq ^ р 'р'
(45)
С помощью стандартных формул перемены ролей зависимых и независимых переменных (аналогичных (34)) из (45) окончательно получается искомая система уравнений на плоскости годографа:
м
1
(46)
pq ?>в = рФя¦
Vq
Исключение из этих уравнений потенциала скоростей ip дает одно независимое уравнение для функции тока ф:
(47)
pq
Уравнения (46) и (47) называются уравнениями Чаплыгина.
В случае политропного газа, с использованием формул (44) и (41), уравнение Чаплыгина (47) для функции тока приводится к следующему:
(с* - q2) Фев + {с\ - 1^т\я2^ Ч2ФЯЯ + ^ - ^ГТ92) ЯФч = 0- (48)
Особенно простую форму принимает уравнение (47) после введения вместо модуля скорости q новой независимой переменной С = С(<?). определенной формулой
где к0 — некоторая положительная константа. С этой переменной уравнение Чаплыгина (47) для функции тока преобразуется в следующее:
(50)
Входящая сюда функция Чаплыгина К определена формулой
1Г
(51)
Цр2
К(0
Плоскость независимых переменных Я2(в, () называется модифицированной плоскостью годографа. Так как в силу определения (49) величина ? является монотонной функцией q, причем
lim С(<?) = +ос,
q-* О
lira С(?) = Сгт
Я-^Ят
(52)
<0,
то полная область годографа {0 < q < qrn• 0 < в < 2тг} отображается на по-луполосу {Cm < С <°0; 0 < 0 < 2тт}. Обычно эту полуполосу продолжают, используя условие периодичности по в с периодом 27Г, на всю полуплоскость С > ?т. При этом окружность критических скоростей q = с* переходит в ось ? = 0. Следовательно, на плоскости R2(6, С) дозвуковым течениям соответствует полуплоскость ? > 0, а сверхзвуковым — полоса Cm < С < О (рис. 3).
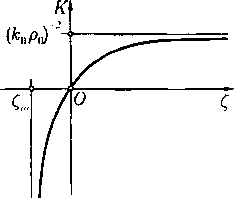
Рис. 4
С
2 7Г в
О
с
Сверхзвуковые
течения
Дозвуковые
течения
Рис. 3
Поведение функции Чаплыгина К (С) определяется тем, что ее производная всюду положительна, и дается формулой (величина m определена в (2.22))
«о
а также предельными значениями
К{ 0) = 0, К{+ос) = (коро)-\ К (Cm) = -оо,
где ро — значение плотности в «точке торможения», т. е. при q = 0. График функции Чаплыгина приведен на рис. 4. Можно показать, что в случае политропного газа K{Q является аналитической функцией во всем интервале Cm < (< ос. Вспомогательная константа к о используется для той или иной нормировки. Обычно она выбирается так, чтобы было либо К(+со) = 1, либо А''(0) = 1.
Групповое свойство. Представляет интерес рассмотрение системы (23) с групповой точки зрения. При этом выявляется принципиальное различие в случаях v = 0 и и = 1. Так как при I/ = 0 система (23) становится линейной в переменных годографа, то она допускает бесконечную группу преобразований, действие которой сводится к сложению и умножению на числа любых решений уравнения (40) или (47). Именно это свойство и делает метод годографа эффективным при исследовании плоскопараллельных течений. Кроме того, в случае и = 0 система (23) допускает однопараметрическую группу вращений (8.5.7°). Следствием этого является тот факт, что коэффициенты уравнений С. А. Чаплыгина (45)-(47) не содержат угловой координаты в. В случае же и = 1 система (23) не допускает ни бесконечной группы, ни группы вращений. Если эти группы преобразований во внимание не принимать, то при любом и остаются допускаемые системой (23) однопараметрические группы переносов по х (в случае и — 0 также и переносов по у) и растяжений с одним параметром а (здесь штрихом обозначены координаты преобразованной точки)
х' = ах, у' = ау. и' = и, г/ = г;. (54)
Эти группы можно использовать как для преобразований одних решений в другие (см. § 8), так и для отыскания классов инвариантных решений (см. § 12) системы (23). Например, группа переносов по х порождает (в случае v = 1) течение, аналогичное рассмотренному в § 11 течению от источника. Поэтому нетривиальным может быть только решение, инвариантное относительно группы (54). В соответствии с определением 13.2 эта группа порождает коническое автомодельное решение вида (32), которое является простой волной. Тем самым при любом v у системы (23) существуют решения, которые будут называться автомодельными простыми волнами. Эти решения и исследуются ниже.
Подстановка выражений (32) в уравнения (23) дает систему обыкновенных дифференциальных уравнений, к решению которой сводится описание автомодельных простых волн:
v' + Хи = О,
{(и - Xv)2 — (А2 + l)c2]u' = vc2v, ^ ^
где штрихом обозначены производные по Л. Здесь необходимо рассмотреть отдельно случаи и = 0 и и = 1.
Течение Прандтля-Мейера. Пусть и — 0. Возможности, когда тождественно v' = 0 или и' = 0, следует исключить, так как они приводят к постоянному решению. Но при v' ф 0 система (55) принимает вид
А = —dv/du, (и — \v)2 = (А2 + 1 )с2. (56)
В силу неравенства Коши (и — Xv)2 < (1 +X2)q2 из (56) следует, что течение является сверхзвуковым. Кроме того, из (56) вытекает, что описание решения сводится к одному обыкновенному дифференциальному уравнению на плоскости годографа. Оказывается, что последнее сводится к квадратуре. Для вывода этого уравнения надо перейти к полярным координатам (39), в которых величина Д равна
tg e + qde/dq
1 - tg9 ¦ qdO/dq
В результате подстановки этого выражения во второе уравнение (56) оно приводится к такому:
q2 = с2( 1 + (qde/dq)2), или, после разрешения относительно производной, к уравнению
<й , ^M2-l
Для интеграла от правой части вводится стандартное обозначение
п
H(q) = J (58)
С*
которое будет играть важную роль в § 24 при анализе характеристик системы (23). С помощью функции (58) решение уравнения (57) с начальным условием 0(с*) = во дается формулой
Тем самым на плоскости годографа получаются два семейства кривых (в зависимости от выбора знака в правой части), зависящих от параметра в0. Так как в есть полярный угол на плоскости годографа, то все кривые, соответствующие фик-~ J" сированному знаку в (59), получаются из одной (например с — во = 0) поворотом вокруг начала координат на угол во¦ Кроме того, кривые в = ±/u(q) получаются одна из другой зеркальным отражением относительно оси v = 0 (заменой в на —в). Поэтому фактически есть Рис. 5 одна стандартная кривая, напри
мер в = —ц(ц)¦ На рис. 5 эта кривая показана жирной линией, а остальные кривые семейства (59) — тонкими линиями.
Введение угла Маха а (11.22), с которым \/М2 — 1 = ctg tv позволяет упростить выражение для А и привести его к виду
А = ctg(6> -fa),
откуда следует более удобная запись уравнения прямых А = const:
у = х tg(0=Fa), (60)
причем в (59) и (60) берутся либо верхние, либо нижние знаки. Так как угол Маха а зависит только от q, то угол /5 = 9 ± а есть угол наклона к оси х того луча А — const, вдоль которого принимаются постоянные значения величин q и в, т. е. вектора скорости и = (и, и). Тем самым формулами (59) и (60) искомое решение полностью определено. Указанные соотношения позволяют построить картину течения газа на плоскости П2(х,у), показанную для стандартной кривой в = -fi{q) на рис. 6.
Плоскопараллельное течение, описываемое полученным решением, — автомодельной простой волной, называется течением Прандтля- Мейера.
Одно из полных течений Прандтля - Мейера и дано на рис. 6. Все остальные течения этого типа получаются из него поворотом на произвольный угол вокруг начала координат (константа во в (59)) и переносом центра течения в любую точку плоскости R2(x,y) (групповое свойство системы (23) при v = 0).
Замечание 2. Когда q qm, то М —> О и интеграл (58) но интервалу (c,,qrn) является несобственным. Вообще говоря, он можег быть и расходящимся. В случае политропного газа интеграл (58) вычисляется явно. Для этого надо сделать подстановку М2 = 1 + z2 и заметить, что 2 — 0 при q —¦ с.. Этим путем получается формула
J л/м2 - 1^ = У 7 - 1
arctg (^2 ~ ') “ arct8 \/м2 - 1.
(61)
Следовательно, в поли гропном газе предельный угол 0т поворота потока в полном течении Прандтля-Мейера конечен и равен
Обтекание выпуклого угла. С помощью течения Прандтля -Мейера решается конически автомодельная (см. § 13) задача обтекания заданного выпуклого угла. В этой задаче требуется найти сверхзвуковое течение, которое было бы непрерывно всюду в области над угловой стенкой АО В с заданным углом во < 0 (рис. 7) и удовлетворяло бы условию обтекания этой стенки. Скорость течения вверх по потоку вдали от угла задана и равна г/i > сь
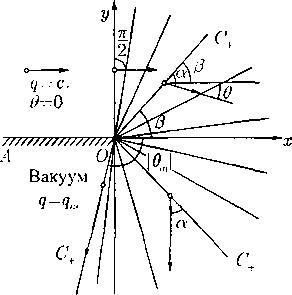
Рис. 6
Решение основано на том, что в течении Прандтля-Мейера вдоль каждого луча р = const вектор скорости постоянен и потому часть течения, заключенная в любом секторе Рх ^ р р2 может быть непрерывно продолжена постоянными течениями в обе стороны.
Для фактического построения решения надо найти угол вi = —ft(qi), а затем вычислить величину q-> из уравнения 01+02 = —^(9г) и взять ту часть полного течения Прандтля-Мейера, показанного на рис. 6, которая заключена между лучами Рх = <•*! +01 и р2 = 0:2 + + $2, где углы Маха извест
ны: sinai = c.\/q\, sina2 = f'2/?/2¦ Непрерывное продолжение этой части в обе стороны постоянным течением и дает искомое решение (см. рис. 7).
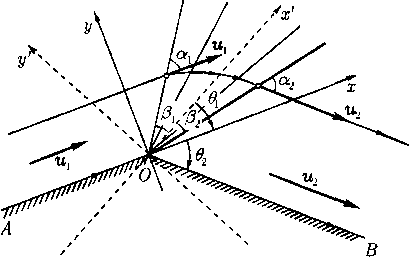
Рис. 7
Течения Буземана. В случае и — 1 необходим качественный анализ решений системы из двух уравнений (55). С введением вспомогательной величины N она переписывается в виде
г/ = —Au', Nu' = c2v, N = (и - Xv)2 - (А2 + 1)с2. (63)
Осесимметричные автомодельные простые волны, описываемые уравнениями (63), называются течениями Буземана.
К системе (63) добавляются начальные данные вида и(Ао) = Щ, v(Xo) = v0. Если при этом N(\0) = (ио — XqVq)2 — (Aq + 1)cq / 0, то система (63) с такими начальными данными имеет единственное решение в некотором интервале, содержащем точку Ао- Анализ всего семейства так получаемых решений не прост ввиду неавтономности системы (63): правые части содержат независимую переменную А. Если же JV(Ао) = 0, то при со ф 0 и конечной и'0 будет г>о = 0. В этом случае луч А = Ао будет характеристикой системы (23) на решении вида (32) и для построения решения системы (63) требуются дополнителные условия.
В частности, система (63) имеет постоянное решение и = щ, v = 0. Представляет интерес вопрос о существовании не постоянного течения Буземана, примыкающего к данному постоянному через слабый или сильный разрыв (последняя возможность будет обсуждаться в § 25). Здесь рассматривается случай слабого разрыва.
Итак, пусть со стороны А < Ао имеется постоянное течение с и = ио > 0, v = 0, к которому вдоль луча А = Ао непрерывно примыкает не постоянное течение Буземана. Так как этот луч должен быть характеристикой (теорема 6.2), то необходимо выполнение равенства N (Ао) = 0 и точка Ао будет особой точкой системы (63). Здесь N(Xq) = Uq — (Aq + 1)cq = = 0, откуда следует qo = щ > со, т. е. течение необходимо должно быть сверхзвуковым. Вычисление производных в точке Ао путем дифференцирования второго уравнения (63) с учетом N(Ао) = 0 дает необходимые и достаточные дополнительные условия
-4 , JV' = -А0с2 , (64)
Ао 4 / Cq
т0 + 2 ul ' V°~ то+ 2 „3
где то > 0 есть значение величины (2.22) в точке Ао- Возможны два варианта течения в зависимости от того, будет Ао > 0 или Ао < 0.
Первый в а р и а н т: Ао > 0. Из (64) следует, что и'0 > 0, v'0 < 0 и No < 0. Поэтому с ростом А вблизи точки Ао величина и возрастает, а v убывает, становясь отрицательной, т. е. |г>| также растет. Значит модуль скорости q растет, а с убывает, причем величина N(А) < 0. Утверждается, что последнее неравенство невозможно при всех А, Ао < А < +оо. Действительно, если N(X) < 0, то |iV(A)j < (А2 + 1)с2 и из первого уравнения (63) следует, что
Интегрирование (65) от некоторой точки Ai > Ао до переменного А > Ai дает неравенство
с некоторой постоянной ki > 0. Так как |г>|2 < q^, то из (66) следует, что неравенство N(А) < 0 возможно лишь до некоторого конечного значения А = А», с которым JV(A*) = 0. Из уравнений (63) получается, что и'(А») = +зо и г/(А„) = — ос, т.е. при А = А» происходит градиентная катастрофа.
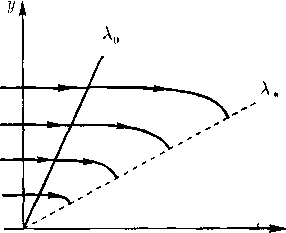
Окончательно получается, что в варианте с Ао > 0 течение Буземана, непрерывно примыкающее к постоянному, является автомодельной волной разрежения, заканчивающейся на луче А = А». Это течение может быть интерпретировано как продольное обтекание части тела вращения, имеющего вид сужающегося цилиндра (А. А. Никольский, 1957). Распределение величин и и I1 в зависимости от А и плоскость течения с линиями тока показаны на рис. 8.
Второй вариант: Ао < 0. Из (64) следует, что здесь и'0 < 0, Vq < 0 и jVg > 0. С ростом А вблизи точки А0 обе величины и и v убывают, т. е. |г>| возрастает и будет N > 0. Это направление изменения величин и, v сохранаяется во всем интервале (Ао,0). Из (63) следует, что г/(0) = 0, а при А > 0 будет v' > 0, т. е. |г>! будет убывать. Как далеко (по А) может существовать такое решение?
Для ответа на этот вопрос сначала устанавливается, что при всех А > 0 пока существует гладкое решение системы (63), знаки неравенств
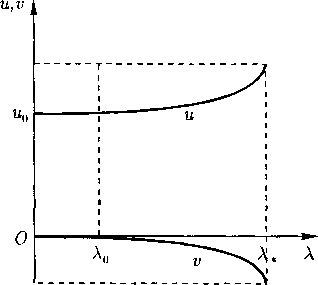
Рис. 8
будут сохраняться. Действительно, пусть Ai (0 < Ai < оо) есть наибольшее значение А, при котором в открытом интервале (0, Ai) выполнены все неравенства (67). Тогда они будут выполнены и при А = Аг. нарушение хотя бы одного из них ведет к противоречию с определением точки Х\. Именно, если v(Ai) = 0, то при N(X\) Ф 0 слева от точки Ai решение системы (63) должно быть постоянным (теорема единственности), а при iV(Ai) = 0 из формул (64), с заменой Ао на Аь следует v'(Xi) < 0 и, в силу непрерывности, г/(А) < 0 для близких к Ai значений А < Х\. Если u'(Ai) = 0, илиг^Ат) = 0,uimiV(Ai) —- 0, то из (63) снова следуетi>(Aj) = 0. Наконец, если u)(Ai) = 0, то будет N(X\) - — (Aj 4- l)cj < 0 и значит величина N должна быть равна нулю при некотором Аз, 0 < Аг < Aj.
Полезно заметить еще, что из (63), (67) следуют соотношения
В частности с ростом А модуль скорости q убывает, а значит скорость звука с растет, т. е. имеет место течение сжатия.
Однако на весь интервал (0, ос) гладкое решение продолжено быть не
может. Это следует из интеграла Бернулли, предписывающего ограничен
ность скорости звука, а значит и плотности р ее максимальным значением. Именно, из интеграла Бернулли и уравнений (63), (68) выводится уравнение для плотности р(А)
Так как N < w2, то из (69) следует неравенство
Но в силу N > 0 будет w2 > (А2 + 1 )с2 и значит при А—>оо будет w = и + Л|г>| —> ос, т. е. |А| —» оо. Поэтому для достаточно больших А > Ai >0 дробь А|и|/эд будет ограничена снизу положительной константой к\, т. е. А|и| > k\w. Значит неравенство (70) при А > Ai приводит к неравенству р / р > 2к\/Х, интегрирование которого дает конечное неравенство
р{\) > к2A2fcl
с некоторой константой к2 >0. Поэтому при А —* оо будет р —> оо, что невозможно.
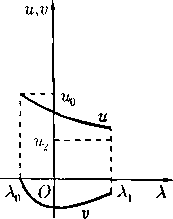
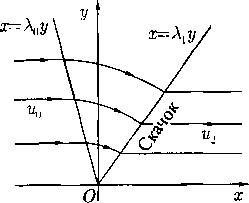
Рис. 9
Оказывается, что здесь существует течение с сильным разрывом (коническим скачком уплотнения, см. § 25), через который ноток переводится в постоянный, идущий вдоль полуоси х > 0. Линия этого разрыва совпадает с некоторым лучом А = Ai (рис. 9). Следовательно, в варианте с Ао < 0 течение Буземана является автомодельной волной сжатия, состоящей из непрерывной волны и конического скачка уплотнения, посредством которых постоянный сверхзвуковой поток со скоростью щ преобразуется снова в постоянный поток со скоростью и2 < Vo- При этом результирующее течение может быть как дозвуковым, так и сверхзвуковым.
В теории дозвуковых установившихся безвихревых изэнтропических (значит — изоэнергетических) двумерных течений газа предполагается, что во всем рассматриваемом течении модуль скорости q меньше соответствующей скорости звука о, т. е. всюду в потоке число Маха М < 1. В зависимости от характера краевых задач в качестве исходных дифференциальных уравнений, описывающих такие течения, берутся либо система уравнений (22.23), либо уравнение для потенциала скоростей (22.28), либо система уравнений метода годографа (22.35), (22.46) и (22.50) или некоторые их модификации. Каждый раз эти дифференциальные уравнения надо рассматривать совместно с интегралом Бернулли (22.24), причем уравнение состояния (которое в теории таких течений принято называть также уравнением адиабаты) р = /(р, So), энтропия So и константа Бернулли считаются фиксированными.
Благодаря строго эллиптическому типу исходных дифференциальных уравнений теория дозвуковых течений с точки зрения постановок ее основных краевых задач во многом аналогична теории течений идеальной несжимаемой жидкости. Здесь будут рассмотрены два класса задач, наиболее хорошо изученных в этой теории: задачи о струях и задачи обтекания. Исторически именно на этих задачах разрабатывались и отшлифовывались математические методы исследования дозвуковых течений газа. Уместно отметить, что первые задачи о дозвуковых плоских газовых струях были решены С. А. Чаплыгиным еще в начале текущего столетия [10].
Задачи о струях. Характерным признаком таких задач является наличие так называемых свободных границ. Этим термином принято называть такие части границы области течения, которые сами заранее неизвестны, но на которых задается два граничных условия: кинематическое и динамическое. Кинематическое условие состоит в требовании, чтобы свободная граница была контактной линией, т. е. состояла все время из одних и тех же частиц. Для установившихся течений это равносильно тому, что свободная граница является линией тока. Динамическое условие заключается в задании распределения давления вдоль свободной границы. Обычно заданное давление считается постоянным. Это позволяет интерпретировать струйное течение как такое, которое происходит в некотором окружающем изобарически покоящемся газе, линия раздела с которым и представляет собой свободную границу, Действительно, тогда линия раздела является контактным разрывом, при переходе через который на ней выполнено условие непрерывности давления. Кроме свободных границ в задачах о струях могут быть и другие участки границы течения, которые считаются заданными твердыми непроницаемыми стенками. На таких участках задается условие обтекания (говорят также: условие непро-текания), равносильное условию, что и эта часть границы является линией тока (заранее заданной). Таким образом, каждая струя, имеющая конечную величину поперечного сечения, течет между двумя линиями тока, и потому расход газа (см. § 22) в ней постоянен. Наконец, в струях, уходящих в бесконечность и имеющих либо обе границы свободными, либо одну из них в виде твердой прямолинейной стенки, требуется выполнение условия выравнивания струи в бесконечности. Оно заключается в том, что вдоль каждой принадлежащей струе линии тока вектор скорости при удалении на бесконечность стремится к одному и тому же предельному значению, не зависящему от выбора линии тока. Другими словами, на бесконечности течение в струе асимптотически стремится к некоторому постоянному течению. При этом модуль скорости q в бесконечно удаленной части струи, так же как и на ее свободной границе, известен: он определяется, через интеграл Бернулли, заданным значением внешнего давления.
Анализ и решение задач о струях сильно облегчаются, если все участвующие твердые стенки являются прямолинейными. Действительно, в этом случае каждый участок границы, вообще говоря, имеет известный годограф: свободная граница, на которой известно постоянное значение модуля скорости q, изображается дугой окружности радиуса q, а прямолинейная твердая стенка, на которой известен постоянный угол наклона в вектора скорости, — отрезком радиуса. Если при этом годограф всей границы ограничивает область на плоскости годографа, то соответствующая задача о струях может быть поставлена, вообще говоря, как некоторая задача для какой-либо из форм основных дифференциальных уравнений на плоскости годографа.
В каждой такой задаче необходим специальный анализ вопросов единственности решения и однолистности отображения плоскости течения на плоскость годографа. Единственность решения обычно устанавливается с помощью принципа максимума и леммы Зарембы о положительности нормальной производной в граничной точке максимума для решений эллиптических уравнений второго порядка. Этими же средствами доказывается отличие от нуля якобиана отображения. Тем самым гарантируется локальная однолистность отображения. Для установления глобальной однолистности используются достаточные условия топологического характера из общей теории дифференцируемых отображений плоских областей. Одним из них является условие односвязности, согласно которому если при непрерывно дифференцируемом отображении с не равным нулю якобианом односвязная область переходит в односвязную, то в этой области отображение взаимно однозначно. Другое условие дается принципом соответствия границ, в котором предполагается, что граница Г области П при непрерывно дифференцируемом отображении замкнутой области П с не равным нулю якобианом переходит в кривую Г', ограничивающую некоторую область S7' (или ее дополнение Q"). Тогда, если Г отображается на Г' взаимно однозначно, то образом П является П' (или П") и отображение П —» П' (или Q —> Q") также взаимно однозначно. Имеются и другие, более тонкие достаточные условия глобальной однолистности. Так как поместить более подробное изложение всего этого математического аппарата в данном тексте не представляется возможным, то читатель отсылается к соответствующим руководствам по уравнениям математической физики. Здесь же приходится ограничиться утверждением о том, что в рассматриваемых ниже задачах о газовых струях свойства единственности решения и глобальной однолистности отображения плоскости течения на плоскость годог рафа могут быть доказаны вышеупомянутыми методами и на самом деле справедливы.
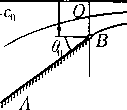
Истечение симметричной струи. Одной из простейших «эталонных» задач о газовых струях является задача об истечении симметричной струи из бесконечного угловидного (или конусовидного) сосуда. Качественная картина всей конфигурации на плоскости течения показана на рис. 1. Здесь АВ и А'В' — стенки симметричного относительно оси х сосуда, ВС и В'С' — свободные границы газовой струи, а сечение В В' представляет собой отверстие, через которое и вытекает газ в окружающее пространство. Заданы ширина (диаметр) отверстия 2/to и угол Оо наклона стснок к оси х, причем 0 < 0О ^ я-- В бесконечности вверх по течению, т. е. в сосуде вдали от отверстия, газ покоится и имеет заданные параметры ро, ро (значит, известна и скорость звука со). Тем самым определена константа qfn — I(cl), интеграл Бернулли (22.24) становится конкретным:
q2 + I(C2) = 1(с2), (1)
и известны также критическая скорость с* (определение 10.2), соответствующие критическая плотность р* и критическое давление pt. На свободных границах задано постоянное давление р\ < ро, а следовательно, и скорость звука d. Поэтому из (1) находится постоянное значение q\ модуля скорости на свободных границах, определяемое формулой
При этом предполагается, что q\ < с\, что равносильно (см. § 10) неравенствам q\ < с* или р* < pi < ро- Требуется дать аналитическое описание (расчет) этого течения, в частности, найти величину расхода газа 2Q.
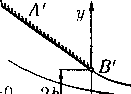
Для построения годографа области искомого течения достаточно заметить, что вдоль стенки АВ (или А1 В') модуль скорости q монотонно возрастает от значения q = 0 до q qi, а вдоль свободной границы ВС угол наклона вектора скорости в монотонно убывает от значения 0 ¦¦¦-- Оо до 0 — 0. Поэтому годографом области течения является круговой сектор, показанный на рис. 2, где соответствующие рис. 1 точки обозначены одинаковыми буквами. Эта область годографа одинакова как для плоскопараллельной, так и для осесимметричной струи.
Пусть 2/ioo — величина сечения (диаметр) струи в бесконечности вниз по течению (сечение С С"). Так как там должно быть асимптотически по-
q-v -
V
О
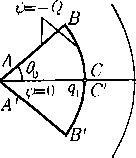
Рис. 2
С
.О/,
с-
q-.q,, с-с, С
;'¦>= 0 9i I С 1с.и
Рис. 1
стоянное течение, то расход газа в струе может быть выражен через величину h0о и,;фдет$но формуле (22.10), имеет значение
![]()
Согласно (22.11) приращение функции тока при переходе от нижней границы струи к верхней равно 2Q, и поэтому граничные значения функции тока могут быть взяты такими:
(3)
Тем самым задача об истечении струи сводится к отысканию функции тока ф = ip(q,0) как решения соответствующего дифференциального уравнения в заданном секторе АВВ'А' плоскости годографа с краевым условием (2), т. е. как решения задачи Дирихле. В силу очевидной симметрии значение ф на оси симметрии равно нулю, и потому достаточно найти решение задачи Дирихле в половине ABC указанного сектора с граничными условиями
0(<?,0о) = -Q< '0{q\,O) = -Q, Ф{я,о) = о.
(4)
Эта постановка краевой задачи для функции тока одна и та же как для плоскопараллельной, так и для осесимметричной струи. Однако решение ее сравнительно просто только в случае плоскопараллельной струи, когда уравнение для функции тока на плоскости годографа (22.47) линейно; этот случай и рассматривается ниже.
Для построения решения вводится вспомогательная функция
которая, так же как и -ф, удовлетворяет уравнению (22.47) и, кроме тою, в силу (4) обращается в нуль при в —¦ 0 и в — во- Далее, методом разделения переменных q и в в уравнении (22.47) находятся частные решения, тоже равные нулю при в = 0 и в = в0'-
n—1
который в случае достаточно хорошей сходимости также представляет ре-шение уравнения (22.47), равное нулю при в = 0 и в = во- Наконец, остается удовлетворить второму краевому условию (4), которое в силу представлений (5) и (8) приводит к соотношению
ОС
Y2anzn{qi)sm(i^ne) = j- - 1 (O<6>s?0o), (9)
П—\
левая часть которого должна быть разложением в ряд Фурье функции, находящейся в правой части. Поэтому коэффициенты ап в (9) определяются по формулам Фурье
00
anz„(qi) = J ^ - 1^ s'm(i/ne)de
о
и оказываются такими:
С коэффициентами (10) по формуле (8) определяется функция ^6циа«яггем из соотношения (5) — и искомая функция тока
где величины vn даны в (6).
Как всегда в методе Фурье, полученное представление решения нуждается в обосновании с точки зрения сходимости ряда (11). С этой целью необходимо выяснить характер асимптотического поведения функций Чаплыгина zn(q) при п —> оо. Известным из теории обыкновенных дифференциальных уравнений приемом получается следующее представление:
где
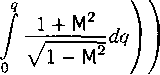
R(q) = exp I i -
1 1 Vl-M2
а функции bn(q) ограничены в интервале 0 ^ q < с» равномерно относительно п — 1,2,... Кроме того, представление (12) можно дифференцировать по q. Отсюда следует, что ряд (11) абсолютно сходится в области АВВ'А' и его можно дифференцировать почленно один и два раза по переменным q ив. Поэтому формула (11) дает решение уравнения (22.47). Легко проверяются также и граничные условия (4).
Итак, решение задачи на плоскости годографа дается формулой (11). Отсюда с помощью формул перехода (22.43) можно вычислить любые величины на плоскости течения. Например, для отыскания расхода согласно (2) достаточно найти величину h^. Это делается интегрированием дифференциала dy вдоль линии ВС, так как (см. рис. 1)
J dy = h0 - hoc.
вс
Для дифференциала dy имеется выражение (22.43), которое на линии ВС принимает вид dy = (sin 0/q)ipode и, в силу второго уравнения (22.46), оказывается таким:
dy | вс = Рг 1 sin в - ibq(qi, 0)d0.
В результате подстановки сюда представления (11) и почленного интегрирования получается соотношение
Q 2sin0o v* *n(?i)(-1)ni'.
![]()
Так как в случае плоскопараллельного течения формула (2) принимает вид Q = hooPiQi, то из этого соотношения следует равенство, определяющее искомую величину /1те:
ho = h0о(1 + Ф(дь0о)),
(13)
где
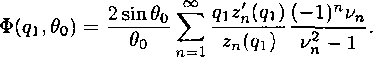
Для некоторых конкретных значений угла во это решение описывает характерные течения. Например, при во = тг/2 — истечение струи газа из полупространства через щель в плоской стенке, а при во = 7г — истечение струи газа из всего пространства в плоский насадок Борда. Решение пригодно для любого qi < с*. Можно показать, что оно справедливо и при q\ = с», причем в этом случае струя выравнивается на конечном расстоянии от отверстия.
Тем же методом, с небольшим усложнением, решается задача об истечении несимметричной струи, когда сечение выходного отверстия не перпендикулярно оси сосуда. Для построения такого решения проще всего задать угол, образуемый вектором скорости в бесконечности вниз по течению с осью сосуда. На годографе рис. 2 это сведется к смещению точки разрыва граничных данных (3) С = С по дуге окружности q = qi от ее симметричного положения в сторону точки В или В'. При совпадении С с В получится задача об истечении струи газа вдоль прямолинейной стенки из-под щита, решение которой фактически дается формулой (11).
Струйное обтекание клина. Аналогично рассматривается задача о симметричном струйном обтекании клиновидной (или конусовидной) стенки конечной длины. Качественно картина течения показана на рис. 3, где CD и CD’ — уходящие струи, на которые натекающая струя ЕЕ' разделяется твердой стенкой ВАВ'. Заданы параметры qQ < cq в натекающей струе, ее ширина (диаметр) 2/io, угол во и ширина (диаметр) основания клина 2/г. Требуется определить силу давления струи на клин и угол в\,
под которым наклонены уходящие струи к оси симметрию Область годографа этого течения показана на рис. 4.
V‘
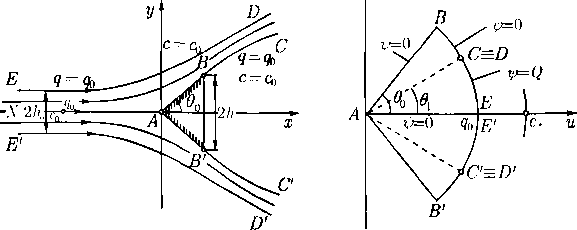
Рис. 3
Рис. 4
Далее рассматривается только плоскопараллельное течение. Снова дело сводится к решению задачи Дирихле для уравнения (22.47), благодаря симметрии, в секторе АВСЕА плоскости годографа (рис. 4) с граничными условиями
Ф\еавс = 0, гр\сЕ = Q,
(14)
где Q — полурасход в натекающей струе, который известен и равен Q = hopoqo. Ясно, что решение этой краевой задачи может быть получено изложенным выше методом.
В этой задаче представляет интерес тот факт, что сила X, действующая на клин, выражается непосредственно через данные задачи И угол в\ простой формулой. Для ее получения надо применить интегральный закон сохранения потока импульса (1.4) к области NABCDEN (предполагая сечения CD и NE находящимися на конечном расстоянии и ортогональными вектору скорости) и затем взять проекцию на ось х (см. рис. 3). При этом следует учесть, что на свободных границах р — ро, и п = 0 и что интегралы вида f pnxds по этим границам сводятся к интегралу J dy и вычисляются явно:
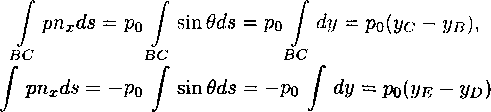
DE
DE
DE
а также заметить, что разность у о - Ус конечна и равна /to cos в\. Этим путем, с учетом того, что сила X по определению равна
X = 2 J pdy,
АВ
в результате элементарного подсчета получается формула
X = 2hp0 + 2(1 - cos0i)/iopo<?o- (15)
Что же касается угла в\, то его можно определить лишь как корень трансцендентного уравнения через решение ip(q,6\ в\) упомянутой краевой задачи. Для этого надо вычислить величину h, например, по формуле h = J dy,
АВ
которая в силу (22.43) и (22.46) преобразуется к виду
40 2
h = sin9q [ --фв{я,в0; 0i)dq. (16)
о
Соотношение (16) при известной h и есть уравнение относительно в\, определяющее этот угол.
Для специальных исходных данных в этой задаче получаются некоторые характерные течения. Например, решение с во = к/2 описывает струйное обтекание пластинки. Можно также сделать клин бесконечным (h = оо) и получить обтекание угла (в этом случае в\ = во). Кроме того, смещая точки С, С' и Е по окружности q = qo на годографе рис. 4, можно тем же методом найти решения целого класса задач о несимметричном обтекании клина. Во всех получаемых течениях точка А является точкой торможения потока; в ней скорость обращается в нуль, т. е. q = 0.
Свободные струи. Представляет интерес также класс свободных струйных течений газа, в которых твердые стенки отсутствуют. Примером служит симметричное течение, возникающее при лобовом столкновении двух свободных струй (рис. 5). Здесь заданы параметры q0 < c.q и ширина 2hi струи АА!, текущей слева направо, и те же параметры и ширина 2/гг струи DD', текущей справа налево. В результате столкновения этих струй возникает точка торможения О и две боковые струи, ВС и В’С'. При этом образуется разделяющая линия тока Е'ОЕ, слева от которой остается весь газ, принесенный струей АА', а справа — весь газ, принесенный етруей DD'. Требуется дать описание течения, в частности, найти угол 9\ наклона боковых струй к оси х, а также разделяющую линию тока Е'ОЕ.

Рис. 5
Оказывается, что в этой задаче угол в\ очень просто выражается через исходные данные, а именно справедлива формула
(17)
cos
hi - h2 hi + h2'
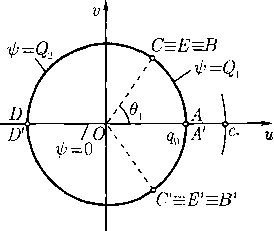
Формула (17) выводится применением интегрального закона сохранения потока импульса (1.4) аналогично тому, как это было сделано в предыдущей задаче. Что же касается разделяющей линии тока, то се можно найти только в результате решения краевой задачи. Область годографа рассматриваемого течения представляет собой круг радиуса qo, показанный на рис. 6. В силу симметрии соответствующую задачу Дирихле достаточно рассмотреть в полукруге DBA с граничными данными
Ф\ва = ^1Ро<7о, Ф\da = 0.
Эта задача легко решается изложенным выше методом, в результате чего определяется функция $(q,0). С ней годограф разделяющей линии тока дается уравнением
(19)
Дифференциальные уравнения разделяющей линии тока согласно определению (22.4) могут быть записаны в виде
![]()
с некоторой функцией Н = Н(в). Вычисление с помощью уравнений (22.43) и (22.46) дает для Н выражение
Я = -i— (q2ibq + (1 - М>!) • PQ~Vq
(21)
Функция Н(в) получается подстановкой в формулу (21) зависимости <7 = q(0), определяемой уравнением (19).
Довольно сложные струйные течения возникают при несимметричном столкновении свободных струй. Решения этого типа могут быть получены смещением точек В, D, В' по окружности q = qo (см. рис. 6) и рассмотрением возникающей задачи Дирихле во всем круге. При этом надо следить за соблюдением интегральных законов сохранения массы и импульса на плоскости течения.
Задачи обтекания. Здесь будут рассмотрены задачи обтекания конечного тела безграничным потоком. Этот класс задач играет важную роль в аэродинамике крыла и снаряда. Результаты анализа и расчета задач обтекания используются при решении ряда актуальных проблем высокоскоростной (реактивной) авиации и внешней баллистики. Общая постановка задачи обтекания уже упоминалась в § 7 и формулируется следующим образом.
Требуется найти непрерывное в замкнутой области Г2 решение системы уравнений (22.23) и (22.24), определенное во внешности Q заданного простого замкнутого контура Т С R2(x,y), удовлетворяющее условию на бесконечности с заданным вектором Uoo
(22)
lim u(rc, у) = Uoo
r—*oc
и условию обтекания контура Т
где г = у/х2 + и2 и п нормаль к Г. Кроме того, предполагаются заданными уравнение состояния р = f(p, So) (ищется изэнтропическое течение) и давление р^ на бесконечности. Тем самым заданы также скорость звука с^о и число Маха М,*, = qx/cx, где = ju^l.
Очевидно, что такое задание условий на бесконечности позволяет найти константу в интеграле Бернулли (22.24), который в силу этого становится вполне определенным. Возможна и другая постановка, когда константа в интеграле Бернулли считается заданной; тогда величина с^о однозначно определяется условием (22).
Из-за специфики рассматриваемых в этом параграфе двумерных дозвуковых течений эта постановка нуждается в уточнении. Прежде всего, требуется, чтобы в любой точке было q < с или, в терминах числа Маха, М < 1. Для этого необходимо выполнение неравенства
Моо < 1,
(24)
которое, однако, не является достаточным. Поэтому условие дозвукового обтекания М < 1 есть дополнительное ограничение, накладываемое на искомое решение. Далее, если на обтекаемом контуре Т есть три угловые точки, представляющие собой вершины выпуклых углов, то непрерывное решение задачи обтекания контура Т не существует. Этот факт аналогичен известному в теории двумерной задачи обтекания тела потенциальным потоком невязкой несжимаемой жидкости. Дело в том, что непрерывное решение в окрестности выпуклого угла обладает следующим свойством: вершина такого угла всегда является точкой разветвления проходящей через нее линии тока. Однако наличие трех (или большего числа) точек разветвления невозможно согласовать одновременно с условием непрерывности решения и условием на бесконечности. Основным является тот случай, когда на контуре Т находятся две точки ветвления, в которых разделяется, а затем соединяется в одну линия тока, образующая Т. Поэтому общая качественная картина течения должна быть такой, как на рис. 7, где показаны линии тока и направление движения частиц вдоль их. Здесь В и С — точки ветвления линии тока ABCD, часть которой образует контур Т.
Циркуляция. Следующая особенность двумерной задачи обтекания состоит в том, что в случае гладкого контура Т ее решение заведомо не единственно; вообще говоря, она имеет однопараметрическое семейство решений. Роль произвольного параметра играет циркуляция вектора скорости по любому простому замкнутому контуру Т', окружающему Т:
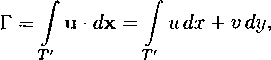
Рис. 7
где контурный интеграл берется в направлении против часовой стрелки; очевидно, что его величина от выбора контура Т' не зависит. Эта неединственность решения, также хорошо известная в теории несжимаемой жидкости, вытекает из возможной неоднозначности потенциала скоростей в силу его особого поведения на бесконечности. Величина циркуляции Г связана с положением точек ветвления на Т. Априори можно задать положение только одной из них; тогда положение другой и циркуляция Г определяются однозначно. В частности, если на Т есть одна угловая точка (типа точки С на рис. 7), то необходимо потребовать, чтобы она была точкой ветвления. Это условие, по аналогии с несжимаемой жидкостью, называется условием Жуковского. Оно определяет величину циркуляции Г однозначно.
В осесимметричной задаче возможны два типа обтекаемых контуров, показанные на рис. 8. Первый из них является сечением односвязного тела вращения (типа снаряда). Обтекание такого контура является бесциркуляционным (Г = 0), а точки ветвления линии тока всегда лежат на оси симметрии. Второй тип представляет кольцевидное (торообразное) тело вращения, от которого на плоскости течения остается лишь его меридиональный профиль (с учетом отмеченной в §22 симметрии). В этом случае положение с циркуляцией и точками ветвления такое же, как и для плоскопараллельной задачи. К сожалению, по осесимметричной задаче обтекания пока еще нет таких результатов, которые можно было бы достаточно просто изложить в данном тексте. Поэтому нижеследующее относится только к плоскопараллельному обтеканию.
Аналог теоремы Янковского. Ввиду отмеченных выше особенностей решения задачи обтекания принципиальное значение имеет вопрос об асимптотическом поведении дозвукового течения на бесконечности. Знание асимптотики позволяет также, как выяснится ниже, вычислить важ-
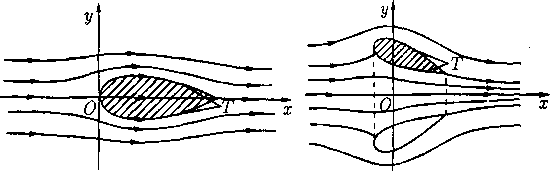
Рис. 8
ную для приложений величину силы, действующей на Т. Получение этой асимптотики — задача довольно трудная, решенная до конца сравнительно недавно, лишь в конце 50-х годов. Оказывается, что асимптотическое поведение потенциала (р и вектора скорости и при г —> оо в системе координат, в которой направление оси х совпадает с направлением вектора и-» (т. е. когда Uqo = («оо- 0)), описывается формулами
<р = UaoX-b J- arctg(fctg/?) + О (г 1+е)
27Г
(26)
Здесь (г, 0) — полярные координаты, вводимые равенствами
х — г cos 0, у = г sin 0, (27)
Г — циркуляция (25), а е > 0 — любое сколь угодно малое число. Символом к обозначена величина
а символ 0(га) означает функцию, которая после деления на га остается ограниченной при г —> оо. Явно выписанные слагаемые асимптотики (26) можно найти сравнительно просто формальным путем, если заметить, что при больших г уравнение для потенциала скоростей (22.28) (с и = 0) приближенно имеет вид
к ipxx + <Руу = 0
с величиной к из (28) и после замены переменной х = кх' превращается в уравнение Лапласа, для которого асимптотика решений известна. Одна-
ко выражения (26) для порядков остаточного члена таким путем получить затруднительно.
Вектор X силы давления газа на контур Т определяется формулой
X = j pnds (29)
т
с нормалью п, направленной внутрь Т. Замечательно, что для силы X получаются такие же формулы, как и в случае обтекания несжимаемой жидкостью, а именно справедлив следующий аналог теоремы Жуковского.
Теорема 1. Компоненты силы X — (X, Y) даются формулами
X = О, Y = -рос^ооГ. (30)
Доказательство. Применение интегрального закона сохранения потока импульса (1.4) к области и, заключенной между контуром Т и окружностью Тц большого радиуса г = R, с учетом равенства и ¦ п = 0 на Т дает для интеграла (29) выражение
У (рп + pu(u • п ))d.s,
Х = -т„
где п — внешняя нормаль к окружности Тц, причем в полярных координатах (27) справедлива формула n = (cos /3, sin /3). На основании асимптотического представления вектора скорости (26) с помощью интеграла Бернулли выводятся соответствующие представления давления и плотности:
Р = Рос Poo Uno ~2 . 2 2 ^ ^ Г ) ’
^ х2 + к2у2
(31)
_ РорЦоо кГ У .
р_ро° <4 ъ-хх2 + itv ( ^
Отсюда следует представление подынтегрального выражения в полярных координатах (27) на окружности Тц:
pn + pu(un) =((роо + Рос'И^о) COS/?, Poo sin/3)+
sin /3 cos /3, l)
, . -г, 'oo5,111 j.; ^ n(iy-2\
"b Poo ^ ос Г , I 2 • 2 /э\ )¦
2тг
J F(x,y)ds = R J F(Rcosp, Rs\aj3)d(3
Тп О
в результате элементарного вычисления интегралов от слагаемых предыдущего выражения и предельного перехода R —» сю получаются формулы (30). ¦
Некоторые качественные результаты. Для любых дозвуковых безвихревых течений справедлив принцип максимума модуля скорости: максимальное значение величины q = |uj достигается только на границе области течения. Применительно к задаче обтекания контура Т это означает, что величина q принимает свое наибольшее значение qs в некоторой точке Е ? Т. Поэтому дозвуковой характер течения во всей области Q гарантируется, если qE <с*.
Теорема единственности решения задачи обтекания справедлива в следующей формулировке: условиями (22) и (23) течение определено единственным образом в случае контура Т с одной угловой точкой; то же верно и для гладкого контура при дополнительном условии, что задана циркуляция Г.
Эта теорема служит основой для моделирования течений. Именно, пусть контур Т\ геометрически нодобен контуру Т и относительно подобно расположен, т. е. получается из Т преобразованием растяжения
х' = ах, у' = ау (а > 0).
Тогда при одинаковых условиях на бесконечности поле скоростей иь будет подобно полю и в том смысле, что
ui (ах,ау) = и(х,у),
а циркуляции будут связаны соотношением Г! = аГ.
Теоремы существования решения задачи обтекания справедливы во всем диапазоне входных данных (включая задание циркуляции Г в случае гладкого контура), гарантирующих неравенство qE < с*.
Упомянутые результаты являются итогом очень глубокого и трудного анализа, использующего современные методы теории функций, функционального анализа и квазиконформных отображений. Подробности можно найти в журнальных статьях, цитированных в [8].
§ 24. Характеристики и простые волны
В этом параграфе изучаются свойства гладких чисто сверхзвуковых двумерных безвихревых изэнтропических течений. Здесь определяющим является свойство гиперболичности основных уравнений и связанные с ним факты локализации возмущений в областях, ограниченных характеристиками. Теория чисто сверхзвуковых течений во многом аналогична теории одномерных движений, рассмотренных в §§ 15, 16. Исследованию возможных вырождений сверхзвукового течения при переходе через звуковые линии или скачки уплотнения будут посвящены дальнейшие параграфы.
Исходные уравнения. Основные уравнения (22.23) здесь удобнее взять в первоначальном виде
иу - vx = 0, (ри)х 4- (pv)y = -jjpv, (1)
присоединяя к ним интеграл Бернулли (22.24) с постоянной константой qm. Согласно (10.8) его дифференциальная форма имеет вид
dp = _р? dq с2
(2)
Из рассмотрений § 10 вытекает, что при q > с (или М > 1) система (1) является гиперболической. Поэтому для нее важно найти характеристики и условия на них, а также построить транспортные уравнения для описания распространения слабых разрывов вдоль характеристик и выяснения возможности градиентной катастрофы. Необходимые для выполнения этой программы выкладки будут более компактными, если сразу ввести в качестве независимых переменных потенциал скоростей ip и функцию тока ф:
Наконец, наряду с декартовым представлением искомого вектора скорости и = (и, v) будет рассматриваться его полярное представление через модуль q и угол наклона в к оси х (полярные координаты на плоскости годографа, уже введенные в § 22):
u = qcos9, v = qsind.
(6)
Естественно, что в этих переменных получится аналог уравнений Чаплыгина (22.45). Однако для охвата также и осесимметричных течений уместно дать краткий вывод преобразованных уравнений. С помощью формул (3), (6) и с учетом соотношений (2), (5) для левых частей уравнений (1) получаются выражения
uy-vx = u<pV - uVy, + yvp(uuф -г ууф) = -q26<p + yvpqqф,
{ри)х + (pv)y =
= u(pu)v + v(pv)v + у'/р{-у{ри)ф + и{ру)ф) =
=q2pv + pqq>fi + y'/p'2q20ф = -pq ctg2 a ¦ qv + yvp2q29^.
Следовательно, после преобразования на плоскость потенциала система (1) оказывается такой:
(7)
Ctg2 a-qч>- yv рчвф = | sin в.
Характеристики. На плоскости потенциала характеристики задаются дифференциальным уравнением вида
d-ф/dip = к.
(8)
Тогда нормальный характеристический вектор с проекциями на оси декартовых координат ((р.гр) есть (—яг, 1) и по правилам, изложенным в §6, находится характеристическая матрица системы (7)
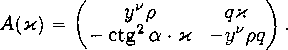
Ее определитель дает следующее характеристическое уравнение:
ctg2 а ¦ х2 — у2"р2 — 0, всегда имеющее два вещественных корня (для v = 1 в области у > 0):
*+ = yl'ptga, х_ = -y"ptga. (9)
Для построения условий на характеристиках находятся соответствующие корням х± левые собственные векторы матрицы А{х), которые могут быть взяты в виде (1, ± tgо). Поэтому условия на характеристиках получаются почленным сложением первого уравнения (7) со вторым, умноженным на ± tg а, и после небольшого преобразования оказываются такими:
(^*-^9*) = T^tg«sin0, (10)
где верхние знаки берутся для корня х+, а нижние — для х.-. В условиях (10) участвует уже рассматривавшаяся в (22.58) вспомогательная функция
Cm
С этой функцией образуются величины, аналогичные инвариантам Римана для одномерных движений (16.6), производные от которых естественно возникли в условиях (10):
r = e-~p,(q), l = e-rfi(q). (12)
В последующем изложении величины г и / будут также называться инвариантами Римана. С ними условия на характеристиках (10) принимают вид
rv + х+Гф = - ~ tg a sill в, 1^ + Х-1Ч, = Щ tg a sin в.
Наконец, вводятся операторы дифференцирования по вдоль характеристик каждого из семейств
и окончательно получается следующая характеристическая форма системы уравнений (7):
(С+) ^ •¦= yv ptga, D+r = - щ tgasintf;
(14)
(С-) ^ = -yvptga, D-l tgasin#.
В дальнейшем будет соблюдаться указанная в (14) маркировка семейств характеристик С±. Уравнения (14) показывают, что г и I действительно являются инвариантами в случае плоскопараллельного течения: при v — О величина г постоянна вдоль каждой характеристики С+, а величина / — вдоль С_.
Для отыскания характеристик на плоскости течения надо просто пересчитать производную dtp/dip и операторы D± согласно формулам (4). Тогда для характеристических направлений получатся выражения
dy = pv + y~vuH± = tg в ± tg а = ±
dx pu-y~vVK± 1 -F tg 0 tg q ' a>'
Операторы D± оказываются такими:
D* = Ша (“»<« ± “) §i + *“<* ± «) Щ
Поэтому если ввести еще модифицированные операторы дифференцирования вдоль характеристик на плоскости R2(x,y)
D± = cos(e ±а)-^~+s\n(e (15)
ox ay
то окончательно получится следующая характеристическая форма системы уравнений (1) на плоскости течения:
(С+) ^ = tg(0 4-ct), D+r = -^ sinasin9: (С-) ^ = tg(0 —а), D-1 - jj sinasin#.
Отсюда следует качественная картина расположения направлений характеристик относительно вектора скорости в каждой точке А плоскости течения, показанная на рис. 1. Здесь АВ\ и АВо — направления характеристик в точке Л и подчеркнуто важное свойство (уже упоминавшееся в § 10), которое очевидным образом следует из формул (16) и (5): абсолютная величина проекции вектора скорости на нормаль к характеристике равна скорости звука.
Уравнения (14) или (16) указывают на еще одно принципиальное различие между плоскопараллельными и осесимметричными течениями. В случае плоскопараллельных течений (и = 0) годографы характеристик являются стандартными кривыми г = const или / = const независимо от конкретного решения. Для это-
_i_ Д> го случая сетка характеристик на плос-
0 4-т-¦> х кости годографа показана на рис. 22.5.
и Для осесимметричных течений (v = 1)
рис j это свойство неверно из-за наличия нену
левых правых частей в уравнениях (16), в силу чего годографы характеристик не совпадают с линиями г = const или I — const и существенно зависят от индивидуального решения.
Транспортные уравнения. В качестве производных по направлению, трансверсальному к любым характеристикам, можно взять производные ПО ifi
R — rv, L = l^. (17)
Общий ход вывода уравнений для этих величин вдоль характеристик аналогичен изложенному в § 15. Ниже для простоты этот вывод дается в случае плоскопараллельных течений (осесимметричный случай предоставляется читателю). Дело сводится к преобразованию уравнения
л
— D+r = r^ + ptga- + (ptga)^^ = 0.
Это преобразование выполняется с использованием равенств
+ ptgar^, = D+R,
(р tg а)ч> = (ptga),^ = {ptga)q ¦ igtga • [L - R),
в силу которых предыдущее уравнение и дает транспортное уравнение, описывающее изменение величины R вдоль характеристики С+:
D+R+±(ptga)q(R-L)R = 0. (18)
Аналогично получается транспортное уравнение, описывающее изменение величины L вдоль характеристики С_:
D-L+±(ptga)q(R-L)L = 0. (19)
Каждое из уравнений (1В), (19) есть уравнение Риккати. Благодаря специальному виду они интегрируются в квадратурах. Более того, аналогично случаю одномерных движений (см. § 16), здесь можно обойтись одной квадратурой. Для этого надо заметить, что справедливы формулы
R=-D-n(q) = -^D-q, L = D+ti(q) = ^D+q. (20)
Действительно, например, первая из формул (20) вытекает из очевидных равенств
?)_r = D_(r — I) = -2 D-fi(q),
D-r = (D+ + D-)r = 2 rv = 2 R,
и аналогично получается вторая.
Для интегрирования уравнения (18) делается подстановка R = 1/z, в результате которой оно становится линейным:
D+z + = Yp^ptg0^q'
С учетом (20) коэффициент при 2 преобразуется к виду
j-(ptgn)qL = — ¦ -
.
lP \Jp tg a
Поэтому предыдущее уравнение упрощается до следующего:
D+(zy/ptga) = ^^ptga(ptga)q.
Для входящей в правую часть производной нетрудно получить выражение
где т — величина, введенная в (2.22). Поэтому правая часть равна
т + 2 y/ptga 4 sin a cos3 q
Теперь интегрирование вдоль характеристики С+ от некоторого значения (при котором все величины отмечаются индексом нуль) до переменного значения ip дает
ч> __
Г-.— /—I--Г т + 2 Vptga
z^ptga = zoVpotgao - / —--:--г-dip.
J 4 sm a cos-5 a
ifio (c „}
Для приложений иногда удобнее иметь результат с интегрированием вдоль характеристики С+ по переменной ф. При такой замене переменной интегрирования будет dtp ¦= dф/ptga. Наконец, возвращение к R = 1/z дает следующее представление решения транспортного уравнения (1В):
Я =
-1 -. (22)
vV-'otur<i, - Ri, f ^j^=J(Kilia)_3^2{C0SQ)~5''2d^
фа(С+) ЧР
Точно такой же вид имеет решение уравнения (19); оно получается из (22) просто заменой R на L и С+ на С_.
На основании (22) можно сделать вывод о том, что неравенства Яо ^ О и Lq < 0 достаточны для того, чтобы первые производные решения оставались ограниченными при движении в сторону dф > 0. Напротив, если хотя бы одна из величин, Rq или Lq, положительна, то со стороны ф > фо можно ожидать наступления градиентной катастрофы в точке, определяемой условием обращения знаменателя в нуль.
Качественные свойства. Очевидно, что гиперболическая система (7) является симметрической (см. § 7). Поэтому для нее справедливы все выводы, полученные для уравнений одномерного движения в § 15. В частности, верны теоремы единственности решения задач Коши и Гурса, а также некоторых смешанных задач. Теорема существования гладкого решения, например, задачи Коши справедлива, вообще говоря, лишь в малом, т. е. в достаточно малой окрестности носителя начальных данных.
Необходимо обратить внимание на то, что система уравнений (7) гиперболична и относительно направления оси р, и относительно направления оси ф. Поэтому для нее корректна задача Коши как с начальными данными при tp = const, так и при ф = const. Это означает, что непрерывные безвихревые сверхзвуковые течения обладают свойством эволюционности как по переменной ip, так и по переменной ф. Однако при рассмотрении течений в целом необходимо учитывать возможность возникновения сильных разрывов, в том числе и контактных, и областей вихревого течения, причем свойства эволюционности могут нарушаться. Для правильного ответа на вопрос об эволюционности следует рассмотреть исходную систему (22.2) без предположений о потенциальности и изэнтроничности.
С этой целью надо заметить, что для любого данного семейства линий тока существует ортогональное семейство кривых, которые могут быть определены как линии уровня функции т = т(х, у), удовлетворяющей уравнениям вида
тх = uN, Ту = vN (23)
с некоторой функцией N > 0, определяемой полем скоростей. Так как якобиан тхфу - Туфх = yvpq2N всюду положителен, то можно перейти к системе уравнений, эквивалентной (22.2), рассматривая искомый вектор U = (и, V, р, S) как функцию переменных (т,ф):
Npq2uT + NupT - yvрурф = О,
N pq2vT + NvpT + у1' pupt, = О, Nbq2pT + NuuT + NvvT - yvpvut + y1'puv4, = ~^jV,
(24)
NST = 0.
В записи системы (24) в матричной форме (здесь U считается векто-ром-столбцом)
ATUT + Афиф = F матрицы-коэффициенты таковы:
Ат
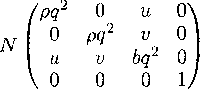
Аф =
У Р
| 0 |
0 | — V |
°\ |
| 0 |
0 | и | 0 |
| -V | и |
0 | 0 |
|
0 | 0 | 0 |
о/ |
Здесь обе матрицы, Ат и А^\ симметричны, но только матрица Ат является положительно определенной при условии, что М > 1, т. е. для сверхзвуко-
вых течений. Поэтому для системы (24) задача Коши с данными при т = = const корректна, а с данными при ф = const, вообще говоря, некорректна. Следовательно, система (24) является эволюционной только по переменной т.
Попутно стоит заметить, что условие совместности уравнений (23) после несложных преобразований приводится к виду
Щ = q~~qmqlmN, (25)
где N рассматривается как функция от (т, г/j), а функция qm = qm(Ф) взята из интеграла Бернулли (22.13). Поэтому функция N в (23) определена однозначно, с точностью до несущественного произвольного множителя, зависящего только от т, если заданы ее значения на какой-нибудь одной линии тока ф = const. В частности, если течение изоэнергетическое, т. е. константа ql не зависит от ф, то уравнение (25) имеет простое решение N — 1, и тогда из (23) следует, что можно принять т — <р. Этот вывод тем более справедлив для безвихревых изэнтропических течений.
Для иллюстрации указанного выше свойства эволюционности системы (24) можно вернуться к уже решенной в § 22 задаче обтекания выпуклого угла и интерпретировать ее как задачу Коши с начальными данными при х = 0, у > 0, задавая их в виде q = q\ > сь в = 0 (см. рис. 22.7). Тогда, проводя аналогию с одномерными движениями, можно трактовать отклоняющуюся часть ОВ обтекаемой стенки как «поршень, выдвигающийся из газа», на котором задано «условие непротекания» 9 = 9\ = const. Подобная аналогия уместна и полезна также в ряде других задач о сверхзвуковых течениях.
Простые волны. В § 22 уже были изучены простые волны для осесимметричных течений и было показано, что все они суть автомодельные решения, зависящие от А = х/у. Поэтому здесь будут рассматриваться простые волны только для плоскопараллельных течений. В этом случае свойства простых волн вполне аналогичны таковым для одномерных изэнптро-пических движений с плоскими волнами, рассмотренных в § 16. Так как, согласно общей теореме 13.1, простые волны должны быть изэнтропически-ми потенциальными течениями, то их можно искать сразу для уравнений (7) с v = 0.
Теорема 1. В каждой простой волне, если она не есть постоянное течение, один и только один из инвариантов Римана, г или I, сохраняет тождественно постоянное значение. Если в простой волне г = const (или I = const), то ее линиями уровня являются характеристики С - (соответственно С+). В обоих случаях характеристики — линии уровня простой волны — прямолинейны как на плоскости течения, так и на плоскости потенциала. Обратно, если в некоторой области течение не постоянно и один из инвариантов Римана тождественно постоянен, то течение в этой области есть простая волна.
Доказательство. Основное предположение, выделяющее простые волны, здесь выглядит так: q = q(А), в = 9(A), где А = А(ip, ip). Подстановка этого представления в (7) дает систему уравнений (штрихом обозначены производные по А)
q9 Av — pq Аф = О, ^
ctg2 а ¦ q Av — pqO'Aip = О, которая может иметь ненулевое решение (А^, А^), только если
q29'2 — ctg2 a-q'2 = 0.
В силу определения (12) это равенство равносильно соотношению г'1' = 0. Значит, один из инвариантов Римана, г или /, должен быть тождественно постоянен. Предположение о том, что постоянны они оба, приводит, очевидно, к постоянному течению.
Если г = const, то q9' = ctg а ¦ q' и уравнения (26) сводятся к одному Ay, — р tg а ¦ Аф = 0 или, в обозначениях (13), к уравнению ?>_ А = 0. Это означает, что параметр простой волны А постоянен вдоль характеристик семейства С_. Но на каждой характеристике С_ сохраняет постоянное значение также инвариант Римана I. Из постоянства инвариантов г и I вдоль С_ следует также постоянство величин q и в, а значит, р и а. Поэтому в дифференциальном уравнении характеристик С_ на плоскости потенциала правая часть постоянна вдоль С_. Следовательно, эти характеристики суть прямые линии на плоскости потенциала с уравнением вида
гр + <рр tg ос = F{q),
где F(q) — произвольная функция. Точно так же в дифференциальном уравнении характеристик С_ на плоскости течения
dy/dx = tg(# — а)
правая часть постоянна вдоль С_. Следовательно, эти характеристики — прямые линии и на плоскости течения с уравнением вида
У ~ ztg(0 - а) = F(q).
Аналогично рассматривается случай I = const, в котором вместо характеристик С_ прямолинейными будут характеристики С+. Наконец, если
в некотором непостоянном течении (заранее не предполагаемом простой волной) выполнено равенство г = const (или I = const, то это означает, что величина в зависит только от q. Значит, если положить q — А, то будет в --- 0(A), т. е. выполнено основное предположение, выделяющее простые волны. ¦
Простая волна, в которой тождественно постоянен инвариант Римана г (соответственно /), называется коротко г-волной (соответственно 1-волной).
В процессе доказательства теоремы 1 получились соотношения, позволяющие дать следующее полное описание всех простых волн.
Уравнения г-волны:
г - в- fi(q) = г0, у - х tg(0 -а) = F(q), ¦ф + ipptga = F(q).
(27)
(28)
Уравнения /-волны:
I = в f p(q) = Z0, у - х tg{9 + а) = F(q), Ф - pptga = F{q).
Входящие сюда произольные функции F(q) в разных уравнениях (27) и (28) могут быть различными.
Для распознавания простых волн служит следующая теорема о примыкании, дающая, аналогично теореме 16.2, достаточное условие существования простой волны.
Теорема 2. Если в непрерывном безвихревом изэнтропическом плоскопараллельном течении есть характеристика С+ (соответственно С_), вдоль которой вектор скорости тождественно постоянен, то в окрестности этой характеристики, с каждой ее стороны, данное течение является либо постоянным, либо простой 1-волной (соответственно г-волной). В частности, непостоянное течение, примыкающее к постоянному, всегда есть простая волна.
Доказательство. С несущественными изменениями повторяется доказательство теоремы 16.2. ¦
Теорема о примыкании справедлива и в усиленной формулировке, без требования потенциальности и изэнтропичности течения в целом, но с дополнительным предположением о том, что вдоль данной характеристики С+ (или С_) вихрь равен нулю и энтропия постоянна.
Простая волна называется центрированной, если все ее прямолинейные характеристики пересекаются в одной точке.
Рассуждение, аналогичное приведенному в § 16 по тому же поводу для простых волн в одномерных движениях, показывает, что справедливо следующее описание центрированных простых волн (для упрощения записи в качестве центра взяты точки (х,у) = (0,0) и (<р,ф) — (0,0); все другие случаи получаются отсюда преобразованиями переноса).
Уравнения центрированной г-волны:
(29)
Уравнения центрированной <-волны:
Итак, центрированные простые волны описываются автомодельными решениями исходных дифференциальных уравнений (1) или (7) (при v = 0). Полная центрированная простая волна уже была найдена в § 22; она называется течением Прандтля-Мейера и на плоскости течения показана на рис. 22.6. Эта картина здесь дополняется ее изображением на плоскости потенциала, приведенным на рис. 2.
Волны сжатия и разрежения. В частице, движущейся вдоль линии тока, плотность газа может возрастать или убывать. Если плотность газа возрастает, то имеет место течение сжатия; если плотность газа убывает — то течение разрежения. Эти понятия в применении к простым волнам приводят к следующему определению (аналогичному 16.3).
Определение 1. Простая волна называется волной сжатия (соответственно волной разрежения), если при движении в направлении вектора скорости вдоль пересекающих эту волну линий тока плотность р возрастает (соответственно убывает).
Так как при указанном направлении движения всегда dip > 0, то различающей величиной является производная р^: течение сжатия (разрежения) характеризуется неравенством pv > 0 (соответственно р. < 0).
При наглядном изображении простых волн в виде «веера» их прямолинейных характеристик можно различать волны сжатия и разрежения по расположению «ручки веера» аналогично тому, как различались такие волны в одномерных движениях (см. § 16). Специфика здесь состоит в том, что положение «ручки веера» определяется но отношению к направлению
e + p{q) = k, tg(e + a)
ф
Ч>'
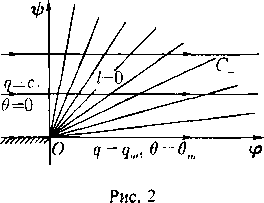
(30)
ptga= -
течения: говорят, что «ручка веера» находится спереди, если сближение прямолинейных характеристик происходит при движении вниз по потоку (в направлении вектора скорости), т. е. со стороны больших значений потенциала <р\ «ручка веера» находится сзади, если сближение прямолинейных характеристик происходит при движении вверх по потоку — со стороны меньших значений потенциала Ясно, что расположение «ручки веера» однозначно описывается направлением изменения, с ростом потенциала '~р, углового коэффициента наклона соответствующих прямолинейных характеристик. Важно, что это направление изменения всегда одинаково на плоскости течения и на плоскости потенциала.
Лемма 1. Угловые коэффициенты dy/dx и dip/dtp прямолинейных характеристик в простой волне с ростом ip всегда изменяются в одном и том же направлении (либо оба возрастают, либо оба убывают).
Доказательство. Для простой г-волны
д dy Q ^
0<pdx dip toV cos2(в — a)
где, как нетрудно вычислить с помощью (2),
т + 2 sirr_a _ 5Q
a'p 2с cos г
Так как здесь в — fx(q) = const, то 6^ = ctg a • q^/q. Следовательно,
Из этой леммы вытекает, что геометрический критерий для различения простых волн сжатия или разрежения на плоскости течения и на плоскости потенциала формулируется одинаково. Он дается следующей теоремой о «ручке веера».
Теорема 3. Простая волна является волной сжатия (соответственно разрежения), если и только если «ручка веера» ее прямолинейных характеристик находится спереди (соответственно сзади).
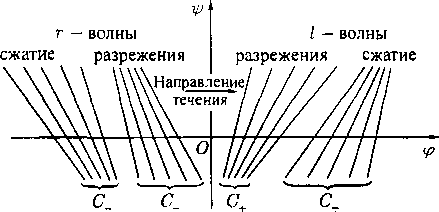
Рис. 3
Доказательство. Очевидно, что (рис. 3) на плоскости потенциала «ручка веера» в любой простой волне находится спереди, если и только если Id^/dtp'^ > 0), и находится сзади, если и только если Ыф/фр>\^ < 0. Так как в любой простой волне для наклона прямолинейных характеристик справедлива формула \d%jj/dip\ = р tga, то из выражений (32) и (2) следует соотношение
_ т + 2 sin а dtp ^ 2 cos a3a^
Поэтому «ручка веера» спереди, если и только если pv > 0, и сзади, если и только если pv < 0. ¦
Например, течение Прандтля - Мейера (см. рис. 2) является простой волной разрежения.
Различение простых волн сжатия и разрежения существенно с точки зрения возможности непрерывного продолжения течения. Нетрудно убедиться в том, что при неограниченном продолжении течения вниз по потоку градиентная катастрофа не наступает в волнах разрежения, но неизбежна в волнах сжатия. Геометрически последнее очевидно, так как в волне сжатия прямые характеристики рано или поздно начнут пересекаться и будут приносить в точку пересечения значения величин q и в. Аналитический вывод основан на замечании, что для простых волн в решении вида (22) транспортного уравнения вдоль прямолинейных характеристик подынтегральное выражение постоянно вдоль пути интегрирования. Поэтому формула (22) упрощается до следующей:
Я=-—---(33)
Но в простой /-волне для величины R справедливо выражение
2
ctg а
R = r4> = -2 -—-q^ = 2-^ct.g a-pv.
4 pq
Поэтому в /-волне разрежения будет R0 < 0 и при всех ф > фо величина R остается ограниченной. Напротив, в /-волне сжатия До > 0 и знаменатель в (33) обращается в нуль при конечном ф.
Плоскость инвариантов Римана. Для анализа сверхзвуковых течений общего характера иногда целесообразно рассматривать величины ю и ф как искомые функции независимых переменных г и /. Плоскость R (г, I) называется плоскостью инвариантов Римана (фактически она является деформированной плоскостью годографа). Ясно, что соответствующие дифференциальные уравнения могут быть выведены непосредственно из уравнений Чаплыгина (22.46) в области их гиперболичности путем перехода к характеристическим переменным (12). Однако проще всего вывести их из уравнений характеристик (14) (при и = 0) тем же приемом, каким были получены уравнения (16.46).
Для этого достаточно заметить, что так как вдоль характеристики С+ меняется только инвариант Римана /, то ее дифференциальное уравнение с1ф ~ ptgadip равносильно уравнению Ф1 = ptga ¦ ipi. Аналогично преобразуются уравнения характеристик С_, и окончательно получается следующая система линейных дифференциальных уравнений сверхзвукового течения на плоскости инвариантов Римана:
Ф1 -- р tg a • ,
фг =• - ptga • (fT.
Так как величины р и а зависят только от q, то их можно рассматривать как известные функции разности / — г. Исключение из системы (34) потенциала <р (путем перекрестного дифференцирования) дает одно линейное дифференциальное уравнение второго порядка для функции тока ф:
Одним из преимуществ записи уравнения (35) является его самосопряженная форма. В раскрытой форме это уравнение принимает вид уравнения Дарбу:
ipir - G(l - r)(ipi - -фг) = 0, (36)
где функция G(z) определена параметрически:
В отличие от его аналога (16.47), уравнение (36) не упрощается сколь-нибудь существенно даже в случае политропного газа. С этим связаны значительные аналитические трудности в исследованиях сверхзвуковых течений.
Задача об истечении струи. Из прямолинейной трубы ширины 2уо, в которой течет постоянный сверхзвуковой поток газа с известным уравнением состояния и заданными параметрами ро, ро, q > со, газ вытекает в окружающую среду (покоящийся газ), в которой задано давление pi < ро. Требуется найти установившееся течение газа вне трубы, считая границу с окружающей средой контактным разрывом.
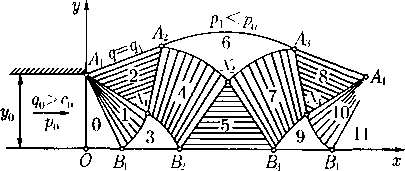
Рис. 4
До тех пор, пока течение в струе остается непрерывным, оно является безвихревым и изэнтропическим. Данные задачи определяют константу q^ в интеграле Бернулли и тем самым все функции параметров состояния от модуля скорости q. Так как при переходе через контактный разрыв давление должно меняться непрерывно, то давление в струе на ее границе также равно рI. Следовательно, вдоль границы известны плотность р\ и скорость звука с 1, а значит, и постоянное значение модуля скорости q\, определяемое интегралом Бернулли
Граничные условия симметричны относительно оси трубы. Из единственности решения следует, что если непрерывное решение существует, то оно должно быть также симметричным. Поэтому можно ограничиться рассмотрением «верхней» половины течения, изображенной на рис. 4. Граница струи и ось симметрии должны быть линиями тока, причем ф = 0 на оси и ф = тра = роЦоУо на границе. Следовательно, задача ставится на плоскости потенциала в полуполосе П = {0 ^ ф фо, ip ^ 0} как смешанная задача Коши с начальными данными при ц> = О
q(0,il>)=qo, в{0,ф)=0 (0 ^ ф ^ ф0) (38)
и граничными условиями
%>,0)=0, q(<p,Vo)=qi {'-р ^ 0). (39)
При движении вниз по течению в вытекающей струе образуется последовательность характерных областей 0,1. ..., 10, ..., показанных на рис. 4. К области 0 постоянного решения q = qo, в = 0 вдоль прямой А\В\ (характеристика С-) примыкает центрированная простая волна 1 с центром в Ах и уравнением г = го- Это течение описывается уравнениями
0 - и(я) = -М<?о); у - уо = xtg(6-а). (40)
В области 2 формируется постоянное течение с параметрами q = qi, в = в2, где угол 02 определяется из (40):
К области 2 вдоль прямой N\A2 (характеристика С+) примыкает простая /-волна 4, уже не являющаяся центрированной, с уравнением
Она заканчивается характеристикой B2N2, вдоль которой в = 0 в силу первого граничного условия (39). Поэтому вдоль B2N2 постоянное значение q = q5 находится из уравнения (41):
В области 5 снова образуется постоянное течение с параметрами q = 95, в = 0, к которому вдоль N2B3 примыкает простая г-волна 7 с уравнением
Область 8 снова есть область постоянного течения, причем так как q = q\ на A3N3, то
В области 10 снова формируется простая /-волна с уравнением
переводящая течение в постоянное в области 11 и т. д. В областях 3, 6. и 9 образуются течения общего характера. Для их расчета требуется решать некоторые краевые задачи, которые могут быть поставлены на плоскости инвариантов Римана. Например, в области 3 вдоль характеристики BiN\ семейства С+ дано г = —/.i(qi), вдоль отрезка В\В2 оси симметрии 0 = 0, т. е. г + I = 0, и вдоль характеристики N\B> семейства С- дано / = ii(qs). Поэтому на плоскости инвариантов Римана область Вi N1В2 имеет вид треугольника, показанного на рис. 5. В нем надо найти решение уравнения (36) по граничным условиям на линиях В1В2, где просто ф = 0, и В\ 1\\, где функция тока известна из описания центрированной простой волны в области 1. Этими данными искомое решение определяется единственным образом, так как в силу симметрии возникающая краевая задача на самом деле сводится к задаче Гурса в квадрате BiN\B2N[ с данными на характеристиках B\N\ и B\N[. Постановка на плоскости инвариантов Римана краевых задач, возникающих в областях 6 и 9, предоставляется читателю.

Важная особенность построенного тече- Рис. 5
ния состоит в том, что простые волны 1 и 4
суть волны разрежения, а простые волны 7 и 10 являются волнами сжатия. Поэтому не исключено, что в них произойдет градиентная катастрофа и дальнейшее непрерывное продолжение течения будет невозможно. Однако окончательное решение этого вопроса до настоящего времени не получено.
Установленные в § 5 свойства ударного перехода связаны с нормальной к фронту ударной волны составляющей вектора скорости. Эти результаты являются окончательными, если движение газа таково, что направление вектора скорости перед волной ортогонально фронту. Однако в общем случае вектор скорости образует с фронтом ударной волны острый угол, и тогда для полного описания движения за волной необходимо учитывать касательную составляющую вектора скорости. Это особенно важно в модели установившегося течения газа, когда за ударной волной могут получаться как сверхзвуковые, так и дозвуковые скорости. В § 10 уже сообщены предварительные сведения о стационарных ударных волнах — скачках уплотнения в установившихся течениях. Они используются в данном параграфе для более детального анализа поведения течения в косых скачках уплотнения (для краткости в дальнейшем слово «уплотнения» опускается).
Основная задача заключается в том, чтобы описать все состояния движения, достигаемые за возможными косыми скачками, через которые может преобразоваться некоторое фиксированное состояние движения перед скачком. При этом, как показано в § 10, течение перед скачком необходимо должно быть сверхзвуковым.
Ударная поляра. Легко сообразить, что упомянутая совокупность состояний за косыми скачками образует однопараметрическое семейство. Действительно, если угол между вектором скорости и поверхностью скачка задан, то состояние движения за скачком полностью определено, гак как касательная к поверхности скачка составляющая вектора скорости при переходе через скачок меняется непрерывно, а нормальная составляющая и термодинамические параметры газа однозначно определяются условием Dn = 0 (теорема 5.5). Кроме того, векторы скорости перед и за скачком и нормаль к поверхности скачка всегда лежат в одной плоскости. Поэтому для описания упомянутого однопараметрического семейства состояний достаточно рассмотреть косые скачки в плоскопараллельном течении (в частности, этим объясняется отнесение обсуждаемых вопросов в раздел двумерных установившихся гчений).
Конфигурация направлений в косом скачке показана на рис. 1. Здесь А •-точка течения, лежащая на линии скачка, и AN — касательная к этой линии в точке А. Предполагается, что передняя сторона скачка (как ударной волны) находится слева от AN, а его задняя сторона • справа от AN. Отрезок ABi длины <7i > Ci, изображает вектор скорости uj перед скачком. Отрезок АВ-> рис j изображает вектор скорости 119 за скач
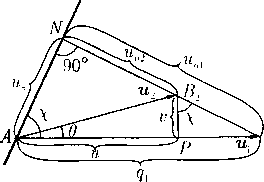
ком. Условие равенства касательных составляющих вектора скорости до и после
скачка равносильно перпендикулярности прямой В\В2 к AN. В системе координат, в которой ось х направлена по вектору скорости иь справедливы представления векторов скорости в компонентах U] = (91,0) и из = (u,v). Тем самым рис. 1 можно рассматривать как совмещение плоскости течения и плоскости годографа с началом координат в точке А. Через х обозначен угол между направлениями линии скачка и вектора скорости в точке А. Отрезки B\N и B2N равны, соответственно, величинам нормальных составляющих и„, и иП2, а отрезок AN — величине касательной составляющей и о.
Изложенные выше соображения показывают, что для заданного угла х положение точки В2 определено однозначно. Поэтому при изменении х точка В2 опишет некоторую кривую, которая называется ударной полярой. На плоскости годографа точки Вi и В2 являются годографами одной и той же точки А плоскости течения: они соответствуют разным сторонам скачка в точке А. Поэтому ударную поляру можно назвать также годографом косых скачков.
Аналитическое представление. Для получения аналитического представления ударной поляры используются все соотношения в ударных волнах, полученные в § 4. В случае установившихся движений соотношения (4.12) и (4.13) могут быть переписаны в виде
PiWn, ^ р2ип2, р2 р\ - PlUni (u„, — иП2).
Для компактности дальнейшей записи вводится амплитуда скачка (19.1), а именно величина
2 = {Р2 -р\)/р\с\, с которой предыдущие уравнения равносильны таким:
cjz г-. Vni{uni - и„2) = и2П1( 1 - V2/Vx), (1)
где V = 1 /р — удельный объем. К уравнениям (1) надо добавить уравнение
адиабаты Гюгонио (4.20) или (5.1), которому здесь целесообразно придать следующую форму:
Vo ~ Vi (1 — Г(г)). (2)
Вводимая уравнением (2) функция Г(г) представляет адиабату Гю
гонио в безразмерном виде. Ее график, вытекающий из установленных в § 5 свойств адиабаты Гюгонио в нормальном газе, показан на рис. 2,
где Zi = pi/picj.
Уравнения ударного перехода по нормали к скачку (1) и (2) замыкаются геометрическими соотношениями, вытекающими из конфигураций рис. 1. Из подобия треугольников В\РВ2 и B\NА следуют равенства
(<?i - и)2
Наконец, подстановка (4) в (5) дает искомое уравнение ударной поляры:
у2 = r(Mi(gi -v)/qi) _
(qi-u)2 (qi-ч i)/q\
Из уравнений (4) и (5) вытекает также следующее параметрическое представление ударной поляры:
u = qi(l-MJ2z), v2 = с2(гГ(г) — M^“2z2). (7)
Геометрическая форма ударной поляры определяется свойствами монотонности и звездности адиабаты Гюгонио, которые равносильны таким же свойствам функции Г(.г). Из них следует, что уравнение
Г(г0) = МГ220 (8)
при любом Mi > 1 имеет единственный корень zq — 2o(Mi) (см. рис. 2).
Поэтому ударная поляра определена в интервале 0 ^ г ^ zq. Из звездно
сти функции Г(г) следует, что ударная поляра также звездна относительно точки В\. Наконец, наклон касательной к ударной поляре в точке В\ определяется из уравнения (5) предельным переходом
lirn \dv/du\ = \/М2 - 1 = ctgai. (9)
z—>0 ' *
Из этих фактов вытекает, что ударная поляра имеет форму овала с угловой точкой В), показанного на рис. 3.
В силу свойства звездности угол наклона х линии скачка к направлению вектора скорости перед скачком U] всегда больше угла Маха а\ для состояния перед скачком. Точка (ц0,0), где
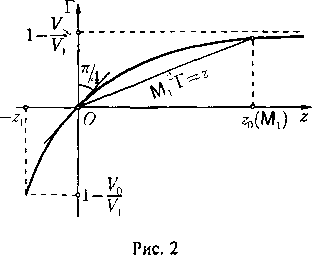
= <?2 = <?i (l _ Mj 22о),
соответствует прямому скачку. Поэтому из теоремы Цемплена 5.4 следует, что ио < С2, т. е. течение за прямым скачком всегда дозвуковое. Что же касается косого скачка, то за ним течение может быть как сверхзвуковым, так и дозвуковым.
Кривую (6) можно рассматривать и для значений 2 < 0. В этом случае, согласно следствию 5.4, состояние «1» должно находиться на задней стороне скачка. На рис. 3 значениям z < 0 соответствуют бесконечные ветви, расположенные в области и > Qi- Вертикальная асимптота этих ветвей связана с поведением функции Г(г) при z < 0 (см. рис. 2) и дается уравнением и = и00 = <?i(l + z\).
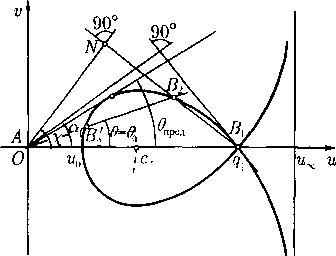
Рис. 3
Важной особенностью косых скачков является то, что угол поворота вектора скорости в не может превосходить наибольшего значения 0„ред, показанного на рис. 3.
В политропном газе функция Г (г) дробно-линейна:
^-зш2х + МГ2
Обтекание вогнутого угла. Постоянное плоскопараллельное сверхзвуковое течение над стенкой В [Л отклоняется, обтекая угол В\АВо, меньший 180° (рис. 4). Задача состоит в построении течения во всей области внутри этого угла. Как краевая задача для системы уравнений (22.23) (при ;/ = 0) с постоянными граничными данными вдоль лучей
01/iBj = 0, = <?i > Съ 9\ав2 = 0о > 0,
она является конически автомодельной (см. § 13). При этом одной из искомых величин будет постоянная скорость дг = <7\ав2- Можно также поставить эту задачу и как задачу Коши на плоскости потенциала в обла
сти {ip ^ 0, 0 ^ 0} с начальными данными при <р — 0
0(0, ф) = 0, <?(0, ф) = <?] > Ci
и граничным условием 0(ip, 0) = 0о > 0. Рассматриваемая задача альтернативна задаче обтекания выпуклого угла (см. § 22); она также является аналогом задачи о поршне, но на этот раз вдвигающемся в газ.
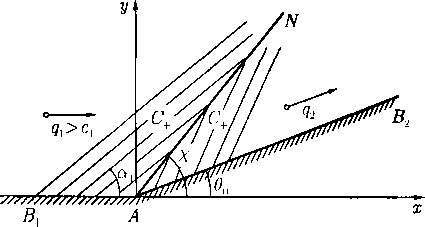
Рис. 4
Непрерывное решение этой задачи не существует. Действительно, в случае непрерывного течения к заданному постоянному сверхзвуковому потоку вдоль выходящей из вершины угла характеристики С® должна примыкать простая /-волна (теорема 24.2). Она обязана быть центрированной в вершине угла, так как иначе вдоль некоторой принадлежащей ей характеристики С+ будет сильный разрыв. Но такая центрированная /-волна может быть только волной разрежения (теорема 24.3), и потому она должна вырабатывать на стенке АВ2 скорость qo > (д. Однако это противоречит факту сохранения инварианта Римана /, в силу которого p(q\) = во + /^(<72) и должно быть qo < qi, так как Оо > 0.
Можно найти решение, в котором постоянное течение вдоль В\ А переводится в постоянное течение вдоль АВ2 посредством косого скачка уплотнения. Для этой цели надо по данным qi, си р\ построить ударную поляру и провести луч из начала координат под заданным углом во (см. рис. 3). Точка пересечения В2 этого луча с ударной полярой дает искомое решение, в котором AN есть линия косого скачка. Это решение и показано на рис. 4, где также изображены (тонкими линиями) характеристики С+ до и после скачка.
Найденное решение используется в задачах обтекания клиновидных тел равномерным сверхзвуковым потоком. Например, в случае бесконечного клина, обращенного острием А навстречу потоку (рис. 5), течение разделяется прямой линией тока В\ А на два течения — обтекания вогнутых углов BiAB2 и В\АВ$.
Здесь возникают следующие важные обстоятельства. Во-первых, пересекающий луч может встречать ударную поляру как минимум дважды, например в точках В2 и В'2, что дает два возможных решения (см. рис. 3). То, которое соответствует точке В2, называется слабым решением, а соответствующее точке В'2 — сильным решением. При этом для отбора един-
ствснного решения требуются какие-то дополнительные условия, которые в настоящее время точно не сформулированы. Во-вторых, указанные решения существуют, только если угол во достаточно мал, точнее, если во ^ ^пред-Для углов во > 0Пред решение (если оно вообще существует) должно резко отличаться от найденного. Здесь положение таково, что решение в точной постановке неизвестно.
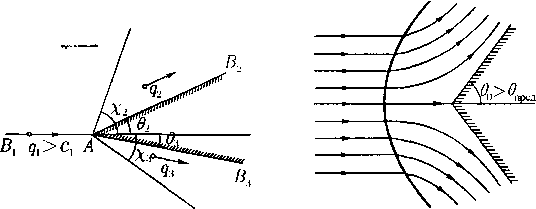
Рис. 6
Рис. 5
Эксперименты с обтеканием конечных клиновидных тел показывают, что при #о < #пред обычно реализуется слабое решение. Если же во > впреа, то возникает так называемый отошедший скачок, линия которого располагается впереди тела, не соприкасаясь с ним (рис. 6). За отошедшим скачком реализуется сложное до- и сверхзвуковое вихревое течение с переменной энтропией, описание которого в настоящее время может быть дано только численными методами.
Отражение косого скачка от стенки. Явление отражения ударной волны от жесткой стенки, рассмотренное в § 18 для падающего фронта, параллельного стенке (нормальное отражение), представляет большой интерес и в случае наклонно падающего фронта. При этом и отраженная волна также будет наклонной. Возникающая здесь задача об описании движения газа за падающим и отраженным фронтами в общем случае достаточно сложна. В ее простейшем варианте предполагается, что падающий фронт и стенка являются плоскими и что газ перед фронтом покоится. Тогда движение может рассматриваться как плоскопараллельное.
Пусть Dn — скорость перемещения падающей ударной волны, А — точка пересечения линии фронта со стенкой и ,\1 — угол между ними (предполагается, что 0 ^ xi ^ тт/2). Тогда скорость перемещения точки А вдоль стенки равна
В системе координат, перемещающейся в ту же сторону вдоль стенки со скоростью <?ь точка пересечения, а с ней и падающий фронт покоятся. В этой системе координат наблюдатель видит движущийся со скоростью q\ вдоль стенки постоянный поток, который отклоняется наклоненным ему навстречу косым скачком уплотнения, образующим со стенкой угол Предполагается, что и дальнейшее течение газа за скачком в этой системе координат является установившимся. Требуется описать это течение при условии, что от точки А отходит второй скачок, приводящий поток за первым скачком к направлению, параллельному стенке (рис. 7).
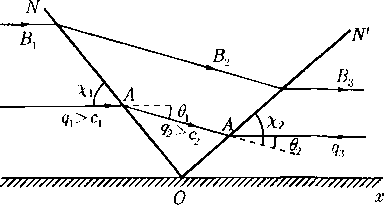
Рис. 7
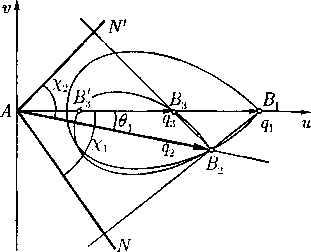
Рис. 8
Решение ищется с помощью ударных поляр. В заданном состоянии газа перед падающим фронтом, согласно предыдущему, известна скорость q\. Тем самым известна и ударная поляра с вершиной В\ (рис. 8). Поэтому за-ланис угла паления \i однозначно определяет угол поворота потока в\ в падающем скачке. За ним все параметры течения, в частности вектор m и скорость q2, становятся вполне определенными. Тем самым известна и ударная поляра с вершиной Во для состояния за падающим скачком. Ее точки пересечения с осью v = 0 определяют ударный переход в отраженном скачке, за которым вектор скорости 113 направлен параллельно стенке. При этом точка Дз дает слабый отраженный скачок, а точка В'л — сильный. Эксперимент показывает, что обычно реализуется слабый отраженный скачок. Такое отражение, картина которого показана на рис. 7, называется правильным отражением.
Правильное отражение возможно не при любых значениях амплитуды падающей волны z\ и угла падения хь Ею реализация лимитируется тем, что ударная поляра с вершиной В2 может не пересечь ось v = 0. Исследование этой ситуации для политропного газа приводит к следующему результату. Если угол х\ достаточно мал, то всегда существует правильное отражение. Для каждого заданного z\ имеется такое предельное значение = X*(2i)> чт0 >ФИ Х\ > X* правильное отражение невозможно.
Качественная зависимость \* от z\ показана на рис. 9. Предельное значение X*izi) ПРИ Zi —> ос для воздуха (7 = 1,4) приблизительно равно 40°.
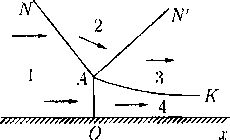
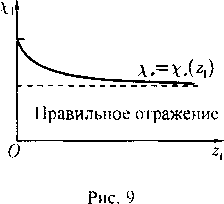
Если xi > т0 картина отражения ударной волны существенно
усложняется. В опыте при этом наблюдается так называемое маховское отражение с «тройной» точкой А пересечения более чем двух линий сильного разрыва. Качественная картина маховского отражения показана на рис. 10, где О А - «почти прямой» скачок, AN и AN' - косые скачки, а АК — линия контактного разрыва. Однако при этом линии скачков в окрестности точки А, вообще говоря, искривляются и течения в областях 2, 3 и 4 не являются постоянными. Это создает значительные трудности при исследовании маховского отражения, и до сих пор неизвестно, существует ли решение вообще (без учета вязкости и теплопроводности). Более подробные сведения
по вопросам, связанным с отражением наклонно падающих ударных волн, можно найти в [4] и в цитированной там литературе.
Осесимметричное обтекание конуса. Бесконечный круговой конус с осью х и полууглом раствора в\ обращен вершиной навстречу равномерному сверхзвуковому потоку, текущему со скоростью ui = (<?i,0). Требуется построить осесимметричное течение — обтекание конуса. Граничное условие на конусе имеет вид
и - Xiv = 0 (Ai--ctg#i).
(15)
Ясно, что так же, как и в случае обтекания клина плоскопараллельным потоком, эта задача принадлежит к классу конически автомодельных (см. § 13) и должна решаться с сильным разрывом — косым скачком уплотнения. Однако есть существенное отличие, так как здесь течение между поверхностями скачка и конуса не может быть постоянным (постоянные осесимметричные течения возможны только в направлении оси х, см. §22). Поэтому
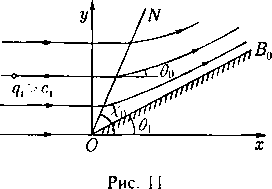
в случае конуса решение усложняется. Оно основано на следующем качественном представлении о геометрии течения (см. рис. 11). К вершине конуса присоединен конический косой скачок ON с уравнением А = Ао, где Ао = ctg хо < Ai, в котором заданное сверхзвуковое течение поворачивает на угол 9q < в\. В интервале Ао ^ А < Ai реализуется некоторое коническое течение Буземана (см. § 22), доворачивающее поток до нужного направления вдоль поверхности обтекаемого конуса.
Для расчета этого конического течения надо обратиться к системе уравнений (22.63). Ее можно свести к одному уравнению второго порядка для функции v = v(u). В этом представлении первое уравнение (22.63) переходит в равенство
А = -¦«„, (16)
а второе приводится к виду
(17)
Уравнение (17) удобно тем, что его интегральные кривые располагаются непосредственно на плоскости годографа. Искомое решение дается инте-
тральной кривой В2В0 (рис. 12), которую при заданной точке Во на ударной
поляре надо искать, решая задачу Коши для уравнения (17) с начальными
условиями
v{u2) ^
v2, vu(u2) =
-~1U2
(18)
Второе равенство (18) следует из уравнения (16) в силу того, что точка В2 лежит на задней стороне линии косого скачка, на котором А = ctg^o, и из равенства касательных составляющих вектора скорости до и после скачка (рис. 12). Эта интегральная кривая должна дойти до конечной точки Bq, где выполнено условие обтекания (15), которое в силу (16) можно переписать в виде
v(u0)vu(u0) + и0 = 0. (19)
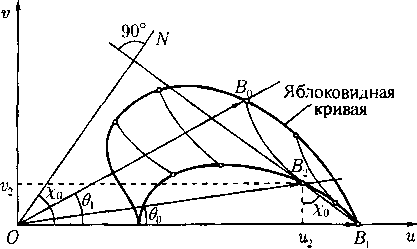
Рис. 12
Совокупность всех конечных точек Во. получаемых, когда точка В пробегает линию ударной поляры, образует яблоковидную кривую, показанную на рис. 12. Ясно, что яблоковидная кривая и семейство интегральных кривых В? Во, получаемые численным решением задачи (17), (18), (19), зависят только от данного невозмущенного сверхзвукового потока и могут считаться известными (см. [3]).
Окончательно решение задачи обтекания конуса сводится к следующему. Заданный луч ОВо образующей поверхности конуса пересекает построенную для данного набегающего потока яблоковидную кривую в точке Во, которой однозначно соответствует точка В2 на ударной поляре с вершиной В\. Нормаль ON к прямой В1В2 дает направление луча образующей поверхности конического скачка. Вектор OBq равен вектору скорости течения на поверхности конуса. Коническое течение между поверхностями скачка и конуса описывается известными из расчета кривой Во Bq зависимостями v(u) и Х(и).
В задаче обтекания конуса возникают те же обстоятельства, связанные с единственностью решения и с существованием решения при больших углах в\, которые отмечены выше по поводу обтекания клина.
Переход через скорость звука представляет собой одно из важнейших газодинамических явлений. С точки зрения теории интерес к этому явлению вызван тем, что основные уравнения модели установившихся течений приобретают дополнительную особенность, связанную с изменением их типа в области определения решения.
Определение 1. Установившееся течение газа называется околозвуковым, если всюду в области этого течения величина ; N1 — 1! мала по сравнению с единицей.
Околозвуковое течение может быть чисто дозвуковым или чисто сверхзвуковым. Однако наибольший интерес представляют трансзвуковые течения, в которых происходит переход через скорость звука. Здесь будут рассматриваться именно такие гладкие околозвуковые течения в рамках модели плоскопараллельного безвихревого изэнтропического течения. Тем не менее надо иметь в виду, что многие из отмеченных ниже фактов и свойств верны и для осесимметричных течений (см. упражнения 20, 21).
Звуковая линия. В плоскопараллельном течении переход через скорость звука осуществляется на некоторой линии, которая называется звуковой линией. Расположение и форма звуковой линии на плоскости течения зависят от решения. На данном решении ее уравнение может быть записано в любой из равносильных форм:
q(x,y) = с{х,у)\ q(x. у) = с»; Щх,у) = 1. (1)
Ясно, что годограф звуковой линии всегда принадлежит фиксированной окружности q = с* (см. рис. 22.2). К звуковой линии может примыкать как дозвуковое, так и сверхзвуковое течение. Прежде всего устанавливаются некоторые особенности такого примыкания.
Если к звуковой линии Z примыкает сверхзвуковое течение, то в каждой точке А € Z выходящие из А характеристики С+ и С- образуют с вектором скорости угол 90° и, следовательно, касаются друг друга (рис. 1). Этот факт очевидным образом следует из определения угла Маха (11.22) и равенства sin а а = 1-
Теорема А. А. Никольского и Г.И.Таганова.
Пусть к звуковой линии Z примыкает дозвуковое течение. Предполагается, что Z не является линией тока. Простой, но весьма важный факт выражается следующим свойством монотонности изменения направления вектора скорости при перемещении вдоль такой звуковой линии.
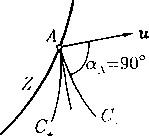
Рис. I
Теорема 1. Если при перемещении вдоль звуковой линии область дозвукового течения останется слева, то вектор скорости монотонно (может быть, не строго монотонно) поворачивается по часовой стрелке.
Доказатнльство. В точках звуковой линии Z уравнения (22.45) принимают вид
и, следовательно, при перемещении вдоль Z
С другой стороны, из второго уравнения (1) следует, что вдоль Z справедливо равенство dq = 0, и так как Z не является линией тока (т. е. вдоль
нее d%l> ф 0), то
ЯФ ~ —qvd<pjdi>.
Подстановка этого выражения в предыдущее показывает, что при перемещении вдоль Z выполнено соотношение
м = <2) Пусть Q есть дозвуковая область течения, частью границы которой является Z. Следует рассмотреть два случая: а) вектор скорости и в точках А € Z направлен вовне П иб) вектор и направлен в область Q (рис. 2, а, б).
В случае а) при перемещении вдоль Z в направлении, указанном в условии теоремы (показано стрелкой на рис. 2), верно неравенство d-ф > 0. Действительно, в местной системе координат с началом в Л и осью х, направленной по ид, в представлении ил = (и, о) будет и = q и v = 0. Поэтому здесь d-ф ~ pq dy, причем dy > 0. Далее, так как q < с, слева от А и q = с* в точке А, то в этой точке производная qv ^ 0. Следовательно,
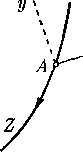
q<C
,-''х
— и
<1ф< О Я,< о
а) б)
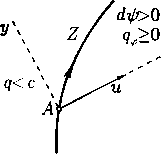
Рис. 2
соотношение (2) влечет неравенство d9 sj 0. Аналогично, в случае б) при обусловленном направлении перемещения вдоль Z (показано стрелкой на рис. 2, б) будет d-ф < 0, qv < 0, и из (2) снова получается d0 ^ 0. ¦
Очевидно, что утверждение теоремы 1 верно и в том случае, когда к звуковой линии Z примыкает сверхзвуковое течение и перемещение вдоль Z происходит так, что область сверхзвукового течения остается справа.
Следствие. Если по обе стороны звуковой линии Z находится дозвуковое (или по обе стороны сверхзвуковое) течение, причем Z не является линией тока, то вдоль Z необходимо в = const; и линия Z совпадает с эквипотенциалью.
Примыкание простой волны. Другой важный факт обнаруживается при изучении вопроса о том, когда к звуковой линии может примыкать простая волна сверхзвукового течения.
Теорема 2. Пусть в области Q. гладкого течения есть звуковая линия Z, к которой примыкает простая волна. Тогда Z является двойной характеристикой С±, причем линия Z — прямая на плоскости течения. Никакая другая характеристика не пересекает Z в области Q. В точках Z вектор скорости ортогонален прямой линии Z.
Доказательство. Пусть к Z примыкает r-волна с уравнением в - n(q) •= г0. Так как //(с*) = 0, то в = г0 вдоль Z. Поэтому Z есть линия уровня простой r-волны и необходимо должна совпадать с некоторой характеристикой С_. Это означает, что вдоль нее справедливы равенства
dy/dx = tg(0 - а) = tg(r0 - тг/2) = - ctg?-0.
Следовательно, если начало координат выбрано в точке А € Z, то линия Z есть прямая у = —ж ctg г0, совпадающая с характеристикой С_.
Характеристика С+, проходящая через точку А, определяется дифференциальным уравнением
dy/dx = tg(0(x, у) + а(х. у))
и начальным условием у(0) = 0. Но прямая у = -xctgro удовлетворяет этому условию и по построению такова, что вдоль нее
0(х, —xctgro) = го, а(х, —xctgro) = тг/2-
Поэтому вдоль этой прямой
dy/dx = - ctgг0 = tg(0(x, -xctgro) + <*(х, -xctgro)),
т. е. предыдущее дифференциальное уравнение превращается в тождество. Следовательно, в силу единственности, решение совпадает с у = —xctgro, т. е. С+ совпадает с Z.
Это же рассуждение показывает, что никакая другая характеристика, проходящая в области О., не может иметь общих точек с Z. Наконец, в силу предыдущего касательный вектор к Z есть 1 = (sinro, cosro), а вектор скорости в точках Z имеет вид и — с» (cos ?-о, sinro). Следовательно, 1 ¦ и = 0. ¦
Итак, примыкание простой волны к звуковой линии возможно, только если последняя есть прямая звуковая линия. В дальнейшем этот вид звуковой линии будет изучен более детально.
Местная сверхзвуковая зона.
Пусть течение определено по одну сторону от некоторой линии тока !? (которую можно считать обтекаемой твердой стенкой) и имеет следующую структуру. Течение всюду дозвуковое, кроме области П, ограниченной участком АВ линии ,СЛ и звуковой линией Z с концами в точках А и В (рис. 3), причем в О. течение сверхзвуковое. Такие местные сверхзвуковые зоны могут возникать, например, на теле при его обтекании безграничным дозвуковым на бесконечности потоком, когда число Маха > Мд (см. §23). Оказывается, что непрерывное течение в местной сверхзвуковой зоне неустойчиво в том смысле, что оно может разрушаться при сколь угодно малом изменении границы !?. Это разрушение связано с появлением скачков уплотнения и нарушением безвихревого изэнтропического характера течения. В частности, справедлив следующий факт: если на сверхзвуковом участке АВ стенки !? имеется сколь угодно малый прямолинейный отрезок, то непрерывное течение в невозможно.
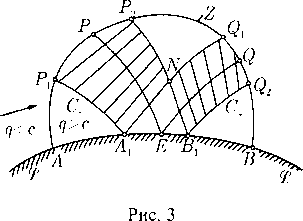
Действительно, пусть A\B\ С АВ — отрезок прямой и точка Е ? А\В\. Характеристики С- и С+, выходящие из Е, не могут пересечься второй раз внутри Q. Этот общий факт следует, например, из того, что угловой коэффициент (24.14) каждой характеристики на плоскости потенциала всегда имеет один и тот же знак, в силу чего никакая характеристика не может дважды пересечь одну и ту же эквипотенциаль. Поэтому они должны достигать звуковой линии Z, соответственно, в точках Р и Q (см. рис. 3). Свойство сохранения значений инварианта I вдоль ЕР и инварианта г вдоль EQ приводит к равенствам
вР = вЕ -(- дд, 0q = вЕ — цЕ, (3)
из которых вытекает соотношение
9р + 9q = 2 Ое- (4)
Так как вЕ = const при перемещении вдоль прямолинейного участка A±Bi, то соотношение (4), в силу теоремы 1, возможно, только если Op — const
и 9q = const. Тогда из (3) получается, что /ле = ц{Че) = const, т. е. qg =
= const. Значит, на отрезке А\В\ скорость постоянна. Из теоремы единственности (см. § 24) следует, что во всем характеристическом треугольнике A\NBi течение является постоянным. По теореме 24.2 к этому постоянному течению должна примыкать вдоль С+ -характеристики A\N простая /-волна. Следовательно, область течения А\Р\ PoN есть простая волна, примыкающая к участку Р\Р2 звуковой линии Z. Но тогда факт пересечения С--характеристики ЕР со звуковой линией в точке Р противоречит теореме 2.
Из соотношения (4) и теоремы 1 следует также невозможность непрерывного течения в местной сверхзвуковой зоне около стенки, на которой есть участки, вогнутые в сторону потока.
Окрестность центра течения. Наиболее замечательные свойства околозвукового течения связаны с его поведением в окрестности так называемого центра течения.
Определение 2. Центром околозвукового течения называется такая точка на звуковой линии Z, в которой вектор скорости ортогонален к Z.
Структура окрестности центра течения рассматривается в предположении, что в этой окрестности компоненты вектора скорости и(х, у) и v(x, у)
трижды непрерывно дифференцируемы. В качестве исходной беретсаьси-стема уравнений на плоскости течения (22.23) при и = 0:
иу - vx - 0,
(и2 — с2)их + 2 uvuy + (у2 — c2)vy — 0.
Система координат (х, у) выбирается так, чтобы начало координат совпадало с центром течения О и ось х была направлена по вектору скорости и0 (в дальнейшем значения всех величин в центре течения отмечаются индексом нуль). В этой системе координат компоненты вектора скорости в центре течения таковы:
Как вскоре выяснится, ответственной за поведение околозвукового потока в окрестности его центра является величина ускорения течения в центре (dq/dt)о = (uqx + vqy)o- Для него в силу (6) справедливо представление (dq/dt)о = с»иХ(). Поэтому величину
«хо = а (7)
также можно назвать ускорением (относительным) околозвукового течения в его центре.
Пусть у = Y{x) есть уравнение проходящей через О линии тока, х = Z(y) — уравнение звуковой линии и х = X(у) — уравнение проходящей через О характеристики. В выбранной системе координат У(0) -- Z(0) = = Х(0) = 0 и из определения центра течения следует, что равны нулю также первые производные:
Для выделения главной части разложений (9) используется моделирование с помощью преобразования растяжения всех переменных
х —» Ах, у —> By, (и - с«) —> Р(и -- с»), v Qv,
где А, В, Р, Q — параметры преобразования. Требование инвариантности первого уравнения (5) приводит к соотношению
Далее, с учетом пропорциональности величины и2 —с? разности и—с* (в силу интеграла Бернулли), выделение главной части второго уравнения (5) вблизи точки О дает
R*(u - с*)их - c*vy = F (R* > 0). (10)
Поэтому требование инвариантности главной (левой) части уравнения (10) влечет соотношение
Кроме того, надо потребовать, чтобы величина ускорения (7) при таком моделировании не менялась. Для этого должно быть Р = А, Следовательно, все параметры выражаются через один из них, например В, и требуемое моделирование, с малым параметром В = 5, определяется формулами
х —> 52:г, у —> 5у, (и — с») —> 52(и — с*), v —> 53v. (11)
В результате подстановки (11) в разложения (9) и сравнения членов с одинаковыми степенями 5 легко устанавливается, что главная часть этих разложений имеет вид
и{х,у) = с„+аюх + а02у2, v{x, у) = 0иху + 0озУ3, (12)
если только выполнены равенства
«01 = 001 = 0ю = 002 = 0. (13)
После этих предварительных замечаний устанавливается следующий точный результат, в формулировке которого участвует положительная величина
где функция гп определена в (2.22) и те* = т(р*).
Теорема 3. Если решение системы уравнений (5) в окрестности центра течения трижды непрерывно дифференцируемо, то для него верны равенства (13), а коэффициенты в представлении (12) таковы:
аю = а, а02 = к„а2, 0ц = 2к,а2, 0Оз = | к^а3. (15)
Кроме того, справедливы формулы а величина Xq имеет два значения:
Х% = -Ка, Х{ = 2 Ка (,17)
для характеристик разных семейств.
Доказательство. Гак как коэффициенты разложений (9) пропорциональны значениям соответствующих частных производных оти и » в точке О, то они получаются в результате дифференцирования уравнений (5) по х и у с последующим переходом в точку О. Например, для получения последней из формул (15) надо дифференцировать второе уравнение (5) трижды по у. При этом используется вытекающее из интеграла Бернулли соотношение
d(c2) = —rnqdq.
справедливое при любом дифференцировании d. Кроме того, вдоль Z верно равенство и2 + v2 = с2, дифференцирование которого один и два раза по у дает в точке О соотношения
иУа = uX(,Zq ~r Uyyo = 0.
Отсюда получается первая формула (16). Далее, дифференцирование уравнения линии тока v = uY' один и два раза по х и учет равенств (13) дает вторую и третью формулы (16). Наконец, для вычисления величины Xq проще всего исходить непосредственно из характеристического уравнения системы (5), которое для характеристик, заданных уравнением х = Х(у), можно записать в виде (нормальный характеристический вектор есть (1, —X'))
(М2 - 1 )(и - vX')2 = [v + uX'f.
Двукратное дифференцирование этого уравнения по у с учетом того, что и = и(Х(у),у) и т.д., и переход в точку О, в силу формул (13) и (15), приводят к соотношению
с. (m. + 2)(2 Ка2 + аХЦ) = 2 с;Х^2.
С величиной 2, вводимой равенством ХЦ = k*az, а также с учетом (14) это соотношение принимает вид квадратного уравнения
z‘2 — z — 2 0.
Его корни z = — 1и2 — 2 и дают формулы (17). ¦
Теорема 3 имеет ряд важных следствий. Точка О называется точкой распрямления проходящей через нее линии тока, если Yq" = 0. Первое следствие вытекает из формул (16), где 2/Зго = vXXo.
Следствие 1. В центре течения кривизна линии тока равна нулю. Центр течения является точкой распрямления проходящей через него линии тока, если и только если vXXo = 0.
Далее, если ускорение а / 0, то звуковая линия Z делит окрестность центра течения на две части, в одной из которых течение дозвуковое, а в другой — сверхзвуковое. Второе следствие вытекает из первой формулы (16).
Следствие 2. Кривизна звуковой линии в центре течения пропорциональна ускорению. Если ускорение отлично от нуля, то в окрестности центра звуковая линия всегда выпукла в сторону сверхзвукового течения.
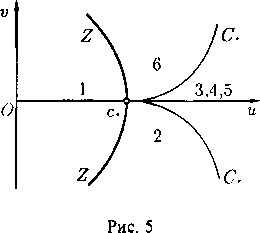

Выявленное этими результатами расположение основных линий в окрестности центра течения показано на рис. 4 в случае а > 0. Здесь обращает на себя внимание тот факт, что характеристика С± (а также характеристика С_) имеет точку О своей точкой перегиба, в которой, как это следует из формул (17), кривизна этой характеристики меняется скачком.
Трехлистность годографа. Еще одно существенное свойство окрестности центра течения выявляется при рассмотрении ее годографа. Из рассмотрения рис. 4 следует, что сверхзвуковая часть годографа не может быть однолистна. Действительно, при однократном обходе вокруг точки О на плоскости течения проходящая через О характеристика С+ встречается дважды (то же верно и для С..). Точная формулировка этого свойства такова.
Следствие 3. Если ускорение а / 0, то годограф сверхзвуковой части течения, расположенной вниз по потоку от первых проходящих через О характеристик, является трехлистным. Каждая из трех областей 3, 4 и 5 на рис. 4 отображается взаимно однозначно на одну и ту же область плоскости годографа (рис. Ъ).
Этот факт устанавливается совсем просто, если ограничиться главной частью отображения R2(x,y) —> R'2(n, v), определенной формулами (12). С учетом (15) эти формулы переписываются в виде
и(х, у) = с» + ах + к*а у , v(x,y) = 2 к*а2ху+ т,к2а3у3
(18)
О
В этом же приближении, в силу (16), уравнение звуковой линии есть
(Z) х = —к^ау2, (19)
а уравнения центральных характеристик С±, в силу (12), таковы:
(С±) х = -}^к*ау2: (С±) х ~ к*ау2. (20)
Исследование отображения R2(x,y) —> R2(u, v), заданного формулами (18), можно выполнить, заметив, что каждой квадратной параболе на плоскости R2(x, у), определяемой заданием вспомогательного параметра А:
х = \к*ау2,
соответствует полукубическая парабола на плоскости R2(u,v), определяемая заданием вспомогательного параметра ц:
v2 = - с»)3.
Действительно, в результате подстановки выражения для х в формулы (18) задаваемое ими отображение сводится к конкретной зависимости р от А:
(А + 1)3
График функции (21) показан на рис. 6. Значениям А < -1 соответствуют значения р. < 0 и и < с». Это есть дозвуковая область течения, в которой отображение (18) взаимно однозначно. Звуковой линии, согласно (19), соответствует значение А = —1 и р = ос. При переходе в сверхзвуковую область, где А > — 1, взаимно однозначный характер соответствия сохраняется до тех пор, пока А < —1/2, ц > 2. Точка А = --1/2 дает, в силу (20), характеристику С±. Значение // = 2 подучается также при А = 1, причем это — двукратное значение, которое дает, согласно (20), характеристику С±. При fj, < 2 соответствие трехзначно: каждое значение /j получается при трех различных значениях А. Поэтому вся область плоскости годографа, определяемая неравенствами 0 < ц < 2, оказывается трижды покрытой образом сверхзвуковой части плоскости течения, соответствующей значениям А > —1/2. Это и утверждается в следствии 3.
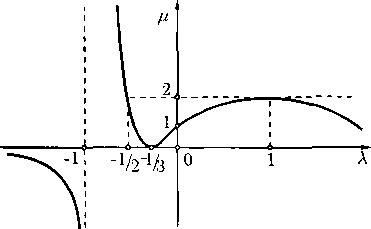
Рис. 6
Указанный характер отображения связан с тем, что якобиан отображения (18) в сверхзвуковой части течения меняет знак, обращаясь в нуль на характеристиках С±. Действительно, из (18) для якобиана следует выражение
uxvy — uyvx = 2k*a3(x - к*ау2) = 2к2аАу2(\ - 1).
Замечание о моделировании. Моделирование (11), использованное при построении главной части течения в окрестности центра, имеет на самом деле более широкое значение. Оно используется для изучения особенностей, которые могут появляться на звуковых линиях в решениях краевых задач о трансзвуковых течениях. Иногда это моделирование дает вполне удовлетворительное приближенное решение задачи в целом.
Необходимая для этого система дифференциальных уравнений получается, если заметить, что первое уравнение (5) инвариантно относительно преобразования (11), а второе имеет вид (10) с инвариантной левой частью. Простое подробное вычисление показывает, что правая часть в (10) после подстановки (11) имеет более высокий порядок малости по сравнению с левой частью при 6 —> 0. Это же вычисление дает величину R* = 2/с* в формуле (10). Поэтому после введения новых переменных
О
Легко проверить, что формулы (25) дают точное решение системы (23).
С помощью стандартных формул перемены ролей зависимых и независимых переменных (22.24) система (23) линеаризуется:
Xv ^ Уи‘ %и ~ Hyvi (26)
и, после исключения х, приводится к уравнению Трикоми для y(u,v):
itVvv Уии = 0. (27)
Оно является простейшим стандартным уравнением смешанного типа. Для уравнения (27) областью эллиптичности (дозвуковые течения) является полуплоскость и < 0, а областью гиперболичности (сверхзвуковые течения) — полуплоскость и > 0. При этом линия вырождения типа есть ось и = 0, изображающая звуковую линию. Соответствие с физическими переменными осуществляется путем «восстановления штрихов» и обращения к формулам (22) и (24).
Прямая звуковая линия. Важная особенность околозвукового течения обнаруживается в случае специального вида звуковой линии, когда все ее точки суть центры течения, а сама она - прямая линия. Именно такого вида течение должно реализоваться, если к звуковой линии примыкает простая волна (теорема 2).
Определение 3. Звуковая линия Z называется прямой звуковой линией, если на плоскости течения Z есть прямая линия и вектор скорости во всех ее точках перпендикулярен Z.
Прежде всего, справедливо следующее замечательное достаточное условие реализации прямой звуковой линии.
Теорема 4. Пусть в окрестности центра течения О решение системы (5) трижды непрерывно дифференцируемо. Если О есть точка распрямления проходящей через нее линии тока и если в О ускорение равно нулю, то точка О принадлежит прямой звуковой линии.
Доказательство. Пусть система координат (х, у) выбрана так же, как и выше при анализе окрестности центра течения. Рассматривается вектор-функция g = g(x, у) с пятью компонентами:
д = (и- с*, v, их, vx, vxx).
(28)
Утверждается, что для любого трижды непрерывно дифференцируемого решения системы (5) при каждом фиксированном х вектор д, как функция величины у, удовлетворяет линейному обыкновенному дифференциальному уравнению вида
![]()
(29)
где Н есть 5 х 5-матрица с элементами, непрерывными в окрестности точки О. В силу предыдущего анализа окрестности центра течения из условий теоремы следует, что р(0,0) = 0. Но единственным решением уравнения (29) с нулевым начальным условием является тождественный нуль, т. е. д(0, у) = 0. Следовательно, на некотором интервале оси у, содержащем точку О, необходимо и = с* и v = 0, т. с. этот интервал есть прямая звуковая линия. Итак, все сводится к доказательству представления (29). Оно выводится последовательным дифференцированием уравнений (5) и справедливо благодаря специальной структуре нелинейных членов во втором уравнении. Для экономии места здесь этот результат приводится для модельной системы (23), где роль и — с* играет и. Именно, для системы (23) соответствующая матрица Н получается тривиально и оказывается такой:
0 0 и 0 0
Wxx 0 Ux 0 0
Из теорем 3 и 4 следует, что на прямой звуковой линии Z производные второго порядка
^ХуVyyi 1'ХУ' Ууу
все обращаются в нуль. Это не так, вообще говоря, для производной ихх. Она характеризует скорость изменения ускорения течения в точках Z, так как простой подсчет дает d2n/dt2.z = c2(uxx\z,0). Ее удобно заменить величиной
w = к„ихх(0,у), (30)
которая будет называться скоростью ускорения течения на прямой звуковой линии. С предположением, что решение в окрестности Z четырежды
непрерывно дифференцируемо, для нее устанавливается следующий замечательный факт.
Теорема 5. Скорость ускорения течения на прямой звуковой линии удовлетворяет уравнению
w" = 6ш2. (31)
Доказательство. Результат получается трехкратным дифференцированием второго уравнения (5) по х, заменой производных vx, vxx, vxy,... производными от и в силу первого уравнения (5) и переходом на Z с учетом предыдущих равенств. Для экономии места здесь этот вывод выполняется для модельной системы (23). В этом случае определение скорости ускорения w надо заменить, согласно (22), таким: 2w — ихх. Дифференцирование второго уравнения (23) по х приводит, в силу первого, к равенству
иуу — Ux -I- иихх.
Еще двукратное дифференцирование по х дает
UXxyy = 3^хх + 4UXUXXX + ииХХХхч
откуда на Z для w = (1/2)ихх получается уравнение (31). ¦
Решениями уравнения (31) являются эллиптические функции, и его полная теория связана с рассмотрением поведения решения на плоскости комплексного переменного у. Для приложений к газовой динамике достаточно заметить, что после умножения на 2w' и интегрирования получается первый интеграл
it/2 - 4-u:3 - 463 (6 -.v const). (32)
Отсюда зависимость между w и у находится квадратурой. Если Ь ф 0, то решение симметрично относительно точки, где w = b и w’ = 0, в качестве которой можно взять у = 0.
w/b
(33>
Интеграл фЗ) сходится, когда w —> ос, и если положить
ОО
то становится ясным, что функция w(y) определена на интервале \у\ <и>/y/b и имеет график, показанный на рис. 7, а. При Ь < 0 квадратура имеет вид
w/\b\
dz
(35)
-1
Можно показать, что с числом и> из (34) верны равенства
0 ОС
dz
= ujs/b.
\/z3 + 1
[ dz _ _uj_ f
J \/z3 +1 ч/з’ J -1 -1
Поэтому здесь функция w(y) определена на интервале \у\ < и>\/3/у/Щ и имеет график, показанный на рис. 7, б. Если же Ь = 0, то решение уравнения (32) дается элементарной функцией (с точностью до переноса по у)
w -- 1 /у2. (36)
В силу теоремы 5 приближенное (главная часть) представление вектора скорости в окрестности прямой звуковой линии х = 0 имеет вид
и = °, t w(y)x2, v = ~w'(y)x\ (37)
Легко проверить с учетом преобразования (22), что формулы (37) дают точное решение системы уравнений (23).
Существование решений (37) указывает на принципиальную особенность течений с прямой звуковой линией: на ней на конечном расстоянии,
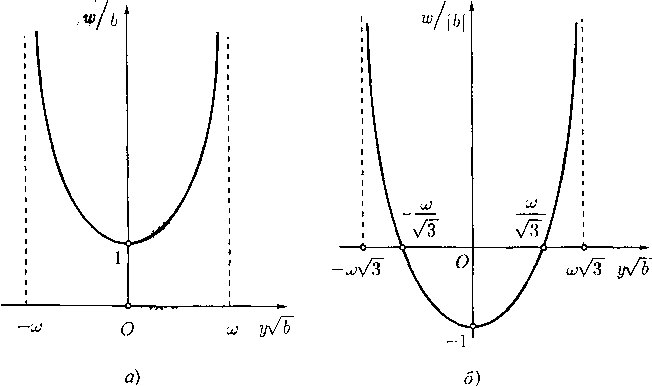
Рис. 7
вообще говоря, существуют особые точки течения, соответствующие обращению функции w(y) в бесконечность. В решениях с Ъ ф 0 таких особых точек всегда две, а при 6 = 0 — одна. Только для нулевого решения (ш = 0) уравнения (31) (т. с. когда скорость ускорения равна нулю) особых точек на прямой звуковой линии может не быть.
При 6 > 0 решение (37) описывает поведение сверхзвукового течения, возникающего при истечении равномерного звукового потока из трубы в пространство с пониженным давлением. Особым точкам соответствуют края отверстия, что позволяет найти скорость ускорения по известной ширине трубы. При 6 = 0 решение с функцией (36) является автомодельной простой волной и представляет собой не что иное, как главную часть течения Прандтля-Мейера, начинающегося со скорости звука (см. рис. 22.6).
Из предыдущих рассмотрений следует еще один важный вывод: прямая звуковая линия Z всегда является двукратной характеристикой С±, и никакая другая характеристика не может пересечь Z в области непрерывного течения.
Сопло Лаваля. Именем шведского инженера П. Лаваля называется вначале сужающийся, а затем расширяющийся канал, предназначенный для непрерывного преобразования дозвукового течения в сверхзвуковое. Такие
каналы используются в конструкциях турбин, ракет и аэродинамических труб.
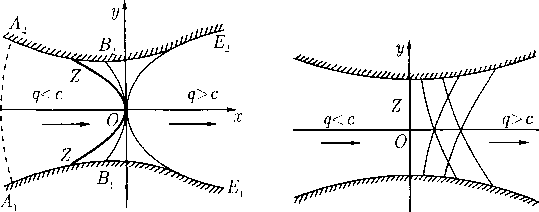
X
Рис. 8
Рис. 9
Симметричное относительно продольной оси сопло Лаваля показано на рис. 8. Переход течения через скорость звука происходит на звуковой линии Z, пересекающей все линии тока и достигающей стенок сопла. Точка пересечения звуковой линии Z с осью симметрии является центром околозвукового течения и называется также центром сопла. Априори возможны два типа течений: с положительным ускорением в центре сопла (структура течения показана на рис. 8) и с нулевым ускорением и прямой звуковой линией (рис. 9). Во втором случае примыкание дозвукового течения к сверхзвуковому вдоль Z происходит, вообще говоря, со слабым разрывом, а именно с разрывом скорости ускорения (30). Возможность такого примыкания обеспечена существованием как дозвукового, так и сверхзвукового решения вида (37) и тем фактом, что прямая звуковая линия Z является характеристикой. Некоторый недостаток сопел Лаваля с прямой звуковой линией заключается в малости продольных градиентов скорости, ввиду чего такие сопла имеют относительно большую длину.
Течение через сопло Лаваля с положительным ускорением в центре сопла определяется, вообще говоря, его заданными стенками А\Е\ и А а ?2 и заданным распределением модуля скорости на входе в сопло (сечение А\А? на рис. 8). Следует заметить, что область влияния участков стенок В\Е\ и В2Е2 совпадает с областью сверхзвукового течения, лежащей вниз по потоку от характеристик В1ОВ2 (соответствующих характеристикам С± на рис. 4). Поэтому течение в дозвуковой области и в части сверхзвуковой области, расположенной вверх по потоку от характеристик В1ОВ2, не зависит от формы частей стенок B\E\ и В2Е2. Следовательно, линия А \ В\ ОВ2А2 ограничивает область независимого (от остальной части сопла) трансзвукового течения. Именно эта область и подлежит
расчету при решении основной задачи об отыскании течения через заданное сопло. Эта задача оказывается очень трудной и, несмотря на имеющиеся разработанные приближенные методы расчета, до настоящего времени удовлетворительного решения не получила. Одна из трудностей здесь состоит в том, что годограф стенок сопла не может быть построен до решения задачи, ввиду чего неизвестна область плоскости годографа, в которой можно было бы ставить и решать краевую задачу для линейного уравнения (22.47).
Истечение сверхзвуковой струи. Рассмотренная в § 23 задача об истечении струи из бесконечного угловидного сосуда допускает постановку на плоскости годографа и в том случае, когда внешнее давление меньше критического, т. е. р\ < р*. Впервые эта задача была поставлена и изучена Ф. И. Франклем.
Постановка такой задачи на плоскости течения аналогична той, которая была дана в § 23 для дозвуковой струи. Однако здесь скорость на свободной границе струи сверхзвуковая, qj > с», и потому в струе должен произойти переход через скорость звука на некоторой звуковой линии Z с центром течения на оси симметрии. Концы линии Z должны совпадать с краями отверстия, так как они не могут лежать ни на свободной границе, где q} > с*, ни на прямолинейной стенке, ибо это несовместимо с предположением о непрерывности течения (аналогично течению в местной сверхзвуковой зоне). Поэтому конфигурация на плоскости течения имеет вид, показанный на рис. 10.
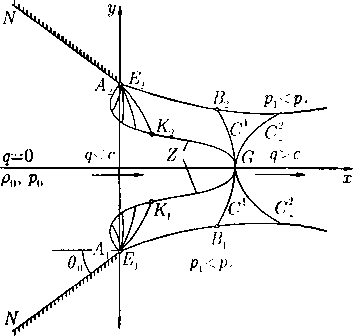
Вдоль стенки N А\ скорость возрастает от q = 0 в N (на бесконечности)
до q = с* в точке А\. Переход к скорости (/, > с, в точке ?’[ на свобод
ной границе происходит посредством центрированной волны разрежения. Эта волна в целом не является простой волной; однако асимптотически, в бесконечно малой близости к точке Ai = Е\, она совпадает с простой /-волной. Волна разрежения заканчивается характеристикой E\Ki, выходящей, вообще говоря, на звуковую линию Z в точке К\. Вместе с тем идущая от центра течения характеристика С\ выходит на свободную границу v
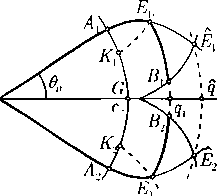
в точке В\. Ввиду симметрии течения
этим определяется область ii независимого трансзвукового течения с границей NA1E1B1GB2E2A2N. Тем самым го- /у дограф области О полностью определен ис- ~0 ходными данными; он показан на рис. 11, где соответствующие точки обозначены теми же буквами, что и на рис. 10. При этом геометрическим точкам Ai = Ei и Лг = Е-z на плоскости течения (краям отверстия) соответствуют дуги характеристик А\Е\ (/ = const) и А‘>Ео (г = const,) на плоскости годографа. Граничные условия для функции тока определяются заданным расходом газа в струе 2 Q и тем, что каждая из линий N Ai Ех Вх и N А2Е2В2 (рис. 10) есть линии тока.
Следовательно, задача об истечении сверхзвуковой струи сводится к следующей краевой задаче для функции тока на плоскости годографа: найти решение уравнения (22.47) в области с границей NA1E1B1GB2E2A2N по граничным условиям
Ф\ыа1е-[11х = -Q, Ф\ь’л2е2В2 -- Q- (38)
В силу очевидной симметрии можно заменить задачу (38) задачей об отыскании решения уравнения (22.47) в области с границей NA\E\B\GN по граничным условиям
Ф\ыв = 0, ^NAtEiB, = -Q- (39)
Понижение внешнего давления pi сопровождается возрастанием скорости qi. Влияние этого изменения передается в область независимого течения через отрезки Е\В\ и E2Bo свободной границы и обуславливает зависимость этого течения от параметра pi. Однако когда <i\ достигает значения q (см. рис. 11), определенного уравнением то точки Е\ и В\ (а также Е-> и Во) сливаются в одну точку Е\ (соответственно Ео). Поэтому дальнейшее понижение внешнего давления уже не влияет на область независимого течения, в частности на его расход. Получаемое течение при q\ =q называется течением с максимальным расходам.
Для течения с максимальным расходом задача (39) несколько упрощается и сводится к следующей: найти решение уравнения (22.47) в области NA\E\GN по граничным условиям
р\мс = о, VInA-iEi = ~Q- (41)
Краевая задача (41) называется задачей Трикоми (для уравнения Чаплыгина (22.47)). В послевоенных работах Ф. И.Франкля и его последователей эта задача получила исчерпывающее решение, причем оказалось, что для нее, как и для задач об истечении дозвуковых струй, эффективен метод Фурье (разделение переменных с последующим представлением решения в виде рядов по частным решениям). Напротив, задача (39) при q\ < q, принадлежащая к классу гак называемых обобщенных задач Трикоми, оказывается очень трудной, хотя и решалась приближенно численными методами рядом авторов. Здесь необходимы дальнейшие аналитические исследования. В частности, представляет большой интерес асимптотическое поведение трансзвукового течения, когда q\ —> с* со стороны q\ > с*.
Аэродинамические явления, происходящие при полете управляемых снарядов, ракет и высокоскоростных самолетов, определяются тем, что числа Маха полета достигают довольно больших значений, порядка 5-10-20. Течения с такими числами Маха получили название гиперзвуковых. Основной задачей теории гиперзвуковых течений является задача обтекания конечного тела сверхзвуковым потоком при больших числах Маха. При установившемся гиперзвуковом обтекании перед телом возникает сильный, вообще говоря, отошедший скачок уплотнения (головная ударная волна), отделяющий невозмущенный набегающий поток от области неравномерного течения между скачком и телом.
В действительности за головной ударной волной образуется область высоких температур (тысячи градусов), вызывающих изменения физико-хи-мических свойств газа (воздуха). Здесь происходят процессы диссоциации и рекомбинации молекул, ионизация и химические реакции. В этих условиях могут быть существенны диффузионные процессы, а также перенос энергии излучением. Может происходить также абляция материала поверхности — его испарение и снос вниз по потоку, вызывающая изменение
формы тела. При расчете движения реальных объектов (например вход спускаемого аппарата в атмосферу) указанные процессы и явления необходимо принимать во внимание. Ясно, что это обстоятельство приводит к существенному усложнению математической модели и делает ее труднодоступной для качественного анализа. В настоящее время гиперзвуковая аэродинамика сформировалась в самостоятельное научное направление с достаточно большим накопленным опытом исследования и обширной литературой
(СМ. [11]).
Тем не менее существенно, что упомянутые сложные физико-химические процессы в газе происходят на общем фоне чисто газодинамического течения, свойства которого во многом являются определяющими и подлежат независимому изучению. Основы такой теории, не учитывающей осложняющие физико-химические факторы, излагаются ниже для модели политропного газа с фиксированным показателем адиабаты 7.
Вопрос о том, за счет какого фактора число Маха невозмущенного сверхзвукового течения Mi = q\/c\ оказывается большим, для теории не очень существен. Для определенности в дальнейшем принимается, что скорость ([\ фиксирована, а скорость звука сЛ относительно мала.
Формулы скачка в политропном газе. Для теории гиперзвуковых течений характерно использование различных приближенных моделей, одна из которых, на формальном уровне, изложена в § 14. Ее обоснование и другие важные особенности гиперзвуковых течений связаны с детальным рассмотрением соотношений в косом скачке уплотнения.
Пусть индекс «1» отмечает значения параметров газа перед скачком. Тогда полученные в § 25 соотношения в косом скачке могут быть переписаны в следующем виде:
![]()
2 + (7 - 1)М2 sin2 х
(i)
![]()
v
v_ = 2 cos х М i sin2 х - 1
Qi 7 - 1 Mj Mj sin x
cos x M2 s^n2 X ~ 1
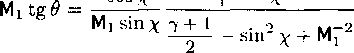
Первая формула (1) следует из определения амплитуды скачка z и выражения для нее согласно (25.10) и (25.12). Вторая формула (1) следует из уравнения адиабаты Гюгонио в политропном газе (25.2) и (25.10). Третья и четвертая формулы (1) следуют из соотношений (25.7) и (25.10). Наконец, последняя формула (1) есть переписанное в другом виде соотношение (25.14).
Параметры гиперзвукового подобия. В связи с формулами (1) обращает на себя внимание ряд важных обстоятельств. Во-первых, в соотношения (1) входит характерное произведение Mi sin X- Далее, если Mi велико, то для слабого скачка его угол наклона хмал, причем х ~* 0, когда Mi ос. Последний факт легко устанавливается путем анализа ударной поляры (25.11) при фиксированном q\ и при Mj —> ос. Кроме того, всегда выполнено неравенство в < в силу которого малость угла х влс_ чет и малость угла поворота потока в. Наконец, для малых углов х и ® можно принять, что sinx = Х>C0SX = 1 и tg# = в с относительной погрешностью 0(х2).
Эти факты наводят на мысль о введении характерных величин
(2)
К = М,0, Kc = MlX-
Они называются параметрами гиперзвукового подобия. Геометрическое истолкование этих параметров вытекает из того, что 1/Mi = sin о при больших Mi приближенно равно углу Маха а. Поэтому К « в/а характеризует относительную величину угла наклона вектора скорости по отношению к углу Маха а, а параметр Кс яз \/а — относительную величину угла наклона скачка.
Параметры К и Кс зависимы. Предельный переход М] —* оо в последнем уравнении (1) при фиксированных параметрах (2) дает соотношение
![]()
Решение этого квадратного уравнения относительно Кс даст
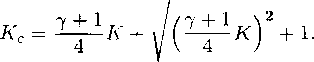
В силу определения параметров (2), уравнения (1) с относительной точностью 0(\2 + Mj~") могут быть переписаны так (здесь использовано соотношение р\с\ = 7pi для политропного газа):
Формулы (5) выражают следующее свойство гиперзвукового подобия косых скачков: стоящие слева величины зависят только от параметра подобия К, но не от значений Mi и в в отдельности. Другими словами, для всех косых скачков с разными М] и в, но с одним и тем же значением параметра К величины в левых частях равенств (5) одинаковы (с относительной точностью 0{х2 + М^~2)).
Классификация моделей. В общем случае головная ударная волна не прямолинейна, а течение между ней и телом не постоянное. При этом параметр подобия К, вычисленный по значению угла в в данной точке, будет переменным. В зависимости от экстремальных значений К в теории гиперзвуковых течений различаются следующие случаи моделирования.
(а) Величина К порядка единицы. Этот случай является основным и приводит к гиперзвуковому приближению, которое уже рассматривалось в § 14 и будет еще изучаться ниже.
(б) Величина К мала по сравнению с единицей. Это означает, что углы наклона вектора скорости много меньше углов Маха. Кроме того, здесь Кс ~ 1, т. е. углы наклона скачков уплотнения близки к соответствующим углам Маха. Поэтому сила разрывов относительно невелика (это видно и из формул (5)). В этом случае применима линейная теория сверхзвукового обтекания тонкого тела.
(в) Величина К велика по сравнению с единицей. Здесь углы наклона линий тока велики по сравнению с углами Маха. Такая модель называется приближением сильных ударных волн. Она может быть рассмотрена в рамках модели (а) гиперзвукового приближения как ее возможный предельный случай.
(г) Величина К велика, а показатель адиабаты 7 близок к единице. Предельное состояние, достигаемое, когда одновременно К —> оо и 7 —» 1, приводит к так называемой теории Ньютона.
Обтекание заостренного тела. Рассматривается задача обтекания тела сверхзвуковым потоком в предположении, что углы наклона поверхности тела к направлению невозмущенного течения всюду малы, а число Маха М] велико, причем параметр подобия К имеет величину порядка единицы. В этом случае головной скачок уплотнения присоединен к переднему острию (рис. 1) и течение между скачком и телом описывается уравнениями гиперзвукового приближения. Для получения этих уравнений вводится малый параметр 8 = 1/М^ и представление основных величин формируется с учетом предельных формул (5). При этом надо еще учесть, что вдоль линий тока dy — tgddx или, в рассматриваемом приближении, dy = 5К dx. Поэтому для правильного представления наклонов линий тока необходимо увеличить ординаты у в 1/5 раз. Эти соображения приводят к следующим форму-
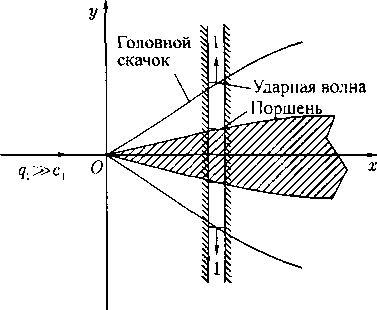
Рис. 1
лам моделирования (для простоты рассматривается плоскопараллельная задача):
х = х\ у = 6у', и = qi + 52и, v = Sv\
р = 52р\ р = р',
в точности совпадающим с формулами (14.15). Здесь формула для давления р получается из (5) в силу того, что в политропном газе
7Pi = Р\с\ = ^P\q\- (7)
Щ
Как было показано в § 14, моделирование (6) приводит к системе уравнений, которая после переобозначения
х -> qit, у'-^х, v'-*u, р'->р, р' -»р (8)
совпадает с уравнениями одномерного неустановившегося движения с плоскими волнами (газ политропный)
щ + иих + ~рх = 0,
(9)
pt + ирх + рих = 0, v '
Pt + ирх + ~fpux = 0.
При этак величина и' вычисляется с помощью интеграла Бернулли
- tV=+^~iel
который в результате моделирования (6) принимает приближенную предельную форму
Здесь возникает вопрос о том, к какой краевой задаче для уравнений (9) сводится при этом исходная задача обтекания. С этой целью надо выяснить соответствующую моделированию (6) предельную форму граничных условий на скачке уплотнения и на теле.
Пусть граница тела задана уравнением у = SY(x). В результате моделирования (6) и переобозначения (8) оно переходит в уравнение
x = Y(qit) (11)
и тем самым задает линию на плоскости событий R2(x, t) — одну из границ области определения решения системы (9). Кроме того, условие обтекания udy = vdx после моделирования (6) и переобозначения (8) принимает
вид
dx/dt = u. (12)
Это показывает, что линия (11) является контактной характеристикой системы (9), т. е. может рассматриваться как поршень.
Аналогично, пусть линия скачка задана уравнением у = 6R(x). В модели это уравнение примет вид х = R(qit), т. е. станет уравнением второй границы области определения решения системы (9). На линии скачка выполнено уравнение dy/dx = tg которое в модели принимает вид dx/dt = q\Kc. Поэтому скорость перемещения точки х = R(q\t) равна
Dn — q\Кс. (13)
В этой точке имеет место разрыв основных (для уравнений (9)) величин и, р, р. Утверждается, что в силу моделирования (6) и переобозначения (8) значения этих величин по разные стороны разрыва удовлетворяют уравнениям сильного разрыва (ударной волны), перемещающегося со скоростью (13). Действительно, если ввести скорость перемещения частиц по нормали к разрыву иП1 и иП2, то будет иП1 = v[ — 0 (перед разрывом). Кроме того, в силу (6) и последнего уравнения (5) будет ип.2 — v' = S~lv — = q\K (за разрывом). Следовательно, для системы (9) значения нормальных скоростей на разрыве таковы:
Что же касается давления и плотности за разрывом, то они даются непосредственно формулами (5).
Легко проверить, что с этими значениями законы сохранения массы и импульса
/02 («П2 Pl(«n, Dn)l
Р2 Pi P\{U-ni Dn)(uni Un’z)
выполнены тождественно в силу соотношения (3) и формулы (7), которая после моделирования (6) принимает вид 7р\ = p[qi ¦ Уравнение адиабаты Гюгонио в политропном газе также легко проверяется и оказывается тождеством в силу соотношения (3).
Итак, задача обтекания заостренного тела в гиперзвуковом приближении оказывается равносильной задаче о неустановившемся движении газа, возникающем под действием поршня, вдвигающегося в покоящийся газ по заданному закону (11) и порождающего впереди себя ударную волну. В этом смысле говорят о поршневой аналогии (или поршневом приближении) при гиперзвуковом обтекании тонких тел. Эта аналогия поясняется на рис. 1, где выделена полоса, играющая роль трубы, в которой по состоянию 1 распространяется ударная волна (элемент головного скачка), когда поршень (элемент поверхности тела) вдвигается в газ 1. При этом полоса считается неподвижной, а тело — движущимся в отрицательном направлении оси х со скоростью сц. Можно показать (см. [11]), что поршневая аналогия справедлива не только для плоскопараллельного обтекания, но также и в общем случае пространственного обтекания с большим числом Маха тонкого тела сложной конфигурации. При этом требуется выполнение только одного условия: всюду в потоке параметр К конечен и имеет порядок единицы.
Отсюда следует важный для приложений закон подобия при гиперзвуковом обтекании тонких тел: описание поля течения в штрихованных переменных (вводимых согласно (6)) для семейства аффинно-подобных тел, определяемых значением угла наклона в\, в фиксированной характерной точке и обтекаемых с различными (большими) числами Маха Mi, зависит только от величины К — М | (9| . Поэтому К и называется параметром ги-перзвукового подобия.
С точки зрения краевой задачи для дифференциальных уравнений упрощение, достигаемое при использовании поршневой аналогии, не очень значительно. Оно сводится к тому, что уравнения (9) содержат на одну искомую функцию меньше, а из граничных условий на ударной волне исключена касательная составляющая вектора скорости. Вообще говоря, решить задачу о поршне не легче, чем исходную задачу обтекания. Поэтому основной выигрыш от перехода к гиперзвуковому приближению заключается в возможности использования накопленного более богатого опыта и многочисленных примеров решения нестационарных задач.
Влияние затупления. Носовая часть реального объекта (тела) по многим причинам не может быть идеально острой. Обтекание такого тела имеет существенно другой характер по сравнению с заостренным телом, так как скачок уплотнения отходит от тела и за ним образуется зона дозвукового течения. В этой зоне параметр К принимает любые значения,
О < К < оо.
Качественная картина течения (точнее, его половины для случая симметричного обтекания) показана на рис. 2. Дозвуковое течение в области ТО A NT заканчивается па звуковой линии AN и переходит в сверхзвуковое. При этом формируется область П независимого трансзвукового течения ТОАБТ, где АВ есть характеристика С+, приходящая в точку А (аналогично течению через сопло Лаваля, см. §26.). Вообще говоря, форма тела ВР вниз по потоку от характеристики АВ не влияет на поле течения в области О.. Анализ и расчет независимого трансзвукового течения весьма сложны из-за того, что линия скачка О А заранее неизвестна, а энтропия за этим криволинейным скачком переменна.
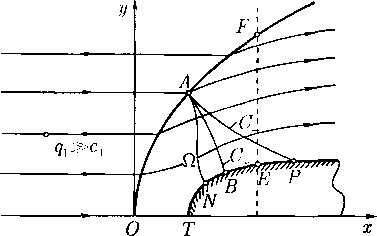
Рис. 2
Тем не менее, если число Маха Mj велико, а характерный размер затупления относительно мал, то область П также мала и ее влияние на течение в целом может быть учтено приближенно. Одно из таких приближений связано с изложенной выше нестационарной аналогией, которую можно считать приемлемой, начиная с некоторого сечения EF, расположенного за линией АВ. Правила выработки начальных данных на линии EF при этом основываются на интерпретации действия затупления как продукто-ра нестационарного течения, возникающего в результате сосредоточенного воздействия на газ путем выделения некоторой энергии Е, импульса I и внезапного движения поршня со скоростью U. Эти вспомогательные параметры должны определяться только формой затупления. Поэтому для данного затупления их можно находить другими методами, например экспериментально, или путем численного расчета, или с использованием других приемлемых приближений. Подробный анализ имеющихся здесь возможностей дан в [11].
Например, если известна полная сила X — (X, Y), действующая на затупление, то можно принять, что в слое единичной ширины выделилась энергия Е = X ¦ 1 и ему сообщен импульс I = q'^Y.
Приближение Ньютона. Когда параметр К, ас ним и К, является большим, то согласно (5) плотность газа за скачком близка к предельно возможному значению p\(~j ¦+ 1)/(7 -- 1). Если при этом 7 близко к единице, то почти вся масса газа, прошедшего через скачок, концентрируется в тонком слое вблизи поверхности скачка — образуется так называемый ударный слой. С другой стороны, при К —> ос и 7 —> 1 из соотношения (3) следует, что К/Кс—» 1. Это означает, что в таком пределе поверхность скачка совпадает с поверхностью обтекаемого тела (равенство Кс — К равносильно равенству х = #¦)¦ При этом из формулы (1) получается, что давление на теле (совпадающее с давлением за скачком) дается формулой
P = PiQiSin29, (15)
которая называется формулой Ньютона. Она была получена знаменитым ученым на основании следующих соображений.
Предполагается, что частицы газа, встречаясь с поверхностью тела, полностью отдают ему свой нормальный к поверхности импульс и затем продолжают двигаться вдоль поверхности, уже не оказывая давления на тело. Пусть а есть элемент площади поверхности тела, наклоненный к набегающему потоку под углом в. Тогда масса газа, сталкивающаяся с площадкой сг за единицу времени, равна т = р\q\<j sin в, а ее импульс есть mui. Его нормальная составляющая к поверхности равна
mqi sin в — cxpig2 sin2 в.
Следовательно, импульс, передаваемый единице площади поверхности тела в направлении нормали, который и равен давлению, дается формулой (15).
Известно, что приближение Ньютона может рассматриваться как предельное также и при газокинетическом подходе к обтеканию тел разреженным газом. Оно справедливо, если течение является свободно-молекулярным (т. е. молекулы между собой не взаимодействуют), а граничное условие взаимодействия молекул с поверхностью тела сводится к неупругому удару. Тем самым изложенная в настоящих лекциях феноменологическая модель газовой динамики в вопросах теории гиперзвуковых течений смыкается с газокинетической моделью.
Задачи и упражнения к главе IV
1. Найти функцию тока и потенциал скоростей течения Прапдтля - Мейера в случае политропного газа.
2. Найти линии тока течения (на плоскости Н2(х,у)), описываемого частным решением уравнения Чаплыгина (22.47) вида
ф = ад + b(q) {а — const).
Рассмотреть случаи а = 0 н b(q) = 0.
3. Показать, что при преобразовании
а( + b cC + d’
ф — (cQ + й)ф'
с постоянными а, Ь, с, d(ad — be ф 0) уравнение Чаплыгина (22.50) переходит в уравнение того же вида с функцией Чаплыгина К', определяемой формулой
KV) -
4. Используя уравнения (22.45), доказать следующий аналог теоремы 20.1 (Никольского и Таганова); если в дозвуковом течении при движении вдоль линии q = const область меньших скоростей находится слева, то вектор скорости монотонно поворачивается по часовой стрелке.
5. Равномерный поток политропного газа, движущийся со скоростью Q\ > ci вдоль прямолинейной стенкн АВ (см. рисунок), обтекает полуокружность ВС. Выяснить, при каких значениях параметров qi, ci и 7 происходит отрыв потока от стенки с образованием зоны вакуума. Найти точку отрыва.
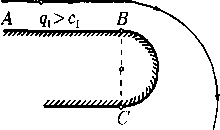
К задаче 5
6. Прямолинейная стенка {ж ^ 0, у = 0}, вдоль которой в направлении оси ж движется равномерный сверхзвуковой поток (расположенный при у > 0), при х > 0 гладко переходит в искривленную стенку у = /(гг). Показать, что если на искривленной
стенке есть вогнутость {/"[х] > 0), то при продолжении потока неизбежна градиентная катастрофа.
7. Найти максимальный угол поворота потока политропного газа 0гфсд в косом скачке в зависимости от Mi (использовать соотношение (25.14)).
8. Показать, что в случае политропного газа скорость за косым скачком с предельным углом поворота потока 0||рСд всегда дозвуковая.
9. Доказать соотношение Прандтля для косых скачков в политропном газе
10. Показать, что если вдоль звуковой линии 0 — const, то она является прямой на плоскости течения.
11. Най ги характеристики уравнения Трикоми (26.27).
12. Показать, что линии у = const (линии гока в околозвуковом приближении) для решения (26.25) на плоскости Я2 (u, v) образуют семейство прямых, огибаюших характеристики
, 2 3/2 V = ±-и
13. Показать, что в полярных координатах (г, в), вводимых соотношениями
![]()
,3/2 _
= rsin t),
2 4
Уве +Г yrr + 7^гуг - 0.
в.
уравнение Трикоми (26.27) принимает вид
14. Найти преобразования растяжения, допускаемые уравнением Трикоми (26.27).
15. Найти предельную форму ударной поляры в случае политроппого газа, когда М1 —> оо при фиксированном qi.
16. Решить задачу обтекания политропным газом выпуклого угла в гиперзву-ковом приближении.
17. Решить задачу симметричного обтекания тонкого ромба равномерным сверхзвуковым потоком политропного газа, направленным вдоль большой диагонали. В гиперзвуковом приближении найти силу сопротивления ромба.
18. Доказать, что в плоскопараллельном установившемся течении политропного газа невозможна конфигурация из трех прямолинейных скачков уплотнения, выходящих из одной точки, если в каждом секторе течение является постоянным.
19. Доказать, что если равномерный сверхзвуковой поток проходит через криволинейный скачок, то течение за скачком вихревое. Вывести формулу для величины вихря, образующегося на скачке:
где иа — касательная составляющая вектора скорости, *г - кривизна линии скачка, а функция P(z) определена равенством (25.2).
20. Показать, что для осесимметричного течения уравнения околозвукового приближения, аналогичные (26.23), имеют вид
Uy = Vx, UUX = Vy -*- v/y.
Проверить, что эти уравнения имеют точное решение
и = 2х + у2, v = 2 ху +
и выяснить свойства отображения (ж, у) —> (и, г;).
21. Показать, что на звуковой плоскости х = 0 осесимметричного течения скорость ускорения w(y) — (1/2)ихх(0, у) удовлетворяет аналогу уравнения (26.31)
w" -ь w' /у = 6-ш2.
Доказать наличие особых точек у решения этого уравнения с начальными данными u>(0) = b, и/(0) = 0.
Основным инструментом использования групп Ли в теории дифференциальных уравнений, в частности, для построения классов точных решений, является соответствие между группами Ли и алгебрами Ли операторов, кратко изложенное здесь с применением к уравнениям газовой динамики (УГД). Доказательства всех формулируемых утверждений можно найти
в [5].
Группы и алгебры Ли. Рассматривается Д'-мерное пространство RN(z) точек (векторов) г = (г1, zN). Пусть о, G R — вещественный параметр. Отображение F : RN х R —> R.,v, действующее по формуле
(1)
z = /(г. а)
называется однопараметрической группой Ли G1 (/), если / € С'00(ДЛ' х R) и обладает свойствами в силу которого для любой (гладкой) функции F(z) верно раввШПЭЭФ
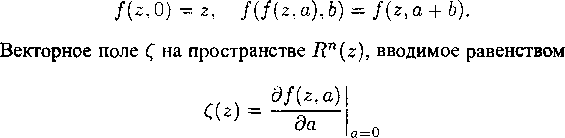
с координатами С = (С1.....CN)> записывается в виде линейного диффе
ренциального оператора

Дифференцирование (2) по параметру 6 в точке Ь = 0, с учетом обозначения (3), приводит к уравнению Ли
Решение уравнения Ли (5) дает отображение (1), обладающее свойствами (2). Тем самым между группами Gl(f) и операторами X существует взаимно однозначное соответствие, которое выражается записью G1(X).
Коммутаторам операторов X и У называется оператор [X, У], определенный (в смысле действия на любую функцию F(z)) формулой
[X, У] = XY - YX. (7)
Конечномерная (r-мерная) группа Ли Gr есть множество однопараметрических групп G1, обладающее свойством
{G1(X)cGr, Gl{Y)cGr}~^G'{\X, У]) с Gr. (8)
Операторы (4) можно складывать и умножать на вещественные числа, образуя их линейные комбинации и векторные пространства (или подпространства) операторов.
Векторное пространство Lr операторов называется r-мерной алгеброй Ли операторов, если выполнено свойство
{X ? и. У ? Lr) => [X, У] е U. (9)
Векторное подпространство К С U называется подалгеброй в U, если для любых X, У ? К также [X, У] ? К.
Число г означает размерность Lr как векторного пространства. Поэтому в Lr существует базис из г линейно независимых операторов Уа (а = 1, .... г). В силу (9) их коммутаторы должны быть линейными комбинациями базисных операторов, т. е. выполняются соотношения (сумма по 7 = L, ..., г)
Wa,Y0\ = ClaY1 (а, 0=1,----г), (10)
где С2д — вещественные числа, называемые структурными колнстанта-ми алгебры Ли Lr. Соотношения (10) определяют таблицу коммутаторов («таблицу умножения») в U. Задание структурных констант вполне определяет алгебру Ли операторов с базисом {Уп}, но эти константы не произвольны: они необходимо удовлетворяют соотношениям (любые а, ,3,
7, 6 = 1, ..., г; суммы по о = 1, ..., г)
второе Ш «Вторых следует из тождества Якоби
[X, [У, Z}] + [У, [Z, Х]\ + [Z, [X, У]] = о,
справедливого для любых операторов X, У, Z вида (4).
Определения (8) и (9) устанавливают соответствие между группами Gr и алгебрами Ли операторов Lr. Это соответствие является взаимно однозначным и продолжается на подгруппы Н С GT и подалгебры К С U.
Применительно к дифференциальным уравнениям вместо «допускаемая группа Ли» говорят также «допускаемая алгебра Ли операторов». Допускаемые операторы вычисляются алгоритмически (см. [5]).
Алгебры Ли, допускаемые УГД. Для УГД пространство RN(z) есть пространство R9(t, х, у, z, u, v, w, р, р). Соответственно указанному в § 8 перечню групп GJ(/1), допускаемых УГД, получается следующий список допускаемых операторов
Xi = дх 'j
Х2 = ду > операторы переносов по х, у, 2
Х4 = tdx 4 ди "j
Х^ ;= tdy 4 д„ > операторы галилеевых переносов
Xq = tdz 4 dw J
Ху — ydz - zdy 4 vdw - wdv Xg = zdx - xdz 4 wdu - udw Xg = xdy - ydx + udv - vdu Xio = dt } оператор переноса no t Хц = tdi + тдх 4 уду •+- zdz \
X 1з = tdt — иди ~ vdv — wdw г 2рдр > операторы растяжений
Х\4 = рдр +рдр )
Ху> = t2dt 4 txdx + tydy + t,zdz-t 'j
J- (x - tu)du + (y - tv)dv+ > «проективный» оператор
4 (z - tw)dw — Ztpdp - btpdp )
Базис в Ln образуют операторы {Xi.....Хц}, в L13 — операто
ры {Xj, ..., Хц, Xl3, Хм} и в LlA - операторы {Xj, .... Х14}.
В нижеследующей таблице 1 коммутаторов для алгебры Ли Ln , для краткости записи, вместо символов операторов Xk написаны только их
номера к (—к означает оператор ~Хк). В коммутаторе Х(] оператор
Xk берется слева, а оператор X; — сверху.
Таблица 1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|
1 | 0 | 0 |
0 | 0 | 0 |
0 | 0 | -3 |
2 | 0 | 1 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | 0 | -1 | 0 | 2 |
| 3 | 0 |
0 | 0 | 0 |
0 | 0 | -2 |
1 | 0 | 0 |
3 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -6 | 5 | -1 | 0 |
| 5 |
0 | 0 | 0 |
0 | 0 | 0 |
6 | 0 | -4 |
-2 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 0 | -5 | 4 | 0 | -3 | 0 |
|
7 | 0 | -3 |
2 | 0 | -6 |
5 | 0 | -9 |
8 | 0 | 0 |
| 8 | 3 | 0 | -1 | 6 | 0 | -4 | 9 | 0 | -7 | 0 | 0 |
| 9 | -2 |
1 | 0 | -5 |
4 | 0 | -8 |
7 | 0 | 0 |
0 |
| 10 | 0 | 0 | 0 | 1 | 2 | 3 | 0 | 0 | 0 | 0 | 10 |
| 11 |
-1 | -2 | -3 |
0 | 0 | 0 |
0 | 0 | 0 |
-10 | 0 |
Инварианты. Функция J(z) называется инвариантом группы Gr, если для любой подгруппы G1(f) с Gr выполнено равенство J(f(z,a)) = = J(z). В силу уравнения (6) это равносильно тому, что для любого оператора X ? Ьг будет XJ(z) = 0. Последнее имеет место если и только если для всех базисных операторов Ya е Ьг выполнены равенства
YaJ(z) = 0 (а = 1.....г). (13)
В совокупности равенства (13) образуют систему из г линейных однородных дифференциальных уравнений первого порядка для одной функции J(z). В силу соотношений (10) эта система всегда совместна. Широта ее общего решения зависит от ранга г х N матрицы из координат операторов Ya
Так как М = M(z), то ее ранг зависит от точки г. Общим рангом матрицы М(z) (обозначается буквами о. р.) называется её максимальный ранг (который ввиду непрерывности функций Со(2) всегда достигается на некотором открытом множестве в /?л (г)). Если о. р. М т, то система (13) имеет N — т функционально независимых решений Jq(z)(q = 1, ..., N — rri), а ее общее решение есть произвольная функция этих решений.
Многообразие Ф с RN называется неособым многообразием груп-
I
пы GT, если ранг М\ = т; если же ранг М < т, то Ф называется ф ф
особым многообразием группы Gr.
Гладкое многообразие Ф С RN называется инвариантным многообразием группы Gr, если для любой точки z ? Ф также z' = f(z,a) € Ф с любым элементом / е Gr. Если Ф задано неявно системой уравнений
Ф : Фа{г) = 0 (а L, ..., 6'), (14)
то критерий его инвариантности состоит в выполнении равенств
= 0 (<т = 1, ..., s)
Yv„{z)
(15)
для любого оператора Y € Ьг. Говорят, что уравнениями (14) многообразие задано регулярно, если
о. р. (dipa/dzk)
s. (16)
Справедлива следующая теорема о представлении: регулярно заданное уравнениями (14) неособое инвариантное многообразие группы G7’ может быть задано системой уравнений
Ja(z)= 0 (а= 1. ..., s), (17)
где ,/сг — инварианты Gr.
Подобие подалгебр. Так как при построении Я-решений нужны только инварианты, то достаточно использовать лишь подалгебры Н допускаемой алгебры Ли LT. В бесконечномерном множестве Q подалгебр Н С Ьг существует важное отношение подобия, позвляющее «сократить» Q до обозримого подмножества.
Автоморфизмом алгебры Ли I/ называется линейное преобразование А векторного пространства Lr, действующее по формуле X' = АХ и обладающее свойством
Каждый фиксированный оператор А' G Lr порождает линейное отображение Lr —» Lr, обозначаемое символом ad X и действующее на векторы У € V по формуле (ad X)Y — [X. Y).
Экспонента exp(adX), где t — вспомогательный параметр, является преобразованием Lr, обладающим при любом t G R свойством (18). Преобразования
А = exp (tad X) (19)
называются внутренними автоморфизмами алгебры Ли Lr. Множество внутренних автоморфизмов, получаемое, когда оператор X пробегает всю Lr, образуют группу, называемую группой внутренних автоморфизмов алгебры Ли Lr и обозначается символом IntLr. В силу (18) автоморфизм А ? Int Z7 переводит каждую подалгебру Н с U в подалгебру АН С Lr.
Подалгебры Н, К С Lr называются подобными (говорят также сопряженными), если существует автоморфизм А е Int Lr, с которым К -- АН.
Формула (1) для преобразований пространства RN, принадлежащих группе Gx(X), может рассматриваться как переход от системы координат (г) в к системе координат (г'). Для любого оператора Y е Lr, записанного в координатах (z) формулой вида (4) символом У', будет обозначаться тот же оператор, преобразованный к координатам (z'). Пусть А — внутренний автоморфизм (19) и J : RN —> R фиксированная функция.
Лемма. Если функция J(z) есть инвариант оператора Y, то J(z') есть инвариант оператора (AY)'.
Другими словами, операторы У и AY имеют одни и тс же инварианты, но записанные в разных системах координат, определяемых формулой (1). То же верно и для подалгебр.
Переход от координат (г) к координатам (г') можно выполнить и в системе дифференциальных уравнений, допускающих LR. При таком переходе эта система должна сохраниться (так как X S Lr), т. е. будет допускать алгебру Ли Lr'. Из леммы следует, что любое Я-решение данной системы, которое определяется набором инвариантов подалгебры Н С U (см. § 8), заменой переменных (1) будет переводиться в Я'-решение преобразованной системы относительно того же самого набора инвариантов. Следовательно, подобные подалгебры производят подобные подмодели.
Оптимальные системы подалгебр. Отношение подобия подалгебр Н с Lr является теоретико-множественным признаком эквивалентности, по которому множество О. всех подалгебр однозначно разбивается на классы подобных. Список этих классов, идентифицируемых их представителями (по одному от каждого класса), называется оптимальной системой подалгебр и обозначается символом 0Lr. Вообще говоря, 077 состоит также из бесконечного множества представителей, но они объединяются в конечное число серий, выделяемых нижеследующими понятиями и фактами.
Подалгебра Я С Ьг называется идеалом подалгебры К С U, если для любого У G Я и любого X е К также [X, У] ? Я (при этом, очевидно, Я С К). Для каждого X ? К отображение Я —> [X, Я] линейно и сохраняет коммутатор. Операторы Х\, Х-i ? К называются эквивалентными, если Х1—Х2 ? Я. По этому признаку подалгебра К разбивается на классы эквивалентных операторов. Множество таких классов называется факто-ралгеброй алгебры К по ее идеалу Я и обозначается символом К/Н. Фак-торалгебра К/Н рассматривается как алгебра Ли операторов X(mod Я). В эти терминах справедливо следующее утверждение.
Если Я есть идеал в К, то Я-подмодель системы уравнений, допускающей алгебру Ли Ьг, допускает факторалгебру К/Н.
Подалгебра К С Ьг максимальной размерности, для которой данная подалгебра Я является ее идеалом, называется нормализатором Я в Lr и обозначается символом Nor Я. Нормализатор любой подалгебры Я определен однозначно и вычисляется алгоритмически. Предыдущее утверждение означает, что Я-подмодель допускает (как минимум) факторалгебру Nor Я/Я. Тем самым симметрия подмодели автоматически оказывается известной (хотя бы частично). Поэтому при построении оптимальной системы подалгебр 0Lr важно, чтобы вместе, с любой подалгеброй Я в 0Lr содержался также её нормализатор ХогЯ. Такая оптимальная система называется нормализованной. Для любой конечномерной алгебры Ли Lr нормализованная 0Lr существует.
Объединение подалгебр в серии подалгебр, зависящие от нескольких параметров, диктуется тем, что при любых значениях этих параметров (с возможными ограничениями) все входящие в серию подалгебры имеют один и тот же нормализатор (быть может зависящий от тех же параметров).
Нормализованная ©L11. В таблице 2 приведена нормализованная оптимальная система подалгебр 0/у11 для алгебры Ли L'1 с базисом (12), допускаемой УГД (всего 223 серии представителей).
Представители классов подобных подалгебр (серии представителей) перечисляются в порядке убывающей размерности г --11,10, ..., 1.
В первом столбце (г) для каждого г указаны порядковые номера г = 1. 2, ..., подалгебр размерности г. Тем самым каждый представитель индексируется парой чисел (г, г).
Во втором столбце (Базис) приведены базисы подалгебр-представи-телей, записанные через операторы (12) в аббревиатурной форме: вместо оператора Хк указывается только его номер к; запись вида а к + 01 означает оператор аХд. + BXi и т. п. Здесь же указаны возможные ограничения значений параметров а, в, ..., серии подалгебр (если для какого-либо параметра ограничений нет, то он может быть любым вещественным числом).
Таблица 2
| г |
Базис | Nor |
| г — 11 | ||
| 1 | 1,2,3; 4,5,6; 7,8,9; 10; 11 | = 11,1 |
|
г = 10 | ||
| 1 | 1,2,3; 4,5,6; 7,8,9; И | = 10,1 |
| 2 |
1,2,3; 4,5,6; 7,8,9; 10 | 11,1 |
| г = 9 | ||
|
1 | 1,2,3; 4,5,6; 7; 10; 11 |
= 9,1 |
| 2 |
1,2,3; 4,5,6; 7,8,9 | 11,1 |
| г = 8 | ||
|
1 | 1,2,3; 7,8,9; 10; 11 |
= 8,1 |
| 2 |
1,2,3; 5,6; а4 + 7; 10; /?4 + 11 |
9Д |
| 3 |
1,2,3; 4,5,6; 7 + all; 10 |
9Д |
| 4 |
1,2,3; 4,5,6; 7; 11 | = 8,4 |
| 5 | 1,2,3; 4,5,6; 10; 11 | 11,1 |
г = 7
| 1 |
1,2,3; 7,8,9; 11 | = 7,1 |
| 2 | 4,5,6; 7,8,9; 11 | = 7,2 |
|
3 | 2,3; 5,6; 7; 10; 11 |
= 7,3 |
| 4 |
1,2,3; 4; 7; 10; 11 | = 7,4 |
| 5 | 1,2,3; 5,6; 10; a4 + 7 + /3ll | 9,1 |
| 6 | 2,3; 4,5,6; 7; 11 |
= 7,6 |
| 7 | 1,2,3; 5,6; a4 + 7; /J4 + 11 |
8,4 |
| 8 |
1,2,3; 4,5,6; 7 + all; a ф 0 |
8,4 |
| 9 |
1,2,3; 7,8,9; 10 | 8,1 |
| 10 | 1,2,3; 5,6; a4 + 7; 4 + 10 | 8,3; a = 0 |
| 11 | 1,2,3; 4,5,6; 7+ 10 | 8,3; a = 0 |
| 12 |
1,2,3; 5,6; 10; a4 + ll | 9,1 |
| 13 | 1,2,3; 4,5,6; 11 | 10,1 |
|
14 | 1,2,3; 4,5,6; 10 |
11,1 |
продолжение таблицы 2
| г |
Базис | Nor |
| 15 | 1,2,3; 4,5,6; 7 | 9Д |
г = 6
| 1 |
1,2,3; а4 +7; 10; 04+11 | 7,4 |
| 2 | 2,3; 5,6; 10; 7 + all; а ^ 0 | 7,3 |
| 3 | 1,2,3; 4; 10; 7 +all | 7,4 |
| 4 | 1; 4,5,6; 7; 11 | = 6,4 |
| 5 |
1,2,3; 4; 7; 11 | = 6,5 |
| 6 | 2,3; 5,6; а4 + 7; /34 + 11 | 7,6 |
|
7 | 2,3; 4,5,6; 7 + all; а ^ 0 | 7,6 |
| 8 |
1,2,3; 5,6; а4 +7 + 011; РфО |
8,4 |
| 9 |
4,5,6; 7,8,9 | 7,2 |
| 10 | 1,2,3; 7,8,9 |
8,1 |
| 11 |
2,3; 5,6; 1 + 7; 10 | 7,5; а = (3 = 0 |
| 12 | 2,3; 5,6; о. 1 + 7; 4 + 10 | 7,10 |
| 13 | 2,3; 5,6; 7; 10 | 8,2; а = Р = 0 |
| 14 | 2,3; 4,5,6; 1 + 7 | 7,15 |
|
15 | 2,3; 4,5,6; 7 |
8,4 |
| 16 |
1,2,3; 5,6; а4 + 7+10 | 7,5; а = (3 = 0 |
| 17 |
2,3; 5,6; 10,11 | 7,3 |
| 18 | 1,2,3; 4; 10; аб + 11; а ф 0 | 8,5 |
| 19 | 1,2,3; 4; 10; 11 | 9Д |
| 20 | 1,2,3; 5,6; а4 + 11 |
8,4 |
| 21 |
2,3; 4,5,6; 11 | 7.6 |
| 22 | 1,2,3; 5,6; 10 | 9,1 |
| 23 | 1,2,3; 5,6; 4 + 10 | 8,3; а - 0 |
| 24 |
1,2,3; 4,5,6 | 11,1 |
| 25 | 1,2,3; 5,6; а4 +7 | 9Д |
|
г = 5 | ||
| 1 |
7,8,9; 10; 11 | = 5,1 |
Приложение продолжение таблицы 2
| г |
Базис | Nor |
| 2 | 1; 4; 7; 10; И | = 5,2 |
| 3 | 2,3; 7; 10; 11 | = 5,3 |
| 4 |
1,2,3; 10; а4 + 7 +/311 | 7,4 |
| 5 | 4,5,6; 7; И | = 5,5 |
|
6 | 2,3; 4; 7; 11 | = 5,6 |
| 7 |
1; 5,6; а4 + 7; /34 + 11 | 6,4 |
| 8 | 1,2,3; с*4 -г 7; /34 + 11 | 6,5 |
| 9 | 1; 4,5,6; 7 + а11 | 6,4 |
|
10 | 2,3; 5,6; а4 + 7 + /311; /3 ф 0 | 7,6 |
| 11 | 1,2,3; 4; 7 + all; а ^ 0 | 6,5 |
|
12 | 1,2,3; а4 + 7; 4+ 10 |
6,3; а = 0 |
| 13 | 2,3; 5,6; а4 + 7; а Ф 0 |
8,4 |
| 14 |
2,3; 5,6; 7 | 9Д |
| 15 | »,2,3; 4; 7 | 7,4 |
|
16 | 1; 4,3 + 5,2 - 6; 7 | = 5,16 |
|
17 | 2,3; 5,6; 1 + 7 |
8,3; а = 0 |
| 18 |
2,3; 5,6; а4 + 7 + а10; а ф 0 | 7,10; а = 0 |
| 19 |
2,3; 5,6; 7+ 10 | 7,5; а = /3 = 0 |
| 20 | 1,2,3; 4; 7+ 10 | 6,3; а = 0 |
| 21 | 2,3; 5; 10; аб + 11 | 6,17 |
|
22 | 1,2,3; 10; 4 + с*11 |
9,1 |
| 23 |
1,2,3; 10; 11 | 11,1 |
| 24 | 1; 4,5,6; 11 |
6.4 |
| 25 |
2,3; а4 5,6; /34 + 11; а ф 0 | 6,21 |
|
26 | 2,3; 5,6, а4 + 11 |
7,6 |
| 27 |
2,3; 4,6; ао + 11 | 6,21 |
| 28 | 1,2,3; 6; а4 + 11; а ф 0 | 7,13 |
| 29 | 1,2,3; 4; 11 | 8,4 |
|
30 | 2,3; а1 + 5,6; 4 + 10; а ^ 0 | 6,23 |
|
т | Приложение продолжение таблицы 2 | |
| i | Базис | Nor |
| 31 | 2,3; 5,6; 4+ 10 | 7,10; a = 0 |
| 32 |
2,3; 1 +5,6; 10 | 6,22 |
| 33 | 2,3; 5,6; 10 |
8,2; a = /? = 0 |
|
34 | 1,2,3; 6; 4+ 10 |
7,14 |
| 35 |
2,3; 4,5,6 | 8,4 |
| 36 | 2,3; 4,5; 1 + 6 | 6,24 |
|
37 | 1,2,3; 5,6 |
9,1 |
| г = |
= 4 | |
| 1 | 7,8,9; 11 | = 4,1 |
| 2 | 1;о4 + 7; 10;/34+ 11 | 5,2 |
|
3 | 2,3; 10; 7 + all; аф 0 | 5,3 |
| 4 | 1; 4; 10; 7 +all |
5,2 |
| 5 |
5,6; a4 + 7; /J4+11 | 5,5 |
| 6 | 1; 4; 7; 11 |
= 4,6 |
| 7 | 2,3;a4 + 7;/?4 + ll |
5,6 |
| 8 |
4,5,6; 7 + all; аф 0 | 5,5 |
| 9 | 1; 5,6; a4 + 7 + /?ll | 6,4 |
| 10 | 2,3; 4; 7 +all |
5,6 |
| 11 |
1,2,3; a4 + 7 + /311; 0 ф 0 |
6,5 |
| 12 |
1,2,3; a4 + 7 | 7,4 |
| 13 | 7,8,9; 10 |
5Д |
| 14 |
2,3; 7; 10 | OS p II il о |
| 15 | 2,3; 1 + 7; 10 | 5,4; a = p = 0 |
| 16 | 2,3; al + 7; 4 + 10 | 5,12; a = 0 |
| 17 | 4,5,6; 7 |
6,4 |
| 18 |
al + 4,5,6; (31 + 7; a2 + (32 = 1 | 5,9; a = 0 |
| 19 | al +4,3+ 5,2-6; pi + 7 | 5,16 |
| 20 | 1; 3 + 5,2-6; a4 + 7 | 5,16 |
|
21 | 2,3; 4; 1+7 |
5,15 |
продолжение таблицы 2
|
г | Базис |
Nor |
| 22 |
1,2,3; q4 + 7+10 | 6,3; а = 0 |
| 23 |
1; 4; 10; 11 | 5,2 |
| 24 | 2,3; 10; а6 + 11;а/0 | 6,17 |
|
25 | 2,3; 10; 11 |
7,3 |
| 26 |
4,5,6; 11 | 7,2 |
| 27 | 1; а4 + 5,6; 04 + 11; а / 0 | 5,24 |
|
28 | 1; 5,6; а4 + 11 |
6,4 |
| 29 |
1; 4,6; q5 + 11 | 5,24 |
| 30 | 2,3; а4 +6; 04+ 55+ 11 | 6,21 |
|
31 | 2,3; 4; а5 + 11; а ф 0 | 6,21 |
|
32 | 2,3; 4; 11 |
7,6 |
| 33 |
1,2,3; а4 + 11; а ф 0 |
8,4 |
| 34 |
1,2,3; 11 | 10,1 |
| 35 | 2,3; а1 + 5; 4 + 06 + 10 | 6,23 |
|
36 | 2,3; а1 + 5;6 + 10 |
6,22 |
| 37 |
2,3; 1+5; 10 | 6,22 |
| 38 | 2,3; 5; 10 |
7,12; а = 0 |
| 39 | 1,2,3; 4+ 10 | 8,3; а = 0 |
| 40 |
1,2,3; 10 | 11,1 |
|
41 | 1; а2 + 03 + 4, стЗ + 5, т2 + 6 а2 + 02 + (а + г)2 - 1 | 6,24 |
| 42 | 1; 4,3 + 5,2 — 6 | 7,15 |
|
43 | 1; 4,5,6 |
8,4 |
| 44 |
2, а1 + 3; 1 + 5,6; а / 0 |
6,24 |
| 45 |
2,3; 1 + 5,6 | 7Д4 |
| 46 | 2,1 + аЗ; 5,6 | 7,13 |
| 47 | 2,3; 5,6 | 9,1 |
| 48 | 1,2; 3 + 5,6 | 6,24 |
|
49 | 1,2,3; 4 |
9,1 |
Приложение продолжение таблицы 2
| г | Базис | Nor |
| г = 3 | ||
| 1 | 7; 10; 11 | = 3,1 |
| 2 | 1; 10; а4 + 7 -г /311 | 5,2 |
| 3 | 4; 7; 11 | = 3,3 |
| 4 | 1; а4+ 7; /34 + 11 |
4,6 |
| 5 |
5,6; q4 + 7 + /311; /3^0 | 5,5 |
| 6 | 1; 4; 7 + all; a ^ 0 |
4,6 |
| 7 | 2,3;a4 + 7 + /3ll;/3^0 | 5,6 |
|
8 | 7,8,9 | 5,1 |
| 9 | 1; a4 + 7; 4+ 10 |
4,4; a = 0 |
| 10 |
5,6; q4 + 7 | 6,4 |
| 11 | 1; 4; 7 | 5,2 |
| 12 | 2,3; q4 + 7; q ^ 0 | 6,5 |
| 13 |
2,3; 7 | 7,4 |
|
14 | 5,6; 1 + 0:4 + 7 | 5,9; a = 0 |
| 15 | 3 + 5,2 —6; al+/34+ 7 | 5,16 |
|
16 | 2,3; 1 + 7 | 6,3; a = 0 |
| 17 | 1; 4; 7 + 10 | 4,4; a = 0 |
| 18 | 2,3; q4 + 7 + alO; а Ф 0 |
5,12; a = 0 |
| 19 |
2,3; 7+ 10 | 5,4; a = /3 = 0 |
| 20 | 1; 10; a4 + 11 |
5,2 |
| 21 | 5,6; q4 + 11 | 5,5 |
| 22 | 1; a4 + 6; /34 + <55 + 11 | 5,24 |
| 23 | 1; 4; q6+11;q/0 | 5,24 |
| 24 |
1; 4; 11 | 6,4 |
|
25 | 2,3; a4 + /35 + 11; /3^0 |
6,21 |
| 26 | 2,3; a4 + 11 | 7,6 |
| 27 | 3; al + ,/32 + 6; 4 + 10 | 5,34 |
| 28 | 1; 2 + 4; 10 | 5,22; a = 0 |
| Приложение продолжение таблицы 2 |
331 | |
| i |
Базис | Nor |
| 29 | 1; 4; 10 | 7,4 |
| 30 | 2,3; 4 + аб + 10; а ф 0 | 6,23 |
| 31 | 2,3; 4 + 10 | 7,10; а = 0 |
| 32 |
2,3; 6 + 10 | 6,22 |
| 33 | 2,3; 10 |
8,2; а = (3 = 0 |
| 34 | —62 + /33 + 4, <51 + <т2 — аЗ + 5, -/31 + а2 + тЗ + 6 а2 + т2 = 1, /З2 + <52 + (ст - г)2 ф 0 at2 + S2 + т2 ф 0, а2 + 02 + а2 Ф 0 |
6,24 |
| 35 |
а1 + 4,3 + 5,2 — 6 |
7,15 |
| 36 |
1 + 4,5,6 | 7,15 |
| 37 | 4,5,6 | 10,1 |
| 38 | al + 3; /31 + 5, al + т2 + 6 (j2 4- о-2 + Т2 = 1 | 6,24 |
| 39 | al + 3; 5, 6 | 7,13 |
|
40 | 1; 3 — 5,а2 + 6; а ф —1 | 6,24 |
|
41 | 1; 3-5,2-6 |
7,15 |
| 42 |
1; 5,6 | 8,4 |
| 43 | al + 3,2; 4 |
7,13 |
| 44 |
2,3; 4 | 8,4 |
| 45 | 1,2; 3 + 4 |
7,14 |
| 46 | 1,2; 4 | 8,5 |
| 47 | 1,2,3 | 11,1 |
| г = | = 2 | |
|
1 | 10; 7 +all; аф 0 |
зд |
| 2 |
а4 + 7; /34 + 11 | 3,3 |
| 3 | 4; 7 -г all; аф 0 | 3,3 |
| • 4 | 1; а4+ 7 + /311; /3^0 | 4,6 |
|
5 | 7; 10 | 4,2; а = /3 = 0 |
| ж | Приложение продолжение таблицы 2 | |
| i | Базис |
Nor |
| 6 |
1 + 7; 10 | 3,2; а = 0 0 |
| 7 | oil + 7; 4 + 10 | 3,9; а = 0 |
| 8 | 4; 7 |
4,6 |
| 9 |
1; q4 + 7 | 5,2 |
| 10 | 4; 1 + 7 |
3,11 |
| 11 |
1; ?*4 + 7 + 10 | 4,4; а = 0 |
| 12 | 10; 11 | 5,1 |
| 13 | 4; 11 | 5,5 |
| 14 | 4; q5 + 11; а ф 0 | 4,26 |
| 15 | 1; а4 + 05 +11;/3^0 | 5,24 |
| 16 | 1; q4 + 11 | 6,4 |
| 17 | 1; 10 | 7,4 |
|
18 | 3; 4 + q6+ 10 |
5,34 |
| 19 |
1; 4 + 10 | 6,3; а = 0 |
| 20 | cvl + стЗ + 5,01 + т2 + 6 а2 + 02 + (и + г)2 = 1 | 6,24 |
| 21 | 3 + 5,2 — 6 |
7,15 |
| 22 |
5,6 | 8,4 |
| 23 | al + 2;3 +4 |
6,24 |
| 24 |
al + 2;4 | 7,13 |
| 25 | 1; 3 + 4 | 7Д4 |
|
26 | 1; 4 |
9,1 |
| 27 |
2,3 | 9,1 |
| г = | = 1 | |
| 1 | Q4 + 7 + 011; /Зф 0 | 3,3 |
|
2 | а4 + 7; а ф 0 | 4,6 |
| 3 | 7 | 5,2 |
| 4 | 1+7 |
4,4; а = 0 |
|
5 | а4 + 7 + а10; а ф 0 | 3,9; а = 0 |
продолжение таблицы 2
| г |
Базис | Nor |
| 6 | 7 + 10 |
3,2; q = в = 0 |
| 7 | а4 + 11; а ф 0 | 5,5 |
|
8 | 11 | 7,2 |
| 9 | 4+10 |
5,12; q = 0 |
|
10 | 10 | 8,1 |
| 11 | 3 + 4 |
6,24 |
| 12 |
4 | 8,4 |
|
13 | 1 | 9,1 |
В третьем столбце (Nor) указан нормализатор каждой подалгебры (серии подалгебр). В силу нормализованности данной 0L173 нормализатор содержится в этой же таблице и потому написан только его индекс (г, г); он может указывать на серию подалгебр, зависящую от «своих» параметров; отмечено, что для получения нормализатора их следует положить равными нулю. Знак «=» означает, что данная подалгебра самонормализована (т. е. совпадает со своим нормализатором).
Справочно: ©L11, приведенная в [13], здесь исправлена. Вычислены также нормализованные оптимальные системы подалгебр 0L13 (политроп-ный газ), состоящие из 1342 представителей [12] и 0L14 (политропный газ с 7 = 5/3), содержащие 1826 представителей [15].
[1] Биркгоф Г. Гидродинамика,— М.: ИЛ, 1954 (к §§ 8, 12-14).
[2] Гудерлпй К. Г. Теория околозвуковых течений — М.: ИЛ, 1960 (к § 26).
[3] КОЧИН Н. Е., КИБЕЛЬ И. А., РОЗЕ Н. В. Теоретическая гидромеханика. Т.Н.- М.: Гостехиздат, 1948 (к §§ 1, 3, 4, 6, 10, 11, 15-17, 22-25).
[4] Курант Р., ФридриХС К. Сверхзвуковое течение и ударные волны.— М.: ИЛ, 1950 (к §§2-7, 15-18,24,25).
[5] Овсянников Л. В. Групповой анализ дифференциальных уравнений.— М.: Наука, 1978 (к §§8, 12, 13, 20, 26).
[6] РОЖДЕСТВЕНСКИЙ Б. Л., Яненко Н. Н. Системы квазилинейных уравнений и их приложения к газовой динамике — М.: Наука, 1978 (к §§ 2, 15-17, 22,24).
[7] Седов Л. И. Методы подобия и размерности в механике,— М.: Наука, 1981 (к §§ 15, 19-21).
[8] Серрин Дж. Математические основы классической механики жидкости.— М.: ИЛ, 1963 (к §§ 10, 11, 22, 23).
[9] Смирнов В. И. Курс высшей математики. T.IV.—М.: Гостехиздат, 1951, (к §§7, 12).
[10] Чаплыгин С. А. О газовых струях,— М.: Гостехиздат, 1949 (к §§22, 23).
[13] ОВСЯННИКОВ Л.В. Программа «Подмодели». Газовая динамика // ПММ. 1994. Т. 58. Вып. 4. С. 30-55.
[14] СИДОРОВ А. Ф. Избранные труды. Математика. Механика. М.: Физмат-лит, 2001.
[15] ЧнРЕВКО А.А. Оптимальная система подалгебр для алгебры Ли операторов, допускаемых уравнениями газовой динамики с уравнением состояния р — f{S)pb/3 // Новосибирск, 1996 (Препр. / СО РАН, Ин-т гидродинамики; № 4-96).
[16] ЧУПАХИН А. П. О барохронных движениях газа // Докл. РАН. 1997. Т. 352, №5. С. 624-626.
Овсянников Лев Васильевич
Лекции по основам газовой динамики
Дизайнер М. В. Ботя Технический редактор А. В. Широбоков Компьютерная верстка Д. П. Вакуленко Корректор М. А. Ложкина
Подписано в печать 31.12.02. Формат 60 х 84 Vj6. Печать офсетная. Уел. печ.л. 19,53. Уч. изд. л. 19,12. Гарнитура Таймс. Бумага офсетная №1.
Тираж 1000 экз. Заказ № 1472.
АНО «Институт компьютерных исследований»
426034, г. Ижевск, ул. Университетская, I.
Лицензия на издательскую деятельность ЛУ \s084 от 03.04.00.
Отпечатано в полном соответствии с качеством предоставленных днапознтнвов на ФГУИПП «Вятка». 610033. г. Киров, ул. Московская. 122.
При интенсификации притока с помощью ГРП
• Обеспечивают связь между пластом и стволом скважины
• В «порванной» скважине, создают связь между трещиной и
стволом
• Задача — минимизировать падения давления в приствольное зоне за счет трения в перфорационном канале, зон микрозазоров с защемлением, многочисленных
взаимовлияющих трещин и извилистости самой трещины

Зоны микрозазоров с защемлением
(SPE 30506)
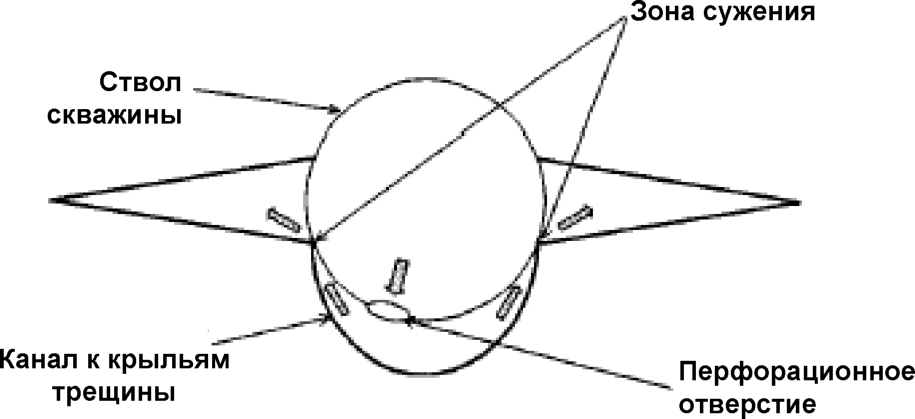
Извилистость трещины в приствольное зоне
(SPE 30506)
р:
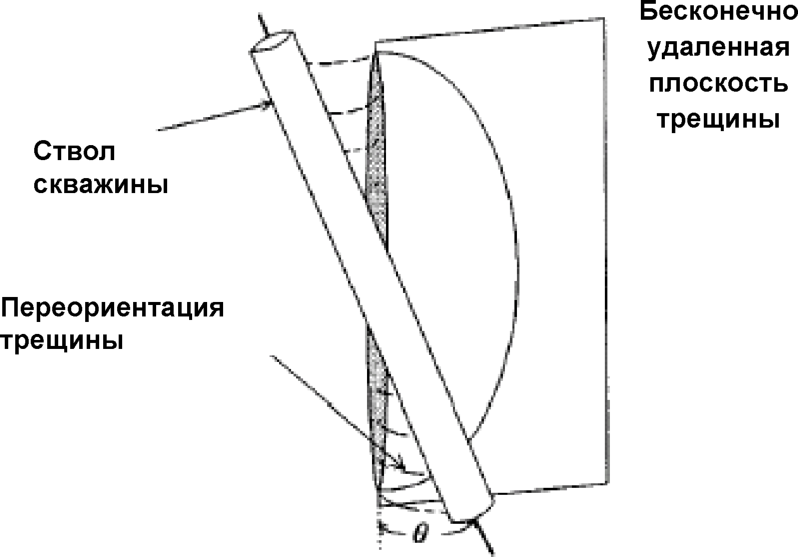
• Недостаточная величина депрессии не позволяет вынести весь песок и шлам из перфорационных каналов.
• Этот оставшийся шлам в процессе нагнетания создает в перфорационном канале фильтрационную корку.
• Возможны значительные падения давления.
Перфорирование может создать микрозазор
Таблица 1 — Перфорационные параметры влияющие на возникновение микрозазора
Создает
| Параметр |
микрозазор |
|
Бескорпусный перфоратор |
Да |
| Корпусной перфоратор | Умеренно |
| Малый зазор перфоратор-колонна | Да |
| Жидкость в стволе |
Да |
| Низкая плотность отверстий | Нет |
| Газ в стволе | Нет |
р
Ширина микрозазора в результате перфорирования
w _ (l + V) dw (-Pm - PR )
2 E
w ширина (дюймы) v Коэффициент Пуассона Pm Давление в микрозазоре (psi) PR Пластовое давление (psi) dw Диаметр скважины (дюймы)
E Модуль Юнга (psi)
Для,
dw = 8,5 дюйма, Pm -PR = 2000 psi v = 0,25, E = 1E06 psi
w = 0,0106 дюйма
что, для скорости жидкости 3,28 фут/с соответствует дебиту 99 бар/день (вязкость 1 cn)
Глубина снижения уровня жидкости [см. (9.36)]
4. Расстояние от устья к месту размещения третьего клапана
1-а0 Yж)
+ а 01 —-1| 1 + а 01 —-1| 1 ~ + 0Д9
2ln—
ra
(2,0391-1,0209га
1\ ; Л Ё- 1; i- 1 S- 1
7
- 0,04046 • 1,9592
+ 0,2350067(0,022401802 - 0,00048364)] = 0,03372. Значит,
4nl ' 1 * 2nnl r П
3 19
1-ra) 4(1-га )4 % Y 7g 7Г!7
ный объем примеси
Основной разработчик методик - фирма MERCK. Методики стандартизованы и имеют сертификаты об утверждении средств измерений.
Раздел составлен по материалам Е.Я. Гаврилова, А.Д. Есикова, В.Г. Козлова, Г.И. Теплинского.
Определение разработано на кафедре геохимии геологического факультета МГУ.
Это условие весьма приближенно описывает процесс остановки станции; на самом деле необходимо учитывать инерционный выбег насосов (см. далее).
1\кинания] между различными группами молекулярных пар нншо не могут быть представлены лишь одной силой притя-'’мин между центрами молекул. Для учета других, нецентрич-мих iu\ вводится ацентрический фактор со. оценивающий м«ФУ отклонения коэффициента сверхсжимаемости природ-жя [«зов от его значения, определяемого по рпр и Гпр:
23 • 10-12 - 3052
Исключение составляют газогидратные месторождения, в которых при разработке разлагаются гидраты.
Знак минус в этой формуле связан с гам, что давление и скорость увеличиваются в разном направлении.
В исследованиях принимали участие А.П. Иванчук, Д.И. Иванов, Е.КЭ. Красновидов и др.
По данным проф. Г.А. Саркисьянца, этот метод широко применялся на грозненских промыслах а начале века.
Как в газе (сепарации, дегазации, дебутанизацни), так и в дебутанизированном конденсате методом газожидкостной хроматографии можно определить содержание вышекипящих углеводородов, например, С* + в (гексан, его изомеры, метилциклопентан,
цнклогексаи и бензол).
При ошибках в 0К[) в координатах ApVQ и получаем вогнутую или выпуклую кривую вместо второго прямолинейного участка. При этом значение О — не должно быть меньше нуля.
Анализ нефти и нефтепродуктов. М., Гостоптехиздат, 1962.
Принципиальным отличием газогидродинамической акустики от обыч
ной является то, что она сопровождается движением среды, что требует учета членов второго приближения 115).
^— APQ - ЬаАРО,
Коротаев Ю.П., Ширковский А.И. Добыча, транспорт и подземное хранение газа. — М.: Недра, 1984. — С. 487.
По уравнению (11.1) при известном объемном расходе газа Qv определяют мощность компрессора
где R = gR в техническом системе единиц имеет размерность м21секг-град. Здесь р в кГ/ж2, р в кГ-сек2/м* и Г в °К.
В ряде случаев оказывается удобным объединить постоянные величины в уравнении состояния (1-1) и записывать его в таком виде:
¦у = «Г, (1-1 а)
Обращаясь к формуле (1-9), мы видим, что выражение для циркуляции скорости напоминает известное уравнение работы вектора силы. Эта внешняя аналогия позволяет понять механический смысл циркуляции (произведение скорости на путь) и дает основание условно называть величину Г работой вектора скорости.
(ккал1кГ) = — i (м2!секг) и т. д., где А — тепловой эквивалент
механической работы.
Уравнение (2-4) справедливо и для адиабатических течений (при наличии трения), сопровождающихся возрастанием энтропии. В этом случае баланс энергии частицы должен быть дополнен двумя членами: одним, учитывающим работу сил сопротивления, и другим, выражающим приращение теплоты в газовом потоке Эти два члена одинаковы по величине, но имеют различные знаки и поэтому взаимно уничтожаются Это означает, что в такой изолированной системе работа сил трения не меняет полной энергии частицы; меняется только соотношение между энергией направленного движения и тепловой энергией. Течение газа является необратимым часть механической энергии необратимо превращается в тепло.
Функция 7t впервые была предложена А Ф Гаг/дельсманом и
использована в работах А. А. Гухмана "н А. Ф. Гандельсмана по исследованию сопротивления труб при адиабатическом течении газа
Размер контура в направлении, нормальном к плоскости чертежа, принят равным единице.
Если пренебречь влиянием вязкости н рассматривать дозвуковое и безотрывное обтекание профиля, как это делается в настоящей главе, то сила лобового сопротивления будет отсутствовать
Соответствующие графики изменения коэффициентов давления по профилю крыла и лопатки приводятся в гл. 5 и 8.
Приведенное ниже доказательство теоремы Н Е. Жуковского предложено Г. Ф. Бураго.
Рассматриваемые силы относим к единице длины крыла.
Формулы (3-44) и (3-45) справедливы в том случае, когда внутренняя и наружная стенки канала имеют кривизну одного знака,
Влиянием массовых сил пренебрегаем.
формулы Дацы М. В- Поликовским-
Рассматривается совершенный газ.
Из формулы (4-ЗЗа) следует, что коэффициент потерь Кс = О при Х,=1 Если ?1=Х1макс = , то формула (4-ЗЗа) дает неоп
ределенность, которая легко раскрывается.
Расчет диаграмм скачков выполнен А. Е. Заряикиным.
При построении процесса в диаграмме is принимаем рг p':i.
См. список литературы. Теоретическое исследование конденсационных скачков впервые было произведено С. 3. Беленьким. В работе Р. Германа дано решение для прямого скачка конденсации. В работе
В. А. Андреева и С. 3. Беленького рассмотрен более общий случай косого скачка. Ф. Росс решнл задачу о косом екачке конденсации с учетом изменений физических свойстр разд.
Под i понимается энтальпия газовой фазы без учета теплоты конденсации.
Рассматриваемый частный случай движения газа называют течением Куэтта.
Размер элемента в направлении оси г принят за единицу.
Вывод дифференциальных уравнений энергии и количества дви
жения можно найти в книге Л. Г. Лойцянскогои др. (см список литера
туры).
В соотношения (5-7а) критерий k не входит, так как согласно
молекулярно-кинетической теории газов условие Рг = Рг' эквивалентно условию k = k'.
Такое допущение оправдывается только в первом приближении.
В действительности ? зависит от чисел Re и М.
Различные системы скачков, образующихся в струе на выходе из трубы, подробно рассмотрены в гл. 6.
Под макрочастицами понимаются частицы жидкости (газа), содержащие достаточно большое число молекул-микрочастиц, — для возможности Применения к ним законов статистики.
Область независимости коэффициента сопротивления от числа
Б. С. Петухов, А. С. Сукомел, В. С. Протопопов, Исследование сопротивления трения и коэффициента восстановления температуры стенки при движении газа в круглой трубе с высокой дозвуковой скоростью, „Теплоэнергетика", 1957, № 3.
Аналогичный характер изменения t, отмечается в начальном участке трубы, где происходит переход ламинарного режима в турбулентный.
Изложенный ииже вывод интегрального соотношения дан А. П. Мельниковым.
Величина Re** введена была ранее при выводе уравнения (5-41)
Исследованию переходной области посвящены работы Л. М. Зы-синой-Моложен и др.
Следует отметить, что в конфузорной области с большими градиентами давления возможен переход турбулентного слоя в ламинарный (стр 227). Такой переход весьма вероятен при M=sl.
Рассматриваемые здесь вопросы обтекания тел при околозвуковых скоростях частично затронуты в гл. 3.
Как указывалось в гл. 4, в неравномерном сверхзвуковом потоке скачок”” криволинейный Поэтому рассматриваемая схема является лишь первым приближением.
Обычно принято картину распределения давлений строить по хорде профиля, причем отрицательные значения коэффициента давления (разрежения) откладываются вверх, а положительные — вниз.
В формулы для сх и су крыловых профилей вводится площадь крыла, равная произведению хорды профиля на длину крыла.
Верхняя граница Re<^3-103 соответствует шару, а нижняя Re <[ 2-103 — цилиндру.
Формула (5-82а) в точке г= 0 дает 7— = —со. Этот резуль-
> 00
Напомним, что весь расчет выполнен без учета пограничного слоя: скорость св берется на внешней границе слоя.
Выделение теплоты трения происходит только в тех областях
потока, где устанавливается неравномерное распределение скоростей, связанное с действием вязкости. /
s Такай задача возникает при исследовании закрученного потока в ступени турбомашииы (турбины или компрессора).
Так же как и в Случае истечения из трубы (гл. 5).
Рассматривается частный случай адиабатического движения газа в трубе без энергетического обмена с окружающей средой. В общем случае условие минимума сеченчя не является необходимым для перехода в область сверхзвуковых скоростей.
Рассматривается случай безотрывного течения за скачком.
Значения е0д могут быть приняты по экспериментальным данным, приведенным в гл. 7.
1 Влияние отрыва на положение скачка может быть учтено опытным путем в уравнение >(6-45|) можмо ввести опытные значения
коэффициента Л,
Частично эти вопросы — затронуты в § 6-2
Изоградиентными диффузорами называются диффузоры с по-. стоянным значением градиента давления dpjdx вдоль оси.
1 Рассматриваемый случай Показан штрихпунктирной линией на диаграмме i — s на рис. 7-20.
Диффузор сверхзвукового эжектора обычно состоит из конического входного участка, цилиндрической горловины и расширяющегося выходного участка,
1 Входную часть и горловину диффузора иногда называют камерой смешения.
Во входной части и в горлов'Ине, кроме основных потерь смешения, возникают потери, вызываемые трением, и волновые потери.
хПр — предельный коэффициент эжекции,
Опыты проводились при различных безразмерных давлениях в камере смешения рк=рк1ра и оптимальных безразмерных расстояниях между срезом сопла и входом в горловину x=xjd\ (di~ диаметр сопла ча выходе).
Рассматриваемые режимы иногда называют режима-ми с постоянным дросселированием на линии всасывания.
Буквой ? условно обозначена величина открытия задвижки ца линии всасывания.
Отрицательные значения х соответствуют такому расположению сопла, когда его выходное сечение находится правее входного сечения горловины.
Легко видеть, что прямая и обратная задачи взаимосвязаны.
См., например, монографию М. Е. Дейча и Г. С. Самойловича «Основы аэродинамики осевых турбомашии» (Машгиз, 1959), а также М. И. Жуковского [Л. 11].
См. § 3-5.
Угол р2 вычисляется по опытным формулам, например, по формуле (8-36) (§ 8-6).
Возможность обобщения теоремы Жуковского на случай течения несжимаемой жидкости через решетку была указана впервые Б. С Стечкиным в 1944 г Точное решение было получено Л И Седовым в 1948 г. Обоснование приближенной теоремы Жуковского для решетки в потоке сжимаемой жидкости было предложено Л. Г. Лоицянским в 1949 г. Изложенное в настоящем параграфе обобщение теоремы Жуковского для решетки в адиабатическом потоке газа дано А. Н Шерстюком
Опыты проведены В. А. Врублевской.
Для решеток с острыми кромками метод расчета профильных потерь разработан Л. Г. Лойцянским. Решение В. С. Елизарова является распространением метода Л. Г. Лойцянского на решетки с кромками конечной толщины.
Анализ вторичных терний в криволинейных каналах дан в § 5-15.
Диффузорно-конфузорные каналы активных решеток впервые предложены ВТИ.
Изло'женная методика разработана совместно с А. Е. Зарян-киным.
При большей кривизне спинки эта линия смещена внутрь канала.
Влияние степени турбулентности на характеристики реактивных решеток при околозвуковых скоростях объясняет несовпадение кри вых ?пр = {(МД получаемых на разных трубах, имеющих различную турбулентность. При низкой турбулентности переход через скорость звука сопровождается резким возрастанием профильных потерь, так как скачки в местной сверхзвуковой зоне иа спиике приводят к отрыву ламинарного пограничного слоя. При высокой турбулентности пограничный слой в сверхзвуковой зоне турбулентный и отрыва, как правило, ие возникает или он смещается по потоку.
Поверхность перехода приближенно совпадает с узким сечением канала. В действительности вследствие неравномерности потока в канале и влияния вязкости поверхность перехода имеет некоторую кривизну и смещается против потока.
Интенсивность первичного и отраженного скачков переменна вдоль фронта, так как они распространяются в неравномерном потоке и взаимодействуют с волмами разрежения.
Решетки группы А рассчитаны на обтекание потоком дозвуковых скоростей.
Проточной частью будем называть направляющую и рабочую решетки ступеии.
Проточной частью будем называть направляющую и рабочую решетки ступеии.
Здесь не рассматриваются влияние центробежных сил на пограничный слой в межлопаточных каналах, а также.и другие особенности пространственного потока вязкой жидкости в ступени при наличии радиальных составляющих скоростей.
Вопросы, изложенные в этом параграфе, разработаны совместно с Г. С. Самойловичем.
dp, ™2и2 — 2uw„2 + «2 __ (w2 COS — Uf _ 4 COS2 a2
p2 fifr r r r ’
(9-52)
где p2 и p2 — давление и плотность, a c2 и a2 — скорость и угол потока за рабочими лопатками в абсолютном движении; и — окружная скорость на текущем радиусе г; Рг — Рг (Г) — УГ0Л выхода в относительном движении, являющийся заданной функцией радиуса; w2 — относительная скорость за рабочей решеткой.
Предполагаем далее, что радиальное смещение струек при переходе из контрольного сечения 1 — 1 в контрольное
где са0, са| — осевые составляющие скорости в сечениях 0 — 0 и 1—/;
р, = pj/р,, — относительная плотность в зазоре.
Функция еа1 в уравнении (9-64) может быть определена по фор
муле
—if]! cos2 ajK(l — r~2)
, —&L(X -7-
Я0к
Эта таблица взята из статьи R. Matteson and W. S. Hanna в журн. „The Oil в метрические И. Е, Ходановичем, В. Н. Раабеном и И. Н. Стрижовым,
Bureau of Mines Technical Paper, № 158.
И. М. Муравьев и А. П. Крылов ,,Курс эксплоатации нефтяных месторождений", стр. 150 и 151, 1940.
рождений и скважин Бугу русла некого района», стр. 8, март, 1944 г.
„Установление оптимального эксплоатационного режима газовых место
Журнал «Нефтяное хозяйство», 1930, № 10» стр. 377.
«Аналитические основы добычи нефти, газа и воды из скважин». В США эта книга была напечатана в 1928 г. В русском переводе она вышла в 1932 г.
Темп понижения давления мы ввели в число факторов установления процента отбора по совету проф. Ф. А. Требина.
«Petroleum Production Engineering», 1939, стр. 129.
Старый тип штуцера Отис изображен и описан на стр. 128 книги «Курс эксплоатации нефтяных месторождений» И. М. Муравьева и А. П. Крылова, 1940. Более новый тип штуцера Отис изображен и описан в книге «Petroleum Production Engineering", by, Lester Uren 1939, стр. 130.
«Back Pressure Data on Natural Gas Wells and Their Aplication to Production Practices», by E. L. Rawlins and M. A. Schellhardt. «U. S. Bureau of Mines», Monograph 7, 1936, revised 1939, стр. 162.
Напечатана в книге Весткотта «Руководство по природному газу» и перепечатана в многочисленных других книгах по газовому делу.
L. С. Lichty. Measurement, Compression and Transmission of Natural Gas, New-Iork, 1924.
Напечатана в ноябрьском номере журнала «Western Gas» за 1929 г. статья Qpen-Flow Measurement of Gas Wells», by Walter Reid.
Описаны в статье «Computation of Pitot Tube Measurments of Gas Wells», by F. K. Bench, в журнале «The Oil Weekly» 1932, 5 сентября, стр. 28.
Bureau of Mines. Report of Investigations, 2229 and 2930, Washington U. S. A.
D. J. Grady and A. L. W i 11 е г. «Experimental Investigation of Gas-Well Gaging».«The Oil and Gasjournal, 1941, March 27, т. 39, № 46, стр. 200—206.
«Natural Gas Handbook», 1927, стр. 291.
«Petroleum Production Engineering», 1939, стр. 84.
«Oil and Gas Journal», 1941, 23 октября, т. 40, № 24, стр. 53.
«Oil and Gas Journal», 3 июля 1941 г., т. 40, № 8, сгр. 37.
Статья «Определение проницаемости путем наблюдений над скважинами». Бюлл. Амер. нефт. инст. № 210, стр. 4.
См. его книгу ,,Petroleum Production Engineering14, 1939, стр. 9.
В книге «Geologv of Natural Gas», by H. A. Ley, изд. «Amer. Ass. Petrol, Geol.», 1935, стр. 741—772.
Конечно, этот подбор месторождений может оказаться имеющим случай ный характер. Всего на земном шаре известно от 1000 до 1200 газовых месторождений.
А. Ф. и В. А. П р и т у л а , Трансп. неф., неф. прод. и газа. Ч. 1, 1938, стр. 129.
Б. А. Бахметьев. О неравномерности движения жидкости. 1928.
Об этом говорится, например, в книге «Petroleum Production» by W. F. Cloud, 1937, стр. 39,
J. Diehl. «Natural Gas Handbook», стр. 380.
I. I. G а г d е s с п. Behavior of Gas Bubbles in Capillary Spaces. Am. Inst-Min. and. Met. Engineers, «Petroleum Development and Technology», 1930, стр. 351— 370.
Напечатано в издании «Амер. института горных инженеров и металлургов», С929 F.
Plummer and Tapp. «Bull. Amer. Ass. Petr. Geol.», 1943, т. 27, № I* стр. 64.
Analytical Principles of1 the Spacing of Oil and Gas Wells, by R. W. Phelps, «Petroleum Development», 1928 — 1929, «Am. Inst. Min. Eng.», 1929, стр. 90.
Эту мысль впоследствии Д. Сюман развил в «The Oil Weekly», 1934, т. 73, № 11.
См. брошюру «Вопросы техники добычи нефти и бурения на промыслах Второго Баку», 1943 г,, стр, 53 и 54.
См. книгу «Geology of Natural Gas », edited by H. A. Ley, 1935, стр. 86 и 87
См. журнал «The Petroleum Engineer», т. XII, № 5, февраль, 1641, стр. 68.
«Установление оптимального эксплоатационного режима газовых и нефтегазовых месторождений и скважин Бугурусланского района», март. 1944, стр. 5.
Описана кратко в журнале «Грозненский нефтяник» в 1923 г., более подробно в 1924 г. в журнале «Нефтяное и сланцевое хозяйство» и в 1928 г. в журнале «The Oil and Gas Journal».
К числу таких же таблиц относятся: табл. 10 на стр. 39 и номограмма фиг. 5 на стр. 37 книги М. X. Шахназарова «Справочник по газобензину», Баку, 1939. табл. 61 на стр. 171 «Справочника по естественному нефтяному газу» М. X. Шахназарова и В. Н. Раабен, Москва, 1939; таблицы в «Hutte» и пр.
Bureau of Mines Report of Investigations, № 3399, май 1938, Washington. U. S. A.
Don В. Carson and Donald L. Katz. «Гидраты углеводородов», «The Oil and Gas Journal», 1941, 23 октября, т. 40, № 24, стр. 56.
Установка сооружается и продается фирмой «Питтсбург Лектродрайер Корпорэшн» в г. Питтербурге (№ 1962, Gulf Building, Pittsburg, Pennsulwania, U. S. А.). Эта фирма является подсобным предприятием наиболее крупной алюминиевой фирмы США «Алорко» («Алюминум ОР Компани»).
Помещена в журнале «The Oil Weekly», 1941, 21 июля т. 102, № 7, стр. 29.
О ней дан реферат № 9 проф. А. С. Смирновым в «Реферативном сборнике по нефтепромысловому делу», 1942, вып. 1.
См. «The Oil and Gas Journal» 1941, 25 сентября, т. 40, № 20, стр. 46—55
Этот рисунок взят из книги Д. Дил «Natural Gas Handbook», 1927, стр. 396.
Вяят из книги Кляуда, стр. 538.
Описан в декабрьском номере жупнала «Gas», Los Angeles, Cal, за 1941 г., т. XVII, № 12, стр. 27.
Доклад Дитона и Фроста напечатан в 1942 i. в издании «Bureau of Mines'* Report of Investigation № 3590. Government Printing Office, Washington, L. S. A.
b = -
kh
q - дебит, баррелей/день, a - слагаемое турбулентности, b - слагаемое потока Дарси.
рг - среднее пластовое давление (статика на забое), psi,
М
Черный Г. Г. Течения газа с большой сверхзвуковой скоростью,— М.: Физматгиз, 1959 (к § 27).
Дополнительная (к 2-му изданию)
